On Fractional Simpson-Type Inequalities via Harmonic Convexity

Abstract

In this paper, we establish some Simpson-type inequalities within the framework of Riemann–Liouville fractional calculus, specifically tailored for differentiable harmonically convex functions. By introducing a novel fractional integral identity for differentiable functions with harmonic arguments, we derive several estimates that generalize and refine existing results in the literature. The theoretical findings are validated through a numerical example supported by graphical illustration, and potential applications in approximation theory and numerical analysis are discussed.

1. Introduction

Convexity is one of the most fundamental and powerful concepts in mathematical analysis, optimization, and applied mathematics. A real-valued function $\varphi :\mathcal{I}\subseteq \mathbb{R}\to \mathbb{R}$ defined on an interval $\mathcal{I}$ is said to be convex if for all ${\mathfrak{i}}_1,{\mathfrak{i}}_2\in \mathcal{I}$ and $\wp \in [0,1]$, the inequality

$$\varphi (\wp {\mathfrak{i}}_1+(1-\wp ){\mathfrak{i}}_2)\le \wp \varphi \left({\mathfrak{i}}_1\right)+(1-\wp )\varphi \left({\mathfrak{i}}_2\right)$$

holds. This elementary definition captures the intuitive notion that the graph of a convex function lies below the chord joining any two points on the graph. Convex functions enjoy numerous desirable properties making them indispensable in variational analysis, economics, engineering, and numerical methods.

Among the most celebrated results in the theory of convex functions is the Hermite–Hadamard inequality, which provides a double-sided estimate for the integral average of a convex function over an interval. Precisely, if $\varphi :[\mathfrak{a},\mathfrak{b}]\to \mathbb{R}$ is convex, then

$$\varphi \left({\displaystyle \frac{\mathfrak{a}+\mathfrak{b}}{2}}\right)\le {\displaystyle \frac{1}{\mathfrak{b}-\mathfrak{a}}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}\varphi \left(\nu \right)\mathrm{d}\nu \le {\displaystyle \frac{\varphi \left(\mathfrak{a}\right)+\varphi \left(\mathfrak{b}\right)}{2}}.$$

This elegant inequality not only characterizes convexity (in the sense that a continuous function satisfying the above for all subintervals is convex) but also serves as a cornerstone for deriving numerous integral inequalities in mathematical analysis. Over the past century, the Hermite–Hadamard inequality has inspired a vast body of research aimed at refining, extending, and generalizing it under various assumptions on the function class and the integration operator.

Simpson-type inequalities provide valuable error estimates for the classical Simpson quadrature rule by leveraging only the first-order derivative. This represents a significant improvement over classical approaches that require boundedness of the fourth-order derivative, as it relaxes smoothness assumptions and extends applicability to functions with lower regularity. Over the past decades, these inequalities have been extensively generalized in various directions, including fractional calculus, multiplicative calculus, and different classes of convex functions such as s-convex, coordinated convex, and exponentially convex functions.

In [1], Sarikaya et al. presented the following Simpson-type inequality:

$$\left|{\displaystyle \frac{1}{6}}\left[\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{\mathfrak{a}+\mathfrak{b}}{2}}\right)+\varphi \left(\mathfrak{b}\right)\right]-{\displaystyle \frac{1}{\mathfrak{b}-\mathfrak{a}}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}\varphi \left(\nu \right)\mathrm{d}\nu \right|\le {\displaystyle \frac{5(\mathfrak{b}-\mathfrak{a})}{72}}\left(\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|+\left|\varphi \left(\mathfrak{b}\right)\right|\right),$$

where $\left|{\varphi }^{\prime }\right|$ is convex on $[\mathfrak{a},\mathfrak{b}]$.

Recent works have established refined versions of Simpson-type inequalities using novel integral identities and advanced analytical techniques, often leading to tighter bounds and broader applicability in numerical integration and special means [2,3,4]. Furthermore, many researchers have devoted their efforts to establish fractional versions of Simpson-type inequality, see [5,6,7,8,9].

In parallel with these developments, researchers have recognized that the classical notion of convexity is often too restrictive for modeling real-world phenomena or capturing the behavior of functions arising in applied contexts. This has led to the introduction of numerous generalized convexity concepts, each relaxing or modifying the standard definition to accommodate broader classes of functions while preserving some of the analytical tractability of convexity. Notable examples include s-convexity, quasi-convexity, log-convexity, P-convexity, and harmonic convexity.

Harmonically convex functions were first systematically studied by İşcan in [10] as a natural counterpart to classical convexity when the argument of the function is transformed via the reciprocal map. A function $\varphi :\mathcal{I}\subseteq \mathbb{R}\setminus \left\{0\right\}\to \mathbb{R}$ is said to be harmonically convex if for all ${\mathfrak{i}}_1,{\mathfrak{i}}_2\in \mathcal{I}$ and $\wp \in [0,1]$,

$$\varphi \left({\displaystyle \frac{{\mathfrak{i}}_1{\mathfrak{i}}_2}{\wp {\mathfrak{i}}_1+(1-\wp ){\mathfrak{i}}_2}}\right)\le \wp \varphi \left({\mathfrak{i}}_1\right)+(1-\wp )\varphi \left({\mathfrak{i}}_2\right).$$

In the same paper, the author established the Hermite–Hadamard inequality for harmonically convex functions: if $\varphi :[\mathfrak{a},\mathfrak{b}]\subseteq \mathbb{R}\setminus \left\{0\right\}\to \mathbb{R}$ is harmonically convex, then

$$\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)\le {\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}{\displaystyle \frac{\varphi \left(\nu \right)}{{\nu }^2}}\mathrm{d}\nu \le {\displaystyle \frac{\varphi \left(\mathfrak{a}\right)+\varphi \left(\mathfrak{b}\right)}{2}}.$$

Here, the harmonic mean ${\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}$ naturally replaces the arithmetic mean ${\displaystyle \frac{\mathfrak{a}+\mathfrak{b}}{2}}$, reflecting the reciprocal structure inherent in harmonic convexity.

Recently, the intersection of generalized convexity and fractional calculus has become a vibrant area of research in recent years. Fractional integrals, such as the Riemann–Liouville [11], Hadamard [12], Katugampola [13], and conformable fractional integrals [14], offer refined tools for modeling memory effects, nonlocal phenomena, and anomalous diffusion. By replacing the classical integral in the Hermite–Hadamard inequality with a fractional integral operator, researchers have obtained fractional Hermite–Hadamard-type inequalities for various classes of convex functions, including harmonically convex, harmonically s-convex functions, and p-harmonic functions (see, e.g., [15,16,17,18,19,20,21]).

In [22], İşcan and Wu established the following Hermite–Hadamard inequalities for harmonically convex functions via fractional integrals: If the function $\varphi :[\mathfrak{a},\mathfrak{b}]\subset \mathbb{R}\setminus \left\{0\right\}\to \mathbb{R}$ is harmonically convex, then

$$\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)\le {\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\le {\displaystyle \frac{\varphi \left(\mathfrak{a}\right)+\varphi \left(\mathfrak{b}\right)}{2}},$$

where $\psi \left(\nu \right)={\displaystyle \frac{1}{\nu }}$, and ${\mathbf{R}}_{{\sigma }^{+}}^{\alpha }$ and ${\mathbf{R}}_{{\sigma }^{-}}^{\alpha }$ denote the left and right Riemann-Liouville fractional integrals [11].

İşcan in [23] presented the following Simpson-type inequality for differentiable harmonically convex functions:

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}{\displaystyle \frac{\varphi \left(\nu \right)}{{\nu }^2}}\mathrm{d}\nu \right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\displaystyle \frac{{\mathfrak{b}}^2-{\mathfrak{a}}^2+4{\mathfrak{a}}^2\mathfrak{b}-4{\mathfrak{a}}^2-4\mathfrak{a}\mathfrak{b}}{3\mathfrak{a}(\mathfrak{a}+\mathfrak{b}){(\mathfrak{b}-\mathfrak{a})}^3}}+{\displaystyle \frac{5\mathfrak{a}+7\mathfrak{b}+11{\mathfrak{a}}^2-{\mathfrak{b}}^2-10\mathfrak{a}\mathfrak{b}}{3{(\mathfrak{b}-\mathfrak{a})}^4}}\ln \left({\displaystyle \frac{18\mathfrak{a}(\mathfrak{a}+\mathfrak{b})}{{(5\mathfrak{a}+\mathfrak{b})}^2}}\right)\right)\left(\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|+\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right).\hfill \end{array}$$

Motivated by the aforementioned studies, this paper aims to establish new Riemann–Liouville fractional Simpson-type inequalities for differentiable harmonically convex functions.

The remainder of this paper is organized as follows: Section 2 recalls essential definitions and preliminary results related to fractional calculus and certain special functions. In Section 3, we present some auxiliary results that are essential for the proofs of our main theorems. Section 4 introduces a novel fractional integral identity, which plays a central role in establishing the inequalities presented in this work. In Section 5, we establish our main result in a form of Riemann–Liouville fractional Simpson-type inequalities based on harmonic convexity. Section 6 provides a numerical example with a graphical illustration that confirm the validity of the theoretical findings. Section 7 discusses practical applications of the derived inequalities, and Section 8 concludes the paper with remarks on possible extensions and future directions.

2. Preliminaries

To ensure self-containment and fix notation, this section recalls key definitions and foundational results concerning Riemann–Liouville fractional integrals and special functions that will be frequently used throughout the paper.

Definition 1

([11]). Let $\varphi \in L^1[\mathfrak{a},\mathfrak{b}]$. The Riemann-Liouville fractional integrals ${\mathbf{R}}_{{\mathfrak{a}}^{+}}^{\alpha }\varphi$ and ${\mathbf{R}}_{{\mathfrak{b}}^{-}}^{\alpha }\varphi$ of order $\alpha >0$ with $\mathfrak{a}\ge 0$ are defined by

$$\begin{array}{cc}\hfill {\mathbf{R}}_{{\mathfrak{a}}^{+}}^{\alpha }\varphi \left(x\right)=& \frac{1}{\Gamma \left(\alpha \right)}\stackrel{x}{\underset{\mathfrak{a}}{\int }}{\left(x-\wp \right)}^{\alpha -1}\varphi (\wp )\mathrm{d}\wp ,x>\mathfrak{a},\hfill \\ \hfill {\mathbf{R}}_{{\mathfrak{b}}^{-}}^{\alpha }\varphi \left(x\right)=& \frac{1}{\Gamma \left(\alpha \right)}\stackrel{\mathfrak{b}}{\underset{x}{\int }}{\left(\wp -x\right)}^{\alpha -1}\varphi (\wp )\mathrm{d}\wp ,\mathfrak{b}>x,\hfill \end{array}$$

respectively, where $\Gamma \left(\alpha \right)=\stackrel{\infty }{\underset{0}{\int }}$ $e^{-\wp }{\wp }^{\alpha -1}\mathrm{d}\wp$, is the Gamma function and ${\mathbf{R}}_{{\mathfrak{a}}^{+}}^0\varphi \left(x\right)={\mathbf{R}}_{{\mathfrak{b}}^{-}}^0\varphi \left(x\right)=\varphi \left(x\right)$.

Definition 2

([24,25]). The Beta function, denoted $B(u,v)$, is a special function defined for real (or complex) numbers $Re\left(u\right)>0$ and $Re\left(v\right)>0$ by the integral

$$B(u,v)=\underset{0}{\stackrel{1}{\int }}{\wp }^{u-1}{(1-t)}^{\wp -1}\mathrm{d}\wp .$$

It is symmetric, i.e., $B(u,v)=B(v,u)$, and is closely related to the Gamma function via the identity

$$B(u,v)={\displaystyle \frac{\Gamma \left(u\right)\Gamma \left(v\right)}{\Gamma (u+v)}}.$$

Definition 3

([24,25]). The integral representation of the hypergeometric function is defined as follows:

$${}_2\mathit{F}_1\left(a,b,c;z\right)={\displaystyle \frac{1}{B\left(b,c-b\right)}}\underset{0}{\stackrel{1}{\int }}{\wp }^{b-1}{\left(1-\wp \right)}^{c-b-1}{\left(1-z\wp \right)}^{-a}\mathrm{d}\wp ,$$

where $c>b>0$, $\left|z\right|<1$ and $B\left(.,.\right)$ is the Beta function.

3. Auxiliary Results

In what follows, we use the following notations

$${\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)=\underset{\varsigma }{\stackrel{\tau }{\int }}{\displaystyle \frac{{\wp }^{\alpha +1}}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp ={\displaystyle \frac{{\tau }^{\alpha +2}\left({}_{2}F_1\left(2,1,\alpha +3,\frac{\tau \left(\mathfrak{b}-\mathfrak{a}\right)}{\mathfrak{a}+\tau \left(\mathfrak{b}-\mathfrak{a}\right)}\right)\right)}{\left(\alpha +2\right){\left(\mathfrak{a}+\tau \left(\mathfrak{b}-\mathfrak{a}\right)\right)}^2}}-{\displaystyle \frac{{\varsigma }^{\alpha +2}\left({}_{2}F_1\left(2,1,\alpha +3,\frac{\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)}{\mathfrak{a}+\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)}\right)\right)}{\left(\alpha +2\right){\left(\mathfrak{a}+\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)\right)}^2}},$$

(1)

with

$${\mathcal{J}}_0\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)=\underset{\varsigma }{\stackrel{\tau }{\int }}{\displaystyle \frac{1}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp ={\displaystyle \frac{\tau -\varsigma }{\left(\mathfrak{a}+\tau \left(\mathfrak{b}-\mathfrak{a}\right)\right)\left(\mathfrak{a}+\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)\right)}}$$

and

$${\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)=\underset{\varsigma }{\stackrel{\tau }{\int }}{\displaystyle \frac{\wp }{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp ={\displaystyle \frac{1}{\mathfrak{b}-\mathfrak{a}}}\left(\ln {\displaystyle \frac{\mathfrak{a}+\tau \left(\mathfrak{b}-\mathfrak{a}\right)}{\mathfrak{a}+\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)}}-{\displaystyle \frac{\mathfrak{a}\left(\tau -\varsigma \right)}{\left(\mathfrak{a}+\tau \left(\mathfrak{b}-\mathfrak{a}\right)\right)\left(\mathfrak{a}+\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)\right)}}\right).$$

$${\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)=\underset{\varsigma }{\stackrel{\tau }{\int }}{\displaystyle \frac{{\wp }^{\alpha +1}}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp ={\displaystyle \frac{{\tau }^{\alpha +2}\left({}_{2}F_1\left(2,\alpha +2,\alpha +3,\frac{\tau \left(\mathfrak{b}-\mathfrak{a}\right)}{\mathfrak{b}}\right)\right)}{\left(\alpha +2\right){\mathfrak{b}}^2}}-{\displaystyle \frac{{\varsigma }^{\alpha +2}\left({}_{2}F_1\left(2,\alpha +2,\alpha +3,\frac{\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)}{\mathfrak{b}}\right)\right)}{\left(\alpha +2\right){\mathfrak{b}}^2}},$$

(2)

with

$${\mathcal{K}}_0\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)=\underset{\varsigma }{\stackrel{\tau }{\int }}{\displaystyle \frac{1}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp ={\displaystyle \frac{\tau -\varsigma }{\left(\mathfrak{b}-\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)\right)\left(\mathfrak{b}-\tau \left(\mathfrak{b}-\mathfrak{a}\right)\right)}}$$

and

$${\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)=\underset{\varsigma }{\stackrel{\tau }{\int }}{\displaystyle \frac{\wp }{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp ={\displaystyle \frac{1}{\mathfrak{b}-\mathfrak{a}}}\left(\ln {\displaystyle \frac{\mathfrak{b}+\tau \left(\mathfrak{a}-\mathfrak{b}\right)}{\mathfrak{b}-\left(\mathfrak{b}-\mathfrak{a}\right)\varsigma }}+{\displaystyle \frac{\mathfrak{b}\left(\tau -\varsigma \right)}{\left(\mathfrak{b}-\varsigma \left(\mathfrak{b}-\mathfrak{a}\right)\right)\left(\mathfrak{b}-\tau \left(\mathfrak{b}-\mathfrak{a}\right)\right)}}\right).$$

$${\mathcal{C}}_1\left(a,b,\alpha \right)=\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\displaystyle \frac{1}{6}}{\mathcal{J}}_1\left(a,b,0,{\left({\displaystyle \frac{1}{6}}\right)}^{{\displaystyle \frac{1}{\alpha }}}\right)-{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ +{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)-{\displaystyle \frac{1}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha \le {\displaystyle \frac{\ln 6}{\ln 2}},\\ {\displaystyle \frac{1}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)-{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha >{\displaystyle \frac{\ln 6}{\ln 2}},\end{array}\right.$$

(3)

$${\mathcal{C}}_2\left(a,b,\alpha \right)=\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\displaystyle \frac{1}{6}}{\mathcal{K}}_0\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)-{\displaystyle \frac{1}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ -{\mathcal{K}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)+{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ +{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)-{\mathcal{K}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)\hfill & & \\ -{\displaystyle \frac{1}{6}}{\mathcal{K}}_0\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{1}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha \le {\displaystyle \frac{\ln 6}{\ln 2}},\\ {\displaystyle \frac{1}{6}}{\mathcal{K}}_0\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)-{\displaystyle \frac{1}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)\hfill & & \\ -{\mathcal{K}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)+{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha >{\displaystyle \frac{\ln 6}{\ln 2}},\end{array}\right.$$

(4)

$${\mathcal{C}}_3\left(a,b,\alpha \right)=\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)-{\displaystyle \frac{5}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha \le {\displaystyle \frac{\ln 6-\ln 5}{\ln 2}},\\ {\displaystyle \frac{5}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)-{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ +{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)-{\displaystyle \frac{5}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha >{\displaystyle \frac{\ln 6-\ln 5}{\ln 2}},\end{array}\right.$$

(5)

$${\mathcal{C}}_4\left(a,b,\alpha \right)=\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\displaystyle \frac{5}{6}}{\mathcal{K}}_0\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)-{\displaystyle \frac{5}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)\hfill & & \\ -{\mathcal{K}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)+{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)\hfill & \mathrm{if}& \alpha \ge {\displaystyle \frac{\ln 6-\ln 5}{\ln 2}},\\ {\displaystyle \frac{5}{6}}{\mathcal{K}}_0\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)-{\displaystyle \frac{5}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)\hfill & & \\ -{\mathcal{K}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)+{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)\hfill & & \\ +{\mathcal{K}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)-{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)\hfill & & \\ -{\displaystyle \frac{5}{6}}{\mathcal{K}}_0\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)+{\displaystyle \frac{5}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)\hfill & \mathrm{if}& \alpha <{\displaystyle \frac{\ln 6-\ln 5}{\ln 2}},\end{array}\right.$$

(6)

$${\mathcal{C}}_5\left(\mathfrak{a},\mathfrak{b},\alpha \right)=\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\displaystyle \frac{1}{6}}{\mathcal{J}}_0\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)-{\displaystyle \frac{1}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ -{\mathcal{J}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)+{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ +{\mathcal{J}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)-{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)\hfill & & \\ -{\displaystyle \frac{1}{6}}{\mathcal{J}}_0\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{1}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha \le {\displaystyle \frac{\ln 6}{\ln 2}},\\ {\displaystyle \frac{1}{6}}{\mathcal{J}}_0\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)-{\displaystyle \frac{1}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)\hfill & & \\ -{\mathcal{J}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)+{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha >{\displaystyle \frac{\ln 6}{\ln 2}},\end{array}\right.$$

(7)

$${\mathcal{C}}_6\left(\mathfrak{a},\mathfrak{b},\alpha \right)=\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\displaystyle \frac{1}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},0,{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }}\right)-{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,1\right)\hfill & & \\ +{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)-{\displaystyle \frac{1}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{1}{6}}\right)}^{\frac{1}{\alpha }},{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha \le {\displaystyle \frac{\ln 6}{\ln 2}},\\ {\displaystyle \frac{1}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)-{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},0,{\displaystyle \frac{1}{2}}\right)\hfill & \mathrm{if}& \alpha >{\displaystyle \frac{\ln 6}{\ln 2}},\end{array}\right.$$

(8)

$${\mathcal{C}}_7\left(\mathfrak{a},\mathfrak{b},\alpha \right)=\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\mathcal{J}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)-{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)\hfill & & \\ -{\displaystyle \frac{5}{6}}{\mathcal{J}}_0\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)+{\displaystyle \frac{5}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)\hfill & \mathrm{if}& \alpha \le {\displaystyle \frac{\ln 6-\ln 5}{\ln 2}},\\ {\displaystyle \frac{5}{6}}{\mathcal{J}}_0\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)-{\displaystyle \frac{5}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ -{\mathcal{J}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)+{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ +{\mathcal{J}}_{\alpha }\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)-{\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)\hfill & & \\ -{\displaystyle \frac{5}{6}}{\mathcal{J}}_0\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)+{\displaystyle \frac{5}{6}}{\mathcal{J}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)\hfill & \mathrm{if}& \alpha >{\displaystyle \frac{\ln 6-\ln 5}{\ln 2}}\end{array}\right.$$

(9)

and

$${\mathcal{C}}_8\left(\mathfrak{a},\mathfrak{b},\alpha \right)=\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp =\left\{\begin{array}{ccc}{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)-{\displaystyle \frac{5}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},1\right)\hfill & \mathrm{if}& \alpha \le {\displaystyle \frac{\ln 6-\ln 5}{\ln 2}},\\ {\displaystyle \frac{5}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)-{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\displaystyle \frac{1}{2}},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }}\right)\hfill & & \\ +{\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)-{\displaystyle \frac{5}{6}}{\mathcal{K}}_1\left(\mathfrak{a},\mathfrak{b},{\left({\displaystyle \frac{5}{6}}\right)}^{\frac{1}{\alpha }},1\right)\hfill & \mathrm{if}& \alpha >{\displaystyle \frac{\ln 6-\ln 5}{\ln 2}},\end{array}\right.$$

where ${\mathcal{J}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)$ and ${\mathcal{K}}_{\alpha +1}\left(\mathfrak{a},\mathfrak{b},\varsigma ,\tau \right)$ are defined as in (1) and (2), respectively.

4. New Riemann–Liouville Fractional Integral Identity

The derivation of our main inequalities relies crucially on a new integral identity involving the Riemann–Liouville fractional integrals.

Lemma 1.

Let $\varphi :\mathcal{I}\subset \mathbb{R}\setminus \left\{0\right\}\to \mathbb{R}$ be a differentiable mapping on ${\mathcal{I}}^{\circ }$ (the interior of $\mathcal{I}$). If ${\varphi }^{\prime }$ is integrable on $\left[\mathfrak{a},\mathfrak{b}\right]$ where $\mathfrak{a},\mathfrak{b}\in {\mathcal{I}}^{\circ }$ with $\mathfrak{a}<\mathfrak{b}$, then the following equality

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{{\displaystyle \frac{1}{\mathfrak{a}}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{{\displaystyle \frac{1}{\mathfrak{b}}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\hfill \\ \hfill =& {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}\left({\displaystyle \frac{\frac{1}{6}-{\wp }^{\alpha }}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)-{\displaystyle \frac{\frac{1}{6}-{\wp }^{\alpha }}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp \right.\hfill \\ \hfill & +\left.\underset{\frac{1}{2}}{\stackrel{1}{\int }}\left({\displaystyle \frac{\frac{5}{6}-{\wp }^{\alpha }}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)-{\displaystyle \frac{\frac{5}{6}-{\wp }^{\alpha }}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp \right)\hfill \end{array}$$

holds where $\psi \left(\nu \right)={\displaystyle \frac{1}{\nu }}$.

Proof. 

Let

$${\mathcal{N}}_1=\underset{0}{\stackrel{\frac{1}{2}}{\int }}\left({\displaystyle \frac{\frac{1}{6}-{\wp }^{\alpha }}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)-{\displaystyle \frac{\frac{1}{6}-{\wp }^{\alpha }}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp$$

and

$${\mathcal{N}}_2=\underset{\frac{1}{2}}{\stackrel{1}{\int }}\left({\displaystyle \frac{\frac{5}{6}-{\wp }^{\alpha }}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)-{\displaystyle \frac{\frac{5}{6}-{\wp }^{\alpha }}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp .$$

Integrating by parts, ${\mathcal{N}}_1$ we obtain

$$\begin{array}{cc}\hfill {\mathcal{N}}_1=& \underset{0}{\stackrel{\frac{1}{2}}{\int }}\left({\displaystyle \frac{\frac{1}{6}-{\wp }^{\alpha }}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)-{\displaystyle \frac{\frac{1}{6}-{\wp }^{\alpha }}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp \hfill \\ \hfill =& {\left.-{\displaystyle \frac{1}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left({\displaystyle \frac{1}{6}}-{\wp }^{\alpha }\right)\left(\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)+\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\right|}_0^{\frac{1}{2}}\hfill \\ \hfill & -{\displaystyle \frac{\alpha }{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\wp }^{\alpha -1}\left(\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)+\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp \hfill \\ \hfill =& {\displaystyle \frac{2}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left({\left({\displaystyle \frac{1}{2}}\right)}^{\alpha }-{\displaystyle \frac{1}{6}}\right)\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+{\displaystyle \frac{1}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left({\displaystyle \frac{1}{6}}\right)\left(\varphi \left(\mathfrak{b}\right)+\varphi \left(\mathfrak{a}\right)\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha }{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\mathrm{d}\wp +\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\mathrm{d}\wp \right).\hfill \end{array}$$

(10)

Similarly, we have

$$\begin{array}{cc}\hfill {\mathcal{N}}_2=& \underset{\frac{1}{2}}{\stackrel{1}{\int }}\left({\displaystyle \frac{\frac{5}{6}-{\wp }^{\alpha }}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)-{\displaystyle \frac{\frac{5}{6}-{\wp }^{\alpha }}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp \hfill \\ \hfill =& {\left.-{\displaystyle \frac{1}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left({\displaystyle \frac{5}{6}}-{\wp }^{\alpha }\right)\left(\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)+\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\right|}_{\frac{1}{2}}^1\hfill \\ \hfill & -{\displaystyle \frac{\alpha }{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\wp }^{\alpha -1}\left(\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)+\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right)\mathrm{d}\wp \hfill \\ \hfill =& {\displaystyle \frac{1}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{2}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left({\left({\displaystyle \frac{1}{2}}\right)}^{\alpha }-{\displaystyle \frac{5}{6}}\right)\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{j}}{\mathfrak{a}+\mathfrak{b}}}\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha }{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\mathrm{d}\wp +\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\mathrm{d}\wp \right).\hfill \end{array}$$

(11)

Adding (10) and (11), we get

$$\begin{array}{cc}\hfill {\mathcal{N}}_1+{\mathcal{N}}_2=& {\displaystyle \frac{2}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left({\displaystyle \frac{1}{6}}\varphi \left(\mathfrak{a}\right)+{\displaystyle \frac{2}{3}}\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+{\displaystyle \frac{1}{6}}\varphi \left(\mathfrak{b}\right)\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha }{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left(\underset{0}{\stackrel{1}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\mathrm{d}\wp +\underset{0}{\stackrel{1}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\mathrm{d}\wp \right).\hfill \end{array}$$

(12)

Using appropriate changes of variable, we obtain

$$\begin{array}{cc}\hfill \underset{0}{\stackrel{1}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\mathrm{d}\wp =& {\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}{\left({\displaystyle \frac{1}{\mu }}-\frac{1}{\mathfrak{b}}\right)}^{\alpha -1}\varphi \left(\mu \right)\frac{\mathrm{d}\mu }{{\mu }^2}\hfill \\ \hfill =& {\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\underset{\frac{1}{\mathfrak{b}}}{\stackrel{\frac{1}{\mathfrak{a}}}{\int }}{\left(u-{\displaystyle \frac{1}{\mathfrak{b}}}\right)}^{\alpha -1}\varphi \left({\displaystyle \frac{1}{u}}\right)\mathrm{d}u.\hfill \end{array}$$

(13)

Similarly, we get

$$\begin{array}{cc}\hfill \underset{0}{\stackrel{1}{\int }}{\wp }^{\alpha -1}\varphi \left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\mathrm{d}\wp =& {\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}{\left({\displaystyle \frac{1}{\mathfrak{a}}}-{\displaystyle \frac{1}{\mu }}\right)}^{\alpha -1}\varphi \left(\mu \right){\displaystyle \frac{\mathrm{d}\mu }{{\mu }^2}}\hfill \\ \hfill =& {\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\underset{\frac{1}{\mathfrak{b}}}{\stackrel{\frac{1}{\mathfrak{a}}}{\int }}{\left({\displaystyle \frac{1}{\mathfrak{a}}}-\nu \right)}^{\alpha -1}\varphi \left({\displaystyle \frac{1}{\nu }}\right)\mathrm{d}\nu .\hfill \end{array}$$

(14)

Combining (12)–(14), we get

$$\begin{array}{cc}\hfill {\mathcal{N}}_1+{\mathcal{N}}_2=& {\displaystyle \frac{1}{3\mathfrak{a}\mathfrak{j}\left(\mathfrak{b}-\mathfrak{a}\right)}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)\hfill \\ \hfill & -{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\frac{1}{\mathfrak{b}}}{\stackrel{\frac{1}{\mathfrak{a}}}{\int }}{\left(\nu -{\displaystyle \frac{1}{\mathfrak{b}}}\right)}^{\alpha -1}\varphi \left({\displaystyle \frac{1}{\nu }}\right)\mathrm{d}\nu +{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\frac{1}{\mathfrak{b}}}{\stackrel{\frac{1}{\mathfrak{a}}}{\int }}{\left({\displaystyle \frac{1}{\mathfrak{a}}}-\nu \right)}^{\alpha -1}\varphi \left({\displaystyle \frac{1}{\nu }}\right)\mathrm{d}\nu \right).\hfill \end{array}$$

(15)

Multiplying (15) by ${\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}$, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\mathcal{N}}_1+{\mathcal{N}}_2\right)=& {\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)\hfill \\ \hfill & -{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right),\hfill \end{array}$$

which is the desired result. □

5. Fractional Simpson-Type Inequality via Harmonic Convexity

Building upon the lemma developed in the previous section, we now present our principal contribution: a family of Simpson-type inequalities in the setting of Riemann–Liouville fractional calculus for differentiable harmonically convex functions.

Theorem 1.

Let $\varphi :\mathcal{I}\subset \mathbb{R}\setminus \left\{0\right\}\to \mathbb{R}$ be a differentiable function on ${\mathcal{I}}^{\circ }$, $\mathfrak{a},\mathfrak{b}\in \mathcal{I}$ with $\mathfrak{a}<\mathfrak{b}$, and ${\varphi }^{\prime }\in L[\mathfrak{a},\mathfrak{b}]$. If $\left|{\varphi }^{\prime }\right|$ is harmonically convex on $\left[\mathfrak{a},\mathfrak{b}\right]$, then we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\mathcal{S}}_1\left(\mathfrak{a},\mathfrak{b},\alpha \right)\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|+{\mathcal{S}}_2\left(\mathfrak{a},\mathfrak{b},\alpha \right)\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right),\hfill \end{array}$$

where $\psi \left(\nu \right)={\displaystyle \frac{1}{\nu }}$.

Here ${\mathcal{S}}_1(\mathfrak{a},\mathfrak{b},\alpha )={\displaystyle \sum _{i=1}^4}{\mathcal{C}}_i(\mathfrak{a},\mathfrak{b},\alpha )$ and ${\mathcal{S}}_2(\mathfrak{a},\mathfrak{b},\alpha )={\displaystyle \sum _{i=5}^8}{\mathcal{C}}_i(\mathfrak{a},\mathfrak{b},\alpha )$, where ${\mathcal{C}}_i(\mathfrak{a},\mathfrak{b},\alpha )$$(i=1,\cdots ,8)$ are defined as in (3)–(10), respectively.

Proof. 

From Lemma 1, absolute value and harmonic convexity of $\left|{\varphi }^{\prime }\right|$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\right|+{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right|\mathrm{d}\wp \right.\hfill \\ \hfill & +\left.\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\right|+{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right|\mathrm{d}\wp \right)\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}\left[{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\left(\wp \left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|+\left(1-\wp \right)\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right)+{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\left(\left(1-\wp \right)\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|+\wp \left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right)\right]\mathrm{d}\wp \right.\hfill \\ \hfill & +\left.\underset{\frac{1}{2}}{\stackrel{1}{\int }}\left[{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\left(\wp \left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|+\left(1-\wp \right)\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right)+{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\left(\left(1-\wp \right)\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|+\wp \left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right)\right]\mathrm{d}\wp \right)\hfill \\ \hfill =& {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left(\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}\left[{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}+{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\right]\mathrm{d}\wp +\underset{\frac{1}{2}}{\stackrel{1}{\int }}\left[{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}+{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\right]\mathrm{d}\wp \right)\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|\right.\hfill \\ \hfill & \left.+\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}\left[{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}+{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}+\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\left(1-\wp \right)}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}+{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|\wp }{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\right]\mathrm{d}\wp \right)\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right)\hfill \\ \hfill =& {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left(\left({\mathcal{C}}_1\left(\mathfrak{a},\mathfrak{b},\alpha \right)+{\mathcal{C}}_2\left(\mathfrak{a},\mathfrak{b},\alpha \right)+{\mathcal{C}}_3\left(\mathfrak{a},\mathfrak{b},\alpha \right)+{\mathcal{C}}_4\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|\right.\hfill \\ \hfill & +\left.\left({\mathcal{C}}_5\left(\mathfrak{a},\mathfrak{b},\alpha \right)+{\mathcal{C}}_6\left(\mathfrak{a},\mathfrak{b},\alpha \right)+{\mathcal{C}}_7\left(\mathfrak{a},\mathfrak{b},\alpha \right)+{\mathcal{C}}_8\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right),\hfill \end{array}$$

where we have used (3)–(10). This completes the proof. □

Corollary 1.

By choosing $\alpha =1$, Theorem 1 becomes

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}{\displaystyle \frac{\varphi \left(\nu \right)}{{\nu }^2}}\mathrm{d}\nu \right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{12}}\left(\left(-{\displaystyle \frac{1}{\mathfrak{b}}}+{\displaystyle \frac{11\mathfrak{a}+\mathfrak{b}}{{\left(\mathfrak{b}-\mathfrak{a}\right)}^2}}\ln {\displaystyle \frac{{\left(5\mathfrak{a}+\mathfrak{b}\right)}^2}{18\mathfrak{a}\left(\mathfrak{a}+\mathfrak{b}\right)}}+{\displaystyle \frac{7\mathfrak{a}+5\mathfrak{b}}{{\left(\mathfrak{b}-\mathfrak{a}\right)}^2}}\ln {\displaystyle \frac{{\left(\mathfrak{a}+5\mathfrak{b}\right)}^2}{18\mathfrak{b}\left(\mathfrak{a}+\mathfrak{b}\right)}}\right)\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|\right.\hfill \\ \hfill & +\left.\left({\displaystyle \frac{1}{\mathfrak{a}}}+{\displaystyle \frac{5\mathfrak{a}+7\mathfrak{b}}{{\left(\mathfrak{b}-\mathfrak{a}\right)}^2}}\ln {\displaystyle \frac{18\mathfrak{a}\left(\mathfrak{a}+\mathfrak{b}\right)}{{\left(5\mathfrak{a}+\mathfrak{b}\right)}^2}}+{\displaystyle \frac{\mathfrak{a}+11\mathfrak{b}}{{\left(\mathfrak{b}-\mathfrak{a}\right)}^2}}\ln {\displaystyle \frac{18\mathfrak{b}\left(\mathfrak{a}+\mathfrak{b}\right)}{{\left(\mathfrak{a}+5\mathfrak{b}\right)}^2}}\right)\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|\right).\hfill \end{array}$$

Theorem 2.

Let $\varphi :\mathcal{I}\subset \mathbb{R}\setminus \left\{0\right\}\to \mathbb{R}$ be a differentiable function on ${\mathcal{I}}^{\circ }$, $\mathfrak{a},\mathfrak{b}\in \mathcal{I}$ with $\mathfrak{a}<\mathfrak{b}$, and ${\varphi }^{\prime }\in L[\mathfrak{a},\mathfrak{b}]$. If ${\left|{\varphi }^{\prime }\right|}^q$ is harmonically convex on $\left[\mathfrak{a},\mathfrak{b}\right]$ where $q>1$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$, then we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left(\left({\left({\mathcal{T}}_1\left(\alpha ,p\right)\right)}^{\frac{1}{p}}+{\left({\mathcal{T}}_4\left(\alpha ,p\right)\right)}^{\frac{1}{p}}\right){\left({\displaystyle \frac{{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+3{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +\left.\left({\left({\mathcal{T}}_2\left(\alpha ,p\right)\right)}^{\frac{1}{p}}+{\left({\mathcal{T}}_3\left(\alpha ,p\right)\right)}^{\frac{1}{p}}\right){\left({\displaystyle \frac{3{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}\right),\hfill \end{array}$$

where $\psi \left(\nu \right)={\displaystyle \frac{1}{\nu }}$, and

$${\mathcal{T}}_1\left(\alpha ,p\right)=\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^{2p}}}\mathrm{d}\wp ,$$

(16)

$${\mathcal{T}}_2\left(\alpha ,p\right)=\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^{2p}}}\mathrm{d}\wp ,$$

(17)

$${\mathcal{T}}_3\left(\alpha ,p\right)=\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^{2p}}}\mathrm{d}\wp$$

(18)

and

$${\mathcal{T}}_4\left(\alpha ,p\right)=\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^{2p}}}\mathrm{d}\wp .$$

(19)

Proof. 

From Lemma 1, absolute value, Hölder’s inequality and harmonic convexity of ${\left|{\varphi }^{\prime }\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^{2p}}}\right)}^{\frac{1}{p}}{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^{2p}}}\right)}^{\frac{1}{p}}{\left(\underset{0}{\stackrel{{\displaystyle \frac{1}{2}}}{\int }}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^{2p}}}\mathrm{d}\wp \right)}^{\frac{1}{p}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +\left.{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}^p}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^{2p}}}\mathrm{d}\wp \right)}^{\frac{1}{p}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\right)\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\left({\mathcal{T}}_1\left(\alpha ,p\right)\right)}^{\frac{1}{p}}{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}\left(\wp {\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}\right.+{\left({\mathcal{T}}_2\left(\alpha ,p\right)\right)}^{\frac{1}{p}}{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}\left(\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\wp {\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\mathcal{T}}_3\left(\alpha ,p\right)\right)}^{\frac{1}{p}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}\left(\wp {\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}+\left.{\left({\mathcal{T}}_4\left(\alpha ,p\right)\right)}^{{\displaystyle \frac{1}{p}}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}\left(\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\wp {\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}\right)\hfill \\ \hfill =& {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\left({\mathcal{T}}_1\left(\alpha ,p\right)\right)}^{\frac{1}{p}}{\left({\displaystyle \frac{{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+3{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}+{\left({\mathcal{T}}_2\left(\alpha ,p\right)\right)}^{\frac{1}{p}}{\left({\displaystyle \frac{3{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +\left.{\left({\mathcal{T}}_3\left(\alpha ,p\right)\right)}^{\frac{1}{p}}{\left({\displaystyle \frac{3{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}+{\left({\mathcal{T}}_4\left(\alpha ,p\right)\right)}^{\frac{1}{p}}{\left({\displaystyle \frac{{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+3{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}\right)\hfill \\ \hfill =& {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left(\left({\left({\mathcal{T}}_1\left(\alpha ,p\right)\right)}^{\frac{1}{p}}+{\left({\mathcal{T}}_4\left(\alpha ,p\right)\right)}^{\frac{1}{p}}\right){\left({\displaystyle \frac{{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+3{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +\left.\left({\left({\mathcal{T}}_2\left(\alpha ,p\right)\right)}^{\frac{1}{p}}+{\left({\mathcal{T}}_3\left(\alpha ,p\right)\right)}^{\frac{1}{p}}\right){\left({\displaystyle \frac{3{\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q}{8}}\right)}^{\frac{1}{q}}\right),\hfill \end{array}$$

where we have used (16)–(19). □

Theorem 3.

Let $\varphi :\mathcal{I}\subset \mathbb{R}\setminus \left\{0\right\}\to \mathbb{R}$ be a differentiable function on ${\mathcal{I}}^{\circ }$, $\mathfrak{a},\mathfrak{b}\in \mathcal{I}$ with $\mathfrak{a}<\mathfrak{b}$, and ${\varphi }^{\prime }\in L[\mathfrak{a},\mathfrak{b}]$. If ${\left|{\varphi }^{\prime }\right|}^q$ is harmonically convex on $\left[\mathfrak{a},\mathfrak{b}\right]$ where $q>1$, then we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}^{\alpha }\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\left({\mathcal{E}}_1\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}{\left({\mathcal{C}}_1\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_5\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left({\mathcal{E}}_2\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}{\left({\mathcal{C}}_2\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_6\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\mathcal{E}}_3\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}\left({\left({\mathcal{C}}_3\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_7\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +\left.{\left({\mathcal{E}}_4\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}{\left({\mathcal{C}}_4\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_8\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\right),\hfill \end{array}$$

where $\psi \left(\nu \right)={\displaystyle \frac{1}{\nu }}$, and

$${\mathcal{E}}_i\left(a,b,\alpha \right)={\mathcal{C}}_i\left(a,b,\alpha \right)+{\mathcal{C}}_{i+4}\left(a,b,\alpha \right)$$

with ${\mathcal{C}}_i\left(\mathfrak{a},\mathfrak{b},\alpha \right)$ are defined as in (3)–(10), respectively.

Proof. 

From (1), absolute value, power mean inequality and harmonic convexity of ${\left|{\varphi }^{\prime }\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{1}{6}}\left(\varphi \left(\mathfrak{a}\right)+4\varphi \left({\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}\right)+\varphi \left(\mathfrak{b}\right)\right)-{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{2}}{\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\right)}^{\alpha }\left({\mathbf{R}}_{{\frac{1}{\mathfrak{a}}}^{-}}\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{b}}}\right)+{\mathbf{R}}_{{\frac{1}{\mathfrak{b}}}^{+}}\left(\varphi \circ \psi \right)\left({\displaystyle \frac{1}{\mathfrak{a}}}\right)\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +\left.{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}{\left|{\varphi }^{\prime }\left({\displaystyle \frac{\mathfrak{a}\mathfrak{b}}{\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}}}\right)\right|}^q\mathrm{d}\wp \right)}^{\frac{1}{q}}\right)\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}\right.\hfill \\ \hfill & \times {\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\left(\wp {\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}{\left(\underset{0}{\stackrel{\frac{1}{2}}{\int }}{\displaystyle \frac{\left|\frac{1}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\left(\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\wp {\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\left(1-\wp \right)\mathfrak{a}+\wp \mathfrak{b}\right)}^2}}\left(\wp {\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}\hfill \\ \hfill & +\left.{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\mathrm{d}\wp \right)}^{1-\frac{1}{q}}{\left(\underset{\frac{1}{2}}{\stackrel{1}{\int }}{\displaystyle \frac{\left|\frac{5}{6}-{\wp }^{\alpha }\right|}{{\left(\wp \mathfrak{a}+\left(1-\wp \right)\mathfrak{b}\right)}^2}}\left(\left(1-\wp \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+\wp {\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)\mathrm{d}\wp \right)}^{\frac{1}{q}}\right)\hfill \\ \hfill =& {\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(\mathfrak{b}-\mathfrak{a}\right)}{2}}\left({\left({\mathcal{E}}_1\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}{\left({\mathcal{C}}_1\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_5\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left({\mathcal{E}}_2\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}{\left({\mathcal{C}}_2\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_6\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\mathcal{E}}_3\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}\left({\left({\mathcal{C}}_3\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_7\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +\left.{\left({\mathcal{E}}_4\left(\mathfrak{a},\mathfrak{b},\alpha \right)\right)}^{1-\frac{1}{q}}{\left({\mathcal{C}}_4\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{a}\right)\right|}^q+{\mathcal{C}}_8\left(\mathfrak{a},\mathfrak{b},\alpha \right){\left|{\varphi }^{\prime }\left(\mathfrak{b}\right)\right|}^q\right)}^{\frac{1}{q}}\right),\hfill \end{array}$$

where we have used (3)–(10). This completes the proof. □

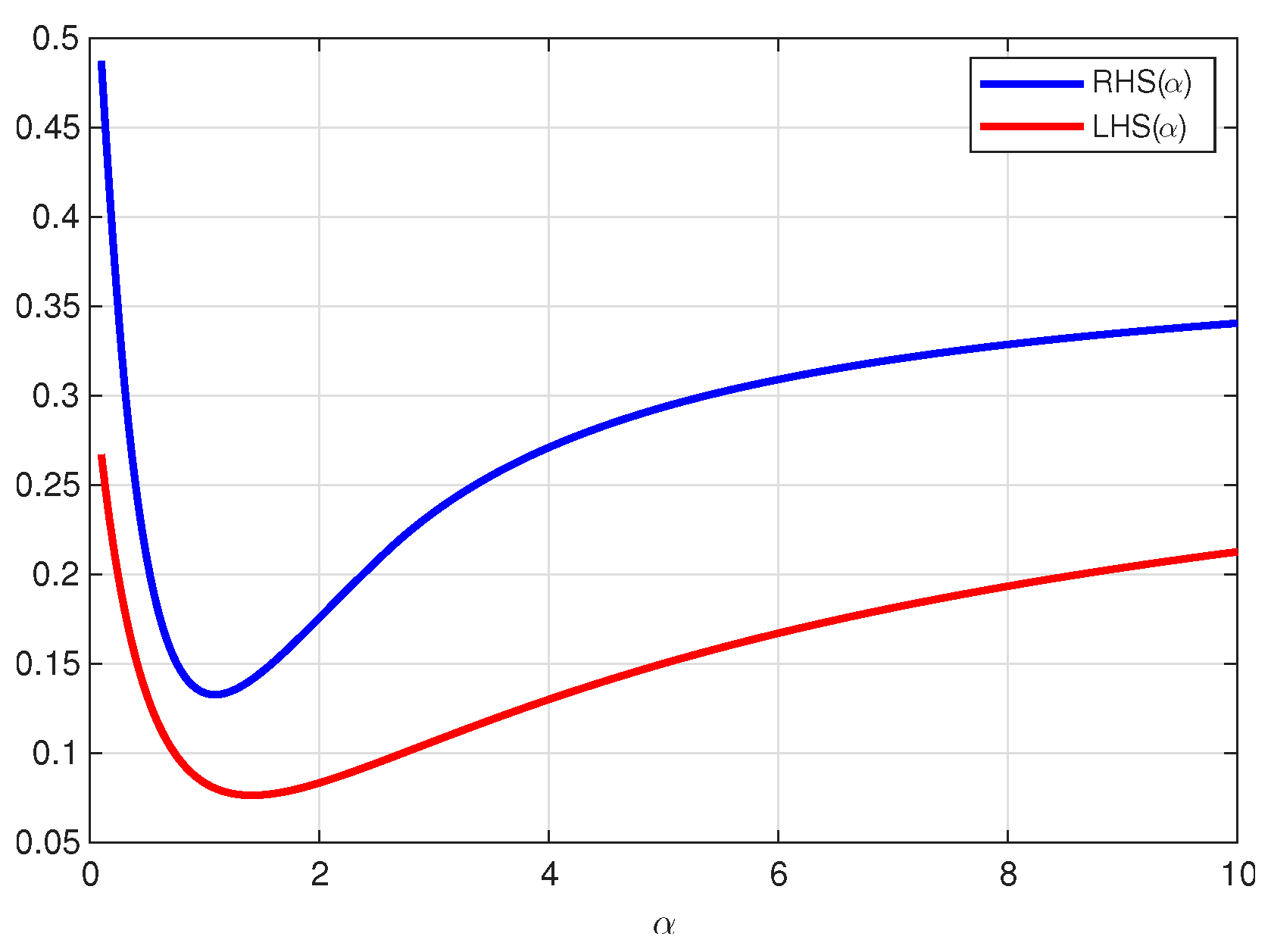
6. Numerical Example

To corroborate the validity of the inequality stated in Theorem 1, we provide a concrete numerical instance together with a visual representation that aligns with the theoretical prediction.

Example 1.

Consider $\mathfrak{a}=1$, $\mathfrak{b}=2$, and the function

$$\varphi \left(\nu \right)={\displaystyle \frac{{\nu }^2}{2}},\nu \in [1,2].$$

Its derivative ${\varphi }^{\prime }\left(\nu \right)=\nu$ is harmonically convex on $(0,\infty )$ (see [10]).

For this setting, the left-hand side (LHS) of the inequality in Theorem 1 reads

$$\mathrm{LHS}\left(\alpha \right)={\displaystyle \frac{1}{2}}\left|{\displaystyle \frac{11}{6}}-{\displaystyle \frac{1}{2}} {}_{2}F_1\left(2,\alpha ;\alpha +1;{\displaystyle \frac{1}{2}}\right)-2 {}_{2}F_1\left(2,\alpha ;\alpha +1;-1\right)\right|.$$

The right-hand side (RHS) is explicitly expressed as

$$\mathrm{RHS}\left(\alpha \right)={\mathcal{S}}_1(1,2,\alpha )+2{\mathcal{S}}_2(1,2,\alpha ),$$

where the terms ${\mathcal{S}}_1={\displaystyle \sum _{i=1}^4}{\mathcal{C}}_i(1,2,\alpha )$ and ${\mathcal{S}}_2={\displaystyle \sum _{i=5}^8}{\mathcal{C}}_i(1,2,\alpha )$, with ${\mathcal{C}}_i$$(i=1,\cdots ,8)$ are defined as in (3)–(10), respectively.

Employing symbolic manipulation and high-precision numerical evaluation, we compute $\mathrm{LHS}\left(\alpha \right)$ and $\mathrm{RHS}\left(\alpha \right)$ over the parameter interval $\alpha \in (0,10]$. The computed surfaces, shown in Figure 1, demonstrate that $\mathrm{LHS}\left(\alpha \right)\le \mathrm{RHS}\left(\alpha \right)$ across the entire sampled domain, offering numerical confirmation of both the correctness and tightness of the derived inequality.

Figure 1. Comparison of the left-hand side and right-hand side of the fractional Simpson-type inequality for $\varphi \left(\nu \right)={\nu }^2/2$ on $[1,2]$, plotted as functions of $\alpha \in (0,10]$. The inequality $\mathrm{LHS}\left(\alpha \right)\le \mathrm{RHS}\left(\alpha \right)$ is satisfied for all tested values of $\alpha$.

7. Applications

Beyond their theoretical interest, the fractional Simpson-type inequalities derived in this work find natural applications in approximation theory and numerical analysis. In this section, we discuss how these estimates can be employed for special means. Let us recall the following means for arbitrary real numbers $\mathfrak{a},\mathfrak{b}$:

The Arithmetic mean: $\mathfrak{a}\left(\mathfrak{a},\mathfrak{b}\right)={\displaystyle \frac{\mathfrak{a}+\mathfrak{b}}{2}}$.

The Harmonic mean: $\mathcal{H}\left(\mathfrak{a},\mathfrak{b}\right)={\displaystyle \frac{2\mathfrak{a}\mathfrak{b}}{\mathfrak{a}+\mathfrak{b}}}$ and $\mathcal{H}\left(\mathfrak{a},\mathfrak{b},c\right)={\displaystyle \frac{3}{\frac{1}{\mathfrak{a}}+\frac{1}{\mathfrak{b}}+\frac{1}{c}}}$.

The Geometric mean: $\mathcal{G}\left(\mathfrak{a},\mathfrak{b}\right)=\sqrt{\mathfrak{a}\mathfrak{b}}$.

The Logarithmic mean: $\mathcal{L}\left(\mathfrak{a},\mathfrak{b}\right)={\displaystyle \frac{\mathfrak{b}-\mathfrak{a}}{\ln \mathfrak{b}-\ln a}}$, $\mathfrak{a},\mathfrak{b}>0,\mathfrak{a}\ne \mathfrak{b}.$

Proposition 1.

Let $\mathfrak{a},\mathfrak{b}\in \mathbb{R}$ with $0<\mathfrak{a}<\mathfrak{b}$, then we have

$$\begin{array}{cc}\hfill & \left|2\mathcal{A}\left({\mathfrak{a}}^2,{\mathfrak{b}}^2\right)+4{\mathcal{H}}^2\left(\mathfrak{a},\mathfrak{b}\right)-6{\mathcal{G}}^2\left(\mathfrak{a},\mathfrak{b}\right){\mathcal{L}}^{-1}\left(\mathfrak{a},\mathfrak{b}\right)\right|\hfill \\ \hfill \le & {\mathfrak{b}}^2-{\mathfrak{a}}^2+{\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(11\mathfrak{a}+7\mathfrak{b}\right)}{\mathfrak{b}-\mathfrak{a}}}\ln {\displaystyle \frac{18\mathfrak{a}\left(\mathfrak{a}+\mathfrak{b}\right)}{{\left(5\mathfrak{a}+\mathfrak{b}\right)}^2}}+{\displaystyle \frac{\mathfrak{a}\mathfrak{b}\left(7\mathfrak{a}+11\mathfrak{b}\right)}{\mathfrak{b}-\mathfrak{a}}}\ln {\displaystyle \frac{18\mathfrak{b}\left(\mathfrak{a}+\mathfrak{b}\right)}{{\left(\mathfrak{a}+5\mathfrak{b}\right)}^2}}.\hfill \end{array}$$

Proof. 

The assertion follows from Corollary 1, applied to the function $\varphi \left(\nu \right)={\nu }^2$. □

Proposition 2.

Let $\mathfrak{a},\mathfrak{b}\in \mathbb{R}$ with $0<\mathfrak{a}<\mathfrak{b}$, then we have

$$\begin{array}{cc}\hfill & \left|2\mathcal{A}\left({\mathfrak{a}}^2,{\mathfrak{b}}^2\right)+4{\mathcal{H}}^2\left(\mathfrak{a},\mathfrak{b}\right)-6{\mathcal{G}}^2\left(\mathfrak{a},\mathfrak{b}\right){\mathcal{L}}^{-1}\left(\mathfrak{a},\mathfrak{b}\right)\right|\hfill \\ \hfill \le & {\displaystyle \frac{\mathfrak{b}-\mathfrak{a}}{2}}+{\displaystyle \frac{3\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\ln {\displaystyle \frac{18\mathfrak{a}\left(\mathfrak{a}+\mathfrak{b}\right)}{{\left(5\mathfrak{a}+\mathfrak{b}\right)}^2}}+{\displaystyle \frac{3\mathfrak{a}\mathfrak{b}}{\mathfrak{b}-\mathfrak{a}}}\ln {\displaystyle \frac{18\mathfrak{b}\left(\mathfrak{a}+\mathfrak{b}\right)}{{\left(\mathfrak{a}+5\mathfrak{b}\right)}^2}}.\hfill \end{array}$$

Proof. 

The assertion follows from Corollary 1, applied to the function $\varphi \left(\nu \right)=\nu$. □

8. Conclusions

In conclusion, we have successfully introduced a new fractional integral identity adapted to harmonic convexity and employed it to derive Riemann–Liouville fractional Simpson-type inequalities. The validity of our theoretical findings is confirmed through a concrete numerical example with graphical support. Future research may explore extensions to other fractional operators (e.g., Caputo, Hadamard) or higher-dimensional settings.