Orthogonality of 1-Types over Sets, Neighborhoods of Sets in 1-Types in Weakly Ordered Minimal Theories

Abstract

This paper examines the relationship between weak orthogonality and almost orthogonality for complete non-algebraic 1-types in weakly ordered minimal theories. A central element of our approach is the concept of neighborhoods, which encapsulate local properties of type realizations. This work contributes to a deeper understanding of the geometry of types in weakly ordered minimal theories and provides tools that may be applied in related model-theoretic contexts.

1. Introduction

This paper investigates weak orthogonality and almost orthogonality in the context of weakly ordered minimal structures. Recall that ordered minimality, introduced in Van den Dries’ work [1], provides a setting in which every definable subset of the domain is a finite union of points and intervals. Weak ordered minimality relaxes this condition by allowing definable subsets to be finite unions of convex sets, a concept introduced by Dickmann [2]. In the study of weak o-minimality, the work of Macpherson, Marker, and Steinhorn [3] was especially important, as it laid the basis for later research on minimality and its applications.

Our focus is on the interaction between non-algebraic complete 1-types. A key tool in our analysis is the study of neighborhoods, which capture local information about realizations of types.

The techniques used in this paper have also been applied in related contexts, such as expansion by unary externally definable predicates, and in the study of conservative extensions and type definability in weakly o-minimal theories.

The notions of orthogonality and almost orthogonality played a significant role in [4]. Furthermore, orthogonality plays an important role in counting countable models, as shown in the work of L. Mayer [5] and in later contributions in [6,7,8].

Our main results characterize the precise relationship between weak and almost orthogonality in $S_1\left(A\right)$ for weakly ordered minimal theories, and provide criteria for their equivalence. We also describe how these notions behave for specific classes of types, such as rational, irrational, solitary, and quasisolitary.

In contrast to the study of expansions, where quasi-neighborhoods play the central role, the investigation of orthogonality focuses on neighborhoods. Orthogonality has been extended to convex orthogonality for incomplete 1-types. In [9], convex orthogonality is considered for the convex closure of a complete type. The results obtained here complement those of [10].

Our results expand upon the framework introduced in an unpublished preprint, completing and extending several of its central arguments.

2. Preliminaries

We adhere to the following convention throughout.

Let $\overline{a}\in M^{\mathcal{l}\left(\overline{a}\right)}$ with $\mathcal{l}\left(\overline{a}\right)=\mathcal{l}$ and $\overline{a}=⟨a_1,\dots ,a_{\mathcal{l}}⟩$, we write $\overline{a}\in M$ to mean $\{a_1,\dots ,a_{\mathcal{l}}\}\subseteq M$. Let $1\le m<\mathcal{l}$, then $\overline{a}\mid m:=⟨a_1,\dots ,a_m⟩$.

Throughout, ${\mathcal{M}}^{\prime }$ is a model of a weakly o-minimal theory T, and $\mathcal{M}$ is a sufficiently large saturated elementary extension of ${\mathcal{M}}^{\prime }$, the Latin letters denote elements of $M^{\prime }$: $\overline{a}$, $\overline{b}$, $\overline{c}$, $\overline{d}\in M$, while the Greek letters denote elements of $M\setminus M^{\prime }$: $\overline{\alpha }$, $\overline{\beta }$, $\overline{\gamma }$, $\overline{\mu }\in M\setminus M^{\prime }$.

For any $C,D\subseteq M$, we write $C<D$ if $c<d$ whenever $c\in C$, $d\in D$. For $c\in M$, we write $c<D$ if $\left\{c\right\}<D$.

For any $D\subseteq M$ set $D^{-}:=\{\beta \in M:\beta <D\}\mathrm{and}{D}^{+}:=\{\beta \in M:\beta >D\}.$

If $A,B\subseteq M$ with $A<B$, write $(A,B):=\{\gamma \in M\mid A<\gamma <B\}$. Note that $(A,B)=A^{+}\cap B^{-}$.

We use $A\subseteq B$ for inclusion, i.e., whenever $a\in A$ implies $a\in B$, and $A\subset B$ for proper inclusion, i.e., if $A\subset B$ if $A\subseteq B$ and $A\ne B$.

Whenever a set of parameters $A\subseteq M$ is fixed, we assume that $\mathcal{M}$ is ${\left|A\right|}^{+}$ -saturated.

Types $p,q,r\in S_1\left(A\right)$ will always be non-algebraic complete 1-types over A. By an isolated type, we mean a non-algebraic isolated type.

${\mathrm{Aut}}_A\left(\mathcal{M}\right)$ is the group of all automorphisms of $\mathcal{M}$ that fix A pointwise, that is, $f\left(a\right)=a$ for any $f\in {\mathrm{Aut}}_A\left(\mathcal{M}\right)$ and any $a\in A$.

We use the following notations:

• $x>F(\mathcal{M},\overline{y})\iff \forall z[F(z,\overline{y})\to z<x]$
• $\mathsf{\Psi }(\mathcal{M},\overline{x})>F(\mathcal{M},\overline{y})\iff \forall z\forall t[F(z,\overline{y})\wedge \mathsf{\Psi }(t,\overline{x})\to z<t]$
• $p\left(\mathcal{M}\right)=\{\gamma \in M\mid \mathrm{for}\mathrm{any}\phi (x)\in p,\mathcal{M}\vDash \phi (\gamma \left)\right\},\alpha \vDash p\iff \alpha \in p\left(\mathcal{M}\right)$

Definition 1.

Let A be a linearly ordered set, and $B\subseteq A$. We say that B is convex if, for all $a,b\in B$, and all $x\in A$,

$$a<x<b\Rightarrow x\in B.$$

Definition 2.

We say that a formula $F(x,y,\overline{a})$, with $\overline{a}\in A$, is convex to the right if

$$\mathcal{M}\vDash \forall y\forall x\left[(F(x,y,\overline{a})\to (y\le x\wedge \forall z(y\le z\le x\to F(z,y,\overline{a}))))\right].$$

We say that a formula $G(x,y,\overline{a})$, with $\overline{a}\in A$, is convex to the left if

$$\mathcal{M}\vDash \forall y\forall x[(G(x,y,\overline{a})\to (y\ge x\wedge \forall z(x\le z\le y\to G(z,y,\overline{a})))].$$

Definition 3

(Baizhanov B.S., Verbovskii V.V., [11]). 1. The convex closure of a formula $\phi (x,\overline{a})$ is the following formula:

$${\phi }^c(x,\overline{a}):=\exists y_1\exists y_2\left(\phi (y_1,\overline{a})\wedge \phi (y_2,\overline{a})\wedge (y_1\le x\le y_2)\right).$$

2. 

The convex closure of a type $p\left(x\right)\in S_1\left(A\right)$ is the following type:

$$p^c\left(x\right):=\left\{{\phi }^c(x,\overline{a})\mid \phi (x,\overline{a})\in p\right\}.$$

Definition 4

(Baizhanov B.S., [12]). Let $p\in S_1\left(A\right)$. We say that a formula $\mathsf{\Phi }(x,y,\overline{a})$, with $\overline{a}\in A$, is p-stable (p-preserving) if

$$\mathit{for}\mathit{any}\alpha \vDash p,\mathit{there}\mathit{exist}{\gamma }_1,{\gamma }_2\vDash p\mathit{such}\mathit{that}{\gamma }_1<\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})<{\gamma }_2.$$

Other recent studies explore formulas from different perspectives, including partial clones of linear formulas [13] and superassociative structures [14].

Definition 5

(Marker D. [15]). A cut $\gamma \left(v\right)\in S_1\left(\mathcal{M}\right)$ is uniquely realizable over $\mathcal{M}$ if and only if, for any c realizing $\gamma \left(v\right)$, c is the only realization of $\gamma \left(v\right)$ in the prime model $Pr(\mathcal{M}\cup \{c\left\}\right)$.

Following Marker’s notion of uniquely realizable types, we generalize this concept to the context of weakly o-minimal theories and refer to such types as solitary.

Definition 6

(Baizhanov B.S. [10]). Let $p\in S_1\left(A\right)$ be a non-algebraic type.

We say that p is semi-quasisolitary to the right if there exists the greatest p-preserving convex to the right 2-A-formula $F(x,y,\overline{a})$, where $\overline{a}\in A$.

We say that p is semi-quasisolitary to the left if there exists the greatest p-preserving convex to the left 2-A-formula $G(x,y,\overline{a})$, where $\overline{a}\in A$.

We say that p is quasisolitary if it is semi-quasisolitary to the right and to the left.

Let $F(y,x,\overline{a})$ be the greatest convex to the right p-preserving formula, and $G(y,x,\overline{a})$ is the greatest convex to the left p-preserving formula. It was proved in [16] that the formula $E_p(x,y,\overline{a}):=F(x,y,\overline{a})\vee G(x,y,\overline{a})$ is an equivalence relation.

Let $p\in S_1\left(A\right)$ be quasisolitary. We say that p is solitary if $E_p(x,y,\overline{a})\equiv (x=y)$.

Definition 7

([16]). A type $p\in S_1\left(A\right)$ is social if there exists no greatest convex to the right (equivalently, convex to the left) on p formula.

Definition 8

([17]). A partition of $A\subset M^{\prime }$ into two convex subsets C and D, such that $C<D$, is said to be a cut in A. If C has a supremum or D has an infimum in $A\cup \{-\infty ,\infty \}$, then the cut $(C,D)$ is said to be rational.

Definition 9

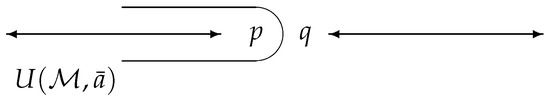
([10]). Let $p\in S_1\left(A\right)$ be non-isolated. We say that p is quasirational to the right if there exists a formula $U(x,\overline{a})$ with $\overline{a}\in A$ such that, for any $\alpha \vDash p$ the following is true:

$$\forall \beta [\alpha <\beta \wedge \mathcal{M}\vDash U(\beta ,\overline{a})\Rightarrow tp(\beta /A)=p].$$

We say that p is quasirational to the left if there exists a formula $U(x,\overline{a})$ with $\overline{a}\in A$ such that, for any $\alpha \vDash p$ the following is true:

$$\forall \beta [\beta <\alpha \wedge \mathcal{M}\vDash U(\beta ,\overline{a})\Rightarrow tp(\beta /A)=p].$$

A non-isolated, non-quasirational type p is said to be irrational (Figure 1).

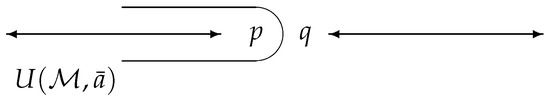
Figure 1. p is a quasirational to the right type and q is a quasirational to the left type.

Remark 1

([16]). 1. If T is o-minimal, then each quasisolitary type is solitary (uniquely realizable [Laskovski M., Steinhorn Ch., [18]).

2. 

There exist the following six essential kinds of non-algebraic 1-types over sets of models with a weakly o-minimal theory:

(1–2) 

isolated (quasisolitary, social);

(3–4) 

quasirational (quasisolitary, social);

(5–6) 

irrational (quasisolitary, social).

Definition 10.

Let $p\in S_1\left(A\right)$, $B\subset M$ such that $\mathcal{M}$ is ${|B\cup A|}^{+}$-saturated. Then a neighborhood of a set B in the type p is the following set:

$$\begin{array}{c}\hfill V_p\left(B\right):=\{\gamma \in M\mid \exists {\gamma }_1,{\gamma }_2\in p\left(\mathcal{M}\right),\mathit{there}\mathit{is}H(x,\overline{b},\overline{c}),\overline{b}\in B,\overline{c}\in A,\\ \hfill {\gamma }_1<H(\mathcal{M},\overline{b},\overline{c})<{\gamma }_2,\gamma \in H(\mathcal{M},\overline{b},\overline{c})\}.\end{array}$$

$$\mathit{Let}\overline{a}=⟨{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k⟩\mathit{then}{V}_p\left(\overline{a}\right):=V_p\left(\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k\}\right).$$

This definition adapts the notion of neighborhoods, which was introduced in the context of semi-isolation.

3. Results

Proposition 1.

Let $p\in S_1\left(A\right)$.

(i) 

Let $\beta \in p\left(\mathcal{M}\right)$. Then $|V_p\left(\beta \right)|=1$ if and only if p is solitary.

(ii) 

p is quasisolitary if and only if there exists $\beta \in p\left(\mathcal{M}\right)$, and $V_p\left(\beta \right)$ is $(A\cup \beta )$-definable set. (In fact $E_p(\mathcal{M},\beta ,{\overline{c}}_p)=V_p\left(\beta \right))$

Proof. 

(i) (⇒) Let p be a solitary type. It follows that, $E_p(x,y,\overline{a})\equiv (x=y)$, which means that for every $\beta \in p\left(\mathcal{M}\right)$, the equivalence class under $E_p$ contains only one element: $\beta$ itself. Since $V_p\left(\beta \right)$ is defined as the equivalence class of $\beta$ under $E_p$, if p is solitary, then

$$V_p\left(\beta \right)=\left\{\beta \right\}\Rightarrow \left|V_p\left(\beta \right)\right|=1$$

•    (⇐)

  Suppose $|V_p\left(\beta \right)|=1$, then $E_p(x,y)$ identifies only trivial equivalences. Consequently, $E_p(x,y)\equiv (x=y)$, and p is solitary.

(ii)

The neighborhood $V_p\left(\beta \right)$ is defined as the equivalence class of $\beta$ under $E_p$, i.e.,:

$$V_p\left(\beta \right)=\{x\in \mathcal{M}|E_p(x,\beta ,\overline{a})\}.$$

(⇒)

Let $\gamma \in V_p\left(\beta \right)$, then there exists a formula $H(x,\beta )$ such that $\gamma \in H(\mathcal{M},\beta )\subset p\left(\mathcal{M}\right)$. Let

$$H^c(x,\beta ):=\exists x_1\exists x_2(H(x_1,\beta )\wedge H(x_2,\beta )\wedge x_1\le x\le x_2).$$

Since $p\left(\mathcal{M}\right)$ is convex $H^c(\mathcal{M},\beta )\subset p\left(\mathcal{M}\right)$. Notice that

$$H^c(x,\beta )\equiv (H^c(x,\beta )\wedge x<\beta )\vee (x=\beta )\vee (H^c(x,\beta )\wedge \beta <x).$$

Then $V_p\left(\beta \right)\subseteq E(\mathcal{M},\beta ).$ On the other hand, by definition, $E(\mathcal{M},\beta )\subseteq V_p\left(\beta \right)$. Hence, $E(\mathcal{M},\beta )=V_p\left(\beta \right)$.

(⇐)

Assume that for some $\beta \in p\left(\mathcal{M}\right)$, the set $V_p\left(\beta \right)$ is $(A\cup \{\beta \left\}\right)$-definable. That is, there exists a formula $\psi (x,\beta )$ such that

$$V_p\left(\beta \right)=\{x\in \mathcal{M}\mid \psi (x,\beta )\}.$$

Moreover, since $V_p\left(\beta \right)$ is an equivalence class under $E_p$, it is convex and contained in $p\left(\mathcal{M}\right)$. Define the formula $E_p(x,y,\overline{c})$ as follows:

$$E_p(x,y,\overline{c})\equiv \forall \beta \left(\psi (x,\beta )\leftrightarrow \psi (y,\beta )\right).$$

Then $E_p(x,y,\overline{c})$ defines an equivalence relation on $p\left(\mathcal{M}\right)$ with convex classes, and for the fixed $\beta$, we have:

$$E_p(\mathcal{M},\beta ,\overline{c})=V_p\left(\beta \right).$$

Therefore, p is quasisolitary.

□

Lemma 1.

$\alpha \in V_p\left(\beta \right)\iff \beta \in V_p\left(\alpha \right)$

Proof. 

Suppose $\alpha \in V_p\left(\beta \right)$. Then there exists a formula $\theta (x,\beta )$ and elements ${\gamma }_1,{\gamma }_2\in p\left(\mathcal{M}\right)$ such that:

$$\begin{gathered} {\gamma }_1<\theta (\mathcal{M},\beta )<{\gamma }_2,\alpha \in \theta (\mathcal{M},\beta )\mathrm{and}\vDash \forall y(\theta (\alpha ,y)\to y<\alpha ). \\ {\theta }^c(x,\beta ):=\exists x_1,x_2((x_1\le x\le x_2)\wedge {\bigwedge }_{i=1}^2\theta (x_i,\beta )). \end{gathered}$$

We know that if $f\subset Au{t}_A\left(\mathcal{M}\right)$ then for every formula $H(x_1,\dots x_n)$ it holds that $\mathcal{M}\vDash H(c_1,\dots c_n)\iff \mathcal{M}\vDash H(f\left(c_1\right),\dots f\left(c_n\right)).$ Now consider an automorphism f of $\mathcal{M}$ fixing A such that $f\left({\gamma }_2\right)={\gamma }_1$, $f\left(\beta \right)={\beta }^{\prime },f\left({\gamma }_1\right)={\gamma }_2^{\prime }$.

$${\gamma }_1^{\prime }<{\theta }^c(\mathcal{M},{\beta }^{\prime })<{\gamma }_2^{\prime }={\gamma }_1<{\theta }^c(\mathcal{M},\beta )<{\gamma }_2$$

It is clear that $\alpha \notin {\theta }^c(\mathcal{M},{\beta }^{\prime })$, consequently $⊭{\theta }^c(\alpha ,{\beta }^{\prime })$. Therefore, there exists $\mu$ such that $\mu <{\theta }^c(\alpha ,\mathcal{M})<{\gamma }_2$.

If $\vDash K({\gamma }_1,\beta ,{\gamma }_2)$ then $\vDash K({\gamma }_1^{\prime },{\beta }^{\prime },{\gamma }_2)$. Thus, the formula ${\theta }^c(\alpha ,y)$ serves as a witness to the fact that $\beta \in V_p\left(\alpha \right)$, since for any $n<\omega$ the formula $\theta (x,f^n\left(\beta \right))$ fails at $x=\alpha$ (such that $⊭\theta (\alpha ,f^n\left(\beta \right))).$ □

Theorem 1

(Compactness Theorem, Henkin L. [19]). If every finite subset of a set T of L-sentences is satisfiable, then T itself is satisfiable.

Lemma 2.

1. Let $p,q\in S_1\left(A\right)$ be non-algebraic, $\alpha \in p\left(\mathcal{M}\right)$, and let $\mathsf{\Phi }(x,y,\overline{a})$, where $\overline{a}\in A$, be such that $\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})\subseteq q\left(\mathcal{M}\right)$ (that is, p isolates q).

$$\mathsf{\Phi }(\mathcal{M},\beta ,\overline{a})\subset q\left(\mathcal{M}\right)\mathit{for}\mathit{each}\beta \vDash p.$$

2. 

If q is irrational to the left, then there is no M-definable formula $C\left(x\right)$ with $C\left(\mathcal{M}\right)=q{\left(\mathcal{M}\right)}^{-},$ and for any formula $\mathsf{\Phi }(x,\overline{\beta })$, where $\overline{\beta }\in M$, with $\mathsf{\Phi }(\mathcal{M},\overline{\beta })\subseteq q\left(\mathcal{M}\right)$, there exists $\gamma \in q\left(\mathcal{M}\right)$ such that $\gamma <\mathsf{\Phi }(\mathcal{M},\overline{\beta }).$

3. 

If q is irrational to the right, that is, there does not exist an M-definable formula $C\left(x\right)$ with $C\left(\mathcal{M}\right)=q{\left(\mathcal{M}\right)}^{+},$ then for any formula $\mathsf{\Phi }(x,\overline{\beta })$, where $\overline{\beta }\in M$, with $\mathsf{\Phi }(\mathcal{M},\overline{\beta })\subseteq q\left(\mathcal{M}\right)$, there exists $\gamma \in q\left(\mathcal{M}\right)$ such that $\gamma >\mathsf{\Phi }(\mathcal{M},\overline{\beta }).$

Proof. 

1. Let $p,q\in S_1\left(A\right)$ be non-algebraic types, $\alpha \vDash p$, and let $\mathsf{\Phi }(x,y,\overline{a})$ be a formula with parameters $\overline{a}\in A$ such that $\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})\subset q\left(\mathcal{M}\right)$ (p isolates q). Let

$$q\left(\mathcal{M}\right)={\bigcap }_{L\in q}L\left(\mathcal{M}\right).$$

Fix any formula $L\left(x\right)\in q$, and define the formula

$$\begin{gathered} K_L\left(\alpha \right):=\forall x(\mathsf{\Phi }(x,\alpha ,\overline{a})\to L\left(x\right)). \\ {K}_L\left(y\right)\in tp(\alpha \setminus A)=p \end{gathered}$$

Since $\beta \in p\left(\mathcal{M}\right)$ then

$$\begin{gathered} \forall \alpha \in q\left(\mathcal{M}\right)\Rightarrow K_L\left(\beta \right) \\ \Rightarrow \mathsf{\Phi }(\mathcal{M},\beta ,\overline{a})\subset L\left(\mathcal{M}\right)=q\left(\mathcal{M}\right) \\ \Rightarrow \beta \in q\left(\mathcal{M}\right). \end{gathered}$$

2.

Let $q\in S_1\left(A\right)$ be irrational to the left. We claim that there is no M-definable formula $C\left(x\right)$ such that $C\left(\mathcal{M}\right)=q{\left(\mathcal{M}\right)}^{-}.$ Suppose there is such formula $C\left(x\right)$, then $\left(C\right(x)\cup q(x\left)\right)$ is consistent because for any finite set of formulas $\left\{{\mathsf{\Phi }}_i\left(x\right)\right|{\mathsf{\Phi }}_i\left(x\right)\in q\}$

$$\vDash \exists x(\bigwedge {\mathsf{\Phi }}_i\left(x\right)\wedge C\left(x\right)).$$

Thus, there is a realization $\mu$ of $\left(C\right(x)\cup q(x\left)\right)$ contradicting the assumption.

Let $\mathsf{\Phi }(x,\overline{\beta })\subseteq q\left(\mathcal{M}\right)$ be any formula with parameters $\overline{\beta }\in M$. This implies that for every $\mathsf{\Phi }(x,\overline{\beta })\subseteq q\left(\mathcal{M}\right)$, there is an element $\gamma \in q\left(\mathcal{M}\right)$ such that $\gamma <\mathsf{\Phi }(\mathcal{M},\overline{\beta }).$

Otherwise $\mathsf{\Phi }(x,\overline{\beta })$ would be bounded below inside $q\left(\mathcal{M}\right)$, contradicting the irrationality of q to the left. Thus, the set

$$\{\forall y(\mathsf{\Phi }(y,\overline{\beta })\to x<y)\}\cup q\left(x\right)$$

is consistent, and therefore there exists some $\gamma$ such that $\gamma <\mathsf{\Phi }(\mathcal{M},\overline{\beta }).$

3.

Let $q\in S_1\left(A\right)$ be irrational to the right. We claim that there is no $\mathcal{M}$-definable formula $C\left(x\right)$ such that $C\left(\mathcal{M}\right)=q{\left(\mathcal{M}\right)}^{+}.$

Suppose such a formula $C\left(x\right)$ exists. Then the set $C\left(x\right)\cup q\left(x\right)$ is consistent because for any finite set of formulas $\{{\mathsf{\Phi }}_i\left(x\right)\mid {\mathsf{\Phi }}_i\left(x\right)\in q\}$, we have

$$\vDash \exists x\left(\bigwedge {\mathsf{\Phi }}_i\left(x\right)\wedge C\left(x\right)\right).$$

Thus, there is a realization $\mu$ of $C\left(x\right)\cup q\left(x\right)$, which contradicts the assumption that q is irrational to the right.

Let $\mathsf{\Phi }(x,\overline{\beta })\subseteq q\left(\mathcal{M}\right)$ be any formula with parameters $\overline{\beta }\in \mathcal{M}$. This implies that for every $\mathsf{\Phi }(x,\overline{\beta })\subseteq q\left(\mathcal{M}\right)$, there is an element $\gamma \in q\left(\mathcal{M}\right)$ such that $\gamma >\mathsf{\Phi }(\mathcal{M},\overline{\beta }).$

Otherwise, $\mathsf{\Phi }(x,\overline{\beta })$ would be bounded above inside $q\left(\mathcal{M}\right)$, contradicting the irrationality of q to the right. Thus, the set

$$\left\{\forall y\left(\mathsf{\Phi }(y,\overline{\beta })\to y<x\right)\right\}\cup q\left(x\right)$$

is consistent, yielding some $\gamma$ such that $\gamma >\mathsf{\Phi }(\mathcal{M},\overline{\beta })$ such that $\gamma \in q\left(\mathcal{M}\right)$.

□

Theorem 2.

Let $p\in S_1\left(A\right)$, $B\subset M$ such that M is ${|A\cup B|}^{+}$-saturated. Then the following holds:

(i) 

$V_p\left(B\right)$ is convex or empty.

(ii) 

Let p be irrational. Then $\forall \overline{a}\in M\setminus M^{\prime }$, for any formula $H(x,\overline{\alpha },\overline{a}),\overline{a}\in A$

$$[H(\mathcal{M},\overline{a},\overline{a})\ne ⌀,H(\mathcal{M},\overline{\alpha },\overline{a})\subseteq p\left(\mathcal{M}\right)\Rightarrow H(\mathcal{M},\overline{\alpha },\overline{a})\subseteq V_p\left(\overline{a}\right)].$$

(iii) 

$V_p\left(B\right)\ne ⌀\Rightarrow \exists {\gamma }_1,{\gamma }_2\in p\left(\mathcal{M}\right),{\gamma }_1<V_p\left(B\right)<{\gamma }_2.$

(iv) 

$\forall \beta \in p\left(\mathcal{M}\right)[V_p\left(B\right)\ne ⌀,\beta \notin V_p\left(B\right)\Rightarrow \forall q\in S_1\left(A\right),V_q\left(\beta \right)\cap V_q\left(B\right)=⌀].$

(v) 

$\forall \alpha \in p\left(\mathcal{M}\right):V_p\left(B\right)<\alpha \Rightarrow \exists {\alpha }_0\in p\left(\mathcal{M}\right)[V_p\left(B\right)<{\alpha }_0<V_p\left(\alpha \right)].$

Proof. 

(i) By Definition 10.

(ii)

By Definition 10 and by Lemma 2 (ii), (iii).

(iii)

By Definition 10 and by Compactness Theorem (Theorem 1).

(iv)

Suppose that there exists $q\in S_1\left(A\right)$ such that $V_q\left(\beta \right)\cap V_q\left(B\right)\ne ⌀$. Then there exists $\mathsf{\Phi }(x,\beta ,\overline{b})$, with $\overline{b}\in A$, and there is $H(x,\overline{a},\overline{c})$, with $\overline{a}\in B$, $\overline{c}\in A$ such that

$$\exists \gamma \in \mathsf{\Phi }(\mathcal{M},\beta ,\overline{b})\cap H(\mathcal{M},\overline{a},\overline{c}),\mathsf{\Phi }(\mathcal{M},\beta ,\overline{b})\subset V_q\left(\beta \right),H(\mathcal{M},\overline{a},\overline{c})\subset V_q\left(B\right).$$

By Definition 10 there are ${\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4\in q\left(\mathcal{M}\right)$ such that

$${\gamma }_1<\mathsf{\Phi }(\mathcal{M},\beta ,\overline{b})<{\gamma }_2,{\gamma }_3<H(\mathcal{M},\overline{a},\overline{c})<{\gamma }_4.$$

Let ${\mu }_1=min\{{\gamma }_1,{\gamma }_3\}$, ${\mu }_2=max\{{\gamma }_2,{\gamma }_4\}$, $f\in {\mathrm{Aut}}_A\left(\mathcal{M}\right)$ be such that $f\left({\mu }_2\right)={\mu }_1$. Define ${\beta }_1:=f\left(\beta \right)$, ${\beta }_2:=f^{-1}\left(\beta \right)$. Then

$$\mathsf{\Phi }(\mathcal{M},{\beta }_1,\overline{b})<{\mu }_1<H(\mathcal{M},\overline{a},\overline{c})<{\mu }_2<\mathsf{\Phi }(\mathcal{M},{\beta }_2,\overline{b}),$$

and either ${\beta }_1<\beta <{\beta }_2$ or ${\beta }_2<\beta <{\beta }_1$. Now let

$$K(y,\overline{a},\overline{b},\overline{c}):=\exists x(H(x,\overline{a},\overline{c})\wedge \mathsf{\Phi }(x,y,\overline{b})).$$

Then $\beta \in K(\mathcal{M},\overline{a},\overline{b},\overline{c})$, while ${\beta }_1,{\beta }_2\notin K(\mathcal{M},\overline{a},\overline{b},\overline{c})$. Let $K_1(x,\overline{a},\overline{b},\overline{c})$ be a convex subformula of $K(x,\overline{a},\overline{b},\overline{c})$ such that $\beta \in K_1(\mathcal{M},\overline{a},\overline{b},\overline{c}).$ Thus

$${\beta }_1<K_1(\mathcal{M},\overline{a},\overline{b},\overline{c})<{\beta }_2 \mathrm{or} {\beta }_2<K_1(\mathcal{M},\overline{a},\overline{b},\overline{c})<{\beta }_1.$$

Then $\beta \in V_p\left(\overline{a}\right)$ and $\beta \in V_p\left(B\right)$. Which is a contradiction.

(v)

Assume $V_p\left(B\right)<\alpha$.

Step 1.

We are going to show that $V_p\left(B\right)<V_p\left(\alpha \right)$. Suppose for contradiction that $V_p\left(B\right)$ and $V_p\left(\alpha \right)$ are not disjoint sets $V_p\left(B\right)\cap V_p\left(\alpha \right)\ne ⌀$. Let $V_p\left(B\right)=\bigcup H_i(\mathcal{M},\overline{b},\overline{c})$ and

$$V_p\left(\alpha \right)=\{\delta \mid \delta \in \mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a}),\exists {\gamma }_1,{\gamma }_2({\gamma }_1<\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})<{\gamma }_2\}.$$

Pick some $\gamma \in H(\mathcal{M},\overline{b},\overline{c})\cap \mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})$. Define

$$K(y,\overline{b},\overline{c}):=\exists x\left(H(x,\overline{b},\overline{c})\wedge \mathsf{\Phi }(x,y,\overline{a})\right).$$

Since $\alpha \vDash K(y,\overline{b},\overline{c},\overline{a})$, with $\overline{b}\in B$, and $\overline{a},\overline{c}\in A$, it follows that $\alpha \in V_p\left(B\right)$.

This is a contradiction, because we assumed $V_p\left(B\right)<\alpha$. Hence, we conclude that $V_p\left(B\right)<V_p\left(\alpha \right)$.

Step 2.

Now we will show that $\exists {\alpha }_0\in p\left(\mathcal{M}\right)[V_p\left(B\right)<{\alpha }_0<V_p\left(\alpha \right)]$.

(a)

$V_p\left(\alpha \right)$ is definable.

(a1)

$V_p\left(B\right)$ is definable.

Let $U\left(\mathcal{M}\right)=V_p{\left(B\right)}^{+}$ be the right border of the neighborhood $V_p\left(B\right)$.

$$\begin{array}{c}\hfill F(y,{\overline{b}}_0,c):=U(x,{\overline{b}}_0,\overline{c})\wedge x<y\wedge \forall x\left[\right(U(\mathcal{M},b_0,c)<z\to \\ \hfill (E_p(z,y)\vee E_p(\mathcal{M},y)<z)]\end{array}$$

Since $\alpha \in F(\mathcal{M},{\overline{b}}_0,\overline{c})$, then $\alpha \in V_p\left(B\right)$.

(a2)

The neighborhood is

$$V_p\left(B\right)={\bigcup }_{i\in I}{H}_i(\mathcal{M},{\overline{b}}_0,\overline{c}).$$

The set of formulas

$$\{(H_{i_1}(\mathcal{M},\overline{b},c)\cup \dots \cup H_{i_n}(\mathcal{M},\overline{b},c))<x<E_p(\mathcal{M},\alpha )\mid i,i_n\in I\}$$

is consistent, and consequently there is ${\alpha }_0$ that satisfies the set. Then

$$V_p\left(B\right)<{\alpha }_0<V_p\left(\alpha \right).$$

(b)

$V_p\left(\alpha \right)$ is non-definable. Since by Step 1 $V_p\left(B\right)<V_p\left(\alpha \right)$, then the lower bound of $V_p\left(\alpha \right)$ is non-definable. The set of formulas

$$\begin{array}{c}\hfill \{H(\mathcal{M},\overline{b},\overline{c})<x<\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})\mid H(\mathcal{M},\overline{b},\overline{c})\subset V_p\left(B\right),\\ \hfill \mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})\subset V_p\left(B\right)\}\end{array}$$

is consistent. Therefore, there is an element that satisfies the set.

□

We will use notations analogous to those in Stability Theory [20,21].

Definition 11.

Let $p,q\in S_1\left(A\right)$. We say that p is weakly orthogonal to q ($p{\perp }^{w}q$) if for any $H(x,y,\overline{a})$, with $\overline{a}\in A$, for any $\alpha \in p\left(\mathcal{M}\right)$, the following holds:

$$[H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀\Rightarrow q\left(\mathcal{M}\right)\subseteq H(\mathcal{M},\alpha ,\overline{a})].$$

If p is not weakly orthogonal to q, we will denote this fact by $p{\perp ̸}^{w}q$.

Lemma 3.

(i) $p{\perp ̸}^{w}q\Rightarrow q{\perp ̸}^{w}p$.

(ii) 

$p{\perp }^{w}q\iff p\left(x\right)\cup q\left(y\right)$ is a complete 2-A-type.

(iii) 

If p is algebraic, then for every $q\in S_1\left(A\right)$, it follows that $p{\perp }^{w}q$.

Proof. 

(i) Assume $p{\perp ̸}^{w}q$. Then there exist an A–formula $H(x,y,\overline{a})$, some $\alpha \in p\left(\mathcal{M}\right)$, and there are ${\beta }_1,{\beta }_2\in q\left(\mathcal{M}\right)$ such that

$$\mathcal{M}\vDash H(\alpha ,{\beta }_1,\overline{a})\mathrm{and}\mathcal{M}\vDash \neg H(\alpha ,{\beta }_2,\overline{a}).$$

• Assume $q{\perp }^{w}p$. Since $\alpha$ satisfies $H({\beta }_1,x,\overline{a})$, then $H({\beta }_1,\mathcal{M},\overline{a})\cap p\left(\mathcal{M}\right)\ne ⌀.$ Let us define the following set of formulas:
  $$\mathsf{\Gamma }:=\{\exists yH(x,y,\overline{a})\wedge {\psi }_i\left(y\right)\mid {\psi }_1\in p\left(y\right)\}\subset q\left(x\right),$$
  ${\beta }_2$ satisfies $\mathsf{\Gamma }$. Then
  $$\{H({\beta }_2,y,\overline{a})\wedge {\psi }_i\left(y\right)\mid {\psi }_i\left(y\right)\in p\left(y\right)\}$$

  is consistent and closed over finite conjunction. Since for any finite $I_0$
  $$\psi \left(y\right):={\bigwedge }_{i\in I_0}{\psi }_i\left(y\right)\in p\left(y\right).$$

  There is some ${\alpha }^{\prime }\vDash p$ that satisfies the set
  $$\{H({\beta }_2,y,\overline{a})\wedge {\psi }_i\left(y\right)\mid {\psi }_i\left(y\right)\in p\left(y\right)\}.$$

  Since $\vDash \neg H({\beta }_2,\alpha ,\overline{a})$, then $p\left(\mathcal{M}\right)⊈H({\beta }_2,y,\overline{a})$. Therefore, $q{\perp ̸}^{w}p$.
  In general the weak orthogonality relation ${\perp ̸}^w$ is symmetric.

(ii)

(⇒)

Assume $p{\perp }^{w}q$, and let $\alpha \in p\left(\mathcal{M}\right)$, $\beta \in q\left(\mathcal{M}\right)$. Then for any A-formula $H(y,x,\overline{a})$, for any $\alpha$ and any $\beta$

$$H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀\Rightarrow q\left(\mathcal{M}\right)\subseteq H(\mathcal{M},\alpha ,\overline{a}).$$

If there exists a realization $\beta$ of q such that $H(y,\alpha ,\overline{a})$ holds, then by weak orthogonality every realization of q also must satisfy $H(y,\alpha ,\overline{a})$. Consequently, for every pair $\alpha \in p\left(\mathcal{M}\right),\beta \in q\left(\mathcal{M}\right)$ we have

$$\begin{gathered} \mathrm{either}\mathcal{M}\vDash H(\beta ,\alpha ,\overline{a})\mathrm{if}H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀ \\ \mathrm{or}\mathcal{M}\vDash \neg H(\beta ,\alpha ,\overline{a})\mathrm{if}H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)=⌀. \end{gathered}$$

Therefore,

$$p\left(x\right)\cup q\left(y\right)⊢H(y,x,\overline{a})\mathrm{or}p\left(x\right)\cup q\left(y\right)⊢\neg H(y,x,\overline{a}).$$

Since $H(y,x,\overline{a})$ was arbitrary, $p\left(x\right)\cup q\left(y\right)$ decides every A-formula in the variables $x,y$. Thus $p\left(x\right)\cup q\left(y\right)$ is a complete 2-A-type.

(⇐)

Assume that $p\left(x\right)\cup q\left(y\right)$ is a complete 2-A-type.

Let $\alpha \vDash p$, and let $H(y,x,\overline{a})$ be any $L\left(A\right)$–formula. Suppose $H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀.$ Let $\beta \vDash q$ with $\mathcal{M}\vDash H(\beta ,\alpha ,\overline{a})$. By completeness of $p\left(x\right)\cup q\left(y\right)$ applied to the formula $H(y,x,\overline{a})$ we have

$$p\left(x\right)\cup q\left(y\right)⊢H(y,x,\overline{a})\mathrm{or}p\left(x\right)\cup q\left(y\right)⊢\neg H(y,x,\overline{a}).$$

The second alternative cannot hold, since $\alpha \vDash p$, $\beta \vDash q$, and $\mathcal{M}\vDash H(\beta ,\alpha ,\overline{a})$. Hence

$$p\left(x\right)\cup q\left(y\right)⊢H(y,x,\overline{a}).$$

Therefore, for every ${\beta }^{\prime }\vDash q$ we have $\mathcal{M}\vDash H({\beta }^{\prime },\alpha ,\overline{a})$, i.e.,

$$q\left(\mathcal{M}\right)\subseteq H(\mathcal{M},\alpha ,\overline{a}).$$

Since $H(y,x,\overline{a})$ and $\alpha$ were arbitrary, this is exactly the definition of $p{\perp }^{w}q$.

(iii)

Let p is algebraic over A. Then there is an A-formula $\varphi \left(x\right)$ whose set of solutions is exactly $p\left(\mathcal{M}\right)$. Then ${\exists }^{!n}x\varphi \left(x\right)$, and $n=1$.

Let suppose there are ${\alpha }_1,\dots ,{\alpha }_n\in p\left(\mathcal{M}\right)$ such that ${\alpha }_1<{\alpha }_2<\dots <{\alpha }_n$. Then

$$\varphi \left(x\right)\wedge \forall x(\varphi \left(x^{\prime }\right)\wedge \neg (x=x^{\prime }))\to (x<x^{\prime })$$

isolates exactly one element.

Suppose there is $H(y,x,\overline{a})$ in p such that $\neg H(y,\alpha ,\overline{a})$ in q.

$$q\left(y\right)\wedge \left\{H(y,\alpha ,\overline{a})\right\}q\left(y\right)\wedge \left\{H(y,\alpha ,\overline{a})\right\}$$

Since x is singular then it is consistent that

$$\begin{gathered} q\left(y\right)\vee \{\exists x(H(y,x,\overline{a})\wedge \varphi \left(x\right))\} \\ q\left(y\right)\vee \{\exists x(\neg H(y,x,\overline{a})\wedge \varphi \left(x\right))\}. \end{gathered}$$

Since the formulas are mutually contradictory, they cannot be used together. Therefore, $p{\perp }^{w}q$.

□

Definition 12.

Let $p,q\in S_1\left(A\right)$. We say that p is almost orthogonal to q ($p{\perp }^{a}q$), if $\exists \alpha \in p\left(\mathcal{M}\right)$ ($\iff \forall \alpha \in p\left(\mathcal{M}\right)$), and $V_q\left(\alpha \right)=⌀$. If p is not almost orthogonal to q, then we denote this fact by $p{\perp ̸}^{a}q$.

From this definition $p{\perp }^{a}q$ if and only if $V_p\left(\alpha \right)\ne ⌀$. And $V_p\left(\alpha \right)\ne ⌀\iff$ there is a formula $\mathsf{\Phi }(x,\alpha ,\overline{a})$ such that there are ${\gamma }_1,{\gamma }_2\in q\left(\mathcal{M}\right)$,

$${\gamma }_1<\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})<{\gamma }_2.$$

Lemma 4.

Let $p,q\in S_1\left(A\right)$. Then the following propositions are true:

(i) 

$p{\perp }^{w}q\Rightarrow p{\perp }^{a}q$.

(ii) 

There exists T — a weakly o-minimal theory such that $p{\perp ̸}^{w}q$, and $p{\perp }^{a}q$.

(iii) 

Let T be o-minimal. Then $p{\perp }^{a}q\iff p{\perp }^{w}q$.

Proof. 

(i) Assume $p{\perp }^{w}q$. By the definition of weak orthogonality, for every A-definable formula $H(x,y,\overline{a})$ and every $\alpha \vDash p$,

$$\left(H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀\right)⟹q\left(\mathcal{M}\right)\subseteq H(\mathcal{M},\alpha ,\overline{a}).$$

(1)

• By the definition of the neighborhood $V_q\left(\alpha \right)$, there exist ${\gamma }_1,{\gamma }_2\in q\left(\mathcal{M}\right)$ and an A-definable formula $H(x,y,\overline{a})$ such that
  $${\gamma }_1<H(\mathcal{M},\alpha ,\overline{a})<{\gamma }_2\mathrm{and}H(\mathcal{M},\alpha ,\overline{a})\subseteq q\left(\mathcal{M}\right).$$
  In particular, $H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀$ but $q\left(\mathcal{M}\right)⊈H(\mathcal{M},\alpha ,\overline{a})$ (since ${\gamma }_1,{\gamma }_2\in q\left(\mathcal{M}\right)$ lie outside the convex set $H(\mathcal{M},\alpha ,\overline{a})$). This contradicts (1).
  Hence $V_q\left(\alpha \right)=⌀$ for (some hence all) $\alpha \vDash p$, which is exactly $p{\perp }^{a}q$ by the definition of almost orthogonality.

(ii)

Let consider $\mathsf{\Sigma }=<=,<,P^1,U^2,c_1,\dots ,c_n{>}_{n<\omega }$, and $\mathcal{M}=<\mathcal{M},\mathsf{\Sigma }>$.

$$\begin{gathered} M=Q\cup Q+\sqrt{2},Q+\sqrt{2}=\{a+\sqrt{2}\mid a\in Q\} \\ P\left(\mathcal{M}\right)=Q,\neg P\left(\mathcal{M}\right)=Q+\sqrt{2} \\ P\left(\mathcal{M}\right)<\neg P\left(\mathcal{M}\right)\Rightarrow \mathrm{elements}\mathrm{of}\mathrm{both}P\left(\mathcal{M}\right)\mathrm{and}\neg P\left(\mathcal{M}\right)\mathrm{are}\mathrm{densely}\mathrm{ordered}. \end{gathered}$$

Let $U^2(x,y)$ is a binary relation such that

$$\begin{gathered} \mathcal{M}\vDash \forall x\forall y[U^2(x,y)\to (P\left(x\right)\wedge \neg P\left(y\right))]. \\ \mathcal{M}\vDash U^2(a,b)\iff a\in Q,b\in Q+\sqrt{2},R\vDash a<b \\ \mathcal{M}\vDash (c_n<c_{n+1})\wedge P\left(c_n\right),n<\omega . \end{gathered}$$

The theory of this structure has quantifier elimination. Let us define non-algebraic 1-types

$$\begin{gathered} p\left(x\right)=\left\{P\left(x\right)\right\}\cup \{c_n<x\mid n<w\} \\ q\left(y\right)=\{\neg P\left(y\right)\}\cup \{U^2(c_n,y)\mid n<\omega \}. \end{gathered}$$

Thus, $p{\perp ̸}^{w}q$, since for an arbitrary $\alpha \vDash p$ the set $q\left(y\right)\cup \left\{U\right(\alpha ,y\left)\right\}$ and the set $q\left(y\right)\cup \{\neg U(\alpha ,y\left)\right\}$ are both consistent.

Let consider an authomorphism f such that $f\left({\gamma }_1\right)={\gamma }_2$, and $f\left(\alpha \right)=\alpha$.

$$\begin{gathered} tp({\gamma }_1/\alpha )=tp({\gamma }_2/\alpha ) \\ {\beta }_1<{\beta }_2,tp({\beta }_1/\alpha )=tp({\beta }_2/\alpha ) \end{gathered}$$

Since we do not have any formula in that type, then $V_q\left(\alpha \right)=⌀$. Therefore, $p{\perp }^{a}q$.

(iii)

(⇒)

Since by (i) $p{\perp }^{w}q\Rightarrow p{\perp }^{a}q$ in any theory, then it is true for o-minimal theories.

(⇐)

Assume $p{\perp }^{a}q$. We must show that $p{\perp }^{w}q$. Let $H(x,y,\overline{a})$ be any A-definable formula and let $\alpha \vDash p$. Suppose

$$H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀.$$

Set $S:=H(\mathcal{M},\alpha ,\overline{a})\subseteq \mathcal{M}$. By o-minimality, S is a finite union of points and open intervals; Hence it is a finite union of convex sets. Since $q\left(\mathcal{M}\right)$ is convex, the intersection $S\cap q\left(\mathcal{M}\right)$ is again a finite union of convex subsets of $q\left(\mathcal{M}\right)$.

We claim that $S\cap q\left(\mathcal{M}\right)=q\left(\mathcal{M}\right)$. Suppose not. Then there exists a nonempty convex component $C\subseteq S\cap q\left(\mathcal{M}\right)$ which is a proper subset of $q\left(\mathcal{M}\right)$. Because $q\left(\mathcal{M}\right)$ is convex, we can choose ${\gamma }_1,{\gamma }_2\in q\left(\mathcal{M}\right)$ with

$${\gamma }_1<C<{\gamma }_2(\mathrm{i}.\mathrm{e}.,\forall y\in C({\gamma }_1<y<{\gamma }_2)).$$

But $C\subseteq S=H(\mathcal{M},\alpha ,\overline{a})$, so ${\gamma }_1<H(\mathcal{M},\alpha ,\overline{a})<{\gamma }_2.$

By the definition of the neighborhood $V_q\left(\alpha \right)$, this implies $V_q\left(\alpha \right)\ne ⌀$, contradicting $p{\perp }^{a}q$. Hence, the assumption was false, and we must have $q\left(\mathcal{M}\right)\subseteq S$.

Since $H(x,y,\overline{a})$, $\alpha$ and $\overline{a}$ were arbitrary, we have shown that for every A-definable $H(x,y,\overline{a})$ and every $\alpha \vDash p$,

$$H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀⟹q\left(\mathcal{M}\right)\subseteq H(\mathcal{M},\alpha ,\overline{a}),$$

which is exactly $p{\perp }^{w}q$ by definition.

□

The following example illustrates that that the inverse of Lemma 4 (i) does not hold.

Example 1.

Let $\mathcal{M}={⟨\mathbb{Q};=,<,U,a_i,b_j,c_i⟩}_{i\in \mathbb{N},j\in \mathbb{Z}}$, where U is a binary predicate, < is the standard relation of dense linear order without endpoints, $a_{i_1}<a_{i_2}<b_{j_1}<b_{j_2}<c_{k_2}<c_{k_1}$ for all $i_1<i_2$, $k_1<k_2$ from $\mathbb{N}$ and all $j_1<j_2$ from $\mathbb{Z}$, and

$${lim}_{i\to \infty }{a}_i={lim}_{i\to -\infty }{b}_j=e,{lim}_{i\to \infty }{b}_i={lim}_{i\to \infty }{c}_i=\pi$$

And let $\mathcal{M}\vDash U(a,b)$ if and only if $\mathbb{R}\vDash b>a-e+\pi$.

Define $p\left(x\right):=\{a_i<x<b_j|i\in \mathbb{N},j\in -\mathbb{N}\}$, and $q\left(y\right):=\{b_j<y<c_k|j,k\in \mathbb{N}\}$. The types p and q are distinct non-isolated types over the empty set. Let ${\mathcal{M}}^{\prime }$ be an arbitrary model of $Th\left(\mathcal{M}\right)$ realizing the type p. For each $\alpha \in p\left({\mathcal{M}}^{\prime }\right)$ the set $U(\alpha ,{\mathcal{M}}^{\prime })$ is a convex set such that $U(\alpha ,{\mathcal{M}}^{\prime })\cap \neg q\left({\mathcal{M}}^{\prime }\right)\ne ⌀$, $U(\alpha ,{\mathcal{M}}^{\prime })\cap q\left({\mathcal{M}}^{\prime }\right)\ne ⌀$, and $q{\left({\mathcal{M}}^{\prime }\right)}^{+}\subset U(\alpha ,{\mathcal{M}}^{\prime })$. Moreover, there is no ∅-definable formula $K(x,y)$ such that $K(\alpha ,{\mathcal{M}}^{\prime })$ is a proper subset of $q\left({\mathcal{M}}^{\prime }\right)$. Then $p{\perp ̸}^{w}q$, but $p{\perp }^{a}q$.

Theorem 3.

Let $p,q\in S_1\left(A\right)$. Then the following propositions are true:

(1) 

Let $p{\perp ̸}^{w}q$. If p is social, then q is social, and $p{\perp ̸}^{a}q$.

(2) 

$p{\perp ̸}^{a}q\Rightarrow q{\perp ̸}^{a}p$.

(3) 

${\perp ̸}^a$ is a relation of equivalence on $S_1\left(A\right)$.

(4) 

${\perp ̸}^w$ is a relation of equivalence on $S_1\left(A\right)$.

In proof of the theorem:

(1)

We will use Lemma 5, Remark 2, Lemmas 6 and 7, and Remark 3.

(2)

Follows from the Lemma 5.

(3)

We already know that ${\perp ̸}^a$ is reflexive and symmetric. We are going to show that ${\perp ̸}^a$ is transitive relation using Lemma 8, Remark 4, and Theorem 2.

(4)

We already know that ${\perp ̸}^w$ is reflexive and symmetric (Note 3). We are going to show that ${\perp ̸}^w$ is transitive relation using Lemma 7, Remark 3.

Proof. 

(1) Consider two cases:

•    (a)

  $p{\perp ̸}^{a}q$,

     (b)

  $p{\perp ̸}^{w}q$, and $p{\perp ̸}^{a}q$.

  Lemma 5 

  (Claim 37 in [16]). Let p isolate q by a formula $\mathsf{\Phi }(x,y,\overline{a})$, with $\overline{a}\in A$, such that there exist $\alpha \in p\left(\mathcal{M}\right)$ and there are ${\gamma }_1$, ${\gamma }_2\in q\left(\mathcal{M}\right)$, such that ${\gamma }_1<\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})<{\gamma }_2$, and $\mathsf{\Phi }(\mathcal{M},\alpha ,\overline{a})\ne ⌀$. Then there exists a formula ${\mathsf{\Phi }}_0(x,y,\overline{a})$ such that for all $\beta \in q\left(\mathcal{M}\right)$ there exist ${\mu }_1$, ${\mu }_2\in p\left(\mathcal{M}\right)$ such that

  $${\mathsf{\Phi }}_0(\beta ,\mathcal{M},\overline{a})\ne ⌀,{\mu }_1<{\mathsf{\Phi }}_0(\beta ,\mathcal{M},\overline{a})<{\mu }_2$$

  and p is quasisolitary if and only if q is quasisolitary.

  If $p{\perp ̸}^{a}q$, then by Lemma 5, if p is social, then q is social.
  Consider the case $p{\perp ̸}^{w}q$, $p{\perp }^{a}q$. We can construct the 2-A-formula $H(x,y,\overline{a})$, with $\overline{a}\in A$ such that for any $\alpha \in p\left(\mathcal{M}\right)$, both $H(\mathcal{M},\alpha ,\overline{a})$, and $\neg H(\mathcal{M},\alpha ,\overline{a})$ are convex,
  $$\begin{gathered} H(\mathcal{M},\alpha ,\overline{a})\cup \neg H(\mathcal{M},\alpha ,\overline{a})=M,\exists {\beta }_1\in H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right), \\ \exists {\beta }_2\in \neg H(\mathcal{M},\alpha ,\overline{a})\cap q\left(\mathcal{M}\right),H(\mathcal{M},\alpha ,\overline{a})<\neg H(\mathcal{M},\alpha ,\overline{a}). \end{gathered}$$

Remark 2.

$\forall \alpha ,\beta \in p\left(\mathcal{M}\right)$

$$[\exists \gamma \in H(\mathcal{M},\alpha ,\overline{a})\setminus H(\mathcal{M},\beta ,\overline{a})\Rightarrow H(\mathcal{M},\beta ,\overline{a})\subset H(\mathcal{M},\alpha ,\overline{a})].$$

Let $\alpha \in p\left(\mathcal{M}\right)$. Consider $f\in {\mathrm{Aut}}_A\left(\mathcal{M}\right)$, such that $f\left({\beta }_1\right)={\beta }_2$. Then

$$H(\mathcal{M},\alpha ,\overline{a})\subset H(\mathcal{M},f\left(\alpha \right),\overline{a}).$$

Lemma 6.

Let $p,q\in S_1\left(A\right)$.

(i) 

If $\alpha \in p\left(\mathcal{M}\right)$, $\beta \in q\left(\mathcal{M}\right)$, then $\alpha \in V_p\left(\beta \right)$ if and only if $\beta \in V_q\left(\alpha \right)$ if and only if $V_p\left(\alpha \right)=V_p\left(\beta \right)$ if and only if $V_q\left(\alpha \right)=V_q\left(\beta \right)$.

(ii) 

If ${\alpha }_1,{\alpha }_2,{\alpha }_3\in p\left(\mathcal{M}\right)$ such that ${\alpha }_1<V_p\left({\alpha }_2\right)<{\alpha }_3$, $V_q\left({\alpha }_1\right)\ne ⌀$, then $V_q\left({\alpha }_1\right)<V_q\left({\alpha }_2\right)<V_q\left({\alpha }_3\right)$ or $V_q\left({\alpha }_3\right)<V_q\left({\alpha }_2\right)<V_q\left({\alpha }_1\right)$.

Proof of Lemma 6

(i) 

This is an immediate corollary of the proof of Theorem 2 (iv).

(ii) 

By Theorem 2 (iv), the following is true:

$$\forall q\in S_1\left(A\right),V_q\left({\alpha }_i\right)\cap V_q\left({\alpha }_j\right)=⌀,i\ne j\in \{1,2,3\},\mathit{and}{V}_p\left({\alpha }_1\right)<V_p\left({\alpha }_2\right)<V_p\left({\alpha }_3\right).$$

Then

$$tp({\alpha }_1/A\cup {\alpha }_3)=tp({\alpha }_2/A\cup {\alpha }_3),tp({\alpha }_2/A\cup {\alpha }_1)=tp({\alpha }_3/A\cup {\alpha }_1).$$

Suppose there is $q\in S_1\left(A\right)$ such that $V_q\left({\alpha }_1\right)<V_q\left({\alpha }_3\right)<V_q\left({\alpha }_2\right)$. Let $H(x,y,\overline{a})$, with $\overline{a}\in A$ be a formula such that $H(\mathcal{M},{\alpha }_1,\overline{a})\subset V_q\left({\alpha }_1\right)$. Consider the following formula:

$$G(y,{\alpha }_3,\overline{a}):=y<{\alpha }_3\wedge \forall x\forall z((H(x,y,\overline{a})\wedge H(z,{\alpha }_3,\overline{a}))\to z<x).$$

Then ${\alpha }_1\notin G(\mathcal{M},{\alpha }_3,\overline{a})$, while ${\alpha }_2\in G(\mathcal{M},{\alpha }_3,\overline{a})$. Consequently, ${\alpha }_2\in V_p\left({\alpha }_3\right)$. Which is a contradiction. Consideration of other cases are the same. Hence, Lemma 6 is proved.

Lemma 7.

If $f\left(\alpha \right)>\alpha$ (respectively, $f\left(\alpha \right)<\alpha$) then for any $\beta <\alpha$ (respectively, $\beta >\alpha$), with $\beta \in p\left(\mathcal{M}\right)$, $H(\mathcal{M},\beta ,\overline{a})\subseteq H(\mathcal{M},\alpha ,\overline{a})$. And there exists $U(x,\alpha ,\overline{c})$, with $\overline{c}\in A$, $U(\mathcal{M},\alpha ,\overline{c})<\alpha$ (respectively, $U(\mathcal{M},\alpha ,\overline{c})>\alpha$) such that

$$\forall \beta <\alpha ,\beta \in p\left(\mathcal{M}\right)[H(\mathcal{M},\beta ,\overline{a})\subseteq H(\mathcal{M},\alpha ,\overline{a})\Rightarrow \beta \in U(\mathcal{M},\alpha ,\overline{c})].$$

Proof of Lemma 7

We suppose that $f\left(\alpha \right)>\alpha$, a consideration of the case $f\left(\alpha \right)<\alpha$ is the same. Let ${\alpha }_0=f^{-1}\left(\alpha \right)$, then $H(\mathcal{M},{\alpha }_0,\overline{a})\subseteq H(\mathcal{M},\alpha ,\overline{a}).$

Suppose there exists $\beta \in p\left(\mathcal{M}\right)$, with $\beta <\alpha$, and $H(\mathcal{M},\alpha ,\overline{a})\subseteq H(\mathcal{M},\beta ,\overline{a})$.

Consider three $<\alpha ,\overline{a}>$-definable sets:

$$\begin{gathered} K_1(\mathcal{M},\alpha ,\overline{a}):=\{\gamma \in M:\gamma <\alpha ,H(\mathcal{M},\alpha ,\overline{a})=H(\mathcal{M},\gamma ,\overline{a})\}, \\ {K}_2(\mathcal{M},\alpha ,\overline{a}):=\{\gamma \in M:\gamma <\alpha ,H(\mathcal{M},\alpha ,\overline{a})\subset H(\mathcal{M},\gamma ,\overline{a})\}, \\ {K}_3(\mathcal{M},\alpha ,\overline{a}):=\{\gamma \in M:\gamma <\alpha ,H(\mathcal{M},\gamma ,\overline{a})\subset H(\mathcal{M},\alpha ,\overline{a})\}. \end{gathered}$$

Clearly,

$${\alpha }_0\in K_3(\mathcal{M},\alpha ,\overline{a})\cap p\left(\mathcal{M}\right),\beta \in K_2(\mathcal{M},\alpha ,\overline{a})\cap p\left(\mathcal{M}\right).$$

Since T is weakly o-minimal, $K_i(\mathcal{M},\alpha ,\overline{a})$, $i=1,2,3$, is a union of convex $\neg K_i(\mathcal{M},\alpha ,\overline{a})$-separable subsets, there are $i\in \{1,2,3\}$, $K_i^j(\mathcal{M},\alpha ,\overline{a})$ is the maximal convex $<\alpha ,\overline{a}>$-definable subset such that

$$\exists \gamma \in K_i^j(\mathcal{M},\alpha ,\overline{a})\cap p\left(\mathcal{M}\right)\Rightarrow \forall \mu [p{\left(\mathcal{M}\right)}^{-}<\mu <\gamma \Rightarrow \mu \in K_i^j(\mathcal{M},\alpha ,\overline{a})].$$

Consider three cases:

$i=1.$

We have two possibilities for p:

a. 

p is irrational to the left. Then there exists $C(x,\overline{c})$, with $\overline{c}\in A$, such that

$$C(\mathcal{M},\overline{c})\subset K_i^j(\mathcal{M},\alpha ,\overline{a}),C(\mathcal{M},\overline{c})<p\left(\mathcal{M}\right).$$

b. 

p is quasirational to the left. Then there exists $C(x,\overline{c})$, with $\overline{c}\in A$, such that

$$C(\mathcal{M},\overline{c})\cup C(\mathcal{M},\overline{c})=p{\left(\mathcal{M}\right)}^{-}.$$

Thus, we obtain:

$$\mathcal{M}\vDash \exists z(C(\mathcal{M},\overline{c})<z<\alpha \wedge \forall x[C(\mathcal{M},\overline{c})<x<z\to H(\mathcal{M},\alpha ,\overline{a})\iff H(\mathcal{M},x,\overline{a})]).$$

Consider the following formula:

$$\mathsf{\Phi }(y,\overline{c},\overline{a}):=\exists z(C(\mathcal{M},\overline{c})<z\wedge \forall x[C(\mathcal{M},\overline{c})<x<z\to \neg H(y,x,\overline{a})]).$$

Then ${\beta }_2\in \mathsf{\Phi }(\mathcal{M},\overline{c},\overline{a})$ and ${\beta }_1\notin \mathsf{\Phi }(\mathcal{M},\overline{c},\overline{a})$. Which is a contradiction.

$i=2.$

Then there is $K_3^m(\mathcal{M},\alpha ,\overline{a})$ — maximal $<\alpha ,\overline{a}>$-definable subset of $K_3(\mathcal{M},\alpha ,\overline{a})$ such that

$$K_3^m(\mathcal{M},\alpha ,\overline{a})\subseteq p\left(\mathcal{M}\right),K_2^j(\mathcal{M},\alpha ,\overline{a})<K_3^m(\mathcal{M},\alpha ,\overline{a}).$$

Let

$$L(x,\alpha ,\overline{a}):=\exists y(K_3^m(y,\alpha ,\overline{a})\wedge \neg H(x,y,\overline{a})\wedge H(x,\alpha ,\overline{a})).$$

It follows that, $L(\mathcal{M},\alpha ,\overline{a})\subseteq q\left(\mathcal{M}\right).$

If $\exists \mu \in q\left(\mathcal{M}\right)$ such that $\mu <L(\mathcal{M},\alpha ,\overline{a})$, then $\mu <{\beta }_2$. This contradicts $p{\perp }^{a}q$. Thus

$$L{(\mathcal{M},\alpha ,\overline{a})}^{-}=q{\left(\mathcal{M}\right)}^{-}.$$

It follows from Lemma 2 (ii) that if q is quasirational to the left or isolated, then there exists a 1-A-formula $G(x,\overline{g})$, with $\overline{g}\in A$ such that

$$G(\mathcal{M},\overline{g})\cup \neg G(\mathcal{M},\overline{g})=q{\left(\mathcal{M}\right)}^{-}.$$

Let

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_1(\alpha ,\overline{a},\overline{g}):=\exists z(G(\mathcal{M},\overline{g})<z\wedge H(z,\alpha ,\overline{a})\wedge \forall x(G(\mathcal{M},\overline{g})<x<z\to \\ \hfill \exists y[K_3^m(y,\alpha ,\overline{a})\wedge \neg H(x,y,\overline{a})]\left)\right).\end{array}$$

It is clear that

$$\mathcal{M}\vDash {\mathsf{\Theta }}_1(\alpha ,\overline{a},\overline{g}).$$

Notice that $\forall \delta \in p\left(\mathcal{M}\right)\mathcal{M}\vDash {\mathsf{\Theta }}_1(\delta ,\overline{a},\overline{g})$.

Consider an arbitrary $\delta \in K_3^j(\mathcal{M},\alpha ,\overline{a})\cap p\left(\mathcal{M}\right)$, then $H(\mathcal{M},\alpha ,\overline{a})\subseteq H(\mathcal{M},\delta ,\overline{a})$ and $K_3^m(\mathcal{M},\delta ,\overline{a})\subset K_2^j(\mathcal{M},\alpha ,\overline{a}).$ Then

$$\forall {\alpha }_1\in K_3^m(\mathcal{M},\delta ,\overline{a}),andH(\mathcal{M},{\alpha }_1,\overline{a})\subseteq H(\mathcal{M},\alpha ,\overline{a}).$$

This contradicts the fact that $\mathcal{M}\vDash {\mathsf{\Theta }}_1(\delta ,\overline{a},\overline{g})$.

i = 3.

Then there is $K_2^m(\mathcal{M},\alpha ,\overline{a})$ — maximal $<\alpha ,\overline{a}>$-definable subset of $K_2(\mathcal{M},\alpha ,\overline{a})$ such that

$$K_2^m(\mathcal{M},\alpha ,\overline{a})\subseteq p\left(\mathcal{M}\right),K_3^j(\mathcal{M},\alpha ,\overline{a})<K_2^m(\mathcal{M},\alpha ,\overline{a}).$$

Let $R(x,\alpha ,\overline{a}):=\exists y(K_2^m(y,\alpha ,\overline{a})\wedge H(x,y,\overline{a})\wedge \neg H(x,\alpha ,\overline{a})).$ So, $R(\mathcal{M},\alpha ,\overline{a})\subseteq q\left(\mathcal{M}\right).$

If $\exists \mu \in q\left(\mathcal{M}\right)(R(\mathcal{M},\alpha ,\overline{a})<\mu )$, then ${\beta }_1<R(\mathcal{M},\alpha ,\overline{a})<\mu$. Contradiction with $p{\perp }^{a}q$.

Thus $R{(\mathcal{M},\alpha ,\overline{a})}^{+}=q{\left(\mathcal{M}\right)}^{+}.$ It follows from Lemma 2 (ii) that if q is quasirational to the left or isolated. Then there is a 1-A-formula $D(x,\overline{d})$, with $\overline{d}\in A$ such that $D{(\mathcal{M},\overline{d})}^{+}=q{\left(\mathcal{M}\right)}^{+}.$

Let

$${\mathsf{\Theta }}_2(\alpha ,\overline{a},\overline{d}):=\forall x(D(x,\overline{d})\wedge \neg H(x,\alpha ,\overline{a})\to \exists y(K_2^m(y,\alpha ,\overline{a})\wedge \neg H(x,y,\overline{a}))).$$

Consider arbitrary $\delta \in K_3^j(\mathcal{M},\alpha ,\overline{a})\cap p\left(\mathcal{M}\right)$, then $\mathcal{M}\vDash {\mathsf{\Theta }}_2(\delta ,\overline{a},\overline{d})$,

$$K_2^m(\mathcal{M},\delta ,\overline{a})\subseteq K_3^j(\mathcal{M},\alpha ,\overline{a})\cap p\left(\mathcal{M}\right).$$

For ${\beta }_2$, there exists ${\alpha }_1\in K_2^m(\mathcal{M},\delta ,\overline{a})$ such that ${\beta }_2\in H(\mathcal{M},{\alpha }_1,\overline{a})$. By Remark 2, we then have $H(\mathcal{M},\alpha ,\overline{a})\subseteq H(\mathcal{M},{\alpha }_1,\overline{a}).$ This leads to a contradiction, since ${\alpha }_1\in K_3^j(\mathcal{M},\alpha ,\overline{a})$. Therefore,

$$p\left(\mathcal{M}\right)\cap K_2(\mathcal{M},\alpha ,\overline{a})=⌀\mathit{and}{K}_1(\mathcal{M},\alpha ,\overline{a})\cap p\left(\mathcal{M}\right)>K_3(\mathcal{M},\alpha ,\overline{a}).$$

It follows that $U(\mathcal{M},\alpha ,\overline{a})$ is the maximal $<\alpha ,\overline{a}>$-definable subset of $K_3(\mathcal{M},\alpha ,\overline{a})$. Clearly, $U(x,\alpha ,\overline{a})$ is the required formula. Hence, Lemma 7 is proved.

Let $G(x,\alpha ,\overline{a}):=U(\mathcal{M},\alpha ,\overline{a})<x\le \alpha$. Then, $G(x,y,\overline{a})$ is maximal convex to the left p-stable 2-A-formula. This implies that p is quasisolitary. Consequently, if p is social and $p{\perp ̸}^{w}q$, then $p{\perp ̸}^{a}q$. By Lemma 5 it follows that q is social.

Remark 3.

Let $p,q\in S_1\left(A\right)$, and $p{\perp ̸}^{w}q$. Then the following hold:

(i) 

If $\alpha \in p\left(\mathcal{M}\right)$ then $[p{\perp }^{a}q\iff V_q\left(\alpha \right)=⌀]$.

(ii) 

If $p{\perp }^{a}q$, and $\alpha ,\beta \in p\left(\mathcal{M}\right)$ then

$$[H(\mathcal{M},\alpha ,\overline{a})=H(\mathcal{M},\beta ,\overline{a})\iff E_p(\alpha ,\beta ,{\overline{c}}_p)].$$

(iii) 

If $p{\perp }^{a}q$, and $B\subset M$ such that $V_p\left(B\right)\ne ⌀$ then

$$[V_q\left(B\right)=⌀\iff \exists \alpha \in p\left(\mathcal{M}\right),V_p\left(B\right)=E_p(\mathcal{M},\alpha ,{\overline{c}}_p)].$$

(2) 

follows from Lemma 5.

(3) 

$p{\perp ̸}^{a}p$ for any $p\in S_1\left(A\right)$ by Definition 12. If $p{\perp ̸}^{a}q$ then $q{\perp ̸}^{a}p$ by Lemma 3 (ii). Suppose $r{\perp ̸}^{a}p$, and $p{\perp ̸}^{a}q$.

Lemma 8.

Let $p\in S_1\left(A\right)$, ${\alpha }_1,{\alpha }_2\in p\left(\mathcal{M}\right)$, $\mathsf{\Phi }(x,\overline{\beta })$, $\overline{\beta }\in M$ such that $V_p\left({\alpha }_1\right)<\mathsf{\Phi }(\mathcal{M},\overline{\beta })<V_p\left({\alpha }_2\right)$. Then for any $q\in S_1\left(A\right)(p\neg {\perp }^{a}q)$, for any $\mathsf{\Psi }(x,y,\overline{a})$, with $\overline{a}\in A$ such that $\mathsf{\Psi }(\mathcal{M},{\alpha }_1,\overline{a})\subset V_q\left({\alpha }_1\right)$ for the formula $K_{\mathsf{\Phi },\mathsf{\Psi }}(y,\overline{\beta },\overline{a}):=\exists x(\mathsf{\Phi }(x,\overline{\beta },\overline{a})\wedge \mathsf{\Psi }(y,x,\overline{a}))$ the following is true:

$$V_q\left({\alpha }_1\right)<K_{\mathsf{\Phi },\mathsf{\Psi }}(\mathcal{M},\overline{\beta },\overline{a})<V_q\left({\alpha }_2\right).$$

Proof of Lemma 8

By Lemma 6 (ii), for any ${\alpha }_0,{\alpha }_0^{\prime }\in \mathsf{\Phi }(\mathcal{M},\overline{\beta })$

$$V_q\left({\alpha }_1\right)<V_q\left({\alpha }_0\right)<V_q\left({\alpha }_2\right)\iff V_q\left({\alpha }_1\right)<V_q\left({\alpha }_0^{\prime }\right)<V_q\left({\alpha }_2\right).$$

Then suppose that for any ${\alpha }_0\in \mathsf{\Phi }(\mathcal{M},\overline{\beta })$

$$V_q\left({\alpha }_1\right)<\mathsf{\Psi }(\mathcal{M},{\alpha }_0,\overline{a})<V_q\left({\alpha }_2\right).$$

Thus,

$$V_q\left({\alpha }_1\right)<{\bigcup }_{{\alpha }_0\in \mathsf{\Phi }(\mathcal{M},\overline{\beta })}\mathsf{\Psi }(\mathcal{M},{\alpha }_0,\overline{a})<V_q\left({\alpha }_2\right).$$

Then

$$V_q\left({\alpha }_1\right)<K_{\mathsf{\Phi },\mathsf{\Psi }}(\mathcal{M},\overline{\beta },\overline{a})<V_q\left({\alpha }_2\right).$$

Hence, Lemma 8 is proved.

Remark 4.

Let $p\in S_1\left(A\right)$, and $B\subset M$, and $V_p\left(B\right)\ne ⌀$ such that M is ${|A\cup B|}^{+}$-saturated.

(i) 

If ${\alpha }_1<V_p\left(B\right)<{\alpha }_2$, with ${\alpha }_1,{\alpha }_2\in p\left(\mathcal{M}\right)$ then for $q\in S_1\left(A\right)$ such that $q{\perp ̸}^{a}p$ the following is true:

$$V_q\left(B\right)\ne ⌀\mathit{and}{V}_q\left({\alpha }_1\right)<V_q\left(B\right)<V_q\left({\alpha }_2\right)\mathit{or}{V}_q\left({\alpha }_2\right)<V_q\left(B\right)<V_q\left({\alpha }_1\right).$$

(ii) 

For every ${\alpha }_0\in V_p\left(B\right)$, and for every type $q\in S_1\left(A\right)$, with $q{\perp ̸}^{a}p$ the following is true: $V_q\left({\alpha }_0\right)\subset V_q\left(B\right).$

Consider $\beta \in r\left(\mathcal{M}\right)$, then $V_p\left(\beta \right)\ne ⌀$ because $r{\perp ̸}^{a}p$. By Remark 4 (i) and Theorem 2 (iii) $V_q\left(\beta \right)\ne ⌀$. Then, $r{\perp ̸}^{a}q$.

(4) 

$p{\perp ̸}^{a}p$ for any $p\in S_1\left(A\right)$ by Definition 1. If $p{\perp ̸}^{w}q$ then $q{\perp ̸}^{w}p$ by Note 3 (i). Suppose $r{\perp ̸}^{w}p$, $p{\perp ̸}^{w}q$, and $p{\perp ̸}^{a}q$. Thus, by Theorem 3 (ii), p and q are quasisolitary. Let $H(x,y,\overline{a})$ be a formula from Lemma 7. Then from Remark 3 (ii), it follows:

$$\begin{array}{c}\hfill \forall {\alpha }_1,{\alpha }_2\in p\left(\mathcal{M}\right)[\vDash \neg E_p({\alpha }_1,{\alpha }_2,{\overline{c}}_p)\Rightarrow H(\mathcal{M},{\alpha }_1,\overline{a})\subset H(\mathcal{M},{\alpha }_2,\overline{a})\\ \hfill \mathit{or}H(\mathcal{M},{\alpha }_2,\overline{a})\subset H(\mathcal{M},{\alpha }_1,\overline{a})].\end{array}$$

Let $\alpha \in p\left(\mathcal{M}\right)$. If there exists ${\alpha }_1\in p\left(\mathcal{M}\right)$ such that ${\alpha }_1<\alpha$, and

$$\mathcal{M}\vDash \neg E_p({\alpha }_1,\alpha ,{\overline{c}}_p),H(\mathcal{M},{\alpha }_1,\overline{a})\subset H(\mathcal{M},\alpha ,\overline{a}),$$

then for any ${\alpha }_2,{\alpha }_3\in p\left(\mathcal{M}\right)$

$$\mathcal{M}\vDash \neg E_p({\alpha }_2,{\alpha }_3,{\overline{c}}_p)\Rightarrow {\alpha }_2\wedge {\alpha }_3\Rightarrow H(\mathcal{M},{\alpha }_2,\overline{a})\subset H(\mathcal{M},{\alpha }_3,\overline{a}).$$

Without loss of generality suppose that $H(x,y,\overline{a})$ is increasing on classes of equivalence $E_p(x,y,{\overline{c}}_p)$ of elements from $p\left(\mathcal{M}\right)$. Consider the following formula:

$$\begin{array}{c}\hfill K(x,\alpha ,{\overline{c}}_p,\overline{b}):=\forall y[x<y<\alpha \wedge \neg E_p(x,y,{\overline{c}}_p)\wedge \neg E_p(y,\alpha ,{\overline{c}}_p)\to \\ \hfill H(\mathcal{M},x,\overline{a})\subset H(\mathcal{M},y,\overline{a})\subset H(\mathcal{M},\alpha ,\overline{a})].\end{array}$$

If p is quasirational to the left then there exists $U_p(x,\overline{b})$ such that $U_p(\mathcal{M},\overline{b})=p{\left(\mathcal{M}\right)}^{-}$.

$$\mathcal{M}\vDash \forall x[U_p(\mathcal{M},\overline{b})<x<\alpha \to K(x,\alpha ,{\overline{c}}_p,\overline{b})].$$

If p is non-quasirational to the left, then there is $C(\mathcal{M},\overline{e})$ such that

$$C(\mathcal{M},\overline{e})\subset K(\mathcal{M},\alpha ,{\overline{c}}_p,\overline{a}),C(\mathcal{M},\overline{e})<p\left(\mathcal{M}\right).$$

It follows that:

$$\mathcal{M}\vDash \forall x[C(\mathcal{M},\overline{e})<x<\alpha \to K(x,\alpha ,{\overline{c}}_p,\overline{a})].$$

By a similar consideration of the formula

$$\begin{array}{c}\hfill K_1(x,\alpha ,{\overline{c}}_p,\overline{a}):=\forall y[(\alpha <y<x\wedge \neg E_p(x,y,{\overline{c}}_p)\wedge \neg E_p(y,\alpha ,{\overline{c}}_p))\to \\ \hfill H(\mathcal{M},\alpha ,\overline{a})\subset H(\mathcal{M},y,\overline{a})\subset H(\mathcal{M},x,\overline{a})].\end{array}$$

we obtain a formula $D(x,\overline{d})$ such that $C(\mathcal{M},\overline{e})<p\left(\mathcal{M}\right)<D(\mathcal{M},\overline{d})$ and

$$\mathcal{M}\vDash \forall x\forall y[C(\mathcal{M},\overline{e})<x<y<D(\mathcal{M},\overline{d})\wedge \neg E_p(x,y,{\overline{c}}_p)\to H(\mathcal{M},x,\overline{a})\subset H(\mathcal{M},y,\overline{a})].$$

Let $\beta \in r\left(\mathcal{M}\right)$. Then there is the formula $\mathsf{\Phi }(x,y,\overline{b})$ such that

$$\mathsf{\Phi }(\mathcal{M},\beta ,\overline{b})\cap p\left(\mathcal{M}\right)\ne ⌀\mathit{and}\neg \mathsf{\Phi }(\mathcal{M},\beta ,\overline{b})\cap p\left(\mathcal{M}\right)\ne ⌀.$$

Suppose ${\gamma }_1\in \mathsf{\Phi }(\mathcal{M},\beta ,\overline{b})\cap p\left(\mathcal{M}\right)$ and ${\gamma }_2\in \neg \mathsf{\Phi }(\mathcal{M},\beta ,\overline{b})\cap p\left(\mathcal{M}\right)$ with ${\gamma }_1<{\gamma }_2$. Let $H_1(x,\beta ,\overline{b})$ be the maximal convex subformula of $\mathsf{\Phi }(x,\beta ,\overline{b})$ such that ${\gamma }_1\in H_1(\mathcal{M},\beta ,\overline{b})$. Then, ${\gamma }_2>H_1(\mathcal{M},\beta ,\overline{b})$. For ${\gamma }_2\in p\left(\mathcal{M}\right)$ there is $\mu \in q\left(\mathcal{M}\right)$ such that $\mu >H(\mathcal{M},{\gamma }_2,\overline{a})$. Hence, $\forall \alpha \in H(\mathcal{M},\beta ,\overline{a})\cap C{(\mathcal{M},\overline{e})}^{+}\cap D{(\mathcal{M},\overline{d})}^{-}$ we have $H(\mathcal{M},\alpha ,\overline{a})<\mu .$ Consider the formula

$$H_2(x,\beta ,\overline{a},\overline{e},\overline{b}):=\exists y[H_1(y,\beta ,\overline{b})\wedge C(\mathcal{M},\overline{e})<y\wedge H(x,y,\overline{a})].$$

Therefore, $H_2(\mathcal{M},\beta ,\overline{b},\overline{d},\overline{e},\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀$, because $H(\mathcal{M},{\gamma }_1,\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀$. Moreover, $\neg H_2(\mathcal{M},\beta ,\overline{b},\overline{d},\overline{e},\overline{a})\cap q\left(\mathcal{M}\right)\ne ⌀$, since $\mu >H_2(\mathcal{M},\beta ,\overline{b},\overline{d},\overline{e},\overline{a})$. Thus, $r{\perp ̸}^{w}q$. Hence, Theorem 3 is proved. □

Corollary 1.

The equivalence relations ${\perp ̸}^a$ and ${\perp ̸}^w$ partition the set of non-algebraic types from $S_1\left(A\right)$ into the classes of equivalence as follows:

(i) 

Every ${\perp ̸}^w$-class contains ${\perp ̸}^a$-classes or it coincides with a ${\perp ̸}^a$-class.

(ii) 

Every ${\perp ̸}^w$-class contains types only of one kind from six basic kinds of Remark 1.

(iii) 

Every ${\perp ̸}^w$-class, which contains social types, is a ${\perp ̸}^a$-class.

Lemma 9 

([16]). Let $p\in S_1\left(A\right)$, and $\psi (x,y,\overline{b})$ is p-stable formula where $\overline{b}\in A$. There is $\varphi (x,\overline{\alpha })$, with $\overline{\alpha }\in M$ and there are ${\mu }_1,{\mu }_2\in p\left(\mathcal{M}\right)$, such that ${\mu }_1<\varphi (\mathcal{M},\overline{a})<{\mu }_2.$ Then there are ${\mu }_1^{\prime }$, ${\mu }_2^{\prime }$ from $p\left(\mathcal{M}\right)$ such that for the formula

$$H_{\varphi ,\psi }(x,\overline{\alpha },\overline{b}):=\exists y(\varphi (y,\overline{\alpha })\wedge \psi (x,y,\overline{b}))$$

the following is true

$${\mu }_1^{\prime }<H_{\varphi ,\psi }(\mathcal{M},\overline{\alpha },\overline{b})<{\mu }_2.$$

Theorem 4.

Let $A,B,C\subset M$ such that M is ${|A\cup B\cup C|}^{+}$-saturated, $p,q\in S_1\left(A\right)$, and $p{\perp ̸}^{w}q$. Then the following hold:

(i) 

If $p{\perp ̸}^{a}q$, then $V_p\left(B\right)\cap V_p\left(C\right)=⌀$ if and only if $V_q\left(B\right)\cap V_q\left(C\right)=⌀$.

(ii) 

If $p{\perp ̸}^{a}q$, $V_p\left(B\right)\cap V_p\left(C\right)=⌀$, $V_q\left(B\right)\cap V_q\left(C\right)\ne ⌀$, then there exists $\delta \in q\left(\mathcal{M}\right)$ such that

$$V_q\left(B\right)\cap V_q\left(C\right)=V_q\left(\delta \right)=E_q(\mathcal{M},\delta ,{\overline{c}}_q),(V_p\left(B\right),V_p\left(C\right))=⌀\mathit{or}(V_p\left(C\right),V_p\left(B\right))=⌀.$$

(iii) 

If $p{\perp ̸}^{a}q$, and there is $\alpha \in p\left(\mathcal{M}\right)$ such that $V_p\left(B\right)<V_p\left(\alpha \right)<V_p\left(C\right)$, then

$$V_q\left(B\right)\cap V_q\left(C\right)=⌀.$$

Proof. 

(i) It follows from Lemma 8 and Remark 4 (ii).

(ii) Let $H(x,y,\overline{b})$ be a formula from Lemma 7, which was obtained from the fact $q{\perp ̸}^{w}p$, and $q{\perp ̸}^{a}p$, such that $\forall {\alpha }_1,{\alpha }_2\in q\left(\mathcal{M}\right)$ the following hold:

• $H(\mathcal{M},{\alpha }_1,\overline{b})<\neg H(\mathcal{M},{\alpha }_1,\overline{b})$
• $\exists {\beta }_1,{\beta }_2\in p\left(\mathcal{M}\right),{\beta }_1\in H(\mathcal{M},{\alpha }_1,\overline{b}),{\beta }_2\in \neg H(\mathcal{M},{\alpha }_2,\overline{b})$
• $H(\mathcal{M},{\alpha }_1,\overline{b})\subset H(\mathcal{M},{\alpha }_2,\overline{b})\Rightarrow \neg E_q({\alpha }_1,{\alpha }_2,{\overline{c}}_q)$

Without loss of generality, as in the proof of Lemma 7, we suppose:

$$H(\mathcal{M},{\alpha }_1,\overline{b})\subset H(\mathcal{M},{\alpha }_2,\overline{b})\iff {\alpha }_1<{\alpha }_2\wedge \neg E_q({\alpha }_1,{\alpha }_2,{\overline{c}}_q).$$

Suppose $⌀\ne V_q\left(B\right)\cap V_q\left(C\right)\ne E_q(\mathcal{M},\delta ,{\overline{c}}_q)$, for all $\delta \in q\left(\mathcal{M}\right)$.

Let $\delta \in V_q\left(B\right)\cap V_q\left(C\right)$. Then there are two formulas $\varphi (x,\overline{\beta })$, and $\psi (x,\overline{\gamma })$, with $\overline{\beta }\in B\cup A,\overline{\gamma }\in C\cup A$ such that $\delta \in \varphi (\mathcal{M},\overline{\beta })\cap \psi (\mathcal{M},\overline{\gamma })$ and there are ${\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4\in q\left(\mathcal{M}\right)$ such that

$${\mu }_1<\varphi (\mathcal{M},\overline{\beta })<{\mu }_2,{\mu }_3<\psi (\mathcal{M},\overline{\gamma })<{\mu }_4.$$

Consider the formula ${\varphi }_1(x,\overline{\beta },{\overline{c}}_q):=\exists y(\varphi (y,\beta )\wedge E_q(x,y,{\overline{c}}_q))$.

Because $E_q(x,y,{\overline{c}}_q)$ is p-stable, Lemma 9 guarantees the existence of of ${\mu }_1^{\prime },{\mu }_2^{\prime }$ such that ${\mu }_1^{\prime }<{\varphi }_1(\mathcal{M},\overline{\beta },{\overline{c}}_q)<{\mu }_2^{\prime }$. Moreover, for every $\delta \in {\varphi }_1(\mathcal{M},\overline{\beta },{\overline{c}}_q)$, it follows that $E_q(\mathcal{M},\delta ,\overline{b})\subseteq {\varphi }_1(\mathcal{M},\overline{\beta },{\overline{c}}_q)$. Let

$${\psi }_1(x,\overline{\gamma },{\overline{c}}_q):=\exists y(\psi (y,\overline{\gamma })\wedge E_q(x,y,{\overline{c}}_q)).$$

Then for any $\delta \in {\varphi }_1(\mathcal{M},\overline{\beta },{\overline{c}}_q)\cap {\psi }_1(\mathcal{M},\overline{\gamma },{\overline{c}}_q)$, we have

$$E_q(\mathcal{M},\delta ,{\overline{c}}_q)\subseteq {\varphi }_1(\mathcal{M},\overline{\beta },{\overline{c}}_q)\cap {\psi }_1(\mathcal{M},\overline{\gamma },{\overline{c}}_q).$$

Thus, there exist ${\alpha }_1,{\alpha }_2\in {\varphi }_1(\mathcal{M},\overline{\beta },{\overline{c}}_q)\cap {\psi }_1(\mathcal{M},\overline{\gamma },{\overline{c}}_q)$ such that $\vDash \neg E_q({\alpha }_1,{\alpha }_2,{\overline{c}}_q).$ Suppose ${\alpha }_1<{\alpha }_2$. Let us define

$$\begin{array}{c}\hfill K_{\varphi }(y,\overline{\beta },\overline{b},{\overline{c}}_q):=\exists x_1\exists x_2({\varphi }_1(x_1,\overline{\beta },{\overline{c}}_q)\wedge {\varphi }_1(x_2,\overline{\beta },{\overline{c}}_q)\wedge \neg E_q(x_1,x_2,{\overline{c}}_q)\wedge \\ \hfill x_1<x_2\wedge \neg H(y,x_1,\overline{b})\wedge \neg H(y,x_2,\overline{b})).\end{array}$$

Then there are ${\beta }_1,{\beta }_2\in p\left(\mathcal{M}\right)$ such that

$$p{\left(\mathcal{M}\right)}^{-}<{\beta }_1<K_{\varphi }(\mathcal{M},\overline{\beta },\overline{b},{\overline{c}}_q)<{\beta }_2<p{\left(\mathcal{M}\right)}^{+}$$

because there are ${\alpha }_3,{\alpha }_4\in q\left(\mathcal{M}\right)$ such that

$${\alpha }_3<V_p\left(B\right)<{\alpha }_4\mathrm{and}\vDash \neg E_q({\alpha }_3,{\alpha }_1,{\overline{c}}_q)\wedge \neg E_q({\alpha }_2,{\alpha }_4,{\overline{c}}_q).$$

Thus, $K_{\varphi }(\mathcal{M},\overline{\beta },\overline{b},{\overline{c}}_q)\ne ⌀$ since there is ${\mu }_0$ such that

$${\mu }_0\in H(\mathcal{M},{\alpha }_2,\overline{b})\setminus H(\mathcal{M},{\alpha }_1,\overline{b}),\mathrm{and}{\mu }_0\in K_{\varphi }(\mathcal{M},\overline{\beta },\overline{b},{\overline{c}}_q).$$

Consider the formula

$$\begin{array}{c}\hfill K_{\psi }(\overline{y},\overline{\gamma },\overline{b},{\overline{c}}_q):=\exists x_1\exists x_2({\psi }_1(x_1,\overline{\gamma },{\overline{c}}_q)\wedge {\psi }_1(x_2,\overline{\gamma },{\overline{c}}_q)\wedge \neg E_q(x_1,x_2,{\overline{c}}_q)\wedge \\ \hfill x_1<x_2\wedge \neg H(y,x_1,\overline{b})\wedge \neg H(y,x_2,\overline{b})).\end{array}$$

Then ${\mu }_0\in K_{\psi }(\mathcal{M},\overline{\gamma },\overline{b},{\overline{c}}_q)$ by the same consideration as for $K_{\varphi }(\mathcal{M},\overline{\beta },\overline{b},{\overline{c}}_q)$. Thus, ${\mu }_0\in V_p\left(B\right)\cap V_p\left(C\right)$. Which is a contradiction.

Thus, $\exists \delta \in q\left(\mathcal{M}\right)$ such that $V_q\left(B\right)\cap V_q\left(C\right)=E_q(\mathcal{M},\delta ,{\overline{c}}_q)$. For quasisolitary type q, $E_q(\mathcal{M},\delta ,{\overline{c}}_q)=V_q\left(B\right)$. Hence, (ii) is proved.

(iii) By Theorem 2 (v), we have $V_p\left(B\right)<V_p\left(\alpha \right)<V_p\left(C\right)$ where $\varphi (\mathcal{M},\overline{\beta })\subseteq V_q\left(B\right)$, $\psi (\mathcal{M},\overline{\gamma })\subseteq \left(C^{\prime }\right)$, and

$$\varphi (\mathcal{M},\overline{\beta })\cap \psi (\mathcal{M},\overline{\gamma })=E_q(\mathcal{M},\delta ,{\overline{c}}_q).$$

The existence of these $\varphi ,\psi ,\delta$ follows from proof of (ii). Let ${\overline{\beta }}_1\in B$ be such that $\mathsf{\Theta }(\mathcal{M},{\overline{\beta }}_1)\subseteq V_p\left(B\right)$ and $V_p\left(B\right)\subseteq H(\mathcal{M},\delta ,\overline{b})$. Suppose $V_p\left(B\right)\subset H(\mathcal{M},\delta ,\overline{b})$. Then $V_p{\left(B\right)}^{+}=H{(\mathcal{M},\delta ,\overline{\beta })}^{+}$. If $V_p{\left(B\right)}^{+}\ne H{(\mathcal{M},\delta ,\overline{\beta })}^{+}$, then there is $\theta (\mathcal{M},{\overline{\beta }}_1)$, with ${\overline{\beta }}_1\in B$, and $\exists \overline{ϵ}\in H(\mathcal{M},\delta ,\overline{b})$ such that $\theta (\mathcal{M},{\overline{\beta }}_1)<\mu$. Consider the following formula:

$$R(x,\overline{\beta },{\overline{\beta }}_1,\overline{b}):=\exists y(\varphi (y,\overline{\beta })\wedge H(x,y,\overline{b})\wedge \theta (\mathcal{M},{\overline{\beta }}_1)<x).$$

Thus, $R(\mathcal{M},\overline{\beta },{\overline{\beta }}_1,\overline{b})\subseteq V_p\left(B\right)$, and $R{(\mathcal{M},\overline{\beta },{\overline{\beta }}_1,\overline{b})}^{+}=H{(\mathcal{M},\delta ,\overline{b})}^{+}$.

Suppose $V_p\left(C\right)=\neg H(\mathcal{M},\delta ,\overline{b})$. Then $V_p\left(C\right)=\neg H{(\mathcal{M},\delta ,\overline{b})}^{-}$. If $V_p{\left(C\right)}^{-}=\neg H(\mathcal{M},\delta ,\overline{b})$, then there is ${\theta }_1(\mathcal{M},{\gamma }_1)$, with ${\gamma }_1\in C$, and $\exists {\mu }_1\in \neg H(\mathcal{M},\delta ,\overline{b})$ such that ${\theta }_1(\mathcal{M},{\gamma }_1)<{\mu }_1$. Consider the following formula:

$$L(x,\overline{\gamma },{\gamma }_1,\overline{b}):=\exists y(\psi (y,\overline{\gamma })\wedge \neg H(x,y,\overline{b})\wedge x<\theta (\mathcal{M},{\gamma }_1,\overline{b})).$$

We then have

$$L(\mathcal{M},\overline{\gamma },{\gamma }_1,\overline{b})\subseteq V_p\left(C\right),L(\mathcal{M},\overline{\gamma },{\gamma }_1,\overline{b})=\neg H{(\mathcal{M},\delta ,\overline{b})}^{-}.$$

Thus, if $V_p{\left(B\right)}^{+}\cap \neg H(\mathcal{M},\delta ,\overline{b})\ne ⌀$, then $V_p\left(B\right)=\neg H(\mathcal{M},\delta ,\overline{b})$, and consequently $V_p\left(B\right)\cap V_q\left(C\right)\ne ⌀$. This yields a contradiction. Hence,

$$V_p{\left(B\right)}^{+}=\neg H(\mathcal{M},\delta ,\overline{b}),\mathrm{and}{V}_q\left(B\right)\cap V_q\left(C\right)=⌀.$$

□

4. Discussion

The main result of this work is the unification of the concepts of type orthogonality and neighborhoods in a type. It can be observed that the notion of a neighborhood of an element within a type generalizes the idea of algebraic closure in a type.

The concept of orthogonality, originally introduced by Shelah S. in [22], is further refined here. In particular, semi-isolation between 1-types splits into two distinct notions: weak orthogonality and almost orthogonality for weakly o-minimal theories.

This paper establishes the connection between p-stable (p-preserving) types and neighborhoods, highlighting how local type behavior can be captured through neighborhood analysis.

The orthogonality properties of types in weakly o-minimal theories, as explored in this article, can be extended to the broader class of NIP theories. In particular, the foundations for this extension, including the notion of ordered stable theories (o-stable theories), were established in works [9,11,23].