Series and Connections Among Central Factorial Numbers, Stirling Numbers, Inverse of Vandermonde Matrix, and Normalized Remainders of Maclaurin Series Expansions ^†

Abstract

This paper presents an extensive investigation into several interrelated topics in mathematical analysis and number theory. The author revisits and builds upon known results regarding the Maclaurin power series expansions for a variety of functions and their normalized remainders, explores connections among central factorial numbers, the Stirling numbers, and specific matrix inverses, and derives several closed-form formulas and inequalities. Additionally, this paper reveals new insights into the properties of these mathematical objects, including logarithmic convexity, explicit expressions for certain quantities, and identities involving the Bell polynomials of the second kind.

1. Brief Review, Motivations, and Aims

We first briefly review and survey some results of the Maclaurin series expansions for the powers of several elementary functions and their normalized remainders, demonstrate our motivations for this paper, and describe the aims of this paper.

1.1. Inverse Sine Function

One of the basic elementary functions in calculus is the inverse sine function $arcsinz$. The Maclaurin power series expansion

$${\displaystyle \frac{arcsinz}{z}}=\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\left|z\right|<1$$

(1)

is common knowledge in analysis; see ([1], p. 444) and ([2], p. 229). However, the Maclaurin power series expansions

$$\begin{array}{cc}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^2\hfill & =\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[\left(2\mathsf{\ell }\right)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+2}{2}\right)}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^3\hfill & =\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }+1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+3}{3}\right)}}\left[\sum _{k=0}^{\mathsf{\ell }}{\displaystyle \frac{1}{{(2k+1)}^2}}\right]{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\hfill \end{array}$$

(3)

$$\begin{array}{cc}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^4\hfill & =\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }+2)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+4}{4}\right)}}\left[\sum _{k=0}^{\mathsf{\ell }}{\displaystyle \frac{1}{{(2k+2)}^2}}\right]{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\hfill \end{array}$$

(4)

and

$${\left({\displaystyle \frac{arcsinz}{z}}\right)}^5={\displaystyle \frac{1}{2}}\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }+3)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+5}{5}\right)}}\left[{\left(\sum _{k=0}^{\mathsf{\ell }+1}{\displaystyle \frac{1}{{(2k+1)}^2}}\right)}^2-\sum _{k=0}^{\mathsf{\ell }+1}{\displaystyle \frac{1}{{(2k+1)}^4}}\right]{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}$$

(5)

of the positive integer power functions ${\left({\displaystyle \frac{arcsinz}{z}}\right)}^q$ for $2\le q\le 5$ and $\left|z\right|<1$ are rare advanced knowledge in analysis. The Maclaurin power series expansions between (2) and (5) have been collected, reviewed, surveyed, traced back, and retrospected in [3,4,5], ([6], Remark 6), ([7], Remark 5.2), ([8], Section 1), ([9], Section 1), and ([10], pp. 279 and 331–333) from a number of studies since a century ago. See also the answer at the site https://math.stackexchange.com/a/4657809 (accessed on 12 March 2023).

In ([6], Theorem 1), ([7], Theorem 2.1), ([11], Section 4), and ([12], Section 6), the general Maclaurin power series expansion

$${\left({\displaystyle \frac{arcsinz}{z}}\right)}^q=1+\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }}{2\mathsf{\ell }}\right)}}{\displaystyle \frac{{\left(2z\right)}^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\left|z\right|<1$$

(6)

for $q\in \mathbb{N}$ was rediscovered multiple times with different ideas and techniques, where

$$\mathcal{Q}(q,2\mathsf{\ell })={(-1)}^{\mathsf{\ell }}\sum _{k=0}^{2\mathsf{\ell }}\left({\displaystyle \genfrac{}{}{0pt}{}{q+k-1}{q-1}}\right)s(q+2\mathsf{\ell }-1,q+k-1){\left({\displaystyle \frac{q+2\mathsf{\ell }-2}{2}}\right)}^k$$

(7)

for $q,\mathsf{\ell }\in \mathbb{N}$, and the Stirling numbers of the first kind $s(\mathsf{\ell }+q,q)$ for $\mathsf{\ell },q\in {\mathbb{N}}_0$ can be analytically generated ([13], Theorem 3.14) by

$${\left[{\displaystyle \frac{ln(1+z)}{z}}\right]}^q=\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{s(\mathsf{\ell }+q,q)}{\left(\genfrac{}{}{0pt}{}{\mathsf{\ell }+q}{q}\right)}}{\displaystyle \frac{z^{\mathsf{\ell }}}{\mathsf{\ell }!}},\left|z\right|<1.$$

(8)

Power series expansion (6) is the unification of the Maclaurin power series expansions beween (1)–(5) and has a better form than those in [4].

In ([11], Theorem 7) (see also ([14]), Example 3.1), the Maclaurin series expansion (6) was generalized as

$${\left({\displaystyle \frac{arcsinz}{z}}\right)}^r=1+\sum _{\mathsf{\ell }=1}^{\infty }\left[\sum _{k=1}^{2\mathsf{\ell }}{\displaystyle \frac{{(-r)}_k}{(2\mathsf{\ell }+k)!}}\sum _{j=1}^k{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{2\mathsf{\ell }+k}{k-j}}\right)\mathcal{Q}(j,2\mathsf{\ell })\right]{\left(2z\right)}^{2\mathsf{\ell }}$$

for $r\in \mathbb{R}$ and $\left|z\right|<1$, where the Pochhammer symbol ${\left(r\right)}_k$, also known as the rising factorial, can be defined ([15], p. 256, Entry 6.1.22) by

$${\left(r\right)}_k=\prod _{\mathsf{\ell }=0}^{k-1}(r+\mathsf{\ell })=\left\{\begin{array}{cc}r(r+1)\dots (r+k-1),\hfill & k\in \mathbb{N}\hfill \\ 1,\hfill & k=0\hfill \end{array}\right.$$

(9)

for $r\in \mathbb{C}$ and $k\in {\mathbb{N}}_0$; see also related texts in papers [16,17].

In ([6], Section 4), ([7], Section 4), [8,9], and ([12], Section 7), several existing applications as well as new applications of series expansions (1)–(6) were reviewed, surveyed, traced back, and carried out.

In the manuscript titled “Monotonicity, convexity, and power series expansions of normalized remainders concerning inverse sine, cosine, and tangent functions” by Liu and Qi, among other things, the normalized remainder

$$f_{1,q}\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{{[\left(2q\right)!!]}^2}{\left(2q\right)!}}{\displaystyle \frac{2q+1}{z^{2q+1}}}\left(arcsinz-{\displaystyle \sum _{k=0}^{q-1}}{\displaystyle \frac{\left(2k\right)!}{{[\left(2k\right)!!]}^2}}{\displaystyle \frac{z^{2k+1}}{2k+1}}\right),\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(10)

for $q\in {\mathbb{N}}_0$ and $\left|z\right|<1$ of the Maclaurin power series expansion of $arcsinz$ at $z=0$ was proved to be logarithmically convex in $x\in (0,1)$, and its logarithm was expanded to a Maclaurin power series at $z=0$. For the history, ideas, and thoughts of initially inventing and designing normalized remainders by Qi and his coauthors, please refer to ([18], Section 1) and ([19], Section 1).

1.2. Inverse Cosine Function

Theorem 4.1 in [12] reads that, for $q\in \mathbb{N}$ and $\left|z\right|<1$, we have

$${\left[{\displaystyle \frac{{(arccosz)}^2}{2(1-z)}}\right]}^q=1+\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{\mathcal{Q}(2q,2\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{2q+2\mathsf{\ell }}{2\mathsf{\ell }}\right)}}{\displaystyle \frac{{\left[2(1-z)\right]}^{\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},$$

where $\mathcal{Q}(q,2\mathsf{\ell })$ is defined by (7).

Theorem 5.2 in [12] states that, for $r\in \mathbb{R}$, we have

$${\left[{\displaystyle \frac{{(arccosz)}^2}{2(1-z)}}\right]}^r=1+\sum _{\mathsf{\ell }=1}^{\infty }\left[\sum _{j=1}^{\mathsf{\ell }}{\displaystyle \frac{{(-r)}_j}{j!}}\sum _{k=1}^j{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{j}{k}}\right){\displaystyle \frac{\mathcal{Q}(2k,2\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{2k+2\mathsf{\ell }}{2\mathsf{\ell }}\right)}}\right]{\displaystyle \frac{{\left[2(1-z)\right]}^{\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},$$

where the Pochhammer symbol ${(-r)}_j$ is defined by (9).

Theorem 6 in [11] confirms that, for $r\in \mathbb{R}$ and $\left|z\right|<1$, we have

$$\begin{array}{cc}{\left({\displaystyle \frac{2arccosz}{\pi }}\right)}^r\hfill & =1+{\displaystyle \frac{{(-r)}_2}{{\pi }^2}}{\displaystyle \frac{{\left(2z\right)}^2}{2!}}+\sum _{j=2}^{\infty }\left[\sum _{\mathsf{\ell }=1}^j{\displaystyle \frac{{(-r)}_{2\mathsf{\ell }}}{{\pi }^{2\mathsf{\ell }}}}\mathcal{Q}(2\mathsf{\ell },2j-2\mathsf{\ell })\right]{\displaystyle \frac{{\left(2z\right)}^{2j}}{\left(2j\right)!}}\hfill \\ \hfill & +\sum _{j=1}^{\infty }\left[\sum _{\mathsf{\ell }=1}^j{\displaystyle \frac{{(-r)}_{2\mathsf{\ell }-1}}{{\pi }^{2\mathsf{\ell }-1}}}\mathcal{Q}(2\mathsf{\ell }-1,2j-2\mathsf{\ell })\right]{\displaystyle \frac{{\left(2z\right)}^{2j-1}}{(2j-1)!}}.\hfill \end{array}$$

In the manuscript titled “Monotonicity, convexity, and power series expansions of normalized remainders concerning inverse sine, cosine, and tangent functions” by Liu and Qi, among other things, the normalized remainder

$$f_{4,q}\left(z\right)=\{\begin{array}{cc}-{\displaystyle \frac{{[\left(2q\right)!!]}^2}{\left(2q\right)!}}{\displaystyle \frac{2q+1}{z^{2q+1}}}\left(arccosz-{\displaystyle \frac{\pi }{2}}+{\displaystyle \sum _{k=0}^{q-1}}{\displaystyle \frac{\left(2k\right)!}{{[\left(2k\right)!!]}^2}}{\displaystyle \frac{z^{2k+1}}{2k+1}}\right),\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(11)

for $q\in {\mathbb{N}}_0$ and $\left|z\right|<1$ was proved to be equal to $f_{1,q}\left(z\right)$, defined by (10), while the even function $ln\left({\displaystyle \frac{2}{\pi }}arccosz\right)$ was expanded to a Maclaurin power series at $z=0$.

1.3. Inverse Tangent Function

Influenced by the techniques, ideas, and thoughts in papers [6,7,8,11,12,14,20], Grishaev and Sazonov established in [21] the Maclaurin power series expansions

$${\left({\displaystyle \frac{arctanz}{z}}\right)}^n=n!\sum _{k=0}^{\infty }{(-1)}^{k}G(n,k)z^{2k},\left|z\right|<1$$

and

$${\left({\displaystyle \frac{arctanz}{z}}\right)}^r=1+\sum _{m=1}^{\infty }{(-1)}^m\left[\sum _{k=1}^{2m}{\displaystyle \frac{{(-r)}_k}{k!}}\sum _{j=1}^k{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{k}{j}}\right)j!G(j,m)\right]z^{2m},\left|z\right|<1$$

for $n\in \mathbb{N}$ and $r\in \mathbb{R}$, where

$$G(n,k)=\sum _{j=0}^{2k}\left({\displaystyle \genfrac{}{}{0pt}{}{2k+n-1}{2k-j}}\right)2^j{\displaystyle \frac{s(j+n,n)}{(j+n)!}}$$

for $n\in \mathbb{N}$ and $k\in {\mathbb{N}}_0$. See also ([11], Remark 12).

In the manuscript titled “Monotonicity, convexity, and power series expansions of normalized remainders concerning inverse sine, cosine, and tangent functions” by Liu and Qi, the normalized remainder

$$f_{2,q}\left(z\right)=\{\begin{array}{cc}{(-1)}^q{\displaystyle \frac{2q+1}{z^{2q+1}}}\left[arctanz-{\displaystyle \sum _{k=0}^{q-1}}{(-1)}^k{\displaystyle \frac{z^{2k+1}}{2k+1}}\right],\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(12)

for $q\in {\mathbb{N}}_0$ and $\left|z\right|<1$ was proved to be positive and decreasing in $z\in (0,1)$. Its logarithm was expanded to a Maclaurin power series at $z=0$, and the function $ln{f}_{2,q}(zi)$ was proved to be convex in $z\in (0,1)$, where $i=\sqrt{-1}$ stands for the imaginary unit.

1.4. Tangent Function

For $z\in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right)$, let

$$F\left(z\right)=\{\begin{array}{cc}ln{\displaystyle \frac{3(tanz-z)}{z^3}},\hfill & 0<\left|z\right|<{\displaystyle \frac{\pi }{2}};\hfill \\ 0,\hfill & z=0.\hfill \end{array}$$

(13)

In ([22], Theorems 1 and 2), the authors presented two forms of the Maclaurin power series expansion of the function $F\left(z\right)$ around $z=0$ in terms of specific determinants and the Bessel zeta functions. In [23], the decreasing property of the function $F\left(z\right)$ was reviewed and surveyed.

In the manuscript titled “Monotonicity, convexity, and power series expansion for logarithms of normalized tails of power series expansion of tangent function” by Qi and his two coworkers, the function $F\left(z\right)$ was generalized as

$$F_q\left(z\right)=\{\begin{array}{cc}ln{\displaystyle \frac{{\displaystyle \left(2q\right)!\left[tanz-\sum _{\mathsf{\ell }=1}^{q-1}\frac{2^{2\mathsf{\ell }-1}(2^{2\mathsf{\ell }}-1)}{\mathsf{\ell }}\left|B_{2\mathsf{\ell }}\right|\frac{z^{2\mathsf{\ell }-1}}{(2\mathsf{\ell }-1)!}\right]}}{2^{2q}\left(2^{2q}-1\right)\left|B_{2q}\right|z^{2q-1}}},\hfill & 0<\left|z\right|<{\displaystyle \frac{\pi }{2}}\hfill \\ 0,\hfill & z=0\hfill \end{array}$$

(14)

for $q\in \mathbb{N}$, where $B_{2\mathsf{\ell }}$ denotes the classical Bernoulli numbers generated ([24], Section 1.1.1) by

$${\displaystyle \frac{z}{e^z-1}}=\sum _{\mathsf{\ell }=0}^{\infty }{B}_{\mathsf{\ell }}{\displaystyle \frac{z^{\mathsf{\ell }}}{\mathsf{\ell }!}}=1-{\displaystyle \frac{z}{2}}+\sum _{\mathsf{\ell }=1}^{\infty }{B}_{2\mathsf{\ell }}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\left|z\right|<2\pi .$$

(15)

The exponential function of $F_q\left(z\right)$ is called the qth normalized remainder of the Maclaurin power series expansion of the tangent function $tanz$ at $z=0$.

The idea to construct the function $F_q\left(z\right)$ in (14) came from the expression in (13) and the first two terms of the Maclaurin power series expansions

$$tanz=\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{2^{2\mathsf{\ell }-1}\left(2^{2\mathsf{\ell }}-1\right)}{\mathsf{\ell }}}\left|B_{2\mathsf{\ell }}\right|{\displaystyle \frac{z^{2\mathsf{\ell }-1}}{(2\mathsf{\ell }-1)!}}=z+{\displaystyle \frac{z^3}{3}}+{\displaystyle \frac{2z^5}{15}}+{\displaystyle \frac{17z^7}{315}}+\dots$$

and

$$ln{\displaystyle \frac{tanz}{z}}=\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{2^{2\mathsf{\ell }}\left(2^{2\mathsf{\ell }-1}-1\right)}{\mathsf{\ell }}}\left|B_{2\mathsf{\ell }}\right|{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}={\displaystyle \frac{z^2}{3}}+{\displaystyle \frac{7z^4}{90}}+{\displaystyle \frac{62z^6}{2835}}+\dots$$

(16)

in ([25], pp. 42 and 55), where $\left|z\right|<{\displaystyle \frac{\pi }{2}}$.

In the manuscript titled “Monotonicity, convexity, and power series expansion for logarithms of normalized tails of power series expansion of tangent function” by Qi and his two collaborators, among other things, the function $F_q\left(z\right)$ was not only proved to be increasing and convex in $z\in \left(0,{\displaystyle \frac{\pi }{2}}\right)$ but also expanded to a Maclaurin power series around the origin $z=0$ with coefficients expressed in terms of determinants of a series of the Hessenberg matrices.

In ([26], p. 798), Brychkov derived the Maclaurin power series expansion

$${tan}^{2}z=\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{2^{2\mathsf{\ell }+1}\left(2^{2\mathsf{\ell }+2}-1\right)}{\mathsf{\ell }+1}}|B_{2\mathsf{\ell }+2}|{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\left|z\right|<{\displaystyle \frac{\pi }{2}}.$$

(17)

In [19], considering the Maclaurin power series expansion (17), as an analog of $F_q\left(z\right)$ in (14), Zhang and Qi created the function

$${\mathfrak{F}}_q\left(z\right)=\{\begin{array}{cc}ln{\displaystyle \frac{{\displaystyle (q+1)\left(2q\right)!\left[{tan}^{2}z-\sum _{\mathsf{\ell }=1}^{q-1}\frac{2^{2\mathsf{\ell }+1}\left(2^{2\mathsf{\ell }+2}-1\right)}{\mathsf{\ell }+1}\left|B_{2\mathsf{\ell }+2}\right|\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}\right]}}{2^{2q+1}(2^{2q+2}-1)\left|B_{2q+2}\right|z^{2q}}},\hfill & z\ne 0\\ 0,\hfill & z=0\end{array}$$

for $q\in \mathbb{N}$ and $\left|z\right|<{\displaystyle \frac{\pi }{2}}$. The exponential function of ${\mathfrak{F}}_q\left(z\right)$ is called the qth normalized remainder of the power series expansion of the square function ${tan}^{2}z$ at $z=0$. From series expansion (16), it is easy to see that

$${\mathfrak{F}}_1\left(z\right)=ln{\left({\displaystyle \frac{tanz}{z}}\right)}^2=\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{2^{2\mathsf{\ell }+1}\left(2^{2\mathsf{\ell }-1}-1\right)}{\mathsf{\ell }}}\left|B_{2\mathsf{\ell }}\right|{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}={\displaystyle \frac{2z^2}{3}}+{\displaystyle \frac{7z^4}{45}}+{\displaystyle \frac{124z^6}{2835}}+\dots$$

for $\left|z\right|<{\displaystyle \frac{\pi }{2}}$. In [19], the even function ${\mathfrak{F}}_q\left(z\right)$ for $q\in \mathbb{N}$ was proved to be increasing and convex in $z\in \left(0,{\displaystyle \frac{\pi }{2}}\right)$, while it was expanded to a Maclaurin power series expansion about $z=0$ with coefficients expressed in terms of specific determinants of a series of the Hessenberg matrices.

For $q\in \mathbb{N}$ and $\left|z\right|<{\displaystyle \frac{\pi }{2}}$, we define

$$\begin{array}{l}{T}_{2q-1}\left[{tan}^{2}z\right]=T_{2q-1}\left[{sec}^{2}z\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\{\begin{array}{cc}{\displaystyle \frac{{\displaystyle (2q+2)!\left[{tan}^{2}z-\sum _{\mathsf{\ell }=1}^{q-1}\frac{2^{2\mathsf{\ell }+2}\left(2^{2\mathsf{\ell }+2}-1\right)(2\mathsf{\ell }+1)}{(2\mathsf{\ell }+2)!}\left|B_{2\mathsf{\ell }+2}\right|z^{2\mathsf{\ell }}\right]}}{2^{2q+2}(2^{2q+2}-1)(2q+1)\left|B_{2q+2}\right|z^{2q}}},\hfill & z\ne 0;\\ 1,\hfill & z=0.\hfill \end{array}\end{array}$$

(18)

It is clear that ${\mathfrak{F}}_q\left(z\right)=ln{T}_{2q-1}\left[{tan}^{2}z\right]=ln{T}_{2q-1}\left[{sec}^{2}z\right]$ for $q\in \mathbb{N}$. In the manuscript titled “Monotonicity results of ratio between two normalized remainders of the Maclaurin series expansion for square of tangent function”, Liu and Qi proved that the ratio ${\displaystyle \frac{T_{2q+1}\left[{tan}^{2}z\right]}{T_{2q-1}\left[{tan}^{2}z\right]}}$ for $q\in \mathbb{N}$ is increasing in $z\in \left(-{\displaystyle \frac{\pi }{2}},0\right)$ and decreasing in $z\in \left(0,{\displaystyle \frac{\pi }{2}}\right)$.

1.5. Sine Function

In ([20], Theorem 1), the authors presented

$${\left({\displaystyle \frac{sinz}{z}}\right)}^q=1+\sum _{\mathsf{\ell }=1}^{\infty }{(-1)}^{\mathsf{\ell }}{\displaystyle \frac{T(q+2\mathsf{\ell },q)}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }}{q}\right)}}{\displaystyle \frac{{\left(2z\right)}^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}$$

(19)

for $q\in {\mathbb{N}}_0$ and $z\in \mathbb{C}$, where central factorial numbers of the second kind $T(i,q)$ for $i,q\in {\mathbb{N}}_0$ can be computed via

$$T(i,q)={\displaystyle \frac{1}{q!}}\sum _{k=0}^q{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{q}{k}}\right){\left({\displaystyle \frac{q}{2}}-k\right)}^i$$

with the conventions $T(0,0)=1$ and $T(i,0)=0$ for $i\in \mathbb{N}$; see ([27], Proposition 2.4, (xii)) and ([28], p. 214, Equation (24)).

In ([20], Theorem 11), power series expansion (19) was generalized to the following forms:

• When $r\ge 0$, the Maclaurin series expansion

  $${\left({\displaystyle \frac{sinz}{z}}\right)}^r=1+\sum _{q=1}^{\infty }{(-1)}^q\left[\sum _{k=1}^{2q}{\displaystyle \frac{{(-r)}_k}{k!}}\sum _{j=1}^k{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{k}{j}}\right){\displaystyle \frac{T(2q+j,j)}{\left(\genfrac{}{}{0pt}{}{2q+j}{j}\right)}}\right]{\displaystyle \frac{{\left(2z\right)}^{2q}}{\left(2q\right)!}}$$

  (20)

  is convergent in $z\in \mathbb{C}$;
• When $r<0$, Maclaurin series expansion (20) is convergent in $\left|z\right|<\pi$.

See also ([14], Example 3.2). The Maclaurin power series expansion of ${\left({\displaystyle \frac{sinz}{z}}\right)}^r$ for $r\in \mathbb{R}$ was applied in [29], for example.

In ([30], Theorem 1), the function

$$G\left(z\right)=\{\begin{array}{cc}ln\left[{\displaystyle \frac{6}{z^2}}\left(1-{\displaystyle \frac{sinz}{z}}\right)\right],\hfill & 0<\left|z\right|<\infty \hfill \\ 0,\hfill & z=0\hfill \end{array}$$

(21)

was expanded to a Maclaurin power series at $z=0$ with coefficients expressed in terms of determinants of a series of specific Hessenberg matrices.

In ([30], Theorem 2), making use of the Maclaurin power series expansion in (19) and other techniques, the authors proved that the even function

$$R\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{ln\left[\frac{6}{z^2}\left(1-\frac{sinz}{z}\right)\right]}{ln\frac{sinz}{z}}},\hfill & \left|z\right|\in (0,\pi )\hfill \\ {\displaystyle \frac{3}{10}},\hfill & z=0\hfill \\ 0,\hfill & z=\pm \pi \hfill \end{array}$$

(22)

is decreasing in z from $[0,\pi ]$ to $\left[0,{\displaystyle \frac{3}{10}}\right]$.

The function $G\left(z\right)$ in (21) can be generalized as

$$G_q\left(z\right)=ln{SinR}_q\left(z\right),q\in {\mathbb{N}}_0,$$

(23)

where

$${SinR}_q\left(z\right)=\{\begin{array}{cc}{(-1)}^q{\displaystyle \frac{(2q+1)!}{z^{2q+1}}}\left[sinz-{\displaystyle \sum _{\mathsf{\ell }=0}^{q-1}}{(-1)}^{\mathsf{\ell }}{\displaystyle \frac{z^{2\mathsf{\ell }+1}}{(2\mathsf{\ell }+1)!}}\right],\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(24)

is called the normalized remainder of the Maclaurin power series expansion

$$sinz=\sum _{\mathsf{\ell }=0}^{\infty }{(-1)}^{\mathsf{\ell }}{\displaystyle \frac{z^{2\mathsf{\ell }+1}}{(2\mathsf{\ell }+1)!}}=z-{\displaystyle \frac{z^3}{6}}+{\displaystyle \frac{z^5}{120}}-{\displaystyle \frac{z^7}{5040}}+\dots ,z\in \mathbb{R}.$$

(25)

Accordingly, the function $R\left(z\right)$ in (22) can be generalized as

$$R_{p,q}\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{G_q\left(z\right)}{G_0\left(z\right)}},\hfill & z\in S\setminus \left\{0\right\},p=0,\mathrm{and}q\in \mathbb{N};\hfill \\ {\displaystyle \frac{G_q\left(z\right)}{G_p\left(z\right)}},\hfill & 0<\left|z\right|<\infty \mathrm{and}q>p\in \mathbb{N};\hfill \\ {\displaystyle \frac{(p+1)(2p+3)}{(q+1)(2q+3)}},\hfill & z=0\mathrm{and}q>p\in {\mathbb{N}}_0,\hfill \end{array}$$

(26)

where S denotes the closed set

$$S=\bigcup _{k=0}^{\infty }[2k\pi ,(2k+1)\pi ]\cup [-(2k+1)\pi ,-2k\pi ].$$

The idea to introduce the functions $G_q\left(z\right)$ and $R_{p,q}\left(z\right)$ in (23) and (26) originated from observing and comparing the expressions of $G\left(z\right)$ and $R\left(z\right)$ in (21) and (22) with the Maclaurin power series expansions (25) and

$$ln{\displaystyle \frac{sinz}{z}}=-\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{2^{2\mathsf{\ell }-1}}{\mathsf{\ell }}}|B_{2\mathsf{\ell }}|{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}=-{\displaystyle \frac{z^2}{6}}-{\displaystyle \frac{z^4}{180}}-{\displaystyle \frac{z^6}{2835}}-\dots ,0<\left|z\right|<\pi$$

collected in ([25], pp. 42 and 55).

In [31], the ratio $R_{0,2}\left(z\right)$ was proved to be decreasing in $z\in (0,\pi )$, while the function $G_q\left(z\right)$ for $q\in {\mathbb{N}}_0$ was expanded to a Maclaurin power series at $z=0$ with coefficients expressed in terms of determinants of a series of the Hessenberg matrices.

In [32], among other things, the normalized remainder ${SinR}_q\left(z\right)$ for $q\in \mathbb{N}$, defined in (24), was proved to be positive in $z\in (0,\infty )$, decreasing in $z\in (0,\infty )$, and concave in $z\in (0,\pi )$. Equivalently, the even function $G_q\left(z\right)$ for $q\in \mathbb{N}$, defined by (23), is negative in $z\in (0,\infty )$, decreasing in $z\in (0,\infty )$, and concave in $z\in (0,\pi )$.

In article [33], among other things, Niu and Qi investigated the monotonic properties of the ratio ${\displaystyle \frac{{SinR}_q\left(x\right)}{{SinR}_{q+1}\left(z\right)}}$ for $q\in {\mathbb{N}}_0$ and $z\in (0,\infty )$.

Some results in [32] were also discussed in ([34], Remark 7).

1.6. Cosine Function

In the proof of ([29], Theorem 8), the following conclusions were established:

• If $r\ge 0$, the Maclaurin power series expansion

  $${cos}^{r}z=\sum _{k=0}^{\infty }{(-1)}^k\left[\sum _{\mathsf{\ell }=0}^{2k}{\displaystyle \frac{{(-r)}_{\mathsf{\ell }}}{\mathsf{\ell }!}}\sum _{m=0}^{\mathsf{\ell }}{\displaystyle \frac{{(-1)}^m}{2^m}}\left({\displaystyle \genfrac{}{}{0pt}{}{\mathsf{\ell }}{m}}\right)\sum _{q=0}^m\left({\displaystyle \genfrac{}{}{0pt}{}{m}{q}}\right){(2q-m)}^{2k}\right]{\displaystyle \frac{z^{2k}}{\left(2k\right)!}}$$

  (27)

  is convergent for $z\in \mathbb{R}$;
• If $r<0$, series expansion (27) is convergent for $\left|z\right|<{\displaystyle \frac{\pi }{2}}$.

In [35], Li and Qi established the following conclusions:

• The even function

  $$\mathfrak{G}\left(z\right)=\{\begin{array}{cc}ln{\displaystyle \frac{2(1-cosz)}{z^2}},\hfill & 0<\left|z\right|<2\pi \hfill \\ 0,\hfill & z=0\hfill \end{array}$$

  (28)

  was expanded to a Maclaurin power series around the origin $z=0$ with coefficients expressed in terms of specific determinants of a series of the Hessenberg matrices.
• The even function

  $$\mathfrak{R}\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{ln\frac{2(1-cosz)}{z^2}}{lncosz}},\hfill & 0<\left|z\right|<{\displaystyle \frac{\pi }{2}}\hfill \\ {\displaystyle \frac{1}{6}},\hfill & z=0\hfill \\ 0,\hfill & z=\pm {\displaystyle \frac{\pi }{2}}\hfill \end{array}$$

  (29)

  was proved to be decreasing in z from $\left[0,{\displaystyle \frac{\pi }{2}}\right]$ to $\left[0,{\displaystyle \frac{1}{6}}\right]$, where the Maclaurin series expansion (19) was employed in one of its two proofs.

In [32,36], the function $\mathfrak{G}\left(z\right)$ in (28) was generalized as

$${\mathfrak{G}}_q\left(z\right)=ln{CosR}_q\left(x\right)$$

(30)

for $q\in {\mathbb{N}}_0$, where

$${CosR}_q\left(z\right)=\{\begin{array}{cc}{(-1)}^q{\displaystyle \frac{\left(2q\right)!}{z^{2q}}}\left[cosz-{\displaystyle \sum _{\mathsf{\ell }=0}^{q-1}}{(-1)}^{\mathsf{\ell }}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\right],\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(31)

is called the qth normalized remainder of the Maclaurin power series expansion

$$cosz=\sum _{\mathsf{\ell }=0}^{\infty }{(-1)}^{\mathsf{\ell }}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}=1-{\displaystyle \frac{z^2}{2}}+{\displaystyle \frac{z^4}{24}}-{\displaystyle \frac{z^6}{720}}+{\displaystyle \frac{z^8}{40320}}-\dots ,z\in \mathbb{R}.$$

(32)

The construction of the function ${\mathfrak{G}}_q\left(z\right)$ in (30) is based on the intrinsic observation and comparison of the function $\mathfrak{G}\left(z\right)$ in (28), the ratio $\mathfrak{R}\left(z\right)$ in (29), and the Maclaurin power series expansions (32) and

$$lncosz=-\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{2^{2\mathsf{\ell }-1}(2^{2\mathsf{\ell }}-1)}{\mathsf{\ell }}}|B_{2\mathsf{\ell }}|{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}=-{\displaystyle \frac{z^2}{2}}-{\displaystyle \frac{z^4}{12}}-{\displaystyle \frac{z^6}{45}}-\dots ,\left|z\right|<{\displaystyle \frac{\pi }{2}}$$

(33)

in ([25], p. 55).

In ([36], Theorem 1), the function ${\mathfrak{G}}_q\left(z\right)$ for $q\in {\mathbb{N}}_0$ was expanded to a Maclaurin power series at $z=0$ with coefficients expressed in terms of determinants of a series of specific Hessenberg matrices.

In ([36], Theorem 2), the decreasing and concave properties of the function ${\mathfrak{G}}_q\left(z\right)$ for $n\ge 0$ were discussed.

In [36], the function $\mathfrak{R}\left(z\right)$ in (29) was generalized as the function ${\mathfrak{R}}_{p,q}\left(z\right)$ for $p>q\in {\mathbb{N}}_0$, which is defined as follows:

• When $p>q=0$, as

  $${\mathfrak{R}}_{p,0}\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{{\mathfrak{G}}_p\left(z\right)}{{\mathfrak{G}}_0\left(z\right)}},\hfill & 0<\left|z\right|<{\displaystyle \frac{\pi }{2}};\hfill \\ {\displaystyle \frac{1}{(p+1)(2p+1)}},\hfill & z=0;\hfill \\ 0,\hfill & z=\pm {\displaystyle \frac{\pi }{2}};\hfill \end{array}$$

  (34)
• When $p>q=1$, as

  $${\mathfrak{R}}_{p,1}\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{{\mathfrak{G}}_p\left(z\right)}{{\mathfrak{G}}_1\left(z\right)}},\hfill & z\in \mathbb{R}\setminus \{\pm 2j\pi ,j=1,2,\dots \};\hfill \\ {\displaystyle \frac{6}{(p+1)(2p+1)}},\hfill & z=0;\hfill \\ 0,\hfill & z\in \{\pm 2j\pi ,j=1,2,\dots \};\hfill \end{array}$$
• When $p>q\ge 2$, as

  $${\mathfrak{R}}_{p,q}\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{{\mathfrak{G}}_p\left(z\right)}{{\mathfrak{G}}_q\left(z\right)}},\hfill & z\ne 0;\hfill \\ {\displaystyle \frac{(q+1)(2q+1)}{(p+1)(2p+1)}},\hfill & z=0.\hfill \end{array}$$

In ([36], Theorem 3), the even function ${\mathfrak{R}}_{2,0}\left(z\right)$ defined by (34) was proved to be decreasing in $z\in \left[0,{\displaystyle \frac{\pi }{2}}\right]$.

In [32], among other things, the following statements were proved to be true:

• The normalized remainder ${CosR}_1\left(z\right)$ is non-negative on $(0,\infty )$ and decreasing in $z\in [0,2\pi ]$. Consequently, the even function ${\mathfrak{G}}_1\left(z\right)$ is decreasing in $z\in [0,2\pi ]$.
• For $q\ge 2$, the normalized remainder ${CosR}_q\left(z\right)$ defined in (31) is positive and decreasing on $(0,\infty )$. Consequently, the even function ${\mathfrak{G}}_q\left(z\right)$ for $q\ge 2$ is decreasing in $z\in (0,\infty )$.
• Both the normalized remainder ${CosR}_1\left(z\right)$ and the even function ${\mathfrak{G}}_1\left(z\right)$ are concave on $(0,z_0)$, where $z_0\in \left({\displaystyle \frac{\pi }{2}},\pi \right)$ is the first positive zero of the equation

  $$\left(z^2-2\right)sinz+2zcosz=0.$$
• For $q\ge 2$, the normalized remainder ${CosR}_q\left(z\right)$ and ${\mathfrak{G}}_q\left(z\right)$ are both concave in $z\in (0,\pi )$.

Some results in [32,36] were also discussed in ([34], Remark 7).

In ([35], Remark 2), Gradimir V. Milovanović, the second author of the paper [14], pointed out that the function $\mathfrak{G}\left(z\right)$ defined by (28) can also be expanded as

$$\mathfrak{G}\left(z\right)=ln{CosR}_1\left(z\right)=-\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{|B_{2\mathsf{\ell }}|}{\mathsf{\ell }}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\left|z\right|<2\pi .$$

(35)

In ([35], Remark 3), based on series expansion (35), the positive and even function

$$H_q\left(z\right)=\{\begin{array}{cc}-{\displaystyle \frac{q+1}{|B_{2q+2}|}}{\displaystyle \frac{(2q+2)!}{z^{2q+2}}}\left[ln{CosR}_1\left(z\right)+{\displaystyle \sum _{\mathsf{\ell }=1}^q}{\displaystyle \frac{|B_{2\mathsf{\ell }}|}{\mathsf{\ell }}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\right],\hfill & 0<\left|z\right|<2\pi \hfill \\ 1,\hfill & z=0\hfill \end{array}$$

(36)

for $q\in \mathbb{N}$ was introduced. In [37], Pei and Guo proved that the normalized remainder $H_q\left(z\right)$ for $q\in \mathbb{N}$ is logarithmically convex in $z\in (0,2\pi )$ and that the ratio ${\displaystyle \frac{H_{q+1}\left(z\right)}{H_q\left(z\right)}}$ for given $q\in \mathbb{N}$ is increasing in $z\in (0,2\pi )$ and decreasing in $z\in (-2\pi ,0)$, while they expanded the logarithm of $H_q\left(z\right)$ for $q\in \mathbb{N}$ to a Maclaurin power series around the origin $z=0$ with coefficients expressed in terms of determinants of a series of the Hessenberg matrices.

In [38], based on Maclaurin series expansion (33), the authors considered the normalized remainder

$${QiR}_q\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{(q+1)(2q+2)!\left[lnsecz-{\sum }_{k=1}^q\frac{2^{2k-1}(2^{2k}-1)}{k\left(2k\right)!}\left|B_{2k}\right|z^{2k}\right]}{2^{2q+1}(2^{2q+2}-1)\left|B_{2q+2}\right|z^{2q+2}}},\hfill & z\ne 0;\\ 1,\hfill & z=0,\end{array}$$

(37)

where an empty sum is understood to be 0. Essentially, the quantity ${QiR}_q\left(z\right)$ defined in (37) is also the normalized remainder for the Maclaurin power series expansion of the logarithm $ln{CosR}_0\left(x\right)=lncosx=-lnsecx$. They proved the following results:

• The normalized remainder ${QiR}_q\left(z\right)$ for given $q\in {\mathbb{N}}_0$ is a logarithmically convex function in $z\in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right)$;
• The ratio ${\displaystyle \frac{{QiR}_{q+1}\left(z\right)}{{QiR}_q\left(z\right)}}$ for $q\in {\mathbb{N}}_0$ is an increasing function of $z\in \left(0,{\displaystyle \frac{\pi }{2}}\right)$ and a decreasing function of $z\in \left(-{\displaystyle \frac{\pi }{2}},0\right)$.

In [33], the authors discussed monotonic properties of the ratios ${\displaystyle \frac{{CosR}_q\left(z\right)}{{SinR}_q\left(z\right)}}$ and ${\displaystyle \frac{{CosR}_q\left(z\right)}{{CosR}_{q+1}\left(z\right)}}$ in $z\in (0,\infty )$ for $q\in {\mathbb{N}}_0$.

1.7. Exponential Function

In [18], the authors considered the normalized remainder

$$f_q\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{q!}{z^q}}\left(e^z-{\displaystyle \sum _{j=0}^{q-1}}{\displaystyle \frac{z^j}{j!}}\right),\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(38)

for $n\in {\mathbb{N}}_0$, the logarithm ${\mathfrak{E}}_q\left(z\right)=ln{f}_q\left(z\right)$ for $n\in {\mathbb{N}}_0$, and the ratio

$${\mathcal{R}}_{p,q}\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{{\mathfrak{E}}_p\left(z\right)}{{\mathfrak{E}}_q\left(z\right)}},\hfill & z\ne 0\\ {\displaystyle \frac{q+1}{p+1}},\hfill & z=0\end{array}$$

(39)

for $p>q\in {\mathbb{N}}_0$ and $z\in \mathbb{C}$.

It is not difficult to derive that

$${\mathfrak{E}}_1\left(z\right)=ln{\displaystyle \frac{e^z-1}{z}}={\displaystyle \frac{z}{2}}+\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{B_{2\mathsf{\ell }}}{2\mathsf{\ell }}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}={\displaystyle \frac{z}{2}}+{\displaystyle \frac{z^2}{24}}-{\displaystyle \frac{z^4}{2880}}+\dots$$

and

$${\mathfrak{E}}_2\left(z\right)=ln{\displaystyle \frac{2(e^z-1-z)}{z^2}}={\displaystyle \frac{z}{3}}+2\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{A_{\mathsf{\ell }+1}}{\mathsf{\ell }+1}}{\displaystyle \frac{z^{\mathsf{\ell }+1}}{(\mathsf{\ell }+1)!}}={\displaystyle \frac{z}{3}}+{\displaystyle \frac{z^2}{36}}+{\displaystyle \frac{z^3}{810}}-\dots ,$$

where the function ${\displaystyle \frac{z^2}{2(e^z-1-z)}}$ is the generating function of the Howard numbers $A_{\mathsf{\ell }}$ for $\mathsf{\ell }\in {\mathbb{N}}_0$; see ([39], p. 979, Equation (2.9)) and related texts in [40].

In ([18], Theorem 1), the function ${\mathfrak{E}}_q\left(z\right)$ for $q\in \mathbb{N}$ was expanded to a Maclaurin power series at $z=0$ with coefficients expressed in terms of specific determinants of a series of the Hessenberg matrices.

In ([18], Corollary 1), the function ${\mathfrak{E}}_q\left(z\right)$ for $q\in \mathbb{N}$ was proved to be increasing and convex in $z\in \mathbb{R}$.

In ([18], Theorem 2), the function ${\mathcal{R}}_{p,0}\left(z\right)$ in (39) for $p\in \mathbb{N}$ was proved to be increasing in $z\in \mathbb{R}$.

Let $I\subseteq \mathbb{R}$ be an interval. A real infinitely differentiable function $f\left(z\right)$ defined on I is said to be absolutely monotonic in $z\in I$ if and only if all of its derivatives satisfy $f^{\left(k\right)}\left(z\right)\ge 0$ for $k\in {\mathbb{N}}_0$ and $z\in I$. When $I=(0,\infty )$ or $I=[0,\infty )$, there have been plenty of classical investigations on absolutely monotonic functions in ([41], Chapter XIII), ([42], Chapter 1), and ([43], Chapter IV). In ([44], Definition 1), the concept of logarithmically absolutely monotonic functions was first introduced; see also [45]. In ([44], Theorem 1), a stronger property than the absolute monotonicity was discovered: a logarithmically absolutely monotonic function must be absolutely monotonic on the same domain, but not conversely. It is clear that if $f\left(z\right)$ is a logarithmically absolutely monotonic function, then $f(-z)$ is a logarithmically complete function that was first invented in [46] and significantly confirmed in [42,47].

In ([48], Theorem 1), it was proved that the ratio ${\displaystyle \frac{f_{q+1}\left(z\right)}{f_q\left(z\right)}}$ for $q\in \mathbb{N}$ is decreasing in $z\in (0,\infty )$. Theorem 2 in [48] reads that the normalized tail $f_q\left(z\right)$ for $q\in \mathbb{N}$ is an absolutely monotonic function in $z\in \mathbb{R}$.

In Theorem 2 of the manuscript titled “Decreasing ratio between two normalized remainders of the Maclaurin series expansion of exponential function”, Qi and his coauthors proved that the ratio ${\displaystyle \frac{f_{q+1}\left(z\right)}{f_q\left(z\right)}}$ for $q\in \mathbb{N}$ is decreasing in $z\in \mathbb{R}$. This result extends ([48], Theorem 1) from $z\in (0,\infty )$ to $z\in \mathbb{R}$.

1.8. Generating Function of Bernoulli Numbers

In paper [49], based on the generating function in (15) of the Bernoulli numbers $B_{\mathsf{\ell }}$ for $\mathsf{\ell }\in {\mathbb{N}}_0$, the function

$$T_q\left(z\right)=\{\begin{array}{cc}{\displaystyle \frac{(2q+2)!}{B_{2q+2}}}{\displaystyle \frac{1}{z^{2q+2}}}\left[{\displaystyle \frac{z}{e^z-1}}-1+{\displaystyle \frac{z}{2}}-{\displaystyle \sum _{\mathsf{\ell }=1}^q}{B}_{2\mathsf{\ell }}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\right],\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(40)

for $q\in \mathbb{N}$ was invented. We call $T_q\left(z\right)$ for $q\in \mathbb{N}$ and $z\in \mathbb{R}$ the normalized remainders of the Maclaurin series expansion (15) of the generating function ${\displaystyle \frac{z}{e^z-1}}-1+{\displaystyle \frac{z}{2}}$ of the classical Bernoulli numbers $B_{\mathsf{\ell }}$ for $\mathsf{\ell }\in {\mathbb{N}}_0$.

In [49], the following properties of the normalized remainder $T_q\left(z\right)$ were discovered:

• The normalized remainder $T_q\left(z\right)$ for $q\in \mathbb{N}$ is positive and decreasing in $z\in (0,\infty )$.
• The ratio ${\displaystyle \frac{T_q\left(z\right)}{T_{q+1}\left(z\right)}}$ for $q\in \mathbb{N}$ is increasing in $z\in (0,\infty )$.

1.9. Complete Elliptic Integrals of the Second Kind

In ([18], Section 5, ([19], Section 1), and ([48], Section 1), a general definition of the normalized remainder for the Maclaurin power series expansion of a real infinitely differentiable function around the origin was defined as follows.

Definition 1.

Suppose that a real infinitely differentiable function $f\left(z\right)$ has a formal Maclaurin power series expansion

$$\sum _{j=0}^{\infty }{f}^{\left(j\right)}\left(0\right){\displaystyle \frac{z^j}{j!}}.$$

(41)

If $f^{(q+1)}\left(0\right)\ne 0$ for some $q\in {\mathbb{N}}_0$, then we call the quantity

$$T_q\left[f\left(z\right)\right]=\{\begin{array}{cc}{\displaystyle \frac{1}{f^{(q+1)}\left(0\right)}}{\displaystyle \frac{(q+1)!}{z^{q+1}}}\left[f\left(z\right)-{\displaystyle \sum _{j=0}^q}{f}^{\left(j\right)}\left(0\right){\displaystyle \frac{z^j}{j!}}\right],\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(42)

the qth normalized remainder (or say, the qth normalized tail) of the Maclaurin power series expansion (41).

The Gauss hypergeometric function ${}_{2}F_1$ is defined by

$${}_{2}F_1(a,b;c;z)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(a\right)}_n{\left(b\right)}_n}{{\left(c\right)}_n}}{\displaystyle \frac{z^n}{n!}},\left|z\right|<1$$

(43)

for given complex numbers $a,b,c\in \mathbb{C}\setminus \{0,-1,-2,\dots \}$; see ([15], Chapter 15) and ([50], Chapter 2). For $r\in [0,1]$, complete elliptic integrals of the second kind $\mathcal{E}\left(r\right)$ can be defined [51,52] by

$$\mathcal{E}\left(r\right)={\int }_0^{\pi /2}\sqrt{1-r^2{sin}^2\varphi }d\varphi ={\displaystyle \frac{\pi }{2}}{}_{2}F_1\left(-{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}};1;r^2\right).$$

For $r\in (0,1)$, let

$$H\left(r\right)={\displaystyle \frac{1-{}_{2}F_1\left(-\frac{1}{2},\frac{1}{2};1;r\right)}{1-(1-r){}_{2}F_1\left(\frac{1}{2},1;\frac{3}{2};r\right)}}={\displaystyle \frac{1-\frac{2}{\pi }\mathcal{E}\left(r\right)}{1+(r-1)\frac{arctanh\sqrt{r}}{\sqrt{r}}}}=\sum _{n=0}^{\infty }{a}_n{r}^n$$

and

$$\begin{array}{cc}G\left(r\right)\hfill & ={\displaystyle \frac{\frac{\pi }{2}\left[{}_{2}F_1\left(-\frac{1}{2},\frac{1}{2};1;r\right)-1\right]+r{}_{2}F_1\left(\frac{1}{2},1;\frac{3}{2};r\right)}{r{}_{2}F_1(1,1;2;r)}}\hfill \\ \hfill & ={\displaystyle \frac{\frac{\pi }{2}-\sqrt{r}arctanh\sqrt{r}-\mathcal{E}\left(r\right)}{ln(1-r)}}\hfill \\ \hfill & =\sum _{n=0}^{\infty }{b}_n{r}^n.\hfill \end{array}$$

In Remarks 2 and 4 of the manuscript titled “Absolute monotonicity of four functions involving the second kind of complete elliptic integrals” by Wang and Qi, the authors observed that the normalized remainder $T_n\left[H\left(r\right)\right]$ for $n\in {\mathbb{N}}_0$ is absolutely monotonic from $(0,1)$ to $\left(1,1+{\displaystyle \frac{{\beta }_n}{{\alpha }_n}}\right)$ and that the normalized remainder $T_n\left[G\left(r\right)\right]$ for $n\in {\mathbb{N}}_0$ is absolutely monotonic from $(0,1)$ to $\left(1,1+{\displaystyle \frac{{\lambda }_n}{{\delta }_n}}\right)$, where

$${\alpha }_n=|a_{n+1}|,{\beta }_n={\displaystyle \frac{2}{\pi }}-1+\sum _{k=0}^n{a}_k,{\delta }_n=\left|b_{n+1}\right|,{\lambda }_n={\displaystyle \frac{\pi -3}{2}}+\sum _{k=0}^n{b}_k.$$

1.10. A General Definition of Normalized Remainders

In ([18], Section 1), ([19], Section 1), ([31], Section 6), and ([48], Section 1), the history, ideas, thoughts, techniques, observations, and related references of normalized remainders of the Maclaurin power series expansions of functions were revised and surveyed.

Definition 1 can be slightly generalized as follows.

Definition 2.

Let $f\left(z\right)$ be a real infinitely differentiable function around the point $z_0\in \mathbb{R}$. Then, its Taylor series is defined by

$$\sum _{j=0}^{\infty }{a}_j{(z-z_0)}^j.$$

(44)

If $a_{q+1}\ne 0$ for some $q\in {\mathbb{N}}_0$, then the qth normalized remainder (or say, the qth normalized tail) of Taylor series (44) is denoted and defined by

$$T_q[f\left(z\right),z_0]=\{\begin{array}{cc}{\displaystyle \frac{1}{a_{q+1}{(z-z_0)}^{q+1}}}\left[f\left(z\right)-{\displaystyle \sum _{j=0}^q}{a}_j{(z-z_0)}^j\right],\hfill & z\ne z_0;\\ 1,\hfill & z=z_0.\end{array}$$

(45)

It is not difficult to see that Definitions 1 and 2 are equivalent to each other.

In terms of the notation $T_q\left[f\left(z\right)\right]=T_q[f\left(z\right),0]$ in (42) and (45), we can uniformly reformulate the normalized remainders in (10)–(12), (14), (18), (24), (31), (36)–(38), and (40) as follows:

$$\begin{array}{c}{T}_{2q}[arcsinz]=T_{2q-1}\left[{\displaystyle \frac{arcsinz}{z}}\right]=T_{2q}\left[{\displaystyle \frac{\pi }{2}}-arccosz\right]=T_{2q-1}\left[{\displaystyle \frac{\frac{\pi }{2}-arccosz}{z}}\right],\\ T_{2q}[arctanz]=T_{2q-1}\left[{\displaystyle \frac{arctanz}{z}}\right],ln{T}_{2q-2}[tanz]=ln{T}_{2q-3}\left[{\displaystyle \frac{tanz}{z}}\right],\\ T_{2q-1}\left[{tan}^{2}z\right]=T_{2q-1}\left[{sec}^{2}z\right]=T_{2q-2}\left[{\displaystyle \frac{{tan}^{2}z}{z}}\right]=T_{2q-3}\left[{\left({\displaystyle \frac{tanz}{z}}\right)}^2\right],\\ T_{2q}[sinz]=T_{2q-1}\left[{\displaystyle \frac{sinz}{z}}\right],T_{2q-1}[cosz],T_{q-1}\left[e^z\right],\\ T_{2q+1}[ln{T}_1[cosz]]=T_{2q}\left[{\displaystyle \frac{ln{T}_1[cosz]}{z}}\right]=T_{2q-1}\left[{\displaystyle \frac{ln{T}_1[cosz]}{z^2}}\right],\\ T_{2q+1}[lnsecz]=T_{2q+1}[-lncosz]=T_{2q}\left[-{\displaystyle \frac{lncosz}{z}}\right]=T_{2q-1}\left[-{\displaystyle \frac{lncosz}{z^2}}\right],\\ T_{2q+1}\left[{\displaystyle \frac{z}{e^z-1}}-1+{\displaystyle \frac{z}{2}}\right]=T_{2q}\left[{\displaystyle \frac{1}{e^z-1}}-{\displaystyle \frac{1}{z}}+{\displaystyle \frac{1}{2}}\right]=T_{2q-1}\left[{\displaystyle \frac{1}{z}}\left({\displaystyle \frac{1}{e^z-1}}-{\displaystyle \frac{1}{z}}+{\displaystyle \frac{1}{2}}\right)\right].\end{array}$$

Stimulated by these concrete examples, we concluded the following theorem.

Theorem 1.

Let α be a constant. Then, the normalized remainder $T_q[f\left(z\right),z_0]$ satisfies

$$T_q[\alpha +f\left(z\right),x_0]=T_q[f\left(z\right),x_0],q\in \mathbb{N}.$$

(46)

For $k,q\in {\mathbb{N}}_0$ such that $k\le q$, if the coefficients $a_j$ in (44) satisfy $a_j=0$ for $0\le j<k$, then the normalized remainder $T_q[f\left(z\right),z_0]$ satisfies

$$T_q[f\left(z\right),z_0]=T_{q-k}\left[{\displaystyle \frac{f\left(z\right)}{{(z-z_0)}^k}},z_0\right].$$

(47)

Proof. 

Let $F\left(z\right)=\alpha +f\left(z\right)$. Equality (46) follows from

$$\begin{array}{c}{\displaystyle \frac{1}{F^{(q+1)}\left(z_0\right)}}{\displaystyle \frac{(q+1)!}{{(z-z_0)}^{q+1}}}\left[F\left(z\right)-\sum _{j=0}^q{F}^{\left(j\right)}\left(z_0\right){\displaystyle \frac{{(z-z_0)}^j}{j!}}\right] \hfill \\ \hfill ={\displaystyle \frac{1}{f^{(q+1)}\left(z_0\right)}}{\displaystyle \frac{(q+1)!}{z^{q+1}}}\left[f\left(z\right)-\sum _{j=0}^q{f}^{\left(j\right)}\left(z_0\right){\displaystyle \frac{z^j}{j!}}\right]\end{array}$$

for $q\in {\mathbb{N}}_0$, where we used the relation $F^{\left(\mathsf{\ell }\right)}\left(z\right)=f^{\left(\mathsf{\ell }\right)}\left(z\right)$ for $\mathsf{\ell }\in \mathbb{N}$.

Making use of expression (45), we arrive at

$$\begin{array}{cc}{T}_q[f\left(z\right),z_0]\hfill & =\{\begin{array}{cc}{\displaystyle \frac{1}{a_{q+1}{(z-z_0)}^{q-k+1}}}\left[{\displaystyle \frac{f\left(z\right)}{{(z-z_0)}^k}}-\sum _{j=0}^q{a}_j{(z-z_0)}^{j-k}\right],\hfill & z\ne z_0\hfill \\ 1,\hfill & z=z_0\hfill \end{array}\hfill \\ & =\{\begin{array}{cc}{\displaystyle \frac{1}{a_{q+1}{(z-z_0)}^{q-k+1}}}\left[{\displaystyle \frac{f\left(z\right)}{{(z-z_0)}^k}}-\sum _{j=0}^{q-k}{a}_{j+k}{(z-z_0)}^j\right],\hfill & z\ne z_0\hfill \\ 1,\hfill & z=z_0\hfill \end{array}\hfill \\ & =T_{q-k}\left[{\displaystyle \frac{f\left(z\right)}{{(z-z_0)}^k}},z_0\right]\hfill \end{array}$$

Equality (47) is thus proved. The required proof is complete. □

1.11. Connections with Generalized Hypergeometric Functions

In terms of the Pochhammer symbol defined by (9), the generalized hypergeometric function ${}_{1}F_2({\alpha }_1;{\beta }_1,{\beta }_2;z)$ is defined ([24], p. 124) by

$${}_{1}F_2({\alpha }_1;{\beta }_1,{\beta }_2;z)=\sum _{q=0}^{\infty }{\displaystyle \frac{{\left({\alpha }_1\right)}_q}{{\left({\beta }_1\right)}_q{\left({\beta }_2\right)}_q}}{\displaystyle \frac{z^q}{q!}},z\in \mathbb{C}$$

for ${\alpha }_1\in \mathbb{C}$ and ${\beta }_1,{\beta }_2\in \mathbb{C}\setminus \{0,-1,-2,\dots \}$. See ([25], p. 1020), ([53], Chapter II), and ([54], Chapter 14).

In ([32], p. 16), Qi and his coauthors derived two relations:

$${SinR}_q\left(z\right)={}_{1}F_2\left(1;q+1,q+{\displaystyle \frac{3}{2}};-{\displaystyle \frac{z^2}{4}}\right),q\in \mathbb{N}$$

(48)

and

$${CosR}_q\left(z\right)={}_{1}F_2\left(1;q+{\displaystyle \frac{1}{2}},q+1;-{\displaystyle \frac{z^2}{4}}\right),q\in \mathbb{N}.$$

(49)

In ([34], Remark 7), making use of relations (48) and (49), the authors restated the main results in [32,36] in terms of the generalized hypergeometric function ${}_{1}F_2\left(1;{\displaystyle \frac{q}{2}},{\displaystyle \frac{q+1}{2}};-z^2\right)$ for $q\in \mathbb{N}$.

In ([31], Section 5), ([33], Section 5), and ([37], Section 6), by virtue of the relations (48) and (49), the authors restated main results in the works [30,31,32,33,35,37] in terms of the generalized hypergeometric functions ${}_{1}F_2\left(1;{\displaystyle \frac{3}{2}},2;-{\displaystyle \frac{z^2}{4}}\right)$ and ${}_{1}F_2\left(1;q+1,q+{\displaystyle \frac{3}{2}};-{\displaystyle \frac{z^2}{4}}\right)$ for $q\in \mathbb{N}$.

1.12. New Results on Riemann Zeta Function and Ratios of Two Bernoulli Numbers and Polynomials

According to ([55], Fact 13.3), for $z\in \mathbb{C}$ such that $\Re \left(z\right)>1$, the Riemann zeta function $\zeta \left(z\right)$ can be defined by

$$\zeta \left(z\right)=\sum _{k=1}^{\infty }{\displaystyle \frac{1}{k^z}}={\displaystyle \frac{1}{1-2^{1-z}}}\sum _{k=1}^{\infty }{\displaystyle \frac{{(-1)}^{k-1}}{k^z}}={\displaystyle \frac{1}{1-2^{1-z}}}\eta \left(z\right),$$

(50)

where $\eta \left(z\right)$ is called the Dirichlet eta function. In ([24], Section 3.5, pp. 57–58), the Riemann zeta function $\zeta \left(z\right)$ is analytically extended from $z\in \mathbb{C}$, such that $\Re \left(z\right)>1$, to the punctured complex plane $\mathbb{C}\setminus \left\{1\right\}$, such that the only singularity $z=1$ is a simple pole with residue 1. In other words, the Riemann zeta function $\zeta \left(z\right)$ is meromorphic with a simple pole at $z=1$. See also ([56], Chapter 6).

While studying the normalized remainders mentioned above, we derived some new results on the Riemann zeta function $\zeta \left(z\right)$ and the ratios ${\displaystyle \frac{B_{2q}}{B_{2q+2}}}$ and ${\displaystyle \frac{B_q\left(t\right)}{B_p\left(t\right)}}$, where the classical Bernoulli polynomials $B_q\left(t\right)$ are generated ([24], p. 3) by

$${\displaystyle \frac{z{e}^{tz}}{e^z-1}}=\sum _{q=0}^{\infty }{B}_q\left(t\right){\displaystyle \frac{z^q}{q!}},\left|z\right|<2\pi$$

and satisfy $B_q\left(0\right)=B_q$ for $q\in {\mathbb{N}}_0$.

In ([19], Lemma 1) and the manuscript titled “Monotonicity, convexity, and power series expansion for logarithms of normalized tails of power series expansion of tangent function” by Qi and his two collaborators, the function $(2^z-1)\zeta \left(z\right)$ was proved to be logarithmically convex on $(1,\infty )$, and the sequence

$${\displaystyle \frac{1}{(\mathsf{\ell }+1)(2\mathsf{\ell }+1)}}{\displaystyle \frac{2^{2\mathsf{\ell }+2}-1}{2^{2\mathsf{\ell }}-1}}\left|{\displaystyle \frac{B_{2\mathsf{\ell }+2}}{B_{2\mathsf{\ell }}}}\right|$$

(51)

was verified to be increasing in $\mathsf{\ell }\in \mathbb{N}$. The first result was also employed in ([38], Lemma 2).

In Lemma 1 of the manuscript titled “Monotonicity results of ratio between two normalized remainders of Maclaurin series expansion for square of tangent function” by Liu and Qi, the function $(z-1)(2^z-1)\zeta \left(z\right)$ was proved to be logarithmically concave in $z\in (0,\infty )$. Consequently, the sequence

$${\displaystyle \frac{1}{(2j-1)(j+1)}}{\displaystyle \frac{2^{2j+2}-1}{2^{2j}-1}}\left|{\displaystyle \frac{B_{2j+2}}{B_{2j}}}\right|$$

(52)

is decreasing in $j\in \mathbb{N}$.

In ([37], Lemma 2), the sequence

$${\displaystyle \frac{j}{{(j+1)}^2(2j+1)}}\left|{\displaystyle \frac{B_{2j+2}}{B_{2j}}}\right|$$

was verified to be increasing in $j\ge 0$. In ([37], Remark 1), it was guessed that the function ${\displaystyle \frac{\zeta \left(z\right)}{z}}$ is decreasing and logarithmically convex in $z>1$.

In ([49], Proposition 1), the ratio ${\displaystyle \frac{B_{2q-1}\left(t\right)}{B_{2q+1}\left(t\right)}}$ for $q\in \mathbb{N}$ was proved to be increasing in $t\in \left(0,{\displaystyle \frac{1}{2}}\right)$ and decreasing in $t\in \left({\displaystyle \frac{1}{2}},1\right)$. In paper [57], plenty of properties related to the ratios ${\displaystyle \frac{B_p\left(t\right)}{B_q\left(t\right)}}$ for $p,q\in \mathbb{N}$ and $p\ne q$ were presented, and some known results were derived. See also paper [58] and several closely related references therein.

1.13. Aims of This Paper

In this paper, based on the first six Maclaurin power series expansions from (1) to (6), motivated by the normalized remainder (10) and the above-mentioned results, and considering Definitions 1 and 2, we invent the function

$$T_{2n+1}\left[{\left({\displaystyle \frac{arcsinz}{z}}\right)}^q\right]=\{\begin{array}{cc}{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{q+2n+2}{2n+2}\right)}{\mathcal{Q}(q,2n+2)}}{\displaystyle \frac{(2n+2)!}{{\left(2z\right)}^{2n+2}}}\left[{\left({\displaystyle \frac{arcsinz}{z}}\right)}^q-1-{\displaystyle \sum _{\mathsf{\ell }=1}^n}{\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }}{2\mathsf{\ell }}\right)}}{\displaystyle \frac{{\left(2z\right)}^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\right],\hfill & z\ne 0\\ 1,\hfill & z=0\end{array}$$

(53)

for $q\in \mathbb{N}$, $n\in {\mathbb{N}}_0$, and $\left|z\right|<1$, where $\mathcal{Q}(q,2\mathsf{\ell })$ is defined by (7). We call the quantity in (53) the normalized remainder of the Maclaurin power series expansion at $z=0$ of the power function ${\left({\displaystyle \frac{arcsinz}{z}}\right)}^q$. For simplicity, we denote

$${\mathfrak{T}}_{q,n}\left(z\right)=T_{2n+1}\left[{\left({\displaystyle \frac{arcsinz}{z}}\right)}^q\right].$$

When $1\le q\le 5$ and $n=0,1$, we have

$$\begin{array}{cccc}{\mathfrak{T}}_{1,0}\left(z\right)\hfill & ={\displaystyle \frac{6(arcsinz-z)}{z^3}},\hfill & {\mathfrak{T}}_{1,1}\left(z\right)\hfill & ={\displaystyle \frac{20\left(6arcsinz-6z-z^3\right)}{9z^5}},\hfill \\ {\mathfrak{T}}_{2,0}\left(z\right)\hfill & ={\displaystyle \frac{3\left({arcsin}^{2}z-z^2\right)}{z^4}},\hfill & {\mathfrak{T}}_{2,1}\left(z\right)\hfill & ={\displaystyle \frac{15\left(3{arcsin}^{2}z-3z^2-z^4\right)}{8z^6}},\hfill \\ {\mathfrak{T}}_{3,0}\left(z\right)\hfill & ={\displaystyle \frac{2\left({arcsin}^{3}z-z^3\right)}{z^5}},\hfill & {\mathfrak{T}}_{3,1}\left(z\right)\hfill & ={\displaystyle \frac{60\left(2{arcsin}^{3}z-2z^3-z^5\right)}{37z^7}},\hfill \\ {\mathfrak{T}}_{4,0}\left(z\right)\hfill & ={\displaystyle \frac{3\left({arcsin}^{4}z-z^4\right)}{2z^6}},\hfill & {\mathfrak{T}}_{4,1}\left(z\right)\hfill & ={\displaystyle \frac{5\left(3{arcsin}^{4}z-3z^4-2z^6\right)}{7z^8}},\hfill \\ {\mathfrak{T}}_{5,0}\left(z\right)\hfill & ={\displaystyle \frac{6\left({arcsin}^{5}z-z^5\right)}{5z^7}},\hfill & {\mathfrak{T}}_{5,1}\left(z\right)\hfill & ={\displaystyle \frac{12\left(6{arcsin}^{5}z-6z^5-5z^7\right)}{47z^9}}.\hfill \end{array}$$

The normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ defined by (53) can be written as a series expansion

$${\mathfrak{T}}_{q,n}\left(z\right)={\displaystyle \frac{(q+2n+2)!}{\mathcal{Q}(q,2n+2)}}\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}{(q+2\mathsf{\ell }+2n+2)!}}{\left(2z\right)}^{2\mathsf{\ell }},\left|z\right|<1$$

(54)

for $q\in \mathbb{N}$ and $n\in {\mathbb{N}}_0$.

It is clear that the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ is an even function in $z\in (-1,1)$. We guess that the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ for $q,\mathsf{\ell }\in \mathbb{N}$ should be positive. If this guess were true, the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ for $q\in \mathbb{N}$ and $n\in {\mathbb{N}}_0$ would be positive, increasing, convex, and absolutely monotonic in $z\in [0,1)$.

More strongly, if the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ for $q,\mathsf{\ell }\in \mathbb{N}$ is positive, we guess that the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ for $q\in \mathbb{N}$ and $n\in {\mathbb{N}}_0$ would be logarithmically absolutely monotonic in $z\in [0,1)$.

In this paper, we aim to prove the last guesses.

2. Known Identities and New Results

In this section, we retrospect some properties of the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ defined in (7) and establish some new results.

We guess that the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ for $q,\mathsf{\ell }\in \mathbb{N}$ should be positive.

2.1. The Quantity $T(r;q,j;\rho )$

In ([7], Theorem 1.1), the quantity

$$T(r;q,j;\rho )={(-1)}^q\left[\sum _{m=q}^r{(-\rho )}^{m}s(r,m)\left({\displaystyle \genfrac{}{}{0pt}{}{m}{q}}\right)\right]\left[\sum _{m=j-q}^r{(-\rho )}^{m}s(r,m)\left({\displaystyle \genfrac{}{}{0pt}{}{m}{j-q}}\right)\right]$$

(55)

was defined for $r,q,j\in \mathbb{N}$ and $\rho \in \mathbb{R}$ such that $r,j\ge q\ge 0$, where $s(r,m)$ denotes the Stirling numbers of the first kind, which can be analytically generated with (8). In ([7], Remark 5.5), two identities

$$\sum _{q=0}^{2\mathsf{\ell }}T\left(\mathsf{\ell };q,2\mathsf{\ell };{\displaystyle \frac{1}{2}}\right)={\displaystyle \frac{{(-1)}^{\mathsf{\ell }}}{4^{\mathsf{\ell }}}}\mathrm{and}\sum _{q=0}^{2\mathsf{\ell }}T(\mathsf{\ell };q,2\mathsf{\ell };1)={(-1)}^{\mathsf{\ell }}$$

(56)

were derived for $\mathsf{\ell }\in {\mathbb{N}}_0$.

2.2. The Quantity $Q(m,k;\alpha )$

In ([6], Theorem 1.1), the quantity

$$Q(m,k;\alpha )=\sum _{\mathsf{\ell }=0}^k\left({\displaystyle \genfrac{}{}{0pt}{}{m+\mathsf{\ell }-1}{m-1}}\right)s(m+k-1,m+\mathsf{\ell }-1){\left({\displaystyle \frac{m+k-\alpha }{2}}\right)}^{\mathsf{\ell }}$$

(57)

was introduced for $m\in \mathbb{N}$, $k\in {\mathbb{N}}_0$, and $\alpha \in \mathbb{R}$ such that $m+k\ne \alpha$. Moreover, we assume

$$Q(m,0;m)=1,m\in \mathbb{N}$$

and

$$Q(m,k;m+k)=0,k,m\in \mathbb{N}.$$

(58)

Corollary 3 in [6] reads that

$$Q(1,2k+1;2)=0\mathrm{and}Q(m+1,2k-1;2)=0$$

(59)

for $k,m\in \mathbb{N}$. The identities in (59) were also proved in the proof of ([6], Theorem 4). We can unify two identities in (59) as

$$Q(j,2k-1;2)=0,(j,k)\in {\mathbb{N}}^2\setminus \left\{(1,1)\right\}.$$

(60)

In the proof of ([6], Theorem 4), two identities

$$Q(1,2k+1;3)=(2k+1)!\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{2k-1}{2}}{2k+1}}\right)\mathrm{and}Q(1,2k+2;3)=0$$

were deduced for $k\in \mathbb{N}$. In ([6], Remark 6), the identity

$$Q(2,2k;2)={(-1)}^k{(k!)}^2,k\in \mathbb{N}$$

(61)

was derived. In ([6], Remark 16), the quantity $Q(m,k;\alpha )$ defined in (57) was further discussed.

Comparing ([6], Theorem 1) with ([7], Theorem 2.1) reveals the relations

$$Q(2\mathsf{\ell }-1,2k;2)={(-1)}^{\mathsf{\ell }+k-1}{2}^{2\mathsf{\ell }-2}\sum _{q=0}^{2\mathsf{\ell }-2}T\left(\mathsf{\ell }+k-1;q,2\mathsf{\ell }-2;{\displaystyle \frac{1}{2}}\right)$$

(62)

and

$$Q(2\mathsf{\ell },2k;2)={(-1)}^{\mathsf{\ell }+k-1}\sum _{q=0}^{2\mathsf{\ell }-2}T(\mathsf{\ell }+k-1;q,2\mathsf{\ell }-2;1)$$

(63)

for $\mathsf{\ell },k\in \mathbb{N}$ between the two quantities $Q(m,k;\alpha )$ and $T(r;q,j;\rho )$, respectively defined in (57) and (55) in sequence. Combining the relations (62) and (63) with two identities in (56) results in the trivial equality

$$Q(m,0;2)=1,m\in \mathbb{N}.$$

2.3. The Quantity $Q(m,k)$

In ([12], Theorem 2.1), the quantity $Q(m,k;2)$ defined in (57) for $\alpha =2$ was written as

$$Q(m,k)=\sum _{\mathsf{\ell }=0}^k\left({\displaystyle \genfrac{}{}{0pt}{}{m+\mathsf{\ell }-1}{m-1}}\right)s(m+k-1,m+\mathsf{\ell }-1){\left({\displaystyle \frac{m+k-2}{2}}\right)}^{\mathsf{\ell }},$$

(64)

with the assumptions $Q(1,1)=0$ and $Q(2,0)=1$, for $m\in \mathbb{N}$ and $k\in {\mathbb{N}}_0$.

In ([12], Remark 3.3), identity (61) was recovered, and another two identities

$$Q(1,2k)={(-1)}^k{\left[{\displaystyle \frac{(2k-1)!!}{2^k}}\right]}^2,k\in \mathbb{N}$$

(65)

and

$$Q(2j-1,2k+1)=0,j,k\in \mathbb{N}$$

(66)

were established.

Combining (60) and (66) with the assumption in (58), we conclude the following proposition.

Proposition 1.

The quantity $Q(m,k)$ defined by (64) satisfies

$$Q(m,2k-1)=0,m,k\in \mathbb{N}.$$

This proposition was also verified in ([11], Theorem 4) via the Bell polynomials of the second kind $B_{q,\mathsf{\ell }}$, which can be found in ([59], Chapter 11).

2.4. The Quantity $\mathcal{Q}(q,2\mathsf{\ell })$

Due to Proposition 1, for determining $Q(m,k)$, it suffices to consider the quantities $Q(m,2k)$ for $m,k\in \mathbb{N}$. Observing the coefficients in the power series expansions (1)–(5), we guess that the coefficients

$$\mathcal{Q}(q,2\mathsf{\ell })={(-1)}^{\mathsf{\ell }}Q(q,2\mathsf{\ell }),q,\mathsf{\ell }\in \mathbb{N}$$

in the series expansion (6) should be positive.

Comparing the coefficients in the power series expansions (1)–(5) with the coefficients in the power series expansion (6) for $q=1,2,3,4,5$, respectively, we determine that

$$\begin{array}{cccc}\mathcal{Q}(1,2\mathsf{\ell })\hfill & ={\left[{\displaystyle \frac{(2\mathsf{\ell }-1)!!}{2^{\mathsf{\ell }}}}\right]}^2,\hfill & \mathcal{Q}(2,2\mathsf{\ell })\hfill & ={\left[{\displaystyle \frac{\left(2\mathsf{\ell }\right)!!}{2^{\mathsf{\ell }}}}\right]}^2={(\mathsf{\ell }!)}^2,\hfill \\ \mathcal{Q}(3,2\mathsf{\ell })\hfill & ={\left[{\displaystyle \frac{(2\mathsf{\ell }+1)!!}{2^{\mathsf{\ell }}}}\right]}^2\sum _{k=0}^{\mathsf{\ell }}{\displaystyle \frac{1}{{(2k+1)}^2}},\hfill & \mathcal{Q}(4,2\mathsf{\ell })\hfill & ={\left[{\displaystyle \frac{(2\mathsf{\ell }+2)!!}{2^{\mathsf{\ell }}}}\right]}^2\sum _{k=0}^{\mathsf{\ell }}{\displaystyle \frac{1}{{(2k+2)}^2}},\hfill \end{array}$$

and

$$\mathcal{Q}(5,2\mathsf{\ell })={\displaystyle \frac{1}{2}}{\left[{\displaystyle \frac{(2\mathsf{\ell }+3)!!}{2^{\mathsf{\ell }}}}\right]}^2\left[{\left(\sum _{k=0}^{\mathsf{\ell }+1}{\displaystyle \frac{1}{{(2k+1)}^2}}\right)}^2-\sum _{k=0}^{\mathsf{\ell }+1}{\displaystyle \frac{1}{{(2k+1)}^4}}\right]$$

for $\mathsf{\ell }\in \mathbb{N}$. The first two of the above five formulas obviously recover identities (65) and (61) in sequence.

The first few numerical values of $\mathcal{Q}(q,2\mathsf{\ell })$ for $1\le q,\mathsf{\ell }\le 6$ are listed in Table 1.

Table 1. The first few values of $\mathcal{Q}(q,2\mathsf{\ell })$ for $1\le q,\mathsf{\ell }\le 6$.

$\mathcal{Q}(\mathit{q},2\mathsf{\ell })$	$\mathsf{\ell }=1$	$\mathsf{\ell }=2$	$\mathsf{\ell }=3$	$\mathsf{\ell }=4$	$\mathsf{\ell }=5$	$\mathsf{\ell }=6$
$q=1$	${\displaystyle \frac{1}{4}}$	${\displaystyle \frac{9}{16}}$	${\displaystyle \frac{225}{64}}$	${\displaystyle \frac{11025}{256}}$	${\displaystyle \frac{893025}{1024}}$	${\displaystyle \frac{108056025}{4096}}$
$q=2$	1	4	36	576	14400	518400
$q=3$	${\displaystyle \frac{5}{2}}$	${\displaystyle \frac{259}{16}}$	${\displaystyle \frac{3229}{16}}$	${\displaystyle \frac{1057221}{256}}$	${\displaystyle \frac{64408383}{512}}$	${\displaystyle \frac{21878089479}{4096}}$
$q=4$	5	49	820	21076	773136	38402064
$q=5$	${\displaystyle \frac{35}{4}}$	${\displaystyle \frac{987}{8}}$	${\displaystyle \frac{86405}{32}}$	${\displaystyle \frac{21967231}{256}}$	${\displaystyle \frac{3841278805}{1024}}$	${\displaystyle \frac{221541455151}{1024}}$
$q=6$	14	273	7645	296296	15291640	1017067024

Remark 1.

Table 1 motivates us to guess that the quantities $\mathcal{Q}(2q,2\mathsf{\ell })$ for $q,\mathsf{\ell }\in \mathbb{N}$ are positive integers, but $\mathcal{Q}(2q-1,2\mathsf{\ell })$ for $q,\mathsf{\ell }\in \mathbb{N}$ are not.

2.5. Identities of $\mathcal{Q}(q,2\mathsf{\ell })$

Some identities expressed in terms of $Q(m,k)$ in paper [11] can be reformulated as

$$\begin{array}{c}\sum _{k=1}^{2n}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{m+2n}{2n+k}}\right)\sum _{i=1}^k{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{2n+k}{k-i}}\right)\mathcal{Q}(i,2n)=\mathcal{Q}(m,2n),m,n\in \mathbb{N},\\ \sum _{j=1}^k{(-1)}^j{\displaystyle \frac{\mathcal{Q}(j,2i)}{(k-j)!(j+2i)!}}=0,k>i\in \mathbb{N},\\ B_{2q,\mathsf{\ell }}\left(0,{\displaystyle \frac{1}{3}},0,{\displaystyle \frac{9}{5}},0,{\displaystyle \frac{225}{7}},0,1225,\dots ,\dots ,{\displaystyle \frac{1+{(-1)}^{\mathsf{\ell }+1}}{2}}{\displaystyle \frac{{[(2q-\mathsf{\ell })!!]}^2}{2q-\mathsf{\ell }+2}}\right)\\ ={\displaystyle \frac{\left(4q\right)!!}{(2q+\mathsf{\ell })!}}\sum _{j=1}^{\mathsf{\ell }}{(-1)}^{\mathsf{\ell }+j}\left({\displaystyle \genfrac{}{}{0pt}{}{2q+\mathsf{\ell }}{\mathsf{\ell }-j}}\right)\mathcal{Q}(j,2q),2q\ge \mathsf{\ell }\in \mathbb{N},\end{array}$$

and

$$\mathcal{Q}(q,2\mathsf{\ell })={\displaystyle \frac{B_{q+2\mathsf{\ell },q}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }-3)!!]}^2,0,{[(2\mathsf{\ell }-1)!!]}^2\right)}{2^{2\mathsf{\ell }}}},$$

(67)

where $B_{q+2\mathsf{\ell },q}$ denotes the Bell polynomials of the second kind ([60], p. 134).

2.6. Connections Between $\mathcal{Q}(q,\mathsf{\ell })$ and Central Factorial Numbers

At the site https://mathoverflow.net/q/456136/#comment1181306_456136 (accessed on 9 October 2023), Ho Boon Suan pointed out that the quantities $\mathcal{Q}(q,2\mathsf{\ell })$ are essentially the central factorial numbers of the first kind $t(q,\mathsf{\ell })$ defined and studied in ([28], pp. 212–217, Section 6.5).

Usually, as in ([28], pp. 212–217, Section 6.5), central factorial numbers of the first kind $t(q,\mathsf{\ell })$ are defined by

$$z\prod _{\mathsf{\ell }=1}^{q-1}\left(z+{\displaystyle \frac{q}{2}}-\mathsf{\ell }\right)=\sum _{\mathsf{\ell }=1}^{q}t(q,\mathsf{\ell })z^{\mathsf{\ell }},q\in \mathbb{N}.$$

(68)

In ([61], p. 44), it was given that

$${\left[2ln\left({\displaystyle \frac{z}{2}}+\sqrt{1+{\left({\displaystyle \frac{z}{2}}\right)}^2}\right)\right]}^q=q!\sum _{\mathsf{\ell }=q}^{\infty }t(\mathsf{\ell },q){\displaystyle \frac{z^{\mathsf{\ell }}}{\mathsf{\ell }!}},q\in \mathbb{N}.$$

(69)

From the oddness of the function $ln\left({\displaystyle \frac{z}{2}}+\sqrt{1+{\left({\displaystyle \frac{z}{2}}\right)}^2}\right)$, it follows that

$$t(2\mathsf{\ell },2q-1)=0,\mathsf{\ell }\ge q\in \mathbb{N}$$

(70)

and

$$t(2\mathsf{\ell }-1,2q)=0,\mathsf{\ell }>q\in \mathbb{N}.$$

(71)

Comparing the thirty-six numerical values in Table 1 with those values in ([28], p. 217, Table 6.1) (see Figure 1) reveals that, just as pointed out by Ho Boon Suan at https://mathoverflow.net/q/456136/#comment1181306_456136 (accessed on 9 October 2023), there must exist some connection between $\mathcal{Q}(q,\mathsf{\ell })$ and central factorial numbers of the first kind $t(q,\mathsf{\ell })$.

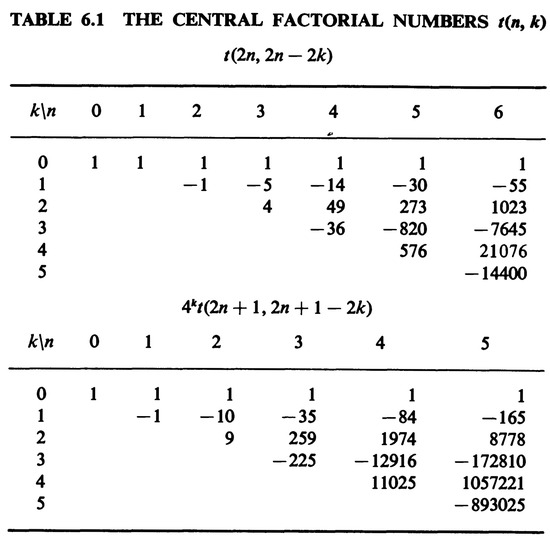
Figure 1. Table 6.1 in ([28], p. 217).

Proposition 2.

For $q,\mathsf{\ell }\in \mathbb{N}$, we have

$$t(q+2\mathsf{\ell }-1,q)=0$$

(72)

and

$$\mathcal{Q}(q,2\mathsf{\ell })={(-1)}^{\mathsf{\ell }}t(q+2\mathsf{\ell },q).$$

(73)

Consequently, for $q\in \mathbb{N}$, we have

$${\left({\displaystyle \frac{arcsinz}{z}}\right)}^q=1+\sum _{\mathsf{\ell }=1}^{\infty }{(-1)}^{\mathsf{\ell }}{\displaystyle \frac{t(q+2\mathsf{\ell },q)}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }}{2\mathsf{\ell }}\right)}}{\displaystyle \frac{{\left(2z\right)}^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\left|z\right|<1.$$

(74)

First Proof. 

Let $i=\sqrt{-1}$ be the imaginary unit. Replacing ${\displaystyle \frac{z}{2}}$ with $zi$ in (69) and rearranging give

$${\left[{\displaystyle \frac{ln\left(zi+\sqrt{1-z^2}\right)}{zi}}\right]}^q=\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{t(q+\mathsf{\ell },q)}{\left(\genfrac{}{}{0pt}{}{q+\mathsf{\ell }}{q}\right)}}{\displaystyle \frac{{(2zi)}^{\mathsf{\ell }}}{\mathsf{\ell }!}}.$$

Since

$$arcsinz=-iln\left[zi+\sqrt{1-z^2}\right],z\in \mathbb{C}\setminus (-\infty ,-1)\cup (1,\infty ),$$

(see ([62], p. 119, Entry 4.23.19)), we deduce

$${\left({\displaystyle \frac{arcsinz}{z}}\right)}^q=\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{t(q+\mathsf{\ell },q)}{\left(\genfrac{}{}{0pt}{}{q+\mathsf{\ell }}{q}\right)}}{\displaystyle \frac{{(2zi)}^{\mathsf{\ell }}}{\mathsf{\ell }!}}.$$

Comparing this series expansion with the one in (6) results in

$${\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }}{2\mathsf{\ell }}\right)}}{\displaystyle \frac{{\left(2z\right)}^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}={\displaystyle \frac{t(q+2\mathsf{\ell },q)}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }}{q}\right)}}{\displaystyle \frac{{(2zi)}^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}$$

and

$${\displaystyle \frac{t(q+2\mathsf{\ell }-1,q)}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }-1}{q}\right)}}{\displaystyle \frac{{(2zi)}^{2\mathsf{\ell }-1}}{(2\mathsf{\ell }-1)!}}=0$$

for $q,\mathsf{\ell }\in \mathbb{N}$. Accordingly, we derive identities (72) and (73). Series expansion (74) comes from combining (73) with (6). The first proof of Proposition 2 is complete. □

Second Proof 

In ([11], Theorem 4 and Remark 10), the first result reads that the Bell polynomials of the second kind $B_{q,\mathsf{\ell }}$ satisfy

$$B_{2j+\mathsf{\ell },\mathsf{\ell }}\left(1,0,1,0,9,0,\dots ,{[(2j-3)!!]}^2,0,{[(2j-1)!!]}^2\right)=2^{2j}\mathcal{Q}(\mathsf{\ell },2j)$$

(75)

and

$$B_{2j+\mathsf{\ell }-1,\mathsf{\ell }}\left(1,0,1,0,9,0,225,0,\dots ,{[(2j-3)!!]}^2,0\right)=0$$

(76)

for $j,\mathsf{\ell }\in \mathbb{N}$. From (75) and the identity

$$B_{q,\mathsf{\ell }}\left(\mu \nu z_1,\mu {\nu }^2{z}_2,\dots ,\mu {\nu }^{q-\mathsf{\ell }+1}{z}_{q-\mathsf{\ell }+1}\right)={\mu }^{\mathsf{\ell }}{\nu }^q{B}_{q,\mathsf{\ell }}(z_1,z_2,\dots ,z_{q-\mathsf{\ell }+1})$$

(77)

for $q\ge \mathsf{\ell }\in {\mathbb{N}}_0$ and $\mu ,\nu \in \mathbb{C}$ in ([59], p. 412) and ([60], p. 135), it follows that

$$\begin{array}{c}{B}_{2j+\mathsf{\ell },\mathsf{\ell }}\left(1,0,-1,0,9,0,-225,0,\dots ,{(-1)}^{j-1}{[(2j-3)!!]}^2,0,{(-1)}^j{[(2j-1)!!]}^2\right)\hfill \\ \begin{array}{cc}& =B_{2j+\mathsf{\ell },\mathsf{\ell }}(1·i^0,0·i^1,1·i^2,0·i^3,9·i^4,0·i^5,225·i^6,0·i^7,\dots ,\hfill \\ & {[(2j-3)!!]}^2{i}^{2j-2},0·i^{2j-1},{[(2j-1)!!]}^2{i}^{2j}),i=\sqrt{-1}\hfill \\ & =i^{2j+\mathsf{\ell }-\mathsf{\ell }}{B}_{2j+\mathsf{\ell },\mathsf{\ell }}\left(1,0,1,0,9,0,\dots ,{[(2j-3)!!]}^2,0,{[(2j-1)!!]}^2\right)\hfill \\ & ={(-1)}^j{2}^{2j}\mathcal{Q}(\mathsf{\ell },2j).\hfill \end{array}\hfill \end{array}$$

(78)

It is standard that

$$\underset{z\to 0}{lim}{\left[ln\left(z+\sqrt{1+z^2}\right)\right]}^{\prime }=\underset{z\to 0}{lim}{\displaystyle \frac{1}{\sqrt{1+z^2}}}=1.$$

From the derivatives

$$\begin{array}{cc}{\left[{\displaystyle \frac{1}{\sqrt{1+z^2}}}\right]}^{\left(q\right)}\hfill & ={\displaystyle \frac{d^q}{d{z}^q}}\sum _{\mathsf{\ell }=0}^{\infty }{(-1)}^{\mathsf{\ell }}{[(2\mathsf{\ell }-1)!!]}^2{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\hfill \\ & \to \{\begin{array}{cc}{(-1)}^m{[(2m-1)!!]}^2,\hfill & q=2m\ge 0;\hfill \\ 0,\hfill & q=2m+1\in \mathbb{N},\hfill \end{array}\hfill \end{array}$$

and by virtue of the Faà di Bruno formula in ([59], p. 412) and ([60], pp. 134–135 and p. 139), we arrive at

$$\begin{array}{c}{\displaystyle \frac{d^n}{d{z}^n}}{\left[2ln\left(z+\sqrt{1+z^2}\right)\right]}^q={\displaystyle \sum _{k=1}^n}{\displaystyle \frac{d^k{u}^q}{d{u}^k}}{B}_{n,k}({\displaystyle \frac{2}{\sqrt{1+z^2}}},{\left({\displaystyle \frac{2}{\sqrt{1+z^2}}}\right)}^{\prime },\hfill \\ {\left({\displaystyle \frac{2}{\sqrt{1+z^2}}}\right)}^{\prime \prime },\dots ,{\left({\displaystyle \frac{2}{\sqrt{1+z^2}}}\right)}^{(n-k)},{\left({\displaystyle \frac{2}{\sqrt{1+z^2}}}\right)}^{(n-k)})\hfill \\ ={\displaystyle \sum _{k=1}^n}{(-1)}^k{(-q)}_k{u}^{q-k}{2}^k{B}_{n,k}({\displaystyle \frac{1}{\sqrt{1+z^2}}},{\left({\displaystyle \frac{1}{\sqrt{1+z^2}}}\right)}^{\prime },\hfill \\ {\left({\displaystyle \frac{1}{\sqrt{1+z^2}}}\right)}^{\prime \prime },\dots ,{\left({\displaystyle \frac{1}{\sqrt{1+z^2}}}\right)}^{(n-k)},{\left({\displaystyle \frac{1}{\sqrt{1+z^2}}}\right)}^{(n-k)})\hfill \\ \to \left\{\begin{array}{cc}0,\hfill & 1\le n<q\hfill \\ \left(2q\right)!!{\mathrm{B}}_{n,q}\left(1,0,-1,0,9,\dots ,{\displaystyle \underset{z\to 0}{lim}}{\left({\displaystyle \frac{1}{\sqrt{1+z^2}}}\right)}^{(n-q)}\right),\hfill & n\ge q\in \mathbb{N}\hfill \end{array}\right.\hfill \\ =\left\{\begin{array}{cc}0,\hfill & 1\le n<q\hfill \\ 0,\hfill & n=2j+q+1>q\in \mathbb{N}\hfill \\ \left(2q\right)!!{\mathrm{B}}_{2j+q,q}\left(1,0,-1,0,9,\dots ,{\displaystyle \underset{z\to 0}{lim}}{\left({\displaystyle \frac{1}{\sqrt{1+z^2}}}\right)}^{\left(2j\right)}\right),\hfill & n=2j+q\ge q\in \mathbb{N}\hfill \end{array}\right.\hfill \\ =\left\{\begin{array}{cc}0,\hfill & 1\le n<q\hfill \\ 0,\hfill & n=2j+q+1>q\in \mathbb{N}\hfill \\ \left(2q\right)!!{\mathrm{B}}_{2j+q,q}\left(1,0,-1,0,9,\dots ,0,{(-1)}^j{[(2j-1)!!]}^2\right),\hfill & n=2j+q\ge q\in \mathbb{N}\hfill \end{array}\right.\hfill \\ =\left\{\begin{array}{cc}0,\hfill & 1\le n<q\hfill \\ 0,\hfill & n=2j+q+1>q\in \mathbb{N}\hfill \\ {(-1)}^j{q}^{\prime }!2^{q+2j}\mathcal{Q}(q,2j),\hfill & n=2j+q\ge q\in \mathbb{N}\hfill \end{array}\right.\hfill \end{array}$$

as $z\to 0$ for $n\in \mathbb{N}$ and $j\in {\mathbb{N}}_0$, where $u=u\left(z\right)=2ln\left(z+\sqrt{1+z^2}\right)\to 0$ as $z\to 0$, and we use identities (76)–(78). This implies that

$${\left[2ln\left(z+\sqrt{1+z^2}\right)\right]}^q=q!\sum _{j=0}^{\infty }{(-1)}^j{2}^{q+2j}\mathcal{Q}(q,2j){\displaystyle \frac{z^{q+2j}}{(q+2j)!}},\left|z\right|<1.$$

Replacing z with ${\displaystyle \frac{z}{2}}$ in the last series expansion gives

$${\left[2ln\left({\displaystyle \frac{z}{2}}+\sqrt{1+{\left({\displaystyle \frac{z}{2}}\right)}^2}\right)\right]}^q=q!\sum _{j=0}^{\infty }{(-1)}^j\mathcal{Q}(q,2j){\displaystyle \frac{z^{q+2j}}{(q+2j)!}},\left|z\right|<2.$$

Comparing this with (69) leads to

$$\begin{array}{cc}\sum _{\mathsf{\ell }=q}^{\infty }t(\mathsf{\ell },q){\displaystyle \frac{z^{\mathsf{\ell }}}{\mathsf{\ell }!}}\hfill & =\sum _{j=0}^{\infty }t(q+2j,q){\displaystyle \frac{z^{q+2j}}{(q+2j)!}}+\sum _{j=0}^{\infty }t(q+2j+1,q){\displaystyle \frac{z^{q+2j+1}}{(q+2j+1)!}}\hfill \\ \hfill & =\sum _{j=0}^{\infty }{(-1)}^j\mathcal{Q}(q,2j){\displaystyle \frac{z^{q+2j}}{(q+2j)!}},q\in \mathbb{N}.\hfill \end{array}$$

Equating the coefficients of $z^{\mathsf{\ell }}$ for $\mathsf{\ell }\ge q$ results in

$$t(q+2j,q)={(-1)}^j\mathcal{Q}(q,2j)=Q(q,2j)\mathrm{and}t(q+2j+1,q)=0$$

for $q\in \mathbb{N}$ and $j\in {\mathbb{N}}_0$. Identities (72) and (73) are proved once again. The second proof of Proposition 2 is complete. □

Identity (72) is a unification of (70) and (71) and recovers the last displayed formula in ([28], p. 216).

Corollary 1.

For $q\ge \mathsf{\ell }\in \mathbb{N}$, central factorial numbers of the first kind $t(q,\mathsf{\ell })$ can be explicitly computed by

$$t(q,\mathsf{\ell })=Q(\mathsf{\ell },q-\mathsf{\ell }),$$

(79)

where $Q(m,k)$ is defined by (64) with two assumptions $Q(1,1)=0$ and $Q(2,0)=1$ for $m\in \mathbb{N}$ and $k\in {\mathbb{N}}_0$.

Proof. 

This follows from the combination of (72) and (73) with expressions (7) and (64) and with Proposition 1. □

2.7. Closed-Form Formulas for Central Factorial Numbers of the First Kind

Formula (79) is a closed-form formula for computing central factorial numbers of the first kind $t(q,\mathsf{\ell })$. We now present two alternative closed-form formulas for computing central factorial numbers of the first kind $t(q,\mathsf{\ell })$.

Proposition 3.

Central factorial numbers of the first kind $t(2q,2\mathsf{\ell })$ can be explicitly computed by

$$t(2q,2\mathsf{\ell })=\sum _{k=2\mathsf{\ell }-1}^{2q-1}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }-1}}\right)s(2q-1,k){(q-1)}^{k-2\mathsf{\ell }+1},q\ge \mathsf{\ell }\in \mathbb{N}$$

(80)

and central factorial numbers of the first kind $t(2q-1,2\mathsf{\ell }-1)$ can be explicitly computed by

$$t(2q+1,2\mathsf{\ell }+1)=\sum _{k=2\mathsf{\ell }}^{2q}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }}}\right)s(2q,k){\left(q-{\displaystyle \frac{1}{2}}\right)}^{k-2\mathsf{\ell }},0\le \mathsf{\ell }\le q,$$

(81)

where the factor $0^0$ for $q=1$ in (80) is assumed to be 1, and $s(q,k)$ denotes the Stirling numbers of the first kind generated in (8).

First Proof. 

Lemma 3.1 in [12] reads that, for $q\in \mathbb{N}$ and $\alpha \in \mathbb{C}$,

$$\prod _{\mathsf{\ell }=1}^q\left({\mathsf{\ell }}^2+{\alpha }^2\right)={(-1)}^q\sum _{\mathsf{\ell }=0}^q{(-1)}^{\mathsf{\ell }}\left[\sum _{k=2\mathsf{\ell }+1}^{2q+1}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }+1}}\right)s(2q+1,k)q^{k-2\mathsf{\ell }-1}\right]{\alpha }^{2\mathsf{\ell }}.$$

(82)

In ([28], p. 233, Problem 8), it was given that

$$\prod _{\mathsf{\ell }=1}^{q-1}\left(z^2-{\mathsf{\ell }}^2\right)=\sum _{\mathsf{\ell }=1}^{q}t(2q,2\mathsf{\ell })z^{2\mathsf{\ell }-2},q\in \mathbb{N}.$$

(83)

Combining this equality with identity (82) and rearranging result in

$$\sum _{\mathsf{\ell }=1}^{q}t(2q,2\mathsf{\ell })z^{2\mathsf{\ell }-2}=\sum _{\mathsf{\ell }=1}^q\left[\sum _{k=2\mathsf{\ell }-1}^{2q-1}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }-1}}\right)s(2q-1,k){(q-1)}^{k-2\mathsf{\ell }+1}\right]z^{2\mathsf{\ell }-2}.$$

As a result, we derive closed-form formula (80).

Lemma 3.2 in [12] states that, for $k\in \mathbb{N}$ and $\alpha \in \mathbb{C}$,

$$\prod _{\mathsf{\ell }=1}^q\left[{(2\mathsf{\ell }-1)}^2+{\alpha }^2\right]={(-1)}^q{2}^{2q}\sum _{\mathsf{\ell }=0}^{2q}{(-1)}^{\mathsf{\ell }}\left[\sum _{k=2\mathsf{\ell }}^{2q}{\displaystyle \frac{s(2q,k)}{2^k}}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }}}\right){(2q-1)}^{k-2\mathsf{\ell }}\right]{\alpha }^{2\mathsf{\ell }}.$$

(84)

In ([28], p. 233, Problem 8), it was found that

$${\displaystyle \frac{1}{4^q}}\prod _{\mathsf{\ell }=1}^q\left[4z^2-{(2\mathsf{\ell }-1)}^2\right]=\sum _{\mathsf{\ell }=0}^{q}t(2q+1,2\mathsf{\ell }+1)z^{2\mathsf{\ell }},q\in \mathbb{N}.$$

(85)

Combining this equality with identity (84) leads to

$$\sum _{\mathsf{\ell }=0}^{q}t(2q+1,2\mathsf{\ell }+1)z^{2\mathsf{\ell }}=\sum _{\mathsf{\ell }=0}^{2q}\left[2^{2\mathsf{\ell }}\sum _{k=2\mathsf{\ell }}^{2q}{\displaystyle \frac{s(2q,k)}{2^k}}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }}}\right){(2q-1)}^{k-2\mathsf{\ell }}\right]z^{2\mathsf{\ell }}.$$

Equating the coefficients of the terms $z^{2\mathsf{\ell }}$ for $1\le \mathsf{\ell }\le 2q$ on both sides produces formula (81). The required proof is complete. □

Second Proof 

Combining (79) with (64), we arrive at

$$\begin{array}{cc}t(2q,2\mathsf{\ell })\hfill & =\sum _{j=0}^{2q-2\mathsf{\ell }}\left({\displaystyle \genfrac{}{}{0pt}{}{2\mathsf{\ell }+j-1}{2\mathsf{\ell }-1}}\right)s(2q-1,2\mathsf{\ell }+j-1){(q-1)}^j\hfill \\ \hfill & =\sum _{k=2\mathsf{\ell }-1}^{2q-1}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }-1}}\right)s(2q-1,k){(q-1)}^{k-2\mathsf{\ell }+1}\hfill \end{array}$$

and

$$\begin{array}{cc}t(2q+1,2\mathsf{\ell }+1)\hfill & =\sum _{j=0}^{2q-2\mathsf{\ell }}\left({\displaystyle \genfrac{}{}{0pt}{}{2\mathsf{\ell }+j}{2\mathsf{\ell }}}\right)s(2q,2\mathsf{\ell }+j){\left(q-{\displaystyle \frac{1}{2}}\right)}^j\hfill \\ \hfill & =\sum _{k=2\mathsf{\ell }}^{2q}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2\mathsf{\ell }}}\right)s(2q,k){\left(q-{\displaystyle \frac{1}{2}}\right)}^{k-2\mathsf{\ell }}.\hfill \end{array}$$

The second proof of Proposition 3 is complete. □

2.8. Central Factorial Numbers and Related Expansions

In ([63], p. 455), Charalambides pointed out that

$$\sum _{q=0}^{\infty }t(q,\mathsf{\ell }){\displaystyle \frac{z^q}{q!}}={\displaystyle \frac{1}{\mathsf{\ell }!}}{\left(2arcsinh{\displaystyle \frac{z}{2}}\right)}^{\mathsf{\ell }}$$

(86)

and

$$\sum _{q=0}^{\infty }T(q,\mathsf{\ell }){\displaystyle \frac{z^q}{q!}}={\displaystyle \frac{1}{\mathsf{\ell }!}}{\left(2sinh{\displaystyle \frac{z}{2}}\right)}^{\mathsf{\ell }},$$

(87)

where $t(q,\mathsf{\ell })$ and $T(q,\mathsf{\ell })$ denote central factorial numbers of the first and second kinds, respectively.

Corollary 2 in [6] reads that, for $q\in \mathbb{N}$ and $\left|z\right|<1$, the function ${\left({\displaystyle \frac{arcsinhz}{z}}\right)}^q$, whose value at $z=0$ is defined to be 1, has a Maclaurin series expansion

$${\left({\displaystyle \frac{arcsinhz}{z}}\right)}^q=1+\sum _{\mathsf{\ell }=1}^{\infty }{\displaystyle \frac{Q(q,2\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{q+2\mathsf{\ell }}{q}\right)}}{\displaystyle \frac{{\left(2z\right)}^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},$$

(88)

where $Q(q,2\mathsf{\ell })$ is defined by (64). Comparing (86) with (88) recovers the relations in (70), (71), (72), and (73).

Corollary 5 in [20] reads that, for $j\in {\mathbb{N}}_0$ and $\mathsf{\ell }\in \mathbb{N}$, we have

$${\displaystyle \frac{T(2j+\mathsf{\ell },\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{2j+\mathsf{\ell }}{\mathsf{\ell }}\right)}}=\sum _{k=0}^{2j}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{2j}{k}}\right){\left({\displaystyle \frac{\mathsf{\ell }}{2}}\right)}^k{\displaystyle \frac{S(2j+\mathsf{\ell }-k,\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{2j+\mathsf{\ell }-k}{\mathsf{\ell }}\right)}},$$

(89)

where $S(q,\mathsf{\ell })$ stands for the Stirling numbers of the second kind that can be analytically generated by

$${\left({\displaystyle \frac{e^z-1}{z}}\right)}^{\mathsf{\ell }}=\sum _{q=0}^{\infty }{\displaystyle \frac{S(q+\mathsf{\ell },\mathsf{\ell })}{\left(\genfrac{}{}{0pt}{}{q+\mathsf{\ell }}{\mathsf{\ell }}\right)}}{\displaystyle \frac{z^q}{q!}},\mathsf{\ell }\ge 0.$$

Substituting (89) into (87) leads to

$$\begin{array}{c}{\left({\displaystyle \frac{sinhz}{z}}\right)}^q=q!\sum _{j=0}^{\infty }T(j,q){\displaystyle \frac{z^{j-q}}{j!}}=q!\sum _{j=q}^{\infty }T(j,q){\displaystyle \frac{z^{j-q}}{j!}}=q!\sum _{j=0}^{\infty }T(j+q,q){\displaystyle \frac{z^j}{(j+q)!}}\\ =q!\sum _{j=0}^{\infty }T(2j+q,q){\displaystyle \frac{z^{2j}}{(2j+q)!}}=\sum _{j=0}^{\infty }{\displaystyle \frac{T(2j+q,q)}{\left(\genfrac{}{}{0pt}{}{2j+q}{q}\right)}}{\displaystyle \frac{z^{2j}}{\left(2j\right)!}}\\ =\sum _{j=0}^{\infty }\left[\sum _{k=0}^{2j}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{2j}{k}}\right){\left({\displaystyle \frac{q}{2}}\right)}^k{\displaystyle \frac{S(2j+q-k,q)}{\left(\genfrac{}{}{0pt}{}{2j+q-k}{q}\right)}}\right]{\displaystyle \frac{z^{2j}}{\left(2j\right)!}}\end{array}$$

for $q\in \mathbb{N}$. This is a special case of the second series expansion in ([20], Theorem 11).

3. Inverse of Specific Vandermonde Matrix

We now give a detailed proof of the problem posted at https://mathoverflow.net/q/456311 (accessed 12 October 2023): What is the inverse of the interesting integer Vandermonde matrix

$$V\left(q\right)=\left(\begin{array}{cccccc}1& 0& 0& \dots & 0& 0\\ 1& 1& 1& \dots & 1& 1\\ 1& 2& 2^2& \dots & 2^{q-1}& 2^q\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& q-1& {(q-1)}^2& \dots & {(q-1)}^{q-1}& {(q-1)}^q\\ 1& q& q^2& \dots & q^{q-1}& q^q\end{array}\right)$$

(90)

for $q\in \mathbb{N}$? The inverse of a general square Vandermonde matrix

$$V(z_1,z_2,\dots ,z_{q-1},z_q)=\left(\begin{array}{cccccc}1& z_1& z_1^2& \dots & z_1^{q-2}& z_1^{q-1}\\ 1& z_2& z_2^2& \dots & z_2^{q-2}& z_2^{q-1}\\ 1& z_3& z_3^2& \dots & z_3^{q-2}& z_3^{q-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& z_{q-1}& z_{q-1}^2& \dots & z_{q-1}^{q-2}& z_{q-1}^{q-1}\\ 1& z_q& z_q^2& \dots & z_q^{q-2}& z_q^{q-1}\end{array}\right),q\in \mathbb{N}$$

is known in the literature (see [64,65] or read the texts at https://en.wikipedia.org/wiki/Vandermonde_matrix#Inverse_Vandermonde_matrix (accessed on 11 October 2023)). We hope to find a simpler form of the inverse of the specific Vandermonde matrix $V\left(q\right)$ for $q\in \mathbb{N}$.

Proposition 4.

For $q\in \mathbb{N}$, the inverse of the specific Vandermonde matrix $V\left(q\right)$ defined in (90) is

$$V^{-1}\left(q\right)=\left(\begin{array}{cc}1& \mathbf{0}\left(q\right)\\ -U\left(q\right){\mathbf{1}}^T\left(q\right)& U\left(q\right)\end{array}\right),$$

(91)

where T stands for the transpose notation, and

$$\begin{array}{c}\mathbf{0}\left(q\right)=(\stackrel{q}{\overbrace{0,0,\dots ,0}}),\mathbf{1}\left(q\right)=(\stackrel{q}{\overbrace{1,1,\dots ,1}}),\\ U\left(q\right)={\left(\begin{array}{c}{u}_{k,i}\left(q\right)\end{array}\right)}_{1\le k\le q,1\le i\le q}={\left(\begin{array}{c}{\displaystyle \frac{1}{i!}\sum _{j=k}^q\frac{{(-1)}^{j-i}}{(j-i)!}s(j,k)}\end{array}\right)}_{1\le k\le q,1\le i\le q},\end{array}$$

where $s(j,k)$ denotes the Stirling numbers of the first kind.

Proof. 

In ([66], pp. 97–98), Macon and Spitzbart established that

$$\begin{array}{cc}{M}^{-1}\left(q\right)\hfill & ={\left(\begin{array}{ccccc}1& 1& \dots & 1& 1\\ 2& 2^2& \dots & 2^{q-1}& 2^q\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ q-1& {(q-1)}^2& \dots & {(q-1)}^{q-1}& {(q-1)}^q\\ q& q^2& \dots & q^{q-1}& q^q\end{array}\right)}^{-1}\hfill \\ \hfill & ={\left(\begin{array}{c}{\displaystyle \sum _{j=k}^q{(-1)}^{j+i}\left(\genfrac{}{}{0pt}{}{j}{i}\right)\frac{s(j,k)}{j!}}\end{array}\right)}_{1\le k\le q,1\le i\le q}\hfill \\ \hfill & =U\left(q\right),q\in \mathbb{N}.\hfill \end{array}$$

See also an unpublished manuscript titled “Inverse of a Vandermonde matrix” by C. M. Bender, D. C. Brody, and B. K. Meister, 2001 (available online: https://www.researchgate.net/publication/240061354 (accessed on 11 October 2023)).

Let $A=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)$ be partitioned as a 2-by-2 block matrix, with $A_{11}$ and $A_{22}$ being square matrices. In ([67], Section 0.7.3), it was stated that if $A_{11}$ and $A_{22}$ are invertible, then the inverse of A is

$$A^{-1}=\left(\begin{array}{cc}{\left(A_{11}-A_{12}{A}_{22}^{-1}{A}_{21}\right)}^{-1}& A_{11}^{-1}{A}_{12}{\left(A_{21}{A}_{11}^{-1}{A}_{12}-A_{22}\right)}^{-1}\\ A_{22}^{-1}{A}_{21}{\left(A_{12}{A}_{22}^{-1}{A}_{21}-A_{11}\right)}^{-1}& {\left(A_{22}-A_{21}{A}_{11}^{-1}{A}_{12}\right)}^{-1}\end{array}\right).$$

According to this, we obtain

$$V^{-1}\left(q\right)={\left(\begin{array}{cc}1& \mathbf{0}\left(q\right)\\ {\mathbf{1}}^T\left(q\right)& M\left(q\right)\end{array}\right)}^{-1}=\left(\begin{array}{cc}1& \mathbf{0}\left(q\right)\\ -M^{-1}\left(q\right){\mathbf{1}}^T\left(q\right)& M^{-1}\left(q\right)\end{array}\right).$$

The proof of Proposition 4 is thus complete. □

Remark 2.

For special cases of $q=2,3,4$, simple but long practical computation shows

$$\begin{array}{cc}{V}^{-1}\left(2\right)\hfill & ={\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 1& 2& 2^2\end{array}\right)}^{-1}=\left(\begin{array}{ccc}1& 0& 0\\ -{\displaystyle \frac{3}{2}}& 2& -{\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{1}{2}}& -1& {\displaystyle \frac{1}{2}}\end{array}\right),\hfill \\ V^{-1}\left(3\right)\hfill & ={\left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 1& 1& 1\\ 1& 2& 2^2& 2^3\\ 1& 3& 3^2& 3^3\end{array}\right)}^{-1}=\left(\begin{array}{cccc}1& 0& 0& 0\\ -{\displaystyle \frac{11}{6}}& 3& -{\displaystyle \frac{3}{2}}& {\displaystyle \frac{1}{3}}\\ 1& -{\displaystyle \frac{5}{2}}& 2& -{\displaystyle \frac{1}{2}}\\ -{\displaystyle \frac{1}{6}}& {\displaystyle \frac{1}{2}}& -{\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{6}}\end{array}\right),\hfill \\ V^{-1}\left(4\right)\hfill & ={\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 1& 1& 1& 1& 1\\ 1& 2& 2^2& 2^3& 2^4\\ 1& 3& 3^2& 3^3& 3^4\\ 1& 4& 4^2& 4^3& 4^4\end{array}\right)}^{-1}=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ -{\displaystyle \frac{25}{12}}& 4& -3& {\displaystyle \frac{4}{3}}& -{\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{35}{24}}& -{\displaystyle \frac{13}{3}}& {\displaystyle \frac{19}{4}}& -{\displaystyle \frac{7}{3}}& {\displaystyle \frac{11}{24}}\\ -{\displaystyle \frac{5}{12}}& {\displaystyle \frac{3}{2}}& -2& {\displaystyle \frac{7}{6}}& -{\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{1}{24}}& -{\displaystyle \frac{1}{6}}& {\displaystyle \frac{1}{4}}& -{\displaystyle \frac{1}{6}}& {\displaystyle \frac{1}{24}}\end{array}\right).\hfill \end{array}$$

Based on these three special inverse matrices, the author observed and examined that the sum of all elements in each row, except the first row, of inverse matrices $V^{-1}\left(2\right)$, $V^{-1}\left(3\right)$, and $V^{-1}\left(4\right)$ is 0:

$$\begin{array}{c}-{\displaystyle \frac{3}{2}}+2-{\displaystyle \frac{1}{2}}=0,{\displaystyle \frac{1}{2}}-1+{\displaystyle \frac{1}{2}}=0,-{\displaystyle \frac{11}{6}}+3-{\displaystyle \frac{3}{2}}+{\displaystyle \frac{1}{3}}=0,1-{\displaystyle \frac{5}{2}}+2-{\displaystyle \frac{1}{2}}=0,\\ -{\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{6}}=0,-{\displaystyle \frac{25}{12}}+4-3+{\displaystyle \frac{4}{3}}-{\displaystyle \frac{1}{4}}=0,{\displaystyle \frac{35}{24}}-{\displaystyle \frac{13}{3}}+{\displaystyle \frac{19}{4}}-{\displaystyle \frac{7}{3}}+{\displaystyle \frac{11}{24}}=0,\\ -{\displaystyle \frac{5}{12}}+{\displaystyle \frac{3}{2}}-2+{\displaystyle \frac{7}{6}}-{\displaystyle \frac{1}{4}}=0,{\displaystyle \frac{1}{24}}-{\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{24}}=0.\end{array}$$

These observations and examinations can be easily seen through from concrete expression (91).

Furthermore, the author also observed and examined that the sum of all elements in each column, except the second column, of inverse matrices $V^{-1}\left(2\right)$, $V^{-1}\left(3\right)$, and $V^{-1}\left(4\right)$ is also 0, but the sum of all elements in the second column of inverse matrices $V^{-1}\left(2\right)$, $V^{-1}\left(3\right)$, and $V^{-1}\left(4\right)$ is 1:

$$\begin{array}{cccccc}\hfill 1-{\displaystyle \frac{3}{2}}+{\displaystyle \frac{1}{2}}& \hfill =0,& \hfill 0+2-1& \hfill =1,& \hfill 0-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}& \hfill =0,\\ \hfill 1-{\displaystyle \frac{11}{6}}+1-{\displaystyle \frac{1}{6}}& \hfill =0,& \hfill 0+3-{\displaystyle \frac{5}{2}}+{\displaystyle \frac{1}{2}}& \hfill =1,& \hfill 0-{\displaystyle \frac{3}{2}}+2-{\displaystyle \frac{1}{2}}& \hfill =0,\\ \hfill 0+{\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{6}}& \hfill =0,& \hfill 1-{\displaystyle \frac{25}{12}}+{\displaystyle \frac{35}{24}}-{\displaystyle \frac{5}{12}}+{\displaystyle \frac{1}{24}}& \hfill =0,& \hfill 0+4-{\displaystyle \frac{13}{3}}+{\displaystyle \frac{3}{2}}-{\displaystyle \frac{1}{6}}& \hfill =1,\\ \hfill 0-3+{\displaystyle \frac{19}{4}}-2+{\displaystyle \frac{1}{4}}& \hfill =0,& \hfill 0+{\displaystyle \frac{4}{3}}-{\displaystyle \frac{7}{3}}+{\displaystyle \frac{7}{6}}-{\displaystyle \frac{1}{6}}& \hfill =0,& 0-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{11}{24}}-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{24}}\hfill & \hfill =0.\end{array}$$

By virtue of explicit expression (91), we can verify these observations as follows. The sum of all elements in the first column of the inverse $V^{-1}\left(q\right)$ for $q\in \mathbb{N}$ is

$$\begin{array}{cc}{C}_1\left(q\right)\hfill & =1-\sum _{k=1}^q\sum _{i=1}^q{u}_{k,i}\left(q\right)\hfill \\ \hfill & =1-\sum _{k=1}^q\sum _{i=1}^q\sum _{j=k}^q{\displaystyle \frac{{(-1)}^{j+i}\left(\genfrac{}{}{0pt}{}{j}{i}\right)s(j,k)}{j!}}\hfill \\ \hfill & =1-\sum _{k=1}^q\sum _{j=k}^q\left[\sum _{i=1}^q{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right)\right]{\displaystyle \frac{{(-1)}^{j}s(j,k)}{j!}}\hfill \\ \hfill & =1-\sum _{k=1}^q\sum _{j=k}^q\left[\sum _{i=1}^j{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right)\right]{\displaystyle \frac{{(-1)}^{j}s(j,k)}{j!}}\hfill \\ \hfill & =1+\sum _{k=1}^q\sum _{j=k}^q{\displaystyle \frac{{(-1)}^{j}s(j,k)}{j!}}\hfill \\ \hfill & =1+\sum _{j=1}^q\left[\sum _{k=1}^{j}s(j,k)\right]{\displaystyle \frac{{(-1)}^j}{j!}}\hfill \\ \hfill & =1+{\displaystyle \frac{{(-1)}^1}{1!}}\hfill \\ \hfill & =0\hfill \end{array}$$

and the sum of all elements in the ℓth column for $2\le \mathsf{\ell }\le q$ is

$$\begin{array}{cc}{C}_{\mathsf{\ell }}\left(q\right)\hfill & =0+\sum _{k=1}^q{u}_{k,\mathsf{\ell }-1}\left(q\right)\hfill \\ \hfill & =\sum _{k=1}^q\sum _{j=k}^q{\displaystyle \frac{{(-1)}^{j+\mathsf{\ell }-1}\left(\genfrac{}{}{0pt}{}{j}{\mathsf{\ell }-1}\right)s(j,k)}{j!}}\hfill \\ \hfill & =\sum _{j=1}^q\left[\sum _{k=1}^{j}s(j,k)\right]{\displaystyle \frac{{(-1)}^{j+\mathsf{\ell }-1}\left(\genfrac{}{}{0pt}{}{j}{\mathsf{\ell }-1}\right)}{j!}}\hfill \\ \hfill & ={\displaystyle \frac{{(-1)}^{1+\mathsf{\ell }-1}\left(\genfrac{}{}{0pt}{}{1}{\mathsf{\ell }-1}\right)}{1!}}\hfill \\ \hfill & =\{\begin{array}{cc}1,\hfill & \mathsf{\ell }=2;\hfill \\ 0,\hfill & 2<\mathsf{\ell }\le q.\hfill \end{array}\hfill \end{array}$$

In other words, those observations in three comments on the problem at https://mathoverflow.net/q/456311 (accessed 12 October 2023) by the author are all verified to be true.

4. Closed-Form Formulas and Positivity of $\mathcal{Q}(\mathbf{q},\mathbf{2}\mathsf{\ell })$

A number of clues motivate us to guess that, for $q,\mathsf{\ell }\in \mathbb{N}$, the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ defined by (7) is positive. This guess was also posted on the web site https://mathoverflow.net/q/456136 (accessed on 9 October 2023). In the comment at https://mathoverflow.net/q/456136/#comment1181306_456136 (accessed on 9 October 2023), Ho Boon Suan pointed out that the positivity of $\mathcal{Q}(q,2\mathsf{\ell })$ follows from ([28], p. 233, Problem 8).

From ([28], p. 233, Problem 8), we derive two closed-form formulas for central factorial numbers of the first kind: $t(2q,2m)$ and $t(2q+1,2m+1)$.

Proposition 5.

Central factorial numbers of the first kind $t(q,m)$ can be explicitly computed by

$$\begin{array}{cc}t(2q,2m)={(-1)}^{q-1}({[(q-1)!]}^2\hfill & \sum _{j=m-1}^{q-1}{\displaystyle \frac{\left|s\right(j,m-1\left)\right|}{j!}}\hfill \\ & +\sum _{i=1}^{q-1}{(-1)}^i\left[\prod _{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]\left[\sum _{j=m-1}^{q-1}\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,m-1\left)\right|}{j!}}\right])\hfill \end{array}$$

(92)

for $q\ge m\in \mathbb{N}$ and

$$\begin{array}{cc}t(2q+1,2m+1)={\displaystyle \frac{{(-1)}^q}{4^{q-m}}}({[(2q-1)!!]}^2\hfill & \sum _{j=m}^q{\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\hfill \\ \hfill & +\sum _{i=1}^q{(-1)}^i\left[\prod _{\mathsf{\ell }=1}^q\left[i+{(2\mathsf{\ell }-1)}^2\right]\right]\left[\sum _{j=m}^q\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\right])\hfill \end{array}$$

(93)

for $q\ge m\in {\mathbb{N}}_0$.

Proof. 

Letting $z\to k^{\theta }i$ for $0\le k\le q-1$ with $q\in \mathbb{N}$ and $\theta >0$ in (83) yields

$${[(q-1)!]}^2={(-1)}^{q-1}t(2q,2)$$

(94)

and

$$\prod _{\mathsf{\ell }=1}^{q-1}\left(k^{2\theta }+{\mathsf{\ell }}^2\right)=\sum _{\mathsf{\ell }=1}^q\left[{(-1)}^{q-\mathsf{\ell }}t(2q,2\mathsf{\ell })\right]k^{2\theta (\mathsf{\ell }-1)},1\le k\le q-1.$$

(95)

Let

$$A_q\left(\mathsf{\ell }\right)={(-1)}^{q-\mathsf{\ell }}t(2q,2\mathsf{\ell }),1\le \mathsf{\ell }\le q.$$

(96)

Then, Equations (94) and (95) can be written as

$$\left(\begin{array}{cccccc}1& 0& 0& \dots & 0& 0\\ 1& 1& 1& \dots & 1& 1\\ 1& 2^{2\theta }& 2^{4\theta }& \dots & 2^{2\theta (q-2)}& 2^{2\theta (q-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& {(q-2)}^{2\theta }& {(q-2)}^{4\theta }& \dots & {(q-2)}^{2\theta (q-2)}& {(q-2)}^{2\theta (q-1)}\\ 1& {(q-1)}^{2\theta }& {(q-1)}^{4\theta }& \dots & {(q-1)}^{2\theta (q-2)}& {(q-1)}^{2\theta (q-1)}\end{array}\right)\left(\begin{array}{c}{A}_q\left(1\right)\\ A_q\left(2\right)\\ A_q\left(3\right)\\ ⋮\\ A_q(q-1)\\ A_q\left(q\right)\end{array}\right)=\left(\begin{array}{c}{\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(0^{2\theta }+{\mathsf{\ell }}^2\right)\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(1^{2\theta }+{\mathsf{\ell }}^2\right)\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(2^{2\theta }+{\mathsf{\ell }}^2\right)\\ ⋮\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left[{(q-2)}^{2\theta }+{\mathsf{\ell }}^2\right]\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left[{(q-1)}^{2\theta }+{\mathsf{\ell }}^2\right]\end{array}\right).$$

Accordingly, setting $\theta ={\displaystyle \frac{1}{2}}$, we obtain

$$\left(\begin{array}{c}{A}_q\left(1\right)\\ A_q\left(2\right)\\ A_q\left(3\right)\\ ⋮\\ A_q(q-1)\\ A_q\left(q\right)\end{array}\right)={\left(\begin{array}{cccccc}1& 0& 0& \dots & 0& 0\\ 1& 1& 1& \dots & 1& 1\\ 1& 2& 2^2& \dots & 2^{q-2}& 2^{q-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& q-2& {(q-2)}^2& \dots & {(q-2)}^{q-2}& {(q-2)}^{q-1}\\ 1& q-1& {(q-1)}^2& \dots & {(q-1)}^{q-2}& {(q-1)}^{q-1}\end{array}\right)}^{-1}\left(\begin{array}{c}{\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(0+{\mathsf{\ell }}^2\right)\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(1+{\mathsf{\ell }}^2\right)\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(2+{\mathsf{\ell }}^2\right)\\ ⋮\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(q-2+{\mathsf{\ell }}^2\right)\\ {\displaystyle {\prod }_{\mathsf{\ell }=1}^{q-1}}\left(q-1+{\mathsf{\ell }}^2\right)\end{array}\right).$$

In view of the closed-form expression (91) in Proposition 4, we acquire

$$\begin{array}{cc}\left(\begin{array}{c}{A}_q\left(1\right)\\ A_q\left(2\right)\\ A_q\left(3\right)\\ ⋮\\ A_q(q-1)\\ A_q\left(q\right)\end{array}\right)\hfill & =\left(\begin{array}{cc}1& \mathbf{0}(q-1)\\ -U(q-1){\mathbf{1}}^T(q-1)& U(q-1)\end{array}\right)\left(\begin{array}{c}{\prod }_{\mathsf{\ell }=1}^{q-1}\left(0+{\mathsf{\ell }}^2\right)\\ {\prod }_{\mathsf{\ell }=1}^{q-1}\left(1+{\mathsf{\ell }}^2\right)\\ {\prod }_{\mathsf{\ell }=1}^{q-1}\left(2+{\mathsf{\ell }}^2\right)\\ ⋮\\ {\prod }_{\mathsf{\ell }=1}^{q-1}\left(q-2+{\mathsf{\ell }}^2\right)\\ {\prod }_{\mathsf{\ell }=1}^{q-1}\left(q-1+{\mathsf{\ell }}^2\right)\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{c}{\prod }_{\mathsf{\ell }=1}^{q-1}\left(0+{\mathsf{\ell }}^2\right)\\ {\sum }_{i=1}^{q-1}\left[u_{1,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]-{\prod }_{\mathsf{\ell }=1}^{q-1}\left(0+{\mathsf{\ell }}^2\right){\sum }_{i=1}^{q-1}{u}_{1,i}(q-1)\\ {\sum }_{i=1}^{q-1}\left[u_{2,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]-{\prod }_{\mathsf{\ell }=1}^{q-1}\left(0+{\mathsf{\ell }}^2\right){\sum }_{i=1}^{q-1}{u}_{2,i}(q-1)\\ ⋮\\ {\sum }_{i=1}^{q-1}\left[u_{q-2,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]-{\prod }_{\mathsf{\ell }=1}^{q-1}\left(0+{\mathsf{\ell }}^2\right){\sum }_{i=1}^{q-1}{u}_{q-2,i}(q-1)\\ {\sum }_{i=1}^{q-1}\left[u_{q-1,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]-{\prod }_{\mathsf{\ell }=1}^{q-1}\left(0+{\mathsf{\ell }}^2\right){\sum }_{i=1}^{q-1}{u}_{q-1,i}(q-1)\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{c}{[(q-1)!]}^2\\ {\sum }_{i=1}^{q-1}\left[u_{1,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]+{[(q-1)!]}^2{\sum }_{j=1}^{q-1}{\displaystyle \frac{{(-1)}^{j}s(j,1)}{j!}}\\ {\sum }_{i=1}^{q-1}\left[u_{2,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]+{[(q-1)!]}^2{\sum }_{j=2}^{q-1}{\displaystyle \frac{{(-1)}^{j}s(j,2)}{j!}}\\ ⋮\\ {\sum }_{i=1}^{q-1}\left[u_{q-2,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]+{[(q-1)!]}^2{\sum }_{j=q-2}^{q-1}{\displaystyle \frac{{(-1)}^{j}s(j,q-2)}{j!}}\\ {\sum }_{i=1}^{q-1}\left[u_{q-1,i}(q-1){\prod }_{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]+{[(q-1)!]}^2{\sum }_{j=q-1}^{q-1}{\displaystyle \frac{{(-1)}^{j}s(j,q-1)}{j!}}\end{array}\right).\hfill \end{array}$$

As a result, we find

$$\begin{array}{c}{A}_q(m+1)=\sum _{i=1}^{q-1}\left[u_{m,i}(q-1)\prod _{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]+{[(q-1)!]}^2\sum _{j=m}^{q-1}{\displaystyle \frac{{(-1)}^{j}s(j,m)}{j!}}\hfill \\ ={(-1)}^m\left[\sum _{i=1}^{q-1}\left(\sum _{j=m}^{q-1}{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\right)\prod _{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)+{[(q-1)!]}^2\sum _{j=m}^{q-1}{\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\right]\hfill \end{array}$$

(97)

for $1\le m\le q-1\in \mathbb{N}$. The closed-form formula (97) is thus proved for $m\in \mathbb{N}$.

Since $s(0,0)=1$, $s(\mathsf{\ell },0)=0$ for $\mathsf{\ell }\in \mathbb{N}$, and $\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right)=0$ for $j<i$, equality (94) can also be deduced from taking $m=0$ in the explicit formula (97).

Combining (97) for $m\in {\mathbb{N}}_0$ with the definition (96) and replacing m with $m-1$ lead to (92) immediately.

Letting $z\to {\displaystyle \frac{k^{\theta }}{2}}i$ for $0\le k\le q$ with $q\in \mathbb{N}$ and $\theta >0$ in (85) yields

$${[(2q-1)!!]}^2=4^q\left[{(-1)}^{q}t(2q+1,1)\right]$$

(98)

and

$$\prod _{\mathsf{\ell }=1}^q\left[k^{2\theta }+{(2\mathsf{\ell }-1)}^2\right]=\sum _{\mathsf{\ell }=0}^q{4}^{q-\mathsf{\ell }}\left[{(-1)}^{q-\mathsf{\ell }}t(2q+1,2\mathsf{\ell }+1)\right]k^{2\theta \mathsf{\ell }},1\le k\le q.$$

(99)

Let

$$B_q\left(\mathsf{\ell }\right)=4^{q-\mathsf{\ell }}\left[{(-1)}^{q-\mathsf{\ell }}t(2q+1,2\mathsf{\ell }+1)\right],0\le \mathsf{\ell }\le q.$$

(100)

Then, the equations in (98) and (99) can be combined as

$$\left(\begin{array}{cccccc}1& 0& 0& \dots & 0& 0\\ 1& 1& 1& \dots & 1& 1\\ 1& 2^{2\theta }& 2^{4\theta }& \dots & 2^{2\theta (q-1)}& 2^{2\theta q}\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& {(q-1)}^{2\theta }& {(q-1)}^{4\theta }& \dots & {(q-1)}^{2\theta (q-1)}& {(q-1)}^{2\theta q}\\ 1& q^{2\theta }& q^{4\theta }& \dots & q^{2\theta (q-1)}& q^{2\theta q}\end{array}\right)\left(\begin{array}{c}{B}_q\left(0\right)\\ B_q\left(1\right)\\ B_q\left(2\right)\\ ⋮\\ B_q(q-1)\\ B_q\left(q\right)\end{array}\right)=\left(\begin{array}{c}{\prod }_{\mathsf{\ell }=1}^q\left[0^{2\theta }+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[1^{2\theta }+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[2^{2\theta }+{(2\mathsf{\ell }-1)}^2\right]\\ ⋮\\ {\prod }_{\mathsf{\ell }=1}^q\left[{(q-1)}^{2\theta }+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[q^{2\theta }+{(2\mathsf{\ell }-1)}^2\right]\end{array}\right).$$

Therefore, letting $\theta ={\displaystyle \frac{1}{2}}$, we acquire

$$\left(\begin{array}{c}{B}_q\left(0\right)\\ B_q\left(1\right)\\ B_q\left(2\right)\\ ⋮\\ B_q(q-1)\\ B_q\left(q\right)\end{array}\right)={\left(\begin{array}{cccccc}1& 0& 0& \dots & 0& 0\\ 1& 1& 1& \dots & 1& 1\\ 1& 2& 2^2& \dots & 2^{q-1}& 2^q\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& q-1& {(q-1)}^2& \dots & {(q-1)}^{q-1}& {(q-1)}^q\\ 1& q& q^2& \dots & q^{q-1}& q^q\end{array}\right)}^{-1}\left(\begin{array}{c}{\prod }_{\mathsf{\ell }=1}^q\left[0+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[1+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[2+{(2\mathsf{\ell }-1)}^2\right]\\ ⋮\\ {\prod }_{\mathsf{\ell }=1}^q\left[q-1+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[q+{(2\mathsf{\ell }-1)}^2\right]\end{array}\right).$$

By means of the closed-form expression (91) in Proposition 4, we determine that

$$\left(\begin{array}{c}{B}_q\left(0\right)\\ B_q\left(1\right)\\ B_q\left(2\right)\\ ⋮\\ B_q(q-1)\\ B_q\left(q\right)\end{array}\right)=\left(\begin{array}{cc}1& \mathbf{0}\left(q\right)\\ -U\left(q\right){\mathbf{1}}^T\left(q\right)& U\left(q\right)\end{array}\right)\left(\begin{array}{c}{\prod }_{\mathsf{\ell }=1}^q\left[0+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[1+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[2+{(2\mathsf{\ell }-1)}^2\right]\\ ⋮\\ {\prod }_{\mathsf{\ell }=1}^q\left[q-1+{(2\mathsf{\ell }-1)}^2\right]\\ {\prod }_{\mathsf{\ell }=1}^q\left[q+{(2\mathsf{\ell }-1)}^2\right]\end{array}\right).$$

This implies that

$$\begin{array}{cc}{B}_q\left(m\right)\hfill & =\sum _{i=1}^q\left[u_{m,i}\left(q\right)\prod _{\mathsf{\ell }=1}^q\left[i+{(2\mathsf{\ell }-1)}^2\right]\right]+{[(2q-1)!!]}^2\sum _{j=m}^q{\displaystyle \frac{{(-1)}^{j}s(j,m)}{j!}}\hfill \\ \hfill & ={(-1)}^m\left[\sum _{i=1}^q\left(\sum _{j=m}^q{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\right)\prod _{\mathsf{\ell }=1}^q\left[i+{(2\mathsf{\ell }-1)}^2\right]+{[(2q-1)!!]}^2\sum _{j=m}^q{\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\right]\hfill \end{array}$$

(101)

for $0\le m\le q$, as discussed about (97). Combining (101) with (100) yields (93). The proof of Proposition 5 is complete. □

Remark 3.

If $\theta \ne {\displaystyle \frac{1}{2}}$ in the proof of Proposition 5, what will happen?

Remark 4.

The closed-form formula (80) is simpler than (92), while formula (81) is simpler than (93).

Different from the manner in ([28], p. 217, Table 6.1) (see Figure 1), we list several values of $t(q+2\mathsf{\ell },q)$ in a new manner in Table 2 and Table 3.

Table 2. The values of $t(2q,2m)$ for $q\ge m\in \mathbb{N}$.

$\mathit{t}(2\mathit{q},2\mathit{m})$	$\mathit{m}=1$	$\mathit{m}=2$	$\mathit{m}=3$	$\mathit{m}=4$	$\mathit{m}=5$	$\mathit{m}=6$	$\mathit{m}=7$
$q=1$	1
$q=2$	−1	1
$q=3$	4	−5	1
$q=4$	−36	49	−14	1
$q=5$	576	−820	273	−30	1
$q=6$	−14400	21076	−7645	1023	−55	1
$q=7$	518400	−773136	296296	−44473	3003	−91	1

Table 3. The values of $t(2q+1,2m+1)$ for $5\ge q\ge m\ge 0$.

$\mathit{t}(2\mathit{q}+1,2\mathit{m}+1)$	$\mathit{m}=0$	$\mathit{m}=1$	$\mathit{m}=2$	$\mathit{m}=3$	$\mathit{m}=4$	$\mathit{m}=5$
$q=0$	1
$q=1$	$-{\displaystyle \frac{1}{4}}$	1
$q=2$	${\displaystyle \frac{9}{16}}$	$-{\displaystyle \frac{5}{2}}$	1
$q=3$	$-{\displaystyle \frac{225}{64}}$	${\displaystyle \frac{259}{16}}$	$-{\displaystyle \frac{35}{4}}$	1
$q=4$	${\displaystyle \frac{11025}{256}}$	$-{\displaystyle \frac{3229}{16}}$	${\displaystyle \frac{987}{8}}$	−21	1
$q=5$	$-{\displaystyle \frac{893025}{1024}}$	${\displaystyle \frac{1057221}{256}}$	$-{\displaystyle \frac{86405}{32}}$	${\displaystyle \frac{4389}{8}}$	$-{\displaystyle \frac{165}{4}}$	1

The signs ± shown in Table 2 and Table 3 help us to prove the following proposition.

Proposition 6.

For $q\ge \mathsf{\ell }\in \mathbb{N}$, central factorial numbers of the first kind $t(q,\mathsf{\ell })$ can be computed by

$$\begin{array}{cc}t(2q,2\mathsf{\ell })\hfill & ={(-1)}^{q-\mathsf{\ell }}\sum _{1\le j_1<j_2<\dots <j_{q-\mathsf{\ell }}\le q-1}\prod _{m=1}^{q-\mathsf{\ell }}{\left(j_m\right)}^2,\hfill \end{array}$$

(102)

$$\begin{array}{cc}t(2q-1,2\mathsf{\ell }-1)\hfill & ={(-1)}^{q-\mathsf{\ell }}\sum _{1\le j_1<j_2<\dots <j_{q-\mathsf{\ell }}\le q-1}\prod _{m=1}^{q-\mathsf{\ell }}{\left(j_m-{\displaystyle \frac{1}{2}}\right)}^2,\hfill \end{array}$$

(103)

and

$$t(q,\mathsf{\ell })={(-1)}^{q-\mathsf{\ell }}\sum _{1\le j_1<j_2<\dots <j_{q-\mathsf{\ell }}\le q-1}\prod _{k=1}^{q-\mathsf{\ell }}\left(j_k-{\displaystyle \frac{q}{2}}\right).$$

(104)

Consequently, for $q\ge \mathsf{\ell }\in \mathbb{N}$, we have

$${(-1)}^{q-\mathsf{\ell }}t(2q,2\mathsf{\ell })>0\mathrm{and}{(-1)}^{q-\mathsf{\ell }}t(2q-1,2\mathsf{\ell }-1)>0.$$

(105)

Proof. 

The idea of this proof originates from the hint in the comment at https://mathoverflow.net/q/456136/#comment1182208_456481 (accessed on 15 October 2023) by Fedor Petrov.

The Vieta theorem ([68], Section 2) states that if $c_q\ne 0$ and

$$f\left(z\right)=c_q{z}^q+c_{q-1}{z}^{q-1}+\dots +c_{1}z+c_0=\prod _{\mathsf{\ell }=1}^q(z-z_{\mathsf{\ell }})$$

for $q\in \mathbb{N}$, then

$${\displaystyle \frac{c_{q-\mathsf{\ell }}}{c_q}}={(-1)}^{\mathsf{\ell }}\sum _{1\le j_1<j_2<\dots <j_{\mathsf{\ell }}\le q}\prod _{m=1}^{\mathsf{\ell }}{z}_{j_m},1\le \mathsf{\ell }\le q.$$

(106)

Applying this theorem to Equations (83) and (85) results in

$$\begin{array}{cc}\sum _{\mathsf{\ell }=0}^{q-1}t(2q,2\mathsf{\ell }+2)z^{2\mathsf{\ell }}\hfill & =\prod _{\mathsf{\ell }=1}^{q-1}\left(z^2-{\mathsf{\ell }}^2\right)\hfill \\ \hfill & =\sum _{\mathsf{\ell }=0}^{q-1}\left[{(-1)}^{q-\mathsf{\ell }-1}\sum _{1\le j_1<j_2<\dots <j_{q-\mathsf{\ell }-1}\le q-1}\prod _{m=1}^{q-\mathsf{\ell }-1}{\left(j_m\right)}^2\right]z^{2\mathsf{\ell }}\hfill \end{array}$$

and

$$\begin{array}{cc}\sum _{\mathsf{\ell }=0}^{q}t(2q+1,2\mathsf{\ell }+1)z^{2\mathsf{\ell }}\hfill & =\prod _{\mathsf{\ell }=1}^q\left[z^2-{\left(\mathsf{\ell }-{\displaystyle \frac{1}{2}}\right)}^2\right]\hfill \\ \hfill & =\sum _{\mathsf{\ell }=0}^q\left[{(-1)}^{q-\mathsf{\ell }}\sum _{1\le j_1<j_2<\dots <j_{q-\mathsf{\ell }}\le q}\prod _{m=1}^{q-\mathsf{\ell }}{\left(j_m-{\displaystyle \frac{1}{2}}\right)}^2\right]z^{2\mathsf{\ell }}\hfill \end{array}$$

for $q\in \mathbb{N}$. Therefore, we deduce Formulas (102) and (103).

Equation (68) can be rewritten as

$$\sum _{\mathsf{\ell }=0}^{q-1}t(q,\mathsf{\ell }+1)z^{\mathsf{\ell }}=\prod _{\mathsf{\ell }=1}^{q-1}\left(z+{\displaystyle \frac{q}{2}}-\mathsf{\ell }\right),q\in \mathbb{N}.$$

By virtue of the Vieta theorem ([68], Section 2) expressed around Equation (106), we derive Formula (104). The proof of Proposition 6 is complete. □

Corollary 2.

For $q,\mathsf{\ell }\in \mathbb{N}$, the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ defined by (7) is positive.

Proof. 

This follows from the combination of two inequalities in (105) with identity (73) in Proposition 2. □

Corollary 3.

For $1\le \mathsf{\ell }\le q\in \mathbb{N}$, we have

$${(-1)}^{\mathsf{\ell }}\left({(q!)}^2\sum _{j=\mathsf{\ell }}^q{\displaystyle \frac{\left|s\right(j,\mathsf{\ell }\left)\right|}{j!}}+\sum _{i=1}^q{(-1)}^i\left[\sum _{j=\mathsf{\ell }}^q\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,\mathsf{\ell }\left)\right|}{j!}}\right]\prod _{k=1}^q\left(i+k^2\right)\right)>0$$

and

$${(-1)}^{\mathsf{\ell }}\left({[(2q-1)!!]}^2\sum _{j=\mathsf{\ell }}^q{\displaystyle \frac{\left|s\right(j,\mathsf{\ell }\left)\right|}{j!}}+\sum _{i=1}^q{(-1)}^i\left[\sum _{j=\mathsf{\ell }}^q\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,\mathsf{\ell }\left)\right|}{j!}}\right]\prod _{k=1}^q\left[i+{(2k-1)}^2\right]\right)>0,$$

where $s(j,\mathsf{\ell })$ is the Stirling numbers of the first kind generated by (8).

Proof. 

From the proof of Proposition 5, we conclude that

$$\begin{array}{cc}{A}_q(m+1)\hfill & =\sum _{i=1}^{q-1}\left[u_{m,i}(q-1)\prod _{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right]-\prod _{\mathsf{\ell }=1}^{q-1}\left(0+{\mathsf{\ell }}^2\right)\sum _{i=1}^{q-1}{u}_{m,i}(q-1)\hfill \\ \hfill & ={(-1)}^m\left[\sum _{i=1}^{q-1}{(-1)}^i|u_{m,i}(q-1)|\prod _{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)-{[(q-1)!]}^2\sum _{i=1}^{q-1}{(-1)}^i|u_{m,i}(q-1)|\right]\hfill \end{array}$$

for $1\le m\le q-1\in \mathbb{N}$ and

$$\begin{array}{cc}{B}_q\left(m\right)\hfill & =\sum _{i=1}^q\left[u_{m,i}\left(q\right)\prod _{\mathsf{\ell }=1}^q\left[i+{(2\mathsf{\ell }-1)}^2\right]\right]-\prod _{\mathsf{\ell }=1}^q\left[0+{(2\mathsf{\ell }-1)}^2\right]\sum _{i=1}^q{u}_{m,i}\left(q\right)\hfill \\ \hfill & ={(-1)}^m\left[\sum _{i=1}^q{(-1)}^i|u_{m,i}\left(q\right)|\prod _{\mathsf{\ell }=1}^q\left[i+{(2\mathsf{\ell }-1)}^2\right]-{[(2q-1)!!]}^2\sum _{i=1}^q{(-1)}^i\left|u_{m,i}\left(q\right)\right|\right]\hfill \end{array}$$

for $1\le m\le q\in \mathbb{N}$, where

$$\begin{array}{cc}{(-1)}^{k-i}{u}_{k,i}\left(q\right)\hfill & ={(-1)}^{k-i}\sum _{j=k}^q{(-1)}^{j+i}\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{s(j,k)}{j!}}\hfill \\ \hfill & =\sum _{j=k}^q\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,k\left)\right|}{j!}}\hfill \\ \hfill & =|u_{k,i}\left(q\right)|\hfill \\ \hfill & >0\hfill \end{array}$$

and

$$\begin{array}{cc}\sum _{i=1}^q{(-1)}^i\left|u_{k,i}\left(q\right)\right|\hfill & =\sum _{i=1}^q{(-1)}^i\sum _{j=k}^q\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,k\left)\right|}{j!}}\hfill \\ \hfill & =\sum _{j=k}^q\left[\sum _{i=1}^q{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right)\right]{\displaystyle \frac{\left|s\right(j,k\left)\right|}{j!}}\hfill \\ \hfill & =\sum _{j=k}^q\left[\sum _{i=1}^j{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right)\right]{\displaystyle \frac{\left|s\right(j,k\left)\right|}{j!}}\hfill \\ \hfill & =-\sum _{j=k}^q{\displaystyle \frac{\left|s\right(j,k\left)\right|}{j!}}\hfill \end{array}$$

for $1\le i,k\le q$. Therefore, the positivity $A_q(m+1)>0$ for $1\le m\le q-1\in \mathbb{N}$ and $B_q\left(m\right)>0$ for $1\le m\le q$ are equivalent to

$${(-1)}^m\left({[(q-1)!]}^2\sum _{j=m}^{q-1}{\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}+\sum _{i=1}^{q-1}{(-1)}^i\left[\sum _{j=m}^{q-1}\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\right]\prod _{\mathsf{\ell }=1}^{q-1}\left(i+{\mathsf{\ell }}^2\right)\right)>0$$

for $1\le m\le q-1\in \mathbb{N}$ and

$${(-1)}^m\left({[(2q-1)!!]}^2\sum _{j=m}^q{\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}+\sum _{i=1}^q{(-1)}^i\left[\sum _{j=m}^q\left({\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right){\displaystyle \frac{\left|s\right(j,m\left)\right|}{j!}}\right]\prod _{\mathsf{\ell }=1}^q\left[i+{(2\mathsf{\ell }-1)}^2\right]\right)>0$$

for $1\le m\le q\in \mathbb{N}$. The required proof is complete. □

5. Logarithmic Convexity of Normalized Remainders

In this section, we demonstrate the logarithmic convexity of the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ in $z\in [0,1)$ for $1\le q\le 5$ and $n\ge 0$, and derive five inequalities involving the power functions ${\left({\displaystyle \frac{arcsinz}{z}}\right)}^q$ for $1\le q\le 5$.

Theorem 2.

For $1\le q\le 5$ and $n\in {\mathbb{N}}_0$, the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ defined by (53) is positive, increasing, convex, absolutely monotonic, and logarithmically convex in $z\in [0,1)$, with the inequalities

$$\begin{array}{c}\left[2n+3+{\displaystyle \frac{{(2n+3)}^2}{(n+2)(2n+5)}}{z}^2\right]{\displaystyle \frac{arcsinz}{z}}\hfill \\ <{\displaystyle \frac{1}{\sqrt{1-z^2}}}+\left[2n+2+{\displaystyle \frac{{(2n+3)}^2}{(n+2)(2n+5)}}{z}^2\right]\\ +{\displaystyle \sum _{\mathsf{\ell }=1}^n}\left[2n-2\mathsf{\ell }+2+{\displaystyle \frac{{(2n+3)}^2}{(n+2)(2n+5)}}{z}^2\right]{\displaystyle \frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}},\end{array}$$

(107)

$$\begin{array}{c}\left[2n+4+{\displaystyle \frac{{(2n+4)}^2}{(2n+5)(n+3)}}{z}^2\right]{\left({\displaystyle \frac{arcsinz}{z}}\right)}^2\hfill \\ <{\displaystyle \frac{2}{\sqrt{1-z^2}}}{\displaystyle \frac{arcsinz}{z}}+\left[2n+2+{\displaystyle \frac{{(2n+4)}^2}{(2n+5)(n+3)}}{z}^2\right]\\ +{\displaystyle \sum _{\ell =1}^n}\left[2n-2\ell +2+{\displaystyle \frac{{(2n+4)}^2}{(2n+5)(n+3)}}{z}^2\right]{\displaystyle \frac{{[(2\ell )!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\ell +2}{2}\right)}}{\displaystyle \frac{z^{2\ell }}{(2\ell )!}},\end{array}$$

(108)

$$\begin{array}{c}\left[2n+5+{\displaystyle \frac{{(2n+5)}^2}{(n+3)(2n+7)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}}}{z}^2\right]{\left({\displaystyle \frac{arcsinz}{z}}\right)}^3\hfill \\ <{\displaystyle \frac{3}{\sqrt{1-z^2}}}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^2+\left[2n+2+{\displaystyle \frac{{(2n+5)}^2}{(n+3)(2n+7)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}}}{z}^2\right]\\ +{\displaystyle \sum _{\ell =1}^n}\left[2n-2\ell +2+{\displaystyle \frac{{(2n+5)}^2}{(n+3)(2n+7)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}}}{z}^2\right]{\displaystyle \frac{{[(2\ell +1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{\ell \ell +3}{3}\right)}}\left[\sum _{k=0}^{\ell }{\displaystyle \frac{1}{{(2k+1)}^2}}\right]{\displaystyle \frac{z^{2\ell }}{(2\ell )!}},\end{array}$$

(109)

$$\begin{array}{c}\left[2n+6+{\displaystyle \frac{{(2n+6)}^2}{(2n+7)(n+4)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}}{z}^2\right]{\left({\displaystyle \frac{arcsinz}{z}}\right)}^4\hfill \\ <{\displaystyle \frac{4}{\sqrt{1-z^2}}}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^3+\left[2n+2+{\displaystyle \frac{{(2n+6)}^2}{(2n+7)(n+4)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}}{z}^2\right]\\ +{\displaystyle \sum _{\ell =1}^n}\left[2n-2\ell +2+{\displaystyle \frac{{(2n+6)}^2}{(2n+7)(n+4)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}}{z}^2\right]{\displaystyle \frac{{[(2\ell +2)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\ell +4}{4}\right)}}\left[\sum _{k=0}^{\ell }{\displaystyle \frac{1}{{(2k+2)}^2}}\right]{\displaystyle \frac{z^{2\ell }}{(2\ell )!}},\end{array}$$

(110)

and

$$\begin{array}{cc}[2n+7+\hfill & {\displaystyle \frac{{(2n+7)}^2}{(n+4)(2n+9)}}{\displaystyle \frac{{\left[{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^4}}{{\left[{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^4}}}{z}^2]{\left({\displaystyle \frac{arcsinz}{z}}\right)}^5\hfill \\ & <{\displaystyle \frac{5}{\sqrt{1-z^2}}}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^4+[2n+2+{\displaystyle \frac{{(2n+7)}^2}{(n+4)(2n+9)}}\hfill \\ & \times {\displaystyle \frac{{\left[{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^4}}{{\left[{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^4}}}{z}^2]+{\displaystyle \frac{1}{2}}\sum _{\mathsf{\ell }=1}^n[2n-2\mathsf{\ell }+2\hfill \\ & +{\displaystyle \frac{{(2n+7)}^2}{(n+4)(2n+9)}}{\displaystyle \frac{{\left[{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^4}}{{\left[{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^4}}}{z}^2]{\displaystyle \frac{{[(2\mathsf{\ell }+3)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+5}{5}\right)}}\hfill \\ & \times \left[{\left({\displaystyle \sum _{k=0}^{\mathsf{\ell }+1}}{\displaystyle \frac{1}{{(2k+1)}^2}}\right)}^2-{\displaystyle \sum _{k=0}^{\mathsf{\ell }+1}}{\displaystyle \frac{1}{{(2k+1)}^4}}\right]{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\hfill \end{array}$$

(111)

for $n\ge 0$ and $0<\left|z\right|<1$.

Proof. 

The positivity, increasing property, convexity, and absolute monotonicity of the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ follow from series expression (54) and the positivity of the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ in Corollary 2.

Let $a_{\mathsf{\ell }}$ and $b_{\mathsf{\ell }}$ for $\mathsf{\ell }\in {\mathbb{N}}_0$ be real numbers and the power series

$$A\left(z\right)=\sum _{\mathsf{\ell }=0}^{\infty }{a}_{\mathsf{\ell }}{z}^{\mathsf{\ell }}\mathrm{and}B\left(z\right)=\sum _{\mathsf{\ell }=0}^{\infty }{b}_{\mathsf{\ell }}{z}^{\mathsf{\ell }}$$

(112)

be convergent on $(-R,R)$ for some $R>0$. If $b_{\mathsf{\ell }}>0$ and the ratio ${\displaystyle \frac{a_{\mathsf{\ell }}}{b_{\mathsf{\ell }}}}$ is increasing for $\mathsf{\ell }\ge 0$, then the function ${\displaystyle \frac{A\left(z\right)}{B\left(z\right)}}$ is also increasing on $(0,R)$. This statement was first established in [69] and is called the monotonicity rule for the ratio of two power series.

Making use of series expansion (1) yields

$$\begin{array}{cc}{\mathfrak{T}}_{1,n}\left(z\right)\hfill & ={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{2n+3}{1}\right)}{{[(2n+1)!!]}^2}}{\displaystyle \frac{(2n+2)!}{z^{2n+2}}}\left[{\displaystyle \frac{arcsinz}{z}}-\sum _{\mathsf{\ell }=0}^n{\displaystyle \frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\right]\hfill \\ \hfill & ={\displaystyle \frac{(2n+3)!}{{[(2n+1)!!]}^2}}\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }+2n+1)!!]}^2}{(2\mathsf{\ell }+2n+3)!}}{z}^{2\mathsf{\ell }},\left|z\right|<1.\hfill \end{array}$$

(113)

Its logarithmic derivative is

$${\displaystyle \frac{{\mathfrak{T}}_{1,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{1,n}\left(z\right)}}={\displaystyle \frac{2z{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+3)!!]}^2}{(2\mathsf{\ell }+2n+5)!}(\mathsf{\ell }+1)z^{2\mathsf{\ell }}}{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+1)!!]}^2}{(2\mathsf{\ell }+2n+3)!}{z}^{2\mathsf{\ell }}}},\left|z\right|<1.$$

Hence, it follows that

$${\mathfrak{Q}}_{1,n}\left(\mathsf{\ell }\right)={\displaystyle \frac{2\frac{{[(2\mathsf{\ell }+2n+3)!!]}^2}{(2\mathsf{\ell }+2n+5)!}(\mathsf{\ell }+1)}{\frac{{[(2\mathsf{\ell }+2n+1)!!]}^2}{(2\mathsf{\ell }+2n+3)!}}}={\displaystyle \frac{2(\mathsf{\ell }+1){(2\mathsf{\ell }+2n+3)}^2}{(2\mathsf{\ell }+2n+4)(2\mathsf{\ell }+2n+5)}}$$

(114)

for $\mathsf{\ell },n\in {\mathbb{N}}_0$. The inequality ${\mathfrak{Q}}_{1,n}\left(\mathsf{\ell }\right)<{\mathfrak{Q}}_{1,n}(\mathsf{\ell }+1)$ is equivalent to

$${\displaystyle \frac{(\mathsf{\ell }+1){(2\mathsf{\ell }+2n+3)}^2}{(2\mathsf{\ell }+2n+4)(2\mathsf{\ell }+2n+5)}}<{\displaystyle \frac{(\mathsf{\ell }+2){(2\mathsf{\ell }+2n+5)}^2}{(2\mathsf{\ell }+2n+6)(2\mathsf{\ell }+2n+7)}}$$

which can be rearranged as

$$\begin{array}{c}8n^4+4(8\mathsf{\ell }+19)n^3+6\left(8{\mathsf{\ell }}^2+40\mathsf{\ell }+47\right)n^2 \hfill \\ +\left(32{\mathsf{\ell }}^3+252{\mathsf{\ell }}^2+620\mathsf{\ell }+481\right)n+8{\mathsf{\ell }}^4+88{\mathsf{\ell }}^3+338{\mathsf{\ell }}^2+542\mathsf{\ell }+311>0\hfill \end{array}$$

for $\mathsf{\ell },n\in {\mathbb{N}}_0$. As a result, the sequence ${\mathfrak{Q}}_{1,n}\left(\mathsf{\ell }\right)$ is increasing in $\mathsf{\ell }\ge 0$ for given $n\ge 0$. Combining this monotonicity of the sequence ${\mathfrak{Q}}_{1,n}\left(\mathsf{\ell }\right)$ in $\mathsf{\ell }\ge 0$ for given $n\ge 0$ with the monotonicity rule stated around (112), we see that the function ${\displaystyle \frac{{\mathfrak{T}}_{1,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{1,n}\left(z\right)}}$, and then the logarithmic derivative ${\displaystyle \frac{{\mathfrak{T}}_{1,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{1,n}\left(z\right)}}$, is increasing in $z\in [0,1)$ for given $n\ge 0$. Consequently, the normalized remainder ${\mathfrak{T}}_{1,n}\left(z\right)$ is logarithmically convex in $z\in [0,1)$ for any given $n\ge 0$.

It is obvious that

$$\underset{z\to 0}{lim}{\displaystyle \frac{{\mathfrak{T}}_{1,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{1,n}\left(z\right)}}=\underset{z\to 0}{lim}{\displaystyle \frac{2{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+3)!!]}^2}{(2\mathsf{\ell }+2n+5)!}(\mathsf{\ell }+1)z^{2\mathsf{\ell }}}{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+1)!!]}^2}{(2\mathsf{\ell }+2n+3)!}{z}^{2\mathsf{\ell }}}}={\displaystyle \frac{{(2n+3)}^2}{(n+2)(2n+5)}}.$$

Using the first expression in (113), taking its logarithm, and differentiating give

$$\begin{array}{cc}{\displaystyle \frac{{\mathfrak{T}}_{1,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{1,n}\left(z\right)}}\hfill & ={\displaystyle \frac{\frac{1}{z\sqrt{1-z^2}}-\frac{arcsinz}{z^2}-{\sum }_{\mathsf{\ell }=1}^n\frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}\frac{z^{2\mathsf{\ell }-1}}{(2\mathsf{\ell }-1)!}}{\frac{arcsinz}{z}-{\sum }_{\mathsf{\ell }=0}^n\frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}-{\displaystyle \frac{2n+2}{z}}.\hfill \end{array}$$

Accordingly, we acquire

$${\displaystyle \frac{\frac{1}{z}\frac{1}{\sqrt{1-z^2}}-\frac{1}{z}\frac{arcsinz}{z}-\frac{1}{z}{\sum }_{\mathsf{\ell }=1}^n\frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}\frac{z^{2\mathsf{\ell }}}{(2\mathsf{\ell }-1)!}}{\frac{arcsinz}{z}-{\sum }_{\mathsf{\ell }=0}^n\frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}-{\displaystyle \frac{2n+2}{z}}>{\displaystyle \frac{{(2n+3)}^2}{(n+2)(2n+5)}}z$$

for $n\ge 0$ and $z\in (0,1)$. Consequently, we obtain the inequality

$${\displaystyle \frac{\frac{1}{\sqrt{1-z^2}}-\frac{arcsinz}{z}-{\sum }_{\mathsf{\ell }=1}^n\frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}\frac{z^{2\mathsf{\ell }}}{(2\mathsf{\ell }-1)!}}{\frac{arcsinz}{z}-{\sum }_{\mathsf{\ell }=0}^n\frac{{[(2\mathsf{\ell }-1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+1}{1}\right)}\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}>2n+2+{\displaystyle \frac{{(2n+3)}^2}{(n+2)(2n+5)}}{z}^2$$

for $n\ge 0$ and $z\in (0,1)$. This inequality can be reformulated as (107).

From series expansion (2), it follows that

$$\begin{array}{cc}{\mathfrak{T}}_{2,n}\left(z\right)\hfill & ={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{2n+4}{2}\right)}{{[(2n+2)!!]}^2}}{\displaystyle \frac{(2n+2)!}{z^{2n+2}}}\left[{\left({\displaystyle \frac{arcsinz}{z}}\right)}^2-\sum _{\mathsf{\ell }=0}^n{\displaystyle \frac{{[\left(2\mathsf{\ell }\right)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+2}{2}\right)}}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\right]\hfill \\ \hfill & ={\displaystyle \frac{(2n+4)!}{{[(2n+2)!!]}^2}}\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }+2n+2)!!]}^2}{(2\mathsf{\ell }+2n+4)!}}{z}^{2\mathsf{\ell }}\hfill \end{array}$$

for $n\ge 0$ and $\left|z\right|<1$. Taking the logarithm and differentiating give

$${\displaystyle \frac{{\mathfrak{T}}_{2,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{2,n}\left(z\right)}}={\displaystyle \frac{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+4)!!]}^2}{(2\mathsf{\ell }+2n+6)!}(2\mathsf{\ell }+2)z^{2\mathsf{\ell }}}{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+2)!!]}^2}{(2\mathsf{\ell }+2n+4)!}{z}^{2\mathsf{\ell }}}}\to {\displaystyle \frac{{(2n+4)}^2}{(2n+5)(n+3)}},z\to 0$$

and

$${\mathfrak{Q}}_{2,n}\left(\mathsf{\ell }\right)={\displaystyle \frac{\frac{{[(2\mathsf{\ell }+2n+4)!!]}^2}{(2\mathsf{\ell }+2n+6)!}(2\mathsf{\ell }+2)}{\frac{{[(2\mathsf{\ell }+2n+2)!!]}^2}{(2\mathsf{\ell }+2n+4)!}}}={\displaystyle \frac{2(\mathsf{\ell }+1){(2\mathsf{\ell }+2n+4)}^2}{(2\mathsf{\ell }+2n+5)(2\mathsf{\ell }+2n+6)}},\mathsf{\ell },n\ge 0.$$

(115)

Regarding ℓ as a variable and differentiating yield

$${\mathfrak{Q}}_{2,n}^{\prime }\left(\mathsf{\ell }\right)={\displaystyle \frac{4(\mathsf{\ell }+n+2)\left[\begin{array}{c}2{\mathsf{\ell }}^3+6{\mathsf{\ell }}^2(n+3)+\mathsf{\ell }\left(6n^2+33n+48\right)\\ +2n^3+15n^2+40n+38]\end{array}\right]}{{(\mathsf{\ell }+n+3)}^2{(2\mathsf{\ell }+2n+5)}^2}}>0$$

for $\mathsf{\ell },n\ge 0$. This means that the sequence ${\mathfrak{Q}}_{2,n}\left(\mathsf{\ell }\right)$ is increasing in $\mathsf{\ell }\ge 0$ for fixed $n\ge 0$. Hence, by the monotonicity rule stated around equation (112), we see that the function ${\displaystyle \frac{{\mathfrak{T}}_{2,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{2,n}\left(z\right)}}$, and then the function ${\displaystyle \frac{{\mathfrak{T}}_{2,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{2,n}\left(z\right)}}$, is increasing in $z\in (0,1)$ for fixed $n\ge 0$. Consequently, the normalized remainder ${\mathfrak{T}}_{2,n}\left(z\right)$ is logarithmically convex in $z\in (0,1)$ for all $n\ge 0$, as well as

$${\displaystyle \frac{{\mathfrak{T}}_{2,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{2,n}\left(z\right)}}>{\displaystyle \frac{{(2n+4)}^2}{(2n+5)(n+3)}},z\in (0,1).$$

Because

$${\displaystyle \frac{{\mathfrak{T}}_{2,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{2,n}\left(z\right)}}={\displaystyle \frac{2}{z}}\left[{\displaystyle \frac{\frac{1}{\sqrt{1-z^2}}\frac{arcsinz}{z}-{\left(\frac{arcsinz}{z}\right)}^2-\frac{1}{2}{\sum }_{\mathsf{\ell }=1}^n\frac{{[\left(2\mathsf{\ell }\right)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+2}{2}\right)}\frac{z^{2\mathsf{\ell }}}{(2\mathsf{\ell }-1)!}}{{\left(\frac{arcsinz}{z}\right)}^2-{\sum }_{\mathsf{\ell }=0}^n\frac{{[\left(2\mathsf{\ell }\right)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+2}{2}\right)}\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}-(n+1)\right],$$

we derive the inequality

$${\displaystyle \frac{\frac{1}{\sqrt{1-z^2}}\frac{arcsinz}{z}-{\left(\frac{arcsinz}{z}\right)}^2-\frac{1}{2}{\sum }_{\mathsf{\ell }=1}^n\frac{{[\left(2\mathsf{\ell }\right)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+2}{2}\right)}\frac{z^{2\mathsf{\ell }}}{(2\mathsf{\ell }-1)!}}{{\left(\frac{arcsinz}{z}\right)}^2-{\sum }_{\mathsf{\ell }=0}^n\frac{{[\left(2\mathsf{\ell }\right)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+2}{2}\right)}\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}-n-1>{\displaystyle \frac{{(2n+4)}^2}{(2n+5)(n+3)}}{\displaystyle \frac{z^2}{2}}$$

which can be reformulated as inequality (108).

From series expansion (3), we derive

$$\begin{array}{cc}{\mathfrak{T}}_{3,n}\left(z\right)\hfill & ={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{2n+5}{3}\right)}{{[(2n+3)!!]}^2}}{\displaystyle \frac{1}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}}}{\displaystyle \frac{(2n+2)!}{z^{2n+2}}}\left\{{\left({\displaystyle \frac{arcsinz}{z}}\right)}^3-\sum _{\mathsf{\ell }=0}^n{\displaystyle \frac{{[(2\mathsf{\ell }+1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+3}{3}\right)}}\left[\sum _{k=0}^{\mathsf{\ell }}{\displaystyle \frac{1}{{(2k+1)}^2}}\right]{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\right\}\hfill \\ \hfill & ={\displaystyle \frac{(2n+5)!}{{[(2n+3)!!]}^2}}{\displaystyle \frac{1}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}}}\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }+2n+3)!!]}^2}{(2\mathsf{\ell }+2n+5)!}}\left[\sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+1)}^2}}\right]z^{2\mathsf{\ell }},\hfill \\ {\displaystyle \frac{{\mathfrak{T}}_{3,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{3,n}\left(z\right)}}\hfill & ={\displaystyle \frac{z{\sum }_{\mathsf{\ell }=0}^{\infty }(2\mathsf{\ell }+2)\frac{{[(2\mathsf{\ell }+2n+5)!!]}^2}{(2\mathsf{\ell }+2n+7)!}\left[{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}\right]z^{2\mathsf{\ell }}}{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+3)!!]}^2}{(2\mathsf{\ell }+2n+5)!}\left[{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+1)}^2}\right]z^{2\mathsf{\ell }}}},\hfill \end{array}$$

and

$$\begin{array}{cc}{\mathfrak{Q}}_{3,n}\left(\mathsf{\ell }\right)\hfill & ={\displaystyle \frac{(2\mathsf{\ell }+2)\frac{{[(2\mathsf{\ell }+2n+5)!!]}^2}{(2\mathsf{\ell }+2n+7)!}{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}}{\frac{{[(2\mathsf{\ell }+2n+3)!!]}^2}{(2\mathsf{\ell }+2n+5)!}{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+1)}^2}}}\hfill \\ \hfill & ={\displaystyle \frac{(2\mathsf{\ell }+2){(2\mathsf{\ell }+2n+5)}^2}{(2\mathsf{\ell }+2n+6)(2\mathsf{\ell }+2n+7)}}{\displaystyle \frac{{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+1)}^2}}}\hfill \end{array}$$

(116)

for $\mathsf{\ell },n\in {\mathbb{N}}_0$. The inequality ${\mathfrak{Q}}_{3,n}\left(\mathsf{\ell }\right)<{\mathfrak{Q}}_{3,n}(\mathsf{\ell }+1)$ is equivalent to

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}8{\mathsf{\ell }}^4+8{\mathsf{\ell }}^3(4n+15)+{\mathsf{\ell }}^2\left(48n^2+348n+638\right)\\ +2\mathsf{\ell }\left(16n^3+168n^2+598n+717\right)\\ +8n^4+108n^3+558n^2+1305n+1158\end{array}\right]{\left[\sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+1)}^2}}\right]}^2\hfill \\ \hfill & +{\displaystyle \frac{2}{{(2\mathsf{\ell }+2n+5)}^2}}\left[\begin{array}{c}4{\mathsf{\ell }}^3(2n+7)+2{\mathsf{\ell }}^2\left(12n^2+74n+123\right)\\ +\mathsf{\ell }\left(24n^3+212n^2+652n+702\right)\\ +8n^4+92n^3+406n^2+825n+654\end{array}\right]\left[\sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+1)}^2}}\right]\hfill \\ \hfill & -{\displaystyle \frac{(\mathsf{\ell }+1)(\mathsf{\ell }+n+4)(2\mathsf{\ell }+2n+9)}{{(2\mathsf{\ell }+2n+5)}^2}}>0\hfill \end{array}$$

(117)

for $\mathsf{\ell },n\in {\mathbb{N}}_0$. Because

$$1\le \sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+1)}^2}}<\sum _{k=0}^{\infty }{\displaystyle \frac{1}{{(2k+1)}^2}}={\displaystyle \frac{{\pi }^2}{8}}=1.233\dots ,$$

replacing ${\sum }_{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+1)}^2}}$ with a smaller scalar 1 in (117) leads to

$$\begin{array}{c}32{\mathsf{\ell }}^6+64{\mathsf{\ell }}^5(3n+10)+16{\mathsf{\ell }}^4\left(30n^2+197n+322\right)\\ +{\mathsf{\ell }}^3\left(640n^3+6208n^2+20064n+21550\right)\\ +{\mathsf{\ell }}^2\left(480n^4+6112n^3+29280n^2+62364n+49735\right)\\ +\mathsf{\ell }\left(192n^5+3008n^4+18976n^3+60078n^2+95227n+60361\right)\\ +32n^6+592n^5+4608n^4+19264n^3+45492n^2+57418n+30222>0\end{array}$$

for $\mathsf{\ell },n\in {\mathbb{N}}_0$. As a result, the sequence ${\mathfrak{Q}}_{3,n}\left(\mathsf{\ell }\right)$ is increasing in ℓ for fixed $n\ge 0$. Hence, by the monotonicity rule stated around Equation (112), we see that the function ${\displaystyle \frac{{\mathfrak{T}}_{3,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{3,n}\left(z\right)}}$, and then the function ${\displaystyle \frac{{\mathfrak{T}}_{3,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{3,n}\left(z\right)}}$, is increasing in $z\in (0,1)$ for fixed $n\ge 0$. Consequently, the normalized remainder ${\mathfrak{T}}_{3,n}\left(z\right)$ is logarithmically convex in $z\in (0,1)$ for all $n\ge 0$, as well as

$${\displaystyle \frac{{\mathfrak{T}}_{3,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{3,n}\left(z\right)}}>{\displaystyle \frac{2\frac{{[(2n+5)!!]}^2}{(2n+7)!}{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}}{\frac{{[(2n+3)!!]}^2}{(2n+5)!}{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}}}={\displaystyle \frac{{(2n+5)}^2}{(n+3)(2n+7)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+1)}^2}}}$$

for $z\in (0,1)$ and $n\ge 0$. On the other hand, it is standard that

$$\begin{array}{cc}{\displaystyle \frac{z}{3}}{\displaystyle \frac{{\mathfrak{T}}_{3,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{3,n}\left(z\right)}}\hfill & ={\displaystyle \frac{\left[\begin{array}{c}\frac{1}{\sqrt{1-z^2}}{\left(\frac{arcsinz}{z}\right)}^2-{\left(\frac{arcsinz}{z}\right)}^3\\ -\frac{1}{3}{\sum }_{\mathsf{\ell }=1}^n\frac{{[(2\mathsf{\ell }+1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+3}{3}\right)}\left[{\sum }_{k=0}^{\mathsf{\ell }}\frac{1}{{(2k+1)}^2}\right]\frac{z^{2\mathsf{\ell }}}{(2\mathsf{\ell }-1)!}\end{array}\right]}{{\left(\frac{arcsinz}{z}\right)}^3-{\sum }_{\mathsf{\ell }=0}^n\frac{{[(2\mathsf{\ell }+1)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+3}{3}\right)}\left[{\sum }_{k=0}^{\mathsf{\ell }}\frac{1}{{(2k+1)}^2}\right]\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}-{\displaystyle \frac{2n+2}{3}}.\hfill \end{array}$$

Consequently, we derive inequality (109).

From series expansion (4), it follows that

$$\begin{array}{cc}{\mathfrak{T}}_{4,n}\left(z\right)\hfill & ={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{2n+6}{4}\right)}{{[(2n+4)!!]}^2}}{\displaystyle \frac{1}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}}{\displaystyle \frac{(2n+2)!}{z^{2n+2}}}\{{\left({\displaystyle \frac{arcsinz}{z}}\right)}^4\hfill \\ \hfill & -\sum _{\mathsf{\ell }=0}^n{\displaystyle \frac{{[(2\mathsf{\ell }+2)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+4}{4}\right)}}\left[\sum _{k=0}^{\mathsf{\ell }}{\displaystyle \frac{1}{{(2k+2)}^2}}\right]{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\}\hfill \\ \hfill & ={\displaystyle \frac{(2n+6)!}{{[(2n+4)!!]}^2}}{\displaystyle \frac{1}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}}\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{{[(2\mathsf{\ell }+2n+4)!!]}^2}{(2\mathsf{\ell }+2n+6)!}}\left[\sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+2)}^2}}\right]z^{2\mathsf{\ell }},\hfill \\ {\displaystyle \frac{{\mathfrak{T}}_{4,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{4,n}\left(z\right)}}\hfill & ={\displaystyle \frac{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+6)!!]}^2}{(2\mathsf{\ell }+2n+8)!}\left[{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+2)}^2}\right](2\mathsf{\ell }+2)z^{2\mathsf{\ell }}}{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{{[(2\mathsf{\ell }+2n+4)!!]}^2}{(2\mathsf{\ell }+2n+6)!}\left[{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+2)}^2}\right]z^{2\mathsf{\ell }}}}\hfill \\ \hfill & \to {\displaystyle \frac{{(2n+6)}^2}{(2n+7)(n+4)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}},z\to 0,\hfill \end{array}$$

and

$${\mathfrak{Q}}_{4,n}\left(\mathsf{\ell }\right)={\displaystyle \frac{(2\mathsf{\ell }+2){(2\mathsf{\ell }+2n+6)}^2}{(2\mathsf{\ell }+2n+7)(2\mathsf{\ell }+2n+8)}}{\displaystyle \frac{{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+2)}^2}}}$$

(118)

for $\mathsf{\ell },n\in {\mathbb{N}}_0$. The inequality ${\mathfrak{Q}}_{4,n}\left(\mathsf{\ell }\right)<{\mathfrak{Q}}_{4,n}(\mathsf{\ell }+1)$ is equivalent to

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}2{\mathsf{\ell }}^4+{\mathsf{\ell }}^3(8n+34)+{\mathsf{\ell }}^2\left(12n^2+99n+206\right)\\ +\mathsf{\ell }\left(8n^3+96n^2+389n+530\right)\\ +2n^4+31n^3+183n^2+487n+491\end{array}\right]{\left[\sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+2)}^2}}\right]}^2\hfill \\ \hfill & +{\displaystyle \frac{\left[\begin{array}{c}4{\mathsf{\ell }}^3(n+4)+{\mathsf{\ell }}^2\left(12n^2+86n+163\right)\\ +\mathsf{\ell }\left(12n^3+124n^2+441n+542\right)\\ +4n^4+54n^3+278n^2+652n+590\end{array}\right]}{4{(\mathsf{\ell }+n+3)}^2}}\left[\sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+2)}^2}}\right]\hfill \\ \hfill & -{\displaystyle \frac{(\mathsf{\ell }+1)(\mathsf{\ell }+n+5)(2\mathsf{\ell }+2n+9)}{16{(\mathsf{\ell }+n+3)}^2}}>0\hfill \end{array}$$

(119)

for $\mathsf{\ell },n\ge 0$. It is apparent that

$${\displaystyle \frac{5}{16}}\le \sum _{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+2)}^2}}<\sum _{k=0}^{\infty }{\displaystyle \frac{1}{{(2k+2)}^2}}={\displaystyle \frac{{\pi }^2}{24}},\mathsf{\ell },n\ge 0.$$

Replacing ${\sum }_{k=0}^{\mathsf{\ell }+n+1}{\displaystyle \frac{1}{{(2k+2)}^2}}$ with ${\displaystyle \frac{5}{16}}$ in (119) leads to

$$\begin{array}{c}50{\mathsf{\ell }}^6+50{\mathsf{\ell }}^5(23+6n)+25{\mathsf{\ell }}^4\left(428+227n+30n^2\right)\\ +{\mathsf{\ell }}^3\left(52088+41855n+11200n^2+1000n^3\right)\\ +{\mathsf{\ell }}^2\left(141049+151856n+61365n^2+11050n^3+750n^4\right)\\ +\mathsf{\ell }\left(202716+273077n+147448n^2+39965n^3+5450n^4+300n^5\right)\\ +121555+195961n+132028n^2+47680n^3+9755n^4+1075n^5+50n^6>0\end{array}$$

for $\mathsf{\ell },n\ge 0$. This means that the sequence ${\mathfrak{Q}}_{4,n}\left(\mathsf{\ell }\right)$ is increasing in $\mathsf{\ell }\ge 0$ for any fixed $n\ge 0$. Using the monotonicity rule stated around equation (112), we acquire that the function ${\displaystyle \frac{{\mathfrak{T}}_{4,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{4,n}\left(z\right)}}$, and then the function ${\displaystyle \frac{{\mathfrak{T}}_{4,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{4,n}\left(z\right)}}$, is increasing in $z\in (0,1)$ for fixed $n\ge 0$. Accordingly, the normalized remainder ${\mathfrak{T}}_{4,n}\left(z\right)$ is logarithmically convex in $z\in (0,1)$ for all $n\ge 0$ and

$${\displaystyle \frac{{\mathfrak{T}}_{4,n}^{\prime }\left(z\right)}{z{\mathfrak{T}}_{4,n}\left(z\right)}}>{\displaystyle \frac{{(2n+6)}^2}{(2n+7)(n+4)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}}$$

for $z\in (0,1)$ and $n\ge 0$. Combining this inequality with

$${\displaystyle \frac{{\mathfrak{T}}_{4,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{4,n}\left(z\right)}}={\displaystyle \frac{1}{z}}{\displaystyle \frac{\frac{4}{\sqrt{1-z^2}}{\left(\frac{arcsinz}{z}\right)}^3-4{\left(\frac{arcsinz}{z}\right)}^4-{\sum }_{\mathsf{\ell }=1}^n\frac{{[(2\mathsf{\ell }+2)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+4}{4}\right)}\left[{\sum }_{k=0}^{\mathsf{\ell }}\frac{1}{{(2k+2)}^2}\right]\frac{z^{2\mathsf{\ell }}}{(2\mathsf{\ell }-1)!}}{{\left(\frac{arcsinz}{z}\right)}^4-{\sum }_{\mathsf{\ell }=0}^n\frac{{[(2\mathsf{\ell }+2)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+4}{4}\right)}\left[{\sum }_{k=0}^{\mathsf{\ell }}\frac{1}{{(2k+2)}^2}\right]\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}-{\displaystyle \frac{2n+2}{z}}$$

results in

$$\begin{array}{c}{\displaystyle \frac{\frac{4}{\sqrt{1-z^2}}{\left(\frac{arcsinz}{z}\right)}^3-4{\left(\frac{arcsinz}{z}\right)}^4-{\sum }_{\mathsf{\ell }=1}^n\frac{{[(2\mathsf{\ell }+2)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+4}{4}\right)}\left[{\sum }_{k=0}^{\mathsf{\ell }}\frac{1}{{(2k+2)}^2}\right]\frac{z^{2\mathsf{\ell }}}{(2\mathsf{\ell }-1)!}}{{\left(\frac{arcsinz}{z}\right)}^4-{\sum }_{\mathsf{\ell }=0}^n\frac{{[(2\mathsf{\ell }+2)!!]}^2}{\left(\genfrac{}{}{0pt}{}{2\mathsf{\ell }+4}{4}\right)}\left[{\sum }_{k=0}^{\mathsf{\ell }}\frac{1}{{(2k+2)}^2}\right]\frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}}-(2n+2)\\ >{\displaystyle \frac{{(2n+6)}^2}{(2n+7)(n+4)}}{\displaystyle \frac{{\sum }_{k=0}^{n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{n+1}\frac{1}{{(2k+2)}^2}}}{z}^2\end{array}$$

which can be reformulated as inequality (110).

By similar arguments as above, we can obtain the logarithmic convexity of the normalized remainder ${\mathfrak{T}}_{5,n}\left(z\right)$ in $z\in (0,1)$ for all $n\ge 0$ and inequality (111). □

Remark 5.

Taking $n=0$ in Theorem 2 results in the following inequalities:

$$\begin{array}{c}\left(3+{\displaystyle \frac{9z^2}{10}}\right){\displaystyle \frac{arcsinz}{z}}<{\displaystyle \frac{1}{\sqrt{1-z^2}}}+\left(2+{\displaystyle \frac{9z^2}{10}}\right),\\ \left(4+{\displaystyle \frac{16z^2}{15}}\right){\left({\displaystyle \frac{arcsinz}{z}}\right)}^2<{\displaystyle \frac{2}{\sqrt{1-z^2}}}{\displaystyle \frac{arcsinz}{z}}+\left(2+{\displaystyle \frac{16z^2}{15}}\right),\\ \left(5+{\displaystyle \frac{37z^2}{30}}\right){\left({\displaystyle \frac{arcsinz}{z}}\right)}^3<{\displaystyle \frac{3}{\sqrt{1-z^2}}}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^2+\left(2+{\displaystyle \frac{37z^2}{30}}\right),\\ \left(6+{\displaystyle \frac{7z^2}{5}}\right){\left({\displaystyle \frac{arcsinz}{z}}\right)}^4<{\displaystyle \frac{4}{\sqrt{1-z^2}}}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^3+\left(2+{\displaystyle \frac{7z^2}{5}}\right),\end{array}$$

and

$$\begin{array}{c}\left(7+{\displaystyle \frac{10633z^2}{5625}}\right){\left({\displaystyle \frac{arcsinz}{z}}\right)}^5<{\displaystyle \frac{5}{\sqrt{1-z^2}}}{\left({\displaystyle \frac{arcsinz}{z}}\right)}^4+\left(2+{\displaystyle \frac{10633z^2}{5625}}\right)\hfill \end{array}$$

for $0<\left|z\right|<1$. These inequalities appear to be quite elegant.

Remark 6.

For given $q\ge 6$ and $n\in {\mathbb{N}}_0$, is the ratio

$${\mathfrak{Q}}_{q,n}\left(\mathsf{\ell }\right)={\displaystyle \frac{8\frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+4)}{(q+2\mathsf{\ell }+2n+4)!}(\mathsf{\ell }+1)2^{2\mathsf{\ell }}}{\frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}{(q+2\mathsf{\ell }+2n+2)!}{2}^{2\mathsf{\ell }}}}=8(\mathsf{\ell }+1){\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+4)}{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}}{\displaystyle \frac{(q+2\mathsf{\ell }+2n+2)!}{(q+2\mathsf{\ell }+2n+4)!}}$$

an increasing sequence in $\mathsf{\ell }\in {\mathbb{N}}_0$? See “one more problem” at https://mathoverflow.net/q/456136 (accessed on 9 October 2023).

6. Ratios of Bell Polynomials and Central Factorial Numbers

In this section, from the proof of Theorem 2, we derive several identities for two consecutive ratios of specific Bell polynomials of the second kind:

$$B_{q+2m,q}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right),m,q\in \mathbb{N}.$$

Theorem 3.

The identities

$$\begin{array}{cc}{\displaystyle \frac{B_{2m+3,1}\left(1,0,1,0,9,0,\dots ,{[(2m-1)!!]}^2,0,{[(2m+1)!!]}^2\right)}{B_{2m+1,1}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right)}}\hfill & ={(1+2m)}^2,\hfill \end{array}$$

$$\begin{array}{cc}{\displaystyle \frac{B_{2m+4,2}\left(1,0,1,0,9,0,\dots ,{[(2m-1)!!]}^2,0,{[(2m+1)!!]}^2\right)}{B_{2m+2,2}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right)}}\hfill & ={(2+2m)}^2,\hfill \end{array}$$

(120)

$$\begin{array}{cc}{\displaystyle \frac{B_{2m+5,3}\left(1,0,1,0,9,0,\dots ,{[(2m-1)!!]}^2,0,{[(2m+1)!!]}^2\right)}{B_{2m+3,3}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right)}}\hfill & ={(3+2m)}^2+{\displaystyle \frac{1}{{\sum }_{k=0}^m\frac{1}{{(2k+1)}^2}}},\hfill \end{array}$$

(121)

$$\begin{array}{cc}{\displaystyle \frac{B_{2m+6,4}\left(1,0,1,0,9,0,\dots ,{[(2m-1)!!]}^2,0,{[(2m+1)!!]}^2\right)}{B_{2m+4,4}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right)}}\hfill & ={(4+2m)}^2+{\displaystyle \frac{1}{{\sum }_{k=0}^m\frac{1}{{(2k+2)}^2}}},\hfill \end{array}$$

(122)

and

$$\begin{array}{cc}{\displaystyle \frac{B_{2m+7,5}\left(1,0,1,0,9,0,\dots ,{[(2m-1)!!]}^2,0,{[(2m+1)!!]}^2\right)}{B_{2m+5,5}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right)}}\hfill & ={(5+2m)}^2{\displaystyle \frac{{\left[{\sum }_{k=0}^{m+2}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{m+2}\frac{1}{{(2k+1)}^4}}{{\left[{\sum }_{k=0}^{m+1}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{m+1}\frac{1}{{(2k+1)}^4}}}\hfill \end{array}$$

(123)

are valid for $m\in \mathbb{N}$.

Proof. 

By relation (67), the ratio ${\mathfrak{Q}}_{q,n}\left(\mathsf{\ell }\right)$ can be rewritten as

$$\begin{array}{cc}{\mathfrak{Q}}_{q,n}\left(\mathsf{\ell }\right)\hfill & =2(\mathsf{\ell }+1){\displaystyle \frac{(q+2\mathsf{\ell }+2n+2)!}{(q+2\mathsf{\ell }+2n+4)!}}\hfill \\ \hfill & \times {\displaystyle \frac{B_{q+2\mathsf{\ell }+2n+4,q}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n+1)!!]}^2,0,{[(2\mathsf{\ell }+2n+3)!!]}^2\right)}{B_{q+2\mathsf{\ell }+2n+2,q}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n-1)!!]}^2,0,{[(2\mathsf{\ell }+2n+1)!!]}^2\right)}}\hfill \end{array}$$

(124)

for $q\in \mathbb{N}$ and $\mathsf{\ell },n\in {\mathbb{N}}_0$.

Combining (114) and (115) reveals that the identity

$${\mathfrak{Q}}_{q,n}\left(\mathsf{\ell }\right)={\displaystyle \frac{2(\mathsf{\ell }+1){(q+2\mathsf{\ell }+2n+2)}^2}{(q+2\mathsf{\ell }+2n+3)(q+2\mathsf{\ell }+2n+4)}}$$

for $q=1,2$ and $\mathsf{\ell },n\in {\mathbb{N}}_0$ is valid. Accordingly, comparing with (124), we deduce that the identity

$${\displaystyle \frac{B_{q+2\mathsf{\ell }+2n+4,q}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n+1)!!]}^2,0,{[(2\mathsf{\ell }+2n+3)!!]}^2\right)}{B_{q+2\mathsf{\ell }+2n+2,q}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n-1)!!]}^2,0,{[(2\mathsf{\ell }+2n+1)!!]}^2\right)}}={(q+2\mathsf{\ell }+2n+2)}^2$$

for $q=1,2$ and $\mathsf{\ell },n\in {\mathbb{N}}_0$, that is, the identity

$${\displaystyle \frac{B_{q+2m+2,q}\left(1,0,1,0,9,0,\dots ,{[(2m-1)!!]}^2,0,{[(2m+1)!!]}^2\right)}{B_{q+2m,q}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right)}}={(q+2m)}^2$$

for $q=1,2$ and $m\in \mathbb{N}$, is valid. This identity was announced on the web site https://mathoverflow.net/q/456701 (accessed on 18 October 2023).

Comparing (116) with (124) for $q=3$ yields

$$\begin{array}{cc}{\mathfrak{Q}}_{3,n}\left(\mathsf{\ell }\right)\hfill & =2(\mathsf{\ell }+1){\displaystyle \frac{(2\mathsf{\ell }+2n+5)!}{(2\mathsf{\ell }+2n+7)!}}{\displaystyle \frac{B_{2\mathsf{\ell }+2n+7,3}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n+1)!!]}^2,0,{[(2\mathsf{\ell }+2n+3)!!]}^2\right)}{B_{2\mathsf{\ell }+2n+5,3}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n-1)!!]}^2,0,{[(2\mathsf{\ell }+2n+1)!!]}^2\right)}}\hfill \\ \hfill & ={\displaystyle \frac{(2\mathsf{\ell }+2){(2\mathsf{\ell }+2n+5)}^2}{(2\mathsf{\ell }+2n+6)(2\mathsf{\ell }+2n+7)}}{\displaystyle \frac{{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+1)}^2}}}\hfill \end{array}$$

which can be reformulated as

$$\begin{array}{c}{\displaystyle \frac{B_{2\mathsf{\ell }+2n+7,3}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n+1)!!]}^2,0,{[(2\mathsf{\ell }+2n+3)!!]}^2\right)}{B_{2\mathsf{\ell }+2n+5,3}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n-1)!!]}^2,0,{[(2\mathsf{\ell }+2n+1)!!]}^2\right)}} \hfill \\ \hfill ={(2\mathsf{\ell }+2n+5)}^2{\displaystyle \frac{{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+1)}^2}}}\end{array}$$

for $\mathsf{\ell },n\in {\mathbb{N}}_0$. Further replacing $\mathsf{\ell }+n+1$ with m gives identity (121). Identity (121) was announced at the site https://mathoverflow.net/a/456784 (accessed on 20 October 2023).

Comparing (118) with (124) gives

$$\begin{array}{c}{\displaystyle \frac{B_{2\mathsf{\ell }+2n+8,4}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n+1)!!]}^2,0,{[(2\mathsf{\ell }+2n+3)!!]}^2\right)}{B_{2\mathsf{\ell }+2n+6,4}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n-1)!!]}^2,0,{[(2\mathsf{\ell }+2n+1)!!]}^2\right)}} \hfill \\ \hfill ={(2\mathsf{\ell }+2n+6)}^2{\displaystyle \frac{{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+2)}^2}}}\end{array}$$

which can be reformulated as (122).

Similarly, we acquire

$$\begin{array}{c}{\displaystyle \frac{B_{2\mathsf{\ell }+2n+9,5}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n+1)!!]}^2,0,{[(2\mathsf{\ell }+2n+3)!!]}^2\right)}{B_{2\mathsf{\ell }+2n+7,5}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n-1)!!]}^2,0,{[(2\mathsf{\ell }+2n+1)!!]}^2\right)}} \hfill \\ \hfill ={(2\mathsf{\ell }+2n+7)}^2{\displaystyle \frac{{\left[{\sum }_{k=0}^{\mathsf{\ell }+n+3}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{\mathsf{\ell }+n+3}\frac{1}{{(2k+1)}^4}}{{\left[{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^4}}}\end{array}$$

(125)

which can be rearranged as (123). The proof of Theorem 3 is finished. □

Theorem 4.

For $m\in \mathbb{N}$ and $1\le \mathsf{\ell }\le 5$, central factorial numbers $t(2m+\mathsf{\ell },\mathsf{\ell })$ satisfy the identities

$$\begin{array}{cccc}{\displaystyle \frac{t(2m+3,1)}{t(2m+1,1)}}\hfill & =-{\displaystyle \frac{{(2m+1)}^2}{4}},\hfill & {\displaystyle \frac{t(2m+5,3)}{t(2m+3,3)}}\hfill & =-{\displaystyle \frac{1}{4}}\left[{(2m+3)}^2+{\displaystyle \frac{1}{{\sum }_{k=0}^m\frac{1}{{(2k+1)}^2}}}\right],\hfill \\ {\displaystyle \frac{t(2m+4,2)}{t(2m+2,2)}}\hfill & =-{\displaystyle \frac{{(2m+2)}^2}{4}},\hfill & {\displaystyle \frac{t(2m+6,4)}{t(2m+4,4)}}\hfill & =-{\displaystyle \frac{1}{4}}\left[{(2m+4)}^2+{\displaystyle \frac{1}{{\sum }_{k=0}^m\frac{1}{{(2k+2)}^2}}}\right],\hfill \end{array}$$

(126)

and

$${\displaystyle \frac{t(2m+7,5)}{t(2m+5,5)}}=-{\displaystyle \frac{{(2m+5)}^2}{4}}{\displaystyle \frac{{\left[{\sum }_{k=0}^{m+2}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{m+2}\frac{1}{{(2k+1)}^4}}{{\left[{\sum }_{k=0}^{m+1}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{m+1}\frac{1}{{(2k+1)}^4}}}.$$

(127)

Proof. 

Using the relation (73) in Proposition 2, we write

$${\mathfrak{Q}}_{q,n}\left(\mathsf{\ell }\right)=-8(\mathsf{\ell }+1){\displaystyle \frac{t(q+2\mathsf{\ell }+2n+4,q)}{t(q+2\mathsf{\ell }+2n+2,q)}}{\displaystyle \frac{(q+2\mathsf{\ell }+2n+2)!}{(q+2\mathsf{\ell }+2n+4)!}}$$

(128)

for $q\in \mathbb{N}$ and $\mathsf{\ell },n\in {\mathbb{N}}_0$. Comparing this for $1\le q\le 4$ with expressions (114)–(116), and (118) results in

$$\begin{array}{cc}{\displaystyle \frac{t(2\mathsf{\ell }+2n+5,1)}{t(2\mathsf{\ell }+2n+3,1)}}\hfill & =-{\displaystyle \frac{{(2\mathsf{\ell }+2n+3)}^2}{4}},\hfill \\ {\displaystyle \frac{t(2\mathsf{\ell }+2n+6,2)}{t(2\mathsf{\ell }+2n+4,2)}}\hfill & =-{\displaystyle \frac{{(2\mathsf{\ell }+2n+4)}^2}{4}},\hfill \\ {\displaystyle \frac{t(2\mathsf{\ell }+2n+7,3)}{t(2\mathsf{\ell }+2n+5,3)}}\hfill & =-{\displaystyle \frac{{(2\mathsf{\ell }+2n+5)}^2}{4}}{\displaystyle \frac{{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}}{{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+1)}^2}}},\hfill \\ {\displaystyle \frac{t(2\mathsf{\ell }+2n+8,4)}{t(2\mathsf{\ell }+2n+6,4)}}\hfill & =-{\displaystyle \frac{{(2\mathsf{\ell }+2n+6)}^2}{4}}{\displaystyle \frac{{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+2)}^2}}{{\sum }_{k=0}^{\mathsf{\ell }+n+1}\frac{1}{{(2k+2)}^2}}}\hfill \end{array}$$

for $\mathsf{\ell },n\ge 0$. Further replacing $\mathsf{\ell }+n+1$ with $m\in \mathbb{N}$ gives those identities in (126).

Comparing (124) with (128) and simplifying lead to

$$\begin{array}{c}{\displaystyle \frac{B_{q+2\mathsf{\ell }+2n+4,q}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n+1)!!]}^2,0,{[(2\mathsf{\ell }+2n+3)!!]}^2\right)}{B_{q+2\mathsf{\ell }+2n+2,q}\left(1,0,1,0,9,0,\dots ,{[(2\mathsf{\ell }+2n-1)!!]}^2,0,{[(2\mathsf{\ell }+2n+1)!!]}^2\right)}} \hfill \\ \hfill =-4{\displaystyle \frac{t(q+2\mathsf{\ell }+2n+4,q)}{t(q+2\mathsf{\ell }+2n+2,q)}}\end{array}$$

(129)

for $q\in \mathbb{N}$ and $\mathsf{\ell },n\in {\mathbb{N}}_0$. Further taking $q=5$ in (129) and employing identity (125) produce

$$-4{\displaystyle \frac{t(2\mathsf{\ell }+2n+9,5)}{t(2\mathsf{\ell }+2n+7,5)}}={(2\mathsf{\ell }+2n+7)}^2{\displaystyle \frac{{\left[{\sum }_{k=0}^{\mathsf{\ell }+n+3}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{\mathsf{\ell }+n+3}\frac{1}{{(2k+1)}^4}}{{\left[{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^2}\right]}^2-{\sum }_{k=0}^{\mathsf{\ell }+n+2}\frac{1}{{(2k+1)}^4}}}.$$

Hence, identity (127) follows. The proof of Theorem 4 is complete. □

Corollary 4.

For $m,q\in \mathbb{N}$, we have the relation

$${\displaystyle \frac{t(q+2m+2,q)}{t(q+2m,q)}}=-{\displaystyle \frac{1}{4}}{\displaystyle \frac{B_{q+2m+2,q}\left(1,0,1,0,9,0,\dots ,{[(2m-1)!!]}^2,0,{[(2m+1)!!]}^2\right)}{B_{q+2m,q}\left(1,0,1,0,9,0,\dots ,{[(2m-3)!!]}^2,0,{[(2m-1)!!]}^2\right)}}.$$

Proof. 

This follows from replacing $\mathsf{\ell }+n+1$ with m in (129). □

7. Maclaurin Power Series Expansion

In this section, we expand the logarithm of the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ into the Maclaurin power series.

Theorem 5.

For $m,n\ge 0$ and $q\in \mathbb{N}$, let

$$\mathfrak{E}\left(m\right)=\mathfrak{E}(m,n,q)=\left(4m\right)!!{\displaystyle \frac{\mathcal{Q}(q,2m+2n+2)}{(q+2m+2n+2)!}}$$

and

$$\mathfrak{D}(m,n,q)=\left|\begin{array}{ccccccc}0& \left({\displaystyle \genfrac{}{}{0pt}{}{0}{0}}\right)\mathfrak{E}\left(0\right)& 0& 0& \dots & 0& 0\\ \mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{1}{1}}\right)\mathfrak{E}\left(0\right)& 0& \dots & 0& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{0}}\right)\mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{2}}\right)\mathfrak{E}\left(0\right)& \dots & 0& 0\\ \mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{3}{1}}\right)\mathfrak{E}\left(1\right)& 0& \dots & 0& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{4}{0}}\right)\mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{4}{2}}\right)\mathfrak{E}\left(1\right)& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ \mathfrak{E}\left(m\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m-1}{1}}\right)\mathfrak{E}(m-1)& 0& \dots & \left({\displaystyle \genfrac{}{}{0pt}{}{2m-1}{2m-1}}\right)\mathfrak{E}\left(0\right)& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m}{0}}\right)\mathfrak{E}\left(m\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m}{2}}\right)\mathfrak{E}(m-1)& \dots & 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m}{2m}}\right)\mathfrak{E}\left(0\right)\\ \mathfrak{E}(m+1)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m+1}{1}}\right)\mathfrak{E}\left(m\right)& 0& \dots & \left({\displaystyle \genfrac{}{}{0pt}{}{2m+1}{2m-1}}\right)\mathfrak{E}\left(1\right)& 0\end{array}\right|,$$

where the quantity $\mathcal{Q}(q,2m+2n+2)$ is defined by (7). Then, the logarithm of the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ for $q\in \mathbb{N}$ and $n\ge 0$ can be expanded to the Maclaurin power series

$$ln{\mathfrak{T}}_{q,n}\left(z\right)=-\sum _{m=1}^{\infty }{\displaystyle \frac{\mathfrak{D}(m-1,n,q)}{{\left[\mathfrak{E}\left(0\right)\right]}^{2m}}}{\displaystyle \frac{z^{2m}}{\left(2m\right)!}},\left|z\right|<1.$$

(130)

Proof. 

Employing series expression (54), we obtain the logarithmic derivative

$$\begin{array}{cc}{\displaystyle \frac{{\mathfrak{T}}_{q,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{q,n}\left(z\right)}}\hfill & ={\displaystyle \frac{{\sum }_{\mathsf{\ell }=1}^{\infty }\frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}{(q+2\mathsf{\ell }+2n+2)!}\left(2\mathsf{\ell }\right)2{\left(2z\right)}^{2\mathsf{\ell }-1}}{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}{(q+2\mathsf{\ell }+2n+2)!}{\left(2z\right)}^{2\mathsf{\ell }}}}\hfill \\ \hfill & ={\displaystyle \frac{4{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+4)}{(q+2\mathsf{\ell }+2n+4)!}(\mathsf{\ell }+1){\left(2z\right)}^{2\mathsf{\ell }+1}}{{\sum }_{\mathsf{\ell }=0}^{\infty }\frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}{(q+2\mathsf{\ell }+2n+2)!}{\left(2z\right)}^{2\mathsf{\ell }}}}\hfill \\ \hfill & \to 0,z\to 0\hfill \end{array}$$

for $q\in \mathbb{N}$, $n\in {\mathbb{N}}_0$, and $\left|z\right|<1$. Furthermore, for $k,m,n\ge 0$, we have

$$\begin{array}{cc}{\left[\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}{(q+2\mathsf{\ell }+2n+2)!}}{\left(2z\right)}^{2\mathsf{\ell }}\right]}^{\left(k\right)}\hfill & =\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+2)}{(q+2\mathsf{\ell }+2n+2)!}}{2}^{2\mathsf{\ell }}{⟨2\mathsf{\ell }⟩}_k{z}^{2\mathsf{\ell }-k}\hfill \\ \hfill & \to \{\begin{array}{cc}0,\hfill & k=2m+1\hfill \\ {\displaystyle \frac{\mathcal{Q}(q,2m+2n+2)}{(q+2m+2n+2)!}}{2}^{2m}\left(2m\right)!,\hfill & k=2m\hfill \end{array}\hfill \\ \hfill & \to \{\begin{array}{cc}0,\hfill & k=2m+1\hfill \\ \mathfrak{E}(m,n,q),\hfill & k=2m\hfill \end{array}\hfill \end{array}$$

and

$$\begin{array}{c}{\left[4\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+4)}{(q+2\mathsf{\ell }+2n+4)!}}(\mathsf{\ell }+1){\left(2z\right)}^{2\mathsf{\ell }+1}\right]}^{\left(k\right)}\hfill \\ =4\sum _{\mathsf{\ell }=0}^{\infty }{\displaystyle \frac{\mathcal{Q}(q,2\mathsf{\ell }+2n+4)}{(q+2\mathsf{\ell }+2n+4)!}}(\mathsf{\ell }+1)2^{2\mathsf{\ell }+1}{⟨2\mathsf{\ell }+1⟩}_k{z}^{2\mathsf{\ell }-k+1}\hfill \\ \to \{\begin{array}{cc}0,\hfill & k=2m\hfill \\ {\displaystyle \frac{\mathcal{Q}(q,2m+2n+4)}{(q+2m+2n+4)!}}{2}^{2m+2}(2m+2)!,\hfill & k=2m+1\hfill \end{array}\hfill \\ =\{\begin{array}{cc}0,\hfill & k=2m\hfill \\ \mathfrak{E}(m+1,n,q),\hfill & k=2m+1\hfill \end{array}\hfill \end{array}$$

as $z\to 0$, where the falling factorial ${⟨z⟩}_n$ for $k\in {\mathbb{N}}_0$ and $z\in \mathbb{C}$ is defined by

$${⟨z⟩}_k=\prod _{\mathsf{\ell }=0}^{k-1}(z-\mathsf{\ell })=\left\{\begin{array}{cc}1,\hfill & k=0;\hfill \\ z(z-1)\dots (z-k+1),\hfill & k\in \mathbb{N}.\hfill \end{array}\right.$$

Let $\varphi \left(z\right)$ and $\phi \left(z\right)\ne 0$ be two m-time differentiable functions on an interval I for given integer $m\ge 0$. Exercise 5 in ([70], p. 40) can be formulated as

$${\displaystyle \frac{{\mathrm{d}}^m}{\mathrm{d}{z}^m}}\left[{\displaystyle \frac{\varphi \left(z\right)}{\phi \left(z\right)}}\right]={(-1)}^m{\displaystyle \frac{\left|{\Omega }_{(m+1)\times (m+1)}\left(z\right)\right|}{{\phi }^{m+1}\left(z\right)}},m\ge 0,$$

(131)

where the matrix

$${\Omega }_{(m+1)\times (m+1)}\left(z\right)={\left(\begin{array}{cc}{\Phi }_{(m+1)\times 1}\left(z\right)& {{\rm Y}}_{(m+1)\times m}\left(z\right)\end{array}\right)}_{(m+1)\times (m+1)},$$

the matrix ${\Phi }_{(m+1)\times 1}\left(z\right)$ is an $(m+1)\times 1$ matrix whose elements satisfy ${\varphi }_{k,1}\left(z\right)={\varphi }^{(k-1)}\left(z\right)$ for $1\le k\le m+1$, the matrix ${{\rm Y}}_{(m+1)\times m}\left(z\right)$ is an $(m+1)\times m$ matrix whose elements are ${\phi }_{\mathsf{\ell },j}\left(z\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{\mathsf{\ell }-1}{j-1}}\right){\phi }^{(\mathsf{\ell }-j)}\left(z\right)$ for $1\le \mathsf{\ell }\le m+1$ and $1\le j\le m$, and the notation $|{\Omega }_{(m+1)\times (m+1)}\left(z\right)|$ denotes the determinant of the $(m+1)\times (m+1)$ matrix ${\Omega }_{(m+1)\times (m+1)}\left(z\right)$. By virtue of derivative formula (131), we acquire

$$\begin{array}{cc}\underset{z\to 0}{lim}{\left[{\displaystyle \frac{{\mathfrak{T}}_{q,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{q,n}\left(z\right)}}\right]}^{(2m+1)}\hfill & =-{\displaystyle \frac{1}{{\left[\mathfrak{E}\left(0\right)\right]}^{2m+2}}}\left|\begin{array}{ccccccc}0& \left({\displaystyle \genfrac{}{}{0pt}{}{0}{0}}\right)\mathfrak{E}\left(0\right)& 0& 0& \dots & 0& 0\\ \mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{1}{1}}\right)\mathfrak{E}\left(0\right)& 0& \dots & 0& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{0}}\right)\mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{2}}\right)\mathfrak{E}\left(0\right)& \dots & 0& 0\\ \mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{3}{1}}\right)\mathfrak{E}\left(1\right)& 0& \dots & 0& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{4}{0}}\right)\mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{4}{2}}\right)\mathfrak{E}\left(1\right)& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ \mathfrak{E}\left(m\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m-1}{1}}\right)\mathfrak{E}(m-1)& 0& \dots & \left({\displaystyle \genfrac{}{}{0pt}{}{2m-1}{2m-1}}\right)\mathfrak{E}\left(0\right)& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m}{0}}\right)\mathfrak{E}\left(m\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m}{2}}\right)\mathfrak{E}(m-1)& \dots & 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m}{2m}}\right)\mathfrak{E}\left(0\right)\\ \mathfrak{E}(m+1)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2m+1}{1}}\right)\mathfrak{E}\left(m\right)& 0& \dots & \left({\displaystyle \genfrac{}{}{0pt}{}{2m+1}{2m-1}}\right)\mathfrak{E}\left(1\right)& 0\end{array}\right|\hfill \\ \hfill & =-{\displaystyle \frac{\mathfrak{D}(m,n,q)}{{\left[\mathfrak{E}\left(0\right)\right]}^{2m+2}}}\hfill \end{array}$$

for $q\in \mathbb{N}$ and $m,n\ge 0$. Consequently, we derive the series expansion

$$\begin{array}{cc}ln{\mathfrak{T}}_{q,n}\left(z\right)\hfill & =\sum _{\mathsf{\ell }=0}^{\infty }\underset{z\to 0}{lim}{[ln{\mathfrak{T}}_{q,n}\left(z\right)]}^{\left(\mathsf{\ell }\right)}{\displaystyle \frac{z^{\mathsf{\ell }}}{\mathsf{\ell }!}}\hfill \\ \hfill & =\sum _{\mathsf{\ell }=1}^{\infty }\underset{z\to 0}{lim}{[ln{\mathfrak{T}}_{q,n}\left(z\right)]}^{\left(2\mathsf{\ell }\right)}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\hfill \\ \hfill & =\sum _{\mathsf{\ell }=1}^{\infty }\underset{z\to 0}{lim}{\left[{\displaystyle \frac{{\mathfrak{T}}_{q,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{q,n}\left(z\right)}}\right]}^{(2\mathsf{\ell }-1)}{\displaystyle \frac{z^{2\mathsf{\ell }}}{\left(2\mathsf{\ell }\right)!}}\hfill \\ \hfill & =\sum _{m=0}^{\infty }\underset{z\to 0}{lim}{\left[{\displaystyle \frac{{\mathfrak{T}}_{q,n}^{\prime }\left(z\right)}{{\mathfrak{T}}_{q,n}\left(z\right)}}\right]}^{(2m+1)}{\displaystyle \frac{z^{2m+2}}{(2m+2)!}}\hfill \\ \hfill & =-\sum _{m=0}^{\infty }{\displaystyle \frac{\mathfrak{D}(m,n,q)}{{\left[\mathfrak{E}\left(0\right)\right]}^{2m+2}}}{\displaystyle \frac{z^{2m+2}}{(2m+2)!}},\hfill \end{array}$$

where we considered the evenness of the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$. The proof of Theorem 5 is complete. □

Remark 7.

Numerical computation shows that

$$\begin{array}{cc}\mathfrak{D}(0,2,5)\hfill & =\left|\begin{array}{cc}0& \left({\displaystyle \genfrac{}{}{0pt}{}{0}{0}}\right)\mathfrak{E}(0,2,5)\\ \mathfrak{E}(1,2,5)& 0\end{array}\right|\hfill \\ \hfill & =-{\displaystyle \frac{241332307}{32362142367744000}},\hfill \\ \mathfrak{D}(1,2,5)\hfill & =\left|\begin{array}{cccc}0& \left({\displaystyle \genfrac{}{}{0pt}{}{0}{0}}\right)\mathfrak{E}\left(0\right)& 0& 0\\ \mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{1}{1}}\right)\mathfrak{E}\left(0\right)& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{0}}\right)\mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{2}}\right)\mathfrak{E}\left(0\right)\\ \mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{3}{1}}\right)\mathfrak{E}\left(1\right)& 0\end{array}\right|\hfill \\ \hfill & =-{\displaystyle \frac{668687533944494501}{3840130281643814511949381632000000}},\hfill \end{array}$$

and

$$\begin{array}{cc}1-1\mathfrak{D}(2,2,5)\hfill & =\left|\begin{array}{cccccc}0& \left({\displaystyle \genfrac{}{}{0pt}{}{0}{0}}\right)\mathfrak{E}\left(0\right)& 0& 0& 0& 0\\ \mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{1}{1}}\right)\mathfrak{E}\left(0\right)& 0& 0& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{0}}\right)\mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{2}{2}}\right)\mathfrak{E}\left(0\right)& 0& 0\\ \mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{3}{1}}\right)\mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{3}{3}}\right)\mathfrak{E}\left(0\right)& 0\\ 0& \left({\displaystyle \genfrac{}{}{0pt}{}{4}{0}}\right)\mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{4}{2}}\right)\mathfrak{E}\left(1\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{4}{4}}\right)\mathfrak{E}\left(0\right)\\ \mathfrak{E}\left(3\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{5}{1}}\right)\mathfrak{E}\left(2\right)& 0& \left({\displaystyle \genfrac{}{}{0pt}{}{5}{3}}\right)\mathfrak{E}\left(1\right)& 0\end{array}\right|\hfill \\ & =-{\displaystyle \frac{15831534362878382639387386703}{1130901070255702099446724532530531200191692800000000}}.\hfill \end{array}$$

Accordingly, the first few terms of series expansion (130) for $(q,n)=(5,2)$ are

$$\begin{array}{cc}ln{\mathfrak{T}}_{5,2}\left(z\right)\hfill & =-{\displaystyle \frac{\mathfrak{D}(0,2,5)}{{\left[\mathfrak{E}(0,2,5)\right]}^2}}{\displaystyle \frac{z^2}{2!}}-{\displaystyle \frac{\mathfrak{D}(1,2,5)}{{\left[\mathfrak{E}(0,2,5)\right]}^4}}{\displaystyle \frac{z^4}{4!}}-{\displaystyle \frac{\mathfrak{D}(2,2,5)}{{\left[\mathfrak{E}(0,2,5)\right]}^6}}{\displaystyle \frac{z^6}{6!}}-\dots \hfill \\ \hfill & ={\displaystyle \frac{153617}{188520}}{z}^2+{\displaystyle \frac{270938584061}{781875388800}}{z}^4+{\displaystyle \frac{4083141709395923773}{20119983742482624000}}{z}^6+\dots \hfill \end{array}$$

for $\left|z\right|<1$.

Remark 8.

In order to prove the logarithmically absolute monotonicity of the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ in $z\in [0,1)$ for $q\in \mathbb{N}$ and $n\in {\mathbb{N}}_0$, an alternative approach is to prove that all coefficients of the Maclaurin power series expansion (130) of $ln{\mathfrak{T}}_{q,n}\left(z\right)$ around $z=0$ are positive. This is equivalent to the negativity of the determinant $\mathfrak{D}(m,n,q)$ for $m,n\ge 0$ and $q\in \mathbb{N}$.

Remark 9.

On 28 December 2024, Izán Péraz asked the author to find the exact value of the improper integral

$${\int }_{-\infty }^{\infty }exp\left[-{\left(x+{\displaystyle \frac{2x}{1-x^2}}\right)}^{2n}\right]dx,n\in \mathbb{N}.$$

It is common knowledge that finding the exact values of improper integrals is conventionally important and interesting in calculus, mathematical analysis, the theory of single-variable complex functions, the theory of special functions, and the like.

Glasser’s master theorem in [71,72] (or see the web sites https://en.wikipedia.org/wiki/Glasser%27s_master_theorem (accessed on 30 December 2024) and https://mathworld.wolfram.com/GlassersMasterTheorem.html (accessed on 30 December 2024)) reads that the identity

$$PV{\int }_{-\infty }^{\infty }F\left(\varphi \left(x\right)\right)dx=PV{\int }_{-\infty }^{\infty }F\left(x\right)dx$$

holds for any integrable function $F\left(x\right)$ and $\varphi \left(x\right)$ of the form

$$\varphi \left(x\right)=\left|a\right|x-\sum _{n=1}^N{\displaystyle \frac{|{\alpha }_n|}{x-{\beta }_n}},$$

with a, ${\left\{{\alpha }_n\right\}}_{n=1}^N$, and ${\left\{{\beta }_n\right\}}_{n=1}^N$ arbitrary constants, where the notation PV denotes a Cauchy principal value. Using Glasser’s master theorem, we easily derive that

$$\begin{array}{cc}{\int }_{-\infty }^{\infty }exp\left[-{\left(x+{\displaystyle \frac{2x}{1-x^2}}\right)}^{2n}\right]dx\hfill & ={\int }_{-\infty }^{\infty }exp\left[-{\left(x-{\displaystyle \frac{1}{x-1}}-{\displaystyle \frac{1}{x+1}}\right)}^{2n}\right]dx\hfill \\ \hfill & =2{\int }_0^{\infty }exp\left(-x^{2n}\right)dx\hfill \\ \hfill & ={\displaystyle \frac{1}{n}}\Gamma \left({\displaystyle \frac{1}{2n}}\right)\hfill \\ \hfill & =2\Gamma \left(1+{\displaystyle \frac{1}{2n}}\right),\hfill \end{array}$$

(132)

where the last equality in (132) follows from the formula

$${\int }_0^{\infty }exp(-x^{\mu })dx={\displaystyle \frac{1}{\mu }}\Gamma \left({\displaystyle \frac{1}{\mu }}\right),\Re \left(\mu \right)>0$$

(133)

in ([25], p. 339), and the Euler gamma function $\Gamma \left(z\right)$ can be defined ([24], Chapter 3) by

$$\Gamma \left(z\right)=\underset{n\to \infty }{lim}{\displaystyle \frac{n!n^z}{{\prod }_{k=0}^n(z+k)}},z\in \mathbb{C}\setminus \{0,-1,-2,\dots \}.$$

The formula in (133) can be verified by

$$\begin{array}{cc}{\int }_0^{\infty }exp\left(-x^{\mu }\right)dx\hfill & ={\int }_0^{\infty }{e}^{-t}d\left(t^{1/\mu }\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\mu }}{\int }_0^{\infty }{e}^{-t}{t}^{1/\mu -1}dt\hfill \\ \hfill & ={\displaystyle \frac{1}{\mu }}\Gamma \left({\displaystyle \frac{1}{\mu }}\right)\hfill \\ \hfill & =\Gamma \left(1+{\displaystyle \frac{1}{\mu }}\right),\hfill \end{array}$$

where we used another definition of the gamma function

$$\Gamma \left(z\right)={\int }_0^{\infty }{e}^{-t}{t}^{z-1}dt,\Re \left(z\right)>0$$

and the recursive relation $z\Gamma \left(z\right)=\Gamma (1+z)$ for $\Re \left(z\right)>0$; see ([15], Section 6.4).

8. Conclusions

In the first section, the author briefly reviewed recent works on the Maclaurin power series expansions for the powers of the inverse sine, inverse cosine, inverse tangent, sine, and cosine functions; concisely surveyed some properties for (the logarithms of) the normalized remainders of the Maclaurin power series expansions for the inverse sine, inverse cosine, inverse tangent, tangent, square of tangent, sine, cosine, exponential function, complete elliptic integrals of the second kind, and the generating function of the Bernoulli numbers; and simply restated those results associated with the sine and cosine functions in terms of the generalized hypergeometric functions.

In the second section, the author retrospected the origin and several known identities of the quantity $\mathcal{Q}(q,2\mathsf{\ell })$ for $\mathsf{\ell },q\in \mathbb{N}$, determined connections between $\mathcal{Q}(q,2\mathsf{\ell })$ and central factorial numbers of the first kind, and derived several closed-form formulas for central factorial numbers of the first kind.

In the third section, the author deduced an elegant inverse of a specific square Vandermonde matrix, relating to the central factorial numbers of the first kind and involving the Stirling numbers of the first kind, and revealed several interesting observations about the elements of the inverse matrix.

In the fourth section, by virtue of the Vieta theorem and the inverse matrix deduced in the third section, the author established several explicit expressions for central factorial numbers of the first kind and proved the positivity of the quantity $\mathcal{Q}(q,2\mathsf{\ell })$.

In the fifth section, the author proved the logarithmic convexity of the normalized remainders $T_{2n+1}\left[{\left({\displaystyle \frac{arcsinz}{z}}\right)}^q\right]$ for $1\le q\le 5$, $n\in {\mathbb{N}}_0$, and $\left|z\right|<1$, and derived five inequalities involving the power functions ${\left({\displaystyle \frac{arcsinz}{z}}\right)}^q$ for $1\le q\le 5$ and $\left|z\right|<1$.

In the sixth section, the author discovered several identities for the ratios of the Bell polynomials of the second kind and central factorial numbers of the first kind.

In the seventh section, the author expanded the logarithm of the normalized remainder ${\mathfrak{T}}_{q,n}\left(z\right)$ into a Maclaurin power series in terms of determinants of specific Hessenberg matrices whose elements involve the quantity $\mathcal{Q}(q,2\mathsf{\ell })$.

This paper introduced several interesting results and explored connections among important mathematical objects. Several results in this paper appear to be novel, particularly the inverse of the specific Vandermonde matrix, the explicit expressions for central factorial numbers, and the logarithmic convexity properties. These findings may provide new tools and perspectives for researchers working with these mathematical structures. The author has presented many detailed derivations, identities, and observations, showcasing a comprehensive understanding of the topics discussed.