DP-4-Colorability on Planar Graphs Excluding 7-Cycles Adjacent to 4- or 5-Cycles

Abstract

In order to resolve Borodin’s Conjecture, DP-coloring was introduced in 2017 to extend the concept of list coloring. In previous works, it is proved that every planar graph without 7-cycles and butterflies is DP-4-colorable. And any planar graph that does not have 5-cycle adjacent to 6-cycle is DP-4-colorable. The existing research mainly focus on the forbidden adjacent cycles that guarantee the DP-4-colorability for planar graph. In this paper, we demonstrate that any planar graph G that excludes 7-cycles adjacent to k-cycles (for each $k=4,5$), and does not feature a Near-bow-tie as an induced subgraph, is DP-4-colorable. This result extends the findings of the previous works mentioned above.

1. Introduction

The graphs discussed are simple, planar graphs. Vertex coloring stands out as a significant area of study within graph theory. A graph G with list assignment allocates a color set $L\left(v\right)$ to each $v\in V\left(G\right)$. Considering $\psi$ to be a proper coloring of G, which ensures that $\psi \left(u\right)$ differs from $\psi \left(v\right)$ across every edge $uv$ in G. If $\psi \left(v\right)\in L\left(v\right)$ in respect to every vertex v, then $\psi$ is defined as a list coloring of G, which proposed by was Vizing et al. [1,2] independently. Considering each list assignment with a size more than k, if G has a list coloring, then we could define G as k-choosable. The least amount k is the choosable number, represented by ${\chi }_l\left(G\right)$. Thomassen [3] demonstrated the 5-choosability of planar graph, while not all planar graphs are 4-choosable, as proven by Voigt [4]. Thus, many experts focus on identifying sufficient conditions under which planar graphs have the property of 4-choosability.

In list coloring, vertex identification cannot be used due to the different lists on vertices. To address this limitation, Dvořák et al. [5] proposed DP-coloring, which enabled them to resolve a long-standing conjecture by Borodin [6], namely that every planar graph G without cycles of lengths 4 to 8 is 3-choosable. Let $X,Y$ be two disjoint vertex sets of G, and $[X,Y]$ denote the collection of edges with one end-vertex in X and the other end-vertex in Y. The following definition of DP-coloring was subsequently provided by Bernshteyn et al. [7].

Definition 1.

Consider that a graph denoted as G along with its respective list assignment L. ${\mathcal{M}}_{(G,L)}$ qualifies as a cover for $(G,L)$ when it meets these criteria:

• $V\left({\mathcal{M}}_{(G,L)}\right)={\bigcup }_{w\in V\left(G\right)}{L}_w$, where $L_w=\left\{w\right\}\times L\left(w\right)=\{(w,c):w\in V\left(G\right)$ and $c\in L\left(w\right)\}$;
• for each vertex w in G, the collection $L_w$ makes up a clique;
• for every edge $uv$, $[L_u,L_v]$ is a matching set (which may be empty), denoted by $M_{uv}$;
• when $uv\notin E\left(G\right)$, $[L_u,L_v]$ is an empty set.

For simplicity, we denote $E_M={\cup }_{u,v\in V\left(G\right)}{M}_{uv}$. Figure 1b,c are two distinct covers of $(C_4,L)$ with $\left|L\right(v\left)\right|=2$ for each vertex of $C_4$.

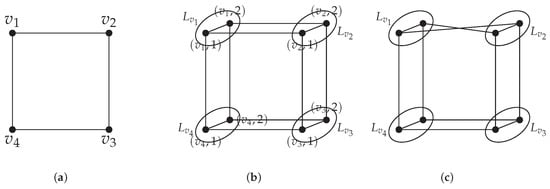
Figure 1. $H_1$ and $H_2$ are two distinct covers of $(C_4,L)$ with $\left|L\right(v_i\left)\right|=2$ for each $i\in \left[4\right]$. (a) 4-cycle $C_4$. (b) $H_1$. (c) $H_2$.

Definition 2.

Considering ${\mathcal{M}}_{(G,L)}$ denoted as a cover of $(G,L)$. Then, the following two conditions are equivalent:

(i) 

${\mathcal{M}}_{(G,L)}$ includes an independent subset I with size $\left|V\right(G\left)\right|$;

(ii) 

G has a coloring ψ on $V\left(G\right)$ satisfying $(v,\psi (v\left)\right)\in I$ across each vertex v. This coloring is said to ${\mathcal{M}}_{(G,L)}$-coloring.

A graph is called DP-k-colorable when it has an ${\mathcal{M}}_{(G,L)}$-coloring for every L with $\left|L\right(u\left)\right|\ge k$ and every cover ${\mathcal{M}}_{(G,L)}$. The minimum such k is the DP-chromatic number, represented as ${\chi }_{DP}\left(G\right)$.

For every $uv\in E\left(G\right)$, distinct matchings between $L_u$ and $L_v$ correspond to different covers of G. If the matching between $L_u$ and $L_v$ is $\left\{\right(u,x\left)\right(v,x\left)\right|$$x\in L\left(u\right)\cap L\left(v\right)\}$, an ${\mathcal{M}}_{(G,L)}$-coloring of G becomes equivalent to a list coloring of G. It indicates that DP-coloring serves as a generalization of list coloring, leading to the conclusion that ${\chi }_l\left(G\right)\le {\chi }_{DP}\left(G\right)$. From Figure 1, $H_1$ has an independent set $\{(v_1,1),(v_2,2),(v_3,1),(v_4,2)\}$; hence, $C_4$ has an $H_1$-coloring with vertices $v_1,v_3$ colored 1 and vertices $v_2,v_4$ colored 2, and this corresponding coloring is also a 2-list coloring of $C_4$. However, $C_4$ does not have an $H_2$-coloring for $H_2$ and has no 4-independent set. So, ${\chi }_{DP}\left(C_4\right)>2$. The fact that ${\chi }_{DP}\left(C_4\right)=3$ and ${\chi }_l\left(C_4\right)=2$ marks an important difference between DP-coloring and list coloring.

Recently, DP-coloring has gained significant attention. Dvořák et al. [5] showed that ${\chi }_{DP}$ does not exceed 5, and it can be reduced to 3 for planar graphs with a girth of at least 5. Li et al. [8] proved that any planar graphs without intersecting 5-cycles is DP-4-colorable. Li et al. [9] discussed the DP-4-colorability of planar graphs with some restrictions on cycles. For more results about DP-colorability, the readers can see in [10,11,12,13,14,15,16,17,18]. Kim and Ozeki [12] improved results about 4-choosability, any planar graph that avoids a k-cycle (where k is in the set $\in \{3,4,5,6\}$) is DP-4-colorable. Moreover, Farzad [19] confirmed the 4-choosability for every planar graph lacking 7-cycles. One naturally asks whether every planar graph lacking 7-cycles has the property of DP-4-colorability. For this purpose, Kim et al. [20] demonstrated the subsequent finding.

Theorem 1.

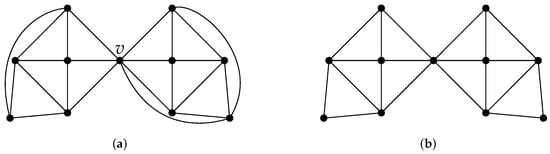
Any planar graph that lacks both butterflies (see Figure 2b) and 7-cycles is DP-4-colorable.

Figure 2. Near-bow-tie and butterfly. (a) Near-bow-tie, where v is a 7-vertex. (b) butterfly.

On the other hand, there is another way to study the sufficient conditions for DP-4-colorability, that is, forbidden adjacent cycles. For more details, the reader can refer to [11,12,13,16,17,18,21].

Theorem 2.

Any planar graph that does not have $k_1$-cycles adjacent to $k_2$-cycles is DP-4-colorable, where $(k_1,k_2)\in \{(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)\}$.

In a planar graph G, a cluster refers to a subgraph formed by a maximal collection of 3-faces, ensuring that no other 3-face shares an edge with any face within this collection. When such a cluster contains k 3-faces, it is designated as k-cluster (see Figure 3). Adjacent cycles (faces) means that they share no less than one edge. A face f is said to be adjacent to one cluster H if there exists a face within H that shares adjacency with f. A Near-bow-tie is a graph isomorphic to the configuration depicted in Figure 2a where v is a 7-vertex. Inspired by Theorems 1 and 2, the subsequent result is formulated.

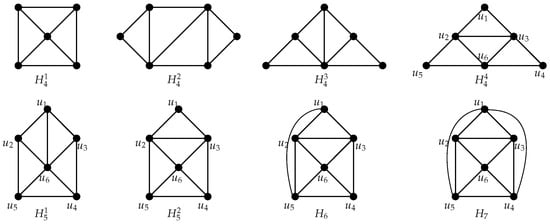
Figure 3. All non-isomorphic k-clusters for each $k\in \{4,5,6,7\}$.

Theorem 3.

Consider a planar graph G without a Near-bow-tie as an induced subgraph. If G lacks 7-cycles that are adjacent to 4- or 5-cycles, then it is DP-4-colorable.

If a graph G is free of 7-cycles that are adjacent to either 4-cycles or 5-cycles, then G may contain 7-cycles and a butterfly. Additionally, if the graph G lacks the Near-bow-tie as an induced subgraph, then it may still contain a butterfly. Therefore, Theorem 3 generalizes Theorem 1.

A 3-cycle C is considered bad provided that it is isomorphic to the bordering of the outer face of $H_7$ in Figure 3; all other 3-cycles are good. Let $K\subseteq G$ denote a portion of graph G. Therefore, G is DP-k-colorable, provided that every DP-k-coloring restricted on K could be expanded to cover the whole G. To demonstrate Theorem 3, a stronger result is established as outlined below.

Theorem 4.

Consider a planar graph G without a Near-bow-tie as an induced subgraph. If G lacks 7-cycles that are adjacent to 4- or 5-cycles, then each DP-4-coloring restricted on one good 3-cycle within G can be extended to the entire graph.

At the conclusion of this section, we will present some definitions and notations. The notation $\left[m\right]$ is defined as $\{1,2,\dots ,m\}$, where m is a positive integer. A k-vertex represents a node whose degree is k, while a $k^{+}$ (or $k^{-}$)-vertex represents a node whose degree is no less (or no more) than k. A face labeled as $(d_1,d_2,\dots ,d_k)$-face corresponds to one k-face $[v_1{v}_2\dots v_k]$ where $v_i$ is $d_i$-vertex for $i\in \left[k\right]$. If $u\in V\left(f\right)$, then u is incident with f. The notation $d\left(C\right)$ denotes the number of edges associated with cycle (or face) C of G.

2. Preliminaries

This section focuses on the corresponding coloring on some small subgraph, which is crucial to the proof of Theorem 4.

Lemma 1.

Consider L as a list assignment on $K_3=v_1{v}_2{v}_3$. If for each $i\in \left[3\right]$, the size of the list $L\left(v_i\right)$ is equal to 2, then $K_3$ has an ${\mathcal{M}}_{(K_3,L)}$-coloring except when the subgraph of ${\mathcal{M}}_{(K_3,L)}$ induced by $E_M$ is a union of two 3-cycles.

Moreover, if $L\left(v_i\right)\ge 2$ for each $i\in \left[3\right]$ and $\left|L\right(v_j\left)\right|>2$ for some $j\in \left[3\right]$, then $K_3$ has an ${\mathcal{M}}_{(K_3,L)}$-coloring for any cover of $(K_3,L)$.

Proof. 

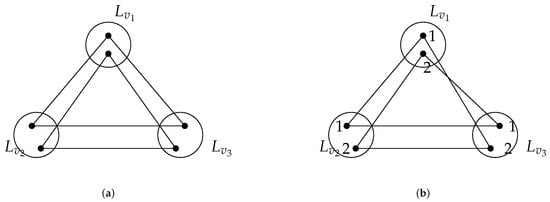
Assume $L\left(v_i\right)=\{1,2\}$ for every index $i\in \left[3\right]$. If the subgraph of ${\mathcal{M}}_{(K_3,L)}$ generated by $E_M$ is a union of two 3-cycles, see Figure 4a, say $\left[(v_1,i)(v_2,i)(v_3,i)\right]$ for each $i=1,2$, then we cannot find a 3-independent set in this cover; hence, $K_3$ does not have an ${\mathcal{M}}_{(K_3,L)}$-coloring for this cover. Thus, we assume that the subgraph of ${\mathcal{M}}_{(K_3,L)}$ induced by $E_M$ is not a union of two 3-cycles. Without loss of generality, suppose $(v_1,1)(v_2,1)(v_3,1)$ forms a 2-path in this cover, but $(v_1,1)(v_3,1)\notin E_M$. Then, $\{(v_1,1),(v_3,1),(v_2,2)\}$ is a 3-independent set of ${\mathcal{M}}_{(K_3,L)}$; see Figure 4b. Hence, we obtain an ${\mathcal{M}}_{(K_3,L)}$-coloring of $K_3$ for this cover.

Figure 4. Different cover ${\mathcal{M}}_{(K_3,L)}$ of $(K_3,L)$, where $L_{v_i}$ is a clique for each $i\in \left[3\right]$. (a) $E_M$ is a union of two 3-cycles. (b) $E_M$ is not a union of two 3-cycles.

If there is one $\left|L\right(v_i\left)\right|\ge 3$, for some $i\in \left[3\right]$, then we can identify a 3-independent set of ${\mathcal{M}}_{(K_3,L)}$ for any cover of $(K_3,L)$. Consequently, an ${\mathcal{M}}_{(K_3,L)}$-coloring of $K_3$ can be achieved for any cover of $(K_3,L)$. □

Lemma 2.

Consider L as a list assignment on $K_4^{-}$, where $K_4^{-}$ comprises two 3-faces $\left[xy{z}_i\right]$ for $i\in \{1,2\}$. If $\left|L\right(z_i\left)\right|\ge 2$ for each $i\in \{1,2\}$ and $\left|L\right(x\left)\right|,\left|L\right(y\left)\right|\ge 3$, then we can assign colors to each $z_i$ using at most one color from $L\left(z_i\right)$, so that $K_4^{-}$ has an ${\mathcal{M}}_{(K_4^{-},L)}$-coloring for any given cover of $K_4^{-}$.

Proof. 

Assuming $L\left(x\right)=L\left(y\right)=\left[3\right]$ and $L\left(z_1\right)=\left[2\right]$ is valid for our analysis. We assume that there is a color, say $1\in L\left(z_2\right)$, which cannot be chosen. This means if we choose $(z_2,1)$ in ${\mathcal{M}}_{(K_4^{-},L)}$, then by Lemma 1, $x,y$ has two available colors and the corresponding vertices of $z_1,x,y$ in ${\mathcal{M}}_{(K_4^{-},L)}$ induce two triangles, say $\left[(x,i)(y,i)(z_1,i)\right]$ for every $i\in \{1,2\}$. In this case, $\left[(z_2,1)(x,3)(y,3)\right]$ is a 3-cycle of ${\mathcal{M}}_{(K_4^{-},L)}$. Then, for each $d\in L\left(z_2\right)-\left\{1\right\}$ and for certain values i and j where $\{i,j\}=\left[2\right]$, the set $\{(z_2,d),(x,3),(z_1,i),(y,j)\}$ is an independent set in ${\mathcal{M}}_{(K_4^{-},L)}$. Thus, each color in $L\left(z_2\right)$ other than 1 can be chosen so that $K_4^{-}$ has an ${\mathcal{M}}_{(K_4^{-},L)}$-coloring. For vertex $z_1$, we can discuss a similar method. □

Lemma 3.

Consider $P=v_1{v}_2{v}_3$ be a 2-path with a list assignment L on P, such that $\left|L\right(v_i\left)\right|\ge 1$ for every $i\in \left[3\right]$. If $|L\left(v_1\right)|+|L\left(v_3\right)|\ge |L\left(v_2\right)|+1$, then we can assign colors to $v_1,v_3$, such that $v_2$ has at least $\left|L\right(v_2\left)\right|-1$ available colors.

Proof. 

If there is a vertex $(v_1,a)$ in ${\mathcal{M}}_{(P,L)}$ such that $(v_1,a)$ is not adjacent to any vertices in $L_{v_2}$, then we have completed this section. Thus, assume each vertex in $L_{v_1}$ is adjacent to a vertex of $L_{v_2}$, and the same holds for $L_{v_3}$. Given that $|L\left(v_1\right)|+|L\left(v_3\right)|\ge |L\left(v_2\right)|+1$, it follows that there exists a vertex in $L_{v_2}$ that is adjacent to at least one vertex from both $L_{v_1}$ and $L_{v_3}$. Without loss of generality, assume $(v_2,b)(v_1,a),(v_2,b)(v_3,c)\in E_M$, where $a\in L\left(v_1\right)$, $c\in L\left(v_3\right)$. Consequently, $v_1$ can be colored with color a and $v_3$ with c, so that $v_2$ has at least $\left|L\right(v_2\left)\right|-1$ available colors. □

Lemma 4.

Let $H_6$ be the graph depicted in Figure 3 with a list assignment L on $H_6$. If $\left|L\right(v\left)\right|\ge 2$ for every 3-vertex of $H_6$, $\left|L\right(u\left)\right|\ge 3$ for some $u\in \{u_3,u_5\}$ and $\left|L\right(v\left)\right|\ge 4$ for other three vertices in $H_6$, then we can color u with all colors but at most two of $L\left(u\right)$, ensuring that $H_6$ has an ${\mathcal{M}}_{(H_6,L)}$-coloring for any given cover of $(H_6,L)$.

Proof. 

Due to symmetry, we can assume that $\left|L\right(u_5\left)\right|\ge 3$. Thus, $\left|L\right(u_i\left)\right|\ge 4$ for each $i\in \{2,3,6\}$ and $\left|L\right(u_i\left)\right|\ge 2$ for each $i\in \{1,4\}$.

For 2-path $u_1{u}_5{u}_4$, if $|L\left(u_1\right)|+|L\left(u_4\right)|\ge |L\left(u_5\right)|+1$, then by Lemma 3, we can color $u_1,u_4$ such that $u_5$ has $\left|L\right(u_5\left)\right|-1\ge 2$ available colors, denoted by $A\left(u_5\right)$. After such coloring, $u_3$ has at least two available colors and $u_i$ has at least three available colors for each $i\in \{2,6\}$. For $\{u_5,u_2,u_3,u_6\}$, by Lemma 2, we can color $u_5$ with at least $|A\left(u_5\right)|-1=|L\left(u_5\right)|-2$ colors such that $\{u_2,u_3,u_6\}$ can be colored. This means we can color $u_5$ with all colors in $L\left(u_5\right)$, except for at most two, ensuring that $H_6$ has an ${\mathcal{M}}_{(H_6,L)}$-coloring for any given cover of $(H_6,L)$, which completes this section.

Thus, $|L\left(u_1\right)|+|L\left(u_4\right)|<|L\left(u_5\right)|+1$. Without loss of generality, we assume $L\left(u_1\right)=L\left(u_4\right)=\left[2\right]$, $L\left(u_5\right)=\left[4\right]$. From the above discussion, we only need to prove the case that after coloring $u_1$ and $u_4$, $u_5$ has exactly two available colors. Without loss of generality, we assume $(u_1,i)(u_5,i),(u_4,i)(u_5,i+2)\in E_M$ for each $i\in \left[2\right]$. For $\{(u_1,1),(u_4,1)\}$, by Lemma 2, we can color $u_5$ with 2 or 4 such that $\{u_2,u_3,u_6\}$ can be colored. For the same reason, for $\{(u_1,2),(u_4,2)\}$, by Lemma 2, we can color $u_5$ with 1 or 3 such that $\{u_2,u_3,u_6\}$ can be colored. This means we can color $u_5$ with all colors in $L\left(u_5\right)$, except for at most two, ensuring that $H_6$ has an ${\mathcal{M}}_{(H_6,L)}$-coloring for any given cover of $(H_6,L)$, which completes this section. □

Lemma 5.

Consider $H_7$ as the 7-cluster shown in Figure 3, along with a list assignment L. Let $S=\{u_1,u_4,u_5\}$. If there is at most one v in S for which $\left|L\right(v\left)\right|=2$, while $\left|L\right(v\left)\right|\ge 3$ for remaining vertices in S, and $\left|L\right(v\left)\right|\ge 4$ for every vertex v in $V\left(H_7\right)$ except S, then $H_7$ admits an ${\mathcal{M}}_{(H_7,L)}$-coloring for any given cover of $(H_7,L)$.

Proof. 

By symmetry, for each $i\in \{4,5\}$, assume that $\left|L\right(u_1\left)\right|=2$ and $\left|L\right(u_i\left)\right|=3$. Furthermore, $\left|L\right(u_i\left)\right|=4$ for each $i\in \{2,3,6\}$. Consequently, set $L\left(u_1\right)=\{1,2\}$, $L\left(u_4\right)=L\left(u_5\right)=\{1,2,3\}$, $L\left(u_2\right)=L\left(u_3\right)=L\left(u_6\right)=\left[4\right]$. Suppose otherwise that $H_7$ does not have an ${\mathcal{M}}_{(H_7,L)}$-coloring for some cover of $(H_7,L)$.

Suppose the subgraph induced by $E_M$ on vertices $L_{u_1},L_{u_4}$ and $L_{u_5}$ contains two triangles in ${\mathcal{M}}_{(H_7,L)}$ since $\left|L\right(u_1\left)\right|=2$; otherwise, by Lemma 1, we can color $u_1$ and $u_5$ such that $u_4$ has two available colors. Then, by Lemma 2, we can color $\{u_2,u_3,u_6,u_4\}$. Therefore, this results in an ${\mathcal{M}}_{(H_7,L)}$-coloring of $H_7$, leading to a contradiction. Let $\left[(u_1,i)(u_4,i)(u_5,i)\right]$ be the two triangles for $i=1,2$ and $(u_4,3)(u_5,3)\in E_M$.

Since $H_7$ does not have an ${\mathcal{M}}_{(H_7,L)}$-coloring, we have the following proposition, Proposition 1, constructed easily using Lemma 1. □

Proposition 1.

If $u_1,u_4,u_5$ are colored, then the subgraph of ${\mathcal{M}}_{(H_7,L)}$ induced by edge $E_M$ between $\{\left\{u_i\right\}\times A\left(u_i\right)|i=2,3,6\}$ is two triangles, where $A\left(u_i\right)$ denotes the available colors in $L\left(u_i\right)$ after coloring $\{u_1,u_4,u_5\}$.

By Proposition 1 and Lemma 1, there are four triangles between $\left\{u_i\right\}\times L\left(u_i\right)$ ($i\in \{2,3,6\}$) in ${\mathcal{M}}_{(H_7,L)}$. Let $\left[(u_2,i)(u_3,i)(u_6,i)\right]$ be the four triangles in ${\mathcal{M}}_{(H_7,L)}$ for each $i\in \left[4\right]$. We assume that $(u_1,1)(u_2,1)\in E_M$. Assume $(u_1,1)(u_3,i)\in E_M$ for some $i\in \left[4\right]$. By symmetry, we only need to discuss two cases: $i=1$ or $i=2$.

If $i=2$, then by Proposition 1, $(u_4,3)(u_3,1)\in E_M$ for 3-independent set $\{(u_1,1),(u_4,3),(u_5,2)\}$ and $(u_4,2)(u_3,1)\in E_M$ for 3-independent set $\{(u_1,1),(u_4,2),(u_5,3)\}$; contrary to this, $[L_{u_3},L_{u_4}]$ is a matching set.

If $i=1$, then by Proposition 1, $(u_5,2)(u_2,j),(u_4,3)(u_3,j)\in E_M$ for some $j\in \{2,3,4\}$, say $j=2$. In this case, for 3-independent set $\{(u_1,2),(u_4,3),(u_5,1)\}$, $(u_1,2)(u_2,2)$, $(u_1,2)(u_3,k)\in E_M$ for some $k\in \{3,4\}$. The independent set $\{(u_1,2),(u_4,1),(u_5,3)\}$, $(u_4,1)(u_3,2)\in E_M$, contrary to $[L_{u_3},L_{u_4}]$, is a matching set.

Lemma 6.

Consider $H_7$ as the 7-cluster shown in Figure 3, along with a list assignment L. If $\left|L\right(u_i\left)\right|\ge 3$ for $i=4,5$ and $\left|L\right(v\left)\right|\ge 4$ for the other vertices of $H_7$, then we can color $u_1$ with all colors but at most one in $L\left(u_1\right)$, ensuring that $H_7$ maintains an ${\mathcal{M}}_{(H_7,L)}$-coloring for any given cover of $(H_7,L)$.

Proof. 

Without loss of generality, we assume that for each $i\in \{4,5\}$, $L\left(u_i\right)=\left[3\right]$ and $L\left(u_j\right)=\left[4\right]$ for each $j\in \{1,2,3,6\}$. For any given cover of $(H_7,L)$, by contradiction, we assume that there are two colors that cannot be chosen in $L\left(u_1\right)$, say $\{1,2\}$. Since $\left[2\right]\subseteq L\left(u_1\right)$, by Lemma 5, there is an ${\mathcal{M}}_{(H_7,L)}$-coloring for any given cover of $(H_7,L)$, a contradiction. This means we can color $u_1$ with all colors, but only use at most one in $L\left(u_1\right)$, ensuring that $H_7$ maintains an ${\mathcal{M}}_{(H_7,L)}$-coloring for any cover of $(H_7,L)$. □

The following definition is due to Sittitrai and Nakprasit [22].

Definition 3.

Let ${\mathcal{M}}_{(G,L)}$ represent a cover of $(G,L)$, with $G^{\prime }$ as an induced subgraph within G. The following definitions apply:

(i) 

A list assignment ${L|}_{G^{\prime }}$ is considered a restriction of L on $G^{\prime }$ if ${L|}_{G^{\prime }}\left(u\right)=L\left(u\right)$ for every vertex of $G^{\prime }$.

(ii) 

A graph ${\mathcal{M}}_{(G,L)}{|}_{G^{\prime }}$ is termed a restriction of ${\mathcal{M}}_{(G,L)}$ on $G^{\prime }$ if ${\mathcal{M}}_{(G,L)}{|}_{G^{\prime }}={\mathcal{M}}_{(G,L)}\left[\{v\times L\left(v\right):v\in V\left(G^{\prime }\right)\}\right]$. According to the cover definition, ${\mathcal{M}}_{(G,L)}{|}_{G^{\prime }}\cong {\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$.

Assuming that $G^{\prime }$ has an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring with an independent set $I^{\prime }$, the residual list assignment $L^{*}$ for $G-G^{\prime }$ is defined as follows:

$L^{*}\left(y\right)=L\left(y\right)-\bigcup _{xy\in E\left(G\right)}\{c^{\prime }\in L\left(y\right):(x,c)(y,c^{\prime })\in E\left(H\right)$ and $(x,c)\in I^{\prime }\}$

for every $y\in V(G-G^{\prime })$. The residual cover ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ is established by ${\mathcal{M}}_{(G,L)}\left[\{w\times L^{*}\left(w\right):w\in V(G-G^{\prime })\}\right]$.

Lemma 7.

([22]). Let ${\mathcal{M}}_{(G,L)}$ represent a cover of $(G,L)$ with $G^{\prime }$ as an induced subgraph of G. If $G^{\prime }$ maintains an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$- coloring, then the residual cover ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ serves as a cover for $(G-G^{\prime },L^{*})$, where $L^{*}$ represents the residual list assignment. Additionally, if $G-G^{\prime }$ is colorable with respect to ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$, then G is also ${\mathcal{M}}_{(G,L)}$-colorable.

For the remainder of this paper, $G^{\prime }$ is regarded as an induced subgraph of $(G,L)$, where $\left|L\right(v\left)\right|\ge 4$ for every vertex v of G. By Lemma 7, to establish that G is ${\mathcal{M}}_{(G,L)}$-colorable, it suffices to demonstrate that $G^{\prime }$ maintains an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring and $G^{*}$ maintains an ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$-coloring.

3. Reducible Configurations

Consider $(G,C_0)$ as a counterexample to Theorem 4, where the number of vertices is minimized, and within that constraint, the number of edges is also minimized, with $C_0$ representing a good 3-cycle. The proof presented in [12] establishes that any planar graph devoid of 3-cycles is DP-4-colorable. Therefore, it is reasonable to assume that G includes a 3-cycle. Indeed, we can always identify a good 3-cycle within G by Lemma 5. Let L represent a 4-list assignment on the vertex set $V\left(G\right)$, and $C_0$ as the outer cycle of G. Let ${\mathcal{M}}_{(G,L)}$ be any cover of $(G,L)$ and ${\varphi }_0$ the ${\mathcal{M}}_{(G,L)}$-coloring restricted on $C_0$. The following lemma holds true when G lacks any 7-cycle that is adjacent to 4- or 5-cycles.

Lemma 8.

G contains no k-cluster for $k\ge 8$; moreover, the graphs of Figure 3 are all k-clusters of G, where $k\in \{4,5,6,7\}$.

Consider C representing a cycle within G. The notation $int\left(C\right)$ (or $ext\left(C\right)$) is employed to indicate the collections of vertices lying inside (or outside) the cycle C. A cycle C is referred to as separating if it divides the vertex set such that both $int\left(C\right)$ and $ext\left(C\right)$ include vertices. A vertex u in G is classified as internal if $u\notin V\left(C_0\right)$. Additionally, a face f is classified as internal if all vertex of f is internal.

Lemma 9.

The statements below are all valid:

(i) 

$V\left(G\right)\ne V\left(C_0\right)$;

(ii) 

G does not have any good 3-cycle that is separating;

(iii) 

the degree of every internal vertex in G is at least 4.

Proof. 

(i) Assume, for the purpose of contradiction, that $V\left(G\right)=V\left(C_0\right)$. Since $C_0$ is a good 3-cycle, the ${\mathcal{M}}_{(G,L)}$-coloring restricted on $C_0$ would also serve as an ${\mathcal{M}}_{(G,L)}$-coloring for G, which contradicts the initial assumption.

(ii) Suppose C is a separating good 3-cycle. Given the property of minimality in G, we can extend ${\varphi }_0$ to ext(C)$\cup C$, say ${\varphi }_1$. This extension can then be restricted to C and further extended to create an ${\mathcal{M}}_{(G,L)}$-coloring ${\varphi }_2$ for $int\left(C\right)$. Consequently, by merging ${\varphi }_1$ and ${\varphi }_2$, we obtain an ${\mathcal{M}}_{(G,L)}$-coloring for G, contrary to the assumption.

(iii) Let v represent an internal $3^{-}$-vertex. Given that G is minimal, the ${\mathcal{M}}_{(G,L)}$-coloring restricted on $C_0$ can be applied to $G-v$. Since $d_G\left(v\right)\le 3$, v has at least one available color for any cover of $(G,L)$. This means that G has an ${\mathcal{M}}_{(G,L)}$-coloring, a contradiction. □

Lemma 10.

No two internal $(4,4,4)$-faces in G can share a common edge.

Proof. 

Assume, for the sake of contradiction, that $f_i=\left[xy{z}_i\right]$ ($i=1,2$) are two internal (4, 4, 4)-faces. Denote $G^{\prime }=G-f_1\cup f_2$. By the minimality of G, the graph $G^{\prime }$ maintains an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring extended by ${\varphi }_0$ on $C_0$, and $L^{*}$, ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ are the residual list assignment and the residual cover of $(f_1\cup f_2,L^{*})$. Since each vertex of $f_1\cup f_2$ is a 4-vertex, $|L^{*}\left(z_i\right)|\ge 2$ for every $i\in \{1,2\}$ and $|L^{*}\left(x\right)|,|L^{*}\left(y\right)|\ge 3$. By Lemmas 2 and 7, we can obtain an ${\mathcal{M}}_{(G,L)}$-coloring for G, which contradicts the original assumption. □

A cluster is special if it is one of $\{H_4^4,H_5^2,H_6,H_7\}$ in Figure 3 with an internal (4, 4, 4)-face $\left[u_2{u}_3{u}_6\right]$ (or $\left[u_2{u}_5{u}_6\right]$ by symmetry if the cluster is $H_6$); otherwise non-special. An internal $4^{+}$-vertex v located inside a cluster H is classified as i-type with respect to H if it is connected to precisely i edges of H. Moreover, if H is a special cluster, then this $4^{+}$-vertex v is referred to as i-type good; otherwise, it is considered i-type bad. The following result is obvious from the fact that G contains no 7-cycle adjacent to a 4- or 5-cycle.

Lemma 11.

(i) 

A 1-cluster is adjacent to no more than a 4-face.

(ii) 

The face of G adjacent to i-cluster should be $8^{+}$-face for each $i\in \{4,5,6,7\}$.

(iii) 

The face of G adjacent to 2- or 3-cluster should be 4-face or $8^{+}$-face; moreover, s 2-cluster is adjacent to no more than two non-adjacent 4-faces, where these two 4-faces are adjacent to different 3-face of this 2-cluster. Similarly, a 3-cluster is adjacent to no more than one 4-face, which is incident to one 4-type 4-vertex to this 3-cluster.

Lemma 12.

No internal 5-vertex of G can belong to two clusters which are special.

Proof. 

Let v represent an internal 5-vertex, and let its neighborhood be $N\left(v\right)=\{v_i:i\in \left[5\right]\}$. Assume, for the purpose of contradiction, that v is a vertex of two special clusters $K_1,K_2$. Without loss of generality, assume the internal (4, 4, 4)-faces of $K_1$ and $K_2$ are $\left[v_1{v}_2{v}_{12}\right]$ and $\left[v_3{v}_4{v}_{34}\right]$, respectively. Define $H_1$ and $H_2$ as the graphs induced by vertex set $\{v_1,v_2,v_{12},v\}$ and $\{v_3,v_4,v_{34},v\}$, respectively. Clearly, $H_i$ is isomorphic to $K_4^{-}$. Let $G^{\prime }=G-H_1\cup H_2$ and $L^{*}$, ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ denote the residual list assignment and the residual cover of $G-G^{\prime }$. Due to the minimality property of $(G,C_0)$, $G^{\prime }$ maintains an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring extended from ${\varphi }_0$. Notably, $|L^{*}\left(v\right)|$ and $|L^{*}\left(v_i\right)|$ are both at least 3 for each $i\in \left[4\right]$, while $|L^{*}\left(v_{12}\right)|,|L^{*}\left(v_{34}\right)|\ge 2$. Applying Lemma 2 to $H_1$, we can color v with at least two colors in $L^{*}\left(v\right)$, ensuring that $H_1$ maintains an ${\mathcal{M}}_{(H_1,L^{*}{|}_{H_1})}$-coloring for every cover of $(H_1,L^{*}{|}_{H_1})$. Applying Lemma 2 to $H_2$ subsequently yields an ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$-coloring for $G-G^{\prime }$. By Lemma 7, this implies that G maintains an ${\mathcal{M}}_{(G,L)}$-coloring, contrary to the assumption. □

Internal 6-vertex v is classified as special if it qualifies as a 4-type good vertex to an internal $6^{+}$-cluster $K_1$ and as a 2-type good vertex in association with a $k_2$-cluster $K_2$, where $4\le k_2\le 5$ (see Figure 5a). Internal 6-vertex v is poor if it is a 3-type good vertex to an internal 6-cluster $K_1$ and a 3-type good vertex to a $k_2$-cluster $K_2$, where $5\le k_2\le 6$ (see Figure 5b).

Figure 5. Special or poor vertex: all $K_1$ is special and internal and $K_2$ is special. (a) Special 6-vertex v. (b) Poor 6-vertex v. (c) Poor 7-vertex v when $u,w\in {\mathcal{A}}_1$. (d) Special 7-vertex v when $u^{\prime }\in {\mathcal{A}}_1$ and $w^{\prime }\in {\mathcal{A}}_2$.

Lemma 13.

Consider v as either a special or poor 6-vertex contained in $K_1$ and $K_2$ (see Figure 5a,b). Let $G^{\prime }=G-K_1$, with $L^{*}$, ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ representing the residual list assignment and residual cover of $G-G^{\prime }$. Then, $|L^{*}\left(v\right)|\ge 3$ if v is a special 6-vertex, and $|L^{*}\left(v\right)|\ge 2$ if v is a poor 6-vertex.

Proof. 

Since v is either a special or poor 6-vertex, $K_2$ is a special cluster. Denote $\left[x^{\prime }{y}^{\prime }{z}^{\prime }\right]$ to represent the (4, 4, 4)-face of $K_2$. Denote $G^{\prime \prime }=G^{\prime }-\{x^{\prime },y^{\prime },z^{\prime }\}=G-K_1\cup \{x^{\prime },y^{\prime },z^{\prime }\}$, with $L^{**}$, ${\mathcal{M}}_{(G-G^{\prime \prime },L^{**})}^{**}$ as the residual list assignment and residual cover for $G-G^{\prime \prime }$. This implies that $|L^{**}\left(x^{\prime }\right)|\ge 2$ and $|L^{**}\left(u\right)|\ge 3$ for each $u\in \{y^{\prime },z^{\prime }\}$.

If v is a special 6-vertex, then $|L^{**}\left(v\right)|\ge 4$. If v is a poor 6-vertex, then $|L^{**}\left(v\right)|\ge 3$. In either case, by Lemma 2, we can precolor v using all colors in $L^{**}\left(v\right)$ except for at most one, allowing the vertices $\{x^{\prime },y^{\prime },z^{\prime }\}$ to be colored as well. This means $|L^{*}\left(v\right)|\ge 3$ when the vertex v is classified as a special 6-vertex and $|L^{*}\left(v\right)|\ge 2$ when v is a poor 6-vertex. □

We use a recursive method to define the poor 7-vertex, the special 7-vertex, and the special 8-vertex.

Definition 4.

Consider v as a 7-vertex of G, which is 4-type good to one internal 6-cluster $K_1$ and 3-type good to one internal 6-cluster $K_2$.

(i) 

v is a  poor $7^0$-vertex  if $K_1$ contains two 3-type vertices, each of which is in {3-type good 5-vertex, 3-type poor 6-vertex};

(ii) 

v is a  poor $7^m$-vertex  if $K_1$ contains one 3-type poor $7^{m-1}$-vertex and one 3-type vertices which is in {3-type good 5-vertex, 3-type poor 6-vertex, 3-type poor $7^k$-vertex $(k\le m-1)$}.

Then, v is called a  3-type poor 7-vertex  if v is a 3-type poor $7^m$-vertex, where $m\in N$.

Let ${\mathcal{A}}_1=\{$3-type good 5-vertex, 3-type poor 6-vertex, 3-type poor 7-vertex}.

Definition 5.

Consider v as a 7-vertex of G which is 4-type good to one internal $6^{+}$-cluster $K_1$ and 3-type good to one internal 6-cluster $K_2$.

(i) 

v is a  special $7^0$-vertex  if $K_2$ contains one vertex of ${\mathcal{A}}_1$ and one vertex of {4-type good 5-vertex, 4-type special 6-vertex};

(ii) 

v is a  special $7^m$-vertex  if $K_2$ contains one vertex of ${\mathcal{A}}_1$ and one special $7^{m-1}$-vertex.

Then, v is called a  4-type special 7-vertex  if v is a 4-type special $7^m$-vertex, where $m\in N$.

Let ${\mathcal{A}}_2=\{$4-type good 5-vertex, 4-type special 6-vertex, 4-type special 7-vertex}.

Definition 6.

Consider v as an 8-vertex of G which is 4-type good to one internal 7-cluster $K_1$ and 4-type good to one internal $6^{+}$-cluster $K_2$.

(i) 

v is a  special $8^0$-vertex  if $K_1$ contains two vertices which are in ${\mathcal{A}}_2$;

(ii) 

v is a  special $8^m$-vertex  if $K_1$ contains one special $8^{m-1}$-vertex and one vertex of ${\mathcal{A}}_2\cup \{$ 4-type special $8^l$-vertex $(l\le m-1)\}$.

Then, v is called a  special 8-vertex  if v is a special $8^m$-vertex, where $m\in N$.

By Definition 6, in order to distinguish the above clusters $K_1$ and $K_2$, $K_1$ is called type I and $K_2$ is called type II.

Lemma 14.

Consider v as a 3-type vertex to an internal cluster K. Let $G^{\prime }=G-K$, with $L^{*}$ and ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ as the residual list assignment and residual cover on $G-G^{\prime }$, respectively. If $v\in {\mathcal{A}}_1$, then $|L^{*}\left(v\right)|\ge 2$.

Proof. 

If v is a 5-vertex, then the cardinality of $L^{*}\left(v\right)$ is at least 2. If v is a 3-type poor 6-vertex, then $|L^{*}\left(v\right)|\ge 2$ by Lemma 13. Then, v is a poor 7-vertex. By Definition 4, assuming v is a poor $7^m$-vertex, $m\in N$. We use the symbol shown in Figure 5c, where $K_2=K$ and $K_1$ are 6-clusters. Let $\left[xyz\right]$ and $\left[x^{\prime }{y}^{\prime }{z}^{\prime }\right]$ be (4, 4, 4)-faces in $K_1$ and $K_2$, respectively. Since v is poor, $K_1$ is also internal, and $u,w\in {\mathcal{A}}_1$. Let $G^{\prime \prime }=G^{\prime }-K_1=G-(K_1\cup K_2)$, and let $L^{**}$ and ${\mathcal{M}}_{(G-G^{\prime \prime },L^{**})}^{**}$ denote the residual list assignment and residual cover of $G-G^{\prime \prime }$. We use the induction hypothesis on m. If $m=0$, then $\{u,w\}$ is a 3-type 5- or poor 6-vertex, by the above discussion, $|L^{**}\left(u\right)|$, $|L^{**}\left(w\right)|\ge 2$. Clearly, $|L^{**}\left(i\right)|=4$ for each $i\in \{x,y,z,v\}$. Lemma 4 provides a minimum of two colors available in $L^{**}\left(v\right)$ to color $K_1$. This means $|L^{*}\left(v\right)|\ge 2$. By the induction hypothesis, it is assumed that the lemma is valid for $m\le n-1$.

Next, we prove that the lemma is valid if $m=n$.

By Definition 4, each of $\{u,w\}$ is a 5-, poor 6-, or $7^l$-vertex $(l\le n-1)$, using Lemma 13 and the induction hypothesis, $|L^{**}\left(u\right)|\ge 2$ and $|L^{**}\left(w\right)|\ge 2$. Then, using Lemma 4, we have completed this section. □

Lemma 15.

Consider v as a 4-type vertex to an internal cluster K. Let $G^{\prime }=G-K$ with $L^{*}$ and ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ representing the residual list assignment and residual cover of $G-G^{\prime }$.

(i) 

If $v\in {\mathcal{A}}_2$, then the cardinality of $L^{*}\left(v\right)$ is at least 3;

(ii) 

If v is a special 8-vertex and K is type II, then $|L^{*}\left(v\right)|\ge 3$.

Proof. 

(i) Clearly, $|L^{*}\left(v\right)|\ge 3$ if v is a 5-vertex. If v is a 4-type special 6-vertex, then $|L^{*}\left(v\right)|\ge 3$ by Lemma 13. Then, v is a special 7-vertex. By Definition 5, assuming v is a special $7^m$-vertex, $m\in N$. We use the labeling shown in Figure 5d, where $K_1=K$ and $K_2$ is an internal 6-cluster. Then, the (4, 4, 4)-face corresponding to the cluster $K_2$ is denoted by $\left[x^{\prime }{y}^{\prime }{z}^{\prime }\right]$ and $u^{\prime }\in {\mathcal{A}}_1$. Let $G^{\prime \prime }=G^{\prime }-K_2=G-(K_1\cup K_2)$, with $L^{**}$ and ${\mathcal{M}}_{(G-G^{\prime \prime },L^{**})}^{**}$ representing the residual list assignment and residual cover of $G-G^{\prime \prime }$. Then, for each vertex $q\in \{v,x^{\prime },y^{\prime },z^{\prime }\}$, $|L^{**}\left(q\right)|=4$. Since $u^{\prime }\in \mathcal{A}{\mathcal{A}}_1$, by Lemma 14, $|L^{**}\left(u^{\prime }\right)|\ge 2$.

Next, we use the induction hypothesis on m.

If $m=0$, then $w^{\prime }$ is a good 5- or special 6-vertex. According to Lemma 13, we have $|L^{**}\left(w^{\prime }\right)|\ge 3$. Without loss of generality, we can take $L^{**}\left(w^{\prime }\right)=\left[3\right],L^{**}\left(u^{\prime }\right)=\left[2\right],L^{**}\left(q\right)=\left[4\right]$ for each $q\in \{x^{\prime },y^{\prime },z^{\prime },v\}$. By Lemma 4, for $\{3,4\}\subseteq L\left(v\right)$, there is an ${\mathcal{M}}_{(K_2,L^{**})}$-coloring, say ${\varphi }_1$, with ${\varphi }_1\left(v\right)=3$. Similarly, for $\{1,2\}\subseteq L\left(v\right)$, there is an ${\mathcal{M}}_{(K_2,L^{**})}$-coloring, say ${\varphi }_2$, with ${\varphi }_2\left(v\right)=1$; for $\{2,4\}\subseteq L\left(v\right)$, there is an ${\mathcal{M}}_{(K_2,L^{**})}$-coloring, say ${\varphi }_3$, with ${\varphi }_3\left(v\right)=2$. Hence, $|L^{*}\left(v\right)|\ge 3$.

By the induction hypothesis, it is assumed that the lemma is valid for $m\le n-1$.

Next we prove that the lemma is valid if $m=n$. By Definition 5, $w^{\prime }$ is a special $7^{n-1}$-vertex. By the induction hypothesis, $|L^{**}\left(w^{\prime }\right)|\ge 3$. By Lemma 4 and the similar reasoning for the case $m=0$, we have $|L^{*}\left(v\right)|\ge 3$.

(ii) Since v is a special 8-vertex, v is a special $8^m$-vertex, $m\in N$. We use the induction hypothesis on m. If $m=0$, then v is a special $8^0$-vertex, K is an internal $6^{+}$-cluster and v is also a vertex of internal 7-cluster $K_1$, and $K_1$ contains two vertices in ${\mathcal{A}}_2$, say $u,w$. Let $G^{\prime \prime }=G^{\prime }-K_1=G-(K\cup K_1)$, with $L^{**}$ and ${\mathcal{M}}_{(G-G^{\prime \prime },L^{**})}^{**}$ representing the residual list assignment and residual cover of $G-G^{\prime \prime }$. Let $\left[xyz\right]$ be the (4, 4, 4)-face in $K_1$. Then, for each vertex $q\in \{v,x,y,z\}$, $|L^{**}\left(q\right)|=4$. Since $u,w\in {\mathcal{A}}_2$, by Lemma 15(i), $|L^{**}\left(u\right)|\ge 3$, $|L^{**}\left(w\right)|\ge 3$. By Lemma 6, we can assign colors to v using all but at most one color, ensuring that $K_1$ maintains an ${\mathcal{M}}_{(K_1,L^{**})}$-coloring for any given cover of $(K_1,L^{**})$. This means $|L^{*}\left(v\right)|\ge 4-1\ge 3$.

By the induction hypothesis, it is assumed that the lemma is valid for $m\le n-1$.

Next, we prove that the lemma is valid if $m=n$. By Definition 6, assuming that u is a special $8^{n-1}$-vertex and w is a vertex from ${\mathcal{A}}_2\cup \{$the 4-type special $8^l$-vertex $(l\le n-1)\}$. By the induction hypothesis, the cardinality of both $L^{**}\left(u\right)$ and $L^{**}\left(w\right)$ is at least 3. By Lemma 6, we have $|L^{*}\left(v\right)|\ge 3$. □

Lemma 16.

If v is a poor 7-vertex in G, then it cannot be a special 7-vertex of G.

Proof. 

Since v is a poor 7-vertex, we will consider v as a good 4-type vertex in relation to the internal 6-cluster $K_1$ and as a good 3-type vertex to internal 6-cluster $K_2$. Clearly, $v\in {\mathcal{A}}_1$. Suppose, on the contrary, that v is also a special 7-vertex. This means $v\in {\mathcal{A}}_2$. Let $G^{\prime }=G-K_1\cup K_2$, with $L^{*}$ and ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ representing the residual list assignment and residual cover for $G-G^{\prime }$. Given the minimal property of G, $G^{\prime }$ has an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring that extends ${\varphi }_0$. Since $v\in {\mathcal{A}}_2$, there are three available colors in $L^{*}\left(v\right)$ to choose, so that $K_2$ can be colored by Lemma 15. Since $v\in {\mathcal{A}}_1$, there are two available colors in $L^{*}\left(v\right)$ to choose, so that $K_1$ can be colored by Lemma 14. Since $|L^{*}\left(v\right)|=4$, we can precolor v so that $K_1\cup K_2$ can be colored. By Lemma 7, G is $(\mathcal{M}$$,L)$-coloring for any given cover of $(G,L)$, leading to a contradiction. □

Lemma 17.

Consider v as a 7-vertex of G, where it is 4-type to a 7-cluster $K_1$ and 3-type to a $6^{-}$-cluster $K_2$. Denote $[x,y,z]$ represent a (4, 4, 4)-face within $K_1$ and $u,w\in V\left(K_1\right)$. If $u,w\in {\mathcal{A}}_2\cup \{$the special 8-vertex and $K_1$ is type II}, then $K_2$ cannot be special.

Proof. 

Assume, to the contrary, that $K_2$ is special. In this case, let $\left[x^{\prime }{y}^{\prime }{z}^{\prime }\right]$ represent the internal (4, 4, 4)-face within $K_2$ with $y^{\prime },z^{\prime }\in N\left(v\right)$. Since $u,w\in {\mathcal{A}}_2\cup \{$the special 8-vertex and $K_1$ is type II}, $K_1$ is internal. Define $G^{\prime }=G-K_1-\{x^{\prime },y^{\prime },z^{\prime }\}$, and let $L^{*}$ and ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ be the residual list assignment and the residual cover of $G-G^{\prime }$. In this setup, $|L^{*}\left(x^{\prime }\right)|\ge 2$ and $|L^{*}\left(y^{\prime }\right)|,|L^{*}\left(z^{\prime }\right)|,|L^{*}\left(v\right)|\ge 3$. By Lemma 15, $|L^{*}\left(u\right)|,|L^{*}\left(w\right)|\ge 3$. Clearly, $|L^{*}\left(x\right)|,|L^{*}\left(y\right)|$ and $|L^{*}\left(z\right)|\ge 4$. According to Lemma 2, v has a minimum of two colors that can be used from $L^{*}\left(v\right)$, allowing for the coloring of the set $\{x^{\prime },y^{\prime },z^{\prime }\}$. Then, by Lemma 5, $K_1$ has an ${\mathcal{M}}_{(K_1,L^{*}{|}_{K_1})}^{*}$-coloring for any cover of $(K_1,L^{*})$. Therefore, $G-G^{\prime }$ maintains an ${\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$-coloring. By the minimality of G, $G^{\prime }$ also maintains an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring. By Lemma 7, G maintains an ${\mathcal{M}}_{(G,L)}$-coloring, a contradiction. □

Lemma 18.

Consider $H_6\subseteq G$ as an internal special 6-cluster with a (4, 4, 4)-face $\left[u_2{u}_3{u}_6\right]$, shown in Figure 3. If $u_i\in \mathcal{A}{\mathcal{A}}_1$ for each $i\in \{1,4\}$, then $d\left(u_5\right)\ge 6$ and $u_5\notin {\mathcal{A}}_2\cup \{$the special 8-vertex, and $H_6$ is type II}.

Proof. 

By Lemma 10, $d\left(u_5\right)\ge 5$. Denote $G^{\prime }=G-H_6$ with $L^{*}$ and ${\mathcal{M}}_{(H_6,L^{*})}^{*}$ as the residual list assignment and residual cover of $G-G^{\prime }$. By the minimal property of G, $G^{\prime }$ maintains an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring that extends ${\varphi }_0$. Suppose otherwise that $u_5\in {\mathcal{A}}_2$ or $u_5$ is a special 8-vertex with $H_6$ type II. Then, by Lemma 15, $|L^{*}\left(u_5\right)|\ge 3$. Since $u_i\in {\mathcal{A}}_1$ for each $i\in \{1,4\}$, by Lemma 14, $|L^{*}\left(u_i\right)|\ge 2$. Note that $|L^{*}\left(u_i\right)|\ge 4$ for each $i\in \{2,3,6\}$. By Lemma 4, $H_6$ has an ${\mathcal{M}}_{(H_6,L^{*})}^{*}$-coloring. According to Lemma 7, G admits an ${\mathcal{M}}_{(G,L)}$-coloring, which is a contradiction. □

Lemma 19.

Consider $H_7\subseteq G$ as an internal 7-cluster (see Figure 3) and $X=\{u_1,u_4,u_5\}$.

(i) 

If X contains two vertices in ${\mathcal{A}}_2\cup \{$the special 8-vertex, and $H_7$ is type II}, then the third vertex of X is a $7^{+}$-vertex;

(ii) 

X does not contain three vertices in ${\mathcal{A}}_2\cup \{$the special 8-vertex, and $H_7$ is type II}.

Proof. 

(i) By symmetry, assume $u_4,u_5\in {\mathcal{A}}_2\cup \{$the special 8-vertex, and $H_7$ is type II}. Suppose, to the contrary, that $d\left(u_1\right)\le 6$.

Define $G^{\prime }=G-H_7$ with $L^{*}$ and ${\mathcal{M}}_{(H_7,L^{*})}^{*}$ as the residual list assignment and the residual cover of $G-G^{\prime }$. By the minimal property of G, $G^{\prime }$ maintains an ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring that extends ${\varphi }_0$, with $|L^{*}\left(u_1\right)|\ge 2$. Note that $|L^{*}\left(u_i\right)|\ge 4$ for each $i\in \{2,3,6\}$. Since $u_4,u_5\in {\mathcal{A}}_2\cup \{$the special 8-vertex, and $H_7$ is type I}, by Lemma 15, $|L^{*}\left(u_i\right)|\ge 3$, for each $i\in \{4,5\}$. By Lemma 5, an ${\mathcal{M}}_{(H_7,L^{*})}^{*}$-coloring of $H_7$ can be achieved. Then, by Lemma 7, G admits an ${\mathcal{M}}_{(G,L)}$-coloring, a contradiction.

(ii) follows easily by Lemmas 5 and 15. □

4. Proof of Theorem 4

Consider V as the family of vertices of G and F as the family of faces. An initial charge is defined as $\mu \left(x\right)=d\left(x\right)-4$ for every $x\in V\cup F\setminus \left\{C_0\right\}$, while $\mu \left(C_0\right)=d\left(C_0\right)+4$, where $C_0$ is designated as the outer face of G. According to Euler’s Formula, the sum ${\sum }_{x\in V\cup F}\mu \left(x\right)=0$. Let ${\mu }^{*}\left(x\right)$ represent the charge of $x\in V\cup F$ after the discharging procedure. To reach a contradiction, the purpose of this is to demonstrate that ${\mu }^{*}\left(x\right)\ge 0$ for all $x\in V\cup F\setminus \left\{C_0\right\}$ and that ${\mu }^{*}\left(C_0\right)>0$.

The discharging rules are as follows:

(R1) 

Every 5- or $8^{+}$-face distributes ${\displaystyle \frac{1}{2}}$ to every neighboring 3-face, while a k-face ($k=6,7$) distributes ${\displaystyle \frac{k-4}{k}}$ to every neighboring 3-face;

Consider v as a vertex of k-face f and let t represent the number of edges of f that are incident to v, such that these edges are not in any 3-faces. In cases where $k\ge 8$, f distributes ${\displaystyle \frac{t}{4}}$ to v; f distributes ${\displaystyle \frac{t(k-4)}{2k}}$ to v when $k\in \{6,7\}$;

(R2) 

Every 2-cluster obtains ${\displaystyle \frac{1}{4}}$ from its 3-type $4^{+}$-vertex and ${\displaystyle \frac{1}{4}}$ from its 2-type $4^{+}$-vertex, which is on a 4-face adjacent to this cluster;

(R3) 

Every 3-cluster which is adjacent to 4-face obtains ${\displaystyle \frac{1}{2}}$ from its 3-type $4^{+}$-vertex and ${\displaystyle \frac{1}{4}}$ from its 2-type $4^{+}$-vertex; otherwise, 3-cluster obtains ${\displaystyle \frac{1}{4}}$ from its 3-type $4^{+}$-vertex;

(R4) 

Every 4-cluster obtains the charge from its incident vertex v, defined by

$$\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}2-\mathrm{type}\mathrm{good}{5}^{+}-\mathrm{vertex}\mathrm{or}\mathrm{a}3-\mathrm{type}{4}^{+}-\mathrm{vertex};\hfill \\ 1,\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}5-\mathrm{type}{5}^{+}-\mathrm{vertex};\hfill \\ {\displaystyle \frac{3}{2}},\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}4-\mathrm{type}{5}^{+}-\mathrm{vertex}.\hfill \end{array}\right.$$

(1)

(R5) 

Every 5-cluster obtains the charge from its incident vertex v defined by

$$\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}2-\mathrm{type}\mathrm{good}{5}^{+}-\mathrm{vertex}\mathrm{or}3-\mathrm{type}4-\mathrm{vertex}\mathrm{or}3-\mathrm{type}\mathrm{bad}5-,6-,7-\mathrm{vertex};\hfill \\ 1,\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}3-\mathrm{type}\mathrm{good}5-,6-,7-\mathrm{vertex}\mathrm{or}3-\mathrm{type}{8}^{+}-\mathrm{vertex}\mathrm{or}5-\mathrm{type}5-\mathrm{vertex};\hfill \\ {\displaystyle \frac{3}{2}},\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}4-\mathrm{type}{5}^{+}-\mathrm{vertex}.\hfill \end{array}\right.$$

(2)

(R6) 

Every 6-cluster K obtains the charge from its incident vertex v defined by

$$\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}3-\mathrm{type}4-\mathrm{vertex}\mathrm{or}3-\mathrm{type}\mathrm{bad}5-,6-,\mathrm{or}7-\mathrm{vertex};\hfill \\ 1,\hfill & \mathrm{if}v\in {\mathcal{A}}_1\mathrm{or}v\mathrm{is}\mathrm{a}3-\mathrm{type}\mathrm{good},\mathrm{non}-\mathrm{poor}6-\mathrm{or}7-\mathrm{vertex},\mathrm{while}K\mathrm{is}\mathrm{not}\mathrm{internal};\hfill \\ 2,\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}4-\mathrm{type}\mathrm{good}{6}^{+}-\mathrm{vertex},\mathrm{while}K\mathrm{is}\mathrm{internal}\mathrm{and}\mathrm{contains}\mathrm{two}\mathrm{vertices}\mathrm{in}{\mathcal{A}}_1,\hfill \\ & \mathrm{or}\mathrm{a}4-\mathrm{type}\mathrm{good}{9}^{+}-\mathrm{vertex};\hfill \\ {\displaystyle \frac{3}{2}},\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}4-\mathrm{type}{5}^{+}-\mathrm{vertex}\mathrm{except}\mathrm{the}\mathrm{above}4-\mathrm{type}\mathrm{vertices},\mathrm{or}3-\mathrm{type}{8}^{+}-\mathrm{vertex},\mathrm{or}\hfill \\ & 3-\mathrm{type}\mathrm{good},\mathrm{non}-\mathrm{poor}6\mathrm{or}7-\mathrm{vertex},\mathrm{while}K\mathrm{is}\mathrm{internal}.\hfill \end{array}\right.$$

(3)

(R7) 

Every 7-cluster K obtains the charge from its incident internal vertex v defined by

$$\left\{\begin{array}{cc}{\displaystyle \frac{3}{2}},\hfill & \mathrm{if}v\in {\mathcal{A}}_2\cup \{\mathrm{the}\mathrm{special}8-\mathrm{vertex}\mathrm{and}K\mathrm{is}\mathrm{type}\mathrm{II}\},\hfill \\ & \mathrm{or}v\mathrm{is}\mathrm{a}7,8-\mathrm{vertex}\mathrm{or}\mathrm{non}-\mathrm{special}6-\mathrm{vertex}\mathrm{while}K\mathrm{is}\mathrm{not}\mathrm{internal},\hfill \\ 2,\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}\mathrm{non}-\mathrm{special}6-\mathrm{vertex}\mathrm{while}K\mathrm{is}\mathrm{internal},\hfill \\ & \mathrm{or}\mathrm{a}\mathrm{non}-\mathrm{special}7,8-\mathrm{vertex}\mathrm{while}K\mathrm{is}\mathrm{internal}\mathrm{and}\hfill \\ & \mathrm{contains}\mathrm{no}\mathrm{two}\mathrm{vertices}\mathrm{in}{\mathcal{A}}_2\cup \{\mathrm{the}\mathrm{special}8-\mathrm{vertex}\mathrm{and}K\mathrm{is}\mathrm{type}\mathrm{II}\},\hfill \\ {\displaystyle \frac{5}{2}},\hfill & \mathrm{if}v\mathrm{is}\mathrm{a}\mathrm{non}-\mathrm{special}7,8-\mathrm{vertex}\mathrm{while}K\mathrm{is}\mathrm{internal}\mathrm{and}\mathrm{contains}\mathrm{two}\mathrm{vertices}(\mathrm{except}v)\hfill \\ & \mathrm{in}{\mathcal{A}}_2\cup \{\mathrm{the}\mathrm{special}8-\mathrm{vertex}\mathrm{and}K\mathrm{is}\mathrm{type}\mathrm{II}\}\mathrm{or}{9}^{+}-\mathrm{vertex}.\hfill \end{array}\right.$$

(4)

(R8) 

$C_0$ receives $\mu \left(v\right)$ from every incident vertex, and distributes 1 to every non-internal 3-face;

(R9) 

At last, each face excepting $C_0$ transfers its present charge to $C_0$.

The following lemma can be easily obtained by discharging rules.

Lemma 20.

Assuming u is a k-type vertex within a cluster, if $d_G\left(u\right)\ge 4$, then u gives at most

$$\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & \mathit{if}k=2,\hfill \\ {\displaystyle \frac{3}{2}},\hfill & \mathit{if}k=3,\hfill \\ {\displaystyle \frac{5}{2}},\hfill & \mathit{if}k=4,\hfill \\ 1,\hfill & \mathit{if}k=5.\hfill \end{array}\right.\mathit{to}\mathit{this}\mathit{cluster}.$$

(5)

We begin by examining the final charge assigned to each vertex of G. Consider v as a vertex of G. If $v\in V\left(C_0\right)$, then according to rule (R8), we have ${\mu }^{*}\left(v\right)\ge 0$. Now, consider the situation in which v is not in $V\left(C_0\right)$. By applying Lemma 9 (iii), the minimal degree of G is 4.

• $d\left(v\right)=4$. Suppose v is a k-type vertex of cluster K for some $k\in \{2,3,4\}$. If $k=4$, then v does not participate in the discharge process, hence ${\mu }^{*}\left(v\right)=\mu \left(v\right)=0$. If $k=3$, then K is a $2^{+}$-cluster and v must be contained in at least one $8^{+}$-face. By (R2)–(R6), v gives ${\displaystyle \frac{1}{4}}$ or ${\displaystyle \frac{1}{2}}$ to K. By (R1), v obtains at least either ${\displaystyle \frac{1}{4}}$ if v is incident with a 4-face or ${\displaystyle \frac{1}{2}}$ otherwise. Therefore, if v is not incident with 4-face, then ${\mu }^{*}\left(v\right)$ is not negative. Assuming v is incident to a single 4-face. It can be inferred from Lemma 11 that K is a 2-cluster. By (R2) and (R1), ${\mu }^{*}\left(v\right)=\mu \left(v\right)+{\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{4}}=0$. If $k=2$, then K is a $1^{+}$-cluster. By (R2)–(R5), v gives a charge to K when K is a 2- or 3-cluster. If K is a 2- or 3-cluster, then v gives ${\displaystyle \frac{1}{4}}$ to K when v is incident with a 4-face adjacent to K according to (R2)–(R3). Given that G lacks 7-cycles that are adjacent to 4- or 5-cycles, and according to Lemma 11, the three other faces incident with v in clockwise direction are 4-, $6^{+}$-, and $8^{+}$-faces, respectively. By applying (R1), we have ${\mu }^{*}\left(v\right)=\mu \left(v\right)-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{4}}>0$.
• $d\left(v\right)=5$. Assume that v represents a k-type vertex of cluster K for some $k\in \{2,3,4,5\}$. By applying Lemma 20, it can be inferred that ${\mu }^{*}\left(v\right)$ is at least $\mu \left(v\right)-1$, which yields ${\mu }^{*}\left(v\right)\ge 0$ when $k=5$. If $k=4$, then K is a $3^{+}$-cluster and v is contained in two $8^{+}$-faces. By (R3)–(R7), v gives at most ${\displaystyle \frac{3}{2}}$ to K. By (R1), v receives ${\displaystyle \frac{1}{4}}$ from each incident $8^{+}$-face, yielding a total of ${\displaystyle \frac{1}{2}}$. Therefore, we find that ${\mu }^{*}\left(v\right)\ge \mu \left(v\right)+{\displaystyle \frac{1}{2}}-{\displaystyle \frac{3}{2}}=0$. If $k=3$, then K is a $2^{+}$-cluster. By rules (R2)–(R6), v contributes no more than 1 to K for $d\left(v\right)=5$. If v is part of only a single cluster, then it follows that ${\mu }^{*}\left(v\right)=\mu \left(v\right)-1=0$. Thus, let us consider the scenario where v is a 2-type vertex of other cluster, referred to as L. By Lemma 11, v is contained in two $8^{+}$-faces. According to rules (R2)–(R5), v contributes ${\displaystyle \frac{1}{2}}$ to L when L is a special 4-, 5-cluster. By Lemma 12, K is not a special cluster. According to rules (R2)–(R6), v contributes no more than ${\displaystyle \frac{1}{2}}$ to K. Then, ${\mu }^{*}\left(v\right)=\mu \left(v\right)-{\displaystyle \frac{1}{2}}\times 2=0$. The case of $k=2$ can be proved similarly as $k=3$.
• $d\left(v\right)=6$. Assume v is contained in no more than three clusters. By (R2)–(R7), v contributes no more than 2 to its incident cluster. Then, ${\mu }^{*}\left(v\right)\ge \mu \left(v\right)-2=0$ when v is contained in only one cluster. If v is contained in three clusters, then it is a 2-type vertex for each cluster. According to Lemma 20, ${\mu }^{*}\left(v\right)=\mu \left(v\right)-{\displaystyle \frac{1}{2}}\times 3>0$. Therefore, we consider the case where v belongs to exactly two clusters, say $K_1,K_2$. Suppose firstly that v is a 2-type vertex for $K_1$. According to Lemma 20, assume v is a 4-type vertex to $K_2$ and v gives more than ${\displaystyle \frac{3}{2}}$ to $K_2$. By (R6)–(R7), v gives 2 to $K_2$, where $K_2$ is an internal 6- or 7-cluster. By (R6) and (R7), either v is a good but not special 6-vertex, or $K_2$ is a special 6-cluster containing two vertices in ${\mathcal{A}}_1$. In the latter situation, by Lemma 18, v is also good but not a special 6-vertex. In either case, v is a non-special 6-vertex, while $K_2$ is internal and special. By the definition of the special 6-vertex, $K_1$ is not a special 4-, 5-cluster. By (R2)–(R5), v gives no charge to $K_1$. In this case, ${\mu }^{*}\left(v\right)=\mu \left(v\right)-2=0$. Now, let us consider the scenario where v acts as a 3-type vertex for $K_1$. Due to the symmetric properties, v is necessarily classified as a 3-type vertex in relation to $K_2$. According to rules (R2)–(R6), we can assume that $K_i$ is $5^{+}$-cluster for each $i\in \{1,2\}$. By (R5)–(R6), assume v gives ${\displaystyle \frac{3}{2}}$ to $K_1$. Then, $K_1$ is an internal 6-cluster and v is a 3-type good 6-vertex which is not poor. By the definition of a poor 6-vertex, $K_2$ is not a special 5- or 6-cluster. Hence, v is a 3-type bad 6-vertex to $K_2$. By (R5)–(R6), v contributes at most ${\displaystyle \frac{1}{2}}$ to $K_2$. Thus, we have ${\mu }^{*}\left(v\right)=\mu \left(v\right)-{\displaystyle \frac{3}{2}}-{\displaystyle \frac{1}{2}}=0$.
• $d\left(v\right)=7$. Then, v is contained in no more than three clusters and $\mu \left(v\right)=3$. By Lemma 20, we only need to discuss the case that v is contained in two clusters, say $K_1$ and $K_2$, and v is classified as a 4-type vertex to $K_1$ and a 3-type vertex to $K_2$. Since v gives at most ${\displaystyle \frac{3}{2}}$ to $K_2$, we need only show the case that v gives at least 2 to $K_1$ cannot occurs by (R2)–(R7). Further, by rules (R2)–(R6), v contributes at most ${\displaystyle \frac{5}{2}}$ to $K_1$. If v contributes ${\displaystyle \frac{5}{2}}$ to $K_1$, then $K_1$ is an internal 7-cluster and contains two vertices in ${\mathcal{A}}_2\cup \{$the special 8-vertex and $K_1$ is type II} by (R7). By Lemma 17, $K_2$ is not special. According to (R2)–(R6), v contributes at most ${\displaystyle \frac{1}{2}}$ to $K_2$. Hence, we find that ${\mu }^{*}\left(v\right)\ge \mu \left(v\right)-{\displaystyle \frac{5}{2}}-{\displaystyle \frac{1}{2}}=0$, and we complete this section. If v gives 2 to $K_1$, then one of the following applies: (i) v is a non-special 7-vertex, while $K_1$ is classified as an internal 7-cluster, lacking two vertices of ${\mathcal{A}}_2\cup \{$the special 8-vertex and $K_1$ is type II} by (R7); (ii) $K_1$ is an internal special 6-cluster that includes two vertices from ${\mathcal{A}}_1$ by (R6). When (i) occurs, $K_2$ is not a 6-cluster for G and contains no Near-bow-tie flaw. Following rules (R2)–(R5), v contributes no more than 1 to $K_2$. Therefore, we have ${\mu }^{*}\left(v\right)\ge \mu \left(v\right)-2-1=0$, concluding our argument. When (ii) occurs, v is poor if $K_2$ is an internal and special 6-cluster. By the same rules (R2)–(R6), v contributes no more than 1 to $K_2$, again leading to ${\mu }^{*}\left(v\right)\ge \mu \left(v\right)-2-1=0$, which completes the proof.
• $d\left(v\right)=8$. Hence, $\mu \left(v\right)=4$. By applying Lemma 20, suppose v belongs to at least two clusters. If v is present in four clusters, then ${\mu }^{*}\left(v\right)\ge 4-4\times {\displaystyle \frac{1}{2}}>0$ according to Lemma 20. For the case where v belongs to three clusters, we have ${\mu }^{*}\left(v\right)\ge 4-2\times {\displaystyle \frac{3}{2}}-{\displaystyle \frac{1}{2}}>0$ or ${\mu }^{*}\left(v\right)\ge 4-{\displaystyle \frac{5}{2}}-2\times {\displaystyle \frac{1}{2}}>0$ by Lemma 20. Thus, suppose v is contained in just two clusters, say $K_1$ and $K_2$. By Lemma 20, suppose v gives ${\displaystyle \frac{5}{2}}$ to $K_1$ and v is a 4-type vertex of $K_1$. According to (R3)–(R7), $K_1$ is an internal 7-cluster and contains two vertices in ${\mathcal{A}}_2\cup \{$the special 8-vertex and $K_1$ is type II}. We only need to prove cases that v gives 2 or ${\displaystyle \frac{5}{2}}$ to $K_2$ cannot occur. Suppose otherwise, by (R2)–(R7), one of the following applies: (i) $K_2$ is an internal and special 6-cluster and contains two vertices in ${\mathcal{A}}_1$; (ii) $K_2$ is an internal 7-cluster and v is a non-special 8-vertex. By Definition 6, v would indeed be a special 8-vertex if $K_2$ is an internal 7-cluster, contradicting the assumption that v is a non-special 8-vertex. This makes the second case (ii) impossible. Therefore, $K_2$ is an internal special 6-cluster containing two vertices from ${\mathcal{A}}_1$. Let $G^{\prime }=G-K_1\cup K_2$, where $L^{*},{\mathcal{M}}_{(G-G^{\prime },L^{*})}^{*}$ be the residual list assignment and the residual cover of $G-G^{\prime }=K_1\cup K_2$. By the minimal property of G, $G^{\prime }$ admits ${\mathcal{M}}_{(G^{\prime },L{|}_{G^{\prime }})}$-coloring extending ${\varphi }_0$ with $|L^{*}\left(v\right)|\ge 4$. By Lemmas 4 and 14, v has at least two available colors to color $K_2$. Thus, by Lemmas 5 and 15, $K_1\cup K_2$ has an ${\mathcal{M}}_{(K_1\cup K_2,L^{*})}^{*}$-coloring. By applying Lemma 7, an ${\mathcal{M}}_{(G,L)}$-coloring of G can be achieved, leading to a contradiction.
• $d\left(v\right)\ge 9$. Then we have $\mu \left(v\right)\ge 5$. According to Lemma 20, ${\mu }^{*}\left(v\right)\ge 5-2\times {\displaystyle \frac{5}{2}}=0$, ${\mu }^{*}\left(v\right)\ge 5-3\times {\displaystyle \frac{3}{2}}>0$ or ${\mu }^{*}\left(v\right)\ge 5-{\displaystyle \frac{5}{2}}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{3}{2}}>0$.

Consider a face $f\ne C_0$ in G. By (R9), ${\mu }^{*}\left(f\right)=0$. Now, we examine ${\mu }^{*}\left(C_0\right)$ in G. Consider that $f_3$ represents the number of 3-faces that have vertices in common with $C_0$ and let b denote the charge transferred to $C_0$ from other faces by (R9). Define s as the size of $[C_0,G-C_0]$. By Lemma 9 (i), $f_3+s\ge 1$. If $f_3\ge 1$, then $s\ge f_3+1$. If $f_3=0$, then $s\ge 1$, and so we also find $s\ge f_3+1$. Using rules (R8) and (R9), we can express ${\mu }^{*}\left(C_0\right)$ as follows:

$${\mu }^{*}\left(C_0\right)=\mu \left(C_0\right)+\sum _{v\in V\left(C_0\right)}(d\left(v\right)-4)-f_3+b$$

(6)

$$=d\left(C_0\right)+4+\sum _{v\in V\left(C_0\right)}(d\left(v\right)-2)-2d\left(C_0\right)-f_3+b$$

$$=4-d\left(C_0\right)+s-f_3+b.$$

Since $s\ge f_3+1$, ${\mu }^{*}\left(C_0\right)\ge 4-d\left(C_0\right)+1+b\ge 2+b$ for $d\left(C_0\right)=3$. If $b\ge 0$, then ${\mu }^{*}\left(C_0\right)>0$, which completes this section.

Next, we prove that $b\ge 0$. Define ${\mu }^{\prime }\left(f\right)$ as the charge assigned to face f following the application of rules (R1)–(R8). Clearly, $b={\displaystyle \sum _{f\in F\setminus \left\{C_0\right\}}}{\mu }^{\prime }\left(f\right)$. To begin with, let us examine the scenario where $d\left(f\right)=4$. In this instance, f is not impacted by the discharging procedure. Thus, ${\mu }^{\prime }\left(f\right)=\mu \left(f\right)=d\left(f\right)-4=0$. If $d\left(f\right)=5$, then f is adjacent to no more than a 3-face for G contains no 7-cycle adjacent to 4- or 5-cycles. By (R1), ${\mu }^{\prime }\left(f\right)=\mu \left(f\right)-{\displaystyle \frac{1}{2}}>0$. Now, assume f is a $6^{+}$-face. Denote f to be adjacent to m 3-faces, meaning f has m edges shared with 3-faces. If f is a 6- or 7-face, then by (R1), ${\mu }^{\prime }\left(f\right)=\mu \left(f\right)-{\displaystyle \frac{\mu \left(f\right)}{d\left(f\right)}}\times m-{\displaystyle \frac{\mu \left(f\right)}{2d\left(f\right)}}\times (d\left(f\right)-m)\times 2=0$. In the case of $d\left(f\right)\ge 8$, we find ${\mu }^{\prime }\left(f\right)=\mu \left(f\right)-{\displaystyle \frac{1}{2}}\times m-{\displaystyle \frac{1}{4}}\times (d\left(f\right)-m)\times 2={\displaystyle \frac{d\left(f\right)}{2}}-4\ge 0$ by (R1). Finally, $d\left(f\right)=3$. If f is a 3-face, then according to Lemma 8, f could be a subgraph of an i-cluster where $i\in \left[7\right]$.

Let K be an l-cluster. Note that $C_0$ is not a face of K. This means $|V\left(K\right)\cap V\left(C_0\right)|\le 2$. We define the initial and the middle charges of K after applying (R1)–(R8), denoted by $\mu \left(K\right)$ and ${\mu }^{\prime }\left(K\right)$, as the sum of the initial and middle charges of l 3-faces in it. Note that the final charge of every 3-face is 0 by (R9). We check ${\mu }^{\prime }\left(K\right)\ge 0$ in the following.

• $l=1$. If K is not internal, then ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+1=0$ by (R8). Thus, assume that K is internal. Assume that $f_i$ is the face adjacent to K for $i=1,2,3$ with $d\left(f_1\right)\le d\left(f_2\right)\le d\left(f_3\right)$. If $d\left(f_1\right)=4$, then $d\left(f_i\right)\ge 5$ and $d\left(f_i\right)\ne 6,7$ for each $i\in \{2,3\}$. By (R1), each $f_i$ ($i=2,3$) gives at least ${\displaystyle \frac{1}{2}}$ to K and ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 2\ge 0$. Thus, $d\left(f_1\right)\ge 5$. By (R1), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+3\times {\displaystyle \frac{1}{3}}=0$.
• $l=2$. Assume that K is not internal. If $|V\left(C_0\right)\cap V\left(K\right)|=2$, then by rule (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+1\times 2=0$. So, suppose $|V\left(C_0\right)\cap V\left(K\right)|=1$. According to Lemma 11(iii), K is adjacent to at least two $8^{+}$-faces. Utilizing (R1) and (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+1+{\displaystyle \frac{1}{2}}\times 2=0$.
  Thus, K is internal. By Lemma 11 (iii), the face adjacent to K is a 4-face or an $8^{+}$-face and there are no more than two 4-faces. If all faces adjacent to K are $8^{+}$-faces, then by (R1), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+4\times {\displaystyle \frac{1}{2}}=0$. Thus suppose one adjacent face is a 4-face. Utilizing (R2) and Lemma 9 (iii), each 3-type vertex of K gives ${\displaystyle \frac{1}{4}}$ to K. Then, according to (R1) and (R2), we find ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 3+{\displaystyle \frac{1}{4}}\times 2=0$ or ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 2+{\displaystyle \frac{1}{4}}\times 2+{\displaystyle \frac{1}{4}}\times 2=0$.
• $l=3$. If $|V\left(C_0\right)\cap V\left(K\right)|=2$, then K must be adjacent to at least two $8^{+}$-faces. Utilizing (R1) and (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+2+{\displaystyle \frac{1}{2}}\times 2=0$. If $|V\left(C_0\right)\cap V\left(K\right)|=1$, then K is adjacent to a minimum of three $8^{+}$-faces. By applying (R1), (R3) and (R8), it can be concluded that ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+1+{\displaystyle \frac{1}{2}}\times 3+{\displaystyle \frac{1}{4}}\times 2\ge 0$ or ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+2+{\displaystyle \frac{1}{2}}\times 3+{\displaystyle \frac{1}{4}}\ge 0$. Thus $|V\left(C_0\right)\cap V\left(K\right)|=0$. If the faces adjacent to K are all $8^{+}$-faces, then ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 5+{\displaystyle \frac{1}{4}}\times 2=0$ by (R1) and (R3). Thus, according to Lemma 11(iii), there exists one adjacent 4-face which contains 4-type vertex of K. By applying (R1) and (R3), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 3+{\displaystyle \frac{1}{4}}\times 2+{\displaystyle \frac{1}{2}}\times 2=0$.
• $l=4$. By Lemma 8, K is a graph of $\{H_4^1,H_4^2,H_4^3,H_4^4\}$ shown in Figure 3. By Lemma 11 (ii), faces adjacent to K are $8^{+}$-faces. If $|V\left(C_0\right)\cap V\left(K\right)|=t$, where $t\in \{1,2\}$, then $C_0$ gives at least t to K when $K\in \{H_4^2,H_4^3,H_4^4\}$, $t+1$ to K when $K\cong H_4^1$ by (R8). If $K\in \{H_4^2,H_4^3,H_4^4\}$, then there are at least $7-t$ edges of K adjacent to $8^{+}$-faces. By (R1) and (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+(7-t)\times {\displaystyle \frac{1}{2}}+t\ge 0$. If $K\cong H_4^1$, ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+(5-t)\times {\displaystyle \frac{1}{2}}+(t+1)\ge 0$ by (R1) and (R8).
  Now, suppose K is internal. Since $H_4^1$ has four 3-type $4^{+}$-vertices and each of $\{H_4^2,H_4^3\}$ has two 3-type $4^{+}$-vertices, ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+4\times {\displaystyle \frac{1}{2}}+4\times {\displaystyle \frac{1}{2}}\ge 0$ or ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+6\times {\displaystyle \frac{1}{2}}+2\times {\displaystyle \frac{1}{2}}\ge 0$ by (R1) and (R4). Suppose $K\cong H_4^4$. If K is special, then by (R1), (R4) and Lemma 10, ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+6\times {\displaystyle \frac{1}{2}}+3\times {\displaystyle \frac{1}{2}}>0$. Otherwise, ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+6\times {\displaystyle \frac{1}{2}}+{\displaystyle \frac{3}{2}}>0$.
• $l=5$. By Lemma 8, K is a graph of $\{H_5^1,H_5^2\}$ shown in Figure 3. By Lemma 11(ii), faces adjacent to K are $8^{+}$-faces. If $|V\left(C_0\right)\cap V\left(K\right)|=2$, then $C_0$ gives 3 to K by (R8). In this case, there are four edges of K adjacent to $8^{+}$-faces. By (R1) and (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+3+4\times {\displaystyle \frac{1}{2}}\ge 0$. If $|V\left(C_0\right)\cap V\left(K\right)|=1$, then there are five edges of K adjacent to $8^{+}$-faces. If K is $H_5^1$, then K has a 5-type 5-vertex and ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+2+5\times {\displaystyle \frac{1}{2}}+1>0$. Assume K is $H_5^2$. If $u_1\in V\left(C_0\right)$, then ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+1+5\times {\displaystyle \frac{1}{2}}+2\times 1>0$ when $H_5^2$ is special; otherwise, ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+1+5\times {\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}+{\displaystyle \frac{3}{2}}>0$. If $u_1\notin V\left(C_0\right)$, then ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+2+5\times {\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\times 2>0$ by (R1), (R5) and (R8).
  Thus, assume K is internal. If $K\cong H_5^1$, then K contains five 3-type bad $4^{+}$-vertices and one 5-type 5-vertex. By (R1) and (R5), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 5+{\displaystyle \frac{1}{2}}\times 5+1>0$. Assume K is $H_5^2$. If K is special, then K contains two 3-type good $5^{+}$-vertices and one 2-type good $5^{+}$-vertex. By (R1) and (R5), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 5+1\times 2+{\displaystyle \frac{1}{2}}=0$. Otherwise, ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+{\displaystyle \frac{1}{2}}\times 5+{\displaystyle \frac{3}{2}}+{\displaystyle \frac{1}{2}}\times 2=0$.
• $l=6$. By Lemma 8, K is the graph $H_6$ shown in Figure 3. By Lemma 11(ii), the faces adjacent to K are $8^{+}$-faces. If $|V\left(C_0\right)\cap V\left(K\right)|=2$, then $C_0$ gives 4 to K by (R8). In this case, there are three edges of K adjacent to $8^{+}$-faces. Due to symmetry, suppose that $u_1,u_3\in V\left(C_0\right)$. Then $u_4$ is a 3-type $4^{+}$-vertex. By (R6), $u_4$ gives at least ${\displaystyle \frac{1}{2}}$ to K. By (R1) and (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+3\times {\displaystyle \frac{1}{2}}+4+{\displaystyle \frac{1}{2}}=0$. If $|V\left(C_0\right)\cap V\left(K\right)|=1$, then $C_0$ contributes at least 2 to K by (R8) and there are four edges of K adjacent to $8^{+}$-faces. Suppose firstly, K is special. Then, K has at least two internal $5^{+}$-vertices. Applying (R1), (R6), and (R8), we find that ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+4\times {\displaystyle \frac{1}{2}}+2+2\times 1\ge 0$. Suppose secondly, that K is not special. Then, K contains one 4-type $5^{+}$-vertex and one 3-type bad $4^{+}$-vertex. Utilizing (R1), (R6), and (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+4\times {\displaystyle \frac{1}{2}}+2+{\displaystyle \frac{3}{2}}+{\displaystyle \frac{1}{2}}\ge 0$.
  Thus, assume K is internal. If K is special, then K contains two 3-type good $5^{+}$-vertices and one 4-type good $5^{+}$-vertex by Lemma 10. If $u_1,u_4\in {\mathcal{A}}_1$, then $d\left(u_5\right)\ge 6$ by Lemma 18. This means $u_5$ is a 4-type good $6^{+}$-vertex and K contains two vertices of ${\mathcal{A}}_1$. In this case, ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+4\times {\displaystyle \frac{1}{2}}+2+2\times 1=0$ by (R1) and (R6). Then, assume $u_1\notin {\mathcal{A}}_1$. By (R6), $u_1$ gives at least ${\displaystyle \frac{3}{2}}$ to K. By (R1) and (R6), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+4\times {\displaystyle \frac{1}{2}}+1+2\times {\displaystyle \frac{3}{2}}=0$. Suppose K is not special. In this situation, $u_i$ is classified as a 4-type $5^{+}$-vertex for each $i\in \{3,5\}$. By (R1) and (R6), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+4\times {\displaystyle \frac{1}{2}}+2\times {\displaystyle \frac{3}{2}}+2\times {\displaystyle \frac{1}{2}}=0$.
• $l=7$. By Lemma 8, K is the graph $H_7$ shown in Figure 3. By Lemma 11(ii), faces adjacent to K are $8^{+}$-faces. If $|V\left(C_0\right)\cap V\left(K\right)|=2$, then $C_0$ gives 5 to K by (R8) and according to Lemma 10, K contains one 4-type $5^{+}$-vertex. If $|V\left(C_0\right)\cap V\left(K\right)|=1$, then $C_0$ contributes 3 to K and K contains two 4-type $5^{+}$-vertices similarly. By (R1), (R7) and (R8), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+5+2\times {\displaystyle \frac{1}{2}}+{\displaystyle \frac{3}{2}}>0$ or ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+3+3\times {\displaystyle \frac{1}{2}}+2\times {\displaystyle \frac{3}{2}}>0$. Thus assume K is internal. By Lemma 10, $d\left(u_i\right)\ge 5$ for each $i\in \{1,4,5\}$. By Lemma 19(ii), there are at most two vertices of $\{u_1,u_4,u_5\}$ in ${\mathcal{A}}_2\cup \{$the special 8-vertex and K is type II}. If any vertex of $\{u_1,u_4,u_5\}$ is not in ${\mathcal{A}}_2\cup \{$the special 8-vertex and K is type II}, then ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+3\times {\displaystyle \frac{1}{2}}+3\times 2>0$. If there is only one vertex in ${\mathcal{A}}_2\cup \{$the special 8-vertex and K is type II}, then ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+3\times {\displaystyle \frac{1}{2}}+{\displaystyle \frac{3}{2}}+2\times 2=0$. Thus assume there are two vertices in ${\mathcal{A}}_2\cup \{$the special 8-vertex and K is type II}, say $u_4,u_5$. By Lemma 19(i), $d\left(u_1\right)\ge 7$. By (R1) and (R7), ${\mu }^{\prime }\left(K\right)\ge \mu \left(K\right)+3\times {\displaystyle \frac{1}{2}}+2\times {\displaystyle \frac{3}{2}}+{\displaystyle \frac{5}{2}}=0$.

5. Conclusions

DP-k-coloring has gained significant attention as a generalization of k-choosability. We demonstrate that any planar graph G, which does not have a Near-bow-tie as an induced subgraph and lacks 7-cycles adjacent to 4-cycles or 5-cycles, is DP-4-colorable. If the planar graph G does not have 7-cycles and a butterfly, then it still satisfies our condition. Thus, our results generalize the findings of Kim et al. [20] and promote research in the area of DP-4-colorability for planar graphs. Future research can focus on determining the DP-4-colorability on planar graphs such as ${\chi }_{DP}\left(G\right)=4$ for any planar graph G without 7-cycles adjacent to 4-cycles.