Abstract
Driven by real-world demands of processing massive high-frequency data and achieving longer forecasting horizons in time series forecasting scenarios, a variety of deep learning architectures designed for time series forecasting have emerged at a rapid pace. However, this rapid development actually leads to a sharp increase in parameter size, and the introduction of numerous redundant modules typically offers only limited contribution to improving prediction performance. Although prediction models have shown a trend towards simplification over a period, significantly improving prediction performance, they remain weak in capturing dynamic relationships. Moreover, the predictive accuracy depends on the quality and extent of data preprocessing, making them unsuitable for handling complex real-world data. To address these challenges, we introduced Treeformer, an innovative model that treats the traditional tree-based machine learning model as an encoder and integrates it with a Transformer-based forecasting model, while also adopting the idea of time–feature two-dimensional information extraction by channel independence and cross-channel modeling strategy. It fully utilizes the rich information across variables to improve the ability of time series forecasting. It improves the accuracy of prediction on the basis of the original deep model while maintaining a low computational cost and exhibits better applicability to real-world datasets. We conducted experiments on multiple publicly available datasets across five domains—electricity, weather, traffic, the forex market, healthcare. The results demonstrate improved accuracy, and provide a better hybrid approach for enhancing predictive performance in Long-term Sequence Forecasting (LSTF) problems.
Keywords:
deep learning; machine learning; multivariate time series forecasting; transformer; multilayer perceptron (MLP) MSC:
68T07; 62M10
1. Introduction
Time series forecasting (TSF) holds a pivotal position in various fields due to its high practicality. By reducing uncertainties about the future through forecasting, TSF enables more efficient resource allocation and improves decision-making processes. For example, during the COVID-19 pandemic, forecasting disease development trends was of great significance for facilitating timely policy interventions. In addition, time series forecasting also plays a key role in daily traffic flow forecasting [1,2], weather forecasting in meteorology [3], and financial risk management [4,5]. The concept of TSF initially appeared as a tool in the disciplines of statistics and finance. With the advent of the information age, the speed of data generation and collection has increased significantly, and early traditional forecasting methods can no longer adequately meet the demands of modern applications. At the same time, it is worth emphasizing that data in the information age is not limited to a single time series (univariate time series). Due to the diversity of data sources, modern TSF not only relies on the analysis of the series itself, but also needs to comprehensively consider the influence of other relevant factors. Over time, researchers have gradually realized the important role of multivariate factors in improving forecasting accuracy. Therefore, multivariate TSF has become one of the key tools for managing the exponential growth of data in the information age. Currently, an in-depth exploration of the effective interactions and dynamic relationships among multiple variables has emerged as a primary focus of research. And moreover, long sequence time series forecasting (hereinafter called LSTF, Informer [6] proposed) has gained growing interest among researchers, it entails leveraging a substantial amount of time series data on historical behavior to generate a long-term forecast. This task not only requires the forecasting models to provide longer forecasting horizons, but also requires more fine-grained predictions of future long-term trends. In particular, the support of LSTF is essential to reducing unnecessary energy consumption in real-world deployment.
In recent years, deep learning models have dominated the field of TSF, overshadowing earlier models such as Autoregressive Integrated Moving Average (ARIMA), Recurrent Neural Network (RNN), and their variants, which appear relatively less competitive. With continuous developments, the Convolutional Neural Network (CNN)-based models [7,8], Transformer-based models [6,9,10], and multilayer perceptron (MLP)-based models [11,12], have all demonstrated promising results. From this perspective, the foundational models for the TSF task have a trend toward simplification over a period, aligning with the overall development direction of deep learning. Although Bengio’s team proposed a pure deep learning model N-BEATS [11] with a core consisting of fully connected layers in 2018. It can be said that, in recent years, Transformer-based TSF models have remained the primary approach achieving major breakthroughs in practical applications. Especially since the introduction of Informer, these kinds of models, specifically designed for TSF tasks, have experienced explosive growth. However, it is well-known that many Transformer-based models applied to multivariate TSF tasks typically focus on modeling temporal dependencies but exhibit limited capacity in capturing cross-variate interactions. This is because the attention weights process all time steps and variable dimensions at the same time, and there is no clear distinction between the two. We have actually found that, there are quite a number of Transformer-based TSF models works for multivariate TSF tasks, but these studies typically focus on decoupling cross-variable dependencies and temporal dependencies during the design of attention mechanisms, aiming to extract critical information from both aspects effectively. For example, some studies capture cross-time and cross-variable dependencies by designing a two-stage attention mechanism (Crossformer [13]), or process cross-variable and cross-time characteristics separately, one of which is modeled by the attention mechanism and the other is completed by other models (Client [14]). Nevertheless, considering that some Transformer-based models have actually achieved relatively significant success on the innovation of the attention mechanism for TSF tasks, further modifications in this part may not yield substantial improvements. Meanwhile, we argue that data embedding often introduces a certain degree of feature entanglement. To address this and extract more predictive information separately from time and variable dimensions, we incorporate the time and variable extraction design in our model framework. Furthermore, the idea utilizes the concepts of channel-independent (CI) and cross-channel interactions to operate on the time dimension and variable dimension (feature dimension), respectively, extracting additional information beneficial for forecasting.
Although Transformer-based models, as a type of neural network, have achieved significant success in processing sequence data, particularly in the field of natural language processing (NLP), they also face certain challenges, especially the widely recognized one: overfitting. This type of model also uses a large number of dropout layers in configuration to alleviate overfitting, but sometimes their effectiveness is not always optimal. Integrating tree-based models into Transformer-based models is conducive to better performance. Transformer-based TSF models involve an encoding–decoding process, where the encoder encodes the historical sequences, enabling it to capture deep representations of the data, which significantly increases the risk of overfitting. In contrast, tree-based models, which are inherently partitioning models, offer a different computational approach. Despite the significant differences between the two model types, their fusion produces a better promotion effect. Tree-based models are widely used in TSF competitions, excelling in projects with strong potential for real-world deployment. One of the drawbacks of tree-based models is their poor extrapolation capability, indicating potential performance degradation when handling data beyond the training range. This limitation arises from the fact that tree-based models are constructed based on training data, and thus may struggle to make accurate predictions for data outside the training range. Therefore, in TSF tasks, situations not observed in the historical data cannot be partitioned correctly, making it challenging for the model to provide accurate predictions under such circumstances. However, unlike tree-based models, neural networks for TSF tasks do not encounter this problem and represent a complementary approach to make up for the shortcomings of tree-based models. It also solves the problem that tree models cannot naturally capture the relationship between distant time steps in the sequence in LSTF task.
Tree-based models are essentially a type of machine learning algorithm that use tree structures to represent decision-making processes. Although it does not directly use the “residual” concept from neural networks, it adopts the Boosting framework. Similar to LighGBM [15], which reduces prediction errors step-by-step through an additive model, it follows a framework based on the Gradient Boosting Decision Tree (GBDT) [16], aiming to minimize the objective function at each iteration. The gradient of the objective function mentioned here can be viewed as the residual of the current model, and the new tree is trained to fit these residuals. Therefore, the implementation of some boosting methods explicitly incorporates the concept of residuals to iteratively optimize the model. This idea actually further enhances the predictive performance of our model. However, another limitation of tree-based models is that they only learn patterns in existing data. Specifically, they perform well on regular and stable data but have limited adaptability to non-stationary data. Furthermore, the dynamic changes are beyond its modeling capabilities to a certain extent. As mentioned earlier, tree-based models themselves are fundamentally based on splitting criteria, which can filter out the most important features of the target variable from high-dimensional data to avoid redundancy. Therefore, GBDT models, such as LightGBM [15], which are based on tree models, perform well on high-dimensional datasets with sufficiently large sample sizes. Additionally, they demonstrate stable performance and effectively handle various input feature distributions, exhibiting strong robustness to noise. Although tree-based models excel in capturing and modeling local features during training, they lack the capability for global forecasting. However, their strength can be effectively complemented by the global forecasting capability of Transformer-based deep learning models. Additionally, Transformer-based deep learning models demonstrate powerful feature learning performance on large datasets, while making up for their limitations in high-noise environments. This synergy aligns well with our expectations for LSTF tasks, effectively compensating for the predictive shortcomings of deep learning models.
Based on the above analysis, we proposed a novel Treeformer model, which incorporates an ensemble approach to address and improve the limitations of the original Transformer-based model. This enhancement further improves the model’s performance on LSTF tasks. The main contributions of this paper are as follows:
- We propose an innovative architecture, Treeformer, which combines channel-independent (CI) and cross-channel modeling strategies to further extract the information across both time and feature dimensions. Additionally, it integrates the tree-based machine learning method with the Transformer-based forecasting model to enhance the performance on LSTF tasks;
- We conducted experiments on multiple public datasets across five major domains, proving the performance of the model on LSTF tasks. In particular, on the Traffic dataset, the model’s improvement even reached 21.77% averaged MAE reduction and 20.13% in MSE, highlighting its adaptability on different types of datasets;
- We conducted in-depth ablation experiments on our model. The results show that our two proposed design components can effectively improve the forecasting performance of the original Transformer-based TSF model.
2. Related Work
Time series forecasting essentially involves using historical observations to predict future values over a specified period. In its early stages, the academia often regarded it as a simple regression problem, ignoring complex patterns in time series data, such as multivariable interactions, nonlinearity, and periodicity. With the advancement of AI, machine learning and deep learning methods have evolved to learn patterns from large amounts of data to make decisions. These models, which demonstrate exceptional capabilities across various domains, have significantly driven progress in the field of TSF. Meanwhile, in recent years, most of the prediction models are designed to address LSTF problems, and this evolution reflects a research focus that shifts in response to the development of real-world data.
Recurrent neural networks based (RNN-based) TSF models, as the earliest model types to achieve breakthroughs in the TSF tasks within the deep learning field, demonstrate strong capabilities in capturing temporal dependencies due to their recursive structure. However, these models are prone to gradient vanishing and gradient explosion when handling LSTF tasks and show insufficient ability in capturing complex temporal patterns. Despite these shortcomings, improvements to this model type significantly contributed to the rapid development of TSF in the field of deep learning for a period of time. LSTNet [17] further combines the efficiency of one-dimension convolution in processing short-term patterns to extract local features, while expanding the temporal span of information by establishing the Recurrent-skip component to enhance the ability to capture long-term dependencies. Some models further enhance the prediction performance through hybrid structures (Hybrid-ES-LSTM [18]) and hierarchical patterns, while others improve RNN-based models by introducing segmentation techniques [19] to optimize point-wise iterations or employing multi-directional Gate Select Cells [20] to integrate and select information, thereby reducing the length of transmission paths to address the performance of RNN-based models in LSTF tasks. CNN-based models were not initially designed for sequence data and were primarily developed to compensate for the limitations of RNN-based models. Early CNN-based TSF models often increased network complexity and training difficulty due to the need to stack many layers to capture global relationships [21]. Instead, these models leveraged their strengths in integrating local information within time series data. As this model type evolved, subsequent designs focused more on mining periodic features of time series [22,23], or employing special tree structures to capture both short-term and long-term dependencies in time series, thereby enhancing performance in prediction tasks [7].
With the validation of Transformer models’ performance in various NLP tasks, their ability to efficiently model long-term dependencies in sequence data has become increasingly prominent. Consequently, the application of these models in TSF area has shown an explosive growth. Early studies primarily focused on directly applying the Transformer [24]. However, subsequent research introduced modifications to address the efficiency and performance challenges arising from modern forecasting needs, especially the LSTF tasks [6,25,26]. Further advancements involved replacing point-level information with segement-level information, thereby improving information utilization while significantly reducing computational complexity [27,28]. Subsequently, approaches leveraging specialized structures (triangle structure or tree structure) for multi-scale modeling emerged, aiming to comprehensively capture both local patterns and global dependencies [29,30]. In addition, some studies have integrated frequency domain analysis from traditional time series into deep learning models, utilizing various Fourier Transforms and inverse Fourier Transforms to achieve conversions between the time and frequency domains. By extracting periodic features of time series in the frequency domain, these approaches enhance the understanding of global properties, as demonstrated by studies such as FEDformer [31], JTFT [32]. The essence of the approach is to transfer effective modeling methods from the time domain to the frequency domain, integrate the independently modeled representations of both domains, and use them for subsequent predictions. For example, some approaches employ Transformer and other architectures to extract information from the frequency and time domains separately, while novel modules are designed to leverage time series patterns to foster the fusion [33]. For multivariate TSF, we have also tried the process from fusion modeling to decoupling modeling and then to optimization. Transformer-based models indeed dominate across research intensity and the depth of exploration.
As TSF models become increasingly complex, multilayer perceptrons (MLPs) have gained attention due to their advantages, including low computational complexity, greater efficiency, and lightweight design. Studies in different fields have demonstrated that simple MLP networks can achieve competitive performance [34]. Given the simplicity of their network structure, research on MLP networks primarily focuses on optimizing the input to enhance the network’s capacity to process more information effectively. For example, after decomposing the data into trends and seasonal parts, they are modeled separately [12]. Likewise, similar modeling techniques can be applied in the frequency domain [35,36]. In addition, innovative applications of foundational time series models have been effectively adapted to MLP-based models, such as multi-scale modeling, segment-level processing, and leveraging the advantages of hybrid models, all of which have contributed to the development of deep learning-based TSF models.
Whereas traditional machine learning models are not specifically designed for sequence data, and require specialized feature engineering and modifications to adapt to transfer across different domains. Tree-based models, as a class of machine learning models, are ensemble learners composed of decision trees. They offer more stable performance in predictions across various domains, exhibit flexible training, and are particularly robust to missing data. Additionally, they are less sensitive to parameter tuning and provide high interpretability. Therefore, although deep learning models have dominated various fields in recent years, the unique characteristics of tree-based models mean that their energy in practical applications should not be underestimated. For example, they remain the preferred choice in domains such as finance. Work has also been performed to utilize feature engineering on the input–output structure of the widely known Gradient Boosting Regression Tree (GBRT) machine learning model, and experiments on multiple datasets demonstrate that simple machine learning models should not be ignored for their predictive effectiveness [37].
As mentioned in the previous section, multivariate TSF can provide higher information entropy, contributing to improved predictive performance. Early studies focused on developing models that extract complex multivariate relationships where multiple values at each time step were encoded and directly fed into subsequent models. While these models demonstrated improved predictive accuracy, the increasing complexity of the model imposes a heavy burden on the training speed of the TSF task, especially for the LSTF task, where significant temporal variations necessitate additional training data for the model to effectively learn useful information from both time and variable dimensions, enabling it to achieve a satisfactory level of prediction accuracy. Actually, it highlights the trade-off inherent in such models, which offer improved performance at the cost of increased data requirements. PatchTST [38] proposed to use the channel-independent (CI) approach to model, which involves predicting each variable in a multivariate time series independently. Surprisingly, this method outperformed channel-dependent (CD) approaches on the same datasets. This finding has motivated further research into modeling relationships among variables. So, it is necessary for us to decouple the variable dimension from the time dimension to prevent entanglement between these two aspects.
Therefore, our model employs a hybrid approach that combines the CI strategy with a method of decoupling time and feature dimensions, and further enhancing the performance of the Transformer-based forecasting model on the LSTF task through the tree-based model.
3. Treeformer Architecture
3.1. Problem Definition
Our model is specifically designed for multivariate time series forecasting tasks, given historical data X containing M () variables (channels/features), , wherein the look-back window size is length T. The goal of our task is to predict the forecasting horizon with length L, denoted as . This means when we input T with M variables (feature dimensions), our model maps the input to the output as , where N () represents the number of predicted variables, and L denotes the forecasting horizon with N dimensions.
3.2. Treeformer Architecture
As illustrated in Figure 1, we begin by performing the channel-independent (CI) strategy on the input data along the time dimension and extract features within this dimension. In this process, the variables (channels/features) are treated independently, meaning that each feature undergoes operations along the time dimension to capture temporal dependencies without introducing interactions between features. Subsequent operations in the feature domain are shared by time steps, enabling cross-variable information interaction through our components. This approach captures the interdependencies among features (variables/channels). Both components utilize the same structure, consisting of a linear layer followed by a ReLU activation function, another linear layer, and a dropout mechanism to prevent overfitting.
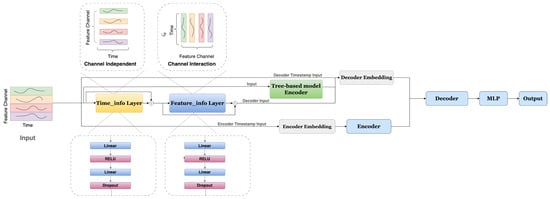
Figure 1.
The diagram outlines the workflow of the Treeformer. First, we perform Time_Info Layer’s operations along the horizontal axis, referred to along the time steps, as shown within the dashed box, to extract information from time dimension. Subsequently, the same operations are applied to the transposed feature channel, representing the variable dimension, to extract cross-variate information. Residual connections are utilized for both time dimension and feature dimension operations to capture deeper-level information while avoiding unnecessary computations. The Tree-based model part can also be viewed as an information-extraction encoder, serving as an effective mechanism for information augmentation with Transformer-based TSF model.
We apply residual connections across both the Time_info layer and the Feature_info layer individually, enabling the network to flexibly learn more important features and capture critical information. These connections also allow the network to avoid redundant computation, thereby improving the efficiency of learning within deep network architectures. Furthermore, we treat the tree-based model as an encoder, utilizing it as an effective tool for feature extraction. Specifically, the tree-based model employed in this study is LightGBM [15], a machine learning model that implements the Gradient Boosted Decision Tree (GBDT) algorithm. Proposed by Microsoft Research Asia (MSRA), LightGBM optimizes GBDT implementation by retaining samples with large gradients to significantly reduce computational costs. Additionally, it employs a feature bundling technique to handle sparse features, thereby reducing the feature dimensions. These optimizations enable LightGBM to achieve faster training speeds and lower memory usage compared to other frameworks, making it particularly suitable for processing large-scale and high-dimensional datasets. Compared to the level-wise tree growth strategy used in XGBoost [39], which splits all nodes at the same depth simultaneously and results in a more balanced tree structure, training on larger datasets is typically slower and has higher resource consumption. In contrast, LightGBM adopts a leaf-wise growth strategy that prioritizes splitting the leaf node with the highest information gain, allowing for faster reduction in the loss function under the same conditions. Additionally, its histogram-based feature binning mechanism significantly reduces memory usage and computational cost. As for CatBoost [40], although it employs oblivious tree structures, which provide better stability and reduce the risk of overfitting on small datasets, its training speed is generally slower and memory consumption is higher when applied to larger datasets. Given the structure of our data and the design of our experiments, LightGBM offers a more balanced trade-off between speed and resource consumption, making it a more suitable choice.
The input features fed into the Tree-based model encoder in our model are not the raw values of the time series, but rather features constructed based on the inherent temporal structure. These include lag features and differenced features. We created multiple lagged versions of the target variable at various time steps, and for each lag, we further derived the corresponding differenced feature to enhance the model’s sensitivity to trend changes and enhance the model’s ability to capture nonlinear relationships. In addition, we explicitly incorporated basic temporal context features, such as hour of day, day of week, and minute, which help LightGBM capture periodic patterns more effectively. For multivariate inputs, we modeled each variable independently to avoid interference from redundant information between variables, resulting in a simpler and more efficient modeling process. As a whole, the tree-based model encoder serves as a domain-informed embedding generator, whose output is incorporated as part of the Transformer decoder’s input. This guides the generative style decoder to initiate prediction from informative and structured embeddings, thereby effectively leveraging temporal structures such as trends and seasonality in the time series. Meanwhile, the method shows some ability to act as a denoiser, achieved through carefully designed feature modeling (including lag, differencing, and temporal context), which helps reduce noise interference. While it incorporates multi-scale structures at the input feature level, its core function remains to guide the Transformer decoder to generate more stable and efficient forecasting by integrating structured prior information. This proposed fusion mechanism provides a method to constrain the decoder’s high-dimensional input space by injecting prior knowledge, effectively serving as a form of structural guidance. This guidance acts similarly to regularization. Specifically, the output of the tree-based model encoder functions as structural regularization. During training, LightGBM selects split features in each tree based on split gain. Features that are not selected across all trees are implicitly ignored, serving as a form of feature selection. This process helps lessen the influence of noisy variables, improves model robustness, and mitigates overfitting. We configure the remaining components and parameters following the settings in [6]. It explicitly embeds timestamp information as input, without requiring additional complex time modeling modules. Furthermore, its attention mechanism is well-designed, demonstrating both strong performance and high efficiency.
4. Experimental Results and Analysis
4.1. Datasets
We validate the effectiveness of the Treeformer model using several publicly available datasets commonly employed for evaluating LSTF problems. Considering the broad applicability of LSTF problems across multiple real-world domains, our experiments cover eight datasets from five domains.
- Traffic (https://pems.dot.ca.gov/ (accessed on 1 January 2023)): This dataset records the hourly road occupancy rates of San Francisco freeways and contains 862 variables. The dataset used in this study covers data sampled from 2016/07/01 02:00 AM to 2018/07/02 01:00 AM, with different sensors collecting data at hourly intervals. The prediction results can be applied to intelligent traffic scheduling, early warning systems, and related applications.
- Electricity Consumption Load (ECL) (https://archive.ics.uci.edu/dataset/321/electricityloaddiagrams20112014 (accessed on 1 January 2023)): It is an hourly-sampled electricity consumption dataset of 321 users, preprocessed by Informer [6]. This dataset includes 321 variables, with a time span from 2012/01/01 to 2014/12/31.
- ETT Series: They originate from Informer [6] and contains the ETTh {ETTh1, ETTh2}, and ETTm1 datasets, which provide hourly data and 15 min sampled data from 2016/07 to 2018/07, respectively. Those datasets contains seven variables including historical loads (covering different types of regions and hierarchical levels), oil temperature, etc. By predicting the oil temperature and studying the extreme load capacity of power transformers, the working conditions of the transformers can be better understood. This approach aims to reduce resource waste caused by decision-making based solely on experience, and indirectly supports power distribution efficiency, which involves demands requiring large-scale resource allocation.
- Weather: The dataset is cited from Informer [6] and has been preprocessed, which is based on U.S. climate records and covers the period from 2010/01/01 to 2013/12/31. It contains 12 meteorological variables, including visibility, wind speed, relative humidity, and station pressure. These indicators are sampled at an hourly resolution.
- Exchange-rate: Collected by LSTNet [17], comprises daily exchange rate data from eights countries including Singapore, Britain, Canada, etc., spanning 26 years since 1990. Each country’s exchange rate is treated as a variable, resulting in a total of eight variables.
- Influenza-like illness(ILI) (https://gis.cdc.gov/grasp/fluview/fluportaldashboard.html (accessed on 1 January 2023)): This dataset preprocessed by Autoformer, is based on the weekly ratio of influenza-like illness data collected by the U.S. CDC. It spans the period from 2002/01/01 to 2020/06/30, with a sampling interval of one week. The dataset includes seven variables, such as the number of medical facilities reporting influenza-related cases to the CDC each week, the number of cases across different age groups, and the total number of patients.
4.2. Implementation Details
To avoid overtuning the hyperparameters, we standardized the input length to 96 across various prediction lengths for the Traffic, ECL, and Exchange-rate datasets. For the ETT Series and Weather datasets, the input length follows the configuration used in Informer [6]. As for the ILI dataset, the input length is set to 104. Different prediction lengths are assigned to each dataset based on their characteristics. For the ETTh and Weather datasets, the prediction lengths are set to {24, 48, 168, 336, 720}, corresponding to 1 day, 2 days, 1 week, 2 weeks, and 30 days (approximately 1 month). For the ETTm1 dataset, the lengths are {24, 48, 96, 288, 672}, representing 6 h, 12 h, 1 day, 3 days, and 7 days, respectively. The Traffic and Exchange-rate datasets were configured with {96, 192, 336, 720}, corresponding to 4, 8, 14, and 30 calendar days, as well as {96, 192, 336, 720} trading days. For the ILL dataset, the prediction lengths are set to {24, 36, 48, 60}.
To facilitate comparison with other models and to ensure that the evaluation metrics intuitively reflect the requirements of time series forecasting scenarios, we adopt Mean Squared Error (MSE) and Mean Absolute Error (MAE) as evaluation metrics in terms of both extreme error situation and overall stability. In order to increase robustness, repeatability, and fairness, experiments on most datasets were repeated five times, except for Traffic and ILL, which were conducted three times. The results were then averaged.
4.3. Results and Analysis
We assessed the performance of Treeformer on the LSTF problem across eight datasets from five domains, which represent some of the most prominent areas where forecasting is widely applied. The results are summarized in Table 1. We maintain a meaningful prediction length, as mentioned in the previous section. Notably, our model is specifically designed for multivariate time series forecasting. We select four baseline models, including three Transformer-based models and LSTNet. Among them, Reformer [41] is not limited to the TSF domain. By leveraging Locality-Sensitive Hashing (LSH) to reduce computational complexity, and incorporating reversible layers [42] and chunking mechanism, Reformer significantly improves in both memory efficiency and performance when processing ultra-long sequence inputs. These characteristics align well with the critical requirements of real-world engineering applications, particularly in scenarios such as financial tick data, which demand high temporal precision and fine-grained information capture. In such settings, every price change is recorded in detail, requiring the model to effectively capture long-range dependencies and subtle variations. Logtrans and Informer apply sparse attention mechanisms from the perspective of time series data. LSTNet captures long-term dependencies through RNN, while simultaneously utilizing CNN to extract local dependencies among multivariate variables. It is still a relatively robust TSF model in many forecasting tasks.

Table 1.
Multivariate time series forecasting results on different datasets with different prediction horizons.
As shown in Table 1, our proposed method exhibits superior performance on most datasets, reflected by lower MSE and MAE values, indicating higher prediction accuracy. To clearly illustrate the performance differences between our method and the second-best approach, we calculated the reduction ratios in MSE and MAE achieved by our method across various datasets and different prediction horizons. Figure 2 shows these findings graphically as bar charts. In the Traffic dataset, we observe that as the prediction length increases, the MSE and MAE decrease more. It is worth noting that the Traffic dataset contains the largest number of variable dimensions, with a total of 821. Under the prediction length of 96, MSE decreased by 23.10% (0.684 → 0.526), and MAE decreased by 20.31% (0.384 → 0.306). When the prediction length is extended to 336, MSE decreased by 21.69% (0.733 → 0.574), and MAE decreased by 23.77% (0.408 → 0.311). The ECL dataset covers the widest range of prediction lengths, spanning from 48 to 960, and ranks second in the number of variables. However, the reduction ratio of MSE and MAE tends to be stable. Compared to the second-best method, at the prediction length of 720, our approach achieves a 28.87% decrease in MSE (0.381 → 0.271) and a 17.60% decrease in MAE (0.409 → 0.337). When the prediction length increases to 960, MSE decreases by 22.31% (0.381 → 0.296), and MAE decreases by 19.77% (0.440 → 0.353).
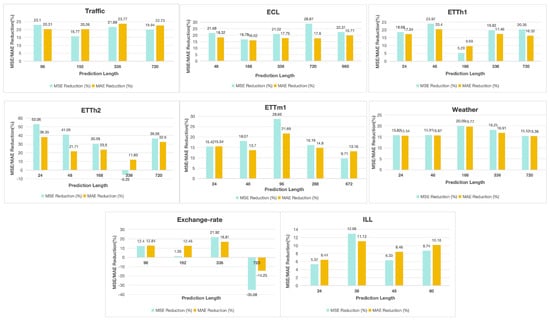
Figure 2.
Percentage reduction in MSE/MAE compared to the second-best model across different datasets on different prediction lengths.
In the ETTh1 dataset, which exhibits distinct seasonal hierarchies (i.e., different seasonality levels), we observe that although the overall prediction performance improves, at the prediction length of 168, the improvements are modest, with MSE reduced by only 5.29% (1.096 → 1.038) and MAE by 9.69% (0.837 → 0.756), suggesting limited effectiveness under this prediction horizon. For other prediction lengths, such as 48 and 720, MSE decreases by 23.97% (0.722 → 0.549) and 20.35% (1.371 → 1.092), while MAE decreases by 20.4% (0.647 → 0.515) and 16.32% (0.950 → 0.795), respectively. This variation in improvement may be attributed to the fact that a prediction horizon of 168 aligns with a full weekly cycle. From a daily time scale perspective, it represents a relatively long forecasting span, whereas from a weekly perspective, it marks the beginning or end of a complete cycle. In contrast, a prediction length of 336 allows the model to capture longer-term temporal interactions, facilitating the learning of cross-week trends more effectively. However, as shown in Figure 3, in the multivariate feature space, the t-SNE [43] and kernel density estimation (KDE) visualizations reveal that ETTh2 gives a more scattered and fragmented sample distribution compared to ETTh1. Specifically, the high-density regions in ETTh2 are more widely separated, with multiple blurred boundaries along the edges, indicating lower compactness and similarity among samples in the low-dimensional space. This reflects weaker inter-variable correlations and more unstable temporal structures. In the original multivariate space, such characteristics may correspond to higher noise levels or stronger non-stationarity, which increases the modeling difficulty. In contrast, the sample distribution of the ETTh1 dataset appears more cohesive and smooth, with multiple high-density regions closely clustered together. These locally cohesive patterns suggest that the time series exhibits stronger temporal regularity (e.g., periodicity). For datasets like ETTh1, which display significant periodicity, the corresponding attention mechanism is better able to stably focus on critical time points, thereby capturing temporal dependencies more effectively and achieving higher predictive accuracy.
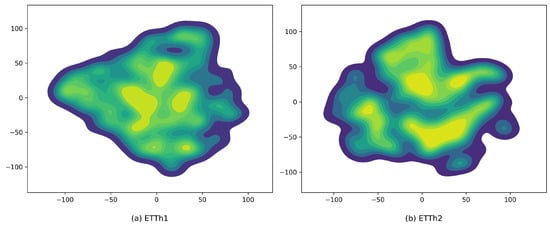
Figure 3.
Data distribution visualization in multivariate feature space using t-SNE and kernel density estimation (KDE).
Treeformer outperforms the second-best model over all forecasting horizons in the Weather dataset and this performance advantage remains highly stable as the prediction length increases. This observed phenomenon has important implications for practical applications, such as weather forecasting, that are highly dependent on warning mechanisms. However, Treeformer exhibits relatively unstable performance on the Exchange-rate dataset. To better understand this, we analyze it from both the dataset and the model aspects. First, the Exchange-rate dataset lacks a stable repetitive structure, displays weak periodicity, shows low inter-variable correlations, and contains a high level of noise. Because the core determinants of exchange rates are actually primarily influenced by a country’s macroeconomic factors and market feedback, it is very challenging to comprehensively collect information about such relevant variables, as the data are scattered across multiple sources without unified standard. Therefore, under the currently available dataset, at the prediction-720 setting, the performance is weaker than that of Reformer. From the model’s perspective, this may be because Reformer is more adept at processing long sequences. As previously mentioned, its design actually uses “LSH Attention”, which implements “local sparseness of similarity”. This design enables the model to pay more attention to similar segments rather than amplifying/reinforcing “random spikes”, making it more robust to “irregular” data. In addition, a 720-step prediction represents a very long forecasting horizon, making the model more prone to error accumulation, thus showing a clear disadvantage under this prediction setting. In ILI, although the dataset is much smaller than others and thus required a different set of parameters, we observed that it performs well across all prediction length settings.
In addition, we conducted additional comparative experiments on the Traffic dataset between Treeformer and several state-of-the-art TSF models, as shown in Table 2, where most of these models incorporate components specifically designed based on the characteristics of time series data. For example, Autoformer [27] integrates a time series decomposition module to enhance its modeling capabilities. FEDformer [31] works in the frequency domain by converting time series data from the time domain. It reconstructs the signal using a small number of learnable frequency components based on the sparsity of the series, thereby minimizing information loss while capturing a more comprehensive global view. Pyraformer [30] is specifically designed with the structural characteristics of time series in mind, particularly their multi-scale nature, by introducing a pyramid-layered attention mechanism. ETSformer [9] further draws inspiration from the classical Holt–Winters method in traditional TSF, and extracts the trend with the help of exponential smoothing to replace the rough trend extraction method previously adopted by simple moving average, making the trend component more stable and predictive. TimesNet [23] is a CNN-based architecture that reshapes 1D time series into a 2D space to simultaneously model intra-period and inter-period variations. Non-stationary Transformer [44] tackles the problem from two perspectives: normalization and de-normalization operations are performed on the input and output, respectively, to restore the statistical characteristics; second, a new De-stationary Attention is designed to approximate the Attention Matrix of the original non-stationary sequence through the Attention Matrix of the stationarized sequence to solve the phenomenon of convergence among attention matrices across different time series caused by traditional normalization methods. DLinear [12] uses a simple structure to improve prediction accuracy and efficiency by combining the time series decomposition mechanism with a linear architecture. However, we still find that the Treeformer we proposed achieves better results than the above models in multivariate LSTF tasks on Traffic, a dataset with high-dimensional variables and inherent temporal patterns. This highlights the hybrid advantages of our model. Moreover, to demonstrate that our results are not simply smoothed by averaging, we present the model’s performance at prediction lengths of 192, 336, and 720 for each run on Traffic. As shown in Figure 4, the results exhibit minimal variation across runs, with performance fluctuations confined to a narrow range. This provides evidence that our experimental outcomes are stable rather than incidental, thereby enhancing the robustness of our conclusions.

Table 2.
Comparison of MAE and MSE across different prediction horizons on the Traffic dataset with other state-of-the-art models specifically designed for the unique properties of time series data.
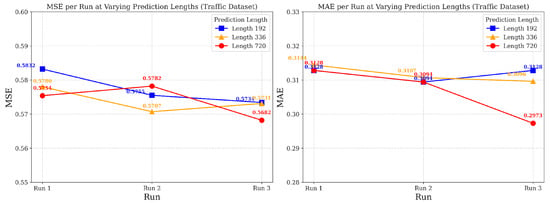
Figure 4.
MSE and MAE results across three runs at different prediction lengths on the Traffic dataset.
4.4. Ablation Studies
4.4.1. Module-Level Ablation
To thoroughly demonstrate the effectiveness of each component and evaluate their impact on the predictive accuracy of Treeformer, we conducted ablation experiments on all datasets, keeping the same configurations described in Treeformer. Specifically, TreeformerT refers to the model variant that retains only the tree-based model encoder component, while TreeformerC denotes the variant that preserves only the time–feature dimension’s decoupling information extraction component. These ablation experiments aim to assess the individual contribution and significance of each module in the proposed framework. The results of the ablation investigations are displayed in Table 3. From the results, it is evident that TreeformerT and TreeformerC consistently achieve the second- and third-best performances across most datasets, outperforming other comparative models. This demonstrates the effectiveness of both components in enhancing the prediction accuracy of the deep learning-based TSF model. Specifically, we observed that on datasets with strong regularity and high variable dimensionality (e.g., Traffic, ECL, Weather), TreeformerC slightly outperforms TreeformerT, indicating that the additional information extracted from decoupling the time and feature dimensions, namely channel-independent and interactive representations, can significantly enhance model capability. However, on datasets such as ILI and ETTh1, TreeformerT slightly outperforms TreeformerC. Nevertheless, the synergistic potential of both components remains evident, contributing substantially to performance improvement and encouraging further exploration of optimal combination strategies.

Table 3.
Ablation study of Treeformer.
4.4.2. Parameter-Level Ablation of Tree-Based Model Encoder
In our original experimental configuration, the maximum tree depth was left unspecified. This was intended to demonstrate that the maximum tree depth was unconstrained, allowing the tree-based model encoder to determine the optimal depth based on the data and its pruning strategy. Unlike traditional level-wise algorithms such as XGBoost, LightGBM adopts a leaf-wise growth strategy that prioritizes splitting the leaf node with the highest potential to reduce the loss function. This can result in some trees growing very deep, but often leads to better overall performance. As a result, max_depth is typically used as the default setting in practice, allowing the model to grow adaptively based on the data. The official practical documentation also highlights this parameter, noting that limiting it is commonly used to reduce the risk of overfitting on small datasets. This choice was motivated by the need to ensure model adaptability across datasets from different domains, as a fixed structural configuration may fail to generalize well. The default depth-setting strategy provides greater flexibility and robustness in such varied scenarios. To evaluate the impact of structural depth on model performance, we conducted an ablation study on the parameter: structure depth (max_depth), while fixing the branching factor (num_leaves) at 64. We tested five depth values: {5, 15, 32, 64, 128}. All ablation experiments in this section adopt a unified prediction setting: a prediction length of 336 on the Traffic dataset. The results of the experiment are illustrated in Figure 5, where the original Treeformer setting (with default max_depth) remains the best-performing configuration overall. Although slight fluctuations are observed across different depths, it is evident that the performance at max_depth = 64, 128 is slightly better than at max_depth = 5, 15, or 32, indicating that forecasting performance is indeed sensitive to tree depth. The lowest MSE is achieved at max_depth = 64, and increasing the depth further to 128 offers limited additional benefit, suggesting diminishing returns with deeper trees. In terms of MAE, both max_depth = 64 and 128 also yield strong performance, falling within the peak performance range, but may stem from an overfitting effect.
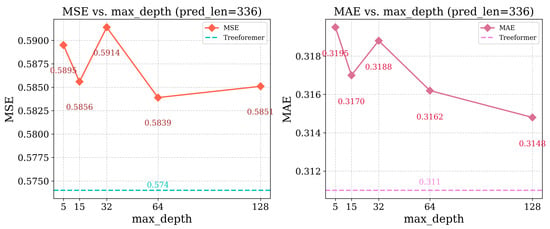
Figure 5.
Ablation study on max_depth for the Traffic dataset (prediction Length = 336, num_leaves = 64).
In addition, we conducted further experiments by fixing max_depth = 64 and varying the number of leaves, with . As the number of leaves increases, the model is theoretically expected to capture more complex patterns due to finer partitioning, which may improve performance, particularly on larger datasets. However, as shown in Figure 6, our results show that num_leaves = 32 achieves the best performance in this setting. This suggests that higher model complexity does not always result in better forecasting accuracy and may instead lead to overfitting or unnecessary computational overhead.
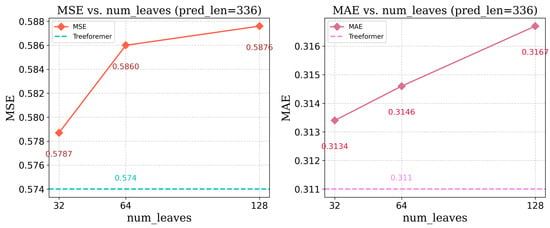
Figure 6.
Ablation study on num_leaves for the Traffic dataset (prediction length = 336, max_depth = 64).
Following this, we conducted experiments with while keeping the structure depth (max_depth) consistent with Treeformer. As shown in Figure 7, the results indicate that our configuration yields the best performance. Regarding computational efficiency, it is evident that increasing the branching factor leads to significantly longer training and inference times when the tree structure depth is fixed. A similar trend is observed under the default tree depth setting of Treeformer. These results highlight a trade-off between forecasting accuracy and computational efficiency, where improved performance comes at the cost of increased computational overhead.
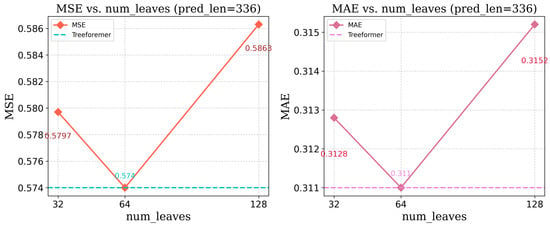
Figure 7.
Ablation study on num_leaves for the Traffic dataset (Default max_depth, consistent with Treeformer).
5. Future Directions
While our work considers the information gain from relationships between multiple variables and utilizes the robust channel-independent modeling method, introducing multivariate relationships into the model may still lead to some degree of information redundancy or interference from irrelevant variables. Repeatedly learning similar information increases complexity and exacerbates the risk of overfitting, thereby limiting the model’s ability to effectively generalize to new datasets. Recent studies have proposed solutions to this problem. The core idea involves clustering the individual variable sequences within multivariate time series data to form similar groups. Based on the degree of similarity between variables, whether the channel-dependent strategy should be used is determined. A channel-dependent strategy is applied within each cluster, while a channel-independent strategy is used to model relationships between clusters. This approach leverages the strengths of both methods effectively. At the same time, this method can be further extended to univariate scenarios by treating each univariate sequence as an individual variable sequence, like those described above. Meanwhile, by performing series-wise clustering, relationships between univariate samples can be captured. This approach is particularly valuable in scenarios where significant dependencies exist between univariate samples, such as in financial markets or similar fields. In addition, this method can be further extended to zero-shot learning. By utilizing the information generated during the clustering process, the model can predict new categories based on its existing knowledge and reasoning ability, even in the absence of any target category data.
6. Conclusions
In this paper, we propose a novel model, Treeformer, specifically designed for multivariate LSTF task. This model effectively enhances the predictive performance of existing deep learning-based approaches and demonstrates superior results across time series datasets from multiple domains. By incorporating the tree-based model as an encoder to enhance the TSF model’s ability to capture local features, we further extract information from two complementary dimensions by employing channel-independent modeling along the time dimension and cross-channel modeling along the feature dimension. These operations, when integrated with the Transformer-based forecasting model, demonstrate a synergistic enhancement in performance. The effectiveness of the Treeformer model has been validated through experiments, particularly achieving competitive performance on the Traffic dataset, which is characterized by high-dimensional features. This highlights the adaptability and efficacy of our approach in addressing complex forecasting tasks. The proposed method not only broadens the research perspective on TSF but also provides a solid foundation for its application and deployment in diverse real-world scenarios. Despite these significant improvements, reducing redundancy among multivariate information remains an important research challenge.
Author Contributions
Conceptualization, X.L.; Methodology, X.L.; Formal analysis, X.L.; Writing—original draft, X.L.; Writing—review & editing, W.W.; Supervision, W.W.; Project administration, W.W.; Funding acquisition, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets used in this study are publicly available and properly cited within the manuscript. However, the source code and experimental implementation are not publicly available at this time, as they will be used in a follow-up research project. Interested readers may contact the authors to request access to the code after publication, and such requests will be considered.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zheng, J.; Huang, M. Traffic Flow Forecast through Time Series Analysis Based on Deep Learning. IEEE Access 2020, 8, 82562–82570. [Google Scholar] [CrossRef]
- Zheng, C.; Fan, X.; Wang, C.; Qi, J. GMAN: A Graph Multi-Attention Network for Traffic Prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 1234–1241. [Google Scholar]
- Nguyen, T.; Shah, R.; Bansal, H.; Arcomano, T.; Maulik, R.; Kotamarthi, R.; Foster, I.; Madireddy, S.; Grover, A. Scaling Transformer Neural Networks for Skillful and Reliable Medium-Range Weather Forecasting. Adv. Neural Inf. Process. Syst. 2024, 37, 68740–68771. [Google Scholar]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial Time Series Forecasting with Deep Learning: A Systematic Literature Review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef]
- Kim, A.; Yang, Y.; Lessmann, S.; Ma, T.; Sung, M.-C.; Johnson, J.E.V. Can Deep Learning Predict Risky Retail Investors? A Case Study in Financial Risk Behavior Forecasting. Eur. J. Oper. Res. 2020, 283, 217–234. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, Number 12. pp. 11106–11115. [Google Scholar]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. SCINet: Time Series Modeling and Forecasting with Sample Convolution and Interaction. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 5816–5828. [Google Scholar]
- Wang, H.; Peng, J.; Huang, F.; Wang, J.; Chen, J.; Xiao, Y. MICN: Multi-Scale Local and Global Context Modeling for Long-Term Series Forecasting. In Proceedings of the Eleventh International Conference on Learning Representations (ICLR 2023), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Woo, G.; Liu, C.; Sahoo, D.; Kumar, A.; Hoi, S. ETSFormer: Exponential Smoothing Transformers for Time-Series Forecasting. arXiv 2022, arXiv:2202.01381. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations (ICLR 2024), Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting. In Proceedings of the Eighth International Conference on Learning Representations (ICLR 2020), Virtual Conference, 26–30 April 2020. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? In Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence (AAAI 2023), Washington, DC, USA, 7–14 February 2023; Volume 37, Number 9. pp. 11121–11128. [Google Scholar]
- Zhang, Y.; Yan, J. Crossformer: Transformer Utilizing Cross-Dimension Dependency for Multivariate Time Series Forecasting. In Proceedings of the Eleventh International Conference on Learning Representations (ICLR 2023), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Gao, J.; Hu, W.; Chen, Y. Client: Cross-Variable Linear Integrated Enhanced Transformer for Multivariate Long-Term Time Series Forecasting. arXiv 2023, arXiv:2305.18838. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.-C.; Yang, Y.; Liu, H. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the 41st International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR 2018), Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Smyl, S. A Hybrid Method of Exponential Smoothing and Recurrent Neural Networks for Time Series Forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Lin, S.; Lin, W.; Wu, W.; Zhao, F.; Mo, R.; Zhang, H. SegRNN: Segment Recurrent Neural Network for Long-Term Time Series Forecasting. arXiv 2023, arXiv:2308.11200. [Google Scholar]
- Jia, Y.; Lin, Y.; Hao, X.; Lin, Y.; Guo, S.; Wan, H. WITRAN: Water-Wave Information Transmission and Recurrent Acceleration Network for Long-Range Time Series Forecasting. In Advances in Neural Information Processing Systems, Proceedings of the Thirty-Seventh Conference on Neural Information Processing Systems (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023; NeurIPS: San Diego, CA, USA, 2023. [Google Scholar]
- Lea, C.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal Convolutional Networks: A Unified Approach to Action Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV 2016) Workshops, Amsterdam, The Netherlands, 8–16 October 2016; Part III. pp. 47–54. [Google Scholar]
- Huang, S.; Wang, D.; Wu, X.; Tang, A. DSANet: Dual Self-Attention Network for Multivariate Time Series Forecasting. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management (CIKM 2019), Beijing, China, 3–7 November 2019; pp. 2129–2132. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the Eleventh International Conference on Learning Representations (ICLR), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case. arXiv 2020, arXiv:2001.08317. [Google Scholar] [CrossRef]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The Long-Document Transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar] [CrossRef]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Virtual Event, 6–14 December 2021; Volume 34, pp. 22419–22430. [Google Scholar]
- Du, D.; Su, B.; Wei, Z. Preformer: Predictive Transformer with Multi-Scale Segment-Wise Correlations for Long-Term Time Series Forecasting. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2023), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Cirstea, R.-G.; Guo, C.; Yang, B.; Kieu, T.; Dong, X.; Pan, S. Triformer: Triangular, Variable-Specific Attentions for Long Sequence Multivariate Time Series Forecasting. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence (IJCAI 2022), Vienna, Austria, 23–29 July 2022; International Joint Conferences on Artificial Intelligence Organization: Vienna, Austria, 2022; pp. 1994–2001. [Google Scholar]
- Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A.X.; Dustdar, S. Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting. In Proceedings of the International Conference on Learning Representations (ICLR 2022), Virtual Event, 25–29 April 2022. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency Enhanced Decomposed Transformer for Long-Term Series Forecasting. In Proceedings of the 39th International Conference on Machine Learning (ICML 2022), Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar]
- Chen, Y.; Liu, S.; Yang, J.; Jing, H.; Zhao, W.; Yang, G. A Joint Time-Frequency Domain Transformer for Multivariate Time Series Forecasting. Neural Netw. 2024, 176, 106334. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Chen, J.; Gong, S.; Jiang, F.; Zhang, T.; Chen, J.; Gao, X. ATFNet: Adaptive Time-Frequency Ensembled Network for Long-Term Time Series Forecasting. arXiv 2024, arXiv:2404.05192. [Google Scholar]
- Tolstikhin, I.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J. MLP-Mixer: An All-MLP Architecture for Vision. In Advances in Neural Information Processing Systems, Proceedings of the Thirty-Fifth Conference on Neural Information Processing Systems (NeurIPS 2021), Virtual, 6–14 December 2021; NeurIPS: San Diego, CA, USA, 2021. [Google Scholar]
- Xu, Z.; Zeng, A.; Xu, Q. FITS: Modeling Time Series with 10k Parameters. arXiv 2023, arXiv:2307.03756. [Google Scholar]
- Yi, K.; Zhang, Q.; Fan, W.; Wang, S.; Wang, P.; He, H.; An, N.; Lian, D.; Cao, L.; Niu, Z. Frequency-Domain MLPs Are More Effective Learners in Time Series Forecasting. In Advances in Neural Information Processing Systems, Proceedings of the Thirty-Seventh Conference on Neural Information Processing Systems (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023; NeurIPS: San Diego, CA, USA; Volume 36, pp. 76656–76679.
- Elsayed, S.; Thyssens, D.; Rashed, A.; Jomaa, H.S.; Schmidt-Thieme, L. Do We Really Need Deep Learning Models for Time Series Forecasting? arXiv 2021, arXiv:2101.02118. [Google Scholar] [CrossRef]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A Time Series Is Worth 64 Words: Long-Term Forecasting with Transformers. arXiv 2022, arXiv:2211.14730. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. Adv. Neural Inf. Process. Syst. 2018, 31, 6639–6649. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The Efficient Transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar] [CrossRef]
- Gomez, A.N.; Ren, M.; Urtasun, R.; Grosse, R.B. The Reversible Residual Network: Backpropagation without Storing Activations. Adv. Neural Inf. Process. Syst. 2017, 30, 2211–2221. [Google Scholar]
- Wang, W. 15.7.6 t-Distributed Stochastic Neighbor Embedding. In Principles of Machine Learning; Springer: Berlin/Heidelberg, Germany, 2024; pp. 501–503. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary Transformers: Exploring the Stationarity in Time Series Forecasting. In Advances in Neural Information Processing Systems (NeurIPS 2022), Proceedings of the Thirty-Sixth Annual Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; NeurIPS: San Diego, CA, USA, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).