Abstract
This article introduces two numerical methods based on the Theory of Functional Connections (TFC) for solving linear ordinary differential equations that involve step discontinuities in the forcing term. The novelty of the first proposed approach lies in the direct incorporation of discontinuities into the free function of the TFC framework, while the second proposed method resolves discontinuities through piecewise constrained expressions comprising particular weighted support functions systematically chosen to enforce continuity conditions. The accuracy of the proposed methods is validated for both a second-order initial value and boundary value problem. As a final demonstration, the methods are applied to a third-order differential equation with non-constant coefficients and multiple discontinuities, for which an analytical solution is known. The methods achieve error levels approaching machine precision, even in the case of equations involving functions whose Laplace transforms are not available.
MSC:
34A36
1. Introduction
Discontinuous differential equations (DDEs) commonly appear in many areas of science and engineering. Some illustrative examples are as follows:
- A mass–spring system subjected to a step load, , where is the Heaviside step function modeling a sudden applied force. This model describes shock responses in structures, such as vehicle collisions or switching mechanisms.
- An RL circuit with a switched voltage source, , that is used in transient circuit analysis, power electronics, and digital devices.
- A rod with piecewise thermal conductivity, , where if and if . This model is common in layered insulation or material systems with abrupt changes in conductivity.
- Wave propagation through layered media, , where and in the wave equation are piecewise functions that model subsurface layers.
- Bang–bang control, , where switches between and according to the control law. This is used in guidance laws for optimal control and rapid switching maneuvers.
- Coulomb friction, , which appears in braking systems, robotics, and dry contact problems.
In general, discontinuities may occur in the forcing term or the coefficients of the differential equation. In the case of discontinuous coefficients, the order of continuity is governed by the structure of the differential equation and its coefficients, which poses significant analytical challenges [1,2]. For second-order linear differential equations, the solution field typically remains continuous across the discontinuity, while the first derivative may be discontinuous depending on the specific expression of the coefficients. Furthermore, the second derivative may contain singular components such as a Dirac delta function, particularly when the discontinuity occurs in the highest-order coefficient. These issues are especially critical in the study of Sturm–Liouville and boundary value problems, where precise matching conditions at points of discontinuity are essential to ensure the mathematical and physical consistency of the solution. Zettl’s work [3] develops a rigorous framework for handling such problems. In the case of the forcing term containing step discontinuities, it has been proven that the solution field of an nth-order differential equation is continuous [4,5,6], so the order of continuity is independent of the associated homogeneous equation. For simplicity and brevity, this article only considers linear nonhomogeneous ordinary differential equations (ODEs) of n-order subject to n linear constraints with simple discontinuities in the forcing function.
Green’s functions [7,8] and Laplace transforms [9,10,11] are the most common analytical methods used to solve such discontinuous ODEs, but these techniques are typically limited to linear problems with known Green’s functions or Laplace transforms, which may be mathematically complex, and simple boundary conditions. Alternatively, within engineering analysis and scientific computing, approximation methods such as the finite difference method (FDM) [12], the finite volume method (FVM) [13], the finite element method (FEM) [14], and spectral methods [15] are frequently employed for modeling a variety of physical systems with varying degrees of complexity. Of particular relevance to this work are spectral methods and FEM.
In spectral methods, the solution field is represented as a weighted sum of smooth global basis functions whose coefficients are chosen to satisfy the differential equation and constraints. Spectral methods are often implemented using a collocation approach, where the function approximation is substituted into the strong form of the differential equation and the residual is forced to zero at select points in the domain. This yields an algebraic system of equations where the unknowns are the coefficients of the basis functions, which can be solved using several numerical techniques, while boundary conditions can be satisfied analytically with a keen choice in basis functions for certain problems; spectral methods commonly employ iterative techniques (i.e., shooting methods) to only approximately satisfy boundary conditions [15]. Since spectral methods typically assume a globally smooth functional form, they do not apply to problems involving discontinuities.
In contrast, the finite element method involves discretizing the global domain into a set of subdomains (i.e., elements) and representing the solution field over each element as a weighted sum of basis functions (i.e., shape functions). Consequently, this piecewise representation of the solution field allows discontinuities to be more easily resolved, while many variations of FEM exist [14]; one of the most common implementations is the Galerkin weighted residual method. This traditional FEM approach involves substituting the function approximation over each element into the differential equation and setting the integral of the corresponding weighted residual to zero with the weighting functions chosen to be identical to the shape functions. Integration by parts is then employed to weaken the differentiability requirements on the shape functions, which simplifies the evaluation of the integral equations that form a set of element equations. Continuity conditions on the field are then directly enforced between elements through an assembly process that forms a global algebraic system of equations, which are then modified to impose boundary conditions via the direct or penalty method. While the finite element method applies to a wider class of problems involving arbitrarily shaped domains and discontinuities, spectral methods are often easier to implement and exhibit better computational efficiency for 1-D and 2-D problems that are smooth, especially over rectilinear domains [16].
In this article, two numerical methods based on the Theory of Functional Connections (TFC) are developed for solving linear nonhomogeneous ODEs with discontinuities in the forcing function that combine principles from spectral and finite element methods. The approaches are similar to spectral methods in that high-order function approximations of the solution field are used to form an algebraic system of equations directly from the strong form of the differential equation; however, the basis functions are defined over subdomains similar to FEM to allow for the resolution of discontinuities. Additionally, all constraints—initial value, boundary value, and continuity—are satisfied analytically. This exploration of TFC addressing discontinuous ordinary differential equations (DDEs) begins with simple, linear DDEs characterized by smooth solution fields and regular constraints, representing an initial and necessary step toward more complex problems. The goal is not to propose a method superior to existing approaches, but rather to demonstrate the potential application of TFC to solving problems involving discontinuities. In particular, the aim is to highlight a novel and significant feature introduced in this study: the ability to encode information (here about discontinuities) directly into the free function of the TFC framework. This capability, presented here for the first time, is general and not limited to the DDEs, which opens new directions for the application of TFC, both theoretically and practically.
Summary of the Theory of Functional Connections
The Theory of Functional Connections was initially introduced in [17], further refined in [18,19], and comprehensively summarized in [20]. It extends the classical interpolation problem—where n constraints are satisfied using n linearly independent support functions—into the broader concept of functional interpolation. TFC provides a systematic approach for constructing functionals representing the entire family of interpolation functions meeting a prescribed set of n linear constraints. These functionals characterize the subspace of functions that inherently satisfy the constraints, effectively reducing the whole solution space to just the subspace where solutions fully comply with all linear constraints. By leveraging these functionals, TFC reformulates constrained optimization problems into unconstrained ones, allowing for more efficient, accurate, and reliable computational techniques. The foundational work in [17] details the application of TFC to univariate constraints involving fixed values, derivatives, and linear combinations thereof. Subsequent developments have expanded TFC to handle integral, infinite, and multivariate constraints, as well as solve ordinary, partial, and integrodifferential equations [21].
In the univariate case, TFC can be expressed by either one of the two equivalent formulations:
where is a functional that satisfies the given n constraints, and is a freely chosen function. Additionally, are user-defined support functions that are linearly independent over the domain, while are the associated coefficient functionals. The functions serve as switching functions that take a value of 1 at their corresponding constraint and 0 at all others, while represent projection functionals that express constraints in terms of the free function. The theoretical foundations and properties of these components are detailed in [18,19,20] and utilized throughout this article without further derivation.
Since the original work in [17], TFC has been widely applied and extended across multiple domains. TFC has enhanced continuation methods [22] and contributed to areas such as indirect optimal control [23], representations of fractional operators [24,25], stiff chemical kinetics modeling [26], epidemiological modeling [27], and aerospace engineering [28,29,30,31,32]. Moreover, TFC has shown promising applications in nonlinear programming [33] and structural mechanics [34,35]. One of its most impactful implementations has been in neural networks [36], where it significantly improves accuracy and enables efficient solutions to high-dimensional problems. In particular, its integration with Physics-Informed Neural Networks (PINNs) [37] enhances computational efficiency by removing constraints from the optimization process, overcoming a key challenge in traditional neural networks [38].
Thus far, however, the development and application of TFC has progressed under the fundamental assumption that the function subject to constraints is continuous. This assumption breaks down when discontinuities appear, so the efficacy of TFC deteriorates, as observed in [39]. Thus, a reconsideration of the theoretical framework is required to extend the application of TFC to discontinuous systems. Admittedly, such considerations were partially explored in [40], which demonstrates how TFC can solve boundary value problems (BVPs) in hybrid systems consisting of a sequence of linear or nonlinear ODEs that are of different orders or contain varying parameters. In contrast, the present study aims to tackle a different class of problems, which arise from physical and engineering applications where discontinuities originate from abrupt changes in terms within the differential equation that represent external stimuli or internal system parameters. The proposed method in [40] illustrates how an ODE can be effectively solved by partitioning the integration domain into multiple subdomains, provided the continuity conditions at the interfaces between successive subdomains are known a priori. This approach has proven to be particularly efficient in addressing stiff equations. While the hybrid TFC approach in [40] was not specifically applied to DDEs, such problems belong to the class of hybrid systems and can be readily achieved by introducing continuity variables as additional unknowns that are solved simultaneously with the unknown coefficients defining the free functions.
In contrast, the two methods presented in this work for solving discontinuous ODEs do not introduce any additional variables, constituting the primary distinction from the approach in [40]. This is accomplished either by coupling free functions associated with successive domains through the imposition of continuity constraints or by modifying the expressions of subsequent free functions such that continuity conditions are directly satisfied. To provide a simple exposition, this article focuses specifically on solving linear nonhomogeneous discontinuous ODEs with simple (i.e., step) discontinuities in the forcing function. The following presentation will first focus on the theoretical development of the proposed methods. Section 2.1 outlines the g-embedded hybrid system approach where continuity is directly embedded within the free function. Section 2.2 outlines the S-embedded hybrid system approach where continuity constraints are imposed by introducing additional support functions. The proposed methods are then implemented numerically in Section 3 for three case studies with known solutions, and this section is then followed by Section 4, which summarizes this present work and outlines future work.
2. Methods
2.1. g-Embedded Hybrid System Approach
As allowed within the TFC framework, the theoretical basis of this work emphasizes that the free function can be any function. Consequently, the proposed method constructs the free functional through a sequence of piecewise local free functions specifically formulated such that continuity constraints across the global domain are intrinsically satisfied. Unlike the hybrid method developed in [40], the proposed g-embedded approach in this section eliminates the need for introducing additional support or switching-projection functions to satisfy local continuity constraints and therefore does not introduce additional unknowns. Thus, the application of TFC to continuous and discontinuous systems is effectively identical.
To illustrate intrinsically satisfying continuity constraints, consider a field defined over the global domain , which is known to contain a simple discontinuity at the coordinate where . Assuming two boundary conditions are imposed on , the constrained functional is
where and are two globally continuous switching functions. Thus, the discontinuity in the constrained functional must be resolved within . This work proposes that two local free functions can be introduced such that and , where and . Thus, the free function is replaced by the free functional , in which the second derivative of the free functional, which includes a discontinuity at , can be expressed piecewise as
where and is the Heaviside function. As derived in Appendix C, integrating Equation (2) over the global domain yields
where , and . Notice that and , so global -continuity is directly embedded into the free functional as shown in Figure 1. Integrating Equation (3) yields the following free functional:
which is necessarily continuous according to the first fundamental theorem of calculus.
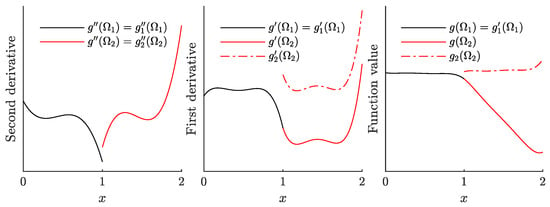
Figure 1.
An example free function (Right) and its first (Center) and second (Left) derivatives as derived in Equations (4), (3) and (2), respectively. Notice that the local free function and its first derivative are different than the global free function and its first derivative, respectively, over the subdomain because continuity is enforced.
As outlined for general cases in Appendix C, Equations (2)–(4) can be conveniently split into two terms such that,
where is the differential operator and the functionals and depend only on and , respectively. In this case, can be expressed as
which reveals a clear algebraic structure that is generalized for simple discontinuities in Equation (A11). Note that this work uses the convention . As demonstrated in Equation (6), the functional describes the contribution of the jth local free function to the global free functional.
Application to Univariate Linear Discontinuous ODEs
Consider the linear differential operator ,
where the are known functions on the 1-dimensional domain . The response of the field subject to a forcing field is governed by the linear differential equation
and satisfies n linear constraints,
In the case of a step-change in at , the field also satisfies the continuity constraints,
Using the switching-projection formulation [20], the unknown field can be expressed as the constrained functional
where all are formulated to directly satisfy the n linear constraints in Equation (9). As previously demonstrated, the free functional can be expressed as the sum of -functionals,
where is the local free function that is continuous in the subdomain and . Since the -functionals are defined such that their summation intrinsically satisfies the continuity constraints in Equation (10), the constrained ODE in Equations (8)–(10) can be rewritten as an unconstrained ODE in terms of the constrained functional as
Without loss of generality, let each local free function be chosen as a linear combination of Legendre orthogonal polynomials such that,
where m is the maximum polynomial degree, and each subdomain is mapped to the interval by the transformation
Thus, the final linear system of equations is of the form
where , comes from the functional (i.e., ) terms, comes from the constraint operator (i.e., ) terms, and comes from the constraint value (i.e., ) terms. Note that according to the TFC framework as applied to optimization problems, the basis functions used to construct the switching functions must be linearly independent of the functions employed to represent the free function [20]. Consequently, when adopting a polynomial basis for the free function, such as the Legendre orthogonal polynomials, and selecting as the basis for the switching functions, the first two Legendre polynomials must be excluded from the expansion of the free function to ensure the required linear independence. Additionally, the matrix is structured as a lower block triangular matrix because the integration scheme that enforces continuity couples the local free function of a particular subdomain to the local free functions of the preceding subdomains. At this point, the unknown field has been represented by the constrained functional , where the function space of has been constrained to a sequence of piecewise Legendre polynomials that directly embed continuity constraints. With this form, a constrained linear DDE is approximated as an algebraic linear system of equations where the unknown coefficients can be solved numerically via linear least squares.
2.2. S-Embedded Hybrid System Approach
In this section, the proposed S-embedded method modifies the original hybrid approach in [40] to avoid introducing additional unknown variables that enforce continuity and is applied to linear DDEs. Unlike the g-embedded approach developed in Section 2.1, the S-embedded method models a univariate field by a piecewise sequence of constrained functionals and all constraints—both boundary and continuity—are satisfied analytically in a classical TFC fashion using the -formulation. Thus, continuity is satisfied within a set of weighted support functions, as opposed to the free function. The advantage of this approach over the g-embedded method is that continuity conditions involving weighted field values and derivatives are more easily resolved.
To facilitate the development of the S-embedded method, consider the second-order BVP, as follows:
with a domain containing three simple discontinuities occurring at , , and . The field is modeled using four piecewise constrained functionals with and selected as the support functions such that
where the free functional is now denoted as for brevity of notation in the remainder of this manuscript. Assuming global continuity of the field and its derivative, the continuity conditions are satisfied by enforcing
From Equations (17)–(19), the following linear system of 8 equations and 8 unknowns (i.e., ) can be constructed, as follows:
where the first two equations correspond to the boundary constraints, and the latter correspond to the continuity constraints.
Thus, the coefficient functionals can be resolved as a linear combination of the local free functions such that Equation (18) satisfies the boundary and continuity constraints for any , as shown in Figure 2.
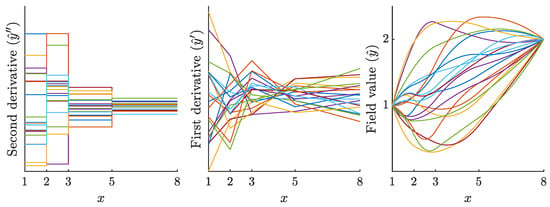
Figure 2.
The field (Right) and its first (Center) and second (Left) derivatives of Equation (18) produced by substituting with randomly weighted second-order Legendre polynomials. The constrained expression satisfies the two boundary constraints in Equation (17), arbitrarily chosen as and , and the six continuity conditions in Equation (19).
Leveraging the notation developed in Section 2.1, this approach can be generalized for nth-order systems with simple discontinuities. Let the constrained functional be expressed as a piecewise sequence of local constrained functionals using the following -formulation:
where, unlike Equation (12), the free functional bears a simple piecewise form of
To distinguish between continuity and boundary value constraints, continuity constraints are denoted as
where the continuity constraint operator is defined as
Without loss of generality, the weighting field is assumed to have a piecewise form , similar to the free functional in Equation (22). Thus, the proposed S-embedded approach implements the continuity constraints as follows:
where . The linear system of equations from which the coefficient functionals are resolved in terms of the local free functions is expressed as follows:
where the first n equations correspond to the boundary constraints, and the remainder correspond to the continuity constraints. Note that denotes the set of n linearly independent support functions in the jth constrained functional, , and (cf. Equation (9)). Additionally, the vectorized constraint operators are of the form
The coefficient functionals can be expressed in terms of the local free functions as
where (i.e., the support matrix) is the coefficient matrix in Equation (26). Using Equation (28), the local constrained functionals in Equation (21) can be rewritten as
where is the submatrix of corresponding to . As previously demonstrated, Equation (29) intrinsically satisfies the n boundary and continuity constraints for any .
Application to Univariate Linear Discontinuous ODEs
Similar to Section Application to Univariate Linear Discontinuous ODEs, consider again the linear DDE in Equation (8) subject to n linear boundary constraints and continuity constraints enforced due to a step-change in or the coefficients (cf. Equation (7)) at . Note that only simple discontinuities in the forcing term will be considered in the subsequent numerical case studies. Over the subdomain , the constrained ODE in Equations (8), (9) and (23) can be rewritten as an unconstrained ODE in terms of the jth local constrained functional as
Assuming the local free functions are a weighted sum of Legendre polynomials as in Section Application to Univariate Linear Discontinuous ODEs, the final system of equations is
where
Additionally, the matrix here is structured as a block diagonal matrix (as opposed to a lower block triangular matrix) because the local free functions are decoupled. At this point, the unknown field has been represented by a piecewise sequence of constrained functionals , each defined over the subdomain to allow for the introduction of additional support functions to enforce continuity. Again, a constrained linear DDE is approximated as an algebraic system of equations where the unknown coefficients can be solved numerically via linear least squares.
3. Results
The proposed g-embedded and S-embedded hybrid system approaches derived in Section 2.1 and Section 2.2, respectively, will now be applied numerically to solve linear DDEs with known solutions and regular constraints. Note that irregular constraints (e.g., integral and linear combinations) are easily incorporated within the TFC framework as studied in prior work [20,21], so they are omitted from the simple studies presented. The first case study is a second-order IVP with a single simple discontinuity, and the second case study converts this problem to an equivalent BVP. The third and final case study is a generic third-order BVP with two simple discontinuities whose solution cannot be obtained using traditional Laplace transform techniques. Since the S-embedded method employs the same classical TFC process applied over a partitioned domain and a simple example derivation is provided in Section 2.2, only the system of equations for the g-embedded method are derived in the first two case studies, and the S-embedded results are only shown for the more complex third-order BVP for conciseness. Finally, the local free functions in each case study are restricted to the same set of Legendre orthogonal polynomials, where m is the maximum degree polynomial (see Equation (14)), and the global domain is discretized using a total of Chebyshev–Gauss–Lobatto (CGL) points that are distributed proportionally to the relative size of each subdomain (see Appendix B).
3.1. Case 1: Second-Order IVP with a Single Discontinuity
The second-order ODE with constant coefficients is
subject to the initial conditions
and the continuity constraints
The analytical solution of this linear IVP, obtained using the Laplace transform and reported in Appendix A, is
and is shown in Figure 3.
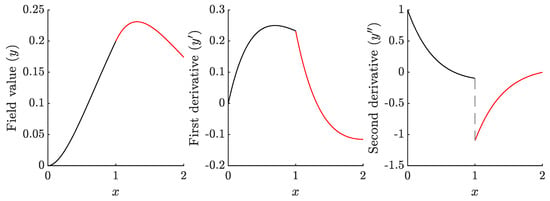
Using Equation (11), the generic TFC-constrained functional for a second-order IVP is
where , and . Using these expressions with Equation (13) and substituting the constraint values in Equation (34) in addition to , the constrained differential equation in Equations (33)–(35) is converted to the unconstrained differential equation,
where the expressions of , , and are provided by Equations (2), (3) and (4), respectively. The system of equations in Equation (16) can be expressed as
where and,
In this case, the matrix terms are zero. After discretizing each subdomain into the set of CGL points and , the resulting algebraic system of equations with unknowns is
where
After removing equations corresponding to , the least-squares problem of Equation (41) can be solved and, the constrained expression approximating the true field can be constructed using Equations (12), (37) and (40). The numerical results are presented in Figure 4 for , which consist of (a) the error distributions of ), ), and ), (b) the -norm of the error vectors , , and with respect to the number of basis functions, (c) the -norm of the residual obtained by substituting the solution estimate and derivatives into the differential equation with respect to the number of basis functions, and (d) the condition number of the matrix inverted within the QR algorithm, derived from the least-squares matrix , with respect to the number of basis functions. The results show that the error values approach machine precision as the number of basis functions increases and that the proposed method is numerically robust as demonstrated by the small condition numbers.
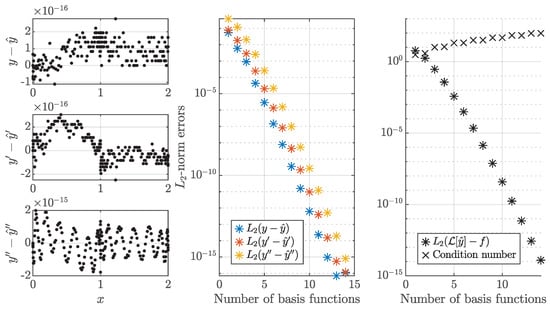
Figure 4.
The numerical results of the g-embedded method applied to the second-order IVP. (Left) The error distributions for 14 basis functions. (Center) The -norm of the error vectors with respect to the number of basis functions. (Right) The -norm of the residual and condition number of the least-squares matrix with respect to the number of basis functions.
3.2. Case 2: Second-Order BVP with a Single Discontinuity
The differential equation presented in Equation (33) is now evaluated as a BVP using the same initial value adopted in the IVP test (i.e., ), while the analytical solution determines the final value,
The generic TFC-constrained functional and its derivatives that always satisfy this BVP are
where
Using the expressions of Equation (43) and substituting and , the differential equation becomes
Notice that the only differences between the IVP and BVP unconstrained ODEs in Equation (38) and Equation (45), respectively, exist in the constraint-related terms. Thus, the matrix for the BVP is identical to that of the IVP in Equation (42), while is modified to
Furthermore, since is non-zero there is an additional forcing term,
which must be accounted for (see Equation (16)). By combining Equations (42), (46) and (47) along with the same choice of basis functions and domain discretization in Section 3.1, the resulting algebraic system of equations with unknowns is
Again, after removing equations corresponding to , the least-squares problem of Equation (48) can be solved, and the constrained expression approximating the true field can be constructed using Equations (12), (40) and (43). The numerical results are presented in Figure 5 and are nearly identical to the IVP results. Additionally, a comparison with a standard central difference method is provided in Appendix D.
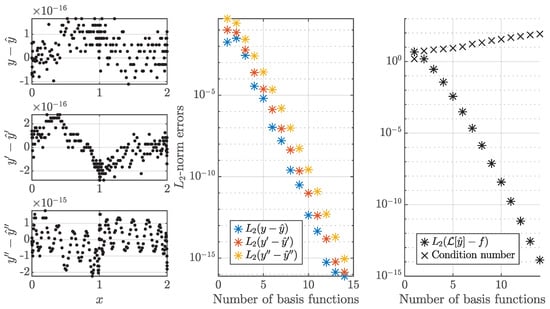
Figure 5.
The numerical results of the g-embedded method applied to the second-order BVP. (Left) The error distributions for 14 basis functions. (Center) The -norm of the error vectors with respect to the number of basis functions. (Right) The -norm of the residual and condition number of the least-squares matrix with respect to the number of basis functions.
3.3. Case 3: Third-Order BVP with Two Discontinuities
Finally, consider the generic third-order linear DDE with non-constant coefficients,
subject to the boundary constraints,
An ODE of this form can be constructed with a known solution by specifying a piecewise continuous such that
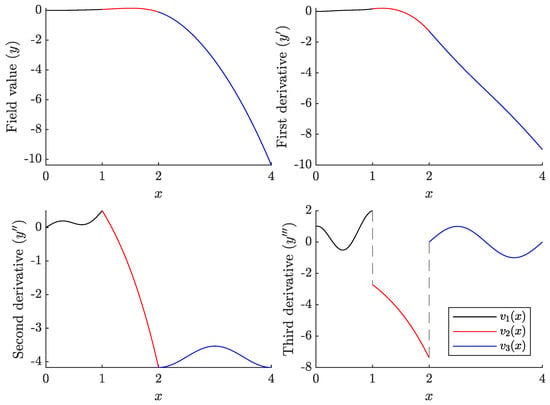
where are arbitrary functions that are continuous over their respective subdomains . By integrating to obtain and specifying the coefficients , the corresponding forcing field in Equation (49) and boundary conditions in Equation (50) are obtained. Consider the case shown in Figure 6 with two simple -discontinuities where the arbitrary functions are chosen, such that
and the coefficients are chosen as
The six continuity constraints are
for . Note that the choice of the coefficient functions in Equation (53) is not arbitrary. The Laplace transform of the function and is unknown, while the Laplace transform of is particularly complex and expressed in terms of the Gamma function. In other words, this differential equation is not well-suited to being solved using the Laplace transform.
3.3.1. g-Embedded Implementation
The constrained functional for this third-order ODE using the g-embedded method is
where
Following the same procedure outlined in the preceding sections, the algebraic system of equations with unknowns is of the form
where , , and are the sets of discretized CGL points. The numerical results are presented in Figure 7 for .
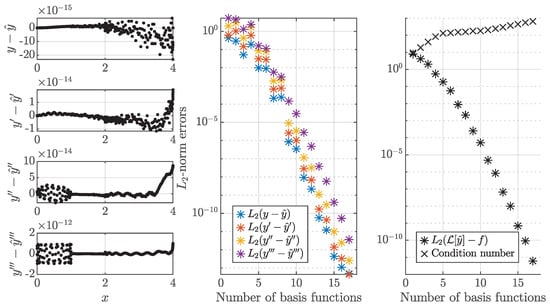
Figure 7.
The numerical results of the g-embedded method applied to the third-order BVP. (Left) The error distributions for 17 basis functions. (Center) The -norm of the error vectors with respect to the number of basis functions. (Right) The -norm of the residual and condition number of the least-squares matrix with respect to the number of basis functions.
3.3.2. S-Embedded Implementation
The constrained functional for this third-order ODE using the S-embedded method is
where the support functions are selected as , , and for all three local constrained functionals. By evaluating the three boundary constraints in Equation (50) and the six continuity constraints in Equation (54), the following system of equations can be formed:
where , , , and . The coefficient functionals can then be obtained in terms of the boundary constraint values and the local free functions, which are then substituted into Equation (58). The typical TFC process of substituting Equation (58) into the differential equation can then be conducted over each subdomain to form the following system of equations:
The numerical results are shown in Figure 8, and the error again approaches machine error as the number of basis functions increases.
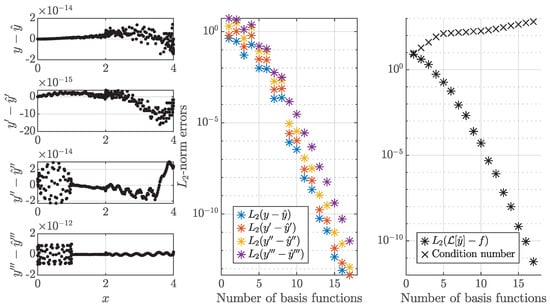
Figure 8.
The numerical results of the S-embedded method applied to the third-order BVP. (Left) The error distributions for 17 basis functions. (Center) The -norm of the error vectors with respect to the number of basis functions. (Right) The -norm of the residual and condition number of the least-squares matrix with respect to the number of basis functions.
4. Discussion
This study introduces two novel numerical methodologies for solving linear nonhomogeneous ODEs of arbitrary order that are subject to simple discontinuities in the forcing function. The approaches are based on the Theory of Functional Connections (TFC), a mathematical framework for embedding constraints into functional representations. The proposed techniques are distinguished by their ability to incorporate discontinuities directly into the structure of the constrained functional either through the free function (i.e., the g-embedded approach) or a set of weighted support functions (i.e., the S-embedded approach), thereby eliminating the need for auxiliary variables that are often employed in conventional methods. Additionally, linearity of the final algebraic system of equations is preserved, provided the original differential equation is linear. Both approaches preserve the fundamental advantage of TFC—transforming constrained differential problems into equivalent unconstrained representations, thereby simplifying the solution process while maintaining analytical precision.
The efficacy of the methods has been evaluated through their application to both initial and boundary value problems for which analytical solutions are known. Numerical experiments confirm that the methods achieve exceptionally high accuracy with error levels approaching machine precision, even in scenarios involving multiple discontinuities and variable coefficients for which no closed-form Laplace transform solutions are available. While the numerical performance of the g-embedded and S-embedded methods are effectively identical, these authors are of the opinion that the g-embedded method is easier to implement, particularly because of its reliance on the switching-projection formulation, and no additional support functions are introduced to resolve the continuity constraints. However, the S-embedded method is expected to more efficiently resolve continuity constraints involving fields and field derivatives that are weighted where, at least within mechanics, the weighting fields represent internal system parameters (e.g., material properties). Nevertheless, both proposed approaches to solving linear nonhomogeneous DDEs exhibit simplicity, robustness, and precision that position them as compelling alternatives to classical numerical techniques. Furthermore, their versatility and ease of implementation suggest promising potential for widespread adoption in various physical and engineering applications.
Beyond application to structural and thermal systems characterized by discontinuities, future research will focus on extending TFC to encompass stiff, nonlinear, and partial DDEs. Such extensions are of particular importance for modeling impact dynamics. These problems typically involve a jump discontinuity in velocity and can be easily resolved for 1-D problems using the present framework (i.e., ), although higher-dimension problems (e.g., 1-D spatial and temporal discontinuities) present the difficult task of embedding discontinuities into higher-dimension functionals. Challenges also arise using the present framework in cases where the time(s) of one or more impact events is unknown, which necessitates an adaptive free functional whose discretization into piecewise local free functions can be updated. Additionally, the performance exhibited within the numerical studies requires support of formal convergence proofs, error estimations, and cost analysis. Though out of the scope of the present work, such investigations will be particularly important for comparing against current state-of-the-art methods and defining the mathematical boundaries of this emerging technique. Finally, the integration of this methodology with machine learning approaches, particularly within the scope of Physics-Informed Neural Networks (PINNs), will be explored. Such advancements are expected to substantially broaden the applicability of TFC-based techniques that enhance their role in addressing complex problems in modern computational science and engineering.
Author Contributions
Conceptualization, T.W. and D.M.; methodology, T.W. and D.M.; software, T.W.; validation, T.W.; writing—original draft preparation, T.W. and D.M.; writing—review and editing, T.W. and D.M.; visualization, T.W.; project administration, D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| TFC | Theory of Functional Connections |
| ODE | Ordinary differential equation |
| DDE | Discontinuous differential equation |
Appendix A
The IVP problem given in Equation (33), subject to and , is here solved in a closed form. The Laplace transform of Equation (33) gives
Substituting and , the equation gives
Since ,
The first term of Equation (A1) can be decomposed as
giving, , , and . Thus,
The second term of Equation (A1) can be written as
The inverse Laplace Transform gives
Specifically, for Equation (A2),
and for Equation (A3),
Combining these results, the solution of Equation (33) and its first and second derivatives are given in Equation (36).
Appendix B
The non-uniformly spaced Chebyshev–Gauss–Lobatto (CGL) point distribution is particularly useful for spectral methods and polynomial approximations because it achieves spectral accuracy, which means the error decreases exponentially for smooth problems due to spectral convergence and provides reduced computational effort compared to uniform grids for the same level of accuracy. CGL point distributions are applied to solve boundary value problems and approximate functions in spectral methods with reduced interpolation errors in polynomial approximations. CGL points are defined on the interval , and the point sequence is given by
These points cluster near the endpoints to minimize approximation errors (Runge’s phenomenon). In this work, a global domain is partitioned into subdomains according to the known locations of discontinuities, and the number of points assigned to each subdomain is proportional to its width. This ensures a balanced distribution of points within each interval. Figure A1 illustrates the point distribution using this technique for a Fibonacci sequence of the discontinuities in the domain.
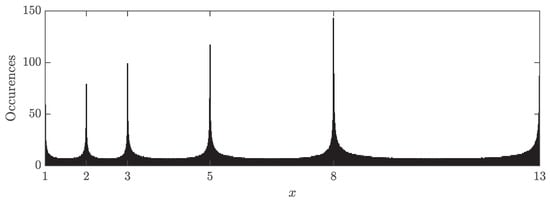
Figure A1.
Histogram of 10,000 CGL points for the Fibonacci sequence.
Appendix C
Consider a function defined over the global domain that contains a set of -discontinuities of the first kind at . The th derivative of can be represented as
where
and is a local function defined over the subdomain . The th derivative of is
Since and , the integrals in Equation (A7) can be rewritten by splitting the domains, assuming , such that
Thus, the th derivative of is
Furthermore, Equation (A9) can be applied recursively for additional integrals where constants such as and must be taken into account. It can be shown that
where c is a constant. Thus, the th derivative of for can be expressed as
which can be substituted into Equation (A5). As discussed in Section 2.1, the purpose of the piecewise functional form in Equations (A5) and (A6) is that continuity constraints in all derivatives of are intrinsically satisfied. To demonstrate this, assume a -discontinuity at . It can be shown that the limits of the first derivatives of and approaching the discontinuity from the left are
and from the right are
Provided the local functions are continuous as implemented in this work, is -continuous over the domain .
Appendix D
For reference, the second-order BVP (see Section 3.2) is used to compare the g-embedded hybrid system approach against a standard finite difference (FD) solver using a central difference approximation of derivatives. To maintain consistency in this comparison, the root mean squared error (RMSE) of the solution field y is plotted in Figure A2 against the number of nodes used to discretize the global domain. Note that the g-embedded approach uses the CGL point distribution from Appendix B, while the finite difference solver uses a uniform grid, and four different sets of Legendre orthogonal polynomials are used with maximum degrees m of 2, 6, 10, and 14. Additionally, it is important to recognize that the size of the matrix inverted for the g-embedded method is dependent upon the number of basis functions and not the number of nodes. These results indicate this second-order BVP requires approximately 30 nodes (i.e., 15 nodes per subdomain) to achieve machine level precision with 13 basis functions up to degree 14 per subdomain. The finite difference solver, on the other hand, achieves an RSME of only with 200 nodes.
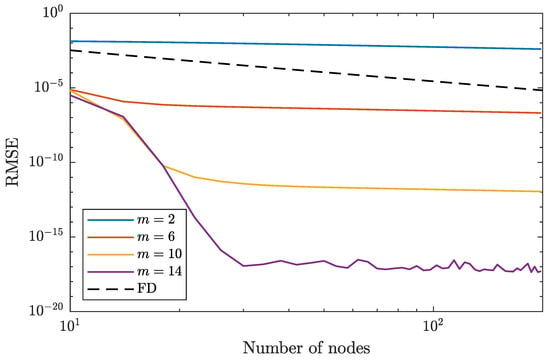
Figure A2.
Convergence comparison of the g-embedded approach with respect to a finite difference solver for the second-order BVP in Section 3.2.
References
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Smirnov, V. On the solutions of linear differential equations with discontinuous coefficients. Russ. Math. Surv. 1970, 25, 221–258. [Google Scholar]
- Zettl, A. Sturm-Liouville Theory; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems, 11th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Zill, D.G. A First Course in Differential Equations with Modeling Applications, 11th ed.; Cengage Learning: Boston, MA, USA, 2017. [Google Scholar]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists, 7th ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Stakgold, I.; Holst, M. Green’s Functions and Boundary Value Problems, 3rd ed.; Wiley: Oxford, UK, 2011. [Google Scholar]
- Herman, R.L. A Second Course in Ordinary Differential Equations: Dynamical Systems and Boundary Value Problems; Green’s Function Construction with Jump Discontinuity Conditions; R.L. Herman: Brooklyn, NY, USA, 2024. [Google Scholar]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- McLachlan, N.W. Laplace Transforms and Their Applications to Differential Equations; Courier Corporation: North Chelmsford, MA, USA, 2014. [Google Scholar]
- Zill, D.G.; Cullen, M.R. Differential Equations with Boundary-Value Problems, 8th ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Versteeg, H.K. An Introduction to Computational Fluid Dynamics the Finite Volume Method, 2nd ed.; Pearson Education India: Noida, India, 2007. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: North Chelmsford, MA, USA, 2001. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods; Springer: Berlin/Heidelberg, Germany, 2006; Volume 285. [Google Scholar]
- Mortari, D. The Theory of Connections: Connecting Points. Mathematics 2017, 5, 57. [Google Scholar] [CrossRef]
- Johnston, H.R. The Theory of Functional Connections: A Journey from Theory to Application. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Leake, C.D. The Multivariate Theory of Functional Connections: An n-Dimensional Constraint Embedding Technique Applied to Partial Differential Equations. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Leake, C.; Johnston, H.; Mortari, D. The Theory of Functional Connections: A Functional Interpolation. Framework with Applications; Lulu: Morrisville, NC, USA, 2022; Available online: https://www.lulu.com/shop/daniele-mortari-and-hunter-johnston-and-carl-leake/the-theory-of-functional-connections/hardcover/product-ve2ren.html?srsltid=AfmBOop9--_QJtbbqYjermg1U2KRFmXSedPxUSOJNQqhylEZ_0dSjwk6 (accessed on 26 October 2024).
- Florio, M.D.; Schiassi, E.; D’Ambrosio, A.; Mortari, D.; Furfaro, R. Theory of Functional Connections applied to Linear ODEs subject to Integral Constraints and Linear Ordinary Integro-Differential Equations. Math. Comput. Appl. 2021, 26, 65. [Google Scholar] [CrossRef]
- Wang, Y.; Topputo, F. A TFC-based homotopy continuation algorithm with application to dynamics and control problems. J. Comput. Appl. Math. 2022, 401, 113777. [Google Scholar] [CrossRef]
- Johnston, H.; Schiassi, E.; Furfaro, R.; Mortari, D. Fuel-efficient powered descent guidance on large planetary bodies via theory of functional connections. J. Astronaut. Sci. 2020, 67, 1521–1552. [Google Scholar] [CrossRef]
- Sivalingam, S.; Govindaraj, V. A novel numerical approach for time-varying impulsive fractional differential equations using theory of functional connections and neural network. Expert Syst. Appl. 2024, 238, 121750. [Google Scholar]
- Sivalingam, S.; Kumar, P.; Govindaraj, V. A novel method to approximate fractional differential equations based on the theory of functional connections. Numer. Algorithms 2024, 95, 527–549. [Google Scholar]
- De Florio, M.; Schiassi, E.; Furfaro, R. Physics-informed neural networks and functional interpolation for stiff chemical kinetics. Chaos 2022, 32. [Google Scholar] [CrossRef]
- Schiassi, E.; Florio, M.D.; D’Ambrosio, A.; Mortari, D.; Furfaro, R. Physics-Informed Neural Networks and Functional Interpolation for Data-Driven Parameters Discovery of Epidemiological Compartmental Models. Mathematics 2021, 9, 2069. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, S.; Zhang, G. Shaping low-thrust multi-target visit trajectories via theory of functional connections. Adv. Space Res. 2023, 72, 257–269. [Google Scholar] [CrossRef]
- Campana, C.; Merisio, G.; Topputo, F. Low-energy Earth–Moon transfers via Theory of Functional Connections and homotopy. Celest. Mech. Dyn. Astron. 2024, 136, 21. [Google Scholar] [CrossRef]
- Li, S.; Yan, Y.; Zhang, K.; Li, X. Fuel-Optimal Ascent Trajectory Problem for Launch Vehicle via Theory of Functional Connections. Int. J. Aerosp. Eng. 2021, 2021, 2734230. [Google Scholar] [CrossRef]
- de Almeida, A.K., Jr.; Aljbaae, S.; Vaillant, T.; Piñeros, J.M.; Coelho, B.; Barbosa, D.; Bergano, M.; Pandeirada, J.; Carvalho, F.C.; Santos, L.B.; et al. Theory of Functional Connections and Nelder–Mead optimization methods applied in satellite characterization. Acta Astronaut. 2024, 215, 548–559. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Y.; Yang, L. A theory of functional connections-based method for orbital pursuit-evasion games with analytic satisfaction of rendezvous constraints. Aerosp. Sci. Technol. 2025, 161, 110142. [Google Scholar] [CrossRef]
- Mai, T.; Mortari, D. Theory of Functional Connections Applied to Quadratic and Nonlinear Programming under Equality Constraints. J. Comput. Appl. Math. 2022, 406, 113912. [Google Scholar] [CrossRef]
- Lombardi, C.; Bevilacqua, R. State space modeling and estimation of flexible structure using the theory of functional connections. Acta Astronaut. 2024, 219, 693–709. [Google Scholar] [CrossRef]
- Yassopoulos, C.; Reddy, J.; Mortari, D. Analysis of nonlinear Timoshenko–Ehrenfest beam problems with von Kármán nonlinearity using the Theory of Functional Connections. Math. Comput. Simul. 2023, 205, 709–744. [Google Scholar] [CrossRef]
- Leake, C.D.; Mortari, D. Deep Theory of Functional Connections: A New Method for Estimating the Solutions of Partial Differential Equations. Mach. Learn. Knowl. Extr. 2020, 2, 37–55. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Min, Y.; Sonar, A.; Azizan, N. Hard-Constrained Neural Networks with Universal Approximation Guarantees. arXiv 2024, arXiv:2410.10807. [Google Scholar] [CrossRef]
- Yassopoulos, C.; Leake, C.; Reddy, J.; Mortari, D. Analysis of Timoshenko-Ehrenfest Beam Problems using the Theory of Functional Connections. J. Eng. Anal. Bound. Elem. 2021, 132, 271–280. [Google Scholar] [CrossRef]
- Johnston, H.R.; Mortari, D. Least-squares Solutions of Boundary-value Problems in Hybrid Systems. J. Comput. Appl. Math. 2021, 393, 113524. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).