Abstract
Recently, a growing number of researchers have focused on multi-view subspace clustering (MSC) due to its potential for integrating heterogeneous data. However, current MSC methods remain challenged by limited robustness and insufficient exploitation of cross-view high-order latent information for clustering advancement. To address these challenges, we develop a novel MSC framework termed TMSC-TNNBDR, a tensorized MSC framework that leverages t-SVD based tensor nuclear norm (TNN) regularization and block diagonal representation (BDR) learning to unify view consistency and structural sparsity. Specifically, each subspace representation matrix is constrained by a block diagonal regularizer to enforce cluster structure, while all matrices are aggregated into a tensor to capture high-order interactions. To efficiently optimize the model, we developed an optimization algorithm based on the inexact augmented Lagrange multiplier (ALM). The TMSC-TNNBDR exhibits both optimized block-diagonal structure and low-rank properties, thereby enabling enhanced mining of latent higher-order inter-view correlations while demonstrating greater resilience to noise. To investigate the capability of TMSC-TNNBDR, we conducted several experiments on certain datasets. Benchmarking on circumscribed datasets demonstrates our method’s superior clustering performance over comparative algorithms while maintaining competitive computational overhead.
MSC:
68T30
1. Introduction
In the field of pattern recognition, subspace clustering (SC) is a very important research topic [1,2,3,4]. In recent decades, scholars have created many subspace clustering algorithms, among which spectral-type methods have shown good performance.
Sparse subspace clustering (SSC) [5] and low-rank representation (LRR) [6], which have achieved significant success, are two typical self-representation subspace clustering methods. Block diagonal structure is a matrix form where non-zero elements are confined to square blocks along the main diagonal, with all elements outside these blocks being zero. Recent studies [7,8] have shown that the block diagonal structure within the learned low-dimensional subspace projection serves the purpose of obtaining the correct clustering results. However, SSC and LRR pursue the block diagonal representation (BDR) matrix indirectly since they only impose nuclear-norm and L1-norm on the subspace representation, respectively. Furthermore, Feng et al. [8] imposed a block diagonal prior on the subspace representation matrices obtained using SSC and LRR, and their clustering performance was improved. However, it is difficult to optimize Feng’s method since the rank constraint is NP-hard. To tackle this problem, Lu et al. [7] developed a simple BDR that relaxes the rank constraint. Compared with Feng’s method, BDR is more easily optimized since it is smooth. Xu et al. [9] developed a learning projective model for BDR to deal with the large-scale subspace clustering problem. Xing et al. [10] proposed an enhanced version of DBSCAN, which is a highly prevalent algorithm in data mining, to improve the clustering process using the block diagonal property of affinity matrices. Meanwhile, Guo et al. [11] put forward a spectral clustering algorithm with BDR for large-scale datasets.
The above-mentioned approaches are single-view-based since they assume that there is only one data source. However, in fact, data are generally sourced from various origins. For instance, one event can be represented by images, text, videos. As such, multi-view clustering (MVC) methods, which often demonstrate a better clustering performance than single-view methods [12,13,14,15,16,17,18,19], are becoming increasingly popular.
The authors of [20] proposed co-training learning to flux the multi-view features. Additionally, the study in [21] investigated the key factors contributing to the success of the co-training method. The co-training learning model is not robust enough against noise pollution, which can lead to error exaggeration. Kumar et al. [17] proposed an MSC framework, in which the clustering hypotheses among views is co-regularized. Graph-based methods are another category MSC methods, which generally use the multiple graph fusion strategy to utilize the information among different views. Sa [22] developed a two-view clustering method, which utilizes different information between two views by constructing bipartite graphs. Moreover, the authors of [13] developed a multi-view spectral clustering algorithm with the help of low-rank and sparse decomposition (RMSC), achieving encouraging success in relation to several real datasets. In the work of Cao et al. [15], the diversity-induced MSC (DiMSC) was presented, leveraging the Hilbert–Schmidt Independence Criterion (HSIC), which plays a key role in utilizing complementary information among different views to enhance the clustering.
By assuming that the different views of an object come from a potential subspace, subspace learning MVC methods can be developed to capture the shared potential subspace. Blaschko and Lampert [23] introduced a novel spectral clustering technique that utilizes canonical correlation analysis (CCA) in its linear and kernel forms for dimensionality reduction. In [24], a low-rank common subspace (LRCS) MVC method is proposed, which can obtain compatible intrinsic information among views by using a common low-rank projection.
These MVC methods shows promising performance in clustering applications; however, they only use paired associations between different views, and may overlook the higher-order associations hidden in multi-view data [12,14,19,25,26,27]. Zhang et al. [12,19] developed a novel multi-view spectral clustering method named LTMSC, incorporating low-rank tensor constraints. In the method, the subspace representations are constructed into a single tensor. It is possible to explore higher-order relationships hidden in the multi-view data. Lu et al. [28] introduced an MSC method with hyper-Laplacian regularization and low-rank tensor constraints (HLR-MSCLRT), which can uncover the local information hidden in the data on the manifold. Nevertheless, the tensor norm employed in both LTMSC and HLR-MSCLRT lacks a clear physical interpretation.
Zhang et al. recently introduced the TNN [29] leveraging the tensor singular value decomposition (t-SVD). The TNN, defined as the summation of singular values, provides a rigorous measure of tensor data low-rankness. In [14], Xie et al. developed a t-SVD based MSC model, namely t-SVD-MSC, which preserves the low-rank property through TNN. With the use of TNN, t-SVD-MSC can more effectively explore the complementary information among all the views [30,31,32,33,34]. Furthermore, in [18], an essential tensor learning method for MSC using a TNN constraint, known as ETLMSC, is proposed. Pan et al. [35] proposed a non-negative non-convex low-rank tensor kernel function in an MSC model (NLRTGC) to reduce the bias from rank. To exploit high-dimensional hidden information, Pan et al. [36] proposed a low-rank fuzzy MSC learning algorithm with the TNN constraint (LRTGFL). Peng et al. [37] designed log-based non-convex functions to approximate tensor rank and tensor sparsity in the Finger-MVC model; these are more precise than the convex ones. Wang et al. [38] integrate noise elimination and subspace learning into a unified MSC framework, holding high-order associations of views constrained by the TNN. Du et al. [39] proposed a robust t-SVD-based multi-view clustering which simultaneously uses low rank and local smooth priors. Luo et al. [40] used an adaptively weighted tensor Schatten-p norm with an adjustable p-value to eliminate the biased estimate of rank.
The optimized BDR structure in affinity matrices inherently encodes cluster information, thereby substantially enhancing clustering efficacy. The low-rank tensor representations intrinsically capture latent high-order correlations across multi-view data through subspace embeddings, resulting in statistically significant clustering improvements. In this paper, inspired by the optimized BDR structure and low-rank tensor representations, we propose a novel MSC method called TMSC-TNNBDR, which integrates the advantages of TNN and BDR. The proposed model imposes BDR constraints on each subspace representation matrix, and all affinity matrices are combined into a tensor regularized by TNN. Finally, an efficient optimization algorithm based on ALM is developed.
The primary contributions of our work are as follows:
- The proposed TMSC-TNNBDR incorporates a BDR regularizer, which promotes a more pronounced block diagonal structure and improves clustering robustness.
- In the TMSC-TNNBDR model, the optimized architecture encodes a TNN constraint, under which TMSC-TNNBDR captures the global structure across all views, thereby effectively exploiting latent complementary information and high-order interactions among views.
- We proposed an ALM optimizer for TMSC-TNNBDR. This approach demonstrates superior clustering performance over comparative algorithms while maintaining competitive computational efficiency.
The remainder of this work is organized as follows. In Section 2, we summarize the notations used and some preliminary definitions. In Section 3, we briefly review two methods, namely the LRR [6] and the BDR [7]. Then, we propose the TMSC-TNNBDR and a solving procedure for TMSC-TNNBDR in Section 4. Subsequently we documented the experimental findings in Section 5. Ultimately, we conclude our work in Section 6.
2. Notations and Preliminaries
2.1. Notations
For a clear explanation of TMSC-TNNBDR, We summarize the notations in Table 1. Bold calligraphy letters, e.g., , are deployed to denote tensors. Bold upper case letters, e.g., W, are deployed to denote matrices. Bold lower case letters, e.g., u, are deployed to denote vectors. Lower case letters, e.g., , are deployed to denote the entries. Among others, is assigned to denote the column vector of one. The diagonal elements of matrix W line up as a column vector, which is referred to as . The column vector w is expanded into a diagonal matrix, which is labeled as .

Table 1.
Notations summarized.
Let denote the nuclear norm operator of matrix W, i.e., , in which is the ith largest singular value of W. Assuming that the singular value decomposition of matrix W is expressed as , then denotes the singular-value thresholding operator applied to matrix W with boundary value , i.e.,, where .
Matrices extend naturally to tensors, which are multidimensional arrays. Mathematically, a matrix is a two-way tensor. Suppose is a three-way tensor, is likely to be regarded as the stack of matrices. Some block-based operators [31] for are defined as follows:
2.2. Preliminaries
We introduced some preliminary definitions [31] as follows:
Definition 1.
Suppose and ; the t-product is , i.e.,
Definition 2.
Suppose ; then, the tensor transpose of is .
Definition 3.
Suppose ; then, is an identity tensor while its first frontal slice is a unit matrix () and all others are zeros.
Definition 4.
If satisfies
Then, is an orthogonal tensor.
Definition 5.
Suppose ; we define as an f-diagonal tensor while all its frontal slices are diagonal.
Definition 6.
Suppose the tensor ; then, the t-SVD is defined as follows:
where , is f-diagonal, while and are both orthogonal.
Definition 7.
Suppose ; then, the TNN of , i.e., , is the summation of the singular values which are decomposed by t-SVD. It has been proven that t-SVD based TNN is the tightest convex relaxation to tensor tubal rank [29].
3. Related Work
Before presenting our method, this section establishes the theoretical foundation by first reviewing two classical methods: LRR [6] and BDR [7].
3.1. Low-Rank Representation (LRR)
Let us assume that is a set of N data points and the dimensionality of the data is d. LRR seeks to find a low-rank factorization of samples for clustering. The objective of LRR can be formulated as follows:
where is the representation of dataset X, E refers to the approximation error, refers to the -norm, and refers to the nuclear norm.
LRR executes spectral clustering via the affinity matrix W, where .
3.2. Block Diagonal Representation (BDR)
The authors of [7] provide the following block diagonal regularizer to chase the optimal representation.
Definition 8.
The k-block diagonal regularizer of the affinity matrix can be formulated as follows:
where , i.e., is the Laplacian matrix of W. refers to the ith eigenvalue of and is in decreasing order. k is the number of subspaces. The loss function of BDR is defined as follows
The affinity matrix W is also defined as .
4. The Proposed TMSC-TNNBDR
In this section, we introduce the TMSC-TNNBDR framework that extends classical LRR and BDR approaches. Subsequently, we derive an ALM-based optimization scheme to solve the resulting non-convex problem.
4.1. Problem Formulation
Let and be, respectively, the feature matrix and subspace coefficient for the vth view. The loss function of TMSC-TNNBDR is demonstrated as follows:
where represents an function that stacks all (v = 1, 2, …, V) into a tensor in then applying a rotation transformation to .
In Equation (10), is the self-representation reconstruction error, denotes the BDR constraint to , denotes TNN low-rank constraint to , and can be seen as a Robust PCA term to remove the noise contained in the H(v). Moreover, , , and are tunable hyperparameters.
4.2. Optimization
The loss function of TMSC-TNNBDR, i.e., Equation (10), can be optimized through the ALM. The theorem relating to is described as follows:
Theorem 1
([41]). Suppose , where L is semi-positive; then, the following holds:
In accordance with Theorem 1, Equation (10) can be rewritten as Equation (12):
To solve Equation (12), an auxiliary tensor variable is introduced to replace . Then, the loss function of TMSC-TNNBDR is converted into the following:
Equation (13) will be converted to the augmented Lagrangian formula, as follows:
where denotes the Lagrange multiplier; is actually the penalty parameter.
We get the resolutions to , , , and by solving each variable alternately in Equation (14). The steps are described as follows:
-subproblem: For computing , we fix the other variables and tackle the following problem:
Differentiating by , we can obtain the following:
-subproblem: will be computed as follows:
For Equation (17), , where is a matrix concatenated from k eigenvectors that correspond to the k smallest eigenvalues of [7].
-subproblem: can be computed as follows:
Equation (18) can be converted into the following:
The theorem in [7] enables the solution of Equation (19).
-subproblem: We fixed the other variables and update as follows:
The solution to Equation (20) can be obtained using the theorem in [14,29].
-subproblem: the Lagrange multiplier can be updated as follows:
Finally, the TMSC-TNNBDR procedure is outlined in Algorithm 1.
| Algorithm 1 TMSC-TNNBDR |
|
4.3. Computational Complexity and Convergence
To calculate , it involves matrix multiplication and matrix inversion, whose complexities are and , respectively. For computing , its complexity is because the main computational burdens are eigenvalue decomposition and matrix product. The computation of is since it mainly depends on matrix multiplication. As for computing , the computational complexity is . Thereafter, the total complexity of TMSC-TNNBDR is .
The procedure of TMSC-TNNBDR is non-convex, which means it cannot achieve a global optimal solution. Nevertheless, TMSC-TNNBDR can converge to a local optimal point. In fact, each variable in Algorithm 1 has a closed-form solution. Following this, the value of the loss function decreases monotonically and remains bounded below. Clustering experiments are performed on some classic datasets, and the results showed that the TMSC-TNNBDR could converge stably.
5. Experimental Results
To evaluate the performance of the TMSC-TNNBDR model, we conduct experiments on abovementioned five image datasets. We compare TMSC-TNNBDR with some representative single-view-based methods, including SPCbest, LRRbest, BDRbest; multi-view-based methods, including Co-Reg SPC, RMSC, LTMSC, and DiMSC; and TNN-based method, i.e., t-SVD-MSC.
- SPCbest: SPCbest is a single-view clustering model using spectral clustering [42] to reach the best capability in all views.
- LRRbest: LRRbest is a single-view clustering model using LRR [6] to reach the best capability in all views.
- BDRbest: BDRbest is a single-view clustering model using BDR [7] to reach the best capability in all views.
- Co-Reg SPC [17]: A co-regularized MVSC method.
- RMSC [13]: RMSC is a multi-view spectral clustering algorithm with the help of low-rank and sparse de-composition.
- LTMSC [12]: LTMSC is a multi-view spectral clustering method incorporating low-rank tensor constraints.
- DiMSC [15]: DiMSC is a multi-view model utilizing HSIC to enhance diversity.
- t-SVD-MSC [14]: A MSC model using t-SVD.
5.1. Description of the Dataset
UCI-Digits: (https://archive.ics.uci.edu/dataset/80/optical+recognition+of+handwritten+digits (accessed on 17 August 2025)). There are a total of 2000 digit images that correspond to 10 classes in this dataset. Similarly to the work in [13], three feature types—morphological features, Fourier coefficients, and pixel averages—are extracted to assemble multi-view data. Ten UCI-Digits samples are shown in Figure 1.
Figure 1.
Example images in UCI-Digits.
ORL: (https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html (accessed on 17 August 2025)). There are a total of 400 face images in ORL, which correspond to 40 people. Firstly, we zoom each image to a resolution of 64 × 64. Then, similarly to the work of [12,14], we retrieved LBP [43], intensity, and Gabor [44] features to formulate multi-view data. Some ORL samples are shown in Figure 2.

Figure 2.
Example images in ORL.
Yale: (https://gitcode.com/open-source-toolkit/885dd (accessed on 17 August 2025)). There are 165 face images in Yale, which correspond to 11 individuals. We zoom each image to a resolution of . Similarly to the work of [12,14], we retrieved LBP [43], intensity, and Gabor [44] features in order to formulate multi-view data. Some Yale samples are shown in Figure 3.

Figure 3.
Example images in Yale.
Extended YaleB: (https://gitcode.com/open-source-toolkit/3d6b2 (accessed on 17 August 2025)). This dataset consists of pictures of 38 people; each individual has about 64 images under different illuminations. Similarly to the work in [12,14], we retrieved LBP [43], intensity, and Gabor [44] features to formulate multi-view data. We zoom each image to a resolution of 32 × 32. Ten examples of YaleB are shown in Figure 4.

Figure 4.
Example images in Extended YaleB.
COIL-20: (https://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php (accessed on 17 August 2025)). There are a total of 1440 pictures in COIL-20, which are associated with 40 object classes. We zoom each picture to a resolution of 32 × 32. Similarly to the work in [12,14], we retrieved LBP [43], intensity, and Gabor [44] features to formulate multi-view data. Some COIL-20 samples are shown in Figure 5.

Figure 5.
Example images in COIL-20.
5.2. Evaluation Metrics
We employ ACC and NMI to compare the performance of various algorithms.
ACC, i.e., accuracy, is defined as follows:
where refers to the true category label of the i-th sample, refers to clustering label, and refers to Kronecker delta, which is defined as follows:
MI, i.e., mutual information, is defined as follows:
where D and refer to two clusters. and refer to the probabilities of belonging to D and . Correspondingly, refers to the joint probability.
NMI, i.e., normalize mutual information, is defined as follows:
where is the entropy of the dataset.
5.3. Experiment Results
Notably, all evaluated clustering methods—specifically TMSC-TNNBDR, LRRbest, SPCbest, BDRbest, t-SVD-MSC, DiMSC, Co-Reg SPC, RMSC, and LTMSC—incorporate K-means procedures in the final step of spectral clustering. Randomness in K-means stems from both the random choice of initial cluster centers and the non-convex objective function. Twenty repetitions typically represent a sound compromise to mitigate the effects of randomness while maintaining computational feasibility. Therefore, we report median performance metrics after 20 experimental repetitions to ensure statistical robustness. Table 2, Table 3, Table 4, Table 5 and Table 6 report the clustering results from five public databases: UCI-digits, ORL, Yale, YaleB, COIL-20. Bold values in the tables indicate the best. The results clearly indicate that TMSC-TNNBDR exceeds the performance of other comparison algorithms. Our observation and analysis are delineated as follows:
- In comparative analyses of single-view clustering methodologies, LRR and BDR consistently outperform conventional spectral clustering (SPC). This performance advantage likely stems from their enhancement of the SPC framework through the incorporation of prior structural knowledge—specifically, low-rank constraints and block-diagonal regularization, respectively.
- Multi-view methods, including TMSC-TNNBDR, demonstrated a superior performance compared with single-view approaches. Our experimental results demonstrate that even selecting the best outcome from all individual single-view clustering procedures still underperforms multi-view clustering in the vast majority of cases. This confirms the superiority of multi-view clustering. It is generally believed that the success of existing multi-view clustering methods involve learning latent cross-view correlations, discovering underlying patterns, and integrating this summarized prior knowledge into clustering models. For instance, Co-Reg SPC embeds co-regularization of clustering consensus into spectral clustering. Similarly, RMSC incorporates both low-rank tensor and sparse constraints into the MSC framework. DiMSC leverages the Hilbert Schmidt Independence Criterion (HSIC) to extract complementary information across views, while LTMSC and t-SVD-MSC employ TNN constraint to explore such complementary information.
- In most cases, multi-view clustering based on tensor representation outperforms co-regularization-based Co-Reg SPC in clustering performance. This superiority is generally attributed to tensor representation’s ability to integrate multiple views into a unified structure, easily capturing complementary information and high-order interactions across views. Experimental results validate this explanation.
- TMSC-TNNBDR achieves superior performance compared to benchmark methods while maintaining favorable time efficiency. This advantage is likely attributed to the complementary interplay between the low-rank property and block-diagonal structure of the similarity matrix—where Tensor Nuclear Norm (TNN) and Block Diagonal Regularization (BDR), as two priori constraints, synergistically enhance the multi-view subspace clustering framework from distinct perspectives.

Table 2.
Clustering results (mean ± standard deviation) on UCI-Digits.
Table 2.
Clustering results (mean ± standard deviation) on UCI-Digits.
| Algorithm | LRRbest | SPCbest | BDRbest |
|---|---|---|---|
| ACC | 0.968 ± 0.001 | 0.740 ± 0.021 | 0.814 ± 0.006 |
| NMI | 0.769 ± 0.002 | 0.639 ± 0.013 | 0.765 ± 0.005 |
| Algorithm | t-SVD-MSC | DiMSC | Co-Reg SPC |
| ACC | 0.953 ± 0.001 | 0.719 ± 0.013 | 0.786 ± 0.007 |
| NMI | 0.929 ± 0.002 | 0.776 ± 0.008 | 0.801 ± 0.004 |
| Algorithm | RMSC | LTMSC | TMSC-TNNBDR |
| ACC | 0.776 ± 0.008 | 0.912 ± 0.003 | 0.994 ± 0.001 |
| NMI | 0.791 ± 0.003 | 0.923 ± 0.002 | 0.984 ± 0.001 |

Table 3.
Clustering results (mean ± standard deviation) on ORL.
Table 3.
Clustering results (mean ± standard deviation) on ORL.
| Algorithm | LRRbest | SPCbest | BDRbest |
|---|---|---|---|
| ACC | 0.773 ± 0.003 | 0.726 ± 0.025 | 0.848 ± 0.003 |
| NMI | 0.895 ± 0.006 | 0.884 ± 0.002 | 0.938 ± 0.002 |
| Algorithm | t-SVD-MSC | DiMSC | Co-Reg SPC |
| ACC | 0.973 ± 0.003 | 0.837 ± 0.001 | 0.715 ± 0.000 |
| NMI | 0.992 ± 0.002 | 0.939 ± 0.003 | 0.853 ± 0.003 |
| Algorithm | RMSC | LTMSC | TMSC-TNNBDR |
| ACC | 0.735 ± 0.006 | 0.793 ± 0.008 | 1.000 ± 0.000 |
| NMI | 0.873 ± 0.011 | 0.932 ± 0.993 | 1.000 ± 0.000 |

Table 4.
Clustering results (mean ± standard deviation) on Yale.
Table 4.
Clustering results (mean ± standard deviation) on Yale.
| Algorithm | LRRbest | SPCbest | BDRbest |
|---|---|---|---|
| ACC | 0.703 ± 0.002 | 0.634 ± 0.015 | 0.712 ± 0.004 |
| NMI | 0.706 ± 0.012 | 0.646 ± 0.009 | 0.716 ± 0.002 |
| Algorithm | t-SVD-MSC | DiMSC | Co-Reg SPC |
| ACC | 0.878 ± 0.013 | 0.703 ± 0.004 | 0.668 ± 0.002 |
| NMI | 0.913 ± 0.009 | 0.728 ± 0.009 | 0.715 ± 0.003 |
| Algorithm | RMSC | LTMSC | TMSC-TNNBDR |
| ACC | 0.639 ± 0.038 | 0.743 ± 0.003 | 0.992 ± 0.002 |
| NMI | 0.685 ± 0.029 | 0.759 ± 0.09 | 0.994 ± 0.001 |

Table 5.
Clustering results (mean ± standard deviation) on Extended YaleB.
Table 5.
Clustering results (mean ± standard deviation) on Extended YaleB.
| Algorithm | LRRbest | SPCbest | BDRbest |
|---|---|---|---|
| ACC | 0.447 ± 0.023 | 0.283 ± 0.035 | 0.464 ± 0.012 |
| NMI | 0.408 ± 0.032 | 0.225 ± 0.043 | 0.432 ± 0.007 |
| Algorithm | t-SVD-MSC | DiMSC | Co-Reg SPC |
| ACC | 0.568 ± 0.003 | 0.470 ± 0.007 | 0.240 ± 0.001 |
| NMI | 0.605 ± 0.002 | 0.397 ± 0.006 | 0.148 ± 0.001 |
| Algorithm | RMSC | LTMSC | TMSC-TNNBDR |
| ACC | 0.223 ± 0.011 | 0.626 ± 0.009 | 0.641 ± 0.002 |
| NMI | 0.161 ± 0.021 | 0.621 ± 0.005 | 0.631 ± 0.004 |

Table 6.
Clustering results (mean ± standard deviation) on COIL-20.
Table 6.
Clustering results (mean ± standard deviation) on COIL-20.
| Algorithm | LRRbest | SPCbest | BDRbest |
|---|---|---|---|
| ACC | 0.767 ± 0.002 | 0.682 ± 0.024 | 0.805 ± 0.002 |
| NMI | 0.870 ± 0.003 | 0.769 ± 0.011 | 0.872 ± 0.003 |
| Algorithm | t-SVD-MSC | DiMSC | Co-Reg SPC |
| ACC | 0.803 ± 0.004 | 0.774 ± 0.014 | 0.720 ± 0.007 |
| NMI | 0.865 ± 0.003 | 0.846 ± 0.002 | 0.809 ± 0.005 |
| Algorithm | RMSC | LTMSC | TMSC-TNNBDR |
| ACC | 0.687 ± 0.043 | 0.802 ± 0.009 | 0.823 ± 0.004 |
| NMI | 0.802 ±0.016 | 0.853 ± 0.005 | 0.892 ± 0.003 |
To evaluate the actual running time of our method, we conducted experiments on the aforementioned five datasets. For fairness in comparison, single-view clustering approaches (e.g., LRRbest, SPCbest, BDRbest) are intentionally excluded. Table 7 summarizes computational times of selected multi-view methods, with bold values indicating the best performance.

Table 7.
Computational time (unit: seconds) of the comparative multi-view methods.
In the experiments, all compared multi-view clustering methods are based on subspace affinity matrix computations using complete graphs and spectral clustering, exhibiting cubic time complexity of N. Results across five datasets indicate that both Co-Reg SPC and our proposed TMSC-TNNBDR achieve optimal time efficiency. While significant performance gaps persist between algorithms, these gaps do not expand drastically with increasing dataset sizes. Considering the noticeable inferior clustering performance of Co-Reg SPC compared to tensor-based multi-view clustering methods, TMSC-TNNBDR delivers exceptionally outstanding results.
5.4. Convergence Analysis
Proving the global convergence of TMSC-TNNBDR is difficult. However, we did conduct some experiments to show the convergence properties. As per the convergence conditions in Algorithm 1, the match error is defined as follows:
The convergence curves of the TMSC-TNNBDR method on ORL and Yale are presented in Figure 6. As shown in Figure 6, the TMSC-TNNBDR method exhibits rapid convergence, achieving stable results within roughly 15 iterations.
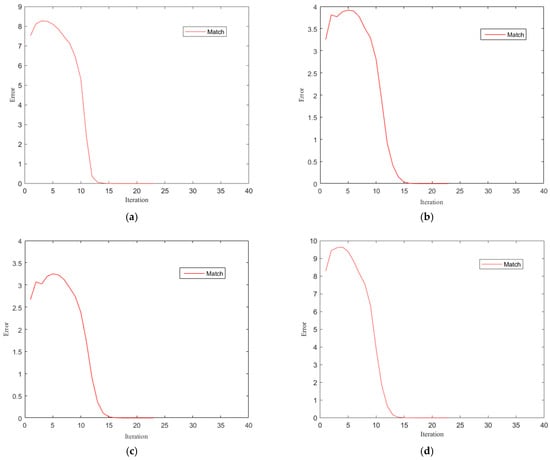
Figure 6.
Convergence curves on different datasets: (a) Convergence curves on UCI-Digits; (b) Convergence curves on ORL; (c) Convergence curves on Yale; (d) Convergence curves on COIL-20.
5.5. Parametric Sensitivity
Three tunable hyperparameters characterize our proposed TMSC-TNNBDR: , and , formally defined in Equation (10). During our optimization, candidate values of , and are selected from . Where applicable, the search space is refined to narrowed ranges based on preliminary selections. The resulting configurations for tunable parameters are documented in Table 8.

Table 8.
Our configurations for tunable parameters.
The clustering performance on the ORL and Yale databases is depicted in Figure 7. As shown in Figure 7, it is evident that the performance of the TMSC-TNNBDR is generally good and insensitive to varying values of and , especially when and are relatively small.
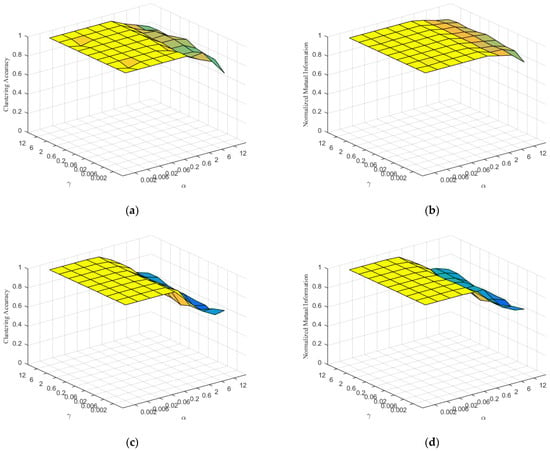
Figure 7.
Clustering performance of TMSC-TNNBDR versus and on different datasets. (a) ACC of TMSC-TNNBDR versus the parameters and on ORL; (b) NMI of TMSC-TNNBDR versus the parameters and on ORL; (c) ACC of TMSC-TNNBDR versus the parameters and on Yale; (d) NMI of TMSC-TNNBDR versus the parameters and on Yale.
6. Conclusions
In this paper, we propose a novel tensorized MSC with tensor nuclear norm and block diagonal representation (TMSC-TNNBDR). In this model, a BDR constraint is utilized to enforce the block diagonal structure of the learned similarity matrix. Additionally, low-rank tensor representations are applied to uncover the high-order correlations within multi-view data, ultimately advancing clustering objectives. Then, we developed an efficient augmented Lagrangian-based procedure for optimizing the TMSC-TNNBDR model. This method harnesses dual priors—block-diagonal structure and low-rank tensor representations—to steer subspace clustering, enabling more thorough exploitation of latent information in multi-view data while significantly alleviating noise interference.
Comparative evaluations demonstrate the superior clustering performance of TMSC-TNNBDR over baseline approaches. While the efficacy of TMSC-TNNBDR is empirically validated, significant challenges persist in multi-view subspace clustering. Our methodology leverages two distinct priors (block-diagonal structure and low-rank tensor constraints), raising new research questions: What additional priors could be incorporated? Is there demonstrable value in integrating more than two priors? Furthermore, algorithmic complexity remains a critical limitation; akin to other classical graph-based multi-view clustering techniques, TMSC-TNNBDR has a cubic time complexity of N. It is inevitably compromised by the curse of dimensionality under real-world data growth conditions. For larger-scale datasets, using anchor graphs instead of full-sample graphs may be an effective alternative. In such scenarios, leveraging prior knowledge to design regularizers remains highly valuable.
Author Contributions
Conceptualization, G.-F.L. and G.-Y.T.; methodology, G.-Y.T., G.-F.L. and Y.W.; software, G.-Y.T. and G.-F.L.; validation, G.-Y.T., G.-F.L., Y.W. and L.-L.F.; formal analysis, G.-Y.T. and G.-F.L.; investigation, G.-Y.T. and L.-L.F.; resources, G.-F.L., Y.W. and G.-Y.T.; data curation, G.-Y.T. and L.-L.F.; writing—original draft preparation, G.-Y.T. and G.-F.L.; writing—review and editing, G.-Y.T., G.-F.L., Y.W. and L.-L.F.; visualization, G.-Y.T. and L.-L.F.; supervision, G.-F.L. and Y.W.; project administration, G.-Y.T.; funding acquisition, G.-F.L., G.-Y.T., Y.W. and L.-L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSFC (No. 61976005), the University Natural Science Research Project of Anhui Province (No. 2022AH050970, KJ2020A0363), the Open Project of Anhui Provincial Medical Big Data Intelligent System Engineering Research Center (No. MBD2024P04), and the 2024 Anhui Provincial Quality Engineering Project for Higher Education Institutions (No. 2024aijy199).
Data Availability Statement
The original data presented in the study are openly available in: UCI Machine Learning Repository—Optical Recognition of Handwritten Digits at https://archive.ics.uci.edu/dataset/80/optical+recognition+of+handwritten+digits (accessed on 17 August 2025). Cambridge University AT&T Lab—ORL Face Database at https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html (accessed on 17 August 2025). GitCode Open Source—Yale Face Database at https://gitcode.com/open-source-toolkit/885dd (accessed on 17 August 2025). GitCode Open Source—YaleB extends Face Database at https://gitcode.com/open-source-toolkit/3d6b2 (accessed on 17 August 2025). Columbia University CAVE Lab—COIL-20 Dataset at https://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php (accessed on 17 August 2025).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ALM | Augmented Lagrange multiplier |
| BDR | Block-diagonal representation |
| Co-Reg SPC | Co-regularized multi-view spectral clustering |
| DiMSC | Diversity-induced multi-view subspace clustering |
| HSIC | Hilbert–Schmidt Independence Criterion |
| LRR | Low-rank representation |
| LTMSC | Low-rank tensor constrained multi-view subspace clustering |
| MSC | Multi-view subspace clustering |
| RMSC | Robust multi-view spectral clustering via low-rank and sparse decomposition |
| SC | Subspace clustering |
| SPC | Spectral clustering |
| SSC | Sparse subspace clustering |
| TMSC-TNNBDR | Tensorized multi-view subspace clustering via tensor nuclear norm and block diagonal representation |
| TNN | Tensor nuclear norm |
| t-SVD | the tensor singular value decomposition |
| t-SVD-MSC | t-SVD based multi-view subspace clustering |
References
- Fu, L.; Lin, P.; Vasilakos, A.V.; Wang, S. An overview of recent multi-view clustering. Neurocomputing 2020, 302, 148–161. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Berkhin, P. Survey of clustering data mining techniques. In Grouping Multidimensional Data: Recent Advances in Clustering; Kogan, J., Nicholas, C., Teboulle, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 25–71. [Google Scholar]
- Wang, J.; Wang, X.; Tian, F.; Liu, C.H.; Yu, H. Constrained low-rank representation for robust subspace clustering. IEEE Trans. Cybern. 2017, 47, 4534–4546. [Google Scholar] [CrossRef] [PubMed]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. 2013, 35, 2765–2781. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. 2013, 35, 171–184. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Lin, Z.; Mei, T.; Yan, S. Subspace clustering by block diagonal representation. IEEE Trans. Pattern Anal. 2019, 41, 487–501. [Google Scholar] [CrossRef]
- Feng, J.; Lin, Z.; Xu, H.; Yan, S. Robust subspace segmentation with block-diagonal prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Xu, Y.Y.; Chen, S.; Li, J.; Li, C.; Yang, J. Fast subspace clustering by learning projective block diagonal representation. Pattern Recogn. 2023, 135, 109152. [Google Scholar] [CrossRef]
- Xing, Z.; Wu, G. Block-diagonal guided DBSCAN clustering. IEEE Trans. Knowl. Data Eng. 2024, 36, 5709–5722. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, S. A restarted large-scale spectral clustering with self-guiding and block diagonal representation. Pattern Recogn. 2023, 156, 110746. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, H.; Liu, S.; Liu, G.; Cao, X. Low-rank tensor constrained multiview subspace clustering. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Xia, R.; Pan, Y.; Du, L.; Yin, J. Robust multi-view spectral clustering via low-rank and sparse decomposition. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence (AAAI), Québec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Xie, Y.; Tao, D.; Zhang, W.; Liu, Y.; Zhang, L.; Qu, Y. On unifying multi-view self-representations for clustering by tensor multi-tank minimization. Int. J. Comput. Vision. 2018, 126, 1157–1179. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, C.; Fu, H.; Liu, S.; Zhang, H. Diversity induced multi-view subspace clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Bickel, S.; Scheffer, T. Multi-view clustering. In Proceedings of the Fourth IEEE International Conference on Data Mining (ICDM), Brighton, UK, 1–4 November 2004. [Google Scholar]
- Kumar, A.; Rai, P.; Daumé, H. Co-regularized multi-view spectral clustering. In Proceedings of the 24th International Conference on Neural Information Processing Systems (NIPS), Granada, Spain, 12–15 December 2011. [Google Scholar]
- Wu, J.; Lin, Z.; Zha, H. Essential tensor learning for multi-view spectral clustering. IEEE Trans. Image Process. 2019, 28, 5910–5922. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, H.; Wang, J.; Li, W.; Cao, X.; Hu, Q. Tensorized multi-view subspace representation learning. Int. J. Comput. Vision. 2020, 128, 2344–2361. [Google Scholar] [CrossRef]
- Ghani, R. Combining labeled and unlabeled data for multiclass text categorization. In Proceedings of the Nineteenth International Conference on Machine Learning, Sydney, Australia, 8–12 July 2002. [Google Scholar]
- Wang, W.; Zhou, Z.H. A new analysis of co-training. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Sa, V.R.d. Spectral clustering with two views. In Proceedings of the ICML Workshop on Learning with Multiple Views, Bonn, Germany, 7–11 August 2005. [Google Scholar]
- Blaschko, M.B.; Lampert, C.H. Correlational spectral clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Ding, Z.; Fu, Y. Low-rank common subspace for multi-view learning. In Proceedings of the IEEE International Conference on Data Mining, Shenzhen, China, 14–17 December 2014. [Google Scholar]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhou, P.; Feng, J. Outlier-robust tensor PCA. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhou, P.; Lu, C.; Lin, Z.; Zhang, C. Tensor factorization for low-rank tensor completion. IEEE Trans. Image Process. 2018, 27, 1152–1163. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.F.; Yu, Q.R.; Wang, Y.; Tang, G.Y. Hyper-Laplacian regularized multi-view subspace clustering with low-rank tensor constraint. Neural Netw. 2020, 125, 214–223. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on Tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Braman, K.S.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. A. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Du, Y.F.; Lu, G.F.; Ji, G.Y. Robust least squares regression for subspace clustering: A multi-view clustering perspective. IEEE Trans. Image Process. 2024, 33, 216–227. [Google Scholar] [CrossRef]
- Cai, B.; Lu, G.F.; Li, H.; Song, W.H. Tensorized scaled simplex representation for multi-view clustering. IEEE Trans. Multimed. 2024, 26, 6621–6631. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. 2020, 42, 925–938. [Google Scholar] [CrossRef]
- Pan, B.; Li, C.; Che, H. Nonconvex low-rank tensor approximation with graph and consistent regularizations for multi-view subspace learning. Neural Networks. 2023, 161, 638–658. [Google Scholar] [CrossRef]
- Pan, B.; Li, C.; Che, H.; Leung, M.F.; Yu, K. Low-rank tensor regularized graph fuzzy learning for multi-view data processing. IEEE Trans. Consum. Electr. 2023, 70, 2925–2938. [Google Scholar] [CrossRef]
- Peng, C.; Kang, K.; Chen, Y.; Kang, Z.; Chen, C.; Cheng, Q. Fine-grained essential tensor learning for robust multi-view spectral clustering. IEEE Trans. Image Process. 2024, 33, 3145–3159. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Y.; Lin, Z.; Cen, Y.; Cao, Q. Robustness meets low-rankness: Unified entropy and tensor learning for multi-view subspace clustering. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 6302–6316. [Google Scholar] [CrossRef]
- Du, Y.F.; Lu, G.F. Joint local smoothness and low-rank tensor representation for robust multi-view clustering. Pattern Recogn. 2025, 157, 110944. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, J.; Zhang, X. Tensor multi-view clustering method for natural image segmentation. Expert Syst. Appl. 2025, 260, 125431. [Google Scholar] [CrossRef]
- Dattorro, J. Convex Optimization & Euclidean Distance Geometry, 2nd ed.; Meboo Publishing: Palo Alto, CA, USA, 2018. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the 15th International Conference on Neural Information Processing Systems: Natural and Synthetic (NIPS), Vancouver, BC, Canada, 3–8 December 2001. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Lades, M.; Vorbruggen, J.C.; Buhmann, J.; Lange, J.; Malsburg, C.v.d.; Wurtz, R.P.; Konen, W. Distortion invariant object recognition in the dynamic link architecture. IEEE Trans. Comput. 1993, 42, 300–311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).