Performance Evaluation of Uplink Cell-Free Massive MIMO Network Under Weichselberger Rician Fading Channel

Abstract

Cell-free massive multiple-input multiple-output (CF M-MIMO) is one of the most promising technologies for future wireless communication such as 5G and beyond fifth-generation (B5G) networks. It is a type of network technology that uses a massive number of distributed antennas to serve a large number of users at the same time. It has the ability to provide high spectral efficiency (SE) as well as improved coverage and interference management, compared to traditional cellular networks. However, estimating the channel with high-performance, low-cost computational methods is still a problem. Different algorithms have been developed to address these challenges in channel estimation. One of the high-performance channel estimators is a phase-aware minimum mean square error (MMSE) estimator. This channel estimator has high computational complexity. To address the shortcomings of the existing estimator, this paper proposed an efficient phase-aware element-wise minimum mean square error (PA-EW-MMSE) channel estimator with QR decomposition and a precoding matrix at the user side. The closed form uplink (UL) SE with the phase MMSE and proposed estimators are evaluated using MMSE combining. The energy efficiency and area throughput are also calculated from the SE. The simulation results show that the proposed estimator achieved the best SE, EE, and area throughput performance with a substantial reduction in the complexity of the computation.

1. Introduction

Future wireless networks will need to manage billions of devices simultaneously, and each one will require high throughput to serve a variety of applications including speech, real-time video, high-definition movies, etc. [1,2]. Cellular networks cannot handle such high connection volumes due to the high levels of interference and the poor performance of user terminals located at the cell boundary. Additionally, traditional cellular systems are primarily built for human users. The Internet of Things, the Internet of Everything, smart X, and other machine-type communication systems are anticipated to be crucial in the development of future wireless networks. Expandable and effective connectivity for billions of units is the primary difficulty in machine-type communications. Since each cell can only serve a certain number of user equipment (UE), a centralized architecture with a cellular topology does not appear to be effective in these situations. Therefore, why not build a cell-free structure with distributed technology? It is called the CF M-MIMO system; it is created by combining M-MIMO technology with cell-free structures [1,2,3,4].

A comparison of traditional and CF M-MIMO technologies is shown in Figure 1 [5]. In cellular M-MIMO, the base station has a lot of antennas installed, allowing for the spatial multiplexing of large user signals in the identical frequency range [6]. Cellular M-MIMO’s performance is, however, constrained by several issues, such as pilot contamination, inter-cell interference, and the requirement for precise channel state data [7]. CF M-MIMO, on the other hand, is not dependent on the conventional cellular network architecture [8,9]. The transmission and reception of signals are instead coordinated across the antennas by the use of signal processing algorithms, which are widely dispersed over the coverage area. By using this strategy, inter-cell interference may be reduced, and the communication lines’ durability can be increased. The CF M-MIMO approach is an excellent fit for indoor and hot-spot coverage situations in the next generation of wireless communication, including locations such as subways, smart factories, shopping malls, railway stations, small towns, hospitals stadiums, community centers, and college campuses [5].

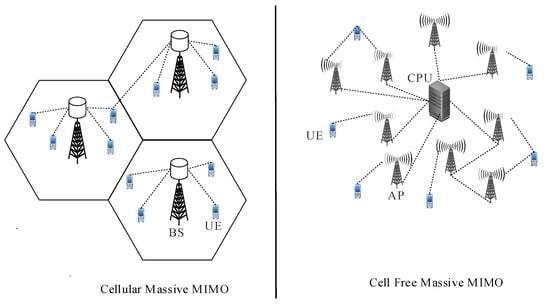
Figure 1. Comparison of CF M-MIMO and cellular M-MIMO systems [5].

Cell-free refers to a situation in which there are no cell borders during UL and downlink transmission, as seen by the UE since every access point (AP) that has an impact on the UE will actively participate in the connection [10,11,12,13]. For instance, all APs that receive an uplink data signal from a UE will work together to decode the signal. Even though not all APs may serve every UE, the network is collectively serving all K-active UE within its coverage region. The infrastructure and signal processing aspects of cellular and cell-free networks differ, although the UE may not be aware of these variations. The same UE should be able to connect to both types of networks without having to update its software [14].

The following are the contributions as a result of the inspirations from the aforementioned observations: (i) The proposed model incorporates two channel estimators to analyze the SE, EE, and area throughput of the CF M-MIMO network under the Weichselberger Rician fading channel with multi-antenna APs and UE, i.e., phase-aware MMSE and phase-aware EW-MMSE; (ii) the performance of the developed estimator with the existing channel estimator based on parameters such as SE, EE, and area throughput is analyzed; (iii) the impact of the pilot reuse factor and the number of users on SE, EE, and area throughput with multi-antenna access point and multi-antenna user equipment studied in details are determined. (iv) The uplink phase-aware MMSE and EW-MMSE channel estimator with MMSE combining is also studied under multi-antenna APs with multi-antenna UE over the Weichselberger Rician fading channel. (v) The performance of CF M-MIMO using the PA-EW-MMSE channel estimator with QR decomposition and a user-side precoding matrix is improved.

The rest of the paper is organized as follows: The related work about the CF M-MIMO system is described in Section 2. In Section 3, the system model is discussed. The results and discussion are covered in Section 4. Finally, the conclusion is discussed in Section 5.

2. Related Work

In this section, the research work on the channel estimation technique of the CF M-MIMO network under 5G and beyond is described. The contribution and drawback of each paper are discussed. Almost all papers considered in this work are on the uplink session of the CF M-MIMO system under fading channels.

In [15], CF M-MIMO with a multi-antenna AP and UE under a Rayleigh fading channel is investigated. The closed-form SE expression with MMSE successive interference cancelation (SIC) and a maximum ratio (MR) combiner is derived. Additionally, MMSE combiner schemes are derived at both the AP and the central processing unit (CPU), which can maximize the achievable SE for the fully centralized and distributed implementations, respectively. Also calculated is the closed-form expression of SE for the two-layer decoding scheme with MR combining. Similarly, the work mentioned in [16,17,18] used a two-layer decoding scheme for further interference reduction in order to enhance the performance of the cell-free massive MIMO system. The author showed the SE performance of different implementations such as fully centralized, distributed, and two-layer decoding with MMSE and MR combining under fading channels that only consider the non-line-of-sight (LoS) path. The author does not address the signal that came in the line-of-sight path, and also the user mobility that leads to the phase shift is not considered. The EE and area throughput is not addressed. The channel estimation in this work is estimated by the MMSE estimator, which does not consider the phase shift or mobility of user equipment. In addition to that, this estimator has high computational complexity.

In [19], the channel estimation of UL CF M-MIMO under the Rician fading channel is analyzed. The channel consists of both the LoS and non-line-of-sight (NLoS) paths. The dynamic cooperative cluster (DCC) is illustrated, where only Aps with the optimal channel conditions with the intended user is permitted to serve it. The DCC in [14,20,21] is also illustrated to make the CF M-MIMO scalable and improve the performance of the CF M-MIMO network. The author proposed a partial channel estimator in which a set of APs with the best channel condition can evaluate the channel estimates. The normalized MSE and the computational complexity for the partial MMSE and partial EW-MMSE are derived. In addition, the author showed that the PEW-MMSE is almost the same as result as of the PMMSE in terms of the normalized MSE. However, the computational complexity of the PEW-MMSE is low compared to that of the PMMSE channel estimator. The author demonstrated that when the number of users increases, the channel estimation reduces. In this paper the analysis is limited to channel estimations only; the energy efficiency, area throughput, and spectral efficiency of the paper are not addressed. The author did not show the channel estimation when the number of antennas per user equipment is more than one.

CF M-MIMO with multiple antennas on both the AP and user devices under Rayleigh fading channels is analyzed [22]. The author investigated the SE for the large-scale fading decoding (LSFD) scheme and fully centralized processing schemes. Iteratively weighted sum-minimum mean square error (I-WMMSE) algorithms have been proposed for two processing schemes in the literature to improve the UL SE in CF M-MIMO systems. The closed-form SE expression is derived. The I-WMMSE precoding scheme has been shown to achieve outstanding performance in CF M-MIMO systems, even with a large number of UE antennas. Importantly, the scheme has been shown to become even more effective with a larger number of UE antennas. The author did not consider the LoS path. The EE and area throughput are not addressed. The MMSE channel estimator used in this work has high computational complexity.

In [23], the multi-antenna AP and multi-antenna UE under the Weichselberger Rician fading channel with random phase shifts are studied. The UL SE for two practical processing strategies, i.e., the fully centralized processing approach with global MMSE or MR combining and the large-scale fading decoding (LSFD) technique with local MMSE or MR combining, is examined. The MMSE and MR combining are studied in [14,21], but the number of antennas per user equipment considered is one, which is not practical. To improve the SE effectiveness of the system, the author proposed an effective UL precoding method that relies only on the UE-side correlation matrices’ eigenvalues. Additionally, the closed-form SE equations for the LSFD scheme with MR combining have been developed. The channel estimation used in this work has high computational complexity. The analysis is only based on the SE; the EE and area throughput are not addressed.

2.1. System Model

In the CF M-MIMO system, M APs and K UE are randomly dispersed over a sizable region, with L as the number of antennas per AP and N as UE. In the system the coherence time–frequency block size has no impact on the channel responses [24]. The system operates in time division duplex (TDD) mode; each block consists of a total of ${\tau }_{\mathrm{c}}$ samples, with ${\tau }_p$ samples set for UL and the remaining ${\tau }_{\mathrm{u}}={\tau }_{\mathrm{c}}-{\tau }_p$ samples used for data transmission. The complex-valued channel between the mth AP and the kth UE is given as $H_{mk}\in {\mathbb{C}}^{L\times N}$, with the assumption that the channel coefficients ${\mathrm{H}}_{mk}$ are not dependent for different AP-UE pairs and independent and identically distributed (IID) across different blocks. The system model for the CF M-MIMO system is shown in Figure 2. In this model, M APs and K UE are randomly dispersed over a sizable region, with L and N denoting the number of antennas per AP and the number of antennas per UE, respectively.

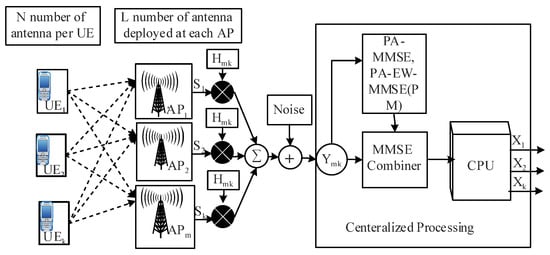
Figure 2. System model for the M access point and K user equipment.

The Weichselberger model is modeled as [15]

$${\mathrm{H}}_{mk}={\overline{\mathrm{H}}}_{mk}{e}^{j{\phi }_{mk}}+\underset{{\tilde{\mathrm{H}}}_{mk}}{\underbrace{{\mathrm{U}}_{mk,r}\left({\tilde{\mathrm{W}}}_{mk}\odot {\mathrm{H}}_{mk,\mathrm{i}\mathrm{i}\mathrm{d}}\right){\mathrm{U}}_{mk,t}^H}}$$

(1)

First, the line of the LoS component of the channel ${\overline{\mathrm{H}}}_{mk}=\left[{\overline{\mathrm{h}}}_{mk1},\dots ,{\overline{\mathrm{h}}}_{mkN}\right]$ is modeled as a deterministic complex vector with L elements, where ${\overline{\mathrm{h}}}_{mkn}\in {\mathbb{C}}^L$ is the channel between the n-th antenna of UE k and AP m, and ${\phi }_{mk}\sim \mathcal{U}\left[-\pi ,\pi \right]$ is a uniformly distributed phase shift [17,25]. Second, the NLoS component of the channel ${\tilde{\mathrm{H}}}_{mk}$ is modeled as a complex random vector with L elements, where ${\mathrm{H}}_{mk,\mathrm{iid}}\in {\mathbb{C}}^{L\times N}$ is a matrix of i.i.d. complex Gaussian entries with zero mean and unit variance.

Third, the unitary matrices ${\mathrm{U}}_{mk,r}\in {\mathbb{C}}^{L\times L}$ and ${\mathrm{U}}_{mk,t}\in {\mathbb{C}}^{N\times N}$ are the eigen basis of the one-sided correlation matrices ${\mathrm{R}}_{mk,\mathrm{r}}\triangleq \mathbb{E}\left\{{\tilde{\mathrm{H}}}_{mk}{\tilde{\mathrm{H}}}_{mk}^H\right\}$ and ${\mathrm{R}}_{mk,\mathrm{t}}\triangleq \mathbb{E}\left\{{\tilde{\mathrm{H}}}_{mk}^T{\tilde{\mathrm{H}}}_{mk}^{\mathrm{*}}\right\}$, respectively, which are defined as the expected values of the outer product of the NLoS component ${\tilde{\mathrm{H}}}_{mk}$ [26]. Fourth, the eigenmode coupling matrix ${\mathrm{W}}_{mk}\triangleq {\tilde{\mathrm{W}}}_{mk}\odot {\tilde{\mathrm{W}}}_{mk}$ is defined as the element-wise product of the matrix ${\mathrm{U}}_{mk,\mathrm{r}}$ and the conjugate transpose of the matrix ${\mathrm{U}}_{mk,\mathrm{t}}$, where the $(i,j)$th element of ${\left[{\mathrm{W}}_{mk}\right]}_{ij}$ specifies the average amount of power coupling from the ith column of ${\mathrm{U}}_{mk,\mathrm{r}}$ to the jth column of ${\mathrm{U}}_{mk,\mathrm{t}}$.

Finally, the full correlation matrix ${\mathrm{R}}_{mk}$ is calculated by taking the Kronecker product of the conjugate transpose of ${\mathrm{U}}_{mk,\mathrm{t}}$ and ${\mathrm{U}}_{mk,\mathrm{r}}$ and then multiplying it by a diagonal matrix formed by the vectorization of the matrix ${\mathrm{W}}_{mk}$. The full correlation matrix is calculated as shown below by taking into consideration the channel between the UE and AP as ${\mathrm{h}}_{mk}=\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathrm{H}}_{mk}\right)\in {\mathbb{C}}^{LN}$.

$${\mathrm{R}}_{mk}\triangleq \mathbb{E}\left\{\mathrm{v}\mathrm{e}\mathrm{c}\left({\tilde{\mathrm{H}}}_{mk}\right)\mathrm{v}\mathrm{e}\mathrm{c}{\left({\tilde{\mathrm{H}}}_{mk}\right)}^H\right\}\in {\mathbb{C}}^{LN\times LN}$$

(2)

$${\mathrm{R}}_{mk}=\left({\mathrm{U}}_{mk,t}^{\mathrm{*}}\otimes {\mathrm{U}}_{mk,r}\right)\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathrm{W}}_{mk}\right)\right){\left({\mathrm{U}}_{mk,t}^{\mathrm{*}}\otimes {\mathrm{U}}_{mk,r}\right)}^H$$

(3)

We use mutually ${\tau }_p$ normal pilot sequences as every pilot matrix contains N mutually orthogonal pilot sequences and is used for channel estimation [27].

$$P_k{P}_{k^{\prime }}=\left\{\begin{array}{c}{\tau }_p{I}_N\\ 0\end{array}\right.\begin{array}{c}{k}^{\prime }=k\\ otherwise\end{array}$$

(4)

where ${\mathrm{P}}_k\in {\mathbb{C}}^{N\times {\tau }_p}$ denotes the pilot matrix of UE $\mathrm{k}$.

In practical CF M-MIMO systems, due to limited system resources, multiple UE may have to use the same pilot matrix. Let ${\mathcal{P}}_k$ denote the set of indices of UE that use the same pilot matrix as UE k, including UE k itself. In this scheme, all UE sends their pilot signals to the AP, and the received signal at the AP can be expressed as ${\mathrm{Y}}_m^p\in {\mathbb{C}}^{L\times {\tau }_p}$; at the AP, $m$ is obtained by Equation (5).

$${\mathrm{Y}}_m^p={\sum }_{k=1}^K {\mathrm{H}}_{mk}{\mathrm{F}}_k{\mathrm{P}}_k+{\mathrm{N}}_m$$

(5)

where ${\mathrm{F}}_k\in {\mathbb{C}}^{N\times N}$ is the UL precoding matrix of UE $k$, which is designed to maximize the received signal power at the AP while satisfying the maximum transmit power constraint $\mathbb{E}\left\{{∥{\mathrm{F}}_k∥}_{\mathrm{F}}^2\right\}\le p_k$, with $p_k$ being the maximum transmit power of UE $k$ and ${\mathrm{N}}_m\in {\mathbb{C}}^{L\times {\tau }_p}$. It represents the noise and interference at the AP, which is modeled as complex Gaussian noise with zero mean and variance with ${\mathcal{N}}_{\mathrm{C}}\left(0,{\sigma }^2\right)$ elements. The integration of the precoding matrix with the user data represents a simple vector multiplication, which performs spatial precoding (or beamforming) at the UE side to improve transmission efficiency and reduce interference.

To find an estimate of ${\mathrm{h}}_{mk}$, AP $m$ matches ${\mathrm{Y}}_m^p$ with ${\mathrm{P}}_k^H$, as shown in Equation (6).

$${\mathrm{Y}}_{mk}^p={\mathrm{Y}}_m^p{\mathrm{P}}_k^H={\sum }_{l\in {\mathcal{P}}_k} {\tau }_p{\mathrm{H}}_{ml}{\mathrm{F}}_l+{\mathrm{N}}_m{\mathrm{P}}_k^H$$

(6)

Since ${\stackrel{\mathrm{ˆ}}{\mathrm{h}}}_{mk}$ $,{\mathrm{R}}_{mk}$, and ${\phi }_{mk}$ are available for AP m, the PA-MMSE estimate of ${\mathrm{h}}_{mk}$ is obtained by Equation (7).

$${\stackrel{\mathrm{ˆ}}{\mathrm{h}}}_{mk}=\mathrm{v}\mathrm{e}\mathrm{c}\left({\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_{mk}\right)={\overline{\mathrm{h}}}_{mk}{e}^{j{\phi }_{mk}}+{\mathrm{R}}_{mk}{\tilde{\mathrm{F}}}_k{\mathsf{\Psi }}_{mk}^{-1}\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathrm{Y}}_{mk}^p\right)$$

(7)

where ${\overline{\mathrm{h}}}_{mk}=\mathrm{vec}\left({\overline{\mathrm{H}}}_{mk}\right),{\tilde{\mathrm{F}}}_k={\mathrm{F}}_k^T\otimes {\mathrm{I}}_L$, and ${\mathsf{\Psi }}_{mk}={\sum }_{l\in {\mathcal{P}}_k} {\tau }_p{\tilde{\mathrm{F}}}_l{\mathrm{R}}_{ml}{\tilde{\mathrm{F}}}_l^H+{\sigma }^2{\mathrm{I}}_{LN}.$

2.2. Uplink Data Transmission

During the data transmission phase in CF M-MIMO systems, all antennas of all UE simultaneously transmit their data symbols to all APs. The received signal at AP m can be expressed as

$${\mathrm{y}}_m=\sum _{k=1}^K {\mathrm{H}}_{mk}{\mathrm{s}}_k+{\mathrm{n}}_m$$

(8)

where ${\mathrm{s}}_k={\mathrm{F}}_k{\mathrm{x}}_k\in {\mathbb{C}}^N$ is the transmitted signal of $\mathrm{U}\mathrm{E} k$, with ${\mathrm{x}}_k\sim {\mathcal{N}}_{\mathbb{C}}\left(0,{\mathrm{I}}_N\right)$ being the data symbol vector of UE $k$, and ${\mathrm{n}}_m\sim {\mathcal{N}}_{\mathbb{C}}\left(0,{\sigma }^2{\mathrm{I}}_L\right)$ is the additive noise vector.

The rationale for selecting the Weichselberger Rician fading model is grounded in its ability to more accurately capture realistic wireless channel conditions compared to conventional models such as the Rayleigh model. Unlike simpler models, the Weichselberger model accounts for joint spatial correlation at both the transmitter and the receiver, making it particularly suitable for scenarios involving large-scale antenna arrays. Additionally, it supports both line-of-sight (LoS) and non-line-of-sight (NLoS) components, incorporating phase shifts that are essential for capturing the dynamic behavior of channels in cell-free massive MIMO (CF M-MIMO) systems, especially in mobility-aware environments. Furthermore, the model is consistent with recent research and industry standards, reinforcing its applicability for simulating spatially correlated channels in practical, real-world deployments of massive MIMO networks.

2.3. MMSE Combining

MMSE combining is a signal processing technique used to combine the signals received from multiple antennas before decoding them. The goal of MMSE combining is to minimize the mean squared error between the sender signal and the received signal, subject to some constraints on the channel model and noise. It can be used to enhance the efficiency of the system by reducing the effects of interference and noise [15].

$${\mathrm{V}}_k={\left({\sum }_{l=1}^K \left({\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_l{\stackrel{\mathrm{ˆ}}{\mathrm{F}}}_l{\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_l^H+{\mathrm{C}}_l^{\prime }\right)+{\sigma }^2{\mathrm{I}}_{ML}\right)}^{-1}{\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_k{\mathrm{F}}_k$$

(9)

2.4. Spectral Efficiency of the System

Under the completely centralized processing setup, APs send all pilot signals from user equipment to the CPU to perform channel estimation, combining, and the data detection process. The APs are only responsible for interfacing the UE and CPU, as shown in Figure 3 below.

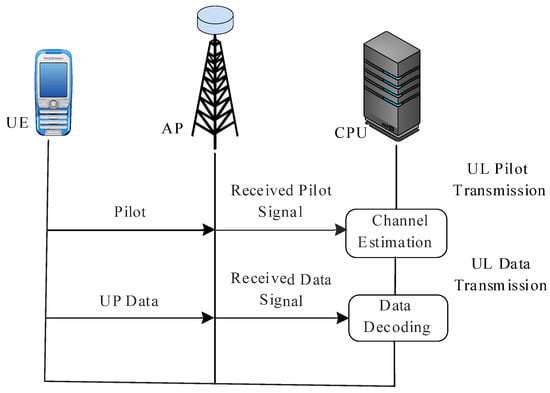
Figure 3. Full centralized processing schemes [20].

The overall channel of UE k is represented as ${\mathrm{h}}_k={\left[{\mathrm{h}}_{1k}^T,\dots ,{\mathrm{h}}_{Mk}^T\right]}^T\in {\mathbb{C}}^{MLN}$, where h_MK $\in {\mathbb{C}}^{LN}$ is the channel matrix between AP M and UE K, with L and N denoting the number of antennas at the AP and UE, respectively. The mean of the collective channel estimate for UE K is denoted as ${\overline{\mathrm{h}}}_k={\left[{\overline{\mathrm{h}}}_{1k}^T{e}^{j{\phi }_{1k}},\dots ,{\overline{\mathrm{h}}}_{Mk}^T{e}^{j{\phi }_{Mk}}\right]}^T$, where ${\phi }_{Mk}$ represents the phase shift in the LoS component of the wireless channel. The full covariance matrix of the collective channel estimate for UE K is denoted as ${\mathrm{R}}_k=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathrm{R}}_{1k},\dots ,{\mathrm{R}}_{Mk}\right)$. For fully centralized implementation, it is assumed that ${\phi }_{Mk}$ is available at the CPU, so channel estimates can be obtained by PA-MMSE estimators at the CPU. The collective channel estimate for UE k can be constructed as ${\stackrel{\mathrm{ˆ}}{\mathrm{h}}}_k={\left[{\stackrel{\mathrm{ˆ}}{\mathrm{h}}}_{1k}^T,\dots ,{\stackrel{\mathrm{ˆ}}{\mathrm{h}}}_{Mk}^T\right]}^T$, where the conditional mean and covariance matrix of the channel estimate given ${\phi }_{Mk}$ is given by

$$\mathbb{E}\left\{{\stackrel{\mathrm{ˆ}}{\mathrm{h}}}_k\mid e^{j{\phi }_k}\right\}={\overline{\mathrm{h}}}_k$$

(10)

$$\mathrm{Cov}\left\{{\stackrel{\mathrm{ˆ}}{\mathrm{h}}}_k\mid e^{j{\phi }_k}\right\}={\tau }_p{\mathrm{R}}_k{\overline{\mathrm{F}}}_k{\mathsf{\Psi }}_k^{-1}{\overline{\mathrm{F}}}_k^H{\mathrm{R}}_k$$

(11)

Here, ${\tau }_p$ represents the pilot length. ${\overline{\mathrm{F}}}_k=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(\underset{M}{\underbrace{{\tilde{\mathrm{F}}}_k,\dots ,{\tilde{\mathrm{F}}}_k}})$ is a diagonal matrix where ${\overline{\mathrm{F}}}_k$ is the precoding matrix for UE K, and ${\mathsf{\Psi }}_k^{-1}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathsf{\Psi }}_{1k}^{-1},\dots ,{\mathsf{\Psi }}_{Mk}^{-1}\right)$ is a diagonal matrix where ΨMK is the variance of the estimation error of H_MK. The received signal available at the CPU can be expressed as

$$\underset{=y}{\underbrace{\left[\begin{array}{c}{y}_1\\ ⋮\\ y_M\end{array}\right]}}={\sum }_{k=1}^K\underset{=H_k}{\underbrace{\left[\begin{array}{c}{H}_{1k}\\ ⋮\\ H_{MK}\end{array}\right]}}{F}_k{x}_k+\underset{=n}{\underbrace{\left[\begin{array}{c}{n}_1\\ ⋮\\ n_M\end{array}\right]}}$$

(12)

The received signal at the AP can be expressed as shown in Equation (12) and can be rewritten as

$$\mathrm{y}={\sum }_{k=1}^K {\mathrm{H}}_k{\mathrm{F}}_k{\mathrm{x}}_k+\mathrm{n}$$

(13)

To decode the data symbol vector ${\mathrm{x}}_k$ for UE k, an arbitrary receive combining matrix ${\mathrm{V}}_k\in {\mathbb{C}}^{LM\times N}$ can be designed by the CPU based on the collective channel estimates. The receive combining matrix Vk is a complex matrix of size LM × N, where LM is the number of antennas at the AP and N is the number of antennas at the UE k. The decoded signal ${\mathrm{x}}_k$ obtained as

$${\stackrel{\mathrm{ˆ}}{\mathrm{x}}}_k={\mathrm{V}}_k^H{\mathrm{H}}_k{\mathrm{F}}_k{\mathrm{x}}_k+{\sum }_{l\ne k}^K {\mathrm{V}}_k^H{\mathrm{H}}_l{\mathrm{F}}_l{\mathrm{x}}_l+{\mathrm{V}}_k^H\mathrm{n}$$

(14)

Based on ${\stackrel{\mathrm{ˆ}}{\mathrm{x}}}_k$, it is possible to derive the achievable SE for UE k in a CF M-MIMO system using standard capacity lower bounds [27,28]. The feasible SE for UE k using the PA-MMSE estimator is given by Equation (7) for the fully centralized processing with a given combining vector Vk defined in Equation (9) for MMSE combining.

$${\mathrm{S}\mathrm{E}}_k^{\left(1\right)}=\left(1-{\displaystyle \frac{{\tau }_p}{{\tau }_c}}\right)\mathbb{E}\left\{{\mathrm{l}\mathrm{o}\mathrm{g}}_2\left|{\mathrm{I}}_N+{\mathrm{D}}_{k,\left(1\right)}^H{\Sigma }_{k,\left(1\right)}^{-1}{\mathrm{D}}_{k,\left(1\right)}\right|\right\}$$

(15)

where ${\mathrm{D}}_{k,\left(1\right)}\triangleq {\mathrm{V}}_k^H{\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_k{\mathrm{F}}_k$,

$${\mathsf{\Sigma }}_{k,\left(1\right)}\triangleq {\mathrm{V}}_k^H\left({\sum }_{l=1}^K {\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_l{\stackrel{\mathrm{ˆ}}{\mathrm{F}}}_l{\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_l^H+{\sum }_{l=1}^K {\mathrm{C}}_l^{\prime }+{\sigma }^2{\mathrm{I}}_{ML}\right){\mathrm{V}}_k-{\mathrm{D}}_{k,\left(1\right)}{\mathrm{D}}_{k,\left(1\right)}^H$$

${\stackrel{\mathrm{ˆ}}{\mathrm{F}}}_l=$ ${\mathrm{F}}_l{\mathrm{F}}_l^H$, and ${\mathrm{C}}_l^{\prime }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathrm{C}}_{1l}^{\prime },\dots ,{\mathrm{C}}_{Ml}^{\prime }\right)$, and the $(i,j)$th element of ${\mathrm{C}}_{ml}^{\prime }$ which is expressed as

$${\left[{\mathrm{C}}_{ml}^{\prime }\right]}_{ij}={\sum }_a^N {\sum }_b^N {\left[{\stackrel{\mathrm{ˆ}}{\mathrm{F}}}_l\right]}_{ba}{\left[{\mathrm{C}}_{ml}^{ba}\right]}_{ij}$$

The MMSE combining stated in Equation (9) can be further minimized as ${\mathrm{M}\mathrm{S}\mathrm{E}}_k=\mathbb{E}\left\{{∥{\mathrm{x}}_k-{\mathrm{V}}_k^H\mathrm{y}∥}^2\mid {\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_k\right\}$ and resulted in the maximization of spectral efficiency defined in Equation (15). The maximized SE using the minimized MMSE combining method can be evaluated as shown in Equation (16),

$${\mathrm{S}\mathrm{E}}_k^{\left(1\right)}=\left(1-{\displaystyle \frac{{\tau }_p}{{\tau }_c}}\right)\mathbb{E}\left\{{\mathrm{l}\mathrm{o}\mathrm{g}}_2\left|{\mathrm{I}}_N+{\left({\mathrm{D}}_{k,\left(1\right)}^{\prime }\right)}^H{\left({\mathsf{\Sigma }}_{k,\left(1\right)}^{\prime }\right)}^{-1}{\mathrm{D}}_{k,\left(1\right)}^{\prime }\right|\right\}$$

(16)

where ${\mathrm{D}}_{k,\left(1\right)}^{\prime }\triangleq {\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_k{\mathrm{F}}_k$ and ${\mathsf{\Sigma }}_{k,\left(1\right)}^{\prime }\triangleq {\sum }_{l\ne k}^K {\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_l{\stackrel{\mathrm{ˆ}}{\mathrm{F}}}_l{\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_l^H+{\sum }_{l=1}^K {\mathrm{C}}_l^{\prime }+{\sigma }^2{\mathrm{I}}_{ML}$.

3. Proposed Method

The performance and complexity of channel estimation algorithms are two key issues in CF M-MIMO systems. The proposed method takes the diagonal of the MMSE matrix, i.e., the element-wise MMSE estimator, and applies QR decomposition to it to find the inverse of the matrix; it then applied it to the estimation process. Since the UE is multi-antenna equipment, a precoding matrix is used at the user side to manage the interference. The estimator is phase-aware because it takes into consideration the received signal’s phase information, which is crucial for correctly predicting the channel in a system with many antennas. The estimator estimates the medium coefficients for every element of the channel separately, making it element-wise as well. The received signal’s phase information is taken into account during the estimating process in the phase-aware version of the estimator, which might increase the channel estimation’s precision. EW-MMSE is a computationally effective method that calculates the channel coefficients of each antenna individually while taking the correlation between several antennas into account. The MMSE estimator may be more successful in capturing this correlation in CF M-MIMO with multi-antenna user equipment since the channel may be highly correlated across antennas. On the other hand, element-wise MMSE may perform better if the channel correlation is minimal by making use of the antennas’ independence. The channel estimator for the element-wise estimator ${\widehat{h}}_{mk}^{ew}$ is defined by

$${\widehat{\mathrm{h}}}_{mk}^{ew}=\mathrm{v}\mathrm{e}\mathrm{c}\left({\stackrel{\mathrm{ˆ}}{\mathrm{H}}}_{mk}\right)={\overline{\mathrm{h}}}_{mk}{e}^{j{\phi }_{mk}}+{\mathrm{R}}_{mk}{\tilde{\mathrm{F}}}_k{\mathsf{\Psi }}_{mk}^{-1}\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathrm{Y}}_{mk}^p\right)$$

(17)

where $R_{mk}$ and ${\Psi }_{mk}^{-1}$ are diagonal matrices defined in Equations (2) and (7), respectively.

3.1. Precoding Matrix Design

To improve the SE performance, UL precoding can be implemented at the UE side in the scenario with multi-antenna UEs. Inspired by CF M-MIMO, the UL precoding scheme can be based on the correlation feature ${\mathrm{U}}_{mk,\mathrm{t}}$ at the UE side as

$${\mathrm{F}}_k=\sqrt{p_k}{∥{\sum }_{m=1}^M {\mathrm{U}}_{mk,\mathrm{t}}∥}_{\mathrm{F}}^{-1}\left({\sum }_{m=1}^M {\mathrm{U}}_{mk,\mathrm{t}}\right)$$

(18)

The correlation feature ${\mathrm{U}}_{mk,\mathrm{t}}$ represents the correlation between the channel vectors at the UE side and can be used to design efficient precoding schemes that take advantage of the spatial diversity of the wireless channel.

To improve computational efficiency and numerical stability, QR decomposition is applied to the PA-EW-MMSE weight matrix. Specifically, it is performed on the diagonal blocks of the covariance matrix, which simplifies the matrix inversion process into a more manageable triangular back substitution. At the user equipment (UE) side, a precoding matrix is applied to enable direct beamforming, enhancing the signal quality and reducing interference. In this configuration, the PA-EW-MMSE estimator not only provides improved estimation accuracy but also significantly lowers computational complexity compared to traditional approaches.

3.2. Performance Metrix of the System

• Area throughput

The data transmission rate per square meter in a wireless network is known as area throughput. Ordinarily, it is expressed in bits per second per square meter (bps/m²). It serves as a gauge for how many users a network can accommodate at once in a specific location.

$$Throughput=B\ast SE\ast D$$

(19)

where SE is the amount of data that can be sent per unit of the spectrum, measured in bits per second per Hertz (bps/Hz), which is evaluated by Equation (16); B is the total amount of spectrum available for transmission, measured in Hertz (Hz); and D is the number of APs deployed per unit area, measured as the number of APs per square meter (APs/m²).

• Computational Complexity

The conventional PA-MMSE estimator achieves high performance but requires the inversion of large matrices, leading to high computational complexity, especially as the system size (number of antennas, subcarriers, or users) increases. The matrix inversion operation typically has a complexity of O(N³), where N is the matrix dimension.

The proposed estimator leverages QR decomposition to avoid direct matrix inversion. QR decomposition reduces the computational burden, as it decomposes the matrix into orthogonal and triangular matrices, which are easier to handle. The complexity of QR decomposition is generally O(N²), which is significantly lower than direct inversion for large matrices. Additionally, the use of a precoding vector at the user side further simplifies receiver processing.

• Energy Efficiency

EE is the capacity of the system to send and receive wireless signals at high data rates while consuming the least amount of energy possible. EE is a crucial factor to take into account when designing wireless communication systems, particularly in the case of M-MIMO, which deploys a lot of antennas to serve several user devices. It can be evaluated as

$$EE=B\ast SE/P$$

(20)

where EE denotes energy efficiency (bit/joule), B is the bandwidth of the system, SE denotes spectral efficiency (bit/s/Hz), and P is the power required to transmit the signal (W). The EE is evaluated from the SE discussed in Equation (16). Also, the spectral efficiency defined in Equation (16) is another performance metric.

The flowchart shown in Figure 4 shows the EW MMSE with QR decomposition and a precoding matrix at the UE side channel estimation process in a CF M-MIMO system. This flowchart outlines the EW-MMSE channel estimation process in a CF M-MIMO system with multi-antenna UE under Rician fading channel conditions. It includes the steps of transmitting pilot signals, receiving and measuring pilot signals, initializing the channel estimation variables, performing QR decomposition on the channel matrix, computing the precoding matrix at the UE side, calculating MMSE weights, performing channel estimation for each element in the channel estimate matrix, and finally sending the estimated channel coefficients back to the central processor.

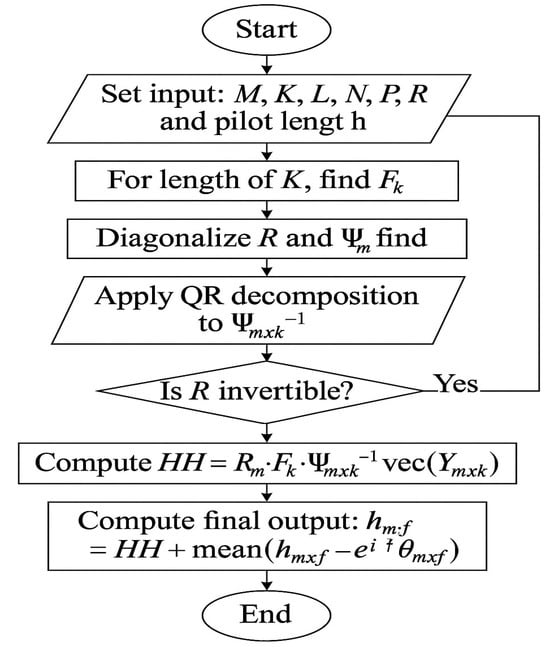
Figure 4. Flow chart of the proposed channel estimator based on element-wise MMSE and QR decomposition with the precoding matrix at the UE side.

4. Results and Discussion

This section describes the simulation outcomes for achieving the study’s specific goal. The simulation results and discussions on how the proposed channel estimator performs in comparison to the current estimate for the CF M-MIMO uplink system based on the SE, EE, and area throughput parameters under the Weichselberger Rician fading channel are provided. Table 1 is a list of the simulation parameters that are used in this paper to compare the proposed channel estimator’s performance and complexity to the previous work channel estimator for a CF M-MIMO UL system. The simulations are carried out in the MATLAB R2022a software with the computer having 16 GB of RAM. Also, Concept Draw is used as a drawing tool.

Table 1. Simulation parameter.

No.	Simulation Parameter	Type and Value
1	Pilot reuse factor (w)	1, 2
2	Uplink transmitter power (p)	200 mW
3	Number of access points (M)	10, 20, 40, 80
4	Number of antennae per UE (N)	1, 2, 3, 4, 5, 6
5	Number of antennae per APs (L)	4
6	Number of user equipment (K)	8, 10, 15, 20
7	Coherence block	200 to 800
8	Bandwidth (B)	1 MHz
9	Coverage area	1 km by 1 km

While QR factorization and user-side precoding can significantly improve system performance and reduce receiver complexity, they introduce notable limitations related to computational demands, power consumption, hardware requirements, channel state information acquisition, signaling overhead, implementation complexity, and scalability. These factors must be carefully considered when designing practical systems, especially for resource-constrained user devices.

4.1. Impact of the Number of Users and the Pilot Reuse Factor per Access Point on Spectral Efficiency

Figure 5 demonstrates the comparison of the proposed estimator with the existing estimator when the number of UE increases. For instance, for N = 3 and M = 40, the average UL SE for the existing estimator decreased from 34.03 bit/s/Hz to 31.72 bit/s/Hz as K increased. Similarly, the average UL SE for the proposed estimator decreased from 35.55 bit/s/Hz to 33.09 bit/s/Hz as K increased. For M = 10, the average UL SE raised to N = 3 and then diminished as N increased. This is due to the number of user antennas being low compared to the number of AP antennas, which increasing the chance of interference occurring between the user antenna and the access point antenna. But the proposed estimator still has better performance than the existing estimator. The proposed estimator obtained the average UL SE = 49.1 bit/s/Hz at N = 5 and M = 80, whereas the MMSE estimator reached the average UL SE = 42.72 bit/s/Hz; i.e., the proposed estimator outperformed the other estimator by 14.93%. The pilot length becomes ${\tau }_p$ = 60; i.e., the pilot length increases as the number of users increases.

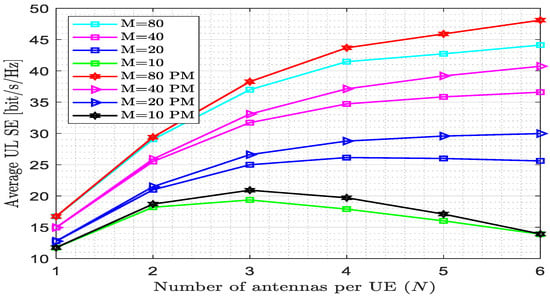
Figure 5. Spectral efficiency versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 1.

Figure 6 shows the comparison of the average UL SE for completely centralized processing as a function of the number of APs (M), with the MMSE combining over varied numbers of antennae per user equipment (N). When the number of users increases to K = 20, the maximum average UL SE achieved by the proposed method is 30.14 bit/s/Hz. For the single-antenna user, the performance is diminished highly from 10.26 bit/s/Hz to 4.408bit/s/Hz for the existing estimator and from 15.07 bit/s/Hz to 30.14 bit/s/Hz for the proposed estimator. This shows that the proposed estimator is not effective for the single-antenna user equipment for a large number of users. The proposed estimator obtained the average UL SE = 30.14 bit/s/Hz at N = 4 and M = 80, whereas the MMSE estimator reached the average UL SE = 28.55 bit/s/Hz; i.e., the proposed estimator outperformed the other estimator by 5.57%. The pilot length is 80 since K = 20 and N = 4.

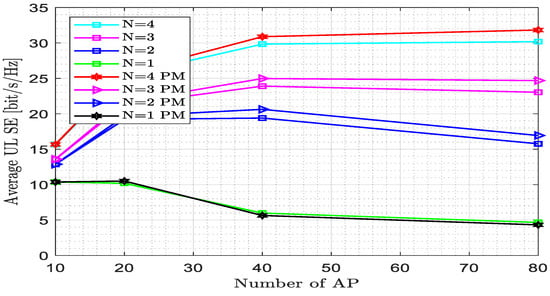
Figure 6. Spectral efficiency versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 20, L = 4, ${\tau }_c$ = 200, and w = 1.

Figure 7 emphasizes the impact of the pilot reuse factor on the SE for different numbers of APs across the number of antennae per UE. The proposed estimator obtained the average UL SE = 17.268 bit/s/Hz at N = 6 and M = 80, whereas the MMSE estimator reached the average UL SE = 15.894 bit/s/Hz; i.e., the proposed estimator outperformed the other estimator by 8.53%. The increment of the pilot reuse factor results in a decrease in average UL SE. The proposed estimator has better performance as compared to the existing estimator when the number of antennae per UE for different numbers of APs is different. The pilot length is 30 since w = 2, K = 1, and N = 6. The pilot length decreases due to the pilot reuse factor; i.e., as the pilot reuse factor increases, the pilot length decreases. The maximum average UL SE achieved for the proposed method is 18.228 bit/s/Hz at N = 4 and M = 80, whereas for the existing one, it is 17.69 bit/s/Hz.

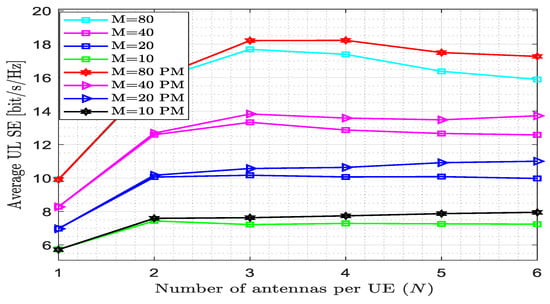
Figure 7. Spectral efficiency versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 2.

Figure 8 describes the impact of the pilot reuse factor on the SE for a different number of UE antennas across a number of APs as the pilot reuse factor increases to two. The proposed estimator obtained the average UL SE = 17.87 bit/s/Hz at N = 4 and M = 80, whereas the MMSE estimator reached the average UL SE = 16.977 bit/s/Hz; i.e., the proposed estimator outperformed the other estimator by 5.27%. The increment of the pilot reuse factor results in a decrease in average UL SE for both the existing and proposed estimators. The proposed estimator has better performance as compared to the existing estimator when the number of APs increases for different numbers of UE. The pilot length is 20 since w = 2, K = 10, and N = 6. The maximum average UL SE achieved for the proposed method is 17.88 bit/s/Hz at N = 4 and M = 40, whereas for the existing one, it is 17.35 bit/s/Hz at N = 4 and M = 80.

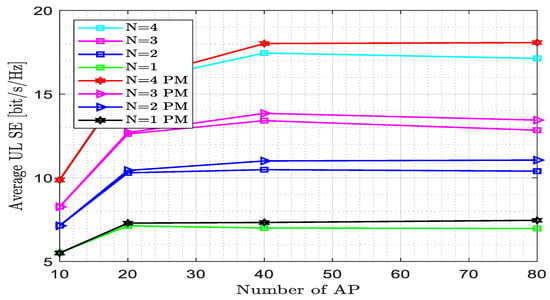
Figure 8. Spectral efficiency versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 20, L = 4, ${\tau }_c$ = 200, and w = 2.

4.2. Impact of the Number of Users and the Pilot Reuse Factor on Energy Efficiency

Figure 9 shows the comparison of the proposed estimator with the existing estimator using the parameter average UL EE with the number of antennae per UE. The simulation result implies that as the number of antennae per UE increases, EE increases for a large value of the number of APs, whereas for a small value of M, EE initially rises and then diminishes as N increases. The MMSE estimator reached the maximum average UL EE = 214.2 Mbit/joule at N = 6 and M = 80, whereas the proposed estimator obtained the average UL EE = 234.5 Mbit/joule; i.e., the proposed estimator outperformed the other estimator by 9.77% at this point. The maximum EE achieved by the proposed estimator for M = 10 is at N = 3, which is 122.8 Mbit/joule, whereas for the existing estimator, it is 114.3 Mbit/joule. The pilot length is 60 since w = 1, N = 6, and K = 10.

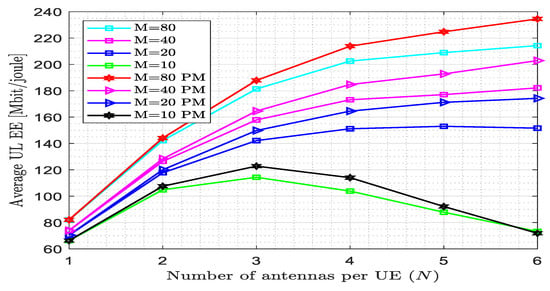
Figure 9. Energy efficiency versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 1.

Figure 10 shows the effect of users on energy efficiency with a varied number of APs and at different numbers of antennae per UE. The proposed estimator achieved energy efficiency EE = 175.249 Mbit/joule at N = 4 and M = 80, whereas for the existing estimator, EE = 165.704 Mbit/joule at N = 4 and M = 80; i.e., the proposed estimator outperformed the existing estimator by 5.76% at this point. At N = 3 and M = 40, the energy efficiency achieved by the existing and proposed estimators became 138.755 Mbit/joule and 144.847 Mbit/joule, respectively. At N = 2 and M = 20, the energy efficiency achieved by the existing and proposed estimators became 98.932 Mbit/joule and 98.932 Mbit/joule, respectively. This indicates that as the number of users increased, the energy efficiency decreased. The pilot length is 60 since K = 15, N = 4, and w = 1. The pilot length depends on the number of users, the number of antennae per UE, and the pilot reuse factor; i.e., as the number of users increased, the pilot length also increased.

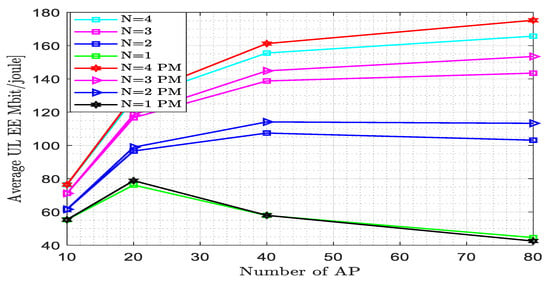
Figure 10. Energy efficiency versus the number of access points for fully centralized processing with the MMSE combiner at K = 15, L = 4, ${\tau }_c$ = 200, and w = 1.

Figure 11 shows that the effect of the pilot reuse factor on the energy efficiency varied across the number of antennae per UE at different numbers of APs when the pilot reuse factor was raised to two. The proposed estimator achieved energy efficiency EE = 176.7 bit/joule at N = 6 and M = 80, whereas for the existing estimator, EE = 162.2 Mbit/joule at N = 6 and M = 80. The proposed estimator improves the performance by 8.94% at this point. At N = 6 and M = 20, the energy efficiency achieved by the existing and proposed estimators became 97.04 Mbit/joule and 108.2 Mbit/joule, respectively. The maximum energy efficiency reached by the proposed estimator occurred at N = 4, i.e., 184.2 Mbit/joule, whereas for the existing estimator, an energy efficiency of 178.2 Mbit/joule was achieved at N = 3. As the pilot reuse factor increased from w = 1 to w = 2, the energy efficiency initially increased and then decreased as the number of antenna per UE increased. The pilot length became 30 since K = 10, N = 6, and w = 2, which means that the pilot length decreased as the pilot reuse factor increased.

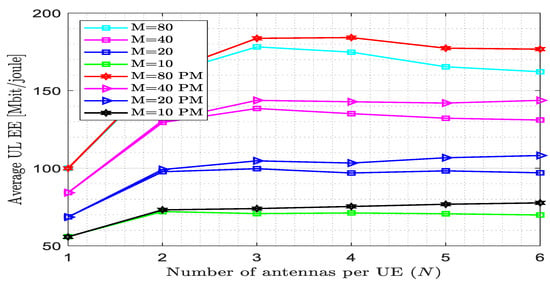
Figure 11. Energy efficiency versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 2.

Figure 12 describes the effect of the pilot reuse factor on the energy efficiency varied across the number of antennae per AP at different numbers of UE when the pilot reuse factor was raised to two. The proposed estimator achieved energy efficiency EE = 87.67 Mbit/joule at N = 4 and M = 80, whereas for the existing estimator, the energy efficiency EE = 83.25 Mbit/joule at N = 4 and M = 80. The proposed estimator improves the performance by 8.94% at this point. At N = 3 and M = 40, the energy efficiency achieved by the existing and proposed estimators became 65.97 Mbit/joule and 68.45 Mbit/joule, respectively. At N = 2 and M = 20, the energy efficiency achieved by the existing and proposed estimators became 49.46 Mbit/joule and 50.03 Mbit/joule, respectively. The energy efficiencies attained by the proposed and existing estimators for N < 2 have nearly the same value. As the pilot reuse factor increased from w = 1 to w = 2, the energy efficiency decreased. When the number of APs increased with the increased pilot reuse factor, the area throughput increased up to some point and diminished after a certain point. The pilot length became 20 since K = 10, N = 4, and w = 2, which means that the pilot length decreased as the pilot reuse factor increased.

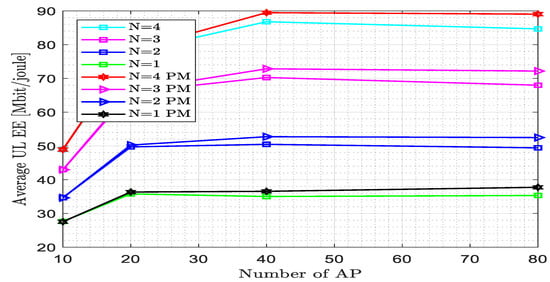
Figure 12. Energy efficiency versus the number of access points for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 2.

4.3. Impact of the Number of Users and the Pilot Reuse Factor on Area Throughput

The comparison between the proposed estimator and the existing estimator utilizing the parameter area throughput with the number of antenna per UE is shown in Figure 13. The area throughput increased as the number of antennae per UE increased for M values of 20, 40, and 80; however for an M value of 10, the area throughput initially increased and then decreased. The suggested estimator attained area throughput AT = 3792 Mbit/s/km² at N = 6 and M = 80, whereas the existing estimator attained AT = 3467 Mbit/s/km² at N = 6 and M = 80. The proposed estimator enhanced the performance by 9.374% at this point. For M = 10, the proposed estimator and the existing estimator maximally reached the area throughput at N = 3, which are 1612 Mbit/s/km² and 1491 Mbit/s/km², respectively. The length of the pilot is 60 since w = 1, N = 6, and K = 10.

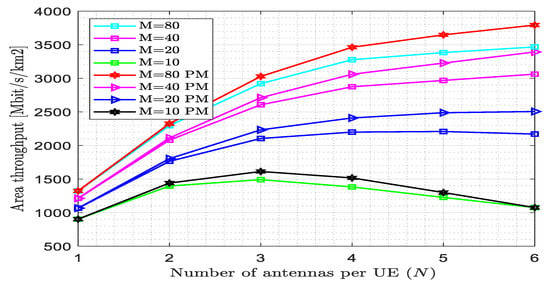
Figure 13. Area throughput versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 1.

Figure 14 shows the effect of users on the area throughput with varied numbers of APs and at different numbers of antennae per UE. When the number of users increased, the area throughput reduced. The proposed estimator achieved area throughput = 3051.17 Mbit/km² at N = 4 and M = 80, whereas for the existing estimator, the area throughput = 2895.84 Mbit/km² at N = 4 and M = 80. As the number of APs increased, the throughput also increased. At N = 3 and M = 40, the area throughput achieved by the existing and proposed estimators became 2405.29 Mbit/km² and 2511.62 Mbit/km², respectively. At N = 4 and M = 20, the area throughput achieved by the existing and proposed estimators became 2226.1 Mbit/km² and 2226.7 Mbit/km², respectively. The area throughput attained by the proposed and existing estimators for M < 20 is similar. The pilot length became 60 since K = 15, N = 4, and w = 1. The pilot length depends on the number of users, the number of antennae per UE, and the pilot reuse factor; i.e., as the number of users increased, the pilot length also increased.

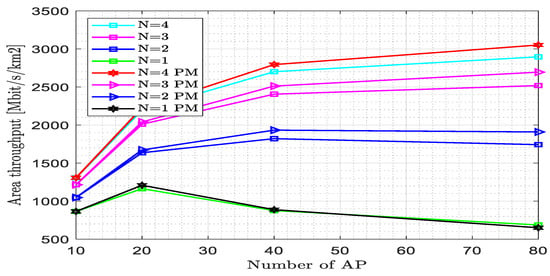
Figure 14. Area throughput versus the number of access points for fully centralized processing with the MMSE combiner at K = 15, L = 4, ${\tau }_c$ = 200, and w = 1.

Figure 15 shows that the effect of the pilot reuse factor on the area throughput varied across the number of antennae per UE at different numbers of APs when the pilot reuse factor was raised to two. The proposed estimator achieved area throughput = 1325 bit/km² at N = 6 and M = 80, whereas for the existing estimator, the area throughput = 1200 Mbit/km² at N = 6 and M = 80. The proposed estimator improves the performance by 10.42% at this point. At N = 4 and M = 40, the area throughput achieved by the existing and proposed estimators became 1050 Mbit/km² and 1150 Mbit/km². The area throughput values attained by the proposed and existing estimators for N < 2 are very close. The maximum area throughput reached by the proposed estimator occurred at N = 3, i.e., 1400 Mbit/km², whereas for the existing estimator, an area throughput of 1350 Mbit/km² was reached. As the pilot reuse factor increased from w = 1 to w = 2, the area throughput decreased. As a result, the gap between the proposed and existing estimators also decreased. The pilot length became 30 since K = 10, N = 6, and w = 2, which means that the pilot length decreased as the pilot reuse factor increased.

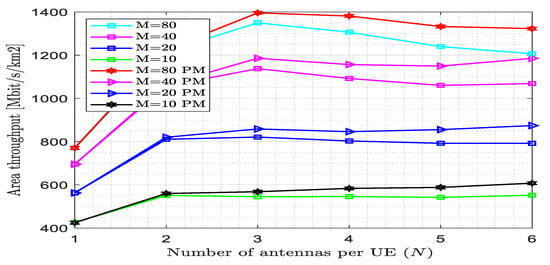
Figure 15. Area throughput versus the number of antennas per UE for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 2.

Figure 16 shows that the effect of the pilot reuse factor on the area throughput varied across the number of antennae per AP at different numbers of UE when the pilot reuse factor was raised to two. The proposed estimator achieved area throughput = 1476 Mbit/km² at N = 4 and M = 80, whereas for the existing estimator, the area throughput = 1399 Mbit/km² at N = 4 and M = 80. The proposed estimator improves the performance by 5.50% at this point. At N = 3 and M = 40, the area throughput achieved by the existing and proposed estimators became 1100 Mbit/km² and 1142 Mbit/km², respectively. At N = 2 and M = 20, the area throughput achieved by the existing and proposed estimators became 837.3 Mbit/km²; i.e., at this point the performance of the two estimators is the same. The area throughput values attained by the proposed and existing estimators for N < 2 are very close. As the pilot reuse factor increased from w = 1 to w = 2, the area throughput decreased. When the number of APs increased with the increased pilot reuse factor, the area throughput increased up to some point and diminished after a certain point. The pilot length became 20 since K = 10, N = 4, and w = 2, which means that the pilot length decreased as the pilot reuse factor increased.

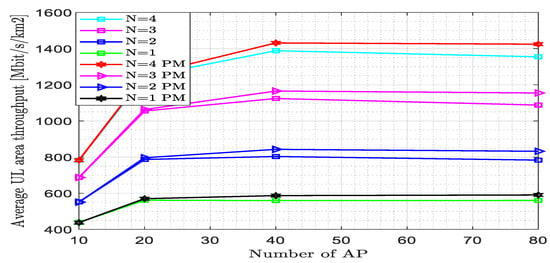
Figure 16. Area throughput versus the number of access points for fully centralized processing with the MMSE combiner at K = 10, L = 4, ${\tau }_c$ = 200, and w = 2.

The use of multi-antenna access points (APs) and user equipment (UE) significantly increases hardware costs, particularly in centralized processing architectures. The multi-antenna configuration at the UE side also adds computational burden, as it requires more complex signal processing. Moreover, establishing efficient connectivity between the APs and the central processing unit (CPU) poses a major challenge. Since the number of APs is typically much larger than the number of UE, this requires high-capacity, low-latency connections such as fiber-optic links with substantial bandwidth. However, deploying and maintaining such a dense and high-speed backhaul network is both technically complex and costly.

5. Conclusions

In this paper, we studied the performance evaluation of an uplink cell-free massive MIMO network under Weichselberger Rician fading channels. This paper analyses the average UL SE, EE, and area throughput for multiple-antenna APs and multiple-antenna UE. As shown in the simulation results, the performance of the proposed estimator is evaluated based on the SE, EE, and area throughput with multi-antenna APs and multi-antenna UE. The fully centralized processing scheme is considered. The performance of the proposed estimator is high when the number of access points and the number of antennae per UE are increased. As the pilot reuse factor increased, the SE, EE, and area throughput are reduced, and the pilot length also decreased due to pilot contamination. The number of antennae per AP, the number of APs, and coherence time have positive effects on the EE, SE, and area throughput; i.e., when those parameters increased, the EE, SE, and area throughput rose. For a small number of antennae per UE, i.e., N < 2, the SE, EE, and area throughput under different numbers of APs for the proposed and existing estimators overlap; i.e., the performance of the proposed estimator is not effective for the single-antenna user equipment, and the performance is reduced as the number of antennae per UE and the number of AP rise due to interference.

In addition to the qualitative trends, simulation results demonstrate clear quantitative benefits of the proposed estimator. The proposed method improved spectral efficiency by up to 14.93% (at N = 5 and M = 80) and energy efficiency by up to 9.77% (at N = 6 and M = 80) compared to the existing MMSE estimator. Area throughput gains reached up to 9.37% in dense AP deployments. However, the advantage is less pronounced for N < 2, where performance overlaps between the estimators. Further, with the increased pilot reuse factor (w = 2), the SE, EE, and AT decreased despite shorter pilot lengths, though the proposed estimator still consistently outperformed the existing one. These findings underline the computational efficiency and scalability of the proposed estimator for large-scale CF massive MIMO networks.