Abstract
In an optomechanical system (OMS), the dynamics of quantum correlations, e.g., quantum discord, can witness synchronized squeezing between the cavity and mechanical modes. We investigate an OMS driven by two coherent fields, and demonstrate that optimal quantum correlations and squeezing synchronization can be achieved by carefully tuning key parameters: the cavity-laser detunings, loss rates, and the effective coupling ratio between the optomechanical interaction and the amplitude drive. By employing the steady-state solution of the covariance matrix within the Lyapunov framework, we identify the conditions under which squeezing becomes stabilized. Furthermore, we demonstrate that synchronized squeezing of the cavity and mechanical modes can be effectively controlled by tuning the loss ratio between the cavity and mechanical subsystems. Alternatively, in the case where the cavity is driven by a single field, we demonstrate that synchronized squeezing in the conjugate quadratures of the cavity and mechanical modes can still be achieved, provided that the cavity is coupled to a squeezed reservoir. The presence of this engineered reservoir compensates the absent driving field, by injecting directional quantum noise, thereby enabling the emergence of steady-state squeezing correlations between the two modes. A critical aspect of our study reveals how the interplay between dissipative and driven-dispersive squeezing mechanisms governs the system’s bandwidth and robustness against decoherence. Our findings provide a versatile framework for manipulating quantum correlations and squeezing in OMS, with applications in quantum metrology, sensing, and the engineering of nonclassical states. This work advances the understanding of squeezing synchronization and offers new strategies for enhancing quantum-coherent phenomena in dissipative environments.
Keywords:
optomechanical system; drive-loss engineering; synchronized squeezing; quantum discord; entanglement MSC:
81V80
1. Introduction
Cavity optomechanics, the study of interactions between electromagnetic fields and mechanical resonators, has emerged as a promising platform for generating and controlling non-classical states of both light and motion degrees of freedom [,,,,,,,]. A key objective in this field is the controlled generation of squeezing and quantum correlations, such as entanglement and quantum discord between the cavity and mechanical modes [,,,,,,,]. Achieving this goal demands a fundamental theoretical understanding and experimentally feasible approaches that preserve conceptual clarity and physical interpretability. Such advancements would pave the way for deeper explorations of quantum hybrid systems and their potential applications in quantum information processing, precision sensing, and foundational tests of quantum mechanics.
The generation of quantum squeezing in OMS has emerged as a key research direction, connecting fundamental quantum physics and applied quantum technologies [,,,,,,,,,,,,,]. Traditional approaches to squeezing in OMS have largely focused on single-mode squeezing, typically realized through drive-dissipation engineering [], dissipative optomechanical coupling [], kicked quadratic optomechanical coupling [], parametric amplification [], quantum measurement [,,,], or a combination of different techniques. Therefore, two principal mechanisms for the generation of such quantum states have been explored. One is through two-tone driving (red and blue cavity-detuned), where the cavity acts as an engineered dissipative reservoir, cooling specific Bogoliubov modes and allowing unconditional steady-state squeezing of the mechanical resonator []. This concept can be extended to multimode and entangled states by engineering a reservoir to simultaneously cool and entangle multiple mechanical or optical modes [,,].
A very detailed theoretical study of a two-tone-driven optomechanical system with backaction-evading (BAE) measurements was presented in []. By going beyond standard analytical approximations—such as the rotating-wave approximation (RWA) and adiabatic cavity elimination—the authors predicted the simultaneous generation of mechanical squeezing, intra-cavity squeezing, and optomechanical entanglement. Similar schemes have been both theoretically developed [,] and experimentally demonstrated, e.g., in [] the authors employed a reservoir engineering technique with two-tone driving to generate and stabilize a quantum squeezed state in a mechanical oscillator. Their results demonstrated squeezing of dB below the zero-point level, surpassing the conventional 3 dB limit. Further works examine the robustness of these strategies under non-ideal conditions, such as in the unresolved sideband regime [], and explore multimode entanglement in hybrid systems [,].
Another major mechanism relies on the parametric effects, in which direct modulation of the mechanical or cavity frequency at twice its resonance frequency implements degenerate parametric amplification. This process can generate strong single-mode squeezing, as analysed in early theoretical proposals using modulated driving fields [,] and further explored with mechanical non-linearities such as Duffing-type interactions []. Additional proposals combine drive-dissipative engineering and parametric mechanisms, leveraging their joint action to enhance and stabilize squeezing or entanglement beyond what is achievable with either approach alone [,,,,]. For example, the theoretical work in [] proposed a hybrid scheme combining two-tone driving with parametric pumping to enhance mechanical squeezing. This joint mechanism not only breaks the 3 dB limit but also improves robustness against thermal noise and mechanical decay. However, challenges remain in optimizing such systems. The study in [] identified a new type of optomechanical instability arising in two-tone BAE measurements. This instability imposes fundamental limitations on measurement sensitivity due to parametric effects, even when intra-cavity fields are perfectly balanced. Addressing these limitations requires refined control strategies. In this direction, ref. [] demonstrated how optimal control theory can maximize mechanical squeezing in a two-tone driven OMS while minimizing the protocol duration. Their findings reveal that the minimal achievable squeezing time is lower-bounded by the inverse cavity decay rate for autonomous drives. The study also provides key insights into the factors limiting squeezing and simplifies the time dependence of external drives, making the protocol experimentally feasible.
A particularly compelling extension of the squeezing paradigm is the joint squeezing of photon and phonon modes [,,,]. This phenomenon is intrinsically linked to the emergence of quantum correlations between these modes and enables measurement precisions that surpass classical limits. Such advancements are crucial for applications in quantum metrology, sensing, and information processing. Therefore, generating dual-mode squeezing, where both the optical and mechanical quadratures simultaneously exhibit noise reduction, remains a significant challenge due to several factors: (i) competing noise sources, such as thermal fluctuations and quantum back-action; (ii) dissipation asymmetry between the cavity and mechanical modes, leading to uneven decoherence rates; and (iii) the need for a delicate balance between amplification and cooling effects to maintain the squeezed correlations. To the best of our knowledge, no reported results have shown synchronized squeezing of both mechanical and optical modes or observed this effect through quantum discord in either (i) a two-tone driven OMS coupled to thermal baths, or (ii) a one-tone driven OM cavity connected to a photon squeezed bath. Our proposal thus uncovers new intrinsic features of driven-dissipative OMSs, paving the way for engineering optimal simultaneous and correlated mechanical-optical squeezing.
In this work, we investigate the synchronized squeezing between the cavity and mechanical modes induced by drive-loss engineering, where two coherent fields drive the cavity mode. Throughout this manuscript, we use the term synchronized squeezing to describe the dynamical phenomenon in which squeezing in both the cavity and mechanical modes occurs not only simultaneously, but also exhibits identical or strongly correlated temporal evolution in magnitude. The term synchronized aptly conveys the notion of an actively co-evolving relationship, where the squeezing in one mode is intrinsically linked to and reflects the behaviour of the other. We discuss in detail the conditions necessary for generating and synchronizing squeezing between the cavity and mechanical modes. The application of two distinct drive fields, tuned to the blue and red sidebands of the OMS, introduces an asymmetry in the system structure, enabling the emergence of quantum correlations. The interplay between coherent driving and dissipation results in squeezing in both the cavity and mechanical quadratures, eventually reaching a steady-state regime. This study demonstrates through numerical simulation and theoretical analysis that the squeezing can be flexibly controlled by adjusting the ratio of effective optomechanical coupling strengths and loss rates. Meanwhile, the robustness of synchronized squeezing against environmental temperature fluctuations can be significantly enhanced by optimizing loss ratios. The key findings of this study demonstrate the successful realization of drive-loss engineering for efficient photon and phonon squeezing synchronization. In particular, our scheme bypasses the need for non-linear parametric amplification [,,], offering a more robust and experimentally feasible alternative. Furthermore, we show that the emergence of synchronized squeezing can be effectively witnessed and characterized through the behaviour of Quantum Discord, providing a reliable indicator of nonclassical correlations.
This paper is structured as follows. In Section 2, we introduce the physical model of an OMS driven by two coherent optical fields. We derive the system’s effective Hamiltonian, emphasizing the key phenomenon of two-mode squeezing, which underpins the quantum correlations in the OMS. Section 3 details the derivation of the dynamical equation governing the covariance matrix of the system’s quadrature operators. Here, we also define the key metrics used to quantify quantum correlations and squeezing in the OMS. In Section 4, we present our main results, analysing both the dynamical evolution and steady-state behaviour of quantum correlations and squeezing between the optical cavity and the mechanical oscillator. In Section 5, we explore an alternative scenario, where the system can be driven by one field and interacting with a squeezing reservoir to reach the synchronized squeezing. We compare its effects with those of the original model, assessing how reservoir engineering influences quantum correlations. Finally, Section 6 summarizes our findings, discusses their implications, and outlines potential directions for future research in quantum optomechanics.
2. Physical Model
Let us consider the OMS schematically illustrated in Figure 1a. The system consists of an optical cavity with resonance frequency , coupled to a mechanical oscillator (MO) of frequency . The strength of the radiation pressure interaction between the cavity field and the mechanical mode is quantified by the single-photon optomechanical coupling constant g. In this setup, the system is driven by a two-tone laser field with frequencies denoted by (). The corresponding drive amplitudes are given by , where represents the decay rate of the optical cavity and P is the power of the external pump driving the system. These drive amplitudes quantify the strength of the coherent input fields interacting with the cavity mode at each frequency component. In the frame rotating at the cavity frequency , the system Hamiltonian takes the form (with ):
where, a () and b () denote the annihilation (creation) bosonic operators of the cavity and MO modes, respectively, and satisfying the usual canonical commutation relations and . Throughout this work, all parameters in the frequency and time domains are normalized to the mechanical oscillator frequency . For numerical simulations, we set , ensuring that all quantities are expressed in dimensionless units.
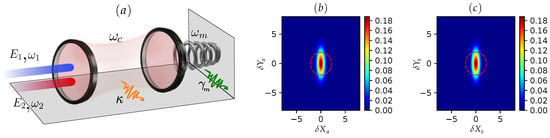
Figure 1.
(a) An OMS driven by two coherent fields tuned to the blue and red sidebands, i.e., at frequencies and , respectively. Wigner function visualization of (b) cavity and (c) MO illustrate the simultaneous squeezing effect for the conditions defined in Figure 3d. For visual comparison with the squeezed state, the red dashed line denotes a thermal state.
Considering the effects of mechanical damping, optical cavity decay, and environmental noise, the system’s evolution is accurately described by a set of nonlinear quantum Langevin equations (QLEs). These equations capture the interplay between coherent dynamics and dissipation, providing a detailed framework for analysing the open quantum behaviour of the coupled system.
where is the decay rate of the MO mode. Here is the input noise operator, satisfying the non-zero correlation functions []:
where and denote the average thermal excitations of the cavity and MO, respectively, at environmental temperature T, with being the Boltzmann constant.
By imposing the resonance conditions and , we selectively address the blue and red sidebands of the OMS, respectively. Under these conditions, we can derive an effective Hamiltonian by applying the rotating wave approximation (RWA), which allows us to neglect rapidly oscillating terms. This approximation significantly simplifies the dynamics while retaining the essential physics of the interaction. Specifically, it captures the coherent interplay between the optical and mechanical modes, mediated by simultaneous red and blue sideband processes. As a result, the system exhibits non-trivial quantum effects such as two-mode squeezing, which is central to the generation of quantum correlations and squeezed states in the OMS. The detailed derivation and assumptions leading to this effective Hamiltonian are provided in Appendix A.
where and represent the effective optomechanical coupling strengths associated with the drive fields through the mean amplitudes , as defined in Equation (A5).
In the following section, we define the key measures employed to quantify nonclassical correlations within the framework of the QLEs. These quantifiers form the basis for our investigation into the dynamics and steady-state of quantum correlations and squeezing phenomena in the OMS setups considered in this work. Specifically, we focus on Entanglement and Quantum Discord as tools to characterize the quantum correlations. In parallel, we explore the conditions for the optimal generation of squeezed states, with particular emphasis on the simultaneous squeezing of both the cavity and MO quadratures. This dual-mode squeezing introduces complex dynamics that can substantially affect the strength and character of nonclassical correlations within the system.
3. Methods
3.1. Dynamics of Quantum Fluctuations
To investigate the dynamics of quantum fluctuations in greater depth, we employ the effective Hamiltonian defined in Equation (6) to derive the set of QLEs governing the fluctuation operators:
In what follows, we introduce the cavity and mechanical quadratures, defined as and , where . The corresponding noise quadratures are given by and .
The Langevin equation can be expressed in a more compact matrix form: , where is a column vector of the system fluctuation operators, and is the corresponding noise operator vector. is the drift matrix governing the system’s dynamics with its explicit form given by:
The stability of the system, in compliance with the Routh-Hurwitz criterion, requires that all eigenvalues of the matrix possess strictly negative real parts [], see details in Appendix C. Due to the linearity of the Langevin equation and the Gaussian nature of the quantum noise, the system asymptotically relaxes to a stable Gaussian state. This state is fully characterized by its covariance matrix [], defined in phase space as: , . The time evolution of the covariance matrix is described by the following equation:
where denotes the transpose of , and the elements of the diffusion matrix are defined by the relation: Therefore, the form of the diffusion matrix becomes:
where the matrix elements are given by: , and , (where denotes the zero matrix, and is the identity matrix).
3.2. Quantifying Quantum Correlations in OMS
In this work, we investigate quantum correlations—specifically entanglement, quantum discord, and quadrature squeezing in the cavity and MO modes. Understanding these correlations is crucial for applications in quantum information processing, metrology, and the development of hybrid quantum systems. To quantify these effects, we employ the covariance matrix , which fully characterizes the Gaussian state of the system and is defined as follows:
where , , and are sub-block matrices of .
3.2.1. Gaussian Entanglement
To quantify the entanglement between the cavity and mechanical modes, we employ the logarithmic negativity , a well-established measure of quantum entanglement for mixed states [,]. This quantity, derived from the negativity of the partially transposed density matrix, is defined as:
where and , with , , , and being symplectic invariants.
3.2.2. Gaussian Quantum Discord
Quantum Discord () is a measure of quantum correlations that extends beyond entanglement, capturing nonclassical interactions even in separable states. Unlike entanglement-based measures, quantifies the disturbance induced by local measurements, revealing quantumness in correlations that classical theories cannot explain. For the Gaussian bipartite system under consideration, the Gaussian is given by [,]:
where the function f is defined as
and
are the two symplectic eigenvalues of , with and
3.2.3. Squeezing
The degree of squeezing in the quadratures of the photon and phonon modes can be quantified in decibels (dB) using the following expression:
where or represents the quadrature fluctuations, and corresponds to the vacuum noise level. A positive squeezing degree () indicates the presence of photon or phonon squeezing, signifying reduced quantum noise below the vacuum limit in the measured quadrature. In general, squeezing levels above 3 dB are considered indicative of strong quantum squeezing.
4. Results
In this section, we analyse the conditions for achieving tunable squeezing in both the cavity and mechanical modes of the OMS. By examining the interplay between driving, dissipation, and coupling strengths, we identify critical thresholds for the emergence of quantum correlations and squeezing, as well as their dynamical evolution.
4.1. Emergence of Quantum Correlations and Squeezing
Figure 2 depicts the evolution of quantum correlations (quantified by and ) and amplitude Squeezing (), as functions of the effective drive-coupling ratio . At low drive-coupling ratios (), the quantum correlations remain suppressed due to dominant losses from the cavity and mechanical oscillators into their respective reservoirs. However, once exceeds this threshold, a gradual buildup of correlations between the cavity field and the mechanical oscillator becomes evident, see Figure 2a,b. This onset indicates that a minimal degree of asymmetry in the coupling strengths is necessary to overcome dissipative noise and enable the emergence of intermode correlations. As the ratio increases further, the system exhibits a progressive enhancement of these correlations, with a clear development of coherence between the cavity field and the MO. This trend highlights the pivotal role of the coupling ratio in mediating and tuning nonclassical correlations within the system.
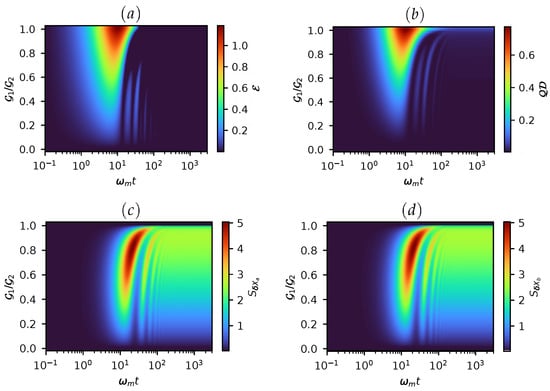
Figure 2.
The evolution of quantum correlations and squeezing (in dB) is analysed as a function of the coupling strength ratio , with the dissipation rates set to . (a) Entanglement ; (b) Quantum Discord ; Squeezing: (c) cavity mode , and (d) MO mode . Other parameters are: , .
Concurrently, the competition between coherent driving and dissipation gives rise to squeezing in both the cavity and mechanical modes. Figure 2c,d demonstrate how this squeezing evolves dynamically, eventually reaching a steady-state regime. For instance, in Figure A1, the case of exemplifies the dynamics where significant squeezing is achieved. During this process, quantum correlations initially rise to a maximum before decaying as the squeezing stabilizes into a steady state. However, there exists a loss regime, e.g., , where finite steady-state entanglement and QD coexist with squeezing for a given ratio, as illustrated in Figure 4b and Figure A1. Additional results and analysis are provided in Appendix B. These findings highlight the intricate and interdependent relationship between the degree of squeezing and the strength of quantum correlations. The dynamic interplay between these two phenomena—governed by the balance between external driving and system losses—offers valuable insights into the mechanisms underlying the emergence and stabilization of nonclassical steady states in driven open quantum systems. All of this not only reflects the interrelation of quantum correlations and squeezing but also underscores how engineered dissipation and coherent control can be harnessed to tailor quantum resources.
4.2. Decay of Squeezing at Strong Coupling Ratios
Interestingly, when the coupling ratio approaches unity (e.g., ), the system enters a regime where squeezing of both cavity and MO modes begins to diminish. This reduction is due to the intensified interaction with the dual drives, which destabilizes the squeezing mechanism while still preserving a residual amount of quantum discord, as indicated in the upper range of Figure 2b. The persistence of despite the decay of squeezing points to a partial retention of quantum correlations, where , underscoring the robustness of discord against certain forms of decoherence [,,]. Therefore, these results demonstrate that the coupling asymmetry serves as a powerful control parameter for tuning both squeezing and quantum correlations in the system. The development, stabilization, and eventual suppression of these quantum features illustrate the subtle interconnection between coherent dynamics and dissipative effects, providing valuable perspectives for the advancement of quantum technologies based on optomechanical systems.
4.3. Controlling Squeezing via Pump and Losses for Cavity–Mechanics Synchronization
To achieve synchronized squeezing of the same quadrature in the cavity and mechanical modes, we find that it is advantageous to operate in the regime , as illustrated in Figure 2c,d, and to maintain a balanced loss rate with . In this regime, the interconnection between the optical and mechanical modes supports coherent energy exchange and correlated squeezing dynamics. To more clearly visualize the squeezing behavior, the Wigner function is especially useful, offering an intuitive phase-space representation of the state that reveals both the degree and orientation of squeezing in each mode. The Wigner function can be expressed as shown in []:
where represents the 2D vector, and is the corresponding covariance matrix (where ).
The squeezing dynamics reveal fundamental constraints imposed by dissipation ratios. In the top panel of Figure 3, we observe that strong steady-state phonon squeezing (>3 dB) occur when the cavity decay rate dominates over the mechanical damping , i.e . This regime benefits from the cavity’s enhanced ability to mediate squeezing interactions before mechanical dissipation destroys quantum coherence. Conversely, the bottom panel of Figure 3 demonstrates a qualitatively different behaviour: optimal squeezing synchronization between optical and mechanical modes occurs precisely at the critical balance point . This equality condition suggests a resonant energy exchange regime where dissipation matching enables: (i) phase-coherent coupling between modes, and (ii) balanced quantum noise redistribution essential for joint squeezing. The inset in Figure 3d presents a magnified view that clearly demonstrates both and remain strictly positive during the early stages of the dynamics. A similar behaviour occurs in the case presented in Figure 3a.
The squeezing synchronization at represents a fundamental trade-off, while individual mode squeezing may not be maximized here, the system achieves maximal cooperativity in its quantum noise suppression. In Section 5, we discuss how certain experimental techniques enable dissipation engineering in the regime ∼. Alternatively, we propose a different model configuration, where synchronized squeezing can be realized for , a condition frequently encountered in optomechanical experiments.
4.4. Steady-State Squeezing
In this section, we explore the relationship between steady-state squeezing and quantum correlations. Specifically, we analyse how these quantities are interrelated when the system reaches its long-time limit. In this regime, the covariance matrix satisfies the Lyapunov Equation (10) in the form
Figure 4 presents the steady-state behaviour of cavity/MO squeezing and quantum correlations as functions of the loss rate ratio for specific values of the drive-coupling ratio , extracted from the broader parameter space depicted in the colour map of Figure A2 (Appendix B). These results reveal a clear dependence on the dissipation balance between the two subsystems. One finds in Figure 4, that the cavity squeezing is enhanced when the cavity losses are lower than those of the mechanical mode (see left panel where ). Conversely, MO squeezing is favoured when the mechanical damping is lower than the cavity decay (see right panel where ). Interestingly, optimal synchronization of squeezing of the cavity and mechanical modes coincides with the maximum quantum correlations, as shown in the central panel of Figure 4. This synchronization peak occurs precisely when the loss rates are balanced, i.e., .

Figure 3.
Tunable squeezing (in dB) through dissipation rate control. (a) Phonon squeezing with asymmetric dissipation rates (, ), showing enhanced mechanical squeezing due to suppressed phonon decoherence. (b,e) and (c,f) Wigner function of the final states of cavity and MO, respectively. (d) Simultaneous photon and phonon squeezing under balanced dissipation (), revealing optimal squeezing synchronization (overlapping of red and blue lines) between optical and mechanical modes. The inset in (d) presents a magnified view that clearly demonstrates both and remain strictly positive during the early stages of the dynamics. All other parameters match those in Figure 2.
For instance, a marked increase in quantum correlations is observed in the region where squeezing synchronization reaches its optimum. Importantly, emerges as a particularly sensitive indicator: it exhibits a sharp rise as squeezing begins to degrade due to system losses. This observation is consistent with the findings reported in Ref. [], where becomes nonzero while synchronization remains optimal, even though entanglement () is still absent. In conclusion, this highlights the role of as a valuable witness to the interplay between dissipation and nonclassical correlations in open quantum systems. Additional results and analysis are provided in Appendix C.
We also explore how the thermal environment affects the squeezing properties of both the cavity and mechanical modes. As shown in Figure 5, optimal squeezing occurs when the average thermal occupation is low, specifically for . These conditions are experimentally achievable in state-of-the-art platforms. For example, OMSs operating in the microwave regime—such as those in Refs. [,]—typically feature mechanical frequencies around . At cryogenic temperatures near T∼, the thermal phonon population can be suppressed to , creating favourable conditions for the observation of squeezing.
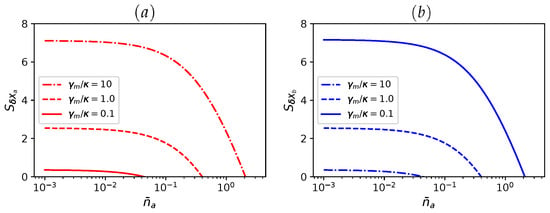
Figure 5.
Steady-state squeezing (in dB): (a) cavity mode , and (b) MO mode as a function of thermal excitations, where , for and different values. Other parameters are the same of Figure 2.
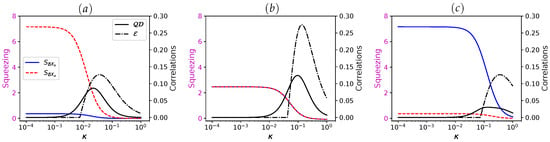
Figure 4.
Steady-state squeezing (in dB, color lines) and quantum correlations (black lines): (a) , (b) , and (c) . Other parameters are the same of Figure 2.
Conversely, when the average thermal excitation exceeds , a notable degradation in squeezing is observed in both modes, eventually leading to its complete suppression, as shown in Figure 5. This trend underscores the harmful effects of thermal noise on quantum coherence and highlights the critical importance of low-temperature environments for preserving features such as squeezing in OMS.
5. Discussion and Outlook
To illustrate the practical applicability of our theoretical framework, we examine an alternative approach for inducing synchronization-like squeezing between the cavity and MO, and contrast it with our original two-tone driving scheme, in which this phenomenon is more easily realized owing to the presence of the thermal reservoirs for both subsystems. In this alternative model, we propose a cavity coupled to a squeezed photon reservoir [,], where the generation of squeezing can be controlled by tuning the driving fields—for instance, by selecting either a single drive or two drives.
Using the covariance matrix formalism (introduced in Section 3.2 and derived for this specific case in Equation (A14) of Appendix D), we investigate the dynamics of squeezing and quantum correlations. The time evolution of squeezing is shown in Figure 6a, which reveals that significant cavity and MO squeezing only emerges when the squeezing parameter r is sufficiently large, see Figure 6b,c. It is worth noting that this effect can be achieved with either coherent single- or two-tone cavity driving, as demonstrated in Figure 6b,c. These plots show how the steady-state squeezing of both modes depends on the ratio and the parameter r, which characterizes the degree of squeezing in the photon reservoir. A particularly striking result is that strong mechanical squeezing persists even with only a single active drive (i.e., and ), with the squeezing of cavity and MO enhancing progressively as r increases. This finding highlights the critical role of input squeezing and asymmetrical driving in engineering nonclassical steady states, offering different strategy for the control of quantum effects in OMS.
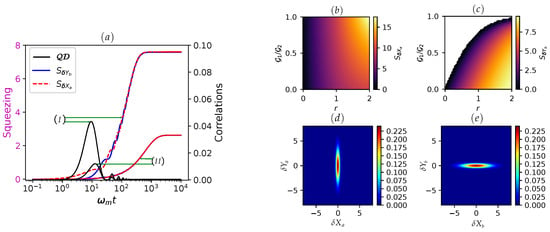
Figure 6.
(a) Dynamics of cavity and MO squeezing (in dB, color lines) and quantum correlations (black lines) for for cases: , and . Density plot of (b) cavity mode , and (c) MO mode as a function of ratios and squeezing parameter r of the cavity bath. Wigner function visualization for the final states of (d) cavity and (e) MO. Here, we observe that optimal squeezing synchronization (overlapping of red and blue lines) between cavity and MO modes occurs with one drive under the squeezed photon reservoir. Other parameters are: , , , and .
Figure 6d,e presents the steady-state phase-space Wigner representation of the system. A key observation is that the mechanical mode exhibits squeezing along the Y-quadrature, whereas the cavity mode displays squeezing along the X-quadrature. This asymmetry in quadrature squeezing can be attributed to the distinct types of reservoirs each subsystem interacts with: the cavity is coupled to a squeezed photon reservoir, while the MO is connected to a thermal reservoir.
In Figure 7, we investigate the impact of introducing a second drive. The panel Figure 7a shows that competition between the two drives disrupts the synchronization of squeezing between the cavity and the mechanical mode, thus altering their collective dynamics. Panel Figure 7b, however, reveals that optimal synchronized squeezing is reached with single-tone drive of the cavity, and also is associated with enhanced quantum correlations. As in the previous case, here also acts as a sensitive witness of the optimal synchronized squeezing, i.e., it emerges when the synchronization disappears, moreover the MO squeezing starts to decay meanwhile cavity squeezing increases as function of the rate , because the back action effect of the photon squeezed reservoir.
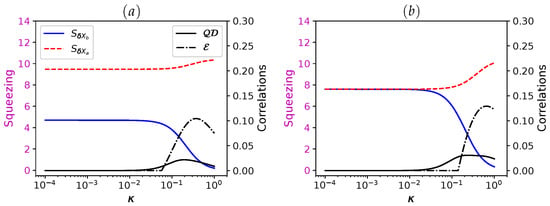
Figure 7.
Steady-state squeezing (in dB, color lines) and quantum correlations (black lines): (a) and (b) . Other parameters are the same of Figure 6.
As in the previous case, also serves as a sensitive indicator of optimal synchronized squeezing, emerging precisely when synchronization breaks down. Remarkably, the mechanical squeezing begins to decay due to decoherence as it interacts with its thermal reservoir, given that . Meanwhile the cavity squeezing increases with the rate , driven by the back-action from the squeezed photon reservoir.
Taken together, these findings illustrate how the interplay between three key factors—cavity reservoir squeezing, drive asymmetry, and coupling strengths—governs both the emergence and robustness of cavity and mechanical squeezing and quantum correlations. This insight provides practical strategies for manipulating nonclassical states in reservoir-engineered OMS.
Finally, we provide a brief discussion on the experimental feasibility of our proposed schemes, outlining the key requirements, potential challenges, and possible implementation strategies within current optomechanical platforms. In the first OMS scheme we analysed, featuring two coherent drives and coupling of both the cavity and the mechanical oscillator to their respective thermal reservoirs, the crucial effect of photon and phonon squeezing synchronization is achieved under the specific condition . This requirement is particularly uncommon in standard OMS, where typically due to the intrinsically low mechanical damping compared to the optical cavity loss. However, such a regime can realistically be expected in certain specialized platforms [,,]. In particular, ultrahigh-Q optical cavities—such as whispering gallery mode resonators and photonic crystal cavities—exhibit extremely low optical losses, effectively reducing to values comparable to . Similarly, in microwave cavity optomechanics (e.g., superconducting circuits coupled to mechanical resonators), photon losses can be engineered to be exceptionally low, again enabling to approach .
All other parameters considered in our model lie well within the range of current experimental capabilities. For instance, the effective couplings can be directly tuned via the driving field amplitude E, and no strong single-photon optomechanical coupling is required. Therefore, this aspect does not pose significant experimental difficulty. The photon loss rate used throughout the manuscript, , is fully compatible with the resolved-sideband regime and aligns with the experimental parameters outlined in the review by Aspelmeyer et al. []. All these conditions provide a favourable platform for observing the predicted squeezing effects.
Moreover, it is possible to intentionally engineer mechanical dissipation in hybrid architectures by coupling the mechanical mode to a designed dissipative bath. Techniques such as active feedback cooling, coupling to auxiliary resonators, or embedding the mechanical mode within tailored thermal environments can be used to enhance the effective mechanical loss rate . This dissipation engineering provides an additional experimental handle for accessing the ∼ regime, thereby facilitating the observation of synchronized photon-phonon squeezing. Under the comparable loss condition , it becomes possible to access a variety of alternative quantum effects beyond synchronized squeezing. These include photon-photon [] and photon-phonon [] asymmetric quantum steering, phonon-photon conversion processes that enable efficient cooling and coherent information transfer [], and the optomechanical preparation of photon number-squeezed states [], among others. Such phenomena highlight the rich landscape of quantum dynamics that can emerge when the mechanical and optical dissipation rates are carefully balanced.
As a natural extension of this work, further investigations could explore additional quantum effects linked to squeezing synchronization in asymmetrically driven optomechanical systems, such as the recently demonstrated phenomenon of asymmetric one-way steering []. Beyond this, other yet-uncovered nonclassical features may emerge in such driven-dissipative settings, offering fertile ground for discovery. This direction not only deepens our understanding of quantum dynamics but also opens intriguing possibilities for quantum control and information processing. Future studies may reveal unexpected phenomena, further enriching the interplay between nonlinear optomechanics, quantum synchronization, and open quantum systems.
6. Conclusions
Our study elucidates the complex relationship between squeezing and quantum correlations—specifically entanglement and quantum discord—in an optomechanical system, highlighting how these quantum features can be precisely controlled by tuning key system parameters. Focusing on a driven-dissipative OMS, we identify the conditions under which squeezed states emerge and become synchronized between the cavity and mechanical oscillator modes. As a key result, we show that in the configuration where the OMS is driven by two coherent fields and both the cavity and mechanical oscillator are coupled to thermal reservoirs, simultaneous squeezing of photon and phonon modes emerges from a delicate interplay among the coherent interference of the driving fields, the optomechanical coupling strength, and the ratio between cavity and mechanical dissipation rates. A comprehensive steady-state analysis offers deeper insight into the fundamental mechanisms underlying these effects, showing how the effects of amplification and noise competition, jointly contribute to the emergence of robust quantum correlations.
We further demonstrate that synchronized squeezing in the conjugate quadratures of the cavity and mechanical modes can be achieved even in a single-tone driven system, provided the cavity is coupled to an engineered squeezed reservoir. In this configuration, the reservoir compensates for the absence of a second driving tone by injecting directional quantum noise, thereby enabling the formation of steady-state squeezing correlations between the two modes. Effectively, the engineered reservoir serves as an external control mechanism, allowing for robust manipulation of quantum states within the one-tone driving scheme.
Interestingly, we find that the effect of synchronized squeezing can be effectively detected and quantified through the behaviour of quantum discord, which serves as a reliable and accessible indicator of nonclassical correlations within the system. This conclusion is consistent with findings from other configurations studied in the context of synchronization effects, e.g., []. Our findings not only deepen the understanding of quantum optomechanics but also open new avenues for the controlled manipulation of photon-phonon correlations and synchronized squeezing. These advances hold significant promise for applications in quantum sensing, noise-resistant quantum communication, and the development of hybrid quantum technologies. Therefore, this work contributes to the broader effort of harnessing OMS for next-generation quantum devices, where precise control over squeezing and correlations is essential.
Author Contributions
Conceptualization, analytical and numerical calculations, writing of original draft, H.M. and V.E. All authors have read and agreed to the published version of the manuscript.
Funding
H.M. acknowledges Universidad de La Frontera and partial financial support from the project “Implementación de una unidad interdisciplinar para el desarrollo de Tecnologías Aplicadas y Ciencias (InTec)”, Code “FRO2395”, from the Ministry of Education of Chile. V.E. acknowledges partial financial support from ANID Fondecyt Regular No. 1221250.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Derivation of the Effective Hamiltonian
The standard linearization procedure is applied by expressing each operator as the sum of its steady-state mean value and quantum fluctuation, i.e., . Substituting this decomposition into Equations (2) and (3) leads to:
Consequently, the standard quantum Langevin equations for the fluctuation operators take the form:
Given that the cavity mode’s amplitude is primarily concentrated at the two-tone driving frequencies and , we approximate the steady-state cavity field as . Moreover, in many experimental setups where the optomechanical coupling strength g is weak, the term contributes negligibly and can thus be safely omitted from the governing equations. Under these approximations, we derive the mean-field amplitudes and , which characterize the cavity’s response to the respective driving frequencies. These amplitudes read:
Using Equations (A3) and (A4), we derive the linearized Hamiltonian by expanding the system dynamics in terms of quantum fluctuation operators. This yields effective interaction terms around the classical averages, resulting in:
Next, we apply the rotating frame defined by the unitary transformation , to obtain:
where and denote the effective optomechanical coupling strengths induced by the drive fields. Without loss of generality, we take to be real and positive. Under the resonance conditions and , the system is described by the effective Hamiltonian:
Under the rotating wave approximation (RWA), the effective Hamiltonian reduces to the form:
Appendix B. Dynamics of Quantum Correlations and Squeezing
In Figure A1, we present the time evolution of quantum correlations and squeezing as a function of the cavity decay rate , under the condition , and for a fixed coupling ratio . The dynamics reveal two distinct regimes governed by the level of dissipation.
In the low-dissipation regime (), quantum correlations ( and ) initially rise, reach significant values, and then gradually decay at long times. In this same regime, Squeezing is initiated shortly after the peak of quantum correlations, evolves dynamically, and eventually stabilizes to a steady-state value. This stabilization marks the onset of cavity-mechanical synchronization due to the condition , clearly visualized in the bottom-right region of the plot with calypso colouring.
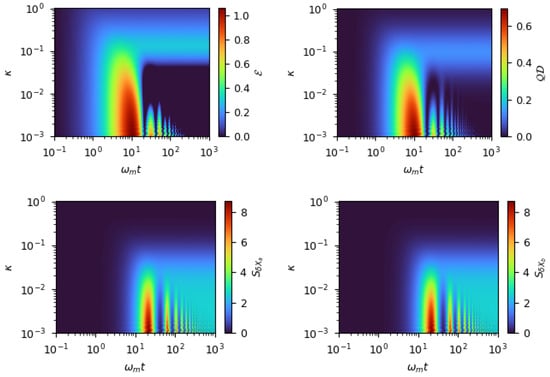
Figure A1.
Density plots illustrating the time evolution of quantum correlations and squeezing (in dB) as a function of the cavity decay rate , under the condition and for a fixed coupling ratio . Other parameters are identical to those used in Figure 2.
In contrast, in the high-dissipation regime (), quantum correlations no longer vanish but instead settle into finite steady-state values—approximately and . However, in this region, squeezing is significantly suppressed, as indicated by (see the dark-blue region in the top-right corner of the lower panel in Figure A1).
These findings highlight that quantum correlations act as a sensitive probe for identifying and characterizing the onset and stabilization of synchronized optomechanical squeezing in this parameter regime.
Appendix C. Steady-State Squeezing Analysis: Drive vs. Losses
According to the Routh–Hurwitz criterion, the system is stable if all the eigenvalues of the drift matrix have negative real parts. For the matrix A defined in Equation (9) of the main text, the eigenvalues are given by:
Since the parameters are strictly positive, the solutions in Equation (A10) satisfy the Routh–Hurwitz (RH) stability criterion. In contrast, solutions in Equation (A11) satisfy the RH criterion under the constraint:
Throughout the manuscript, we have consistently considered the relation , which is fully compatible with the constraint Equation (A12). Therefore, we conclude that the parameter regime adopted in this study ensures the existence of a stable steady-state.
In Figure A2, we present a detailed density plot illustrating the steady-state behaviour of both squeezing and quantum correlations as functions of the drive-optomechanical coupling ratio and the loss ratio . This two-dimensional landscape provides a comprehensive view of how the interplay between coherent coupling and dissipation influences the emergence and stabilization of nonclassical correlations and synchronized squeezing in the OMS. In the first row, where cavity squeezing is shown, we observe a clear enhancement when the cavity dissipation is lower than that of the mechanical mode (). Conversely, in the second row, the mechanical oscillator exhibits stronger squeezing in the opposite regime, i.e., when the cavity dissipation dominates (). This complementary behaviour highlights the role of dissipation tailoring in localizing squeezing to one subsystem.
The most striking behaviour emerges in the central panels, corresponding to the balanced dissipation case (). Here, we observe the emergence of synchronized squeezing—simultaneous and time-correlated squeezing in both the optical and mechanical modes. This balanced regime also coincides with the maximal build-up of quantum correlations, as previously seen in Figure A1, confirming that balanced drive-loss conditions promote coherent quantum interactions between the subsystems.
Remarkably, quantum discord continues to serve as a highly sensitive indicator of nonclassical behaviour in this case. It not only captures the emergence and enhancement of quantum correlations beyond Entanglement, but also reliably monitors the degradation of squeezing as system losses increase. This makes it a robust and insightful witness for both the onset and breakdown of quantum synchronization between cavity and mechanical modes, even in regimes where other indicators may fail to detect subtle quantum features.
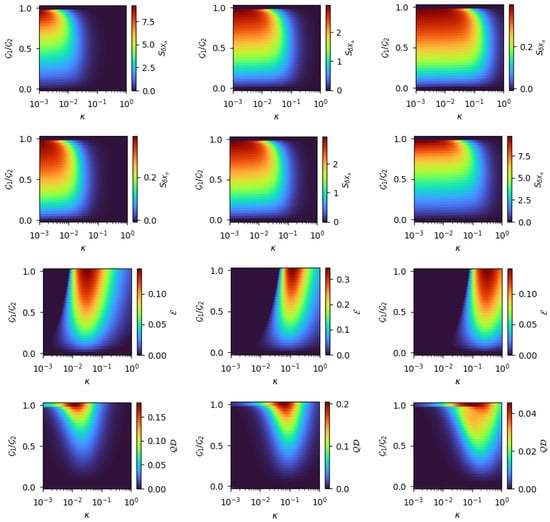
Figure A2.
Density plots illustrating the steady-state squeezing (in dB) and quantum correlations. (Left panel) , (center panel) and (right panel) . Other parameters are identical to those used in Figure 2.
Appendix D. Synchronized Optomechanical Squeezing via Single Drive and Squeezed Photon Reservoir
In this Appendix, we explore an alternative configuration for generating squeezing and inducing synchronization between the cavity and mechanical modes. Specifically, we consider a scenario in which the cavity is coherently driven by one or two fields, while the mechanical oscillator remains coupled solely to its thermal reservoir, as described in the main text (see Equations (4)). Distinct from the configuration studied earlier, the cavity is now incoherently coupled to a squeezed photonic reservoir.
In this setup, the input noise operator acquires modified statistical properties due to its transformation into the squeezed frame. This transformation is implemented by applying the squeezing operator , where is the squeezing parameter that quantifies the degree of reservoir squeezing. As a consequence, the cavity mode is subjected to nontrivial input noise correlations that differ from the standard thermal or vacuum noise and play a significant role in shaping the quantum dynamics of the coupled OMS. These altered noise correlations lead to an effective modification of the system’s dissipative dynamics, enabling the engineering of enhanced steady-state squeezing in both the cavity and mechanical modes. Interestingly, this configuration supports the emergence of squeezing synchronization, a regime in which both modes exhibit correlated squeezing along orthogonal quadratures, despite being coupled to reservoirs with fundamentally different statistical properties.
This analysis reveals that by tuning the squeezing parameter r and the relative strengths of the coherent drives, it is possible to access new regimes of nonclassical behavior and improved synchronization between the photonic and phononic subsystems. The corresponding noise correlation functions in the squeezed frame take the form []:
Building upon the considerations outlined above, we now derive the dynamical equation governing the evolution of the covariance matrix , which takes the form:
where drift matrix is defined in Equation (9), and for the diffusion matrix we get, This equation captures the interplay between coherent quantum interactions and dissipative processes within the system, providing a fundamental basis for investigating quantum correlations and squeezing dynamics in the optomechanical framework considered here.
References
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 2008, 321, 1172–1176. [Google Scholar] [CrossRef] [PubMed]
- Kronwald, A.; Marquardt, F.; Clerk, A.A. Arbitrarily large steady-state bosonic squeezing via dissipation. Phys. Rev. A 2013, 88, 063833. [Google Scholar] [CrossRef]
- Woolley, M.J.; Clerk, A.A. Two-mode squeezed states in cavity optomechanics via engineering of a single reservoir. Phys. Rev. A 2014, 89, 063805. [Google Scholar] [CrossRef]
- Bowen, W.P.; Milburn, G.J. Quantum Optomechanics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Lin, Q.; He, B.; Ghobadi, R.; Simon, C. Fully quantum approach to optomechanical entanglement. Phys. Rev. A 2014, 90, 022309. [Google Scholar] [CrossRef]
- Wollman, E.E.; Lei, C.U.; Weinstein, A.J.; Suh, J.; Kronwald, A.; Marquardt, F.; Clerk, A.A.; Schwab, K.C. Quantum squeezing of motion in a mechanical resonator. Science 2015, 349, 952–955. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Xuereb, A.; Gröblacher, S.; Paternostro, M.; Regal, C.A.; Weig, E.M. Optomechanics for quantum technologies. Nat. Phys. 2022, 18, 15–24. [Google Scholar] [CrossRef]
- Mancini, S.; Giovannetti, V.; Vitali, D.; Tombesi, P. Entangling Macroscopic Oscillators Exploiting Radiation Pressure. Phys. Rev. Lett. 2002, 88, 120401. [Google Scholar] [CrossRef]
- Wang, Y.D.; Clerk, A.A. Reservoir-Engineered Entanglement in Optomechanical Systems. Phys. Rev. Lett. 2013, 110, 253601. [Google Scholar] [CrossRef]
- Lei, C.U.; Weinstein, A.J.; Suh, J.; Wollman, E.E.; Kronwald, A.; Marquardt, F.; Clerk, A.A.; Schwab, K.C. Quantum Nondemolition Measurement of a Quantum Squeezed State Beyond the 3 dB Limit. Phys. Rev. Lett. 2016, 117, 100801. [Google Scholar] [CrossRef]
- Chen, Z.X.; Lin, Q.; He, B.; Lin, Z.Y. Entanglement dynamics in double-cavity optomechanical systems. Opt. Express 2017, 25, 17237–17248. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Sarma, A.K. Enhancing quantum correlations in an optomechanical system via cross-Kerr nonlinearity. J. Opt. Soc. Am. B 2017, 34, 1503–1510. [Google Scholar] [CrossRef]
- Ockeloen-Korppi, C.F.; Damskägg, E.; Pirkkalainen, J.M.; Asjad, M.; Clerk, A.A.; Massel, F.; Woolley, M.J.; Sillanpää, M.A. Stabilized entanglement of massive mechanical oscillators. Nature 2018, 556, 478–482. [Google Scholar] [CrossRef] [PubMed]
- Bemani, F.; Roknizadeh, R.; Motazedifard, A.; Naderi, M.H.; Vitali, D. Quantum correlations in optomechanical crystals. Phys. Rev. A 2019, 99, 063814. [Google Scholar] [CrossRef]
- Amazioug, M.; Maroufi, B.; Daoud, M. Creating mirror–mirror quantum correlations in optomechanics. Eur. Phys. J. D 2020, 74, 54. [Google Scholar] [CrossRef]
- Purdy, T.P.; Yu, P.L.; Peterson, R.W.; Kampel, N.S.; Regal, C.A. Strong Optomechanical Squeezing of Light. Phys. Rev. X 2013, 3, 031012. [Google Scholar] [CrossRef]
- Schnabel, R. Squeezed states of light and their applications in laser interferometers. Phys. Rep. 2017, 684, 1–51. [Google Scholar] [CrossRef]
- Mason, D.; Chen, J.; Rossi, M.; Tsaturyan, Y.; Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 2019, 15, 745–749. [Google Scholar] [CrossRef]
- Brunelli, M.; Malz, D.; Nunnenkamp, A. Conditional Dynamics of Optomechanical Two-Tone Backaction-Evading Measurements. Phys. Rev. Lett. 2019, 123, 093602. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Thourhout, D.V.; Baets, R.; Laer, R.V. Controlling phonons and photons at the wavelength scale: Integrated photonics meets integrated phononics. Optica 2019, 6, 213–232. [Google Scholar] [CrossRef]
- Aggarwal, N.; Cullen, T.J.; Cripe, J.; Cole, G.D.; Lanza, R.; Libson, A.; Follman, D.; Heu, P.; Corbitt, T.; Mavalvala, N. Room-temperature optomechanical squeezing. Nat. Phys. 2020, 16, 784–788. [Google Scholar] [CrossRef]
- Huber, J.S.; Rastelli, G.; Seitner, M.J.; Kölbl, J.; Belzig, W.; Dykman, M.I.; Weig, E.M. Spectral Evidence of Squeezing of a Weakly Damped Driven Nanomechanical Mode. Phys. Rev. X 2020, 10, 021066. [Google Scholar] [CrossRef]
- Maccone, L.; Riccardi, A. Squeezing metrology: A unified framework. Quantum 2020, 4, 292. [Google Scholar] [CrossRef]
- Xiong, B.; Li, X.; Chao, S.L.; Yang, Z.; Zhang, W.Z.; Zhang, W.; Zhou, L. Strong mechanical squeezing in an optomechanical system based on Lyapunov control. Photon. Res. 2020, 8, 151–159. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X. Photon-assisted entanglement and squeezing generation and decoherence suppression via a quadratic optomechanical coupling. Opt. Express 2020, 28, 2732–2743. [Google Scholar] [CrossRef]
- Li, B.B.; Ou, L.; Lei, Y.; Liu, Y.C. Cavity optomechanical sensing. Nanophotonics 2021, 10, 2799–2832. [Google Scholar] [CrossRef]
- Wu, Z.; Yi, Z.; Gu, W.; Sun, L.; Ficek, Z. Enhancement of Optomechanical Squeezing of Light Using the Optical Coherent Feedback. Entropy 2022, 24, 1741. [Google Scholar] [CrossRef]
- Marchese, M.M.; Belenchia, A.; Paternostro, M. Optomechanics-Based Quantum Estimation Theory for Collapse Models. Entropy 2023, 25, 500. [Google Scholar] [CrossRef]
- Gu, W.J.; Li, G.X.; Yang, Y.P. Generation of squeezed states in a movable mirror via dissipative optomechanical coupling. Phys. Rev. A 2013, 88, 013835. [Google Scholar] [CrossRef]
- Asjad, M.; Agarwal, G.S.; Kim, M.S.; Tombesi, P.; Giuseppe, G.D.; Vitali, D. Robust stationary mechanical squeezing in a kicked quadratic optomechanical system. Phys. Rev. A 2014, 89, 023849. [Google Scholar] [CrossRef]
- Szorkovszky, A.; Doherty, A.C.; Harris, G.I.; Bowen, W.P. Mechanical Squeezing via Parametric Amplification and Weak Measurement. Phys. Rev. Lett. 2011, 107, 213603. [Google Scholar] [CrossRef] [PubMed]
- Ruskov, R.; Schwab, K.; Korotkov, A.N. Squeezing of a nanomechanical resonator by quantum nondemolition measurement and feedback. Phys. Rev. B 2005, 71, 235407. [Google Scholar] [CrossRef]
- Clerk, A.A.; Marquardt, F.; Jacobs, K. Back-action evasion and squeezing of a mechanical resonator using a cavity detector. New J. Phys. 2008, 10, 095010. [Google Scholar] [CrossRef]
- Szorkovszky, A.; Brawley, G.A.; Doherty, A.C.; Bowen, W.P. Strong Thermomechanical Squeezing via Weak Measurement. Phys. Rev. Lett. 2013, 110, 184301. [Google Scholar] [CrossRef]
- Meng, C.; Brawley, G.A.; Bennett, J.S.; Vanner, M.R.; Bowen, W.P. Mechanical Squeezing via Fast Continuous Measurement. Phys. Rev. Lett. 2020, 125, 043604. [Google Scholar] [CrossRef]
- Gu, W.J.; Yi, Z.; Yan, Y.; Sun, L.H. Generation of Optical and Mechanical Squeezing in the Linear-and-Quadratic Optomechanics. Ann. Der Phys. 2019, 531, 1800399. [Google Scholar] [CrossRef]
- Zhang, R.; Fang, Y.; Wang, Y.Y.; Chesi, S.; Wang, Y.D. Strong mechanical squeezing in an unresolved-sideband optomechanical system. Phys. Rev. A 2019, 99, 043805. [Google Scholar] [CrossRef]
- Liao, C.G.; Chen, R.X.; Xie, H.; Lin, X.M. Reservoir-engineered entanglement in a hybrid modulated three-mode optomechanical system. Phys. Rev. A 2018, 97, 042314. [Google Scholar] [CrossRef]
- Molinares, H.; He, B.; Eremeev, V. Transfer of quantum states and stationary quantum correlations in a hybrid optomechanical network. Mathematics 2023, 11, 2790. [Google Scholar] [CrossRef]
- Nunnenkamp, A.; Børkje, K.; Harris, J.G.E.; Girvin, S.M. Cooling and squeezing via quadratic optomechanical coupling. Phys. Rev. A 2010, 82, 021806. [Google Scholar] [CrossRef]
- Liao, J.Q.; Law, C.K. Parametric generation of quadrature squeezing of mirrors in cavity optomechanics. Phys. Rev. A 2011, 83, 033820. [Google Scholar] [CrossRef]
- Lü, X.Y.; Liao, J.Q.; Tian, L.; Nori, F. Steady-state mechanical squeezing in an optomechanical system via Duffing nonlinearity. Phys. Rev. A 2015, 91, 013834. [Google Scholar] [CrossRef]
- You, X.; Li, Z.; Li, Y. Strong quantum squeezing of mechanical resonator via parametric amplification and coherent feedback. Phys. Rev. A 2017, 96, 063811. [Google Scholar] [CrossRef]
- Wu, X.J.; Cheng, H.H.; Wu, Q.; Bai, C.H.; Wu, S.X. Generation of strong mechanical squeezing through the joint effect of two-tone driving and parametric pumping. Opt. Express 2024, 32, 35663–35677. [Google Scholar] [CrossRef]
- Shomroni, I.; Youssefi, A.; Sauerwein, N.; Qiu, L.; Seidler, P.; Malz, D.; Nunnenkamp, A.; Kippenberg, T.J. Two-Tone Optomechanical Instability and Its Fundamental Implications for Backaction-Evading Measurements. Phys. Rev. X 2019, 9, 041022. [Google Scholar] [CrossRef]
- Halaski, A.; Krauss, M.G.; Basilewitsch, D.; Koch, C.P. Quantum optimal control of squeezing in cavity optomechanics. Phys. Rev. A 2024, 110, 013512. [Google Scholar] [CrossRef]
- Molinares, H.; Eremeev, V.; Orszag, M. High-fidelity synchronization and transfer of quantum states in optomechanical hybrid systems. Phys. Rev. A 2022, 105, 033708. [Google Scholar] [CrossRef]
- Gardiner, C.W.; Zoller, P. Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics; Springer: Berlin/Heidelberg, Germany, 2004; Available online: https://link.springer.com/book/9783540223016 (accessed on 30 April 2025).
- DeJesus, E.X.; Kaufman, C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 1987, 35, 5288–5290. [Google Scholar] [CrossRef]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical Entanglement between a Movable Mirror and a Cavity Field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Adesso, G.; Serafini, A.; Illuminati, F. Extremal entanglement and mixedness in continuous variable systems. Phys. Rev. A 2004, 70, 022318. [Google Scholar] [CrossRef]
- Giorda, P.; Paris, M.G.A. Gaussian Quantum Discord. Phys. Rev. Lett. 2010, 105, 020503. [Google Scholar] [CrossRef] [PubMed]
- Adesso, G.; Datta, A. Quantum versus Classical Correlations in Gaussian States. Phys. Rev. Lett. 2010, 105, 030501. [Google Scholar] [CrossRef] [PubMed]
- Werlang, T.; Souza, S.; Fanchini, F.F.; Villas Boas, C.J. Robustness of quantum discord to sudden death. Phys. Rev. A 2009, 80, 024103. [Google Scholar] [CrossRef]
- Ferraro, A.; Aolita, L.; Cavalcanti, D.; Cucchietti, F.M.; Acín, A. Almost all quantum states have nonclassical correlations. Phys. Rev. A 2010, 81, 052318. [Google Scholar] [CrossRef]
- Xu, J.S.; Xu, X.Y.; Li, C.F.; Zhang, C.J.; Zou, X.B.; Guo, G.C. Experimental investigation of classical and quantum correlations under decoherence. Nat. Commun. 2010, 1, 7. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621–669. [Google Scholar] [CrossRef]
- Mari, A.; Farace, A.; Didier, N.; Giovannetti, V.; Fazio, R. Measures of Quantum Synchronization in Continuous Variable Systems. Phys. Rev. Lett. 2013, 111, 103605. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Sipahigil, A.; Kalaee, M.; Painter, O. Superconducting qubit to optical photon transduction. Nature 2020, 588, 599–603. [Google Scholar] [CrossRef]
- Riedinger, R.; Hong, S.; Norte, R.A.; Slater, J.A.; Shang, J.; Krause, A.G.; Anant, V.; Aspelmeyer, M.; Gröblacher, S. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 2016, 530, 313–316. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, X.; Li, G. Steady-state one-way Einstein-Podolsky-Rosen steering in optomechanical interfaces. Phys. Rev. A 2015, 91, 032121. [Google Scholar] [CrossRef]
- Zheng, T.A.; Zheng, Y.; Wang, L.; Liao, C.G. Dissipative generation of significant amount of photon-phonon asymmetric steering in magnomechanical interfaces. EPJ Quantum Technol. 2023, 10, 19. [Google Scholar] [CrossRef]
- Ferreri, A.; Bruschi, D.E.; Wilhelm, F.K.; Nori, F.; Macrì, V. Phonon-photon conversion as mechanism for cooling and coherence transfer. Phys. Rev. Res. 2024, 6, 023320. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, K.; Zhang, W. Optomechanical preparation of photon number-squeezed states with a pair of thermal reservoirs of opposite temperatures. Photon. Res. 2023, 11, A26–A34. [Google Scholar] [CrossRef]
- Gardiner, C.W. Inhibition of Atomic Phase Decays by Squeezed Light: A Direct Effect of Squeezing. Phys. Rev. Lett. 1986, 56, 1917–1920. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).