Applying λ-Statistical Convergence in Fuzzy Paranormed Spaces to Supply Chain Inventory Management Under Demand Shocks ($\mathcal{D}\mathcal{S}$)

Abstract

This paper introduces and analyzes the concept of $\lambda$-statistical convergence in fuzzy paranormed spaces, demonstrating its relevance to supply chain inventory management under demand shocks. We establish key relationships between generalized convergence methods and fuzzy convex analysis, showing how these results extend classical summability theory to uncertain demand environments. By exploring $\lambda$-statistical Cauchy sequences and $(V,\lambda )$-summability in fuzzy paranormed spaces, we provide new insights applicable to adaptive inventory optimization and decision-making in supply chains. Our findings bridge theoretical aspects of fuzzy convexity with practical convergence tools, advancing the robust modeling of demand uncertainty.

1. Introduction and Background

The idea of convergence plays a crucial role in mathematical analysis and its applications. Conventional convergence, which studies how sequences approach a certain limit, is a well-established concept. Nevertheless, classical convergence can be limiting in some situations. To overcome these constraints, various alternative types of convergence have been proposed, with statistical convergence being particularly notable for its flexibility and wider applicability.

Statistical convergence was first introduced by Steinhaus and Fast in 1951 [1,2]. It broadens the concept of classical convergence by focusing on the density of terms in a sequence rather than their exact positions. A sequence is considered statistically convergent if the indices at which the sequence deviates significantly from the limit form a set with zero density. This method not only extends the scope of convergence but also finds applications in fields such as number theory, functional analysis, and approximation theory.

Over the years, the concept of statistical convergence has been extended to various frameworks, including normed spaces, metric spaces, fuzzy normed spaces, paranormed spaces, and fuzzy paranormed spaces [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].

Recent advances have significantly expanded these concepts, including higher-order statistical convergence in fuzzy difference sequence spaces with applications to fuzzy number theory [26], weighted statistical convergence of fractional order for double sequences in paranormed spaces [27], $\lambda$-statistical convergence in fuzzy n-normed linear spaces [28], generalizations to triple sequences via $M{\lambda }_{m,n,p}$-statistical convergence [29], and Tauberian theory for statistically Cesàro summable triple sequences of fuzzy numbers [30].

These contributions underscore the ongoing evolution of statistical convergence, particularly in multidimensional settings (double and triple sequences), advanced fuzzy structures, and Tauberian theory, reinforcing its interdisciplinary relevance.

Building upon statistical convergence, the concept of $\lambda$-statistical convergence was introduced by Mursaleen [31] as a more generalized framework. Here, $\lambda =\left({\lambda }_k\right)$ represents a sequence that determines the weighted density of terms in a sequence. This extension provides greater flexibility in analyzing convergence behavior, allowing the study of sequences under nonuniform density conditions. The $\lambda$-statistical convergence framework has been further explored in various mathematical settings, such as paranormed spaces and fuzzy spaces, offering new insights and tools for sequence analysis [32,33,34,35,36,37,38,39,40,41].

Despite these advancements, existing frameworks for $\lambda$-statistical convergence exhibit critical limitations in handling complex uncertainties. For instance, studies in fuzzy normed spaces (e.g., [25]) lack the flexibility to model non-homogeneous uncertainty distributions, while works in paranormed spaces (e.g., [8]) cannot capture gradual membership transitions inherent in imprecise data. Furthermore, recent extensions to n-normed spaces [28] or triple sequences [29] focus primarily on theoretical generalizations without providing adaptive convergence criteria for real-world volatility.

In contrast, our work bridges these gaps by unifying $\lambda$-statistical convergence with fuzzy paranormed spaces. This synthesis enables:

(i)

Dynamic density-based weighting (via $\lambda$-sequences) for irregular demand patterns;

(ii)

Fuzzy paranormed structures to quantify partial or transitional uncertainties; and

(iii)

Robust convergence criteria for sequences with abrupt, nonuniform fluctuations—addressing rigidity in earlier models [5,15].

This framework thus overcomes the key constraint of prior approaches: their inability to jointly model stochastic volatility and fuzzy imprecision in a unified topology.

In practical supply chain inventory management, sudden demand shocks and imprecise demand forecasting often lead to significant stockouts or overstocking. Therefore, applying the framework of $\lambda$-statistical convergence in fuzzy paranormed spaces provides a robust tool for modeling such uncertainties and designing adaptive replenishment policies that maintain desired service levels under fluctuating demand.

The illustrative inventory case study serves to demonstrate the practical application of the theoretical framework; full-scale industrial implementations and empirical validations are postponed to future work.

This paper aims to extend the concept of $\lambda$-statistical convergence to fuzzy paranormed spaces, providing a comprehensive framework for analyzing convergence in these settings. The main results include new definitions, theorems, and illustrative examples that demonstrate the applicability and significance of this generalization.

The subsequent sections are organized as follows: Section 2 provides the necessary preliminaries, including key definitions and foundational concepts. Section 3 presents the fundamental definitions and propositions underpinning the theoretical framework of our study. In Section 4, we establish the core theorems that offer critical insights into $\lambda$-statistical convergence within this context. Finally, Section 5 summarizes the implications of these theorems and outlines directions for future research.

2. Preliminaries

This section introduces the foundational concepts of paranormed spaces, fuzzy normed spaces, fuzzy paranormed spaces, statistical convergence, and $\lambda$-statistical convergence. We begin by defining paranormed and fuzzy normed spaces, followed by the notion of statistical convergence within these spaces. Finally, we extend these concepts to $\lambda$-statistical convergence in both classical and generalized settings, including fuzzy paranormed spaces.

2.1. Paranormed Spaces

Let $\wp :X\to \mathbb{R}$ be a function, and let X be a real or complex linear space. If all $p,q\in X$ satisfy the following requirements, then ℘ is a paranorm and the pair $(X,\wp )$ is called a paranormed space.

• $\wp \left(\theta \right)=0$;
• $\wp (-p)=\wp \left(p\right)$;
• $\wp (p+q)\le \wp \left(p\right)+\wp \left(q\right)$;
• $\wp ({\gamma }_k{p}_k-\gamma p)\to 0$ as $k\to \infty$ if $\left({\gamma }_k\right)$ is a sequence of scalars with ${\gamma }_k\to \gamma$ as $k\to \infty$ and $\left(p_k\right)$ is a sequence in X with $\wp (p_k-p)\to 0$ as $k\to \infty$.

If $\wp \left(p\right)=0$ implies $p=\theta$, then ℘ is said to be a total paranorm, where $\theta$ is the zero vector of X.

In paranormed spaces, the concept of convergence is defined similarly to normed spaces.

A sequence $p=\left(p_k\right)$ is considered convergent (or ℘-convergent) to the element $\xi$ in $(X,\wp )$ if, for each $\epsilon >0$, there exists a positive integer $k_0$ such that $\wp (p_k-\xi )<\epsilon$ whenever $k\ge k_0$. In this case, we write ℘-lim $p=\xi$, and $\xi$ is referred to as the ℘-limit of p.

2.2. Fuzzy Normed Spaces

The fuzzy norm introduced by Felbin [42], further developed by Xiao and Zhu [43] and finalized by Şençimen and Pehlivan [17], is given as follows.

Here, $\tilde{0}$ denotes the zero fuzzy number, i.e., a fuzzy number whose membership function is fully concentrated at 0, typically represented as the degenerate fuzzy set

$${\mu }_{\tilde{0}}\left(x\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}x=0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Let X be a vector space over $\mathbb{R}$. Let $\parallel ·\parallel :X\to L^{*}\left(\mathbb{R}\right)$ be a mapping, and let L and R be mappings (respectively, the left norm and right norm) from $[0,1]\times [0,1]$ to $[0,1]$, which are symmetric, nondecreasing in both arguments and satisfy $L(0,0)=0$ and $R(1,1)=1$.

The quadruple $(X,\parallel ·\parallel ,L,R)$ is called a fuzzy normed linear space (briefly $(X,\parallel ·\parallel )\mathrm{FNS}$), and $\parallel ·\parallel$ is called a fuzzy norm if the following axioms are satisfied.

• $\parallel x\parallel =\tilde{0}$ if and only if $x=\theta$;
• $\parallel rx\parallel =\left|r\right|·\parallel x\parallel$ for $x\in X$, $r\in \mathbb{R}$;
• For all $x,y\in X$:

  a.

  $\parallel x+y\parallel (s+t)\ge L(\parallel x\parallel (s),\parallel y\parallel (t\left)\right)$, whenever $s\le {\parallel x\parallel }_1^{-}$, $t\le {\parallel y\parallel }_1^{-}$, and $s+t\le {\parallel x+y\parallel }_1^{-}$;

  b.

  $\parallel x+y\parallel (s+t)\le R(\parallel x\parallel (s),\parallel y\parallel (t\left)\right)$, whenever $s\ge {\parallel x\parallel }_1^{-}$, $t\ge {\parallel y\parallel }_1^{-}$, and $s+t\ge {\parallel x+y\parallel }_1^{-}$.

Write ${[\parallel x\parallel ]}_{\alpha }={[\parallel x\parallel }_{\alpha }^{-}{,\parallel x\parallel }_{\alpha }^{+}]$ for $x\in X$ and $0\le \alpha \le 1$. Suppose that for all $x\in X$, $x\ne \theta$, we have ${inf}_{\alpha \in [0,1]}{\parallel x\parallel }_{\alpha }^{-}>0$, where $\theta$ is the zero vector of X.

Şençimen and Pehlivan [17] modified conditions 3-a and 3-b in the fuzzy norm definition as follows:

For all $x,y\in X$:

3-a.

${\parallel x+y\parallel }_0^{-}\le {\parallel x\parallel }_0^{-}+{\parallel y\parallel }_0^{-}$;

3-b.

${\parallel x+y\parallel }_0^{+}\le {\parallel x\parallel }_0^{+}+{\parallel y\parallel }_0^{+}$.

Thus, in an FNS $(X,\parallel ·\parallel )$, the triangle inequality of the fuzzy norm definition (3) implies $\parallel x+y\parallel ⪯\parallel x\parallel \oplus \parallel y\parallel$. According to this definition, $x=\theta$ if and only if ${\parallel x\parallel }_{\alpha }^{-}={\parallel x\parallel }_{\alpha }^{+}=0$ for all $\alpha \in [0,1]$. Furthermore, ${\parallel x\parallel }_0^{-}>0$ whenever $x\ne \theta$.

Now, if $r=0$, then

$${[\parallel rx\parallel ]}_{\alpha }={[\parallel \theta \parallel ]}_{\alpha }=[0,0]={\left[\right|r|\parallel x\parallel ]}_{\alpha }$$

for all $\alpha \in [0,1]$ and $x\in X$. For $r\ne 0$, we have

$${[\parallel rx\parallel ]}_{\alpha }={\left[\right|r|\parallel x\parallel ]}_{\alpha }$$

for each $\alpha \in [0,1]$, i.e.,

$${[\parallel rx\parallel ]}_{\alpha }^{-}={\left[\right|r|\parallel x\parallel ]}_{\alpha }^{-}\mathrm{and}{[\parallel rx\parallel ]}_{\alpha }^{+}={\left[\right|r|\parallel x\parallel ]}_{\alpha }^{+}$$

for each $\alpha \in [0,1]$, where $L=min$ and $R=max$.

Along with this definition, Şençimen and Pehlivan [17] defined convergence in fuzzy normed spaces by using the distance framework developed by Kaleva [44] and Felbin [42]. Throughout this paper, we denote that distance by $\mathrm{D}(·,·)$. Specifically, if A and B are fuzzy numbers with $\alpha$–cuts ${\left[A\right]}_{\alpha }=[A_{\alpha }^{-},A_{\alpha }^{+}]$ and ${\left[B\right]}_{\alpha }=[B_{\alpha }^{-},B_{\alpha }^{+}]$, we set

$$\mathrm{D}(A,B)=\underset{0\le \alpha \le 1}{sup}max\left\{|A_{\alpha }^{-}-B_{\alpha }^{-}|,|A_{\alpha }^{+}-B_{\alpha }^{+}|\right\},$$

so that $\mathrm{D}(\parallel p_k-\ell \parallel ,\tilde{0})$ measures the deviation of the fuzzy norm $\parallel p_k-\ell \parallel$ from the zero fuzzy number $\tilde{0}$.

A sequence $\left(p_k\right)$ (in the fuzzy normed space $(X,\parallel ·\parallel )$) is convergent to $\ell \in X$ provided that

$$\left(\mathrm{D}\right)-\underset{k\to \infty }{lim}\parallel p_k-\ell \parallel =\tilde{0};$$

i.e., for all $\epsilon >0$, there exists $p_0\in \mathbb{N}$ such that

$$\mathrm{D}(\parallel p_k-\ell \parallel ,\tilde{0})<\epsilon$$

for all $k\ge p_0$. We denote this by $p_k\stackrel{FN}{\to }\ell$.

This means that for every $\epsilon >0$, there exists $k_0\left(\epsilon \right)\in \mathbb{N}$ such that

$$\underset{\alpha \in [0,1]}{sup}\parallel p_k{-\ell \parallel }_{\alpha }^{+}={\parallel p_k-\ell \parallel }_0^{+}<\epsilon$$

for all $k\ge k_0$. In terms of neighborhoods, we have $p_k\stackrel{FN}{\to }\ell$ provided that for each $\epsilon >0$, there exists $p_0\left(\epsilon \right)\in \mathbb{N}$ such that $p_k\in {\aleph }_{\ell }(\epsilon ,0)$ whenever $k\ge p_0$.

2.3. Fuzzy Paranormed Spaces

Çınar et al. [23] introduced the notion of a fuzzy paranorm—a paranorm-type extension of the classical fuzzy norms of Felbin [42] and Xiao–Zhu [43] that replaces the homogeneity axiom with a paranorm-continuity requirement—and their definition is recalled below as follows.

Let $\wp :X\to L^{*}\left(\mathbb{R}\right)$ be a paranorm and let $X\subset \mathbb{R}$ be a vector space. Let the mappings L and $R:[0,1]\times [0,1]\to [0,1]$ be symmetric, non-decreasing, and satisfy $L(0,0)=0$ and $R(1,1)=1$. Write

$${[\wp \left(x\right)]}_{\alpha }=[\wp {\left(x\right)}_{\alpha }^{-},\wp {\left(x\right)}_{\alpha }^{+}]$$

for $p\in X$ and $\alpha \in (0,1]$. Suppose that for all $p\in X$, $p\ne \theta$ (where $\theta$ is the zero vector of X),

$$\underset{\alpha \in [0,1]}{inf}\wp {\left(p\right)}_{\alpha }^{-}>0,sup\wp {\left(p\right)}_{\alpha }^{+}<\infty .$$

The quadruple $(X,\wp ,L,R)$ is called a fuzzy paranormed space and ℘ is a fuzzy paranorm if the following conditions hold:

• $\wp \left(p\right)=\tilde{0}$ if $p=\theta$;
• $\wp (-p)=\wp \left(p\right)$ for all $p\in X$;
• For all $p,q\in X$;

  (a)

  If $s\le \wp {\left(p\right)}_1^{-}$, $t\le \wp {\left(q\right)}_1^{-}$, and $s+t\le \wp {(p+q)}_1^{-}$, then

  $$\wp (p+q)(s+t)\ge L(\wp (p\left)\right(s),\wp (q\left)\right(t\left)\right);$$

  (b)

  If $s\ge \wp {\left(p\right)}_1^{-}$, $t\ge \wp {\left(q\right)}_1^{-}$, and $s+t\ge \wp {(p+q)}_1^{-}$, then

  $$\wp (p+q)(s+t)\le R(\wp (p\left)\right(s),\wp (q\left)\right(t\left)\right);$$

• If $\left({\gamma }_k\right)$ is a sequence in $\mathbb{R}$ with ${\gamma }_k\to \gamma$ as $k\to \infty$ and $p_k,\ell \in X$ for all $k\in \mathbb{N}$ with $\wp (p_k-\ell )\to \tilde{0}$ as $k\to \infty$, then

  $$\wp ({\gamma }_k{p}_k-\gamma \ell )\to \tilde{0}\mathrm{as}k\to \infty .$$

If $\wp \left(p\right)=\tilde{0}$ implies $p=\theta$, then the fuzzy paranorm is referred to as a totally fuzzy paranorm.

2.4. Statistical Convergence

A set K of positive integers has a natural density defined by

$$\delta \left(K\right)=\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}\left|\{k\in K:k\le n\}\right|,$$

where $\left|\right\{k\in K:k\le n\left\}\right|$ represents the count of elements of K not exceeding n. It is evident that $\delta \left(K\right)=0$ for any finite set K.

Statistical convergence using natural density was defined by Fast [2] as follows.

If the set

$$\{n\in \mathbb{N}:|p_k-\varsigma |>\epsilon \}$$

has natural density zero for every $\epsilon >0$, then the real number sequence $\left(p_k\right)$ is said to be statistically convergent to $\varsigma \in \mathbb{R}$. In this case, we write

$$st-lim{p}_k=\varsigma .$$

The definition of statistical convergence in paranormed spaces is given by Alotaibi and Alroqi [13] as follows.

If, for each $\epsilon >0$, we have

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}\left|\{k\le n:\wp (p_k-\xi )>\epsilon \}\right|=0,$$

then the sequence $p=\left(p_k\right)$ is statistically convergent to $\xi$ in $(X,\wp )$ (or $\wp \left(st\right)$-convergent). We write

$$\wp \left(st\right)-limp=\xi .$$

The set of all $\wp \left(st\right)$-convergent sequences is denoted by $S_{\wp }$.

Next, we give the definitions of statistical convergence in fuzzy normed spaces [17] and fuzzy paranormed spaces [23], which form the basis of our study.

Assume that $(X,\parallel ·\parallel )$ is a fuzzy normed space. If

$$st-lim\parallel p_k-\varsigma \parallel =\tilde{0},$$

then a sequence $\left(p_k\right)$ in X is statistically convergent to $\varsigma \in X$, and we write

$$p_k\stackrel{st\left(FN\right)}{\to }\varsigma ,$$

i.e., for each $\epsilon >0$,

$$\delta \left(\{k\in \mathbb{N}:\mathrm{D}(\parallel p_k-\varsigma \parallel ,\tilde{0})\ge \epsilon \}\right)=0.$$

This means that for any $\epsilon >0$, the natural density of the set

$$\{k\in \mathbb{N}:\parallel p_k-\varsigma {\parallel }_0^{+}\ge \epsilon \}$$

is zero. In other words, for each $\epsilon >0$, the condition

$$\parallel p_k{-\varsigma \parallel }_0^{+}<\epsilon$$

holds for almost all k. In terms of neighborhoods, $p_k\stackrel{st\left(FN\right)}{\to }\varsigma$ means that for each $\epsilon >0$,

$$\delta \left(\{k\in \mathbb{N}:p_k\notin {\aleph }_{\varsigma }(\epsilon ,0)\}\right)=0,$$

i.e., $p_k\in {\aleph }_{\varsigma }(\epsilon ,0)$ for almost all k.

A useful equivalent form is:

$$p_k\stackrel{st\left(FN\right)}{\to }\varsigma \iff st-lim{\parallel p_k-\varsigma \parallel }_0^{+}=0.$$

When $st-lim\parallel p_k{-\varsigma \parallel }_0^{+}=0$, it implies that for every $\alpha \in [0,1]$,

$$st-lim\parallel p_k{-\varsigma \parallel }_{\alpha }^{-}=st-lim{\parallel p_k-\varsigma \parallel }_{\alpha }^{+}=0,$$

as for all $k\in \mathbb{N}$ and $\alpha \in [0,1]$, we have

$$0\le \parallel p_k{-\varsigma \parallel }_{\alpha }^{-}\le \parallel p_k{-\varsigma \parallel }_{\alpha }^{+}\le {\parallel p_k-\varsigma \parallel }_0^{+}.$$

Let $(X,\wp )$ be a fuzzy paranormed space. A sequence $p=\left(p_k\right)$ is statistically convergent to $\varsigma \in X$ if, for each $\epsilon >0$,

$$\delta \left(\{k\in \mathbb{N}:\mathrm{D}(\wp (p_k-\varsigma ),\tilde{0})\ge \epsilon \}\right)=0.$$

In this case, we write

$$p_k\stackrel{st\left(FP\right)}{\to }\varsigma \mathrm{or}st\stackrel{FP}{-}\underset{k\to \infty }{lim}\wp (p_k-\varsigma )=\tilde{0}.$$

This implies that for each $\epsilon >0$, the set

$$K\left(\epsilon \right)=\{k\in \mathbb{N}:\wp {(p_k-\varsigma )}_0^{+}\ge \epsilon \}$$

has natural density zero. In other words, for each $\epsilon >0$, we have

$$\wp {(p_k-\varsigma )}_0^{+}\le \epsilon$$

for almost all k, where

$$\wp {(p_k-\varsigma )}_0^{+}=\underset{\alpha \in [0,1]}{sup}\wp {(p_k-\varsigma )}_{\alpha }^{+}.$$

According to the above definition,

$$p_k\stackrel{st\left(FP\right)}{\to }\varsigma \iff st-\underset{k\to \infty }{lim}\wp {(p_k-\varsigma )}_0^{+}=0.$$

Note that

$$st-\underset{k\to \infty }{lim}\wp {(p_k-\varsigma )}_0^{+}=0$$

implies

$$st-\underset{k\to \infty }{lim}\wp {(p_k-\varsigma )}_{\alpha }^{-}=st-\underset{k\to \infty }{lim}\wp {(p_k-\varsigma )}_{\alpha }^{+}=0$$

for each $\alpha \in (0,1]$ as

$$0\le \wp {(p_k-\varsigma )}_{\alpha }^{-}\le \wp {(p_k-\varsigma )}_{\alpha }^{+}\le \wp {(p_k-\varsigma )}_0^{+}$$

holds for every $k\in \mathbb{N}$ and each $\alpha \in (0,1]$. We denote the set of all statistically convergent sequences by $S\left(FP\right)$.

2.5. $\lambda$-Statistical Convergence

The concept of $\lambda$-statistical convergence generalizes statistical convergence by introducing a weight sequence $\lambda =\left({\lambda }_n\right)$.

Let $\lambda =\left({\lambda }_n\right)$ be a sequence of positive real numbers that is non-decreasing and tends to infinity, with the condition that ${\lambda }_{n+1}\le {\lambda }_n+1$ and ${\lambda }_1=1$. The collection of all such sequences is denoted by $\Lambda$.

The idea of $\lambda$-statistical convergence was proposed by Mursaleen [31] as follows.

A sequence $p=\left(p_k\right)$ is said to be $\lambda$-statistically convergent or $S_{\lambda }$-convergent to $\varsigma$ if for every $\epsilon >0$,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\left|\left\{k\in I_n:|p_k-\varsigma |\ge \epsilon \right\}\right|=0,$$

where $I_n=[n-{\lambda }_n+1,n]$. In this case, we write $S_{\lambda }-limp=\varsigma$ or $p_k\to \varsigma \left(S_{\lambda }\right)$ and define

$$S_{\lambda }:=\left\{p:\exists \varsigma \in \mathbb{R},S_{\lambda }-limp=\varsigma \right\}.$$

Alghamdi and Mursaleen [36] defined $\lambda$-statistical convergence in paranormed spaces as follows.

A sequence $p=\left(p_k\right)$ is said to be $\lambda$-statistically convergent to the number $\xi$ in the paranormed space $(X,\wp )$ if, for each $\epsilon >0$,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\left|\left\{k\in I_n:\wp (p_k-\xi )\ge \epsilon \right\}\right|=0.$$

In this case, we write $s{t}_{\lambda }(\wp )-limp=\xi$.

Türkmen and Çınar [34] defined the concept of $\lambda$-statistical convergence within fuzzy normed spaces as follows.

Let $(X,\parallel ·\parallel )$ be a fuzzy normed space (FNS) and $\lambda \in \Lambda$. A sequence $p=\left(p_k\right)$ in X is considered $\lambda$-statistically convergent to $\varsigma \in X$ with respect to the fuzzy norm on X, or $F{S}_{\lambda }$-convergent, if for every $\epsilon >0$,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\left|\left\{k\in I_n:\mathrm{D}\left(\parallel p_k-\varsigma \parallel ,\tilde{0}\right)\ge \epsilon \right\}\right|=0,$$

and we write

$$p_k\stackrel{F{S}_{\lambda }}{\to }\varsigma ,$$

or

$$p_k\to \varsigma \left(F{S}_{\lambda }\right),$$

or

$$S_{\lambda }\stackrel{FN}{-}lim{p}_k=\varsigma ,$$

where $I_n=[n-{\lambda }_n+1,n]$.

This indicates that for every $\epsilon >0$, the set

$$K\left(\epsilon \right)=\{k\in I_n:\parallel p_k-\varsigma {\parallel }_0^{+}\ge \epsilon \}$$

has natural density zero, which means that for each $\epsilon >0$, $\parallel p_k{-\varsigma \parallel }_0^{+}<\epsilon$ holds for almost all k.

In this case, we express $S_{\lambda }\stackrel{FN}{-}lim{p}_k$ as $\varsigma$. The collection of all sequences that converge statistically with respect to the fuzzy norm on X is denoted by $F{S}_{\lambda }$.

The element $\varsigma \in X$ serves as the $F{S}_{\lambda }$-limit of the sequence $\left(p_k\right)$. In terms of neighborhoods, we say $\left(p_k\right)$ converges to $\varsigma \left(F{S}_{\lambda }\right)$ if for every $\epsilon >0$, $p_k$ lies in ${\aleph }_{\varsigma }(\epsilon ,0)$ for almost all k.

An equivalent way to express this is:

$$p_k\stackrel{F{S}_{\lambda }}{\to }\varsigma \mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{S}_{\lambda }\stackrel{FN}{-}lim{\parallel p_k-\varsigma \parallel }_0^{+}=0.$$

Note that

$$S_{\lambda }\stackrel{FN}{-}lim{\parallel p_k-\varsigma \parallel }_0^{+}=0$$

implies

$$S_{\lambda }\stackrel{FN}{-}lim\parallel p_k{-\varsigma \parallel }_{\alpha }^{-}=S_{\lambda }\stackrel{FN}{-}lim{\parallel p_k-\varsigma \parallel }_{\alpha }^{+}=0$$

for each $\alpha \in [0,1]$, as

$$0\le \parallel p_k{-\varsigma \parallel }_{\alpha }^{-}\le \parallel p_k{-\varsigma \parallel }_{\alpha }^{+}\le {\parallel p_k-\varsigma \parallel }_0^{+}$$

holds for every $k\in I_n$ and each $\alpha \in [0,1]$.

3. Main Definitions and Propositions

In this section, we present the concept of $\lambda$-statistical convergence for sequences in fuzzy paranormed spaces. Furthermore, we explore its relationship with $\lambda$-statistically Cauchy sequences and $\lambda$-summability within this framework.

Definition 1.

Let $(X,\wp )$ be a fuzzy paranormed space and $\lambda \in \Lambda$. A sequence $p=\left(p_k\right)$ in X is said to be λ-statistically convergent to $\xi \in X$ with respect to the fuzzy paranorm on X, or $FP{S}_{\lambda }$-convergent, if for each $\epsilon >0$,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\left|\left\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \right\}\right|=0,$$

and we write

$$p_k\stackrel{FP{S}_{\lambda }}{\to }\xi ,p_k\to \xi \left(FP{S}_{\lambda }\right),\mathit{or}{S}_{\lambda }\stackrel{FP}{-}lim{p}_k=\xi ,$$

where $I_n=[n-{\lambda }_n+1,n]$.

For every $\epsilon >0$, the natural density of the set

$$\{k\in I_n:\wp {(p_k-\xi )}_0^{+}\ge \epsilon \}$$

is zero, meaning that for each $\epsilon >0$, $\wp {(p_k-\xi )}_0^{+}<\epsilon$ holds for almost all k.

In this case, we denote it as $S_{\lambda }\stackrel{FP}{-}lim{p}_k=\xi$. The set of all statistically convergent sequences with respect to the fuzzy paranorm on X is denoted by $FP{S}_{\lambda }$.

The element $\xi \in X$ is the $FP{S}_{\lambda }$-limit of $\left(p_k\right)$. In terms of neighborhoods, we have

$$p_k\stackrel{FP{S}_{\lambda }}{\to }\xi$$

provided that for each $\epsilon >0$, $p_k\in {\aleph }_{\xi }(\epsilon ,0)$ for almost all k.

A useful way to interpret the above definition is:

$$p_k\stackrel{FP{S}_{\lambda }}{\to }\xi \mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{S}_{\lambda }\stackrel{FP}{-}lim\wp {(p_k-\xi )}_0^{+}=0.$$

Note that

$$S_{\lambda }\stackrel{FP}{-}lim\wp {(p_k-\xi )}_0^{+}=0$$

implies

$$S_{\lambda }\stackrel{FP}{-}lim\wp {(p_k-\xi )}_{\alpha }^{-}=S_{\lambda }\stackrel{FP}{-}lim\wp {(p_k-\xi )}_{\alpha }^{+}=0$$

for each $\alpha \in [0,1]$, as

$$0\le \wp {(p_k-\xi )}_{\alpha }^{-}\le \wp {(p_k-\xi )}_{\alpha }^{+}\le \wp {(p_k-\xi )}_0^{+}$$

holds for every $k\in I_n$ and each $\alpha \in [0,1]$.

Throughout this paper, we say that $\left(p_k\right)$ is statistically convergent to $\xi \in X$ with respect to the fuzzy paranorm on X if it is $FP{S}_{\lambda }$-convergent to $\xi$.

Because the natural density of a finite set is zero, every convergent sequence in $FPS$ is also $\lambda$-statistically convergent. However, the converse is not always true. Çınar et al. [23] demonstrated this for the case of statistical convergence in Example 3.4. If we take $\lambda =\left({\lambda }_n\right)=\left(n\right)\in \Lambda$, we show that not every $\lambda$-statistically convergent sequence is convergent.

Proposition 1.

Let $\left(p_k\right)$ and $\left(q_k\right)$ be sequences in a fuzzy paranormed space $(X,\wp )$ such that

$$p_k\stackrel{FP{S}_{\lambda }}{\to }\xi \mathit{and}{q}_k\stackrel{FP{S}_{\lambda }}{\to }\varsigma ,$$

where $\xi ,\varsigma \in X$. Then, the following holds:

(i) 

$(p_k+q_k)\stackrel{FP{S}_{\lambda }}{\to }\xi +\varsigma$;

(ii) 

$t{p}_k\stackrel{FP{S}_{\lambda }}{\to }t\xi$ for all $t\in \mathbb{R}$;

(iii) 

$S_{\lambda }\stackrel{FP}{-}lim\wp \left(p_k\right)=\wp \left(\xi \right)$.

Definition 2.

Let $(X,\wp )$ be a fuzzy paranormed space (FPS). A sequence $\left(p_k\right)$ in X is called λ-statistically Cauchy with respect to the fuzzy paranorm on X if for every $\epsilon >0$ there exists a number $p_0=p_0\left(\epsilon \right)\in \mathbb{N}$ such that

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\left|\left\{k\in I_n:\wp {(p_k-p_{p_0})}_0^{+}\ge \epsilon \right\}\right|=0.$$

In the fuzzy paranorm on X, the fact that $\left(p_k\right)$ is $FP{S}_{\lambda }$-Cauchy implies that it is λ-statistically Cauchy.

Proposition 2.

All $FP{S}_{\lambda }$-convergent sequences in $(X,\wp )$ are also $FP{S}_{\lambda }$-Cauchy sequences.

Proof. 

Let $p_k\stackrel{FP{S}_{\lambda }}{\to }\xi$ and $\epsilon >0$. Then, we have $\wp {(p_k-\xi )}_0^{+}<\epsilon /2$ for almost all k. Choose $n_0\in \mathbb{N}$ such that $\wp {(p_{n_0}-\xi )}_0^{+}<\epsilon /2$.

Because $\wp {(·)}_0^{+}$ is a paranorm in the conventional sense, we have

$$\wp {(p_k-p_{n_0})}_0^{+}=\wp {\left((p_k-\xi )+(\xi -p_{n_0})\right)}_0^{+}\le \wp {(p_k-\xi )}_0^{+}+\wp {(p_{n_0}-\xi )}_0^{+}<{\displaystyle \frac{\epsilon }{2}}+{\displaystyle \frac{\epsilon }{2}}=\epsilon$$

for almost all k. This shows that $\left(p_k\right)$ is $FP{S}_{\lambda }$-Cauchy. □

Definition 3.

Let $(X,\wp )$ be an FPS and let $\lambda =\left({\lambda }_n\right)$ be a non-decreasing sequence of positive numbers tending to ∞, satisfying ${\lambda }_{n+1}\le {\lambda }_n+1$ and ${\lambda }_1=1$. Let $p=\left(p_k\right)$ be a sequence in the set X.

This sequence p is said to be strongly λ-summable with respect to the fuzzy paranorm on X if there exists $\xi \in X$ such that

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\sum _{k\in I_n}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})=0,$$

where $I_n=[n-{\lambda }_n+1,n]$.

In this context, we express ${\left[V,\lambda \right]}_{FP}-lim{p}_k=\xi$. The collection of all fuzzy paranorms on X that are strongly $\left(V,\lambda \right)$ summable is referred to as ${\left[V,\lambda \right]}_{FP}$.

We say that X is strongly $\lambda$-summable to $\xi$ with respect to the fuzzy paranorm on X. If ${\lambda }_n=n$, then strong $\lambda$-summability reduces to strong Cesàro summability with respect to the fuzzy paranorm on X, which is defined as follows:

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}\sum _{k=1}^n\mathrm{D}(\wp (p_k-\xi ),\tilde{0})=0.$$

In this case, we write

$${[C,1]}_{FP}-lim{p}_k=\xi .$$

The collection of all strongly $(C,1)$ summable fuzzy paranorm sequences on X is denoted by ${[C,1]}_{FP}$.

Therefore, we express them as follows:

$${[V,\lambda ]}_{FP}=\left\{p=\left(p_k\right):\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\sum _{k\in I_n}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})=0\mathrm{for}\mathrm{some}\xi \right\},$$

$${[C,1]}_{FP}=\left\{p=\left(p_k\right):\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}\sum _{k=1}^n\mathrm{D}(\wp (p_k-\xi ),\tilde{0})=0\mathrm{for}\mathrm{some}\xi \right\}.$$

4. Core Theorems

In this section, we will give and prove important theorems using the definitions and propositions given in the previous section.

Theorem 1.

If a sequence $p=\left(p_k\right)$ is ${\left[V,\lambda \right]}_{FP}$-summable to ξ, then

$$p_k\stackrel{FP{S}_{\lambda }}{⟶}\xi .$$

Proof. 

Let $\epsilon >0$. From ${\left[V,\lambda \right]}_{FP}$-summability, we have

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)=0.$$

On the other hand, by positivity of $\mathrm{D}$,

$$\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\ge \sum _{\begin{array}{c}k\in I_n\\ \mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \end{array}}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\ge \epsilon ·\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|.$$

Dividing both sides by ${\lambda }_n$ and taking the limit as $n\to \infty$,

$$0=\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\ge \epsilon ·\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|.$$

Because $\epsilon >0$ was arbitrary, it follows that

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|=0,$$

i.e., $p_k$ converges to $\xi$ in the $FP{S}_{\lambda }$ sense. □

Theorem 2.

If a bounded sequence $p=\left(p_k\right)$ converges λ-statistically to ξ in a fuzzy paranormed space, and $\lambda =\left({\lambda }_n\right)$ satisfies ${\lambda }_n\to \infty$ and ${\lambda }_n/n\to 0$, then it is ${\left[V,\lambda \right]}_{FP}$-summable to ξ, which also implies that p is ${\left[C,1\right]}_{FP}$-summable to ξ.

Proof. 

Boundedness implies that there exists $M>0$ such that

$$\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)<M$$

for all k. For $\epsilon >0$, we have

$${\displaystyle \frac{1}{{\lambda }_n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\le {\displaystyle \frac{M}{{\lambda }_n}}\left|\left\{k\in I_n:\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\ge \epsilon \right\}\right|+\epsilon .$$

The first term vanishes by $\lambda$-statistical convergence, proving ${\left[V,\lambda \right]}_{FP}$-summability.

For ${\left[C,1\right]}_{FP}$, observe that

$${\displaystyle \frac{1}{n}}\sum _{k=1}^n\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)=\underset{\le {\displaystyle \frac{n-{\lambda }_n}{n}}M\to 0}{\underbrace{{\displaystyle \frac{1}{n}}\sum _{k=1}^{n-{\lambda }_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)}}+\underset{\le {\displaystyle \frac{{\lambda }_n}{n}}M\to 0}{\underbrace{{\displaystyle \frac{1}{n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)}}.$$

Both terms vanish, completing the proof. □

Theorem 3.

If a sequence $p=\left(p_k\right)$ converges statistically to ξ with respect to the fuzzy paranorm on X, and if

$$\underset{n\to \infty }{lim\; inf}\left({\displaystyle \frac{{\lambda }_n}{n}}\right)>0,$$

then p is $FP{S}_{\lambda }$-convergent to ξ.

Proof. 

For the given $\epsilon >0$, note that the set

$$\{k\le n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}$$

contains the set

$$\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}.$$

Therefore,

$${\displaystyle \frac{1}{n}}\left|\{k\le n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\ge {\displaystyle \frac{1}{n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\ge {\displaystyle \frac{{\lambda }_n}{n}}·{\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|.$$

Taking the limit as $n\to \infty$, and using the fact that

$$\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{{\lambda }_n}{n}}>0,$$

we conclude that p converges to $\xi$ in the $FP{S}_{\lambda }$ sense. □

In this paper, unless otherwise specified, the phrase “for all $n\in {\mathbb{N}}_{n_0}$” means “for all $n\in \mathbb{N}$ except for finitely many positive integers,” where

$${\mathbb{N}}_{n_0}=\{n_0,n_0+1,n_0+2,\cdots \}$$

for some fixed $n_0\in \mathbb{N}=\{1,2,3,\cdots \}$.

Theorem 4.

Let $\lambda =\left({\lambda }_n\right)$ and $\mu =\left({\mu }_n\right)$ be two sequences in Λ such that for every $n\in {\mathbb{N}}_{n_0}$, it holds that ${\lambda }_n\le {\mu }_n$.

i. 

If

$$\underset{n\to \infty }{lim\; inf}{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}>0,$$

(1)

then

$$FP{S}_{\mu }\subseteq FP{S}_{\lambda };$$

ii. 

If

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}=1,$$

(2)

then

$$FP{S}_{\lambda }\subseteq FP{S}_{\mu }.$$

Proof. 

(i) Assume that ${\lambda }_n\le {\mu }_n$ for every $n\in {\mathbb{N}}_{n_0}$ and condition (1) holds. Consequently, $I_n\subseteq J_n$, where $I_n=[n-{\lambda }_n+1,n]$ and $J_n=[n-{\mu }_n+1,n]$.

Thus, for any $\epsilon >0$, we have

$$\left|\{k\in J_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\ge \left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|.$$

Dividing both sides by ${\mu }_n$ and using ${\lambda }_n\le {\mu }_n$, we get

$${\displaystyle \frac{1}{{\mu }_n}}\left|\{k\in J_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\ge {\displaystyle \frac{{\lambda }_n}{{\mu }_n}}·{\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|.$$

Taking the limit inferior as $n\to \infty$ and applying (1), it follows that

$$FP{S}_{\mu }\subseteq FP{S}_{\lambda }.$$

(ii) Let $\left(p_k\right)\in FP{S}_{\lambda }$ and suppose condition (2) holds. As $I_n\subseteq J_n$, for any $\epsilon >0$ we can write

$$\begin{array}{cc}& {\displaystyle \frac{1}{{\mu }_n}}\left|\{k\in J_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\hfill \\ & ={\displaystyle \frac{1}{{\mu }_n}}\left|\{n-{\mu }_n+1\le k\le n-{\lambda }_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\hfill \\ & +{\displaystyle \frac{1}{{\mu }_n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\hfill \\ & \le {\displaystyle \frac{{\mu }_n-{\lambda }_n}{{\mu }_n}}+{\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|\hfill \\ & =\left(1-{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}\right)+{\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|.\hfill \end{array}$$

Because ${lim}_{n\to \infty }{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}=1$ by (2) and $\left(p_k\right)\in FP{S}_{\lambda }$, the right-hand side tends to zero as $n\to \infty$.

Therefore,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{{\mu }_n}}\left|\{k\in J_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|=0,$$

which means $\left(p_k\right)\in FP{S}_{\mu }$, and so

$$FP{S}_{\lambda }\subseteq FP{S}_{\mu }.$$

□

5. Conclusions

In this section, we summarize the main results from the theorems presented in the previous section. Additionally, we state important corollaries derived from these results.

Corollary 1.

Let $\lambda =\left({\lambda }_n\right)$ and $\mu =\left({\mu }_n\right)$ be two sequences in Λ such that ${\lambda }_n\le {\mu }_n$ for all sufficiently large n. If

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}=1,$$

(3)

then

$$FP{S}_{\lambda }=FP{S}_{\mu }.$$

Corollary 2.

Let $\lambda =\left({\lambda }_n\right)\in \Lambda$ satisfy ${\lambda }_n\le n$ for all sufficiently large n and

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\lambda }_n}{n}}=1.$$

Then, $FP{S}_{\lambda }=FPS$.

This result follows immediately from Corollary 1 by taking ${\mu }_n=n$.

Theorem 5.

Let $\lambda =\left({\lambda }_n\right)$ and $\mu =\left({\mu }_n\right)$ be elements of Λ such that ${\lambda }_n\le {\mu }_n$ for all sufficiently large n.

1. 

If condition (1) holds, then

$${\left[V,\mu \right]}_{FP}\subseteq {\left[V,\lambda \right]}_{FP};$$

2. 

If condition (2) holds, then

$${\ell }_{\infty }\cap {\left[V,\lambda \right]}_{FP}\subseteq {\left[V,\mu \right]}_{FP}.$$

Proof. 

(i) Because ${\lambda }_n\le {\mu }_n$ for all sufficiently large n, it follows that $I_n=[n-{\lambda }_n+1,n]$ is a subset of $J_n=[n-{\mu }_n+1,n]$. Therefore, for all such n,

$${\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in J_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\ge {\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right).$$

Taking the limit as $n\to \infty$ and applying condition (1), we conclude that

$${\left[V,\mu \right]}_{FP}\subseteq {\left[V,\lambda \right]}_{FP}.$$

(ii) Let $p=\left(p_k\right)\in {\ell }_{\infty }\cap {\left[V,\lambda \right]}_{FP}$ so there exists $M>0$ such that

$$\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\le M\mathrm{for}\mathrm{all}k.$$

Because ${\lambda }_n\le {\mu }_n$, we have ${\displaystyle \frac{1}{{\mu }_n}}\le {\displaystyle \frac{1}{{\lambda }_n}}$, and $I_n\subseteq J_n$ for all large n. Hence,

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in J_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)& ={\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in J_n\setminus I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)+{\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\hfill \\ & \le {\displaystyle \frac{{\mu }_n-{\lambda }_n}{{\mu }_n}}·M+{\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\hfill \\ & \le \left(1-{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}\right)·M+{\displaystyle \frac{1}{{\lambda }_n}}\sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right).\hfill \end{array}$$

By condition (2), the first term tends to zero as $n\to \infty$, and because $p\in {\left[V,\lambda \right]}_{FP}$, the second term also tends to zero. (Note that $1-{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}\ge 0$ for all sufficiently large n.)

Therefore,

$${\ell }_{\infty }\cap {\left[V,\lambda \right]}_{FP}\subseteq {\left[V,\mu \right]}_{FP},$$

which implies

$${\ell }_{\infty }\cap {\left[V,\lambda \right]}_{FP}\subseteq {\ell }_{\infty }\cap {\left[V,\mu \right]}_{FP}.$$

□

Corollary 3.

Let $\lambda ,\mu \in \Lambda$ be such that ${\lambda }_n\le {\mu }_n$ for all sufficiently large $n\in {\mathbb{N}}_{n_0}$. If condition (2) holds, then

$${\ell }_{\infty }\cap {\left[V,\lambda \right]}_{FP}={\ell }_{\infty }\cap {\left[V,\mu \right]}_{FP}.$$

Theorem 6.

Let $\lambda ,\mu \in \Lambda$ such that ${\lambda }_n\le {\mu }_n$ for all $n\in {\mathbb{N}}_{n_0}$.

1. 

If condition (1) holds, then

$$p_k\to \xi \mathrm{in}{\left[V,\mu \right]}_{FP}\Rightarrow p_k\to \xi \mathrm{in}FP{S}_{\lambda },$$

and the inclusion ${\left[V,\mu \right]}_{FP}\subset FP{S}_{\lambda }$ is strict for some $\lambda ,\mu \in \Lambda$;

2. 

If $\left(p_k\right)\in {\ell }_{\infty }$ and $p_k\to \xi$ in $FP{S}_{\lambda }$, then

$$p_k\to \xi \mathrm{in}{\left[V,\mu \right]}_{FP},$$

whenever condition (2) holds.

Proof. 

(i) Let $\epsilon >0$ and suppose $p_k$ converges to $\xi$ in ${\left[V,\mu \right]}_{FP}$. For every $n\in {\mathbb{N}}_{n_0}$, we have

$$\sum _{k\in J_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\ge \sum _{k\in I_n}\mathrm{D}\left(\wp (p_k-\xi ),\tilde{0}\right)\ge \epsilon \left|\{k\in I_n:\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \}\right|.$$

Taking limits as $n\to \infty$ and applying (1), it follows that $p_k\to \xi$ in $FP{S}_{\lambda }$.

To show strictness of the inclusion, take ${\lambda }_n=\sqrt{n}$, ${\mu }_n=n$ and define

$$p_k=\left\{\begin{array}{cc}k,\hfill & k=n^2,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Then, clearly $p_k\to 0$ in $FP{S}_{\lambda }$, but

$${\displaystyle \frac{1}{{\mu }_n}}\sum _{j\in J_n}\mathrm{D}\left(\wp (p_k-0),\tilde{0}\right)={\displaystyle \frac{1}{n}}\sum _{k=1}^n\wp {\left(p_k\right)}_0^{+}={\displaystyle \frac{1}{n}}\left(1+0+0+4+\cdots +{\left[\sqrt{n}\right]}^2\right).$$

Using the formula for sum of squares,

$$1^2+2^2+\cdots +m^2={\displaystyle \frac{m(m+1)(2m+1)}{6}},$$

we get

$${\displaystyle \frac{1}{n}}\sum _{k=1}^n\wp {\left(p_k\right)}_0^{+}={\displaystyle \frac{1}{n}}·{\displaystyle \frac{\left[\sqrt{n}\right](\left[\sqrt{n}\right]+1)(2\left[\sqrt{n}\right]+1)}{6}}.$$

Because $\sqrt{n}<\left[\sqrt{n}\right]+1$ and $\sqrt{n}<2\left[\sqrt{n}\right]+1$, it follows that

$${\displaystyle \frac{1}{n}}>{\displaystyle \frac{1}{(\left[\sqrt{n}\right]+1)(2\left[\sqrt{n}\right]+1)}},$$

hence

$${\displaystyle \frac{1}{{\mu }_n}}\sum _{j\in J_n}\mathrm{D}\left(\wp (p_k-0),\tilde{0}\right)>{\displaystyle \frac{\left[\sqrt{n}\right]}{6}}\to \infty ,$$

so $p\notin {\left[V,\mu \right]}_{FP}$.

(ii) Suppose $p_k\to \xi$ in $FP{S}_{\lambda }$ and $p=\left(p_k\right)\in {\ell }_{\infty }$, so there exists $M>0$ such that $\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\le M$ for all k. Because ${\displaystyle \frac{1}{{\mu }_n}}\le {\displaystyle \frac{1}{{\lambda }_n}}$ and $I_n\subseteq J_n$, for each $\epsilon >0$ and every $n\in {\mathbb{N}}_{n_0}$,

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in J_n}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})& ={\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in J_n\setminus I_n}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})+{\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in I_n}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\hfill \\ & \le {\displaystyle \frac{{\mu }_n-{\lambda }_n}{{\mu }_n}}M+{\displaystyle \frac{1}{{\mu }_n}}\sum _{k\in I_n}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\hfill \\ & \le \left(1-{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}\right)M+{\displaystyle \frac{1}{{\lambda }_n}}\sum _{k\in I_n}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})\hfill \\ & \le \left(1-{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}\right)M+{\displaystyle \frac{1}{{\lambda }_n}}\sum _{\begin{array}{c}k\in I_n\\ \mathrm{D}(\wp (p_k-\xi ),\tilde{0})\ge \epsilon \end{array}}\mathrm{D}(\wp (p_k-\xi ),\tilde{0})+\epsilon .\hfill \end{array}$$

Taking the limit as $n\to \infty$ and applying (2), the right side tends to zero as $p_k\to \xi$ in $FP{S}_{\lambda }$.

Thus,

$${\ell }_{\infty }\cap FP{S}_{\lambda }\subseteq {\left[V,\mu \right]}_{FP}.$$

By setting ${\mu }_n=n$ for all $n\in {\mathbb{N}}_{n_0}$, we obtain subsequent results. Note that

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}=1\Rightarrow \underset{n\to \infty }{lim}inf{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}=1>0,$$

that is, (2) implies (1). □

Corollary 4.

Let ${lim}_{n\to \infty }{\displaystyle \frac{{\lambda }_n}{{\mu }_n}}=1$. Then:

1. 

If $\left(p_k\right)\in {\ell }_{\infty }$ and $p_k\to \xi$ in $FP{S}_{\lambda }$, then $p_k\to \xi$ in ${\left[C,1\right]}_{FP}$;

2. 

If $p_k\to \xi$ in ${\left[C,1\right]}_{FP}$, then $p_k\to \xi$ in $FP{S}_{\lambda }$.

Example 1.

In Çınar et al.’s [23] definition, let $X=\mathbb{R}$ with zero vector $\theta =0$ and define

$$L(a,b)=min\{a,b\},R(a,b)=max\{a,b\}.$$

For each $x\in \mathbb{R}$, set its α-cut by

$${[\wp \left(x\right)]}_{\alpha }=\left[{\displaystyle \frac{\left|x\right|}{1+\alpha }},{\displaystyle \frac{\left|x\right|}{1-\alpha }}\right],\alpha \in (0,1).$$

Moreover, define the 0-cut as the limit

$${[\wp \left(x\right)]}_0:=\underset{\alpha \to 0^{+}}{lim}{[\wp \left(x\right)]}_{\alpha }=\left[\right|x|,|x\left|\right].$$

Then, $(\mathbb{R},\wp ,L,R)$ is a fuzzy paranormed space.

Consider the sequence

$$p_k=\left\{\begin{array}{cc}1,\hfill & k=n^2\mathit{for}\mathit{some}n\in \mathbb{N},\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

The 0-level function of the sequence $\left(p_k\right)$ is given by

$${\wp }_0^{+}\left(p_k\right)=sup\{t\ge 0:t\in {[\wp \left(p_k\right)]}_0\}=\left|p_k\right|=\left\{\begin{array}{cc}1,\hfill & k=n^2\mathit{for}\mathit{some}n\in \mathbb{N},\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Let ${\lambda }_n=\lfloor \sqrt{n}\rfloor$ and

$$I_n=\{k\in \mathbb{N}:n-{\lambda }_n<k\le n\}.$$

Then, for any $\epsilon >0$,

$$\left|\{k\in I_n:{\wp }_0^{+}\left(p_k\right)\ge \epsilon \}\right|=\left|\{k\in I_n:p_k=1\}\right|\le 1,$$

so

$${\displaystyle \frac{\left|\right\{k\in I_n:{\wp }_0^{+}\left(p_k\right)\ge \epsilon \left\}\right|}{{\lambda }_n}}\le {\displaystyle \frac{1}{{\lambda }_n}}\to 0\mathit{as}n\to \infty .$$

Hence, $\left(p_k\right)$ is λ-statistically convergent to 0 in $(\mathbb{R},\wp ,L,R)$, but it does not converge to 0 in the classical sense.

As illustrated in Figure 1, the sequence $p_k$ takes the value 1 exactly at perfect square indices and 0 elsewhere. This highlights the “sparse shock” character of the example: infinitely many isolated peaks separated by arbitrarily large gaps.

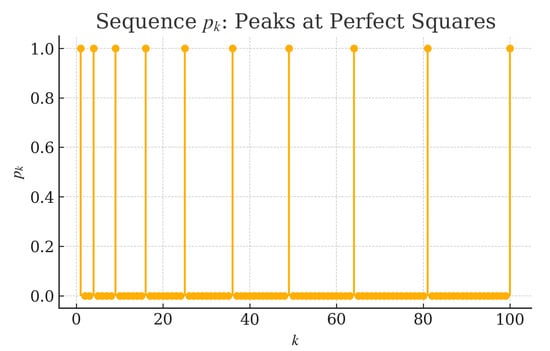
Figure 1. Sequence $p_k$ with peaks at perfect squares.

Figure 2 depicts the theoretical upper bound $1/{\lambda }_n$ as a function of n. This monotone decrease to zero confirms the theoretical upper bound property, ensuring that

$${\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\le n:p_k\ge \epsilon \}\right|\le {\displaystyle \frac{1}{{\lambda }_n}}\to 0,$$

for every fixed $\epsilon >0$.

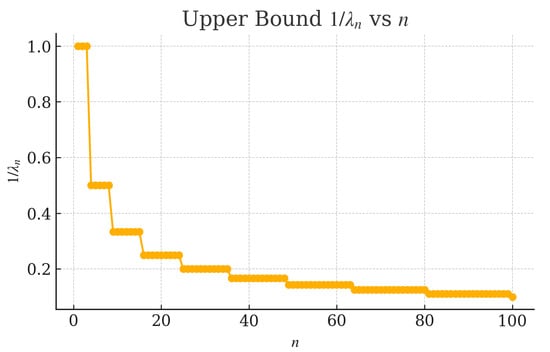
Figure 2. Upper bound $1/{\lambda }_n$ versus n.

Example 2

(Fuzzy inventory planning). Consider a retailer forecasting period-by-period demand modeled as a triangular fuzzy number:

$$D_k=(80,100,120)\mathit{units}.$$

The adaptive inventory policy is defined as follows:

1. 

Initial stock: $Q_1=100$;

2. 

For each period k, observe actual demand $D_k^{\left(\mathrm{act}\right)}$ and compute the shortfall:

$$p_k=max\{0,D_k^{\left(\mathrm{act}\right)}-Q_k\};$$

3. 

Update inventory with learning rate $t=0.5$:

$$Q_{k+1}=Q_k+0.5p_k.$$

A 10-period simulation reveals only two shortfalls exceeding 5 units. Defining ${\lambda }_n=\lfloor n/2\rfloor$, we observe

$${\displaystyle \frac{1}{{\lambda }_n}}\left|\{k\le {\lambda }_n:p_k>5\}\right|\to 0\mathit{as}n\to \infty ,$$

which implies that the shortfall sequence $\left\{p_k\right\}$λ-statistically converges to zero.

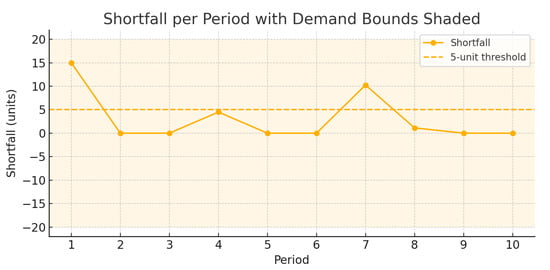
Figure 3 shows period-by-period shortfalls (orange circles) alongside the 5-unit threshold (dashed line). The shaded region indicates the fuzzy demand bounds (80–120 units). Notice that only periods 1, 4, and 7 exceed the threshold, with rapid correction thereafter.

Figure 3. Period-by-period shortfalls with 5-unit threshold (dashed) and fuzzy demand bounds (shaded).

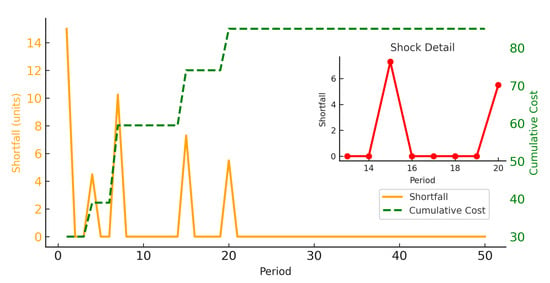
Figure 4 presents the shortfall trajectory (orange line, left axis) and cumulative holding cost (green dashed line, right axis; unit cost = 2). The inset zooms in on periods 13–20, highlighting the impact of a demand shock around $n=15$.

Figure 4. Shortfall vs. cumulative cost over 50 periods. Inset focuses on demand shock near $n=15$.

Verification of Convergence Conditions:

Extending the simulation to 50 periods, the λ-statistical convergence condition, expressed probabilistically, is:

$$\underset{n\to \infty }{lim}P\left({\displaystyle \frac{1}{{\lambda }_n}}\sum _{k=1}^{{\lambda }_n}{\mathbf{1}}_{\{p_k>5\}}\ge \epsilon \right)=0,\forall \epsilon >0.$$

In the simulation,

$$\underset{n>30}{max}{s}_n\le 2.1,{\displaystyle \frac{1}{25}}\left|\{k\le 25:s_k>5\}\right|=0.08.$$

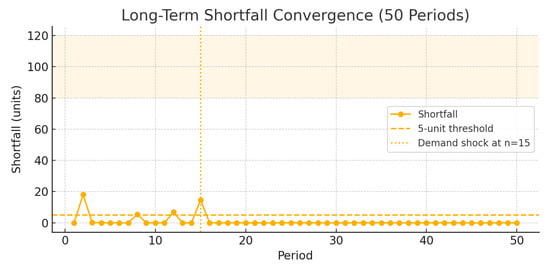
Figure 5 illustrates the long-term shortfall behavior over 50 periods. The red dashed line marks the 5-unit threshold; the shaded band shows fuzzy demand bounds. The dotted vertical line at $n=15$ indicates a significant demand shock. After period 20, all shortfalls remain below the threshold, confirming λ-statistical convergence in practice.

Figure 5. Long-term shortfall convergence over 50 periods. Red dashed line: 5-unit threshold; shaded band: fuzzy demand bounds (80–120). Vertical dotted line at $n=15$ marks a demand shock.

In addition, the adaptive system satisfies standard convergence properties:

1. 

Contraction property: $\mathbb{E}\left[\right|s_{k+1}|\mid {\mathcal{F}}_k]\le |s_k|-\eta$ for some $\eta >0$;

2. 

Martingale stability: ${\sum }_{k=1}^{\infty }P(s_k>ϵ)<\infty$ for each $ϵ>5$;

3. 

Parameter robustness: Convergence holds for learning rates $t\in (0.3,0.7)$.

In practice, serial correlation is removed by pre-processing, and λ-statistical convergence is analyzed on the residuals.

Remark 1.

The λ-statistical convergence of the shortfall sequence depends solely on the finiteness of $\mathrm{D}\left(\wp (·),\tilde{0}\right)$; hence, it remains valid if the triangular demand numbers are replaced by any bounded fuzzy profile, such as trapezoidal or Gaussian-shaped membership functions.

5.1. Key Contributions and Practical Implications

Beyond theoretical advances, our work demonstrates practical value for adaptive inventory optimization under uncertain, shock-driven demand. By applying $\lambda$-statistical convergence within a fuzzy paranorm framework, inventory policies can dynamically adjust safety stocks based on observed demand fluctuations, thereby improving service levels while controlling holding costs. This bridges rigorous convergence theory with real-world replenishment strategies and lays the groundwork for further empirical validation.

5.2. Future Work

Classical EOQ (economic order quantity) and bullwhip mitigation rules typically rely on deterministic or linear forecasting assumptions. In contrast, the $\lambda$-statistical approach specifically addresses fuzzy, shock-driven demand. Consequently, a quantitative comparison of costs and service levels necessitates a dedicated simulation study with fully specified cost parameters and lead time structures, which we plan to undertake in future research.

Building on the current $\lambda$-statistical framework, we will explore two broader convergence concepts in fuzzy paranormed spaces:

(i)

Lacunary statistical convergence, allowing the gaps between index blocks to grow super-linearly, thus isolating highly clustered, sporadic demand shocks that may be obscured by uniform windowing;

(ii)

Ideal convergence, permitting the exclusion of a pre-specified negligible subset of indices (e.g., holiday blackouts or data outages), thereby enhancing robustness against irregular disruptions.

These extensions promise a more flexible toolkit for modeling real-world demand volatility and will be pursued in future empirical work.