Spectral ℝ-Linear Problems: Applications to Complex Permittivity of Coated Cylinders

Abstract

A composite-coated inclusion is embedded in a matrix, where the conductivity (permittivity) of the phases is assumed to be complex-valued. The purpose of this paper is to demonstrate that a non-zero flux can arise under specific conditions related to the conductivities of the components in the absence of external sources. These conditions are unattainable with conventional positive conductivities but can be satisfied when the conductivities are negative or complex—a scenario achievable in the context of metamaterials. The problem is formulated as a spectral boundary value problem for the Laplace equation, featuring a linear conjugation condition defined on a smooth curve L. This curve divides the plane ${\mathbb{R}}^2$ into two regions, $D^{+}$ and $D^{-}\ni \infty$. The spectral parameter appears in the boundary condition, drawing parallels with the Steklov eigenvalue problem. The case of a circular annulus is analyzed using the method of functional equations. The complete set of eigenvalues is derived by applying the classical theory of self-adjoint operators in Hilbert space.

1. Introduction

One of the most prominent models in the theory of composites, the coated disk (or sphere) assemblage, represents a composite structure comprising circular inclusions of one phase embedded within a matrix of another phase. This model was first introduced by Hashin [1] and developed in [2] (Chapter 7) and [3,4,5]. The problem can be approached as a neutral inclusion problem, wherein researchers sought a specific non-zero solution to illustrate the cloaking phenomenon, the process of concealing an object from detection. This perspective played a pivotal role in the advancement of the metamaterial theory [6,7], a rapidly evolving domain in modern physics. In the quasistatic limit, the electromagnetic wave propagation equations are simplified to standard conductivity equations, albeit with complex local fields and complex-valued conductivity (or permittivity). Veselago first observed the negative permittivity values [8]. Complex permittivity values emerge due to energy loss in certain materials. The real part of permittivity represents the traditional dielectric constant, while the imaginary part characterizes energy dissipation, also known as loss permittivity [2,9]. Although the number of pure substances in nature is finite, their diverse compositions give rise to an infinite variety of materials at the macroscale. Consequently, the classical theory of composites covers a broad range of material property constants, including complex-valued parameters for metamaterials that adhere to some bounds [2]. In previous studies, analytical formulas and simulations of local fields were employed to demonstrate the physical attributes of the structures examined. The current work extends this exploration by linking such problems to a classical spectral framework.

Spectral boundary value problems for PDEs are classic analysis topics [10,11,12,13]. We omit an extended study on spectral problems for ODEs and instead refer to one of the latest papers [14]. To present the significance of the new result obtained in this paper, first, we outline three types of spectral problems and describe the third type related to a new physical trend concerning metamaterials.

Spectral problems involving a spectral parameter $\lambda$ that is a control parameter of a partial differential equation have been sufficiently well studied. Equation $\Delta u+\lambda u=0$ in a domain D with the Dirichlet boundary condition $u=0$ on $\partial D$ is one of the fundamental spectral problems. The main keys of the theory for this problem in a Riemannian manifold D are presented in [15]. A recent review of this problem can be found in [10,11,12,13], and the works cited therein.

The study of spectral boundary value problems with the spectral parameter in the boundary condition begins with the Steklov eigenvalue problem for the Laplace equation $\Delta u=0$ in D with the boundary condition ${\displaystyle \frac{\partial u}{\partial n}}u=\lambda u$ on $\partial D$, where ${\displaystyle \frac{\partial }{\partial n}}$ denotes the normal derivative. Recent results on this problem can be found in [16,17,18,19], and the works cited therein. The present paper is devoted to the third type of spectral problem when, instead of a boundary condition, the following linear conjugation condition is given on a smooth curve L, dividing the plane ${\mathbb{R}}^2\equiv \mathbb{C}$ into two domains $D^{+}$ and $D^{-}$ [20,21,22,23]:

$$u^{+}=u^{-},{\displaystyle \frac{\partial u^{+}}{\partial n}}=\lambda {\displaystyle \frac{\partial u^{-}}{\partial n}}\mathrm{on}L=\partial D^{+},$$

(1)

where the signs ± correspond to the limit values of the function u harmonic in $D^{\pm }$ and continuously differentiable in the closures of $D^{\pm }$. Here, it is convenient to consider the extended complex plane $\widehat{\mathbb{C}}=\mathbb{C}\cup \{\infty \}$ and assume that $\infty \in D^{-}$. It should be noted that the domain $D^{+}$ may not be connected, and the constants $\lambda$ may be different in the different components of L. The conjugation condition is called the perfect contact or transmission condition in the theory of composites.

Schiffer [24] considered an eigenvalue problem for a double-layer potential on a set of curves and showed that this problem can be reduced to the spectral problem (1). The spectral parameter $\lambda$ was supposed to be the same for all components of the curve.

The present paper is devoted to studying a coated composite with complex-valued conductivity (permittivity) phases. This physical problem is stated as a spectral $\mathbb{R}$-linear problem. The problem is reduced to an iterative functional equation [25]. It is established that the theory of neutral inclusion related to metamaterials may be considered a new type of spectral problem with the spectral parameter $\lambda$ in the conjugation condition (1).

2. Functional Spaces

Let ${\mathcal{H}}^2\left(\mathbb{U}\right)$ denote the classic Hardy space of analytic functions in the unit disk $\mathbb{U}=\{\mathbb{C}:|z|<1\}$ [26], and let ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$ be the corresponding space on the disk ${\mathbb{U}}_r=\{\mathbb{C}:|z|<r\}$. The Hilbert space ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$ is endowed with the norm

$$\parallel f\parallel =\underset{0\le r_0<r}{\sup }{\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }\left|f\right(r_0{\exp \left(i\theta \right)|}^{2}d\theta .$$

(2)

Introduce a sequence space $h_r^2$ isomorphic to ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$ as follows. Let a function

$$F\left(z\right)=\sum _{k=1}^{\infty }{\alpha }_k{z}^k$$

(3)

belong to ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$. Then, the coefficients ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ of the function (3) can be considered as elements of a discrete space. The sets of these coefficients ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ form the space $h_r^2$ isomorphic to ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$.

The isomorphism ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)\equiv h_r^2$ has to be checked on the level of the scalar product since the considered spaces are Hilbert. Consider the radial limit of $F\left(z\right)$ on the circle $z=r\exp \theta$ existing for almost every argument $\theta \in [0,2\pi )$:

$$f\left(\theta \right):=F\left(r{e}^{i\theta }\right),0\le \theta <2\pi .$$

(4)

The scalar product $(F,G)$ in the Hardy space ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$ coincides with the scalar product $(f,g)$ in the space $L_2$ given by the integral

$$(f,g)={\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }f\left(\theta \right)\overline{g\left(\theta \right)}d\theta .$$

(5)

Using (4), find

$$(F,G)=(f,g)={\displaystyle \frac{1}{2\pi i}}{\int }_{\left|z\right|=r}F\left(z\right)\overline{G\left(z\right)}{\displaystyle \frac{dz}{z}}.$$

(6)

Transform the integral (6)

$$(F,G)={\displaystyle \frac{1}{2\pi i}}{\int }_{\left|z\right|=r}F\left(z\right)\overline{G\left({\displaystyle \frac{r^2}{\overline{z}}}\right)}{\displaystyle \frac{dz}{z}}.$$

(7)

By substituting the Taylor series of functions $F\left(z\right)$ and $G\left(z\right)$, we find that

$$F\left(z\right)=\sum _{k=1}^{\infty }{\alpha }_k{z}^k,G\left(z\right)=\sum _{k=1}^{\infty }{\beta }_k{z}^k,\left|z\right|<r.$$

(8)

Find

$$\overline{G\left({\displaystyle \frac{r^2}{\overline{z}}}\right)}=\sum _{k=1}^{\infty }\overline{{\beta }_k}{\displaystyle \frac{r^{2k}}{z^k}},\left|z\right|=r$$

(9)

and substitute the first expressions of (8) and (9) into (7). The obtained integral can be calculated by the residue theorem, by the coefficient in ${\displaystyle \frac{1}{z}}$ of the integrand

$$(F,G)=\sum _{k=1}^{\infty }{r}^{2k}{\alpha }_k\overline{{\beta }_k}.$$

(10)

Consequently, the norms in the considered spaces can be written in the form

$$\parallel f\parallel =\parallel F\parallel =\sum _{k=0}^{\infty }{r}^{2k}{\left|{\alpha }_k\right|}^2.$$

(11)

3. Spectral Problem

Let $D_1=\{z\in \mathbb{C}:|z|<r\}$, $D_2=\{z\in \mathbb{C}:|z|>1\}$ and $D=\{z\in \mathbb{C}:r<|z|<1\}$ be domains in the extended complex plane $\widehat{\mathbb{C}}=\mathbb{C}\cup \{\infty \}$ (see Figure 1). We are looking for functions $u_1(x_1,x_2)$, $u_2(x_1,x_2)$ and $u(x_1,x_2)$ that are harmonic in $D_1$, $D_2$, and D, respectively, and belonging to the Sobolev spaces $W^{(1,2)}$ [27] in the corresponding domains.

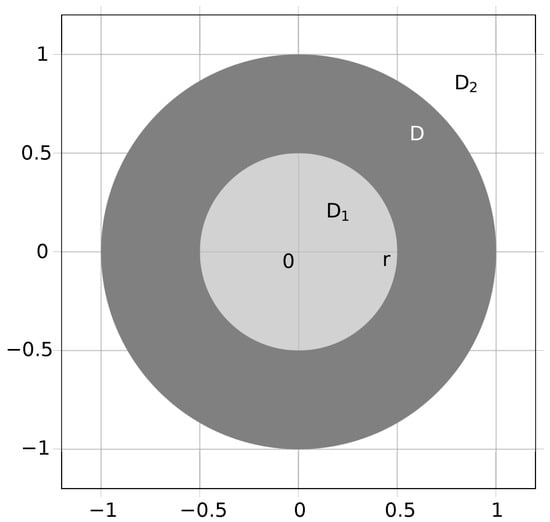
Figure 1. A coated composite on the complex plane. The domains $D_1$ and $D_2$ are occupied by materials of conductivities ${\sigma }_1$ and ${\sigma }_2$, respectively. The conductivity of the annulus $r<\left|z\right|<1$ is normalized to unity.

Consider the following conductivity problem. Let the domains $D_1$, $D_2$, and D be occupied by the materials of conductivities ${\sigma }_1$ and ${\sigma }_2$, and the normalized conductivity $\sigma =1$, respectively. The perfect contact between the components of the considered composite has the form [21]

$$u_1=u,{\sigma }_1{\displaystyle \frac{\partial u_1}{\partial n}}={\displaystyle \frac{\partial u}{\partial n}},\left|z\right|=r,$$

(12)

$$u_2=u,{\sigma }_2{\displaystyle \frac{\partial u_2}{\partial n}}={\displaystyle \frac{\partial u}{\partial n}},\left|z\right|=1,$$

(13)

where ${\displaystyle \frac{\partial }{\partial n}}$ are the outward normal derivatives to the circles. It is supposed that

$$u_2(\infty )=0.$$

(14)

The boundary value problem in Equations (12)–(14) can be stated for the spectral parameter ${\sigma }_1$ or ${\sigma }_2$. We will demonstrate below its equivalence for a complex boundary value problem in relation to Equations (12)–(14).

Following [21], we introduce complex potentials analytically in the considered domain:

$$u\left(z\right)+iv\left(z\right)=\phi \left(z\right),z\in D,$$

(15)

$$u_k\left(z\right)+i{v}_k\left(z\right)={\displaystyle \frac{2}{{\sigma }_k+1}}{\phi }_k\left(z\right),z\in D_k(k=1,2),$$

(16)

where $v_k$ are the imaginary parts of the considered analytic functions. Let ${\displaystyle \frac{\partial }{\partial s}}$ denote a tangent derivative, where s is a natural length parameter of arcs. The Riemann–Cauchy conditions on the circles $L_1=\{z\in \mathbb{C}:|z|=r\}$ and $L_2=\{z\in \mathbb{C}:|z|=1\}$ have the form

$${\displaystyle \frac{\partial u}{\partial n}}={\displaystyle \frac{\partial v}{\partial s}},{\displaystyle \frac{\partial u}{\partial s}}=-{\displaystyle \frac{\partial v}{\partial n}}.$$

(17)

Then, the second Equations (12) and (13) become

$${\displaystyle \frac{\partial v}{\partial s}}\left(t\right)={\sigma }_k{\displaystyle \frac{\partial v_k}{\partial s}}\left(t\right),t\in L_k(k=1,2),$$

(18)

By integrating (18), we get

$$v\left(t\right)={\sigma }_k{v}_k\left(t\right)+d_k,t\in L_k,$$

(19)

where $d_k$ are arbitrary constants.

We then introduce the contrast parameters

$${\varrho }_k={\displaystyle \frac{{\sigma }_k-1}{{\sigma }_k+1}},\mathrm{on}{L}_k(k=1,2).$$

(20)

The first real Equation (12) and the real Equation (19) for $k=1$ can be written in the first of one complex equation. The same concerns the second pair of real equations for $k=2$. The obtained complex equations can be written in the form of the $\mathbb{R}$–linear problem:

$$\phi \left(t\right)={\phi }_k\left(t\right)-{\varrho }_k\overline{{\phi }_k\left(t\right)}+C_k,t\in L_k(k=1,2),$$

(21)

where $C_k$ are constants. The function ${\phi }_2\left(z\right)$ is bounded at infinity.

We introduce the complex velocity

$$\psi \left(z\right)={\phi }^{\prime }\left(z\right)={\displaystyle \frac{\partial u}{\partial x_1}}\left(z\right)-i{\displaystyle \frac{\partial u}{\partial x_2}}\left(z\right),z\in D,$$

(22)

and

$${\psi }_k\left(z\right)={\phi }_k^{\prime }\left(z\right),z\in D_k(k=1,2).$$

(23)

The boundary conditions (21) can be differentiated along the curves $L_k$. It was shown in [20,21] that

$$\psi \left(t\right)={\psi }_k\left(t\right)+{\varrho }_k\overline{n{\left(t\right)}^2}\overline{{\psi }_k\left(t\right)},t\in L_k(k=1,2),$$

(24)

where the unit outward normal vectors $n\left(t\right)$ are expressed in terms of complex values.

4. Functional Equation

In the present section, the boundary value problem is reduced to a functional equation that will be solved.

The normal vector can be written as follows:

$$n\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{t}{r}},\hfill & \left|t\right|=r,\hfill \\ \\ t,\hfill & \left|t\right|=1.\hfill \end{array}\right.$$

(25)

Substitute (25) into (24) and write the resulting equation in the extended form:

$$\begin{array}{cc}\hfill & \psi \left(t\right)={\psi }_1\left(t\right)+{\varrho }_1{\displaystyle \frac{r^2}{t^2}}\overline{{\psi }_1\left(t\right)},\left|t\right|=r,\hfill \\ \hfill & \psi \left(t\right)={\psi }_2\left(t\right)+{\varrho }_2{\displaystyle \frac{1}{t^2}}\overline{{\psi }_2\left(t\right)},\left|t\right|=1.\hfill \end{array}$$

(26)

The function ${\phi }_2\left(z\right)$ near infinity is represented by the series

$${\phi }_2\left(z\right)=constant+{\displaystyle \frac{c_1}{z}}+{\displaystyle \frac{c_2}{z^2}}+\dots .$$

(27)

Hence,

$${\psi }_2\left(z\right)=-{\displaystyle \frac{c_1}{z^2}}-{\displaystyle \frac{2c_2}{z^3}}+\dots ,$$

(28)

in particular,

$${\psi }_2(\infty )=0.$$

(29)

The spectral problem for the complex velocity can be stated as follows. It is required to find ${\psi }_1,{\psi }_2$ and constants such as ${\varrho }_1$ and ${\varrho }_2$ that the boundary value problem given by Equations (26) and (29) has a non-zero solution. One of the parameters ${\varrho }_1$ and ${\varrho }_2$ can be fixed. For example, ${\varrho }_1$ is fixed, and ${\varrho }_2$ has to be found. In the case of the unknown ${\varrho }_1={\varrho }_2=\varrho$, we arrive at the Schiffer spectral problem [24].

Introduce the analytic function separately in $\left|z\right|<r$, $r<\left|z\right|<1$, and $\left|z\right|>1$, and ensure that it is separately continuous in the closures of the considered domains:

$$\mathsf{\Phi }\left(z\right)=\left\{\begin{array}{cc}{\psi }_1\left(z\right)-{\varrho }_2{\displaystyle \frac{1}{z^2}}\overline{{\psi }_2\left({\displaystyle \frac{1}{\overline{z}}}\right)},\hfill & \left|z\right|⩽r,\hfill \\ \\ {\psi }_2\left(z\right)-{\varrho }_1{\displaystyle \frac{r^2}{z^2}}\overline{{\psi }_1\left({\displaystyle \frac{r^2}{\overline{z}}}\right)},\hfill & \left|z\right|⩾1,\hfill \\ \\ \psi \left(z\right)-{\varrho }_1{\displaystyle \frac{r^2}{z^2}}\overline{{\psi }_1\left({\displaystyle \frac{r^2}{\overline{z}}}\right)}-{\varrho }_2{\displaystyle \frac{1}{z}}\overline{{\psi }_2\left({\displaystyle \frac{1}{\overline{z}}}\right)},\hfill & r<\left|z\right|<1.\hfill \end{array}\right.$$

(30)

Calculate the jump of $\mathsf{\Phi }\left(z\right)$ across $\left|t\right|=r$ using the relation $t={\displaystyle \frac{r^2}{\overline{t}}}$,

$$\begin{array}{cc}\hfill & {\mathsf{\Phi }}^{+}\left(t\right)-{\mathsf{\Phi }}^{-}\left(t\right)={\psi }_1\left(t\right)-\psi \left(t\right)+{\varrho }_1{\displaystyle \frac{r^2}{t^2}}\overline{{\psi }_1\left({\displaystyle \frac{r^2}{\overline{t}}}\right)}=\hfill \\ \hfill & ={\psi }_1\left(t\right)+{\varrho }_1{\displaystyle \frac{r^2}{t^2}}\overline{{\psi }_1\left(t\right)}-\psi \left(t\right)=0,\hfill \end{array}$$

(31)

according the first relation (26). Therefore, $\mathsf{\Phi }\left(z\right)$ is analytically continued through the circle $\left|z\right|=r$ by the principle of analytic continuation. In the same way, one can check that $\mathsf{\Phi }\left(z\right)$ is analytically continued through the circle $\left|z\right|=1$. Find $\mathsf{\Phi }(\infty )=0$ using Equation (29). By Liouville’s theorem, $\mathsf{\Phi }\left(z\right)=0$ everywhere in the extended complex plane. Writing $\mathsf{\Phi }\left(z\right)=0$ in the extended form (30) in $\left|z\right|⩽r$ and $\left|z\right|⩾1$, we obtain the system of functional equations

$$\begin{array}{cc}{\psi }_1\left(z\right)={\varrho }_1{\displaystyle \frac{1}{z^2}}\overline{{\psi }_2\left({\displaystyle \frac{1}{\overline{z}}}\right)},\hfill & \left|z\right|⩽r,\hfill \\ \\ {\psi }_2\left(z\right)={\varrho }_2{\displaystyle \frac{r^2}{z^2}}\overline{{\psi }_1\left({\displaystyle \frac{r^2}{\overline{z}}}\right)},\hfill & \left|z\right|⩾1.\hfill \end{array}$$

(32)

Substituting ${\displaystyle \frac{1}{\overline{z}}}$ instead of z in the second Equation (32), we obtain

$$\overline{{\psi }_2\left({\displaystyle \frac{1}{\overline{z}}}\right)}=\overline{{\varrho }_2}{r}^2{z}^2{\psi }_1\left(r^{2}z\right),\left|z\right|⩽1.$$

(33)

Substituting Equation (33) into the first Equation (32) yields the functional equation

$${\psi }_1\left(z\right)={\varrho }_1\overline{{\varrho }_2}{r}^2{\psi }_1\left(r^{2}z\right),\left|z\right|⩽r.$$

(34)

The unknown function ${\psi }_1\left(z\right)$ is analytic in the disk $\left|z\right|<r$ and continuous in $\left|z\right|⩽r$. One can consider the functional equation in the wider Hardy space ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$. The result does not depend on the space since the function ${\psi }_1\left(z\right)$ is analytically continued to the complex plane $\mathbb{C}$ by Equation (34).

4.1. Case of Equal Contrast Parameters

In the present section, consider the case $\varrho :={\varrho }_1={\varrho }_2$. Introduce the operator

$$\left(A{\psi }_1\right)\left(z\right)=r^2{\psi }_1\left(r^{2}z\right)$$

(35)

acting on ${\psi }_1\left(z\right)$ in the written part of Equation (34). This is a shift operator inside the domain of analyticity. According to Shapiro [28], the shift operator is a compact operator in ${\mathcal{H}}^2\left({\mathbb{U}}_r\right)$. Thus, we arrive at the eigenvalue problem for the operator A:

$$\lambda {\psi }_1=A{\psi }_1⟺\lambda {\psi }_1\left(z\right)=r^2{\psi }_1\left(r^{2}z\right),\left|z\right|⩽r$$

(36)

with the spectral parameter $\lambda ={\left|\varrho \right|}^{-2}$.

Represent the unknown function in the form of its Taylor series as follows:

$${\psi }_1\left(z\right)=\sum _{k=0}^{\infty }{\alpha }_k{z}^k,\left|z\right|<r,$$

(37)

Substitute it into Equation (36) and take the coefficients in the same power of z:

$$\lambda {\alpha }_k=r^2{\alpha }_k{r}^{2k},k=0,1,\dots .$$

(38)

Equation (38) has a countable number of non-zero solutions:

$${\lambda }_k=r^{2(k+1)},k=0,1,\dots .$$

(39)

The corresponding solutions of the functional Equation (36) have the form

$${\psi }_1^{\left(k\right)}\left(z\right)=z^k,k=0,1,\dots .$$

(40)

Theorem 1. 

The compact operator A defined by Equation (35) is self-adjoint in ${\mathcal{H}}_2$. Its simple eigenvalues are given by Equation (39) and the eigenfunctions in (40). The relation (39) can be written in the form

$${\left|\varrho \right|}^2{r}^{2(k+1)}=1,k=0,1,\dots .$$

(41)

Proof. 

Find an operator $A^{*}$ adjoint to the operator A by the definition of the scalar product (5)

$$(Af,g)=(f,A^{*}g).$$

(42)

It will be shown that $A=A^{*}$.

We have

$$(f,g)=\sum _{k=0}^{\infty }{f}_k{\overline{g}}_k{r}^{2k}.$$

(43)

Using (35), calculate

$$(Af,g)=\left(r^{2}f\left(r^{2}z\right),g\left(z\right)\right)=\sum _{k=0}^{\infty }{f}_k{\overline{g}}_k{r}^{2(k+1)}{r}^{2k}.$$

(44)

Equate the latter expression to $\left(f,A^{*}g\right)$

$$\left(A^{*}g\right)\left(z\right)=r^2\sum _{k=0}^{\infty }{g}_k{r}^{2k}{z}^k=r^{2}g\left(r^{2}z\right).$$

(45)

Hence, $A=A^{*}$. Therefore, the operator A is self-adjoint.

It follows from the properties of the compact self-adjoint operators in the Hilbert space that the spectrum of the operator A consists of the eigenvalues in (39) satisfying the inequality

$${\lambda }_0>{\lambda }_1>{\lambda }_2>\dots {\lambda }_k>\dots .$$

(46)

One can see that ${\lambda }_k\to 0$, as $k\to \infty$, corresponds to the general theory. The eigenvalues given by (40) are simple since the monomials $z^k$ are orthogonal with respect to the inner product (5), and form a basis for ${\mathcal{H}}^2\left(D_1\right)$.

The theorem is proved. □

4.2. Case of Different Contrast Parameters

In the present section, the parameter ${\varrho }_1$ is fixed and ${\varrho }_2$ is considered as a spectral parameter.

Introduce the operator

$$\left(B{\psi }_1\right)\left(z\right)=\overline{{\varrho }_1}{r}^2{\psi }_1\left(r^{2}z\right),$$

(47)

acting on ${\psi }_1\left(z\right)$ in the right part of (34).

Theorem 2. 

The compact operator B defined by Equation (47) is self-adjoint in ${\mathcal{H}}_2$. Its eigenvalues are given by

$${\lambda }_k=\overline{{\varrho }_1}{r}^{2(k+1)}(k=0,1,\dots ),$$

(48)

the corresponding eigenfunctions $z^k$. The relation (48) can be written in the form

$${\varrho }_2\overline{{\varrho }_1}{r}^{2(k+1)}=1(k=0,1,\dots ).$$

(49)

Proof. 

Substitute the series (37) into Equation (34)

$$\lambda \sum _{k=0}^{\infty }{\alpha }_k{z}^k=\overline{{\varrho }_1}{r}^2\sum _{k=0}^{\infty }{\alpha }_k{r}^{2k}{z}^k,$$

(50)

where $\lambda ={\displaystyle \frac{1}{{\varrho }_2}}$. In Equation (50), the coefficients with the same powers z are taken as

$$\lambda {\alpha }_k=\overline{{\varrho }_1}{r}^2{\alpha }_k{r}^{2k},k=0,1,\dots$$

(51)

This yields Equation (48) and ${\lambda }_k\to 0$, as $k\to \infty$.

The operator $B=B^{*}$ is self-conjugate. It is proven in a similar way to Theorem 1 for the operator A.

The theorem is proved. □

Consider the particular case when ${\varrho }_1>0$. Then,

$${\lambda }_0>{\lambda }_1>{\lambda }_2>\dots .$$

(52)

A numerical example of the vector field for $k=1$ is presented in Figure 2 and Figure 3. It is worth noting that the domains $D_1$ and $D_2$ are occupied by conducting and absorbing materials, respectively. This serves as the physical explanation of the non-vanishing field in the free-source medium. The vector field is expressed by the complex velocity. The gradient (22) can be calculated by the formula

$$\left({\displaystyle \frac{\partial u}{\partial x_1}}\left(z\right),{\displaystyle \frac{\partial u}{\partial x_2}}\left(z\right)\right)=\left(\mathrm{Re}\psi \left(z\right),-\mathrm{Im}\psi \left(z\right)\right),z\in D,$$

(53)

and

$$\left({\displaystyle \frac{\partial u_j}{\partial x_1}}\left(z\right),{\displaystyle \frac{\partial u_j}{\partial x_2}}\left(z\right)\right)={\displaystyle \frac{2}{{\sigma }_j+1}}\left(\mathrm{Re}{\psi }_j\left(z\right),-\mathrm{Im}\psi \left(z\right)\right),z\in D_j(j=1,2).$$

(54)

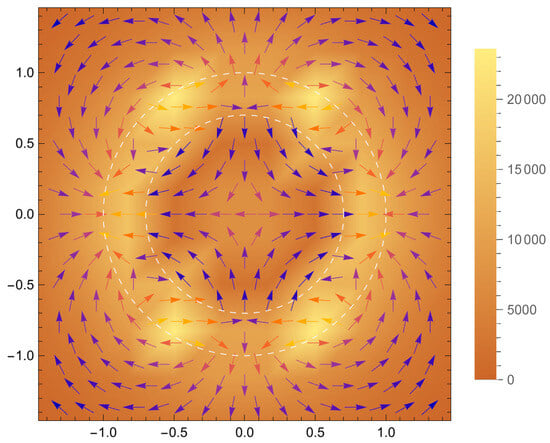
Figure 2. Vector field in the plane calculated by Formulas (53), (22), (23), and (39) for $k=1$. The circles $\left|z\right|=0.7$ and $\left|z\right|=1$ are shown by dashed white lines. The domains $\left|z\right|<0.7$ and $\left|z\right|>1$ are occupied by materials of conductivities ${\sigma }_1=20$ and ${\sigma }_2=-1.555$, respectively. The conductivity of the annulus $0.7<\left|z\right|<1$ is normalized to unity. The legend scale shows the intensity of the field, which is equal to $\left|\psi \right(z\left)\right|$ in D and $|{\psi }_j\left(z\right)|$ in $D_j$ ($j=1,2$).

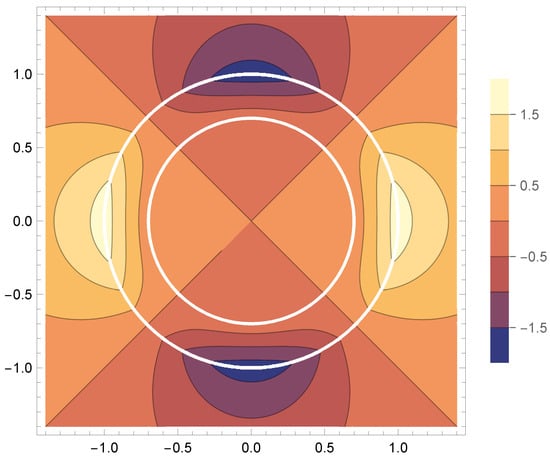
Figure 3. The contour plot illustrating the potentials $u\left(z\right)=\mathrm{Re}\phi \left(z\right)$ and $u_k\left(z\right)={\displaystyle \frac{2}{{\sigma }_k+1}}\mathrm{Re}{\phi }_k\left(z\right)$ ($k=1,2$) of the vector field from Figure 2.

4.3. Hashin–Shtrikman Assemblage

The Hashin–Shtrikman assemblage is not governed by the spectral problem considered above. The condition (29) means that the external flux at infinity is absent. Replace Equation (29) by the condition of the non-vanishing external flux parallel to the $OX$-axes:

$${\psi }_2(\infty )=1.$$

(55)

Then, we arrive at the Hashin–Shtrikman problem. Its solution is then written in terms of complex potentials in the corresponding domains:

$${\psi }_1\left(z\right)=1,{\psi }_2\left(z\right)=1,\psi \left(z\right)=1+{\displaystyle \frac{{\varrho }_2}{z^2}}.$$

(56)

The analog of spectral relation (49) has the form

$${\varrho }_2={\varrho }_1{r}^2⟺{\displaystyle \frac{{\sigma }_2-1}{{\sigma }_2+1}}={\displaystyle \frac{{\sigma }_1-1}{{\sigma }_1+1}}{r}^2.$$

(57)

Here, ${\sigma }_1$ and 1 are the conductivities of the core and the coating, respectively. In the framework of the Hashin–Shtrikman model, ${\sigma }_2$ yields the effective conductivity of neutral non-overlapping, coated inclusions distributed in the plane. It can be written in the form of the Hashin–Shtrikman bound and, equivalently, as the Clausius–Mossotti (Maxwell) approximation [2] (Chapter 7). It is worth noting that condition (57) can be fulfilled for positive conductivities ${\sigma }_1$ and ${\sigma }_2$.

5. Conclusions and Discussion

The coated inclusions in the theory of composites distinguish many exceptional properties. In the present paper, we consider a composite, displayed in Figure 1, with complex-valued conductivities under the absence of any sources and sinks in the whole plane, including infinity. It is established that a non-zero flux takes place under the conditions (49) or (41) on the contrast parameters ${\varrho }_1$ and ${\varrho }_2$ expressed through the conductivity of components by Equation (20). The relations (49) and (41) cannot be fulfilled for the traditional positive conductivities ${\sigma }_1$ and ${\sigma }_2$ and can hold only for negative and complex values. Such a case takes place for metamaterials [6,8].

A boundary value problem is stated with the spectral parameter on the boundary. Complex potentials are introduced in the considered domain through analytic functions. Next, the boundary value problem is reduced to a spectral problem for a functional equation that has been solved. Equal and different contrast parameters are considered. Using the classic theory of self-adjoint operators in the Hilbert space, the complete set of eigenvalues and eigenfunctions modeling special fields are written without external sources.

The classic spectral problem with the parameter $\lambda$ in the partial differential equation, e.g., Laplace’s equation, models wave processes for the special frequencies when an initial mode holds in a medium. In the considered model, Laplace’s equation is not perturbed, which corresponds to a stationary process. However, the wave mode is hidden in the imaginary parts of the material constants ${\sigma }_1$ and ${\sigma }_2$ [9]. Hence, the main physical mechanism, wave mode, is the main reason for the occurrence of unusual phenomena in materials. It is interesting to study the general geometric configurations to check this hypothesis.

The Hashin–Shtrikman assemblage discussed in Section 4.3 is an example of neutral inclusions [2,3] with the classical case of positive material constants ${\sigma }_1$ and ${\sigma }_2$. It is worth noting that the complex velocity is bounded at infinity, e.g., Equation (55). At the same time, the complex potential ${\phi }_2\left(z\right)$ defined by Equation (16) has a pole at infinity. This observation distinguishes the neutral inclusion from others.

The results obtained highlight the significance of the eigenvalue problem in metamaterial theory. This approach helps refine the range of specific metamaterial constants, contributing to a more precise characterization.