Error Estimate for a Finite-Difference Crank–Nicolson–ADI Scheme for a Class of Nonlinear Parabolic Isotropic Systems

Abstract

To understand phase-transition processes like solidification, phase-field models are frequently employed. In this paper, we study a finite-difference Crank–Nicolson–ADI scheme for a class of nonlinear parabolic isotropic systems. We establish an error estimate for this scheme, demonstrating its effectiveness in solving phase-field models. Our analysis provides rigorous mathematical justification for the numerical method’s reliability in simulating phase transitions.

1. Introduction

Phase-transition phenomena, such as solidification, are effectively modeled using phase-field methods [1,2,3,4,5]. These approaches introduce a continuous scalar field—the phase variable—which smoothly interpolates between distinct thermodynamic states, typically adopting values close to zero in the solid phase and close to one in the liquid phase. The evolution of this variable is governed by a nonlinear parabolic partial differential equation (PDE) coupled with the classical heat equation for temperature, thereby enabling a unified treatment of interfacial dynamics and thermal diffusion.

The strength of the phase-field framework lies in its ability to represent complex interface motion without explicitly tracking the interface location [1,5,6]. This is achieved through the diffuse interface paradigm, wherein the transition between phases occurs over a narrow but finite width. As a result, the model naturally accommodates the formation of intricate morphologies, such as dendritic structures and branching patterns, that emerge during solidification processes. The spatial distribution and temporal evolution of these patterns are intrinsically linked to the underlying thermodynamic driving forces and kinetic parameters encoded within the coupled system of equations.

Phase field models [7] possess a high degree of flexibility, allowing their adaptation to a broad class of phase-transition mechanisms beyond solidification. Examples include melting, solid-state transformations, precipitation, and multiphase alloy formation. Their capacity to incorporate material-specific parameters, anisotropic effects, and various types of boundary conditions renders them suitable not only for theoretical investigations but also for quantitative simulations in computational materials science. Through this framework, the influence of temperature gradients, interface kinetics, and latent heat release on microstructural evolution can be systematically explored.

The governing equations are typically posed as an initial-boundary value problem on a fixed computational domain, and the resulting solution exhibits steep gradients near the phase interface. Capturing this behavior with sufficient fidelity requires refined spatial discretizations and small time steps, particularly in two- and three-dimensional settings. The interface dynamics are characterized by sharp transitions and moving fronts, whose evolution must be resolved accurately in both time and space. Consequently, the development of efficient numerical schemes—such as implicit-explicit or alternating direction methods—is essential to reduce the computational burden while preserving stability and accuracy.

In practice, the solution initialized from given data should exhibit a propagating interface whose morphology reflects the nonlinear coupling between the thermal and phase fields. The interface region often dominates the computational effort due to the need for high resolution. Recent advances in error estimation techniques [8,9,10,11] have provided rigorous frameworks for analyzing such numerical schemes, particularly for parabolic equations on complex geometries. Nevertheless, the phase-field method provides a rigorous and thermodynamically consistent tool for simulating such processes, bridging the gap between macroscopic behavior and microscopic structure formation.

In this note, we consider a specific system in two dimensions, simplifying a model by McFadden, Wheeler, Sekerka, Wang, and others [3,4,5,12]. This “isotropic” model consists of a system of two PDEs of the form

$$\left\{\begin{array}{cc}\hfill {\varphi }_t& =\nabla ·\left(A\left(\varphi \right)\nabla \varphi \right)+f(\varphi ,u),\hfill \\ \hfill u_t& =\Delta u+{\left[p\left(\varphi \right)\right]}_t,\hfill \end{array}\right.$$

(1)

where $\varphi :\Omega \times [0,T]\to \mathbb{R}$ represents the phase-field variable, $u:\Omega \times [0,T]\to \mathbb{R}$ denotes the temperature, $A:\mathbb{R}\to \mathbb{R}$ is a mobility function, $f:{\mathbb{R}}^2\to \mathbb{R}$ is a nonlinear coupling term, and $p:\mathbb{R}\to \mathbb{R}$ is a function related to latent heat release. The functions f and p are given smooth scalar functions of their arguments, and A is a $2\times 2$ matrix given by

$$A\left(\varphi \right)=\left(\begin{array}{cc}a\left(\varphi \right)& 0\\ 0& b\left(\varphi \right)\end{array}\right),$$

where a and b are smooth functions of $\varphi$ satisfying the bounds $0<c_a^0\le a\left(\xi \right)\le c_a^1$ and $0<c_b^0\le b\left(\xi \right)\le c_b^1$ for all $\xi \in \mathbb{R}$. The functions f and p are smooth functions defined on ${\mathbb{R}}^2$ and $\mathbb{R}$, respectively, with $f(0,0)=0$ and $p\left(0\right)=0$. Additionally, we require that $g^{\varphi }=g^u=0$ on $\partial \Omega$. Let $\Omega =(\alpha ,\beta )\times (\alpha ,\beta )$. For $(x,y,t)\in \overline{\Omega }\times [0,T]$, where $T>0$, we consider the following initial-boundary-value problem:

$$\left\{\begin{array}{cccc}\hfill {\displaystyle \frac{\partial \varphi }{\partial t}}& -{\displaystyle \frac{\partial }{\partial x}}\left(a\left(\varphi \right){\displaystyle \frac{\partial \varphi }{\partial x}}\right)-{\displaystyle \frac{\partial }{\partial y}}\left(b\left(\varphi \right){\displaystyle \frac{\partial \varphi }{\partial y}}\right)=f(\varphi ,u),\hfill & \hfill & (x,y,t)\in \overline{\Omega }\times [0,T],\hfill \\ \hfill {\displaystyle \frac{\partial u}{\partial t}}& -{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}={\displaystyle \frac{\partial }{\partial t}}p\left(\varphi \right),\hfill & \hfill & (x,y,t)\in \overline{\Omega }\times [0,T],\hfill \\ \hfill \varphi (x,y,t)& =0,u(x,y,t)=0,\hfill & \hfill & (x,y,t)\in \partial \Omega \times [0,T],\hfill \\ \hfill \varphi (x,y,0)& =g^{\varphi }(x,y),\hfill & \hfill & (x,y)\in \overline{\Omega },\hfill \\ \hfill u(x,y,0)& =g^u(x,y),\hfill & \hfill & (x,y)\in \overline{\Omega },\hfill \end{array}\right.$$

(2)

Here, a and b are smooth functions of $\varphi$, satisfying

$$0<c_a^0\le a\left(\xi \right)\le c_a^1,0<c_b^0\le b\left(\xi \right)\le c_b^1,\mathrm{for}\mathrm{all}\xi \in \mathbb{R},$$

and f and p are smooth functions defined on ${\mathbb{R}}^2$ and $\mathbb{R}$, respectively, with $f(0,0)=0$ and $p\left(0\right)=0$. We assume that $g^{\varphi }=g^u=0$ on $\partial \Omega$.

Furthermore, to simplify the proofs of the error estimates, we assume that the functions f, a, b, and p are globally Lipschitz continuous. Specifically, there exists a constant C such that the following inequalities hold:

$$|f(z_1,z_2)-f(Z_1,Z_2)|\le C\left(|z_1-Z_1|+|z_2-Z_2|\right),$$

(3)

$$|a\left(z_1\right)-a\left(Z_1\right)|\le C|z_1-Z_1|,$$

(4)

$$|b\left(z_1\right)-b\left(Z_1\right)|\le C|z_1-Z_1|,$$

(5)

$$|p\left(z_1\right)-p\left(Z_1\right)|\le C|z_1-Z_1|.$$

(6)

We assume that the initial-boundary-value problem (2) for the system of equations admits a unique solution $(u,\varphi )$ that is sufficiently smooth for the purposes of the numerical approximations. Aspects of numerical methods, error estimation, and phase field modeling have also been addressed in the literature [10,11,13,14,15,16,17,18,19].

2. Notation and Preliminary Results

We discretize the initial-boundary-value problem for the system of Equation (2) as follows. Let $h=(\beta -\alpha )/(J+1),$ where J is a positive integer and

$$\begin{array}{cc}\hfill x_i& =\alpha +ih,y_j=\alpha +jh,0\le i,j\le J+1,\hfill \\ \hfill {\Omega }_h& =\{(x_i,y_j):i,j=1,\dots ,J\},\hfill \\ \hfill \partial {\Omega }_h& =\{(x_i,y_j):i=0\mathrm{or}i=J+1\mathrm{or}j=0\mathrm{or}j=J+1\}.\hfill \end{array}$$

Let N be positive integer and $t^n=n\Delta t,$$n=0,\dots ,N,$ where $\Delta t=T/N,$ and define $t^{n+{\displaystyle \frac{1}{2}}}=t^n+\Delta t/2,$$x_{i\pm {\displaystyle \frac{1}{2}}}=x_i\pm h/2,$$y_{j\pm {\displaystyle \frac{1}{2}}}=y_j\pm h/2,$ and ${\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}:=\left\{U={(U_{00},\dots ,U_{J+1,J+1})}^T\in \mathrm{I}{\mathrm{R}}^{(J+2)\times (J+2)}:\right.$ $\left.U_{ij}=0on\partial {\Omega }_h\right\}.$ We approximate the solution $u,\varphi$ of the system of Equation (2) by mesh functions $U^n,{\Phi }^n\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}$ as follows: For $n=0,1,2,\dots ,N,$ we approximate the vectors ${(u(x_0,y_0,t^n),\dots ,u(x_{J+1},y_{J+1},t^n))}^T,$${(\varphi (x_0,y_0,t^n),\dots ,\varphi (x_{J+1},y_{J+1},t^n))}^T$ by $U^n,{\Phi }^n\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}$ satisfying the following finite-difference scheme:

$$\left.\begin{array}{cc}\left(\mathrm{i}\right){\Phi }_{ij}^0=g^{\varphi }(x_i,y_j),\hfill & (x_i,y_j)\in {\Omega }_h\bigcup \partial {\Omega }_h,\\ \left(\mathrm{ii}\right)U_{ij}^0=g^u(x_i,y_j),\hfill & (x_i,y_j)\in {\Omega }_h\bigcup \partial {\Omega }_h,\\ \mathrm{F}\mathrm{o}\mathrm{r} n=0,1,\dots ,N-1:\hfill & \\ {\displaystyle \left(\mathrm{iii}\right)\frac{{\Phi }_{ij}^{n+\frac{1}{2}}-{\Phi }_{ij}^n}{\frac{1}{2}\Delta t}-{\delta }_x(a_{i-\frac{1}{2},j}^n{\delta }_{\overline{x}}{\Phi }_{ij}^{n+\frac{1}{2}})}\hfill & \\ {\displaystyle \phantom{\left(\mathrm{iii}\right)}-{\delta }_y(b_{i,j-\frac{1}{2}}^n{\delta }_{\overline{y}}{\Phi }_{ij}^n)=F_{ij}^n,}\hfill & (x_i,y_j)\in {\Omega }_h,\\ {\displaystyle \left(\mathrm{iv}\right)\frac{{\Phi }_{ij}^{n+1}-{\Phi }_{ij}^{n+\frac{1}{2}}}{\frac{1}{2}\Delta t}-{\delta }_x(a_{i-\frac{1}{2},j}^n{\delta }_{\overline{x}}{\Phi }_{ij}^{n+\frac{1}{2}})}\hfill & \\ {\displaystyle \phantom{\left(\mathrm{iv}\right)}-{\delta }_y(b_{i,j-\frac{1}{2}}^n{\delta }_{\overline{y}}{\Phi }_{ij}^{n+1})=F_{ij}^n,}\hfill & (x_i,y_j)\in {\Omega }_h,\\ \left(\mathrm{v}\right){\Phi }_{ij}^{n+{\displaystyle \frac{1}{2}}}={\Phi }_{ij}^{n+1}=0,\hfill & (x_i,y_j)\in \partial {\Omega }_h,\\ {\displaystyle \left(\mathrm{vi}\right)\frac{U_{ij}^{n+\frac{1}{2}}-U_{ij}^n}{\frac{1}{2}\Delta t}-{\delta }_{x\overline{x}}{U}_{ij}^{n+\frac{1}{2}}}\hfill & \\ {\displaystyle \phantom{\left(vi\right)}-{\delta }_{y\overline{y}}{U}_{ij}^n=\frac{P_{ij}^{n+1}-P_{ij}^n}{\Delta t},}\hfill & (x_i,y_j)\in {\Omega }_h,\\ {\displaystyle \left(\mathrm{vii}\right)\frac{U_{ij}^{n+1}-U_{ij}^{n+\frac{1}{2}}}{\frac{1}{2}\Delta t}-{\delta }_{x\overline{x}}{U}_{ij}^{n+\frac{1}{2}}}\hfill & \\ {\displaystyle \phantom{\left(\mathrm{vii}\right)}-{\delta }_{y\overline{y}}{U}_{ij}^{n+1}=\frac{P_{ij}^{n+1}-P_{ij}^n}{\Delta t},}\hfill & (x_i,y_j)\in {\Omega }_h,\\ \left(\mathrm{viii}\right)U_{ij}^{n+{\displaystyle \frac{1}{2}}}=U_{ij}^{n+1}=0,\hfill & (x_i,y_j)\in \partial {\Omega }_h,\end{array}\right\}$$

(7)

where $P_{i,j}^n:=p\left({\Phi }_{i,j}^n\right),$${\delta }_x{v}_{ij}:={\displaystyle \frac{v_{i+1,j}-v_{i,j}}{h}},$${\delta }_{\overline{x}}{v}_{ij}:={\displaystyle \frac{v_{i,j}-v_{i-1,j}}{h}},$${\delta }_y{v}_{ij}:={\displaystyle \frac{v_{i,j+1}-v_{i,j}}{h}},{\delta }_{\overline{y}}{v}_{ij}:={\displaystyle \frac{v_{i,j}-v_{i,j-1}}{h}},$${\delta }_{x\overline{x}}{v}_{ij}:={\displaystyle \frac{v_{i+1,j}-2v_{i,j}+v_{i-1,j}}{h^2}},$${\delta }_{y\overline{y}}{v}_{ij}:={\displaystyle \frac{v_{i,j+1}-2v_{i,j}+v_{i,j-1}}{h^2}},$${\Delta }_h{v}_{ij}:={\delta }_{x\overline{x}}{v}_{ij}+{\delta }_{y\overline{y}}{v}_{ij}.$ We also let for $(x_i,y_j)\in {\Omega }_h$ $a_{i+{\displaystyle \frac{1}{2}},j}^n:=a({\displaystyle \frac{{\Phi }_{i+1,j}^n+{\Phi }_{i,j}^n}{2}}),$ $a_{i-{\displaystyle \frac{1}{2}},j}^n:=a({\displaystyle \frac{{\Phi }_{i,j}^n+{\Phi }_{i-1,j}^n}{2}}),$ $a_{i,j+{\displaystyle \frac{1}{2}}}^n:=a({\displaystyle \frac{{\Phi }_{i,j+1}^n+{\Phi }_{i,j}^n}{2}}),$ $a_{i,j-{\displaystyle \frac{1}{2}}}^n:=a({\displaystyle \frac{{\Phi }_{i,j}^n+{\Phi }_{i,j-1}^n}{2}}).$ (The quantities $b_{i\pm {\displaystyle \frac{1}{2}},j}^n,$ $b_{i,j\pm {\displaystyle \frac{1}{2}}}^n$ are defined analogously.) In addition, we let

$$F_{ij}^n:=\left\{\begin{array}{cc}f({\check{\Phi }}_{ij}^{{\displaystyle \frac{1}{2}}},{\check{U}}_{ij}^{{\displaystyle \frac{1}{2}}}),\hfill & \mathrm{if}n=0,\\ f({\displaystyle \frac{3}{2}}{\Phi }_{ij}^n-{\displaystyle \frac{1}{2}}{\Phi }_{ij}^{n-1},{\displaystyle \frac{3}{2}}{U}_{ij}^n-{\displaystyle \frac{1}{2}}{U}_{ij}^{n-1}),\hfill & \mathrm{if}n\ge 1,\end{array}\right.$$

where

$${\check{\Phi }}_{ij}^{{\displaystyle \frac{1}{2}}}:=g^{\varphi }(x_i,y_j)+{\displaystyle \frac{\Delta t}{2}}\left\{a\left(g^{\varphi }(x_i,y_j)\right)g_{xx}^{\varphi }(x_i,y_j)+b\left(g^{\varphi }(x_i,y_j)\right)g_{yy}^{\varphi }(x_i,y_j)\right.$$

$$\left.+a^{\prime }\left(g^{\varphi }(x_i,y_j)\right){\left(g_x^{\varphi }(x_i,y_j)\right)}^2+b^{\prime }\left(g^{\varphi }(x_i,y_j)\right){\left(g_y^{\varphi }(x_i,y_j)\right)}^2+f(g^{\varphi }(x_i,y_j),g^u(x_i,y_j)\right\}$$

and

$${\check{U}}_{ij}^{{\displaystyle \frac{1}{2}}}:=g^u(x_i,y_j)+{\displaystyle \frac{\Delta t}{2}}\left\{\Delta g^u(x_i,y_j)+{\displaystyle \frac{2}{\Delta t}}{p}^{\prime }\left(g^{\varphi }(x_i,y_j)\right)[{\check{\Phi }}_{ij}^{{\displaystyle \frac{1}{2}}}-g^{\varphi }(x_i,y_j)]\right\}.$$

Subtracting Equation (7) part (vi) from Equation (7) part (vii) we have for $(x_i,y_j)\in {\Omega }_h$

$${\displaystyle \frac{U_{ij}^{n+1}-2U_{ij}^{n+\frac{1}{2}}+U_{ij}^n}{\frac{1}{2}\Delta t}}-{\delta }_{y\overline{y}}(U_{ij}^{n+1}-U_{ij}^n)=0.$$

Solving for $U_{ij}^{n+{\displaystyle \frac{1}{2}}}$ we obtain

$$U_{ij}^{n+{\displaystyle \frac{1}{2}}}={\displaystyle \frac{U_{ij}^{n+1}+U_{ij}^n}{2}}-{\displaystyle \frac{\Delta t}{4}}{\delta }_{y\overline{y}}(U_{ij}^{n+1}-U_{ij}^n).$$

(8)

Replacing the above relation in Equation (7) part (vi) we obtain

$${\displaystyle \frac{U_{ij}^{n+1}-U_{ij}^n}{\Delta t}}-{\Delta }_h{\displaystyle \frac{U_{ij}^{n+1}+U_{ij}^n}{2}}+{\displaystyle \frac{\Delta t}{4}}{\delta }_{x\overline{x}}{\delta }_{y\overline{y}}(U_{ij}^{n+1}-U_{ij}^n)={\displaystyle \frac{P_{ij}^{n+1}-P_{ij}^n}{\Delta t}},(x_i,y_j)\in {\Omega }_h.$$

(9)

Conversely, suppose that Equation (9) holds. Then, defining $U^{n+{\displaystyle \frac{1}{2}}}$ from Equation (8), we see that Equation (7) parts (vi) and (vii) are valid. Hence Equation (7) parts (vi)–(vii) are equivalent to Equations (8) and (9). Similarly, subtracting Equation (7) part (iii) from Equation (7) part (iv), we see, for $(x_i,y_j)\in {\Omega }_h$

$${\displaystyle \frac{{\Phi }_{ij}^{n+1}-2{\Phi }_{ij}^{n+\frac{1}{2}}+{\Phi }_{ij}^n}{\frac{1}{2}\Delta t}}-{\delta }_y(b_{i,j-{\displaystyle \frac{1}{2}}}^n{\delta }_{\overline{y}}({\Phi }_{ij}^{n+1}-{\Phi }_{ij}^n))=0,$$

and therefore

$${\Phi }_{ij}^{n+{\displaystyle \frac{1}{2}}}={\displaystyle \frac{{\Phi }_{ij}^{n+1}+{\Phi }_{ij}^n}{2}}-{\displaystyle \frac{\Delta t}{4}}{\delta }_y(b_{i,j-{\displaystyle \frac{1}{2}}}^n{\delta }_{\overline{y}}({\Phi }_{ij}^{n+1}-{\Phi }_{ij}^n)).$$

(10)

Finally, substituting in Equation (7) part (iii) we obtain for $0\le n\le N-1,(x_i,y_j)\in {\Omega }_h:$

$${\displaystyle \frac{{\Phi }_{ij}^{n+1}-{\Phi }_{ij}^n}{\Delta t}}-{\delta }_x\left(a_{i-{\displaystyle \frac{1}{2}},j}^n{\delta }_{\overline{x}}\left({\displaystyle \frac{{\Phi }_{ij}^{n+1}+{\Phi }_{ij}^n}{2}}\right)\right)$$

$$-{\delta }_y\left(b_{i,j-{\displaystyle \frac{1}{2}}}^n{\delta }_{\overline{y}}\left({\displaystyle \frac{{\Phi }_{ij}^{n+1}+{\Phi }_{ij}^n}{2}}\right)\right)$$

$$+{\displaystyle \frac{\Delta t}{4}}{\delta }_x\left(a_{i-{\displaystyle \frac{1}{2}},j}^n\left({\delta }_{\overline{x}}\left({\delta }_y\left(b_{i,j-{\displaystyle \frac{1}{2}}}^n\left({\delta }_{\overline{y}}({\Phi }_{ij}^{n+1}-{\Phi }_{ij}^n)\right)\right)\right)\right)\right)=F_{ij}^n.$$

(11)

Conversely, let Equation (11) hold. Then, if we define ${\Phi }^{n+{\displaystyle \frac{1}{2}}}$ from Equation (10), we see that Equation (7) parts (iii) and (iv) are equivalent to Equation (11) and Equation (10).

While the solution algorithm is given by Equation (7), the error analysis will be based on Equations (9) and (11). It is clear that solving in Equation (7) for ${\Phi }^{n+{\displaystyle \frac{1}{2}}},$${\Phi }^{n+1},$$U^{n+{\displaystyle \frac{1}{2}}},$$U^{n+1}$ requires the solution of $J,$ $J\times J$ symmetric tridiagonal systems of equations in each case. Their systems are clearly invertible in view of our assumptions on the functions a and $b.$

In what follows, we list a few auxiliary helpful results whose proofs are standard and may be found in [20].

Lemma 1.

(a) Let $\varphi \in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},\psi \in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}.$ Then

$$\sum _{i=1}^J({\varphi }_{i+1,j}-{\varphi }_{i,j}){\psi }_{ij}=-\sum _{i=1}^{J+1}{\varphi }_{ij}({\psi }_{i,j}-{\psi }_{i-1,j}).$$

(b) 

Let $\varphi \in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},\psi \in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}.$ Then

$$\sum _{j=1}^J({\varphi }_{i,j+1}-{\varphi }_{i,j}){\psi }_{ij}=-\sum _{j=1}^{J+1}{\varphi }_{ij}({\psi }_{i,j}-{\psi }_{i,j-1}).$$

(c) 

If $\varphi ,v\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},$ then for $(x_i,y_j)\in {\Omega }_h:$

(i) 

${\delta }_{x\overline{x}}{v}_{ij}:={\delta }_x{\delta }_{\overline{x}}{v}_{ij}={\delta }_{\overline{x}}{\delta }_x{v}_{ij},{\delta }_{y\overline{y}}{v}_{ij}:={\delta }_y{\delta }_{\overline{y}}{v}_{ij}={\delta }_{\overline{y}}{\delta }_y{v}_{ij}.$

(ii) 

${\delta }_x{\delta }_y{v}_{ij}={\delta }_y{\delta }_x{v}_{ij},$${\delta }_{\overline{x}}{\delta }_y{v}_{ij}={\delta }_y{\delta }_{\overline{x}}{v}_{ij},$${\delta }_{\overline{y}}{\delta }_x{v}_{ij}={\delta }_x{\delta }_{\overline{y}}{v}_{ij}.$

(iii) 

${\delta }_{\overline{x}\overline{y}}{v}_{ij}:={\delta }_{\overline{x}}{\delta }_{\overline{y}}{v}_{ij}={\delta }_{\overline{y}}{\delta }_{\overline{x}}{v}_{ij}.$

(iv) 

${\delta }_{\overline{x}}\left({\varphi }_{ij}\left({\delta }_{\overline{y}}{v}_{ij}\right)\right)=\left[{\delta }_{\overline{x}}{\varphi }_{ij}{\delta }_{\overline{y}}{v}_{ij}+{\varphi }_{ij}{\delta }_{\overline{x}\overline{y}}{v}_{ij}\right]-h{\delta }_{\overline{x}}{\varphi }_{i,j}{\delta }_{\overline{x}\overline{y}}{v}_{i,j},$

${\delta }_{\overline{y}}\left({\varphi }_{ij}\left({\delta }_{\overline{x}}{v}_{ij}\right)\right)=\left[{\delta }_{\overline{y}}{\varphi }_{ij}{\delta }_{\overline{x}}{v}_{ij}+{\varphi }_{ij}{\delta }_{\overline{x}\overline{y}}{v}_{ij}\right]-h{\delta }_{\overline{y}}{\varphi }_{i,j}{\delta }_{\overline{x}\overline{y}}{v}_{i,j}.$

(v) 

${\delta }_x\left({\varphi }_{ij}{v}_{ij}\right)=v_{ij}{\delta }_x{\varphi }_{ij}+{\varphi }_{ij}{\delta }_x{v}_{ij}+h\left({\delta }_x{\varphi }_{i,j}\right)\left({\delta }_x{v}_{i,j}\right).$

For $v,w\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},$ define the ${\ell }_2$ inner product on ${\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}$ by ${\displaystyle {(v,w)}_h:=h^2\sum _{i=1}^J\sum _{j=1}^J{v}_{ij}{w}_{ij},}$ with corresponding norm ${\displaystyle {\parallel v\parallel }_h:=h{\left(\sum _{i=1}^J\sum _{j=1}^J{v}_{ij}^2\right)}^{\frac{1}{2}}.}$

Lemma 2.

Define ${\Delta }_h:{\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}\to {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}$ by

$${\left({\Delta }_{h}v\right)}_{i,j}:=\left\{\begin{array}{cc}{\displaystyle \frac{v_{i+1,j}+v_{i-1,j}+v_{i,j+1}+v_{i,j-1}-4v_{ij}}{h^2},}\hfill & (x_i,y_j)\in {\Omega }_h,\\ 0,\hfill & (x_i,y_j)\in \partial {\Omega }_h\end{array}\right.$$

Then, there hold that

$${({\Delta }_{h}v,w)}_h={(v,{\Delta }_{h}w)}_h\forall v,w\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},$$

(12)

and

$${({\Delta }_{h}v,v)}_h=-{\left|v\right|}_{1,h}^2\forall v\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},$$

(13)

where ${\left|v\right|}_{1,h}^2:=h^2{\sum }_{i=1}^{J+1}{\sum }_{j=1}^{J+1}[{\left({\delta }_{\overline{x}}{v}_{ij}\right)}^2+{\left({\delta }_{\overline{y}}{v}_{ij}\right)}^2]$ is a discrete $H_1$ norm.

Lemma 3.

Define $L_h^n:{\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}\to {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}$ by

$${\left(L_h^{n}v\right)}_{i,j}:=\left\{\begin{array}{cc}{\displaystyle {\delta }_x(a_{i-\frac{1}{2},j}^n{\delta }_{\overline{x}}{v}_{ij})+{\delta }_y(b_{i,j-\frac{1}{2}}^n{\delta }_{\overline{y}}{v}_{ij})}\hfill & (x_i,y_j)\in {\Omega }_h,\\ 0\hfill & (x_i,y_j)\in \partial {\Omega }_h.\end{array}\right.$$

Then, there holds that

$${(L_h^{n}v,w)}_h={(v,L_h^{n}w)}_h\forall v,w\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}$$

(14)

and

$${(L_h^{n}v,v)}_h=-h^2\sum _{j=1}^{J+1}\sum _{i=1}^{J+1}\left\{a_{i+{\displaystyle \frac{1}{2}},j}^n{\left({\delta }_{\overline{x}}{v}_{ij}\right)}^2+b_{i,j+{\displaystyle \frac{1}{2}}}^n{\left({\delta }_{\overline{y}}{v}_{ij}\right)}^2\right\}\le 0\forall v\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}}.$$

(15)

Lemma 4.

Define, for $v,w\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},$ the bilinear form ${\beta }_h(v,w)$ as

$${\displaystyle {\beta }_h^n(v,w):={\left({\delta }_x\left(a^n\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left({\delta }_{\overline{y}}v\right)\right)\right)\right)\right),w\right)}_h:=}$$

$${\displaystyle h^2\sum _{i=1}^J\sum _{j=1}^J{\delta }_x\left(a_{i-\frac{1}{2},j}^n\left({\delta }_{\overline{x}}\left({\delta }_y\left(b_{i,j-\frac{1}{2}}^n\left({\delta }_{\overline{y}}{v}_{ij}\right)\right)\right)\right)\right)w_{ij}.}$$

Then, for some constants $\lambda ,\mu$ independent of $h,$ there holds that

$${\beta }_h^n(v,v)\ge {\lambda \left|v\right|}_{\overline{x}\overline{y},h}^2-\mu {\left|v\right|}_{1,h}^2\forall v\in {\mathbf{X}}_{\mathbf{h}}^{\mathbf{0}},$$

(16)

where ${\displaystyle {\left|v\right|}_{\overline{x}\overline{y},h}^2:=h^2\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left({\delta }_{\overline{x}\overline{y}}v\right)}^2.}$

3. Error Estimation

In this section, we establish error bounds for our numerical approximation scheme. We begin by analyzing the local truncation error and then proceed to derive global error estimates.

3.1. Local Truncation Error

We first establish bounds on the local truncation error terms ${\zeta }^n$ and ${\epsilon }^n$.

$$\parallel {\zeta }^n{\parallel }_h\le C(\Delta t^2+h^2),1\le n\le N-1,$$

(17)

$$\parallel {\epsilon }^n{\parallel }_h\le C(\Delta t^2+h^2),0\le n\le N-1,$$

(18)

where C is a constant independent of h and $\Delta t$.

3.2. Global Error Estimates

Having established bounds on the local truncation error, we now proceed to derive global error estimates. The following theorem provides the main convergence result of our numerical scheme.

Theorem 1.

Let $(u,\varphi )$ be a sufficiently smooth solution of the system of Equation (2) for the system of equations, and let $(U^n,{\Phi }^n)$ be the solution of our numerical scheme. Under the stability condition ${\displaystyle \frac{\Delta t}{h}}\le \sigma$, there exist positive constants $C_1$ and $C_2$, independent of h and $\Delta t$, such that:

$$\underset{0\le n\le N}{max}{\parallel u^n-U^n\parallel }_h\le C_1(\Delta t^2+h^2),$$

(19)

$$\underset{0\le n\le N}{max}{|{\varphi }^n-{\Phi }^n|}_{1,h}\le C_2(\Delta t^2+h^2).$$

(20)

These inequalities establish second-order convergence in both the discrete $L^2$ norm for the temperature u and the discrete $H^1$ norm for the phase field ϕ.

Throughout this proof, we denote by C any generic constant that is independent of $\Delta t$ and h. We proceed by establishing a series of estimates that will lead to the desired error bounds. At various points in the proof, we follow some techniques of Dendy [6], extending them from the case of a single parabolic equation considered in [6] to the case of the parabolic system considered herein. Let us define the numerical error terms $e^n:=u^n-U^n$ for the temperature and $z^n:={\varphi }^n-{\Phi }^n$ for the phase field. From Equations (7) and (11), for $1\le n\le N-1$ and $1\le i,j\le J$, we obtain:

$$\left.\begin{array}{c}{\displaystyle \frac{z_{ij}^{n+1}-z_{ij}^n}{\Delta t}}\hfill \\ -{\delta }_x\left(a(x_{i-{\displaystyle \frac{1}{2}}},y_j,t^{n+{\displaystyle \frac{1}{2}}},{\displaystyle \frac{\tilde{\varphi }(x_i,y_j,t^n)+\tilde{\varphi }(x_{i-1},y_j,t^n)}{2}}){\delta }_{\overline{x}}\left({\displaystyle \frac{{\varphi }_{ij}^{n+1}+{\varphi }_{ij}^n}{2}}\right)\right)\hfill \\ -{\delta }_y\left(b(x_i,y_{j-{\displaystyle \frac{1}{2}}},t^{n+{\displaystyle \frac{1}{2}}},{\displaystyle \frac{\tilde{\varphi }(x_i,y_j,t^n)+\tilde{\varphi }(x_i,y_{j-1},t^n)}{2}}){\delta }_{\overline{y}}\left({\displaystyle \frac{{\varphi }_{ij}^{n+1}+{\varphi }_{ij}^n}{2}}\right)\right)\hfill \\ +{\delta }_x\left(a(x_{i-{\displaystyle \frac{1}{2}}},y_j,t^{n+{\displaystyle \frac{1}{2}}},{\displaystyle \frac{\tilde{\Phi }(x_i,y_j,t^n)+\tilde{\Phi }(x_{i-1},y_j,t^n)}{2}}){\delta }_{\overline{x}}\left({\displaystyle \frac{{\Phi }_{ij}^{n+1}+{\Phi }_{ij}^n}{2}}\right)\right)\hfill \\ +{\delta }_y\left(b(x_i,y_{j-{\displaystyle \frac{1}{2}}},t^{n+{\displaystyle \frac{1}{2}}},{\displaystyle \frac{\tilde{\Phi }(x_i,y_j,t^n)+\tilde{\Phi }(x_i,y_{j-1},t^n)}{2}}){\delta }_{\overline{y}}\left({\displaystyle \frac{{\Phi }_{ij}^{n+1}+{\Phi }_{ij}^n}{2}}\right)\right)\hfill \\ +{\displaystyle \frac{\Delta t}{4}}{\delta }_x\left(a(x_{i-{\displaystyle \frac{1}{2}}},y_j,t^{n+{\displaystyle \frac{1}{2}}},{\displaystyle \frac{\tilde{\varphi }(x_i,y_j,t^n)+\tilde{\varphi }(x_{i-1},y_j,t^n)}{2}})\right.\hfill \\ \left.\ast \left({\delta }_{\overline{x}}\left({\delta }_y\left(b({\displaystyle \frac{\tilde{\varphi }(x_i,y_j,t^n)+\tilde{\varphi }(x_i,y_{j-1},t^n)}{2}})\left({\delta }_{\overline{y}}({\varphi }_{ij}^{n+1}-{\varphi }_{ij}^n)\right)\right)\right)\right)\right)\hfill \\ -{\displaystyle \frac{\Delta t}{4}}{\delta }_x\left(a(x_{i-{\displaystyle \frac{1}{2}}},y_j,t^{n+{\displaystyle \frac{1}{2}}},{\displaystyle \frac{\tilde{\Phi }(x_i,y_j,t^n)+\tilde{\Phi }(x_{i-1},y_j,t^n)}{2}})\right.\hfill \\ \left.\ast \left({\delta }_{\overline{x}}\left({\delta }_y\left(b({\displaystyle \frac{\tilde{\Phi }(x_i,y_j,t^n)+\tilde{\Phi }(x_i,y_{j-1},t^n)}{2}})\left({\delta }_{\overline{y}}({\Phi }_{ij}^{n+1}-{\Phi }_{ij}^n)\right)\right)\right)\right)\right)\hfill \\ =f(x_i,y_j,t^{n+{\displaystyle \frac{1}{2}}},\tilde{\varphi }(x_i,y_j,t^n),\tilde{u}(x_i,y_j,t^n))\hfill \\ -f(x_i,y_j,t^{n+{\displaystyle \frac{1}{2}}},\tilde{\Phi }(x_i,y_j,t^n),\tilde{U}(x_i,y_j,t^n))+{\zeta }_{ij}^n\hfill \end{array}\right\}$$

(21)

For $n\ge 1$, we define the following discrete approximations: ${\varphi }_{i,j}^n:=\varphi (x_i,y_j,t^n)$ and ${\tilde{\varphi }}_{ij}^n:={\displaystyle \frac{3}{2}}{\varphi }_{ij}^n-{\displaystyle \frac{1}{2}}{\varphi }_{ij}^{n-1}$.

The coefficients at the half-points are defined as: $a_{i-{\displaystyle \frac{1}{2}},j}^n\left(\widehat{\varphi }\right):=a({\displaystyle \frac{{\tilde{\varphi }}_{ij}^n+{\tilde{\varphi }}_{i-1,j}^n}{2}})=a({\widehat{\varphi }}_{i-{\displaystyle \frac{1}{2}},j}^n)$ for $i=1,\dots ,J+1,j=0,\dots ,J+1$, and $b_{i,j-{\displaystyle \frac{1}{2}}}^n\left(\widehat{\varphi }\right):=b({\displaystyle \frac{{\tilde{\varphi }}_{ij}^n+{\tilde{\varphi }}_{i,j-1}^n}{2}})=b({\widehat{\varphi }}_{i,j-{\displaystyle \frac{1}{2}}}^n)$ for $i=0,\dots ,J+1,j=1,\dots ,J+1$, where the half-point values $\widehat{\varphi }$ are computed as weighted averages:

$${\widehat{\varphi }}_{i-{\displaystyle \frac{1}{2}},j}^n={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{3}{2}}{\varphi }_{ij}^n-{\displaystyle \frac{1}{2}}{\varphi }_{ij}^{n-1}+{\displaystyle \frac{3}{2}}{\varphi }_{i-1,j}^n-{\displaystyle \frac{1}{2}}{\varphi }_{i-1,j}^{n-1}\right)$$

$$={\displaystyle \frac{3}{4}}\left({\varphi }_{ij}^n+{\varphi }_{i-1,j}^n\right)-{\displaystyle \frac{1}{4}}\left({\varphi }_{ij}^{n-1}+{\varphi }_{i-1,j}^{n-1}\right),$$

$${\widehat{\varphi }}_{i,j-{\displaystyle \frac{1}{2}}}^n={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{3}{2}}{\varphi }_{ij}^n-{\displaystyle \frac{1}{2}}{\varphi }_{ij}^{n-1}+{\displaystyle \frac{3}{2}}{\varphi }_{i,j-1}^n-{\displaystyle \frac{1}{2}}{\varphi }_{i,j-1}^{n-1}\right)$$

$$={\displaystyle \frac{3}{4}}\left({\varphi }_{ij}^n+{\varphi }_{i,j-1}^n\right)-{\displaystyle \frac{1}{4}}\left({\varphi }_{ij}^{n-1}+{\varphi }_{i,j-1}^{n-1}\right),$$

Similar expressions define the discrete quantities $\tilde{\Phi }$, $\widehat{\Phi }$, $a_{i-{\displaystyle \frac{1}{2}},j}^n\left(\widehat{\Phi }\right)$, and $b_{i,j-{\displaystyle \frac{1}{2}}}^n\left(\widehat{\Phi }\right)$. For notational convenience, we write:

$$F_{ij}^n(\tilde{\varphi },\tilde{u})-F_{ij}^n(\tilde{\Phi },\tilde{U}):=f({\tilde{\varphi }}_{ij}^n,{\tilde{u}}_{ij}^n)-f({\tilde{\Phi }}_{ij}^n,{\tilde{U}}_{ij}^n).$$

We finally define for $1\le \nu \le N$

$$\parallel z^{\nu }{\parallel }_n^2:=h^2\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}\left(a_{i-{\displaystyle \frac{1}{2}},j}^n\left({\widehat{\Phi }}^n\right){\left({\delta }_{\overline{x}}{z}_{ij}^{\nu }\right)}^2+b_{i,j-{\displaystyle \frac{1}{2}}}^n\left({\widehat{\Phi }}^n\right){\left({\delta }_{\overline{y}}{z}_{ij}^{\nu }\right)}^2\right).$$

(22)

We now proceed with an inductive proof. Let us assume the following induction hypothesis holds for $1\le m\le M$:

$$\begin{array}{c}{\displaystyle \frac{1}{\Delta t}}\sum _{n=1}^{m-1}\parallel z^{n+1}-z^n{\parallel }_h^2+\parallel z^m{\parallel }_{m-1}^2+\Delta t{\displaystyle \frac{\lambda }{4}}\sum _{n=1}^{m-1}{|z^{n+1}-z^n|}_{\overline{x}\overline{y},h}^2\\ \le C_2\Delta t\sum _{n=1}^{m-1}{\parallel z^n\parallel }_{n-1}^2+C_2(\Delta t^4+h^4).\end{array}$$

(23)

Obviously, (23) holds for $m=1.$ To proceed with the proof, we take the discrete ${\ell }^2$ inner product of Equation (21) with the difference $z^{n+1}-z^n$ for $n\ge 2$, which yields:

$$\left.\begin{array}{c}\parallel z^{n+1}-z^n{\parallel }_h^2\hfill \\ -\Delta t{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right){\delta }_{\overline{x}}\left({\displaystyle \frac{z^{n+1}+z^n}{2}}\right)\right)+{\delta }_y\left(b^n\left(\widehat{\Phi }\right){\delta }_{\overline{y}}\left({\displaystyle \frac{z^{n+1}+z^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{y}}(z^{n+1}-z^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ =\Delta t{\left(F^n(\tilde{\varphi },\tilde{u})-F^n(\tilde{\Phi },\tilde{U}),z^{n+1}-z^n\right)}_h+\Delta t{\left({\zeta }^n,z^{n+1}-z^n\right)}_h\hfill \\ +\Delta t{\left({\delta }_x\left([a^n\left(\widehat{\varphi }\right)-a^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{x}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ +\Delta t{\left({\delta }_y\left([b^n\left(\widehat{\varphi }\right)-b^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{y}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ -{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h.\hfill \end{array}\right\}$$

(24)

Applying Lemma 3 and using the symmetry property (14) and negativity property (15) of $L_h^n$, along with our hypotheses on a and b, we obtain the following. Please note that we use the equivalence of the norms ${\parallel ·\parallel }_n$ and ${|·|}_{1,h}$ with constants independent of h and $\Delta t$. Let us denote ${\widehat{z}}^n:={\widehat{\varphi }}^n-{\widehat{\Phi }}^n$. Then:

$$\parallel z^n{\parallel }_n^2:=h^2\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}\left(a_{i-{\displaystyle \frac{1}{2}},j}^n\left({\widehat{\Phi }}^n\right){\left({\delta }_{\overline{x}}{z}_{ij}^n\right)}^2+b_{i,j-{\displaystyle \frac{1}{2}}}^n\left({\widehat{\Phi }}^n\right){\left({\delta }_{\overline{y}}{z}_{ij}^n\right)}^2\right)\le$$

$$\le \parallel z^n{\parallel }_{n-1}^2+C{\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{x}}{z}^n,{\delta }_{\overline{x}}{z}^n\right)}_h$$

$$+C{\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{y}}{z}^n,{\delta }_{\overline{y}}{z}^n\right)}_h+C\Delta t{\parallel z^n\parallel }_{n-1}^2.$$

Therefore

$$-{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right){\delta }_{\overline{x}}\left({\displaystyle \frac{z^{n+1}+z^n}{2}}\right)\right)+{\delta }_y\left(b^n\left(\widehat{\Phi }\right){\delta }_{\overline{y}}\left({\displaystyle \frac{z^{n+1}+z^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\ge$$

$$\ge {\displaystyle \frac{1}{2}}\parallel z^{n+1}{\parallel }_n^2-{\displaystyle \frac{1}{2}}[\parallel z^n{\parallel }_{n-1}^2+C{\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{x}}{z}^n,{\delta }_{\overline{x}}{z}^n\right)}_h$$

$$+C{\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{y}}{z}^n,{\delta }_{\overline{y}}{z}^n\right)}_h+C^{\prime }\Delta t\parallel z^n{\parallel }_{n-1}^2].$$

(25)

In addition, there holds that

$$\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{x}}{z}^n,{\delta }_{\overline{x}}{z}^n\right)\le {\displaystyle \frac{C}{h^{1/3}}}(|{\widehat{z}}^n{|}_{1,h}+|{\widehat{z}}^{n-1}{|}_{1,h})\parallel z^n{\parallel }_{n-1}^2.$$

(26)

To see this consider Hölder’s inequality:

$$\left|\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{f}_{ij}{g}_{ij}\right|\le {\left(\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|f_{ij}\right|}^p\right)}^{{\displaystyle \frac{1}{p}}}{\left(\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|g_{ij}\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\mathrm{for}{\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1.$$

(27)

and

$$\left|\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{f}_{ij}{g}_{ij}{r}_{ij}\right|\le {\left(\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|f_{ij}\right|}^p\right)}^{{\displaystyle \frac{1}{p}}}{\left(\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|g_{ij}\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}{\left(\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|r_{ij}\right|}^s\right)}^{{\displaystyle \frac{1}{s}}}$$

(28)

for ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}+{\displaystyle \frac{1}{s}}=1.$ Applying Equation (28) with the specific choice of exponents $p=6$, $q={\displaystyle \frac{12}{5}}$, and $s=12$ (which satisfy ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}+{\displaystyle \frac{1}{s}}=1$), we obtain:

$$\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{x}}{z}^n,{\delta }_{\overline{x}}{z}^n\right)\le \parallel {\widehat{z}}^n-{\widehat{z}}^{n-1}{\parallel }_{6,h}\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_{{\displaystyle \frac{12}{5}},h}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_{{\displaystyle \frac{12}{5}},h},$$

where for $v\in {\mathbb{R}}^{{(J+1)}^2}$, we define the discrete ${\ell }^p$ norm:

$${\parallel v\parallel }_{p,h}:={\left(h^2\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|v_{ij}\right|}^p\right)}^{1/p}$$

(note that when $p=2$, this reduces to our standard discrete $L^2$ norm: ${\parallel v\parallel }_{2,h}\equiv {\parallel v\parallel }_h$). Therefore,

$$\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{x}}{z}^n,{\delta }_{\overline{x}}{z}^n\right)\le \parallel {\widehat{z}}^n-{\widehat{z}}^{n-1}{\parallel }_{6,h}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_{{\displaystyle \frac{12}{5}},h}^2.$$

From Equation (27) we have

$$\left|\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{f}_{ij}^r{g}_{ij}^s\right|\le {\left(\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|f_{ij}\right|}^{rp}\right)}^{{\displaystyle \frac{1}{p}}}{\left(\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}{\left|g_{ij}\right|}^{sq}\right)}^{{\displaystyle \frac{1}{q}}}\mathrm{for}{\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1.$$

(29)

Using Equation (29) with $r={\displaystyle \frac{9}{5}},s={\displaystyle \frac{3}{5}},p={\displaystyle \frac{10}{9}},q=10$ we see that

$$\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_{{\displaystyle \frac{12}{5}},h}\le \parallel {\delta }_{\overline{x}}{z}^n{\parallel }^{3/4}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_{6,h}^{1/4}.$$

We now apply the inverse inequality for discrete norms, which states that

$${\parallel v\parallel }_{p,h}\le C{h}^{-N({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{p}})}{\parallel v\parallel }_h$$

holds on ${\mathbb{R}}^{{(J+1)}^2}$, where $N=2$ is the dimension. Setting $p=6$, we obtain:

$$\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_{6,h}\le C{h}^{-2({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{6}})}\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_h=C{h}^{-{\displaystyle \frac{2}{3}}}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_h.$$

Hence

$$\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_{{\displaystyle \frac{12}{5}},h}\le C\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_h^{3/4}(h^{-{\displaystyle \frac{2}{3}}}\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_h{)}^{1/4}=C{h}^{-{\displaystyle \frac{2}{12}}}\parallel {\delta }_{\overline{x}}{z}^n{\parallel }_h=C{h}^{-{\displaystyle \frac{1}{6}}}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_h.$$

Combining these inequalities, we conclude:

$$\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{x}}{z}^n,{\delta }_{\overline{x}}{z}^n\right)\le \parallel {\widehat{z}}^n-{\widehat{z}}^{n-1}{\parallel }_{6,h}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_{{\displaystyle \frac{12}{5}},h}^2$$

$$\le C|{\widehat{z}}^n-{\widehat{z}}^{n-1}{|}_{1,h}{(C{h}^{-{\displaystyle \frac{1}{6}}}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_h)}^2=C{h}^{-{\displaystyle \frac{1}{3}}}|{\widehat{z}}^n-{\widehat{z}}^{n-1}{|}_{1,h}{\parallel {\delta }_{\overline{x}}{z}^n\parallel }_h^2$$

$$\le C{h}^{-{\displaystyle \frac{1}{3}}}|{\widehat{z}}^n-{\widehat{z}}^{n-1}{|}_{1,h}{\parallel z^n\parallel }_{n-1}^2,$$

from which inequality (26) follows.

Using the induction hypothesis $\left(I\right)$, we will now establish bounds for three key quantities when $n\le M$:

• The discrete $H^1$ norms $|{\widehat{z}}^n{|}_{1,h}$ and $|{\widehat{z}}^{n-1}{|}_{1,h}$
• The maximum discrete derivatives ${\displaystyle max\{\underset{i,j}{max}|{\delta }_{\overline{x}}{\widehat{\Phi }}_{ij}^n|,\underset{i,j}{max}|{\delta }_{\overline{y}}{\widehat{\Phi }}_{ij}^n|\}}$

Indeed, from hypothesis $\left(I\right)$, for a sufficiently small fixed $ϵ>0$, we have:

$$\parallel z^m{\parallel }_{m-1}^2\le C\Delta t\sum _{n=1}^m{\parallel z^n\parallel }_{n-1}^2+C\Delta t^4,m\le M.$$

Applying Gronwall’s lemma to this inequality yields:

$$|z^m{|}_{1,h}^2\le e^{Cm\Delta t}\Delta t^4\mathrm{for}m\le M.$$

(30)

Furthermore, using the CFL stability condition ${\displaystyle \frac{\Delta t}{h}}\le \sigma$, we obtain:

$$\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}|\left[{\left({\delta }_{\overline{x}}{\widehat{z}}_{ij}^m\right)}^2+{\left({\delta }_{\overline{y}}{\widehat{z}}_{ij}^m\right)}^2\right]\le C{\displaystyle \frac{\Delta t^4}{h^2}}\le C\Delta t^2.$$

Hence

$$max\left(\underset{i,j}{max}|{\delta }_{\overline{x}}{\widehat{z}}_{ij}|,\underset{i,j}{max}\left|{\delta }_{\overline{y}}{\widehat{z}}_{ij}\right|\right)\le \sqrt{\sum _{i=1}^{J+1}\sum _{j=1}^{J+1}\left[{\left({\delta }_{\overline{x}}{\widehat{z}}_{ij}^m\right)}^2+{\left({\delta }_{\overline{y}}{\widehat{z}}_{ij}^m\right)}^2\right]}\le C\Delta t,$$

and therefore

$$|{\delta }_{\overline{x}}{\widehat{\Phi }}_{ij}^n|\le |{\delta }_{\overline{x}}{\widehat{z}}_{ij}^n|+|{\delta }_{\overline{x}}{\widehat{\varphi }}_{ij}^n|\le C,$$

(31)

since $|{\delta }_{\overline{x}}{\widehat{\varphi }}_{ij}^n|$ is bounded by the regularity of the exact solution $\varphi$. Similarly, we obtain the bound $|{\delta }_{\overline{y}}{\widehat{\Phi }}_{ij}^n|\le C$.

Returning to Equation (30), for $n\le M$, we can use the Poincaré inequality to obtain:

$$\parallel {\widehat{z}}^n{\parallel }_h\le C{\left|{\widehat{z}}^n\right|}_{1,h}\le C{e}^{CT}\Delta t^2.$$

and a similar bound for the term $\left(|{\widehat{z}}^n-{\widehat{z}}^{n-1}|{\delta }_{\overline{y}}{z}^n,{\delta }_{\overline{y}}{z}^n\right).$ Substituting (37) in (25) we have, for $n\le M$

$$-{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right){\delta }_{\overline{x}}\left({\displaystyle \frac{z^{n+1}+z^n}{2}}\right)\right)+{\delta }_y\left(b^n\left(\widehat{\Phi }\right){\delta }_{\overline{y}}\left({\displaystyle \frac{z^{n+1}+z^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h$$

$$\ge {\displaystyle \frac{1}{2}}\parallel z^{n+1}{\parallel }_n^2-{\displaystyle \frac{1}{2}}(\parallel z^n{\parallel }_{n-1}^2+C\Delta t\parallel z^n{\parallel }_{n-1}^2)$$

(32)

Hence, from (24) and (32) we obtain, for $n\le M$

$$\begin{array}{c}\parallel z^{n+1}-z^n{\parallel }_h^2\hfill \\ +\Delta t\left[{\displaystyle \frac{1}{2}}\parallel z^{n+1}{\parallel }_n^2-{\displaystyle \frac{1}{2}}(\parallel z^n{\parallel }_{n-1}^2+C\Delta t\parallel z^n{\parallel }_{n-1}^2)\right]\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{y}}(z^{n+1}-z^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ \le \Delta t{\left(F^n(\tilde{\varphi },\tilde{u})-F^n(\tilde{\Phi },\tilde{U}),z^{n+1}-z^n\right)}_h+\Delta t{\left({\zeta }^n,z^{n+1}-z^n\right)}_h\hfill \\ +\Delta t{\left({\delta }_x\left([a^n\left(\widehat{\varphi }\right)-a^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{x}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ +\Delta t{\left({\delta }_y\left([b^n\left(\widehat{\varphi }\right)-b^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{y}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ -{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h.\hfill \end{array}$$

(33)

Therefore, using Lemma 4, we conclude for $n\le M$ that

$$\left.\begin{array}{c}\parallel z^{n+1}-z^n{\parallel }_h^2+\Delta t\left[{\displaystyle \frac{1}{2}}\parallel z^{n+1}{\parallel }_n^2-{\displaystyle \frac{1}{2}}(\parallel z^n{\parallel }_{n-1}^2+C\Delta t\parallel z^n{\parallel }_{n-1}^2)\right]\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}(\lambda |z^{n+1}-z^n{|}_{\overline{x}\overline{y},h}^2-\mu |z^{n+1}-z^n{|}_{1,h}^2)\le \hfill \\ \le \Delta t{\left(F^n(\tilde{\varphi },\tilde{u})-F^n(\tilde{\Phi },\tilde{U}),z^{n+1}-z^n\right)}_h+\Delta t{\left({\zeta }^n,z^{n+1}-z^n\right)}_h\hfill \\ +\Delta t{\left({\delta }_x\left([a^n\left(\widehat{\varphi }\right)-a^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{x}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ +\Delta t{\left({\delta }_y\left([b^n\left(\widehat{\varphi }\right)-b^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{y}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ -{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h.\hfill \end{array}\right\}$$

(34)

We now define the following quantities

$$\begin{array}{ccc}I& :=& {\left({\delta }_x\left([a^n\left(\widehat{\varphi }\right)-a^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{x}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h\hfill \\ & & +{\left({\delta }_y\left([b^n\left(\widehat{\varphi }\right)-b^n\left(\widehat{\Phi }\right)]{\delta }_{\overline{y}}\left({\displaystyle \frac{{\varphi }^{n+1}+{\varphi }^n}{2}}\right)\right),z^{n+1}-z^n\right)}_h,\hfill \\ II& :=& {\left({\delta }_x\left(a^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\varphi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h,\hfill \\ III& :=& {\left({\delta }_x\left(a^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{x}}\left({\delta }_y\left(b^n\left(\widehat{\Phi }\right)\left({\delta }_{\overline{y}}({\varphi }^{n+1}-{\varphi }^n)\right)\right)\right)\right)\right),z^{n+1}-z^n\right)}_h.\hfill \end{array}$$

After lengthy but straightforward calculations, we can establish that for any $\epsilon >0$:

$$\Delta t\left|I\right|\le C_{\epsilon }\Delta t^6+\epsilon {\parallel z^{n+1}-z^n\parallel }_h^2,$$

(35)

and similarly,

$$\Delta t^2|III-II|\le C_{\epsilon }\Delta t^6+\epsilon \Delta t^2{|z^{n+1}-z^n|}_{\overline{x}\overline{y},h}^2.$$

(36)

Substituting these bounds into Equation (32), we obtain:

$$\begin{array}{c}\parallel z^{n+1}-z^n{\parallel }_h^2+\Delta t\left[{\displaystyle \frac{1}{2}}\parallel z^{n+1}{\parallel }_n^2-{\displaystyle \frac{1}{2}}(\parallel z^n{\parallel }_{n-1}^2+C\Delta t\parallel z^n{\parallel }_{n-1}^2)\right]\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}(\lambda |z^{n+1}-z^n{|}_{\overline{x}\overline{y},h}^2-\mu |z^{n+1}-z^n{|}_{1,h}^2)\le \hfill \\ \le \Delta t{\left(F^n(\tilde{\varphi },\tilde{u})-F^n(\tilde{\Phi },\tilde{U}),z^{n+1}-z^n\right)}_h+\Delta t{\left({\zeta }^n,z^{n+1}-z^n\right)}_h\hfill \\ +C_{{\epsilon }^{\prime }}\Delta t^6+{\epsilon }^{\prime }{\parallel z^{n+1}-z^n\parallel }_h^2\hfill \\ +C_{{\epsilon }^{\prime \prime }}\Delta t^6+{\epsilon }^{\prime \prime }\Delta t^2{|z^{n+1}-z^n|}_{\overline{x},\overline{y},h}^2,\hfill \end{array}$$

(37)

where ${\epsilon }^{\prime }$ and ${\epsilon }^{″}$ are arbitrary positive constants. Applying the Cauchy-Schwarz inequality and the arithmetic-geometric mean inequality with parameter ${\epsilon }^{‴}$, we obtain:

$$\begin{array}{c}\parallel z^{n+1}-z^n{\parallel }_h^2+\Delta t\left[{\displaystyle \frac{1}{2}}\parallel z^{n+1}{\parallel }_n^2-{\displaystyle \frac{1}{2}}(\parallel z^n{\parallel }_{n-1}^2+C\Delta t\parallel z^n{\parallel }_{n-1}^2)\right]\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}(\lambda |z^{n+1}-z^n{|}_{\overline{x}\overline{y},h}^2-\mu |z^{n+1}-z^n{|}_{1,h}^2)\hfill \end{array}$$

Furthermore, since the partial derivatives are bounded ($|F_{\varphi }|\le c$ and $|F_u|\le c$), applying the mean value theorem yields:

$$\parallel F^n(\tilde{\varphi },\tilde{u})-F^n(\tilde{\Phi },\tilde{U}){\parallel }_h\le L_1\parallel {\tilde{z}}^n{\parallel }_h+L_2{\parallel {\tilde{e}}^n\parallel }_h$$

$$\le L_1^{\prime }(\parallel z^n{\parallel }_h+\parallel z^{n-1}{\parallel }_h)+L_2^{\prime }(\parallel e^n{\parallel }_h+\parallel e^{n-1}{\parallel }_h).$$

Recalling from Equation (30) that for $n\le M$, we have $\parallel z^n{\parallel }_h\le C{\left|z^n\right|}_{1,h}\le e^{CT}\Delta t^2$. Therefore, for any ${\epsilon }^{‴}>0$:

$$\parallel F^n(\tilde{\varphi },\tilde{u})-F^n(\tilde{\Phi },\tilde{U}){\parallel }_h^2\le C\Delta t^4+C(\parallel e^n{\parallel }_h^2+\parallel e^{n-1}{\parallel }_h^2),$$

$$\begin{array}{c}\parallel z^{n+1}-z^n{\parallel }_h^2\hfill \\ +\Delta t\left[{\displaystyle \frac{1}{2}}\parallel z^{n+1}{\parallel }_n^2-{\displaystyle \frac{1}{2}}(\parallel z^n{\parallel }_{n-1}^2+C\Delta t\parallel z^n{\parallel }_{n-1}^2)\right]\hfill \\ +{\displaystyle \frac{\Delta t^2}{4}}\left(\lambda \right|z^{n+1}-z^n{|}_{\overline{x}\overline{y},h}^2-\mu |z^{n+1}-z^n{|}_{1,h}^2)\hfill \\ \le \left({\displaystyle \frac{\Delta t^2}{4{\epsilon }^{\prime \prime \prime }}}(C\Delta t^4+C(\parallel e^n{\parallel }_h^2+\parallel e^{n-1}{\parallel }_h^2\left)\right)+{\epsilon }^{\prime \prime \prime }{\parallel z^{n+1}-z^n\parallel }_h^2\right)\hfill \\ +\left({\displaystyle \frac{\Delta t^2}{4{\epsilon }^{\prime \prime \prime }}}\parallel {\zeta }^n{\parallel }_h^2+{\epsilon }^{\prime \prime \prime }{\parallel z^{n+1}-z^n\parallel }_h^2\right)\hfill \\ +C_{{\epsilon }^{\prime },{\epsilon }^{\prime \prime }}\Delta t^6+{\epsilon }^{\prime }\parallel z^{n+1}-z^n{\parallel }_h^2+{\epsilon }^{\prime \prime }\Delta t^2{|z^{n+1}-z^n|}_{\overline{x},\overline{y},h}^2.\hfill \end{array}$$

Choosing the parameters ${\epsilon }^{\prime }$, ${\epsilon }^{″}$, and ${\epsilon }^{‴}$ to be of order $\epsilon$ (where $\epsilon$ is sufficiently small), we obtain:

$$\begin{array}{c}(1-\epsilon )\parallel z^{n+1}-z^n{\parallel }_h^2\hfill \\ +{\displaystyle \frac{\Delta t}{2}}\left[\parallel z^{n+1}{\parallel }_n^2-{\parallel z^n\parallel }_{n-1}^2\right]+\Delta t^2({\displaystyle \frac{\lambda }{4}}-\epsilon ){|z^{n+1}-z^n|}_{\overline{x}\overline{y},h}^2\hfill \\ \le C\Delta t^2\parallel z^n{\parallel }_{n-1}^2+\Delta t^2{C}_{\epsilon }(\parallel e^n{\parallel }_h^2+\parallel e^{n-1}{\parallel }_h^2)\hfill \\ +\Delta t^2{C}_{\epsilon }{\parallel {\zeta }^n\parallel }_h^2+C_{\epsilon }\Delta t^6,n\le M.\hfill \end{array}$$

Summing these inequalities for n ranging from 1 to m, we obtain:

$$\begin{array}{c}{\displaystyle \frac{2(1-\epsilon -C^{\prime }{\sigma }^2)}{\Delta t}}\sum _{n=1}^m\parallel z^{n+1}-z^n{\parallel }_h^2+\parallel z^{m+1}{\parallel }_m^2+2\Delta t({\displaystyle \frac{\lambda }{4}}-\epsilon )\sum _{n=1}^m{|z^{n+1}-z^n|}_{\overline{x}\overline{y},h}^2\hfill \\ \le C\Delta t\sum _{n=1}^m\parallel z^n{\parallel }_{n-1}^2+C_{\epsilon }\Delta t\sum _{n=1}^m\parallel e^n{\parallel }_h^2+C_{\epsilon }\Delta t\sum _{n=1}^m{\parallel {\zeta }^n\parallel }_h^2+C_{\epsilon }\Delta t^4,\hfill \end{array}$$

which holds for all $1\le m\le M$ and any $\epsilon >0$. Now, turning to the error equation for e, from Equations (9) and (11), we have for $0\le n\le N-1$ and $1\le i,j\le J$:

$${\displaystyle \frac{e_{ij}^{n+1}-e_{ij}^n}{\Delta t}}-{\Delta }_h\left({\displaystyle \frac{e_{ij}^{n+1}+e_{ij}^n}{2}}\right)+{\displaystyle \frac{\Delta t}{4}}{\delta }_{x\overline{x}}{\delta }_{y\overline{y}}(e_{ij}^{n+1}-e_{ij}^n)$$

$$={\displaystyle \frac{1}{\Delta t}}\left\{[P(x_i,y_j,t^{n+1},\varphi (x_i,y_j,t^{n+1}))-P(x_i,y_j,t^n,\varphi (x_i,y_j,t^n))]\right\}$$

$$-{\displaystyle \frac{1}{\Delta t}}\left\{[P(x_i,y_j,t^{n+1},\Phi (x_i,y_j,t^{n+1}))-P(x_i,y_j,t^n,\Phi (x_i,y_j,t^n))]\right\}+{\epsilon }_{ij}^n.$$

Let us define the temporal difference operator $\widehat{P}$ as:

$${\widehat{P}}_{ij}{\left(v\right)}^n:=P(x_i,y_j,t^{n+1},v(x_i,y_j,t^{n+1}))-P(x_i,y_j,t^n,v(x_i,y_j,t^n)).$$

Taking the discrete ${\ell }^2$ inner product of both sides with $e^{n+1}+e^n$ (which represents a centered discretization), we obtain:

$$\begin{array}{c}{\left(e^{n+1}-e^n,e^{n+1}+e^n\right)}_h-\Delta t{\left({\Delta }_h\left({\displaystyle \frac{e^{n+1}+e^n}{2}}\right),e^{n+1}+e^n\right)}_h\hfill \end{array}$$

$$+{\displaystyle \frac{\Delta t^2}{4}}{\left({\delta }_{x\overline{x}}{\delta }_{y\overline{y}}(e^{n+1}-e^n),e^{n+1}+e^n\right)}_h$$

$$={\left(\widehat{P}{\left(\varphi \right)}^n-\widehat{P}{(\Phi )}^n,e^{n+1}+e^n\right)}_h+\Delta t{\left({\epsilon }^n,e^{n+1}+e^n\right)}_h.$$

(38)

Using the symmetry of the bilinear form ${\beta }_h(·,·)$, applying Lemma 4 with $a\equiv 1$ and $b\equiv 1$, and invoking Lemma 2, we sum the above relation from $n=0$ to $m^{\prime }-1$. Please note that $e^0=0$ by initial conditions.

$$\parallel e^{m^{\prime }}{\parallel }_h^2+{\displaystyle \frac{\Delta t}{2}}\sum _{n=0}^{m^{\prime }-1}{|e^{n+1}+e^n|}_{1,h}^2$$

$$\le \sum _{n=0}^{m^{\prime }-1}{\left(\widehat{P}{\left(\varphi \right)}^n-\widehat{P}{(\Phi )}^n,e^{n+1}+e^n\right)}_h+\Delta t\sum _{n=0}^{m^{\prime }-1}{\left({\epsilon }^n,e^{n+1}+e^n\right)}_h$$

$$\le \sum _{n=0}^{m^{\prime }-1}\parallel \widehat{P}{\left(\varphi \right)}^n-\widehat{P}{(\Phi )}^n{\parallel }_h\parallel e^{n+1}+e^n{\parallel }_h+\Delta t\sum _{n=0}^{m^{\prime }-1}\parallel {\epsilon }^n{\parallel }_h{\parallel e^{n+1}+e^n\parallel }_h$$

$$\le {\displaystyle \frac{1}{4\epsilon \Delta t}}\sum _{n=0}^{m^{\prime }-1}\parallel \widehat{P}{\left(\varphi \right)}^n-\widehat{P}{(\Phi )}^n{\parallel }_h^2+\epsilon \Delta t\sum _{n=0}^{m^{\prime }-1}{\parallel e^{n+1}+e^n\parallel }_h^2$$

$$+{\displaystyle \frac{\Delta t}{4\epsilon }}\sum _{n=0}^{m^{\prime }-1}\parallel {\epsilon }^n{\parallel }_h^2+\Delta t\epsilon \sum _{n=0}^{N-1}{\parallel e^{n+1}+e^n\parallel }_h^2$$

$$\le {\displaystyle \frac{1}{4\epsilon \Delta t}}\sum _{n=0}^{m^{\prime }-1}\parallel \widehat{P}{\left(\varphi \right)}^n-\widehat{P}{(\Phi )}^n{\parallel }_h^2+C_{\epsilon }\Delta t\sum _{n=0}^{m^{\prime }-1}\parallel {\epsilon }^n{\parallel }_h^2+\Delta t\epsilon \sum _{n=0}^{N-1}{\parallel e^{n+1}+e^n\parallel }_h^2.$$

In view of Equation (38) we have

$$\parallel e^{m^{\prime }}{\parallel }_h^2\le C\left(C_{\epsilon }\Delta t\sum _{n=0}^{m^{\prime }-1}\parallel e^n{\parallel }_h^2+C_{\epsilon }\Delta t\sum _{n=1}^{m^{\prime }-1}\parallel {\zeta }^n{\parallel }_h^2+C_{\epsilon }\Delta t^4+{\parallel z^1\parallel }_0^2\right)$$

$$+c\Delta t\sum _{n=0}^{m^{\prime }-1}{\parallel {\epsilon }^n\parallel }_h^2.$$

Applying Gronwall’s lemma to this inequality yields:

$$\underset{0\le n\le m^{\prime }}{max}{\parallel e^n\parallel }_h^2\le C\left[\Delta t\sum _{n=1}^{m-1}\parallel {\zeta }^n{\parallel }_h^2+\Delta t\sum _{n=0}^{m-1}\parallel {\epsilon }^n{\parallel }_h^2+\Delta t^4+{\parallel z^1\parallel }_0^2\right].$$

Therefore, applying estimates (17) and (18), we obtain:

$$\begin{array}{c}\underset{0\le n\le m}{max}{\parallel e^n\parallel }_h^2\le C\left[\Delta t\sum _{n=1}^{m-1}{(\Delta t^2+h^2)}^2+\Delta t^4+{\parallel z^1\parallel }_0^2\right]\le C\left({(\Delta t^2+h^2)}^2+{\parallel z^1\parallel }_0^2\right).\hfill \end{array}$$

Using the fact that $\parallel z^1{\parallel }_0=O(\Delta t^2+h^2)$, we conclude:

$$\underset{0\le n\le m}{max}{\parallel e^n\parallel }_h\le C(\Delta t^2+h^2).$$

(39)

Moreover, we have the following bound on the time-summed error:

$$\Delta t\sum _{n=0}^m{\parallel e^n\parallel }_h^2\le C{(\Delta t^2+h^2)}^2.$$

(40)

Finally, substituting bounds (40) and (18) into inequality (37), we obtain:

$${\displaystyle \frac{2(1-\epsilon -C^{\prime }{\sigma }^2)}{\Delta t}}\sum _{n=1}^m\parallel z^{n+1}-z^n{\parallel }_h^2+\parallel z^{m+1}{\parallel }_m^2+2\Delta t({\displaystyle \frac{\lambda }{4}}-\epsilon )\sum _{n=1}^m{|z^{n+1}-z^n|}_{\overline{x}\overline{y},h}^2$$

$$\le C\Delta t\sum _{n=1}^m{\parallel z^n\parallel }_{n-1}^2+C_{\epsilon }(\Delta t^4+h^4)$$

(41)

Let us choose $\epsilon >0$ sufficiently small such that $2(1-\epsilon -C^{\prime }{\sigma }^2)\ge 1$ and $2({\displaystyle \frac{\lambda }{4}}-\epsilon )\ge {\displaystyle \frac{\lambda }{4}}$. Then inequality (41) yields:

$$\begin{array}{c}{\displaystyle \frac{1}{\Delta t}}\sum _{n=1}^m\parallel z^{n+1}-z^n{\parallel }_h^2+\parallel z^{m+1}{\parallel }_m^2+\Delta t{\displaystyle \frac{\lambda }{4}}\sum _{n=1}^m{|z^{n+1}-z^n|}_{\overline{x}\overline{y},h}^2\hfill \\ \le C\Delta t\sum _{n=1}^m{\parallel z^n\parallel }_{n-1}^2+C(\Delta t^4+h^4),\hfill \end{array}$$

which establishes the inductive hypothesis $\left(I\right)$ for index m. Thus, $\left(I\right)$ holds for all $1\le m\le N$.

From Equation (38), we conclude that estimate (19) holds. Moreover, from $\left(I\right)$ we obtain:

$$\parallel z^m{\parallel }_{m-1}^2\le C\Delta t\sum _{n=1}^{m-1}{\parallel z^n\parallel }_{n-1}^2+C(\Delta t^4+h^4),1\le m\le N$$

Applying Gronwall’s lemma to this inequality yields:

$$\underset{1\le m\le N}{max}{\parallel z^m\parallel }_{m-1}\le C(\Delta t^2+h^2),$$

which establishes estimate (20).

We note that by Taylor’s theorem, we can construct a first-step approximation satisfying:

$$\parallel z^1{\parallel }_h=O(\Delta t^2+h^2).$$

4. Numerical Verification of Convergence Order

In this section, we present numerical experiments to verify the theoretical convergence rates established in the previous sections. We solve the system of Equation (2) with Neumann boundary conditions on $\partial \Omega$ (similar convergence rates were observed for Dirichlet boundary conditions).

The computational domain is set to $\Omega =[0,1]\times [0,1]$ with final time $T=0.1$. We consider the isotropic case where $a=b=1$, with nonlinear terms:

$$f(\varphi ,u)={\displaystyle \frac{\varphi (1-\varphi )u}{1+0.25u}},p\left(\varphi \right)={\varphi }^3(10-15\varphi +6{\varphi }^2).$$

To facilitate error analysis, we construct an exact solution by adding appropriate source terms such that the solution to the initial-boundary-value problem with Neumann conditions is:

$$(\varphi ,u)=(e^{-t}cos\left(x(x-1)\right)cos\left(y(y-1)\right),e^{-t}cos\left(\pi x\right)cos\left(\pi y\right)).$$

Table 1 presents the numerical errors and convergence rates for solutions computed using the ADI–ADI scheme. We measure the errors in both the discrete maximum norm ${\parallel ·\parallel }_{\infty }$ and the discrete ${\ell }^2$ norm ${\parallel ·\parallel }_h$. The spatial discretization parameter is taken as $h=1/(J+1)$ for $J=50,75,\dots ,567$, with the time step chosen as $\Delta t=0.01h$ to maintain a fixed ratio. For both variables $\varphi$ and u, we observe second-order convergence in both norms, confirming our theoretical analysis.

Table 1. Errors and convergence rates for the ADI–ADI scheme in discrete norms ($T=0.1$).

	${\parallel ·\parallel }_{\mathit{\infty }}$		${\parallel ·\parallel }_{\mathit{h}}$
J	Errors	Order	Errors	Order
50	$\varphi :1.920\times {10}^{-4}$	$--$	$8.664\times {10}^{-5}$	$--$
	$u:1.047\times {10}^{-4}$	$--$	$4.762\times {10}^{-5}$	$--$
75	$\varphi :8.708\times {10}^{-5}$	$1.95$	$3.851\times {10}^{-5}$	$1.99$
	$u:4.725\times {10}^{-5}$	$1.96$	$2.119\times {10}^{-5}$	$1.99$
112	$\varphi :3.979\times {10}^{-5}$	$1.93$	$1.731\times {10}^{-5}$	$1.97$
	$u:2.143\times {10}^{-5}$	$1.94$	$9.513\times {10}^{-6}$	$1.97$
168	$\varphi :1.806\times {10}^{-5}$	$1.94$	$7.747\times {10}^{-6}$	$1.98$
	$u:9.622\times {10}^{-6}$	$1.97$	$4.231\times {10}^{-6}$	$1.99$
252	$\varphi :8.254\times {10}^{-6}$	$1.93$	$3.486\times {10}^{-6}$	$1.96$
	$u:4.320\times {10}^{-6}$	$1.97$	$1.883\times {10}^{-6}$	$1.99$
378	$\varphi :3.814\times {10}^{-6}$	$1.90$	$1.582\times {10}^{-6}$	$1.94$
	$u:1.944\times {10}^{-6}$	$1.96$	$8.383\times {10}^{-7}$	$1.99$
567	$\varphi :1.795\times {10}^{-6}$	$1.85$	$7.300\times {10}^{-7}$	$1.90$
	$u:8.783\times {10}^{-7}$	$1.95$	$3.736\times {10}^{-7}$	$1.99$

For each refinement level, the experimental order of convergence is computed as:

$$\mathrm{rate}={\displaystyle \frac{log(e_2/e_1)}{log(h_2/h_1)}},$$

where $e_1$, $e_2$ are the errors and $h_1$, $h_2$ are the mesh sizes for two consecutive refinements. In the numerical solution of phase-field models, the ADI–ADI order $\Delta t^2+h^2$ method demonstrates notable advantages over both the Euler-Euler order $\Delta t+h$ and Euler-ADI schemes order $\Delta t+h^2$. As detailed in Sfyrakis et al. [19], the ADI–ADI approach achieves second-order accuracy in both time and space while maintaining unconditional stability. This allows for larger time steps without compromising accuracy, leading to enhanced computational efficiency. In contrast, the fully explicit Euler-Euler method requires significantly smaller time steps to ensure stability, resulting in increased computational costs. While the semi-implicit Euler-ADI method offers improved stability over Euler-Euler, it still falls short in terms of accuracy and efficiency, particularly when addressing nonlinearities and higher-dimensional problems. Therefore, the ADI–ADI method provides a more robust and efficient framework for simulating complex phase-transition phenomena. In Table 2 they are shown the computing times (in seconds) required by the two schemes in a parallel implementation to achieve the error levels close to those shown in Table 1 on one, two, and four CPUs.

Table 2. Computing time (in seconds) to obtain the results of Table 1 on 1, 2, and 4 CPUs.

J	Euler-ADI	Euler-ADI	Euler-ADI	ADI–ADI	ADI–ADI	ADI–ADI
	CPU 1	CPU 2	CPU 4	CPU 1	CPU 2	CPU 4
50	9	9	20	5	4	8
75	38	33	62	16	12	17
112	179	139	220	52	37	47
168	874	605	800	177	115	126
252	4384	2800	3181	609	378	369
378	22559	13907	13525	2155	1541	1286
567	111202	66821	57504	6934	4221	3435

The results clearly indicate the tremendous superiority of the ADI–ADI scheme.

5. Additional Numerical Experiments

We now present numerical experiments with physically relevant initial conditions. Following Wang [5], we consider the computational domain $\Omega =[0,1]\times [0,1]$ with the initial phase field:

$${\varphi }_0(x,y)={\displaystyle \frac{1}{2}}\left[1+tanh{\displaystyle \frac{r-R_0}{2\sqrt{2}\epsilon }}\right],$$

where $r=\sqrt{x^2+y^2}$ and:

$$u_0\left(r\right)=\left\{\begin{array}{cc}{t}_s\hfill & \mathrm{if}r<R_0\hfill \\ {\displaystyle \frac{ln(r/R_0)+t_{s}ln(r/R_{00})}{ln(R_0/R_{00})}}\hfill & \mathrm{if}{R}_0\le r<R_{00}\hfill \\ -1\hfill & \mathrm{if}r\ge R_{00}\hfill \end{array}\right.$$

The model parameters are set to $a=b=1$ with anisotropic mobility:

$$q={\displaystyle \frac{1}{m(1+{\delta }_{\mu }cos\left(4\theta \right))}},\theta =arctan({\varphi }_y/{\varphi }_x),$$

and nonlinear terms:

$$f={\displaystyle \frac{1}{{\epsilon }^2}}\varphi (1-\varphi )\left(\varphi -{\displaystyle \frac{1}{2}}+30\epsilon \alpha S{\displaystyle \frac{u}{1+0.25u}}\varphi (1-\varphi )\right),$$

$$p={\displaystyle \frac{{\varphi }^3(10-15\varphi +6{\varphi }^2)}{S}}.$$

Here, S is the dimensionless supercooling of the melt, m is the ratio of capillary to kinetic length, and $\epsilon$ represents the ratio of the average interface thickness.

For the isotropic case (${\delta }_{\mu }=0$), we use the following physical parameters:

• Initial condition: $t_s=0.01$, $R_0=0.1$, $R_{00}=2R_0$
• Model parameters: $S=0.8$, $m=0.1$, $\alpha =70$, $\epsilon =1/400$
• Numerical parameters: $h={10}^{-3}$, $\Delta t=2·{10}^{-5}$

The evolution of the solution is shown in Figure 1 and Figure 2.

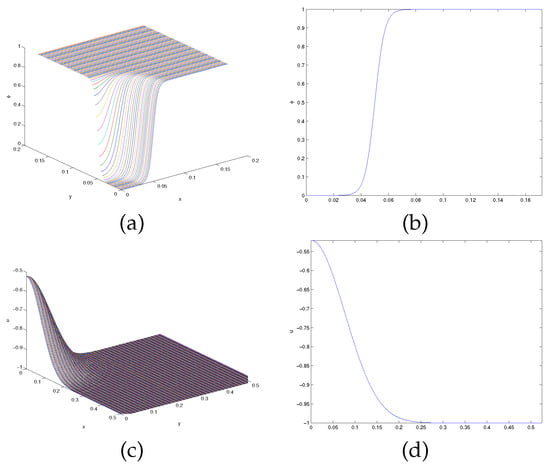
Figure 1. Phase field $\varphi$ and temperature u in the isotropic case at $t=2·{10}^{-3}$: (a) 3D plot of $\varphi$, (b) cross-section at $x=0.1$ of $\varphi$, (c) 3D plot of u, (d) cross-section at $x=0.1$ of u.

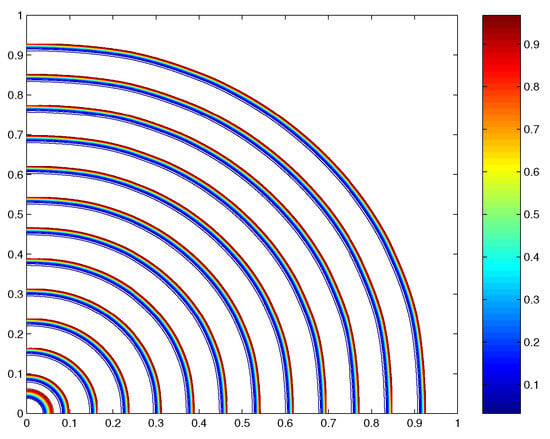
Figure 2. Time evolution of the interface: contours plotted every 100 time steps for the isotropic case.