Metric Dimension of Circulant Graphs with 5 Consecutive Generators

Abstract

The problem of finding the metric dimension of circulant graphs with t generators $1,2,\dots ,t$ (and their inverses) has been extensively studied. The problem is solved for $t=2,3,4$, and some exact values and bounds are known also for $t=5$. We solve all the open cases for $t=5$.

1. Introduction

The metric dimension is an invariant that has wide applications, for example, in pharmaceutical chemistry [1], Sonar and coast guard Loran [2], and robot navigation [3]. Applications of the metric dimension to the problem of pattern recognition and image processing can be found in [4]. The concept of metric dimension was introduced by Slater [2] in 1975.

For a graph G with set of vertices $V\left(G\right)$, the distance $d(u,v)$ between two vertices $u,v\in V\left(G\right)$ is the number of edges in a shortest path between u and v. The vertices u and v are resolved by a vertex w if $d(u,w)\ne d(v,w)$. For an ordered set $W=\{w_1,w_2,\dots ,w_z\}$, the representation of distances of v with respect to W is the ordered z-tuple

$$r\left(v\right|W)=(d(v,w_1),d(v,w_2),\dots ,d(v,w_z)).$$

The set $W\subset V\left(G\right)$ is a resolving set of G if all the vertices of G have distinct representations (if every pair of vertices of G is resolved by a vertex of W). The number of vertices in a smallest resolving set is the metric dimension $\dim \left(G\right)$.

Circulant graphs have been extensively studied because they are particularly symmetric, and it is easy to set up such networks and check their properties. For $t\ge 2$ and $n\ge 2t+1$, the circulant graph $C_n(1,2,\dots ,t)$ has vertices $v_0,v_1$, $v_2,\dots ,v_{n-1}$ and edges $v_i{v}_{i+1}$, $v_i{v}_{i+2},\dots ,v_i{v}_{i+t}$, where $i=0,1,2,\dots ,n-1$, and the subscripts are taken modulo n. The integers $\pm 1,\pm 2,\dots ,\pm t$ are the generators of $C_n(1,2,\dots ,t)$.

Let us suppose that $n\ge 2t+2$ since $C_n(1,2,\dots ,t)$ is a complete graph for $n=2t+1$. We present the known results on $\dim \left(C_n(1,2,\dots ,t)\right)$ for small t (and $n\ge 2t+2$). By [5,6], we have

$$\dim \left(C_n(1,2)\right)=\left\{\begin{array}{cc}3\hfill & \mathrm{if}n\equiv 0,2,3\left(\mathrm{mod}4\right),\hfill \\ 4\hfill & \mathrm{if}n\equiv 1\left(\mathrm{mod}4\right).\hfill \end{array}\right.$$

By [5,7],

$$\dim \left(C_n(1,2,3)\right)=\left\{\begin{array}{cc}4\hfill & \mathrm{if}n\equiv 0,2,3,4,5\left(\mathrm{mod}6\right),\hfill \\ 5\hfill & \mathrm{if}n\equiv 1\left(\mathrm{mod}6\right).\hfill \end{array}\right.$$

For $n\notin \{11,19\}$, by [8],

$$\dim \left(C_n(1,2,3,4)\right)=\left\{\begin{array}{cc}4\hfill & \mathrm{if}n\equiv 2\left(\mathrm{mod}8\right),\hfill \\ 5\hfill & \mathrm{if}n\equiv 0,1,3,4\left(\mathrm{mod}8\right),\hfill \\ 6\hfill & \mathrm{if}n\equiv 5,6,7\left(\mathrm{mod}8\right),\hfill \end{array}\right.$$

and $\dim \left(C_{11}(1,2,3,4)\right)=\dim \left(C_{19}(1,2,3,4)\right)=4$.

The metric dimension of $C_n(1,2,3,4)$ was studied also in [9], the graphs $C_n(1,3)$ were investigated in [10], $C_n(2,3)$ in [11], $C_n(1,4)$ in [12], $C_n(1,\frac{n}{2})$ where n is even in [13], $C_n(1,2,4)$ in [14], and $C_n(1,2,5)$ in [15].

In [16], it was shown that $\dim \left(C_n(1,2,\dots ,t)\right)\ge ⌈\frac{2t}{3}⌉+2$ for $t\ge 6$, and by [17], for each $t\ge 6$ there exists an n such that the bound is sharp. However, this bound does not hold for $t=5$. Therefore, we are very interested in the case $t=5$, and we solve all the open cases for $\dim \left(C_n(1,2,3,4,5)\right)$.

Let us denote $C_n(1,2,3,4,5)$ by $G_n$. Since $n\ge 2t+2$, we have $n\ge 12$. From Theorem 2.5 given in [18], we have $\dim \left(G_n\right)\ge 6$ for $n\equiv 0,1,7,8,9\left(\mathrm{mod}10\right)$. This result was extended by Chau and Gosselin [19], who proved in their Theorem 2.7 that $\dim \left(G_n\right)\ge 6$ also for $n\equiv 2,6\left(\mathrm{mod}10\right)$. By Theorem 2.13 from [19], $\dim \left(G_n\right)\ge 6$ for $n\equiv 3\left(\mathrm{mod}10\right)$, where $n\ge 23$. By Lemma 8 and Theorem 10 given in [16], $\dim \left(G_n\right)\ge 6$ for $n\equiv 4,5\left(\mathrm{mod}10\right)$. Thus, by [16,18,19], for $n\ge 12$ where $n\ne 13$,

$$\dim \left(G_n\right)\ge 6.$$

(1)

From Table 3 presented in [19], we have $\dim \left(G_{13}\right)=5$.

By Grigorious et al. [20] (see Proposition 1.2 in [19]), we have

$$\dim \left(G_n\right)\le 6\mathrm{if}n\equiv 2,3,4,5,6,7\left(\mathrm{mod}10\right).$$

By Theorem 2.9 presented in [19], $\dim \left(G_n\right)\le 6$ for $n\equiv 8\left(\mathrm{mod}10\right)$. Thus, by [16,19,20], for $n\ge 12$ where $n\ne 13$,

$$\dim \left(G_n\right)=6\mathrm{if}n\equiv 2,3,4,5,6,7,8\left(\mathrm{mod}10\right),\mathrm{and}\dim \left(G_{13}\right)=5.$$

(2)

In this paper, we study $\dim \left(G_n\right)$ for $n\equiv 0,1,9\left(\mathrm{mod}10\right)$.

2. Results

First, we prove an upper bound on $\dim \left(G_n\right)$ for $n\equiv 9\left(\mathrm{mod}10\right)$.

Theorem 1. 

Let $n=10k+9$ where $k\ge 2$. Then, $\dim \left(G_n\right)\le 6$.

Proof. 

We show that $W=\{v_0,v_3,v_7,v_{5k},v_{5k+4},v_{5k+7}\}$ is a resolving set of $G_n$. Representations of distances of all the vertices in $V\left(G_n\right)\setminus W$ with respect to W are given in Table 1.

Table 1. Representations of vertices in $V\left(G_n\right)\setminus W$ with respect to W.

Representation	${\mathit{v}}_0$	${\mathit{v}}_3$	${\mathit{v}}_7$	${\mathit{v}}_{5\mathit{k}}$	${\mathit{v}}_{5\mathit{k}+4}$	${\mathit{v}}_{5\mathit{k}+7}$
$v_1$	1	1	2	k	$k+1$	$k+1$
$v_2$	1	1	1	k	$k+1$	$k+1$
$v_4$	1	1	1	k	k	$k+1$
$v_5$	1	1	1	$k-1$	k	$k+1$
$v_6$	2	1	1	$k-1$	k	$k+1$
$v_{5i+1}$$(2\le i\le k-1)$	$i+1$	i	$i-1$	$k-i$	$k-i+1$	$k-i+2$
$v_{5i+2}$$(2\le i\le k-1)$	$i+1$	i	$i-1$	$k-i$	$k-i+1$	$k-i+1$
$v_{5i+3}$$(1\le i\le k-1)$	$i+1$	i	i	$k-i$	$k-i+1$	$k-i+1$
$v_{5i+4}$$(1\le i\le k-1)$	$i+1$	$i+1$	i	$k-i$	$k-i$	$k-i+1$
$v_{5i+5}$$(1\le i\le k-2)$	$i+1$	$i+1$	i	$k-i-1$	$k-i$	$k-i+1$
$v_{5k+1}$	$k+1$	k	$k-1$	1	1	2
$v_{5k+2}$	$k+1$	k	$k-1$	1	1	1
$v_{5k+3}$	$k+1$	k	k	1	1	1
$v_{5k+5}$	$k+1$	$k+1$	k	1	1	1
$v_{5k+6}$	$k+1$	$k+1$	k	2	1	1
$v_{5k+8}$	$k+1$	$k+1$	$k+1$	2	1	1
$v_{5k+9}$	k	$k+1$	$k+1$	2	1	1
$v_{5k+10}$	k	$k+1$	$k+1$	2	2	1
$v_{10k-5i+6}$$(1\le i\le k-1)$	$i+1$	$i+2$	$i+2$	$k-i+2$	$k-i+1$	$k-i$
$v_{10k-5i+7}$$(1\le i\le k-1)$	$i+1$	$i+1$	$i+2$	$k-i+2$	$k-i+1$	$k-i$
$v_{10k-5i+8}$$(1\le i\le k-1)$	$i+1$	$i+1$	$i+2$	$k-i+2$	$k-i+1$	$k-i+1$
$v_{10k-5i+9}$$(1\le i\le k-1)$	i	$i+1$	$i+2$	$k-i+2$	$k-i+1$	$k-i+1$
$v_{10k-5i+10}$$(1\le i\le k-1)$	i	$i+1$	$i+2$	$k-i+2$	$k-i+2$	$k-i+1$
$v_{10k+6}$	1	2	2	$k+1$	$k+1$	k
$v_{10k+7}$	1	1	2	$k+1$	$k+1$	k
$v_{10k+8}$	1	1	2	$k+1$	$k+1$	$k+1$

Since any two vertices have different representations, $\dim \left(G_n\right)\le 6$. ☐

Let $v_x$ be a vertex from a resolving set W. Then, $v_x$ resolves $v_{x+5}$ and $v_{x+6}$, but it does not resolve any pair from $v_{x+1},v_{x+2},\dots ,v_{x+5}$. Analogously, $v_x$ resolves $v_{x+10}$ and $v_{x+11}$, but it does not resolve any pair from $v_{x+6},v_{x+7},\dots ,v_{x+10}$. If $v_y$ and $v_{y+1}$ are resolved by $v_x$ and $v_x\notin \{v_y,v_{y+1}\}$, then we say that $v_x$ creates a border between $v_y$ and $v_{y+1}$. Observe that borders caused by $v_x$ split the vertices of $G_n$ into sequences of non-resolved vertices (by $v_x$). The only exception is $v_x$ itself since it does not create borders between $v_{x-1}$ and $v_x$ and between $v_x$ and $v_{x+1}$ (recall that we require $v_x\notin \{v_y,v_{y+1}\}$ in the definition of borders). The reason is that $v_x$ does not distinguish $v_{x-1}$ and $v_{x+1}$. Of course, $v_x$ does not distinguish also $v_{x-6}$ from $v_{x+6}$ though in the sequence $v_{x-6},v_{x-5},\dots ,v_{x+6}$ there are two borders caused by $v_x$. But our aim is to construct a lower bound, so we need a necessary condition, not a sufficient.

So take all vertices of W and create all borders caused by these vertices. Then, these borders split $V\left(G_n\right)$ around the cycle $C_n=(v_0,v_1,\dots ,v_{n-1})$ into many small sequences, which we call states. And the necessary condition for W to be a resolving set is that every state contains at most one vertex which is not in W. We use this condition in the proofs of the next theorems.

We need to distinguish the distance in $G_n$ from the distance in a subgraph $C_n$ ($=(v_0,v_1,\dots ,v_{n-1})$) of $G_n$. Therefore, by the index distance, we call the distance between the vertices of $G_n$ in $C_n$. For example, $v_x$ and $v_{x+5}$ (the indices are always taken modulo n) have distance 1 in $G_n$, but their index distance is 5.

We start with a lower bound on $\dim \left(G_n\right)$ for $n\equiv 1\left(\mathrm{mod}10\right)$.

Theorem 2. 

Let $n=10d+1$, where $d\ge 2$. Then, $\dim \left(G_n\right)\ge 8$.

Proof. 

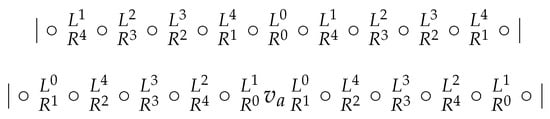
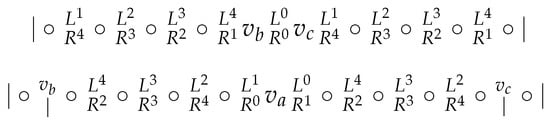
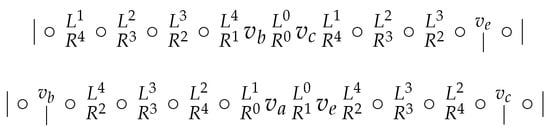
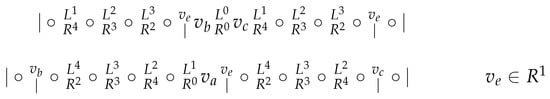
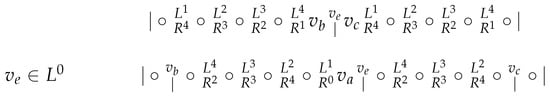
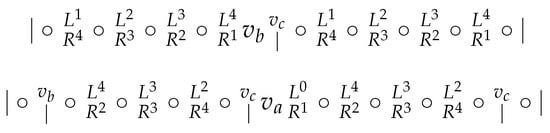
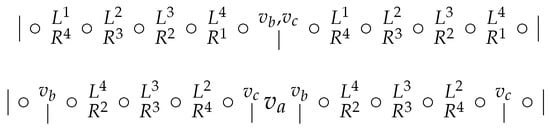
By way of contradiction, suppose that $V\left(G_n\right)$ contains a subset W containing 7 vertices which are resolving. Observe that $G_n$ has diameter d and for every vertex $v_x$, the vertices at distance d from $v_x$ are the 10 consecutive vertices (consecutive by index distance) $v_{x+n^{\prime }-4},v_{x+n^{\prime }-3},\dots ,v_{x+n^{\prime }},v_{x-n^{\prime }},v_{x-n^{\prime }+1},\dots ,v_{x-n^{\prime }+4}$, where $n^{\prime }=\frac{n-1}{2}$.

Let $v_x\in W$. Since W must distinguish $v_{x-n^{\prime }}$ from $v_{x+n^{\prime }}$, we have $v_{x-n^{\prime }}\in W$ or $v_{x+n^{\prime }}\in W$ or there is a vertex $v_y\in W$ at index distance $5k$ from $v_x$ for some $k\in \mathrm{\mathbb{N}}$. But since both $v_{x-n^{\prime }}$ and $v_{x+n^{\prime }}$ have index distance $n^{\prime }=\frac{n-1}{2}=5d$ from $v_x$, we conclude that W must contain a vertex at index distance $5k$ from $v_x$.

So for every $v_x\in W$, there is $v_y\in W$ such that the index distance between $v_x$ and $v_y$ is a multiple of 5. Obviously, such a role as that which $v_y$ plays for $v_x$ is played also by $v_x$ for $v_y$. And since $\left|W\right|=7$, there must be a vertex in W, say $v_a$, such that two vertices from W, say $v_b$ and $v_c$, have an index distance that is a multiple of 5 from $v_a$.

Not only this, but let $L=\{v_{a-1},v_{a-2},\dots ,v_{a-n^{\prime }}\}$ and $R=\{v_{a+1},v_{a+2},\dots ,v_{a+n^{\prime }}\}$. Then, L, R, $\left\{v_a\right\}$ is a partition of $V\left(G_n\right)$. If both $v_b$ and $v_c$ are in R (or if they are both in L), then all mutual index distances between pairs of vertices of $\{v_a,v_b,v_c\}$ are multiples of 5. Hence, by symmetry, we may assume that $v_b\in L$, $v_c\in R$, and we may also assume that $a=0$.

Now, we split L and R, each into five sets according to the index distance from $v_0$ ($=v_a$). Let $0\le i\le 4$. By $L^i$ (by $R^i$), we denote vertices of L (of R) whose index distance from $v_0$ is congruent to $i(mod5)$. (Observe that the index distance cannot be greater than $n^{\prime }$.) Hence, $v_b\in L^0$ and $v_c\in R^0$.

As mentioned above, for every $v_z\in W\setminus \{v_a,v_b,v_c\}$, to distinguish $v_{z-n^{\prime }}$ from $v_{z+n^{\prime }}$, there must be a vertex in W which is at index distance $5k$ from $v_z$. For instance, if $v_z\in L^0$, then to distinguish $v_{z-n^{\prime }}$ from $v_{z+n^{\prime }}$, W contains a vertex, say $v_y$, such that either $v_y\in L^0$ (if $v_y$ is in L), or $v_y\in R^0$ (when $v_y\in R$ and the shortest index distance $v_z-v_y$ path contains $v_a$), or $v_y\in R^1$ (when $v_y\in R$ and the shortest index distance $v_z-v_y$ path does not contain $v_a$). In Table 2, we have all 10 cases according to $v_z$ being in $L^0$, $L^1$, …, $R^4$. In each case, the vertex $v_y$ is from the union of the three sets.

Table 2. The 10 cases according to $v_z$ being in $L^0$, $L^1$, …, $R^4$.

${\mathit{L}}^0$: ${\mathit{L}}^0,{\mathit{R}}^0,{\mathit{R}}^1$	${\mathit{R}}^0$: ${\mathit{R}}^0,{\mathit{L}}^0,{\mathit{L}}^1$
$L^1$: $L^1,R^4,R^0$	$R^1$: $R^1,L^4,L^0$
$L^2$: $L^2,R^3,R^4$	$R^2$: $R^2,L^3,L^4$
$L^3$: $L^3,R^2,R^3$	$R^3$: $R^3,L^2,L^3$
$L^4$: $L^4,R^1,R^2$	$R^4$: $R^4,L^1,L^2$

Let $i\le 4$. Suppose that we have borders caused by $7-i$ vertices of W and the borders caused by the remaining i vertices of W are not considered yet. Moreover, suppose that there is a sequence of $i+1$ vertices, say $v_x,v_{x+1},\dots ,v_{x+i}$, such that none of the $7-i$ already considered vertices is in $\{v_x,v_{x+1},\dots ,v_{x+i}\}$ and the already considered vertices do not create borders between any consecutive pair from $\{v_x,v_{x+1},\dots ,v_{x+i}\}$. Then, $v_{x+i-n^{\prime }-5},v_{x+i-n^{\prime }-4},\dots ,v_{x-n^{\prime }+4}$ cannot be among the remaining vertices of W. The reason is that each of the remaining i vertices of W causes, at most, one border in the sequence $v_x,v_{x+1},\dots ,v_{x+i}$ and if it is in $\{v_{x+i-n^{\prime }-5},v_{x+i-n^{\prime }-4},\dots ,v_{x-n^{\prime }+4}\}=\{v_{x+i+n^{\prime }-4}$, $v_{x+i+n^{\prime }-3},\dots ,v_{x+n^{\prime }+5}\}$, then it causes no border in the sequence since every member of the sequence is at distance d from all the vertices from $\{v_{x+i-n^{\prime }-5},v_{x+i-n^{\prime }-4},\dots ,v_{x-n^{\prime }+4}\}$.

Denote 11 vertices which are at distance at most 1 from $v_a$ by $\alpha$, and denote 10 vertices which are at distance d from $v_a$ by $\beta$. Then, both $\alpha$ and $\beta$ form sequences of consecutive vertices. We consider the situation in $\alpha$ and $\beta$. In Figure 1, we describe $\alpha$ and $\beta$ as they occur in the cycle $C_n\left(1\right)$ (the other vertices are not depicted). Circles represent vertices of $G_n$, and those whose position is already known, such as $v_a$, are depicted instead of circles. Vertical lines are borders caused by $v_a$, and in the space between vertices, we indicate which vertices may form the border. In fact, such vertices cause borders if and only if they are not in $\alpha$ or $\beta$, and therefore, situations when W contains vertices of $\alpha$ or $\beta$ should be considered separately.

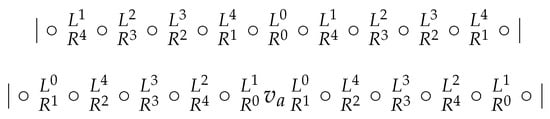
Figure 1. Initial distribution.

Regarding the position of $v_b$ and $v_c$ in $\beta$, by symmetry, we distinguish three main cases.

Case 1. $v_b,v_c\in \beta$.

See Figure 2, where we specify also the borders in $\alpha$ caused by $v_b$ and $v_c$.

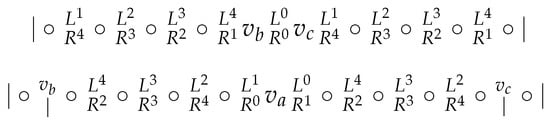
Figure 2. Case 1.

The vertices $v_{-1}$ and $v_1$ must be distinguished, so there must be a border on the left-hand side of $v_a$ (or $v_{a-1}\in W$) or on the right-hand side of $v_a$ (or $v_{a+1}\in W$). By symmetry, we may assume that this border is on the right-hand side of $v_a$. So for the next vertex $v_e\in W$, we have either $e=a+1$, or $v_e\in R^1$ but $v_e\notin \alpha$, or $v_e\in L^0$. We consider these subcases separately.

Subcase 1.1. $e=a+1$.

So, $v_e=v_{a+1}=v_1\in R^1$. Now, the positions of four vertices of W are determined, see Figure 3. It remains to be determined the positions of the last three vertices, say, $v_f$, $v_g$ and $v_h$.

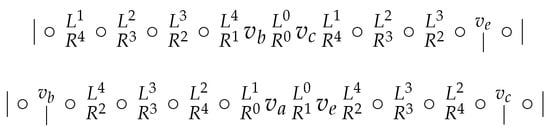
Figure 3. Subcase 1.1.

At the moment, there is a sequence of four consecutive vertices in $L\cap \alpha$ without a border, namely, $v_{-4},v_{-3},v_{-2},v_{-1}$, so $R\cap \beta \cap W=\left\{v_c\right\}$ since it remains to be determined the three vertices of W. Also, there is a sequence of four consecutive vertices in $L\cap \beta$ without a border, namely $v_{-n^{\prime }+1},v_{-n^{\prime }+2},v_{-n^{\prime }+3},v_{-n^{\prime }+4}$, so $R\cap \alpha \cap W=\left\{v_e\right\}$. Thus, there is a border between $v_2$ and $v_3$, and also a border between $v_3$ and $v_4$. This yields four possibilities.

(a) $v_f\in L^3$ and $v_g\in L^2$. Since $v_{-n^{\prime }+1}$ must be distinguished from $v_{n^{\prime }-1}$, we have $v_h\in L^4\cup R^1\cup L^0\cup R^0\cup L^1\cup R^4$ or $v_h=v_{-n^{\prime }+1}\in L^4$. In any case, by Table 2, W does not contain a vertex at index distance $5k$ from $v_f$.

(b) $v_f\in L^3$ and $v_g\in R^4$. By Table 2, $v_h\in L^3\cup R^2\cup R^3$ since W must contain a vertex at index distance $5k$ from $v_f$. At the same time, $v_h\in R^4\cup L^1\cup L^2$ since W must contain a vertex at index distance $5k$ from $v_g$, a contradiction.

(c) $v_f\in R^3$ and $v_g\in L^2$. Since $v_{n^{\prime }-2}$ must be distinguished from $v_{n^{\prime }-3}$ and $v_{n^{\prime }-2},v_{n^{\prime }-3}\notin W$, we have $v_h\in L^3\cup R^2$. On the other hand, $v_{n^{\prime }+1}$ must be distinguished from $v_{n^{\prime }-1}$ and so $v_h\in L^4\cup R^1\cup L^0\cup R^0\cup L^1\cup R^4$, a contradiction.

(d) $v_f\in R^3$ and $v_g\in R^4$. Since $v_{n^{\prime }-2}$ must be distinguished from $v_{n^{\prime }-3}$, we have $v_h\in L^3\cup R^2$. However, by Table 2, W does not contain a vertex at index distance $5k$ from $v_g$.

Subcase 1.2. $v_e\in R^1$ but $v_e\notin \alpha$ (see Figure 4).

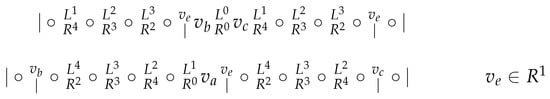
Figure 4. Subcase 1.2.

At the moment, there are sequences of four consecutive vertices without a border in $L\cap \alpha$ ($v_{-4},v_{-3},v_{-2},v_{-1}$), in $R\cap \alpha$ ($v_1,v_2,v_3,v_4$), and in $L\cap \beta$ ($v_{-n^{\prime }+1},v_{-n^{\prime }+2},v_{-n^{\prime }+3},v_{-n^{\prime }+4}$). Therefore, $R\cap \beta \cap W=\left\{v_c\right\}$, $L\cap \beta \cap W=\left\{v_b\right\}$ and $R\cap \alpha \cap W=\varnothing$. Hence, there is a border between $v_2$ and $v_3$ and also a border between $v_3$ and $v_4$. Analogously as in Subcase 1.1, we consider four possibilities.

(a) $v_f\in L^3$ and $v_g\in L^2$. Since $v_{-n^{\prime }+4}$ must be distinguished from $v_{-n^{\prime }+3}$ and $L\cap \beta \cap W=\left\{v_b\right\}$, we have $v_h\in L^1\cup R^4$. In any case, by Table 2, W does not contain a vertex at index distance $5k$ from $v_f$.

(b) $v_f\in L^3$ and $v_g\in R^4$. This case can be solved analogously as in Subcase 1.1.

(c) $v_f\in R^3$ and $v_g\in L^2$. Since $v_{n^{\prime }-2}$ must be distinguished from $v_{n^{\prime }-3}$ and $v_{n^{\prime }-2},v_{n^{\prime }-3}\notin W$, we have $v_h\in L^3\cup R^2$. On the other hand, $v_1$ must be distinguished from $v_2$ and $v_1,v_2\notin W$, and so $v_h\in L^4\cup R^2$. Consequently, $v_h\in R^2$, and by Table 2, W does not contain a vertex at index distance $5k$ from $v_h$.

(d) $v_f\in R^3$ and $v_g\in R^4$. This case can be solved analogously as in Subcase 1.1.

Subcase 1.3. $v_e\in L^0$.

This situation is presented in Figure 5. Here, $v_e\in \alpha$ if $v_e=v_{-5}$, or $v_e\notin \alpha$. In any case, $v_e\notin \beta$.

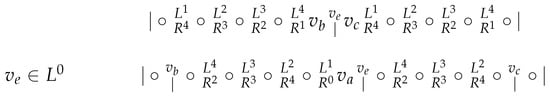
Figure 5. Subcase 1.3.

In this subcase, we have four consecutive vertices without a border in all $L\cap \alpha$, $R\cap \alpha$, $L\cap \beta$ and $R\cap \beta$, and so $\alpha \cap W=\left\{v_a\right\}$ and $\beta \cap W=\{v_b,v_c\}$. Hence, there is a border between $v_2$ and $v_3$, and also a border between $v_3$ and $v_4$. This gives the same possibilities as in the previous two subcases, and they can be solved analogously as in Subcase 1.2.

Case 2. $v_b\in \beta$ but $v_c\notin \beta$ (see Figure 6).

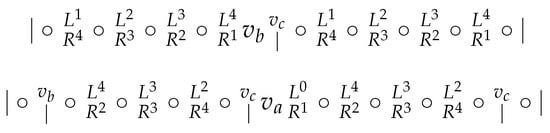
Figure 6. Case 2.

The positions of three vertices of W are determined, and it remains to be determined the last four vertices. But at the moment, there is a sequence of five consecutive vertices without a border in $R\cap \beta$, namely $v_{n^{\prime }-4},v_{n^{\prime }-3},v_{n^{\prime }-2},v_{n^{\prime }-1},v_{n^{\prime }}$, and so $L\cap \alpha =\varnothing$. Thus, we distinguish eight possibilities.

(a) $v_e\in L^4$, $v_f\in L^3$ and $v_g\in L^2$. By Table 2, $v_h\in L^4\cup R^1\cup R^2$ since W must contain a vertex at index distance $5k$ from $v_e$. At the same time, $v_h\in L^2\cup R^3\cup R^4$ since W must contain a vertex at index distance $5k$ from $v_g$, a contradiction.

(b) $v_e\in L^4$, $v_f\in L^3$ and $v_g\in R^4$. By Table 2, $v_h\in L^4\cup R^1\cup R^2$ since W must contain a vertex at index distance $5k$ from $v_e$. At the same time, $v_h\in R^4\cup L^1\cup L^2$ since W must contain a vertex at index distance $5k$ from $v_g$, a contradiction.

(c) $v_e\in L^4$, $v_f\in R^3$ and $v_g\in L^2$. Since $v_{n^{\prime }}$ must be distinguished from $v_{n^{\prime }-1}$, we have $v_h\in L^1\cup R^4$ or $v_h=v_{n^{\prime }}$ or $v_h=n_{n^{\prime }-1}$. Summing up, $v_h\in L^1\cup R^4\cup R^0$. At the same time, $v_h\in L^4\cup R^1\cup R^2$ since W must contain a vertex at index distance $5k$ from $v_e$, a contradiction.

(d) $v_e\in L^4$, $v_f\in R^3$ and $v_g\in R^4$. By Table 2, $v_h\in L^4\cup R^1\cup R^2$ since W must contain a vertex at index distance $5k$ from $v_e$. At the same time, $v_h\in R^4\cup L^1\cup L^2$ since W must contain a vertex at index distance $5k$ from $v_g$, a contradiction.

(e) $v_e\in R^2$, $v_f\in L^3$ and $v_g\in L^2$. To distinguish $v_{n^{\prime }}$ from $v_{n^{\prime }-1}$, we have $v_h\in L^1\cup R^4$ or $v_h=v_{n^{\prime }}$ or $v_h=v_{n^{\prime }-1}$. But the case $v_h=v_{n^{\prime }}$ was already considered in Case 1. Hence, $v_h\in L^1\cup R^4$. At the same time, W must contain a vertex at index distance $5k$ from $v_g$, and so $v_h\in R^4$. To distinguish $v_{n^{\prime }-3}$ from $v_{n^{\prime }-4}$, W must contain a vertex in $L^4\cup R^1$ or $v_h=v_{n^{\prime }-3}$ or $v_h=v_{n^{\prime }-4}$. Consequently, $v_e=v_{n^{\prime }-3}$. However, then, $v_e$ does not create the border between $v_{-4}$ and $v_{-3}$. Since W does not contain a vertex in $L^4$ and $v_{-4},v_{-3}\notin W$, the vertices $v_{-4}$ and $v_{-3}$ are not resolved, a contradiction.

(f) $v_e\in R^2$, $v_f\in L^3$ and $v_g\in R^4$. First, suppose that $v_e\ne v_{n^{\prime }-3}$. To distinguish $v_{n^{\prime }-3}$ from $v_{n^{\prime }-4}$, we have $v_h\in L^4\cup R^1$ or $v_h=v_{n^{\prime }-3}$ or $v_h=v_{n=-4}$. Hence, $v_h\in L^4\cup R^1\cup R^2$. At the same time, $v_h\in R^4\cup L^1\cup L^2$ since W must contain a vertex at index distance $5k$ from $v_g$, a contradiction. So $v_e=v_{n^{\prime }-3}$. But then, $v_e$ does not create a border between $v_{-4}$ and $v_{-3}$ since $v_{-4},v_{-3}\notin W$, $v_h\in L^4\cup R^2$. But then, W does not contain a vertex at index distance $5k$ from $v_g$, a contradiction.

(g) $v_e\in R^2$, $v_f\in R^3$ and $v_g\in L^2$. To distinguish $v_{n^{\prime }}$ from $v_{n^{\prime }-1}$, we must have $v_h\in L^1\cup R^4$ or $v_h=v_{n^{\prime }}$ or $v_h=v_{n^{\prime }-1}$. Summing up, $v_h\in L^1\cup R^4\cup R^0$. At the same time $v_h\in R^2\cup L^3\cup L^4$ since W must contain a vertex at index distance $5k$ from $v_e$, a contradiction.

(h) $v_e\in R^2$, $v_f\in R^3$ and $v_g\in R^4$. By Table 2, $v_h\in R^2\cup L^3\cup L^4$ since W must contain a vertex at index distance $5k$ from $v_e$. At the same time $v_h\in R^4\cup L^1\cup L^2$ since W must contain a vertex at index distance $5k$ from $v_g$, a contradiction.

Case 3. $v_b,v_c\notin \beta$ (see Figure 7).

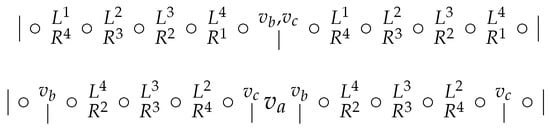
Figure 7. Case 3.

Analogously as in Case 2, at the moment there are sequences of five consecutive vertices without a border in $L\cap \beta$ and $R\cap \beta$, and so $R\cap \alpha =\varnothing$ and $L\cap \alpha =\varnothing$. Thus, we distinguish eight possibilities analogously as in Case 2. And we can use the proofs from Case 2 since in Case 3, we have more restrictions (so it is even easier to obtain a contradiction). ☐

Finally, we present a lower bound on $\dim \left(G_n\right)$ for $n\equiv 0\left(\mathrm{mod}10\right)$.

Theorem 3. 

Let $n=10d$, where $d\ge 2$. Then, $\dim \left(G_n\right)\ge 7$.

Proof. 

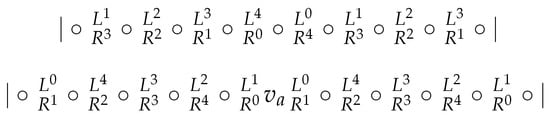
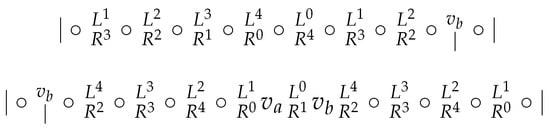
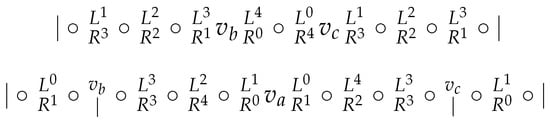
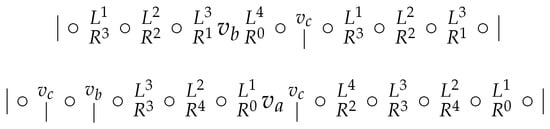
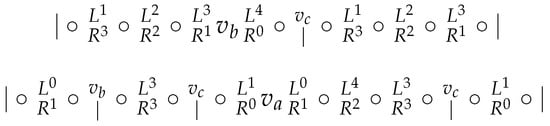
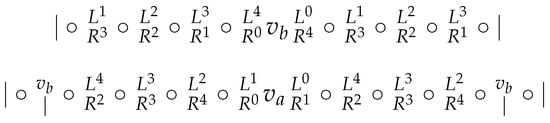
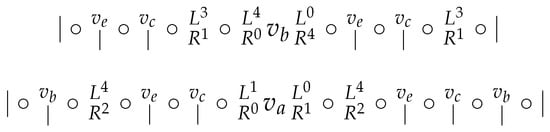
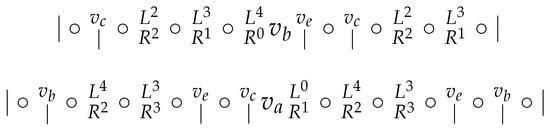
We proceed analogously as in the proof of Theorem 2. Let $n^{\prime }=\frac{n}{2}$. Observe that the index distance is at most $n^{\prime }$ in $G_n$. Obviously, $G_n$ has diameter d and for every vertex $v_x$. There are nine consecutive vertices at distance d from $v_x$, namely, $v_{x+n^{\prime }-4},v_{x+n^{\prime }-3},\dots ,v_{x+n^{\prime }+4}$.

By way of contradiction, suppose that $V\left(G_n\right)$ contains a subset W of six vertices, which is resolving. Let $v_a\in W$. Denote $L=\{v_{a-1},v_{a-2},\dots ,v_{a-n^{\prime }}\}$ and $R=\{v_{a+1},v_{a+2},\dots ,v_{a+n^{\prime }}\}$. Hence, $L\cap R=\left\{v_{a+n^{\prime }}\right\}$. Analogously as in the proof of Theorem 2, we split L and R each into five sets according to the index distance from $v_a$. Let $0\le i\le 4$. By $L^i$ (by $R^i$), we denote vertices of L (of R) whose index distance from $v_a$ is congruent to $i(mod5)$. (Recall that the index distance does not exceed $n^{\prime }$.) To simplify the notation, we assume that $a=0$.

Let $i\le 4$. Suppose that we have borders caused by $6-i$ vertices of W and the borders caused by the remaining i vertices of W are not considered yet. Moreover, suppose that there is a sequence of $i+1$ vertices, say $v_x,v_{x+1},\dots ,v_{x+i}$ such that none of the $6-i$ already considered vertices is in $\{v_x,v_{x+1},\dots ,v_{x+i}\}$ and the already considered vertices do not form borders between any consecutive pair from $\{v_x,v_{x+1},\dots ,v_{x+i}\}$. Then, $v_{x+n^{\prime }+i-4},v_{x+n^{\prime }+i-3},\dots ,v_{x+n^{\prime }+4}$ cannot be among the remaining vertices of W. The reason is that each of the remaining i vertices of W causes at most one border in the sequence $v_x,v_{x+1},\dots ,v_{x+i}$ and if it is in $\{v_{x+n^{\prime }+i-4},v_{x+n^{\prime }+i-3},\dots ,v_{x+n^{\prime }+4}\}$, then it causes no border in the sequence since every member of the sequence is at distance d from all the vertices from $\{v_{x+n^{\prime }+i-4},v_{x+n^{\prime }+i-3},\dots ,v_{x+n^{\prime }+4}\}$.

Denote 11 vertices which are at distance at most 1 from $v_a$ by $\alpha$, and denote 9 vertices which are at distance d from $v_a$ by $\beta$. Then, both $\alpha$ and $\beta$ form sequences of vertices, where neighboring vertices have index distance 1. We consider mainly the situation in $\alpha$ and $\beta$. In Figure 8, we describe $\alpha$ and $\beta$ analogously as in the proof of Theorem 2. Circles represent vertices of $G_n$, and those whose position is already known, such as $v_a$, are depicted instead of circles. Vertical borders are borders caused by $v_a$, and in the space between vertices, we indicate which vertices may form the border. Again, such vertices cause borders if and only if they are not in $\alpha$ or $\beta$, and therefore situations when W contains vertices of $\alpha$ or $\beta$ should be considered separately.

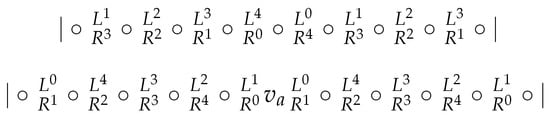
Figure 8. Initial distribution.

Before we start with cases, we exclude the possibility that two consecutive vertices are in W. So by way of contradiction, suppose that $v_a,v_{a+1}\in W$, see Figure 9.

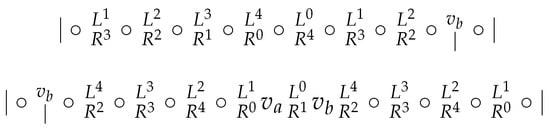
Figure 9. $v_a,v_{a+1}\in W$.

This yields a sequence of six consecutive vertices $v_{n^{\prime }-1},v_{n^{\prime }},\dots ,v_{n^{\prime }+4}$ without a border caused by $v_a$ or $v_b$. However, any vertex from $W\setminus \{v_a,v_b\}$ creates at most one border in this sequence, and so W cannot distinguish all the vertices in this sequence, a contradiction.

To distinguish the three vertices $v_{n^{\prime }-1},v_{n^{\prime }},v_{n^{\prime }+1}$, we need two vertices of W, say, $v_b$ and $v_c$. In the following cases, we distinguish their position with respect to $\beta$.

Case 1. $v_b,v_c\notin \beta$. (By symmetry, we consider three subcases.)

Subcase 1.1. $v_b\in L^4$ and $v_c\in R^4$ (see Figure 10).

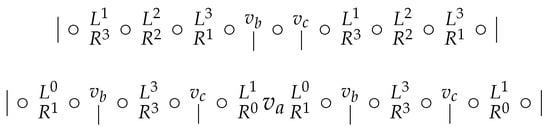
Figure 10. Subcase 1.1.

At the moment, there is a sequence of four vertices without a border in $L\cap \beta$, namely, $v_{n^{\prime }+1},v_{n^{\prime }+2},v_{n^{\prime }+3},v_{n^{\prime }+4}$. Thus, $v_{n^{\prime }+1+n^{\prime }+3-4}=v_0,v_1,\dots ,v_{n^{\prime }+1+n^{\prime }+4}=v_5$ are not among the vertices of $W\setminus \{v_a,v_b,v_c\}$, and so $R\cap \alpha \cap (W\setminus \left\{v_c\right\})=\varnothing$. Analogously, $v_{n^{\prime }-4},v_{n^{\prime }-3},v_{n^{\prime }-4}$, $v_{n^{\prime }-1}$ form a sequence of 4 consecutive vertices without a border in $R\cap \beta$, and so $L\cap \alpha \cap (W\setminus \left\{v_b\right\})=\varnothing$.

Observe that $v_b\notin \{v_{-3},v_{-2}\}$ even if $v_b\in \alpha$. Hence, to distinguish $v_{-3}$ from $v_{-2}$, we need $v_e\in L^3\cup R^3$. By now, this subcase is symmetric, so we may assume that $v_e\in L^3$. Recall that as mentioned above, $v_e\notin \alpha$. Now, we consider four possibilities with respect to $\{v_b,v_c\}\cap \alpha$.

(a) $v_b,v_c\notin \alpha$. Recall that $v_f,v_g\notin \alpha$. Since $v_{-5}$ must be distinguished from $v_{-4}$, we have $v_f\in L^0\cup R^1$, and since $v_4$ must be distinguished from $v_5$, we have $v_g\in L^1\cup R^0$. However, also $v_{n^{\prime }-3}$ must be distinguished from $v_{n^{\prime }-2}$, and so W must contain a vertex in $L^2\cup R^2\cup \{v_{n^{\prime }-3},v_{n^{\prime }-2}\}$, that is a vertex in $L^2\cup R^2\cup R^3$, a contradiction.

(b) $v_b\in \alpha$ and $v_c\notin \alpha$. In this case $v_b=v_{-4}$. To distinguish $v_{-5}$ from $v_{-3}$ we have $v_f\in L^0\cup L^4\cup R^1\cup R^2$, and to distinguish $v_4$ from $v_5$ we have $v_g\in L^1\cup R^0$. However, to distinguish $v_{n^{\prime }-2}$ from $v_{n^{\prime }-3}$ we conclude that $v_f\in R^2$, and to distinguish $v_{n^{\prime }+3}$ from $v_{n^{\prime }+4}$, we conclude that $v_g\in L^1$.

So we have $v_b=v_{-4}$, $v_c\in R^4$, $v_e\in L^3$, $v_f\in R^2$ and $v_g\in L^1$. This choice works well in $\alpha \cup \beta$, see Figure 11. So denote ${\alpha }_a=\alpha$, ${\beta }_a=\beta$, $L_a=L$, $R_a=R$, $L_a^i=L^i$ and $R_a^i=R^i$, $0\le i\le 4$, and analogously construct ${\alpha }_x$, ${\beta }_x$, $L_x$, $R_x$, $L_x^i$ and $R_x^i$ where $x\in \{b,c,e,f,g\}$.

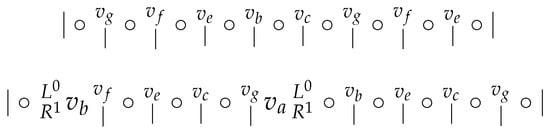
Figure 11. Subcase 1.1.

Consider $v_g$. We have $v_a\in R_g^1$, $v_b\in R_g^2$, $v_c\in L_g^0\cup R_g^0$, $v_e\in L_g^2\cup R_g^3$ and $v_f\in L_g^2\cup R_g^3$. Observe that W does not contain a vertex in $L_g^4\cup R_g^4$. Thus, the unique vertex $v_c$ must distinguish three consecutive vertices $v_{g+n^{\prime }-1},v_{g+n^{\prime }},v_{g+n^{\prime }+1}$ in ${\beta }_g$ (see Figure 8), a contradiction.

(c) $v_b\notin \alpha$ and $v_c\in \alpha$. In this case, $v_c=v_4$. To distinguish $v_{-5}$ from $v_{-4}$, we have $v_f\in L^0\cup R^1$, and to distinguish $v_3$ from $v_5$, we have $v_g\in L^1\cup L^2\cup R^0\cup R^4$. However, to distinguish $v_{n^{\prime }-3}$ from $v_{n^{\prime }-2}$ we conclude that $v_g\in L^2$, and to distinguish $v_{n^{\prime }-2}$ from $v_{n^{\prime }-1}$, we need a vertex of W in $L^1\cup R^3$ or $v_{n^{\prime }-1}\in R^4$ (different from $v_c$) or $v_{n^{\prime }-2}\in R^3$, a contradiction.

(d) $v_b,v_c\in \alpha$, that is $v_b=v_{-4}$ and $v_c=v_4$. To distinguish $v_{-5}$ from $v_{-3}$, we have $v_f\in L^0\cup L^4\cup R^1\cup R^2$, and to distinguish $v_3$ from $v_5$, we have $v_g\in L^1\cup L^2\cup R^0\cup R^4$. However, to distinguish $v_{n^{\prime }-2}$ from $v_{n^{\prime }-1}$, the set W must contain a vertex of $L^1\cup R^3$ or $v_{n^{\prime }-2}\in R^3$ or $v_{n^{\prime }-1}\in R^4$ (different from $v_c$). Thus, $v_g=v_{n^{\prime }-1}$ or $v_g\in L^1$. And to distinguish $v_{n^{\prime }-3}$ from $v_{n^{\prime }-2}$, the set W must contain a vertex in $L^2\cup R^2$ or $v_{n^{\prime }-3}\in R^3$ or $v_{n^{\prime }-2}\in R^2$, and so $v_f\in R^2$. Now, if $v_g=v_{n^{\prime }-1}$, then $v_{n^{\prime }+3}$ is not distinguished from $v_{n^{\prime }+4}$, so we conclude that $v_g\in L^1$. This yields a situation which was already solved in case (b) above.

Subcase 1.2. $v_b\in L^0$ and $v_c\in R^0$ (see Figure 12).

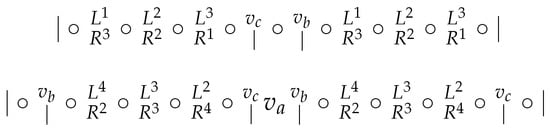
Figure 12. Subcase 1.2.

In each $L\cap \alpha$, $R\cap \alpha$, $L\cap \beta$ and $R\cap \beta$, there are four consecutive vertices which are not resolved by $v_a,v_b,v_c$, even if $v_b\in \alpha$ or $v_c\in \alpha$. Since the sequence $v_1,v_2,v_2,v_4$ yields $\{v_{n^{\prime }},v_{n^{\prime }+1},\dots ,v_{n^{\prime }+5}\}\cap (W\setminus \{v_a,v_b,c_c\})=\varnothing$, and the sequence $v_{n^{\prime }+1},v_{n^{\prime }+2},v_{n^{\prime }+3},v_{n^{\prime }+4}$ yields $\{v_0,v_1,\dots ,v_5\}\cap (W\setminus \{v_a,v_b,c_c\})=\varnothing$, we have $\{v_e,v_f,v_g\}\cap (\alpha \cup \beta )=\varnothing$.

Hence, to distinguish $v_{n^{\prime }+3}$ from $v_{n^{\prime }+4}$, we have $v_e\in L^1\cup R^3$; to distinguish $v_{n^{\prime }+2}$ from $v_{n+3}$, we have $v_f\in L^2\cup R^2$; and to distinguish $v_{n^{\prime }+1}$ from $v_{n^{\prime }+2}$, we have $v_g\in L^3\cup R^1$. But also, $v_{-4}$ must be distinguished from $v_{-3}$, and so $v_f\in R^2$. And since $v_{-2}$ must be distinguished from $v_{-1}$, W must contain a vertex in $L^2\cup R^4$, a contradiction.

Subcase 1.3. $v_b\in L^0$ and $v_c\in L^4$, see Figure 13 (the case $v_b\in R^0$ and $v_c\in R^4$ is analogous, by symmetry).

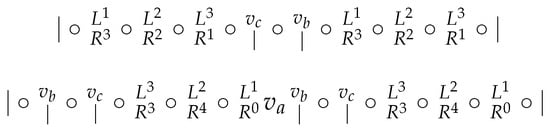
Figure 13. Subcase 1.3.

Recall that $v_b,v_c\notin \beta$. So at the moment, the vertices $v_{n^{\prime }+1},v_{n^{\prime }+2},v_{n^{\prime }+3},v_{n^{\prime }+4}$ are not distinguished, and so $\{v_0,v_1\dots ,v_5\}\cap \{v_e,v_f,v_g\}=\varnothing$. That is, $v_e,v_f,v_g\notin R\cap \alpha$. Analogously $v_2,v_3,v_4,v_5$ are not distinguished since $v_b,v_c\in L$, and so $v_e,v_f,v_g\notin \{v_{n^{\prime }+1},v_{n^{\prime }+2},\dots ,v_{n^{\prime }+6}\}$.

Hence, to distinguish $v_2$ from $v_3$, we have $v_e\in L^3\cup R^3$; to distinguish $v_3$ from $v_4$, we have $v_f\in L^2\cup R^4$; and to distinguish $v_4$ from $v_5$, we have $v_g\in L^1\cup R^0$. On the other hand, also $v_{n^{\prime }+1}$ must be distinguished from $v_{n^{\prime }+2}$, and so $v_e\in L^3$. Since $v_{n^{\prime }+2}$ must be distinguished from $v_{n^{\prime }+3}$, we have $v_f\in L^2$. And since $v_{n^{\prime }+3}$ must be distinguished from $v_{n^{\prime }+4}$, we have $v_g\in L^1$.

So we have $v_b\in L^0$, $v_c\in L^4$, $v_e\in L^3$, $v_f\in L^2$ and $v_g\in L^1$. Observe that if $x\in \{b,c,e,f,g\}$, then $v_{x+n^{\prime }-1},v_{x+n^{\prime }},v_{x+n^{\prime }+1}\notin W$. Hence, relabeling a with x, we remain in Case 1, and in four out of these five possible relabelings, not all remaining vertices of W are in $L_x$ and also they are not all in $R_x$. So, each of the four relabelings reduces this case to one of the previous ones.

Case 2. $v_b=v_{n^{\prime }+1}$ and $v_c=v_{n^{\prime }-1}$ (see Figure 14).

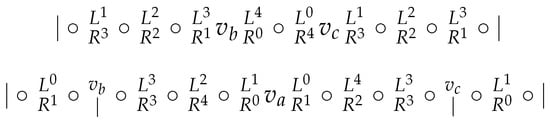
Figure 14. Case 2.

First, we focus on $\alpha$. To distinguish $v_{-1}$ from $v_1$ we have $v_e\in L^0{\cup }^1\cup R^0\cup R^1$. Recall that consecutive vertices cannot be in W. So, to distinguish $v_{-2}$ from $v_{-1}$ we have $v_f\in L^2\cup R^4$, which covers also the case $v_f=v_{-2}$. And to distinguish $v_1$ from $v_2$, we have $v_g\in L^4\cup R^2$, which covers also the case $v_g=v_2$. But we need to distinguish also $v_{-3}$ from $v_{-2}$, for which we need a vertex of $L^3\cup R^3\cup \{v_{-3},v_{-2}\}$. Consequently, $v_f=v_{-2}\in L^2$. But to distinguish $v_{-3}$ from $v_{-1}$ we need a vertex in $L^2\cup L^3\cup R^3\cup R^4$ other than $v_f$, a contradiction.

Case 3. $v_b=v_{n^{\prime }+1}$ and $v_c\notin \beta$.

Thus, $v_c\in L^0\cup R^4$. We distinguish two subcases.

Subcase 3.1. $v_c\in L^0$ (see Figure 15).

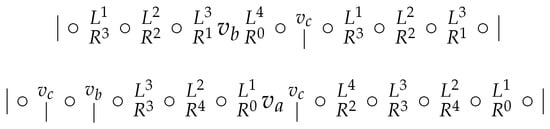
Figure 15. Subcase 3.1.

At the moment, we have a sequence of 5 consecutive vertices $v_1,v_2,\dots ,v_5$ without a border. The vertices in this sequence should be distinguished by three remaining vertices of W, which is impossible.

Subcase 3.2. $v_c\in R^4$, but $v_c\ne v_{n^{\prime }-1}$ (see Figure 16).

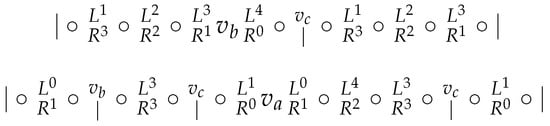
Figure 16. Subcase 3.2.

At the moment, there is a sequence of four vertices without a border $v_{n^{\prime }-4},v_{n^{\prime }-3},v_{n^{\prime }-2}$, $v_{n^{\prime }-1}$, and so $v_e,v_f,v_g\notin \{v_{-5},v_{-4},\dots ,v_0\}$. To distinguish $v_{-5}$ from $v_{-4}$, we have $v_e\in L^0\cup R^1$, and to distinguish $v_{-3}$ from $v_{-2}$, we have $v_f\in L^3\cup R^3$. Finally, to distinguish $v_1$ from $v_2$, we have $v_g\in L^4\cup R^2$ which covers also the case $v_g=v_2$ (recall that $v_1\notin W$ since W does not contain consecutive vertices).

Now, we consider $\beta$. To distinguish $v_{n^{\prime }-2}$ from $v_{n^{\prime }-1}$, W must contain a vertex of $L^1\cup R^3$, which covers also $v_{n^{\prime }-2}$ (recall that the case $v_{n^{\prime }-1}\in W$ was already considered in Case 2), and so $v_f\in R^3$. To distinguish $v_{n^{\prime }+2}$ from $v_{n^{\prime }+3}$, W must contain a vertex of $L^2\cup R^2$ (since $v_{n^{\prime }+2}\notin W$), and so $v_g\in R^2$.

Now, if $v_e\in R^1$, then $v_c,v_e,v_f,v_g\in R$. So considering ${\alpha }_e$ and ${\beta }_e$ instead of ${\alpha }_a$ and ${\beta }_a$ reduces the problem to Case 1 (recall that $v_e\ne v_1$). Hence, $v_e\in L^0$.

So $v_c\in R^4$, $v_e\in L^0$, $v_f\in R^3$ and $v_g\in R^2$. But to distinguish $v_{n^{\prime }}$ from $v_{n^{\prime }+2}$, W must contain a vertex in $L^3\cup L^4\cup R^0\cup R^1$ other than $v_b$, a contradiction.

Thus, it remains to consider the last case, namely, when $v_{n^{\prime }}\in W$. But since all the other cases were solved already, we may assume that $v_e=v_{c+n^{\prime }}$ and $v_g=v_{f+n^{\prime }}$.

Case 4. $v_b=v_{n^{\prime }}$, $v_e=v_{c+n^{\prime }}$ and $v_g=v_{f+n^{\prime }}$ (see Figure 17).

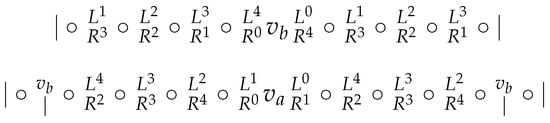
Figure 17. Case 4.

Obviously, two vertices from $v_c,v_e,v_f,v_g$ are in L, and two are in R. We assume that $v_c,v_f\in L$ and $v_e,v_g\in R$. To distinguish $v_{-2}$ from $v_{-1}$, W must contain a vertex in $L^2\cup R^4$, which covers also the case $v_{-2}$. So we distinguish 2 subcases.

Subcase 4.1. $v_c\in L^2$.

Then, $v_e\in R^3$; see Figure 18.

Figure 18. Subcase 4.1.

To distinguish $v_1$ from $v_2$, W must contain a vertex in $L^4\cup R^2$, and so either $v_f\in L^4$ and $v_g\in R^1$, or $v_g\in R^2$ and $v_f\in L^3$. Since in the later case $v_{-1}$ and $v_1$ are not distinguished, we conclude that $v_f\in L^4$ and $v_g\in R^1$.

Now, consider ${\alpha }_c$ and ${\beta }_c$. We have $v_a\in R_c^2$, $v_b\in L_c^3$, and either $v_f\in L_c^2$ and $v_g\in R_c^3$ or $v_f\in R_c^3$ and $v_g\in L_c^2$. However, both cases were already excluded in the previous paragraph.

Subcase 4.2. $v_e\in R^4$.

Then, $v_c\in L^1$; see Figure 19.

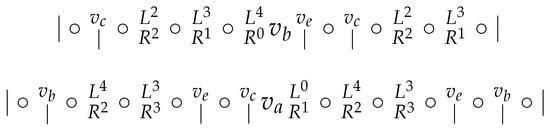
Figure 19. Subcase 4.2.

To distinguish $v_1$ from $v_2$, W must contain a vertex in $L^4\cup R^2$, and so either $v_f\in L^4$ and $v_g\in R^1$, or $v_g\in R^2$ and $v_f\in L^3$. Since in the former case $v_{n^{\prime }+2}$ and $v_{n^{\prime }+3}$ are not distinguished, we conclude that $v_f\in L^3$ and $v_g\in R^2$.

Now consider ${\alpha }_f$ and ${\beta }_f$. We have $v_a\in R_f^3$, $v_b\in L_f^2$, and either $v_c\in R_f^2$ and $v_e\in L_f^3$, or $v_c\in L_f^3$ and $v_e\in R_f^2$. However, both cases were already excluded, which completes the proof. ☐

3. Conclusions

From our Theorem 1, we have $\dim \left(G_n\right)\le 6$ for $n\equiv 9\left(\mathrm{mod}10\right)$ where $n\ge 29$. By (1), we have $\dim \left(G_n\right)\ge 6$, and thus,

$$\dim \left(G_n\right)=6\mathrm{if}n\equiv 9\left(\mathrm{mod}10\right)\mathrm{where}n\ge 29.$$

(3)

By Theorems 2.18 and 2.19 from [19], $\dim \left(G_n\right)\le 8$ for $n\equiv 0,1\left(\mathrm{mod}10\right)$. By Theorem 2.17 given in [19], $\dim \left(G_n\right)\ge 7$ for $n\equiv 1\left(\mathrm{mod}10\right)$. We improved the lower bound in our Theorem 2 by proving that $\dim \left(G_n\right)\ge 8$ for $n\equiv 1\left(\mathrm{mod}10\right)$. Thus,

$$\dim \left(G_n\right)=8\mathrm{if}n\equiv 1\left(\mathrm{mod}10\right).$$

(4)

From our Theorem 3, we obtain $\dim \left(G_n\right)\ge 7$ for $n\equiv 0\left(\mathrm{mod}10\right)$. By [21], for the same values of n, we have $\dim \left(G_n\right)\le 7$, and thus

$$\dim \left(G_n\right)=7\mathrm{if}n\equiv 0\left(\mathrm{mod}10\right).$$

(5)

Hence, by (2), (3), (4) and (5), for $n\ge 12$ where $n\notin \{13,19\}$,

$$\dim \left(G_n\right)=\left\{\begin{array}{cc}6\hfill & \mathrm{if}n\equiv 2,3,4,5,6,7,8,9\left(\mathrm{mod}10\right),\hfill \\ 7\hfill & \mathrm{if}n\equiv 0\left(\mathrm{mod}10\right),\hfill \\ 8\hfill & \mathrm{if}n\equiv 1\left(\mathrm{mod}10\right).\hfill \end{array}\right.$$

Note that from Table 3 given in [19], we have $\dim \left(G_{13}\right)=5$ and $\dim \left(G_{19}\right)=7$.

Thus, the problem of finding the metric dimension of $C_n(1,2,\dots ,t)$ is now completely solved for $t\le 5$ and any n. We suggest continuing to try to solve the problem completely for $t>5$.

Problem 1. 

Find the metric dimension of $C_n(1,2,\dots ,t)$ for $t\ge 6$ and any n.