Embedding Secret Data in a Vector Quantization Codebook Using a Novel Thresholding Scheme

Abstract

In recent decades, information security has become increasingly valued, including many aspects of privacy protection, copyright protection, and digital forensics. Therefore, many data hiding schemes have been proposed and applied to various carriers such as text, images, audio, and videos. Vector Quantization (VQ) compression is a well-known method for compressing images. In previous research, most methods related to VQ compressed images have focused on hiding information in index tables, while only a few of the latest studies have explored embedding data in codebooks. We propose a data hiding scheme for VQ codebooks. With our approach, a sender XORs most of the pixel values in a codebook and then applies a threshold to control data embedding. The auxiliary information generated during this process is embedded alongside secret data in the index reordering phase. Upon receiving the stego codebook and the reordered index table, the recipient can extract the data and reconstruct the VQ-compressed image using the reverse process. Experimental results demonstrate that our scheme significantly improves embedding capacity compared to the most recent codebook-based methods. Specifically, we observe an improvement rate of 223.66% in a small codebook of size 64 and an improvement rate of 85.19% in a codebook of size 1024.

1. Introduction

With the widespread usage of digital media in daily life, protecting the security and privacy of data has become increasingly important. Artificial intelligence-based watermarking [1], cryptography systems [2], and data hiding [3,4,5,6,7,8] have become effective means of safeguarding confidential data and personal privacy at a time when AI is rapidly evolving. These new techniques are used in many fields, such as privacy protection, copyright protection, and digital forensics.

Vector Quantization (VQ) [9] is a data compression technology. The basic principle of VQ-compressed images is to divide the image into non-overlapping pixel blocks, and then treat each pixel block as a vector. An algorithm, such as the Linde–Buzo–Gray (LBG) algorithm [10] or another improved algorithm [11], is used to train images into a codebook. The image’s pixel blocks are then mapped to the closest codeword in the codebook, and the indices of these codewords are stored as an index table. During decompression, the VQ compressed image can be reconstructed based on the stored codebook and the index table. In recent years, data hiding in the compression domain of VQ-compressed images has been an active area of research. This technique not only achieves image compression but also embeds data into the compression domain to enhance data security. Most of this research employed techniques to hide data within the index tables [12,13,14,15,16], while some recent studies explored methods for hiding data within the codebooks [17,18]. In 2023, Liu et al. [17] proposed a novel approach that focused on data embedding and extraction through sorting and reordering codewords of a VQ codebook. When a codebook size was 64, they achieved a bit rate of 0.2578 bits per pixel (bpp). Building upon this work, in 2024, Chang et al. [18] introduced a method for data embedding by employing pairwise adjustments of pixels within codewords. When a codebook size was 64, their method achieved a higher bit rate of 0.5820 bpp, indicating improved performance in terms of data capacity.

The key carrier of the proposed scheme is a VQ codebook which is not a common medium for data embedding due to its size. Even though its embedding capacity is relatively small compared to that of a cover image, it is very interesting to find ways to improve the capacity. Therefore, we propose a scheme that utilizes a threshold. First, codewords are preprocessed to reduce their pixel values through XOR operations. Then, data embedding is performed by looking up a rule table. Compared with the previous methods, it not only significantly improves the embedding capacity but also allows adapting to different situations by adjusting of the threshold to meet different requirements.

This particular study makes several significant contributions, as follows:

• Compared with a more recent compatible method, the embedding capacity is significantly improved. On a codebook of size 64, the embedding bit rate is 1.8838 bpp, which makes the improvement rate go as high as 223.66%. Even for a codebook of size 1024, the improvement rate can be as high as 85.19%.
• Our proposed scheme provides an adjustable threshold that can be adjusted to suit various requirements and reflects the flexibility of our approach.
• Our proposed scheme can losslessly reconstruct a VQ-compressed image. Achieving a PSNR of +∞ between a VQ-compressed image and the reconstructed VQ-compress image using the original codebook indicates that the two VQ-compressed images are exactly the same.

In Section 2, we introduce some methods related to our proposed scheme. Section 3 describes the details of data embedding and the reverse process of our proposed scheme. Experimental results demonstrate the good performance of our proposed scheme in Section 4. Finally, in Section 5, our proposed scheme is concluded.

2. Related Work

In this section, we review some technologies related to our scheme. In Section 2.1, we introduce the training method of the VQ codebook using the LBG algorithm [10]. Section 2.2 introduces the VQ codeword index reordering scheme proposed by Liu et al. [17] in 2023. In Section 2.3, we discuss the extended run-length encoding compression algorithm proposed by Chen and Chang [19] back in 2019.

2.1. Vector Quantization Codebook Training

VQ is a well-known lossy data compression technique. It is also called “block quantization” because media are divided into blocks first. A simple VQ training algorithm is as follows:

(a)

Pick a random sample point $P$

(b)

Let the distance between $P$ and a VQ centroid $c_i$ be $d\left(P,c_i\right)$

(c)

Find the VQ centroid $c_i$ with the shortest distance

(d)

Repeat

Figure 1 demonstrates the process of codebook creation.

Figure 1. Process of training a codebook.

Linde–Buzo–Gray (LBG) [10] is an algorithm designed based on k-means clustering in 1980 and is frequently used to train VQ codebooks. The process involves collecting a small set of vectors to represent a large set of vectors through iterations. The large set is known as a training set, and the small set collected is called a codebook. Lossy compressed images can then be reconstructed using the codebook and an index table.

2.2. VQ Codeword Index Reordering

Liu et al. [17], in 2023, used an index reordering technique to embed data in well-trained codebooks. The codebook embedding capacity is highly dependent on the size of a codebook. In order to extract embedded data and recover the original codebook from a stego codebook, the codebook needs to be sorted before manipulating the index orders to hide data.

2.2.1. Codebook Sorting

There are different ways of ordering a codebook. Liu et al. simply used a line, projected the codebook vectors to the line to gain the project values, and obtained a sorted codebook by sorting these projected values. Their experiment results showed that the sorting method was effective for the purpose of retrieving the original sorted codebook from a stego codebook. The sorted codebook is then employed to encode/decode images for the compression and recovery process.

2.2.2. VQ Codebook Data Embedding

The embedding capacitor can be calculated by the size of a sorted codebook $CB$. If the size of a sorted codebook is ${size}_{CB}$, the total embedding capacity $EC$ is calculated by Equation (1), where $i$ represents the index being processed.

$$EC={\sum }_{i=1}^{{size}_{CB}}⌊{\log }_{2}i⌋$$

(1)

Figure 2 illustrates a simple example of how a codebook embeds data, assuming there is secret data $S=\left\{1011000010010\right\}$ in its binary form and the size of a sorted codebook $CB$ is 8. Codewords are single dimension values defined as ${cw}_0=\left\{0\right\}, {cw}_1=\left\{1\right\}, \cdots ,{cw}_7=\left\{7\right\}$. The stego codebook $SCB$ is generated after data embedding. In our example, the first embeddable bit count is $e_8=⌊{\log }_{2}8⌋=3$. The first three bits of secret data $S$, ${\left(101\right)}_2={\left(5\right)}_{10}$ will be embedded in the first round. Take the converted decimal value five as the index value, the codeword ${cw}_5$ of the original codebook $CB$ to the stego codebook $SCB$ as ${scw}_0$. After the embedding, the indices of $CB$ are adjusted accordingly. Since there are only 7 codewords left in $CB$, the embeddable bit count is now $e_7=⌊{\log }_{2}7⌋=2$. Take the value of the fourth bit and the fifth bit and convert them to decimal value ${\left(10\right)}_2={\left(2\right)}_{10}$. The second codeword ${cw}_2$ is moved from $CB$ to $SCB$ as ${scw}_1$. The process continues until all secret bits are embedded or there are no more codewords in the original codebook.

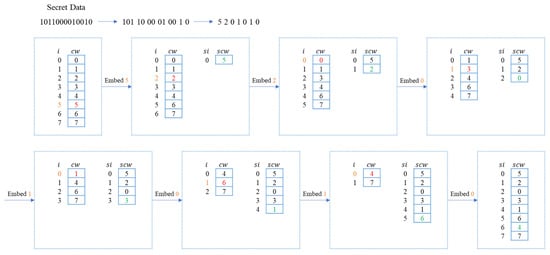
Figure 2. Embedding using VQ codeword index reordering.

2.2.3. VQ Codebook Data Extraction

To recover the data from the stego codebook, the same sorting algorithm is used to sort the stego codebook and generate a sorted codebook $CW$ as a reference for data extraction. By the order of the codewords in the stego codebook, the data embedding order is determined. By matching a codeword from the stego codebook and the sorted reference codebook, the embedded data is the index of the codeword in the sorted reference codebook. Convert the index to binary format and append it to the recovered secret data. Remove the matched codeword from both the stego codebook and the sorted reference codebook for continuous recovery stages. Repeat until there are no more codewords in the stego codebook.

Figure 3 explains the data extraction portion using the stego codebook generated from Figure 2. Sort the stego codebook $SCB$ after receiving and obtaining the sorted reference codebook $CB$. Match the first codeword ${scw}_0$ of $SCB$ in $CB$ and obtain the index $i=5$ from $CB$. Convert into binary format ${\left(5\right)}_{10}={\left(101\right)}_2$ and append it to the recovered secret $S=\left\{101\right\}$. Remove the codeword from both codebooks before the next round of extraction. Repeat the process of matching the first codeword ${scw}_0$ of $SCB$ in $CB$ and obtain the index of the matched codeword from $CB$. The secret data are extracted. The extracting process ends when there are no codewords in the stego codebook $SCB$.

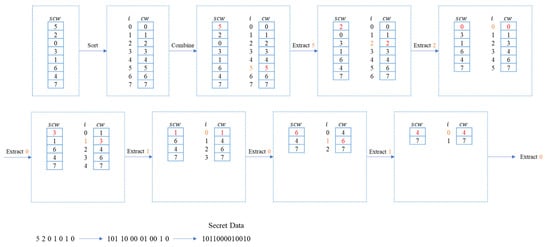
Figure 3. Data extraction using VQ codeword index reordering.

2.3. Extended Run-Length Encoding

Run-length encoding (RLE) is an effective lossless data compression technology. The run length represents the length of a sequence of consecutive identical symbols. Compression can be achieved by storing symbols and their respective quantities. Since its inception, there have been numerous improvements in RLE-based techniques. In 2019, Chen and Chang proposed the Extended Run-Length Encoding (ERLE) algorithm [19] which categorizes input into two types, fixed-length codewords and variable-length codewords, to further enhance compression performance.

When a run-length $L_r<4$, the ERLE algorithm defines it as a fixed-length codeword; conversely, when a run-length $L_r\ge 4$, it is a variable-length codeword. For fixed-length codewords, the prefix length code is recorded as 0, and then the fixed length $L_{fix}$ bits are directly scanned afterward from the current position. For variable-length codewords, the prefix length code $L_{pre}$ is first calculated using Equation (2). The prefix encoding begins with a 1 in the $(L_{pre}-1)$ bit and ends with a 0. The length of the length symbol is the same as the prefix code, and the value of the length symbol ${Symbol}_{length}$ is as shown in Equation (3). Finally, one bit is used to represent consecutive identical symbols. The sequence is processed differently based on the codeword type and the sequence compressed by the ERLE algorithm is ultimately obtained.

$$L_{pre}=⌊{log}_2\left(L_r\right)⌋$$

(2)

$${Symbol}_{length}=L_r-2^{L_{pre}}$$

(3)

The same process applies in the decompression stage. First, the prefix code is observed to determine the codeword type. If the prefix code starts with 0, it indicates it is a fixed-length codeword, and the fixed-length $L_{fix}$ bits need to be scanned afterward. If the prefix code starts with one, it indicates it is a variable-length codeword. The scan needs to continue until it reaches 0, and the length from the starting position to the end position determines the length of the prefix code, $L_{pre}$. Then, scan the following $L_{pre}$ bits to obtain the binary sequence of the length symbol ${Symbol}_{length}$, convert it to decimal, and calculate using Equation (4) to obtain the run length, $L_r$. Finally, read the following bit to represent the consecutive identical symbols. After decompression is complete, the original sequence can be restored losslessly.

$$L_r={2^{L_{pre}}+Symbol}_{length}$$

(4)

Figure 4 presents a specific example of $L_{fix}=4$. In Figure 4a, input the original sequence first, and consecutively scan identical symbols. When $L_r=2$, bit length 2 is less than 4 and 4 bits are scanned, which results in 0010 with 0 as the prefix code. Continue to scan to identify consecutive identical symbols resulting in $L_r=13$. Since 13 is larger than 4, $L_{pre}$ is calculated as $⌊{log}_2\left(13\right)⌋=3$, and ${Symbol}_{length}$ is then computed as $13-2^3=5$ represented by 3 bits. The last added bit represents the repeated symbol 1. Figure 4b illustrates the decompression phase. Initially, 0 is scanned, indicating a fixed-length codeword, and the following 4 bits are scanned. The scan continues until it reaches a 1, then stops when it reaches a 0, yielding $L_{pre}=3$. Subsequently, 3 bits are scanned resulting in ${Symbol}_{length}=5$. Thus, $L_r$ is calculated as $2^3+5=13$. Finally, 1 bit is scanned and a symbol 1 is obtained, indicating that the original sequence comprises 13 consecutive 1s.

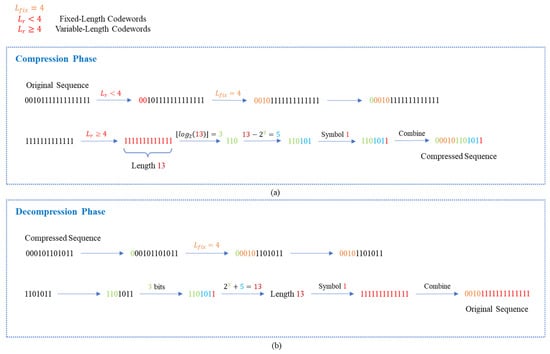
Figure 4. An example of ERLE algorithm. (a) Compression Phase. (b) Decomposition Phase.

3. Proposed Scheme

In this section, we introduce a novel data hiding scheme in VQ codebooks. The preprocessing phase, which reduces the pixel values of codewords through XOR operations, is described in Section 3.1. Section 3.2 details the data embedding phase, in which we utilize an adjustable threshold to flexibly accommodate different requirements. Section 3.3 outlines the data extraction and image recovery phase after a receiver receives the stego codebook and the reordered index table. Figure 5 shows the flow of our proposed scheme.

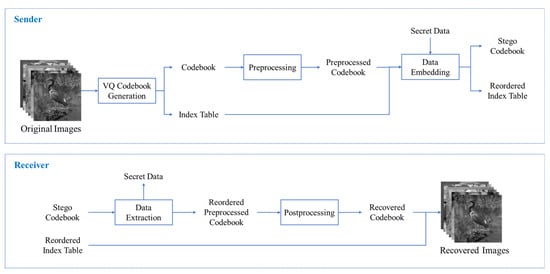
Figure 5. Flow of Our Proposed Scheme.

3.1. Preprocessing Phase

The sender begins a codebook training process using the original images by employing the LBG algorithm [10]. This process entails partitioning the original images into $4\times 4$ blocks and iteratively refining a codebook to accurately represent these blocks of data. The VQ codebook $CB$ and the corresponding index tables $IT$ for VQ compressed images are generated after the process. Since the VQ codebook exhibits a characteristic that most pixel values in a codeword are very similar, we utilize XOR to condense these values to assist in achieving better embedding results. In Equation (5), where $i$ represents the current codeword and $j$ represents the location of pixel $p$ in the current codeword, we preserve the first pixel of the codeword $i$ as the reference pixel and leave its value unchanged. Meanwhile, we XOR the remaining pixels with the first one to derive the preprocessed pixel values, denoted as $pp$. Figure 6 presents an example of four codewords in a codebook. It fulfills our requirement that the values of other pixels mostly become very small after XORing with the first pixel.

$${pp}_{ij}=\left\{\begin{array}{c}{p}_{ij} ,\\ p_{ij}\oplus p_{i1} ,\end{array} \begin{array}{c}if j=1\\ otherwise\end{array}\right.$$

(5)

Figure 6. An example of preprocessing phase in a segment of the codebook.

3.2. Data Embedding Phase

Our scheme supports adjustable embedding rules by setting different thresholds to flexibly adapt to various application scenarios. We utilize encoding rules similar to prefix codes to establish correspondence between the data and the label. Figure 7 illustrates encoding rules for different thresholds, where $t$ represents the threshold, $l$ represents the label, and $d$ represents the data.

Figure 7. Encoding Rules for Different Thresholds.

To ensure successful recovery of the codeword, the first pixel within each codeword, acting as a reference, must remain unchanged. Before utilizing the embedding process ${sp}_{ij}=p{p}_{ij}\times t+l$ to embed data, it is essential to first ascertain whether the embedded pixel value, ${sp}_{ij}$, will cause an overflow. If an overflow is anticipated, the embedding is deemed unacceptable, and the pixel value remains unchanged. Otherwise, embedding can proceed. Equation (6) encapsulates this mathematical process, where $sp$ represents the stego pixel, $pp$ represents the preprocessed pixel, $i$ and $j$ represent the positions of the pixel in the codebook, and $t$ is the threshold specified.

$${sp}_{ij}=\left\{\begin{array}{c}p{p}_{ij} ,\\ p{p}_{ij}\times t+l ,\end{array} \begin{array}{c}if j=1 or \left(p{p}_{ij}\times t+l \right)>255\\ otherwise\end{array}\right.$$

(6)

While calculating $sp$, we need to check whether the output $sp$ conforms to the input rules of $pp$ to ensure correct recovery. In terms of mathematical formulas, it is necessary to check the $sp$ of all non-reference pixels ($j\ne 1$). If ${sp}_{ij}\times t\in \left[\mathrm{0,255}\right]$, it means that it is naturally known that it can be embedded without additional auxiliary information. If ${sp}_{ij}\times t>255$, further checking shown in Equation (7) is required. If it is not embeddable, let the indicator ${ind}_k=0$ be saved as auxiliary information; otherwise, if it is embeddable, let the indicator ${ind}_k=1$, where $k$ is the current indicator, and $k$ is automatically incremented every time an indicator is added. Finally, we obtain a binary sequence composed of indicators. Because most preprocessed pixel values in the codebook are relatively close, there will be many consecutive 0’s or consecutive 1’s in the binary sequence. We can utilize the ERLE algorithm [19] for auxiliary information compression to conserve capacity and allocate more capacity for embedded data.

$${ind}_k=\left\{\begin{array}{c}0 ,\\ 1 ,\end{array} \begin{array}{c}if \left(p{p}_{ij}\times t+l \right)>255\\ otherwise\end{array}\right.$$

(7)

Figure 8 provides a codeword example that covers all embedding cases when $t=3$. In this codeword, the first pixel ($j=1$) circled in yellow serves as the reference pixel which remains unchanged. The pixel circled in orange is a case of non-embeddable because its pixel value would overflow after embedding. To avoid confusion during the data extraction and image recovery phases for the non-embeddable case, auxiliary information ${ind}_k=0$ is required to be recorded. Circles in light green and dark green indicate pixels are embeddable, and Equation (6) is the mathematical formula for embedding. Taking the row in light green, when $t=3$ and the data $d$ embedded is 00, the corresponding label $l=0$ according to Figure 7; therefore, the embedded pixel value $sp=60\times 3+0=180$. Similarly, in the dark green row, the corresponding label $l=1$ when the data $d$ embedded is 01, so $sp=8\times 3+1=25$. The light green row indicates that it needs to check whether the output obeys the input rules, ${sp}_{ij}\times t>255$. To prevent confusion with non-embeddable situations, it is necessary to use ${ind}_k=1$ as the auxiliary information. Finally, the dark green row indicates that the embedded pixel can be known directly without any auxiliary information.

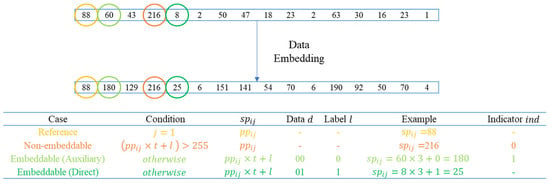
Figure 8. An example of data embedding phase in a codeword ($t=3$).

After our scheme completes embedding, the stego codebook is sorted using Liu et al.’s method [17] and then more data can be embedded using VQ reordering. It should be noted that there are very important technical details in the process. During embedding, we first retain the reference pixels and record indicators for non-embeddable pixels. Then, we embed the embeddable pixel, represented by light green in Figure 8, which requires an indicator. At this point, a portion of the secret data has been embedded and all indicators have been obtained. After applying ERLE algorithm compression, we embed the auxiliary information as data into pixels that can be directly known to be embeddable, represented by dark green in Figure 8. If the capacity does not support embedding all auxiliary information, the remaining auxiliary information can also be embedded using VQ reordering. If there is remaining capacity, additional secret data can be embedded. Eventually, the sender will transmit the stego codebook and the reordered index table to the receiver.

Algorithm 1 describes the process of our proposed scheme in the data embedding phase, outlining how data is encoded and embedded into the stego data.

Algorithm 1 Data Embedding
Input	Preprocessed codebook $PCB$, index table $IT$, secret $S$, and threshold $t$.
Output	Stego codebook $SCB$ and reordered index table $RIT$.
Step 1	Preserve reference pixels and pixels causing overflow. Hide secret data in pixels flagged by indicators according to encoding rules. Record all indicators. $k=1$; for $i\in \{1,2,\dots , {size}_{PCB}\}$    for $j\in \{1,2,\dots ,16\}$      Obtain the label $l$ according to the encoding rules.      if $j=1$ or $({pp}_{ij}\times t+l)>255$         ${sp}_{ij}={pp}_{ij}$;      else         if ${sp}_{ij}\times t>255$           ${sp}_{ij}={pp}_{ij}\times t+l$;           if $({pp}_{ij}\times t+l)>255$             indicator ${ind}_k=0$;           else             indicator ${ind}_k=1$;           end if           $k=k+1$;         end if        end if     end for end for
Step 2	Compress the indicator sequence using the ERLE algorithm to obtain compressed auxiliary information.
Step 3	Similar to Step 1, but here, $l$ is first used for auxiliary information. Any remaining space can be used to embed the secret. for $i\in \{1,2,\dots , {size}_{PCB}\}$    for $j\in \{1,2,\dots ,16\}$      Obtain the label $l$ according to the encoding rules.      if $j=1$ or $({pp}_{ij}\times t+l)>255$        ${sp}_{ij}={pp}_{ij}$;      else        if ${sp}_{ij}\times t\le 255$            ${sp}_{ij}={pp}_{ij}\times t+l$;        end if      end if     end for end for
Step 4	Utilize reordering for additional data embedding. Embed any remaining auxiliary information not fully embedded in Step 3, and use available spaces to embed secret data.
Step 5	Output stego codebook $SCB$ and reordered index table $RIT$.

3.3. Data Extraction and Image Recovery Phase

When the receiver has a stego codebook and a reordered index table, the stego codebook must first be reordered to extract data, which may include both secret data and auxiliary information. Then, it proceeds to extract data from pixel values that can be directly identified as embedded, which may also include both secret data and auxiliary information. After extracting all auxiliary information, ERLE algorithm decompression is applied to retrieve all indicators. Subsequently, all pixels other than references are examined with $s{p}_{ij}\times t>255$. If ${ind}_k=0$, the pixel remains unchanged. If ${ind}_k=1$, data extraction occurs. The mathematical formulas for data extraction are depicted in Equations (8) and (9). It is evident that when pixels are references or non-embedded ones, they remain unchanged. Otherwise, they are embedded pixels, and extraction operations are executed, denoted as ${rp}_{ij}=⌊s{p}_{ij}÷t⌋$, where $rpp$ represents the pixel of the reordered preprocessed codebook. Subsequently, the label $l={s{p}_{ij}-rp}_{ij}\times t$ can be calculated, and then the data can be extracted by referring to the encoding rules depicted in Figure 7.

$${rpp}_{ij}=\left\{\begin{array}{c}s{p}_{ij} ,\\ ⌊s{p}_{ij}÷t⌋ ,\end{array} \begin{array}{c}if j=1 or (s{p}_{ij}\times t>255 and {ind}_k=0)\\ otherwise\end{array}\right.$$

(8)

$$l={s{p}_{ij}-rpp}_{ij}\times t$$

(9)

Figure 9 provides an example of the data extraction phase in a codeword when $t=3$. Circled in yellow are the reference pixels, which remain unchanged. Subsequently, the other pixels are checked. If $s{p}_{ij}\times t>255$, then the indicator is further examined. If ${ind}_k=0$, it indicates non-embeddable pixels, which remain unchanged and are represented in orange in the figure. If ${ind}_k=1$, it indicates the presence of embedding. For the pixels circled in light green in the picture, first, calculate ${rpp}_{ij}=⌊180÷3⌋=$ 60, then compute the label $l=180-60\times 3=0$, and subsequently refer to the encoding rules to extract the data as 00. Similarly, the same applies to pixels directly identified as embedded, represented in dark green. First, calculate ${rpp}_{ij}=⌊25÷3⌋=$8, then compute the label $l=25-8\times 3=1$. According to the encoding rules, the extracted data is 01.

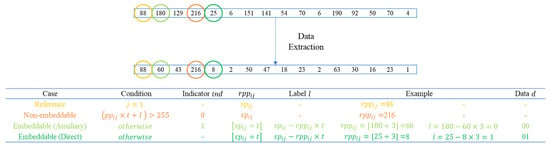
Figure 9. An example of data extraction phase in a codeword ($t=3$).

After the data is extracted, we obtain the reordered preprocessed codebook. Subsequently, we only need to perform post-processing to restore the pixels. As shown in Equation (10), the reference pixel remains unchanged, while the remaining pixels and the first pixel are XORed to obtain the recovered pixel, $rp$. After processing all pixels, the receiver can obtain the recovered codebook, and then compare the reordered index table with it to recover the VQ compressed image. After processing all pixels, the receiver can obtain the recovered codebook. Then, the receiver compares the reordered index table with it to reconstruct the VQ compressed image.

$${rp}_{ij}=\left\{\begin{array}{c}{rpp}_{ij} ,\\ {rpp}_{ij}\oplus {rpp}_{i1} ,\end{array} \begin{array}{c}if j=1\\ otherwise\end{array}\right.$$

(10)

Algorithm 2 describes the process of our proposed scheme in the data extraction phase, outlining how data is decoded and extracted from the stego data, and then recovers the codebook.

Algorithm 2 Data Extraction
Input	Stego codebook $SCB$, reordered index table $RIT$, and threshold $t$.
Output	Secret $S$ and reordered codebook $RCB$.
Step 1	Use reordering of the stego codebook $SCB$ to extract data.
Step 2	Keep reference pixels unchanged and recover the pixels that can be directly known to be embedded and extract data. for $i\in \{1,2,\dots , {size}_{SCB}\}$    for $j\in \{1,2,\dots ,16\}$      if $j=1$        ${rpp}_{ij}={sp}_{ij}$;      else        if ${sp}_{ij}\times t\le 255$          ${rpp}_{ij}=⌊s{p}_{ij}÷t⌋$;          $l={s{p}_{ij}-rpp}_{ij}\times t$;          Obtain the data according to the encoding rules.        end if      end if    end for end for
Step 3	Similar to Step 2, the situation of $s{p}_{ij}\times t>255$ needs to be judged based on the indicator. for $i\in \{1,2,\dots ,{size}_{SCB}\}$    for $j\in \{1,2,\dots ,16\}$      if $j=1$        ${rpp}_{ij}={sp}_{ij}$;      else        if ${sp}_{ij}\times t>255$          if ${ind}_k=0$           ${rpp}_{ij}={sp}_{ij}$;          else            ${rpp}_{ij}=⌊s{p}_{ij}÷t⌋$;            $l={s{p}_{ij}-rpp}_{ij}\times t$;            Obtain the data according to the encoding rules.          end if        Obtain the secret $S$ and the reordered preprocessed codebook $RPCB$.        end if      end if    end for end for
Step 4	Post-processing for reordered preprocessed codebook $RPCB$ for $i\in \{1,2,\dots , {size}_{SCB}\}$    for $j\in \{1,2,\dots ,16\}$      if $j=1$        ${rp}_{ij}={rpp}_{ij}$;      else        ${rp}_{ij}={rpp}_{ij}\oplus {rpp}_{i1}$;      end if    end for end for Obtain the recovered codebook $RCB$.
Step 5	Output secret $S$ and recovered codebook $RCB$.

4. Experimental Results

This section shows the experimental results of our proposed scheme. Figure 10 displays six grayscale images of size 512 × 512 used as test images, trained to generate a VQ codebook. Our experimental environment runs on a Windows 11 operating system with an AMD Ryzen 7 5800H CPU with Radeon Graphics, 16 GB of memory, and MATLAB R2023B software.

Figure 10. Six 512 × 512 test images: (a) Egretta, (b) Elaine, (c) peppers, (d) Tiffany, (e) woodland, (f) Zelda.

Table 1 presents comparisons of PSNR values between a reconstructed image and its original image (OI), as well as between the reconstructed image and its VQ image (VI) reconstructed using the original codebook. It can be clearly observed from the table that the PSNR values for all VI images are +∞, which shows that our proposed scheme can reconstruct VQ-compressed images fully.

Table 1. PSNR comparisons of reconstructed images with their original images and reconstructed images with the VQ images reconstructed using the original codebook.

Codebook Size	64		128		256		512		1024
Image	OI	VI	OI	VI	OI	VI	OI	VI	OI	VI
Egretta	29.6811	+∞	30.4843	+∞	31.1983	+∞	31.9952	+∞	32.7203	+∞
Elaine	29.3081	+∞	30.1569	+∞	30.8513	+∞	31.4101	+∞	32.1139	+∞
Peppers	28.2237	+∞	29.1556	+∞	30.4569	+∞	31.3893	+∞	32.3213	+∞
Tiffany	27.0808	+∞	27.7653	+∞	28.4232	+∞	29.6245	+∞	30.4309	+∞
Woodland	31.1364	+∞	32.2857	+∞	33.0819	+∞	33.8991	+∞	34.6139	+∞
Zelda	31.8216	+∞	32.8539	+∞	33.6891	+∞	34.5065	+∞	35.2775	+∞

Our scheme supports adjustable thresholds. Table 2 shows embedded capacities (ECs) for codebook sizes 64, 128, 256, 512, and 1024, with different thresholds from 2 to 8. It is worth mentioning that with codebook sizes 512 and 1024, we observe that the ECs of $t=5$ decreases compared with the ECs of $t=4$. The main reason is that when $t$ is larger, the number of embeddable pixels decreases even the embedded bits for a pixel may increase. The combination of these factors leads to the changes in the ECs. We also observe that when $t=8$, the embedding capacity is the largest regardless of the codebook size and this result is in line with the methodology of our proposed scheme. We can see the reason from Figure 7, as when $t=8$, every label can embed 3 bits, so a high embedding capacity can be achieved. With a codebook size of 1024, the embedding capacity can be as high as 27,425 bits.

Table 2. Embedding capacity comparison under different codebook sizes and different thresholds.

Codebook Size		64	128	256	512	1024
$\mathrm{Threshold} t$	2	1098	2206	4727	9888	20,478
	3	1449	2819	5833	12,022	24,413
	4	1581	3169	6470	13,312	26,846
	5	1745	3336	6560	12,889	26,185
	6	1834	3545	6714	13,119	26,374
	7	1885	3655	6943	13,456	26,809
	8	1929	3738	7114	13,821	27,425

Table 3 shows the comparison between our scheme with $t=8$ and those of Liu et al. [17] and Chang et al. [18]. We compared the embedding capacity (EC) and embedding rate (ER) for codebooks of sizes 64, 128, 256, 512, and 1024. The ER is expressed in bits per pixel (bpp), calculated as the total embedded bits divided by the total number of pixels in the codebook, as shown in Equation (11). It can be intuitively illustrated from the table that the embedding capacity of our scheme is far better than the other two schemes for codebooks of any size. For a 64-size codebook, the embedding rate is as high as 1.8838 bpp. Compared with the latest scheme by Chang et al., the improvement rate reaches as high as 223.66%. Even for a codebook of size 1024, the improvement rate is as high as 85.19% which fully reflects the superior performance of our scheme.

$$ER=\frac{EC}{total number of pixels}$$

(11)

Table 3. Comparison with other data embedding schemes in the codebook.

Codebook Size		64	128	256	512	1024
EC	Liu et al. [17]	264	649	1546	3595	8204
	Chang et al. [18]	596	1433	3128	6876	14,809
	Proposed Scheme	1929	3738	7114	13,821	27,425
ER	Liu et al. [17]	0.2578	0.3169	0.3774	0.4388	0.5007
	Chang et al. [18]	0.5820	0.6997	0.7637	0.8394	0.9039
	Proposed Scheme	1.8838	1.8252	1.7368	1.6871	1.6739
Improvement Rate		223.66%	160.85%	127.43%	101.00%	85.19%

We randomly sampled 12 images from the USC-SIPI image database [20], comprising images of various sizes (256 × 256, 512 × 512, and 1024 × 1024). These images were utilized to train codebooks sized 64, 128, 256, 512, and 1024. Figure 11 illustrates the comparisons of ECs with other codebook-based data embedding schemes.

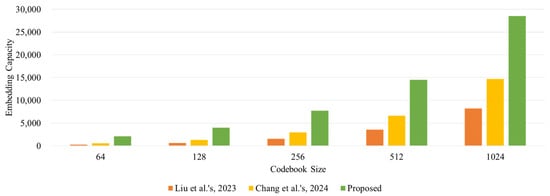
Figure 11. Comparisons with other data embedding schemes [17,18] in the codebook trained by 12 random images from the USC-SIPI image database.

5. Conclusions

Our proposed scheme introduces a novel approach for embedding data in VQ codebooks. We achieve this by XORing most pixel values in the codebook and applying a threshold to regulate data embedding. Through this method, we efficiently integrate both secret data and auxiliary information during the index reordering step of embedding. Upon receiving the stego codebook and the reordered index table, the recipient can losslessly extract the data and reconstruct the VQ-compressed image using the reverse process. Experimental validation of our scheme demonstrates a substantial enhancement in embedding capacity compared to state-of-the-art codebook-based methods. Specifically, we achieve an embedding rate of 1.8838 bpp with an impressive improvement rate of 223.66% using small codebooks of size 64. Similarly, we observe a notable improvement rate of 85.19% in larger codebooks of size 1024. These findings highlight the superior performance and efficacy of our proposed scheme when using VQ codebooks to embed data. Future research directions may encompass more study of carrier characteristics, achieving higher embedding capacity, and expanding towards verifiability. These endeavors hold significant implications for privacy protection, copyright preservation, and digital forensics.