Abstract
A graph’s edge labeling involves the allocation of symbols (colors or numbers) to the edges of a graph governed by specific criteria. Such labeling of a graph G with order n and size m is named edge odd graceful if there is a bijective map from the set of edges to the set in a way that the derived transformation from the vertex-set to the set given by is injective. Any graph is named edge odd graceful if it permits an edge odd graceful allocation (Solairaju and Chithra). The primary aim of this study is to define and explore the edge odd graceful labeling of five new families of wheel-related graphs. Consequently, necessary and sufficient conditions for these families to be edge odd graceful are provided.
MSC:
05C78
1. Introduction
Let be a simple, connected, finite, and undirected graph, where n is the number of its vertices and m is the number of its edges. An edge labeling of G is an allocation of symbols (integers) to the edges of G, governed by specific criteria. Graph labeling, whether it is vertex or edge labeling, plays a significant role in understanding and resolving issues associated with graphs and networks across a wide range of fields. It facilitates effective representation, identification of patterns, optimization, and communication in diverse applications. As a fundamental tool in graph theory, graph labeling holds important practical implications (see [1,2,3]). Although graph labeling is crucial for applications, it remains an active area of research within graph theory. Two fundamental questions for edge labeling are: What is the family of graphs that admit an edge labeling? What are the necessary and sufficient conditions for these graphs to have such labeling?
The paper is organized into two main sections and multiple subsections to ensure a clear structure of the content. The introductory part offers contextual information concerning graph labeling, elucidating the importance of the present study and introducing the research problem, which focuses on investigating the edge odd graceful labeling in diverse graph families. The results section is further divided into subsections numbered Section 2.1, Section 2.2, Section 2.3, Section 2.4 and Section 2.5. Within each of these subsections, we define specific categories of graphs, namely, closed flower graphs, cog wheel graphs, triangulated wheel graphs, double crown-wheel graphs, and crown-triangulated wheel graphs, respectively. For every graph family, we provide comprehensive conditions that are both necessary and sufficient to establish their edge odd graceful nature. It is worth noting that all the graphs examined in this paper have no loops, no multi-edges, and no weighted edges.
Most of the references in the literature attribute the beginning of graph labeling to the work of Rosa [4] in 1967. In Rosa’s paper, a labeling of G called -valuation was introduced as an injection from the set of vertices to the set such that when each edge is designated as , the derived edges are assigned distinct symbols. The same labeling is named “graceful labeling” by Solomon W. Golomb [5].
Another kind of labeling was defined in 1991 by Gnanajothi [6]. It is called an odd graceful labeling, which is an injection from the set of vertices to the set such that when each edge is designated as , the derived edges are assigned .
In 1985, Lo [7] considered a modified version of the graceful labeling of a graph G and called it edge graceful labeling. It is defined as a bijection from the set of edges to the set in a way that the derived transformation from the set of vertices to given by is a bijection.
In 2009, Solairaju and Chithra [8] defined a new labeling of G by combining the ideas of Gnanajothi and Lo and they call it edge odd graceful labeling. This labeling is a bijection from the set of edges to the set in a way that the derived transformation from the vertex-set to the set given by is injective. A graph is named an edge odd graceful if it admits an edge odd graceful labeling. A graph is called graceful (resp. odd graceful, edge graceful) if it admits a labeling that is graceful (resp. odd graceful, edge graceful). For more results on edge odd graceful graphs, see [9,10,11,12,13].
It is not difficult to see that not all graphs are edge odd graceful. For instance, not all stars are edge odd graceful, as we can observe in the following:
Observation 1.
For the star graph is edge odd graceful if and only if n is an even integer.
Proof.
Let be a star graph with the vertex set , where . Then . Each edge in is incident with and exactly one leaf vertex for . All the ways to label the edges of are equivalent.
Now, each leaf vertex has the same labeling as the edge incident with it. Therefore, the outer vertices receive distinct labels from , while the central vertex is labeled as . Therefore, is labeled as 0 if n is even, which means that is edge odd graceful in this case. However, if n is odd, , where k is an odd positive integer less than , this means that is not edge odd graceful in this case. □
Note that identifying the outer vertices of a star with the vertices of an n-cycle, , with vertex set , results in the wheel . For the graph , the vertices and are combined into a single vertex . It was shown in [14] that the wheel graph is edge odd graceful. This manuscript investigates some graphs that are defined in a similar way.
2. Results
2.1. Closed Flower Graphs
The first graph is the closed flower graph, error. It is obtained by connecting a cycle with vertex set and a star graph with vertex set , such that each vertex is connected to vertices and for . In addition the vertex is adjacent to and .
Theorem 1.
The closed flower graph, , is edge odd graceful for n greater than or equal to 3.
Proof.
Let be a closed flower graph, where n is an integer greater than or equal to 3. The size of is . Assume that the vertex set of is . We show that this graph is edge odd graceful by considering three different cases:
- Case (1): Let be as in Figure 1 and .
 Figure 1. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the closed flower graph is edge odd graceful when .
Figure 1. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the closed flower graph is edge odd graceful when . - Case (2): Let be as in Figure 2 and .
 Figure 2. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:
Figure 2. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:
In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Consequently, is a bijective function, and the closed flower graph exhibits an edge odd graceful property when . After considering case (1) and case (2), it can be concluded that every closed flower graph possesses the property of being edge odd graceful for values of n greater than or equal to □
Examples: The closed flower graphs , , …, and their explicit labeling are depicted in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, respectively.
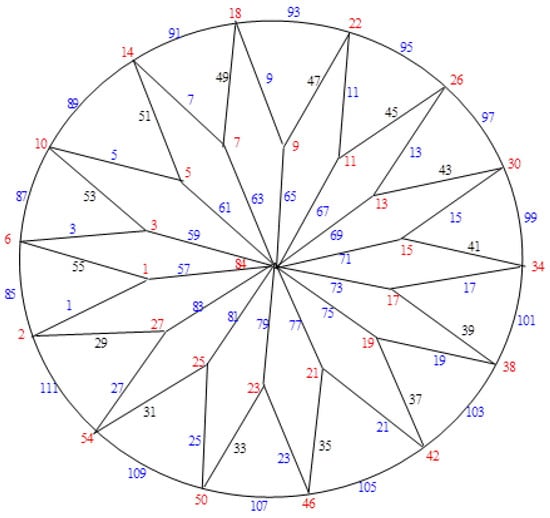
Figure 3.
.

Figure 4.
.

Figure 5.
.
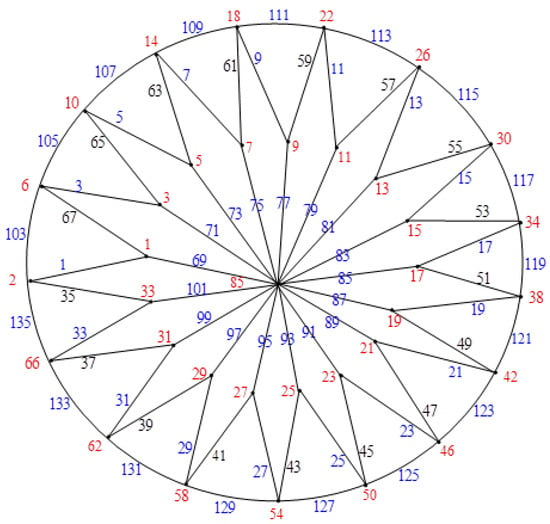
Figure 6.
.

Figure 7.
.
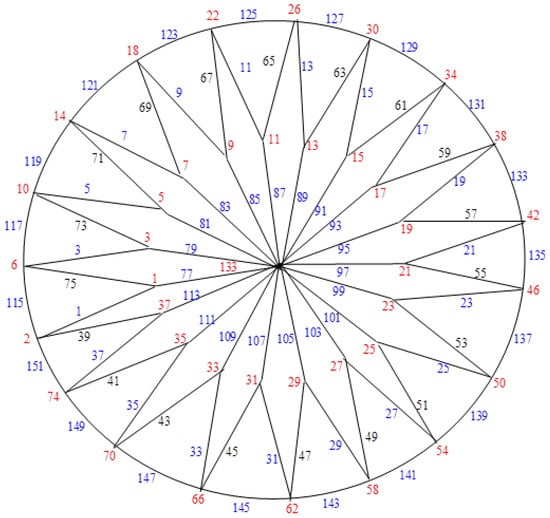
Figure 8.
.
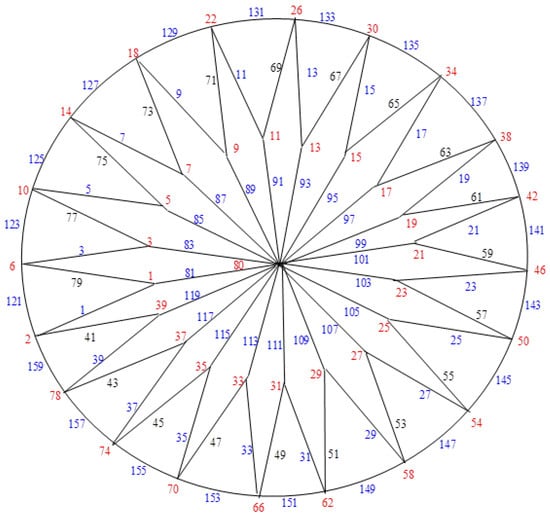
Figure 9.
.

Figure 10.
.
2.2. Cog Wheel Graphs
The second graph is the cog wheel graph, . It is obtained by combining a wheel graph with a set of vertices such that a vertex is adjacent to vertices and , for Furthermore, the vertex is adjacent to vertices and .
Theorem 2.
The Cog wheel graph, , is edge odd graceful for n greater than or equal to 3.
Proof.
Let be a cog wheel graph where n is an integer greater than or equal to 3. It has a size of . Assuming that the vertex set of is , we divide the proof into two cases and provide explicit edge labeling in each case.
- Case (1): Let be as in Figure 11 and .
 Figure 11. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the cog wheel graph is edge odd graceful when .
Figure 11. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the cog wheel graph is edge odd graceful when . - Case (2): Let be as in Figure 12 and .
 Figure 12. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:
Figure 12. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:
In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Consequently, is a bijective function, and the cog wheel graph exhibits an edge odd graceful property when . After considering case (1) and case (2), it can be concluded that every cog wheel graph possesses the property of being edge odd graceful for values of n greater than or equal to □
Examples: The cog wheel graphs and their explicit labeling are depicted in Figure 9, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20, respectively.
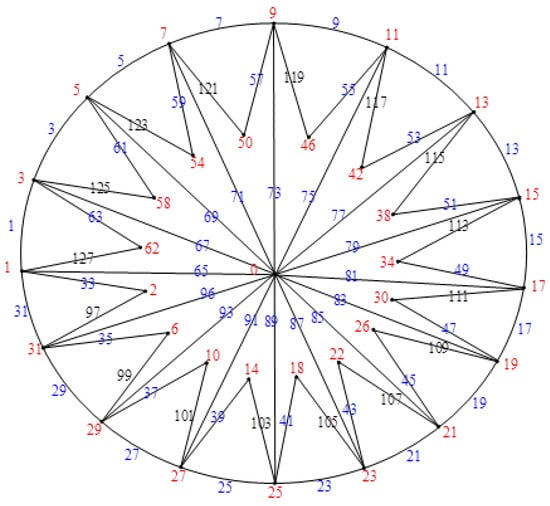
Figure 13.
.
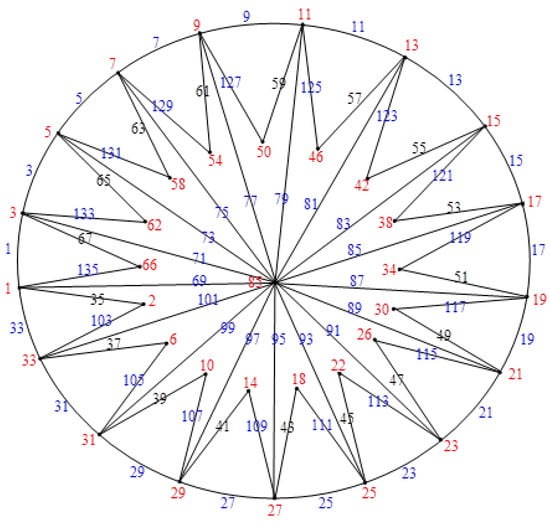
Figure 14.
.
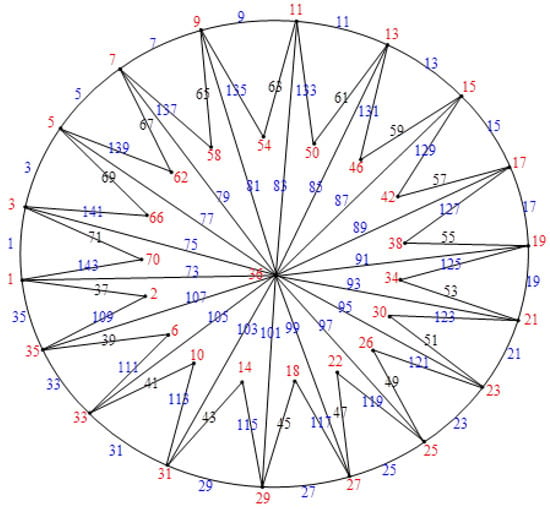
Figure 15.
.

Figure 16.
.

Figure 17.
.
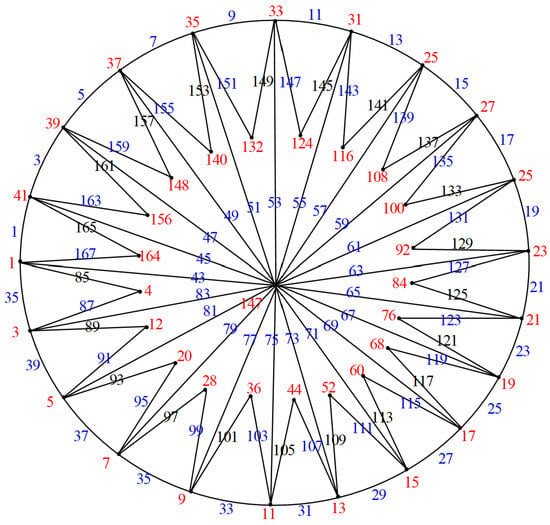
Figure 18.
.
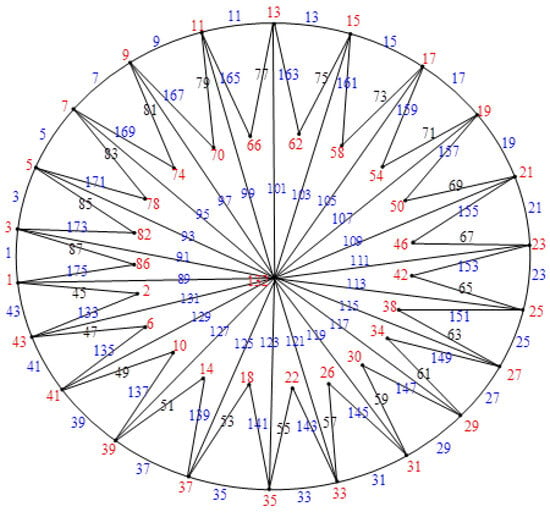
Figure 19.
.

Figure 20.
.
2.3. Triangulated Wheel Graphs
The third graph is the triangulated wheel graph,. It is obtained by combining the wheel graph with a set of vertices such that vertex is adjacent to vertices and , and vertex is adjacent to vertices and . Additionally, each vertex is adjacent to the vertex .
Theorem 3.
The triangulated wheel graph, is edge odd graceful for n greater than or equal to 3.
Proof.
Let be a triangulated wheel graph where n is an integer greater than or equal to 3. It has a size of . Assuming that the vertex set of is , we provide an explicit edge odd labeling in three different cases based on the number of vertices.
- Case (1): Let be as in Figure 21 and .
 Figure 21. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:FurthermoreIn this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the triangulated wheel graph is edge odd graceful when .
Figure 21. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:FurthermoreIn this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the triangulated wheel graph is edge odd graceful when . - Case (2): Let be as in Figure 22 and .
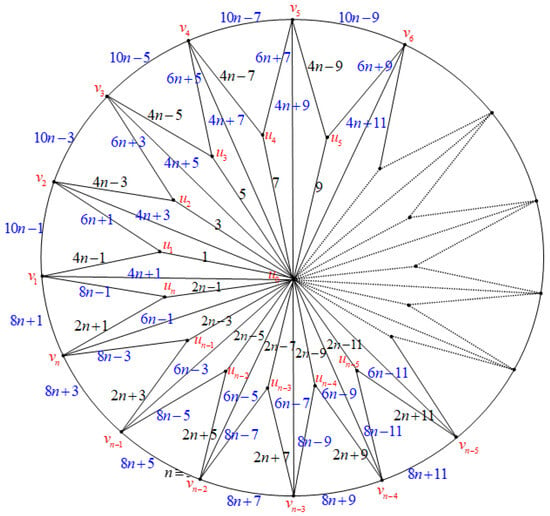 Figure 22. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the triangulated wheel graph is edge odd graceful when .
Figure 22. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the triangulated wheel graph is edge odd graceful when . - Case (3): Let be as in Figure 23 and .
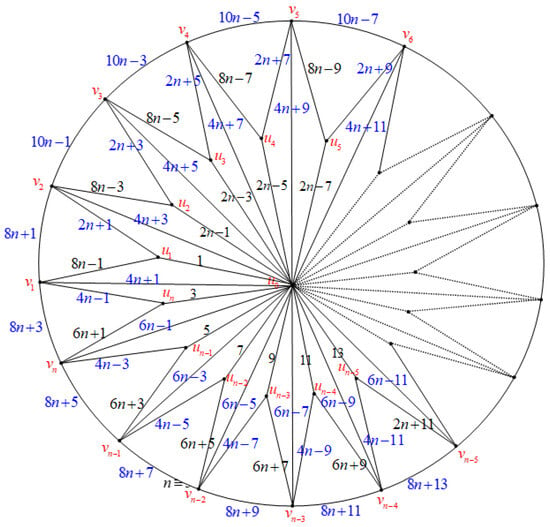 Figure 23. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,
Figure 23. .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,
In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the triangulated wheel graph is edge odd graceful when . After considering case (1), case (2), and case (3), it can be concluded that every triangulated wheel graph possesses the property of being edge odd graceful for values of n greater than or equal to □
Examples: The triangulated wheel graphs and , and their explicit labeling are depicted in Figure 24, Figure 25 and Figure 26, respectively.

Figure 24.
.
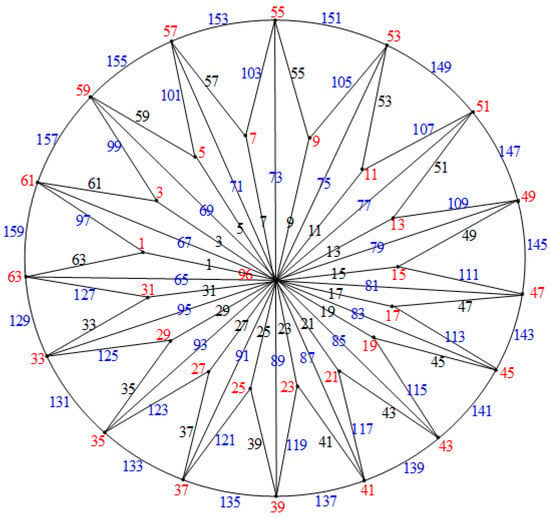
Figure 25.
.
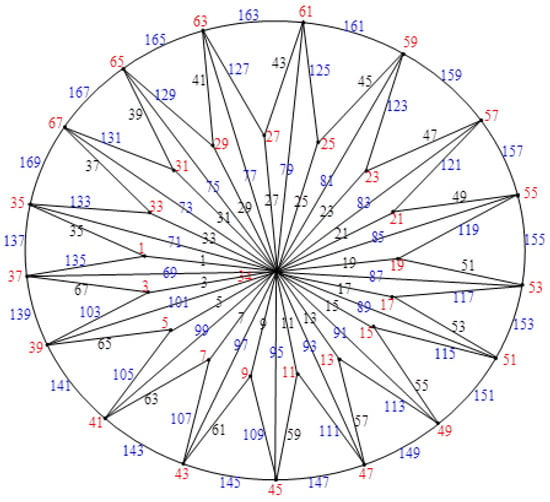
Figure 26.
.
2.4. Double Crown-Wheel Graphs
The fourth graph is the double crown-wheel graph, . It is obtained by combining a wheel graph with two sets of vertices. The first set is , where each vertex is adjacent to vertices and , for , and the vertex is adjacent to vertices and . The second set is , where each vertex is adjacent to vertices and , for , and the vertex is adjacent to vertices and .
Theorem 4.
The double crown-wheel graph, is edge odd graceful for n greater than or equal to 3.
Proof.
Clearly, ; assuming that the set of vertices of is , we provide an explicit edge odd labeling in two different cases based on the number of vertices.
- Case (1): Let be as in Figure 27 and .
 Figure 27. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:In this case, the map from to , respectively is one to one. Additionally, it is one to one map from to , respectively. It is evident that and do not share any common elements. Consequently, is a bijective function, and the double crown-wheel graph is edge odd graceful when .
Figure 27. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:In this case, the map from to , respectively is one to one. Additionally, it is one to one map from to , respectively. It is evident that and do not share any common elements. Consequently, is a bijective function, and the double crown-wheel graph is edge odd graceful when . - Case (2): Let be as in Figure 28 and .
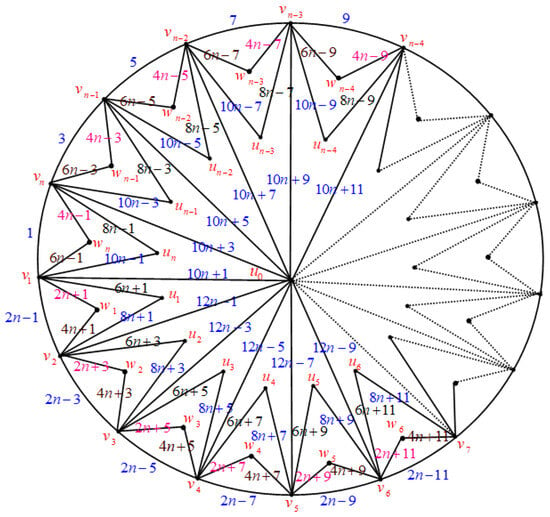 Figure 28. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:
Figure 28. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:
In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the double crown-wheel graph is edge odd graceful when . After considering case (1) and case (2), it can be concluded that every double crown-wheel graph possesses the property of being edge odd graceful for values of n greater than or equal to □
Examples: The double crown-wheel graphs and and their explicit labeling are depicted in Figure 29, Figure 30, Figure 31, Figure 32 and Figure 33, respectively.
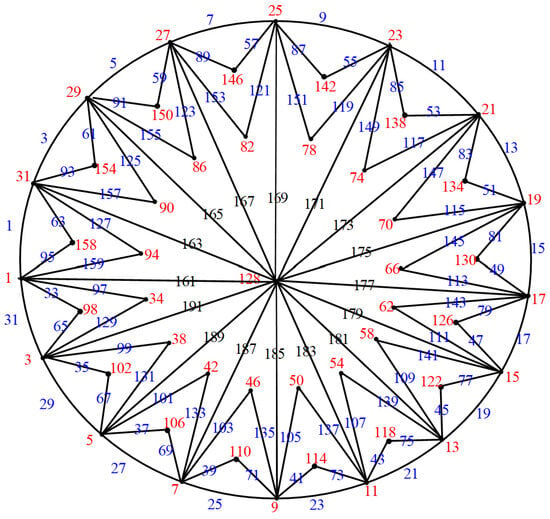
Figure 29.
.
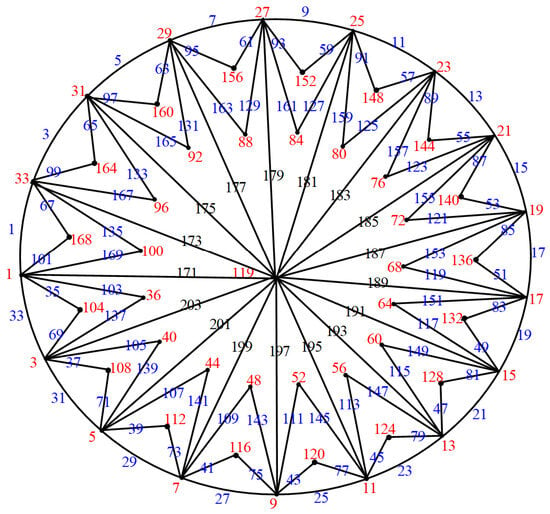
Figure 30.
.
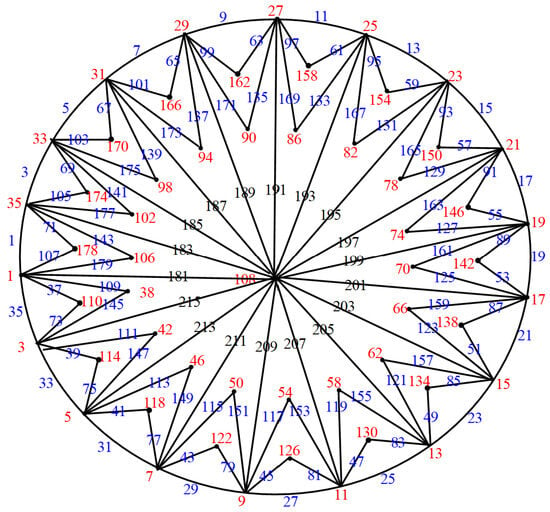
Figure 31.
.

Figure 32.
.
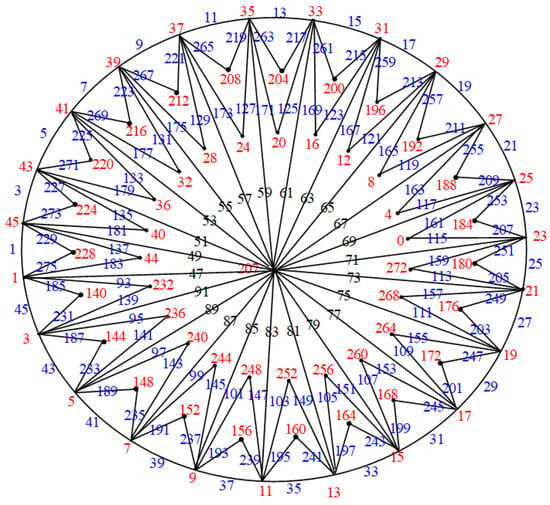
Figure 33.
.
2.5. Crown-Triangulated Wheel Graphs
The fifth graph is the crown-triangulated wheel graph, . It is obtained by combining the triangulated wheel graphs with the set , where each vertex is adjacent to vertices and , for , and the vertex is adjacent to vertices and .
Theorem 5.
The crown-triangulated wheel graph, is edge odd graceful for n greater than or equal to 3.
Proof.
Clearly, , the set of vertices of is
There are two cases:
- Case (1): Let be as in Figure 34 and .
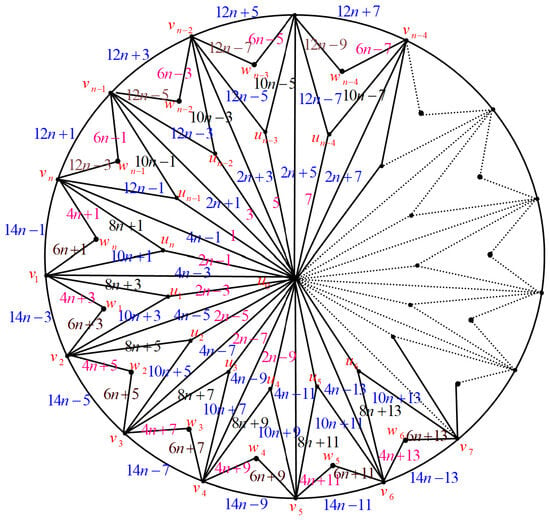 Figure 34. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is one to one map from to , respectively. It is evident that and do not share any common elements. Consequently, is a bijective function, and the crown-triangulated wheel graph is edge odd graceful when .
Figure 34. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,In this case, the map from to , respectively, is one to one. Additionally, it is one to one map from to , respectively. It is evident that and do not share any common elements. Consequently, is a bijective function, and the crown-triangulated wheel graph is edge odd graceful when . - Case (2): Let be as in Figure 35 and .
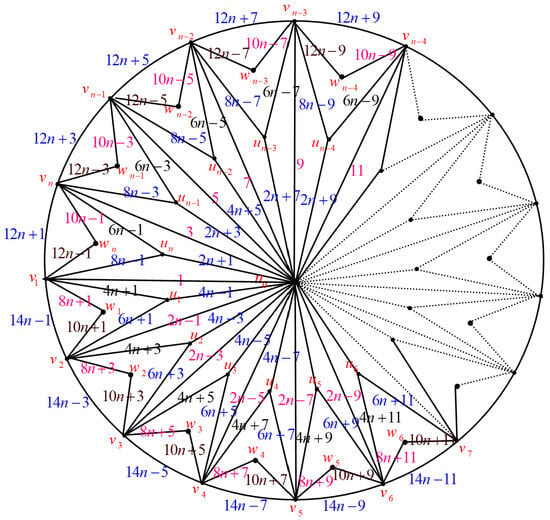 Figure 35. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,Furthermore,
Figure 35. , .Define the mapTherefore, the derived transformation on the set of vertices is given in the following manner:Furthermore,Furthermore,
In this case, the map from to , respectively, is one to one. Additionally, it is a one to one map from to , respectively. It is evident that and do not share any common elements. Moreover, belongs to , and has no elements in common with or . Consequently, is a bijective function, and the crown-triangulated wheel graph is edge odd graceful when . After considering case (1) and case (2), it can be concluded that every crown-triangulated wheel graph possesses the property of being edge odd graceful for values of n greater than or equal to □
Examples: The crown-triangulated wheel graphs and their explicit labeling are depicted in Figure 36, Figure 37, Figure 38 and Figure 39, respectively.

Figure 36.
.
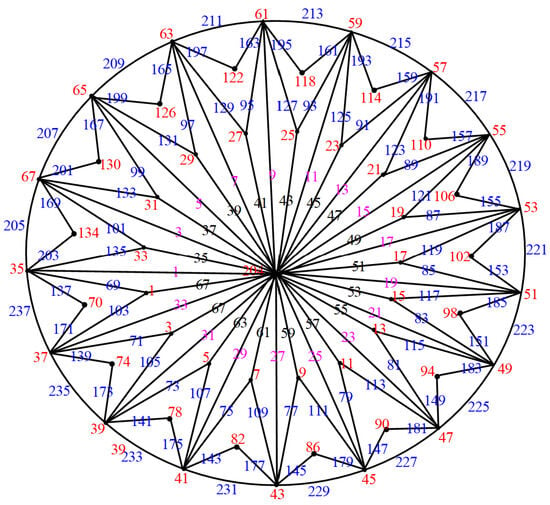
Figure 37.
.
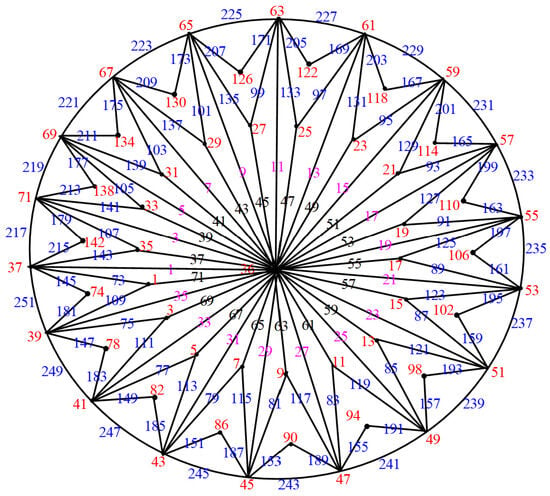
Figure 38.
.
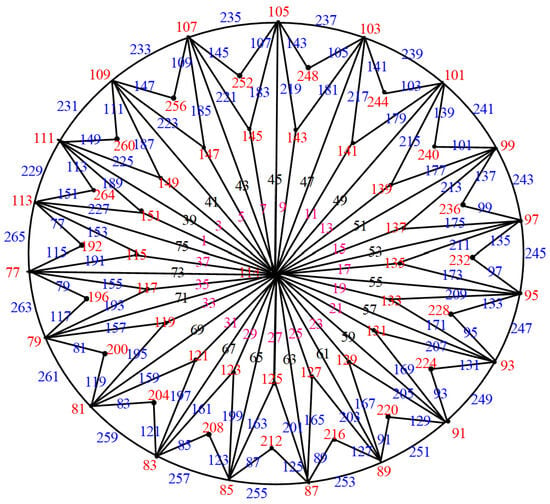
Figure 39.
.
3. Conclusions
The concepts of edge graceful labeling and edge odd graceful labeling have been recognized in the field of graph theory since 2009. Despite numerous studies on these topics, the edge-odd-gracefulness of many graphs remains unknown. One particular group of graphs, stars , is proven to not be edge odd graceful if n is odd, as illustrated in Observation 1. In this research, we introduce five novel graph families that bear some resemblance to wheels. These families encompass closed flower graphs, cogwheel graphs, triangulated wheel graphs, double crown-wheel graphs, and crown-triangulated wheel graphs. By providing explicit labeling for each class, we establish the edge-odd-gracefulness of these graphs. Theorems 1–5 serve as the basis for demonstrating the edge-odd-gracefulness of their respective graph classes.
Author Contributions
Conceptualization, M.A. and S.N.D.; methodology, M.A. and S.N.D.; software, M.A. and S.N.D.; validation, M.A. and S.N.D.; formal analysis, M.A. and S.N.D.; investigation, M.A. and S.N.D.; resources, M.A. and S.N.D.; data curation, M.A. and S.N.D.; writing—original draft preparation, M.A. and S.N.D.; writing—review and editing, M.A. and S.N.D.; visualization, M.A. and S.N.D.; supervision, M.A. and S.N.D.; project administration, M.A. and S.N.D.; funding acquisition, M.A. and S.N.D. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number 445-9-935.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We sincerely thank the referees for their invaluable advice and feedback, which greatly improved the quality of this paper. Their expertise and careful evaluation were instrumental in refining our research.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Bloom, G.S.; Golomb, S.W. Numbered complete graphs, unusual rulers and assorted applications. In Theory and Applications of Graphs; Lecture Notes in Math; Alavi, Y., Lick, D.R., Eds.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 53–65. [Google Scholar]
- Sutton, M. Summable Graphs Labelings and their Applications. Ph.D. Thesis, Department of Computer Science, The University of Newcastle, Newcastle, UK, 2001. [Google Scholar]
- Bloom, G.S.; Golomb, S.W. Applications of numbered undirected graphs. Proc. IEEE 1977, 65, 562–570. [Google Scholar] [CrossRef]
- Rosa, A. On certain valuations of the vertices of a graph. In Theory of Graphs (International Symposium, Rome, Italy, July 1966); Dunod Gordon & Breach Science Publishers, Inc.: New York, NY, USA; Paris, France, 1966; pp. 349–355. [Google Scholar]
- Golomb, S.W. How to Number a Graph. In Graph Theory and Computing; Academic Press: Cambridge, MA, USA, 1972; pp. 23–37. [Google Scholar]
- Gnanajothi, R.B. Topics in Graph Theory. Ph.D. Thesis, Madurai Kamaraj University, Palkalai Nagar, India, 1991. [Google Scholar]
- Lo, S.P. On edge-graceful labelings of graphs. Congr. Numer. 1985, 50, 231–241. [Google Scholar]
- Solairaju, A.; Chithra, K. Edge-Odd Graceful Graphs. Electron. Notes Discret. Math. 2009, 33, 15–20. [Google Scholar] [CrossRef]
- Gallian, J.A. Dynamic survey of graph labeling electronic. J. Comb. 2002, 5, D56. [Google Scholar]
- Jesintha, J.J.; Yogalakshmi, C. Edge-odd graceful labeling of Jahangir graph. South East Asian Math. Math. Sci. 2021, 17, 347–354. [Google Scholar]
- Mirajkar, K.G.; Sthavarmath, P.G. Edge odd gracefulness of lict and litact graphs for few types of graphs. AIP Conf. Proc. 2022, 2385, 130039. [Google Scholar]
- Soleha, M.; Purwanto; Rahmadani, D. Edge odd graceful of alternate snake graphs. J. Phys. Conf. Ser. 2022, 2157, 012002. [Google Scholar] [CrossRef]
- Daoud, S.N. Edge odd graceful labeling of cylinder and torus grid graphs. IEEE Access 2018, 7, 10568–10592. [Google Scholar] [CrossRef]
- Daoud, S.N. Edge odd graceful labeling of some path and cycle related graphs. AKCE Int. J. Graphs Comb. 2017, 14, 178–203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).