Explicit P₁ Finite Element Solution of the Maxwell-Wave Equation Coupling Problem with Absorbing b. c.

Abstract

In this paper, we address the approximation of the coupling problem for the wave equation and Maxwell’s equations of electromagnetism in the time domain in terms of electric field by means of a nodal linear finite element discretization in space, combined with a classical explicit finite difference scheme for time discretization. Our study applies to a particular case where the dielectric permittivity has a constant value outside a subdomain, whose closure does not intersect the boundary of the domain where the problem is defined. Inside this subdomain, Maxwell’s equations hold. Outside this subdomain, the wave equation holds, which may correspond to Maxwell’s equations with a constant permittivity under certain conditions. We consider as a model the case of first-order absorbing boundary conditions. First-order error estimates are proven in the sense of two norms involving first-order time and space derivatives under reasonable assumptions, among which lies a CFL condition for hyperbolic equations. The theoretical estimates are validated by numerical computations, which also show that the scheme is globally of the second order in the maximum norm in time and in the least-squares norm in space.

1. Introduction

The aim of this article is to show that an explicit $P_1$ lumped-mass finite element scheme can be a reliable method to solve Maxwell’s equations of electromagnetism in the time domain and in a bounded domain in ${\Re }^N$, $N=2,3$. This fact is illustrated here, assuming a constant magnetic permeability. It is well known that, in this case, these equations can be expressed as a second-order system in terms of sole electric field. Moreover, the study is conducted in a particular case where the dielectric permittivity is constant in a region of the computational domain contiguous to its boundary. As a consequence, the wave equation holds therein, and for this reason, we address the case of a coupling problem for Maxwell’s equations in the inner domain and the wave equation in the outer domain. However, if it happens that the Maxwell system also holds in the latter, then our study will directly apply to Maxwell’s equations in the whole domain. Moreover, although it extends to other boundary conditions with minor modifications, as a model, we consider in this work first-order absorbing boundary conditions.

The main contribution of this article is justifying the adequacy of a relatively low-cost formulation and underlying finite element solution scheme for the coupling problem at hand, which encompasses Maxwell’s equations as a particular case. Incidentally, from the authors’ point of view, our strategy lines up among the cheapest possible ways to solve the latter equations in arbitrary geometries, as compared with those advocated in the vast literature on their finite element solution [1,2,3]. It is not superfluous to emphasize that, in this article, we carry out this justification from a rigorously mathematical point of view, although numerical validations were not neglected.

Standard conforming linear finite elements are a priori an attractive tool to solve Maxwell’s equations, as an inexpensive method, especially in a three-dimensional space. However, this is not always a good choice for such a purpose. A primary explanation for this assertion is the fact that, in general, the electric field cannot be searched for in the Sobolev space ${\left\{H^1\right\}}^N$, but rather in a subspace of $\mathbf{H}\left(curl\right)\cap \mathbf{H}\left(div\right)$ consisting of vector fields satisfying certain boundary conditions. As a consequence, if the spacial domain in which the equations are defined has re-entrant corners, the subspace of ${\left\{H^1\right\}}^N\cap (\mathbf{H}\left(curl\right)\cap \mathbf{H}\left(div\right))$, incorporating, for instance, zero tangential boundary conditions, is a proper subspace of the corresponding subspace of $\mathbf{H}\left(curl\right)\cap \mathbf{H}\left(div\right)$ owing to the so-called corner paradox (see, e.g., refs. [4,5]). This was one of the main motivations of different authors who looked into the design of finite element methods to cope with the issue. A celebrated contribution in this direction is due to Nédélec [3], namely, a family of $\mathbf{H}\left(curl\right)$-conforming methods to solve these equations, commonly known as edge elements. The crucial point in the discussion on discretization methods to tackle the problem is how to get rid of spurious solutions and other instabilities usually caused by nodal elements, such as the $P_1$ FEM. A detailed study of these questions, together with methods especially designed to solve Maxwell’s equations, is given, for instance, in [2,6]. However, the edge elements are less attractive for solving time-dependent problems, since a linear system of equations should be solved at every time iteration. In contrast, $P_1$ elements can be efficiently used in a fully explicit finite element scheme with a lumped-mass matrix [7,8]. On the other hand, it is also well known that the numerical solution of Maxwell’s equations with nodal finite elements can result in unstable spurious solutions [9,10]. Nevertheless, a number of techniques are available to remove them, and in this respect, we refer, for example, to [10,11,12,13,14]. In the current work, similar to [15], the spurious solutions are removed from the finite element scheme by adding the divergence-free condition to the model equation for the electric field. Numerical tests given in [15] show that spurious solutions are removable indeed, in case an explicit $P_1$ finite element solution scheme is employed.

The first stable time domain decomposition method for the solution of Maxwell’s equations was proposed in [16,17,18]. This method combined the finite difference time domain method (FDTD) on the structured part of the mesh with tetrahedral edge elements on the unstructured part. In [16,17,18], a finite element method was implemented using edge elements of Nédélec [3] on a hexahedral mesh for the $\mathbf{H}\left(curl\right)$-conforming discretization of the electric field. In  [16,17,18], implicit time stepping was used inside a finite element domain to obtain stability of the whole hybrid scheme in time.

In this work, we rule out the aforementioned shortcoming by taking advantage of the fact that the solution of the wave equation lies in ${\left\{H^1\right\}}^N$ irrespective of boundary conditions. Hence, in our case, we can show that the $P_1$ finite element method is indeed an accurate numerical solution tool, provided that the coupled equations are written in a suitable VF (variational form). Actually, the VF employed in this work is similar but not equal to the AVF-augmented variational formulation thoroughly studied by Ciarlet Jr. (cf. [19]) in the static and time-harmonic cases and by Jamelot [20] and Ciarlet Jr.–Jamelot [21]) in the time-dependent case. However, non-negligible additional complexities must be dealt with, stemming from the fact that the dielectric permittivity varies in space. This is one of the main reasons that compelled the authors to carry out here a rigorous analysis of the $P_1$ lumped-mass approximation of Maxwell’s equations. As a matter of fact, to the best of their knowledge, such results were lacking. Indeed, the case of a variable dielectric permittivity was addressed in [7,22], but not for nodal finite elements, while in [21,23,24], nodal finite elements were dealt with, though for constant coefficients and formulations different from ours.

Conforming nodal finite elements were considered to handle the time-dependent case in the early 1990s (cf. [23]) for convex domains. Later on, specialists studied formulations of the static or the time-harmonic Maxwell equations suitable for a numerical solution with nodal elements, even for nonconvex domains. In this respect, we refer to [20,21,25,26]. Such studies revealed the adequacy of nodal elements, at least in some relevant practical situations. Underlying this work lies precisely one such a case, characterized by the fact that the dielectric permittivity is constant in a neighborhood of the boundary of the domain of interest. On the other hand, we emphasize again that there are not many studies of nodal elements as applied to the time-dependent Maxwell equations with variable coefficients. Hence, this paper also gives a contribution in this direction. In short, by applying a lumped-mass explicit $P_1$ finite element scheme to the Maxwell equations in terms of electric field recast in a suitable VF, we establish that, at least in the above case, reliable numerical solutions are generated, as long as a classical stability condition is fulfilled. Here, the purpose of the mass lumping technique is just to provide a fully explicit time marching solver. It should be noted, however, that mass lumping finite element schemes also have nice properties, such as the preservation of the positivity of certain physical variables (see, e.g., ref. [27]).

Before pursuing, it should be pointed out that we described and assessed our method in [28,29] without giving mathematical proofs of reliability. Here, we present the main lines of its formal numerical analysis, though not for the same boundary conditions. For this reason, the numerical examples shown in both articles are different from those presented in this work. We also observe that, akin to [29], we study here a Maxwell-wave equation coupling problem posed in two contiguous disjoint subdomains, which happens to simplify into Maxwell’s equations in the union of both subdomains under certain conditions. The mathematical grounds of our VF, in particular its equivalence with the strong form of Maxwell’s equations, follow the main lines of [29].

As a matter of fact, this work somehow validates a numerical solution procedure described in [15] applied to a kind of CIP—coefficient inverse problem—for the time-dependent Maxwell equations in the particular configuration underlined above. Let us briefly recall it below. For more details, we refer to [30,31,32,33] and references therein.

Assume that in a vast nonconducting homogeneous medium with a given dielectric permittivity, an unknown object is searched for. The  object’s material is also supposedly nonconducting, though with a different dielectric permittivity. Solenoidal electric waves of a regular pattern are sufficiently emitted far away from the search region during a certain time. In the absence of a hidden object, such a pattern will be observed at all times in a certain location closer to the search zone. However, if there is indeed a hidden object, waves will be reflected and back-scattered onto the observation zone. Schematically, such a process may be thought of as governed by the Maxwell system of equations of electromagnetism in an unbounded domain with a constant dielectric permittivity, except in a region surrounding the hidden object where the dielectric permittivity varies. The CIP consists of determining the spacial distribution of an unknown dielectric permittivity—i.e., a coefficient of Maxwell’s equations—with the aim of locating the hidden object, on the basis of measurements of back-scattered waves at a small observation zone. In principle, the far electric field will still be as regular as the emitted one. However, we may conveniently solve the problem by taking a bounded computational domain consisting of two subdomains, namely, an inner domain where the hidden object lies and a surrounding outer domain on whose outer boundary—that is, the boundary of the computational domain—absorbing boundary conditions are prescribed (see, e.g., refs. [34,35]). It is noticeable that, since the dielectric permittivity is constant in the outer domain, N wave equations hold therein. Moreover, since the far field is solenoidal, in practical terms, it can be thought of as being also solenoidal on the boundary of the computational domain, as long as it is large enough. However, strictly speaking, such a condition cannot be prescribed, and hence, it is mathematically inconsistent to consider that the full Maxwell system of equations holds in the outer domain, as it does in the inner domain. That is why we address in this article a Maxwell-wave coupling problem posed simultaneously in the inner and the outer subdomains, bearing in mind that, at least for the CIP in view, Maxwell’s equations are expected to hold in the union of both.

An outline of this paper is as follows: In Section 2, we describe the model problem being solved and study its equivalent VF employed in the sequel. In Section 3, we set up the discretizations of the model problem in both space and time. Section 4 is devoted to the formal reliability analysis of the explicit scheme considered in the previous section. A priori error estimates are given therein under the realistic assumption that the time step varies linearly with the mesh size as the mesh is refined. In Section 5, we present a numerical validation of our scheme. Finally, we conclude in Section 6 with a few comments on the whole work.

2. The Model Problem

The Maxwell-wave equation coupling problem for a field $\mathbf{e}$ in a bounded Lipschitz domain $\mathsf{\Omega }$ of ${\Re }^N,N=2,3$ with boundary $\mathsf{\Gamma }$, that we consider in this work is posed in the following setting. First, we consider that $\mathsf{\Omega }={\overline{\mathsf{\Omega }}}_{in}\cup {\mathsf{\Omega }}_{out}$, where ${\mathsf{\Omega }}_{in}$ is an interior open set whose boundary ${\mathsf{\Gamma }}_{in}$ does not intersect $\mathsf{\Gamma }$ and ${\mathsf{\Omega }}_{out}$ is the complementary set of ${\overline{\mathsf{\Omega }}}_{in}$ with respect to $\mathsf{\Omega }$ (the boundary of ${\mathsf{\Gamma }}_{out}$ is $\mathsf{\Gamma }\cup {\mathsf{\Gamma }}_{in}$). The dielectric permittivity denoted by $\epsilon$ is assumed to belong to $C^2\left(\overline{\mathsf{\Omega }}\right)$ and to fulfill the following conditions:

$$\epsilon \equiv 1 \mathrm{in} {\mathsf{\Omega }}_{out} \mathrm{and} \epsilon \ge 1 \mathrm{otherwise}.$$

(1)

Let $\mathbf{n}$ be the unit outer normal vector on $\mathsf{\Gamma }$. We denote by ${\partial }_n(·)$ the outer normal derivative of a field on $\mathsf{\Gamma }$. Taking into account conditions (1), we may prescribe wave-equation first-order absorbing boundary conditions ${\partial }_n\mathbf{e}=-{\partial }_t\mathbf{e}$ on $\mathsf{\Gamma }\times (0,T)$ [34,35], as seen hereafter.

Now, we are given ${\mathbf{e}}_0\in {\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$ and ${\mathbf{e}}_1\in \mathbf{H}(div,\mathsf{\Omega })$ satisfying $\nabla ·\left(\epsilon {\mathbf{e}}_0\right)=\nabla ·\left(\epsilon {\mathbf{e}}_1\right)\equiv 0$, together with $\mathbf{f}\in L^2[(0,T);\mathbf{H}(div,\mathsf{\Omega })]$ satisfying $\nabla ·\mathbf{f}\equiv 0$. Then, setting $\mathbf{V}:={\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$, the problem to solve is as follows:

$$\left\{\begin{array}{cc}\mathrm{Find} \mathbf{e}\in \mathcal{V}:=H^2[(0,T);{\left\{L^2\left(\mathsf{\Omega }\right)\right\}}^N]\cap L^2[(0,T);\mathbf{V}]\hfill & \\ \mathrm{such} \mathrm{that}\hfill & \\ \left.\begin{array}{c}\epsilon {\partial }_{tt}\mathbf{e}+\nabla \times \nabla \times \mathbf{e}=\mathbf{f},\hfill \\ \nabla ·\left\{\epsilon \mathbf{e}\right\}=0.\hfill \end{array}\right\}\hfill & \mathrm{in} {\mathsf{\Omega }}_{in}\times (0,T),\hfill \\ {\partial }_{tt}\mathbf{e}-\Delta \mathbf{e}=\mathbf{f}\hfill & \mathrm{in} {\mathsf{\Omega }}_{out}\times (0,T),\hfill \\ \mathrm{with} \mathrm{the} \mathrm{initial} \mathrm{conditions}\hfill & \\ \mathbf{e}(·,0)={\mathbf{e}}_0(·), \mathrm{and} {\partial }_t\mathbf{e}(·,0)={\mathbf{e}}_1(·)\hfill & \mathrm{in} \mathsf{\Omega }\hfill \\ \mathrm{and} \mathrm{the} \mathrm{boundary} \mathrm{conditions}\hfill & \\ {\partial }_n\mathbf{e}+{\partial }_t\mathbf{e}=\mathbf{0}\hfill & \mathrm{on} \mathsf{\Gamma }\times (0,T).\hfill \end{array}\right.$$

(2)

Equation (2) tells us that the wave equation holds in ${\mathsf{\Omega }}_{out}\times (0,T)$. On the other hand, the equations in braces of (2) make up Maxwell’s equations in ${\mathsf{\Omega }}_{in}\times (0,T)$ for the sole electric field. It is noticeable that, since $\mathbf{f}$ is solenoidal by assumption, the second equation in ${\mathsf{\Omega }}_{in}\times (0,T)$ is superfluous, i.e., redundant. Indeed, taking the divergence of both sides of the first equation in ${\mathsf{\Omega }}_{in}\times (0,T)$ and denoting by u the function $\nabla ·\left(\epsilon \mathbf{e}\right)$, we have ${\partial }_{tt}u=0 \mathrm{in} {\mathsf{\Omega }}_{in}\times (0,T)$. Taking into account that $u_{|t=0}={{\partial }_{t}u}_{|t=0}=0$ by our assumption on ${\mathbf{e}}_0$ and ${\mathbf{e}}_1$, it must hold $\nabla ·\left(\epsilon \mathbf{e}\right)=0$ in ${\mathsf{\Omega }}_{in}\times (0,T)$. However, the same conclusion cannot be drawn for ${\mathsf{\Omega }}_{out}\times (0,T)$. This is because, in this subdomain, $u:=\nabla ·\mathbf{e}$ solves a wave equation $u_{tt}-\Delta u=0$ with zero initial conditions. Since zero boundary conditions do not necessarily hold for u, this is not sufficient to infer that $u\equiv 0$ in ${\mathsf{\Omega }}_{out}\times (0,T)$. However, of course, nothing prevents Maxwell’s equations from holding indeed in this domain too, as pointed out at the end of Section 1.

2.1. Notations and Reminders

Before pursuing, we introduce some notations and recall a couple of results to be used hereafter.

We denote the standard seminorm of $C^n\left(\overline{\mathsf{\Omega }}\right)$ by ${|·|}_{n,\infty }$ for $n>0$ and the standard norm of $C^0\left(\overline{\mathsf{\Omega }}\right)$ by ${\parallel ·\parallel }_{0,\infty }$. A subset of $\overline{\mathsf{\Omega }}$ will be denoted by an uppercase Latin letter with or without a subscript. For any $D\subset \mathsf{\Omega }$, we denote the standard inner product of ${\left\{L^2\left(D\right)\right\}}^N$ by ${(·,·)}_D$ and the corresponding norm by ${\Vert \{·\}\Vert }_D$; if $D=\mathsf{\Omega }$, we drop the subscript D. $meas\left(D\right)$ represents the measure of D, which accounts for the length, the area, or the volume of D, according to the case.

Any scalar function defined in $\mathsf{\Omega }$ will be denoted by a lowercase Greek letter combined or not with other symbols different from uppercase letters. For a given non-negative function $\omega \in L^{\infty }\left(\mathsf{\Omega }\right)$, we introduce the weighted $L^2\left(\mathsf{\Omega }\right)$-seminorm ${\parallel \{·\}\parallel }_{\omega }:=\sqrt{{\int }_{\mathsf{\Omega }}\omega {|\{·\}|}^2}$, which is actually a norm if $\omega \ne 0$ everywhere in $\overline{\mathsf{\Omega }}$. The notation ${(\mathcal{A},\mathcal{B})}_{\omega }$ expresses ${\int }_{\mathsf{\Omega }}\omega \mathcal{A}·\mathcal{B}$, $\mathcal{A},\mathcal{B}$ being two square-integrable fields in $\mathsf{\Omega }$. If $\omega$ is strictly positive, this expression defines an inner product associated with the norm ${\parallel \{·\}\parallel }_{\omega }$.

We denote by $<·,·{>}_{s,{\mathsf{\Gamma }}_{in}}$ the duality product of $H^s\left({\mathsf{\Gamma }}_{in}\right)-H^{-s}\left({\mathsf{\Gamma }}_{in}\right)$ for $s\in {\Re }^{+}$.

In the sequel, we shall repeatedly employ a well-known operator identity applying to vector fields, namely,

$$-\Delta \equiv -\nabla \nabla ·+\nabla \times \nabla \times .$$

(3)

Let D be a bounded domain of ${\Re }^N$ with boundary $\partial D$. We recall that, according to the trace theorem (cf. [36]) and well-known results, if a given function $\chi \in L^2\left(D\right)$ has a well-defined trace on $\partial D$ in the space $H^{1/2}(\partial D)$ and $\Delta \chi \in H^{-1}\left(D\right)$, then necessarily, $\chi \in H^1\left(D\right)$.

2.2. Well-Posedness Considerations

The well-posedness of (2) will be taken for granted. However, it can be established by means of an argument similar to the one exploited in [29]. Since it is rather laborious, for the sake of brevity, we skip the details of such an analysis. Nevertheless, we next sketch its main lines, which rely on the well-posedness of the following problem.

Let $\mathbf{R}:=\{(\mathbf{v},\mathbf{z})|\mathbf{v}\in {\left\{H^1\left({\mathsf{\Omega }}_{out}\right)\right\}}^N,\mathbf{z}\in \mathbf{H}(curl;{\mathsf{\Omega }}_{in})\cap \mathbf{H}(div;{\mathsf{\Omega }}_{in}),{\int }_{{\mathsf{\Omega }}_{out}}\mathbf{u}+{\int }_{{\mathsf{\Omega }}_{in}}\mathbf{w}=\mathbf{0}\}$, and let ${\mathbf{R}}_{\epsilon }$ be the subspace of $\mathbf{R}$ of the pairs $(\mathbf{v};\mathbf{z})$ satisfying $\nabla ·\left(\epsilon \mathbf{z}\right)=0$ in ${\mathsf{\Omega }}_{in}$. Noticing that the trace over ${\mathsf{\Gamma }}_{in}$ of a field in $\mathbf{H}(curl;{\mathsf{\Omega }}_{in})\cap \mathbf{H}(div;{\mathsf{\Omega }}_{in})\}$ lies in ${\left\{H^{-1/2}\left({\mathsf{\Gamma }}_{in}\right)\right\}}^N$ (cf. [37]), recalling the space $L_0^2\left(\mathsf{\Omega }\right):=\{v|v\in L^2\left(\mathsf{\Omega }\right),{\int }_{\mathsf{\Omega }}v=0\}$, we set the following problem:

$$\left\{\begin{array}{c}\mathrm{Given} \mathrm{a} \mathrm{solenoidal} \mathbf{g}\in {\left\{L_0^2\left(\mathsf{\Omega }\right)\right\}}^N, \mathrm{find} ((\mathbf{u};\mathbf{w});\mathbf{p})\in {\mathbf{R}}_{\epsilon }\times {\left\{H^{1/2}\left({\mathsf{\Gamma }}_{in}\right)\right\}}^N\hfill \\ \mathrm{such} \mathrm{that} \forall ((\mathbf{v};\mathbf{z});\mathbf{q})\in {\mathbf{R}}_{\epsilon }\times {\left\{H^{1/2}\left({\mathsf{\Gamma }}_{in}\right)\right\}}^N\hfill \\ {(\nabla \mathbf{u},\nabla \mathbf{v})}_{{\mathsf{\Omega }}_{out}}+{(\nabla \times \mathbf{w},\nabla \times \mathbf{z})}_{{\mathsf{\Omega }}_{in}}+<\mathbf{p},\mathbf{v}-\mathbf{z}{>}_{1/2,{\mathsf{\Gamma }}_{in}}={({\mathbf{g}}_{|{\mathsf{\Omega }}_{out}},\mathbf{v})}_{{\mathsf{\Omega }}_{out}}+{({\mathbf{g}}_{|{\mathsf{\Omega }}_{in}},\mathbf{z})}_{{\mathsf{\Omega }}_{in}},\hfill \\ <\mathbf{q},\mathbf{u}-\mathbf{w}{>}_{1/2,{\mathsf{\Gamma }}_{in}}=0.\hfill \end{array}\right.$$

(4)

Using the theory of saddle-point linear problems (cf. [38]), we have checked that (4) has a unique solution; moreover, by the same theory, it is equivalent to the following system:

$$\left\{\begin{array}{c}\mathrm{Given} \mathrm{a} \mathrm{solenoidal} \mathbf{g}\in {\left\{{\mathbf{L}}_0^2\left(\mathsf{\Omega }\right)\right\}}^N, \mathrm{find} ((\mathbf{u};\mathbf{w});r;\mathbf{p})\in \mathbf{R}\times L^2\left({\mathsf{\Omega }}_{in}\right)\times {\left\{H^{1/2}\left({\mathsf{\Gamma }}_{in}\right)\right\}}^N\hfill \\ \mathrm{such} \mathrm{that} \forall ((\mathbf{v};\mathbf{z});s;\mathbf{q})\in \mathbf{R}\times L^2\left({\mathsf{\Omega }}_{in}\right)\times {\left\{H^{1/2}\left({\mathsf{\Gamma }}_{in}\right)\right\}}^N\hfill \\ {(\nabla \mathbf{u},\nabla \mathbf{v})}_{{\mathsf{\Omega }}_{out}}+{(\nabla \times \mathbf{w},\nabla \times \mathbf{z})}_{{\mathsf{\Omega }}_{in}}+{(r,\nabla ·\left(\epsilon \mathbf{z}\right))}_{{\mathsf{\Omega }}_{in}}+<\mathbf{p},\mathbf{v}-\mathbf{z}{>}_{1/2,{\mathsf{\Gamma }}_{in}}\hfill \\ ={({\mathbf{g}}_{|{\mathsf{\Omega }}_{out}},\mathbf{v})}_{{\mathsf{\Omega }}_{out}}+{({\mathbf{g}}_{|{\mathsf{\Omega }}_{in}},\mathbf{z})}_{{\mathsf{\Omega }}_{in}},\hfill \\ {(\nabla ·\left(\epsilon \mathbf{w}\right),s)}_{{\mathsf{\Omega }}_{in}}=0,\hfill \\ <\mathbf{q},\mathbf{u}-\mathbf{w}{>}_{1/2,{\mathsf{\Gamma }}_{in}}=0.\hfill \end{array}\right.$$

(5)

It is clear that the solution of (5) solves the following problem:

$$\left\{\begin{array}{cc}\mathrm{Given} \mathbf{g}\in {\left\{{\mathbf{L}}_0^2\left(\mathsf{\Omega }\right)\right\}}^N \mathrm{fulfilling} \nabla ·\mathbf{g}=0 \mathrm{in} \mathsf{\Omega },\hfill & \mathrm{find} (\mathbf{u};\mathbf{w})\in \mathbf{R} \mathrm{such} \mathrm{that}\hfill \\ -\Delta \mathbf{u}={\mathbf{g}}_{|{\mathsf{\Omega }}_{out}}\hfill & \mathrm{in} {\mathsf{\Omega }}_{out}\hfill \\ \left.\begin{array}{c}\nabla \times \nabla \times \mathbf{w}={\mathbf{g}}_{|{\mathsf{\Omega }}_{in}},\hfill \\ \nabla ·\left(\epsilon \mathbf{w}\right)=0.\hfill \end{array}\right\}\hfill & \mathrm{in} {\mathsf{\Omega }}_{in},\hfill \\ \mathbf{u}=\mathbf{w}\hfill & \mathrm{on} {\mathsf{\Gamma }}_{in},\hfill \\ {\partial }_n\mathbf{u}=\mathbf{0}\hfill & \mathrm{on} \mathsf{\Gamma },\hfill \\ {\int }_{{\mathsf{\Omega }}_{out}}\mathbf{u}+{\int }_{{\mathsf{\Omega }}_{in}}\mathbf{w}=\mathbf{0}.\hfill \end{array}\right.$$

(6)

Thus, from classical results (cf. [39]), any linear second-order hyperbolic counterpart of (6) assorted with proper initial conditions also has a unique solution. Let us consider a field $\mathbf{e}$ defined in $\mathsf{\Omega }$ such that ${\mathbf{e}}_{|{\mathsf{\Omega }}_{out}}=\mathbf{u}$ and ${\mathbf{e}}_{|{\mathsf{\Omega }}_{in}}=\mathbf{w}$. Since $\nabla ·\mathbf{w}=-\nabla log\left(\epsilon \right)·\mathbf{w}\in L^2\left({\mathsf{\Omega }}_{in}\right)$ from the assumed regularity of $\epsilon$, we have $\nabla \nabla ·\mathbf{w}\in {\left\{H^{-1}\left({\mathsf{\Omega }}_{in}\right)\right\}}^N$. This implies that $\Delta \mathbf{w}\in {\left\{H^{-1}\left({\mathsf{\Omega }}_{in}\right)\right\}}^N$ by the identity (3), since $\nabla \times \nabla \times \mathbf{w}\in \{L^2{\left({\mathsf{\Omega }}_{in}\right\}}^N$. Therefore, $\mathbf{w}\in {\left\{H^1\left({\mathsf{\Omega }}_{in}\right)\right\}}^N$ owing to the coincidence of $\mathbf{u}$ and $\mathbf{w}$ on ${\mathsf{\Gamma }}_{in}$. Hence, $\mathbf{e}$ lies in ${\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$; moreover, it solves a well-posed elliptic problem in $\mathsf{\Omega }$. Thus, the well-posedness of (2) follows from the fact that it is a second-order hyperbolic counterpart of (6).

Remark 1.

As already pointed out in Section 1, the study that follows also applies to several types of boundary conditions, for which such an $H^1$-regularity is known to hold. As pointed out in Section 1, the choice of absorbing boundary conditions here was motivated by the fact that they correspond to practical situations addressed in [32] and references therein.

2.3. Variational Form

Throughout this article, we work with variational problem (7) stated below, supposedly equivalent to (2).

Requiring that ${\tilde{\mathbf{e}}}_{|t=0}={\mathbf{e}}_0$ and ${\left\{{\partial }_t\tilde{\mathbf{e}}\right\}}_{|t=0}={\mathbf{e}}_1$, we wish to perform the following:

$$\left\{\begin{array}{c}\mathrm{Find} \mathbf{e}\in \tilde{\mathcal{V}}, \mathrm{where}\hfill \\ \tilde{\mathcal{V}}:=\{\mathbf{v}|\mathbf{v}\in H^2[(0,T);{\left\{L^2\left(\mathsf{\Omega }\right)\right\}}^N]\cap H^1[(0,T);\mathbf{V}]\}\hfill \\ \mathrm{such} \mathrm{that} \forall \mathbf{v}\in {\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N \mathrm{and} \forall t\in (0,T)\hfill \\ {\left({\partial }_{tt}\tilde{\mathbf{e}},\mathbf{v}\right)}_{\epsilon }+(\nabla \tilde{\mathbf{e}},\nabla \mathbf{v})+(\nabla ·\epsilon \tilde{\mathbf{e}},\nabla ·\mathbf{v})-(\nabla ·\tilde{\mathbf{e}},\nabla ·\mathbf{v})+{({\partial }_t\tilde{\mathbf{e}},\mathbf{v})}_{\mathsf{\Gamma }}=(\mathbf{f},\mathbf{v}).\hfill \end{array}\right.$$

(7)

Under the conditions assumed in this work, problem (7) is equivalent to the coupling problem (2). Indeed, we have the following:

Proposition 1.

If the solution $\mathbf{e}$ to (2) belongs to $\tilde{\mathcal{V}}$, the following assertions hold:

1. 

$\mathbf{e}$ is also a solution to (7).

2. 

Any solution to (7) is unique, and thus, it is the solution to Equation (2).

Proof. 

1. Using the operator identity (3), we rewrite the second equation of (2) as follows:

$$\epsilon {\partial }_{tt}\mathbf{e}-\Delta \mathbf{e}+\nabla \nabla ·\mathbf{e}=\mathbf{f} \mathrm{in} {\mathsf{\Omega }}_{in}\times (0,T).$$

(8)

We know that the solution of (2) satisfies $\nabla \nabla ·\left(\epsilon \mathbf{e}\right)=\mathbf{0}$ in ${\mathsf{\Omega }}_{in}\times (0,T)$. If we subtract this equation from (8), we obtain the following:

$$\epsilon {\partial }_{tt}\mathbf{e}-\Delta \mathbf{e}-\nabla \nabla ·\left(\epsilon \mathbf{e}\right)+\nabla \nabla ·\mathbf{e}=\mathbf{f} \mathrm{in} {\mathsf{\Omega }}_{in}\times (0,T).$$

(9)

Since $\epsilon \equiv 1$, in ${\mathsf{\Omega }}_{out}$, it is readily seen that (9) also holds in the whole $\mathsf{\Omega }\times (0,T)$.

Thus, taking an arbitrary $\mathbf{v}\in \mathbf{V}$ and using Green’s first identity, together with the absorbing boundary conditions satisfied by $\mathbf{e}$, we readily obtain $\forall \mathbf{v}\in \mathbf{V}$:

$$\left(\epsilon {\partial }_{tt}\mathbf{e},\mathbf{v}\right)+(\nabla \mathbf{e},\nabla \mathbf{v})-(\nabla ·\mathbf{e},\nabla ·\mathbf{v})+(\nabla ·\left\{\epsilon \mathbf{e}\right\},\nabla ·\mathbf{v})+{({\partial }_t\mathbf{e},\mathbf{v})}_{\mathsf{\Gamma }}=(\mathbf{f},\mathbf{v})\forall t\in (0,T),$$

(10)

which establishes that $\mathbf{e}$ solves (7).

2. In order to prove the uniqueness of a solution to (7), we resort to the following energy estimate demonstrated in [15] for variational problem (7):

$$\begin{array}{c}{\displaystyle \forall t\in (0,T]\left\{\Vert {\partial }_t\tilde{\mathbf{e}}{\Vert }_{\epsilon }^2+\Vert \nabla \tilde{\mathbf{e}}{\Vert }^2+{\Vert \nabla ·\tilde{\mathbf{e}}\Vert }_{\epsilon -1}^2\right\}\left(t\right)}\hfill \\ {\displaystyle \le \mathcal{E}\left\{{\int }_0^T{\Vert \mathbf{f}(·,t)\Vert }^{2}dt+\Vert {\mathbf{e}}_0{\Vert }^2+\Vert \nabla {\mathbf{e}}_0{\Vert }^2+\Vert \nabla ·{\mathbf{e}}_0{\Vert }_{\epsilon -1}^2+{\Vert {\mathbf{e}}_1\Vert }_{\epsilon }^2\right\},}\hfill \end{array}$$

(11)

where $\mathcal{E}$ is a constant independent of ${\mathbf{e}}_0$ and ${\mathbf{e}}_1$.

The uniqueness follows from (11) owing to the linearity of problem (7). □

3. Space–Time Discretization

We next describe our numerical scheme to solve (7). Henceforth, for the sake of simplicity, we assume that both $\mathsf{\Omega }$ and ${\mathsf{\Omega }}_{in}$ are polytopes, and without loss of generality, we take $\mathbf{f}\equiv \mathbf{0}$.

3.1. Space Semidiscretization

Let ${\mathcal{T}}_h$ be a mesh fitting $\mathsf{\Omega }$, consisting of N-simplices with the maximum edge length h, belonging to a quasi-uniform family of meshes (cf. [1]). Each element $K\in {\mathcal{T}}_h$ is to be understood as a closed set. Practical calculations are certainly simplified in case ${\mathsf{\Omega }}_{in}$ is the union of N-simplices belonging to ${\mathcal{T}}_h$, which we also assume, even though such an assumption is not essential. We denote by $V_h$ the $P_1$ FE-space of continuous functions related to ${\mathcal{T}}_h$.

Setting ${\mathbf{V}}_h:={\left\{V_h\right\}}^N$, we define ${\mathbf{e}}_{0h}$ (resp. ${\mathbf{e}}_{1h}$) to be the standard ${\mathbf{V}}_h$-interpolate of ${\mathbf{e}}_0$ (resp. ${\mathbf{e}}_1$). Then the space semidiscretized problem to solve consists of finding ${\mathbf{e}}_h\in {\mathbf{V}}_h$ such that $\forall t\in (0,T]$:

$$\begin{array}{c}{\left({\partial }_{tt}{\mathbf{e}}_h,\mathbf{v}\right)}_{\epsilon }+(\nabla {\mathbf{e}}_h,\nabla \mathbf{v})+(\nabla ·\left\{\epsilon {\mathbf{e}}_h\right\},\nabla ·\mathbf{v})-(\nabla ·{\mathbf{e}}_h,\nabla ·\mathbf{v})+{({\partial }_t{\mathbf{e}}_h,\mathbf{v})}_{\mathsf{\Gamma }}=0\hfill \\ \forall \mathbf{v}\in {\mathbf{V}}_h,\hfill \\ \mathrm{with} \hfill \\ {\mathbf{e}}_h(·,0)={\mathbf{e}}_{0h}(·) \mathrm{and} {\partial }_t{\mathbf{e}}_h(·,0)={\mathbf{e}}_{1h}(·) \mathrm{in} \mathsf{\Omega }.\hfill \end{array}$$

(12)

3.2. Full Discretization

To begin with, we consider a natural centered time discretization scheme to solve (12); namely, given a number M of time steps, we define the time increment $\tau :=T/M$. Then we approximate ${\mathbf{e}}_h\left(k\tau \right)$ by ${\mathbf{e}}_h^k$ for $k=1,2,\dots ,M$ according to the following FE scheme for $k=1,2,\dots ,M-1$:

$$\begin{array}{c}{\displaystyle {\left(\frac{{\mathbf{e}}_h^{k+1}-2{\mathbf{e}}_h^k+{\mathbf{e}}_h^{k-1}}{{\tau }^2},\mathbf{v}\right)}_{\epsilon }+(\nabla {\mathbf{e}}_h^k,\nabla \mathbf{v})+(\nabla ·\epsilon {\mathbf{e}}_h^k,\nabla ·\mathbf{v})-(\nabla ·{\mathbf{e}}_h^k,\nabla ·\mathbf{v})}\hfill \\ {\displaystyle +{\left(\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}}{2\tau },\mathbf{v}\right)}_{\mathsf{\Gamma }}=0\forall \mathbf{v}\in {\mathbf{V}}_h,}\hfill \\ \mathrm{with} \hfill \\ {\mathbf{e}}_h^0={\mathbf{e}}_{0h} \mathrm{and} {\mathbf{e}}_h^1={\mathbf{e}}_h^0+\tau {\mathbf{e}}_{1h} \mathrm{in} \mathsf{\Omega }.\hfill \end{array}$$

(13)

Owing to its coupling with ${\mathbf{e}}_h^k$ and ${\mathbf{e}}_h^{k-1}$ on the left-hand side of (13), ${\mathbf{e}}_h^{k+1}$ cannot be determined explicitly by this scheme at every time step. In order to enable an explicit solution, we resort to the classical mass lumping technique. We recall that this consists of replacing on the left-hand side the inner product $(\mathbf{u},\mathbf{v})$ (resp. ${(\mathbf{u},\mathbf{v})}_{\mathsf{\Gamma }}$) by an inner product ${(\mathbf{u},\mathbf{v})}_h$ using the trapezoidal rule to approximate the integral of ${\int }_K{\mathbf{u}}_{|K}·{\mathbf{v}}_{|K}d\mathbf{x}$, for every element K in ${\mathcal{T}}_h$, for $(\mathbf{u};\mathbf{v})\in {\left\{C^0\left(\overline{\mathsf{\Omega }}\right)\right\}}^N\times {\left\{C^0\left(\overline{\mathsf{\Omega }}\right)\right\}}^N$. In the case of (13), $\mathbf{u}$ stands for $\epsilon ({\mathbf{e}}_h^{k+1}-2{\mathbf{e}}_h^k+{\mathbf{e}}_h^{k-1})$ and $\mathbf{v}$ is an arbitrary field in ${\mathbf{V}}_h$. It is well known that, in this case, the matrix associated with ${(\epsilon {\mathbf{e}}_h^{k+1},\mathbf{v})}_h$ is a diagonal matrix. Similarly, a mass lumping approximation ${({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1},\mathbf{v})}_{\mathsf{\Gamma },h}$ must be used for the inner product ${({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1},\mathbf{v})}_{\mathsf{\Gamma }}$.

The expression ${(\epsilon \mathbf{u},\mathbf{v})}_h$ for continuous $\mathbf{u}$ and $\mathbf{v}$ gives rise to an approximation of the inner product ${(\mathbf{u},\mathbf{v})}_{\epsilon }$, henceforth denoted by ${(\mathbf{u},\mathbf{v})}_{\epsilon ,h}$. In order to simplify the calculations, we further approximate the inner product ${(\mathbf{u},\mathbf{v})}_{\epsilon ,h}$ by the inner product ${(\mathbf{u},\mathbf{v})}_{{\epsilon }_h,h}$, whose definition is given below, followed by the expression ${(\mathbf{u},\mathbf{v})}_{\mathsf{\Gamma },h}$ approximating the inner product ${(\mathbf{u},\mathbf{v})}_{\mathsf{\Gamma }}$ for every $(\mathbf{u};\mathbf{v})\in {\left\{C^0\left(\overline{\mathsf{\Omega }}\right)\right\}}^N\times {\left\{C^0\left(\overline{\mathsf{\Omega }}\right)\right\}}^N$.

$${\displaystyle {(\mathbf{u},\mathbf{v})}_{{\epsilon }_h,h}:=\sum _{K\in {\mathcal{T}}_h}\epsilon \left(G_K\right)meas\left(K\right)\sum _{i=1}^{N+1}\frac{\mathbf{u}\left(S_{K,i}\right)·\mathbf{v}\left(S_{K,i}\right)}{N+1},}$$

where $S_{K,i}$ are the vertexes of K, $i=1,\dots ,N+1$ and $G_K$ is the centroid of K.

Generically denoting by $F^K$ the edges for $N=2$ or the faces for $N=3$ of an N -simplex K, let ${\mathcal{S}}_h$ be the subset of ${\mathcal{T}}_h$ consisting of K such that $\mathsf{\Gamma }\cap K\ne \varnothing$. Then we set the following:

$${\displaystyle {(\mathbf{u},\mathbf{v})}_{\mathsf{\Gamma },h}:=\sum _{K\in {\mathcal{S}}_h}\sum _{F^K\cap \mathsf{\Gamma }\ne \varnothing }meas\left(F^K\right)\sum _{i=1}^N\frac{\mathbf{u}\left(R_{F^K,i}\right)·\mathbf{v}\left(R_{F^K,i}\right)}{N},}$$

where $R_{F^K,i}$ are the vertexes of $F^K$, $i=1,\dots ,N$.

For coherence, ${\epsilon }_h$ is defined to be the function whose value in each $K\in {\mathcal{T}}_h$ is constant equal to $\epsilon \left(G_K\right)$. Furthermore, we introduce the norms ${\Vert \{·\}\Vert }_{{\epsilon }_h,h}$ and ${\Vert \{·\}\Vert }_h$ of $V_h$, given by ${(\{·\},\{·\})}_{{\epsilon }_h,h}^{1/2}$ and ${(\{·\},\{·\})}_h^{1/2}$, respectively. Similarly, we denote by ${\Vert \{·\}\Vert }_{\mathsf{\Gamma },h}$ the norm defined by ${(\{·\},\{·\})}_{\mathsf{\Gamma },h}^{1,2}$. Then still denoting the approximation of ${\mathbf{e}}_h\left(k\tau \right)$ by ${\mathbf{e}}_h^k$, for $k=1,2,\dots ,M$, we determine ${\mathbf{e}}_h^{k+1}$ by the following:

$$\begin{array}{c}{\displaystyle {\left(\frac{{\mathbf{e}}_h^{k+1}-2{\mathbf{e}}_h^k+{\mathbf{e}}_h^{k-1}}{{\tau }^2},\mathbf{v}\right)}_{{\epsilon }_h,h}+(\nabla {\mathbf{e}}_h^k,\nabla \mathbf{v})+(\nabla ·\epsilon {\mathbf{e}}_h^k,\nabla ·\mathbf{v})-(\nabla ·{\mathbf{e}}_h^k,\nabla ·\mathbf{v})}\hfill \\ {\displaystyle +{\left(\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}}{2\tau },\mathbf{v}\right)}_{\mathsf{\Gamma },h}=0\forall \mathbf{v}\in {\mathbf{V}}_h,}\hfill \\ \mathrm{with} \hfill \\ {\mathbf{e}}_h^0={\mathbf{e}}_{0h} \mathrm{and} {\mathbf{e}}_h^1={\mathbf{e}}_h^0+\tau {{\mathbf{e}}_1}_h \mathrm{in} \mathsf{\Omega }.\hfill \end{array}$$

(14)

Now we adapt a result given in Lemma 3 of [40], which allows us to assert that the following upper bounds hold:

$${\Vert v\Vert }_{{\epsilon }_h}\le {\Vert v\Vert }_{{\epsilon }_h,h}\forall v\in V_h.$$

(15)

Similarly, we have the following:

$${\Vert v\Vert }_{\mathsf{\Gamma }}\le {\Vert v\Vert }_{\mathsf{\Gamma },h}\forall v\in V_h.$$

(16)

4. Reliability Analysis

We next show that, under very reasonable conditions, optimal-order error estimates in a natural sense hold for approximations of the solution of problem (7) generated by scheme (14).

4.1. Scheme Stability

In order to conveniently prepare the subsequent steps of the reliability study of (14), following a technique thoroughly exploited in [41], we carry out the stability analysis of a more general form thereof, encompassing scheme (14) as a particular case, namely,  

$$\begin{array}{c}{\displaystyle {\left(\frac{{\mathbf{e}}_h^{k+1}-2{\mathbf{e}}_h^k+{\mathbf{e}}_h^{k-1}}{{\tau }^2},\mathbf{v}\right)}_{{\epsilon }_h,h}+(\nabla {\mathbf{e}}_h^k,\nabla \mathbf{v})+(\nabla ·\epsilon {\mathbf{e}}_h^k,\nabla ·\mathbf{v})-(\nabla ·{\mathbf{e}}_h^k,\nabla ·\mathbf{v})}\hfill \\ {\displaystyle +{\left(\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}}{2\tau },\mathbf{v}\right)}_{\mathsf{\Gamma },h}={\mathbf{F}}^k\left(\mathbf{v}\right)+(d^k,\nabla ·\mathbf{v})+{\mathbf{G}}^k\left(\mathbf{v}\right)\forall \mathbf{v}\in {\mathbf{V}}_h,}\hfill \\ \\ {\mathbf{e}}_h^0={\mathbf{e}}_{0h} \mathrm{and} {\mathbf{e}}_h^1={\mathbf{e}}_h^0+\tau {\mathbf{e}}_{1h} \mathrm{in} \mathsf{\Omega }.\hfill \end{array}$$

(17)

where, for every $k\in \{1,2,\dots ,N-1\}$, ${\mathbf{F}}^k$ and ${\mathbf{G}}^k$ are given bounded linear functionals over ${\mathbf{V}}_h$ and the space of traces over $\mathsf{\Gamma }$ of fields in ${\mathbf{V}}_h$ equipped with the norms ${\parallel ·\parallel }_h$ and ${\parallel ·\parallel }_{\mathsf{\Gamma },h}$, respectively. We denote by $|{\mathbf{F}}^k{|}_h$ and $|{\mathbf{G}}^k{|}_{\mathsf{\Gamma },h}$ the underlying norms of both functionals. $d^k$, in turn, is a given function in $L^2\left(\mathsf{\Omega }\right)$ for $k\in \{1,2,\dots ,M-1\}.$

Taking $\mathbf{v}={\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}$ in (17), we obtain for $k=1,2,\dots ,M-1$:

$$\begin{array}{c}{\displaystyle {\left({\displaystyle \frac{{\mathbf{e}}_h^{k+1}-2{\mathbf{e}}_h^k+{\mathbf{e}}_h^{k-1}}{\tau },\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}}{\tau }}\right)}_{{\epsilon }_h,h}+(\nabla {\mathbf{e}}_h^k,\nabla {\mathbf{e}}_h^{k+1}-\nabla {\mathbf{e}}_h^{k-1})}\hfill \\ \\ {\displaystyle +(\nabla ·\{\epsilon -1\}{\mathbf{e}}_h^k,\nabla ·{\mathbf{e}}_h^{k+1}-\nabla ·{\mathbf{e}}_h^{k-1})+{\left(\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}}{2\tau },{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\right)}_{\mathsf{\Gamma },h}}\hfill \\ \\ ={\mathbf{F}}^k({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1})+(d^k,\nabla ·\{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\})+{\mathbf{G}}^k({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1})\hfill \end{array}$$

(18)

Noting that ${\mathbf{e}}_h^{k+1}-2{\mathbf{e}}_h^k+{\mathbf{e}}_h^{k-1}=({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k)-({\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1})$ and that ${\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}=({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k)+({\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1})$, the following estimate trivially holds for Equation (17):

$$\begin{array}{c}{\displaystyle {∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}_{{\epsilon }_h,h}^2-{∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+I_1+I_2+2\tau {∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}}{2\tau }∥}_{\mathsf{\Gamma },h}^2}\hfill \\ \le |{\mathbf{F}}^k{|}_h{∥{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}∥}_h+\parallel d^k\parallel \parallel \nabla ·({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1})\parallel \hfill \\ +|{\mathbf{G}}^k{|}_{\mathsf{\Gamma },h}{∥{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}∥}_{\mathsf{\Gamma },h}\hfill \\ \mathrm{where}\hfill \\ I_1:=(\nabla {\mathbf{e}}_h^k,\nabla \{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\});\hfill \\ \mathrm{and}\hfill \\ I_2:=(\nabla ·\{\epsilon -1\}{\mathbf{e}}_h^k,\nabla ·\{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\}).\hfill \end{array}$$

(19)

Next, we estimate the terms $I_1$ and $I_2$ given by (19).

First of all, it is easy to see the following:

$$\begin{array}{c}{\displaystyle I_1=\frac{1}{2}(\parallel \nabla {\mathbf{e}}_h^{k+1}{\parallel }^2+\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2-\parallel \nabla ({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k){\parallel }^2)}\hfill \\ {\displaystyle -\frac{1}{2}(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+\parallel \nabla {\mathbf{e}}_h^{k-1}{\parallel }^2-\parallel \nabla ({\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}){\parallel }^2).}\hfill \end{array}$$

(20)

Next, we note the following:

$$\begin{array}{c}{I}_2=J_1+J_2\hfill \\ \mathrm{where}\hfill \\ J_1:={(\nabla ·{\mathbf{e}}_h^k,\nabla ·\{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\})}_{\epsilon -1}\hfill \\ \mathrm{and}\hfill \\ J_2:=(\nabla \epsilon ·{\mathbf{e}}_h^k,\nabla ·\{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\}).\hfill \end{array}$$

(21)

Similar to (20), we can write the following:

$$\begin{array}{c}{\displaystyle J_1=\frac{1}{2}(\parallel \nabla ·{\mathbf{e}}_h^{k+1}{\parallel }_{\epsilon -1}^2+\parallel \nabla ·{\mathbf{e}}_h^k{\parallel }_{\epsilon -1}^2-\parallel \nabla ·({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k){\parallel }_{\epsilon -1}^2)}\hfill \\ {\displaystyle -\frac{1}{2}(\parallel \nabla ·{\mathbf{e}}_h^k{\parallel }_{\epsilon -1}^2+\parallel \nabla ·{\mathbf{e}}_h^{k-1}{\parallel }_{\epsilon -1}^2-\parallel \nabla ·({\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}){\parallel }_{\epsilon -1}^2)}\hfill \end{array}$$

(22)

Now observing that $\nabla \epsilon \equiv \mathbf{0}$ on $\mathsf{\Gamma }$, we integrate by parts $J_2$ given by (21) to obtain the following:

$$\begin{array}{c}{J}_2=-(\nabla \{\nabla \epsilon ·{\mathbf{e}}_h^k\},{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}).\hfill \end{array}$$

(23)

Let us rewrite $J_2$ as follows:

$$\begin{array}{c}{J}_2=M_1+M_2\hfill \\ \mathrm{where}\hfill \\ M_1:=-\left(\nabla \nabla \epsilon {\mathbf{e}}_h^k,{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\right)\hfill \\ \mathrm{and}\hfill \\ M_2:=-\left({\{\nabla {\mathbf{e}}_h^k\}}^{\mathcal{T}}\nabla \epsilon ,{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\right)\hfill \end{array}$$

(24)

$M_1$, in turn, can be rewritten as follows:

$$\begin{array}{c}{M}_1=N_1+N_2\hfill \\ \mathrm{where}\hfill \\ {\displaystyle N_1:=-\tau \left(\nabla \nabla \epsilon {\mathbf{e}}_h^k,\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }\right)}\hfill \\ \mathrm{and}\hfill \\ {\displaystyle N_2:=-\tau \left(\nabla \nabla \epsilon {\mathbf{e}}_h^k,\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }\right).}\hfill \end{array}$$

(25)

Then, we further observe the following:

$${\displaystyle N_1=-{\tau }^2\sum _{i=1}^k\left(\nabla \nabla \epsilon \frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau },\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }\right)-\tau \left(\nabla \nabla \epsilon {\mathbf{e}}_h^0,\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }\right).}$$

(26)

Hence,

$${\displaystyle N_1\ge -{\tau }^2{|\epsilon |}_{2,\infty }∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥\sum _{i=1}^k∥\frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau }∥+{\tau |\epsilon |}_{2,\infty }\parallel {\mathbf{e}}_h^0\parallel ∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}$$

or yet

$${\displaystyle N_1\ge -\tau {|\epsilon |}_{2,\infty }∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥\left\{\tau \sqrt{k}{\left({\displaystyle \sum _{i=1}^k{∥\frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau }∥}^2}\right)}^{1/2}+\parallel {\mathbf{e}}_h^0\parallel \right\},}$$

and noting that $k\le T/\tau$, we obtain the following:

$$\begin{array}{c}{\displaystyle N_1\ge -\tau {|\epsilon |}_{2,\infty }∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥\left\{\tau \sqrt{\frac{T}{\tau }}{\left({\displaystyle \sum _{i=1}^k{∥\frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau }∥}^2}\right)}^{1/2}+\parallel {\mathbf{e}}_h^0\parallel \right\}.}\hfill \end{array}$$

(27)

Applying to (27) Young’s inequality $ab\le \delta a^2/2+b^2/\left(2\delta \right)$$\forall a,b\in \Re$ and $\delta >0$ with $\delta =1$, we easily conclude as follows:

$$\begin{array}{c}{\displaystyle N_1\ge -\frac{\tau }{2}{|\epsilon |}_{2,\infty }\left({\displaystyle 2{∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}^2+\tau T\sum _{i=1}^k{∥\frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau }∥}^2+{\parallel {\mathbf{e}}_h^0\parallel }^2}\right).}\hfill \end{array}$$

(28)

Similar to (28),

$$\begin{array}{c}{\displaystyle N_2\ge -\frac{\tau }{2}{|\epsilon |}_{2,\infty }\left({\displaystyle 2{∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}^2+\tau T\sum _{i=1}^k{∥\frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau }∥}^2+{\parallel {\mathbf{e}}_h^0\parallel }^2}\right).}\hfill \end{array}$$

(29)

Combining (28) and (29), we come up with the following:

$$\begin{array}{c}{M}_1\ge -\tau {|\epsilon |}_{2,\infty }\left({\displaystyle {∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}^2+{∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}^2+L_k}\right),\hfill \\ \mathrm{where}\hfill \\ {\displaystyle L_k:=\tau T\sum _{i=1}^k{∥\frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau }∥}^2+{\parallel {\mathbf{e}}_h^0\parallel }^2.}\hfill \end{array}$$

(30)

As for $M_2$ given by (24), we have the following:

$${\displaystyle M_2\ge -{\left|\epsilon \right|}_{1,\infty }∥\nabla {\mathbf{e}}_h^k∥∥{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}∥\ge -\tau {|\epsilon |}_{1,\infty }∥\nabla {\mathbf{e}}_h^k∥\left({\displaystyle ∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥+∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}\right)}$$

or yet

$${\displaystyle M_2\ge -\frac{\tau }{2}{|\epsilon |}_{1,\infty }\left({\displaystyle 2\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}^2+{∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}^2}\right).}$$

(31)

Now, we recall (19) together with (16) and notice that, for every square-integrable field $\mathbf{A}$ in $\mathsf{\Omega }$, we have $\parallel \mathbf{A}\parallel \le {\parallel \mathbf{A}\parallel }_{{\epsilon }_h}$. Then taking into account that $\parallel \nabla ·\mathbf{v}\parallel \le \sqrt{N}\parallel \nabla \mathbf{v}\parallel$$\forall \mathbf{v}\in {\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$, and using Young’s inequality with $\delta =\tau$, $\delta =1/\tau$ and $\delta =\tau$, respectively, we easily obtain the following estimates:

$$\begin{array}{c}{\displaystyle |{\mathbf{F}}^k{|}_h\parallel {\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}\parallel \le \frac{\tau }{2}{|{\mathbf{F}}^k|}_h^2+\tau \left({\displaystyle {∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}_h^2+{∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_h^2}\right),}\hfill \\ \\ {\displaystyle \parallel d^k\parallel \parallel \nabla ·({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1})\parallel \le \frac{N}{2\tau }\parallel d^k{\parallel }^2+\tau (\parallel \nabla {\mathbf{e}}_h^{k+1}{\parallel }^2+\parallel \nabla {\mathbf{e}}_h^{k-1}{)\parallel }^2),}\hfill \\ \\ {\displaystyle |{\mathbf{G}}^k{|}_{\mathsf{\Gamma },h}{∥{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}∥}_{\mathsf{\Gamma },h}\le \frac{\tau }{2}{|{\mathbf{G}}^k|}_{\mathsf{\Gamma },h}^2+2\tau {∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^{k-1}}{2\tau }∥}_{\mathsf{\Gamma },h}^2,}\hfill \end{array}$$

(32)

where, in the first and the second inequality, we also used the fact that ${\parallel \mathbf{A}\pm \mathbf{B}\parallel }^2\le {2(\parallel \mathbf{A}\parallel }^2+{\parallel \mathbf{B}\parallel }^2)$ for all square-integrable fields $\mathbf{A}$ and $\mathbf{B}$.

Now, we collect Equations (20)–(24) and (30)–(32) to plug them into (19). Using the fact that $\parallel ·\parallel \le {\parallel ·\parallel }_h\le {\parallel ·\parallel }_{{\epsilon }_h}\le {\parallel ·\parallel }_{{\epsilon }_h,h}$, we obtain for $1\le k\le M-1$ the following:

$$\begin{array}{c}{\displaystyle (A_k-B_k)+(C_k-D_k)\le \frac{\tau }{2}|{\mathbf{F}}^k{|}_h^2+\frac{N}{2\tau }{\parallel d^k\parallel }^2+\frac{\tau }{2}{\left|{\mathbf{G}}^k\right|}_{{\mathsf{\Gamma }}_h}^2,}\hfill \\ \mathrm{where}\hfill \\ {\displaystyle A_k:={∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}_{{\epsilon }_h,h}^2-\frac{\tau }{2}\left(2+{|\epsilon |}_{1,\infty }+2{|\epsilon |}_{2,\infty }\right){∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}_{{\epsilon }_h,h}^2}\hfill \\ {\displaystyle +\frac{1}{2}\left\{(1-2\tau )\parallel \nabla {\mathbf{e}}_h^{k+1}{\parallel }^2{+(1-\tau |\epsilon |}_{1,\infty })\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2\right\}}\hfill \\ \\ {\displaystyle B_k:={∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\left(2+{|\epsilon |}_{1,\infty }+2{|\epsilon |}_{2,\infty }\right){∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2}\hfill \\ {\displaystyle +\frac{1}{2}\left\{\left(1+2\tau \right)\parallel \nabla {\mathbf{e}}_h^{k-1}{\parallel }^2+\left(1+{\tau |\epsilon |}_{1,\infty }\right){\parallel \nabla {\mathbf{e}}_h^k\parallel }^2\right\}+\tau {|\epsilon |}_{2,\infty }{L}_k}\hfill \\ \\ {\displaystyle C_k:=-\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k)\parallel }_{\epsilon -1}^2\right\}+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^{k+1}{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^k\parallel }_{\epsilon -1}^2\right)}\hfill \\ \\ {\displaystyle D_k:=-\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1})\parallel }_{\epsilon -1}^2\right\}+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^k{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^{k-1}\parallel }_{\epsilon -1}^2\right).}\hfill \end{array}$$

(33)

Setting

$$\begin{array}{c}\eta :=2+{|\epsilon |}_{1,\infty }+2{|\epsilon |}_{2,\infty };\hfill \\ \theta :={|\epsilon |}_{1,\infty };\hfill \\ \rho :=T^2{|\epsilon |}_{2,\infty },\hfill \end{array}$$

(34)

we can rewrite $A_k$ and $B_k$ as follows:

$$\begin{array}{c}{\displaystyle A_k:={∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}_{{\epsilon }_h,h}^2-\frac{\tau }{2}\eta {∥\frac{{\mathbf{e}}_h^{k+1}-{\mathbf{e}}_h^k}{\tau }∥}_{{\epsilon }_h,h}^2}\hfill \\ {\displaystyle +\frac{1}{2}\left(\parallel \nabla {\mathbf{e}}_h^{k+1}{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^k\parallel }^2\right)-\tau \left(\parallel \nabla {\mathbf{e}}_h^{k+1}{\parallel }^2+\frac{\theta }{2}{\parallel \nabla {\mathbf{e}}_h^k\parallel }^2\right);}\hfill \\ \\ {\displaystyle B_k:={∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\eta {∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2}\hfill \\ {\displaystyle +\frac{1}{2}\left(\parallel \nabla {\mathbf{e}}_h^{k-1}{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^k\parallel }^2\right)+\tau \left(\parallel \nabla {\mathbf{e}}_h^{k-1}{\parallel }^2+\frac{\theta }{2}{\parallel \nabla {\mathbf{e}}_h^k\parallel }^2\right)+\frac{\tau \rho }{T^2}{L}_k}\hfill \end{array}$$

(35)

Then we note that, for $1\le k\le m-1$ with $2\le m\le M-1$,

$$\begin{array}{c}{\displaystyle A_{k-1}-B_k=-\tau \eta {∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2-\tau \left(1+\frac{\theta }{2}\right)\left(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)-\frac{\tau \rho }{T^2}{L}_k.}\hfill \end{array}$$

(36)

It follows that

$$\begin{array}{c}{\displaystyle \sum _{k=1}^m(A_k-B_k)=A_m-B_1+\sum _{k=2}^m(A_{k-1}-B_k)}\hfill \\ {\displaystyle =\frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{1}{2}\left(1-2\tau \right)\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+\frac{1}{2}\left(1-\tau \theta \right){\parallel \nabla {\mathbf{e}}_h^m\parallel }^2}\hfill \\ {\displaystyle -\frac{1}{2}\left(2+\tau \eta \right){∥\frac{{\mathbf{e}}_h^1-{\mathbf{e}}_h^0}{\tau }∥}_{{\epsilon }_h,h}^2-\frac{1}{2}\left(1+2\tau \right)\parallel \nabla {\mathbf{e}}_h^0{\parallel }^2-\frac{1}{2}\left(1+\tau \theta \right){\parallel \nabla {\mathbf{e}}_h^1\parallel }^2-\frac{\tau \rho }{T^2}{L}_1}\hfill \\ {\displaystyle -\sum _{k=2}^m\left\{{\displaystyle \tau \eta {∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\left(2+\theta \right)\left(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)+\frac{\tau \rho }{T^2}{L}_k}\right\}.}\hfill \end{array}$$

(37)

Now, we extend to $k=1$ the summation range on the right-hand side of (37) to obtain the following:

$$\begin{array}{c}{\displaystyle \sum _{k=1}^m(A_k-B_k)}\hfill \\ {\displaystyle =\frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{1}{2}\left(1-2\tau \right)\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+\frac{1}{2}\left(1-\tau \theta \right){\parallel \nabla {\mathbf{e}}_h^m\parallel }^2}\hfill \\ {\displaystyle -\frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^1-{\mathbf{e}}_h^0}{\tau }∥}_{{\epsilon }_h,h}^2-\frac{1}{2}\left(1-\tau \theta \right)\parallel \nabla {\mathbf{e}}_h^0{\parallel }^2-\frac{1}{2}\left(1-2\tau \right){\parallel \nabla {\mathbf{e}}_h^1\parallel }^2}\hfill \\ {\displaystyle -\sum _{k=1}^m\left\{{\displaystyle \tau \eta {∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\left(2+\theta \right)\left(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)+\frac{\tau \rho }{T^2}{L}_k}\right\}.}\hfill \end{array}$$

(38)

Moreover, since $C_{k-1}=D_k$ for all $m\ge k\ge 2$, recalling (33), we easily come up with the following:

$$\begin{array}{c}{\displaystyle \sum _{k=1}^m(C_k-D_k)=C_m-D_1}\hfill \\ {\displaystyle =-\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m)\parallel }_{\epsilon -1}^2\right\}+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^{m+1}{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^m\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle +\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^1-{\mathbf{e}}_h^0){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^1-{\mathbf{e}}_h^0)\parallel }_{\epsilon -1}^2\right\}-\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^1{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^0\parallel }_{\epsilon -1}^2\right).}\hfill \end{array}$$

(39)

Combining (38) and (39), we obtain for $2\le m\le -1$ the following:

$$\begin{array}{c}{\displaystyle \sum _{k=1}^m(A_k+C_k)-\sum _{k=1}^m(B_k+D_k)}\hfill \\ {\displaystyle =\frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{1}{2}\left(1-2\tau \right)\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+\frac{1}{2}\left(1-\tau \theta \right){\parallel \nabla {\mathbf{e}}_h^m\parallel }^2}\hfill \\ {\displaystyle -\frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^1-{\mathbf{e}}_h^0}{\tau }∥}_{{\epsilon }_h,h}^2-\frac{1}{2}\left(1-\tau \theta \right)\parallel \nabla {\mathbf{e}}_h^0{\parallel }^2-\frac{1}{2}\left(1-2\tau \right){\parallel \nabla {\mathbf{e}}_h^1\parallel }^2}\hfill \\ {\displaystyle -\sum _{k=1}^m\left\{{\displaystyle \tau \eta {∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\left(2+\theta \right)\left(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)+\frac{\tau \rho }{T^2}{L}_k}\right\}}\hfill \\ {\displaystyle -\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m)\parallel }_{\epsilon -1}^2\right\}+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^{m+1}{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^m\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle +\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^1-{\mathbf{e}}_h^0){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^1-{\mathbf{e}}_h^0)\parallel }_{\epsilon -1}^2\right\}-\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^1{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^0\parallel }_{\epsilon -1}^2\right).}\hfill \end{array}$$

(40)

On the other hand, recalling (30), we note that, for $2\le m\le M-1$,

$$\begin{array}{c}{\displaystyle \sum _{k=1}^m{L}_k\le \sum _{k=1}^m\left({\displaystyle \tau T\sum _{i=1}^m{∥\frac{{\mathbf{e}}_h^i-{\mathbf{e}}_h^{i-1}}{\tau }∥}^2+{\parallel {\mathbf{e}}_h^0\parallel }^2}\right)=Tm\tau \sum _{k=1}^m{∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}^2+m{\parallel {\mathbf{e}}_h^0\parallel }^2}\hfill \end{array}$$

(41)

In short, since $m\tau \le T$, from (41), we easily obtain for $2\le m\le M-1$ the following:

$$\begin{array}{c}{\displaystyle \frac{\tau \rho }{T^2}\sum _{k=1}^m{L}_k\le \tau \rho \sum _{k=1}^m{∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}^2+\frac{\rho }{T}{\parallel {\mathbf{e}}_h^0\parallel }^2.}\hfill \end{array}$$

(42)

Plugging (42) into (40) and summing up both sides of (33) from $k=1$ through $k=m$ for $2\le m\le N-1$ by using (35) and (40) yields the following:

$$\begin{array}{c}{\displaystyle \frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{1}{2}\left(1-2\tau \right)\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+\frac{1}{2}\left(1-\tau \theta \right){\parallel \nabla {\mathbf{e}}_h^m\parallel }^2}\hfill \\ {\displaystyle -\frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^1-{\mathbf{e}}_h^0}{\tau }∥}_{{\epsilon }_h,h}^2-\frac{1}{2}\left(1-\tau \theta \right)\parallel \nabla {\mathbf{e}}_h^0{\parallel }^2-\frac{1}{2}\left(1-2\tau \right){\parallel \nabla {\mathbf{e}}_h^1\parallel }^2}\hfill \\ {\displaystyle -\sum _{k=1}^m\left\{{\displaystyle \tau \left(\eta +\rho \right){∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\left(2+\theta \right)\left(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)}\right\}}\hfill \\ {\displaystyle -\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m)\parallel }_{\epsilon -1}^2\right\}+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^{m+1}{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^m\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle +\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^1-{\mathbf{e}}_h^0){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^1-{\mathbf{e}}_h^0)\parallel }_{\epsilon -1}^2\right\}-\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^1{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^0\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle \le \sum _{k=1}^m\left({\displaystyle \frac{\tau }{2}|{\mathbf{F}}^k{|}_h^2+\frac{N}{2\tau }{\parallel d^k\parallel }^2+\frac{\tau }{2}{\left|{\mathbf{G}}^k\right|}_{{\mathsf{\Gamma }}_h}^2}\right)+\frac{\rho }{T}{\parallel {\mathbf{e}}_h^0\parallel }^2.}\hfill \end{array}$$

(43)

Thus, taking into account that ${\mathbf{e}}_h^1-{\mathbf{e}}_h^0=\tau {\mathbf{e}}_{1h}$, leaving on the left-hand side only the terms with the superscripts $m+1$ and m, and increasing the coefficients of $\parallel \nabla {\mathbf{e}}_h^j{\parallel }^2$ for $j=0,1$ and $\parallel {\mathbf{e}}_{1h}{\parallel }_{{\epsilon }_h,h}^2$, for $2\le m\le M-1$, we come up with the following:

$$\begin{array}{c}{\displaystyle \frac{1}{2}\left(2-\tau \eta \right){∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{1}{2}\left(1-2\tau \right)\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+\frac{1}{2}\left(1-\tau \theta \right){\parallel \nabla {\mathbf{e}}_h^m\parallel }^2}\hfill \\ {\displaystyle -\frac{1}{2}\left\{\parallel \nabla ({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m)\parallel }_{\epsilon -1}^2\right\}+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^{m+1}{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^m\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle \le \sum _{k=1}^m\left\{{\displaystyle \tau \left(\eta +\rho \right){∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\left(2+\theta \right)\left(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)}\right.}\hfill \\ {\displaystyle \left.{\displaystyle +\frac{\tau }{2}|{\mathbf{F}}^k{|}_h^2+\frac{N}{2\tau }{\parallel d^k\parallel }^2+\frac{\tau }{2}{\left|{\mathbf{G}}^k\right|}_{\mathsf{\Gamma },h}^2}\right\}+{∥{\mathbf{e}}_{1h}∥}_{{\epsilon }_h,h}^2+\frac{{\tau }^2}{2}\left(\parallel \nabla {\mathbf{e}}_{1h}{\parallel }^2+{\parallel \nabla ·{\mathbf{e}}_{1h}\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle +\frac{1}{2}\left(\parallel \nabla {\mathbf{e}}_h^1{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^0\parallel }^2\right)+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^1{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^0\parallel }_{\epsilon -1}^2\right)+\frac{\rho }{T}{\parallel {\mathbf{e}}_h^0\parallel }^2.}\hfill \end{array}$$

(44)

Now, we recall a classical inverse inequality (cf. [1]), according to which,

$$\parallel \nabla v\parallel \le C{h}^{-1}\parallel v\parallel \le C{h}^{-1}{\parallel v\parallel }_{{\epsilon }_h,h} \mathrm{for} \mathrm{all} v\in V_h,$$

(45)

where C is a mesh-independent constant, and we apply the trivial upper bound ${\parallel \nabla ·\mathbf{v}\parallel }_{\epsilon -1}\le \sqrt{{N\parallel \epsilon -1\parallel }_{\infty }}\parallel \nabla \mathbf{v}\parallel$ for all $\mathbf{v}\in {\mathbf{V}}_h$.

Let us assume that $\tau$ satisfies the following CFL condition:

$$\tau \le h/\nu \mathrm{with} \nu ={C(1+N\parallel \epsilon -1\parallel }_{\infty }{)}^{1/2}.$$

(46)

Then we have $\forall \mathbf{v}\in {\mathbf{V}}_h$:

$${\displaystyle {\parallel \nabla \mathbf{v}\parallel }^2+{\parallel \nabla ·\mathbf{v}\parallel }_{\epsilon -1}^2\le {\nu }^2\frac{{\tau }^2}{h^2}\frac{{\parallel \mathbf{v}\parallel }^2}{{\tau }^2}\le \frac{{\parallel \mathbf{v}\parallel }_{{\epsilon }_h,h}^2}{{\tau }^2}}$$

(47)

This means that

$${\displaystyle \parallel \nabla ({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m){\parallel }^2+{\parallel \nabla ·({\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m)\parallel }_{\epsilon -1}^2\le {∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2}$$

(48)

Plugging (48) into (44), we obtain the following:  

$$\begin{array}{c}{\displaystyle \frac{1}{2}\left(1-\tau \eta \right){∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{1}{2}\left(1-2\tau \right)\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+\frac{1}{2}\left(1-\tau \theta \right){\parallel \nabla {\mathbf{e}}_h^m\parallel }^2}\hfill \\ {\displaystyle \le \sum _{k=1}^m\left\{{\displaystyle \tau \left(\eta +\rho \right){∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\frac{\tau }{2}\left(2+\theta \right)\left(\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)}\right.}\hfill \\ {\displaystyle \left.{\displaystyle +\frac{\tau }{2}|{\mathbf{F}}^k{|}_h^2+\frac{N}{2\tau }{\parallel d^k\parallel }^2+\frac{\tau }{2}{\left|{\mathbf{G}}^k\right|}_{\mathsf{\Gamma },h}^2}\right\}+{∥{\mathbf{e}}_{1h}∥}_{{\epsilon }_h,h}^2+\frac{{\tau }^2}{2}\left(\parallel \nabla {\mathbf{e}}_{1h}{\parallel }^2+{\parallel \nabla ·{\mathbf{e}}_{1h}\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle +\frac{1}{2}\left(\parallel \nabla {\mathbf{e}}_h^1{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^0\parallel }^2\right)+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^1{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^0\parallel }_{\epsilon -1}^2\right)+\frac{\rho }{T}{\parallel {\mathbf{e}}_h^0\parallel }^2.}\hfill \end{array}$$

(49)

Next, we note that both $1-2\tau$ and $1-\tau \theta$ are bounded below by $1-\tau \eta$; moreover, $\frac{1}{2}(2+\theta )$ is obviously bounded above by $\eta +\rho$. Therefore, it is easy to see that (49) can be transformed into the following:

$$\begin{array}{c}{\displaystyle \frac{1}{2}\left(1-\tau \eta \right)\left({∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^m\parallel }^2\right)}\hfill \\ {\displaystyle \le S_M+E_0+\sum _{k=1}^m\tau \left(\eta +\rho \right)\left({∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right),}\hfill \end{array}$$

(50)

where

$$\begin{array}{c}{\displaystyle S_M:=\sum _{k=1}^{M-1}\left({\displaystyle \frac{\tau }{2}|{\mathbf{F}}^k{|}_h^2+\frac{N}{2\tau }{\parallel d^k\parallel }^2+\frac{\tau }{2}{\left|{\mathbf{G}}^k\right|}_{\mathsf{\Gamma },h}^2}\right)}\hfill \\ \\ {\displaystyle E_0:={∥{\mathbf{e}}_{1h}∥}_{{\epsilon }_h,h}^2+\frac{{\tau }^2}{2}\left(\parallel \nabla {\mathbf{e}}_{1h}{\parallel }^2+{\parallel \nabla ·{\mathbf{e}}_{1h}\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle +\frac{1}{2}\left(\parallel \nabla {\mathbf{e}}_h^1{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^0\parallel }^2\right)+\frac{1}{2}\left(\parallel \nabla ·{\mathbf{e}}_h^1{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\mathbf{e}}_h^0\parallel }_{\epsilon -1}^2\right)+\frac{\rho }{T}{\parallel {\mathbf{e}}_h^0\parallel }^2.}\hfill \end{array}$$

(51)

Let us assume that ${\displaystyle \tau \le \frac{1}{2\eta }}$. Then from (51), we have the following:

$$\begin{array}{c}{\displaystyle {∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}_{{\epsilon }_h,h}^2+\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^m\parallel }^2}\hfill \\ \le 4\left\{{\displaystyle S_M+E_0+\sum _{k=1}^m\tau \left(\eta +\rho \right)\left({∥\frac{{\mathbf{e}}_h^k-{\mathbf{e}}_h^{k-1}}{\tau }∥}_{{\epsilon }_h,h}^2+\parallel \nabla {\mathbf{e}}_h^k{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^{k-1}\parallel }^2\right)}\right\}.\hfill \end{array}$$

(52)

Now we set the following:

$$\beta =4M\tau (\eta +\rho )=4T\left\{2+{|\epsilon |}_{1,\infty }+(2+T^2){|\epsilon |}_{2,\infty }\right\}.$$

(53)

From the discrete Grönwall lemma and (15) from (52), we infer that $\forall m\le M-1$:

$$\begin{array}{|c|}\hline {\displaystyle {∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }∥}^2+\parallel \nabla {\mathbf{e}}_h^{m+1}{\parallel }^2+{\parallel \nabla {\mathbf{e}}_h^m\parallel }^2\le 4(S_M+E_0)e^{\beta },}\\ \hline\end{array}$$

(54)

as long as $\tau \le min\{h/\nu ,1/(2\eta \left)\right\}$, where $\nu$, $\eta$-$\rho$, and $\beta$ are defined in (34), (46) and (53), respectively, and in the expression of $E_0$, ${\mathbf{e}}_h^1$ is to be replaced by ${\mathbf{e}}_h^0+\tau {\mathbf{e}}_{1h}$.

Remark 2.

Since our scheme is based on nodal elements, at each time step, the numerical complexity of our fully explicit scheme is proportional to the number of vertexes in the mesh. In contrast, it would be proportional to an integer power greater than one of the same number of vertexes, in case an implicit scheme was employed. Even with an explicit scheme in time, the numerical complexity would be proportional to the much larger number of edges in the mesh, in case classical edge elements for Maxwell’s equations are used, such as Nédélec’s (cf. [3]).

4.2. Scheme Consistency

Before pursuing the reliability study of our scheme, we need some approximation results related to Maxwell’s equations. The arguments employed in this section found their inspiration in Thomée [42] and in Ruas [41].

4.2.1. Preliminaries

Henceforth, we assume that $\mathsf{\Omega }$ is a convex polygon for $N=2$ or a convex polyhedron for $N=3$.

In this case, one may reasonably assert that, for every $\mathbf{g}\in {\left\{L_0^2\left(\mathsf{\Omega }\right)\right\}}^N$, the solution ${\mathbf{v}}_{\mathbf{g}}\in {\{H^1\left(\mathsf{\Omega }\right)\cap L_0^2\left(\mathsf{\Omega }\right)\}}^N$ of the following equation:

$$\begin{array}{cc}-\Delta {\mathbf{v}}_{\mathbf{g}}-\nabla \{(\epsilon -1)\nabla ·{\mathbf{v}}_{\mathbf{g}}\}=\mathbf{g}\hfill & \mathrm{in} \mathsf{\Omega }\hfill \\ {\partial }_n{\mathbf{v}}_{\mathbf{g}}=\mathbf{0}\hfill & \mathrm{on} \mathsf{\Gamma }\hfill \end{array}$$

(55)

belongs to ${\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$.

Another result that we take for granted in this section is the existence of a constant $C_{\epsilon }$ such that

$$\forall \mathbf{g}\in {\left\{L_0^2\left(\mathsf{\Omega }\right)\right\}}^N \mathrm{it} \mathrm{holds} \parallel \mathcal{H}\left({\mathbf{v}}_{\mathbf{g}}\right)\parallel \le C_{\epsilon }\parallel \mathbf{g}\parallel ,$$

(56)

where $\mathcal{H}(·)$ is the Hessian of a function or vector field.

Equation (56) is a result whose grounds are found in analogous inequalities for convex polytopes applying to both the scalar Poisson problem and the linear elasticity system (or yet to the Stokes system) (cf. [43]). In fact, (55) can be viewed as a problem halfway between the vector Poisson equation with homogeneous Neumann boundary conditions whenever $\epsilon \equiv 1$ and a modified linear elasticity system with a smoothly varying Poisson ratio $\epsilon -1$ whenever $\epsilon >1$. This fully justifies (56).

Now, in order to establish the consistency of the explicit scheme (14), we first introduce an auxiliary field ${\widehat{\mathbf{e}}}_h(·,t)$ belonging to ${\mathbf{V}}_h$ for every $t\in [0,T]$, uniquely defined up to an additive field depending only on t as follows:

$$(\nabla {\widehat{\mathbf{e}}}_h\{·,t\},\nabla \mathbf{v})+{(\nabla ·{\widehat{\mathbf{e}}}_h\{·,t\},\nabla ·\mathbf{v})}_{\epsilon -1}=(\nabla \mathbf{e}\{·,t\},\nabla \mathbf{v})+{(\nabla ·\mathbf{e}\{·,t\},\nabla ·\mathbf{v})}_{\epsilon -1}\forall \mathbf{v}\in {\mathbf{V}}_h.$$

(57)

The time-dependent additive field up to which ${\widehat{\mathbf{e}}}_h\{·,t\}$ is defined can be determined by requiring that ${\int }_{\mathsf{\Omega }}\{{\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\}d\mathbf{x}=\mathbf{0}$$\forall t\in [0,T]$.

Let us further assume that for every $t\in [0,T]$$\mathbf{e}(·,t)\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$. In this case, from classical approximation results based on the interpolation error, we can assert the following:

$$\parallel \nabla \{{\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\}\parallel +\parallel \nabla ·\{{\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\}{\parallel }_{\epsilon -1}\le {\widehat{C}}_{1}h\parallel \mathcal{H}\left(\mathbf{e}\right)(·,t)\parallel \forall t\in [0,T],$$

(58)

where ${\widehat{C}}_1$ is a mesh-independent constant.

Let us show that there exists another mesh-independent constant ${\widehat{C}}_0$ such that, for every $t\in [0,T]$, it holds as follows:

$$\parallel {\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\parallel \le {\widehat{C}}_0{h}^2\parallel \mathcal{H}\left(\mathbf{e}\right)(·,t)\parallel \forall t\in [0,T].$$

(59)

Since ${\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\in {\left\{L_0^2\left(\mathsf{\Omega }\right)\right\}}^N$ for every t, we may write as follows:

$${\displaystyle \parallel {\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\parallel =\underset{\mathbf{g}\in {\left\{L_0^2\left(\mathsf{\Omega }\right)\right\}}^N\setminus \left\{\mathbf{0}\right\}}{sup}\frac{({\widehat{\mathbf{e}}}_h\{·,t\}-\mathbf{e}\{·,t\},\mathbf{g})}{\parallel \mathbf{g}\parallel }\forall t\in [0,T].}$$

(60)

Defining $\mathbf{W}:=\{\mathbf{w}|\mathbf{w}\in {\{H^2\left(\mathsf{\Omega }\right)\cap L_0^2\left(\mathsf{\Omega }\right)\}}^N{\partial }_n\mathbf{w}=\mathbf{0} \mathrm{on} \mathsf{\Gamma }\}$, owing to (56), we have $\forall t\in [0,T]$ the following:

$${\displaystyle \parallel {\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\parallel \le C_{\epsilon }\underset{\mathbf{w}\in \mathbf{W}\setminus \left\{\mathbf{0}\right\}}{sup}\frac{({\widehat{\mathbf{e}}}_h\{·,t\}-\mathbf{e}\{·,t\},-\Delta \mathbf{w}-\nabla (\epsilon -1)\nabla ·\mathbf{w})}{\parallel \mathcal{H}\left(\mathbf{w}\right)\parallel }.}$$

(61)

Since ${\partial }_n\mathbf{w}=\mathbf{0}$ and $\epsilon =1$ on $\mathsf{\Gamma }$, we may integrate by parts the numerator in (61) to obtain for every $t\in [0,T]$ the following:

$${\displaystyle \parallel {\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\parallel \le C_{\epsilon }\underset{\mathbf{w}\in \mathbf{W}\setminus \left\{\mathbf{0}\right\}}{sup}\frac{(\nabla \{{\widehat{\mathbf{e}}}_h\{·,t\}-\mathbf{e}\{·,t\}\},\nabla \mathbf{w})+{(\nabla ·\{{\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\},\nabla ·\mathbf{w})}_{\epsilon -1}}{\parallel \mathcal{H}\left(\mathbf{w}\right)\parallel }.}$$

(62)

Taking into account (57), the numerator of (62) can be rewritten as follows:

$$(\nabla \{{\widehat{\mathbf{e}}}_h\{·,t\}-\mathbf{e}\{·,t\}\},\nabla \{\mathbf{w}-\mathbf{v}\})+{(\nabla ·\{{\widehat{\mathbf{e}}}_h\{·,t\}-\mathbf{e}\{·,t\}\},\nabla ·\{\mathbf{w}-\mathbf{v}\})}_{\epsilon -1}\forall \mathbf{v}\in {\mathbf{V}}_h.$$

Then choosing $\mathbf{v}$ to be the ${\mathbf{V}}_h$-interpolate of $\mathbf{w}$, taking into account (58), we easily establish (59) with ${\widehat{C}}_0=C_{\epsilon }{\widehat{C}}_1^2$.

To conclude these preliminary considerations, we refer to Chapter 5 of [41] to infer that the second-order time derivative ${\partial }_{tt}{\widehat{\mathbf{e}}}_h(·,t)$ is well defined in ${\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$ for every $t\in [0,T]$, as long as ${\partial }_{tt}\mathbf{e}(·,t)$ lies in ${\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$ for every $t\in [0,T]$. Moreover, provided that ${\partial }_{tt}\mathbf{e}\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$ for every $t\in [0,T]$, the following estimate holds:

$$\parallel {\partial }_{tt}\{{\widehat{\mathbf{e}}}_h(·,t)-\mathbf{e}(·,t)\}\parallel \le {\widehat{C}}_0{h}^2\parallel \mathcal{H}\left({\partial }_{tt}\mathbf{e}\right)(·,t)\parallel \forall t\in [0,T].$$

(63)

In addition to the results given in this subsection, we recall that, according to the Sobolev embedding theorem, there exists a constant $C_T$ depending only on T such that it holds as follows:

$${\parallel u\parallel }_{L^{\infty }(0,T)}\le C_T{\{\parallel u\parallel }_{L^2(0,T)}^2+\parallel u_t{{\parallel }_{L^2(0,T)}^2\}}^{1/2}\forall u\in H^1(0,T).$$

(64)

In the remainder of this work, we assume a certain regularity of $\mathbf{e}$, namely,

Assumption 1.

The solution $\mathbf{e}$ to Equation (2) belongs to ${\left\{H^4(\mathsf{\Omega }\times (0,T))\right\}}^N$.

Now taking $u=\parallel \mathcal{H}\left(\mathbf{e}\right)(·,t)\parallel$, we have ${\displaystyle u_t\left(t\right)=\frac{{\int }_{\mathsf{\Omega }}\{\mathcal{H}\left(\mathbf{e}\right):\mathcal{H}\left({\partial }_t\mathbf{e}\right)\}(\mathbf{x},t)d\mathbf{x}}{\parallel \left\{\mathcal{H}\right(\mathbf{e}\left)\right\}(·,t)\parallel }}$, where : denotes the inner product of two constant tensors of order greater than or equal to three. Then by the Cauchy–Schwarz inequality and taking into account Assumption 1, it trivially follows from (64) that the following upper bound holds:

$$\parallel \left\{\mathcal{H}\left(\mathbf{e}\right)\right\}(·,t)\parallel \le C_T{\{\parallel \parallel \mathcal{H}\left(\mathbf{e}\right)\parallel \parallel }_{L^2(0,T)}^2+\parallel \parallel \mathcal{H}\left({\partial }_t\mathbf{e}\right){\parallel \parallel }_{L^2(0,T)}^2{\}}^{1/2}\forall t\in (0,T).$$

(65)

In complement to the above ingredients, we extend the inner products ${(·,·)}_{{\epsilon }_h,h}$ and ${(·,·)}_{\mathsf{\Gamma },h}$, and associated norms ${\Vert ·\Vert }_{{\epsilon }_h,h}$ and ${\Vert ·\Vert }_{\mathsf{\Gamma },h}$ in a semidefinite manner, to fields in ${\left\{L^2\left(\mathsf{\Omega }\right)\right\}}^N$, $N=2,3$ as follows: First of all, $\forall K\in {\mathcal{T}}_h$, let ${\Pi }_K:L^2\left(K\right)\to P_1\left(K\right)$ be the standard orthogonal projection operator onto the space $P_1\left(K\right)$ of linear functions in K. We set the following:

$${\displaystyle \forall \mathbf{u} \mathrm{and} \mathbf{v}\in {\left\{L^2\left(\mathsf{\Omega }\right)\right\}}^N,{(\mathbf{u},\mathbf{v})}_{{\epsilon }_h,h}:=\sum _{K\in {\mathcal{T}}_h}\frac{\epsilon \left(G_K\right)meas\left(K\right)}{N+1}\sum _{i=1}^{N+1}{\Pi }_K\mathbf{u}\left(S_{K,i}\right)·{\Pi }_K\mathbf{v}\left(S_{K,i}\right).}$$

Let us generically denote by $F\subset \mathsf{\Gamma }$ an edge of a triangle or a face of a tetrahedron K such that $meas(K\cap \mathsf{\Gamma })>0$. Moreover, we denote by ${\Pi }_F\left(v\right)$ the standard orthogonal projection of a function $v\in L^2\left(F\right)$ onto the space of linear functions on F. Similarly we define the following:

$${\displaystyle \forall \mathbf{u} \mathrm{and} \mathbf{v}\in {\left\{L^2\left(\mathsf{\Gamma }\right)\right\}}^N,{(\mathbf{u},\mathbf{v})}_{\mathsf{\Gamma },h}:=\sum _{F\subset \mathsf{\Gamma }}\frac{meas\left(F\right)}{N}\sum _{i=1}^N{\Pi }_F\mathbf{u}\left(R_{F,i}\right)·{\Pi }_F\mathbf{v}\left(R_{F,i}\right).}$$

It is noteworthy that whenever $\mathbf{u}$ and $\mathbf{v}$ belong to ${\mathbf{V}}_h$, both semidefinite inner products coincide with the inner products previously defined for such fields.

The following results hold in connection to the above inner products:

Lemma 1.

Let ${\Delta }_{{\epsilon }_h}(\mathbf{u},\mathbf{v}):={(\mathbf{u},\mathbf{v})}_{{\epsilon }_h,h}-{(\mathbf{u},\mathbf{v})}_{{\epsilon }_h}$ for $\mathbf{u},\mathbf{v}\in {\left\{L^2\left(\mathsf{\Omega }\right)\right\}}^N$. There exists a mesh-independent constant $c_{\mathsf{\Omega }}$ such that $\forall \mathbf{u}\in {\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$ and $\forall \mathbf{v}\in {\mathbf{V}}_h$:

$$|{\Delta }_{{\epsilon }_h}(\mathbf{u},\mathbf{v})|\le c_{\mathsf{\Omega }}{\Vert \epsilon \Vert }_{0,\infty }{h\Vert \nabla \mathbf{u}\Vert \Vert \mathbf{v}\Vert }_h$$

(66)

Lemma 2.

Let ${\Xi }_h(\gamma \left\{\mathbf{u}\right\},\gamma \left\{\mathbf{v}\right\}):={(\gamma \left\{\mathbf{u}\right\},\gamma \left\{\mathbf{v}\right\})}_{\mathsf{\Gamma },h}-{(\gamma \left\{\mathbf{u}\right\},\gamma \left\{\mathbf{v}\right\})}_{\mathsf{\Gamma }}$ for $\mathbf{u},\mathbf{v}\in {\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$, where $\gamma \left\{w\right\}$ represents the trace on Γ of a function $w\in H^1\left(\mathsf{\Omega }\right)$. Let also ${\nabla }_{\mathsf{\Gamma }}$ be the tangential gradient operator over Γ. There exists a mesh-independent constant ${\tilde{c}}_{\mathsf{\Gamma }}$ such that $\forall \mathbf{u}\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$ and $\forall \mathbf{v}\in {\mathbf{V}}_h$:

$$|{\Xi }_h(\gamma \left\{\mathbf{u}\right\},\gamma \left\{\mathbf{v}\right\})|\le {\tilde{c}}_{\mathsf{\Gamma }}h\Vert {\nabla }_{\mathsf{\Gamma }}{\gamma \left\{\mathbf{u}\right\}\Vert }_{\mathsf{\Gamma }}{\Vert \gamma \left\{\mathbf{v}\right\}\Vert }_{\mathsf{\Gamma },h}.$$

(67)

The proof of Lemma 1 is based on the Bramble–Hilbert lemma, and we refer to [40] for more details. Lemma 2, in turn, follows from the same arguments combined with the trace theorem, which ensures that ${\nabla }_{\mathsf{\Gamma }}\gamma \left\{\mathbf{u}\right\}$ is well defined in ${\left\{L^2\left(\mathsf{\Gamma }\right)\right\}}^N$ if $\mathbf{u}\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$. Incidentally, the trace theorem allows us to bound above the right-hand side of (67) in such a way that the following estimate also holds for another mesh-independent constant $c_{\mathsf{\Gamma }}$:

$$|{\Xi }_h(\gamma \left\{\mathbf{u}\right\},\gamma \left\{\mathbf{v}\right\})|\le c_{\mathsf{\Gamma }}{h\{\Vert \nabla \mathbf{u}\Vert }^2+{\Vert \mathcal{H}\left(\mathbf{u}\right)\Vert }^2{\}}^{1/2}{\Vert \gamma \left\{\mathbf{v}\right\}\Vert }_{\mathsf{\Gamma },h}.$$

(68)

To conclude, we prove the validity of the following upper bounds:

Lemma 3.

$\forall \mathbf{v}\in {\left\{L^2\left(\mathsf{\Omega }\right)\right\}}^N$, it holds as follows:

$${\parallel \mathbf{v}\parallel }_{{\epsilon }_h,h}\le \sqrt{N+2}{\Vert \mathbf{v}\Vert }_{{\epsilon }_h}.$$

Proof. 

Denoting by ${\Pi }_h\left(\mathbf{v}\right)$ the function defined in $\mathsf{\Omega }$ whose restriction to every $K\in {\mathcal{T}}_h$ is ${\Pi }_K\left(\mathbf{v}\right)$ for a given $\mathbf{v}\in {\left\{L^2\left(\mathsf{\Omega }\right)\right\}}^N$, from an elementary property of the orthogonal projection, we have the following:

$$\Vert {\Pi }_h{\left(\mathbf{v}\right)\Vert }_{{\epsilon }_h}\le {\Vert \mathbf{v}\Vert }_{{\epsilon }_h},\forall \mathbf{v}\in \left\{L^2\left(\mathsf{\Omega }\right)\right\}N.$$

(69)

Now taking v such that $v_{|K}\in P_1\left(K\right)\forall K\in {\mathcal{T}}_h$, by a straightforward calculation using the expression of $v_{|K}$ in terms of barycentric coordinates, we have the following:

$${\displaystyle {\int }_K\epsilon \left(G_K\right)v_{|K}^{2}d\mathbf{x}=\frac{2\epsilon \left(G_K\right)meas\left(K\right)}{(N+2)(N+1)}\left\{{\displaystyle \sum _{i=1}^{N+1}{|v\left(S_{K,i}\right)|}^2+\sum _{i=1}^N\sum _{j=i+1}^{N+1}v\left(S_{K,i}\right)v\left(S_{K,j}\right)}\right\}.}$$

It trivially follows that

$${\displaystyle {\int }_K\epsilon \left(G_K\right)v_{|K}^{2}d\mathbf{x}=\frac{\epsilon \left(G_K\right)meas\left(K\right)}{(N+2)(N+1)}\left\{{\displaystyle \sum _{i=1}^{N+1}{|v\left(S_{K,i}\right)|}^2+{\left(\sum _{i=1}^{N+1}v\left(S_{K,i}\right)\right)}^2}\right\},}$$

and finally,

$${\displaystyle (N+2){\int }_K\epsilon \left(G_K\right)v_{|K}^{2}d\mathbf{x}\ge \frac{\epsilon \left(G_K\right)meas\left(K\right)}{N+1}\sum _{i=1}^{N+1}{|v\left(S_{K,i}\right)|}^2.}$$

This immediately yields Lemma 3, taking into account (69). □

Lemma 4.

$\forall \mathbf{v}\in {\left\{L^2\left(\mathsf{\Gamma }\right)\right\}}^N$, it holds ${\parallel \mathbf{v}\parallel }_{\mathsf{\Gamma },h}\le \sqrt{N+1}{\Vert \mathbf{v}\Vert }_{\mathsf{\Gamma }}$.

The proof of this lemma is based on arguments entirely analogous to Lemma 3.

4.2.2. Residual Estimation

To begin with, we define for $k=0,1,\dots ,N$ functions ${\widehat{\mathbf{e}}}_h^k\in {\mathbf{V}}_h$ by ${\widehat{\mathbf{e}}}_h^k(·):={\widehat{\mathbf{e}}}_h(·,k\tau )$. In the sequel for any function or field $\mathcal{A}$ defined in $\mathsf{\Omega }\times (0,T)$, ${\mathcal{A}}^k(·)$ denotes $\mathcal{A}(·,k\tau )$, except for other quantities carrying the subscript h such as ${\mathbf{e}}_h^k$.

Let us substitute ${\mathbf{e}}_h^k$ by ${\widehat{\mathbf{e}}}_h^k$ for $k=2,3,\dots ,N$ on the left-hand side of the first equation of (14) and take also as initial conditions ${\widehat{\mathbf{e}}}_h^j$ instead of ${\mathbf{e}}_h^j$, $j=0,1$.

The case of the initial conditions will be dealt with in the next section in the framework of the convergence analysis. As for the variational residual $E_h^k\left(\mathbf{v}\right)$ resulting from the above substitution, where $E_h^k$ is a linear functional acting on ${\mathbf{V}}_h$, it can be expressed in the following manner:

$$\begin{array}{c}{E}_h^k\left(\mathbf{v}\right)={({\left\{{\partial }_{tt}\mathbf{e}\right\}}^k,\mathbf{v})}_{\epsilon }+(\nabla {\mathbf{e}}^k,\nabla \mathbf{v})+{(\nabla ·{\mathbf{e}}^k,\nabla ·\mathbf{v})}_{\epsilon -1}+(\nabla \epsilon ·{\mathbf{e}}^k,\nabla ·\mathbf{v})+{({\left\{{\partial }_t\mathbf{e}\right\}}^k,\mathbf{v})}_{\mathsf{\Gamma }}\hfill \\ \\ -{\overline{\mathbf{F}}}^k\left(\mathbf{v}\right)-({\overline{d}}^k,\nabla ·\mathbf{v})-{\overline{\mathbf{G}}}^k\left(\mathbf{v}\right)\forall \mathbf{v}\in {\mathbf{V}}_h,\hfill \end{array}$$

(70)

where

$$\begin{array}{c}{\overline{d}}^k=\nabla \epsilon ·\{{\widehat{\mathbf{e}}}_h^k-{\mathbf{e}}^k\},\hfill \end{array}$$

(71)

and ${\overline{\mathbf{F}}}^k\left(\mathbf{v}\right)$ and ${\overline{\mathbf{G}}}^k\left(\mathbf{v}\right)$ can be written as follows:

$$\begin{array}{c}{\overline{\mathbf{F}}}^k\left(\mathbf{v}\right)={\mathbf{F}}_1^k\left(\mathbf{v}\right)+{\mathbf{F}}_2^k\left(\mathbf{v}\right)+{\mathbf{F}}_3^k\left(\mathbf{v}\right)+{\mathbf{F}}_4^k\left(\mathbf{v}\right),\hfill \\ \mathrm{with}\hfill \\ {\mathbf{F}}_1^k\left(\mathbf{v}\right)={({\mathbf{T}}^k({\widehat{\mathbf{e}}}_h-\mathbf{e}),\mathbf{v})}_{{\epsilon }_h,h};\hfill \\ {\mathbf{F}}_2^k\left(\mathbf{v}\right)={\Delta }_{{\epsilon }_h}({\mathbf{T}}^k\left(\mathbf{e}\right),\mathbf{v});\hfill \\ {\mathbf{F}}_3^k\left(\mathbf{v}\right)=(({\epsilon }_h-\epsilon ){\mathbf{T}}^k\left(\mathbf{e}\right),\mathbf{v});\hfill \\ {\mathbf{F}}_4^k\left(\mathbf{v}\right)={({\mathbf{T}}^k\left(\mathbf{e}\right)-{\left\{{\partial }_{tt}\mathbf{e}\right\}}^k,\mathbf{v})}_{\epsilon },\hfill \end{array}$$

(72)

${\mathbf{T}}^k$ being the finite difference operator defined by the following:

$${\displaystyle {\mathbf{T}}^k(·):=\frac{{\{·\}}^{k+1}-2{\{·\}}^k+{\{·\}}^{k-1}}{{\tau }^2},}$$

(73)

and

$$\begin{array}{c}{\overline{\mathbf{G}}}^k\left(\mathbf{v}\right)={\mathbf{G}}_1^k\left(\mathbf{v}\right)+{\mathbf{G}}_2^k\left(\mathbf{v}\right)+{\mathbf{G}}_3^k\left(\mathbf{v}\right),\hfill \\ \mathrm{with}\hfill \\ {\mathbf{G}}_1^k\left(\mathbf{v}\right)={({\mathbf{Q}}^k({\widehat{\mathbf{e}}}_h-\mathbf{e}),\mathbf{v})}_{\mathsf{\Gamma },h};\hfill \\ {\mathbf{G}}_2^k\left(\mathbf{v}\right)={\mathsf{\Gamma }}_h({\mathbf{Q}}^k\left(\mathbf{e}\right),\mathbf{v});\hfill \\ {\mathbf{G}}_3^k\left(\mathbf{v}\right)={({\mathbf{Q}}^k\left(\mathbf{e}\right)-{\left\{{\partial }_t\mathbf{e}\right\}}^k,\mathbf{v})}_{\mathsf{\Gamma }},\hfill \end{array}$$

(74)

${\mathbf{Q}}^k$ being the finite difference operator defined by the following:

$${\displaystyle {\mathbf{Q}}^k(·):=\frac{{\{·\}}^{k+1}-{\{·\}}^{k-1}}{2\tau }.}$$

(75)

Notice that, under Assumption 1, both ${\partial }_t\mathbf{e}(·,t)$ and ${\partial }_{tt}\mathbf{e}(·,t)$ belong to ${\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$ for every $t\in [0,T]$. Hence, we can define ${\partial }_t{\widehat{\mathbf{e}}}_h$ from ${\partial }_t\mathbf{e}$ and ${\partial }_{tt}{\widehat{\mathbf{e}}}_h$ from ${\partial }_{tt}\mathbf{e}$ in the same way as ${\widehat{\mathbf{e}}}_h$ is defined from $\mathbf{e}$. Moreover, straightforward calculations lead to the following:

$${\displaystyle {\mathbf{T}}^k(·)=\frac{1}{{\tau }^2}\left\{{\displaystyle {\int }_{(k-1)\tau }^{k\tau }\left({\int }_t^{k\tau }{\partial }_{tt}\{·\}ds\right)dt+{\int }_{k\tau }^{(k+1)\tau }\left({\int }_{k\tau }^t{\partial }_{tt}\{·\}ds\right)dt}\right\}.}$$

(76)

Furthermore, another straightforward calculation allows us to write the following:

$${\displaystyle \begin{array}{c}{\mathbf{T}}^k\left(\mathbf{e}\right)={\left\{{\partial }_{tt}\mathbf{e}\right\}}^k+{\mathbf{R}}^k\left(\mathbf{e}\right)\hfill \\ \mathrm{where}\hfill \\ {\mathbf{R}}^k\left(\mathbf{e}\right):=\frac{1}{2{\tau }^2}\left\{-{\int }_{(k-1)\tau }^{k\tau }{\{t-(k-1)\tau \}}^2{\partial }_{ttt}\mathbf{e}dt+{\int }_{k\tau }^{(k+1)\tau }{\{(k+1)\tau -t\}}^2{\partial }_{ttt}\mathbf{e}dt\right\}.\hfill \end{array}}$$

(77)

Similarly,

$${\displaystyle {\mathbf{Q}}^k(·)=\frac{1}{2\tau }{\int }_{(k-1)\tau }^{(k+1)\tau }{\partial }_t\{·\}dt,}$$

(78)

and

$$\begin{array}{c}{\mathbf{Q}}^k\left(\mathbf{e}\right)={\left\{{\partial }_t\mathbf{e}\right\}}^k+{\mathbf{S}}^k\left(\mathbf{e}\right),\hfill \\ \mathrm{where}\hfill \\ {\displaystyle {\mathbf{S}}^k\left(\mathbf{e}\right)=\frac{1}{2\tau }\left\{-{\int }_{(k-1)\tau }^{k\tau }\{t-(k-1)\tau \}{\partial }_{tt}\mathbf{e}dt+{\int }_{k\tau }^{(k+1)\tau }\{(k+1)\tau -t\}{\partial }_{tt}\mathbf{e}dt\right\}.}\hfill \end{array}$$

(79)

Now, we note that the sum of the terms on the first line of the expression of $E_h^k\left(\mathbf{v}\right)$ equals zero because they are just the left-hand side of (7) at time $t=k\tau$. Therefore, the functions ${\widehat{\mathbf{e}}}_h^k\in {\mathbf{V}}_h$ are the solution of the following problem for $k=1,2,\dots ,M-1$:

$$\begin{array}{c}{\displaystyle \left(\epsilon \frac{{\widehat{\mathbf{e}}}_h^{k+1}-2{\widehat{\mathbf{e}}}_h^k+{\widehat{\mathbf{e}}}_h^{k-1}}{{\tau }^2},\mathbf{v}\right)+(\nabla {\widehat{\mathbf{e}}}_h^k,\nabla \mathbf{v})+(\nabla ·\left\{\epsilon {\widehat{\mathbf{e}}}_h^k\right\},\nabla ·\mathbf{v})-(\nabla ·{\widehat{\mathbf{e}}}_h^k,\nabla ·\mathbf{v})}\hfill \\ {\displaystyle +{\left(\frac{{\widehat{\mathbf{e}}}_h^{k+1}-{\widehat{\mathbf{e}}}_h^{k-1}}{2\tau },\mathbf{v}\right)}_{\mathsf{\Gamma }}={\overline{\mathbf{F}}}^k\left(\mathbf{v}\right)+({\overline{d}}^k,\nabla ·\mathbf{v})+{\overline{\mathbf{G}}}^k\left(\mathbf{v}\right)\forall \mathbf{v}\in {\mathbf{V}}_h,}\hfill \\ \\ {\widehat{\mathbf{e}}}_h^0(·)={\widehat{\mathbf{e}}}_h(·,0) \mathrm{and} {\widehat{\mathbf{e}}}_h^1(·)={\widehat{\mathbf{e}}}_h(·,\tau ) \mathrm{in} \mathsf{\Omega },\hfill \end{array}$$

(80)

${\overline{d}}^k$, ${\overline{\mathbf{F}}}^k$ and ${\overline{\mathbf{G}}}^k$ being given by Equations (71)–(75).

Estimating $\parallel {\overline{d}}^k\parallel$ is a trivial matter. Indeed, since ${\mathbf{e}}^k\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$, from (59), we immediately obtain the following:

$$\parallel {\overline{d}}^k\parallel \le {\widehat{C}}_0{h}^2{|\epsilon |}_{1,\infty }\parallel \mathcal{H}\left({\mathbf{e}}^k\right)\parallel .$$

(81)

Therefore, consistency of the scheme will result from suitable estimations of $|{\overline{\mathbf{F}}}^k{|}_h$ and $|{\overline{\mathbf{G}}}^k{|}_{\mathsf{\Gamma },h}$ in terms of $\mathbf{e}$, $\epsilon$, $\tau$, and h, which we next carry out.

First of all, we search for upper bounds for the operators ${\mathbf{T}}^k(·)$, ${\mathbf{Q}}^k(·)$, ${\mathbf{R}}^k(·)$, and ${\mathbf{S}}^k(·)$. With this aim, we denote by $|·|$ the Euclidean norm of ${\Re }^n$ for $n\ge 1$.

From (76) and the Cauchy–Schwarz inequality, we easily obtain for every $\mathbf{x}\in \mathsf{\Omega }$ and $\mathbf{u}$ such that $\left\{{\partial }_{tt}\mathbf{u}\right\}(·,t)\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$$\forall t\in (0,T)$:

$$\begin{array}{c}{\displaystyle |{\mathbf{T}}_h^k\left\{\mathbf{u}\left(\mathbf{x}\right)\right\}|\le \frac{1}{{\tau }^2}\left\{{\displaystyle {\int }_{(k-1)\tau }^{k\tau }\left({\int }_t^{k\tau }\left|\left\{{\partial }_{tt}\mathbf{u}\right\}\left(\mathbf{x}\right)\right|ds\right)dt+{\int }_{k\tau }^{(k+1)\tau }\left({\int }_{k\tau }^t\left|\left\{{\partial }_{tt}\mathbf{u}\right\}\left(\mathbf{x}\right)\right|ds\right)dt}\right\}}\hfill \\ {\displaystyle \le \frac{1}{{\tau }^2}\left\{{\displaystyle {\int }_{(k-1)\tau }^{k\tau }\left({\int }_{(k-1)\tau }^{k\tau }\left|\left\{{\partial }_{tt}\mathbf{u}\right\}\left(\mathbf{x}\right)\right|ds\right)dt+{\int }_{k\tau }^{(k+1)\tau }\left({\int }_{k\tau }^{(k+1)\tau }\left|\left\{{\partial }_{tt}\mathbf{u}\right\}\left(\mathbf{x}\right)\right|ds\right)dt}\right\}}\hfill \\ {\displaystyle =\frac{1}{\tau }{\int }_{(k-1)\tau }^{(k+1)\tau }\left|\left\{{\partial }_{tt}\mathbf{u}\right\}\left(\mathbf{x}\right)\right|dt.}\hfill \end{array}$$

It follows that, for every $\mathbf{u}$ such that $\left\{{\partial }_{tt}\mathbf{u}\right\}(·,t)\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$$\forall t\in (0,T)$, we have the following:

$${\displaystyle |{\mathbf{T}}_h^k\left\{\mathbf{u}\left(\mathbf{x}\right)\right\}|\le \sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\left\{{\partial }_{tt}\mathbf{u}\right\}\left(\mathbf{x}\right)\right|}^{2}dt\right\}}^{1/2}.}$$

(82)

Furthermore, from (77) and the inequality $a+b\le {\left\{2(a^2+b^2)\right\}}^{1/2}\forall a,b\in \Re$, for every $\mathbf{x}\in \mathsf{\Omega }$, we obtain the following:

$$\begin{array}{c}{\displaystyle |{\mathbf{R}}^k\left\{\mathbf{e}\left(\mathbf{x}\right)\right\}|\le \frac{1}{2}\left\{{\displaystyle {\int }_{(k-1)\tau }^{k\tau }\left|\left\{{\partial }_{ttt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|dt+{\int }_{k\tau }^{(k+1)\tau }\left|\left\{{\partial }_{ttt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|dt}\right\}}\hfill \\ {\displaystyle \le \frac{\sqrt{\tau }}{2}\left\{{\left({\displaystyle {\int }_{(k-1)\tau }^{k\tau }{\left|\left\{{\partial }_{ttt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|}^{2}dt}\right)}^{1/2}+{\left({\displaystyle {\int }_{k\tau }^{(k+1)\tau }{\left|\left\{{\partial }_{ttt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|}^{2}dt}\right)}^{1/2}\right\}.}\hfill \end{array}$$

It follows that

$${\displaystyle |{\mathbf{R}}^k\left\{\mathbf{e}\left(\mathbf{x}\right)\right\}|\le \sqrt{\frac{\tau }{2}}{\left\{{\displaystyle {\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\left\{{\partial }_{ttt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|}^{2}dt}\right\}}^{1/2}.}$$

(83)

On the other hand, from (78) and the Cauchy–Schwarz inequality, we trivially have for every $\mathbf{x}\in \mathsf{\Gamma }$ and $\mathbf{u}$ such that $\gamma \left\{{\partial }_t\mathbf{u}\right\}(·,t)\in {\left\{H^{3/2}\left(\mathsf{\Gamma }\right)\right\}}^N$$\forall t\in (0,T)$:

$${\displaystyle |{\mathbf{Q}}^k\left\{\mathbf{u}\left(\mathbf{x}\right)\right\}|\le \frac{1}{\sqrt{2\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{|\left\{{\partial }_t\mathbf{u}\right\}\left(\mathbf{x}\right)|}^{2}dt\right\}}^{1/2}.}$$

(84)

Finally, similar to (83), from (79), for every $\mathbf{x}$ in $\mathsf{\Gamma }$, we successively derive the following:

$$\begin{array}{c}{\displaystyle |{\mathbf{S}}^k\left\{\mathbf{e}\left(\mathbf{x}\right)\right\}|\le \frac{1}{2}\left\{{\displaystyle {\int }_{(k-1)\tau }^{k\tau }\left|\left\{{\partial }_{tt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|dt+{\int }_{k\tau }^{(k+1)\tau }\left|\left\{{\partial }_{tt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|dt}\right\}}\hfill \\ {\displaystyle \le \frac{\sqrt{\tau }}{2}\left\{{\left({\displaystyle {\int }_{(k-1)\tau }^{k\tau }{\left|\left\{{\partial }_{tt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|}^{2}dt}\right)}^{1/2}+{\left({\displaystyle {\int }_{k\tau }^{(k+1)\tau }{\left|\left\{{\partial }_{tt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|}^{2}dt}\right)}^{1/2}\right\}.}\hfill \end{array}$$

Therefore, it holds as follows:

$${\displaystyle |{\mathbf{S}}^k\left\{\mathbf{e}\left(\mathbf{x}\right)\right\}|\le \sqrt{\frac{\tau }{2}}{\left\{{\displaystyle {\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\left\{{\partial }_{tt}\mathbf{e}\right\}\left(\mathbf{x}\right)\right|}^{2}dt}\right\}}^{1/2}.}$$

(85)

Notice that bounds entirely analogous to (82) and (84) hold for $\nabla {\mathbf{T}}^k(·)={\mathbf{T}}^k(\nabla ·)$ and ${\nabla }_{\mathsf{\Gamma }}{\mathbf{Q}}^k(·)={\mathbf{Q}}^k({\nabla }_{\mathsf{\Gamma }}·)$, that is, $\forall \mathbf{x}\in \mathsf{\Omega }$,

$$\begin{array}{c}{\displaystyle |\nabla {\mathbf{T}}_h^k\left(\mathbf{e}\right)\left(\mathbf{x}\right)|\le \sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\{{\partial }_{tt}\nabla \mathbf{e}\}\left(\mathbf{x}\right)\right|}^{2}dt\right\}}^{1/2},}\hfill \end{array}$$

(86)

and $\forall \mathbf{x}\in \mathsf{\Gamma }$,

$${\displaystyle |{\nabla }_{\mathsf{\Gamma }}{\mathbf{Q}}^k\left(\mathbf{e}\right)\left(\mathbf{x}\right)|\le \frac{1}{\sqrt{2\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{|\left\{{\partial }_t{\nabla }_{\mathsf{\Gamma }}\mathbf{e}\right\}\left(\mathbf{x}\right)|}^{2}dt\right\}}^{1/2}.}$$

(87)

Next, we estimate the four terms in the expression (72) of ${\mathbf{F}}^k\left(\mathbf{v}\right)$.

With the use of (82) and of Lemma 3, followed by a trivial manipulation, we successively have the following:

$$\begin{array}{c}{\displaystyle |{\mathbf{F}}_1^k{\left(\mathbf{v}\right)|\le \Vert \epsilon \Vert }_{0,\infty }\sqrt{\frac{2}{\tau }}{∥{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\left\{{\partial }_{tt}({\widehat{\mathbf{e}}}_h-\mathbf{e})\right\}(·,t)\right|}^{2}dt\right\}}^{1/2}∥}_h{\Vert \mathbf{v}\Vert }_h}\hfill \\ {\displaystyle \le \sqrt{N+2}{\Vert \epsilon \Vert }_{0,\infty }\sqrt{\frac{2}{\tau }}∥{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\left\{{\partial }_{tt}({\widehat{\mathbf{e}}}_h-\mathbf{e})\right\}(·,t)\right|}^{2}dt\right\}}^{1/2}∥{\Vert \mathbf{v}\Vert }_h}\hfill \\ {\displaystyle \le \sqrt{N+2}{\Vert \epsilon \Vert }_{0,\infty }\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{∥\left\{{\partial }_{tt}({\widehat{\mathbf{e}}}_h-\mathbf{e})\right\}(·,t)∥}^{2}dt\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_h}\hfill \end{array}$$

(88)

Recalling (72) and applying (63) to (88), we come up with the following:

$${\displaystyle |{\mathbf{F}}_1^k\left(\mathbf{v}\right)|\le {\widehat{C}}_0{h}^2\sqrt{\frac{2(N+2)}{\tau }}{\Vert \epsilon \Vert }_{0,\infty }{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\Vert \left\{\mathcal{H}\left({\partial }_{tt}\mathbf{e}\right)\right\}(·,t)\Vert }^{2}dt\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_h.}$$

(89)

Next, combining (66) and (86), we immediately obtain the following:

$${\displaystyle |{\mathbf{F}}_2^k\left(\mathbf{v}\right)|\le c_{\mathsf{\Omega }}{h\Vert \epsilon \Vert }_{0,\infty }\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\{{\partial }_{tt}\nabla \mathbf{e}\}(·,t)\right.∥}^{2}dt\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_h.}$$

(90)

Further, taking into account (15), (76) and (86) and the standard estimate $\Vert {\epsilon }_h{-\epsilon \Vert }_{0,\infty }\le C_{\infty }h{|\epsilon |}_{1,\infty }$, where $C_{\infty }$ is a mesh-independent constant, it holds as follows:

$${\displaystyle |{\mathbf{F}}_3^k\left(\mathbf{v}\right)|\le C_{\infty }{h|\epsilon |}_{1,\infty }\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{∥\left\{{\partial }_{tt}\mathbf{e}\right\}(·,t)∥}^{2}dt\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_h}$$

(91)

Finally, by (15), (77) and (83), we have the following:

$${\displaystyle |{\mathbf{F}}_4^k{\left(\mathbf{v}\right)|\le \Vert \epsilon \Vert }_{0,\infty }\sqrt{\frac{\tau }{2}}{\left\{{\displaystyle {\int }_{(k-1)\tau }^{(k+1)\tau }{∥\left\{{\partial }_{ttt}\mathbf{e}\right\}(·,t)∥}^{2}dt}\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_h.}$$

(92)

Now, we turn our attention to the three terms in the expression (74) of ${\mathbf{G}}^k\left(\mathbf{v}\right)$. First of all, owing to Assumption 1 and standard error estimates, we can write for a suitable mesh-independent constant ${\widehat{C}}_1$:

$$\Vert \{\nabla {\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})\}(·,t)\Vert \le {\widehat{C}}_{1}h\Vert \left\{\mathcal{H}\left({\partial }_t\mathbf{e}\right)\right\}(·,t))\Vert ,\forall t\in [0,T].$$

(93)

On the other hand, by the trace theorem, there exists a constant $C_{Tr}$ depending only on $\mathsf{\Omega }$ such that

$$\Vert \left\{{\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})\right\}(·,t){\Vert }_{\mathsf{\Gamma }}\le C_{Tr}\{\Vert \left\{{\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})\right\}(·,t){\Vert }^2+\Vert \{\nabla {\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})\}(·,t){{\Vert }^2\}}^{1/2}\forall t\in [0,T].$$

(94)

Hence, by (63), (93) and (94), we have, for a suitable mesh-independent constant $C_B$, the following:

$$\Vert \left\{{\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})\right\}(·,t){\Vert }_{\mathsf{\Gamma }}\le C_{B}h\Vert \left\{\mathcal{H}\left({\partial }_t\mathbf{e}\right)\right\}(·,t)\Vert \forall t\in [0,T].$$

(95)

Now recalling (72) and taking into account (87) and Lemma 4, similar to (88), we first obtain the following:

$${\displaystyle |{\mathbf{G}}_1^k\left(\mathbf{v}\right)|\le \frac{2}{\sqrt{2\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{∥\left\{{\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})\right\}(·,t)∥}_{\mathsf{\Gamma }}^{2}dt\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_{\mathsf{\Gamma },h}.}$$

(96)

Then using (95), we immediately establish the following:

$${\displaystyle |{\mathbf{G}}_1^k\left(\mathbf{v}\right)|\le C_{B}h\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\Vert \left\{\mathcal{H}\left({\partial }_t\mathbf{e}\right)\right\}(·,t)\Vert }^{2}dt\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_{\mathsf{\Gamma },h}.}$$

(97)

Next, we switch to ${\mathbf{G}}_2^k$. Similar to (90), (68) and (87) yield the following:

$${\displaystyle |{\mathbf{G}}_2^k\left(\mathbf{v}\right)|\le c_{\mathsf{\Gamma }}h\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }\left(\Vert \{\nabla {\partial }_t\mathbf{e}\}(·,t){\Vert }^2+{\Vert \left\{\mathcal{H}\left({\partial }_t\mathbf{e}\right)\right\}(·,t)\Vert }^2\right)dt\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_{\mathsf{\Gamma },h}.}$$

(98)

As for $G_3^k$, taking into account (79) together with (85) and (16), we obtain the following:

$${\displaystyle |{\mathbf{G}}_3^k\left(\mathbf{v}\right)|\le \sqrt{\frac{\tau }{2}}{\left\{{\displaystyle {\int }_{(k-1)\tau }^{(k+1)\tau }{∥\left\{{\partial }_{tt}\mathbf{e}\right\}(·,t)∥}_{\mathsf{\Gamma }}^{2}dt}\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_{\mathsf{\Gamma },h}.}$$

(99)

Then using the trace theorem (cf. (94)), we finally establish the following:

$${\displaystyle |{\mathbf{G}}_3^k\left(\mathbf{v}\right)|\le C_{Tr}\sqrt{\frac{\tau }{2}}{\left\{{\displaystyle {\int }_{(k-1)\tau }^{(k+1)\tau }\left(\Vert \left\{{\partial }_{tt}\mathbf{e}\right\}(·,t){\Vert }^2+{\Vert \{\nabla {\partial }_{tt}\mathbf{e}\}(·,t)\Vert }^2\right)dt}\right\}}^{1/2}{\Vert \mathbf{v}\Vert }_{\mathsf{\Gamma },h}.}$$

(100)

Now, collecting F1,F2,F3,F4, we can write the following:

$$\begin{array}{c}{\displaystyle |{\overline{\mathbf{F}}}^k{|}_h\le {\widehat{C}}_0{h}^2\sqrt{\frac{2(N+2)}{\tau }}{\Vert \epsilon \Vert }_{0,\infty }{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\Vert \left\{\mathcal{H}\left({\partial }_{tt}\mathbf{e}\right)\right\}(·,t)\Vert }^{2}dt\right\}}^{1/2}}\hfill \\ {\displaystyle +c_{\mathsf{\Omega }}h{\Vert \epsilon \Vert }_{0,\infty }\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\left|\{{\partial }_{tt}\nabla \mathbf{e}\}(·,t)\right.∥}^{2}dt\right\}}^{1/2}}\hfill \\ {\displaystyle +C_{\infty }h{|\epsilon |}_{1,\infty }\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{∥\{{\partial }_{tt}\nabla \mathbf{e}\}(·,t)∥}^{2}dt\right\}}^{1/2}}\hfill \\ {\displaystyle +{\Vert \epsilon \Vert }_{0,\infty }\sqrt{\frac{\tau }{2}}{\left\{{\displaystyle {\int }_{(k-1)\tau }^{(k+1)\tau }{∥\left\{{\partial }_{ttt}\mathbf{e}\right\}(·,t)∥}^{2}dt}\right\}}^{1/2}.}\hfill \end{array}$$

(101)

On the other hand, (97), (98), and (100) yield the following:

$$\begin{array}{c}{\displaystyle |{\overline{\mathbf{G}}}^k{|}_{\mathsf{\Gamma },h}\le C_{B}h\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }{\Vert \left\{\mathcal{H}\left({\partial }_t\mathbf{e}\right)\right\}(·,t)\Vert }^{2}dt\right\}}^{1/2}}\hfill \\ {\displaystyle +c_{\mathsf{\Gamma }}h\sqrt{\frac{2}{\tau }}{\left\{{\int }_{(k-1)\tau }^{(k+1)\tau }\left(\Vert \{\nabla {\partial }_t\mathbf{e}\}(·,t){\Vert }^2+{\Vert \left\{\mathcal{H}\left({\partial }_t\mathbf{e}\right)\right\}(·,t)\Vert }^2\right)dt\right\}}^{1/2}}\hfill \\ {\displaystyle +C_{Tr}\sqrt{\frac{\tau }{2}}{\left\{{\displaystyle {\int }_{(k-1)\tau }^{(k+1)\tau }\left(\Vert \left\{{\partial }_{tt}\mathbf{e}\right\}(·,t){\Vert }^2+{\Vert \{\nabla {\partial }_{tt}\mathbf{e}\}(·,t)\Vert }^2\right)dt}\right\}}^{1/2}.}\hfill \end{array}$$

(102)

Then, taking into account (80) and the stability condition (46), by inspection, we can assert that the consistency of scheme (14) is an immediate consequence of (81), (101) and (102).

4.3. Convergence Results

In order to establish the convergence of scheme (14), we combine the stability and consistency results obtained in the previous subsections. With this aim, we define ${\overline{\mathbf{e}}}_h^k:={\widehat{\mathbf{e}}}_h^k-{\mathbf{e}}_h^k$ for $k=0,1,2,\dots ,M$. By linearity, we can assert that the variational residual on the left-hand side of the first equation of (14) for $k=2,3,\dots ,M$, when ${\mathbf{e}}_h^k$s are replaced with ${\overline{\mathbf{e}}}_h^k$s and ${\mathbf{e}}_h^j$ is replaced with ${\overline{\mathbf{e}}}_h^j$ for $j=0,1$, is exactly $E_h^k\left(\mathbf{v}\right)$, since the residual corresponding to ${\mathbf{e}}_h^k$’s vanishes by definition. The initial conditions ${\overline{\mathbf{e}}}_h^j$ for $j=0$ and $j=1$ corresponding to the thus modified problem have to be estimated. This is the purpose of the next subsection.

4.3.1. Initial Condition Deviations

Here, we turn our attention to the estimate of ${\overline{E}}_0$, which accounts for the deviation in the initial conditions appearing in the stability inequality (54) that applies to the modification of (14) when ${\mathbf{e}}_h^k$ is replaced by ${\overline{\mathbf{e}}}_h^k$.

Let us first define the following:

$$\begin{array}{c}{\widehat{\mathbf{e}}}_{1h}:=({\widehat{\mathbf{e}}}_h^1-{\widehat{\mathbf{e}}}_h^0)/\tau \hfill \\ {\overline{\mathbf{e}}}_{1h}:={\widehat{\mathbf{e}}}_{1h}-{\mathbf{e}}_{1h},\hfill \\ {\displaystyle {\overline{E}}_0:={∥{\overline{\mathbf{e}}}_{1h}∥}_{{\epsilon }_h,h}^2+\frac{{\tau }^2}{2}\left(\parallel \nabla {\overline{\mathbf{e}}}_{1h}{\parallel }^2+{\parallel \nabla ·{\overline{\mathbf{e}}}_{1h}\parallel }_{\epsilon -1}^2\right)}\hfill \\ {\displaystyle +\frac{1}{2}\left(\parallel \nabla {\overline{\mathbf{e}}}_h^1{\parallel }^2+{\parallel \nabla {\overline{\mathbf{e}}}_h^0\parallel }^2\right)+\frac{1}{2}\left(\parallel \nabla ·{\overline{\mathbf{e}}}_h^1{\parallel }_{\epsilon -1}^2+{\parallel \nabla ·{\overline{\mathbf{e}}}_h^0\parallel }_{\epsilon -1}^2\right)+{T|\epsilon |}_{2,\infty }{\parallel {\overline{\mathbf{e}}}_h^0\parallel }^2}\hfill \end{array}$$

(103)

Recalling that ${\mathbf{e}}_h^1={\mathbf{e}}_h^0+\tau {\mathbf{e}}_{1h}$, we have ${\overline{\mathbf{e}}}_h^1={\overline{\mathbf{e}}}_h^0+\tau {\overline{\mathbf{e}}}_{1h}$. Thus, taking either $\mathcal{A}=\nabla {\overline{\mathbf{e}}}_h^0$ or $\mathcal{A}=\nabla ·{\overline{\mathbf{e}}}_h^0$ and either $\mathcal{B}=\tau \nabla {\overline{\mathbf{e}}}_{1h}$ or $\mathcal{B}=\tau \nabla ·{\overline{\mathbf{e}}}_{1h}$, we apply twice the inequality ${\parallel \mathcal{A}+\mathcal{B}\parallel }^2/2\le {\parallel \mathcal{A}\parallel }^2+{\parallel \mathcal{B}\parallel }^2$ to (103) together with Lemma 3 to obtain the following:

$$\begin{array}{c}{\displaystyle {\overline{E}}_0\le \frac{3}{2}\left\{\parallel \nabla {\overline{\mathbf{e}}}_h^0{\parallel }^2+{\parallel \nabla ·{\overline{\mathbf{e}}}_h^0\parallel }_{\epsilon -1}^2+{\tau }^2\left(\parallel \nabla {\overline{\mathbf{e}}}_{1h}{\parallel }^2+{\parallel \nabla ·{\overline{\mathbf{e}}}_{1h}\parallel }_{\epsilon -1}^2\right)\right\}}\hfill \\ +{T|\epsilon |}_{2,\infty }\parallel {\overline{\mathbf{e}}}_h^0{\parallel }^2+{(N+2)\parallel \epsilon \parallel }_{0,\infty }{\parallel {\overline{\mathbf{e}}}_{1h}\parallel }^2.\hfill \end{array}$$

(104)

Finally, using the inequality ${\parallel \nabla ·\mathbf{v}\parallel }_{\epsilon -1}^2\le {N\parallel \epsilon -1\parallel }_{0,\infty }{\parallel \nabla \mathbf{v}\parallel }^2$$\forall \mathbf{v}\in {\left\{H^1\left(\mathsf{\Omega }\right)\right\}}^N$, after straightforward manipulations, we easily infer from (104) the following:

$$\begin{array}{c}{\displaystyle {\overline{E}}_0\le \frac{{3+3N\parallel \epsilon -1\parallel }_{0,\infty }}{2}\left(\parallel \nabla {\overline{\mathbf{e}}}_h^0{\parallel }^2+{\tau }^2{\parallel \nabla {\overline{\mathbf{e}}}_{1h}\parallel }^2\right)+{T|\epsilon |}_{2,\infty }\parallel {\overline{\mathbf{e}}}_h^0{\parallel }^2+{(N+2)\parallel \epsilon \parallel }_{0,\infty }{\parallel {\overline{\mathbf{e}}}_{1h}\parallel }^2.}\hfill \end{array}$$

(105)

We next use the obvious splitting ${\overline{\mathbf{e}}}_h^0=({\widehat{\mathbf{e}}}_h^0-{\mathbf{e}}_0)+({\mathbf{e}}_0-{\mathbf{e}}_h^0)$, together with the trivial one:

$${\displaystyle {\overline{\mathbf{e}}}_{1h}=\frac{{\widehat{\mathbf{e}}}_h^1-{\widehat{\mathbf{e}}}_h^0}{\tau }-{\mathbf{e}}_{1h}=({\left\{{\partial }_t{\widehat{\mathbf{e}}}_h\right\}}_{|t=0}-{\mathbf{e}}_1)+\frac{1}{\tau }{\int }_0^{\tau }(\tau -t){\partial }_{tt}{\widehat{\mathbf{e}}}_{h}dt+({\mathbf{e}}_1-{\mathbf{e}}_{1h}).}$$

(106)

Then plugging (106) into (105), since ${\left\{{\sum }_{i=1}^p\parallel {\mathcal{A}}_i\parallel \right\}}^2\le p{\sum }_{i=1}^p{\parallel {\mathcal{A}}_i\parallel }^2$ for any set of p functions or fields ${\mathcal{A}}_i$, we obtain the following:

$$\begin{array}{c}{\displaystyle {\overline{E}}_0\le \frac{{3+3N\parallel \epsilon -1\parallel }_{0,\infty }}{2}\left\{2\left\{\parallel \nabla ({\widehat{\mathbf{e}}}_h^0-{\mathbf{e}}_0){\parallel }^2+{\parallel \nabla ({\mathbf{e}}_0-{\mathbf{e}}_h^0)\parallel }^2\right\}\right.}\hfill \\ \left.{\displaystyle 3{\tau }^2\left\{{\displaystyle \parallel \nabla {\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})(·,0){\parallel }^2+\frac{1}{{\tau }^2}{∥{\int }_0^{\tau }(\tau -t){\partial }_{tt}\nabla {\widehat{\mathbf{e}}}_{h}dt∥}^2+{\parallel \nabla ({\mathbf{e}}_1-{\mathbf{e}}_{1h})\parallel }^2}\right\}}\right\}\hfill \\ +{2T|\epsilon |}_{2,\infty }\left(\parallel {\widehat{\mathbf{e}}}_h^0-{\mathbf{e}}_0{\parallel }^2+{\parallel {\mathbf{e}}_0-{\mathbf{e}}_h^0\parallel }^2\right)\hfill \\ {\displaystyle +{3(N+2)\parallel \epsilon \parallel }_{0,\infty }\left\{{\displaystyle \parallel {\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})(·,0){\parallel }^2+\frac{1}{{\tau }^2}{∥{\int }_0^{\tau }(\tau -t){\partial }_{tt}{\widehat{\mathbf{e}}}_{h}dt∥}^2+{\parallel {\mathbf{e}}_1-{\mathbf{e}}_{1h}\parallel }^2}\right\}.}\hfill \end{array}$$

(107)

Owing to a trivial upper bound and to the Cauchy–Schwarz inequality, we easily come up with the following:

$$\begin{array}{c}{\displaystyle \frac{1}{{\tau }^2}{∥{\int }_0^{\tau }(\tau -t)\nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_{h}dt∥}^2\le {∥{\int }_0^{\tau }|\nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_h|dt∥}^2\le \tau {∥{\displaystyle {\left\{{\int }_0^{\tau }{|\nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_h|}^{2}dt\right\}}^{1/2}}∥}^2.}\hfill \end{array}$$

It follows that

$${\displaystyle \frac{1}{{\tau }^2}{∥{\int }_0^{\tau }(\tau -t)\nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_{h}dt∥}^2\le \tau {\int }_0^{\tau }{∥\nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_h∥}^{2}dt\le {(1+N\parallel \epsilon -1\parallel }_{0,\infty })\tau {\int }_0^{\tau }{∥\nabla {\partial }_{tt}\mathbf{e}∥}^{2}dt.}$$

(108)

The last inequality in (108) follows from the definition of ${\widehat{\mathbf{e}}}_h$. Indeed, we know the following:

$$(\nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_h,\nabla \mathbf{v})+{(\nabla ·{\partial }_{tt}{\widehat{\mathbf{e}}}_h,\nabla ·\mathbf{v})}_{\epsilon -1}=(\nabla {\partial }_{tt}\mathbf{e},\nabla \mathbf{v})+{(\nabla ·{\partial }_{tt}\mathbf{e},\nabla ·\mathbf{v})}_{\epsilon -1}\forall \mathbf{v}\in {\mathbf{V}}_h.$$

(109)

Taking $\mathbf{v}=\left\{{\partial }_{tt}{\widehat{\mathbf{e}}}_h\right\}(·,t)$, by the Cauchy–Schwarz inequality, we easily obtain the following:

$$\{\parallel \nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_h{\parallel }^2+\parallel \nabla ·{\partial }_{tt}{\widehat{\mathbf{e}}}_h{\parallel }_{\epsilon -1}^2{\}}^{1/2}\le \{\parallel \nabla {\partial }_{tt}{\mathbf{e}\parallel }^2+\parallel \nabla ·{\partial }_{tt}\mathbf{e}{{\parallel }_{\epsilon -1}^2\}}^{1/2},$$

(110)

or yet

$$\parallel \nabla {\partial }_{tt}{\widehat{\mathbf{e}}}_h\parallel \le \sqrt{{1+N\parallel \epsilon -1\parallel }_{0,\infty }}\parallel \nabla {\partial }_{tt}\mathbf{e}\parallel ,$$

(111)

which validates (108).

On the other hand, according to (63), we have $\parallel {\partial }_{tt}{\widehat{\mathbf{e}}}_h\parallel \le \parallel {\partial }_{tt}\mathbf{e}\parallel +{\widehat{C}}_0{h}^2\parallel \mathcal{H}\left({\partial }_{tt}\mathbf{e}\right)\parallel$. This yields the following:

$${∥{\int }_0^{\tau }(\tau -t){\partial }_{tt}{\widehat{\mathbf{e}}}_{h}dt∥}^2\le \tau {\int }_0^{\tau }{∥{\partial }_{tt}{\widehat{\mathbf{e}}}_h∥}^{2}dt\le 2\tau \left\{{\int }_0^{\tau }{∥{\partial }_{tt}\mathbf{e}∥}^{2}dt+{\widehat{C}}_0^2{h}^4{\int }_0^{\tau }{∥\mathcal{H}\left({\partial }_{tt}\mathbf{e}\right)∥}^{2}dt\right\}.$$

(112)

Incidentally, we point out that Assumption 1 and (64) allow us to assert the following:

• ${\partial }_{tt}\nabla \mathbf{e}\in {\left\{L^2(\mathsf{\Omega }\times (0,T))\right\}}^N$;
• $\parallel {\partial }_{tt}\mathbf{e}\parallel \in {\left\{L^{\infty }(0,T)\right\}}^N$;
• ${\left\{{\partial }_t\mathbf{e}\right\}}_{|t=0}={\mathbf{e}}_1\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$;
• ${\left\{\mathbf{e}\right\}}_{|t=0}={\mathbf{e}}_0\in {\left\{H^2\left(\mathsf{\Omega }\right)\right\}}^N$.

Clearly enough, besides (59) and (58), we will apply to (107) standard estimates based on the interpolation error in Sobolev norms (cf. [1]), together with the following obvious variants of (58) and (63), namely,

$$\begin{array}{c}∥\nabla {\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})(·,0)∥\le {\widehat{C}}_{1}h∥\mathcal{H}\left({\mathbf{e}}_1\right)∥,\hfill \\ ∥{\partial }_t({\widehat{\mathbf{e}}}_h-\mathbf{e})(·,0)∥\le {\widehat{C}}_0{h}^2∥\mathcal{H}\left({\mathbf{e}}_1\right)∥.\hfill \end{array}$$

(113)

Then taking into account that $\tau \le 1/\left(2\eta \right)$, from (107), (108), (112) and (113) and Assumption 1, we conclude that there exists a constant ${\overline{C}}_0$ depending on $\mathsf{\Omega }$, T, and $\epsilon$, but neither on h nor on $\tau$, such that

$$\begin{array}{c}{\displaystyle {\overline{E}}_0\le {\overline{C}}_0^2\left\{(h^2+\tau h^2+h^4)\parallel \mathcal{H}\left({\mathbf{e}}_0\right){\parallel }^2+(h^2+{\tau }^2{h}^2)\parallel \mathcal{H}\left({\mathbf{e}}_1\right){\parallel }^2+{\tau }^3\parallel \parallel \nabla {\partial }_{tt}\mathbf{e}{\parallel \parallel }_{L^2(0,T)}^2\right.}\hfill \\ \left.+{\tau }^2\parallel \parallel {\partial }_{tt}\mathbf{e}{\parallel \parallel }_{L^{\infty }(0,T)}^2+\tau h^4{\int }_0^{\tau }{∥\mathcal{H}\left({\partial }_{tt}\mathbf{e}\right)∥}^{2}dt\right\}.\hfill \end{array}$$

(114)

Notice that, starting from (64) with $u=\parallel \nabla {\partial }_{tt}\mathbf{e}\parallel$, similar to (65), we obtain the following:

$$\parallel \parallel {\partial }_{tt}{\mathbf{e}\parallel \parallel }_{L^{\infty }(0,T)}\le C_T\{\parallel \parallel {\partial }_{tt}{\mathbf{e}\parallel \parallel }_{L^2(0,T)}^2+\parallel \parallel {\partial }_{ttt}{\mathbf{e})\parallel \parallel }_{L^2(0,T)}^2{\}}^{1/2}.$$

Thus, noting that $h\le diam\left(\mathsf{\Omega }\right)$, using again the upper bound $\tau \le 1/\left(2\eta \right)$ and extending the integral to the whole interval $(0,T)$ in (114), from the latter inequality, we infer the existence of another constant $C_0$ independent of h and $\tau$ such that

$$\begin{array}{c}{\displaystyle {\overline{E}}_0\le C_0^2\{h^2\{\parallel \mathcal{H}\left({\mathbf{e}}_0\right){\parallel }^2+\parallel \mathcal{H}\left({\mathbf{e}}_1\right){\parallel }^2+\parallel \mathcal{H}\left({\partial }_{tt}\mathbf{e}\right){\parallel }_{L^2(\mathsf{\Omega }\times (0,T))}^2\}}\hfill \\ +{\tau }^2\{\parallel {\partial }_{tt}{\mathbf{e}\parallel }_{L^2(\mathsf{\Omega }\times (0,T))}^2+\parallel {\partial }_{ttt}{\mathbf{e}\parallel }_{L^2(\mathsf{\Omega }\times (0,T))}^2+\parallel \nabla {\partial }_{tt}\mathbf{e}{\parallel }_{L^2(\mathsf{\Omega }\times (0,T))}^2\}\}.\hfill \end{array}$$

(115)

4.3.2. Error Estimates

In order to fully exploit the stability inequality (54), we further define the following:

$${\displaystyle {\overline{S}}_M:=\sum _{k=1}^{M-1}\left({\displaystyle \frac{\tau }{2}|{\overline{\mathbf{F}}}^k{|}_h^2+\frac{N}{2\tau }{\parallel {\overline{d}}^k\parallel }^2+\frac{\tau }{2}{\left|{\overline{\mathbf{G}}}^k\right|}_{\mathsf{\Gamma },h}^2}\right).}$$

(116)

According to (80), in order to estimate ${\overline{S}}_M$ under the regularity Assumption 1 on $\mathbf{e}$, we resort to the estimates (81), (101) and (102). Using the inequality $|\mathbf{a}·\mathbf{b}|\le |\mathbf{a}||\mathbf{b}|$ for $\mathbf{a},\mathbf{b}\in {\Re }^n$, it is easy to see that there exist two constants ${\overline{C}}_F$ and ${\overline{C}}_G$ independent of h and $\tau$ such that

$${\displaystyle \sum _{k=1}^{M-1}\frac{\tau }{2}|{\overline{\mathbf{F}}}^k{|}_h^2\le {\overline{C}}_F\left(h^2+{\tau }^2\right){|\mathbf{e}|}_{H^4(\mathsf{\Omega }\times (0,T))}^2,}$$

(117)

$${\displaystyle \sum _{k=1}^{M-1}\frac{\tau }{2}|{\overline{\mathbf{G}}}^k{|}_{\mathsf{\Gamma },h}^2\le {\overline{C}}_G\left(h^2+{\tau }^2\right){|\mathbf{e}|}_{H^3(\mathsf{\Omega }\times (0,T))}^2.}$$

(118)

On the other hand, recalling (65), we have $k=1,2,\dots ,M-1$:

$${\displaystyle \parallel \mathcal{H}\left({\mathbf{e}}^k\right){\parallel }^2\le C_T^2{\int }_0^T\left\{{\parallel \mathcal{H}\left(\mathbf{e}\right)\parallel }^2+{\parallel \mathcal{H}\left({\partial }_t\mathbf{e}\right)\parallel }^2\right\}dt.}$$

(119)

Therefore, since $M=T/\tau$, we have the following:

$${\displaystyle \sum _{k=1}^{M-1}{\parallel \mathcal{H}\left({\mathbf{e}}^k\right)\parallel }^2\le \frac{C_T^{2}T}{\tau }{\int }_0^T\left\{{\parallel \mathcal{H}\left(\mathbf{e}\right)\parallel }^2+{\parallel \mathcal{H}\left({\partial }_t\mathbf{e}\right)\parallel }^2\right\}dt}$$

(120)

It follows from (120) and (81) that

$${\displaystyle \sum _{k=1}^{M-1}\frac{N}{2\tau }\parallel {\overline{\mathbf{d}}}^k{\parallel }^2\le {\widehat{C}}_0^2{C}_T^{2}T{|\epsilon |}_{1,\infty }^2\frac{N{h}^4}{2{\tau }^2}\left({|\mathbf{e}|}_{H^2(\mathsf{\Omega }\times (0,T))}^2+{|\mathbf{e}|}_{H^3(\mathsf{\Omega }\times (0,T))}^2\right)}$$

(121)

Plugging (117), (118) and (121) into (116), we can assert that there exists a constant $\tilde{C}$ depending on $\mathsf{\Omega }$, T, and $\epsilon$, but neither on h nor on $\tau$ such that

$$\begin{array}{c}{\displaystyle {\overline{S}}_M\le {\tilde{C}}^2\left(h^2+{\tau }^2+\frac{h^4}{{\tau }^2}\right){\parallel \mathbf{e}\parallel }_{H^4(\mathsf{\Omega }\times (0,T))}^2}\hfill \end{array}$$

(122)

Now recalling (54) and (53), provided that (46) holds, together with $\tau \le 1/\left(2\eta \right)$, we have the following:

$${\displaystyle {\left\{{∥\frac{{\overline{\mathbf{e}}}_h^{m+1}-{\overline{\mathbf{e}}}_h^m}{\tau }∥}^2+\parallel \nabla {\overline{\mathbf{e}}}_h^{m+1}{\parallel }^2+{\parallel \nabla {\overline{\mathbf{e}}}_h^m\parallel }^2\right\}}^{1/2}\le 2\sqrt{{\overline{S}}_M+{\overline{E}}_0}{e}^{\beta /2}.}$$

(123)

This implies that, for $m=1,2,\dots ,M-1$, it holds as follows:

$$\begin{array}{c}{\displaystyle {\left\{{∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }-\frac{{\mathbf{e}}^{m+1}-{\mathbf{e}}^m}{\tau }∥}^2+\parallel \nabla \left({\mathbf{e}}_h^{m+1}-{\mathbf{e}}^{m+1}\right){\parallel }^2+{\parallel \nabla \left({\mathbf{e}}_h^m-{\mathbf{e}}^m)\right)\parallel }^2\right\}}^{1/2}}\hfill \\ {\displaystyle \le {\left\{{∥\frac{{\widehat{\mathbf{e}}}_h^{m+1}-{\mathbf{e}}^{m+1}}{\tau }-\frac{{\widehat{\mathbf{e}}}_h^m-{\mathbf{e}}^m}{\tau }∥}^2+\parallel \nabla \left({\widehat{\mathbf{e}}}_h^{m+1}-{\mathbf{e}}^{m+1}\right){\parallel }^2+{\parallel \nabla \left({\widehat{\mathbf{e}}}_h^m-{\mathbf{e}}^m\right)\parallel }^2\right\}}^{1/2}}\hfill \\ +2\sqrt{{\overline{S}}_M+{\overline{E}}_0}{e}^{\beta /2}.\hfill \end{array}$$

(124)

Let us define a function ${\mathbf{e}}_h$ in $\overline{\mathsf{\Omega }}\times [0,T]$ whose value at $t=k\tau$ equals ${\mathbf{e}}_h^k$ for $k=1,2,\dots ,M$ and that varies linearly with t in each time interval $\left[\right(k-1)\tau ,k\tau ]$ in such a way that ${\displaystyle {\partial }_t{\mathbf{e}}_h(\mathbf{x},t)=\frac{{\mathbf{e}}_h^k\left(\mathbf{x}\right)-{\mathbf{e}}_h^{k-1}\left(\mathbf{x}\right)}{\tau }}$ for every $\mathbf{x}\in \overline{\mathsf{\Omega }}$ and $t\in \left(\right(k-1)\tau ,k\tau )$.

Now, we define ${\tilde{\mathcal{A}}}^{m-1/2}(·)$ for any function or field $\mathcal{A}(·,t)$ to be the mean value of $\mathcal{A}(·,t)$ in $(m\tau ,(m+1)\tau$, that is, ${\tilde{\mathcal{A}}}^{m+1/2}={\tau }^{-1}{\int }_{m\tau }^{(m+1)\tau }\mathcal{A}(·,t)dt$. Clearly enough, we have the following:

$${\displaystyle {∥\frac{{\mathbf{e}}_h^{m+1}-{\mathbf{e}}_h^m}{\tau }-\frac{{\mathbf{e}}^{m+1}-{\mathbf{e}}^m}{\tau }∥}^2={∥{\left\{\widetilde{{\partial }_t{\mathbf{e}}_h}\right\}}^{m+1/2}-{\left\{\widetilde{{\partial }_t\mathbf{e}}\right\}}^{m+1/2}∥}^2,}$$

(125)

and also recalling (120) and (65),

$$\begin{array}{c}{\displaystyle {∥\frac{{\widehat{\mathbf{e}}}_h^{m+1}-{\mathbf{e}}^{m+1}}{\tau }-\frac{{\widehat{\mathbf{e}}}_h^m-{\mathbf{e}}^m}{\tau }∥}^2={∥{\displaystyle {\int }_{m\tau }^{(m+1)\tau }\frac{{\partial }_t{\widehat{\mathbf{e}}}_h-{\partial }_t\mathbf{e}}{\tau }dt}∥}^2}\hfill \\ {\displaystyle \le {∥{\displaystyle \frac{{\left\{{\int }_{m\tau }^{(m+1)\tau }{({\partial }_t{\widehat{\mathbf{e}}}_h-{\partial }_t\mathbf{e})}^{2}dt\right\}}^{1/2}}{\sqrt{\tau }}}∥}^2=\frac{1}{\tau }{\int }_{m\tau }^{(m+1)\tau }{∥{\partial }_t{\widehat{\mathbf{e}}}_h-{\partial }_t\mathbf{e}∥}^{2}dt}\hfill \\ {\displaystyle \le \frac{{\widehat{C}}_0^2{h}^4}{\tau }{\int }_{m\tau }^{(m+1)\tau }\parallel \mathcal{H}\left({\partial }_t\mathbf{e}\right){\parallel }^{2}dt\le C_T^2{\widehat{C}}_0^2{h}^4{\int }_0^T\{\parallel \mathcal{H}\left({\partial }_t\mathbf{e}\right){\parallel }^2+\parallel \mathcal{H}\left({\partial }_{tt}\mathbf{e}\right){\parallel }^2\}dt,}\hfill \end{array}$$

which implies the following:

$$\begin{array}{c}{\displaystyle {∥\frac{{\widehat{\mathbf{e}}}_h^{m+1}-{\mathbf{e}}^{m+1}}{\tau }-\frac{{\widehat{\mathbf{e}}}_h^m-{\mathbf{e}}^m}{\tau }∥}^2\le C_T^2{\widehat{C}}_0^2{h}^2{|diam\left(\mathsf{\Omega }\right)|}^2{\parallel \mathbf{e}\parallel }_{H^4(\mathsf{\Omega }\times (0,T))}^2.}\hfill \end{array}$$

(126)

On the other hand, from (58) and (65), we have for $j=m$ or $j=m+1$ the following:

$${\displaystyle \parallel \nabla ({\widehat{\mathbf{e}}}_h^j-{\mathbf{e}}^j){\parallel }^2\le {\widehat{C}}_1^2{h}^2{\parallel \mathcal{H}\left({\mathbf{e}}^j\right)\parallel }^2\le {\widehat{C}}_1^2{C}_T^2{h}^2{\int }_0^T\left\{{\parallel \mathcal{H}\left(\mathbf{e}\right)\parallel }^2+{\parallel \mathcal{H}\left({\partial }_t\mathbf{e}\right)\parallel }^2\right\}dt,}$$

which yields the following:

$$\parallel \nabla ({\widehat{\mathbf{e}}}_h^j-{\mathbf{e}}^j){\parallel }^2\le C_T^2{\widehat{C}}_1^2{h}^2{\parallel \mathbf{e}\parallel }_{H^3(\mathsf{\Omega }\times (0,T))}^2.$$

(127)

Now, using Taylor expansions about $t=(m+1/2)\tau$ together with some arguments already exploited in this work, it is easy to establish that for a certain constant $\tilde{\mathcal{C}}$ independent of h and $\tau$, it holds as follows:

$$∥{\left\{\widetilde{{\partial }_t\mathbf{e}}\right\}}^{m+1/2}-{\left\{{\partial }_t\mathbf{e}\right\}}^{m+1/2}∥\le \tilde{\mathcal{C}}{\tau }^2{∥\mathbf{e}∥}_{H^4(\mathsf{\Omega }\times (0,T))},$$

(128)

where, for every function g defined in $\overline{\mathsf{\Omega }}\times [0,T]$ and $s\in {\Re }^{+}$, $g^s$ is the function defined in $\mathsf{\Omega }$ by $g^s(·)=g(·,s\tau )$.

Noting that ${\left\{\widetilde{{\partial }_t{\mathbf{e}}_h}\right\}}^{m+1/2}(·)$ is nothing but ${\left\{{\partial }_t{\mathbf{e}}_h\right\}}^{m+1/2}(·)$, collecting (124)–(128), together with (115) and (122), we have thus proved the following convergence result for scheme (14):

Provided that the CFL condition (46) is satisfied and $\tau$ also satisfies $\tau \le 1/\left(2\eta \right)$, under Assumption 1 on $\mathbf{e}$, there exists a constant $\mathcal{C}$ depending only on $\mathsf{\Omega }$, $\epsilon$, and T such that

$$\begin{array}{|c|}\hline \begin{array}{c}{\displaystyle \underset{1\le m\le M-1}{max}∥{\left\{{\partial }_t({\mathbf{e}}_h-\mathbf{e})\right\}}^{m+1/2}∥+\underset{2\le m\le M}{max}\parallel \nabla ({\mathbf{e}}_h^m-{\mathbf{e}}^m)\parallel }\hfill \\ {\displaystyle \le \mathcal{C}(\tau +h+h^2/\tau )\left\{{\parallel \mathbf{e}\parallel }_{H^4(\mathsf{\Omega }\times (0,T))}+\parallel \mathcal{H}\left({\mathbf{e}}_0\right)\parallel +\parallel \mathcal{H}\left({\mathbf{e}}_1\right)\parallel \right\}.}\hfill \end{array}\\ \hline\end{array}$$

(129)

In short, as long as $\tau$ varies linearly with h, the first-order convergence of scheme (14) in terms of either $\tau$ or h is established in the sense of the norms on the left-hand side of (129).

5. Assessment of the Scheme

The purpose of this section is to validate the theoretical results given in Section 4 by means of numerical experiments for $N=2$. With this aim, every partition ${\mathcal{T}}_h$ is assumed to fit both $\mathsf{\Omega }$ and ${\mathsf{\Omega }}_{in}$ in the usual way. Let ${\mathsf{\Omega }}_h$ be the union of all the triangles in ${\mathcal{T}}_h$. If we replace $\mathsf{\Omega }$ by ${\mathsf{\Omega }}_h$ in scheme (14), it is not difficult to see that, in the case of convex domains, the error estimates (129) extend to a curved domain $\mathsf{\Omega }$, as long as the norm $\parallel ·\parallel$ is replaced by the norm ${\parallel ·\parallel }_{{\mathsf{\Omega }}_h}$. Actually, unlike what we did so far, in this section, the notation ${\parallel ·\parallel }_h$ will rather stand for the later norm for the sake of brevity.

We performed numerical tests for the model problem (2), taking $T=0.5$ and $\mathsf{\Omega }$ to be the unit disk given by $\mathsf{\Omega }=\{(x_1;x_2)|r<1\}$, where $r:=\sqrt{x_1^2+x_2^2}$. $H_{1/2}$ being the Heaviside function, for an integer $m>1$, we take the following (Figure 1):

$$\begin{array}{c}\epsilon \left(r\right)=1+{(1-4r^2)}^m(1-H_{1/2}\left(r\right))\\ \mathrm{and} \mathrm{set} v_{\theta }(r,t):=\frac{e^{r-2t}}{\epsilon \left(r\right)}.\end{array}$$

(130)

We consider that the exact solution $\mathbf{e}=(e_1,e_2)$ of (2) is given by the following:

$$e_1=-x_2{v}_{\theta }(r,t) \mathrm{and} e_2=x_1{v}_{\theta }(r,t).$$

It is easy to check that $\mathbf{e}$ satisfies absorbing conditions on the boundary of the unit disk.

Figure 1. The Function $\epsilon (x,y)$ in the domain $\mathsf{\Omega }=(0,1)\times (0,1)$ for different values of m in (130) on the mesh with $h=2^{-5}$.

The initial data ${\mathbf{e}}_0$ and ${\mathbf{e}}_1$ are given by the following:

$${\displaystyle {\mathbf{e}}_0:={\mathbf{e}}_{|t=0}=\frac{(-x_2,x_1)e^r}{\epsilon \left(r\right)} \mathrm{and} {\mathbf{e}}_1:={\left\{{\partial }_t\mathbf{e}\right\}}_{|t=0}=\frac{2(x_2,-x_1)e^r}{\epsilon \left(r\right)}}$$

Since $\nabla ·\left(\epsilon \mathbf{e}\right)\equiv 0$ in $\mathsf{\Omega }$ by construction, the right-hand side $\mathbf{f}=(f_1;f_2)$ is given by $\mathbf{f}:=\epsilon {\partial }_{tt}\mathbf{e}-\Delta \mathbf{e}+\nabla (\nabla ·\mathbf{e})$, that is,  

$$\begin{array}{cc}\hfill \mathbf{f}=& (-4x_2{e}^{r-2t}-\Delta e_1;4x_1{e}^{r-2t}-\Delta e_2),\hfill \\ \hfill \mathrm{where}& {\displaystyle (\Delta e_1;\Delta e_2)=(-\frac{3x_2}{r}{v}_{\theta }^{\prime }-x_2{v}_{\theta }^{″};\frac{3x_1}{r}{v}_{\theta }^{\prime }+x_1{v}_{\theta }^{″});}\hfill \\ \hfill \mathrm{with}& {\displaystyle v_{\theta }^{\prime }=\frac{\epsilon -{\epsilon }^{\prime }}{{\epsilon }^2}{e}^{r-2t},v_{\theta }^{″}=\frac{{\epsilon }^2-2\epsilon {\epsilon }^{\prime }-\epsilon {\epsilon }^{{\epsilon }^{″}}+2{\left({\epsilon }^{\prime }\right)}^2}{{\epsilon }^3}{e}^{r-2t}}\hfill \\ \hfill \mathrm{and}& {\epsilon }^{\prime }=-8mr{(1-4r^2)}^{m-1}(1-H_{1/2}\left(r\right)),\hfill \\ \hfill & {\epsilon }^{″}=8m(8m^2{r}^2-4r^2-1){(1-4r^2)}^{m-2}(1-H_{1/2}\left(r\right)).\hfill \end{array}$$

In our computations, we used the software package Waves [44] for the finite element method applied to the solution of the model problem (2). The spatial domain $\mathsf{\Omega }$ is discretized by a family of quasi-uniform meshes consisting of $2\times 2^{2l+2}$ triangles K for $l=1,\dots ,6$, constructed as a certain mapping of the same number of triangles of the uniform mesh of the square $(-1,1)\times (-1,1)$, which is symmetric with respect to the Cartesian axes and has their edges parallel to those axes and either to the line $x_1=x_2$ if $x_1{x}_2\ge 0$ or to the line $x_1=-x_2$ otherwise. The above mapping is defined by means of a suitable transformation of Cartesian into polar coordinates. For each value of l, we define a reference mesh size $h_l$ equal to $2^{-l}$.

We considered a partition of the time domain $(0,T)$ into time intervals $J=(t_{k-1},t_k]$ of equal length ${\tau }_l$ for a given number of time intervals $M,l=1,\dots ,6$. We performed numerical tests taking $m=2,3,4,5$ in (130). We chose the time step ${\tau }_l=0.025\times 2^{-l},l=1,\dots ,6$, which provides numerical stability for all meshes. We computed the maximum value over the time steps of the relative errors measured in the $L^2$-norms of the function, its gradient, and its time derivative in the polygon ${\mathsf{\Omega }}_h$ for the different meshes in use. Now, $\mathbf{e}$ and ${\mathbf{e}}_h$ being the exact and approximate solution of (2), setting $M:=T/{\tau }_l$, these quantities are represented by the following:

$$\begin{array}{cc}\hfill e_l^1& {\displaystyle =\frac{{\displaystyle \underset{1\le k\le M}{max}{\parallel {\mathbf{e}}^k-{\mathbf{e}}_h^k\parallel }_h}}{{\displaystyle \underset{1\le k\le M}{max}{\parallel {\mathbf{e}}^k\parallel }_h}},}\hfill \\ \hfill e_l^2& {\displaystyle =\frac{{\displaystyle \underset{1\le k\le M}{max}{\parallel \nabla ({\mathbf{e}}^k-{\mathbf{e}}_h^k)\parallel }_h}}{{\displaystyle \underset{1\le k\le M}{max}{\parallel \nabla {\mathbf{e}}^k\parallel }_h}},}\hfill \\ \hfill e_l^3& {\displaystyle =\frac{{\displaystyle \underset{1\le k\le M-1}{max}{\parallel {\left\{{\partial }_t(\mathbf{e}-{\mathbf{e}}_h)\right\}}^{k+1/2}\parallel }_h}}{{\displaystyle \underset{1\le k\le M-1}{max}{\parallel {\left\{{\partial }_t\mathbf{e}\right\}}^{k+1/2}\parallel }_h}}.}\hfill \end{array}$$

(131)

In Table 1, Table 2, Table 3 and Table 4, the method’s convergence in these three senses is observed, taking $m=2,3,4,5$ in (130). Figure 2 shows convergence rates of our numerical scheme based on a $P_1$ space discretization, taking the function $\epsilon$ defined by (130) with $m=2$ (on the left) and $m=3$ (on the right) for $\epsilon \left(r\right)$. Similar convergence results are presented in Figure 3, taking $m=4$ (on the left) and $m=5$ (on the right) in (130).

Table 1. Computed maximum relative errors $e_l$ in maximum energy, maximum $L^2$, and maximum in broken time error on different meshes with mesh sizes $h_l=2^{-l},l=1,\dots ,6$ for the function $\epsilon$ with $m=2$ in (130).

l	$\mathit{nel}$	$\mathit{nno}$	${\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(1\right)}/{\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(2\right)}/{\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(3\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(3\right)}/{\mathit{e}}_{\mathit{l}}^{\left(3\right)}$
1	32	25	0.6057		2.2827		3.1375
2	128	81	0.1499	4.0418	1.0769	2.1198	1.1536	2.7196
3	512	289	0.0333	4.5007	0.4454	2.4178	0.5776	1.9972
4	2048	1089	0.0078	4.2466	0.2077	2.1449	0.2802	2.0617
5	8192	4225	0.0019	4.1288	0.1066	1.9483	0.1379	2.0313
6	32,768	16,641	0.0005	4.0653	0.0535	1.9905	0.0690	1.9981

Table 2. Computed maximum relative errors $e_l$ in maximum energy, maximum $L^2$, and maximum in broken time error on different meshes with mesh sizes $h_l=2^{-l},l=1,\dots ,6$ for the function $\epsilon$ with $m=3$ in (130).

l	$\mathit{nel}$	$\mathit{nno}$	${\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(1\right)}/{\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(2\right)}/{\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(3\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(3\right)}/{\mathit{e}}_{\mathit{l}}^{\left(3\right)}$
1	32	25	0.6144		1.8851		3.0462
2	128	81	0.1511	4.0666	1.0794	1.7464	1.1417	2.6682
3	512	289	0.0339	4.4553	0.4713	2.2904	0.5680	2.0099
4	2048	1089	0.0080	4.2216	0.2166	2.1753	0.2760	2.0583
5	8192	4225	0.0019	4.1207	0.1137	1.9049	0.1354	2.0381
6	32,768	16,641	0.0005	4.0615	0.0566	2.0092	0.0677	1.9997

Table 3. Computed maximum relative errors $e_l$ in maximum energy, maximum $L^2$, and maximum in broken time error on different meshes with mesh sizes $h_l=2^{-l},l=1,\dots ,6$ for the function $\epsilon$ with $m=4$ in (130).

l	$\mathit{nel}$	$\mathit{nno}$	${\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(1\right)}/{\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(2\right)}/{\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(3\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(3\right)}/{\mathit{e}}_{\mathit{l}}^{\left(3\right)}$
1	32	25	0.6122		1.9517		3.0545
2	128	81	0.1529	4.0027	1.0896	1.7912	1.1445	2.6689
3	512	289	0.0346	4.4266	0.4879	2.2331	0.5639	2.0296
4	2048	1089	0.0082	4.2069	0.2234	2.1839	0.2728	2.0667
5	8192	4225	0.0020	4.1151	0.1183	1.8879	0.1336	2.0418
6	32,768	16,641	0.0005	4.0585	0.0595	1.9890	0.0668	2.0008

Table 4. Computed maximum relative errors $e_l$ in maximum energy, maximum $L^2$, and maximum in broken time error on different meshes with mesh sizes $h_l=2^{-l},l=1,\dots ,6$ for the function $\epsilon$ with $m=5$ in (130).

l	$\mathit{nel}$	$\mathit{nno}$	${\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(1\right)}/{\mathit{e}}_{\mathit{l}}^{\left(1\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(2\right)}/{\mathit{e}}_{\mathit{l}}^{\left(2\right)}$	${\mathit{e}}_{\mathit{l}}^{\left(3\right)}$	${\mathit{e}}_{\mathit{l}-1}^{\left(3\right)}/{\mathit{e}}_{\mathit{l}}^{\left(3\right)}$
1	32	25	0.6107		1.9930		3.0603
2	128	81	0.1546	3.9505	1.1006	1.8108	1.1464	2.6696
3	512	289	0.0351	4.4031	0.4982	2.2090	0.5619	2.0403
4	2048	1089	0.0084	4.1954	0.2288	2.1777	0.2706	2.0765
5	8192	4225	0.0020	4.1106	0.1223	1.8715	0.1325	2.0417
6	32,768	16,641	0.0005	4.0561	0.0607	2.0139	0.0662	2.0011

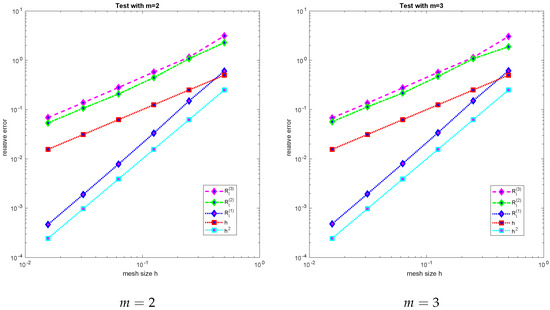
Figure 2. Convergence rates $R_l^{\left(i\right)},i=1,2,3;l=1,\dots ,6$, for $m=2$ (left) and $m=3$ (right).

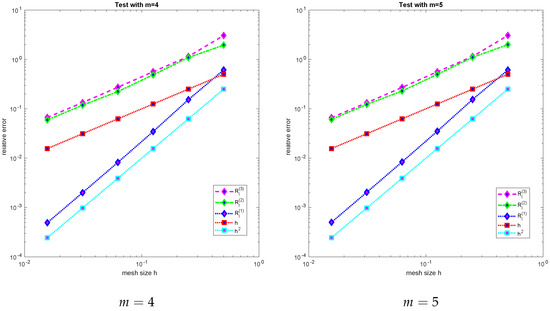
Figure 3. Convergence rates $R_l^{\left(i\right)},i=1,2,3;l=1,\dots ,6$, for $m=4$ (left) and $m=5$ (right).

Convergence rates $R_l^{\left(j\right)},j=1,2,3;l=1,\dots ,6$, of Figure 2 and Figure 3 are computed according to [28,29] as follows:

$$\begin{array}{c}\hfill R_l^{\left(j\right)}=\frac{\left|log\frac{e_{l-1}^{\left(j\right)}}{e_l^{\left(j\right)}}\right|}{|log(2)|},\end{array}$$

(132)

where $e_l^{\left(j\right)},j=1,2,3;l=1,\dots ,6$, are defined in (131).

Observation of these tables and figures clearly indicates that our scheme behaves like a first-order method in the (semi-)norm of $L^{\infty }[(0,T);H^1\left(\mathsf{\Omega }\right)]$ for $\mathbf{e}$ and in the norm of $L^{\infty }[(0,T);L^2\left(\mathsf{\Omega }\right)]$ for ${\partial }_t\mathbf{e}$ for all the chosen values of m. As far as the values of m greater or equal to 4 are concerned, this perfectly conforms to the a priori error estimates given in Section 4. However, those tables and figures also show that such theoretical predictions extend to cases not considered in our analysis, such as $m=2$ and $m=3$, in which the regularity of the exact solution is lower than assumed. Otherwise stated, some of our assumptions seem to be of academic interest only, and a lower regularity of the solution, such as $H^2(\mathsf{\Omega }\times (0,T))$, should be sufficient to attain optimal first-order convergence in both senses. On the other hand, second-order convergence can be expected from our scheme in the norm of $L^{\infty }[(0,T);L^2\left(\mathsf{\Omega }\right)]$ for $\mathbf{e}$, according to Table 1, Table 2, Table 3 and Table 4 and Figure 2 and Figure 3.

Algorithm 1 presents the main steps in the computation of convergence rates (132) for the explicit scheme (14). We refer to [31] for full details of the finite element implementation of this scheme.

Algorithm 1: Computation of convergence rates for explicit scheme (14)

Remark 3.

The authors are not able to supply comparative studies for the numerical results shown in this section since, to the best of their knowledge, there is no other work available in the literature addressing the numerical solution of the Maxwell-wave equation coupling problem in a similar context. Nevertheless, the reliability of the approach advocated in this article has been fully demonstrated, which was its main purpose.

6. Final Remarks and Conclusions

As previously noted, the approach advocated in this work was extensively and successfully tested in the framework of the solution of CIPs governed by Maxwell’s equations. More specifically, it was used with minor modifications to solve both the direct problem and the adjoint problem as steps of an adaptive algorithm to determine the unknown dielectric permittivity. More details on this procedure can be found in [32] and references therein.

In practical terms, our scheme combining a finite element spatial discretization with a finite difference time discretization is globally of the second order in the maximum norm. It is likely that known schemes for the Maxwell equations based only on finite difference discretizations could be adapted to the Maxwell-wave equation coupling problem at hand, thereby yielding higher-order approximations in the same sense. However, this would mean restricting the application of the numerical solution method to particular geometries, such as Cartesian ones.

As a matter of fact, the method studied in this paper was designed to handle composite dielectrics structured in such a way that layers with a higher permittivity are completely surrounded by layers with a (constant) lower permittivity, say $\epsilon =1$. It should be noted, however, that the assumption that $\epsilon$ attains a minimum in the outer layer was made here only to simplify things. Actually, under the same assumptions, (129) also applies to the case where $\epsilon$ in inner layers is allowed to be smaller than in the outer layer, say $\epsilon <1$. We refer to [45] for further details.

Another issue that is worth a comment is the practical calculation of the term $(\nabla ·\epsilon {\mathbf{e}}_h^k,\nabla ·\mathbf{v})$ in (14). Unless $\epsilon$ is a simple function, such as a polynomial, it is not possible to compute this term exactly. That is why we recommend the use of the trapezoidal rule to carry out these computations. At the price of small adjustments in some terms involving norms of $\epsilon$, the thus modified scheme is stable in the same sense as (54). Moreover, the qualitative convergence result (129) remains unchanged, provided that a little more regularity is required from $\epsilon$. We skip details for the sake of brevity.

In conclusion, besides the numerical validation provided in Section 5, a rather large number of experiments have been conducted by using the scheme studied in this article. They are reported in several papers on the solution of inverse problems governed by the coupling problem at hand; see [31,32,33] and references therein. The analysis carried out in this paper completely corroborates the adequacy of such a numerical choice from a rigorous and strictly mathematical point of view.

Future work can be related to the application of the proposed approach to different types of hyperbolic PDEs. For example, the scheme considered in the current work can be studied with other boundary conditions and other additional terms in Maxwell’s system, for example, terms with conductivity.