Uncertain Asymptotic Stability Analysis of a Fractional-Order System with Numerical Aspects

Abstract

We apply known special functions from the literature (and these include the Fox $\mathbb{H}–$function, the exponential function, the Mittag-Leffler function, the Gauss Hypergeometric function, the Wright function, the $\mathbb{G}–$function, the Fox–Wright function and the Meijer $\mathbb{G}–$function) and fuzzy sets and distributions to construct a new class of control functions to consider a novel notion of stability to a fractional-order system and the qualified approximation of its solution. This new concept of stability facilitates the obtention of diverse approximations based on the various special functions that are initially chosen and also allows us to investigate maximal stability, so, as a result, enables us to obtain an optimal solution. In particular, in this paper, we use different tools and methods like the Gronwall inequality, the Laplace transform, the approximations of the Mittag-Leffler functions, delayed trigonometric matrices, the alternative fixed point method, and the variation of constants method to establish our results and theory.

1. Introduction

Stability analysis depends on the control of a system’s behavior in response to changes or perturbations. It includes analyzing the equilibrium state of a problem, assessing its ability to recover from disturbances, and maintaining stability over time when acted upon by forces tending to displace it. Generally, stability theory addresses the stability of solutions under small perturbations of initial conditions.

In mathematics and engineering, stability concepts are categorized as follows [1,2,3,4,5,6,7,8,9,10]:

• Lyapunov stability: if the solutions that start out near an equilibrium point $x_e$ stay near forever, then $x_e$ is Lyapunov stable.
• Asymptotic stability: if $x_e$ is Lyapunov stable and all solutions that start out near $x_e$ converge to $x_e,$ then $x_e$ is said to be asymptotically stable.
• Exponential stability: this stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge.
• Probability stability: a property of probability distributions.
• Algebraic geometry stability: this stability is a notion which characterizes when a geometric object has some desirable properties for the purpose of classifying them.
• Numerical stability: a property of numerical algorithms which describes how errors in the input data propagate through the algorithm.
• K-stability: a stability condition for algebraic varieties.
• Radius stability: a property of continuous polynomial functions.
• Learning theory stability: a property of machine learning algorithms.

Stability in the Ulam sense is important since it introduces analytical approximate solutions for diverse problems where exact solutions are difficult to obtain. If a system is Ulam stable, then essential properties hold in the vicinity of the exact solution (see [11,12,13] and their references) and this is seen in optimization, biology and economics (especially when very little is known in regards to exact solutions). Ulam-type stability was first proposed in Ulam’s talk at a conference in 1940 [14], and he phrased it as follows: Let M be a group and N a metric group with metric $d.$ Given $\epsilon >0,$ is there a $\delta >0,$ such that if a mapping $g:M\to N$ satisfies $d\left(g\right(yx),g(y\left)g\right(x\left)\right)\le \delta ,$ for every $y,x\in M,$ then, there exists a homomorphism $h:M\to N$ with $d\left(g\right(x),h(x\left)\right)\le \epsilon ,$ for all $x\in M?$

The first answer was given by Hyers [15]. Let $Y_1$ and $Y_2$ be Banach spaces and let $\epsilon >0$. Then, for all $g:Y_1\to Y_2$ with

$$\underset{y,x\in Y_1}{sup}\parallel g(y+x)-g\left(y\right)-g\left(x\right)\parallel \le \epsilon ,$$

there exists a unique additive mapping $h:Y_1\to Y_2,$ such that

$$\underset{x\in Y_1}{sup}\parallel g\left(x\right)-h\left(x\right)\parallel \le \epsilon .$$

The Ulam stability of differential equations was first studied by Ger and Alsina [16] and they noted the following. Let $\epsilon >0,$ J be an open real-valued interval and $g:J\to \mathbb{R}$ be a differentiable function. If g satisfies

$$\parallel g\left(x\right)-g^{\prime }\left(x\right)\parallel \le \epsilon ,x\in J,$$

then, there exists a differentiable function $g_0:J\to \mathbb{R}$ such that $g_0^{\prime }\left(x\right)=g_0\left(x\right)$ and

$$\parallel g\left(x\right)-g_0\left(x\right)\parallel \le 3\epsilon ,x\in J.$$

The stability of differential linear equations of the first order was studied in [16,17], Riccati equations were studied in [18], Bernoulli equations in [19], and Ulam stability of partial differential equations was investigated by Rassias and Prastaro in [20,21,22]; the authors presented a different concept of perturbation stability in the Ulam sense.

To obtain an affective decision about the best approximation of a fractional-order system, one has to enhance reliable and applicable information on various facets of it. In this paper, to obtain useful information about the quality and the certainty of approximating the solution of a fractional-order system, we apply the concept of fuzzy systems and probability theory. As will be shown, by introducing the concept of time-stamped fuzzy sets and distribution functions that have a dynamic state, we can choose the best approximation of the solution of a fractional-order system at any time. Motivated by [21,22], we study the following fractional-order system:

$$\begin{array}{ccc}\hfill & & D_0{\mathbf{G}}_1\left(\chi \right)={\mathbf{H}}_0{\mathbf{G}}_2(\chi ,{\mathbf{G}}_1\left(\chi \right),D_1{\mathbf{G}}_1\left(\chi \right),\dots ,D_m{\mathbf{G}}_1\left(\chi \right))+{\mathbf{H}}_1{\mathbf{G}}_1\left(\chi \right)\hfill \\ & & +{\mathbf{H}}_2{\mathbf{G}}_3\left(\chi \right){\mathbf{G}}_1\left(\chi \right)+{\mathbf{H}}_3{\mathbf{G}}_1(\chi -\mathcal{Y}).\hfill \end{array}$$

(1)

A brief discussion on fractional calculus can be found in Section 2.6 and Section 2.7. Here, we apply known special functions and use the concept of fuzzy sets and distribution functions to construct a new class of control functions to consider the stability of (1) and the qualified approximation of its solution. Let ${[.]}_{n\times n}$ be a square matrix. Let us consider the following special cases:

Case 1:

• $m=1,D_0=D_1:={}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }$ ($\delta$–Hilfer derivative).
• $I_{{\alpha }^{+}}^{1-{\mathcal{P}}_3;\delta }{\mathbf{G}}_1\left({\alpha }^{+}\right)={\mathbf{G}}_0\in \mathbb{R}$ ($\delta$–Riemann–Liouville integral).
• ${\mathcal{P}}_1\in (0,1],{\mathcal{P}}_2\in [0,1],{\mathcal{P}}_3={\mathcal{P}}_1+{\mathcal{P}}_2(1-{\mathcal{P}}_1).$
• ${\mathbf{H}}_0:={\left[\mathbf{1}\right]}_{1\times 1},{\mathbf{H}}_i={\left[\mathbf{0}\right]}_{1\times 1},i=1,2,3.$
• ${\mathbf{G}}_1:\mathbb{I}\to \mathbb{R},$ ${\mathbf{G}}_2:\mathbb{I}\times {\mathbb{R}}^2\to \mathbb{R}$.
• $\mathbb{I}:=[\alpha ,\beta ]$ (and $\mathbb{I}:=\mathbb{R}).$

Case 2:

• $\chi =({\chi }_1,{\chi }_2).$
• $m=3,D_0=D_{{\chi }_2}^{\mathcal{P}}$ (Conformable derivative), $D_1=\frac{d}{d{\chi }_1},D_2=\frac{d^2}{d{\chi }_1^2},D_3=\frac{d^3}{d{\chi }_1^3}.$
• $\mathcal{P}\in (0,1].$
• ${\mathbf{H}}_0:={\left[\mathbf{1}\right]}_{1\times 1},{\mathbf{H}}_i={\left[\mathbf{0}\right]}_{1\times 1},i=1,2,3.$

Case 3:

• $D_0={}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}}$ (Riemann–Liouville derivative).
• ${}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}-\ell }{\mathbf{G}}_1\left(\chi \right){|}_{\chi ={\chi }_0}={\mathbf{G}}_{1(\ell -1)},\ell =1,2.$
• $\mathcal{P}\in (1,2),\chi >{\chi }_0.$
• ${\mathbf{H}}_1\in {\mathbb{R}}^{n\times n},{\mathbf{H}}_i={\left[\mathbf{0}\right]}_{n\times n},i=0,2,3.$
• ${\mathbf{G}}_1\in {\mathbb{R}}^n.$

Case 4:

• $D_0={}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}}$ (Riemann–Liouville derivative).
• ${}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}-\ell }{\mathbf{G}}_1\left(\chi \right){|}_{\chi ={\chi }_0}={\mathbf{G}}_{1(\ell -1)},\ell =1,2.$
• $\mathcal{P}\in (1,2),\chi >{\chi }_0.$
• ${\mathbf{H}}_1\in {\mathbb{R}}^{n\times n},{\mathbf{H}}_2={\left[\mathbf{1}\right]}_{n\times n},{\mathbf{H}}_i={\left[\mathbf{0}\right]}_{n\times n},i=0,3.$
• ${\mathbf{G}}_1\in {\mathbb{R}}^n,{\mathbf{G}}_3:\mathbb{I}\to {\mathbb{R}}^{n\times n}.$
• $\mathbb{I}:=[{\chi }_0,\infty ).$

Case 5:

• $D_0={}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}\left({}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}\right)$ (Caputo derivative).
• ${}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}\left({}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}\right){\mathbf{G}}_1\left(\chi \right)={\mathbf{H}}_3{\mathbf{G}}_1(\chi -\mathcal{Y}),\chi >0,\mathcal{Y}>0.$
• ${\mathbf{G}}_1\left(\chi \right)=\mathcal{U}\left(\chi \right),{\mathbf{G}}_1^{\prime }\left(\chi \right)={\mathcal{U}}^{\prime }\left(\chi \right),\chi \in [-\mathcal{Y},0],\mathcal{Y}>0.$
• ${\mathbf{H}}_3:=-{\mathbf{H}}^2,\mathbf{H}\in {\mathbb{R}}^{n\times n},{\mathbf{H}}_i={\left[\mathbf{0}\right]}_{n\times n},i=0,1,2.$
• ${\mathbf{G}}_1\in {\mathbb{R}}^n,$$\mathcal{U}\in C([-\mathcal{Y},0],{\mathbb{R}}^n).$
• $\mathbb{I}:=[0,T],T>0.$

The goal in this paper is to effectively generalize stability problems and to evaluate optimized controllability and stability. Our mathematical stability results (based on fixed point theory) can be found in Theorems 1–7. In the following sections, we present the theory and some comparison results to tackle this. In Case 1, we begin with the theory and present fuzzy multistability and Fox-type stability results via aggregate special controllers and fixed point theory. We discuss both finite and infinite domains and controllability and optimal error estimates are also presented here. In Case 2, we illustrate the numerical theory by considering a modified nonlinear Schrödinger equation and we apply the first Kudryashov-type method to obtain numerical solutions. In Cases 3 and 4, we present the theory of fuzzy stability and the fuzzy asymptotic stability and our results are achieved via the Gronwall inequality, the Laplace transform, and some approximations of Mittag-Leffer functions. In Case 5, we present random finite-time stability theory via the delayed matrix cosine and sine functions.

We now present two results as an example of the theorems established in this paper.

Result 1. In Section 2, we discuss

$${}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\mathbf{G}}_1\left(\chi \right)={\mathbf{G}}_2(\chi ,{\mathbf{G}}_1\left(\chi \right),{}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\mathbf{G}}_1\left(\chi \right)),$$

$$I_{{\alpha }^{+}}^{{\mathcal{P}}_3;\delta }{\mathbf{G}}_1\left({\alpha }^{+}\right)={\mathbf{G}}_0,{\mathbf{G}}_0\in \mathbb{R},$$

and in Theorem 1, under appropriate assumptions, we establish a unique solution and, in addition, we obtain that it is multistable. To achieve this, we use fixed point theory and our argument makes use of aggregation maps on special functions which define our class of controllers. Comparison and optimality is discussed after the main result is presented.

Result 2. In Section 5, we discuss

$$\begin{array}{ccc}& & {}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}}{\mathbf{G}}_1\left(\chi \right)={\mathbf{H}}_1{\mathbf{G}}_1\left(\chi \right),\chi >{\chi }_0,\hfill \\ & & {}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}-\ell }{\mathbf{G}}_1\left(\chi \right){|}_{\chi ={\chi }_0}={\mathbf{G}}_{1(\ell -1)},\ell =1,2,\hfill \end{array}$$

where $1<\mathcal{P}<2,$ ${\mathbf{H}}_1\in {\mathbb{R}}^{n\times n},$ and ${\mathbf{G}}_1\in {\mathbb{R}}^n,$ and in Theorem 3, under appropriate assumptions, we consider a relationship between stability, asymptotic stability and critical eigenvalues.

2. Preliminaries

2.1. Fox’s $\mathbb{H}$–Functions

We define the Fox’s $\mathbb{H}$-function ( see [23,24,25,26,27,28]) as

$$\begin{array}{ccc}\hfill & & {}_C{}^A\mathbb{H}_D^B\left[\chi {|}_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]\hfill \\ & & :={\displaystyle \frac{1}{2\pi i}}{\int }_{\mathcal{X}}\varpi \left(S\right)\exp \left(S\right[i\arg \left(\chi \right)+\log \left|\chi \right|\left]\right)\hfill \\ & & ·{\displaystyle \frac{{\prod }_{j=1}^A\Gamma (N_j-M_{j}S){\prod }_{j=1}^B\Gamma (1-V_j+W_{j}S)}{{\prod }_{j=A+1}^D\Gamma (1-N_j+M_{j}S){\prod }_{j=B+1}^C\Gamma (V_j-W_{j}S)}}dS,\hfill \end{array}$$

(2)

in which $C,B,D,A\in \mathbb{N},$ $0\le B\le C,$ $1\le A\le D$, $\underset{\underset{j=1,\dots ,C}{⏟}}{W_j,V_j}>0$ and $\underset{\underset{j=1,\dots ,D}{⏟}}{M_j,N_j}>0,$ and $\mathcal{X}$ are a contour of a Mellin–Barnes-type integral in the complex S-plane.

The following special cases of Fox’s $\mathbb{H}$-function have an important role in our results:

• Exponential map ${}_0\mathbb{H}_0\left[\chi \right].$
• Mittag-Leffler function ${}_0\mathbb{H}_1[\chi ;N_1],$ with 1 parameter.
• Gauss Hypergeometric function ${}_2\mathbb{H}_1[\chi ;N_1;V_1,V_2].$
• Wright function ${}_1\mathbb{H}_1[\chi ;N_1;V_1].$
• $\mathbb{G}$–function ${}_C\mathbb{H}_D[\chi ;N_1,\dots ,N_C;V_1,\dots ,V_C].$
• Fox–Wright function ${}_C\mathbb{H}_D\left[\chi {|}_{(N_1,M_1),\dots ,(N_D,M_D)}^{(V_1,W_1),\dots ,(V_C,W_C)}\right].$
• Meijer $\mathbb{G}$-function ${}_C{}^A\mathbb{H}_D^B\left[\chi {|}_{(N_1,1),\dots ,(N_D,1)}^{(V_1,1),\dots ,(V_C,1)}\right].$

2.2. Generalized Triangular Norms (GTNs)

Assume $ϵ:=[0,1]$ and

$$\mathrm{diag}{M}_n\left(ϵ\right):=\left\{\left[\begin{array}{ccccc}{R}_{11}& 0& 0& \cdots & 0\\ 0& R_{22}& 0& \cdots & 0\\ 0& 0& R_{33}& \cdots & 0\\ ⋮& ⋮& ⋮& & ⋮\\ 0& 0& 0& \cdots & R_{nn}\end{array}\right]=\mathrm{diag}[R_{11},\cdots ,R_{nn}],\underset{\underset{\underset{1\le i\le n}{1\le j\le n}}{⏟}}{R_{ij}}\in ϵ\right\},$$

with the following partial order relation:

$$\mathbf{R}:=\mathrm{diag}[R_{11},\cdots ,R_{nn}],\mathbf{S}:=\mathrm{diag}[S_{11},\cdots ,S_{nn}]\in \mathrm{diag}{M}_n\left(ϵ\right),$$

$$\mathbf{R}⪯\mathbf{S}⟺R_{ij}\le S_{ij},1\le i,j\le n.$$

Definition 1 

([22]). A GTN is a mapping ⨂ from ${\left(\mathit{diag}{M}_n\left(ϵ\right)\right)}^2$ to $\mathit{diag}{M}_n\left(ϵ\right)$, s.t. for every $\mathbf{R},\mathbf{S},\mathbf{E},\mathbf{K}\in \mathit{diag}{M}_n\left(ϵ\right),$ we have

$\left(1\right)$$\mathbf{R}⨂\mathbf{1}=\mathbf{R},$

(2) $\mathbf{R}⨂\mathbf{S}=\mathbf{S}⨂\mathbf{R}$,

(3) $\mathbf{R}⨂(\mathbf{S}⨂\mathbf{E})=(\mathbf{R}⨂\mathbf{S})⨂\mathbf{E},$

(4) $\mathbf{R}⪯\mathbf{S}\mathrm{and}\mathbf{E}⪯\mathbf{K}⟹\mathbf{R}⨂\mathbf{E}⪯\mathbf{S}⨂\mathbf{K}.$

For each sequence $\left\{{\mathbf{R}}_m\right\}$, $\left\{{\mathbf{S}}_m\right\}$ converging to $\mathbf{R},\mathbf{S}\in \mathrm{diag}{M}_n\left(ϵ\right)$, if we obtain

$$\underset{m}{lim}({\mathbf{R}}_m⨂{\mathbf{S}}_m)=\mathbf{R}⨂\mathbf{S},$$

then ⨂ on diagonal matrices is continuous.

We define the continuous GTN ${⨂}_M:{\left(\mathrm{diag}{M}_n\left(ϵ\right)\right)}^2\to \mathrm{diag}{M}_n\left(ϵ\right),$ as follows:

$$\begin{array}{ccc}& & \mathbf{R}\underset{M}{⨂}\mathbf{S}\hfill \\ & & =\mathrm{diag}[R_{11},\cdots ,R_{nn}]\underset{M}{⨂}\mathrm{diag}[S_{11},\cdots ,S_{nn}]\hfill \\ & & =\mathrm{diag}[min\{R_{11},S_{11}\},\cdots ,min\{R_{nn},S_{nn}\}].\hfill \end{array}$$

In the rest of the paper, we consider $⨂:={⨂}_M.$

2.3. Fuzzy Normed Spaces

Consider the following assumptions:

• $\mathfrak{J}$ is a linear space.
• $\mathfrak{G}$ is a family of matrix-valued fuzzy (shortly, MVF) sets $\Phi :\mathfrak{J}\times (0,+\infty )\to \mathrm{diag}{M}_n\left(ϵ\right)$.
• $\Phi$ is a continuous increasing function.
• ${lim}_{\varphi \to \infty }\Phi (\chi ,\varphi )=\mathbf{1},$ for all $\chi \in \mathfrak{J},$ and $\varphi >0$.
• $\Phi ⪯{\Phi }^{\prime }⟺\Phi (\chi ,\varphi )⪯{\Phi }^{\prime }(\chi ,\varphi ),$ for each $\chi \in \mathfrak{J},$ $\varphi >0$, and $\Phi ,{\Phi }^{\prime }\in \mathfrak{G}.$

A triple $(\mathfrak{J},\Phi ,⨂)$ is said to be a MVF normed space (MVFN space), if for each $\varphi ,{\varphi }^{\prime }>0,$ $\chi ,{\chi }^{\prime }\in \mathfrak{J},$ and $0\ne \upsilon \in \mathbb{C},$ we have

(i) $\Phi (\chi ,\varphi )=\mathrm{diag}{[1,\cdots ,1]}_{n^2},\iff \chi =0.$

(ii) $\mathrm{diag}{[0,\cdots ,0]}_{n^2}\prec \Phi (\chi ,\varphi )$.

(iii) $\Phi ({\chi }^{\prime },{\varphi }^{\prime })⨂\Phi (\chi ,\varphi )⪯\Phi ({\chi }^{\prime }+\chi ,{\varphi }^{\prime }+\varphi ),$

(iv) $\Phi (\upsilon \chi ,\varphi )=\Phi (\chi ,{\displaystyle \frac{\varphi }{\left|\upsilon \right|}})$.

2.4. MV Random Normed (MVRN) Spaces

Consider the following assumptions:

• $\mathfrak{J}$ is a vector space.
• $\mathfrak{E}$ is a set of MV distribution functions (MVDFs) $\kappa :\mathbb{R}\cup \{-\infty ,+\infty \}⟶\mathrm{diag}{M}_n\left(ϵ\right).$
• $\kappa$ is a left-continuous and non-decreasing function.
• $\kappa (-\infty )=\mathbf{0}$ and $\kappa (+\infty )=\mathbf{1}.$
• ${\mathfrak{E}}^{+}\subseteq \mathfrak{E}$ contains functions $\Psi \in \mathfrak{E},$ s.t., ${lim}_{\psi ⟶+{\infty }^{-}}{\Psi }_{\psi }=\mathbf{1}.$
• $\kappa ⪯{\kappa }^{\prime }\iff \kappa \left(\psi \right)⪯{\kappa }^{\prime }\left(\psi \right),$ for every $\psi \in \mathbb{R},$ and $\kappa ,{\kappa }^{\prime }\in {\mathfrak{E}}^{+}.$
• the maximal element of ${\mathfrak{E}}^{+}$ is ${\mathcal{E}}_0\left(\psi \right)=\left\{\begin{array}{c}\begin{array}{cc}\mathbf{1},& \psi >0,\\ \mathbf{0},& \psi \le 0.\end{array}\hfill \end{array}\right.$

The MVRN space $(\mathfrak{J},\Psi ,⨂)$ is defined and studied in [21,29]. A triple $(\mathfrak{J},\Psi ,⨂)$ is said to be an MVRN space if for each $\chi ,{\chi }^{\prime }\in \mathfrak{J},$ and $\psi >0,$ we have

(1)

${\Psi }_{\chi }\left(\psi \right)={\mathcal{E}}_0\left(\psi \right),$ iff $\chi =0.$

(2)

${\Psi }_{\upsilon \chi }\left(\psi \right)={\Psi }_{\chi }\left(\frac{\psi }{\left|\upsilon \right|}\right),$ for every $0\ne \upsilon \in \mathbb{C}.$

(3)

${\Psi }_{\chi +{\chi }^{\prime }}(\psi +{\psi }^{\prime })⪰{\Psi }_{\chi }\left(\psi \right)⨂{\Psi }_{{\chi }^{\prime }}\left({\psi }^{\prime }\right)$.

A complete MVRN space is said to be an MVR-Banach (MVRB) space.

2.5. Mittag-Leffler Function and Its Approximations

Consider the two-parameter Mittag-Leffler function

$$\begin{array}{ccc}\hfill {\mathbb{M}}_{{\mathcal{P}}_1,{\mathcal{P}}_2}\left(\chi \right)& =& \sum _{k=0}^{\infty }{\displaystyle \frac{{\chi }^k}{\Gamma ({\mathcal{P}}_{1}k+{\mathcal{P}}_2)}},\hfill \end{array}$$

for ${\mathcal{P}}_1,{\mathcal{P}}_2\in \mathbb{C},$ and $\Re \left({\mathcal{P}}_1\right),\Re \left({\mathcal{P}}_2\right)>0.$

Lemma 1 

([30]). Let $\mathcal{P}>0,{\mathcal{P}}_1\in (0,2),{\mathcal{P}}_2\in \mathbb{C},$ and $\sigma \in \mathbb{R},$ s.t., $\sigma \in (0.5\pi \mathcal{P},min\{\pi ,\pi \mathcal{P}\left\}\right).$ Then, for integer $m\ge 1,$ we obtain

$$\begin{array}{c}\hfill {\mathbb{M}}_{{\mathcal{P}}_1,{\mathcal{P}}_2}\left(\chi \right)=\frac{1}{\mathcal{P}}{\chi }^{\frac{1-{\mathcal{P}}_2}{{\mathcal{P}}_1}}exp({\chi }^{\frac{1}{{\mathcal{P}}_1}})-\sum _{n=1}^m\frac{{\chi }^{-n}}{\Gamma ({\mathcal{P}}_2-{\mathcal{P}}_{1}n)}+{O\left(\right|\chi |}^{-m-1}),\end{array}$$

with $\left|\chi \right|\to \infty$ and $\left|\mathit{arg}\right(\chi \left)\right|<\sigma ,$ and

$$\begin{array}{c}\hfill {\mathbb{M}}_{{\mathcal{P}}_1,{\mathcal{P}}_2}\left(\chi \right)=-\sum _{n=1}^m\frac{{\chi }^{-n}}{\Gamma ({\mathcal{P}}_2-{\mathcal{P}}_{1}n)}+{O\left(\right|\chi |}^{-m-1}),\end{array}$$

with $\left|\chi \right|\to \infty$ and $\sigma \le \left|\mathit{arg}\right(\chi \left)\right|\le \pi .$

In view of Lemma 1 and the derivatives of the two-parameter Mittag-Leffler function, we have

$$\begin{array}{c}\hfill {\chi }^{{\mathcal{P}}_1\nu +{\mathcal{P}}_2-1}{\mathbb{M}}_{{\mathcal{P}}_1,{\mathcal{P}}_2}^{\left(\nu \right)}\left(\gamma {\chi }^{{\mathcal{P}}_1}\right)\simeq {\left(\frac{\partial }{\partial \gamma }\right)}^{\nu }\left[\frac{1}{{\mathcal{P}}_1}{\gamma }^{\frac{1-{\mathcal{P}}_2}{{\mathcal{P}}_1}}exp\left({\gamma }^{\frac{1}{{\mathcal{P}}_1}}\chi \right)\right],\end{array}$$

(3)

with $\chi \to \infty$ and $\left|\arg \right(\chi \left)\right|<\sigma ,$ and

$$\begin{array}{c}\hfill {\chi }^{{\mathcal{P}}_1\nu +{\mathcal{P}}_2-1}{\mathbb{M}}_{{\mathcal{P}}_1,{\mathcal{P}}_2}^{\left(\nu \right)}\left(\gamma {\chi }^{{\mathcal{P}}_1}\right)\simeq {(-1)}^{\nu +1}\left[\frac{\nu !{\gamma }^{-\nu -1}}{\Gamma ({\mathcal{P}}_2-{\mathcal{P}}_1)}{\chi }^{{\mathcal{P}}_2-{\mathcal{P}}_1-1}+\frac{(\nu +1)!{\gamma }^{-\nu -2}}{\Gamma ({\mathcal{P}}_2-2{\mathcal{P}}_1)}{\chi }^{{\mathcal{P}}_2-2{\mathcal{P}}_1-1}\right],\end{array}$$

(4)

with $\chi \to \infty ,$ $\sigma \le \left|\arg \right(\chi \left)\right|\le \pi ,$ and $\nu =0,1,2,\cdots .$

2.6. Fractional Derivatives

2.6.1. Hilfer Derivative

Consider a real interval $({\Xi }_1,{\Xi }_2)$. Let $\delta \left(\chi \right)$ be an increasing and positive monotone function on $({\Xi }_1,{\Xi }_2]$ that has a continuous derivative ${\delta }^{\prime }\left(\chi \right)$ on $({\Xi }_1,{\Xi }_2)$. We define the fractional-order Riemann–Liouville integral with respect to $\delta$ on $[{\Xi }_1,{\Xi }_2]$ as follows:

$$I_{{\Xi }_1^{+}}^{\mathcal{P};\delta }\mathbf{G}\left(\chi \right)={\displaystyle \frac{1}{\Gamma \left(\mathcal{P}\right)}}{\int }_{{\Xi }_1}^{\chi }{\delta }^{\prime }(\Theta ){(\delta \left(\chi \right)-\delta (\Theta ))}^{\mathcal{P}-1}\mathbf{G}(\Theta )d\Theta ,\mathcal{P}>0.$$

Let ${\mathcal{P}}_1\in (\Xi -1,\Xi )$ with $\Xi \in \mathbb{N}$, ${\mathcal{P}}_2\in [0,1]$ and $h,\delta \in C^{\Xi }[{\Xi }_1,{\Xi }_2],$ be two functions, s.t. $\delta$ is increasing and ${\delta }^{\prime }\left(\chi \right)\ne 0,$ for all $\chi \in [{\Xi }_1,{\Xi }_2]$. Then, the $\delta$-Hilfer fractional derivative [21] ${}^{\mathcal{H}}D_{{\Xi }_1^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }(.)$ is defined by

${}^{\mathcal{H}}D_{{\Xi }_1^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }\mathbf{G}\left(\chi \right)=I_{{\Xi }_1^{+}}^{{\mathcal{P}}_2(\Xi -{\mathcal{P}}_1);\delta }{\left({\displaystyle \frac{1}{{\delta }^{\prime }\left(\chi \right)}}{\displaystyle \frac{d}{d\chi }}\right)}^{\Xi }{I}_{{\Xi }_1^{+}}^{(1-{\mathcal{P}}_2)(\Xi -{\mathcal{P}}_1);\delta }\mathbf{G}\left(\chi \right)$.

2.6.2. Conformable Derivative

The conformable derivative of order $\mathcal{P}$ for a given function $\mathbf{G}:[0,\infty )⟶\mathbb{R}$ is given by [31]

$$\begin{array}{c}\hfill D_{\xi }^{\mathcal{P}}\left(\mathbf{G}\right)=\underset{ϵ⟶0}{lim}{\displaystyle \frac{\mathbf{G}(\xi +ϵ{\xi }^{1-\mathcal{P}})-\mathbf{G}\left(\xi \right)}{ϵ}},0<\mathcal{P}⩽1,\xi >0.\end{array}$$

2.6.3. Riemann–Liouville Derivative

The Riemann–Liouville derivative [30] is defined by

$$\begin{array}{c}\hfill {}^{RL}D_{\chi ,{\chi }_0}^{\mathcal{P}}\mathbf{G}\left(\chi \right)=\frac{1}{\Gamma (n-\mathcal{P})}\frac{dn}{d{\chi }^n}{\int }_{{\chi }_0}^{\chi }{(\chi -s)}^{n-\mathcal{P}-1}\mathbf{G}\left(s\right)ds,\end{array}$$

(5)

where $\mathcal{P}\in [n-1,n),n\in \mathbb{N}.$

The Laplace transforms of (5) for ${\chi }_0=0,$ are given by [30]

$$\begin{array}{c}\hfill L\{{}^{RL}D_{\chi ,{\chi }_0}^{\mathcal{P}}\mathbf{G}\left(\chi \right),\rho \}={\rho }^{\mathcal{P}}L\left\{\mathbf{G}\left(\chi \right)\right\}-\sum _{i=0}^{n-1}{\rho }^i{\left[{}^{RL}D_{0,\chi }^{\mathcal{P}-i-1}\mathbf{G}\left(\chi \right)\right]}_{\chi =0},\end{array}$$

where $\mathcal{P}\in [n-1,n),n\in \mathbb{N}.$

2.6.4. Caputo Derivative

The fractional-order Caputo derivative [22] for $\mathbf{G}:[-\mathcal{Y},\infty )\to \mathbb{R}$ is given by

$$\begin{array}{c}\hfill {}^{\mathcal{C}}D_{-\mathcal{Y}}^{\mathcal{P}}\mathbf{G}\left(\chi \right)=\frac{1}{\Gamma (1-\mathcal{P})}{\int }_{-\mathcal{Y}}^{\chi }\frac{{\mathbf{G}}^{\prime }\left(s\right)}{{(\chi -s)}^{\mathcal{P}}}ds,\chi >-\mathcal{Y},\end{array}$$

(6)

where $\mathcal{P}\in (0,1].$

2.7. Fractional-Order Delayed Matrix Sine and Cosine

Here, we introduce the parametric Mittag-Leffler matrices, and then, we present the fractional-order delayed matrix cosine, the fractional-order delayed matrix sine, and some of their properties [32,33,34,35,36,37].

Let $\mathbf{0}$ and I (or $\mathbf{1}$) be the zero and identity matrices, respectively.

Here, we consider the Mittag-Leffler matrices [21] with parameters ${\mathcal{P}}_1,{\mathcal{P}}_2>0,$ and ${\left[\mathbf{H}\right]}_{n\times n}$ which are defined by

$$\begin{array}{ccc}\hfill {\mathbb{M}}_{{\mathcal{P}}_1}\left(\mathbf{H}\right)& =& \sum _{k=0}^{\infty }{\displaystyle \frac{{\mathbf{H}}^k}{\Gamma ({\mathcal{P}}_{1}k+1)}}\hfill \\ & =& I+{\displaystyle \frac{\mathbf{H}}{\Gamma (1+{\mathcal{P}}_1)}}+{\displaystyle \frac{{\mathbf{H}}^2}{\Gamma (1+2{\mathcal{P}}_1)}}+\cdots ,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\mathbb{M}}_{{\mathcal{P}}_1,{\mathcal{P}}_2}\left(\mathbf{H}\right)& =& \sum _{k=0}^{\infty }{\displaystyle \frac{{\mathbf{H}}^k}{\Gamma ({\mathcal{P}}_{1}k+{\mathcal{P}}_2)}}\hfill \\ & =& I+{\displaystyle \frac{\mathbf{H}}{\Gamma ({\mathcal{P}}_1+{\mathcal{P}}_2)}}+{\displaystyle \frac{{\mathbf{H}}^2}{\Gamma (2{\mathcal{P}}_1+{\mathcal{P}}_2)}}+\cdots .\hfill \end{array}$$

Definition 2 

([38]). The fractional-order delayed matrix cosine, and the fractional-order delayed matrix sine of a polynomial of degree $2j\mathcal{P}$ on $\chi \in \left[\right(j-1)\mathcal{Y},j\mathcal{Y})$ identified at the nodes $\chi =j\mathcal{Y}$, $j=0,1,\cdots ,$ are, respectively, given by

$$\begin{array}{c}\hfill {cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}=\left\{\begin{array}{c}\begin{array}{cc}\mathbf{0},& -\infty <\chi <-\mathcal{Y},\\ I,& -\mathcal{Y}\le \chi \le 0,\\ I-{\mathbf{H}}^2\frac{{\chi }^{2\mathcal{P}}}{\Gamma (1+2\mathcal{P})}+\cdots +{(-1)}^j{\mathbf{H}}^{2j}\frac{{(\chi -(j-1)\mathcal{Y})}^{2j\mathcal{P}}}{\Gamma (2j\mathcal{P}+1)},& (j-1)\mathcal{Y}\le \chi <j\mathcal{Y}.\end{array}\hfill \end{array}\right.\end{array}$$

(7)

and

$$\begin{array}{c}\hfill {sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}=\left\{\begin{array}{c}\begin{array}{cc}\mathbf{0},& -\infty <\chi <-\mathcal{Y},\\ \mathbf{H}\frac{{(\chi +\mathcal{Y})}^{\mathcal{P}}}{\Gamma (\mathcal{P}+1)},& -\mathcal{Y}\le \chi \le 0,\\ \mathbf{H}\frac{{(\chi +\mathcal{Y})}^{\mathcal{P}}}{\Gamma (\mathcal{P}+1)}-{\mathbf{H}}^3\frac{{\chi }^{3\mathcal{P}}}{\Gamma (1+3\mathcal{P})}+\cdots +{(-1)}^j{\mathbf{H}}^{2j+1}\frac{{(\chi -(j-1)\mathcal{Y})}^{(2j+1)\mathcal{P}}}{\Gamma \left(\right(2j+1)\mathcal{P}+1)},& (j-1)\mathcal{Y}\le \chi <j\mathcal{Y}.\end{array}\hfill \end{array}\right.\end{array}$$

(8)

Lemma 2. 

For $\chi \in \left[\right(j-1)\mathcal{Y},j\mathcal{Y}],$ and $j,\alpha ,\beta \in \mathbb{R},$ we obtain

$$\begin{array}{c}\hfill \lambda \left(\chi \right):={\int }_{j\mathcal{Y}}^{\chi }{(\chi -s)}^{\alpha }{(s-j\mathcal{Y})}^{\beta }ds={(\chi -j\mathcal{Y})}^{\beta +\alpha +1}\mathbb{B}[\alpha +1,\beta +1],\end{array}$$

in which $\mathbb{B}[\alpha ,\beta ]={\int }_0^1{t}^{\alpha -1}{(1-t)}^{1-\beta }dt$ is the Beta function.

Proof. 

$$\begin{array}{ccc}\hfill \lambda \left(\chi \right)& =& {\int }_0^{\chi -j\mathcal{Y}}{(\chi -j\mathcal{Y}-\varpi )}^{\alpha }{\varpi }^{\beta }d\varpi (\varpi =s-j\mathcal{Y})\hfill \\ & =& {\int }_0^{\chi -j\mathcal{Y}}{(\chi -j\mathcal{Y})}^{\alpha }{(1-\frac{\varpi }{\chi -j\mathcal{Y}})}^{\alpha }{\varpi }^{\beta }d\varpi \hfill \\ & =& {\int }_0^1{(\chi -j\mathcal{Y})}^{\alpha +\beta +1}{(1-\theta )}^{\alpha }{\theta }^{\beta }d\theta (\theta (\chi -j\mathcal{Y})=\theta )\hfill \\ & =& {(\chi -j\mathcal{Y})}^{\beta +\alpha +1}\mathbb{B}[\alpha +1,\beta +1].\hfill \end{array}$$

□

Lemma 3. 

The Caputo derivative of the fractional-order delayed matrix cosine ${cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}$ and the fractional-order delayed matrix sine ${sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}$ are given by

$$\begin{array}{ccc}& & {}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}=-\mathbf{H}{sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y})}^{\mathcal{P}},\hfill \\ & & {}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}{sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}=\mathbf{H}{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}.\hfill \end{array}$$

Proof. 

By repeating the computation in Lemma 2, for every $\chi \in \left[\right(E-1)\mathcal{Y},E\mathcal{Y}]$ and $E\in \mathbb{N},$ we obtain

$$\begin{array}{ccc}& & {}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}\hfill \\ & =& \frac{1}{\Gamma (1-\mathcal{P})}{\int }_{-\mathcal{Y}}^0{(\chi -s)}^{-\mathcal{P}}\Xi ds+\frac{1}{\Gamma (1-\mathcal{P})}{\int }_0^{\mathcal{Y}}{(\chi -s)}^{-\mathcal{P}}[-{\mathbf{H}}^2\frac{s^{2\mathcal{P}-1}}{\Gamma \left(2\mathcal{P}\right)}]ds\hfill \\ & & +\frac{1}{\Gamma (1-\mathcal{P})}{\int }_{\mathcal{Y}}^{2\mathcal{Y}}{(\chi -s)}^{-\mathcal{P}}\left[-{\mathbf{H}}^2\frac{s^{2\mathcal{P}-1}}{\Gamma \left(2\mathfrak{P}\right)}+{\mathbf{H}}^4\frac{{(s-\mathcal{Y})}^{4\mathcal{P}-1}}{\Gamma \left(4\mathcal{P}\right)}\right]ds+\dots \hfill \\ & & +\frac{1}{\Gamma (1-\mathcal{P})}{\int }_{(E-1)\mathcal{Y}}^{\chi }{(\chi -s)}^{-\mathcal{P}}\left[-{\mathbf{H}}^2\frac{s^{2\mathcal{P}-1}}{\Gamma \left(2\mathcal{P}\right)}+\dots +{(-1)}^E{\mathbf{H}}^{2E}\frac{{(s-(E-1)\mathcal{Y})}^{2E\mathcal{P}-1}}{\Gamma \left(2E\mathcal{P}\right)}\right]ds\hfill \end{array}$$

$$\begin{array}{ccc}& =& \frac{1}{\Gamma (1-\mathcal{P})}{\int }_{-\mathcal{Y}}^{\chi }{(\chi -s)}^{-\mathcal{P}}\Xi ds+\frac{1}{\Gamma (1-\mathcal{P})}{\int }_0^{\chi }{(\chi -s)}^{\mathcal{P}}\left[-{\mathbf{H}}^2\frac{s^{2\mathcal{P}-1}}{\Gamma \left(2\mathcal{P}\right)}\right]ds\hfill \\ & & +\frac{1}{\Gamma (1-\mathcal{P})}{\int }_{\mathcal{Y}}^{\chi }{(\chi -s)}^{-\mathcal{P}}\left[{\mathbf{H}}^4\frac{{(s-\mathcal{Y})}^{4\mathcal{P}-1}}{\Gamma \left(4\mathcal{P}\right)}\right]ds+\dots \hfill \\ & & +\frac{1}{\Gamma (1-\mathcal{P})}{\int }_{(E-1)\mathcal{Y}}^{\chi }{(\chi -s)}^{-\mathcal{P}}\left[{(-1)}^E{\mathbf{H}}^{2E}\frac{{(s-(E-1)\mathcal{Y})}^{2E\mathcal{P}-1}}{\Gamma \left(2E\mathcal{P}\right)}\right]ds\hfill \\ & =& -{\mathbf{H}}^2\frac{{\chi }^{\mathcal{P}}}{\Gamma (\mathcal{P}+1)}+-{\mathbf{H}}^4\frac{{(\chi -\mathcal{Y})}^{3\mathcal{P}}}{\Gamma (3\mathcal{P}+1)}+\dots +{(-1)}^E{\mathbf{H}}^{2E}\frac{{(\chi -(E-1)\mathcal{Y})}^{(2E-1)\mathcal{P}}}{\Gamma \left(\right(2E-1)\mathcal{P}+1)}\hfill \\ & =& -\mathbf{H}{sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y})}^{\mathcal{P}}.\hfill \end{array}$$

□

Lemma 4. 

For $\chi \in \left[\right(j-1)\mathcal{Y},j\mathcal{Y}),j\in \mathbb{N},$ and $\overrightarrow{\varphi }>\overrightarrow{0},$ we have that

$$\begin{array}{ccc}& & \Phi ({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}},\overrightarrow{\varphi })⪰\Phi ({\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right),\overrightarrow{\varphi }),\hfill \\ & & \Phi ({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}},\overrightarrow{\varphi })⪰\Phi ({\mathbb{M}}_{\mathcal{P}}\left(\mathbf{H}{(\chi +\mathcal{Y})}^{\mathcal{P}}\right)-{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{(\chi +\mathcal{Y})}^{2\mathcal{P}}\right),\overrightarrow{\varphi }).\hfill \end{array}$$

Proof. 

For every $\overrightarrow{\varphi }>\overrightarrow{0},$ we obtain

$$\begin{array}{ccc}& & \Phi ({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}},\overrightarrow{\varphi })\hfill \\ & & \Phi \left(I+{\mathbf{H}}^2\frac{{\chi }^{2\mathcal{P}}}{\Gamma (2\mathcal{P}+1)}+\cdots +{\mathbf{H}}^{2j}\frac{{\chi }^{2j\mathcal{P}}}{\Gamma (2j\mathcal{P}+1)},\overrightarrow{\varphi }\right)\hfill \\ & & ⪰\Phi \left(\sum _{j=0}^{\infty }\frac{{\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)}^j}{\Gamma (2j\mathcal{P}+1)},\overrightarrow{\varphi }\right)\hfill \\ & & =\Phi ({\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right),\overrightarrow{\varphi }),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & \Phi ({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}},\overrightarrow{\varphi })\hfill \\ & & \Phi \left(\mathbf{H}\frac{{(\chi +\mathcal{Y})}^{\mathcal{P}}}{\Gamma (\mathcal{P}+1)}+{\mathbf{H}}^3\frac{{(\chi +\mathcal{Y})}^{3\mathcal{P}}}{\Gamma (3\mathcal{P}+1)}+\cdots +{\mathbf{H}}^{2j+1}\frac{{(\chi +\mathcal{Y})}^{(2j+1)\mathcal{P}}}{\Gamma \left(\right(2j+1)\mathcal{P}+1)},\overrightarrow{\varphi }\right)\hfill \\ & & ⪰\Phi \left(\sum _{j=0}^{\infty }\frac{{\left(\mathbf{H}{(\chi +\mathcal{Y})}^{\mathcal{P}}\right)}^j}{\Gamma (j\mathcal{P}+1)}-\sum _{j=0}^{\infty }\frac{{\left({\mathbf{H}}^2{(\chi +\mathcal{Y})}^{2\mathcal{P}}\right)}^j}{\Gamma (2j\mathcal{P}+1)},\overrightarrow{\varphi }\right)\hfill \\ & & =\Phi ({\mathbb{M}}_{\mathcal{P}}\left(\mathbf{H}{(\chi +\mathcal{Y})}^{\mathcal{P}}\right)-{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{(\chi +\mathcal{Y})}^{2\mathcal{P}}\right),\overrightarrow{\varphi }).\hfill \end{array}$$

□

2.8. Aggregate Maps

Assume $\mathrm{{\rm Y}}=\mathrm{diag}[{\mathrm{{\rm Y}}}_1,\cdots ,{\mathrm{{\rm Y}}}_n],$ ${\mathrm{{\rm Y}}}_i\in ϵ,$ $1\le i\le n,$ and $n\in \mathbb{N}.$ A mapping ${\mathtt{AG}}^{\left(n\right)}:\mathrm{diag}{M}_n\left(ϵ\right)⟶ϵ$ is called an n-ary aggregation map [22] if ${\mathtt{AG}}^{\left(1\right)}\left(\mathrm{{\rm Y}}\right)=\mathrm{{\rm Y}},$ and

$$\begin{array}{c}\hfill \underset{{\mathrm{{\rm Y}}}_i\in ϵ}{inf}{\mathtt{AG}}^{\left(n\right)}\left(\mathrm{{\rm Y}}\right)=infϵ,\mathrm{and}\underset{{\mathrm{{\rm Y}}}_i\in ϵ}{sup}{\mathtt{AG}}^{\left(n\right)}\left(\mathrm{{\rm Y}}\right)=supϵ.\end{array}$$

Note, for each $\mathrm{{\rm Y}},{\mathrm{{\rm Y}}}^{\prime }\in \mathrm{diag}{M}_n\left(ϵ\right),$ if ${\mathrm{{\rm Y}}}_i\le {\mathrm{{\rm Y}}}_i^{\prime },$ then ${\mathtt{AG}}^{\left(n\right)}\left(\mathrm{{\rm Y}}\right)\le {\mathtt{AG}}^{\left(n\right)}\left({\mathrm{{\rm Y}}}^{\prime }\right).$

Consider the following well-known aggregation functions ${\mathtt{AG}}_i:\mathrm{diag}{M}_n\left({ϵ}^n\right)⟶ϵ,$$1\le i\le 8:$

• Geometric mean functions ${\mathtt{AG}}_1\left(\mathrm{{\rm Y}}\right)={\left({\prod }_{i=1}^n{\mathrm{{\rm Y}}}_i\right)}^{\frac{1}{n}}.$
• Arithmetric mean functions ${\mathtt{AG}}_2\left(\mathrm{{\rm Y}}\right)={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\mathrm{{\rm Y}}}_i.$
• Maximum functions ${\mathtt{AG}}_3\left(\mathrm{{\rm Y}}\right)=max\{{\mathrm{{\rm Y}}}_1,\cdots ,{\mathrm{{\rm Y}}}_n\}.$
• Minimum functions ${\mathtt{AG}}_4\left(\mathrm{{\rm Y}}\right)=min\{{\mathrm{{\rm Y}}}_1,\cdots ,{\mathrm{{\rm Y}}}_n\}.$
• Median of odd numbers ${\mathtt{AG}}_5\left(\mathrm{diag}[{\mathrm{{\rm Y}}}_1,\cdots ,{\mathrm{{\rm Y}}}_{2n-1}]\right)={min}_{\underset{\left|N\right|=n}{N\subseteq [2n-1]}}{max}_{i\in n}{\mathrm{{\rm Y}}}_i.$
• Median of even numbers ${\mathtt{AG}}_6\left(\mathrm{diag}[{\mathrm{{\rm Y}}}_1,\cdots ,{\mathrm{{\rm Y}}}_{2n}]\right)={min}_{\underset{\left|N\right|=n}{N\subseteq \left[2n\right]}}{max}_{i\in n}{\mathrm{{\rm Y}}}_i.$
• Sum functions: ${\mathtt{AG}}_7\left(\mathrm{{\rm Y}}\right)={\sum }_{i=1}^n{\mathrm{{\rm Y}}}_i.$
• Product functions: ${\mathtt{AG}}_8\left(\mathrm{{\rm Y}}\right)={\prod }_{i=1}^n{\mathrm{{\rm Y}}}_i.$

2.9. Alternative Fixed Point Theory [22]

Consider the complete $[0,\infty ]$-valued metric ⋔ on $\omega$ and the strictly contractive mapping $\Lambda$ on $\omega$ with the Lipschitz constant $k<1,$ s.t.

$$⋔(\Lambda {\chi }_1,\Lambda {\chi }_2)\le k⋔({\chi }_1,{\chi }_2),$$

for every ${\chi }_1,{\chi }_2\in \omega .$ If we get a $N_0\in \mathbb{N}$, s.t.

$$⋔({\Lambda }^N{\chi }_1,{\Lambda }^{N+1}{\chi }_1)<\infty ,$$

for every $N\ge N_0$, then, we have the following results for every ${\chi }_1,{\chi }_2\in \omega$:

(1)

The fixed point $\chi \ast$ of $\Lambda$ is the convergence point of $\left\{{\Lambda }^N{\chi }_1\right\}$;

(2)

In the set $\{{\chi }_2\in \omega :⋔({\Lambda }^{N_0}{\chi }_1,{\chi }_2)<\infty \}$, $\chi \ast$ is the unique fixed point of $\Lambda$;

(3)

$(1-k)⋔({\chi }_2,{\chi }^{*})\le ⋔({\chi }_2,\Lambda {\chi }_2)$.

2.10. The First Kudryashov-Type  Method

Here, we propose the process of the first Kudryashov-type technique [39] for a nonlinear PDE:

We consider an NPDE of the following type:

$$\begin{array}{c}\hfill \mathsf{N}(\mathbf{G},D_{{\chi }_2}^{{\mathcal{P}}_1}\mathbf{G},D_{{\chi }_1}^{{\mathcal{P}}_1}\mathbf{G},D_{{\chi }_1}^{{\mathcal{P}}_2}\mathbf{G},D_{{\chi }_1}^{{\mathcal{P}}_1}{D}_{{\chi }_1}^{{\mathcal{P}}_2}\mathbf{G},D_{{\chi }_2}^{{\mathcal{P}}_1}{D}_{{\chi }_2}^{{\mathcal{P}}_2}\mathbf{G},\cdots )=0,0<{\mathcal{P}}_1,{\mathcal{P}}_2⩽1,\end{array}$$

(9)

where $\mathbf{G}=\mathbf{G}({\chi }_1,{\chi }_2).$ Convert the nonlinear PDE (9) into an ODE through

$$\begin{array}{c}\hfill \mu ={\displaystyle \frac{d{\chi }_1^{d{\mathcal{P}}_1}}{\Gamma (1+{\mathcal{P}}_1)}}+{\displaystyle \frac{c{\chi }_2^{c{\mathcal{P}}_2}}{\Gamma (1+{\mathcal{P}}_2)}},\mathbf{G}({\chi }_1,{\chi }_2)=\mathbf{G}\left(\mu \right),\end{array}$$

(10)

in which c and d are fixed. Rewrite (9) as follows:

$$\begin{array}{c}\hfill \tilde{\mathsf{N}}(\mathbf{G},{\mathbf{G}}^{\prime },{\mathbf{G}}^{″},{\mathbf{G}}^{‴},\dots )=0.\end{array}$$

(11)

Assume the general solution of (11) can be expressed as

$$\begin{array}{c}\hfill \mathbf{G}\left(\mu \right)=a_0+a_1\mathbb{k}\left(\mu \right)+a_2{\mathbb{k}}^2\left(\mu \right)+\cdots +a_N{\mathbb{k}}^N\left(\mu \right).\end{array}$$

(12)

where $\underset{\underset{1\le i\le N}{⏟}}{a_i}$ are retrieved later, and the value of $N\in \mathbb{N}$ can be computed through the homogeneous balance principle, and

$$\begin{array}{c}\hfill \mathbb{k}\left(\mu \right)={\displaystyle \frac{1}{1+d{a}^{\mu }}}\end{array}$$

(13)

which satisfies

$$\begin{array}{c}\hfill {\mathbb{k}}^{\prime }\left(\mu \right)=\mathbb{k}\left(\mu \right)(\mathbb{k}\left(\mu \right)-1)ln\left(a\right).\end{array}$$

(14)

According to (11) and (12), a nonlinear system of algebraic type is obtained, and by solving it, solutions of (12) are obtained.

2.11. Gronwall Inequality

Suppose $\alpha \left(\chi \right)\le \beta \left(\chi \right)+{\int }_{{\chi }_0}^{\chi }\gamma \left(\tau \right)\alpha \left(\tau \right)d\tau ,$ for $\chi \in [{\chi }_0,\mathcal{T}),\mathcal{T}\le +\infty ,$ in which all the above functions are continuous on $[{\chi }_0,\mathcal{T}),$ $\gamma \left(\chi \right)\ge 0,$ and $\beta \left(\chi \right)$ is nondecreasing. Then,

$$\alpha \left(\chi \right)\le \beta \left(\chi \right)exp({\int }_{{\chi }_0}^{\chi }\gamma \left(\tau \right)d\tau ),$$

(15)

for every $\chi \in [{\chi }_0,\mathcal{T}).$ (See [40]).

3. Fuzzy Stability Results of (1) for Case 1

Taking into account Case 1 of (1), we have

$${}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\mathbf{G}}_1\left(\chi \right)={\mathbf{G}}_2(\chi ,{\mathbf{G}}_1\left(\chi \right),{}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\mathbf{G}}_1\left(\chi \right)),$$

(16)

$$I_{{\alpha }^{+}}^{{\mathcal{P}}_3;\delta }{\mathbf{G}}_1\left({\alpha }^{+}\right)={\mathbf{G}}_0,{\mathbf{G}}_0\in \mathbb{R},$$

(17)

(see [28,41,42,43,44,45,46,47,48,49,50]). Now, consider the fuzzy inequality below:

$$\begin{array}{ccc}\hfill & & \Phi \left({}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\mathbf{G}}_1\left(\chi \right)-{\mathbf{G}}_2(\chi ,{\mathbf{G}}_1\left(\chi \right),{}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\mathbf{G}}_1\left(\chi \right)),\overrightarrow{\varphi }\right)\hfill \\ & & ⪰\mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_8{\varphi }_8)\right)],\hfill \end{array}$$

(18)

where $\chi \in \mathbb{I}$, $\overrightarrow{\varphi }=({\varphi }_1,\cdots ,{\varphi }_8),$ ${\varphi }_i\in (0,+\infty ),{\mathfrak{S}}_i>0,i=1,\cdots ,8,$ and the fuzzy Fox-type controller $\mathfrak{Z}$ is given by

$$\begin{array}{ccc}\hfill & & \mathfrak{Z}(\chi ,\overrightarrow{\varphi }):=\mathrm{diag}[{}_2\mathbb{H}_1\left[V_1,V_2;N_1;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_1}\right],{}_0\mathbb{H}_0\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_2}\right],\hfill \\ & & {}_0\mathbb{H}_1\left[N_1;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_3}\right],{}_C{}^A\mathbb{H}_D^B\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_4}{|}_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right],\hfill \\ & & {}_1\mathbb{H}_1\left[V_1;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_5}\right],{}_C\mathbb{H}_D\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_6}{|}_{(N_1,M_1),\dots ,(N_D,M_D)}^{(V_1,W_1),\dots ,(V_C,W_C)}\right]\hfill \\ & & {}_C{}^A\mathbb{H}_D^B\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_7}{|}_{(N_1,1),\dots ,(N_D,1)}^{(V_1,1),\dots ,(V_C,1)}\right],\hfill \\ & & {}_C\mathbb{H}_D\left[V_1,\dots ,V_C;N_1,\dots ,N_C;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_8}\right]].\hfill \end{array}$$

(19)

Definition 3. 

The fractional-order Equations (16) and (17) is multistable with respect to

$$\mathit{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,\overrightarrow{\varphi })\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}\left((\chi ,\overrightarrow{\varphi })\right)\right],$$

if there exist ${\mathfrak{S}}_i>0$, s.t., for any ${\overline{\mathfrak{S}}}_i>0$ and each solution $\widehat{\mathbf{G}}\in C(\mathbb{I},\mathbb{R})$ to (18) and $I_{{\alpha }^{+}}^{1-{\mathcal{P}}_3;\delta }\widehat{\mathbf{G}}\left({\alpha }^{+}\right)={\mathbf{G}}_0$, there exist a solution ${\mathbf{G}}_1\in C(\mathbb{I},\mathbb{R})$ to (16) and (17) with

$$\begin{array}{c}\hfill \Phi (\widehat{\mathbf{G}}\left(\chi \right)-{\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })⪰\mathit{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_1{\overline{\mathfrak{S}}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_8{\overline{\mathfrak{S}}}_8{\varphi }_8)\right)],\end{array}$$

for every $\chi \in \mathbb{I},$ and ${\varphi }_i\in (0,+\infty ),i=1,\cdots ,8.$

3.1. Fuzzy Multistability Results for Finite Domains

Here, let $\mathbb{I}:=[\alpha ,\beta ].$

Lemma 5 

([45,46,47]). The fractional-order Equations (16) and (17) are equivalent to

$${\mathbf{G}}_1\left(\chi \right)={\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(\alpha \right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+I_{{\alpha }^{+}}^{{\mathcal{P}}_1;\delta }{\mathcal{U}}_{{\mathbf{G}}_1}\left(\chi \right),$$

(20)

in which ${\mathcal{U}}_{{\mathbf{G}}_1}\in C(\mathbb{I},\mathbb{R})$ satisfies

$${\mathcal{U}}_{{\mathbf{G}}_1}\left(\chi \right)={\mathbf{G}}_2\left(\chi ,{\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(\alpha \right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+I_{{\alpha }^{+}}^{{\mathcal{P}}_1;\delta }{\mathcal{U}}_{{\mathbf{G}}_1}\left(\chi \right),{\mathcal{U}}_{{\mathbf{G}}_1}\left(\chi \right)\right).$$

(21)

Remark 1 

([45,46,47]). Suppose ${\mathbf{G}}_1\in C(\mathbb{I},\mathbb{R})$ is a solution of (18) and $I_{{\alpha }^{+}}^{1-{\mathcal{P}}_3;\delta }{\mathbf{G}}_1\left(\alpha \right)={\mathbf{G}}_0$. Thus, ${\mathbf{G}}_1$ is a solution of

$$\begin{array}{ccc}& & \Phi \left({\mathbf{G}}_1\left(\chi \right)-{\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0-{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left(\tau \right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{{\mathbf{G}}_1}\left(\tau \right)d\tau ,\overrightarrow{\varphi }\right)\hfill \\ & & ⪰\mathit{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_8{\varphi }_8)\right)]\hfill \end{array}$$

in which ${\varphi }_i\in (0,+\infty ),{\mathfrak{S}}_i>0,i=1,\cdots ,8,$ and ${\mathcal{U}}_{{\mathbf{G}}_1}\in C(\mathbb{I},\mathbb{R})$ satisfies (21).

Let us consider the following assumptions:

$\left({\mathcal{E}}_1\right)$${\mathbf{G}}_2:\mathbb{I}\times {\mathbb{R}}^2\to \mathbb{R}$ is continuous.

$\left({\mathcal{E}}_2\right)$ There exists $0<{\mathfrak{P}}_i<1,i=1,\cdots ,8,$ s.t. $I_{{\alpha }^{+}}^{{\mathcal{P}}_3;\delta }{\mathtt{AG}}_i\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_i{\varphi }_i)\right)⪰{\mathtt{AG}}_i\left(\mathfrak{Z}(\chi ,\frac{{\mathfrak{S}}_i}{{\mathfrak{P}}_i}{\varphi }_i)\right),$ for every $\chi \in \mathbb{I},{\mathfrak{S}}_i>0,$ and $\overrightarrow{\varphi }>\overrightarrow{0}$.

$\left({\mathcal{E}}_3\right)$ There exists $0<{\Theta }_1,{\Theta }_2,$ s.t. $\frac{{\mathfrak{P}}_i}{({\Theta }_1+{\Theta }_2)}<1,i=1,\cdots ,8,$ and

$$\begin{array}{c}\hfill \Phi ({\mathbf{G}}_2(\chi ,\kappa ,\upsilon )-{\mathbf{G}}_2(\chi ,\overline{\kappa },\overline{\upsilon }),\overrightarrow{\varphi })⪰\Phi ({\Theta }_1(\kappa -\overline{\kappa }),\overrightarrow{\varphi }))\underset{\mathtt{GTN}}{⨂}\Phi ({\Theta }_2(\upsilon -\overline{\upsilon }),\overrightarrow{\varphi })),\end{array}$$

for each $\kappa ,\upsilon ,\overline{\kappa },\overline{\upsilon }\in \mathbb{R}$, $\chi \in \mathbb{I}$ and $\overrightarrow{\varphi }>\overrightarrow{0}$.

Theorem 1. 

Assume $\left({\mathcal{E}}_1\right),\left({\mathcal{E}}_2\right)$ and $\left({\mathcal{E}}_3\right)$ hold. Then, (16) and (17) have a unique solution $\widehat{\mathbf{G}}$ in $C(\mathbb{I},\mathbb{R}),$ s.t.

$$\widehat{\mathbf{G}}\left(\chi \right)={\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(\alpha \right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+I_{{\alpha }^{+}}^{{\mathcal{P}}_1;\delta }{\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\chi \right),$$

(22)

in which ${\mathcal{U}}_{\widehat{\mathbf{G}}}\in C(\mathbb{I},\mathbb{R})$ is given by

${\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\chi \right)={\mathbf{G}}_2\left(\chi ,{\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(\alpha \right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+I_{{\alpha }^{+}}^{{\mathcal{P}}_1;\delta }{\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\chi \right),{\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\chi \right)\right)$

and for each $\chi \in \mathbb{I}$ and $\overrightarrow{\varphi }>\overrightarrow{0}$,

$$\begin{array}{c}\hfill \Phi ({\mathbf{G}}_1\left(\chi \right)-\widehat{\mathbf{G}}\left(\chi \right),\overrightarrow{\varphi })⪰\mathit{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)],\end{array}$$

(23)

where

$${\mathcal{D}}_i:={(1-{\displaystyle \frac{{\mathfrak{P}}_i}{({\Theta }_1+{\Theta }_2)}})}^{-1},i=1,\cdots ,8.$$

(24)

Proof. 

Consider $\Xi =C(\mathbb{I},\mathbb{R})$ and a mapping $\lambda :{\Xi }^2\to [0,+\infty ],$ given by

$$\begin{array}{ccc}\hfill & & \lambda (\nu ,{\nu }^{\prime })=inf\{({\complement }_1,\cdots ,{\complement }_8)\in {(0,+\infty )}^8:\Phi (\nu \left(\chi \right)-{\nu }^{\prime }\left(\chi \right),\overrightarrow{\varphi })\hfill \\ & & ⪰\mathrm{diag}\left[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,\frac{{\mathfrak{S}}_1}{{\complement }_1}{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,\frac{{\mathfrak{S}}_8}{{\complement }_8}{\varphi }_8)\right)\right],\nu ,{\nu }^{\prime }\in \Xi ,\chi \in \mathbb{I},\overrightarrow{\varphi }>\overrightarrow{0}\}.\hfill \end{array}$$

(25)

We have that the double $(\Xi ,\lambda )$ is a complete generalized metric space (see [46]).

In view of Lemma 5, we have that (16) and (17) are equivalent to (20). Consider $\mathrm{{\rm Y}}:\Xi ⟶\Xi ,$ s.t. for every ${\hslash }_1\in \Xi$,

$$\begin{array}{c}\hfill \mathrm{{\rm Y}}\left({\hslash }_1\left(\chi \right)\right)={\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{{\hslash }_1}\left(\tau \right)d\tau \end{array}$$

(26)

in which ${\mathcal{U}}_{{\hslash }_1}\in C(\mathbb{I},\mathbb{R})$ is defined by

$${\mathcal{U}}_{{\hslash }_1}\left(\chi \right)={\mathbf{G}}_2(\chi ,{\hslash }_1\left(\chi \right),{\mathcal{U}}_{{\hslash }_1}\left(\chi \right)).$$

(27)

We now show that the self–mapping $\mathrm{{\rm Y}}$ is contractive on $\Xi$. Consider $\mathrm{{\rm Y}}:\Xi ⟶\Xi$ given in (26). Let ${\hslash }_1,{\hslash }_2\in C(\mathbb{I},\mathbb{R}),{\mathbb{k}}_i\in [0,+\infty ],i=1,\dots ,8$, and $\lambda ({\hslash }_1\left(\chi \right),{\hslash }_2\left(\chi \right))\le ({\mathbb{k}}_1,\cdots ,{\mathbb{k}}_8).$ For every $\chi \in \mathbb{I}$ and $\overrightarrow{\varphi }>\overrightarrow{0}$, we obtain

$$\begin{array}{ccc}\hfill & & \Phi (\mathrm{{\rm Y}}\left({\hslash }_1\left(\chi \right)\right)-\mathrm{{\rm Y}}\left({\hslash }_2\left(\chi \right)\right),\overrightarrow{\varphi })\hfill \\ & & ⪰\Phi \left({\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}({\mathcal{U}}_{{\hslash }_1}\left(\tau \right)-{\mathcal{U}}_{{\hslash }_2}\left(\tau \right))d\tau ,\overrightarrow{\varphi }\right)\hfill \end{array}$$

(28)

in which ${\mathcal{U}}_{{\hslash }_j}\left(\chi \right)={\mathbf{G}}_2(\chi ,{\hslash }_j\left(\chi \right),{\mathcal{U}}_{{\hslash }_j}\left(\chi \right)),j=1,2.$ Making use of $\left({\mathcal{E}}_3\right),$ for every $\chi \in \mathbb{I}$ and $\overrightarrow{\varphi }\in {(0,+\infty )}^8$, we obtain

$$\begin{array}{ccc}& & \Phi ({\mathcal{U}}_{{\hslash }_1}\left(\chi \right)-{\mathcal{U}}_{{\hslash }_2}\left(\chi \right),\overrightarrow{\varphi })⪰\Phi ({\Theta }_1({\hslash }_1\left(\chi \right)-{\hslash }_2\left(\chi \right)),\overrightarrow{\varphi })\underset{\mathtt{GTN}}{⨂}\Phi ({\Theta }_2({\mathcal{U}}_{{\hslash }_1}\left(\chi \right)-{\mathcal{U}}_{{\hslash }_2}\left(\chi \right)),\overrightarrow{\varphi }),\hfill \end{array}$$

which can be written as

$$\begin{array}{ccc}\hfill & & \Phi ({\mathcal{U}}_{{\hslash }_1}\left(\mathfrak{F}\right)-{\mathcal{U}}_{{\hslash }_2}\left(\chi \right),\overrightarrow{\varphi })⪰\Phi (({\Theta }_1+{\Theta }_2)({\hslash }_1\left(\chi \right)-{\hslash }_2\left(\chi \right)),\overrightarrow{\varphi }).\hfill \end{array}$$

(29)

In view of Remark 1, (28) and (29), we obtain

$$\begin{array}{ccc}& & \Phi (\mathrm{{\rm Y}}\left({\hslash }_1\left(\chi \right)\right)-\mathrm{{\rm Y}}\left({\hslash }_2\left(\chi \right)\right),\overrightarrow{\varphi })\hfill \\ & ⪰& \Phi \left(\frac{{\Theta }_1+{\Theta }_2}{\Gamma \left({\mathcal{P}}_1\right)}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}({\hslash }_1\left(\tau \right)-{\hslash }_2\left(\tau \right))d\tau ,\overrightarrow{\varphi }\right)\hfill \\ & ⪰& {\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}\hfill \\ & & \times \mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}\left(\chi ,\frac{({\Theta }_1+{\Theta }_2){\mathfrak{S}}_1}{{\mathbb{k}}_1}{\varphi }_1\right)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}\left(\chi ,\frac{({\Theta }_1+{\Theta }_2){\mathfrak{S}}_8}{{\mathbb{k}}_8}{\varphi }_8\right)\right]d\tau \hfill \\ & ⪰& \mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}\left(\chi ,\frac{({\Theta }_1+{\Theta }_2){\mathfrak{S}}_1}{{\mathfrak{P}}_1{\mathbb{k}}_1}{\varphi }_1\right)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}\left(\chi ,\frac{({\Theta }_1+{\Theta }_2){\mathfrak{S}}_8}{{\mathfrak{P}}_8{\mathbb{k}}_8}{\varphi }_8\right)\right],\hfill \end{array}$$

which infers

$$\begin{array}{ccc}\hfill \lambda (\mathrm{{\rm Y}}\left({\hslash }_1\left(\chi \right)\right)-\mathrm{{\rm Y}}\left({\hslash }_2\left(\chi \right)\right))& \le & \left({\displaystyle \frac{{\mathfrak{P}}_1}{({\Theta }_1+{\Theta }_2)}},\cdots ,{\displaystyle \frac{{\mathfrak{P}}_8}{({\Theta }_1+{\Theta }_2)}}\right)\lambda ({\hslash }_1\left(\chi \right)-{\hslash }_2\left(\chi \right)).\hfill \end{array}$$

Thus, we conclude the contractive property of $\mathrm{{\rm Y}}$, because ${\displaystyle \frac{{\mathfrak{P}}_i}{({\Theta }_1+{\Theta }_2)}}<1$, $i=1,\dots ,8$.

Assume ${\mathbf{G}}_1\in \Xi$. We now prove $\lambda (\mathrm{{\rm Y}}{\mathbf{G}}_1,{\mathbf{G}}_1)<\underset{\underset{8}{⏟}}{(\infty ,\cdots ,\infty )}$. Based on (18) and Remark 1, we obtain

$$\begin{array}{ccc}& & \Phi (\mathrm{{\rm Y}}\left({\mathbf{G}}_1\left(\chi \right)\right)-{\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })\hfill \\ & ⪰& \Phi \left({\mathbf{G}}_1\left(\chi \right)-{\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0-{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{{\mathbf{G}}_1}\left(\tau \right)d\tau ,\overrightarrow{\varphi }\right)\hfill \\ & ⪰& \mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathfrak{S}}_8{\varphi }_8)\right)],\hfill \end{array}$$

for each $\overrightarrow{\varphi }\in {(0,+\infty )}^8,{\mathfrak{S}}_i>0,i=1,\dots ,8,$ and $\chi \in \mathbb{I}$. Thus, we conclude that $\lambda (\mathrm{{\rm Y}}{\mathbf{G}}_1,{\mathbf{G}}_1)\le \underset{\underset{8}{⏟}}{(1,\cdots ,1)}$. In view of the alternative fixed point theory, we can find $\widehat{\mathbf{G}}\in \Xi ,$ s.t. the following applies:

(1) $\widehat{\mathbf{G}}$ is a fixed point of $\mathrm{{\rm Y}}$, i.e.,

$$\begin{array}{ccc}& & \mathrm{{\rm Y}}\left(\widehat{\mathbf{G}}\left(\chi \right)\right)\hfill \\ & =& {\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\tau \right)d\tau \hfill \end{array}$$

(30)

in which ${\mathcal{U}}_{\widehat{\mathbf{G}}}\in C(\mathbb{I},\mathbb{R})$ is given by

$${\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\chi \right)={\mathbf{G}}_2\left(\chi ,{\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+I_{{\alpha }^{+}}^{{\mathcal{P}}_1;\delta }{\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\chi \right),{\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\chi \right)\right),$$

(31)

which is unique in the set ${\Xi }^{\ast }=\{\hslash \in \Xi :\lambda (\mathrm{{\rm Y}}{\mathbf{G}}_1,\hslash )<\underset{\underset{8}{⏟}}{(\infty ,\cdots ,\infty )}\}.$

(2) $\lambda ({\mathrm{{\rm Y}}}^m\left({\mathbf{G}}_1\right),\widehat{\mathbf{G}})\to \underset{\underset{8}{⏟}}{(0,\cdots ,0)},$ as $m\to \infty$.

(3) We obtain

$$\begin{array}{ccc}\hfill \lambda ({\mathbf{G}}_1,\widehat{\mathbf{G}})& \le & \underset{\underset{8}{⏟}}{(\frac{1}{1-{\mathfrak{P}}_1({\Theta }_1+{\Theta }_2)},\cdots ,\frac{1}{1-{\mathfrak{P}}_8({\Theta }_1+{\Theta }_2)})}\lambda (\mathrm{{\rm Y}}{\mathbf{G}}_1,{\mathbf{G}}_1)\hfill \\ & \le & \underset{\underset{8}{⏟}}{(\frac{1}{1-{\mathfrak{P}}_1({\Theta }_1+{\Theta }_2)},\cdots ,\frac{1}{1-{\mathfrak{P}}_8({\Theta }_1+{\Theta }_2)}),}\hfill \end{array}$$

which infers

$$\begin{array}{c}\hfill \Phi ({\mathbf{G}}_1\left(\chi \right)-\widehat{\mathbf{G}}\left(\chi \right),\overrightarrow{\varphi })⪰\mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)],\end{array}$$

(32)

where

$${\mathcal{D}}_i:=\frac{1}{1-\frac{{\mathfrak{P}}_i}{({\Theta }_1+{\Theta }_2)}},i=1,\cdots ,8,$$

(33)

for each $\chi \in \mathbb{I}$ and $\overrightarrow{\varphi }\in {(0,+\infty )}^8$. We now show the fixed point in ${\Xi }^{\ast }$ is unique. Let $\tilde{\mathbf{G}}\in \Xi$ satisfy (22) and (23). We prove $\tilde{\mathbf{G}}=\widehat{\mathbf{G}}$ and $\tilde{\mathbf{G}}\in {\Xi }^{\ast }$. According to (22), we obtain

$$\tilde{\mathbf{G}}\left(\chi \right)={\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{\tilde{\mathbf{G}}}\left(\tau \right)d\tau ,$$

(34)

in which ${\mathcal{U}}_{\tilde{\mathbf{G}}}\in C(\mathbb{I},\mathbb{R})$ is defined as

$${\mathcal{U}}_{\tilde{\mathbf{G}}}\left(\chi \right)={\mathbf{G}}_2\left(\chi ,{\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+I_{{\alpha }^{+}}^{{\mathcal{P}}_1;\delta }{\mathcal{U}}_{\tilde{\mathbf{G}}}\left(\chi \right),{\mathcal{U}}_{\tilde{\mathbf{G}}}\left(\chi \right)\right),$$

(35)

and so

$$\mathrm{{\rm Y}}\left(\tilde{\mathbf{G}}\left(\chi \right)\right)={\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\Xi }_{\tilde{\mathbf{G}}}\left(\tau \right)d\tau .$$

(36)

Now, we prove

$$\tilde{\mathbf{G}}\in \{\hslash \in \Xi :\lambda (\mathrm{{\rm Y}}\left({\mathbf{G}}_1\right),\hslash )<\underset{\underset{8}{⏟}}{(\infty ,\cdots ,\infty )}\},$$

i.e., $\lambda (\mathrm{{\rm Y}}\left({\mathbf{G}}_1\right),\tilde{\mathbf{G}})<\underset{\underset{8}{⏟}}{(\infty ,\cdots ,\infty )}$. From (23) we have

$$\begin{array}{ccc}\hfill & & \Phi ({\mathbf{G}}_1\left(\chi \right)-\tilde{\mathbf{G}}\left(\chi \right),\overrightarrow{\varphi })⪰\mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)],\hfill \end{array}$$

(37)

where ${\mathcal{D}}_i,i=1,\cdots ,8$ are given in (33), for each $\chi \in \mathbb{I}$ and $\overrightarrow{\varphi }\in {(0,+\infty )}^8$.

Based on the triangle inequality, (18), (36) and (37), and Remark 1, we obtain

$$\begin{array}{ccc}& & \Phi (\mathrm{{\rm Y}}\left({\mathbf{G}}_1\left(\chi \right)\right)-\tilde{\mathbf{G}}\left(\chi \right),\overrightarrow{\varphi })\hfill \\ & & =\Phi ({\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0\hfill \\ & & +{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{{\mathbf{G}}_1}\left(\tau \right)d\tau +{\mathbf{G}}_1\left(\chi \right)-{\mathbf{G}}_1\left(\chi \right)-\tilde{\mathbf{G}}\left(\chi \right),\overrightarrow{\varphi })\hfill \\ & & ⪰\Phi \left({\displaystyle \frac{{(\delta \left(\chi \right)-\delta \left(0\right))}^{{\mathcal{P}}_1-1}}{\Gamma \left({\mathcal{P}}_1\right)}}{\mathbf{G}}_0+{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{{\mathbf{G}}_1}\left(\tau \right)d\tau -{\mathbf{G}}_1\left(\chi \right),{\displaystyle \frac{\overrightarrow{\varphi }}{2}}\right)\hfill \\ & & \underset{\mathtt{GTN}}{⨂}\Phi ({\mathbf{G}}_1\left(\chi \right)-\tilde{\mathbf{G}}\left(\chi \right),\frac{\overrightarrow{\varphi }}{2})\hfill \\ & & ⪰\mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,2{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,2{\mathfrak{S}}_8{\varphi }_8)\right)]\hfill \\ & & \underset{\mathtt{GTN}}{⨂}\mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,2{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,2{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)]\hfill \\ & & ⪰\mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,2max\{1,{\mathcal{D}}_1\}{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,2max\{1,{\mathcal{D}}_8\}{\mathfrak{S}}_8{\varphi }_8)\right)],\hfill \end{array}$$

for each $\varphi \in \mathbb{I}$ and $\overrightarrow{\varphi }>\overrightarrow{0}$. This infers $\lambda (\mathrm{{\rm Y}}{\mathbf{G}}_1,\tilde{\mathbf{G}})\le (2max\{1,{\mathcal{D}}_1\},\cdots ,2max\{1,{\mathcal{D}}_8\})<\infty$, then, $\tilde{\mathbf{G}}\in {\Xi }^{\ast }$. Here, we conclude the existence, uniqueness and the multistability property of solutions of fractional-order Equations (16) and (17).

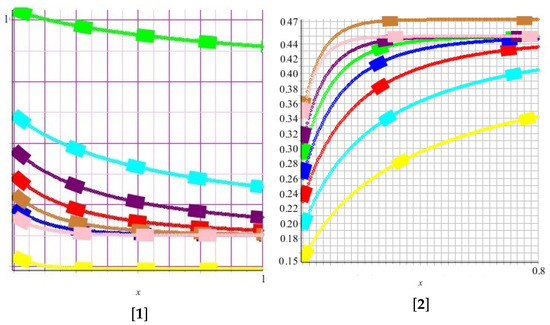
The plots of the aggregate special functions ${\mathtt{AG}}_i\left(\mathfrak{Z}\right),i=1,\dots ,8$ are shown in the sub-figure [1] of Figure 1. As you can observe, ${\mathtt{AG}}_4\left(\mathfrak{Z}\right)$ (yellow) and ${\mathtt{AG}}_3\left(\mathfrak{Z}\right)$ (green) include the lowest and highest values, respectively, and ${\mathtt{AG}}_i\left(\mathfrak{Z}\right),i=1,2,5,6,7,8$ are placed between them. Therefore, this infers that ${\mathtt{AG}}_4\left(\mathfrak{Z}\right)$ can present a better approximation for the governing fractional-order system than others. Thus, based on (32), we obtain

$$\begin{array}{ccc}& & \mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)]\hfill \\ & & ⪰\mathrm{diag}[{\mathtt{AG}}_4\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_4\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)].\hfill \end{array}$$

Figure 1. [1] displays the plots of aggregation maps ${\mathtt{AG}}_i\left(\mathfrak{Z}\right),i=1,\dots ,8$, in which the minimum aggregation map ${\mathtt{AG}}_4\left(\mathfrak{Z}\right)$ and the maximum aggregation map ${\mathtt{AG}}_3\left(\mathfrak{Z}\right)$ are shown in yellow and green colors, respectively, and the rest are in between. [2] displays the plots of aggregation map ${\mathtt{AG}}_4$ on special functions given in the the main diagonal of square matrix $\mathfrak{Z},$ in which the diagram of $\mathbb{H}$-Fox function and the Wright function are displayed in yellow and brown colors, and the rest are in between.

The plots of ${\mathtt{AG}}_4$ on special functions given in the the main diagonal of square matrix $\mathfrak{Z}$ are shown in the sub-figure [2] of Figure 1. As you can see, the diagram of the $\mathbb{H}$-Fox function ${}_C{}^A\mathbb{H}_D^B\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\varphi }_4}{|}_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]$ (yellow) can present a better approximation than the other special functions. Then, we can conclude that

$$\begin{array}{ccc}& & \mathrm{diag}[{\mathtt{AG}}_4\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_4\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)]\hfill \\ & & ⪰\mathrm{daig}\left[{}_C{}^A\mathbb{H}_D^B\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1}{|}_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right],\cdots ,{}_C{}^A\mathbb{H}_D^B\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8}{|}_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]\right].\hfill \end{array}$$

This means the governing fractional-order system is Fox-type stable with respect to Fox’s $\mathbb{H}$ function.

In the Table 1 below, we present some numerical results for (19). As mentioned earlier, the Fox function shows an optimal error estimate compared to the others.

Table 1. Numerical results for $\varphi =0.05,{\mathcal{P}}_1=0.5,$ and $\delta (.)=exp(.)$.

$\mathit{\chi }$	(0, 0.025)	(0.025, 0.050)	(0.050, 0.075)	(0.075, 0.100)
${}_0\mathbb{H}_0\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }\right]$	0.0317	0.0620	0.0829	0.0857
${}_0\mathbb{H}_1\left[N_1;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }\right]$	0.0286	0.0579	0.0764	0.0810
${}_1\mathbb{H}_1\left[V_1;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }\right]$	0.0214	0.0548	0.0705	0.0789
${}_2\mathbb{H}_1\left[V_1,V_2;N_1;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }\right]$	0.0198	0.0413	0.0507	0.0696
${}_C\mathbb{H}_D\left[V_1,\dots ,V_C;N_1,\dots ,N_C;\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }\right]$	0.0129	0.0364	0.0489	0.0601
${}_C\mathbb{H}_D\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }{|}_{(N_1,M_1),\dots ,(N_D,M_D)}^{(V_1,W_1),\dots ,(V_C,W_C)}\right]$	0.0107	0.0207	0.0360	0.0549
${}_C{}^A\mathbb{H}_D^B\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }{|}_{(N_1,1),\dots ,(N_D,1)}^{(V_1,1),\dots ,(V_C,1)}\right]$	0.0095	0.0199	0.0317	0.0501
${}_C{}^A\mathbb{H}_D^B\left[\frac{{-|\delta \left(\chi \right)-\delta \left(0\right)|}^{{\mathcal{P}}_1}}{\varphi }{|}_{{(N_j,M_j)}_{1,D}}^{{(V_j,W_j)}_{1,C}}\right]$	0.0048	0.0076	0.0221	0.0449

□

3.2. Fuzzy Multi-Stability Results for Unbounded Domains

Here, let $\mathsf{S}=C\left(\mathbb{I}\right),$ in which $\mathbb{I}:=\mathbb{R}.$

Theorem 2. 

Suppose $\left({\mathcal{E}}_1\right)$, $\left({\mathcal{E}}_2\right)$ and $\left({\mathcal{E}}_3\right)$ are satisfied. If ${\mathbf{G}}_1$ in $\mathsf{S}$ satisfies (18) and also $I_{{\alpha }^{+}}^{1-{\mathcal{P}}_3;\delta }{\mathbf{G}}_1\left({\alpha }^{+}\right)={\mathbf{G}}_0$, then, there is a unique function $\widehat{\mathbf{G}}$ satisfying (16) and (17), s.t. (23) is satisfied for each $\chi \in \mathbb{R}$.

Proof. 

For all $n\in \mathbb{N},$ and $\mathfrak{I}>0,$ we let ${\mathbb{J}}_n=[\mathfrak{I}-n,\mathfrak{I}+n].$ As stated in Theorem 1, there is a unique function ${\widehat{\mathbf{G}}}_n\in C({\mathbb{J}}_n,\mathbb{R}),$ s.t.

$${}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\widehat{\mathbf{G}}}_n\left(\chi \right)={\mathbf{G}}_2(\chi ,{\widehat{\mathbf{G}}}_n\left(\chi \right),{}^{\mathcal{H}}D_{{\alpha }^{+}}^{{\mathcal{P}}_1,{\mathcal{P}}_2;\delta }{\widehat{\mathbf{G}}}_n\left(\chi \right)),\chi \in {\mathbb{J}}_n,$$

(38)

$$I_{{\alpha }^{+}}^{1-{\mathcal{P}}_3;\delta }{\widehat{\mathbf{G}}}_n\left({\alpha }^{+}\right)={\mathbf{G}}_0,{\mathbf{G}}_0\in \mathbb{R},$$

(39)

and

$$\begin{array}{ccc}\hfill & & \Phi ({\widehat{\mathbf{G}}}_n\left(\chi \right)-{\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })⪰\mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)],\hfill \end{array}$$

(40)

where ${\mathcal{D}}_i:={(1-\frac{{\mathfrak{P}}_i}{({\Theta }_1+{\Theta }_2)})}^{-1}$ for each $\chi \in {\mathbb{J}}_n,{\mathfrak{S}}_i,{\mathfrak{P}}_i,{\varphi }_i>0,i=1,\dots ,8$. The uniqueness of ${\widehat{\mathbf{G}}}_n$ infers that if $\chi \in {\mathbb{J}}_n,$ then,

$${\widehat{\mathbf{G}}}_n\left(\chi \right)={\widehat{\mathbf{G}}}_{n+1}\left(\chi \right)={\widehat{\mathbf{G}}}_{n+2}\left(\chi \right)=\cdots .$$

(41)

Define $n\left(\chi \right)\in \mathbb{N}$ as $n\left(\chi \right)=min\{n\in \mathbb{N}|\chi \in {\mathbb{J}}_n\}.$ In addition, define a function $\widehat{\mathbf{G}}$, given by $\widehat{\mathbf{G}}\left(\chi \right)={\widehat{\mathbf{G}}}_{n\left(\chi \right)}\left(\chi \right).$ We claim that $\widehat{\mathbf{G}}\in \mathsf{S}$. For ${\chi }_1\in \mathbb{R},$ we consider the integer $n_1=n\left({\chi }_1\right).$ Then, ${\chi }_1$ belongs to the interior of ${\mathbb{J}}_{n_1+1}$ and there is an $ϵ>0,$ s.t. $\widehat{\mathbf{G}}\left(\chi \right)={\widehat{\mathbf{G}}}_{n_1+1}\left(\chi \right),$ for each $\chi$ with ${\chi }_1-ϵ<\chi <{\chi }_1+ϵ$. We now prove $\widehat{\mathbf{G}}$ satisfies (16), (17) and (23) for each $\chi \in \mathbb{R}.$ For each $\chi \in \mathbb{R},$ we consider the integer $n\left(\chi \right).$ Thus, it infers $\chi \in {\mathbb{J}}_{n\left(\chi \right)}$ and also, it infers from (38) and (39) that for ${\mathcal{U}}_{\widehat{\mathbf{G}}},{\mathcal{U}}_{{\widehat{\mathbf{G}}}_{n\left(\chi \right)}}\in \mathsf{S},$ defined as (31), we obtain

$$\begin{array}{ccc}& \widehat{\mathbf{G}}\left(\chi \right)& ={\widehat{\mathbf{G}}}_{n\left(\chi \right)}\left(\chi \right)\hfill \\ & & ={\displaystyle \frac{{(\delta \left(\mathfrak{F}\right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{{\widehat{\mathbf{G}}}_{n\left(\chi \right)}}\left(\tau \right)d\tau \hfill \\ & & ={\displaystyle \frac{{(\delta \left(\mathfrak{F}\right)-\delta \left(0\right))}^{{\mathcal{P}}_3-1}}{\Gamma \left({\mathcal{P}}_3\right)}}{\mathbf{G}}_0+{\displaystyle \frac{1}{\Gamma \left({\mathcal{P}}_1\right)}}{\int }_0^{\chi }{\delta }^{\prime }\left({\mathcal{P}}_1\right){(\delta \left(\chi \right)-\delta \left(\tau \right))}^{{\mathcal{P}}_1-1}{\mathcal{U}}_{\widehat{\mathbf{G}}}\left(\tau \right)d\tau ,\hfill \end{array}$$

(42)

where the equality above remains true because $n\left(\tau \right)\le n\left(\chi \right)$ for all $\tau \in {\mathbb{J}}_{n\left(\chi \right)},$ and it infers from (41) that $\widehat{\mathbf{G}}\left(\tau \right)={\widehat{\mathbf{G}}}_{n\left(\tau \right)}\left(\tau \right)={\widehat{\mathbf{G}}}_{n\left(\chi \right)}\left(\tau \right).$ Since $\widehat{\mathbf{G}}\left(\chi \right)={\widehat{\mathbf{G}}}_{n\left(\chi \right)}\left(\chi \right)$ and $\chi \in {\mathbb{J}}_{n\left(\chi \right)},$ for all $\chi \in \mathbb{R}$ and $\overrightarrow{\varphi }\in {(0,+\infty )}^8,$ (40) infers that

$$\begin{array}{ccc}\hfill \Phi (\widehat{\mathbf{G}}\left(\chi \right)-{\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })& =& \Phi ({\widehat{\mathbf{G}}}_{n\left(\chi \right)}\left(\chi \right)-{\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })\hfill \\ & ⪰& \mathrm{diag}[{\mathtt{AG}}_1\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_1{\mathfrak{S}}_1{\varphi }_1)\right),\cdots ,{\mathtt{AG}}_8\left(\mathfrak{Z}(\chi ,{\mathcal{D}}_8{\mathfrak{S}}_8{\varphi }_8)\right)].\hfill \end{array}$$

Finally, we prove $\widehat{\mathbf{G}}$ is unique. Let $\tilde{\mathbf{G}}\in \mathsf{S}$ be another function, which satisfies (16), (17) and (23) for each $\chi \in \mathbb{R}.$ Since $\widehat{\mathbf{G}}{|}_{{\mathbb{J}}_{n\left(\chi \right)}}(={\widehat{\mathbf{G}}}_{n\left(\chi \right)})$ and $\tilde{\mathbf{G}}{|}_{{\mathbb{J}}_{n\left(\chi \right)}}$ both satisfy (16), (17) and (23), for each $\chi \in {\mathbb{J}}_{n\left(\chi \right)},$ the uniqueness of ${\widehat{\mathbf{G}}}_{n\left(\chi \right)}=\widehat{\mathbf{G}}{|}_{{\mathbb{J}}_{n\left(\chi \right)}}$ infers that

$$\widehat{\mathbf{G}}\left(\chi \right)=\widehat{\mathbf{G}}{{|}_{{\mathbb{J}}_{n\left(\chi \right)}}\left(\chi \right)=\tilde{\mathbf{G}}|}_{{\mathbb{J}}_{n\left(\chi \right)}}\left(\chi \right)=\tilde{\mathbf{G}}\left(\chi \right),$$

as required. □

4. Results of (1) for Case 2

Taking into account Case 2 of (1), we consider the following conformable time-modified nonlinear Schrödinger equation (CTFMNLSE) [51,52,53,54]:

$$\mathrm{i}{D}_{{\chi }_2}^{\mathcal{P}}{\mathbf{G}}_1+{\sigma }_1{\left({\mathbf{G}}_1\right)}_{{\chi }_1{\chi }_1}+{\sigma }_2|{\mathbf{G}}_1{|}^2{\mathbf{G}}_1-\mathrm{i}{\delta }_1{\left({\mathbf{G}}_1\right)}_{{\chi }_1{\chi }_1{\chi }_1}-\mathrm{i}{\delta }_2{\mathbf{G}}_1^2{\left({\mathbf{G}}_1\right)}_{{\chi }_1}^{\ast }+\mathrm{i}{\delta }_3{\left|{\mathbf{G}}_1\right|}^2{\left({\mathbf{G}}_1\right)}_{{\chi }_1}-{\delta }_4{\mathbf{G}}_1=0,$$

(43)

where $0<\mathcal{P}\le 1,$ ${\sigma }_1={\displaystyle \frac{{\Xi }_0}{8{\Omega }_0^2(-3cos\left(\theta \right)+2)}},{\sigma }_2={\displaystyle \frac{-{\Xi }_0{\Omega }_0^2}{2}}$, ${\delta }_1={\displaystyle \frac{{\Xi }_{0}cos\left(\theta \right)}{16{\Omega }_0^3(-5{cos}^2\left(\theta \right)-6)}}$, ${\delta }_2={\displaystyle \frac{{\Xi }_0{\Omega }_{0}cos\left(\theta \right)}{4}},{\delta }_3={\displaystyle \frac{3{\Xi }_0{\Omega }_0}{2}},{\delta }_4={\Omega }_0{\left|{\mathbf{G}}_1\right|}_{{\chi }_1}^2{|}_{{\chi }_1=0}$, and ${\Omega }_0$ is the wave number and ${\Xi }_0$ is the frequency of the carrier wave.

The original applications of CTFMNLSE are to model the water wave propagation in ocean engineering and study small-amplitude gravity waves on the surface of water.

We start with

$${\mathbf{G}}_1({\chi }_1,{\chi }_2)=\mathbf{G}\left(\mu \right){\mathrm{e}}^{\mathrm{i}\mathcal{Y}}$$

(44)

where $\mu =\eta ({\chi }_1-{\displaystyle \frac{\rho }{\mathcal{P}}}{\chi }_2^{\mathcal{P}})$ and $\mathcal{Y}=-\omega {\chi }_1+{\displaystyle \frac{\varsigma }{\mathcal{P}}}{\chi }_2^{\mathcal{P}}+\epsilon$, and $\epsilon$ is the phase constant, $\varsigma$ is the frequency and $\omega$ is the wave number. Setting (44) in (43), we get the imaginary and real parts as

$${\eta }^2({\sigma }_1-3{\delta }_1\omega ){\mathbf{G}}^{″}+({\sigma }_2+({\delta }_2+{\delta }_3)\omega ){\mathbf{G}}^3+(-\varsigma -{\sigma }_1{\omega }^2+{\delta }_1{\omega }^3-{\delta }_4)\mathbf{G}=0,$$

(45)

and

$$(3{\delta }_1{\omega }^2-\rho -2{\sigma }_1\omega ){\mathbf{G}}^{\prime }-{\delta }_1{\eta }^2{\mathbf{G}}^{‴}+({\delta }_3-{\delta }_2){\mathbf{G}}^2{\mathbf{G}}^{\prime }=0.$$

(46)

By integrating (45) and taking the constant equal to zero, we obtain

$$3(3{\delta }_1{\omega }^2-\rho -2{\sigma }_1\omega )\mathbf{G}-3{\delta }_1{\eta }^2{\mathbf{G}}^{″}+({\delta }_3-{\delta }_2){\mathbf{G}}^3=0.$$

(47)

From (45) and (47), we have that

$${\displaystyle \frac{{\omega }^3{\delta }_1-\varsigma -{\sigma }_1{\omega }^2-{\delta }_4}{3(3{\delta }_1{\omega }^2-\rho -2{\sigma }_1)\omega }}={\displaystyle \frac{{\sigma }_1-3{\delta }_1\omega }{-3{\delta }_1}}={\displaystyle \frac{\omega {\delta }_2+\omega {\delta }_3+{\sigma }_2}{{\delta }_3-{\delta }_2}}.$$

(48)

From the above, we have that

$$\rho =-{\displaystyle \frac{{\delta }_1\varsigma +{\delta }_1{\delta }_4+2\omega {({\sigma }_1-2{\delta }_1\omega )}^2}{{\sigma }_1-3{\delta }_1\omega }},$$

$$\omega ={\displaystyle \frac{{\sigma }_1({\delta }_2-{\delta }_3)-3{\sigma }_2{\delta }_1}{6{\delta }_1{\delta }_2}}.$$

Rewrite (45) into the following form:

$${\mathbf{G}}^{″}+c_1{\mathbf{G}}^3-c_2\mathbf{G}=0$$

(49)

or

$${\mathbf{G}}^{″}=c_2\mathbf{G}-c_1{\mathbf{G}}^3$$

(50)

where $c_1={\displaystyle \frac{{\sigma }_2+({\delta }_2+{\delta }_3)\omega }{{\eta }^2({\sigma }_1-3{\delta }_1\omega )}}$ and $c_2=-{\displaystyle \frac{-\varsigma -{\sigma }_1{\omega }^2+{\delta }_1{\omega }^3-{\delta }_4}{{\eta }^2({\sigma }_1-3{\delta }_1\omega )}}$.

Application of the First Kudryashov-Type Method

Balancing ${\mathbf{G}}^{″}$ in (50) with ${\mathbf{G}}^3$, we obtain the balancing number $3N=N+2$ or $N=1.$

Suppose the solution of (50) can be given by

$$\begin{array}{c}\hfill \mathbf{G}\left(\mu \right)=a_0+a_1\mathbb{k}\left(\mu \right),\end{array}$$

(51)

in which $a_0,$ and $a_1$ are constants to be determined later.

Making use of (14), (47) and (51), we obtain

$$\begin{array}{ccc}& & 9{\omega }^2{a}_0{\delta }_1-a_0^3{\delta }_2+a_0^3{\delta }_3-6\omega a_0{\sigma }_1-3\rho a_0=0,\hfill \\ & & -3ln{\left(a\right)}^2{\eta }^2{a}_1{\delta }_1+9{\omega }^2{a}_1{\delta }_1+9{\omega }^2{a}_1{\delta }_1-3{\delta }_2{a}_0^2{a}_1+3{\delta }_3{a}_0^2{a}_1-6\omega a_1{\sigma }_1-3\rho a_1=0,\hfill \\ & & 9ln{\left(a\right)}^2{\eta }^2{a}_1{\delta }_1-3{\delta }_2{a}_0{a}_1^2+3{\delta }_3{a}_0{a}_1^2=0,\hfill \\ & & -6ln{\left(a\right)}^2{\eta }^2{a}_1{\delta }_1-{\delta }_2{a}_1^3+{\delta }_3{a}_1^3=0.\hfill \end{array}$$

Solving the above system, we obtain

$$\begin{array}{ccc}& & \rho ={\displaystyle \frac{1}{2}}ln{\left(a\right)}^2{\eta }^2{\delta }_1+3{\delta }_1{\omega }^2-2{\sigma }_1\omega \hfill \\ & & a_0=\pm {\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-(6{\delta }_2-6{\delta }_3){\delta }_1}\eta ln\left(a\right)}{{\delta }_2-{\delta }_3}},\hfill \\ & & a_1=\pm {\displaystyle \frac{\sqrt{-(6{\delta }_2-6{\delta }_3){\delta }_1}\eta ln\left(a\right)}{{\delta }_2-{\delta }_3}}.\hfill \end{array}$$

Based on the above results, the following solution to CTFMNLSE (43) is obtained by

$$\begin{array}{ccc}\hfill {\mathbf{G}}_1({\chi }_1,{\chi }_2)& =& [\pm {\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-(6{\delta }_2-6{\delta }_3){\delta }_1}\eta ln\left(a\right)}{{\delta }_2-{\delta }_3}}\pm {\displaystyle \frac{\sqrt{-(6{\delta }_2-6{\delta }_3){\delta }_1}\eta ln\left(a\right)}{{\delta }_2-{\delta }_3}}\times \hfill \\ & & {\displaystyle \frac{1}{1+d{a}^{\eta ({\chi }_1-{\displaystyle \frac{{\displaystyle \frac{1}{2}}ln{\left(a\right)}^2{\eta }^2{\delta }_1+3{\delta }_1{\omega }^2-2{\sigma }_1\omega }{\mathcal{P}}}{\chi }_2^{\mathcal{P}})}}}]e^{i(-\omega {\chi }_1+{\displaystyle \frac{\varsigma }{\mathcal{P}}}{\chi }_2^{\mathcal{P}}+\epsilon )}.\hfill \end{array}$$

(52)

The Figure 2, Figure 3 and Figure 4 display the plots of (52), for specific values and $\alpha =0,1,0.2,0.3,\cdots ,0.9.$

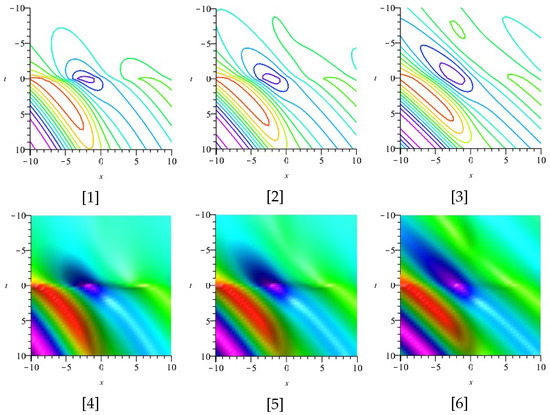
Figure 2. The [1]–[6] display the plots of the imaginary parts of (52), for $\alpha =0.7,0.8,0.9$.

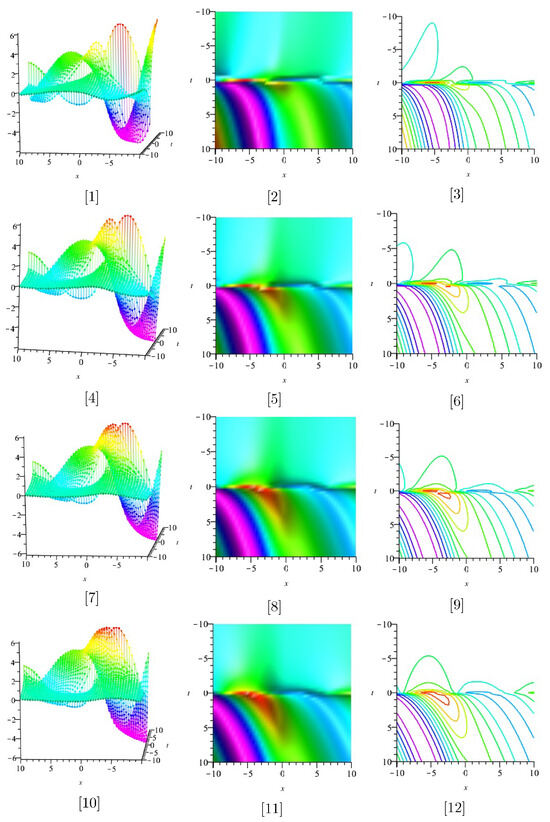
Figure 3. The [1]–[12] display the plots of the real parts of (52), for $\alpha =0.2,0.3,0.4,0.5$.

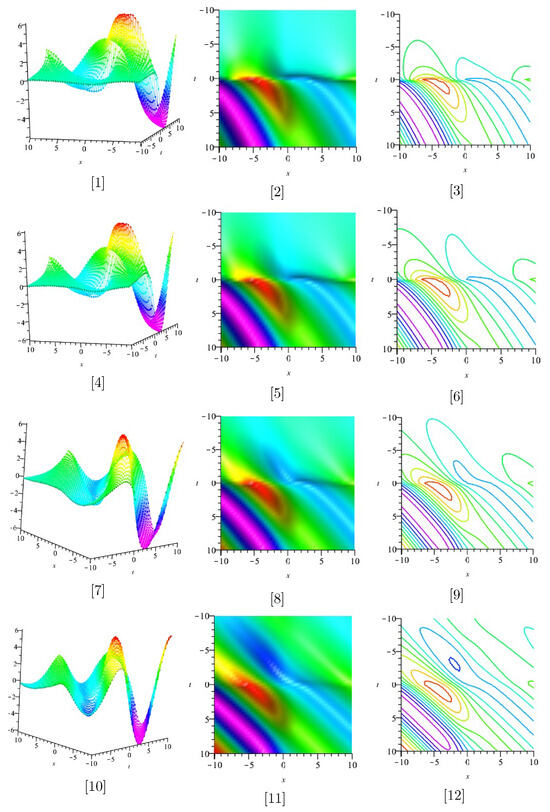
Figure 4. The [1]–[12] display the plots of the real parts of (52), for $\alpha =0.6,0.7,0.8,0.9$.

5. Fuzzy Asymptotic Stability Results of (1) for Case 3

Taking into account Case 3 of (1), we have that

$$\begin{array}{ccc}& & {}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}}{\mathbf{G}}_1\left(\chi \right)={\mathbf{H}}_1{\mathbf{G}}_1\left(\chi \right),\chi >{\chi }_0,\hfill \end{array}$$

(53)

$$\begin{array}{ccc}& & {}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}-\ell }{\mathbf{G}}_1\left(\chi \right){|}_{\chi ={\chi }_0}={\mathbf{G}}_{1(\ell -1)},\ell =1,2,\hfill \end{array}$$

(54)

where $1<\mathcal{P}<2,$ ${\mathbf{H}}_1\in {\mathbb{R}}^{n\times n},$ and ${\mathbf{G}}_1\in {\mathbb{R}}^n.$

Definition 4 

([22]). The zero solution of fractional-order Equations (53) and (54) is stable if there is a positive $M,$ s.t. $\Phi ({\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })⪰\Phi (M,\overrightarrow{\varphi })$ for every $\chi >{\chi }_0$ and $\overrightarrow{\varphi }>0.$ The zero solution of fractional-order Equations (53) and (54) is asymptotically stable if it is stable and $\Phi ({\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })\to \mathbf{1},$ as $\chi \to +\infty ,$ for every $\overrightarrow{\varphi }>0.$

Lemma 6 

([36]). Consider the square complex matrix ${\mathbf{H}}_1.$ Then, there is an invertible matrix $\alpha ,$ s.t. ${\alpha }^{-1}{\mathbf{H}}_1\alpha ={\beta }_1\oplus \cdots \oplus {\beta }_j,$ in which ${\beta }_{ı}$ are the Jordan blocks of matrix ${\mathbf{H}}_1,$ with the eigenvalues of ${\mathbf{H}}_1$ on the diagonal.

Note that $\mathrm{spec}\left(\mathbf{H}\right)$ means the spectrum of the matrix $\mathbf{H}$. In the next theorem, we consider a relationship between stability, asymptotically stability and critical eigenvalues [55].

Theorem 3. 

The fractional–order differential Equations (53) and (54) is asymptotically stable if and only if $\left|\mathit{arg}\right(\mathit{spec}\left({\mathbf{H}}_1\right)\left)\right|>0.5\pi \mathcal{P}.$ In addition, the fractional–order differential Equations (53) and (54) is stable if and only if either it is asymptotically stable, or those critical eigenvalues that satisfy $\left|\mathit{arg}\right(\mathit{spec}\left({\mathbf{H}}_1\right)\left)\right|=0.5\pi \mathcal{P},$ have the same geometric and algebraic multiplicities.

Proof. 

Making use of the Laplace transform, the solution of fractional-order Equations (53) and (54) can be expressed as

$$\begin{array}{ccc}\hfill {\mathbb{G}}_1\left(\chi \right)& =& {(\chi -{\chi }_0)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{10}+{(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-1}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{11}\hfill \\ & =& \sum _{\ell =0}^1{(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{1\ell }.\hfill \end{array}$$

(55)

With respect to ${\mathbf{H}}_1,$ there is an invertible matrix $\alpha$, s.t.

$${\mathbf{H}}_1=\alpha \beta {\alpha }^{-1}=\alpha ({\beta }_1,\cdots ,{\beta }_j){\alpha }^{-1},$$

(56)

in view of Lemma 6, where the Jordan block

$${\beta }_{ı}={\left[\begin{array}{cccc}{\gamma }_{ı}& 1& & \\ & {\gamma }_{ı}& \ddots & \\ & & \ddots & 1\\ & & & {\gamma }_{ı}\end{array}\right]}_{n_{ı}\times n_{ı}},$$

$\mathit{ı}=1,\cdots ,j,$${\sum }_{\mathit{ı}=1}^j{n}_{\mathit{ı}}=n,$ and ${\gamma }_{\mathit{ı}}\in \mathbb{C}$ are the eigenvalue of ${\mathbf{H}}_1.$ Inserting (56) in ${(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{1\ell },$ we get

$$\begin{array}{ccc}& & {(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right)\hfill \\ & =& {(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\alpha \sum _{\mathbb{k}=0}^{\infty }\frac{\mathrm{diag}[{\beta }_1^{\mathbb{k}},\cdots ,{\beta }_j^{\mathbb{k}}]{(\chi -{\chi }_0)}^{\mathcal{P}\mathbb{k}}}{\Gamma (\mathcal{P}\mathbb{k}+\mathcal{P}-\ell )}\hfill \\ & =& {(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\alpha \mathrm{diag}[{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\beta }_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right),\dots ,{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\beta }_j{(\chi -{\chi }_0)}^{\mathcal{P}}\right)]{\alpha }^{-1},\hfill \end{array}$$

(57)

in which $\ell =1,2.$ The matrix ${(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\beta }_{ı}{(\chi -{\chi }_0)}^{\mathcal{P}}\right)$ can be given by

$$\begin{array}{c}\hfill \mathcal{Y}\left({\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left(\gamma {(\chi -{\chi }_0)}^{\mathcal{P}}\right)\right){|}_{\gamma ={\gamma }_{ı}},\end{array}$$

(58)

in which

$$\begin{array}{c}\hfill \mathcal{Y}={(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\left[\begin{array}{ccccc}1& \frac{\partial }{\partial \gamma }& \frac{1}{2!}{\left(\frac{\partial }{\partial \gamma }\right)}^2& \cdots & \frac{1}{(n_{ı}-1)!}{\left(\frac{\partial }{\partial \gamma }\right)}^{n_{ı}-1}\\ & 1& \frac{\partial }{\partial \gamma }& \cdots & \frac{1}{(n_{ı}-2)!}{\left(\frac{\partial }{\partial \gamma }\right)}^{n_{ı}-2}\\ & & \ddots & \ddots & ⋮\\ & & & 1& \frac{\partial }{\partial \gamma }\\ & & & & 1\end{array}\right].\end{array}$$

(59)

The non–zero elements of ${(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\beta }_{ı}{(\chi -{\chi }_0)}^{\mathfrak{P}}\right)$ can be written by

$$\begin{array}{c}\hfill {(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\frac{1}{(\nu -1)!}\left\{{(\frac{\partial }{\partial \beta })}^{\nu -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }(\gamma {(\chi -{\chi }_0)}^{\mathfrak{P}})\right\}{|}_{\beta ={\beta }_{ı}},(\nu =1,2,\cdots ,n_{ı}).\end{array}$$

(60)

Now, consider the following cases:

(1) If ${\gamma }_{ı}=0,$ then (60) is equal to $\lambda :=\frac{{(\chi -{\chi }_0)}^{\nu \mathcal{P}-\ell -1}}{\Gamma (\nu \mathcal{P}-\ell )},$ and $\lambda \to \infty ,$ when $\chi \to \infty ,$ for every $\ell =0,$ and $\nu \ge 1.$ Then, $\Phi ({\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })\cancel{\to }\mathbf{1},$ when $\chi \to \infty ,$ for every $\overrightarrow{\varphi }>\overrightarrow{0}.$

(2) If ${\gamma }_{ı}\ne 0,$ we have the following cases:

(2-i) If $|\arg \left(\mathrm{spec}\left({\mathbf{H}}_1\right)\right)|=|\arg \left({\gamma }_{ı}\right)|>0.5\pi \mathcal{P},$ and $\chi \to \infty ,$ then, based on (4), (60) is equivalent to ${(-1)}^{\nu }[\frac{{\gamma }_{ı}^{-\nu }{(\chi -{\chi }_0)}^{-\ell -1}}{\Gamma (-\ell )}+\frac{\nu {\gamma }_{ı}^{-\nu -1}{(\chi -{\chi }_0)}^{-\ell -\mathcal{P}-1}}{\Gamma (-\ell -\mathcal{P})}].$ Then, $\Phi ({\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })\to \mathbf{1},$ when $\chi \to \infty ,$ for every $\overrightarrow{\varphi }>\overrightarrow{0}.$

(2-ii) If $|\arg \left(\mathrm{spec}\left({\mathbf{H}}_1\right)\right)|=|\arg \left({\gamma }_{ı}\right)|<0.5\pi \mathcal{P},$ and $\chi \to \infty ,$ based on (3), we obtain

$$\begin{array}{ccc}\hfill & & {(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\frac{1}{(\nu -1)!}\left\{{(\frac{\partial }{\partial \beta })}^{\nu -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left(\gamma {(\chi -{\chi }_0)}^{\mathfrak{P}}\right)\right\}{|}_{\beta ={\beta }_{ı}}\hfill \\ & =& \frac{{(\chi -{\chi }_0)}^{\nu \mathcal{P}-\ell -1}}{(\nu -1)!}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }^{(\nu -1)}\left(\gamma {(\chi -{\chi }_0)}^{\mathfrak{P}}\right){|}_{\beta ={\beta }_{ı}}\hfill \\ & \approx & \frac{1}{(\nu -1)!}\left\{{(\frac{\partial }{\partial \beta })}^{\nu -1}\left[\frac{1}{\mathcal{P}}{\gamma }^{\frac{1-\mathcal{P}+\ell }{\mathcal{P}}}exp\left({\gamma }^{\frac{1}{\mathcal{P}}}(\chi -{\chi }_0)\right)\right]\right\}{|}_{\beta ={\beta }_{ı}}\hfill \\ & =& \frac{1}{(\nu -1)!}\{\frac{(1+\ell -\mathcal{P})(1+\ell -2\mathcal{P})\cdots (1+\ell -(\nu -1\left)\mathcal{P}\right)}{{\mathcal{P}}^{\nu }}{\gamma }_{ı}^{\frac{1+\ell -\nu \mathcal{P}}{\mathcal{P}}}+\cdots \hfill \\ & & +\frac{\frac{\nu (\nu -1)}{2}-(\nu -1)(\mathcal{P}-\ell )-\frac{(\nu -1)(\nu -2)\mathcal{P}}{2}}{{\mathcal{P}}^{\nu }}\hfill \\ & & \times {\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell -1}{\mathcal{P}}}{(\chi -{\chi }_0)}^{\nu -2}+\frac{1}{{\mathcal{P}}^{\nu }}{\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell }{\mathcal{P}}}{(\chi -{\chi }_0)}^{\nu -1}\}exp({\gamma }_{ı}^{\frac{1}{\mathcal{P}}}(\chi -{\chi }_0)),\hfill \end{array}$$

(61)

then,

$$\begin{array}{ccc}& & \Phi \left({(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\frac{1}{(\nu -1)!}\left\{{(\frac{\partial }{\partial \beta })}^{\nu -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left(\gamma {(\chi -{\chi }_0)}^{\mathfrak{P}}\right)\right\}{|}_{\beta ={\beta }_{ı}},\overrightarrow{\varphi }\right)\hfill \\ & ⪰& \Phi \left(\frac{1}{(\nu -1)!}\right\{\frac{(1+\ell -\mathcal{P})(1+\ell -2\mathcal{P})\cdots (1+\ell -(\nu -1\left)\mathcal{P}\right)}{{\mathcal{P}}^{\nu }}{\gamma }_{ı}^{\frac{1+\ell -\nu \mathcal{P}}{\mathcal{P}}}+\cdots \hfill \\ & & +\frac{\frac{\nu (\nu -1)}{2}-(\nu -1)(\mathcal{P}-\ell )-\frac{(\nu -1)(\nu -2)\mathcal{P}}{2}}{{\mathcal{P}}^{\nu }}\hfill \\ & & \left.\times ,{\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell -1}{\mathcal{P}}},{(\chi -{\chi }_0)}^{\nu -2},+,\frac{1}{{\mathcal{P}}^{\nu }},{\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell }{\mathcal{P}}},{(\chi -{\chi }_0)}^{\nu -1}\right\},\frac{\overrightarrow{\varphi }}{exp\left(|{\gamma }_{ı}{|}^{\frac{1}{\mathcal{P}}}cos\left(\frac{\arg \left({\gamma }_{ı}\right)}{\mathcal{P}}\right)(\chi -{\chi }_0)\right)})\hfill \\ & \cancel{\to }& 1,\mathrm{as}\chi \to \infty ,\hfill \end{array}$$

for every $\nu =1,2,\cdots ,n_{ı}.$ Note that $cos\left(\frac{\arg \left({\gamma }_{ı}\right)}{\mathcal{P}}\right)>0,$ for $\frac{\arg \left({\gamma }_{ı}\right)}{\mathcal{P}}<0.5\pi .$ Thus, $\Phi ({\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })=\Phi ({\sum }_{\ell =0}^1{(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{1\ell },\overrightarrow{\varphi })\cancel{\to }\mathbf{1},(\chi \to \infty ).$

(2-iii) Let $|\arg \left(\mathrm{spec}\left({\mathbf{H}}_1\right)\right)|=|\arg \left({\gamma }_{ı}\right)|=0.5\pi \mathcal{P},$ and ${\gamma }_{ı}=r(isin\left(0.5\pi \mathcal{P}\right)+cos\left(0.5\pi \mathcal{P}\right)),$ where $r:=|{\gamma }_{ı}|.$ Now, we have two cases:

(2-iii-a) Suppose the critical eigenvalue ${\gamma }_{\mathit{ı}}$ has the same geometric and algebraic multiplicities. In this case, ${\beta }_{ı}$ is a diagonal matrix. Making use of (58), we obtain

$$\begin{array}{c}\hfill {(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\beta }_{ı}{(\chi -{\chi }_0)}^{\mathcal{P}}\right)={(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\gamma }_{ı}{(\chi -{\chi }_0)}^{\mathcal{P}}\right)\mathrm{diag}[1,\cdots ,1].\end{array}$$

(62)

If $\left|\arg \right(\gamma ı\left)\right|=0.5\pi \mathcal{P},$ based on (3), we obtain

$$\Phi ({(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\gamma }_{ı}{(\chi -{\chi }_0)}^{\mathcal{P}}\right),\overrightarrow{\varphi })⪰\Phi (r^{(1+\ell -\mathcal{P}){\mathcal{P}}^{-1}},\mathcal{P}\overrightarrow{\varphi }),(\chi \to \infty ).$$

Thus, the solution of (53) and (54) is stable.

(2-iii-b) Suppose the geometric multiplicity of the critical eigenvalue is not equal to the algebraic multiplicity. Here, ${\beta }_{ı}$ is a Jordan block matrix and ${(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\beta }_{ı}{(\chi -{\chi }_0)}^{\mathcal{P}}\right)$ is the same as (58). Thus, according to (61), the nondiagonal elements of ${(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\beta }_{ı}{(\chi -{\chi }_0)}^{\mathcal{P}}\right),$ can be given by

$$\begin{array}{ccc}& & {(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\frac{1}{(\nu -1)!}\left\{{(\frac{\partial }{\partial \beta })}^{\nu -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left(\gamma {(\chi -{\chi }_0)}^{\mathfrak{P}}\right)\right\}{|}_{\beta ={\beta }_{ı}}\hfill \\ & \simeq & \frac{1}{(\nu -1)!}\{\frac{(1+\ell -\mathcal{P})(1+\ell -2\mathcal{P})\cdots (1+\ell -(\nu -1\left)\mathcal{P}\right)}{{\mathcal{P}}^{\nu }}{\gamma }_{ı}^{\frac{1+\ell -\nu \mathcal{P}}{\mathcal{P}}}+\cdots \hfill \\ & & +\frac{\frac{\nu (\nu -1)}{2}-(\nu -1)(\mathcal{P}-\ell )-\frac{(\nu -1)(\nu -2)\mathcal{P}}{2}}{{\mathcal{P}}^{\nu }}\hfill \\ & & \times {\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell -1}{\mathcal{P}}}{(\chi -{\chi }_0)}^{\nu -2}+\frac{1}{{\mathcal{P}}^{\nu }}{\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell }{\mathcal{P}}}{(\chi -{\chi }_0)}^{\nu -1}\}exp(i{r}^{\frac{1}{\mathcal{P}}}(\chi -{\chi }_0)),\nu =2,\cdots ,n_{ı}.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}& & \Phi \left({(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}\frac{1}{(\nu -1)!}\left\{{(\frac{\partial }{\partial \beta })}^{\nu -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left(\gamma {(\chi -{\chi }_0)}^{\mathfrak{P}}\right)\right\}{|}_{\beta ={\beta }_{ı}},\overrightarrow{\varphi }\right)\hfill \\ & ⪰& \Phi \left(\frac{1}{(\nu -1)!}\right\{\frac{(1+\ell -\mathcal{P})(1+\ell -2\mathcal{P})\cdots (1+\ell -(\nu -1\left)\mathcal{P}\right)}{{\mathcal{P}}^{\nu }}{\gamma }_{ı}^{\frac{1+\ell -\nu \mathcal{P}}{\mathcal{P}}}+\cdots \hfill \\ & & +\frac{\frac{\nu (\nu -1)}{2}-(\nu -1)(\mathcal{P}-\ell )-\frac{(\nu -1)(\nu -2)\mathcal{P}}{2}}{{\mathcal{P}}^{\nu }}\hfill \\ & & \times {\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell -1}{\mathcal{P}}}{(\chi -{\chi }_0)}^{\nu -2}+\frac{1}{{\mathcal{P}}^{\nu }}{\gamma }_{ı}^{\frac{\nu (1-\mathcal{P})+\ell }{\mathcal{P}}}{(\chi -{\chi }_0)}^{\nu -1}\},\overrightarrow{\varphi })\hfill \\ & \cancel{\to }& \mathbf{1},\mathrm{as}\chi \to \infty ,\hfill \end{array}$$

for every $\nu =2,\cdots ,n_{ı}.$ Thus, $\Phi \left({\mathbf{G}}_1\left(\chi \right)\right),\overrightarrow{\varphi })\cancel{\to }\mathbf{1},$ as $\chi \to \infty .$

□

6. Fuzzy Asymptotic Stability Results of (1) for Case 4

Taking into account Case 4 of (1), we have that

$$\begin{array}{ccc}& & {}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}}{\mathbf{G}}_1\left(\chi \right)={\mathbf{H}}_1{\mathbf{G}}_1\left(\chi \right)+{\mathbf{G}}_3\left(\chi \right){\mathbf{G}}_1\left(\chi \right),\chi >{\chi }_0,\hfill \end{array}$$

(63)

$$\begin{array}{ccc}& & {}^{RL}D_{{\chi }_0,\chi }^{\mathcal{P}-\ell }{\mathbf{G}}_1\left(\chi \right){|}_{\chi ={\chi }_0}={\mathbf{G}}_{1(\ell -1)},\ell =1,2,\hfill \end{array}$$

(64)

where $1<\mathcal{P}<2,$ ${\mathbf{H}}_1\in {\mathbb{R}}^{n\times n},$ ${\mathbf{G}}_1\in {\mathbb{R}}^n,$ and ${\mathbf{G}}_3:[{\chi }_0,\infty )\to {\mathbb{R}}^{n\times n}$ is a continuous matrix.

Theorem 4. 

Consider the matrix ${\mathbf{H}}_1,$ s.t., $\left|\mathit{spec}\right({\mathbf{H}}_1\left)\right|\ne 0,$ and $\left|\mathit{arg}\right(\mathit{spec}\left({\mathbf{H}}_1\right)\left)\right|\ge 0.5\pi \mathcal{P}.$ Let the critical eigenvalues that satisfy $\left|\mathit{arg}\right(\mathit{spec}\left({\mathbf{H}}_1\right)\left)\right|=0.5\pi \mathcal{P}$ have the same geometric and algebraic multiplicities, and ${\int }_{{\chi }_0}^{\infty }{\mathbf{G}}_3\left(\chi \right)d\chi$ be bounded. Thus, the zero solution of (63) and (64) is stable.

Proof. 

Making use of the Laplace transform, the solution of (63) and (64) can be given by

$$\begin{array}{ccc}\hfill {\mathbf{G}}_1\left(\chi \right)& =& {(\chi -{\chi }_0)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{10}+{(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-1}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{11}\hfill \\ & & +{\int }_{{\chi }_0}^{\chi }{(\chi -s)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -s)}^{\mathcal{P}}\right){\mathbf{G}}_3\left(s\right){\mathbf{G}}_1\left(s\right)ds\hfill \\ & =& \sum _{\ell =0}^1{(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{1\ell }\hfill \\ & & +{\int }_{{\chi }_0}^{\chi }{(\chi -s)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -s)}^{\mathcal{P}}\right){\mathbf{G}}_3\left(s\right){\mathbf{G}}_1\left(s\right)ds.\hfill \end{array}$$

(65)

In view of the Gronwall inequality (15), we obtain

$$\begin{array}{ccc}\hfill {\mathbf{G}}_1\left(\chi \right)& \le & \sum _{\ell =0}^1{(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{1\ell }\hfill \\ & & exp\left({\int }_{{\chi }_0}^{\chi }{(\chi -s)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -s)}^{\mathcal{P}}\right){\mathbf{G}}_3\left(s\right)ds\right).\hfill \end{array}$$

According to the proof of Theorem 3, ${(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right),\ell =0,1$ is bounded. Thus, there is positive $M_{\ell },$ s.t. $\Phi \left({(\chi -{\chi }_0)}^{\mathcal{P}-\ell -1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-\ell }\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right),\overrightarrow{\varphi }\right)⪰\Phi (1,\frac{\overrightarrow{\varphi }}{M_{\ell }}),\ell =0,1.$ Therefore, we have that

$$\begin{array}{ccc}\hfill & & \Phi ({\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })\hfill \\ & ⪰& \Phi ({(\chi -{\chi }_0)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{10},\hfill \\ & & \frac{\overrightarrow{\varphi }}{2exp\left({\int }_{{\chi }_0}^{\chi }{(\chi -s)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -s)}^{\mathcal{P}}\right){\mathbf{G}}_3\left(s\right)ds\right)})\hfill \\ & & ⨂\Phi ({(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbb{M}}_{\mathcal{P},\mathcal{P}-1}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right){\mathbf{G}}_{11},\hfill \\ & & \frac{\overrightarrow{\varphi }}{2exp\left({\int }_{{\chi }_0}^{\chi }{(\chi -s)}^{\mathcal{P}-1}{\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -s)}^{\mathcal{P}}\right){\mathbf{G}}_3\left(s\right)ds\right)})\hfill \\ & ⪰& \Phi \left({\mathbf{G}}_{10},\frac{\overrightarrow{\varphi }}{2M_{0}exp\left(M_0{\int }_{{\chi }_0}^{\chi }{\mathbf{G}}_3\left(s\right)ds\right)}\right)⨂\Phi \left({\mathbf{G}}_{11},\frac{\overrightarrow{\varphi }}{2M_{1}exp\left(M_0{\int }_{{\chi }_0}^{\chi }{\mathbf{G}}_3\left(s\right)ds\right)}\right).\hfill \end{array}$$

(66)

Thus, $\Phi ({\mathbf{G}}_1\left(\chi \right),\overrightarrow{\varphi })$ is bounded and then the zero solution of (63) and (64) is stable. □

Theorem 5. 

Consider the matrix ${\mathbf{H}}_1,$ s.t. $\left|\mathit{spec}\right({\mathbf{H}}_1\left)\right|\ne 0,$ and $\left|\mathit{arg}\right(\mathit{spec}\left({\mathbf{H}}_1\right)\left)\right|>0.5\pi \mathcal{P}.$ Let ${\mathbf{G}}_3\left(\chi \right)=O{(\chi -{\chi }_0)}^{\kappa },$ $\kappa \in (-1,1-\mathcal{P}),$ for $\chi >{\chi }_0>0.$ Thus, the zero solution of (63) and (64) is asymptotically stable.

Proof. 

Based on the proof of Theorem 3, we obtain

$$\begin{array}{ccc}& & \Phi (\chi ,\overrightarrow{\varphi })\hfill \\ & ⪰& \Phi \left({(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbf{G}}_{10},\frac{\overrightarrow{\varphi }}{3L_1}\right)⨂\Phi \left({(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbf{G}}_{11},\frac{\overrightarrow{\varphi }}{3L_2}\right)\hfill \\ & & \Phi \left({\int }_{{\chi }_0}^{\chi }{(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbf{G}}_3\left(s\right){\mathbf{G}}_1\left(s\right)ds,\frac{\overrightarrow{\varphi }}{3L_1}\right),\hfill \end{array}$$

(67)

in which $L_1,L_2,$ are positive s.t. $\Phi ((\chi -{\chi }_0){\mathbb{M}}_{\mathcal{P},\mathcal{P}}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right),\overrightarrow{\varphi })⪰\Phi (L_1,\overrightarrow{\varphi })$ and $\Phi ({\mathbb{M}}_{\mathcal{P},\mathcal{P}-1}\left({\mathbf{H}}_1{(\chi -{\chi }_0)}^{\mathcal{P}}\right),\overrightarrow{\varphi })⪰\Phi (L_2,\overrightarrow{\varphi }).$ Making use of the proof of Theorem 4, we have

$$\begin{array}{ccc}& & \Phi \left({\int }_{{\chi }_0}^{\chi }{(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbf{G}}_3\left(s\right){\mathbf{G}}_1\left(s\right)ds,\frac{\overrightarrow{\varphi }}{3L_1}\right)\hfill \\ & ⪰& \Phi \left({\mathbf{G}}_{10}{\int }_{{\chi }_0}^{\chi }{(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbf{G}}_3\left(s\right)exp\left(L_1{\int }_{{\chi }_0}^s{(s-E)}^{\mathcal{P}-2}{\mathbf{G}}_3\left(E\right)dE\right)ds,\frac{\overrightarrow{\varphi }}{6L_1{M}_0}\right)\hfill \\ & & ⨂\Phi \left({\mathbf{G}}_{11}{\int }_{{\chi }_0}^{\chi }{(\chi -{\chi }_0)}^{\mathcal{P}-2}{\mathbf{G}}_3\left(s\right)exp\left(L_1{\int }_{{\chi }_0}^s{(s-E)}^{\mathcal{P}-2}{\mathbf{G}}_3\left(E\right)dE\right)ds,\frac{\overrightarrow{\varphi }}{6L_1{M}_1}\right)\hfill \\ & ⪰& \Phi \left({\mathbf{G}}_{10}{\int }_{{\chi }_0}^{\chi }{(\chi -{\chi }_0)}^{\mathcal{P}-2}O{(\chi -s)}^{\kappa }ds,\frac{\overrightarrow{\varphi }}{6L_1{M}_{0}exp\left(L_{1}M\right)}\right)\hfill \\ & & ⨂\Phi \left({\mathbf{G}}_{11}{\int }_{{\chi }_0}^{\chi }{(\chi -{\chi }_0)}^{\mathcal{P}-2}O{(\chi -s)}^{\kappa }ds,\frac{\overrightarrow{\varphi }}{6L_1{M}_{1}exp\left(L_{1}M\right)}\right)\hfill \\ & ⪰& \Phi \left({\mathbf{G}}_{10}\frac{\Gamma (\mathcal{P}-1)\Gamma (1+\kappa )}{\Gamma (\mathcal{P}+\kappa )}O{(\chi -{\chi }_0)}^{\kappa +\mathcal{P}-1},\frac{\overrightarrow{\varphi }}{6L_1{M}_{0}exp\left(L_{1}M\right)}\right)\hfill \\ & & ⨂\Phi \left({\mathbf{G}}_{11}\frac{\Gamma (\mathcal{P}-1)\Gamma (1+\kappa )}{\Gamma (\mathcal{P}+\kappa )}O{(\chi -{\chi }_0)}^{\kappa +\mathcal{P}-1},\frac{\overrightarrow{\varphi }}{6L_1{M}_{1}exp\left(L_{1}M\right)}\right),\hfill \end{array}$$

in which $M>0.$ Thus, the zero solution of (63) and (64) is asymptotically stable. □

7. Random Finite-Time Stability Results of (1) for Case 5

Taking into account Case 5 of (1), we have (see [29,38,56,57,58,59])

$$\begin{array}{ccc}& & {}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}\left({}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}{\mathbf{G}}_1\right)\left(\chi \right)=-{\mathbf{H}}^2{\mathbf{G}}_1(\chi -\mathcal{Y}),\chi \ge 0,\mathcal{Y}>0,\hfill \end{array}$$

(68)

$$\begin{array}{ccc}& & {\mathbf{G}}_1\left(\chi \right)=\mathcal{U}\left(\chi \right),{\mathbf{G}}_1^{\prime }\left(\chi \right)={\mathcal{U}}^{\prime }\left(\chi \right),\chi \in [-\mathcal{Y},0],\hfill \end{array}$$

(69)

in which ${\mathbf{G}}_1\in {\mathbb{R}}^n,$ $\mathbf{H}\in {\mathbb{R}}^{n\times n},$ $\mathcal{P}\in (0,1],$ and $\mathcal{U}\in C([-\mathcal{Y},0],{\mathbb{R}}^n).$

Here, we study the fractional-order system (68) and (69), on $\mathbb{I}:=[0,\mathcal{T}],\mathcal{T}>0.$

Definition 5. 

The fractional system (68) and (69) is random finite-time stable with respect to $\{0,\mathbb{I},\mathcal{Y},M_1,M_2\},$ if ${\Psi }_{\lambda }\left(\overrightarrow{\psi }\right)⪰{\Psi }_{M_1}\left(\overrightarrow{\psi }\right)$ infers that ${\Psi }_{\mathbf{G}\left(\chi \right)}\left(\overrightarrow{\psi }\right)⪰{\Psi }_{M_2}\left(\overrightarrow{\psi }\right)$, for every $\chi \in \mathbb{I},\overrightarrow{\psi }>\overrightarrow{0},$ and positive $M_i,i=1,2,$ and $\lambda :={max}_{\chi \in [-\mathcal{Y},0]}\{\mathcal{U}\left(\chi \right),{\mathcal{U}}^{\prime }\left(\chi \right)\}.$

In view of Lemma 3, we obtain the following results:

(i)

${cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}$ is a solution of the fractional-order system (68) and (69), satisfying ${cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}=I,$ and ${\left({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}\right)}^{\prime }=\mathbf{0},$ for $\chi \in [-\mathcal{Y},0].$ In other words, we have that

$${}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}\left({}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}\right)=-{\mathbf{H}}^2{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y})}^{\mathcal{P}}.$$

(ii)

${sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}$ is a solution of the fractional-order systems (68) and (69), satisfying ${sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}=\mathbf{H}\frac{{(\chi +\mathcal{Y})}^{\mathcal{P}}}{\Gamma (1+\mathcal{P})},$ and ${\left({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}\right)}^{\prime }=\mathbf{H}\frac{{(\chi +\mathcal{Y})}^{\mathcal{P}-1}}{\Gamma \left(\mathcal{P}\right)},$ for $\chi \in [-\mathcal{Y},0].$ In other words, we have that

$${}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}\left({}^{\mathcal{C}}D_{-{\mathcal{Y}}^{+}}^{\mathcal{P}}{sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}\right)=-{\mathbf{H}}^2{sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y})}^{\mathcal{P}}.$$

Applying the variation of parameters technique, the authors in [57,58], introduced the explicit formula of solution for (68) and (69), as

Theorem 6. 

The solution of the fractional system (68) and (69) has the following form:

$$\begin{array}{ccc}\hfill & & {\mathbf{G}}_1\left(\chi \right)\hfill \\ & & =\left({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}\right)\mathcal{U}(-\mathcal{Y})+{\mathbf{H}}^{-1}\left({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y})}^{\mathcal{P}}\right){\mathcal{U}}^{\prime }\left(0\right)+{\int }_{-\mathcal{Y}}^0{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}{\mathcal{U}}^{\prime }\left(s\right)ds,\hfill \end{array}$$

(70)

where $\mathbf{H}$ is a nonsingular matrix.

Proof. 

In view of the variation of parameters technique, set

$$\begin{array}{ccc}\hfill & & {\mathbf{G}}_1\left(\chi \right)\hfill \\ & & =\left({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +C)}^{\mathcal{P}}\right)A+\left({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +D)}^{\mathcal{P}}\right)B+{\int }_{-\mathcal{Y}}^0{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}{\varpi }^{\prime }\left(s\right)ds,\hfill \end{array}$$

(71)

in which $C,D\in \mathbb{R},$ $A,B\in {\mathbb{R}}^n$ and $\varpi \in C([-\mathcal{Y},0],{\mathbb{R}}^n).$

Using Definition 2, ${cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}$ and ${sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}$ are solutions of (68) and (69); therefore, (71) is also a solution of (68) and (69).

We now obtain $A,B,C,D$ and $\varpi ,$ s.t. (71) satisfies ${\mathbf{G}}_1\left(\chi \right)=\mathcal{U}\left(\chi \right)$ and ${\mathbf{G}}_1^{\prime }\left(\chi \right)={\mathcal{U}}^{\prime }\left(\chi \right),$ for every $\chi \in [-\mathcal{Y},0].$ In other words, for every $\chi \in [-\mathcal{Y},0],$

$$\begin{array}{ccc}\hfill & & \left({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +C)}^{\mathcal{P}}\right)A+\left({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +D)}^{\mathcal{P}}\right)B\hfill \\ & & +{\int }_{-\mathcal{Y}}^0{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}{\varpi }^{\prime }\left(s\right)ds=\mathcal{U}\left(\chi \right),\hfill \end{array}$$

(72)

and

$$\begin{array}{ccc}& & \frac{d}{d\chi }\{\left({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +C)}^{\mathcal{P}}\right)A+\left({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +D)}^{\mathcal{P}}\right)B\hfill \\ & & +{\int }_{-\mathcal{Y}}^0{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}{\varpi }^{\prime }\left(s\right)ds\}={\mathcal{U}}^{\prime }\left(\chi \right).\hfill \end{array}$$

(73)

For $\chi \in [-\mathcal{Y},0],$ via the definition of ${cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\left(\chi \right)}^{\mathcal{P}},$ when $s\in [-\mathcal{Y},\chi ],$ we obtain $-\mathcal{Y}\le \chi -\mathcal{Y}-s\le \chi \le 0,$ and ${cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}=I,$ and when $s\in (\chi ,0],$ we have $\chi -\mathcal{Y}\le \chi -\mathcal{Y}-s\le -\mathcal{Y},$ and ${cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}=\mathbf{0}.$

Then, we have that

$$\begin{array}{ccc}\hfill & & {\int }_{-\mathcal{Y}}^0{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}{\varpi }^{\prime }\left(s\right)ds\hfill \\ & =& {\int }_{-\mathcal{Y}}^{\chi }{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}{\varpi }^{\prime }\left(s\right)ds\hfill \\ & =& {\int }_{-\mathcal{Y}}^{\chi }{\varpi }^{\prime }\left(s\right)ds\hfill \\ & =& \varpi \left(\chi \right)-\varpi (-\mathcal{Y}).\hfill \end{array}$$

(74)

Setting (74) in (72) and (73), we obtain

$$\begin{array}{ccc}\hfill & & \left({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +C)}^{\mathcal{P}}\right)A+\left({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +D)}^{\mathcal{P}}\right)B+\varpi \left(\chi \right)-\varpi (-\mathcal{Y})=\mathcal{U}\left(\chi \right),\hfill \end{array}$$

(75)

and

$$\begin{array}{ccc}& & \frac{d}{d\chi }\left\{\left({cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +C)}^{\mathcal{P}}\right)A+\left({sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi +D)}^{\mathcal{P}}\right)B+\varpi \left(\chi \right)-\varpi (-\mathcal{Y})\right\}={\mathcal{U}}^{\prime }\left(\chi \right),\hfill \end{array}$$

(76)

for every $\chi \in [-\mathcal{Y},0].$ Thus, (75) and (76) hold if we put $C=0,D=-\mathcal{Y},A=\mathcal{U}(-\mathcal{Y})$, $B={\mathbf{H}}^{-1}{\mathcal{U}}^{\prime }\left(0\right),$ and $\varpi \left(\chi \right)=\mathcal{U}\left(\chi \right).$ □

Now, we present the random finite-time stability results for (68) and (69) as

Theorem 7. 

The fractional systems (68) and (69) are random finite-time stable with respect to $\{0,\mathbb{I},\mathcal{Y},M_1,M_2\},$ if $min\{{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right),{\mathbf{H}}^{-1}[{\mathbb{M}}_{\mathcal{P}}\left(\mathbf{H}{\chi }^{\mathcal{P}}\right)-{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)],\mathcal{Y}{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)\}\times 3M_1<M_2.$

Proof. 

In view of Lemma 4, we obtain

$$\begin{array}{ccc}\hfill {\Psi }_{{\mathbf{G}}_1\left(\chi \right)}\left(\overrightarrow{\psi }\right)& ⪰& {\Psi }_{{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{\chi }^{\mathcal{P}}\mathcal{U}(-\mathcal{Y})}(\frac{\overrightarrow{\psi }}{3})⨂{\Psi }_{{\mathbf{H}}^{-1}{sin}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y})}^{\mathcal{P}}{\mathcal{U}}^{\prime }\left(0\right)}(\frac{\overrightarrow{\psi }}{3})\hfill \\ & & ⨂{\Psi }_{{\int }_{-\mathcal{Y}}^0{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}{\mathcal{U}}^{\prime }\left(s\right)ds}(\frac{\overrightarrow{\psi }}{3})\hfill \\ & ⪰& {\Psi }_{{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)}(\frac{\overrightarrow{\psi }}{3M_1})⨂{\Psi }_{{\mathbf{H}}^{-1}[{\mathbb{M}}_{\mathcal{P}}\left(\mathbf{H}{\chi }^{\mathcal{P}}\right)-{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)]}(\frac{\overrightarrow{\psi }}{3M_1})\hfill \\ & & ⨂{\Psi }_{\mathcal{Y}{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)}(\frac{\overrightarrow{\psi }}{3M_1})\hfill \\ & ⪰& {\Psi }_{min\{{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right),{\mathbf{H}}^{-1}[{\mathbb{M}}_{\mathcal{P}}\left(\mathbf{H}{\chi }^{\mathcal{P}}\right)-{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)],\mathcal{Y}{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)\}\times 3M_1}\left(\overrightarrow{\psi }\right)\hfill \\ & ⪰& {\Psi }_{M_2}\left(\overrightarrow{\psi }\right),\hfill \end{array}$$

for every $\overrightarrow{\psi }>\overrightarrow{0}.$ Note that

$$\begin{array}{ccc}\hfill {\Psi }_{{cos}_{\mathcal{Y},\mathcal{P}}\mathbf{H}{(\chi -\mathcal{Y}-s)}^{\mathcal{P}}}\left(\overrightarrow{\psi }\right)& ⪰& {\Psi }_{{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{(\chi -\mathcal{Y}-s)}^{2\mathcal{P}}\right)}\left(\overrightarrow{\psi }\right)\hfill \\ & ⪰& {\Psi }_{{\mathbb{M}}_{2\mathcal{P}}\left({\mathbf{H}}^2{\chi }^{2\mathcal{P}}\right)}\left(\overrightarrow{\psi }\right),\hfill \end{array}$$

for $s\in [-\mathcal{Y},0]$ and $\overrightarrow{\psi }>\overrightarrow{0}.$ □

8. Conclusions

We presented a new definition of stability which allows us to obtain diverse approximations depending on various special functions that are initially chosen. This allows us to evaluate maximal stability and minimal error which enable us to obtain a unique optimal solution of fractional equations. To effectively generalize stability problems and to evaluate optimized controllability and stability is a reasonable goal, so in this paper, we present ideas and theory to tackle this. This concept of stability considers the optimization of problems which are used in natural sciences and engineering disciplines.