Abstract
The primary objective of introducing metaheuristic algorithms into traditional systematic logic is to minimize the cost function. However, there is a lack of research on the impact of introducing metaheuristic algorithms on the cost function under different proportions of positive literals. In order to fill in this gap and improve the efficiency of the metaheuristic algorithm in systematic logic, we proposed a metaheuristic algorithm based on mutation tabu search and embedded it in probabilistic satisfiability logic in discrete Hopfield neural networks. Based on the traditional tabu search algorithm, the mutation operators of the genetic algorithm were combined to improve its global search ability during the learning phase and ensure that the cost function of the systematic logic converged to zero at different proportions of positive literals. Additionally, further optimization was carried out in the retrieval phase to enhance the diversity of solutions. Compared with nine other metaheuristic algorithms and exhaustive search algorithms, the proposed algorithm was superior to other algorithms in terms of time complexity and global convergence, and showed higher efficiency in the search solutions at the binary search space, consolidated the efficiency of systematic logic in the learning phase, and significantly improved the diversity of the global solution in the retrieval phase of systematic logic.
MSC:
68T07; 68T27; 68T20
1. Introduction
In recent years, the rapid development of artificial intelligence has made artificial neural networks a focal point of interest within the academic community [,]. Artificial neural networks (ANNs) are an application of learning intelligence from biological brains and have gradually become the frontier in the field of artificial intelligence. In the early 1980s, J.J. Hopfield proposed the Hopfield neural network and made a first attempt to introduce the concept of “energy function” to analyze the stability of dynamic neural networks, and obtained the conditions for determining the stability of the system, which played a crucial role in the research and development of neural networks. Hopfield networks allow machines to store “memories”. The network is similar to the way the human brain processes information, and it is able to “recall” its complete information through incomplete information. Hopfield neural networks have been applied to many other disciplines, such as image processing [,], combinatorial optimization [], and Boolean function optimization []. Discrete Hopfield neural networks (DHNNs) are a type of fully connected neural network, which means that each neuron is connected to every other neuron in the network, and the strength of the neuron connections is represented by synaptic weights. These synaptic weights are part of the content-addressable memory (CAM) in DHNNs. As the number of neurons increases, the DHNN suffers from more capacity issues with CAM. Therefore, an optimal symbolic instruction is required to ensure the appropriate connectivity of neurons without compromising the networks’ behavior.
Satisfiability (SAT) was designed as a symbolic instruction for the neuronal connections of DHNNs. The logic rules were firstly introduced to DHNNs by Wan Abdullah []. In this paper, an artificial neural network (ANN) was formulated by leveraging the correlation between logical variables and the minimized final energy function. Through a comparative analysis between the cost function derived from logical rules and the final energy function, one can determine the synaptic weights that facilitate the modulation of the final neuron state’s direction. The emergence of this study laid the key foundation for the further rapid development of systematic and nonsystematic logics of DHNNs. Typical Systematic Logical rules are available in 2 Satisfiability (2SAT), which requires each clause to contain only a fixed quantity of literals. Chen et al. [] proposed Probabilistic 2 Satisfiability (PRO2SAT), in which probabilities were introduced to control the proportion of positive literals and the generation position, aiming to improve the satisfiability of systematic logical clauses. At present, PRO2SAT has successfully embedded the probability-based systematic logic into DHNNs. However, the learning efficacy of the PRO2SAT model remains unsatisfactory when addressing a large number of neurons. Additionally, research findings from reference [,] indicate that, as the number of neurons increases, the retrieval capability of systemic logic during the learning phase gradually approaches zero. Hence, there is a necessity to explore new methods for enhancing the learning efficiency of systemic logic.
Fueled by the effectiveness of the learning phase in showing direct contribution to that of the retrieval phase, the optimization of the learning phase plays a crucial part in DHNNs. To solve this problem, metaheuristics are embedded into systematic and non-systematic logic rules to minimize the valence function and obtain the optimal salient weights, thus enhancing the ability to obtain the uppermost final state of neurons. Metaheuristic algorithm refers to a method for the optimal or satisfactory solutions to complex optimization problems based on an intelligent computation mechanism [,], and it is also sometimes referred to as intelligent optimization algorithm, which is admired by more researchers for its accessibility to implement and provide feasible solutions to problems at a reasonable cost (computation time and space). Metaheuristic algorithms typically do not depend on the specific structure of the problem but adapt to the characteristics of various problems through a flexible iterative search process. Currently, more metaheuristic algorithms have been applied to systematic and non-systematic logics of DHNNs. As proposed by [], the GA algorithm was imbedded in the logic phase and learning phase of DHNNs. During the logic phase, the GA algorithm assists in constructing the logical rules of r2SAT according to the desired ratio of negative literals. In the learning phase, the GA algorithm aids r2SAT in finding satisfied assignments of the proposed logic. According to [], the EA algorithm was also embedded in the random maximum 2 satisfiability logic for minimizing the cost function. As defined in [], the artificial bee colony algorithm (ABC) was used in the logic stage of r2SAT to control the distribution of negative literals in the logical structure and find the correct logical structure based on the initialization proportion of negative literals. The ant colony algorithm (ACO) was introduced in [] for minimizing the cost function corresponding to the logic rules in DHNNs and finding the optimal path to the zero cost function. The gray wolf algorithm (GWO) was used in [] in a rotor Hopfield neural network (RDHNN). Using the rotor Hopfield neural network and grey wolf optimization algorithm to identify solid oxide fuel cell models, the results show that this hybrid model has advantages in terms of accuracy and computational efficiency. Overall, these studies demonstrated the auxiliary optimization function of metaheuristic algorithms in DHNNs, and they played a primary role in the logic phase and learning phase of DHNNs. Although there is a plethora of metaheuristic algorithms available, their application in both systematic and non-systematic logic is relatively limited. In order to obtain suitable metaheuristic algorithms in terms of solution quality and solution efficiency, more extensive explorations are needed to apply the metaheuristic algorithms to DHNNs. Therefore, a comprehensive survey of metaheuristic algorithms applied in DHNNs is necessary to identify the most suitable algorithms.
Tabu search (TS) is a metaheuristic algorithm starting from a single solution [], which has been successfully applied to solve many combinatorial optimization problems []. TS conducts similar search activities as a human performs which are based on a global stepwise optimization algorithm for local domain search, and creates a stored list (tabu table) to record the search process. The data accessed in the tabu list are not accessed again in the next few iterations. In this way, repetitive search is avoided by the TS algorithm, which directs its search toward the local optimal solution. The selection of parameters and the design of neighborhood operation plays crucial roles in the TS algorithm []. An aspiration criterion will be used in TS during its use to release some excellent tabu solutions and avoid the loss of optimal solutions. The TS algorithm has the advantages of fast convergence and exemption from local minimal values. Since the TS algorithm was proposed, substantial optimization has been conducted for it by the researchers. Meeran et al. [] proposed a hybrid TS algorithm which combines the TS algorithm with the evolutionary algorithm and the ant colony optimization (ACO) algorithm to solve the travelling salesman problem (TSP), providing the method and idea of the TS algorithm for the searching solution in binary search space. Žulj et al. [] proposed a hybrid algorithm based on adaptive large neighborhood search or tabu search (ALNS/TS) to solve the order batching problem (OBP). Initially, multiple destruction and repair operators are employed for the solution search. As iterations proceed, the probabilities of selecting these operators are adaptively adjusted based on their performance in the search process to optimize the search. After a certain number of iterations, the TS algorithm is executed to explore the neighborhood of the current solution to find a better solution. In ALNS/MTS, the diversification capability of ALN was combined with the intensification capability of TS. Compared with state-of-the-art algorithms, ALNS/TS showed the most obvious advantages over larger instances. Lin et al. [] proposed the hybrid binary particle swarm algorithm (HBPSO/TS) based on TS for solving the set-union knapsack problem (SUKP). A tabu-based mutation process was designed as part of this algorithm to guide the search into the new promising regions, and the MTS algorithm was employed to enhance the capabilities of local exploitation. In addition, a gain update strategy was used to reduce the solution time. Experiments have shown that HBPSO/TS performs much better than other algorithms in terms of solution quality. These two studies provided useful ideas for improving the quality and efficiency of the MTS algorithm in solving problems. Although these hybrid metaheuristic algorithms show potential in improving search efficiency and tackling complex problems, they typically involve combinations of multiple operators or operations, thereby resulting in higher algorithmic complexity and more pronounced challenges in parameter tuning.
In this paper, we introduced MTS to the latest systematic logic PRO2SAT [] to extensively explore the application of metaheuristic arithmetic in systematic logic. The contributions of this paper are as follows:
- (a)
- To propose a modified metaheuristic algorithm, namely the hybrid mutation tabu search algorithm, which integrates a mutation operator and segment operation as neighborhood operations. Through these newly constructed neighborhood operations, the tabu search algorithm has been successfully incorporated into the systematic logic for minimizing the cost function.
- (b)
- To optimize the retrieval phase by introducing a mutation operator. The mutation operator randomly flips the literals in unsatisfied clauses, aiming to disrupt the bias in the final state of neurons and enhance the diversity of the global minimum.
- (c)
- To propose the average similarity metric to evaluate the variability and diversity of solutions in the retrieval phase by calculating the similarity between non-repeated solutions and benchmark solutions.
- (d)
- This study examined the effectiveness of the mutation tabu search algorithm through the analysis of different performance measures. The performance of the proposed approach was thoroughly evaluated against that of the leading logical rule in both the learning and retrieval phase.
The organization of this paper is as follows. Section 2 highlights the motivation of this study. Section 3 presents the general formula of PRO2SAT. Section 4 describes the logical structure of PRO2SAT in DHNNs, referred to as PRO2SAT. Section 5 provides the objective function of the metaheuristic algorithm in the learning phase. Section 6 details the metaheuristic algorithms used in the proposed model for the optimization process in the learning phase. Section 7 introduces the experimental setup and parameter settings as well as the performance evaluation indicators used in this paper. Section 8 discusses and analyzes the experimental results of the proposed model and the comparison model. It should be noted that the organization of this experiment is based on the listed contributions. This paper is not intended to replace the existing logical structure of neuron representation in DHNNs, but it will provide critical explorations on the different metaheuristics in the proposed logical phase with the improved DHNN model, which may contribute to the quality of the final neuron states retrieved.
2. Motivation
2.1. Inefficient Learning Phase of DHNNs
For DHNNs, effective learning phases can lead the network to optimal synaptic weight management. A satisfactory explanation of SAT logical rules ensures a zero-cost function for DHNNs, which, when compared with the Lyapunov energy function, yields the optimal synaptic weight. As the scale of neurons in the learning phase expands, most existing systematic and non-systematic logical rules employ metaheuristic algorithms as optimization training algorithms, iteratively finding consistent interpretation. The existing work of Zamri et al. [] initially employs a genetic algorithm (GA) as the logic phase and learning phase algorithm for RAN2SAT in the DHNN model, known as DHNN-r2SAT. This model is compared with traditional exhaustive search (ES) and demonstrates superior retrieval performance. Unfortunately, the genetic algorithm mutation operator proposed in this paper easily falls into local optima when the number of neurons is large, meaning that the fitness of the neuron state before mutation may be better than after mutation. The study by Someetheram et al. [] introduces a novel non-satisfiability logical rule for the first time and successfully embeds the election algorithm within it. This approach enhances the capability of minimizing the cost function through the election algorithm to seek consistent interpretations. The research findings demonstrate the significant superiority of the election algorithm in the training process of the discrete Hopfield neural network compared to genetic algorithms and exhaustive searches. Currently, existing optimization training algorithms typically rely on probability to explore the consistency solutions in the learning phase of both system and non-system logics, which indeed plays a role in improving learning efficiency. However, this probabilistic dependency can easily lead to being influenced by randomness and trapped in local optima, thus requiring more iterations and computational time. Therefore, from an innovative perspective, introducing a non-probabilistic approach to explore new solution methods is of significant importance. With this concept in mind, we propose a tabu search algorithm integrated with a mutation operator, which utilizes non-probabilistic operations such as a tabu list and aspiration rules to guide the search process, aiming to enhance the efficiency and robustness of learning for PRO2SAT.
2.2. Limited Solution Diversity in Retrieval Phase of DHNN
The optimal retrieval capability of the DHNN ensures that the final neuron states always converge to the global minimum energy. Currently, most systematic or non-systematic logics follow the retrieval phase training mechanism proposed by Abdullah [], known as the Wan Abdullah (WA) method. For example, the PRO2SAT by Chen et al. [], the 2SAT by Zamri et al. [], and the RANkSAT by Someetheram et al. [] all adopt this approach. These models update neuron states using the hyperbolic tangent activation function (HTAF) after local field computation. The combination of local field and HTAF results in good stability during the retrieval phase. However, unfortunately, the presence of positive literals in second or third-order clauses leads to bias in the final neuron states obtained during the retrieval phase, meaning that the solutions generated during the retrieval phase will be excessively similar. This bias becomes more pronounced when there are more positive literal clauses. To address this issue, this paper introduces a mutation strategy to improve the diversity of neurons after local field computation, thereby enhancing solution diversity.
3. Probabilistic 2 Satisfiability (PRO2SAT)
PRO2SAT belongs to systematic logic, which consists of variables, literals, probabilities, AND operators (conjunction, also denoted by), OR operators and non-operators. Compared with the traditional systematic logic 2SAT, PRO2SAT has a fixed number of positive literals, where the probability that is used to control the uniform distribution of positive literals in the clauses is introduced. Equation (1) shows the general formula of PRO2SAT, where is a clause, n is the number of second-order clauses, and the composition of clauses is represented by Equation (2).
where is a set of literals. The literal is either positive literal or negative literal . The conjunction formula of the two literals is the clause. The literals are bipolar, i.e., they can take value , which represents , respectively. represents the probability, which determines the positive and negative literals. For example, when , the probability of is 0.8, whereas has a probability of 0.2. The calculation is shown in Equations (3)–(5):
where l, i, and j are integers greater than zero. Variable in Equation (5) is used to mark the positive literals, and variable in Equation (4) is used to record the number of positive literals in the first i variables. Variable in Equation (3) is the preset proportion of positive literals in PRO2SAT, and the value range is [0.1, 0.9]. It is worth mentioning that the step size of variable n is set to 0.1, ensuring that the number of positive literals is not duplicated. When the step size is less than 0.1 (), the number of positive literals () will have a significant number of replicates, which will cause redundancy in the model’s classification. When the step size is more than 0.1 (), fewer values will be assigned to the number of positive literals to reduce the number of classifications of the model. is used to avoid too much negative literals and two positive literals in one clause, i.e., avoiding . In addition, when is assigned as , it means that the number of positive literals does not reach the preset value, and it is necessary to continue generating the positive literals. When the neuron is 8, the example of is shown in Table 1.

Table 1.
Examples of PRO2SAT.
4. in Discrete Hopfield Neural Network (DHNN)
A discrete Hopfield neural network (DHNN) is a single-layer symmetric full feedback network where each neuron has the same function and is interconnected with each other. The DHNN employs an asynchronous approach for adjusting network states, and it utilizes a symmetric matrix for the synaptic weight matrix. In this section, will be embedded in the DHNN, and the newly generated neural network is called PRO2SAT. The asynchronous update method for the neurons of PRO2SAT is shown in Equation (6):
where and are two interconnected neurons, denoting the states of the i-th and j-th neurons, respectively. signifies the synaptic weight between neuron i and neuron j, with “” serving as the predetermined threshold value. Taking the value of 0 can effectively ensure the energy monotonic reduction in the network and allow the network to reach a stable state []. It is worth mentioning that the synaptic weight of PRO2SAT has no self-loop where , . The synaptic weight will be stored as control-addressable memory (CAM). When the neuron is in the active state, it can be assigned as 1; otherwise, the neuron is in the inhibited state and can be assigned as −1. The cost function represents the “inconsistency” in the logic rule. Therefore, the inconsistency in the logic needs to be reduced by minimizing the cost function (). In PRO2SAT, every neuron is connected to one another through the following cost function:
where n represents the number of second-order clauses and is the inconsistency of . It is calculated as shown in Equation (8).
where represents the state of the j-th neuron whose value is bipolar with . It is worth noting that means that all clauses in the logic rule are satisfied. , , which means that y clauses in the logic rule are not satisfied. The cost function is crucial in the learning phase, and its minimization can assist PRO2SAT to find the optimal synaptic weights and generate a good energy profile in the retrieval phase. The minimized probability of for PRO2SAT is , and it is small as the number of neurons and clause n becomes larger. PRO2SAT calculates the final state of the neuron by means of a local field, as shown in Equation (9):
In the retrieval phase, PRO2SAT uses the hyperbolic activation function (HTAF) to assist the local field to calculate the neuron final state, because the HTAF can help reduce the neuron oscillation tendency and assist PRO2SAT to converge to the global minimum energy. The final state of the neuron is shown in Equation (10) and the HTAF is shown in Equation (11):
The final energy of PRO2SAT can be calculated using Equation (12), which is called Lyapunov energy function. It is worth mentioning that, according to the WA method, the cost function () is compared with the Lyapunov energy function () to compute the optimal synaptic weights and . Section 6 introduces the MTS metaheuristic algorithm, which will assist PRO2SAT in the learning phase to find the consistent interpretation when the neurons are large.
where represents the number of neurons. According to Equation (12), we can derive the calculation of the minimum energy, as shown in Equation (13). In the learning phase, the Lyapunov energy function obtains the minimum value when , where n represents the number of second-order clauses. According to Jamaluddin et al. [], the energy of the DHNN always converges to near the global minimum energy in the search phase. Therefore, we need to focus on PRO2SAT to find the global minimum energy as much as possible.
The expression for the global minimum energy error of PRO2SAT is provided as Equation (14):
Global minimum energy error is used to determine whether the correct final neuron state is obtained, where is the tolerance value determined by the researcher, and the values is assigned as 0.001 [].
5. Objective Function of PRO2SAT in Learning Phase
The main objective of the learning phase of PRO2SAT is to find a set of optimal synaptic weights. With the increase in the number of neurons, however, especially when it is greater than or equal to 60 neurons, it is difficult for PRO2SAT to find optimal synaptic weights anymore. Therefore, the metaheuristic algorithm is implemented into PRO2SAT to find the consistent interpretation. From this, the optimal synaptic weights can be obtained by comparing the cost function and the energy function. The objective function of the metaheuristic algorithm in PRO2SAT is shown in Equation (15):
where is the solution string; for example, when the number of neurons is 6, its value can be expressed as . represents the fitness function. is used as input to obtain the fitness, and its specific calculation process is shown in Equation (16):
where n is the number of second-order clauses, Ci represents the i-th second-order clauses, and represents the fitness value of the i-th clause of PRO2SAT, which is calculated as shown in Equation (17):
In , a clause is considered to obtain the consistent interpretation when it is satisfied at an input value of . Take 1 for the fitness value of MTS. Otherwise, the clause is not consistent and the fitness is −1. The purpose embedding PRO2SAT in the learning phase of the metaheuristic algorithm is to find the maximum fitness n, where n represents the number of second-order clauses.
6. Proposed Metaheuristics
Inspired by different natural phenomena, mathematical models are built in metaheuristic algorithms. Based on this, metaheuristic algorithms can be classified into three categories: evolutionary algorithms, physical mechanism algorithms, and swarm intelligence algorithms [], where the primary role of evolutionary algorithms is to simulate the computation model of the biological evolution process by natural selection and genetic mechanism of Darwin’s theory of biological evolution. Such algorithms are mainly meant to eliminate the individuals with poor fitness values and retain those with good genes through the continuous evolution of individuals. The evolutionary algorithms used in this paper involved GA, DE, and EDA. Physical mechanism algorithms are algorithms based on physical phenomena and physical laws, which optimize the answers to the problems mainly by simulating physical phenomena, such as temperature, energy, and force. The physical mechanism algorithm used in this paper encompassed the SA algorithm. Swarm intelligence algorithms are algorithms that simulate group behavior, which optimize the answers to the problems mainly by simulating group behavior. The swarm intelligence algorithms used in this paper included EA, GWO, ant algorithm, PSO, and ABC.
6.1. Proposed Mutation Tabu Search Algorithm (MTS)
The TS algorithm is an intelligent metaheuristic algorithm proposed by Glover, a famous American scholar, in the 1990s. The algorithm is a typical stochastic search algorithm [], which mimics the human thought process and extends the scope of local domain search. In the search process, the TS algorithm first searches for some local optimal solutions, and records these objects by the tabu table, avoiding these local optimal solutions that have been searched for in the following iteration process, obtaining a variety of regions and improving the efficiency of the search. It is worth noting that a flouting rule is introduced into the MTS algorithm to release some excellent tabu solutions and avoid the loss of optimal solutions. The MTS algorithm has the advantages of fast convergence and the capability of avoiding local minima. In view of this, in this paper, the MTS algorithm is embedded into the systematic logic (PRO2SAT) for the first time, where mutation operators are embedded into MTS to assist in the faster convergence of the systematic logic PRO2SAT in the learning phase and to guarantee the optimal solution in the retrieval phase.
6.1.1. Initialization
Initialization of the initial solutions: the MTS algorithm starts from one initial solution. The convergence of this algorithm is closely related to the quality of the initial solution. A high-quality initial solution facilitates the rapid convergence of the algorithm during execution, while a lower-quality initial solution slows down the search speed. In order to better utilize the performance of the MTS algorithm, it is necessary to select one superior initial solution. In the PRO2SAT model, c solution strings are randomly generated in the learning phase, and each solution string is denoted by , , , , where fitness , is calculated for each solution. Therefore, we selected the solution with the maximum fitness value as the initial solution, as shown in Equation (18):
Initialization of the local optimal solution and the global optimal solution: and are defined to represent the local optimal solution and the global optimal solution, respectively. stores the solution with the maximum fitness among the neighborhood solutions under a certain cycle of the MTS algorithm, and stores the solution with the maximum fitness among all iterations of the MTS algorithm. The initial values of the local optimal solution and the global optimal solution are the initial solutions, as shown in Equation (19).
By initializing the local and global optimal solutions with the initial solution, it ensures that the algorithm starts its search from a reasonable starting point and gradually optimizes to find better solutions.
6.1.2. Generation Strategy to Neighborhood Solution
A new solution can be obtained by performing certain operations on the initial solution, and these operations are called neighborhood operations. The option is critical in neighborhood operation, and the neighborhood operations vary from the results. Inspired by GA, we used mutation operations to generate neighborhood solutions. Firstly, the initial solution was divided into w segments equally by neurons, x segments were randomly selected among them, and y neurons were randomly selected in the selected segment for mutation operations, i.e., flipping the values of the selected neurons. For example, if the value of the selected neuron is −1, the mutation becomes 1. On the contrary, if the value of the selected neuron is 1, the mutation becomes −1. Figure 1 shows the generation process of the neighborhood solution when w takes the value of 5, x takes the value of 2, and y takes the value of 1. In this step, N replicates generate N neighborhood solutions, denoted by .
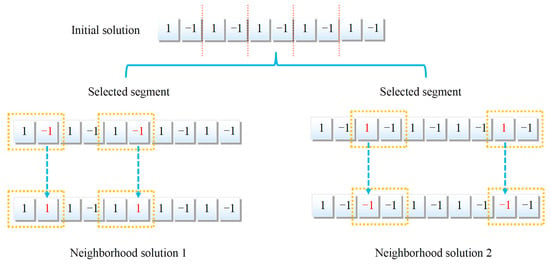
Figure 1.
Generation process of neighborhood solution.
6.1.3. Generation Strategy to Candidate Solution
Candidate solution : the neighborhood solution with the maximum fitness is selected as the candidate solution, as defined in Equation (20).
Tabu table (TBT): it refers to the storage structure used to store the tabu operations, where two main indicators are available: tabu operations (TBS) and tabu length (L). In this paper, the mutation segment number of the neighborhood solution was used as the tabu operation to avoid the repeated search of the obtained solution, expand the search area of the algorithm, and escape the local optimum. The tabu length is usually set to a positive integer; too short a tabu length tends to fall into the local optimal solution prematurely, and too long a tabu length leads to prolonged computation. As a result, all the neighborhood solutions are tabued, and it is impossible to continue computing. Therefore, according to [], we set the tabu length to 3.
where i takes an integer and , ns takes an integer, and .
Update of the local optimal solution and the global optimal solution: it determines whether the mutation segment number of the candidate solution has been stored in TBT when implementing the neighborhood operation. If not, it is written to TBT. The local optimal solution is updated and the candidate solution values are assigned to the local optimal solution. Note that, if the new local optimal solution outperforms the global optimal solution, it is necessary to update the global solution, and assign the new local optimal solution value to the global optimal solution. If the mutation segment number of the candidate solution has been recorded in TBT, in order to expand the search domain of the MTS algorithm, the current candidate solution should be discarded and the solution with the maximum fitness among the remaining solutions in the neighborhood solution should be selected as the new candidate solution . The above process is repeated until the local optimal solution and the global optimal solution are generated.
Flouting rule: If the mutation segments number of the candidate solution is available in TBT, but the fitness is greater than the current global optimal solution, the tabu operations can be neglected. The mutation segment number of the candidate solution is written to TBT, and the local optimal solution and the global optimal solution are updated accordingly, as defined in Equations (24) and (25).
The flouting rule is typically executed after a certain number of iterations, aiming to revoke previously tabu neighborhood operations. It allows for the algorithm to tolerate neighborhood operations previously deemed prohibitive, provided that the fitness is sufficiently satisfactory, thus preventing undue constraints during the search process. This facilitates the algorithm’s escape from local optimal solutions. The generation process of candidate solution is shown in Figure 2.
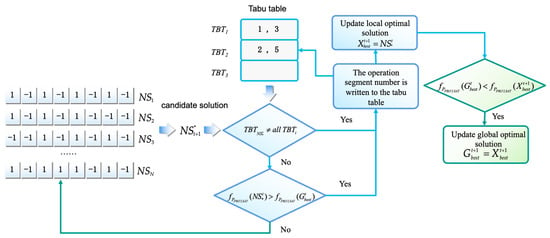
Figure 2.
Generation strategy to candidate solution.
6.1.4. Fitness Assessment
The fitness value of is calculated according to Equation (16). If the solution fails to reach the maximum fitness and the algorithm fails to reach the maximum number of iterations, return to 5.1.1 and continue to the next round.
6.1.5. Mutation
At the beginning of the test phase, 100 solution strings will be generated randomly in PRO2SAT in order to increase the diversity of the solutions in the retrieval phase. The MTS metaheuristic algorithm will flip the satisfied clauses of the global minimum solution by virtue of the mutation operators after calculating the local field in the retrieval phase as shown in Equations (26) and (27):
6.2. Baseline Model
The model proposed in this paper will be compared with other established existing algorithms. The baseline models in this paper include genetic algorithm (GA), election algorithm (EA), ant colony optimization (ACO), estimation of distribution algorithm (EDA), differential evolution algorithm (DE), grey wolf optimization algorithm (GWO), particle swarm optimization (PSO), simulated annealing algorithm (SA), and artificial bee colony algorithm (ABC). The following content summarizes their working principles.
- (a)
- GA []: This study integrated the strengths of the genetic algorithm and Hopfield neural network to efficiently find solutions to the logic satisfiability problem. The genetic algorithm is a global search algorithm which usually uses a binary encoding technique for optimization problems []. At the time of solving, the initial solution to the actual problem is coded to form a gene string, i.e., a chromosome, which is selected, crossed, and mutated to form a new chromosome. The resulting chromosome will be retained if it is closer to the maximum fitness than the previous one.
- (b)
- EA []: The EA algorithm is inspired by the election of a national president. The algorithm was proposed by Emami, H [], which combined the features of evolutionary algorithms and SIA. In this algorithm [], positive advertisement, negative advertisement, and coalition were used to implement intelligent search in a synergy mechanism. All solutions will be considered as voters from whom candidates will be selected, and each candidate determines his own voters based on his social relationship to the voters, thus forming a political party. As the leader of this party, the candidate will positively influence his own supporters (voters) through positive advertisement and positively influence the supporters (voters) for the leaders of other parties through negative advertisement in order to expand the search space and increase their probability of being elected. The most popular candidate will ultimately receive the most votes.
- (c)
- ACO []: Kho introduced the ACO algorithm in HDNNs (Kho, 2021). In this work, the ant colony algorithm is used to minimize the cost function of the corresponding logic rule in DHNNs. In the ACO algorithm, the pheromone density is used to find the optimal path, thus achieving a zero-cost function without consuming more learning iterations. In this study, the potential application of the ACO algorithm was fully demonstrated in optimization problems, including propositional logic.
- (d)
- EDA []: This algorithm is a probability-based population evolution algorithm. By generating a new population through random sampling, the evolution of the population is achieved through iterations. The main function of MTS is to estimate and predict the distribution of the data. This algorithm is able to predict future data trends by inferring the distribution of the data through statistical analysis. The standard EDA has two important operations, namely the selection operations and the modeling of the probability distribution. The selection operation is the same as the selection strategy in GA. The probability distribution model can be a univariate marginal distribution algorithm (UMDA), which is calculated.
- (e)
- DE []: A novel binary differential evolution algorithm based on Taper-shaped transfer functions (T-NBDE) is proposed to address the knapsack problem in []. The DE and GA algorithms are both evolutionary algorithms, which are adaptive global search algorithms first proposed by Price and Storn in the 1990s to solve the real number solution optimization problems. The DE algorithm has the main features of a simple structure, easy implementation, robustness and fast convergence, etc. In addition, the DE algorithm also has memory function, which can dynamically track the search situation, and the control parameters mainly include population size, variation operator, crossover operator, and selection operator. Unlike the GA algorithm, the variation operators of DE randomly select three individuals as parents for mutation operation to form new individuals.
- (f)
- GWO []: The GWO algorithm has been successfully applied to RDHNNs in the work by Ba et al. []. Therefore, we used GWO in the learning phase of PRO2SAT for comparative analysis. It is a heuristic optimization algorithm based on the behavior of grey wolf packs in nature, which simulates the social hierarchy of grey wolves and divides the individuals within the pack into four classes: head wolf (), subordinate wolf (), common wolf (), and bottom wolf (). In the GWO algorithm, each grey wolf represents a potential solution, and each wolf has an adaptation value. The higher the adaptation value, the better the indicated solution. Starting from any position in the solution space, the individual with the best fitness is set as the leader wolf , the one with the second fitness is set as the subordinate wolf , the one with the third fitness is set as the ordinary wolf , and the rest are the bottom wolves . The leader wolf is responsible for guiding the behavior of the pack, the subordinate wolf assists the leader wolf in making decisions, the ordinary wolf obeys the leader wolf and the subordinate wolf, and dominates the bottom wolf to catch and hunt the target. The bottom wolf needs to obey the guidance of other wolves and follows other wolves to complete hunting, and mainly takes charge of the balance of intra-pack relationships.
- (g)
- (PSO []: The PSO algorithm, proposed by Eberhart and Kenndy in 1995, is a type of SIA algorithm, which is widely used in the field of combinatorial optimization, and it can be applied to PRO2SAT. Inspired by the foraging behavior of a flock of birds, this algorithm includes evolutionary theory. The idea of the PSO algorithm is that each individual searches for a better solution based on the optimal solution that has been found and compares the optimal solution currently found by the population to update its speed. The algorithm searches for the global optimal solution by constantly updating the position and velocity of the population, which is a process of movement from simple individuals to complex global solutions.
- (h)
- SA []: The SA algorithm is a probability-based search algorithm proposed by Kirkpatrick, Gelatt, and Vecchi in 1983 to describe the physical annealing process of an object. It can be used to solve complex optimization problems. The basic idea is the process of finding the global optimal solution of the objective function randomly in the space of all local solutions starting from an initial solution (annealing point) in an isothermal process combined with the probabilistic sudden jump property, i.e., the ability to probabilistically jump out of each local solution and finally obtain the global optimal solution. The advantage of the SA algorithm is that it can find the global optimal solution and have a relatively large search space to find a better solution.
- (i)
- ABC []: This study introduces the combination of the artificial bee colony algorithm with the Hopfield network to minimize or maximize the cost function of any combinatorial problem. With this literature approach, we processed the secondary values using the ABC algorithm. Each bee was assigned an initial nectar source, and the employed bee dances through the solution space to compute the new nectar source. This explores the solution space of consistent solutions during the learning phase of the Hopfield neural network and identifies potential solutions. The combination of the ABC algorithm and the Hopfield neural network demonstrates the superior performance of the artificial bee colony in solving the 2 Satisfiability problem.
7. Experimental Setup
In this experiment, we verified the validity of the MTS model proposed in this paper in the learning phase and the retrieval phase, and considered the metaheuristic algorithm to achieve a single objective function, i.e., the proposed model achieved the maximum fitness.The flowchart of MTS model is shown in Figure 3. To ensure the reproducibility and fairness of the experiment, our experimental setup is as follows.
7.1. Simulation Design
All simulations were conducted using the same set of features to prevent bias during the experiments, encompassing three specific characteristics. Experimental environment and programming language: We opted for PyCharm as our development tool, and all experimental models were coded using Python. The operating environment of the experiment was mac OS Monterey (12.1) with an apple M1 pro CPU, an apple M1 pro graphics card, and 16 GB of RAM. Note that the experimental models operated on the same devices to ensure fairness in the comparison of performance metrics. Setup for the number of neurons: The number of neurons is taken in the range of . PRO2SAT consists of the second-order logical clauses only, and this fixed structure is beneficial to the stability and fairness of the experimental results. It is worth mentioning that PRO2SAT specifies the proportion of the number of positive literals in the logic structure. Similarly, to ensure the fairness of the experiment, we divided PRO2SAT into nine types (The proportion of positive literals is taken in the range of [0.1, 0.9] and the step size is taken as 0.1). Each PRO2SAT was applied to 10 metaheuristics and exhaustive search algorithms proposed in this paper for comparison experiments. Maximum iteration limit: We set the maximum iteration limit to 100 for all metaheuristics.
7.2. Parameters Assignment
Table 2 lists the parameters used in the learning phase of MTS. It was found by a certain study [] that an increased size of populations contributes to the chance of the algorithm to obtain the optimal solution. Therefore, in order to make the evaluation of each algorithm more objective and convincing, we set the populations of all algorithms except ABC to 100.

Table 2.
List of parameters for PRO2SAT-TS model.
7.3. Performance Evaluation Metrics
In order to comprehensively evaluate the performance of PRO2SAT with the assistance of different metaheuristic algorithms, nine metrics were selected to analyze PRO2SAT. Since the metaheuristic algorithms acted in the learning phase of PRO2SAT and were used to assist in finding consistent explanations, the metrics were mainly meant to evaluate the number, quality, and efficiency of the solutions obtained by the proposed metaheuristic algorithm versus the baseline metaheuristic algorithm. The performance of all PRO2SAT models was evaluated based on different computational phases, each with the following two objectives:
Firstly, during the learning phase, we evaluate the efficiency and quality of the metaheuristic algorithm to minimize the cost function from macro (logic rules) and micro (clauses) perspectives. Secondly, an effective learning phase will help PRO2SAT to obtain better final neuron states and have better convergence in the retrieval phase. Therefore, we mainly evaluated the ability of the metaheuristic algorithm to facilitate PRO2SAT to obtain globally optimal solutions with small energy differences in the retrieval phase.
7.3.1. Learning Phase Metrics
- (a)
- Mean absolute error of clause adaptation ()
This metric is used to measure the ability of the metaheuristic algorithm to search for clause interpretations during the learning phase, i.e., the ability to find clause fitness, and to analyze PRO2SAT from a microscopic perspective. Good metaheuristic algorithms can rapidly improve the fitness of PRO2SAT clauses until they reach the maximum fitness (all clauses are satisfied).
where is the maximum fitness of a logic rule, and the value is equal to the number of second-order logic clauses. is the actual fitness, and the value is equal to the number of second-order logical satisfiable clauses. is the number of combinations, i.e., the number of times needed to generate . is the number of trials when .
- (b)
- Mean absolute error of the adaptation of logic rules ()
This metric is used to measure the ability of the metaheuristic algorithm to search for a consistent interpretation of the logical rules in the learning phase. It analyzes PRO2SAT from a macro perspective, focused on the ability of the metaheuristic algorithm to obtain a solution.
where represents whether the consistency explanation is found in 100 trials, and the value is 1 if found; otherwise, it is 0.
- (c)
- Mean similarity of consistency interpretations ()
It can be seen that the benchmark state is only related to the positive and negative literals. The benchmark state is “1” for positive literals and “−1” for negative literals. For example, if the logic rule is , the benchmark state is (−1,1,−1,−1,−1,−1). In this paper, we analyzed the diversity of solutions by comparing the consistency interpretation obtained by benchmark states and the metaheuristic algorithms, and the specific method for comparison is shown in Equation (44).
In order to analyze the quality of the solutions obtained by the metaheuristic algorithm in the learning phase, the similarity metrics were used to observe the diversity of solutions. It is worth mentioning that a certain logical rule has more than one consistent interpretation in the learning phase, but they have multiple benchmark states obtained by Equation (31):
where m represents the number of neurons and represents the state value of the neuron when the metaheuristic algorithm obtains a consistent interpretation. The standard canonical variables in the comparison process can be determined by the following method:
- l indicates the overall occurrence count of in ;
- m indicates the overall occurrence count of in ;
- n indicates the overall occurrence count of in ;
- o indicates the overall occurrence count of in .
According to the calculation of the standard specification variables above, the similarity metric GLI is calculated as shown in Equation (19), where the larger GLI represents a more diverse solution and the opposite represents a solution closer to the standard solution. From the point of view of the quality of the solution required, we hope to find the solution with a higher quality, i.e., the solution obtained is closer to the standard solution. This can be expressed by the average similarity metric in Equation (33).
where is the number of solutions.
- (d)
- Computational Time ()
This metric is used to determine the effectiveness of the proposed model. It implies the capability and stability of the model. It is calculated as shown in Equation (34):
where is the average time for 100 trails performed by the metaheuristic algorithm for a given number of neurons. The time is expressed in seconds.
- (e)
- Average iterations ()
This metric is used to demonstrate the speed of convergence of the algorithm and will be analyzed together with the metric CT to determine the efficiency of the metaheuristic algorithm. It is calculated as shown in Equation (35). It has been shown that the better the metaheuristic algorithm, the fewer iterations it will have.
where represents the number of iterations when the metaheuristic algorithm finds a one-time explanation under each combination. It is worth noting that we set the maximum number of iterations for the metaheuristic algorithm, and is counted as the maximum number of iterations when the maximum metaheuristic algorithm reaches the maximum number of iterations and still does not obtain a consistent explanation.
7.3.2. Retrieval Phase Metrics
- (f)
- Global minimum proportion ()
The global minimum solution is obtained by converging to the optimal final neuron state in a good retrieval phase. In this paper, we use this metric to demonstrate the ability of the neural network to obtain the global minimum solution. The general form of global minimum proportion is shown in Equation (36):
where stands for the count of neuron states in the model achieving the global minimum energy, while a denotes the number of combinations, and b signifies the total number of trials.
- (g)
- The average similarity of solutions ()
In addition to considering the number of global minimum solutions obtained by the model in the retrieval phase, the average similarity metric of solutions was first proposed to calculate the similarity between the non-repeated solutions and the benchmark solutions in the retrieval phase. The larger the value of this metric indicates that the solution is more identical to the standard solution, and the worse the variability ability to the solutions and diversities is. On the contrary, the larger the difference between the solution and the standard solution, the better the variation ability and diversity of the solution.
where is the number of non-repeating solutions in the retrieval phase, and l and o have the same meanings as (c).
- (h)
- Mean Absolute Error of Logic Rule Energy ()
This metric is used to evaluate the energy error generated by the neuron, which will obtain the final energy after the final state of the nerve is obtained via the local field. The smaller energy error represents the better quality of the final state of the neuron. It is calculated according to Equation (38):
where is the minimum energy and is the final energy.
- (i)
- Friedman Statistical Analysis ()
Friedman statistical analysis is a non-parametric test that determines whether there is a significant difference in the effectiveness of the metaheuristics by counting and rating the results of the metrics in the learning and retrieval phases of each metaheuristic algorithm. The Friedman test is represented in Equation (39) in its general form.
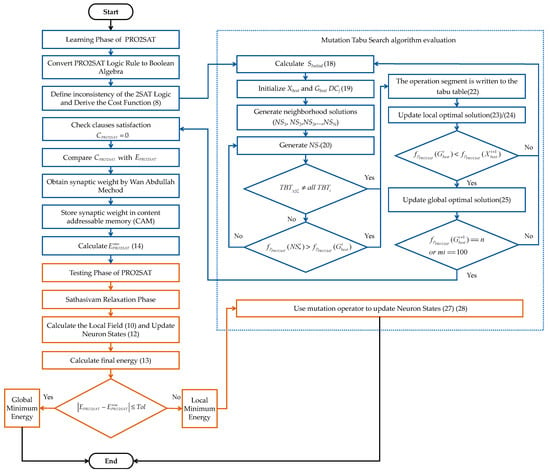
Figure 3.
Flowchart of MTS.
7.4. Simulation Dataset
In this paper, we conducted the experiments by using simulated data in which the initial values of the neurons are bipolar and randomly generated. The simulated dataset is typically used to simulate and evaluate the performance of a newly proposed logic programming models with 100 randomly generated initial data in both the learning phase and the retrieval phase. This simulated dataset was employed following the works of Zamri et al. [] and Someetheram et al. [], allowing the learning phase metaheuristic algorithm to have an unbiased start, so that the final state of neurons in the retrieval phase can be determined by the optimal synaptic weights. The metaheuristic algorithm acts upon the learning phase of PRO2SAT, where each iteration is aimed to minimize the cost function. Since different proportions of positive literals were proposed in the PRO2SAT model, the randomized simulated experiment data make each simulation of the model independent and do not cause the experiment to converge early or fail to converge due to too many positive or negative literals.
8. Result and Discussions
In this section, we will discuss the performance of the metaheuristic algorithm in the learning phase of PRO2SAT and the impact on the retrieval phase. MTS algorithms were first embedded into the systematic logic PRO2SAT, and nine typical meta-inspired algorithms embedded into PRO2SAT were compared and analyzed as baseline models. Our experiments were conducted to understand the effectiveness of the proposed MTS metaheuristic algorithm by limiting the number of neurons (). In this section, the abbreviations of the metaheuristic algorithms were used directly to represent the experimental models, e.g., MTS for PRO2SAT-MTS and GA for PRO2SAT-GA. In order to assess the algorithms’ average performance and stability, we conducted five runs of each set of experiments, and the final result was determined as the average. It is important to note that the data used in these experiments were derived from a simulated dataset with a space size of .
8.1. Learning Phase
The metaheuristic algorithm was embedded into the learning phase of PRO2SAT and was used to improve the ability of PRO2SAT to find consistent interpretation. We used performance metrics to analyze the variation in the fitness of PRO2SAT embedded in the metaheuristic algorithm for different proportions of positive literals in clauses, with the smaller representing the higher satisfied interpretation.
We used a line graph to show all the experimental models of , as shown in Figure 4. Since was used to describe the change in fitness, it was also referred to as fitness error. From the figure, we can see that, among them, the ES model has the maximum fitness error, which is due to the fact that an exhaustive search method is used in this model to generate the 100 sets of initial neuron states. No metaheuristic algorithm was used to explore the solution space, but it would be used as the most dominant comparison model. It is worth mentioning that, at , all experimental models have no fundamental difference in the fitness error for different proportions of positive literal values; this is due to the stipulation in our code that the 10 metaheuristic algorithms of the experiment are implemented only if a consistent interpretation cannot be found in the set of 100 sets of initial neuronal states. Therefore, the metaheuristic algorithm was substantially not implemented in the experimental model at .
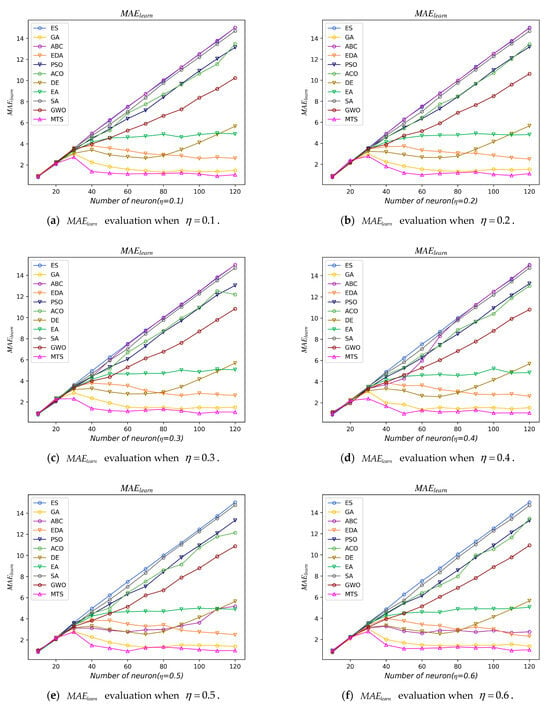
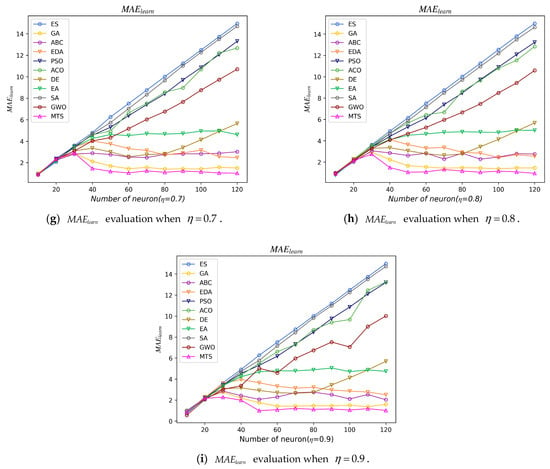
Figure 4.
evaluation for all experimental models.
Five models spanning PSO, ACO, SA, GWO, and DE show a linear increase in fitness error as the number of neurons increases. This indicates that the clauses of these algorithms are affected by the number of neurons. What is more interesting is that, in the ABC model, the fitness error is larger when , but smaller and stable when . This is because the ABC algorithm bees dance to find the new honey source operator , where the operator represents OR. It can be seen that, if the old honey source is positive, the new honey source must be positive. The neuron state will change toward +1 as the iterations progress, which directly leads to poor satisfiability of the clause when and good satisfiability of the clause when . In the four models involving EDA, EA, GA, and MTS, their fitness errors are presented as a horizontal line, indicating that the algorithm is better stabilized and does not iteratively swing with the increase in the number of neurons, and still has good clause satisfiability. Among these four models, the MTS model proposed in this paper has the best performance, attributed to the fact that the MTS metaheuristic algorithm begins the operation by selecting the optimal solution from 100 initial solutions. In contrast, other metaheuristic algorithms in this paper involve multiple solutions in each iteration, extensively exploring potential high-quality solutions across the solution space. This characteristic endows the MTS metaheuristic algorithm with higher retrieval efficiency. Additionally, leveraging the characteristics of metaheuristic algorithms [], conducting local search based on high-quality solutions enables the rapid discovery of consistent interpretations. Considering the structural characteristics of second-order logical clauses, reducing the value to find consistent interpretations necessitates increasing the number of satisfiable clauses. To increase the number of satisfiable clauses, flipping any literal in unsatisfiable clauses suffices. Based on this property, the mutation operator in the MTS algorithm is set to have a mutation probability of 1 for flipping clause literals. Simultaneously, segment operations are employed to ensure that the mutation operator operates on different clauses, directing the exploration of the local solution space. Consequently, the MTS algorithm exhibits superior stability and performance in terms of the indicator compared to other algorithms.
Table 3 and Table 4 show the results of the experimental model with different proportions of positive literals () and number of neurons for . The values of the number of neurons were taken in consistency with the values of , and the optimal value of was 1. In the table, Max, Min, and Mean represent the maximum, minimum, and intermediate values of in the model, respectively. The larger these three values, the stronger the ability of the experimental model to find consistent explanations. It is worth noting that measures the ability of the experimental model to find consistent explanations in terms of clauses, and measures the ability of the experimental model to find consistent explanations in terms of logic (), which is more important than , because it maps the ability of the model to obtain the optimal salient weights. Std refers to the standard deviation, which reflects the degree of dispersion of the dataset. A larger Std represents a larger difference between most of the L values and their means; a smaller Std means that these values are closer to the mean, and the better the stability of the model. Avg Rank represents the average ranking of the Friedman test of the model with the same proportion of positive literals and number of neurons highlighted.

Table 3.
The average value of all proposed algorithms in the learning phase for . The bold values indicate the superior result among the mentioned metrics.

Table 4.
The average value of all proposed algorithms in the learning phase for . The bold values indicate the superior result among the mentioned metrics.
- (a)
- Experimental model for
The optimal data in Table 3 are identified in bold. As described in the table, we know that the three models MTS, GA, and EA have the same performance and are the best among all models. The values of Max, Min, and Mean are 1, which means that is optimal for all values of neuron number, and the value of Std is 0, meaning that the models are absolutely stable in finding consistent explanations. Meanwhile, the values of Avg Rank for these three models are 3.667, 3.625, 3.583, and 3.833, respectively, which are the minimum among the experimental models under the corresponding values of positive literal occupancy. The results validate the advantages of the MTS, GA, and EA models in finding consistent interpretations.
- (b)
- Experimental model for
The optimal data in Table 4 are identified in bold. As described in the table, MTS, GA, ABC, and EA perform well and are the most satisfactory among all models. The optimal value of is achieved for all values of the number of neurons. All of the values Max, Min, and Mean have a value of 1. The Std value of 0 means that the model is absolutely stable in finding consistent explanations. Similarly, the values of Avg Rank for these four models are 4.042, 4.083, 4.000, and 4.167, respectively, which are the minimum among the experimental models under the corresponding values of positive literals. The results validate the advantages of the MTS, GA, and EA models in finding consistent interpretations.
Combined with the results of (a) and (b), it can be observed that the ABC model performs poorly at and well at . The reason for this phenomenon is still the OR operator used in the generation of new nectar sources, and we have explained in the analysis section. In addition, the MTS, GA, and EA models optimize values for all positive literal proportion. The key to achieving the optimal value of lies in the ability of metaheuristic algorithms to escape the local optimum solution. The MTS, GA, and EA algorithms all possess good capabilities for escaping the local optimum solution. The MTS metaheuristic algorithm achieves this goal by utilizing the mutation operator, while the GA metaheuristic algorithm employs crossover and mutation operators to avoid premature convergence to local solutions. It is worth noting that, due to the mutation probability of 0.01 in the GA metaheuristic algorithm, the crossover operator plays a major role. In contrast, the EA metaheuristic algorithm uses an advertising strategy to confine the search scope of solutions around the optimal solution and alternates between positive and negative advertisements to avoid premature convergence to the local optimum solution. Therefore, compared to other metaheuristic algorithms, these three metaheuristic algorithms all have useful strategies to avoid the local optimum solution, allowing them to explore unknown areas as much as possible. Even with a large number of neurons, they still possess good capabilities for finding consistent interpretations. However, acquiring this capability typically requires more iterations. Regarding the number of iterations, we will discuss this further in the AI indicator section.
Figure 5 depicts the values obtained for the different experimental models. measures the similarity of the solutions with respect to the benchmark state. For this case, the higher the value is, the more favorable it is to study the similarity index, indicating that the smaller the difference between the solution found by the metaheuristic algorithm and the standard solution, the better the ability of the model to obtain high-quality solutions. In our analysis, it is easier to obtain solutions for all experimental models when . On the contrary, when , the six models ES, ABC, SA, DE, PSO, and GWO are unstable in their solving ability. These models will have null values of when the models are trapped in the local optimal solution. In addition, the average similarity index values of the solutions of the five models including MTS, GA, EDA, ACO, and EA do not have null values and increase linearly with the number of neurons, indicating that these models can search for solutions in the learning phase and the solution diversity is greater with the increase in the number of neurons. The diversity of solutions is greater as the number of neurons increases. Among them, the EDA model has the lowest solution quality, which is due to the EDA algorithm showing the selection rate of 0.1, with the statistical fitness of the largest 10 solutions to obtain the probability of the neuron state taking values. This method to obtain the neuron state is guided by these 10 maximum fitness solutions, indicating that the arithmetic exploration ability is weaker. It can also be seen that the MTS and EA models are the best performers among all the models. To observe the results of these two models more clearly, we used the matrix diagram to show their specific results, as shown in Table 5 and Table 6.
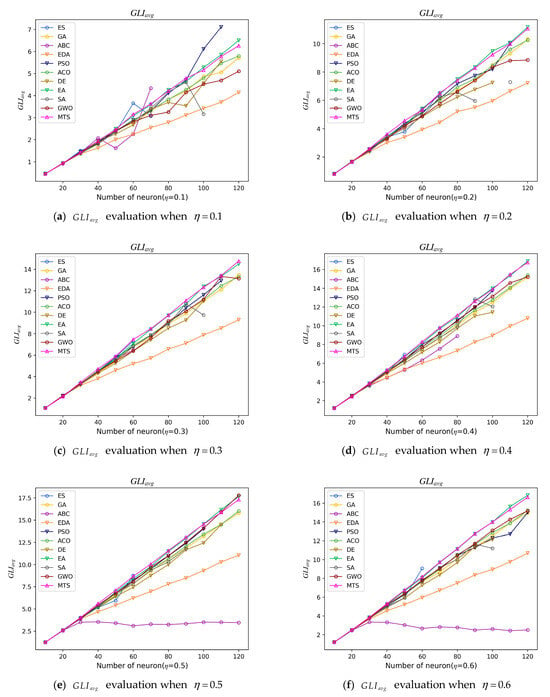
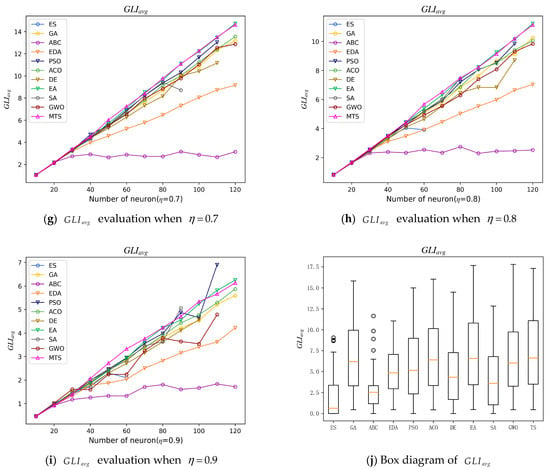
Figure 5.
evaluation for all experimental models.

Table 5.
Matrix diagram of for MTS and EA models. The bold value indicates the superior result among the mentioned metrics.

Table 6.
Matrix representing the frequency of the maximum . The bold value indicates the superior result among the mentioned metrics.
We plotted the box plots summarizing the data for each model , as shown in (j) in Figure 5, from which we can see that the box of the MTS model is longer, indicating that the data are more concentrated, and the median of the MTS model is the highest compared to all experimental models, indicating that the model solution has the best quality. In additionally, the ES model and ABC model values are biased and the data are more discrete, indicating that the model-solving ability is not stable.
Table 5 depicts the values obtained for the MTS and EA models with different positive literal proportions. The best values are expressed in bold following the comparison between MTS and EA. It can be seen that the MTS metaheuristic algorithm has more obvious advantages when , and the EA algorithm performs even better when the neuron value is equal to 120. Note that Table 6 counts the number of times that the model obtains the maximum value, and the chance that MTS obtains the optimal value is 69%. Thus, it can be seen that the quality of solutions obtained by the MTS metaheuristic algorithm is overall higher than that of the EA metaheuristic algorithm. This is because, in the EA algorithm, each voter may be influenced by the assimilation of the party leader they support (positive advertisement) or by the assimilation of other party leaders (negative advertisement), leading to frequent superposition operations. In the worst-case scenario, a voter may be subject to assimilation operations from all party leaders, resulting in unstable changes in party membership direction and consequently causing larger differences between generated solutions and standard solutions. In contrast, the MTS algorithm’s process of finding the optimal solution is more direct and explicit. Firstly, by using segment operations and the mutation operator to flip the states of four neurons, new solutions are directly generated, avoiding repetitive superposition operations and ensuring the stability of solution generation. Secondly, the use of a tabu table as short-term “memory” avoids using operation segments stored in the tabu table in the next iterations, thereby avoiding repetitive searches in the short term and providing exploration directions for solution generation, thus yielding high-quality solutions. In summary, the MTS metaheuristic algorithm demonstrates superior solution quality among all experimental models.
In this paper, we used two metrics, CT and AI, to measure the efficiency of all experimental models in the retrieval phase. An efficient and stable model can be run in a short time, i.e., the value of both metrics is small. CT is the average time to execute the metaheuristic algorithm in 100 logical combination (). The values of these two metrics are demonstrated for the 10 experimental models. It is worth mentioning that the absence of data for the ES model in Figure 6 is due to the fact that the ES algorithm does not run a metaheuristic algorithm.
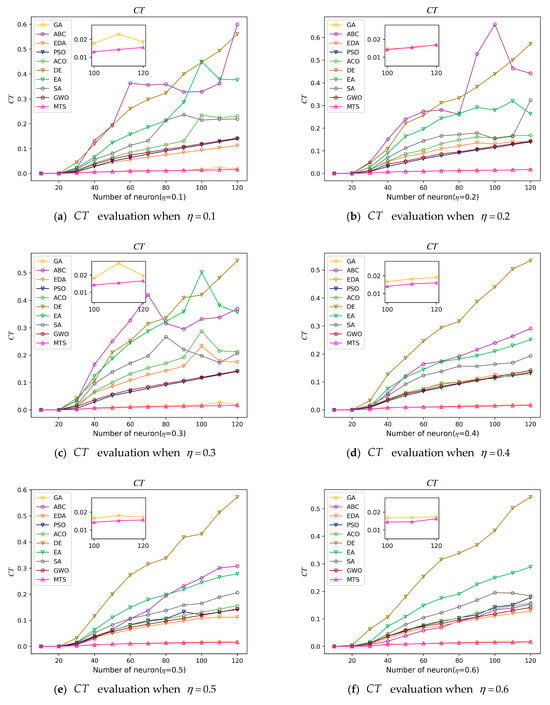
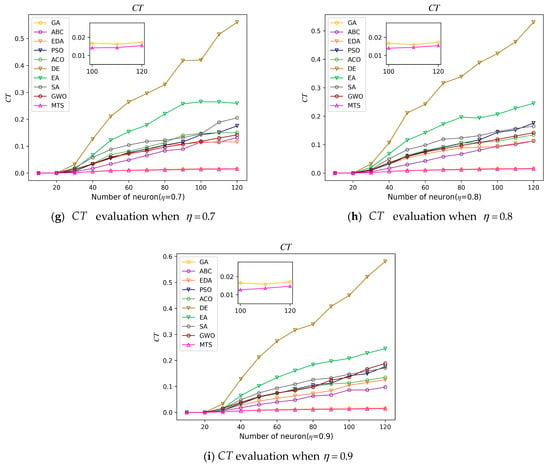
Figure 6.
evaluation for all PRO2SAT embedded in metaheuristic algorithms.
From Figure 6, it can be known that all experimental models have a gradual increase in the CT value with the increase in the number of neurons. Among them, the DE model takes the most time among all experimental models for one iteration and changes unstably as the number of neurons increases, because the optimal solution in the learning phase is not a definite combination of neurons. The DE algorithm randomly selects three fathers to generate the new generation solution, and the quality of the new generation solution depends on the quality of the parent fitness. Random fathers leads the DE algorithm to easily stay in the local optimal solution and be unable to effectively find the global optimal solution []. Furthermore, the DE algorithm requires a longer computation time per iteration []. This is because it is the only model among all others that performs mutation and crossover calculations for each neuron of every generation of solutions. Therefore, the DE algorithm necessitates more iterations and computation time for solving. Secondly, we can see from the figure that the CT values of the models GA and MTS are the smallest and basically overlap. As the number of neurons increases, their CT values basically remain as a straight line with a very small increase, indicating that these two algorithms have good computational scalability. Similarly, as the number of neurons increases, the computation time of the algorithms can remain basically constant without much impact on the computation time. After zooming on the result locally, we can clearly observe that the CT value of MTS is the smallest among the metaheuristics, and the algorithm time has a much lower complexity.
We will further compare the time complexity of GA and MTS algorithms to more intuitively assess their performance. The calculation mainly considers the time complexity of the major steps in one iteration of the algorithm under the worst-case scenario, where c represents the number for learning, n represents the number of offspring chromosomes, and m represents the number of excellent parent chromosomes in each iteration process. In this experiment, the values are set to 50 []. NN represents the number of neurons, and w represents the number of domain solutions, with a value of 14 as introduced in Table 2. The time complexity of the GA and MTS algorithms is represented as GATC and MTSTC, respectively. For a more intuitive comparison of algorithm time complexity, we set n and w to the same value. By comparing GATC and MTSTC, it can be observed that MTSTC has a smaller time complexity. The advantage of the MTS algorithm mainly manifests in the aspect of the fitness evaluation. This advantage stems from the feedback correction mechanism implemented in the MTS algorithm during computation, specifically the guided search for the highest-quality solution using a tabu list. In contrast, the GA algorithm generates multiple offspring chromosomes in each iteration, leading to increased computational complexity in evaluating the fitness of the next generation, thus consuming more time. Additionally, the mutation operation in the GA algorithm requires traversing every gene in all chromosomes, directly resulting in a more significant time gap compared to the MTS algorithm. Therefore, the MTS algorithm exhibits higher search efficiency and performance, especially in terms of fitness evaluation.
At the same time, we can also see that the CT value visibly varies as the ABC model changes with the proportion value of the positive literal. The CT value is larger when . However, as the positive literal share increases , it becomes smaller, but it still larger than the GA and MTS models. This is because, when the proportion of the positive literals proportion is small, the ABC metaheuristic algorithm requires many iterations and even reaches the maximum iteration limit. When the proportion of positive literals is large, the ABC algorithm usually converges in one to two iterations. From this, we know that the MTS model in this paper is more efficient and stable, and the value remains stable as the number of neurons increases.
In this experiment, Figure 7a–i show the convergence trend to all experimental models, and the number of iterations required for convergence of the experimental models mostly tends to increase as the number of neurons increases. It is worth noting that, when , can be satisfied among the 100 initial solutions of PRO2SAT. At this point, no metaheuristic algorithm is executed and the AI value of the experimental model is mostly 0. From the figure, we can divide the experimental models into two categories. The first category “parameter-sensitive models”, which are influenced by the number of neurons, including SA, DE, PSO, GWO. These four models are influenced by the proportion of positive literals. The second category of “stable models”, where the number of iterations is less influenced by the number of neurons and the proportion of positive literals, including EDA, ACO, EA, GA, and MTS. The part of the parameter-sensitive model that is influenced by the number of neurons falls into a local solution after a certain number of iterations and is unable to jump out of the local solution. The convergence of the ABC model also significantly fluctuates depending on the proportion of positive literals. This convergence bias of the ABC metaheuristic algorithm is not suitable for PRO2SAT, because PRO2SAT includes nine positive literal proportion settings, and the desired metaheuristic algorithm is meant to satisfy all occupancy proportions of the positive literals of PRO2SAT.
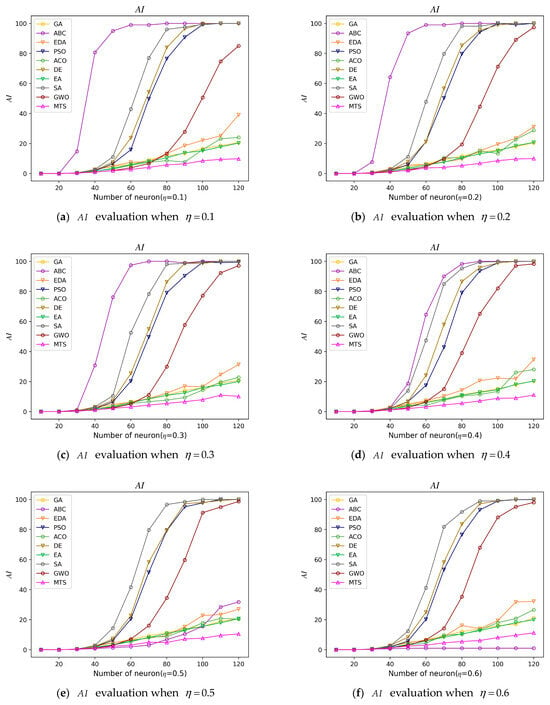
Figure 7.
evaluation for all PRO2SAT embedded in metaheuristic algorithms.
Stable metaheuristic algorithms are required, in which the most outstanding performance is the MTS algorithm proposed in this paper, which has the fastest convergence speed and is equally stable. When , , the consistency interpretation can be found by calculating an average of 10.48 iterations of the MTS algorithm for a neuron value of 120. This is because the MTS algorithm constructs a search feedback strategy, which is specifically manifested as short-term “memory” and long-term “memory”. Firstly, based on the tabu table to achieve short-term “memory”, the tabu table is used to record the recently accessed segment numbers, enabling adaptive adjustment of the search direction when selecting segments, actively choosing segments that have not been operated on recently to facilitate a faster solution search. Secondly, based on to achieve long-term “memory”, stores the solutions with the highest fitness in each iteration; combined with the flouting rule, when the local solution is greater than the global solution ( > ), the excellent domain operations banned by the tabu are pardoned, allowing repeated access to segment numbers that were recently accessed, thereby ensuring diverse and effective exploration and avoiding missing better solutions. Short-term “memory” functions within each iteration, while long-term “memory” functions between iterations, enabling the MTS algorithm to possess intelligent search capabilities throughout the entire process. In contrast, other comparative models only calculate fitness between each iteration to determine if a solution has been found, lacking effective search guidance. Thus, the MTS metaheuristic algorithm achieves a more balanced exploration and exploitation of the solution space, exhibiting efficient and stable characteristics.
In summary, for the performance analysis of all experimental models in the learning phase, the MTS model proposed in this paper has three advantages in the learning phase. Firstly, it has the strongest ability to find consistent explanations. Secondly, the solutions found have high quality and the highest diversity. Finally, it has the highest efficiency in finding consistent explanations, that is, the iteration time and the number of iterations is minimized. Therefore, the MTS model is the best among all experimental models when examined comprehensively.
8.2. Retrieval Phase
ZM is the core metric of the experimental model in the retrieval phase. Table 7 and Table 8 show the results of the ZM metric for 11 experimental models with different proportions of positive literal () and number of neurons. The ideal value for ZM is 1. A higher value for this metric indicates a greater presence of global minimum solutions within the solution set and a reduced number of local minimum solutions. Note that the data following the ‘/’ symbol in the table represent the number of neurons at the time the value was obtained. It is worth noting that the experimental models in this paper start the metaheuristic algorithm only when they cannot find consistent explanations within the default learning (a). All models will not start the metaheuristic algorithm for PRO2SAT at .

Table 7.
The time complexity of the GA and MTS algorithms.

Table 8.
The average value of all proposed algorithms during the retrieval phase at . The bold value indicates the superior result among the mentioned metrics.
The optimal data in Table 8 are marked in bold. We analyzed and classified the experimental models into three different classes. The first rank models include GA, EA, and MTS, which reaches the optimal value of ZM under all neuron takes, i.e., the value of ZM is always 1. In the table, their Max, Min, and Mean values are all 1, which means that these three models can always obtain the global minimum solution. In addition, their standard deviation values are all 0, indicating that these three models have absolute stability and are not affected by the change in the number of neurons in the experiments. Further observing the average rank values of the first rank models, it can be found that their Ava Rank values are equal and the minimum among the results under the condition of the same proportion of positive literals. All the results show the superiority of these three models in ZM metrics. The second-level models include ACO, EDA, and GWO. The second-level models have a slightly inferior performance compared to first-level models, which is mainly reflected in their inability to obtain the optimal value of ZM as the number of neurons increases. The third-level models include ES, ABC, PSO, DE, and SA, which have poorer performance, and the ZM value will gradually take 0 as the number of neurons increases. Notably, it is important to highlight that the results presented in this paper differ from the conclusions reported in the literature []. In the literature [], researchers have found that the ZM value of the PRO2SAT model increases as the proportion of positive literals increases. This is because traditional activation functions tend to lead the final neuron states toward suboptimal states, which may likely converge to local minimum energy, But such a phenomenon is not observed in our experiment. This difference can be attributed to the new activation function used in this paper. When the value of Equation (11) is taken as 0, the final state of the neuron in Equation (12) remains the same as the initial state. The new activation function leads to the correct update of the final neuron states in clauses containing negated literals, thereby converging to the global minimum energy, resulting in higher ZM values.
Based on the optimal data identified in bold in Table 9, we performed a comprehensive analysis according to the same model hierarchical classification method as in Table 7. Notably, The ABC model is elevated from the third to the first rank, while the ZM metrics data of the other models present the same performance as in Table 7, with no change in rank attribution. Despite the ABC model’s stronger performance seen in Table 8, this merely highlights its superiority in situations wherein there is a high proportion of positive literals. Nevertheless, with a low proportion of positive literals, the model’s ZM performance deteriorates, indicating its instability. Overall, only three metaheuristic algorithms, namely GA, EA, and MTS, with LRTR taking the max value of 1 for different proportion values of positive literals and number of neurons, were able to provide optimal synaptic weights for the retrieval phase. Under the guidance of the optimal synaptic weights and the new activation function, the three models GA, EA, and MTS show excellent performance in obtaining the global minimum solution. Consequently, we analyzed the quality of the global minimum solution obtained by the models using the new metrics .

Table 9.
The average value of all proposed algorithms during the retrieval phase at . The bold value indicates the superior result among the mentioned metrics.
Figure 8 illustrates the metric, which is used to analyze the quality of the solutions generated during the retrieval phase. Accordingly, we calculated the similarity between the non-repeated solution and the benchmark solution. If the solution is less different from the benchmark solution (the larger the value is), the resultant solution has poorer variability and diversity, and vice versa, the resultant solution has better variability and diversity. Firstly, the linear trend of values for all experimental models is due to the logical stable clause structure of the system. Furthermore, the ES, ABC, PSO, DE, and SA models take the value as null in the case of neurons that are available. We zoomed in on these plots and observed that the line plots of these models are suddenly interrupted. This is because the value of ZM affects the value obtained by the final neuron states, as only the final neuron states reaching the global minimum solution are used to calculate . Finally, the distribution of the value in the MTS model is around 0.58, and the distribution of this value of all the remaining comparison models is around 0.75, meaning that the MTS model outperforms among all the experimental models in terms of solving variability and solution diversity due to the fact that the MTS model has embedded a mutation operator when generating the solution in the test phase. Otherwise, under the influence of the new activation function, the final neuron states of all models may tend to converge to the benchmark solution. The mutation operator during the retrieval phase is responsible for searching for clauses that match the benchmark solution after the local field computation of neuron strings and randomly flipping neuron states. This operation enhances the diversity of model solutions while maintaining the same number of global minimum solutions.
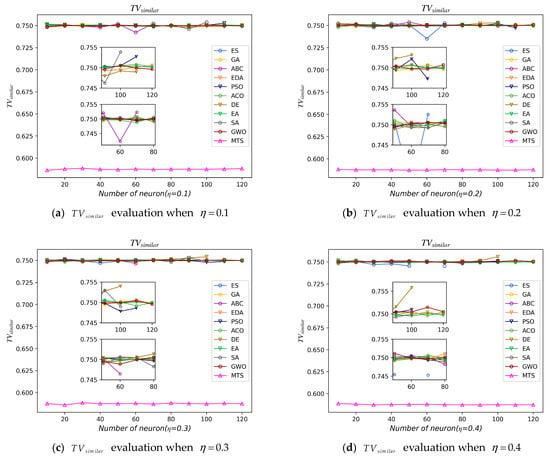
Figure 8.
evaluation for all experimental models.
Table 10 and Table 11 show the energy error for 11 experimental models taking different proportions of positive literal () and number of neurons. This comparison is vital for assessing the model’s convergence during the retrieval phase, with lower metric values signifying improved model convergence.

Table 10.
The average value of all proposed algorithms during the retrieval phase at . The bold values indicate the superior result among the mentioned metrics.

Table 11.
The average value of all proposed algorithms during the retrieval phase at . The bold values indicate the superior result among the mentioned metrics.
The optimal data in Table 10 and Table 11 are identified in bold. As described in the table, we can see that the models GA, EA, and MTS perform more prominently than the other models in terms of energy error, which consistently takes the value of 0 for different numbers of neurons. From , the energy error value is equivalent to the cost function value, and the value of is equal to the sum of unsatisfiable clauses in the range of [0, n]. n represents the number of second-order clauses. As the clause satisfaction rate of PRO2SAT increases during the retrieval phase, the energy error value decreases. When the optimal prominence weights are obtained, all types of clauses will be satisfied. This shows that the model that performs well in the learning phase will have a smaller energy error in the retrieval phase. With the analysis of the retrieval phase, we learn that the GA, EA, and MTS models all have better performance, thanks to the excellent performance of these models in the learning phase. While ABC also performs well in terms of energy error, it has a biased final state of neurons and is not suitable for all PRO2SAT models under positive literal occupancy.
8.3. Friedman Test
We conducted the Friedman test for all metric values with different values in the learning and retrieval phases. It can be seen that the Chi-square value takes the interval [64.303, 77.455] for , [71.525, 78.046] for , [40.920, 63.445] for , [87.320, 100.993] for CT, [71.021, 81.908] for AI, [71.689, 80.273] for ZM, [27.707, 52.180] for , and [68.753, 78.643] for . The degree of freedom of these indicators is 10. Most importantly, the p-value values for all metrics are less than 0.05 (), as shown in Table 12, representing that the null hypothesis of similar performance between MTS and all compared models is rejected, that is, the results of all models are significantly different across metrics.

Table 12.
Performing a Friedman test on MTS using various comparison algorithms.
8.4. Conclusions
In this paper, the MTS metaheuristic algorithm was introduced in systematic logic for the first time. Taking the representative systematic logic programming PRO2SAT as an example, we introduced the MTS metaheuristic algorithm and nine advanced metaheuristics (GA, EA, ACO, ED, DE, GWO, PSO, SA, and ABC). What is more, the ES algorithm was added to carry out experiments and comparisons from two dimensions in both the learning and retrieval phases, giving all the experimental model calculations and quantitatively analyzing the results. Finally, we used the Friedman test to test the significant difference between the experimental results in these two dimensions.
Based on the experimental results presented in Section 8.1, Section 8.2 and Section 8.3, the MTS model demonstrated superior performance over other models in both the learning and retrieval phases, particularly surpassing the exhaustive search approach. In the learning phase, the MTS metaheuristic algorithm exhibits higher retrieval efficiency by starting from a high-quality solution. The neighborhood solution generation strategy makes the process of solution generation simple, direct, and adaptive, resulting in high-quality solutions during the learning phase. Due to the short-term “memory” and long-term “memory” of the MTS algorithm, it can balance efficiency and stability. The overall algorithm structure of the MTS metaheuristic algorithm was simple and with low computational complexity, providing faster search speed compared with other metaheuristic algorithms and finding the optimal solution faster. These characteristics were reflected in the , , CT, AI, and metrics, due to the fact that the active role of the MTS algorithm in the learning phase provided advantages to the retrieval phase of the MTS model.
A successful new metaheuristic algorithm introduced into logic programming, the MTS algorithm has achieved excellent performance in systematic logic and is also expected to be introduced into non-systematic logic to enhance the performance of non-systematic logic. The enhancement of metaheuristic algorithms for DHNN-SAT models is not limited to finding consistent interpretations, but can also be used to enhance solution diversity, logic construction regularity, etc. For future work, metaheuristic algorithms can be used to enhance logic programming from more dimensions. PRO2SAT’s powerful architecture provides a new perspective on the application of knowledge in real life. For the future work, the proposed PRO2SAT can be embedded in logic mining to extract the best logic rules to classify and predict palm oil.
Author Contributions
Conceptualization, Project Administration, Writing—Original Draft, J.C.; Visualization, Y.G.; Resources, M.S.M.K.; Formal Analysis, Investigation, C.Z.; Methodology, Writing—Review & Editing, N.A.R.; Validation, M.A.M. and N.E.Z.; Funding Acquisition, C.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Xinglin Scholar, Chengdu University of Traditional Chinese Medicine with Project number (QNXZ2018042).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to express special thanks to all researchers in the AI Research Development Group for their continued support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Beam, A.L.; Kohane, I.S. Big Data and Machine Learning in Health Care. JAMA 2018, 319, 1317–1318. [Google Scholar] [CrossRef] [PubMed]
- Vigilante, K.; Escaravage, S.; McConnell, M. Big Data and the Intelligence Community-Lessons for Health Care. N. Engl. J. Med. 2019, 380, 1888–1890. [Google Scholar] [CrossRef] [PubMed]
- Egmont-Petersen, M.; de Ridder, D.; Handels, H. Image processing with neural networks—A review. Pattern Recognit. 2002, 35, 2279–2301. [Google Scholar] [CrossRef]
- Dang, X.; Tang, X.; Hao Ren, J. Discrete Hopfield neural network based indoor Wi-Fi localization using CSI. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 76. [Google Scholar] [CrossRef]
- Mérida-Casermeiro, E.; Galán-Marín, G.; Muoz-Pérez, J. An Efficient Multivalued Hopfield Network for the Traveling Salesman Problem. Neural Process. Lett. 2001, 14, 203–216. [Google Scholar] [CrossRef]
- Chu, P.P. Applying Hopfield network to find the minimum cost coverage of a Boolean function. In Proceedings of the First Great Lakes Symposium on VLSI, Kalamazoo, MI, USA, 1–2 March 1991; IEEE Computer Society: Washington, DC, USA, 1991; pp. 182–183. [Google Scholar]
- Abdullah, W.A.T.W. Logic programming on a neural network. Int. J. Intell. Syst. 1992, 7, 513–519. [Google Scholar] [CrossRef]
- Chen, J.; Kasihmuddin, M.S.M.; Gao, Y.; Mansor, M.A.; Romli, N.A.; Chen, W.; Zheng, C. PRO2SAT: Systematic Probabilistic Satisfiability logic in Discrete Hopfield Neural Network. Adv. Eng. Softw. 2023, 175, 103355. [Google Scholar] [CrossRef]
- Hussain, K.; Mohd Salleh, M.N.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic algorithms: A comprehensive review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2018; pp. 185–231. [Google Scholar]
- Zamri, N.E.; Azhar, S.A.; Mansor, M.A.; Alway, A.; Kasihmuddin MS, M. Weighted Random k Satisfiability for k = 1, 2 (r2SAT) in Discrete Hopfield Neural Network. Appl. Soft Comput. 2022, 126, 109312. [Google Scholar] [CrossRef]
- Someetheram, V.; Marsani, M.F.; Mohd Kasihmuddin, M.S.; Zamri, N.E.; Muhammad Sidik, S.S.; Mohd Jamaludin, S.Z.; Mansor, M.A. Random Maximum 2 Satisfiability Logic in Discrete Hopfield Neural Network Incorporating Improved Election Algorithm. Mathematics 2022, 10, 4734. [Google Scholar] [CrossRef]
- Muhammad Sidik, S.S.; Zamri, N.E.; Mohd Kasihmuddin, M.S.; Wahab, H.A.; Guo, Y.; Mansor, M.A. Non-Systematic Weighted Satisfiability in Discrete Hopfield Neural Network Using Binary Artificial Bee Colony Optimization. Mathematics 2022, 10, 1129. [Google Scholar] [CrossRef]
- Kho, L.C.; Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Propositional Satisfiability Logic via Ant Colony Optimization in Hopfield Neural Network. Malays. J. Math. Sci. 2022, 16, 37–53. [Google Scholar]
- Ba, S.; Xia, D.; Gibbons, E.M. Model identification and strategy application for Solid Oxide Fuel Cell using Rotor Hopfield Neural Network based on a novel optimization method. Int. J. Hydrogen Energy 2020, 45, 27694–27704. [Google Scholar] [CrossRef]
- Glover, F. Tabu search: A tutorial. Interfaces 1990, 20, 74–94. [Google Scholar] [CrossRef]
- Glover, F.; Laguna, M. Tabu search. In Handbook of Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 1998; pp. 2093–2229. [Google Scholar]
- Gopalakrishnan, M.; Mohan, S.; He, Z. A tabu search heuristic for preventive maintenance scheduling. Comput. Ind. Eng. 2001, 40, 149–160. [Google Scholar] [CrossRef]
- Meeran, S.; Morshed, M.S. A hybrid genetic tabu search algorithm for solving job shop scheduling problems: A case study. J. Intell. Manuf. 2012, 23, 1063–1078. [Google Scholar] [CrossRef]
- Žulj, I.; Kramer, S.; Schneider, M. A hybrid of adaptive large neighborhood search and tabu search for the order-batching problem. Eur. J. Opeproportionnal Res. 2018, 264, 653–664. [Google Scholar] [CrossRef]
- Lin, G.; Guan, J.; Li, Z.; Feng, H. A hybrid binary particle swarm optimization with tabu search for the set-union knapsack problem. Expert Syst. Appl. 2019, 135, 201–211. [Google Scholar] [CrossRef]
- Mohd Jamaludin, S.Z.; Mohd Kasihmuddin, M.S.; Md Ismail, A.I.; Mansor, M.A.; Md Basir, M.F. Energy based logic mining analysis with hopfield neural network for recruitment evaluation. Entropy 2021, 23, 40. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Gendreau, M.; Iori, M.; Laporte, G.; Martello, S. A Tabu search heuristic for the vehicle routing problem with two-dimensional loading constraints. Int. J. 2008, 51, 4–18. [Google Scholar] [CrossRef]
- Misevicius, A. A tabu search algorithm for the quadratic assignment problem. Comput. Optim. Appl. 2005, 30, 95–111. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms and the optimal allocation of trials. SIAM J. Comput. 1973, 2, 88–105. [Google Scholar] [CrossRef]
- Emami, H.; Derakhshan, F. Election algorithm: A new socio-politically inspired strategy. AI Commun. 2015, 28, 591–603. [Google Scholar] [CrossRef]
- Pelikan, M.; Sastry, K.; Goldberg, D.E. Multiobjective estimation of distribution algorithms. In Scalable Optimization via Probabilistic Modeling; Springer: Berlin/Heidelberg, Germany, 2006; pp. 223–248. [Google Scholar]
- He, Y.; Zhang, F.; Mirjalili, S.; Zhang, T. Novel binary differential evolution algorithm based on taper-shaped transfer functions for binary optimization problems. Swarm Evol. Comput. 2022, 69, 101022. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2008, 13, 398–417. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).