Solitary Wave Solutions of a Hyperelastic Dispersive Equation

Abstract

This paper explores solitary wave solutions arising in the deformations of a hyperelastic compressible plate. Explicit traveling wave solution expressions with various parameters for the hyperelastic compressible plate are obtained and visualized. To analyze the perturbed equation, we employ geometric singular perturbation theory, Melnikov methods, and invariant manifold theory. The solitary wave solutions of the hyperelastic compressible plate do not persist under small perturbations for wave speed $c>-\beta k^2$. Further exploration of nonlinear models that accurately depict the persistence of solitary wave solution on the significant physical processes under the K-S perturbation is recommended.

1. Introduction

Nonlinear elasticity is a pivotal field in continuum mechanics that holds paramount significance in comprehending the intricate behaviors of deformable materials beyond the linear regime. Nonlinear elasticity wave equations are generated by the elastic wave propagation in inelastic material. These equations provide a specific explanation of material response under large deformations and elucidate complex nonlinear phenomena observed in various engineering applications, including structural engineering, aerospace engineering, and geological engineering [1,2,3,4].

A fundamental topic of nonlinear elasticity is unraveling the profound connections between three-dimensional theoretical frameworks and the specialized theories governing lower-dimensional entities such as plates [5]. Researching this topic contributes to predict, model, and design materials effectively, enabling more accurate equation-based simulations for material design and structural analysis in practical engineering applications. Numerous theoretical studies about exact solutions have been conducted [5,6,7,8,9]. In particular, Chen [8] derived a new family of two-dimensional nonlinear dispersive equations

$${[u_t-u_{xxt}+3u{u}_x-\gamma (2u_x{u}_{xx}+u{u}_{xxx})]}_x-\alpha u_{yy}+\beta u_{xxyy}=0,$$

(1)

whose family includes the KdV, Kadomtsev–Petviashvili (KP), and Camassa–Holm (C-H) equations. Chen [7] demonstrated global well-posedness of the Cauchy problem for Equation (1), establishing the existence of solitary wave solutions derived from an associated variational problem. In Equation (1), u represents the displacement along the z-direction, while x and y denote rescaled longitudinal and lateral coordinates in the horizontal plane, respectively. The equation encompasses four crucial material parameters, denoted by $\gamma ,\alpha ,\beta$. The parameter $\alpha$ and $\beta$ are material constants measuring subtle transverse effects. The parameter $\gamma$ represents the coupling strength between the nonlinear and dispersive terms. Specifically, $\gamma$ controls the relative contributions of the nonlinear and dispersive terms, thereby influencing the behavior of the solutions, described as follows:

(1)

When $\gamma >0$, the coupling between the nonlinear and dispersive terms is positive, indicating a forward interaction between the nonlinear and dispersive effects. In this case, the solutions may exhibit more complex behaviors, such as the formation and interaction of solitary waves.

(2)

When $\gamma <0$, the coupling between the nonlinear and dispersive terms is negative, implying an opposite interaction. In such a scenario, the behavior of the solutions may be simpler, potentially exhibiting stable behaviors such as asymptotic or periodic solutions. This paper discusses the case of $\gamma <0$.

It is noteworthy that the derived equation is an approximate two-dimensional plate equation designed to simulate the behavior of the complete three-dimensional field space. Therefore, we make the assumption that small perturbations applied to the pre-stressed state primarily manifest in the vertical direction (z-direction) and a singular horizontal direction (x-direction), which implies that variations in waves within the transverse direction (y-direction) are considered to be small.

In practical engineering simulations, models inevitably experience perturbations from various features. Therefore, investigating the persistence of traveling wave solutions for nonlinear differential equations under different small perturbations is crucial. Apart from parameter $\gamma$ balancing nonlinearity and dispersion, in cases of strong dispersion compared to the backward diffusion and dissipation, we add Kuramoto–Sivashinsky (KS) perturbation [10] ($u_{xx}+u_{xxxx}$) to the equation to mimic real engineering scenarios.

Geometric singular perturbation theory (GSP) has been widely applied in the study of perturbation problems. The basic principles and theories of GSP are introduced in detail by Fenichel [11], while application fields and methods of GSP are introduced by Kuehn [12], Jones [13], and Hek [14]. Moreover, GSP has found extensive use in exploring the existence and persistence of traveling wave solutions in water wave equations [15,16,17,18,19].

Under certain specific parameter constraints, Equation (1) generalizes several well-known models of water waves equations. The explicit solutions and persistence of some of these models have been extensively studied, described as follows:

(1)

When $\gamma =\beta =0$, (1) is reduced to the regularized long-wave KP equation [6]. Mahmood and Ur-Rehman [20] investigated the existence and propagation characteristics of ion-acoustic KP solitons; Anco and Gandarias [21] discussed Kinematic properties of all of the different types of compactons and solitary waves, along with conservation laws of the generalized KP equation.

(2)

When $\gamma =\alpha =\beta =0$, (1) is reduced to the the BBM equation [22]. Chen et al. [23] proved the existence of solitary waves and periodic waves for a generalized BBM equation with KS perturbation with the method of GSP; Buhe and Chaolu [24] used a hybrid approach to obtain the approximate solitary wave solutions of a perturbed BBM equations.

(3)

When $\gamma =1$, and $\alpha =\beta =0$, (1) is reduced to the the Camassa–Holm equation [25]. Lenells [26] classified all weak traveling wave solutions of the CH equation, determined the wavelength of the traveling waves for the peaked solutions, and detailed analyzed the phase diagram of the CH equation. Du et al. [27,28] analyzed a CH equation with KS perturbation and a delayed CH equations with methods of GSP. Sun et al. [29] depicted bifurcation portraits of a CH–DP-type equation and proved that the portraits exhibit all possible exact explicit bounded solutions. Wang [30] obtained the exact traveling-wave solution of the non-differential type for the local fractional Camassa–Holm–Kadomtsev–Petviashvili equation by employing the local fractional wave method.

Inspired by the above references, in this paper we study the perturbed equation as the following form

$${[u_t-u_{xxt}+3u{u}_x-\gamma (2u_x{u}_{xx}+u{u}_{xxx})+ϵ(u_{xx}+u_{xxxx})]}_x-\alpha u_{yy}+\beta u_{xxyy}=0,$$

(2)

where $\epsilon$ is sufficiently small. $u_{xx}$ and $u_{xxxx}$ represent the backward diffusion term and dissipation term, respectively. We prove that the Melnikov function of (2) lacks a simple zero point for the wave speed c. Thus, the solitary wave on the homoclinic orbit is not persistent in the perturbed Equation (2) under the parameter conditions $\gamma <0,\alpha =\beta$ for wave speed $c>-\beta k^2$ with perturbation $\epsilon$ being sufficiently small.

The innovations of this paper can be summarized as follows:

(1)

Departing from calculating the exact solution of the hyperelastic dispersion equation [5,8], this paper expresses traveling solutions in terms of the relationship between u and y, studying the persistence of homoclinic orbits under real disturbances simulated by KS perturbation.

(2)

In contrast to traditional GSP methods for proving the existence and persistence of solutions in water wave equations with perturbations, the paper uses Melnikov functions to demonstrate the non-persistence of homoclinic orbits for wave speed c satisfying certain conditions.

(3)

In the process of calculating the Melnikov function, which involves numerous complex parameters, the paper simplifies the function and breaks down the parameter range for $\gamma$, eventually obtaining the specific expression of the Melnikov function concerning the wave speed c when $\alpha =\beta$.

The paper follows the structure outlined below. In Section 2, we simplify Equation (1) into ordinary differential equations and transform it into the fast and slow system. Then we depict the bifurcation and phase portraits under various parameter ranges, ultimately obtaining the precise expression for homoclinic orbits. In Section 3, we utilize GSP and invariant manifold theory to reduce the dimension of (2). Moreover, we employ Melnikov function theory to demonstrate the non-persistence of solitary solutions on the homoclinic orbit $\Gamma$ of Equation (2) for $\gamma <0,\alpha =\beta$. In Section 4, we conduct numerical simulations to verify our results. In Section 5, we summarize the conclusion of this paper and potential directions for future work. In Appendix A, we describe the Theorem 3.1(2) cited in this paper regarding reference [31].

2. Solitary Wave Solutions of (1)

In this section, we consider the traveling wave solutions of (1). We utilize the traveling wave transformation $\xi =x+ky-ct$, where k is the directional constant and c is the wave speed. We then integrate $\xi$ twice on both sides of the equation, introducing the integral constant as 0. Equation (1) transforms into

$$\frac{3}{2}{u}^2-(\alpha k^2+c)u+(\beta k^2+c)u_{\xi \xi }-\frac{\gamma }{2}{\left(u_{\xi }\right)}^2-\gamma u{u}_{\xi \xi }=0.$$

(3)

Let

$$A=\alpha k^2+c,B=\beta k^2+c,A=B+(\alpha -\beta )k^2.$$

(4)

Equation (3) can be expressed more succinctly as follows:

$$\frac{3}{2}{u}^2-Au+B{u}_{\xi \xi }-\frac{\gamma }{2}{\left(u_{\xi }\right)}^2-\gamma u{u}_{\xi \xi }=0.$$

(5)

Equation (5) corresponds to the subsequent first-order system

$$\left\{\begin{array}{c}\frac{du}{d\xi }=y,\hfill \\ (B-\gamma u)\frac{dy}{d\xi }=\frac{\gamma }{2}{y}^2+Au-\frac{3}{2}{u}^2.\hfill \end{array}\right.$$

(6)

By the transformation $\frac{\xi }{B-\gamma u}=\eta$, we obtain the equivalent system

$$\left\{\begin{array}{c}\frac{du}{d\eta }=(B-\gamma u)y,\hfill \\ \frac{dy}{d\eta }=\frac{\gamma }{2}{y}^2+Au-\frac{3}{2}{u}^2.\hfill \end{array}\right.$$

(7)

The system (7) is a Hamiltonian system with the first integral function

$$H(u,y)=-\frac{y^2}{2}(B-\gamma u)+\frac{A}{2}{u}^2-\frac{u^3}{2}.$$

Let $(u_i,0)(i=1,2)$ represent the equilibrium point of (7)

$$u_1=0,u_2=\frac{2A}{3}.$$

At each equilibrium point $(u_i,0)$, the linearized representation of system (7) can be formulated as

$$\left(\begin{array}{cc}0& B-\gamma u_i\\ A-3u_i& 0\end{array}\right).$$

(8)

Theorem 1.

For system (7) with $A>0$ and $\gamma <0$, we have the following results:

(a) 

If $B>0$, (7) has a saddle at (0, 0) and a center at ($\frac{2A}{3}$, 0). System (7) has a homoclinic orbit Γ surrounding the center, which is from (0, 0) to (0, 0) and intersects with the u-axis at (A, 0) (see Figure 1a).

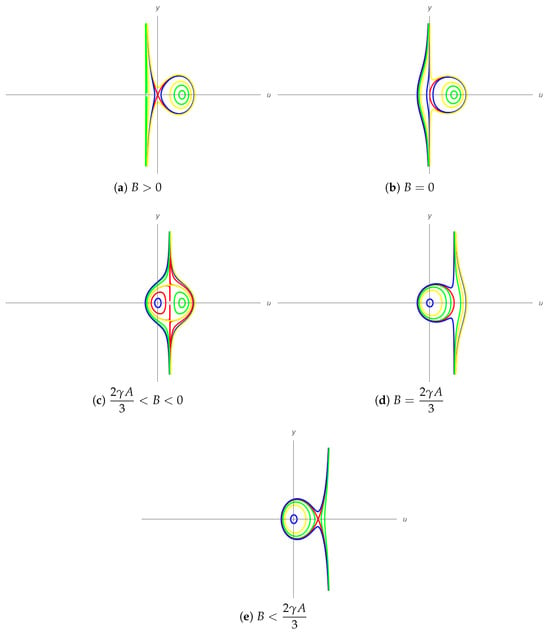Figure 1. The bifurcation and phase portraits of waves with different starting points of system (7).

(b) 

If $B=0$, (7) has a cusp at (0, 0) and a center at ($\frac{2A}{3}$, 0). System (7) has period orbits surrounding the center (see Figure 1b).

(c) 

If ${\displaystyle \frac{2\gamma A}{3}}<B<0$, (7) has a center at (0, 0) and a center at ($\frac{2A}{3}$, 0). System (7) has period orbits surrounding the centers (see Figure 1c).

(d) 

If $B={\displaystyle \frac{2\gamma A}{3}}$, (7) has a center at (0, 0) and a cusp at ($\frac{2A}{3}$, 0). System (7) has period orbits surrounding the center (see Figure 1d).

(e) 

If $B<{\displaystyle \frac{2\gamma A}{3}}$, (7) has a center at (0, 0) and a saddle at ($\frac{2A}{3}$, 0). System (7) has a homoclinic orbit ${\Gamma }_0$ surrounding the center, which is from ($\frac{2A}{3}$, 0) to ($\frac{2A}{3}$, 0) and intersects with the u-axis at (${\displaystyle \frac{\sqrt[3]{27A{u}^2-4A^3}}{3}}$, 0) (see Figure 1e).

Corollary 1.

For system (7) with $A<0$ and $\gamma <0$, we have the following results:

(a) 

If $B>{\displaystyle \frac{2\gamma A}{3}}$, (7) has a center at (0, 0) and a saddle at ($\frac{2A}{3}$, 0). System (7) has a homoclinic orbit Γ surrounding the center, which is from ($\frac{2A}{3}$, 0) to ($\frac{2A}{3}$, 0) and intersects with the u-axis at (${\displaystyle \frac{\sqrt[3]{27A{u}^2-4A^3}}{3}}$, 0).

(b) 

If $B={\displaystyle \frac{2\gamma A}{3}}$, (7) has a center at (0, 0) and a cusp at ($\frac{2A}{3}$, 0). System (7) has period orbits surrounding the center.

(c) 

If $0<B<{\displaystyle \frac{2\gamma A}{3}}$, (7) has a center at (0, 0) and a center at ($\frac{2A}{3}$, 0). System (7) has period orbits surrounding the centers.

(d) 

If $B=0$, (7) has a cusp at (0, 0) and a center at ($\frac{2A}{3}$, 0). System (7) has period orbits surrounding the center.

(e) 

If $B<0$, (7) has a saddle at (0, 0) and a center at ($\frac{2A}{3}$, 0). System (7) has a homoclinic orbit surrounding the center, which is from (0, 0) to (0, 0) and intersects with the u-axis at (A, 0).

From Theorem 1 and Figure 1, we observe the existence of the homoclinic orbit $\Gamma$ when the parameters satisfy $A>0,\gamma <0,B>0$, and the homoclinic orbit ${\Gamma }_0$ when the parameters satisfy $A>0,\gamma <0,B<\frac{2\gamma A}{3}$ for system (7). Both $\Gamma$ and ${\Gamma }_0$ share identical properties and characteristics.

Next, we will present the explicit expression of the homoclinic orbit $\Gamma$ using the Hamiltonian function. For $A>0,\gamma <0,B>0$ (see Figure 1a), homoclinic orbit $\Gamma$ satisfies

$$\underset{\xi \to \infty }{lim}u\left(\xi \right)=0.$$

The Hamiltonian function of the point on the homoclinic orbit $\Gamma$ is characterized by

$$H(u,y)=H(0,0)=0.$$

(9)

${\Gamma }_{+}$ represents the segment of the homoclinic orbit $\Gamma$ above the u-axis which the homoclinic orbit is from $(0,0)$ to $(A,0)$. The expression of y along the ${\Gamma }_{+}$ deduced from (9) is

$$y=\sqrt{\frac{A{u}^2-u^3}{B-\gamma u}}.$$

(10)

${\Gamma }_{-}$ represents the part of the homoclinic orbit $\Gamma$ below the u-axis which the homoclinic orbit is from $(A,0)$ to $(0,0)$. The expression of y along the ${\Gamma }_{-}$ deduced from (9) is

$$y=-\sqrt{\frac{A{u}^2-u^3}{B-\gamma u}}.$$

(11)

Since homoclinic orbits determine solitary wave solutions, we will discuss the persistence of homoclinic orbit $\Gamma$ for (2) ${|}_{\epsilon \ne 0}$, where $\epsilon$ is sufficiently small.

3. Non-Persistence of Solitary Wave Solutions of (2) ${|}_{\mathbf{\epsilon }\ne \mathbf{0}}$

In this section, we will prove that solitary wave solutions of the hyperelastic compressible plate on the homoclinic orbit $\Gamma$ (Theorem 1 (a)) do not persist under small perturbations.

By using the identical transformation as detailed in Section 2, we attain the equivalent formulation of (2)

$$\frac{3}{2}{u}^2-Au+B{u}_{\xi \xi }-\frac{\gamma }{2}{\left(u_{\xi }\right)}^2-\gamma u{u}_{\xi \xi }+\epsilon (u_{\xi }+u_{\xi \xi \xi })=0,$$

(12)

which is equivalent to the following slow system

$$\left\{\begin{array}{c}\frac{du}{d\xi }=y,\hfill \\ \frac{dy}{d\xi }=w,\hfill \\ \epsilon \frac{dw}{d\xi }=-(B-\gamma u)w+Au-\frac{3}{2}{u}^2+\frac{\gamma }{2}{y}^2-\epsilon y.\hfill \end{array}\right.$$

(13)

Let $\frac{\xi }{\epsilon }=\sigma$. We obtain the equivalent fast system

$$\left\{\begin{array}{c}\frac{du}{d\sigma }=\epsilon y,\hfill \\ \frac{dy}{d\sigma }=\epsilon w,\hfill \\ \frac{dw}{d\sigma }=-(B-\gamma u)w+Au-\frac{3}{2}{u}^2+\frac{\gamma }{2}{y}^2-\epsilon y.\hfill \end{array}\right.$$

(14)

The linearization of system (14) with $\epsilon =0$ is

$$\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ A-3u+\gamma w& \gamma y& \gamma u-B\end{array}\right)$$

(15)

It can be directly calculated that the eigenvalues of (15) are ${\lambda }_1=0$, ${\lambda }_2=0$, and ${\lambda }_3=\gamma u-B$.

The critical manifold of (14) is as follows:

$$M_0=\{(u,y,w)\in R^3|(B-\gamma u)w=Au-\frac{3}{2}{u}^2+\frac{\gamma }{2}{y}^2\}.$$

The dimension of $M_0$ is equal to the number of zero eigenvalues of (15). Thus, $M_0$ is normally hyperbolic.

By Fenichel’s Invariant Manifold Theorem (Theorem 1, [13]), (14) has a slow manifold $M_{\epsilon }$

$$M_{\epsilon }=\{(u,y,w)\in R^3|(B-\gamma u)w=Au-\frac{3}{2}{u}^2+\frac{\gamma }{2}{y}^2+\epsilon h_1+O\left({\epsilon }^2\right)\},$$

(16)

which is diffeomorphic to $M_0$ and locally invariant under the flow of system (14).

By substituting (16) into the slow system (13), we obtain

$$\begin{array}{cc}\hfill h_1& =(\frac{3u-A-2\gamma w}{\gamma u-B}+1)y,\hfill \\ \hfill & =-\frac{y}{{(B-\gamma u)}^2}({\gamma }^2{u}^2+{\gamma }^2{y}^2+B^2+A\gamma u-2B\gamma u-3Bu+AB).\hfill \end{array}$$

(17)

Hence, the three-dimensional system (13) reduces to the following two-dimensional system on $M_{\epsilon }$

$$\left\{\begin{array}{c}\frac{du}{d\xi }=y,\hfill \\ (B-\gamma u)\frac{dy}{d\xi }=Au-\frac{3}{2}{u}^2+\frac{\gamma }{2}{y}^2-\epsilon \frac{y}{{(B-\gamma u)}^2}({\gamma }^2{u}^2+{\gamma }^2{y}^2+B^2+A\gamma u-2B\gamma u-3Bu+AB).\hfill \end{array}\right.$$

(18)

Let $\frac{\xi }{B-\gamma u}=\eta$. We obtain the equivalent two-dimensional system

$$\left\{\begin{array}{c}\frac{du}{d\eta }=(B-\gamma u)y,\hfill \\ \frac{dy}{d\eta }=Au-\frac{3}{2}{u}^2+\frac{\gamma }{2}{y}^2-\epsilon \frac{y}{{(B-\gamma u)}^2}({\gamma }^2{u}^2+{\gamma }^2{y}^2+B^2+A\gamma u-2B\gamma u-3Bu+AB).\hfill \end{array}\right.$$

(19)

Theorem 2.

For $\gamma <0$, $\alpha =\beta$, there does not exist wave speed $c>-\beta k^2$ such that (19) has homoclinic orbits near Γ (Theorem 1(a)) with ε that is small enough. That is, the solitary wave solution of (2) is not persistent.

Proof. 

We shall compete the proof by using the Melnikov method. Consider the Melnikov function in homoclinic orbit $\Gamma$ (Theorem 1(a))

$$M\left(B\right)={\int }_{-\infty }^{+\infty }-\frac{y^2}{B-\gamma u}({\gamma }^2{u}^2+{\gamma }^2{y}^2+B^2+A\gamma u-2B\gamma u-3Bu+AB)d\eta .$$

By substituting (10), (11) and the first equation of system (19) into $M\left(B\right)$, we obtain

$$\begin{array}{cc}\hfill M\left(B\right)& ={\int }_{{\Gamma }_{+}}-\frac{y}{{(B-\gamma u)}^2}({\gamma }^2{u}^2+{\gamma }^2{y}^2+B^2+A\gamma u-2B\gamma u-3Bu+AB)du\hfill \\ \hfill & +{\int }_{{\Gamma }_{-}}-\frac{y}{{(B-\gamma u)}^2}({\gamma }^2{u}^2+{\gamma }^2{y}^2+B^2+A\gamma u-2B\gamma u-3Bu+AB)du\hfill \\ \hfill & ={\int }_0^A-\sqrt{\frac{A{u}^2-u^3}{{(B-\gamma u)}^5}}({\gamma }^2{u}^2+{\gamma }^2{\displaystyle \frac{A{u}^2-u^3}{B-\gamma u}}+B^2+A\gamma u-2B\gamma u-3Bu+AB)du\hfill \\ \hfill & +{\int }_A^0\sqrt{\frac{A{u}^2-u^3}{{(B-\gamma u)}^5}}({\gamma }^2{u}^2+{\gamma }^2{\displaystyle \frac{A{u}^2-u^3}{B-\gamma u}}+B^2+A\gamma u-2B\gamma u-3Bu+AB)du\hfill \\ \hfill & =-2{\int }_0^A\sqrt{\frac{A{u}^2-u^3}{{(B-\gamma u)}^5}}({\gamma }^2{u}^2+{\gamma }^2{\displaystyle \frac{A{u}^2-u^3}{B-\gamma u}}+B^2+A\gamma u-2B\gamma u-3Bu+AB)du\hfill \\ \hfill & =-2{\int }_0^A\sqrt{\frac{A{u}^2-u^3}{{(B-\gamma u)}^7}}((1+{\displaystyle \frac{1}{\gamma }}){(B-\gamma u)}^3+B(AB-{\displaystyle \frac{B^2}{\gamma }}))du\hfill \\ \hfill & =-2{\int }_0^A\sqrt{\frac{A{u}^2-u^3}{B-\gamma u}}(1+{\displaystyle \frac{1}{\gamma }}+{\displaystyle \frac{B(AB-{\displaystyle \frac{B^2}{\gamma }})}{{(B-\gamma u)}^3}})du.\hfill \end{array}$$

(20)

Take the transform $B-\gamma u=z$. Since $\alpha =\beta$ ($A=B$), we obtain

$$\begin{array}{cc}\hfill M\left(B\right)& =-{\displaystyle \frac{2}{{\gamma }^2}}{\int }_B^{(1-\gamma )B}(z-B)\sqrt{{\displaystyle \frac{z-(1-\gamma )B}{\gamma z}}}(1+{\displaystyle \frac{1}{\gamma }}-\frac{B^3(1-\gamma )}{\gamma z^3})dz\hfill \\ \hfill & =-{\displaystyle \frac{2}{{\gamma }^2}}{\int }_B^{(1-\gamma )B}(z-B)\sqrt{{\displaystyle \frac{z-(1-\gamma )B}{\gamma z}}}\left({\displaystyle \frac{(\gamma +1)z^3-B^3(1-\gamma )}{\gamma z^3}}\right)dz.\hfill \end{array}$$

(21)

(a)

For $\gamma \le {\displaystyle \frac{1-\sqrt{5}}{2}}$, we have

$$z^3\le {(1-\gamma )}^3{B}^3\le {\displaystyle \frac{1-\gamma }{1+\gamma }}{B}^3.$$

$$(z-B)\ge 0,\sqrt{{\displaystyle \frac{z-(1-\gamma )B}{\gamma z}}}\ge 0,\left({\displaystyle \frac{(\gamma +1)z^3-B^3(1-\gamma )}{\gamma z^3}}\right)\ge 0.$$

Thus, $M\left(B\right)<0$, $M\left(B\right)$ has no simple zero point with respect to $B>0$.

(b)

For ${\displaystyle \frac{1-\sqrt{5}}{2}}\le \gamma <0$, (21) can be integrated

$$\begin{array}{cc}\hfill M\left(B\right)& =-{\displaystyle \frac{2}{{\gamma }^2}}{\int }_B^{(1-\gamma )B}(z-B)\sqrt{{\displaystyle \frac{z-(1-\gamma )B}{\gamma z}}}\left({\displaystyle \frac{(\gamma +1)z^3-B^3(1-\gamma )}{\gamma z^3}}\right)dz\hfill \\ \hfill & =-{\displaystyle \frac{2}{{\gamma }^2}}·\frac{B^2\left(\sqrt{\gamma }\left(-45+\gamma \left(15+(61-15\gamma )\gamma \right)\right)+15{(-1+\gamma )}^2(1+\gamma )(3+\gamma )\mathrm{ArcTanh}\left(\sqrt{\gamma }\right)\right)}{60(-1+\gamma ){\gamma }^{3/2}}.\hfill \end{array}$$

(22)

$M\left(B\right)\ne 0$ for any $B>0$.

Thus, for ${\displaystyle \frac{1-\sqrt{5}}{2}}\le \gamma <0$, $M\left(B\right)$ does not possess a simple zero point with respect to B($B>0$).

The proof is completed by (a) and (b). By Theorem 3.1 (2) [31] (see Appendix A Lemma A1), $M\left(B\right)$ has no zero point for $\alpha =\beta$, $B=c+\beta k^2>0$, $\gamma <0$. In other words, when $\alpha =\beta$, the homoclinic orbit $\Gamma$ (Theorem 1(a)) of (2) does not persist under small perturbations for arbitrary wave speed $c>-\beta k^2$ since $B=c+\beta k^2>0$. □

4. Numerical Simulations

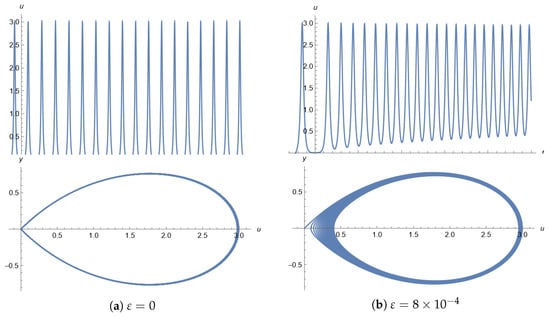
In this section, we verify the results above through numerical simulations conducted using Mathematica 13. Let $\gamma =-2.0$, $B=A=3.0$. From Theorem 1(a), we know that when $\epsilon =0$, Equation (1) has a homoclinic orbit $\Gamma$ from the saddle (0, 0) to (0, 0). To capture the bifurcation, we set $(u\left(0\right),y\left(0\right))=({10}^{-3},0)$. Consequently, we obtain the bifurcation and phase portrait (see Figure 2a).

Figure 2. The initial condition is $(u\left(0\right),y\left(0\right))=({10}^{-3},0)$. The phase portraits of (1) and (2) with $\gamma =-2.0$, $B=A=3.0$.

To simulate the case of Equation (2), we set $\epsilon =8·{10}^{-4}$. From Theorem 2, we know that the phase diagram trajectory breaks for any $c>-\beta k^2$($B>0$). The result is verified by numerical simulation (see Figure 2b).

5. Conclusions

In this paper, we derived the precise expressions of the homoclinic orbits $\Gamma$ for $\gamma <0,A>0,c>-\beta k^2$ and the homoclinic orbit ${\Gamma }_0$ for $\gamma <0,A>0,c<-\beta k^2+\frac{2\gamma A}{3}$ by analyzing the bifurcation and phase portraits of the hyperelastic compressible plate model (1) under specific parameter conditions. Then we proved that, although the solitary wave solutions on the homoclinic orbit $\Gamma$ (Theorem 1(a)) of the system (1) exists, it is not persistent on the perturbed system (2) under the parameters $\gamma <0,\alpha =\beta$ for wave speed $c>-\beta k^2$.

In future research, we may explore the persistence of solitary solutions on the homoclinic orbit $\Gamma$ in more intricate scenarios, such as on the condition of $\alpha \ne \beta$. Additionally, investigating the persistence of solitary solutions on the homoclinic orbit ${\Gamma }_0$ could be another promising direction.