Certain Novel Dynamic Inequalities Applicable in the Theory of Retarded Dynamic Equations and Their Applications

Abstract

In this article, we establish certain time-scale-retarded dynamic inequalities that contain nonlinear retarded integral equations on various time scales. These inequalities extend and generalize some significant inequalities existing in the literature to their more general forms. The qualitative and quantitative characteristics of solutions to various dynamic equations on time scales involving retarded integrals can be studied using these inequalities. The results presented in this manuscript furnish a powerful tool to analyze the boundedness of nonlinear integral equations with retarded integrals on several time scales. In the end, we also include numerical illustrations to signify the applicability of these results to power nonlinear retarded integral equations on real and quantum time scales.

1. Introduction

Throughout the history of mathematics, inequality has been a major factor in its growth. The primary factor behind the effective development of inequalities in the theory of fractional difference equations, integral equations, partial differential equations, and ordinary differential equations is their capacity to analyze the unknown function that appears in the aforementioned equations for both qualitative and quantitative properties.

In the annals of mathematics, integral equations have acquired immense importance. In the year 1812, Abel shaped notable research by developing an integral equation for a certain mechanical problem, signifying the beginning of the theory of integral equations. This branch further witnessed a huge growth due to several mathematicians, with the remarkable contributions of Volterra (1895) and Fredholm (1900). Integral equations have shown to be quite helpful in a variety of applied domains, including control theory, network theory, nuclear reactor dynamics, etc. However, it remained a difficult task for many years to find an exact analytical solution for such an equation. In 1919, Gronwall [1] made a revolutionary discovery of an inequality to obtain an explicit bound for a class of integral and differential equations. Since then, several mathematicians contributed remarkably to the development and exploration of new inequalities to study certain properties like boundedness, existence, and stability of the solutions of the aforementioned equation, viz., Bellman (1943), Bihari (1956), Pachpatte (1973), to mention a few.

Similarly, a number of mathematicians have explored integral equations, integro-differential equations, and partial integro-differential equations with retarded arguments, and numerous approaches have been brought forward for the investigation of their various characteristics on the real domain.

A general integral equation with retarded arguments is of the form

$$\begin{array}{c}\hfill \mathfrak{u}\left(t\right)=f\left(t\right)+\underset{\alpha \left(x_0\right)}{\overset{\alpha \left(x\right)}{\int }}g\left(s\right)\mathfrak{u}\left(s\right)ds.\end{array}$$

If we consider the same equation on a certain time-scale, it is regarded as a retarded dynamic equation.

However, considering the methods and resources at hand, it is not always possible to determine the precise solution of the integral equations in question. Integral inequalities are essential in this situation because they provide a clear bound on the unknown function and help to analyze the solution for boundedness, stability, and continuous dependency on initial data.

In 2000, Lipovan [2] obtained the bound on the Gronwall-type retarded inequality, which reads as

$$\begin{array}{c}\hfill \mathfrak{u}\left(t\right)\le k+\underset{\alpha \left(t_0\right)}{\overset{\alpha \left(t\right)}{\int }}h\left(s\right)\mathfrak{u}\left(s\right)ds,t_0<t<T_0,\end{array}$$

where k is a constant, $\mathfrak{u},h\in C([t_0,T_0],{\mathbb{R}}_{+})$ and $\alpha \in C([t_0,T_0],[t_0,T_0]).$

In 2006, Pachpatte [3] studied and obtained the bound on the Volterra–Fredholm-type integral inequality of the form

$$\begin{array}{c}\hfill \mathfrak{u}\left(\tau \right)\le a_1\left(\tau \right)+{\int }_{l_1}^{\tau }{a}_2\left(\delta \right)\mathfrak{u}\left(\delta \right)d\delta +{\int }_{l_1}^{l_2}{a}_3\left(\delta \right)\mathfrak{u}\left(\delta \right)d\delta .\end{array}$$

Further, in 2014, Kendre et al. [4] extended Pachpatte’s inequality and studied the bound on an integral inequality of the type

$$\begin{array}{c}\hfill {\mathfrak{u}}^p\left(t\right)\le a_1\left(t\right)+{\int }_{\alpha }^t{a}_2\left(s\right)\mathfrak{u}\left(s\right)ds+{\int }_{\alpha }^{\beta }{a}_3\left(s\right){\mathfrak{u}}^p\left(s\right)ds.\end{array}$$

Later, in 2017, El-Deeb and A. Ahmed [5] used Lipovan’s inequality as the base and established a bound on retarded integral inequality of the kind

$$\begin{array}{c}\hfill {\mathfrak{u}}^p\left(t\right)\le a_1\left(t\right)+{\int }_{\alpha }^{\alpha \left(t\right)}{a}_2\left(s\right)\mathfrak{u}\left(s\right)ds+{\int }_{\alpha }^{\beta }{a}_3\left(s\right){\mathfrak{u}}^p\left(s\right)ds.\end{array}$$

Recently, there has been a great deal of interest in the research of time scale calculus and related dynamic inequalities, a branch of mathematics that can be traced all the way back to Stefan Hilger [6,7]. The goal is to demonstrate a solution of dynamic equations on arbitrary time scales, which are any nonempty and closed subset of the $\mathbb{R}$ (see [8,9]). The merging of continuous and discrete analysis is one goal of the theory of time scales. Differential calculus ($\mathbb{T}=\mathbb{R}$), difference calculus ($\mathbb{T}=\mathbb{Z}$), and quantum calculus ($\mathbb{T}=\overline{q^{\mathbb{Z}}}=\left\{0\right\}\cup \{q^{\vartheta },\vartheta \in \mathbb{Z}\},q>1$) are the three most common applications of calculus over time scales (see [9,10,11]). Time scale calculus is largely organized and summarized in Agarwal, Bohner, and Peterson’s books [9,10] on the subject. A number of dynamic inequalities have been created during the past decade by many researchers, who were inspired by various applications. As an example, we recommend the reader review [5,12,13,14,15,16,17] for contributions and the references included therein.

Recently, in 2022, Wang et al. [12] extended and presented a time scale version of inequality attributed to El-Deeb and Ahmed [5], which reads as

$$\begin{array}{c}\hfill {\mathfrak{u}}^p\left(t\right)\le a_1\left(t\right)+{\int }_{\alpha }^{{\alpha }_1\left(t\right)}{a}_2\left(s\right)\mathfrak{u}\left(s\right)\mathrm{\Delta }s+{\int }_{\alpha }^{{\alpha }_2\left(t\right)}{a}_3\left(s\right){\mathfrak{u}}^p\left(s\right)\mathrm{\Delta }s.\end{array}$$

(1)

Nevertheless, Wang et al.’s inequalities [12] are insufficient to derive explicit bounds on the retarded dynamic equations; within which, the integrals on the right-hand side of Wang’s inequality (1), which involve nonlinear unknown functions, are either raised to additional powers or, in the case of nonlinear unknown functions linked to another function, raised to yet another power. With this shortcoming in mind, the main goal of this manuscript is to present several inequalities to solve some important delayed dynamic equations that contain the aforementioned scenarios. Our findings not only expand and broaden Wang’s inequalities, but they also offer a powerful instrument for analyzing important delayed dynamic equations that are beyond the scope of Wang’s existing inequalities.

The layout of this article is as follows. We will review fundamental calculus on time scales in Section 2, present our results with their methodology in Section 3, discuss useful numerical illustrations of the established findings in Section 4, and then draw conclusions.

2. An Overview of Time Scales and Some Fundamental Theorems

Any nonempty and closed subset of $\mathbb{R}$ is regarded as a time scale $\mathbb{T}.$ Further, for any $\tau \in \mathbb{T},$ $\sigma \left(\tau \right)=\mathrm{infimum} \mathrm{of} \mathrm{the} \mathrm{set}\{{\tau }^{\prime }\in \mathbb{T}:{\tau }^{\prime }>\tau \}$ is referred as a forward jump operator on $\mathbb{T}$ and $\sigma (\varnothing )=sup\mathbb{T}$. A point $\tau$ is classified as right-scattered and right-dense if $\sigma \left(\tau \right)>\tau$ and $\sigma \left(\tau \right)=\tau ,$ where $\tau <sup\mathbb{T},$ respectively. Similar definitions apply to the left-scattered and left-dense points as well as the backward jump operator. Furthermore, $\mu \left(t\right):=\sigma \left(t\right)-t,$ where $\mu :\mathbb{T}\to [0,\infty )$ is referred as a graininess operator. We symbolize ${\mathbb{T}}^{\kappa },{\mathbb{T}}_{\kappa }$, and ${\mathbb{T}}_{\kappa }^{\kappa }$ as

• ${\mathbb{T}}^{\kappa }:$ $\mathbb{T}-l_{smax}$, where $l_{smax}$ is the left scattered maximum of $\mathbb{T};$
• ${\mathbb{T}}_{\kappa }:$ $\mathbb{T}-r_{smin}$, where $r_{smin}$ is the right scattered minimum of $\mathbb{T};$
• ${\mathbb{T}}_{\kappa }^{\kappa }={\mathbb{T}}^{\kappa }\cap {\mathbb{T}}_{\kappa }.$

Definition 1. 

(delta derivative of $\mathfrak{f}$) A number ${\mathfrak{f}}^{\mathrm{\Delta }}\left(t\right),t\in {\mathbb{T}}^{\kappa }$ (provided it exists) such that for $ϵ>0$ one can determine some neighorhood of τ (nbd$\left({\mathcal{U}}_{\tau }\right)$) wherein

$$\left|[\mathfrak{f}\left(\sigma \left(\tau \right)\right)-\mathfrak{f}\left(\delta \right)]-{\mathfrak{f}}^{\mathrm{\Delta }}\left(\tau \right)[\sigma \left(\tau \right)-\delta ]\right|\le ϵ|\sigma \left(\tau \right)-\delta |\mathit{for}\mathit{all}\delta \in \mathrm{nbd}\left({\mathcal{U}}_{\tau }\right)$$

is called a delta derivative of $\mathfrak{f}$.

Let $\mathfrak{f},\mathfrak{g}$ be real-valued mappings on $\mathbb{T}$. We note the following for $\tau \in {\mathbb{T}}^{\kappa },$

(i)

$\mathfrak{f}$ is continuous at $\tau$ if it is differentiable at $\tau$.

(ii)

The delta derivative of a continuous function $\mathfrak{f}$ at right-scattered point $\tau \in {\mathbb{T}}^{\kappa }$ is ${\mathfrak{f}}^{\mathrm{\Delta }}\left(\tau \right)=\frac{\mathfrak{f}\left(\sigma \right(\tau \left)\right)-\mathfrak{f}\left(\tau \right)}{\mu \left(\tau \right)}$ and the delta derivative of a differentiable function $\mathfrak{f}$ at right-dense point $\tau \in {\mathbb{T}}^{\kappa }$ is ${\mathfrak{f}}^{\mathrm{\Delta }}\left(\tau \right)=\underset{s\to \tau }{lim}\frac{\mathfrak{f}\left(\tau \right)-\mathfrak{f}\left(s\right)}{\tau -s}.$

(iii)

If both $\mathfrak{f},\mathfrak{g}$ are delta-differentiable, then for any $\tau \in {\mathbb{T}}^{\kappa },$ ${\mathfrak{f}}^{\sigma }\left(\tau \right)=\mathfrak{f}\left(\tau \right)+\mu \left(\tau \right){\mathfrak{f}}^{\mathrm{\Delta }}\left(\tau \right),$ where ${\mathfrak{f}}^{\sigma }:=\mathfrak{f}\circ \sigma$ and ${\left(\mathfrak{f}\mathfrak{g}\right)}^{\mathrm{\Delta }}\left(\tau \right)={\mathfrak{f}}^{\mathrm{\Delta }}\left(\tau \right)\mathfrak{g}\left(\tau \right)+{\mathfrak{f}}^{\sigma }\left(\tau \right){\mathfrak{g}}^{\mathrm{\Delta }}\left(\tau \right).$

Definition 2. 

(rd-continuous function) A real-valued function defined on $\mathbb{T}$, which is continuous at every right-dense point in $\mathbb{T}$ and has finite left limit at every left-dense point in $\mathbb{T}$ is referred to as an rd-continuous function. In this manuscript, we symbolize the collection of all rd-continuous functions on $\mathbb{T}$ as $C_{\mathrm{R}\mathrm{D}}\left(\mathbb{T}\right)$.

Definition 3. 

An antiderivative of a real-valued function $\mathfrak{f}$ on $\mathbb{T}$ is F wherein $F^{\mathrm{\Delta }}\left(\tau \right)=\mathfrak{f}\left(\tau \right)$ for $\tau \in {\mathbb{T}}^{\kappa },$ and we write

$${\int }_{\delta }^{\tau }\mathfrak{f}\left(\tau \right)\mathrm{\Delta }\tau =F\left(\tau \right)-F\left(\delta \right)\mathit{for}\delta ,\tau \in \mathbb{T}.$$

Definition 4. 

If for $\tau \in \mathbb{T},$ $1+\mathfrak{p}\left(\tau \right)\mu \left(\tau \right)\ne 0$ for a real valued function $\mathfrak{p}$ on $\mathbb{T}$, then $\mathfrak{p}$ is regarded as a regressive function. The set of all regressive and rd-continuous functions is denoted by $\mathcal{R}$.

Definition 5. 

If for $\tau \in \mathbb{T},$ $1+\mathfrak{p}\left(\tau \right)\mu \left(\tau \right)>0$ for a real valued function $\mathfrak{p}$ on $\mathbb{T}$, then $\mathfrak{p}$ is regarded as a positively regressive function. The collection of all positively regressive functions is denoted by ${\mathcal{R}}^{+}$.

Definition 6. 

For any $\mathfrak{p}, \mathfrak{q}\in \mathcal{R},$ the addition ($\mathfrak{p}\oplus \mathfrak{q}$), additive inverse of $\mathfrak{p}$ ($\ominus \mathfrak{p}$), and subtraction ($\mathfrak{p}\ominus \mathfrak{q}$) on $\mathcal{R}$ are defined as

$$\mathfrak{p}\oplus \mathfrak{q}=\mathfrak{p}+\mathfrak{q}+\mu \mathfrak{p}\mathfrak{q},\ominus \mathfrak{p}=-\frac{\mathfrak{p}}{1+\mu \mathfrak{p}},\mathit{and}\mathfrak{p}\ominus \mathfrak{q}=\mathfrak{p}\oplus (\ominus \mathfrak{q})$$

respectively.

Remark 1. 

If we consider an initial value problem on $\mathbb{T}$ as

$$x^{\mathrm{\Delta }}=\mathfrak{p}\left(\tau \right)x,x\left({\tau }_0\right)=1,\tau \in \mathbb{T},$$

where $\mathfrak{p}:\mathbb{T}\to \mathbb{R}$ is rd-continuous and a regressive function, then it has a unique solution, and it is denoted by the exponential function $e_{\mathfrak{p}}\left(·,{\tau }_0\right),$ for any fixed ${\tau }_0\in \mathbb{T}$.

The Four Theorems of Bohner and Peterson [9] are now listed, followed by a fundamental dynamic inequality on time scales and lemmas due to Zhao [18]. These results are important for our discussion because they are used in the technique of proofs of our main theorems to establish an explicit bound on the unknown function of concerned inequality.

Theorem 1. 

If $\mathfrak{p},\mathfrak{q}\in \mathcal{R},$ then

(i) 

The value of $e_{\mathfrak{p}}(\tau ,\tau )$ and $e_0(\tau ,\delta )$ is 1;

(ii) 

$e_{\mathfrak{p}}(\sigma \left(\tau \right),\delta )=(1+\mathfrak{p}\left(\tau \right)\mu \left(\tau \right))e_{\mathfrak{p}}(\tau ,\delta )$;

(iii) 

$\frac{1}{e_{\mathfrak{p}}(\tau ,\delta )}=e_{\ominus \mathfrak{p}}(\tau ,\delta )=e_{\mathfrak{p}}(\delta ,\tau )$;

(iv) 

$\frac{e_{\mathfrak{p}}(\tau ,\delta )}{e_{\mathfrak{q}}(\tau ,\delta )}=e_{\mathfrak{p}\ominus \mathfrak{q}}(\tau ,\delta )$;

(v) 

$e_{\mathfrak{p}}(\tau ,\delta )e_{\mathfrak{q}}(\tau ,\delta )=e_{\mathfrak{p}\oplus \mathfrak{q}}(\tau ,\delta )$;

(vi) 

$e_{\mathfrak{p}}\left(\tau ,{\tau }_0\right)>0$ for $\mathfrak{p}\in {\mathcal{R}}^{+}$.

Theorem 2. 

Let $\mathfrak{p}\in \mathcal{R}$ and ${\tau }_1,{\tau }_2,{\tau }_3\in \mathbb{T}$, then

$$\underset{{\tau }_1}{\overset{{\tau }_2}{\int }}\mathfrak{p}\left(\tau \right)e_{\mathfrak{p}}({\tau }_3,\sigma \left(\tau \right))\mathrm{\Delta }\tau =e_{\mathfrak{p}}({\tau }_3,{\tau }_1)-e_{\mathfrak{p}}({\tau }_3,{\tau }_2).$$

Theorem 3. 

If ${\tau }_1,{\tau }_2\in \mathbb{T}$ and $f\in {\mathrm{C}}_{\mathrm{rd}}$ such that $f\left(t\right)\ge 0$ for all ${\tau }_1\le \tau <{\tau }_2$, then

$$\underset{{\tau }_1}{\overset{{\tau }_2}{\int }}f\left(\tau \right)\mathrm{\Delta }\tau \ge 0.$$

Theorem 4. 

Let $\mathcal{K}:\mathbb{T}\times {\mathbb{T}}^{\kappa }\to \mathbb{R}$ be a continuous map at $(s,s),$ where $s\in {\mathbb{T}}^{\kappa }$ and $s>s_0$ for fixed $s_0\in {\mathbb{T}}^{\kappa }.$ If $\mathcal{K}(s,·)$ is rd-continuous on an interval $\left[s_0,\sigma \left(s\right)\right]$ and for $ϵ>0$ one can determine a neighborhood of s (nbd$\left({\mathcal{U}}_s\right)$), not depending on $s\in \left[t_0,\sigma \left(s\right)\right]$ such that

$$\left|\mathcal{K}(\sigma \left(s\right),{\tau }^{\prime })-\mathcal{K}(s,{\tau }^{\prime })-{\mathcal{K}}^{\mathrm{\Delta }}(s,{\tau }^{\prime })(\sigma \left(s\right)-t)\right|\le \epsilon |\sigma \left(s\right)-t|\mathit{for}\mathit{all}s\in \mathcal{U},$$

where ${\mathcal{K}}^{\mathrm{\Delta }}$ is delta-derivative of $\mathcal{K}$ with respect to t then

$$g\left(s\right):=\underset{s_0}{\overset{s}{\int }}\mathcal{K}(s,\tau )\mathrm{\Delta }\tau \mathit{implies}{g}^{\mathrm{\Delta }}\left(s\right)=\underset{s_0}{\overset{s}{\int }}{\mathcal{K}}^{\mathrm{\Delta }}(s,\tau )\mathrm{\Delta }\tau +\mathcal{K}(\sigma \left(s\right),s).$$

Theorem 5. 

(Fundamental dynamic inequality on time scales)

$$x^{\mathrm{\Delta }}\left(\mathfrak{s}\right)\le a_1\left(\mathfrak{s}\right)x\left(\mathfrak{s}\right)+a_2\left(\mathfrak{s}\right),\mathit{for}\mathit{all}\mathfrak{s}\in {\mathbb{T}}_0$$

implies

$$x\left(\mathfrak{s}\right)\le x\left({\mathfrak{s}}_0\right)e_{a_1}\left(\mathfrak{s},{\mathfrak{s}}_0\right)+{\int }_{{\mathfrak{s}}_0}^{\mathfrak{s}}{e}_{a_1}(\mathfrak{s},\sigma \left(t\right))a_2\left(t\right)\mathrm{\Delta }t,\mathit{for}\mathit{all}\mathfrak{s}\in {\mathbb{T}}_0,$$

where $x, a_2\in {\mathrm{C}}_{\mathrm{rd}}$ and $a_1\in {\mathcal{R}}^{+}$.

Lemma 1 

(Zhao [18]).

$$\begin{array}{c}\hfill z^{\frac{1}{r}}\le \frac{1}{r}{l}^{\frac{1-r}{r}}z+\frac{r-1}{r}{l}^{\frac{1}{r}},l>0,\end{array}$$

for $z\ge 0,r\ge 1.$

Lemma 2 

(Zhao [18]).

$$\begin{array}{c}\hfill z^{\frac{r^{\prime }}{r}}\le \frac{r^{\prime }}{r}{l}^{\frac{r^{\prime }-r}{r}}z+\frac{r-r^{\prime }}{r}{l}^{\frac{r^{\prime }}{r}},l>0,\end{array}$$

for $z\ge 0,r\ge r^{\prime }\ge 0,r\ne 0.$

Let us begin with our main findings.

3. Main Results

In the subsequent discussion, we present the main findings of our research. In order to establish the proofs for our main results, we have used Zhao’s lemmas coupled with a fundamental inequality on various time scales. Through the combination of these mathematical tools, we have systematically established the framework of our inequalities.

Theorem 6. 

Let $u,f_1,f_2,g,{\alpha }_1,{\alpha }_2\in C_{\mathrm{R}\mathrm{D}}({[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{\mathbb{T}}^{\kappa },{\mathbb{R}}^{+}),\mathrm{where}\mathring{{\zeta }_1},\mathring{{\zeta }_2}\in {\mathbb{T}}_{\kappa }^{\kappa }(\mathring{{\zeta }_1}<\mathring{{\zeta }_2})$ be provided such that the delta-derivatives of $g,{\alpha }_1$, and ${\alpha }_2$ exist on $\mathbb{T}$ and are non-negative with $\tau \ge {\alpha }_1\left(\tau \right),\tau \ge {\alpha }_2\left(\tau \right)$ wherein ${\alpha }_1(\mathring{{\zeta }_1})=\mathring{{\zeta }_1},{\alpha }_2(\mathring{{\zeta }_1})=\mathring{{\zeta }_2}$ with constants $p\ge q\ge 1$. If $u\left(\tau \right)$ on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^{\kappa }}$ satisfies

$$\begin{array}{c}\hfill u^p\left(\tau \right)\le g\left(\tau \right)+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{f}_1\left(\delta \right)u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}{f}_2\left(\delta \right)u^q\left(\delta \right)\mathrm{\Delta }\delta ,\end{array}$$

(2)

then

$$\begin{array}{c}\hfill u\left(\tau \right)\le {\left\{H{e}_F(\tau ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\tau }{e}_F(\tau ,\sigma \left(\delta \right))G\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{p}},\end{array}$$

(3)

where

$$\begin{array}{cc}\hfill F\left(\tau \right)& =m_1{\mathring{{\zeta }_1}}^{\mathrm{\Delta }}\left(\tau \right)f_1(\mathring{{\zeta }_1}\left(\tau \right))+n_1{\mathring{{\zeta }_2}}^{\mathrm{\Delta }}\left(\tau \right)f_2(\mathring{{\zeta }_2}\left(\tau \right)),\hfill \\ \hfill G\left(\tau \right)& =g^{\mathrm{\Delta }}\left(\tau \right)+m_2{\mathring{{\zeta }_1}}^{\mathrm{\Delta }}\left(\tau \right)f_1(\mathring{{\zeta }_1}\left(\tau \right))+n_2{\mathring{{\zeta }_2}}^{\mathrm{\Delta }}\left(\tau \right)f_2(\mathring{{\zeta }_2}\left(\tau \right)),\hfill \end{array}$$

$$\begin{array}{cc}\hfill H& =\frac{g(\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{f}_2\left(\delta \right)\left(\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{n}_1{e}_F(\delta ,\sigma \left(r\right))G\left(r\right)\mathrm{\Delta }r+n_2\right)\mathrm{\Delta }\delta }{\left(1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_1{f}_2\left(\delta \right)e_F(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta \right)}\mathit{such}\mathit{that}\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_1{f}_2\left(\delta \right)e_F(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta <1,\hfill \end{array}$$

$$\begin{array}{c}\hfill m_1=\frac{1}{p}{l}^{\frac{1-p}{p}},m_2=\frac{p-1}{p}{l}^{\frac{1}{p}},n_1=\frac{q}{p}{l}^{\frac{q-p}{p}},n_2=\frac{p-q}{p}{l}^{\frac{q}{p}},l>0.\end{array}$$

Proof. 

Let $z\left(t\right)$ indicate the right-side of Equation (2). The nondecreasing nature of $z\left(t\right)⩾0$ on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^{\kappa }}$ is immediately apparent. We derive from $z\left(t\right)$ that

$$\begin{array}{c}\hfill z(\mathring{{\zeta }_1})=g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{f}_2\left(s\right)u^q\left(s\right)\mathrm{\Delta }s.\end{array}$$

(4)

From (2) and (4), we find that $u\left(t\right)\le {\left(z\left(t\right)\right)}^{\frac{1}{p}},u\left({\alpha }_1\left(t\right)\right)\le {\left(z\left(t\right)\right)}^{\frac{1}{p}}$ and $u\left({\alpha }_2\left(t\right)\right)\le {\left(z\left(t\right)\right)}^{\frac{1}{p}}$. So, at this point, by Lemma’s 1 and 2,

$$\begin{array}{cc}\hfill z^{\mathrm{\Delta }}\left(\tau \right)& =g^{\mathrm{\Delta }}\left(\tau \right)+{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)u\left({\alpha }_1\left(\tau \right)\right)+{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right)u^q\left({\alpha }_2\left(t\right)\right)\hfill \\ \hfill & \le g^{\mathrm{\Delta }}\left(\tau \right)+{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)z^{\frac{1}{p}}\left(\tau \right)+{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right)z^{\frac{q}{p}}\left(t\right)\hfill \\ \hfill & \le g^{\mathrm{\Delta }}\left(\tau \right)+m_1{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)z\left(\tau \right)+m_2{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)\hfill \\ \hfill & +n_1{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right)z\left(\tau \right)+n_2{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(t\right)\right)=F\left(\tau \right)z\left(\tau \right)+G\left(\tau \right).\hfill \end{array}$$

(5)

Applying Theorem 5 to (5) gives

$$\begin{array}{c}\hfill z\left(\tau \right)\le z(\mathring{{\zeta }_1})e_F(\tau ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\tau }{e}_F(\tau ,\sigma \left(\delta \right)G\left(\delta \right)\mathrm{\Delta }\delta ).\end{array}$$

(6)

As $u\left(\tau \right)\le z^{\frac{1}{p}}\left(\tau \right)$, from inequality (6), we get

$$\begin{array}{cc}\hfill u^q\left(\tau \right)\le z^{\frac{q}{p}}\left(\tau \right)& \le n_{1}z\left(\tau \right)+n_2\le n_1\left(z(\mathring{{\zeta }_1})e_F(\tau ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\tau }{e}_F(\tau ,\sigma \left(\delta \right))G\left(\delta \right)\mathrm{\Delta }\delta \right)+n_2.\hfill \end{array}$$

(7)

From the expression of $z\left(\alpha \right)$ and (7), we deduce that

$$\begin{array}{cc}\hfill z(\mathring{{\zeta }_1})=& g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{f}_2\left(\delta \right)u^q\left(\delta \right)\mathrm{\Delta }\delta \hfill \\ \hfill \le & g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{f}_2\left(\delta \right)\left[n_1\left(z(\mathring{{\zeta }_1})e_F(\delta ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\delta }{e}_F(\delta ,\sigma \left(r\right))G\left(r\right)\mathrm{\Delta }r\right)+n_2\right]\mathrm{\Delta }\delta .\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill z(\mathring{{\zeta }_1})& \le \frac{g(\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{f}_2\left(\delta \right)\left(\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{n}_1{e}_F(\delta ,\sigma \left(r\right))G\left(r\right)\mathrm{\Delta }r+n_2\right)\mathrm{\Delta }\delta }{\left(1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_1{f}_2\left(\delta \right)e_F(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta \right)}=H.\hfill \end{array}$$

(8)

By employing $u\left(\tau \right)\le z^{\frac{1}{p}}\left(\tau \right)$, (6), and (8), we thus obtain the required bound shown in (3). □

Remark 2. 

Some Important Remarks:

(1) 

For $\mathbb{T}=\mathbb{R},{\alpha }_1\left(\tau \right)=\tau ,{\alpha }_2\left(\tau \right)=\mathring{{\zeta }_2},{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)=1,{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)=0$ and $p=q=1,$ the inequality in Theorem 6 reduces to the inequality by Pachpatte [3] (p. 40, Theorem 1.5.1).

(2) 

If we substitute $q=p$, then the inequality by G. Wang ([12], Theorem 3.2) turns out as a particular case of the above inequality.

(3) 

For $\mathbb{T}=\mathbb{R},{\alpha }_1\left(\tau \right)=\tau ,{\alpha }_2\left(\tau \right)=\mathring{{\zeta }_2},{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)=1,{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)=0$ and $q=p,$ the inequality proved above can be shrinked to the inequality due to Kendre et al. ([4], Theorem 2.1).

Theorem 7. 

Let us assume $\mathring{{\zeta }_1},\mathring{{\zeta }_2}\in {\mathbb{T}}_{\kappa }^{\kappa },$ considering $\mathring{{\zeta }_1}<\mathring{{\zeta }_2}.$ For some constants $p,q,r,$ and $m,$ suppose $u,f_1,f_2,g,{\alpha }_1,{\alpha }_2\in C_{\mathrm{R}\mathrm{D}}({[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{\mathbb{T}}^{\kappa },{\mathbb{R}}^{+})$ wherein delta-derivatives of ${\alpha }_1,{\alpha }_2,g$ exist and are non-negative on $\mathbb{T},$ such that ${\alpha }_1(\mathring{{\zeta }_1})=\mathring{{\zeta }_1},{\alpha }_2(\mathring{{\zeta }_1})=\mathring{{\zeta }_2},\tau \ge {\alpha }_1\left(\tau \right),\tau \ge {\alpha }_2\left(\tau \right),p\ge r\ge 1,p\ge mr\ge 1$, and $p\ge qr\ge 1.$ If $u\left(\tau \right)$ on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^{\kappa }}$ is such that

$$\begin{array}{c}\hfill u^p\left(\tau \right)\le {\left[g\left(\tau \right)+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{f}_1\left(\delta \right)u^m\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}{f}_2\left(\delta \right)u^q\left(\delta \right)\mathrm{\Delta }\delta \right]}^r,\end{array}$$

(9)

then

$$\begin{array}{c}\hfill u\left(\tau \right)\le {\left\{\overline{H}{e}_{\overline{F}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\overline{F}}(\tau ,\sigma \left(\delta \right))\overline{G}\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{r}{p}},\end{array}$$

(10)

where

$$\begin{array}{cc}\hfill \overline{F}\left(\tau \right)& =m_3{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)+n_3{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right),\hfill \\ \hfill \overline{G}\left(\tau \right)& =g^{\mathrm{\Delta }}\left(\tau \right)+m_4{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)+n_4{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill \overline{H}& =\frac{g(\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{f}_2\left(\delta \right)\left(\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{n}_3{e}_{\overline{F}}(\delta ,\sigma \left(\tilde{r}\right))\overline{G}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}+n_4\right)\mathrm{\Delta }\delta }{\left(1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_3{f}_2\left(\delta \right)e_{\overline{F}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta \right)}\mathit{wherein}\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_3{f}_2\left(\delta \right)e_{\overline{F}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta <1,\hfill \end{array}$$

and

$$\begin{array}{c}\hfill m_3=\frac{rm}{p}{l}^{\frac{rm-p}{p}},m_4=\frac{p-rm}{p}{l}^{\frac{m}{p}},n_3=\frac{rq}{p}{l}^{\frac{rq-p}{p}},n_4=\frac{p-rq}{p}{l}^{\frac{rq}{p}},l>0.\end{array}$$

Proof. 

Let $z\left(\tau \right)$ symbolize the right-side of (9). It is instantly clear that on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^{\kappa }},$ $z\left(\tau \right)$ is nondecreasing and $0\le z\left(\tau \right).$ From $z\left(\tau \right)$, we infer that

$$\begin{array}{c}\hfill z(\mathring{{\zeta }_1})=g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{f}_2\left(\delta \right)u^q\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(11)

We can derive from (9) that $u\left(\tau \right)\le z^{\frac{r}{p}}\left(\tau \right)$, and for $j=1,2,$ $u\left({\alpha }_j\left(\tau \right)\right)\le z^{\frac{r}{p}}\left(\tau \right)$. On differentiating $z\left(\tau \right)$ and using Lemmas 1 and 2, we find that

$$\begin{array}{cc}\hfill z^{\mathrm{\Delta }}\left(\tau \right)& =g^{\mathrm{\Delta }}\left(\tau \right)+{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)u^m\left({\alpha }_1\left(\tau \right)\right)+{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right)u^q\left({\alpha }_2\left(\tau \right)\right)\hfill \\ \hfill & \le g^{\mathrm{\Delta }}\left(\tau \right)+{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)z^{\frac{rm}{p}}\left(\tau \right)+{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right)z^{\frac{rq}{p}}\left(\tau \right)\hfill \\ \hfill & \le g^{\mathrm{\Delta }}\left(\tau \right)+m_3{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)z\left(\tau \right)+m_4{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_1\left({\alpha }_1\left(\tau \right)\right)\hfill \\ \hfill & +n_3{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right)z\left(\tau \right)+n_4{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_2\left(\tau \right)\right)=\overline{F}\left(\tau \right)z\left(\tau \right)+\overline{G}\left(\tau \right).\hfill \end{array}$$

(12)

Theorem 5 applied to (12) provides that

$$\begin{array}{c}\hfill z\left(\tau \right)\le z(\mathring{{\zeta }_1})e_{\overline{F}}(\tau ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\tau }{e}_{\overline{F}}(\tau ,\sigma \left(\delta \right))\overline{G}\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(13)

Also, $u^p\left(\tau \right)\le z^r\left(\tau \right)$ implies $u^q\left(\tau \right)\le z^{\frac{qr}{p}}\left(\tau \right)$, so from Equations (11) and (13), we get

$$\begin{array}{cc}\hfill z(\mathring{{\zeta }_1})& =g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{f}_2\left(\delta \right)z^{\frac{qr}{p}}\left(\delta \right)\mathrm{\Delta }\delta \hfill \\ \hfill \le & g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{f}_2\left(\delta \right)\left[n_3\left(z(\mathring{{\zeta }_1})e_{\overline{F}}(\delta ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\delta }{e}_{\overline{F}}(\delta ,\sigma \left(\tilde{r}\right))\overline{G}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}\right)+n_4\right]\mathrm{\Delta }\delta .\hfill \end{array}$$

After simplification, it gives

$$\begin{array}{c}\hfill z(\mathring{{\zeta }_1})\le \frac{g(\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{f}_2\left(\delta \right)\left(\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{n}_3{e}_{\overline{F}}(\delta ,\sigma \left(\tilde{r}\right))\overline{G}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}+n_4\right)\mathrm{\Delta }\delta }{\left(1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_3{f}_2\left(\delta \right)e_{\overline{F}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta \right)}=\overline{H}.\end{array}$$

(14)

From (14), one can eventually notice that $z(\mathring{{\zeta }_1})\le exp\left(\overline{H}\right)$, however, it will result in a remarkable increase in the explicit bound on the $u\left(\tau \right)$. Thus, we can then obtain the necessary bound as stated in (10) by using $u\left(\tau \right)\le z^{\frac{r}{p}}\left(\tau \right)$, (13) and (14). □

Theorem 8. 

Assume $\mathring{{\zeta }_1},\mathring{{\zeta }_2}$ in ${\mathbb{T}}_{\kappa }^{\kappa }$ such that $\mathring{{\zeta }_1}<\mathring{{\zeta }_2}$. Consider constants $p,q,r,\lambda ,\mu$ wherein $p\ge q>0,p\ge \lambda >0,0<r\le 1,0<\mu \le 1$ and suppose $u,f_1,f_2,f_3,f_4,f_5,g,{\alpha }_1,{\alpha }_2\in C_{\mathrm{R}\mathrm{D}}({[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{\mathbb{T}}^{\kappa },{\mathbb{R}}^{+}),$ where delta-derivatives of $g,{\alpha }_1,{\alpha }_2$ exist and are nonnegative on $\mathbb{T},$ with $\tau \ge {\alpha }_1\left(\tau \right),\tau \ge {\alpha }_2\left(\tau \right),{\alpha }_1(\mathring{{\zeta }_1})=\mathring{{\zeta }_1}$ and ${\alpha }_2(\mathring{{\zeta }_1})=\mathring{{\zeta }_2}.$ If $u\left(\tau \right)$ on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^{\kappa }}$ satisfies

$$\begin{array}{cc}\hfill u^p\left(\tau \right)& \le g\left(\tau \right)+{\int }_{\mathring{{\zeta }_1}}^{\tau }{f}_1\left(\delta \right)u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{\left(f_2\left(\delta \right)u^q\left(\delta \right)+f_3\left(\delta \right)\right)}^r\mathrm{\Delta }\delta \hfill \\ \hfill & +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}{\left(f_4\left(\delta \right)u^{\lambda }\left(\delta \right)+f_5\left(\delta \right)\right)}^{\mu }\mathrm{\Delta }\delta ,\hfill \end{array}$$

(15)

then

$$\begin{array}{c}\hfill u\left(\tau \right)\le {\left\{\widehat{H}{e}_{\widehat{F}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\widehat{F}}(\tau ,\sigma \left(\delta \right))\widehat{G}\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{p}},\end{array}$$

(16)

where

$$\begin{array}{cc}\hfill \widehat{F}\left(\tau \right)& =m_1{f}_1\left(\tau \right)+m_1^{\prime }{n}_1{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_1\left(\tau \right)\right)+n_1^{\prime }{l}_1{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_4\left({\alpha }_2\left(\tau \right)\right),\hfill \\ \hfill \widehat{G}\left(\tau \right)& =g^{\mathrm{\Delta }}\left(\tau \right)+m_2{f}_1\left(\tau \right)+m_1^{\prime }{n}_2{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_1\left(\tau \right)\right)+m_1^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_3\left({\alpha }_1\left(\tau \right)\right)+m_2^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\hfill \\ \hfill & +n_1^{\prime }{l}_2{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_4\left({\alpha }_2\left(\tau \right)\right)+n_1^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_5\left({\alpha }_2\left(\tau \right)\right)+n_2^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{H}& =\frac{g(\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_1^{\prime }{l}_2{f}_4\left(\delta \right)+n_1^{\prime }{f}_5\left(\delta \right)+n_2^{\prime }+n_1^{\prime }{l}_1{f}_4\left(\delta \right)\left(\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\widehat{F}}(\delta ,\sigma \left(\tilde{r}\right))\widehat{G}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}\right)\mathrm{\Delta }\delta }{1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{l}_1{n}_1^{\prime }{f}_4\left(\delta \right)e_{\widehat{F}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta },\hfill \end{array}$$

wherein $\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{l}_1{n}_1^{\prime }{f}_4\left(\delta \right)e_{\widehat{F}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta <1,$ $m_1,m_2$ are the same values as in Theorem 6 and $m_1^{\prime }=r{l}^{r-1},m_2^{\prime }=(1-r)l^r,n_1^{\prime }=\mu l^{\mu -1},n_2^{\prime }=(1-\mu )l^{\mu },n_1=\frac{q}{p}{l}^{\frac{q-p}{p}},n_2=\frac{p-q}{p}{l}^{\frac{q}{p}},l_1=\frac{\lambda }{p}{l}^{\frac{\lambda -p}{p}},l_2=\frac{p-\lambda }{p}{l}^{\frac{\lambda }{p}},l>0$.

Proof. 

Let us set $z\left(\tau \right)$ as the RHS of inequality (15), then $u^p\left(\tau \right)\le z\left(\tau \right)$. It is immediately clear that on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^k}$, $0\le z\left(\tau \right)$ is nondecreasing. It is straightforward that

$$\begin{array}{c}\hfill z(\mathring{{\zeta }_1})=g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{\left(f_4\left(\delta \right)u^{\lambda }\left(\delta \right)+f_5\left(\delta \right)\right)}^{\mu }\mathrm{\Delta }\delta .\end{array}$$

(17)

Since $u\left(\tau \right)\le z^{\frac{1}{p}}\left(\tau \right),$ and for $j=1,2,u\left({\alpha }_j\left(\tau \right)\right)\le z^{\frac{1}{p}}\left(\tau \right),$ we can infer from the delta derivative of $z\left(\tau \right)$ and Lemmas 1 and 2 that

$$\begin{array}{cc}\hfill z^{\mathrm{\Delta }}\left(\tau \right)& =g^{\mathrm{\Delta }}\left(\tau \right)+f_1\left(\tau \right)u\left(\tau \right)+{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right){\left(f_2\left({\alpha }_1\left(\tau \right)\right)u^q\left({\alpha }_1\left(\tau \right)\right)+f_3\left({\alpha }_1\left(\tau \right)\right)\right)}^r\hfill \\ \hfill & +{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right){\left(f_4\left({\alpha }_2\left(\tau \right)\right)u^{\lambda }\left({\alpha }_2\left(\tau \right)\right)+f_5\left({\alpha }_2\left(\tau \right)\right)\right)}^{\mu }\hfill \\ \hfill & \le g^{\mathrm{\Delta }}\left(\tau \right)+f_1\left(\tau \right)u\left(\tau \right)+\left(m_1^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\left(f_2\left({\alpha }_1\left(\tau \right)\right)u^q\left({\alpha }_1\left(\tau \right)\right)+f_3\left({\alpha }_1\left(\tau \right)\right)\right)+m_2\right)\hfill \\ \hfill & +\left(n_1^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)\left(f_4\left({\alpha }_2\left(\tau \right)\right)u^{\lambda }\left({\alpha }_2\left(\tau \right)\right)+f_5\left({\alpha }_2\left(\tau \right)\right)+n_2^{\prime }\right)\right)\hfill \\ \hfill & \le g^{\mathrm{\Delta }}\left(\tau \right)+f_1\left(\tau \right)z^{\frac{1}{p}}\left(\tau \right)+\left(m_1^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_1\left(\tau \right)\right)z^{\frac{q}{p}}\left(\tau \right)+m_1^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_3\left({\alpha }_1\left(\tau \right)\right)+m_2^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\right)\hfill \\ \hfill & +\left(n_1^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)(f_4\left({\alpha }_2\left(\tau \right)\right)z^{\frac{\lambda }{p}}\left(\tau \right)+n_1^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_5\left({\alpha }_2\left(\tau \right)\right)+n_2^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right))\right)\hfill \\ \hfill & \le g^{\mathrm{\Delta }}\left(\tau \right)+f_1\left(\tau \right)(m_{1}z\left(\tau \right)+m_2)+(m_1^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_2\left({\alpha }_1\left(\tau \right)\right)\left(n_{1}z\left(\tau \right)+n_2\right)+m_2^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\hfill \\ \hfill & +m_1^{\prime }{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)f_3\left({\alpha }_1\left(\tau \right)\right))+(n_1^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_4\left({\alpha }_2\left(\tau \right)\right)\left(l_{1}z\left(\tau \right)+l_2\right)+n_2^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)\hfill \\ \hfill & +n_1^{\prime }{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f_5\left({\alpha }_2\left(\tau \right)\right))=\widehat{F}\left(\tau \right)z\left(\tau \right)+\widehat{G}\left(\tau \right).\hfill \end{array}$$

(18)

When Theorem 5 is applied to (18), it yields

$$\begin{array}{c}\hfill z\left(\tau \right)\le z(\mathring{{\zeta }_1})e_{\widehat{F}}(\tau ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\tau }{e}_{\widehat{F}}(\tau ,\sigma \left(\delta \right))\widehat{G}\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(19)

Now, from (17), (19), and Lemmas 1 and 2, we derive that

$$\begin{array}{cc}\hfill z(\mathring{{\zeta }_1})& \le g(\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}\left(n_1^{\prime }{l}_2{f}_4\left(\delta \right)+n_1^{\prime }{f}_5\left(\delta \right)+n_2^{\prime }\right)\mathrm{\Delta }\delta \hfill \\ \hfill & +{\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}{l}_1{n}_1^{\prime }{f}_4\left(\delta \right)\left(z(\mathring{{\zeta }_1})e_{\widehat{F}}(\delta ,\mathring{{\zeta }_1})+{\int }_{\mathring{{\zeta }_1}}^{\delta }{e}_{\widehat{F}}(\delta ,\sigma \left(\tilde{r}\right))\widehat{G}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}\right)\mathrm{\Delta }\delta .\hfill \end{array}$$

Upon further simplification, it gives

$$\begin{array}{cc}\hfill z(\mathring{{\zeta }_1})& \le \frac{g(\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{n}_1^{\prime }{l}_2{f}_4\left(\delta \right)+n_1^{\prime }{f}_5\left(\delta \right)+n_2^{\prime }+n_1^{\prime }{l}_1{f}_4\left(\delta \right)\left(\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\widehat{F}}(\delta ,\sigma (\tilde{r}))\widehat{G}(\tilde{r})\mathrm{\Delta }\tilde{r}\right)\mathrm{\Delta }\delta }{1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}{l}_1{n}_1^{\prime }{f}_4\left(\delta \right)e_{\widehat{F}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta }=\widehat{H}.\hfill \end{array}$$

(20)

Using $u\left(\tau \right)\le z^{\frac{1}{p}}\left(\tau \right)$, (19), and (20), we can then achieve the requisite bound indicated in (16). □

Remark 3. 

If we assume $f_1=0=f_3=f_5,\mu =1=r,q=m,$ and $\lambda =q$ in Theorem 8, then Theorem 7, under the circumstance that $r=1$, constitutes a specific case of Theorem 7.

Theorem 9. 

Let us assume $\mathring{{\zeta }_1},\mathring{{\zeta }_2}\in {\mathbb{T}}_{\kappa }^{\kappa }(\mathring{{\zeta }_1}<\mathring{{\zeta }_2})$, and for some constants $p,q,$ consider $u,g,f,{\alpha }_1,{\alpha }_2\in C_{\mathrm{R}\mathrm{D}}({[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^k},{\mathbb{R}}^{+}),$ wherein delta-derivatives of ${\alpha }_1,{\alpha }_2,g$ exist and are non-negative on $\mathbb{T},$ such that ${\alpha }_1(\mathring{{\zeta }_1})=\mathring{{\zeta }_1},{\alpha }_2(\mathring{{\zeta }_1})=\mathring{{\zeta }_2},\tau \ge {\alpha }_1\left(\tau \right),\tau \ge {\alpha }_2\left(\tau \right),p\ge 1$ and $q\ge 1.$ If for $\mathcal{K}(\tau ,\delta ),{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )\in C_{\mathrm{R}\mathrm{D}}({[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^k}\times {[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^k},{\mathbb{R}}^{+}),\mathring{{\zeta }_1}\le \delta \le \tau \le \mathring{{\zeta }_2}$, $u\left(\tau \right)$ on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^{\kappa }}$ satisfies

$$\begin{array}{c}\hfill u^p\left(\tau \right)⩽g\left(\tau \right)+{\left\{{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}\mathcal{K}(\tau ,\delta )u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}f\left(\delta \right)u^p\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{q}},\end{array}$$

(21)

then

$$\begin{array}{c}\hfill u\left(\tau \right)\le {\left(g\left(\tau \right)+{\left\{\overline{\overline{H}}{e}_{\overline{\overline{F}}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\overline{\overline{F}}}(\tau ,\sigma \left(\delta \right))\overline{\overline{G}}\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{q}}\right)}^{\frac{1}{p}},\end{array}$$

(22)

where

$$\begin{array}{cc}\hfill \overline{\overline{F}}\left(\tau \right)& =m_1{n}_1{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right))+n_1{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f\left({\alpha }_2\left(\tau \right)\right)+\underset{\mathring{{\zeta }_1}}{\overset{{\alpha }_1\left(\tau \right)}{\int }}{m}_1{n}_1{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )\mathrm{\Delta }\delta ,\hfill \\ \hfill \overline{\overline{G}}\left(t\right)& =\left(m_{1}c\left(\tau \right)+m_1{n}_2+m_2\right){\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right))+{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f\left({\alpha }_2\left(\tau \right)\right)(c\left(\tau \right)+n_2)\hfill \\ \hfill & +\underset{\mathring{{\zeta }_1}}{\overset{{\alpha }_1\left(\tau \right)}{\int }}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )\left[m_{1}g\left(\delta \right)+m_1{n}_2+m_2\right]\mathrm{\Delta }\delta ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \overline{\overline{H}}& =\frac{\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)\left(n_2+g\left(\delta \right)+n_1\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\overline{\overline{F}}}(\delta ,\sigma \left(r\right))\overline{\overline{G}}\left(r\right)\mathrm{\Delta }r\right)\mathrm{\Delta }\delta }{1-n_1\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)e_{\overline{\overline{F}}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta },\hfill \end{array}$$

wherein $\left(n_1\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)e_{\overline{\overline{F}}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta \right)<1,$ $n_1=\frac{1}{q}{l}^{\frac{1-q}{q}},n_2=\frac{q-1}{q}{l}^{\frac{1}{q}},l>0,$ and $m_1,m_2$ are the same values as in Theorem 6.

Proof. 

Assign

$$\begin{array}{c}\hfill z\left(\tau \right)={\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}\mathcal{K}(\tau ,\delta )u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}f\left(\delta \right)u^p\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(23)

It is readily apparent that $0\le z\left(\tau \right)$ is nondecreasing on $[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]$. Further, (21) and (23) simply assert that

$$\begin{array}{c}\hfill u\left(\tau \right)\le {\left(g\left(\tau \right)+z^{\frac{1}{q}}\left(\tau \right)\right)}^{\frac{1}{p}}\mathrm{and}z(\mathring{{\zeta }_1})={\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}f\left(\delta \right)u^p\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(24)

Then,

$$\begin{array}{cc}\hfill z^{\mathrm{\Delta }}\left(\tau \right)& ={\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}\left(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right)\right)u\left({\alpha }_1\left(\tau \right)\right)+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )u\left(\delta \right)\mathrm{\Delta }\delta +{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f\left({\alpha }_2\left(\tau \right)\right)u^p\left({\alpha }_2\left(\tau \right)\right)\hfill \\ \hfill & \le {\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}\left(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right)\right){\left(g\left(\tau \right)+z^{\frac{1}{q}}\left(\tau \right)\right)}^{\frac{1}{p}}+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta ){\left(g\left(\delta \right)+z^{\frac{1}{q}}\left(\delta \right)\right)}^{\frac{1}{p}}\mathrm{\Delta }\delta \hfill \\ \hfill & +{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f\left({\alpha }_2\left(\tau \right)\right)\left(g\left(\tau \right)+z^{\frac{1}{q}}\left(\tau \right)\right)\hfill \\ \hfill & \le {\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right))\left[m_1\left(g\left(\tau \right)+n_{1}z\left(\tau \right)+n_2\right)+m_2\right]+\underset{\mathring{{\zeta }_1}}{\overset{{\alpha }_1\left(\tau \right)}{\int }}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )[m_1(g\left(\delta \right)\hfill \\ \hfill & +n_{1}z\left(\delta \right)+n_2)+m_2]\mathrm{\Delta }\delta +{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)f\left({\alpha }_2\left(\tau \right)\right)\left(g\left(\tau \right)+n_{1}z\left(\tau \right)+n_2\right)\hfill \\ \hfill & =\overline{\overline{F}}\left(\tau \right)z\left(\tau \right)+\overline{\overline{G}}\left(\tau \right).\hfill \end{array}$$

(25)

We utilize Theorem 5 on inequality (25) and deduce that

$$\begin{array}{c}\hfill z\left(\tau \right)\le z(\mathring{{\zeta }_1})e_{\overline{\overline{F}}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\overline{\overline{F}}}(\tau ,\sigma \left(\delta \right))\overline{\overline{G}}\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(26)

From (24), (26), and Lemma 1, we derive that

$$\begin{array}{cc}\hfill z(\mathring{{\zeta }_1})& \le \underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)\left(g\left(\delta \right)+z^{\frac{1}{q}}\left(\delta \right)\right)\mathrm{\Delta }\delta \hfill \\ \hfill & \le \underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)\left(n_2+g\left(\delta \right)+n_{1}z\left(\delta \right)\right)\mathrm{\Delta }\delta \hfill \\ \hfill & \le \underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)\left(n_2+g\left(\delta \right)+n_1\left\{z(\mathring{{\zeta }_1})e_{\overline{\overline{F}}}(\delta ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\overline{\overline{F}}}(\delta ,\sigma \left(r\right))\overline{\overline{G}}\left(r\right)\mathrm{\Delta }r\right\}\right)\mathrm{\Delta }\delta \hfill \\ \hfill & \le n_{1}z\left(\mathring{{\zeta }_1}\right)\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)e_{\overline{\overline{F}}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta +\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)\left(n_2+g\left(\delta \right)+n_1\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\overline{\overline{F}}}(\delta ,\sigma \left(r\right))\overline{\overline{G}}\left(r\right)\mathrm{\Delta }r\right)\mathrm{\Delta }\delta .\hfill \end{array}$$

(27)

So, from (27), we acquire that

$$\begin{array}{c}\hfill z(\mathring{{\zeta }_1})\le \frac{\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)\left(n_2+g\left(\delta \right)+n_1\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\overline{\overline{F}}}(\delta ,\sigma \left(r\right))\overline{\overline{G}}\left(r\right)\mathrm{\Delta }r\right)\mathrm{\Delta }\delta }{1-n_1\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}f\left(\delta \right)e_{\overline{\overline{F}}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta }=\overline{\overline{H}}.\end{array}$$

(28)

Consequently, we eventually obtain the requisite bound given in (22) from (24), (26), and (28). □

Theorem 10. 

Consider that $\mathring{{\zeta }_1},\mathring{{\zeta }_2},u,g,{\alpha }_1,{\alpha }_2,p,q$ and $\mathcal{K}(\tau ,\delta )$ correspond to their respective definitions in Theorem 9, and let $\tilde{\mathcal{K}}(\tau ,\delta ),{\tilde{\mathcal{K}}}^{\mathrm{\Delta }}(\tau ,\delta )\in C_{\mathrm{R}\mathrm{D}}({[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^k}\times {[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^k},{\mathbb{R}}^{+}),$ wherein $\mathring{{\zeta }_1}\le \delta \le \tau \le \mathring{{\zeta }_2}$. If for $r\ge 1,$ $u\left(\tau \right)$ on ${[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]}_{{\mathbb{T}}^{\kappa }}$ is such that

$$\begin{array}{c}\hfill u^p\left(\tau \right)⩽{\left(g\left(\tau \right)+{\left\{{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}\mathcal{K}(\tau ,\delta )u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}\tilde{\mathcal{K}}(\tau ,\delta )u^p\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{q}}\right)}^{\frac{1}{r}},\end{array}$$

(29)

then

$$\begin{array}{c}\hfill u\left(\tau \right)⩽{\left(g\left(\tau \right)+{\left\{\widehat{\widehat{H}}{e}_{\widehat{\widehat{F}}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\widehat{\widehat{F}}}(\tau ,\sigma \left(\delta \right))\widehat{\widehat{G}}\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{q}}\right)}^{\frac{1}{rp}},\end{array}$$

(30)

where

$$\begin{array}{cc}\hfill \widehat{\widehat{H}}& =\frac{\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}\tilde{\mathcal{K}}(\tau ,\delta )\left({\lambda }_{1}g\left(\delta \right)+{\lambda }_1{n}_1\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\widehat{\widehat{F}}}(\delta ,\sigma \left(\tilde{r}\right))\widehat{\widehat{G}}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}+{\lambda }_1{n}_2+{\lambda }_2\right)\mathrm{\Delta }\delta }{1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}\tilde{\mathcal{K}}(\tau ,\delta ){\lambda }_1{n}_1{e}_{\widehat{\widehat{F}}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta },\hfill \end{array}$$

wherein

$$\begin{array}{c}\hfill \underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}\tilde{\mathcal{K}}(\tau ,\delta ){\lambda }_1{n}_1{e}_{\widehat{\widehat{F}}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta <1\end{array}$$

and

$$\begin{array}{cc}\hfill \widehat{\widehat{F}}\left(\tau \right)& =l_1{n}_1{\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}\left(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right)\right)+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )(l_1{n}_1+l_1{n}_2+l_2)\mathrm{\Delta }\delta \hfill \\ \hfill & +{\lambda }_1{n}_1{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)\tilde{\mathcal{K}}\left(\sigma \left(\tau \right),{\alpha }_2\left(\tau \right)\right)+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}{\lambda }_1{n}_1{\tilde{\mathcal{K}}}^{\mathrm{\Delta }}(\tau ,\delta )\mathrm{\Delta }\delta ,\hfill \\ \hfill \widehat{\widehat{G}}\left(\tau \right)& ={\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}\left(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right)\right)(l_{1}g\left(\tau \right)+l_1{n}_2+l_2)+{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)\tilde{\mathcal{K}}\left(\sigma \left(\tau \right),{\alpha }_2\left(\tau \right)\right)({\lambda }_{1}g\left(\tau \right)+{\lambda }_1{n}_2+{\lambda }_2)\hfill \\ \hfill & +\underset{\mathring{{\zeta }_1}}{\overset{{\alpha }_1\left(\tau \right)}{\int }}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )(l_{1}g\left(\delta \right)+l_1{n}_2+l_2)\mathrm{\Delta }\delta +\underset{\mathring{{\zeta }_1}}{\overset{{\alpha }_2\left(\tau \right)}{\int }}{\tilde{\mathcal{K}}}^{\mathrm{\Delta }}(\tau ,\delta )({\lambda }_{1}g\left(\delta \right)+{\lambda }_1{n}_2+{\lambda }_2)\mathrm{\Delta }\delta ,\hfill \end{array}$$

where ${\lambda }_1=\frac{1}{r}{l}^{\frac{1-r}{r}},{\lambda }_2=\frac{r-1}{r}{l}^{\frac{1}{r}},l_1=\frac{1}{rp}{l}^{\frac{1-rp}{rp}},l_2=\frac{rp-1}{rp}{l}^{\frac{1}{rp}},l>0,$ and $n_1,n_2$ are the same values as in Theorem 9.

Proof. 

Assign

$$\begin{array}{c}\hfill z\left(\tau \right)={\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}\mathcal{K}(\tau ,\delta )u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}\tilde{\mathcal{K}}(\tau ,\delta )u^p\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(31)

The nondecreasing nature on the set $[\mathring{{\zeta }_1},\mathring{{\zeta }_2}]$ of the function $0\le z\left(\tau \right)$ is intuitively obvious. Furthermore, (29) and (31) simply state that

$$\begin{array}{c}\hfill u\left(\tau \right)⩽{\left(g\left(\tau \right)+z^{\frac{1}{q}}\left(\tau \right)\right)}^{\frac{1}{rp}}\mathrm{and}z(\mathring{{\zeta }_1})={\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}\tilde{\mathcal{K}}(\tau ,\delta )u^p\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(32)

Then,

$$\begin{array}{cc}\hfill z^{\mathrm{\Delta }}\left(\tau \right)& ={\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}\left(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right)\right)u\left({\alpha }_1\left(\tau \right)\right)+{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)\tilde{\mathcal{K}}\left(\sigma \left(\tau \right),{\alpha }_2\left(\tau \right)\right)u^p\left({\alpha }_2\left(\tau \right)\right)\hfill \\ \hfill & +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}{\tilde{\mathcal{K}}}^{\mathrm{\Delta }}(\tau ,\delta )u^p\left(\delta \right)\mathrm{\Delta }\delta \hfill \\ \hfill & \le {\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}\left(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right)\right){\left(g\left(\tau \right)+z^{\frac{1}{q}}\left(\tau \right)\right)}^{\frac{1}{rp}}+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta ){\left(g\left(\delta \right)+z^{\frac{1}{q}}\left(\delta \right)\right)}^{\frac{1}{rp}}\mathrm{\Delta }\delta \hfill \\ \hfill & +{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)\tilde{\mathcal{K}}\left(\sigma \left(\tau \right),{\alpha }_2\left(\tau \right)\right){\left(g\left(\tau \right)+z^{\frac{1}{q}}\left(\tau \right)\right)}^{\frac{1}{r}}+{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}{\tilde{\mathcal{K}}}^{\mathrm{\Delta }}(\tau ,\delta ){\left(g\left(\delta \right)+z^{\frac{1}{q}}\left(\delta \right)\right)}^{\frac{1}{r}}\mathrm{\Delta }\delta \hfill \\ \hfill & \le {\alpha }_1^{\mathrm{\Delta }}\left(\tau \right)\mathcal{K}\left(\sigma \left(\tau \right),{\alpha }_1\left(\tau \right)\right)(l_{1}g\left(\tau \right)+l_1{n}_{1}z\left(\tau \right)+l_1{n}_2+l_2)\hfill \\ \hfill & +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_1\left(\tau \right)}{\mathcal{K}}^{\mathrm{\Delta }}(\tau ,\delta )(l_{1}g\left(\delta \right)+l_1{n}_{1}z\left(\delta \right)+l_1{n}_2+l_2)\mathrm{\Delta }\delta \hfill \\ \hfill & +{\alpha }_2^{\mathrm{\Delta }}\left(\tau \right)\tilde{\mathcal{K}}\left(\sigma \left(\tau \right),{\alpha }_2\left(\tau \right)\right)({\lambda }_{1}g\left(\tau \right)+{\lambda }_1{n}_{1}z\left(\tau \right)+{\lambda }_1{n}_2+{\lambda }_2)\hfill \\ \hfill & +{\int }_{\mathring{{\zeta }_1}}^{{\alpha }_2\left(\tau \right)}{\tilde{\mathcal{K}}}^{\mathrm{\Delta }}(\tau ,\delta )({\lambda }_{1}g\left(\delta \right)+{\lambda }_1{n}_{1}z\left(\delta \right)+{\lambda }_1{n}_2+{\lambda }_2)\mathrm{\Delta }\delta =\widehat{\widehat{F}}\left(\tau \right)z\left(\tau \right)+\widehat{\widehat{G}}\left(\tau \right).\hfill \end{array}$$

(33)

Using Theorem 5 on inequality (33), we identify that

$$\begin{array}{c}\hfill z\left(\tau \right)\le z(\mathring{{\zeta }_1})e_{\widehat{\widehat{F}}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\widehat{\widehat{F}}}(\tau ,\sigma \left(\delta \right))\widehat{\widehat{G}}\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(34)

From (32), (34), and Lemma 1, we can figure out that

$$\begin{array}{cc}\hfill z(\mathring{{\zeta }_1})& ={\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}\tilde{\mathcal{K}}(\tau ,\delta )u^p\left(\delta \right)\mathrm{\Delta }\delta \hfill \\ \hfill & \le {\int }_{\mathring{{\zeta }_1}}^{\mathring{{\zeta }_2}}\tilde{\mathcal{K}}(t,\delta )({\lambda }_{1}g\left(\delta \right)+{\lambda }_1{n}_{1}z\left(\delta \right)+{\lambda }_1{n}_2+{\lambda }_2)\mathrm{\Delta }\delta \hfill \\ \hfill & \le {\int }_{\alpha }^{\beta }\tilde{\mathcal{K}}(t,\delta )({\lambda }_{1}g\left(\delta \right)+{\lambda }_1{n}_1\left\{z\left(\alpha \right)e_{\widehat{\widehat{F}}}(\delta ,\alpha )+\underset{\alpha }{\overset{\delta }{\int }}{e}_{\widehat{\widehat{F}}}(\delta ,\sigma \left(\tilde{r}\right))\widehat{\widehat{G}}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}\right\}\hfill \\ \hfill & +{\lambda }_1{n}_2+{\lambda }_2)\mathrm{\Delta }\delta .\hfill \end{array}$$

(35)

From (35), we find that

$$\begin{array}{c}\hfill z(\mathring{{\zeta }_1})\le \frac{\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}\tilde{\mathcal{K}}(\tau ,\delta )\left({\lambda }_{1}g\left(\delta \right)+{\lambda }_1{n}_1\underset{\mathring{{\zeta }_1}}{\overset{\delta }{\int }}{e}_{\widehat{\widehat{F}}}(\delta ,\sigma \left(\tilde{r}\right))\widehat{\widehat{G}}\left(\tilde{r}\right)\mathrm{\Delta }\tilde{r}+{\lambda }_1{n}_2+{\lambda }_2\right)\mathrm{\Delta }\delta }{1-\underset{\mathring{{\zeta }_1}}{\overset{\mathring{{\zeta }_2}}{\int }}\tilde{\mathcal{K}}(\tau ,\delta ){\lambda }_1{n}_1{e}_{\widehat{\widehat{F}}}(\delta ,\mathring{{\zeta }_1})\mathrm{\Delta }\delta }=\widehat{\widehat{H}}.\end{array}$$

(36)

From (32), (34), and (36), we find that

$$\begin{array}{cc}\hfill u\left(\tau \right)& ⩽{\left(g\left(\tau \right)+z^{\frac{1}{q}}\left(\tau \right)\right)}^{\frac{1}{rp}}\hfill \\ \hfill & ⩽{\left(g\left(\tau \right)+{\left\{z(\mathring{{\zeta }_1})e_{\widehat{\widehat{F}}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\widehat{\widehat{F}}}(\tau ,\sigma \left(\delta \right))\widehat{\widehat{G}}\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{q}}\right)}^{\frac{1}{rp}}\hfill \\ \hfill & ⩽{\left(g\left(\tau \right)+{\left\{\widehat{\widehat{H}}{e}_{\widehat{\widehat{F}}}(\tau ,\mathring{{\zeta }_1})+\underset{\mathring{{\zeta }_1}}{\overset{\tau }{\int }}{e}_{\widehat{\widehat{F}}}(\tau ,\sigma \left(\delta \right))\widehat{\widehat{G}}\left(\delta \right)\mathrm{\Delta }\delta \right\}}^{\frac{1}{q}}\right)}^{\frac{1}{rp}}.\hfill \end{array}$$

(37)

This provides us with the required bound on $u\left(\tau \right)$ as in (30). □

4. Applications

Example 1. 

Take into consideration the dynamic equation on a time scale $\mathbb{T}=\mathbb{R}$,

$$\begin{array}{c}\hfill u^3\left(\tau \right)=(\tau +1)+{\int }_0^{\frac{\sqrt{\tau }}{2}}\delta u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_0^{\sqrt{\tau }}2s{u}^2\left(\delta \right)\mathrm{\Delta }\delta .\end{array}$$

(38)

We observe that, on $\mathbb{T}=\mathbb{R},$

$$\begin{array}{c}\hfill \sigma \left(\tau \right)=\tau ,{\mathfrak{f}}^{\mathrm{\Delta }}\left(\tau \right)={\mathfrak{f}}^{\prime }\left(\tau \right),{\int }_{\alpha }^{\beta }\mathfrak{f}\left(\tau \right)\mathrm{\Delta }\tau ={\int }_{\alpha }^{\beta }\mathfrak{f}\left(\tau \right)dt\mathrm{and}{e}_{\mathfrak{f}}(\tau ,\delta )=exp\left(\underset{s}{\overset{\tau }{\int }}\mathfrak{f}\left(\vartheta \right)d\vartheta \right).\end{array}$$

Thus, from (38), we obtain

$$\begin{array}{c}\hfill u^3\left(\tau \right)=(\tau +1)+{\int }_0^{\frac{\sqrt{\tau }}{2}}\delta u\left(\delta \right)d\delta +{\int }_0^{\sqrt{\tau }}2s{u}^2\left(\delta \right)d\delta .\end{array}$$

(39)

The inequality shown in Theorem 6 may be used to obtain the exact bound on solution $u\left(\tau \right)$ of (39), letting $p=3,q=2,g\left(\tau \right)=\tau +1,{\alpha }_1\left(\tau \right)=\frac{\sqrt{\tau }}{2},{\alpha }_2\left(\tau \right)=\sqrt{\tau },f_1\left(\tau \right)=\tau$ and $f_2\left(\tau \right)=2\tau$. We find that

$$\begin{array}{c}\hfill m_1=\frac{1}{3}{l}^{\frac{-2}{3}},m_2=\frac{2}{3}{l}^{\frac{1}{3}},n_1=\frac{2}{3}{l}^{\frac{-1}{3}},n_2=\frac{1}{3}{l}^{\frac{2}{3}},l>0.\end{array}$$

Assuming $l=1,$ we obtain $F\left(\tau \right)=\frac{17}{24},e_F(\tau ,\delta )=exp\left(\frac{17}{24}\left(\frac{{\tau }^2}{2}-\frac{{\delta }^2}{2}\right)\right),G\left(\tau \right)=\frac{17}{12},H=1.$

The outcome is the bound

$$\begin{array}{cc}\hfill u\left(\tau \right)& \le {\left\{exp\left(\frac{17{\tau }^2}{48}\right)+\underset{0}{\overset{\tau }{\int }}exp\left(\frac{17}{24}\left(\frac{{\tau }^2}{2}-\frac{{\delta }^2}{2}\right)\right)\frac{17}{12}d\delta \right\}}^{\frac{1}{3}}\hfill \\ \hfill & ={\left\{exp\left(\frac{17{\tau }^2}{48}\right)+\frac{1}{2}\sqrt{\frac{17\pi }{3}}{e}^{\frac{17{\tau }^2}{48}}\mathrm{erf}\left(\frac{1}{4}\sqrt{\frac{17}{3}}\tau \right)\right\}}^{\frac{1}{3}},\hfill \end{array}$$

(40)

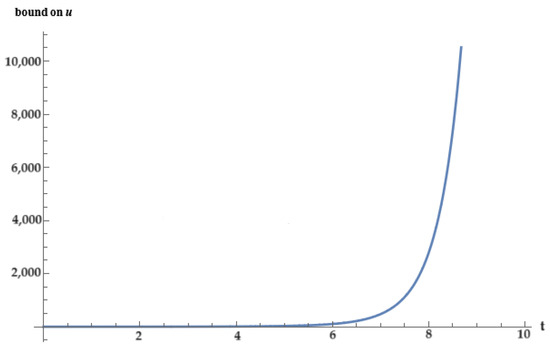
where erf$\left(x\right)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-t^2}dt$ is the error funtion of x. This further results in the plot below.

We can infer from Figure 1 that the solution does not attain an undefined value at any point of the domain. Thus, there is never a blow-up at any $\tau \in \mathbb{R}$; hence, the solution is always constrained.

Figure 1. Blow-up analysis of the bound of the solution of (38).

Example 2. 

Suppose $\mathbb{T}=\overline{q^{\mathbb{Z}}}=\left\{0\right\}\cup \{q^{\vartheta },\vartheta \in \mathbb{Z}\},q>1.$ On $\overline{q^{\mathbb{Z}}}$,

$$\begin{array}{c}\hfill \sigma \left(\tau \right)=q\tau ,{\mathfrak{f}}^{{\mathrm{\Delta }}_q}\left(\tau \right)=\frac{\mathfrak{f}\left(qt\right)-\mathfrak{f}\left(\tau \right)}{(q-1)\tau },{\int }_{\alpha }^{\beta }\mathfrak{f}\left(\tau \right){\mathrm{\Delta }}_q\tau =\sum _{\vartheta ={log}_q\left(\alpha \right)}^{{log}_q\left(\beta \right)-1}{q}^{\vartheta }\mathfrak{f}\left(q^{\vartheta }\right)\end{array}$$

and

$$\begin{array}{c}\hfill e_{\mathfrak{f}}(\tau ,\delta )=\prod _{\vartheta =\delta }^{\tau -1}(1+(q-1)\vartheta \mathfrak{f}\left(\vartheta \right))\end{array}$$

are noted. Take a retarded dynamic equation

$$\begin{array}{c}\hfill u^3\left(\tau \right)={\left(1+5\delta +{\int }_1^{\tau }5u\left(\delta \right)\mathrm{\Delta }\delta +{\int }_1^{\tau }7u\left(\delta \right)\mathrm{\Delta }\delta \right)}^2.\end{array}$$

(41)

Equation (41) may be transformed into equation

$$\begin{array}{c}\hfill u^3\left(\tau \right)={\left(1+5\delta +{\int }_1^{\tau }5u\left(\delta \right){\mathrm{\Delta }}_q\left(\delta \right)+{\int }_1^{\tau }7{\mathrm{\Delta }}_q\left(\delta \right)\right)}^2,\end{array}$$

(42)

by setting $\mathbb{T}=\overline{q^{\mathbb{Z}}}$. We obtain for $l=1,$

$$\begin{array}{cc}\hfill & m_3=\frac{2}{3},m_4=\frac{1}{3},n_3=\frac{2}{3},n_4=\frac{1}{3},\overline{F}\left(\tau \right)=8,\overline{G}\left(\tau \right)=9\mathit{and}\overline{H}=1\hfill \\ \hfill & e_{\overline{F}}(\tau ,1)=8^{\tau -1}{(q-1)}^{\tau -1}{\left(1+\frac{1}{8(q-1)}\right)}_{\tau -1}.\hfill \end{array}$$

By subsequently adopting Theorem 7 to (42), and hence, the bound by using Theorem 7 in this situation is

$$\begin{array}{cc}\hfill u\left(\tau \right)& \le {\left\{e_{\overline{F}}(\tau ,\alpha )+\underset{1}{\overset{\tau }{\int }}9e_{\overline{F}}(\tau ,q\delta ){\mathrm{\Delta }}_q\left(\delta \right)\right\}}^{\frac{2}{3}}\hfill \\ \hfill & ={\left({\left(8(q-1)\right)}^{\tau -1}{\left(\frac{8q-7}{8q-8}\right)}_{\tau -1}+\sum _{k=0}^{\frac{log\left(\tau \right)}{log\left(q\right)}-1}{\left(8(q-1)\right)}^{q^k-1}{q}^k{\left(\frac{8q-7}{8q-8}\right)}_{q^k-1}\right)}^{\frac{2}{3}},\hfill \end{array}$$

(43)

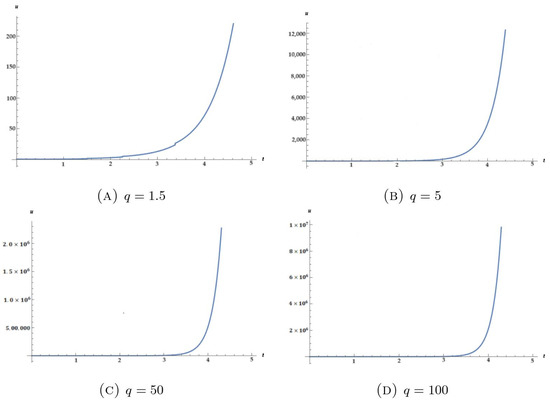
where ${\left(x\right)}_n=\frac{x+n}{x}$ is the Pochhmmer symbol, certainly referred to as a rising factorial. The plots of the above-mentioned bound for various q values are shown below.

We have assumed specific values of q in accordance with the requirements of quantum calculus, and we have examined the boundedness of the solution in each of these scenarios. We derive from the plots in the Figure 2 that $u\left(\tau \right)$ does not take an undefined value for any of the values of q. This demonstrates that for every q, Equation (42) does not reach a blow. Thus, for any q and τ in $\overline{q^{\mathbb{Z}}}$, the solution of (42) is bounded. Furthermore, we may determine that the boundedness of the solution relies on the time scale under consideration by comparing the blow-up analyses of Examples 1 and 2.

Figure 2. Blow-up analysis of the bound of the solution of (41).

5. Conclusions

In conclusion, this study has investigated a class of new nonlinear retarded dynamic inequalities in which powers of delayed integrals with unknown functions and the association of function with an unknown function raised to a nonlinear power are involved. These inequalities generalize and improve upon recent and important findings in the literature on dynamic inequalities within time scales. Our study’s main findings offer a reliable instrument for handling a certain class of nonlinear retarded dynamic equations. These inequalities can be used to examine both qualitative and quantitative properties of solutions to different nonlinear delayed dynamic equations, including boundedness, stability, and continuous dependence on initial data. Furthermore, by altering the base time scale, these conclusions can be easily applied to integrodifferential and difference equations. Looking ahead, these inequalities can be extended and generalized for more nonlinear delayed dynamic equations over time scales in this field of study. Furthermore, the practical application of these results to real-world issues continues to be a fascinating area of research.