The m-Component Connectivity of Leaf-Sort Graphs

Abstract

Connectivity plays an important role in measuring the fault tolerance of interconnection networks. As a special class of connectivity, m-component connectivity is a natural generalization of the traditional connectivity of graphs defined in terms of the minimum vertex cut. Moreover, it is a more advanced metric to assess the fault tolerance of a graph G. Let $G=\left(V\right(G),E(G\left)\right)$ be a non-complete graph. A subset F$(F\subseteq V(G\left)\right)$ is called an m-component cut of G, if $G-F$ is disconnected and has at least m components $(m\ge 2)$. The m-component connectivity of G, denoted by $c{\kappa }_m\left(G\right)$, is the cardinality of the minimum m-component cut. Let $C{F}_n$ denote the n-dimensional leaf-sort graph. Since many structures do not exist in leaf-sort graphs, many of their properties have not been studied. In this paper, we show that $c{\kappa }_3\left(C{F}_n\right)=3n-6$ $(n$ is odd) and $c{\kappa }_3\left(C{F}_n\right)=3n-7$ $(n$ is even) for $n\ge 3$; $c{\kappa }_4\left(C{F}_n\right)=\frac{9n-21}{2}$ $(n$ is odd) and $c{\kappa }_4\left(C{F}_n\right)=\frac{9n-24}{2}$ $(n$ is even) for $n\ge 4$.

1. Introduction

An interconnection network is usually modeled as an undirected graph, in which vertices and edges correspond to processor and communication links, respectively. Let $G=\left(V\right(G),E(G\left)\right)$ be a graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. As an application, graphs can also be used to study many issues related to interconnection networks [1,2]. For a graph G, the failure of vertices or edges is inevitable. In order to have an unimpeded interconnection network, we must think about the fault tolerance of a graph. There are many references focused on the fault tolerance of interconnection networks (see, for example [3,4,5,6,7,8,9,10]).

The connectivity of a graph is an important topology parameter in graph theory. The connectivity can be used to assess the vulnerability of corresponding networks, and is an important measurement for the reliability and fault tolerance of the network. A subgraph obtained from G by removing a set F of vertices and all associated incident edges is denoted by $G-F$. In particular, F is called a vertex cut of a connected graph G, if $G-F$ becomes disconnected or has only one vertex. If F is a vertex cut of a graph G, then the biggst component of $G-F$ is called the big component. Furthermore, when G is not a complete graph, the traditional connectivity $\kappa \left(G\right)$ is defined to be the cardinality of a minimum vertex cut of G. By convention, the connectivity of a complete graph with n vertices is defined to be $n-1$. A graph G is k-connected if $\kappa \left(G\right)\ge k$.

However, traditional connectivity is not enough to evaluate the reliability of networks [11,12]. To further analyze the detailed situation of the disconnected graph caused by a vertex cut F, it is natural to generalize the traditional connectivity by introducing some conditions or restrictions on the vertex cut F and/or the components of $G-F$. The notion concerning the number of components associated with the disconnected graph $G-F$ was first introducted by Chartrand et al. [13] and Sampathkumar [14]. Furthermore, in order to figure out how many sizes of a vertex cut can result in a disconnected graph with a certain number of components, Hsu et al. [15] proposed the definition of m-component connectivity. For a non-complete graph G, a subset F$(F\subseteq V(G\left)\right)$ is called an m-component cut of G, if $G-F$ is disconnected and has at least m components $(m\ge 2)$. The m-component connectivity of G, denoted by $c{\kappa }_m\left(G\right)$, is the cardinality of the minimum m-component cut. By this definition, it is obvious that $c{\kappa }_2\left(G\right)=\kappa \left(G\right)$ and $c{\kappa }_{m+1}\left(G\right)\ge c{\kappa }_m\left(G\right)$ for every positive integer m.

In recent years, the exact values of m-component connectivity have been studied for many graphs. For example, Hsu et al. [15] and Zhao et al. [16] studied the n-dimensional hypercube $Q_n$ for $2\le m\le n+1$ and $n+2\le m\le 2n-4$, respectively. Zhao and Yang studied the n-dimensional folded hypercube $F{Q}_n$ for $1\le m\le n-1$ and $n\ge 8$ [17]. Zhang et al. [18] determined the $(m+1)$-component connectivity of augmented cubes. In addition, the m-component connectivity $(m=3,m=4)$ has been studied for many graphs: alternating group networks $A{N}_n$ [19,20], split-star networks [20], hierarchical star networks [21], balanced hypercube [22], bubble-sort star graphs, and burnt pancake graphs [23]. However, most of these results are related to $m=3$ and $m=4$. For $m=5$, there are a few results. Furthermore, it is worth noting that some scholars have studied the relationship between m-component $\left(edge\right)$ connectivity $c{\kappa }_m\left(G\right)$ and m-extra $\left(edge\right)$ connectivity [24,25,26]. The m-extra connectivity, denoted by ${\kappa }_m\left(G\right)$, is defined as the minimum number of vertices whose removal from G results in every component in $G-F$ having at least $(m+1)$ vertices [27].

In this paper, we study the m-component connectivity of leaf-sort graphs, which will be defined later in Section 2. Although this graph has been proposed for a long time, many properties related to it have not been studied due to its unique structure. The biggest feature of leaf-sort graphs is as follows: let $u\in V\left(C{F}_n^i\right)$, if n is odd, u has two outgoing neighbors in other subgraphs; if n is even, u only has one outgoing neighbor in other subgraphs (Proposition 2 in Section 2). Due to this special feature, many structures which exist in other graphs do not exist in leaf-sort graphs. This leads to many difficulties when studying this graph. Meanwhile, there are some conclusions about leaf-sort graphs [28,29]. It is worth noting that there are many scholars working on the domination number of a graph [30], which is a very interesting research topic, and we can try to do more research in this direction.

The remaining part of this paper is organized as follows: Section 2 introduces the definition of $C{F}_n$ and gives some properties of $C{F}_n$. In Section 3, we first prove that the following conclusion is true: when n is odd, $|N_{C{F}_n}\left(S\right)|\ge 3n-6$; when n is even, $|N_{C{F}_n}\left(S\right)|\ge 3n-7$ $(S$ is an $Ind-set)$. Then, we get the exact value of $c{\kappa }_3\left(C{F}_n\right)$. In Section 4, we prove certain structures do not exist in leaf-sort graphs firstly, and then get the exact value of $c{\kappa }_4\left(C{F}_n\right)$. Section 5 concludes this paper.

2. Preliminaries

Let $G=\left(V\right(G),E(G\left)\right)$ be a simple connected graph, where $V\left(G\right)$ is the vertex set and $E\left(G\right)$ is the edge set. For a vertex $v\in V\left(G\right)$, $N_G\left(v\right)=\{u|(u,v)\in E\left(G\right)\}$ is the set of neighbors of v. Let $de{g}_G\left(v\right)=|N_G\left(v\right)|$ be the degree of v and $\delta \left(G\right)=min\{de{g}_G\left(v\right)|v\in V\left(G\right)\}$ be the minimum degree of G. If $de{g}_G\left(v\right)=k$ for every $v\in V\left(G\right)$, then G is k-regular. A singleton of G is a vertex v with $de{g}_G\left(v\right)=0$. For a vertex set X, $N_G\left(X\right)=\left\{{\cup }_{x\in X}{N}_G\left(x\right)\right\}-X$ is the neighbor of X. The distance between any two vertices u and v, denoted by $d_G(u,v)$, is the length of the shortest path from u to v. G is bipartite if there exist two vertex subsets $V_1,V_2$ with $V_1\cap V_2=\varnothing$ such that $V\left(G\right)=V_1\cup V_2$ and for each edge $(u,v)\in E\left(G\right)$, $|\{u,v\}\cap V_1|=|\{u,v\}\cap V_2|=1$. It is well known that bipartite graphs contain no odd cycles. We use Bondy and Murty [31] for terminology and notation not defined here.

2.1. Definition of Leaf-Sort Graphs

Let $l_1$, $l_2$ be two integers with $1\le l_1\le l_2$. Set $[l_1,l_2]=\{l|l$ as an integer with $l_1\le l\le l_2\}$. In the permutation $\left(\begin{array}{cccc}1& 2& \cdots & n\\ p_1& p_2& \cdots & p_n\end{array}\right)$, $i\to p_i$. For convenience, we denote the permutation $\left(\begin{array}{cccc}1& 2& \cdots & n\\ p_1& p_2& \cdots & p_n\end{array}\right)$ by $p_1{p}_2\cdots p_n$. In [32], every permutation can be denoted by a product of disjoint cycles. For example, $\left(\begin{array}{c}123\\ 231\end{array}\right)=\left(123\right)$. In particular, $\left(\begin{array}{c}12\cdots n\\ 12\cdots n\end{array}\right)=\left(1\right)$. The product $\sigma \tau$ of two permutations is the composition function $\tau$ followed by $\sigma$, e.g., $\left(12\right)\left(13\right)=\left(132\right)$. Let $S_n$ be the symmetric group on $[1,n]$ containing all permutations $p=p_1{p}_2\cdots p_n$ of $[1,n]$. It is well known that $\left\{\right(1i):i=2,3,\cdots ,n\}$ is a generating set for $S_n$. So $\left\{\right(1,i):i=2,3,\cdots ,n\}\cup \left\{\right(j,j+1):j=2,4,\cdots ,n-1\}$ (n is odd) is also a generating set for $S_n$ and $\left\{\right(1,i):i=2,3,\cdots ,n\}\cup \left\{\right(j,j+1):j=2,4,\cdots ,n-2\}$ (n is even) is also a generating set for $S_n$. For terminology and notation not defined here, we follow [32]. Now, we give the definition of n-dimensional leaf-sort graphs $C{F}_n$.

Definition 1 

([29]). The n-dimensional leaf-sort graph $C{F}_n$ is a graph with vertex set $V\left(C{F}_n\right)=S_n$ in which two vertices $u,v$ are adjacent if and only if $u=v(1,i),2\le i\le n$, or $u=v(j,j+1),$ $2\le j\le n-1$ when j is even and n is odd, or $u=v(j,j+1),$ $2\le j\le n-2$ when j and n are even.

By definition, we can obtain $C{F}_n$ as a $\frac{3n-3}{2}$-regular graph on $n!$ vertices for odd n, and $\frac{3n-4}{2}$-regular graph on $n!$ vertices for even n. The graphs $C{F}_2$, $C{F}_3$ and $C{F}_4$ are depicted in Figure 1.

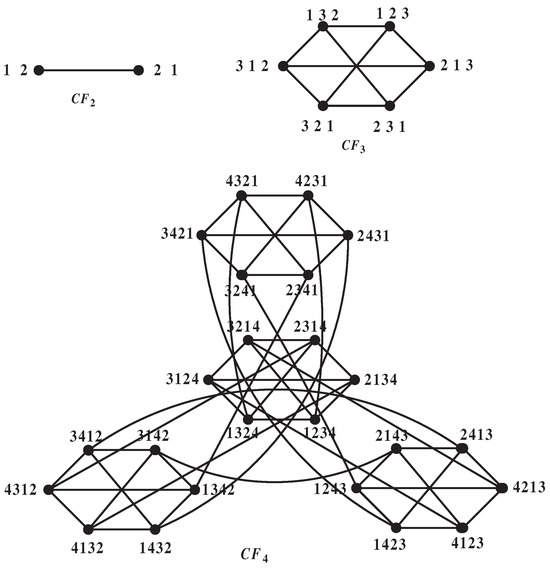
Figure 1. The leaf-sort graphs $C{F}_2$, $C{F}_3$ and $C{F}_4$.

2.2. Structural Properties of $C{F}_n$

We can partition $C{F}_n$ into n subgraphs $C{F}_n^1,C{F}_n^2,\cdots ,C{F}_n^n$, where every vertex $u=x_1{x}_2\cdots x_n$ $\in C{F}_n^i$ has a fixed integer i in the last position $x_n$ for $i\in [1,n]$. It is obvious that $C{F}_n^i$ is isomorphic to $C{F}_{n-1}$ for $i\in [1,n]$ [29]. The edges’ end vertices in different $C{F}_n^i{\hspace{0.17em}}^{\prime }s$ are called cross-edges. Two edges are said to be independent if they do not share the same vertex. For $i,j\in [1,n]$ with $i\ne j$, we denote by $E_{i,j}\left(C{F}_n\right)$ the set of edges between $C{F}_n^i$ and $C{F}_n^j$. For each vertex $u\in V\left(C{F}_n^i\right)$, two vertices adjacent to u via out-edges are called the outgoing neighbors of u, and are denoted by $u^{+}=u(1,n)$, $u^{-}=u(n-1,n)$. Let $N_u^{+}=\{u^{+},u^{-}\}$.

Proposition 1 

([29]). Let $C{F}_n^i$ $(1\le i\le n)$ be defined as above. Then, there are $2(n-2)!$ independent cross-edges between two different $C{F}_n^i{\hspace{0.17em}}^{\prime }s$ when n is odd; there are $(n-2)!$ independent cross-edges between two different $C{F}_n^i{\hspace{0.17em}}^{\prime }s$ when n is even.

Proposition 2 

([29]). Let $v\in V\left(C{F}_n^i\right)$ $(1\le i\le n)$, which is defined as above. Then, $v(1,n)$ and $v(n-1,n)$ belong to two different $C{F}_n^j$’s$(j\ne i)$ when n is odd; $v(1,n)$ belong to $C{F}_n^j$ $(j\ne i)$ when n is even.

Proposition 3. 

For any $u,v\in V\left(C{F}_n^i\right)$, $N_u^{+}\cap N_v^{+}=\varnothing$ when n is odd; $u^{+}\ne v^{+}$ when n is even.

Proof. 

Let $u=u_1{u}_2\cdots u_{n-1}i$ and $v=v_1{v}_2\cdots v_{n-1}i$, where $u_j\ne v_j$ for some $j\in [1,n-1]$. Then, $u^{+}=i{u}_2\cdots u_{n-1}{u}_1\ne i{v}_2\cdots v_{n-1}{v}_1=v^{+}$, $u^{-}=u_1{u}_2\cdots i{u}_{n-1}\ne v_1{v}_2\cdots i{v}_{n-1}=v^{-}$. Moreover, $u^{+}\ne v^{-}$ and $v^{+}\ne u^{-}$. Hence, when n is odd, $N_u^{+}\cap N_v^{+}=\varnothing$; when n is even, $u^{+}\ne v^{+}$. □

Proposition 4 

([29]). For any integer $n\ge 2$, $C{F}_n$ is bipartite.

Proposition 5. 

For any two vertices $x,y\in V\left(C{F}_n\right)$ $(n\ge 3)$, $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|\le 3$.

Proof. 

If $d_{C{F}_n}(x,y)=1$ or $d_{C{F}_n}(x,y)\ge 3$, then $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|=0$; otherwise, (i.e., $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|\ge 1$) there will be a 3-circle or $d_{C{F}_n}(x,y)=2$, a contradiction. So we only consider the situation: $d_{C{F}_n}(x,y)=2$. Next, we prove this result by induction on n.

For $n=3$, $|N_{C{F}_3}\left(x\right)\cap N_{C{F}_3}\left(y\right)|=3$ as $C{F}_3\cong K_{3,3}$ and $d_{C{F}_3}(x,y)=2$.

For $n=4$, if $x,y\in V\left(C{F}_4^i\right)$, $|N_{C{F}_4}\left(x\right)\cap N_{C{F}_4}\left(y\right)|=3$ as $C{F}_4^i\cong C{F}_3$ and $x^{+}\ne y^{+}$. If $x\in V\left(C{F}_4^i\right)$, $y\in V\left(C{F}_4^j\right)$ $(i\ne j)$, let $x=x_1{x}_2{x}_{3}i$ and $y=y_1{y}_2{y}_{3}j$, we know $x^{+}\ne y^{+}$. If $y^{+}\in C{F}_4^i$ or $x^{+}\in C{F}_4^j$, then $N_{C{F}_4}\left(x\right)\cap N_{C{F}_4}\left(y\right)\subseteq \{x^{+},y^{+}\}$. Thus, $|N_{C{F}_4}\left(x\right)\cap N_{C{F}_4}\left(y\right)|\le 2$.

Now, we assume $n\ge 5$ and the result holds for $C{F}_{n-1}$. If $x,y\in V\left(C{F}_n^i\right)$ for $i\in [1,n]$, then by Proposition 3 and the inductive hypothesis, the result holds. So we let $x\in V\left(C{F}_n^i\right)$, $y\in V\left(C{F}_n^j\right)$ $(i\ne j)$, $x=x_1{x}_2\cdots x_{n-1}i$, $y=y_1{y}_2\cdots y_{n-1}j$. Then, $x^{+}=i{x}_2\cdots x_{n-1}{x}_1$, $x^{-}=x_1{x}_2\cdots i{x}_{n-1}$, $y^{+}=j{y}_2\cdots y_{n-1}{y}_1$, $y^{-}=y_1{y}_2\cdots j{y}_{n-1}$. We know $x^{+}\ne x^{-}$ and $y^{+}\ne y^{-}$ since $i\ne j$, $x^{+}\ne y^{+}$ and $x^{-}\ne y^{-}$. As $d_{C{F}_n}(x,y)=2$ and $N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)\subseteq \{x^{+},x^{-},y^{+},y^{-}\}$, we can assume $y^{+}\in N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)$.

When n is odd. If $y^{+}=x^{-}$, then $j{y}_2{y}_3\cdots y_{n-1}{y}_1=x_1{x}_2\cdots i{x}_{n-1}$, $x_1=j,$ $y_2=x_2,$ $y_3=x_3,\cdots ,y_{n-2}=x_{n-2},y_{n-1}=i,y_1=x_{n-1}$. Thus, $x^{+}=y_{n-1}{y}_2{y}_3\cdots y_{n-2}{y}_{1}j\in C{F}_n^j$ and $y^{-}=x_{n-1}{x}_2{x}_3\cdots x_{n-2}{x}_{1}i\in C{F}_n^i$, $y{x}^{+}\in E\left(C{F}_n^j\right)$, $x{y}^{-}\in E\left(C{F}_n^i\right)$. So $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|=3$. If $y^{+}\in C{F}_n^i$ and adjacent to x, then $y^{+}=j{y}_2\cdots y_{n-1}i$, $N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)\subseteq \{x^{+},y^{+},x^{-}\}$. Thus, $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|\le 3$. Furthermore, $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|=3$ holds if and only if $y^{-}=x^{+}$; this is similar to the situation $y^{+}=x^{-}$. When $y^{-}\ne x^{+}$, $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|\le 2$. So when n is odd, this result holds.

When n is even, note that $x^{+}\ne y^{+}$. If $y^{+}\in C{F}_n^i$ or $x^{+}\in C{F}_n^j$, then $N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)\subseteq \{x^{+},y^{+}\}$. Thus, $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|\le 2$.

In summary, this proposition is proven. □

Corollary 1. 

When $n\ge 4$ is even, if x and y belong to two different subgraphs in $C{F}_n$, then $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|\le 2$.

Corollary 2. 

When $n\ge 3$ is odd, for any two vertices $x,y\in V\left(C{F}_n\right)$, where $x\in V\left(C{F}_n^i\right)$, $y\in V\left(C{F}_n^j\right)$ $(i\ne j)$. Then, $|N_{C{F}_n}\left(x\right)\cap N_{C{F}_n}\left(y\right)|=3$ holds if and only if $y^{+}=x^{-}$ or $y^{-}=x^{+}$.

Proposition 6 

([29]). Let $C{F}_n$ be the leaf-sort graph. Then, the connectivity $\kappa \left(C{F}_n\right)=\frac{3n-3}{2}$ when n is odd and $\kappa \left(C{F}_n\right)=\frac{3n-4}{2}$ when n is even.

Lemma 1 

([28]). Let $F\subseteq V\left(C{F}_n\right)$ with $|F|\le 3n-6$ when n is odd $(n\ge 5)$ and $|F|\le 3n-7$ when n is even $(n\ge 4)$. If $C{F}_n-F$ is disconnected, then $C{F}_n-F$ satisfies one of the following conditions:

$\left(1\right)$ $C{F}_n-F$ has two components, one of which is a singleton;

$\left(2\right)$ $C{F}_n-F$ has three components, two of which are singletons.

The conclusion of Lemma 1 is closely related to the m-component connectivity of $C{F}_n$, which is why we listed it here.

3. The 3-Component Connectivity of ${\mathit{CF}}_{\mathit{n}}$

In this section, we will discuss the 3-component connectivity of $C{F}_n$, and will prove that, when n is odd, $c{\kappa }_3\left(C{F}_n\right)=3n-6$ for $n\ge 3$; when n is even, $c{\kappa }_3\left(C{F}_n\right)=3n-7$ for $n\ge 3$. Before proving our main results, we prove some useful lemmas firstly. Let S be a subset of $V\left(G\right)$ (i.e., $S\subseteq V\left(G\right))$; S is called an independent set $(Ind-set)$ if any two vertices $x_1,x_2\in V\left(S\right)$ are nonadjacent.

Lemma 2. 

When n is odd, if $x_1\in V\left(C{F}_n^i\right)$, then there exists only $(n-3)$ vertices in $C{F}_n^i$, which can satisfy that $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|=3$; when n is even, if $x_1\in V\left(C{F}_n^i\right)$, then there exists only $(n-2)$ vertices in $C{F}_n^i$ such that $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|=3$. In addition, these vertices are all regular.

Proof. 

Note that $C{F}_n^i\cong C{F}_{n-1}$. When n is odd, $n-1$ is even, $\{x_1,x_2\}\subseteq V\left(C{F}_n^i\right)$. Since $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|=3$, by Corollary 1 we know that $x_1,x_2$ must belong to a common subgraph in $C{F}_n^i$; otherwise, if $x_1,x_2$ belong to different subgraphs in $C{F}_n^i$, then $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|\le 2$. So we can assume $x_1=i_1{i}_2{i}_3\cdots i_{n-2}ji$, $x_2=j_1{j}_2{j}_3\cdots j_{n-2}ji$. Now, we let $x_1^{\prime }=i_1{i}_2{i}_3\cdots i_{n-2}$, $x_2^{\prime }=j_1{j}_2{j}_3\cdots j_{n-2}$, then $\{x_1^{\prime },x_2^{\prime }\}\subseteq V\left(G_1\right)$, $G_1\cong C{F}_{n-2}$, $n-2$ is odd. Since $|N_{G_1}\left(x_1^{\prime }\right)\cap N_{G_1}\left(x_2^{\prime }\right)|=3$, by the proof process of Proposition 5, we now $x_1^{\prime },x_2^{\prime }$ have two different situations:

Case 1. 

$x_1^{\prime },x_2^{\prime }$ belong to two different subgraphs in $G_1$, and ${\left(x_1^{\prime }\right)}^{+}={\left(x_2^{\prime }\right)}^{-}$ or ${\left(x_1^{\prime }\right)}^{-}={\left(x_2^{\prime }\right)}^{+}$.

In this case, we have $i_{n-2}\ne j_{n-2}$. If ${\left(x_1^{\prime }\right)}^{+}=i_{n-2}{i}_2{i}_3\cdots i_{n-3}{i}_1={\left(x_2^{\prime }\right)}^{-}=j_1{j}_2{j}_3\cdots j_{n-2}$ $j_{n-3}$, then $j_1=i_{n-2},j_2=i_2$,…,$j_{n-4}=i_{n-4},j_{n-3}=i_1,j_{n-2}=i_{n-3}$. Thus, $x_2=i_{n-2}{i}_2{i}_3\cdots i_{n-4}$ $i_1{i}_{n-3}ji$. If ${\left(x_1^{\prime }\right)}^{-}=i_1{i}_2{i}_3\cdots i_{n-2}{i}_{n-3}={\left(x_2^{\prime }\right)}^{+}=j_{n-2}{j}_2{j}_3\cdots j_{n-3}{j}_1$, then $j_{n-2}=i_1,$ $j_2=i_2,$ $\dots ,j_{n-4}=i_{n-4},j_{n-3}=i_{n-2},j_1=i_{n-3}$. Thus, $x_2=i_{n-3}{i}_2{i}_3\cdots i_{n-4}{i}_{n-2}{i}_{1}ji$.

Case 2. 

$x_1^{\prime },x_2^{\prime }$ belong to the same subgraph in $G_1$.

In this case, we have $i_{n-2}=j_{n-2}$, $x_1^{\prime }=i_1{i}_2{i}_3\cdots i_{n-2}$, $x_2^{\prime }=j_1{j}_2{j}_3\cdots i_{n-2}$. As $G_1^{i_{n-2}}\cong C{F}_{n-3}$, $n-3$ is even, $|N_{G_1^{i_{n-2}}}\left(x_1^{\prime }\right)\cap N_{G_1^{i_{n-2}}}\left(x_2^{\prime }\right)|=3$, we can obtain $x_1^{\prime },x_2^{\prime }$ belonging to a common subgraph in $G_1^{i_{n-2}}$. Then, $i_{n-3}=j_{n-3}$. Let $x_1^{\prime \prime }=i_1{i}_2{i}_3\cdots i_{n-4}$, $x_2^{\prime \prime }=j_1{j}_2{j}_3\cdots j_{n-4}$, then $\{x_1^{\prime \prime },x_2^{\prime \prime }\}\subseteq V\left(G_2\right)$, $G_2\cong C{F}_{n-4}$ and $|N_{G_2}\left(x_1^{\prime \prime }\right)\cap N_{G_2}\left(x_2^{\prime \prime }\right)|=3$. As $(n-4)$ is odd, there are two different situations:

Subcase 2.1. 

$x_1^{\prime \prime },x_2^{\prime \prime }$ belong to two different subgraphs in $G_2$, and ${\left(x_1^{\prime \prime }\right)}^{+}={\left(x_2^{\prime \prime }\right)}^{-}$ or ${\left(x_1^{\prime \prime }\right)}^{-}={\left(x_2^{\prime \prime }\right)}^{+}$.

If ${\left(x_1^{\prime \prime }\right)}^{+}={\left(x_2^{\prime \prime }\right)}^{-}$, we can get $j_1=i_{n-4},j_2=i_2,\dots ,j_{n-6}=i_{n-6},j_{n-4}=i_{n-5},j_{n-5}=i_1$. Thus, $x_2=i_{n-4}{i}_2{i}_3\cdots i_{n-6}{i}_1{i}_{n-5}{i}_{n-3}{i}_{n-2}ji$. If ${\left(x_1^{\prime \prime }\right)}^{-}={\left(x_2^{\prime \prime }\right)}^{+}$, then $j_1=i_{n-5},j_2=i_2,\dots ,j_{n-4}=i_1,j_{n-5}=i_{n-4}$. Thus, $x_2=i_{n-5}{i}_2{i}_3\cdots i_{n-6}{i}_{n-4}{i}_1{i}_{n-3}{i}_{n-2}ji$.

Subcase 2.2. 

$x_1^{\prime \prime },x_2^{\prime \prime }$ belong to a same subgraph in $G_2$.

This case is similar to case 2; this is a finite cycle process.

Finally, when n is odd, we can obtain $(n-3)$ vertices such that $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|=3$, they are $i_{n-2}{i}_2{i}_3\cdots i_{n-4}{i}_1{i}_{n-3}ji$, $i_{n-3}{i}_2{i}_3\cdots i_{n-4}{i}_{n-2}{i}_{1}ji$, $i_{n-4}{i}_2{i}_3\cdots i_{n-6}{i}_1{i}_{n-5}{i}_{n-3}{i}_{n-2}ji$, $i_{n-5}{i}_2{i}_3\cdots i_{n-4}{i}_1{i}_{n-3}{i}_{n-2}ji$,…,$i_3{i}_1{i}_2{i}_4\cdots i_{n-2}ji$, $i_2{i}_3{i}_1{i}_4\cdots i_{n-2}ji$.

When n is even, $n-1$ is odd, $C{F}_n^i\cong C{F}_{n-1}$. Let $x_1=i_1{i}_2{i}_3\cdots i_{n-1}i$, $x_2=j_1{j}_2{j}_3\cdots j_{n-1}i$, $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|=3$. Assume $x_1^{\prime }=i_1{i}_2{i}_3\cdots i_{n-1}$, $x_2^{\prime }=j_1{j}_2{j}_3\cdots j_{n-1}$, then $\{x_1^{\prime },x_2^{\prime }\}\subseteq V\left(G_1\right)$, $G_1\cong C{F}_{n-1}$; similarly, we can also divide it into two different situations:

Case 1. 

$x_1^{\prime },x_2^{\prime }$ belong to two different subgraphs in $G_1$, and ${\left(x_1^{\prime }\right)}^{+}={\left(x_2^{\prime }\right)}^{-}$ or ${\left(x_1^{\prime }\right)}^{-}={\left(x_2^{\prime }\right)}^{+}$.

In this case, we have $i_{n-1}\ne j_{n-1}$. If ${\left(x_1^{\prime }\right)}^{+}={\left(x_2^{\prime }\right)}^{-}$, then $j_1=i_{n-1},j_2=i_2,\dots ,j_{n-1}=i_{n-2},j_{n-2}=i_1$. Thus, $x_2=i_{n-1}{i}_2{i}_3\cdots i_{n-3}{i}_1{i}_{n-2}i$. If ${\left(x_1^{\prime }\right)}^{-}={\left(x_2^{\prime }\right)}^{+}$, then $j_1=i_{n-2},j_2=i_2,\dots ,j_{n-2}=i_{n-1},j_{n-1}=i_1$. Thus, $x_2=i_{n-2}{i}_2{i}_3\cdots i_{n-3}{i}_{n-1}{i}_{1}i$.

Case 2. 

$x_1^{\prime },x_2^{\prime }$ belong to a same subgraph in $G_1$.

In this case, $i_{n-1}=j_{n-1}$. Since $G_1^{i_{n-1}}\cong C{F}_{n-2}$ and $|N_{G_1^{i_{n-1}}}\left(x_1^{\prime }\right)\cap N_{G_1^{i_{n-1}}}\left(x_2^{\prime }\right)|=3$, $x_1^{\prime }$ and $x_2^{\prime }$ are in a same subgraph in $G_1^{i_{n-1}}$. So $i_{n-2}=j_{n-2}$. Let $x_1^{\prime \prime }=i_1{i}_2{i}_3\cdots i_{n-3}$, $x_2^{\prime \prime }=j_1{j}_2{j}_3\cdots j_{n-3}$, then $\{x_1^{\prime \prime },x_2^{\prime \prime }\}\subseteq V\left(G_2\right)$, $G_2\cong C{F}_{n-3}$, $n-3$ is odd. As $|N_{G_2}\left(x_1^{\prime \prime }\right)\cap N_{G_2}\left(x_2^{\prime \prime }\right)|=3$, we can also consider the following two situations:

Subcase 2.1. 

$x_1^{\prime \prime }$ and $x_2^{\prime \prime }$ belong to two different subgraphs in $G_2$, and ${\left(x_1^{\prime \prime }\right)}^{+}={\left(x_2^{\prime \prime }\right)}^{-}$ or ${\left(x_1^{\prime \prime }\right)}^{-}={\left(x_2^{\prime \prime }\right)}^{+}$.

If ${\left(x_1^{\prime \prime }\right)}^{+}={\left(x_2^{\prime \prime }\right)}^{-}$, then $j_1=i_{n-3},j_2=i_2,\dots ,j_{n-3}=i_{n-4},j_{n-4}=i_1$. Thus $x_2=i_{n-3}{i}_2{i}_3\cdots i_{n-5}$ $i_1{i}_{n-4}{i}_{n-2}{i}_{n-1}i$. If ${\left(x_1^{\prime \prime }\right)}^{-}={\left(x_2^{\prime \prime }\right)}^{+}$, then $j_1=i_{n-4},j_2=i_2,\dots ,j_{n-3}=i_1,j_{n-4}=i_{n-3}$. Thus $x_2=i_{n-4}{i}_2{i}_3\cdots i_{n-5}{i}_{n-3}{i}_1{i}_{n-2}{i}_{n-1}i$.

Subcase 2.2. 

$x_1^{\prime \prime }$ and $x_2^{\prime \prime }$ belong to a same subgraph in $G_2$.

This case is similar to case 2; this is also a finite cycle process.

Finally, when n is even, we can obtain $(n-2)$ vertices such that $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|=3$, they are $i_{n-1}{i}_2{i}_3\cdots i_{n-3}{i}_1{i}_{n-2}i$, $i_{n-2}{i}_2{i}_3\cdots i_{n-3}{i}_{n-1}{i}_{1}i$, $i_{n-3}{i}_2{i}_3\cdots$ $i_{n-5}{i}_1{i}_{n-4}{i}_{n-2}{i}_{n-1}i$, $i_{n-4}{i}_2{i}_3\cdots$ $i_{n-5}{i}_{n-3}{i}_1{i}_{n-2}{i}_{n-1}i$,…, $i_3{i}_1{i}_2{i}_4\cdots i_{n-2}{i}_{n-1}i$, $i_2{i}_3{i}_1{i}_4\cdots i_{n-2}{i}_{n-1}i$. □

Corollary 3. 

Let $C{F}_n$ is an n-dimension leaf-sort graph, $\{x_1,x_2\}\subseteq V\left(C{F}_n^i\right)$. If $x_1=i_1{i}_2{i}_3\cdots i_{n-1}i$, $x_2=j_1{j}_2{j}_3\cdots j_{n-1}i$ and $|N_{C{F}_n^i}\left(x_1\right)\cap N_{C{F}_n^i}\left(x_2\right)|=3$, then $j_1\ne i_1$.

Lemma 3. 

For $n\ge 3$, let S is an $Ind$-set and $|S|=2$, then when n is odd, $|N_{C{F}_n}\left(S\right)|\ge 3n-6$; when n is even, $|N_{C{F}_n}\left(S\right)|\ge 3n-7$.

Proof. 

Let $S=\{x_1,x_2\}$, as S is an $Ind$-set, so $x_1$ and $x_2$ are nonadjacent. By Proposition 5 and the definition of $C{F}_n$, we know that $|N_{C{F}_n}\left(x_1\right)\cap N_{C{F}_n}\left(x_2\right)|\le 3$ and $C{F}_n$ is a $\frac{3n-3}{2}$-regular graph $(n$ is odd) or $\frac{3n-4}{2}$-regular graph $(n$ is even). So, when n is odd, $|N_{C{F}_n}\left(S\right)|=|N_{C{F}_n}\left(x_1\right)|+|N_{C{F}_n}\left(x_2\right)|-|N_{C{F}_n}\left(x_1\right)\cap N_{C{F}_n}\left(x_2\right)|\ge 2\times \frac{3n-3}{2}-3=3n-6$. When n is even, $|N_{C{F}_n}\left(S\right)|=|N_{C{F}_n}\left(x_1\right)|+|N_{C{F}_n}\left(x_2\right)|-|N_{C{F}_n}\left(x_1\right)\cap N_{C{F}_n}\left(x_2\right)|\ge 2\times \frac{3n-4}{2}-3=3n-7$. □

Corollary 4. 

For $n\ge 4$, let F be a subset of $V\left(C{F}_n\right)$ (i.e., $F\subseteq V\left(C{F}_n\right)$) and when n is odd, $|F|\le 3n-7$; when n is even, $|F|\le 3n-8$, then $C{F}_n-F$ contains a big component C, which satisfies $|V(C)|\ge n!-|F|-1$.

Theorem 1. 

For $n\ge 3$, when n is odd, $c{\kappa }_3\left(C{F}_n\right)=3n-6$; when n is even, $c{\kappa }_3\left(C{F}_n\right)=3n-7$.

Proof. 

For $n=3$, since $c{\kappa }_{l+1}\left(C{F}_n\right)\ge c{\kappa }_l\left(C{F}_n\right)$, we can obtain $c{\kappa }_3\left(C{F}_3\right)\ge \frac{3n-3}{2}=3=3n-6$ by Proposition 6. For $n\ge 4$, by Corollary 4, we can also obtain $c{\kappa }_3\left(C{F}_n\right)\ge 3n-6$ when n is odd and $c{\kappa }_3\left(C{F}_n\right)\ge 3n-7$ when n is even. Next, we will prove that, when n is odd, $c{\kappa }_3\left(C{F}_n\right)\le 3n-6$ and when n is even, $c{\kappa }_3\left(C{F}_n\right)\le 3n-7$. Since $|N_{C{F}_n}\left(x_1\right)\cap N_{C{F}_n}\left(x_2\right)|\le 3$, we can choose two different vertices $x_1,x_2\in V\left(C{F}_n\right)$, such that $|N_{C{F}_n}\left(x_1\right)\cap N_{C{F}_n}\left(x_2\right)|=3$. From the definition of $C{F}_n$, we know that $C{F}_n$ is a $\frac{3n-3}{2}$-regular $(n$ is odd) and $\frac{3n-4}{2}$-regular graph $(n$ is even), so when n is odd, $|N_{C{F}_n}\left(\{x_1,x_2\}\right)|=2\times \frac{3n-3}{2}-3=3n-6$; when n is even, $|N_{C{F}_n}\left(\{x_1,x_2\}\right)|=2\times \frac{3n-4}{2}-3=3n-7$. Let $F=N_{C{F}_n}\left(\{x_1,x_2\}\right)$; we know $C{F}_n-F$ contains three components and two of them only have a singleton. So we can obtain $c{\kappa }_3\left(C{F}_n\right)\le 3n-6$ $(n$ is odd) and $c{\kappa }_3\left(C{F}_n\right)\le 3n-7$ $(n$ is even). □

4. The 4-Component Connectivity of ${\mathit{CF}}_{\mathit{n}}$

Lemma 4. 

When $n=4$, let S be an $Ind$-set and $|S|=3$, $|N_{C{F}_4}\left(S\right)|\ge 6$.

Proof. 

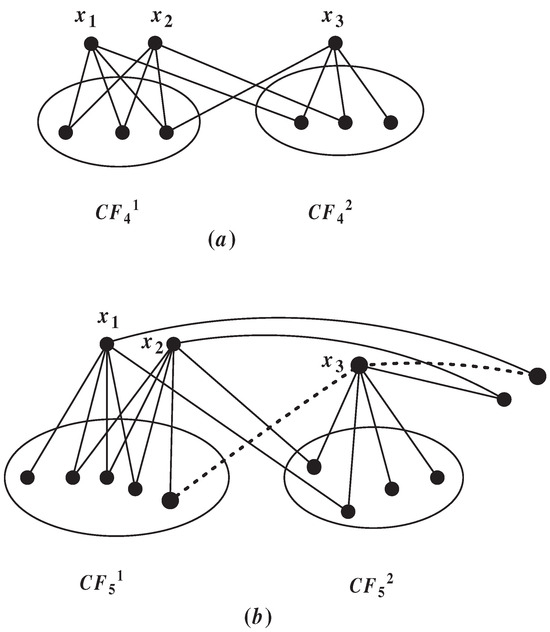
Let $S=\{x_1,x_2,x_3\}$; since S is an $Ind$-set, $x_1,x_2,x_3$ are nonadjacent with each other. Note that $C{F}_4^i\cong C{F}_3$, $C{F}_3\cong K_{3,3}$. Next, we will think about the following three cases.

Case 1. 

$x_1,x_2,x_3$ belong to the same subgraph $C{F}_4^i$.

In this case, since $C{F}_4^i\cong K_{3,3}$ and S is an $Ind$-set, $|N_{C{F}_4^i}\left(S\right)|=3$. By Proposition 3, we know the outgoing neighbors of $\{x_1,x_2,x_3\}$ are different. Thus, $|N_{C{F}_4}\left(S\right)|=3+3=6$.

Case 2. 

$x_1,x_2,x_3$ belong to two different subgraphs $C{F}_4^i$, $C{F}_4^j$ $(i\ne j)$.

In this case, we can let $\{x_1,x_2\}\subseteq V\left(C{F}_4^1\right)$, $x_3\in V\left(C{F}_4^2\right)$. Since $x_1$ and $x_2$ are nonadjacent, we can obtain $|N_{C{F}_4^1}\left(\{x_1,x_2\}\right)|=3$, $|N_{C{F}_4^2}\left(x_3\right)|=3$. By the definition of $C{F}_n$, we know $x_i$ $(i\in \{1,2,3\left\}\right)$ only has one outgoing neighbor. If the structure shown in Figure 2a exists, $|N_{C{F}_4}\left(S\right)|\ge |N_{C{F}_4^1}\left(\{x_1,x_2\}\right)|+|N_{C{F}_4^2}\left(x_3\right)|=6$. Now, we can show that this structure does not exist. As $|N_{C{F}_4^1}\left(\{x_1,x_2\}\right)|=3$ and $\{x_1,x_2\}\subseteq V\left(C{F}_4^1\right)$, we assume $x_1=2341$, then $x_2=4231$ or $x_2=3421$. Thus, $x_1^{+}\in V\left(C{F}_4^2\right)$, $x_2^{+}\notin V\left(C{F}_4^2\right)$, and the structure shown in Figure 2a does not exist. Thus, $|N_{C{F}_4}\left(S\right)|\ge 7$.

Figure 2. (a) is an illustration of $|N_{C{F}_4}\left(S\right)|=|N_{C{F}_4^1}\left(\{x_1,x_2\}\right)|+|N_{C{F}_4^2}\left(x_3\right)|=6$ in Lemma 4 and (b) is an illustration of Case 2 in Lemma 5.

Case 3. 

$x_1,x_2,x_3$ belong to three different subgraphs $C{F}_4^i$, $C{F}_4^j$, $C{F}_4^k$ $(i,j,k$ are different from each other).

In this case, we can let $x_i\in V\left(C{F}_4^i\right)$. By the definition of $C{F}_n$, we know $|N_{C{F}_4^i}\left(x_i\right)|=3$, thus $|N_{C{F}_4}\left(S\right)|\ge 3\times 3=9$.

Combining the above three situations, we can obtain $|N_{C{F}_4}\left(S\right)|\ge 6$. □

Lemma 5. 

When $n=5$, let S be an $Ind$-set and $|S|=3$, $|N_{C{F}_5}\left(S\right)|\ge 12$.

Proof. 

Let $S=\{x_1,x_2,x_3\}$, since S is an $Ind$-set, $x_1,x_2,x_3$ are nonadjacent with each other. Note that $C{F}_5^i\cong C{F}_4$ $(1\le i\le 5)$. We think about the following three cases.

Case 1. 

$x_1,x_2,x_3$ belong to the same subgraph $C{F}_5^i$.

Since $C{F}_5^i\cong C{F}_4$, by Lemma 4, we can obtain $|N_{C{F}_5^i}\left(S\right)|\ge 6$. By the definition of $C{F}_n$ and Proposition 3, we know the outgoing neighbors of $\{x_1,x_2,x_3\}$ are different and every vertex has two different outgoing neighbors. Thus, $|N_{C{F}_5}\left(S\right)|=|N_{C{F}_5^i}\left(S\right)|+6\ge 6+6=12$.

Case 2. 

$x_1,x_2,x_3$ belong to two different subgraphs $C{F}_5^i$, $C{F}_5^j$ $(i\ne j)$.

In this case, we can let $\{x_1,x_2\}\subseteq V\left(C{F}_5^1\right)$, $x_3\in V\left(C{F}_5^2\right)$. Since $C{F}_5^1\cong C{F}_4$, by Lemma 3, we know that $|N_{C{F}_5^1}\left(\{x_1,x_2\}\right)|\ge 3(n-1)-7=3\times 5-10=5$. By the definition of $C{F}_n$, we can obtain $|N_{C{F}_5^2}\left(x_3\right)|=\frac{3(n-1)-4}{2}=4$. By Proposition 2, we can ascertain that $x_1$ and $x_2$ have, at most, two neighbors which belong to $C{F}_5^2$. In other words, there are at least two neighbors of $x_1$ and $x_2$ belonging to $C{F}_5-C{F}_5^1-C{F}_5^2$. If the structure shown in Figure 2b exists, then $|N_{C{F}_5}\left(S\right)|\ge |N_{C{F}_5^1}\left(\{x_1,x_2\}\right)|+|N_{C{F}_5^2}\left(x_3\right)|+2=5+4+2=11$. Furthermore, $|N_{C{F}_5}\left(S\right)|=11$ holds if and only if this structure exists. Now, we can prove this structure does not exist.

Since $\{x_1,x_2\}\subseteq V\left(C{F}_5^1\right)$ and $|N_{C{F}_5^1}\left(x_1\right)\cap N_{C{F}_5^1}\left(x_2\right)|=3$, by Lemma 2, we can ascertain whether $x_1=i_1{i}_2{i}_3{i}_{4}1$, $x_2=i_3{i}_1{i}_2{i}_{4}1$ or $x_2=i_2{i}_3{i}_1{i}_{4}1$ $(i_1,i_2,i_3,i_4$ are different from each other).

If $x_2=i_3{i}_1{i}_2{i}_{4}1$, then $x_2^{+}=1i_1{i}_2{i}_4{i}_3$, $x_2^{-}=i_3{i}_1{i}_{2}1i_4$. Since $x_1^{+}=1i_2{i}_3{i}_4{i}_1$, $x_1^{-}=i_1{i}_2{i}_{3}1i_4$ and one of the two outgoing neighbors of $x_1,x_2$ belong to $C{F}_5^2$, we can obtain $i_4=2$. Thus, $\{x_1^{-},x_2^{-}\}\subseteq V\left(C{F}_5^2\right)$. As $x_1^{-},x_2^{-}$ are adjacent to $x_3$, so $x_3=i_2{i}_1{i}_{3}12$ or $x_3=i_3{i}_2{i}_{1}12$ or $x_3=i_1{i}_3{i}_{2}12$. When $x_3=i_2{i}_1{i}_{3}12$, $x_3^{+}=2i_1{i}_{3}1i_2\in V\left(C{F}_5^{i_2}\right)$, $x_3^{-}=i_2{i}_1{i}_{3}21\in V\left(C{F}_5^1\right)$, and $x_3^{-}$ is adjacent to $x_2$. Since $x_1^{+}=1i_2{i}_{3}2i_1\in V\left(C{F}_5^{i_1}\right)$, $x_2^{+}=1i_1{i}_{2}2i_3\in V\left(C{F}_5^{i_3}\right)$, $x_3^{+}\ne x_1^{+}$, $x_3^{+}\ne x_2^{+}$. Thus, this structure does not exist. When $x_3=i_3{i}_2{i}_{1}12$, $x_3^{+}=2i_2{i}_{1}1i_3\in V\left(C{F}_5^{i_3}\right)$, $x_3^{-}=i_3{i}_2{i}_{1}21\in V\left(C{F}_5^1\right)$, and $x_3^{-}$ is adjacent to $x_1$. Since $x_1^{+}=1i_2{i}_{3}2i_1$, $x_2^{+}=1i_1{i}_{2}2i_3$ and $1\ne 2$, $x_3^{+}\ne x_1^{+}$, $x_3^{+}\ne x_2^{+}$. When $x_3=i_1{i}_3{i}_{2}12$, $x_3^{+}=2i_3{i}_{2}1i_1\in V\left(C{F}_5^{i_1}\right)$, $x_3^{-}=i_1{i}_3{i}_{2}21\in V\left(C{F}_5^1\right)$, and $x_3^{-}$ is adjacent to $x_2$. Since $x_1^{+}=1i_2{i}_{3}2i_1$, $x_2^{+}=1i_1{i}_{2}2i_3$ and $1\ne 2$, $x_3^{+}\ne x_1^{+}$, $x_3^{+}\ne x_2^{+}$. So this structure does not exist.

If $x_2=i_2{i}_3{i}_1{i}_{4}1$, then $x_2^{+}=1i_3{i}_1{i}_4{i}_2$, $x_2^{-}=i_2{i}_3{i}_{1}1i_4$. Since $x_1^{+}=1i_2{i}_3{i}_4{i}_1$, $x_1^{-}=i_1{i}_2{i}_{3}1i_4$ and one of the two outgoing neighbors of $x_1,x_2$ belong to $C{F}_5^2$, we can obtain $i_4=2$. Thus, $\{x_1^{-},x_2^{-}\}\subseteq V\left(C{F}_5^2\right)$. As $x_1^{-},x_2^{-}$ are adjacent to $x_3$, so $x_3=i_3{i}_2{i}_{1}12$ or $x_3=i_1{i}_3{i}_{2}12$ or $x_3=i_2{i}_1{i}_{3}12$. As discussed above, we can also conclude that this structure does not exist.

Thus, the structure shown in Figure 2b does not exist, $|N_{C{F}_5}\left(S\right)|\ge 12$.

Case 3. 

$x_1,x_2,x_3$ belong to three different subgraphs $C{F}_5^i$, $C{F}_5^j$, $C{F}_5^k$ $(i,j,k$ are different from each other).

Without loss of generality, we can let $x_1\in V\left(C{F}_5^1\right)$, $x_2\in V\left(C{F}_5^2\right)$, $x_3\in V\left(C{F}_5^3\right)$. By the definition of $C{F}_n$, we can obtain $|N_{C{F}_5^i}\left(x_i\right)|=\frac{3(n-1)-4}{2}=4$ $(i\in \{1,2,3\left\}\right)$, thus $|N_{C{F}_5}\left(S\right)|\ge |N_{C{F}_5^1}\left(x_1\right)|+|N_{C{F}_5^2}\left(x_2\right)|+|N_{C{F}_5^3}\left(x_3\right)|=12$.

Combining the above three situations, we can obtain $|N_{C{F}_5}\left(S\right)|\ge 12$. □

Lemma 6. 

When n is odd, let $S=\{x_1,x_2,x_3\}$ be an $Ind$-set, where $\{x_1,x_2\}\subseteq V\left(C{F}_n^i\right)$, $x_3\in V\left(C{F}_n^j\right)$ $(i\ne j)$ and $|N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|=3n-10$. Then, $|N_{C{F}_n}\left(S\right)|\ne \frac{9n-23}{2}$.

Proof. 

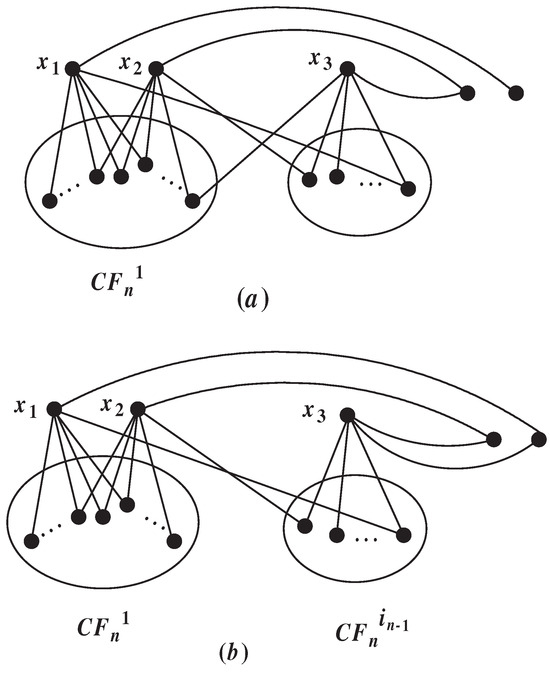
When n is odd, $|N_{C{F}_n}\left(S\right)|=\frac{9n-23}{2}$ occurs if and only if the structure in Figure 3 appears. Next, we will prove that these structures cannot appear.

Figure 3. (a,b) are the two cases of $|N_{C{F}_n}\left(S\right)|=\frac{9n-23}{2}$ in Lemma 6.

Firstly, we prove that the structure shown in Figure 3a does not exist. Suppose, on the contrary, we assume this structure exists and $\{x_1,x_2\}\subseteq V\left(C{F}_n^1\right)$, then $x_1=i_1{i}_2{i}_3\cdots i_{n-2}{i}_{n-1}1$, $x_2=j_1{j}_2{j}_3\cdots j_{n-2}{j}_{n-1}1$. As $|N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|=3n-10$, by the proof process of Lemma 3, we can know that $x_1,x_2$ must have three common neighbors in $C{F}_n^1$. Note that n is odd, then $n-1$ is even, and $C{F}_n^i\cong C{F}_{n-1}$. By Corollary 1, we can ascertain that $x_1,x_2$ must belong to a common subgraph in $C{F}_n^1$; otherwise, if $x_1,x_2$ belongs to two different subgraphs in $C{F}_n^1$, then $|N_{C{F}_n^1}\left(\{x_1,x_2\}\right)|\le 2$, which is a contradiction. So $j_{n-1}=i_{n-1}$, $x_1^{+}=1i_2{i}_3\cdots i_{n-2}{i}_{n-1}{i}_1$, $x_1^{-}=i_1{i}_2{i}_3\cdots i_{n-2}1i_{n-1}$, $x_2^{+}=1j_2{j}_3\cdots j_{n-2}{i}_{n-1}{j}_1$, $x_2^{-}=j_1{j}_2{j}_3\cdots j_{n-2}1i_{n-1}$. By Corollary 3, we know $j_1\ne i_1$. As one of the two outgoing neighbors of $x_1$ and $x_2$ belong to a common subgraph with $x_3$, $\{x_1^{-},x_2^{-}\}\subseteq V\left(C{F}_n^{i_{n-1}}\right)$ and $x_3\in V\left(C{F}_n^{i_{n-1}}\right)$. Now, we assume $x_3=k_1{k}_2{k}_3\cdots k_{n-2}{k}_{n-1}{i}_{n-1}$. As one of the two outgoing neighbors of $x_3$ belongs to $C{F}_n^1$, $x_3=k_1{k}_2{k}_3\cdots k_{n-2}1i_{n-1}$ or $x_3=1k_2{k}_3\cdots k_{n-2}{k}_{n-1}{i}_{n-1}$. When $x_3=k_1{k}_2{k}_3\cdots k_{n-2}1i_{n-1}$, $x_3^{+}=i_{n-1}{k}_2{k}_3\cdots k_{n-2}1k_1$, $x_3^{-}=k_1{k}_2{k}_3\cdots k_{n-2}{i}_{n-1}1$. In this situation, $x_3^{-}\in V\left(C{F}_n^1\right)$, $x_3^{+}\in V\left(C{F}_n^{k_1}\right)$, since $i_{n-1}\ne 1$, we have $x_3^{+}\ne x_1^{+}$, $x_3^{+}\ne x_2^{+}$. Thus, this structure does not exist. When $x_3=1k_2{k}_3\cdots k_{n-2}{k}_{n-1}{i}_{n-1}$, as $x_1^{-},x_2^{-}$ are adjacent to $x_3$, we can obtain $x_1^{-}=x_3(1,n-1)$, $x_2^{-}=x_3(1,n-1)$; this contradicts the fact that $x_1^{-}\ne x_2^{-}$, thus this structure does not exist.

Next, we will prove that the structure in Figure 3b does not exist. Similarly, we know that $j_1\ne i_1$, $j_{n-1}=i_{n-1}$, $\{x_1^{-},x_2^{-}\}\subseteq V\left(C{F}_n^{i_{n-1}}\right)$ and $x_3\in V\left(C{F}_n^{i_{n-1}}\right)$. We let $x_3=k_1{k}_2{k}_3\cdots k_{n-2}{k}_{n-1}{i}_{n-1}$, then $x_3^{+}=i_{n-1}{k}_2{k}_3\cdots k_{n-2}{k}_{n-1}{k}_1$, $x_3^{-}=k_1{k}_2{k}_3\cdots k_{n-2}{i}_{n-1}{k}_{n-1}$. Thus, $x_3^{+}$ $\ne x_1^{+}$ and $x_3^{+}$ $\ne x_2^{+}$; the structure in Figure 3b does not exist. □

Lemma 7. 

When n is even, let $S=\{x_1,x_2,x_3\}$ be an $Ind$-set, where $\{x_1,x_2\}\subseteq V\left(C{F}_n^i\right)$, $x_3\in V\left(C{F}_n^j\right)$ $(i\ne j)$ and $|N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|=3n-9$. Then, $|N_{C{F}_n}\left(S\right)|\ne \frac{9n-24}{2}$.

Proof. 

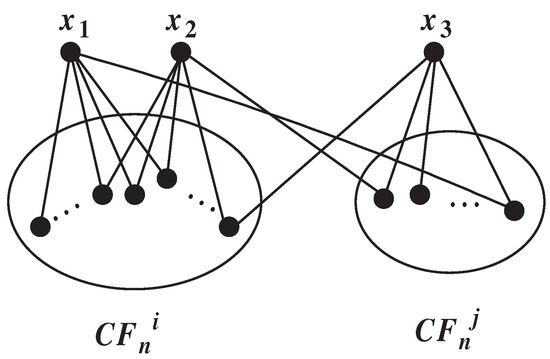
When n is even, $|N_{C{F}_n}\left(S\right)|=\frac{9n-24}{2}$ occurs if and only if the structure in Figure 4 appears. Next, we will prove that this structure does not exist. Note that $C{F}_n^i\cong C{F}_{n-1}$; $n-1$ is odd.

Figure 4. The case of $|N_{C{F}_n}\left(S\right)|=\frac{9n-24}{2}$ in Lemma 7.

Suppose, on the contrary, we assume this structure exists; as $|N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|=3n-9$, we know $x_1,x_2$ must have three common neighbors in $C{F}_n^i$ by Lemma 3. Now, we let $x_1=i_1{i}_2{i}_3\cdots i_{n-2}{i}_{n-1}i$, $x_2=j_1{j}_2{j}_3\cdots j_{n-2}{j}_{n-1}i$. By Corollary 3, we know $j_i\in [i_1,i_{n-1}]$ and $j_1\ne i_1$. Thus, $x_1^{+}\in V\left(C{F}_n^{i_1}\right)$, $x_2^{+}\in V\left(C{F}_n^{j_1}\right)$, $x_1^{+}$ and $x_2^{+}$ can not belong to a common subgraph in $C{F}_n$; this contradicts this structure. Thus, $|N_{C{F}_n}\left(S\right)|\ne \frac{9n-24}{2}$. □

Lemma 8. 

When $n\ge 4$, let S be an $Ind$-set and $|S|=3$, then when n is odd, $|N_{C{F}_n}\left(S\right)|\ge \frac{9n-21}{2}$; when n is even, $|N_{C{F}_n}\left(S\right)|\ge \frac{9n-24}{2}$.

Proof. 

Let $S=\{x_1,x_2,x_3\}$; since S is an $Ind$-set, $x_1,x_2,x_3$ are nonadjacent to each other. We prove this result by induction on n. By Lemmas 4 and 5, we know when $n=4,5$, this result holds. Now, we assume that $n\ge 6$ and the result holds for $C{F}_{n-1}$. Note that $C{F}_n^i\cong C{F}_{n-1}$. Next, we think about the following three cases:

Case 1. 

$x_1,x_2,x_3$ belong to a same subgraph $C{F}_n^i$.

When n is odd, by the induction hypothesis, we have $|N_{C{F}_n^i}\left(S\right)|\ge \frac{9(n-1)-24}{2}=\frac{9n-33}{2}$. By Proposition 3 and the definition of $C{F}_n$, we know the neighbors of $x_1,x_2,x_3$ in $C{F}_n-C{F}_n^i$ are different and every vertex has two outgoing neighbors. Thus, $|N_{C{F}_n}\left(S\right)|=|N_{C{F}_n^i}\left(S\right)|+|N_{C{F}_n-C{F}_n^i}\left(S\right)|\ge \frac{9n-33}{2}+6=\frac{9n-21}{2}$.

When n is even, by the induction hypothesis, we have $|N_{C{F}_n^i}\left(S\right)|\ge \frac{9(n-1)-21}{2}=\frac{9n-30}{2}$. By Proposition 3 and the definition of $C{F}_n$, we know the neighbors of $x_1,x_2,x_3$ in $C{F}_n-C{F}_n^i$ are different and every vertex has only one outgoing neighbor. Thus, $|N_{C{F}_n}\left(S\right)|=|N_{C{F}_n^i}\left(S\right)|+|N_{C{F}_n-C{F}_n^i}\left(S\right)|\ge \frac{9n-30}{2}+3=\frac{9n-24}{2}$.

Case 2. 

$x_1,x_2,x_3$ belong to two different subgraphs $C{F}_n^i$, $C{F}_n^j$ $(i\ne j)$.

In this case, we can let $\{x_1,x_2\}\subseteq V\left(C{F}_n^i\right)$, $x_3\in V\left(C{F}_n^j\right)$. By Lemma 3, we can obtain the following: when n is odd, $|N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|\ge 3(n-1)-7=3n-10$; when n is even, $|N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|\ge 3(n-1)-6=3n-9$. By the definition of $C{F}_n$, we know that, when n is odd, $|N_{C{F}_n^j}\left(x_3\right)|=\frac{3(n-1)-4}{2}=\frac{3n-7}{2}$; when n is even, $|N_{C{F}_n^j}\left(x_3\right)|=\frac{3(n-1)-3}{2}=\frac{3n-6}{2}$. When n is odd, by Proposition 2, we know $x_1,x_2$ that, at most, two outgoing neighbors can belong to $C{F}_n^j$; in other words, there are at least two outgoing neighbors of $\{x_1,x_2\}$ that can belong to $C{F}_n-C{F}_n^i-C{F}_n^j$. So $|N_{C{F}_n}\left(S\right)|\ge |N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|+|N_{C{F}_n^j}\left(x_3\right)|+2=\frac{9n-23}{2}$. By Lemma 6, we know $|N_{C{F}_n}\left(S\right)|\ne \frac{9n-23}{2}$, thus $|N_{C{F}_n}\left(S\right)|\ge \frac{9n-23}{2}+1=\frac{9n-21}{2}$. When n is even, if the structure of Figure 4 exists, then $|N_{C{F}_n}\left(S\right)|\ge |N_{C{F}_n^i}\left(\{x_1,x_2\}\right)|+|N_{C{F}_n^j}\left(x_3\right)|=3n-9+\frac{3n-6}{2}=\frac{9n-24}{2}$. By Lemma 7, we know this structure does not exist, so $|N_{C{F}_n}\left(S\right)|\ge \frac{9n-24}{2}+1=\frac{9n-22}{2}$.

Case 3. 

$x_1,x_2,x_3$ belong to three different subgraphs $C{F}_n^i$, $C{F}_n^j$, $C{F}_n^k$ $(i,j,k$ are different from each other).

Without loss of generality, we can let $x_1\in V\left(C{F}_n^1\right)$, $x_2\in V\left(C{F}_n^2\right)$, $x_3\in V\left(C{F}_n^3\right)$. By Proposition 6, we have, when n is odd, $|N_{C{F}_n^i}\left(x_i\right)|=\frac{3n-7}{2}$ $(i\in \{1,2,3\left\}\right)$; when n is even, $|N_{C{F}_n^i}\left(x_i\right)|=\frac{3n-6}{2}$ $(i\in \{1,2,3\left\}\right)$. Thus, when n is odd, $|N_{C{F}_n}\left(S\right)|\ge 3\times \frac{3n-7}{2}=\frac{9n-21}{2}$; when n is even, $|N_{C{F}_n}\left(S\right)|\ge 3\times \frac{3n-6}{2}=\frac{9n-18}{2}$.

Thus, the result holds. □

Corollary 5. 

When n is even, let $S=\{x_1,x_2,x_3\}$ be an $Ind$-set, if $|N_{C{F}_n}\left(S\right)|=\frac{9n-24}{2}$, then $x_1,x_2,x_3$ belong to the same subgraph in $C{F}_n$.

Lemma 9. 

For $n=5$, if $|F|\le 11$, then $C{F}_5-F$ contains a big component C, which satisfies the result $|V(C)|\ge 5!-|F|-2$. In other words, $C{F}_5-F$ satisfies one of the following conditions: $\left(1\right)$ $C{F}_5-F$ has two components, one of which is a singleton or an edge; $\left(2\right)$ $C{F}_5-F$ has three components, two of which are singletons.

Proof. 

We are not going to think about $C{F}_5-F$ being connected for the moment, so we assume that $C{F}_5-F$ is disconnected. Let $F_i=F\cap V\left(C{F}_5^i\right)$ for $i=1,2,3,4,5$ with $|F_{i_1}|\ge |F_{i_2}|\ge |F_{i_3}|\ge |F_{i_4}|\ge |F_{i_5}|$, where $i_j\in \{1,2,3,4,5\}$. If $|F_{i_3}|=0$, then $|F_{i_4}|=|F_{i_5}|=0$ and $C{F}_5^{[i_3,i_5]}-F^{[i_3,i_5]}$ is connected. By Proposition 2, we know every vertex in $C{F}_5^{i_1}-F_{i_1}$ $(resp.,C{F}_5^{i_2}-F_{i_2})$ has an neighbor in $C{F}_5^{[i_3,i_5]}-F^{[i_3,i_5]}$. So $C{F}_5-F$ is connected, which is a contradiction. Hence, we consider $|F_{i_3}|\ge 1$. Since $|F|\le 11$, we have $|F_{i_5}|\le 2$, $|F_{i_4}|\le 2$, $1\le |F_{i_3}|\le 3$, $1\le |F_{i_2}|\le 5$, $1\le |F_{i_1}|\le 9$. Firstly, we prove the following claim is correct. □

Claim 1. 

If $|F_{i_j}|\le 3$ for some $i_j\in [i_1,i_4]$, then $C{F}_5^{[i_j,i_5]}-F^{[i_j,i_5]}$ is connected.

Proof of Claim 1. 

By Proposition 6, we can ascertain that $C{F}_5^j-F_j$ is connected for each $j\in [i_j,i_5]$. On the other hand, as $|F_{i_5}|\le 2$, we can obtain $|E_{p,i_5}\left(C{F}_5\right)|=12>5\ge |F_p|+|F_{i_5}|$, which implies $E_{p,i_5}(C{F}_5-F)\ne \varnothing$ for $p\in [i_j,i_4]$. Hence, $C{F}_5^{[i_j,i_5]}-F^{[i_j,i_5]}$ is connected.

Since $|F_{i_5}|\le |F_{i_4}|\le |F_{i_3}|\le 3$, by Claim 1, we can ascertain that $C{F}_5^{[i_3,i_5]}-F^{[i_3,i_5]}$ is connected. If $C{F}_5^{i_1}-F_{i_1}$ and $C{F}_5^{i_2}-F_{i_2}$ are all connected, we know $C{F}_5-F$ is connected. As $|E_{i_2,i_3}\left(C{F}_5\right)|=12>8\ge |F_{i_2}\cup F_{i_3}|$, $C{F}^{[i_2,i_5]}-F^{[i_2,i_5]}$ is connected. As $|E_{i_1,i_5}\left(C{F}_5\right)|=12>9+2=11\ge |F_{i_1}\cup F_{i_5}|$, we establish that $C{F}_5-F$ is connected. Since $C{F}_5-F$ is disconnected, at least one of $C{F}_5^i-F_i,i\in \{i_1,i_2\}$ is disconnected, which leads to the following two cases.

Note that, if $|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\le 1$, by Proposition 3, we can ascertain that $C{F}_5^i-F_i$ $(i\in \{i_1,i_2\})$ has a big component $C_i$ and, at most, one vertices, which has a neighbor in $F_{i_3}\cup F_{i_4}\cup F_{i_5}$. Thus, if $C{F}_5^{i_1}-F_{i_1}$ or $C{F}_5^{i_2}-F_{i_2}$ is connected, then $C{F}_5-F$ satisfies the condition $\left(1\right)$. If $C{F}_5^{i_1}-F_{i_1}$ and $C{F}_5^{i_2}-F_{i_2}$ are all disconnected, then $C{F}_5-F$ satisfies the condition $\left(2\right)$. Hence, we only think about this situation: $|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\ge 2$.

Case 1. 

Both $C{F}_5^{i_1}-F_{i_1}$ and $C{F}_5^{i_2}-F_{i_2}$ are disconnected.

In this case, we know $|F_{i_1}|\ge |F_{i_2}|\ge 4$. Since $|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\ge 2$, $|F_{i_1}\cup F_{i_2}|\le |F|-|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\le 11-2=9$. Hence, $|F_{i_2}|=4$, $4\le |F_{i_1}|\le 5$. By Corollary 4, we know $C{F}_5^{i_2}-F_{i_2}$ has a big component $C_2$ and a singleton $x_2$. By Lemma 1, $C{F}_5^{i_1}-F_{i_1}$ should consider the following two situations: $\left(1\right)$ $C{F}_5^{i_1}-F_{i_1}$ has two components, one of which is a singleton. $\left(2\right)$ $C{F}_5^{i_1}-F_{i_1}$ has three components, two of which are singletons. For $\left(1\right)$, let $C_1$ be the big component and $x_1$ be the singleton of $C{F}_5^{i_1}-F_{i_1}$; since $|V\left(C_1\right)|=|V\left(C_2\right)|=|V\left(C{F}_5^i\right)-F_i-\left\{x_i\right\}|\ge 4!-5-1=18$ $(i\in \{i_1,i_2\})$ and $|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\le 3$, by Proposition 3, we can ascertain that $C{F}_5[V(C{F}_5^{[i_3,i_5]}-F^{[i_3,i_5]})\cup V\left(C_1\right)]$ is connected. Similarly, we can also ascertain that $C{F}_5[V(C{F}_5^{[i_3,i_5]}-F^{[i_3,i_5]})\cup V\left(C_2\right)]$ is connected. Thus, the result holds. For $\left(2\right)$, let $C_1$ be the big component and $x_1$, $x_3$ be singletons of $C{F}_5^{i_1}-F_{i_1}$. If $x_2$ is nonadjacent to $\{x_1,x_3\}$, then $\{x_1,x_2,x_3\}$ are three singletons in $C{F}_5-F$. By Lemma 5, we can obtain $|F|\ge 12$; this contradicts the fact that $|F|\le 11$. If $x_2$ is adjacent to $\{x_1,x_3\}$, say $(x_1,x_2)\in E(C{F}_5-F)$, then $C{F}_5-F$ only has two components; otherwise, we let $C{F}_5-F$ have three components, then $x_3$ is a singleton in $C{F}_5-F$. By Proposition 5, we have $|F|\ge |N_{C{F}_5}\left(\{x_1,x_2\}\right)\cup N_{C{F}_5}\left(x_3\right)|\ge 5\times 2+6-3=13>11$, which is a contradiction. Thus, the result holds.

Case 2. 

Only $C{F}_5^{i_2}-F_{i_2}$ is disconnected.

Since $|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\ge 2$, $|F_{i_1}\cup F_{i_2}|\le 9$. As $C{F}_5^{i_2}-F_{i_2}$ is disconnected, we have $|F_{i_2}|\ge 4$ and then $|F_{i_1}|\le 5$. If $|F_{i_2}|=5$, then $|F_{i_1}|\ge 5$, $|F|\ge |F_{i_1}|+|F_{i_2}|+|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\ge 5+5+2=12$, which is a contradiction. Thus, $|F_{i_2}|=4$. Since $|E_{i_1,i_3}\left(C{F}_5\right)|=12>8\ge |F_{i_1}\cup F_{i_3}|$, $C{F}_5[V(C{F}_5^{[i_3,i_5]}-F^{[i_3,i_5]})\cup V(C{F}_5^{i_1}-F_{i_1})]$ is connected. As $|F_{i_2}|=4$, by Corollary 4, we know $C{F}_5^{i_2}-F_{i_2}$ has a big component S and, at most, one singleton. By the same argument as that of Case 1, we can ascertain that $C{F}_5[V(C{F}_5^{[i_3,i_5]}-F^{[i_3,i_5]})\cup V(C{F}_5^{i_1}-F_{i_1})\cup V\left(S\right)]$ is connected. Then, $C{F}_5-F$ must satisfy condition $\left(1\right)$.

Case 3. 

Only $C{F}_5^{i_1}-F_{i_1}$ is disconnected.

By Proposition 6, we have $|F_{i_1}|\ge 4$. Since $|F|\le 11$ and $|F_{i_3}\cup F_{i_4}\cup F_{i_5}|\ge 2$, $|F_{i_2}|\le 4$. As $|E_{i_2,i_3}\left(C{F}_5\right)|=12>7\ge |F_{i_2}\cup F_{i_3}|$, we can see that $C{F}_5^{[i_2,i_5]}-F^{[i_2,i_5]}$ is connected.

If $|F_{i_1}|\le 5$, by Lemma 1, $C{F}_5^{i_1}-F_{i_1}$ has a big component S and one single and two singletons. By the same argument as that of Case 1, we can see that $C{F}_5[V(C{F}_5^{[i_2,i_5]}-F^{[i_2,i_5]})\cup V\left(S\right)]$ is connected. Then, $C{F}_5-F$ must be one of conditions $\left(1\right)$ and $\left(2\right)$.

Now, we suppose $|F_{i_1}|\ge 6$. Then, $|F_{i_2}\cup F_{i_3}\cup F_{i_4}\cup F_{i_5}|\le 5$. Let W be the union of components of $C{F}_5-F$, whose vertices, which are totally contained in $C{F}_5^{i_1}-F_{i_1}$, are not connected with $C{F}_5^{[i_2,i_5]}-F^{[i_2,i_5]}$. By Propositions 2 and 3, we know $2|W|\le |F-F_{i_1}|\le 5$, which implies $|W|\le 2$. Thus, $C{F}_5-F$ satisfies $\left(1\right)$ or $\left(2\right)$.

Combining the above three cases, we know this result holds. □

Lemma 10. 

For $n=6$, if $|F|\le 14$, then $C{F}_6-F$ contains a big component C, which satisfies the result $|V(C)|\ge 6!-|F|-2$. In other words, $C{F}_6-F$ satisfies one of the following conditions: $\left(1\right)$ $C{F}_6-F$ has two components, one of which is a singleton or an edge; $\left(2\right)$ $C{F}_6-F$ has three components, two of which are singletons.

Proof. 

Similarly, we do not think about the situation $C{F}_6-F$ being connected, so we let $C{F}_6-F$ be disconnected. Let $F_i=F\cap V\left(C{F}_6^i\right)$ for $i\in [1,6]$ with $|F_{i_1}|\ge |F_{i_2}|\ge |F_{i_3}|\ge |F_{i_4}|\ge |F_{i_5}|\ge |F_{i_6}|$, where $i_j\in \{1,2,3,4,5,6\}$. If $|F_{i_2}|=0$, then $|F_{i_3}|=|F_{i_4}|=\cdots =|F_{i_6}|=0$ and $C{F}^{[i_2,i_6]}-F^{[i_2,i_6]}$ is connected. By Proposition 2, we can ascertain that $C{F}_6-F$ is connected. So we assume $|F_{i_2}|\ge 1$. Since $|F|\le 14$, we have $|F_{i_6}|\le 2$, $|F_{i_5}|\le 2$, $|F_{i_4}|\le 3$, $|F_{i_3}|\le 4$, $1\le |F_{i_2}|\le 7$, $1\le |F_{i_1}|\le 13$. Firstly, we prove the following claim is correct. □

Claim 2. 

If $|F_{i_j}|\le 5$, then $C{F}_6^{[i_j,i_6]}-F^{[i_j,i_6]}$ is connected.

Proof of Claim 2. 

By Proposition 6, we know $C{F}_6^j-F_j$ is connected for each $j\in [i_j,i_6]$. On the other hand, since $|E_{p,i_6}\left(C{F}_6\right)|=(6-2)!=24>7\ge |F_p\cup F_{i_6}|$ for $p\in [i_j,i_5]$, we can obtain $E_{p,i_6}(C{F}_6-F)\ne \varnothing$. Thus, $C{F}_6^{[i_j,i_6]}-F^{[i_j,i_6]}$ is connected.

By Claim 2, we know $C{F}_6^{[i_3,i_6]}-F^{[i_3,i_6]}$ is connected. If both $C{F}_6^{i_1}-F_{i_1}$ and $C{F}_6^{i_2}-F_{i_2}$ are connected, we can establish that $C{F}_6-F$ is connected, which is a contradiction. Thus, at least one of $C{F}_6^i-F_i$ $(i\in \{i_1,i_2\})$ is disconnected, which leads to the following cases.

Case 1. 

Both $C{F}_6^{i_1}-F_{i_1}$ and $C{F}_6^{i_2}-F_{i_2}$ are disconnected.

In this case, we know $6\le |F_{i_2}|\le |F_{i_1}|\le |F|-|F_{i_2}|\le 8<9$. By Corollary 4, we know that $C{F}_6^{i_1}-F_{i_1}$ $(resp.,C{F}_6^{i_2}-F_{i_2})$ has a big component $C_1$ $(resp.,C_2)$ and one singleton $x_1$ $(resp.,x_2)$. As $|E_{C{F}_6-F}(V\left(C_1\right),V(C{F}_6^{i_3}-F_{i_3}))|\ge 24-2-8-1=13>1$, thus $C{F}_6-F[V(C{F}_6^{[i_3,i_6]}-F^{[i_3,i_6]})\cup V\left(C_1\right)]$ is connected. Similarly, we can see that $C{F}_6-F[V(C{F}_6^{[i_3,i_6]}-F^{[i_3,i_6]})\cup V\left(C_2\right)]$ is also connected. Thus, the result holds.

Case 2. 

Only $C{F}_6^{i_2}-F_{i_2}$ is disconnected.

As $C{F}_6^{i_2}-F_{i_2}$ is disconnected, we have $|F_{i_2}|\ge 6$ and then $|F_{i_1}|\le 8$. Since $|E_{i_1,i_3}\left(C{F}_6\right)|=24>10\ge |F_{i_1}\cup F_{i_3}|$, $C{F}_6[V(C{F}_6^{[i_3,i_6]}-F^{[i_3,i_6]})\cup V(C{F}_6^{i_1}-F_{i_1})]$ is connected. Since $|F_{i_2}|\le |F_{i_1}|\le 8$, by Corollary 4, $C{F}_6^{i_2}-F_{i_2}$ has a big component C and one singleton. Since $|E_{i_2,i_3}\left(C{F}_6\right)|=24>11\ge |F_{i_2}\cup F_{i_3}|+1$, we can ascertain that $C{F}_6[V(C{F}_6^{[i_3,i_6]}-F^{[i_3,i_6]})\cup V(C{F}_6^{i_1}-F_{i_1})\cup V\left(C\right)]$ is connected. Then, $C{F}_6-F$ must be one of the conditions $\left(1\right)$.

Case 3. 

Only $C{F}_6^{i_1}-F_{i_1}$ is disconnected.

In this case, $6\le |F_{i_1}|\le 13$, $|F_{i_2}|\le 8$. As $|E_{i_2,i_3}\left(C{F}_6\right)|=24>11>|F_{i_2}\cup F_{i_3}|$, we can see that $C{F}_6^{[i_2,i_6]}-F^{[i_2,i_6]}$ is connected.

If $|F_{i_1}|\le 11$, by Lemma 9, $C{F}_6^{i_1}-F_{i_1}$ has a big component C with $|V\left(C\right)|\ge 5!-|F_{i_1}|-2$. By the same argument as that of Case 2, we can see that $C{F}_6[V(C{F}_6^{[i_2,i_6]}-F^{[i_2,i_6]})\cup V\left(C\right)]$ is connected. Thus, the result holds.

If $|F_{i_1}|\ge 12$, then $|F_{i_2}\cup F_{i_3}\cup F_{i_4}\cup F_{i_5}\cup F_{i_6}|\le 2$. Let W be the union of components of $C{F}_6-F$, whose vertices, which are totally contained in $C{F}_6^{i_1}-F_{i_1}$, and are not connected with $C{F}_6^{[i_2,i_6]}-F^{[i_2,i_6]}$. By Propositions 2 and 3, we have $|W|\le |F-F_{i_1}|\le 2$. Thus, the result holds. □

Lemma 11. 

Let $|F|\le \frac{9n-23}{2}$ for odd n$(n\ge 5)$ and $|F|\le \frac{9n-26}{2}$ for even n$(n\ge 6)$, then $C{F}_n-F$ contains a big component C, which satisfies that $|V(C)|\ge n!-|F|-2$. In other words, $C{F}_n-F$ satisfies one of the following conditions: $\left(1\right)$ $C{F}_n-F$ has two components, one of which is a singleton or an edge; $\left(2\right)$ $C{F}_n-F$ has three components, two of which are singletons.

Proof. 

By Lemmas 9 and 10, the result holds for $n=5,6$. We prove this result by induction on n. Assume $n\ge 7$ and that the result holds for $C{F}_{n-1}$. Now, we suppose $C{F}_n-F$ is disconnected for any $F\subseteq V\left(C{F}_n\right)$ with $|F|\le \frac{9n-23}{2}$ or $|F|\le \frac{9n-26}{2}$. Let $F_i=F\cap V\left(C{F}_n^i\right)$ for $i\in [1,n]$ with $|F_{i_1}|\ge |F_{i_2}|\ge \cdots \ge |F_{i_n}|$, where $i_j\in [1,n]$.

When n is odd, if $|F_{i_3}|=0$, then $|F_{i_4}|=|F_{i_5}|=\cdots =|F_{i_n}|=0$ and $C{F}^{[i_3,i_n]}-F^{[i_3,i_n]}$ is connected; thus, by Proposition 2, we can establish that $C{F}_n-F$ is connected. Now, we assume $|F_{i_3}|\ge 1$; when n is even, if $|F_{i_2}|=0$, then $|F_{i_3}|=|F_{i_4}|=\cdots =|F_{i_n}|=0$ and $C{F}^{[i_2,i_n]}-F^{[i_2,i_n]}$ is connected, and thus, by Proposition 2, we can see that $C{F}_n-F$ is connected. Now, we assume $|F_{i_2}|\ge 1$. □

Claim 3. 

When n is even, if $|F_{i_j}|\le \frac{3n-8}{2}$ $(i_j\in [i_1,i_{n-1}])$ , then $C{F}_n^{[i_j,i_n]}-F^{[i_j,i_n]}$ is connected; when n is odd, if $|F_{i_j}|\le \frac{3n-9}{2}$ $(i_j\in [i_1,i_{n-1}])$, then $C{F}_n^{[i_j,i_n]}-F^{[i_j,i_n]}$ is connected.

Proof of Claim 3. 

By Proposition 6, we know $C{F}_n^j-F_j$ is connected for each $j\in [i_j,i_n]$. On the other hand, since $|E_{p,i_n}\left(C{F}_n\right)|=(n-2)!>3n-8>|F_p\cup F_{i_n}|$ for $p\in [i_j,i_{n-1}]$ $(n$ is even) and $|E_{p,i_n}\left(C{F}_n\right)|=2(n-2)!>3n-9>|F_p\cup F_{i_n}|$ for $p\in [i_j,i_{n-1}]$ $(n$ is odd), we can obtain $E_{p,i_n}(C{F}_n-F)\ne \varnothing$. Thus, $C{F}_n^{[i_j,i_n]}-F^{[i_j,i_n]}$ is connected.

Since $|F|\le \frac{9n-26}{2}$ $(n$ is even) and $|F|\le \frac{9n-23}{2}$ $(n$ is odd), we have $\frac{3n-8}{2}>|F_{i_3}|\ge |F_{i_4}|\ge \cdots \ge |F_{i_n}|$ for even n and $\frac{3n-9}{2}\ge |F_{i_3}|\ge |F_{i_4}|\ge \cdots \ge |F_{i_n}|$ for odd n. By Claim 3, we can ascertain that $C{F}_n^{[i_3,i_n]}-F^{[i_3,i_n]}$ is connected. If $C{F}_n^{i_1}-F_{i_1}$ and $C{F}_n^{i_2}-F_{i_2}$ are all connected, as $|E_{i_2,i_3}\left(C{F}_n\right)|=(n-2)!>\frac{9n-26}{2}>|F_{i_2}\cup F_{i_3}|$ $(n$ is even) and $|E_{i_2,i_3}\left(C{F}_n\right)|=2(n-2)!>\frac{9n-23}{2}>|F_{i_2}\cup F_{i_3}|$ $(n$ is odd), then $C{F}_n^{[i_2,i_n]}-F^{[i_2,i_n]}$ is connected. Similarly, we can also see that $C{F}_n-F$ is connected. So, at least one of $C{F}_n^i-F_i$ $(i\in \{i_1,i_2\})$ is disconnected, which leads to the following cases.

Note that, when n is odd, if $|F_{i_3}\cup F_{i_4}\cup F_{i_5}\cup \cdots \cup F_{i_n}|\le 1$, by the same argument of Lemma 9, we know $C{F}_n-F$ satisfies condition $\left(1\right)$ or $\left(2\right)$. Hence, we assume that $|F_{i_3}\cup F_{i_4}\cup F_{i_5}\cup \cdots \cup F_{i_n}|\ge 2$.

Case 1. 

Both $C{F}_n^{i_1}-F_{i_1}$ and $C{F}_n^{i_2}-F_{i_2}$ are disconnected.

When n is even, we have $\frac{3n-6}{2}\le |F_{i_2}|\le |F_{i_1}|\le |F|-|F_{i_2}|\le \frac{9n-26}{2}-\frac{3n-6}{2}=3n-10$. By Corollary 4, we know $C{F}_n^{i_1}-F_{i_1}$ and $C{F}_n^{i_2}-F_{i_2}$ all have a big component $C_1,C_2$ and one singleton. As $|E_{C{F}_n-F}(V\left(C_1\right),V(C{F}_n^{i_3}-F_{i_3}))|\ge (n-2)!-1-\frac{9n-26}{2}>1$, $|E_{C{F}_n-F}(V\left(C_2\right),V(C{F}_n^{i_3}-F_{i_3}))|\ge (n-2)!-1-\frac{9n-26}{2}>1$. Thus, $C{F}_n-F[V(C{F}_n^{[i_3,i_n]}-F^{[i_3,i_n]})\cup V\left(C_1\right)\cup V\left(C_2\right)]$ is connected and the result holds.

When n is odd, we have $\frac{3n-7}{2}\le |F_{i_2}|\le |F_{i_1}|\le |F|-|F_{i_2}|-|F_{i_3}\cup F_{i_4}\cup \cdots \cup F_{i_n}|\le \frac{9n-23}{2}-\frac{3n-7}{2}-2=3n-10$. So, by Lemma 1, we would consider the following three subcases: $\left(1\right)$ both $C{F}_n^{i_1}-F_{i_1}$ and $C{F}_n^{i_2}-F_{i_2}$ have three components, two of which are singletons; $\left(2\right)$ only one of $C{F}_n^{i_1}-F_{i_1}$ and $C{F}_n^{i_2}-F_{i_2}$ has three components, two of which are singletons; and $\left(3\right)$ both $C{F}_n^{i_1}-F_{i_1}$ and $C{F}_n^{i_2}-F_{i_2}$ have two components, one of which is a singleton. Now, we just prove the first subcase and the other two subcases can be proved by the same argument. Let $x_1,y_1,C_1$ (resp., $x_2,y_2,C_2$) be the two singletons and the other big component of $C{F}_n^{i_1}-F_{i_1}$ (resp., $C{F}_n^{i_2}-F_{i_2}$). Since $|V\left(C_1\right)|=|V\left(C{F}_n^{i_1}\right)-F_{i_1}-\{x_1,y_1\}|\ge (n-1)!-(3n-10)-2$ and $|F_{i_3}\cup F_{i_4}\cup \cdots \cup F_{i_n}|\le \frac{3n-9}{2}$, by Proposition 3, we know $C{F}_n[V(C{F}_n^{[i_3,i_n]}-F^{[i_3,i_n]})\cup V\left(C_1\right)]$ is connected. Similarly, we can ascertain that $C{F}_n[V(C{F}_n^{[i_3,i_n]}-F^{[i_3,i_n]})\cup V\left(C_2\right)]$ is connected.

If $x_1,x_2,y_1,y_2$ are four singletons in $C{F}_n-F$, then by Proposition 5, we know $|F|\ge |N_{C{F}_n^{i_1}}\left(\{x_1,y_1\}\right)\cup N_{C{F}_n^{i_2}}\left(\{x_2,y_2\}\right)\cup (F_{i_3}\cup F_{i_4}\cup \cdots \cup F_{i_n})|\ge [\frac{3(n-1)-4}{2}\times 2-3]\times 2+2=6n-18>\frac{9n-23}{2}$, which is a contradiction.

If $C{F}_n-F$ has three singletons, then by Lemma 8, we can obtain $|F|\ge \frac{9n-21}{2}$; this contradicts the fact that $|F|\le \frac{9n-23}{2}$. So, $C{F}_n-F$ has two singletons or only one singleton. □

Claim 4. 

 If $(C{F}_n-F)\left[\{x_1,y_1,x_2,y_2\}\right]$ has at least one edge, say $(x_1,x_2)\in E(C{F}_n-F)$, then $C{F}_n-F$ only has two components.

Proof of Claim 4. 

Suppose $C{F}_n-F$ has at least three components. Then, $y_1$ is a singleton or $(y_1,y_2)\in E(C{F}_n-F)$. If $y_1$ is a singleton, then $|F|\ge |N_{C{F}_n}\left(\{x_1,x_2\}\right)\cup N_{C{F}_n}\left(y_1\right)|\ge (\frac{3n-3}{2}-1)\times 2+\frac{3n-3}{2}-3=\frac{9n-19}{2}>\frac{9n-23}{2}$, which is a contradiction. If $(y_1,y_2)\in E(C{F}_n-F)$, then $|F|\ge |N_{C{F}_n}\left(\{x_1,x_2\}\right)\cup N_{C{F}_n}\left(\{y_1,y_2\}\right)|\ge (\frac{3n-3}{2}-1)\times 4-3\times 2=6n-16>\frac{9n-23}{2}$, which is a contradiction.

• Thus, by Claim 4, the result holds.

Case 2. 

Only $C{F}_n^{i_2}-F_{i_2}$ is disconnected.

As $C{F}_n^{i_2}-F_{i_2}$ is disconnected, we have $|F_{i_2}|\ge \frac{3n-6}{2}$ for even n and $|F_{i_2}|\ge \frac{3n-7}{2}$ for odd n, then $|F_{i_1}|\le 3n-10<3n-9$ $(n$ is even) and $|F_{i_1}|\le 3n-10$ $(n$ is odd). Since $|E_{i_1,i_3}\left(C{F}_n\right)|=(n-2)!>\frac{9n-26}{2}\ge |F_{i_1}\cup F_{i_3}|$ $(n$ is even) and $|E_{i_1,i_3}\left(C{F}_n\right)|=2(n-2)!>\frac{9n-23}{2}\ge |F_{i_1}\cup F_{i_3}|$ $(n$ is odd), $C{F}_n[V(C{F}_n^{[i_3,i_n]}-F^{[i_3,i_n]})\cup V(C{F}_n^{i_1}-F_{i_1})]$ is connected. Since $|F_{i_2}|\le |F_{i_1}|\le 3n-10$, when n is even, by Corollary 4, we know $C{F}_n^{i_2}-F_{i_2}$ has a big component C and one singleton; when n is odd, by Lemma 1, we know $C{F}_n^{i_2}-F_{i_2}$ has a big component C and at most two singletons. By the same argument as that of Case 1, we can establish that $C{F}_n[V(C{F}_n^{[i_3,i_n]}-F^{[i_3,i_n]})\cup V(C{F}_n^{i_1}-F_{i_1})\cup V\left(C\right)]$ is connected. Then, $C{F}_n-F$ must be one of conditions $\left(1\right)$ and $\left(2\right)$.

Case 3. 

Only $C{F}_n^{i_1}-F_{i_1}$ is disconnected.

In this case, $\frac{3n-6}{2}\le |F_{i_1}|\le \frac{9n-28}{2}$ for even n and $\frac{3n-7}{2}\le |F_{i_1}|\le \frac{9n-29}{2}$ for odd n. As $|E_{i_2,i_3}\left(C{F}_n\right)|=(n-2)!>\frac{9n-26}{2}\ge |F_{i_2}\cup F_{i_3}|$ $(n$ is even) and $|E_{i_2,i_3}\left(C{F}_n\right)|=2(n-2)!>\frac{9n-23}{2}\ge |F_{i_2}\cup F_{i_3}|$ $(n$ is odd), we know that $C{F}_n^{[i_2,i_n]}-F^{[i_2,i_n]}$ is connected.

When n is even, if $|F_{i_1}|\le \frac{9n-32}{2}$, by introduction, we know $C{F}_n^{i_1}-F_{i_1}$ has a big component C with $|V\left(C\right)|\ge (n-1)!-|F_{i_1}|-2$. By the same argument as that of Case 1, we can establish that $C{F}_n[V(C{F}_n^{[i_2,i_n]}-F^{[i_2,i_n]})\cup V\left(C\right)]$ is connected. Thus, the result holds. If $|F_{i_1}|\ge \frac{9n-30}{2}$, then $|F_{i_2}\cup F_{i_3}\cup \cdots \cup F_{i_n}|\le 2$. Let W be the union of components of $C{F}_n-F$, whose vertices are totally contained in $C{F}_n^{i_1}-F_{i_1}$ and are not connected with $C{F}_n^{[i_2,i_n]}-F^{[i_2,i_n]}$. By Propositions 2 and 3, we have $|W|\le |F-F_{i_1}|\le 2$. Thus, the result holds.

When n is odd, if $|F_{i_1}|\le \frac{9n-35}{2}$, by introduction, $C{F}_n^{i_1}-F_{i_1}$ has a big component C with $|V\left(C\right)|\ge (n-1)!-|F_{i_1}|-2$. By the same argument as that of Case 1, we can see that $C{F}_n[V(C{F}_n^{[i_2,i_n]}-F^{[i_2,i_n]})\cup V\left(C\right)]$ is connected. Thus, the result holds. If $|F_{i_1}|\ge \frac{9n-33}{2}$, then $|F_{i_2}\cup F_{i_3}\cup \cdots \cup F_{i_n}|\le 5$. Let W be the union of components of $C{F}_n-F$, whose vertices are totally contained in $C{F}_n^{i_1}-F_{i_1}$ and are not connected with $C{F}_n^{[i_2,i_n]}-F^{[i_2,i_n]}$. By Proposition 3, $2|W|\le |F-F_{i_1}|\le 5$. Then, we have $|W|\le 2$. Thus, the result holds. □

Theorem 2. 

For $n\ge 4$, when n is odd, $c{\kappa }_4\left(C{F}_n\right)=\frac{9n-21}{2}$; when n is even, $c{\kappa }_4\left(C{F}_n\right)=\frac{9n-24}{2}$.

Proof. 

By Lemma 1, we have $c{\kappa }_4\left(C{F}_4\right)\ge 6=\frac{9\times 4-24}{2}$. For $n\ge 5$, by Lemma 11, we can obtain, when n is odd, $c{\kappa }_4\left(C{F}_n\right)\ge \frac{9n-21}{2}$; when n is even, $c{\kappa }_4\left(C{F}_n\right)\ge \frac{9n-24}{2}$. Next, we will prove that $c{\kappa }_4\left(C{F}_n\right)\le \frac{9n-21}{2}$ and $c{\kappa }_4\left(C{F}_n\right)\le \frac{9n-24}{2}$. For $n=4$, if we let $F=\{2314,3124,1234,4213,4132,4321\}$, then $C{F}_n-F$ has three singletons: $x_1=3214,$ $x_2=2134,$ $x_3=1324$. Thus, $c{\kappa }_4\left(C{F}_4\right)\le 6=\frac{9\times 4-24}{2}$. For $n\ge 5$, when n is odd, let $S=\{x_1,x_2,x_3\}$, where $x_1=i_1{i}_2{i}_3\cdots i_{n-4}3214$, $x_2=2i_2{i}_3\cdots i_{n-4}{i}_{1}314$, $x_3=2i_2{i}_3\cdots i_{n-4}3i_{1}41$, then $|N_{C{F}_n}\left(S\right)|=3n-10+\frac{3n-7}{2}+3=\frac{9n-21}{2}$ and there are three singletons $\{x_1,x_2,x_3\}$ in $C{F}_n-N_{C{F}_n}\left(S\right)$. Thus when n is odd, $c{\kappa }_4\left(C{F}_n\right)\le \frac{9n-21}{2}$. When n is even, let $S=\{x_1,x_2,x_3\}$, where $x_1=i_1{i}_2{i}_3\cdots i_{n-4}3214j$, $x_2=2i_2{i}_3\cdots i_{n-4}{i}_{1}314j$, $x_3=2i_2{i}_3\cdots i_{n-4}3i_{1}41j$, then $\{x_1,x_2,x_3\}\subseteq V\left(C{F}_n^j\right)$ and $|N_{C{F}_n^j}\left(S\right)|=\frac{9(n-1)-21}{2}=\frac{9n-30}{2}$. As $x_1,x_2,x_3$ belong to a common subgraph, by Proposition 3, we know $x_1,x_2,x_3$ have different outgoing neighbors. So, $|N_{C{F}_n}\left(S\right)|=\frac{9n-30}{2}+3=\frac{9n-24}{2}$ and $x_1,x_2,x_3$ are three singletons in $C{F}_n-N_{C{F}_n}\left(S\right)$. Thus, when n is even, $c{\kappa }_4\left(C{F}_n\right)\le \frac{9n-24}{2}$. □

5. Conclusions

It is very useful to study the connectivity of a graph. In this paper, we study the m-component connectivity of $C{F}_n$. The leaf-sort graph is a special Cayley graph that has many special properties. We have shown that, for $n\ge 3$, $c{\kappa }_3\left(C{F}_n\right)=3n-6$ $(n$ is odd) and $c{\kappa }_3\left(C{F}_n\right)=3n-7$ $(n$ is even); for $n\ge 4$, $c{\kappa }_4\left(C{F}_n\right)=\frac{9n-21}{2}$ $(n$ is odd) and $c{\kappa }_4\left(C{F}_n\right)=\frac{9n-24}{2}$ $(n$ is even). So far, we only obtained the value of $c{\kappa }_3\left(C{F}_n\right)$, $c{\kappa }_4\left(C{F}_n\right)$; for $m\ge 5$, this problem is still unsolved. Therefore, we can seriously think about whether we can use a similar method to study $c{\kappa }_m\left(C{F}_n\right)$ $(m\ge 5)$ on this basis. Furthermore, by referring to the references, we can find that there is a regularity between $c{\kappa }_m\left(B{S}_n\right)$ and ${\kappa }^{\left(m\right)}\left(B{S}_n\right)$. Similarly, $c{\kappa }_m\left(B{P}_n\right)$ and ${\kappa }^{\left(m\right)}\left(B{P}_n\right)$ also have regularity. So, we can think about whether there some sort of relationship between $c{\kappa }_m\left(C{F}_n\right)$ and ${\kappa }^{\left(m\right)}\left(C{F}_n\right)$.