On Bond Incident Degree Indices of Fixed-Size Bicyclic Graphs with Given Matching Number

Abstract

A connected graph with p vertices and q edges satisfying $q=p+1$ is referred to as a bicyclic graph. This paper is concerned with an optimal study of the BID (bond incident degree) indices of fixed-size bicyclic graphs with a given matching number. Here, a BID index of a graph G is the number ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)={\sum }_{vw\in E\left(G\right)}\mathfrak{f}(d_G\left(v\right),d_G\left(w\right))$, where $E\left(G\right)$ represents G’s edge set, $d_G\left(v\right)$ denotes vertex v’s degree, and $\mathfrak{f}$ is a real-valued symmetric function defined on the Cartesian square of the set of all different members of G’s degree sequence. Our results cover several existing indices, including the Sombor index and symmetric division deg index.

1. Introduction

Throughout this study, the considered graphs are connected. The books [1,2,3] and [4,5,6] can be consulted for the fundamental concepts of graph theory and chemical graph theory, respectively.

A graph with size m is referred to as an m-size graph. Similarly, an n-order graph is the one having order n. The notations $E\left(G\right)$ and $V\left(G\right)$ are used for the sets of edges and vertices of a graph G, respectively. For a vertex $w\in V\left(G\right)$, its degree is represented by $d_G\left(w\right)$.

A graph invariant $\mathcal{GI}$ is a property associated with graphs in such a way that the equation $\mathcal{GI}\left(G\right)=\mathcal{GI}\left(G^{\prime }\right)$ holds for every two isomorphic graphs G and $G^{\prime }$ [3]. The graph invariants that take only real numbers are often referred to as topological indices or molecular descriptors by chemical graph theorists [4,5,6]. Chemical graph theory is a subfield of mathematical chemistry that models and investigates the structures of chemical compounds using graph theory. Atoms (of chemical compounds) are commonly represented in this discipline as vertices in a graph, and bonds (of chemical compounds) are represented as edges between the vertices. Important chemical characteristics can be derived by applying graph-theoretical principles to structures of chemical compounds; for example, see some most recent papers in this research direction including [7,8].

In the current study, we are concerned with bond incident degree indices (BID indices for short), which form a special collection of topological indices. For a graph G, the general form of a bond incident degree index (for example, see [9,10,11]) is as follows:

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=\sum _{wv\in E\left(G\right)}\mathfrak{f}(d_G\left(w\right),d_G\left(v\right)),$$

where $\mathfrak{f}:D\left(G\right)\times D\left(G\right)\to (-\infty ,\infty )$ is a symmetric function, and $D\left(G\right)$ represents the set of all different elements of the degree sequence of G. We note here that such indices are also known as graphical edge-weight-function indices [12]. Also, we remark that the aforementioned class of indices is a proper subclass of the class of all degree-based topological indices; for example, see [13].

A connected m-size graph of order $m-1$ is referred to as a bicyclic graph. In other words, a connected graph containing at least two cycles is said to be a bicyclic graph if the removal of its exactly two edges yields a tree (a connected graph without any cycle). Here, we remark that a bicyclic graph may have more than two cycles. The present paper is concerned with an optimal study of the BID indices of fixed-size bicyclic graphs with a given matching number. Our results can be divided into the following two categories: (i) results about perfect matching, and (ii) results about a given matching number. Our results from each of the aforementioned two categories cover the SO (Sombor) index [14,15,16], the reduced Sombor index [16], the Euler Sombor (ES) index [17], the arithmetic-geometric index (for example, see [18]), the symmetric division deg (SDD) index [19,20], and the modified symmetric division deg (MSDD) index [21]. In other words, our results generalize a few existing results and provide particular new cases for several existing indices. As there are a lot of particular BID indices and, in many cases, the extremal results with respect to them, including their proofs, are considerably similar to one another, it is natural to think of adopting a unified technique to obtain those results and hence generalize them, which is the primary motivation of the current study.

2. Preliminaries

In the current section, we give the definitions and notions that are used in the subsequent section.

A vertex of degree one in a graph is known as a pendent vertex. An edge that is incident to a pendent vertex is called a pendent edge. For a vertex u of a graph G, we define $N_G\left(u\right):=\{x:xu\in E\left(G\right)\}$. Every vertex $x\in N_G\left(u\right)$ is called the neighbor of u. A subset U of the edge set of a graph is said to be a matching if U contains no two adjacent edges. A matching consisting of $\alpha$ edges is known as an $\alpha$-matching. A matching U in a graph G is said to be maximum if G contains no matching of size larger than $\left|U\right|$. The number of edges in a maximum matching of a graph G is referred to as the matching number of G. A vertex incident to an edge of a matching U is referred to as U-saturated; in particular, if every vertex of the graph is U-saturated, then U is referred to as a perfect matching. A vertex that is not U-saturated is referred to as a U-unsaturated vertex.

For two vertices v and w of a graph G, we use $G-\{v,w\}$ to denote the graph formed by dropping $v,w,$ and all the edges incident with them. Similarly, $G-\left\{w\right\}$ is defined. For simplicity, we write $G-w$ instead of writing $G-\left\{w\right\}$. Also, if $pq$ is an edge of G, then the graph formed by dropping $pq$ is represented as $G-pq$.

A connected m-size graph of order m is referred to as a unicyclic graph. Let $S_n^{+}$ denote the n-size unicyclic graph constructed by adding precisely one edge to the n-order start graph, where $n\ge 4$. Let $U_{n,\nu }$ denote the graph generated by inserting one vertex of degree 2 on each of the $\nu -2$ pendent edges of the graph $S_{n-\nu +2}^{+}$, where $4\le 2\nu \le n$. Figure 1 shows the graph $U_{n,\nu }$.

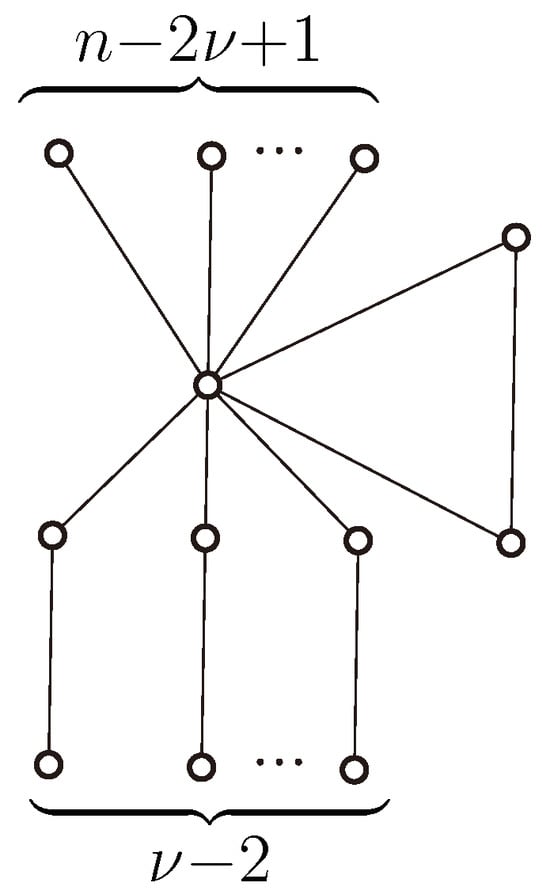
Figure 1. The unicyclic graph $U_{n,\nu }$.

Let $S_n^{-+}$ denote the $(n+1)$-size bicyclic graph constructed by inserting two non-adjacent edges to the n-order star graph $S_n$. Let $B_{n,\nu }$ denote the graph generated by inserting one vertex of degree 2 on each of the $\nu -3$ pendent edges of the graph $S_{n-\nu +3}^{-+}$, where $6\le 2\nu \le n$. Figure 2 shows the graph $B_{n,\nu }$. We end this preliminary section by noting that both the graphs $U_{2\nu ,\nu }$ and $B_{2\nu ,\nu }$ have perfect matching.

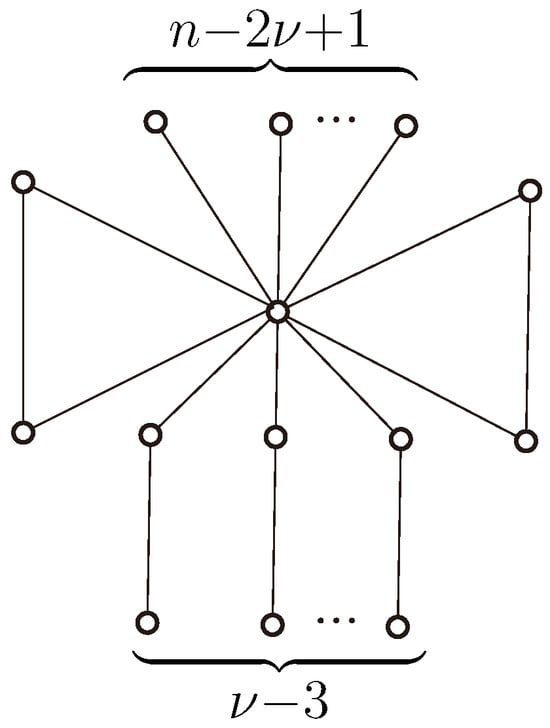
Figure 2. The bicyclic graph $B_{n,\nu }$.

3. Main Results

We start this section by giving a result for fixed-size bicyclic graphs having a matching number 2. Let $S_n^{++}$ denote the bicyclic graph formed by inserting two adjacent edges to the n-order star graph $S_n$.

Theorem 1.

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. If $S_n^{++}$ uniquely possesses the maximum value of ${\mathcal{BID}}_{\mathfrak{f}}$ among all $(n+1)$-size bicyclic graphs, then

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le (n-4)\mathfrak{f}(n-1,1)+2\mathfrak{f}(n-1,2)+\mathfrak{f}(n-1,3)+2\mathfrak{f}(2,3).$$

(1)

for every $(n+1)$-size bicyclic graph G having a matching number 2. The equality in (1) holds iff $G\cong S_n^{++}$.

Proof. 

Since $S_n^{++}$ uniquely possesses the maximum value of ${\mathcal{BID}}_{\mathfrak{f}}$ among all $(n+1)$-size bicyclic graphs and ${\mathcal{BID}}_{\mathfrak{f}}\left(S_n^{++}\right)=(n-4)\mathfrak{f}(n-1,1)+2\mathfrak{f}(n-1,2)+\mathfrak{f}(n-1,3)+2\mathfrak{f}(2,3)$, the required conclusion follows from the fact that the matching number of $S_n^{++}$ is 2. □

Next, we have a minimal version of Theorem 1.

Theorem 2.

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. If $S_n^{++}$ uniquely possesses the minimum value of ${\mathcal{BID}}_{\mathfrak{f}}$ among all $(n+1)$-size bicyclic graphs, then

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\ge (n-4)\mathfrak{f}(n-1,1)+2\mathfrak{f}(n-1,2)+\mathfrak{f}(n-1,3)+2\mathfrak{f}(2,3)$$

(2)

for every $(n+1)$-size bicyclic graph G having a matching number 2. The equality in (2) holds iff $G\cong S_n^{++}$.

Proof. 

Similar to the proof of Theorem 1. □

In order to prove our next two results, we need the following two known results about unicyclic graphs:

Lemma 1 

([22]). Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. If the following hold:

(i) 

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)<0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(ii) 

${\eta }_1[\mathfrak{f}(1,3)+\mathfrak{f}(3,3)]<{\eta }_1\mathfrak{f}({\eta }_1+1,2)+({\eta }_1-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_1+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_1\ge 3$;

(iii) 

the function g, defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly decreasing in ${\eta }_1$ for ${\eta }_2\ge 2$ and ${\eta }_1\ge 1$;

(iv) 

the function ℏ, defined as

$$\hslash \left({\eta }_1\right)=\mathfrak{f}({\eta }_1,2)+\mathfrak{f}({\eta }_1,1)-\mathfrak{f}({\eta }_1-1,1)+({\eta }_1-2)\left[\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1-1,2)\right],$$

is strictly increasing for ${\eta }_1\ge 2$;

then, for every $2\nu$-size unicyclic graph G having a matching number $\nu (\ge 2)$,

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le \nu \mathfrak{f}(\nu +1,2)+(\nu -2)\mathfrak{f}(1,2)+\mathfrak{f}(\nu +1,1)+\mathfrak{f}(2,2),$$

with equality iff $G\cong U_{2\nu ,\nu }$ (see Figure 1).

Lemma 2

([22]). Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. If the following hold:

(i) 

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)>0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(ii) 

${\eta }_1[\mathfrak{f}(1,3)+\mathfrak{f}(3,3)]>{\eta }_1\mathfrak{f}({\eta }_1+1,2)+({\eta }_1-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_1+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_1\ge 3$;

(iii) 

the function g, defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly increasing in ${\eta }_1$ for ${\eta }_2\ge 2$ and ${\eta }_1\ge 1$;

(iv) 

the function ℏ, defined as

$$\hslash \left({\eta }_1\right)=\mathfrak{f}({\eta }_1,2)+\mathfrak{f}({\eta }_1,1)-\mathfrak{f}({\eta }_1-1,1)+({\eta }_1-2)\left[\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1-1,2)\right],$$

is strictly decreasing for ${\eta }_1\ge 2$;

then, for every $2\nu$-size unicyclic graph G having a matching number $\nu (\ge 2)$,

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\ge \nu \mathfrak{f}(\nu +1,2)+(\nu -2)\mathfrak{f}(1,2)+\mathfrak{f}(\nu +1,1)+\mathfrak{f}(2,2),$$

with equality iff $G\cong U_{2\nu ,\nu }$ (see Figure 1).

In order to prove the next result, we also define five particular classes of bicyclic graphs. Let ${\mathbb{B}}_q^{\left(1\right)}$, ${\mathbb{B}}_q^{\left(2\right)}$, ${\mathbb{B}}_q^{\left(3\right)}$, ${\mathbb{B}}_q^{\left(4\right)}$, and ${\mathbb{B}}_q^{\left(5\right)}$ denote the classes of all those q-order graphs that are formed by the following, respectively:

• Inserting an edge between two non-adjacent vertices of the q-order cycle graph $C_q$, provided that $q\ge 4$;
• Inserting a path of length at least 2 between two non-adjacent vertices of a cycle graph of order at least 4;
• Connecting two disjoint cycles via a path of length at least 2;
• Identifying one vertex of two disjoint cycles;
• Inserting an edge between two vertices of two disjoint cycles.

For every $i\in \{1,2,\dots ,5\}$, the general form $B_q^{\left(i\right)}$ of the graphs of ${\mathbb{B}}_q^{\left(i\right)}$ is depicted in Figure 3.

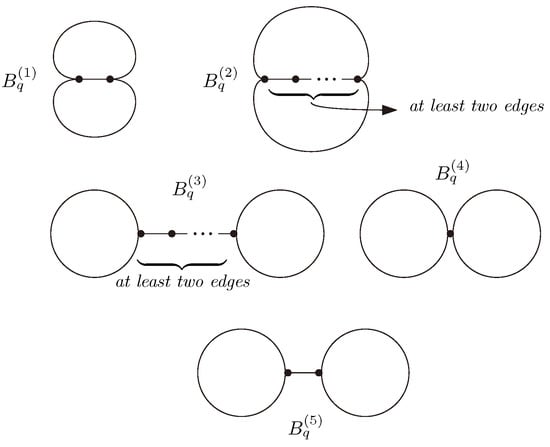
Figure 3. The general form $B_q^{\left(i\right)}$ of the q-order graphs of ${\mathbb{B}}_q^{\left(i\right)}$, where $i\in \{1,2,\dots ,5\}$.

Lemma 3.

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. Let ${\eta }_1\ge 1$ and ${\eta }_2\ge 2$. Assume that the following conditions involving $\mathfrak{f}$ hold:

(i).

${\eta }_2[\mathfrak{f}(3,3)+\mathfrak{f}(1,3)]<{\eta }_2\mathfrak{f}({\eta }_2+1,2)+({\eta }_2-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_2+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_2\ge 3$;

(ii).

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)<0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(iii).

Function g, defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly decreasing in ${\eta }_1$;

(iv).

$2\mathfrak{f}(3,1)+2\mathfrak{f}(4,1)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)-5\mathfrak{f}(6,2)-\mathfrak{f}(6,1)-2\mathfrak{f}(2,2)-\mathfrak{f}(1,2)<0$;

(v).

${\Theta }_1\left(\eta \right)<\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_1\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -4)\mathfrak{f}(3,3)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)+2\mathfrak{f}(4,1)$ and $\Theta \left(\eta \right)=\mathfrak{f}(\eta +2,1)+(\eta +1)\mathfrak{f}(\eta +2,2)+(\eta -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2)$;

(vi).

${\Theta }_2\left(\eta \right)<\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_2\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -5)\mathfrak{f}(3,3)+6\mathfrak{f}(3,4)+2\mathfrak{f}(4,1)$ and $\Theta \left(\eta \right)$ is defined in condition (v);

(vii).

${\Theta }_3\left(\eta \right)<\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_3\left(\eta \right)=(\eta -1)\mathfrak{f}(3,1)+(\eta -3)\mathfrak{f}(3,3)+4\mathfrak{f}(3,5)+\mathfrak{f}(5,1)$ and $\Theta \left(\eta \right)$ is defined in condition (v);

(viii).

The function ℏ, defined as

$$\hslash \left({\eta }_2\right)=\mathfrak{f}({\eta }_2,2)+\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)+({\eta }_2-2)\left[\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right],$$

is strictly increasing;

(ix).

${\eta }_1\mathfrak{f}({\eta }_1+1,2)+\mathfrak{f}({\eta }_1+1,1)-\mathfrak{f}({\eta }_1+2,1)-({\eta }_1+1)\mathfrak{f}({\eta }_1+2,2)+4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)<0$ for ${\eta }_1\ge 4$;

(x).

$({\eta }_1-1)[\mathfrak{f}({\eta }_1,4)-\mathfrak{f}({\eta }_1+1,4)]+\mathfrak{f}(2,{\eta }_2)-\mathfrak{f}({\eta }_1+1,{\eta }_2)+\mathfrak{f}(2,{\eta }_1)-\mathfrak{f}(1,{\eta }_1+1)<0$ for ${\eta }_1,{\eta }_2\in \{2,3,4\}$.

If G is a $(2\nu +1)$-size bicyclic graph having a matching number $\nu (\ge 3)$ such that it does not contain any pendent vertex adjacent to a vertex of degree 2, then ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le \Theta \left(\nu \right)$, with equality iff $G\cong B_{6,3}$ (see Figure 2), where $\Theta \left(\nu \right)$ is defined in condition (v).

Proof. 

We observe that no two pendent edges of G can be adjacent. Let $\mathcal{M}$ be a $\nu$-matching in G. Since $\mathcal{M}$ is a perfect matching and G does not contain any pendent vertex adjacent to a vertex of degree 2, G must be a graph formed by attaching at most one pendent vertex to every vertex of a graph $B_q\in {\cup }_{i=1}^5{\mathbb{B}}_q^{\left(i\right)}$ such that $\nu \le q\le 2\nu$, where the general form $B_q^{\left(i\right)}$ of the q-order graphs of ${\mathbb{B}}_q^{\left(i\right)}$ for every $i\in \{1,2,\dots ,5\}$ is depicted in Figure 3. Therefore, the maximum degree of G is at most 5.

Case 1.

The graph G contains no vertex of degree 2.

In the present case, we observe that either $q=\nu$ or $q=\nu +1$. If $q=\nu$, then G is a graph formed by attaching exactly one pendent vertex to every vertex of a graph $B_q\in {\cup }_{i=1}^5{\mathbb{B}}_q^{\left(i\right)}$. However, if $q=\nu +1$, then G is a graph formed by attaching exactly one pendent vertex to every vertex of degree 2 of a graph $B_q\in {\mathbb{B}}_q^{\left(1\right)}\cup {\mathbb{B}}_q^{\left(5\right)}$.

Subcase 1.1.

$\nu =3$.

In the present subcase, we note that $q=4$, and thus G is the 6-order graph formed by attaching exactly one pendent vertex to every vertex of degree 2 of the unique graph in ${\mathbb{B}}_4^{\left(1\right)}$. We note that

$$\begin{array}{cc}\hfill \Theta \left(3\right)-5\mathfrak{f}(3,3)-2\mathfrak{f}(1,3)& >\mathfrak{f}(2,2)-\mathfrak{f}(3,3)+2\left[\mathfrak{f}\right(1,3)-\mathfrak{f}(1,2\left)\right]\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & >\mathfrak{f}(2,3)-\mathfrak{f}(3,3)+\mathfrak{f}(1,3)-\mathfrak{f}(1,2)\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & >\mathfrak{f}(2,2)-\mathfrak{f}(3,2)+\mathfrak{f}(1,3)-\mathfrak{f}(1,2)\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & >0,\hfill \end{array}$$

(6)

where inequality (3) is obtained by taking ${\eta }_2=4$ in condition (i) of the lemma, inequalities (4) and (6) follow from condition (iii) (particularly, from $g(1,3)>g(2,3)$), and inequality (5) also follows from condition (iii) (particularly, from $g(2,3)>g(3,3)$). Therefore, we have

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=2\mathfrak{f}(3,1)+5\mathfrak{f}(3,3)<\Theta \left(3\right),$$

as desired.

Subcase 1.2.

$\nu =4$.

In the present subcase, $q\in \{4,5\}$, and thus, by keeping in mind the fact that G does not contain any vertex of degree 2, we observe that G is the 8-order graph formed by attaching exactly one pendent vertex to either every vertex of the unique graph in ${\mathbb{B}}_4^{\left(1\right)}$, or every vertex of degree 2 of the unique graph in ${\mathbb{B}}_5^{\left(1\right)}$. Hence, we have

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=\left\{\begin{array}{cc}2\mathfrak{f}(3,1)+2\mathfrak{f}(4,1)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)\hfill & \mathrm{if}q=4,\hfill \\ 3\mathfrak{f}(3,1)+6\mathfrak{f}(3,3)<\Theta \left(\nu \right)\hfill & \mathrm{if}q=5,\hfill \end{array}\right.$$

If $q=4$, then the required inequality, that is ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)<\Theta \left(4\right)$, follows from condition (iv). If $q=5$, then we note that

$$\begin{array}{cc}\hfill \Theta \left(5\right)-6\mathfrak{f}(3,3)-3\mathfrak{f}(1,3)& >\mathfrak{f}(2,2)-\mathfrak{f}(3,3)+2\left[\mathfrak{f}\right(1,3)-\mathfrak{f}(1,2\left)\right],\hfill \end{array}$$

(7)

where (7) is obtained by taking ${\eta }_2=5$ in condition (i). We note that the right-hand sides of (3) and (7) are the same. Therefore, based on (3)–(7), we have

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=3\mathfrak{f}(3,1)+6\mathfrak{f}(3,3)<\Theta \left(5\right).$$

Subcase 1.3.

$\nu \ge 5$.

In this subcase, we have

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=\left\{\begin{array}{cc}{\Theta }_1\left(\nu \right)<\Theta \left(\nu \right)\hfill & \mathrm{if}{B}_{\nu }\in {\mathbb{B}}_{\nu }^{\left(1\right)}\cup {\mathbb{B}}_{\nu }^{\left(5\right)},\hfill \\ (\nu -1)\mathfrak{f}(3,1)+(\nu +2)\mathfrak{f}(3,3)<\Theta \left(\nu \right)\hfill & \mathrm{if}{B}_{\nu +1}\in {\mathbb{B}}_{\nu +1}^{\left(1\right)}\cup {\mathbb{B}}_{\nu +1}^{\left(5\right)},\hfill \\ {\Theta }_2\left(\nu \right)<\Theta \left(\nu \right)\hfill & \mathrm{if}{B}_{\nu }\in {\mathbb{B}}_{\nu }^{\left(2\right)}\cup {\mathbb{B}}_{\nu }^{\left(3\right)},\hfill \\ {\Theta }_3\left(\nu \right)<\Theta \left(\nu \right)\hfill & \mathrm{if}{B}_{\nu }\in {\mathbb{B}}_{\nu }^{\left(4\right)},\hfill \end{array}\right.$$

where the first, third, and fourth inequalities follow from conditions (v), (vi), and (vii), respectively. In the rest of the considered subcase, we prove the inequality corresponding to the situation, when $B_{\nu +1}\in {\mathbb{B}}_{\nu +1}^{\left(1\right)}\cup {\mathbb{B}}_{\nu +1}^{\left(5\right)}$. The choice ${\eta }_2=\nu +1$ in condition (i) yields

$$\Theta \left(\nu \right)-(\nu +2)\mathfrak{f}(3,3)-(\nu -1)\mathfrak{f}(1,3)>\mathfrak{f}(2,2)-\mathfrak{f}(3,3)+2\left[\mathfrak{f}\right(1,3)-\mathfrak{f}(1,2\left)\right].$$

(8)

We note that the right-hand sides of (3) and (8) are the same, which is positive based on (3)–(6).

Case 2.

The graph G contains at least one vertex of degree 2.

We choose a vertex $x\in V\left(G\right)$ of degree 2 in the following way: if at least one cycle of G contains at least one vertex of degree 2, then we assume that x lies on a cycle of G; otherwise, we suppose that x is any vertex of degree 2. Take $N_G\left(x\right)=\{y,z\}$. Then $min\{d_G\left(y\right),d_G\left(z\right)\}\ge 2$ because G contains no pendent vertex adjacent to a vertex of degree 2. Since exactly one of the edges incident to x belongs to $\mathcal{M}$, without loss of generality, we suppose that $xy\in \mathcal{M}$.

Subcase 2.1.

No cycle of G contains any vertex of degree 2.

Since G does not contain any pendent vertex adjacent to a vertex of degree 2, its induced subgraph without pendent vertices must belong to ${\mathbb{B}}_q^{\left(3\right)}$, and thus, there is a unique path between the vertices $y,z\in V\left(G\right)$. Let $G^{\prime }$ denote the graph formed by dropping the edge $xz$ and adding $yz$. We note that the matching number of $G^{\prime }$ is also $\nu$. Only the degrees of the vertices x and y are changed in $G^{\prime }$ after applying the aforementioned transformation on G, and every other vertex has the same degree in both G and $G^{\prime }$. We note that the maximum degree of G is at most 4 in the current subcase. Therefore, by conditions (iii) and (x), we have

$$\begin{array}{cc}\hfill {\mathcal{BID}}_{\mathfrak{f}}\left(G\right)-{\mathcal{BID}}_{\mathfrak{f}}\left(G^{\prime }\right)& =\sum _{y^{\prime }\in N_G\left(y\right)\setminus \left\{x\right\}}[\mathfrak{f}(d_G\left(y\right),d_G\left(y^{\prime }\right))-\mathfrak{f}(d_G\left(y\right)+1,d_G\left(y^{\prime }\right))]\hfill \\ \hfill & +\mathfrak{f}(2,d_G\left(z\right))-\mathfrak{f}(d_G\left(y\right)+1,d_G\left(z\right))+\mathfrak{f}(2,d_G\left(y\right))-\mathfrak{f}(1,d_G\left(y\right)+1)\hfill \\ \hfill & \le (d_G\left(y\right)-1)[\mathfrak{f}(d_G\left(y\right),4)-\mathfrak{f}(d_G\left(y\right)+1,4)]\hfill \\ \hfill & +\mathfrak{f}(2,d_G\left(z\right))-\mathfrak{f}(d_G\left(y\right)+1,d_G\left(z\right))+\mathfrak{f}(2,d_G\left(y\right))-\mathfrak{f}(1,d_G\left(y\right)+1)<0.\hfill \end{array}$$

This means that the above transformation reduces the number of vertices of degree 2 present in G by exactly 1 without changing its matching number. Consequently, we conclude that after applying this transformation a finite number of times on G, we obtain a graph $G^{*}$ containing no vertex of degree 2 such that ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)<{\mathcal{BID}}_{\mathfrak{f}}\left(G^{*}\right)$. Now, by Case 1, we have ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)<{\mathcal{BID}}_{\mathfrak{f}}\left(G^{*}\right)<\Theta \left(\nu \right)$, as desired.

Subcase 2.2.

At least one cycle of G contains at least one vertex of degree 2.

In this subcase, the vertex x lies on a cycle of G. Thus, the graph $G-xz$ is a $2\nu$-size unicyclic graph having a matching number $\nu$. Since z has at most one pendent neighbor, by condition (iii) of the lemma, we have

$$\begin{array}{cc}\hfill {\mathcal{BID}}_{\mathfrak{f}}\left(G\right)-{\mathcal{BID}}_{\mathfrak{f}}(G-xz)& =\sum _{z^{\prime }\in N_G\left(z\right)\setminus \left\{x\right\}}[\mathfrak{f}(d_G\left(z\right),d_G\left(z^{\prime }\right))-\mathfrak{f}(d_G\left(z\right)-1,d_G\left(z^{\prime }\right))]\hfill \\ \hfill & +\mathfrak{f}(2,d_G\left(y\right))-\mathfrak{f}(1,d_G\left(y\right))+\mathfrak{f}(2,d_G\left(z\right))\hfill \\ \hfill & \le [(d_G\left(z\right)-2)\{\mathfrak{f}(d_G\left(z\right),2)-\mathfrak{f}(d_G\left(z\right)-1,2)\}\hfill \\ \hfill & +\mathfrak{f}(d_G\left(z\right),1)-\mathfrak{f}(d_G\left(z\right)-1,1)+\mathfrak{f}(2,d_G\left(z\right))]\hfill \\ & +\mathfrak{f}(2,2)-\mathfrak{f}(1,2).\hfill \end{array}$$

(9)

We recall the definition of the function ℏ given in condition (viii) of the lemma and note that the expression given within the square brackets on the right-hand side of (9) is equal to $\hslash \left(d_G\left(z\right)\right)$. Since $2\le d_G\left(z\right)\le 5$, we have $\hslash \left(d_G\left(z\right)\right)\le \hslash \left(5\right)$, and hence (9) gives

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)-{\mathcal{BID}}_{\mathfrak{f}}(G-xz)\le 4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)+\mathfrak{f}(2,2)-\mathfrak{f}(1,2),$$

which yields the following inequality (because of Lemma 1):

$$\begin{array}{cc}\hfill {\mathcal{BID}}_{\mathfrak{f}}\left(G\right)& \le \nu \mathfrak{f}(\nu +1,2)+(\nu -3)\mathfrak{f}(1,2)+\mathfrak{f}(\nu +1,1)+2f(2,2)\hfill \\ \hfill & +4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1),\hfill \end{array}$$

(10)

where the equality in (10) holds iff z has $d_G\left(z\right)-1$ neighbors of degree 2 and one pendent neighbor, $d_G\left(y\right)=2$, $d_G\left(z\right)=5$, and $G-xz\cong U_{2\nu ,\nu }$. By keeping in mind condition (ix), for $\nu \ge 3$, we have

$$\begin{array}{cc}\hfill & \nu \mathfrak{f}(\nu +1,2)+(\nu -3)\mathfrak{f}(1,2)+\mathfrak{f}(\nu +1,1)+2f(2,2)\hfill \\ \hfill & +4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)\le \Theta \left(\nu \right),\hfill \end{array}$$

(11)

with equality iff $\nu =3$. Now, the required conclusion follows from (10) and (11). □

Proof of the following result uses Lemma 2, and is totally similar to that of Lemma 3, and hence we omit it.

Lemma 4.

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. Let ${\eta }_1\ge 1$ and ${\eta }_2\ge 2$. Assume that the following conditions involving $\mathfrak{f}$ hold:

(i).

${\eta }_2[\mathfrak{f}(3,3)+\mathfrak{f}(1,3)]>{\eta }_2\mathfrak{f}({\eta }_2+1,2)+({\eta }_2-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_2+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_2\ge 3$;

(ii).

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)>0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(iii).

Function g, defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly increasing in ${\eta }_1$;

(iv).

$2\mathfrak{f}(3,1)+2\mathfrak{f}(4,1)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)-5\mathfrak{f}(6,2)-\mathfrak{f}(6,1)-2\mathfrak{f}(2,2)-\mathfrak{f}(1,2)>0$;

(v).

$min\{{\Theta }_1\left(\eta \right),{\Theta }_2\left(\eta \right),{\Theta }_3\left(\eta \right)\}>\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_1\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -4)\mathfrak{f}(3,3)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)+2\mathfrak{f}(4,1)$, ${\Theta }_2\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -5)\mathfrak{f}(3,3)+6\mathfrak{f}(3,4)+2\mathfrak{f}(4,1)$, ${\Theta }_3\left(\eta \right)=(\eta -1)\mathfrak{f}(3,1)+(\eta -3)\mathfrak{f}(3,3)+4\mathfrak{f}(3,5)+\mathfrak{f}(5,1)$ and $\Theta \left(\eta \right)=\mathfrak{f}(\eta +2,1)+(\eta +1)\mathfrak{f}(\eta +2,2)+(\eta -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2)$;

(vi).

${\Theta }_1\left(\eta \right)>\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_1\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -4)\mathfrak{f}(3,3)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)+2\mathfrak{f}(4,1)$ and $\Theta \left(\eta \right)=\mathfrak{f}(\eta +2,1)+(\eta +1)\mathfrak{f}(\eta +2,2)+(\eta -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2)$;

(vii).

${\Theta }_2\left(\eta \right)>\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_2\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -5)\mathfrak{f}(3,3)+6\mathfrak{f}(3,4)+2\mathfrak{f}(4,1)$, and $\Theta \left(\eta \right)$ is defined in condition (v);

(viii).

${\Theta }_3\left(\eta \right)>\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_3\left(\eta \right)=(\eta -1)\mathfrak{f}(3,1)+(\eta -3)\mathfrak{f}(3,3)+4\mathfrak{f}(3,5)+\mathfrak{f}(5,1)$, and $\Theta \left(\eta \right)$ is defined in condition (v);

(ix).

The function ℏ, defined as

$$\hslash \left({\eta }_2\right)=\mathfrak{f}({\eta }_2,2)+\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)+({\eta }_2-2)\left[\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right],$$

is strictly decreasing;

(x).

${\eta }_1\mathfrak{f}({\eta }_1+1,2)+\mathfrak{f}({\eta }_1+1,1)-\mathfrak{f}({\eta }_1+2,1)-({\eta }_1+1)\mathfrak{f}({\eta }_1+2,2)+4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)>0$ for ${\eta }_1\ge 4$;

(xi).

$({\eta }_1-1)[\mathfrak{f}({\eta }_1,4)-\mathfrak{f}({\eta }_1+1,4)]+\mathfrak{f}(2,{\eta }_2)-\mathfrak{f}({\eta }_1+1,{\eta }_2)+\mathfrak{f}(2,{\eta }_1)-\mathfrak{f}(1,{\eta }_1+1)>0$ for ${\eta }_1,{\eta }_2\in \{2,3,4\}$.

If G is a $(2\nu +1)$-size bicyclic graph having a matching number $\nu (\ge 3)$ such that it does not contain any pendent vertex adjacent to a vertex of degree 2, then ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\ge \Theta \left(\nu \right)$, with equality iff $G\cong B_{6,3}$ (see Figure 2).

Theorem 3.

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. Let ${\eta }_1\ge 1$ and ${\eta }_2\ge 2$. Assume that the following conditions involving $\mathfrak{f}$ hold:

(i).

${\eta }_2[\mathfrak{f}(3,3)+\mathfrak{f}(1,3)]<{\eta }_2\mathfrak{f}({\eta }_2+1,2)+({\eta }_2-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_2+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_2\ge 3$;

(ii).

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)<0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(iii).

Function g, defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly decreasing in ${\eta }_1$;

(iv).

$2\mathfrak{f}(3,1)+2\mathfrak{f}(4,1)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)-5\mathfrak{f}(6,2)-\mathfrak{f}(6,1)-2\mathfrak{f}(2,2)-\mathfrak{f}(1,2)<0$;

(v).

$max\{{\Theta }_1\left(\eta \right),{\Theta }_2\left(\eta \right),{\Theta }_3\left(\eta \right)\}<\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_1\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -4)\mathfrak{f}(3,3)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)+2\mathfrak{f}(4,1)$, ${\Theta }_2\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -5)\mathfrak{f}(3,3)+6\mathfrak{f}(3,4)+2\mathfrak{f}(4,1)$, ${\Theta }_3\left(\eta \right)=(\eta -1)\mathfrak{f}(3,1)+(\eta -3)\mathfrak{f}(3,3)+4\mathfrak{f}(3,5)+\mathfrak{f}(5,1)$, and $\Theta \left(\eta \right)=\mathfrak{f}(\eta +2,1)+(\eta +1)\mathfrak{f}(\eta +2,2)+(\eta -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2)$;

(vi).

$\Theta \left(3\right)>max\left\{\mathfrak{f}\right(1,2)+3\mathfrak{f}(2,3)+3\mathfrak{f}(3,3),\mathfrak{f}(1,2)+3\mathfrak{f}(2,4)+2\mathfrak{f}(2,3)+\mathfrak{f}(3,4\left)\right\}$;

(vii).

The function ℏ, defined as

$$\hslash \left({\eta }_2\right)=\mathfrak{f}({\eta }_2,2)+\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)+({\eta }_2-2)\left[\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right],$$

is strictly increasing;

(viii).

${\eta }_1\mathfrak{f}({\eta }_1+1,2)+\mathfrak{f}({\eta }_1+1,1)-\mathfrak{f}({\eta }_1+2,1)-({\eta }_1+1)\mathfrak{f}({\eta }_1+2,2)+4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)<0$ for ${\eta }_1\ge 4$;

(ix).

$({\eta }_1-1)[\mathfrak{f}({\eta }_1,4)-\mathfrak{f}({\eta }_1+1,4)]+\mathfrak{f}(2,{\eta }_2)-\mathfrak{f}({\eta }_1+1,{\eta }_2)+\mathfrak{f}(2,{\eta }_1)-\mathfrak{f}(1,{\eta }_1+1)<0$ for ${\eta }_1,{\eta }_2\in \{2,3,4\}$.

If G is a $(2\nu +1)$-size bicyclic graph having a matching number $\nu (\ge 3)$, then ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le \Theta \left(\nu \right)$, with equality iff $G\cong B_{2\nu ,\nu }$ (see Figure 2).

Proof. 

We use induction on $\nu$ to prove the theorem. Assume first that $\nu =3$. If G does not contain any pendent vertex adjacent to a vertex of degree 2, then the desired conclusion is valid based on Lemma 3 (for $\nu =3$). However, if G contains a pendent vertex adjacent to a vertex of degree 2, then G can be formed by attaching a path of length 2 to a vertex of the unique graph of ${\mathbb{B}}_4^{\left(1\right)}$ (see Figure 3). Hence, either

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=\mathfrak{f}(1,2)+3\mathfrak{f}(2,3)+3\mathfrak{f}(3,3)\mathrm{or}$$

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=\mathfrak{f}(1,2)+3\mathfrak{f}(2,4)+2\mathfrak{f}(2,3)+\mathfrak{f}(3,4).$$

In either case, based on condition (vi), we have ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)<\Theta \left(3\right)$, which completes the base step of the induction. Let us now assume that $\nu >3$ and that the theorem’s conclusion holds for all $(2\nu -1)$-size bicyclic graphs having $\nu -1$ matching numbers. We next consider a $(2\nu +1)$-size bicyclic graph G with a matching number $\nu (>3)$. If G has no pendent vertex adjacent to a vertex of degree 2, then the desired conclusion holds because of Lemma 3. In the rest of the proof, we assume that G has at least one pendent vertex adjacent to a vertex of degree 2. Take $x,y\in V\left(G\right)$ such that $xy\in E\left(G\right)$, $d_G\left(x\right)=1$ and $d_G\left(y\right)=2$. Let $N_G\left(y\right):=\{x,z\}$. Let $\mathcal{M}$ be a $\nu$-matching of G. Since G consists of $2\nu +1$ edges and because z is not incident with at least $\nu -1$ edges belonging to $\mathcal{M}$, we have $d_G\left(z\right)\le 2\nu +1-(\nu -1)=\nu +2$. Clearly, $xy\in \mathcal{M}$. Since $G^{★}:=G-\{x,y\}$ has $2\nu -1$ edges and because its matching number is $\nu -1$, the induction hypothesis implies the following:

$${\mathcal{BID}}_{\mathfrak{f}}\left(G^{★}\right)\le \Theta (\nu -1),$$

(12)

where the equality is satisfied iff $G\cong B_{2(\nu -1),\nu -1}$. Since z has at most one pendent neighbor, by using conditions (iii) and (vii) of the theorem, we have

$$\begin{array}{c}{\mathcal{BID}}_{\mathfrak{f}}\left(G\right)-{\mathcal{BID}}_{\mathfrak{f}}\left(G^{★}\right)\hfill \\ =\mathfrak{f}(1,2)+\mathfrak{f}(d_G\left(z\right),2)+{\displaystyle \sum _{z^{\prime }\in N_G\left(z\right)\setminus \left\{y\right\}}}\left[\mathfrak{f}(d_G\left(z\right),d_G\left(z^{\prime }\right))-\mathfrak{f}(d_G\left(z\right)-1,d_G\left(z^{\prime }\right))\right]\hfill \\ \le \mathfrak{f}(1,2)+\mathfrak{f}(d_G\left(z\right),2)+(d_G\left(z\right)-2)\left[\mathfrak{f}(d_G\left(z\right),2)-\mathfrak{f}(d_G\left(z\right)-1,2)\right]\hfill \\ +\left[\mathfrak{f}(d_G\left(z\right),1)-\mathfrak{f}(d_G\left(z\right)-1,1)\right]\hfill \\ \le \mathfrak{f}(1,2)+\mathfrak{f}(\nu +2,2)+\nu \left[\mathfrak{f}(\nu +2,2)-\mathfrak{f}(\nu +1,2)\right]+\left[\mathfrak{f}(\nu +2,1)-\mathfrak{f}(\nu +1,1)\right].\hfill \end{array}$$

(13)

From (12) and (13), we obtain ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le \Theta \left(\nu \right)$ with equality iff $G\cong B_{2\nu ,\nu }$. □

Proof of the following theorem uses Lemma 4 and is completely analogous to that of Theorem 3, and thus we omit it.

Theorem 4. 

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. Let ${\eta }_1\ge 1$ and ${\eta }_2\ge 2$. Assume that the following conditions involving $\mathfrak{f}$ hold:

(i).

${\eta }_2[\mathfrak{f}(3,3)+\mathfrak{f}(1,3)]>{\eta }_2\mathfrak{f}({\eta }_2+1,2)+({\eta }_2-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_2+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_2\ge 3$;

(ii).

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)>0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(iii).

Function g defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly increasing in ${\eta }_1$;

(iv).

$2\mathfrak{f}(3,1)+2\mathfrak{f}(4,1)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)-5\mathfrak{f}(6,2)-\mathfrak{f}(6,1)-2\mathfrak{f}(2,2)-\mathfrak{f}(1,2)>0$;

(v).

$min\{{\Theta }_1\left(\eta \right),{\Theta }_2\left(\eta \right),{\Theta }_3\left(\eta \right)\}>\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_1\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -4)\mathfrak{f}(3,3)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)+2\mathfrak{f}(4,1)$, ${\Theta }_2\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -5)\mathfrak{f}(3,3)+6\mathfrak{f}(3,4)+2\mathfrak{f}(4,1)$, ${\Theta }_3\left(\eta \right)=(\eta -1)\mathfrak{f}(3,1)+(\eta -3)\mathfrak{f}(3,3)+4\mathfrak{f}(3,5)+\mathfrak{f}(5,1)$, and $\Theta \left(\eta \right)=\mathfrak{f}(\eta +2,1)+(\eta +1)\mathfrak{f}(\eta +2,2)+(\eta -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2)$;

(vi).

$\Theta \left(3\right)<min\left\{\mathfrak{f}\right(1,2)+3\mathfrak{f}(2,3)+3\mathfrak{f}(3,3),\mathfrak{f}(1,2)+3\mathfrak{f}(2,4)+2\mathfrak{f}(2,3)+\mathfrak{f}(3,4\left)\right\}$;

(vii).

The function ℏ, defined as

$$\hslash \left({\eta }_2\right)=\mathfrak{f}({\eta }_2,2)+\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)+({\eta }_2-2)\left[\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right],$$

is strictly decreasing;

(viii).

${\eta }_1\mathfrak{f}({\eta }_1+1,2)+\mathfrak{f}({\eta }_1+1,1)-\mathfrak{f}({\eta }_1+2,1)-({\eta }_1+1)\mathfrak{f}({\eta }_1+2,2)+4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)>0$ for ${\eta }_1\ge 4$;

(ix).

$({\eta }_1-1)[\mathfrak{f}({\eta }_1,4)-\mathfrak{f}({\eta }_1+1,4)]+\mathfrak{f}(2,{\eta }_2)-\mathfrak{f}({\eta }_1+1,{\eta }_2)+\mathfrak{f}(2,{\eta }_1)-\mathfrak{f}(1,{\eta }_1+1)>0$ for ${\eta }_1,{\eta }_2\in \{2,3,4\}$.

If G is a $(2\nu +1)$-size bicyclic graph having a matching number $\nu (\ge 3)$, then ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\ge \Theta \left(\nu \right)$, with equality iff $G\cong B_{2\nu ,\nu }$ (see Figure 2).

We notice that ${\mathcal{BID}}_{\mathfrak{f}}$ coincides with the SO (Sombor) index [14,16], or the RSO (reduced Sombor) index [16], or the Euler Sombor (ES) index [17], or the arithmetic-geometric (AG) index (for example, see [18]), or the symmetric division deg (SDD) index [19,20], or the modified symmetric division deg (MSDD) index [21], when $\mathfrak{f}({\xi }_1,{\xi }_2)=\sqrt{{\xi }_1^2+{\xi }_2^2}$, or $\mathfrak{f}({\xi }_1,{\xi }_2)=\sqrt{{({\xi }_1-1)}^2+{({\xi }_2-1)}^2}$, or $\mathfrak{f}({\xi }_1,{\xi }_2)=\sqrt{{\xi }_1^2+{\xi }_2^2+{\xi }_1{\xi }_2}$, or $\mathfrak{f}({\xi }_1,{\xi }_2)={\left(2\sqrt{{\xi }_1{\xi }_2}\right)}^{-1}$$({\xi }_1+{\xi }_2)$, or $\mathfrak{f}({\xi }_1,{\xi }_2)={\left({\xi }_1{\xi }_2\right)}^{-1}$$({\xi }_1^2+{\xi }_2^2)$, or $\mathfrak{f}({\xi }_1,{\xi }_2)=\sqrt{{\left(2{\xi }_1{\xi }_2\right)}^{-1}({\xi }_1^2+{\xi }_2^2)}$, respectively. We verified all the conditions of Theorem 3 for all the aforementioned choices of $\mathfrak{f}$, and hence we have the next result (which follows from Theorem 3).

Corollary 1.

Let ${\mathcal{BID}}_{\mathfrak{f}}$ be one of the following: SO index, RSO index, ES index, AG index, SDD index, or MSDD index. If G is any $(2\nu +1)$-size bicyclic graph having a matching number $\nu (\ge 3)$, then

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le \mathfrak{f}(\nu +2,1)+(\nu +1)\mathfrak{f}(\nu +2,2)+(\nu -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2),$$

with equality iff $G\cong B_{2\nu ,\nu }$ (see Figure 2).

Before proceeding further, we recall the following known lemma that will be used in proving our next main result:

Lemma 5

([23]). If G is an $(n+1)$-size bicyclic graph possessing a matching number ν and at least one pendent vertex, provided that $n>2\nu \ge 6$, then G contains a ν-matching $\mathcal{M}$ and a pendent vertex w such that w is $\mathcal{M}$-unsaturated.

Theorem 5. 

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. Let ${\eta }_1\ge 1$ and ${\eta }_2\ge 2$. Also, assume that the following conditions involving $\mathfrak{f}$ hold:

(i).

${\eta }_2[\mathfrak{f}(3,3)+\mathfrak{f}(1,3)]<{\eta }_2\mathfrak{f}({\eta }_2+1,2)+({\eta }_2-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_2+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_2\ge 3$;

(ii).

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)<0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(iii).

Function g, defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly decreasing in ${\eta }_1$;

(iv).

$2\mathfrak{f}(3,1)+2\mathfrak{f}(4,1)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)-5\mathfrak{f}(6,2)-\mathfrak{f}(6,1)-2\mathfrak{f}(2,2)-\mathfrak{f}(1,2)<0$;

(v).

$max\{{\Theta }_1\left(\eta \right),{\Theta }_2\left(\eta \right),{\Theta }_3\left(\eta \right)\}<\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_1\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -4)\mathfrak{f}(3,3)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)+2\mathfrak{f}(4,1)$, ${\Theta }_2\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -5)\mathfrak{f}(3,3)+6\mathfrak{f}(3,4)+2\mathfrak{f}(4,1)$, ${\Theta }_3\left(\eta \right)=(\eta -1)\mathfrak{f}(3,1)+(\eta -3)\mathfrak{f}(3,3)+4\mathfrak{f}(3,5)+\mathfrak{f}(5,1)$, and $\Theta \left(\eta \right)=\mathfrak{f}(\eta +2,1)+(\eta +1)\mathfrak{f}(\eta +2,2)+(\eta -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2)$;

(vi).

$\Theta \left(3\right)>max\left\{\mathfrak{f}\right(1,2)+3\mathfrak{f}(2,3)+3\mathfrak{f}(3,3),\mathfrak{f}(1,2)+3\mathfrak{f}(2,4)+2\mathfrak{f}(2,3)+\mathfrak{f}(3,4\left)\right\}$;

(vii).

The function ℏ, defined as

$$\hslash \left({\eta }_2\right)=\mathfrak{f}({\eta }_2,2)+\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)+({\eta }_2-2)\left[\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right],$$

is strictly increasing;

(viii).

${\eta }_1\mathfrak{f}({\eta }_1+1,2)+\mathfrak{f}({\eta }_1+1,1)-\mathfrak{f}({\eta }_1+2,1)-({\eta }_1+1)\mathfrak{f}({\eta }_1+2,2)+4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)<0$ for ${\eta }_1\ge 4$;

(ix).

$({\eta }_1-1)[\mathfrak{f}({\eta }_1,4)-\mathfrak{f}({\eta }_1+1,4)]+\mathfrak{f}(2,{\eta }_2)-\mathfrak{f}({\eta }_1+1,{\eta }_2)+\mathfrak{f}(2,{\eta }_1)-\mathfrak{f}(1,{\eta }_1+1)<0$ for ${\eta }_1,{\eta }_2\in \{2,3,4\}$,

(x).

$max\left\{\right(2\eta -3\left)\mathfrak{f}\right(2,2)+4\mathfrak{f}(2,3)+\mathfrak{f}(3,3);2(\eta -2\left)\mathfrak{f}\right(2,2)+6\mathfrak{f}(2,3),2(\eta -1\left)\mathfrak{f}\right(2,2)+$$4\mathfrak{f}(2,4)\}<2\mathfrak{f}(\eta +3,1)+(\eta +1\left)\mathfrak{f}\right(\eta +3,2)+(\eta -3\left)\mathfrak{f}\right(1,2)+2\mathfrak{f}(2,2)$ for $\eta \ge 3$;

(xi).

The function Ψ, defined as $\Psi ({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2-1,1)+{\eta }_1[\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)]+({\eta }_2-{\eta }_1)\left(\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right)$, is strictly increasing in ${\eta }_2$ for ${\eta }_2\ge {\eta }_1+1\ge 2$.

If G is an $(n+1)$-size bicyclic graph having a matching number $\nu (\ge 3)$, then

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le (n-2\nu +1)\mathfrak{f}(n-\nu +2,1)+(\nu +1)\mathfrak{f}(n-\nu +2,2)+(\nu -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2),$$

with equality iff $G\cong B_{n,\nu }$ (see Figure 2).

Proof. 

We define

$$\Phi (n,\nu ):=(n-2\nu +1)\mathfrak{f}(n-\nu +2,1)+(\nu +1)\mathfrak{f}(n-\nu +2,2)+(\nu -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2).$$

The result will be proved by using induction on n. Since all the conditions of Theorem 3 are listed in the statement of the current theorem, the desired conclusion is true for $n=2\nu$ because of Theorem 3. Let us now assume that $n>2\nu$ and that the result holds for all n-size bicyclic graphs having a matching number $\nu$. We next consider an $(n+1)$-size bicyclic graph possessing a matching number $\nu$ such that $n>2\nu$. We note that the minimum degree of G is either 1 or 2.

Case. 1.

The minimum degree of G is 2.

In the current case, it holds that $n=2\nu +1$, and hence $G\in {\mathbb{B}}_{2\nu +1}^{\left(i\right)}$ for some $i\in \{1,2,\dots ,5\}$ (see Figure 3). Here, we have

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)=\left\{\begin{array}{cc}(2\nu -3)\mathfrak{f}(2,2)+4\mathfrak{f}(2,3)+\mathfrak{f}(3,3)\hfill & \mathrm{if}G\in {\mathbb{B}}_{2\nu +1}^{\left(1\right)}\cup {\mathbb{B}}_{2\nu +1}^{\left(5\right)},\hfill \\ 2(\nu -2)\mathfrak{f}(2,2)+6\mathfrak{f}(2,3)\hfill & \mathrm{if}G\in {\mathbb{B}}_{2\nu +1}^{\left(2\right)}\cup {\mathbb{B}}_{2\nu +1}^{\left(3\right)},\hfill \\ 2(\nu -1)\mathfrak{f}(2,2)+4\mathfrak{f}(2,4)\hfill & \mathrm{if}G\in {\mathbb{B}}_{2\nu +1}^{\left(4\right)}.\hfill \end{array}\right.$$

In any of the above three possibilities, by condition (x) of the theorem, we have

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)<\Phi (2\nu +1,\nu ),$$

as desired.

Case. 2.

The minimum degree of G is 1.

Based on Lemma 5, G contains a $\nu$-matching $\mathcal{M}$ and a pendent vertex x such that x is $\mathcal{M}$-unsaturated. Thus, the matching number of G is the same as the one that $G-x$ has. Hence, by the inductive hypothesis, we obtain

$${\mathcal{BID}}_{\mathfrak{f}}(G-x)\le \Phi (n-1,\nu )$$

(14)

with equality iff $G-x\cong B_{n-1,\nu }$. Let y denote the unique neighbor of x. We observe that $\mathcal{M}$ must contain an edge incident to y as $\mathcal{M}$ is a maximum matching and $yx\notin \mathcal{M}$. Hence, because G has $n+1$ edges, we have $d_G\left(y\right)\le n+1-\left(\right|\mathcal{M}|-1)$; that is,

$$d_G\left(y\right)\le n-\nu +2.$$

Take $N_G\left(y\right):=\{y_1,y_2,\cdots ,y_p,y_{p+1},\cdots ,y_r\}$, where the vertices $y_1(=x),y_2,\cdots ,y_p$ are pendent, and all the remaining vertices of $N_G\left(y\right)$ are non-pendent. Since the total number of $\mathcal{M}$-unsaturated vertices of G is $n-2\nu$, and because at least $p-1$ pendent neighbors of y are $\mathcal{M}$-unsaturated, we have $p-1\le n-2\nu$. Based on condition (iii), we have

$$\begin{array}{cc}\hfill {\mathcal{BID}}_{\mathfrak{f}}\left(G\right)-{\mathcal{BID}}_{\mathfrak{f}}(G-x)& =\mathfrak{f}(d_G\left(y\right),1)+(p-1)[\mathfrak{f}(d_G\left(y\right),1)-\mathfrak{f}(d_G\left(y\right)-1,1)]\hfill \\ \hfill & +\sum _{i=p+1}^{d_G\left(y\right)}\left(\mathfrak{f}(d_G\left(y\right),d_G\left(y_i\right))-\mathfrak{f}(d_G\left(y\right)-1,d_G\left(y_i\right))\right)\hfill \\ \hfill & \le \mathfrak{f}(d_G\left(y\right)-1,1)+p[\mathfrak{f}(d_G\left(y\right),1)-\mathfrak{f}(d_G\left(y\right)-1,1)]\hfill \\ \hfill & +(d_G\left(y\right)-p)\left(\mathfrak{f}(d_G\left(y\right),2)-\mathfrak{f}(d_G\left(y\right)-1,2)\right).\hfill \end{array}$$

(15)

Since $p+1\le d_G\left(y\right)\le n-\nu +2$, by keeping in mind condition (xi), from (15) we obtain

$$\begin{array}{cc}\hfill {\mathcal{BID}}_{\mathfrak{f}}\left(G\right)-{\mathcal{BID}}_{\mathfrak{f}}(G-x)& \le \mathfrak{f}(n-\nu +1,1)+p\left(\mathfrak{f}(n-\nu +2,1)-\mathfrak{f}(n-\nu +1,1)\right)\hfill \\ \hfill & +(n-\nu -p+2)\left(\mathfrak{f}(n-\nu +2,2)-\mathfrak{f}(n-\nu +1,2)\right).\hfill \end{array}$$

(16)

By keeping in mind condition (iii), and the fact that $p\le n-2\nu +1$, from (16) we obtain

$$\begin{array}{cc}\hfill {\mathcal{BID}}_{\mathfrak{f}}\left(G\right)-{\mathcal{BID}}_{\mathfrak{f}}(G-x)& \le \mathfrak{f}(n-\nu +1,1)+(n-2\nu +1)\left(\mathfrak{f}(n-\nu +2,1)-\mathfrak{f}(n-\nu +1,1)\right)\hfill \\ \hfill & +(\nu +1)\left(\mathfrak{f}(n-\nu +2,2)-\mathfrak{f}(n-\nu +1,2)\right).\hfill \end{array}$$

(17)

From (14) and (17), it follows that ${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le \Phi (n,\nu )$, with equality iff $G\cong B_{n,\nu }$. □

The next result’s proof utilizes Theorem 4, and is completely similar to that of Theorem 5, and hence we omit it.

Theorem 6.

Let $\mathfrak{f}:[1,\infty )\times [1,\infty )\to (-\infty ,\infty )$ be a function such that $\mathfrak{f}({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2,{\eta }_1)$. Let ${\eta }_1\ge 1$ and ${\eta }_2\ge 2$. Also, assume that the following conditions involving $\mathfrak{f}$ hold:

(i).

${\eta }_2[\mathfrak{f}(3,3)+\mathfrak{f}(1,3)]>{\eta }_2\mathfrak{f}({\eta }_2+1,2)+({\eta }_2-2)\mathfrak{f}(1,2)+\mathfrak{f}({\eta }_2+1,1)+\mathfrak{f}(2,2)$ for ${\eta }_2\ge 3$;

(ii).

$\mathfrak{f}({\eta }_1,2)-\mathfrak{f}({\eta }_1,3)+\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2,3)+\mathfrak{f}(2,2)-\mathfrak{f}(1,3)>0$ for ${\eta }_1,{\eta }_2\in \{2,3\}$;

(iii).

Function g, defined as $g({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_1,{\eta }_2)-\mathfrak{f}({\eta }_1,{\eta }_2-1)$, is strictly increasing in ${\eta }_1$;

(iv).

$2\mathfrak{f}(3,1)+2\mathfrak{f}(4,1)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)-5\mathfrak{f}(6,2)-\mathfrak{f}(6,1)-2\mathfrak{f}(2,2)-\mathfrak{f}(1,2)>0$;

(v).

$min\{{\Theta }_1\left(\eta \right),{\Theta }_2\left(\eta \right),{\Theta }_3\left(\eta \right)\}>\Theta \left(\eta \right)$ for $\eta \ge 5$, where ${\Theta }_1\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -4)\mathfrak{f}(3,3)+4\mathfrak{f}(3,4)+\mathfrak{f}(4,4)+2\mathfrak{f}(4,1)$, ${\Theta }_2\left(\eta \right)=(\eta -2)\mathfrak{f}(3,1)+(\eta -5)\mathfrak{f}(3,3)+6\mathfrak{f}(3,4)+2\mathfrak{f}(4,1)$, ${\Theta }_3\left(\eta \right)=(\eta -1)\mathfrak{f}(3,1)+(\eta -3)\mathfrak{f}(3,3)+4\mathfrak{f}(3,5)+\mathfrak{f}(5,1)$, and $\Theta \left(\eta \right)=\mathfrak{f}(\eta +2,1)+(\eta +1)\mathfrak{f}(\eta +2,2)+(\eta -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2)$;

(vi).

$\Theta \left(3\right)<min\left\{\mathfrak{f}\right(1,2)+3\mathfrak{f}(2,3)+3\mathfrak{f}(3,3),\mathfrak{f}(1,2)+3\mathfrak{f}(2,4)+2\mathfrak{f}(2,3)+\mathfrak{f}(3,4\left)\right\}$;

(vii).

The function ℏ, defined as

$$\hslash \left({\eta }_2\right)=\mathfrak{f}({\eta }_2,2)+\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)+({\eta }_2-2)\left[\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right],$$

is strictly decreasing;

(viii).

${\eta }_1\mathfrak{f}({\eta }_1+1,2)+\mathfrak{f}({\eta }_1+1,1)-\mathfrak{f}({\eta }_1+2,1)-({\eta }_1+1)\mathfrak{f}({\eta }_1+2,2)+4\mathfrak{f}(5,2)-3\mathfrak{f}(4,2)+\mathfrak{f}(5,1)-\mathfrak{f}(4,1)>0$ for ${\eta }_1\ge 4$;

(ix).

$({\eta }_1-1)[\mathfrak{f}({\eta }_1,4)-\mathfrak{f}({\eta }_1+1,4)]+\mathfrak{f}(2,{\eta }_2)-\mathfrak{f}({\eta }_1+1,{\eta }_2)+\mathfrak{f}(2,{\eta }_1)-\mathfrak{f}(1,{\eta }_1+1)>0$ for ${\eta }_1,{\eta }_2\in \{2,3,4\}$;

(x).

$min\left\{\right(2\eta -3\left)\mathfrak{f}\right(2,2)+4\mathfrak{f}(2,3)+\mathfrak{f}(3,3),2(\eta -2\left)\mathfrak{f}\right(2,2)+6\mathfrak{f}(2,3),2(\eta -1\left)\mathfrak{f}\right(2,2)+$$4\mathfrak{f}(2,4)\}>2\mathfrak{f}(\eta +3,1)+(\eta +1\left)\mathfrak{f}\right(\eta +3,2)+(\eta -3\left)\mathfrak{f}\right(1,2)+2\mathfrak{f}(2,2)$ for $\eta \ge 3$;

(xi).

The function Ψ, defined as $\Psi ({\eta }_1,{\eta }_2)=\mathfrak{f}({\eta }_2-1,1)+{\eta }_1[\mathfrak{f}({\eta }_2,1)-\mathfrak{f}({\eta }_2-1,1)]+({\eta }_2-{\eta }_1)\left(\mathfrak{f}({\eta }_2,2)-\mathfrak{f}({\eta }_2-1,2)\right)$, is strictly decreasing in ${\eta }_2$ for ${\eta }_2\ge {\eta }_1+1\ge 2$.

If G is an $(n+1)$-size bicyclic graph having a matching number $\nu (\ge 3)$, then

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\ge (n-2\nu +1)\mathfrak{f}(n-\nu +2,1)+(\nu +1)\mathfrak{f}(n-\nu +2,2)+(\nu -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2),$$

with equality iff $G\cong B_{n,\nu }$ (see Figure 2).

We verified all the conditions in Theorem 5 for the functions corresponding to the SO, AG, RSO, SDD, ES, and MSDD indices (see the paragraph right before Corollary 1 for the definitions of these indices), and hence we have the next result (which follows from Theorem 5).

Corollary 2.

Let ${\mathcal{BID}}_{\mathfrak{f}}$ be the SO index, or the AG index, or the MSDD index, or the RSO index, or the SDD index, or the ES index. If G is an $(n+1)$-size bicyclic graph having a matching number $\nu (\ge 3)$, then

$${\mathcal{BID}}_{\mathfrak{f}}\left(G\right)\le (n-2\nu +1)\mathfrak{f}(n-\nu +2,1)+(\nu +1)\mathfrak{f}(n-\nu +2,2)+(\nu -3)\mathfrak{f}(1,2)+2\mathfrak{f}(2,2),$$

with equality iff $G\cong B_{n,\nu }$ (see Figure 2).

We end this paper with the remark given below.

Remark 1.

We remark that most of our primary results might have their constraints simpler without affecting their conclusions and without making any considerable changes in their proofs. For example, in the statement of Theorem 5, the addition of the assumption that “the function $\mathfrak{f}$ is strictly increasing” may simplify its several conditions without affecting the theorem’s conclusion. However, the assumption that “the function $\mathfrak{f}$ is strictly increasing” is not satisfied by the AG index, for instance. Because of these kinds of observations, we did not simplify the existing conditions of our results. Nevertheless, it would be nice to either reduce the number of conditions given in our results (without affecting their conclusions) or modify those conditions in such a way that the resulting statements of these results cover additional BID indices (in addition to the ones mentioned in Corollary 2).