Brauer Configuration Algebras Induced by Integer Partitions and Their Applications in the Theory of Branched Coverings

Abstract

Brauer configuration algebras are path algebras induced by appropriated multiset systems. Since their structures underlie combinatorial data, the general description of some of their algebraic invariants (e.g., their dimensions or the dimensions of their centers) is a hard problem. Integer partitions and compositions of a given integer number are examples of multiset systems which can be used to define Brauer configuration algebras. This paper gives formulas for the dimensions of Brauer configuration algebras (and their centers) induced by some integer partitions. As an application of these results, we give examples of Brauer configurations, which can be realized as branch data of suitable branched coverings over different surfaces.

1. Introduction

Green and Schroll [1] introduced Brauer configuration algebras to investigate algebras of the wild representation type. These algebras are generalizations of some biserial algebras introduced previously by them, named Brauer graph algebras [2]. Afterward, Espinosa [3] used Brauer configuration algebras to obtain applications in different fields of science and mathematics.

In particular, Espinosa [3] introduced the notion of the message of a Brauer configuration. He used this concept to give formulas for the number of perfect matchings of some snake graphs or to describe the determinant of a given matrix as the specialized message of a Brauer configuration.

The study of the algebraic invariants associated with Brauer configuration algebras gives rise to the so-called Brauer analysis or Brauer data analysis [4]. It was used to describe the dimensions of Brauer configuration algebras induced by special settings designed by Zeilinger et al. [5] to model some quantum entangled states. In [4], Brauer analysis is also applied to some real-world network architecture models.

Brauer analysis was extended and applied by Cañadas et al. [6] to define Dynkin functions introduced previously by Ringel [7] to study algebraic invariants of Dynkin algebras, i.e., path algebras defined by Dynkin diagrams of the types ${\mathbb{A}}_n,{\mathbb{B}}_n,{\mathbb{C}}_n,{\mathbb{D}}_n,{\mathbb{E}}_6,{\mathbb{E}}_7,{\mathbb{E}}_8,{\mathbb{F}}_4$, and ${\mathbb{G}}_2$.

A relationship between Brauer configuration algebras and the theory of branched coverings arises from the fact that any branched covering of a degree of an integer d between closed surfaces determines a collection $\mathfrak{D}$ (branch data) of integer partitions of d.

This paper gives examples of a question (the realizability problem) proposed by Edmonds et al. [8], which asks for conditions for a collection of integer partitions $\mathfrak{D}$ to be realized as branch data of a suitable branched covering. This problem goes back to Hurwitz [9], who introduced the well-known Hurwitz necessary condition for the realization of branch data.

Gonçalves et al. [10] studied the problem from a purely algebraic point of view, an approach that has been intensively studied in the last few years. For instance, in [11], it was proven that an indecomposable primitive branched covering on a connected closed surface N with Euler characteristic $\chi \left(N\right)\le 0$ realizes any branch data, and their decomposability property was studied in [12]. Similarly, characterizations of primitive branched coverings with minimal defects over the projective plane have been explored in [13].

It is worth noting that finding formulas for the dimensions of Brauer configuration algebras induced by particular subsets of partitions of an integer n is an open problem. For instance, to date, there is no known formula for the dimension of a Brauer configuration algebra induced by the set of binary partitions of an integer n (i.e., partitions of n into parts of the form $2^j$, $j\ge 0$). An additional invariant associated with the proposed Brauer analysis is the defect of subsets of partitions defined by a suitable branched covering. Computing this defect allows for a straight connection between Brauer configuration algebras and the theory of branched coverings.

This paper gives formulas for the dimensions of Brauer configuration algebras induced by some restricted integer partitions and compositions (according to Andrews [14], integer compositions are partitions for which the order of the parts matters). In particular, Brauer analysis is applied to some subsets of binary compositions.

Contributions

This paper defines Brauer configuration algebras induced by integer partitions and compositions describing their Brauer quivers, dimensions, and centers. The analysis of these invariants is said to be a Brauer data analysis. This analysis allows for classifying integer partitions as branch data of suitable branched coverings over the projective plane $\mathbb{R}{P}^2$ and the sphere $S^2$.

The main results of this paper are Theorems 5–12 and Corollary 2.

Theorems 5, 7, 8 and 10 and Corollary 2 are devoted to giving formulas for the dimensions of Brauer configuration algebras induced by several kinds of integer partitions and compositions.

Theorems 6, 9, 11 and 12 give criteria for restricted integer compositions to be realizable as branched data over the projective plane $\mathbb{R}{P}^2$ or the sphere $S^2$.

The organization of this paper is as follows: the background, main definitions, and notations are given in Section 2; we remind the reader of the definitions of multisets (Section 2.4), integer partitions, compositions (Section 2.2), and Brauer configuration algebras (Section Brauer Configuration Algebras). We present the main results in Section 3. The concluding remarks are given in Section 4.

2. Preliminaries

In this section, we describe the developments in the research of the realization problem and basic definitions and notations regarding integer partitions, compositions, multisets, and Brauer configuration algebras.

2.1. Background

Green and Schroll [1] introduced Brauer configuration algebras to study algebras of the wild representation type. They gave some of their main properties, which describe algebraic invariants, such as their dimensions, the structure of the corresponding indecomposable projective modules, and their Jacobson radicals. Afterward, Sierra [15] found a formula for the dimension of the Brauer configuration algebras centers.

Espinosa [3] defined an appropriate message (Brauer message) induced by a Brauer configuration and used it to give alternative formulas for the number of perfect matchings of snake graphs. These ideas allowed Cañadas et al. [16,17,18,19,20] to obtain applications of the Brauer configuration algebras theory in different fields of mathematics and sciences. For example, they used Brauer messages to study the trace norm of some $\{0,1\}$-matrices [16] or implement some cybersecurity applications [17]. In [18], the structure of Brauer configuration algebras is used to design Human Interaction Proofs (HIPs), whose development allows for the construction of CAPTCHAs (Completely Automated Public Turing Test to Tell Computers and Humans Apart). In [19], mutations of Brauer configuration algebras were introduced for cryptanalysis of the Advanced Encryption Standard (AES), a well-known tool for enabling Wi-Fi security. In [20], the authors used Brauer messages to describe set-theoretical solutions of the Yang–Baxter equation.

Brauer configuration algebra theory embraces the hypergraph theory used recently to model cyber network data. These structures can be used to analyze data using techniques similar to those presented in topological data analysis [21].

The analysis of algebraic invariants associated with Brauer configuration algebras is said to be a Brauer analysis of the data given by the multisets inducing such algebras [4]. This analysis was extended by adding tools such as the covering graph and some graph degree-based entropies [6].

According to Edmonds et al. [8], if M and N denote closed connected surfaces, then a smooth map $\varphi :M\to N$ is a degree d branched covering if for each $x\in N$, there is a partition $L\left(x\right)=\{a_1,a_2,\dots ,a_r\}$ of d such that over a neighborhood of x in N, $\varphi$ is equivalent to the map $f:\{1,2,\dots ,r\}\times \mathbb{C}\to \mathbb{C}$ where $f(i,z)=z^{a_i}$ and x corresponds to 0 in $\mathbb{C}$. The set of points $x\in N$ for which $L\left(x\right)$ is not the trivial partition $\{1,1,\dots ,1\}$ of d constitutes the branch set $B_{\varphi }$ of $\varphi$. The collection $\mathfrak{D}=\{L\left(x\right)\mid x\in B_{\varphi }\}$ is called the branch data of $\varphi$ (repetitions allowed).

Edmonds et al. [8] proposed the following problem called the realizability problem:

Given a closed, connected surface N and a collection $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$ of partitions of a positive integer d, is there a branched covering $\varphi :M\to N$ with $\mathfrak{D}$ as its branch data?

The problem goes back to Hurwitz [9], who reformulated the question to one regarding integer partitions. In fact, there are well-known necessary conditions based on the Riemann–Hurwitz formula:

If $\varphi :M\to N$ is a degree d branched covering of closed, connected surfaces with branch data $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$, then the total branching or defect $\nu \left(\varphi \right)={\displaystyle \sum _{j=1}^m}\nu \left(L_j\right)=md-{\displaystyle \sum _{j=1}^m}{r}_j$ of the branched covering is even; where $L_j=\{{\lambda }_{j,1},{\lambda }_{j,2},\dots ,{\lambda }_{j,r_j}\}\in \mathfrak{D}$ is a partition of d and for each $1\le j\le m$, it holds that $\nu \left(L_j\right)=d\chi \left(N\right)-\chi \left(M\right)=d-r_j={\displaystyle \sum _{i=1}^{r_j}}({\lambda }_{j,i}-1)$.

Gonçalves et al. [10,11,12,13] also studied the realizability problem. In [10], the authors followed the Hurwitz approach to study the problem of primitive branched coverings. In particular, they studied the problem of the torus and the Klein bottle. In [11], it is proven that any branch data set can be realized by an indecomposable primitive branched covering over a closed surface S with Euler characteristic $\chi \left(S\right)\le 0$. In [12], the decomposability property of a branched covering over the projective plane with a covering surface having Euler characteristic zero was studied. In [13], the authors characterized primitive branched coverings with minimal defects over the projective plane with respect to the decomposability property of primitive branched coverings.

This paper applies Brauer analysis to some integer partitions and compositions. Such an analysis allows formulas for the dimensions of the corresponding Brauer configuration algebras. As an application, we present Brauer configurations as examples of branch data of some branched coverings.

2.2. Integer Partitions and Compositions

This section reminds the reader of the notation, definitions, and facts regarding integer partitions and compositions and their enumeration. The authors refer to [14,22] for more insights regarding these subjects.

An integer partition $\lambda$ of a positive integer n is a nonincreasing sequence of positive integers $\lambda =\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r\}$ such that $n={\displaystyle \sum _{i=1}^r}{\lambda }_i$. $p\left(n\right)$ denotes the number of partitions of an integer n. If $n=0$, it is considered that $\lambda =⌀$ and $p\left(0\right)=1$, $p\left(n\right)=0$, if $n<0$ [14]. If $\mathcal{S}$ denotes the set of all partitions, then $p(S;n)$ denotes the number of partitions of n that belong to a subset S of $\mathcal{S}$ [14].

Elements ${\lambda }_i\in \lambda$ are said to be parts of the partition. Particularly, if $\lambda =\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r\}$ is a partition of n, then we write $\lambda ⊢n$. Sometimes, it is possible to write

$$\lambda =(1^{f_1}{2}^{f_2}\dots )$$

(1)

to specify the number of times $f_i$ that a given part ${\lambda }_i$ occurs in $\lambda$, in such a way that $n={\displaystyle \sum _{i\ge 1}}i{f}_i$.

If the order of the parts matters, then a partition $\lambda$ is said to be a composition [14,22]. For example, $\left\{\right\{3\},\{2,1\},\{1,1,1\left\}\right\}$ are partitions of 3, whereas $\left\{\right\{3\},\{2,1\},\{1,2\},\{1,1,1\left\}\right\}$ are its compositions.

Hardy, Ramanujan, and Rademacher (see [14], Theorem 5.1, and [23] Theorem (1.71)) gave the following formula for $p\left(n\right)$:

$$p\left(n\right)={\displaystyle \frac{1}{\pi \sqrt{2}}}{\displaystyle \sum _{j=1}^{\infty }}{A}_j\left(n\right)j^{1/2}{[{\displaystyle \frac{d}{dx}}{\displaystyle \frac{sinh((\pi /j){\left(\frac{2}{3}(x-1/24)\right)}^{1/2}}{{(x-1/24)}^{1/2}}}]}_{x=n},$$

(2)

where

$$A_j\left(n\right)=\sum _{\underset{(h,j)=1}{hmodj}}{w}_{h,j}{e}^{-2\pi inh/j}$$

(3)

where with $w_{h,j}$, there is a certain 24th root of unity.

For instance, the number of partitions of n into, at most, two parts is $p\left(\right\{1,2\},n)=[n/2]+1$ and the number of partitions of n into, at most, three parts is $p(\{1,2,3\},n)=\{1/12{(n+3)}^2\}$, where $\left[x\right]$ is the largest integer not exceeding x ($\left\{x\right\}$ the nearest integer to x). In particular, there are $2^{n-1}$ compositions of n [14].

The following formula gives $c_j(m,n)$ the number of compositions of n into exactly m parts, each $\ge j$.

$$c_j(m,n)=\left({\displaystyle \genfrac{}{}{0pt}{}{n-(j-1)m-1}{m-1}}\right).$$

(4)

Particularly, the number of compositions of n, $c(m,n)$ with exactly m parts is given by the following formula:

$$c(m,n)=\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{m-1}}\right).$$

(5)

According to Andrews [14], Meinardus gave the following asymptotic formula for $p\left(n\right)$, which includes numerous partition formulas.

$$p\left(n\right)\sim {\displaystyle \frac{1}{4n\sqrt{3}}}{e}^{\pi {(\frac{2}{3})}^{1/2}{n}^{1/2}}.$$

(6)

The following result is known as the Elder’s theorem [24]:

Theorem 1

([24] Result 2, [25] Corollary 2). The total number of occurrences of an integer j among all unordered partitions of n equals the number of occasions that a part occurs j or more times in a partition.

We let ${\mathcal{Q}}_j\left(n\right)$ denote the number of occurrences of the part j in all partitions of n. $S\left(n\right)={\mathcal{Q}}_1\left(n\right)$ denotes the sum of distinct numbers in the partitions of n [24].

We note that

$${\mathcal{Q}}_j\left(n\right)={\mathcal{Q}}_j(n-j)+p(n-j).$$

(7)

The generating function $G_j\left(x\right)$ of ${\mathcal{Q}}_j\left(n\right)$ is given by the following identity [24]:

$$G_j\left(x\right)={\displaystyle \sum _{m=0}^{\infty }}{\mathcal{Q}}_j\left(m\right)x^m={\displaystyle \frac{x^j}{1-x^j}}{\displaystyle \prod _{n=1}^{\infty }}{\displaystyle \frac{1}{1-x^n}}.$$

(8)

Let $p(m_1,m_2;n)$ be the number of partitions of n into, at most, $m_2$ parts, each $\le m_1$, and $inv(m_1,m_2;n)$ the number of permutations ${\psi }_{m_1}{\psi }_{m_2}\dots {\psi }_{m_1+m_2}$ of $\left\{1^{m_1}{2}^{m_2}\right\}$ in which there are exactly n pairs $({\psi }_i,{\psi }_j)$ such that $i<j$ and ${\psi }_i>{\psi }_j$ [14].

The following result holds:

Theorem 2

([14] Theorem 3.5). $inv(m_1,m_2;n)=p(m_1,m_2;n)$.

As an example, we note that the sequence 111211221111122122 corresponds to the partition $8+6+6+1+1$ of type $p(11,7;22)$, where the number of 1s after the first 2 tells us the first part of the partition, the number of 1s after the second 2 tells us the second part of the partition, and so on.

Cañadas et al. [26] defined integer compositions of type $\mathcal{O}\left(\right(r,s),(n,n);1)$ of an integer m with $m={\mathcal{O}}_n+{\mathcal{O}}_n+1={\mathcal{O}}_{nn1}$ and $1\le r\le s\le n$. In such a case, ${\mathcal{O}}_h=\frac{h(2h^2+1)}{3}$ is the hth octahedral number, $h\ge 1$.

A composition of type $\mathcal{O}\left(\right(r,s),(n,n);1)$ satisfies the following conditions:

• $z_0={\mathcal{O}}_{111}=3$.
• $$\begin{array}{cc}\hfill m& ={\mathcal{O}}_{rs1}+z_1+\cdots +z_t\hfill \end{array}$$

  (9)

  where $1\le r\le s\le n$; $z_i=h^2+{(h+1)}^2$, for some positive integer h.
• The ith partial sum $s_i$ is of the form ${\mathcal{O}}_{pq1}$, $1\le p\le q\le n$, with $s_1=z_0$. Furthermore, if $s_i={\mathcal{O}}_{pq1}$, then $s_{i+1}$ is either ${\mathcal{O}}_{(p+1)q1}$ or ${\mathcal{O}}_{p(q+1)1}$ ($s_2={\mathcal{O}}_{121}=8$).
• ${\mathcal{O}}_{nn1}$ is a trivial composition of m.

Example 1.

As an example, the following are the compositions of type $\mathcal{O}\left(\right(r,s),(3,3);1)$ of $39={\mathcal{O}}_{331}={\mathcal{O}}_3+{\mathcal{O}}_3+1$:

39,

$13+2^2+3^2+2^2+3^2$,

$26+2^2+3^2$,

$21+1^2+2^2+2^2+3^2$,

$8+2^2+3^2+1^2+2^2+2^2+3^2$,

$8+1^2+2^2+2^2+3^2+2^2+3^2$,

$3+1^2+2^2+1^2+2^2+2^2+3^2+2^2+3^2$,

$3+1^2+2^2+2^2+3^2+1^2+2^2+2^2+3^2$.

2.3. Branched Coverings of the Sphere and the Projective Plane

This section reminds the reader of the criteria for a branched datum to be realizable over connected surfaces such as the sphere and the projective plane.

Theorem 3

([8], Theorem 5.1). Let $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$ be a collection of partitions of a positive integer d. Then, there is a branched covering $M\to \mathbb{R}{P}^2$ of degree d, with M connected, and with branch data $\mathfrak{D}$ if and only if ${\displaystyle \sum _{i=1}^m}\nu \left(L_i\right)\ge d-1$ and ${\displaystyle \sum _{i=1}^m}\nu \left(L_i\right)$ is even. Moreover, M can be chosen to be nonorientable.

According to Desmond et al. [8], a collection $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$ of partitions of d is said to be realizable if $\mathfrak{D}$ arises as the branch data of a connected branched covering of $S^2$. They proved the following results (Propositions 1 and 2, Theorem 4, and Corollary 1) regarding these types of coverings.

Proposition 1

([8], Proposition 5.2). A collection $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$ of partitions of d, with some $L_i=\left\{d\right\}$ is realizable if and only if $\nu \left(\mathfrak{D}\right)\ge 2d-2$ and $\nu \left(\mathfrak{D}\right)\equiv 0mod2$.

Proposition 2

([8], Proposition 5.3). A collection $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$ of partitions of d, with some $L_i=\{d-1,1\}$, is realizable if and only if $\nu \left(\mathfrak{D}\right)\ge 2d-2$, $\nu \left(\mathfrak{D}\right)\equiv 0mod2$ and $\mathfrak{D}$ is not

1. 

$\mathfrak{D}=\{2,2\},\dots ,\{2,2\},\{3,1\}$ ($d=4$, $m\ge 3$);

2. 

$\mathfrak{D}=\{2,\dots ,2\},\{2,\dots ,2\},\{d-1,1\}$ ($d=2r$, $m=3$).

Theorem 4

([8], Theorem 5.4). A collection $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$ of partitions of $d\ge 2$, $d\ne 4$, is realizable provided $\nu \left(\mathfrak{D}\right)\ge 3(d-1)$ and $\nu \left(\mathfrak{D}\right)\equiv 0mod2$.

Corollary 1

([8], Corollary 6.4). If $d=2r$, then the data {{x, 2r − x}, {2,…, 2}, {2,…, 2} } with $x\le r$ are realizable as the branch data for a connected branched covering of $S^2$ if and only if $x=r$.

Table 1 shows the examples given by Desmond et al. [8] of realizable branch data described by Corollary 1.

Table 1. Examples of realizable branch data given by Corollary 1.

Degree	Data
9	$\{4,4,1\}$	$\{3,3,3\}$	$\{2,2,2,2,1\}$
9	$\{3,3,3\}$	$\{3,3,3\}$	$\{2,2,2,2,1\}$
10	$\{4,4,2\}$	$\{3,3,3,1\}$	$\{2,2,2,2,2\}$
16	$\{5,5,5,1\}$	$\{3,3,3,3,3,1\}$	$\{2,2,2,2,2,2,2,2\}$
16	$\{4,4,4,4\}$	$\{3,3,3,3,3,1\}$	$\{2,2,2,2,2,2,2,2\}$
18	$\{4,4,4,4,2\}$	$\{3,3,3,3,3,3\}$	$\{2,2,2,2,2,2,2,2,2\}$
21	$\{5,5,5,5,1\}$	$\{3,3,3,3,3,3,3\}$	$\{2,2,2,2,2,2,2,2,2,2,1\}$
25	$\{5,5,5,5,5\}$	$\{3,3,3,3,3,3,3,3,1\}$	$\{2,2,2,2,2,2,2,2,2,2,2,2,1\}$
36	$\{5,5,\dots ,5,1\}$	$\{3,3,\dots ,3,3\}$	$\{2,2,\dots ,2,2\}$
40	$\{5,5,\dots ,5,5\}$	$\{3,3,\dots ,3,1\}$	$\{2,2,\dots ,2,2\}$
45	$\{5,5,\dots ,5,5\}$	$\{3,3,\dots ,3,3\}$	$\{2,2,\dots ,2,1\}$

2.4. Multisets

In this section, we recall the basic definitions associated with multisets. For more details about them, their messages, and their operations, we refer the interested reader to [3,14,22,27].

Intuitively, a multiset is a set with repeated elements. Formally speaking, a finite multiset M on a set S is a function $\mathfrak{f}:S\to \mathbb{N}$ such that ${\displaystyle \sum _{x\in S}}\mathfrak{f}\left(x\right)<\infty$. One regards $\mathfrak{f}\left(x\right)$ as the number of repetitions of x [22]. Thus, integer partitions and compositions are examples of multisets.

The integer ${\displaystyle \sum _{x\in S}}\mathfrak{f}\left(x\right)$ is called the cardinality or number of elements of M and is denoted as $\left|M\right|$, $\#M$ or $\mathrm{card}M$. This paper assumes that $\left|M\right|>1$ for any multiset M.

If $S=\{m_1,m_2,\dots ,m_s\}$ and $\mathfrak{f}\left(m_i\right)=f_i$, then we write $M=\{m_1^{f_1},m_2^{f_2},\dots ,m_s^{f_s}\}$ [22].

Andrews [14] gives an alternative definition of a multiset. According to him, a multiset is an ordered pair $(M,\mathfrak{f})$ where M is a set and $\mathfrak{f}$ is a function from M to the non-negative integers $\mathbb{N}$.

For each $m\in M$, $\mathfrak{f}\left(m\right)$ would be called the multiplicity of m. When M is a finite set, a multiset $(M=\{m_1,m_2,\dots ,m_s\},\mathfrak{f})$ can be written as a word w whose letters are the elements of M with letter occurrences given by the map $\mathfrak{f}$. In this paper, we assume that words associated with multisets have the following form:

$$w\left(M\right)=m_1^{\mathfrak{f}\left(m_1\right)}{m}_2^{\mathfrak{f}\left(m_2\right)}\dots m_s^{\mathfrak{f}\left(m_s\right)}.$$

(10)

Let $\mathcal{M}=\{M_1,M_2,\dots ,M_h\}$ be a collection of nonempty finite sets, $M={\displaystyle \bigcup _{i=1}^h}{M}_i$, and $\mathcal{M}=\{(M_1,{\mathfrak{f}}_1),(M_2,{\mathfrak{f}}_2),\dots ,(M_h,{\mathfrak{f}}_h)\}$ be a collection of multisets defined by the collection $\mathcal{M}$. Then, the valency $val\left(y\right)$ of an element $y\in M$ is given by the following identity [1]:

$$val\left(y\right)={\displaystyle \sum _{i=1}^h}{\mathfrak{f}}_i\left(y\right).$$

(11)

If $y\in M$, then we let ${\mathfrak{I}}_y$ denote the set of all the multisets $(M_i,{\mathfrak{f}}_i)\in \mathcal{M}$ with $y\in M_i$. In other words, ${\mathfrak{I}}_y=\{(M_i,{\mathfrak{f}}_i)\in \mathcal{M}\mid y\in M_i\}$.

The collection of multisets $\mathcal{M}$ as described above is said to be a multiset system of type M, if it is endowed with a map $\kappa :M\to {\mathbb{N}}^{+}\times {\mathbb{N}}^{+}$ such that $\kappa \left(m\right)=(j_m,val\left(m\right))$ for each $m\in M$. And for any $y\in M$, the set ${\mathfrak{I}}_y$ is endowed with a linear order <.

The elements of M are named vertices by Green and Schroll [1]. The integer $j_m>0$ in a pair $(j_m,val\left(m\right))$ associated with a vertex m corresponds to the multiplicity value $\mu \left(m\right)$ in their work. Note that $\mu \left(m\right)$ does not say anything about the multiplicity of m as an element of a multiset. A vertex $m\in M$ is nontruncated (truncated) if $\mu \left(m\right)val\left(m\right)>1$ ($\mu \left(m\right)val\left(m\right)=1$). Therefore, the multiplicity function $\mu$ permits us to classify the set of vertices M into the set of truncated and nontruncated vertices. In this paper, if $val\left(m\right)=1$, then $\mu \left(m\right)=j_m=2$, otherwise, $\mu \left(m\right)=j_m=1$. Thus, the considered vertices are nontruncated [6].

Each $(M_i,{\mathfrak{f}}_i)\in {\mathfrak{I}}_y$ has an expansion ${\mathfrak{M}}_{i,y}$ of the following form:

$${\mathfrak{M}}_{i,y}=M_i^{\left(1\right)}<M_i^{\left(2\right)}<\cdots <M_i^{\left({\mathfrak{f}}_i\left(y\right)\right)}.$$

(12)

Note that, if $(M_i,{\mathfrak{f}}_i)<(M_{i+1},{\mathfrak{f}}_{i+1})$ is a covering in ${\mathfrak{I}}_y$, then the following identity holds:

$${\mathfrak{M}}_{i,y}<{\mathfrak{M}}_{i+1,y}=M_i^{\left(1\right)}<\cdots <M_i^{{\mathfrak{f}}_i\left(y\right)}<M_{i+1}^{\left(1\right)}<\cdots <M_{i+1}^{\left({\mathfrak{f}}_{i+1}\left(y\right)\right)}.$$

(13)

Since $({\mathfrak{I}}_y,<)$ is a well-ordered set each element $M_i^{\left(r\right)}\in {\mathfrak{I}}_y$ has a unique successor $Suc\left(M_i^{\left(r\right)}\right)$ and the following identities hold:

$$\begin{array}{cc}\hfill Suc(M_i^{\left(r\right)})& =M_i^{(r+1)},\mathrm{if}r<{\mathfrak{f}}_i\left(y\right),\hfill \\ \hfill Suc(M_j^{\left({\mathfrak{f}}_j\left(y\right)\right)})& =M_{j+1}^{\left(1\right)},\mathrm{if}j<\left|{\mathfrak{I}}_y\right|.\hfill \end{array}$$

(14)

For each $y\in M$, the chain $S_y=({\mathfrak{I}}_y,<)$ can be written as follows:

$$\begin{array}{cc}\hfill & {\mathfrak{M}}_{1,y}<{\mathfrak{M}}_{2,y}<\cdots <{\mathfrak{M}}_{|{\mathfrak{I}}_y|,y}=\hfill \\ \hfill & M_1^{\left(1\right)}<\cdots <M_1^{\left({\mathfrak{f}}_1\left(y\right)\right)}<M_2^{\left(1\right)}<\cdots <M_{|{\mathfrak{I}}_y|}^{\left(1\right)}<\cdots <M_{|{\mathfrak{I}}_y|}^{({\mathfrak{f}}_{|{\mathfrak{I}}_y|}\left(y\right))}.\hfill \end{array}$$

(15)

${\mathfrak{M}}_{1,y}<{\mathfrak{M}}_{2,y}<\cdots <{\mathfrak{M}}_{|{\mathfrak{I}}_y|,y}$ is said to be the compressed successor sequence at vertex y and $M_1^{\left(1\right)}<\cdots <M_1^{\left({\mathfrak{f}}_1\left(y\right)\right)}<M_2^{\left(1\right)}<\cdots <M_{|{\mathfrak{I}}_y|}^{\left(1\right)}<\cdots <M_{|{\mathfrak{I}}_y|}^{\left({\mathfrak{f}}_{|{\mathfrak{I}}_y|}\left(y\right)\right)}$ is the successor sequence at vertex y. Note that $|S_y|=val\left(y\right)$.

Each successor sequence of type $({\mathfrak{I}}_y,<)$ induces a circular ordering by adding a relation of the form $M_{|{\mathfrak{I}}_y|}^{({\mathfrak{f}}_{|{\mathfrak{I}}_y|}\left(y\right))}<M_1^{\left(1\right)}$. In such a case, $Suc(M_{|{\mathfrak{I}}_y|}^{({\mathfrak{f}}_{|{\mathfrak{I}}_y|}\left(y\right))})=M_1^{\left(1\right)}$.

This paper assumes that if $y\in M$ and ${\mathfrak{I}}_y=\{(M_{i_1},{\mathfrak{f}}_{i_1}),(M_{i_2},{\mathfrak{f}}_{i_2}),\dots (M_{i_n},{\mathfrak{f}}_{i_n})\}$, $\{i_1,i_2,\dots ,i_n\}\subseteq \{1,2,\dots ,n\}$ and $i_1<i_2<\cdots <i_n$ with the usual order of the natural numbers, then $S_y={\mathfrak{M}}_{i_1,y}<{\mathfrak{M}}_{i_2,y}<\cdots <{\mathfrak{M}}_{i_n,y}$.

Example 2.

As an example, let us consider the following partitions of 10 as branch data over $S^2$ given in Table 1. Where

$$\begin{array}{cc}\hfill L_1& =\left(4^{\left(2\right)}{2}^{\left(1\right)}\right),\hfill \\ \hfill L_2& =\left(3^{\left(3\right)}{1}^{\left(1\right)}\right),\hfill \\ \hfill L_3& =\left(2^{\left(5\right)}\right),\hfill \\ \hfill L_1\cap L_3& =\left\{2\right\},L_i\cap L_j=⌀\mathit{for}\mathit{the}\mathit{remaining}\mathit{cases}.\hfill \end{array}$$

(16)

Vertices $i\in M$ are nontruncated in this case. Note that the successor sequences $S_i$ associated with the set $M=\{1,2,3,4\}$ are

$$\begin{array}{cc}\hfill S_1& =L_2^{\left(1\right)}=L_2,\hfill \\ \hfill S_2& =L_1^{\left(1\right)}<L_3^{\left(1\right)}<L_3^{\left(2\right)}<L_3^{\left(3\right)}<L_3^{\left(4\right)}<L_3^{\left(5\right)},\hfill \\ \hfill S_3& =L_2^{\left(1\right)}<L_2^{\left(2\right)}<L_2^{\left(3\right)},\hfill \\ \hfill S_4& =L_1^{\left(1\right)}<L_1^{\left(2\right)}.\hfill \end{array}$$

(17)

Furthermore,

$$\begin{array}{cc}\hfill val\left(1\right)& =1,val\left(2\right)=6,val\left(3\right)=3,val\left(4\right)=2,\hfill \\ \hfill \mu \left(1\right)& =2,\mu \left(i\right)=1,\mathrm{for}i\in \{2,3,4\}.\hfill \end{array}$$

(18)

Brauer Configuration Algebras

In this section, we recall the basic definitions and notation of the Brauer configurations and their induced Brauer configuration algebras. See [1,2,3,4] for more details on those topics.

Following Green and Schroll [1], a Brauer configuration is a combinatorial data $\Gamma =({\Gamma }_0,{\Gamma }_1,\mu ,\mathcal{O})$, with ${\Gamma }_0$ being the (finite) set of vertices of $\Gamma$; ${\Gamma }_1$ is a finite collection of finite labeled multisets; the polygons, whose elements are in ${\Gamma }_0$, $\mu :{\Gamma }_0\to {\mathbb{N}}^{+}$ is a map known as the multiplicity function; and $\mathcal{O}$ is an orientation for $\Gamma$. In this case, every vertex in ${\Gamma }_0$ is a vertex in at least one polygon, and every polygon in ${\Gamma }_1$ has at least two vertices. Every polygon in ${\Gamma }_1$ has at least one nontruncated vertex $\alpha$ with the condition that $val\left(\alpha \right)\mu \left(\alpha \right)>1$. The role of the function $\mu$ was already described.

An orientation $\mathcal{O}$ for $\Gamma$ is a selection for each vertex $\alpha \in {\Gamma }_0$ of a cycling ordering of the polygons in which $\alpha$ is a vertex, including repetitions. In such a case, if $\alpha$ occurs in polygons or multisets of the form $(U_1,{\mathfrak{h}}_1),\dots ,(U_m,{\mathfrak{h}}_m)$, then the polygon $(U_i,{\mathfrak{h}}_i)$ occurs ${\mathfrak{h}}_i\left(\alpha \right)$ times in the list. The cyclic order at vertex $\alpha$ is obtained by linearly ordering the list, say $(U_{i_1},{\mathfrak{h}}_{i_1})<(U_{i_2},{\mathfrak{h}}_{i_2})<\cdots <(U_{i_m},{\mathfrak{h}}_{i_m})$, and by adding the relation $(U_{i_m},{\mathfrak{h}}_{i_m})<(U_{i_1},{\mathfrak{h}}_{i_1})$, $m=val\left(\alpha \right)$.

As stated by Green and Schroll [1], the cyclic ordered list of polygons $(U_1,{\mathfrak{h}}_1),\dots ,(U_m,{\mathfrak{h}}_m)$ or just $U_1,U_2,\dots ,U_m$ is the succesor sequence at α. In that case, if $U_1<U_2<\cdots <U_m$ is the successor sequence at a nontruncated vertex $\alpha$ such that $val\left(\alpha \right)=m$, then $U_{i+1}$ is the successor of $U_i$ at $\alpha$, for $1\le i\le m$, with $U_{m+1}=U_1$. For a vertex $\alpha$ in a polygon U such that $val\left(\alpha \right)=1$, the successor sequence at $\alpha$ is U.

The concepts defined in this section let us conclude that multiset systems of type M are Brauer configurations, known as Brauer configurations of type M (or Brauer configurations, for simplicity), with vertices given by a set $M={\displaystyle \bigcup _{i=1}^m}{M}_i$ and $\{(M_1,{\mathfrak{h}}_1),\dots ,(M_m,{\mathfrak{h}}_m)\}$ being the set of polygons. The multiplicity function $\mu$ is given by the first coordinate of the function $\kappa$ (see Section 2.4). In this case, the orientation is provided by successor sequences (15).

Given that the function $\kappa$ associated with multiset systems of type M includes the multiplicity function $\mu$, we can accept the notation (19) for this type of configuration.

$$\mathcal{M}=(M,{\mathcal{M}}_1,\mu ,\mathcal{O}).$$

(19)

The message or Brauer message $M\left(\mathcal{M}\right)$ of a Brauer configuration is the concatenation of the fixed words $w\left(M_i\right)$ [3], i.e.,

$$M\left(\mathcal{M}\right)=w\left(M_1\right)w\left(M_2\right)\dots w\left(M_h\right).$$

(20)

Remark 1.

This paper assumes that Brauer configurations are all multiset systems of type M with successor sequences defined by Formulas (12)–(15).

Desmond et al. [8] gave the following result where word concatenation is used to characterize branch data of some branched coverings:

Proposition 3

([8] Proposition 2.7). Let d be an even integer, $\mathfrak{D}=\{L_1,L_2,\dots ,L_m\}$, a collection of partitions of d, and N is a closed, connected, nonorientable surface. Then, a necessary and sufficient condition that there exists a degree d branched covering $\varphi :M\to N$ with branch data $\mathfrak{D}$ and M orientable is that for each i, $1\le i\le m$, one can express $L_i$ as a concatenation $L_{i,1}{L}_{i,2}$ of two partitions of $d/2$, such that $\{L_{1,1},L_{2,1},\dots ,L_{m,1},L_{1,2},L_{2,2},\dots ,L_{m,2}\}$ is the branch data of a degree $d/2$ branched covering of the orientable double covering of N.

The Brauer quiver $Q_{\mathcal{M}}=(Q_0,Q_1,s,t)$ (or simply Q) induced by a Brauer configuration $\mathcal{M}=(M,{\mathcal{M}}_1,\mu ,\mathcal{O})$ is obtained through a bijective correspondence between its set of vertices $Q_0$ and the collection of polygons ${\mathcal{M}}_1$. In other words, vertices in a Brauer quiver are given by the multisets in ${\mathcal{M}}_1$. Furthermore, each pair $\left\{\right(M,\mathfrak{f}),Suc((M,\mathfrak{f})\left)\right\}$ in a circular ordering defines an arrow from $(M,\mathfrak{f})$ to $Suc\left(\right(M,\mathfrak{f}\left)\right)$ in $Q_1$. In particular, if $val\left(y\right)>1$, then a covering of the form $(M_i,{\mathfrak{f}}_i)<(M_j,{\mathfrak{f}}_j)\in {\mathfrak{I}}_y$ defines an arrow from $(M_i,{\mathfrak{f}}_i)$ to $(M_j,{\mathfrak{f}}_j)$ in $Q_1$ [1].

Henceforth, if no confusion arises, we will write $\mathcal{M}$ instead of $(\mathcal{M},\mathfrak{f})$ to denote a multiset with multiplicity function $\mathfrak{f}$.

The covering graph or nerve of a Brauer quiver $Q_{\mathcal{M}}$ gotten from a fixed Brauer configuration $\mathcal{M}$ (or the covering graph of a Brauer configuration $\mathcal{M}$) is a graph $\mathfrak{c}\left(Q_{\mathcal{M}}\right)=(V_{\mathfrak{c}\left(Q_{\mathcal{M}}\right)},E_{\mathfrak{c}\left(Q_{\mathcal{M}}\right)})$ with a set of vertices $V_{\mathfrak{c}\left(Q_{\mathcal{M}}\right)}$ consisting of polygons in ${\mathcal{M}}_1$. We define an edge $M_i-M_j\in E_{\mathfrak{c}\left(Q_{\mathcal{M}}\right)}$ to connect the polygons $M_i,M_j\in {\mathcal{M}}_1$ if and only if there exists $y\in M$ and a covering ${\mathfrak{M}}_{i,y}<{\mathfrak{M}}_{j,y}$ at vertex y. Note that $\mathfrak{c}\left(Q_{\mathcal{M}}\right)$ has no multiple edges nor loops. Thus, we write only one edge to represent all the coverings of a given form [6]. Alternative conditions for the vertices and edges of a covering graph are given in (21).

$$\begin{array}{cc}\hfill & V_{\mathfrak{c}\left(Q_{\mathcal{M}}\right)}={\mathcal{M}}_1.\hfill \\ \hfill & {\{M_i,M_j\}}_{i<j}\in E_{\mathfrak{c}\left(Q_{\mathcal{M}}\right)},\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{M}_i^{\left({\mathfrak{f}}_i\left(y\right)\right)}<M_j^{\left(1\right)}\mathrm{is}\mathrm{a}\mathrm{covering}\mathrm{in}\mathrm{a}\mathrm{successor}\mathrm{sequence}\hfill \\ \hfill & \mathrm{at}\mathrm{some}\mathrm{vertex}y\mathrm{with}\mu \left(y\right)=1.\hfill \end{array}$$

(21)

Example 3.

The Brauer configuration ${\mathcal{M}}_{\mathfrak{D}}=(M,{\mathcal{M}}_1,\mu ,\mathcal{O})$ defined by the system of partitions in Example 2 is such that $M=\{1,2,3,4\}$, ${\mathcal{M}}_1=\{L_1,L_2,L_3\}$ with $\mathcal{O}$ and μ given by identities (17) and (18), respectively. Figure 1 shows the Brauer quiver $Q_{\mathcal{M}}$ induced by the Brauer configuration ${\mathcal{M}}_{\mathfrak{D}}$.

Figure 1. Brauer quiver induced by branch data realizable as branched covering of $S^2$. See Example 2, identities (16), and successor sequences (17).

A Brauer configuration $\mathcal{M}=(M,{\mathcal{M}}_1,\mu ,\mathcal{O})$ is said to be reduced if the set M has no truncated vertices. It is connected if the corresponding Brauer quiver is. A Brauer configuration algebra ${\Lambda }_{\mathcal{M}}$ (or simply $\Lambda$, if no confusion arises) is a bound quiver algebra ${\Lambda }_{\mathcal{M}}=k{Q}_{\mathcal{M}}/I_{\mathcal{M}}$ induced by a Brauer quiver $Q_{\mathcal{M}}$ bounded by an admissible ideal $I_{\mathcal{M}}=⟨\rho ⟩$ generated by a set of relations $\rho$ of the following types [1,2]:

$\left({\rho }_1\right)$

$C_i^{\mu \left(i\right)}-C_j^{\mu \left(j\right)}$ if i and j are vertices in the same polygon $M_i$ and $C_x$ is a cycle (starting and ending at $M_i$) defined by an appropriate circular ordering. These cycles are said to be special cycles.

$\left({\rho }_2\right)$

$C_i^{\mu \left(i\right)}a$ if a is the first arrow of a special cycle $C_i$ associated with a vertex i. In particular, $C_i^3\in I_{\mathcal{M}}$ if $val\left(i\right)=1$.

$\left({\rho }_3\right)$

$ab$ if $a,b\in Q_1$ are arrows of different special cycles and $ab$ is an element of the path algebra induced by $Q_{\mathcal{M}}$.

We say that a Brauer configuration algebra is indecomposable (as an algebra) and reduced if it is induced by a connected and reduced Brauer configuration.

Example 4.

As an example, the Brauer configuration algebra ${\Lambda }_{\mathcal{M}}$ induced by the Brauer configuration $\mathcal{M}$ defined in Example 2 by identities (16) and (17) and the Brauer quiver $Q_{\mathcal{M}}$ shown in Figure 1 is bounded by an admissible ideal $I_{\mathcal{M}}$. The following are examples of $I_{\mathcal{M}}$ generators:

1. 

$l_{j_1}^4{l}_{j_2}^4-{\alpha }_1^2{l}_{h_1}^2{l}_{h_2}^2{l}_{h_3}^3{l}_{h_4}^2{\alpha }_3^2$; ${\left(l_1^1\right)}^2-l_{i_1}^3{l}_{i_2}^3{l}_{i_3}^3$, $i_1,i_2,i_3\in \{1,2,3\}$, $j_1,j_2\in \{1,2\}$, $h_1,h_2,h_3,h_4\in \{1,2,3,4\}$.

2. 

${\left(l_1^1\right)}^3$; ${\left(l_j^i\right)}^2$, for all possible values of j if $2\le i\le 4$.

3. 

$l_{j_1}^4{l}_{j_2}^4{l}_{j_1}^4$; ${\alpha }_1^2{l}_{h_1}^2{l}_{h_2}^2{l}_{h_3}^3{l}_{h_4}^4{\alpha }_3^2{\alpha }_1^2$; $l_{i_1}^3{l}_{i_2}^3{l}_{i_3}^3{l}_{i_1}^3$; $l_{h_1}^2{l}_{h_2}^2{l}_{h_3}^3{l}_{h_4}^2{l}_{h_1}^2$.

4. 

$l_{j_1}^4{\alpha }_1^2$; ${\alpha }_3^2{l}_{j_1}^4$; $l_1^1{l}_{i_1}^3$; $l_{i_1}^3{l}_1^1$.

We remind [1] that a multiserial algebra is defined to be a finite-dimensional algebra $\mathcal{A}$ such that, for every indecomposable projective left and right $\mathcal{A}$-module P, the corresponding radical $radP$ is a sum of uniserial modules (an $\mathcal{A}$-module M is said to be uniserial if it has a unique composition series), i.e., $radP={\displaystyle \sum _{j=1}^m}{V}_j$, where for some integer m and uniserial modules $V_j$, it holds that if $i\ne j$, then $V_i\cap V_j$ is either 0 or a simple $\mathcal{A}$-module.

Remark 2.

The following results were found by Green and Schroll [1] and Sierra [15] (see [1] Theorem B, Proposition 2.7, Theorem 3.10, Corollary 3.12, and [15] Theorem 4.9). For all of them, we assume the notation ${\Lambda }_{\mathcal{M}}$ for a Brauer configuration algebra induced by a Brauer configuration $\mathcal{M}$.

$\left({\mathfrak{B}}_1\right)$

There is a bijection between the set of indecomposable projective ${\Lambda }_{\mathcal{M}}$-modules and the polygons in $\mathcal{M}$.

$\left({\mathfrak{B}}_2\right)$

If P is an indecomposable projective ${\Lambda }_{\mathcal{M}}$-module corresponding to a polygon V in ${\mathcal{M}}_1$, then the Jacobson radical $\mathrm{rad}P$ is a sum of r indecomposable uniserial modules, where r is the number of (nontruncated) vertices of V and where the intersection of any two of the uniserial modules is a simple ${\Lambda }_{\mathcal{M}}$-module.

$\left({\mathfrak{B}}_3\right)$

A Brauer configuration algebra is a multiserial algebra.

$\left({\mathfrak{B}}_4\right)$

The number of summands in the heart $ht\left(P\right)=\mathrm{rad}P/\mathrm{soc}P$ of an indecomposable projective ${\Lambda }_{\mathcal{M}}$-module P such that ${\mathrm{rad}}^{2}P\ne 0$ equals the number of nontruncated vertices of the polygons in $\mathcal{M}$ corresponding to P counting repetitions.

$\left({\mathfrak{B}}_5\right)$

Let ${\Lambda }_{\mathcal{M}}$ be the Brauer configuration algebra induced by a connected Brauer configuration $\mathcal{M}$. The algebra ${\Lambda }_{\mathcal{M}}$ has a length grading induced from the path algebra $k{Q}_{\mathcal{M}}$ if and only if there is a positive integer N such that for each nontruncated vertex $m\in M$, it holds that $val\left(m\right)\mu \left(m\right)=N$. In such a case, we say that the algebra ${\Lambda }_{\mathcal{M}}$ satisfies the length grading property.

$\left({\mathfrak{B}}_6\right)$

The dimension of a Brauer configuration algebra ${\Lambda }_{\mathcal{M}}$ is given by the following formula (see Formula (11) and notation (19)):

$${\dim }_k{\Lambda }_{\mathcal{M}}=2\left|{\mathcal{M}}_1\right|+\sum _{m_i\in M}val\left(m_i\right)(\mu \left(m_i\right)val\left(m_i\right)-1)$$

(22)

$\left({\mathfrak{B}}_7\right)$

Sierra [15] gave the following Formula (23) for the center of a Brauer configuration algebra ${\Lambda }_{\mathcal{M}}$ induced by a connected and reduced Brauer configuration $\mathcal{M}$.

$${\dim }_{k}Z\left({\Lambda }_{\mathcal{M}}\right)=1+\sum _{m\in M}\mu \left(m\right)+|{\mathcal{M}}_1|-|M|+\#\left(Loops{Q}_{\mathcal{M}}\right)-\left|{\mathcal{C}}_{\mathcal{M}}\right|.$$

(23)

where ${\mathcal{C}}_{\mathcal{M}}=\{m\in \mathcal{M}\mid val\left(m\right)=1,and\mu \left(m\right)>1\}$ and the number of vertices $|{\left(Q_{\mathcal{M}}\right)}_1|$ of the Brauer quiver $Q_{\mathcal{M}}$ is given by the number of multisets or polygons in ${\mathcal{M}}_1$.

Example 5.

According to Remark 2, the analysis of the data (known as Brauer analysis) inducing the Brauer configuration algebra ${\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}$ and the Brauer quiver $Q_{{\mathcal{M}}_{\mathfrak{D}}}$ (see Figure 1) gives the following information (see Examples 2–4):

1. 

${\Lambda }_{\mathcal{M}}$ is multiserial. Particularly, the Jacobson radical of the indecomposable projective ${\Lambda }_{\mathcal{M}}$-modules, $P_1,P_2$, and $P_3$ induced by partitions $L_1,L_2$, and $L_3$, respectively, is a sum of $3,4$ and 5 indecomposable uniserial modules, respectively.

2. 

${\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}$ does not satisfy the length grading property.

3. 

The Brauer quiver $Q_{{\mathcal{M}}_{\mathfrak{D}}}$ has two components and four vertices $1,2,3$, and 4 with $val\left(1\right)=1$, $val\left(2\right)=6$, $val\left(3\right)=3$, $val\left(4\right)=2$; $\mu \left(1\right)=2$, and $\mu \left(i\right)=1$, $i\in \{2,3,4\}$.

4. 

${\dim }_k{\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}=2\left(3\right)+1(2-1)+6\left(5\right)+3\left(2\right)+2\left(1\right)=45$.

5. 

$\#\left(Loops{Q}_{{\mathcal{M}}_{\mathfrak{D}}}\right)=10$.

6. 

${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}\right)=1+5-4+3+10-1=14$.

3. Main Results

This section provides a Brauer analysis of some integer partitions and compositions and defines Brauer configurations as realizable branch data over some surfaces.

Table 2 gives a Brauer analysis of realizable branch data over $S^2$ defined by Corollary 1. Note that the defect $\nu \left(\mathfrak{D}\right)$ deals with the number of summands in the heart $ht\left(P_i\right)$, $i\in \{1,2,3\}$ of the corresponding indecomposable projective modules and $\mathfrak{e}$ ($\mathfrak{c}\left(Q_{\mathcal{M}}\right)$) is the number of components (covering graph) of the corresponding Brauer quiver $Q_{\mathfrak{D}}$.

Table 2. Brauer analysis of Brauer configuration ${\mathcal{M}}_{\mathfrak{D}}$ induced by realizable branch data $\mathfrak{D}$ over $S^2$. See Table 1 and Corollary 1.

	Brauer Analysis of Branch Data $\mathfrak{D}$
Degree	${\mathbf{dim}}_{\mathit{k}}$${\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}$	$\mathbf{\#}\mathbf{Loops}\mathbf{\left(}{\mathit{Q}}_{{\mathcal{M}}_{\mathfrak{D}}}\mathbf{\right)}$	$\mathfrak{e}$	$\nu \left(\mathfrak{D}\right)$	$\mathfrak{c}\left({\mathit{Q}}_{{\mathcal{M}}_{\mathfrak{D}}}\right)$
9	28	6	2	16	∘ − ∘  ∘
9	49	8	2	16	∘   ∘   ∘
10	45	8	2	18	∘ − ∘  ∘
16	90	13	2	26	∘ − ∘  ∘
16	89	14	3	30	∘   ∘   ∘
18	138	16	2	34	∘ − ∘  ∘
21	152	18	2	40	∘ − ∘  ∘
25	216	22	2	48	∘ − ∘  ∘
36	487	35	3	70	∘   ∘   ∘
40	599	39	3	78	∘   ∘   ∘
45	751	44	3	108	∘   ∘   ∘

Let ${\mathcal{M}}_{p\left(n\right)}=(M\left(p\left(n\right)\right),{\mathcal{M}}_1\left(p\left(n\right)\right),\mu ,\mathcal{O})$ be the Brauer configuration defined by the integer partitions of a positive integer n ($\left\{n\right\}$ excluded as a partition). We assume that ${\mathcal{M}}_1\left(p\left(n\right)\right)=\{L_1\left(n\right),L_2\left(n\right),\dots ,L_{p\left(n\right)-1}\left(n\right)\}$; therefore, $p\left(n\right)-1$ is the number $|{\mathcal{M}}_1\left(p\left(n\right)\right)|$ of polygons (see Formula (22)). We also assume that $L_i\left(n\right)<L_j\left(n\right)$ if $i<j$ in successor sequences. Then, the following result holds:

Theorem 5.

Let ${\Lambda }_{p\left(n\right)}$ be the Brauer configuration algebra induced by the Brauer configuration ${\mathcal{M}}_{p\left(n\right)}$; then, ${\Lambda }_{p\left(n\right)}$ is indecomposable as an algebra and

$${\displaystyle \frac{{\dim }_k{\Lambda }_{p\left(n\right)}+1}{2}}=p\left(n\right)+\sum _{j\in \underset{j\ne n-1}{M\left(p\right(n\left)\right)}}{t}_{{\mathcal{Q}}_j\left(n\right)-1},$$

(24)

where ${\mathcal{Q}}_j\left(n\right)$ denotes the number of occurrences of the part j in the partitions of n (see (8)).

Proof. 

The covering graph $\mathfrak{c}\left(Q_{{\mathcal{M}}_{p\left(n\right)}}\right)$ induced by the Brauer configuration ${\mathcal{M}}_{p\left(n\right)}$ is connected. Note that, if $L_i\left(n\right)\cap L_j\left(n\right)\ne ⌀$, then by definition, there is an edge in $\mathfrak{c}\left(Q_{{\mathcal{M}}_{p\left(n\right)}}\right)$ connecting $L_i\left(n\right)=\{{\lambda }_{i,1},{\lambda }_{i,2},\dots ,{\lambda }_{i,r_i}\}$ and $L_j\left(n\right)=\{{\lambda }_{j,1},{\lambda }_{j,2},\dots ,{\lambda }_{j,r_j}\}$. On the other hand, if $L_i\left(n\right)\cap L_j\left(n\right)=⌀$ and the largest parts of $L_i\left(n\right)$ and $L_j\left(n\right)$ are ${\lambda }_{i,1}$ and ${\lambda }_{j,1}$, respectively, with ${\lambda }_{i,1}<{\lambda }_{j,1}$, then ${\lambda }_{j,1}={\lambda }_{i,1}+\underset{({\lambda }_{j,1}-{\lambda }_{i,1})-\mathrm{times}}{\underbrace{1+1+\cdots +1}}$ and there exists a partition $L_m\left(n\right)=\{{\lambda }_{i,1},{\lambda }_{j,2},\dots ,{\lambda }_{j,r_j},\underset{({\lambda }_{j,1}-{\lambda }_{i,1})-\mathrm{times}}{\underbrace{1,1,\dots ,1}}\}$ of n. Thus, there exists an edge connecting $L_i\left(n\right)$ with $L_m\left(n\right)$; if $L_m\left(n\right)\cap L_j\left(n\right)\ne ⌀$, then there is an edge connecting $L_m\left(n\right)$ and $L_j\left(n\right)$. Therefore, there exists a path $\{L_i\left(n\right),L_m\left(n\right),L_j\left(n\right)\}$ connecting $L_i\left(n\right)$ and $L_j\left(n\right)$. If $L_j\left(n\right)\cap L_m\left(n\right)=⌀$ and ${\lambda }_{j,r_j}$ is the less part of $L_j\left(n\right)$, then there exists a partition of n, $L_q\left(n\right)$ such that $L_q\left(n\right)=\{{\lambda }_{j,1},{\lambda }_{j,2},\dots ,{\lambda }_{j,r_{j-1}},\underset{{\lambda }_{j,r_j}-\mathrm{times}}{\underbrace{1,1,\dots ,1}}\}$. Then, there is an edge connecting $L_j\left(n\right)$ and $L_q\left(n\right)$ and a path of the form $\{L_i\left(n\right),L_m\left(n\right),L_q\left(n\right),L_j\left(n\right)\}\subset \mathfrak{c}\left(Q_{{\mathcal{M}}_{p\left(n\right)}}\right)$ connecting $L_i\left(n\right)$ and $L_j\left(n\right)$. Thus, the Brauer quiver $Q_{{\mathcal{M}}_{p\left(n\right)}}$ is connected and the induced Brauer configuration algebra ${\Lambda }_{p\left(n\right)}$ is indecomposable as an algebra.

Since the number of polygons in ${\mathcal{M}}_1\left(p\left(n\right)\right)$ equals $p\left(n\right)-1$ and $n-1$ is the only vertex j in the Brauer configuration ${\mathcal{M}}_{p\left(n\right)}$ with $val\left(j\right)=1$ and $val\left(j\right)={\mathcal{Q}}_j\left(n\right)$ for the remaining vertices, then the Formula (25) holds. □

Let ${\mathcal{M}}_{c\left(n\right)}=(M\left(c\left(n\right)\right),{\mathcal{M}}_1\left(c\left(n\right)\right),\mu ,\mathcal{O})$ be the Brauer configuration induced by the compositions of a positive integer n ($n\notin M\left(c\right(n\left)\right)$), with ${\mathcal{M}}_1\left(c\left(n\right)\right)=\{c_1\left(n\right),c_2\left(n\right),\dots ,c_{2^{n-1}-1}\}$ and $c_i\left(n\right)<c_j\left(n\right)$ if $i<j$ in successor sequences.

The following result regarding integer compositions holds:

Corollary 2.

Let ${\Lambda }_{c\left(n\right)}$ be the Brauer configuration algebra induced by the Brauer configuration ${\mathcal{M}}_{c\left(n\right)}$; then, ${\Lambda }_{c\left(n\right)}$ is indecomposable as an algebra and

$${\dim }_k{\Lambda }_{c\left(n\right)}+2\le 2^n+\sum _{j\in M\left(c\right(n\left)\right)}{\mathcal{Q}}_j{N}_{L_i\left(n\right)}({\mathcal{Q}}_j{N}_{L_i\left(n\right)}-1).$$

(25)

where $N_{L_i}\left(n\right)={\displaystyle \frac{(f_1+f_2+\cdots +f_r)!}{f_1!f_2!\dots f_r!}}$ is the size of the largest family of compositions of n induced by a fixed partition with the form $L_i\left(n\right)=\{{\lambda }_{i,1}^{f_1},{\lambda }_{i,2}^{f_2},\dots ,{\lambda }_{i,r}^{f_r}\}$.

Proof. 

The arguments posed in Theorem 5 prove that ${\Lambda }_{c\left(n\right)}$ is indecomposable as an algebra. On the other hand, we note that $c\left(n\right)=2^{n-1}$ and that $N_{L_i\left(n\right)}$ is the number of compositions of n defined by $L_i\left(n\right)$. Each composition is associated with a unique partition; then, each composition $L_j\left(n\right)$ of n gives rise to at most $N_{L_i}\left(n\right)$ copies of its corresponding partition. Thus, the compositions of n define at most $N_{L_i}\left(n\right)$ repetitions of ${\mathcal{M}}_1\left(p\left(n\right)\right)$ since each part occurs ${\mathcal{Q}}_j\left(n\right)$ times in each of these copies. We conclude that for each $j\in M\left(c\right(n\left)\right)=M\left(p\right(n\left)\right)$, it holds that $val\left(j\right)\le {\mathcal{Q}}_j\left(n\right)N_{L_i}\left(n\right)$. Therefore, the inequality (2) holds, and we are finished. □

Let ${\mathcal{M}}_{c(m,n)}=(M\left(c(m,n)\right),{\mathcal{M}}_1\left(c(m,n)\right),\mu ,\mathcal{O})$ be the Brauer configuration induced by the compositions of a positive integer n into exactly $m\ge 2$ parts. Then, the following result holds:

Theorem 6.

If $n-m$ is even, then there exists a branched covering $\varphi :M\to \mathbb{R}{P}^2$ over the projective plane $\mathbb{R}{P}^2$ of degree n with M connected and ${\mathcal{M}}_1\left(c(m,n)\right)$ as branch data.

Proof. 

$\nu \left({\mathcal{M}}_1\left(c(m,n)\right)\right)=(n-m)\left(\genfrac{}{}{0pt}{}{n-1}{m-1}\right)\equiv 0mod2$. Moreover, $(n-m)\left(\genfrac{}{}{0pt}{}{n-1}{m-1}\right)=$$\frac{(n-1)!}{(n-m-1)!(m-1)!}=\frac{(n-m)(n-m+1)\dots (n-2)(n-1)}{(m-1)!}$. Since $(n-m)(n-m+1)\dots (n-2)=t(m-1)!$, with $t\ge 1$, it holds that ${\displaystyle \sum _{i=1}^{\left(\genfrac{}{}{0pt}{}{n-1}{m-1}\right)}}\nu \left(L_i\right)=(n-m)\left(\genfrac{}{}{0pt}{}{n-1}{m-1}\right)\ge n-1$. We are finished. □

Let ${\mathcal{M}}_{inv(m_1,m_2;n)}=(M\left(inv(m_1,m_2;n)\right),{\mathcal{M}}_1\left(inv(m_1,m_2;n)\right),\mu ,\mathcal{O})$ be the Brauer configuration induced by permutations ${\psi }_{m_1}{\psi }_{m_2}\dots {\psi }_{m_1+m_2}$ of $\left\{1^{m_1}{2}^{m_2}\right\}$ in which there are exactly n pairs $({\psi }_i,{\psi }_j)$ such that $i<j$ and ${\psi }_i>{\psi }_j$. In this case, $M\left(inv(m_1,m_2;n)\right)=\{1,2\}$ and the words associated with the polygons in ${\mathcal{M}}_1\left(inv(m_1,m_2;n)\right)$ are permutations of $1^{m_1}{2}^{m_2}$ (see Theorem 2). If the orientation $\mathcal{O}$ is given for partitions and compositions of an integer n, then the following result holds:

Theorem 7.

Let ${\Lambda }_{inv(m_1,m_2;n)}$ be the Brauer configuration algebra induced by the Brauer configuration ${\mathcal{M}}_{inv(m_1,m_2;n)}$. Then,

$${\dim }_k{\Lambda }_{inv(m_1,m_2;n)}=p(m_1,m_2;n)((m_1^2+m_2^2)p(m_1,m_2;n)-(m_1+m_2)+2)$$

(26)

Proof. 

The number of polygons in ${\mathcal{M}}_1\left(inv(m_1,m_2;n)\right)$ is $inv(m_1,m_2;n)=p(m_1,m_2;n)$ (see Theorem 2) and $val\left(i\right)=m_{i}p(m_1,m_2;n)$, $i\in \{1,2\}$. □

Let ${\mathcal{M}}_{\mathcal{O}\left(\right(r,s),(n,n);1)}=(M\left(\mathcal{O}((r,s),(n,n);1)\right),{\mathcal{M}}_1\left(\mathcal{O}((r,s),(n,n);1)\right),\mu ,\mathcal{O})$ be the Brauer configuration defined by the compositions of type $\mathcal{O}\left(\right(r,s),(n,n);1)$ of ${\mathcal{O}}_n+{\mathcal{O}}_n+{\mathcal{O}}_1$, where ${\mathcal{O}}_i$ denotes the ith octahedral number, $n\ge 1$. Furthermore, any composition $c({\mathcal{O}}_n+{\mathcal{O}}_n+{\mathcal{O}}_1)\in {\mathcal{M}}_1(\mathcal{O}((r,s),(n,n);1)$ ($\{{\mathcal{O}}_n+{\mathcal{O}}_n+{\mathcal{O}}_1\}$ excluded as composition) is a sequence of the form $\{{\mathcal{O}}_{rs1},z_1,z_2,\dots ,z_t\}$ with $z_p=\{j^2,{(j+1)}^2\}$, $1\le p\le t$, $j\le n-1$.

We let $C(n,j)=\left(\genfrac{}{}{0pt}{}{n+j}{j}\right)-\left(\genfrac{}{}{0pt}{}{n+j}{j-1}\right)$ denote the $(n,j)$-entry of the Catalan triangle encoded as A001263 in the On-Line Encyclopedia of Integer Sequences (OEIS) [28].

The following result gives the properties of a Brauer configuration algebra induced by compositions of type $\mathcal{O}\left(\right(r,s),(n,n);1)$.

Theorem 8.

Let ${\Lambda }_{{\mathcal{M}}_{\mathcal{O}\left(\right(r,s),(n,n);1)}}$ be the Brauer configuration algebra induced by the Brauer configuration ${\mathcal{M}}_{\mathcal{O}\left(\right(r,s),(n,n);1)}$. Then, the following identities hold:

$${\mathfrak{v}}_j=val\left(j^2\right)=val\left({(j-1)}^2\right)+R(n,j^2),\mathrm{with}R(n,j^2)={\displaystyle \sum _{j_i=0}^{n-i}\sum _{i=0}^{n-1}}{Q}_i(n-i,j_i)C(n-i,j_i).$$

(27)

where

$$Q_i(n-i,j_i)=\left\{\begin{array}{cc}1,\hfill & 0\le j_i\le n-j,\hfill \\ 2,\hfill & n-j+1\le j_i\le n-i.\hfill \end{array}\right.$$

$$val\left({\mathcal{O}}_{rs1}\right)=C(n-r,n-s),1\le r\le s\le n.$$

(28)

$${\displaystyle \frac{{\dim }_k{\Lambda }_{{\mathcal{M}}_{\mathcal{O}\left(\right(r,s),(n,n);1)}}}{2}}={\displaystyle \sum _{m=1}^{n-1}}\sum _{j\le m}C(m,j)+t_{{\mathfrak{v}}_j-1}+t_{C(n-r,n-s)-1}+n,n-s\ne 0,1\le r\le s\le n.$$

(29)

where $t_i={\displaystyle \frac{i(i+1)}{2}}$ denotes the ith triangular number.

$${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathcal{O}\left(\right(r,s),(n,n);1)}}\right)={\displaystyle \sum _{m=1}^{n-1}}\sum _{j\le m}C(m,j)+n+1.$$

(30)

Proof. 

We let ${\mathcal{M}}_n$ denote the poset $\left(\delta \right(J(\mathbf{2}\times \mathbf{n})),⪯)$, where $\mathbf{2}$ and $\mathbf{n}$ are chains or linear ordered sets with 2 and n points, respectively. Furthermore, for positive integers $i,j,i^{\prime },j^{\prime }$, it holds that

$$\begin{array}{cc}\hfill (i,j)⪯(i^{\prime },j^{\prime })& \mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}1\le i\le i^{\prime }\mathrm{and}1\le j\le j^{\prime }.\hfill \end{array}$$

(31)

${\mathcal{M}}_n$ is a lattice and there exists a bijection ${\delta }_n:{\mathcal{L}}_n\to \mathcal{O}((r,s),(n,n);1)$ between the set of lattice paths ${\mathcal{L}}_n$ connecting points $(x,y)\in {\mathcal{M}}_n$ and the maximal point $(n,n)\in {\mathcal{M}}_n$. And the set of compositions of type $\mathcal{O}\left(\right(r,s),(n,n);1)$ of ${\mathcal{O}}_n+{\mathcal{O}}_n+1$. In such a case, if $P=\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)=(n,n)\}\in {\mathcal{L}}_n$, then

$${\delta }_n\left(P\right)=\left\{{\mathcal{O}}_{x_1{y}_{1}1}\right\}\cup A_1\cup A_2\cdots \cup A_t.$$

(32)

Sets $A_i$ are given by the set of edges $E\left(P\right)$ of the lattice path P. In such a case, an edge of the form $\{(x_{i-1},y_{i-1}),(x_{i-1},y_i)\}$ has assigned a two-point set consisting of consecutive squares of the form $\{y_i^2,y_{i+1}^2\}$. If the edge is of the form $\{(x_{i-1},y_{i-1}),(x_{i-1},y_i)\}$, then elements of $A_i$ are of the form $\{x_i^2,{(x_i+1)}^2\}$. Particularly, $A_t={(n-1)}^2+n^2$. Note that compositions associated with a given lattice path P with the same starting point have the same parts. Thus, the first identity (27) holds provided that consecutive squares occur consecutively, the square numbers $x_1^2$ and $n^2$ occur just once, and the remaining parts occur twice.

The second identity (28) holds taking into account that each point $(x_i,y_i)$ gives rise to the entry $C(n-x_i,n-y_i)$ in the Catalan triangle, which is the number of lattice paths connecting $(x_1,y_1)$ with $(n,n)$. This is also the number of compositions of type $\mathcal{O}((x_1,y_1),(n,n);1)$.

The third identity (29) and fourth identity (30) hold as consequences of Formulas (22) and (23) and the valency values given above. Note that ${\Lambda }_{{\mathcal{M}}_{\mathcal{O}\left(\right(r,s),(n,n);1)}}$ is indecomposable as an algebra, the number of compositions of type $\mathcal{O}\left(\right(r,s),(n,n);1)$ is ${\displaystyle \sum _{m=1}^{n-1}}{\displaystyle \sum _{j\le m}}C(m,j)$, and the number of loops is given by parts of the form ${\mathcal{O}}_{in1}$ and ${\mathcal{O}}_{(n-1)(n-1)1}$ provided that $val\left({\mathcal{O}}_{in1}\right)\mu \left({\mathcal{O}}_{in1}\right)=val\left({\mathcal{O}}_{(n-1)(n-1)1}\right)\mu \left({\mathcal{O}}_{in1}\right)=2$, $i<n$. Figure 2 shows the poset ${\mathcal{M}}_5$ labeled by compositions of type $\mathcal{O}\left(\right(r,s),(5,5);1)$. We are finished. □

Figure 2. Poset ${\mathcal{M}}_5$ labeled with compositions of type $\mathcal{O}\left(\right(r,s),(5,5),1)$.

For the following result, we assume that the parts of compositions of type $\mathcal{O}\left(\right(r,s),(n,n);1)$ consist of parts of the forms $\{{\mathcal{O}}_{rs1},z_1,\dots ,z_t\}$, where $z_i=j^2+{(j+1)}^2$ is a sum of two suitable consecutive square numbers, $1\le i\le t$.

Theorem 9.

If $n\equiv 1mod4$ and $n\ge 5$, then the collection of polygons ${\mathcal{M}}_1\left(\mathcal{O}((r,s),(n,n);1)\right)$ associated with the Brauer configuration ${\mathcal{M}}_{\mathcal{O}\left(\right(r,s),(n,n);1)}$ is realizable as the branch data of a branched covering $M\to \mathbb{R}{P}^2$ of degree n over the projective plane $\mathbb{R}{P}^2$ with M connected.

Proof. 

Note that if L is a composition of type $\mathcal{O}\left(\right(r,s),(n,n);1)$, then L has the form ${\mathcal{O}}_{r^{\prime }{s}^{\prime }1}+z_1+z_2+\dots +z_t$, where $z_j=h^2+{(h+1)}^2$ for some $h>0$ and $r\le r^{\prime }\le s^{\prime }\le s$. Therefore, $z_j-1\equiv 0mod2$ for any $1\le j\le t$. That is, ${\displaystyle \sum _{h=1}^t}{z}_h=2p$, for some suitable $p>0$ and $\nu \left({\mathcal{M}}_1\left(\mathcal{O}((r,s),(n,n);1)\right)\right)={\displaystyle \sum _{r\le v\le w\le s}}{\mathcal{O}}_{vw}+2m$, for some $m>0$. Since ${\displaystyle \sum _{r\le v\le w\le s}}{\mathcal{O}}_{vw}=(n+1){\displaystyle \sum _{j=1}^{n-1}}{\mathcal{O}}_j+(n-1){\mathcal{O}}_n$ is an even number, we conclude that $\nu \left({\mathcal{M}}_1\left(\mathcal{O}((r,s),(n,n);1)\right)\right)$ is an even number and $\nu \left({\mathcal{M}}_1\left(\mathcal{O}((r,s),(n,n);1)\right)\right)>(n-1){\mathcal{O}}_n>2{\mathcal{O}}_n={\mathcal{O}}_{nn1}-1$; then, the result holds as a consequence of Theorem 3. We are finished. □

Let ${\Lambda }_{\mathcal{B}(j,m;n)}$ be the Brauer configuration algebra induced by the Brauer configuration $\mathcal{B}(j,m;n)=(M\left(\mathcal{B}(j,m;n)\right),{\mathcal{M}}_1\left(\mathcal{B}(j,m;n)\right),\mu ,\mathcal{O})$ defined by compositions of a positive integer $n\ge 6$ with the form $\{\underset{m-\mathrm{times}}{\underbrace{2^j,2^j,\dots ,2^j}},\underset{i-\mathrm{times}}{\underbrace{2^s,2^s,\dots ,2^s}},\underset{u-\mathrm{times}}{\underbrace{2^0,2^0,\dots ,2^0}}\mid j\ge 1,s<j,1\le m\le m_0,i,u\ge 0,m_0{2}^j\le n<(m_0+1)2^j\}$. Note that $M\left(\mathcal{B}(j,m;n)\right)=\{1,2,4,\dots ,2^j\}$ and $\left\{n\right\}\notin {\mathcal{M}}_1\left(\mathcal{B}(j,m;n)\right)$.

Example 6.

The following are compositions of type $\mathcal{B}(2,2;10)$:

1. 

{4,4,2};

2. 

{4,4,1,1};

3. 

{4,2,2,2};

4. 

{4,2,2,1,1};

5. 

{4,1,1,2,1,1};

6. 

{4,1,1,1,1,1,1}.

For $n\ge 6$ fixed, we let $n_{m{2}^j,i{2}^s}$ denote the positive integer with the following form:

$$n_{m{2}^j,i{2}^s}=(n-3)-(2^2+2^3+\dots +2^{j-1})-7(m-1)-3(s-1)i,j\ge 3;m,s\ge 1,s<j.$$

(33)

We let $A(j,s,m,i;n)$ denote a sequence of positive integers, such that

$$\begin{array}{cc}\hfill A(0,0,1,0;n)& =1,\hfill \\ \hfill A(1,0,m,1;n)& =\left({\displaystyle \genfrac{}{}{0pt}{}{n-m}{m}}\right),0\le m\le M,2+2M\le n<2+2(M+1),\hfill \\ \hfill A(2,1,m,i;n)& =\left({\displaystyle \genfrac{}{}{0pt}{}{n-3m-i}{i+m}}\right),1\le m\le M^{\prime },0\le i\le M,4M^{\prime }\le n<4\left(M^{\prime }+1\right),\hfill \\ \hfill 4m+2M& \le n<4m+2(M+1),\hfill \\ \hfill A(j,s,m,i;n)& =\left({\displaystyle \genfrac{}{}{0pt}{}{n_{m{2}^j,i{2}^s}}{i+m}}\right),a\le i\le Mm{2}^j+M{2}^s\le n<m{2}^j+(M+1)2^s,\hfill \end{array}$$

(34)

where

$$a=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}s=1,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

We let ${\mathfrak{b}}_j$ denote the sequence of positive integers, such that

$${\mathfrak{b}}_j=\sum _{j\mathrm{fixed},s,m,i}A(j,s,m,i;n)b(j,s,m,i;n)+\sum _{h>j,s=j\mathrm{fixed},m,i}A(h,s,m,i;n)b(j,s,m,i;n).$$

(35)

For $(j,s,m,i;n)\ne (0,0,1,0;n)$, it holds that

$$b(j,s,m,i;n)=\left\{\begin{array}{cc}m,\hfill & \mathrm{if}s=0,\hfill \\ i+m,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Particularly, $b(0,0,1,0;n)=n$.

We let $\mathfrak{L}$ denote a map with the domain being the sequence $A(j,s,m,i;n)$ and such that

$$\begin{array}{cc}\hfill \mathfrak{L}\left(A\right(0,0,1,0;n\left)\right)& =n-1,\hfill \\ \hfill \mathfrak{L}\left(A\right(1,0,m,1;n\left)\right)& =n-m-1,0\le m\le M,2+2M\le n<2+2(M+1),\hfill \\ \hfill \mathfrak{L}\left(A\right(2,1,m,i;n\left)\right)& =n-3(m+i+1),1\le m\le M^{\prime },0\le i\le M,4M^{\prime }\le n<4\left(M^{\prime }+1\right),\hfill \\ & 4m+2M\le n<4m+2(M+1),\hfill \\ \hfill \mathfrak{L}\left(A\right(j,s,m,i;n\left)\right)& =n+m(1-2^j)+i(1-2^s)-3,a\le i\le M\hfill \\ \hfill & m{2}^j+M{2}^s\le n<m{2}^j+(M+1)2^s.\hfill \end{array}$$

(36)

The following result gives the dimensions of Brauer configuration algebras induced by compositions of type $\mathcal{B}(j,m;n)$.

Theorem 10.

Let ${\Lambda }_{\mathcal{B}(j,m;n)}$ be the Brauer configuration algebra induced by the Brauer configuration $\mathcal{B}(j,m;n)$; then, ${\Lambda }_{\mathcal{B}(j,m;n)}$ is indecomposable as an algebra and

$${\dim }_k{\Lambda }_{\mathcal{B}(j,m;n)}=\sum _{j,s,m,i}A(j,s,m,i;n)+\sum _j{\mathfrak{b}}_j({\mathfrak{b}}_j-1).$$

(37)

$${\dim }_{k}Z\left({\Lambda }_{\mathcal{B}(j,m;n)}\right)=1+\sum _{j,s,m,i}A(j,s,m,i;n)+\sum _{j,s,m,i}\mathfrak{L}\left(A(j,s,m,i;n)\right).$$

(38)

Proof. 

If $c_i$ and $c_j$ are compositions of type $c\in \mathcal{B}(j,m;n)$ such that $c_i\cap c_j\ne ⌀$, then there is an arrow in the corresponding Brauer quiver $Q_{\mathcal{B}(j,m;n)}$ connecting $c_i$ and $c_j$. On the other hand, if $c_i\cap c_j=⌀$ and ${\lambda }_i$ and ${\lambda }_j$ are the smallest parts of $c_i$ and $c_j$, respectively, then there are partitions $c_i^{\prime }$ and $c_j^{\prime }$ with 1 as the smallest part. It occurs ${\lambda }_i$ (${\lambda }_j$) times in $c_i$ ($c_j$). Then, there is a path in $Q_{\mathcal{B}(j,m;n)}$ connecting $c_i,c_i^{\prime },c_j$ and $c_j^{\prime }$. Thus, $Q_{\mathcal{B}(j,m;n)}$ is connected and the algebra ${\Lambda }_{\mathcal{B}(j,m;n)}$ is indecomposable.

Since $A(j,s,m,i;n)$ equals the number of compositions of n into m parts of the form $2^j$, i parts of the form $2^s$ and $n-m{2}^j-i{2}^s$, 1s. Then, $={\displaystyle \sum _{j,s,m,i}}A(j,s,m,i;n)$ is the number of vertices of the Brauer quiver $Q_{\mathcal{B}(j,m;n)}$ induced by compositions of type $\mathcal{B}(j,m;n)$ and, by definition, ${\mathfrak{b}}_j$ is the valency of j for any j and the identity (37) holds.

Finally, note that, by definition, ${\displaystyle \sum _{j,s,m,i}}\mathfrak{L}\left(A(j,s,m,i;n)\right)$ is the number of loops in $Q_{\mathcal{B}(j,m;n)}$ and $val\left(j\right)\ne 1$ for any vertex $j\in \mathcal{B}(j,m;n)$. Thus, the identity (38) holds. We are finished. □

The following result is a consequence of Theorem 3, which regards branched coverings over the projective plane.

Theorem 11.

If ${\displaystyle \sum _{j,s,m,i}}n-n_{m{2}^j,i{2}^s}$ is even, then there is a branched covering $\varphi :M\to \mathbb{R}{P}^2$ of degree n with M connected and with compositions of type $\mathcal{B}(j,m;n)$ of an integer $n\ge 6$ as branch data.

Proof. 

According to Theorem 3, it suffices to note that $n-n_{2,1}=A(1,0,1,1;n)=n-1$. Thus, $\nu \left(\mathcal{B}\right(j,m,n\left)\right)>n-1$. We are finished. □

Example 7.

The following are compositions of type $\mathcal{B}(j,m;6)$:

• $\{4,2\}$, $\{4,1,1\}$, $\{2,2,2\}$, $\{2,2,1,1\}$, $\{2,1,1,1,1\}$, $\{1,1,1,1,1,1\}$.

The following are compositions of type $\mathcal{B}(j,m;7)$:

• $L_1=\{4,2,1\}$, $L_2=\{4,1,1,1\}$, $L_3=\{2,2,2,1\}$, $L_4=\{2,2,1,1,1\}$, $L_5=\{2,1,1,1,1,1\}$, $L_6=\{1,1,1,1,1,1,1\}$.

$\nu \left(\mathcal{B}\right(j,m;6\left)\right)=37$ and $\nu \left(\mathcal{B}\right(j,m;7\left)\right)=62>7$. Then, there is not a branched covering $\varphi :M\to \mathbb{R}{P}^2$ of degree 6 provided that the compositions of this type do not satisfy the Hurwitz condition. According to Theorem 3, such a branched covering exists with $\mathcal{B}(j,m;7)$ as branch data.

Figure 3 shows the Brauer quiver induced by the compositions ${\mathcal{M}}_{\mathfrak{D}}=\{L_1,L_2,L_3,L_4\}$ whose defect $\nu \left({\mathcal{M}}_{\mathfrak{D}}\right)=12$ satisfies the Hurwitz condition, since $\nu \left({\mathcal{M}}_{\mathfrak{D}}\right)=12>6$, ${\mathcal{M}}_{\mathfrak{D}}$ is a branch data of a branched covering of degree 7 over the projective plane.Note that the collection of compositions $\mathfrak{E}=\{L_1,L_2,L_3,L_4,L_5,L_6\}$ does not satisfy the Hurwitz condition, provided that $\nu \left(\mathfrak{E}\right)=13$.

Note that the Brauer configuration algebra ${\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}$ induced by the quiver $Q_{{\mathcal{M}}_{\mathfrak{D}}}$ shown in Figure 3 is bounded by relations of the following forms:

• $C_i-C_j$, where $C_x$ denotes a special cycle at the vertex x, $i\ne j$, $i,j\in \{1,2,4\}$.
• $C_{i}f$, if f is the first arrow of the special cycle $C_i$.
• ${\alpha }_x^i{\alpha }_y^j$, if $i\ne j$ for any $x,y$.

Table 3 shows a Brauer analysis for compositions ${\mathcal{M}}_{\mathfrak{D}}=\{L_1,L_2,L_3,L_4\}$ described above. Note that $val\left(1\right)=8$, $val\left(2\right)=6$, and $val\left(4\right)=2$. $C_3[(L_1,L_2,L_3);(1,1,2)]$ denotes the covering graph $\mathfrak{c}\left(Q_{{\mathcal{M}}_{\mathfrak{D}}}\right)$, which is a hair graph obtained by attaching a two-point linear path to the vertex $L_3$ of the cycle $C_3=\{L_1,L_2,L_3\}$ (see Figure 4).

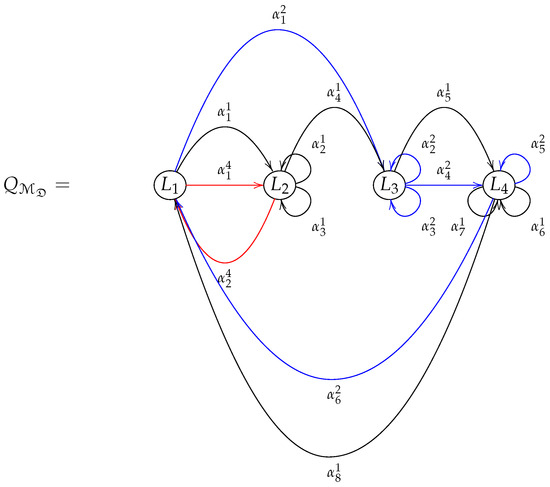
Figure 3. Brauer quiver induced by branch data ${\mathcal{M}}_{\mathfrak{D}}=\{L_1,L_2,L_3,L_4\}$ realizable as branched covering of the projective plane.

Figure 4. Covering graph $\mathfrak{c}\left(Q_{{\mathcal{M}}_{\mathfrak{D}}}\right)$ defined by the Brauer quiver $Q_{{\mathcal{M}}_{\mathfrak{D}}}$ (see Figure 3).

Table 3. Brauer analysis of the Brauer configuration ${\mathcal{M}}_{\mathfrak{D}}$ induced by compositions $L_1,L_2,L_3$, and $L_4$.

	Brauer Analysis of Branch Data ${\mathcal{M}}_{\mathfrak{D}}$
Degree	${\mathbf{dim}}_{\mathit{k}}$${\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}$	$\mathbf{\#}\mathbf{Loops}\mathbf{\left(}{\mathit{Q}}_{{\mathcal{M}}_{\mathfrak{D}}}\mathbf{\right)}$	${\mathbf{dim}}_{\mathit{k}}$$\mathit{Z}\left({\mathbf{\Lambda }}_{{\mathcal{M}}_{\mathfrak{D}}}\right)$	$\nu \left(\mathfrak{D}\right)$	$\mathfrak{c}\left({\mathit{Q}}_{{\mathcal{M}}_{\mathfrak{D}}}\right)$
7	96	7	12	12	$C_3[(L_1,L_2,L_3);(1,1,2)]$

Table 3. Brauer analysis of the Brauer configuration ${\mathcal{M}}_{\mathfrak{D}}$ induced by compositions $L_1,L_2,L_3$, and $L_4$.

	Brauer Analysis of Branch Data ${\mathcal{M}}_{\mathfrak{D}}$
Degree	${\mathbf{dim}}_{\mathit{k}}$${\Lambda }_{{\mathcal{M}}_{\mathfrak{D}}}$	$\mathbf{\#}\mathbf{Loops}\mathbf{\left(}{\mathit{Q}}_{{\mathcal{M}}_{\mathfrak{D}}}\mathbf{\right)}$	${\mathbf{dim}}_{\mathit{k}}$$\mathit{Z}\left({\mathbf{\Lambda }}_{{\mathcal{M}}_{\mathfrak{D}}}\right)$	$\nu \left(\mathfrak{D}\right)$	$\mathfrak{c}\left({\mathit{Q}}_{{\mathcal{M}}_{\mathfrak{D}}}\right)$
7	96	7	12	12	$C_3[(L_1,L_2,L_3);(1,1,2)]$

The following result is a consequence of Proposition 2.

Theorem 12.

If $n=2^h+1$, $h>2$, and ${\displaystyle \sum _{j,s,m,i}}n-n_{m{2}^j,i{2}^s}$ is even. Then, any composition of type $\mathcal{B}(j,m;2^h+1)$ with $h>2$ is realizable.

Proof. 

Note that $n=2^h+1$ is an odd number $>4$, and the number of compositions of type $\mathcal{B}(j,m;n)$ is greater than 3. Furthermore, there are two compositions $L_1=\{2^h,1\}$ and $L_2=\{1,2^h\}$ of type $\mathcal{B}(j,m;n)$, such that $\nu \left(L_i\right)=2^h-1$, $i\in \{1,2\}$. Then, $\nu \left(L_1\right)+\nu \left(L_2\right)=2^{h+1}-2=2n-4$. Thus, $2n-2<\nu \left(\mathcal{B}\right(j,m;n\left)\right)$. Therefore, the result follows as a consequence of Proposition 2. We are finished. □

Example 8.

Suppose that $\mathfrak{H}=\{H_1,H_2,\dots ,H_t\}$ is a subset of binary partitions of a fixed integer h with the form $\{{\lambda }_i,{\lambda }_i,\dots ,{\lambda }_i,1\}$, $|L_j|>1$, $1\le j\le t$, ${\lambda }_i>1$, ${\lambda }_i\ne {\lambda }_j$ if $i\ne j$; then, if ${\Lambda }_{{\mathcal{M}}_{\mathfrak{H}}}$ is the Brauer configuration algebra induced by $\mathfrak{H}$, then ${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathfrak{H}}}\right)-(t+1)={\displaystyle \sum _{i=1}^t}(\frac{\nu \left(H_i\right)}{{\lambda }_i-1}-1)$.

For instance, if $\mathfrak{H}=\{H_1=\{2,2,2,2,1\},H_2=\{4,4,1\}\}$, then $\nu \left(H_1\right)=4$, $\nu \left(H_2\right)=6$, $t=2$, and ${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathfrak{H}}}\right)=1+2+4=7$. Therefore, $(\frac{\nu \left(H_1\right)}{1}-1)+(\frac{\nu \left(H_2\right)}{3}-1)=4=7-(2+1)$.

Theorem 13.

If $\mathfrak{W}=\{W_1,W_2,\dots ,W_s\}$ is a collection of partitions of a fixed integer $w\ge 4$ with $W_i=1^{i_1}{2}^{i_2}$, $i_1\ge 0$, $i_2>1$, $1\le i\le s$, and ${\Lambda }_{{\mathcal{M}}_{\mathfrak{W}}}$ is the Brauer configuration algebra induced by $\mathfrak{W}$, then ${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathfrak{W}}}\right)+s-\mathfrak{r}=\nu \left(\mathfrak{W}\right)$. Where

$$\mathfrak{r}=\left\{\begin{array}{cc}{(h-1)}^2,\hfill & \mathrm{if}w=2h+1,\hfill \\ 2t_{h-2}=(h-2)(h-1),\hfill & \mathrm{if}w=2h.\hfill \end{array}\right.$$

Proof. 

The number $\#\mathrm{Loops}\left(Q_{{\mathcal{M}}_{\mathfrak{W}}}\right)$ of loops contained in the induced Brauer quiver $Q_{{\mathcal{M}}_{\mathfrak{W}}}$ is given by a sum of the form ${\displaystyle \sum _{j=1}^s}(j_1+j_2-2)$. Thus, $\#\mathrm{Loops}\left(Q_{{\mathcal{M}}_{\mathfrak{W}}}\right)={\displaystyle \sum _{j=1}^s}(j_1-1)+{\displaystyle \sum _{j=1}^s}(j_2-1)=\mathfrak{r}+\nu \left(\mathfrak{W}\right)-2s$, with $\mathfrak{r}={\displaystyle \sum _{i=2}^h}2i-3$ ($\mathfrak{r}=2{\displaystyle \sum _{i=0}^{h-2}}h)$, if $w=2h+1$ ($w=2h$). Therefore, ${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathfrak{W}}}\right)=\mathfrak{r}+\nu \left(\mathfrak{W}\right)-s+1$. Thus, $\nu \left(\mathfrak{W}\right)+1={\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathfrak{W}}}\right)+s-\mathfrak{r}$. We are finished. □

Example 9.

Note that, if $\mathfrak{W}=\{W_1=\{2,2,1,1,1,1,1\},W_2=\{2,2,2,1,1,1\},\{2,2,2,2,1\}\}$, then $w=9$, $h=4$, $val\left(1\right)=9$, $val\left(2\right)=9$, $s=3$, and $\mathrm{Loops}\left(Q_{{\mathcal{M}}_{\mathfrak{W}}}\right)=12$, and then ${\dim }_{k}Z\left({\Lambda }_{{\mathcal{M}}_{\mathfrak{W}}}\right)=16$. Thus, according to Theorem 13, it holds that $\nu \left(\mathfrak{W}\right)+1=16+3-{(4-1)}^2=19-9=10$.

4. Concluding Remarks

This paper gives formulas for the dimensions of Brauer configuration algebras induced by restricted partitions and compositions, which makes it possible to give formulas for the number of occurrences of their parts.

Elder’s theorem, the Hardy–Ramanujan–Rademacher formula, and the Catalan triangle allow for finding formulas for the dimension of Brauer configuration algebras induced by integer partitions. It is an open problem, giving a closed formula for the center of these algebras.

We classify the defined integer partitions and compositions as realizable branch data of branched coverings over the projective plane $\mathbb{R}{P}^2$ and the sphere $S^2$ via the Hurwitz condition and some restrictions imposed on the associated defects. Giving a criterion to determine the parity of the defect of general integer partitions or compositions is still an open problem.

5. Future Work

The following are interesting problems to be addressed in the future:

• The first problem is giving a closed formula for the center of Brauer configuration algebras induced by general integer partitions and compositions.
• Another interesting task consists of giving formulas for the defect of general integer compositions of type $\mathcal{O}((p,q),(r,s);m_0)$ and $\mathcal{B}(j,m;n)$, establishing for them some parity criteria.