Large Sample Behavior of the Least Trimmed Squares Estimator

Abstract

The least trimmed squares (LTS) estimator is popular in location, regression, machine learning, and AI literature. Despite the empirical version of least trimmed squares (LTS) being repeatedly studied in the literature, the population version of the LTS has never been introduced and studied. The lack of the population version hinders the study of the large sample properties of the LTS utilizing the empirical process theory. Novel properties of the objective function in both empirical and population settings of the LTS and other properties, are established for the first time in this article. The primary properties of the objective function facilitate the establishment of other original results, including the influence function and Fisher consistency. The strong consistency is established with the help of a generalized Glivenko–Cantelli Theorem over a class of functions for the first time. Differentiability and stochastic equicontinuity promote the establishment of asymptotic normality with a concise and novel approach.

1. Introduction

In classical multiple linear regression analysis, it is assumed that there is a relationship for a given data set $\{{({\mathit{x}}_i^{\top },y_i)}^{\top },i\in \{1,\cdots ,n\}\}$:

$$y_i=(1,{\mathit{x}}_i^{\top }){\mathit{\beta }}_0+e_i,i\in \{1,\cdots ,n\},$$

(1)

where $y_i$ and $e_i$ (an error term, a random variable, and is assumed to have a zero mean and unknown variance ${\sigma }^2$ in the classic regression theory) are in ${\mathbb{R}}^1$, ⊤ stands for the transpose, ${\mathit{\beta }}_0={({\beta }_{01},\cdots ,{\beta }_{0p})}^{\top }$, the true unknown parameter, and ${\mathit{x}}_{\mathit{i}}={(x_{i1},\cdots ,x_{i(p-1)})}^{\top }$ is in ${\mathbb{R}}^{p-1}$ ($p\ge 2$) and could be random. It is seen that ${\beta }_{01}$ is the intercept term. Writing ${\mathit{w}}_i={(1,{\mathit{x}}_i^{\top })}^{\top }$, one has $y_i={\mathit{w}}_i^{\top }{\mathit{\beta }}_0+e_i$. The classic assumptions such as linearity and homoscedasticity are implicitly assumed here. Others will be considered later when they are needed.

The goal is to estimate the ${\mathit{\beta }}_0$ based on the given sample ${\mathbf{z}}^{\left(n\right)}:=\{{({\mathit{x}}_i^{\top },y_i)}^{\top },i\in \{1,\cdots ,n\}\}$ (hereafter, it is implicitly assumed that they are i.i.d. from parent $(\mathit{x},y)$). For a candidate coefficient vector $\mathit{\beta }$, call the difference between $y_i$ (observed) and ${\mathit{w}}_{\mathit{i}}^{\top }\mathit{\beta }$ (predicted), the ith residual, $r_i\left(\mathit{\beta }\right)$, ($\mathit{\beta }$ is often suppressed). That is,

$$r_i:=r_i\left(\mathit{\beta }\right)=y_i-{\mathit{w}}_{\mathit{i}}^{\top }\mathit{\beta }.$$

(2)

To estimate ${\mathit{\beta }}_0$, the classic least squares (LS) minimizes the sum of squares of residuals,

$${\widehat{\mathit{\beta }}}_{ls}:=arg\underset{\mathit{\beta }\in {\mathbb{R}}^p}{min}\sum _{i=1}^n{r}_i^2.$$

Alternatively, one can replace the square above with the absolute value to obtain the least absolute deviations estimator (aka, $L_1$ estimator, in contrast to the $L_2$ (LS) estimator).

Due to its great computability and optimal properties when the error $e_i$ follows a Gaussian distribution, the LS estimator is popular in practice across multiple disciplines. It, however, can misbehave when the error distribution slightly departs from the Gaussian assumption, particularly when the errors are heavy-tailed or contain outliers. Both $L_1$ and $L_2$ estimators have the worst $0\%$ asymptotic breakdown point, in sharp contrast to the $50\%$ of the least trimmed squares estimator [1]. The latter is one of the most robust alternatives to the LS estimator. Robust alternatives to the LS estimator are abundant in the literature. The most popular are M-estimators [2]), least median squares (LMS) and least trimmed squares (LTS) estimators [3]), S-estimators [4]), MM-estimators [5]), $\tau$-estimators [6]) and maximum depth estimators [7,8,9]), among others.

Although the M-estimator is the first robust alternative to the LS estimator, it has a poor breakdown point, $1/n$, just as the LS whereas the MM-estimator could have a higher breakdown point but it depends on the initial estimator, which must have a high breakdown robustness such as the LTS. So the MM-estimator can have a better efficiency than the LTS but not robustness.

Due to the cube-root consistency of LMS in R84 and its other drawbacks, LTS is preferred over LMS (see [10]). LTS is popular in the literature in view of its fast computability and high robustness and often serves as the initial estimator for many high breakdown iterative procedures (e.g., S- and MM- estimators). The LTS is defined as the minimizer of the sum of h trimmed squares of residuals. Namely,

$${\widehat{\mathit{\beta }}}_{lts}:=arg\underset{\mathit{\beta }\in {\mathbb{R}}^p}{min}\sum _{i=1}^h{r}_{i:n}^2,$$

(3)

where $r_{1:n}^2\le r_{2:n}^2\le \cdots \le r_{n:n}^2$ are the ordered squared residuals and $\lceil n/2\rceil \le h<n$ and $\lceil x\rceil$ is the ceiling function.

There are copious studies on the LTS in the literature. Most are focused on its computation, e.g., [1,10,11,12,13,14,15,16,17,18];

The LTS has been extended to penalized regression setting with a sparse model where dimension p (in thousands) is much larger than sample size n (in tens, or hundreds), see, e.g., [19,20]. The resulting estimator performs outstanding, especially in terms of robustness.

Other studies on LTS sporadically addressed the asymptotics, e.g., Refs. [1,21] addressed the asymptotic normality of the LTS, but limited to the location case, that is, when $p=1$. Refs. [22,23,24] also addressed the asymptotics of the LTS without employing advanced technical tools in a series (three) of lengthy articles for consistency, root-n consistency, and asymptotic normality, respectively. The analysis is technically demanding and with difficult-to-verify assumptions $\mathcal{A},\mathcal{B},\mathcal{C}$. Furthermore, the analysis is limited to the non-random vector ${\mathit{x}}_i$s case. In this article, without those assumptions and limitations, those results are established concisely with the help of advanced empirical process theory.

Replacing $(1,{\mathit{x}}_i^{\top }){\mathit{\beta }}_0$ by a unspecified nonlinear function $h({\mathit{x}}_i,{\mathit{\beta }}_0)$, Refs. [25,26,27] discussed the asymptotics of the LTS in a nonlinear regression setting. Now that the more general non-linear case has been addressed, one might wonder if there are any merits to discussing the special linear case in this article.

There are at least three merits: (i) the nonlinear function $h({\mathit{x}}_i,{\mathit{\beta }}_0)$ cannot always cover the linear case of $(1,{\mathit{x}}_i^{\top }){\mathit{\beta }}_0$ for the usual LTS (e.g., in the exponential and power regression cases); (ii) many assumptions for the nonlinear case (see A1, A2, A3, A4 in [25]; H1, H2, H3, H4, H5, H6; D1, D2; I1, I2 in [26,27]) (which are usually difficult to verify) can be dropped for the linear case as demonstrated in this article. (iii) A key assumption that $\left\{h\right(\mathit{x},\mathit{\beta }),\mathit{\beta }\in \mathrm{\Theta }\}$ form a VC class of functions over a compact parameter space $\mathrm{\Theta }$ (see [25,26,27]) can be verified directly in this article.

To avoid all the drawbacks and limitations discussed above and take advantage of the standard results of the empirical process theory, this article defines the population version of the LTS (Section 2.1), introduces the novel partition of the parameter space (Section 2.2), and investigates the primary properties of the objective function for the LTS both in the empirical and population settings (Section 2) for the first time. The obtained novel results facilitate the versification of some fundamental assumptions conveniently made previously in the literature. The major contributions of this article thus include the following

(a)

Introducing a novel partition of the parameter space and defining an original population version of the LTS for the first time;

(b)

Investigating primary properties of the sample and population versions of the objective function for the LTS, obtaining original results;

(c)

For the first time, obtaining the influence function ($p\ge 2$) and Fisher consistency for the LTS;

(d)

For the first time, establishing the strong consistency of the sample LTS via a generalized Glivenko-Cantelli Theorem without artificial assumptions; and

(e)

For the first time, employing a novel and concise approach based on the empirical process theory to establish the asymptotic normality of the sample LTS.

The rest of the article is organized as follows. Section 2 introduces for the first time, the population version of LTS and addresses the properties of the LTS estimator in both empirical and population settings, including the global continuity and local differentiability and convexity of its objective function; its influence function (in $p>2$ cases) and Fisher consistency are established for the first time. Section 3 establishes the strong consistency via a generalized Glivenko–Cantelli Theorem and the asymptotic normality of the estimator is re-established in a very different and concise approach (via stochastic equicontinuity) rather than the previous approaches in the literature. Section 4 addresses the asymptotic inference procedures based on the asymptotic normality and bootstrapping. Concluding remarks in Section 5 end the article. Major proofs are deferred to Appendix A.

2. Definition and Properties of the LTS

2.1. Definition

Denote by $F_{({\mathbf{x}}^{\top },y)}$ the joint distribution of ${\mathbf{x}}^{\top }$ and y in model (1). Throughout, $F_{\mathbf{Z}}$ stands for the distribution function of the random vector ${\mathbf{Z}}^{\top }$. For a given $\mathit{\beta }\in {\mathbb{R}}^p$ and an $\alpha \in [1/2,c]$, $1/2<c<1$, let $q(\mathit{\beta },\alpha )=F_W^{-1}\left(\alpha \right)$ be the $\alpha$th quantile of $F_W$ with $W:=W\left(\mathit{\beta }\right)={(y-{\mathit{w}}^{\top }\mathit{\beta })}^2$, where ${\mathit{w}}^{\top }=(1,{\mathit{x}}^{\top })$. The constant $c=1$ case is excluded to avoid unbounded $q(\mathit{\beta },\alpha )$ and the LS cases. Define an objective function

$$O(F_{({\mathbf{x}}^{\top },y)},\mathit{\beta },\alpha )=\int {(y-(1,{\mathit{x}}^{\top })\mathit{\beta })}^2\mathbb{1}\left({(y-(1,{\mathit{x}}^{\top })\mathit{\beta })}^2\le q(\mathit{\beta },\alpha )\right)d{F}_{({\mathbf{x}}^{\top },y)}(\mathbf{x},y),$$

(4)

and a regression functional

$${\mathit{\beta }}_{lts}(F_{({\mathbf{x}}^{\top },y)},\alpha )=arg\underset{\mathit{\beta }\in {\mathbb{R}}^p}{min}O(F_{({\mathbf{x}}^{\top },y)},\mathit{\beta },\alpha ),$$

(5)

where $\mathbb{1}\left(A\right)$ is the indicator of A (i.e., it is one if A holds and zero otherwise). Let $F_{({\mathbf{x}}^{\top },y)}^n$ be the sample version of the $F_{({\mathbf{x}}^{\top },y)}$ based on a sample ${\mathbf{z}}^{\left(n\right)}:=\{{({\mathbf{x}}_i^{\top },y_i)}^{\top },i\in \{1,2,\cdots ,n\}\}$. $F_{({\mathbf{x}}^{\top },y)}^n$ and ${\mathbf{z}}^{\left(n\right)}$ will be used interchangeably. Using $F_{({\mathbf{x}}^{\top },y)}^n$, one obtains the sample versions

$$O(F_{({\mathbf{x}}^{\top },y)}^n,\mathit{\beta },\alpha )={\displaystyle \frac{1}{n}}\sum _{i=1}^{\lfloor \alpha n\rfloor +1}{r}_{i:n}^2,$$

(6)

where $\lfloor x\rfloor$ is the floor function. Further

$${\widehat{\mathit{\beta }}}_{lts}^n:={\mathit{\beta }}_{lts}(F_{({\mathbf{x}}^{\top },y)}^n,\alpha )=arg\underset{\mathit{\beta }\in {\mathbb{R}}^p}{min}O(F_{({\mathbf{x}}^{\top },y)}^n,\mathit{\beta },\alpha ).$$

(7)

It is readily seen that the ${\widehat{\mathit{\beta }}}_{lts}^n$ above is identical to the ${\widehat{\mathit{\beta }}}_{lts}$ in (3) with $h=\lfloor \alpha n\rfloor +1$. Henceforth, we prefer to treat the ${\widehat{\mathit{\beta }}}_{lts}^n$ rather than the ${\widehat{\mathit{\beta }}}_{lts}$ in (3).

The first natural question is the existence of the minimizer in the right-hand side (RHS) of (7), or the existence of the ${\widehat{\mathit{\beta }}}_{lts}^n$. Does it always exist? If it exists, will it be unique? Unique existence is a key precondition for the study of asymptotics of an estimator.

One might take the existence for granted since the objective is non-negative and has a finite infimum that can be approximated by objective values of a sequence of $\mathit{\beta }$s. There is a sub-sequence of $\mathit{\beta }$s with its objective values converging to the infimum that is a minimum due to the continuity of the objective function. The sub-sequence of $\mathit{\beta }$s converges to a point ${\mathit{\beta }}^{*}$, which is the minimizer of the RHS. However, there are multiple issues with the arguments above. The existence and the convergence of the $\mathit{\beta }$ sub-sequence (to a minimum) and continuity of objective function need to be proved. In the sequel, we take a different approach.

2.2. Properties in the Empirical Case

Write $O^n\left(\mathit{\beta }\right)$ and ${\mathbb{1}}_i$ for the $O(F_{({\mathbf{x}}^{\prime },y)}^n,\mathit{\beta },\alpha )$ and the $\mathbb{1}\left(r_i^2\le r_{h:n}^2\right)$, respectively. It is seen that

$$O^n\left(\mathit{\beta }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{r}_i^2\mathbb{1}\left(r_i^2\le r_{h:n}^2\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{r}_i^2{\mathbb{1}}_i,$$

(8)

where $h=\lfloor \alpha n\rfloor +1$. The fraction $1/n$ will often be ignored in the following discussion.

• Existence and uniqueness
• Partition parameter space

For a given sample $z^{\left(n\right)}$, an $\alpha$ (or h), and any ${\mathit{\beta }}^1\in {\mathbb{R}}^p$, let $r_{i:n}^2\left({\mathit{\beta }}^1\right)=r_{k_i}^2\left({\mathit{\beta }}^1\right)$ for an integer $k_i$. Note that $r_j$ and $k_i$ depend on ${\mathit{\beta }}^1$, i.e., $r_j:=r_j\left({\mathit{\beta }}^1\right)$, $k_i:=k_i\left({\mathit{\beta }}^1\right)$. Obviously $r_{k_1}^2\le r_{k_2}^2\le \cdots \le r_{k_n}^2$. Call $\{k_i,1\le i\le h\}$ ${\mathit{\beta }}^1$-h-integer set. If $r_i^2\ne r_j^2$ for any distinct i and j, then the h-integer set is unique. Hereafter, we assume (A0): $\mathit{W}$ has a density for any given $\mathit{\beta }$. Then, almost surely (a.s.), the h-integer set is unique.

Consider the unique cases. There are other $\mathit{\beta }$s in ${\mathbb{R}}^p$ that share the same h-integer set as that of the ${\mathit{\beta }}^1$. Denote the set of such points that have the same h integers as ${\mathit{\beta }}^1$ by

$$S_{{\mathit{\beta }}^1}:=\left\{\mathit{\beta }\in {\mathbb{R}}^p:k_i\left(\mathit{\beta }\right)=k_i\left({\mathit{\beta }}^{\mathbf{1}}\right)=k_i,i\in \{1,2,\cdots ,h\}\{k_i,1\le i\le h\}\mathrm{is}\mathrm{unique}.\right\}$$

(9)

If (A0) holds, then $S_{{\mathit{\beta }}^1}\ne \varnothing$ (a.s.). If it is ${\mathbb{R}}^p$, then we have a trivial case (see Remark 1 below). Otherwise, there are only finitely many such sets (for a fixed n) that partition ${\mathbb{R}}^p$. Let ${\cup }_{l=1}^L{\overline{S}}_{{\mathit{\beta }}^l}={\mathbb{R}}^p$, where $S_{{\mathit{\beta }}^l}$s are defined similarly to (9) and are disjoint for different l, $1\le l\le L:=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{h}}\right)$, and $\overline{A}$ is the closure of the set A. Write ${\mathbf{X}}_n={({\mathit{w}}_1,\cdots ,{\mathit{w}}_n)}^{\prime }$, an $n\times p$ matrix. Assume (A1): ${\mathbf{X}}_{\mathit{n}}$ and any its h rows have a full rank $\mathit{p}$. As in the R function ltsReg in the R package robustbase version 99-4-1, hereafter, we assume that $p<n/2$.

Lemma 1.

Assume that (A0) and (A1) hold, then

(i) 

(a) For any l ($1\le l\le L$), $r_{k_1\left({\mathit{\beta }}^l\right)}^2<r_{k_2\left({\mathit{\beta }}^l\right)}^2<\cdots <r_{k_h\left({\mathit{\beta }}^l\right)}^2$ over $S_{{\mathit{\beta }}^l}$.

(b) For any $\mathit{\eta }\in S_{{\mathit{\beta }}^l}$, there exists an open ball $B(\mathit{\eta },\delta )$ centered at η with a radius $\delta >0$ such that for any $\mathit{\beta }\in B(\mathit{\eta },\delta )$

$$O^n\left(\mathit{\beta }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^h{r}_{k_i\left(\mathit{\beta }\right)}^2\left(\mathit{\beta }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^h{r}_{k_i\left(\mathit{\eta }\right)}^2\left(\mathit{\beta }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^h{r}_{k_i\left({\mathit{\beta }}^l\right)}^2\left(\mathit{\beta }\right),(a.s.)$$

(10)

(ii) 

The graph of $O^n\left(\mathit{\beta }\right)$ over $\mathit{\beta }\in {\mathbb{R}}^p$ is composed of the L closures of graphs of the quadratic function of β: ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^h{r}_{k_i\left({\mathit{\beta }}^l\right)}^2\left(\mathit{\beta }\right)$ for $O^n\left({\mathit{\beta }}^l\right)$ and any l ($1\le l\le L$), joined together.

(iii) 

$O^n\left(\mathit{\beta }\right)$ is continuous in $\mathit{\beta }\in {\mathbb{R}}^p$.

(iv) 

$O^n\left(\mathit{\beta }\right)$ is differentiable and strictly convex over each $S_{{\mathit{\beta }}^l}$ for any $1\le l\le L$.

Proof. 

See the Appendix A. □

Remark 1.

(a) If $S_{{\mathit{\beta }}^0}={\mathbb{R}}^p$, then $O^n\left(\mathit{\beta }\right)$ is a twice differentiable and strictly convex quadratic function of β, the existence and the uniqueness of ${\widehat{\mathit{\beta }}}_{lts}^n$ are trivial as long as ${\mathbf{X}}_n$ has a full rank.

(b) Replacing ${(1,{\mathit{x}}_i)}^{\prime }\mathit{\beta }$ by a nonlinear $h({\mathit{x}}_i,\mathit{\beta })$, conveniently assuming that (i) $F_W$ is twice differentiable around the points corresponding to the square roots of the α-quantiles of W, (ii) $h({\mathit{x}}_i,\mathit{\beta })$ is continuous over parameter space B, (iii) $h({\mathit{x}}_i,\mathit{\beta })$ is twice differentiable in β for $\mathit{\beta }\in B({\mathit{\beta }}_0,\delta )$ a.s., and (iv) $\partial h({\mathit{x}}_i,\mathit{\beta })/\partial \mathit{\beta }$ is continuous in β, Refs. [26,27] also addressed the continuity and differentiability of the objective function of the LTS. All assumptions were never verified in [26,27], though; however, they are proved (or not required) in Lemma 1.

(c) Continuity and differentiability inferred just based on $O^n\left(\mathit{\beta }\right)$ being the sum of h continuous and differentiable functions (squares of residual) without (i) or (10) might not be flawless. In general, $O^n\left(\mathit{\beta }\right)$ is not differentiable nor convex in β globally.

Let ${\mathbf{y}}_n:={(y_1,\cdots ,y_n)}^{\top }$, ${\mathit{M}}_n:=\mathit{M}({\mathbf{y}}_n,{\mathbf{X}}_n,\mathit{\beta },\alpha )={\sum }_{i=1}^n{\mathit{w}}_i{\mathit{w}}_i^{\top }{\mathbb{1}}_i={\sum }_{i=1}^h{\mathit{w}}_{k_i\left(\mathit{\beta }\right)}{\mathit{w}}_{k_i\left(\mathit{\beta }\right)}^{\top }$. Note that ${\mathbb{1}}_i$ depends on $\mathit{\beta }$.

Theorem 1.

Assume that (A0) and (A1) hold. Then,

(i) 

${\widehat{\mathit{\beta }}}_{lts}^n$ exists and is the local minimum of $O^n\left(\mathit{\beta }\right)$ over $S_{{\mathit{\beta }}^{l_0}}$ for some $l_0$ ($1\le l_0\le L$).

(ii) 

Over $S_{{\mathit{\beta }}^{l_0}}$, ${\widehat{\mathit{\beta }}}_{lts}^n$ is the solution of the system of equations

$$\sum _{i=1}^n(y_i-{\mathit{w}}_i^{\top }\mathit{\beta }){\mathit{w}}_i{\mathbb{1}}_i=\mathbf{0},$$

(11)

(iii) 

Over $S_{{\mathit{\beta }}^{l_0}}$, the unique solution is

$${\widehat{\mathit{\beta }}}_{lts}^n={\mathit{M}}_n{({\mathbf{y}}_n,{\mathbf{X}}_n,{\widehat{\mathit{\beta }}}_{lts}^n,\alpha )}^{-1}\sum _{i=1}^h{y}_{k_i\left({\mathit{\beta }}^{l_0}\right)}{\mathit{w}}_{k_i\left({\mathit{\beta }}^{l_0}\right)}.$$

(12)

Proof. 

The given conditions and Lemma 1 allow one to focus on a piece $S_{{\mathit{\beta }}^l}$, $1\le l\le L$, all results follow in a straightforward fashion. For more details, see Appendix A. □

Remark 2.

(a) Unique existence, which is often implicitly assumed or ignored in the literature, is central for the discussion of asymptotics of ${\widehat{\mathit{\beta }}}_{lts}^n$. Existence of ${\widehat{\mathit{\beta }}}_{lts}^n$ could also be established under the assumption that there are no $\lfloor (n+1)/2\rfloor$ sample points of $z^{\left(n\right)}$ contained in any $(p-1)$-dimensional hyperplane, similarly to that of Theorem 2.2 for LST in [28]. It is established here without such an assumption nevertheless.

(b) A sufficient condition for the invertibility of ${\mathit{M}}_n$ is that any h rows of ${\mathit{X}}_n$ form a full rank sub-matrix. The latter is true if (A1) holds.

(c) Ref. [22] also addressed the existence of ${\widehat{\mathit{\beta }}}_{lts}^n$ (Assertion 1) for non-random covariates (carriers) satisfying many demanding assumptions ($\mathcal{A},\mathcal{B}$) that are never verified. The uniqueness was left unaddressed, though.

2.3. Properties in the Population Case

The best breakdown point of the LTS (see p. 132 of [1]) reflects its global robustness. We now examine its local robustness via the influence function to depict its complete robust picture.

2.3.1. Definition of Influence Function

For a distribution F on ${\mathbb{R}}^p$ and an $\epsilon \in (0,1/2)$, the version of F contaminated by an $\epsilon$ amount of an arbitrary distribution G on ${\mathbb{R}}^p$ is denoted by $F(\epsilon ,G)=(1-\epsilon )F+\epsilon G$ (an $\epsilon$ amount deviation from the assumed F). $F(\epsilon ,G)$ is actually a convex contamination of F. There are other types of contamination such as contamination by total variation or Hellinger distances. We cite the definition given in [29].

Definition 1

([29]). The influence function (IF) of a functional $\mathbf{t}$ at a given point $\mathit{x}\in {\mathbb{R}}^p$ for a given F is defined as

$$\mathit{IF}(\mathit{x};\mathbf{t},F)=\underset{\epsilon \to 0^{+}}{lim}{\displaystyle \frac{\mathbf{t}\left(F(\epsilon ,{\delta }_{\mathit{x}})\right)-\mathbf{t}\left(F\right)}{\epsilon }},$$

(13)

where ${\delta }_{\mathit{x}}$ is the point-mass probability measure at $\mathit{x}\in {\mathbb{R}}^p$.

The function $\mathrm{IF}(\mathit{x};\mathbf{t},F)$ describes the relative effect (influence) on $\mathbf{t}$ of an infinitesimal point-mass contamination at $\mathit{x}$ and measures the local robustness of $\mathbf{t}$.

To establish the IF for the functional ${\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\top },y)},\alpha )$, we need to first show its existence and uniqueness with or without point-mass contamination. To that end, write

$$F_{\epsilon }\left(\mathbf{z}\right):=F(\epsilon ,{\delta }_{\mathbf{z}})=(1-\epsilon )F_{({\mathit{x}}^{\top },y)}+\epsilon {\delta }_{\mathbf{z}},$$

with $\mathbf{u}={({\mathbf{s}}^{\top },t)}^{\top }\in {\mathbb{R}}^p$, $\mathbf{s}\in {\mathbb{R}}^{p-1}$, $t\in {\mathbb{R}}^1$ as the corresponding random vector (i.e., $F_{\mathbf{u}}=F_{\epsilon }\left(\mathbf{z}\right)=F(\epsilon ,{\delta }_{\mathbf{z}})$). The versions of (4) and (5) at the contaminated $F(\epsilon ,{\delta }_{\mathbf{z}})$ are, respectively,

$$O(F_{\epsilon }\left(\mathbf{z}\right),\mathit{\beta },\alpha )=\int {(t-(1,{\mathit{s}}^{\top })\mathit{\beta })}^2\mathbb{1}\left({(t-(1,{\mathit{s}}^{\top })\mathit{\beta })}^2\le q_{\epsilon }(\mathbf{z},\mathit{\beta },\alpha )\right)d{F}_{\mathbf{u}}(\mathbf{s},t),$$

(14)

with $q_{\epsilon }(\mathbf{z},\mathit{\beta },\alpha )$ being the $\alpha$th quantile of the distribution function of ${(t-{\mathit{v}}^{\top }\mathit{\beta })}^2$, $\mathit{v}={(1,{\mathit{s}}^{\top })}^{\top }$, and

$${\mathit{\beta }}_{lts}(F_{\epsilon }\left(\mathbf{z}\right),\alpha )=arg\underset{\mathit{\beta }\in {\mathbb{R}}^p}{min}O(F_{\epsilon }\left(\mathbf{z}\right),\mathit{\beta },\alpha ).$$

(15)

For ${\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\top },y)},\alpha )$ defined in (5) and ${\mathit{\beta }}_{lts}(F_{\epsilon }\left(\mathbf{z}\right),\alpha )$ above, we have an analogous result to Theorem 1. (Assume that the counterpart of model (1) is $y=(1,{\mathit{x}}^{\top }){\mathit{\beta }}_0+e={\mathit{w}}^{\top }{\mathit{\beta }}_0+e$). Before we derive the influence function, we need to establish existence and uniqueness.

2.3.2. Existence and Uniqueness

Write $O\left(\mathit{\beta }\right)$ for $O(F_{({\mathit{x}}^{\top },y)},\mathit{\beta },\alpha )$ in (4). To have a counterpart of Lemma 1, we need (A2): $\mathit{W}$ has a positive density around a small neighborhood of $\mathit{q}(\mathit{\beta },\mathit{\alpha })$ for the given $\mathit{\alpha }$, $\mathit{\beta }$.

Lemma 2.

Assume (A2) holds and $E\left(\mathit{w}{\mathit{w}}^{\top }\right)$ exists. Then,

(i) $O\left(\mathit{\beta }\right)$ is continuous in $\mathit{\beta }\in {\mathbb{R}}^p$;

(ii) $O\left(\mathit{\beta }\right)$ is twice differentiable in $\mathit{\beta }\in {\mathbb{R}}^p$,

$${\partial }^{2}O\left(\mathit{\beta }\right)/\partial {\mathit{\beta }}^2=2E(\mathit{w}{\mathit{w}}^{\top }\mathbb{1}({(y-{\mathit{w}}^{\top }\mathit{\beta })}^2\le q(\mathit{\beta },\alpha )));$$

(iii) $O\left(\mathit{\beta }\right)$ is strictly convex in $\mathit{\beta }\in {\mathbb{R}}^p$.

Proof. 

The boundedness of the integrand in (4), given conditions, and the Lebesgue-dominated convergence theorem leads to the desired results. For the details, see Appendix A. □

Note that (ii) and (iii) above are global in $\mathit{\beta }$, stronger than the empirical counterparts, and all are attributed to the boundary of $S_{{\mathit{\beta }}^l}$ issue. We now treat the existence and uniqueness of ${\mathit{\beta }}_{lts}$, which is central to the study of the asymptotics.

Theorem 2.

Assume (A2) holds and $E\left(\mathit{w}{\mathit{w}}^{\top }\right)$ exists, $q_{\epsilon }(\mathbf{z},\mathit{\beta },\alpha )$ is continuous in β, and $P({(t-{\mathit{v}}^{\top }\mathit{\beta })}^2=q_{\epsilon }(\mathbf{z},\mathit{\beta },\alpha ))=0$ for any $\mathit{\beta }\in {\mathbb{R}}^p$ and the given α. Then,

(i) ${\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\top },y)},\alpha )$ and ${\mathit{\beta }}_{lts}(F_{\epsilon }\left(\mathbf{z}\right),\alpha )$ exist.

(ii) Furthermore, they are the solution of a system of equations, respectively,

$$\begin{array}{cc}\hfill \int (y-(1,{\mathit{x}}^{\top })\mathit{\beta }){(1,{\mathit{x}}^{\top })}^{\top }\mathbb{1}\left({(y-(1,{\mathit{x}}^{\top })\mathit{\beta })}^2\le q(\mathit{\beta },\alpha )\right)d{F}_{({\mathit{x}}^{\top },y)}(\mathit{x},y)& =\mathbf{0},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \int (t-(1,{\mathit{s}}^{\top })\mathit{\beta }){(1,{\mathit{s}}^{\top })}^{\top }\mathbb{1}\left({(t-(1,{\mathit{s}}^{\top })\mathit{\beta })}^2\le q_{\epsilon }(\mathbf{z},\mathit{\beta },\alpha )\right)d{F}_{\mathbf{u}}(\mathbf{s},t)& =\mathbf{0}.\hfill \end{array}$$

(17)

(iii) ${\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\top },y)},\alpha )$ and ${\mathit{\beta }}_{lts}(F_{\epsilon }\left(\mathbf{z}\right),\alpha )$ are unique provided that

$$\begin{array}{cc}\hfill \int {(1,{\mathit{x}}^{\top })}^{\top }(1,{\mathit{x}}^{\top })\mathbb{1}\left({(y-(1,{\mathit{x}}^{\top })\mathit{\beta })}^2\le q(\mathit{\beta },\alpha )\right)d{F}_{({\mathit{x}}^{\top },y)}(\mathit{x},y)& ,\hfill \end{array}$$

(18)

$$\begin{array}{c}\hfill \int {(1,{\mathit{s}}^{\top })}^{\top }(1,{\mathit{s}}^{\top })\mathbb{1}\left({(t-(1,{\mathit{s}}^{\top })\mathit{\beta })}^2\le q_{\epsilon }(\mathbf{z},\mathit{\beta },\alpha )\right)d{F}_{\mathbf{u}}(\mathbf{s},t)\end{array}$$

(19)

are invertible for β in a small neighborhood of ${\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\top },y)},\alpha )$ and ${\mathit{\beta }}_{lts}(F_{\epsilon }\left(\mathbf{z}\right),\alpha )$, respectively.

Proof. 

In light of Lemma 2, the proof is straightforward, see Appendix A. □

The continuity of $q_{\epsilon }(\mathbf{z},\mathit{\beta },\alpha )$ in $\mathit{\beta }$ is necessary for the differentiability of $O(F_{\epsilon }\left(\mathbf{z}\right),\mathit{\beta },\alpha )$. In the non-contaminated case, the continuity of $q(\mathit{\beta },\alpha )$ is guaranteed by (A2).

Does the population version of the LTS, ${\mathit{\beta }}_{lts}$, defined in (5), have something to do with ${\mathit{\beta }}_0$? It turns out that under some conditions, they are identical, which is called Fisher consistency.

2.3.3. Fisher Consistency

Theorem 3.

Assume (A2) holds and $E\left(\mathit{w}{\mathit{w}}^{\top }\right)$ exists, then, ${\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\top },y)},\alpha )={\mathit{\beta }}_0$ provided that

(i) 

$E_{({\mathit{x}}^{\top },y)}\left(\mathit{w}{\mathit{w}}^{\top }\mathbb{1}(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right))\right)$ is invertible, and

(ii) 

$E_{({\mathit{x}}^{\top },y)}\left(e\mathit{w}\mathbb{1}(e^2\le F_{e^2}^{-1}\left(\alpha \right))\right)=\mathbf{0}$, where $r\left(\mathit{\beta }\right)=y-{\mathit{w}}^{\top }\mathit{\beta }$.

Proof. 

Theorem 2 leads directly to the desired result, see the Appendix A. □

2.3.4. Influence Function

Theorem 4.

Assume that the assumptions in Theorem 2 hold. Set ${\mathit{\beta }}_{lts}:={\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\top },y)},\alpha )$. Then, for any ${\mathbf{z}}_0:={({\mathbf{s}}_0^{\top },t_0)}^{\top }\in {\mathbb{R}}^p$, we have that

$$IF({\mathbf{z}}_0;{\mathit{\beta }}_{lts},F_{({\mathit{x}}^{\top },y)})=\left\{\begin{array}{cc}\mathbf{0},\hfill & if{(t_0-{\mathit{v}}_0^{\top }{\mathit{\beta }}_{lts})}^2>q({\mathit{\beta }}_{lts},\alpha ),\hfill \\ M^{-1}(t_0-{\mathit{v}}_0^{\top }{\mathit{\beta }}_{lts}){\mathit{v}}_0,\hfill & otherwise,\hfill \end{array}\right.$$

provided that $\mathit{M}=E_{({\mathit{x}}^{\top },y)}\left(\mathit{w}{\mathit{w}}^{\top }\mathbb{1}\left(r{\left({\mathit{\beta }}_{lts}\right)}^2\le q({\mathit{\beta }}_{lts},\alpha )\right)\right)$ is invertible, where ${\mathit{v}}_0={(1,{\mathit{s}}_0^{\top })}^{\top }$.

Proof. 

The connection to the derivative of a functional is the key, see Appendix A. □

Remark 3.

(a) When $p=1$, the problem in our model (1) becomes a location problem (see p. 158 of [1]) and the IF of the LTS estimation functional is given on p. 191 of [1]. In the location setting, Ref. [30] also studied the IF of the LTS. When $p=2$, namely in the simple regression case, Ref. [31] studied IF of the sparse-LTS functional under the assumption that $\mathit{x}$ and e are independent and normally distributed. Under stringent assumptions on the error terms $e_i$ and on $\mathit{x}$, Ref. [21] also addressed the IF of LTS for any p, but the point mass at $({\mathit{x}}^{\top },z)$ with z being the error term, an unusual contaminating point. The above result is much more general and valid for any $p\ge 1$, ${\mathit{x}}^{\prime }$, and e.

(b) The influence function of ${\mathit{\beta }}_{lts}$ remains bounded if the contaminating point $({\mathit{s}}_0^{\prime },t_0)$ does not follow the model (i.e., its residual is extremely large), in particular for bad leverage points and vertical outliers. This shows the good robust properties of the LTS.

(c) The influence function of ${\mathit{\beta }}_{lts}$, unfortunately, might be unbounded (in $p>1$ case), sharing the drawback of the sparse-LTS (in the p = 2 case). The latter was shown in [31]. Trimming based on the residuals (or squared residuals) will have this type of drawback since the term ${\mathit{w}}^{\top }\mathit{\beta }$ can be bounded, but $\parallel \mathit{x}\parallel$ might not.

3. Asymptotic Properties

Refs. [22,23,24] rigorously addressed the consistency, root-n consistency, and normality of the LTS under a restrictive setting (${\mathit{x}}_i$s are non-random covariates) plus many assumptions on ${\mathit{x}}_i$s and on the distribution of $e_i$ in a series of three lengthy papers.

Refs. [26,27] also addressed asymptotic properties of an extended LTS under $\mathit{\beta }$-mixing conditions for ${\mathit{x}}_i$ with nonlinear regression function $h({\mathit{x}}_i,\mathit{\beta })$, a seemingly more general setting, but with numerous artificial assumptions (H1, H2, H3, H4, H5, H6; D1, D2; I1, I2) that are never verified in any concrete example and not even for the linear LTS case. That is, Refs. [26,27] do not cover the LTS in (3).

Here, we address asymptotic properties of ${\widehat{\mathit{\beta }}}_{lts}^n$ without the artificial assumptions that were made in the literature for LTS with a nonlinear regression function. Strong consistency has been addressed in [25] in a nonlinear setting without verifying any of their conveniently assumed key assumptions for the linear LTS. We now rigorously establish strong consistency.

3.1. Strong Consistency

Following the notations of [32], write

$$\begin{array}{cc}\hfill O(\mathit{\beta },P):& =O(F_{({\mathit{x}}^{\top },y)},\mathit{\beta },\alpha )=P\left[{(y-{\mathit{w}}^{\top }\mathit{\beta })}^2\mathbb{1}(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right))\right]=Pf,\hfill \\ \hfill O(\mathit{\beta },P_n):& =O(F_{({\mathit{x}}^{\top },y)}^n,\mathit{\beta },\alpha )={\displaystyle \frac{1}{n}}\sum _{i=1}^n{r}_i^2\mathbb{1}\left(r_i^2\le {\left(r\right)}_{h:n}^2\right)=P_{n}f,\hfill \end{array}$$

where $f:=f(\mathit{x},y,\mathit{\beta },\alpha )={(y-{\mathit{w}}^{\top }\mathit{\beta })}^2\mathbb{1}(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right))$, $\alpha$ and $h=\lfloor \alpha n\rfloor +1$ are fixed.

Under corresponding assumptions in Theorems 1 and 2, ${\widehat{\mathit{\beta }}}_{lts}^n$ and ${\mathit{\beta }}_{lts}$ are unique minimizers of $O(\mathit{\beta },P_n)$ and $O(\mathit{\beta },P)$, respectively.

To show that ${\widehat{\mathit{\beta }}}_{lts}^n$ converges to ${\mathit{\beta }}_{lts}$ a.s., one can take the approach given in Section 4.2 of [28]. However, here, we take a different and more direct approach.

To show that ${\widehat{\mathit{\beta }}}_{lts}^n$ converges to ${\mathit{\beta }}_{lts}$ a.s., it will suffice to prove that $O({\widehat{\mathit{\beta }}}_{lts}^n,P)\to O({\mathit{\beta }}_{lts},P)$ a.s., because $O(\mathit{\beta },P)$ is bounded away from $O({\mathit{\beta }}_{lts},P)$ outside each neighborhood of ${\mathit{\beta }}_{lts}$ in light of continuity and compactness. Let $\mathrm{\Theta }$ be a closed ball centered at ${\mathit{\beta }}_{lts}$ with a radius $r>0$. Define a class of functions

$$\mathcal{F}(\mathit{\beta },\alpha )=\left\{f(\mathit{x},y,\mathit{\beta },\alpha )={(y-{\mathit{w}}^{\top }\mathit{\beta })}^2\mathbb{1}(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right)):\mathit{\beta }\in \mathrm{\Theta },\alpha \in [1/2,c]\right\}$$

If we prove uniform almost sure convergence of $P_n$ to P over $\mathcal{F}$ (see Lemma 3 below), then we can deduce that $O({\widehat{\mathit{\beta }}}_{lts}^n,P)\to O({\mathit{\beta }}_{lts},P)$ a.s. from

$$\begin{array}{cc}\hfill O({\widehat{\mathit{\beta }}}_{lts}^n,P_n)-O({\widehat{\mathit{\beta }}}_{lts}^n,P)& \to 0(\mathrm{in} \mathrm{light} \mathrm{of} \mathrm{Lemma} 3),\mathrm{and}\hfill \\ \hfill O({\widehat{\mathit{\beta }}}_{lts}^n,P_n)\le O({\mathit{\beta }}_{lts},P_n)& \to O({\mathit{\beta }}_{lts},P)\le O({\widehat{\mathit{\beta }}}_{lts}^n,P).\hfill \end{array}$$

The above discussions and arguments have led to the following

Theorem 5.

Under corresponding assumptions in Theorems 1 and 2 for the uniqueness of ${\widehat{\mathit{\beta }}}_{lts}^n$ and ${\mathit{\beta }}_{lts}$, respectively, we have ${\widehat{\mathit{\beta }}}_{lts}^n$ converges a.s. to ${\mathit{\beta }}_{lts}$ (i.e., ${\widehat{\mathit{\beta }}}_{lts}^n-{\mathit{\beta }}_{lts}=o\left(1\right)$, a.s.).

The above is based on the following generalized Glivenko–Cantelli Theorem.

Lemma 3.

${sup}_{f\in \mathcal{F}}|P_{n}f-Pf|\to 0$ a.s., provided that (A2) holds.

Proof. 

Verifying two requirements in Theorem 24 in II.5 of [32] leads to the result. Showing the covering number for functions in $\mathcal{F}$ is bounded is challenging. Essentially, one needs to show that the graphs of functions in $\mathcal{F}$ form a VC class of sets (this was avoided in the literature, e.g., in [22,23,24,25,26,27]). For details, see Appendix A. □

3.2. Root-n Consistency and Asymptotic Normality

Instead of treating the root-n consistency separately as in [22,23,24], we will establish the asymptotic normality of ${\widehat{\mathit{\beta }}}_{lts}^n$ directly via stochastic equicontinuity (see p. 139 of [32]).

Stochastic equicontinuity refers to a sequence of stochastic processes $\{Z_n\left(t\right):t\in T\}$ whose shared index set T comes equipped with a semi-metric $d(·,·)$.

Definition 2

(IIV. 1, Def. 2 of [32]). Call $Z_n$ stochastically equicontinuous at $t_0$ if for each $\eta >0$ and $ϵ>0$ there exists a neighborhood U of $t_0$ for which

$$lim\; supP\left(\underset{U}{sup}|Z_n\left(t\right)-Z_n\left(t_0\right)|>\eta \right)<ϵ.$$

(20)

It is readily seen (see [32]) that if ${\tau }_n$ is a sequence of random elements of T that converges in probability to $t_0$, then,

$$Z_n\left({\tau }_n\right)-Z_n\left(t_0\right)\to 0\mathrm{in} \mathrm{probability},$$

(21)

because, with probability tending to one, ${\tau }_n$ will belong to each U. The form above will be easier to apply, especially when the behavior of a particular ${\tau }_n$ sequence is under investigation.

Suppose $\mathcal{F}=\left\{f\right(·,t):t\in T\}$, with T a subset of ${\mathbb{R}}^k$, is a collection of real, P-integrable functions on the set S where P (probability measure) lives. Denote by $P_n$ the empirical measure formed from n independent observations on P, and define the empirical process $E_n$ as the signed measure $n^{1/2}(P_n-P)$. Define

$$\begin{array}{cc}\hfill F\left(t\right)& =Pf(·,t),\hfill \\ \hfill F_n\left(t\right)& =P_{n}f(·,t).\hfill \end{array}$$

Suppose $f(·,t)$ has a linear approximation near the $t_0$ at which $F(·)$ takes on its minimum value:

$$f(·,t)=f(·,t_0)+{(t-t_0)}^{\top }\nabla f(·,t)+|t-t_0|r(·,t).$$

(22)

For completeness, set $r(·,t_0)=0$, where ∇ (differential operator) is a vector of k real functions on S. We cite theorem 5 in VII.1 of [32] (p. 141) for the asymptotic normality of ${\tau }_n$.

Lemma 4

([32]). Suppose $\left\{{\tau }_n\right\}$ is a sequence of random vectors converging in probability to the value $t_0$ at which $F(·)$ has its minimum. Define $r(·,t)$ and the vector of functions $\nabla (·,t)$ by (22). If

(i) 

$t_0$ is an interior point of the parameter set T;

(ii) 

$F(·)$ has a non-singular second derivative matrix V at $t_0$;

(iii) 

$F_n\left({\tau }_n\right)=o_p\left(n^{-1}\right)+{inf}_t{F}_n\left(t\right)$;

(iv) 

The components of $\nabla f(·,t)$ all belong to ${\mathcal{L}}^2\left(P\right)$;

(v) 

The sequence $\left\{E_{n}r(·,t)\right\}$ is stochastically equicontinuous at $t_0$;

then,

$$n^{1/2}({\tau }_n-t_0)\stackrel{d}{⟶}N(\mathbf{0},V^{-1}[P(\nabla {\nabla }^{\top })-(P\nabla ){(P\nabla )}^{\top }]V^{-1}).$$

By Theorems 1 and 5, assume, without loss of generality (w.l.o.g.), that ${\widehat{\mathit{\beta }}}_{lts}^n$ and ${\mathit{\beta }}_{lts}$ belong to a ball centered at ${\mathit{\beta }}_{lts}$ with a large enough radius $r_0$, $B({\mathit{\beta }}_{lts},r_0)$, and that $\mathrm{\Theta }=B({\mathit{\beta }}_{lts},r_0)$ is our parameter space of $\mathit{\beta }$, hereafter. In order to apply the Lemma, we first realize that in our case, ${\widehat{\mathit{\beta }}}_{lts}^n$ and ${\mathit{\beta }}_{lts}$ correspond to ${\tau }_n$ and $t_0$ (assume, w.l.o.g. that ${\mathit{\beta }}_{lts}=\mathbf{0}$ in light of regression equivariance, see Section 4); $\mathit{\beta }$ and $\mathrm{\Theta }$ correspond to t and T; $f(·,t):=f({\mathit{x}}^{\top },y,\mathit{\beta },\alpha )={(y-{\mathit{w}}^{\top }\mathit{\beta })}^2\mathbb{1}(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right))$. In our case,

$$\nabla f(·,t):=\nabla f(\mathit{x},y,\mathit{\beta },\alpha )={\displaystyle \frac{\partial }{\partial \mathit{\beta }}}f(\mathit{x},y,\mathit{\beta },\alpha )=-2(y-{\mathit{w}}^{\top }\mathit{\beta })\mathit{w}\mathbb{1}\left(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right)\right).$$

We will have to assume that $P\left({\nabla }_i^2\right)=P(4{(y-{\mathit{w}}^{\top }\mathit{\beta })}^2{w}_i^2\mathbb{1}(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right)))$ exists to meet (iv) of the lemma, where $i\in \{1,\cdots ,p\}$ and ${\mathit{w}}^{\top }=(1,{\mathit{x}}^{\top })=(1,x_1,\cdots ,x_{p-1})$. It is readily seen that a sufficient condition for this assumption to hold is the existence of $P\left(x_i^2\right)$. In our case, $V=2P(\mathit{w}{\mathit{w}}^{\top }\mathbb{1}(r{\left(\mathit{\beta }\right)}^2\le F_{r{\left(\mathit{\beta }\right)}^2}^{-1}\left(\alpha \right)))$, and we will have to assume that it is invertible when $\mathit{\beta }$ is replaced by ${\mathit{\beta }}_{lts}$ (this is covered by (18)) to meet (ii) of the lemma. In our case,

$$r(·,t)=\left({\displaystyle \frac{{\mathit{\beta }}^{\top }}{\parallel \mathit{\beta }\parallel }}V/2{\displaystyle \frac{\mathit{\beta }}{\parallel \mathit{\beta }\parallel }}\right)\parallel \mathit{\beta }\parallel .$$

We will assume that ${\lambda }_{min}$ and ${\lambda }_{max}$ are the minimum and maximum eigenvalues of positive semidefinite matrix V over all $\mathit{\beta }\in \mathrm{\Theta }$ and $\alpha \in [1/2,c]$.

Theorem 6.

Assume that

(i) 

The uniqueness assumptions for ${\widehat{\mathit{\beta }}}_{lts}^n$ and ${\mathit{\beta }}_{lts}$ in Theorems 1 and 2 hold respectively;

(ii) 

$P\left(x_i^2\right)$ exists with $\mathit{x}=(x_1,\cdots ,x_{p-1})$;

then

$$n^{1/2}({\widehat{\mathit{\beta }}}_{lts}^n-{\mathit{\beta }}_{lts})\stackrel{d}{⟶}N(\mathbf{0},V^{-1}[P(\nabla {\nabla }^{\top })-(P\nabla ){(P\nabla )}^{\top }]V^{-1}),$$

where β in V and ∇ is replaced by ${\mathit{\beta }}_{lts}$ (which could be assumed to be zero).

Proof. 

The key to applying this Lemma is to verify (v). For details, see Appendix A. □

Remark 4.

(a) In the case of $p=1$, that is in the location case, the asymptotic normality of the LTS has been studied in [21,33,34].

(b) Ref. [35], under the rank-based optimization framework and stringent assumptions on error term $e_i$ (even density that is strictly decreasing for positive value, bounded absolute first moment) and on ${\mathbf{x}}_i$ (bounded fourth moment), covers the asymptotic normality of the LTS. Ref. [24] also treated the general case $p\ge 1$ and obtained the asymptotic normality of the LTS under many stringent conditions on the non-random covariates ${\mathbf{x}}_i$s and the distributions of $e_i$ in a 27-page article. The assumption $\mathcal{C}$ is quite artificial and never verified there. Conversely, Refs. [26,27] also addressed the asymptotic normality of LTS in the nonlinear regression under a dependence setting. For these extensions, many artificial assumptions (D1, D2, H1, H2, H3, H4, H5, H6, I1, I2) are imposed, but they are never verified even for the linear LTS case. So those results do not cover the LTS in (3).

(c) Furthermore, since there was no population version like (4) and (5) before, empirical process theory could not be employed to verify the VC class of functions in [22,23,24,26,27]. Our approach here is quite different from former classical analyses and much more neat and concise (employing the standard empirical process theory that was asserted to be not applicable in [26,27]).

4. Inference Procedures

In order to utilize the asymptotic normality result in Theorem 6, we need to figure out the asymptotic covariance. For simplicity, assume that $\mathit{z}={({\mathit{x}}^{\top },y)}^{\top }$ follows elliptical distributions $E(g;\mathit{\mu },\mathbf{\Sigma })$ with density

$$f_{\mathit{z}}({\mathit{x}}^{\top },y)={\displaystyle \frac{g({({({\mathit{x}}^{\top },y)}^{\top }-\mathit{\mu })}^{\top }{\mathbf{\Sigma }}^{-1}({({\mathit{x}}^{\top },y)}^{\top }-\mathit{\mu }))}{\sqrt{det\left(\mathbf{\Sigma }\right)}}},$$

where $\mathit{\mu }\in {\mathbb{R}}^p$ and $\mathbf{\Sigma }$ is a positive definite matrix of size p which is proportional to the covariance matrix if the latter exists. We assume $f_{\mathit{z}}$ is unimodal.

4.1. Equivariance

A regression estimation functional $\mathit{t}(·)$ is said to be regression, scale, and affine equivariant (see [8]) if, respectively,

$$\begin{array}{ccc}\hfill \mathit{t}\left(F_{(\mathit{w},y+{\mathit{w}}^{\top }b)}\right)& =& \mathit{t}\left(F_{(\mathit{w},y)}\right)+\mathit{b},\forall \mathit{b}\in {\mathbb{R}}^p;\hfill \\ \hfill \mathit{t}\left(F_{(\mathit{w},sy)}\right)& =& s\mathit{t}\left(F_{(\mathit{w},y)}\right),\forall s\in \mathbb{R};\hfill \\ \hfill \mathit{t}\left(F_{({\mathit{A}}^{\top }\mathit{w},y)}\right)& =& {\mathit{A}}^{-1}\mathit{t}\left(F_{(\mathit{w},y)}\right),\forall \mathrm{n}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r} \mathit{A}\in {\mathbb{R}}^{p\times p};\hfill \end{array}$$

Theorem 7.

${\mathit{\beta }}_{lts}(F_{({\mathit{x}}^{\prime },y)},\alpha )$ is regression, scale, and affine equivariant.

Proof. 

See the empirical version treatment given in [1] (p. 132). □

4.2. Transformation

Assume the Cholesky decomposition of $\mathbf{\Sigma }$ yields a non-singular lower triangular matrix $\mathit{L}$ of the form

$$\left(\begin{array}{cc}\mathit{A}& \mathbf{0}\\ {\mathit{v}}^{\top }& c\end{array}\right)$$

with $\mathbf{\Sigma }=\mathit{L}{\mathit{L}}^{\top }$. Hence, $det\left(\mathit{A}\right)\ne 0\ne c$. Now, transfer $({\mathit{x}}^{\top },y)$ to $({\mathit{s}}^{\top },t)$ with ${({\mathit{s}}^{\top },t)}^{\top }={\mathit{L}}^{-1}({({\mathit{x}}^{\top },y)}^{\top }-\mathit{\mu })$. It is readily seen that the distribution of ${({\mathit{s}}^{\top },t)}^{\top }$ follows $E(g;\mathbf{0},{\mathit{I}}_{\mathit{p}\times \mathit{p}})$.

Note that ${({\mathit{x}}^{\top },y)}^{\top }=\mathit{L}{({\mathit{s}}^{\top },t)}^{\top }+{({\mathit{\mu }}_1^{\top },{\mu }_2)}^{\top }$ with $\mathit{\mu }={({\mathit{\mu }}_1^{\top },{\mu }_2)}^{\top }$. That is,

$$\begin{array}{cc}\hfill \mathit{x}& =\mathit{A}\mathit{s}+{\mathit{\mu }}_1,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill y& ={\mathit{v}}^{\top }\mathit{s}+ct+{\mu }_2.\hfill \end{array}$$

(24)

Equivalently,

$$\begin{array}{cc}\hfill {(1,{\mathit{s}}^{\top })}^{\top }& ={\mathit{B}}^{-1}{(1,{\mathit{x}}^{\top })}^{\top },\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill t& ={\displaystyle \frac{y-(1,{\mathit{s}}^{\top }){({\mu }_2,{\mathit{v}}^{\top })}^{\top }}{c}},\hfill \end{array}$$

(26)

where

$$\mathit{B}=\left(\begin{array}{cc}1& {\mathbf{0}}^{\top }\\ {\mu }_1& \mathit{A}\end{array}\right),{\mathit{B}}^{-1}=\left(\begin{array}{cc}1& {\mathbf{0}}^{\top }\\ -{\mathit{A}}^{-1}{\mu }_1& {\mathit{A}}^{-1}\end{array}\right),$$

It is readily seen that (25) is an affine transformation on $\mathit{w}$ and (26) is first an affine transformation on $\mathit{w}$ then a regression transformation on y followed by a scale transformation on y. In light of Theorem 7, we can assume, hereafter, w.l.o.g. that $({\mathit{x}}^{\top },y)$ follows an $E(g;\mathbf{0},{\mathit{I}}_{p\times p})$ (spherical) distribution and ${\mathit{I}}_{p\times p}$ is the covariance matrix of $({\mathit{x}}^{\top },y)$.

Theorem 8.

Assume that $e\sim \mathcal{N}(0,{\sigma }^2)$, e, and $\mathit{x}$ are independent. Then,

(1) 

$P\nabla =\mathbf{0}$ and $P(\nabla {\nabla }^{\prime })=8{\sigma }^{2}C{\mathit{I}}_{p\times p}$,

with $C=\mathrm{\Phi }\left(c\right)-1/2-c{e}^{-c^2/2}/\sqrt{2\pi }$, where $c=\sqrt{F_{{\chi }^2\left(1\right)}^{-1}\left(\alpha \right)}$ and $\mathrm{\Phi }\left(x\right)$ is the CDF of $\mathcal{N}(0,1)$, ${\chi }^2\left(1\right)$ is a chi-square random variable with one degree of freedom.

(2) 

$\mathbf{V}=2C_1{\mathit{I}}_{p\times p}$ with $C_1=2\mathrm{\Phi }\left(c\right)-1$.

(3) 

$n^{1/2}({\widehat{\mathit{\beta }}}_{lts}^n-{\mathit{\beta }}_{lts})\stackrel{d}{⟶}\mathcal{N}(\mathbf{0},{\displaystyle \frac{2C{\sigma }^2}{C_1^2}}{\mathit{I}}_{p\times p})$, where C and $C1$ are defined in (1) and (2) above.

Proof. 

See Appendix A. □

4.3. Approximate $100(1-\gamma )\%$ Confidence Region

(i) Based on the asymptotic normality. Under the setting of Theorem 8, an approximate $100(1-\gamma )\%$ confidence region for the unknown regression parameter ${\mathit{\beta }}_0$ is:

$$\left\{\mathit{\beta }\in {\mathbb{R}}^p:\parallel \mathit{\beta }-{\widehat{\mathit{\beta }}}_{lts}^n\parallel \le \sqrt{{\displaystyle \frac{2C{\sigma }^2}{C_1^{2}n}}}{F}_{{\chi }^2\left(p\right)}^{-1}\left(\gamma \right)\right\},$$

where $\parallel ·\parallel$ stands for the Euclidean distance. Without asymptotic normality, one can appeal to the next procedure.

(ii) Based on bootstrapping scheme and depth-median and depth-quantile. Here, no assumptions on the underlying distribution are needed. This approximate procedure first re-samples n points with replacement from the given original sample points and calculates an ${\widehat{\mathit{\beta }}}_{lts}^n$. Repeat this m (a large number, say ${10}^4$) times and obtain m such ${\widehat{\mathit{\beta }}}_{lts}^n$s.

The next step is to calculate the depth, concerning a location depth function (e.g., halfspace depth [36] or projection depth [37,38]), of these m points in the parameter space of $\mathit{\beta }$. Trimming $\lfloor \gamma m\rfloor$ of the least deep points among the m points, the left points form a convex hull, that is an approximate $100(1-\gamma )\%$ confidence region for the unknown regression parameter ${\mathit{\beta }}_0$ in the location case and low dimensions.

Example 1.

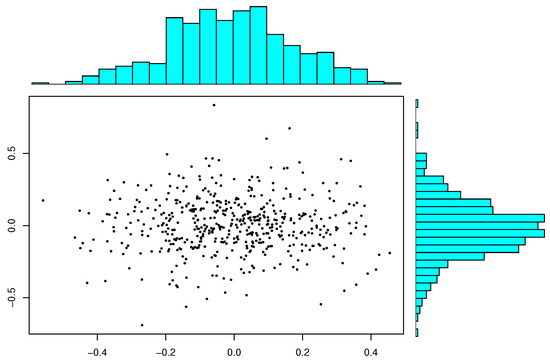
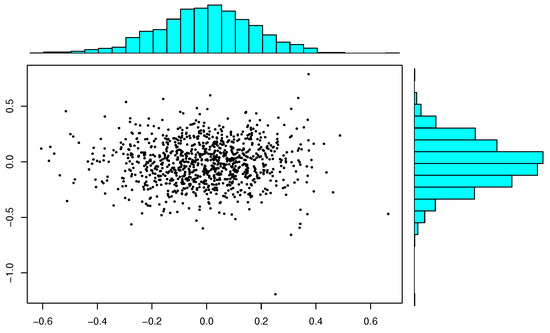
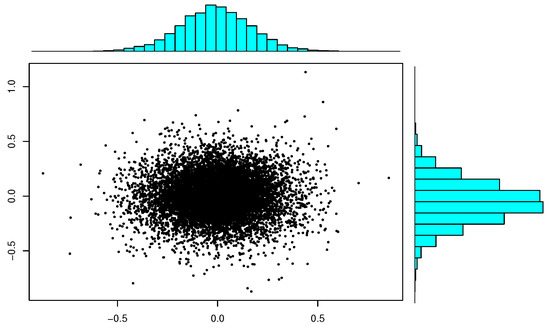
To illustrate the normality of ${\widehat{\mathit{\beta }}}_{lts}^n$, here, we carry out a small-scale simulation. We will generate $N=500,1000,10000$ ${\widehat{\mathit{\beta }}}_{lts}^n$s, each obtained based on a bivariate standard normal sample $\left\{({\mathit{x}}_i,y_i)\right\}$ of size $n=50$. For each N, we provide scatter plots of N ${\widehat{\mathit{\beta }}}_{lts}^n$s and marginal histgrams. Inspecting Figure 1, Figure 2 and Figure 3 reveals that the plots of ${\widehat{\mathit{\beta }}}_{lts}^n$s more and more resemble a bivariate normal pattern when the number of ${\widehat{\mathit{\beta }}}_{lts}^n$ increases. The marginal histograms confirm the normality.

Figure 1. Marginal histograms and scatter plot of 500 ${\widehat{\mathit{\beta }}}_{lts}^n$ with sample size $n=50$.

Figure 2. Marginal histograms and scatter plot of 1000 ${\widehat{\mathit{\beta }}}_{lts}^n$ with sample size $n=50$.

Figure 3. Marginal histograms and scatter plot of 10000 ${\widehat{\mathit{\beta }}}_{lts}^n$ with sample size $n=50$.

5. Concluding Remarks

Without the population version of the LTS (see (5)), it will be difficult to apply the empirical process theory to study the asymptotics of the LTS, e.g, to verify the key result, the VC-class property of regression function class (indexed by $\mathit{\beta }$) will be challenging. To avoid this challenge, some authors addressed the asymptotics of the nonlinear LTS, where without an explicit regression function (unlike the linear case), they can conveniently assume this VC-class property. Refs. [26,27] even believed that the standard empirical process theory does not apply to the asymptotics of LTS, while Refs. [22,23,24], addressed the asymptotics without any advanced tools, employing elementary tools with numerous artificial, difficult-to-verify assumptions and lengthy articles.

By partitioning the parameter space and introducing the population version for the LTS, this article establishes some fundamental and primary properties for the objective function of the LTS in both empirical and population settings. These newly obtained original results verify some key facts that were conveniently assumed (but never verified) in nonlinear regression literature for the LTS and facilitate the application of standard empirical process theory to the establishment of asymptotic normality for the sample LTS concisely and neatly. Some of the newly obtained results, such as Fisher and strong consistency, and influence function, are original and obtained as by-products.

The asymptotic normality is applied in Theorem 8 for the practical inference procedure of confidence regions of the regression parameter ${\mathit{\beta }}_0$. There are open problems left here; one is the estimation of the variance of e, which is now unrealistically assumed to be known, and the other is the testing of the hypothesis on ${\mathit{\beta }}_0$.