Some Results on Multivalued Proximal Contractions with Application to Integral Equation

Abstract

In this manuscript, for the purpose of investigating the coincidence best proximity point, best proximity point, and fixed point results via alternating distance $\varphi$, we discuss some multivalued ${(\varphi -{\mathcal{F}}_{\tau })}_{C_P}$ and ${(\varphi -{\mathcal{F}}_{\tau })}_{B_P}-$proximal contractions in the context of rectangular metric spaces. To ascertain the coincidence best proximity point, best proximity point, and the fixed point for single-valued mappings, we reduce these findings using ${({\mathcal{F}}_{\tau })}_{C_P}$ and ${({\mathcal{F}}_{\tau })}_{B_P}-$proximal contractions. To make our work more understandable, examples of both single- and multivalued mappings are provided. These examples support our core findings, which rely on coincidence points, as well as the corollaries that address fixed point conclusions. In the final phase of our study, we use the obtained results to verify that a solution to a Fredholm integral equation exists. This application highlights the theoretical framework we built throughout our study.

1. Introduction

An essential tool for solving equations of the kind $\mathcal{T}\mathcal{x}=\mathcal{x}$ is fixed point theory, in which $\mathcal{T}$ denotes a mapping that is defined on a subset of a topological vector space or a metric space. However, it should be noted that not all mappings have a fixed point, for example, when under restricted conditions, and some other mappings (such as translation mappings and non-self-mappings with two distinct sets) may not have fixed points. While it might be difficult to locate exact fixed points in some situations, under some conditions, it is possible to find an approximation of fixed points. The application of the best approximation theory facilitates the study of these approximate fixed points. Recent advancements in fixed point theory have introduced several innovative approaches and applications, as discussed in [1,2].

It is possible that a non-self-mapping $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$ lacks a fixed point by nature. Fundamentally, though, an element $\mathcal{x}$ closer to $\mathcal{T}\mathcal{x}$ always advances. In this scenario, the importance of the best proximity theorem and the idea of the best proximity point become quite apparent. The essence of the best proximity point theorem resides in achieving a globally optimized solution of factual components, symbolized by $\mathcal{x}\to \mathcal{d}(\mathcal{x},\mathcal{T}\mathcal{x})$. This property indicates the degree of inaccuracy in the approximate solution of the operator $\mathcal{T}\mathcal{x}=\mathcal{x}$. The metric $\mathcal{d}(\mathcal{x},\mathcal{T}\mathcal{x})$ for a non-self-mapping $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$ is at least $\mathcal{d}(\mathcal{P},\mathcal{Q})$ for every $\mathcal{x}$ in $\mathcal{P}$. The condition $\mathcal{d}(\mathcal{x},\mathcal{T}\mathcal{x})=\mathcal{d}(\mathcal{P},\mathcal{Q})$ is imposed by limiting an approximate solution $\mathcal{x}$, to the equation $\mathcal{T}\mathcal{x}=\mathcal{x}$.

The concept of the best proximity point had initially been laid out by Sadiq Basha et al. [3,4] in 1997. Eldred et al. [5] proposed a technique for identifying the best proximity point for non-self-mappings $\mathcal{T}$ in the framework of a uniformly convex Banach space. Baria gave the concept of a new type of contraction named Cyclic Meir–Keeler contractions in [6], whereas Kikkawa et al. [7] characterized the connections between contractions and Kannan mappings. The concept of proximal pointwise contraction was initially introduced by Anuradha et al. [8], and the UC property was introduced by Suzuki et al. [9]. The presence of the best proximity points and the convergence of asymptotic cyclic contractions with the UC property were established by Abkar et al. [10]. Theorems on the best proximity points were initially given by Basha et al. in [11,12], offering the best possible approximation solutions. Samet et al. [13] introduced the notion of $\alpha$-admissible mappings, while the investigation of $\alpha$-proximal admissible mapping was started by Jleli et al. [14].

A foundational theorem on best approximation, initially presented by Fan [15], states that there exists an element $\mathcal{x}$ in a compact convex subset $\mathcal{P}\ne \varphi$ of a Hausdorff locally convex topological vector space $(\mathcal{X},\mathcal{p})$, where $\mathcal{p}$ is a semi-norm. The theorem states that for a continuous mapping $\mathcal{T}:\mathcal{P}\to \mathcal{X}$, the distance between $\mathcal{x}$ and $\mathcal{T}\mathcal{x}$ equals the distance between $\mathcal{T}\mathcal{x}$ and $\mathcal{P}$, i.e., $\mathcal{d}(\mathcal{x},\mathcal{T}\mathcal{x})=\mathcal{d}(\mathcal{T}\mathcal{x},\mathcal{P}).$ In the investigation of generalized Geraghty proximal cyclic contractions, Komal et al. [16] established results pertaining to coincidence best proximity points within the structure of a complete metric space. In their work [17], Latif et al. gave the idea of partially ordered metric space and produced findings for coincidence best approximation points for ${\mathcal{F}}_{\mathcal{g}}$-weak contractive mappings. Fan’s theory has been the subject of several subsequent changes and adaptations, as evidenced by publications like [18], wherein Ahmad et al. utilized rational-type Ćirić-contractive-type contractions in the context of controlled metric-type spaces to generate novel fixed point results with an application to a second-order differential equation. In [19], Kirk et al. presented best proximity pair theorems in hyperconvex metric spaces and in Hilbert spaces. In [20], Naeem et al. discussed some (coincidence) best proximity point results for generalized proximal contractions and $\lambda -\mu -$proximal Geraghty contractions in controlled metric-type spaces. In [21], Suzuki et al. proved three generalizations of Matkowski’s fixed point theorems for weakly contractions. In [22], Wani et al. established the approximation by Durrmeyer-type Jakimovski–Leviatan operators involving the Brenke-type polynomials. The positive linear operators are constructed for the Brenke polynomials, and thus, approximation properties for these polynomials are obtained.

Recently, numerous authors have made valuable contributions to the best proximity theory. In [23], S. Laha introduced concepts such as topologically Berinde weak proximal contractions and topologically proximal weakly contractive mappings with respect to $\mathcal{g}$, providing conditions for the existence and uniqueness of best proximity points for these mappings. In [24], M. Asim generalized the $PIV-$metric and $\mathcal{S}-$metric spaces through a partial idempotent-valued $\mathcal{S}-$metric space, establishing a fixed point and best proximity point theorem. In [25], A. Das applied the $\varphi -$metric to measure distances on non-planar surfaces, extending best proximity point concepts to $\varphi -$metric spaces and proving corresponding proximity point results.

Building upon the insights gleaned from our extensive literature review, we have derived notable coincidence best proximity point results within rectangular metric space. Distinguished by our innovative approach, we apply $\mathcal{F}$-type proximal contractions paired with an alternating distance function $\varphi$ for multivalued mappings. Additionally, we improve upon our contributions by obtaining findings for fixed points, which we summarize as corollaries to the concept of optimum proximity points. Importantly, we advance the concept of multivalued coincidence points to single-valued coincidence points. We give descriptive instances of the change from coincidence points to fixed points to support the importance of our main results. These illustrations not only help to make sense of our results but also strengthen the validity and relevance of the findings we give in this manuscript.

Imagine that there are two nonempty subsets in the complete rectangular metric space $(\mathcal{X},\mathcal{d})$, which are $\mathcal{P}$ and $\mathcal{Q}$. The distance between the elements in this space is determined by the metric $\mathcal{d}$. The sets ${\mathcal{P}}_0$ and ${\mathcal{Q}}_0$ are defined as

$$\begin{array}{ccc}\hfill {\mathcal{P}}_0& =& \{ɱ\in \mathcal{P}:\mathcal{d}(ɱ,ȵ)=\mathcal{d}(\mathcal{P},\mathcal{Q})\mathrm{for}\mathrm{some}ȵ\in \mathcal{Q}\},\hfill \\ \hfill {\mathcal{Q}}_0& =& \{ȵ\in \mathcal{Q}:\mathcal{d}(ɱ,ȵ)=\mathcal{d}(\mathcal{P},\mathcal{Q})\mathrm{for}\mathrm{some}\mathcal{x}\in \mathcal{P}\},\hfill \end{array}$$

where

$$\mathcal{d}(\mathcal{P},\mathcal{Q})=inf\{\mathcal{d}(ɱ,ȵ):ɱ\in \mathcal{P},ȵ\in \mathcal{Q}\},$$

which represents the distance from set $\mathcal{P}$ to set $\mathcal{Q}$.

2. Preliminaries

We introduce essential definitions to start off our conversation that contribute to the development of our results. Our starting point is the definition of a metric space.

Definition 1

([26]). Upon satisfying the given conditions, a function $\mathcal{d}:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$, with a range of non-negative real numbers, is considered a metric, such that the following occur:

1.

$\mathcal{d}(ɱ,ȵ)\ge 0$;

2.

$\mathcal{d}(ɱ,ȵ)=0$ iff $ɱ=ȵ$;

3.

$\mathcal{d}(ɱ,ȵ)=\mathcal{d}(ȵ,ɱ)$;

4.

$\mathcal{d}(ɱ,\zeta )+\mathcal{d}(\zeta ,ȵ)\ge \mathcal{d}(ɱ,ȵ)$, for each $ɱ,ȵ,\zeta \in \mathcal{X}.$

Here, $\mathcal{d}$ is a metric on $\mathcal{X}$, and the pair $(\mathcal{X},\mathcal{d})$ defines the metric space, with $\mathcal{X}$ identified as the ground set. The individual elements $ɱ,ȵ,\zeta \in \mathcal{X}$ are recognized as points within this metric space. Consequently, the notation $\mathcal{X}$ encompasses the metric space $(\mathcal{X},\mathcal{d})$.

Few examples are also presented from the literature [26] to explain the distance or metric.

Example 1.

We have few functions ${\mathcal{d}}_1,{\mathcal{d}}_2,{\mathcal{d}}_3:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ given as

$$\begin{array}{ccc}\hfill {\mathcal{d}}_1(ɱ,ȵ)& =& \sqrt{\left|ɱ-ȵ\right|,}\hfill \\ \hfill {\mathcal{d}}_2(ɱ,ȵ)& =& \left|ɱ-ȵ\right|,\hfill \\ \hfill {\mathcal{d}}_3(ɱ,ȵ)& =& \left|{\displaystyle \frac{1}{ɱ}}-{\displaystyle \frac{1}{ȵ}}\right|,\hfill \end{array}$$

where ${\mathcal{d}}_1$ and ${\mathcal{d}}_2$ are metrics defined by the set of real numbers, $\mathbb{R}$. Furthermore, ${\mathcal{d}}_3$ is a metric defined by the real numbers excluding zero, denoted as $\mathbb{R}\setminus \{0\}$.

Example 2.

Suppose ${\mathcal{x}}_1=(\mathcal{a},\mathcal{b})$ and ${\mathcal{x}}_2=(\mathcal{c},\mathcal{h})$ for each $\mathcal{a},\mathcal{b},\mathcal{c},\mathcal{h}\in \mathbb{R},$ then $\mathcal{d}({\mathcal{x}}_1,{\mathcal{x}}_2)$ is defined as

$$\mathcal{d}({\mathcal{x}}_1,{\mathcal{x}}_2)=\left|\mathcal{a}-\mathcal{c}\right|+\left|\mathcal{b}-\mathcal{h}\right|,$$

where $\mathcal{d}$ is a metric on ${\mathbb{R}}^2=\mathcal{X}.$

Example 3.

Let $\mathcal{X}$ be a nonempty set furnished with a metric space structure, denoted as $(\mathcal{X},{\mathcal{d}}_0)$. In the present case, the function ${\mathcal{d}}_0:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$ is defined as follows:

$${\mathcal{d}}_0(ɱ,ȵ)=\left\{\begin{array}{c}0,\mathrm{if}ɱ=ȵ\\ 1,\mathrm{if}ɱ\ne ȵ,\end{array}\right.$$

The metric ${\mathcal{d}}_0$ establishes a discrete metric and the pair $(\mathcal{X},{\mathcal{d}}_0)$ represents a discrete metric space.

A unique generalization of metric spaces was established by Branciari [27] in 2000. It is explained as follows.

Definition 2.

Consider a set $\mathcal{X}$ that is not empty. If a function $\mathcal{d}:\mathcal{X}\times \mathcal{X}\to {\mathbb{R}}^{+}$ meets the following criteria, it is referred to as a rectangular metric:

1.

$\mathcal{d}(ɱ,ȵ)\ge 0;$

2.

$\mathcal{d}(ɱ,ȵ)=0$ if and only if $ɱ=ȵ;$

3.

$\mathcal{d}(ɱ,ȵ)=\mathcal{d}(ȵ,ɱ);$

4.

$\mathcal{d}(ɱ,\zeta )+\mathcal{d}(\zeta ,\mathcal{u})+\mathcal{d}(\mathcal{u},ȵ)\ge \mathcal{d}(ɱ,ȵ)$ for all $ɱ,ȵ\in \mathcal{X}\setminus \{\zeta ,\mathcal{u}\},$ then the space $(\mathcal{X},\mathcal{d})$ is known to be a rectangular metric space.

Definition 3

([27]). Consider a rectangular metric space $(\mathcal{X},\mathcal{d})$. If $\mathcal{x}\in \mathcal{X}$ and $\mathcal{X}$ possesses a sequence $\{{\mathcal{x}}_n\}$, then the following holds:

(i)

The sequence $\{{\mathcal{x}}_n\}$ converges to point $\mathcal{x}$ if and only if ${lim}_{n\to \infty }{\mathcal{x}}_n=\mathcal{x}.$

(ii)

The sequence $\{{\mathcal{x}}_n\}$ is known to be a Cauchy sequence if and only if $\underset{n,m\to \infty }{lim}\mathcal{d}({\mathcal{x}}_n,{\mathcal{x}}_m)=0$.

(iii)

The rectangular metric space $\mathcal{X}$ is complete if and only if every Cauchy sequence in $\mathcal{X}$ is convergent.

(iv)

Every convergent sequence in a rectangular metric space $\mathcal{X}$ has a unique limit.

Definition 4

([28]). In a rectangular metric space with nonempty subsets represented by the pair $(\mathcal{P},\mathcal{Q})$, where ${\mathcal{P}}_0$ is nonempty, $(\mathcal{P},\mathcal{Q})$ is said to satisfy the $\mathcal{P}$-property if

$$\mathcal{d}({\mathcal{x}}_1,{\mathcal{y}}_1)=\mathcal{d}({\mathcal{x}}_2,{\mathcal{y}}_2)=\mathcal{d}(\mathcal{P},\mathcal{Q})$$

implies that

$$\mathcal{d}({\mathcal{x}}_1,{\mathcal{x}}_2)=\mathcal{d}({\mathcal{y}}_1,{\mathcal{y}}_2)$$

where ${\mathcal{y}}_1,{\mathcal{y}}_2\in \mathcal{Q}$ and ${\mathcal{x}}_1,{\mathcal{x}}_2\in \mathcal{P}$.

Definition 5

([29]). Let $\varphi :[0,+\infty )⟶[0,+\infty )$ be a function. If ϕ satisfies the given axioms:

(i)

$\varphi$ is continuous.

(ii)

If $ɱ\le ȵ$, then $\varphi (ɱ)\le \varphi (ȵ).$

(iii)

For all $ɱ\ge 0$, $\varphi (ɱ)\ge 0$.

Then, we say that it is an alternating distance function.

Definition 6

([30]). Given that the mapping $\mathcal{F}:{\mathbb{R}}^{+}\to \mathbb{R}$ is considered as an $\mathcal{F}-$contraction if it adheres to the specified criteria:

(F1)

For all positive real numbers, $\mathcal{F}$ is a strictly increasing function.

(F2)

For all $\{{\mathcal{x}}_n\}\subseteq \mathbb{R},\underset{n\to \infty }{lim}$${\mathcal{x}}_n=0$, if and only if $\underset{n\to \infty }{lim}$$\mathcal{F}({\mathcal{x}}_n)=-\infty .$

(F3)

For $\underset{\mathcal{x}\to 0^{+}}{lim}$${\mathcal{x}}^k\mathcal{F}(\mathcal{x})=0,$ there exists $k\in (0,1)$.

The set of all functions that fulfill the above given conditions is denoted by ${\mathcal{F}}_i.$

A mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ defined on a rectangular metric space $(\mathcal{X},\mathcal{d})$ is known to be an $\mathcal{F}-$contraction with $\mathcal{F}\in {\mathcal{F}}_i$ and $\tau \in (0,+\infty )$ such that

$$\mathcal{d}(\mathcal{T}(ɱ),\mathcal{T}(ȵ))>0,\Rightarrow \tau +\mathcal{F}(\mathcal{d}(\mathcal{T}(ɱ),\mathcal{T}(ȵ)))\le \mathcal{F}(\mathcal{d}(ɱ,ȵ)),$$

where $ɱ$ and $ȵ$ are elements of $\mathcal{X}.$

Example 4.

Let $\mathcal{F}:(0,+\infty )\to \mathbb{R}$ be a function, given as

$$\mathcal{F}(\mathcal{x})=log\mathcal{x}+\mathcal{x},$$

and the mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ be constructed on a complete rectangular metric space, with the metric

$$\mathcal{d}(\mathcal{x},\mathcal{y})=\left|\mathcal{x}-\mathcal{y}\right|,$$

by $\mathcal{T}(\mathcal{x})={\displaystyle \frac{\mathcal{x}}{3}}.$ Clearly, $\mathcal{T}$ satisfies the $\mathcal{F}$ contraction condition.

Definition 7

([31]). Consider a set of all closed and bounded subsets of $\mathcal{X}$, denoted as $\mathcal{CB}(\mathcal{X})$ within the space $\mathcal{X}$. Assume that $\mathcal{H}$ represents the Pompeiu–Hausdorff metric with metric $\mathcal{d}$, defined as

$$\mathcal{H}(\mathcal{P},\mathcal{Q})=max\{\underset{\zeta \in \mathcal{P}}{sup}\mathcal{D}(\zeta ,\mathcal{Q}),\underset{\sigma \in \mathcal{Q}}{sup}\mathcal{D}(\sigma ,\mathcal{P})\},$$

for $\mathcal{P},\mathcal{Q}\subseteq \mathcal{CB}(\mathcal{X}),$ where

$$\mathcal{D}(\zeta ,\mathcal{Q})=inf\{\mathcal{d}(\zeta ,\sigma ):\sigma \in \mathcal{Q}\},$$

and in this manuscript, we will denote

$${\mathcal{D}}^{*}(\zeta ,\sigma )=\mathcal{D}(\zeta ,\sigma )-\mathcal{d}(\mathcal{P},\mathcal{Q}),$$

for $\zeta \in \mathcal{P}$ and $\sigma \in \mathcal{Q}.$

From the beginning to the end of this manuscript, we suspect that the rectangular metric $\mathcal{d}$ is a continuous mapping.

3. For Multivalued Mappings

In this section, we introduce new definitions and theorems pertaining to best proximity points, fixed points, and multivalued coincidence points within the framework of a complete rectangular metric space $(\mathcal{X},\mathcal{d})$, utilizing the concepts and results established in the previous section.

Definition 8.

In a rectangular metric space $(\mathcal{X},\mathcal{d}),$ consider closed nonempty subsets $\mathcal{P}$ and $\mathcal{Q}$. Let $(\mathcal{g},\mathcal{T})$ be a pair of mappings such that $\mathcal{T}:\mathcal{P}\to \mathcal{CB}(\mathcal{Q})$ is a multivalued mapping and $\mathcal{g}:\mathcal{P}\to \mathcal{P}$ is a self-mapping. The mappings here satisfy the following:

$$\mathcal{D}(\mathcal{g}\mathcal{x},\mathcal{T}\mathcal{x})=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

Then,$\mathcal{x}\in \mathcal{P}$ is known as a coincidence best proximity point for $(\mathcal{g},\mathcal{T}).$

Remark 1.

The coincidence-best-proximity-point results refer to a wider notion that includes fixed points and best proximity points. When $\mathcal{g}=I_{\mathcal{P}}$ is taken into account, this becomes clear since any closest proximity point that coincides becomes the closest proximity point for mapping $\mathcal{T}$. Moreover, the idea of a best proximity point reduces to that of a fixed point in the scenario, where $\mathcal{T}$ is a self-mapping.

Definition 9.

Let $\mathcal{T}:\mathcal{P}\to \mathcal{CB}(\mathcal{Q})$ be a multivalued mapping and $\mathcal{g}:\mathcal{P}\to \mathcal{P}$ be a self-mapping. The pair of mappings $(\mathcal{g},\mathcal{T})$ is known to be satisfied ${(\varphi -{\mathcal{F}}_{\tau })}_{C_P}-$proximal contraction if there is a non-negative real number τ and for all $\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}$ in $\mathcal{P}$ such that

$$\begin{array}{c}\mathcal{D}\left(\mathcal{g}\mathcal{u},\mathcal{T}\mathcal{x}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\\ \mathcal{D}\left(\mathcal{g}\mathcal{v},\mathcal{T}\mathcal{y}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\end{array}$$

implies that

$$\tau +\mathcal{F}(\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}))),$$

where

$$\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})=max\{\mathcal{d}(\mathcal{g}\mathcal{u},\mathcal{g}\mathcal{v}),\mathcal{d}(\mathcal{g}\mathcal{x},\mathcal{g}\mathcal{y}),{\mathcal{D}}^{*}(\mathcal{g}\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{D}(\mathcal{g}\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{g}\mathcal{u},\mathcal{g}\mathcal{v})-\mathcal{D}(\mathcal{g}\mathcal{y},\mathcal{T}\mathcal{u})\}.$$

Definition 10.

A multivalued mapping $\mathcal{T}:\mathcal{P}\to \mathcal{CB}(\mathcal{Q})$ is known to be satisfied ${(\varphi -{\mathcal{F}}_{\tau })}_{B_P}-$ proximal contraction if there exists a non-negative real number τ and for all $\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}$ in $\mathcal{P}$, such that

$$\begin{array}{c}\mathcal{D}\left(\mathcal{u},\mathcal{T}\mathcal{x}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\\ \mathcal{D}\left(\mathcal{v},\mathcal{T}\mathcal{y}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\end{array}$$

implies that

$$\tau +\mathcal{F}(\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}))),$$

where

$$\begin{array}{c}\hfill \mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})=max\{\mathcal{d}(\mathcal{u},\mathcal{v}),\mathcal{d}(\mathcal{x},\mathcal{y}),{\mathcal{D}}^{*}(\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{D}(\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{u},\mathcal{v})-\mathcal{D}(\mathcal{y},\mathcal{T}\mathcal{u})\}.\end{array}$$

Observe that each ${(\varphi -\mathcal{F}\tau )}_{C_P}$-proximal contraction simplifies to a ${(\varphi -\mathcal{F}\tau )}_{B_P}$-proximal contraction upon selecting $\mathcal{g}={\mathcal{I}}_{\mathcal{P}}$ (where ${\mathcal{I}}_{\mathcal{P}}$ indicates the identity mapping on $\mathcal{P}$). Furthermore, we see that if

$$\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})=max\{\mathcal{d}(\mathcal{u},\mathcal{v}),\mathcal{d}(\mathcal{x},\mathcal{y}),{\mathcal{D}}^{*}(\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{D}(\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{u},\mathcal{v})-\mathcal{D}(\mathcal{y},\mathcal{T}\mathcal{u})\}=\mathcal{d}(\mathcal{x},\mathcal{y})$$

and ϕ is an identity map, then our contraction is reduced to $\mathcal{F}-$contraction for multivalued mappings.

Theorem 1.

Consider nonempty closed subsets $\mathcal{P}$ and $\mathcal{Q}$ in the complete rectangular metric space $(\mathcal{X},\mathcal{d})$, both of which fulfill the $\mathcal{P}$-property, where ${\mathcal{P}}_0\ne \varphi$. Let $\mathcal{T}:\mathcal{P}\to \mathcal{CB}(\mathcal{Q})$ and $\mathcal{g}:\mathcal{P}\to \mathcal{P}$ be continuous mappings with ${\mathcal{P}}_0\subseteq \mathcal{g}({\mathcal{P}}_0)$ and $\mathcal{T}({\mathcal{P}}_0)\subseteq {\mathcal{Q}}_0$. Additionally, assume that $\mathcal{g}$ is an injective continuous mapping, and $(\mathcal{g},\mathcal{T})$ fulfill the ${(\varphi -\mathcal{F}\tau )}_{C_P}$-proximal contraction condition with alternating distance ϕ. Then, the pair $(\mathcal{g},\mathcal{T})$ attains a coincidence best proximity point.

Proof. 

Select an arbitrary element ${\mathcal{x}}_0\in {\mathcal{P}}_0.$ Given that $\mathcal{T}({\mathcal{P}}_0)$ is a subset of ${\mathcal{Q}}_0$ and ${\mathcal{P}}_0$ is within $\mathcal{g}({\mathcal{P}}_0),$ there exists an element ${\mathcal{x}}_1\in {\mathcal{P}}_0$ such that

$$\mathcal{D}(\mathcal{g}{\mathcal{x}}_1,\mathcal{T}{\mathcal{x}}_0)=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

Furthermore, given that $\mathcal{T}{\mathcal{x}}_1\in \mathcal{T}({\mathcal{P}}_0)$, which is a subset of ${\mathcal{Q}}_0$, and that ${\mathcal{P}}_0$ is within $\mathcal{g}({\mathcal{P}}_0),$ this suggests that there is an element ${\mathcal{x}}_2$ in ${\mathcal{P}}_0$ such that

$$\mathcal{D}(\mathcal{g}{\mathcal{x}}_2,\mathcal{T}{\mathcal{x}}_1)=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

Using the $\mathcal{P}-$property $\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)=\mathcal{H}(\mathcal{T}{\mathcal{x}}_0,\mathcal{T}{\mathcal{x}}_1)$. Since, $(\mathcal{g},\mathcal{T})$ provides the ${(\varphi -{\mathcal{F}}_{\tau })}_{C_p}-$ proximal contraction condition, we obtain

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)))\le \mathcal{F}(\varphi (\mathcal{N}({\mathcal{x}}_1,{\mathcal{x}}_2,{\mathcal{x}}_0,{\mathcal{x}}_1)))-\tau ,$$

(1)

where

$$\begin{array}{ccc}\hfill \mathcal{N}({\mathcal{x}}_1,{\mathcal{x}}_2,{\mathcal{x}}_0,{\mathcal{x}}_1)& =& max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),{\mathcal{D}}^{*}(\mathcal{g}{\mathcal{x}}_1,\mathcal{T}{\mathcal{x}}_0),\\ \mathcal{D}(\mathcal{g}{\mathcal{x}}_0,\mathcal{T}{\mathcal{x}}_0)-\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1)-\mathcal{D}(\mathcal{g}{\mathcal{x}}_2,\mathcal{T}{\mathcal{x}}_0),\end{array}\right\},\hfill \\ & \le & max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),\mathcal{D}(\mathcal{g}{\mathcal{x}}_1,\mathcal{T}{\mathcal{x}}_0)-\mathcal{D}(\mathcal{P},\mathcal{Q}),\\ \mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1)+\mathcal{d}(\mathcal{g}{x}_1,\mathcal{g}{x}_2)+\mathcal{D}(\mathcal{g}{\mathcal{x}}_1,\mathcal{T}{\mathcal{x}}_0)\\ -\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1)-\mathcal{D}(\mathcal{g}{\mathcal{x}}_2,\mathcal{T}{\mathcal{x}}_0),\end{array}\right\}\hfill \\ & \le & max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),0,\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)\end{array}\right\}\hfill \\ & \le & max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)\right\},\hfill \end{array}$$

and so, we can say that

$$\mathcal{N}({\mathcal{x}}_1,{\mathcal{x}}_2,{\mathcal{x}}_0,{\mathcal{x}}_1)\le max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)\right\}.$$

If we choose $max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)\right\}=\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),$ then the inequality (1) becomes

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)))-\tau$$

which is impossible.

If $max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)\right\}=\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1),$ then the inequality (1) will be

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1)))-\tau ,$$

then we obtain

$$\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)\le \mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1).$$

Now, an arbitrary element ${\mathcal{x}}_1\in {\mathcal{P}}_0.$ Given that $\mathcal{T}({\mathcal{P}}_0)$ is a subset of ${\mathcal{Q}}_0$ and ${\mathcal{P}}_0$ is within $\mathcal{g}({\mathcal{P}}_0),$ there exists an element ${\mathcal{x}}_2\in {\mathcal{P}}_0$ such that

$$\mathcal{D}(\mathcal{g}{\mathcal{x}}_2,\mathcal{T}{\mathcal{x}}_1)=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

Furthermore, given that $\mathcal{T}{\mathcal{x}}_2\in \mathcal{T}({\mathcal{P}}_0)$, which is a subset of ${\mathcal{Q}}_0$, and that ${\mathcal{P}}_0$ being within $\mathcal{g}({\mathcal{P}}_0),$ this suggests that there is an element ${\mathcal{x}}_3$ in ${\mathcal{P}}_0$ such that:

$$\mathcal{D}(\mathcal{g}{\mathcal{x}}_3,\mathcal{T}{\mathcal{x}}_2)=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

Using the $\mathcal{P}-$property $\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)=\mathcal{H}(\mathcal{T}{\mathcal{x}}_1,\mathcal{T}{\mathcal{x}}_2)$.

Since $(\mathcal{g},\mathcal{T})$ fulfills the ${(\varphi -{\mathcal{F}}_{\tau })}_{C_p}-$proximal contraction condition, we obtain

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)))\le \mathcal{F}(\varphi (\mathcal{N}({\mathcal{x}}_2,{\mathcal{x}}_3,{\mathcal{x}}_1,{\mathcal{x}}_2)))-\tau ,$$

(2)

where

$$\begin{array}{ccc}\hfill \mathcal{N}({\mathcal{x}}_2,{\mathcal{x}}_3,{\mathcal{x}}_1,{\mathcal{x}}_2)& =& max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_1),\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3),{\mathcal{D}}^{*}(\mathcal{g}{\mathcal{x}}_2,\mathcal{T}{\mathcal{x}}_1),\\ \mathcal{D}(\mathcal{g}{\mathcal{x}}_1,\mathcal{T}{\mathcal{x}}_1)-\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)-\mathcal{D}(\mathcal{g}{\mathcal{x}}_3,\mathcal{T}{\mathcal{x}}_1),\end{array}\right\},\hfill \\ & \le & max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3),\mathcal{D}(\mathcal{g}{\mathcal{x}}_2,\mathcal{T}{\mathcal{x}}_1)-\mathcal{D}(\mathcal{P},\mathcal{Q}),\\ \mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)+\mathcal{d}(\mathcal{g}{x}_2,\mathcal{g}{x}_3)+\mathcal{D}(\mathcal{g}{\mathcal{x}}_2,\mathcal{T}{\mathcal{x}}_1)\\ -\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)-\mathcal{D}(\mathcal{g}{\mathcal{x}}_3,\mathcal{T}{\mathcal{x}}_1),\end{array}\right\}\hfill \\ & \le & max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3),0,\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)\end{array}\right\}\hfill \\ & \le & max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)\right\},\hfill \end{array}$$

so we can say that

$$\mathcal{N}({\mathcal{x}}_2,{\mathcal{x}}_3,{\mathcal{x}}_1,{\mathcal{x}}_2)\le max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)\right\}.$$

If we choose $max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)\right\}=$$\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3),$ then the inequality (2) becomes

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)))-\tau$$

which is impossible.

If $max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)\right\}=\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2),$ then the inequality (2) will be

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2)))-\tau ,$$

then we obtain

$$\mathcal{d}(\mathcal{g}{\mathcal{x}}_2,\mathcal{g}{\mathcal{x}}_3)\le \mathcal{d}(\mathcal{g}{\mathcal{x}}_1,\mathcal{g}{\mathcal{x}}_2).$$

Similarly, for ${\mathcal{x}}_n\in {\mathcal{P}}_0$ with $\mathcal{T}({\mathcal{P}}_0)\subseteq {\mathcal{Q}}_0,$ there exists ${\mathcal{x}}_{n+1}\in {\mathcal{P}}_0$ such that

$$\mathcal{D}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{T}{\mathcal{x}}_n)=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

(3)

Having selected $\{{\mathcal{x}}_{n+1}\}$ and satisfying the condition, there is an element ${\mathcal{x}}_{n+2}\in {\mathcal{P}}_0$ that fulfills the condition that

$$\mathcal{D}(\mathcal{g}({\mathcal{x}}_{n+2}),\mathcal{T}({\mathcal{x}}_{n+1}))=\mathcal{d}(\mathcal{P},\mathcal{Q})$$

(4)

for all n (where n represents positive integers).

Using the $\mathcal{P}-$property $\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})=\mathcal{H}(\mathcal{T}{\mathcal{x}}_n,\mathcal{T}{\mathcal{x}}_{n+1})$.

Since $(\mathcal{g},\mathcal{T})$ fulfills the ${(\varphi -{\mathcal{F}}_{\tau })}_{C_p}-$proximal contraction condition, from Equations (3) and (4), we obtain

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))\le \mathcal{F}(\varphi (\mathcal{N}({\mathcal{x}}_{n+1},{\mathcal{x}}_{n+2},{\mathcal{x}}_n,{\mathcal{x}}_{n+1})))-\tau ,$$

(5)

where

$$\begin{array}{ccc}\hfill \mathcal{N}({\mathcal{x}}_{n+1},{\mathcal{x}}_{n+2},{\mathcal{x}}_n,{\mathcal{x}}_{n+1})& =& max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2}),{\mathcal{D}}^{*}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{T}{\mathcal{x}}_n),\\ \mathcal{D}(\mathcal{g}{\mathcal{x}}_n,\mathcal{T}{\mathcal{x}}_n)-\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1})-\mathcal{D}(\mathcal{g}{\mathcal{x}}_{n+2},\mathcal{T}{\mathcal{x}}_n)\end{array}\right\}\hfill \\ & \le & max\left\{\begin{array}{c}\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2}),\mathcal{D}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{T}{\mathcal{x}}_n)\\ -\mathcal{D}(\mathcal{P},\mathcal{Q}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1})+\mathcal{d}(\mathcal{g}{x}_{n+1},\mathcal{g}{x}_{n+2})\\ +\mathcal{D}(\mathcal{g}{\mathcal{x}}_{n+2},\mathcal{T}{\mathcal{x}}_n)-\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1})-\mathcal{D}(\mathcal{g}{\mathcal{x}}_{n+2},\mathcal{T}{\mathcal{x}}_n)\end{array}\right\}\hfill \\ & \le & max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2}),0,\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\right\}\hfill \\ & \le & max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\right\}.\hfill \end{array}$$

So, we can say that

$$\mathcal{N}({\mathcal{x}}_{n+1},{\mathcal{x}}_{n+2},{\mathcal{x}}_n,{\mathcal{x}}_{n+1})\le max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\right\}.$$

If we choose $max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\right\}=$$\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2}),$ then the inequality (5) becomes

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))-\tau$$

which is impossible.

If $max\left\{\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\right\}=$$\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}),$ then the inequality (5) will be

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1})))-\tau$$

(6)

then we obtain

$$\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\le \mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1}).$$

Hence, the sequence is $\{(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\}$ monotonic nonincreasing and bounded below. Therefore, we have a $\lambda \ge 0$ such that

$$\underset{n\to \infty }{lim}\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})=\lambda \ge 0.$$

(7)

Consider ${lim}_{n\to \infty }\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})=\lambda >0$, and, by using (6) and (7), we obtain

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n-1},\mathcal{g}{\mathcal{x}}_n)))-2\tau .$$

Continuing the procedure, we obtain

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1)))-n\tau .$$

(8)

We can conclude from the previous equation that

$$\underset{n\to \infty }{lim}\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))=-\infty .$$

Using (F2) of Definition 6 gives

$$\underset{n\to \infty }{lim}\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2}))=0.$$

(9)

Again, using (F3) of Definition 6, there exists $k\in (0,1)$, such that

$$\begin{array}{ccc}\hfill \underset{\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})\to 0}{lim}{(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))}^k\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))& =& 0,\hfill \\ \hfill \underset{n\to \infty }{lim}{(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))}^k\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))& =& 0.\hfill \end{array}$$

(10)

By using (8), we obtain

$$\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))\le \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1)))-n\tau$$

$$\begin{array}{ccc}\hfill \Rightarrow {(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))}^k[\mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2})))& -& \mathcal{F}(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_0,\mathcal{g}{\mathcal{x}}_1)))]\hfill \\ & \le & -{(\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_n,\mathcal{g}{\mathcal{x}}_{n+1})))}^{k}n\tau .\hfill \end{array}$$

Assume that ${\varsigma }_n=\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_{n+1},\mathcal{g}{\mathcal{x}}_{n+2}))$ from the above inequality is given as

$${({\varsigma }_n)}^k(\mathcal{F}({\varsigma }_n)-\mathcal{F}({\varsigma }_0))\le -{({\varsigma }_n)}^{k}n\tau .$$

From Equations (9) and (10) and $\underset{n\to \infty }{lim},$ we have

$$\underset{n\to \infty }{lim}{({\varsigma }_n)}^k(\mathcal{F}({\varsigma }_n)-\mathcal{F}({\varsigma }_0))\le \underset{n\to \infty }{lim}-{({\varsigma }_n)}^{k}n\tau \le 0,$$

so, the above inequality is

$$\underset{n\to \infty }{lim}n{({\varsigma }_n)}^k=0.$$

(11)

It is clear from the Equation (11) that we obtain an $n_1\in \mathbb{N}$ such that, for each given $\epsilon >0$,

$$\begin{array}{ccc}\hfill \left|n{({\varsigma }_n)}^k-0\right|& <& \epsilon ,\mathrm{for}\mathrm{all}n\ge n_1\hfill \\ \hfill \left|n{({\varsigma }_n)}^k\right|& <& \epsilon \hfill \\ \hfill ({\varsigma }_n)& <& {\displaystyle \frac{\epsilon }{n^{\frac{1}{k}}}}.\hfill \end{array}$$

Now, we want to show that $\{\mathcal{g}{\mathcal{x}}_n\}$ is a Cauchy sequence, where $(\mathcal{X},\mathcal{d})$ is a complete rectangular metric space for all $n,m\in \mathbb{N}$:

$$\begin{array}{ccc}\hfill \varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_m,\mathcal{g}{\mathcal{x}}_n))& \le & \varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_m,\mathcal{g}{\mathcal{x}}_{n+2}))+{\varsigma }_{n+1}+{\varsigma }_n\hfill \\ & \le & \varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_m,\mathcal{g}{\mathcal{x}}_{n+4}))+{\varsigma }_{n+3}+{\varsigma }_{n+2}+{\varsigma }_{n+1}+b{\varsigma }_n\hfill \\ & & ⋮\hfill \\ & \le & {\varsigma }_{m-1}+{\varsigma }_{m-2}+\dots +{\varsigma }_{n+1}+{\varsigma }_n\hfill \\ & =& \sum _{i=n}^{m-1}{\varsigma }_i\le \sum _{i=n}^{\infty }{\displaystyle \frac{\epsilon }{i^{\frac{1}{k}}}}.\hfill \end{array}$$

Hence, for all non-negative integers $n\ge n_1,$$p\in \mathbb{N}$ and $\mathcal{k}\in (0,1)$, the above inequality will be as follows:

$$\varphi (\mathcal{d}(\mathcal{g}{\mathcal{x}}_m,\mathcal{g}{\mathcal{x}}_n))\le \sum _{i=n}^{\infty }{\displaystyle \frac{\epsilon }{i^{\frac{1}{k}}}}.$$

By using the P-series test, we can determine that ${\displaystyle \sum _{i=n}^{\infty }}{\displaystyle \frac{\epsilon }{i^{\frac{1}{\mathcal{k}}}}}$ is convergent for ${\displaystyle \frac{1}{\mathcal{k}}}>1$. Consequently, the Cauchy sequence $\{\mathcal{g}{\mathcal{x}}_n\}$ converges in the complete rectangular metric space $(\mathcal{X},\mathcal{d})$. Let us assume that it converges to ${\mathcal{x}}^{*}$ within ${\mathcal{P}}_0\subseteq \mathcal{P}$ (given that the set $\mathcal{P}$ is closed), implying that the sequence $\{{\mathcal{x}}_n\}\subseteq {\mathcal{P}}_0$ as ${\mathcal{x}}_n\to {\mathcal{x}}^{*}$. Since $(\mathcal{g},\mathcal{T})$ are continuous mappings, it follows that

$$\mathcal{D}(\mathcal{g}{\mathcal{x}}^{*},\mathcal{T}{\mathcal{x}}^{*})=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

Thus, ${\mathcal{x}}^{*}$ is a coincidence point of the pair of mappings $(\mathcal{g},\mathcal{T})$. □

Example 5.

Consider the set $\mathcal{X}=\{0,1,2,3,4,5\}$ with the metric $\mathcal{d}:\mathcal{X}\times \mathcal{X}\to [0,\infty )$ defined as

$\mathcal{d}$	0	1	2	3	4	5
0	0	3	4	2	6	7
1	3	0	5	8	2	6
2	4	5	0	7	8	2
3	2	8	7	0	3	4
4	6	2	8	3	0	5
5	7	6	2	4	5	0

Clearly, $(\mathcal{X},\mathcal{d})$ is a complete rectangular metric space. Assuming the nonempty closed subsets $\mathcal{P}=\{0,1,2\}$ and $\mathcal{Q}=\{3,4,5\}$ of the given rectangular metric space $(\mathcal{X},\mathcal{d})$ and fulfill the $\mathcal{P}-$property condition, where ${\mathcal{P}}_0=\mathcal{P}$, ${\mathcal{Q}}_0=\mathcal{Q}$. After a few simple steps of calculation, we obtain $\mathcal{d}(\mathcal{P},\mathcal{Q})=2.$ The mapping $\mathcal{T}:\mathcal{P}\to \mathcal{CB}(\mathcal{Q})$ is given as follows:

$$\mathcal{T}\mathcal{x}=\left\{\begin{array}{cc}4,\hfill & \mathit{when}\mathcal{x}\in \{0,1\}\hfill \\ \{3,5\},\hfill & \mathit{when}\mathcal{x}\in \{2\},\hfill \end{array}\right.$$

and $\mathcal{g}:\mathcal{P}\to \mathcal{P}$, given as

$$\mathcal{g}\mathcal{x}=\left\{\begin{array}{c}0,\mathit{when}\mathcal{x}=2\\ 1,\mathit{when}\mathcal{x}=1\\ 2,\mathit{when}\mathcal{x}=0.\end{array}\right.$$

Clearly, $\mathcal{T}({\mathcal{P}}_0)\subseteq {\mathcal{Q}}_0$ and $\mathcal{g}({\mathcal{P}}_0)\subseteq {\mathcal{P}}_0.$ Then, $(\mathcal{g},\mathcal{T})$ satisfy the ${(\varphi -{\mathcal{F}}_{\tau })}_{C_P}-$proximal contraction condition

$$\tau +\mathcal{F}(\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}))),$$

(12)

for all elements $\mathcal{x},\mathcal{y},\mathcal{u},\mathcal{v}\in \mathcal{P}$. Since,

$$\begin{array}{ccc}\hfill \mathcal{D}(\mathcal{g}1,\mathcal{T}0)& =& \mathcal{d}(\mathcal{P},\mathcal{Q}),\hfill \\ \hfill \mathcal{D}(\mathcal{g}0,\mathcal{T}2)& =& \mathcal{d}(\mathcal{P},\mathcal{Q}),\hfill \end{array}$$

where $\mathcal{x}=0$, $\mathcal{y}=2$$\mathcal{u}=1,$ and $\mathcal{v}=0$. After simple calculation, we obtain

$$\mathcal{H}(\mathcal{T}0,\mathcal{T}2)=\mathcal{H}(4,\{3,5\})=3,$$

and

$$\begin{array}{ccc}\hfill \mathcal{N}(1,0,0,2)& =& max\left(\begin{array}{c}\mathcal{d}(\mathcal{g}0,\mathcal{g}2),\mathcal{d}(\mathcal{g}2,\mathcal{g}0),{\mathcal{D}}^{*}(\mathcal{g}1,\mathcal{T}0),\\ \mathcal{D}(\mathcal{g}0,\mathcal{T}0)-\mathcal{d}(\mathcal{g}0,\mathcal{g}2)-\mathcal{D}(\mathcal{g}0,\mathcal{T}0)\end{array}\right)\hfill \\ & =& max\left(\begin{array}{c}\mathcal{d}(2,0),\mathcal{d}(0,2),\mathcal{D}(1,4)-\mathcal{d}(\mathcal{P},\mathcal{Q}),\\ \mathcal{D}(2,4)-\mathcal{d}(2,0)-\mathcal{D}(2,4)\end{array}\right)\hfill \\ & =& max\left(4,4,0,-4\right)=4.\hfill \end{array}$$

Let the function $\mathcal{F}$ be as follows:

$$\begin{array}{c}\hfill \mathcal{F}(\varsigma )=log\varsigma +\varsigma .\end{array}$$

For $\varphi =2\mathcal{t}$ and $\tau =1$, we obtain $\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y}))=6$, $\varphi (\mathcal{N}(u,v,\mathcal{x},\mathcal{y}))=8$, and then the inequality (12) will be

$$\tau +\mathcal{F}(6)\le \mathcal{F}(8).$$

As a result, all of the circumstances of Theorem 1 are fulfilled, where the two points 1 and 2 are the coincidence points for $(\mathcal{g},\mathcal{T}).$

Corollary 1.

Within a complete rectangular metric space $(\mathcal{X},\mathcal{d})$, consider nonempty closed subsets $\mathcal{P}$ and $\mathcal{Q}$, both of which fulfill the $\mathcal{P}$-property with a nonempty set ${\mathcal{P}}_0$. Let $\mathcal{T}:\mathcal{P}\to \mathcal{CB}(\mathcal{Q})$ be a continuous mapping with $\mathcal{T}({\mathcal{P}}_0)\subseteq {\mathcal{Q}}_0$. We can say that $\mathcal{T}$ permits a best proximity point if it fulfills the ${(\varphi -\mathcal{F}\tau )}_{B_P}-$proximal contraction condition with an alternating distance function ϕ.

Proof. 

Assuming that $\mathcal{g}=I_{\mathcal{P}}$ ($\mathcal{g}$ is an identity on $\mathcal{P}),$ then the remainder of the proof follows Theorem 1.

Example 6.

Consider $\mathcal{X}={\mathbb{R}}^2$, then $(\mathcal{X},\mathcal{d})$ is a complete rectangular metric space, where $\mathcal{d}$ is defined as

$$\mathcal{d}(\mathcal{x},\mathcal{y})=\left\{\begin{array}{cc}\sqrt{{({\mathcal{x}}_2-{\mathcal{x}}_1)}^2+{({\mathcal{y}}_2-{\mathcal{y}}_1)}^2},\hfill & \mathit{if}\mathcal{x},\mathcal{y}\in {\mathbb{R}}^2/(2,3)\hfill \\ 1,\hfill & \mathit{if}\mathcal{x},\mathcal{y}\in \{(2,3)\},\hfill \\ 0,\hfill & \mathit{if}\mathcal{x}=\mathcal{y}.\hfill \end{array}\right.$$

Now, $\mathcal{P}=\{(1,\mathcal{a}):\mathcal{a}\in \mathbb{R}\}$ and $\mathcal{Q}=\{(0,\mathcal{b}):\mathcal{b}\in \mathbb{R}\}$ are clearly closed sets, and $\mathcal{d}(\mathcal{P},\mathcal{Q})=1.$ Further, ${\mathcal{P}}_0=\mathcal{P}$ and ${\mathcal{Q}}_0=\mathcal{Q}$, and the pair $(\mathcal{P},\mathcal{Q})$ has $\mathcal{P}-$property. A multivalued mapping $\mathcal{T}:\mathcal{P}\to \mathcal{CB}(\mathcal{Q})$, such that

$$\mathcal{T}(1,\mathcal{a})=\left\{(0,\mathcal{b}):\mathcal{b}\ge \mathcal{a}\right\}.$$

Now, the mapping $\mathcal{T}$ satisfies ${(\varphi -{\mathcal{F}}_{\tau })}_{B_P}-$proximal contraction

$$\tau +\mathcal{F}(\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})))$$

(13)

for all $\mathcal{x},\mathcal{y}\in \mathcal{X}$. Let the function $\mathcal{F}$ be as follows:

$$\begin{array}{c}\hfill \mathcal{F}(\varsigma )=log\varsigma +\varsigma .\end{array}$$

For $\varphi =2\mathcal{t}$ and $\tau =1$, we have the following simple calculation:

Let $\mathcal{x}=(1,\mathcal{a})$, then $\mathcal{T}(\mathcal{x})=(0,b)$ and we choose $\mathcal{y}=\mathcal{u}=(1,\mathcal{b})$. Then, clearly, $\mathcal{T}\mathcal{y}=\mathcal{T}\mathcal{u}=\{(0,\mathcal{c}):\mathcal{c}\ge \mathcal{b}\}$, and we take $\mathcal{v}=(1,\mathcal{c})$. So,

$$\begin{array}{cc}\hfill \mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})& =\mathcal{b}-\mathcal{a}\hfill \\ \hfill & \le max\{\mathcal{d}(\mathcal{u},\mathcal{v}),\mathcal{d}(\mathcal{x},\mathcal{y}),{\mathcal{D}}^{*}(\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{D}(\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{u},\mathcal{v})-\mathcal{D}(\mathcal{y},\mathcal{T}\mathcal{u})\}.\hfill \\ \hfill & =\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})\hfill \end{array}$$

Equation (13) is satisfied by this. All of the requirements listed in Corollary 1 are therefore satisfied, identifying 1 as the fixed point of the mapping $\mathcal{T}$.

Note that in Theorem 1, if we embrace $\mathcal{P}=\mathcal{Q}=\mathcal{X},$ we obtain the corresponding findings described below. □

Corollary 2.

Consider a multivalued mapping $\mathcal{T}:\mathcal{X}\to \mathcal{CB}(\mathcal{X})$ defined on a complete rectangular metric space. Suppose that it fulfilled the ${({\mathcal{F}}_{\tau })}_{Bp}$-proximal contraction condition with the alternating distance function ϕ. Under these conditions, the existence of a fixed point for the mapping $\mathcal{T}$ is guaranteed.

Proof. 

Consider $\mathcal{P}=\mathcal{Q}=\mathcal{X}$. The remaining part of the proof precisely matches Theorem 1. □

Example 7.

Consider $\mathcal{X}=\{1,2,3,4\}$, then $(\mathcal{X},\mathcal{d})$ is a complete rectangular metric space, where $\mathcal{d}$ is defined as

$$\mathcal{d}(\mathcal{x},\mathcal{y})=\mathcal{d}(\mathcal{y},\mathcal{x})=\left\{\begin{array}{cc}0,\hfill & \mathit{if}\mathcal{x}=\mathcal{y},\hfill \\ 1,\hfill & \mathit{if}(\mathcal{x},\mathcal{y})\in \{(1,3),(2,3)\},\hfill \\ 2,\hfill & \mathit{if}(\mathcal{x},\mathcal{y})\in \{(1,4),(2,4),(3,4)\},\hfill \\ 3,\hfill & \mathit{if}(\mathcal{x},\mathcal{y})=(1,2).\hfill \end{array}\right.$$

A multivalued mapping $\mathcal{T}:\mathcal{X}\to \mathcal{CB}(\mathcal{X})$, such that

$$\mathcal{T}\mathcal{x}=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\mathcal{x}=\{1,2,3\}\hfill \\ \{2,3\},\hfill & \mathit{if}\mathcal{x}=4.\hfill \end{array}\right.$$

Now, the mapping $\mathcal{T}$ satisfies the ${(\varphi -{\mathcal{F}}_{\tau })}_{B_P}-$proximal contraction

$$\tau +\mathcal{F}(\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{x},\mathcal{y}))),$$

(14)

for all $\mathcal{x},\mathcal{y}\in \mathcal{X}$. Let the function $\mathcal{F}$ be as follows:

$$\begin{array}{c}\hfill \mathcal{F}(\varsigma )=log\varsigma +\varsigma .\end{array}$$

For $\varphi =2\mathcal{t}$ and $\tau =1$, we have the following simple calculation:

Let $\mathcal{x}\in \{1,2,3\}$ and $\mathcal{y}=4$, then, clearly, $\mathcal{T}\mathcal{x}=1$, and $\mathcal{T}\mathcal{y}=\{2,3\}$. So, $\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})=1$. On the other hand, we obtain the following:

$$\begin{array}{cc}\hfill \mathcal{N}(\mathcal{x},\mathcal{y})& =max\{\mathcal{d}(\mathcal{x},\mathcal{y}),\mathcal{d}(y,\mathcal{T}y),\mathcal{d}(\mathcal{x},\mathcal{T}y)-\mathcal{d}(\mathcal{x},\mathcal{y})\}\hfill \\ \hfill & =max\{2,\mathcal{d}(4,1),\mathcal{d}(2,1)-\mathcal{d}(2,4)\}\hfill \\ \hfill & =max\{2,2,3-2\}=2.\hfill \end{array}$$

Therefore,

$$\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y}))=\varphi (1)=2(1)=2,$$

and

$$\varphi (\mathcal{N}(\mathcal{x},\mathcal{y}))=\varphi (2)=2(2)=4.$$

Now, apply $\mathcal{F}$, and we obtain

$$\mathcal{F}(\varphi (\mathcal{H}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))=\mathcal{F}(2)=log2+2=2.30103,$$

and

$$\mathcal{F}(\varphi (\mathcal{N}(\mathcal{x},\mathcal{y})))=\mathcal{F}(4)=log(4)+4=4.60206.$$

Equation (14) is satisfied by this. All of the requirements listed in Corollary 2 are therefore satisfied, identifying 1 as the fixed point of the mapping $\mathcal{T}$.

4. For Single-Valued Mappings

This section is devoted to examining coincidence best proximity point results in complete rectangular metric spaces, specifically for single-valued mappings. Recognizing that multivalued mappings produce sets as outputs, which behave as single-valued mappings when these outputs are singleton sets, we leverage this property to establish new results for single-valued mappings. These results are developed in relation to those introduced in the previous section.

Definition 11.

A pair of mappings $(\mathcal{g},\mathcal{T}),$ where $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$ and $\mathcal{g}:\mathcal{P}\to \mathcal{P}$ is said to be a ${(\tau -\mathcal{F})}_{C_p}-$proximal contraction, if there exists a $\tau \in (0,+\infty )$ such that

$$\begin{array}{c}\mathcal{d}\left(\mathcal{g}\mathcal{u},\mathcal{T}\mathcal{x}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\\ \mathcal{d}\left(\mathcal{g}\mathcal{v},\mathcal{T}\mathcal{y}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\end{array},$$

then this implies that

$$\tau +\mathcal{F}(\varphi (\mathcal{d}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}))),$$

where

$$\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})=max\{\mathcal{d}(\mathcal{g}\mathcal{u},\mathcal{g}\mathcal{v}),\mathcal{d}(\mathcal{g}\mathcal{x},\mathcal{g}\mathcal{y}),{\mathcal{d}}^{*}(\mathcal{g}\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{d}(\mathcal{g}\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{g}\mathcal{u},\mathcal{g}\mathcal{v})-\mathcal{d}(\mathcal{g}\mathcal{y},\mathcal{T}\mathcal{u})\}$$

for all $\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}$ in $\mathcal{P}.$

Definition 12.

A mapping $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$ is said to be ${({\mathcal{F}}_{\tau })}_{B_P}-$proximal contraction if there exists a $\tau \in (0,+\infty )$ such that

$$\begin{array}{c}\mathcal{d}\left(\mathcal{u},\mathcal{T}\mathcal{x}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\\ \mathcal{d}\left(\mathcal{v},\mathcal{T}\mathcal{y}\right)=\mathcal{d}(\mathcal{P},\mathcal{Q})\end{array},$$

which implies that

$$\tau +\mathcal{F}(\varphi (\mathcal{d}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}))),$$

where

$$\begin{array}{c}\hfill \mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})=max\{\mathcal{d}(\mathcal{u},\mathcal{v}),\mathcal{d}(\mathcal{x},\mathcal{y}),{\mathcal{d}}^{*}(\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{d}(\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{u},\mathcal{v})-\mathcal{d}(\mathcal{y},\mathcal{T}\mathcal{u})\}\end{array}$$

for all $\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}$ in $\mathcal{P}.$

When $\mathcal{g}$ is selected as $I_{\mathcal{P}}$, signaling the identity mapping on $\mathcal{P}$, it results in the transformation of all ${({\mathcal{F}}_{\tau })}_{C_p}$-proximal contractions into a unified form of ${({\mathcal{F}}_{\tau })}_{B_p}$-proximal contractions. Furthermore, we see that if

$$\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y})=max\{\mathcal{d}(\mathcal{u},\mathcal{v}),\mathcal{d}(\mathcal{x},\mathcal{y}),{\mathcal{d}}^{*}(\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{d}(\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{u},\mathcal{v})-\mathcal{d}(\mathcal{y},\mathcal{T}\mathcal{u})\}=\mathcal{d}(\mathcal{x},\mathcal{y})$$

and $\varphi$ is an identity map, then our contraction is reduced to $\mathcal{F}-$contraction for single-valued mappings.

Theorem 2.

Consider the mappings $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$ and $\mathcal{g}:\mathcal{P}\to \mathcal{P}$, where both $\mathcal{P}$ and $\mathcal{Q}$ are nonempty closed subsets of a complete rectangular metric space $(\mathcal{X},\mathcal{d})$. These mappings fulfill the $\mathcal{P}$-property, with $\mathcal{T}({\mathcal{P}}_0)\subseteq {\mathcal{Q}}_0$ and ${\mathcal{P}}_0\subseteq \mathcal{g}({\mathcal{P}}_0)$. If the pair of continuous mappings $(\mathcal{g},\mathcal{T})$, where $\mathcal{g}$ is an injective mapping, the ${({\mathcal{F}}_{\tau })}_{C_p}$-proximal contraction condition is fulfilled with an alternating distance function ϕ. Under these conditions, it follows that $(\mathcal{g},\mathcal{T})$ admits a coincidence point.

Proof. 

Multivalued mappings produce sets as outputs. When the output is a singleton set, the mapping behaves like a single-valued mapping. Since all single-valued mappings fall into the category known as multivalued mappings, the rest of the proof aligns with the methodology outlined in Theorem 1. □

Example 8.

Determine the complete rectangular metric space $(\mathcal{X},\mathcal{d})$ by taking the set $\mathcal{X}=\{11,12,13,14,15,16\}$. The metric function $\mathcal{d}:\mathcal{X}\times \mathcal{X}\to [0,\infty )$ is formed as

$$\mathcal{d}(\mathcal{x},\mathcal{y})=\left\{\begin{array}{cc}\sqrt{|\mathcal{x}-\mathcal{y}|}\hfill & \mathit{if}\mathcal{x}\ne \mathcal{y},\hfill \\ 0,\hfill & \mathit{if}\mathcal{x}=\mathcal{y}.\hfill \end{array}\right.$$

Suppose that $\mathcal{Q}=\{12,14,16\}$ and $\mathcal{P}=\{11,13,15\}$ are closed subsets of rectangular metric space $(\mathcal{X},\mathcal{d}).$ Simply, we calculate $\mathcal{d}(\mathcal{P},\mathcal{Q})=1,$ and satisfy the $\mathcal{P}-$property, where ${\mathcal{P}}_0=\mathcal{P}$ and ${\mathcal{Q}}_0=\mathcal{Q}$. A mapping $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$ such that

$$\mathcal{T}\mathcal{x}=\left\{\begin{array}{cc}14,\hfill & \mathit{if}\mathcal{x}=15\hfill \\ 12,\hfill & \mathit{if}\mathcal{x}=\{11,13\},\hfill \end{array}\right.$$

and also, $\mathcal{g}:\mathcal{P}\to \mathcal{P}$:

$$\mathcal{g}\mathcal{x}=\left\{\begin{array}{c}15,\mathit{if}\mathcal{x}=13\\ 13,\mathit{if}\mathcal{x}=15\\ 11,\mathit{if}\mathcal{x}=11\end{array}.\right.$$

We clearly see that $\mathcal{T}({\mathcal{P}}_0)\subseteq {\mathcal{Q}}_0$ and $\mathcal{g}({\mathcal{P}}_0)\subseteq {\mathcal{P}}_0.$ Now, we want to show the pair $(\mathcal{g},\mathcal{T})$ fulfills the ${({\mathcal{F}}_{\tau })}_{C_p}-$proximal contraction condition

$$\tau +\mathcal{F}(\varphi (\mathcal{d}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}))),$$

(15)

for all $\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}\in \mathcal{P}$. Since,

$$\begin{array}{ccc}\hfill \mathcal{d}(\mathcal{g}11,\mathcal{T}13)& =& \mathcal{d}(\mathcal{P},\mathcal{Q}),\hfill \\ \hfill \mathcal{d}(\mathcal{g}13,\mathcal{T}15)& =& \mathcal{d}(\mathcal{P},\mathcal{Q}),\hfill \end{array}$$

where $\mathcal{u}=11,$$\mathcal{v}=13,$$\mathcal{x}=13$ and $\mathcal{y}=15$. After routine calculation, we obtain

$$\mathcal{d}(\mathcal{T}13,\mathcal{T}15)=\mathcal{d}(12,14)=\sqrt{2},$$

and

$$\begin{array}{ccc}\hfill \mathcal{N}(11,13,13,15)& =& max\left(\begin{array}{c}\mathcal{d}(\mathcal{g}11,\mathcal{g}13),\mathcal{d}(\mathcal{g}13,\mathcal{g}15),{\mathcal{d}}^{*}(\mathcal{g}13,\mathcal{T}11),\\ \mathcal{d}(\mathcal{g}11,\mathcal{T}11)-\mathcal{d}(\mathcal{g}11,\mathcal{g}13)-\mathcal{d}(\mathcal{g}15,\mathcal{T}11)\end{array}\right)\hfill \\ & =& max\left(\begin{array}{c}\mathcal{d}(\mathcal{g}11,\mathcal{g}13),\mathcal{d}(\mathcal{g}13,\mathcal{g}15),\mathcal{d}(\mathcal{g}13,\mathcal{T}11)-\mathcal{d}(\mathcal{P},\mathcal{Q}),\\ \mathcal{d}(\mathcal{g}11,\mathcal{T}11)-\mathcal{d}(\mathcal{g}11,\mathcal{g}13)-\mathcal{d}(\mathcal{g}15,\mathcal{T}11)\end{array}\right)\hfill \\ & =& max\left(\begin{array}{c}\mathcal{d}(11,15),\mathcal{d}(15,13),\mathcal{d}(15,12)-\mathcal{d}(\mathcal{P},\mathcal{Q}),\\ \mathcal{d}(11,12)-\mathcal{d}(11,15)-\mathcal{d}(13,12)\end{array}\right)\hfill \\ & =& max\left(2,\sqrt{2},\sqrt{3}-1,1-2-\sqrt{2}\right)=2.\hfill \end{array}$$

Let the function $\mathcal{F}(\varsigma )$ be defined as

$$\mathcal{F}(\varsigma )=log\varsigma +\varsigma .$$

For $\varphi =2\mathcal{t}$ and $\tau =1$, we conclude that $\varphi (\mathcal{d}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y}))=2\sqrt{2}$, $\varphi (\mathcal{N}(\mathcal{u},\mathcal{v},\mathcal{x},\mathcal{y}))=4$, then the inequality (15) will be

$$\tau +\mathcal{F}(2\sqrt{2})\le \mathcal{F}(4).$$

Hence, all the conditions specified in Theorem 2 are satisfied, establishing 11 as the coincidence best proximity point of the pair $(\mathcal{g},\mathcal{T}).$

Corollary 3.

Consider a mapping $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$, where both $\mathcal{P}$ and $\mathcal{Q}$ are nonempty closed subsets of a complete rectangular metric space $(\mathcal{X},\mathcal{d})$ and fulfill the $\mathcal{P}$-property. Furthermore, suppose $\mathcal{T}({\mathcal{P}}_0)\subseteq {\mathcal{Q}}_0$. $\mathcal{T}$ permits a best proximity point if it is a continuous mapping with an alternating distance function ϕ that fulfills the ${({\mathcal{F}}_{\tau })}_{B_p}-$proximal contraction.

Proof. 

When we consider the mapping $\mathcal{g}=I_{\mathcal{P}}$ (where $\mathcal{g}$ represents the identity mapping on $\mathcal{P}$), the rest of the proof follows a similar structure as presented in Theorem 1. □

Example 9.

Let us have $\mathcal{X}=C[0,3]$, and define metric $\mathcal{d}(\mathcal{a},\mathcal{b})={sup}_{t\in [0,1]}|{\mathcal{a}}^8(t)-{\mathcal{b}}^8(t)|$. Let

$$\mathcal{P}=\{\alpha t:\alpha \in [0,1]\}$$

and

$$\mathcal{Q}=\{\alpha (t-2):\alpha \in [0,1]\}.$$

So, we can calculate $\mathcal{d}(\mathcal{P},\mathcal{Q})=2$; therefore, ${\mathcal{P}}_0=\mathcal{P}$ and ${\mathcal{Q}}_0=\mathcal{Q}$. Now, define a non-self-map $\mathcal{T}:\mathcal{P}\to \mathcal{Q}$, given as

$$\mathcal{T}(\mathcal{a}(t))={\displaystyle \frac{8}{9}}(t-2)+(t-2){\int }_0^1({\mathcal{a}}^8(s))ds.$$

So, $\mathcal{T}({\mathcal{P}}_0)\subset {\mathcal{Q}}_0.$ Now, take $\mathcal{a}(t),\mathcal{b}(t),\mathfrak{w}(t),\mathfrak{u}(t)\in \mathcal{P}$, such that

$$\mathcal{d}(\mathfrak{w}(t),\mathcal{T}(\mathcal{a}(t)))=\mathcal{d}(\mathcal{P},\mathcal{Q})$$

$$\mathcal{d}(\mathfrak{u}(t),\mathcal{T}(\mathcal{b}(t)))=\mathcal{d}(\mathcal{P},\mathcal{Q}).$$

Now,

$$\begin{array}{cc}\hfill \mathcal{d}(\mathcal{T}(\mathcal{a}(t)),\mathcal{T}(\mathcal{b}(t)))& =\underset{t\in [0,1]}{sup}\left|\alpha (t-2)+(t-2){\int }_0^1({\mathcal{a}}^8(s))ds-\alpha (t-2)-(t-2){\int }_0^1({\mathcal{b}}^8(s))ds\right|\hfill \\ \hfill & =\underset{t\in [0,1]}{sup}\left|(t-2){\int }_0^1({\mathcal{a}}^8(s))ds-(t-2){\int }_0^1({\mathcal{b}}^8(s))ds\right|\hfill \\ \hfill & \le \underset{t\in [0,1]}{sup}(t-2){\int }_0^1\left|{\mathcal{a}}^8(s)-{\mathcal{b}}^8(s)\right|ds\hfill \\ \hfill & =(t-2)\underset{t\in [0,1]}{sup}\left|{\mathcal{a}}^8(t)-{\mathcal{b}}^8(t)\right|{\int }_0^{1}ds\hfill \\ \hfill & =(t-2)\mathcal{d}(\mathcal{a}(t),\mathcal{b}(t))\hfill \\ \hfill & \le (t-2)max\left\{\begin{array}{cc}\hfill & \mathcal{d}(\mathcal{a}(t),\mathcal{b}(t)),\mathcal{d}(\mathfrak{w}(t),\mathfrak{u}(t)),\mathcal{d}(\mathfrak{w}(t),\mathcal{T}(\mathfrak{w}(t)))\hfill \\ & -\mathcal{d}(\mathfrak{w}(t),\mathfrak{u}(t))-\mathcal{d}(\mathcal{b}(t),\mathcal{T}(\mathfrak{w}(t))),{\mathcal{d}}^{*}(\mathfrak{u}(t),\mathcal{T}(\mathfrak{w}(t)))\hfill \end{array}\right\}\hfill \\ \hfill & \le (t-2)\mathcal{N}\left(\mathcal{a}(t),\mathcal{b}(t),\mathfrak{w}(t),\mathfrak{u}(t)\right)\hfill \\ \hfill & \le t\mathcal{N}\left(\mathcal{a}(t),\mathcal{b}(t),\mathfrak{w}(t),\mathfrak{u}(t)\right).\hfill \end{array}$$

Now, taking $\varphi (\mathfrak{t})=2\mathfrak{t}$, and $\mathcal{F}(\varsigma )=log\varsigma +\varsigma$, implies

$$\tau +\mathcal{F}\left(\varphi \left(\mathcal{d}(\mathcal{T}(\mathcal{a}(t)),\mathcal{T}(\mathcal{b}(t))\right)\right)\le \mathcal{F}\left(\varphi \left(\mathcal{N}(\mathcal{a}(t),\mathcal{b}(t),\mathfrak{w}(t),\mathfrak{u}(t),)\right)\right).$$

Hence, ${({\mathcal{F}}_{\tau })}_{B_P}$ holds.

5. Fixed Point Results

If we use $\mathcal{Q}=\mathcal{P}=\mathcal{X}$ in Theorem 2 given in the previous section, then we acquire the fixed point in this section and we also achieve the preceding considerations accordingly. For an in-depth investigation of the significance of fixed point theorems in various engineering applications, we refer to [32].

Definition 13.

A mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ is deemed an ${(\mathcal{F}\tau )}_{F_P}$ contraction if there is a positive real number τ, satisfying the condition

$$\tau +\mathcal{F}(\varphi (\mathcal{d}(\mathcal{T}\mathcal{u},\mathcal{T}\mathcal{v})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{u},\mathcal{v}))),$$

where, for all $\mathcal{u},\mathcal{v}$ in $\mathcal{X}$

$$\begin{array}{ccc}\hfill \mathcal{N}(\mathcal{u},\mathcal{v})& =& max\{\mathcal{d}(\mathcal{u},\mathcal{v}),\mathcal{d}(\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{d}(\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{u},\mathcal{v})\}.\hfill \end{array}$$

We see that if

$$\mathcal{N}(\mathcal{u},\mathcal{v})=max\{\mathcal{d}(\mathcal{u},\mathcal{v}),\mathcal{d}(\mathcal{v},\mathcal{T}\mathcal{u}),\mathcal{d}(\mathcal{u},\mathcal{T}\mathcal{u})-\mathcal{d}(\mathcal{u},\mathcal{v})\}=\mathcal{d}(\mathcal{u},\mathcal{v})$$

and $\varphi$ is an identity map, then our contraction is reduced to $\mathcal{F}-$contraction.

Theorem 3.

Consider a single-valued self-mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ defined on a complete rectangular metric space that satisfies the ${(\mathcal{F}\tau )}_{F_P}$-proximal contraction with an alternating distance function ϕ. Under these conditions, it follows that $\mathcal{T}$ possesses a fixed point.

Proof. 

In the scenario that $\mathcal{P}=\mathcal{Q}=\mathcal{X}$ is used, the remaining portions of the proof replicate Theorem 2. □

Example 10.

: If we take $\mathcal{A}=\{{\displaystyle \frac{1}{n}}:n=\{1,2,3,4,5\}\}$ and $\mathcal{B}=[1,2]$, the metric function $\mathcal{d}:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$ is given as

$$\mathcal{d}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{3}}\right)=0.03=\mathcal{d}\left({\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{5}}\right),$$

$$\mathcal{d}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}}\right)=0.02=\mathcal{d}\left({\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{4}}\right),$$

$$\mathcal{d}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{4}}\right)=0.06=\mathcal{d}\left({\displaystyle \frac{1}{5}},{\displaystyle \frac{1}{3}}\right),$$

and

$$\mathcal{d}(\mathcal{x},\mathcal{y})=|\mathcal{x}-\mathcal{y}|,\mathrm{all}\mathrm{other}\mathcal{x},\mathcal{y}\in \mathcal{X}.$$

Here, $\mathcal{X}=\mathcal{A}\cup \mathcal{B}$. Clearly, $(\mathcal{X},\mathcal{d})$ is a rectangular metric space but not a metric space. If we take $\mathcal{x}={\displaystyle \frac{1}{2}},\mathcal{y}={\displaystyle \frac{1}{4}}$ and $\mathcal{z}={\displaystyle \frac{1}{3}}$, then

$$\mathcal{d}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{4}}\right)=0.06.$$

On the other hand,

$$\mathcal{d}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{3}}\right)+\mathcal{d}\left({\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{4}}\right)=0.03+0.02=0.05$$

which gives,

$$\mathcal{d}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{4}}\right)\ge \mathcal{d}\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{3}}\right)+\mathcal{d}\left({\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{4}}\right),$$

which shows that $(\mathcal{X},\mathcal{d})$ are not metric but clearly satisfy the rectangular metric conditions. Now, we define a mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$, where $\mathcal{X}=\mathcal{A}\cup \mathcal{B}$, such that

$$\mathcal{T}\mathcal{x}=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\mathcal{x}\in \mathcal{A}\hfill \\ {\displaystyle \frac{1}{2}}x+{\displaystyle \frac{1}{2}},\hfill & \mathit{if}\mathcal{x}\in \mathcal{B}.\hfill \end{array}\right.$$

The mapping $\mathcal{T}$ satisfies ${({\mathcal{F}}_{\tau })}_{F_p}-$proximal contraction

$$\tau +\mathcal{F}(\varphi (\mathcal{d}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{x},\mathcal{y}))),$$

(16)

for all $\mathcal{x},\mathcal{y}\in \mathcal{X}$.

Case (i): If $\mathcal{x}\in \mathcal{A}$ and $\mathcal{y}\in \mathcal{B}$, we take the points as $\mathcal{x}={\displaystyle \frac{1}{2}}$ and $\mathcal{y}=1.5$. Then, $\mathcal{d}(\mathcal{T}x,\mathcal{T}y)=0.25$ and $\mathcal{N}(2,4)=1.$

Case (ii): If both elements are from set $\mathcal{B}$, then there are two further cases; in the first case, we choose elements that are very near to each other, and in the other, we pick up points far away from each other.

(a)

$\mathcal{x}=1$ and $\mathcal{y}=1.1$, then $\mathcal{d}$$(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})=0.05$ and $\mathcal{N}(\mathcal{x},\mathcal{y})=0.1.$

(b)

$\mathcal{x}=1$ and $\mathcal{y}=2$, then $\mathcal{d}(\mathcal{T}\mathcal{x},\mathcal{T}\mathcal{y})=0.5$ and $\mathcal{N}(\mathcal{x},\mathcal{y})=1.$

For all cases, let $\mathcal{F}$ be a function as

$$\mathcal{F}(\varsigma )=log\varsigma +\varsigma .$$

For $\varphi (\mathcal{t})=2\mathcal{t}$ and $\tau =1$, we obtain the inequality (16) for all cases.

Hence, all the assumptions of Theorem 3 are fulfilled and $\mathcal{T}$ concedes 1 as the fixed point.

In the subsequent analysis, we investigate the convergence behavior of the sequence under consideration, employing various initial points. The tabulated results given below in   Table 1  clearly depict the distinctive convergence patterns exhibited by the sequences.

Table 1. Numerical convergence behavior of sequences with different initial points.

Sr. No.	${\mathcal{x}}_0=2$	${\mathcal{x}}_0=1.8$	${\mathcal{x}}_0=1.6$	${\mathcal{x}}_0=1.4$	${\mathcal{x}}_0=1.2$
1	1.5	1.4	1.3	1.2	1.1
2	1.25	1.2	1.15	1.1	1.05
3	1.125	1.1	1.075	1.05	1.025
4	1.0625	1.05	1.0375	1.025	1.0125
5	1.03125	1.025	1.01875	1.00125	1.00625
6	1.01563	1.0125	1.00938	1.00625	1.00313
7	1.00781	1.00625	1.00468	1.00313	1.00157
8	1.00391	1.00313	1.00234	1.00157	1.00079
9	1.00196	1.00157	1.00117	1.00079	1.00040
⋮	⋮	⋮	⋮	⋮	⋮
16	1.00002	1.00001	1.00001	1	1
17	1.00001	1	1	1	1
18	1	1	1	1	1

A graph demonstrating the behavior of sequences created from various starting points is shown in Figure 1. The graph gives valuable insights into the convergence patterns exhibited by these distinct sequences.

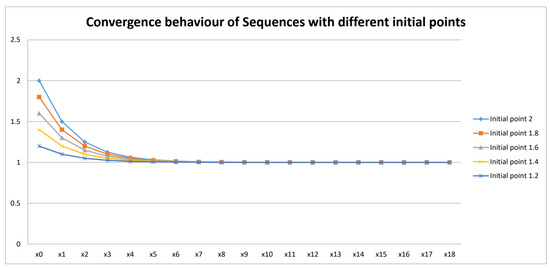
Figure 1. Convergence behavior of sequences with different initial points.

6. Application to the Fredholm Integral Equation

In this section, we rigorously assess the existence and uniqueness of solutions to a Fredholm integral equation within a function space by applying the results which were established in the previous section.

The Fredholm integral equation is given as

$$\mathcal{a}(\mathfrak{t})=\phi (\mathfrak{t})+{\int }_0^1\mathcal{G}(\mathfrak{t},\mathcal{s},\mathcal{a}(\mathfrak{t}))d\mathcal{s},\mathcal{a}(\mathfrak{t})\in \mathcal{X}.$$

(17)

The continuous function $\mathcal{G}$ is defined across the space $[\mathcal{a},b]\times [\mathcal{a},\mathcal{b}]$ in the present scenario, but the continuous function $\phi$ is on the interval $[\mathcal{a},\mathcal{b}]$.

We present a numerical example that clearly illustrates the usefulness of our findings to highlight the importance of our contributions. The study of function spaces as the selected metric space gives our research a fascinating new dimension. In this regard, we utilize the strength of Theorem 3 to investigate in detail the existence and uniqueness of solutions to the Fredholm integral equation, therefore making a valuable contribution to the field’s general knowledge.

Consider the function space $\mathcal{X}=\mathcal{C}([0,1],\mathbb{R})$ and ${\mathcal{d}}_{\mathfrak{t}}:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$, defined by

$${\mathcal{d}}_{\mathfrak{t}}(\mathcal{a},\mathcal{b})=\underset{\mathfrak{t}\in [0,1]}{sup}|{\mathcal{a}}^8(\mathfrak{t})-{\mathcal{b}}^8(\mathfrak{t})|.$$

Clearly, $(\mathcal{X},{\mathcal{d}}_{\mathfrak{t}})$ form a rectangular metric space. Now, we introduce a self-mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ given by

$$\mathcal{T}(\mathcal{a}(\mathfrak{t}))=\phi (\mathfrak{t})+{\int }_0^1\mathcal{G}(\mathfrak{t},\mathcal{s},\mathcal{a}(\mathfrak{t}))d\mathcal{s},\mathcal{a}(\mathfrak{t})\in \mathcal{X}.$$

(18)

Let $\phi (\mathfrak{t})={\displaystyle \frac{8}{9}}\mathfrak{t}$ and $\mathcal{G}(\mathfrak{t},\mathcal{s},\mathcal{a}(\mathfrak{t}))=\mathfrak{t}{\mathcal{a}}^8(\mathcal{s})$, where $\mathfrak{t}<{\displaystyle \frac{1}{{exp}^{\tau }}}$. Equation (18) is then given by

$$\begin{array}{cc}\hfill \mathcal{T}(\mathcal{a}(\mathfrak{t}))& ={\displaystyle \frac{8}{9}}\mathfrak{t}+{\int }_0^1\mathfrak{t}{\mathcal{a}}^8(\mathcal{s})d\mathcal{s},\hfill \end{array}$$

where ${\displaystyle \frac{8}{9}}\mathfrak{t}$ and $\mathfrak{t}{\mathcal{a}}^8(\mathcal{s})$ are continuous functions. Now, consider

$$\begin{array}{cc}\hfill \mathcal{d}(\mathcal{T}(\mathcal{a}(\mathfrak{t})),\mathcal{T}(\mathcal{b}(\mathfrak{t})))& =\left|\mathcal{T}(\mathcal{a}(\mathfrak{t}))-\mathcal{T}(\mathcal{b}(\mathfrak{t}))\right|\hfill \\ \hfill & =\left|{\displaystyle \frac{8}{9}}\mathfrak{t}+{\int }_0^1\mathfrak{t}{\mathcal{a}}^8(\mathcal{s})-{\displaystyle \frac{8}{9}}\mathfrak{t}-{\int }_0^1\mathfrak{t}{\mathcal{b}}^8(\mathcal{s})\right|\hfill \\ \hfill & =\left|{\int }_0^1\mathfrak{t}{\mathcal{a}}^8(\mathcal{s})-{\int }_0^1\mathfrak{t}{\mathcal{b}}^8(\mathcal{s})\right|\hfill \\ \hfill & \le {\int }_0^1\mathfrak{t}\left|{\mathcal{a}}^8(\mathcal{s})-{\mathcal{b}}^8(\mathcal{s})\right|ds\hfill \\ \hfill & =\mathcal{d}(\mathcal{a}(\mathfrak{t}),\mathcal{b}(\mathfrak{t}))\hfill \\ \hfill & \le \mathfrak{t}max\{\mathcal{d}(\mathcal{a}(\mathfrak{t}),\mathcal{b}(\mathfrak{t})),\mathcal{d}(\mathcal{b}(\mathfrak{t}),\mathcal{T}\mathcal{a}(\mathfrak{t})),\mathcal{d}(\mathcal{a}(\mathfrak{t}),\mathcal{T}\mathcal{a}(\mathfrak{t}))-\mathcal{d}(\mathcal{a}(\mathfrak{t}),\mathcal{b}(\mathfrak{t}))\}\hfill \\ \hfill & =\mathfrak{t}\mathcal{N}(\mathcal{a}(\mathfrak{t}),\mathcal{b}(\mathfrak{t})).\hfill \end{array}$$

The alternating function is $\varphi (\mathfrak{t})=2\mathfrak{t}$ and $\mathfrak{t}<{\displaystyle \frac{1}{{exp}^{\tau }}}$, leading to

$$\varphi (\mathcal{d}(\mathcal{T}(\mathcal{a}(\mathfrak{t})),\mathcal{T}(\mathcal{b}(\mathfrak{t}))))\le {\displaystyle \frac{1}{{exp}^{\tau }}}\varphi (\mathcal{N}(\mathcal{a}(\mathfrak{t}),\mathcal{b}(\mathfrak{t}))).$$

(19)

Now, let $\mathcal{F}(\mathcal{x})=log(\mathcal{x})$; applying it on both sides of the inequality (19), we obtain

$$log({exp}^{\tau })+log(\varphi (\mathcal{d}(\mathcal{T}(\mathcal{a}(\mathfrak{t})),\mathcal{T}(\mathcal{b}(\mathfrak{t})))))\le log(\varphi (\mathcal{N}(\mathcal{a}(\mathfrak{t}),\mathcal{b}(\mathfrak{t}))),$$

which implies that

$$\tau +\mathcal{F}(\varphi (\mathcal{d}(\mathcal{T}(\mathcal{a}(\mathfrak{t})),\mathcal{T}(\mathcal{b}(\mathfrak{t}))))\le \mathcal{F}(\varphi (\mathcal{N}(\mathcal{a}(\mathfrak{t}),\mathcal{b}(\mathfrak{t}))).$$

Hence, it satisfies the ${({\mathcal{F}}_{\tau })}_{F_P}-$proximal contraction, and, by Theorem 3, the Fredholm integral equation has a unique solution. Equation (17) clearly has an exact solution, which is $\mathcal{a}(\mathfrak{t})=\mathfrak{t}$.

We next highlight the importance of our findings by showing that the numerical solution converges. The iterative scheme is defined by

$${\mathcal{a}}_{n+1}(\mathfrak{t})=\mathcal{T}({\mathcal{a}}_n(\mathfrak{t}))={\displaystyle \frac{8}{9}}\mathfrak{t}+{\int }_0^1\mathfrak{t}{\mathcal{a}}_n^8(\mathcal{s})d\mathcal{s},\mathcal{a}(\mathfrak{t})\in \mathcal{X}.$$

(20)

We select ${\mathcal{a}}_0=0$ as the initial guess to start the procedure. When $n=1,2,3,\dots$ are substituted into Equation (20), we obtain the values shown in Table 2.

Table 2. Numerical convergence behavior of the sequence.

Sr. No.	${\mathcal{a}}_{\mathit{n}}$	Values
0	${\mathcal{a}}_0$	${\displaystyle \frac{8}{9}}\mathfrak{t}$
1	${\mathcal{a}}_1$	$0.8889\mathfrak{t}$
2	${\mathcal{a}}_2$	$0.9322\mathfrak{t}$
3	${\mathcal{a}}_3$	$0.9522\mathfrak{t}$
4	${\mathcal{a}}_4$	$0.9640\mathfrak{t}$
5	${\mathcal{a}}_5$	$0.9717\mathfrak{t}$
6	${\mathcal{a}}_6$	$0.9772\mathfrak{t}$
7	${\mathcal{a}}_7$	$0.9813\mathfrak{t}$
8	${\mathcal{a}}_7$	$0.9844\mathfrak{t}$
9	${\mathcal{a}}_9$	$0.9869\mathfrak{t}$
10	${\mathcal{a}}_{10}$	$0.9888\mathfrak{t}$
⋮	⋮	⋮
31	${\mathcal{a}}_{31}$	$0.9995\mathfrak{t}$
32	${\mathcal{a}}_{32}$	$0.9996\mathfrak{t}$
33	${\mathcal{a}}_{33}$	$0.9997\mathfrak{t}$
34	${\mathcal{a}}_{34}$	$0.9998\mathfrak{t}$
35	${\mathcal{a}}_{35}$	$\mathfrak{t}$

Upon examination, we conclude that the unique solution is $\mathcal{a}(\mathfrak{t})=\mathfrak{t}$. This finding supports the answer to Equation (17) and is unique. Subsequently, we provide visual evidence of the convergence behavior of all iterations in Figure 2.

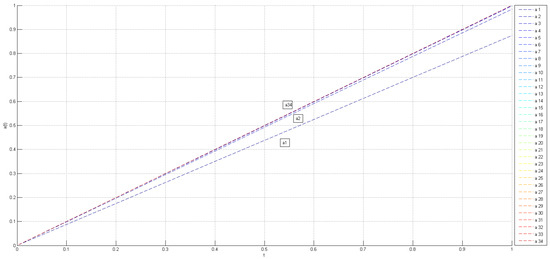
Figure 2. Convergence behavior of iterations.

7. Conclusions

In this article, we examine the existence of coincidence best proximity points for multivalued mappings using the newly developed ${(\varphi -{\mathcal{F}}_{\tau })}_{C_P}$-proximal contraction, and the best proximity points for multivalued mappings through the ${(\varphi -\mathcal{F})}_{B_P}$-proximal contraction approach within a rectangular metric space, employing the alternating distance function $\varphi$. We also introduce contractions for single-valued mappings to establish results on coincidence best proximity points, best proximity points, and fixed points, such as ${({\mathcal{F}}_{\tau })}_{C_P}$ and ${({\mathcal{F}}_{\tau })}_{B_P}$. To enhance adaptability, we provide examples illustrating multivalued and single-valued proximity points and fixed points. Additionally, we apply these results to prove the solution existence for Fredholm integral equations and provide graphical and numerical illustrations showing the convergence behavior of iterations. These findings are valuable for theoretical research in fixed point theory and practical challenges in mechanics and engineering.

Future Direction

Readers may extend this work to Hilbert spaces by employing maximal monotone operators, potentially broadening its applicability within functional analysis.

This work can also be extended by using iterative procedures other than the Picard process to claim a faster convergence.

This work can be generalized into different metric structure settings such as Fuzzy metric spaces, probabilistic metric spaces, etc. These extensions offer opportunities for a deeper exploration of diverse mathematical frameworks.

For application purposes, it would be interesting if the results in this article were utilized to discuss the chaotic dynamics of different models, especially Chua’s attractor model, as discussed in [33].