Abstract
The spatiotemporal dynamics of a three-component model of a food web are considered. The model describes the interactions between populations of resources, prey, and predators that consume both species. It assumes that the predator responds to the spatial change in the resource and prey densities by occupying areas where species density is higher (prey-taxis) and that the prey population avoids areas with a high predator density (predator-taxis). This work studies the conditions for the taxis-driven instability leading to the emergence of stationary patterns resulting from Turing instability and autowaves caused by wave instability. The existence of nonconstant positive steady states for the system is assessed through a rigorous bifurcation analysis. Meanwhile, the conditions for the existence of both types of instabilities are obtained by linear stability analysis. It is shown that the presence of cross-diffusion in the system supports the formation of spatially heterogeneous patterns. For low values of the resource-tactic and predator-tactic coefficients, Turing and wave instabilities coexist. The system undergoes only Turing instability for high levels of these parameters.
Keywords:
food web model; prey- and predator-taxis; nonconstant positive steady states; Turing and wave instability; pattern formation MSC:
37N30; 35B32; 92D25
1. Introduction
An ecological community is a part of an ecosystem containing different species of organisms interacting in space and time. The need to consider the spatial organization of a community along with its trophic structure is recognized in mathematical ecology and has been the subject of analysis in the modeling of ecological systems over the past decades. The interplay between trophic and spatial heterogeneity might induce contrasting effects depending on the internal dynamics of the system [1,2].
Among the mathematical tools for studying spatiotemporal processes in ecosystems are partial differential equations (PDEs). PDE models allow the description of numerous fundamental population processes such as dispersal, ecological invasions, dispersal-mediated coexistence, and emergence of spatial patterns [3]. Skellam’s analogy [4] between the movement of molecules and the random movements of individual members of biological species gave impetus to the use of reaction–diffusion models in theoretical ecology.
Diffusive predator–prey models assume that species move randomly in their habitats. However, in real predator–prey communities, directed movements of predator and prey populations often occurs, which is usually shown by the predator pursuing the prey and the prey escaping from the predator. The spatial behavior of the predator moving toward the gradient direction of the prey distribution is classified as prey-taxis. Predator-taxis means that the prey moves opposite to the gradient of the predator distribution.
Starting with the classical model [5], directed movement of predators has attracted much attention in recent years and has inspired numerous works on population dynamics models of one-predator and one-prey systems with prey-taxis [6,7,8,9]. These studies analyzed the prey-taxis effects on pattern formation when a spatially homogeneous equilibrium loses its stability. In [10], necessary conditions for pattern formation with diverse prey birth rates, predator mortality rates, and functional responses were investigated. The authors found that with an increase in the taxis coefficient, spatial structures disappeared, and the system stabilized. However, the taxis role as a stabilizing factor is unobvious. It is generally accepted that the ability for self-organization of a system is determined by nonlinear trophic functions. However, [11] provided a method for modeling spatial patterns emerging in trophic systems due to the directed movements of the consumer species.
The influence of taxis on system dynamics has also been studied for three-species systems. In [12], a model of a two-predator–one-prey ecosystem with cross-diffusion and a prey defense mechanism was considered. The authors obtained conditions for the emergence of stationary inhomogeneous structures with an increasing taxis coefficient. The work [13] also modeled a system in which two predators consume one prey, and the prey-taxis of both predators can be either positive or negative. Negative taxis was interpreted as a predator’s avoidance of areas where the prey population accumulates because prey can defend themselves as a group (see [14,15]). The authors established that the formation of stationary and periodic structures is possible when the taxis of one predator is positive and that of the other is negative.
The interactions among more than two species are modeled by food chain models. Various types of food chain models consisting of three species are available: one of which is a food chain with omnivory. A special kind of omnivory known as intraguild predation [16] is characterized by predators that feed on one or more of the resources of their own prey. This approach can be applied to model a tritrophic food chain, such as a planktivorous fish that feeds on planktonic food, including phytoplankton and zooplankton, or herbivorous and carnivorous zooplankton [17,18]. A similar model can describe the interaction between phytoplankton, microzooplankton, and mesozooplankton.
This study continues the analysis of the nonspatial model [19] proposed by the author and takes into account the spatial movements of species. The presented model considers relationships between the resource, prey, and a predator that feeds on both species. This model differs from previous ones in that the predator’s functional response depends on the density of one species. The use of a one-prey functional responses allows us to model the various feeding behaviors of predators that can shift from one feeding mode to another. The previous study revealed that the proposed model with self-limitation of the prey or predators and saturated consumption of them can reproduce coexistence between the three species in a resource-rich environment. Additionally, the model considers movement of the predator toward the gradient direction of both species’ distributions and the anti-predator behavior of prey moving away from the direction with a high predator density. Recently, Wu et al. [20] investigated the global existence of and the boundedness in a reaction–diffusion model with predator-taxis and showed that the presence of predator-taxis can induce the disappearance of spatial patterns. Fuest [21] investigated global solutions and convergence near homogeneous steady states in a spatial predator–prey model with predator- and prey-taxis. The spatiotemporal patterns in a predator–prey model including predator- and prey-taxis were studied by Wang et al. [22].
A number of works [13,23,24] studying the effect of taxis on the model dynamics state the stabilizing role of this factor in the case of positive values and the possibility of pattern formation in the case of negative ones. The purpose of this study is to determine the effects of positive prey-taxis and negative predator-taxis on the spatiotemporal dynamics of the system and pattern formation. The reason for the Turing pattern occurrence is the existence of nonconstant positive steady states of a model as a result of diffusion. Stationary structures can also be formed under the influence of taxis pressure. The system’s ability to self-organize into spatial patterns forms a mechanism of species coexistence. Through biodiversity conservation, therefore, the influence of taxis pressure on the existence of nonconstant positive solutions is of interest as the coexistence mechanism.
The remainder of this paper is organized as follows: Section 2 introduces a model of a food chain and its dimensionless form. In Section 3, the linear bifurcation analysis is carried out and the existence of a nonconstant positive equilibrium is investigated. In Section 4, the conditions for Turing and wave instabilities are obtained. Pattern formation is numerically illustrated in Section 5.
2. Model Formulation and Preliminary Analysis
The model consists of three coupled partial differential equations describing the changes to the densities of the resource , prey , and predator at time t and position x:
Here, , and a homogeneous Neumann boundary condition is imposed to describe an enclosed domain; are the diffusion coefficients. The term shows the tendency of prey to move away from the high gradient of predator density with taxis rate , and the term shows the tendency of predators to move towards the direction of resource and prey gradients with rates and , respectively. The nonlinear functions represent the interactions between the predators, prey, and resources as follows:
Here, r is the maximum growth rate of the resource population, K is the resource carrying capacity, and are the predation rates and half-saturation constants of prey and predator; are the assimilation coefficients, and and are the rates of natural mortality and intraspecies predation of prey and predator, respectively. All the parameters are assumed to be positive.
Introducing the dimensionless variables and parameters
and dropping the over-bars, we obtain the nondimensional model as
Here, and
The spatially homogeneous non-negative steady states of System (3) are given by: , , , and , where
and are positive roots of the following equations:
The positive steady state is given by , where
is a positive root of the equation:
and is a positive root of the following equation:
Proposition 1.
We have the following results:
- There exist equilibria and for any parameters.
- There exists equilibrium if .
- There exists equilibrium if .
- There exists equilibrium if and Equation (9) has a positive root such that the following conditions are satisfied:
3. Classical Bifurcation Analysis
The main purpose of this section is to investigate the bifurcation structure of positive solutions to System (3) by regarding as a bifurcation parameter and fixing all other parameters.
3.1. Linear Analysis
Here, are small spatiotemporal perturbations away from , and
The Jacobian matrix evaluated at is:
where and , , , , , , , , .
Since , the solutions for System (12) can be expanded into a Fourier series [25]:
where are the Fourier coefficients, denotes the growth rate of the solution, and k is the wavenumber corresponding to mode number n. Substituting (14) into (12) leads to the following system:
The characteristic equation for the above system can be written as:
where
with , , , and
According to the Routh–Hurwitz criteria, the equilibrium point is stable with respect to spatially homogeneous and nonhomogeneous perturbations if the following conditions hold:
The local stability of the positive equilibrium for the homogeneous model is a necessary condition for Turing and wave instability. Let ; then (16) are satisfied for , and is the stable homogeneous stationary state. Moreover, . The equilibrium loses its stability if one of the two remaining conditions in (16) is violated. If for some , then Equation (15) has one positive real root: this implies that Turing instability occurs, and there exist nonconstant positive steady states for System (3). If for some , then Equation (15) has a pair of complex roots with a positive real part: this means that wave instability occurs.
3.2. Existence of Nonconstant Positive Steady States
In this subsection, the existence of a nonconstant interior equilibrium is considered. In the following, the bifurcation theory of Crandall–Rabinovitz [26] and its application to the bifurcation analysis of elliptic systems developed in [27] are applied to prove the existence of a Turing bifurcation with as the bifurcation parameter. I study a positive nonconstant solution for the following system:
Here, prime denotes differentiation with respect to x. System (17) can be rewritten in the following form:
where
and
Note that , is a continuously differentiable mapping, and for any . The Fréchet derivative of for any is given by
where .
Theorem 1.
Suppose that all parameters in (17) are positive and there exists a positive constant equilibrium . Assume that
Here, can be found in the proof of the theorem.
Proof.
Since , ; then (22) is strictly elliptic, and it satisfies Agmons’s condition according to Remark 2.5 of Case 2 with in [27]. Therefore, (22) is a Fredholm operator with zero index thanks to Theorem 3.3 and Remark 3.4 in [27]. The necessary condition for the existence of bifurcation is that the null space of is nonempty, where . By taking in (20), one has
Its null space consists of solutions for the following system:
Because Problem (24) is linear, we now consider the solution of (24) in the form
where are the Fourier coefficients. Substituting these series into (24) gives rise to
There exists a nontrivial solution of (25) if the coefficient matrix in (25) is singular. For each , this condition holds if there exists positive , where
with
Moreover, we have that , where denotes the null space, and , where
with
Then, in accordance with bifurcation from the simple eigenvalue [26], to prove the theorem, it remains to show the validity of the following transversality condition
Differentiating (23) with respect to , we get
Suppose that condition (28) fails. Then, there exists a nontrivial such that
Let , where . Substituting these series into (29) gives rise to
We observe that the coefficient matrix in (30) with is singular, while the right-hand side is nonzero: then this leads to a contradiction. Consequently, the transversality condition (28) is verified. Then, according to the Crandall–Rabinowitz bifurcation theory [26], there exist nonconstant positive solutions that can be parameterized as
where are constants, is an element in the closed complement of in :
with , and given in (27).
Finally, we require for all positive in order to apply the bifurcation theory from a simple eigenvalue; therefore,
which is equivalent to (21). □
4. Pattern Formation
4.1. Conditions for Turing Instability
In this section, the effect of taxis on pattern formation is studied. According to Theorem 1, positive equilibrium loses its stability through bifurcation as crosses the critical bifurcation value . It is widely known that a reaction–diffusion system with two or more agents with largely different diffusion coefficients can generate spatially heterogeneous patterns. The aim of this study is to investigate the occurrence of stationary patterns as a result of taxis pressure. Therefore, I consider a special case of Model (3) with equal diffusion coefficients for all components: , and resource-tactic sensitivity depends on prey-tactic coefficient . Turing bifurcation occurs when , which is analogous to
Note that (32) is equivalent to (26). Then System (3) undergoes Turing instability when for some . If the denominator in (32) is negative (positive), then is analogous to (). The following theorem provides sufficient conditions for Turing instability.
Theorem 2.
System (3) undergoes Turing instability around the uniform steady-state if one of the following sets of conditions holds:
- and ;
- , , and there exist , such that .
Here, , and , can be found in the proof of the theorem.
Proof.
Note that and . Then for some if or . In this case the equation either possesses no positive roots or has two positive roots: namely, and for all . The coefficients and can be rewritten as:
where
Let us introduce the following notation:
Then if when or when ; if when or when since .
Consider the following limit:
If for some , then there exists such that System (3) undergoes Turing instability when . Let . If there exist and such that , then for all , where
and
If , then , so is not valid. Let , then for all and . □
4.2. Conditions for Wave Instability
In three-component models, not only can Turing bifurcation occur, but wave bifurcation (or finite wavenumber Hopf bifurcation) can also occur. Wave bifurcation breaks spatial and temporal symmetries, and the system generates patterns that are oscillatory in space and time. This bifurcation occurs when , which is analogous to
where , , . Condition (33) is equivalent to
where
Then System (3) undergoes wave instability when for some . If the denominator in (34) is negative (positive), then is analogous to (). The following theorem provides sufficient conditions for wave instability.
Theorem 3.
System (3) undergoes wave instability around the uniform steady-state if one of the following sets of conditions holds:
- and ;
- , , and there exist and such that .
Here, , and can be found in the proof of the theorem.
Proof.
The proof is similar to that of Theorem 2. Since and , then for some if or . The coefficients and can be written as:
Let us introduce the following notation:
Then if when or when ; if when or when since .
Consider the following limit:
If for some , then there exists such that System (3) undergoes wave instability when . Let . If there exist and such that , then for all , where
and
If , then , so is not valid. Let ; then for all and . □
5. Numerical Simulations
5.1. Numerical Scheme
I simulated System (4) using the method of lines with an -point spatial grid for a domain , i.e., , , and . For spatial discretization, the second-order central difference is used for the diffusive terms:
where , , and the first-order upwind scheme is used for the taxis terms:
where if and if ; , , . The result of spatial discretization is the autonomous semi-discrete system:
The splitting method [28,29] is used for solving this system. The function is split as , where function contains the taxis term, and contains the diffusion and reaction terms. In the time integration, the taxis term is treated explicitly, and the remaining terms are treated linearly implicitly by approximate matrix factorization and operator splitting. Then, given an approximation at time and a step size , we compute
Here and are approximate evolution operators of and , respectively. Specifically, approximates the solution of the initial-value problem . As a result, we obtain . For approximation of , the Runge–Kutta fourth-order method is used. Then, approximates the solution of the initial-value problem . The right-hand side of the ODE can be written as , where contains the terms arising from the discretization of diffusion terms, and contains the reaction terms. A linearly implicit variant of the trapezoidal splitting method was used for approximation of :
Here, , are first-order approximations of the Jacobians and of and , respectively. The solution to Problem (36) is obtained by again using the operator : . The approximation (36) is consistent with order two (see [28]).
5.2. Spatiotemporal Patterns
Now, I investigate the effect of prey- and predator-taxis on the formation of stationary and oscillatory patterns. In the simulations to be presented below, I have taken the following parameters: , , , , , , . For the given set of parameter values, the equilibrium point for the spatially homogeneous model is stable. The initial condition is always the steady-state with small perturbations: , , where are small-amplitude random perturbations at one percent from the steady-state .
In accordance with Theorem 2, we get the following conditions for Turing instability:
or
In accordance with Theorem 3, we get the conditions for wave instability as
Figure 1 shows stability/instability domains with . When , the system undergoes wave instability (domain ) for small . Turing bifurcation occurs if (domain ). When , the system undergoes Turing instability for almost all . The right panel in Figure 1 shows the wave bifurcation curves for ; instability occurs below these curves. Both instabilities are possible when .
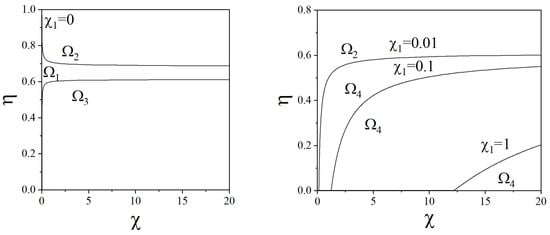
Figure 1.
Stability/instability domains: —stability area, —Turing instability, —wave instability, and —Turing and wave instabilities.
Figure 2 demonstrates the system dynamics for and and three variants of . When , the system undergoes wave instability. The top panel in the figure shows that after a long period of spatially homogeneous oscillations, a standing wave regime is established. With an increase in , both instabilities are possible. The system generates standing waves (middle panel) and a stationary structure (bottom panel) when and , respectively.
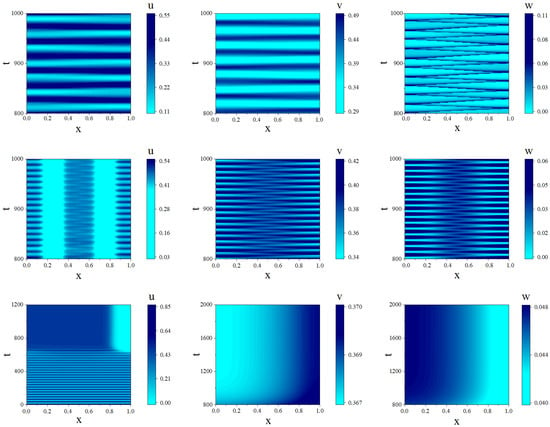
Figure 2.
Stationary and oscillatory patterns for and . Top panel: ; middle panel: ; bottom panel: .
Figure 3 shows the spatial patterns for ; in this case, Turing and wave bifurcations are possible. For and , after a certain incubation period, stationary patterns emerge. When , only Turing bifurcation occurs. Figure 4 demonstrates the system dynamics for and . For (), the system generates a spatiotemporal pattern oscillating in space and time (top panel). This behavior indicates that nonlinear effects arising from the interaction between the Turing and wave modes cause the pure Turing mode to lose its stability before the wave bifurcation occurs. With an increase in , the spatial structures achieve equilibrium (bottom panel).
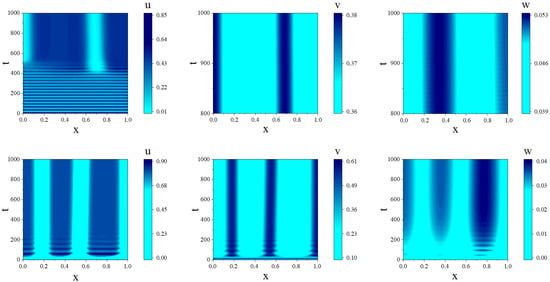
Figure 3.
Stationary and oscillatory patterns for , . Top panel: ; bottom panel: .
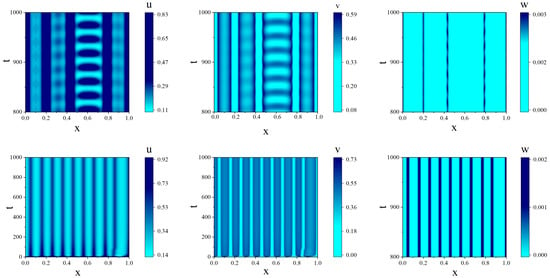
Figure 4.
System dynamics for , . Top panel: ; bottom panel: .
The initial condition for all the simulations discussed above is the stable spatially homogeneous equilibrium with small perturbations. Now, consider the system dynamics when taking an unstable spatially homogeneous equilibrium as the initial state. In the simulations to be presented below, I have taken the same set of parameter values as in the previous ones; the only exceptions are and . For the given set of parameter values, the equilibrium point for the spatially homogeneous model is unstable. Oscillatory dynamics of the system without diffusion and taxis are presented in Figure 5a. As diffusion and taxis are incorporated into the system, the system behavior changes as follows. When only prey-taxis is considered, we observe a solution that is oscillatory in time and homogeneous in space (Figure 5b). When predator-taxis is considered, stationary structures are formed. Figure 6 demonstrates the solution to System (3) for and three variants of prey-taxis coefficients.
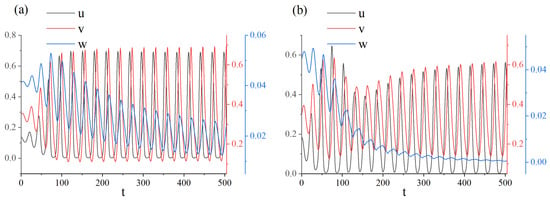
Figure 5.
Spatially homogeneous solutions to System (3) with an unstable spatially homogeneous equilibrium as the initial state: (a) , ; (b) , , .
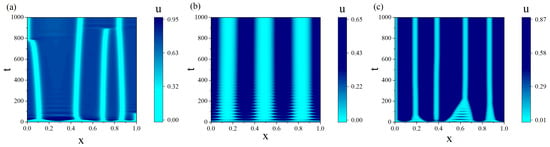
Figure 6.
Spatially nonhomogeneous solutions to System (3) with an unstable spatially homogeneous equilibrium as the initial state with : (a) ; (b) , ; (c) , .
6. Discussion and Conclusions
This paper presents a model of a three-trophic food chain with an omnivorous predator and with consideration of spatial heterogeneity. The model considers the movements of the predator to be directed towards the areas with high densities of the resource and the prey, and the prey moves opposite to the gradient of the predator distribution. The proposed model provides a way to represent the dynamics of a community in which the predator can use different foraging strategies. This model, which takes into account the movement of the predator towards the gradient direction of both species’ distributions, displays qualitatively different behavior of the system as the taxis coefficients change. Moreover, the model allows the assessment of the cumulative effect of prey-taxis and anti-predator mechanisms on the community dynamics.
A linear analysis of the system stability under small spatially inhomogeneous disturbances is carried out. The existence of a nonconstant positive equilibrium as a result of Turing bifurcation is proved. Sufficient conditions for Turing and wave instabilities are obtained. It is shown that the system can lose stability with a high level of prey-taxis. Analysis of the taxis coefficients’ effects on the system dynamics reveals the following properties of the system.
If only the prey-taxis is considered, then either Turing or wave instability may occur depending on the resource-tactic rate. When the predator-taxis is taken into account, stationary structures are formed when the resource-tactic coefficient is high. If this parameter is less than the prey-tactic coefficient, then Turing patterns and wave modes may exist.
Numerical simulations reveal that an increase in leads to a regime shift in which oscillations in the population abundances change to equilibrium spatially heterogeneous structures. A further increase in at a fixed does not lead to a change in the stationary structures. As increases, the dynamics of the system achieve equilibrium, but the structures change along with changes to the resource-tactic coefficient. The real parts of the eigenvalues plotted in Figure 7 show that with increasing , the range of wavenumbers for unstable modes and growth rates of these modes also increase. An increase in leads only to growth of for the most unstable mode, and the range of unstable wavenumbers practically does not change. From a biological point of view, as increases, the predator switches its preference to the resource, and the fear-driven behavioral avoidance of predators forces prey competing for the resource and predator-free-area species to converge on a narrower suite of resource that is associated with low predation risk [30]. An increase in the predator-taxis sensitivity leads to an increase in the growth rates of the most unstable modes, resulting in a decrease in the incubation time for the structures to emerge, while the spatial distribution pattern remains virtually unchanged.
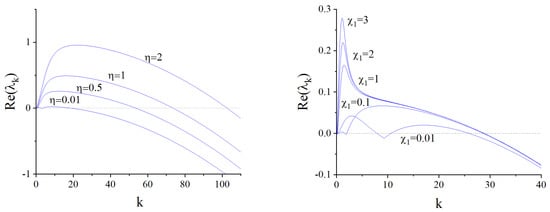
Figure 7.
The real parts of the eigenvalues for Equation (15) as a function of k.
In real communities, such spatial heterogeneity can be caused by various reasons, both physical and biological. The heterogeneity of planktonic communities is initiated by turbulent advection [31] or the behavior of zooplankton in response to the presence of toxic phytoplankton [32]. The propagation of spatial waves caused by taxis is observed in bacterial populations responding to changes in the gradient of an attractant or repellent [33]. Wave solutions are demonstrated by models of the invasion of species [34] or infections [35].
The numerical simulations demonstrate a variety of system dynamics, including the formation of stable and unstable stationary and oscillatory patterns. When the parameters are selected from the Turing instability area and are close to the wave instability line, the purely stationary Turing structures become modulated (Figure 4). Similar system behavior was established in [36]. The stability of Turing structures depends on whether subcritical or supercritical bifurcation occurs; the determination of the nature of bifurcation requires a weakly nonlinear analysis. This analysis can also determine the type of wave—namely, a traveling or standing wave—that arises when a homogeneous steady state goes through that bifurcation (see [37] and references therein). Such nonlinear analysis is beyond the scope of this work, which has focused exclusively on studying the existence of a nonconstant steady state to the system and the patterns appearing at the onset of Turing and wave instability, but it will form the subject of future work by the present author.
As a final comment, I would like to note one more property of the presented model. A system’s ability to form patterns is considered one of the mechanisms that allows species to coexist. The anti-predator behavior of prey promotes the formation of stationary structures. The effects of refuges used by prey increase the equilibrium density of the prey population. However, the presented model demonstrates a decline in the prey population with an increase in predator-tactic sensitivity when resource-tactic sensitivity is low. This decline may be caused by the fact that prey aggregated in refuge habitats may strongly compete for limited resources [30]. With an increase in the resource-tactic coefficient, the prey population begins to grow, and the predator, whose diet consists mainly of the resource, begins to decline catastrophically. Nevertheless, the system stabilizes, and all species in the community survive.
Funding
This work was carried out within the framework of the state targets of the Institute of Automation and Control Processes of the Far Eastern Branch of the Russian Academy of Sciences.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declare no conflicts of interest.
References
- Nathan, R.; Getz, W.M.; Revilla, E.; Holyoak, M.; Kadmon, R.; Saltz, D.; Smouse, P.E. A movement ecology paradigm for unifying organismal movement research. Proc. Natl. Acad. Sci. USA 2008, 105, 19052–19059. [Google Scholar] [CrossRef] [PubMed]
- Quévreux, P.; Pigeault, R.; Loreau, M. Predator avoidance and foraging for food shape synchrony and response to perturbations in trophic metacommunities. J. Theor. Biol. 2021, 528, 110836. [Google Scholar] [CrossRef] [PubMed]
- Holmes, E.E.; Lewis, M.A.; Banks, J.E.; Veit, R.R. Partial Differential Equations in Ecology: Spatial Interactions and Population Dynamics. Ecology 1994, 75, 17–29. [Google Scholar] [CrossRef]
- Skellam, J.G. Random Dispersal in Theoretical Populations. Biometrika 1951, 38, 196–218. [Google Scholar] [CrossRef] [PubMed]
- Kareiva, P.; Odell, G. Swarms of predators exhibit “preytaxis” if individual predators use area restricted search. Am. Nat. 1987, 130, 233–270. [Google Scholar] [CrossRef]
- Berezovskaya, F.S.; Karev, G.P. Bifurcations of travelling waves in population taxis models. Phys. Uspekhi 1999, 42, 917–929. [Google Scholar] [CrossRef]
- Turchin, P. Quantitative Analysis of Movement: Measuring and Modeling Population Redistribution in Animals and Plants; Sinauer Associates: Sunderland, MA, USA, 1998. [Google Scholar]
- Wang, Q.; Song, Y.; Shao, L. Nonconstant positive steady states and pattern formation of 1d prey-taxis systems. J. Nonlinear Sci. 2017, 27, 71–97. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Zhang, G. Global bifurcation of solutions for a predator–prey model with prey-taxis. Math. Methods Appl. Sci. 2015, 38, 431–443. [Google Scholar] [CrossRef]
- Lee, J.M.; Hillen, T.; Lewis, M.A. Pattern formation in prey-taxis systems. J. Biol. Dyn. 2009, 3, 551–573. [Google Scholar] [CrossRef]
- Tyutyunov, Y.V.; Titova, L.I.; Senina, I.N. Prey-taxis destabilizes homogeneous stationary state in spatial Gause–Kolmogorov-type model for predator–prey system. Ecol. Complex. 2017, 31, 170–180. [Google Scholar] [CrossRef]
- Pang, P.Y.H.; Wang, M. Strategy and stationary pattern in a three-species predator–prey model. J. Differ. Equ. 2004, 200, 245–273. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Q.; Yu, F. Stationary and time-periodic patterns of two-predator and one-prey systems with prey-taxis. Discret. Contin. Dyn. Syst. 2017, 37, 505–543. [Google Scholar] [CrossRef]
- Hamilton, W.D. Geometry of the selfish herd. J. Theor. Biol. 1971, 31, 295–311. [Google Scholar] [CrossRef]
- Xiao, D.; Ruan, S. Codimension two bifurcations in a predator–prey system with group defense. Int. J. Bifurc. Chaos 2001, 11, 2123–2131. [Google Scholar] [CrossRef]
- Hsu, S.B.; Ruan, S.; Yang, T.H. Analysis of three species Lotka–Volterra food web models with omnivory. J. Math. Anal. Appl. 2015, 426, 659–687. [Google Scholar] [CrossRef]
- Kumari, S.; Upadhyay, R.K. Dynamics comparison between non-spatial and spatial systems of the plankton–fish interaction model. Nonlinear Dyn. 2020, 99, 2479–2503. [Google Scholar] [CrossRef]
- Mortoja, S.G.; Panja, P.; Mondal, S.K. Stability Analysis of Plankton–Fish Dynamics with Cannibalism Effect and Proportionate Harvesting on Fish. Mathematics 2023, 11, 3011. [Google Scholar] [CrossRef]
- Giricheva, E. Stability and bifurcation analysis of a tri-trophic food chain model with intraguild predation. Int. J. Biomath. 2023, 16, 2250073. [Google Scholar] [CrossRef]
- Wu, C.J.; Chiang, K.P.; Liu, H. Diel feeding pattern and prey selection of mesozooplankton on microplankton community. J. Exp. Mar. Biol. Ecol. 2010, 390, 134–142. [Google Scholar] [CrossRef]
- Fuest, M. Global Solutions near Homogeneous Steady States in a Multidimensional Population Model with Both Predator- and Prey-Taxis. SIAM J. Math. Anal. 2020, 52, 5865–5891. [Google Scholar] [CrossRef]
- Wang, J.F.; Wu, S.N.; Shi, J.P. Pattern formation in diffusive predator-prey systems with predator-taxis and prey-taxis. Discret. Contin. Dyn. Syst. Ser. B 2021, 26, 1273–1289. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. Dynamics and pattern formations in diffusive predator-prey models with two prey-taxis. Math. Methods Appl. Sci. 2019, 42, 4197–4212. [Google Scholar] [CrossRef]
- Han, R.; Röst, G. Stationary and oscillatory patterns of a food chain model with diffusion and predator-taxis. Math. Methods Appl. Sci. 2023, 46, 9652–9675. [Google Scholar] [CrossRef]
- Malchow, H.; Petrovskii, S.V.; Venturino, E. Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, and Simulation; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Crandall, M.G.; Rabinowitz, P.H. Bifurcation from simple eigenvalues. J. Funct. Anal. 1971, 8, 321–340. [Google Scholar] [CrossRef]
- Shi, J.; Wang, X. On global bifurcation for quasilinear elliptic systems on bounded domains. J. Differ. Equ. 2009, 246, 2788–2812. [Google Scholar] [CrossRef]
- Gerisch, A.; Griffiths, D.F.; Weiner, R.; Chaplain, M.A. A positive splitting method for mixed hyperbolic-parabolic systems. Numer. Methods Partial. Differ. Equ. Int. J. 2001, 17, 152–168. [Google Scholar] [CrossRef]
- Hundsdorfer, W.H.; Verwer, J.G.; Hundsdorfer, W.H. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations; Springer: Berlin/Heidelberg, Germany, 2003; Volume 33. [Google Scholar]
- Orrock, J.L.; Preisser, E.L.; Grabowski, J.H.; Trussell, G.C. The cost of safety: Refuges increase the impact of predation risk in aquatic systems. Ecology 2013, 94, 573–579. [Google Scholar] [CrossRef]
- Abraham, E.R. The generation of plankton patchiness by turbulent stirring. Nature 1998, 391, 577–580. [Google Scholar] [CrossRef]
- Semplice, M.; Venturino, E. Travelling waves in plankton dynamics. Math. Model. Nat. Phenom. 2013, 8, 64–79. [Google Scholar] [CrossRef]
- Ivanitsky, G.R.; Medvinskii, A.B.; Tsyganov, M.A. From the dynamics of population autowaves generated by living cells to neuroinformatics. Phys. Uspekhi 1994, 37, 961–989. [Google Scholar] [CrossRef]
- Morozov, A.; Petrovskii, S.; Li, B.L. Spatiotemporal complexity of patchy invasion in a predator-prey system with the Allee effect. J. Theor. Biol. 2006, 238, 18–35. [Google Scholar] [CrossRef] [PubMed]
- Bate, A.M.; Hilker, F.M. Preytaxis and travelling waves in an eco-epidemiological model. Bull. Math. Biol. 2019, 81, 995–1030. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.A. Pattern formation arising from interactions between Turing and wave instabilities. J. Chem. Phys. 2002, 117, 7259–7265. [Google Scholar] [CrossRef]
- Kaminaga, A.; Vanag, V.K.; Epstein, I.R. A reaction–diffusion memory device. Angew. Chem. 2006, 45, 3087–3089. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).