Abstract
The Salp Swarm Algorithm (SSA) is a bio-inspired metaheuristic optimization technique that mimics the collective behavior of Salp chains hunting for food in the ocean. While it demonstrates competitive performance on benchmark problems, the SSA faces challenges with slow convergence and getting trapped in local optima like many population-based algorithms. To address these limitations, this study proposes the locally weighted Salp Swarm Algorithm (LWSSA), which combines two mechanisms into the standard SSA framework. First, a locally weighted approach is introduced and integrated into the SSA to guide the search toward locally promising regions. This heuristic iteratively probes high-quality solutions in the neighborhood and refines the current position. Second, a mutation operator generates new positions for Salp followers to increase randomness throughout the search. In order to assess its effectiveness, the proposed approach was evaluated against the state-of-the-art metaheuristics using standard test functions from the IEEE CEC 2021 and IEEE CEC 2017 competitions. The methodology is also applied to a risk assessment of cardiovascular disease (CVD). Seven optimization strategies of the extreme gradient boosting (XGBoost) classifier are evaluated and compared to the proposed LWSSA-XGBoost model. The proposed LWSSA-XGBoost achieves superior prediction performance with 94% F1 score, 94% recall, 93% accuracy, and 93% area under the ROC curve in comparison with state-of-the-art competitors. Overall, the experimental results demonstrate that the LWSSA enhances SSA’s optimization ability and XGBoost predictive power in automated CVD risk assessment.
Keywords:
swarm intelligence; Salp swarm optimizer; global optimization; locally weighted approach; risk assessment; XGBoost classifier MSC:
68T20
1. Introduction
Cardiovascular disease (CVD) remains the leading cause of mortality worldwide, responsible for over 18 million deaths per year according to the World Health Organization [1]. Early identification of at-risk individuals allows for timely lifestyle and pharmaceutical interventions to control modifiable risk factors such as hypertension, diabetes, and smoking. Conventionally, risk is assessed manually using factors like age, sex, family history, blood pressure, cholesterol, and smoking status [2]. However, this approach suffers from limited scalability and predictive ability [3].
Machine learning has emerged as a promising solution to automate CVD risk prediction from electronic health records at a population scale. A variety of supervised algorithms have been explored, including logistic regression, decision trees, support vector machines, naïve Bayes classifiers, and ensemble methods [4]. Among these, ensemble techniques such as random forests and gradient boosting machines have achieved state-of-the-art performance due to their ability to handle complex interactions between risk variables [5]. In particular, extreme gradient boosting (XGBoost) has proven highly effective for medical applications through its efficient implementation of regularized model fitting [6]. Nonetheless, machine learning models remain limited by the improper selection of hyperparameters that determine model complexity, learning, and regularization strategies [7]. Conventional grid searches exhaustively evaluate a fixed set of predefined parameter combinations but scale poorly with dimensions and fail to explore interactions between settings effectively [8]. Random searches offer superior coverage of the search space but evaluate many suboptimal configurations without exploiting promising regions [8]. To address these limitations, metaheuristic techniques have emerged as automated approaches to nonlinear, multimodal hyperparameter optimization problems [9,10,11,12,13]. The class of optimization methods known as metaheuristic algorithms has seen widespread adoption. These methods can be broken down into nine classes, with contributions from fields as varied as biology, physics, sociology, music, chemistry, sports, mathematics, collective behaviors (swarm-based), and hybrid approaches that combine elements from several of these classes [14]. In particular, metaheuristic algorithms are useful for solving high-dimensional, nonlinear, constrained optimization problems that arise in the real world. Metaheuristic algorithms have gained substantial recognition and utilization in diverse fields of research and practical applications. One area where these algorithms have shown promise is in the domain of cardiovascular disease (CVD) risk assessment, a critical healthcare concern worldwide. The use of metaheuristic algorithms in CVD risk assessment presents an opportunity to enhance the accuracy and efficiency of predictive models, enabling healthcare professionals to better identify individuals at high risk of developing cardiovascular diseases. Recent studies have explored the application of metaheuristic algorithms, such as Genetic Algorithms, Particle Swarm Optimization, and Artificial Neural Networks, in developing CVD risk prediction models [15]. These algorithms can effectively process large datasets containing diverse risk factors, biomarkers, and clinical parameters, thereby providing a more comprehensive assessment of an individual’s risk profile [16]. The use of these algorithms helps not only with predicting the risk of CVD but also in identifying the key contributing factors and their complex interactions, which can be instrumental in tailoring personalized prevention and treatment strategies [17]. Recent research has also emphasized the importance of integrating data from various sources, including clinical records, medical imaging, and genomic information. Metaheuristic algorithms can aid in fusing these heterogeneous data sources to build more holistic and accurate CVD risk prediction models [18]. Furthermore, considering the rapid advancements in medical technology and the increasing availability of health-related data, the application of metaheuristic algorithms in CVD risk assessment is expected to evolve. This evolution includes the incorporation of deep learning and hybrid models that combine the strengths of different metaheuristic techniques to enhance prediction accuracy and robustness [19].
Bio-inspired swarm intelligence algorithms take inspiration from social behaviors observed in nature to robustly solve complex optimization tasks. The domain of bio-inspired swarm intelligence research is experiencing burgeoning growth, with an increasing number of scholars amalgamating machine learning techniques with optimization algorithms rooted in swarm intelligence in pursuit of enhancing the efficacy and efficiency of machine learning methods [20]. Annually, a plethora of novel swarm intelligence algorithms are introduced with the primary aim of addressing a myriad of optimization problems, including but not limited to Particle Swarm Optimization (PSO), which Kennedy and Eberhart initially introduced [21], or Genetic Algorithms (GAs) [22], Salp Swarm Algorithm (SSA) [23], Artificial Bee Colonies (ABCs) [24], Ant Colony optimization (ACO) [25], differential evolution (DE) [26], and others. Other types that can be listed here include Black Holes (BHs) [27], Thermal Exchange Optimization (TEO) [28], Chemical Reaction Optimization (CRO) [29], etc., all of which are examples of techniques that are based on physics or chemistry. More sophisticated examples include those based on the social behaviors of a human like Teaching–Learning-Based Optimization (TLBO) [30] and Imperialist Competitive Algorithm (ICA) [31], and music-based examples such as Melody Search [32] and Salp Swarm Algorithm (SSA) [23].
The Salp Swarm Algorithm (SSA) constitutes a notable advancement in the realm of bio-inspired swarm intelligence. Developed from the inspiration drawn from the collective behavior of Salps, a type of marine organism, the SSA has garnered considerable attention within the academic community. This algorithm has demonstrated its prowess in addressing complex optimization problems by employing a population of virtual Salps that emulate the biological characteristics and interactions observed in their natural counterparts. The SSA leverages these principles to guide the search process, facilitating the identification of optimal solutions across a spectrum of domains. The algorithm’s unique features, including its adaptive mechanisms and its capacity to adapt to dynamic environments, render it a compelling subject of investigation and application within various scientific disciplines [10,33,34,35,36]. Nonetheless, the standard SSA faces some limitations that hinder its search abilities. Like many population-based metaheuristics, the SSA can become stuck in local optima and exhibit slow convergence characteristics [37]. This is due in part to the lack of fine-grained neighborhood information incorporated into Salps’ movement updates, which focus exploration more globally without sufficient local refinement [38]. Recent studies have also shown that the SSA’s performance degrades for highly multimodal problems with many local optima due to its tendency to converge prematurely to suboptimal solutions [39]. Additionally, the use of fixed control parameters facilitates exploitation but constrains exploration over time, restricting flexibility when tackling diverse problem landscapes [40]. To address these drawbacks, localized adaptations guiding Salps towards high-quality neighboring solutions have been explored as an effective means of balancing exploration and exploitation abilities [38]. To address these drawbacks, in the past few years, multiple modified forms of the SSA have been developed by researchers with the aim of enhancing its performance, rectifying its shortcomings, and augmenting its capabilities.
This paper presents a novel variant of the Salp Swarm Algorithm (SSA) and applies it to the important real-world application domain of cardiovascular disease risk prediction through automated machine learning. The core innovation of the LWSSA resides in its integration of two distinct mechanisms into the Salp Swarm Algorithm (SSA), thereby mitigating well-known challenges such as slow convergence and susceptibility to local optima. The first mechanism introduces a locally weighted approach that enhances the search process by effectively guiding it towards locally promising regions, thereby facilitating a more efficient exploration of the solution space. The iterative probing and refinement of high-quality solutions in the neighborhood contribute to the algorithm’s enhanced performance. The second mechanism incorporates a mutation operator, injecting randomness into the search process and thus further improving the algorithm’s ability to escape local optima.
Below is a list of the main contributions of this study:
- This research introduces the Locally Weighted Salp Swarm Algorithm (LWSSA), an enhancement of the Salp Swarm Algorithm (SSA), which combines two mechanisms to mitigate issues like slow convergence and local optima.
- The LWSSA introduces a new Local Search (LS) Algorithm known as the “Locally Weighted approach” that guides the search process toward promising local regions, improving search efficiency by iteratively probing and refining high-quality solutions. This local search strategy is employed to refine individual solutions after each iteration of the optimization process.
- The LWSSA incorporates a mutation operator to inject randomness into the search process, enhancing its ability to escape local optima and explore the solution space more effectively.
- This research extends its contributions to practical applications by evaluating the LWSSA-XGBoost model for cardiovascular disease (CVD) risk assessment, showcasing its superior predictive performance.
The rest of the paper is arranged as follows: Section 2 discusses the related work regarding the SSA and its variants. Section 3 provides the essential theory of the original Salp Swarm Algorithm. The new Local Search (LS) Algorithm is explained in Section 4. Section 4 also provides a description of the proposed algorithm (LWSSA) in detail. Section 5 provides the experimental results and analysis of CEC2021 and CEC2017. Section 6 provides the experimental results and analysis results of the CVD dataset and the classification of 16 datasets. The conclusion and future work are outlined in Section 7.
2. Related Work
Algorithms inspired by nature have unique characteristics that have attracted the interest of researchers in many fields, since they may be used for a wide variety of problems. Furthermore, the No Free Lunch Theorem states that there is no silver bullet for optimization problems [41], citing a lack of optimal solutions. Therefore, it is still a challenging task to create novel optimization algorithms suited to the requirements of practical application settings. As a result, there has been a rise in interest in developing new optimization techniques by combining existing, simpler meta-algorithms. Hybridization is gaining popularity because it combines the best features of different algorithms into one, creating new systems with improved efficiency and accuracy. Since its invention in 2017, the Salp Swarm Algorithm (SSA) has been improved iteratively by incorporating many adjustments proposed by researchers. These additions have been carefully selected to strengthen the algorithm’s flexibility and efficiency across a wide range of problem-solving domains by catering to specific optimization issues. According to [42], the conventional Salp Swarm Algorithm’s (SSA) performance was improved by using the DE algorithm’s operators in order to avoid becoming stuck in local optimum solutions and hasten the convergence to the global optimum. The SSAGWO approach was proposed by [34] to adjust the locations of Salp followers using the GWO search strategy. Differential evolution and the SSA are integrated into the proposed study [43] to improve accuracy and convergence rate. El-Shorbagy et al. improved the SSA method to achieve this goal by utilizing a chaotic collection of functions to expand the algorithm’s capacity to search across wide regions for the best solutions [44]. QSSALEO [33] presents a novel hybrid that improves the Salp swarm by combining Local Escape Operator (LEO) and Quadratic Interpolation (QI), where the QI technique enhanced the new algorithm’s capacity to exploit and the precision of the optimal solution. The LEO was employed on the site of QI of the ideal search element at the same time to solve the local optima problem. The TBLSBCL [35] is a novel search technique that aims to show issues of population diversity, imbalanced exploitation and exploration, and premature convergence in the SSA. The hybridization process includes two stages: The first stage is temporary dynamic fundaments used to represent the hierarchy of followers and leaders in the SSA. This approach raises the number of leaders and decreases the number of followers linearly. The leader’s position in the population is also edited using the effective exploitation capabilities of the SSA. The second stage, a competitive learning strategy, is employed to revise the condition of the followers by allowing them to learn from the leading member. Problems with population diversity, unequal exploration and exploitation, and premature convergence are all handled by the one-of-a-kind search strategy known as SSALEO [36]. The SSA has these issues, but SSALEO is able to solve them. The LEO (Local Escape Operator) is the component that contributes to SSALEO by streamlining the search procedure in the Salp Swarm Algorithm and boosting the local search effectiveness of the swarm members. The utilization of the SSA has been widely observed across many applications due to its notable optimization potential. Table 1 presents a comprehensive compilation of various modifications and hybridizations within the field of the SSA. In the majority of instances, the initial Salp Swarm Algorithm (SSA) was suitably enhanced prior to its implementation. However, it was uncommon for the unmodified SSA to be explicitly implemented. The concept of the No Free Lunch (NFL) theorem effectively exemplifies this notion. This serves as an incentive for academics to participate in the endeavor of enhancing the SSA.

Table 1.
SSA modifications and hybridizations.
Following an analysis of the relevant published material, one can reach the conclusion that there is a significant body of work devoted to the Salp Swarm Algorithm. Although the SSA has proven its efficacy in a variety of contexts by outperforming conventional optimizers, it is not immune to the influence of local optima. In response to this issue, numerous distinct iterations of the SSA have been devised. These versions vary the mechanism in order to improve the rate of convergence, strike a balance between exploration and exploitation, and steer clear of locally optimal solutions. Moreover, diversity techniques are used in complex optimization algorithms in order to increase search quality and decrease the impacts of genetic drift, which can result in a loss of diversity in bio-inspired algorithms. This is performed in order to maximize the potential of the algorithms.
In this paper, a technique known as the Locally Weighted Salp Swarm Algorithm (LWSSA) is suggested in order to address these deficiencies. The LWSSA method is different from other works in a number of ways:
- For more accurate fine-tuning of solutions, the Salp Swarm Algorithm (SSA) incorporates the locally weighted approach as a local search tool. The method is able to better solve difficult optimization problems and converge more quickly because of the concentrated exploration.
- The implementation of the mutation scheme within the SSA adds an extra layer of randomness to the Salps, which in turn improves the latter’s capacity for conducting global searches. This helps to diversify the exploration process, which enables the algorithm to break free from local optimal solutions and investigate a wider range of possible solutions.
- The performance of the SSA’s global search is improved thanks to the synergistic effect of the combination of the locally weighted technique and the mutation scheme. The method is made more robust and successful in tackling difficult optimization problems with multiple local optima as a result of the integration of both strategies.
The LWSSA algorithm that was proposed was evaluated using CEC2021 and CEC2017, in addition to a risk assessment of cardiovascular disease and 19 dataset classifications. According to the findings, the LWSSA algorithm appears to be capable of efficiently addressing the issues posed by the SSA. The performance of the suggested method is superior to that of previous SSA variations and optimization strategies in the vast majority of cases.
3. Preliminaries
In this segment, the algorithm pertaining to Salp Swarm optimization, as well as the articulation of the problem statement, are dissected into their constituent elements.
Principles of Salp Swarm Optimization (SSA)
The Salp Swarm Algorithm (SSA) [23] is a nature-inspired optimization algorithm that models the collective behavior of Salps, marine invertebrates known for their swarming patterns. SSA is designed to tackle optimization problems by mimicking the social interactions and cooperation observed in Salp swarms. The algorithm employs mathematical formulations to govern the movement and decision-making processes of virtual Salps within a search space. The basic mathematical representation of the SSA involves the update of each Salp’s position in the solution space based on its current position, the influence of the best solution encountered so far, and the collective influence of the entire swarm. The position update equation is as follows:
and denote the coordinates of the first Salp position and the location of the food source in the jth dimension, respectively. The upper bounds and lower bounds are represented by and , respectively. The two scales and are random in the interval [0, 1]. Parameter is used to achieve constancy in the process of exploitation and exploration, also representing a critical point parameter.
The maximum number of iterations is denoted by , and the present iteration is . Equation (1), mentioned previously, pertains exclusively to the updating of the position of the leading Salp. To determine the position update relative to the follower Salps, Equation (3) is utilized and provided as follows.
is the location of the th follower in the th dimension, is the location of the th −1 follower in the th dimension. Equation (3) depends on Equation (4) (Newton’s law of movement):
is the location of the th follower in the th dimension, variable denotes the time per iteration, is the initial speed, and is calculated as follows:
is the initial speed, and is the final speed. It is vital to note that the leader and follower Salp positions are updated by using Equations (1) and (3). Follower Salps are programmed to mimic the leader’s actions until the maximum number of iterations is reached, while the leader Salp itself is updated depending on the availability of food sources. During the iterations, the exploratory phase of the algorithm gives way to the exploitative phase, which is marked by a downward trend in the parameter . To avoid becoming stuck at local optimums and instead find the best approximation to the global optimum, it is essential to strike a balance between global and local search strategies.
4. Proposed Algorithm
The locally weighted approach (LW) and proposed approach are introduced in this section.
4.1. Locally Weighted Approach ()
The locally weighted approach, also known as local search, is a heuristic algorithm used to find the solution to complex optimization issues. It involves continuously changing the present solution with a neighboring solution in the search space. The number of potential neighbors for a solution is often infinite, so the key to a successful local search is to find an effective way to select the appropriate neighbors. The proposed algorithm, called the local search algorithm (LW), uses this local search strategy to develop the current solution, or Salp, after all iterations of the optimization process. Algorithm 1 outlines the steps for the LW local search method.
Initially, in each iteration t, a population with the size of Npop Salps and a solution will be optimized by the SSA according to the proposed algorithm and become ; after that, this Salp will be improved by the LW to become by using this formula:
where i = 1, 2, … Npop, are two particles chosen randomly from the population (except the current particle ). In addition, is random numbers generated by the magenta method based on Levy distribution [56] by the following equation:
where b and q are drawn from normal distributions as , and is generated by the following equation:
where is the index of stability , also referred to as the Levy index.
4.2. Update Salp Followers’ Position
Due to the benefits that the SSA enjoys, such as its adaptability [57] and ease of implementation [32], which result from its straightforward mathematical formula and usage of fewer parameters than other algorithms [58], the efficiency of the search for the food site is decreased through continuous iterations of updating the leader’s location, which results in a stagnation process. Additionally, in the SSA mathematical model, the line between exploration and exploitation is not clearly defined, and the use of the SSA to improve high-dimensional problems is not clear [40]. The problem of local stagnation has been taken into consideration in this paper; we proposed a modification to the formula for updating followers’ positions in Equation (5) in a Salp chain through a mutation factor as follows:
where is the constant mutation factor set equal to 0.5, is a random value within the interval , and and are two random locations within the population that different from location .
As can be seen, can communicate with and about the whereabouts of others. When there is a large gap between and , the individual receiving the update is more likely to update somewhere in the middle of that range. This sort of conduct is helpful in the exploration process. When the distance between and is small, on the other hand, the individual is more likely to look nearby for possible solutions. This attitude fosters exploitation. When the principle is applied, individuals as a whole are led to the best possible results, and inequality gradually decreases as a result. Instead of depending solely on the efforts of individual actors, communities can more effectively investigate and establish potential locations. Concurrently, a value from the interval [0, 1] is integrated to shift the food supply position and take advantage of the inherent randomness of the initial SSA Equation (1), proactively avoiding the local optimum problem, and permitting the convergence process to be resumed. It is worth noting that the proposed algorithm optimization scenario is fully described in the next section.
| Algorithm 1: The developed Locally Weighted Approach |
| For i = 1: If random < 0.5: Randomly choose two positions and from Calculate for position i by Equation (6) Calculate for position i by Equation (8) Calculate the new position of particle i by Equation (7) End For |
4.3. LWSSA Optimization Scenario
The proposed algorithm, shown in Figure 1, combines local search, the SSA, and mutation to efficiently find optimal solutions and avoid getting stuck in local minima. In the first stage, the population is divided into two groups. The first group includes the first half of the population (leaders) updated using Equation (1), and the second half of the population (followers) updated using the proposed mutation Equation (10). In the second stage, the “local weight” (LW) technique is used to enhance solutions and determine the optimal location for individuals, and it is updated with a probability of 0.5 for all populations. The combination of these techniques aims to quicken the search process and find optimal solutions quickly, while also avoiding local minima. The steps of the proposed technique are outlined in Algorithm 2.
| Algorithm 2: The LWSSA |
| Each search agent’s dimension (D), as well as its upper bound (ub) and lower bound (lb), as well as the evaluation fitness function (Fitness), as well as the maximum number of iterations (T), are input. Optimal individual (Food Location), and optimal cost function (Food Fitness) are the final results. According to Dimensions D, population size N, ub, lb, initial the Salp population. According to the fitness function, select the least costly individual in the population as the Food Fitness. while (stopping condition is not hold) compute w1 by Equation (2) for (all Salp (Salp Location)) if () then Update the location of the Salp leaders by Equation (1) else Update the Location of the followers Salp by Equation (10) if (random < 0.5) Apply (LW) technique as Algorithm (2) Compute the value of the fitness of and reported it as NewFitness if (NewFitness < Food Fitness) then Update the Food Location and Food Fitness end endend |
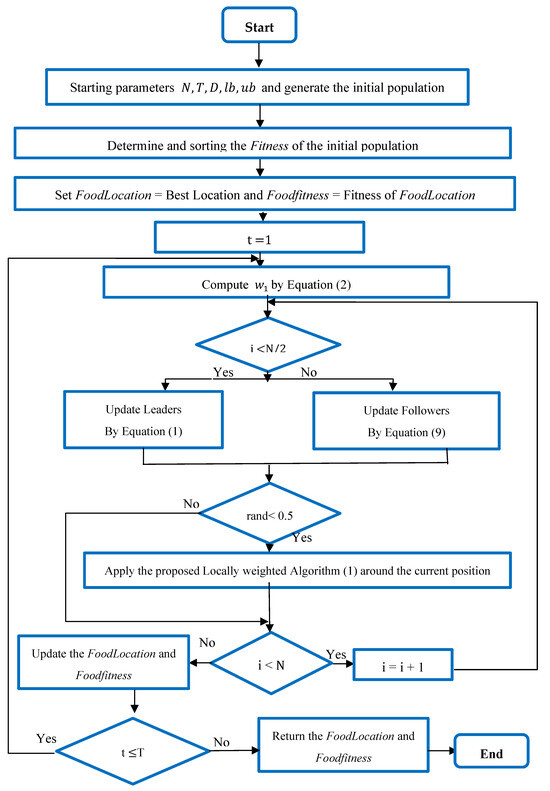
Figure 1.
LWSSA flowchart.
5. Experimental Results and Analysis
To assess the efficacy of the LWSSA, a series of tests were managed using the IEEE CEC 2017 and IEEE CEC 2021 function groups. These tests were designed to evaluate the optimization performance of the LWSSA and were managed under the same operating conditions, with a number of sophisticated algorithms used for comparison. The LWSSA was also applied as a search algorithm to find and localize the values of the optimal hyperparameters for the XGBoost Classifier for risk assessment of cardiovascular disease classification. Further information about the risk assessment of cardiovascular disease problems and their characteristics can be found in a subsequent subsection.
The experiments were conducted on a computer running the Windows operating system using an Inter(R) Intel Core i5-7300U (2.50 GHz) processor and 8 GB of memory. Both the LWSSA and the comparison algorithms were implemented in Python. The IEEE CEC 2021 functions, which include 20 dimensions and evaluate the performance of algorithms on shifted, rotated, and biased functions, and the IEEE CEC 2017 test suite, which includes 50 dimensions, were used to thoroughly examine the performance of the LWSSA. Further details about the IEEE CEC 2017 and IEEE CEC 2021 functions can be found in [59,60], respectively. The results of the experiment were obtained through 30 independent runs, each comprising 2500 iterations, for statistical analysis. When the LWSSA reached the highest number of permitted iterations, the algorithm terminated. To compare the effectiveness of different algorithms, it is common to use statistical measures such as the average solution (Avg), median solution (Med), and standard deviation (Std) in the analysis.
The two non-parametric statistical hypothesis assessments, the Friedman test and the Wilcoxon signed-rank test, were performed to analyze the outcomes of the LWSSA and its competitors. The Wilcoxon signed-rank technique was performed to determine if there was a great difference in the usage of each function by the LWSSA and its rivals and if the LWSSA is better than its competitors. The Friedman test’s final rankings for algorithms on all equations can be used to check for significant divergences in overall performance among the techniques. In this paper, the effectiveness of the LWSSA is compared to seven Salp variant optimization techniques, including ESSA [61], HSSASCA [62], ISSA [63], ISSA-OBL [64], TVSSA [65], SSALEO [36], and SSA-FGWO [34], and eight other recent algorithms: GBO [66], EGBO [67], SMA [68], PSO [69], EO [70], SADE [71], CL-PSO [72], and HPSO_TVAC [72]. The parameters related to the competing algorithms, which were suggested by their respective authors, were adopted and are listed in Table 2 for reference in this paper.

Table 2.
Parameter settings for the competitors.
5.1. Experiment 1: Benchmark Examination for the IEEE CEC 2021
There are a total of 10 various functions included in the IEEE CEC 2021 benchmark suite. The associated technical paper [60] contains in-depth explanations of each and every one of these functions. The extra material includes an illustration that provides a summary of all 10 functions in total. Some of the Salp variants, and GBO, EGBO, SMA, PSO, EO, SADE, CL-PSO, and HPSO_TVAC, are the algorithms that are competing in this examination. All of the participants had their parameters determined, as can be shown in Table 2. The size of the population and number of members for these optimization techniques were both over 30 and 2500, respectively.
5.1.1. Comparison of LWSSA with Some SSA Variants
In this subsection, the effectiveness of the LWSSA in solving mathematical CEC2021 test functions is compared to seven other optimization techniques: ESSA [61], HSSASCA [62], ISSA [63], ISSA-OBL [64], TVSSA [65], SSALEO [36], and SSA-FGWO [34]. The size of the population and number of members for these optimization techniques were both over 30 and 2500, respectively.
The outcomes presented in Appendix A.1 show that the LWSSA performed well in terms of average values for most of the test functions, except for f8. In terms of standard deviation, the LWSSA significantly outperformed the other algorithms in almost all cases. These results suggest that the LWSSA is a reliable, robust, and scalable optimization algorithm that performs well compared to the other algorithms included in the comparison.
The outcomes of the Wilcoxon signed-rank test, with an importance level of 0.05, are outlined in Appendix A.2. These results indicate that the LWSSA outperformed several other algorithms, including ISSA, ISSA_OBL, ESSA, SSALEO, SSA-FGWO, and HSSASCA, on all of the CEC 2021 test functions. In addition, the LWSSA outperformed TVSSA in terms of nine functions. These results suggest that the LWSSA is a strong performer among the algorithms included in the comparison. The Wilcoxon signed-rank test showed that the LWSSA is a highly reliable optimization technique as compared to the seven other algorithms. Figure 2 illustrates the convergence behaviors of the LWSSA and its competitors on the CEC 2021 test functions. It can be seen that the LWSSA significantly outperforms the other algorithms in both initial and final iterations, indicating strong exploration and exploitation capabilities. Additionally, as presented in Figure 2, the LWSSA is able to find the global optimal solution and avoid becoming stuck in local optima thanks to its new local search feature.
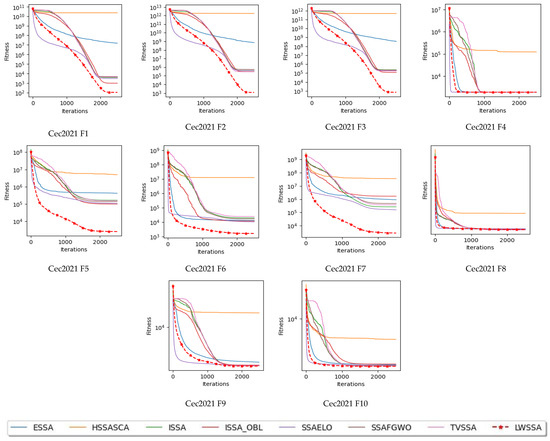
Figure 2.
LWSSA convergence curves vs. some Salps variants during 2500 iterations.
5.1.2. Comparison of LWSSA with State-of-the-Art Competitors
The LWSSA was extensively evaluated using the IEEE CEC 2021 functions and compared to the application of eight other algorithms. The outcomes, displayed in Appendix A.3, indicate that the LWSSA performed well in terms of average values for most of the test functions, except for f8 and f10. In terms of standard deviation, the LWSSA significantly outperformed the other algorithms in almost all cases. Overall, these results suggest that the LWSSA is a reliable, robust, and scalable optimization algorithm that performs well compared to the other algorithms included in the correlation and differences.
The outcomes of the Wilcoxon signed-rank test, with an importance level of 0.05, are outlined in Appendix A.4. These results indicate that the LWSSA outperformed several other algorithms, including EGBO, GBO, HPSO_TVAC, CL-PSO and PSO, on all of the CEC 2021 equations. In addition, the LWSSA outperformed SMA and EO on nine functions and SADE on seven functions. These results suggest that the LWSSA is a strong performer among the algorithms included in the comparison. The Wilcoxon signed-rank test showed that the LWSSA is a highly reliable optimization technique as compared to the eight other algorithms. Figure 3 illustrates the convergence behaviors of the LWSSA and its competitors on the CEC 2021 test functions. It can be seen that the LWSSA significantly outperformed the other algorithms in both initial and final iterations, indicating strong exploration and exploitation capabilities. Additionally, as presented in Figure 3, the LWSSA was able to find the global optimal solution and avoid becoming stuck in local optima thanks to its new local search feature.
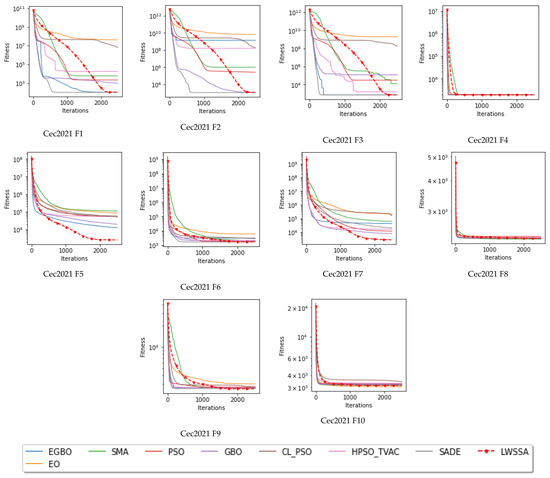
Figure 3.
LWSSA convergence curves vs. some basic and advanced algorithms during 2500 iterations.
5.2. Experiment 2: Benchmark Examination for the IEEE CEC 2017
There are a total of 29 various functions included in the IEEE CEC 2017 benchmark suite. The range [−100, 100] was used to determine the search zone for each variable and function in each dimension. The associated technical paper [59] contains in-depth explanations of each and every one of these functions. The extra material includes an illustration that provides a summary of all 29 functions in total. ESSA, HSSASCA, ISSA OBL, ISSA, SSALEO, TVSSA, and QSSALEO are some of the algorithms that are competing in this examination. All of the participants had their parameters determined, as can be seen in Table 2. The size of the population and the number of members for these optimization techniques were both over 30 and 2500, respectively.
Friedman’s rank test was utilized since there was a strong feeling that the LWSSA algorithm was the best option. In addition, the Wilcoxon signed-rank test with a significance level of 5% was taken into consideration in order to investigate the statistical differences between the results obtained by the LWSSA and those obtained by its rivals. Appendix A.5 contains a report that details the results of the LWSSA’s comparison with those of its competitors. Appendix A.6 contains the p-value that was determined using the Wilcoxon signed-rank test. In Appendix A.7, the symbol “<0.05” indicates whether the LWSSA performed substantially better than its peers, significantly worse, or about the same as its contemporaries.
In comparison to SSALEO and QSSALEO, the newly suggested algorithm LWSSA demonstrated superior performance across all 26 of the evaluations. In addition, the average ranking that is shown in Appendix A.6 shows that the LWSSA received the highest ranking, while the HSSASCA and ISSA-OBL had the lowest ranking. This reveals that all SSA variants enhance the performance of the regular SSA, with the LWSSA boosting it the most. According to Appendix A.7, there is hardly any p-value larger than 0.05, which demonstrates that the differences between the LWSSA and the comparison methods are statistically significant. This can be seen as evidence that the LWSSA is superior to the comparison methods.
5.3. LWSSA Computation Complexity
The computation complexity of the LWSSA was analyzed stage by stage, where the population size is N, the dimension of the given problem is D, and the maximum iteration number is L. The computational complexity under the worst situation of computation time is computed as follows.
In the initialization stage, the LWSSA obtains one phase, one random initialization with the same computational complexity O (N × D) as the original SSA, and the computational complexity of obtaining the optimal solution is O(N), the same as the original SSA. So, in the initialization stage, the computational complexity of the LWSSA is O(N × D + N).
In each iteration stage, first, the position of the agent is renewed according to Equation (1) or Equation (9); therefore, the computational complexity is O(N × D), and then, the location of each agent is further renewed by a LW strategy with O(N) computational complexity. So, in each iteration, the computational complexity of LWSSA is O(N × D + N).
Because of this, the computational complexity of the original LWSSA is O(L × N × D + L × N), which can be condensed to be read as O(L × N × N × (D)).
5.4. Qualitative Analysis
This paper presents a novel optimization strategy called the LWSSA that combines a locally weighted approach with a mutation scheme to overcome the limitations of traditional SSA methods. The LWSSA aims to address issues such as early convergence, uneven exploration and exploitation, and population heterogeneity. The paper investigates the performance of the LWSSA in five functions (Function 1, Function 2, Function 3, Function 8, and Function 9) from the CEC 2017 benchmark (see Figure 4a), specifically focusing on both uni-modal and multimodal functions. These examples were chosen due to their representative nature and significant influence. The qualitative results of the investigation are displayed in Figure 4, which shows the LWSSA’s expected exploration and exploitation phases and its average global best fitness level as it traverses along its first-dimensional trajectory.
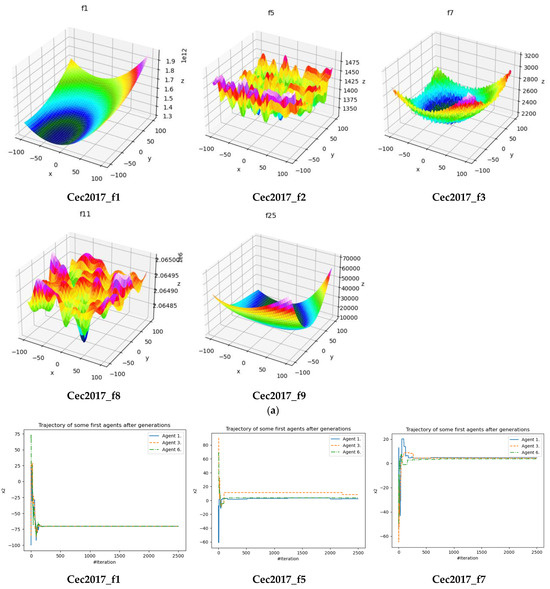
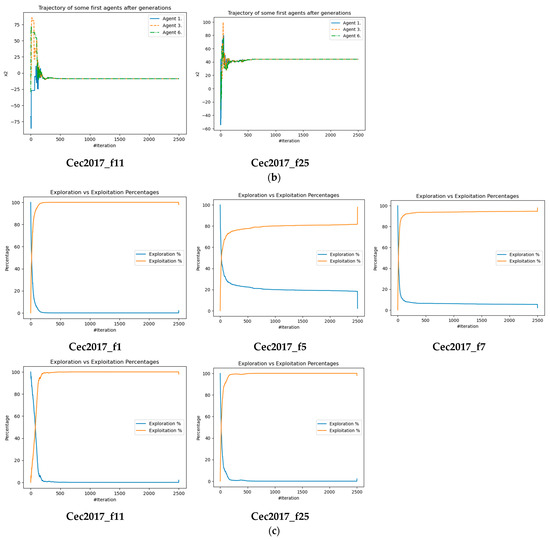
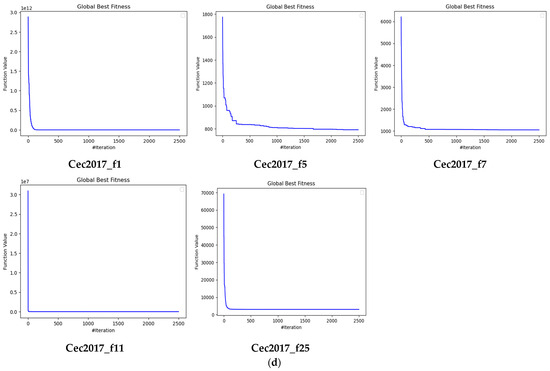
Figure 4.
(a) LWSSA qualitative analysis (Cec2017_functions). (b) LWSSA qualitative analysis (1st-dimensional trajectory). (c) LWSSA qualitative analysis (phase of exploration and exploitation). (d) LWSSA qualitative analysis (global best fitness—average). # denotes to the number of iteration.
Figure 4b also demonstrates the adaptability and resilience of the LWSSA in various contexts, as its trajectory shows rapid oscillation during the exploration phase and moderate oscillation during the exploitation phase, enabling it to efficiently seek out the best solution. The LWSSA’s position amplitude in the first few iterations has the potential to encompass half of the exploration space, and its subsequent adjustments are slower but still effective.
The graphical representation in Figure 4c also highlights the LWSSA’s planned exploitation and exploitation phases, with the initial algorithm having a high exploration ratio but a low exploitation ratio. However, as iterations progress, the focus shifts towards exploitation for most of the chosen functions, and the LWSSA strikes a balance between exploration and exploitation.
Furthermore, Figure 4d shows that the LWSSA’s global fitness has a tendency to fluctuate during iterative approaches, but its average fitness value decreases and oscillation frequency decreases with increasing iterations, allowing it to thoroughly search the entire space and rapidly arrive at a trustworthy conclusion.
In conclusion, this paper presents the LWSSA as a promising optimization strategy that can overcome the limitations of traditional SSA methods, and its performance is demonstrated through the investigation of five functions. The qualitative results presented in Figure 4 provide a comprehensive understanding of the LWSSA’s growth pattern in exploration and exploitation.
5.5. Demonstrated Effectiveness
The Locally-Weighted Salp Search Algorithm (LWSSA) distinguishes itself from existing algorithms through several key innovations in its design and optimization strategies. The notable differences include:
- Population Division and Dynamic Mutation:
- -
- LWSSA approach: The LWSSA employs a unique population division strategy, categorizing individuals into leaders and followers. Leaders are updated using a specific equation, while followers undergo a distinct mutation strategy. This dynamic population management introduces a nuanced exploration–exploitation balance.
- -
- Contrast with existing algorithms: Unlike conventional algorithms with uniform population treatment, the LWSSA’s tailored approach enhances diversity within the population, fostering a more effective search process.
- Local Weight (LW) Technique:
- -
- LWSSA approach: The LWSSA introduces the LW technique, functioning as a form of local search with a 50% update probability for all individuals. This technique strategically enhances solutions and determines optimal locations, providing adaptability and responsiveness to the optimization process.
- -
- Contrast with existing algorithms: Many existing algorithms lack a dedicated local search strategy. The LWSSA’s integration of the LW technique contributes to its ability to navigate the search space dynamically.
- Robustness and Local Minima Avoidance:
- -
- LWSSA approach: The LWSSA demonstrates enhanced robustness, effectively avoiding local minima through its dynamic population strategies and local search capabilities.
- -
- Contrast with existing algorithms: Some existing algorithms may struggle in complex landscapes, leading to premature convergence to local minima. The LWSSA’s adaptability and strategic updates contribute to its robust performance.
- Convergence Speed and Solution Quality:
- -
- LWSSA approach: The LWSSA consistently exhibits superior convergence speed, rapidly approaching optimal solutions. This can be attributed to the innovative combination of population division, mutation, and the LW technique.
- -
- Contrast with existing algorithms: While many algorithms may converge more slowly or struggle to reach high-quality solutions, the LWSSA’s distinctive techniques contribute to its efficiency in reaching optimal outcomes.
- Versatility and Competitive Performance:
- -
- LWSSA approach: The LWSSA competes favorably against state-of-the-art Salps algorithm variants and advanced optimization algorithms, showcasing its versatility and competitiveness across diverse benchmark problems.
- -
- Contrast with existing algorithms: The LWSSA’s performance consistently outpaces existing solutions, substantiating its effectiveness in addressing a wide range of optimization challenges.
In summary, the LWSSA’s differentiation from existing algorithms lies in its dynamic population division, unique mutation strategies, incorporation of the LW technique for local search, enhanced robustness, accelerated convergence speed, and competitive performance across various benchmarks. These distinctive features collectively position the LWSSA as a novel and effective optimization algorithm in the landscape of swarm intelligence and metaheuristic algorithms.
6. Risk Assessment Method for CVD Using LWSSA-XGBoost Model
In this part, we present a novel CVD risk assessment method called LWSSA-XGBoost, which is based on machine learning and swarm intelligence algorithms. The XGBoost model is used in this approach to differentiate between healthy individuals and those with cardiovascular disease. However, imprecise parameterization of the XGBoost model can negatively affect the prediction accuracy. To address this issue, we propose an improved version of the SSA (LWSSA) to ensure a more reliable prediction of cardiovascular disease. The LWSSA integrates the Salp algorithm into the finder position update formula and uses the LW strategy to enhance the searchability of the worst individual. Ultimately, we apply the proposed LWSSA to optimize the parameters of the XGBoost model, resulting in more precise disease prediction outcomes. This can help medical professionals make more informed decisions and decrease the misdiagnosis rate. In this section, this work details the XGBoost classifier and the CVD dataset employed. Following this, to find out the efficiency of the proposed LWSSA in this work, it was compared with some results of swarm intelligence optimization algorithms, including SSA-XGBoost, GWO-XGBoost, ESSA-XGBoost, TVSSA-XGBoost, SSALEO-XGBoost, ISSA-XGBoost, and SSAFGWO- XGBoost. Moreover, the proposed LWSSA is compared with some basic ML classifiers, such as KNN, LR, RF, SVM, and LGB.
6.1. Dataset Description
The CVD dataset, which includes data on combined instances of heart failure, is used here to validate the model that has been developed. The dataset contains 11 features, including age, gender, the type of chest pain experienced, resting blood pressure, and a few others. There are a total of 918 instances, 508 of which are sick while the other 410 are not. Table 3 contains in-depth information regarding the features that are currently available.

Table 3.
Description of the characteristics/attributes of the dataset.
6.2. The XGBoost Method
XGBoost is a type of gradient boosting machine (gbm) that is widely recognized as one of the top-performing algorithms used in supervised learning. It can be employed for both regression and classification tasks. Data scientists often favor XGBoost due to its ability to execute computations at high speeds, even when dealing with large datasets that require out-of-core computation. To use XGBoost, the algorithm operates in the following manner: if a dataset, , contains m features and n examples, the function that we aim to minimize at iteration t, which consists of the loss function and regularization, is expressed as follows:
Suppose that represents the predicted output of an ensemble tree model produced using the following equations:
In Equation (10), denotes the quantity of trees present in the model, while represents the k-th tree. In order to address the aforementioned equation, the optimal set of functions must be determined through the minimization of the loss and regularization objective.
The symbol refers to the loss function, which is determined by the variance between the predicted output () and the actual output (). The symbol is used to gauge the complexity of the model, which is important in preventing overfitting. The complexity is calculated using a specific formula.
The symbol in the equation mentioned earlier indicates the leaf count of the tree, while represents the weight of each leaf. Boosting is utilized during the training of decision tree models to reduce the objective function. This approach involves incorporating a new function (in the form of a tree) into the model as it continues to learn. During the t-th iteration, a new function (tree) is added in the following manner:
6.3. Objective Function and LWSSA-XGBoost Parameter Settings
Creating an optimization issue requires thoughtful study of the objective function as it is being developed. In this investigation, the LWSSA technique that was proposed was used in order to retrieve the most optimal settings for XGBoost. The F1 score was utilized in order to ascertain how beneficial the LWSSA is to one’s fitness, with a higher score being preferred. The parameters that were determined by the method were utilized in subsequent iterations of the LWSSA to produce an improved version of the optimal solution. The XGBoost model parameters that resulted in the greatest average F1 score were the ones that were considered to be the optimal solution. After that, a predetermined test set was used to assess the performance of the final model which had received the highest F1 score. Parameters and settings for the search space are detailed in Table 4.

Table 4.
Search space and hyperparameter settings.
6.4. Methodology
The initial step involves cleansing the CVD dataset of outliers and processing the data. Since the CVD dataset comprises primarily numerical features, only five features—Sex, ChestPainType, RestingECG, ExerciseAngina, and ST_Slope—are categorical and require preprocessing for classification purposes. To convert these categorical features into numerical values, one-hot encoding was utilized. Subsequently, to optimize the performance of XGBoost techniques, a suggested approach was employed to identify the optimal XGBoost hyperparameters. A search process was used with a train and test data split, and the classifier’s parameters were explored by minimizing the F1 score error value “1-F1-score”. The search process was repeated for every combination of parameters, and the parameter set with the lowest fitness value was considered the best combination for XGBoost. The methodology’s approach is demonstrated in Figure 5, and further details about the techniques are discussed in subsequent sections.
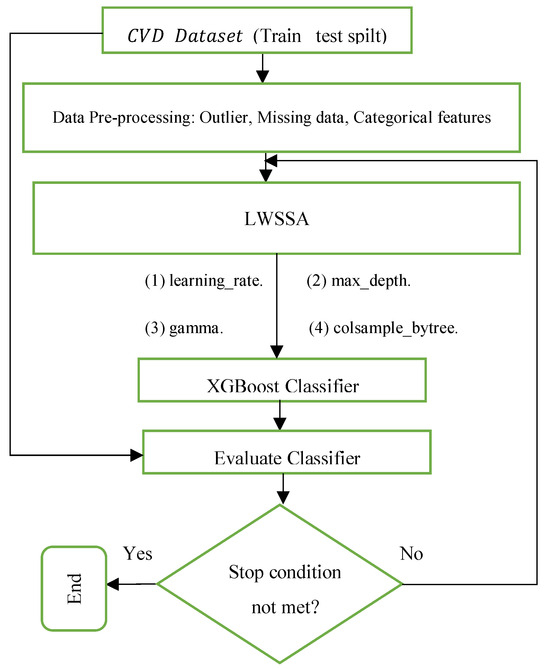
Figure 5.
Suggested methodology.
6.5. Measure of Performance
The following metrics were utilized in order to make a comparison between the proposed algorithm and the following ones: SSA, GWO, WOA, ISSA, ESSA, TVBSSA, SSALEO, and SSA-FGWO.
6.5.1. Classification Evaluation Indicators Based on the Confusion Matrix
To measure the precision of a predictive model, experts typically use a confusion matrix and a Rating Evaluation Index. The proposed method is evaluated in comparison to preexisting algorithms using the following criteria:
Accuracy
The proposed algorithm was put through rigorous testing and analysis based on precise calculations, with accuracy and quality of the solution being key factors. Accuracy was determined by calculating the proportion of correctly predicted samples (for both those with and without cardiovascular diseases) out of the total number of samples analyzed. The accuracy of the calculation was determined using the following formula.
TP represents the number of correctly identified sick people (true positives), FN represents the number of incorrectly identified normal people, TN represents the number of correctly identified normal people (true negatives), and FP represents the number of incorrectly identified sick people (false positives). The model’s ability to predict the presence or absence of CVD is measured by TP and TN.
Precision
The precision is the proportion of individuals correctly identified as having an illness compared to the total number of individuals expected to have the illness. This is calculated using the following formula:
Recall
The recall rate is the percentage of patients with cardiovascular disease who are correctly identified among all patients with the disease. Classifiers that have a higher recall rate will prioritize correctly identifying patients with cardiovascular disease to minimize the chances of misclassifying those with the disease as healthy individuals.
F1 Score
The F1 score percentage is the mean of both precision and recall rates and ranges [0, 1]. The equation used to calculate it is displayed below.
6.5.2. ROC Area and AUC Area
The ROC curve is a plot of the true positive rate (TPR) versus the false positive rate (FPR) calculated from a confusion matrix. The TPR, also known as sensitivity, is the proportion of individuals with cardiovascular disease who are correctly identified as having the disease (TP/(TP + FN)). The FPR is the proportion of individuals without cardiovascular disease who are incorrectly identified as having the disease (FP/(FP + TN)), where TN is the number of true negatives. The AUC value, which represents the area under the ROC curve, is often used as a measure of model performance. AUC ranges from 0.5 to 1, with values closer to 1 indicating better detection efficiency. An AUC of 0.5 suggests that the method is not effective in distinguishing between individuals with and without cardiovascular disease.
6.6. Analysis and Outcomes
In this subsection, the CVD dataset and four evaluation criteria are employed to test the proposed algorithm’s effectiveness in this study. The proposed method’s performance is compared with other methods. Firstly, it is compared against the outcomes of other swarm intelligence optimization algorithms that are designed to improve XGBoost. Secondly, it is compared against various machine learning classifiers.
6.6.1. Comparison with Most Advanced Optimization Techniques
In this section, the effectiveness and efficiency of the proposed LWSSA are examined and compared to other optimization techniques such as SSA, WOA, GWO, ESSA, ISSA, TVBSSA, SSALEO, and SSA-FGWO in terms of optimizing the performance of XGBoost. The efficacy and efficiency of the LWSSA is the focus of this particular investigation. Table 5 contains the findings of the comparisons, with the conclusion that was deemed to be the most advantageous for each comparison being highlighted in bold text. It is worth mentioning that the “Fitness” column in Table 5 represents the cost function (1 − f1_score).

Table 5.
A comparison of the statistical outcomes of the classification test’s accuracy, F1 score, recall, precision, and area under the curve for each optimizer throughout 30 runs on the CVD dataset (on average).
Table 5 compares the best fitness results of various optimization algorithms. The proposed approach, the LWSSA, performed better than the others with the lowest average fitness value of 0.069; this clearly shows that the LWSSA’s optimization effect on XGBoost is particularly noteworthy, and that the LWSSA-XGBoost can search for more parameter values and yield better results than the other competitors. The second-best algorithm was GWO with an average fitness value of 0.072. SSALEO and TVSSA were the third-best algorithms with the same average fitness of 0.073. ISSA and SSA-FGWO were the fourth-best algorithms with the same average fitness value of 0.074. SSA, WOA, and ESSA were in the worst position with average fitness values of 0.075, 0.076, and 0.079, respectively. The convergence of the suggested method is compared to SSA, GWO, WOA, ISSA, ESSA, TVSSA, SSALEO, and SSA-FGWO in Figure 6. This comparison is available, and it is evident that the proposed LWSSA approach can achieve swift convergence for the CVD dataset.
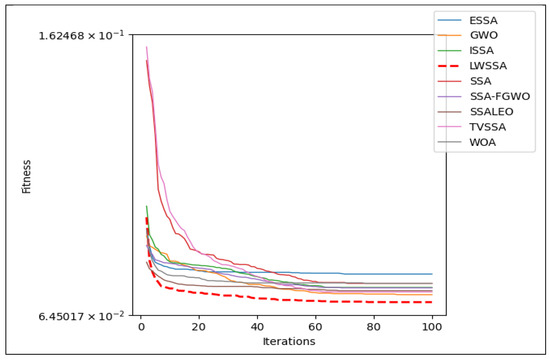
Figure 6.
Convergence curves for LWSSA and other competitors during 100 iterations on CVD dataset.
According to Figure 6, the LWSSA performs significantly better than the other approaches, jumping out of the local optimum and achieving a fitness value. This is due to the LWSSA’s enhanced global search and ability to jump out of the local optimum, making it a promising optimization algorithm.
The optimal prediction model was determined by final parameter selection, and the model with the highest average F1 score was evaluated on a specialized test set. The results are presented in Table 5. It is evident that LWSSA-XGBoost had the highest F1 score in the test set, surpassing other models by 1.0%. These findings demonstrate the effectiveness and strong generalization ability of LWSSA-XGBoost. Therefore, using this model to predict CVD can significantly reduce misdiagnosis rates, which can ultimately prevent, reverse, and reduce the spread of CVD and associated health risks. Additionally, Table 5 also shows the accuracy and AUC (area under the receiver operating characteristic curve) of the LWSSA, and other optimization algorithms based on the XGBoost classifier were compared in a test set as seen in Figure 7. The LWSSA-XGBoost approach achieved the highest accuracy (92.30%), AUC (92.10%), recall (94.0%), and precision (92.2%), outperforming other methods. Figure 8 shows that the LWSSA shows a good performance, and the improved SSA used in the LWSSA-XGBoost model enhances its global search capabilities and achieves better results. The improved model performance can help in the early detection of CVD, reducing the risk of CVD in advance.
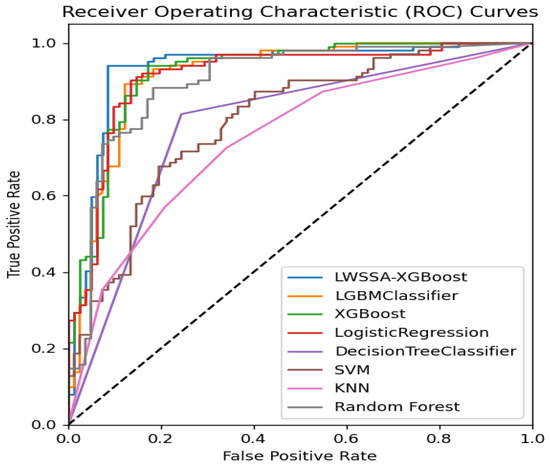
Figure 7.
ROC curves of the LWSSA-XGBoost and other competitors.
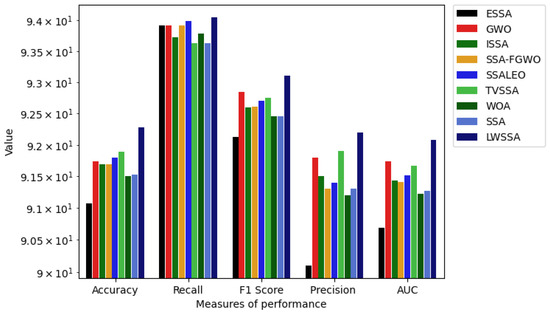
Figure 8.
Measures of performance test accuracy, recall, F1 score, precision, and AUC for LWSSA and other methods.
Average Run Time
When determining whether or not an algorithm is effective, the amount of time it takes to calculate results is an essential parameter. Figure 9 demonstrates how effective the LWSSA is by presenting the average amount of time that it takes for the CPU to compute each of the alternative algorithms that are being considered for use in optimizing the performance of the XGBoost classifier. The experiments were carried out on a computer that featured a 2.50 GHz Inter(R) Intel Core i5-7300U processor, 8 GB of memory, and a Python implementation running on Windows 10. The amount of time required by each algorithm to successfully solve the problem differed according to the model. The LWSSA has the lowest computational time, whereas SSA-FGWO has the longest average CPU calculation time compared to the other algorithms. However, the SSA has the longest average CPU calculation time in comparison to the LWSSA. Because of this, the LWSSA demonstrates highly competitive performance and requires less computational time than the other algorithms. As a result, we are in a position to confidently draw the conclusion that the LWSSA is an algorithm with considerable potential and adequate computational efficiency.
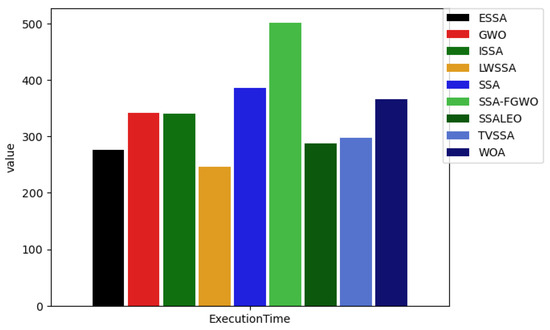
Figure 9.
Average CPU time of different algorithms on CVD dataset.
6.6.2. Comparing to ML Models Currently Used
Prior to evaluating the proposed method, six commonly used classifiers, including RF, LR, KNN, SVM, DT, LGB, and XGBoost with the default parameters for each classifier, were tested on the test set of the CVD dataset. LWSSA-XGBoost was then tested under the same experimental conditions (see Section 6.4), and the prediction results and corresponding indicators were presented in Table 6. As shown in Table 6, LWSSA-XGBoost achieved the best accuracy results among all models. The accuracy rates for RF, LR, KNN, SVM, DT, LGB, and XGBoost were 0.885, 0.695, 0.755, 0.880, 0.717, 0.869, and 0.858, respectively. KNN had the poorest accuracy performance at 0.695. LR and RF had the highest accuracy rates of 0.885 and 0.880 among these basic classification models. LWSSA-XGBoost with the optimal parameters ({‘learning_rate’: 0.46001000000000003, ‘max_depth’: 6, ‘gamma’: 0.2, ‘colsample_bytree’: 0.30000000000000004, ‘reg_alpha’: 6.400000100000001, ‘reg_lambda’: 3.7400001}) achieved an accuracy of 0.929 on the CVD dataset, meaning that 168 out of 180 people were correctly classified. The experiments showed that the LWSSA could optimize the XGBoost model with parameters, thereby enhancing its accuracy. The F1 score is the average of precision and recall. As demonstrated in Table 6, the F1 score obtained by LWSSA-XGBoost was the highest. The F1 scores of RF, LR, KNN, SVM, DT, LGB, and XGBoost were 0.901, 0.725, 0.774, 0.911, 0.735, 0.872, and 0.862, respectively. Among them, KNN and SVM had the poorest F1 score performance, while RF had the highest F1 score. This indicates that XGBoost has certain advantages in predicting CVD compared with other classifiers. Furthermore, after being optimized by the LWSSA proposed in this paper, the F1 score of XGBoost reached 0.936, which was 2.20% to 19.70% higher than the other classifiers, demonstrating the superiority of LWSSA-XGBoost in CVD classification.

Table 6.
Comparison of LWSSA-XGBoost with other classification models.
6.6.3. Evaluation of LWSSA Algorithm with Various Kinds of Datasets
To demonstrate the efficacy of metaheuristic algorithms in optimizing the performance of the XGBoost classifier in large feature spaces, the LWSSA’s efficiency was compared to that of other such algorithms. Sixteen benchmark datasets of various kinds, obtained from UCI’s machine learning repository [73], were used for this purpose, and each dataset is summarized in Table 7. To ensure a fair comparison, all algorithms began with the same population, and their remaining parameters are presented in Table 2. Each algorithm was run 20 times on an Intel Core i3 with 4GB of RAM, using a fixed number of iterations (100) and initial population (30). The parameters and settings for the search space are provided in Table 4, while the methodology and performance measures employed are consistent with those of the preceding section.
This section compares the proposed LWSSA algorithm with other optimization techniques such as the SSA, WOA, GWO, ESSA, ISSA, TVBSSA, and SSALEO for optimizing the performance of XGBoost in terms of effectiveness and efficiency. The main focus of this investigation is to evaluate the efficacy and efficiency of the LWSSA algorithm. The results of the comparisons are presented in Table 8, Table 9 and Table 10, with the most advantageous conclusion for each comparison highlighted in bold text. It should be noted that the “Fitness” column in Table 10 represents the cost function (1 − f1_score).

Table 7.
Dataset characteristics.
Table 7.
Dataset characteristics.
| ID | Dataset Name | No. Classes | No. Attributes | No. of Samples |
|---|---|---|---|---|
| DS1 | Zoo | 7 | 16 | 101 |
| DS2 | Wine | 3 | 13 | 178 |
| DS3 | Heart | 2 | 13 | 270 |
| DS4 | Vehicle | 4 | 18 | 846 |
| DS5 | Breastcancer | 2 | 9 | 699 |
| DS6 | Soybean small | 4 | 35 | 47 |
| DS7 | Spambase | 2 | 57 | 4601 |
| DS8 | Dermatology | 6 | 34 | 366 |
| DS9 | fri_c0_500_10 | 2 | 10 | 500 |
| DS10 | fri_c0_1000_10 | 2 | 10 | 1000 |
| DS11 | fri_c1_1000_10 | 2 | 10 | 1000 |
| DS12 | Pc1 | 2 | 21 | 1109 |
| DS13 | stock | 2 | 9 | 950 |
| DS14 | CLEAN | 2 | 166 | 476 |
| DS15 | Semeion | 10 | 256 | 1593 |
| DS16 | Waveform | 3 | 40 | 5000 |
Test Accuracy and Precision Analysis
In Table 8, we compare the accuracy of classification achieved by LWSSA-XGBoost and other methods across all available datasets. According to the findings, LWSSA-XGBoost performed better than any other method in 14 out of 16 datasets, which is equivalent to 87.5% of all datasets combined. In addition, LWSSA-XGBoost, ESSA-XGBoost, and SSA-XGBoost all managed to achieve accuracy rates of 100% across three different datasets (Zoo, Wine, and Soybean small). The SSALEO-XGBoost algorithm came in second place because it achieved the highest accuracy in 2 of the 16 datasets and obtained 100% accuracy in the Zoo, Wine, and Soybean small datasets. This was the same level of accuracy that was achieved by the GWO-XGBoost algorithm, which came in third place. ISSA-XGBoost came in at position four across all three datasets, achieving results that were comparable to those of GWO-XGBoost while, on the whole, outperforming WOA-XGBoost, TVSSA-XGBoost, and SSA-XGBoost. Even though the remaining methods produced good results, their performance was not as good as the performance of the other methods across all of the matching datasets. Based on these findings, it appears that the approach that was proposed has the potential to achieve superior results when compared to other methods, particularly for both small and large datasets.

Table 8.
Statistical outcome comparison, average test accuracy, and precision values for 20 runs for all methods.
Table 8.
Statistical outcome comparison, average test accuracy, and precision values for 20 runs for all methods.
| ID | GWO-XGBoost | ISSA-XGBoost | ESSA-XGBoost | TVSSA-XGBoost | SSA-XGBoost | WOA-XGBoost | SSALEO-XGBoost | LWSSA-XGBoost | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc. | Preci. | Acc. | Preci. | Acc. | Preci. | Acc. | Preci. | Acc. | Preci. | Acc. | Preci. | Acc. | Preci. | Acc. | Preci. | |
| DS1 | 1.000 | 1.000 | 1.000 | 1.000 | 0.964 | 0.905 | 1.000 | 1.000 | 0.876 | 0.811 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| DS2 | 1.000 | 1.000 | 1.000 | 1.000 | 0.994 | 0.995 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| DS3 | 0.877 | 0.876 | 0.888 | 0.887 | 0.852 | 0.854 | 0.885 | 0.884 | 0.840 | 0.813 | 0.870 | 0.871 | 0.884 | 0.883 | 0.889 | 0.888 |
| DS4 | 0.820 | 0.820 | 0.816 | 0.816 | 0.791 | 0.785 | 0.813 | 0.814 | 0.805 | 0.804 | 0.808 | 0.808 | 0.819 | 0.820 | 0.826 | 0.826 |
| DS5 | 0.970 | 0.963 | 0.971 | 0.964 | 0.965 | 0.959 | 0.971 | 0.964 | 0.968 | 0.962 | 0.969 | 0.962 | 0.972 | 0.965 | 0.971 | 0.964 |
| DS6 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.940 | 0.910 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| DS7 | 0.958 | 0.956 | 0.956 | 0.954 | 0.950 | 0.949 | 0.956 | 0.954 | 0.955 | 0.953 | 0.956 | 0.954 | 0.957 | 0.956 | 0.958 | 0.955 |
| DS8 | 0.987 | 0.987 | 0.991 | 0.990 | 0.989 | 0.989 | 0.984 | 0.983 | 0.973 | 0.971 | 0.986 | 0.985 | 0.994 | 0.993 | 0.989 | 0.989 |
| DS9 | 0.964 | 0.957 | 0.959 | 0.959 | 0.901 | 0.901 | 0.954 | 0.954 | 0.946 | 0.946 | 0.949 | 0.949 | 0.960 | 0.960 | 0.974 | 0.964 |
| DS10 | 0.903 | 0.901 | 0.897 | 0.897 | 0.883 | 0.883 | 0.897 | 0.897 | 0.892 | 0.893 | 0.895 | 0.895 | 0.902 | 0.902 | 0.904 | 0.904 |
| DS11 | 0.957 | 0.955 | 0.954 | 0.953 | 0.945 | 0.944 | 0.954 | 0.953 | 0.950 | 0.949 | 0.954 | 0.952 | 0.959 | 0.958 | 0.961 | 0.959 |
| DS12 | 0.959 | 0.873 | 0.959 | 0.883 | 0.948 | 0.760 | 0.959 | 0.892 | 0.955 | 0.864 | 0.957 | 0.876 | 0.959 | 0.878 | 0.961 | 0.886 |
| DS13 | 0.988 | 0.988 | 0.988 | 0.988 | 0.968 | 0.968 | 0.989 | 0.989 | 0.976 | 0.976 | 0.987 | 0.987 | 0.990 | 0.990 | 0.991 | 0.991 |
| DS14 | 0.969 | 0.970 | 0.969 | 0.970 | 0.965 | 0.967 | 0.969 | 0.970 | 0.967 | 0.968 | 0.967 | 0.967 | 0.969 | 0.970 | 0.970 | 0.970 |
| DS15 | 0.972 | 0.974 | 0.973 | 0.975 | 0.967 | 0.968 | 0.958 | 0.961 | 0.957 | 0.960 | 0.959 | 0.962 | 0.962 | 0.964 | 0.974 | 0.976 |
| DS16 | 0.872 | 0.872 | 0.868 | 0.868 | 0.869 | 0.870 | 0.867 | 0.867 | 0.869 | 0.870 | 0.867 | 0.868 | 0.872 | 0.872 | 0.876 | 0.876 |
Acc. refers to test accuracy, and Preci. indicates precision. Bold denotes to the best results.
Recall, Precision, F1 Score, and AUC Analysis
According to the recall and F1 score measures, LWSSA-XGBoost performed significantly better than the regular SSA-XGBoost in every dataset, as shown in Table 9. The proposed method achieved better results in terms of recall and F1 score measures than contemporary variants of the SSA, such as ESSA-XGBoost, ISSA-XGBoost, and TVBSSA-XGBoost. Because of the hybridization procedure that was applied, the LWSSA-XGBoost that was recommended was successful in achieving a higher recall and F1 score measures. The LW method, which is centered on the best search agent, improves the LWSSA’s capability of exploitation and the correctness of the solution in each iteration, whereas the mutation operator uses random operators to get away from local optima. As a direct consequence of this, the best solution can be enhanced by accomplishing better performance criteria measurements.

Table 9.
Statistical outcomes of comparison, average recall, and F1 score values for 20 runs for all methods.
Table 9.
Statistical outcomes of comparison, average recall, and F1 score values for 20 runs for all methods.
| ID | GWO-XGBoost | ISSA-XGBoost | ESSA-XGBoost | TVSSA-XGBoost | SSA-XGBoost | WOA-XGBoost | SSALEO-XGBoost | LWSSA-XGBoost | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Recall | F1 Score | Recall | F1 Score | Recall | F1 Score | Recall | F1 Score | Recall | F1 Score | Recall | F1 Score | Recall | F1 Score | Recall | F1 Score | |
| DS1 | 1.000 | 1.000 | 1.000 | 1.000 | 0.911 | 0.907 | 1.000 | 1.000 | 0.829 | 0.816 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| DS2 | 1.000 | 1.000 | 1.000 | 1.000 | 0.995 | 0.995 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| DS3 | 0.879 | 0.876 | 0.887 | 0.887 | 0.858 | 0.852 | 0.885 | 0.884 | 0.837 | 0.819 | 0.873 | 0.870 | 0.885 | 0.883 | 0.888 | 0.888 |
| DS4 | 0.821 | 0.819 | 0.817 | 0.816 | 0.793 | 0.784 | 0.814 | 0.812 | 0.806 | 0.804 | 0.809 | 0.807 | 0.820 | 0.819 | 0.827 | 0.826 |
| DS5 | 0.972 | 0.967 | 0.973 | 0.968 | 0.964 | 0.961 | 0.972 | 0.968 | 0.968 | 0.965 | 0.970 | 0.966 | 0.974 | 0.969 | 0.973 | 0.968 |
| DS6 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.925 | 0.914 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| DS7 | 0.954 | 0.955 | 0.953 | 0.954 | 0.946 | 0.948 | 0.954 | 0.954 | 0.952 | 0.952 | 0.953 | 0.953 | 0.955 | 0.955 | 0.955 | 0.956 |
| DS8 | 0.985 | 0.985 | 0.989 | 0.989 | 0.986 | 0.987 | 0.981 | 0.982 | 0.971 | 0.970 | 0.986 | 0.985 | 0.993 | 0.993 | 0.986 | 0.988 |
| DS9 | 0.958 | 0.957 | 0.959 | 0.958 | 0.901 | 0.900 | 0.954 | 0.953 | 0.946 | 0.945 | 0.950 | 0.949 | 0.961 | 0.960 | 0.961 | 0.963 |
| DS10 | 0.901 | 0.900 | 0.897 | 0.897 | 0.883 | 0.883 | 0.897 | 0.897 | 0.892 | 0.892 | 0.895 | 0.895 | 0.902 | 0.902 | 0.907 | 0.903 |
| DS11 | 0.957 | 0.956 | 0.955 | 0.954 | 0.944 | 0.944 | 0.954 | 0.953 | 0.951 | 0.950 | 0.953 | 0.953 | 0.960 | 0.959 | 0.961 | 0.960 |
| DS12 | 0.772 | 0.813 | 0.765 | 0.810 | 0.644 | 0.676 | 0.757 | 0.806 | 0.736 | 0.782 | 0.754 | 0.799 | 0.763 | 0.807 | 0.776 | 0.820 |
| DS13 | 0.988 | 0.988 | 0.988 | 0.988 | 0.968 | 0.968 | 0.989 | 0.989 | 0.976 | 0.976 | 0.987 | 0.987 | 0.990 | 0.990 | 0.991 | 0.991 |
| DS14 | 0.967 | 0.968 | 0.968 | 0.969 | 0.963 | 0.964 | 0.967 | 0.968 | 0.965 | 0.967 | 0.965 | 0.966 | 0.968 | 0.969 | 0.968 | 0.969 |
| DS15 | 0.972 | 0.972 | 0.973 | 0.973 | 0.967 | 0.967 | 0.959 | 0.959 | 0.957 | 0.957 | 0.960 | 0.960 | 0.962 | 0.962 | 0.974 | 0.975 |
| DS16 | 0.872 | 0.871 | 0.868 | 0.868 | 0.869 | 0.868 | 0.867 | 0.867 | 0.870 | 0.869 | 0.867 | 0.867 | 0.872 | 0.872 | 0.877 | 0.876 |
Bold denotes to the best results.
In a similar vein, the LWSSA-XGBoost fitness values improved as a result of the adjustments and the gained search balance. Table 10 compares the average fitness values and AUC of all competing methods, indicating that LWSSA-XGBoost exceeded all other techniques. Furthermore, these findings indicate the LWSSA-XGBoost algorithm’s robustness and repeatability across multiple datasets.

Table 10.
Statistical outcomes of comparison, average fitness, and AUC values for 20 runs for all methods.
Table 10.
Statistical outcomes of comparison, average fitness, and AUC values for 20 runs for all methods.
| ID | GWO-XGBoost | ISSA-XGBoost | ESSA-XGBoost | TVSSA-XGBoost | SSA-XGBoost | WOA-XGBoost | SSALEO-XGBoost | LWSSA-XGBoost | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fitness | AUC. | Fitness | AUC. | Fitness | AUC. | Fitness | AUC. | Fitness | AUC. | Fitness | AUC. | Fitness | AUC. | Fitness | AUC. | |
| DS1 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0933 | 0.999 | 0.0000 | 0.998 | 0.1842 | 0.898 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0000 | 1.000 |
| DS2 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0051 | 0.999 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0000 | 1.000 |
| DS3 | 0.1240 | 0.879 | 0.1134 | 0.887 | 0.1484 | 0.858 | 0.1160 | 0.885 | 0.1807 | 0.837 | 0.1304 | 0.873 | 0.1167 | 0.885 | 0.1125 | 0.888 |
| DS4 | 0.1809 | 0.936 | 0.1841 | 0.938 | 0.2165 | 0.927 | 0.1876 | 0.936 | 0.1958 | 0.935 | 0.1932 | 0.934 | 0.1814 | 0.938 | 0.1745 | 0.938 |
| DS5 | 0.0329 | 0.972 | 0.0318 | 0.973 | 0.0386 | 0.964 | 0.0322 | 0.972 | 0.0350 | 0.968 | 0.0341 | 0.970 | 0.0310 | 0.974 | 0.0318 | 0.973 |
| DS6 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0857 | 0.950 | 0.0000 | 1.000 | 0.0000 | 1.000 | 0.0000 | 1.000 |
| DS7 | 0.0444 | 0.955 | 0.0463 | 0.953 | 0.0523 | 0.946 | 0.0460 | 0.954 | 0.0476 | 0.952 | 0.0465 | 0.953 | 0.0446 | 0.955 | 0.0452 | 0.954 |
| DS8 | 0.0145 | 0.998 | 0.0107 | 0.998 | 0.0131 | 0.997 | 0.0184 | 0.998 | 0.0297 | 0.997 | 0.0152 | 0.998 | 0.0069 | 0.998 | 0.0123 | 0.998 |
| DS9 | 0.0430 | 0.958 | 0.0415 | 0.959 | 0.0995 | 0.901 | 0.0465 | 0.954 | 0.0545 | 0.946 | 0.0510 | 0.950 | 0.0400 | 0.961 | 0.0365 | 0.964 |
| DS10 | 0.0995 | 0.901 | 0.1033 | 0.897 | 0.1173 | 0.883 | 0.1030 | 0.897 | 0.1078 | 0.892 | 0.1048 | 0.895 | 0.0978 | 0.902 | 0.0968 | 0.903 |
| DS11 | 0.0439 | 0.957 | 0.0464 | 0.955 | 0.0562 | 0.944 | 0.0467 | 0.954 | 0.0505 | 0.951 | 0.0472 | 0.953 | 0.0414 | 0.960 | 0.0401 | 0.961 |
| DS12 | 0.1873 | 0.772 | 0.1899 | 0.765 | 0.3240 | 0.644 | 0.1944 | 0.757 | 0.2179 | 0.736 | 0.2006 | 0.754 | 0.1928 | 0.763 | 0.1803 | 0.776 |
| DS13 | 0.0121 | 0.988 | 0.0119 | 0.988 | 0.0321 | 0.968 | 0.0113 | 0.989 | 0.0242 | 0.976 | 0.0134 | 0.987 | 0.0097 | 0.990 | 0.0087 | 0.991 |
| DS14 | 0.0318 | 0.967 | 0.0313 | 0.968 | 0.0356 | 0.963 | 0.0318 | 0.967 | 0.0334 | 0.965 | 0.0340 | 0.965 | 0.0313 | 0.968 | 0.0308 | 0.968 |
| DS15 | 0.0276 | 0.998 | 0.0269 | 0.997 | 0.0332 | 0.997 | 0.0412 | 0.996 | 0.0428 | 0.997 | 0.0403 | 0.996 | 0.0377 | 0.997 | 0.0255 | 0.998 |
| DS16 | 0.1286 | 0.973 | 0.1319 | 0.970 | 0.1318 | 0.973 | 0.1333 | 0.974 | 0.1308 | 0.973 | 0.1329 | 0.972 | 0.1284 | 0.974 | 0.1237 | 0.974 |
AUC—Area Under Curve. Bold denotes to the best results.
After taking into account all of the preliminary results, it is clear that the LWSSA-XGBoost is a strong candidate in the effort to improve the performance of the XGBoost classifier on a variety of datasets. In addition, the LWSSA-exploitation XGBoost ability and solution accuracy were both improved by the mutation operator agent, while the exploration of the method was improved by the local search operator LW agent. Because of these enhancements, the LWSSA was better able to deliver high-quality solutions in comparison to other optimization algorithms. This can be seen in the increased average classification accuracy, fitness function values, area under the curve (AUC), precision, and F1 score. Based on these findings, it appears that the LWSSA may be a workable strategy for tackling problems that occur in the real world.
7. Problematic Constraints and Difficulties
While the LWSSA did outperform several competing algorithms in our hand-picked tests, it is not without its flaws. Here are some of our thoughts on the most important constraints that we believe the algorithm imposes:
- Computational Overhead: Because of the increased complexity of the optimization process, the locally weighted technique and the mutation strategy could result in the introduction of additional computing overhead. This could result in a greater amount of processing time compared to some of the simpler forms of the Salp Swarm Algorithm, depending on the size of the problem and the number of iterations.
- Parameter Tuning: The success of the strategy that has been suggested is strongly dependent on the accurate tuning of parameters linked to the locally weighted strategy and the mutation scheme. Finding the ideal values for the parameters may need additional work and trial and error, particularly when dealing with a variety of distinct optimization situations.
- Sensitivity to Problem Characteristics: In the same way that the performance of any algorithm can be affected by the specifics of the optimization problems it is applied to, the performance of the suggested approach could be susceptible to those features. It is very useful in some circumstances, but its usefulness may vary depending on the nature of the problem and the structure it has.
- Comparative Performance: Comprehensive comparative studies are required so that an in-depth evaluation may be carried out to determine whether or not the proposed method is preferable to the various other Salp Swarm versions. This requires testing the algorithm on a wide variety of benchmark issues and contrasting its results with those of previously developed variants of the Salp Swarm Algorithm as well as other cutting-edge optimization strategies.
In order to provide a full evaluation of the suggested method and its potential contributions to the field of optimization, addressing these constraints with respect to other variants of Salp Swarm that are similar will be of great assistance.
8. Conclusions and Future Work
This study aims to introduce an improved version of the Salp Search Algorithm called the LWSSA, which is designed to optimize XGBoost parameters. The LWSSA optimization approach is achieved through two modifications. Firstly, the mutation operator in the SSA is used to develop the searching ability of half of the individuals, which enhances convergence potential and accuracy. Secondly, the LWSSA technique utilizes a novel locally weighted technique (LW) to overcome the problem of sticking at local optima and improve overall performance. To evaluate its performance and compare it to other well-established metaheuristics, the proposed technique was tested on the latest Competitions on Evolutionary Computation (CEC) benchmark functions, including CEC 2021 and CEC 2017. Additionally, the LWSSA algorithm was applied to optimize the performance of the XGBoost classifier in the risk assessment of cardiovascular disease and classification of 16 datasets.
The final results demonstrate that the LWSSA-XGBoost model was highly effective in predicting cardiovascular disease risk. This research is valuable for predicting the risk of developing cardiovascular disease (CVD) and has the potential to guide individuals and encourage high-risk groups to modify their lifestyle behaviors, thus reducing the risk of CVD. Additionally, it can help clinicians identify potential risks and patterns, enabling them to identify high-risk groups more and reduce misdiagnosis rates. However, there are some limitations and opportunities for future research. For instance, healthcare big data can take on various structural forms—including structured, semi-structured, and unstructured data—which may be used for assessing the risk of CVD. However, the approach presented in this paper has only been validated on datasets that may contain a single type of data structure. Additionally, the study focuses on XGBoost as the primary model and demonstrates that the LWSSA effectively optimizes its parameters. It is unclear if the LWSSA can similarly optimize parameters for other classifiers. Future work for the Locally-Weighted Salp Search Algorithm (LWSSA) involves exploring its applicability in diverse domains beyond cardiovascular risk assessment. The algorithm’s unique features, including dynamic population division, a local weight technique, and a tailored mutation strategy, position it as a versatile optimization tool. Future research endeavors could focus on evaluating the LWSSA in areas such as financial modeling, supply chain optimization, and energy management, where adaptive and efficient solutions are crucial. Additionally, a thorough comparative analysis against state-of-the-art algorithms in these diverse application areas would provide valuable insights into the LWSSA’s relative efficacy. Collaborative efforts across disciplines could enhance the LWSSA’s adaptability, opening avenues for innovative problem-solving methodologies and fostering interdisciplinary research initiatives. This future work aims to advance the field of optimization algorithms and contribute to the algorithm’s broader utility across various domains.
Author Contributions
Conceptualization, M.Q. and N.K.H.; methodology, M.Q., M.A.A. and S.I.M.; software, M.A.A., M.Q. and M.A.; validation, M.A., M.Q. and N.K.H.; formal analysis, M.A.; investigation, S.I.M., O.H. and M.A.; resources, M.A. and O.H.; data curation, O.H., M.A.A., S.I.M., M.A. and M.Q.; writing—original draft preparation, N.K.H. and O.H.; writing—review and editing, M.Q., S.I.M., O.H., M.A.A., M.A. and N.K.H.; visualization, M.Q., S.I.M., M.A., M.A.A. and N.K.H.; supervision, M.Q., S.I.M., M.A. and N.K.H.; project administration, M.Q. and N.K.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia, project number 445-9-777.
Data Availability Statement
We have made the code for this research project available on GitHub at https://github.com/MohammedQaraad/LWSSA-algorithm (accessed on 5 January 2024). Readers interested in accessing the code can download it from this repository.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia, for funding this research work through project number 445-9-777.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Comparison of the LWSSA with Some Improved SSA Algorithms during 2500 Iterations (cec2021)
| F1 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F2 | Avg | ||||||||
| Std | |||||||||
| Med | 1.345 | 1.100 | |||||||
| F3 | Avg | 2.151 | 1.692 | 7.002 | |||||
| Std | 1.499 | 2.206 | 9.574 | 1.844 | 2.304 | 2.379 | 6.716 | ||
| Med | 2.647 | 4.791 | 1.418 | 8.691 | 1.444 | 1.104 | 6.491 | 7.002 | |
| F4 | Avg | 1.909 | 1.233 | 1.904 | 1.912 | 1.904 | 1.904 | 1.904 | 1.904 |
| Std | 4.635 | 1.719 | 1.296 | 3.376 | 1.308 | 1.516 | 1.254 | ||
| Med | 1.907 | 3.900 | 1.904 | 1.911 | 1.904 | 1.904 | 1.904 | 1.904 | |
| F5 | Avg | 4.169 | 5.002 | 1.640 | 9.883 | 1.062 | 1.350 | 1.548 | 2.555 |
| Std | 4.740 | 5.063 | 9.887 | 7.492 | 6.638 | 9.461 | 8.765 | 5.437 | |
| Med | 3.010 | 3.666 | 1.507 | 7.715 | 9.471 | 1.042 | 1.379 | 2.456 | |
| F6 | Avg | 1.346 | 1.287 | 2.017 | 1.208 | 1.060 | 1.741 | 2.514 | 1.686 |
| Std | 9.198 | 2.874 | 1.716 | 5.195 | 7.099 | 1.343 | 1.530 | 1.576 | |
| Med | 1.032 | 8.938 | 1.546 | 1.013 | 8.698 | 1.365 | 2.420 | 1.606 | |
| F7 | Avg | 9.040 | 3.593 | 2.653 | 1.688 | 1.561 | 4.767 | 3.723 | 2.796 |
| Std | 9.564 | 6.567 | 1.418 | 6.874 | 6.675 | 4.554 | 3.031 | 3.971 | |
| Med | 5.997 | 1.035 | 2.114 | 1.717 | 1.435 | 3.859 | 2.905 | 2.712 | |
| F8 | Avg | 2.326 | 2.717 | 2.315 | 2.333 | 2.337 | 2.313 | 2.315 | 2.321 |
| Std | 4.287 | 6.736 | 1.636 | 1.752 | 1.540 | 1.653 | 1.705 | 1.423 | |
| Med | 2.326 | 2.576 | 2.303 | 2.338 | 2.338 | 2.300 | 2.303 | 2.328 | |
| F9 | Avg | 2.944 | 1.631 | 2.606 | 2.662 | 2.621 | 2.600 | 2.622 | 2.567 |
| Std | 1.498 | 3.795 | 3.427 | 1.276 | 5.598 | 4.968 | 6.926 | 4.795 | |
| Med | 2.948 | 1.678 | 2.600 | 2.600 | 2.600 | 2.600 | 2.600 | 2.600 | |
| F10 | Avg | 3.265 | 6.061 | 3.162 | 3.307 | 3.215 | 3.170 | 3.156 | 3.132 |
| Std | 8.030 | 1.312 | 3.603 | 1.440 | 7.049 | 4.920 | 3.858 | 1.452 | |
| Med | 3.258 | 5.942 | 3.157 | 3.273 | 3.221 | 3.158 | 3.142 | 3.123 | |
| 5.879 | 7.938 | 3.886 | 4.886 | 3.779 | 3.983 | 3.852 | 1.797 | ||
| 7.000 | 8.000 | 4.000 | 6.000 | 2.000 | 5.000 | 3.000 | 1.000 | ||
| Bold denotes to the best results. | |||||||||
Appendix A.2. Wilcoxon Rank-Sum of the LWSSA vs. Some Improved SSA Algorithms on CEC2021
| Fun | |||||||
| 1 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 2 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 3 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 4 | <0.05 | <0.05 | <0.05 | <0.05 | 0.15475248 | 0.61326587 | 0.3629539 |
| 5 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 6 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 7 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 8 | 0.91948423 | <0.05 | 0.22811625 | <0.05 | <0.05 | 0.05478402 | 0.23417446 |
| 9 | <0.05 | <0.05 | 0.74987697 | <0.05 | 0.52880743 | 0.83371254 | 0.63527561 |
| 10 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
Appendix A.3. Comparison between LWSSA and Some State-of-the-Art Algorithms during 2500 Iterations (cec2021)
| GBO | EGBO | SMA | PSO | EO | SADE | CLPSO | HPSO_TVAC | LWSSA | ||
| F1 | Avg | 9.217 | 1.499 | 7.679 | 2.137 | 4.280 | 1.000 | 6.292 | 1.754 | 1.000 |
| Std | 1.415 | 2.704 | 3.384 | 2.187 | 1.346 | 0.000 | 2.358 | 6.309 | 4.336 | |
| Med | 4.134 | 1.000 | 8.933 | 1.453 | 4.233 | 1.000 | 7.389 | 2.327 | 1.000 | |
| F2 | Avg | 1.122 | 1.398 | 9.045 | 2.590 | 6.700 | 1.100 | 2.040 | 1.575 | 1.100 |
| Std | 6.650 | 7.657 | 7.804 | 3.880 | 1.369 | 0.000 | 5.861 | 8.617 | 6.938 | |
| Med | 1.101 | 1.100 | 6.705 | 1.351 | 2.509 | 1.100 | 9.251 | 1.646 | 1.100 | |
| F3 | Avg | 1.183 | 1.183 | 9.370 | 2.991 | 1.897 | 7.000 | 1.753 | 1.554 | 7.000 |
| Std | 6.442 | 6.442 | 1.662 | 1.418 | 2.781 | 0.000 | 3.641 | 3.196 | 9.569 | |
| Med | 7.000 | 7.000 | 1.305 | 7.000 | 5.883 | 7.000 | 7.717 | 7.000 | 7.002 | |
| F4 | Avg | 1.907 | 1.908 | 1.905 | 1.905 | 1.907 | 1.905 | 1.913 | 1.926 | 1.904 |
| Std | 3.669 | 5.142 | 1.525 | 1.161 | 1.179 | 7.251 | 3.100 | 1.612 | 1.042 | |
| Med | 1.906 | 1.907 | 1.903 | 1.903 | 1.903 | 1.905 | 1.906 | 1.922 | 1.904 | |
| F5 | Avg | 1.946 | 1.280 | 1.073 | 5.173 | 8.561 | 5.156 | 5.718 | 5.280 | 2.638 |
| Std | 1.119 | 1.259 | 4.806 | 2.961 | 4.972 | 2.661 | 2.007 | 2.411 | 6.982 | |
| Med | 1.944 | 7.881 | 1.053 | 4.306 | 6.680 | 4.570 | 5.562 | 4.808 | 2.548 | |
| F6 | Avg | 2.115 | 3.107 | 2.309 | 1.788 | 6.070 | 1.672 | 2.920 | 2.163 | 1.634 |
| Std | 5.474 | 3.569 | 8.531 | 2.248 | 2.584 | 1.763 | 1.306 | 7.765 | 9.759 | |
| Med | 2.013 | 2.341 | 2.006 | 1.677 | 5.359 | 1.604 | 2.649 | 2.000 | 1.604 | |
| F7 | Avg | 7.997 | 4.270 | 5.924 | 1.203 | 2.166 | 2.068 | 1.580 | 1.678 | 2.838 |
| Std | 5.292 | 9.986 | 2.737 | 6.035 | 6.129 | 1.239 | 7.703 | 8.566 | 7.969 | |
| Med | 7.122 | 8.697 | 5.601 | 1.063 | 6.654 | 1.719 | 1.648 | 1.326 | 2.611 | |
| F8 | Avg | 2.332 | 2.337 | 2.303 | 2.362 | 2.320 | 2.318 | 2.328 | 2.339 | 2.319 |
| Std | 8.092 | 4.241 | 6.499 | 5.505 | 1.135 | 1.442 | 2.165 | 8.417 | 1.403 | |
| Med | 2.334 | 2.336 | 2.300 | 2.342 | 2.324 | 2.328 | 2.328 | 2.338 | 2.327 | |
| F9 | Avg | 2.642 | 2.622 | 2.614 | 2.715 | 3.014 | 2.605 | 2.739 | 2.647 | 2.530 |
| Std | 1.117 | 8.419 | 4.880 | 3.634 | 5.436 | 3.009 | 3.289 | 1.382 | 4.661 | |
| Med | 2.600 | 2.600 | 2.601 | 2.600 | 2.738 | 2.600 | 2.602 | 2.600 | 2.500 | |
| F10 | Avg | 3.216 | 3.208 | 3.160 | 3.278 | 3.035 | 3.164 | 3.423 | 3.298 | 3.132 |
| Std | 6.647 | 8.238 | 4.418 | 1.597 | 7.140 | 4.642 | 9.664 | 1.214 | 1.581 | |
| Med | 3.213 | 3.183 | 3.149 | 3.232 | 3.017 | 3.158 | 3.443 | 3.281 | 3.123 | |
| 4.690 | 4.366 | 5.845 | 4.988 | 6.541 | 3.359 | 6.807 | 6.162 | 2.243 | ||
| 4.000 | 3.000 | 6.000 | 5.000 | 8.000 | 2.000 | 9.000 | 7.000 | 1.000 | ||
| Bold denotes to the best results. | ||||||||||
Appendix A.4. Wilcoxon Rank-Sum of the LWSSA vs. Some State-of-the-Art Algorithms during 2500 Iterations
| Fun | GBO | EGBO | SMA | PSO | EO | SADE | CLPSO | HPSO_TVAC |
| 1 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | 1 | <0.05 | <0.05 |
| 2 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | 1 | <0.05 | <0.05 |
| 3 | <0.05 | 0.821595 | <0.05 | 0.651998 | <0.05 | 1 | <0.05 | <0.05 |
| 4 | <0.05 | <0.05 | 0.266174 | <0.05 | 0.5809 | <0.05 | <0.05 | <0.05 |
| 5 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 6 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | 0.240346 | <0.05 | <0.05 |
| 7 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 8 | <0.05 | <0.05 | <0.05 | <0.05 | 0.931838 | 0.432254 | 0.301061 | <0.05 |
| 9 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 10 | <0.05 | <0.05 | 0.228116 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
Appendix A.5. Results from 2500 Iterations of the LWSSA vs. Some Salp Variants on IEEE CEC2017
| F | Cr. | ESSA | HSSASCA | ISSA_OBL | ISSA | SSALEO | TVSSA | QSSALEO | LWSSA |
| F1 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F2 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| AF3 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F4 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F5 | Avg | ||||||||
| Std | 7.28669 | ||||||||
| Med | |||||||||
| F6 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F7 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F8 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F9 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F10 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F11 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F12 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F13 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F14 | Avg | 2.76966 × 103 | |||||||
| Std | |||||||||
| Med | |||||||||
| F15 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F16 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F17 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F18 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F19 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F20 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F21 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F22 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F23 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F24 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F25 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F26 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F27 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F28 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| F29 | Avg | ||||||||
| Std | |||||||||
| Med | |||||||||
| Bold denotes to the best results. | |||||||||
Appendix A.6. Wilcoxon Rank-Sum of the LWSSA vs. Salp Variant Algorithms on CEC2017
| Fun | ESSA | HSSASCA | ISSA_OBL | ISSA | SSALEO | TVSSA | QSSALEO |
| 1 | <0.05 | <0.05 | <0.05 | <0.05 | 0.907149516 | <0.05 | 0.379592005 |
| 2 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 3 | <0.05 | <0.05 | <0.05 | 0.93183835 | 0.450706377 | <0.05 | 0.539032803 |
| 4 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 5 | 0.624228823 | <0.05 | 0.065354024 | <0.05 | <0.05 | <0.05 | 0.058827192 |
| 6 | <0.05 | <0.05 | <0.05 | 0.703198218 | 0.894837154 | 0.323393973 | <0.05 |
| 7 | <0.05 | <0.05 | 0.785508454 | 0.858063401 | 0.141670776 | <0.05 | 0.591599389 |
| 8 | 0.323393973 | <0.05 | 0.956592944 | <0.05 | <0.05 | 0.821595142 | <0.05 |
| 9 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 10 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 11 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 12 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 13 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 14 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 15 | <0.05 | <0.05 | <0.05 | 0.749876972 | <0.05 | 0.388084142 | <0.05 |
| 16 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 17 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 18 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 19 | 0.845869569 | <0.05 | 0.646404177 | 0.104139005 | 0.129455778 | <0.05 | 0.129455778 |
| 20 | <0.05 | <0.05 | 0.070028526 | <0.05 | <0.05 | <0.05 | 0.178564788 |
| 21 | <0.05 | <0.05 | <0.05 | 0.222170531 | <0.05 | 0.346779952 | <0.05 |
| 22 | 0.870291194 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | 0.371215114 |
| 23 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
| 24 | <0.05 | <0.05 | <0.05 | 0.498735035 | <0.05 | 0.054784023 | <0.05 |
| 25 | 0.591599389 | <0.05 | <0.05 | <0.05 | 0.286756545 | 0.121777891 | 0.423194286 |
| 26 | <0.05 | <0.05 | <0.05 | 0.22811625 | <0.05 | 0.968987463 | <0.05 |
| 27 | <0.05 | <0.05 | <0.05 | <0.05 | 0.293850289 | <0.05 | 0.060939894 |
| 28 | 0.272918441 | <0.05 | <0.05 | 0.15475248 | <0.05 | <0.05 | <0.05 |
| 29 | 0.749876972 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 | <0.05 |
Appendix A.7. Friedman Test Result of the LWSSA vs. Salp Variant Algorithms on CEC2017
| Fun | ESSA | HSSASCA | ISSA_OBL | ISSA | SSALEO | TVSSA | QSSALEO | LWSSA |
| 1 | 6.9655 | 8.0000 | 6.0345 | 3.4483 | 2.3448 | 3.8966 | 2.8276 | 2.4828 |
| 2 | 6.6207 | 8.0000 | 4.2759 | 5.1034 | 1.0000 | 6.0000 | 2.8966 | 2.1034 |
| 3 | 6.7586 | 8.0000 | 6.0690 | 2.7931 | 3.0690 | 3.5172 | 3.0345 | 2.7586 |
| 4 | 2.8621 | 8.0000 | 4.6207 | 2.7931 | 3.5862 | 3.4483 | 5.0345 | 5.6552 |
| 5 | 4.8621 | 8.0000 | 6.2069 | 2.6552 | 2.7931 | 2.8966 | 3.8276 | 4.7586 |
| 6 | 4.3103 | 7.9655 | 7.0345 | 2.6552 | 2.7241 | 2.8966 | 5.6897 | 2.7241 |
| 7 | 3.4138 | 8.0000 | 4.6552 | 4.4483 | 3.6897 | 2.7241 | 4.4483 | 4.6207 |
| 8 | 5.5862 | 8.0000 | 4.8621 | 3.7241 | 1.5172 | 4.8276 | 2.7586 | 4.7241 |
| 9 | 3.7586 | 8.0000 | 5.3448 | 3.7931 | 3.5517 | 4.1034 | 5.1724 | 2.2759 |
| 10 | 6.8966 | 8.0000 | 6.0690 | 4.3103 | 2.5862 | 3.9310 | 2.5172 | 1.6897 |
| 11 | 4.8966 | 8.0000 | 6.1034 | 4.9310 | 2.8621 | 4.9655 | 3.2414 | 1.0000 |
| 12 | 7.0000 | 8.0000 | 2.1034 | 4.8621 | 4.0000 | 4.9310 | 4.1034 | 1.0000 |
| 13 | 7.4483 | 7.5517 | 5.1379 | 4.3103 | 3.0690 | 4.3103 | 3.1724 | 1.0000 |
| 14 | 7.0000 | 8.0000 | 2.0345 | 5.1724 | 3.6207 | 5.1724 | 4.0000 | 1.0000 |
| 15 | 4.5172 | 8.0000 | 5.8276 | 3.0345 | 4.5172 | 3.0345 | 4.5862 | 2.4828 |
| 16 | 3.7241 | 8.0000 | 4.1379 | 4.5172 | 4.2414 | 4.7241 | 4.2759 | 2.3793 |
| 17 | 6.8621 | 7.9310 | 5.7241 | 4.2759 | 2.9655 | 4.0345 | 3.2069 | 1.0000 |
| 18 | 3.6897 | 8.0000 | 2.2069 | 6.0345 | 4.7586 | 6.0345 | 4.2759 | 1.0000 |
| 19 | 3.6897 | 7.8621 | 4.0345 | 4.4138 | 3.4483 | 4.9655 | 3.6207 | 3.9655 |
| 20 | 3.4828 | 8.0000 | 5.8621 | 1.8966 | 4.2414 | 2.4828 | 4.5862 | 5.4483 |
| 21 | 4.2414 | 8.0000 | 6.1379 | 3.2759 | 3.8621 | 3.5517 | 4.2759 | 2.6552 |
| 22 | 3.9655 | 7.9310 | 6.6897 | 1.6897 | 5.4138 | 1.9655 | 4.2414 | 4.1034 |
| 23 | 5.5862 | 8.0000 | 6.6207 | 2.1724 | 5.4483 | 1.5517 | 3.0690 | 3.5517 |
| 24 | 6.4828 | 8.0000 | 6.5172 | 2.3103 | 3.5862 | 3.0000 | 3.8276 | 2.2759 |
| 25 | 3.8276 | 8.0000 | 6.4483 | 2.9655 | 3.4828 | 3.5517 | 3.6552 | 4.0690 |
| 26 | 4.1724 | 8.0000 | 6.6552 | 1.7586 | 5.7586 | 2.3793 | 4.7241 | 2.5517 |
| 27 | 6.2069 | 8.0000 | 6.7931 | 3.3793 | 2.6552 | 3.3448 | 3.0690 | 2.5517 |
| 28 | 2.2069 | 8.0000 | 6.0000 | 2.8276 | 5.5345 | 3.7586 | 5.5345 | 2.1379 |
| 29 | 1.4828 | 8.0000 | 5.9310 | 5.2759 | 4.1207 | 5.5517 | 4.1207 | 1.5172 |
| Avg. | 4.9144 | 7.9738 | 5.3841 | 3.6147 | 3.6017 | 3.8466 | 3.9239 | 2.7408 |
| Rank | 6.0000 | 8.0000 | 7.0000 | 3.0000 | 2.0000 | 4.0000 | 5.0000 | 1.0000 |
| Bold denotes to the best results. | ||||||||
References
- Cardiovascular Diseases (CVDs). Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 10 November 2023).
- D’Agostino, R.B.; Vasan, R.S.; Pencina, M.J.; Wolf, P.A.; Cobain, M.; Massaro, J.M.; Kannel, W.B. General Cardiovascular Risk Profile for Use in Primary Care: The Framingham Heart Study. Circulation 2008, 117, 743–753. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Jones, D.M. Cardiovascular Risk Prediction. Circulation 2010, 121, 1768–1777. [Google Scholar] [CrossRef] [PubMed]
- Ward, A.; Sarraju, A.; Chung, S.; Li, J.; Harrington, R.; Heidenreich, P.; Palaniappan, L.; Scheinker, D.; Rodriguez, F. Machine Learning and Atherosclerotic Cardiovascular Disease Risk Prediction in a Multi-Ethnic Population. npj Digit. Med. 2020, 3, 125. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. Undefined Xgboost: A Scalable Tree Boosting System. In Proceedings of the 2nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Probst, P.; Boulesteix, A.; Bischl, B. Tunability: Importance of Hyperparameters of Machine Learning Algorithms. J. Mach. Learn. Res. 2019, 20, 1934–1965. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Farag, M.A.; Mirjalili, S.; Elhosseini, M.A. Quadratic Interpolation and a New Local Search Approach to Improve Particle Swarm Optimization: Solar Photovoltaic Parameter Estimation. Expert Syst. Appl. 2024, 236, 121417. [Google Scholar] [CrossRef]
- Qaraad, M.; Aljadania, A.; Elhosseini, M. Large-Scale Competitive Learning-Based Salp Swarm for Global Optimization and Solving Constrained Mechanical and Engineering Design Problems. Mathematics 2023, 11, 1362. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Badawy, M.; Mirjalili, S.; Elhosseini, M.A. Photovoltaic Parameter Estimation Using Improved Moth Flame Algorithms with Local Escape Operators. Comput. Electr. Eng. 2023, 106, 108603. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Mirjalili, S.; Elhosseini, M.A. An Innovative Time-Varying Particle Swarm-Based Salp Algorithm for Intrusion Detection System and Large-Scale Global Optimization Problems. Artif. Intell. Rev. 2022, 56, 8325–8392. [Google Scholar] [CrossRef]
- Ojha, V.K.; Abraham, A.; Snášel, V. Metaheuristic Design of Feedforward Neural Networks: A Review of Two Decades of Research. Eng. Appl. Artif. Intell. 2017, 60, 97–116. [Google Scholar] [CrossRef]
- Akyol, S.; Alatas, B. Plant Intelligence Based Metaheuristic Optimization Algorithms. Artif. Intell. Rev. 2017, 47, 417–462. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, V. Application of Genetic Algorithms in Healthcare: A Review. Stud. Comput. Intell. 2022, 1039, 75–86. [Google Scholar] [CrossRef]
- Kumar, S.; Sahoo, G. A Random Forest Classifier Based on Genetic Algorithm for Cardiovascular Diseases Diagnosis (RESEARCH NOTE). Int. J. Eng. 2017, 30, 1723–1729. [Google Scholar]
- Amma, N.G.B. Cardiovascular Disease Prediction System Using Genetic Algorithm and Neural Network. In Proceedings of the 2012 International Conference on Computing, Communication and Applications, Dindigul, India, 22–24 February 2012. [Google Scholar] [CrossRef]
- Ay, Ş.; Ekinci, E.; Garip, Z. A Comparative Analysis of Meta-Heuristic Optimization Algorithms for Feature Selection on ML-Based Classification of Heart-Related Diseases. J. Supercomput. 2023, 79, 11797–11826. [Google Scholar] [CrossRef] [PubMed]
- Sheeba, P.T.; Roy, D.; Syed, M.H. A Metaheuristic-Enabled Training System for Ensemble Classification Technique for Heart Disease Prediction. Adv. Eng. Softw. 2022, 174, 103297. [Google Scholar] [CrossRef]
- Tharwat, A.; Schenck, W. A Conceptual and Practical Comparison of PSO-Style Optimization Algorithms. Expert Syst. Appl. 2021, 167, 114430. [Google Scholar] [CrossRef]
- Okwu, M.O.; Tartibu, L.K. Particle Swarm Optimisation. Stud. Comput. Intell. 2021, 927, 5–13. [Google Scholar] [CrossRef]
- Tang, K.S.; Man, K.F.; Kwong, S.; He, Q. Genetic Algorithms and Their Applications. IEEE Signal Process. Mag. 1996, 13, 22–37. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Grandgirard, J.; Poinsot, D.; Krespi, L.; Nénon, J.P.; Cortesero, A.M. Costs of Secondary Parasitism in the Facultative Hyperparasitoid Pachycrepoideus Dubius: Does Host Size Matter? Entomol. Exp. Appl. 2002, 103, 239–248. [Google Scholar] [CrossRef]
- Hatamlou, A. Black Hole: A New Heuristic Optimization Approach for Data Clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A Novel Meta-Heuristic Optimization Algorithm: Thermal Exchange Optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Lam, A.Y.S.; Member, S.; Li, V.O.K. Chemical-Reaction-Inspired Metaheuristic for Optimization. IEEE Trans. Evol. Comput. 2009, 14, 381–399. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Abdollahi, M.; Isazadeh, A.; Abdollahi, D. Imperialist Competitive Algorithm for Solving Systems of Nonlinear Equations. Comput. Math. Appl. 2013, 65, 1894–1908. [Google Scholar] [CrossRef]
- Ashrafi, S.M.; Dariane, A.B. A Novel and Effective Algorithm for Numerical Optimization: Melody Search (MS). In Proceedings of the 2011 11th International Conference on Hybrid Intelligent Systems (HIS), Melacca, Malaysia, 5–8 December 2011; pp. 109–114. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Elhosseini, M.A. An Innovative Quadratic Interpolation Salp Swarm-Based Local Escape Operator for Large-Scale Global Optimization Problems and Feature Selection. Neural Comput. Appl. 2022, 34, 17663–17721. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Elhosseini, M.A. Large Scale Salp-Based Grey Wolf Optimization for Feature Selection and Global Optimization. Neural Comput. Appl. 2022, 34, 8989–9014. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Elhosseini, M.A. Addressing Constrained Engineering Problems and Feature Selection with a Time-Based Leadership Salp-Based Algorithm with Competitive Learning. J. Comput. Des. Eng. 2022, 9, 2235–2270. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Mirjalili, S.; Halima, N.B.; Elhosseini, M.A. Comparing SSALEO as a Scalable Large Scale Global Optimization Algorithm to High-Performance Algorithms for Real-World Constrained Optimization Benchmark. IEEE Access 2022, 10, 95658–95700. [Google Scholar] [CrossRef]
- Chen, J.; Luo, Q.; Zhou, Y.; Huang, H. Firefighting Multi Strategy Marine Predators Algorithm for the Early-Stage Forest Fire Rescue Problem. Appl. Intell. 2023, 53, 15496–15515. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Alabool, H. Salp Swarm Algorithm: A Comprehensive Survey. Neural Comput. Appl. 2020, 32, 11195–11215. [Google Scholar] [CrossRef]
- Cuevas, E. An Optimization Algorithm Inspired by the States of Matter That Improves the Balance between Exploration and Exploitation. Appl. Intell. 2014, 40, 256–272. [Google Scholar] [CrossRef]
- Castelli, M.; Manzoni, L.; Mariot, L.; Nobile, M.S.; Tangherloni, A. Salp Swarm Optimization: A Critical Review. Expert Syst. Appl. 2022, 189, 116029. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Fathi, R.; Tousi, B.; Galvani, S. Allocation of Renewable Resources with Radial Distribution Network Reconfiguration Using Improved Salp Swarm Algorithm. Appl. Soft Comput. 2023, 132, 109828. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, T.; Ye, X.; Asghar, A.; Guoxi, H.; Huiling, L.; Zhifang, C. Differential Evolution-Assisted Salp Swarm Algorithm with Chaotic Structure for Real-World Problems; Springer: London, UK, 2022; ISBN 0123456789. [Google Scholar]
- El-Shorbagy, M.A.; Eldesoky, I.M.; Basyouni, M.M.; Nassar, I.; El-Refaey, A.M. Chaotic Search-Based Salp Swarm Algorithm for Dealing with System of Nonlinear Equations and Power System Applications. Mathematics 2022, 10, 1368. [Google Scholar] [CrossRef]
- Nautiyal, B.; Prakash, R.; Vimal, V.; Liang, G.; Chen, H. Improved Salp Swarm Algorithm with Mutation Schemes for Solving Global Optimization and Engineering Problems. Eng. Comput. 2021, 38, 3927–3949. [Google Scholar] [CrossRef]
- Kansal, V.; Dhillon, J.S. Emended Salp Swarm Algorithm for Multiobjective Electric Power Dispatch Problem. Appl. Soft Comput. 2020, 90, 106172. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Chen, W.; Heidari, A.A.; Wang, M.; Zhao, X.; Liang, G.; Chen, H.; Zhang, X. Ensemble Mutation-Driven Salp Swarm Algorithm with Restart Mechanism: Framework and Fundamental Analysis. Expert Syst. Appl. 2021, 165, 113897. [Google Scholar] [CrossRef]
- Wang, C.; Xu, R.-Q.; Ma, L.; Zhao, J.; Wang, L.; Xie, N.-G.; Cheong, K.H. An Efficient Salp Swarm Algorithm Based on Scale-Free Informed Followers with Self-Adaption Weight. Appl. Intell. 2023, 53, 1759–1791. [Google Scholar] [CrossRef]
- Ren, H.; Li, J.; Chen, H.; Li, C.Y. Adaptive Levy-Assisted Salp Swarm Algorithm: Analysis and Optimization Case Studies. Math. Comput. Simul. 2021, 181, 380–409. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Ibrahim, A.M. Improved Salp Swarm Algorithm Combined with Chaos. Math. Comput. Simul. 2022, 202, 113–148. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.; Zhao, K.; Wang, Y. A Salp Swarm Algorithm Based on Harris Eagle Foraging Strategy. Math. Comput. Simul. 2023, 203, 858–877. [Google Scholar] [CrossRef]
- Neggaz, N.; Ewees, A.A.; Elaziz, M.A.; Mafarja, M. Boosting Salp Swarm Algorithm by Sine Cosine Algorithm and Disrupt Operator for Feature Selection. Expert Syst. Appl. 2020, 145, 113103. [Google Scholar] [CrossRef]
- Si, T.; Miranda, P.B.C.; Bhattacharya, D. Novel Enhanced Salp Swarm Algorithms Using Opposition-Based Learning Schemes for Global Optimization Problems. Expert Syst. Appl. 2022, 207, 117961. [Google Scholar] [CrossRef]
- Abbassi, A.; Abbassi, R.; Heidari, A.A.; Oliva, D.; Chen, H.; Habib, A.; Jemli, M.; Wang, M. Parameters Identification of Photovoltaic Cell Models Using Enhanced Exploratory Salp Chains-Based Approach. Energy 2020, 198, 117333. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K.; Heidari, A.A.; Moayedi, H.; Chen, H. Harmonized Salp Chain-Built Optimization. Eng. Comput. 2021, 37, 1049–1079. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Havlin, S.; Da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. Lévy Flights in Random Searches. Phys. A Stat. Mech. Appl. 2000, 282, 1–12. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An Efficient Salp Swarm-Inspired Algorithm for Parameters Identification of Photovoltaic Cell Models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Luo, X. Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm. Water 2018, 10, 815. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Techical Report; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Mohamed, A.W.; Sallam, K.M.; Agrawal, P.; Hadi, A.A.; Mohamed, A.K. Evaluating the Performance of Meta-Heuristic Algorithms on CEC 2021 Benchmark Problems. Neural Comput. Appl. 2022, 35, 1493–1517. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Enhanced Salp Swarm Algorithm: Application to Variable Speed Wind Generators. Eng. Appl. Artif. Intell. 2019, 80, 82–96. [Google Scholar] [CrossRef]
- Singh, N.; Son, L.H.; Chiclana, F.; Magnot, J.P. A New Fusion of Salp Swarm with Sine Cosine for Optimization of Non-Linear Functions. Eng. Comput. 2020, 36, 185–212. [Google Scholar] [CrossRef]
- Tubishat, M.; Ja’afar, S.; Alswaitti, M.; Mirjalili, S.; Idris, N.; Ismail, M.A.; Omar, M.S. Dynamic Salp Swarm Algorithm for Feature Selection. Expert Syst. Appl. 2021, 164, 113873. [Google Scholar] [CrossRef]
- Tubishat, M.; Idris, N.; Shuib, L.; Abushariah, M.A.M.; Mirjalili, S. Improved Salp Swarm Algorithm Based on Opposition Based Learning and Novel Local Search Algorithm for Feature Selection. Expert Syst. Appl. 2020, 145, 113122. [Google Scholar] [CrossRef]
- Faris, H.; Heidari, A.A.; Al-Zoubi, A.M.; Mafarja, M.; Aljarah, I.; Eshtay, M.; Mirjalili, S. Time-Varying Hierarchical Chains of Salps with Random Weight Networks for Feature Selection. Expert Syst. Appl. 2020, 140, 112898. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-Based Optimizer: A New Metaheuristic Optimization Algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Gong, W.; Heidari, A.A.; Golilarz, N.A.; Samadi-Koucheksaraee, A.; Chen, H. Gradient-Based Optimization with Ranking Mechanisms for Parameter Identification of Photovoltaic Systems. Energy Rep. 2021, 7, 3979–3997. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime Mould Algorithm: A New Method for Stochastic Optimization. Futur. Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Frank, A.; Asuncion, A. UCI Machine Learning Repository. 2010. Available online: https://archive.ics.uci.edu/ (accessed on 5 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).