Godeaux and Campedelli Surfaces via Deformations

Abstract

In this paper, we construct two deformations of the Godeaux surface with ${\pi }_1\cong {\mathbb{Z}}_4$, such that each central fibre contains a family of conics. We show that surfaces that are birational to these Godeaux surfaces exist in two connected components of the moduli space of the Campedelli surfaces with a fundamental group of order 8. The whole construction is simplified by the use of key varieties.

1. Introduction

Understanding moduli spaces is an important step for completing the classification process in algebraic geometry, a problem which is not yet settled, even in dimension 2. One of the interesting classes in dimension 2 consists of the surfaces of general type. In [1], Gieseker proved the existence of the modulus varieties ${\mathcal{M}}_{K^2,\chi }$, parameterising the surfaces of general type with given invariants $K^2$ and $\chi$. The ultimate goal is to understand its compactification ${\overline{\mathcal{M}}}_{K^2,\chi }$—the moduli space of stable surfaces that, intuitively, are the limits of smooth surfaces. One of the basic questions about the geometry of ${\overline{\mathcal{M}}}_{K^2,\chi }$ is to find and analyze the codimension 1 components of the boundary. One important boundary divisor consists of normal surfaces with Wahl singularities, also known as T-singularities [2].

In this work, we are interested in studying the moduli space of Campedelli surfaces, which are the surfaces of general type with $p_g=q=0$ and $K^2=2$. Campedelli surfaces are the first example of non-rational surfaces with $p_g=q=0$ [3]. Every finite group of order ≤9 can occur as the fundamental group for such surfaces, except for Dihedral groups of order 6 and 8. We consider only the Campedelli surfaces with a fundamental group of order 8 [4].

Two minimal surfaces of general type belong to the same connected component of the Gieseker moduli scheme iff they are deformation equivalent. Moreover, surfaces in the same connected component have the same fundamental group. We aim to find two deformations of the Godeaux surface with ${\pi }_1\cong {\mathbb{Z}}_4$ such that the central fibre contains the resolution graph of a T-singularity. Using unprojection, we then show that there exist two connected components at the boundary of ${\overline{\mathcal{M}}}_{2,1}$ that contain surfaces birational to Godeaux surfaces. In [5], Alexeev and Pardini showed that, in the compactification of the moduli space of the Campedelli surfaces with ${\pi }_1\cong {\mathbb{Z}}_2^3$, Godeaux surface T with ${\pi }_1\cong {\mathbb{Z}}_4$ does not appear. There are three Campedelli surfaces corresponding to Abelian fundamental groups of order 8. In this work, we consider the other two cases. There are Campedelli surfaces with non-Abelian fundamental groups of order 8, which are not considered.

The key idea in the present work is derived from [6] (Lemma 2.3) which describes how different T-singularities change $K^2$ in the case of canonically embedded algebraic surfaces. Based on this, there are two possible directions. The forward part is to consider the $\mathbb{Q}$-Gorenstein deformations of a surface such that the central fibre contains a desired T-singularity, then resolving the central fibre decrease $K^2$ by a specified positive integer. The reverse part is to deform a surface so that it contains the resolution graph of a desired T-singularity, contracting the resolution graph increase $K^2$. In [6], we adapted the forward way and constructed some deformations of Campedelli surfaces with two different fundamental groups to contain ${\displaystyle \frac{1}{4}}(1,1)$ singularities and, thus, proved the existence of the surfaces birational to the Godeaux surface with ${\pi }_1\cong {\mathbb{Z}}_4$ in two different connected components of ${\mathcal{M}}_{2,1}$. In this work, we consider the reverse part, that is, constructing the deformations of the Godeaux surface with ${\pi }_1\cong {\mathbb{Z}}_4$ to contain the resolution graphs of ${\displaystyle \frac{1}{4}}(1,1)$. For the canonically embedded surfaces, these resolution graphs are conics. As a consequence of our deformation construction, we are able to construct Campedelli surfaces, with higher $K^2$, from a Godeaux surface, a surface with a low value of $K^2$. In general, the reverse part is important since the construction of these surfaces of general type is harder for higher values of $K^2$.

One of the main challenges is that the deformation spaces of such surfaces of general type satisfy Murphy’s law and can be arbitrarily singular [7]. We aim to find the deformations of the universal cover of a Godeaux surface T such that each central fibre contains specific resolution graphs without any additional singularities. We use the group action on the canonical ring of the universal cover of the Godeaux surface T to achieve our goal. Here is the main result which addresses this issue.

Theorem 1.

There exist two deformations of Godeaux surface T with fundamental group ${\pi }_1\cong {\mathbb{Z}}_4$, such that each central fibre contains a conic.

To contract these conics, we use unprojection. To unproject these conics and to find the fundamental group of the unprojections, we use key varieties constructed using Triple Tom & Jerry [8], an unprojection format introduced by Reid et al. These key varieties are sixfold and make our constructions explicit in the sense that the generators and relations of polarised graded rings are given at each stage.

In Section 2, we recall the basics of unprojection and Tom & Jerry, a format for unprojection. Section 3 is our main section, where we use group action on the graded rings to find two deformation families of a sixfold. Using the central fibres of these deformations and the theory of unprojection, we construct our key varieties in Section 4. In Section 5, we first review the construction of the Godeaux surfaces T with fundamental group ${\mathbb{Z}}_4$ from [9], and then construct two families inside ${\mathcal{H}}_{2,0,T}$ using previous constructions. We then construct stable surfaces with ${\displaystyle \frac{1}{4}}(1,1)$ singularities in Section 6. Using these families and $\mathbb{Q}$-Gorenstein smoothing, introduced by Lee and Park in this context [10,11], we construct Campedelli surfaces [12,13] with fundamental groups ${\mathbb{Z}}_8$ and ${\mathbb{Z}}_4\times {\mathbb{Z}}_2$.

Notation: We work over the field of complex numbers $\mathbb{C}$.

2. A Brief on Kustin–Miller Parallel Unprojection

In 2012, Reid et al. [14] introduced a theory of unprojection for constructing high-codimension varieties. Consider projectively Gorenstein varieties $\Gamma \subset W$, where $\Gamma$ is a codimension 1 divisor, such that we have the following:

$$0\to {\mathcal{I}}_{\Gamma }\to {\mathcal{O}}_W\to {\mathcal{O}}_{\Gamma }\to 0.$$

Applying $\mathcal{H}om(-,{\omega }_X)$ and using the adjunction formula gives us

$$0\to {\omega }_W\to \mathcal{H}om({\mathcal{I}}_{\Gamma },{\omega }_W)\stackrel{res}{\to }{\omega }_{\Gamma }\to 0.$$

The ${\mathcal{O}}_X$-module $\mathcal{H}om({\mathcal{I}}_{\Gamma },{\omega }_W)$ is generated by two elements $\{i,s\}$, where i is the basis of ${\omega }_X$ and $s:{\mathcal{I}}_{\Gamma }\to {\omega }_X$ is an injection such that the Poincaré residue $res\left(s\right)$ is the basis of ${\omega }_D$. This element s is our unprojection variable, which defines a rational map

$$W⤏W_1\subset \mathbb{P}\left[s\right]=Projk[x_0,\cdots ,x_n,s],$$

such that $\Gamma$ is mapped to $P_s=(0:\cdots :0:1)$. The variety $W_1$ is projectively Gorenstein [14,15]. The existence of s can also be seen using complexes if we further assume that $\Gamma$ and W are contained in an ambient local scheme A, with ${\mathcal{O}}_{\Gamma }$ and W having finite projective dimension over ${\mathcal{O}}_A$. [14] (p. 8).

Tom & Jerry Parallel Unprojection

In 2012, Reid et al. introduced two formats for unprojection, namely, Tom and Jerry. Both these formats provide a way to specify unprojection data, that is, a divisor $\Gamma$ contained in a scheme W defined by $4\times 4$ Pfaffians of a $5\times 5$ skew-symmetric matrix. Here, W is codimension 3 and $\Gamma$ is a complete intersection. Let

$$M=\left(\begin{array}{cccc}{m}_{12}& m_{13}& m_{14}& m_{15}\\ & m_{23}& m_{24}& m_{25}\\ -Sym& & m_{34}& m_{35}\\ & & & m_{45}\end{array}\right),$$

(1)

under the assumption that entries $m_{ij}$ belong to a regular ambient ring. The two formats are defined as follows:

${\mathrm{Tom}}_i$:

For fixed $i\in 1,\cdots ,5$, the entries $m_{lm}\in I_{\Gamma }$ for all $l,m\ne i$;

${\mathrm{Jer}}_{ij}$:

For fixed $1\le i<j\le 5$, the entries $m_{lk}\in I_{\Gamma }$ if either l or k equal to i or j.

One can naturally ask if W contains more than one Tom or Jerry type of divisor. One such construction exists in [16] (p. 75), but the first formal appearance is due to Petrotou [8], where they introduced a format for triple Tom and Jerry and used parallel unprojection theory, introduced by Papadakis et al. [17], for their unprojection constructions in high codimensions.

3. Deformation Using Group Action

Group Action and the Graded Ring

Let V be a normal projective variety such that the locus of the fixed points of group action by a finite Abelian group has codimension $\ge 2$. Consider an ample line bundle $\mathcal{L}$. Henceforth, we let G be a cyclic group of order n that acts on the graded ring of the polarised variety $(V,\mathcal{L})$, which is given as

$$R(V,\mathcal{L})=\underset{m\ge 0}{⨁}{H}^0(V,{\mathcal{L}}^{\otimes m}).$$

(2)

Each summand can be decomposed as the direct sum of eigenspaces

$$H^0(V,{\mathcal{L}}^{\otimes m})=\underset{g\in G}{⨁}{U}_m\left(g\right),$$

(3)

where $U_m\left(g\right)$ denotes the eigenspace corresponding to the element g in G. For the cyclic group G, each character ${\chi }_k$ is given by ${\chi }_k\left(g\right)=e^{2\pi ikg/n}$ for $k=0,1,\dots ,n-1$. Therefore, the entire graded ring $R(V,\mathcal{L})$ can be decomposed as

$$R(V,\mathcal{L})=\underset{m\ge 0}{⨁}{H}^0(V,{\mathcal{L}}^{\otimes m})=\underset{m\ge 0}{⨁}\underset{k=0}{\overset{n-1}{⨁}}{H}^0{(V,{\mathcal{L}}^{\otimes m})}_{{\chi }_k},$$

where $H^0{(V,{\mathcal{L}}^m)}_{{\chi }_k}$ is the eigenspace and the action of G is via the character ${\chi }_k$.

Definition 1.

For an element $x\in H^0(V,{\mathcal{L}}^{\otimes m})$, define the principal length $pl\left(x\right)$ of the orbit $Orb\left(x\right)$ to be the cardinality of the following set:

$$\left\{div\left(f\right):f\in Orb\left(x\right)\right\}.$$

Observe that $pl\left(x\right)\le |Orb(x\left)\right|$. For example, if $G=⟨g:g^4=1⟩$, then, for general $x\in U\left(g\right)\oplus U\left(g^3\right)$, the principal length is $pl\left(x\right)=2$, whereas $|Orb(x\left)\right|=4$.

To construct our required key varieties in the following section, we start by deforming the following sixfold, given by the complete intersection of two quartics:

$$W:\mathbb{V}(F,G)\subset \mathbb{P}(1^3,2^6),$$

(4)

with coordinates $x_1,x_2,x_3$ of weight 1 and $u_0,u_1,u_2,u_3,w_0,w_1$ of weight 2. Then, $K_W=-7A$, where $A=\mathcal{O}\left(1\right)$. Moreover, we define the following actions of ${\mathbb{Z}}_4$ on W, such that, in each action, $F,G$ denote the invariant and anti-invariant quartics, respectively. We consider two different group actions of ${\mathbb{Z}}_4$ for the deformations ${\Psi }^1$ and ${\Psi }^2$. For ${\Psi }^i:\mathcal{W}\to {\Delta }_i$, we take the following diagonalised group action:

$$x_j\mapsto {\epsilon }^j{x}_j,u_j\mapsto {\epsilon }^j{u}_j,w_j\mapsto {\epsilon }^{2j+(i-1)}{w}_j,$$

(5)

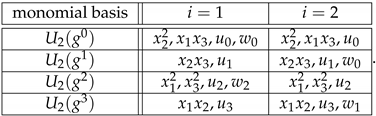
where $\epsilon$ is a primitive fourth root of unity. The monomial basis for $U_2\left(g^i\right)$ is explicitly given in the following table.

(6)

Theorem 2.

Let W be as above. There exist two distinct deformations of W, say, ${\Psi }^i:\mathcal{W}\to {\Delta }_i$, for $i=1,2$, such that the central fibre of each of the deformation ${\Psi }^i$ contains four loci, namely, ${\Gamma }_0^i,\cdots ,{\Gamma }_3^i$. Each ${\Gamma }_i$ is defined by a complete intersection of three quadrics, permuted by ${\mathbb{Z}}_4$, that intersect with each other in codimension $\ge 5$.

Proof. 

Taking $\mathcal{L}=\mathcal{O}\left(A\right)$, where $K_W=-7A$ and $m=2$, Equation (3), under the action of ${\mathbb{Z}}_4=⟨g⟩$, becomes the following:

$$H^0(W,{\mathcal{L}}^{\otimes 2})=\underset{i=0}{\overset{3}{⨁}}{U}_2\left(g^i\right).$$

(7)

A general element of the above space has a principal length of 4. Elements with principal length 2 belong to one of the following spaces:

$$U_{2,1}=U_2\left(g^0\right)\oplus U_2\left(g^2\right),U_{2,2}=U_2\left(g\right)\oplus U_2\left(g^3\right).$$

(8)

This leads to two different deformations ${\Psi }^i:\mathcal{W}\to {\Delta }_i$, for $i=1,2$, of W; the general fibre for both deformations is a complete intersection of two quartics, one invariant and the other invariant, under an action of ${\mathbb{Z}}_4$. We now discuss the central fibres for both deformations one by one. Let

$$W_0^i=\mathbb{V}(F_0^i,G_0^i)$$

(9)

be the central fibre of ${\Psi }^i$.

• Case 1 (${\Psi }^1$): Let $Q_1\in \oplus U_2\left(g^i\right)$ be a general element with $Orb\left(Q_1\right)=\{Q_{1,i}=g^i{Q}_1:i=0,\cdots ,3\}$, that is, its elements are permuted in the following way:

  $$Q_{1,0}\to Q_{1,1}\to Q_{1,2}\to Q_{1,3}\to Q_{1,0}.$$

  (10)

  Let $R_1\in U_{2,1}$ be an arbitrary element with $R_{1,i}=g^i{R}_1,$ for $i=0,1$. The quartic $R_{1,0}{R}_{1,1}$ is invariant since the action of ${\mathbb{Z}}_4$ permutes $R_{1,0}$ and $R_{1,1}$. The central fibre $W_0^1$ is then constructed as follows:

  $$F_0^1=R_{1,0}{R}_{1,1}-{\displaystyle \frac{1}{2}}(Q_{1,0}{Q}_{1,2}+Q_{1,1}{Q}_{1,3}),G_0^1=Q_{1,0}{Q}_{1,2}-Q_{1,1}{Q}_{1,3},$$

  (11)

  Here, the quartics $F_0^1$ and $G_0^1$ are invariant and anti-invariant, respectively.
• Case 2 (${\Psi }^2$): Let $P\in {\oplus }_{i=0}^3{U}_2\left(g^i\right)$ be a general element with $pl\left(P\right)=4$ and $P_i=g^{i}P$. Using these quadrics, we define the following quadrics:

  $$\begin{array}{c}\hfill Q_{2,0}=P_0,Q_{2,1}=-P_1,Q_{2,2}=P_2,Q_{2,3}=P_3.\end{array}$$

  (12)

  such that

  $$Q_{2,0}\to -Q_{2,1},Q_{2,1}\to -Q_{2,2},Q_{2,2}\to Q_{2,3},Q_{2,3}\to Q_{2,0}.$$

  (13)

  For a general $R_2\in U_{2,2}$, the quartic $R_{2,0}{R}_{2,1}$ is anti-invariant, where $R_{2,i}=g^i{R}_2$, for $i=0,1$. We construct $W_0^2$ as the following complete intersection:

  $$F_0^2=Q_{2,0}{Q}_{2,2}-Q_{2,1}{Q}_{2,3},G_0^2=R_{2,0}{R}_{2,1}-{\displaystyle \frac{1}{2}}(Q_{2,0}{Q}_{2,2}+Q_{2,1}{Q}_{2,3}).$$

  (14)

  It can be seen that $F_0^2$ is invariant and $G_0^2$ is anti-invariant.

For each central fibre $W_0^i$, there are four families ${\Gamma }_0^i,\cdots ,{\Gamma }_3^i$, defined as follows:

$${\Gamma }_m^i:\mathbb{V}(Q_{i,m},Q_{{i,(m+1)}_4},R_{{i,(m+1)}_2})\subset \mathbb{P}(1^3,2^n),\mathrm{for}0\le m\le 3,$$

(15)

where ${\left(a\right)}_n:=a\left(\mathrm{mod}n\right)$. Under the action of ${\mathbb{Z}}_4$, the ${\Gamma }_m^i$ are permuted in the following way:

$${\Gamma }_{{\left(m\right)}_4}^i\to {\Gamma }_{{(m+1)}_4}^i,\mathrm{for}m=0,\cdots ,3,\mathrm{and}i=1,2.$$

(16)

The generators of $\mathbb{I}({\Gamma }_i\cap {\Gamma }_j)$ form a regular sequence of length 5 and, hence, the ${\Gamma }_{i}s$ intersect each other in codimension 5. □

Remark 1.

There are many choices for quartics in (11) and (14) that satisfy the conditions of Theorem 2. These choices are required for Proposition 1.

4. Key Varieties

We start from the central fibres $W_0^i$ (9), and unproject from the divisors ${\Gamma }_m^i$ (15). The constructions of $W_0^1$ and $W_0^2$ allow us to perform unprojection for both n-folds simultaneously. Let $W_{m+1}^i$ be the n-fold obtained from unprojecting ${\Gamma }_m^i\subset W_m^i$.

We perform unprojections in two stages: in the first stage, we unproject from ${\Gamma }_0^i$, and, in the second stage, we use the theory of triple Tom and Jerry to unproject the three divisors ${\Gamma }_1^i,{\Gamma }_2^i,{\Gamma }_3^i$.

4.1. Stage 1: $W_1^i$

Due to our choices of coefficients from Equations (11)–(14), we have

$$F_0^i=G_0^i=0\iff Q_{i,0}{Q}_{i,2}-Q_{i,1}{Q}_{i,3}=R_{i,0}{R}_{i,1}-Q_{i,1}{Q}_{i,3}=0.$$

(17)

The unprojection ${\Gamma }_0^i\subset W_0^i$ is the ring ${\mathcal{O}}_{W_0^i}\left[s_0^{\left(i\right)}\right]$. To find relations expressing $s_0^{\left(i\right)}$ as a rational function, we follow [18] and write the right hand side of (17) as $A_0{X}_0=0$, where

$$A_0=\left(\begin{array}{ccc}0& -Q_{i,3}& R_{i,0}\\ Q_{i,2}& -Q_{i,3}& 0\end{array}\right)\mathrm{and}{X}_0=\left(\begin{array}{ccc}{Q}_{i,0}& Q_{i,1}& R_{i,1}\end{array}\right),$$

(18)

where the entries of the column matrix $X_0$ are the defining equations of ${\Gamma }_0^i$. Since $W_0^i$ is a complete intersection, the equations of $W_1^i$ involving $s_0^{\left(i\right)}$ can be described using Cramer’s rule as

$$s_0^{\left(i\right)}=A_1/Q_{i,0},s_0^{\left(i\right)}=A_2/Q_{i,1},s_0^{\left(i\right)}=A_3/R_{i,1},$$

(19)

where the $A_m$ are the $2\times 2$ minors of $A_0$. The homogenous coordinate ring of $W_1^i$ is then given as

$$k\left[W_1^i\right]=k[x_1,x_2,x_3,u_0\cdots ,u_3,w_0,w_1,s_0^{\left(i\right)}]/r_1^i,$$

where $r_1^i$ is the ideal generated by $4\times 4$ Pfaffians of the following anti-symmetric matrix:

$$J_1^i=\left(\begin{array}{cccc}{s}_0^{\left(i\right)}& 0& -Qi,3& R_{i,0}\\ & Q_{i,2}& -Q_{i,3}& 0\\ -Sym& & R_{i,1}& -Q_{i,1}\\ & & & Q_{i,0}\end{array}\right).$$

(20)

Moreover, $W_1^i$ is Gorenstein by [15].

4.2. Triple Tom Parallel Unprojection

The n-fold $W_1^i$ contains the following three divisors:

$${\Gamma }_m^i:\mathbb{V}(Q_{i,m},Q_{{i,(m+1)}_4},R_{{i,(m+1)}_2})\subset \mathbb{P}(1^3,2^n),\mathrm{for}1\le m\le 3,$$

(21)

Observe that, ${\Gamma }_1^i,{\Gamma }_2^i$, and ${\Gamma }_3^i$ appear in the $5\times 5$ skew-symmetric matrix $J_1^i$ (20) as ${\mathrm{Tom}}_4$, ${\mathrm{Tom}}_5$, and ${\mathrm{Tom}}_3$ formats, respectively. Using Theorem 2, it can be seen that these three divisors satisfy the conditions of parallel unprojection [17] (Theorem 2.3).

Following constructions from [8,18], the homogenous coordinate ring of $W_{m+1}^i$, for $0\le m\le 3$, is given as

$$k\left[W_{m+1}^i\right]=k[x_1,x_2,x_3,y_0,\cdots ,y_3,w_0,w_1,s_0^{\left(i\right)},\cdots ,s_m^{\left(i\right)}]/r_m^i,$$

(22)

where the ideal $r_m^i$ is generated by the $4\times 4$ Pfaffians of the antisymmetric matrices $J_1^i,\cdots ,J_{m+1}^i$, where

$$J_{m+1}^i=\left(\begin{array}{cccc}{s}_m^{\left(i\right)}& -{\left(m\right)}_2{Q}_{i,{(m+2)}_4}& -{(m+1)}_2{Q}_{i,{(m+3)}_4}& R_{i,{\left(m\right)}_2}\\ & {(-1)}^m{Q}_{i,{(m+2)}_4}& {(-1)}^{m+1}{Q}_{i,{(m+3)}_4}& 0\\ -Sym& & R_{i,{(m+1)}_2}& -Q_{i,{(m+1)}_4}\\ & & & Q_{i,{\left(m\right)}_4}\end{array}\right),$$

(23)

Here, ${\left(a\right)}_n:=a\left(\mathrm{mod}n\right)$, and the relations are quadratic in $s_0^{\left(i\right)},\cdots ,s_m^{\left(i\right)}$:

$$\begin{array}{ccc}{s}_3^{\left(i\right)}{s}_2^{\left(i\right)}-{\left(Q_{i,1}\right)}^2=0,& s_3^{\left(i\right)}{s}_1^{\left(i\right)}-{\left(R_{i,1}\right)}^2=0,& s_3^{\left(i\right)}{s}_0^{\left(i\right)}-{\left(Q_{i,2}\right)}^2=0\\ s_2^{\left(i\right)}{s}_1^{\left(i\right)}-{\left(Q_{i,0}\right)}^2=0,& s_2^{\left(i\right)}{s}_0^{\left(i\right)}-{\left(R_{i,0}\right)}^2=0,& s_1^{\left(i\right)}{s}_0^{\left(i\right)}-{\left(Q_{i,3}\right)}^2=0.\end{array}$$

(24)

Here, $wt{s}_m^{\left(i\right)}=2,\forall m,\forall i$. Moreover, the group ${\mathbb{Z}}_4$ acts on the $s_0^{\left(i\right)}\cdots ,s_4^{\left(i\right)}$ in the following way:

$$\begin{array}{c}\hfill s_0^{\left(1\right)}\mapsto -s_1^{\left(1\right)},s_1^{\left(1\right)}\mapsto -s_2^{\left(1\right)},s_2^{\left(1\right)}\mapsto -s_3^{\left(1\right)},s_3^{\left(1\right)}\mapsto -s_0^{\left(1\right)},\end{array}$$

(25)

$$\begin{array}{c}\hfill s_0^{\left(2\right)}\mapsto s_1^{\left(2\right)},s_1^{\left(2\right)}\mapsto s_2^{\left(2\right)},s_2^{\left(2\right)}\mapsto s_3^{\left(2\right)},s_3^{\left(2\right)}\mapsto s_0^{\left(2\right)}.\end{array}$$

(26)

Remark 2.

The defining relations for $W_0^i,W_1^i,\cdots ,W_4^i$ depend on the choice of action of ${\mathbb{Z}}_4$ and on the weights of variables.

Proposition 1.

For fixed $0\le m\le 3$, the n-fold $W_{m+1}^i$ is a section of $wGr(2,5+m)$.

Proof. 

The ideal $r_{m+1}^i$ generated by $4\times 4$ Pfaffians of $J_0^i,\cdots ,J_{m+1}^i$, and the associated relations of unprojection variables (24), can also be generated by $4\times 4$ Pfaffians of the submatrix of the following matrix obtained by deleting the top $3-m$ rows and columns:

$$M=\left(\begin{array}{ccccccc}-Q_{i,0}& -Q_{i,1}& -R_{i,0}& -R_{i,0}& -Q_{i,1}& 0& s_2^{\left(i\right)}\\ & 0& Q_{i,2}& 0& s_3^{\left(i\right)}& R_{i,1}& 0\\ & & Q_{i,3}& 0& R_{i,1}& s_1^{\left(i\right)}& 0\\ & & & -s_0^{\left(i\right)}& 0& Q_{i,3}& R_{i,0}\\ & & & & Q_{i,2}& Q_{i,3}& 0\\ & -\mathrm{Sym}& & & & R_{i,1}& Q_{i,1}\\ & & & & & & Q_{i,0}\end{array}\right).$$

(27)

□

The following can be seen using a magma [19] computation.

Lemma 1.

The ideal $r_4^i$ is generated by $2\times 2$ minors of the following symmetric matrix A:

$$A=\left(\begin{array}{cccc}{s}_3^{\left(i\right)}& Q_{i,1}& R_{i,1}& Q_{i,2}\\ & s_2^{\left(i\right)}& Q_{i,0}& R_{i,0}\\ Sym& & s_1^{\left(i\right)}& Q_{i,3}\\ & & & s_0^{\left(i\right)}\end{array}\right).$$

(28)

Lemma 2.

The sixfolds $W_m^i$, for $0\le m\le 3$, are invariant under ${\mathbb{Z}}_4$ action.

Proof. 

All the $2\times 2$ minors of the matrix A (28) are invariant under the ${\mathbb{Z}}_4$ group action. □

5. Families of Conics Inside a Godeaux Surface

Using Theorem 2, we construct two deformation families of a Godeaux surface with ${\pi }_1\cong {\mathbb{Z}}_4$, such that each central fibre contains families of four conics.

Godeaux Surface with ${\pi }_1={\mathbb{Z}}_4$

A Godeaux surface is a general-type surface with $p_g=0$ and $K^2=1$. Bombieri showed in [20] that, in the case of Godeaux surfaces, $|TorsT|\le 5$. Reid in [9] proved that $TorsT\cong {\mathbb{Z}}_m$ and also gave a complete description of the cases ${\mathbb{Z}}_3$, ${\mathbb{Z}}_4$, ${\mathbb{Z}}_5$.

Let T be a Godeaux surface with $TorsT={\mathbb{Z}}_4:=⟨\sigma :{\sigma }^4=1⟩$, and $S\to T$ be an etale Galois cover such that $q\left(S\right)=0$, $p_g\left(S\right)=3$, and $K_S^2=4$. The canonical ring of S is given by

$$\begin{array}{ccc}\hfill R(S,K_S)& =& \underset{n\ge 0}{⨁}{H}^0(S,\mathcal{O}\left(n{K}_S\right))\hfill \end{array}$$

(29)

$$\begin{array}{ccc}& =& \underset{n\ge 0,\sigma \in TorsT}{⨁}{H}^0(T,\mathcal{O}(n{K}_T+\sigma ))\hfill \end{array}$$

(30)

$$\begin{array}{ccc}& =& k[x_1,x_2,x_3,u_1,u_3]/(f_4,g_4),\hfill \end{array}$$

(31)

where $x_j\in H^0\left({\mathcal{O}}_T(K+j)\right)$, $u_j\in H^0\left({\mathcal{O}}_T(2K+j)\right)$. Moreover, the relations $f_4$ and $g_4$ are invariant and anti-invariant quartics, respectively [9].

Finding a non-singular conic on T is the same as finding a non-singular conic $\Gamma$ on the ${\mathbb{Z}}_4$-cover S such that the sets $\Gamma ,\sigma ·\Gamma ,{\sigma }^2·\Gamma ,{\sigma }^3·\Gamma$ are mutually disjoint. It is not a straightforward task to find $f_4,g_4$ containing four desired families of conics. Consider a conic given by the image of $\varphi :{\mathbb{P}}_{u,v}^1\to \mathbb{P}(1^3,2^2),$ defined by

$$p\mapsto (x_1\left(p\right):x_2\left(p\right):x_3\left(p\right):u_1\left(p\right):u_3\left(p\right)),$$

where $x_1,x_2,x_3\in {Sym}^2⟨u,v⟩,u_1,u_3\in {Sym}^4⟨u,v⟩$. Let $D_4$ be a quartic in $\mathbb{P}(1^3,2^2)$; restricting $D_4$ to $Im\varphi$ gives a polynomial of degree 8 and, hence, imposes 9 conditions on the coefficients of $D_4$. Hence, if we impose three general conics, we can only expect to find a three-dimensional family of quartics, and, if we fix four general conics, then we expect to obtain none. Another way to define a conic in $\mathbb{P}(1^3,2^2)$ is the intersection of three quadrics. The following Lemma discusses this situation.

Lemma 3.

A general quartic $D_4$ in $\mathbb{P}(1^3,2^2)$ contains a 6-dimensional family of conics.

Proof. 

We assume that a conic in $\mathbb{P}(1^3,2^2)$ is given by the intersection of three quadrics. Consider the incidence variety

$$I:=\left\{(D_4,\Gamma )|D_4\in H^0(\mathbb{P}(1^3,2^2),\mathcal{O}\left(4\right)),\Gamma \in Gr(3,V),\Gamma \subset D_4\right\}$$

(32)

where $V=H^0(\mathbb{P}(1^3,2^2),\mathcal{O}\left(2\right))$, with two projections, ${\pi }_1:I\to H^0(\mathbb{P}(1^3,2^2),\mathcal{O}\left(4\right))$, and ${\pi }_2:I\to Gr(3,V)$. Here, $dim{H}^0(\mathbb{P}(1^3,2^2),\mathcal{O}\left(4\right))=30$, and $dim{H}^0(\mathbb{P}(1^3,2^2),\mathcal{O}\left(2\right))=8$, implying $dimGr(3,V)=15$.

For a fixed $\Gamma \in Gr(3,V)$, the fibre of ${\pi }_2$ imposes nine conditions on $D_4$. The fibre has dimension 21-1, which makes the dimension of I to be 15+20. Hence, the result is proven. □

To construct our required deformations, we use sixfolds, as constructed in Section 4.

Lemma 4.

There exist two deformations ${\Phi }^i:\mathcal{S}\to {\Delta }_i$, for $i=0,1$, such that the fibres are etale Galois covers of the Godeaux with ${\pi }_1\cong {\mathbb{Z}}_4$. Moreover, the central fibre, denoted as $S_0^i$, contains four disjoint conics permuted by the action of ${\mathbb{Z}}_4$.

Proof. 

Using deformations ${\Psi }^i:\mathcal{W}\to {\Delta }_i$, we can further define two deformations ${\Phi }^i:\mathcal{S}\to {\Delta }_i$, such that the general fibre is

$${\left({\Phi }^i\right)}^{-1}\left(t\right)=\left({\cap }_{m=0}^1{q}_{2m}\cap p_{2m+(i-1)}\right)\cap {\left({\Psi }^i\right)}^{-1}\left(t\right),$$

(33)

where the $q_n$s and $p_n$s are quadrics belonging to the following eigenspaces (see Equation (6)):

$$q_{2m}\in U_2\left(g^{2m}\right),p_{2m+(i-1)}\in U\left(g^{2m+(i-1)}\right)\mathrm{for}m=0,1.$$

(34)

The central fibres are given by

$$S_0^i=\left({\cap }_{m=0}^1{q}_{2m}\cap p_{2m+(i-1)}\right)\cap W_0^i\subset \mathbb{P}(1^3,2^6).$$

(35)

Under some appropriate projective transformation (which eliminates four weight 2 variables using four quadric $q_n$s and $p_n$s), all fibres become an intersection of two quartics in $\mathbb{P}(1^3,2^2)$, one invariant and the other invariant. Thus, the central fibres $S_0^i$ are etale Galois covers of the Godeaux surface, containing the following conics:

$$C_m^i={\cap }_{m=0}^1(q_{2m}\cap p_{2m+(i-1)})\cap {\Gamma }_m^i\subset \mathbb{P}(1^3,2^6),\mathrm{for}0\le m\le 3,$$

(36)

where the ${\Gamma }_m^i$ are given in (15), which become conics under some appropriate projective transformation. Furthermore, the conics are permuted by the group action as follows:

$$C_0^i\mapsto C_1^i\mapsto C_2^i\mapsto C_3^i\mapsto C_0^i.$$

(37)

□

Theorem 3.

There exist two deformations of Godeaux surface T with fundamental group ${\pi }_1\cong {\mathbb{Z}}_4$, such that each central fibre contains a conic.

Proof. 

From Lemma 4, we have deformations ${\Phi }^i:\mathcal{S}\to {\Delta }_i$, for $i=0,1$, such that the fibres are etale Galois covers of the Godeaux with ${\pi }_1\cong {\mathbb{Z}}_4$. Moreover, the fibres of ${\Phi }^i$ are invariant under the respective ${\mathbb{Z}}_4$ actions. The general fibres ${\left({\Psi }^i\right)}^{-1}$ are non-singular and the action of ${\mathbb{Z}}_4$ is fixed-point-free [9]. As such, there exist deformations ${\Theta }^i$ such that the general fibre is ${\left({\Theta }^i\right)}^{-1}\left(t\right)={\left({\Phi }^i\right)}^{-1}\left(t\right)/{\mathbb{Z}}_4$. For central fibres, namely, $S_0^i$, we proceed as follows.

We first show that $S_0^i$ are non-singular. The surface $S_0^1$ is given by

$$S_0^1:\mathbb{V}\left(q_0,q_2,p_0,p_2,F_0^1,G_0^1\right)\subset \mathbb{P}(x_1,x_2,x_3,u_0,\cdots ,u_3,w_0,w_1),$$

(38)

where, from (11), we have

$$F_0^1=R_{1,0}{R}_{1,1}-{\displaystyle \frac{1}{2}}(Q_{1,0}{Q}_{1,2}+Q_{1,1}{Q}_{1,3}),G_0^1=Q_{1,0}{Q}_{1,2}-Q_{1,1}{Q}_{1,3},$$

(39)

Using quadrics $q_0,p_0,q_2,p_2$, given in (34), we write $u_0,w_0$ in terms of $x_2^2,x_1{x}_3$, and $u_2,w_2$ in terms of $x_1^2,x_3^2$ (see Equation (6)). The above quartics become the general elements of the following vector spaces:

$$F_0^1\in ⟨x_1^4,x_2^4,x_3^4,x_1{x}_2^2{x}_3,x_1^2{x}_3^2,u_1{u}_3⟩,G_0^1\in ⟨x_1^2{x}_2^2,x_1^3{x}_3,x_2^2{x}_3^2,x_1{x}_3^3,u_1^2,u_3^2⟩.$$

(40)

By observing the monomials, we can say that the linear system of quartics has an empty base locus; hence, it is quasi-smooth. Moreover, none of the ambient singularities lie on $S_0^1$. Hence, $S_0^1$ is non-singular. On the same lines, we show that the conics, given in (36), are non-singular. Moreover, (37) shows that the conics are permuted by the action of ${\mathbb{Z}}_4$. It remains to be shown that there is a fixed-point-free action of ${\mathbb{Z}}_4$ on $S_0^i$, $i=1,2$. The fixed locus of the action of ${\mathbb{Z}}_4$ on $\mathbb{P}(x_1,x_2,x_3,u_0,\cdots ,u_3,w_0,w_1)$, defined in (5), is given belowL

$$\begin{array}{cc}\hfill \mathrm{for}i=1;& {\mathbb{P}}_{u_0,w_0}\bigsqcup {\mathbb{P}}_{x_1,u_1}\bigsqcup {\mathbb{P}}_{x_2,u_2,w_2}\bigsqcup {\mathbb{P}}_{x_3,u_3},\end{array}$$

(41)

$$\begin{array}{cc}\hfill \mathrm{for}i=2;& {\mathbb{P}}_{u_0}\bigsqcup {\mathbb{P}}_{x_1,u_1,w_1}\bigsqcup {\mathbb{P}}_{x_2,u_2}\bigsqcup {\mathbb{P}}_{x_3,u_3,w_3}.\end{array}$$

(42)

For $i=1$, using $q_0,p_0,$ we can express $u_0,w_0$ in terms of $x_2^2,x_1{x}_3$ so any point of ${\mathbb{P}}_{u_0,w_0}$ does not lie on $S_0^1$. The presence of the monomial term $x_2^4$ in $F_0^1$ and the expression of $u_2,w_2$ in terms of $x_1^2,x_3^2$ using quadrics $q_2,p_2$ guarantees that no point from ${\mathbb{P}}_{x_2,u_2,w_2}$ lies on $S_0^1$. The presence of $x_1^4,u_1^2$ and $x_3^4,u_3^2$ implies that the points of ${\mathbb{P}}_{x_1,u_1}$ and ${\mathbb{P}}_{x_3,u_3}$ have empty intersection with $S_0^1$, respectively. The other case is similar. Hence, the central fibres of $\Theta$ are $S_0^i/{\mathbb{Z}}_4$, which is a deformation of the Godeaux surface with ${\pi }_1\cong {\mathbb{Z}}_4$ containing a family of conics. □

6. Constructing Campedelli Surfaces from Godeaux with ${\mathbf{\pi }}_{\mathbf{1}}\cong {\mathbb{Z}}_{\mathbf{4}}$

A Campedelli surface is a surface of general type with $p_g=q=0$, and the order of the algebraic fundamental group ${\pi }_1^{\mathrm{alg}}$ is at most 9 [21]. Our focus is on Campedelli surfaces with $|{\pi }_1^{\mathrm{alg}}|=8$.

Theorem 4

([12]). Let X be a Campedelli surface, and $\pi :Z\to X$ be an etale cover of degree 8. The canonical model $\overline{Z}$ of Z is isomorphic to a complete intersection of four quadrics $\overline{Z}={\cap }_{i=1}^4{Q}_i\subset {\mathbb{P}}^6$. Moreover, Z is the universal cover of X and the covering group $G=Gal(Z/X)$ is the topological fundamental group ${\pi }_{1}X$.

We denote by $X^i$ the Campedelli surfaces with fundamental groups $G^1:={\pi }_1\left(X^1\right)\cong {\mathbb{Z}}_4\times {\mathbb{Z}}_2$ and $G^2:={\pi }_1\left(X^2\right)\cong {\mathbb{Z}}_8$. Let $Z^i\to X^i$ be the etale Galois cover for $i=1,2$, such that $p_g\left(Z^i\right)=7,K_{Z^i}^2=16$.

Lemma 5.

Unprojecting $C_m^i\subset S_0^i$, for $0\le m\le 3$, we obtain surfaces $Y_0^i$ with $p_g\left(Y_0^i\right)=3$ and $K_{Y_0^i}^2=8$ containing $4\times {\displaystyle \frac{1}{4}}(1,1)$ singularities with a ${\mathbb{Z}}_4$ action. The singularities form an orbit under the action.

Proof. 

The surfaces $S_0^i$ (35) have invariants $p_g\left(S_0^i\right)=3$, $K_{S_0^i}^2=4$, containing four conics $C_m^i\subset S_0^i$ (36) permuted by ${\mathbb{Z}}_4$ action (37). Since

$$S_0^i=\left({\cap }_{m=0}^1{q}_{2m}\cap p_{2m+(i-1)}\right)\cap W_0^i.$$

and

$$C_m^i=\left({\cap }_{m=0}^1{q}_{2m}\cap p_{2m+(i-1)}\right)\cap {\Gamma }_m^i,\mathrm{for}0\le m\le 3,$$

the unprojection $C_m^i\subset S_0^i$ can be obtained by using the unprojection of ${\Gamma }_m^i\subset W_0^i$ given in (22). Using key varieties $W_4^i$, the surfaces after the unprojection of all four conics are given by

$$Y_0^i=\left({\cap }_{m=0}^1{q}_{2m}\cap p_{2m+(i-1)}\right)\cap W_4^i.$$

(43)

Using [6] (Lemma 2.3), we obtain $p_g\left(Y_0^i\right)=3$ and $K_{Y_0^i}^2=8$. The four singularities form an orbit because of the action of ${\mathbb{Z}}_4$ on the unprojection variables given in (25). □

Theorem 5.

There exist $\mathbb{Q}$-Gorenstein smoothings ${{\rm Y}}^i:{\mathcal{Y}}^i\to {\Lambda }^i$ of $Y_0^i$ such that the fibres are invariant under the respective group actions of ${\mathbb{Z}}_4$.

Proof. 

To obtain a $\mathbb{Q}$-Gorenstein smoothing of $Y_0^i$, we move the quadric sections (34); the new quadrics are given as

$$\begin{array}{ccc}\hfill q_{2m}^{\prime }& :=& q_{2m}+c_m\sum _{j=1}^4{\epsilon }^{2mj}{s}_{j-1}^{\left(i\right)},m=0,1\hfill \\ \hfill p_{2m+(i-1)}^{\prime }& :=& p_{2m+(i-1)}+d_{m,i}\sum _{j=1}^4{\epsilon }^{j\left(3\right(i-1)+2m)}{s}_{j-1}^{\left(i\right)},m=0,1.\hfill \end{array}$$

where $c_m,d_{m,i}$ are parameters. It can be seen that

$$q_{2m}^{\prime }\in U_2\left(g^{2m}\right),p_{2m+(i-1)}^{\prime }\in U\left(g^{2m+(i-1)}\right)\mathrm{for}m=0,1,$$

(44)

and, hence, the general fibre, given below, is invariant under the action of ${\mathbb{Z}}_4$:

$$Y^i:={\left({{\rm Y}}^i\right)}^{-1}\left(t\right)=\left({\cap }_{m=0}^1{q}_{2m}^{\prime }\cap p_{2m+(i-1)}^{\prime }\right)\cap W_4^i.$$

(45)

The coordinate ring of the general fibre is given by

$$R(Y^i,K_{Y^i})=k[x_1,x_2,x_3,u_k,w_0,w_1,s_k^{\left(i\right)}]/(q_{2j}^{\prime },p_{2j+(i-1)}^{\prime },E),$$

(46)

where $j=0,1$, $0\le k\le 3$, and E are $2\times 2$ minors of Matrix (28).

The sixfold $W_4^i$ is obtained through unprojection from $W_0^i$, which is Gorenstein since it is a complete intersection. Also, an unprojection of a Gorenstein is a Gorenstein. Hence, $Y^i$ is Gorenstein, being a complete intersection with a Gorenstein. □

Theorem 6.

The fundamental group of the general fibre $Y^i$ is ${\mathbb{Z}}_2$. Moreover, there exists an etale Galois cover $Z^i$ of $Y^i$ given as an intersection of four quadrics in ${\mathbb{P}}^6$.

Proof. 

For $i=1$, the key variety $W_4^1$ is constructed in terms of the general elements of $Q\in H^0(W,{\mathcal{L}}^{\otimes 2})$ and $R_1\in U_{2,1}$. We can take

$$\begin{array}{ccc}{R}_1& =& w_0+w_1,\\ Q& =& u_0+u_1+u_2+u_3,\end{array}$$

(47)

with orbits $\{Q_{1,0},Q_{1,1},Q_{1,2},Q_{1,3}\}$ and $\{R_{1,0},R_{1,1}\}$, such that

$$\begin{array}{ccc}\hfill Q_{1,0}& =& u_0+u_1+u_2+u_3,\hfill \\ \hfill Q_{1,1}& =& \epsilon u_0+\epsilon u_1+{\epsilon }^2{u}_2+{\epsilon }^3{u}_3,\hfill \\ \hfill Q_{1,2}& =& u_0+{\epsilon }^2{u}_1+u_2+{\epsilon }^2{u}_3,\hfill \\ \hfill Q_{1,3}& =& u_0+{\epsilon }^3{u}_1+{\epsilon }^2{u}_2+\epsilon u_3,\hfill \\ \hfill R_{1,0}& =& w_0+w_1,\hfill \\ \hfill R_{1,1}& =& w_0+{\epsilon }^2{w}_1.\hfill \end{array}$$

Let $T^i$ be the square matrix of the coefficients of $Q_{1,0}\cdots ,Q_{1,3},R_{1,0},R_{1,1}$ with respect to variables $u_0,u_1,u_2,u_3,w_0,w_1$. The $T^i$ are non-singular so we can express $u_0,\cdots ,u_3,w_0,w_1$ in terms of the symbols $Q_{1,0}\cdots ,Q_{1,3},R_{1,0},R_{1,1}$, and use these as our new variables. Similarly, for $i=2$, the symbols become $Q_{2,0}\cdots ,Q_{2,3},R_{2,0},R_{2,1}$.

Let $q_{2m}^{″},p_{2m+(i-1)}^{″}$, for $m=0,1$, be the quadrics in terms of $Q_{i,0}\cdots ,Q_{i,3},R_{i,0},R_{i,1}$. Then,

$$R(Y^i,K_{Y^i})\cong k[x_1,x_2,x_3,s_0^{\left(i\right)},\cdots ,s_3^{\left(i\right)},Q_{i,0},\cdots ,Q_{i,3},R_{i,0},R_{i,1}]/(q_0^{″},q_2^{″},p_{i-1}^{″},p_{i+1}^{″},E),$$

(48)

where E is given as the $2\times 2$ minors of the following matrix:

$$\left(\begin{array}{cccc}{s}_3^{\left(i\right)}& Q_{i,1}& R_{i,1}& Q_{i,2}\\ & s_2^{\left(i\right)}& Q_{i,0}& R_{i,0}\\ Sym& & s_1^{\left(i\right)}& Q_{i,3}\\ & & & s_0^{\left(i\right)}\end{array}\right).$$

(49)

Thus,

$$R(Y^i,K_{Y^i})\cong {\left[k[x_1,x_2,x_3,z_j]/({\mathcal{Q}}_0,{\mathcal{Q}}_2,{\mathcal{P}}_{i-1}^{″},{\mathcal{P}}_{i+1}^{″})\right]}^{{\mathbb{Z}}_2},$$

(50)

where ${\mathcal{Q}}_0,{\mathcal{Q}}_2,{\mathcal{P}}_{i-1}^{″},{\mathcal{P}}_{i+1}^{″}$ are the quadrics in our new variables. Let $Z^i$ be the surface defined by these four quadrics. The surfaces $Z^i$ are smooth by Bertini’s theorem. The action of ${\mathbb{Z}}_2$ on $Z^i$ is given by

$$x_k\mapsto x_k,z_j\mapsto -z_j,\forall k,j.$$

(51)

Moreover, the group ${\mathbb{Z}}_4$ acts on $Z^i$ as (5) and, from the matrix $T^i$, we have

$$z_3\mapsto z_2\to z_1\to z_0\to {(-1)}^i{z}_3.$$

(52)

□

Corollary 1.

The surface $Z^i$, together with the action of $G^i$, gives a construction of Campedelli with ${\pi }_1\cong G^i$.

Proof. 

The action of $G^1\cong Z_4\times {\mathbb{Z}}_2$ on $Z^1\subset {\mathbb{P}}_{x_1,x_2,x_2,z_1,\cdots ,z_4}^6$ is obtained by combining the action of ${\mathbb{Z}}_2$ given in (51) and of ${\mathbb{Z}}_4$ given as

$$z_3\mapsto z_2\to z_1\to z_0\to -z_3,x_i\mapsto {\epsilon }^i{x}_i.$$

(53)

This gives a construction of Campedelli with fundamental group $G^1$ (c.f. page 13 in [13]). The situation is similar for $i=2$. □

7. Conclusions

We constructed two deformations of the Godeaux surface with ${\mathbb{Z}}_4$, each containing a family of conics in the central fiber. By using $\mathbb{Q}$-Gorenstein smoothing and unprojection techniques, we linked families of surfaces birational to these Godeaux surface to two distinct components of the Campedelli surfaces with fundamental group of order 8.

These deformations provide insight into the birational geometry of Godeaux and Campedelli surfaces. While our study focuses on explicit constructions using deformation and unprojection methods, our results may have broader implications for the study of algebraic cycles and cohomological invariants, potentially offering new examples relevant to motivic cohomology.

Additionally, our work explores the structure of polynomial rings under the action of the fundamental group. By using graded rings with group actions, we provide explicit constructions. This provides a new perspective on the interplay between group actions and the study of varieties.