The Various Radii Circle Packing Problem in a Triangle

Abstract

Malfatti’s problem is the problem of fitting three circles into a triangle such that they are tangent to each other and each circle is also tangent to a pair of the triangle’s sides. This problem has been extended to include T_n = 1 + 2 + … + n circles inside the triangle with special tangency properties among the circles and triangle sides; this problem is referred to as the extended Malfatti problem or the Tri(T_n) problem. In the extended Malfatti problem, the number of circles in the triangle is a triangle number because the tangency properties between the internal circles and the three sides of the triangle have a special type of structure; that is, the corner circle is tangent to two sides of the triangle and two other circles, the boundary circles are tangent to one side of the triangle and four other circles, and the inner circles are always tangent to six other circles. The circles we find in the extended Malfatti problem have the following property: the smallest and largest radii of the circles differ to a great extent. In the study presented herein, we propose algorithms to solve the problem that the tangency properties between the circles and the sides of the triangle are not fixed, so that the number of circles in the triangle is not necessarily a triangle number. The purpose of this change is to attempt to establish the radii of the circles in the triangle within a small range.

1. Introduction

Before we explain the problem in detail, we will introduce related materials such as the extended Malfatti problem.

1.1. Malfatti’s Problem and the Extended General Malfatti Problem

The circles-in-an-area problem has been investigated for a number of years. Circles may comprise equal circles or circles of different radii. The area can be a triangle [1,2,3,4], square [5], circle [6], or other area [7].

In 1803, Gian Francesco Malfatti [8] proposed the following problem: how to find the maximum total volume of three cylindrical columns out of a triangular prism of marble.

Identically, the problem can be recognized as finding three circles that fit into a specific triangle and ensuring that the total area is at its maximum. Malfatti theorized that the solution was to make three circles tangent to each other and to make each circle tangent to two sides of the triangle. One case is shown in Figure 1 [9].

Figure 1. Malfatti’s problem.

In fact, Malfatti’s hypothesis is incorrect. In 1930, Lob and Richmond [10] established a method to obtain a larger area of some triangles by using a greedy algorithm that inscribes a single circle of the maximal radius within the triangle; inscribes a second circle within one of the three remaining corners of the triangle—the one with the smallest angle; and inscribes a third circle within the largest of the five remaining areas. The difference in area for an equilateral triangle is roughly over 1% (as shown in Figure 2) [11]; however, as Howard Eves (1946) stated, for an isosceles triangle with a very sharp apex, the optimal solution has nearly twice the area of the Malfatti circles (as shown in Figure 3) [12]. As stated in the 1960s, later proven firmly, the Lob–Richmond procedure always gives the largest area and solves the problem. In the literature, Malfatti’s hypothesis has become understood as Malfatti’s problem [13,14,15].

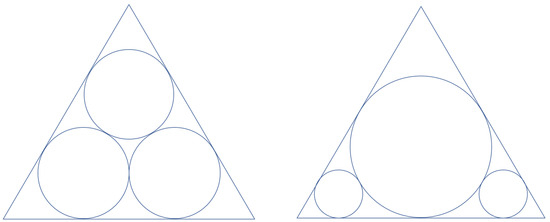
Figure 2. Circles in an equilateral triangle.

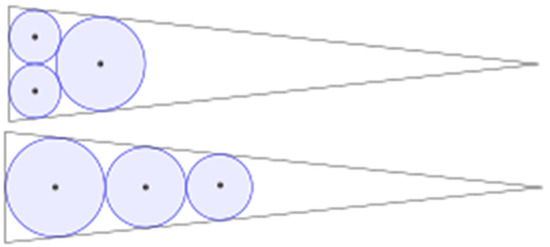
Figure 3. Malfatti’s problem and the max area problem.

There are several known solutions to Malfatti’s problem. In their work, Fukagawa and Pedoe [15] state that Chokuen Ajima actually formulated and solved Malfatti′s problem. For a detailed history of the problem and explanations of various solutions and generalizations, interested readers are referred to [16,17,18].

The extended Malfatti problem [19] aims to determine T_n circles that can be inscribed inside a triangle while maintaining tangency among the circles and the triangle’s sides. When considering the problem with T_n = ${\sum }_1^{n}i$ circles, it is referred to as the Tri(T_n) n problem (as shown in Figure 4). Notably, when n = 1, the problem seeks to find the inscribed circle of a triangle, and when n = 2, it is precisely Malfatti’s problem.

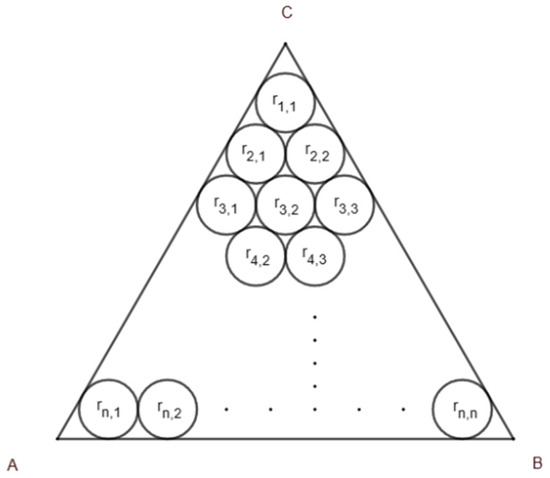
Figure 4. The tangency property of the Tri(T_n) problem.

There are closed forms for finding inscribed circles and Malfatti’s circles. Therefore, when n = 1 or n = 2, it is easy to propose a constant time algorithm to solve these problems. Chiang [19] proposed algorithms to solve the Tri(T_n) problem when n > 2.

There are three types of circles—corner circles, edge circles, and inner circles. Corner circles are tangent to two other circles and two sides of the triangle (Figure 5a). Edge circles are tangent to four other circles and one side of the triangle (Figure 5b). Inner circles are tangent to six other circles. Let SA(C) represent the sum of the surrounding angles for circle C. Then, SA(C) is the sum of 4, 5, and 6 angles, as shown in Figure 5a, Figure 5b, and Figure 5c, respectively. Specifically, if C is a corner circle, then SA(C) = α₁ + α₂ + α₃ + α₄, as depicted in Figure 5a. The definition of SA(C) is similar when C is an edge circle or an inner circle.

Figure 5. Calculation of the total surrounding angles for 3 types of circles. (a) Corner Circle; (b) Edge Circle; (c) Inner Circle.

Chiang proposed an algorithm [19] that requested three vertices of the triangle and a value n as the inputs. From these inputs, we know the triangle (from three vertices), number of circles (from n), and the tangency relation between the circles and the sides of the triangle (from n). However, we do not know the radii of the circles. The initial radii are given for all circles and since then, the algorithm adjusts the radii so that SA(C) is equal to 2π for all circles, C. Chiang uses the following approach to adjust the radii: If SA(C) is greater than 2π, the radius of C should be enlarged. If SA(C) is less than 2π, the radius of C should be reduced. This approach is repeated until SA(C) is equal to 2π for all circles, C [19]. There are different methods to compute SA(C) when C is a corner circle, an edge circle [19], or an inner circle [20].

When considering the Tri(T₂) problem, only corner circles are involved in this problem (see Figure 1). Assuming that these three circles have radii r₁, r₂, and r₃, when we multiply these radii by a constant k, the angle computation (in Figure 5a) for α₁, α₂, α₃, and α₄ shows the same result. This means that there are infinitely many solutions in this case. One more constraint is required to find one solution only. The constant k can be computed by comparing the length of one side of the triangle with the corresponding side of the triangle bounded by these three circles, as shown in Figure 6. The constant k is referred to as the change ratio for the current solution and the real solution.

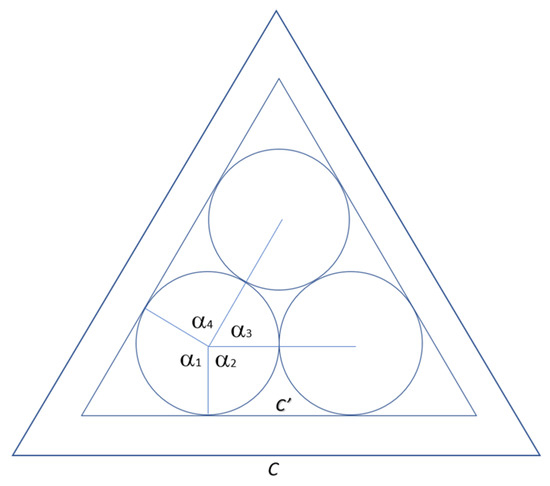
Figure 6. Tri(T₂) problem; change ratio = c/c′.

The Algorithm 1 proposed by Chiang [19] is as follows:

Algorithm 1. Chiang’s Algorithm

1. The coordinate of three vertices A, B, and C are inputted; angles A, B, and C, as well as edge length c, are calculated; 2. A tolerance variable eps = 0.01 is set; 3. An initial radius list r = [ri,j| where 1 ≤ i ≤ n, 1 ≤ j≤ i.] is created; 4. A surrounding angle list is created for all circles Ci,j (whose associated radius is ri,j) and they are named θi,j; 5. While one of |θi,j − 2| > eps: 5.1       The radius list is modified; all radii values are computed by the current radii and are assigned to the new radius list concurrently; 5.2       A surrounding angle list is calculated for all circles Ci,j (using the new radii) and assign to θi,j; 5.3       From the radius list, the change ratio is calculated and the radius list from the change ratio is modified; 6 The result is displayed.

The result for the Tri(T_n) problem, n = 2, 3, 4, 8, 30, using Chiang’s algorithm [19] is shown in Figure 7.

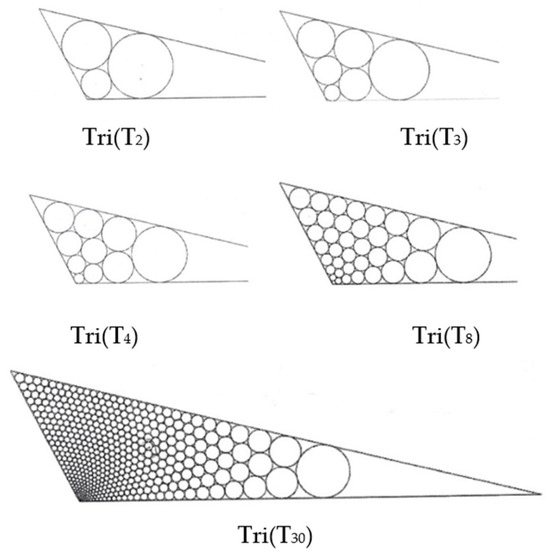
Figure 7. Tri(T_n) problem, where n = 2, 3, 4, 8, and 30.

1.2. Problem Statement

We would like to take the main concept of Chiang’s algorithm and propose a new algorithm to ensure that the radii of these circles have a small range. Based on the results shown in Figure 7, the smallest angle of a triangle corresponds to the biggest circle. Conversely, the largest angle corresponds to the smallest circle, especially for the acute angle. In the circle packing area, some problems fix the radius of the circles inside the specified area or at least in similar-sized circles. Therefore, we propose a new algorithm based on the concept of Chiang’s algorithm to ensure that the circle’s radii have a small range. In Chiang’s algorithm, because the structure of circles inside the triangle is fixed, it is not necessary to establish a tangency graph (explained in further detail below) before finding the solution.

Circle packing inside a triangle can be applied to some applications, such as wireless transmitter location design. The centers of the circles are the position of the transmitter locations and the radii are the distance the transmitter can transmit. If the radii of the circles vary, different types of transmitters with different transmission distances are needed. Therefore, our aim is for the radius range of these circles to be small. The same concept can be applied in radar location design so that nothing can pass this triangle area. Other applications include logo design and circle-cutting design to reduce material wastage. There is an intermediate process needed to create a triangle mesh; therefore, many applications of mesh can also be treated in the same manner as the application in this paper. We will give an example at the end of this paper.

This paper comprises four sections. In Section 1, Malfatti’s problem is illustrated and extended. In Section 2, some terms, derived theories, and proposed algorithms for the new problem are defined. In Section 3, details of algorithm implementation are described. In Section 4, conclusions are drawn.

2. Terms, Theories, and Algorithms

Our aim is to find circles inside a triangle, where there are specified tangency constraints between these circles and the three sides of the triangle. We use a tangency graph to show the tangency constraints. Consider a graph G (V, E), where V corresponds to the vertices that represent the circles or the sides of the triangles and E represents the edges connecting the vertices. When an edge connects two vertices, this means that these two geometric objects are tangent to each other. That is, the circle is externally tangent to the circle if these two geometric objects are circles or if the circle is tangent to the side of the triangle. When a circle is tangent to two, one, or zero sides of a triangle, we refer to it as a corner circle, edge circle, or inner circle, respectively.

We use Tri(T₂) and its tangency graph G(V, E) as an example (see Figure 8a), where V = {c₁, c₂, c₃, e₁, e₂, e₃} and E = {(c₁, c₂), (c₁, c₃), (c₂, c₃), (c₁, e₂), (c₁, e₃), (c₂, e₁), (c₂, e₃), (c₃, e₁), (c₃, e₂)}, as shown in Figure 8b. To see the edge circle or corner circle tangent to the side of the triangle more clearly, we drew a tangency graph, as shown in Figure 8c.

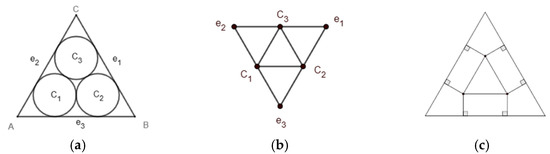
Figure 8. Tri(T₂) problem and its tangency graphs. (a) Tri(T₂) problem; (b) Tangency graph; (c) Our tangency graph.

The main concept of the new proposed algorithm is to generate a tangency graph, to find solution radii for all circles that satisfy the constraints specified by the tangency graph, and then to display them. The purpose of this algorithm is to find circles with a small range of radii. At the start of the process, it is necessary to set a real number r, with the aim of generating circles inside the triangle that have a radius near r. Our proposed algorithm comprises four parts, including data inputting, the generation of a tangency graph, the use of Chiang’s algorithm, and result generation.

Thus, the main concept of the proposed Algorithm 2 is as follows:

Algorithm 2. Proposed Algorithm

1. The coordinates of three vertices, A, B, and C are input; the angles A, B, and C, as well as the edge length c, are calculated. 2. A tolerance variable eps = 0.0001, epsR = 0.3 is set. A value r is set. A value of i = 1 is set. 3. The one-offset of the triangle is generated. It is named Ti. 3.1       The vertices on Ti are generated. 3.2       The edges for vertices on Ti are generated, including the edges connecting two neighbors of vertices A, B, and C. 3.3       Edges for vertices on Ti to the side of the triangle $\overline{AB}$, $\overline{BC}$, and $\overline{CA}$ are generated. 4. While Ti does not satisfy some conditions: 4.1       The $\sqrt{3}$R-offset of the triangle Ti is generated and it is named Ti+1. 4.2       The vertices and edges on Ti+1 are generated, as performed in steps 3.1 and 3.2. 4.3       The edge connect vertices on Ti to vertices on Ti+1 are generated 4.4       i = i + 1 5. It is decided whether the last triangle contains only one vertex (circle) or three vertices (circles). The last triangle is named Tlast. 6. The edge of the graph is established to connect Ti−1 and Tlast. 7. Chiang’s algorithm is used with tolerance eps to find the solution. 8. The results are displayed.

Steps one and two are the inputs of the algorithm; steps three, four, five, and six generate the tangency graph of this problem; and step seven involves the use of Chiang’s algorithm to find the solution for the tangency graph. The final step involves displaying the results.

We will describe the above algorithm in more detail, including the solution to the following four problems:

• How to find the R-offset of a triangle (step 3, 4.1).
• How to construct the tangency graph (vertices and edges) for the same layer.
• How to construct the tangency (vertices and edges) for two consecutive layers.
• How to stop the while loop in step 4.

The above four problems will be described in Section 2.1, Section 2.2, Section 2.3 and Section 2.4.

2.1. Offset a Triangle

Consider three different terms—line, ray, and line segment. There is no endpoint for a line, one endpoint for a ray, and two endpoints for a line segment. Consider the parametric forms of a line, ray, and line segment passing through two points, P₁ and P₂; these parametric forms are the same (1 − t) P₁ + tP₂ with different parameter ranges. There is a line, ray, and line segment when t∈R, t ≥ 0, and 0 ≤ t ≤ 1, respectively. Note that the ray has P₁ as its endpoint, denoted as Ray(P₁, P₂); with the orientation of Ray(P₁, P₂), we can define the left side and the right side of Ray(P₁, P₂). Let L = Ray(P₁, P₂); we denote the point P₁′ as the point moving P₁ to the left side of the Ray(P₁, P₂) R distance, and we denote P₁′ = Move(P₁, L, R). Ray(P₁′, P₂′), also denoted as Ray_r(P₁, P₂), is referred to as the R-offset of Ray(P₁,P₂).

Before providing a detailed description of the proposed algorithm, we present the following theorem:

Theorem 1. 

R-offset of a ray. Given Ray_r (P₁, P₂), where P₁ = (x₁, y₁) and P₂ = (x₂, y₂), the parametric form of Ray_r(P₁, P₂) is (1 − t)P₁ + tP₂ + r × n_L, $0\le t$, where n_L = ${\displaystyle \frac{1}{\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}}}$ ($y_1-y_2$, $x_2-x_1$). The implicit form for the line cover Ray_r(P₁, P₂) is a′x + b′y + c′ = 0, where a′ = (y₂ − y₁), b′ = (x₁ − x₂), and c′ = $-\left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|+\left(r\times \sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}\right)$.

Proof of Theorem 1. 

The direction of the ray is P₂ − P₁ = $(x_2-x_1,y_2-y_1)$. The two vectors n_L = ${\displaystyle \frac{1}{\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}}}(y_1-y_2,x_2-x_1)$ and n_R = ${\displaystyle \frac{1}{\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}}}(y_2-y_1,x_1-x_2)$ are perpendicular to P₂-P₁. These two vectors point to the left (n_L) and the right (n_R). We can move points on Ray(P₁, P₂) along the n_L direction R distance; therefore, the parametric form for Ray_r (P₁, P₂) is (1 − t) P₁ + tP₂ + R × n_L. Consider two points, P₁′ and P₂′, which are points P₁ and P₂, moving to left side of Ray(P₁, P₂); that is, P_i′ = (x_i′,y_i′) = P_i + R × n_L, I = 1, 2. The implicit form for Ray(P₁, P₂) is ax + by + c = 0, where a = y₂ − y₁, b = x₁ − x₂, and c = $-\left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|$. Let the R-offset of Ray(P₁, P₂) be denoted as Ray_r(P₁, P₂) = a′x + b′y + c′ = 0, where a′ = y₂′ − y₁′ = a, b′ = x₁′ − x₂′ = b, and c′ = $-\left|\begin{array}{cc}{x_1}^{\prime }& {y_1}^{\prime }\\ {x_2}^{\prime }& {y_2}^{\prime }\end{array}\right|$ = $\mathrm{c}+\left(r\ast \sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}\right)$. Thus, the implicit form of Ray_r(P₁, P₂) is (y₂ − y₁)x + (x₁ − x₂)y − $\left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|$ +$\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}\times \mathrm{R}$ = 0. □

Example 1. 

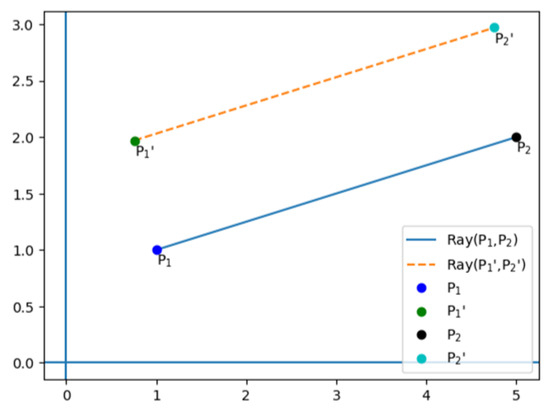
Given two points, P₁ = (1, 1) and P₂ = (5, 2), let L = Ray₁ (P₁, P₂). The points P₁′ = Move(P₁, L, 1) = (0.757, 1.970), and P₂′ = Move(P₂, L, 1) = (4.757, 2.970). In Figure 9, L is shown in blue with implicit form x + 4y + 3 = 0. Furthermore, Ray₁(P₁,P₂) = Ray(P₁′, P₂′) is shown in orange with implicit form x + 4y + 7.123 = 0. So, Ray₁(P₁, P₂) is the 1-offset of the ray from P₁ to P₂, and Ray(P₁′, P₂′) is the ray from P₁′ to P₂′; they are the same ray because P₁′ and P₂′ are the points that move P₁, P₂ to the left side of the ray from P₁ to P₂ for a distance equal to one.

Figure 9. R-offset of a ray.

We refer to Ray(P₁′, P₂′) as the R-offset of Ray(P₁, P₂).

The following theorem is taken directly from [21].

Theorem 2. 

Intersection of two lines from four points [11]. Given four points, P₁ (x₁, y₁), P₂ (x₂, y₂), P₃ (x₃, y₃), and P₄ (x₄, y₄), there are two lines, L₁ and L₂, where L₁ passes through P₁, P₂, and L₂ passes through P₃, P₄. Then, if $\left|\begin{array}{cc}\left(x_1-x_2\right)& \left(y_1-y_2\right)\\ \left(x_3-x_4\right)& {(y}_3-y_4)\end{array}\right|=0$, L₁, L₂ are parallel to each other. Otherwise, these two lines intersect each other at (x,y), where $x={\displaystyle \frac{\left|\begin{array}{cc}\left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|& \left|\begin{array}{cc}{x}_3& y_3\\ x_4& y_4\end{array}\right|\\ \left(x_1-x_2\right)& {(x}_3-x_4)\end{array}\right|}{\left|\begin{array}{cc}\left(x_1-x_2\right)& \left(y_1-y_2\right)\\ \left(x_3-x_4\right)& {(y}_3-y_4)\end{array}\right|}},y={\displaystyle \frac{\left|\begin{array}{cc}\left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|& \left|\begin{array}{cc}{x}_3& y_3\\ x_4& y_4\end{array}\right|\\ \left(y_1-y_2\right)& {(y}_3-y_4)\end{array}\right|}{\left|\begin{array}{cc}\left(x_1-x_2\right)& \left(y_1-y_2\right)\\ \left(x_3-x_4\right)& {(y}_3-y_4)\end{array}\right|}}.$

Theorem 3. 

Intersection of two R-offset rays from three points. Given Ray(P₁, P₂) and Ray(P₂, P₃), where Pi = (x_i,y_i) and I = 1, 2, 3, the intersection of Ray_r(P₁, P₂) and Ray_r(P₂, P₃) is (x, y) = (${\displaystyle \frac{{∆}_x}{∆}},{\displaystyle \frac{{∆}_y}{∆}}$) if $∆$ ≠ 0, where

$$∆=\left|\begin{array}{cc}\left(x_1-x_2\right)& \left(y_1-y_2\right)\\ \left(x_2-x_3\right)& {(y}_2-y_3)\end{array}\right|$$

(1)

$${∆}_x=\left|\begin{array}{cc}\left|\begin{array}{ccc}{x}_1& y_1& -r\\ x_2& y_2& -r\\ n_{12x}& n_{12y}& 1\end{array}\right|& \left|\begin{array}{ccc}{x}_2& y_2& -r\\ x_3& y_3& -r\\ n_{23x}& n_{23y}& 1\end{array}\right|\\ \left(x_1-x_2\right)& {(x}_2-x_3)\end{array}\right|$$

(2)

$${∆}_y=\left|\begin{array}{cc}\left|\begin{array}{ccc}{x}_1& y_1& -r\\ x_2& y_2& -r\\ n_{12x}& n_{12y}& 1\end{array}\right|& \left|\begin{array}{ccc}{x}_2& y_2& -r\\ x_3& y_3& -r\\ n_{23x}& n_{23y}& 1\end{array}\right|\\ \left(y_1-y_2\right)& {(y}_2-y_3)\end{array}\right|$$

(3)

$$n_{12}=(n_{12x}{n}_{12y})={\displaystyle \frac{1}{\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}}}(y_1-y_2,x_2-x_1)$$

(4)

$$n_{23}=(n_{23x}{n}_{23y})={\displaystyle \frac{1}{\sqrt{{(x_3-x_2)}^2+{(y_3-y_2)}^2}}}(y_2-y_3,x_3-x_2)$$

(5)

Proof of Theorem 3. 

Let L₁ = Ray(P₁, P₂), L₂ = Ray(P₂, P₃), L₃ = Ray_r(P₁, P₂), and L₄ = Ray_r(P₂, P₃). Let P₁′ = Move(P₁, L₁, r), P₂′ = Move(P₂, L₁, r), P₃′ = Move(P₂, L₂, r), and P₄′ = Move(P₃, L₂, r); then, P₁′ = P₁ + r × n₁₂, P₂′ = P₂ + r × n₁₂, P₃′ = P₂ + r × n₂₃, and P₄′ = P₃ + r × n₂₃, where n₁₂ = ${\displaystyle \frac{1}{\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}}}\left(y_1-y_2,x_2-x_1\right)$ and n₂₃ = ${\displaystyle \frac{1}{\sqrt{{(x_3-x_2)}^2+{(y_3-y_2)}^2}}}$($y_2-y_3$,$x_3-x_2)$. The proof can be easily derived using Theorem 2 with the following four points—P₁′, P₂′, P₃′_, and P₄′. □

$$\mathrm{Denote}∆=\left|\begin{array}{cc}{x}_1^{\prime }-x_2^{\prime }& y_1^{\prime }-y_2^{\prime }\\ x_3^{\prime }-x_4^{\prime }& y_3^{\prime }-y_4^{\prime }\end{array}\right|=\left|\begin{array}{cc}\left(x_1-x_2\right)& \left(y_1-y_2\right)\\ \left(x_2-x_3\right)& {(y}_2-y_3)\end{array}\right|$$

(6)

$${∆}_x=\left|\begin{array}{cc}\left|\begin{array}{ccc}{x}_1& y_1& -r\\ x_2& y_2& -r\\ n_{12x}& n_{12y}& 1\end{array}\right|& \left|\begin{array}{ccc}{x}_2& y_2& -r\\ x_3& y_3& -r\\ n_{23x}& n_{23y}& 1\end{array}\right|\\ \left(x_1-x_2\right)& {(x}_2-x_3)\end{array}\right|$$

(7)

$${∆}_y=\left|\begin{array}{cc}\left|\begin{array}{ccc}{x}_1& y_1& -r\\ x_2& y_2& -r\\ n_{12x}& n_{12y}& 1\end{array}\right|& \left|\begin{array}{ccc}{x}_2& y_2& -r\\ x_3& y_3& -r\\ n_{23x}& n_{23y}& 1\end{array}\right|\\ \left(y_1-y_2\right)& {(y}_2-y_3)\end{array}\right|$$

(8)

The intersection P(x, y) = (${\displaystyle \frac{{∆}_x}{∆}},{\displaystyle \frac{{∆}_y}{∆}}$) when $∆\ne 0$.

Example 2. 

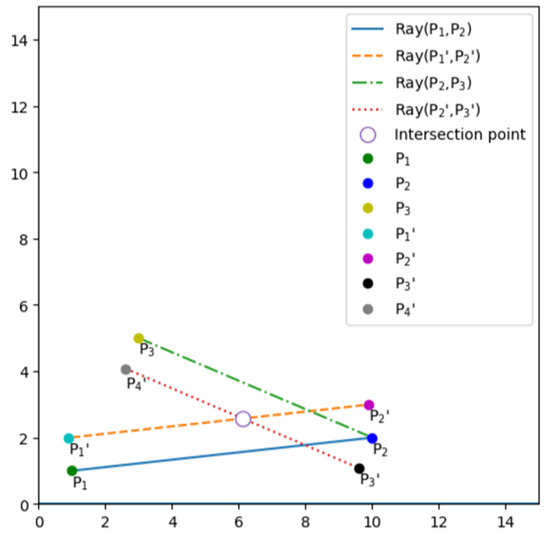
Given three points, P₁ = (1, 1), P₂ = (10, 2), and P₃ = (3, 5), P₁′ = (0.889, 1.993), P₂′ = (9.889, 2.993), P₃′ = (9.606, 1.080), and P₄′ = (2.606, 4.080). The intersection point P for Ray₁(P₁, P₂) and Ray₁(P₂, P₃) is at (6.119, 2.575), as shown in Figure 10.

Figure 10. Intersection of two R-offset rays from three points.

We denote P = Ray₁(P₁, P₂) ∩ Ray₁(P₂, P₃).

From △ABC, we can find three points—B′ = Ray_r(A,B) ∩ Ray_r(B,C), C′ = Ray_r(B,C) ∩ Ray_r(C,A), and A′ = Ray_r(C,A) ∩ Ray_r(A,B). △A′B′C′ is referred to as the R-offset triangle for △ABC.

Example 3. 

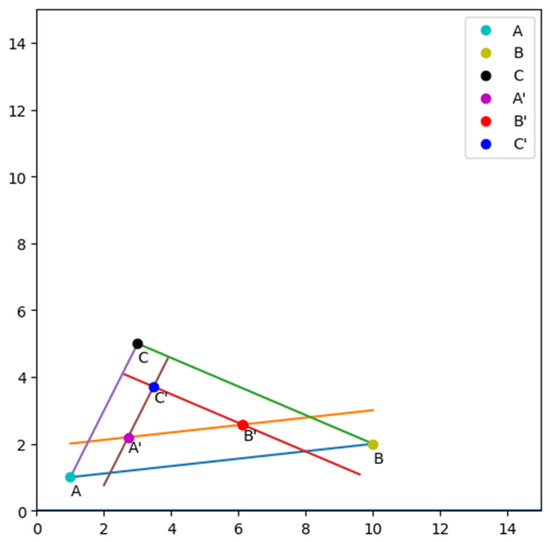
Given A = (1, 1), B = (10, 2), and C = (3, 5), the 1-offset triangle for ΔABC is a triangle with vertices A′ = (2.716, 2.196), B′ = (6.119,2.575), and C′ = (3.472, 3.709); see Figure 11.

Figure 11. The result of the R-offset triangle.

2.2. How to Construct Vertices and Edges on the Same Layer

The primary purpose of the proposed algorithm is to generate the tangency graph G (V, E) to ensure that circles in the triangle have a small range of radii. Thus, it was necessary to generate the vertices, as well as the edges that connect the vertices. We generated the vertices layer by layer and generated the edges for the same layer, as well as the edges that connect two consecutive layers. Given a triangle △ABC and circles with radius r, where r is much smaller than the shortest length of three sides of the triangle, and given that △A′B′C′ is the R-offset of △ABC, then the circles centered at the sides of △A′B′C′ with radius r are tangent to △ABC. At this stage, our aim is to find the vertices on edge A’B’ (steps one to three in the following description) and △A′B′C′ (steps four and five). Furthermore, the edges of these two consecutive layers, △ABC and △A′B′C′, must be generated (step six).

• Find n circles with radius r’, where r’ is close to r, so that these circles can be lined up tangent to two circles on the vertices A’ and B’ with radius r, as shown in Figure 12. That is, find integer n and r′ so that |r − r′| is at a minimum and 2(r + n ∗ r′) is equal to the length of A′B′.
  

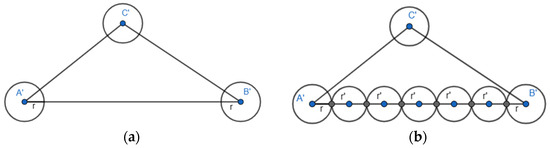  Figure 12. Vertex setup for one side of the triangle. (a) Add three vertices; (b) Find vertices in between one side.
• All centers of the circles shown in Figure 12b are the vertices belonging to V.
• Connect two consecutive vertices in Figure 12b belonging to E.
• It is also necessary to carry out these four steps for B’C’ and C’A’ to generate more vertices and edges for the graph G(V,E).
• Connect two neighbors of the vertices of △A′B′C′.
• Connect edges from $\overline{A^{\prime }{B}^{\prime }}$ to $\overline{AB}$, from $\overline{B^{\prime }{C}^{\prime }}$ to $\overline{BC},$ and from $\overline{C^{\prime }{A}^{\prime }}$ to $\overline{CA}$ (described in Section 2.3)

Using the above approach, starting from △ABC, the 1-offset of △ABC is T₁ (△A′B′C′); the vertices and edges for T₁ are shown in Figure 13a. Note that the three vertices of triangle T₁ have a circle center at these three vertices with radius r tangent to △ABC.

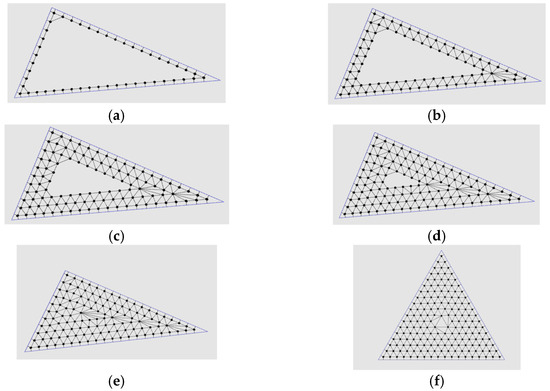
Figure 13. Generating the tangency tree for triangles. (a) ΔABC to T₁; (b) T₁ to T₂; (c) T₂ to T₃; (d) T₃ to T₄; (e) T_last contains 1 vertex; (f) T_last contains 3 vertices.

Next, consider triangle T₂, which is the $\sqrt{3}$R-offset of T₁. The method used for generating vertices and edges for T₂ is identical to the method used to generate vertices and edges for T₁. Thereafter, we generate edges between vertices in T₁ and vertices in T₂ (which will be described in the following section), with the tangency graph shown in Figure 13b.

2.3. How to Construct Edges on Two Consecutive Layers

The next step in the process involves generating edges between the vertices on T₁ and the vertices on T₂. Before we explain our strategy to connect the vertices on these two triangles, we present the following theorem.

Theorem 4. 

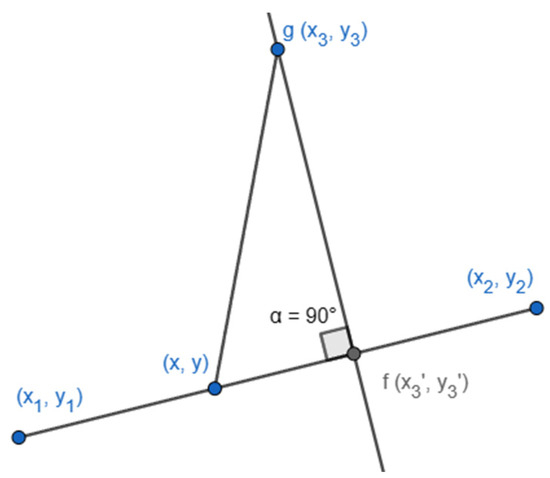
Find the foot point of a point onto a line. Given a point g (x₃, y₃) and a line L (g∉L) passing through two points, (x₁, y₁) and (x₂, y₂), the nearest point, also called the foot point, of g onto L is at $\left(x,y\right)=\left(1-t\right)\left(x_1,y_1\right)+t\left(x_2,y_2\right),wheret={\displaystyle \frac{(x_3-x_1)(x_2-x_1)+(y_3-y_1)(y_2-y_1)}{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}}$, as shown in Figure 14.

Figure 14. Establishment of the foot point f of point g.

Proof of Theorem 4. 

With a point (x,y) on L, we can generate the square of the distance function from (x,y) to point g, as follows: f(t) = ${(x-x_3)}^2+{(y-y_3)}^2$ = ${[\left(1-t\right)x_1+t{x}_2-x_3]}^2+{[\left(1-t\right)y_1+t{y}_2-y_3]}^2$. We aim to find the value t at which f(x) is the minimum; that is, ${\displaystyle \frac{d}{dt}}f(t)=0$. The parameter value t can be computed from ${\displaystyle \frac{d}{dt}}f(t)=0.$ □

Consider the correspondence edge $\overline{A^{\prime }{B}^{\prime }}$ on T₁ and $\overline{A”B”}$ on T₂. Assume the parameter values for the vertices on $A^{\prime }{B}^{\prime }$ are t₀, t₁, …, t_m, and the parameter values for the foot points of vertices on $\overline{A”B”}$ onto $\overline{A^{\prime }{B}^{\prime }}$are t₀′, t₁′, …, t_n′. We explain the details with m = 7 and n = 3, as shown in Figure 15. To simplify our description, we use the parameter values as the vertex name hereafter. The vertices t₀ and t₇ are the vertices on $\overline{A^{\prime }{B}^{\prime }}$; at this point, no vertices on $\overline{A”B”}$(T₂) are connected. When we construct edges for △A′B′C′, we construct one edge from t₁ to the last vertex on $\overline{C^{\prime }{A}^{\prime }}$ and from t₆ to the first vertex on $\overline{B^{\prime }{C}^{\prime }}$. Next, it was necessary to construct the edges for t_i, I = 1…, 6 and t_j′, j = 0, 3. We used the following approach to connect edges between vertices generated on T₁ and T₂. Note that we tried to connect vertices in $\overline{A”B”}$ to the vertices close to it in $\overline{A^{\prime }{B}^{\prime }}$. We employed the same process for vertices in $\overline{B”C”}$ to the vertices close to it in $\overline{B^{\prime }{C}^{\prime }}$, as well as for vertices in $\overline{C”A”}$ to the vertices close to it in $\overline{C^{\prime }{A}^{\prime }}$.

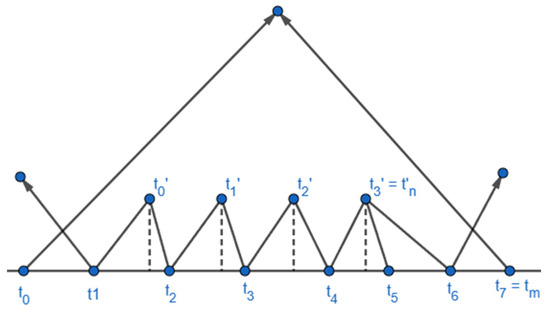
Figure 15. Relation between vertices.

We define the floor and ceiling for the vertices ${\mathrm{t}}_{\mathrm{i}}^{\prime }$ as follows:

$⌊t_i^{\prime }⌋=\mathit{max}\left\{t_j\right|t_j<{t_i}^{\prime }\};⌈t_j^{\prime }⌉=\mathit{min}\left\{t_j\right|t_j>{t_i}^{\prime }\},$where$\left\{\begin{array}{c}⌈t_n^{\prime }⌉=t_{m-1}\\ ⌈t_{-1}^{\prime }⌉=t_1\end{array}\right.$. With the above definition, we connect vertices ${\mathrm{t}}_{\mathrm{i}}^{\prime }$ to all vertices from $⌈{\mathrm{t}}_{\mathrm{i}-1}^{\prime }⌉ \mathrm{t}\mathrm{o} ⌈{\mathrm{t}}_{\mathrm{i}}^{\prime }⌉{\forall }_{\mathrm{i}}$ = 0, …, n. Therefore, in Figure 15, ${\mathrm{t}}_0^{\prime }$ connects vertices from $⌈{\mathrm{t}}_{-1}^{\prime }⌉$ = t₁ to $⌈{\mathrm{t}}_0^{\prime }⌉$ = t₂, and ${\mathrm{t}}_3^{\prime }$ connects vertices from $⌈{\mathrm{t}}_2^{\prime }⌉$ = t₄ to $⌈{\mathrm{t}}_3^{\prime }⌉$ = t₆. Therefore, the vertex with parameter ${\mathrm{t}}_3^{\prime }in{A}^{″}{B}^{″}$ has three edges connected to the vertices on $\overline{A\prime B\prime }$.

The results following the connection of the edges between T₁ and T₂ are shown in Figure 13b. We continued to generate vertices on T₃ = $\sqrt{3}$R-offset(T₂) and T₄ = $\sqrt{3}$R-offset(T₃) and generated vertices and edges for the tangency graph G(V,E). We increased the number of vertices on V and the number of edges connecting vertices on the same layer and previous layer; see Figure 13c,d. At this point, it is appropriate to determine how to stop the process.

2.4. How to Stop the While Loop

It is already established that any triangle contains an inscribed circle and three Malfatti circles. The criterion to stop the algorithm depends on the radius of the inscribed circle and the minimum radius of the three Malfatti circles.

This process specifies the tangency properties between circles, representing vertices on G(V,E). Let r₁ be the radius of the inscribed circle for T_last, and let r₂ be the minimum radius of the three Malfatti circles for T_last. If one of these two radii is less than (1 + epsR)r—eqpR —a small value set by us—we stop the process and leave the loop. If r₁ is close to r, we use one vertex for T_last (see Figure 13e; otherwise, we use three vertices for T_last (see Figure 13f)). The final aspect involved in constructing a tangency graph is connecting the edges for the vertices of T_last with the previous layer triangle (see Figure 13e,f).

3. Examples

We used “Intel^® Core™”i7-10750H CPU, 16G Ram, and Anaconda 23.5.2 (https://www.anaconda.com/products/distribution, accessed on 28 August 2024) with Python 3.11.3 (https://www.python.org) to implement the algorithm. We provide two examples below.

Example 4. 

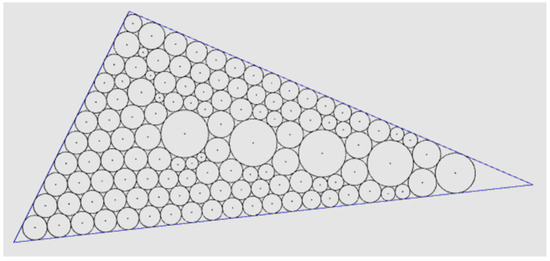
Given a triangle with vertices at A = (10, 10), B = (100, 20), and C = (30, 50) and initial r = 2, set epsR = 0.3 and eps = 0.0001; the tangency graph these values generate is shown in Figure 13a–e. Following angle computation for every circle, including corner circles, boundary, and inner circles, a figure is produced, as shown in Figure 16. It takes 144.9, 6.140, and 0.288 s to construct a tangency graph, to find the radii for all circles, and to display the results, respectively. All of the circles generated have the radii range (0.829, 4.129), which is (0.415r, 2.065r).

Figure 16. Output display for Example 4.

In this case, on the final layer, the radius of the inscribed circle is 2.22, which is less than (1 + epsR)r = 2.6, and the radii of the Malfatti circles are 1.432, 1.099, and 1.766, with the minimum radius being 1.099. The value 2.22 is closer to r = 2 compared to 1.099. Thus, the final generated layer contains one vertex only. The output is shown in Figure 16.

Note that there are four circles in Figure 16 that contain larger inner circles. We found that when a circle has a large number of surrounding circles, there is a high likelihood that its radius is large. Therefore, if we add more circles in close proximity, this raises the question as to whether it is possible to reduce the range of the radii for the problem. Thus, after constructing the tangency graph, we checked the degree of each vertex; if the degree is larger than 15 or between 12 and 15, we construct two vertices/circles or one new vertex/circle with this vertex. Next, we use two different algorithms—one is used before adjustment and the other is used after adjustment. For the latter, we present the following example.

Example 5. 

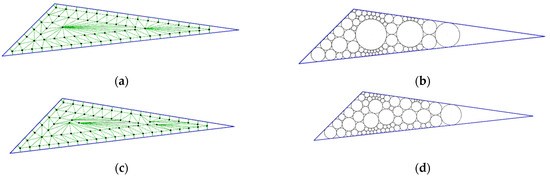
Given a triangle with vertices at A = (10, 10), B = (100, 20), and C = (30, 30) and initial r = 1.9, set epsR = 0.3 and eps = 0.0001. The tangency graph before the adjustment constructs is shown in Figure 17a, and its associated tangency circles in the triangle are shown in Figure 17b. Note that two vertices contain more than 15 vertices; in this case, we add two more vertices for each of these two vertices, as shown in Figure 17c; their associated tangency circles in the triangle are shown in Figure 17d. Note that the range of the radii shown in Figure 17d is smaller than the range of the radii shown in Figure 17b.

Figure 17. Before and after the adjustment in Example 5. (a) Tangency graph before adjustment; (b) Result for the tangency graph in (a); (c) Tangency graph after adjustment; (d) Result for the tangency graph in (c).

We can see the clear difference between Figure 17b,d. Herein, we would like to compare the range of the radii with numerical numbers. There are 66 circles in Figure 17b; thus, we compared our results with Chiang’s result to solve the Tri(T₁₁) problem because T₁₁ = 65, which is close to 66. The result for Tri(figureT₁₁) using Chiang’s algorithm is shown in Figure 18.

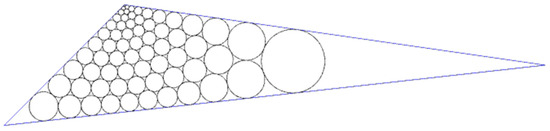
Figure 18. The solution for Tri(T₁₁).

A comparison of the range of the radii using three different algorithms is shown in Table 1. The first algorithm is Chiang’s algorithm to solve the Tri(T₁₁) problem. The second and third algorithms are the proposed algorithm before and after adjustment before using Chiang’s algorithm, respectively. We refer to these as Algorithm 1 and Algorithm 2. Shown are the minimum, lower quartile, median, third quartile, and maximum values of the circle radii from these three algorithms. We also show the range of the radii in the final column. Note that from Tri(T₁₁) to Algorithm 1, the radius for the smallest circle varies from 0.147 to 0.52, and the median varies from 1.397 to 0.945. However, the maximum values vary from 5.28 to 5.684. At this point, we found that the large circle has more neighboring circles, which is the reason as to why we added one adjustment before using Chiang’s algorithm. Below, we compare Chiang’s algorithm with Algorithm 2, where the range of the radii (max–min) drops to 3.8 from 5.133.

Table 1. Comparison of the radii from the three different algorithms.

	Min	Q1	Median	Q3	Max	Max–Min
Chiang’s Algorithm Tri(T11)	0.147	0.97	1.397	1.676	5.28	5.133
Algorithm 1 (r = 1.9)	0.52	0.715	0.945	1.674	5.684	5.164
Algorithm 2 (r = 1.9)	0.452	0.775	1.129	1.992	4.252	3.8

Example 6. 

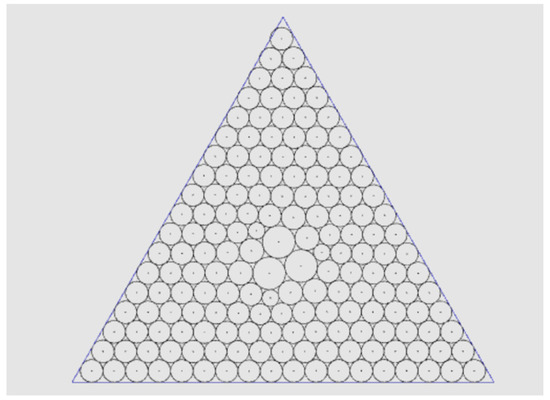
Given a triangle with vertices at A = (0, 0), B = (37.5, 64.952), and C = (75, 0), set r = 2, epsR = 0.4, and eps = 0.0001; the tangency graph these values generate is similar to the previous example, except for the final step, as shown in Figure 13f. The resulting figure following angle computation for every circle, including corner circles, boundary circles, and inner circles, is shown in Figure 19. It takes 127.106, 1.430, and 0.130 s to construct a tangency graph, to find the radii for all circles, and to display the results, respectively. All of the circles generated have the radii range (1.506, 2.194), which is (0.753r, 1.097r).

Figure 19. Output for Example 6.

In this case, on the final layer, the radius of the inscribed circle is 4.330, and the minimum radius of the Malfatti circles is 2.745. Because 4.330 > 2.8 and 2.745 < 2.8, the final generated layer has three vertices, and we connected these three vertices to the vertices in the previous layer triangle. The output is shown in Figure 17.

Note that Figure 17a,c generate the triangle mesh. This meshed triangle can be used in games to enable NPCs (non-player characters) to navigate through a triangle without walking directly from A on one side of the triangle to a point B on the other side. We can find a path from point at T₀ to T₁, then T₁ to T₂, up until T_last. When there is more than one choice, we select any one because we did not ask for the shortest path. Using this approach, we can find a path for a robot from A to T_last, and a path from B to T_last. Connecting these two paths, it generates a path from A to B. Using this approach and the tangency graph shown in Figure 17c, the path from A to B is shown in Figure 20.

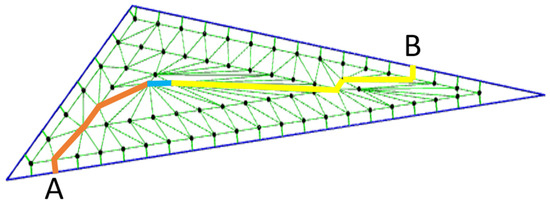
Figure 20. Non straigt path for robots from A to B.

4. Conclusions and Future Research

Herein, we propose an algorithm to generate a tangency graph to specify the tangency relationship among all circles and triangle boundaries. The purpose of this proposed algorithm is to reduce the range of the radii among all circles. The process of generating a tangency graph takes more CPU time compared to the time spent constructing and displaying circles.

There are some ways to extend the research presented herein. For example, we can extend the problem from a triangular area to a circular triangle (including the Reuleaux triangle) or the area bounded by three Bezier curves. Another direction of future research could be to change the area from a triangle to a convex polygon.