Global Existence of Solutions to a Free Boundary Problem for Viscous Incompressible Magnetohydrodynamics for Small Data

Abstract

The motion of viscous incompressible magnetohydrodynamics (MHD) is considered in a domain that is bounded by a free surface. The motion interacts through the free surface with an electromagnetic field located in a domain exterior to the free surface and bounded by a given fixed surface. Some electromagnetic fields are prescribed on this fixed boundary. On the free surface, jumps in the magnetic and electric fields are assumed. The global existence of solutions to this problem assuming appropriate smallness conditions on the initial and boundary data is proved.

1. Introduction

We prove the global existence of solutions to equations of magnetohydrodynamics (MHD) in domain ${\stackrel{1}{\mathrm{\Omega }}}_t$ with a free boundary $S_t$. The motion interacts with the electromagnetic field in domain ${\stackrel{2}{\mathrm{\Omega }}}_t$, which is exterior to ${\stackrel{1}{\mathrm{\Omega }}}_t$ with a fixed boundary B. The magnetic fields in ${\stackrel{1}{\mathrm{\Omega }}}_t$ and ${\stackrel{2}{\mathrm{\Omega }}}_t$ are coupled by transmission conditions on $S_t$. We prove the existence of solutions such that the velocity and magnetic fields are continuous with their time and space derivatives.

On boundary B, there is a magnetic field prescribed.

The motion in ${\stackrel{1}{\mathrm{\Omega }}}_t$ is described by velocity v and magnetic field $\stackrel{1}{H}$. The electromagnetic field in ${\stackrel{2}{\mathrm{\Omega }}}_t$ is described by magnetic field $\stackrel{2}{H}$.

Now, we describe the technical and physical background of the considered problem:

1.

We model plasma as an MHD fluid and drop heat sources so that our problem models controlled thermonuclear fusion. The most important requirement is to keep the plasma in a region located at a positive distance from B by magnetic forces.

This property is shown in (238).

2.

The magnetic field on B is a restriction to B of a magnetic field generated by some electromagnets located at some distance from B. This kind of technical construction, although in a different geometrical framework, can be seen in CERN, where the motion of protons and antiprotons is confined to some torus thanks to a special magnetic field generated by strong electromagnets.

3.

The considered problem is also realized in galaxies, where the motion of ionised gas is concentrated in some region and maintained by a magnetic field. This phenomenon is close to the model considered in this paper up to the point where gravitation must be taken into account.

4.

The electromagnetic field from the Sun meets the magnitosphere, where similar transmission conditions appear. In this case, charged particles pass through the boundary of the magnetosphere.

Formulas (2)–(9) in Section 2 describe the considered problem. Next, the problem is transformed into problems (10) and (12), for which the solvability is proved in [1].

It is difficult to show the existence of solutions and derive appropriate estimates of problem (12) because we have jumps in the magnetic field and a current on $S_t$. This can be carried out by applying the technique of the regularizer.

In Section 5, we derive necessary estimates by the energy method. The linearized problem (10) is the Stokes system with the Neumann boundary conditions. To find energy type estimates for solutions to (10), we need the Korn inequality, which is shown in Section 3.3.

Coupling estimates from Section 4 and Section 5, we prove a differential inequality in Section 6. The differential inequality yields a global estimate by applying a step-by-step approach in time for all $t\in {\mathbb{R}}_{+}$ and using sufficiently small data. The estimate guarantees a global existence. A non-small-data approach is not possible because the regularity problem of the Navier–Stokes equations is still open.

The first results on the existence of solutions to dissipative incompressible MHD in a complex domain were given by Ladyzhenskaya and Solonnikov [2]. The motions were considered in domains composed of two different materials separated by a fixed surface. On the surface, they assumed the continuity of the tangent components of the magnetic field, the continuity of the normal component of magnetic induction and the continuity of the tangent components of the electric field.

Moreover, the boundary of the domain was treated as an ideal conductor, so the normal component of the magnetic field and tangent components of the electric field vanish. They proved the existence of weak solutions. A necessary technique to solve the problem can be found in [3].

Padula and Solonnikov [4] proved the existence of local solutions to problems (2)–(9), where $\stackrel{2}{H}$ is a solution to the system

$$\mathrm{rot}\stackrel{2}{H}=0,\mathrm{div}\stackrel{2}{H}=0$$

(1)

and the continuity of the tangent components of the magnetic field and the normal component of induction were assumed on $S_t$.

Free boundary problems for MHD equations were also considered in [5,6], where the external magnetic field satisfies the elliptic system (1). In [7], using the Weis theory of Fourier multipliers and the semigroup technique, two different MHD fluids interacting through a free surface are considered.

Since the paper is very technical and long, we write a short review of its methods and results. In Section 2, the considered problem is formulated. Moreover, the main result is presented in Theorem 1. The considered problem is expressed in the form of two problems: problem (10) (for velocity $(v)$ and pressure $(p)$ for a given magnetic field $(\stackrel{1}{H})$) and problem (12) (for magnetic fields $(\stackrel{1}{H},\stackrel{2}{H})$ in terms of a given velocity $(v)$). Estimates for solutions to (10) and (12) are derived in Section 4 and Section 5, respectively. The estimates are made by the energy method, so only the $L_2$-Sobolev spaces are used. To prove the estimates in Section 4, we need Korn inequalities. Different variants of Korn inequalities can be found in Section 3.3. In Lemmas 14–16, energy-type estimates for $\stackrel{1}{H}$ and $\stackrel{2}{H}$ are found (in terms of some nonlinear expressions). To derive them, integration by parts is necessary, so some boundary terms on $S_t$ appear. They can be cancelled by applying the transmission conditions (see Lemma 15).

To describe the geometry of the considered problem we present its two-dimensional version in Figure 1.

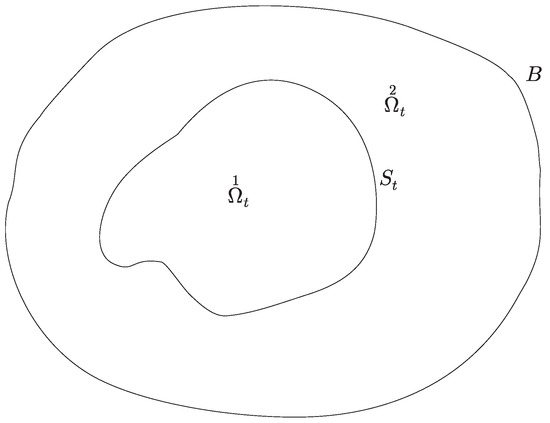
Figure 1. Description of the two-dimensional intersection of the space shape of the considered problem.

To estimate $L_2$-norms of $\stackrel{1}{H}$ and $\stackrel{2}{H}$ by applying the Poincaré inequality it is convenient to use the geometry of the considered problem presented in Figure 2. It is clear that the boundary B, in the form of a cylinder makes an application of the Poincaré inequality simple.

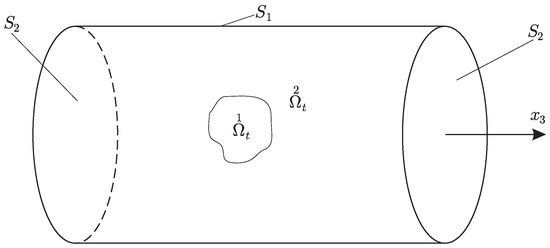
Figure 2. Special space geometry of the considered problem convenient for the proof of estimates for the magnetic fields.

To estimate the second- and the third-space derivatives of $\stackrel{1}{H}$ and $\stackrel{2}{H}$, we need the partition of unity described in Figure 3.

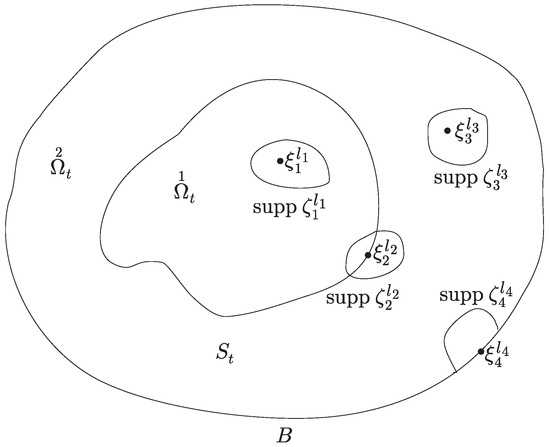
Figure 3. Partition of unity necessary for application of the regularizer technique.

Consequently, local $H^2,H^3$ estimates for $\stackrel{1}{H}$, $\stackrel{2}{H}$ are found in the proof of Lemma 17. By the collection of the estimates by the technique of the regularizer, we prove Lemma 17.

Finally, we derive estimate (229), which for small data gives a global estimate and, thus, global existence. Furthermore, inequality (234) guarantees that the free boundary remains at a positive distance from the fixed boundary B at all times.

2. Statement of the Problem

We are concerned with MHD motions in ${\stackrel{1}{\mathrm{\Omega }}}_t$ and the electromagnetic field in ${\stackrel{2}{\mathrm{\Omega }}}_t$ coupled through the free surface $S_t$ by transmission conditions.

The MHD equations in ${\stackrel{1}{\mathrm{\Omega }}}_t$ read

$$\begin{array}{cc}& v_{,t}+v·\nabla v-\mathrm{div}\mathbb{T}(v,p)-{\mu }_1\stackrel{1}{H}·\nabla \stackrel{1}{H}+{\displaystyle \frac{1}{2}}{\mu }_1\nabla {\stackrel{1}{H}}^2=f,\hfill \\ & \mathrm{div}v=0,\hfill \\ & {\mu }_1{\stackrel{1}{H}}_{,t}=-\mathrm{rot}\stackrel{1}{E},\hfill \\ & \mathrm{rot}\stackrel{1}{H}={\sigma }_1(\stackrel{1}{E}+{\mu }_{1}v\times \stackrel{1}{H}),\hfill \\ & \mathrm{div}\stackrel{1}{H}=0,\hfill \end{array}$$

(2)

where $v=v(x,t)\in {\mathbb{R}}^3$ denotes the velocity of the fluid, $p=p(x,t)\in \mathbb{R}$ denotes the pressure, $\stackrel{1}{H}=\stackrel{1}{H}(x,t)\in {\mathbb{R}}^3$ denotes the magnetic field, $\stackrel{1}{E}=\stackrel{1}{E}(x,t)\in {\mathbb{R}}^3$ denotes the electric field, $f=f(x,t)\in {\mathbb{R}}^3$ denotes the external force field, and $x=(x_1,x_2,x_3)$ are Cartesian coordinates.

Furthermore, ${\mu }_1$ is the constant magnetic permeability, ${\sigma }_1$ is the constant electrical conductivity, and $\mathbb{T}(v,p)$ is the stress tensor and has the form

$$\mathbb{T}(v,p)=\nu \mathbb{D}(v)-p\mathbb{I},$$

(3)

where $\nu$ is the positive viscosity coefficient, $\mathbb{I}$ is the unit matrix, and $\mathbb{D}(v)$ is the dilatation tensor:

$$\mathbb{D}(v)={\{v_{i,x_j}+v_{j,x_i}\}}_{i,j=1,2,3}.$$

(4)

We assume the following initial and boundary conditions

$$\begin{array}{cc}& \overline{n}·\mathbb{T}(v,p)+{\mu }_1\overline{n}·\mathbb{T}(\stackrel{1}{H})=p_0\overline{n},\hfill \\ & {v|}_{t=0}=v(0),\stackrel{1}{H}{|}_{t=0}=\stackrel{1}{H}(0),\mathrm{div}\stackrel{1}{H}(0)=0,\hfill \\ & {\stackrel{1}{\mathrm{\Omega }}}_t{{|}_{t=0}={\stackrel{1}{\mathrm{\Omega }}}_0,S_t|}_{t=0}=S_0,\hfill \end{array}$$

(5)

where $\overline{n}$ is the unit vector outward to ${\stackrel{1}{\mathrm{\Omega }}}_t$ and normal to $S_t$, and

$$\mathbb{T}(\stackrel{1}{H})={\left\{{\stackrel{1}{H}}_i{\stackrel{1}{H}}_j-{\displaystyle \frac{1}{2}}{\stackrel{1}{H}}^2{\delta }_{ij}\right\}}_{i,j=1,2,3}.$$

(6)

From (5)₁, the compatibility condition follows

$$\overline{n}(0)·\mathbb{D}(v(0))·\overline{\tau }(0)+{\mu }_1\overline{n}(0)·\stackrel{1}{H}(0)\overline{\tau }(0)·\stackrel{1}{H}(0)=0\mathrm{on}{S}_0,$$

where $\overline{n}(0)=\overline{n}{|}_{t=0}$, $\overline{\tau }(0)=\overline{\tau }{|}_{t=0}$, and $\overline{\tau }$ is a tangent vector to $S_t$.

In ${\stackrel{2}{\mathrm{\Omega }}}_t$, which is occupied by a dielectric gas, we have a motionless electromagnetic field described by

$$\begin{array}{cc}& {\mu }_2{\stackrel{2}{H}}_{,t}=-\mathrm{rot}\stackrel{2}{E},\hfill \\ & {\sigma }_2\stackrel{2}{E}=\mathrm{rot}\stackrel{2}{H},\hfill \\ & \mathrm{div}\stackrel{2}{H}=0\hfill \end{array}$$

(7)

with the following initial and boundary conditions:

$$\begin{array}{cc}& \stackrel{2}{H}{{|}_{t=0}=\stackrel{2}{H}(0),\mathrm{div}\stackrel{2}{H}(0)=0,{\stackrel{2}{\mathrm{\Omega }}}_t|}_{t=0}={\stackrel{2}{\mathrm{\Omega }}}_0,\hfill \\ & \stackrel{2}{H}·{\overline{\tau }}_{\alpha }{{|}_B=H_{\ast \alpha },\alpha =1,2,\mathrm{div}\stackrel{2}{H}|}_B=0,\hfill \end{array}$$

(8)

where ${\overline{\tau }}_{\alpha }$, $\alpha =1,2$, are tangent vectors to B.

Electromagnetic fields in ${\stackrel{1}{\mathrm{\Omega }}}_t$ and ${\stackrel{2}{\mathrm{\Omega }}}_t$ are coupled at $S_t$ by the following transmission conditions:

$${\stackrel{1}{a}}_{\alpha }\stackrel{1}{E}·{\overline{\tau }}_{\alpha }={\stackrel{2}{a}}_{\alpha }\stackrel{2}{E}·{\overline{\tau }}_{\alpha }{{|}_{S_t},{\stackrel{1}{b}}_{\beta }{\stackrel{1}{H}}_{\beta }={\stackrel{2}{b}}_{\beta }{\stackrel{2}{H}}_{\beta }|}_{S_t},\alpha =1,2,\beta =1,2,3,$$

(9)

where ${\overline{\tau }}_1$, ${\overline{\tau }}_2$, $\overline{n}$ is an orthonormal system of vector fields in a neighbourhood of $S_t$ such that $\overline{n}{|}_{S_t}$ is normal and ${\overline{\tau }}_1,{\overline{\tau }}_2{|}_{S_t}$ are tangent to $S_t$.

In addition, we assume that ${\stackrel{i}{a}}_{\alpha }$, ${\stackrel{i}{b}}_{\beta }$, $i=1,2$, $\alpha =1,2$, $\beta =1,2,3$, are constants. Non-vanishing of the differences ${\stackrel{1}{a}}_{\alpha }-{\stackrel{2}{a}}_{\alpha }$, ${\stackrel{1}{b}}_{\beta }-{\stackrel{2}{b}}_{\beta }$ means that there are jumps in the tangent components of the electric field and components of the magnetic field on the free surface $S_t$. The transmission conditions (9) are very general, but they are admissible because the energy inequality holds for the solutions to problem (2)–(9) (see [1], Lemma 1.1). The first condition in (9) describes a current jump.

It is crucial to acknowledge that in magnetohydrodynamics, the displacement current $E_{,t}$ is omitted.

Problem (2)–(9) can be transformed into two problems:

The first problem is to identify v, p for a given $\stackrel{1}{H}$:

$$\begin{array}{ccc}& v_{,t}+v·\nabla v-\mathrm{div}\mathbb{T}(v,p)=f+{\mu }_1\mathrm{div}\mathbb{T}(\stackrel{1}{H})\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}v=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \overline{n}·\mathbb{T}(v,p)=-{\mu }_1\overline{n}·\mathbb{T}(\stackrel{1}{H})\hfill & \mathrm{on}{S}_t,\hfill \\ & {v|}_{t=0}=v(0)\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_0,\hfill \end{array}$$

(10)

where we assumed that $p_0$ is already absorbed by p.

The second problem is to identify $\stackrel{1}{H}$, $\stackrel{2}{H}$ for a given v, p:

$$\begin{array}{ccc}& {\mu }_1{\stackrel{1}{H}}_{,t}=-\mathrm{rot}\stackrel{1}{E},\mathrm{rot}\stackrel{1}{H}={\sigma }_1(\stackrel{1}{E}+{\mu }_{1}v\times \stackrel{1}{H}),\mathrm{div}\stackrel{1}{H}=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & {\mu }_2{\stackrel{2}{H}}_{,t}=-\mathrm{rot}\stackrel{2}{E},{\sigma }_2\stackrel{2}{E}=\mathrm{rot}\stackrel{2}{H},\mathrm{div}\stackrel{2}{H}=0\hfill & \mathrm{in}{\stackrel{2}{\mathrm{\Omega }}}_t,\hfill \\ & \stackrel{1}{H}{|}_{t=0}=\stackrel{1}{H}(0),\mathrm{div}\stackrel{1}{H}(0)=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_0,\hfill \\ & \stackrel{2}{H}{|}_{t=0}=\stackrel{2}{H}(0),\mathrm{div}\stackrel{2}{H}(0)=0\hfill & \mathrm{in}{\stackrel{2}{\mathrm{\Omega }}}_0,\hfill \\ & \stackrel{2}{H}·{\overline{\tau }}_{\alpha }^{\prime }=H_{\ast \alpha },\mathrm{div}\stackrel{2}{H}{|}_B=0,{\overline{\tau }}_{\alpha }^{\prime },\alpha =1,2,\mathrm{is}\mathrm{a}\mathrm{tangent}\mathrm{vector}\mathrm{to}B\hfill & \mathrm{on}B,\hfill \\ & {\stackrel{1}{a}}_{\alpha }\stackrel{1}{E}·{\overline{\tau }}_{\alpha }={\stackrel{2}{a}}_{\alpha }\stackrel{2}{E}·{\overline{\tau }}_{\alpha },{\stackrel{1}{b}}_{\beta }{\stackrel{1}{H}}_{\beta }={\stackrel{2}{b}}_{\beta }{\stackrel{2}{H}}_{\beta },{\overline{\tau }}_{\alpha },\alpha =1,2,\mathrm{is}\mathrm{a}\mathrm{tangent}\mathrm{vector}\mathrm{to}{S}_t,\alpha =1,2,\beta =1,2,3\hfill & \mathrm{on}{S}_t.\hfill \end{array}$$

(11)

In this problem, it is possible to formulate very general anisotropic transmission conditions.

In Section 5, the conditions are reduced to a more simplified form.

The elimination of electric fields $\stackrel{1}{E}$, $\stackrel{2}{E}$ from (11) takes the form

$$\begin{array}{ccc}& {\mu }_1{\stackrel{1}{H}}_{,t}+{\displaystyle \frac{1}{{\sigma }_1}}\mathrm{rot}{}^2\stackrel{1}{H}={\displaystyle \frac{{\mu }_1}{{\sigma }_1}}\mathrm{rot}(\stackrel{1}{v}\times \stackrel{1}{H})\hfill & \mathrm{in}\bigcup _t{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}\stackrel{1}{H}=0\hfill & \mathrm{in}\bigcup _t{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & {\mu }_2{\stackrel{2}{H}}_{,t}+{\displaystyle \frac{1}{{\sigma }_2}}\mathrm{rot}{}^2\stackrel{2}{H}=0\hfill & \mathrm{in}\bigcup _t{\stackrel{2}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}\stackrel{2}{H}=0\hfill & \mathrm{in}\bigcup _t{\stackrel{2}{\mathrm{\Omega }}}_t,\hfill \\ & \stackrel{2}{H}·{\overline{\tau }}_{\alpha }=H_{\ast \alpha },\mathrm{div}\stackrel{2}{H}{|}_B=0,{\tau }_{\alpha },\alpha =1,2\mathrm{is}\mathrm{a}\mathrm{tangent}\mathrm{vector}\mathrm{to}{B}^t\hfill & \mathrm{on}{B}^t,\hfill \\ & {\stackrel{1}{a}}_{\alpha }\left({\displaystyle \frac{1}{{\sigma }_1}}\mathrm{rot}\stackrel{1}{H}-{\mu }_{1}v\times \stackrel{1}{H}\right)·{\overline{\tau }}_{\alpha }={\stackrel{2}{a}}_{\alpha }{\displaystyle \frac{1}{{\sigma }_2}}\mathrm{rot}\stackrel{2}{H}·{\overline{\tau }}_{\alpha },\alpha =1,2\hfill & \mathrm{on}\bigcup _t{S}_t,\hfill \\ & {\stackrel{1}{b}}_{\beta }{\stackrel{1}{H}}_{\beta }={\stackrel{2}{b}}_{\beta }{\stackrel{2}{H}}_{\beta },\beta =1,2,3\hfill & \mathrm{on}\bigcup _t{S}_t,\hfill \\ & \stackrel{1}{H}{|}_{t=0}=\stackrel{1}{H}(0),\mathrm{div}\stackrel{1}{H}(0)=0\hfill & \mathrm{in}{\mathrm{\Omega }}_0,\hfill \\ & \stackrel{2}{H}{|}_{t=0}=\stackrel{2}{H}(0),\mathrm{div}\stackrel{2}{H}(0)=0\hfill & \mathrm{in}{\mathrm{\Omega }}_0,\hfill \\ & {\stackrel{i}{\mathrm{\Omega }}}_t{{|}_{t=0}={\stackrel{i}{\mathrm{\Omega }}}_0,i=1,2,S_t|}_{t=0}=S_0.\hfill \end{array}$$

(12)

In this paper, we prove the global existence of solutions to problems (10) and (12) assuming sufficient smallness of the initial data, the external force and the magnetic field prescribed on B. Since local existence is proved in [1], our goal is to find a global estimate of the local solutions.

The proof is divided into the following steps:

1.

In Section 4, we derive a differential inequality for solutions to (10) by applying the energy method and appropriate Korn inequalities.

2.

In Section 5, we derive a differential inequality for solutions to problem (12). Since we are interested in considering problem (12) with transmission conditions on the free surface $S_t$, we need to use much more sophisticated methods than the energy method. To examine solutions to (12) in a neighbourhood of a flattened part of $S_t$, we use the $L_2$-Sobolev spaces in the language of Fourier–Laplace transforms. It helps us to consider a transmission condition with jumps in the magnetic field on $S_t$.

3.

Finally, in Section 6, we derive a differential inequality that combines the differential inequalities from Section 4 and Section 5. The differential inequality by the step-by-step-in-time argument implies a global estimate. The local existence and the global estimate yield a global existence for sufficiently small initial data, an external force and the magnetic field prescribed on B.

Theorem 1. 

Assume that

(1) 

$v(0)\in H^2({\stackrel{1}{\mathrm{\Omega }}}_0)$, $v_{,t}(0)\in H^1({\stackrel{1}{\mathrm{\Omega }}}_0)$, and $v_{,tt}(0)\in L_2({\stackrel{1}{\mathrm{\Omega }}}_0)$;

(2) 

$\stackrel{i}{H}(0)\in H^2({\stackrel{1}{\mathrm{\Omega }}}_0)$, ${\stackrel{i}{H}}_{,t}(0)\in H^1({\stackrel{1}{\mathrm{\Omega }}}_0)$, ${\stackrel{i}{H}}_{,t}(0)\in H^1({\stackrel{1}{\mathrm{\Omega }}}_0)$, ${\stackrel{i}{H}}_{,tt}(0)\in L_2({\stackrel{1}{\mathrm{\Omega }}}_0)$, and $i=1,2$;

(3) 

$f=0$;

(4) 

$G_{\ast \alpha }^2\equiv {\sum }_{i=0}^2{\parallel {\partial }_t^i{H}_{\ast \alpha }\parallel }_{3/2,B}^2<\infty$, and $\alpha =1,2$;

(5) 

The transmission conditions

$${\alpha }_1\stackrel{1}{H}={\alpha }_2\stackrel{2}{H},{\alpha }_1{\stackrel{1}{H}}_{,\tau }={\alpha }_2{\stackrel{2}{H}}_{,\tau }$$

where ${\alpha }_1$, ${\alpha }_2$ are arbitrary positive numbers, ${\partial }_{\tau }=\overline{\tau }·\nabla$, and $\overline{\tau }$ is any tangent vector to the boundary $S_t$;

(6) 

B is a box.

Let

$$X^2(t)={\displaystyle \sum _{i=0}^2}\left(\parallel {\partial }_t^i{v(t)\parallel }_{H^{2-i}({\stackrel{1}{\mathrm{\Omega }}}_t)}^2+{\displaystyle \sum _{\alpha =1}^2}{\parallel {\partial }_t^i\stackrel{\alpha }{H}(t)\parallel }_{H^{2-i}({\stackrel{\alpha }{\mathrm{\Omega }}}_t)}^2\right);$$

(7) 

$X^2(0)={\sum }_{i=0}^2(\parallel {\partial }_t^i{v(0)\parallel }_{H^{2-i}({\stackrel{1}{\mathrm{\Omega }}}_0)}^2+{\sum }_{\alpha =1}^2\parallel {\partial }_t^i\stackrel{\alpha }{H}(0){\parallel }_{H^{2-i}({\stackrel{\alpha }{\mathrm{\Omega }}}_0)}^2)$.

Let $X^2(0)\le \gamma$, $G_{\ast \alpha }^2\le \gamma$, with γ being sufficiently small.

Then there exists a global solution to problems (10) and (12) such that

$$X^2(t)<\infty ,{\displaystyle \underset{kT}{\overset{(k+1)T}{\int }}}{Y}^2(t)<\infty$$

for any $k\in \mathbb{N}\cup \left\{0\right\}$ and a fixed T, where

$$Y^2(t)={\displaystyle \sum _{i=0}^2}\left(\parallel {\partial }_t^i{v\parallel }_{H^{3-i}({\stackrel{1}{\mathrm{\Omega }}}_t)}^2+{\displaystyle \sum _{\alpha =1}^2}{\parallel {\partial }_t^i\stackrel{\alpha }{H}\parallel }_{H^{3-i}({\stackrel{\alpha }{\mathrm{\Omega }}}_t)}^2\right)$$

Remark 1. 

The aim of this note is to describe the following initial conditions:

$$v(0)\in H^2({\stackrel{1}{\mathrm{\Omega }}}_0),v_{,t}(0)\in H^1({\stackrel{1}{\mathrm{\Omega }}}_0),v_{,tt}(0)\in L_2({\stackrel{1}{\mathrm{\Omega }}}_0).$$

To describe the condition $v_{,t}(0)$, we consider (10)₁. Projecting it on $t=0$, we have

$$\begin{array}{cc}\parallel v_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill & \le {\parallel v(0)·\nabla v(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}+{\parallel \mathbb{D}eltav(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill \\ & +{\parallel \nabla p(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}+\parallel \stackrel{1}{H}(0)·\nabla \stackrel{1}{H}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}+{\parallel f(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill \\ & \le {c\parallel v(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+{\parallel v(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}+{\parallel p(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}+c{\parallel \stackrel{1}{H}(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\hfill \\ & +{\parallel f(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}.\hfill \end{array}$$

(13)

It is necessary to estimate ${\parallel p(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}$. In order to achieve this, we apply the div operator to (10) and project the result on $t=0$. Then we have

$$\begin{array}{cc}\mathrm{\Delta }p(0)\hfill & =-(\nabla v·\nabla v)(0)+{\mu }_1({\nabla }_j{\stackrel{1}{H}}_i·{\nabla }_i{\stackrel{1}{H}}_j+\stackrel{1}{H}\mathrm{\Delta }\stackrel{1}{H}\hfill \\ & +{\nabla }_i{\stackrel{1}{H}}_j{\nabla }_i{\stackrel{1}{H}}_j)(0)+\mathrm{div}f(0).\hfill \end{array}$$

(14)

Furthermore, (10) implies the boundary condition for $p(0)$:

$${p(0)|}_{S_0}=\overline{n}·\mathbb{D}(v(0))\overline{n}+{\mu }_1\overline{n}·\mathbb{T}(\stackrel{1}{H}(0))\overline{n}.$$

(15)

For the solutions to problems (14) and (15), the following estimate is valid:

$${\parallel p(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\le {c(\parallel v(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+\parallel \stackrel{1}{H}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+{|\mathrm{div}f(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}+{\parallel v(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}).$$

(16)

Using (16) in (13) yields

$$\parallel v_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}\le {c(\parallel v(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+{\parallel v(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}+\parallel \stackrel{1}{H}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+{\parallel f(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}).$$

(17)

In the next step, we examine the condition $v_{,tt}(0)\in L_2({\stackrel{1}{\mathrm{\Omega }}}_0)$. Differentiating (10)₁ with respect to t and projecting the result on $t=0$, we have

$$\begin{array}{cc}|v_{,tt}{(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill & \le |(v·\nabla v_{,t}+v_{,t}·\nabla v)(0){|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}+{|\mathrm{\Delta }{v}_{,t}(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill \\ & +|\nabla p_{,t}{(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}+|({\stackrel{1}{H}}_{,t}\nabla \stackrel{1}{H}+\stackrel{1}{H}·\nabla {\stackrel{1}{H}}_{,t})(0){|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}+{|f_{,t}(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill \\ & \le {c\parallel v(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\parallel v_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}+\parallel v_{,t}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}+{|\nabla p_{,t}(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill \\ & +c\parallel \stackrel{1}{H}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\parallel {\stackrel{1}{H}}_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}+{|f_{,t}(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}.\hfill \end{array}$$

(18)

Because we calculate $v_{,t}(0)$, $p_{,t}(0)$, ${\stackrel{1}{H}}_{,t}(0)$ step by step, the above projection is possible.

From (12)₁, we have

$$\parallel {\stackrel{1}{H}}_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}\le c\parallel \stackrel{1}{H}{(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}+c\parallel \stackrel{1}{v}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}{\parallel \stackrel{1}{H}(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}$$

(19)

and (10)₁ yields

$$\begin{array}{cc}\parallel v_{,t}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill & \le {c\parallel v(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}{\parallel v(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}+c{\parallel v(0)\parallel }_{4,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill \\ & +c\parallel \stackrel{1}{H}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\parallel \stackrel{1}{H}{(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}+{c\parallel p(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}+c{\parallel f(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}.\hfill \end{array}$$

(20)

From problems (14) and (15), we have

$$\begin{array}{cc}{\parallel p(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill & \le {c\parallel v(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}{\parallel v(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}+c\parallel \stackrel{1}{H}{(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}{\parallel \stackrel{1}{H}(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}\hfill \\ & +{c\parallel f(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}+c{\parallel v(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}.\hfill \end{array}$$

(21)

On the right-hand side of (18), we have the norm $|\nabla p_{,t}{(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}$. Therefore, we have to consider the problem

$$\begin{array}{cc}& \mathrm{\Delta }{p}_{,t}(0)=-\mathrm{div}[{(v·\nabla v)}_{,t}(0)-{(\stackrel{1}{H}·\nabla \stackrel{1}{H})}_{,t}(0)-f_{,t}(0)]\hfill \\ & p_{,t}{(0)|}_S=\overline{n}·\mathbb{D}(v_{,t}(0))·\overline{n}+\overline{n}·\mathbb{T}{(\stackrel{1}{H})}_{,t}(0)·\overline{n}.\hfill \end{array}$$

(22)

To derive a weak-type estimate of solutions to (22), we construct the function η such that

$$\eta =(\overline{n}·\mathbb{D}(v_{,t}(0))·\overline{n}+\overline{n}·\mathbb{T}{(\stackrel{1}{H})}_{,t}(0)·\overline{n}){|}_S.$$

Subsequently, we define the function

$$q(0)=p_{,t}(0)-\tilde{\eta }$$

where $\tilde{\eta }$ is an extension of η such that $\tilde{\eta }{|}_S=\eta$, and $q(0)$ is a solution to the problem

$$\begin{array}{cc}& \mathrm{\Delta }q(0)=-\mathrm{div}({(v·\nabla v)}_{,t}(0)-{(\stackrel{1}{H}·\nabla \stackrel{1}{H})}_{,t}(0)-f_{,t}(0))+\mathrm{\Delta }\tilde{\eta },\hfill \\ & {q(0)|}_S=0.\hfill \end{array}$$

(23)

Multiplying (23)₁ by $q(0)$ and integrating over ${\stackrel{1}{\mathrm{\Omega }}}_0$ and by parts, we have

$$\begin{array}{cc}{|\nabla q(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\hfill & \le |\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }{(v·\nabla v)}_{,t}(0)·\nabla q(0)dx|+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }{(\stackrel{1}{H}·\nabla \stackrel{1}{H})}_{,t}(0)\nabla q(0)dx|\hfill \\ & +|\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }{f}_{,t}(0)\nabla q(0)dx|+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }\nabla \tilde{\eta }\nabla q(0)dx|.\hfill \end{array}$$

(24)

By continuing and using the Poincaré inequality, we obtain

$$\begin{array}{cc}{\parallel q(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\hfill & \le c(|{(v·\nabla v)}_{,t}(0){|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+|{(\stackrel{1}{H}·\nabla \stackrel{1}{H})}_{,t}(0){|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\hfill \\ & +|f_{,t}{(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+\parallel \tilde{\eta }{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}^2)\hfill \\ & \le c(\parallel v(0){\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\parallel v_{,t}(0){\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+\parallel \stackrel{1}{H}(0){\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\parallel {\stackrel{1}{H}}_{,t}(0){\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\hfill \\ & +\parallel f_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}^2+\parallel v_{,t}(0){\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}^2)\equiv I.\hfill \end{array}$$

(25)

Hence,

$$\parallel p_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}^2\le I$$

(26)

Using (19)–(21) and (26) in (18) implies

$$|v_{,tt}{(0)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}\le {\varphi (\parallel v(0)\parallel }_{4,{\stackrel{1}{\mathrm{\Omega }}}_0},\parallel \stackrel{1}{H}{(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}{,\parallel f(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0},\parallel f_{,t}(0){\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}).$$

(27)

Finally, using (21) in (20) yields

$$\parallel v_{,t}{(0)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_0}\le {\varphi (\parallel v(0)\parallel }_{4,{\stackrel{1}{\mathrm{\Omega }}}_0},\parallel \stackrel{1}{H}{(0)\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_0}{,\parallel f(0)\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_0}).$$

(28)

This concludes the note.

The equations of magnetohydrodynamics can be found in [8]. We use Sobolev spaces, theorems of imbedding and traces introduced in [9].

3. Notation and Auxiliary Results

3.1. Spaces and a Partition of Unity

To simplify the presentation, we introduce the following notation:

Notation 1. 

Let Ω be a domain in ${\mathbb{R}}^3$. We use the Lebesque and Sobolev spaces.

$$L_p(\mathrm{\Omega })=\left\{u:{\left(\underset{\mathrm{\Omega }}{\int }{|u(x)|}^{p}dx\right)}^{1/p}\equiv {\parallel u\parallel }_{L_p(\mathrm{\Omega })}\equiv {|u|}_{p,\mathrm{\Omega }}<\infty \right\},$$

where $p\in [1,\infty ]$. Next, we introduce $L_2$-Sobolev spaces:

$$H^l(\mathrm{\Omega })=\left\{u:{\left(\sum _{|\alpha |\le l}\underset{\mathrm{\Omega }}{\int }{|D_x^{\alpha }u|}^{2}dx\right)}^{1/2}\equiv \sum _{|\alpha |\le l}|D_x^{\alpha }{u|}_{2,\mathrm{\Omega }}\equiv {\parallel u\parallel }_{l,\mathrm{\Omega }}<\infty \right\},$$

where $l\in \mathbb{N}$, $D_x^{\alpha }={\partial }_{x_1}^{{\alpha }_1}{\partial }_{x_2}^{{\alpha }_2}{\partial }_{x_3}^{{\alpha }_3}$, ${\alpha }_i\in \mathbb{N}\cup \left\{0\right\}$, $i=1,2,3$, $\alpha =({\alpha }_1,{\alpha }_2,{\alpha }_3)$ is the multi-index, and $|\alpha |={\alpha }_1+{\alpha }_2+{\alpha }_3$.

We frequently use the embedding $H^k(\mathrm{\Omega })\subset L_p(\mathrm{\Omega })$, which holds for

$${\displaystyle \frac{3}{2}}-{\displaystyle \frac{3}{p}}\le k.$$

By $W_q^s(\mathrm{\Omega })$, we denote the standard Sobolev space with the norm

$${\parallel u\parallel }_{W_q^s(\mathrm{\Omega })}=\sum _{|\alpha |\le s}{|D^{\alpha }u|}_{q,\mathrm{\Omega }},$$

where $s\in \mathbb{N}\cup \left\{0\right\}$, $q\in [1,\infty ]$.

We also need the embedding

$$H^k(\mathrm{\Omega })\subset W_q^s(\mathrm{\Omega })\mathrm{if}{\displaystyle \frac{3}{2}}-{\displaystyle \frac{3}{q}}+s\le k.$$

We also have direct and inverse theorems of traces (see [10,11]).

Let $u\in W_p^l(\mathrm{\Omega })$, $l\in {\mathbb{R}}_{+}$, $p\in (1,\infty )$. Let $S=\partial \mathrm{\Omega }$. Then $\tilde{u}{=u|}_S\in W_p^{l-1/p}(S)$ and

$$\parallel \tilde{u}{\parallel }_{W_p^{1-1/p}(S)}\le c{\parallel u\parallel }_{W_p^l(\mathrm{\Omega })}.$$

Let $\tilde{u}\in W_p^{l-1/p}(S)$. Then there exists $u\in W_p^l(\mathrm{\Omega })$ such that ${u|}_S=\tilde{u}$ and

$${\parallel u\parallel }_{W_p^l(\mathrm{\Omega })}\le c{\parallel \tilde{u}\parallel }_{W_p^{l-1/p}(S)}.$$

Furthermore, by ϕ we denote an increasing positive function.

We apply the energy method to prove the existence of solutions to (10) and (12). Therefore, we use the $L_2$-Sobolev spaces.

In order to examine problem (12) in a neighbourhood of the free surface $S_t$, we need Sobolev spaces $H^k$ expressed by the Fourier transforms. Let

$$\tilde{u}(\xi )=\underset{{\mathbb{R}}^3}{\int }u(x)e^{-ix·\xi }dx$$

be the Fourier transform of u, $\xi =({\xi }_1,{\xi }_2,{\xi }_3)$, $x=(x_1,x_2,x_3)$, and $x·\xi =x_1{\xi }_1+x_2{\xi }_2+x_3{\xi }_3$.

Then, by the Parseval identity, we have the equivalence

$${\parallel u\parallel }_{H^k({\mathbb{R}}^3)}={\left(\underset{{\mathbb{R}}^3}{\int }|\tilde{u}{|}^2{\displaystyle \sum _{j=0}^k}{|\xi |}^{2j}d\xi \right)}^{1/2}.$$

Consider functions defined in ${\mathbb{R}}_{+}^3=\{x\in {\mathbb{R}}^3:x_3>0\}$. Then

$${\parallel u\parallel }_{H^k({\mathbb{R}}_{+}^3)}={\left({\displaystyle \sum _{s=0}^k}{\displaystyle \sum _{j=0}^s}\underset{{\mathbb{R}}^2}{\int }|{\left({\displaystyle \frac{\partial }{\partial x_3}}\right)}^j\tilde{u}(\xi ,x_3){|}^2{|\xi |}^{2(s-j)}d\xi \right)}^{1/2},$$

where $\xi =({\xi }_1,{\xi }_2)$.

Let ${\mathrm{\Gamma }}_l^k(\mathrm{\Omega })={\{u:|u|}_{k,l,\mathrm{\Omega }}<\infty \}$, where

$${|u|}_{k,l,\mathrm{\Omega }}=\sum _{i\le k-l}{|{\partial }_t^{i}u|}_{H^{k-i}(\mathrm{\Omega })}\mathrm{and}k,l\in \mathbb{N}\cup \left\{0\right\}.$$

We introduce the notation

$$\begin{array}{cc}& X_1^2={|v|}_{2,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|p|}_{1,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|\stackrel{1}{H}|}_{2,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^2,\hfill \\ & Y_1^2={|v|}_{3,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|p|}_{2,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|\stackrel{1}{H}|}_{3,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.\hfill \end{array}$$

(29)

Now, we introduce a partition of unity in ${\mathrm{\Omega }}_0={\stackrel{1}{\mathrm{\Omega }}}_0\cup {\stackrel{2}{\mathrm{\Omega }}}_0$ (see [12] Ch. 4, Sect. 4). We consider two collections of open subsets $\left\{{\omega }^{(k)}\right\}$ and $\left\{{\mathrm{\Omega }}^{(k)}\right\}$, $k\in \mathcal{M}\cup \mathcal{N}$, such that ${\overline{\omega }}^{(k)}\subset {\mathrm{\Omega }}^{(k)}\subset {\mathrm{\Omega }}_0$, ${\bigcup }_k{\omega }^{(k)}={\bigcup }_k{\mathrm{\Omega }}^{(k)}={\mathrm{\Omega }}_0$. For $k\in {\mathcal{M}}_1$, ${\mathrm{\Omega }}^{(k)}\subset {\stackrel{1}{\mathrm{\Omega }}}_0$ and ${\overline{\mathrm{\Omega }}}^{(k)}\cap S_0=\varphi$, for $k\in {\mathcal{M}}_2$${\mathrm{\Omega }}^{(k)}\subset {\stackrel{2}{\mathrm{\Omega }}}_0$, ${\overline{\mathrm{\Omega }}}^{(k)}\cap S_0=\varphi$ and ${\overline{\mathrm{\Omega }}}^{(k)}\cap B=\varphi$, ${\overline{\mathrm{\Omega }}}^{(k)}\cap S_0\ne \varphi$ for $k\in {\mathcal{N}}_1$, and ${\overline{\mathrm{\Omega }}}^{(k)}\cap B\ne \varphi$ for $k\in {\mathcal{N}}_2$.

We assume that at most $N_0$ of the ${\mathrm{\Omega }}^{(k)}$ have nonempty intersections, ${sup}_k\mathrm{diam}{\mathrm{\Omega }}^{(k)}\le 2\lambda$, and ${sup}_k\mathrm{diam}{\omega }^{(k)}\le \lambda$ for some $\lambda >0$. Let ${\zeta }^{(k)}(x)$ be a smooth function such that $0\le {\zeta }^{(k)}(x)\le 1$, ${\zeta }^{(k)}(x)=1$ for $x\in {\omega }^{(k)}$, ${\zeta }^{(k)}(x)=0$ for $x\in {\mathrm{\Omega }}_0\setminus {\mathrm{\Omega }}^{(k)}$ and $|D_x^{\nu }{\zeta }^{(k)}(x)|\le c/{\lambda }^{|\nu |}$, where $D^{\nu }={\partial }_{x_1}^{{\nu }_1}{\partial }_{x_2}^{{\nu }_2}{\partial }_{x_3}^{{\nu }_3}$, $|\nu |={\nu }_1+{\nu }_2+{\nu }_3$. Then $1\le {\sum }_k{({\zeta }^{(k)}(x))}^2\le N_0$. Introducing the function

$${\eta }^{(k)}(x)={\displaystyle \frac{{\zeta }^{(k)}(x)}{{\sum }_l{({\zeta }^{(l)}(x))}^2}},$$

we have that ${\eta }^{(k)}(x)=0$ for $x\in {\mathrm{\Omega }}_0\setminus {\mathrm{\Omega }}^{(k)}$, ${\sum }_k{\eta }^{(k)}(x){\zeta }^{(k)}(x)=1$, and $|D_x^{\nu }{\eta }^{(k)}(x)|\le c/{\lambda }^{|\nu |}$.

We denote by ${\xi }^{(k)}$ an interior point of ${\omega }^{(k)}$ and ${\mathrm{\Omega }}^{(k)}$ for $k\in \mathcal{M}$, an interior point of ${\overline{\omega }}^{(k)}\cap S_0$ and of ${\overline{\mathrm{\Omega }}}^{(k)}\cap S_0$ for $k\in {\mathcal{N}}_1$, and an interior point of ${\overline{\omega }}^{(k)}\cap B$ and of ${\overline{\mathrm{\Omega }}}^{(k)}\cap B$ for $k\in {\mathcal{N}}_2$. For $k\in {\mathcal{M}}_i$, ${\xi }^{(k)}\in {\stackrel{i}{\mathrm{\Omega }}}_0$, $i=1,2$.

Let $x=(x_1,x_2,x_3)$ be a Cartesian coordinate system with its origin located at the interior point of ${\mathrm{\Omega }}_0$. Then, using translations and rotations, we introduce a local coordinate system $y=(y_1,y_2,y_3)$ with the origin at ${\xi }^{(k)}\in {\mathrm{\Omega }}^{(k)}\cap S_0$, $k\in {\mathcal{N}}_1$, such that the part ${\tilde{S}}_0^{(k)}=S_0\cap {\mathrm{\Omega }}^{(k)}$ of the boundary $S_0$ is described by $y_3=F_k(y_1,y_2)$. We call the transformation $y=Y_k(x)$. Then we introduce new coordinates defined by

$$z_i=y_i,i=1,2,z_3=y_3-F_k(y_1,y_2),k\in {\mathcal{N}}_1.$$

We denote this transformation by ${\widehat{\mathrm{\Omega }}}^{(k)}\ni z={\mathrm{\Phi }}_k(y)$, where $y\in {\mathrm{\Omega }}^{(k)}$.

We assume that the sets ${\widehat{\omega }}^{(k)}$, ${\widehat{\mathrm{\Omega }}}^{(k)}$ are described in local coordinates at ${\xi }^{(k)}$ by the inequalities

$$\begin{array}{cc}& |y_i|<\lambda ,i=1,2,|y_3-F_k(y_1,y_2)|<\lambda ,\hfill \\ & |y_i|<2\lambda ,i=1,2,|y_3-F_k(y_1,y_2)|<2\lambda ,\hfill \end{array}$$

respectively. Furthermore, $(y_1,y_2,y_3)\in {\stackrel{1}{\mathrm{\Omega }}}_0$ if $y_3>F_k(y_1,y_2)$ and $(y_1,y_2,y_3)\in {\stackrel{2}{\mathrm{\Omega }}}_0$ for $y_3<F_k(y_1,y_2)$.

Let ${\mathrm{\Psi }}_k={\mathrm{\Phi }}_k\circ Y_k$. Then $z={\mathrm{\Psi }}_k(x)$ and ${\widehat{u}}^{(k)}(z,t)=u({\mathrm{\Phi }}_k^{-1}(z),t)$, ${\tilde{u}}^{(k)}(z,t)={\widehat{u}}^{(k)}(z,t){\widehat{\zeta }}^{(k)}(z,t)$.

For $k\in \mathcal{M}$, we have

$${\tilde{u}}^{(k)}(x,t)=u^{(k)}(x,t){\zeta }^{(k)}(x,t).$$

For $k\in {\mathcal{N}}_2$, we introduce new local coordinates with the origin at ${\xi }^{(k)}\in B\cap {\overline{\mathrm{\Omega }}}^{(k)}$ such that $y_3=F_k(y_1,y_2)$ describes locally $B\cap {\overline{\mathrm{\Omega }}}^{(k)}$. We also introduce the transformation $z_i=y_i$, $i=1,2$, $z_3=y_3-F_k(y_1,y_2)$ and assume that $z={\mathrm{\Phi }}_k(y)$ belongs to ${\widehat{\mathrm{\Omega }}}^{(k)}$ for $y\in {\mathrm{\Omega }}^{(k)}$.

Finally, ${\widehat{\omega }}^{(k)}$, ${\widehat{\mathrm{\Omega }}}^{(k)}$ are described by the inequalities

$$\begin{array}{cc}& |y_i|<\lambda ,i=1,2,0<y_3-F_k(y_1,y_2)<\lambda ,\hfill \\ & |y_i|<2\lambda ,i=1,2,0<y_3-F_k(y_1,y_2)<2\lambda ,\hfill \end{array}$$

respectively.

In this paper, by $\varphi$, we denote an increasing positive function such that $\varphi (0)\ne 0$, and it can change its form from formula to formula.

3.2. Eulerian and Lagrangian Coordinates

Let $x=(x_1,x_2,x_3)$ be Eulerian coordinates. By Lagrangian coordinates, we mean the initial data of the problem

$${\displaystyle \frac{dx}{dt}}{=v(x,t),x|}_{t=0}=\xi .$$

(30)

Solving (30) yields

$$x=\xi +{\displaystyle \underset{0}{\overset{t}{\int }}}v(x(\xi ,t^{\prime }),t^{\prime })d{t}^{\prime }=\xi +{\displaystyle \underset{0}{\overset{t}{\int }}}\overline{v}(\xi ,t^{\prime })d{t}^{\prime }\equiv x(\xi ,t),$$

(31)

where $\overline{v}(\xi ,t)=v(x(\xi ,t),t)$.

Domain ${\stackrel{1}{\mathrm{\Omega }}}_t$ and its boundary $S_t$ are described as follows:

$${\stackrel{1}{\mathrm{\Omega }}}_t=\{x=x(\xi ,t):\xi \in {\stackrel{1}{\mathrm{\Omega }}}_0\},S_t=\{x=x(\xi ,t):\xi \in S_0\}.$$

(32)

By $\left\{x_{\xi }\right\}$, we denote the Jacobi matrix of the transformation (31). Let $J=det\left\{x_{\xi }\right\}$ be the Jacobian of this transformation. Then

$${\displaystyle \frac{dJ}{dt}}=J\mathrm{div}v.$$

(33)

For a divergence-free vector, we have $J(t)=1$. Let ${\mathrm{\Omega }}_t$ replace either ${\stackrel{1}{\mathrm{\Omega }}}_t$ or ${\stackrel{2}{\mathrm{\Omega }}}_t$. Then we have

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\underset{{\mathrm{\Omega }}_t}{\int }f(x,t)dx={\displaystyle \frac{d}{dt}}\underset{\mathrm{\Omega }}{\int }f(x(\xi ,t),t)Jd\xi \hfill \\ & =\underset{\mathrm{\Omega }}{\int }\left({\displaystyle \frac{\partial f}{\partial t}}+v·\nabla f+\mathrm{div}v\right)Jd\xi =\underset{{\mathrm{\Omega }}_t}{\int }(f_t(x,t)+v·\nabla f+f\mathrm{div}v)dx.\hfill \end{array}$$

(34)

Using (34), we calculate

$${\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }dx={\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }d\xi =0.$$

Hence,

$$|{\stackrel{1}{\mathrm{\Omega }}}_t|=|{\stackrel{1}{\mathrm{\Omega }}}_0|.$$

(35)

Lemma 1. 

Assume that v is a solution to (10). Assume that ${\displaystyle {\int }_0^t}{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}f·\phi dxd{t}^{\prime }$, ${\int }_{{\stackrel{1}{\mathrm{\Omega }}}_0}v(0)\phi (0)d\xi$ are finite, where

$$\phi =(x-\overline{x})\times \overline{e},$$

(36)

where $x=(x_1,x_2,x_3)$, $\overline{x}={\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\left({\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{x}_{1}dx,{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{x}_{2}dx,{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{x}_{3}dx\right)$, ${\overline{e}}_i=({\delta }_{i1},{\delta }_{i2},{\delta }_{i3})$, $i=1,2,3$, and ${\delta }_{ij}$ is the Kronecker delta. Moreover, $\phi (0)=\left(\xi -{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_0|}}{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_0}\xi d\xi \right)\times \overline{e}$.

Then

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\phi dx={\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_{t^{\prime }}}{\int }f·\phi dxd{t}^{\prime }+\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)\phi (0)d\xi .$$

(37)

Proof. 

We calculate

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\phi dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\partial }_t(v·\phi )dx+v·\nabla (v·\phi )dx\hfill \\ & =\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }({\partial }_{t}v+v·\nabla v)·\phi dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(v·{\phi }_{,t}dx+v·\nabla \phi ·vdx)\equiv I_1+I_2.\hfill \end{array}$$

(38)

First, we consider $I_1$. Using (10)₁ yields

$$I_1=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{div}(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))·\phi dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·\phi dx.$$

Integrating by parts in $I_1$ and using the boundary condition (10)₃ yields

$$I_1=-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))·\nabla \phi dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·\phi dx,$$

where the first integral vanishes because $\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H})$ is a symmetric tensor and $\nabla \phi$ is an antisymmetric tensor.

Hence,

$$I_1=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·\phi dx.$$

To consider $I_2$, we see that

$$\begin{array}{cc}{\partial }_t\overline{x}\hfill & ={\partial }_t{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }xdx={\displaystyle \frac{1}{|{\mathrm{\Omega }}_0|}}{\partial }_t\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }x(\xi ,t)d\xi \hfill \\ & ={\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_0|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(x(\xi ,t),t)d\xi ={\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v(x,t)dx.\hfill \end{array}$$

(39)

The second term in $I_2$ equals

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_i{v}_j{\nabla }_i{\phi }_{j}dx=0$$

because $\nabla \phi$ is an antisymmetric tensor.

To consider the first term in $I_2$, we calculate

$${\phi }_t={\partial }_t(x-\overline{x})\times \overline{e}=({\overline{x}}_t-{\partial }_t\overline{x})\times \overline{e}=\left[v-{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v(x,t)dx\right]\times \overline{e}.$$

Then the first term in $I_2$ equals

$$\begin{array}{cc}& \underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\left(v-{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v(x,t)dx\right)\times \overline{e}dx\hfill \\ & =-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }vdx·{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v(x,t)dx\times \overline{e}=-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }vdx·{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }vdx\times \overline{e}=0.\hfill \end{array}$$

Using the above results in (38) yields the equality

$${\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\phi dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·\phi dx.$$

(40)

Integrating (40) with respect to time implies (37). This completes the proof. □

Remark 2. 

We derive an energy-type inequality for solutions to problem (10) assuming that the tensor of the magnetic field $\mathbb{T}(\stackrel{1}{H})$ is given.

Multiplying (10)₁ by v, integrating over ${\stackrel{1}{\mathrm{\Omega }}}_t$, and using boundary conditions (10)₃, we obtain

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}^{2}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{|\mathbb{D}(v)|}^{2}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathbb{T}(\stackrel{1}{H})·\mathbb{D}(v)dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·vdx.$$

(41)

Applying the Hölder and Young inequalities to the last term on the left-hand side of (41) implies

$${\displaystyle \frac{d}{dt}}{|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|\mathbb{D}(v)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c{|\mathbb{T}(\stackrel{1}{H})|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·vdx.$$

(42)

3.3. The Korn Inequalities

Using ideas from [13,14], we derive Korn-type inequalities necessary for the existence of solutions.

Lemma 2. 

Let ${\stackrel{1}{\mathrm{\Omega }}}_t$ be a given bounded domain. Let

$${\phi }_i=(x-\overline{x})\times {\overline{e}}_i,i=1,2,3,$$

(43)

where $x=(x_1,x_2,x_3)$, $\overline{x}={\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\left({\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{x}_{1}dx,{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{x}_{2}dx,{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{x}_{3}dx\right)$, ${\overline{e}}_i=({\delta }_{i1},{\delta }_{i2},{\delta }_{i3})$, $i=1,2,3$, and ${\delta }_{ij}$ is the Kronecker delta.

Let w be a given vector function such that

$$E_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w)=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(w_{i,x_j}+w_{j,x_i})}^{2}dx<\infty ,$$

(44)

and the following quantities are finite:

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx,\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }w·{\phi }_{i}dx,i=1,2,3.$$

(45)

Then

$${\parallel w\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c\left(E_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w)+{\left(\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx\right)}^2+{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }w·{\phi }_{i}dx{|}^2\right),$$

(46)

where c does not depend on w.

Proof. 

Let

$$u={\displaystyle \sum _{i=1}^3}{b}_i{\phi }_i(x)+w.$$

(47)

Define $b=(b_1,b_2,b_3)$ by

$$b={\displaystyle \frac{1}{2|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{rot}wdx.$$

(48)

Since $\mathrm{rot}{\phi }_i=-2{\overline{e}}_i$, $i=1,2,3$, Equations (47) and (48) imply

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{rot}udx=0.$$

(49)

From (43), we have $\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\phi }_{i}dx=0$, $i=1,2,3$; so

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }udx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx.$$

(50)

and also $E_{{\stackrel{1}{\mathrm{\Omega }}}_t}({\phi }_i)=0$, $i=1,2,3$; so

$$E_{{\stackrel{1}{\mathrm{\Omega }}}_t}(u)=E_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w).$$

(51)

Theorem 1 from [13] implies

$${\partial }_{x_j}{(\mathrm{rot}u)}_i={\epsilon }_{ikl}{\partial }_{x_k}{D}_{jl}(u),i,j=1,2,3,$$

(52)

where $D_{ij}(u)=u_{j,x_i}+u_{i,x_j}$, and ${\epsilon }_{ijk}$ is the antisymmetric Ricci tensor.

Hence, (49) and Lemma 2.4 from [3] yield

$${|\mathrm{rot}u|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c{\displaystyle \sum _{i,j=1}^3}{|D_{ij}(u)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\equiv c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(u)=c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w).$$

(53)

Using the identity

$$u_{i,x_j}={\displaystyle \frac{1}{2}}(u_{i,x_j}+u_{j,x_i})+{\displaystyle \frac{1}{2}}(u_{i,x_j}-u_{j,x_i})$$

and (53), we have

$$\begin{array}{cc}{|\nabla u|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill & \le c(E_{{\stackrel{1}{\mathrm{\Omega }}}_t}(u)+{|\mathrm{rot}u|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)\le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(u)=c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w).\hfill \end{array}$$

(54)

Given (47) and (54), we obtain

$${|\nabla w|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le {c|\nabla u|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{c|b|}^2\le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w)+c{|b|}^2.$$

(55)

From (47), we derive the algebraic system

$${\displaystyle \sum _{i=1}^3}{b}_i\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\phi }_i(x)·{\phi }_j(x)dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(u-w)·{\phi }_{j}dx,j=1,2,3.$$

(56)

Since det $\mathrm{\Gamma }\ne 0$, where $\mathrm{\Gamma }={\left\{{\mathrm{\Gamma }}_{ij}\right\}}_{i,j=1,2,3}$ and ${\mathrm{\Gamma }}_{ij}=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\phi }_i(x)·{\phi }_j(x)dx$, we calculate

$${\left|b\right|}^2\le c{\displaystyle \sum _{i=1}^3}\left(|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }u(x)·{\phi }_i(x)dx{|}^2+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }w(x)·{\phi }_i(x)dx{|}^2\right).$$

(57)

By the Poincaré inequality, (50) and (54), we obtain

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }u·{\phi }_{i}dx{|}^2\le c{\left|u\right|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le c|u-{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t}}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }udx{|}^2+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }udx{|}^2\hfill \\ & \le {c|\nabla u|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx{|}^2\le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w)+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx{|}^2.\hfill \end{array}$$

(58)

Using (58) in (57) yields

$$b^2\le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w)+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx{|}^2+c{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }w·{\phi }_{i}dx{|}^2.$$

(59)

Then (55) gives

$$\begin{array}{cc}& {|\nabla w|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(w)+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx{|}^2+c{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }w·{\phi }_{i}dx{|}^2.\hfill \end{array}$$

(60)

Next,

$$\begin{array}{cc}{|w|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill & \le |w-{\displaystyle \frac{1}{|{\stackrel{1}{\mathrm{\Omega }}}_t|}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx{|}^2+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx{|}^2\hfill \\ & \le {c|\nabla w|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }wdx{|}^2.\hfill \end{array}$$

(61)

Inequalities (60) and (61) imply (46). This concludes the proof. □

Corollary 1. 

From (10), we have

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }vdx={\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }fdxd{t}^{\prime }+\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)dx$$

(62)

and (37) yields

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·{\phi }_{i}dx={\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_{t^{\prime }}}{\int }f·{\phi }_{i}dxd{t}^{\prime }+\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)·{\phi }_i(0)dx,$$

(63)

where $i=1,2,3$.

Using Lemma 2 with $w=v$ and equalities (62) and (63), we have

$$\begin{array}{cc}{\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill & \le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(v)+c|{\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_{t^{\prime }}}{\int }fdxd{t}^{\prime }{|}^2+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)dx{|}^2\hfill \\ & +c{\displaystyle \sum _{i=1}^3}\left(|{\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_{t^{\prime }}}{\int }f·{\phi }_{i}dxd{t}^{\prime }{|}^2+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)·{\phi }_i(0)dx{|}^2\right).\hfill \end{array}$$

(64)

Corollary 2. 

From (2)₁, we have

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,t}dx=-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\nabla vdx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }fdx,$$

(65)

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,t}·{\phi }_{i}dx=-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(v·\nabla v)·{\phi }_{i}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·{\phi }_{i}dx,i=1,2,3.$$

(66)

Using Lemma 2 with $w=v_t$ and also (65) and (66), we have

$$\begin{array}{cc}\parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill & \le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(v_{,t})+{c|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{|\nabla v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }fdx{|}^2+c{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·{\phi }_{i}dx{|}^2.\hfill \end{array}$$

(67)

Lemma 3. 

For sufficiently regular solutions to (2) such that $E_{{\stackrel{1}{\mathrm{\Omega }}}_t}(v_{,tt})<\infty$, $|{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{f}_{,t}dx|<\infty$, $|{\int }_{{\stackrel{1}{\mathrm{\Omega }}}_t}{f}_{,t}·{\phi }_{i}dx|<\infty$, $i=1,2,3$, $v\in {\mathrm{\Gamma }}_1^2({\stackrel{1}{\mathrm{\Omega }}}_t)$, $p\in H^1({\stackrel{1}{\mathrm{\Omega }}}_t)$, and $\stackrel{1}{H}\in {\mathrm{\Gamma }}_0^1({\stackrel{1}{\mathrm{\Omega }}}_t)$, the following inequality holds:

$$\begin{array}{cc}\parallel v_{,tt}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill & \le c{E}_{{\stackrel{1}{\mathrm{\Omega }}}_t}(v_{,tt})+{c(|v|}_{2,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4\hfill \\ & +{|v|}_{2,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2·{(\parallel p\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4)+c|\stackrel{1}{H}{|}_{1,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^4\hfill \\ & +c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}dx|+c{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}·{\phi }_{i}dx{|}^2.\hfill \end{array}$$

(68)

Proof. 

From (2)₁, we have

$$\begin{array}{cc}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,tt}dx\hfill & =-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(v·\nabla v)}_{,t}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{div}{(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))}_{,t}dx\hfill \\ & +\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}dx.\hfill \end{array}$$

(69)

Integrating by parts in the second term on the right-hand side of (69) yields

$$\begin{array}{cc}& \underset{S_t}{\int }\overline{n}·{(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))}_{,t}d{S}_t\hfill \\ & =\underset{S_t}{\int }{[\overline{n}·(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))]}_{,t}d{S}_t-\underset{S_t}{\int }{\overline{n}}_{,t}(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))d{S}_t,\hfill \end{array}$$

(70)

where the first term vanishes because (10)₃ holds.

To examine the second integral in (70), we use the kinematic condition

$$v·\nabla \varphi =-{\varphi }_{,t},$$

(71)

where $\varphi (x,t)$ describes the boundary $S_t$.

The condition means that the free boundary $S_t$ is a material surface. Hence, $S_t$ consists of moving particles. Therefore,

$$S_t=\left\{x:x=x(\xi ,t)=\xi +{\displaystyle \underset{0}{\overset{t}{\int }}}\overline{v}(\xi ,\tau )d\tau ,\xi \in S_0\right\}.$$

Since $\varphi (x,t)$ describes $S_t$, we have

$$0={\displaystyle \frac{d}{dt}}\varphi (x,t)=v·\nabla \varphi +{\varphi }_{,t},$$

(72)

where we used

$${\displaystyle \frac{dx}{dt}}{=v(x,t),x|}_{t=0}=\xi .$$

(73)

Hence, (72) implies (71). Furthermore, $v(x,t)$ for $x=x(\xi ,t)\in S_t$ is tangent to $S_t$.

The normal vector to $S_t$ has the following form:

$$\overline{n}={\displaystyle \frac{\nabla \varphi }{|\nabla \varphi |}}.$$

(74)

Therefore,

$${\overline{n}}_{,t}={\displaystyle \frac{\nabla {\varphi }_{,t}}{|\nabla \varphi |}}-{\displaystyle \frac{\nabla \varphi \nabla \varphi ·\nabla {\varphi }_{,t}}{{|\nabla \varphi |}^2}}.$$

Since

$$\nabla {\varphi }_{,t}=-\nabla v·\nabla \varphi -v{\nabla }^2\varphi$$

we obtain

$$|{\overline{n}}_{,t}|\le c(|\nabla v|+|v|).$$

(75)

Consequently, the second term on the right-hand side of (70) is bounded by

$$c\underset{S_t}{\int }(|v|+|\nabla v|)(|\nabla v|+|p|+|\stackrel{1}{H}{|}^2)d{S}_t.$$

(76)

Finally, we obtain

$$\begin{array}{cc}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,tt}dx|\hfill & \le c\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(|v_{,t}||\nabla v|+|v||\nabla v_{,t}|)dx\hfill \\ & +c\underset{S_t}{\int }(|v|+|\nabla v|)(|\nabla v|+|p|+|\stackrel{1}{H}{|}^2)d{S}_t+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}dx|\hfill \\ & \le c|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\nabla v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{c|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}|\nabla v_t{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{c(|v|}_{2,S_t}\hfill \\ & +{|\nabla v|}_{2,S_t}{)·(|\nabla v|}_{2,S_t}+{|p|}_{2,S_t}+|\stackrel{1}{H}{|}_{4,S_t}^2)+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}dx|.\hfill \end{array}$$

(77)

From (2)₁, we have

$$\begin{array}{cc}& \underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,tt}·{\phi }_{i}dx=-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(v·\nabla v)}_{,t}{\phi }_{i}dx\hfill \\ & +\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{div}{(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))}_{,t}{\phi }_{i}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·{\phi }_{i}dx,i=1,2,3,\hfill \end{array}$$

(78)

where function ${\phi }_i$, $i=1,2,3$, is introduced in (43).

Integrating by parts in the second term on the right-hand side of (78) gives

$$\begin{array}{cc}& \underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{div}\left[{(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))}_{,t}{\phi }_i\right]dx\hfill \\ & -\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))}_{,t}·\nabla {\phi }_{i}dx\equiv I_1+I_2.\hfill \end{array}$$

(79)

Since $\mathbb{T}(v_{,t},p_{,t})$ is symmetric and $\nabla {\phi }_i$ is antisymmetric, the integral $I_2$ equals

$$I_2=-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathbb{T}{(\stackrel{1}{H})}_{,t}·\nabla {\phi }_{i}dx.$$

Using boundary condition (10)₃, the integral $I_1$ takes the form

$$I_1=-\underset{S_t}{\int }{\overline{n}}_{,t}·(\mathbb{T}(v,p)+\mathbb{T}(\stackrel{1}{H}))·{\phi }_{i}d{S}_t.$$

Therefore,

$$\begin{array}{cc}& |\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,tt}·{\phi }_{i}dx|\le {c|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}|\nabla v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\nabla v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +{c(|v|}_{2,S_t}+{|\nabla v|}_{2,S_t}{)(|\nabla v|}_{2,S_t}+{|p|}_{2,S_t}+|\stackrel{1}{H}{|}_{4,S_t}^2)\hfill \\ & +c|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}{|{\stackrel{1}{H}}_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}·{\phi }_{i}dx|,i=1,2,3.\hfill \end{array}$$

(80)

Using (77) and (80) in Lemma 2 with $w=v_{tt}$, we obtain

$$\begin{array}{cc}\parallel v_{,tt}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill & \le c|\mathbb{D}(v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c|v{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2|\nabla v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2|\nabla v{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{(|v|}_{2,S_t}^2+{|\nabla v|}_{2,S_t}^2{)·(|\nabla v|}_{2,S_t}^2+{|p|}_{2,S_t}^2+|\stackrel{1}{H}{|}_{4,S_t}^4))\hfill \\ & +c|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{|{\stackrel{1}{H}}_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}dx{|}^2+c{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}·{\phi }_{i}dx{|}^2.\hfill \end{array}$$

(81)

This inequality implies (68) and concludes the proof. □

3.4. Estimates for ${\overline{n}}_{,t}$ and ${\overline{n}}_{,tt}$

Next, we calculate

$$\begin{array}{cc}{\overline{n}}_{,tt}\hfill & ={\displaystyle \frac{\nabla {\varphi }_{,tt}}{|\nabla \varphi |}}-{\displaystyle \frac{\nabla {\varphi }_{,t}}{{|\nabla \varphi |}^3}}\nabla \varphi \nabla {\varphi }_{,t}-{\left({\displaystyle \frac{\nabla \varphi ·\nabla {\varphi }_{,t}\nabla \varphi }{{|\nabla \varphi |}^2}}\right)}_{,\nabla {\varphi }_{,t}}\nabla {\varphi }_{,tt}\hfill \\ & -{\left({\displaystyle \frac{\nabla \varphi ·\nabla {\varphi }_{,t}·\nabla \varphi }{{|\nabla \varphi |}^2}}\right)}_{,\nabla \varphi }\nabla {\varphi }_{,t}.\hfill \end{array}$$

Using

$$\nabla {\varphi }_{,tt}=-\nabla v_{,t}·\nabla \varphi -\nabla v·\nabla {\varphi }_{,t}-v_{,t}·{\nabla }^2\varphi -v{\nabla }^2{\varphi }_{,t}$$

and

$$-{\nabla }^2{\varphi }_{,t}={\nabla }^{2}v·\nabla \varphi +2\nabla v·{\nabla }^2\varphi +v{\nabla }^3\varphi$$

we obtain

$$|{\overline{n}}_{,tt}|\le c(|\nabla v_{,t}|+|\nabla v|+|v|+|v_{,t}|+|{\nabla }^{2}v|)(|\nabla v|+|v|).$$

(82)

3.5. Poincaré Inequality for the Pressure

From boundary condition (5)₁ and $p_0=0$, we have

$$\begin{array}{cc}p\hfill & =\nu \overline{n}·\mathbb{D}(v)·\overline{n}-{\mu }_1\overline{n}·\mathbb{T}(\stackrel{1}{H})·\overline{n}\hfill \\ & =\nu \overline{n}·\mathbb{D}(v)·\overline{n}-{\mu }_1{(\stackrel{1}{H}·\overline{n})}^2+{\mu }_1{\displaystyle \frac{{\stackrel{1}{H}}^2}{2}}\equiv p_{\ast }.\hfill \end{array}\mathrm{on}{S}_t$$

(83)

Knowing that p is defined on $S_t$, we can derive the following Poincaré inequality:

Lemma 4. 

Let $X_1$ be defined as in Notation 1. Let $v\in H^2({\stackrel{1}{\mathrm{\Omega }}}_t)$, $v_{,t}\in H^2({\stackrel{1}{\mathrm{\Omega }}}_t)$, $p_{,x}\in L_2({\stackrel{1}{\mathrm{\Omega }}}_t)$, and $p_{,xt}\in L_2({\stackrel{1}{\mathrm{\Omega }}}_t)$. Then

$${|p|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le \epsilon |v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(1/\epsilon )|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(X_1^2+|p_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})$$

(84)

and

$$|p_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le \epsilon |v_{,xxt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(1/\epsilon )|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(X_1^2(1+X_1)+|p_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}).$$

(85)

Proof. 

First, we show (84). From the Poincaré inequality and (83), we have

$$\begin{array}{cc}{|p|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill & \le c(|p_{\ast }{|}_{2,S_t}+|p_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\le c(|v_{,x}{|}_{2,S_t}+|\stackrel{1}{H}{|}_{4,S_t}^2+|p_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\hfill \\ & \le \epsilon |v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(1/\epsilon )|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|p_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\hfill \\ & \le \epsilon |v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(1/\epsilon )|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(X_1^2+|p_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}).\hfill \end{array}$$

This inequality implies (84).

Next, using (83), we have

$$\begin{array}{cc}|p_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill & \le c(|p_{\ast t}{|}_{2,S_t}+|p_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\hfill \\ & \le c(|v_{,xt}{|}_{2,S_t}+|{\overline{n}}_{,t}{v}_{,x}{|}_{2,S_t}+|\stackrel{1}{H}{|}_{4,S_t}|{\stackrel{1}{H}}_{,t}{|}_{4,S_t}\hfill \\ & +|{\overline{n}}_{,t}{\stackrel{1}{H}}^2{|}_{2,S_t}+|p_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\equiv I_1.\hfill \end{array}$$

Considering (75) and the results on traces yields

$$\begin{array}{cc}{I}_1\hfill & \le \epsilon |v_{,xxt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(1/\epsilon )|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(|v{v}_{,x}{|}_{2,S_t}\hfill \\ & +|v_{,x}{|}_{4,S_t}^2+\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\parallel {\stackrel{1}{H}}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v{\stackrel{1}{H}}^2{|}_{2,S_t}+|v_{,x}{\stackrel{1}{H}}^2{|}_{2,S_t}+|p_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

This inequality implies (85) and concludes the proof. □

4. Differential Inequalities for Solutions to (10)

Lemma 5. 

Assume that $\stackrel{1}{H}\in L_4({\stackrel{1}{\mathrm{\Omega }}}_t)$, $f\in L_{6/5}({\stackrel{1}{\mathrm{\Omega }}}_t)$, and

$$\begin{array}{cc}{A}_1^2\hfill & =|{\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_{t^{\prime }}}{\int }fdxd{t}^{\prime }{|}^2+{\displaystyle \sum _{i=1}^3}|{\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_{t^{\prime }}}{\int }f·{\phi }_{i}dxd{t}^{\prime }{|}^2+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)dx{|}^2\hfill \\ & +{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)·{\phi }_i(0)dx{|}^2<\infty .\hfill \end{array}$$

Then

$${\displaystyle \frac{d}{dt}}{|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c(|\stackrel{1}{H}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}^4+{|f|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+A_1^2).$$

(86)

Proof. 

Multiply (10)₁ by v and integrate over ${\stackrel{1}{\mathrm{\Omega }}}_t$. Integrating by parts and using boundary conditions (10)₃, we obtain

$${\displaystyle \frac{d}{dt}}{|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+E_{{\stackrel{1}{\mathrm{\Omega }}}_t}(v)\le c{|\mathbb{T}(\stackrel{1}{H})|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·vdx.$$

(87)

Using the Korn inequality (64) and the form of the tensor $\mathbb{T}(\stackrel{1}{H})$, we obtain

$${\displaystyle \frac{d}{dt}}{|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c|\stackrel{1}{H}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}^4+c{|f|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+A_1^2,$$

(88)

where the Hölder and Young inequalities are applied to the last term on the right-hand side of (87). This ends the proof. □

Lemma 6. 

Assume that v, p, $\stackrel{1}{H}$ are sufficiently regular. Let $f_t\in L_{6/5}({\stackrel{1}{\mathrm{\Omega }}}_t)$.Let

$$A_2^2=|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }fdx{|}^2+{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }f·{\phi }_{i}dx{|}^2.$$

Then

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\nu \parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le {c(|v|}_{2,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4+{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel p\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4+|{\stackrel{1}{H}}_{,t}{|}_{2,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4+|f_{,t}{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+A_2^2).\hfill \end{array}$$

(89)

Proof. 

By differentiating (10)₁ with respect to t, multiplying by $v_{,t}$, integrating over ${\stackrel{1}{\mathrm{\Omega }}}_t$, and using (34), we obtain

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{|v_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{div}{(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))}_{,t}·v_{,t}dx\hfill \\ & =-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,t}·\nabla v·v_{,t}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}·v_{,t}dx.\hfill \end{array}$$

(90)

Integrating by parts in the second term on the left-hand side of (90) yields

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{|v_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2-\underset{S_t}{\int }\overline{n}·{(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))}_{,t}·v_{,t}d{S}_t\hfill \\ & +\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }[\mathbb{T}(v_{,t},p_{,t})+{\mu }_1\mathbb{T}{(\stackrel{1}{H})}_{,t}]·\nabla v_{,t}dx=-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,t}·\nabla v·v_{,t}dx\hfill \\ & +\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}·v_{,t}dx.\hfill \end{array}$$

(91)

The use of boundary condition (10)₃ implies

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\nu {|\mathbb{D}(v_{,t})|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2=-\underset{S_t}{\int }{\overline{n}}_{,t}·(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))·v_{,t}d{S}_t\hfill \\ & -{\mu }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathbb{T}{(\stackrel{1}{H})}_{,t}·\nabla v_{,t}dx-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,t}·\nabla v·v_{,t}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}·v_{,t}dx.\hfill \end{array}$$

(92)

Given of the Korn inequality (67) and (75), we obtain

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\nu {\parallel v_{,t}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le c\underset{S_t}{\int }(|v|+|\nabla v|)(|\nabla v|+|p|+|\stackrel{1}{H}{|}^2)|v_{,t}|d{S}_t\hfill \\ & +c\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|\stackrel{1}{H}||{\stackrel{1}{H}}_{,t}||\nabla v_{,t}|dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|v_{,t}||\nabla v||v_{,t}|dx\hfill \\ & +\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|f_{,t}||v_{,t}|dx+c{A}_2^2.\hfill \end{array}$$

(93)

The first term on the right-hand side of (93) is bounded by

$${\epsilon }_1|v_{,t}{|}_{4,S_t}^2+c(1/{\epsilon }_1){(\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^4+{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel p\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4),$$

the second by

$${\epsilon }_2|\nabla v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_2)\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel {\stackrel{1}{H}}_{,t}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2,$$

the third by

$${\epsilon }_3|v_{,t}{|}_{6,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_3)|v_t{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel \nabla v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2$$

and the fourth by

$${\epsilon }_4|v_{,t}{|}_{6,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_4){|f_{,t}|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

Using the above estimates in (93) and assuming that ${\epsilon }_1-{\epsilon }_4$ are sufficiently small, we have

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\nu {\parallel v_{,t}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le {c(\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^4+{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{(\parallel p\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4)\hfill \\ & +\parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel {\stackrel{1}{H}}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,t}{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+c{A}_2^2.\hfill \end{array}$$

(94)

Using Notation 1 we obtain (89). This concludes the proof. □

Lemma 7. 

Assume that v, p, $\stackrel{1}{H}$ are sufficiently regular. Let

$$A_3^2=|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}dx{|}^2+{\displaystyle \sum _{i=1}^3}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}·{\phi }_{i}dx{|}^2$$

Then

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\nu {\parallel v_{,tt}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c(X_1^2+X_1^4+X_1^6)Y_1^2\hfill \\ & +c{X}_1^4(1+X_1^2)+c{A}_3^2+c{|f_{,tt}|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.\hfill \end{array}$$

(95)

Proof. 

Differentiating (10)₁ twice with respect to t, multiplying by $v_{,tt}$, integrating over ${\stackrel{1}{\mathrm{\Omega }}}_t$ and using (34), we obtain

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{|v_{,tt}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{div}{(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))}_{,tt}·v_{,tt}dx\hfill \\ & =-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(v_{,tt}·\nabla v+2v_{,t}·\nabla v_{,t})·v_{,tt}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,tt}·v_{,tt}dx.\hfill \end{array}$$

(96)

Integrate by parts in the second term on the left-hand side of (96). Then it takes the form

$$\begin{array}{cc}& -\underset{S_t}{\int }\overline{n}·{(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))}_{,tt}·v_{,tt}d{S}_t\hfill \\ & +\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }[\mathbb{T}(v_{,tt},p_{,tt})+{\mu }_1\mathbb{T}{(\stackrel{1}{H})}_{,tt}]·\nabla v_{,tt}dx\equiv I_1+I_2.\hfill \end{array}$$

Applying boundary conditions (10)₃, we write $I_1$ in the form

$$\begin{array}{cc}{I}_1\hfill & =-\underset{S_t}{\int }{[\overline{n}·(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))]}_{,tt}·v_{,tt}d{S}_t\hfill \\ & +\underset{S_t}{\int }{\overline{n}}_{,tt}·(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))·v_{,tt}d{S}_t\hfill \\ & +2\underset{S_t}{\int }{\overline{n}}_{,t}·{(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))}_{,t}·v_{,tt}d{S}_t\hfill \\ & \equiv I_1^1+I_1^2+I_1^3,\hfill \end{array}$$

where $I_1^1=0$. Using (75) and (82), we have

$$\begin{array}{cc}{I}_1^2\hfill & \le c\underset{S_t}{\int }(|\nabla v_{,t}|+|v_{,t}|+|{\nabla }^{2}v|+|\nabla v|+|v|)(|v|+|\nabla v|)·\hfill \\ & ·(|\nabla v|+|p|+|\stackrel{1}{H}{|}^2)|v_{,tt}|d{S}_t\hfill \\ & \le \epsilon |v_{,tt}{|}_{4,S_t}^2+c(1/\epsilon )(|\nabla v_{,t}{|}_{4,S_t}^2+|{\nabla }^2{v|}_{4,S_t}^2+{|\nabla v|}_{4,S_t}^2+{|v_{,t}|}_{4,S_t}^2\hfill \\ & +{|v|}_{4,S_t}^2{)(|v|}_{4,S_t}^2+{|\nabla v|}_{4,S_t}^2{)(|\nabla v|}_{4,S_t}^2+{|p|}_{4,S_t}^2+|\stackrel{1}{H}{|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}^2|\stackrel{1}{H}{|}_{4,S_t}^2)\hfill \\ & \le \epsilon \parallel v_{,tt}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/\epsilon )(\parallel v_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\parallel v\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{)\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2·\hfill \\ & ·(\parallel v{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel p{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^4).\hfill \end{array}$$

Next, we examine $I_1^3$. Using (75), we have

$$\begin{array}{cc}{I}_1^3\hfill & \le c\underset{S_t}{\int }(|\nabla v|+|v|)(|v_{,xt}|+|p_{,t}|+|\stackrel{1}{H}||{\stackrel{1}{H}}_{,t}|)|v_{,tt}|d{S}_t\hfill \\ & \le \epsilon |v_{,tt}{|}_{4,S_t}^2+{c(1/\epsilon )\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2(\parallel v_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel p_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel {\stackrel{1}{H}}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

Next, we have

$$I_2={|\mathbb{D}(v_{,tt})|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+2\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }({\stackrel{1}{H}}_{,tt}\stackrel{1}{H}+{\stackrel{1}{H}}_{,t}^2)\nabla v_{,tt}dx,$$

where the second term is bounded by

$$\epsilon |\nabla v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/\epsilon )(|{\stackrel{1}{H}}_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel {\stackrel{1}{H}}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4).$$

The first term on the right-hand side of (96) is bounded by

$$\epsilon |v_{,tt}{|}_{6,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/\epsilon )(|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^4).$$

Finally, we estimate the last term on the right-hand side of (96) by

$$\epsilon |v_{,tt}{|}_{6,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/\epsilon ){|f_{,tt}|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

Using (29), we have

$$\begin{array}{cc}& I_1^2\le \epsilon {\parallel v_{,tt}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/\epsilon )X_1^2(X_1^2+X_1^4)Y_1^2,\hfill \\ & I_1^3\le \epsilon {\parallel v_{,tt}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/\epsilon )X_1^2(Y_1^2+X_1^4).\hfill \end{array}$$

The first term on the right-hand side of (96) is bounded by

$$\epsilon \parallel v_{,tt}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/\epsilon )(X_1^2{Y}_1^2+X_1^4).$$

Finally, using Notation 1 in the Korn inequality (81) yields

$$\parallel v_{,tt}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c{|\mathbb{D}(v_{,tt})|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(X_1^4+X_1^6)+c{A}_3^2.$$

Using the above estimates in (96) yields

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\nu {\parallel v_{,tt}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le c(X_1^2+X_1^4+X_1^6)Y_1^2\hfill \\ & +c(X_1^4+X_1^6)+c{A}_3^2+c{|f_{,tt}|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.\hfill \end{array}$$

(97)

The above inequality implies (95) and concludes the proof. □

Corollary 3. 

From Lemmas 5–7, we have

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}{(|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{)+\nu (\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel v_{,tt}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)\hfill \\ & \le c(X_1^2+X_1^4+X_1^6)Y_1^2+c{X}_1^4(1+X_1^2)+c(A_1^2+A_2^2+A_3^2)\hfill \\ & +c(|f{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,t}{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,tt}{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

(98)

Lemma 8. 

For sufficiently regular solutions to (10), we obtain

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le \epsilon (|v_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+c(1/\epsilon )(|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+X_1^4),\hfill \end{array}$$

(99)

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}|v_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le \epsilon (|v_{,xtt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xxt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+c(1/\epsilon )(|v_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+X_1^4).\hfill \end{array}$$

(100)

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\le \epsilon (|v_{,xxt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xxx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+c(1/\epsilon )(|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+X_1^4).\hfill \end{array}$$

(101)

Proof. 

From (34), we have

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,x}^{2}dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\partial }_t{v}_{,x}^{2}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\nabla v_{,x}^{2}dx\hfill \\ & \le \epsilon (|v_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+c(1/\epsilon )(|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel v_{,x}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

Using the definition of $X_1$ yields (99). In view of (34), we obtain

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,xt}^{2}dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\partial }_t{v}_{,xt}^{2}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\nabla v_{,xt}^{2}dx\hfill \\ & \le \epsilon (|v_{,xtt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xxt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+c(1/\epsilon )\left(|v_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}^2{v}_{,xt}^{2}dx\right),\hfill \end{array}$$

where the last term is bounded by

$${|v|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{|v_{,xt}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

Exploiting the definition (29) of $X_1$ gives (100).

Finally, we prove (101). Using again (34) implies

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,xx}^{2}dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\partial }_t{v}_{,xx}^{2}dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }v·\nabla v_{,xx}^{2}dx\hfill \\ & \le \epsilon (|v_{,xxt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xxx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+c(1/\epsilon )\left(|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}^2{v}_{,xx}^{2}dx\right),\hfill \end{array}$$

where the last term is bounded by

$${|v|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{|v_{,xx}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

Using the definition of $X_1$, we obtain (101). This ends the proof. □

Consider the stationary Stokes system:

$$\begin{array}{ccc}\hfill -& \mathrm{div}\mathbb{T}(v,p)=-v_{,t}-v·\nabla v+{\mu }_1\mathrm{div}\mathbb{T}(\stackrel{1}{H})+f\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}v=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \overline{n}·\mathbb{T}(v,p)=-\mu \overline{n}·\mathbb{T}(\stackrel{1}{H})\hfill & \mathrm{on}{S}_t,\hfill \end{array}$$

(102)

where t is fixed.

Lemma 9. 

To prove the existence of solutions to (102) and to derive appropriate estimates, we need the following compatibility condition:

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }vdx={\displaystyle \underset{0}{\overset{t}{\int }}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }fdxd{t}^{\prime }+\underset{{\stackrel{1}{\mathrm{\Omega }}}_0}{\int }v(0)dx.$$

(103)

Proof. 

We express (102) in the form

$$\begin{array}{ccc}& -\mathrm{div}(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))=-v_{,t}-v·\nabla v+f\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}v=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \overline{n}·(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))=0\hfill & \mathrm{on}{S}_t.\hfill \end{array}$$

(104)

Integrating (104)₁ over ${\stackrel{1}{\mathrm{\Omega }}}_t$ and using boundary condition (104)₃, we obtain

$$-\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(v_{,t}+v·\nabla v)dx+\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }fdx=0$$

so

$${\displaystyle \frac{d}{dt}}\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }vdx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }fdx.$$

Hence, the compatibility condition (103) holds. This ends the proof. □

Lemma 10. 

For solutions to (102), the following inequality holds:

$${\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel p\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+X_1^2+{|f|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+A_1^2).$$

(105)

Proof. 

Since the compatibility condition (103) holds, we obtain for solutions to problem (102) the following inequality:

$$\begin{array}{cc}& {\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel p\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|v·\nabla v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +|\mathrm{div}\mathbb{T}(\stackrel{1}{H}){|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|f|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel \overline{n}·\mathbb{T}(\stackrel{1}{H}){\parallel }_{1/2,S_t}+A_1^2),\hfill \end{array}$$

(106)

where we used the Korn inequality described by Lemma 5 and the Poincaré inequality (84) derived in Lemma 4.

Using the estimates

$$\begin{array}{cc}& {|v·\nabla v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le {|v|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\nabla v|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{X}_1^2,\hfill \\ & |\mathrm{div}\mathbb{T}(\stackrel{1}{H}){|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c|\stackrel{1}{H}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\nabla \stackrel{1}{H}|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{X}_1^2,\hfill \\ & \parallel \overline{n}·\mathbb{T}(\stackrel{1}{H}){\parallel }_{1/2,S_t}\le c{\parallel \mathbb{T}(\stackrel{1}{H})\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{X}_1^2\hfill \end{array}$$

in (106) yields (105). This ends the proof. □

Lemma 11. 

For solutions to (102), we have

$$\begin{array}{cc}& {\parallel v\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel p\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(\parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel v_{,x}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel f\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+X_1^2+A_1^2).\hfill \end{array}$$

(107)

Proof. 

Considering compatibility (103), the Korn inequality in Lemma 5 and the Poincaré inequality in Lemma 4, we obtain for solutions to (102) the inequality

$$\begin{array}{cc}& {\parallel v\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel p\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(\parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel v_{,x}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel v·\nabla v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +\parallel \mathrm{div}\mathbb{T}(\stackrel{1}{H}){\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel f\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel \overline{n}·\mathbb{T}(\stackrel{1}{H}){\parallel }_{3/2,S_t}+A_1^2).\hfill \end{array}$$

(108)

Now, we estimate the nonlinear terms from the right-hand side of (108):

$$\begin{array}{cc}{\parallel v·\nabla v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill & \le c{\left(\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(v^2{v}_{,x}^2+v_{,x}^4+v^2{v}_{,xx}^2)dx\right)}^{1/2}\hfill \\ & \le {c(|v|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|v|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\le c{X}_1^2,\hfill \end{array}$$

$$\begin{array}{cc}\parallel \mathrm{div}\mathbb{T}(\stackrel{1}{H}){\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill & \le c\parallel \mathbb{T}(\stackrel{1}{H}){\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le c{\left(\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }({\stackrel{1}{H}}^4+{\stackrel{1}{H}}^2{\stackrel{1}{H}}_{,x}^2+H_{,x}^4+{\stackrel{1}{H}}^2{\stackrel{1}{H}}_{,xx}^2)dx\right)}^{1/2}\le c{X}_1^2,\hfill \end{array}$$

$$\parallel \overline{n}·\mathbb{T}(\stackrel{1}{H}){\parallel }_{3/2,S_t}\le c{\parallel T(\stackrel{1}{H})\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{X}_1^2.$$

Using the estimates in (108) yields (107). This ends the proof. □

Differentiating (102) with respect to time yields

$$\begin{array}{cc}& -{(\mathrm{div}\mathbb{T}(v,p)+{\mu }_1\mathrm{div}\mathbb{T}(\stackrel{1}{H}))}_t=-{(v_{,t}+v·\nabla v-f)}_{,t},\hfill \\ & {(\mathrm{div}v)}_{,t}=0,\hfill \\ & {(\overline{n}·(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H})))}_{,t}=0.\hfill \end{array}$$

(109)

First, we find compatibility conditions for solutions to problem (109).

Remark 3. 

Integrating (109)₁ over ${\stackrel{1}{\mathrm{\Omega }}}_t$ yields

$$\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(\mathrm{div}\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H})){)}_{,t}dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(v_{,t}+v·\nabla v-f)}_{,t}dx.$$

(110)

In the case of Eulerian coordinates, space and time variables are independent.

By the Green theorem, we have

$$-\underset{S_t}{\int }\overline{n}·{(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))}_{,t}dx=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(v_{,t}+v·\nabla v-f)}_{,t}dx.$$

(111)

Using boundary conditions (109)₃ in (111) implies the following compatibility condition for problem (109).

$$\underset{S_t}{\int }{\overline{n}}_{,t}·(\mathbb{T}(v,p)+{\mu }_1\mathbb{T}(\stackrel{1}{H}))d{S}_t=\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(v_{,t}+v·\nabla v-f)}_{,t}dx.$$

(112)

Estimate (75) used in (112) implies

$$\begin{array}{cc}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,tt}dx|\hfill & \le |\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }(v·\nabla v_{,t}+v_{,t}·\nabla v)dx|+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{f}_{,t}dx|\hfill \\ & +c\underset{S_t}{\int }(|\nabla v|+|v|)(|\nabla v|+|p|+{\stackrel{1}{H}}^2)d{S}_t.\hfill \end{array}$$

In view of Notation 1, we have

$$\begin{array}{cc}|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,tt}dx|\hfill & \le {c|v|}_{2,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c{|f_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +{c(|\nabla v|}_{2,S_t}+{|v|}_{2,S_t}{)(|\nabla v|}_{2,S_t}+{|p|}_{2,S_t}+|\stackrel{1}{H}{|}_{4,S_t}^2).\hfill \end{array}$$

Applying again Notation 1 and theorems on traces, we finally derive the inequality

$$|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{v}_{,tt}dx|\le c(X_1^2+X_1^3)+c{|f_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}.$$

(113)

Lemma 12. 

For sufficiently regular solutions to problem (10), solutions to (109) satisfy the inequality

$$\begin{array}{cc}& \parallel v_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel p_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|f_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\hfill \\ & +c(X_1^2+X_1^3+X_1{Y}_1).\hfill \end{array}$$

(114)

Proof. 

To prove the lemma, we write (109) in the form

$$\begin{array}{cc}& \mathrm{div}\mathbb{T}(v_{,t},p_{,t})=v_{,tt}+v·\nabla v_{,t}+v_{,t}·\nabla v\hfill \\ & -{\mu }_1\mathrm{div}\mathbb{T}{(\stackrel{1}{H})}_{,t}-f_i\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}{v}_t=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \overline{n}·\mathbb{T}(v_{,t},p_{,t})=-{\overline{n}}_{,t}·\mathbb{T}(v,p)-{\mu }_1{\overline{n}}_{,t}·\mathbb{T}(\stackrel{1}{H})\hfill \\ & -{\mu }_1\overline{n}·\mathbb{T}{(\stackrel{1}{H})}_{,t}\hfill & \mathrm{on}{S}_t.\hfill \end{array}$$

(115)

Using the compatibility condition (112), the Korn inequality from Lemma 5 and the Poincaré inequality from Lemma 4, we obtain the following inequality for solutions to (115):

$$\begin{array}{cc}& \parallel v_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel p_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|v·\nabla v_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +|v_{,t}{·\nabla v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|\mathrm{div}\mathbb{T}{(\stackrel{1}{H})}_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|f_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +\parallel {\overline{n}}_{,t}{·\mathbb{T}(v,p)\parallel }_{1/2,S_t}+\parallel {\overline{n}}_{,t}·\mathbb{T}(\stackrel{1}{H}){\parallel }_{1/2,S_t}+{\parallel \overline{n}·\mathbb{T}{(\stackrel{1}{H})}_{,t}\parallel }_{1/2,S_t}\hfill \\ & +X_1^2(1+X_1)).\hfill \end{array}$$

(116)

The nonlinear terms from the right-hand side of (116) are bounded by

$$\begin{array}{cc}& |v·\nabla v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le {|v|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\nabla v_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{X}_1^2,\hfill \\ & |v_{,t}{·\nabla v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le |v_{,t}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\nabla v|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{X}_1^2,\hfill \\ & |\mathrm{div}\mathbb{T}{(\stackrel{1}{H})}_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c|{(\stackrel{1}{H}\stackrel{1}{H})}_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|{\stackrel{1}{H}}_{,x}{\stackrel{1}{H}}_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +|\stackrel{1}{H}{\stackrel{1}{H}}_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})\le c|{\stackrel{1}{H}}_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}|{\stackrel{1}{H}}_{,t}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}+|\stackrel{1}{H}{|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}{|{\stackrel{1}{H}}_{,xt}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le c{X}_1^2.\hfill \end{array}$$

Finally, we estimate the boundary terms in the right-hand side of (116).

$$\begin{array}{cc}& \parallel {\overline{n}}_{,t}{·\mathbb{T}(v,p)\parallel }_{1/2,S_t}\le c{\parallel {\overline{n}}_{,t}·\mathbb{T}(v,p)\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le c|{\overline{n}}_{,t}{·\mathbb{T}(v,p)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|{\overline{n}}_{,tx}{·\mathbb{T}(v,p)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c{|{\overline{n}}_{,t}·\mathbb{T}(v_{,x},p_{,x})|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le c|(|v|+|v_{,x}|)(|v_{,x}{|+|p|)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|(|v|+|v_{,x}|+|v_{,xx})(|v_{,x}{|+|p|)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c|(|v|+|v_{,x}|)(|v_{,xx}|+|p_{,x}{|)|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\equiv I_1,\hfill \end{array}$$

where we used

$$|{\overline{n}}_{,tx}|\le c(|v|+|v_{,x}|+|v_{,xx}|).$$

Continuing, we have

$$\begin{array}{cc}{I}_1\hfill & \le {c(|v|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{(|v|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{)|p|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +|v_{,xx}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,xx}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|p|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +{|v|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|v|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}|p_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|p_{,x}|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le c{X}_1^2+c{X}_1{(|p|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}+|p_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|p_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t})\hfill \\ & +c|v_{,xx}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}(|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|p|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t})\hfill \\ & \le c{X}_1^2+c{X}_1(X_1+Y_1)+c{X}_1{Y}_1=c{X}_1^2+c{X}_1{Y}_1.\hfill \end{array}$$

Next, we examine

$$\begin{array}{cc}& \parallel {\overline{n}}_{,t}\mathbb{T}(\stackrel{1}{H}){\parallel }_{1/2,S_t}\le c\parallel {\overline{n}}_{,t}\mathbb{T}(\stackrel{1}{H}){\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{|{\overline{n}}_{,t}{\stackrel{1}{H}}^2|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c|{\overline{n}}_{,tx}{\stackrel{1}{H}}^2{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c{|{\overline{n}}_{,t}{\stackrel{1}{H}}_{,x}\stackrel{1}{H}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le c|(|v|+|v_{,x}|){\stackrel{1}{H}}^2{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|(|v|+|v_{,x}|+|v_{,xx}|){\stackrel{1}{H}}^2{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c|(|v|+|v_{,x}|){\stackrel{1}{H}}_{,x}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le {c(|v|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})|\stackrel{1}{H}{|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +c|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}|\stackrel{1}{H}{|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{c|v|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}|{\stackrel{1}{H}}_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\stackrel{1}{H}|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}|{\stackrel{1}{H}}_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\stackrel{1}{H}|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{X}_1^3.\hfill \end{array}$$

Finally, we calculate

$$\begin{array}{cc}& \parallel \overline{n}·\mathbb{T}{(\stackrel{1}{H})}_{,t}{\parallel }_{1/2,S_t}\le \parallel \overline{n}·\mathbb{T}{(\stackrel{1}{H})}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c{|\overline{n}{\stackrel{1}{H}}_{,t}\stackrel{1}{H}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c|{\overline{n}}_{,x}{\stackrel{1}{H}}_{,t}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|\overline{n}{\stackrel{1}{H}}_{,tx}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c{|\overline{n}{\stackrel{1}{H}}_{,t}{\stackrel{1}{H}}_{,x}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le c|(1+|v|+|v_{,x}|){\stackrel{1}{H}}_{,t}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|{\stackrel{1}{H}}_{,xt}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c{|{\stackrel{1}{H}}_{,t}{\stackrel{1}{H}}_{,x}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & \le {c(1+|v|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t})|{\stackrel{1}{H}}_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}|\stackrel{1}{H}{|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|v_{,x}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}|{\stackrel{1}{H}}_{,t}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|\stackrel{1}{H}|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c|{\stackrel{1}{H}}_{,xt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}|\stackrel{1}{H}{|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}+c|{\stackrel{1}{H}}_{,t}{|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}{|{\stackrel{1}{H}}_{,x}|}_{4,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(X_1^2+X_1^3).\hfill \end{array}$$

Using the above estimates in (116) yields

$$\begin{array}{cc}& \parallel v_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel p_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|v_{,t}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +|f_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(X_1^2+X_1^3+X_1{Y}_1).\hfill \end{array}$$

(117)

The above inequality implies (114) and ends the proof. □

Lemma 13. 

For sufficiently regular solutions to (10), we have

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}{|v|}_{2,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|v|}_{3,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|p|}_{2,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le c(X_1^2+X_1^4+X_1^6)Y_1^2+c{X}_1^4(1+X_1^2)+c(A_1^2+A_2^2+A_3^2)\hfill \\ & +c(|f{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,tt}{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

(118)

Proof. 

From Corollary 3 and Lemma 8, we obtain the inequality

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}{|v|}_{2,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\nu (\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel v_{,tt}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)\hfill \\ & \le \epsilon (|v_{,xx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xxt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|v_{,xxx}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)\hfill \\ & +c{X}_1^2(1+X_1^2+X_1^4)Y_1^2+c{X}_1^4(1+X_1^2)+c(A_1^2+A_2^2+A_3^2)\hfill \\ & +c(|f{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,t}{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,tt}{|}_{6/5,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

(119)

Lemma 10 yields

$${\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel p\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|v_{,x}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})+c(X_1^2+{|f|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+A_1).$$

(120)

Lemma 11 implies

$${\parallel v\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel p\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(\parallel v_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel v_{,x}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t})+c(X_1^2+{\parallel f\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+A_1).$$

(121)

Finally, Lemma 12 gives

$$\begin{array}{cc}& \parallel v_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel p_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c(|v_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +|v_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|f_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t})+c(X_1^2+X_1^3+X_1{Y}_1).\hfill \end{array}$$

(122)

From (119)–(122), we obtain (118). This ends the proof. □

5. Differential Inequality for Solutions to Problem (12)

First, we derive some inequalities using the energy method. For this, we need the Dirichlet data on B to be homogeneous. To solve this, we need local curvilinear coordinates. We introduce them near $S_t$ and B independently.

Remark 4. 

We introduce systems of curvilinear coordinates ${\tau }_1$, ${\tau }_2$, n and ${\tau }_1^{\prime }$, ${\tau }_2^{\prime }$, $n^{\prime }$ in neighbourhoods of $S_t$ and B, respectively. Let $x=(x_1,x_2,x_3)$ be a Cartesian coordinate system. Then, in these neighbourhoods wehave diffeomorphisms $x=x({\tau }_1,{\tau }_2,n)$ and $x=x({\tau }_1^{\prime },{\tau }_2^{\prime },n^{\prime })$ such that $n=n(x_1,x_2,x_3)=0$ describes locally $S_t$ and $n^{\prime }=n^{\prime }(x_1,x_2,x_3)=0$ describes locally B.

These curvilinear coordinates correspond to systems of orthonormal vectors ${\overline{\tau }}_1$, ${\overline{\tau }}_2$, $\overline{n}$ and ${\overline{\tau }}_1^{\prime }$, ${\overline{\tau }}_2^{\prime }$, ${\overline{n}}^{\prime }$, respectively. Furthermore, the following relations hold:

$$\begin{array}{cc}& x_{,{\tau }_{\alpha }}=L_{\alpha }{\overline{\tau }}_{\alpha },\alpha =1,2,x_{,n}=L_n\overline{n}\mathrm{and}\hfill \\ & x_{,{\tau }_{\alpha }^{\prime }}=L_{\alpha }^{\prime }{\overline{\tau }}_{\alpha }^{\prime },\alpha =1,2,x_{,n^{\prime }}=L_n^{\prime }{\overline{n}}^{\prime },\hfill \end{array}$$

where $L_1$, $L_2$, $L_n$ and $L_1^{\prime }$, $L_2^{\prime }$, $L_n^{\prime }$ are the Lamé coefficients.

We describe operators rot and div in the curvilinear coordinates. We only need the formulations in a neighbourhood of $S_t$. Let u be any vector. We can decompose $\mathrm{rot}u$ in the form

$$\mathrm{rot}u={(\mathrm{rot}u)}_{{\tau }_1}{\overline{\tau }}_1+{(\mathrm{rot}u)}_{{\tau }_2}{\overline{\tau }}_2+{(\mathrm{rot}u)}_n\overline{n},$$

(123)

where ${(\mathrm{rot}u)}_{{\tau }_{\alpha }}$, $\alpha =1,2$, ${(\mathrm{rot}u)}_n$ are curvilinear coordinates of $\mathrm{rot}u$.

They can be expressed as follows:

$$\begin{array}{cc}& {(\mathrm{rot}u)}_{{\tau }_1}={\displaystyle \frac{1}{L_2{L}_n}}({\partial }_{{\tau }_2}(u_n{L}_n)-{\partial }_n(u_{{\tau }_2}{L}_2)),\hfill \\ & {(\mathrm{rot}u)}_{{\tau }_2}={\displaystyle \frac{1}{L_1{L}_n}}({\partial }_n(u_{{\tau }_1}{L}_1)-{\partial }_{{\tau }_1}(u_n{L}_n)),\hfill \\ & {(\mathrm{rot}u)}_n={\displaystyle \frac{1}{L_1{L}_2}}({\partial }_{{\tau }_1}(u_{{\tau }_2}{L}_2)-{\partial }_{{\tau }_2}(u_{{\tau }_1}{L}_1)).\hfill \end{array}$$

(124)

Similarly, operator $\mathrm{div}u$ is expressed in the form

$$\mathrm{div}u={\displaystyle \frac{1}{L_1{L}_2{L}_n}}[{(u_{{\tau }_1}{L}_2{L}_n)}_{,{\tau }_1}+{(u_{{\tau }_2}{L}_n{L}_1)}_{,{\tau }_2}-{(u_n{L}_1{L}_2)}_{,n}],$$

(125)

where we used that the parameter n increases in the direction exterior to the considered domain.

Now, we recall the boundary conditions on B.

$$\begin{array}{ccc}& {\stackrel{2}{H}}_{{\tau }_{\alpha }}=H_{\ast \alpha },\alpha =1,2,\hfill & \mathrm{on}B,\hfill \\ & \mathrm{div}\stackrel{2}{H}=0\hfill & \mathrm{on}B.\hfill \end{array}$$

(126)

Expressing (126)₂ in the curvilinear coordinates, we have

$${\stackrel{2}{H}}_{n,n}+{\stackrel{2}{H}}_n\mathrm{div}\overline{n}=-{\displaystyle \sum _{\alpha =1}^2}(H_{\ast \alpha ,\alpha }+H_{\ast \alpha }\mathrm{div}{\overline{\tau }}_{\alpha })\equiv B_{\ast }.$$

(127)

To simplify, we assume that B is the boundary of a box. Then, $\mathrm{div}\overline{n}=0$. Hence, (127) takes the form

$${\stackrel{2}{H}}_{n,n}=B_{\ast }.$$

(128)

To allow any integration by parts in problem (12) to be possible, we introduce the following extension $\mathrm{\Phi }$:

$$\begin{array}{ccc}& {\mathrm{\Phi }}_{\alpha }=H_{\ast \alpha },\alpha =1,2,{\mathrm{\Phi }}_{n,n}=B_{\ast }\hfill & \mathrm{on}B,\hfill \\ & \mathrm{div}\mathrm{\Phi }=0,\hfill \\ & \mathrm{\Phi }=0\hfill & \mathrm{in}\mathrm{a}\mathrm{neighbourhood}\mathrm{of}{S}_t.\hfill \end{array}$$

(129)

Then the function

$$\stackrel{2}{H^{\prime }}=\stackrel{2}{H}-\mathrm{\Phi }$$

(130)

is such that

$$\begin{array}{cc}& \stackrel{2}{H_{\alpha }^{\prime }}{{|}_B=0,\alpha =1,2,{\stackrel{2}{H^{\prime }}}_{n,n}|}_B=0,\mathrm{div}{H}^{\prime }=0,\hfill \\ & \stackrel{2}{H^{\prime }}=\stackrel{2}{H}\mathrm{in}\mathrm{a}\mathrm{neighbourhood}\mathrm{of}{S}_t.\hfill \end{array}$$

(131)

A construction of such $\mathrm{\Phi }$ is given in the following remark:

Remark 5. 

First, we define a vector-valued function δ such that

$$\delta ={\displaystyle \sum _{\alpha =1}^2}{\delta }_{\alpha }{\overline{\tau }}_{\alpha }+{\delta }_n\overline{n},$$

(132)

where

$$\begin{array}{cc}& {\delta }_{\alpha }(x)=\underset{{\mathbb{R}}^2}{\int }{H}_{\ast \alpha }({\tau }_1+tn,{\tau }_2+tn)K_{\alpha }(t)dt,\alpha =1,2,\hfill \\ & {\delta }_n(x)=n\underset{{\mathbb{R}}^2}{\int }{B}_{\ast }({\tau }_1+tn,{\tau }_2+tn)K_n(t)dt,\hfill \end{array}$$

(133)

where $K_1,K_2,K_n\in C_0^{\infty }({\mathbb{R}}^2)$ are such that

$$\underset{{\mathbb{R}}^2}{\int }{K}_{\alpha }(t)dt=1,\alpha =1,2,\underset{{\mathbb{R}}^2}{\int }{K}_n(t)dt=1.$$

Let $\zeta =\zeta (x)$ be a smooth function equal to 1 near B and vanishing at a positive distance from $S_t$. Then we define

$${\delta }^{\prime }=\zeta \delta .$$

(134)

Then we look for a function Φ in the form

$$\mathrm{\Phi }=\zeta \delta +\phi$$

(135)

which is a solution to the problem

$$\begin{array}{cc}\hfill -& \mathrm{\Delta }\mathrm{\Phi }+\nabla \sigma =0,\hfill \\ & \mathrm{div}\mathrm{\Phi }=0,\hfill \\ & \mathrm{\Phi }·{\overline{\tau }}_{\alpha }{|}_B=H_{\ast \alpha },\alpha =1,2,\hfill \\ & {\mathrm{\Phi }}_{n,n}{|}_B=B_{\ast },\hfill \\ & {\mathrm{\Phi }|}_{S_d}=0,\hfill \end{array}$$

(136)

where surface $S_d\in {\stackrel{1}{\mathrm{\Omega }}}_t$ and is located at some positive distance from $S_t$. The function σ is artificial, but it helps to make Φ divergence-free.

Since $\delta$ and $\zeta$ are known, problem (136) yields the following problem for $\phi$ and $\sigma$:

$$\begin{array}{cc}\hfill -& \mathrm{\Delta }\phi +\nabla \sigma =\mathbb{D}elta(\zeta \delta ),\hfill \\ & \mathrm{div}\phi =-\mathrm{div}(\zeta \delta ),\hfill \\ & \phi ·{\overline{\tau }}_{\alpha }{|}_B=0,\alpha =1,2,\hfill \\ & {\phi }_{n,n}{|}_B=0,\hfill \\ & {\phi |}_{S_d}=0.\hfill \end{array}$$

(137)

Since (137) is the well-known Stokes system, the existence of its solutions is also well-known.

Problem (12) for $\stackrel{1}{H}$, $\stackrel{2}{H^{\prime }}$ takes the form

$$\begin{array}{cc}& {\sigma }_1{\mu }_1({\stackrel{1}{H}}_{,t}+\stackrel{1}{v}·\nabla \stackrel{1}{H})+\mathrm{rot}{}^2\stackrel{1}{H}={\mu }_1\mathrm{rot}(\stackrel{1}{v}\times \stackrel{1}{H})+{\sigma }_1{\mu }_1\stackrel{1}{v}·\nabla \stackrel{1}{H},\hfill \\ & \mathrm{div}\stackrel{1}{H}=0\hfill \\ & {\sigma }_2{\mu }_2(\stackrel{2}{H_{,t}^{\prime }}+\stackrel{2}{v}·\nabla \stackrel{2}{H^{\prime }})+\mathrm{rot}{}^2\stackrel{2}{H^{\prime }}={\sigma }_2{\mu }_2\stackrel{2}{v}·\nabla \stackrel{2}{H^{\prime }}\hfill \\ & -{\sigma }_2{\mu }_2{\mathrm{\Phi }}_{,t}-\mathrm{rot}{}^2\mathrm{\Phi },\hfill \\ & \mathrm{div}\stackrel{2}{H^{\prime }}=0\hfill \\ & \stackrel{2}{H^{\prime }}·{\overline{\tau }}_{\alpha }^{\prime }{{|}_B=0,\alpha =1,2,\mathrm{div}\stackrel{2}{H^{\prime }}|}_B=0,\hfill \\ & {\stackrel{1}{\alpha }}_1(\mathrm{rot}\stackrel{1}{H}-{\sigma }_1{\mu }_{1}v\times \stackrel{1}{H})·{\overline{\tau }}_{\alpha }={\stackrel{1}{\alpha }}_2\mathrm{rot}\stackrel{2}{H}·{\overline{\tau }}_{\alpha },\alpha =1,2,\mathrm{on}{S}_t,\hfill \\ & {\stackrel{2}{\alpha }}_1\stackrel{1}{H}={\stackrel{2}{\alpha }}_2\stackrel{2}{H}\mathrm{on}{S}_t,\hfill \\ & \stackrel{1}{H}{|}_{t=0}=\stackrel{1}{H}(0),\mathrm{div}\stackrel{1}{H}(0)=0,\hfill \\ & \stackrel{2}{H^{\prime }}{|}_{t=0}=\stackrel{2}{H^{\prime }}(0),\mathrm{div}\stackrel{2}{H^{\prime }}(0)=0,\hfill \end{array}$$

(138)

where ${\stackrel{i}{\alpha }}_j$, $i,j=1,2$, are parameters, ${\overline{\tau }}_1$, ${\overline{\tau }}_2$ are tangent vectors to $S_t$, and ${\overline{\tau }}_1^{\prime }$, ${\overline{\tau }}_2^{\prime }$ are tangent to B.

Now, we derive an energy-type inequality for solutions to problem (138).

Lemma 14. 

Let B be a box. Let $\stackrel{1}{H}$, $\stackrel{2}{H^{\prime }}$ be a solution to (138). Assume that ${\alpha }_i={\stackrel{1}{\alpha }}_i{\stackrel{2}{\alpha }}_i$, $i=1,2$, ${\beta }_i={\alpha }_i{\sigma }_i{\mu }_i$, $i=1,2$, $\stackrel{i}{v}\in H^1({\stackrel{i}{\mathrm{\Omega }}}_t)$, $\stackrel{1}{H}\in H^1({\stackrel{1}{\mathrm{\Omega }}}_t)$, $\stackrel{2}{H^{\prime }}\in H^1({\stackrel{2}{\mathrm{\Omega }}}_t)$, $H_{\ast \alpha }$, $H_{\ast \alpha ,t}\in H^{3/2}(B)$, $\alpha =1,2$, $B_{\ast },B_{\ast ,t}\in H^{1/2}(B)$, $B_{\ast }=-{\sum }_{\alpha =1}^2(H_{\ast ,{\tau }_{\alpha }}+H_{\ast \alpha }\mathrm{div}{\overline{\tau }}_{\alpha })$. Then there exists a constant ${\overline{\epsilon }}_1$, assumed to be small, such that

$$\begin{array}{cc}& {\beta }_1{\displaystyle \frac{d}{dt}}|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\beta }_2{\displaystyle \frac{d}{dt}}|\stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2+{\alpha }_1|\mathrm{rot}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\alpha }_2{|\mathrm{rot}\stackrel{2}{H^{\prime }}|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le {\overline{\epsilon }}_1(\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)+c(1/{\overline{\epsilon }}_1)(\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +\parallel \stackrel{2}{v}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)+{\displaystyle \sum _{\alpha =1}^2}(\parallel H_{\ast \alpha ,t}{\parallel }_{3/2,B}^2+\parallel H_{\ast \alpha }{\parallel }_{3/2,B}^2)\hfill \\ & +c(\parallel B_{\ast }{\parallel }_{1/2,B}^2+\parallel B_{\ast ,t}{\parallel }_{1/2,B}^2).\hfill \end{array}$$

(139)

Proof. 

Multiply (138)₁ by ${\alpha }_1\stackrel{1}{H}$ and integrate over ${\stackrel{1}{\mathrm{\Omega }}}_t$. Multiply (138)₂ by ${\alpha }_2\stackrel{2}{H^{\prime }}$ and integrate over ${\stackrel{2}{\mathrm{\Omega }}}_t$. Adding the results and using (34) gives

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\alpha }_1{\sigma }_1{\mu }_1{\displaystyle \frac{d}{dt}}|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\displaystyle \frac{1}{2}}{\alpha }_2{\sigma }_2{\mu }_2{\displaystyle \frac{d}{dt}}{|\stackrel{2}{H^{\prime }}|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{\alpha }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{rot}{}^2\stackrel{1}{H}·\stackrel{1}{H}dx+{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }\mathrm{rot}{}^2\stackrel{2}{H^{\prime }}·\stackrel{2}{H^{\prime }}dx\hfill \\ & ={\alpha }_1{\mu }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{rot}(\stackrel{1}{v}\times \stackrel{1}{H})·\stackrel{1}{H}dx\hfill \\ & +{\alpha }_1{\sigma }_1{\mu }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\stackrel{1}{v}·\nabla \stackrel{1}{H}·\stackrel{1}{H}dx+{\alpha }_2{\sigma }_2{\mu }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }\stackrel{2}{v}·\nabla \stackrel{2}{H^{\prime }}·\stackrel{2}{H^{\prime }}dx\hfill \\ & -{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }({\sigma }_2{\mu }_2{\mathrm{\Phi }}_{,t}+\mathrm{rot}{}^2\mathrm{\Phi })·\stackrel{2}{H^{\prime }}dx.\hfill \end{array}$$

(140)

Integrating by parts in the last two terms on the left-hand side of (140) yields

$$\begin{array}{cc}& {\alpha }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|\mathrm{rot}\stackrel{1}{H}{|}^{2}dx+{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }{|\mathrm{rot}\stackrel{2}{H^{\prime }}|}^{2}dx\hfill \\ & +\underset{S_t}{\int }({\alpha }_1\mathrm{rot}\stackrel{1}{H}·\overline{n}\times \stackrel{1}{H}-{\alpha }_2\mathrm{rot}\stackrel{2}{H}·\overline{n}\times \stackrel{2}{H})d{S}_t,\hfill \end{array}$$

(141)

where $\overline{n}$ is a unit normal vector to $S_t$.

The boundary term in (141) equals

$$I\equiv \underset{S_t}{\int }({\stackrel{1}{\alpha }}_1\mathrm{rot}\stackrel{1}{H}·{\stackrel{2}{\alpha }}_1\overline{n}\times \stackrel{1}{H}-{\stackrel{1}{\alpha }}_2\mathrm{rot}\stackrel{2}{H}·{\stackrel{2}{\alpha }}_2\overline{n}\times \stackrel{2}{H})d{S}_t.$$

To apply transmission conditions (138)_6,7 in I, we use the orthonormal system of vectors ${\overline{\tau }}_1$, ${\overline{\tau }}_2$, $\overline{n}$ in a neighbourhood of $S_t$ such that ${\overline{\tau }}_i{|}_{S_t}$, $i=1,2$, is tangent to $S_t$ and $\overline{n}{|}_{S_t}$ is normal. Furthermore, the vectors satisfy the relations

$$\overline{n}\times {\overline{\tau }}_1={\overline{\tau }}_2,\overline{n}\times {\overline{\tau }}_2=-{\overline{\tau }}_1.$$

Therefore, any vector can be decomposed as follows:

$$H=H_1{\overline{\tau }}_1+H_2{\overline{\tau }}_2+H_n\overline{n}.$$

Using the properties of the orthonormal system, we can write I in the form

$$\begin{array}{cc}I\hfill & =-\underset{S_t}{\int }[{\stackrel{1}{\alpha }}_1\mathrm{rot}\stackrel{1}{H}·{\overline{\tau }}_2{\stackrel{2}{\alpha }}_1{\stackrel{1}{H}}_1-{\stackrel{1}{\alpha }}_1\mathrm{rot}\stackrel{1}{H}·{\overline{\tau }}_1{\stackrel{2}{\alpha }}_1{\stackrel{1}{H}}_2\hfill \\ & -({\stackrel{1}{\alpha }}_2\mathrm{rot}\stackrel{2}{H}·{\overline{\tau }}_2{\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_1-{\stackrel{1}{\alpha }}_2\mathrm{rot}\stackrel{1}{H}·{\overline{\tau }}_1{\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_2)]d{S}_t.\hfill \end{array}$$

Considering transmission conditions (138)_6,7, we have

$$I=-\underset{S_t}{\int }[{\stackrel{1}{\alpha }}_1{\sigma }_1{\mu }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_2{\stackrel{2}{\alpha }}_1{\stackrel{1}{H}}_1-{\stackrel{1}{\alpha }}_1{\sigma }_1{\mu }_1(v\times \stackrel{1}{H})·{\overline{\tau }}_1{\stackrel{2}{\alpha }}_1{\stackrel{1}{H}}_2]d{S}_t.$$

Hence,

$$|I|\le {\epsilon }_1\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_1){\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel H\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

Applying the Hölder and Young inequalities to the first two terms on the right-hand side of (140), we bound the result with

$${\epsilon }_2\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_2)\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel H\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2$$

and the third term on the right-hand side of (140) is estimated by

$${\epsilon }_3\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_3)\parallel \stackrel{2}{v}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2.$$

Integrating by parts in the last term on the right-hand side of (140) yields

$$I_1\equiv -{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }({\sigma }_2{\mu }_2{\mathrm{\Phi }}_{,t}\stackrel{2}{H^{\prime }}+\mathrm{rot}\mathrm{\Phi }\mathrm{rot}\stackrel{2}{H^{\prime }})dx,$$

where we have used that the tangent components of $\underset{ }{\overset{2}{H}}$′ vanish on B.

Hence,

$$|I_1|\le {\epsilon }_4\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_4)(|{\mathrm{\Phi }}_{,t}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2+{|\mathrm{rot}\mathrm{\Phi }|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)\equiv I_2.$$

In consideration of the form of $\mathrm{\Phi }$, the second term in $I_2$ can be estimated as follows:

$$\begin{array}{cc}& c(1/{\epsilon }_4)(|{\mathrm{\Phi }}_{,t}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2+{\parallel \mathrm{\Phi }\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)\le c(1/{\epsilon }_4)(\parallel H_{\ast ,t}{\parallel }_{3/2,B}^2\hfill \\ & +\parallel H_{\ast }{\parallel }_{3/2,B}^2+\parallel B_{\ast }{\parallel }_{1/2,B}^2+\parallel B_{\ast ,t}{\parallel }_{1/2,B}^2).\hfill \end{array}$$

Using the above estimates in (140) yields

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}{\alpha }_1{\sigma }_1{\mu }_1{\displaystyle \frac{d}{dt}}|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\displaystyle \frac{1}{2}}{\alpha }_2{\sigma }_2{\mu }_2{\displaystyle \frac{d}{dt}}{|\stackrel{2}{H^{\prime }}|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{\alpha }_1|\mathrm{rot}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\alpha }_2{|\mathrm{rot}\stackrel{2}{H^{\prime }}|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le ({\epsilon }_1+{\epsilon }_2)\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_1,1/{\epsilon }_2)\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +({\epsilon }_3+{\epsilon }_4)\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_3,1/{\epsilon }_4)(\parallel \stackrel{2}{v}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2{\parallel \stackrel{2}{H^{\prime }}\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\hfill \\ & +\parallel H_{\ast ,t}{\parallel }_{3/2,B}^2+\parallel H_{\ast }{\parallel }_{3/2,B}^2+\parallel B_{\ast ,t}{\parallel }_{1/2,B}^2+\parallel B_{\ast }{\parallel }_{1/2,B}^2).\hfill \end{array}$$

(142)

The above inequality implies (139) and concludes the proof. □

Consider the problem

$$\begin{array}{cc}& \mathrm{rot}\stackrel{1}{H}\in L_2({\stackrel{1}{\mathrm{\Omega }}}_t),\mathrm{rot}\stackrel{2}{H^{\prime }}\in L_2({\stackrel{2}{\mathrm{\Omega }}}_t),\hfill \\ & \mathrm{div}\stackrel{1}{H}=0,\mathrm{div}\stackrel{2}{H^{\prime }}=0,\hfill \\ & \stackrel{2}{H^{\prime }}·{\overline{\tau }}_{\alpha }^{\prime }{{|}_B=0,\alpha =1,2,\mathrm{div}\stackrel{2}{H^{\prime }}|}_B=0,\hfill \\ & {\stackrel{1}{\alpha }}_1(\mathrm{rot}\stackrel{1}{H}-{\sigma }_1{\mu }_{1}v\times \stackrel{1}{H})·{\overline{\tau }}_{\alpha }={\stackrel{1}{\alpha }}_2\mathrm{rot}\stackrel{2}{H}·{\overline{\tau }}_{\alpha },\alpha =1,2,\hfill & \mathrm{on}{S}_t,\hfill \\ & {\stackrel{2}{\alpha }}_1\stackrel{1}{H}={\stackrel{2}{\alpha }}_2\stackrel{2}{H}\hfill & \mathrm{on}{S}_t,\hfill \end{array}$$

(143)

where ${\alpha }_1={\stackrel{1}{\alpha }}_1{\stackrel{2}{\alpha }}_1$, ${\alpha }_2={\stackrel{1}{\alpha }}_2{\stackrel{2}{\alpha }}_2$, ${\overline{\tau }}_{\alpha }^{\prime }$ is a tangent vector to B, ${\overline{\tau }}_{\alpha }$ is a tangent vector to $S_t$, and $\alpha =1,2$.

The transmission conditions in (9) are very general. To simplify the considerations in this paper, we restrict the parameters from (9) to parameters from (143)_4,5. This makes the proof of Lemma 15 much easier.

Lemma 15. 

Solutions to (143) satisfy the following inequality:

$$\begin{array}{cc}& |\nabla \stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|\nabla \stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\le c(|\mathrm{rot}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|\mathrm{rot}\stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)\hfill \\ & +\epsilon |\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{c(1/\epsilon )\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\equiv D_1^2,\hfill \end{array}$$

(144)

where ε can be assumed to be arbitrarily small, and we assume the following compatibility conditions:

$$\begin{array}{cccc}& \sqrt{{\alpha }_1}\stackrel{1}{H}=\sqrt{{\alpha }_2}\stackrel{2}{H},\hfill & {\stackrel{1}{\alpha }}_i={\stackrel{2}{\alpha }}_i=\sqrt{{\alpha }_i},\hfill & i=1,2\hfill \\ & \sqrt{{\alpha }_1}{\stackrel{1}{H}}_{\tau }=\sqrt{{\alpha }_2}{\stackrel{2}{H}}_{\tau },\hfill & \sqrt{{\alpha }_1}{\stackrel{1}{H}}_n=\sqrt{{\alpha }_2}{\stackrel{2}{H}}_n,\hfill \\ & \sqrt{{\alpha }_1}{\stackrel{1}{H}}_{n,\tau }=\sqrt{{\alpha }_2}{\stackrel{2}{H}}_{n,\tau },\hfill & \sqrt{{\alpha }_1}{\stackrel{1}{H}}_{\tau ,\tau }=\sqrt{{\alpha }_2}{\stackrel{2}{H}}_{\tau ,\tau },\hfill \end{array}$$

where $H_{\tau }$ denotes the tangent component of H to $S_t$, $H_n$ is the normal component, and ${\partial }_{\tau }$ means the tangent derivative.

Proof. 

Consider the identities. (The idea of this proof is taken from [10])

$$\begin{array}{cc}& \mathrm{rot}{}^2\stackrel{1}{H}=-\mathrm{\Delta }\stackrel{1}{H},\hfill \\ & \mathrm{rot}{}^2\stackrel{2}{H^{\prime }}=-\mathrm{\Delta }\stackrel{2}{H^{\prime }}.\hfill \end{array}$$

(145)

Multiply (145)₁ by ${\alpha }_1\stackrel{1}{H}$ and integrate over ${\stackrel{1}{\mathrm{\Omega }}}_t$. Next, multiply (145)₂ by ${\alpha }_2\stackrel{2}{H^{\prime }}$ and integrate over ${\stackrel{2}{\mathrm{\Omega }}}_t$. By adding the results, we obtain

$$\begin{array}{cc}& {\alpha }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{rot}{}^2\stackrel{1}{H}·\stackrel{1}{H}dx+{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }\mathrm{rot}{}^2\stackrel{2}{H^{\prime }}·\stackrel{2}{H^{\prime }}dx\hfill \\ & =-{\alpha }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\mathrm{\Delta }\stackrel{1}{H}·\stackrel{1}{H}dx-{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }\mathrm{\Delta }\stackrel{2}{H^{\prime }}·\stackrel{2}{H^{\prime }}dx.\hfill \end{array}$$

(146)

Integrating by parts yields

$$\begin{array}{cc}& {\alpha }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|\mathrm{rot}\stackrel{1}{H}{|}^{2}dx+{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }{|\mathrm{rot}\stackrel{2}{H^{\prime }}|}^{2}dx\hfill \\ & +\underset{S_t}{\int }({\alpha }_1\mathrm{rot}\stackrel{1}{H}·\overline{n}\times \stackrel{1}{H}-{\alpha }_2\mathrm{rot}\stackrel{2}{H}·\overline{n}\times \stackrel{2}{H})d{S}_t\hfill \\ & +{\alpha }_2\underset{B}{\int }\mathrm{rot}\stackrel{2}{H^{\prime }}·{\overline{n}}^{\prime }\times \stackrel{2}{H^{\prime }}dB\hfill \\ & ={\alpha }_1\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|\nabla \stackrel{1}{H}{|}^{2}dx+{\alpha }_2\underset{{\stackrel{2}{\mathrm{\Omega }}}_t}{\int }{|\nabla \stackrel{2}{H^{\prime }}|}^{2}dx\hfill \\ & -\underset{S_t}{\int }({\alpha }_1\overline{n}·\nabla \stackrel{1}{H}·\stackrel{1}{H}-{\alpha }_2\overline{n}·\nabla \stackrel{2}{H}·\stackrel{2}{H})d{S}_t\hfill \\ & -{\alpha }_2\underset{B}{\int }{\overline{n}}^{\prime }·\nabla \stackrel{2}{H^{\prime }}·\stackrel{2}{H^{\prime }}dB.\hfill \end{array}$$

(147)

The boundary term on $S_t$ on the left-hand side of (147) equals I (see the proof of Lemma 14).

Then, it is estimated by

$$|I|\le {\epsilon }_1\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_1){\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

(148)

To examine the other boundary terms in (147), we introduce systems of curvilinear coordinates ${\tau }_1$, ${\tau }_2$, n and ${\tau }_1^{\prime }$, ${\tau }_2^{\prime }$, $n^{\prime }$ in neighbourhoods of $S_t$ and B, respectively, as described in Remark 4.

These curvilinear coordinates correspond to systems of orthonormal vectors ${\overline{\tau }}_1$, ${\overline{\tau }}_2$, $\overline{n}$ and ${\overline{\tau }}_1^{\prime }$, ${\overline{\tau }}_2^{\prime }$, ${\overline{n}}^{\prime }$, respectively. Furthermore, the following relations $x_{,{\tau }_{\alpha }}=L_{\alpha }{\overline{\tau }}_{\alpha }$, $\alpha =1,2$, $x_{,n}=L_n\overline{n}$ and $x_{,{\tau }_{\alpha }^{\prime }}=L_{\alpha }^{\prime }{\overline{\tau }}_{\alpha }^{\prime }$, $\alpha =1,2$, $x_{,n^{\prime }}=L_n^{\prime }{\overline{n}}^{\prime }$ hold, where $L_1$, $L_2$, $L_n$ and $L_1^{\prime }$, $L_2^{\prime }$, $L_n^{\prime }$ are the Lamé coefficients.

We assume that systems of vectors ${\overline{\tau }}_1$, ${\overline{\tau }}_2$, $\overline{n}$ and ${\overline{\tau }}_1^{\prime }$, ${\overline{\tau }}_2^{\prime }$, ${\overline{n}}^{\prime }$ are orthonormal.

The last term on the left-hand side of (147) vanishes because $\stackrel{2}{H^{\prime }}·{\overline{\tau }}_{\alpha }^{\prime }=0$ and $\alpha =1,2$.

Using the curvilinear coordinates, the last term on right-hand side of (147) equals

$$M=\underset{B}{\int }{\overline{n}}^{\prime }·\nabla \left({\displaystyle \sum _{\alpha =1}^2}\stackrel{2}{H_{{\tau }_{\alpha }^{\prime }}^{\prime }}{\overline{\tau }}_{\alpha }^{\prime }+\stackrel{2}{H_{n^{\prime }}^{\prime }}{\overline{n}}^{\prime }\right)\left({\displaystyle \sum _{\alpha =1}^2}\stackrel{2}{H_{{\tau }_{\alpha }^{\prime }}^{\prime }}{\overline{\tau }}_{\alpha }^{\prime }+\stackrel{2}{H_{n^{\prime }}^{\prime }}{\overline{n}}^{\prime }\right)dB.$$

Since ${\stackrel{2}{H}}_{{\tau }_{\alpha }^{\prime }}^{\prime }=0$, $\alpha =1,2$, we have

$$M=\underset{B}{\int }{\overline{n}}^{\prime }·\nabla \left({\displaystyle \sum _{\alpha =1}^2}\stackrel{2}{H_{{\tau }_{\alpha }^{\prime }}^{\prime }}{\overline{\tau }}_{\alpha }^{\prime }+\stackrel{2}{H_{n^{\prime }}^{\prime }}{\overline{n}}^{\prime }\right)\stackrel{2}{H_{n^{\prime }}^{\prime }}{\overline{n}}^{\prime }dB=\underset{B}{\int }{\overline{n}}^{\prime }·\nabla \stackrel{2}{H_{n^{\prime }}^{\prime }}\stackrel{2}{H_{n^{\prime }}^{\prime }}dB.$$

In view of (131), we have that $M=0$.

Using the curvilinear coordinates, the third term on the right-hand side of (147) takes the form

$$\begin{array}{cc}N\hfill & =\underset{S_t}{\int }[{\alpha }_1\overline{n}·\nabla \left({\displaystyle \sum _{\alpha =1}^2}{\stackrel{1}{H}}_{{\tau }_{\alpha }}{\overline{\tau }}_{\alpha }+{\stackrel{1}{H}}_n\overline{n}\right)·\left({\displaystyle \sum _{\alpha =1}^2}{\stackrel{1}{H}}_{\alpha }{\overline{\tau }}_{\alpha }+{\stackrel{1}{H}}_n\overline{n}\right)\hfill \\ & -{\alpha }_2\overline{n}·\nabla \left({\displaystyle \sum _{\alpha =1}^2}{\stackrel{2}{H}}_{{\tau }_{\alpha }}{\overline{\tau }}_{\alpha }+{\stackrel{2}{H}}_n\overline{n}\right)·\left({\displaystyle \sum _{\alpha =1}^2}{\stackrel{2}{H}}_{\alpha }{\overline{\tau }}_{\alpha }+{\stackrel{2}{H}}_n\overline{n}\right)]d{S}_t.\hfill \end{array}$$

Next, we write it in the more explicit form

$$\begin{array}{cc}N\hfill & =\underset{S_t}{\int }\left({\alpha }_1{\displaystyle \sum _{\alpha =1}^2}\overline{n}·\nabla {\stackrel{1}{H}}_{{\tau }_{\alpha }}{\stackrel{1}{H}}_{{\tau }_{\alpha }}-{\alpha }_2{\displaystyle \sum _{\alpha =1}^2}\overline{n}·\nabla {\stackrel{2}{H}}_{{\tau }_{\alpha }}{\stackrel{2}{H}}_{{\tau }_{\alpha }}\right)d{S}_t\hfill \\ & +\underset{S_t}{\int }\sum _{\alpha ,\beta =1}({\alpha }_1{\stackrel{1}{H}}_{{\tau }_{\alpha }}\overline{n}·\nabla {\overline{\tau }}_{\alpha }·({\stackrel{1}{H}}_{{\tau }_{\beta }}{\overline{\tau }}_{\beta }+{\stackrel{1}{H}}_n\overline{n})\hfill \\ & -{\alpha }_2{\stackrel{2}{H}}_{{\tau }_{\alpha }}\overline{n}·\nabla {\overline{\tau }}_{\alpha }({\stackrel{2}{H}}_{{\tau }_{\beta }}{\overline{\tau }}_{\beta }+{\stackrel{2}{H}}_n\overline{n}))d{S}_t\hfill \\ & +\underset{S_t}{\int }({\alpha }_1\overline{n}·\nabla {\stackrel{1}{H}}_n{\stackrel{1}{H}}_n-{\alpha }_2\overline{n}·\nabla {\stackrel{2}{H}}_n{\stackrel{2}{H}}_n)d{S}_t\hfill \\ & +\underset{S_t}{\int }\left[\overline{n}·\nabla \overline{n}\left({\alpha }_1{\stackrel{1}{H}}_n·{\displaystyle \sum _{\alpha =1}^2}{\stackrel{1}{H}}_{{\tau }_{\alpha }}{\overline{\tau }}_{\alpha }-{\alpha }_2{\stackrel{2}{H}}_n{\displaystyle \sum _{\alpha =1}^2}{\stackrel{2}{H}}_{{\tau }_{\alpha }}{\overline{\tau }}_{\alpha }\right)\right]d{S}_t\hfill \\ & \equiv N_1+N_2+N_3+N_4.\hfill \end{array}$$

Using the transmission conditions

$$\sqrt{{\alpha }_1}\stackrel{1}{H}=\sqrt{{\alpha }_2}\stackrel{2}{H}$$

(149)

we obtain

$$N_2=N_4=0$$

(150)

To examine $N_1$ and $N_3$, we recall the form of the rotation operator in curvilinear coordinates (see Remark 4):

$$\begin{array}{cc}& {(\mathrm{rot}\stackrel{i}{H})}_{{\tau }_1}={\displaystyle \frac{1}{L_2{L}_n}}({\partial }_{{\tau }_2}({\stackrel{i}{H}}_n{L}_n)-{\partial }_n({\stackrel{i}{H}}_{{\tau }_2}{L}_2)),\hfill \\ & {(\mathrm{rot}\stackrel{i}{H})}_{{\tau }_2}={\displaystyle \frac{1}{L_1{L}_n}}({\partial }_n({\stackrel{i}{H}}_{{\tau }_1}{L}_1)-{\partial }_{{\tau }_1}({\stackrel{i}{H}}_n{L}_n)),\hfill \\ & {(\mathrm{rot}\stackrel{i}{H})}_n={\displaystyle \frac{1}{L_1{L}_2}}({\partial }_{{\tau }_1}({\stackrel{i}{H}}_{{\tau }_2}{L}_2)-{\partial }_{{\tau }_2}({\stackrel{i}{H}}_{{\tau }_1}{L}_1)).\hfill \end{array}$$

(151)

We have the following transmission condition:

$${\stackrel{1}{\alpha }}_1[{(\mathrm{rot}\stackrel{1}{H})}_{{\tau }_{\alpha }}-{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_{\alpha }]={\stackrel{1}{\alpha }}_2{(\mathrm{rot}\stackrel{2}{H})}_{{\tau }_{\alpha }},\alpha =1,2.$$

(152)

Using (151) in (152) yields

$$\begin{array}{cc}& {\stackrel{1}{\alpha }}_1\left[{\displaystyle \frac{1}{L_2{L}_n}}({\partial }_{{\tau }_2}({\stackrel{1}{H}}_n{L}_n)-{\partial }_n({\stackrel{1}{H}}_{{\tau }_2}{L}_2))-{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_1\right]\hfill \\ & ={\stackrel{1}{\alpha }}_2{\displaystyle \frac{1}{L_2{L}_n}}({\partial }_{{\tau }_2}({\stackrel{2}{H}}_n{L}_n)-{\partial }_n({\stackrel{2}{H}}_{{\tau }_2}{L}_2))\hfill \end{array}$$

(153)

and

$$\begin{array}{cc}& {\stackrel{1}{\alpha }}_1\left[{\displaystyle \frac{1}{L_1{L}_n}}({\partial }_n({\stackrel{1}{H}}_{{\tau }_1}{L}_1)-{\partial }_{{\tau }_1}({\stackrel{1}{H}}_n{L}_n))-{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_2\right]\hfill \\ & ={\stackrel{1}{\alpha }}_2{\displaystyle \frac{1}{L_1{L}_n}}({\partial }_n({\stackrel{2}{H}}_{{\tau }_1}{L}_1)-{\partial }_{{\tau }_1}({\stackrel{2}{H}}_n{L}_n)).\hfill \end{array}$$

(154)

We write (153) in the form

$$\begin{array}{cc}& {\stackrel{1}{\alpha }}_1[{\displaystyle \frac{1}{L_n}}{\stackrel{1}{H}}_{{\tau }_2,n}+{\displaystyle \frac{1}{L_2{L}_n}}{L}_{2,n}{\stackrel{1}{H}}_{{\tau }_2}-{\displaystyle \frac{1}{L_2}}{\stackrel{1}{H}}_{n,{\tau }_2}-{\displaystyle \frac{1}{L_2{L}_n}}{L}_{n,{\tau }_2}{\stackrel{1}{H}}_n\hfill \\ & +{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_1]\hfill \\ & ={\stackrel{1}{\alpha }}_2\left[{\displaystyle \frac{1}{L_n}}{\stackrel{2}{H}}_{{\tau }_2,n}+{\displaystyle \frac{1}{L_2{L}_n}}{L}_{2,n}{\stackrel{2}{H}}_{{\tau }_2}-{\displaystyle \frac{1}{L_2}}{\stackrel{2}{H}}_{n,{\tau }_2}-{\displaystyle \frac{1}{L_2{L}_n}}{L}_{n,{\tau }_2}{\stackrel{2}{H}}_n\right].\hfill \end{array}$$

Multiplying the above equality by $L_n$ yields

$$\begin{array}{cc}& {\stackrel{1}{\alpha }}_1\left[{\stackrel{1}{H}}_{{\tau }_2,n}-{\displaystyle \frac{L_n}{L_2}}{\stackrel{1}{H}}_{n,{\tau }_2}\right]={\stackrel{1}{\alpha }}_2\left[{\stackrel{2}{H}}_{{\tau }_2,n}-{\displaystyle \frac{L_n}{L_2}}{\stackrel{2}{H}}_{n,{\tau }_2}\right]\hfill \\ & +\{{\stackrel{1}{\alpha }}_1\left[-{\displaystyle \frac{1}{L_2}}{L}_{2,n}{\stackrel{1}{H}}_{{\tau }_2}+{\displaystyle \frac{1}{L_2}}{L}_{n,{\tau }_2}{\stackrel{1}{H}}_n-L_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_1\right]\hfill \\ & +{\stackrel{1}{\alpha }}_2\left[{\displaystyle \frac{1}{L_2}}{L}_{2,n}{\stackrel{2}{H}}_{{\tau }_2}-{\displaystyle \frac{1}{L_2}}{L}_{n,{\tau }_2}{\stackrel{2}{H}}_n\right]\}.\hfill \end{array}$$

(155)

Next, we write (154) in the form

$$\begin{array}{cc}& {\stackrel{1}{\alpha }}_1[{\displaystyle \frac{1}{L_n}}{\stackrel{1}{H}}_{{\tau }_1,n}+{\displaystyle \frac{L_{1,n}}{L_1{L}_n}}{\stackrel{1}{H}}_{{\tau }_1}-{\displaystyle \frac{1}{L_1}}{\stackrel{1}{H}}_{n,{\tau }_1}-{\displaystyle \frac{L_{n,{\tau }_1}}{L_1{L}_n}}{\stackrel{1}{H}}_n\hfill \\ & -{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_2]\hfill \\ & ={\stackrel{1}{\alpha }}_2\left[{\displaystyle \frac{1}{L_n}}{\stackrel{2}{H}}_{{\tau }_1,n}+{\displaystyle \frac{L_{1,n}}{L_1{L}_n}}{\stackrel{2}{H}}_{{\tau }_1}-{\displaystyle \frac{1}{L_1}}{\stackrel{2}{H}}_{n,{\tau }_1}-{\displaystyle \frac{L_{n,{\tau }_1}}{L_1{L}_n}}{\stackrel{2}{H}}_n\right]\hfill \end{array}$$

Multiplying the above equality by $L_n$ yields

$$\begin{array}{cc}& {\stackrel{1}{\alpha }}_1\left[{\stackrel{1}{H}}_{{\tau }_1,n}-{\displaystyle \frac{L_n}{L_1}}{\stackrel{1}{H}}_{n,{\tau }_1}\right]={\stackrel{1}{\alpha }}_2\left[{\stackrel{2}{H}}_{{\tau }_1,n}-{\displaystyle \frac{L_n}{L_1}}{\stackrel{2}{H}}_{n,{\tau }_1}\right]\hfill \\ & +\{{\stackrel{1}{\alpha }}_1\left[-{\displaystyle \frac{L_{1,n}}{L_1}}{\stackrel{1}{H}}_{{\tau }_1}+{\displaystyle \frac{L_{n,{\tau }_1}}{L_1}}{\stackrel{1}{H}}_n+L_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_2\right]\hfill \\ & +{\stackrel{1}{\alpha }}_2\left[{\displaystyle \frac{L_{1,n}}{L_1}}{\stackrel{2}{H}}_{{\tau }_1}-{\displaystyle \frac{L_{n,{\tau }_1}}{L_1}}{\stackrel{2}{H}}_n\right]\},\hfill \end{array}$$

(156)

We write $N_1$ in the explicit form

$$\begin{array}{cc}{N}_1\hfill & =\underset{S_t}{\int }[{\alpha }_1{\stackrel{1}{H}}_{{\tau }_1,n}{\stackrel{1}{H}}_{{\tau }_1}+{\alpha }_1{\stackrel{1}{H}}_{{\tau }_2,n}{\stackrel{1}{H}}_{{\tau }_2}-{\alpha }_2{\stackrel{2}{H}}_{{\tau }_1,n}{\stackrel{2}{H}}_{{\tau }_1}-{\alpha }_2{\stackrel{2}{H}}_{{\tau }_2,n}{\stackrel{2}{H}}_{{\tau }_2}]d{S}_t\hfill \\ & =\underset{S_t}{\int }({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_1,n}{\stackrel{2}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_1}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1,n}{\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1})d{S}_t\hfill \\ & +\underset{S_t}{\int }({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_2,n}{\stackrel{2}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_2}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1,n}{\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_2})d{S}_t.\hfill \end{array}$$

Using the transmission

$${\stackrel{2}{\alpha }}_1{\stackrel{1}{H}}_{\tau }-{\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_{\tau }=0$$

(157)

we can write $N_1$ in the form

$$\begin{array}{cc}{N}_1\hfill & =\underset{S_t}{\int }({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_1,n}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1,n}){\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1}d{S}_t\hfill \\ & +\underset{S_t}{\int }({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_2,n}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_2,n}){\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_2}d{S}_t\hfill \\ & \equiv \underset{S_t}{\int }{R}_1{\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1}d{S}_t+\underset{S_t}{\int }{R}_2{\stackrel{2}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_2}d{S}_t\equiv {\overline{N}}_1+{\overline{N}}_2.\hfill \end{array}$$

From (156), we have

$$\begin{array}{cc}{R}_1\hfill & \equiv {\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_1,n}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1,n}={\displaystyle \frac{L_n}{L_1}}({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{n,{\tau }_1}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{n,{\tau }_1})\hfill \\ & {\displaystyle \frac{L_{1,n}}{L_1}}(-{\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_1}+{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_1})+{\displaystyle \frac{L_{n,{\tau }_1}}{L_1}}({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_n-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_n)\hfill \\ & +{\stackrel{1}{\alpha }}_1{L}_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_2\hfill \end{array}$$

and

$$\begin{array}{cc}{R}_2\hfill & \equiv {\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_2,n}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_2,n}={\displaystyle \frac{L_n}{L_2}}({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{n,{\tau }_2}-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{n,{\tau }_2})\hfill \\ & +{\displaystyle \frac{L_{2,n}}{L_2}}(-{\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_{{\tau }_2}+{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_{{\tau }_2})+{\displaystyle \frac{L_{n,{\tau }_2}}{L_2}}({\stackrel{1}{\alpha }}_1{\stackrel{1}{H}}_n-{\stackrel{1}{\alpha }}_2{\stackrel{2}{H}}_n)\hfill \\ & -{\stackrel{1}{\alpha }}_1{L}_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_1.\hfill \end{array}$$

In consideration of the transmission

$${\stackrel{2}{\alpha }}_1\stackrel{1}{H}={\stackrel{2}{\alpha }}_2\stackrel{2}{H}$$

(158)

we obtain

$$\begin{array}{cc}& R_1={\stackrel{1}{\alpha }}_1{L}_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_2,\hfill \\ & R_2=-{\stackrel{1}{\alpha }}_1{L}_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_1.\hfill \end{array}$$

(159)

From (149) and (158), we have that ${\stackrel{1}{\alpha }}_1={\stackrel{2}{\alpha }}_1$, ${\stackrel{1}{\alpha }}_2={\stackrel{2}{\alpha }}_2$.

Since ${\alpha }_1={\stackrel{1}{\alpha }}_1{\stackrel{2}{\alpha }}_1$, ${\alpha }_2={\stackrel{1}{\alpha }}_2{\stackrel{2}{\alpha }}_2$, we obtain

$$\begin{array}{cc}& {\stackrel{1}{\alpha }}_1={\stackrel{2}{\alpha }}_1=\sqrt{{\alpha }_1},\hfill \\ & {\stackrel{1}{\alpha }}_2={\stackrel{2}{\alpha }}_2=\sqrt{{\alpha }_2}\mathrm{and}\hfill \\ & \sqrt{{\alpha }_1}{\stackrel{1}{H}}_{{\tau }_{\alpha }}=\sqrt{{\alpha }_2}{\stackrel{2}{H}}_{{\tau }_{\alpha }},\sqrt{{\alpha }_1}{\stackrel{1}{H}}_n=\sqrt{{\alpha }_2}{\stackrel{2}{H}}_n,\mathrm{and}\hfill \\ & \sqrt{{\alpha }_1}{\stackrel{1}{H}}_{n,{\tau }_{\alpha }}=\sqrt{{\alpha }_2}{\stackrel{2}{H}}_{n,{\tau }_{\alpha }},\alpha =1,2.\hfill \end{array}$$

(160)

Using (159) in $N_1$ yields

$$N_1=\underset{S_t}{\int }(-{\alpha }_1{L}_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_1{\stackrel{1}{H}}_{{\tau }_2}+{\alpha }_2{L}_n{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_2{\stackrel{1}{H}}_{{\tau }_1}).$$

(161)

Hence,

$$|N_1|\le \epsilon \parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{c(1/\epsilon )\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

(162)

Next, we consider

$$N_3=\underset{S_t}{\int }({\alpha }_1{\stackrel{1}{H}}_{n,n}{\stackrel{1}{H}}_n-{\alpha }_2{\stackrel{2}{H}}_{n,n}{\stackrel{2}{H}}_n)d{S}_t.$$

To examine $N_3$, we use $\mathrm{div}\stackrel{i}{H}$, $i=1,2$, in the curvilinear coordinates (see Remark 4):

$$\begin{array}{cc}0\hfill & =\mathrm{div}\stackrel{i}{H}={\displaystyle \frac{1}{L_1{L}_2{L}_n}}[{({\stackrel{i}{H}}_{{\tau }_1}{L}_2{L}_n)}_{,{\tau }_1}+{({\stackrel{i}{H}}_{{\tau }_2}{L}_n{L}_1)}_{,{\tau }_2}-{({\stackrel{i}{H}}_n{L}_1{L}_2)}_{,n}]\hfill \\ & =-{\stackrel{i}{H}}_{n,n}{\displaystyle \frac{1}{L_n}}+{\stackrel{i}{H}}_{{\tau }_1,{\tau }_1}{\displaystyle \frac{1}{L_1}}+{\stackrel{i}{H}}_{{\tau }_2,{\tau }_2}{\displaystyle \frac{1}{L_2}}\hfill \\ & +\left[{\displaystyle \frac{1}{L_1{L}_2{L}_n}}(-{(L_1{L}_2)}_{,n}{\stackrel{i}{H}}_n+{(L_n{L}_1)}_{,{\tau }_2}{\stackrel{i}{H}}_{{\tau }_2}+{(L_2{L}_n)}_{,{\tau }_1}{\stackrel{i}{H}}_{{\tau }_1})\right],\hfill \end{array}$$

(163)

where $i=1,2$, and parameter n increases in the direction that is normal exterior to ${\stackrel{i}{\mathrm{\Omega }}}_t$, $i=1,2$.

Multiplying (163) by $L_n$, we have

$$\begin{array}{cc}& {\stackrel{i}{H}}_{n,n}=+{\displaystyle \frac{L_n}{L_1}}{\stackrel{i}{H}}_{{\tau }_1,{\tau }_1}+{\displaystyle \frac{L_n}{L_2}}{\stackrel{i}{H}}_{{\tau }_2,{\tau }_2}\hfill \\ & +\left[-{\displaystyle \frac{1}{L_1{L}_2}}({(L_1{L}_2)}_{,n}{\stackrel{i}{H}}_n+{(L_n{L}_1)}_{,{\tau }_2}{\stackrel{i}{H}}_{{\tau }_2}+{(L_2{L}_n)}_{,{\tau }_1}{\stackrel{i}{H}}_{{\tau }_1})\right].\hfill \end{array}$$

(164)

Using (149) in $N_3$ yields

$$\begin{array}{cc}& N_3=\underset{S_t}{\int }[{\alpha }_1\left(+{\displaystyle \frac{L_n}{L_1}}{\stackrel{1}{H}}_{{\tau }_1,{\tau }_1}+{\displaystyle \frac{L_n}{L_2}}{\stackrel{1}{H}}_{{\tau }_2,{\tau }_2}\right){\stackrel{1}{H}}_n\hfill \\ & -{\alpha }_2\left(+{\displaystyle \frac{L_n}{L_1}}{\stackrel{2}{H}}_{{\tau }_1,{\tau }_1}+{\displaystyle \frac{L_n}{L_2}}{\stackrel{2}{H}}_{{\tau }_2,{\tau }_2}\right){\stackrel{2}{H}}_n]d{S}_t\hfill \\ & +\underset{S_t}{\int }\{{\alpha }_1\left[-{\displaystyle \frac{1}{L_1{L}_2}}({(L_1{L}_2)}_{,n}{\stackrel{1}{H}}_n+{(L_n{L}_1)}_{,{\tau }_2}{\stackrel{1}{H}}_{{\tau }_2}+{(L_2{L}_n)}_{,{\tau }_1}{\stackrel{1}{H}}_{{\tau }_1})\right]{\stackrel{1}{H}}_n\hfill \\ & -{\alpha }_2\left[-{\displaystyle \frac{1}{L_1{L}_2}}({(L_1{L}_2)}_{,n}{\stackrel{2}{H}}_n+{(L_n{L}_1)}_{,{\tau }_2}{\stackrel{2}{H}}_{{\tau }_2}+{(L_2{L}_n)}_{,{\tau }_1}{\stackrel{2}{H}}_{{\tau }_1}\right]{\stackrel{2}{H}}_n\}d{S}_t.\hfill \end{array}$$

In view of transmission conditions (160), we obtain

$$N_3=0.$$

(165)

Finally, we prove that (147) implies (144). The third term on the left-hand side of (147), denoted by I, is estimated in (148).

In consideration of (131), the last terms on the left-hand side and right-hand side of (147) vanish.

The third term on the right-hand side of (147) is denoted by N, where $N=N_1+N_2+N_3+N_4$.

The transmission conditions imply that $N_2=N_3=N_4=0$, and $N_1$ is described by (161). Next, $N_1$ is estimated in (162).

The above considerations imply that the following inequality results from (147).

$$\begin{array}{cc}& {\alpha }_1|\nabla \stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\alpha }_2|\nabla \stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\le {\alpha }_1{|\mathrm{rot}\stackrel{1}{H}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{\alpha }_2|\mathrm{rot}\stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2+\epsilon |\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{c(1/\epsilon )\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.\hfill \end{array}$$

(166)

The above inequality yields (144) and concludes the proof. □

Lemma 16. 

Assume that B is a boundary of a cylinder and

$$|\nabla \stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+{|\nabla \stackrel{2}{H^{\prime }}|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}\le D_1,$$

(167)

where $D_1$ is a given quantity.

Then

$$\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+{\parallel \stackrel{2}{H^{\prime }}\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c{D}_1.$$

(168)

Proof. 

To prove (168), we need to show that

$$|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|\stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c(|\nabla \stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+|\nabla \stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t})\le c{D}_1.$$

(169)

To simplify the proof of (169), we assume that boundary $B=S_1\cup S_2$ is such that $S_1$ is parallel and $S_2$ is perpendicular to the $x_3$-axis.

In Note 4, we assumed that B is the boundary of a box.

Since $\stackrel{2}{H_{{\tau }_{\alpha }}^{\prime }}=0$, $\alpha =1,2$, on $S_1\cup S_2$, we have that $\stackrel{2}{H_3^{\prime }}{|}_{S_1}=0$ and $\stackrel{2}{H_{\alpha }^{\prime }}{|}_{S_2}=0$, $\alpha =1,2$.

Hence, the Poincaré inequality yields

$$|\stackrel{2}{H^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c{|\nabla \stackrel{2}{H^{\prime }}|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}.$$

(170)

Therefore,

$$\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c{D}_1.$$

(171)

Hence, $\stackrel{2}{H}{|}_{S_t}\in H^{1/2}(S_t)$ and

$$\parallel \stackrel{2}{H}{\parallel }_{1/2,S_t}\le c{D}_1,$$

(172)

where we used that $\stackrel{2}{H^{\prime }}{{|}_{S_t}=\stackrel{2}{H}|}_{S_t}$.

Transmission condition (138)₇ yields

$${\stackrel{2}{\alpha }}_1\stackrel{1}{H}={\stackrel{2}{\alpha }}_2\stackrel{2}{H}\mathrm{on}{S}_t.$$

Using the Poincaré inequality, we have

$$|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c|\nabla \stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c{|\stackrel{2}{H}|}_{2,S_t}\le c{D}_1.$$

(173)

Hence, (171), (173) and (167) imply (168). This concludes the proof. □

Consider problem (12). We write it in the form of the elliptic problem

$$\begin{array}{ccc}& \mathrm{rot}{}^2\stackrel{1}{H}={\mu }_1\mathrm{rot}(v\times \stackrel{1}{H})-{\mu }_1{\sigma }_1{\stackrel{1}{H}}_{,t}\equiv f_1\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}\stackrel{1}{H}=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{rot}{}^2\stackrel{2}{H^{\prime }}=-{\mu }_2{\sigma }_2\stackrel{2}{H_{,t}^{\prime }}\equiv f_2\hfill & \mathrm{in}{\stackrel{2}{\mathrm{\Omega }}}_t,\hfill \\ & \mathrm{div}\stackrel{2}{H^{\prime }}=0\hfill & \mathrm{in}{\stackrel{2}{\mathrm{\Omega }}}_t,\hfill \\ & \stackrel{2}{H^{\prime }}·{\overline{\tau }}_{\alpha }{{|}_B=0,\alpha =1,2,\mathrm{div}\stackrel{2}{H^{\prime }}|}_B=0\hfill & \mathrm{on}B,\hfill \\ & {\stackrel{1}{a}}_{\alpha }({\displaystyle \frac{1}{{\sigma }_1}}\mathrm{rot}\stackrel{1}{H}-{\mu }_{1}v\times \stackrel{1}{H})·{\overline{\tau }}_{\alpha }={\stackrel{2}{a}}_{\alpha }\left({\displaystyle \frac{1}{{\sigma }_2}}\mathrm{rot}\stackrel{2}{H^{\prime }}\right)·{\overline{\tau }}_{\alpha },\alpha =1,2,\hfill & \mathrm{on}{S}_t,\hfill \\ & {\stackrel{1}{b}}_{\beta }{\stackrel{1}{H}}_{\beta }={\stackrel{2}{b}}_{\beta }{\stackrel{2}{H}}_{\beta },\beta =1,2,3,\hfill & \mathrm{on}{S}_t,\hfill \end{array}$$

(174)

where t is fixed and is treated as a parameter.

Lemma 17. 

Assume that t is a fixed parameter.

(a) 

Assume that $\stackrel{1}{H}\in H^2({\stackrel{1}{\mathrm{\Omega }}}_t)$, $v\in H^2({\stackrel{1}{\mathrm{\Omega }}}_t)$, ${\stackrel{1}{H}}_{,t}\in L_2({\stackrel{1}{\mathrm{\Omega }}}_t)$, $\stackrel{2}{H_{,t}^{\prime }}\in L_2({\stackrel{2}{\mathrm{\Omega }}}_t)$. Then for solutions to problem (174), the following inequality holds:

$$\begin{array}{cc}& \parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel \stackrel{2}{H^{\prime }}{\parallel }_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+c(|{\stackrel{1}{H}}_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +|\stackrel{2}{H_{,t}^{\prime }}{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t})+c(\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}).\hfill \end{array}$$

(175)

(b) 

Assume that $\stackrel{1}{H}\in H^2({\stackrel{1}{\mathrm{\Omega }}}_t)$, $v\in H^2({\stackrel{1}{\mathrm{\Omega }}}_t)$, ${\stackrel{1}{H}}_{,t}\in \stackrel{1}{H}({\stackrel{1}{\mathrm{\Omega }}}_t)$, $\stackrel{2}{H_{,t}^{\prime }}\in \stackrel{1}{H}({\stackrel{2}{\mathrm{\Omega }}}_t)$. Then solutions to (174) satisfy the following inequality:

$$\begin{array}{cc}& \parallel \stackrel{1}{H}{\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel \stackrel{2}{H^{\prime }}{\parallel }_{3,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}{\parallel \stackrel{1}{v}\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c(\parallel {\stackrel{1}{H}}_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel \stackrel{2}{H_{,t}^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t})+c(\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}+\parallel \stackrel{2}{H^{\prime }}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}).\hfill \end{array}$$

(176)

Proof. 

To prove the lemma, we use the technique of the regularizer. In the proof, we replace $\stackrel{2}{H^{\prime }}$ with $\stackrel{2}{H}$. We use only $\stackrel{2}{H^{\prime }}$ in the formulation of this lemma. To make calculations easier, we write (174) in the simpler form

$$\begin{array}{ccc}& -\mathrm{\Delta }\stackrel{1}{H}=\stackrel{1}{f},\mathrm{div}\stackrel{1}{H}=0,\mathrm{div}\stackrel{1}{f}=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & -\mathrm{\Delta }\stackrel{2}{H}=\stackrel{2}{f},\mathrm{div}\stackrel{2}{H}=0,\mathrm{div}\stackrel{2}{f}=0\hfill & \mathrm{in}{\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ & \stackrel{2}{H}·{\overline{\tau }}_{\alpha }{{|}_B=0,\alpha =1,2,\mathrm{div}\stackrel{2}{H}|}_B=0\hfill & \mathrm{on}B,\hfill \\ & {\stackrel{1}{a}}_{\alpha }(\mathrm{rot}\stackrel{1}{H}-{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H})·{\overline{\tau }}_{\alpha }={\stackrel{2}{a}}_{\alpha }\mathrm{rot}\stackrel{2}{H}·{\overline{\tau }}_{\alpha },\alpha =1,2,\hfill & \mathrm{on}{S}_t,\hfill \\ & {\stackrel{1}{b}}_{\beta }{\stackrel{1}{H}}_{\beta }={\stackrel{2}{b}}_{\beta }{\stackrel{2}{H}}_{\beta },\beta =1,2,3\hfill & \mathrm{on}{S}_t.\hfill \end{array}$$

(177)

To examine problem (177), we introduce the following partition of unity

$${\displaystyle \sum _{j=1}^4}{\displaystyle \sum _{l_j=1}^{L_j}}{\zeta }_j^{l_j}(x)=1,$$

as described in Figure 3.

Now, we examine problem (177) in subdomains $\mathrm{supp}{\zeta }_j^{l_j}$, $j=1,2,3,4$, $l_j=1,\dots ,L_j$. We introduce the notation

$${\stackrel{i}{H}}^{(j,l_j)}=\stackrel{i}{H}{\zeta }_j^{l_j},i=1,2.$$

In subdomain $\mathrm{supp}{\zeta }_1^{l_1}$, problem (177) takes the form

$$\begin{array}{cc}-\hfill & \mathrm{\Delta }{\stackrel{1}{H}}^{(1,l_1)}=-2\nabla \stackrel{1}{H}\nabla {\zeta }_1^{l_1}-\stackrel{1}{H}\mathrm{\Delta }{\zeta }_1^{l_1}+{\stackrel{1}{f}}^{(1,l_1)},\mathrm{in}\mathrm{supp}{\zeta }_1^{l_1}\hfill \\ & \mathrm{div}{\stackrel{1}{H}}^{(1,l_1)}=\stackrel{1}{H}\nabla {\zeta }_1^{l_1}.\hfill \end{array}$$

(178)

Since $\mathrm{supp}{\zeta }_1^{l_1}\subset {\stackrel{1}{\mathrm{\Omega }}}_t$ and $\mathrm{supp}{\zeta }_1^{l_1}\cap S_t=\varphi$, we can treat problem (178) as a problem in ${\mathbb{R}}^3$ such that all terms in (178) have compact supports equal to $\mathrm{supp}{\zeta }_1^{l_1}$.

We can drop equation $\mathrm{div}\stackrel{i}{H}$, $i=1,2$, in any subdomain of the partition of unity because if $\mathrm{div}\stackrel{i}{H}=0$ initially, then $\mathrm{div}\stackrel{i}{H}=0$ in ${\stackrel{i}{\mathrm{\Omega }}}_t$ follows automatically for any $t>0$ as long as solutions exist.

Therefore, we can write problem (178) in the form

$$-\mathrm{\Delta }{\stackrel{1}{H}}^{(1,l_1)}=-2\nabla \stackrel{1}{H}\nabla {\zeta }_1^{l_1}-\stackrel{1}{H}\mathrm{\Delta }{\zeta }_1^{l_1}+{\stackrel{1}{f}}^{(1,l_1)}\mathrm{in}{\mathbb{R}}^3.$$

(179)

In subdomain $\mathrm{supp}{\zeta }_3^{l_3}$, problem (148) reads

$$-\mathrm{\Delta }{\stackrel{2}{H}}^{(3,l_3)}=-2\nabla \stackrel{2}{H}\nabla {\zeta }_3^{l_3}-\stackrel{2}{H}\mathrm{\Delta }{\zeta }_3^{l_3}+{\stackrel{2}{f}}^{(3,l_3)}\mathrm{in}{\mathbb{R}}^3.$$

(180)

Problem (177) in subdomain $\mathrm{supp}{\zeta }_2^{l_2}$ takes the form

$$\begin{array}{cc}-\hfill & \mathrm{\Delta }{\stackrel{1}{H}}^{(2,l_2)}=-2\nabla \stackrel{1}{H}\nabla {\zeta }_2^{l_2}-\stackrel{1}{H}\mathrm{\Delta }{\zeta }_2^{l_2}+{\stackrel{1}{f}}^{(2,l_2)}\hfill \\ & \equiv {\stackrel{1}{g}}^{(2,l_2)}\hfill & \mathrm{in}\mathrm{supp}{\zeta }_2^{l_2}\cap {\stackrel{1}{\mathrm{\Omega }}}_t,\hfill \\ -\hfill & \mathrm{\Delta }{\stackrel{2}{H}}^{(2,l_2)}=-2\nabla \stackrel{2}{H}\nabla {\zeta }_2^{l_2}-\stackrel{2}{H}\mathrm{\Delta }{\zeta }_2^{l_2}+{\stackrel{2}{f}}^{(2,l_2)}\hfill \\ & \equiv {\stackrel{2}{g}}^{(2,l_2)}\hfill & \mathrm{in}\mathrm{supp}{\zeta }_2^{l_2}\cap {\stackrel{2}{\mathrm{\Omega }}}_t,\hfill \\ & ({\stackrel{1}{a}}_{\alpha }\mathrm{rot}{\stackrel{1}{H}}^{(2,l_2)}-{\stackrel{2}{a}}_{\alpha }\mathrm{rot}{\stackrel{2}{H}}^{(2,l_2)})·{\overline{\tau }}_{\alpha }\hfill \\ & =[({\stackrel{1}{a}}_{\alpha }\mathrm{rot}{\stackrel{1}{H}}^{(2,l_2)}-{\stackrel{2}{a}}_{\alpha }\mathrm{rot}{\stackrel{2}{H}}^{(2,l_2)})\hfill \\ & -({\stackrel{1}{a}}_{\alpha }\mathrm{rot}\stackrel{1}{H}-{\stackrel{2}{a}}_{\alpha }\mathrm{rot}\stackrel{2}{H})·{\zeta }_2^{l_2}]·{\overline{\tau }}_{\alpha }\hfill \\ & +{\mu }_1{\sigma }_{1}v\times \stackrel{1}{H}·{\overline{\tau }}_{\alpha }{\zeta }_2^{l_2}\equiv h^{(2,l_2)},\alpha =1,2,\hfill & \mathrm{on}\mathrm{supp}{\zeta }_2^{l_2}\cap S_t,\hfill \\ & {\stackrel{1}{b}}_{\beta }{\stackrel{1}{H}}_{\beta }^{(2,l_2)}-{\stackrel{2}{b}}_{\beta }{\stackrel{2}{H}}_{\beta }^{(2,l_2)}=0,\beta =1,2,3,\hfill & \mathrm{on}\mathrm{supp}{\zeta }_2^{l_2}\cap S_t.\hfill \end{array}$$

(181)

Finally, we write problem (177) in $\mathrm{supp}{\zeta }_4^{l_4}$:

$$\begin{array}{ccc}& -\mathrm{\Delta }{\stackrel{2}{H}}^{(4,l_4)}=-2\nabla \stackrel{2}{H}\nabla {\zeta }_4^{l_4}-\stackrel{2}{H}\mathrm{\Delta }{\zeta }_4^{l_4}+{\stackrel{2}{f}}^{(4,l_4)}\hfill & \mathrm{in}\mathrm{supp}{\zeta }_4^{l_4}\cap {\stackrel{2}{\mathrm{\Omega }}}_t,\hfill \\ & {\stackrel{2}{H}}^{(4,l_4)}·{\overline{\tau }}_{\alpha }=0,\alpha =1,2,\hfill & \mathrm{on}B\cap \mathrm{supp}{\zeta }_4^{l_4},\hfill \\ & \overline{n}·\nabla {\stackrel{2}{H}}^{(4,l_4)}-\stackrel{2}{H}\overline{n}·\nabla {\zeta }_4^{l_4}=0\hfill & \mathrm{on}B\cap \mathrm{supp}{\zeta }_4^{l_4}.\hfill \end{array}$$

(182)

Using the forms of $\stackrel{1}{f}$ and $\stackrel{2}{f}$, we obtain the following inequalities for solutions to (179), (180) and (182):

$$\parallel {\stackrel{1}{H}}^{(1,l_1)}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{1}{H}{\parallel }_{1,\mathrm{supp}{\zeta }_1^{l_1}}+{c\parallel v\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\parallel \stackrel{1}{H}{\parallel }_{2,\mathrm{supp}{\zeta }_1^{l_1}}+c{|{\stackrel{1}{H}}_{,t}|}_{2,\mathrm{supp}{\zeta }_1^{l_1}},$$

(183)

$$\parallel {\stackrel{1}{H}}^{(1,l_1)}{\parallel }_{3,{\stackrel{1}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{1}{H}{\parallel }_{2,\mathrm{supp}{\zeta }_1^{l_1}}+{c\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\parallel \stackrel{1}{H}{\parallel }_{2,\mathrm{supp}{\zeta }_1^{l_1}}+c{\parallel {\stackrel{1}{H}}_{,t}\parallel }_{1,\mathrm{supp}{\zeta }_1^{l_1}},$$

(184)

$$\parallel {\stackrel{2}{H}}^{(3,l_3)}{\parallel }_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{2}{H}{\parallel }_{1,\mathrm{supp}{\zeta }_3^{l_3}}+c{|{\stackrel{2}{H}}_{,t}|}_{2,\mathrm{supp}{\zeta }_3^{l_3}},$$

(185)

$$\parallel {\stackrel{2}{H}}^{(3,l_3)}{\parallel }_{3,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{2}{H}{\parallel }_{2,\mathrm{supp}{\zeta }_3^{l_3}}+c{\parallel {\stackrel{2}{H}}_{,t}\parallel }_{1,\mathrm{supp}{\zeta }_3^{l_3}},$$

(186)

$$\parallel {\stackrel{2}{H}}^{(4,l_4)}{\parallel }_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{2}{H}{\parallel }_{1,\mathrm{supp}{\zeta }_4^{l_4}}+c{|{\stackrel{2}{H}}_{,t}|}_{2,\mathrm{supp}{\zeta }_4^{l_4}},$$

(187)

$$\parallel {\stackrel{2}{H}}^{(4,l_4)}{\parallel }_{3,{\stackrel{2}{\mathrm{\Omega }}}_t}\le c\parallel \stackrel{2}{H}{\parallel }_{2,\mathrm{supp}{\zeta }_4^{l_4}}+c{\parallel {\stackrel{2}{H}}_{,t}\parallel }_{1,\mathrm{supp}{\zeta }_4^{l_4}}.$$

(188)

Now, we examine problem (181). First we introduce such coordinates that $S_t\cap \mathrm{supp}{\zeta }_2^{l_2}$ becomes flat. Introducing coordinates $y=(y_1,y_2,y_3)$ with origin at ${\xi }_2^{l_2}$ such that $S_t\cap \mathrm{supp}{\zeta }_2^{l_2}$, the form has

$$y_3=F_{{\zeta }_2^{l_2}}(y_1,y_2).$$

(189)

Define global Cartesian coordinates $x=(x_1,x_2,x_3)$ in ${\stackrel{1}{\mathrm{\Omega }}}_t\cup {\stackrel{2}{\mathrm{\Omega }}}_t\cup S_t$. Then the transformation $y=Y(x)$ is a composition of a rotation and a translation.

Next, we introduce new coordinates $z=(z_1,z_2,z_3)$ as defined by the relations

$$\begin{array}{cc}& z_{\alpha }=y_{\alpha },\alpha =1,2,\hfill \\ & z_3=y_3-F_{{\zeta }_2^{l_2}}(y_1,y_2).\hfill \end{array}$$

(190)

In these coordinates, interface $S_t$, which is locally expressed by (189), is described by the equation

$$z_3=0.$$

(191)

Transformation (190) is defined by

$$z=\mathrm{\Phi }(y)=\mathrm{\Phi }\circ Y(x)\equiv \mathrm{\Psi }(x).$$

(192)

Let ${\widehat{\mathrm{\Omega }}}_t^i=\{z\in {\mathbb{R}}^3:z=\mathrm{\Psi }(x),x\in {\stackrel{i}{\mathrm{\Omega }}}_t\}$, $i=1,2$.

We assume that $z=(z_1,z_2,z_3)\in {\widehat{\mathrm{\Omega }}}_t^2$ for $z_3>0$, and for $z_3<0$ we have that $z\in {\widehat{\mathrm{\Omega }}}_t^1$.

Let $u=u(x)$. Then $\widehat{u}(z)=u({\mathrm{\Psi }}^{-1}(z))$ and $\tilde{u}(z)=\widehat{u}(z)\widehat{\zeta }(z)$, where $\zeta$ is any function from the partition of unity introduced in Section 3.1.

Let h be a quantity such that $h=\stackrel{i}{h}(x)$ for $x\in {\stackrel{i}{\mathrm{\Omega }}}_t$, $i=1,2$. Let $x_0\in S_t$. Then a jump of h across the interface $S_t$ is defined as follows:

$$\left[h\right](x_0)=\underset{{\displaystyle \genfrac{}{}{0pt}{}{x\to x_0}{x\in {\stackrel{2}{\mathrm{\Omega }}}_t}}}{lim}\stackrel{2}{h}(x)-\underset{{\displaystyle \genfrac{}{}{0pt}{}{x\to x_0}{x\in {\stackrel{1}{\mathrm{\Omega }}}_t}}}{lim}\stackrel{1}{h}(x).$$

(193)

We introduce the transformed operator

$$\widehat{\nabla }=z_x{|}_{x={\mathrm{\Psi }}^{-1}(z)}·{\nabla }_z,$$

where ${\nabla }_z={({\partial }_{z_1},{\partial }_{z_2},{\partial }_{z_3})}^T$.

To introduce the transformed tangent and normal vectors, we recall that

$$\overline{n}={\displaystyle \frac{\nabla \varphi }{|\nabla \varphi |}},$$

where $\nabla ={\nabla }_x$ and $\varphi (x)=0$ describes $S_t$ locally, and the index t is omitted for simplicity. Then the transformed normal vector has the form

$$\widehat{\overline{n}}={\displaystyle \frac{\widehat{\nabla }\widehat{\varphi }}{|\widehat{\nabla }\widehat{\varphi }|}},$$

where $\widehat{\varphi }(z)=\varphi ({\mathrm{\Psi }}^{-1}(z))$ and

$${\widehat{\overline{\tau }}}_1={\overline{e}}_2\times \widehat{\overline{n}},{\widehat{\overline{\tau }}}_2={\overline{e}}_1\times \widehat{\overline{n}},$$

where ${\overline{e}}_1=(1,0,0)$, ${\overline{e}}_2=(0,1,0)$.

The transformed locally boundary has the form

$$z_3=0.$$

Hence, ${\overline{\tau }}_{z1}=(1,0,0)$, ${\overline{\tau }}_{z2}=(0,1,0)$.

To describe problem (181) using variable z, for simplicity, we drop the index $(2,l_2)$. Next, we pass to variable z and use the notation $\widehat{\sigma }=\sigma ({\psi }^{-1}(z))$, where $\sigma$ replaces any function in (181).

Then (181) takes the form

$$\begin{array}{ccc}-\hfill & {\nabla }_z^2\stackrel{1}{\widehat{H}}=-({\nabla }_z^2-{\widehat{\nabla }}^2)\stackrel{1}{\widehat{H}}+\stackrel{1}{\widehat{g}}\equiv \stackrel{1}{\overline{g}}\hfill & \mathrm{in}{z}_3>0,\hfill \\ -\hfill & {\nabla }_z^2\stackrel{2}{\widehat{H}}=-({\nabla }_z^2-{\widehat{\nabla }}^2)\stackrel{2}{\widehat{H}}+\stackrel{2}{\widehat{g}}\equiv \stackrel{2}{\overline{g}}\hfill & \mathrm{in}{z}_3<0,\hfill \\ & ({\stackrel{1}{a}}_{\alpha }\mathrm{rot}{}_z\stackrel{1}{\widehat{H}}-{\stackrel{2}{a}}_{\alpha }\mathrm{rot}{}_z\stackrel{2}{\widehat{H}})·{\overline{\tau }}_{z\alpha }\hfill \\ & =({\stackrel{1}{a}}_{\alpha }\mathrm{rot}{}_z\stackrel{1}{\widehat{H}}-{\stackrel{2}{a}}_{\alpha }\mathrm{rot}{}_z\stackrel{2}{\widehat{H}}){\overline{\tau }}_{z\alpha }\hfill \\ & -({\stackrel{1}{a}}_{\alpha }\widehat{\mathrm{rot}}\stackrel{1}{\widehat{H}}-{\stackrel{2}{a}}_{\alpha }\widehat{\mathrm{rot}}\stackrel{2}{\widehat{H}}){\widehat{\overline{\tau }}}_{\alpha }+{\widehat{h}}_{\alpha }\equiv {\widehat{k}}_{\alpha },\alpha =1,2,\hfill & z_3=0,\hfill \\ & {\mu }_1\mathrm{div}{}_z\stackrel{1}{\widehat{H}}-{\mu }_2\mathrm{div}{}_z\stackrel{1}{\widehat{H}}\hfill \\ & ={\mu }_1\mathrm{div}{}_z\stackrel{1}{\widehat{H}}-{\mu }_2\mathrm{div}{}_z\stackrel{2}{\widehat{H}}-({\mu }_1\widehat{\mathrm{div}}\stackrel{1}{\widehat{H}}-{\mu }_2\widehat{\mathrm{div}}\stackrel{2}{\widehat{H}})\equiv \widehat{b}\hfill & z_3=0,\hfill \\ & ({\stackrel{1}{b}}_{\beta }{\stackrel{1}{\widehat{H}}}_{\beta }-{\stackrel{2}{b}}_{\beta }{\stackrel{2}{\widehat{H}}}_{\beta }){\tau }_{z\alpha \beta }\hfill \\ & =({\stackrel{1}{b}}_{\beta }{\stackrel{1}{\widehat{H}}}_{\beta }-{\stackrel{2}{b}}_{\beta }{\stackrel{2}{\widehat{H}}}_{\beta })({\tau }_{z\alpha \beta }-{\widehat{\tau }}_{\alpha \beta })\equiv {\widehat{d}}_{\alpha },\alpha =1,2,\hfill & z_3=0,\hfill \\ & ({\stackrel{1}{b}}_{\beta }{\stackrel{1}{\widehat{H}}}_{\beta }-{\stackrel{2}{b}}_{\beta }{\stackrel{2}{\widehat{H}}}_{\beta })n_{z\beta }\hfill \\ & =({\stackrel{1}{b}}_{\beta }{\stackrel{1}{\widehat{H}}}_{\beta }-{\stackrel{2}{b}}_{\beta }{\stackrel{2}{\widehat{H}}}_{\beta })(n_{z\beta }-{\widehat{n}}_{\beta })\equiv {\widehat{d}}_3,\hfill & z_3=0,\hfill \end{array}$$

(194)

where the condition (194)₄ is only important in local space considerations, since in the exit problem (174), $\stackrel{1}{H}$ and $\stackrel{2}{H^{\prime }}$ are divergence free and the summation over $\beta$ is assumed.

Extending functions $\stackrel{i}{\overline{g}}$, $i=1,2$, on ${\mathbb{R}}^3$, we look for solutions to the problem

$${\nabla }_z^2\stackrel{i}{w}=\stackrel{i}{\tilde{g}},i=1,2,$$

(195)

where $\stackrel{i}{\tilde{g}}$ is an extension of $\stackrel{i}{\overline{g}}$, $i=1,2$, on ${\mathbb{R}}^3$.

We introduce the functions

$$\stackrel{i}{u}=\stackrel{i}{\widehat{H}}-\stackrel{i}{w},i=1,2.$$

(196)

Then functions $\stackrel{i}{u}$, $i=1,2$, are solutions to the problem

$$\begin{array}{cc}& {\nabla }_z^2\stackrel{1}{u}=0z_3>0,\hfill \\ & {\nabla }_z^2\stackrel{2}{u}=0z_3<0,\hfill \\ & [\mathrm{rot}{}_{z}u·{\overline{\tau }}_{z\alpha }]=-[\mathrm{rot}{}_{z}w·{\overline{\tau }}_{z\alpha }]+{\widehat{k}}_{\alpha }=k_{\alpha },\alpha =1,2,z_3=0,\hfill \\ & \left[\mu \mathrm{div}{}_{z}u\right]=-\left[\mu \mathrm{div}{}_{z}w\right]+\widehat{b}\equiv b,z_3=0,\hfill \\ & [u·{\overline{\tau }}_{z\alpha }]=-[w·{\overline{\tau }}_{z\alpha }]+{\widehat{d}}_{\alpha }=d_{\alpha },\alpha =1,2,z_3=0,\hfill \\ & [\mu u·{\overline{n}}_z]=-[w·{\overline{n}}_z]+{\widehat{d}}_3=d_3{z}_3=0,\hfill \end{array}$$

(197)

where we assume for simplicity that ${\stackrel{i}{a}}_{\alpha }$, ${\stackrel{i}{b}}_{\alpha }=1$, $\alpha =1,2$, $i=1,2$ and ${\stackrel{i}{\widehat{b}}}_3={\mu }_i$, $i=1,2$.

Let us define the Fourier transform

$$\stackrel{j}{v}({\xi }_1,{\xi }_2,z_3)={\displaystyle \frac{1}{2\pi }}\underset{{\mathbb{R}}^2}{\int }\stackrel{j}{u}(z_1,z_2,z_3)e^{-i({\xi }_1{z}_1+{\xi }_2{z}_2)}d{z}_{1}d{z}_2,j=1,2,$$

and its inverse

$$\stackrel{j}{u}(z_1,z_2,z_3)={\displaystyle \frac{1}{2\pi }}\underset{{\mathbb{R}}^2}{\int }\stackrel{j}{v}({\xi }_1,{\xi }_2,z_3)e^{i({\xi }_1{z}_1+{\xi }_2{z}_2)}d{\xi }_{1}d{\xi }_2,j=1,2.$$

Applying the Fourier transform to (197) yields

$$\begin{array}{ccc}& {\xi }^2\stackrel{1}{v}-{\stackrel{1}{v}}_{,z_3{z}_3}=0\hfill & z_3>0,\hfill \\ & {\xi }^2\stackrel{2}{v}-{\stackrel{2}{v}}_{,z_3{z}_3}=0\hfill & z_3<0,\hfill \\ & {\stackrel{1}{v}}_{2,z_3}-i{\xi }_2{\stackrel{1}{v}}_3-({\stackrel{2}{v}}_{2,z_3}-i{\xi }_2{\stackrel{2}{v}}_3)={\tilde{k}}_1\hfill & z_3=0,\hfill \\ & i{\xi }_1{\stackrel{1}{v}}_3-{\stackrel{1}{v}}_{1,z_3}-(i{\xi }_1{\stackrel{2}{v}}_3-{\stackrel{2}{v}}_{1,z_3})={\tilde{k}}_2\hfill & z_3=0,\hfill \\ & {\mu }_1(i{\xi }_{\alpha }{\stackrel{1}{v}}_{\alpha }+{\stackrel{1}{v}}_{3,z_3})-{\mu }_2(i{\xi }_{\alpha }{\stackrel{2}{v}}_{\alpha }+{\stackrel{2}{v}}_{3,z_3})=\tilde{b}\hfill & z_3=0,\hfill \\ & {\stackrel{1}{v}}_{\alpha }-{\stackrel{2}{v}}_{\alpha }={\tilde{d}}_{\alpha },\alpha =1,2,\hfill & z_3=0,\hfill \\ & {\mu }_1{\stackrel{1}{v}}_3-{\mu }_2{\stackrel{2}{v}}_3={\tilde{d}}_3\hfill & z_3=0,\hfill \end{array}$$

(198)

where

$$\tilde{f}(\xi ,z_3)={\displaystyle \frac{1}{2\pi }}\underset{{\mathbb{R}}^2}{\int }\tilde{f}(z^{\prime },z_3)e^{-i{z}^{\prime }·\xi }d{z}_{1}d{z}_2,z^{\prime }=(z_1,z_2).$$

Solving (198)_1,2, we obtain

$$\stackrel{1}{v}=\stackrel{1}{A}({\xi }_1,{\xi }_2)e^{-|\xi |z_3},\stackrel{2}{v}=\stackrel{2}{A}({\xi }_1,{\xi }_2)e^{|\xi |z_3},$$

(199)

where $|\xi |=\sqrt{{\xi }_1^2+{\xi }_2^2}$, $\xi =({\xi }_1,{\xi }_2)$ and we used the Shapiro–Lopatinskii conditions.

To calculate coefficients $\stackrel{1}{A}$ and $\stackrel{2}{A}$, we insert (199) to transmission conditions (198)_3,4,5,6,7, where we dropped index ∼ in the right-hand side terms. Then we obtain

$$\begin{array}{cc}-\hfill & |\xi |{\stackrel{1}{A}}_2-i{\xi }_2{\stackrel{1}{A}}_3-(|\xi |{\stackrel{2}{A}}_2-i{\xi }_2{\stackrel{2}{A}}_3)=k_1,\hfill \\ & i{\xi }_1{\stackrel{1}{A}}_3+|\xi |{\stackrel{1}{A}}_1-(i{\xi }_1{\stackrel{2}{A}}_3-|\xi |{\stackrel{2}{A}}_1)=k_2,\hfill \\ & {\mu }_1(i{\xi }_{\alpha }{\stackrel{1}{A}}_{\alpha }-|\xi |{\stackrel{1}{A}}_3)-{\mu }_2(i{\xi }_{\alpha }{\stackrel{2}{A}}_{\alpha }+|\xi |{\stackrel{2}{A}}_3)=b,\hfill \\ & {\stackrel{1}{A}}_{\alpha }-{\stackrel{2}{A}}_{\alpha }=d_{\alpha },\alpha =1,2,\hfill \\ & {\mu }_1{\stackrel{1}{A}}_3-{\mu }_2{\stackrel{2}{A}}_3=d_3.\hfill \end{array}$$

(200)

Using that

$$\begin{array}{cc}& {\stackrel{1}{A}}_{\alpha }={\stackrel{2}{A}}_{\alpha }+d_{\alpha },\alpha =1,2,\hfill \\ & {\stackrel{1}{A}}_3={\displaystyle \frac{{\mu }_2}{{\mu }_1}}{\stackrel{2}{A}}_3+{\displaystyle \frac{1}{{\mu }_1}}{d}_3\hfill \end{array}$$

(201)

we write (200)_1,2,3 in the form

$$\begin{array}{cc}-\hfill & |\xi |({\stackrel{2}{A}}_2+d_2)-i{\xi }_2\left({\displaystyle \frac{{\mu }_2}{{\mu }_1}}{\stackrel{2}{A}}_3+{\displaystyle \frac{1}{{\mu }_1}}{d}_3\right)-(|\xi |{\stackrel{2}{A}}_2-i{\xi }_2{\stackrel{2}{A}}_3)=k_1,\hfill \\ & i{\xi }_1\left({\displaystyle \frac{{\mu }_2}{{\mu }_1}}{\stackrel{2}{A}}_3+{\displaystyle \frac{1}{{\mu }_1}}{d}_3\right)+|\xi |({\stackrel{2}{A}}_1+d_1)-(i{\xi }_1{\stackrel{2}{A}}_3-|\xi |{\stackrel{2}{A}}_1)=k_2,\hfill \\ & {\mu }_1\left(i{\xi }_{\alpha }({\stackrel{2}{A}}_{\alpha }+d_{\alpha })-|\xi |\left({\displaystyle \frac{{\mu }_2}{{\mu }_2}}{\stackrel{2}{A}}_3+{\displaystyle \frac{1}{{\mu }_1}}{d}_3\right)\right)\hfill \\ & -{\mu }_2(i{\xi }_{\alpha }{\stackrel{2}{A}}_{\alpha }+|\xi |{\stackrel{2}{A}}_3)=b.\hfill \end{array}$$

(202)

Simplifying (202) yields

$$\begin{array}{cc}-\hfill & 2|\xi |{\stackrel{2}{A}}_2-i{\xi }_2\left({\displaystyle \frac{{\mu }_2}{{\mu }_1}}-1\right){\stackrel{2}{A}}_3=k_1+|\xi |d_2-{\displaystyle \frac{i{\xi }_2}{{\mu }_1}}{d}_3,\hfill \\ & i{\xi }_1\left({\displaystyle \frac{{\mu }_2}{{\mu }_1}}-1\right){\stackrel{2}{A}}_3+2|\xi |{\stackrel{2}{A}}_1=k_2-|\xi |d_1-{\displaystyle \frac{i{\xi }_1}{{\mu }_1}}{d}_3,\hfill \\ & ({\mu }_1-{\mu }_2)i{\xi }_{\alpha }{\stackrel{2}{A}}_{\alpha }-|\xi |\left({\displaystyle \frac{{\mu }_2}{{\mu }_1}}+1\right){\stackrel{2}{A}}_3=b-{\displaystyle \frac{1}{{\mu }_1}}|\xi |d_3-{\mu }_{1}i{\xi }_{\alpha }{d}_{\alpha }.\hfill \end{array}$$

(203)

We write some comments on deriving problem (202). Applying the Fourier transform to problem (197) along directions perpendicular to $z_3$, we derive (198). The solutions to the first two equations (198) have the form (199). Using them, we derive (200). Using solutions of the last two equations of (200), described by (201), implies (202).

Problem (203) is a simple consequence of (202).

We prove Lemma 17 in the simpler case ${\mu }_1={\mu }_2$ because in the general case ${\mu }_1\ne {\mu }_2$, the assertions of Lemma 17 also hold.

Setting ${\mu }_1={\mu }_2$ in (203) yields

$$\begin{array}{cc}& {\stackrel{2}{A}}_1={\displaystyle \frac{1}{2|\xi |}}\left(k_2-|\xi |d_1-{\displaystyle \frac{i{\xi }_1}{{\mu }_1}}{d}_3\right),\hfill \\ & {\stackrel{2}{A}}_2=-{\displaystyle \frac{1}{2|\xi |}}\left(k_1+|\xi |d_2-{\displaystyle \frac{i{\xi }_2}{{\mu }_1}}{d}_3\right),\hfill \\ & {\stackrel{2}{A}}_3=-{\displaystyle \frac{1}{2|\xi |}}\left(b-i{\mu }_1{\xi }_{\alpha }{d}_{\alpha }-{\displaystyle \frac{1}{{\mu }_1}}|\xi |d_3\right).\hfill \end{array}$$

(204)

Now, we prove (175). Let

$$\lambda =\underset{k}{sup}\mathrm{diam}\mathrm{supp}{\zeta }_k.$$

(205)

From (195), it follows that

$$\parallel \stackrel{i}{w}{\parallel }_{2,R^3}\le c\lambda \parallel \stackrel{i}{\widehat{H}}{\parallel }_{2,{\mathbb{R}}^3}+c\parallel \widehat{v}{\parallel }_{2,{\mathbb{R}}^3}\parallel \stackrel{i}{\widehat{H}}{\parallel }_{2,{\mathbb{R}}^3}+c\parallel \stackrel{i}{\widehat{H}}{\parallel }_{1,{\mathbb{R}}^3}+c{|{\stackrel{i}{\widehat{H}}}_{,t}|}_{2,{\mathbb{R}}^3}.$$

(206)

Next, we examine

$$\parallel \stackrel{i}{\widehat{H}}{\parallel }_{2,{\mathbb{R}}^3}\le c\parallel \stackrel{i}{w}{\parallel }_{2,{\mathbb{R}}^3}+c{\parallel \stackrel{i}{u}\parallel }_{2,{\mathbb{R}}^3}.$$

(207)

To estimate $\parallel \stackrel{i}{u}{\parallel }_{2,{\mathbb{R}}^3}$, we examine the Fourier transforms of $\stackrel{i}{u}$, $i=1,2$, described by (198) because norms $\parallel \stackrel{i}{u}{\parallel }_{2,{\mathbb{R}}^3}$ and $\parallel \stackrel{i}{v}{\parallel }_{2,{\mathbb{R}}^3}$ are equivalent. To estimate $\parallel \stackrel{i}{v}{\parallel }_{2,{\mathbb{R}}^3}$, $i=1,2$, we use expressions of $\stackrel{1}{A}$, $\stackrel{2}{A}$ calculated in (204) and (201).

We prove Lemma 17 in the simpler case ${\mu }_1={\mu }_2$. It is clear that in the general case ${\mu }_1\ne {\mu }_2$, the assertions of Lemma 17 also hold.

By the Parseval identity, the norm ${\sum }_{i=1}^2{\parallel \stackrel{i}{u}\parallel }_{H^2({\mathbb{R}}_{+}^3)}$ is equivalent to the following one:

$${\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{u}{\parallel }_{2,{\mathbb{R}}_{+}^3}^2={\displaystyle \sum _{j=0}^2}\underset{{\mathbb{R}}^2}{\int }d{\xi }_{1}d{\xi }_2{|\xi |}^{2(2-j)}\left(\underset{{\mathbb{R}}_{+}}{\int }|{\partial }_{z_3}^j\stackrel{1}{v}{|}^{2}d{z}_3+\underset{{\mathbb{R}}_{-}}{\int }{|{\partial }_{z_3}^j\stackrel{2}{v}|}^{2}d{z}_3\right),$$

(208)

where $\stackrel{i}{v}$ is the Fourier transform of $\stackrel{i}{u}$, $i=1,2$, and ${\mathbb{R}}_{-}=\{x:x_3<0\}$.

Since $\stackrel{1}{v}=\stackrel{1}{A}({\xi }_1,{\xi }_2)e^{-|\xi |z_3}$, we restrict our considerations to estimating only the term

$${\stackrel{1}{v}}_1={\stackrel{1}{A}}_1({\xi }_1,{\xi }_2)e^{-|\xi |z_3}$$

(209)

because the other terms can be treated in a similar way. From (201) and (204), we have

$${\stackrel{1}{A}}_1={\stackrel{2}{A}}_1+d_1={\displaystyle \frac{1}{2|\xi |}}\left(k_2-|\xi |d_1-{\displaystyle \frac{i{\xi }_1}{{\mu }_1}}{d}_3\right)+d_1.$$

(210)

Since $\stackrel{1}{v_1}$ is described by (209) and (210), we shall examine the following part of $\stackrel{1}{v_1}$:

$$\stackrel{1}{v_1^{\prime }}={\displaystyle \frac{1}{|\xi |}}{k}_2{e}^{-|\xi |z_3}.$$

Applying norm (208) to $\stackrel{1}{v_1^{\prime }}$ yields

$$\begin{array}{cc}& {\displaystyle \sum _{j=0}^2}\underset{{\mathbb{R}}^2}{\int }d{\xi }_{1}d{\xi }_2{|\xi |}^{2(2-j)}\underset{{\mathbb{R}}_{+}}{\int }{|{\partial }_{z_3}^j\stackrel{1}{v_1^{\prime }}|}^{2}d{z}_3\hfill \\ & ={\displaystyle \sum _{j=0}^2}\underset{{\mathbb{R}}^2}{\int }d{\xi }_{1}d{\xi }_2{|\xi |}^{2(2-j)}{\displaystyle \frac{1}{{|\xi |}^2}}|k_2{|}^2\underset{{\mathbb{R}}_{+}}{\int }{|{\partial }_{z_3}^j{e}^{-|\xi |z_3}|}^{2}d{z}_3\hfill \\ & ={\displaystyle \sum _{j=0}^2}\underset{{\mathbb{R}}^2}{\int }d{\xi }_{1}d{\xi }_2{|\xi |}^{2(2-j)}{|\xi |}^{2j}{\displaystyle \frac{1}{{|\xi |}^2}}|k_2{|}^2\underset{{\mathbb{R}}_{+}}{\int }{|e^{-|\xi |z_3}|}^{2}d{z}_3\hfill \\ & =\underset{{\mathbb{R}}^2}{\int }d{\xi }_{1}d{\xi }_2{|\xi |}^4{|\xi |}^{-2}{k}_2^2\underset{{\mathbb{R}}_{+}}{\int }{e}^{-2|\xi |z_3}d{z}_3\hfill \\ & \le c\underset{{\mathbb{R}}^2}{\int }d{\xi }_{1}d{\xi }_2{|\xi |}^2{\displaystyle \frac{1}{2|\xi |}}{k}_2^2=c\underset{{\mathbb{R}}^2}{\int }d{\xi }_{1}d{\xi }_2|\xi |k_2^2=c{\parallel k_1\parallel }_{1/2,{\mathbb{R}}^2}^2.\hfill \end{array}$$

Continuing the estimates for solutions to problem (198), we derive the estimate

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^3}\parallel \stackrel{i}{v}{\parallel }_{2,{\mathbb{R}}^3}\le c{\displaystyle \sum _{i=1}^2}(\parallel {\tilde{k}}_i{\parallel }_{1/2,{\mathbb{R}}^2}+\parallel {\tilde{d}}_i{\parallel }_{3/2,{\mathbb{R}}^2})\hfill \\ & +c(\parallel \tilde{b}{\parallel }_{1/2,{\mathbb{R}}^2}+\parallel {\tilde{d}}_3{\parallel }_{3/2,{\mathbb{R}}^2}).\hfill \end{array}$$

(211)

By the Parseval identity estimate, (211) takes the form

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{u}{\parallel }_{2,{\mathbb{R}}^3}\le c{\displaystyle \sum _{i=1}^2}(\parallel k_i{\parallel }_{1/2,{\mathbb{R}}^2}+\parallel d_i{\parallel }_{3/2,{\mathbb{R}}^2})\hfill \\ & +c(\parallel b{\parallel }_{1/2,{\mathbb{R}}^2}+\parallel d_3{\parallel }_{3/2,{\mathbb{R}}^2}).\hfill \end{array}$$

(212)

From (194), we have

$$\parallel {\widehat{k}}_{\alpha }{\parallel }_{1/2,{\mathbb{R}}^2}\le c\lambda (\parallel \stackrel{1}{\widehat{H}}{\parallel }_{3/2,{\mathbb{R}}^2}+\parallel \stackrel{2}{\widehat{H}}{\parallel }_{3/2,{\mathbb{R}}^2})+c\parallel {\widehat{h}}_{\alpha }{\parallel }_{1/2,{\mathbb{R}}^2}$$

and (183)₃ implies

$$\begin{array}{cc}& \parallel {\widehat{h}}_{\alpha }{\parallel }_{1/2,{\mathbb{R}}^2}\le c\lambda (\parallel \stackrel{1}{\widehat{H}}{\parallel }_{3/2,{\mathbb{R}}^2}+\parallel \stackrel{2}{\widehat{H}}{\parallel }_{3/2,{\mathbb{R}}^2}{)+c\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}{\parallel \stackrel{1}{H}\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}\hfill \\ & +c(|{\stackrel{1}{\widehat{H}}}_{,t}{|}_{2,{\mathbb{R}}^3}+|{\stackrel{2}{\widehat{H}}}_t{|}_{2,{\mathbb{R}}^3}).\hfill \end{array}$$

We also have

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^2}\parallel d_i{\parallel }_{3/2,{\mathbb{R}}^2}+{\parallel b\parallel }_{1/2,{\mathbb{R}}^2}+\parallel d_3{\parallel }_{3/2,{\mathbb{R}}^2}\le c\lambda (\parallel \stackrel{1}{\widehat{H}}{\parallel }_{2,{\mathbb{R}}^3}+\parallel \stackrel{2}{\widehat{H}}{\parallel }_{2,{\mathbb{R}}^3})\hfill \\ & +c\parallel \widehat{v}{\parallel }_{2,{\mathbb{R}}^3}\parallel \stackrel{1}{\widehat{H}}{\parallel }_{2,{\mathbb{R}}^3}+c(|{\stackrel{1}{\widehat{H}}}_{,t}{|}_{2,{\mathbb{R}}^3}+|{\stackrel{2}{\widehat{H}}}_{,t}{|}_{2,{\mathbb{R}}^3}).\hfill \end{array}$$

Using the above estimates in (212), using (206) and (207), and passing to variables x, we obtain

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^2}\parallel {\stackrel{i}{H}}^{(2,l_2)}{\parallel }_{2,{\mathbb{R}}^3}\le \lambda {\displaystyle \sum _{i=1}^2}\parallel {\stackrel{i}{H}}^{(2,l_2)}{\parallel }_{2,{\mathbb{R}}^3}+{c\parallel v\parallel }_{2,{\mathbb{R}}^3\cap \mathrm{supp}{\zeta }^{(2,l_2)}}{\parallel {\stackrel{1}{H}}^{(2,l_2)}\parallel }_{2,{\mathbb{R}}^3}\hfill \\ & +c{\displaystyle \sum _{i=1}^2}{|{\stackrel{i}{H}}_{,t}^{(2,l_2)}|}_{2,{\mathbb{R}}^3}.\hfill \end{array}$$

Finally, using (183)–(188) and the above inequality, exploiting properties of the partition of unity and with $\lambda$ sufficiently small (see Section 3.1), we derive (175). Similar considerations imply (176). This concludes the proof. □

Finally, we derive a differential inequality for magnetic fields.

Lemma 18. 

Assume that the following quantities are finite:

$$\begin{array}{cc}& X_2(t)={\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{H}{\parallel }_{{\mathrm{\Gamma }}_0^2({\stackrel{i}{\mathrm{\Omega }}}_t)}+{\parallel v\parallel }_{{\mathrm{\Gamma }}_0^2({\stackrel{1}{\mathrm{\Omega }}}_t)},\hfill \\ & Y_2(t)={\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{H}{\parallel }_{{\mathrm{\Gamma }}_1^3({\stackrel{i}{\mathrm{\Omega }}}_t)}+{\parallel v\parallel }_{{\mathrm{\Gamma }}_1^3({\stackrel{1}{\mathrm{\Omega }}}_t)},\hfill \end{array}$$

where $\stackrel{2}{H}$ must be replaced by $\stackrel{2}{H^{\prime }}$. Then the following differential inequality holds:

$${\displaystyle \frac{d}{dt}}{X}_2^2+Y_2^2\le c{X}_2^2{Y}_2^2+G_{\ast }^2,$$

(213)

where

$$G_{\ast }^2={\displaystyle \sum _{i=0}^2}(\parallel {\partial }_t^i{H}_{\ast }{\parallel }_{3/2,B}^2+\parallel {\partial }_t^i{H}_{\ast ,t}{\parallel }_{3/2,B}^2+\parallel {\partial }_t^i{B}_{\ast }{\parallel }_{1/2,B}^2+\parallel {\partial }_t^i{B}_{\ast ,t}{\parallel }_{1/2,B}^2).$$

Proof. 

In the proof, we replace $\stackrel{2}{H^{\prime }}$ by $\stackrel{2}{H}$. Inequality (139) implies

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}(|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|H_2^2{|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)+{\displaystyle \frac{1}{{\sigma }_1}}|\mathrm{rot}\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{\displaystyle \frac{1}{{\sigma }_2}}{|\mathrm{rot}\stackrel{2}{H}|}_{2,{\stackrel{2}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le {\overline{\epsilon }}_1(\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{2}{H}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)+c(1/{\overline{\epsilon }}_1)(\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +\parallel \stackrel{2}{v}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}\parallel \stackrel{2}{H}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)+c(\parallel H_{\ast }{\parallel }_{3/2,B}^2+{\parallel H_{\ast ,t}\parallel }_{3/2,B}^2\hfill \\ & +\parallel B_{\ast }{\parallel }_{1/2,B}+\parallel B_{\ast ,t}{\parallel }_{1/2,B}^2).\hfill \end{array}$$

(214)

Inequality (144) yields

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^2}|\nabla \stackrel{i}{H}{|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\le c{\displaystyle \sum _{i=1}^2}|\mathrm{rot}\stackrel{i}{H}{|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+{\overline{\epsilon }}_2{|\stackrel{1}{H}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +c\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}{\parallel \stackrel{1}{H}\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.\hfill \end{array}$$

(215)

Inequalities (214) and (215) imply

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\left({\displaystyle \sum _{i=1}^2}{|\stackrel{i}{H}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\right)+{\displaystyle \sum _{i=1}^2}{|\nabla \stackrel{i}{H}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le {\overline{\epsilon }}_2|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{2}{v}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}\parallel \stackrel{2}{H}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)+G_0^2,\hfill \end{array}$$

(216)

where

$$G_0^2=c(\parallel H_{\ast }{\parallel }_{3/2,B}^2+\parallel H_{\ast ,t}{\parallel }_{3/2,B}^2+\parallel B_{\ast }{\parallel }_{1/2,B}^2+\parallel B_{\ast ,t}{\parallel }_{1/2,B}^2).$$

From (168), we have

$${\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{H}{\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\le {\overline{\epsilon }}_2|\stackrel{1}{H}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c\parallel \stackrel{2}{v}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}{\parallel \stackrel{2}{H}\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}.$$

(217)

Inequalities (216) and (217) imply

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\left({\displaystyle \sum _{i=1}^2}{|\stackrel{i}{H}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\right)+{\displaystyle \sum _{i=1}^2}{\parallel \stackrel{i}{H}\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le c(\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{2}{v}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}\parallel \stackrel{2}{H}{\parallel }_{1,{\stackrel{2}{\mathrm{\Omega }}}_t}^2)+G_0^2.\hfill \end{array}$$

(218)

We differentiate (138)_1,3 with respect to t. Then (218) is replaced by

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\left({\displaystyle \sum _{i=1}^2}{|{\stackrel{i}{H}}_{,t}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\right)+{\displaystyle \sum _{i=1}^2}{\parallel {\stackrel{i}{H}}_{,t}\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le |{\displaystyle \sum _{i=1}^2}\underset{{\stackrel{i}{\mathrm{\Omega }}}_t}{\int }{(\stackrel{i}{v}·\nabla \stackrel{i}{H})}_{,t}{\stackrel{i}{H}}_{,t}dx|+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(\stackrel{1}{H}·\nabla \stackrel{1}{v})}_{,t}{\stackrel{1}{H}}_{,t}dx|+G_1^2,\hfill \end{array}$$

(219)

where

$$G_1^2=c(\parallel H_{\ast ,t}{\parallel }_{3/2,B}^2+\parallel H_{\ast ,tt}{\parallel }_{3/2,B}^2+\parallel B_{\ast ,t}{\parallel }_{1/2,B}^2+\parallel B_{\ast ,tt}{\parallel }_{1/2,B}^2).$$

We estimate the first term on the right-hand side of (219) by

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^2}|\underset{{\stackrel{i}{\mathrm{\Omega }}}_t}{\int }\stackrel{i}{v}·\nabla {\stackrel{i}{H}}_{,t}{\stackrel{i}{H}}_{,t}dx|+{\displaystyle \sum _{i=1}^2}|\underset{{\stackrel{i}{\mathrm{\Omega }}}_t}{\int }{\stackrel{i}{v}}_{,t}·\nabla \stackrel{i}{H}·{\stackrel{i}{H}}_{,t}dx|\hfill \\ & \le {\epsilon }_1{\displaystyle \sum _{i=1}^2}|\nabla {\stackrel{i}{H}}_{,t}{|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_1){\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{v}{\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2{\parallel {\stackrel{i}{H}}_{,t}\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{\epsilon }_2{\displaystyle \sum _{i=1}^2}|{\stackrel{i}{H}}_{,t}{|}_{6,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_2){\displaystyle \sum _{i=1}^2}\parallel {\stackrel{i}{v}}_{,t}{\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2{\parallel \nabla \stackrel{i}{H}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \end{array}$$

and the second by

$$\begin{array}{cc}& |\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{\stackrel{1}{H}}_{,t}·\nabla \stackrel{1}{v}{\stackrel{1}{H}}_{,t}dx|+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }\stackrel{1}{H}·\nabla {\stackrel{1}{v}}_{,t}·{\stackrel{1}{H}}_{,t}dx|\hfill \\ & \le {\epsilon }_3|{\stackrel{1}{H}}_{,t}{|}_{6,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_3)(\parallel {\stackrel{1}{H}}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel \stackrel{1}{v}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{1}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel {\stackrel{1}{v}}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

Considering the above estimates and with ${\epsilon }_1-{\epsilon }_3$ sufficiently small, inequality (219) takes the form

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\left({\displaystyle \sum _{i=1}^2}{|{\stackrel{i}{H}}_{,t}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\right)+{\displaystyle \sum _{i=1}^2}{\parallel {\stackrel{i}{H}}_{,t}\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le c{\displaystyle \sum _{i=1}^2}(\parallel \stackrel{i}{v}{\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\parallel {\stackrel{i}{H}}_{,t}{\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+\parallel \stackrel{i}{H}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\parallel {\stackrel{i}{v}}_{,t}{\parallel }_{1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2)+G_1^2.\hfill \end{array}$$

(220)

It is necessary to differentiate (138) twice with respect to time.

Then (190) is replaced by

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\left({\displaystyle \sum _{i=1}^2}{|{\stackrel{i}{H}}_{,tt}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\right)+{\displaystyle \sum _{i=1}^2}{\parallel {\stackrel{i}{H}}_{,tt}\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le |{\displaystyle \sum _{i=1}^2}\underset{{\stackrel{i}{\mathrm{\Omega }}}_t}{\int }{(\stackrel{i}{v}·\nabla \stackrel{i}{H})}_{,tt}·{\stackrel{i}{H}}_{,tt}dx|+|\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }{(\stackrel{1}{H}·\nabla \stackrel{1}{v})}_{,tt}·{\stackrel{1}{H}}_{,tt}dx|+G_2^2,\hfill \end{array}$$

(221)

where

$$G_2^2=c(\parallel H_{\ast ,tt}{\parallel }_{3/2,B}^2+\parallel H_{\ast ,ttt}{\parallel }_{3/2,B}^2+\parallel B_{\ast ,tt}{\parallel }_{1/2,B}^2+\parallel B_{\ast ,ttt}{\parallel }_{1/2,B}^2).$$

We bound the first term on the right-hand side of (221) by

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^2}[\underset{{\stackrel{i}{\mathrm{\Omega }}}_t}{\int }|{\stackrel{i}{v}}_{,tt}·\nabla \stackrel{i}{H}·{\stackrel{i}{H}}_{,tt}|dx+2\underset{{\stackrel{i}{\mathrm{\Omega }}}_t}{\int }|{\stackrel{i}{v}}_{,t}·\nabla {\stackrel{i}{H}}_{,t}·{\stackrel{i}{H}}_{,tt}|dx\hfill \\ & +\underset{{\stackrel{i}{\mathrm{\Omega }}}_t}{\int }|\stackrel{i}{v}·\nabla {\stackrel{i}{H}}_{,tt}·{\stackrel{i}{H}}_{,tt}|dx]\hfill \\ & \le {\displaystyle \sum _{i=1}^2}[{\epsilon }_1|{\stackrel{i}{H}}_{,tt}{|}_{6,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_1)|\nabla \stackrel{i}{H}{|}_{3,{\stackrel{i}{\mathrm{\Omega }}}_t}^2{|{\stackrel{i}{v}}_{,tt}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{\epsilon }_2|{\stackrel{i}{H}}_{,tt}{|}_{6,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_2)|{\stackrel{i}{v}}_{,t}{|}_{3,{\stackrel{i}{\mathrm{\Omega }}}_t}^2{|\nabla {\stackrel{i}{H}}_{,t}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & +{\epsilon }_3|\nabla {\stackrel{i}{H}}_{,tt}{|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_3)|\stackrel{i}{v}{|}_{\infty ,{\stackrel{i}{\mathrm{\Omega }}}_t}^2|{\stackrel{i}{H}}_{,tt}{|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2]\hfill \end{array}$$

and the second by

$$\begin{array}{cc}& \underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|{\stackrel{1}{H}}_{,tt}·\nabla \stackrel{1}{v}·{\stackrel{1}{H}}_{,tt}|dx+2\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|{\stackrel{1}{H}}_{,t}·\nabla {\stackrel{1}{v}}_{,t}·{\stackrel{1}{H}}_{,tt}|dx\hfill \\ & +\underset{{\stackrel{1}{\mathrm{\Omega }}}_t}{\int }|\stackrel{1}{H}·\nabla {\stackrel{1}{v}}_{,tt}·{\stackrel{1}{H}}_{,tt}|dx\hfill \\ & \le {\epsilon }_4|{\stackrel{1}{H}}_{,tt}{|}_{6,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c(1/{\epsilon }_4)(|{\stackrel{1}{H}}_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{|\nabla \stackrel{1}{v}|}_{3,{\stackrel{1}{\mathrm{\Omega }}}_t}^2\hfill \\ & +|{\stackrel{1}{H}}_{,t}{|}_{3,\stackrel{1}{\mathrm{\Omega }}{|}_t}^2|\nabla {\stackrel{1}{v}}_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|\stackrel{1}{H}{|}_{\infty ,{\stackrel{1}{\mathrm{\Omega }}}_t}^2|\nabla {\stackrel{1}{v}}_{,tt}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2).\hfill \end{array}$$

Applying the above estimates in (221) and choosing a ${\epsilon }_1-{\epsilon }_4$ that is sufficiently small yields

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}\left({\displaystyle \sum _{i=1}^2}{|{\stackrel{i}{H}}_{,tt}|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\right)+{\displaystyle \sum _{i=1}^2}{\parallel {\stackrel{i}{H}}_{,tt}\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\hfill \\ & \le c{\displaystyle \sum _{i=1}^2}|\stackrel{i}{H}{|}_{2,0,{\stackrel{i}{\mathrm{\Omega }}}_t}^2|\stackrel{i}{v}{|}_{2,0,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+c\parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{|\nabla {\stackrel{1}{v}}_{,tt}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+G_2^2.\hfill \end{array}$$

(222)

We differentiate (174)_1,3 with respect to time. Then (175) is replaced by

$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^2}\parallel {\stackrel{i}{H}}_{,t}{\parallel }_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2\le c{\displaystyle \sum _{i=1}^2}(\parallel {\stackrel{i}{H}}_{,t}{\parallel }_{1,{\stackrel{i}{\mathrm{\Omega }}}_t}^2+|{\stackrel{i}{H}}_{,tt}{|}_{2,{\stackrel{i}{\mathrm{\Omega }}}_t}^2)\hfill \\ & +c\parallel {\stackrel{1}{H}}_{,t}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel v\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+c\parallel \stackrel{1}{H}{\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2{\parallel v_t\parallel }_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.\hfill \end{array}$$

(223)

Finally, we also have inequality (176) for ${\stackrel{1}{H}}_{,t}$, ${\stackrel{2}{H^{\prime }}}_{,t}$.

We introduce the notation

$$\begin{array}{cc}& X_2(t)={\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{H}{\parallel }_{{\mathrm{\Gamma }}_0^2({\stackrel{i}{\mathrm{\Omega }}}_t)}+{\parallel v\parallel }_{{\mathrm{\Gamma }}_0^2({\stackrel{1}{\mathrm{\Omega }}}_t)},\hfill \\ & Y_2(t)={\displaystyle \sum _{i=1}^2}\parallel \stackrel{i}{H}{\parallel }_{{\mathrm{\Gamma }}_1^3({\stackrel{i}{\mathrm{\Omega }}}_t)}+{\parallel v\parallel }_{{\mathrm{\Gamma }}_1^3({\stackrel{i}{\mathrm{\Omega }}}_t)},\hfill \end{array}$$

(224)

where $\stackrel{2}{H}$ should be replaced by $\stackrel{2}{H^{\prime }}$.

Using that $\stackrel{1}{v}=v$ and $\parallel \stackrel{2}{v}{\parallel }_{{\mathrm{\Gamma }}_0^2({\stackrel{2}{\mathrm{\Omega }}}_t)}\le c{\parallel v\parallel }_{{\mathrm{\Gamma }}_0^2({\stackrel{1}{\mathrm{\Omega }}}_t)}$, $\parallel \stackrel{2}{v}{\parallel }_{{\mathrm{\Gamma }}_1^3({\stackrel{2}{\mathrm{\Omega }}}_t)}\le c{\parallel v\parallel }_{{\mathrm{\Gamma }}_1^3({\stackrel{1}{\mathrm{\Omega }}}_t)}$, and taking into account all of the above estimates, we obtain

$${\displaystyle \frac{d}{dt}}{X}_2^2+Y_2^2\le c{X}_2^2{Y}_2^2+G_{\ast }^2,$$

(225)

$$G_{\ast }^2={\displaystyle \sum _{i=0}^2}{G}_i^2,$$

where $G_0$ is defined below (216), $G_1$ is defined below (219), and $G_2$ is defined below (221). This gives (213) and completes the proof. □

Remark 6. 

Inequality (213) is not optimal with respect to the regularity of $H_{\ast }$ and $B_{\ast }$. To derive an appropriate regularity of these terms, we need advanced result of a potential theory applied to problem (136).

6. Global Estimate

Recall that

$$\begin{array}{ccc}& {\widehat{X}}_1^2(t)={|v|}_{2,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^2,\hfill & {\overline{X}}_1^2(t)={|\stackrel{1}{H}|}_{2,0,{\stackrel{1}{\mathrm{\Omega }}}_t}^2,\hfill \\ & {\widehat{Y}}_1^2(t)={|v|}_{3,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2,\hfill & {\overline{Y}}_1^2(t)={|\stackrel{1}{H}|}_{3,1,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.\hfill \end{array}$$

(226)

Eliminating p, (118) implies

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}}{\widehat{X}}_1^2+{\widehat{Y}}_1^2\le c({\widehat{X}}_1^2+{\overline{X}}_1^2+{\widehat{X}}_1^4+{\overline{X}}_1^4\hfill \\ & +{\widehat{X}}_1^6+{\overline{X}}_1^6)({\widehat{Y}}_1^2+{\overline{Y}}_1^2)+c({\widehat{X}}_1^4+{\overline{X}}_1^4)(1+{\widehat{X}}_1^2+{\overline{X}}_1^2)\hfill \\ & +c{A}^2+c{F}^2,\hfill \end{array}$$

(227)

where

$$A^2=A_1^2+A_2^2+A_3^2,F^2={|f|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+|f_{,t}{|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2+{|f_{,tt}|}_{2,{\stackrel{1}{\mathrm{\Omega }}}_t}^2.$$

Introducing the notation

$$\begin{array}{cc}& X^2(t)={\widehat{X}}_1^2(t)+X_2^2(t),\hfill \\ & Y^2(t)={\widehat{Y}}_1^2(t)+Y_2^2(t),\hfill \end{array}$$

(228)

where $X_2$, $Y_2$ are introduced in (224); we obtain from (227) and (225) the inequality

$${\displaystyle \frac{d}{dt}}{X}^2+\overline{\nu }{Y}^2\le c_0(X^2+X^4+X^6)Y^2+c_0{G}^2,$$

(229)

where

$$G^2=c_0(A^2+F^2+G_{\ast }^2).$$

We can write (229) in the form

$${\displaystyle \frac{d}{dt}}{X}^2\le -(\overline{\nu }-c_0(X^2+X^4+X^6))Y^2+G^2.$$

(230)

Lemma 19. 

Let $c_{\ast }>0$ be a given positive number. Let ${\gamma }_{\ast }>0$ satisfy

$$\overline{\nu }-c_0({\gamma }_{\ast }^2+{\gamma }_{\ast }^4+{\gamma }_{\ast }^6)\ge {\displaystyle \frac{c_{\ast }}{2}}.$$

(231)

Let $\gamma \in (0,{\gamma }_{\ast }]$ and $X^2(0)\le \gamma$, $G^2(t)\le c_{\ast }{\displaystyle \frac{\gamma }{4}}$ for any $t\in {\mathbb{R}}_{+}$.

Then

$$X^2(t)\le \gamma \mathrm{for}\mathrm{any}t\in {\mathbb{R}}_{+}.$$

(232)

Proof. 

Let

$$t_{\ast }=inf\{t\in {\mathbb{R}}_{+}:X^2(t)>\gamma \}.$$

We can write (230) in the form

$${\displaystyle \frac{d}{dt}}{X}^2\le -{\displaystyle \frac{c_{\ast }}{2}}{X}^2+G^2.$$

(233)

For $t=t_{\ast }$, we have

$${\displaystyle \frac{d}{dt}}{X}^2{|}_{t=t_{\ast }}\le -{\displaystyle \frac{c_{\ast }}{2}}\gamma +{\displaystyle \frac{c_{\ast }}{4}}\gamma =-{\displaystyle \frac{c_{\ast }}{4}}\gamma <0.$$

Hence, we have a contradiction with the definition of $t_{\ast }$. Hence,

$$X^2(t)\le \gamma \mathrm{for}t\in {\mathbb{R}}_{+}.$$

This concludes the proof. □

To control the free boundary $S_t$, we recall its definition:

$$S_t=\left\{x\in {\mathbb{R}}^3:x=\xi +{\displaystyle \underset{0}{\overset{t}{\int }}}\overline{v}(\xi ,\tau )d\tau ,\xi \in S_0\right\}.$$

Since the free boundary $S_t$ changes with time, we have to show that it does not meet the boundary B at any time.

Otherwise, we would not have a global existence.

For this purpose, we need to show that

$$|x(t)-\xi |<\eta <\mathrm{dist}\{S_0,B\}\mathrm{for}\mathrm{any}t\in {\mathbb{R}}_{+}.$$

Lemma 20. 

Assume that $G(t)\le \delta e^{-\mu t}$, where $\delta >0$, $\mu >0$.

Then

$$X(t)\le c_{\ast \ast }{e}^{-\mu t},$$

(234)

where $c_{\ast \ast }=\delta /({\displaystyle \frac{c_{\ast }}{2}}-\mu )+X^2(0)$ and

$${\displaystyle \underset{0}{\overset{t}{\int }}}X(t^{\prime })d{t}^{\prime }\le {\displaystyle \frac{c_{\ast \ast }}{\mu }},$$

(235)

where ${\displaystyle \frac{c_{\ast \ast }}{\mu }}<\mathrm{dist}\{S_0,B\}$.

Proof. 

From (233), we have

$${\displaystyle \frac{d}{dt}}{X}^2+{\displaystyle \frac{c_{\ast }}{2}}{X}^2\le \delta e^{-\mu t}.$$

Hence,

$${\displaystyle \frac{d}{dt}}\left(X^2{e}^{{\displaystyle \frac{c_{\ast }}{2}}t}\right)\le \delta e^{({\displaystyle \frac{c_{\ast }}{2}}-\mu )t}.$$

(236)

Integrating (236) with respect to time yields

$$X^2(t)\le e^{-{\displaystyle \frac{c_{\ast }}{2}}t}\left(\delta {\displaystyle \underset{0}{\overset{t}{\int }}}{e}^{({\displaystyle \frac{c_{\ast }}{2}}-\mu )t^{\prime }}d{t}^{\prime }+X^2(0)\right).$$

Then

$$X^2(t)\le {\displaystyle \frac{\delta }{\frac{c_{\ast }}{2}-\mu }}{e}^{-\mu t}+X^2(0)e^{-{\displaystyle \frac{c_{\ast }}{2}}t}.$$

For $\mu <{\displaystyle \frac{c_{\ast }}{2}}$ and $c_{\ast \ast }={\displaystyle \frac{\delta }{\frac{c_{\ast }}{2}-\mu }}+X^2(0)$, we have

$$X^2(t)\le c_{\ast \ast }{e}^{-\mu t}$$

(237)

so (234) holds. Integrating (237) with respect to time yields (235). This ends the proof. □

From (235), it follows that $|x(t)-\xi |\le {\displaystyle \frac{c{c}_{\ast \ast }}{\mu }}$, where c is the constant from the embedding $H^2(\mathrm{\Omega })\subset L_{\infty }(\mathrm{\Omega })$.

Hence, we need

$${\displaystyle \frac{c{c}_{\ast \ast }}{\mu }}<\mathrm{dist}\{S_0,B\}.$$

(238)

7. Conclusions

We prove the existence of global regular solutions to problems (2)–(9) (see Theorem 1). In reality, we only find the estimate, because existence follows by standard arguments. To prove the existence, we replace problem (2)–(9) with two problems: problem (10) for v, p for a given $\stackrel{1}{H}$ and problem (12) for $\stackrel{1}{H}$, $\stackrel{2}{H}$ with a given v. Problem (10) is the Neumann problem for the Stokes system with nonlinear terms that depend on v and $\stackrel{1}{H}$.

To derive the necessary energy method estimates for solutions to (10), we need Korn inequalities (see Lemma 2 and (64), (67) and (68)).

The estimate is described in (118).

Problem (12) is composed of two problems: the problems of $\stackrel{1}{H}$ and $\stackrel{2}{H}$ with nonlinear right-hand sides, which are coupled by the transmission conditions. To prove the existence of solutions to linearized problem (12), we need to apply the technique of the regularizer (see [1,15,16]). We use the energy method to find estimates for solutions to (12). Since in this method integration by parts is used, we derive some boundary terms on $S_t$. We have to cancel them because otherwise there is no estimate. Applying the transmission conditions, we cancel the boundary terms on $S_t$ (see Lemmas 14 and 15). Furthermore, we use the energy method to eliminate the Lagrangian coordinates and to derive such a global estimate that the motion of $S_t$ can be controlled for all $t\in {\mathbb{R}}_{+}$. This is important because we need to know that $S_t$ remains far from the fixed boundary B for all $t\in {\mathbb{R}}_{+}$.