Robust a Posteriori Error Estimates of Time-Dependent Poisson–Nernst–Planck Equations

Abstract

The paper considers the a posteriori error estimates for fully discrete approximations of time-dependent Poisson–Nernst–Planck (PNP) equations, which provide tools that allow for optimizing the choice of each time step when working with adaptive meshes. The equations are discretized by the Backward Euler scheme in time and conforming finite elements in space. Overcoming the coupling of time and the space with a full discrete solution and dealing with nonlinearity by taking G-derivatives of the nonlinear system, the computable, robust, effective, and reliable space–time a posteriori error estimation is obtained. The adaptive algorithm constructed based on the estimates realizes the parallel adaptations of time steps and mesh refinements, which are verified by numerical experiments with the time singular point and adaptive mesh refinement with boundary layer effects.

1. Introduction

In this work, we focus on the Poisson–Nernst–Planck (PNP) equations, which are among the models for charge transport. The system serves as the basis for modeling many devices, such as semiconductor studies, electrodiffusion problems, and the dynamics of ion transport in biological membrane channels [1,2,3]. The system and its modifications have been studied with the existence, uniqueness, and stability of a solution [4,5,6].

A variety of numerical methods have been used extensively for solving PNP equations [7,8,9]. In the application of time-dependent PNP equations, the boundary layer effect due to the thin Debye layer will arbitrarily change their positions in space with the flow of time, which causes the computational cost of the solving process being very large, and the methods in [7,8,9] lose effectiveness. Therefore, solving time-dependent PNP equations with boundary layers is valuable and challenging.

The adaptive finite element method can reduce the computational complexity through nonuniform mesh distributions, which is a good method to solve time-dependent PNP equations with boundary layers. For time-dependent problem, the solving process with the parallel adaptations of time steps and mesh refinements will make the calculation more efficient. The aim of this paper is to propose an adaptive finite element method for fully discrete time-dependent PNP equations, more precisely, to provide tools that allow for optimizing the choice of each time step when working with adaptive meshes.

The a posteriori error analysis plays an important role in adaptivity techniques, which can measure the actual discrete errors without knowledge of the exact solution. With the nonlinearity and strong coupling properties of PNP equations, the a posteriori estimates and associated adaptive algorithms for time-dependent PNP equations are challenging, both for theory and computations. Such issues are, for instance, the way to analyze the a posterior error estimation of fully discrete approximations, robust estimates for strongly coupled nonlinear parabolic problems, and the algorithms for both the time step and the spatial mesh adaptivity. Then, we will explore methods to solve the difficulties through a literature review.

There have been considerable efforts devoted to overcoming the coupling of time and space for a posteriori error estimates of fully discrete approximations. Picasso [10], Verfürth [11], Chen and Jia [12], and Chami and Sayah [13] have managed to bound the error by the spatial estimators at each time step based on the error equation. Bergam, Bernardi and Mghazli [14] established an approach, and the main idea consists of uncoupling time and space errors as much as possible. According to the idea of [14], Bernardi and Verfürth [15] and Bernardi and Sayah [16,17] derived estimates of time-dependent Stokes problem, time-dependent Stokes equations with mixed boundary conditions, and time-dependent Navier–Stokes equations with mixed boundary conditions, respectively. The main estimate tool in Lakkis and Makridakis [18] is the elliptic reconstruction technique introduced by Makridakis and Nochetto [19] for the model problem of semi-discrete finite element approximation. The elliptic reconstruction leads to an appropriate pointwise representation of the error equation. Akrivis [20], and Makridakis and Nochetto [21] have applied the reconstruction technique into Crank–Nicolson and Runge–Kutta schemes. Bnsch, Karakatsani and Makridakis [22] devoted their work to an a posteriori error analysis of fully discrete finite element approximations to the time-dependent Stokes system, where estimates are based on the methodology developed in [18,19] for space discrete and in [20,21] for time discrete schemes.

For nonlinear time-dependent problem, the construction of a posteriori error estimators for fully discrete approximations is a challenge. The pioneering work of Moore [23] and Eriksso and Johnsone [24] discussed a class of nonlinear scalar problem. Verfürth [25] showed that estimates for fully discrete approximations of certain quasilinear parabolic paroblems and estimators are not computable. Moreover, ref. [25] used the framework in [26]. Babuška, Feistauer and Šolín [27] converted a parabolic or hyperbolic problem to a system of ordinary differential equations, and gave a posteriori error estimates for a general nonlinear parabolic problem with a strongly monotonic elliptic operator. Bernardi and Sayah in [17] used the theory of Pousin and Rappaz [28] to handle the nonlinear term of time-dependent Navier–Stokes equations. It is worth noting that the techniques dealing with the nonlinearity in [28] are similar to those in [26]. The situation for fully discrete nonlinear time-dependent problems, however, has not yet been as thoroughly explored.

It is worth noting that a small positive perturbation parameter $ϵ$ leading to the solutions of PNP equations typically contains layers. We expect to have a robust a posteriori analysis of PNP equations with respect to the singular perturbation parameter. For the boundary layer effect, there are many studies on the a posterior estimation of stationary linear singular perturbation problems [29,30,31] and the nonstationary convection dominated convection–diffusion equation [27,32]. Time-dependent PNP equations have received less attention, and coupling and nonlinearity properties make the problem more difficult.

In this paper, we consider the time-dependent PNP equations which are discretized by the Backward Euler scheme in time and conforming finite elements in space. For PNP equations, the way to construct the error equation [10,11,12,13] and build elliptic reconstruction [18,19,20,21,22] by the properties of linear equations is not a good choice due to the nonlinearity and strong coupling properties of the system. Instead of using the time semi-discrete solution to decouple the error [14,15,16,17], our method consists of associating with a full discrete solution. With the full discrete solution, we can obtain a posteriori estimates through the solution existence and uniqueness of linearized equations derived by taking G-derivatives of the nonlinear system. Meanwhile, the efficient and reliable a posteriori error estimators are proved, referring to the techniques in [17,26]. The robustness of the estimator is demonstrated with an improved energy norm in view of the coupling properties of PNP equations. Based on the adaptive algorithm in [10,12], numerical experiments are conducted. Numerical results show the phenomenon of adaptive time step adjustment due to the time singular point and adaptive mesh refinement with boundary layer effects.

The paper is organized as follows. We begin in Section 2 by defining the PNP equations, its variational form, and the finite element spaces to be used. In Section 3, we verify the solution existence and uniqueness of linearized equations with details presented in Appendix A, and further develop the a poteriori error estimate with time and space. The computable, robust, effective and reliable space–time a posteriori error estimations are derived. We introduce the adaptive algorithm in Section 4, and numerical experiments are reported with showing the adaptive phenomenon in time and space, respectively. Conclusion remarks and future work are finally given in Section 5.

2. The Poisson–Nernst–Planck Equations and Their Discretization

In this work, we consider the time-dependent Poisson–Nernst–Planck (PNP) equations [9]:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & {\displaystyle \frac{\partial C_i}{\partial t}}-\nabla ·D_i(\nabla C_i+\beta z_{i}e{C}_i\nabla \psi )=0,i=1,\dots ,K,\hfill \\ \hfill & -\nabla ·({\epsilon }_r{\epsilon }_0\nabla \psi )-{\displaystyle \sum _{i=1}^K}{z}_{i}e{C}_i=F^f,\hfill \end{array}\hfill \end{array}\right.$$

(1)

which describe the nonlinear coupling of the electric potential $\psi$ and the ionic concentration $C_i$ of the i-th species, where the number of ion species is K. The first equation is called the Nernst–Planck equation for species i, and the second one is named Poisson’s equation. Here, $D_i$ and $z_i$ are the diffusivity and valence, respectively. $\beta =1/\left(k_B{T}_{abs}\right)$, where $k_B$ is the Boltzmann constant and $T_{abs}$ is the absolute temperature. e is the elementary charge, ${\epsilon }_r$ and ${\epsilon }_0$ are the relative and vacuum dielectric permittivities, and $F^f$ is generally the fixed charges.

The boundary conditions are a critical component of the PNP model and determine important qualitative behavior of the solution. Let $\Omega$ be a bounded domain with Lipschitz boundary $\partial \Omega$. Homogeneous no-flux conditions are considered for each charged species, i.e.,

$$\begin{array}{c}\hfill (\nabla C_i+z_i{C}_i\nabla \psi )·\overrightarrow{\mathit{n}}=0,\mathit{x}\in \partial \Omega ,i=1,\dots ,K,\end{array}$$

(2)

where $\mathit{n}$ is the outward unit normal vector on the boundary $\partial \Omega$.

The external electrostatic potential $\psi$ is influenced by applied potential, which can be modeled by prescribing a Dirichlet boundary condition, i.e.,

$$\psi =0,\partial \Omega \times (0,T].$$

For nonhomogeneous Dirichlet boundary conditions such as ${\psi |}_{\partial \Omega }=g$, they can be transformed into homogeneous Dirichlet boundary conditions. Since the PNP equations is assumed to satisfy the no-flux boundary condition for the charge carrier concentrations, it is known that the charge carrier concentrations satisfy the conservation of mass [33].

For convenience, assuming

$$\begin{array}{c}\hfill K=2;D_i=1,i=1,2;\beta =e=1;ϵ:={ϵ}_r·{ϵ}_o,\end{array}$$

$ϵ$ is a constant in system (1). Let $(C_1^0,C_2^0,{\psi }_0)$ be the initial ionic concentrations and electric potential. We use standard notations for Sobolev spaces $W^{1,2}(\Omega )=H^1(\Omega )$, and the associated norms and semi-norms. Here, $H_0^1(\Omega )=\{v\in H^1(\Omega ):v{|}_{\partial \Omega }=0\}$ and $H^{-1}(\Omega )={\left(H_0^1(\Omega )\right)}^{*}$, which means the dual space of $H_0^1(\Omega )$. The variational form of system (1) is as follows.

To find $C_i\in L^2(0,T;H^1(\Omega )),i=1,2,\psi \in L^2(0,T;H_0^1(\Omega ))$ such that

$$\left\{\begin{array}{c}\begin{array}{c}({\displaystyle \frac{\partial C_i}{\partial t}},v_i)+(\nabla C_i,\nabla v_i)+(z_i{C}_i\nabla \psi ,\nabla v_i)=0,\forall v_i\in H^1(\Omega ),i=1,2,\hfill \\ (ϵ\nabla \psi ,\nabla v_3)-{\displaystyle \sum _{i=1}^2}(z_i{C}_i,v_3)=(F^f,v_3),\forall v_3\in H_0^1(\Omega ),\hfill \end{array}\hfill \end{array}\right.$$

(3)

where $z_i$ is the valence of $C_i,i=1,2$, the scalar product $(.,.)$ is the standard $L^2$-scalar product, and $(C_1^0,C_2^0,{\psi }^0)$ is the initial value. When $F^f\in L^{\infty }(0,T;{\mathbb{R}}^d)$, there is a unique solution to the variational problem [4]. For simplicity, in the following, we choose $z_1=1$ and $z_2=-1$.

Let the quasi-uniform mesh of $\Omega$ be ${\mathcal{T}}_h$ with mesh size $0<h<1$ [34] and the corresponding finite element space be

$$V_h=\{v\in H^1(\Omega ):v{|}_{\tau }\in {\mathcal{P}}_1\left(\tau \right),\forall \tau \in {\mathcal{T}}_h\},$$

and

$$V_{h,0}=\{v\in H_0^1(\Omega ):v{|}_{\tau }\in {\mathcal{P}}_1\left(\tau \right),\forall \tau \in {\mathcal{T}}_h\},$$

where $V_h\subset H^1(\Omega )$ and $V_{h,0}\subset H_0^1(\Omega )$.

For the time discretization, define a partition of the time domain,

$$\begin{array}{c}\hfill 0=t_0<t_1<\cdots <t_m=T,\end{array}$$

where $t_n={\displaystyle \sum _{j=1}^m}{\tau }_i$ and ${\tau }_j:=t_j-t_{j-1}$.

$\mathit{Y}:=H^1(\Omega )\times H^1(\Omega )\times H_0^1(\Omega ),{\mathit{Y}}_h:=V_h\times V_h\times V_{h,0}$. For all $u\in L^2(0,T;H^1(\Omega ))$, $u^n:=u(\mathit{x},t_n)$, $u_h\left(t\right):=u_h(·,t),t\ge 0$, and $u_h^n:=u_h(\mathit{x},t_n)$. Define the following scheme:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u^n}{\partial t}}={\displaystyle \frac{u^n-u^{n-1}}{{\tau }_n}},\end{array}$$

and using the Backward Euler scheme, the fully discrete form of the variational problem is as follows.

For $n=1,2,\dots ,N$, find ${\mathit{u}}_h^n=(C_{1,h}^n,C_{2,h}^n,{\psi }_h^n)\in {\mathit{Y}}_h$ such that

$$\left\{\begin{array}{c}\begin{array}{c}\left({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}},v_{i,h}\right)+(\nabla C_{i,h}^n,\nabla v_{i,h})+(z_i{C}_{i,h}^n\nabla {\psi }_h^n,\nabla v_{i,h})=0,\forall v_{i,h}\in V_h,i=1,2,\hfill \\ (ϵ\nabla {\psi }_h^n,\nabla v_{3,h})-{\displaystyle \sum _{i=1}^2}(z_i{C}_{i,h}^n,v_{3,h})=(F^{f,n},v_{3,h}),\forall v_{3,h}\in V_{h,0}.\hfill \end{array}\hfill \end{array}\right.$$

(4)

The initial value $(C_{1,h}^0,C_{2,h}^0,{\psi }_h^0)$ is the interpolation of $(C_1^0,C_2^0,{\psi }^0)$ in ${\mathit{Y}}_h$. Ref. [35] proved the existence and uniqueness of solutions to the above problems. By setting the test functions $(v_{1,h},v_{2,h},v_{3,h})=(1,1,0)$, we have ${\int }_{\Omega }{C}_{i,h}^{n}d\mathit{x}={\int }_{\Omega }{C}_{i,h}^{0}d\mathit{x},i=1,2$, that is, the global mass conservation property is satisfied.

Assuming $\mathit{u}=(C_1,C_2,\psi )$ is the weak solution of system (3), where $\mathit{u}\in L^2(0,T;\mathit{Y})$ if and only if $\forall \mathit{v}\in \mathit{Y}$, $\forall t\in [0,T]$, $\mathit{u}$ satisfies

$$\begin{array}{ccc}\hfill \left(\mathit{F}\right(\mathit{u}),\mathit{v})& :=& {\int }_{\Omega }(\sum _{i=1}^2\left({\displaystyle \frac{\partial C_i}{\partial t}}{v}_i+\nabla C_i·\nabla v_i+z_i{C}_i\nabla \psi ·\nabla v_i\right)+ϵ\nabla \psi ·\nabla v_3\hfill \\ & & -\sum _{i=1}^2{z}_i{C}_i{v}_3-F^f{v}_3)d\mathit{x}\hfill \\ & =& 0.\hfill \end{array}$$

(5)

Hence, the weak problem of the system (3) is to find $\mathit{u}=(C_1,C_2,\psi )\in L^2(0,T;\mathit{Y})$ such that

$$\left(\mathit{F}\right(\mathit{u}),\mathit{v})=0,\forall \mathit{v}\in \mathit{Y},$$

(6)

where $\mathit{F}$ is a nonlinear operator from $L^2(0,T;\mathit{Y})$ to ${\mathit{Y}}^{*}.$

Similarly, the finite element approximation of system (4) indicates that the full discrete approximation of problem (6) is to find ${\mathit{u}}_h^n\in {\mathit{Y}}_h$ satisfying,

$$\begin{array}{c}\hfill (\mathit{F}\left({\mathit{u}}_h^n\right),{\mathit{v}}_h)=0,\forall {\mathit{v}}_h=(v_{h,1},v_{h,2},v_{h,3})\in {\mathit{Y}}_h,\end{array}$$

(7)

where

$$\begin{array}{ccc}\hfill (\mathit{F}\left({\mathit{u}}_h^n\right),{\mathit{v}}_h)& =& {\int }_{\Omega }(\sum _{i=1}^2({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}{v}_{i,h}+\nabla C_{i,h}^n·\nabla v_{i,h}+z_i{C}_{i,h}^n\nabla {\psi }_h^n\nabla v_{i,h})\hfill \\ & & +ϵ\nabla {\psi }_h^n·\nabla v_{3,h}-\sum _{i=1}^2{z}_i{C}_{i,h}^n{v}_{3,h}-F^f{v}_{3,h})d\mathit{x}.\hfill \end{array}$$

The error in this work is measured in following the norm, i.e., $\forall \varphi \in H^1(\Omega )$,

$${\left|\right|\varphi \left|\right|}_{ϵ,\Omega }:={\left({\parallel \varphi \parallel }_{L^2(\Omega )}^2+ϵ{\left|\varphi \right|}_{1,\Omega }^2\right)}^{1/2},$$

$${\left|\right|\varphi \left|\right|}_{*,\Omega }:={\left|\right|\varphi \left|\right|}_{ϵ,\Omega }+\underset{v\in H^1(\Omega )\setminus 0}{sup}{\displaystyle \frac{(\nabla \varphi ,\nabla v)}{{\parallel v\parallel }_{ϵ,\Omega }}},$$

and

$${\left|\right|\mathit{u}\left|\right|}_{ϵ,\Omega }:={\left({\parallel C_1\parallel }_{1,\Omega }^2+{\parallel C_2\parallel }_{1,\Omega }^2+{\parallel \psi \parallel }_{ϵ,\Omega }^2\right)}^{1/2},$$

$${\left|\right|\mathit{u}\left|\right|}_{*,\Omega }:={\left({\parallel C_1\parallel }_{1,\Omega }^2+{\parallel C_2\parallel }_{1,\Omega }^2+{\parallel \psi \parallel }_{*,\Omega }^2\right)}^{1/2},$$

where $0<ϵ\le 1$.

And $\forall f\in H^{-1}(\Omega )$, we define

$${\left|\right|f\left|\right|}_{-ϵ,\Omega }:=\underset{v\in H_0^1(\Omega )}{sup}{\displaystyle \frac{\left|\right(f,v\left)\right|}{{\parallel v\parallel }_{ϵ,\Omega }}},$$

and $\forall \mathit{F}\in {\mathit{Y}}^{*}$ where ${\mathit{Y}}^{*}$ is the dual space of $\mathit{Y}$,

$${\left|\right|\mathit{F}\left|\right|}_{-ϵ,\Omega }:=\underset{\mathit{v}\in \mathit{Y}}{sup}{\displaystyle \frac{\left|\right(\mathit{F},\mathit{v}\left)\right|}{{\parallel \mathit{v}\parallel }_{ϵ,\Omega }}},$$

$\forall \mathit{u}\in L^2(0,T;X),$

$${\parallel \mathit{u}\parallel }_{L^2(0,T;X)}:=({\int }_0^T{\parallel \mathit{u}\parallel }_X^2{ds)}^{{\displaystyle \frac{1}{2}}},$$

where ${\parallel \mathit{u}\parallel }_X=({\displaystyle \sum _{i=1}^3}\parallel u_i{{\parallel }_X^2)}^{{\displaystyle \frac{1}{2}}}$.

For brevity, we introduce the space

$$V(a,b)=\left\{\mathit{\kappa }=({\kappa }_1,{\kappa }_2,{\kappa }_3)\in L^2(a,b;\mathit{Y}):{\partial }_t{\kappa }_1,{\partial }_t{\kappa }_2\in L^2(a,b;H^{-1}(\Omega ))\right\},$$

which is a Banach space [36] with respect to the norm defined by

$${\parallel \mathit{\kappa }\parallel }_{V(a,b)}={\left\{{\int }_a^b(\parallel {\kappa }_1{\parallel }_{1,\Omega }^2+\parallel {\kappa }_2{\parallel }_{1,\Omega }^2+\parallel {\kappa }_3{\parallel }_{*,\Omega }^2)ds+\sum _{i=1}^2{\int }_a^b{\parallel {\partial }_t{\kappa }_i\parallel }_{-ϵ,\Omega }^{2}ds\right\}}^{{\displaystyle \frac{1}{2}}}.$$

A similar definition can be found in [11,37].

For the system (3), we have ${\displaystyle \frac{\partial C_1}{\partial t}},{\displaystyle \frac{\partial C_2}{\partial t}}\in L^2(0,T;H^{-1}(\Omega ))$ with $L^2(\Omega )\subset H^{-1}(\Omega )$, and $\mathit{u}\in V(0,T)$.

3. The a Posteriori Error Estimates

In this section, we present a posteriori error estimates for PNP equations. In Section 3.1, we bound the error by the computable error estimator $\eta$. And the lower bound of the local error in space and time is proved, respectively, in Section 3.2.

3.1. Upper Bound of Errors

For the a posteriori error studies, we use the piecewise affine function ${\mathit{u}}_{h,\tau }$, which takes the values in the interval $[t_{n-1},t_n]$ as follows:

$$\begin{array}{ccc}\hfill {\mathit{u}}_{h,\tau }{|}_{[t_{n-1},t_n]}& =& {\displaystyle \frac{t-t_{n-1}}{{\tau }_n}}((C_{1,h}^n-C_{1,h}^{n-1}),(C_{2,h}^n-C_{2,h}^{n-1}),({\psi }_h^n-{\psi }_h^{n-1}))\hfill \\ & & +(C_{1,h}^{n-1},C_{2,h}^{n-1},{\psi }_h^{n-1})\hfill \\ & =& {\displaystyle \frac{t-t_{n-1}}{{\tau }_n}}({\mathit{u}}_h^n-{\mathit{u}}_h^{n-1})+{\mathit{u}}_h^{n-1}.\hfill \end{array}$$

(8)

And we consider the a posteriori error estimate for the error $\parallel \mathit{u}-{\mathit{u}}_{h,\tau }{\parallel }_{ϵ,\Omega }$.

Our method consists of associating with ${\mathit{u}}_h^n$ such that

$$\begin{array}{c}\hfill \mathit{e}:=\mathit{u}-{\mathit{u}}_{h,\tau }\end{array}$$

can be split as

$$\begin{array}{c}\hfill \mathit{\rho }:={\mathit{\rho }}_1-{\mathit{\rho }}_2,\end{array}$$

and

$$\begin{array}{c}\hfill {\mathit{\rho }}_1:=\mathit{u}-{\mathit{u}}_h^n,{\mathit{\rho }}_2:={\mathit{u}}_h^n-{\mathit{u}}_{h,\tau }.\end{array}$$

Furthermore, for a posterior error estimates of $\mathit{\rho }$, it can be observed that ${\mathit{\rho }}_2$ can only be reduced by changing the time step at a fixed time, then we treat the estimates of ${\mathit{\rho }}_2$ as the time a posterior error estimates. Meanwhile, the remaining part ${\mathit{\rho }}_1$ is handled as a posterior error estimates of the space. In the following discussion, we will deal with the estimates of ${\mathit{\rho }}_1$ firstly.

For the estimate about ${\mathit{\rho }}_1$, we deal with the nonlinearity through the property of the linearized equations derived by taking G derivatives of the nonlinear system. The definition of $\mathit{DF}(·)$ at $\mathit{u}$ is as follows [38]:

$$(\mathit{DF}\left(\mathit{u}\right)\mathit{\varphi },\mathit{w})=\underset{\tilde{\epsilon }\to 0}{lim}{\displaystyle \frac{(\mathit{F}(\mathit{u}+\tilde{\epsilon }\mathit{\varphi })-\mathit{F}\left(\mathit{u}\right),\mathit{w})}{\tilde{\epsilon }}},\forall \mathit{\varphi }\in L^2(0,T;{\left[H_0^1(\Omega )\right]}^3),\mathit{w}\in \mathit{Y},$$

(9)

which leads to the following linear problem:

$\forall \mathit{R}\in L^2(0,T;{\left[L^2(\Omega )\right]}^3)\subset L^2(0,T;{\left[H^{-1}(\Omega )\right]}^3)$, to find $\mathit{\varphi }=({\varphi }_1,{\varphi }_2,{\varphi }_3)\in L^2(0,T;$${\left[H_0^1(\Omega )\right]}^3)$, such that

$$\left(\mathit{DF}\right(\mathit{u})\mathit{\varphi },\mathit{v})=(\mathit{R},\mathit{v}),\forall \mathit{v}\in \mathit{Y},$$

(10)

where $\mathit{u}=(C_1,C_2,\psi )$ satisfies Equation (6), ${\varphi }_1(\mathit{x},0)={\varphi }_2(\mathit{x},0)=0$ and

$$\begin{array}{ccc}\hfill \left(\mathit{DF}\right(\mathit{u})\mathit{\varphi },\mathit{v})& =& \sum _{i=1}^2(({\displaystyle \frac{\partial {\varphi }_i}{\partial t}},v_i)+(\nabla {\varphi }_i,\nabla v_i)+z_i(C_i\nabla {\varphi }_3,\nabla v_i)+z_i({\varphi }_i\nabla \psi ,\nabla v_i))\hfill \\ & & +(ϵ\nabla {\varphi }_3,\nabla v_3)-\sum _{i=1}^2{z}_i({\varphi }_i,v_3).\hfill \end{array}$$

(11)

Meanwhile, $\forall v_i\in H^1(\Omega )\subset L^2(\Omega ),{\displaystyle \frac{\partial {\varphi }_i}{\partial t}}\in L^2(\Omega )\subset H^{-1}(\Omega ),i=1,2$, that is $\mathit{\varphi }\in V(0,T)$.

For the estimate about ${\mathit{\rho }}_1$, Lemma 2 is proved firstly. One of the important tools used in the proof of Lemma 2 is the solution existence and uniqueness of the linear problem (10), which is verified in Lemma 1. In all proofs, $a\lesssim b$ means $a\le Cb$, where C is a constant independent of $ϵ$.

Lemma 1.

If $C_1$, $C_2\in L^{\infty }(\Omega )$ and $\psi \in W^{1,\infty }(\Omega )$, there exists a unique solution of Equation (10) in $V(0,T)$.

Proof. 

The proof of the lemma is referred to in [4]; see Appendix A for details. □

Lemma 2.

If $C_1$, $C_2$, and ψ satisfy the condition in Lemma 1, we have the regularity conclusion for Equation (10) that $\forall \mathit{R}\in L^2(0,T;{\left[L^2(\Omega )\right]}^3)$:

$${\parallel \mathit{\varphi }\parallel }_{V(0,T)}\le M_1({\int }_0^T{\parallel \mathit{R}\parallel }_{-ϵ,\Omega }^2{ds)}^{1/2},$$

(12)

where constant $M_1$ is independent of $\mathit{u}$, $\mathit{\varphi }$, $\mathit{R}$, and ϵ.

Proof. 

Due to the variational form of Equation (10) as Equation (11), we have $\forall \mathit{v}\in \mathit{Y},$

$$\begin{array}{ccc}\hfill \left|\right(\mathit{DF}\left(\mathit{u}\right)\mathit{\varphi },\mathit{v}\left)\right|& \lesssim & |{\varphi }_1{|}_{1,\Omega }|v_1{|}_{1,\Omega }+|{\varphi }_3{|}_{1,\Omega }|v_1{|}_{1,\Omega }+\parallel {\varphi }_1{\parallel }_{L^2(\Omega )}{\left|v_1\right|}_{1,\Omega }\hfill \\ & & +|{\varphi }_2{|}_{1,\Omega }{\left|v_2\right|}_{1,\Omega }+|{\varphi }_3{|}_{1,\Omega }|v_2{|}_{1,\Omega }+\parallel {\varphi }_2{\parallel }_{L^2(\Omega )}{\left|v_2\right|}_{L^2(\Omega )}\hfill \\ & & +ϵ|{\varphi }_3{|}_{1,\Omega }|v_3{|}_{1,\Omega }+\parallel {\varphi }_1{\parallel }_{L^2(\Omega )}{\parallel v_3\parallel }_{L^2(\Omega )}+\parallel {\varphi }_2{\parallel }_{L^2(\Omega )}{\parallel v_3\parallel }_{L^2(\Omega )}\hfill \\ & & +\parallel {\displaystyle \frac{\partial {\varphi }_1}{\partial t}}{\parallel }_{-ϵ,\Omega }\parallel v_1{\parallel }_{1,\Omega }+\parallel {\displaystyle \frac{\partial {\varphi }_2}{\partial t}}{\parallel }_{-ϵ,\Omega }{\parallel v_2\parallel }_{1,\Omega }\hfill \\ & \lesssim & {\parallel \mathit{\varphi }\parallel }_{*,\Omega }{\parallel \mathit{v}\parallel }_{ϵ,\Omega }.\hfill \end{array}$$

Due to Lemma 1, we have the one-to-one mapping $\mathit{DF}\left(\mathit{u}\right):V[0,T]\to L^2(0,T;{\mathit{Y}}^{*})$. By the bounded inverse theorem, there exists an inverse $\mathit{DF}{\left(\mathit{u}\right)}^{-1}:L^2(0,T;{\mathit{Y}}^{*})$→$V[0,T]$ and $\forall \mathit{R}\in L^2(0,T;{\left[L^2(\Omega )\right]}^3)\subset L^2(0,T;{\mathit{Y}}^{*})$,

$$\begin{array}{c}\hfill {\parallel \mathit{\varphi }\parallel }_{V(0,T)}={\parallel \mathit{G}\mathit{R}\parallel }_{V(0,T)}\le M_2{\parallel \mathit{R}\parallel }_{L^2(0,T;{\mathit{Y}}^{*})},\end{array}$$

with ${\parallel \mathit{R}\parallel }_{{\mathit{Y}}^{*}}=\underset{\mathit{v}\in \mathit{Y}}{sup}{\displaystyle \frac{(\mathit{R},\mathit{v})}{{\parallel \mathit{v}\parallel }_{*,\Omega }}}$ and ${\parallel \mathit{v}\parallel }_{ϵ,\Omega }\le {\parallel \mathit{v}\parallel }_{*,\Omega },\forall \mathit{v}\in {\left[H_0^1(\Omega )\right]}^3$, we have

$$\begin{array}{c}\hfill {\parallel \mathit{\varphi }\parallel }_{V(0,T)}\le M_2({\int }_0^T{\parallel \mathit{R}\parallel }_{-ϵ,\Omega }^2{ds)}^{1/2},\end{array}$$

and Equation (12) is proved with $M_1$ independent of $\mathit{u}$, $\mathit{\varphi }$, $ϵ$, and $\mathit{R}$. □

Theorem 1.

If $C_1$, $C_2$, and ψ satisfy the condition in Lemma 1, and $\underset{i=1,2}{max}\{\parallel z_i{e}_i{\parallel }_{L^{\infty }(\Omega )}\}\le ϵ/\left(2\sqrt{2}{M}_2\right)$, then

$$\parallel \mathit{u}-{\mathit{u}}_h^n{\parallel }_{V(0,T)}\le 2M_1({\int }_0^T\parallel \mathit{F}\left({\mathit{u}}_h^n\right){{\parallel }_{-ϵ,\Omega }^{2}ds)}^{{\displaystyle \frac{1}{2}}},$$

(13)

where $M_1$ are constants in Equation (12) in taking $\mathit{\varphi }=\mathit{u}-{\mathit{u}}_h^n$.

Proof. 

Denote ${\mathit{\rho }}_1=\mathit{u}-{\mathit{u}}_h^n:=(e_1,e_2,e_3)$. The definition of the G derivative [38] indicates that $\forall \mathit{w}\in \mathit{Y}$,

$$\begin{array}{c}\hfill {\int }_0^1(\mathit{DF}(\mathit{u}-l{\mathit{\rho }}_1){\mathit{\rho }}_1,\mathit{w})dl=(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{w})-(\mathit{F}\left(\mathit{u}\right),\mathit{w}).\end{array}$$

With Equation (6), we have

$$\begin{array}{c}\hfill (\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{w})={\int }_0^1(\mathit{DF}(\mathit{u}-l{\mathit{\rho }}_1){\mathit{\rho }}_1,\mathit{w})dl,\end{array}$$

(14)

and thus

$$\begin{array}{c}\hfill (\mathit{DF}\left(\mathit{u}\right){\mathit{\rho }}_1,\mathit{w})={\int }_0^1(\mathit{DF}\left(\mathit{u}\right){\mathit{\rho }}_1-\mathit{DF}(\mathit{u}-l{\mathit{\rho }}_1){\mathit{\rho }}_1,\mathit{w})dl+(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{w}).\end{array}$$

(15)

Then, we define $(\mathit{DF}\left(\mathit{u}\right){\mathit{\rho }}_1,\mathit{w})=(\tilde{\mathit{R}},\mathit{w})$. The integral part in Equation (15) is estimated, i.e.,

$$\begin{array}{cc}& \left|\right(\mathit{DF}\left(\mathit{u}\right){\mathit{\rho }}_1-\mathit{DF}(\mathit{u}-l{\mathit{\rho }}_1){\mathit{\rho }}_1,\mathit{w}\left)\right|\hfill \\ \le & 2l\left|{\int }_{\Omega }\left(\sum _{i=1}^2{z}_i{e}_i\nabla e_3·\nabla w_i\right)d\mathit{x}\right|\hfill \\ \le & 2\sqrt{2}l\parallel \nabla e_3{\parallel }_{L^{\infty }(\Omega )}\left(\right||e_1{\left|\right|}_{L^2(\Omega )}\left|\right|\nabla w_1{\left|\right|}_{L^2(\Omega )}+\left|\right|e_1{\left|\right|}_{L^2(\Omega )}\left|\right|\nabla w_2{\left|\right|}_{L^2(\Omega )})\hfill \\ \le & 2\sqrt{2}l\parallel \nabla e_3{\parallel }_{L^{\infty }(\Omega )}{\parallel \mathit{\rho }\parallel }_{ϵ,\Omega }{\parallel \mathit{w}\parallel }_{ϵ,\Omega },\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill & \underset{{\mathit{w}\in \mathit{W};\parallel \mathit{w}\parallel }_{ϵ,\Omega }=1}{sup}\left(\left|{\int }_0^1(\mathit{DF}\left(\mathit{u}\right){\mathit{\rho }}_1-\mathit{DF}(\mathit{u}-l{\mathit{\rho }}_1){\mathit{\rho }}_1,\mathit{w})dl\right|+\left|(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{w})\right|\right)\hfill \\ \hfill \le & \underset{\mathit{w}\in {\mathit{W};\parallel \mathit{w}\parallel }_{ϵ,\Omega }=1}{sup}(\sqrt{2}max\{\parallel \nabla e_3{\parallel }_{L^{\infty }(\Omega )}\left\}\right||{\mathit{\rho }}_1{\left|\right|}_{ϵ,\Omega }{\left|\right|\mathit{w}\left|\right|}_{ϵ,\Omega })+||\mathit{F}\left({\mathit{u}}_h^n\right){\left|\right|}_{-ϵ,\Omega }\hfill \\ \hfill =& \sqrt{2}max\{\parallel \nabla e_3{\parallel }_{L^{\infty }(\Omega )}\left\}\right||{\mathit{\rho }}_1{\left|\right|}_{ϵ,\Omega }+\left|\right|\mathit{F}\left({\mathit{u}}_h\right){\left|\right|}_{-ϵ,\Omega }.\hfill \end{array}$$

The second inequality of (12) in Lemma 2 leads to $\parallel {\mathit{\rho }}_1{\parallel }_{V(0,T)}\le M_1({\int }_0^T\parallel \tilde{\mathit{R}}{{\parallel }_{-ϵ,\Omega }^{2}ds)}^{{\displaystyle \frac{1}{2}}}$ as taking $\mathit{\varphi }={\mathit{\rho }}_1$. Hence,

$$\begin{array}{c}\hfill \parallel {\mathit{\rho }}_1{\parallel }_{V(0,T)}\le \sqrt{2}{M}_{1}max\{\parallel \nabla e_3{\parallel }_{L^{\infty }(\Omega )}\}\parallel {\mathit{\rho }}_1{\parallel }_{V(0,T)}+M_1({\int }_0^T\left|\right|F\left({\mathit{u}}_h^n\right){\left|\right|}_{-ϵ,\Omega }^2{ds)}^{{\displaystyle \frac{1}{2}}}.\end{array}$$

Notably, we shall have $\parallel {\mathit{\rho }}_1{\parallel }_{V(0,T)}\lesssim ({\int }_0^T\parallel \mathit{F}\left({\mathit{u}}_h^n\right){{\parallel }_{-ϵ,\Omega }^{2}ds)}^{{\displaystyle \frac{1}{2}}}$ if $\underset{i=1,2}{max}\{\parallel z_i{e}_i{\parallel }_{L^{\infty }(\Omega )}\}<(ϵ/\sqrt{2}{M}_1)$; however, we restrict the condition as $\underset{i=1,2}{max}\{\parallel z_i{e}_i{\parallel }_{L^{\infty }(\Omega )}\}\le ϵ/\left(2\sqrt{2}{M}_1\right)$, for simplicity, and have

$$\begin{array}{c}\hfill \parallel {\mathit{\rho }}_1{\parallel }_{V(0,T)}\le 2M_1({\int }_0^T\parallel \mathit{F}\left({\mathit{u}}_h^n\right){{\parallel }_{-ϵ,\Omega }^{2}ds)}^{{\displaystyle \frac{1}{2}}}.\end{array}$$

This proves the inequality (13).  □

For the sake of discussion, let us define some symbols. For a regular triangle subdivision ${\mathcal{T}}_h$ of $\Omega$, ${\mathcal{N}}_h$ represents the set of all vertices divided, ${\mathcal{E}}_h$ represents all edges contained in ${\mathcal{T}}_h$, and ${\mathcal{I}}_h:={\mathcal{E}}_h\setminus \partial \Omega$ contains the inner edges of ${\mathcal{T}}_h$. We set ${\tilde{w}}_K:={\bigcup }_{K\cap K^{\prime }\ne ⌀}{K}^{\prime }$, $w_E:={\bigcup }_{E\in \partial K^{\prime }}{K}^{\prime }$, and ${\tilde{w}}_E:={\bigcup }_{K^{\prime }\in w_E}{\bigcup }_{K^{\prime \prime }\cap K^{\prime }\ne ⌀}{K}^{\prime \prime }$. $h_B:=\mathrm{diam}\left(B\right)$ denotes the diameter of any set B. Let E be the shared edge of K and $\tilde{K}$, i.e., $E=K\cap \tilde{K}$, and ${\mathit{n}}_E$ represent the outward normal vector of E in K. We define the jump across the edge by

$$\begin{array}{c}\hfill [\nabla v·{\mathit{n}}_E]:=\nabla v·{\mathit{n}}_E{{|}_K-\nabla v·{\mathit{n}}_E|}_{\tilde{K}},\forall v\in H_0^1(\Omega ),\end{array}$$

and $\forall E\in \partial \Omega$; we set $[\nabla v·{\mathit{n}}_E]=0$ for convenience.

The a posteriori estimates of the space can be derived from the right end of Theorem 1 by quite standard arguments [26] with $Cl\acute{e}ment$ interpolation and the bubble functions.

Lemma 3

(The estimation of $Cl\acute{e}ment$ interpolation [39]). Let $R_h$ be the $Cl\acute{e}ment$ interpolation operator for a regular partition, then, $\forall v\in H_0^1(\Omega )$,

$$\begin{array}{ccc}\hfill \parallel v-R_h{v\parallel }_{L^2\left(K\right)}& \le & {\tilde{M}}_1{h}_K{\parallel v\parallel }_{1,{\tilde{w}}_K},\forall K\in {\mathcal{T}}_h,\hfill \\ \hfill \parallel v-R_h{v\parallel }_{L^2\left(E\right)}& \le & {\tilde{M}}_2{h}_E^{1/2}{\parallel v\parallel }_{1,{\tilde{w}}_E},\forall E\in {\mathcal{E}}_h,\hfill \\ \hfill \parallel v-R_h{v\parallel }_{L^2\left(K\right)}& \le & {\tilde{M}}_3{\alpha }_K{\parallel v\parallel }_{ϵ,{\tilde{w}}_K},\forall K\in {\mathcal{T}}_h,\hfill \\ \hfill \parallel v-R_h{v\parallel }_{L^2\left(E\right)}& \le & {\tilde{M}}_4{ϵ}^{-1/4}{\alpha }_E^{1/2}{\parallel v\parallel }_{ϵ,{\tilde{w}}_E},\forall E\in {\mathcal{E}}_h,\hfill \end{array}$$

where ${\alpha }_S=min\{1,h_S{ϵ}^{-1/2}\}$ and S represent the edge E or element K. Constants ${\tilde{M}}_1$, ..., ${\tilde{M}}_4$ only depend on the reference element and regular partition.

Let ${\lambda }_{K,i}$ ($i=1,2,3$) be the area coordinates on the reference element K. We define the bubble functions $b_K$ and $b_E$ as follows:

$$\begin{array}{ccc}\hfill b_K\left(\mathit{x}\right)& =& \left\{\begin{array}{c}\begin{array}{cc}27{\lambda }_{K,1}{\lambda }_{K,2}{\lambda }_{K,3},& \mathit{x}\in K,\hfill \\ 0,& \mathit{x}\in \Omega \setminus K,\hfill \end{array}\hfill \end{array}\right.\hfill \\ \hfill b_E\left(\mathit{x}\right)& =& \left\{\begin{array}{c}\begin{array}{cc}4{\lambda }_{K_1,j}{\lambda }_{K_1,k},& \mathit{x}\in K_1,\hfill \\ 4{\lambda }_{K_2,l}{\lambda }_{K_2,m},& \mathit{x}\in K_2,\hfill \\ 0,& \mathit{x}\in \Omega \setminus w_E,\hfill \end{array}\hfill \end{array}\right.\hfill \end{array}$$

where j and k are the indices of E’s two vertexes associated with $K_1$ while l and m are that with $K_2$, and $w_E=K_1\cup K_2$. The space of vector bubble functions is then denoted by ${\tilde{\mathit{Y}}}_h:={\left({\tilde{Y}}_h^0\right)}^3$ with ${\tilde{Y}}_h^0=span\{b_{K}u,b_{E}Pw:\forall u\in {\mathcal{P}}_k\left(K\right),\forall w\in {\mathcal{P}}_k\left(E\right),\forall K\in {\mathcal{T}}_h,\forall E\in {\mathcal{I}}_h\}$. Here, ${\mathcal{P}}_k\left(K\right)$ and ${\mathcal{P}}_k\left(E\right)$ are spaces of linear polynomials on K and E, respectively, and $P:L^{\infty }\left(E\right)\to L^{\infty }\left(K\right)$ is a continuation operator.

Lemma 4

(Bubble function space [40]). $\forall u\in {\mathcal{P}}_1\left(K\right)$ and $\forall w\in {\mathcal{P}}_1\left(E\right)$, where $K\in {\mathcal{T}}_h$ and $E\in {\mathcal{I}}_h$,

$$\begin{array}{ccc}& & {\tilde{C}}_1{\parallel u\parallel }_{L^2\left(K\right)}\le \parallel b_K{u\parallel }_{L^2\left(K\right)}\le {\parallel u\parallel }_{L^2\left(K\right)},\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & {\tilde{C}}_2{\parallel u\parallel }_{L^2\left(K\right)}\le \underset{v\in {\mathcal{P}}_1\left(K\right)}{sup}{\displaystyle \frac{{\int }_{K}u{b}_{K}vd\mathit{x}}{{\parallel v\parallel }_{L^2\left(K\right)}}}\le {\parallel u\parallel }_{L^2\left(K\right)},\hfill \end{array}$$

(18)

$$\begin{array}{ccc}& & {\tilde{C}}_3{\parallel w\parallel }_{L^2\left(E\right)}\le \underset{\tau \in {\mathcal{P}}_1\left(E\right)}{sup}{\displaystyle \frac{{\int }_{E}w{b}_{E}P\tau ds}{{\parallel \tau \parallel }_{L^2\left(E\right)}}}\le {\parallel w\parallel }_{L^2\left(E\right)},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}& & {\tilde{C}}_4{h}_K^{-1}{\parallel u\parallel }_{L^2\left(K\right)}\le \parallel \nabla \left(b_{K}u\right){\parallel }_{L^2\left(K\right)}\le {\tilde{C}}_5{h}_K^{-1}{\parallel u\parallel }_{L^2\left(K\right)},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}& & {\tilde{C}}_6{h}_K^{-1}\parallel b_E{Pw\parallel }_{L^2\left(K\right)}\le \parallel \nabla \left(b_{E}Pw\right){\parallel }_{L^2\left(K\right)}\le {\tilde{C}}_7{h}_K^{-1}{\parallel b_{E}Pw\parallel }_{L^2\left(K\right)},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}& & \parallel \nabla \left(b_{K}u\right){\parallel }_{L^2\left(K\right)}\le {\tilde{C}}_8{h}_K^{-1}{\parallel u\parallel }_{L^2\left(K\right)},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& & \parallel b_E{Pw\parallel }_{L^2\left(K\right)}\le {\tilde{C}}_9{h}_K^{1/2}{\parallel w\parallel }_{L^2\left(E\right)},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& & {\tilde{C}}_{10}{\parallel u\parallel }_{L^2\left(K\right)}\le \parallel b_K^{1/2}{u\parallel }_{L^2\left(K\right)}\le {\parallel u\parallel }_{L^2\left(K\right)},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}& & {\tilde{C}}_{11}{\parallel u\parallel }_{L^2\left(E\right)}\le \parallel b_E^{1/2}{Pu\parallel }_{L^2\left(K\right)}\le {\parallel u\parallel }_{L^2\left(E\right)},\hfill \end{array}$$

(25)

where constants ${\tilde{C}}_1,\dots ,{\tilde{C}}_{11}$ depend on the reference element and regular partition only.

Theorem 2.

There exists a constant $M_2$ independent of ${\mathit{u}}_h$, $\mathit{f}$ and ϵ such that

$$\begin{array}{c}\hfill {\left({\int }_0^T{\parallel \mathit{F}\left({\mathit{u}}_h^n\right)\parallel }_{-ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}\le M_2{\left(\sum _{n=1}^N({\tau }_n{\left({\eta }_{space}^n\right)}^2+{\epsilon }^2)\right)}^{1/2},\end{array}$$

where ${\eta }_{space}^n:={\left({\displaystyle \sum _{K\in {\mathcal{T}}_h}}{\eta }_K^2+{\displaystyle \sum _{E\in {\mathcal{I}}_h}}{\eta }_E^2\right)}^{1/2}$, and the oscillation term $\epsilon :={\left({\displaystyle \sum _{K\in {\mathcal{T}}_h}}{\int }_{t_{n-1}}^{t_n}{\epsilon }_K^{2}ds\right)}^{1/2}$, with $F_K^{f,n}={\int }_K{F}^{f,n}d\mathit{x}/\left|K\right|,$ $F^{f,n}=F^f(\mathit{x},t_n)$, and 

$$\begin{array}{ccc}\hfill {\eta }_K^2& :=& h_K^2\sum _{i=1}^2\left|\right|{\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}^n+z_i\nabla ·(C_{i,h}^n\nabla {\psi }^n){\left|\right|}_{L^2\left(K\right)}^2+{\alpha }_K^2\left|\right|\sum _{i=1}^2{z}_i{C}_{i,h}^n-F_T^{f,n}{\left|\right|}_{L^2\left(K\right)}^2,\hfill \\ \hfill {\eta }_E^2& :=& h_E\sum _{i=1}^2\left|\right|[\nabla C_{i,h}^n·{\mathit{n}}_E]+z_i[C_{i,h}^n\nabla {\psi }_h^n·{\mathit{n}}_E]{\left|\right|}_{L^2\left(K\right)}^2+{ϵ}^{-1/2}{\alpha }_E\left|\right|\alpha [\nabla {\psi }_h^n·{\mathit{n}}_E]{\left|\right|}_{L^2\left(E\right)}^2,\hfill \\ \hfill {\epsilon }_K^2& :=& {\alpha }_K^2{\parallel F^f-F_K^{f,n}\parallel }_{L^2\left(K\right)}^2.\hfill \end{array}$$

Here, $\left|K\right|$ denotes the area of K.

Proof. 

With Equation (5), $\forall v\in \mathit{Y},$

$$\begin{array}{ccc}\hfill (\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v})& =& {\int }_{\Omega }(\sum _{i=1}^2({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}{v}_i+\nabla C_{i,h}^n·\nabla v_i+z_i{C}_{i,h}^n\nabla {\psi }_h^n·\nabla v_i)+ϵ\nabla {\psi }_h^n·\nabla v_3\hfill \\ & & -\sum _{i=1}^2{z}_i{C}_{i,h}^n{v}_3-F^f{v}_3)d\mathit{x}.\hfill \end{array}$$

We denote ${\mathit{R}}_h\mathit{\varphi }:=(R_h{\varphi }_1,R_h{\varphi }_2,R_h{\varphi }_3),\forall \mathit{\varphi }\in \mathit{Y}$ with $R_h$ a $Cl\acute{e}ment$ interpolation and have ${\mathit{R}}_h\in \mathcal{L}(\mathit{Y},{\mathit{Y}}_h)$. We denote by ${\mathit{Y}}_h^{*}$ and ${({\mathrm{Id}}_{\mathit{Y}}-{\mathit{R}}_h)}^{*}$ the dual space of ${\mathit{Y}}_h$ and the dual operator of $({\mathrm{Id}}_{\mathit{Y}}-{\mathit{R}}_h)$, respectively. $\mathcal{L}(\mathit{Y},{\mathit{Y}}_h)$ is the Banach space of continuous linear maps of $\mathit{Y}$ in ${\mathit{Y}}_h$.

For Equation (7) with ${\mathit{v}}_h={\mathit{R}}_h\mathit{v}$, $(\mathit{F}\left({\mathit{u}}_h^n\right),{\mathit{R}}_h\mathit{v})=0$, then

$$\begin{array}{cc}\hfill (\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v})=& (\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v}-{\mathit{R}}_h\mathit{v})=(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v}-{\mathit{R}}_h\mathit{v})-({\mathit{F}}^{\prime },\mathit{v}-{\mathit{R}}_h\mathit{v}),\hfill \end{array}$$

(26)

where $({\mathit{F}}^{\prime },\mathit{v})=((F^f-F_T^{f,n}),v_3)$, and 

$$\begin{array}{ccc}\hfill (\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})& =& \sum _{K\in {\mathcal{T}}_h}{\int }_K(\sum _{i=1}^2({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}{v}_i+\nabla C_{i,h}^n·\nabla v_i+z_i{C}_{i,h}^n\nabla {\psi }_h^n·\nabla v_i)\hfill \\ & & +ϵ\nabla {\psi }_h^n·\nabla v_3-\sum _{i=1}^2{z}_i{C}_{i,h}^n{v}_3-F_K^{f,n}{v}_3)d\mathit{x}.\hfill \end{array}$$

(27)

Then,

$$\begin{array}{cc}\hfill \parallel \mathit{F}\left({\mathit{u}}_h^n\right){\parallel }_{-ϵ,\Omega }\le & \parallel {({\mathrm{Id}}_{\mathit{Y}}-{\mathit{R}}_h)}^{*}\left(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right)\right){\parallel }_{-ϵ,\Omega }+{\parallel {(I{d}_{\mathit{Y}}-{\mathit{R}}_h)}^{*}\left({\mathit{F}}^{\prime }\right)\parallel }_{-ϵ,\Omega }.\end{array}$$

(28)

The two terms on the right-hand side (RHS) of the above inequality are considered one by one as shown below. The first term is

$$\begin{array}{ccc}& & \parallel {({\mathrm{Id}}_{\mathit{Y}}-{\mathit{R}}_h)}^{*}\left(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right)\right){\parallel }_{-ϵ,\Omega }\hfill \\ & =& \underset{\mathit{\varphi }\in {\mathit{Y},\parallel \mathit{\varphi }\parallel }_{ϵ,\Omega }=1}{sup}|\sum _{K\in {\mathcal{T}}_h}\{{\int }_K[\sum _{i=1}^2({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}^n+z_i\nabla ·(C_{i,h}^n\nabla {\psi }_h^n))({\varphi }_i-R_h{\varphi }_i)\hfill \\ & & +(-ϵ\Delta {\psi }_h^n-\sum _{i=1}^2{z}_i{C}_{i,h}^n-F_K^{f,n})({\varphi }_3-R_h{\varphi }_3)]d\mathit{x}\hfill \\ & & +\sum _{E\in {\mathcal{I}}_h\cap \partial K}{\int }_E[\sum _{i=1}^2([\nabla C_{i,h}^n·{\mathit{n}}_E]+z_i[C_{i,h}^n\nabla {\psi }_h^n·{\mathit{n}}_E])({\varphi }_i-R_h{\varphi }_i)\hfill \\ & & +ϵ[\nabla {\psi }_h^n·{\mathit{n}}_E]({\varphi }_3-R_h{\varphi }_3)\left]ds\right\}|\hfill \\ & \lesssim & \underset{\mathit{\varphi }\in {\mathit{Y},\parallel \mathit{\varphi }\parallel }_{ϵ,\Omega }=1}{sup}\{\sum _{K\in {\mathcal{T}}_h}(h_K\sum _{i=1}^2\Vert {\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}^n+z_i\nabla ·(C_{i,h}^n\nabla {\psi }_h^n){\Vert }_{L^2\left(K\right)}{\parallel {\varphi }_i\parallel }_{1,{\tilde{w}}_K}\hfill \\ & & +{\alpha }_K\Vert -ϵ\Delta {\psi }_h^n-\sum _{i=1}^2{z}_i{C}_{i,h}^n-F_K^{f,n}{\Vert }_{L^2\left(K\right)}\parallel {\varphi }_3{\parallel }_{1,{\tilde{w}}_K})\hfill \\ & & +\sum _{E\in {\mathcal{I}}_h}(h_E^{1/2}\sum _{i=1}^2\Vert [\nabla C_{i,h}^n·{\mathit{n}}_E]+z_i[C_{i,h}^n\nabla {\psi }_h^n·{\mathit{n}}_E]{\Vert }_{L^2\left(E\right)}{\parallel {\varphi }_i\parallel }_{1,{\tilde{w}}_E}\hfill \\ & & +{ϵ}^{-1/4}{\alpha }_E^{1/2}\Vert ϵ[\nabla {\psi }_h^n·{\mathit{n}}_E]{\Vert }_{L^2\left(E\right)}\parallel {\varphi }_3{\parallel }_{1,{\tilde{w}}_E})\}\hfill \\ & \lesssim & \underset{\mathit{\varphi }\in {\mathit{Y},\parallel \mathit{\varphi }\parallel }_{ϵ,\Omega }=1}{sup}\{\sum _{K\in {\mathcal{T}}_h}{\eta }_K{\left(\parallel {\varphi }_1{\parallel }_{ϵ,{\tilde{w}}_K}^2+\parallel {\varphi }_2{\parallel }_{ϵ,{\tilde{w}}_K}^2+{\parallel {\varphi }_3\parallel }_{ϵ,{\tilde{w}}_K}^2\right)}^{1/2}\hfill \\ & & +\sum _{E\in {\mathcal{I}}_h}{\eta }_E{\left(\parallel {\varphi }_1{\parallel }_{ϵ,{\tilde{w}}_E}^2+\parallel {\varphi }_2{\parallel }_{ϵ,{\tilde{w}}_E}^2+{\parallel {\varphi }_3\parallel }_{ϵ,{\tilde{w}}_E}^2\right)}^{1/2}\}\hfill \\ & \lesssim & \eta .\hfill \end{array}$$

(29)

In the second term of the RHS of (28),

$$\begin{array}{ccc}& & \parallel {({\mathrm{Id}}_{\mathit{Y}}-{\mathit{R}}_{\mathit{h}})}^{*}{\mathit{F}}^{\prime }{\parallel }_{-ϵ,\Omega }\hfill \\ & =& \underset{\mathit{\varphi }\in {\mathit{Y},\parallel \mathit{\varphi }\parallel }_{ϵ,\Omega }=1}{sup}\left|\sum _{K\in {\mathcal{T}}_h}{\int }_K\left[(F^f-F_K^{f,n})({\varphi }_3-R_h{\varphi }_3)\right]d\mathit{x}\right|\hfill \\ & \lesssim & \underset{\mathit{\varphi }\in {\mathit{Y},\parallel \mathit{\varphi }\parallel }_{ϵ,\Omega }=1}{sup}\sum _{K\in {\mathcal{T}}_h}{\alpha }_K\left(\parallel F^f-F_K^{f,n}{\parallel }_{L^2\left(K\right)}{\parallel {\varphi }_3\parallel }_{ϵ,{\tilde{w}}_K}\right)\hfill \\ & \lesssim & \sum _{K\in {\mathcal{T}}_h}{\epsilon }_K.\hfill \end{array}$$

Therefore, according to the above analysis and Equation (26),

$$\begin{array}{cc}\hfill ({\int }_0^T\parallel \mathit{F}\left({\mathit{u}}_h^n\right){{\parallel }_{-ϵ,\Omega }^{2}ds)}^{{\displaystyle \frac{1}{2}}}\lesssim & {\left(\sum _{n=1}^N{\int }_{t_{n-1}}^{t_n}({{\eta }_{space}^n}^2+\sum _{K\in {\mathcal{T}}_h}{\epsilon }_K^2)ds\right)}^{1/2}\hfill \\ \hfill \le & M_2{\left(\sum _{n=1}^N({\tau }_n{\left({\eta }_{space}^n\right)}^2+{\epsilon }^2)\right)}^{1/2}.\hfill \end{array}$$

 □

Theorem 3.

If $C_1,C_2,\psi$ and $\mathit{e}$ satisfy the conditions in Theorem 1, there exists a constant $M_3$ independent of ${\mathit{u}}_h$, $\mathit{f}$ and ϵ such that

$$\begin{array}{c}\hfill {\left({\int }_0^T{\parallel \mathit{u}-{\mathit{u}}_{h,\tau }\parallel }_{ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}\le M_3{\left\{\sum _{n=1}^N({\tau }_n{\left({\eta }_{space}^n\right)}^2+{\tau }_n{\left({\eta }_{time}^n\right)}^2+{\epsilon }^2)\right\}}^{1/2},\end{array}$$

(30)

where ${\eta }_{time}^n:={\left({\displaystyle \frac{1}{3}}{\parallel {\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}\parallel }_{\mathit{Y}}^2\right)}^{1/2}$.

Proof. 

Equation (8) gives for $t\in [t_{n-1},t_n]$

$$\begin{array}{c}\hfill {\mathit{u}}_h^n-{\mathit{u}}_{h,\tau }={\displaystyle \frac{t_n-t}{{\tau }_n}}({\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}).\end{array}$$

Then, we have

$$\begin{array}{ccc}\hfill \parallel {\mathit{u}}_h^n-{\mathit{u}}_{h,\tau }{\parallel }_{L^2(0,T;\mathit{Y})}& =& {\left\{\parallel {\displaystyle \frac{t_n-t}{{\tau }_n}}({\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}){\parallel }_{L^2(0,T;\mathit{Y})}^2\right\}}^{{\displaystyle \frac{1}{2}}}\hfill \\ & =& {\left\{\sum _{n=1}^N{\displaystyle \frac{1}{3}}{\tau }_n{\parallel ({\mathit{u}}_h^n-{\mathit{u}}_h^{n-1})\parallel }_{\mathit{Y}}^2\right\}}^{{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

According to Theorem 1,

$$\begin{array}{c}\hfill {\left({\int }_0^T{\parallel \mathit{u}-{\mathit{u}}_h^n\parallel }_{ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}\le {\parallel \mathit{u}-{\mathit{u}}_h^n\parallel }_{V(0,T)}\le 2\sqrt{2}{M}_2{\left({\int }_0^T{\parallel \mathit{F}\left({\mathit{u}}_h^n\right)\parallel }_{-ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}.\end{array}$$

Therefore, with Theorem 2, we have

$$\begin{array}{ccc}& & {\left({\int }_0^T{\parallel \mathit{u}-{\mathit{u}}_{h,\tau }\parallel }_{ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}\hfill \\ & \lesssim & {\left({\int }_0^T{\parallel \mathit{u}-{\mathit{u}}_h^n\parallel }_{ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}+{\left({\int }_0^T{\parallel {\mathit{u}}_{\mathit{h}}^{\mathit{n}}-{\mathit{u}}_{h,\tau }\parallel }_{ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}\hfill \\ & \lesssim & {\left({\int }_0^T{\parallel \mathit{u}-{\mathit{u}}_h^n\parallel }_{ϵ,\Omega }^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}+{\left({\int }_0^T{\parallel {\mathit{u}}_{\mathit{h}}^{\mathit{n}}-{\mathit{u}}_{h,\tau }\parallel }_{\mathit{Y}}^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}\hfill \\ & \lesssim & {\left(\sum _{n=1}^N({\tau }_n{\left({\eta }_{space}^n\right)}^2+{\epsilon }^2)\right)}^{1/2}+{\left\{\sum _{n=1}^N{\displaystyle \frac{1}{3}}{\tau }_n{\parallel {\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}\parallel }_{\mathit{Y}}^2\right\}}^{1/2}\hfill \\ & \lesssim & {\left\{\sum _{n=1}^N({\tau }_n{\left({\eta }_{space}^n\right)}^2+{\epsilon }^2+{\displaystyle \frac{1}{3}}{\tau }_n\parallel {\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}{\parallel }_{\mathit{Y}}^2)\right\}}^{1/2}\hfill \\ & \le & M_3{\left\{\sum _{n=1}^N({\tau }_n{\left({\eta }_{space}^n\right)}^2+{\tau }_n{\left({\eta }_{time}^n\right)}^2+{\epsilon }^2)\right\}}^{1/2},\hfill \end{array}$$

with $M_3$ independent of ${\mathit{u}}_h$, $\mathit{f}$ and $ϵ$. □

Remark 1.

For the oscillation term ϵ in inequality (30), $ϵ=\mathcal{O}\left(h^{1+s}\right)$ when $f_i$ is piecewise $H^s\left(K\right)(0<s\le 1)$, $\forall K\in {\mathcal{T}}_h$ [41]. Specially, $\parallel f_i-f_{K,i}{\parallel }_{L^2\left(K\right)}\lesssim h{\parallel f_i\parallel }_{1,K},\forall f_i\in H^1\left(K\right)$ and $\parallel f_i-f_{K,i}{\parallel }_{L^2\left(K\right)}=0$ when $f_i$ is a piecewise constant function on ${\mathcal{T}}_h$.

3.2. Upper Bounds of the Estimators

In this subsection, we prove the upper bounds of the space and time estimators, respectively. We now begin with the space estimator. The special bubble function [42] is defined before discussions.

Given any number $\mu \in (0,1]$, we denote the transformation $F_{\mu }:R^2\to R^2$, which meets

$$F_{\mu }\left((x,y)\right)=B_{\mu }{(x,y)}^{\tau },\forall (x,y)\in R^2,$$

where $B_{\mu }:=diag(\mu ,1)$. $\forall K\in {\mathcal{T}}_h$, we set invertible affine map [43] on reference element $\widehat{K}$ that

$$F_K(\widehat{x},\widehat{y})=B_K{(\widehat{x},\widehat{y})}^{\tau }+\mathit{b}={(x,y)}^{\tau }\in K,\forall (\widehat{x},\widehat{y})\in \widehat{K}.$$

Set ${\widehat{K}}_{\mu }:=F_{\mu }\left(\widehat{K}\right)$ for the edge bubble function on $\widehat{E}$, $\forall \widehat{E}\in \widehat{K}$,

$$b_{\widehat{E},\mu }:=b_{\widehat{E}}\circ F_{\mu }^{-1}(\mu \widehat{x},\widehat{y}),$$

and we call $b_{\widehat{E},\mu }$ the special edge bubble function on ${\widehat{K}}_{\mu }$. We set $b_{\widehat{E},\mu }=0$ on $\widehat{K}\setminus {\widehat{K}}_{\mu }$ for simplicity defining the function on $w_E=K_1\cup K_2$ with $w\in H^1\left(E\right)$ as follows:

$$\begin{array}{cc}\hfill b_{E,\mu }w\left(\mathit{x}\right)& =\left\{\begin{array}{c}\begin{array}{cc}{b}_{E,{\mu }_1}Pw,& \mathit{x}\in K_1,\hfill \\ b_{E,{\mu }_2}Pw,& \mathit{x}\in K_2,\hfill \end{array}\hfill \end{array}\right.\end{array}$$

and $b_{E,{\mu }_1}{|}_E=b_{E,{\mu }_2}{{|}_E=b_E|}_E$.

Lemma 5

(Special bubble function [42]). T is the element and E is one of its edge, then $\forall w\in P_1\left(E\right)$,

$$\begin{array}{cc}& \parallel b_{E,\mu }{Pw\parallel }_{L^2\left(T\right)}\le {\tilde{M}}_5{h}_E^{1/2}{\mu }^{1/2}{\parallel w\parallel }_E,\\ & \parallel \nabla \left(b_{E,\mu }Pw\right){\parallel }_{L^2\left(T\right)}\le {\tilde{M}}_6{h}_E^{-1/2}{\mu }^{-1/2}{\parallel w\parallel }_E,\end{array}$$

where constants ${\tilde{M}}_5$ and ${\tilde{M}}_6$ only depend on the reference element and regular partition.

The weak problem of the system (3) at $t_n$ can be represented so as to find ${\mathit{u}}^n=(C_1^n,C_2^n,{\psi }^n)\in \mathit{Y}$ such that

$$(\mathit{F}\left({\mathit{u}}^n\right),\mathit{v})=0,\forall \mathit{v}\in \mathit{Y}.$$

(31)

Corresponding to problem (31), we obtain the following linear problem at $t_n$ by the G derivative: $\forall \mathit{R}\in {\left[L^2(\Omega )\right]}^3$, to find $\mathit{\phi }=({\phi }_1,{\phi }_2,{\phi }_3)\in {\left[H_0^1(\Omega )\right]}^3$, such that

$$\begin{array}{cc}\hfill (\mathit{DF}\left({\mathit{u}}^n\right)\mathit{\phi },\mathit{v})=& (\mathit{R},\mathit{v}),\hfill \end{array}$$

(32)

where ${\mathit{u}}^n=(C_1^n,C_2^n,{\psi }^n)$ satisfies Equation (31) and

$$\begin{array}{ccc}\hfill (\mathit{DF}\left({\mathit{u}}^n\right)\mathit{\phi },\mathit{v})& :=& (\mathit{DF}\left(\mathit{u}(\mathit{x},t_n)\right)\mathit{\phi },\mathit{v})\hfill \\ & =& {\int }_{\Omega }(\sum _{i=1}^2(\nabla {\phi }_i·\nabla v_i+z_i{C}_i^n\nabla {\phi }_3·\nabla v_i+z_i{\phi }_i\nabla {\psi }^n·\nabla v_i)\hfill \\ & & +ϵ\nabla {\phi }_3·\nabla v_3-\sum _{i=1}^2{z}_i{\phi }_i{v}_3)d\mathit{x}.\hfill \end{array}$$

To build the relationship between $\parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{ϵ,\Omega }$ and ${\eta }_{space}$, we discuss the relationship between $\parallel \mathit{F}\left({\mathit{u}}_h^n\right){\parallel }_{-ϵ,\Omega }$ and $\parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{ϵ,\Omega }$ at first.

Theorem 4.

Denoting ${\mathit{e}}^n={\mathit{u}}^n-{\mathit{u}}_h^n$. If $C_1^n$, $C_2^n\in L^{\infty }(\Omega )$, ${\psi }^n\in W^{1,\infty }(\Omega )$, and $\underset{i=1,2}{max}\{\parallel z_i{e}_i^n{\parallel }_{L^{\infty }(\Omega )}\}\le ϵ/2\sqrt{2}{M}_1$, we have

$$\begin{array}{c}\hfill \parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{*,\Omega }\ge M_4\underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v})\right|,\end{array}$$

where constant $M_4$ is independent of $\mathit{u}$, $\mathit{\varphi }$ and ϵ.

Proof. 

Due to the variational form of Equation (10) as Equation (32), $\forall \mathit{v}\in \mathit{Y}$,

$$\begin{array}{c}\hfill |(\mathit{DF}\left({\mathit{u}}^n\right)\mathit{\phi },\mathit{v})|\lesssim {\parallel \mathit{\phi }\parallel }_{*,\Omega }{\parallel \mathit{v}\parallel }_{*,\Omega }.\end{array}$$

(33)

The definition of the G derivative [38] indicates that, $\forall \mathit{v}\in \mathit{Y}$,

$$\begin{array}{c}\hfill {\int }_0^1(\mathit{DF}({\mathit{u}}^n-l{\mathit{e}}^n){\mathit{e}}^n,\mathit{v})dl=(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v})-(\mathit{F}\left({\mathit{u}}^n\right),\mathit{v}).\end{array}$$

By means of the fact that $(\mathit{F}\left({\mathit{u}}^n\right),\mathit{v})=0,\forall \mathit{v}\in \mathit{Y}$ (Equation (6)), we have

$$\begin{array}{c}\hfill (\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v})={\int }_0^1(\mathit{DF}({\mathit{u}}^n-l{\mathit{e}}^n){\mathit{e}}^n,\mathit{v})dl,\end{array}$$

and thus

$$(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v})=(\mathit{DF}\left({\mathit{u}}^n\right){\mathit{e}}^n,\mathit{v})-{\int }_0^1(\mathit{DF}\left({\mathit{u}}^n\right){\mathit{e}}^n-\mathit{DF}({\mathit{u}}^n-l{\mathit{e}}^n){\mathit{e}}^n,\mathit{v})dl.$$

(34)

Then, with inequality (33) and (16) choosing $\mathit{\phi }={\mathit{e}}^n$ and ${\mathit{\rho }}_1={\mathit{e}}^n$, respectively, we have

$$\begin{array}{cc}\hfill \underset{\mathit{v}\in {\mathit{Y}}_h,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v})\right|\le & \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}|(\mathit{DF}\left({\mathit{u}}^n\right){\mathit{e}}^n,\mathit{v})|+\sqrt{2}max\{\parallel \nabla e_3{\parallel }_{L^{\infty }(\Omega )}\}\parallel {\mathit{e}}^n{\parallel }_{ϵ,\Omega }\hfill \\ \hfill \lesssim & \parallel {\mathit{e}}^n{\parallel }_{*,\Omega },\hfill \end{array}$$

where the second inequality is provided by using the first inequality in (12).

Consequently,

$$\begin{array}{c}\hfill \parallel {\mathit{e}}^n{\parallel }_{*,\Omega }\ge M_4\underset{\mathit{v}\in {\mathit{Y}}_h,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})\right|,\end{array}$$

and $M_4$ independent of $\mathit{u}$, $\mathit{\varphi }$, and $ϵ$. □

Theorem 5.

If $C_1,C_2,\psi$ and $\mathit{e}$ satisfy the conditions in Theorem 4, there exist constants $M_5,M_6$ independent of ${\mathit{u}}_h$, $\mathit{f}$, and ϵ such that

$$\begin{array}{c}\hfill {\eta }_K\le M_5(\parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{*,K}+{\epsilon }_K+{\rho }_K),\end{array}$$

(35)

and

$$\begin{array}{c}\hfill {\eta }_E\le M_6(\parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{*,{\tilde{w}}_E}+{\epsilon }_{w_E}+{\rho }_{w_E}),\end{array}$$

(36)

where ${\epsilon }_{w_E}:={\left({\displaystyle \sum _{K\in w_E}}{\epsilon }_K^2\right)}^{1/2}$, ${\rho }_K:=h_K\left|\right|F^f-F_K^{f,n}{\left|\right|}_{L^2\left(K\right)}$ and ${\rho }_{w_E}:=h_K{|}_{w_E}\left|\right|F^f-F_K^{f,n}{\left|\right|}_{L^2\left(w_E\right)}$.

Proof. 

For ${\tilde{\mathit{F}}}_h\left({\mathit{u}}_h^n\right)$ defined in Equation (27), the relationship between ${\tilde{\mathit{F}}}_h\left({\mathit{u}}_h^n\right)$ and each term of ${\eta }_{space}^n$ is considered. Then, we have

$$\begin{array}{cc}\hfill & h_K\parallel {\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}^n+z_i\nabla ·(C_{i,h}^n\nabla {\psi }^n){\parallel }_{L^2\left(K\right)}\hfill \\ \hfill \lesssim & h_K\underset{\varphi \in {\mathcal{P}}_1\left(K\right)\setminus \left\{0\right\}}{sup}\left|({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}+z_i\nabla ·(C_{i,h}\nabla {\psi }_h),b_K\varphi {)}_K\right|·{\parallel \varphi \parallel }_{L^2\left(K\right)}^{-1}\hfill \\ \hfill \lesssim & \underset{\varphi \in {\mathcal{P}}_1\left(K\right)\setminus \left\{0\right\}}{sup}\left|({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}+z_i\nabla ·(C_{i,h}\nabla {\psi }_h),b_K\varphi {)}_K\right|·{\left|b_K\varphi \right|}_{1,K}^{-1}\hfill \\ \hfill \lesssim & \underset{\varphi \in {\mathcal{P}}_1\left(K\right)\setminus \left\{0\right\},{\parallel b_K\varphi \parallel }_{1,K}=1}{sup}\left|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),(b_K\varphi ,0,0){)}_K\right|\hfill \\ \hfill \lesssim & \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|{(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})}_K\right|,\hfill \end{array}$$

where inequality (18) is applied for having the first inequality, and inequalities (17) and (20) are used for obtaining the second inequality.

Let $w:=b_K({\displaystyle \sum _{i=1}^2}{z}_i{C}_{i,h}^n+F_K^{f,n})$, then

$$\begin{array}{ccc}& & {\int }_K(\sum _{i=1}^2{z}_i{C}_{i,h}^n+F_K^{f,n})wd\mathit{x}\hfill \\ & =& {\int }_K(\sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n})wd\mathit{x}-{\int }_K(F^{f,n}-F_K^{f,n})wd\mathit{x}\hfill \\ & =& {\int }_K(\sum _{i=1}^2{z}_i(C_{i,h}^n-C_i^n)+ϵ\nabla {\psi }^n·\nabla w)d\mathit{x}-{\int }_K(F^{f,n}-F_K^{f,n})wd\mathit{x}\hfill \\ & =& {\int }_K(\sum _{i=1}^2{z}_i(C_{i,h}^n-C_i^n)+ϵ\nabla ({\psi }^n-{\psi }_h^n)·\nabla w)d\mathit{x}+{\int }_K(F^{f,n}-F_K^{f,n})wd\mathit{x}\hfill \\ & \le & \sum _{i=1}^2\parallel C_{i,h}^n-C_i^n{\parallel }_{L^2\left(K\right)}{\parallel w\parallel }_{L^2\left(K\right)}+ϵ\parallel \nabla ({\psi }_h^n-{\psi }^n){\parallel }_{L^2\left(K\right)}{\parallel \nabla w\parallel }_{L^2\left(K\right)}\hfill \\ & & +\parallel F^{f,n}-F_K^{f,n}{\parallel }_{L^2\left(K\right)}{\parallel w\parallel }_{L^2\left(K\right)}\hfill \\ & \le & (\sum _{i=1}^2\parallel C_{i,h}^n-C_i^n{\parallel }_{L^2\left(K\right)}+\parallel F^{f,n}-F_K^{f,n}{\parallel }_{L^2\left(K\right)})\parallel \sum _{i=1}^2{z}_i{C}_{i,h}^n+F_K^{f,n}{\parallel }_{L^2\left(K\right)}\hfill \\ & & +ϵh_K^{-1}\parallel \nabla ({\psi }_h^n-{\psi }^n){\parallel }_{L^2\left(K\right)}{\parallel \sum _{i=1}^2{z}_i{C}_{i,h}^n+F_K^{f,n}\parallel }_{L^2\left(K\right)},\hfill \end{array}$$

(37)

where the last inequality is obtained by inequalities (17) and (22).

With the left side of inequality (24) and ${\alpha }_Kϵh_K^{-1}=ϵ{ϵ}^{-1/2}min\{1,{ϵ}^{1/2}{h}_K^{-1}\}\le {ϵ}^{1/2}$, we have

$$\begin{array}{c}\hfill {\alpha }_K\parallel n_h-p_h-f_{K,3}{\parallel }_{L^2\left(K\right)}\lesssim {\parallel {\mathit{u}}^n-{\mathit{u}}_h^n\parallel }_{ϵ,K}+{\epsilon }_K.\end{array}$$

On the side of ${\eta }_E$, we have

$$\begin{array}{ccc}& & h_E^{1/2}\left|\right|[\nabla C_{i,h}·{\mathit{n}}_E]+[C_{i,h}\nabla {\psi }_h·{\mathit{n}}_E]{\left|\right|}_{L^2\left(E\right)}\hfill \\ & \lesssim & h_E^{1/2}\underset{\delta \in {\mathcal{P}}_1\left(E\right)\setminus \left\{0\right\}}{sup}{\left|\right|\delta \left|\right|}_{L^2\left(E\right)}^{-1}\left|{\int }_E([\nabla C_{i,h}·{\mathit{n}}_E]+[C_{i,h}\nabla {\psi }_h·{\mathit{n}}_E])b_{E}P\delta ds\right|\hfill \\ & \lesssim & h_E^{1/2}{h}_K^{1/2}\underset{\delta \in {\mathcal{P}}_1\left(E\right)\setminus \left\{0\right\}}{sup}\left|\right|b_{E}P\delta {\left|\right|}_{L^2\left(K\right)}^{-1}\left|{\int }_E([\nabla C_{i,h}·{\mathit{n}}_E]+[C_{i,h}\nabla {\psi }_h·{\mathit{n}}_E])b_{E}P\delta ds\right|\hfill \\ & \lesssim & h_K\underset{\delta \in {\mathcal{P}}_1\left(E\right)\setminus \left\{0\right\}}{sup}\left|\right|b_{E}P\delta {\left|\right|}_{L^2\left(K\right)}^{-1}|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),(b_{E}P\delta ,0,0){)}_{{\tilde{w}}_E}.\hfill \\ & & -{\int }_{{\tilde{w}}_E}({\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}^n+z_i\nabla ·(C_{i,h}^n\nabla {\psi }^n))b_{E}P\delta d\mathit{x}|\hfill \\ & \lesssim & \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h,{\parallel \mathit{v}\parallel }_{1,\Omega }=1}{sup}|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})|+h_K{|}_{{\tilde{w}}_E}\left|\right|{\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}^n+z_i\nabla ·(C_{i,h}^n\nabla {\psi }^n){\left|\right|}_{L^2\left({\tilde{w}}_E\right)}\hfill \\ & \lesssim & \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})\right|,\hfill \end{array}$$

where $h_K{|}_{{\tilde{w}}_E}$ represents the maximal diameter of K in ${\tilde{w}}_E$. Inequalities (19) and (23) are applied for showing the first and second inequalities, respectively. Inequality (21) is used to obtain the fourth inequality.

Denote $r=b_{E,\mu }ϵ[\nabla {\psi }_h^n·{\mathit{n}}_E]$, with the constant $\mu$ to be determined later. Based on the Green formulation and Lemma 5, then

$$\begin{array}{ccc}& & {\int }_E\left(ϵ[\nabla {\psi }_h^n·{\mathit{n}}_E]\right)rds={\int }_{{\tilde{w}}_E}ϵ\nabla {\psi }_h^n·\nabla rd\mathit{x}\hfill \\ & =& {\int }_{{\tilde{w}}_E}ϵ\nabla {\psi }_h^n·\nabla rd\mathit{x}-\sum _{K\in {\tilde{w}}_E}{\int }_K(\sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n})rd\mathit{x}+\sum _{K\in {\tilde{w}}_E}{\int }_K(\sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n})rd\mathit{x})\hfill \\ & =& {\int }_{{\tilde{w}}_E}ϵ\nabla {\psi }_h^n·\nabla rd\mathit{x}-\sum _{K\in {\tilde{w}}_E}{\int }_K(\sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n})rd\mathit{x}+\sum _{K\in {\tilde{w}}_E}{\int }_K(\sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n})rd\mathit{x}\hfill \\ & & +{\int }_{{\tilde{w}}_E}\sum _{i=1}^2{z}_i{C}_i^{n}d\mathit{x}+{\int }_{{\tilde{w}}_E}{F}^{f,n}rd\mathit{x}-{\int }_{{\tilde{w}}_E}ϵ\nabla {\psi }^n·\nabla rd\mathit{x}\hfill \\ & =& {\int }_{{\tilde{w}}_E}ϵ\nabla ({\psi }_h^n-{\psi }^n)·\nabla rd\mathit{x}+{\int }_{{\tilde{w}}_E}\sum _{i=1}^2{z}_i(C_i^n-C_{i,h}^n)rd\mathit{x}-\sum _{K\in {\tilde{w}}_E}{\int }_K(\sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n})rd\mathit{x}\hfill \\ & \le & {ϵ}^{1/2}\parallel \nabla ({\psi }_h^n-{\psi }^n){\parallel }_{L^2\left({\tilde{w}}_E\right)}{ϵ}^{1/2}{\parallel \nabla r\parallel }_{L^2\left({\tilde{w}}_E\right)}+(\sum _{i=1}^2|z_i|\parallel C_i^n-C_{i,h}^n{\parallel }_{L^2\left({\tilde{w}}_E\right)}\hfill \\ & & +\sum _{K\in {\tilde{w}}_E}\parallel \sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n}{\parallel }_{L^2\left(K\right)}{)\parallel r\parallel }_{L^2\left({\tilde{w}}_E\right)}\hfill \\ & \lesssim & \sum _{i=1}^2({ϵ}^{1/2}\parallel \nabla ({\psi }_h^n-{\psi }^n){\parallel }_{L^2\left({\tilde{w}}_E\right)}{ϵ}^{1/2}{\mu }_i^{-1/2}{h}_E^{-1/2}{\parallel ϵ[\nabla {\psi }_h^n·{\mathit{n}}_E]\parallel }_{L^2\left(E\right)}\hfill \\ & & +(\sum _{i=1}^2|z_i|\parallel C_i^n-C_{i,h}^n{\parallel }_{L^2\left({\tilde{w}}_E\right)}\hfill \\ & & +\sum _{K\in {\tilde{w}}_E}\parallel \sum _{i=1}^2{z}_i{C}_{i,h}^n+F^{f,n}{\parallel }_{L^2\left(K\right)}{\mu }_i^{1/2}{h}_E^{1/2}\parallel ϵ[\nabla {\psi }_h^n·{\mathit{n}}_E]{\parallel }_{L^2\left(E\right)}).\hfill \end{array}$$

(38)

Choosing ${\mu }_i={ϵ}^{1/2}{h}_E^{-1}{\alpha }_E<1$, it reads

$$\begin{array}{cc}\hfill & {ϵ}^{-1/4}{\alpha }_E^{1/2}\parallel ϵ[\nabla {\psi }_h^n·{\mathit{n}}_E]{\parallel }_{L^2\left(E\right)}\lesssim {\parallel {\mathit{u}}^n-{\mathit{u}}_h^n\parallel }_{ϵ,{\tilde{w}}_E}+{\epsilon }_K.\hfill \end{array}$$

In summary,

$$\begin{array}{c}\hfill {\eta }_T\lesssim \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})|+\parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{ϵ,K}+{\epsilon }_K,\end{array}$$

(39)

and

$$\begin{array}{c}\hfill {\eta }_E\lesssim \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h,{\parallel \mathit{v}\parallel }_{*,{\tilde{w}}_E}=1}{sup}|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})|+\parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{ϵ,{\tilde{w}}_E}+{\epsilon }_{{\tilde{w}}_E}.\end{array}$$

(40)

For the first term on the right side of inequalities (39) and (40),

$$\begin{array}{ccc}\hfill \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h{|}_K,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v}{)}_K\right|& \le & \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h{|}_K,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\mathit{F}\left({\mathit{u}}_h^n\right),\mathit{v}{)}_K\right|\hfill \\ & & +\underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h{|}_K,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\mathit{F}\left({\mathit{u}}_h^n\right)-\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v}{)}_K\right|,\hfill \end{array}$$

with Theorem 4 and

$$\begin{array}{ccc}\hfill \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h{|}_K,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|(\mathit{F}\left({\mathit{u}}_h^n\right)-\tilde{\mathit{F}}\left({\mathit{u}}_h^n\right),\mathit{v})\right|& =& \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h{|}_K,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}\left|{\int }_K(F^f-F_K^{f,n})v_{3}d\mathit{x}\right|\hfill \\ & \lesssim & \underset{\mathit{v}\in {\tilde{\mathit{Y}}}_h{|}_K,{\parallel \mathit{v}\parallel }_{*,K}=1}{sup}{h}_K(\parallel F^f-F_K^{f,n}{\parallel }_{L^2\left(K\right)}{\parallel v_3\parallel }_{1,K})\hfill \\ & \lesssim & {\rho }_K,\hfill \end{array}$$

we have

$$\begin{array}{c}\hfill {\eta }_K\le M_5(\parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{*,K}+{\epsilon }_K+{\rho }_K).\end{array}$$

Analogously, we can obtain inequality (36). □

Remark 2.

According to Theorem 3, Remark 1, and the numerical integration formula, at a fixed time $t_n$, we can have the conclusion that

$$\begin{array}{c}\hfill \parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{ϵ,\Omega }\lesssim ({\eta }_{space}^n+{\eta }_{time}^n),\end{array}$$

and

$$\begin{array}{c}\hfill \parallel {\mathit{u}}^n-{\mathit{u}}_h^n{\parallel }_{*,\Omega }\lesssim ({\eta }_{space}^n+{\eta }_{time}^n).\end{array}$$

Recalling that robust means that the estimators yield upper and lower bounds on the error such that the ratio of the upper and lower bounds is bounded from below and from above by constants which depend neither on any mesh size nor on the perturbation parameter [42], and combined with the conclusion in Theorem 5, we verify that our work ensures the robustness for the a posteriori estimates of space under the improved energy norm.

To finish the proof of the upper bound, we have to estimate the term ${\eta }_{time}^n$. In our a posteriori error estimates, for fixed time-step ${\tau }_n$, we control the error between ${\mathit{u}}_h^n$ and ${\mathit{u}}^n$. A mature analytical method is presented in [17], and here, we give a brief proof.

Theorem 6.

Each ${\eta }_{time}^n$ defined in Lemma 2 satisfies the following upper bound

$$\begin{array}{c}\hfill {\eta }_{time}^n\le \sqrt{6}(\parallel \mathit{u}-{\mathit{u}}_h^n{\parallel }_{L^2(t_{n-1},t_n;\mathit{Y})}+\parallel \mathit{u}-{\mathit{u}}_{h,\tau }{\parallel }_{L^2(t_{n-1},t_n;\mathit{Y})}).\end{array}$$

Proof. 

Equation (8) gives for $t\in [t_{n-1},t_n]$,

$$\begin{array}{c}\hfill {\mathit{u}}_h^n-{\mathit{u}}_{h,\tau }={\displaystyle \frac{t_n-t}{{\tau }_n}}({\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}).\end{array}$$

Then, we have

$$\begin{array}{c}\hfill |{\displaystyle \frac{t_n-t}{{\tau }_n}}\left|\right|{\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}{|}_{1,\Omega }\le |\mathit{u}-{\mathit{u}}_h^n{|}_{1,\Omega }+{|\mathit{u}-{\mathit{u}}_{h,\tau }|}_{1,\Omega }.\end{array}$$

Furthermore, we obtain the bound

$$\begin{array}{c}\hfill |{\displaystyle \frac{t_n-t}{{\tau }_n}}{|}^2\parallel {\mathit{u}}_h^n-{\mathit{u}}_h^{n-1}{\parallel }_{\mathit{Y}}^2\le 2(\parallel \mathit{u}-{\mathit{u}}_h^n{\parallel }_{\mathit{Y}}^2+|\mathit{u}-{\mathit{u}}_{h,\tau }{|}_{\mathit{Y}}^2).\end{array}$$

We integrate between $t_{n-1}$ and $t_n$, and obtain

$$\begin{array}{ccc}\hfill {\left({\eta }_{time}^n\right)}^2& \le & 6(\parallel \mathit{u}-{\mathit{u}}_h^n{\parallel }_{L^2(t_{n-1},t_n;\mathit{Y})}^2+\parallel \mathit{u}-{\mathit{u}}_{h,\tau }{\parallel }_{L^2(t_{n-1},t_n;\mathit{Y})}^2)\hfill \\ & \le & 6(\parallel \mathit{u}-{\mathit{u}}_h^n{\parallel }_{L^2(t_{n-1},t_n;\mathit{Y})}+\parallel \mathit{u}-{\mathit{u}}_{h,\tau }{{\parallel }_{L^2(t_{n-1},t_n;\mathit{Y})})}^2,\hfill \end{array}$$

and thus, Theorem 5 is proved. □

4. Adaptive Algorithm and Numerical Experiments

In this section, we provide one possible implementation of the adaptive algorithm for PNP equations and give numerical experiments to validate the algorithm.

Considering the algorithm for time-step size control, the time discretization error is equally distributed to each time interval $(t_{n-1},t_n),n=1,\dots ,N$. Let $To{l}_{time}$ be the total tolerance to the time discretization, then

$$\begin{array}{c}\hfill \sum _{n=1}^N({\tau }_n{\left({\eta }_{time}^n\right)}^2+{\tau }_n{\epsilon }^2)\le To{l}_{time}.\end{array}$$

(41)

With $To{l}_{time}={\displaystyle \sum _{n=1}^N}{\tau }_n{\displaystyle \frac{To{l}_{time}}{T}}$, a natural way to achieve inequality (41) is to adjust the time step size ${\tau }_n$ such that the following relations are satisfied

$$\begin{array}{c}\hfill {\left({\eta }_{time}^n\right)}^2\le {\displaystyle \frac{To{l}_{time}}{2T}}\mathrm{and}{\epsilon }^2\le {\displaystyle \frac{To{l}_{time}}{2T}}.\end{array}$$

(42)

Let $To{l}_{space}$ be the tolerance allowed for the space discretization. The usual stopping criterion for the mesh adaption is to satisfy

$$\begin{array}{c}\hfill \sum _{n=1}^N\left({\tau }_n{\left({\eta }_{space}^n\right)}^2\right)\le To{l}_{space}.\end{array}$$

(43)

With $To{l}_{space}={\displaystyle \sum _{n=1}^N}{\tau }_n{\displaystyle \frac{To{l}_{space}}{T}}$, the relation in inequality (43) converts into

$$\begin{array}{c}\hfill {\left({\eta }_{space}^n\right)}^2\le {\displaystyle \frac{To{l}_{space}}{T}}.\end{array}$$

(44)

A natural way to achieve adaptive algorithm for time-dependent PNP equations is to adjust the time step size and ${\mathcal{T}}_h$, satisfying Equations (42) and (44). The method also appears in [12].

At each time step, the well-known cycle of the adaptive method for the space is “SOLVE →ESTIMATE→MARK→ REFINE”. The difficulty in solving time-dependent PNP equations lies in how to deal with the nonlinear term. We choose Picard’s linearization in [44] for the nonlinear term in system (3). It is important to mention that the equations with $ϵ<1$ lead to systems that are potentially convection dominated, which leads to potential algorithmic difficulties in solving the system. Here, we use the edge-averaged finite element (EAFE) scheme in [45]. The method has been discussed in [33,46] for PNP equations. Algorithm 1 provides one possible implementation of time and space adaptivity for the time-dependent PNP equations at each time step referred to in [10,12,31].

Some numerical experiments are presented to verify the viability and efficiency of the a posteriori estimations. For these experiments, we use the following model to verify our theory.

To find $C_i\in L^2(0,T;H_0^1(\Omega )),i=1,2;\psi \in L^2(0,T;H_0^1(\Omega ))$ such that

$$\left\{\begin{array}{c}\begin{array}{c}({\displaystyle \frac{\partial C_i}{\partial t}},v_i)+(\nabla C_i,\nabla v_i)+(z_i{C}_i\nabla \psi ,\nabla v_i)=(f_i,v),\forall v_i\in H_0^1(\Omega ),i=1,2\hfill \\ (ϵ\nabla \psi ,\nabla v_3)-{\displaystyle \sum _{i=1}^2}(q_i{C}_i,v_3)=(f_3,v_3),\forall v_3\in H_0^1(\Omega )\hfill \end{array}\hfill \end{array}\right.$$

(45)

where $z_1=1$ and $z_2=-1$.

Compared with the previous system (3), the system (45) has the right end term $f_i,i=1,2$ and the boundary condition becomes a homogeneous Dirichlet condition. Because the homogeneous Dirichlet condition is a special case of the boundary condition (2), the analysis in our previous sections can be adapted to the system (45). According to the analysis of Theorem 2, the forms of ${\epsilon }_K$ and ${\eta }_K$ change as

$$\begin{array}{cc}\hfill {\epsilon }_K^2:=& h_K^2\sum _{i=1}^2\left|\right|f_i-f_{K,i}{\left|\right|}_{L^2\left(K\right)}^2+{\alpha }_K^2\left|\right|f_3-f_{K,3}{\left|\right|}_{L^2\left(K\right)}^2,\hfill \end{array}$$

where $f_{K,i}^n={\int }_K{f}_i(\mathit{x},t_n)d\mathit{x}/\left|K\right|$ and

$$\begin{array}{ccc}\hfill {\eta }_K^2:& =& h_K^2\sum _{i=1}^2\parallel {\displaystyle \frac{C_{i,h}^n-C_{i,h}^{n-1}}{{\tau }_n}}-\Delta C_{i,h}^n+z_i\nabla ·(C_{i,h}^n\nabla {\psi }^n)-f_{K,i}^n{\parallel }_{L^2\left(K\right)}^2\hfill \\ & & +{\alpha }_K^2\parallel \sum _{i=1}^2{z}_i{C}_{i,h}^n-f_{K,3}^n{\parallel }_{L^2\left(K\right)}^2.\hfill \end{array}$$

The first experiment presented here is designed to verify the adaptive effect in the time step adjustment due to the time singular point, and the time and space parallel adaptive adjustment with the flow structure changing caused by time. The second numerical experiment verifies the problem with the boundary layer effect. All experiments are in two dimensions, and simulations are performed with the software MATLAB 7.0 based on an integrated finite element method package iFEM.

Algorithm 1 Time and space adaptive algorithm.

Prescribe deadline T, tolerances $To{l}_{time}$ and $To{l}_{space}$, maximum number of space division cycles $MaxIt$, maximum number of mesh points in space division $MaxN$, cycles parameters ${\delta }_1>1,{\delta }_2\in (0,1),{\delta }_3\in (0,1)$ and ${\theta }_{time}\in (0,1)$. Let ${\mathit{u}}_h^{n-1}$ be computed from the previous time step at time $t_{n-1}$ with the mesh ${\mathcal{T}}_h^{n-1}$ and the time-step size $\tau$. Step 1: Initialization      ${\mathcal{T}}_h^n:={\mathcal{T}}_h^{n-1},{\tau }_n:=\tau ,t_n:=t_{n-1}+{\tau }_n$,      Solve ${\mathit{u}}_h^n$ with the mesh ${\mathcal{T}}_h^n$ where let $(C_{1,h}^{n,0},C_{2,h}^{n,0},{\varphi }_h^{n,0})={\mathit{u}}_h^{n-1}$, and compute time error estimator. Step 2: The current time step is too small      While $max({\left({\eta }_{time}^n\right)}^2,{\epsilon }^2)\le {\theta }_{time}\ast To{l}_{time}/(2\ast T)$ do         ${\tau }_n:={\delta }_1{\tau }_n$;         $t_n:=t_{n-1}+{\tau }_n$;         Solve ${\mathit{u}}_h^n$ similar with Step 1 and compute time error estimator;      End while. Step 3: Time iteration with smaller time step      While ${\left({\eta }_{time}^n\right)}^2<To{l}_{time}/(2\ast T)$ or ${\epsilon }^2<Toltime/(2\ast T)$ do         If ${\tau }_n=\tau$, which means the iteration dose not go through Step2,             ${\tau }_n:={\delta }_2{\tau }_n$;         Else             ${\tau }_n:={\delta }_3{\tau }_n$;         End If             $t_n:=t_{n-1}+{\tau }_n$;             Solve ${\mathit{u}}_h^n$ similar with Step 1 and compute time error estimator;      End while. Step 4: Adaptive method for the space      While ${\left({\eta }_{space}^n\right)}^2\le {\displaystyle \frac{To{l}_{space}}{T}}$ and the number of space division cycles ≤$MaxIt$ do         MARK: The maximum marking strategy [47] is utilized to remark the grid.         REFINE: The latest vertex bisection method [48] is used to refine the marked grid.                    Simultaneously, the new grid ${\mathcal{T}}_h^n$ is created.         SOLVE: Solve ${\mathit{u}}_h^n$, ${\mathit{u}}_h^{n-1}$ with the mesh ${\mathcal{T}}_h^n$.         ESTIMATE: Compute the a posterior error estimator ${\left({\eta }_{space}^n\right)}^2$.         If $(INOF>MaxN)$, where $INOF$ is the number of mesh points.             break;         End if,      End while. Step 5: Time marching      Stop if $t^n=T$, otherwise, set $n+1\leftarrow n$ and go to Step 1.

Example 1

([12]). Considering the case with $ϵ=1$ in system (45), we take

$$\begin{array}{c}\hfill \beta \left(t\right)=0.03\ast (1-e^{(-10000\ast {(t-0.5)}^2)}),\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{C}_1=\beta \left(t\right)e^{(-({(x-t+0.5)}^2+{(y-t+0.5)}^2)/0.1)},\hfill \\ C_2=\beta \left(t\right)e^{(-({(x-t+0.5)}^2+{(y-t+0.5)}^2)/0.4)},\hfill \\ \psi =\beta \left(t\right)e^{(-({(x-t+0.5)}^2+{(y-t+0.5)}^2)/0.6)},\hfill \end{array}\right.\end{array}$$

as an exact solution of system (45) in the domain $\Omega =(-1,1)\times (-1,1)$ with homogeneous Dirichlet boundary conditions. Consequently, functions $f_1,f_2$ and $f_3$ on the RHS are determined by the exact solution.

For Algorithm 1, we choose $T=1,{\delta }_1=2,{\delta }_2=0.5,{\delta }_3=0.75,{\theta }_{time}=0.5$ in Example 1 and give some specific cases of time-step adaptation. Firstly, we constrain the time step to be extended only once when the time step is too small at each time step. Figure 1 shows the number of nodes and the time step size at each time step n with $\tau =0.0025,0.01$, respectively, when $To{l}_{space}=0.0025$ and $To{l}_{time}=0.01$. We note that the time step size drops in a small time interval around $t=0.5$ and is constant in the rest of the interval. It is not a surprise, as $\beta \left(t\right)$ changes exponentially from $0.03$ to 0 and then from 0 to $0.03$ around $t=0.5$. The ratio of the maximum time step size to the minimum is $0.02/0.00125=16$ when $\tau =0.01$. That means the efficiency of the adaptation can increase by an order of magnitude. Then, Figure 2 shows the number of nodes of ${\mathcal{T}}_h^n$ at each time step when $To{l}_{space}=0.0025$, $To{l}_{time}=0.01$, $MaxIt=15$ and $\tau =0.0025$ without the constrains on the number of time extensions.

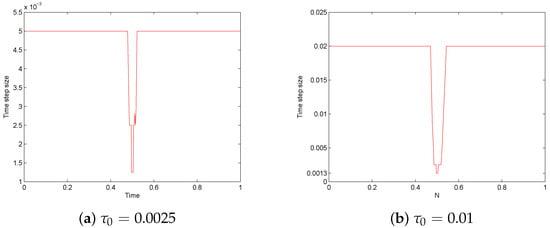
Figure 1. The time step size ${\tau }_n$ at each time step n with different initial step size ${\tau }_0$ when $To{l}_{time}=0.0002$ and $To{l}_{space}=0.01$. The total numbers of the calculation time are $N_{time}=213$ and $N_{time}=69$, respectively.

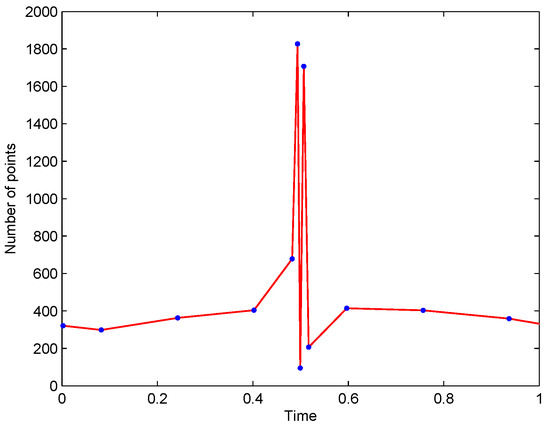
Figure 2. The number of nodes of ${\mathcal{T}}_h^n$ at each time step when $To{l}_{space}=0.0025$, $To{l}_{time}=0.01$, $MaxIt=15$ and initial time step ${\tau }_0=0.0025$.

In Figure 3, the surface plots of discrete solutions $C_1$ and the corresponding meshes at $t=0.0825,0.5169,0.9369$ are displayed. It clearly indicates the ability of Algorithm 1 to capture the singularity of the solutions by locally refining and coarsening the meshes, and to realize the adaptive adjustments of time steps and mesh sizes simultaneously.

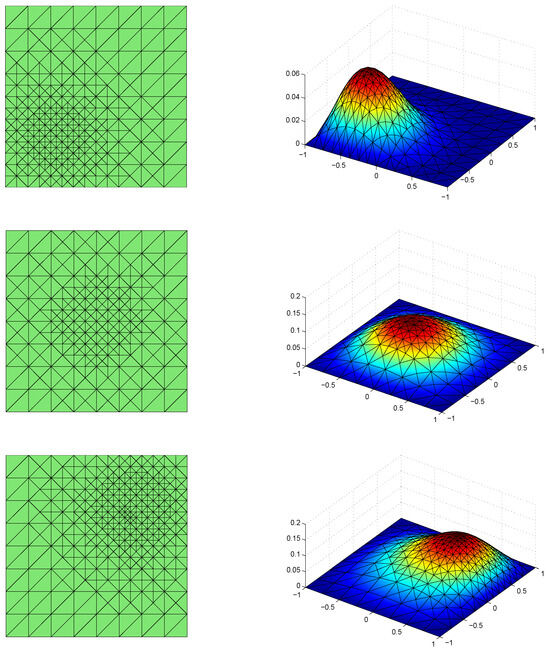
Figure 3. Surface plots of discrete solutions $C_1$ (right) and the corresponding meshes (left) at $t=0.0825,0.5169,0.9369$ (from top to bottom). The numbers of nodes of the meshes are $298,206,359$ for $t=0.0825,0.5169,0.9369$, respectively.

In summary, Figure 1 shows the adaptive effect in time step adjustment due to the time singular point. The time and space parallel adaptive adjustments with the flow structure are verified in Figure 2 and Figure 3. The numerical results mean Algorithm 1 can realize adaptive adjustments of the time steps and mesh sizes simultaneously.

Example 2

([31]). Considering the boundary layer changing with time, we take

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{c}{C}_1=C_2=e^{-xt/\epsilon }+e^{-yt/\epsilon },\hfill \\ \psi =e^{-3xt/\epsilon }+e^{-3yt/\epsilon },\hfill \end{array}\hfill \end{array}\right.\end{array}$$

to be the exact solution to system (45) on $\Omega =(0,1)\times (0,1)$. Correspondingly, the right-hand side functions $f_1$, $f_2$, and $f_3$ are determined by the above exact solution.

Here, we focus on the adaptivity in the space and choose uniform time refined with ${\tau }_n=0.01,T=1$ in Example 2, and Figure 4 shows that the boundary layer is perfectly captured, and the mesh adaptation is realized. The first two lines in Figure 4 show the surface plots of discrete solutions $\psi$ (right) and the corresponding meshes (left) at $t=0.16,0.96$ (from top to bottom) for $ϵ={10}^{-4}$. As time goes on, we observe more grids near the original point than other parts of the boundary when degrees of freedom are close to each other. Furthermore, in order to observe the boundary layer with the decrease of $ϵ$ at the same time, we give the surface plots of discrete solutions $\psi$ (top right) and the corresponding meshes (top left) at $t=0.96$ for $ϵ={10}^{-1}$ in the third line of Figure 4. The adaptivity can be demonstrated as more condensed grids near the boundaries as $ϵ$ decreases. For the case with $t=0.96,ϵ={10}^{-4}$, the mesh refinements are well observed in the boundary, i.e., $x=0$ and $y=0$, as the number of meshes is increased to be large enough. The corresponding surface plots of discrete solutions $\psi$ (bottom right) and the corresponding meshes (bottom left) are shown in the last line of Figure 4.

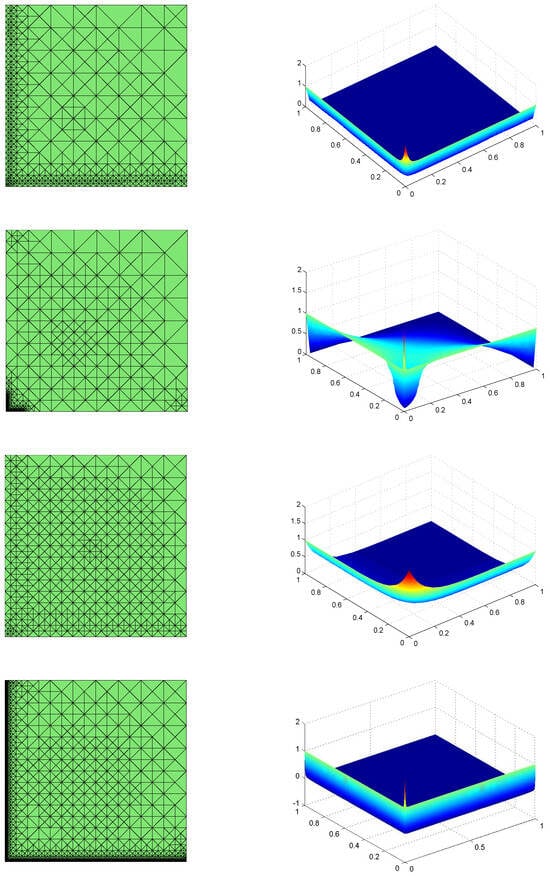
Figure 4. For the first two lines, surface plots of discrete solutions $\psi$ (right) and the corresponding meshes (left) at t = 0.16, 0.96 (from top to bottom) for $ϵ={10}^{-4}$. The numbers of the mesh nodes are 579, 568 for t = 0.16, 0.96, respectively. For the last two lines, the surface plots of discrete solutions $\psi$ (right) and the corresponding meshes (left) at t = 0.96 for $ϵ={10}^{-1},{10}^{-4}$ (from top to bottom). The numbers of the meshes nodes are 573, 11,398 for $ϵ={10}^{-1},{10}^{-4}$, respectively.

5. Conclusions

In this paper, the a posteriori error estimation is adopted for the adaptive analysis of time-dependent PNP equations, where the nonlinearity and strong coupling are focused. During the theoretical study of the a posteriori error estimation, we establish two types of computable error estimators which bound the time and space error, respectively. The estimates for the upper bounds of the time and space estimator are derived, respectively, so as to demonstrate the efficiency and reliability of the error estimator. In particular, the a posterior error estimate in space is robust under the improved energy norm. The adaptive algorithm is constructed based on the estimates and realizes the parallel adaptivity of time steps and mesh refinements. Numerical experiments show the phenomenon of adaptive time step and mesh size adjustments due to the time singular point and the flow structure with time, and successfully capture boundary layers arbitrarily changing with the flow of time. Although our work can solve the boundary layer problem well, it is still valuable to find a method with lower computational complexity. In the future, we plan to explore various a posterior error estimation methods and seek more effective methods to solve such problems through comparative analysis. We will use different control algorithms to achieve adaptive time steps, and extend the theoretical analysis to anisotropic meshes, which are more efficient for real physical problems.