An Integrated T-Spherical Fuzzy Einstein Interaction Aggregator Group Decision-Making Approach: A Case Study of Concrete 3D Printing Robot Application in Vietnam

Abstract

This study introduces the integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach, a novel framework designed to enhance multi-criteria decision-making (MCDM). Implementing the case study of concrete 3D printing technology in Vietnam, this approach integrates T-spherical fuzzy sets with Einstein aggregation operators to handle the complexities of uncertain and subjective expert judgments effectively. The methodology provides a robust mechanism for evaluating and prioritizing the barriers and strategies associated with the implementation of concrete 3D printing. Findings from this study underline the significance of technological advancements and strategic financial incentives, with R&D strategy emerging as the top priority. This research contributes to both theoretical advancements in decision-making frameworks and offers practical insights for industries looking to integrate emerging technologies. Moreover, it demonstrates the application of advanced fuzzy set theories in real-world settings, providing a valuable tool for decision-makers facing similar technological adoption challenges.

1. Introduction

The journey of fuzzy sets began with Zadeh’s introduction of a system where objects possess degrees of membership, extending beyond traditional binary classifications [1,2]. His fundamental advancement significantly enhanced the applicability of set theory, particularly in areas where binary logic proved overly restrictive. Building on this foundational concept, Atanassov developed intuitionistic fuzzy sets (IFS), which featured both membership and non-membership functions, providing a richer framework for expressing uncertainties [3]. However, the requirement that the sum of these degrees not exceed one posed certain limitations, prompting further innovations in the field. Yager’s introduction of Pythagorean fuzzy sets (PyFS) marked a significant evolution, as it relaxed the constraints by allowing the square sum of membership and non-membership degrees to remain within the unit interval [0, 1] [4]. This modification granted decision-makers greater flexibility and maintained the necessary logical consistency for effective decision-making. Yager continued to expand the fuzzy set framework by proposing the q-rung orthopair fuzzy set (q-ROFS), which removed the overall limitations on the assignment of membership and non-membership values, thus providing an even richer and more nuanced framework for representing uncertainty [5]. Following this, Cuong introduced the picture fuzzy set (PFS), which added dimensions of abstention and refusal [6]. However, like its predecessors, it faced limitations when the sum of these dimensions exceeded one, indicating a need for further refinement. Addressing this issue, Kutlu et al. introduced spherical fuzzy sets (SFS) and subsequently developed T-spherical fuzzy sets (T-SFS) [7,8,9]. These advancements allowed for the square sum of membership, abstention, and non-membership degrees to fit within the unit interval, offering decision-makers unprecedented flexibility in quantifying uncertainty.

All the fuzzy structures mentioned previously are employed to address numerous challenges in the field of decision-making. In 2012, Pei and Zheng proposed a ranking method based on revised score and accuracy functions for IFS [10]. Meanwhile, Shen et al. introduced a method to construct an intuitionistic fuzzy outranking relation using support, risk, and credibility functions [11]. In 2017, Liang and Xu proposed hesitant Pythagorean fuzzy sets (HPFSs) to handle uncertain information in decision-making, combining the strengths of PFSs and hesitant fuzzy sets [12]. Hussain et al. proposed new aggregation operators for multi-attribute decision-making (MADM) under PyFSs, leveraging the flexibility of Aczel–Alsina operators for handling incomplete information. They introduced Aczel–Alsina sum, product, averaging, and geometric operators, proving their properties and demonstrating effectiveness through an example and comparisons with existing methods [13]. In 2018, Garg proposed HPFSs for decision-making, combining the strengths of hesitant and Pythagorean fuzzy sets. He develops new aggregation operators for HPFSs and establishes a MADM approach using them [14]. In the same year, Peng et al. developed a new score function and operational law for q-ROFNs to address shortcomings in comparing q-ROFNs and solve multi-criteria decision-making problems [15]. Garg and Chen illustrated the adaptability of q-ROFSs in decision-making by introducing operational laws and aggregation operators that enhance decision processes and demonstrated the superiority of these methods over traditional fuzzy sets through numerical examples and a comparative review [16]. Akram et al. introduced the complex picture fuzzy set (CPFS) as an enhancement to complex intuitionistic fuzzy sets by incorporating a neutral membership degree, expanding the scope of membership values, and developing aggregation operators for multiple criteria decision-making (MCDM) problems, demonstrating their effectiveness in selecting the best enterprise resource planning (ERP) system and affirming their methods’ consistency and superiority through comparisons [17]. In 2022, Le and Nhieu aimed to enhance multi-criteria decision-making methods by proposing a novel extension using SFS to account for decision-makers’ psychological behavior. They employed the spherical fuzzy Decision-Making Trial and Evaluation Laboratory (SF DEMATEL) method to weigh evaluation criteria and the spherical fuzzy Interactive Multi-Criteria Decision-Making method in a Monte Carlo simulation environment (SF TODIM’MC) to evaluate alternatives [18]. Wang et al. address the need for sustainable and resilient production systems amidst pandemic-induced disruptions, advocating for the deployment of smart technologies to reduce reliance on human labor. Their study proposes an integrated spherical fuzzy bounded rationality decision-making approach, combining SF DEMATEL and the spherical fuzzy regret theory-based combined compromise solution (R-SF CoCoSo) methods, to prioritize smart technologies for manufacturing in Vietnam [19]. In 2021, Garg et al. introduced power aggregation operators for T-SFSs, which offer enhanced handling of uncertain information with four membership functions. Their work defines various weighted averaging and geometric power aggregation operators, including T-spherical fuzzy weighted, ordered weighted, hybrid averaging, and geometric operators [20]. Rani and Mishra develop an integrated decision-making method for selecting electric vehicle charging station (EVCS) locations under the Fermatean fuzzy set (FFS) context, effectively handling uncertainty. Their approach combines multi-objective optimization, maximizing deviation method, and novel Einstein aggregation operators within the FFS environment, demonstrating its effectiveness through an illustrative study [21]. Recently, Razzaq and Riaz presented a picture of fuzzy soft-max Einstein interactive weighted average and fuzzy soft-max Einstein interactive weighted geometric operators to improve decision-making for sustainable biomass resource selection. These operators blend the soft-max function and Einstein interactive operations to manage uncertainty and accommodate decision-maker preferences [22].

Focus on the Einstein operators for fuzzy information aggregation. Wang and Liu (2012) introduced new operations within Atanassov’s intuitionistic fuzzy set (AIFS) theory, such as the Einstein sum, product, and scalar multiplication, and developed intuitionistic fuzzy aggregation operators like the intuitionistic fuzzy Einstein weighted averaging and ordered weighted averaging operators [23]. These operators are designed to aggregate intuitionistic fuzzy values in decision-making processes, extending traditional methods and demonstrating their applications with numerical examples. In 2016, Garg extended the fuzzy set theory to PFSs, introducing advanced aggregator operators like the Pythagorean fuzzy Einstein weighted averaging and its ordered and generalized versions, which accommodate the relaxed conditions on membership functions [24]. These new operators are utilized in decision-making scenarios where experts’ preferences are expressed in a Pythagorean fuzzy context, demonstrating their effectiveness and providing comparisons with existing methods. Later, Gümüş and Bali explore MCDM in an intuitionistic fuzzy environment, introducing operations like Einstein sum, product, and exponentiation and defining new dynamic intuitionistic fuzzy Einstein averaging operators (DIFWA and DIFWG). These operators are designed to aggregate intuitionistic fuzzy values across different periods using Einstein operations, with their applicability demonstrated in MCDM problems through an illustrative example and comparison with existing methods. Additionally, Khan et al. examined information aggregation operators in group decision-making within a picture fuzzy environment, introducing operators like picture fuzzy Einstein weighted and Einstein ordered weighted [25]. In 2020, Riaz et al. expanded the Pythagorean and intuitionistic fuzzy sets into q-ROFS, useful for handling vague information in real-world scenarios, by introducing aggregation operators that include several versions of the q-rung orthopair fuzzy Einstein weighted and ordered averaging operators [26]. These operators leverage the flexibility of Einstein operations to enable robust MCDM, with the applicability and effectiveness of these methods demonstrated through a numerical example in sustainable energy planning. Currently, Fatima et al. introduce spherical fuzzy Z-numbers (SFZNs) and establish basic operational rules, emphasizing their effectiveness in reflecting fuzzy data and facilitating ambiguous judgments in decision-making. They also develop spherical fuzzy Einstein Z-number weighted averaging/geometric aggregation operators along with their key axioms and propose algorithms based on these operators to handle uncertain information in decision-making problems [27]. According to existing literature, the integration of Einstein aggregation operators with T-spherical fuzzy sets marks a significant advancement in multi-criteria decision-making (MCDM). These operators provide flexibility in combining multiple criteria represented as fuzzy numbers, handle non-linear relationships effectively, and prevent information loss during aggregation, making them ideal for complex decision-making environments [28].

In recent years, the Criteria Importance Through Intercriteria Correlation (CRITIC) and Combined Compromise Solution (CoCoSo) methods have garnered increasing attention in the field of MCDM [29,30]. These methods have risen to prominence due to their ability to address some of the limitations of traditional MCDM approaches and offer more nuanced and robust decision-making frameworks. One of the key advantages of the CRITIC method lies in its ability to capture the interdependencies among criteria, thereby providing a more accurate and comprehensive assessment of their relative importance [31]. By analyzing the correlations between criteria, CRITIC helps decision-makers better understand the underlying relationships and trade-offs involved in the decision-making process. This leads to more informed decisions that account for the complex interactions between different criteria, ultimately improving the quality of outcomes. Similarly, the CoCoSo method offers several advantages over traditional MCDM techniques by focusing on finding compromise solutions that balance competing objectives [32]. Unlike methods that prioritize the optimization of a single criterion, CoCoSo seeks solutions that are acceptable across multiple criteria, accommodating diverse stakeholder preferences and objectives [33]. This flexibility allows decision-makers to explore a wider range of potential solutions and make more robust decisions that account for the inherent uncertainties and trade-offs present in complex decision environments [34,35]. By combining the strengths of both methods, decision-makers can gain a more comprehensive understanding of the decision space and identify compromise solutions that not only reflect the relative importance of criteria but also account for their interdependencies. This integrated approach enables decision-makers to navigate complex decision problems more effectively, leading to more robust and well-informed decisions that align with stakeholder preferences and objectives.

Based on this motivation, the primary objective of this study is to introduce and validate a novel integrated T-Spherical fuzzy Einstein interaction aggregator group decision-making approach that is inspired by CRITIC and CoCoSo methods. As a secondary objective, this study aims to apply this newly proposed method to systematically identify barriers that impede the widespread adoption of 3D printing technology in Vietnam’s construction practices. Additionally, this study aims to prioritize strategies to overcome these barriers. This secondary objective serves to validate the practicality and effectiveness of the proposed decision-making approach, ultimately facilitating the broader integration of 3D printing technology into construction practices. The key novel contributions of this research are outlined as follows:

• Integration of T-Spherical Fuzzy Sets with Einstein Aggregation Operators: This study is one of the first to apply T-Spherical Fuzzy Weighted Einstein Geometric Aggregation (TSFWEIGA) and T-Spherical Fuzzy Weighted Einstein Interaction Aggregation Approach (TSFWEIAA) within established MCDM frameworks (CRITIC and CoCoSo methods). This integration allows for more refined and accurate handling of uncertainties and interdependencies in decision-making data.
• By enhancing the CRITIC and CoCoSo methods with advanced fuzzy aggregation operators, this study addresses specific challenges in evaluating and implementing new technologies in the construction sector, offering a methodological advancement that can be adapted for other industries.
• This study focuses on the practical application of these enhanced decision-making frameworks to the specific case of adopting concrete 3D printing technology in Vietnam, providing context-specific insights that are valuable for stakeholders in similar emerging markets.
• This research not only identifies but also prioritizes the barriers and strategies for the adoption of 3D printing technology in construction, utilizing a novel decision-making approach that combines expert judgment with sophisticated fuzzy logic techniques.
• The approach developed in this study contributes to both the theoretical literature on fuzzy MCDM and offers practical tools for decision-makers facing complex decisions regarding new technology implementations.

This study is structured into four sections: Introduction, Methodology, Case Study and Discussion, and Conclusions. The introduction provides background, motivation, and objectives. The methodology details the proposed approach. The Case Study and Discussion Section analyzes findings, followed by the Conclusions summarizing key insights and implications.

2. Methodology

2.1. Preliminaries

Definition 1

([36]). A T-spherical fuzzy set $\tilde{A}$ on the universe of discourse $X$ is defined as

$$\tilde{A}=\left\{\right(x,\alpha \left(x\right), \gamma \left(x\right),\beta \left(x\right)\left)\right|x\in X\}$$

(1)

$$\begin{gathered} \mathit{where} \alpha ,\gamma ,\beta : X\to \left[0,1\right] \mathit{and} 0\le {\alpha }^t\left(x\right)+{\gamma }^t\left(x\right)+{\beta }^t\left(x\right)\le 1 \\ \forall t\in \mathbb{N},x\in X. \end{gathered}$$

(2)

The notation $\alpha \left(x\right),\gamma \left(x\right),$ and $\beta \left(x\right)$ are the degree of membership, hesitancy, and non-membership of $x$ to $\tilde{A}$, respectively. The refusal degree of $x$ in $\tilde{A}$ is defined as

$$r\left(x\right)={\left(1-\left({\alpha }^t\left(x\right)+{\gamma }^t\left(x\right)+{\beta }^t\left(x\right)\right)\right)}^{\frac{1}{t}}$$

(3)

and the $\tilde{A}=(\alpha ,\gamma ,\beta )$ is known as T-spherical number (T-SFN).

Definition 2

([36]). The score value $\left(SV\right)$ of the T-SFN $\tilde{A}=(\alpha ,\gamma ,\beta )$ is defined as

$$SV\left(\tilde{A}\right)={\alpha }^t-{\beta }^t$$

(4)

and the accuracy value $\left(AV\right)$ of the T-SFN $\tilde{A}=(\alpha ,\gamma ,\beta )$ is defined as

$$AV\left(\tilde{A}\right)={\alpha }^t+{\gamma }^t+{\beta }^t.$$

(5)

Remark 1.

Definitions 1 and 2 can be reduced for

(1) 

PFS if $t=1$;

(2) 

SFS if $t=2$;

(3) 

q-ROFS if $\gamma =0$;

(4) 

PyFS if $t=2$and$\gamma =0$;

(5) 

IFS if $t=1$ and $\gamma =0$;

(6) 

FS if $t=1$, $\gamma =0$, and $\beta =0.$

Definition 3

([36]). Consider two T-SFN ${\tilde{A}}_1=({\alpha }_1,{\gamma }_1,{\beta }_1)$ and ${\tilde{A}}_2=({\alpha }_2,{\gamma }_2,{\beta }_2)$, the comparison is defined as

$$\begin{gathered} {\tilde{A}}_1<{\tilde{A}}_2 if and only if \\ i. SV\left({\tilde{A}}_1\right)<SV\left({\tilde{A}}_2\right) or \\ ii. SV\left({\tilde{A}}_1\right)=SV\left({\tilde{A}}_2\right) and AV\left({\tilde{A}}_1\right)<AV\left({\tilde{A}}_2\right). \end{gathered}$$

(6)

Definition 4

([37]). Consider two T-SFN ${\tilde{A}}_1=({\alpha }_1,{\gamma }_1,{\beta }_1)$ and ${\tilde{A}}_2=({\alpha }_2,{\gamma }_2,{\beta }_2)$, the Einstein interaction operations are defined as

$$\begin{gathered} {\tilde{A}}_1\oplus {\tilde{A}}_2= \\ \left(\begin{array}{c}{\left(\frac{\left(1+{\alpha }_1^t\right)\left(1+{\alpha }_2^t\right)-\left(1-{\alpha }_1^t\right)\left(1-{\alpha }_2^t\right)}{\left(1+{\alpha }_1^t\right)\left(1+{\alpha }_2^t\right)+\left(1-{\alpha }_1^t\right)\left(1-{\alpha }_2^t\right)}\right)}^{\frac{1}{t}}, {\left(\frac{\left(1+{\gamma }_1^t\right)\left(1+{\gamma }_2^t\right)-\left(1-{\gamma }_1^t\right)\left(1-{\gamma }_2^t\right)}{\left(1+{\gamma }_1^t\right)\left(1+{\gamma }_2^t\right)+\left(1-{\gamma }_1^t\right)\left(1-{\gamma }_2^t\right)}\right)}^{\frac{1}{t}},\\ {\left(\frac{2\left(\left(1-{\alpha }_1^t-{\gamma }_1^t\right)\left(1-{\alpha }_2^t-{\gamma }_2^t\right)-\left(1-{\alpha }_1^t-{\gamma }_1^t-{\beta }_1^t\right)\left(1-{\alpha }_2^t-{\gamma }_2^t-{\beta }_2^t\right)\right)}{\left(1+{\alpha }_1^t\right)\left(1+{\alpha }_2^t\right)+\left(1-{\alpha }_1^t\right)\left(1-{\alpha }_2^t\right)}\right)}^{\frac{1}{t}}\end{array}\right) \end{gathered}$$

(7)

$$\begin{gathered} {\tilde{A}}_1\otimes {\tilde{A}}_2= \\ \left(\begin{array}{c}{\left(\frac{2\left(\left(1-{\beta }_1^t-{\gamma }_1^t\right)\left(1-{\beta }_2^t-{\gamma }_2^t\right)-\left(1-{\alpha }_1^t-{\gamma }_1^t-{\beta }_1^t\right)\left(1-{\alpha }_2^t-{\gamma }_2^t-{\beta }_2^t\right)\right)}{\left(1+{\beta }_1^t\right)\left(1+{\beta }_2^t\right)+\left(1-{\beta }_1^t\right)\left(1-{\beta }_2^t\right)}\right)}^{\frac{1}{t}}, \\ {\left(\frac{\left(1+{\gamma }_1^t\right)\left(1+{\gamma }_2^t\right)-\left(1-{\gamma }_1^t\right)\left(1-{\gamma }_2^t\right)}{\left(1+{\gamma }_1^t\right)\left(1+{\gamma }_2^t\right)+\left(1-{\gamma }_1^t\right)\left(1-{\gamma }_2^t\right)}\right)}^{\frac{1}{t}},{\left(\frac{\left(1+{\beta }_1^t\right)\left(1+{\beta }_2^t\right)-\left(1-{\beta }_1^t\right)\left(1-{\beta }_2^t\right)}{\left(1+{\beta }_1^t\right)\left(1+{\beta }_2^t\right)+\left(1-{\beta }_1^t\right)\left(1-{\beta }_2^t\right)}\right)}^{\frac{1}{t}}\end{array}\right) \end{gathered}$$

(8)

$$\begin{gathered} \omega {\tilde{A}}_1= \\ \left(\begin{array}{c}{\left(\frac{{\left(1+{\alpha }_1^t\right)}^{\omega }-{\left(1-{\alpha }_1^t\right)}^{\omega }}{{\left(1+{\alpha }_1^t\right)}^{\omega }+{\left(1-{\alpha }_1^t\right)}^{\omega }}\right)}^{\frac{1}{t}},{\left(\frac{{\left(1+{\gamma }_1^t\right)}^{\omega }-{\left(1-{\gamma }_1^t\right)}^{\omega }}{{\left(1+{\alpha }_1^t\right)}^{\omega }+{\left(1-{\alpha }_1^t\right)}^{\omega }}\right)}^{\frac{1}{t}},\\ {\left(\frac{2\left({\left(1-{\alpha }_1^t-{\gamma }_1^t\right)}^{\omega }-{\left(1-{\alpha }_1^t-{\gamma }_1^t-{\beta }_1^t\right)}^{\omega }\right)}{{(1+{\alpha }_1^t)}^{\omega }+{(1-{\alpha }_1^t)}^{\omega }}\right)}^{\frac{1}{t}} \end{array}\right), \omega >0 \end{gathered}$$

(9)

$$\begin{gathered} {\left({\tilde{A}}_1\right)}^{\omega }= \\ \left(\begin{array}{c}{\left(\frac{2\left({\left(1-{\beta }_1^t-{\gamma }_1^t\right)}^{\omega }-{\left(1-{\alpha }_1^t-{\gamma }_1^t-{\beta }_1^t\right)}^{\omega }\right)}{{\left(1+{\beta }_1^t\right)}^{\omega }+{\left(1-{\beta }_1^t\right)}^{\omega }}\right)}^{\frac{1}{t}},\\ {\left(\frac{{\left(1+{\gamma }_1^t\right)}^{\omega }-{\left(1-{\gamma }_1^t\right)}^{\omega }}{{\left(1+{\gamma }_1^t\right)}^{\omega }+{\left(1-{\gamma }_1^t\right)}^{\omega }}\right)}^{\frac{1}{t}},{\left(\frac{{\left(1+{\beta }_1^t\right)}^{\omega }-{\left(1-{\beta }_1^t\right)}^{\omega }}{{\left(1+{\beta }_1^t\right)}^{\omega }+{\left(1-{\beta }_1^t\right)}^{\omega }}\right)}^{\frac{1}{t}}\end{array}\right), \omega >0. \end{gathered}$$

(10)

Remark 2.

Definition 3 can be reduced for

(1) 

PFSs if $t=1$;

(2) 

SFSs if $t=2$;

(3) 

q-ROFSs if $\gamma =0$;

(4) 

PyFSs if $t=2$and$\gamma =0$;

(5) 

IFSs if $t=1$ and $\gamma =0$;

(6) 

FSs if $t=1$, $\gamma =0$, and $\beta =0.$

Definition 5

([37]). Consider T-SFNs ${\tilde{A}}_i=({\alpha }_i,{\gamma }_i,{\beta }_i)$ with $i=1\dots m$, the T-spherical fuzzy weighted Einstein interactive geometric aggregator (TSFWEIGA) and the T-spherical fuzzy weighted Einstein interactive arithmetic aggregator (TSFWEIAA) with the weight vector $w=\left(w_1,w_2,\dots ,w_m\right)$ are defined as

$$\begin{gathered} {TSFWEIGA}_w\left({\tilde{A}}_1,{\tilde{A}}_2,\dots ,{\tilde{A}}_m\right)={\otimes }_{i=1}^m{\tilde{A}}_i^{w_i}= \\ \left(\begin{array}{c}{\left(\frac{2\left(\prod _{i=1}^m{\left(1-{\beta }_1^t-{\gamma }_1^t\right)}^{w_i}-\prod _{i=1}^m{\left(1-{\alpha }_1^t-{\gamma }_1^t-{\beta }_1^t\right)}^{w_i}\right)}{\prod _{i=1}^m{\left(1+{\beta }_1^t\right)}^{w_i}+\prod _{i=1}^m{\left(1-{\beta }_1^t\right)}^{w_i}}\right)}^{\frac{1}{t}},\\ {\left(\frac{\prod _{i=1}^m{\left(1+{\gamma }_1^t\right)}^{w_i}-\prod _{i=1}^m{\left(1-{\gamma }_1^t\right)}^{w_i}}{\prod _{i=1}^m{\left(1+{\gamma }_1^t\right)}^{w_i}+\prod _{i=1}^m{\left(1-{\gamma }_1^t\right)}^{w_i}}\right)}^{\frac{1}{t}},{\left(\frac{\prod _{i=1}^m{\left(1+{\beta }_1^t\right)}^{w_i}-\prod _{i=1}^m{\left(1-{\beta }_1^t\right)}^{w_i}}{\prod _{i=1}^m{\left(1+{\beta }_1^t\right)}^{w_i}+\prod _{i=1}^m{\left(1-{\beta }_1^t\right)}^{w_i}}\right)}^{\frac{1}{t}}\end{array}\right) \end{gathered}$$

(11)

$$\begin{gathered} {TSFWEIAA}_w\left({\tilde{A}}_1,{\tilde{A}}_2,\dots ,{\tilde{A}}_m\right)={\oplus }_{i=1}^m{w}_i{\tilde{A}}_i= \\ \left(\begin{array}{c}{\left(\frac{\prod _{i=1}^m{\left(1+{\alpha }_1^t\right)}^{w_i}-\prod _{i=1}^m{\left(1-{\alpha }_1^t\right)}^{w_i}}{\prod _{i=1}^m{\left(1+{\alpha }_1^t\right)}^{w_i}+\prod _{i=1}^m{\left(1-{\alpha }_1^t\right)}^{w_i}}\right)}^{\frac{1}{t}},{\left(\frac{\prod _{i=1}^m{\left(1+{\gamma }_1^t\right)}^{w_i}-\prod _{i=1}^m{\left(1-{\gamma }_1^t\right)}^{w_i}}{\prod _{i=1}^m{\left(1+{\alpha }_1^t\right)}^{w_i}+\prod _{i=1}^m{\left(1-{\alpha }_1^t\right)}^{w_i}}\right)}^{\frac{1}{t}},\\ {\left(\frac{2\left(\prod _{i=1}^m{\left(1-{\alpha }_1^t-{\gamma }_1^t\right)}^{w_i}-\prod _{i=1}^m{\left(1-{\alpha }_1^t-{\gamma }_1^t-{\beta }_1^t\right)}^{w_i}\right)}{\prod _{i=1}^m{(1+{\alpha }_1^t)}^{w_i}+\prod _{i=1}^m{(1-{\alpha }_1^t)}^{w_i}}\right)}^{\frac{1}{t}} \end{array}\right) \end{gathered}$$

(12)

where

$$0\le w_i\le 1, i=1\dots m$$

(13)

and

$$\sum _{i=1}^m{w}_i=1.$$

(14)

2.2. The Integrated T-Spherical Fuzzy Einstein Interaction Aggregator Group Decision-Making Approach

This section comprehensively details the novel approach, providing a step-by-step description accompanied by Figure 1 for visual reference. In this study, the integration of TSFWEIGA and TSFWEIAA into the CRITIC and CoCoSo methods is proposed. For the CRITIC method, which typically determines the weight of criteria based on their variability and correlation, TSFWEIGA has been utilized to enhance the handling of fuzzy data characteristics such as uncertainty and hesitancy. This integration allows for a more sophisticated evaluation of the criteria’ importance, taking into account the subtle nuances and interdependencies among criteria that traditional methods might overlook. Detailed mathematical formulations are included to demonstrate how the TSFWEIGA modifies the calculation of criteria weights, thereby enhancing the robustness and accuracy of the method in capturing the complexities of expert judgments in a fuzzy environment. Similarly, the CoCoSo method, used for selecting and ranking alternatives based on a combination of compromise solutions, has been augmented by incorporating TSFWEIAA. This operator facilitates a more dynamic interaction among multiple decision criteria, reflecting the real-world complexities and dependencies of the criteria in the decision-making process. The revised section includes a step-by-step explanation of how TSFWEIAA is implemented within CoCoSo, detailing the operational improvements and providing justification for its use over more traditional aggregation operators. These enhancements are supported by a theoretical discussion on the benefits of employing these fuzzy aggregation operators, particularly their capability to handle multi-dimensional fuzzy data more effectively.

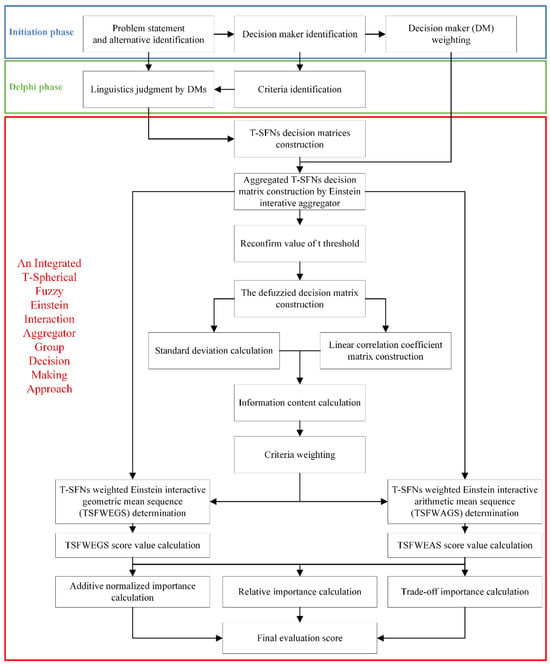
Figure 1. The integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach.

Step 1. Define the group decision-making problem with $I$ alternatives $(i=1\dots I)$.

Step 2. Define the group of $K$ decision-makers ($k=1\dots K)$.

Step 3. Let a given T-SFNs ${\tilde{Q}}_k=({\alpha }_k,{\gamma }_k,{\beta }_k)$ is the degree of expertise of $k$th decision-maker. The weight $\left({\omega }_k\right)$ of $k$th decision-maker is determined as

$${\omega }_k=\frac{1-{\left(\frac{\left(\left(1-{\alpha }_k^t\right)+{\beta }_k^t+{\gamma }_k^t\right)}{3}\right) }^{\frac{1}{t}}}{\sum _{k=1}^K\left(1-{\left(\frac{\left(\left(1-{\alpha }_k^t\right)+{\beta }_k^t+{\gamma }_k^t\right)}{3}\right) }^{\frac{1}{t}}\right)}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}k=1\dots K$$

(15)

Step 4. Through the Delphi method procedure, the $J$ evaluation criteria $(j=1\dots J)$ are defined from the perspectives of the decision-makers.

Step 5. Decision-makers provide linguistic judgments on alternatives for each criterion.

Step 6. Linguistic judgments are converted into T-SFNs. For example, in this study, the relationship between the linguistic judgments and T-SFNs is applied according to Table 1 $(t=2)$. As a result, the T-SFN decision matrix of $k$th decision-maker is established and shown in Equation (16).

$$X_k={\left[{\tilde{x}}_{kij}\right]}_{IxJ}$$

(16)

where

$${\tilde{x}}_{kij}=\left({\alpha }_{kij},{\gamma }_{kij},{\beta }_{kij}\right)\hspace{1em}\hspace{1em}\hspace{1em}k=1\dots K, i=1\dots I, j=1\dots J$$

(17)

Table 1. The corresponding T-SFN and linguistic judgments.

Linguistic Judgments	Notation	T-SFN $(\mathit{\alpha },\mathit{\gamma },\mathit{\beta })$
Extremely low	EL	0.040, 0.040, 0.960
Very low	VL	0.155, 0.155, 0.845
Low	L	0.270, 0.270, 0.730
Slightly low	SL	0.385, 0.385, 0.615
Medium	M	0.500, 0.500, 0.500
Slightly high	SH	0.615, 0.385, 0.385
Very high	VH	0.730, 0.270, 0.270
High	H	0.845, 0.155, 0.155
Extremely high	EH	0.960, 0.040, 0.040

Step 7. By applying the T-spherical fuzzy weighted Einstein interactive arithmetic aggregator, as shown in Equation (12), the aggregated T-SFN decision matrix is established.

$$Y={TSFWEIAA}_{{\omega }_k}\left({\tilde{x}}_{1ij},{\tilde{x}}_{2ij},\dots ,{\tilde{x}}_{3ij}\right)={\oplus }_{k=1}^K{\omega }_k{\tilde{x}}_{kij}={\left[{\tilde{y}}_{ij}\right]}_{IxJ}$$

(18)

where

$${\tilde{y}}_{ij}=\left({\alpha }_{ij},{\gamma }_{ij},{\beta }_{ij}\right)\hspace{1em}\hspace{1em}i=1\dots I, j=1\dots J$$

(19)

Step 8. Recheck the value of $t$ because the properties of T-SFNs may change after aggregation. Thus, the value of t is determined such that:

$$0\le {\alpha }_{ij}^t+{\gamma }_{ij}^t+{\beta }_{ij}^t\le 1\hspace{1em}\hspace{1em}i=1\dots I, j=1\dots J$$

(20)

where

$${\tilde{y}}_{ij}=\left({\alpha }_{ij},{\gamma }_{ij},{\beta }_{ij}\right)\hspace{1em}\hspace{1em}i=1\dots I, j=1\dots J$$

(21)

Step 9. Determine the score value of the aggregated T-SFN decision matrix according to Equation (4). Then, the defuzzied decision matrix is constructed as

$$Z={\left[z_{ij}\right]}_{IxJ}$$

(22)

where

$$z_{ij}={\alpha }_{ij}^t-{\beta }_{ij}^t\hspace{1em}\hspace{1em}i=1\dots I, j=1\dots J$$

(23)

Step 10. Calculate the standard deviation of alternatives according to each criterion.

$${\sigma }_j=\sqrt{\frac{\sum _{i=1}^I{\left|z_{ij}-{\overline{z}}_j\right|}^2}{I}}\hspace{1em}\hspace{1em}j=1\dots J$$

(24)

where

$${\overline{z}}_j=\frac{\sum _{i=1}^I{z}_{ij}}{I}\hspace{1em}\hspace{1em}j=1\dots J$$

(25)

Step 11. Determine the linear correlation coefficient for each pair of $j$th criterion and $l$th criterion. The correlation coefficient matrix $\left(CR\right)$ is obtained as follows:

$$CR={\left[r_{jl}\right]}_{JxJ}$$

(26)

where

$$r_{jl}=\frac{\sum _{i=1}^I\left(z_{ij}-{\overline{z}}_j\right)\left(z_{il}-{\overline{z}}_l\right)}{ \sqrt{{\sum }_{i=1}^I{\left(z_{ij}-{\overline{z}}_j\right)}^2} \sqrt{{\sum }_{i=1}^I{\left(z_{il}-{\overline{z}}_l\right)}^2}}\hspace{1em}\hspace{1em}j=1\dots J, l=1\dots J$$

(27)

Step 12. Calculate the amount of information content of each criterion as

$${\phi }_j={\sigma }_j\sum _{l=1}^J(1-r_{jl}) j=1\dots J$$

(28)

Step 13. Determine the weight of the criteria as

$$w_j=\frac{{\phi }_j}{\sum _{j=1}^J{\phi }_j} j=1\dots J$$

(29)

Step 14. Based on the T-SFN aggregated decision matrix $\left(Y\right)$ and obtained the criteria weight $\left(w_j\right)$, the T-spherical fuzzy weighted Einstein interactive arithmetic mean sequence $\left({TSFWEAS}_i\right)$ and the T-spherical fuzzy weighted Einstein interactive geometric mean sequence $\left({TSFEWGS}_i\right)$ of each alternative are determined as

$${TSFWEAS}_i={TSFWEIAA}_{w_j}\left({\tilde{y}}_{1j},{\tilde{y}}_{2j},\dots ,{\tilde{y}}_{Ij}\right)={\oplus }_{j=1}^J{w}_j{\tilde{y}}_{ij} i=1\dots I$$

(30)

$${TSFWEGS}_i={TSFWEIGA}_{w_j}\left({\tilde{y}}_{1j},{\tilde{y}}_{2j},\dots ,{\tilde{y}}_{Ij}\right)={\otimes }_{j=1}^J{\tilde{y}}_{ij}^{w_j} i=1\dots I$$

(31)

Step 15. The score values of ${TSFWEAS}_i$ and ${TSFWEGS}_i$ are calculated according to Equation (4).

Step 16. Determine the additive normalized importance $\left({\theta }_i\right)$, the relative importance $\left({\pi }_i\right)$, and the trade-off importance $\left({\tau }_i\right)$ of each alternative with the trade-off coefficient $\left(\lambda \right)$.

$${\theta }_i=\frac{{TSFWEAS}_i+{TSFWEGS}_i}{\sum _{i=1}^I({TSFWEAS}_i+{TSFWEGS}_i)} i=1\dots I$$

(32)

$${\pi }_i=\frac{{TSFEAS}_i}{\underset{i}{\min }\left({TSFWEAS}_i\right)}+\frac{{TSFEGS}_i}{\underset{i}{\min }\left({TSFWEGS}_i\right)} i=1\dots I$$

(33)

$${\tau }_i=\frac{(\lambda {)TSFWEAS}_i+(1-\lambda ){TSFWEGS}_i}{\left(\lambda \right)\underset{i}{\max }\left({TSFWEAS}_i\right)+(1-\lambda )\underset{i}{\max }\left({TSFWEGS}_i\right)} i=1\dots I$$

(34)

Step 17. Calculate the final evaluation score of alternatives as

$${\kappa }_i=\frac{{\theta }_i+{\pi }_i+{\tau }_i}{3}+\sqrt[3]{{\theta }_i+{\pi }_i+{\tau }_i} i=1\dots I$$

(35)

3. Results

3.1. The Proposed Approach Application

In the practical application of our theoretical framework, this study conducts a case study focusing on the deployment of concrete 3D printing robots in Vietnam’s construction industry. This segment aims to illustrate how the novel integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach can be effectively applied to real-world scenarios. This case study explores a specific construction project where concrete 3D printing technology is being considered, providing an in-depth analysis of the operational, economic, and regulatory environments that influence technology adoption.

In the beginning, a group of ten experts from relevant fields was invited to participate in the Delphi method procedures as decision-makers (DM), and their expertise is detailed in Table 2. Accordingly, the analyst provides linguistic assessments of the experts’ qualifications and converts them into T-SFNs. Based on these T-SFNs, the weight of decision-makers is computed according to Equation (15), as presented in Table 3.

Table 2. The decision-makers and their expertise.

DM No.	Highest Degree	Work Position	Years of Experience	Field
1	Ph.D.	Chief Technology Officer	20	Robotics and Automation
2	Ph.D.	Professor of Civil Engineering	25	Civil Engineering
3	M.Sc.	Senior Project Manager	15	Construction Management
4	Ph.D.	Director of R&D	18	Material Science
5	Ph.D.	Innovation Strategist	12	Construction Technology
6	M.Eng.	Construction Technology Consultant	10	Sustainable Building Practices
7	Ph.D.	Lead Structural Engineer	22	Structural Engineering
8	Ph.D.	Head of Advanced Manufacturing	19	Advanced Manufacturing Technologies
9	Ph.D.	Urban Planning Expert	20	Urban Development and Planning
10	M.Eng.	Robotics Integration Specialist	8	Robotics

Table 3. The linguistic assessment of DM’s qualifications, corresponding T-SFN, and weight.

Expert No.	Linguistic Assessment of Qualification	T-SFN	DM’s Weight
1	Very high	(0.730, 0.270, 0.270)	0.103
2	High	(0.845, 0.155, 0.155)	0.125
3	Slightly high	(0.615, 0.385, 0.385)	0.084
4	Very high	(0.730, 0.270, 0.270)	0.103
5	Slightly high	(0.615, 0.385, 0.385)	0.084
6	Medium	(0.500, 0.500, 0.500)	0.066
7	High	(0.845, 0.155, 0.155)	0.125
8	High	(0.845, 0.155, 0.155)	0.125
9	High	(0.845, 0.155, 0.155)	0.125
10	Slightly low	(0.385, 0.385, 0.615)	0.060

In the next phase, the three-round in-depth interview process in the Delphi method procedure is conducted with each decision-maker independently. In the first round of interviews, the experts participating helped establish a list of ten potential barriers to the adoption of concrete 3D printing robots in the construction industry in Vietnam, as described in Table 4. In the second round of interviews, experts were provided with a comprehensive list of potential barriers. Based on that information, experts have proposed six strategies to address them, including:

• Subsidies and financial incentives (ST1): Governments and industry associations can provide subsidies, grants, or tax incentives to offset the high initial costs and encourage investment in 3D printing technology. This can make the technology more accessible to smaller firms and startups.
• Training and education programs (ST2): Develop comprehensive training programs in collaboration with educational institutions and technology providers to equip current and future construction workers with the necessary skills to operate and manage 3D printing technologies. This can help mitigate the lack of expertise in the field.
• Regulatory framework adjustments (ST3): Work with regulatory bodies to update and adapt building codes and standards to include provisions for 3D-printed structures. This can ensure that these innovative construction methods are legally compliant and can be more readily adopted.
• Research and development (ST4): Encourage partnerships between universities, research institutions, and construction firms to advance the technology, improve the quality and durability of 3D-printed structures, and expand the range of designs that can be realized. This could involve developing new materials or enhancing printer capabilities.
• Pilot projects and demonstrations (ST5): Implement pilot projects to showcase the capabilities and benefits of concrete 3D printing. This can help build trust and acceptance among stakeholders by demonstrating the practical applications and effectiveness of the technology in real-world settings.
• Sustainability initiatives (ST6): Promote the environmental benefits of 3D printing, such as reduced waste and the potential for using recycled materials, to address environmental and safety concerns. Establishing clear guidelines and best practices for the sustainable use of 3D printing in construction can also help overcome related barriers.

Table 4. The potential barriers to the adoption of concrete 3D printing robots in the construction industry in Vietnam.

No.	Potential Barriers	Notation	Description
1	High initial costs	B1	The upfront investment in 3D printing technology, including the cost of robots and materials, can be significant.
2	Technical challenges	B2	There may be technical limitations related to the precision, speed, and quality of 3D printing with concrete that need to be overcome.
3	Supply chain issues	B3	Ensuring a reliable supply of specialized materials that are required for concrete 3D printing can be challenging.
4	Lack of expertise	B4	There may be a shortage of professionals trained to operate 3D printing equipment and to integrate this technology into current construction practices.
5	Regulatory barriers	B5	The existing regulatory frameworks may not be adapted for buildings constructed with 3D printing technologies, leading to approval and compliance issues.
6	Cultural resistance	B6	Traditional construction industries may show resistance to adopting new technologies due to entrenched practices and a reluctance to change.
7	Maintenance and operational challenges	B7	Maintaining and operating sophisticated 3D printing equipment in rugged construction environments can be difficult.
8	Quality and durability concerns	B8	There could be concerns about the long-term durability and structural integrity of buildings constructed using 3D-printed concrete.
9	Limited design flexibility	B9	While 3D printing allows for innovative designs, there might be limitations in terms of scale and complexity that can be achieved with current technology.
10	Environmental and safety Issues	B10	Ensuring that the technology is environmentally sustainable and adheres to safety standards, especially in a construction environment, can be a substantial barrier.

Table 4. The potential barriers to the adoption of concrete 3D printing robots in the construction industry in Vietnam.

No.	Potential Barriers	Notation	Description
1	High initial costs	B1	The upfront investment in 3D printing technology, including the cost of robots and materials, can be significant.
2	Technical challenges	B2	There may be technical limitations related to the precision, speed, and quality of 3D printing with concrete that need to be overcome.
3	Supply chain issues	B3	Ensuring a reliable supply of specialized materials that are required for concrete 3D printing can be challenging.
4	Lack of expertise	B4	There may be a shortage of professionals trained to operate 3D printing equipment and to integrate this technology into current construction practices.
5	Regulatory barriers	B5	The existing regulatory frameworks may not be adapted for buildings constructed with 3D printing technologies, leading to approval and compliance issues.
6	Cultural resistance	B6	Traditional construction industries may show resistance to adopting new technologies due to entrenched practices and a reluctance to change.
7	Maintenance and operational challenges	B7	Maintaining and operating sophisticated 3D printing equipment in rugged construction environments can be difficult.
8	Quality and durability concerns	B8	There could be concerns about the long-term durability and structural integrity of buildings constructed using 3D-printed concrete.
9	Limited design flexibility	B9	While 3D printing allows for innovative designs, there might be limitations in terms of scale and complexity that can be achieved with current technology.
10	Environmental and safety Issues	B10	Ensuring that the technology is environmentally sustainable and adheres to safety standards, especially in a construction environment, can be a substantial barrier.

After the second round of interviews, the main components of an MCDM problem were identified, as depicted in Figure 2. In the final round of interviews, experts provide linguistic judgments about the effectiveness of the strategies for each potential barrier. The linguistic judgments of the first expert are shown in Table 5. In the next step, the linguistic judgments are transformed into the corresponding T-SFNs, according to Table 1. As a result, the K T-SFN decision matrices are established for each expert. The first expert’s T-SFN decision matrix is shown in Table 6, while the remaining linguistic judgments and T-SFN decision matrix are presented in Appendix A.

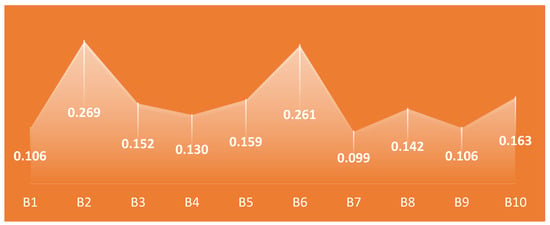
Figure 2. The standard deviation in Barriers’ data.

Table 5. The linguistic judgments of the first expert.

Strategy	Barriers
	B1	B2	B3	B4	B5	B6	B7	B8	B9	B10
ST1	VH	L	SL	EH	M	H	L	SL	L	EH
ST2	SH	H	SH	EH	VH	SH	SH	EH	SH	L
ST3	H	H	SL	L	EH	EH	SH	H	EH	SL
ST4	M	SL	SH	SL	VH	VH	VH	EH	H	M
ST5	H	SL	VH	SH	M	VH	EH	EH	L	L
ST6	EH	L	SL	VH	H	VH	SH	SH	L	SL

Table 6. The T-SFN decision matrix of the first expert.

Strategy	Barriers
	B1	B2	B3	B4	B5
ST1	(0.730, 0.270, 0.270)	(0.270, 0.270, 0.730)	(0.385, 0.385, 0.615)	(0.960, 0.040, 0.040)	(0.500, 0.500, 0.500)
ST2	(0.615, 0.385, 0.385)	(0.845, 0.155, 0.155)	(0.615, 0.385, 0.385)	(0.960, 0.040, 0.040)	(0.730, 0.270, 0.270)
ST3	(0.845, 0.155, 0.155)	(0.845, 0.155, 0.155)	(0.385, 0.385, 0.615)	(0.270, 0.270, 0.730)	(0.960, 0.040, 0.040)
ST4	(0.500, 0.500, 0.500)	(0.385, 0.385, 0.615)	(0.615, 0.385, 0.385)	(0.385, 0.385, 0.615)	(0.730, 0.270, 0.270)
ST5	(0.845, 0.155, 0.155)	(0.385, 0.385, 0.615)	(0.730, 0.270, 0.270)	(0.615, 0.385, 0.385)	(0.500, 0.500, 0.500)
ST6	(0.960, 0.040, 0.040)	(0.270, 0.270, 0.730)	(0.385, 0.385, 0.615)	(0.730, 0.270, 0.270)	(0.845, 0.155, 0.155)
Strategy	B6	B7	B8	B9	B10
ST1	(0.845, 0.155, 0.155)	(0.270, 0.270, 0.730)	(0.385, 0.385, 0.615)	(0.270, 0.270, 0.730)	(0.960, 0.040, 0.040)
ST2	(0.615, 0.385, 0.385)	(0.615, 0.385, 0.385)	(0.960, 0.040, 0.040)	(0.615, 0.385, 0.385)	(0.270, 0.270, 0.730)
ST3	(0.960, 0.040, 0.040)	(0.615, 0.385, 0.385)	(0.845, 0.155, 0.155)	(0.960, 0.040, 0.040)	(0.385, 0.385, 0.615)
ST4	(0.730, 0.270, 0.270)	(0.730, 0.270, 0.270)	(0.960, 0.040, 0.040)	(0.845, 0.155, 0.155)	(0.500, 0.500, 0.500)
ST5	(0.730, 0.270, 0.270)	(0.960, 0.040, 0.040)	(0.960, 0.040, 0.040)	(0.270, 0.270, 0.730)	(0.270, 0.270, 0.730)
ST6	(0.730, 0.270, 0.270)	(0.615, 0.385, 0.385)	(0.615, 0.385, 0.385)	(0.270, 0.270, 0.730)	(0.385, 0.385, 0.615)

After the Delphi procedure is completed, the aggregation is deployed using a T-spherical fuzzy weighted Einstein interactive arithmetic aggregator with experts’ weight according to Equation (18). Thus, the aggregated T-SFN decision matrix is established, as shown in Table 7. As discussed in Section 2, the properties of T-SFNs can be changed by the aggregation process. Therefore, the $t$ threshold of T-SFNs needs to be redefined by checking the condition of Equation (2) in Definition 1. According to Equation (2), let $\mathsf{\Omega }={\alpha }^t\left(x\right)+{\gamma }^t\left(x\right)+{\beta }^t\left(x\right)$ be the T-SFNs verification coefficient for Definition 1. As shown in Table 8, the $t$ threshold with values of 2 and 3 satisfies Equation (2). Therefore, the following calculations can be implemented with $t=2$ or $t=3$.

Table 7. The aggregated T-SFN decision matrix.

Strategy	Barriers
	B1	B2	B3	B4	B5
ST1	(0.743, 0.342, 0.341)	(0.859, 0.197, 0.255)	(0.787, 0.306, 0.311)	(0.746, 0.335, 0.375)	(0.586, 0.379, 0.477)
ST2	(0.728, 0.304, 0.345)	(0.809, 0.228, 0.251)	(0.688, 0.323, 0.409)	(0.795, 0.314, 0.285)	(0.685, 0.339, 0.381)
ST3	(0.806, 0.273, 0.241)	(0.692, 0.300, 0.398)	(0.591, 0.338, 0.487)	(0.621, 0.358, 0.431)	(0.767, 0.346, 0.347)
ST4	(0.680, 0.350, 0.415)	(0.791, 0.324, 0.297)	(0.640, 0.329, 0.435)	(0.772, 0.295, 0.335)	(0.736, 0.321, 0.336)
ST5	(0.689, 0.373, 0.378)	(0.669, 0.327, 0.412)	(0.664, 0.307, 0.412)	(0.784, 0.286, 0.339)	(0.815, 0.307, 0.304)
ST6	(0.720, 0.318, 0.394)	(0.499, 0.368, 0.556)	(0.582, 0.403, 0.472)	(0.689, 0.390, 0.389)	(0.691, 0.294, 0.427)
Strategy	B6	B7	B8	B9	B10
ST1	(0.812, 0.269, 0.304)	(0.655, 0.322, 0.444)	(0.702, 0.362, 0.381)	(0.731, 0.279, 0.401)	(0.842, 0.265, 0.259)
ST2	(0.651, 0.348, 0.475)	(0.610, 0.350, 0.463)	(0.749, 0.297, 0.369)	(0.599, 0.366, 0.449)	(0.658, 0.290, 0.405)
ST3	(0.741, 0.318, 0.380)	(0.694, 0.295, 0.386)	(0.762, 0.297, 0.317)	(0.696, 0.314, 0.402)	(0.696, 0.347, 0.421)
ST4	(0.839, 0.264, 0.272)	(0.719, 0.339, 0.363)	(0.610, 0.374, 0.483)	(0.740, 0.318, 0.359)	(0.699, 0.358, 0.396)
ST5	(0.479, 0.378, 0.560)	(0.728, 0.327, 0.376)	(0.707, 0.370, 0.356)	(0.760, 0.299, 0.337)	(0.631, 0.311, 0.497)
ST6	(0.693, 0.389, 0.393)	(0.631, 0.335, 0.443)	(0.606, 0.383, 0.461)	(0.714, 0.350, 0.390)	(0.708, 0.316, 0.380)

Table 8. The T-SFNs verification coefficient.

t Threshold	Strategy	Barriers
		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10
1	ST1	1.426	1.311	1.405	1.456	1.442	1.384	1.421	1.446	1.411	1.367
	ST2	1.376	1.287	1.420	1.395	1.405	1.474	1.423	1.414	1.414	1.354
	ST3	1.320	1.391	1.417	1.411	1.459	1.439	1.374	1.376	1.413	1.464
	ST4	1.445	1.412	1.404	1.401	1.393	1.374	1.421	1.467	1.418	1.454
	ST5	1.440	1.408	1.383	1.409	1.426	1.416	1.432	1.433	1.395	1.439
	ST6	1.432	1.422	1.457	1.468	1.412	1.474	1.409	1.450	1.454	1.403
2	ST1	0.785	0.842	0.810	0.809	0.714	0.824	0.729	0.770	0.773	0.847
	ST2	0.741	0.769	0.745	0.813	0.729	0.770	0.709	0.785	0.694	0.682
	ST3	0.782	0.728	0.701	0.700	0.828	0.795	0.717	0.769	0.745	0.782
	ST4	0.757	0.818	0.707	0.795	0.758	0.847	0.764	0.745	0.779	0.774
	ST5	0.756	0.725	0.705	0.811	0.850	0.685	0.779	0.763	0.780	0.741
	ST6	0.775	0.693	0.724	0.778	0.746	0.785	0.707	0.726	0.785	0.745
3	ST1	0.490	0.658	0.546	0.505	0.364	0.583	0.402	0.449	0.477	0.633
	ST2	0.454	0.556	0.428	0.557	0.415	0.425	0.369	0.496	0.354	0.376
	ST3	0.558	0.422	0.361	0.366	0.534	0.494	0.417	0.500	0.433	0.453
	ST4	0.429	0.554	0.380	0.523	0.469	0.629	0.459	0.392	0.485	0.450
	ST5	0.432	0.405	0.392	0.544	0.598	0.339	0.474	0.449	0.503	0.404
	ST6	0.466	0.345	0.368	0.445	0.434	0.452	0.376	0.376	0.466	0.441

Following the $t$ threshold verification, the score value of the aggregated T-SFN decision matrix according to Equation (4) is shown in Table 9. Based on the score value matrix, the standard deviations in each criterion and the linear correlation coefficients between criteria can be determined according to Equations (24)–(27). Those results are illustrated in Figure 2 and Table 10. Then, according to Equations (28)–(29), the weights of potential barriers are computed as shown in Figure 3.

Table 9. The score value matrix.

Strategy	Barriers
	B1	B2	B3	B4	B5	B6	B7	B8	B9	B10
ST1	0.436	0.672	0.522	0.416	0.116	0.567	0.231	0.348	0.374	0.642
ST2	0.411	0.591	0.306	0.551	0.323	0.199	0.158	0.424	0.157	0.269
ST3	0.592	0.321	0.113	0.201	0.468	0.405	0.333	0.480	0.323	0.307
ST4	0.290	0.537	0.219	0.484	0.428	0.630	0.386	0.139	0.419	0.332
ST5	0.331	0.278	0.271	0.499	0.572	−0.084	0.389	0.373	0.463	0.151
ST6	0.363	−0.060	0.116	0.323	0.296	0.325	0.201	0.154	0.358	0.356

Table 10. The linear correlation coefficients between criteria.

Barrier	B1	B2	B3	B4	B5	B6	B7	B8	B9	B10
B1	1.000	0.051	0.051	−0.716	−0.098	0.122	−0.176	0.735	−0.393	0.197
B2	0.051	1.000	0.741	0.484	−0.322	0.365	−0.024	0.314	−0.253	0.391
B3	−0.115	0.741	1.000	0.502	−0.605	0.148	−0.238	0.188	−0.014	0.619
B4	−0.716	0.484	0.502	1.000	−0.001	−0.276	−0.065	−0.140	−0.099	−0.190
B5	−0.098	−0.322	−0.605	−0.001	1.000	−0.544	0.728	0.145	0.314	−0.898
B6	0.122	0.365	0.148	−0.276	−0.544	1.000	−0.038	−0.382	0.020	0.724
B7	−0.176	−0.024	−0.238	−0.065	0.728	−0.038	1.000	−0.085	0.759	−0.378
B8	0.735	0.314	0.188	−0.140	0.145	−0.382	−0.085	1.000	−0.419	−0.134
B9	−0.393	−0.253	−0.014	−0.099	0.314	0.020	0.759	−0.419	1.000	0.001
B10	0.197	0.391	0.619	−0.190	−0.898	0.724	−0.378	−0.134	0.001	1.000

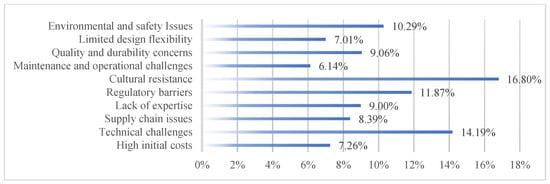
Figure 3. The weight of potential barriers obtained by the proposed approach.

The barrier weighting results from the integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach provide valuable insights into the challenges facing the adoption of concrete 3D printing robots in Vietnam’s construction industry. Cultural resistance, with the highest weight of 16.80%, underscores a significant reluctance within the industry to shift from traditional construction practices to innovative technologies. Addressing this barrier requires comprehensive educational initiatives and demonstrations to showcase the technology’s benefits. Technical challenges, the second most significant barrier at 14.19%, suggest that precision, speed, and quality of 3D printing need enhancements through continuous research and collaboration with experts. Regulatory barriers, weighing 11.87%, highlight the necessity for updated standards and codes that accommodate 3D printing technologies, necessitating collaboration with regulatory bodies. Environmental and safety issues, carrying a weight of 10.29%, point towards the importance of aligning 3D printing processes with stringent environmental and safety standards to foster sustainable and safe practices. The close weights of lack of expertise and quality and durability concerns, both around 9%, emphasize the need for skilled workforce development and rigorous quality assurance to ensure structural integrity. Supply chain issues, at 8.39%, indicate challenges in securing a steady supply of specialized materials, suggesting the establishment of robust local supply chains. High initial costs and limited design flexibility, weighted at 7.26% and 7.01%, respectively, imply financial and technological constraints that could be mitigated through strategic investments and technological advancements. Finally, maintenance and operational challenges, the least weighted barrier at 6.14%, point to the need for regular training and maintenance to ensure the smooth operation of sophisticated equipment. These findings reveal that while technological and financial issues are critical, the more significant challenges are human and regulatory factors.

The purpose of the next phase is to prioritize strategies to overcome the barriers. Then, the T-spherical fuzzy weighted Einstein interactive arithmetic mean sequence $\left({TSFWEAS}_i\right)$ and the T-spherical fuzzy weighted Einstein interactive geometric mean sequence $\left({TSFEWGS}_i\right)$ of each strategy are determined according to Equations (30) and (31). After this step, the score values of those mean sequences are calculated according to Equation (4). Those mean sequences and their score values are shown in Table 11. Based on Table 11, the additive normalized importance $\left({\theta }_i\right)$, the relative importance $\left({\pi }_i\right)$, the trade-off importance $\left({\tau }_i\right)$, and the final evaluation score (${\kappa }_i$) of each strategy are determined according to Equations (32)–(35), as shown in Table 12.

Table 11. The T-SFN Einstein interactive mean sequences and their score values.

Strategy	${\mathit{T}\mathit{S}\mathit{F}\mathit{W}\mathit{E}\mathit{A}\mathit{S}}_{\mathit{i}}$	${\mathit{T}\mathit{S}\mathit{F}\mathit{E}\mathit{W}\mathit{G}\mathit{S}}_{\mathit{i}}$	$\mathit{S}\mathit{V}\left({\mathit{T}\mathit{S}\mathit{F}\mathit{W}\mathit{E}\mathit{A}\mathit{S}}_{\mathit{i}}\right)$	$\mathit{S}\mathit{V}\left({\mathit{T}\mathit{S}\mathit{F}\mathit{E}\mathit{W}\mathit{G}\mathit{S}}_{\mathit{i}}\right)$
ST1	(0.770, 0.304, 0.342)	(0.762, 0.304, 0.353)	0.47566	0.45564
ST2	(0.711, 0.315, 0.382)	(0.706, 0.315, 0.389)	0.35881	0.34692
ST3	(0.715, 0.321, 0.383)	(0.714, 0.321, 0.387)	0.36510	0.35963
ST4	(0.745, 0.324, 0.354)	(0.741, 0.324, 0.363)	0.42973	0.41686
ST5	(0.691, 0.333, 0.409)	(0.684, 0.333, 0.421)	0.31017	0.29061
ST6	(0.656, 0.359, 0.433)	(0.653, 0.359, 0.439)	0.24251	0.23338

Table 12. The strategy’s importance and rank.

Strategy	The Additive Normalized Importance $\left({\mathit{\theta }}_{\mathit{i}}\right)$	The Relative Importance $\left({\mathit{\pi }}_{\mathit{i}}\right)$	The Trade-Off Importance $\left({\mathit{\tau }}_{\mathit{i}}\right)$ with $\mathit{\lambda }=\mathbf{0.5}$	The Final Evaluation Score $\left({\mathit{\kappa }}_{\mathit{i}}\right)$	Rank
ST1	0.217	3.914	1.000	2.658	2
ST2	0.165	2.966	0.852	2.074	4
ST3	0.169	3.046	0.311	1.719	6
ST4	0.198	3.558	1.943	3.009	1
ST5	0.140	2.524	1.681	2.289	3
ST6	0.111	2.000	1.532	1.913	5

The prioritization of strategies for the adoption of concrete 3D printing technology in Vietnam, as determined by the integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach, reveals insightful trends about the perceived challenges and key areas of opportunity within this emerging field. The analysis indicates a strategic emphasis on developing technological capabilities and creating an enabling environment for the adoption of 3D printing in construction. Research and development (ST4), which emerged as the highest-ranked strategy with a score of 3.009, underscores a critical focus on enhancing the technological foundations of 3D printing. This priority reflects an understanding among experts that breakthroughs in material science, printer technology, and design capabilities are pivotal. Enhancements in these areas can significantly address the technical challenges currently limiting the precision, speed, and architectural versatility of 3D printers. Furthermore, continuous innovation can lead to the development of new applications and methods, potentially transforming construction practices and outcomes. Subsidies and financial incentives (ST1), with a score of 2.658, highlight the importance of reducing the financial barriers associated with the adoption of this technology. High initial costs of equipment and materials are significant hurdles, especially for small to medium enterprises. By providing subsidies, grants, or tax incentives, governments and industry associations can lower these barriers, making the technology more accessible and fostering a more competitive market. This strategy is not just about easing adoption but also about stimulating a broader ecosystem of innovation and enterprise around 3D printing in construction. Pilot projects and demonstrations (ST5), ranking third with a score of 2.289, are crucial for gaining the trust and buy-in of industry stakeholders. Demonstrating the practical benefits and real-world applications of 3D printing through pilot projects can help dispel doubts and showcase the effectiveness of this technology in improving construction efficiency, reducing waste, and enhancing design capabilities. These projects serve as tangible proof points that can accelerate industry acceptance and integration. Training and education programs (ST2), which received a score of 2.074, reflect the need for a skilled workforce capable of operating new technologies. As 3D printing becomes more integral to construction processes, the demand for professionals who are adept at these new technologies will increase. Collaborative efforts between educational institutions, industry bodies, and technology providers to develop targeted training programs can equip workers with the necessary skills, thus supporting a smooth transition to more technologically advanced construction methods. Sustainability initiatives (ST6), with a score of 1.913, point to the growing importance of environmental considerations in construction. Promoting the environmental benefits of 3D printing, such as its ability to reduce material waste and incorporate recycled materials into new construction, aligns with global sustainability goals and can enhance the social license to operate for businesses in this sector. Establishing best practices and guidelines for sustainable use also helps in mitigating potential environmental and safety concerns associated with new construction technologies. Lastly, regulatory framework adjustments (ST3), though ranked lowest with a score of 1.719, remain a foundational strategy for the long-term integration of 3D printing in construction. The adaptation of building codes and regulatory standards is essential to ensuring that 3D-printed structures are recognized under law, meet safety and quality standards, and are insurable. While this strategy might not provide immediate benefits like the others, it is crucial for ensuring that the operational and commercial integration of 3D printing technology is sustainable and compliant.

3.2. Discussion

The integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach in this study represents a significant advancement in the field of MCDM, particularly tailored for evaluating complex technological adoptions in sectors like construction. This approach is novel in its integration of T-spherical fuzzy sets with Einstein aggregation operators, which enhances the handling of uncertain and subjective expert opinions more flexibly and accurately than traditional methods. T-spherical fuzzy sets extend beyond conventional fuzzy logic by introducing an additional parameter of hesitancy, enriching the representation of uncertainty. Meanwhile, Einstein operators facilitate sophisticated aggregation of multi-criteria data, considering the interdependencies among criteria to provide a balanced evaluative outcome.

This method stands out for its comprehensive modeling of uncertainty, superior decision support capabilities, and flexibility and scalability across various decision-making scenarios. It is particularly adept at summarizing complex data into actionable decision metrics, thereby aiding in managing the information overload that often accompanies extensive decision-making processes. The approach’s theoretical robustness—rooted in advanced mathematical principles—ensures reliable and credible decision-making support, enhancing the integrity and dependability of outcomes. Moreover, it is designed to accommodate iterative refinements, allowing updates and adjustments in response to new data or changing project parameters, thus maintaining relevance and accuracy over time.

4. Conclusions

This study commenced with a detailed exploration of the evolution of fuzzy sets and their applications in decision-making processes, highlighting the development from simple fuzzy sets to more sophisticated models like T-spherical fuzzy sets. As outlined in the introduction, these advanced mathematical tools, particularly when combined with Einstein interaction aggregators, facilitate enhanced MCDM by more accurately modeling uncertainty and aggregating diverse expert opinions. This methodology is especially pertinent in sectors like construction, where technological innovations, such as concrete 3D printing, present both significant opportunities and complex challenges. The methodology employed the integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach, a novel framework designed to tackle the intricacies of evaluating technology adoption barriers and strategies in the construction industry. This innovative method enhances decision-making quality by more accurately handling the uncertainty and imprecision inherent in human judgment, which is often overlooked by deterministic methods. Unlike standard fuzzy methods that may not fully capture the nuances of expert hesitation or the complexity of interrelated criteria, the T-spherical fuzzy sets provide a more sophisticated representation of uncertainty through three-dimensional membership, non-membership, and hesitancy degrees. Furthermore, the use of Einstein aggregation operators allows for an interaction-aware aggregation process, enhancing the capability to synthesize diverse opinions and criteria into a cohesive decision-making framework. This approach not only results in more reliable and nuanced decision outcomes but also offers greater flexibility in dealing with complex decision environments typical of technology adoption scenarios. Consequently, the adoption of this method represents a significant advancement over traditional techniques, offering a robust tool that aligns more closely with the real-world complexities faced by decision-makers in the construction industry and beyond.

The application of this methodology yielded insightful results regarding the prioritization of barriers and strategies for the adoption of concrete 3D printing technology in Vietnam. Key findings indicated that technical advancements and addressing financial constraints are critical. This study effectively ranked the strategies, identifying ‘Research and Development’ as a pivotal area that aligns with the global push towards innovation in construction methodologies.

The primary contribution of this research is the introduction and validation of the integrated T-spherical fuzzy Einstein interaction aggregator group decision-making approach. This approach not only advances theoretical frameworks in decision-making but also offers a practical tool for analyzing complex decision environments. The secondary contribution involves applying this innovative decision-making framework to a concrete case study, thus demonstrating its practical value and adaptability in real-world settings.

As for this study’s limitations, the dependence on expert inputs, while invaluable for incorporating professional insights, introduces a degree of subjectivity that could impact the replicability and objectivity of the findings. Moreover, the rapid evolution of technology could potentially render some of the analysis obsolete unless the model is continuously updated. Additionally, the focus on Vietnam’s construction industry means that the results might not directly translate to other markets or regions without modifications to account for local variances in economic, regulatory, and market conditions.