You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Mathematics
Download PDF
  • Article
  • Open Access

26 June 2024

Three-Step Iterative Algorithm for the Extended Cayley–Yosida Inclusion Problem in 2-Uniformly Smooth Banach Spaces: Convergence and Stability Analysis

,
and
1
Department of Engineering Mathematics, College of Engineering, Koneru Lakshmaiah Education Foundation, Vaddeswaram 522302, Andhra Pradesh, India
2
School of Mathematical Sciences, Zhejiang Normal University, Jinhua 321004, China
3
Mathematics Department of Humanities College, Zhejiang Guangsha Vocational and Technical University of Construction, Jinhua 321004, China
4
Department of Mathematics, Aligarh Muslim University, Aligarh 202002, Uttar Pradesh, India
Mathematics2024, 12(13), 1977;https://doi.org/10.3390/math12131977
This article belongs to the Special Issue Advanced Research in Functional Analysis and Operator Theory
Version Notes
Order Reprints

Abstract

In this article, we investigate and study an extended Cayley–Yosida inclusion problem. We show that our problem is equivalent to a fixed-point equation. Based on the fixed-point equation, we develop a three-step iterative algorithm to solve our problem. Finally, we illustrate the convergence of the proposed algorithm with an example, computational table, and convergence graph by using MATLAB 2018b.

1. Introduction

Variational inclusion represents a valuable and significant generalization of the variational inequality, playing a crucial role in various fields such as engineering science, economics, transportation equilibrium, and optimization and control. For more detail, we direct readers to [1,2,3] and the references therein. The multi-valued inclusion problem is to find a ^ ∈ H ^ such that
0 ∈ M ( a ^ ) ,
where M : H ^ → 2 H ^ is the multi-valued mapping. This problem serves as a versatile model for a broad spectrum of challenges in both pure and applied sciences. For detail, we refer to [4,5,6,7] and the references therein.
Resolvent and Yosida approximation operators have important roles in convex analysis, partial differential equations, and other analytical problems, as illustrated in [8,9,10,11]. In 1994, Hassouni and Moudafi [12] explored variational inclusions, a type of variational inequality with single-valued mappings, using the resolvent operator approach for maximal monotone mappings. The initial method employed to address problem (1) was the forward–backward splitting algorithm. Subsequently, various iterative methods, including the Douglas–Rachford splitting method [13], the Peaceman–Rachford splitting method [14], and others, have been developed to tackle mixed inclusion problems (MIPs).
Tseng [15] introduced the modified forward–backward approach in 2000, demonstrated weak convergence. In 2018, Gibali and Thong [16] obtained a modified version of Tseng’s splitting method, showcasing its strong convergence. In 2019, Ahmad et al. [17] developed an XOR operation-based, three-step iterative technique for generalized mixed ordered quasi-variational inclusion and independently demonstrated the existence, convergence, and stability results. In 1989, Glowinski et al. [18] demonstrated that three-step iterative methods outperformed and gave better numerical results than two- and one-step iterative schemes.
Due to the Cayley operators’ [19] widespread applicability in fundamental and allied sciences, encompassing fields such as financial modeling, computer programming, economics, and engineering, among others, we investigate a generalized Cayley operator. This operator incorporates a generalized resolvent operator initially introduced by Fang and Huang [20].
Motivated by the above-mentioned work, our aim is to introduce and study an extended Cayley–Yosida inclusion problem. We formulate the proposed problem into a fixed-point equation by using a generalized Yosida approximation operator and a generalized resolvent operator. Based on the fixed-point equation, we develop a three-step iterative algorithm. We provide proof of stability analysis results and strong convergence for the sequence generated by the three-step iterative algorithm. Additionally, convergence graphs and a numerical example are provided, implemented through MATLAB programming.

2. Background and Problem Formulation

The majority of splitting methods are founded on the resolvent operator of type [ I + λ M ( f , g ) ] − 1 , where M is a multi-valued monotone mapping, λ > 0 constant, and I is an identity operator. Thus, the resolvent operator, R I , λ M ( f , g ) : H ^ → H ^ , where H ^ is a Hilbert space, is defined as
R I , λ M ( f , g ) ( a ^ ) = [ I + λ M ( f , g ) ] − 1 ( a ^ ) , f o r a l l a ^ ∈ H ^ .
The Yosida approximation operator, Y I , λ M ( f , g ) , is defined as
Y I , λ M ( f , g ) ( a ^ ) = 1 λ I − R I , λ M ( f , g ) ( a ^ ) , f o r a l l a ^ ∈ H ^ .
The Cayley operator, C I , λ M ( f , g ) , is defined as
C I , λ M ( f , g ) ( a ^ ) = 2 R I , λ M ( f , g ) − I ( a ^ ) , f o r a l l a ^ ∈ H ^ .
We consider R I , λ M ( f , g ) , Y I , λ M ( f , g ) , and C I , λ M ( f , g ) defined by (2), (3), and (4), respectively, in the context of 2-Uniformly Smooth Banach Spaces in this article.
Throughout this work, we suppose E ^ to be a real 2-Uniformly Smooth Banach Space (in short, 2-USBS) whose norm is denoted by ∥ · ∥ , where   E ^ ∗ is the topological dual of E ^ , ⟨ · , · ⟩ is the duality pairing between E ^ and E ^ ∗ , and J : E ^ → 2 E ^ ∗ is the normalized duality mapping, which is defined as
J ( a ^ ) = f ^ ∈ E ^ ∗ : ⟨ a ^ , f ^ ⟩ = ∥ a ^ ∥ 2 , ∥ f ^ ∥   =   ∥ a ^ ∥ and a ^ ∈ E ^ .
The function τ E ^ : [ 0 , ∞ ) → [ 0 , ∞ ) measures the modulus of smoothness of the Banach space E and is defined as
τ E ^ ( t ) = sup ∥ a ^ + b ^ ∥ − ∥ a ^ − b ^ ∥ 2 − 1 : a ^ , b ^ ∈ E ^ , ∥ a ^ ∥ ≤ 1 , ∥ b ^ ∥ ≤ t .
The Banach space E ^ is called the following:
(i)
Uniformly Smooth if  lim t → 0 τ E ^ ( t ) t = 0 ;
(ii)
2-uniformly smooth if there exists a positive real constant k such that τ E ^ ( t ) ≤ k t 2 .
The Lemma stated below plays a significant role in the proof of our main result.
Lemma 1
([21,22]). Let E ^ be a 2-Uniformly Smooth Banach Space and J : E ^ → 2 E ^ ∗ be the normalized duality mapping. Then, for any a ^ , b ^ , ∈ E ^ ,
(i)
∥ a ^ + b ^ ∥ 2 ≤ ∥ a ^ ∥ 2 + 2 ⟨ b ^ , j ( a ^ + b ^ ) ⟩ + k ∥ b ^ ∥ 2 , for all j ( a ^ + b ^ ) ∈ J ( a ^ + b ^ ) ;
(ii)
⟨ a ^ − b ^ , j ( a ^ ) − j ( b ^ ) ⟩ ≤ 2 d 2 τ E ^ 4 ∥ a ^ − b ^ ∥ d , where d = ( ∥ a ^ ∥ 2 + ∥ b ^ ∥ 2 ) 2 , j ( a ^ ) ∈ J ( a ^ ) and j ( b ^ ) ∈ J ( b ^ ) .
Definition 1
([21,22]). A single-valued mapping F : E ^ × E ^ → E ^ is said to be mixed ( ∧ 1 , ∧ 2 ) -Lipschitz continuous if F ( a ^ , . ) is ∧ 1 -Lipschitz continuous in the first component and F ( . , a ^ ) is ∧ 2 -Lipschitz continuous in the second component. That is,
∥ F ( a ^ , z ^ ) − F ( b ^ , z ^ ) ∥ ≤ ∧ 1 ∥ a ^ − b ^ ∥ ,
and
∥ F ( w ^ , a ^ ) − F ( w ^ , b ^ ) ∥ ≤ ∧ 2 ∥ a ^ − b ^ ∥ , ∀ a ^ , b ^ , w ^ , z ^ ∈ E ^ a n d ∧ 1 , ∧ 2 > 0 .
For ∧ 1 = 1 and ∧ 2 = 1 , F is non-expansive in both arguments, respectively.
Definition 2
([23]). A multi-valued mapping M : E ^ × E ^ → 2 E ^ with regard to single-valued mappings f , g : E ^ → E ^ is said to be as follows:
(i)
α-strongly accretive with regard to f if there is a constant α > 0 such that
⟨ u ^ − v ^ , j ( a ^ − b ^ ) ⟩ ≥ α ∥ a ^ − b ^ ∥ 2 , ∀ a ^ , b ^ ∈ E ^ , ∀ u ^ ∈ M ( f ( a ^ ) , z ^ ) , v ^ ∈ M ( f ( b ^ ) , z ^ ) ;
(ii)
β-relaxed strongly accretive with regard to g if there is a constant β > 0 such that
⟨ u ^ − v ^ , j ( a ^ − b ^ ) ⟩ ≥ − β ∥ a ^ − b ^ ∥ 2 , ∀ a ^ , b ^ ∈ E ^ , ∀ u ^ ∈ M ( z ^ , g ( a ^ ) ) , v ^ ∈ M ( z ^ , g ( b ^ ) ) ;
(iii)
α β -symmetric accretive with regard to f , g if M ( f , . ) is α-strongly accretive, and M ( . , g ) is β-relaxed accretive with α ≥ β if and only if a ^ = b ^ .
Definition 3
([23]). A multi-valued mapping M : E ^ × E ^ → 2 E ^ is said to be α β –I-accretive with regard to f and g if M ( f , g ) is α β -symmetric accretive and for all λ > 0 , [ I + λ M ( f , g ) ] ( E ^ ) = E ^ , where f , g : E ^ → E ^ are the single-valued mappings and I : E ^ → E ^ is an identity mapping.
Definition 4.
The generalized resolvent operator R I , λ M ( f , g ) : E ^ → E ^ in terms of I and M is defined as
R I , λ M ( f , g ) ( a ^ ) = [ I + λ M ( f , g ) ] − 1 ( a ^ ) , for all a ^ ∈ E ^ ,
where f , g : E ^ → E ^ are single-valued mappings, I : E ^ → E ^ is an identity mapping, and M : E ^ × E ^ → 2 E ^ is α β –I-accretive with regard to f and g .
Definition 5
([24]). For a ^ 0 ∈ H ^ , let a ^ n + 1 = G ( T , p ^ n ) , where T : H ^ → H ^ is a single-valued mapping and G : H ^ × H ^ → H ^ is the bimapping. Assume that the fixed-point set S ( T ) ≠ ∅ and { a ^ n } → a ^ ∗ ( a ^ ∗ ∈ S ( T ) ) . Let { u ^ n } ⊂ H ^ and
ϑ ^ n = ∥ u ^ n + 1 − G ( T , u ^ n ) ∥ .
Define an iterative scheme that generates a sequence of points { a ^ n } in H ^ . Assume that lim n → ∞ ϑ ^ n = 0 implies u ^ n → a ^ ∗ ; then, the sequence { a ^ n } is said to be stable with respect to T .
Lemma 2
([25]). Let { ξ n } ⊆ R + be a sequence in R + and { φ n } ⊆ [ 0 , 1 ] be a sequence in [ 0 , 1 ] such that ∑ n = 0 ∞ φ n = ∞ . If there is a natural number m such that
ξ n ≤ ( 1 − φ n ) ξ n + φ n η n , ∀ n ≥ m ,
where η n ≥ 0 , for all n ≥ 0 and η n → 0 ( n → 0 ) , then lim n → ∞ ξ n = 0 .
Theorem 1.
Let f , g : E ^ → E ^ be the single-valued mappings and I : E ^ → E ^ be an identity mapping. Let M : E ^ × E ^ → 2 E ^ be α β –I-accretive with regard to f and g . Then, R I , λ M ( f , g ) : E ^ → E ^ is θ-Lipschitz continuous. That is,
R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ≤ θ ∥ a ^ − b ^ ∥ , f o r a l l a ^ , b ^ ∈ E ^ ,
where θ = 1 1 + λ ( α − β ) , and λ , α , and β are non-negative real numbers with α ≥ β .
Proof. 
Let a ^ ∈ E ^ . It follows that
R I , λ M ( f , g ) ( a ^ ) = [ I + λ M ( f , g ) ] − 1 ( a ^ )
and
R I , λ M ( f , g ) ( b ^ ) = [ I + λ M ( f , g ) ] − 1 ( b ^ ) .
This implies that
1 λ a ^ − R I , λ M ( f , g ) ( a ^ ) ∈ M f ( R I , λ M ( f , g ) ( a ^ ) , g ( R I , λ M ( f , g ) ( a ^ ) ,
1 λ b ^ − R I , λ M ( f , g ) ( b ^ ) ∈ M f ( R I , λ M ( f , g ) ( b ^ ) , g ( R I , λ M ( f , g ) ( b ^ ) .
Since M ( . , . ) is α β -symmetric with respect to f and g , we have
( α − β ) R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) 2 ≤ 1 λ a ^ − R I , λ M ( f , g ) ( a ^ ) ) − ( b ^ − R I , λ M ( f , g ) ( b ^ ) , j R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ≤ 1 λ ( a ^ − b ^ ) , j R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) + 1 λ R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) , j R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) .
On the other hand, we calculate
∥ a ^ − b ^ ∥ R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ≥ 1 λ ( a ^ − b ^ ) , j R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ≥ λ ( α − β ) R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) 2 + ⟨ R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) , j R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ⟩ ≥ λ ( α − β ) R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) 2 + R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) 2 .
Hence,
R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ≤ 1 [ 1 + λ ( α − β ) ] ∥ a ^ − b ^ ∥ .
That is, R I , λ M ( f , g ) is θ = 1 [ 1 + λ ( α − β ) ] -Lipschitz continuous.    □
We now demonstrate certain properties of the generalized Yosida approximation and the Cayley operators.
Proposition 1
([26]). The Yosida approximation operator defined by (3) is as follows:
(i)
θ Y -Lipschitz continuous, where θ Y = 1 + θ λ ;
(ii)
m -strongly accretive, where m = 1 − θ λ .
Proof. 
The definition of the generalized Yosida approximation operator leads directly to the proof.    □
Proposition 2
([26]). The Cayley operator defined by (4) is θ C -Lipschitz continuous, where θ C = 2 θ + 1 .
Proof. 
The definition of the generalized Cayley operator leads directly to the proof.    □

Problem Formulation

Let F : E ^ × E ^ → E ^ be the single-valued bimapping, f , g : E ^ → E ^ be single-valued mappings, and M : E ^ × E ^ → 2 E ^ be a multi-valued mapping. Let C I , λ M ( f , g ) and Y I , λ M ( f , g ) be generalized Cayley and Yosida approximation operators, respectively. We consider the following problem:
Find a ^ ∈ E ^ such that
0 ∈ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + M ( f ( a ^ ) , g ( a ^ ) ) .
Problem (9) is called an extended Cayley–Yosida inclusion problem.
Additionally, we summarize a few specific examples of our problem below to demonstrate the generality of problem (9).
(i)
If M ( f ( a ^ ) , g ( a ^ ) ) = M ( a ^ ) and F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ) = C I , λ M ( f , g ) ( a ^ ) , then problem (9) reduces to the problem of finding a ^ ∈ E ^ such that
0 ∈ C I , λ M ( a ^ ) + M ( a ^ ) .
Problem (10) was investigated and studied by Ahmad et al. [26], and the results were published in Applicable Analysis.
(ii)
If M ( f ( a ^ ) , g ( a ^ ) ) = M ( a ^ ) and F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ) = Y I , λ M ( f , g ) ( a ^ ) , then problem (9) reduces to the problem of finding a ^ ∈ E ^ such that
0 ∈ Y I , λ M ( a ^ ) + M ( a ^ ) .
Problem (11) was investigated and studied by Arvind et al. [27] in 2023, and the results were published in Mathematics.

3. Fixed-Point Equation and Three-Step Iterative Algorithm

The subsequent lemma presents a fixed-point formulation for the extended Cayley–Yosida inclusion problem, (9), incorporating the generalized resolvent and Yosida approximation operators defined by (3) and (4), respectively.
Lemma 3.
The extended Cayley–Yosida inclusion problem in (9) has a solution a ^ ∈ E ^ if and only if the following equation holds:
a ^ = R I , λ M ( f , g ) λ Y I , λ M ( f , g ) ( a ^ ) − F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ) + R I , λ M ( f , g ) ( a ^ ) .
Proof. 
Let a ^ ∈ E ^ satisfy Equation (12); then,
a ^ = R I , λ M ( f , g ) λ Y I , λ M ( f , g ) ( a ^ ) − F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ) + R I , λ M ( f , g ) ( a ^ ) a ^ = ( I + λ M ( f , g ) ) − 1 [ λ Y I , λ M ( f , g ) ( a ^ ) − F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ) + R I , λ M ( f , g ) ( a ^ ) ] ,
which implies that
I ( a ^ ) + λ M ( f ( a ^ ) , g ( a ^ ) ) = λ 1 λ I ( a ^ ) − R I , λ M ( f , g ) ( a ^ ) − λ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) 0 ∈ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + M ( f ( a ^ ) , g ( a ^ ) ) .
Conversely, suppose that a ^ is the solution of problem (9). That is,
0 ∈ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + M ( f ( a ^ ) , g ( a ^ ) ) .
From above, we have
− F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ∈ M ( f ( a ^ ) , g ( a ^ ) ) I ( a ^ ) − λ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ∈ I ( a ^ ) + λ M ( f ( a ^ ) , g ( a ^ ) ) , = [ I + λ M ( f , g ) ] ( a ^ ) ,
which implies that
[ I + λ M ( f , g ) ] − 1 I ( a ^ ) − λ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) = a ^
or
a ^ = R I , λ M ( f , g ) I ( a ^ ) − R I , λ M ( f , g ) ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) − λ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) a ^ = R I , λ M ( f , g ) λ 1 λ { I − R I , λ M ( f , g ) } ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) − λ F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) a ^ = R I , λ M ( f , g ) λ Y I , λ M ( f , g ) ( a ^ ) − F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) ) + R I , λ M ( f , g ) ( a ^ ) .
Thus, Equation (12) is fulfilled.    □

3.1. Existence Result

The following theorem gives the guarantee for the existence of the solution of problem (9).
Theorem 2.
Let E ^ be a real 2-USBS with a modulus of smoothness τ E ^ ( t ) ≤ k t 2 for some constant k > 0 . Let f , g : E ^ → E ^ be the single-valued mappings and I : E ^ → E ^ be an identity mapping. Let F : E ^ × E ^ → E ^ be a ( ∧ 1 , ∧ 2 ) -Lipschitz continuous mapping with non-negative constants ∧ 1 , ∧ 2 > 0 . Let M : E ^ × E ^ → 2 E ^ be α β –I-accretive with regard to f and g . Then, the extended Cayley–Yosida inclusion problem has a unique solution a ^ in E ^ if
θ − ( − £ 2 ) < £ 2 + 4 2 ,
where
£ = λ [ ▵ + ∧ 1 θ C + ∧ 2 θ Y + 1 ] , ▵ = 1 − 2 m + 64 k θ Y 2 + k θ Y , θ C = 2 θ + 1 ,
θ Y = 1 + θ λ , m = 1 − θ λ , θ = 1 1 + λ ( α − β ) , and λ , α , a n d β a r e n o n - n e g a t i v e   c o n s t a n t s
with α ≥ β .
Proof. 
Let us define P ( a ^ ) = Y I , λ M ( f , g ) ( a ^ ) − F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) . For any a ^ , b ^ ∈ E ^ , we will prove that R I , λ M ( f , g ) λ P + R I , λ M ( f , g ) is a contraction mapping.
R I , λ M ( f , g ) λ P ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) λ P ( b ^ ) + R I , λ M ( f , g ) ( b ^ ) ≤ θ λ P ( a ^ ) − P ( b ^ ) + R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ≤ θ λ ∥ P ( a ^ ) − P ( b ^ ) ∥ + R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ≤ θ λ ∥ P ( a ^ ) − P ( b ^ ) ∥ + θ ∥ a ^ − b ^ ∥ .
On the other hand, we have
∥ P ( a ^ ) − P ( b ^ ) ∥ ≤ Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) − ( a ^ − b ^ ) + ∥ F C I , λ M ( f , g ) ( b ^ ) , Y I , λ M ( f , g ) ( b ^ ) − F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + ( a ^ − b ^ ) ∥ .
Using the strong accretivity of the Yosida approximation operator, we obtain
( a ^ − a ^ ) − Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( a ^ ) 2 ≤ ∥ b ^ − a ^ ∥ 2 + 2 ⟨ − Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) , j ( a ^ − b ^ ) − Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) ⟩ + k ∥ Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) ∥ 2 = ∥ a ^ − b ^ ∥ 2 + 2 − Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( a ^ ) , j ( a ^ − b ^ ) + 2 ⟨ − Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) , j ( a ^ − b ^ ) − Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) − j ( a ^ − b ^ ) ⟩ + k ∥ Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) ∥ 2 ≤ ∥ a ^ − b ^ ∥ 2 − 2 m ∥ a ^ − b ^ ∥ 2 + 4 d 2 τ E ^ 4 Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) d + k θ Y ∥ a ^ − b ^ ∥ 2 ≤ ∥ a ^ − b ^ ∥ 2 − 2 m ∥ a ^ − b ^ ∥ 2 + 64 k Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) 2 + k θ Y ∥ a ^ − b ^ ∥ 2 ≤ [ 1 − 2 m + 64 k θ Y 2 + k θ Y ] ∥ a ^ − b ^ ∥ 2 .
Since F , C I , λ M ( f , g ) and Y I , λ M ( f , g ) are ( ∧ 1 , ∧ 2 ) -, θ C - and θ Y -Lipschitz continuous, respectively, we have
F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) − F C I , λ M ( f , g ) ( b ^ ) , Y I , λ M ( f , g ) ( b ^ ) + ( a ^ − b ^ ) ≤ ∥ a ^ − b ^ ∥ + F C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) − F C I , λ M ( f , g ) ( b ^ ) , Y I , λ M ( f , g ) ( a ^ ) + F C I , λ M ( f , g ) ( b ^ ) , Y I , λ M ( f , g ) ( a ^ ) − F C I , λ M ( f , g ) ( b ^ ) , Y I , λ M ( f , g ) ( b ^ ) ≤ ∥ a ^ − b ^ ∥ + ∧ 1 C I , λ M ( f , g ) ( a ^ ) − C I , λ M ( f , g ) ( b ^ ) + ∧ 2 Y I , λ M ( f , g ) ( a ^ ) − Y I , λ M ( f , g ) ( b ^ ) ≤ ∥ a ^ − b ^ ∥ + ∧ 1 θ C ∥ a ^ − b ^ ∥ + ∧ 2 θ Y ∥ a ^ − b ^ ∥ = [ 1 + ∧ 1 θ C + ∧ 2 θ Y ] ∥ a ^ − b ^ ∥ ,
Using (16) and (17) in (15), we obtain
∥ P ( a ^ ) − P ( b ^ ) ∥ ≤ [ 1 − 2 m + 64 k θ Y 2 + k θ Y ] + [ 1 + ∧ 1 θ C + ∧ 2 θ Y ] ∥ a ^ − b ^ ∥ .
From (18) and (14), we obtain
R I , λ M ( f , g ) λ P ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) λ P ( b ^ ) + R I , λ M ( f , g ) ( b ^ ) ≤ ∥ a ^ − b ^ ∥ ,
where
= θ λ [ 1 − 2 m + 64 k θ Y 2 + k θ Y ] + [ 1 + ∧ 1 θ C + ∧ 2 θ Y ] + θ .
From (13), < 1 . Hence, R I , λ M ( f , g ) λ P + R I , λ M ( f , g ) is a contraction mapping. Since E ^ is a 2-Uniformly Smooth Banach Space, from Lemma 3, problem (9) has a unique solution a ^ which is a fixed point of R I , λ M ( f , g ) λ P + R I , λ M ( f , g ) .    □

3.2. Three-Step Iterative Algorithm

Drawing upon Lemma 3 as a cornerstone, we formulate a three-step iterative algorithm to ascertain the solution of the extended Cayley–Yosida inclusion problem in (9). This iterative algorithm incorporates both the generalized resolvent and Yosida approximation operators, presenting itself as a novel approach.
The following result is from the convergence and stability analysis of Cayley–Yosida inclusion problem (9).
Theorem 3.
Assume E ^ , f , g , F , I , and M are all the same as as in Theorem 2, such that all the conditions specified in Theorem 2 are fulfilled. Moreover, the following condition is satisfied:
θ − ( − £ 2 ) < £ 2 + 4 6 ,
where £ is the same as in (13) and l i m n → ∞ δ 1 ^ n = l i m n → ∞ δ 2 ^ n = l i m n → ∞ δ 3 ^ n . Then, we have the following:
(I)
The sequence { a ^ n } produced by Algorithm 1 converges strongly to the unique solution of problem (9).
(II)
Additionally, the sequence { a ^ n } produced by Algorithm 1 is stable with respect to R I , λ M ( f , g ) .
Proof. 
(I)  Convergence  of a ^ n :
On the basis of Lemma 3, we can write
a ^ ∗ = ( 1 − α n ) a ^ ∗ + α n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( a ^ ∗ ) − F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) ) + R I , λ M ( f , g ) ( a ^ ∗ ) ] .
Now, from Algorithm 1 and Theorem 1, we have
∥ a ^ n + 1 − a ^ ∗ ∥ = ∥ ( 1 − α n ) a ^ n + α n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( b ^ n ) − F ( C I , λ M ( f , g ) ( b ^ n ) , Y I , λ M ( f , g ) ( b ^ n ) ) + R I , λ M ( f , g ) ( b ^ n ) ] + α n δ 1 ^ n − { ( 1 − α n ) a ^ ∗ + α n R I , λ M ( f , g ) [ λ ( Y I , λ M ( f , g ) ( a ^ ∗ ) − F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) ) ) + R I , λ M ( f , g ) ( a ^ ∗ ) ] } ∥ ≤ | ( 1 − α n ) | ∥ a ^ n − a ^ ∗ ∥ + | α n | ∥ R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( b ^ n ) − F ( C I , λ M ( f , g ) ( b ^ n ) , Y I , λ M ( f , g ) ( b ^ n ) + R I , λ M ( f , g ) ( b ^ n ) ] − R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( a ^ ∗ ) − F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) + R I , λ M ( f , g ) ( a ^ ∗ ) ] ∥ + ∥ α n δ 1 ^ n ∥ .
Using a Lipschitz continuity of R I , λ M ( f , g ) , we have
≤ | ( 1 − α n ) | ∥ a ^ n − a ^ ∗ ∥ + | α n | θ ∥ ∥ λ Y I , λ M ( f , g ) ( b ^ n ) − Y I , λ M ( f , g ) ( a ^ ∗ ) − λ F ( C I , λ M ( f , g ) ( b ^ n ) , Y I , λ M ( f , g ) ( b ^ n ) ) + λ F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) ) + R I , λ M ( f , g ) ( b ^ n ) − R I , λ M ( f , g ) ( a ^ ∗ ) ∥ + ∥ α n δ 1 ^ n ∥ ≤ | ( 1 − α n ) | ∥ a ^ n − a ^ ∗ ∥ + | α n | θ λ ∥ ( Y I , λ M ( f , g ) ( b ^ n ) − Y I , λ M ( f , g ) ( a ^ ∗ ) ) − ( a ^ n − a ^ ∗ ) ∥ + λ ∥ F ( C I , λ M ( f , g ) ( b ^ n ) , Y I , λ M ( f , g ) ( b ^ n ) ) − F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) ) + ( b ^ n − a ^ ∗ ) ∥ + ∥ R I , λ M ( f , g ) ( b ^ n ) − R I , λ M ( f , g ) ( a ^ ∗ ) ∥ + ∥ α n δ 1 ^ n ∥ .
Since F is ( ∧ 1 , ∧ 2 ) -Lipschitz continuous, C I , λ M ( f , g ) is θ C -Lipschitz continuous, and Y I , λ M ( f , g ) is m -strongly accretive and θ Y -Lipschitz continuous, from Lemma 1, we obtain
∥ a ^ n + 1 − a ^ ∗ ∥ ≤ | ( 1 − α n ) | ∥ a ^ n − a ^ ∗ ∥ + | α n | θ λ [ 1 − 2 m + 64 k θ Y 2 + k θ Y ] ∥ b ^ n − x ∗ ∥ + | α n | θ λ [ 1 + ∧ 1 θ C + ∧ 2 θ Y ] ∥ b ^ n − a ^ ∗ ∥ + | α n | θ 2 ∥ b ^ n − a ^ ∗ ∥ + ∥ α n δ 1 ^ n ∥ = | ( 1 − α n ) | ∥ a ^ n − a ^ ∗ ∥ + | α n | ∥ b ^ n − a ^ ∗ ∥ + ∥ α n δ 1 ^ n ∥ ,
where
= θ λ [ 1 − 2 m + 64 k θ Y 2 + k θ Y ] + [ 1 + ∧ 1 θ C + ∧ 2 θ Y ] + θ .
From Algorithm 1, we calculate
∥ b ^ n − a ^ ∗ ∥ = ∥ ( 1 − β n ) a ^ n + β n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( z ^ n ) − F ( C I , λ M ( f , g ) ( z ^ n ) , Y I , λ M ( f , g ) ( z ^ n ) + R I , λ M ( f , g ) ( z ^ n ) ] + β n δ 2 ^ n − { ( 1 − β n ) a ^ ∗ + β n R I , λ M ( f , g ) [ λ ( Y I , λ M ( f , g ) ( a ^ ∗ ) − F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) ) + R I , λ M ( f , g ) ( a ^ ∗ ) ] } ∥ ≤ | ( 1 − β n ) | ∥ a ^ n − a ^ ∗ ∥ + | β n | θ λ ∥ ( Y I , λ M ( f , g ) ( z ^ n ) − Y I , λ M ( f , g ) ( a ^ ∗ ) ) − ( b ^ − a ^ ∗ ) ∥ + λ ∥ F ( C I , λ M ( f , g ) ( z ^ n ) , Y I , λ M ( f , g ) ( z ^ n ) − F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) ) + ( b ^ − a ^ ∗ ) ∥ + | β n | ∥ R I , λ M ( f , g ) ( b ^ n ) − R I , λ M ( f , g ) ( a ^ ∗ ) ∥ + ∥ β n δ 2 ^ n ∥ .
By using the same argument as above, we obtain
∥ b ^ n − a ^ ∗ ∥ ≤ | ( 1 − β n ) | ∥ a ^ n − a ^ ∗ ∥ + | β n | θ λ [ 1 − 2 m + 64 k θ Y 2 + k θ Y ] ∥ z ^ n − a ^ ∗ ∥ + [ 1 + ∧ 1 θ C + ∧ 2 θ Y ] ∥ b ^ n − a ^ ∗ ∥ + ∥ β n δ 2 ^ n ∥ = | ( 1 − β n ) | ∥ a ^ n − a ^ ∗ ∥ + | β n | ∥ z ^ n − a ^ ∗ ∥ + ∥ β n δ 2 ^ n ∥ .
Similarly, we may calculate
∥ z ^ n − a ^ ∗ ∥ ≤ | ( 1 − γ n ) | ∥ a ^ n − a ^ ∗ ∥ + | γ n | ∥ z ^ n − a ^ ∗ ∥ + ∥ γ n δ 3 ^ n ∥ .
Algorithm 1 Three-Step Iterative Algorithm
Let a ^ 0 ∈ E ^ ,   λ > 0 , F : E ^ × E ^ → E ^ be a single-valued mapping, and M : E ^ × E ^ → 2 E be a multi-valued mapping. Let C I , λ M ( f , g ) and Y I , λ M ( f , g ) be the generalized Cayley and Yosida approximation operators defined in (3) and (4), respectively. Then, we develop the following iterative scheme:
a ^ n + 1 = ( 1 − α n ) a ^ n + α n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( b ^ n ) − F ( C I , λ M ( f , g ) ( b ^ n ) , Y I , λ M ( f , g ) ( b ^ n ) ) + R I , λ M ( f , g ) ( b ^ n ) ] + α n δ 1 ^ n b ^ n = ( 1 − β n ) a ^ n + β n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( z ^ n ) − F ( C I , λ M ( f , g ) ( z ^ n ) , Y I , λ M ( f , g ) ( z ^ n ) ) + R I , λ M ( f , g ) ( z ^ n ) ] + β n δ 2 ^ n z ^ n = ( 1 − γ n ) a ^ n + γ n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( a ^ n ) − F ( C I , λ M ( f , g ) ( a ^ n ) , Y I , λ M ( f , g ) ( a ^ n ) ) + R I , λ M ( f , g ) ( a ^ n ) ] + γ n δ 3 ^ n .
Let { u ^ n } ⊆ E ^ be a sequence and define { v ^ n } by
v ^ n = ∥ u ^ n + 1 − { ( 1 − α n ) a ^ n + α n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( t ^ n ) − F ( C I , λ M ( f , g ) ( t ^ n ) , Y I , λ M ( f , g ) ( t ^ n ) ) + R I , λ M ( f , g ) ( t ^ n ) ] + α n δ 1 ^ n } ∥ t ^ n = ( 1 − β n ) u ^ n + β n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( s ^ n ) − F ( C I , λ M ( f , g ) ( s ^ n ) , Y I , λ M ( f , g ) ( s ^ n ) ) + R I , λ M ( f , g ) ( s ^ n ) ] + β n δ 2 ^ n s ^ n = ( 1 − γ n ) u ^ n + γ n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( u ^ n ) − F ( C I , λ M ( f , g ) ( u ^ n ) , Y I , λ M ( f , g ) ( u ^ n ) ) + R I , λ M ( f , g ) ( u ^ n ) ] + γ n δ 3 ^ n ,
where α n , β n , γ n ∈ [ 0 , 1 ] , ∑ n = 0 ∞ α n = ∞ , a n d ∀ n ≥ 0 . Here, { δ 1 ^ n } , { δ 2 ^ n } , { δ 3 ^ n } ⊆ E ^ are sequences in E ^ considered to accommodate possible computational inaccuracies.
Using (24) and (25), (22) becomes
∥ a ^ n + 1 − a ^ ∗ ∥ ≤ { ( 1 − α n ) + α n ( 1 − β n ) + 2 α n β n ( 1 − γ n ) + 3 α n β n γ n + 2 α n β n δ 3 ^ n γ n } ∥ a ^ n − a ^ ∗ ∥ + α n β n δ 2 ^ n + δ 1 ^ n α n ≤ 1 − α n ( 1 − 3 ) ∥ a ^ n − a ^ ∗ ∥ + α n ( 1 − 3 ) β n δ 2 ^ n + δ 1 ^ n 1 − 3 .
On setting η n : = β n δ 2 ^ n + δ 1 ^ n 1 − 3 , ξ n = ∥ a ^ n − a ^ ∗ ∥ , and ζ n : = { 1 − α n ( 1 − 3 ) } , then (26) can be written as
ξ n ≤ ( 1 − ζ n ) ξ n + ζ n η n .
By Lemma 2, we can conclude that ξ n → 0 , as n → ∞ , and so { a ^ n } → a ^ ∗ strongly.
(II) Stability of a ^ n :
Let H ( a ^ ∗ ) = R I , λ M ( f , g ) λ Y I , λ M ( f , g ) ( a ^ ∗ ) − F ( C I , λ M ( f , g ) ( a ^ ∗ ) , Y I , λ M ( f , g ) ( a ^ ∗ ) + R I , λ M ( f , g ) ( a ^ ∗ ) . From Algorithm 1, we have
∥ u ^ n + 1 − a ^ ∗ ∥ = ∥ u ^ n + 1 − { ( 1 − α n ) a ^ ∗ + α n H ( a ^ ∗ ) } ∥ ≤ u ^ n + 1 − ( 1 − α n ) u ^ n − α n H ( t n ) − δ 1 ^ n α n + ( 1 − α n ) u ^ n + α n H ( t ^ n ) + δ 1 ^ n α n − ( 1 − α n ) a ^ ∗ − α n H ( a ^ ∗ ) ≤ u ^ n + 1 − ( 1 − α n ) u ^ n − α n H ( t ^ n ) − δ 1 ^ n α n + | 1 − α n | ∥ u ^ n − a ^ ∗ ∥ + α n ∥ H ( t ^ n ) − H ( a ^ ∗ ) ∥ + ∥ δ 1 ^ n α n ∥ ≤ u ^ n + 1 − ( 1 − α n ) u ^ n − α n H ( t ^ n ) − δ 1 ^ n α n + | 1 − α n | ∥ δ 1 ^ n − a ^ ∗ ∥ + | α n | ∥ t ^ n − a ^ ∗ ∥ + ∥ δ 1 ^ n α n ∥ ,
where
= θ λ [ 1 − 2 m + 64 k θ Y 2 + k θ Y ] + [ 1 + ∧ 1 θ C + ∧ 2 θ Y ] + θ .
∥ t ^ n − a ^ ∗ ∥ ≤ ( 1 − β n ) u ^ n + β n H ( s ^ n ) + δ 2 ^ n β n − ( 1 − β n ) a ^ ∗ − β n H ( a ^ ∗ ) ≤ | 1 − β n | ∥ u ^ n − a ^ ∗ ∥ + β n ∥ H ( s ^ n ) − H ( a ^ ∗ ) ∥ + ∥ δ 2 ^ n β n ∥ ≤ | 1 − β n | ∥ u ^ n − a ^ ∗ ∥ + | β n | ∥ s ^ n − a ^ ∗ ∥ ∥ δ 2 ^ n β n ∥ .
Similarly, we obtain
∥ s ^ n − a ^ ∗ ∥ ≤ ( 1 − γ n ) u ^ n + γ n H ( u ^ n ) + δ 3 ^ n γ n − ( 1 − γ n ) a ^ ∗ − γ n H ( a ^ ∗ ) ≤ | 1 − γ n | ∥ u ^ n − a ^ ∗ ∥ + γ n ∥ H ( u ^ n ) − H ( a ^ ∗ ) ∥ + ∥ δ 3 ^ n γ n ∥ ≤ | 1 − γ n | ∥ u ^ n − a ^ ∗ ∥ + | γ n | ∥ u ^ n − a ^ ∗ ∥ ∥ δ 3 ^ n γ n ∥ .
Using (28) and (29) in (27), we have
∥ u ^ n + 1 − a ^ ∗ ∥ ≤ u ^ n + 1 − ( 1 − α n ) u ^ n − α n H ( t ^ n ) − δ 1 ^ n α n + | ( 1 − α n ) ∥ u ^ n − a ^ ∗ ∥ + ( α n ( 1 − β n ) + 2 α n β n ( 1 − γ n ) + β n α n γ n 3 ) ∥ u ^ n − a ^ ∗ ∥ + α n β n ∥ δ 3 ^ n γ n ∥ + ∥ δ 1 ^ n α n ∥ ∥ u ^ n + 1 − a ^ ∗ ∥ ≤ v ^ n + ( 1 − α n ( 1 − 3 ) ) ∥ u ^ n − a ^ ∗ ∥ + α n ( 1 − 3 ) × β n δ 2 ^ n + δ 1 ^ n 1 − 3
Assume that l i m n → ∞ v ^ n = 0 . Hence, l i m n → ∞ u ^ n = a ^ ∗ , where l i m n → ∞ δ 1 ^ n = l i m n → ∞ δ 2 ^ n = l i m n → ∞ δ 3 ^ n = 0 . Similarly, one can prove that if l i m n → ∞ u ^ n = a ^ ∗ and condition (19) holds then l i m n → ∞ v ^ n = 0 . Hence, the convergence of { a ^ n } is stable with regard to R I , λ M ( f , g ) . □

4. Numerical Example

We now present the following numerical example to illustrate the convergence analysis of the sequence { a ^ n } towards the solution of problem (9).
Example 1.
Assume E ^ = R , f , g : E ^ → E ^ are single-valued mappings, and M : E ^ × E ^ → 2 E ^ is a multi-valued mapping defined by
f ( a ^ ) = 6 a ^ 5 , g ( a ^ ) = 5 a ^ 3 , M ( a ^ , b ^ ) = a ^ + b ^ 3 .
Now, for λ = 1 / 2 , the associate resolvent operator
R I , λ M ( f , g ) ( a ^ ) = [ I + λ M ( f , g ) ] − 1 ( a ^ ) = 90 a ^ 133 .
Furthermore,
∥ R I , λ M ( f , g ) ( a ^ ) − R I , λ M ( f , g ) ( b ^ ) ∥ = 90 133 a ^ − 90 133 b ^ = 90 133 a ^ − b ^ ≤ 9 11 ∥ a ^ − b ^ ∥ ,
i.e., R I , λ M ( f , g ) is Lipschitz continuous with constant θ = 9 11 .
Now, we define the Yosida approximation operator as
Y I , λ M ( f , g ) ( a ^ ) = 1 λ [ I − R I , λ M ( f , g ) ] ( a ^ ) = 43 a ^ 266 .
Next, the Cayley operator is defined as
C I , λ M ( f , g ) ( a ^ ) = 2 R I , λ M ( f , g ) ( a ^ ) − I ( a ^ ) = 47 a ^ 133 .
It is straightforward that Y I , λ M ( f , g ) and C I , λ M ( f , g ) are Lipschitz continuous with constants θ Y = 40 11 and θ C = 29 11 , respectively.
For λ = 1 2 , we calculate
R I , λ M ( f , g ) λ Y I , λ M ( f , g ) ( a ^ ) − F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) = 90 133 1 2 Y I , λ M ( f , g ) ( a ^ ) − F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) = 90 133 1 2 43 266 ( a ^ ) − C I , λ M ( f , g ) ( a ^ ) + Y I , λ M ( f , g ) ( a ^ ) 3 + 90 133 ( a ^ ) = 90 133 1 2 43 266 ( a ^ ) − 137 266 × 3 ( a ^ ) + 90 133 ( a ^ ) = 8040 17689 ( a ^ ) .
Clearly, 0 is the fixed point of R I , λ M ( f , g ) λ Y I , λ M ( f , g ) ( a ^ ) − F ( C I , λ M ( f , g ) ( a ^ ) , Y I , λ M ( f , g ) ( a ^ ) + R I , λ M ( f , g ) ( a ^ ) .
Let δ 1 ^ n = 1 2 n , δ 2 ^ n = n + 2 n + 3 , δ 3 ^ n = 2 n 2 n + 1 , α n = n 2 n + 1 , β n = 1 n + 1 , and γ n = n + 1 n ( n + 2 ) . It is clear that the sequences δ 1 ^ n , δ 2 ^ n , δ 3 ^ n , α n , β n , a n d γ n satisfy condition (19). We compute the sequence { p ^ n } using the following iterative scheme:
a ^ n + 1 = ( 1 − α n ) a ^ n + α n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( b ^ n ) − F ( C I , λ M ( f , g ) ( b ^ n ) , Y I , λ M ( f , g ) ( b ^ n ) + R I , λ M ( f , g ) ( b ^ n ) ] + α n δ 1 ^ n a ^ n + 1 = n + 1 2 n + 1 a ^ n + 8040 n 17689 ( 2 n + 1 ) b ^ n + 1 2 ( 2 n + 1 ) ,
b ^ n = ( 1 − β n ) a ^ n + β n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( z ^ n ) − F ( C I , λ M ( f , g ) ( z ^ n ) , Y I , λ M ( f , g ) ( z ^ n ) + R I , λ M ( f , g ) ( z ^ n ) ] + β n δ 2 ^ n b ^ n = n n + 1 a ^ n + 8040 17689 ( n + 1 ) z ^ n + n + 2 ( n + 1 ) ( n + 3 ) ,
and
z ^ n = ( 1 − γ n ) a ^ n + γ n R I , λ M ( f , g ) [ λ Y I , λ M ( f , g ) ( a ^ n ) − F ( C I , λ M ( f , g ) ( a ^ n ) , Y I , λ M ( f , g ) ( a ^ n ) + R I , λ M ( f , g ) ( a ^ n ) ] + γ n δ 3 ^ n . z ^ n = n 2 + n − 1 n ( n + 2 ) a ^ n + 8040 ( n + 1 ) 17689 n ( n + 2 ) a ^ n + 2 ( n + 1 ) ( n + 2 ) ( 2 n + 1 ) .
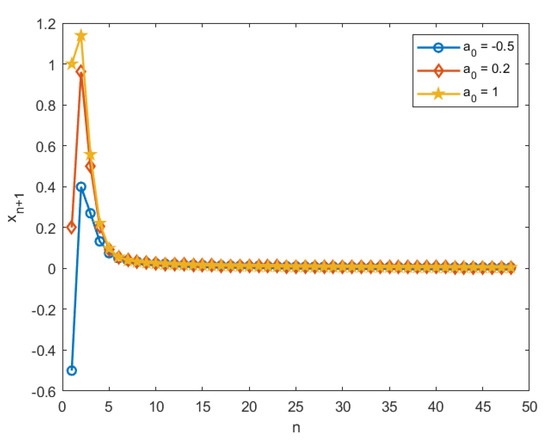
All codes were written in MATLAB 2018b, for the following different initial values: a ^ 0 = − 0.5 , a ^ 0 = 0.2 , and a ^ 0 = 1.0 . The sequence { a ^ n } → 0 , which is a fixed point of R I , λ M ( f , g ) [ λ ( Y I , λ M ( f , g ) − F ( C I , λ M ( f , g ) , Y I , λ M ( f , g ) ) + R I , λ M ( f , g ) ] . That is, the solution of problem (9), a ^ ∗ = 0 , exists. In this regard, a computational table (Table 1) and convergence graph (Figure 1) are shown below.
Table 1. The computational table of { a ^ n } starting with a ^ 0 = − 0.5 ,   a ^ 0 = 0.2 , and a ^ 0 = 1 .
Figure 1. Convergence of { a ^ n } starting with values a 0 = − 0.5 ,   a 0 = 0.2 , and a 0 = 1 .

5. Discussion

We selected the same operators as those in Example 1 and will now conduct a comparison between our proposed Algorithm 1 and the Ishikawa- and-Mann type algorithms. By setting γ n = 0 , we may compute { a ^ n } and { b ^ n } using the Ishikawa-type schemes outlined below:
a ^ n + 1 = n + 1 2 n + 1 a ^ n + 8040 n 17689 ( 2 n + 1 ) b ^ n + 1 2 ( 2 n + 1 ) , b ^ n = 17689 n + 8040 17689 ( n + 1 ) a ^ n + n + 2 ( n + 1 ) ( n + 3 ) .
Furthermore, on selecting β n = γ n = 0 , we may approximate { a ^ n } by the Mann-type iterative scheme:
a ^ n + 1 = 25729 n + 17689 17689 ( 2 n + 1 ) a ^ n + 1 2 ( 2 n + 1 ) .
When the stopping criterion ∥ a ^ n + 1 − a ^ n ∥ ≤ 10 − 10 is achieved, the iteration methods will cease. Table 2 and Figure 2 compare Algorithm 1 with the Ishikawa-type algorithm (32) and the Mann-type algorithm (33), all initiated with the initial value a ^ 0 = 1 .
Table 2. The computational table of { a ^ n } with starting value a ^ 0 = 1 .
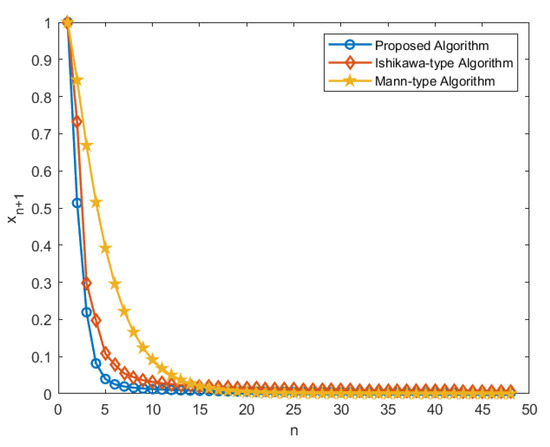
Figure 2. Convergence of { a ^ n } with starting value a ^ 0 = 1 .

6. Conclusions

We examined and demonstrated the existence of a solution to an extended Cayley–Yosida inclusion problem in a real 2-USBS. For the extended Cayley–Yosida inclusion problem, we also developed a three-step iterative method. This algorithm is much more comprehensive than the Mann- and Ishikawa-type iterative schemes, as well as numerous other iterative schemes that have been examined by different writers (see, e.g., [28,29,30]). We proved that our suggested algorithm converges to a unique solution of the problem under some suitable consideration and that this convergence is stable with respect to R I , λ M ( f , g ) . Lastly, we supported our main result with a numerical example.

Author Contributions

Conceptualization, I.A.; Methodology, I.A. and Y.W.; Validation, Y.W. and R.A.; Writing—original draft, I.A.; Funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant number 12171435).

Data Availability Statement

No new data were created or analyzed in this study. Data is not applicable for this article.

Acknowledgments

The authors are grateful to the anonymous reviewers for their valuable remarks which improved the results and presentation of this paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ansari, Q.H.; Yao, J.C. A fixed point theorem and its applications to system of variational inequalities. Bull. Aust. Math. Soc. 1999, 59, 433–442. [Google Scholar] [CrossRef]
  2. Pang, J.S. Asymmetric variational inequality problems over product of sets: Applications and iterative methods. Math. Program. 1985, 31, 206–219. [Google Scholar] [CrossRef]
  3. Yan, W.Y.; Fang, Y.P.; Huang, N.J. A new system of set-valued variational inclusions with H-monotone operators. Math. Inequal. Appl. 2005, 8, 537–546. [Google Scholar] [CrossRef]
  4. Abubakar, J.; Kumam, P.; Deepho, J. Multistep hybrid viscosity method for split monotone variational inclusion and fixed point problems in Hilbert spaces. AIMS Math. 2020, 5, 5969–5992. [Google Scholar] [CrossRef]
  5. Agarwal, R.P.; Verma, R.U. Generalized system of (A, η)-maximal relaxed monotone variational inclusion problems based on generalized hybrid algorithms. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 238–251. [Google Scholar] [CrossRef]
  6. Rockafellar, R.T. On the maximality of sums ofnonlinear monotone operators. Trans. Am. Math. Soc. 1970, 149, 75–88. [Google Scholar] [CrossRef]
  7. Lan, H.Y.; Kim, J.H.; Cho, Y.J. On a new system of nonlinear A-monotone multivalued variational inclusions. J. Math. Anal. Appl. 2007, 327, 481–493. [Google Scholar] [CrossRef]
  8. De, A. Hille-Yosida Theorem and Some Applications. Ph.D. Thesis, Department of Mathematics and its Applications, Central European University, Budapest, Hungary, 2015. [Google Scholar]
  9. Balooee, J. Resolvent algorithms for system of generalized nonlinear variational inclusions and fxed point problems. Afr. Mat. 2014, 25, 1023–1042. [Google Scholar] [CrossRef]
  10. Cao, H.W. Yosida approximation equations technique for system of generalized set-valued variational inclusions. J. Inequal. Appl. 2013, 2013, 455. [Google Scholar] [CrossRef][Green Version]
  11. Lan, H.Y. Generalized Yosida approximation based on relatively A-maximal m-relaxed monotonicity frameworks. Abs. Appl. Anal. 2013, 2013, 157190. [Google Scholar]
  12. Hassouni, A.; Moudafi, A. A perturbed algorithm for variational inclusions. J. Math. Anal. Appl. 1994, 183, 706–712. [Google Scholar] [CrossRef]
  13. Douglas, J.; Rachford, H.H. On the numerical solution of heat conduction problems in two and three space variables. Trans. Am. Math. Soc. 1956, 82, 421–439. [Google Scholar] [CrossRef]
  14. Peaceman, D.W.; Rachford, H.H., Jr. The numerical solution of parabolic and elliptic differential equations. J. Appl. Ind. Math. 1955, 3, 28–41. [Google Scholar] [CrossRef]
  15. Tseng, P. A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 2000, 38, 431–446. [Google Scholar] [CrossRef]
  16. Gibali, A.; Thong, D.V. Tseng type methods for solving inclusion problems and its applications. Calcolo 2018, 55, 49. [Google Scholar] [CrossRef]
  17. Ahmad, I.; Rahaman, M.; Ahmad, R.; Ali, I. Convergence analysis and stability of perturbed three-step iterative algorithm for generalized mixed ordered quasi-variational inclusion involving XOR operator. Optimization 2020, 69, 821–845. [Google Scholar] [CrossRef]
  18. Glowinski, G.; Tallec, P.L. Augmented Lagrangian and Operator Spliting Methods in Nonlinear Mechanics; SIAM: Philadelphia, PA, USA, 1989. [Google Scholar]
  19. Helmberg, G. Introduction to Spectral Theory in Hilbert Space: The Cayley Transform; North-Holland Series in Applied Mathematics and Mechanics, Applied Mathematics and Mechanics #6; North-Holland Publishing Company: Amsterdam, The Netherlands, 1969. [Google Scholar]
  20. Fang, Y.P.; Huang, N.J. H-accretive operator and resolvent operator technique for variational inclusions in Banach spaces. Appl. Math. Lett. 2004, 17, 647–653. [Google Scholar] [CrossRef]
  21. Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Fixed Point Theory for Lipschitzian-Type Mappings with Applications; Springer: New York, NY, USA, 2009; Volume 6. [Google Scholar]
  22. Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. Theory Methods Appl. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
  23. Kazmi, K.R.; Khan, F.A.; Shahzad, M. A system of generalized variational inclusions involving generalized H(·, ·)-accretive mapping in real q-uniformly smooth Banach spaces. Appl. Math. Comput. 2011, 217, 9679–9688. [Google Scholar] [CrossRef]
  24. Osilike, M.O. Stability results for the Ishikawa fixed point iteration procedure. Ind. J. Pure Appl. Math. 1995, 26, 937–945. [Google Scholar]
  25. Weng, X.L. Fixed point iteration for local srictly pseudocontractive mapping. Proc.Am.Math.Soc. 1991, 113, 727–731. [Google Scholar] [CrossRef]
  26. Ahmad, R.; Ali, I.; Rahaman, M.; Ishtyak, M.; Yao, J.C. Cayley inclusion problem with its corresponding generalized resolvent equation problem in uniformly smooth Banach spaces. Appl. Anal. 2022, 101, 1354–1368. [Google Scholar] [CrossRef]
  27. Rajpoot, A.K.; Ishtyak, M.; Ahmad, R.; Wang, Y.; Yao, J.C. Convergence analysis for Yosida variational inclusion problem with its corresponding Yosida resolvent equation problem through inertial extrapolation scheme. Mathematics 2023, 11, 763. [Google Scholar] [CrossRef]
  28. Akram, M.; Dilshad, M.; Rajpoot, A.K.; Babu, F.; Ahmad, R.; Yao, J.C. Modified Iterative Schemes for a Fixed-Point Problem and a Split Variational Inclusion Problem. Mathematics 2022, 10, 2098. [Google Scholar] [CrossRef]
  29. Zhao, X.; Sahu, D.R.; Wen, C.F. Iterative methods for system of variational inclusions involving accretive operators and applications. Fixed Point Theory 2018, 19, 801–822. [Google Scholar] [CrossRef]
  30. Iqbal, J.; Ali, I.; Arora, P.K.; Mir, W.A. Set-valued variational inclusion problem with fuzzy mappings involving XOR-operation. AIMS Math. 2021, 6, 3288–3304. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Deceptive Path Planning via Count-Based Reinforcement Learning under Specific Time Constraint
Previous
Prediction of Carbon Emissions Level in China’s Logistics Industry Based on the PSO-SVR Model
Next