Linear Combination of Order Statistics Moments from Log-Extended Exponential Geometric Distribution with Applications to Entropy

Abstract

Moments of order statistics (OSs) characterize the Weibull–geometric and half-logistic families of distributions, of which the extended exponential–geometric (EEG) distribution is a particular case. The EEG distribution is used to create the log-extended exponential–geometric (LEEG) distribution, which is bounded in the unit interval (0, 1). In addition to the generalized Stirling numbers of the first kind, a few years ago, the polylogarithm function and the Lerch transcendent function were used to determine the moments of order statistics of the LEEG distributions. As an application based on the L-moments, we expand the features of the LEEG distribution in this work. In terms of the Gauss hypergeometric function, this work presents the precise equations and recurrence relations for the single moments of OSs from the LEEG distribution. Along with recurrence relations between the expectations of function of two OSs from the LEEG distribution, it also displays the truncated and conditional distribution of the OSs. Additionally, we use the L-moments to estimate the parameters of the LEEG distribution. We further fit the LEEG distribution on three practical data sets from medical and environmental sciences areas. It is seen that the estimated parameters through L-moments of the OSs give a superior fit. We finally determine the correspondence between the entropies and the OSs.

1. Introduction

Over the last several years, many different and modified statistical models have been deployed to fit practical data sets from different domains. However, some types of these data may not be fitted by the classical distributions. Because of this, many authors have generalized such distributions or combined two or more classical distributions to add new parameters for data flexibility. Among these models is exponential distribution, which is a popular choice because of its flexibility. The exponential distribution has various applications, and, even in recent years, a large number of authors have contributed to its generalizations. A survey of the literature is provided below, which includes some well-known generalizations of the exponential distribution shown in Table 1.

Table 1. A review on the generalization of the exponential distribution in chronological order.

Author (s)	Distribution
Adamidis and Loukas [1]	Exponential–geometric (EG) distribution
Gupta and Kundu [2]	Generalized exponential (GE) distribution
Nadarajah [3]	Generalized exponential (GE) distribution: A survey
Adamidis et al. [4]	Extended exponential–geometric (EEG) distribution
Nadarajah and Haghighi [5]	Extended exponential (EE) distribution or NH distribution
Louzada et al. [6]	Complementary exponential–geometric (CEG) distribution
Lemonte [7]	Exponentiated NH (ENH) distribution
Jodrá and Jiménez-Gamero [8]	Log-extended exponential–geometric (LEEG) distribution
Bakouch et al. [9]	A new exponential distribution with trigonometric functions
Chesneau et al. [10]	The polynomial–exponential distribution
Bakouch et al. [11]	A new weighted exponential distribution

The probability density function (pdf) of the LEEG distribution is defined by Jodrá and Jiménez-Gamero [12] as

$$f\left(x\right|\alpha ,\beta )=\frac{\alpha (1+\beta )x^{\alpha -1}}{{(1+\beta x^{\alpha })}^2},\mathit{if}0<\mathrm{x}<1,\alpha >0\mathrm{and}\beta >-1,$$

(1)

the distribution function $\left(df\right)$ as

$$F\left(x\right|\alpha ,\beta )=\frac{(1+\beta )x^{\alpha }}{1+\beta x^{\alpha }},\mathit{if}0<\mathrm{x}<1,\alpha >0\mathrm{and}\beta >-1,$$

(2)

and the survival function $\left(sf\right)$ is given as

$$1-F\left(x\right|\alpha ,\beta )=\frac{1-x^{\alpha }}{1+\beta x^{\alpha }},\mathit{if}0<\mathrm{x}<1,\alpha >0\mathrm{and}\beta >-1.$$

(3)

Figure 1 represents the $pdf$ of the LEEG distribution for several values of the parameters. The power function and the uniform distributions are special cases, with $\beta =0$ and $\alpha =1$, respectively. As one may further note, for a negative value of $\beta$, the pdf strictly increases over the entire range. For positive and higher values of $\beta$, the pdf achieves its peak earlier (small values of x), where the peak is also seen to be substantially higher than in cases where $\beta$ is positive but small.

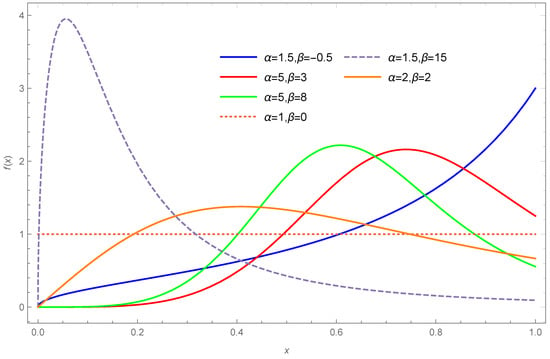
Figure 1. Behavior of the LEEG distribution at different values of different parameters.

Now, using Equations (1)–(3), we get

$$x(1-x^{\alpha })f\left(x\right|\alpha ,\beta )=x(1-x^{\alpha })\frac{\alpha (1+\beta )x^{\alpha -1}}{{(1+\beta x^{\alpha })}^2}=\alpha \left(\frac{1-x^{\alpha }}{1+\beta x^{\alpha }}\right)\left(\frac{(1+\beta )x^{\alpha }}{1+\beta x^{\alpha }}\right).$$

Thus, it can be noted that

$$x(1-x^{\alpha })f\left(x\right|\alpha ,\beta )=\alpha [1-F\left(x\right|\alpha ,\beta )]\left[F\left(x\right|\alpha ,\beta )\right].$$

(4)

Equation (4) is a characterizing equation, which is used for finding the recurrence relations of the LEEG distribution for the moments of the OSs.

This paper is summarized as follows. Section 2 presents some supporting lemmas, which are needed to establish the main results. In Section 3, we obtain some explicit expressions and recurrence relations of the OSs for the single moments of the LEEG distribution with numerical computations. Section 4 contains applications based on L-moments applied on different data sets, entropies and projective future data. Finally, Section 5 contains a few concluding remarks and future work.

2. Supporting Results

The following lemma is needed to calculate OSs’ moments from the LEEG distribution.

Lemma 1.

(See Gradshteyn and Ryzhik [13])

We have

$$\begin{array}{c}\hfill {\int }_0^u\frac{x^{\lambda -1}}{{(1+\beta x)}^{\nu }}dx=\frac{u^{\lambda }}{\lambda }{}_{2}F_1(\nu ;\lambda ;1+\lambda ;-\beta u)\end{array}$$

for $\lambda >0$, where ${}_{2}F_1(a,b;c;x)$ denote the Gauss hypergeometric function defined by

$$\begin{array}{c}\hfill {}_{2}F_1(a,b;c;x)=\sum _{i=0}^{\infty }\frac{{\left(a\right)}_i{\left(b\right)}_i}{{\left(c\right)}_i}\frac{x^i}{i!},\end{array}$$

where ${\left(p\right)}_i=p(p+1)\cdots (p+i-1)=\frac{\mathsf{\Gamma }(p+i)}{\mathsf{\Gamma }\left(p\right)}$ denotes the ascending factorial.

The hypergeometric function [see Mathai and Saxena [14]] can be also written as

$${}_{p}F_q[a_1,\cdots ,a_p;b_1,\cdots ,b_q;x]=\sum _{r=0}^{\infty }\left[\prod _{j=1}^p\frac{\mathsf{\Gamma }(a_j+r)}{\mathsf{\Gamma }\left(a_j\right)}\right]\left[\prod _{j=1}^q\frac{\mathsf{\Gamma }\left(b_j\right)}{\mathsf{\Gamma }(b_j+r)}\right]\frac{x^r}{r!}.$$

Following Mathai and Saxena [14], the series ${}_{p}F_q[a_1,\cdots ,a_p;b_1,\cdots ,b_q;x]$ converges for $\left|x\right|<1$, diverges for $\left|x\right|>1$ and, for $\left|x\right|=1$, ${}_{p}F_q$ converges only for $p=q+1$ and ${\sum }_{j=1}^q{b}_j-{\sum }_{j=1}^p{a}_j>0$.

At $p=2$ and $q=1$, this ${}_{2}F_1(a,b;c;x)$ is known as a Gauss hypergeometric series, which is defined above.

Lemma 2.

(See Jodrá and Jiménez-Gamero [8])

For any real numbers $a\ge 0$, $s\ge 1$ and $z>-1$, we consider

$${\mathsf{\Gamma }}_n\left(z,s,a\right)={\int }_0^1\frac{x^a{log}^{s-1}(1/x)}{{(1+zx)}^{n+1}}dx,n=0,1,\cdots .$$

(5)

Jodrá and Jiménez-Gamero [8] expressed the ${\mathsf{\Gamma }}_n(z,s,a)$ in a finite sum involving the Lerch transcendent function $\mathsf{\Phi }(z,\lambda ,\nu )$ with the generalized Stirling numbers of the first kind $R_n^j(\rho ,\tau )$ and the polylogarithm function $L{i}_{\lambda }\left(z\right)$. Those expressions are

$${\mathsf{\Gamma }}_n\left(z,s,a\right)=\frac{\mathsf{\Gamma }\left(s\right)}{\mathsf{\Gamma }(n+1)}\sum _{j=0}^n{R}_n^j(a-n+1,1)\mathsf{\Phi }(-z,s-j,a+1),n=0,1,\cdots ,$$

(6)

and

$${\mathsf{\Gamma }}_n\left(z,s,a\right)=\frac{\mathsf{\Gamma }\left(s\right)}{\mathsf{\Gamma }(n+1)}\sum _{j=0}^n{R}_n^j(i+r+\frac{k}{\alpha }-n,1){\mathit{Li}}_{1-j}(-\beta ),n=0,1,\cdots .$$

(7)

As a special case,

$${\mathsf{\Gamma }}_n\left(z,s,a\right)=\left\{\begin{array}{c}\mathsf{\Gamma }\left(s\right)\mathsf{\Phi }(-z,s,a+1)\mathit{if}n=0,\hfill \\ \frac{\mathsf{\Gamma }\left(s\right)}{{(a+1)}^s}\mathit{if}z=0.\hfill \end{array}\right.$$

The Lerch transcendent function $\mathsf{\Phi }(.)$ is defined as the analytic continuation of the series

$$\mathsf{\Phi }(z,\lambda ,\nu )=\sum _{i=0}^{\infty }\frac{z^i}{{(i+\nu )}^{\lambda }},$$

(8)

which converges for any real number $\nu >0$ if z and λ are any complex numbers with either $\left|z\right|<1$, or $\left|z\right|=1$ and $Re\left(\lambda \right)>1$.

The polylogarithm function of order λ and argument z is defined by the Dirichlet series

$$L{i}_{\lambda }\left(z\right)=\sum _{i=1}^{\infty }\frac{z^i}{i^{\lambda }},$$

(9)

which is absolutely convergent for all complex λ and z inside the unit circle in the complex z-plane. It is clear that the Lerch transcendent function includes as a particular case the polylogarithm function, specifically, $L{i}_{\lambda }\left(z\right)=z\mathsf{\Phi }(z,\lambda ,1)$. For more details on the Lerch transcendent, the polylogarithm function and the generalized Stirling numbers of the first kind, see Erdélyi et al. [15], Apostol [16] and Pickard [17].

The moment properties derived in Section 3.1 involve Lemmas 1 and 2, which are an infinite series. In general, the problem of finding closed-form expressions for computing the moments of order statistics has attracted a great deal of attention in statistics. All these functions can be computed numerically, and computations are available in mathematical and statistical packages, such as MATHEMATICA 13.1 and R software R-4.4.0. Hence, the expressions derived in Section 3.1 are seen to be convenient.

3. Order Statistics

In the statistical sciences, OSs are highly helpful. They have a wide range of applications, including modeling, manufacturing, insurance, optimizing production processes, estimating parameters of distributions. OSs and their uses have been extensively discussed in the popular books by Arnold et al. [18] and David and Nagarajah [19].

When the magnitude of the random variables $X_1,X_2,\cdots ,X_n$ of size n from the LEEG distribution with $pdf$ $f\left(x\right)$ and $cdf$ $F\left(x\right)$ as in (1) and (2), respectively, are arranged in an increasing order as $X_{1:n}\le X_{2:n}\le \cdots \le X_{n:n}$, they are called as the OSs from the LEEG distribution. The $pdf$ of $X_{r:n}$, the $r^{th}$ order statistic, denoted by $f_{r:n}\left(x\right)$, for $1\le r\le n$ is given in [Arnold et al. [18] and David and Nagaraja [19]] as

$$f_{r:n}\left(x\right)=C_{r:n}{\left[F\left(x\right)\right]}^{r-1}{[1-F\left(x\right)]}^{n-r}f\left(x\right),0<x<\infty ,$$

(10)

where

$$C_{r:n}=\frac{n!}{(r-1)!(n-r)!}.$$

Now, we shall denote,

$${\mu }_{r:n}^{\left(k\right)}=E\left(X_{r:n}^k\right);1\le r\le n;k\in \mathbb{N},$$

the $k^{th}$ single moment of the $r^{th}$ order statistic from the LEEG distribution.

In statistical literature, the explicit expression and recurrence relations for the moments of order statistics are frequently utilized, such as statistical modelling, statistical inferences, decision procedures, nonparametric statistics, among others. Many authors have established the exact expressions and recurrence relations for several distributions. For example, see Khan et al. [20,21], Ali and Khan [22], Khan and Khan [23], Nadarajah [24], Genç [25], Nagaraja [26], MirMostafaee [27], Akhter et al. [28,29], Alam et al. [30], Singh et al. [31] and references therein.

3.1. Exact Moments of Order Statistics from of the LEEG Distribution

In this section, we obtain the results for the single moments of order statistics for the underlying distribution. The results are presented in the form of the following theorems.

Theorem 1.

For $1\le r\le n$ and $k\in \mathbb{N}$, we have

$${\mu }_{r:n}^{\left(k\right)}=C_{r:n}{(1+\beta )}^r\sum _{i=0}^{n-r}\frac{{(-1)}^i}{i+r+k/\alpha }\left(\genfrac{}{}{0pt}{}{n-r}{i}\right){}_{2}F_1\left(n+1,i+r+\frac{k}{\alpha };i+r+\frac{k}{\alpha }+1;-\beta \right),$$

(11)

where $C_{r:n}$ is as defined in (10) and ${}_{2}F_1(a,b;c;x)$ is the Gauss hypergeometric function, defined in Lemma 1.

Proof. 

Using (10), we have

$${\mu }_{r:n}^{\left(k\right)}=C_{r:n}{\int }_0^1{x}^k{\left[F\right(x\left)\right]}^{r-1}{[1-F(x\left)\right]}^{n-r}f\left(x\right)dx.$$

Now, using (1)–(4), we get

$${\mu }_{r:n}^{\left(k\right)}=\alpha C_{r:n}{(1+\beta )}^r{\int }_0^1\frac{x^{k+\alpha r-1}}{{(1+\beta x^{\alpha })}^{n+1}}{(1-x^{\alpha })}^{n-r}dx.$$

(12)

Substituting $t=x^{\alpha }$, we find that

$${\mu }_{r:n}^{\left(k\right)}=C_{r:n}{(1+\beta )}^r{\int }_0^1\frac{t^{r+k/\alpha -1}}{{(1+\beta t)}^{n+1}}{(1-t)}^{n-r}dt.$$

Using the binomial expression, we get

$${\mu }_{r:n}^{\left(k\right)}=C_{r:n}{(1+\beta )}^r\sum _{i=0}^{n-r}{(-1)}^i\left(\genfrac{}{}{0pt}{}{n-r}{i}\right){\int }_0^1\frac{t^{i+r+k/\alpha -1}}{{(1+\beta t)}^{n+1}}dt.$$

(13)

Since, using Lemma 1, the resulting expression can be viewed as (11). This proves the theorem. □

Theorem 2.

For $1\le r\le n$ and $k\in \mathbb{N}$, we obtain the following representations:

$${\mu }_{r:n}^{\left(k\right)}=C_{r:n}{(1+\beta )}^r\sum _{i=0}^{n-r}{(-1)}^i\left(\genfrac{}{}{0pt}{}{n-r}{i}\right){\mathsf{\Gamma }}_n\left(\beta ,1,i+r+\frac{k}{\alpha }-1\right),$$

(14)

where ${\mathsf{\Gamma }}_n\left(a,b,c\right)$ and $C_{r:n}$ are defined as before.

$${\mu }_{r:n}^{\left(k\right)}=\frac{{(1+\beta )}^r}{(r-1)!(n-r)!}\sum _{i=0}^{n-r}{(-1)}^i\left(\genfrac{}{}{0pt}{}{n-r}{i}\right)\sum _{j=0}^n{R}_n^j(i+r+\frac{k}{\alpha }-n,1)\mathsf{\Phi }\left(-\beta ,1-j,i+r+\frac{k}{\alpha }\right),$$

(15)

where $R_n^j(i+r+\frac{k}{\alpha }-n,1)$ and $\mathsf{\Phi }\left(-\beta ,1-j,i+r+\frac{k}{\alpha }\right)$ are defined in Section 2.

$${\mu }_{r:n}^{\left(k\right)}=\frac{{(1+\beta )}^r}{(r-1)!(n-r)!}\sum _{i=0}^{n-r}{(-1)}^i\left(\genfrac{}{}{0pt}{}{n-r}{i}\right)\sum _{j=0}^n{R}_n^j(i+r+\frac{k}{\alpha }-n,1){\mathit{Li}}_{1-j}(-\beta ),$$

(16)

where ${\mathit{Li}}_{1-j}(-\beta )$ are defined in Section 2.

Proof. 

Proofs are straightforward, in line with Jodránez-Gamero [8,12]. By using the (13), we get

$${\mu }_{r:n}^{\left(k\right)}=C_{r:n}{(1+\beta )}^r\sum _{i=0}^{n-r}{(-1)}^i\left(\genfrac{}{}{0pt}{}{n-r}{i}\right){\int }_0^1\frac{t^{i+r+k/\alpha -1}}{{(1+\beta t)}^{n+1}}dt.$$

(17)

By utilizing Lemma 2, the resulting expression can be viewed as (14)–(16). This proves the theorem. □

Remark 1.

When $n=r=1$ in (11), we get

$$\begin{array}{c}\hfill {\mu }_{1:1}^{\left(k\right)}=\mathbb{E}\left(X^k\right)=\frac{1+\beta }{1+k/\alpha }{}_{2}F_1\left(2,1+\frac{k}{\alpha };2+\frac{k}{\alpha };-\beta \right),\end{array}$$

(18)

which is the k-th moments of the LEEG distribution.

At $k=1,2,3$ and $k=4$ in (18), we obtain the first four moments of the LEEG distribution as

$$\begin{array}{c}\hfill {\mu }_{1:1}^{\left(1\right)}=\mathbb{E}\left(X\right)=\frac{1+\beta }{1+1/\alpha }{}_{2}F_1\left(2,1+\frac{1}{\alpha };2+\frac{1}{\alpha };-\beta \right)\end{array}$$

(19)

and

$$\begin{array}{c}\hfill {\mu }_{1:1}^{\left(2\right)}=\mathbb{E}\left(X^2\right)=\frac{1+\beta }{1+2/\alpha }{}_{2}F_1\left(2,1+\frac{2}{\alpha };2+\frac{2}{\alpha };-\beta \right),\end{array}$$

(20)

which, upon using (19) and (20), together with $\mathbb{V}\left[X\right]=\mathbb{E}\left(X^2\right)-{\left(\mathbb{E}\left(X\right)\right)}^2$, gives the variance of the LEEG distribution as

$$\mathbb{V}\left[X\right]=\frac{1+\beta }{1+2/\alpha }{}_{2}F_1\left(2,1+\frac{2}{\alpha };2+\frac{2}{\alpha };-\beta \right)-{\left[\frac{1+\beta }{1+1/\alpha }{}_{2}F_1\left(2,1+\frac{1}{\alpha };2+\frac{1}{\alpha };-\beta \right)\right]}^2.$$

(21)

Remark 2.

At $r=1$, in (11), we get

$${\mu }_{1:n}^{\left(k\right)}=n(1+\beta )\sum _{i=0}^{n-1}\frac{{(-1)}^i}{i+1+k/\alpha }\left(\genfrac{}{}{0pt}{}{n-1}{i}\right){}_{2}F_1\left(n+1,i+\frac{k}{\alpha }+1;i+\frac{k}{\alpha }+2;-\beta \right)$$

(22)

and at $r=n$, in (11), we get

$${\mu }_{n:n}^{\left(k\right)}=\frac{n{(1+\beta )}^n}{n+k/\alpha }{}_{2}F_1\left(n+1,n+\frac{k}{\alpha };n+\frac{k}{\alpha }+1;-\beta \right).$$

(23)

The expressions in (22) and (23) are the extreme k-th moments of the LEEG distribution.

3.2. Recurrence Relations of the LEEG Distribution

In this section, we obtain the recurrence relations for the single moments of order statistics for the LEEG distribution. Recurrence relations are particularly helpful in minimizing the amount of direct computation, which lessens labor and time. They also offer a few easy ways to verify that the computation of moments of OSs is accurate. The results are presented in the form of the following theorems.

Theorem 3.

For $1<r\le n$ and $k\in \mathbb{N}$, we have

$${\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n-1}^{\left(k\right)}=\frac{k}{\alpha (r-1)}\left[{\mu }_{r-1:n-1}^{\left(k\right)}-{\mu }_{r-1:n-1}^{(k+\alpha )}\right]$$

(24)

and consequently,

$${\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n}^{\left(k\right)}=\frac{nk}{\alpha (n-r+1)(r-1)}\left[{\mu }_{r-1:n-1}^{\left(k\right)}-{\mu }_{r-1:n-1}^{(k+\alpha )}\right].$$

(25)

Proof. 

Khan et al. [20] have shown that for $1\le r\le n$,

$${\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n-1}^{\left(k\right)}=\left(\genfrac{}{}{0pt}{}{n-1}{r-1}\right)k{\int }_0^{\infty }{x}^{k-1}{\left[F\right(x\left)\right]}^{r-1}{[1-F(x\left)\right]}^{n-r+1}dx.$$

(26)

Now, using (4) in (26), we get

$$\begin{array}{cc}\hfill {\mu }_{r:n}^{\left(k\right)}-{\mu }_{r-1:n-1}^{\left(k\right)}& =\left(\genfrac{}{}{0pt}{}{n-1}{r-1}\right)\frac{k}{\alpha }{\int }_0^1{x}^k{\left[F\right(x\left)\right]}^{r-2}{[1-F(x\left)\right]}^{n-r}f\left(x\right)dx\hfill \\ & -\left(\genfrac{}{}{0pt}{}{n-1}{r-1}\right)\frac{k}{\alpha }{\int }_0^1{x}^{k+\alpha }{\left[F\right(x\left)\right]}^{r-2}{[1-F(x\left)\right]}^{n-r}f\left(x\right)dx,\hfill \end{array}$$

which, after simplification, yields (24). □

Now, by using the following well-known moment recurrence relation,

$$n{\mu }_{r:n-1}^{\left(k\right)}=(n-r){\mu }_{r:n}^{\left(k\right)}+r{\mu }_{r+1:n}^{\left(k\right)},$$

[see, e.g., David and Nagaraja [19]], we obtain (25). This completes the proof of the theorem.

Corollary 1.

For $n>1$ and $k\in \mathbb{N}$,

$${\mu }_{2:n}^{\left(k\right)}-{\mu }_{1:n-1}^{\left(k\right)}=\frac{k}{\alpha }\left[{\mu }_{1:n-1}^{\left(k\right)}-{\mu }_{1:n-1}^{(k+\alpha )}\right]$$

(27)

and

$${\mu }_{n:n}^{\left(k\right)}-{\mu }_{n-1:n}^{\left(k\right)}=\frac{nk}{\alpha (n-1)}\left[{\mu }_{n-1:n-1}^{\left(k\right)}-{\mu }_{n-1:n-1}^{(k+\alpha )}\right].$$

(28)

Proof. 

Relations (27) and (28) are the simple consequences of (24) and can be established by putting $r=2$ and $r=n$, respectively, in (24). □

3.3. Truncated and Conditional Distribution of the OSs

We refer to the following identities pertaining to the LEEG distribution

$${\int }_0^{Q_1}f\left(x\right)dx=\frac{(1+\beta )Q_1^{\alpha }}{1+\beta Q_1^{\alpha }}=Q\left(\mathrm{say}\right),{\int }_0^{P_1}f\left(x\right)dx=\frac{(1+\beta )P_1^{\alpha }}{1+\beta P_1^{\alpha }}=P\left(\mathrm{say}\right).$$

This implies

$${\int }_{Q_1}^{P_1}f\left(x\right)dx=\frac{(1+\beta )P_1^{\alpha }}{1+\beta P_1^{\alpha }}-\frac{(1+\beta )Q_1^{\alpha }}{1+\beta Q_1^{\alpha }}=\frac{(P_1^{\alpha }-Q_1^{\alpha })(1+\beta )}{(1+\beta P_1^{\alpha })(1+\beta Q_1^{\alpha })},$$

or, equivalently,

$${\left[\frac{(P_1^{\alpha }-Q_1^{\alpha })(1+\beta )}{(1+\beta P_1^{\alpha })(1+\beta Q_1^{\alpha })}\right]}^{-1}{\int }_{Q_1}^{P_1}f\left(x\right)dx=1.$$

Thus, the doubly truncated pdf of the LEEG distribution is given by

$$g\left(x\right)={\left[\frac{(P_1^{\alpha }-Q_1^{\alpha })(1+\beta )}{(1+\beta P_1^{\alpha })(1+\beta Q_1^{\alpha })}\right]}^{-1}\frac{\alpha (1+\beta )x^{\alpha -1}}{{(1+\beta x^{\alpha })}^2},x\in (Q_1,P_1),$$

and the corresponding cdf is given by

$$G\left(x\right)={\left[\frac{(P_1^{\alpha }-Q_1^{\alpha })(1+\beta )}{(1+\beta P_1^{\alpha })(1+\beta Q_1^{\alpha })}\right]}^{-1}\left[\frac{(x^{\alpha }-Q_1^{\alpha })(1+\beta )}{(1+\beta x^{\alpha })(1+\beta Q_1^{\alpha })}\right],x\in (Q_1,P_1),$$

where $0\le Q_1\le 1,0\le P_1\le 1$ such that $Q_1\le P_1$ are the lower and upper truncation points. If we fix $Q_1=0$, the distribution will be truncated to the right. Similarly, if $P_1=1$, the distribution will be truncated to the left. Finally, if $Q_1=0$ and $P_1=1$, we get the non-truncated distribution. The following remarks give a connection between the truncated distributions given above and the conditional distributions of the OSs pertaining to the LEEG distribution. All these are based on similar results derived in David and Nagaraja [19].

Remark 3.

Let $X_1,X_2,...,X_n$ be a random sample from the LEEG distribution with pdf and cdf as given in (1) and (2). Let $X_{1:n},X_{2:n},...,X_{n:n}$ denote the OSs obtained from this sample. Then, the conditional distribution of $X_{r:n}$ given $X_{s:n}=y$ for $s>r$ is the same as the distribution of the r-th order statistic obtained from a sample of size $(s-1)$ from a population whose distribution is truncated on the right at y.

Remark 4.

We consider a random sample from the LEEG distribution, such as $X_1,X_2,...,X_n$, with pdf and df given in (1) and (2). Let $X_{1:n},X_{2:n},...,X_{n:n}$ denote the OSs obtained from this sample. Then, the conditional distribution of $X_{s:n}$ given $X_{r:n}=x$ for $s>r$ is the same as the distribution of the $(s-r)$-th OSs obtained from a sample of size $(n-r)$ from a population whose distribution is truncated on the left at x.

Remark 5.

Let $X_1,X_2,...,X_n$ be a random sample from the LEEG distribution with pdf and df as given in (1) and (2). Let $X_{1:n},X_{2:n},...,X_{n:n}$ denote the order statistics obtained from this sample. Then, the conditional distribution of $X_{s:n}$ given $X_{r:n}=x$ and $X_{t:n}=z$ for $1\le r<s<t\le n$ is the same as the distribution of the $(s-r)$-th order statistic obtained from a sample of size $(t-r-1)$ from a population whose distribution is truncated on the left at x and on the right at z.

One can find the proofs of the above remarks in Kumar [32].

3.4. Recurrence Relations between Expectations of Function of Two OSs from the LEEG Distribution

The df of the LEEG distribution can be written as

$$\begin{array}{c}F\left(x\right)=\frac{(1+\beta )x^{\alpha }}{1+\beta x^{\alpha }}=(1+\beta ){(x^{-\alpha }+\beta )}^{-1}={\left[\frac{1}{1+\beta }\left(x^{-\alpha }+\beta \right)\right]}^{-1}\\ ={\left(\frac{x^{-\alpha }}{1+\beta }+\frac{\beta }{1+\beta }\right)}^{-1},\end{array}$$

which can be seen in the form ${[ah\left(x\right)+b]}^c,$ where $a={(1+\beta )}^{-1},h\left(x\right)=x^{-\alpha },b=\beta {(1+\beta )}^{-1}$ and $c=-1$. Using the results of Ali and Khan [33], we can write the following theorems:

Theorem 4.

For $1\le r<s\le n,n=1,2,...$, we get

$$\begin{array}{cc}\hfill E\left[g(X_{r:n},X_{s:n})\right]& - E\left[g(X_{r:n},X_{s-1:n})\right]\hfill \\ \hfill & =-\frac{n{P}_3}{n-s+1}\{E\left[g(X_{r:n-1},X_{s:n-1})\right]-E\left[g(X_{r:n-1},X_{s-1:n-1})\right]\}\hfill \\ \hfill & +\frac{1}{(n-s+1){(1+\beta )}^{-1}}E\left[m(X_{r:n},X_{s:n})\right],\hfill \end{array}$$

where $m(x,y)$ is a function defined as

$$m(x,y)=[ah\left(y\right)+b]\frac{\frac{\partial }{\partial y}g(x,y)}{h^{\prime }\left(y\right)},$$

and $g(.,.)$ is a Borel measurable function from ${\mathbb{R}}^2$ to $\mathbb{R}$. Further, $P_3=\frac{P}{P-Q}$, where $P,Q$ are as defined in Section 3.3.

Theorem 5.

For $1\le r<s\le n,n=1,2,...$,

$$\begin{array}{c}\hfill E\left[g(X_{r:n},X_{s:n})\right]=E\left[g(X_{r:n},X_{s-1:n})\right]-\frac{P-Q}{(n+1){(1+\beta )}^{-1}}E\left[z(X_{r:n+1},X_{s:n+1})\right],\end{array}$$

where $z(x,y)$ is a function defined as

$$z(x,y)={[ah\left(y\right)+b]}^2\frac{\frac{\partial }{\partial y}g(x,y)}{h^{\prime }\left(y\right)},$$

and $g(.,.)$ is defined as previously.

The proofs of above theorems can be seen to be in line with Kumar [32].

3.5. Numerical Computations

Here, we have calculated means, second moments and variances of OSs (Table 2). All computations were obtained using Mathematica. Mathematica, like other algebraic manipulation packages, allows for arbitrary precisions, so the accuracy of the given values is not an issue. In the case of OSs, following identities are used to check the calculation of mean and variances (see David and Nagarajah [19]).

$$\begin{array}{c}\hfill \sum _{r=0}^n{\mu }_{r:n}^k=n{\mu }^k,k=1,2\mathrm{and}{\mu }^k=E\left(X^k\right).\end{array}$$

Table 2. Means, second moments and variances of OSs.

		$\mathit{\alpha }=1.50,\mathit{\beta }=0.40$			$\mathit{\alpha }=5,\mathit{\beta }=0.40$
n	r	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$
1	1	$0.548921$	$0.371862$	$0.070548$	$0.806808$	$0.673138$	$0.022199$
3	1	$0.316831$	$0.136715$	$0.036333$	$0.675731$	$0.477462$	$0.020849$
	2	$0.553745$	$0.347130$	$0.040496$	$0.823602$	$0.688779$	$0.010459$
	3	$0.776188$	$0.631739$	$0.029271$	$0.921092$	$0.853172$	$0.004761$
5	1	$0.234086$	$0.076740$	$0.021944$	$0.615173$	$0.396778$	$0.018340$
	2	$0.402834$	$0.190005$	$0.027730$	$0.745738$	$0.566609$	$0.010484$
	3	$0.555288$	$0.336698$	$0.028353$	$0.829057$	$0.694125$	$0.006789$
	4	$0.702599$	$0.518166$	$0.024520$	$0.894193$	$0.803823$	$0.004242$
	5	$0.849799$	$0.737699$	$0.015541$	$0.949881$	$0.904354$	$0.002080$
		$\mathsf{\alpha }=\mathbf{1}.\mathbf{50},\mathsf{\beta }=-\mathbf{0}.\mathbf{40}$			$\mathsf{\alpha }=\mathbf{5},\mathsf{\beta }=-\mathbf{0}.\mathbf{40}$
n	r	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$	${\mu }_{r:n}^{\left(1\right)}$	${\mu }_{r:n}^{\left(2\right)}$	$V\left[X_{r:n}\right]$
1	1	$0.674306$	$0.517040$	$0.062351$	$0.869459$	$0.772059$	$0.016100$
3	1	$0.451748$	$0.254138$	$0.050061$	$0.760745$	$0.598528$	$0.019795$
	2	$0.699640$	$0.522882$	$0.033386$	$0.890339$	$0.799267$	$0.006563$
	3	$0.871532$	$0.774099$	$0.014531$	$0.957292$	$0.918382$	$0.001974$
5	1	$0.354707$	$0.163094$	$0.037277$	$0.703683$	$0.514651$	$0.019481$
	2	$0.559940$	$0.345673$	$0.032140$	$0.829386$	$0.696149$	$0.008268$
	3	$0.709414$	$0.525798$	$0.022530$	$0.897189$	$0.808922$	$0.003974$
	4	$0.826306$	$0.696205$	$0.013423$	$0.942158$	$0.889510$	$0.001848$
	5	$0.921164$	$0.854430$	$0.005886$	$0.974876$	$0.951061$	$0.000678$

For any fixed sample size n, the increase in r results in increase in moments. For any fixed r, an increase in sample size n leads to a decrease in variance, which is universally true.

4. Applications

In this section, we estimate the parameters of the LEEG distribution through L-moments of OSs. Furthermore, we fit the distribution to flood levels data, clinical trial data and the testosterone level data, which were already studied by several authors (cf. Asgharzadeha et al. [34], Makouei et al. [35]) and are commonly used in the OSs area. Compared to ordinary moments, L-moments exhibit less sample variance and are better adapted to outliers. Additionally, model specification probability distributions can be characterized using L-moments for parameter estimation and hypothesis testing. The L-moments are expectations of certain linear combinations of OSs (see Hosking [36]). The r-th L-moment of a distribution can be defined as OSs appearing in several areas of study and provide the suitable and appropriate solution for many problems, such as detection of outlier, robustness, quality control, reliability analysis, breaking strength analysis and so on.

4.1. L-Moments

Let $X_1,X_2,\cdots ,X_n$ be a random sample from the LEEG distribution given in (1) and $X_{1:n},X_{2:n},\cdots ,X_{n:n}$ denote the corresponding OSs. Hosking [36] defined L-moments as linear combinations of OSs. When there are outliers in the data, L-moments are more accurate than ordinary moments. The L-moments of a distribution are given by

$$\begin{array}{c}\hfill L_r=\frac{1}{r}\sum _{j=0}^{r-1}{(-1)}^j\left(\genfrac{}{}{0pt}{}{r-1}{j}\right){\mu }_{r-j:r},r\ge 1,\end{array}$$

(29)

where ${\mu }_{r:n}$ is defined in (11) for $k=1$.

For $r=1,2$ in (29), the first and second L-moments are given as

$$\begin{array}{c}\hfill L_1=E\left(X_{1:1}\right)\mathrm{and}{L}_2=\frac{1}{2}E(X_{2:2}-X_{1:2}).\end{array}$$

(30)

According to Hosking [36], the first and second sample L-moments are calculated as

$$l_1=\frac{1}{n}\sum _{i=1}^n{x}_{i:n}\mathrm{and}{l}_2=\frac{2}{n(n-1)}\sum _{i=2}^n(i-1)x_{i:n}-l_1.$$

(31)

By solving (30) and (31), one can obtain the L-moment estimators $\widehat{\alpha }$ and $\widehat{\beta }$ for the parameters $\alpha$ and $\beta$, respectively, of the LEEG distribution. The expression is not in a compact form, so we solve the underlying equations using the statistical software R [37].

4.2. Examples

Flood levels data: The data represent the maximum flood levels (in millions of cubic feet per second) of the Susquehenna River at Harrisburg, Pennsylvania over 20 four-year periods (1890–1969) as follows: 0.654, 0.613, 0.315, 0.449, 0.297, 0.402, 0.379, 0.423, 0.379, 0.324, 0.269, 0.740, 0.418, 0.412, 0.494, 0.416, 0.338, 0.392, 0.484 and 0.265, assuming the data to be independent. From Table 3 and Table 4, one can see that the flood data are leptokurtic and fit the LEEG distribution.

Table 3. Summaries of the data.

Data	Min.	Median	Mean	Variance	Max.	Skewness	Kurtosis
Flood data	0.265	0.407	0.423	0.0157	0.740	1.068	3.600
Relief time	0.29	0.60	0.61	0.0232	0.87	–0.27	2.40
Testosterone level	0.18	0.37	0.45	0.0381	0.90	0.78	2.61

Table 4. Estimates, KS statistic and their p-values for the data.

Data	Model	Estimates	KS  Test Statistic	KS  p-Value
Flood data	$LEEG(\alpha ,\beta )$	$\widehat{\alpha }=0.85,\widehat{\beta }=0.24$	0.40	0.0815
Relief time	$LEEG(\alpha ,\beta )$	$\widehat{\alpha }=1.37,\widehat{\beta }=-0.18$	0.28	0.1057
Testosterone level	$LEEG(\alpha ,\beta )$	$\widehat{\alpha }=0.92,\widehat{\beta }=0.20$	0.30	0.1344

Clinical trials data: The data display the relief time (in hours) for 50 arthritic patients as follows: 0.70, 0.84, 0.58, 0.50, 0.55, 0.82, 0.59, 0.71, 0.72, 0.61, 0.62, 0.49, 0.54, 0.72, 0.36, 0.71, 0.35, 0.64, 0.85, 0.55, 0.59, 0.29, 0.75, 0.53, 0.46, 0.60, 0.60, 0.36, 0.52, 0.68, 0.80, 0.55, 0.84, 0.70, 0.34, 0.70, 0.49, 0.56, 0.71, 0.61, 0.57, 0.73, 0.75, 0.58, 0.44, 0.81, 0.80, 0.87, 0.29 and 0.50. The data summary and fitting to the LEEG distribution are provided in Table 3 and Table 4.

The testosterone level in infertile women data: The data show the testosterone level ($\mathsf{\mu }$g/dL) in 30 infertile women in Alzahra hospital in Tabriz, Iran, as follows: 0.33, 0.37, 0.51, 0.30, 0.45, 0.18, 0.67, 0.20, 0.33, 0.38, 0.35, 0.25, 0.33, 0.68, 0.32, 0.35, 0.35, 0.31, 0.38, 0.35, 0.19, 0.70, 0.50, 0.50, 0.73, 0.83, 0.77, 0.45, 0.50 and 0.90. Table 3 and Table 4 give the summary of the data and fit them to the LEEG distribution.

The conclusion that can be drawn from the p-values of the three data sets is that the LEEG can fit the data with acceptable estimations.

4.3. The Predictive Moments of OSs

The most significant use of estimation is the prediction of upcoming events. In the case of the prediction of future emergencies related to extreme events, it is of interest to have the largest observations of the OSs. For this purpose, we used the moments of some OSs for the earlier data sets using Equation (11) of the LEEG distribution, where the parameters of the LEEG distribution are replaced by their corresponding L-moments estimates for the earlier data set. Those OSs are given in Table 5, where the moments increase with increasing r.

Table 5. The predictive moments of OSs.

${\widehat{\mathit{\mu }}}_{\mathit{r}:20}$	Flood Data	Relief Time	Testosterone Level
r = 1	0.0239282	0.113663	0.0316463
r = 2	0.0526336	0.195225	0.0666027
r = 3	0.0844921	0.264589	0.103675
r = 4	0.11890	0.326658	0.14245
r = 5	0.155551	0.383581	0.182724
r = 6	0.194268	0.436547	0.224382
r = 7	0.234941	0.486309	0.267354
r = 8	0.277501	0.533379	0.311596
r = 9	0.321908	0.578135	0.357081
r = 10	0.368138	0.620859	0.403794
r = 11	0.416182	0.661776	0.451727
r = 12	0.466041	0.701066	0.500881
r = 13	0.517724	0.738877	0.55126
r = 14	0.571248	0.775335	0.602871
r = 15	0.626637	0.810544	0.655728
r = 16	0.683918	0.844598	0.709844
r = 17	0.743123	0.877574	0.765237
r = 18	0.804291	0.909543	0.821926
r = 19	0.867463	0.940568	0.879934
r = 20	0.932682	0.970704	0.939283

4.4. Entropies

Entropy is a scientific concept as well as a measurable physical property that provides a measure of the average amount of information associated with a state of disorder, randomness or uncertainty. The classical entropy is the information that is mathematically calculated by C. E. Shannon and called the Shannon entropy. If X is a non-negative absolutely continuous random variable associated with the information, then the Shannon entropy is defined by [38] as

$$H\left(X\right)=E[-ln\left(X\right)]=-{\int }_0^{+\infty }f\left(x\right)lnf\left(x\right)dx.$$

There are different types of entropies, each suitable for a specific situation. Recently, various authors have discussed different versions of entropies and their applications. For more details, the reader may see [39,40,41,42,43]. The cumulative residual entropy (CRE) of X given by Rao et al. [44] and the cumulative entropy (CE) of X given by Di Crescenzo and Longobardi [45] are one of the most important versions of entropy. These entropies are defined, respectively, as

$$\mathcal{E}\left(X\right)=-{\int }_0^{+\infty }\overline{F}\left(x\right)ln\left(\overline{F}\left(x\right)\right)dx\mathrm{and}C\mathcal{E}\left(X\right)=-{\int }_0^{+\infty }F\left(x\right)ln\left(F\left(x\right)\right)dx.$$

(32)

4.4.1. Relationships between Entropies and OSs of the LEEG Distribution

Theorem 6.

Let X follow the LEEG distribution with a finite mean, noting $\beta >-1$. Then, the CRE of X is given by

$$\mathcal{E}\left(X\right)=(1+\beta )\left[\sum _{n=1}^{\infty }\frac{{(1+\beta )}^n}{n(n+1+1/\alpha )}{\mathsf{\Delta }}_{n+1}^{n+1}(\alpha ,\beta )-\frac{1}{1+1/\alpha }\mathsf{\Delta }(\alpha ,\beta )\right],$$

and the CE of X is given by

$$\mathcal{CE}\left(X\right)=-(1+\beta )\left[\sum _{n=1}^{\infty }\sum _{i=0}^n\frac{{(-1)}^i}{i+1+1/\alpha }\left(\genfrac{}{}{0pt}{}{n}{i}\right){\mathsf{\Delta }}_{i+1}^{n+1}(\alpha ,\beta )-\frac{1}{1+1/\alpha }\mathsf{\Delta }(\alpha ,\beta )\right],$$

where ${\mathsf{\Delta }}_i^n(\alpha ,\beta )={}_{2}F_1\left(n+1,i+\frac{1}{\alpha };i+\frac{1}{\alpha }+1;-\beta \right)$ and $\mathsf{\Delta }(\alpha ,\beta )={\mathsf{\Delta }}_1^1(\alpha ,\beta )$.

Proof. 

In view of [46], we have

$$\mathcal{E}\left(X\right)=\sum _{n=1}^{\infty }\frac{1}{n(n+1)}{\mu }_{n+1:n+1}-\mu$$

and

$$C\mathcal{E}\left(X\right)=-\sum _{n=1}^{\infty }\frac{1}{n(n+1)}{\mu }_{1:n+1}+\mu .$$

 □

Thus, the proof follows by applying Theorem 1 and for $k=1$. This completes the proof of the theorem.

4.4.2. The Estimated Values of the CRE and the CE for the Considered Data Sets

In this section, we estimated the CRE and CE for the given data sets, using the formulas given in Theorem 6 that represent the relationship between the measures of entropy and OSs from the LEEG distribution. Since both the formulas contain summation over the summand index (n) up to infinity, we picked different values of n to outline different situations. The results are given in Table 6. One can note that both entropies’ estimated values grow as the summand index (n) increases. For all data sets, the estimated values of the CRE are bigger than the corresponding values of the CE.

Table 6. The estimated values of the CRE and the CE for the data sets.

	Flood Data		Relief Time		Testosterone Level
Summand Index $\left(\mathit{n}\right)$	$\widehat{\mathcal{E}}\left(\mathit{X}\right)$	$\widehat{\mathit{C}\mathcal{E}}\left(\mathit{X}\right)$	$\widehat{\mathcal{E}}\left(\mathit{X}\right)$	$\widehat{\mathit{C}\mathcal{E}}\left(\mathit{X}\right)$	$\widehat{\mathcal{E}}\left(\mathit{X}\right)$	$\widehat{\mathit{C}\mathcal{E}}\left(\mathit{X}\right)$
5	0.113638	1.57443	0.0565906	4.67586	0.107623	1.74851
10	0.178327	2.26484	0.127177	13.8214	0.173297	2.61238
20	0.217831	2.88377	0.168787	76.0661	0.213163	3.47566
50	0.244567	3.32477	0.196252	12561.6	0.240027	4.17617

5. Conclusions and Future Work

The moments of OSs from the LEEG distribution were obtained by Jodrá and Jiménez-Gamero [12]. This current work presented an adaptable approach to find the exact moments of the OSs using a suitable Gauss hypergeometric function. Some recursive relations for single moments were also developed to simplify the computation of moments. Such computations were obtained and also verified as per the result of David and Nagaraja [19]. The LEEG distribution was also applied through the moments of OSs. The L-moments were used for estimating the parameters, which turned out to be more efficient in the case of outliers. The LEEG distribution was successfully fitted on some practical data sets from different fields. Moreover, we established the relation between the OSs, entropies and estimated the entropies.

As a few future research directions, these studies may be extended to generalized OSs, which contain OSs recording and progressive censoring of the LEEG distribution. One may also look at some other members of the Weibull–geometric or half-logistic families of distributions to obtain the moments of OSs similarly.