Symmetric Quantum Inequalities on Finite Rectangular Plane

Abstract

Finding the range of coordinated convex functions is yet another application for the symmetric Hermite–Hadamard inequality. For any two-dimensional interval $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$, we introduce the notion of partial ${\mathrm{q}}_{\theta }$-, ${\mathrm{q}}_{\varphi }$-, and ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric derivatives and a ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric integral. Moreover, we will construct the ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric Hölder’s inequality, the symmetric quantum Hermite–Hadamard inequality for the function of two variables in a rectangular plane, and address some of its related applications.

1. Introduction

The study of convex functions is an important field in mathematics which occurs almost everywhere in pure and applied branches of mathematics, but mainly it plays a key role in predicting the approximate solutions for linear and non-linear programming. A well known inequality called the Hermite–Hadamard inequality, introduced first by Hadamard [1], states:

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\subseteq \Re ⟶\Re$ be a convex function on $[{\mathrm{a}}_0,{\mathrm{a}}_1]$, then

$$\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2}\right)⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x}\right)d\mathrm{x}⩽\frac{\mathfrak{f}\left({\mathrm{a}}_0\right)+\mathfrak{f}\left({\mathrm{a}}_1\right)}{2}$$

(1)

inequality holds.

Over the last three decades, a number of researchers concentrated their research on various types of Hadamard’s inequality and its related applications. But we are able to acknowledge with confidence that the actual work on it was diversified by Dragomir in 1992 (see [2]). Many interested researchers have generalized (1) and constructed multiple formulations in different forms as a result of this progressive work. Dragomir established a number of Hermite–Hadamard-type inequalities for many kinds of functions using various assumptions, like convex functions defined on a disc in the plane and on a ball in the space. See Ref. [2] for further details. The Hermite–Hadamard-type inequalities for convex functions on n-dimensional convex bodies were investigated in 2006 by de la Cal and Cárcamo [3]. They derived two main results; the first one is related to mappings on polytopes in ${\Re }^n$, and the second one is related (1) via symmetric random vectors on arbitrary norms on ${\Re }^n$. Another extension of (1) for a function defined on a convex subset of ${\Re }^3$ was introduced by Yang in 2012 [4]. Furthermore, matrix and operator inequalities of the Hermite–Hadamard type were introduced by Moslehian recently in [5]. The idea of a coordinated convex function was given by Dragomir [6]; it is defined as follows:

For any two-dimensional interval $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$, with ${\mathrm{a}}_0<{\mathrm{a}}_1$ and ${\mathrm{c}}_0<{\mathrm{c}}_1$. A function $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]⟶\Re$ is a coordinated convex if the partial mappings ${\mathfrak{f}}_{\mathrm{y}}:[{\mathrm{a}}_0,{\mathrm{a}}_1]⟶\Re$, ${\mathfrak{f}}_{\mathrm{y}}\left(\mathrm{u}\right)=\mathfrak{f}(\mathrm{u},\mathrm{y})$ and ${\mathfrak{f}}_{\mathrm{x}}:[{\mathrm{c}}_0,{\mathrm{c}}_1]⟶\Re$, ${\mathfrak{f}}_{\mathrm{x}}\left(\mathrm{u}\right)=\mathfrak{f}(\mathrm{x},\mathrm{u})$ are convex for all $\mathrm{x}\in [{\mathrm{a}}_0,{\mathrm{a}}_1]$ and $\mathrm{y}\in [{\mathrm{c}}_0,{\mathrm{c}}_1]$.

Using this definition, Dragomir derived the Hermite–Hadamard inequality on a coordinated convex function, which is stated as follows:

Theorem 1

([6]). Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function, then

$$\begin{array}{cc}\hfill \mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)& ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)\mathrm{d}\mathrm{x}+\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right)\mathrm{d}\mathrm{y}\right]\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y})\mathrm{d}\mathrm{y}\mathrm{d}\mathrm{x}\hfill \\ & ⩽\frac{1}{4({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0)\mathrm{d}\mathrm{x}+\frac{1}{4({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1)\mathrm{d}\mathrm{x}\hfill \\ & +\frac{1}{4({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y})\mathrm{d}\mathrm{y}+\frac{1}{4({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y})\mathrm{d}\mathrm{y}\hfill \\ & ⩽{\displaystyle \frac{\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)+\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)}{4}}\hfill \end{array}$$

(2)

inequalities hold.

In the current era, the study of quantum calculus is also a center of attention for researchers. Euler (1707–1783) was the first person to propose the concept of quantum calculus after the 17th century. Its role provides a bridge between physics and mathematics. F. H. Jackson and others focused more on quantum calculus in the early 20th century. Quantum calculus ($\mathrm{q}$-calculus), a subfield of time-scale calculus, deals with the study of difference equations and provides solutions to a wide range of dynamical problems. Furthermore, we can state that q-calculus generalizes the derivative and integration of classical calculus and that we retrieve the classical conclusions as $\mathrm{q}\to 1$. The Euler notion was first studied by Jackson [7] in 1910. He used it to define $\mathrm{q}$-integration and $\mathrm{q}$-derivatives for continuous functions over an interval (0, ∞), commonly called calculus without limits. Al-Salam [8] introduced the concepts of $\mathrm{q}$-fractional and $\mathrm{q}$-Riemann–Liouville fractional inequalities in 1966. The fundamental principles of $\mathrm{q}$-calculus were first discussed by Kac and Cheung in their book [9]. We recommend reading [10,11] for some details on quantum calculus.

The $\mathrm{q}$-integral and $\mathrm{q}$-derivative of continuous functions over finite intervals were specifically presented in 2013 by Tariboon and Ntouyas.

Definition 1

([12]). For a continuous function $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\to \Re$, suppose that for $0<\mathrm{q}<1$

$$\underset{\mathrm{x}\to {\mathrm{a}}_0}{lim}{\displaystyle \frac{\mathfrak{f}\left(\mathrm{x}\right)-\mathfrak{f}\left(\mathrm{q}\mathrm{x}+(1-\mathrm{q}){\mathrm{a}}_0\right)}{(1-\mathrm{q})(\mathrm{x}-{\mathrm{a}}_0)}}=b.$$

Then, ${}_{{\mathrm{a}}_0}D_{\mathrm{q}}\mathfrak{f}\left(\mathrm{x}\right)$ is defined as follows:

$$\begin{array}{c}\hfill {}_{{\mathrm{a}}_0}D_{\mathrm{q}}\mathfrak{f}\left(\mathrm{x}\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\mathfrak{f}\left(\mathrm{x}\right)-\mathfrak{f}\left(\mathrm{q}\mathrm{x}+(1-\mathrm{q}){\mathrm{a}}_0\right)}{(1-\mathrm{q})(\mathrm{x}-{\mathrm{a}}_0)}},\hfill & \mathit{if}\mathrm{x}\ne {\mathrm{a}}_0,\hfill \\ b,\hfill & \mathit{if}\mathrm{x}={\mathrm{a}}_0.\hfill \end{array}\right.\end{array}$$

(3)

If we put ${\mathrm{a}}_0=0$, (3) becomes

$$\begin{array}{c}\hfill D_q\mathfrak{f}\left(\mathrm{x}\right)={\displaystyle \frac{\mathfrak{f}\left(\mathrm{x}\right)-\mathfrak{f}\left(\mathrm{q}\mathrm{x}\right)}{(1-\mathrm{q})\left(\mathrm{x}\right)}}.\end{array}$$

Definition 2

([12]). For a continuous function $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\to \Re$, the $\mathrm{q}$-integral on $[{\mathrm{a}}_0,{\mathrm{a}}_1]$ can be obtained by

$${\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}\left(\mathrm{t}\right){\mathrm{a}}_0{d}_{\mathrm{q}}\mathrm{t}=(1-\mathrm{q})(\mathrm{x}-{\mathrm{a}}_0)\sum _{n=0}^{\infty }{\mathrm{q}}^n\mathfrak{f}\left({\mathrm{q}}^n\mathrm{x}+\left(1-{\mathrm{q}}^n\right){\mathrm{a}}_0\right),$$

(4)

If we put ${\mathrm{a}}_0$ = 0, (4) becomes

$${\int }_0^{\mathrm{x}}\mathfrak{f}\left(\mathrm{t}\right)d_{\mathrm{q}}\mathrm{t}=(1-\mathrm{q})\mathrm{x}\sum _{n=0}^{\infty }{\mathrm{q}}^n\mathfrak{f}\left({\mathrm{q}}^n\mathrm{x}\right).$$

Furthermore, Jackson [7] derived its subsequent form:

$${\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{t}\right)d_{\mathrm{q}}\mathrm{t}={\int }_0^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{t}\right)d_{\mathrm{q}}\mathrm{t}-{\int }_0^{{\mathrm{a}}_0}\mathfrak{f}\left(\mathrm{t}\right)d_{\mathrm{q}}\mathrm{t}.$$

Utilizing the above essentials of quantum calculus, Tariboon and Ntouyas developed various well-known inequalities on finite intervals in [13] and the Hermite–Hadamard inequality is one of them. But there is an error in the first form of the quantum Hermite–Hadamard inequality, which was pointed out by Alp et al. in [14], where they gave a counter-example to the previously established form of this inequality. Thus, they formulated the corrected form of Hermite–Hadamard inequality in quantum calculus, which can be presented as

Theorem 2

([14]). For $\mathfrak{f}:\left[{\mathrm{a}}_0,{\mathrm{a}}_1\right]\to \Re$ being a convex function on $\left[{\mathrm{a}}_0,{\mathrm{a}}_1\right]$, then

$$\mathfrak{f}\left(\frac{\mathrm{q}{\mathrm{a}}_0+{\mathrm{a}}_1}{1+\mathrm{q}}\right)\le \frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}\underset{{\mathrm{a}}_0}{\overset{{\mathrm{a}}_1}{\int }}\mathfrak{f}\left(\mathrm{t}\right)\begin{array}{c}{}_{{\mathrm{a}}_0}d_{\mathrm{q}}\mathrm{t}\hfill \end{array}\le \frac{\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_0\right)+\mathfrak{f}\left({\mathrm{a}}_1\right)}{1+\mathrm{q}},$$

inequality holds for $\mathrm{q}\in (0,1)$.

Dragomir et al., in [15], published some work on quantum calculus. They provided some definitions of the partial ${\mathrm{q}}_{\theta }$-derivative, ${\mathrm{q}}_{\varphi }$-derivative, ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-derivative, and ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-integral and shifted the notion of quantum calculus on finite intervals with work on bi-intervals (i.e., coordinates in plane).

Definition 3

([15]). Let $\mathfrak{f}$ be a continuous function of two variables from $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$ to ℜ and $0<{\mathrm{q}}_{\theta }<1,0<{\mathrm{q}}_{\varphi }<1$, then

$$\frac{{}_{{\mathrm{a}}_0}𝜕_{{\mathrm{q}}_{\theta }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}𝜕_{{\mathrm{q}}_{\theta }}\mathrm{x}}=\frac{\mathfrak{f}({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0,\mathrm{y})-\mathfrak{f}(\mathrm{x},\mathrm{y})}{(1-{\mathrm{q}}_{\theta })(\mathrm{x}-{\mathrm{a}}_0)},\mathrm{x}\ne {\mathrm{a}}_0,$$

$$\frac{{}_{{\mathrm{c}}_0}𝜕_{{\mathrm{q}}_{\varphi }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{c}}_0}𝜕_{{\mathrm{q}}_{\varphi }}\mathrm{y}}=\frac{\mathfrak{f}(\mathrm{x},{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0)-\mathfrak{f}(\mathrm{x},\mathrm{y})}{(1-{\mathrm{q}}_{\varphi })(\mathrm{y}-{\mathrm{c}}_0)},\mathrm{y}\ne {\mathrm{c}}_0,$$

and

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}𝜕_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}𝜕_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}𝜕_{{\mathrm{q}}_{\varphi }}\mathrm{y}}& =\frac{1}{(1-{\mathrm{q}}_{\theta })(1-{\mathrm{q}}_{\varphi })(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\times \left[\mathfrak{f}({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0)\right.\hfill \\ & -\left.\mathfrak{f}({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0,\mathrm{y})-\mathfrak{f}(\mathrm{x},{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0)+\mathfrak{f}(\mathrm{x},\mathrm{y})\right],\mathrm{x}\ne {\mathrm{a}}_0,\mathrm{y}\ne {\mathrm{c}}_0,\hfill \end{array}$$

are called the partial ${\mathrm{q}}_{\theta }$-derivative, ${\mathrm{q}}_{\varphi }$-derivative, and ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-derivative at $(\mathrm{x},\mathrm{y})\in [{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$.

Definition 4

([15]). Let $\mathfrak{f}$ be a continuous function from $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$ to ℜ, then

$$\begin{array}{cc}\hfill {\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}d_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}d_{{\mathrm{q}}_{\varphi }}\mathrm{y}& =(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta })(1-{\mathrm{q}}_{\varphi })\hfill \\ & \times \sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^n{\mathrm{q}}_{\varphi }^m\mathfrak{f}\left({\mathrm{q}}_{\theta }^n\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^n\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^m\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^m\right){\mathrm{c}}_0\right)\hfill \end{array}$$

is called the ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-integral on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$.

With the help of these definitions, they derived the Hermite–Hadamard inequality for the convex function of two variables.

Theorem 3.

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$, then for $0<{\mathrm{q}}_{\theta }<1$ and $0<{\mathrm{q}}_{\varphi }<1$, the following inequalities hold:

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)\hfill \\ \hfill & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}){}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi })}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi })}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta })}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{1}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta })}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽{\displaystyle \frac{{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)}{(1+{\mathrm{q}}_{\theta })(1+{\mathrm{q}}_{\varphi })}}.\hfill \end{array}$$

(5)

In July 2020, N. Alp and M. Z. Sarikaya [16] published an article in which they gave a counter-example that disproves the (5) and derived the correct form of the Hermite–Hadamard inequality.

Theorem 4

([16]). Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$, then for $0<{\mathrm{q}}_{\theta }<1$ and $0<{\mathrm{q}}_{\varphi }<1$, the following inequalities hold:

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{{\mathrm{a}}_0{\mathrm{q}}_{\theta }+{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }},\frac{{\mathrm{c}}_0{\mathrm{q}}_{\varphi }+{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }}\right)\hfill \\ & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{{\mathrm{c}}_0{\mathrm{q}}_{\varphi }+{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }}){}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{{\mathrm{a}}_0{\mathrm{q}}_{\theta }+{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }},\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi })}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi })}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\mathrm{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta })}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{1}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta })}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\mathrm{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽{\displaystyle \frac{{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)}{(1+{\mathrm{q}}_{\theta })(1+{\mathrm{q}}_{\varphi })}}.\hfill \end{array}$$

(6)

In the recent past, a number of publications have been presented regarding the improvement and development of different variants of the quantum Hermite–Hadamard and related inequalities (see [17,18,19,20], and references therein). However, in the present article we are interested in exploring such findings under the new and latest perspective of symmetric quantum calculus.

2. Preliminaries and New Results in Symmetric Quantum Calculus

The symmetric partial derivatives of the function are defined below.

Definition 5

([21]). Let $\mathfrak{f}(\mathrm{x},\mathrm{y})$ be a function which is defined on ${\Re }^2$, then

$$\begin{array}{c}\hfill {\displaystyle \frac{{𝜕}^{*}\mathfrak{f}}{𝜕\mathrm{x}}}=\underset{\mathrm{h}\to 0}{lim}{\displaystyle \frac{\mathfrak{f}(\mathrm{x}+\mathrm{h},\mathrm{y})-\mathfrak{f}(\mathrm{x}-\mathrm{h},\mathrm{y})}{2\mathrm{h}}}\end{array}$$

(7)

$$\begin{array}{c}\hfill {\displaystyle \frac{{𝜕}^{*}\mathfrak{f}}{𝜕\mathrm{y}}}=\underset{\mathrm{h}\to 0}{lim}{\displaystyle \frac{\mathfrak{f}(\mathrm{x},\mathrm{y}+\mathrm{h})-\mathfrak{f}(\mathrm{x},\mathrm{y}-\mathrm{h})}{2\mathrm{h}}}\end{array}$$

(8)

are said to be symmetric partial derivatives of $\mathfrak{f}$ with respect to $\mathrm{x}$ and $\mathrm{y}$, respectively.

Da Cruz et al. introduced a new concept called symmetric quantum calculus in [22]. It plays an important role in developing hypergeometric and a class of harmonic functions in complex analysis [23]. The symmetric quantum analogue of any number $\mathrm{m}$ can be defined as [9]

$$\begin{array}{c}\hfill \widetilde{\left[m\right]}=\frac{{\mathrm{q}}^{\mathrm{m}}-{\mathrm{q}}^{-\mathrm{m}}}{\mathrm{q}-{\mathrm{q}}^{-1}}where\mathrm{m}\in N.\end{array}$$

In addition to this, the $\mathrm{q}$-differential and $\mathrm{h}$-differential for $\mathrm{q}\ne 1$ and $\mathrm{h}\ne 0$ can be defined as

$$\begin{array}{c}{\tilde{d}}_{\mathrm{q}}{\mathfrak{f}}_1\left(\mathrm{x}\right)={\mathfrak{f}}_1\left(\mathrm{q}\mathrm{x}\right)-{\mathfrak{f}}_1\left({\mathrm{q}}^{-1}\mathrm{x}\right),\mathrm{x}\ne {\mathrm{a}}_0,\\ {\tilde{d}}_{\mathrm{h}}{\mathfrak{f}}_2\left(\mathrm{x}\right)={\mathfrak{f}}_2(\mathrm{x}+\mathrm{h})-{\mathfrak{f}}_2(\mathrm{x}-\mathrm{h}),\mathrm{x}\ne {\mathrm{a}}_0.\end{array}$$

The derivative and integral in symmetric quantum calculus can be derived as

Definition 6

([24]). For a continuous function $\mathfrak{f}:\left[{\mathrm{a}}_0,{\mathrm{a}}_1\right]\to \Re$, then the $\tilde{\mathrm{q}}$-derivative or ${}_{{\mathrm{a}}_0}\mathrm{q}$-symmetric derivative on $\left[{\mathrm{a}}_0,{\mathrm{a}}_1\right]$ is defined as

$${}_{{\mathrm{a}}_0}\tilde{D}_{\mathrm{q}}\mathfrak{f}\left(\mathrm{x}\right)=\frac{{\tilde{d}}_{\mathrm{q}}\mathfrak{f}\left(\mathrm{x}\right)}{{\tilde{d}}_{\mathrm{q}}\mathrm{x}}=\frac{\mathfrak{f}(\mathrm{q}\mathrm{x}+(1-\mathrm{q}){\mathrm{a}}_0)-\mathfrak{f}({\mathrm{q}}^{-1}\mathrm{x}+(1-{\mathrm{q}}^{-1}){\mathrm{a}}_0)}{(\mathrm{q}-{\mathrm{q}}^{-1})(\mathrm{x}-{\mathrm{a}}_0)},\mathrm{x}\ne {\mathrm{a}}_0,$$

if ${\mathrm{a}}_0=0$, this becomes

$${\tilde{D}}_{\mathrm{q}}\mathfrak{f}\left(\mathrm{x}\right)=\frac{{\tilde{d}}_{\mathrm{q}}\mathfrak{f}\left(\mathrm{x}\right)}{{\tilde{d}}_{\mathrm{q}}\mathrm{x}}=\frac{\mathfrak{f}\left(\mathrm{q}\mathrm{x}\right)-\mathfrak{f}\left({\mathrm{q}}^{-1}\mathrm{x}\right)}{(\mathrm{q}-{\mathrm{q}}^{-1})\mathrm{x}},\mathrm{x}\ne 0.$$

Definition 7

([24]). For a continuous function $\mathfrak{f}:\left[{\mathrm{a}}_0,{\mathrm{a}}_1\right]\to \Re$, then the $\tilde{\mathrm{q}}$-integral or ${}_{{\mathrm{a}}_0}\mathrm{q}$-symmetric integral on $\left[{\mathrm{a}}_0,{\mathrm{a}}_1\right]$ is defined as

$${\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}\left(\mathrm{t}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{t}=({\mathrm{q}}^{-1}-\mathrm{q})(\mathrm{x}-{\mathrm{a}}_0)\sum _{n=0}^{\infty }{\mathrm{q}}^{2n+1}\mathfrak{f}\left({\mathrm{q}}^{2n+1}\mathrm{x}+\left(1-{\mathrm{q}}^{2n+1}\right){\mathrm{a}}_0\right);$$

here, $\mathrm{x}\in [{\mathrm{a}}_0,{\mathrm{a}}_1]$ or

$${\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}\left(\mathrm{t}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{t}=(1-{\mathrm{q}}^2)(\mathrm{x}-{\mathrm{a}}_0)\sum _{n=0}^{\infty }{\mathrm{q}}^{2n}\mathfrak{f}\left({\mathrm{q}}^{2n+1}\mathrm{x}+\left(1-{\mathrm{q}}^{2n+1}\right){\mathrm{a}}_0\right).$$

In this section, with the help of all of the notions above, we will define some new definitions in symmetric quantum calculus that assist in constructing the ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric Hölder’s inequality and Hermite–Hadamard inequalities.

We introduce and provide definitions below.

Definition 8.

Let $\mathfrak{f}$ be a continuous function of two variables from $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$ to ℜ and $0<{\mathrm{q}}_{\theta }<1,0<{\mathrm{q}}_{\varphi }<1$, then

$$\frac{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}}=\frac{\mathfrak{f}({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0,\mathrm{y})-\mathfrak{f}({\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0,\mathrm{y})}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})(\mathrm{x}-{\mathrm{a}}_0)},\mathrm{x}\ne {\mathrm{a}}_0,$$

$$\frac{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}=\frac{\mathfrak{f}(\mathrm{x},{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0)-\mathfrak{f}(\mathrm{x},{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0)}{({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{y}-{\mathrm{c}}_0)},\mathrm{y}\ne {\mathrm{c}}_0,$$

and

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}& =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\times \left[\mathfrak{f}({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }\mathrm{y}\right.\hfill \\ & +(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0)-\mathfrak{f}({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0)\hfill \\ & -\mathfrak{f}({\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0)\hfill \\ & +\left.\mathfrak{f}({\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0)\right],\mathrm{x}\ne {\mathrm{a}}_0,\mathrm{y}\ne {\mathrm{c}}_0,\hfill \end{array}$$

(9)

are called the partial ${\mathrm{q}}_{\theta }$-, ${\mathrm{q}}_{\varphi }$-, and ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric derivatives at $(\mathrm{x},\mathrm{y})\in [{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$.

If $\frac{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}},\frac{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}$, and $\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}$ exist for all $(\mathrm{x},\mathrm{y})\in [{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$, then $\mathfrak{f}$ is called partially ${\mathrm{q}}_{\theta }$-, ${\mathrm{q}}_{\varphi }$-, and ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric differentiable on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$.

Example 1.

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a function.

Case 1. 

If $\mathfrak{f}$ is a non-convex function. Suppose that $\mathfrak{f}(\mathrm{x},\mathrm{y})=\mathrm{x}\mathrm{y}$, then the partial ${\mathrm{q}}_{\theta }$-symmetric derivative of $\mathfrak{f}(\mathrm{x},\mathrm{y})$ is

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}}& =\frac{({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0)\mathrm{y}-({\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0)\mathrm{y}}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})(\mathrm{x}-{\mathrm{a}}_0)}\hfill \\ \hfill & =\frac{\mathrm{y}[{\mathrm{q}}_{\theta }\mathrm{x}+{\mathrm{a}}_0-{\mathrm{q}}_{\theta }{\mathrm{a}}_0-{\mathrm{q}}_{\theta }^{-1}\mathrm{x}-{\mathrm{a}}_0+{\mathrm{q}}_{\theta }^{-1}{\mathrm{a}}_0]}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})(\mathrm{x}-{\mathrm{a}}_0)}=\mathrm{y}.\hfill \end{array}$$

The partial ${\mathrm{q}}_{\varphi }$-symmetric derivative of $\mathfrak{f}(\mathrm{x},\mathrm{y})$ is

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}& =\frac{\mathrm{x}({\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0)-\mathrm{x}({\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0)}{({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{y}-{\mathrm{c}}_0)}\hfill \\ \hfill & =\frac{\mathrm{x}[{\mathrm{q}}_{\varphi }\mathrm{y}+{\mathrm{c}}_0-{\mathrm{q}}_{\varphi }{\mathrm{c}}_0-{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}-{\mathrm{c}}_0+{\mathrm{q}}_{\varphi }^{-1}{\mathrm{c}}_0)]}{({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{y}-{\mathrm{c}}_0)}=\mathrm{x}.\hfill \end{array}$$

And also, the partial ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric derivative of $\mathfrak{f}(\mathrm{x},\mathrm{y})$ is

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}& =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[\{{\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0\}\{{\mathrm{q}}_{\varphi }\mathrm{y}\right.\hfill \\ & +(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0\}-\{{\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0\}\{{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}\hfill \\ & -\{{\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}\{{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0\}\hfill \\ & +\left.\{{\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}\{{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[\{{\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0\}\{{\mathrm{q}}_{\varphi }\mathrm{y}\right.\hfill \\ & +(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0-{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}-(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}-\{{\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}\hfill \\ & \times \left.\{{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0-{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}-(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[\{{\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0-{\mathrm{q}}_{\theta }^{-1}\mathrm{x}\right.\hfill \\ & -\left.(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}\{{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0-{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}-(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}\right]\hfill \\ \hfill & =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[\{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})\mathrm{x}+(1-{\mathrm{q}}_{\theta }-1+{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}\right.\hfill \\ & \times \left.\{({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})\mathrm{y}+(1-{\mathrm{q}}_{\varphi }-1+{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}\right]\hfill \\ \hfill & =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[\{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})\mathrm{x}-({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}\right.\hfill \\ & \times \left.\{({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})\mathrm{y}-({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}\right],\hfill \end{array}$$

and finally,

$$\begin{array}{c}\hfill \frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}=1.\end{array}$$

Case 2. 

If $\mathfrak{f}$ is a convex function. Suppose that $\mathfrak{f}(\mathrm{x},\mathrm{y})={\mathrm{x}}^2+{\mathrm{y}}^2$, then the partial ${\mathrm{q}}_{\theta }$-symmetric derivative of $\mathfrak{f}(\mathrm{x},\mathrm{y})$ is

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}}& =\frac{{({\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0)}^2+{\mathrm{y}}^2-{({\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0)}^2-{\mathrm{y}}^2}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})(\mathrm{x}-{\mathrm{a}}_0)}\hfill \\ \hfill & =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})(\mathrm{x}-{\mathrm{a}}_0)}[{\left({\mathrm{q}}_{\theta }\right)}^2{\mathrm{x}}^2+{\mathrm{a}}_0^2+{\left({\mathrm{q}}_{\theta }\right)}^2{\mathrm{a}}_0^2-2{\mathrm{q}}_{\theta }{\mathrm{a}}_0^2+2{\mathrm{q}}_{\theta }\mathrm{x}{\mathrm{a}}_0-2{\left({\mathrm{q}}_{\theta }\right)}^2\mathrm{x}{\mathrm{a}}_0\hfill \\ \hfill & -{\left({\mathrm{q}}_{\theta }^{-1}\right)}^2{\mathrm{x}}^2-{\mathrm{a}}_0^2-{\left({\mathrm{q}}_{\theta }^{-1}\right)}^2{\mathrm{a}}_0^2+2{\mathrm{q}}_{\theta }^{-1}{\mathrm{a}}_0^2-2{\mathrm{q}}_{\theta }^{-1}\mathrm{x}{\mathrm{a}}_0+2{\left({\mathrm{q}}_{\theta }^{-1}\right)}^2\mathrm{x}{\mathrm{a}}_0]\hfill \\ \hfill & =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})(\mathrm{x}-{\mathrm{a}}_0)}[\{{\left({\mathrm{q}}_{\theta }\right)}^2-{\left({\mathrm{q}}_{\theta }^{-1}\right)}^2\}{\mathrm{x}}^2+\{{\left({\mathrm{q}}_{\theta }\right)}^2-{\left({\mathrm{q}}_{\theta }^{-1}\right)}^2\}{\mathrm{a}}_0^2-2{\mathrm{a}}_0^2({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})\hfill \\ \hfill & +2({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})\mathrm{x}{\mathrm{a}}_0-2\{{\left({\mathrm{q}}_{\theta }\right)}^2-{\left({\mathrm{q}}_{\theta }^{-1}\right)}^2\}\mathrm{x}{\mathrm{a}}_0]\hfill \\ \hfill & =\frac{({\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^{-1}){\mathrm{x}}^2+({\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0^2-2{\mathrm{a}}_0^2+2\mathrm{x}{\mathrm{a}}_0-2({\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^{-1})\mathrm{x}{\mathrm{a}}_0}{\mathrm{x}-{\mathrm{a}}_0}.\hfill \end{array}$$

Similarly, the partial ${\mathrm{q}}_{\varphi }$-symmetric derivative of $\mathfrak{f}(\mathrm{x},\mathrm{y})$ is

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}& =\frac{({\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^{-1}){\mathrm{y}}^2+({\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0^2-2{\mathrm{c}}_0^2+2\mathrm{y}{\mathrm{c}}_0-2({\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^{-1})\mathrm{y}{\mathrm{c}}_0}{\mathrm{y}-{\mathrm{c}}_0}.\hfill \end{array}$$

And also, the partial ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric derivative of $\mathfrak{f}(\mathrm{x},\mathrm{y})$ is

$$\begin{array}{cc}\hfill \frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{x},\mathrm{y})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}& =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[{\{{\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0\}}^2+\{{\mathrm{q}}_{\varphi }\mathrm{y}\right.\hfill \\ & +(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0{\}}^2-{\{{\mathrm{q}}_{\theta }\mathrm{x}+(1-{\mathrm{q}}_{\theta }){\mathrm{a}}_0\}}^2-{\{{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}}^2\hfill \\ & -{\{{\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}}^2-{\{{\mathrm{q}}_{\varphi }\mathrm{y}+(1-{\mathrm{q}}_{\varphi }){\mathrm{c}}_0\}}^2\hfill \\ & +\left.{\{{\mathrm{q}}_{\theta }^{-1}\mathrm{x}+(1-{\mathrm{q}}_{\theta }^{-1}){\mathrm{a}}_0\}}^2+{\{{\mathrm{q}}_{\varphi }^{-1}\mathrm{y}+(1-{\mathrm{q}}_{\varphi }^{-1}){\mathrm{c}}_0\}}^2\right]=0.\hfill \end{array}$$

Remark 1.

If ${\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }⟶1$ in both cases of Example 1, then the results will coincide with the symmetric partial derivatives of such functions coming from (7) and (8), respectively.

Definition 9.

Let $\mathfrak{f}$ be a continuous function from $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$ to ℜ, then for $(\mathrm{x},\mathrm{y})\in [{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$,

$$\begin{array}{cc}\hfill {\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}& =(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)({\mathrm{q}}_{\theta }^{-1}-{\mathrm{q}}_{\theta })({\mathrm{q}}_{\varphi }^{-1}-{\mathrm{q}}_{\varphi })\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n+1}\hfill \\ & \times {\mathrm{q}}_{\varphi }^{2m+1}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+1}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\hfill \end{array}$$

or

$$\begin{array}{cc}\hfill {\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}& =(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\hfill \\ & \times \sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+1}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\hfill \end{array}$$

(10)

is called ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric integral on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$.

From (10), we can say that

$${\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}={\int }_{{\mathrm{a}}_0}^{\mathrm{x}}{\int }_{{\mathrm{c}}_0}^{\mathrm{y}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}.$$

Moreover, for any point $({\mathrm{x}}_0,{\mathrm{y}}_0)\in ({\mathrm{a}}_0,\mathrm{x})\times ({\mathrm{c}}_0,\mathrm{y})$, we can write

$$\begin{array}{cc}\hfill {\int }_{{\mathrm{y}}_0}^{\mathrm{y}}{\int }_{{\mathrm{x}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}& ={\int }_{{\mathrm{y}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}-{\int }_{{\mathrm{y}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{{\mathrm{x}}_0}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ \hfill & ={\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}-{\int }_{{\mathrm{c}}_0}^{{\mathrm{y}}_0}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ \hfill & -{\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{{\mathrm{x}}_0}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+{\int }_{{\mathrm{c}}_0}^{{\mathrm{y}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{x}}_0}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}.\hfill \end{array}$$

(11)

Some results that are given below hold for Definitions 8 and 9.

Theorem 5.

Let $\mathfrak{f}$ be a continuous function from $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$ to ℜ, then

$$\begin{array}{cc}\hfill & \left(1\right)\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{u},\mathrm{v}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}=\mathfrak{f}(\mathrm{x},\mathrm{y})\hfill \\ \hfill & \left(2\right){\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{v}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}=\mathfrak{f}(\mathrm{x},\mathrm{y})\hfill \\ \hfill & \left(3\right){\int }_{{\mathrm{y}}_0}^{\mathrm{y}}{\int }_{{\mathrm{x}}_0}^{\mathrm{x}}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{v}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}=\mathfrak{f}(\mathrm{x},\mathrm{y})-\mathfrak{f}(\mathrm{x},{\mathrm{y}}_0)-\mathfrak{f}({\mathrm{x}}_0,\mathrm{y})+\mathfrak{f}({\mathrm{x}}_0,{\mathrm{y}}_0)\hfill \end{array}$$

for $({\mathrm{x}}_0,{\mathrm{y}}_0)\in ({\mathrm{a}}_0,{\mathrm{a}}_1)\times ({\mathrm{c}}_0,{\mathrm{c}}_1)$.

Proof. 

(1) Using (10), and then, (9),

$$\begin{array}{cc}\hfill & \frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\mathfrak{f}(\mathrm{u},\mathrm{v}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}=\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}\left[(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\right.\hfill \\ & \times \left.\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+1}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\right]\hfill \\ \hfill & =\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\right.\hfill \\ & \times \sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+2}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+2}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+2}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+2}\right){\mathrm{c}}_0\right)\hfill \\ & -{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }^{-1}(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\hfill \\ & \times \sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+2}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+2}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ & -{\mathrm{q}}_{\theta }^{-1}{\mathrm{q}}_{\varphi }(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\hfill \\ & \times \sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+2}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+2}\right){\mathrm{c}}_0\right)\hfill \\ & +{\mathrm{q}}_{\theta }^{-1}{\mathrm{q}}_{\varphi }^{-1}(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\hfill \\ & \times \left.\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\right]\hfill \\ \hfill & =\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n+2}{\mathrm{q}}_{\varphi }^{2m+2}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+2}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+2}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+2}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+2}\right){\mathrm{c}}_0\right)\hfill \\ & -\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n+2}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+2}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+2}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ & -\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m+2}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+2}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+2}\right){\mathrm{c}}_0\right)\hfill \\ & +\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ & =\mathfrak{f}(\mathrm{x},\mathrm{y}).\hfill \end{array}$$

(2)

Using (9), and then, (10),

$$\begin{array}{cc}\hfill & {\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}\hfill \\ & ={\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\frac{1}{({\mathrm{q}}_{\theta }-{\mathrm{q}}_{\theta }^{-1})({\mathrm{q}}_{\varphi }-{\mathrm{q}}_{\varphi }^{-1})(\mathrm{x}-{\mathrm{a}}_0)(\mathrm{y}-{\mathrm{c}}_0)}\left[\mathfrak{f}\left({\mathrm{q}}_{\theta }\mathrm{u}+\left(1-{\mathrm{q}}_{\theta }\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }\mathrm{v}+\left(1-{\mathrm{q}}_{\varphi }\right){\mathrm{c}}_0\right)\right.\hfill \\ & -\mathfrak{f}\left({\mathrm{q}}_{\theta }^{-1}\mathrm{u}+\left(1-{\mathrm{q}}_{\theta }^{-1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }\mathrm{v}+\left(1-{\mathrm{q}}_{\varphi }\right){\mathrm{c}}_0\right)-\mathfrak{f}\left({\mathrm{q}}_{\theta }\mathrm{u}+\left(1-{\mathrm{q}}_{\theta }\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{-1}\mathrm{v}+\left(1-{\mathrm{q}}_{\varphi }^{-1}\right){\mathrm{c}}_0\right)\hfill \\ & +\left.\mathfrak{f}\left({\mathrm{q}}_{\theta }^{-1}\mathrm{u}+\left(1-{\mathrm{q}}_{\theta }^{-1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{-1}\mathrm{v}+\left(1-{\mathrm{q}}_{\varphi }^{-1}\right){\mathrm{c}}_0\right)\right]\hfill \\ \hfill & =\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }\left[\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+2}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+2}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+2}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+2}\right){\mathrm{c}}_0\right)\right.\hfill \\ \hfill & -\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+2}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m+2}\right){\mathrm{c}}_0\right)\hfill \\ & -\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n+2}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n+2}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ & -\left.\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\right]\hfill \\ \hfill & =\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ & -\sum _{m=1}^{\infty }\sum _{n=0}^{\infty }\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ \hfill & -\sum _{m=0}^{\infty }\sum _{n=1}^{\infty }\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ & +\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }\mathfrak{f}\left({\mathrm{q}}_{\theta }^{2n}\mathrm{x}+\left(1-{\mathrm{q}}_{\theta }^{2n}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m}\mathrm{y}+\left(1-{\mathrm{q}}_{\varphi }^{2m}\right){\mathrm{c}}_0\right)\hfill \\ & =\mathfrak{f}(\mathrm{x},\mathrm{y}).\hfill \end{array}$$

(3)

Using (11), and then, (2) results in

$$\begin{array}{cc}\hfill & {\int }_{{\mathrm{y}}_0}^{\mathrm{y}}{\int }_{{\mathrm{x}}_0}^{\mathrm{x}}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}\hfill \\ & ={\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}-{\int }_{{\mathrm{c}}_0}^{{\mathrm{y}}_0}{\int }_{{\mathrm{a}}_0}^{\mathrm{x}}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}\hfill \\ & -{\int }_{{\mathrm{c}}_0}^{\mathrm{y}}{\int }_{{\mathrm{a}}_0}^{{\mathrm{x}}_0}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}+{\int }_{{\mathrm{c}}_0}^{{\mathrm{y}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{x}}_0}\frac{{}_{{\mathrm{a}}_0,{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }}^2\mathfrak{f}(\mathrm{u},\mathrm{v})}{{}_{{\mathrm{a}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\widetilde{𝜕}_{{\mathrm{q}}_{\varphi }}\mathrm{y}}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{u}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{v}\hfill \\ & =\mathfrak{f}(\mathrm{x},\mathrm{y})-\mathfrak{f}(\mathrm{x},{\mathrm{y}}_0)-\mathfrak{f}({\mathrm{x}}_0,\mathrm{y})+\mathfrak{f}({\mathrm{x}}_0,{\mathrm{y}}_0).\hfill \end{array}$$

□

Hölder’s inequality for the double sum can be stated as

Theorem 6

([15]). For any two real or complex sequences ${\left({\mathrm{a}}_{\mathrm{s}\mathrm{t}}\right)}_{\mathrm{s},\mathrm{t}\in N}$, ${\left({\mathrm{c}}_{\mathrm{s}\mathrm{t}}\right)}_{\mathrm{s},\mathrm{t}\in N}$ and $\frac{1}{{\mathrm{r}}_{\theta }}+\frac{1}{{\mathrm{r}}_{\varphi }}=1$, with ${\mathrm{r}}_{\theta }>1,{\mathrm{r}}_{\varphi }>1$

$$\begin{array}{c}\hfill \sum _{\mathrm{s}=0}^{\infty }\sum _{\mathrm{t}=0}^{\infty }\left|{\mathrm{a}}_{\mathrm{s}\mathrm{t}}{\mathrm{c}}_{\mathrm{s}\mathrm{t}}\right|⩽{\left(\sum _{\mathrm{s}=0}^{\infty }\sum _{\mathrm{t}=0}^{\infty }{\left|{\mathrm{a}}_{\mathrm{s}\mathrm{t}}\right|}^{{\mathrm{r}}_{\theta }}\right)}^{\frac{1}{{\mathrm{r}}_{\theta }}}{\left(\sum _{\mathrm{s}=0}^{\infty }\sum _{\mathrm{t}=0}^{\infty }{\left|{\mathrm{c}}_{\mathrm{s}\mathrm{t}}\right|}^{{\mathrm{r}}_{\varphi }}\right)}^{\frac{1}{{\mathrm{r}}_{\varphi }}}\end{array}$$

(12)

inequality holds for finite sums.

Now, with the help of Theorem 5, we construct Hölder’s inequality for the function of two variables in symmetric quantum calculus.

Theorem 7.

(${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-Symmetric Hölder’s Inequality). Let ${\mathfrak{f}}_1$ and ${\mathfrak{f}}_2$ be continuous functions from $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2$ to ℜ, then for $0<{\mathrm{q}}_{\theta }<1$, $0<{\mathrm{q}}_{\varphi }<1$, and $\frac{1}{{\mathrm{r}}_{\theta }}+\frac{1}{{\mathrm{r}}_{\varphi }}$ = 1, with ${\mathrm{r}}_{\theta }>1,{\mathrm{r}}_{\varphi }>1$, then

$$\begin{array}{cc}\hfill & {\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\left|{\mathfrak{f}}_1(\mathrm{x},\mathrm{y}){\mathfrak{f}}_2(\mathrm{x},\mathrm{y})\right|{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽{\left({\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\left|{\mathfrak{f}}_1(\mathrm{x},\mathrm{y})\right|}^{{\mathrm{r}}_{\theta }}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right)}^{\frac{1}{{\mathrm{r}}_{\theta }}}{\left({\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\left|{\mathfrak{f}}_2(\mathrm{x},\mathrm{y})\right|}^{{\mathrm{r}}_{\varphi }}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right)}^{\frac{1}{{\mathrm{r}}_{\varphi }}}\hfill \end{array}$$

(13)

inequality holds.

Proof. 

Using the definition of a ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric integral and (12), we have

$$\begin{array}{cc}\hfill & {\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\left|{\mathfrak{f}}_1(\mathrm{x},\mathrm{y}){\mathfrak{f}}_2(\mathrm{x},\mathrm{y})\right|{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & =({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\hfill \\ & \times \sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\left|{\mathfrak{f}}_1\left({\mathrm{q}}_{\theta }^{2n+1}{\mathrm{a}}_1+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}{\mathrm{c}}_1+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\right|\hfill \\ & \times \left|{\mathfrak{f}}_2\left({\mathrm{q}}_{\theta }^{2n+1}{\mathrm{a}}_1+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}{\mathrm{c}}_1+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\right|\hfill \\ & =\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\left\{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\right\}}^{\frac{1}{{\mathrm{r}}_{\theta }}}{\left\{{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\right\}}^{\frac{1}{{\mathrm{r}}_{\theta }}}\hfill \\ & \times \left|{\mathfrak{f}}_1\left({\mathrm{q}}_{\theta }^{2n+1}{\mathrm{a}}_1+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}{\mathrm{c}}_1+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\right|\hfill \\ & \times {\left\{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\right\}}^{\frac{1}{{\mathrm{r}}_{\varphi }}}{\left\{{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}\right\}}^{\frac{1}{{\mathrm{r}}_{\varphi }}}\hfill \\ & \times \left|{\mathfrak{f}}_2\left({\mathrm{q}}_{\theta }^{2n+1}{\mathrm{a}}_1+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}{\mathrm{c}}_1+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\right|\hfill \\ & ⩽\left[({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\right.\hfill \\ & \times {\left.\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}{\left|{\mathfrak{f}}_1\left({\mathrm{q}}_{\theta }^{2n+1}{\mathrm{a}}_1+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}{\mathrm{c}}_1+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\right|}_{\theta }^{\mathrm{r}}\right]}^{\frac{1}{{\mathrm{r}}_{\theta }}}\hfill \\ & \times \left[({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\right.\hfill \\ & \times {\left.\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m}{\left|{\mathfrak{f}}_2\left({\mathrm{q}}_{\theta }^{2n+1}{\mathrm{a}}_1+\left(1-{\mathrm{q}}_{\theta }^{2n+1}\right){\mathrm{a}}_0,{\mathrm{q}}_{\varphi }^{2m+1}{\mathrm{c}}_1+\left(1-{\mathrm{q}}_{\varphi }^{2m+1}\right){\mathrm{c}}_0\right)\right|}_{\varphi }^{\mathrm{r}}\right]}^{\frac{1}{{\mathrm{r}}_{\varphi }}}\hfill \\ & ={\left({\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\left|{\mathfrak{f}}_1(\mathrm{x},\mathrm{y})\right|}^{{\mathrm{r}}_{\theta }}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right)}^{\frac{1}{{\mathrm{r}}_{\theta }}}{\left({\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\left|{\mathfrak{f}}_2(\mathrm{x},\mathrm{y})\right|}^{{\mathrm{r}}_{\varphi }}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right)}^{\frac{1}{{\mathrm{r}}_{\varphi }}}.\hfill \end{array}$$

□

In our previous work [25], we derived some results in symmetric quantum calculus which are given below.

For any function $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\to \Re$ which is convex differentiable on $({\mathrm{a}}_0,{\mathrm{a}}_1)$ and $0<\mathrm{q}<1$, then

$$\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}⩽\frac{(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_1\right)}{1+{\mathrm{q}}^2}$$

(14)

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{\mathrm{q}{\mathrm{a}}_0+(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)-\frac{{(1-\mathrm{q})}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{1+{\mathrm{q}}^2}{\mathfrak{f}}^{\prime }\left(\frac{\mathrm{q}{\mathrm{a}}_0+(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)\hfill \\ \hfill & ⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}⩽\frac{(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{b}}_0\right)+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_1\right)}{1+{\mathrm{q}}^2}\hfill \end{array}$$

(15)

$$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2}\right)-\frac{{(1-\mathrm{q})}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{2(1+{\mathrm{q}}^2)}{\mathfrak{f}}^{\prime }\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2}\right)\\ \hfill ⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}⩽\frac{(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_1\right)}{1+{\mathrm{q}}^2}.\end{array}$$

(16)

3. Hermite–Hadamard Inequalities for Coordinated Convex Function in Symmetric Quantum Calculus

In this section, we will construct the Hermite–Hadamard inequality for the convex coordinated function in symmetric quantum calculus and its types. For this, let $\Omega$ be a class of continuous functions from a one- or two-dimensional interval to ℜ that satisfies some of the following properties of symmetric quantum integrals:

(i)

For ${\mathfrak{f}}_1,{\mathfrak{f}}_2\in \Omega$ with ${\mathfrak{f}}_1⩽{\mathfrak{f}}_2$ and $[{\mathrm{a}}_0,{\mathrm{a}}_1]\subseteq \Re$, then ${\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\mathfrak{f}}_1\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}⩽{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\mathfrak{f}}_2\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}$ for all $\mathrm{x}\in [{\mathrm{a}}_0,{\mathrm{a}}_1]$.

(ii)

For ${\mathfrak{f}}_1\in \Omega$, then $\left|{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\mathfrak{f}}_1\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}\right|⩽{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\left|{\mathfrak{f}}_1\left(\mathrm{x}\right)\right|{}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}$.

It is important to mention here that throughout the rest of the paper all the functions that we will consider belong to the class $\Omega$.

Theorem 8.

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$, then for $0<{\mathrm{q}}_{\theta }<1$ and $0<{\mathrm{q}}_{\varphi }<1$,

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \\ & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽{\displaystyle \frac{1}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\left[(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)\right.\hfill \\ & +\left.{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right]\hfill \end{array}$$

(17)

inequalities hold.

Proof. 

Let ${\mathfrak{h}}_{\mathrm{x}}$ be a convex function from $[{\mathrm{c}}_0,{\mathrm{c}}_1]$ to ℜ and defined as ${\mathfrak{h}}_{\mathrm{x}}\left(\mathrm{y}\right)=\mathfrak{f}(\mathrm{x},\mathrm{y})$. Then, using (14), we have

$$\begin{array}{c}{\mathfrak{h}}_{\mathrm{x}}\left(\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)⩽\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\mathfrak{h}}_{\mathrm{x}}\left(\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}⩽\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathfrak{h}}_{\mathrm{x}}\left({\mathrm{c}}_0\right)+{\mathrm{q}}_{\varphi }{\mathfrak{h}}_{\mathrm{x}}\left({\mathrm{c}}_1\right)}{1+{\mathrm{q}}_{\varphi }^2},\\ \mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)⩽\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}⩽\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1)}{1+{\mathrm{q}}_{\varphi }^2}\end{array}$$

(18)

for $0<{\mathrm{q}}_{\varphi }<1$ and for all $\mathrm{x}\in [{\mathrm{a}}_0,{\mathrm{a}}_1]$. For any $0<{\mathrm{q}}_{\theta }<1$, taking the symmetric ${\mathrm{q}}_{\theta }$-integral on $[{\mathrm{a}}_0,{\mathrm{a}}_1]$

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1)}{1+{\mathrm{q}}_{\varphi }^2}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ \hfill & =\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}.\hfill \end{array}$$

(19)

Similarly, let ${\mathfrak{h}}_{\mathrm{y}}$ be a convex function from $[{\mathrm{a}}_0,{\mathrm{a}}_1]$ to ℜ and defined as ${\mathfrak{h}}_{\mathrm{y}}\left(\mathrm{x}\right)=\mathfrak{f}(\mathrm{x},\mathrm{y})$. Then, again using (14), we have

$$\begin{array}{c}{\mathfrak{h}}_{\mathrm{y}}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2}\right)⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\mathfrak{h}}_{\mathrm{y}}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathfrak{h}}_{\mathrm{y}}\left({\mathrm{a}}_0\right)+{\mathrm{q}}_{\theta }{\mathfrak{h}}_{\mathrm{y}}\left({\mathrm{a}}_1\right)}{1+{\mathrm{q}}_{\theta }^2},\\ \mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right)⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,\mathrm{y})+{\mathrm{q}}_{\theta }\mathfrak{f}({\mathrm{a}}_1,\mathrm{y})}{1+{\mathrm{q}}_{\theta }^2}\end{array}$$

(20)

for $0<{\mathrm{q}}_{\theta }<1$ and for all $\mathrm{y}\in [{\mathrm{c}}_0,{\mathrm{c}}_1]$, for any $0<{\mathrm{q}}_{\varphi }<1$.

Taking the symmetric ${\mathrm{q}}_{\varphi }$-integral on $[{\mathrm{c}}_0,{\mathrm{c}}_1]$,

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,\mathrm{y})+{\mathrm{q}}_{\theta }\mathfrak{f}({\mathrm{a}}_1,\mathrm{y})}{1+{\mathrm{q}}_{\theta }^2}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & =\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}.\hfill \end{array}$$

(21)

Adding (19) and (21):

$$\begin{array}{cc}\hfill & \frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}.\hfill \end{array}$$

(22)

Replacing $\mathrm{x}$ by $\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2}$ in (18) and $\mathrm{y}$ by $\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}$ in (20), then adding, we have

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \\ & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & ⩽\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_1)}{1+{\mathrm{q}}_{\varphi }^2}\hfill \\ & +\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2})+{\mathrm{q}}_{\theta }\mathfrak{f}({\mathrm{a}}_1,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2})}{2(1+{\mathrm{q}}_{\theta }^2)}.\hfill \end{array}$$

(23)

Applying (14) on the right-hand side of (22):

$$\begin{array}{cc}\hfill & \frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2(1+{\mathrm{q}}_{\varphi }^2)}\left[\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)}{1+{\mathrm{q}}_{\theta }^2}\right]\hfill \\ & +\frac{{\mathrm{q}}_{\varphi }}{2(1+{\mathrm{q}}_{\varphi }^2)}\left[\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)}{1+{\mathrm{q}}_{\theta }^2}\right]\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2(1+{\mathrm{q}}_{\theta }^2)}\left[\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)}{1+{\mathrm{q}}_{\varphi }^2}\right]\hfill \\ & +\frac{{\mathrm{q}}_{\theta }}{2(1+{\mathrm{q}}_{\theta }^2)}\left[\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)}{1+{\mathrm{q}}_{\varphi }^2}\right]\hfill \\ & ={\displaystyle \frac{1}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\left[(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)\right.\hfill \\ & +\left.{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right].\hfill \end{array}$$

(24)

Joining (22)–(24), we obtain the desired result. □

Remark 2.

If ${\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }$ approach 1 in Theorem 8, then it is reconstructed into the classical one (2).

Now, we derive another new result of symmetric quantum calculus which will assist in proving some related results of Hermite–Hadamard inequalities.

Theorem 9.

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]⟶\Re$ be a convex function on $({\mathrm{a}}_0,{\mathrm{a}}_1)$ and differentiable as well, then for $0<\mathrm{q}<1$

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}\hfill \\ & ⩽\frac{\mathrm{q}(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)+{\mathrm{q}}^2\mathfrak{f}\left({\mathrm{a}}_1\right)}{{(1+{\mathrm{q}}^2)}^2}+\left(\frac{1-\mathrm{q}+{\mathrm{q}}^2}{1+{\mathrm{q}}^2}\right)\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)\hfill \\ & ⩽\frac{(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_1\right)}{1+{\mathrm{q}}^2}\hfill \end{array}$$

(25)

inequalities hold.

Proof. 

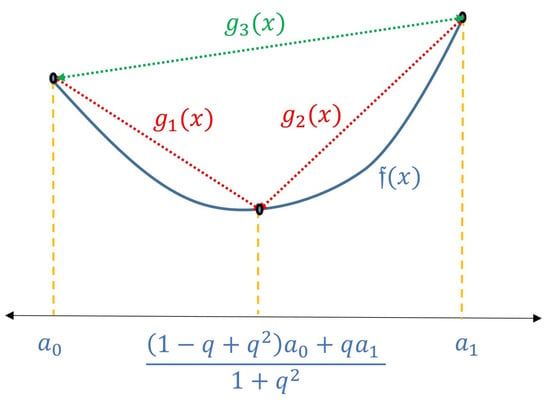
Let ${\mathfrak{g}}_1\left(\mathrm{x}\right)$ and ${\mathfrak{g}}_2\left(\mathrm{x}\right)$ be the line segments joining the points $({\mathrm{a}}_0,\mathfrak{f}\left({\mathrm{a}}_0\right)),(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2},\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}))$ and $(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2},\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})),({\mathrm{a}}_1,\mathfrak{f}\left({\mathrm{a}}_1\right))$, respectively. Owing to the convexity of $\mathfrak{f}$ on $[{\mathrm{a}}_0,{\mathrm{a}}_1]$, $\mathfrak{f}$ is always below the line segments ${\mathfrak{g}}_1\left(\mathrm{x}\right)$ and ${\mathfrak{g}}_2\left(\mathrm{x}\right)$. The equations of these line segments are ${\mathfrak{g}}_1\left(\mathrm{x}\right)=\frac{\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_0\right)}{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}-{\mathrm{a}}_0}(\mathrm{x}-{\mathrm{a}}_0)+\mathfrak{f}\left({\mathrm{a}}_0\right)$ and ${\mathfrak{g}}_2\left(\mathrm{x}\right)=\frac{\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_1\right)}{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}-{\mathrm{a}}_1}(\mathrm{x}-{\mathrm{a}}_1)+\mathfrak{f}\left({\mathrm{a}}_1\right)$.

From Figure 1, we can write the equations of ${\mathfrak{g}}_1\left(\mathrm{x}\right),{\mathfrak{g}}_2\left(\mathrm{x}\right)$, and ${\mathfrak{g}}_3\left(\mathrm{x}\right)$ using the two-point form formula of the equation of a line as

$$\begin{array}{cc}\hfill {\mathfrak{g}}_1\left(\mathrm{x}\right)& =(1+{\mathrm{q}}^2)\frac{\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_0\right)}{\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}(\mathrm{x}-{\mathrm{a}}_0)+\mathfrak{f}\left({\mathrm{a}}_0\right),\hfill \\ \hfill {\mathfrak{g}}_2\left(\mathrm{x}\right)& =(1+{\mathrm{q}}^2)\frac{\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_1\right)}{(1-\mathrm{q}+{\mathrm{q}}^2)({\mathrm{a}}_0-{\mathrm{a}}_1)}(\mathrm{x}-{\mathrm{a}}_1)+\mathfrak{f}\left({\mathrm{a}}_1\right),\hfill \\ \hfill {\mathfrak{g}}_3\left(\mathrm{x}\right)& ={\displaystyle \frac{\mathfrak{f}\left({\mathrm{a}}_1\right)-\mathfrak{f}\left({\mathrm{a}}_0\right)}{{\mathrm{a}}_1-{\mathrm{a}}_0}}(\mathrm{x}-{\mathrm{a}}_0)+\mathfrak{f}\left({\mathrm{a}}_0\right).\hfill \end{array}$$

Also, from Figure 1, from ${\mathrm{a}}_0$ to $\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}$,

$$\begin{array}{c}\hfill \mathfrak{f}\left(\mathrm{x}\right)⩽{\mathfrak{g}}_1\left(\mathrm{x}\right)=(1+{\mathrm{q}}^2)\frac{\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_0\right)}{\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}(\mathrm{x}-{\mathrm{a}}_0)+\mathfrak{f}\left({\mathrm{a}}_0\right).\end{array}$$

(26)

Similarly, from $\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}$ to ${\mathrm{a}}_1,$

$$\begin{array}{c}\hfill \mathfrak{f}\left(\mathrm{x}\right)⩽{\mathfrak{g}}_2\left(\mathrm{x}\right)=(1+{\mathrm{q}}^2)\frac{\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_1\right)}{(1-\mathrm{q}+{\mathrm{q}}^2)({\mathrm{a}}_0-{\mathrm{a}}_1)}(\mathrm{x}-{\mathrm{a}}_1)+\mathfrak{f}\left({\mathrm{a}}_1\right).\end{array}$$

(27)

Taking the symmetric $\mathrm{q}$-integral, the inequalities (26) and (27) from ${\mathrm{a}}_0$ to $\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}$ and $\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}$ to ${\mathrm{a}}_1$, respectively, then from Figure 1,

$$\begin{array}{c}\hfill {\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}⩽{\int }_{{\mathrm{a}}_0}^{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}{\mathfrak{g}}_1\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}+{\int }_{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}^{{\mathrm{a}}_1}{\mathfrak{g}}_2\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x},\end{array}$$

(28)

where $\mathrm{x}\in [{\mathrm{a}}_0,{\mathrm{a}}_1]$.

$$\begin{array}{cc}\hfill & {\int }_{{\mathrm{a}}_0}^{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}{\mathfrak{g}}_1\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}=\frac{1+{\mathrm{q}}^2}{\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}\left[\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_0\right)\right]\hfill \\ & \times \left[{\int }_{{\mathrm{a}}_0}^{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}\mathrm{x}{}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}-{\mathrm{a}}_0\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}-{\mathrm{a}}_0\right)\right]\hfill \\ & +\mathfrak{f}\left({\mathrm{a}}_0\right)\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}-{\mathrm{a}}_0\right)\hfill \\ & =\frac{1+{\mathrm{q}}^2}{\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}\left[\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_0\right)\right]\left[(1-{\mathrm{q}}^2)\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}-{\mathrm{a}}_0\right)\sum _{n=0}^{\infty }{\mathrm{q}}^{2n}\right.\hfill \\ & \times \left.\left\{(1-{\mathrm{q}}^{2n+1}){\mathrm{a}}_0+{\mathrm{q}}^{2n+1}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)\right\}-{\mathrm{a}}_0\mathrm{q}\left(\frac{{\mathrm{a}}_1-{\mathrm{a}}_0}{1+{\mathrm{q}}^2}\right)\right]+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_0\right)\left(\frac{{\mathrm{a}}_1-{\mathrm{a}}_0}{1+{\mathrm{q}}^2}\right)\hfill \\ & =\frac{1+{\mathrm{q}}^2}{\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}\left[\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_0\right)\right]\left[\frac{(1-{\mathrm{q}}^2)\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}{1+{\mathrm{q}}^2}\left\{\left(\frac{1}{1-{\mathrm{q}}^2}-\frac{\mathrm{q}}{1-{\mathrm{q}}^4}\right){\mathrm{a}}_0\right.\right.\hfill \\ & +\left.\left.\frac{\mathrm{q}}{1-{\mathrm{q}}^4}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)\right\}-{\mathrm{a}}_0\mathrm{q}\left(\frac{{\mathrm{a}}_1-{\mathrm{a}}_0}{1+{\mathrm{q}}^2}\right)\right]+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_0\right)\left(\frac{{\mathrm{a}}_1-{\mathrm{a}}_0}{1+{\mathrm{q}}^2}\right)\hfill \\ & =\left[\mathfrak{f}(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2})-\mathfrak{f}\left({\mathrm{a}}_0\right)\right]\left[\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0}{1+{\mathrm{q}}^2}+\frac{\mathrm{q}}{1+{\mathrm{q}}^2}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)-{\mathrm{a}}_0\right]\hfill \\ & +\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_0\right)\left(\frac{{\mathrm{a}}_1-{\mathrm{a}}_0}{1+{\mathrm{q}}^2}\right)\hfill \\ & =\left[\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)-\mathfrak{f}\left({\mathrm{a}}_0\right)\right]\left[\frac{{\mathrm{q}}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{{(1+{\mathrm{q}}^2)}^2}\right]+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_0\right)\left(\frac{{\mathrm{a}}_1-{\mathrm{a}}_0}{1+{\mathrm{q}}^2}\right)\hfill \\ & =\frac{\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}{{(1+{\mathrm{q}}^2)}^2}\left[\mathrm{q}\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)-\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_0\right)+\mathfrak{f}\left({\mathrm{a}}_0\right)(1+{\mathrm{q}}^2)\right]\hfill \\ & =\frac{\mathrm{q}({\mathrm{a}}_1-{\mathrm{a}}_0)}{{(1+{\mathrm{q}}^2)}^2}\left[\mathrm{q}\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)+(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)\right].\hfill \end{array}$$

(29)

Similarly,

$$\begin{array}{c}\hfill {\int }_{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}^{{\mathrm{a}}_1}{\mathfrak{g}}_2\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}=\frac{{\mathrm{a}}_1-{\mathrm{a}}_0}{{(1+{\mathrm{q}}^2)}^2}\left[{\mathrm{q}}^2\mathfrak{f}\left({\mathrm{a}}_1\right)+(1-\mathrm{q}+{\mathrm{q}}^2-{\mathrm{q}}^3+{\mathrm{q}}^4)\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)\right].\end{array}$$

(30)

Adding (29) and (30):

$$\begin{array}{cc}\hfill & {\int }_{{\mathrm{a}}_0}^{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}{\mathfrak{g}}_1\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}+{\int }_{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}^{{\mathrm{a}}_1}{\mathfrak{g}}_2\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}\hfill \\ & =({\mathrm{a}}_1-{\mathrm{a}}_0)\left[\frac{\mathrm{q}(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)+{\mathrm{q}}^2\mathfrak{f}\left({\mathrm{a}}_1\right)}{{(1+{\mathrm{q}}^2)}^2}+\left(\frac{1-\mathrm{q}+{\mathrm{q}}^2}{1+{\mathrm{q}}^2}\right)\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)\right].\hfill \end{array}$$

(31)

So, inequality (28) becomes

$$\begin{array}{cc}\hfill {\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}& ⩽({\mathrm{a}}_1-{\mathrm{a}}_0)\left[\frac{\mathrm{q}(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)+{\mathrm{q}}^2\mathfrak{f}\left({\mathrm{a}}_1\right)}{{(1+{\mathrm{q}}^2)}^2}\right.\hfill \\ & +\left.\left(\frac{1-\mathrm{q}+{\mathrm{q}}^2}{1+{\mathrm{q}}^2}\right)\mathfrak{f}\left(\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}\right)\right].\hfill \end{array}$$

(32)

From Figure 1, we can also conclude that

$$\begin{array}{cc}\hfill {\int }_{{\mathrm{a}}_0}^{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}{\mathfrak{g}}_1\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}+{\int }_{\frac{(1-\mathrm{q}+{\mathrm{q}}^2){\mathrm{a}}_0+\mathrm{q}{\mathrm{a}}_1}{1+{\mathrm{q}}^2}}^{{\mathrm{a}}_1}{\mathfrak{g}}_2\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}& ⩽{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\mathfrak{g}}_3\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{\mathrm{q}}\mathrm{x}\hfill \\ & =({\mathrm{a}}_1-{\mathrm{a}}_0)\frac{(1-\mathrm{q}+{\mathrm{q}}^2)\mathfrak{f}\left({\mathrm{a}}_0\right)+\mathrm{q}\mathfrak{f}\left({\mathrm{a}}_1\right)}{1+{\mathrm{q}}^2}.\hfill \end{array}$$

(33)

Finally, if we combine the left-hand side of (14) with (32) and (33), we obtain the desired result. □

Remark 3.

If $\mathrm{q}$ approaches 1 in Theorem 9, then it is reconstructed into corollary 2.1 from [26].

Theorem 10.

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$, then for $0<{\mathrm{q}}_{\theta }<1$ and $0<{\mathrm{q}}_{\varphi }<1$,

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \\ & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{2({\mathrm{a}}_1-{\mathrm{a}}_0){(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0){(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)}{2({\mathrm{c}}_1-{\mathrm{c}}_0){(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0){(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ \hfill & ⩽{\displaystyle \frac{1}{{(1+{\mathrm{q}}_{\theta }^2)}^2{(1+{\mathrm{q}}_{\varphi }^2)}^2}}\left[{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{q}}_{\varphi }^2\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)\right.\hfill \\ & +\left.{\mathrm{q}}_{\theta }^2{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }^2{\mathrm{q}}_{\varphi }^2\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right]\hfill \\ & +{\displaystyle \frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{(1+{\mathrm{q}}_{\theta }^2){(1+{\mathrm{q}}_{\varphi }^2)}^2}}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_0\right)\hfill \\ & +{\displaystyle \frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{q}}_{\varphi }^2}{(1+{\mathrm{q}}_{\theta }^2){(1+{\mathrm{q}}_{\varphi }^2)}^2}}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_1\right)\hfill \\ & +{\displaystyle \frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{{(1+{\mathrm{q}}_{\theta }^2)}^2(1+{\mathrm{q}}_{\varphi }^2)}}\mathfrak{f}\left({\mathrm{a}}_0,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \\ & +{\displaystyle \frac{{\mathrm{q}}_{\theta }^2(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{{(1+{\mathrm{q}}_{\theta }^2)}^2(1+{\mathrm{q}}_{\varphi }^2)}}\mathfrak{f}\left({\mathrm{a}}_1,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \\ & \hspace{1em}\hspace{1em}+{\displaystyle \frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \end{array}$$

(34)

inequalities hold.

Proof. 

Let ${\mathfrak{h}}_{\mathrm{x}}$ be a convex function from $[{\mathrm{c}}_0,{\mathrm{c}}_1]$ to ℜ and defined as ${\mathfrak{h}}_{\mathrm{x}}\left(\mathrm{y}\right)=\mathfrak{f}(\mathrm{x},\mathrm{y})$. Then, using (32), we have

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\mathfrak{h}}_{\mathrm{x}}\left(\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}⩽\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathfrak{h}}_{\mathrm{x}}\left({\mathrm{c}}_0\right)+{\mathrm{q}}_{\varphi }^2{\mathfrak{h}}_{\mathrm{x}}\left({\mathrm{c}}_1\right)}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}\hfill \\ & +\left(\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2}\right){\mathfrak{h}}_{\mathrm{x}}\left(\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \\ \hfill & \frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}⩽\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }^2\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1)}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}\hfill \\ & +\left(\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2}\right)\mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \end{array}$$

holds for all $\mathrm{x}\in [{\mathrm{a}}_0,{\mathrm{a}}_1]$ and $0<{\mathrm{q}}_{\varphi },{\mathrm{q}}_{\theta }<1$. Taking the symmetric ${\mathrm{q}}_{\theta }$-integral from ${\mathrm{a}}_0$ to ${\mathrm{a}}_1$:

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }^2}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\left(\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2}\right){\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}.\hfill \end{array}$$

(35)

Similarly, let ${\mathfrak{h}}_{\mathrm{y}}$ be a convex function from $[{\mathrm{a}}_0,{\mathrm{a}}_1]$ to ℜ and defined as ${\mathfrak{h}}_{\mathrm{y}}\left(\mathrm{x}\right)=\mathfrak{f}(\mathrm{x},\mathrm{y})$. Then, again using (32), we have

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\mathfrak{h}}_{\mathrm{y}}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathfrak{h}}_{\mathrm{y}}\left({\mathrm{a}}_0\right)+{\mathrm{q}}_{\theta }^2{\mathfrak{h}}_{\mathrm{y}}\left({\mathrm{a}}_1\right)}{{(1+{\mathrm{q}}_{\theta }^2)}^2}\hfill \\ & +\left(\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2}\right){\mathfrak{h}}_{\mathrm{y}}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2}\right)\hfill \\ \hfill & \frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,\mathrm{y})+{\mathrm{q}}_{\theta }^2\mathfrak{f}({\mathrm{a}}_1,\mathrm{y})}{{(1+{\mathrm{q}}_{\theta }^2)}^2}\hfill \\ & +\left(\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2}\right)\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right)\hfill \end{array}$$

holds for all $\mathrm{y}\in [{\mathrm{c}}_0,{\mathrm{c}}_1]$ and $0<{\mathrm{q}}_{\varphi },{\mathrm{q}}_{\theta }<1$. Now, taking the symmetric ${\mathrm{q}}_{\varphi }$-integral from ${\mathrm{c}}_0$ to ${\mathrm{c}}_1$.

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}{}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)}{{(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }^2}{{(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}+\left(\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2}\right){\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}.\hfill \end{array}$$

(36)

Now, $\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}$ (35) + $\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}$ (36), we have

$$\begin{array}{cc}\hfill \frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}& ⩽\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{2({\mathrm{a}}_1-{\mathrm{a}}_0){(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0){(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}\hfill \\ & \times {\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)}{2({\mathrm{c}}_1-{\mathrm{c}}_0){(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & +\frac{{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0){(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}\hfill \\ & \times {\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}.\hfill \end{array}$$

(37)

Now, applying (32) on the right-hand side of (37), we have

$$\begin{array}{cc}\hfill \frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{2({\mathrm{a}}_1-{\mathrm{a}}_0){(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}& ⩽\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)}{2{(1+{\mathrm{q}}_{\varphi }^2)}^2}\left[\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }^2\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)}{{(1+{\mathrm{q}}_{\theta }^2)}^2}\right.\hfill \\ & +\left.\left(\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2}\right)\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_0\right)\right],\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \frac{{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0){(1+{\mathrm{q}}_{\varphi }^2)}^2}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}& ⩽\frac{{\mathrm{q}}_{\varphi }^2}{2{(1+{\mathrm{q}}_{\varphi }^2)}^2}\left[\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }^2\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)}{{(1+{\mathrm{q}}_{\theta }^2)}^2}\right.\hfill \\ & +\left.\left(\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2}\right)\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_1\right)\right],\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill \frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)}{2({\mathrm{c}}_1-{\mathrm{c}}_0){(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}& ⩽\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)}{2{(1+{\mathrm{q}}_{\theta }^2)}^2}\left[\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }^2\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}\right.\hfill \\ & +\left.\left(\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2}\right)\mathfrak{f}\left({\mathrm{a}}_0,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\right],\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill \frac{{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0){(1+{\mathrm{q}}_{\theta }^2)}^2}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}& ⩽\frac{{\mathrm{q}}_{\theta }^2}{2{(1+{\mathrm{q}}_{\theta }^2)}^2}\left[\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)+{\mathrm{q}}_{\varphi }^2\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}\right.\hfill \\ & +\left.\left(\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2}\right)\mathfrak{f}\left({\mathrm{a}}_1,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\right],\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & \frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2(1+{\mathrm{q}}_{\varphi }^2)}\left[\frac{{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}\left({\mathrm{a}}_0,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)+{\mathrm{q}}_{\theta }^2\mathfrak{f}\left({\mathrm{a}}_1,\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)}{{(1+{\mathrm{q}}_{\theta }^2)}^2}\right.\hfill \\ & +\left.\left(\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2}\right)\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\right],\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & \frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2(1+{\mathrm{q}}_{\theta }^2)}\left[\frac{{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_0\right)+{\mathrm{q}}_{\varphi }^2\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},{\mathrm{c}}_1\right)}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}\right.\hfill \\ & +\left.\left(\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2}\right)\mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\right].\hfill \end{array}$$

(43)

Adding (38)–(43), and then, combining the obtained result with (37) and the left-hand sides of (22) and (23), we obtain the desired result. □

Remark 4.

If ${\mathrm{q}}_{\theta },{\mathrm{q}}_{\varphi }$ approach 1 in Theorem 10, then it is reconstructed into the classical one of theorem 2.2 from [26].

Theorem 11.

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$, then for $0<{\mathrm{q}}_{\theta }<1$ and $0<{\mathrm{q}}_{\varphi }<1$,

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{x}}}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{y}}}-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ \hfill & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ \hfill & -\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽{\displaystyle \frac{1}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\left[(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)\right.\hfill \\ & +\left.{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right]\hfill \end{array}$$

(44)

inequalities hold.

Proof. 

Let ${\mathfrak{h}}_{\mathrm{x}}$ be a convex function from $[{\mathrm{c}}_0,{\mathrm{c}}_1]$ to ℜ and defined as ${\mathfrak{h}}_{\mathrm{x}}\left(\mathrm{y}\right)=\mathfrak{f}(\mathrm{x},\mathrm{y})$. Then, using (16), we have

$$\begin{array}{c}\hfill {\mathfrak{h}}_{\mathrm{x}}\left(\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)-\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{2(1+{\mathrm{q}}_{\varphi }^2)}{\displaystyle \frac{𝜕{\mathfrak{h}}_{\mathrm{x}}\left(\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{y}}}⩽\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\mathfrak{h}}_{\mathrm{x}}\left(\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y},\\ \hfill \mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)-\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{2(1+{\mathrm{q}}_{\varphi }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{y}}}⩽\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y},\end{array}$$

(45)

for $0<{\mathrm{q}}_{\varphi }<1$ and for all $\mathrm{x}\in [{\mathrm{a}}_0,{\mathrm{a}}_1]$. For any $0<{\mathrm{q}}_{\theta }<1$.

Taking the symmetric ${\mathrm{q}}_{\theta }$-integral on $[{\mathrm{a}}_0,{\mathrm{a}}_1]$ and dividing by $({\mathrm{a}}_1-{\mathrm{a}}_0)$, we have

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}-\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{2(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ \hfill & ⩽\frac{1}{({\mathrm{c}}_1-{\mathrm{c}}_0)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}.\hfill \end{array}$$

(46)

Similarly, let ${\mathfrak{h}}_{\mathrm{y}}$ be a convex function from $[{\mathrm{a}}_0,{\mathrm{a}}_1]$ to ℜ and defined as ${\mathfrak{h}}_{\mathrm{y}}\left(\mathrm{x}\right)=\mathfrak{f}(\mathrm{x},\mathrm{y})$. Then, again using (16), we have

$$\begin{array}{c}\hfill {\mathfrak{h}}_{\mathrm{y}}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2}\right)-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{2(1+{\mathrm{q}}_{\theta }^2)}{\displaystyle \frac{𝜕{\mathfrak{h}}_{\mathrm{y}}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2}\right)}{𝜕\mathrm{x}}}⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\mathfrak{h}}_{\mathrm{y}}\left(\mathrm{x}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x},\\ \hfill \mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right)-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{2(1+{\mathrm{q}}_{\theta }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right)}{𝜕\mathrm{x}}}⩽\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x},\end{array}$$

(47)

for $0<{\mathrm{q}}_{\theta }<1$ and for all $\mathrm{y}\in [{\mathrm{c}}_0,{\mathrm{c}}_1]$, for any $0<{\mathrm{q}}_{\varphi }<1$.

Taking the symmetric ${\mathrm{q}}_{\varphi }$-integral on $[{\mathrm{c}}_0,{\mathrm{c}}_1]$ and dividing by $({\mathrm{c}}_1-{\mathrm{c}}_0)$, we have

$$\begin{array}{cc}\hfill & \frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{2(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ \hfill & ⩽\frac{1}{({\mathrm{c}}_1-{\mathrm{c}}_0)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}.\hfill \end{array}$$

(48)

Adding (46) and (48), we have

$$\begin{array}{cc}\hfill & \frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ \hfill & ⩽\frac{1}{({\mathrm{c}}_1-{\mathrm{c}}_0)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}.\hfill \end{array}$$

(49)

Replacing $\mathrm{x}$ by $\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2}$ and $\mathrm{y}$ by $\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}$ in (45) and (47), respectively, then adding, we have

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{x}}}-\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{y}}}\hfill \\ \hfill & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ \hfill & \Rightarrow \mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{x}}}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right)}{𝜕\mathrm{y}}}-\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ \hfill & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ \hfill & -\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{4(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{a}}_0+{\mathrm{a}}_1}{2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{4(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{c}}_0+{\mathrm{c}}_1}{2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}.\hfill \end{array}$$

(50)

Finally, by (22), (24), (49), and (50) we obtain the desired result. □

Theorem 12.

Let $\mathfrak{f}:[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function on $[{\mathrm{a}}_0,{\mathrm{a}}_1]\times [{\mathrm{c}}_0,{\mathrm{c}}_1]$, then for $0<{\mathrm{q}}_{\theta }<1$ and $0<{\mathrm{q}}_{\varphi }<1$,

$$\begin{array}{cc}\hfill & \mathfrak{f}\left(\frac{{\mathrm{q}}_{\theta }{\mathrm{a}}_0+(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{{\mathrm{q}}_{\varphi }{\mathrm{c}}_0+(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{2(1+{\mathrm{q}}_{\theta }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{q}}_{\theta }{\mathrm{a}}_0+(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{{\mathrm{q}}_{\varphi }{\mathrm{c}}_0+(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)}{𝜕\mathrm{x}}}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{2(1+{\mathrm{q}}_{\varphi }^2)}{\displaystyle \frac{𝜕\mathfrak{f}\left(\frac{{\mathrm{q}}_{\theta }{\mathrm{a}}_0+(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{{\mathrm{q}}_{\varphi }{\mathrm{c}}_0+(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)}{𝜕\mathrm{y}}}\hfill \\ \hfill & -\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{2(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{q}}_{\theta }{\mathrm{a}}_0+(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{2(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{q}}_{\varphi }{\mathrm{c}}_0+(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ \hfill & ⩽\frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{q}}_{\varphi }{\mathrm{c}}_0+(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}\left(\frac{{\mathrm{q}}_{\theta }{\mathrm{a}}_0+(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ \hfill & -\frac{{(1-{\mathrm{q}}_{\theta })}^2({\mathrm{a}}_1-{\mathrm{a}}_0)}{2(1+{\mathrm{q}}_{\theta }^2)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{x}}}\mathfrak{f}\left(\frac{{\mathrm{q}}_{\theta }{\mathrm{a}}_0+(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}\right){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & -\frac{{(1-{\mathrm{q}}_{\varphi })}^2({\mathrm{c}}_1-{\mathrm{c}}_0)}{2(1+{\mathrm{q}}_{\varphi }^2)({\mathrm{a}}_1-{\mathrm{a}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\displaystyle \frac{𝜕}{𝜕\mathrm{y}}}\mathfrak{f}\left(\mathrm{x},\frac{{\mathrm{q}}_{\varphi }{\mathrm{c}}_0+(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽\frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & ⩽{\displaystyle \frac{1}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\left[(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)\right.\hfill \\ & +\left.{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right]\hfill \end{array}$$

(51)

inequalities hold.

Proof. 

Using (15) and same methodology of Theorem 5, we will get the desired result. □

Now, we will investigate our main result (17) through examples.

Example 2.

Let $\mathfrak{f}:[1,2]\times [3,4]\subseteq {\Re }^2⟶\Re$ be a convex coordinated function on $[1,2]\times [3,4]$ and defined as $\mathfrak{f}(\mathrm{x},\mathrm{y})={\mathrm{x}}^2+{\mathrm{y}}^2$, applying it on (17). Let ${\mathrm{a}}_0=1$, ${\mathrm{a}}_1=2$, ${\mathrm{c}}_0=3$, and ${\mathrm{c}}_1=4$.

Case 1. 

If ${\mathrm{q}}_{\theta }<{\mathrm{q}}_{\varphi }$, put ${\mathrm{q}}_{\theta }=\frac{1}{3}$ and ${\mathrm{q}}_{\varphi }=\frac{1}{2}$.

Then, the term on the left-hand side of (17) becomes

$$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)=\mathfrak{f}\left(\frac{13}{10},\frac{17}{5}\right)=\frac{169}{100}+\frac{289}{25}=13.25.\end{array}$$

(52)

The right-hand part of the extreme left term of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ \hfill & =\frac{1}{2}\left[{\int }_1^2\mathfrak{f}(\mathrm{x},\frac{17}{5}){}_1\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+{\int }_3^4\mathfrak{f}(\frac{13}{10},\mathrm{y}){}_3\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & =\frac{1}{2}\left[{\int }_1^2{\mathrm{x}}^2{}_1\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+{\left(\frac{17}{5}\right)}^2(2-1)+{\left(\frac{13}{10}\right)}^2(4-3)+{\int }_3^4{\mathrm{y}}^2{}_3\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & =\frac{1}{2}\left[(2-1)(1-{\mathrm{q}}_{\theta }^2)\sum _{n=0}^{\infty }{\mathrm{q}}_{\theta }^{2n}{\left\{(1-{\mathrm{q}}_{\theta }^{2n+1}).1+{\mathrm{q}}_{\theta }^{2n+1}.2\right\}}^2+\frac{289}{25}+\frac{169}{100}\right.\hfill \\ & +\left.(4-3)(1-{\mathrm{q}}_{\varphi }^2)\sum _{m=0}^{\infty }{\mathrm{q}}_{\varphi }^{2m}{\left\{(1-{\mathrm{q}}_{\varphi }^{2m+1}).3+{\mathrm{q}}_{\varphi }^{2m+1}.4\right\}}^2\right]\hfill \\ & =\frac{1}{2}\left[(1-{\mathrm{q}}_{\theta }^2)\left\{\frac{1}{1-{\mathrm{q}}_{\theta }^2}+\frac{{\mathrm{q}}_{\theta }^2}{1-{\mathrm{q}}_{\theta }^6}+\frac{2{\mathrm{q}}_{\theta }}{1-{\mathrm{q}}_{\theta }^4}\right\}+\frac{1325}{100}+(1-{\mathrm{q}}_{\varphi }^2)\left\{\frac{9}{1-{\mathrm{q}}_{\varphi }^2}+\frac{{\mathrm{q}}_{\varphi }^2}{1-{\mathrm{q}}_{\varphi }^6}+\frac{6{\mathrm{q}}_{\varphi }}{1-{\mathrm{q}}_{\varphi }^4}\right\}\right]\hfill \\ & =\frac{1}{2}\left[1+\frac{{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2+{\mathrm{q}}_{\theta }^4}+\frac{2{\mathrm{q}}_{\theta }}{1+{\mathrm{q}}_{\theta }^2}+\frac{1325}{100}+9+\frac{{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2+{\mathrm{q}}_{\varphi }^4}+\frac{6{\mathrm{q}}_{\varphi }}{1+{\mathrm{q}}_{\varphi }^2}\right]\hfill \\ & =\frac{1}{2}\left[10+\frac{9}{91}+\frac{3}{5}+\frac{1325}{100}+\frac{4}{21}+\frac{12}{5}\right]=13.27.\hfill \end{array}$$

(53)

The middle term of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & =\frac{1}{(2-1)(4-3)}{\int }_1^2{\int }_3^4({\mathrm{x}}^2+{\mathrm{y}}^2){}_3\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_1\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & =(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\varphi }^{2m}{\mathrm{q}}_{\theta }^{2n}\left[{\left\{1-{\mathrm{q}}_{\theta }^{2n+1}+2{\mathrm{q}}_{\theta }^{2n+1}\right\}}^2+{\left\{3-3{\mathrm{q}}_{\varphi }^{2m+1}+4{\mathrm{q}}_{\varphi }^{2m+1}\right\}}^2\right]\hfill \\ & =(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\mathrm{q}}_{\varphi }^{2m}\left[{\mathrm{q}}_{\theta }^{2n}+{\mathrm{q}}_{\theta }^{6n+2}+2{\mathrm{q}}_{\theta }^{4n+1}+9{\mathrm{q}}_{\theta }^{2n}+6{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{2m+1}+{\mathrm{q}}_{\theta }^{2n}{\mathrm{q}}_{\varphi }^{4m+2}\right]\hfill \\ & =(1-{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }^2)\sum _{m=0}^{\infty }{\mathrm{q}}_{\varphi }^{2m}\left[\frac{1}{1-{\mathrm{q}}_{\theta }^2}+\frac{{\mathrm{q}}_{\theta }^2}{1-{\mathrm{q}}_{\theta }^6}+\frac{2{\mathrm{q}}_{\theta }}{1-{\mathrm{q}}_{\theta }^4}+\frac{9}{1-{\mathrm{q}}_{\theta }^2}+\frac{6{\mathrm{q}}_{\varphi }^{2m+1}}{1-{\mathrm{q}}_{\theta }^2}+\frac{{\mathrm{q}}_{\varphi }^{4m+2}}{1-{\mathrm{q}}_{\theta }^2}\right]\hfill \\ & =(1-{\mathrm{q}}_{\varphi }^2)\sum _{m=0}^{\infty }\left[10{\mathrm{q}}_{\varphi }^{2m}+\frac{{\mathrm{q}}_{\theta }^2{\mathrm{q}}_{\varphi }^{2m}}{1+{\mathrm{q}}_{\theta }^2+{\mathrm{q}}_{\theta }^4}+\frac{2{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }^{2m}}{1+{\mathrm{q}}_{\theta }^2}+6{\mathrm{q}}_{\varphi }^{4m+1}+{\mathrm{q}}_{\varphi }^{6m+2}\right]\hfill \\ & =10+\frac{{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2+{\mathrm{q}}_{\theta }^4}+\frac{2{\mathrm{q}}_{\theta }}{1+{\mathrm{q}}_{\theta }^2}+\frac{6{\mathrm{q}}_{\varphi }}{1+{\mathrm{q}}_{\varphi }^2}+\frac{{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2+{\mathrm{q}}_{\varphi }^4}=10+\frac{9}{91}+\frac{3}{5}+\frac{12}{5}+\frac{4}{21}=13.29.\hfill \end{array}$$

(54)

The second term from the right-hand side of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & =\frac{3}{10}\left[{\int }_1^2{\mathrm{x}}^2{}_1\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+3^2(2-1)\right]+\frac{1}{5}\left[{\int }_1^2{\mathrm{x}}^2{}_1\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+4^2(2-1)\right]+\frac{7}{20}\left[1^2(4-3)+{\int }_3^4{\mathrm{y}}^2{}_3\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & +\frac{3}{20}\left[2^2(4-3)+{\int }_3^4{\mathrm{y}}^2{}_3\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ & =\frac{3}{10}\left[1+\frac{{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2+{\mathrm{q}}_{\theta }^4}+\frac{2{\mathrm{q}}_{\theta }}{1+{\mathrm{q}}_{\theta }^2}+9\right]+\frac{1}{5}\left[1+\frac{{\mathrm{q}}_{\theta }^2}{1+{\mathrm{q}}_{\theta }^2+{\mathrm{q}}_{\theta }^4}+\frac{2{\mathrm{q}}_{\theta }}{1+{\mathrm{q}}_{\theta }^2}+16\right]\hfill \\ & +\frac{7}{20}\left[1+9+\frac{{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2+{\mathrm{q}}_{\varphi }^4}+\frac{6{\mathrm{q}}_{\varphi }}{1+{\mathrm{q}}_{\varphi }^2}\right]+\frac{3}{20}\left[4+9+\frac{{\mathrm{q}}_{\varphi }^2}{1+{\mathrm{q}}_{\varphi }^2+{\mathrm{q}}_{\varphi }^4}+\frac{6{\mathrm{q}}_{\varphi }}{1+{\mathrm{q}}_{\varphi }^2}\right]\hfill \\ & =\frac{3}{10}\left(10+\frac{9}{91}+\frac{3}{5}\right)+\frac{1}{5}\left(17+\frac{9}{91}+\frac{3}{5}\right)+\frac{7}{20}\left(10+\frac{4}{21}+\frac{12}{5}\right)+\frac{3}{20}\left(13+\frac{4}{21}+\frac{12}{5}\right)\hfill \\ \hfill & =13.49.\hfill \end{array}$$

(55)

The extreme right-hand term of (17) becomes

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\left[(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)\right.\hfill \\ & +\left.{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right]\hfill \\ & ={\displaystyle \frac{\left(\frac{7}{9}\right)\left(\frac{3}{4}\right)\left(10\right)+\left(\frac{1}{3}\right)\left(\frac{3}{4}\right)\left(13\right)+\left(\frac{1}{2}\right)\left(\frac{7}{9}\right)\left(17\right)+\left(\frac{1}{3}\right)\left(\frac{1}{2}\right)\left(20\right)}{\left(\frac{10}{9}\right)\left(\frac{5}{4}\right)}}=13.7.\hfill \end{array}$$

(56)

From (52)–(56), we have

$$\begin{array}{c}\hfill 13.25<13.27<13.29<13.49<13.7.\end{array}$$

Which endorses our result.

Case 2. 

If ${\mathrm{q}}_{\theta }>{\mathrm{q}}_{\varphi }$, put ${\mathrm{q}}_{\theta }=\frac{1}{2}$ and ${\mathrm{q}}_{\varphi }=\frac{1}{3}$.

Then, the term on the left-hand side of (17) becomes

$$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)=\mathfrak{f}\left(\frac{7}{5},\frac{33}{10}\right)=12.85.\end{array}$$

(57)

The right-hand part of the extreme left term of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ \hfill & =\frac{1}{2}\left[10+\frac{4}{21}+\frac{9}{91}+\frac{1089}{100}+\frac{49}{25}+\frac{13}{5}\right]=12.87.\hfill \end{array}$$

(58)

The middle term of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}=10+\frac{4}{21}+\frac{4}{5}+\frac{9}{91}+\frac{9}{5}=12.89.\hfill \end{array}$$

(59)

The second term from the right-hand side of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & =\frac{7}{20}\left(10+\frac{4}{21}+\frac{4}{5}\right)+\frac{3}{20}\left(17+\frac{4}{21}+\frac{4}{5}\right)+\frac{3}{10}\left(10+\frac{9}{91}+\frac{9}{5}\right)+\frac{1}{5}\left(13+\frac{9}{91}+\frac{9}{5}\right)\hfill \\ \hfill & =13.09.\hfill \end{array}$$

(60)

The extreme right-hand term of (17) becomes

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\left[(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)\right.\hfill \\ & +\left.{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right]\hfill \\ & ={\displaystyle \frac{\left(\frac{3}{4}\right)\left(\frac{7}{9}\right)\left(10\right)+\left(\frac{1}{2}\right)\left(\frac{7}{9}\right)\left(13\right)+\left(\frac{1}{3}\right)\left(\frac{3}{4}\right)\left(17\right)+\left(\frac{1}{2}\right)\left(\frac{1}{3}\right)\left(20\right)}{\left(\frac{5}{4}\right)\left(\frac{10}{9}\right)}}=13.3.\hfill \end{array}$$

(61)

From (57)–(61), we have

$$12.85<12.87<12.89<13.09<13.3.$$

Which also endorses our result.

Case 3. 

If ${\mathrm{q}}_{\theta }={\mathrm{q}}_{\varphi }$, put ${\mathrm{q}}_{\theta }={\mathrm{q}}_{\varphi }=\frac{1}{2}$.

Then, the term on the left-hand side of (17) becomes

$$\begin{array}{c}\hfill \mathfrak{f}\left(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}\right)=\mathfrak{f}\left(\frac{7}{5},\frac{17}{5}\right)=13.52.\end{array}$$

(62)

The right-hand part of the extreme left term of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1}{2}\left[\frac{1}{{\mathrm{a}}_1-{\mathrm{a}}_0}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},\frac{(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2){\mathrm{c}}_0+{\mathrm{q}}_{\varphi }{\mathrm{c}}_1}{1+{\mathrm{q}}_{\varphi }^2}){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\right.\hfill \\ & +\left.\frac{1}{{\mathrm{c}}_1-{\mathrm{c}}_0}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2){\mathrm{a}}_0+{\mathrm{q}}_{\theta }{\mathrm{a}}_1}{1+{\mathrm{q}}_{\theta }^2},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\right]\hfill \\ \hfill & =\frac{1}{2}\left[10+\frac{4}{21}+\frac{4}{5}+\frac{289}{25}+\frac{49}{25}+\frac{4}{21}+\frac{12}{5}\right]=13.55.\hfill \end{array}$$

(63)

The middle term of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1}{({\mathrm{a}}_1-{\mathrm{a}}_0)({\mathrm{c}}_1-{\mathrm{c}}_0)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}(\mathrm{x},\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}=10+\frac{4}{21}+\frac{4}{5}+\frac{4}{21}+\frac{12}{5}=13.58.\hfill \end{array}$$

(64)

The second term from the right-hand side of (17) becomes

$$\begin{array}{cc}\hfill & \frac{1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_0){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}+\frac{{\mathrm{q}}_{\varphi }}{2({\mathrm{a}}_1-{\mathrm{a}}_0)(1+{\mathrm{q}}_{\varphi }^2)}{\int }_{{\mathrm{a}}_0}^{{\mathrm{a}}_1}\mathfrak{f}(\mathrm{x},{\mathrm{c}}_1){}_{{\mathrm{a}}_0}\tilde{d}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & +\frac{1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_0,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}+\frac{{\mathrm{q}}_{\theta }}{2({\mathrm{c}}_1-{\mathrm{c}}_0)(1+{\mathrm{q}}_{\theta }^2)}{\int }_{{\mathrm{c}}_0}^{{\mathrm{c}}_1}\mathfrak{f}({\mathrm{a}}_1,\mathrm{y}){}_{{\mathrm{c}}_0}\tilde{d}_{{\mathrm{q}}_{\varphi }}\mathrm{y}\hfill \\ & =\frac{3}{10}\left(10+\frac{4}{21}+\frac{4}{5}\right)+\frac{1}{5}\left(17+\frac{4}{21}+\frac{4}{5}\right)+\frac{3}{10}\left(10+\frac{4}{21}+\frac{12}{5}\right)+\frac{1}{5}\left(13+\frac{4}{21}+\frac{12}{5}\right)\hfill \\ \hfill & =13.79.\hfill \end{array}$$

(65)

The extreme right-hand term of (17) becomes

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}\left[(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_0)+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_0)\right.\hfill \\ & +\left.{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathfrak{f}({\mathrm{a}}_0,{\mathrm{c}}_1)+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }\mathfrak{f}({\mathrm{a}}_1,{\mathrm{c}}_1)\right]\hfill \\ & ={\displaystyle \frac{\left(\frac{3}{4}\right)\left(\frac{3}{4}\right)\left(10\right)+\left(\frac{1}{2}\right)\left(\frac{3}{4}\right)\left(13\right)+\left(\frac{1}{2}\right)\left(\frac{3}{4}\right)\left(17\right)+\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(20\right)}{\left(\frac{5}{4}\right)\left(\frac{5}{4}\right)}}=14.\hfill \end{array}$$

(66)

From (62)–(66), we have

$$13.52<13.55<13.58<13.79<14.$$

Which also endorses our result.

4. Application

Like a quantum Hermite–Hadamard inequality [15], the inequality (17) can also be used to find the range for coordinated convex functions whose symmetric quantum integrals cannot be calculated.

Example 3.

Let $\mathfrak{f}(\mathrm{x},\mathrm{y})={\mathrm{e}}^{{\mathrm{x}}^2+{\mathrm{y}}^2}$ be a coordinated convex function whose quantum and symmetric quantum integrals cannot be calculated on $\Delta =[0,1]\times [0,1]$. But the range of this function for ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$- and ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric integrals can be calculated with the help of the Hermite–Hadamard inequality in quantum and symmetric quantum calculus, respectively.

In Quantum Calculus:

In example 2 from [15], we have

$$\begin{array}{c}\hfill {\mathrm{e}}^{\frac{1}{{(1+{\mathrm{q}}_{\theta })}^2}+\frac{1}{{(1+{\mathrm{q}}_{\varphi })}^2}}⩽{\int }_0^1{\int }_0^1{\mathrm{e}}^{{\mathrm{x}}^2+{\mathrm{y}}^2}{\mathrm{d}}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{\mathrm{d}}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽\frac{{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\theta }\mathrm{e}+{\mathrm{q}}_{\varphi }\mathrm{e}+{\mathrm{e}}^2}{(1+{\mathrm{q}}_{\theta })(1+{\mathrm{q}}_{\varphi })}\end{array}$$

(67)

Case 1. 

If ${\mathrm{q}}_{\theta }={\mathrm{q}}_{\varphi }=\frac{1}{2}$, then (67) becomes

$$\begin{array}{c}\hfill 2.432⩽{\int }_0^1{\int }_0^1{\mathrm{e}}^{{\mathrm{x}}^2+{\mathrm{y}}^2}{\mathrm{d}}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{\mathrm{d}}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽4.603.\end{array}$$

(68)

Case 2. 

If ${\mathrm{q}}_{\theta }\ne {\mathrm{q}}_{\varphi }$ and ${\mathrm{q}}_{\theta }=\frac{1}{3}$, ${\mathrm{q}}_{\varphi }=\frac{1}{2}$, then (67) becomes

$$\begin{array}{c}\hfill 2.737⩽{\int }_0^1{\int }_0^1{\mathrm{e}}^{{\mathrm{x}}^2+{\mathrm{y}}^2}{\mathrm{d}}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{\mathrm{d}}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽4.911.\end{array}$$

(69)

In Symmetric Quantum Calculus: 

We have

$$\begin{array}{cc}\hfill & {\mathrm{e}}^{\frac{{\mathrm{q}}_{\theta }^2}{{(1+{\mathrm{q}}_{\theta }^2)}^2}+\frac{{\mathrm{q}}_{\varphi }^2}{{(1+{\mathrm{q}}_{\varphi }^2)}^2}}⩽{\int }_0^1{\int }_0^1{\mathrm{e}}^{{\mathrm{x}}^2+{\mathrm{y}}^2}{\tilde{d}}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{\tilde{d}}_{{\mathrm{q}}_{\theta }}\mathrm{x}\hfill \\ & ⩽{\displaystyle \frac{(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathrm{e}+{\mathrm{q}}_{\theta }(1-{\mathrm{q}}_{\varphi }+{\mathrm{q}}_{\varphi }^2)\mathrm{e}+{\mathrm{q}}_{\varphi }(1-{\mathrm{q}}_{\theta }+{\mathrm{q}}_{\theta }^2)\mathrm{e}+{\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }{\mathrm{e}}^2}{(1+{\mathrm{q}}_{\theta }^2)(1+{\mathrm{q}}_{\varphi }^2)}}.\hfill \end{array}$$

(70)

Case 1. 

If ${\mathrm{q}}_{\theta }={\mathrm{q}}_{\varphi }=\frac{1}{2}$, then (70) becomes

$$\begin{array}{c}\hfill 1.338⩽{\int }_0^1{\int }_0^1{\mathrm{e}}^{{\mathrm{x}}^2+{\mathrm{y}}^2}{\tilde{d}}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{\tilde{d}}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽2.847.\end{array}$$

(71)

Case 2. 

If ${\mathrm{q}}_{\theta }\ne {\mathrm{q}}_{\varphi }$ and ${\mathrm{q}}_{\theta }=\frac{1}{3}$, ${\mathrm{q}}_{\varphi }=\frac{1}{2}$, then (70) becomes

$$\begin{array}{c}\hfill 1.28⩽{\int }_0^1{\int }_0^1{\mathrm{e}}^{{\mathrm{x}}^2+{\mathrm{y}}^2}{\tilde{d}}_{{\mathrm{q}}_{\varphi }}\mathrm{y}{\tilde{d}}_{{\mathrm{q}}_{\theta }}\mathrm{x}⩽2.234.\end{array}$$

(72)

5. Conclusions

In this work, we develop the calculus of symmetric quantum calculus on coordinates in plane that helps us to construct the ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric Hölder’s and Hermite–Hadamard inequalities for functions of two variables. We provide examples to justify our novel results. Moreover, the ${\mathrm{q}}_{\theta }{\mathrm{q}}_{\varphi }$-symmetric Hermite–Hadamard inequality can also be used for finding the range of coordinated convex functions. In the second example, we can see that the range set of coordinated convex functions in symmetric quantum calculus is smaller than in quantum calculus.