The Equivalence of Two Modes of Order Convergence

Abstract

It is well known that if a poset satisfies Property A and its dual form, then the o-convergence and $o_2$-convergence in the poset are equivalent. In this paper, we supply an example to illustrate that a poset in which the o-convergence and $o_2$-convergence are equivalent may not satisfy Property A or its dual form, and carry out some further investigations on the equivalence of the o-convergence and $o_2$-convergence. By introducing the concept of the local Frink ideals (the dually local Frink ideals) and establishing the correspondence between ID-pairs and nets in a poset, we prove that the o-convergence and $o_2$-convergence of nets in a poset are equivalent if and only if the poset is ID-doubly continuous. This result gives a complete solution to the problem of E.S. Wolk in two modes of order convergence, which states under what conditions for a poset the o-convergence and $o_2$-convergence in the poset are equivalent.

1. Introduction

Let P be a poset and ${\left(x_i\right)}_{i\in I}$ a net on an up-directed set I with value in the poset P. The concept of order convergence of nets in a poset P was introduced by Birkhoff [1], Mcshane [2], Frink [3], Rennie [4] and Ward [5]. It is worth noting that the authors may have attached different meanings to the order convergence. Following the formulation of Wolk [6], we correspond to the following two modes of order convergence:

Definition 1

([1,2,3]). A net ${\left(x_i\right)}_{i\in I}$ in a poset P is said to o-converge to an element $x\in P$ (in symbol ${\left(x_i\right)}_{i\in I}\stackrel{o}{\to }x$) if there exist subsets M and N of P such that

(A0)

M is up-directed and N is down-directed;

(B0)

$supM=x=infN$;

(C0)

For every $m\in M$ and $n\in N$, $m⩽x_i⩽n$ holds eventually, i.e., there is $i_0\in I$ such that $m⩽x_i⩽n$ for all $i\geqq i_0$.

Definition 2

([4,5,6]). A net ${\left(x_i\right)}_{i\in I}$ in a poset P is said to $o_2$-converge to an element $x\in P$ (in symbol ${\left(x_i\right)}_{i\in I}\stackrel{o_2}{\to }x$) if there exist subsets M and N of P such that

(A2)

$supM=x=infN$;

(B2)

For every $m\in M$ and $n\in N$, $m⩽x_i⩽n$ holds eventually.

A research topic concerning the o-convergence and $o_2$-convergence, which are closely related to our work, is from the topological aspect. The o-convergence in a poset P may not be topological, i.e., there does not exist a topology $\tau$ on the poset P such that the o-convergent class and the convergent class with respect to the topology $\tau$ are equivalent. In [7], based on the introduction of Condition(*) and the double continuity for posets, Zhou and Zhao proved that, for a double continuous poset P with Condition(*), the o-convergence in the poset P is topological. As a further result, Condition (Δ), a weaker condition than Condition(*), and the $\mathcal{O}$-doubly continuous posets were defined in [8]. It was shown that, for a poset P with Condition (Δ), the o-convergence in the poset P is topological if and only if the poset P is $\mathcal{O}$-doubly continuous. Following the ideal in [8], Sun and Li [9] studied the B-topology on posets and found that the o-convergence in a poset P is topological if and only if the poset P is $S^{*}$-doubly continuous, which demonstrates the equivalence between the o-convergence being topological and the $S^{*}$-double continuity of a poset. Moreover, the ideal-o-convergence, a generalized form of o-convergence established via ideals, was defined in posets by Georgiou et al. [10,11]. Also, the authors obtained that the ideal-o-convergence in a poset P is topological if and only if the poset P is $S^{*}$-doubly continuous. This generalized the previous results on the o-convergence.

On the other hand, the $o_2$-convergence is also not topological generally. To characterize these posets so that the $o_2$-convergence is topological, Zhao and Li [12] studied the notions of $\alpha$-double continuous posets and ${\alpha }^{*}$-double continuous posets. Under some additional conditions, the $o_2$-convergence in these posets is topological. Ulteriorly, Li and Zou [13] proposed the concept of $O_2$-doubly continuous posets and showed that the $o_2$-convergence in a poset P is topological if and only if the poset P is $O_2$-doubly continuous, meaning that they gave a sufficient and necessary condition for the $o_2$-convergence to be topological. Further, Georgiou et al. [14] extended the $o_2$-convergence to be the ideal-$o_2$-convergence via ideals, and showed that the $O_2$-double continuity can equivalently characterize such a convergence to be topological.

From the order-theoretical aspect, by the definitions, one can readily verify that the o-convergence implies the $o_2$-convergence, i.e., if a net ${\left(x_i\right)}_{i\in I}$ in a poset P o-converges to an element $x\in P$, then it $o_2$-converges to x. However, the converse implication is not true. This fact can be demonstrated by the example in [6]. Hence, in [6], Wolk posed the following fundamental problem:

Problem 1.

Under what conditions for a poset P do the o-convergence and $o_2$-convergence in P agree?

A well-known result on this problem is that the o-convergence and $o_2$-convergence in a lattice are equivalent. Then, Wolk [6] obtained a result on the characterization of posets for the associated o-inf convergence (a counterpart of o-convergence) and $o_2$-inf convergence (a counterpart of $o_2$-convergence) being equivalent, which provides an approximate solution to the fundamental problem, using the concepts of Frink ideals and dual Frank ideals [15].

Motivated by these results toward the problem mentioned above, in this paper, we continue to make some further investigations on the o-convergence and $o_2$-convergence, hoping to clarify the order-theoretical condition of a poset P, which is sufficient and necessary for the o-convergence and $o_2$-convergence to be equivalent.

To this end, in Section 2, following the Frink ideal (the dual Frink ideal), the concepts of local Frink ideals (dually local Frink ideals) and ID-pairs in posets are further proposed, and then the relationship between ID-pairs and nets is presented. Section 3 is devoted to the order-theoretical characterization of the local Frink ideal (the dually local Frink ideal) generated by a general set. Using this characterization, we prove that the ID-double continuity is the precise feature for those posets for which the two modes of order convergence are equivalent.

For the unexplained notions and concepts, one can refer to [6,16,17].

2. Local Frink Ideal (Dually Local Frink Ideal) in Posets

We appoint some conventional notations to be used in the sequel. Let X be a set. We take $F⊑X$ to mean that F is a finite subset of the set X, including the empty set ∅. Given a poset P and $K,L\subseteq P$. The notations $K^u$ and $L^l$ are used to denote the set of all upper bounds of K and the set of all lower bounds of L, respectively, i.e., $K^u=\{y\in P:(\forall p\in K)y⩾p\}$ and $L^l=\{z\in P:(\forall p\in L)z⩽p\}$. Particularly, if the sets K and L are all reduced to be a singleton $\left\{y\right\}$, then the notations $\uparrow y$ and $\downarrow y$ are reserved to denote the sets ${\left\{y\right\}}^u$ and ${\left\{y\right\}}^l$, respectively.

Since the Frink ideal (the dual Frink ideal) in posets plays a fundamental role in the discussion of this section, we first review its definition.

Definition 3

([15]). Let P be a poset.

(1)

A subset K of the poset P is called a Frink ideal if, for every $F⊑K$, we have ${\left(F^u\right)}^l\subseteq K$. Furthermore, a Frink ideal K is said to be normal if ${\left(K^u\right)}^l=K$.

(2)

A subset L of the poset P is called a dual Frink ideal if, for every $S⊑L$, we have ${\left(S^l\right)}^u\subseteq L$. Furthermore, a dual Frink ideal L is said to be normal if ${\left(L^l\right)}^u=L$.

Based on the Frink ideal (the dual Frink ideal), we further define the local Frink ideal (the dually local Frink ideal) in posets.

Definition 4.

Let P be a poset and $K,L\subseteq P$.

(1)

The subset K is called a local Frink ideal in Li f, for every $F⊑K$ and every $S⊑L$, we have ${(F^u\bigcap S^l)}^l\subseteq K$.

(2)

The subset L is called a dually local Frink ideal in K if, for every $F⊑K$ and every $S⊑L$, we have ${(F^u\bigcap S^l)}^u\subseteq L$.

Example 1.

Let $\mathbb{R}$ be the set of all real numbers, in its usual order, and let $a\in \mathbb{R}$. If we take $K=(-\infty ,a]$ and $L=[a,+\infty )$, then, by Definition 4, the interval K is a local Frink ideal in L and the interval L is a dually local Frink ideal in K.

Given a poset P and $K,L\subseteq P$. We simply denote by $\mathfrak{L}\left(L\right)$ the family of all local Frink ideals in L and, by $\mathfrak{D}\left(K\right)$, the family of all dually local Frink ideals in K.

Remark 1.

Let P be a poset and $K,L\subseteq P$. Then,

(1)

From the logic viewpoint, it is reasonable to stipulate that ${\varnothing }^u={\varnothing }^l=P$. Thus, for every $L\subseteq P$ and every $K\in \mathfrak{L}\left(L\right)$, we have $\perp \in K$ if the poset P has the least element ⊥. Dually, for every $K\subseteq P$ and every $L\in \mathfrak{D}\left(K\right)$, we have $\top \in L$ if the greatest element ⊤ exists in the poset P.

(2)

If $K\in \mathfrak{L}\left(L\right)$, then $K\in \mathfrak{L}\left(L_0\right)$ for every $L_0\subseteq L$. And, dually, if $L\in \mathfrak{D}\left(K\right)$, then $L\in \mathfrak{D}\left(K_0\right)$ for every $K_0\subseteq K$.

(3)

The subset K is a Frink ideal if and only if $K\in \mathfrak{L}(\varnothing )$. And, dually, the subset L is a dual Frink ideal if and only if $L\in \mathfrak{D}(\varnothing )$.

Proposition 1.

Let P be a poset and $K,L\subseteq P$.

(1)

If $K\in \mathfrak{L}\left(L\right)$, then the subset K is a Frink ideal.

(2)

If $L\in \mathfrak{D}\left(K\right)$, then the subset L is a dual Frink ideal.

Proof. 

(1): Suppose that $K\in \mathfrak{L}\left(L\right)$. Then, we have ${(F^u\bigcap S^l)}^l\subseteq K$ for every $F⊑K$ and $S⊑L$. This implies that ${\left(F^u\right)}^l\subseteq {(F^u\bigcap S^l)}^l\subseteq K$. Thus, we conclude that ${\left(F^u\right)}^l\subseteq K$ for every $F⊑K$. This shows that the subset K is a Frink ideal.

(2): The proof is similar to that of (1). □

However, the converse implications of Proposition 1 may not be true. This fact can be clarified in Example 7.

Definition 5.

Let P be a poset. A pair $(K,L)$ consisting of subsets K and L of P is called an ID-pair in P if $K\in \mathfrak{L}\left(L\right)$ and $L\in \mathfrak{D}\left(K\right)$. Moreover, an ID-pair $(K,L)$ in P is said to be nontrivial if one of the following conditions is exactly satisfied:

(1)

$\left|P\right|=1$, where $\left|P\right|$ denotes the cardinal of the poset P;

(2)

$\left|P\right|\ge 2$ and $(K,L)\ne (P,P)$.

Example 2.

Let $P=\{a,b\}\bigcup \{\perp ,\top \}$, with the partial order ≤ defined by

• $\perp ⩽a⩽\top$;
• $\perp ⩽b⩽\top$.

Take $K=\{\perp \}$ and $L=\{\top \}$. Then, it is easy to see from Definitions 4 and 5 that the pair $(K,L)=\left(\right\{\perp \},\{\top \left\}\right)$ is a nontrivial ID-pair.

Proposition 2.

Let $(K,L)$ be an ID-pair in a poset P. Then, the ID-pair $(K,L)$ is nontrivial if and only if $F^u\bigcap S^l\ne \varnothing$ for every $F⊑K$ and every $S⊑L$.

Proof. 

(⇒): Let $(K,L)$ be a nontrivial ID-pair in a poset P. We consider the following cases:

(i)

$\left|P\right|=1$, i.e., the poset $P=\left\{p\right\}$ contains only one element p.

It is easy to check that $F^u\bigcap S^l=\left\{p\right\}\ne \varnothing$ for every $F⊑K$ and every $S⊑L$.

(ii)

$\left|P\right|\ge 2$.

Suppose that ${\left(F_0\right)}^u\bigcap {\left(S_0\right)}^l=\varnothing$ for some $F_0⊑K$ and $S_0⊑L$. Then, we have ${[{\left(F_0\right)}^u\bigcap {\left(S_0\right)}^l]}^l=P\subseteq K$ and ${[{\left(F_0\right)}^u\bigcap {\left(S_0\right)}^l]}^u=P\subseteq L$ since $(K,L)$ is an ID-pair in the poset P. This implies that $(K,L)=(P,P)$, which is a contradiction to the assumption that the ID-pair $(K,L)$ is nontrivial. Hence, we have that $F^u\bigcap S^l\ne \varnothing$ for every $F⊑K$ and every $S⊑L$.

By (i) and (ii), we conclude that $F^u\bigcap S^l\ne \varnothing$ for every $F⊑K$ and every $S⊑L$.

(⇐): Suppose that $(K,L)$ is an ID-pair such that $F^u\bigcap S^l\ne \varnothing$ for every $F⊑K$ and every $S⊑L$. If $(K,L)\ne (P,P)$, then the ID-pair $(K,L)$ is nontrivial by Definition 5. If $(K,L)=(P,P)$, i.e., $K=L=P$, then, by the assumption, we have ${\left\{p\right\}}^u\bigcap {\left\{q\right\}}^l=\uparrow p\bigcap \downarrow q\ne \varnothing$ and ${\left\{q\right\}}^u\bigcap {\left\{p\right\}}^l=\uparrow q\bigcap \downarrow p\ne \varnothing$ for all $p,q\in P$. It follows that $p=q$ for all $p,q\in P$. Hence, we conclude that $\left|P\right|=1$. This shows, by Definition 5, that the ID-pair $(K,L)$ is nontrivial. □

In fact, given a poset P and a Frink ideal K (resp. a dual Frink ideal L) of the poset P, we can select a subset L (resp. a subset K) of P such that the pair $(K,L)$ is a nontrivial ID-pair.

Theorem 1.

Let P be a poset.

(1)

If K is a Frink ideal of the poset P, then the pair $(K,L)$ is a nontrivial ID-pair for some subset L of the poset P;

(2)

If L is a dual Frink ideal of the poset P, then the pair $(K,L)$ is a nontrivial ID-pair for some subset K of the poset P.

Proof. 

(1): Suppose that K is a Frink ideal of P. Set $L=\bigcup \{{\left(F^u\right)}^u:F⊑K\}$. Now, we process to show that the pair $(K,L)$ is an ID-pair. Let $F_0⊑K$ and $S_0⊑L$. We consider the following two cases:

(i)

$S_0=\varnothing$.

Since K is a Frink ideal, by the definition of L, we have

$${[{\left(F_0\right)}^u\cap {\left(S_0\right)}^l]}^l={[{\left(F_0\right)}^u\cap P]}^l={\left[{\left(F_0\right)}^u\right]}^l\subseteq K,$$

and

$${[{\left(F_0\right)}^u\cap {\left(S_0\right)}^l]}^u={[{\left(F_0\right)}^u\cap P]}^u={\left[{\left(F_0\right)}^u\right]}^u\subseteq L.$$

(ii)

$S_0=\{s_1,s_2,\dots ,s_m\}\ne \varnothing$.

By the definition of L, there exists $F_i⊑K$ such that $s_i\in {\left[{\left(F_i\right)}^u\right]}^u$ for every $i\in \{1,2,\dots ,m\}$. This means that ${\left(F_i\right)}^u\subseteq \downarrow s_i$ for every $i\in \{1,2,\dots ,m\}$. Thus, we have ${(F_1\cup F_2\cup \dots \cup F_m)}^u\subseteq {\left(S_0\right)}^l$, which implies that

$$\begin{array}{cc}\hfill {({\left(F_0\right)}^u\cap {\left(S_0\right)}^l)}^l\subseteq & {[{(F_0\cup F_1\cup F_2\cup \dots \cup F_m)}^u\cap {\left(S_0\right)}^l]}^l\hfill \\ \hfill =& {\left[{(F_0\cup F_1\cup F_2\cup \dots \cup F_m)}^u\right]}^l\hfill \\ \hfill \subseteq & K,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {({\left(F_0\right)}^u\cap {\left(S_0\right)}^l)}^u\subseteq & {[{(F_0\cup F_1\cup F_2\cup \dots \cup F_m)}^u\cap {\left(S_0\right)}^l]}^u\hfill \\ \hfill =& {\left[{(F_0\cup F_1\cup F_2\cup \dots \cup F_m)}^u\right]}^u\hfill \\ \hfill \subseteq & L.\hfill \end{array}$$

The combination of (i) and (ii) shows that the pair $(K,L)$ is an ID-pair in P. Finally, we prove that the ID-pair $(K,L)$ is nontrivial. Assume that $(K,L)=(P,P)$. Let $x,y\in L=P$. Then, by the definition of L, there exists $F_y⊑P$ such that $y\in {\left[{\left(F_y\right)}^u\right]}^u$, which implies that ${\left(F_y\right)}^u\subseteq \downarrow y$. Since ${(\left\{x\right\}\cup F_y)}^u\subseteq {\left(F_y\right)}^u\subseteq \downarrow y$, we have $x\in \downarrow y$, i.e., $x⩽y$. Similarly, we can prove that $y⩽x$. This means that $x=y$, and thus we have $\left|P\right|=1$. By Definition 5, it follows that the ID-pair $(K,L)$ is nontrivial.

(2): By a similar verification to that of (1). □

Example 3.

Let P be a chain, i.e., for all $x,y\in P$, either $x⩽y$ or $y⩽x$. For every $x\in P$, by Definition 4 we have that the set $\downarrow x$ is a Frink ideal. Obviously, by Definitions 4 and 5, the set $\uparrow x$ can be selected such that the pair $(\downarrow x,\uparrow x)$ is a nontrivial ID-pair in P.

Given a poset P and a net ${\left(x_i\right)}_{i\in I}$ in the poset P, an element $p\in P$ is called an eventually lower bound of the net ${\left(x_i\right)}_{i\in I}$ provided that there exists $i_0\in I$ such that $x_i⩾p$ for all $i\geqq i_0$. An eventually upper bound of the net ${\left(x_i\right)}_{i\in I}$ is defined dually. Following the notations of Wolk [6], we also take the symbols $P_x$ and $Q_x$ to mean the set of all eventually lower bounds of the net ${\left(x_i\right)}_{i\in I}$ and the set of all eventually upper bounds of the net ${\left(x_i\right)}_{i\in I}$, respectively. If we denote $E_x\left(i_0\right)=\{x_i\in P:i\geqq i_0\}$, then $P_x=\bigcup \{{\left[E_x\left(i\right)\right]}^l:i\in I\}$ and $Q_x=\bigcup \{{\left[E_x\left(i\right)\right]}^u:i\in I\}$. For a set X, the symbol $Y\subset X$ means that Y is a proper subset of the set X, i.e., $Y\subseteq X$ and $Y\ne X$. In the following, we always take ${\ge }_o$ to represent the ordinary order on $\mathbb{N}$, the set of all positive integers.

Now, we can establish a correspondence between the nets and the ID-pairs:

Theorem 2.

Let P be a poset. Then, a pair $(K,L)$ in P is a nontrivial ID-pair if and only if there exists a net ${\left(x_i\right)}_{i\in I}$ in P such that $P_x=K$ and $Q_x=L$.

Proof. 

(⇐): Let $(K,L)$ be a pair of subsets of the poset P. Suppose also that ${\left(x_i\right)}_{i\in I}$ is a net in the P such that $P_x=K$ and $Q_x=L$. For every $F⊑P_x=K$ and every $S⊑Q_x=L$, we consider the following cases:

(i)

$F=S=\varnothing$.

Since $F=\varnothing$ and $S=\varnothing$, we have that $E_x\left(i\right)\subseteq F^u\bigcap S^l=P\ne \varnothing$ for all $i\in I$. This implies that ${(F^u\bigcap S^l)}^l\subseteq {\left[E_x\left(i\right)\right]}^l$ and ${(F^u\bigcap S^l)}^u\subseteq {\left[E_x\left(i\right)\right]}^u$ for all $i\in I$. Hence, ${(F^u\bigcap S^l)}^l\subseteq P_x$ and ${(F^u\bigcap S^l)}^u\subseteq Q_x$.

(ii)

$F=\varnothing ⊑P_x$ and $S=\{s_1,s_2,\dots ,s_n\}⊑Q_x$.

Since $S=\{s_1,s_2,\dots ,s_n\}⊑Q_x$, for every $1{\le }_{o}t{\le }_{o}n$, there exists $i_t\in I$ such that $E_x\left(i_t\right)\subseteq \downarrow s_t$. Take $i_0\in I$ such that $i_0\geqq i_t$ for all $1{\le }_{o}t{\le }_{o}n$. Then, we have $E_x\left(i_0\right)\subseteq \bigcap \{E_x\left(i_t\right):1{\le }_{o}t{\le }_{o}n\}\subseteq \bigcap \{\downarrow s_t:1{\le }_{o}t{\le }_{o}n\}=S^l$, which implies that $E_x\left(i_0\right)\subseteq F^u\bigcap S^l=S^l\ne \varnothing$, ${(F^u\bigcap S^l)}^l\subseteq {\left[E_x\left(i_0\right)\right]}^l$ and ${(F^u\bigcap S^l)}^u\subseteq {\left[E_x\left(i_0\right)\right]}^u$. It follows that ${(F^u\bigcap S^l)}^l\subseteq P_x$ and ${(F^u\bigcap S^l)}^u\subseteq Q_x$.

(iii)

$F=\{e_1,e_2,\dots ,e_m\}⊑P_x$ and $S=\varnothing ⊑Q_x$.

By a similar verification to that of (ii), we can also prove that $F^u\bigcap S^l\ne \varnothing$, ${(F^u\bigcap S^l)}^l\subseteq P_x$ and ${(F^u\bigcap S^l)}^u\subseteq Q_x$.

(iv)

$F=\{e_1,e_2,\dots ,e_m\}⊑P_x$ and $S=\{s_1,s_2,\dots ,s_n\}⊑Q_x$.

Since $F=\{e_1,e_2,\dots ,e_m\}⊑P_x$ and $S=\{s_1,s_2,\dots ,s_n\}⊑Q_x$, there exist $i_r,i_t\in I$ such that $E_x\left(i_r\right)\subseteq \uparrow e_r$ and $E_x\left(i_t\right)\subseteq \downarrow s_t$ for all $1{\le }_{o}r{\le }_{o}m$ and $1{\le }_{o}t{\le }_{o}n$. Take $i_0\in I$ such that $i_0\geqq i_r,i_t$ for all $1{\le }_{o}r{\le }_{o}m$ and $1{\le }_{o}t{\le }_{o}n$. Then, we have $E_x\left(i_0\right)\subseteq \bigcap \{\uparrow e_r:1{\le }_{o}r{\le }_{o}m\}\bigcap \bigcap \{\downarrow s_t:1{\le }_{o}t{\le }_{o}n\}=F^u\bigcap S^l$, which implies that $F^u\bigcap S^l\ne \varnothing$, ${(F^u\bigcap S^l)}^l\subseteq {\left[E_x\left(i_0\right)\right]}^l$ and ${(F^u\bigcap S^l)}^u\subseteq {\left[E_x\left(i_0\right)\right]}^u$. Thus, ${(F^u\bigcap S^l)}^l\subseteq P_x$ and ${(F^u\bigcap S^l)}^u\subseteq Q_x$.

By (i)–(iv), Definition 4 and Proposition 2, we conclude that the pair $(P_x,Q_x)=(K,L)$ is a nontrivial ID-pair in the poset P.

(⇒): Assume that the pair $(K,L)$ is a nontrivial ID-pair in the poset P. We take the following cases into consideration:

(v)

Either the set K or the set L is infinite.

Without loss of generality, we can assume that the set K is infinite. As the ID-pair $(K,L)$ is nontrivial, we have that $F^u\bigcap S^l\ne \varnothing$ for every $F⊑K$ and every $S⊑L$ by Proposition 2. Let ${\kappa }_F^S$ be the cardinal, linearly ordered by ${\ge }_F^S$, of the set $F^u\bigcap S^l$, and $a_F^S:{\kappa }_F^S\to F^u\bigcap S^l$ be a one-to-one function from ${\kappa }_F^S$ onto $F^u\bigcap S^l$ for every $F⊑K$ and every $S⊑L$. Put $I=\{(F,S,\lambda ):F⊑K,S⊑L,\lambda \in {\kappa }_F^S\}$. For any $(F_1,S_1,{\lambda }_1),(F_2,S_2,{\lambda }_2)\in I$, we define $(F_2,S_2,{\lambda }_2)\geqq (F_1,S_1,{\lambda }_1)$ if and only if one of the following conditions is satisfied:

(1)

$F_1=F_2$, $S_1=S_2$ and ${\lambda }_2{\ge }_{F_1}^{S_1}{\lambda }_1$;

(2)

$F_1\subset F_2$ and $S_1\subseteq S_2$.

Now, one can readily check that the ordered set I is up-directed. Let the net ${\left(x_i\right)}_{i\in I}$ in the poset P be defined by $x_{(F,S,\lambda )}=a_F^S\left(\lambda \right)$ for every $(F,S,\lambda )\in I$. Next, we proceed to prove that $P_x=K$ and $Q_x=L$. Let $p\in P_x$. Then, there exists $(F_1,S_1,{\lambda }_1)\in I$ such that $p\in {\left[E_x\left((F_1,S_1,{\lambda }_1)\right)\right]}^l$. Take $S_2=S_1$ and $F_2⊑K$ with $F_1\subset F_2$. Then, we have ${[{\left(F_2\right)}^u\bigcap {\left(S_2\right)}^l]}^l\subseteq K$ since the pair $(K,L)$ is a nontrivial ID-pair. According to the definition of I, it follows that $(F_2,S_2,{\lambda }_2)\geqq (F_1,S_1,{\lambda }_1)$ for every ${\lambda }_2\in {\kappa }_{F_2}^{S_2}$, which implies that $x_{(F_2,S_2,{\lambda }_2)}=a_{F_2}^{S_2}\left({\lambda }_2\right)\in E_x\left((F_1,S_1,{\lambda }_1)\right)$ for every ${\lambda }_2\in {\kappa }_{F_2}^{S_2}$. Hence, we conclude that ${\left(F_2\right)}^u\bigcap {\left(S_2\right)}^l\subseteq E_x\left((F_1,S_1,{\lambda }_1)\right)$. This shows that $p\in {\left[E_x\left((F_1,S_1,{\lambda }_1)\right)\right]}^l\subseteq {[{\left(F_2\right)}^u\bigcap {\left(S_2\right)}^l]}^l\subseteq K$. Thus, $P_x\subseteq K$. Conversely, let $q\in K$. Set $F_0=\left\{q\right\}⊑K$ and $S_0=\varnothing ⊑L$. Then, by the definition of I, it is easy to see that $(F_0,S_0,{\lambda }_0)\in I$ for all ${\lambda }_0\in {\kappa }_{F_0}^{S_0}$. For every $(F,S,\lambda )\in I$ with $(F,S,\lambda )\geqq (F_0,S_0,{\lambda }_0)$, by the definition of I, we have $F_0\subseteq F$ and $S_0\subseteq S$, which implies that $F^u\bigcap S^l\subseteq {\left(F_0\right)}^u\bigcap {\left(S_0\right)}^l=\uparrow q$. It follows that $x_{(F,S,\lambda )}=a_F^S\left(\lambda \right)\in F^u\bigcap S^l\subseteq \uparrow q$ for every $(F,S,\lambda )\geqq (F_0,S_0,{\lambda }_0)$. This means that $q\in P_x$. Hence, we conclude that $K\subseteq P_x$. This shows that $P_x=K$. It can be similarly proved that $Q_x=L$.

(vi)

Both the sets K and L are finite.

Since the pair $(K,L)$ is a nontrivial ID-pair in the poset P, it follows that $K^u\bigcap L^l\ne \varnothing$, ${(K^u\bigcap L^l)}^l\subseteq K$ and ${(K^u\bigcap L^l)}^u\subseteq L$. Let ${\kappa }_K^L$, well ordered by ${\ge }_K^L$, denote the cardinal of the set $K^u\bigcap L^l$, and $a_K^L:{\kappa }_K^L\to K^u\bigcap L^l$ be a one-to-one function from the cardinal ${\kappa }_K^L$ onto the set $K^u\bigcap L^l$. Set $I=\{(n,\lambda ):n\in \mathbb{N},\lambda \in {\kappa }_K^L\}$. For any $(n_1,{\lambda }_1),(n_2,{\lambda }_2)\in I$, we define $(n_2,{\lambda }_2)\geqq (n_1,{\lambda }_1)$ if and only if one of the following conditions is satisfied:

(3)

$n_1=n_2$ and ${\lambda }_2{\ge }_K^L{\lambda }_1$;

(4)

$n_1\ne n_2$ and $n_2{\ge }_o{n}_1$.

It can easily be checked that the ordered I is up-directed. Let ${\left(x_i\right)}_{i\in I}$ be the net in the poset P by defining $x_{(n,\lambda )}=a_K^L\left(\lambda \right)\in K^u\bigcap L^l$ for all $\lambda \in {\kappa }_K^L$. Now, it remains to show that $K=P_x$ and $L=Q_x$. Let $q\in K$. Then, we have $K^u\bigcap L^l\subseteq \uparrow q$. By the definition of the net ${\left(x_i\right)}_{i\in I}$, it follows that $x_{(n,\lambda )}=a_K^L\left(\lambda \right)\in K^u\bigcap L^l\subseteq \uparrow q$ for all $(n,\lambda )\in I$. This means that $q\in {\left[E_x\left((n,\lambda )\right)\right]}^l$ for all $(n,\lambda )\in I$. Hence, we conclude that $q\in P_x$, which shows that $K\subseteq P_x$. Conversely, let $p\in P_x$. Then, there exists $(n_0,{\lambda }_0)\in I$ such that $p\in {\left[E_x\left((n_0,{\lambda }_0)\right)\right]}^l$. Since $(n_0+1,\lambda )\geqq (n_0,{\lambda }_0)$, for all $\lambda \in {\kappa }_K^L$, it follows that $x_{(n_0+1,\lambda )}=a_K^L\left(\lambda \right)\in K^u\bigcap L^l$ for all $\lambda \in {\kappa }_K^L$. This implies that $K^u\bigcap L^l\subseteq E_x\left((n_0,{\lambda }_0)\right)$. Hence, we have $p\in {\left[E_x\left((n_0,{\lambda }_0)\right)\right]}^l\subseteq {(K^u\bigcap L^l)}^l\subseteq K$. This shows that $P_x\subseteq K$. Therefore, $P_x=K$. A similar verification can show that $Q_x=L$.

By (v) and (vi), we can conclude that there exists a net ${\left(x_i\right)}_{i\in I}$ in the poset P such that $P_x=K$ and $Q_x=L$. Thus, the proof is completed. □

Example 4.

Let $P=\{\top \}\bigcup \{a_1,a_2,\dots ,a_n,\dots \}$ with the partial order ≤ defined by

• $(\forall n)a_n⩽\top$.

Consider the net ${\left(x_n\right)}_{n\in \mathbb{N}}$ defined by

$$(\forall n\in \mathbb{N})x_n=a_n,$$

where the up-directed set $\mathbb{N}$ is the set of all positive integers in its usual order. By the definition of the net ${\left(x_n\right)}_{n\in \mathbb{N}}$, we have $P_x=\varnothing$ and $Q_x=\{\top \}$. On the other hand, it follows from Definition 4 and Definition 5 that the pair $(\varnothing ,\{\top \left\}\right)$ is a nontrivial ID-pair. This demonstrates Theorem 2 in the case.

The combination of Proposition 1 and Theorems 1 and 2 indicates that the eventually lower bounds $P_x$ and eventually upper bounds $Q_x$ of a net ${\left(x_i\right)}_{i\in I}$ are precisely a Frink ideal and a dual Frink ideal, respectively (see Corollary 1). However, they are not independent. Theorem 2 clarifies the correlation between the Frink ideal $P_x$ and the dual Frink ideal $Q_x$ from the point of view of order; that is, the Frink ideal $P_x$ and the dual Frink ideal $Q_x$ must be matched as a nontrivial ID-pair. Also, this is the initial motivation of introducing the local Frink ideal (the dually local Frink ideal) and ID-pair for posets in the sequel.

Corollary 1

([6]). Let P be a poset and $K,L\subseteq P$. Then,

(1)

The subset K is a Frink ideal if and only if $P_x=K$ for some net ${\left(x_i\right)}_{i\in I}$ in the poset P;

(2)

The subset L is a dual Frink ideal if and only if $Q_y=L$ for some net ${\left(y_j\right)}_{j\in J}$ in the poset P.

3. ID-Doubly Continuous Posets

Given a poset P and $M,N\subseteq P$, let ${\mathfrak{L}}_M\left(N\right)=\{K\in \mathfrak{L}\left(N\right):M\subseteq K\}$. Then, one can readily verify by Definition 4 that the intersection $\bigcap {\mathfrak{L}}_M\left(N\right)$ contains the set M and is again a local Frink ideal in the set N. This local Frink ideal is called the local Frink ideal generated by the set M and denoted by $I{G}_N\left(M\right)$. Thedually local Frink ideal generated by the set N is defined dually, and denoted by $D{G}_M\left(N\right)$. Next, we clarify the structure of $I{G}_N\left(M\right)$ and $D{G}_M\left(N\right)$:

Proposition 3.

Let P be a poset and $M,N\subseteq P$. Then,

(1)

$I{G}_N\left(M\right)=\{p\in P:(\exists M_0⊑M)(\exists N_0⊑N){\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l\subseteq \uparrow p\}$;

(2)

$D{G}_M\left(N\right)=\{q\in P:(\exists M_{00}⊑M)(\exists N_{00}⊑N){\left(M_{00}\right)}^u\bigcap {\left(N_{00}\right)}^l\subseteq \downarrow q\}$.

Proof. 

(1): Denote the set $\{p\in P:(\exists M_0⊑M)(\exists N_0⊑N){\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l\subseteq \uparrow p\}$ by ${\overline{M}}_N$. Then, it is easy to see that $M\subseteq {\overline{M}}_N$. Now, we proceed to prove that ${\overline{M}}_N\in \mathfrak{L}\left(N\right)$. Let $F⊑{\overline{M}}_N$ and $S⊑N$. We should consider the following cases:

(i)

$F=\varnothing$.

Since $F=\varnothing$, it follows that ${\left(M_a\right)}^u\bigcap S^l\subseteq F^u\bigcap S^l=S^l$ for all $M_a⊑M$, which implies that ${(F^u\bigcap S^l)}^l\subseteq {[{\left(M_a\right)}^u\bigcap S^l]}^l$ for all $M_a⊑M$. This means that ${\left(M_a\right)}^u\bigcap S^l\subseteq \uparrow p^{\prime }$ for all $p^{\prime }\in {(F^u\bigcap S^l)}^l$. Hence, we infer that ${(F^u\bigcap S^l)}^l\subseteq {\overline{M}}_L$.

(ii)

$F=\{e_1,e_2,\dots ,e_m\}\ne \varnothing$.

It follows by the definition of ${\overline{M}}_N$ that, for every $1{\le }_{o}r{\le }_{o}m$, there exist $M_r⊑M$ and $N_r⊑N$ such that ${\left(M_r\right)}^u\bigcap {\left(N_r\right)}^l\subseteq \uparrow e_r$. Take $M_F=\bigcup \{M_r:1{\le }_{o}r{\le }_{o}m\}$ and $N_F=\bigcup \{N_r:1{\le }_{o}r{\le }_{o}m\}\bigcup S$. Then, we have that $M_F⊑M$, $N_F⊑N$ and

$$\begin{array}{cc}\hfill {\left(M_F\right)}^u\bigcap {\left(N_F\right)}^l=& \bigcap \{{\left(M_r\right)}^u\bigcap {\left(N_r\right)}^l:1{\le }_{o}r{\le }_{o}m\}\bigcap S^l\hfill \\ \hfill \subseteq & \bigcap \{\uparrow e_r:1{\le }_{o}r{\le }_{o}m\}\bigcap S^l\hfill \\ \hfill =& F^u\bigcap S^l.\hfill \end{array}$$

This implies that ${(F^u\bigcap S^l)}^l\subseteq {[{\left(M_F\right)}^u\bigcap {\left(N_F\right)}^l]}^l$, which means that ${\left(M_F\right)}^u\bigcap {\left(N_F\right)}^l\subseteq \uparrow p^{\prime }$ for all $p^{\prime }\in {(F^u\bigcap S^l)}^l$. Thus, we conclude that ${(F^u\bigcap S^l)}^l\subseteq {\overline{M}}_N$ by the definition of ${\overline{M}}_N$.

According to (i), (ii) and Definition 4, we show that ${\overline{M}}_N\in \mathfrak{L}\left(N\right)$.

To complete the proof, it suffices to prove that ${\overline{M}}_N\subseteq K$ for every $K\in \mathfrak{L}\left(N\right)$ with $M\subseteq K$. Let $p\in {\overline{M}}_N$. Then, by the definition of ${\overline{M}}_N$, there exist $M_0⊑M$ and $N_0⊑N$ such that ${\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l\subseteq \uparrow p$. This means that $p\in {[{\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l]}^l$. Since $M\subseteq K$ and $K\in \mathfrak{L}\left(N\right)$, it follows that $p\in {[{\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l]}^l\subseteq K$. So, we have that ${\overline{M}}_N\subseteq K$. Consequently, we infer that $I{G}_N\left(M\right)={\overline{M}}_N=\{p\in P:(\exists M_0⊑M)(\exists N_0⊑N){\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l\subseteq \uparrow p\}$.

(2): The proof is similar to that of (1). □

Lemma 1.

Let P be a poset and $M,N\subseteq P$. Then, we have that $I{G}_N\left(M\right)\in \mathfrak{L}\left(D{G}_M\left(N\right)\right)$ and $D{G}_M\left(N\right)\in \mathfrak{D}\left(I{G}_N\left(M\right)\right)$, i.e., the pair $(I{G}_N\left(M\right),D{G}_M\left(N\right))$ is an ID-pair in the poset P.

Proof. 

We only show that $I{G}_N\left(M\right)\in \mathfrak{L}\left(D{G}_M\left(N\right)\right)$; the fact $D{G}_M\left(N\right)\in \mathfrak{D}\left(I{G}_N\left(M\right)\right)$ can be similarly proved. Let $F⊑I{G}_N\left(M\right)$ and $S⊑D{G}_M\left(N\right)$. We consider the following cases:

(i)

$F=\varnothing$ and $S=\varnothing$.

If the least element ⊥ exists in the poset P, then we have that $\perp \in I{G}_N\left(M\right)$ by Remark 1. It follows that ${(F^u\bigcap S^l)}^l=\{\perp \}\subseteq I{G}_N\left(M\right)$. If the poset P has no least element, then ${(F^u\bigcap S^l)}^l=\varnothing \subseteq I{G}_N\left(M\right)$ by Remark 1 again. This shows that ${(F^u\bigcap S^l)}^l\subseteq I{G}_N\left(M\right)$.

(ii)

$F=\{e_1,e_2,\dots ,e_m\}\ne \varnothing$ and $S=\varnothing$.

By Proposition 3, there exist $M_r⊑M$ and $N_r⊑N$ such that ${\left(M_r\right)}^u\bigcap {\left(N_r\right)}^l\subseteq \uparrow e_r$ for all $1{\le }_{o}r{\le }_{o}m$. Take $M_0=\bigcup \{M_r:1{\le }_{o}r{\le }_{o}m\}$ and $N_0=\bigcup \{N_r:1{\le }_{o}r{\le }_{o}m\}$. Then, we have that $M_0⊑M$, $N_0⊑N$ and

$$\begin{array}{cc}\hfill {\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l=& \bigcap \{{\left(M_r\right)}^u\bigcap {\left(N_r\right)}^l:1{\le }_{o}r{\le }_{o}m\}\hfill \\ \hfill \subseteq & \bigcap \{\uparrow e_r:1{\le }_{o}r{\le }_{o}m\}\hfill \\ \hfill =& F^u=F^u\bigcap S^l.\hfill \end{array}$$

It follows that ${(F^u\bigcap S^l)}^l\subseteq {[{\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l]}^l$, which implies that ${\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l\subseteq \uparrow p$ for all $p\in {(F^u\bigcap S^l)}^l$. Thus, by Proposition 3, we have that $p\in I{G}_N\left(M\right)$ for all $p\in {(F^u\bigcap S^l)}^l$. This means that ${(F^u\bigcap S^l)}^l\subseteq I{G}_N\left(M\right)$.

(iii)

$F=\varnothing$ and $S=\{s_1,s_2,\dots ,s_n\}\ne \varnothing$.

Proceeding as in the proof of (ii), we can again have ${(F^u\bigcap S^l)}^l\subseteq I{G}_N\left(M\right)$.

(iv)

$F=\{e_1,e_2,\dots ,e_m\}\ne \varnothing$ and $S=\{s_1,s_2,\dots ,s_n\}\ne \varnothing$.

By Proposition 3, there exist $M_r^F,M_t^S⊑M$ and $N_r^F,N_t^S⊑N$ such that ${\left(M_r^F\right)}^u\bigcap {\left(N_r^F\right)}^l\subseteq \uparrow e_r$ and ${\left(M_t^S\right)}^u\bigcap {\left(N_t^S\right)}^l\subseteq \downarrow s_t$ for all $1{\le }_{o}r{\le }_{o}m$ and $1{\le }_{o}t{\le }_{o}n$. Set $M_0=\bigcup \{M_r^F:1{\le }_{o}r{\le }_{o}m\}\bigcup \bigcup \{M_t^S:1{\le }_{o}t{\le }_{o}n\}$ and $N_0=\bigcup \{N_r^F:1{\le }_{o}r{\le }_{o}m\}\bigcup \bigcup \{N_t^S:1{\le }_{o}t{\le }_{o}n\}$. Then, we have that $M_0⊑M$, $N_0⊑N$ and

$$\begin{array}{cc}\hfill {\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l=& \bigcap \{{\left(M_r^F\right)}^u\bigcap {\left(N_r^F\right)}^l:1{\le }_{o}r{\le }_{o}m\}\hfill \\ \hfill & \bigcap \bigcap \{{\left(M_t^S\right)}^u\bigcap {\left(N_t^S\right)}^l:1{\le }_{o}t{\le }_{o}n\}\hfill \\ \hfill \subseteq & \bigcap \{\uparrow e_r:1{\le }_{o}r{\le }_{o}m\}\bigcap \bigcap \{\downarrow s_t:1{\le }_{o}t{\le }_{o}n\}\hfill \\ \hfill =& F^u\bigcap S^l.\hfill \end{array}$$

This implies that ${(F^u\bigcap S^l)}^l\subseteq {[{\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l]}^l$, which concludes that ${\left(M_0\right)}^u\bigcap {\left(N_0\right)}^l\subseteq \uparrow p$ for all $p\in {(F^u\bigcap S^l)}^l$. Hence, by Proposition 3, we have ${(F^u\bigcap S^l)}^l\subseteq I{G}_N\left(M\right)$.

According to (i)–(iv) and Definition 4, we infer that $I{G}_N\left(M\right)\in \mathfrak{L}\left(D{G}_M\left(N\right)\right)$. □

Lemma 2.

Let P be a poset and $M,N\subseteq P$. If $supM=x=infN\in P$, then we have $supI{G}_N\left(M\right)=x=infD{G}_M\left(N\right)$.

Proof. 

Let $supM=x=infN\in P$. Then, one can readily check, by Proposition 3, that $M\subseteq I{G}_N\left(M\right)\subseteq \downarrow x$ and $N\subseteq D{G}_M\left(N\right)\subseteq \uparrow x$. It follows that $supI{G}_N\left(M\right)=x=infD{G}_M\left(N\right)$. □

We turn to define the ID-double continuity for posets. Since the ID-double continuity has a close relationship to Property A, proposed by Wolk, we review Property A and its dual form for posets in the following:

Definition 6

([6]). A poset P has Property A if, for every non-normal Frink ideal K with $supK=x\in P$, there exists an up-directed subset $K_U\subseteq K$ such that $sup{K}_U=x$. Dually, a poset P has Property DAif, for every non-normal dual Frink ideal L with $infL=y\in P$, there exists a down-directed subset $L_D\subseteq L$ such that $inf{L}_D=y$.

Definition 7.

A poset P is called an ID-doubly continuous poset if, for every ID-pair $(K,L)$ in the poset P with $supK=x=infL\in P$, there exist an up-directed subset $K_U\subseteq K$ and a down-directed subset $L_D\subseteq L$ such that $sup{K}_U=x=inf{L}_D$.

Example 5. (1) Every finite poset is ID-doubly continuous;

(2) Every lattice is ID-doubly continuous.

Suppose that P is a finite poset and $(K,L)$ is an ID-pair with $supK=x=infL\in P$. Then, we have that $K,L⊑P$ and $K^u\bigcap L^l=\left\{x\right\}$. Since the pair $(K,L)$ is an ID-pair, by Definition 4 and Definition 5, it follows that ${(K^u\bigcap L^l)}^l=\downarrow x\subseteq K$ and ${(K^u\bigcap L^l)}^u=\uparrow x\subseteq L$, which implies that $x\in K$ and $x\in L$. This means that the singleton $\left\{x\right\}$ is an up-directed subset of K and also a down-directed subset of L such that $sup\left\{x\right\}=x=inf\left\{x\right\}$. So, by Definition 7, the finite poset P is ID-doubly continuous.

The fact that every lattice is ID-doubly continuous can also be readily checked by Definition 7.

Proposition 4.

Let P be a poset. If the poset P has Property A and Property DA, then it is an ID-doubly continuous poset.

Proof. 

Let $(K,L)$ be an ID-pair in the poset P with $supK=x=infL\in P$. Then, by Proposition 1, the set K is a Frink ideal. If $x\in K$, then we have that $\left\{x\right\}$ is an up-directed subset of K and $sup\left\{x\right\}=x$. If $x\notin K$, then K is a non-normal Frink ideal since $x\in {\left(K^u\right)}^l=\downarrow x\ne K$. By Property A, it follows that there exists an up-directed subset $K_U\subseteq K$ such that $sup{K}_U=x$. A similar verification can prove that there exists a down-directed subset $L_D\subseteq L$ such that $inf{L}_D=x$. Hence, the poset P is ID-doubly continuous. □

In general, an ID-doubly continuous poset may not possess Property A and Property DA. For such an example, one can refer to Example 7 in Section 4.

Now, we arrive at the main result:

Theorem 3.

A poset P is ID-doubly continuous if and only if the o-convergence and $o_2$-convergence in the poset P are equivalent.

Proof. 

(⇒): Suppose that a poset P is ID-doubly continuous. To prove the equivalence between the o-convergence and $o_2$-convergence, it suffices to show that, for every net ${\left(x_i\right)}_{i\in I}$ in the poset P, we have

$${\left(x_i\right)}_{i\in I}\stackrel{o_2}{\to }x\in P\Rightarrow {\left(x_i\right)}_{i\in I}\stackrel{o}{\to }x.$$

Let ${\left(x_i\right)}_{i\in I}\stackrel{o_2}{\to }x$. Then, by Definition 2, there exist subsets $M,N\subseteq P$ such that $supM=x=infN$, and, for every $m\in M$ and every $n\in N$, $m⩽x_i⩽n$ holds eventually. This means that $M\subseteq P_x$ and $N\subseteq Q_x$, which implies that $I{G}_N\left(M\right)\subseteq P_x$ and $D{G}_M\left(N\right)\subseteq Q_x$ by Remark 1 and Theorem 2. According to Lemma 1 and 2, it follows that $(I{G}_N\left(M\right),D{G}_M\left(N\right))$ is an ID-pair with $supI{G}_N\left(M\right)=x=infD{G}_M\left(N\right)$. Since the poset P is ID-doubly continuous, we have that $sup{M}_U=x=inf{N}_D$ for some up-directed subset $M_U\subseteq I{G}_N\left(M\right)\subseteq P_x$ and some down-directed subset $N_D\subseteq D{G}_M\left(N\right)\subseteq Q_x$. This concludes ${\left(x_i\right)}_{i\in I}\stackrel{o}{\to }x$.

(⇐): Assume that the o-convergence and $o_2$-convergence in a poset P are equivalent. Let $(K,L)$ be an ID-pair in the poset P with $supK=x=infL\in P$. Since $x\in F^u\bigcap S^l\ne \varnothing$ for all $F⊑K$ and $S⊑L$, the pair $(K,L)$ is a nontrivial ID-pair by Proposition 2. According to Theorem 2, there exists a net ${\left(x_i\right)}_{i\in I}$ in the poset P such that $K=P_x$ and $L=Q_x$. Thus, we have ${\left(x_i\right)}_{i\in I}\stackrel{o_2}{\to }x$. By the hypothesis, it follows that ${\left(x_i\right)}_{i\in I}\stackrel{o}{\to }x$. This means that $sup{K}_U=x=inf{L}_D$ for some up-directed subset $K_U\subseteq K=P_x$ and some down-directed subset $L_D\subseteq L=Q_x$. So, the poset P is an ID-doubly continuous poset. □

By Example 5 and Theorem 3, we immediately have the following:

Example 6. (1) In every finite poset, the o-convergence and the $o_2$-convergence are equivalent;

(2) In every lattice, the o-convergence and the $o_2$-convergence are equivalent.

By Proposition 4 and Theorem 3, or by Definition 2 and Theorem 2 and 5 in [6], we readily have the following:

Corollary 2.

If a poset P has Property A and Property DA, then the o-convergence and $o_2$-convergence in the poset P are equivalent.

4. Example

In this section, we mainly give an example to clarify the following facts:

(1)

A Frink ideal K of a poset P may not be a local Frink ideal in every nonempty subset L of P; Dually, a dual Frink ideal K need not be a dually local Frink ideal in every nonempty subset K of P.

(2)

An ID-doubly continuous poset fails to satisfy Property A and Property DA.

Example 7.

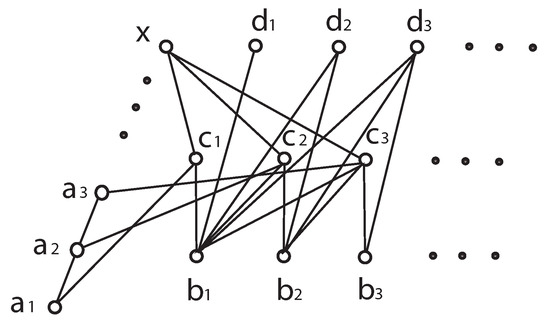
Let $P=\left\{x\right\}\bigcup \{a_1,a_2,\dots ,a_n,\dots \}\bigcup \{b_1,b_2,\dots ,b_n,\dots \}\bigcup \{c_1,c_2,\dots ,c_n,\dots \}$$\bigcup \{d_1,d_2,\dots ,d_n,\dots \}$ (see Figure 1). Define the partial order ≤ on P by setting

Figure 1. The diagram for the poset in Example 7.

• $\downarrow x=\left\{x\right\}\bigcup \{a_1,a_2,\dots ,a_n,\dots \}\bigcup \{b_1,b_2,\dots ,b_n,\dots \}\bigcup \{c_1,c_2,\dots ,c_n,\dots \}$;
• $(\forall n)\downarrow a_n=\{a_1,a_2,\dots ,a_n\}$;
• $(\forall n)\downarrow b_n=\left\{b_n\right\}$;
• $(\forall n)\downarrow c_n=\left\{c_n\right\}\bigcup \{a_1,a_2,\dots ,a_n\}\bigcup \{b_1,b_2,\dots ,b_n\}$;
• $(\forall n)\downarrow d_n=\left\{d_n\right\}\bigcup \{b_1,b_2,\dots ,b_n\}$.

Let $K=\{b_1,b_2,\dots ,b_n,\dots \}$. Then, the set K is a non-normal Frink ideal by Definition 3 and the definition of the poset P. However, the poset P does not process Property A since we can easily see that $supK=x$, and $sup{K}_U\ne x$ for every up-directed subset $K_U\subseteq K$. We next show that $K\notin \mathfrak{L}\left(L\right)$ for any nonempty subset L of the poset P by analyzing the following cases:

(i)

$a_i\in L$ (resp. $b_i\in L$, $c_i\in L$, $d_i\in L$) for some $i\in \mathbb{N}$.

Take $j\in \mathbb{N}$ such that $j{>}_{o}i$. Then, we have $\left\{b_j\right\}⊑K$, $\left\{a_i\right\}⊑L$ (resp. $\left\{b_i\right\}⊑L$, $\left\{c_i\right\}⊑L$, $\left\{d_i\right\}⊑L$) and ${({\left\{b_j\right\}}^u\bigcap {\left\{a_i\right\}}^l)}^l=P⊈K$ (resp. ${({\left\{b_j\right\}}^u\bigcap {\left\{b_i\right\}}^l)}^l=P⊈K$, ${({\left\{b_j\right\}}^u\bigcap {\left\{c_i\right\}}^l)}^l=P⊈K$, ${({\left\{b_j\right\}}^u\bigcap {\left\{d_i\right\}}^l)}^l=P⊈K$). This implies that $K\notin \mathfrak{L}\left(L\right)$ by Definition 4.

(ii)

$x\in L$.

It is easy to see that $\{b_1,b_2\}⊑K$, $\left\{x\right\}⊑L$ and ${({\{b_1,b_2\}}^u\bigcap {\left\{x\right\}}^l)}^l=\{a_1,a_2\}\bigcup \{b_1,b_2\}⊈K$. This implies that $K\notin \mathfrak{L}\left(L\right)$ by Definition 4.

The combination of (i) and (ii) shows that the set K is not a local Frink ideal in any nonempty subset L of the poset P.

Now, we are going to verify that P is an ID-doubly continuous poset. Let $(K^{\prime },L^{\prime })$ be an ID-pair in the poset P with $sup{K}^{\prime }=p=inf{L}^{\prime }$. We consider the following cases:

(iii)

$p=a_i$ (resp. $p=b_i,c_i,d_i$) for some $i\in \mathbb{N}$.

It is easy to see, by the definition of the poset P, that there exist $K_0⊑K^{\prime }$ and $L_0⊑L^{\prime }$ such that $sup{K}_0=inf{L}_0=p=a_i$. Since the pair $(K^{\prime },L^{\prime })$ is an ID-pair, we have ${[{\left(K_0\right)}^u\bigcap {\left(L_0\right)}^l]}^l=\downarrow a_i\subseteq K^{\prime }$ and ${[{\left(K_0\right)}^u\bigcap {\left(L_0\right)}^l]}^u=\uparrow a_i\subseteq L^{\prime }$, i.e., $a_i\in K^{\prime }$ and $a_i\in L^{\prime }$. Take $K_U^{\prime }=L_D^{\prime }=\left\{a_i\right\}$. Then, the set $K_U^{\prime }$ is an up-directed subset of the set $K^{\prime }$, the set $L_D^{\prime }$ is a down-directed subset of the set $L^{\prime }$ and $sup{K}_U^{\prime }=a_i=inf{L}_D^{\prime }$.

(iv)

$p=x$ and $x\in K^{\prime }$.

Since $inf{L}^{\prime }=x$, one can readily check that $L^{\prime }=\left\{x\right\}$. Take $K_U^{\prime }=L_D^{\prime }=\left\{x\right\}$. Then, we have that the set $K_U^{\prime }$ is an up-directed subset of the set $K^{\prime }$, the set $L_D^{\prime }$ is a down-directed subset of the set $L^{\prime }$ and $sup{K}_U^{\prime }=x=inf{L}_D^{\prime }$.

(v)

$p=x$ and $a_i\in K^{\prime }$ for some $i\in \mathbb{N}$.

Since $inf{L}^{\prime }=x$, it is easy to see that $L^{\prime }=\left\{x\right\}$. If the set $K^{\prime }\bigcap \{a_1,a_2,\dots \}$ is infinite, then we have that the set $K_U^{\prime }=K^{\prime }\bigcap \{a_1,a_2,\dots \}$ is an up-directed subset of the set $K^{\prime }$, the set $L_D^{\prime }=\left\{x\right\}$ is a down-directed subset of the set $L^{\prime }$ and $sup{K}_U^{\prime }=x=inf{L}_D^{\prime }$.

If the set $K^{\prime }\bigcap \{a_1,a_2,\dots \}$ is finite, then we have that the set $K^{\prime }\bigcap \{b_1,b_2,\dots \}$ is also finite. Otherwise, suppose that the set $K^{\prime }\bigcap \{b_1,b_2,\dots \}$ is infinite. Then, there exists $\{b_{i_1},b_{i_2},\dots \}\subseteq K^{\prime }$. Since the pair $(K^{\prime },L^{\prime })$ is an ID-pair in the poset P, we have that $a_{i_k}\in {({\{b_{i_1},b_{i_k}\}}^u\bigcap {\left\{x\right\}}^l)}^l$ for every $k\in \mathbb{N}$ with $k{\ge }_{o}2$. This means that $\{a_{i_2},a_{i_3},\dots \}\subseteq K^{\prime }\bigcap \{a_1,a_2,\dots \}$, contradicting the hypothesis that the set $K^{\prime }\bigcap \{a_1,a_2,\dots \}$ is finite. Let $\{a_{j_1},a_{j_2},\dots ,a_{j_m}\}=K^{\prime }\bigcap \{a_1,a_2,\dots \}$ and $\{b_{i_1},b_{i_2},{\dots }_{i_n}\}=K^{\prime }\bigcap \{b_1,b_2,\dots \}$, and let $j_0=max\{j_1,j_2,\dots ,j_m\}$ and $i_0=max\{i_1,i_2,\dots ,i_n\}$. Since $sup{K}^{\prime }=x$, we also take the following cases into consideration:

(v1)

$x\in K^{\prime }$.

In this case, we can return the verification to Case (iv).

(v2)

$c_{i^0}\in K^{\prime }$ for some $i^0\in \mathbb{N}$ with $i^0{<}_o{j}_0$.

In this case, if we take $K_0=\{a_{j_0},c_{i^0}\}$ and $L_0=\left\{x\right\}$, then we have $K_0⊑K^{\prime }$ and $L_0⊑L^{\prime }$ with $sup{K}_0=x=inf{L}_0$. By a similar verification to that of Case (iii), there exist an up-directed subset $K_U^{\prime }$ of the set $K^{\prime }$ and a down-directed subset $L_D^{\prime }$ of the set $L^{\prime }$ such that $sup{K}_U^{\prime }=x=inf{L}_D^{\prime }$.

(v3)

$c_{i^1}\in K^{\prime }$ for some $i^1\in \mathbb{N}$ with $i^1{<}_o{i}_0$.

In this case, if we take $K_0=\{b_{i_0},c_{i^1}\}$ and $L_0=\left\{x\right\}$, then we have $K_0⊑K^{\prime }$ and $L_0⊑L^{\prime }$ with $sup{K}_0=x=inf{L}_0$. By a similar verification to that of (iii), there exist an up-directed subset $K_U^{\prime }$ of the set $K^{\prime }$ and a down-directed subset $L_D^{\prime }$ of the set $L^{\prime }$ such that $sup{K}_U^{\prime }=x=inf{L}_D^{\prime }$.

(v4)

$c_{i^2},c_{i^3}\in K^{\prime }$ for some $i^2,i^3\in \mathbb{N}$.

In this case, if we take $K_0=\{c_{i^2},c_{i^3}\}$ and $L_0=\left\{x\right\}$, then we have $K_0⊑K^{\prime }$ and $L_0⊑L^{\prime }$ with $sup{K}_0=x=inf{L}_0$. By a similar verification to (iii), there exist an up-directed subset $K_U^{\prime }$ of the set $K^{\prime }$ and a down-directed subset $L_D^{\prime }$ of the set $L^{\prime }$ such that $sup{K}_U^{\prime }=x=inf{L}_D^{\prime }$.

(vi)

$p=x$ and $c_i\in K^{\prime }$ for some $i\in \mathbb{N}$.

Since the pair $(K^{\prime },L^{\prime })$ is an ID-pair, we have $a_i\in {({\left\{c_i\right\}}^u\bigcap {\left\{x\right\}}^l)}^l\subseteq K^{\prime }$. So, we can return the verification to Case (v).

(vii)

$p=x$ and $b_i\in K^{\prime }$ for some $i\in \mathbb{N}$.

We consider the following cases:

(vii1)     

$b_i,b_j\in K^{\prime }\bigcap \{b_1,b_2,\dots \}$ for some $i,j\in \mathbb{N}$.

Since the pair $(K^{\prime },L^{\prime })$ is an ID-pair, we have $a_i\in {({\{b_i,b_j\}}^u\bigcap {\left\{x\right\}}^l)}^l\subseteq K^{\prime }$. So, we can return the verification to Case (v).

(vii2)

$\left\{b_i\right\}=K^{\prime }\bigcap \{b_1,b_2,\dots \}$.

Since $sup{K}^{\prime }=x$, there exists $j\in \mathbb{N}$ such that $a_j\in K^{\prime }$ (resp. $c_j\in K^{\prime }$, $x\in K^{\prime }$). So, we can return the verification to Case (v) (resp. Case (vi), Case (iv)).

By Definition 7 and the combination of Cases (iii)–(vii), we conclude that the poset P is an ID-doubly continuous poset.

5. Discussion

This paper introduced the notion of ID-pairs in posets. It was shown that the set of all eventually lower bounds and the set of all eventually upper bounds of a net in a given poset can be precisely paired to be an ID-pair. This result provides a potential approach for dealing with the general nets in posets, since some kinds of order convergent nets, such as the o-convergent nets and $o_2$-convergent nets, are uniquely determined by their eventually lower bounds sets and eventually upper bounds sets.

Furthermore, in order to characterize these posets in which the o-convergence and $o_2$-convergence are equivalent, the concept of ID-doubly continuous posets is proposed. It is proved that the equivalence of the o-convergence and $o_2$-convergence in a poset is equivalent to the ID-double continuity of the poset. This result provides a sufficient and necessary condition for the o-convergence and $o_2$-convergence to be equivalent.

However, it may be complicated to verify the ID-double continuity for some posets, such as the poset in Example 7. On the contrary, the lattices, a special kind of poset, can be easily proved to be ID-double continuous. This indicates that the ID-double continuity has some close relationships with some special kinds of posets. These relationships deserve further investigation.