Maximum Packing of λ-Fold Complete 3-Uniform Hypergraph with a Special Tetrahedron

Abstract

Let $K_v^{(3)}=(V,E)$ be the complete 3-uniform hypergraph, where the vertex set is $V=\{x_1,x_2,\cdots ,x_v\}$, in which the edge set $E$ is of all triples. Let $ST$ denote the special tetrahedron with four edges, where each edge contains three vertices of degree 2. In this paper, we consider the decomposition and packing of a complete 3-uniform hypergraph of an $\lambda \text{-}$fold special tetrahedron. Firstly, the necessary conditions for the existence of the $\lambda \text{-}$fold $ST\text{-}$decomposition are discussed in four distinct cases. Secondly, according to the recursive constructions, the required designs of small orders are found. For hypergraphs with large orders, they can be recursively generated using some designs of small orders. Then, it is proven that the above necessary conditions are sufficient. Finally, we prove that a maximum $ST\text{-}$packing of a complete 3-uniform hypergraph $K_v^{(3)}$ exists for all $v\ge 6$ and $\lambda \ge 1$.

1. Introduction

As efficient relational representation structures, graphs have been widely used for modeling pairwise relations. However, non-paired relations are difficult to effectively express using general simple graph structures. The emergence of hypergraphs provides a natural advantage for the expression of such relationships.

A hypergraph is defined as an ordered binary group $(V,E)$, where $V$ is a finite set $V=\{x_1,x_2,x_3,\cdots ,x_v\}$, the elements in $V$ are called vertices, $E$ is a family of finite non-empty subsets of $V$, and the elements in $E$ are called hyperedges. If a hypergraph does not contain multiple hyperedges, that is, there are no repeated elements in its hyperedge $E$, the hypergraph is called a simple hypergraph.

For a hypergraph, if every hyperedge has exactly $t$ vertices, such a hypergraph is called $t\text{-}$uniform. A 2-uniform hypergraph is a graph. A $t\text{-}$uniform hypergraph is called a complete $t\text{-}$uniform hypergraph if its hyperedge contains every $t\text{-}$subset of vertices exactly once. When $\left|V\right|=v$, a completely $t\text{-}$uniform hypergraph is denoted as $K_v^{(t)}$, where $v$ is the order of the hypergraph. Therefore, a complete 3-uniform hypergraph $K_v^{(3)}$ is a hypergraph with a vertex set $V=\{x_1,x_2,x_3,\cdots ,x_v\}$, and its hyperedge set is 3-subsets of the vertex set $V$. Each 3-subset occurs only once; that is to say, a complete 3-uniform hypergraph has $\left(\begin{array}{c}v\\ 3\end{array}\right)$ hyperedges.

Let $\lambda$ be a positive integer and $H=K_v^{(t)}$ be a $t\text{-}$uniform hypergraph, that is, $\lambda H$ is a hypergraph derived from $H$, the vertices of which are those of $H$, and the edges of which contain every edge of $H$ exactly $\lambda$ times.

A commonly studied problem in combinatorics is the decomposition of hypergraphs into edge-disjoint sub-hypergraphs. Let $\lambda H$ be a $t\text{-}$uniform hypergraph and $\Gamma$ be a set of the $t\text{-}$uniform hypergraph. The $\Gamma \text{-}$decomposition of the hypergraph $\lambda H$ is its partitioning into sub-hypergraphs, each of which is isomorphic to a certain hypergraph of $\Gamma$, which is denoted by $(\lambda H,\Gamma )\text{-}$design or $S_{\lambda }(t,\Gamma ,H)$. If $\Gamma$ only contains one type of hypergraph $K$, it is denoted by $S_{\lambda }(t,K,H)$. When $\lambda =1$, $S(t,K,H)$ is replaced with $S_{\lambda }(t,K,H)$.

Keevash [1] recently showed that for all $t$ and $k$, the obvious necessary conditions for the existence of an $S(t,k,v)\text{-}$design are sufficient for sufficiently large values of $v$. Similar results were obtained by Glock, Kuhn, Lo, and Osthus [2,3], which included the corresponding asymptotic results for $H\text{-}$designs of order $v$ for all uniform hypergraphs $H$. These results for $t\text{-}$uniform hypergraphs mirror the celebrated results of Wilson [4] for graphs. For $t=3$, Feng Tao and Chang Yanxun [5] summed up the necessary conditions for the existence of $S(3,\Gamma ,v)$.

Let $s (\le \mathrm{v})$ be a non-negative integer. A $(K_v^{(t)}\backslash K_s^{(t)},\Gamma )\text{-}$design is an ordered triple $(X,Y,\mathcal{B})$, where $X$ is the set of vertices of $K_v^{(t)}\backslash K_s^{(t)}$, $Y$ is the set of vertices of $K_s^{(t)}$, $Y$ is called a hole, and $\mathcal{B}$ is the set sub-hypergraphs of $K_v^{(t)}\backslash K_s^{(t)}$, where each sub-hypergraph is isomorphic to a hypergraph in $\Gamma$, each sub-hypergraph is called a block, and every edge of $K_v^{(t)}\backslash K_s^{(t)}$ is required to be contained in a block of $\mathcal{B}$. Such a design is denoted as $HS(t,\Gamma ;v,s)$.

Let $n$ and $t$ be positive integers. Let $X$ be a set of vertices and $\mathcal{B}$ be a family of hypergraphs whose vertices are defined on some subsets of $X$. Then, every hypergraph in $\mathcal{B}$ is isomorphic to a hypergraph in $\Gamma$. Every hypergraph in $\mathcal{B}$ is called a block. Let $\mathcal{G}$ be a partition of $X$, where $X$ is divided into $n$ non-empty subsets. Each non-empty subset is called a group. For an ordered triple $(X,\mathcal{G},\mathcal{B})$, if each edge in the edge set of each block intersects any given group by one point at most, and, for any $t\text{-}$subset $T$ of $X$, if the $t$ points in $T$ are from $t$ different groups, then $T$ is contained in exactly one block. Such a design is called a group-divisible $(\Gamma ,t)\text{-}$design.

We use the usual exponential notation for the group-divisible $(\Gamma ,t)\text{-}$designs. Then, type $g_1^{a_1}{g}_2^{a_2}\cdots g_m^{a_m}$ denotes that there are $a_i$ groups of size $g_i$, $1\le i\le m$. A group-divisible $(\Gamma ,t)\text{-}$design of type $g_1^{a_1}{g}_2^{a_2}\cdots g_m^{a_m}$ can be denoted by $\mathrm{GDD}(t,\Gamma ,v)$, where the vertex set is $v=a_1{g}_1+a_2{g}_2+\cdots +a_m{g}_m$. If $\Gamma$ contains only one hypergraph $J$, we write $\mathrm{GDD}(t,\{J\},v)$ as $\mathrm{GDD}(t,J,v)$.

Let $H$ be a complete $t\text{-}$uniform hypergraph, $H=K_v^{(t)}$. Then, $(\lambda H,\Gamma )\text{-}$packing is a binary $(X,\mathcal{B})$, where $X$ is the finite vertex set of $\lambda H$, and $\mathcal{B}$ is the set of some sub-hypergraphs of $\lambda H$, where each hypergraph of $\mathcal{B}$ is isomorphic to a hypergraph in $\Gamma$, called a block, and each edge of $H$ is contained in, at most, one block of $\mathcal{B}$. In this case, an $(\lambda H,\Gamma )\text{-}$packing design can be denoted by $P_{\lambda }(t,\Gamma ,v)$. When there is no packing $(X,\mathcal{A})$ such that the number of blocks in $\mathcal{B}$ and the number of blocks in $\mathcal{A}$ satisfy condition $\left|\mathcal{B}\right|<\left|\mathcal{A}\right|$, then packing $(X,\mathcal{B})$ is called the maximum packing, denoted by $M{P}_{\lambda }(t,\Gamma ,v)$. When $\lambda =1$, $MP(t,\Gamma ,v)$ is replaced with $M{P}_{\lambda }(t,\Gamma ,v)$. The same applies to hypergraph decomposition; when considering the packing design of hypergraphs, we mainly focus on the number of blocks.

For any $t\text{-}$subset $e=\{v_1,v_2,\cdots ,v_t\}$ of $X$, let $I$ be the number of blocks containing $e$. The leave of a packing $P_{\lambda }(t,\Gamma ,v)$ is the $t\text{-}$uniform hypergraph spanned by all $t\text{-}$subsets $e$ of $X$ with multiplicity $\lambda$ $-I$.

To enhance the understanding of hypergraph maximum packing, we give the following examples. First, in this paper, the symbol $ST$ always denotes a hypergraph with vertices $\{a,b,c,d,e,f\}$ and edges $\{(a,c,e),(b,c,e),(a,d,f),(b,d,f)\}$, and such a hypergraph can be denoted as an ordered hextuple $(a,b,c,d,e,f)$.

Example 1.

In this example, we first construct an $MP(3,ST,7)$ on the point set  $\{0,1,2,3,4,5,6\}$. Its  $⌊\left(\begin{array}{c}7\\ 3\end{array}\right)/6⌋=8$ blocks, listed as follows:

$$\begin{gathered} (0,3,5,2,6,4),(0,6,1,4,2,5),(5,6,0,3,1,4),(1,2,0,4,3,6),(5,6,0,1,2,3) \\ (4,5,1,0,2,3),(3,5,2,4,6,1),(3,4,2,0,5,6) \end{gathered}$$

It can be verified that the leave of the above packing contains three edges, $\{1,2,3\}$, $\{1,0,4\}$, and $\{1,5,6\}$. Then, the above blocks form a maximum packing of $ST$.

In the theory of combinatorial mathematics, the study of graphs has been greatly improved. At present, many studies focus on the related problems of complete 3-uniform hypergraphs. Several authors have obtained many results on the $\Gamma \text{-}$decomposition, packing, and covering problems of 3-uniform hypergraphs, where $\Gamma$ is $K_4^{(3)}-e$, $W_4^{(3)}$ and $K_4^{(3)}+e$ [5,6,7,8,9,10]. In 1987, Zbigniew LONC [11] defined the hyperstar, which is a 3-uniform hypergraph consisting of one vertex of degree $m$ and $2m$ vertices of degree one, and it is denoted by $S_m^{(3)}$. Necessary and sufficient conditions for the existence of $S_m^{(3)}\text{-}$decompositions of $K_v^{(3)}$ are given in [12] for $m\in \{4,5,6\}$ and settled in [13] for any $m$. Some results on maximum $S_m^{(3)}\text{-}$packings of $K_v^{(3)}$ are given in [14]. In 2014, Hoffman solved the packing and covering problems of any $k\text{-}$star [15]. Amber Armstrong [16] found the maximum packings of $\lambda K_v^{(3)}$ with copies of the symmetric triple-hyperstar with four edges. Ryan C. Bunge [17] resolved the problem of a maximum loose 3-cycle packing of a λ-fold complete 3-uniform hypergraph of order $v$. The corresponding problems of tight six-cycle and tight nine-cycle decompositions of $K_v^{(3)}$ were resolved in [18,19].

Here, we are interested in the maximum $ST\text{-}$packings of $\lambda K_v^{(3)}$, where $ST$ is a 3-uniform special tetrahedron with four edges [20]. The special tetrahedron is a hypergraph with a vertex set of $(a,b,c,d,e,f)$, and its hyperedge set contains $\{(a,c,e),(b,c,e),(a,d,f),$$(b,d,f)\}$, as shown in Figure 1. The three vertices contained in each hyperedge appear twice, that is, vertex $a$ is contained in both the hyperedge $(a,c,e)$ and the hyperedge $(a,d,f)$, so we call vertex “$a$” a vertex of degree 2. Thus, each hyperedge of special tetrahedron contains three vertices of degree 2.

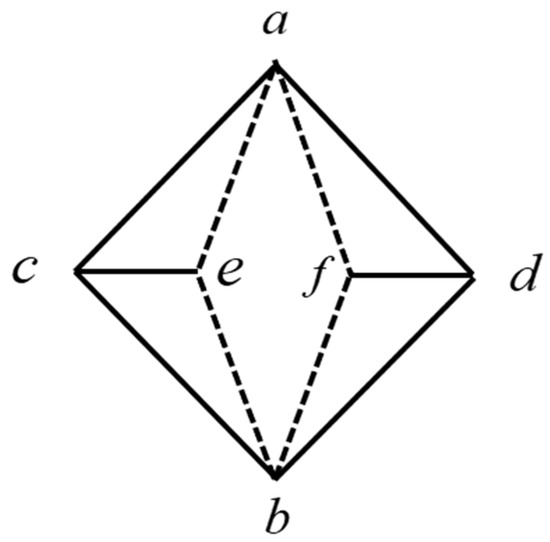
Figure 1. The special tetrahedron (ST) of size 4, denoted as $\left(a,b,c,d,e,f\right)$.

In this paper, we prove that for all $v\ge 6$, $\lambda \ge 1$, a maximum $ST\text{-}$packing of $\lambda K_v^{(3)}$ exists, where the leave has fewer than four edges. The rest of this paper is outlined as follows. Section 2 presents some related preliminaries, including notations, notions, and the method of analysis. In Section 3, we provide some small-order designs that are used to help prove the main conclusions of this paper. Other designs are listed in Appendix A. In Section 4, we prove the main results. We first show the decompositions and packings of simple hypergraphs. Based on the simple hypergraphs, we consider the $ST$ decomposition of $\lambda K_v^{(3)}$ and its maximum packing of $ST$. In Section 5, we provide the conclusions of this work. In Section 6, we discuss the practical implications of the findings, especially their application in neural networks.

2. Preliminaries

2.1. Additional Notations and Terminology

Let $V=V_1\cup V_2\cup V_3$. The complete tripartite 3-uniform hypergraph $H$ consists of the vertex set $V$ and the hyperedge set $E$, where $V=V_1\cup V_2\cup V_3$, $V_i\cap V_j=\varnothing$, and $E=\left\{e\right|e\subseteq V,\left|e\right|=3,e\cap V_i\ne \varnothing \}$ for $1\le i<j\le 3$. The hypergraph is denoted by $K_{v_1,v_2,v_3}^{(3)}$. Currently, this partition of $V$ is denoted by $GDD(3,ST,v)$, where $v=v_1+v_2+v_3$.

Let $V=V_1\cup V_2$. The complete bipartite 3-uniform hypergraph $H$ consists of the vertex set $V$ and the hyperedge set $E$, where $V=V_1\cup V_2$, $V_1\cap V_2=\varnothing$, and $E=\left\{e\right|e\subseteq V,\left|e\right|=3,e\cap V_i\ne \varnothing \}$ for $i=1,2$. The hypergraph is denoted by $L_{v_1,v_2}^{(3)}$. Currently, this partition of $V$ is denoted by $S(3,ST,v_1,v_2)$.

For the complete 3-uniform hypergraph $K_v^{(3)}$, the $\lambda$-fold maximum packing of the special tetrahedron is denoted by $M{P}_{\lambda }(3,ST,v)$, and the $\lambda$-fold decomposition of the special tetrahedron is denoted by $S_{\lambda }(3,ST,v)$. When $\lambda =1$, $M{P}_{\lambda }(3,ST,v)$ is denoted by $MP(3,ST,v)$, and $S_{\lambda }(3,ST,v)$ is denoted by $S(3,ST,v)$.

2.2. Method of Analysis

Theorem 1.

Let $a$, $r$, and $l$ be non-negative integers. Let $v=ar+l$ and $v\ge 3$. Under the given conditions, a partition of $K_{ar+l}^{(3)}$ exists, as shown as Figure 2, which comprises isomorphic copies of each of the following:

Figure 2. The partition of $K_{ar+l}^{(3)}$.

• $K_l^{(3)}$ if $r=0$;
• $K_{a+l}^{(3)}$ if $r=1$;
• $K_l^{(3)}$, $K_{a+l}^{(3)}$, $K_{a+l}^{(3)}\backslash K_l^{(3)}$, $K_{l,a,a}^{(3)}\cup L_{a,a}^{(3)}$ if $r=2$;
• $K_l^{(3)}$, $K_{a+l}^{(3)}$, $K_{a+l}^{(3)}\backslash K_l^{(3)}$, $K_{l,a,a}^{(3)}\cup L_{a,a}^{(3)}$, $K_{a,a,a}^{(3)}$ if $r\ge 3$.

Proof of Theorem 1.

When $a=0$ and $l\ge 3$, then $K_l^{(3)}=K_{a+l}^{(3)}=K_{ar+l}^{(3)}$, and $K_{a+l}^{(3)}\backslash K_l^{(3)}$, $K_{l,a,a}^{(3)}\cup L_{a,a}^{(3)}$, and $K_{a,a,a}^{(3)}$ are empty (i.e., without any edges), and the decomposition is trivial. Let $A_0$, $A_1$, $A_2$, $\cdots$, and $A_r$ be pairwise-disjoint sets of vertices with $\left|A_0\right|=l$, $\left|A_1\right|=\left|A_2\right|=\cdots =\left|A_r\right|=a$. Then, the above theorem has five cases:

• Case 1: When $r=0$, $a\ge 1$, $K_{ar+l}^{(3)}=K_l^{(3)}$, the partition of $K_{ar+l}^{(3)}$ is $K_l^{(3)}$with the vertex set $A_0$, and the decomposition is trivial.
• Case 2: When $r=1$, $a\ge 1$, $K_{ar+l}^{(3)}=K_{a+l}^{(3)}$. Let $V=A_0\cup A_1$, where the partition of $K_{ar+l}^{(3)}$ is $K_{a+l}^{(3)}$ with the vertex set $A_0\cup A_1$, and the decomposition is trivial.
• Case 3: When $r=2$, $a\ge 1$, $K_{ar+l}^{(3)}=K_{2a+l}^{(3)}$. Let $V=A_0\cup A_1\cup A_2$, where the partitions of $K_{ar+l}^{(3)}$ are two $K_{a+l}^{(3)}$ with each vertex set $A_0\cup A_1$, two $K_{a+l}^{(3)}\backslash K_l^{(3)}$ with each vertex set $A_1\cup A_0$ and the hole set $A_0$, one $L_{a,a}^{(3)}$ with the vertex set $A_1\cup A_2$, and one $K_{l,a,a}^{(3)}$ with the vertex set $A_0\cup A_1\cup A_2$.
• Case 4: When $r=3$, $a\ge 1$, $K_{ar+l}^{(3)}=K_{3a+l}^{(3)}$. Let $V=A_0\cup A_1\cup A_2\cup A_3$, where the partitions of $K_{ar+l}^{(3)}$ are three $K_{a+l}^{(3)}$ with each vertex set $A_0\cup A_1$, three $K_{a+l}^{(3)}\backslash K_l^{(3)}$ with each vertex set $A_1\cup A_0$ and the hole set $A_0$, three $L_{a,a}^{(3)}$ with each vertex set $A_1\cup A_2$, three $K_{l,a,a}^{(3)}$ with each vertex set $A_0\cup A_1\cup A_2$, and one $K_{a,a,a}^{(3)}$ with the vertex set $A_1\cup A_2\cup A_3$.
• Case 5: When $r\ge 3$, $a\ge 1$, $K_{ar+l}^{(3)}=K_{3a+l}^{(3)}$. Let $V=A_0\cup A_1\cup A_2\cup \cdots \cup A_r$, where the partition of $K_{ar+l}^{(3)}$ is $\left(\begin{array}{c}r\\ 1\end{array}\right)$  $K_{a+l}^{(3)}$ with each vertex set $A_0\cup A_1$, $\left(\begin{array}{c}r\\ 1\end{array}\right)$  $K_{a+l}^{(3)}\backslash K_l^{(3)}$ with each vertex set $A_1\cup A_0$ and the hole set $A_0$, $\left(\begin{array}{c}r\\ 2\end{array}\right)$  $L_{a,a}^{(3)}$ with each vertex set $A_1\cup A_2$, $\left(\begin{array}{c}r\\ 2\end{array}\right)$  $K_{l,a,a}^{(3)}$ with each vertex set $A_0\cup A_1\cup A_2$, and $\left(\begin{array}{c}r\\ 3\end{array}\right)$  $K_{a,a,a}^{(3)}$ with the vertex set $A_1\cup A_2\cup A_3.$

According to Theorem 1, as long as $v=ar+l$ and $r\ge 1$, the hypergraph $K_v^{(3)}$ can be decomposed to the union of the following subgraphs: $K_l^{(3)}$, $K_{a+l}^{(3)}$, $K_{a+l}^{(3)}\backslash K_l^{(3)}$, $K_{l,a,a}^{(3)}\cup L_{a,a}^{(3)}$, and $K_{a,a,a}^{(3)}$.

Combined with the number of hyperedges of $ST$ and the characteristics of $ST$, we have $4|\left(\begin{array}{c}v\\ 3\end{array}\right)$ and $2|\left(\begin{array}{c}v-1\\ 2\end{array}\right)$. When the order $v$ of $K_v^{(3)}$ satisfies the above conditions, the decomposition of hypergraph $K_v^{(3)}$ exists. At this point, in order to obtain the decomposition of the hypergraph $K_v^{(3)}$, $v=ar+l$, we need to find the following design: $S(3,TS,a+l)$, $S(3,TS,a,a)$, $HS(3,TS;8+l,l)$, and $GDD(3,ST,2a+l)$ of type $a^2{l}^1$ and $GDD(3,ST,24)$ of type $8^3$.

If the order $v$ of $K_v^{(3)}$ does not satisfy the above conditions, for these hypergraphs $K_v^{(3)}$, their packing design is considered. To obtain the maximum packing of the hypergraph $K_v^{(3)}$, we need to consider the following design: $MP(3,TS,a+l)$, $S(3,TS,a,a)$, $HS(3,TS;8+l,l)$, and $GDD(3,ST,2a+l)$ of type $a^2{l}^1$ and $GDD(3,ST,24)$ of type $8^3$.

Moreover, we can know that the $\Gamma \text{-}$decomposition of the hypergraph is the maximum $\Gamma \text{-}$packing without a leave. □

3. Some Small Orders

Next, we provide some small-order designs of $ST\text{-}$packing, the decomposition design of which is the special packing design without a leave. The designs in the following and in Appendix A were constructed directly and are used to prove the main conclusions of this paper.

Example 1.

$S(3,ST,4,4)$ exists.

Proof of Example 1.

Let $X=\{0,2,4,6\}\cup \{1,3,5,7\}$. All blocks consist of the base block $(1,7,0,4,2,6)$ under the action of +1 modulo 8 and the base block $(5,1,0,2,4,6)$ under the action of $j\to j+i$, where $i=1,2,3,4$. □

Example 2.

$GDD(3,ST,12)$ of type  $4^3$ exists.

Proof of Example 2.

Let $X=\{0,2,4,6\}\cup \{1,3,5,7\}\cup \{{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4\}$. The base blocks for this design are given below. All other blocks can be obtained using the following base blocks of +1 modulo 8, where ${\infty }_i+1={\infty }_i$. $({\infty }_1,{\infty }_2,3,2,6,1)$, $({\infty }_3,{\infty }_4,4,0,3,5)$. □

Example 3.

$MP(3,ST,v)$ exists, where $v=7$.

Proof of Example 3.

Let $X=\{0,1,2,3,4,5,6\}$. The base blocks for this design are given below. The maximum packing of $K_7^{(3)}$ consists of the following base blocks, and the leave consists of the edge $\{1,2,3\}$, $\{1,0,4\}$, and $\{1,5,6\}.$

$$\begin{gathered} (0,3,5,2,6,4), (0,6,1,4,2,5), (5,6,0,3,1,4),(1,2,0,4,3,6),(5,6,0,1,2,3), \\ (4,5,1,0,2,3), (3,5,2,4,6,1), \mathrm{and} (3,4,2,0,5,6). \end{gathered}$$

Meanwhile, another $MP(3,ST,7)$ exists. Let $X=\{0,1,2,3,4,5,6\}$. The base blocks for this design are given below. The maximum packing of $K_7^{(3)}$ consists of the following base blocks and the leave consists of the edge $\{1,2,6\}$, $\{5,6,3\}$, and $\{3,0,4\}$. $(1,4,2,5,0,6)$, $(1,2,0,4,3,6)$, $(5,6,0,1,2,3)$, $(3,5,2,4,6,1)$, $(5,6,0,3,1,4)$, $(5,4,2,0,1,6)$, $(1,5,2,0,3,4)$, and $(3,5,2,0,4,6).$ □

Example 4.

$MP(3,ST,v)$ exists, where  $v=8$.

Proof of Example 4.

Let $X=\{0,1,2,3,4,5,6,7\}$. The base blocks for this design are given below. The maximum packing of $K_8^{(3)}$ consists of the following base blocks, and the leave $H$ consists of the edge $\{2,3,7\}$, $\{2,4,5\}$, $\{7,2,6\}$, and $\{7,0,1\}$.

$$\begin{gathered} (0,7,1,3,2,6), (0,5,1,7,3,2), (6,1,0,2,4,3), (0,4,5,2,1,6), (7,0,1,5,6,4), \\ (2,3,0,6,4,1),(2,3,5,1,0,4), (2,6,1,4,5,7), (4,5,2,7,3,0), (2,7,0,6,3,5), \\ (5,7,3,0,4,6), (3,1,4,7,6,5), \mathrm{and} (3,4,1,6,7,5). \end{gathered}$$

Meanwhile, another $MP(3,ST,8)$ exists, where $v=8$. Let $X=\{0,1,2,3,4,5,6,7\}$. The base blocks for this design are given below. The maximum packing of $K_7^{(3)}$ consists of the following base blocks, and the leave consists of the edge $\{6,7,3\}$, $\{6,0,1\}$, $\{3,2,6\}$, and $\{4,5,3\}.$

$$\begin{gathered} (4,3,5,7,6,2), (4,1,5,3,7,6), (2,5,4,6,0,7), (0,4,5,2,1,6), (3,4,5,1,2,0), \\ (6,7,4,2,0,5),(6,7,1,5,4,0), (2,6,5,0,1,3), (0,1,6,3,7,4), (6,3,4,2,7,1), \\ (7,5,0,3,2,1), (7,0,5,2,3,1), \mathrm{and} (3,1,7,4,0,2). \end{gathered}$$

□

Example 5.

$S(3,ST,11)$ of type  $4^2{3}^1$ exists.

Proof of Example 5.

Let $X=\{0,2,4,6\}\cup \{1,3,5,7\}\cup \{{\infty }_1,{\infty }_2,{\infty }_3\}$. The base blocks for this design are given below. All other blocks can be obtained using the following base blocks of +1 modulo 8, where ${\infty }_i+1={\infty }_i.$

$$({\infty }_1,3,4,2,7,1), ({\infty }_2,{\infty }_3,4,0,7,1), \mathrm{and} (5,7,0,6,2,3).$$

□

4. Main Results

4.1. Decompositions and Packings of Simple Hypergraphs

There are no repeated elements in the hyperedge set of the hypergraph of 1-fold $ST$, so it is a simple hypergraph. In this section, we consider the 1-fold $ST$ decomposition and packing of complete 3-uniform hypergraphs $K_v^{(3)}$.

Theorem 2

([20]). $S(3,ST,v)$ exists if, and only if,  $v=1,2,6 (\mathrm{mod} 8)$.

Proof of Theorem 2.

We can easily know that the necessary conditions for the existence of $S(3,ST,v)$ are $v=1,2,6 (\mathrm{mod} 8)$. Therefore, we need to prove its sufficiency. Let $v=8r+l$, where $r\ge 1$ and $l\in \{1,2,6\}$. According to Theorem 1, it suffices to find the $ST\text{-}$decompositions of $K_{8+l}^{(3)}$, $K_{8+l}^{(3)}\backslash K_l^{(3)}$, $K_{l,8,8}^{(3)}\cup L_{8,8}^{(3)}$, and $K_{8,8,8}^{(3)}$, that is, $S(3,ST,8+l)$, $HS(3,ST;8+l,l)$, and $GDD(3,ST,16+l)$ of type $8^2{l}^1$ and $GDD(3,ST,24)$ of type $8^3$. According to Examples A1–A9 and A12, we know that $S(3,ST,v)$ exists. □

Theorem 3.

If $v\ge 6$ is an integer, then an $MP(3,ST,v)$ of $K_v^{(3)}$ exists, where the leave has fewer than four edges.

Proof of Theorem 3.

According to Theorem 2, when $v=1,2,6 (\mathrm{mod} 8)$, the $ST\text{-}$decomposition of $K_v^{(3)}$ is the maximum $ST\text{-}$packing, where the leave is empty. Hence, we need to only consider the maximum $ST\text{-}$packing when $v=0,3 (\mathrm{mod} 4)$, $v\ge 7$, and $v=5 (\mathrm{mod} 8)$.

Let $v=4r$, where $v\ge 7$. According to Theorem 1, we only need to consider the maximum $ST\text{-}$packing of $K_8^{(3)}$, where a leave has four edges, and the $ST\text{-}$decompositions of $L_{4,4}^{(3)}$ and $K_{4,4,4}^{(3)}$, that is, $MP(3,ST,8)$, $S(3,ST,4,4)$, and $GDD(3,ST,12)$ of type $4^3$. According to Examples 1, 2, and 4, $MP(3,ST,8)$, $S(3,ST,4,4)$, and $GDD(3,ST,12)$ of type $4^3$ exist.

Let $v=4r+3$, where $r\ge 1$. According to Theorem 1, we only need to consider the maximum $ST\text{-}$packing of $K_7^{(3)}$ where a leave has three edges, and the $ST\text{-}$decompositions of $K_{4,4,4}^{(3)}$ and $K_{3,4,4}^{(3)}\cup L_{4,4}^{(3)}$, that is, $MP(3,ST,7)$, $S(3,ST,4,4)$, and $GDD(3,ST,11)$ of type $4^2{3}^1$ and $GDD(3,ST,12)$ of type $4^3$. According to Examples 1, 2, 3, and 5, $MP(3,ST,7)$, $S(3,ST,4,4)$, and $GDD(3,ST,11)$ of type $4^2{3}^1$ and $GDD(3,ST,12)$ of type $4^3$ exist.

Let $v=8r+5$ where $r\ge 1$. According to Theorem 1, we only need to consider the maximum $ST\text{-}$packing of $K_{13}^{(3)}$, where a leave has two edges and the $ST\text{-}$decompositions of $K_{13}^{(3)}\backslash K_5^{(3)}$, $K_{5,8,8}^{(3)}\cup L_{8,8}^{(3)}$, and $K_{8,8,8}^{(3)}$, that is, $MP(3,ST,13)$, $HS(3,ST;13,5)$, $S(3,ST,8,8)$, and $GDD(3,ST,21)$ of type $8^2{5}^1$ and $GDD(3,ST,24)$ of type $8^3$. According to Examples A5, A9, A10, A11, and A14 in Appendix A, the above construction exists. Thus, for $v\ge 6$, $MP(3,ST,v)$ of $K_v^{(3)}$ exists, where the leave has fewer than four edges. □

4.2. Decompositions of $\lambda \text{-}$Fold Hypergraphs

The leave of the maximum packing of a complete 3-uniform hypergraph is related to the decomposition of the $\lambda$-fold complete 3-uniform hypergraph. Without the loss of generality, let $a,b,c,d,e,f\in \{V(K_v^3)\}$, where both a maximum $ST\text{-}$packing, say ${\mathcal{C}}_{\mathbf{1}}$, with a leave consisting of two edges $\{(a,c,e),(b,c,e)\}$ and a maximum $ST\text{-}$packing, say ${\mathcal{C}}_2$, with a leave consisting of two vertex-disjoint edges $\{(a,d,f),(b,d,f)\}$ exist [17]. Hence,

$$({\mathcal{C}}_{\mathbf{1}}\backslash E(H_1))\cup ({\mathcal{C}}_{\mathbf{2}}\backslash E(H_2))\cup \{E(H_1)\cup E(H_2)\}$$

is the decomposition of a 2-fold complete 3-uniform hypergraph.

Theorem 4.

Let $v\ge 6$ be an integer. The necessary conditions for the existence of $S_{\lambda }(3,ST,v)$ are as follows:

• If $\lambda =1,3(\mathrm{mod}4)$, then $v=1,2,6(\mathrm{mod}8)$;
• If $\lambda =2(\mathrm{mod}4)$, then $v=0,1,2(\mathrm{mod}4)$;
• If $\lambda =0(\mathrm{mod}4)$, then $v\ge 6$.

Proof of Theorem 4.

Because $|E(ST)|=4$ and $\gcd \{d(x):x\in V(ST)\}=2$, we must have $4|\lambda \left(\begin{array}{c}v\\ 3\end{array}\right)=4|(\lambda v(v-1)(v-2)/6)$ and $2|\lambda \left(\begin{array}{c}v-1\\ 2\end{array}\right)=2|(\lambda v(v-1)(v-2)/2)$, that is, $24|\lambda v(v-1)(v-2)$ and $4|\lambda (v-1)(v-2)$. Because of $3|v(v-1)(v-2)$, for $\lambda$ and $v$, $8|\lambda v(v-1)(v-2)$ and $4|\lambda (v-1)(v-2)$ exist. $\lambda$ denotes that the hyperedge set of a hypergraph $\lambda H$ is repeated $\lambda$ times by the hyperedge set of a hypergraph $H$. Because $|E(ST)|=4$, for the necessary conditions for the existence of $S_{\lambda }(3,ST,v)$, the following four cases exist:

• Case 1: When $\lambda =1 (\mathrm{mod} 4)$, $\lambda =4k+1$. Because of $8\cancel{|}\lambda$, we need to consider $8|v(v-1)(v-2)$ and $4|(v-1)(v-2)$; thus, $v=1,2,6 (\mathrm{mod} 8)$.
• Case 2: When $\lambda =2 (\mathrm{mod} 4)$, $\lambda =4k+2$. Because of $2|\lambda$, we need to consider $4|v(v-1)(v-2)$ and $2|(v-1)(v-2)$; thus, $v=0,1,2 (\mathrm{mod} 4)$.
• Case 3: When $\lambda =3 (\mathrm{mod} 4)$, $\lambda =4k+3$. Because of $8\cancel{|}\lambda$, we need to consider $8|v(v-1)(v-2)$ and $4|(v-1)(v-2)$; thus, $v=1,2,6 (\mathrm{mod} 8)$.
• Case 4: When $\lambda =0 (\mathrm{mod} 4)$, $\lambda =4k$. Because of $4|\lambda$, we need to consider $2|v(v-1)(v-2)$ and $1|(v-1)(v-2)$; thus, $v\ge 6$. □

According to the above Theorem 4, we can first consider the sufficiency of $S_{\lambda }(3,ST,v)$, $\lambda =1,2,3,4$. We can observe that when $\lambda =3$, the case of $v$ is the same as that for $\lambda =1$. We already know that $S(3,ST,v)$ exists according to Theorem 2. Then, the design in $S(3,ST,v)$ is repeated three times to obtain the design that $S_3(3,ST,v)$ needs. Thus, $S_3(3,ST,v)$ exists. We need to consider the sufficiency of $S_{\lambda }(3,ST,v)$, and $\lambda =2,4$.

Theorem 5.

$S_2(3,ST,v)$ exists if, and only if, $v=0,1,2 (\mathrm{mod} 4)$.

Proof of Theorem 5.

When $v=1,2,6 (\mathrm{mod} 8)$, the result follows from the fact that there are 2 copies of $S(3,ST,v)$. Thus, we need to consider the cases of $v=0 (\mathrm{mod} 4)$ and $v=5 (\mathrm{mod} 8)$.

When $v=8$, two types of $MP(3,ST,8)$ exist according to Example 4, denoted as ${\mathcal{C}}_{\mathbf{1}}$ and ${\mathcal{C}}_2$. Let $H_1$ and $H_2$ be the edges in the leaves of ${\mathcal{C}}_{\mathbf{1}}$ and ${\mathcal{C}}_2$, where both $H_1$ and $H_2$ have four edges. Then,

$$({\mathcal{C}}_{\mathbf{1}}\backslash E(H_1))\cup ({\mathcal{C}}_{\mathbf{2}}\backslash E(H_2))\cup \{(2,3,4,6,5,7),(7,6,0,2,1,3)\}$$

is a set of $ST\text{-}$blocks such that each edge of $K_8^{(3)}$ is represented exactly twice. Therefore, we have an $ST\text{-}$decomposition of $2K_8^{(3)}$.

When $v=13$, let $V_1,V_2,V_3,V_4,V_5,V_6,V_7,V_8,V_9\in \{V(K_v^{(3)})\}$. According to Example A14, both a maximum $ST\text{-}$packing of $K_{13}^{(3)}$, say ${\mathcal{C}}_{\mathbf{1}}$, with a leave consisting of two edges that share a single vertex, and a maximum $ST\text{-}$packing of $K_{13}^{(3)}$, say ${\mathcal{C}}_2$, with a leave consisting of two vertex-disjoint edges exist [17]. Let $H_1$ and $H_2$ be the leaves of ${\mathcal{C}}_{\mathbf{1}}$ and ${\mathcal{C}}_2$, respectively. Without the loss of generality, we may assume that $E(H_1)=\{(V_1,V_2,V_3),(V_1,V_4,V_5)\}$, $E(H_2)=\{(V_6,V_2,V_3),(V_6,V_4,V_5)\}$. Hence,

$$({\mathcal{C}}_{\mathbf{1}}\backslash E(H_1))\cup ({\mathcal{C}}_{\mathbf{2}}\backslash E(H_2))\cup \{E(H_1)\cup E(H_2)\}$$

is a set of $ST\text{-}$blocks such that each edge of $K_{13}^{(3)}$ is represented exactly twice. Therefore, we have an $ST\text{-}$decomposition of $2K_{13}^{(3)}$.

Now, let $v=4r$, $r\ge 2$. It suffices to find the $ST\text{-}$decompositions of (2-fold) $K_8^{(3)}$, $L_{4,4}^{(3)}$, and $K_{4,4,4}^{(3)}$, that is, $S_2(3,ST,v)$, $S_2(3,ST,4,4)$, and $GD{D}_2(3,ST,12)$ of type $4^3$. We already found $2K_8^{(3)}$. According to Examples 1 and 2, $S(3,ST,4,4)$ and $GDD(3,ST,12)$ exist. We know that the $S_2(3,ST,4,4)$ and $GD{D}_2(3,ST,12)$ follow from the fact that there are two copies of $S(3,ST,4,4)$ and $GDD(3,ST,12)$. Hence, when $v=0 (\mathrm{mod} 4)$, $S_2(3,ST,v)$ exists.

Now, let $v=8x+5$. It suffices to find the $ST\text{-}$decompositions of (2-fold) $K_{13}^{(3)}$, $K_{13}^{(3)}\backslash K_5^{(3)}$, $K_{5,8,8}^{(3)}\cup L_{8,8}^{(3)}$, and $K_{8,8,8}^{(3)}$, that is, $HS(3,ST;13,5)$, $S(3,ST,8,8)$, and $GDD(3,ST,21)$ of type $8^2{5}^1$ and $GDD(3,ST,24)$ of type $8^3$. We already found $2K_{13}^{(3)}$. According to Examples A5, A9, A10, A11, and A14, $HS(3,ST;13,5)$, $S(3,ST,8,8)$, and $GDD(3,ST,21)$ of type $8^2{5}^1$ and $GDD(3,ST,24)$ of type $8^3$ exist. We know that $H{S}_2(3,ST;13,5)$, $S_2(3,ST,8,8)$, $GD{D}_2(3,ST,21)$, and $GD{D}_2(3,ST,24)$ follow from the fact that there are two copies of $HS(3,ST;13,5)$, $S(3,ST,8,8)$, $GDD(3,ST,21)$, and $GDD(3,ST,24)$. Hence, when $v=0 (\mathrm{mod} 4)$, $S_2(3,ST,v)$ exists. □

Theorem 6.

$S_4(3,ST,v)$ exists, if and only if $v\ge 6$.

Proof of Theorem 6.

When $v=0,1,2 (\mathrm{mod} 4)$, the result follows from the fact that there are two copies of $S_2(3,ST,v)$. Hence, we need to only consider the $ST\text{-}$decomposition when $v=3 (\mathrm{mod} 4)$.

Now, let $v=4r+3$ and $v\ge 7$. It suffices to find the $ST\text{-}$decompositions of (4-fold) $K_7^{(3)}$, $K_{3,8,8}^{(3)}\cup L_{8,8}^{(3)}$, and $K_{8,8,8}^{(3)}$, that is, $S_4(3,ST,4,4)$ and $GD{D}_4(3,ST,11)$ of type $4^2{3}^1$ and $GD{D}_4(3,ST,12)$ of type $4^3$. We already found $S_4(3,ST,7)$ using Example A13. According to Examples 1, 2, and 5, $S(3,ST,4,4)$, $GDD(3,ST,11)$, and $GDD(3,ST,12)$ exist. We know that $S_4(3,ST,4,4)$, $GD{D}_4(3,ST,11)$, and $GD{D}_4(3,ST,12)$ follow from the fact that there are four copies of $S(3,ST,4,4)$, $GDD(3,ST,11)$, and $GDD(3,ST,12)$. Thus, for $v=3 (\mathrm{mod} 4)$, $S_4(3,ST,v)$ exists. To sum up, for $v\ge 6$, $S_4(3,ST,v)$ exists. □

4.3. Maximum Packing of $\lambda \text{-}$Fold Hypergraphs

Theorem 7.

For $v\ge 6$, $M{P}_2(3,ST,v)$ exists.

Proof of Theorem 7.

According to Theorem 6, when $v=0,1,2 (\mathrm{mod} 4)$, the $ST\text{-}$decomposition of $2K_v^{(3)}$ is the maximum $ST\text{-}$packing, the leave of which is empty. Thus, we only need to consider the case of $v=3 (\mathrm{mod} 4)$.

When $v=7$, two types of $MP(3,ST,7)$ exist according to Example 3. Then, we denote the two types of packing as ${\mathcal{C}}_{\mathbf{1}}$  and ${\mathcal{C}}_2$. Let $H_1$  and $H_2$  be the edges in the leaves of ${\mathcal{C}}_{\mathbf{1}}$  and ${\mathcal{C}}_2$, where both $H_1$  and $H_2$  have three edges. Then,

$$({\mathcal{C}}_{\mathbf{1}}\backslash E(H_1))\cup ({\mathcal{C}}_{\mathbf{2}}\backslash E(H_2))\cup \{(1,3,0,5,4,6)\}$$

is the maximum $ST\text{-}$packing with the leave consisting of two edges $\{(1,2,3),(1,2,6)\}$. Therefore, $M{P}_2(3,ST,7)$  exists.

Now, let $v=4r+3$, $r\ge 1$. It suffices to find $ST\text{-}$decompositions of (2-fold) $K_{4+l}^{(3)}$, $K_{3,4,4}^{(3)}\cup L_{4,4}^{(3)}$, and $K_{4,4,4}^{(3)}$, that is, $M{P}_2(3,ST,7)$, $S(3,ST,4,4)$, and $GDD(3,ST,11)$  of type $4^2{3}^1$  and $GDD(3,ST,12)$  of type $4^3$. We already found $M{P}_2(3,ST,7)$. According to Examples 1, 2, and 5, $S(3,ST,4,4)$  and $GDD(3,ST,11)$  of type $4^2{3}^1$  and $GDD(3,ST,12)$  of type $4^3$  exist. Therefore, for $v\ge 6$, $M{P}_2(3,ST,v)$  exists. □

Theorem 8.

For $v\ge 6$, $M{P}_3(3,ST,v)$ exists.

Proof of Theorem 8.

When $v=1,2,6 (\mathrm{mod} 8)$, the result follows from the fact that there are three copies of $S(3,ST,v)$, and the $ST\text{-}$decomposition of $K_v^{(3)}$  is the maximum $ST\text{-}$packing, the leave of which is empty. Hence, we need to only consider the 3-fold maximum $ST\text{-}$packing when $v=0,3 (\mathrm{mod} 4)$  and $v=5 (\mathrm{mod} 8)$.

When $v=7$, let ${\mathcal{C}}_{\mathbf{1}}$  be a $MP(3,ST,7)$  with the leave consisting of three edges, which exists according to Example 3, and let ${\mathcal{C}}_2$  be $M{P}_2(3,ST,7)$  with the leave consisting of two edges, which exists according to Theorem 7. Let $H_1$  and $H_2$  be the edges in the leaves of ${\mathcal{C}}_{\mathbf{1}}$  and ${\mathcal{C}}_2$. Without the loss of generality, we may assume that

$$\begin{array}{l}E(H_1)=\{(V_1,V_2,V_3),(V_1,V_4,V_5),(V_6,V_2,V_3)\}\\ E(H_2)=\{(V_6,V_4,V_5),(V_4,V_2,V_3)\}\end{array}$$

Thus, according to the edge set $E(H_1)\cup E(H_2)$, we can obtain a new block and an edge, denoted as $H_3$  and consisting of the edge $(V_4,V_2,V_3)$. Then, the (multi-)set

$$({\mathcal{C}}_{\mathbf{1}}\backslash E(H_1))\cup ({\mathcal{C}}_{\mathbf{2}}\backslash E(H_2))\cup \{(E(H_1)\cup E(H_2))\backslash E(H_3),E(H_3)\}$$

is the maximum $ST\text{-}$packing with the leave consisting of one edge. Thus, $M{P}_3(3,ST,7)$  exists.

When $v=8$, let ${\mathcal{C}}_{\mathbf{1}}$  be $MP(3,ST,8)$  with the leave consisting of four edges, which exists according to Example 4, and let ${\mathcal{C}}_2$  be $M{P}_2(3,ST,7)$  with the empty leave, which exists according to Theorem 7. Let $H_1$  be the edges in the leave of ${\mathcal{C}}_{\mathbf{1}}$. Then, the (multi-)set

$$({\mathcal{C}}_{\mathbf{1}}\backslash E(H_1))\cup ({\mathcal{C}}_{\mathbf{2}})\cup \{(E(H_1)\}$$

is the maximum $ST\text{-}$packing with the leave consisting of four edges. Hence, $M{P}_3(3,ST,8)$  exists.

When $v=13$, let ${\mathcal{C}}_{\mathbf{1}}$  be $MP(3,ST,13)$, consisting of two leaves, which exists according to Example 4, and let ${\mathcal{C}}_2$  be $M{P}_2(3,ST,13)$, consisting of empty leaves, which exists according to Theorem 7. Let $H_1$  be the leaves of ${\mathcal{C}}_{\mathbf{1}}$. Then, the (multi-)set

$$({\mathcal{C}}_{\mathbf{1}}\backslash E(H_1))\cup ({\mathcal{C}}_{\mathbf{2}})\cup \{(E(H_1)\}$$

is the maximum $ST\text{-}$packing consisting of two leaves. Hence, $M{P}_3(3,ST,13)$  exists.

Let $v=4r$  where $v\ge 7$. According to Theorem 1, we only need to consider the 3-fold maximum $ST\text{-}$packing of $K_8^{(3)}$  where a leave has four edges and the 3-fold $ST\text{-}$decompositions of $L_{4,4}^{(3)}$  and $K_{4,4,4}^{(3)}$, that is, $M{P}_3(3,ST,v)$, $S_3(3,ST,4,4)$, and $GD{D}_3(3,ST,12)$  of type $4^3$. We already found $M{P}_3(3,ST,8)$. According to Examples 1 and 2, $S(3,ST,4,4)$  and $GDD(3,ST,12)$  of type $4^3$  exist. We know that $S_3(3,ST,4,4)$  and $GD{D}_3(3,ST,12)$  follow from the fact that there are three copies of $S(3,ST,4,4)$  and $GDD(3,ST,12)$. Thus, for $v=0 (\mathrm{mod} 4)$, $M{P}_3(3,ST,v)$  exists.

Let $v=4r+3$ where $r\ge 1$. According to Theorem 1, we only need to consider the 3-fold maximum $ST\text{-}$packing of $K_7^{(3)}$ where a leave consists of one edge, and the 3-fold $ST\text{-}$decompositions of $K_{3,4,4}^{(3)}\cup L_{4,4}^{(3)}$  and $K_{4,4,4}^{(3)}$, that is, $M{P}_3(3,ST,7)$, $S_3(3,ST,4,4)$, and $GD{D}_3(3,ST,11)$  of type $4^2{3}^1$  and $GD{D}_3(3,ST,12)$  of type $4^3$. We already found $M{P}_3(3,ST,7)$. According to Examples 1, 2, and 5, $S(3,ST,4,4)$  and $GDD(3,ST,11)$  of type $4^2{3}^1$  and $GDD(3,ST,12)$  of type $4^3$  exist. We know that $S_3(3,ST,4,4)$, $GD{D}_3(3,ST,11)$, and $GD{D}_3(3,ST,12)$  follow from the fact that there are three copies of $S(3,ST,4,4)$, $GDD(3,ST,11)$, and $GDD(3,ST,12)$. Thus, for $v=3 (\mathrm{mod} 4)$, $M{P}_3(3,ST,v)$  exists.

Let $v=8r+5$ where $r\ge 1$. According to Theorem 1, we only need to consider the maximum $ST\text{-}$packing of $K_{13}^{(3)}$  where a leave has two edges and the 3-fold $ST\text{-}$decompositions of $K_{13}^{(3)}\backslash K_5^{(3)}$, $K_{5,8,8}^{(3)}\cup L_{8,8}^{(3)}$, and $K_{8,8,8}^{(3)}$, that is, $M{P}_3(3,ST,13)$, $HS(3,ST;13,5)$, and $GD{D}_3(3,ST,21)$  of type $8^2{5}^1$  and $S_3(3,ST,8,8)$  and $GDD(3,ST,24)$ of type $8^3$. We already found $M{P}_3(3,ST,13)$. According to Examples A5, A9, A10 and A11, $HS(3,TS;13,5)$ and $GDD(3,ST,21)$ of type $8^2{5}^1$ and $S(3,ST,8,8)$ and $GDD(3,ST,24)$ of type $8^3$ exist. We know that $S_3(3,ST,8,8)$, $H{S}_3(3,ST;13,5)$, $GD{D}_3(3,ST,21)$, and $GD{D}_3(3,ST,24)$ follow from the fact that there are three copies of $S(3,ST,8,8)$, $HS(3,ST;13,5)$, $GDD(3,ST,21)$, and $GDD(3,ST,24)$. Thus, for $v=5 (\mathrm{mod} 8)$, $M{P}_3(3,ST,v)$ exists. □

5. Conclusions

Theorem 9.

$S_{\lambda }(3,ST,v)$ exists if, and only if, the following cases are true:

• If $\lambda =1,3(\mathrm{mod}4)$, then $v=1,2,6(\mathrm{mod}8)$;
• If $\lambda =2(\mathrm{mod}4)$, then $v=0,1,2(\mathrm{mod}4)$;
• If $\lambda =0(\mathrm{mod}4)$, then $v\ge 6$.

Proof of Theorem 9.

According to Theorem 4, we obtained the necessary conditions for the existence of $S_{\lambda }(3,ST,v)$. For sufficiency, we will consider the following cases.

• Case 1. When $\lambda =0 (\mathrm{mod} 4)$, let $\lambda =4k$, where $k$ is a positive integer. The result follows from the fact that there are $k$ copies of $S_4(3,ST,v)$. According to Theorem 6, we prove that $S_4(3,ST,v)$  exists for all $v\ge 6$.
• Case 2. When $\lambda =1,3 (\mathrm{mod} 4)$, we have $v=1,2,6 (\mathrm{mod} 8)$. Let $\lambda =4k+l, l\in \{1,3\}$ and $k\ge 0$. The result follows from the fact that there are $k$ copies of $S_4(3,ST,v)$ and $l$ copies of $S(3,ST,v)$. According to Theorem 4 and Theorem 6, we prove that $S(3,ST,v)$ and $S_4(3,ST,v)$ exist.
• Case 3. When $\lambda =2 (\mathrm{mod} 4)$, we have $v=0,1,2 (\mathrm{mod} 4)$. Let $\lambda =4k+2$ and $k\ge 0$. The result follows from the fact that there are $k$ copies of $S_4(3,ST,v)$ and one copy of $S_2(3,ST,v)$. According to Theorem 5 and Theorem 6, we prove that $S_2(3,ST,v)$ and $S_4(3,ST,v)$ exist. □

Theorem 10.

$M{P}_{\lambda }(3,ST,v)$ exists for all $v\ge 6$ and $\lambda \ge 1$.

Proof of Theorem 10.

When $\lambda =\{1,2,3\}$, according to Theorem 3, Theorem 7, and Theorem 8, we found that $MP(3,ST,v)$, $M{P}_2(3,ST,v)$, and $M{P}_3(3,ST,v)$ exist. For $\lambda =4$, we prove that t $S_4(3,ST,v)$ exists according to Theorem 6, that is, $M{P}_4(3,ST,v)$ exists with an empty leave. For $\lambda >4$, let $\lambda =4k+l$ and $l\in \{1,2,3\}$. We prove that the result follows from the fact that there are $k$ copies of $S_4(3,ST,v)$ and one copy of the ($l$-fold) maximum $ST\text{-}$packing, that is, $M{P}_l(3,ST,v)$. According to Theorem 3, Theorem 7, and Theorem 8, $MP(3,ST,v)$, $M{P}_2(3,ST,v)$ and $M{P}_3(3,ST,v)$ exist.

This completes the proof. □

6. Discussion

The decomposition and packing theory of hypergraphs not only accurately captures the non-pairedness of complex data relations but also provides more abundant expression means for neural networks to optimize their performance. Therefore, with the continuous development of data science and artificial intelligence, the research and application prospects of hypergraphs will be broader.