An Approach to Multidimensional Discrete Generating Series

Abstract

We extend existing functional relationships for the discrete generating series associated with a single-variable linear polynomial coefficient difference equation to the multivariable case.

1. Introduction

An approach to build the general theory of a discrete generating series of one variable and its connection with the linear difference equations was introduced in [1]. We extend those results to the multidimensional case. We define a discrete generating series for $f:{\mathbb{Z}}^n\to \mathbb{C}$ and derive functional relations for such series.

The general theory of linear recurrences with constant coefficients and the Stanley hierarchy [2,3] of its generating functions (rational, algebraic, D-finite) depending on the initial data function was considered in [4]. Difference equations with polynomial coefficients is an effective means to study lattice paths with restriction [5,6]. Some properties of linear difference operators whose coefficients have the form of infinite two-sided sequences over a field of characteristic zero are considered in [7]. An effective method of obtaining explicit formulas for the coefficients of a generating function related to the Aztec diamond and a generating function related to the permutations with cycles was derived in [8,9]. Using the notion of amoeba [10] of the characteristic polynomial of a difference equation, a description for the solution space of a multidimensional difference equation with constant coefficients was obtained in [11]. A generalization to several variables of the classical Poincaré theorem on the asymptotic behavior of solutions of a linear difference equation is presented in [12]. We can also note that the almost periodic and the almost automorphic solutions to the difference equations depending on several variables are not well explored in the existing literature [13].

Let ${\mathbb{Z}}_{⩾}$ denote the non-negative integers, ${\mathbb{Z}}^n=\mathbb{Z}\times \cdots \times \mathbb{Z}$ be the n-dimensional integers, and ${\mathbb{Z}}_{⩾}^n={\mathbb{Z}}_{⩾}\times \cdots \times {\mathbb{Z}}_{⩾}$ for $n\in {\mathbb{Z}}_{⩾}$ be its non-negative orthant. For any $z\in \mathbb{C}$ and $n\in {\mathbb{Z}}_{⩾}$, we define the falling factorial $z^{\underline{n}}$$=z(z-1)\cdots (z-n+1)$ with $z^{\underline{0}}$$=1$ and the Pochhammer symbol (or rising factorial) is defined by ${\left(z\right)}_n=z(z+1)\cdots (z+n-1)$ with ${\left(z\right)}_0=1$. Throughout, we will use the multidimensional notation for convience of expressions: $x=(x_1,\dots ,x_n)\in {\mathbb{Z}}_{⩾}^n$, $z=(z_1,\dots ,z_n)\in {\mathbb{C}}^n$, $\xi =({\xi }_1,\dots ,{\xi }_n)\in {\mathbb{C}}^n$, ${\xi }^x={\xi }_1^{x_1}\cdots {\xi }_n^{x_n}$, $z^{\underline{x}}=z_1^{\underline{x_1}}\cdots z_n^{\underline{x_n}}$, $\ell =({\ell }_1,\dots ,{\ell }_n)\in {\mathbb{Z}}_{⩾}^n$, $x!=x_1!\dots x_n!$. We also will use $x\le y$ for $x,y\in {\mathbb{Z}}^n$ componentwise, i.e., that $x_i\le y_i$ for all $i=1,\dots ,n$.

Given a function $f:{\mathbb{Z}}_{⩾}^n\to \mathbb{C}$, we define the associated multidimensional discrete generating series of f as

$$F(\xi ;\ell ;z)=\sum _{x\in {\mathbb{Z}}_{⩾}^n}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}=\sum _{x_1=0}^{\infty }\dots \sum _{x_n=0}^{\infty }f(x_1,\dots ,x_n){\xi }_1^{x_1}\cdots {\xi }_n^{x_n}{z}_1^{\underline{{\ell }_1{x}_1}}\cdots z_n^{\underline{{\ell }_n{x}_n}}.$$

Let $p_{\alpha }\in \mathbb{C}\left[z\right]$ denote polynomials with complex coefficients. The difference equation under consideration in this work is

$$\sum _{\alpha \in A}{p}_{\alpha }\left(x\right)f(x-\alpha )=0,$$

(1)

where set $A\subset {\mathbb{Z}}_{⩾}^n$ is finite and there is $m\in A$ such that for all $\alpha \in A$, the inequality $\alpha ⩽m,$ which means ${\alpha }_j⩽m_j,j=1,\dots ,n,$ holds. Occasionally we will use an equivalent notation $0⩽\alpha ⩽m$, assuming that for some $\alpha$ coefficients, $p_{\alpha }\left(x\right)$ vanishes and only $p_m\left(x\right)\not\equiv 0$. In Section 2, we will particularly consider a homogeneous difference equation with constant coefficients.

The special case where each $p_{\alpha }=c_{\alpha }$ is a constant

$$\sum _{\alpha \in A}{c}_{\alpha }f(x-\alpha )=0$$

(2)

arises in a wide class of combinatorial analysis problems [3], for instance, in lattice path problems [4], the theory of digital recursive filters [14], and the wavelet theory [15]. The question about correctness and well-posedness of (2) was considered in [16,17,18].

We equip (1) with initial data on a set named $X_m$, which is used often enough. We introduce the notation ${\mathbb{Z}}_{\ngeqq }$ as $X_m={\mathbb{Z}}_{⩾}^n\setminus \left(m+{\mathbb{Z}}_{⩾}^n\right)=\left\{x\in {\mathbb{Z}}_{⩾}^n:x\ngeqq m\right\}$ (see Figure 1) and we define the initial data function $\phi :X_m\to \mathbb{C}$ so that

$$f\left(x\right)=\phi \left(x\right),x\in X_m.$$

(3)

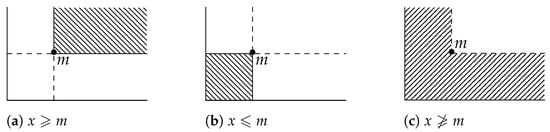
Figure 1. Illustration of the sets $x⩾m$, $x⩽m$, and $x\ngeqq m$.

For convenience, we extend $\phi$ to the whole of ${\mathbb{Z}}^n$ by taking it to be identically zero outside of $X_m$. The Cauchy problem is to find a solution to difference Equation (1) that coincides with $\phi$ on $X_m$, i.e., $f\left(x\right)=\phi \left(x\right)$, for all $x\in X_m$.

In Section 2, functional equations for the discrete generating series are derived for the solution of the difference equations with constant coefficients. In Section 3, a case of difference equations with polynomial coefficients is considered. Section 4 contains two examples that illustrate our approach to discrete generating series.

2. Discrete Generating Series for Linear Difference Equations with Constant Coefficients

In this section, we consider a homogeneous difference equation with constant coefficients (2) and introduce the shift operator by

$$\mathcal{P}(\xi ;\ell ;z)=\sum _{0⩽\alpha ⩽m}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }.$$

(4)

Also useful is its truncation for $\tau \in {\mathbb{Z}}^n$, defined by the formula

$${\mathcal{P}}_{\tau }(\xi ;\ell ;z)=\sum _{\begin{array}{c}0⩽\alpha ⩽m\\ \alpha \ngeqq \tau \end{array}}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha },$$

and the discrete generating series of the initial data for $\tau \in X_m$ by

$${\Phi }_{\tau }(\xi ;\ell ;z)=\sum _{x\ngeqq \tau }\phi \left(x\right){\xi }^x{z}^{\underline{\ell x}}.$$

(5)

Let ${\delta }_j:x\to x+e^j$ be the forward shift operator for $j=1,\dots ,n$ with multidimensional notation ${\delta }^{\alpha }={\delta }_1^{{\alpha }_1}\dots {\delta }_n^{{\alpha }_n}$ and define the polynomial difference operator

$$P\left(\delta \right)=\sum _{0⩽\alpha ⩽m}{c}_{\alpha }{\delta }^{\alpha }.$$

With this notation, Equation (2) is represented compactly as

$$P\left({\delta }^{-1}\right)f\left(x\right)=0,x⩾m.$$

The case of generating series ${\sum }_{x}f\left(x\right)z^x$ and exponential generating series ${\sum }_x\frac{f\left(x\right)}{x!}{z}^x$ is well-studied for both one and several variables: one of the first convenient formulas to derive the generating series exploiting the characteristic polynomial and the initial data function was proven in [19]. We will prove analogues of these formulas for the discrete generating series $F(\xi ;\ell ;z)$.

Theorem 1.

The discrete generating series $F(\xi ;\ell ;z)$ for the solution to the Cauchy problem for Equation (2) with initial data (3) satisfies the functional equations:

$$\begin{array}{}\mathrm{(6)}& \hfill \mathcal{P}(\xi ;\ell ;z)F(\xi ;\ell ;z)& =\sum _{0⩽\alpha ⩽m}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }{\Phi }_{m-\alpha }(\xi ;\ell ;z)\hfill \mathrm{(7)}& & =\sum _{x\ngeqq m}P\left({\delta }^{-1}\right)\phi \left(x\right){\xi }^x{z}^{\underline{\ell x}}\hfill \mathrm{(8)}& & =\sum _{x\ngeqq m}{\mathcal{P}}_{m-x}(\xi ;\ell ;z)\phi \left(x\right)z^{\underline{\ell x}}.\hfill \end{array}$$

Proof. 

By multiplying (2) by ${\xi }^x{z}^{\underline{\ell x}}$ and summing over $x⩾m$, we obtain

$$\begin{array}{cc}\hfill 0& =\sum _{x⩾m}\sum _{0⩽\alpha ⩽m}{c}_{\alpha }f(x-\alpha ){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{0⩽\alpha ⩽m}{c}_{\alpha }\sum _{x⩾m}f(x-\alpha ){\xi }^x{z}^{\underline{\ell x}}.\hfill \end{array}$$

Now, substituting x with $x+\alpha$ yields

$$\begin{array}{cc}\hfill 0& =\sum _{0⩽\alpha ⩽m}{c}_{\alpha }\sum _{x⩾m-\alpha }f\left(x\right){\xi }^{x+\alpha }{z}^{\underline{\ell (x+\alpha )}}\hfill \\ \hfill & =\sum _{0⩽\alpha ⩽m}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }\sum _{x⩾m-\alpha }f\left(x\right){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{0⩽\alpha ⩽m}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }\left(\sum _{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}-\sum _{x\ngeqq m-\alpha }\phi \left(x\right){\xi }^x{z}^{\underline{\ell x}}\right)\hfill \\ \hfill & =\underset{=\mathcal{P}(\xi ;\ell ;z)}{\underbrace{{\sum }_{0⩽\alpha ⩽m}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }}}\underset{=F(\xi ;\ell ;z)}{{\displaystyle \underbrace{{\sum }_{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}}}}-{\displaystyle \sum _{0⩽\alpha ⩽m}}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }\underset{={\Phi }_{m-\alpha }(\xi ;\ell ;z)}{{\displaystyle \underbrace{{\sum }_{x\ngeqq m-\alpha }\phi \left(x\right){\xi }^x{z}^{\underline{\ell x}}}}}.\hfill \end{array}$$

Thus, by (5), we have established (6). Since

$$\begin{array}{cc}\hfill \sum _{0⩽\alpha ⩽m}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }\sum _{x\ngeqq m-\alpha }\phi \left(x\right){\xi }^x{z}^{\underline{\ell x}}& =\sum _{0⩽\alpha ⩽m}{c}_{\alpha }\sum _{x\ngeqq m-\alpha }\phi \left(x\right){\xi }^{x+\alpha }{z}^{\underline{\ell (x+\alpha )}}\hfill \\ \hfill & =\sum _{0⩽\alpha ⩽m}{c}_{\alpha }\sum _{x\ngeqq m}\phi (x-\alpha ){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{x\ngeqq m}\underset{=P\left({\delta }^{-1}\right)\phi \left(x\right)}{\underbrace{\left[{\sum }_{0⩽\alpha ⩽m}{c}_{\alpha }\phi (x-\alpha )\right]}}{\xi }^x{z}^{\underline{\ell x}},\hfill \end{array}$$

which yields (7). Finally, collecting (6) by $\phi \left(x\right)$ yields

$$\begin{array}{c}\hfill \sum _{0⩽\alpha ⩽m}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }\sum _{x\ngeqq m-\alpha }\phi \left(x\right){\xi }^x{z}^{\underline{\ell x}}=\sum _{x\ngeqq m}\underset{={\mathcal{P}}_{m-x}(\xi ;\ell ;z)}{\underbrace{{\sum }_{\begin{array}{c}0⩽\alpha ⩽m\\ \alpha \ngeqq m-x\end{array}}{c}_{\alpha }{\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }}}\phi \left(x\right)z^{\underline{\ell x}},\end{array}$$

completing the proof of (8). □

For $z=(z_1,\dots ,z_n)$, we denote the projection operator ${\pi }_{j}z=(z_1,\dots ,z_{j-1},0,z_{j+1},\dots ,z_n)$ and we introduce the notation

$${\pi }_{j}F(\xi ;\ell ;z)=F(\xi ;\ell ;{\pi }_{j}z)=\sum _{\begin{array}{c}x⩾0\\ x_j=0\end{array}}f\left(x\right){\xi }^x{z}^{\underline{\ell x}},$$

and we define the combined projection $\Pi =(1-{\pi }_1)\circ \cdots \circ (1-{\pi }_n)$ as the composition of $1-{\pi }_j$ for all $j=1,\dots ,n$.

For the next result, we introduce the symbols $I=(1,1,\dots ,1)\in {\mathbb{Z}}^n$ and the unit vectors $e_j=(0,\dots ,0,1,0,\dots ,0)$ for $j=1,2,\dots ,n$, which is nonzero only for the jth component. In these two lemmas, we will prove some useful properties of the combined projection $\Pi$.

Lemma 1.

The following formula holds:

$$\begin{array}{c}\hfill \Pi \sum _{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}=\sum _{x⩾I}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}.\end{array}$$

Proof. 

First, compute for any $j=1,2,\dots ,n$,

$$\begin{array}{cc}\hfill (1-{\pi }_j)\sum _{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}& =\sum _{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}-{\pi }_j\sum _{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{x⩾e_j}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}.\hfill \end{array}$$

Thus, we see that applying $\Pi$ to ${\displaystyle \sum _{x\ge 0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}}$ yields the desired result. □

We now obtain a similar result as Lemma 1 but for a shifted discrete generating series.

Lemma 2.

The following formula holds:

$$\begin{array}{c}\hfill \Pi {\xi }_j{z}_j^{\underline{{\ell }_j}}{\rho }^{{\ell }_j}F(\xi ;\ell ;z)=\sum _{x⩾I}f(x-e^j){\xi }^x{z}^{\underline{\ell x}}.\end{array}$$

Proof. 

First, compute

$$\begin{array}{cc}\hfill (1-{\pi }_j){\xi }_j{z}_j^{\underline{{\ell }_j}}{\rho }^{{\ell }_j}F(\xi ;\ell ;z)& ={\xi }_j{z}_j^{\underline{{\ell }_j}}{\rho }^{{\ell }_j}F(\xi ;\ell ;z)-{\pi }_j{\xi }_j{z}_j^{\underline{{\ell }_j}}{\rho }^{{\ell }_j}F(\xi ;\ell ;z)\hfill \\ \hfill & ={\xi }_j{z}_j^{\underline{{\ell }_j}}{\rho }^{{\ell }_j}\sum _{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{x⩾0}f\left(x\right){\xi }^{x+e_j}{z}^{\underline{\ell (x+e^j)}}\hfill \\ \hfill & =\sum _{x⩾e^j}f(x-e^j){\xi }^x{z}^{\underline{\ell x}}.\hfill \end{array}$$

Thus, we see that applying $\Pi$ to ${\xi }_j{z}_j^{\underline{{\ell }_j}}{\rho }^{{\ell }_j}F(\xi ;\ell ;z)$ completes the proof. □

We introduce the inner product

$$⟨c,\xi z^{\underline{\ell }}{\rho }^{\ell }⟩=c_1{\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}+\cdots +c_n{\xi }_n{z}_n^{\underline{{\ell }_n}}{\rho }_n^{{\ell }_n}$$

and

$$⟨c,{\delta }^{-I}⟩=c_1{\delta }_1^{-1}+\cdots +c_n{\delta }_n^{-1}.$$

We are now prepared to prove an analogue of [20], [Theorem 1.1].

Theorem 2.

The following formula holds:

$$\Pi \left[(1-⟨c,\xi z^{\underline{\ell }}{\rho }^{\ell }⟩)F(\xi ;\ell ;z)\right]=\sum _{x⩾I}(1-⟨c,{\delta }^{-I}⟩)f\left(x\right){\xi }^x{z}^{\underline{\ell x}}.$$

(9)

Proof. 

Applying $\Pi$ to $(1-⟨c,\xi z^{\underline{\ell }}{\rho }^{\ell }⟩)F(\xi ;\ell ;z)$ yields

$$\begin{array}{cc}\hfill \Pi \left[(1-\right.& \left.⟨c,\xi z^{\underline{\ell }}{\rho }^{\ell }⟩)F(\xi ;\ell ;z)\right]=\Pi F(\xi ;\ell ;z)-⟨c,\Pi \xi z^{\underline{\ell }}{\rho }^{\ell }⟩F(\xi ;\ell ;z)\hfill \\ \hfill & =\Pi F(\xi ;\ell ;z)-c_1\Pi {\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}F(\xi ;\ell ;z)-\cdots -c_n\Pi {\xi }_n{z}_n^{\underline{{\ell }_n}}{\rho }_n^{{\ell }_n}F(\xi ;\ell ;z)\hfill \\ \hfill & =\sum _{x⩾I}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}-c_1\sum _{x⩾I}f(x-e^1){\xi }^x{z}^{\underline{\ell x}}-\cdots -c_n\sum _{x⩾I}f(x-e^n){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{x⩾I}\left(f\left(x\right)-c_{1}f(x-e^1)-\cdots -c_{n}f(x-e^n)\right){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{x⩾I}(1-⟨c,{\delta }^{-I}⟩)f\left(x\right){\xi }^x{z}^{\underline{\ell x}},\hfill \end{array}$$

thereby completing the proof. □

The following corollary is straightforward.

Corollary 1.

If f solves $(1-⟨c,{\delta }^{-I}⟩)f\left(x\right)=0$, then

$$\Pi \left[(1-⟨c,\zeta ⟩)F(\xi ;\ell ;z)\right]=0.$$

(10)

3. Discrete Generating Series for Linear Difference Equations with Polynomial Coefficients

We define the componentwise forward difference operators ${\Delta }_j$ by

$${\Delta }_{j}F\left(z\right)=F(z+e^j)-F\left(z\right),j=1,\dots ,n.$$

If $z^{\underline{x}}=z_1^{\underline{x_1}}\dots z_n^{\underline{x_n}}$, then ${\Delta }_j{z}^{\underline{x}}=x_j{z}^{\underline{x-e^j}}$. Thus, we can regard ${\Delta }_j$ as a discrete analogue of a partial derivative operator. Now, compute

$$\begin{array}{cc}\hfill {\Delta }_{j}F(\xi ;\ell ;z)& ={\Delta }_j\sum _{x⩾0}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{x⩾0}f\left(x\right){\xi }^x{\Delta }_j{z}^{\underline{\ell x}}\hfill \\ \hfill & =\sum _{x⩾0}{\ell }_j{x}_{j}f\left(x\right){\xi }^x{z}^{\underline{\ell x-e^j}}.\hfill \end{array}$$

We denote the componentwise backward jump ${\rho }_j$ by

$${\rho }_{j}F\left(z\right)=F(z-e^j)$$

and we define the componentwise operators ${\theta }_j={\ell }_j^{-1}{z}_j{\rho }_j{\Delta }_j$, which generalizes the single-variable one defined earlier in [21,22]. Now, we prove some useful properties of the operator ${\theta }^k:={\theta }_1^k\dots {\theta }_n^k$.

Lemma 3.

If $k=(k_1,\dots ,k_n)\in {\mathbb{Z}}_{⩾}^n$, then the following formula holds:

$$\begin{array}{c}\hfill {\theta }^{k}F(\xi ;\ell ;z)=\sum _{x⩾0}{x}^{k}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}.\end{array}$$

(11)

Proof. 

We obtain:

$$\begin{array}{cc}\hfill {\theta }^{k}F(\xi ;\ell ;z)& ={\theta }_1^{k_1}\dots {\theta }_n^{k_n}F(\xi ;\ell ;z)\hfill \\ \hfill & ={\theta }_1^{f{k}_1}\dots {\theta }_{n-1}^{k_{n-1}}{\left({\ell }_n^{-1}{z}_n{\rho }_n{\Delta }_n\right)}^{k_n-1}{\ell }_n^{-1}{z}_n{\rho }_n{\Delta }_{n}F(\xi ;\ell ;z)\hfill \\ \hfill & ={\theta }_1^{k_1}\dots {\theta }_{n-1}^{k_{n-1}}{\left({\ell }_n^{-1}{z}_n{\rho }_n{\Delta }_n\right)}^{k_n-1}{\ell }_n^{-1}{z}_n{\rho }_n\sum _{x⩾0}{\ell }_n{x}_{n}f\left(x\right){\xi }^x{z}^{\underline{\ell x-e^n}}\hfill \\ \hfill & ={\theta }_1^{k_1}\dots {\theta }_{n-1}^{k_{n-1}}{\left({\ell }_n^{-1}{z}_n{\rho }_n{\Delta }_n\right)}^{k_n-1}\sum _{x⩾0}{x}_{n}f\left(x\right){\xi }^x{z}^{\underline{\ell x}}.\hfill \end{array}$$

Continuing this process $k_n-1$ times for ${\theta }_n$ and in $k_j$ times in turn for the powers of ${\theta }_j$, $j=1,\dots ,n-1$ completes the proof. □

The proof of the following lemma resembles the proof of Lemma 3 but for the operator ${\displaystyle p\left(\theta \right)=\sum _{\alpha \in A\subset {\mathbb{Z}}_{⩾}^n}{c}_{\alpha }{\theta }^{\alpha }}$, so we omit explicitly writing the proof.

Lemma 4.

The following formula holds:

$$\begin{array}{c}\hfill p\left(\theta \right)F(\xi ;\ell ;z)=\sum _{x⩾0}p\left(x\right)f\left(x\right){\xi }^x{z}^{\underline{\ell x}}.\end{array}$$

(12)

We define an operator ${\mathcal{P}}_A$ by

$${\mathcal{P}}_A(\xi ;\ell ;z;\theta ;\rho )=\sum _{\alpha \in A}{p}_{\alpha }(\theta +\alpha ){\xi }^{\alpha }{z}^{\underline{\ell \alpha }}{\rho }^{\ell \alpha }.$$

Theorem 3.

The discrete generating series $F(\xi ;\ell ;·)$ of the Cauchy problem for Equation (1) with initial data (3) satisfies the functional equation

$${\mathcal{P}}_A(\xi ;\ell ;z;\theta ;\rho )F(\xi ;\ell ;z)=\sum _{\alpha \in A}\sum _{x\ngeqq m-\alpha }{p}_{\alpha }(x-\alpha )\phi \left(x\right){\xi }^x{z}^{\underline{\ell (x+\alpha )}}.$$

(13)

Proof. 

Similar to the proof of Theorem 1, we multiply (1) by ${\xi }^x{z}^{\underline{\ell x}}$ and sum over $x⩾m$ to obtain

$$0=\sum _{x⩾m}\sum _{\alpha \in A}{p}_{\alpha }\left(x\right)f(x-\alpha ){\xi }^x{z}^{\underline{\ell x}}=\sum _{\alpha \in A}\sum _{x⩾m-\alpha }{p}_{\alpha }(x-\alpha )f\left(x\right){\xi }^{x+\alpha }{z}^{\underline{\ell (x+\alpha )}}.$$

Replacing x with $x+\alpha$ then leads to

$$\begin{array}{cc}\hfill 0& =\sum _{\alpha \in A}{\xi }^{\alpha }\left(\sum _{x⩾0}{p}_{\alpha }(x-\alpha )f\left(x\right){\xi }^x{z}^{\underline{\ell (x+\alpha )}}-\sum _{x\ngeqq m-\alpha }{p}_{\alpha }(x-\alpha )\phi \left(x\right){\xi }^x{z}^{\underline{\ell (x+\alpha )}}\right)\hfill \end{array}$$

and routine algebraic manipulation completes the proof. □

4. Examples

Example 1.

We will derive the functional equation for the discrete generating series

$$F(;;z_1,z_2)=F({\xi }_1,{\xi }_2;{\ell }_1,{\ell }_2;z_1,z_2)$$

for the basic combinatorial recurrence

$$f(x_1,x_2)-f(x_1-1,x_2)-f(x_1,x_2-1)=0.$$

(14)

Multiplying both sides of (14) by ${\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}$ and summing over $(x_1,x_2)⩾(1,1)$ yields

$$\begin{array}{c}\sum _{(x_1,x_2)⩾(1,1)}f(x_1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}-\sum _{(x_1,x_2)⩾(1,1)}f(x_1-1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill -\sum _{(x_1,x_2)⩾(1,1)}f(x_1,x_2-1){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}=0.\end{array}$$

We consider each sum separately:

$$\begin{array}{cc}\hfill & \sum _{(x_1,x_2)⩾(1,1)}f(x_1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ & \phantom{AAAAAAAAA}=F(;;z_1,z_2)-F(;;0,z_2)-F(;;z_1,0)+F(;;0,0);\hfill \\ \hfill & \sum _{(x_1,x_2)⩾(1,1)}f(x_1-1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill & \phantom{AAAAAAAAA}=\sum _{(x_1,x_2)⩾(0,1)}f(x_1,x_2){\xi }_1^{x_1+1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1(x_1+1)}}{z}_2^{\underline{{\ell }_2{x}_2}}=\hfill \\ \hfill & \phantom{AAAAAAAAA}={\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}\sum _{(x_1,x_2)⩾(0,1)}f(x_1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill & \phantom{AAAAAAAAA}={\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}\left(F(;;z_1,z_2)-F(;;z_1,0)\right);\hfill \\ \hfill & \sum _{(x_1,x_2)⩾(1,1)}f(x_1,x_2-1){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill & \phantom{AAAAAAAAA}={\xi }_2{z}_2^{\underline{{\ell }_2}}{\rho }_2^{{\ell }_2}\left(F(;;z_1,z_2)-F(;;0,z_2)\right).\hfill \end{array}$$

Finally, we obtain

$$\begin{array}{cc}\hfill F(;;z_1,z_2)& -F(;;0,z_2)-F(;;z_1,0)+F(;;0,0)\hfill \\ & -{\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}\left(F(;;z_1,z_2)-F(;;z_1,0)\right)-{\xi }_2{z}_2^{\underline{{\ell }_2}}{\rho }_2^{{\ell }_2}\left(F(;;z_1,z_2)-F(;;0,z_2)\right)=0,\hfill \end{array}$$

which yields the functional equation on $F(;;z_1,z_2)$:

$$\begin{array}{cc}\hfill (1-{\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}-{\xi }_2& z_2^{\underline{{\ell }_2}}{\rho }_2^{{\ell }_2})F(;;z_1,z_2)\hfill \\ & -(1-{\xi }_2{z}_2^{\underline{{\ell }_2}}{\rho }_2^{{\ell }_2})F(;;0,z_2)-(1-{\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1})F(;;z_1,0)+F(;;0,0)=0.\hfill \end{array}$$

Example 2.

We consider a difference equation with polynomial coefficients whose solution is a p-recursive series [23]:

$$f(x_1,x_2)-(1+x_1{x}_2)f(x_1-1,x_2)-x_2^{2}f(x_1,x_2-1)=0.$$

(15)

Multiplying both sides of (15) by ${\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}$ and summing over $(x_1,x_2)⩾(1,1)$ yields

$$\begin{array}{c}\sum _{(x_1,x_2)⩾(1,1)}f(x_1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}-\sum _{(x_1,x_2)⩾(1,1)}(1+x_1{x}_2)f(x_1-1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill -\sum _{(x_1,x_2)⩾(1,1)}{x}_2^{2}f(x_1,x_2-1){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}=0.\end{array}$$

The first sum is the same as in the previous example. We consider the second and third sum separately:

$$\begin{array}{cc}\hfill & \sum _{(x_1,x_2)⩾(1,1)}(1+x_1{x}_2)f(x_1-1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill & \phantom{AAAAAAAAA}=\sum _{(x_1,x_2)⩾(0,1)}(1+(x_1+1)x_2)f(x_1,x_2){\xi }_1^{x_1+1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1(x_1+1)}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill & \phantom{AAAAAAAAA}=(1+({\theta }_1+1){\theta }_2){\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}\sum _{(x_1,x_2)⩾(0,1)}f(x_1,x_2){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill & \phantom{AAAAAAAAA}=(1+({\theta }_1+1){\theta }_2){\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}\left(F(;;z_1,z_2)-F(;;z_1,0)\right);\hfill \\ \hfill & \sum _{(x_1,x_2)⩾(1,1)}{x}_2^{2}f(x_1,x_2-1){\xi }_1^{x_1}{\xi }_2^{x_2}{z}_1^{\underline{{\ell }_1{x}_1}}{z}_2^{\underline{{\ell }_2{x}_2}}\hfill \\ \hfill & \phantom{AAAAAAAAA}={({\theta }_2+1)}^2{\xi }_2{z}_2^{\underline{{\ell }_2}}{\rho }_2^{{\ell }_2}\left(F(;;z_1,z_2)-F(;;0,z_2)\right),\hfill \end{array}$$

which yields the functional equation

$$\begin{array}{cc}\hfill (1-(1+{\theta }_1{\theta }_2+{\theta }_2){\xi }_1& z_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}-{({\theta }_2+1)}^2{\xi }_2{z}_2^{\underline{{\ell }_2}}{\rho }_2^{{\ell }_2})F(;;z_1,z_2)\hfill \\ & -(1-(1+{\theta }_1{\theta }_2+{\theta }_2\left){\xi }_1{z}_1^{\underline{{\ell }_1}}{\rho }_1^{{\ell }_1}\right)F(;;0,z_2)\hfill \\ & -\left(1-{({\theta }_2+1)}^2{\xi }_2{z}_2^{\underline{{\ell }_2}}{\rho }_2^{{\ell }_2}\right)F(;;z_1,0)+F(;;0,0)=0.\hfill \end{array}$$

5. Conclusions

We have initiated the theory of discrete generating series for multidimensional polynomial coefficient difference equations. We introduced a multidimensional polynomial shift operator and established three functional equations that these new discrete generating series obey, revealing some of their structural properties. A strong direction for future research is to generalize to the time scales calculus [24]. The falling factorial functions here are called generalized $h_k$ polynomials in time scales. This suggests some directions for the time scales analogue of this research, which was arguably anticipated with the definition of a moment-generating series for distributions in [25]. One particularly interesting question is what the proper analogue of (1) is for an arbitrary time scale, and perhaps analysis from a generating series perspective would reveal new insights to this problem.