Optimal Weak Order and Approximation of the Invariant Measure with a Fully-Discrete Euler Scheme for Semilinear Stochastic Parabolic Equations with Additive Noise

Abstract

In this paper, we consider the ergodic semilinear stochastic partial differential equation driven by additive noise and the long-time behavior of its full discretization realized by a spectral Galerkin method in spatial direction and an Euler scheme in the temporal direction, which admits a unique invariant probability measure. Under the condition that the nonlinearity is once differentiable, the optimal convergence orders of the numerical invariant measures are obtained based on the time-independent weak error, but not relying on the associated Kolmogorov equation. More precisely, the obtained convergence orders are $O({\lambda }_N^{-\gamma })$ in space and $O({\tau }^{\gamma })$ in time, where $\gamma \in (0,1]$ from the assumption $\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2}$ is used to characterize the spatial correlation of the noise process. Finally, numerical examples confirm the theoretical findings.

1. Introduction

(Stochastic) Differential equations are widely used in various fields of science (e.g., [1,2,3]). In order to find the hiding information of (stochastic) differential equations, it is necessary for us to analyze the properties of their solution (e.g., [4,5,6,7]). However, the solutions of most (stochastic) differential equations cannot be explicitly expressed, so we need to find numerical solutions (e.g., [8,9,10,11,12]). Over the last two decades, there have been plenty of research articles focusing on the design and analysis of approximations of invariant measures for stochastic differential equations (SDEs) and stochastic partial differential equations (SPDEs) (see [13,14,15,16,17,18,19,20,21,22]). In contrast to stochastic differential equations, approximations of invariant measures for SPDEs is, in our opinion, at an early stage and far from being well-understood. In the present paper, our aim is to make a further contribution to numerical invariant measures for SPDEs.

Let $\mathcal{D}\subset {\mathbb{R}}^d$, d = 1, 2, 3 be a bounded open spatial domain with smooth boundary and let $H:=L^2(D,\mathbb{R})$ be a real separable Hilbert space endowed with the usual inner product and norm. Through the present paper, we consider the following semilinear SPDEs

$$\left\{\begin{array}{c}\mathrm{d}X(t)+AX(t)\mathrm{d}t=F(X(t))\mathrm{d}t+\mathrm{d}W(t),\hfill \\ X(0)=X_0\in H\hfill \end{array}\right.$$

(1)

where $A:D(A)\subset H\to H$ is a linear, densely defined, positive self-adjoint unbounded operator with compact inverse (e.g., $A=-\Delta$ with homogeneous Dirichlet boundary condition) in H, generating an analytic semigroup $\mathcal{S}(t)=e^{-tA}$ in H and $F:H\to H$ is a deterministic mapping. Moreover, ${\left\{W(t)\right\}}_{t\ge 0}$ is an H-valued Q-Wiener process on a filtered probability space $(\Omega ,\mathcal{F},\mathbb{P},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0})$ with respect to the normal filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$. Under further assumptions specified later, particularly including

$$\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2}<\infty ,forsome\gamma \in (0,1],$$

(2)

it was shown in (Section 8.6 in [23]) that the mild solution ${\left\{X(t)\right\}}_{t\ge 0}$ is ergodic and it admits a unique invariant probability measure $\nu$ on $(H,\mathcal{B}(H))$. Moreover, if $\overline{\nu }$ is the unique invariant measure of some numerical solution $\overline{X}(t)$ in a Hilbert space $\overline{H}\subset H$, the definition of ergodicity implies

$$\begin{array}{cc}\hfill & \left|{\int }_H\Phi (y)\nu (dy)-{\int }_{\overline{H}}\Phi (y)\overline{\nu }(dy)\right|\hfill \\ \hfill & \le \underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T|\mathbb{E}[\Phi \left(X(t)\right)]-\mathbb{E}[\Phi \left(\overline{X}(t)\right)]|dt,forall\Phi \in C_b^2(H,\mathbb{R}).\hfill \end{array}$$

(3)

Hence, to conduct the time-independent weak error analysis is a key to driving the error of the numerical invariant measure. However, this is not an easy thing.

Let $P_N$ be a projection operator from H to the finite-dimensional space $H_N\subset H$, which is spanned by the first N eigenvectors of A. Then the fully-discretization of (1) is to find $X_N^m\in H_N$ such that, for $m\in \{1,2,3,\cdots ,M\}$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_N^m-X_N^{m-1}+\tau A_N{X}_N^m=\tau P_{N}F(X_N^{m-1})+P_N\Delta W_m,\hfill & \\ X_N^0=P_N{X}_0,\hfill \end{array}\right.\end{array}$$

(4)

where $\tau :=\frac{T}{M}$ represents the time step size. The solution of (4) is ergodic and it admits a unique invariant measure ${\nu }_{\tau }^N$ (see Lemma 3). By applying the strategy in [24] without using the associated Komogorov equation, we do the time-independent weak error analysis and obtain the following weak error

$$\left|\mathbb{E}\right[\Phi (X(T))]-\mathbb{E}[\Phi (X_N^M)\left]\right|\le C({\lambda }_N^{-\gamma }+{\tau }^{\gamma }),$$

(5)

where $C>0$ is a constant independent of $N,T,M$. Note, that the weak error analysis in [24] was conducted on a finite time interval, but here it is time-independent and holds over a long time. Then, by using the time-independent weak error estimate (5) and the ergodicity, we obtain the error between $\nu$ and ${\nu }_{\tau }^M$ as follows

$$\begin{array}{c}\hfill |{\int }_H\Phi (y)\mathrm{d}\nu (y)-{\int }_{H_N}\Phi (y)\mathrm{d}{\nu }_{\tau }^N(y)|\le C({\lambda }_N^{-\gamma }+{\tau }^{\gamma }).\end{array}$$

(6)

This indicates that the error of invariant measures has the same order as the time-independent weak error and that the convergence order relies on the regularity of the driven noise process. In particular, for the trace-class additive noise when (2) is fulfilled with $\gamma =1$, a classical convergence rate of order $O({\lambda }_N^{-1}+\tau )$ can be reached, even in multiple dimensions. The optimal convergence order is derived by a very careful use of the smoothing property of the semigroup $E(t)=e^{-tA}$ and a family operators $E_N^m={(I+\tau A_N)}^{-m}{P}_N$ (see (10) and (79)) and the deterministic error estimates (see (100)).

Finally, we give some comments on a few works related to invariant measures for (1). The linear implicit Euler time semi-discretization was examined in [14] for (1) with space-time white noise. In [15], the authors studied a full discretization realized by a spectral Galerkin method in spatial direction and an Euler scheme in temporal direction for (1) with space-time white noise. In [25], a full-discrete exponential Euler approximation of the invariant measure for (1) driven by additive noise was analyzed. The analysis in [14,15,25] was based on the condition that the nonlinearity F is supposed to be twice Fréchet differentiable in H, i.e., $\parallel F^{\prime \prime }{(u)\parallel }_{\mathcal{L}(H\times H;{\dot{H}}^{-\eta })}$, for all $u\in H$ for some $\eta \in [0,2)$. Here we relax conditions on F by assuming that F is a differentiable mapping (see Remarks 1–3). We stress that, to the best of our knowledge, in all articles which deal with the error of numerical invariant measures of (1), the obtained order of convergence is of the suboptimal form $\gamma -ϵ$ (see [14,15,25]). Hence, our improved results are derived based on a weaker condition.

The outline of this paper is organized as follows. In the next section, some preliminaries and assumptions are collected to ensure the ergodicity of the mild solution to the problem (1) and a brief introduction to the Malliavin calculus is also given, which plays an insignificant role in the error analysis of the invariant measures. In Section 3 we prove that the weak error of the spatial-spectral Galerkin method does not depend on the time interval, which enables us to achieve the same order as the weak error for the error of invariant measure. Similarly to the semi-discretization, the time-independent weak error together with the error of invariant measures is given in Section 4 for the full discretization. Finally, numerical examples are presented to verify the theoretical results.

2. Stochastic Problem and Malliavin Calculus

Given a separable $\mathbb{R}$-Hilbert space $\left(H,⟨·,·⟩,\parallel ·\parallel \right)$, let $\mathcal{L}(H)$ be the Banach space of all linear bounded operators from H to H and by ${\mathcal{B}}_b(H)$ (resp. $C_b(H)$) we denote the Banach space of all Borel bounded mappings (resp. a space of uniformly continuous and bounded mappings) $\Phi :H\to \mathbb{R}$ endowed with the norm ${\parallel \Phi \parallel }_0={sup}_{x\in H}|\Phi (x)|$. Also, we denote by ${\mathcal{L}}_2(H)$ the Hilbert space consisting of all Hilbert–Schmidt operators from H into H, equipped with the scalar product and the norm

$$\begin{array}{c}\hfill {⟨{\Gamma }_1,{\Gamma }_2⟩}_{{\mathcal{L}}_2(H)}=\sum _{j=1}^{\infty }⟨{\Gamma }_1{\varphi }_j,{\Gamma }_2{\varphi }_j⟩,{\parallel \Gamma \parallel }_{{\mathcal{L}}_2(H)}={\left(\sum _{j=1}^{\infty }\parallel \Gamma {\varphi }_j{\parallel }^2\right)}^{\frac{1}{2}},\end{array}$$

(7)

independent of the choice of orthonormal basis $\left\{{\varphi }_j\right\}$ of H. If $\Gamma \in {\mathcal{L}}_2(H)$ and $L\in \mathcal{L}(H)$, then $\Gamma L,L\Gamma \in {\mathcal{L}}_2(H)$ and

$$\begin{array}{c}\hfill {\parallel \Gamma L\parallel }_{{\mathcal{L}}_2(H)}\le {\parallel L\parallel }_{\mathcal{L}(H)}{\parallel \Gamma \parallel }_{{\mathcal{L}}_2(H)}{,\parallel L\Gamma \parallel }_{{\mathcal{L}}_2(H)}\le {\parallel L\parallel }_{\mathcal{L}(H)}{\parallel \Gamma \parallel }_{{\mathcal{L}}_2(H)}.\end{array}$$

(8)

2.1. Main Assumptions

In this subsection, we formulate main assumptions concerning the operator A, the nonlinear term $F(·)$, the noise process $W(t)$ and the initial data $X_0$, which will be used throughout this paper.

Assumption 1 

(Linear operator A). Let $\mathcal{D}\subset {\mathbb{R}}^d,d\in \{1,2,3\}$ be a bounded open spatial domain with smooth boundary and let $H:=L^2(\mathcal{D},\mathbb{R})$ be the real separable Hilbert space endowed with the usual inner product $⟨·,·⟩$ and the associated norm $\parallel ·\parallel ={⟨·,·⟩}^{\frac{1}{2}}$. Let $A:D(A)\subset H\to H$ be a densely defined, positive self-adjoint unbounded operator on H with compact inverse.

Such assumptions imply the existence of a sequence of nondecreasing positive real numbers ${\left\{{\lambda }_k\right\}}_{k\ge 1}$ and an orthonormal basis ${\left\{e_k\right\}}_{k\ge 1}$ of H such that

$$\begin{array}{c}\hfill A{e}_k={\lambda }_k{e}_k,\underset{k\to \infty }{lim}{\lambda }_k=+\infty .\end{array}$$

(9)

Furthermore, $-A$ generates an analytic semigroup $E(t)=e^{-tA}$ satisfying, (see [14,15])

$$\begin{array}{c}\hfill \begin{array}{c}\parallel A^{\mu }{E(t)\parallel }_{\mathcal{L}(H)}\le C{e}^{-\frac{{\lambda }_{1}t}{2}}{t}^{-\mu },t>0,\mu \ge 0,\\ \parallel A^{-\nu }{(E(t)-E(s))\parallel }_{\mathcal{L}(H)}\le C{(t-s)}^{\nu }{e}^{-\frac{{\lambda }_{1}s}{2}},0\le s<t,\nu \in [0,1],\end{array}\end{array}$$

(10)

and for any $\rho \in [0,1]$, (see [26])

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\int }_{{\tau }_1}^{{\tau }_2}{\parallel A^{\frac{\rho }{2}}E({\tau }_2-\sigma )x\parallel }^2\mathrm{d}\sigma \le C{({\tau }_2-{\tau }_1)}^{1-\rho }{\parallel x\parallel }^2,0\le {\tau }_1<{\tau }_2,\\ \hfill \parallel A^{\rho }{\int }_{{\tau }_1}^{{\tau }_2}E({\tau }_2-\sigma )x\mathrm{d}\sigma \parallel \le C{({\tau }_2-{\tau }_1)}^{1-\rho }\parallel x\parallel ,0\le {\tau }_1<{\tau }_2.\end{array}\end{array}$$

(11)

Throughout this article, we use generic constants which may vary at each appearance but are always independent of discretization parameters and t. By means of the spectral decomposition of A, we can also define the fractional powers $s\in \mathbb{R}$ of A in a simple way, e.g., $A^{s}v={\sum }_{k=1}^{\infty }{\lambda }_k^s⟨v,e_k⟩e_k$. Then denote the Hilbert space ${\dot{H}}^s:=D(A^{\frac{s}{2}})$ with the inner product $⟨A^{\frac{s}{2}}·,A^{\frac{s}{2}}·⟩$ and the associated norm ${\parallel ·\parallel }_s:=\parallel A^{\frac{s}{2}}·\parallel$.

Assumption 2 

(Nonlinearity). Suppose that $F:H\to H$ is assumed to be a differentiable mapping satisfying, for some $\gamma \in (0,1]$ and $\eta \in (\frac{3}{2},2)$

$$\begin{array}{cc}\hfill \parallel F^{\prime }(\phi )\psi \parallel & \le L\parallel \psi \parallel ,\phi ,\psi \in \dot{H},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \parallel A^{-\frac{\eta }{2}}{F}^{\prime }(\phi )\psi \parallel & \le L_{\eta }{(\parallel \phi \parallel }_{{\dot{H}}^{\gamma }}+{1)\parallel \psi \parallel }_{{\dot{H}}^{-\gamma }},\phi \in {\dot{H}}^{\gamma },\psi \in \dot{H}.\hfill \end{array}$$

(13)

Further, let F satisfy a one-sided Lipschitz condition

$$\begin{array}{c}\hfill ⟨\phi -\psi ,F(\phi )-F(\psi )⟩\le L_F\parallel \phi -\psi \parallel ,with{L}_F<{\lambda }_1,\phi ,\psi \in H.\end{array}$$

(14)

Assumption 3 

(Q-Wiener process). Let $W(t)$ be a standard H-valued Q-Wiener process on the stochastic basis $\left(\Omega ,\mathcal{F},\mathbb{P},{\left\{\mathcal{F}\right\}}_{t\ge 0}\right)$, where $Q\in \mathcal{L}(H)$ is a self-adjoint and positive definite bounded linear operator. Furthermore, let A and Q be commutable and satisfy

$$\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2(H)}<\infty ,$$

(15)

where $\gamma \in (0,1]$ is the parameter from (13).

It is well known that ${\left\{W(t)\right\}}_{t\ge 0}$ can be expressed in terms of its Fourier series, given by

$$W(t)=:\sum _{i=1}^{\infty }\sqrt{q_i}{\beta }_i(t)e_i,t\ge 0,$$

(16)

where ${\left\{{\beta }_i(t)\right\}}_{i\in \mathbb{N}}$ for $t\ge 0$ is a sequence of real-valued independently and identically distributed Brownian motions, ${\left\{e_i\right\}}_{i\in \mathbb{N}}$ also is an orthonormal basis of eigenvectors of the operator Q and ${\left\{q_i\right\}}_{i\in \mathbb{N}}$ is a corresponding sequence of positive eigenvalues. Therefore, Q possesses a unique positive square root. Then we are able to introduce the real Hilbert space $U_0=Q^{\frac{1}{2}}(H)$ with the inner product ${⟨u,v⟩}_{U_0}:={⟨Q^{-\frac{1}{2}}u,Q^{-\frac{1}{2}}v⟩}_H$, for all $u,v\in H$ and the space ${\mathcal{L}}_2^0={\mathcal{L}}_2(U_0,H)$ consisting of all Hilbert Schmidt operators from $U_0$ to H. The above assumption is sufficient to ensure that the stochastic convolution $\mathcal{O}(t):={\int }_0^{t}E(t-s)\mathrm{d}W(s)$ enjoys the following spatial-temporal regularity results (see Lemma 2.1 in [27], (3.10) in [25]), for any $p\in (1,\infty )$

$$\begin{array}{c}\hfill \underset{s\in (0,\infty )}{sup}{\parallel \mathcal{O}(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}\le C,\end{array}$$

(17)

and for any $\beta \in [0,\gamma ]$

$$\begin{array}{c}\hfill {\parallel \mathcal{O}(t)-\mathcal{O}(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\beta })}\le C{|t-s|}^{\frac{\gamma -\beta }{2}},\end{array}$$

(18)

where C is a positive constant independent of $t,s$.

Assumption 4 

(Initial data). Let the initial value $X_0$ be deterministic and for $\gamma \in (0,1]$ from (13), it holds

$$\begin{array}{c}\hfill \parallel X_0{\parallel }_{{\dot{H}}^{2\gamma }}<\infty .\end{array}$$

(19)

Remark 1. 

Note that (14) is a sufficient condition to ensure that ${\left\{X(t)\right\}}_{t\ge 0}$ is ergodic (see Section 8.6 in [23]) and there exist plenty of nonlinear Nemytskii operators, which satisfy Assumption 2 (see Example 3.2 in [28]). In the most literature on the weak convergence ([14,15,25,29,30]), the mapping F is usually assumed to be two differentiable and satisfies (12) and (13) with an additional condition: there exists a constant $\delta \in [0,2)$

$$\begin{array}{c}\hfill \parallel A^{-\frac{\delta }{2}}{F}^{\prime \prime }(\phi )({\phi }_1,{\phi }_2)\parallel \le L\parallel {\phi }_1\parallel \parallel {\phi }_2\parallel ,forall\phi ,{\phi }_1,{\phi }_2\in H.\end{array}$$

(20)

2.2. Regularity Results of the Model

This part is devoted to the space-time regularity properties of the mild solution to the underlying problem (1) over a long time. Existence, uniqueness, and regularity of mild solutions to (1) have been studied in [23]. A preliminary theorem is stated as follows.

Theorem 1. 

Under Assumptions 1–4, the problem (1) admits a unique mild solution $X(t)$, given by

$$X(t)=E(t)X_0+{\int }_0^{t}E(t-s)F(X(s))\mathrm{d}s+{\int }_0^{t}E(t-s)\mathrm{d}W(s),a.s,t\ge 0.$$

(21)

Moreover, there exists a constant $C=C(X_0,\gamma )$ such that, for any $p\ge 1$

$$\underset{s\in [0,\infty )}{sup}{\parallel X(s)\parallel }_{L^p(\Omega ;H)}\le C.$$

(22)

By a slight modification of the proof of (Theorem 3.1 in [25]), we can easily show (22). The temporal-spatial regularity of mild solution (21) over a period of time is discussed in (Theorems 3.1 and 4.1 in [31]) and (Theorem 2.4 in [32]). Furthermore, following the standard argument in [31] combining with very careful use of the smoothing property of the corresponding semigroup $E(t)$, we can desire further regularity results over a long time.

Theorem 2. 

Under Assumptions 1–4, the mild solution (21) enjoys the following regularity, for $p\in (1,\infty )$

$$\begin{array}{c}\hfill \underset{s\in [0,\infty )}{sup}{\parallel X(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}<\infty ,\end{array}$$

(23)

and, for $\beta \in [0,\gamma ]$

$$\begin{array}{c}\hfill {\parallel X(t)-X(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\beta })}\le C{|t-s|}^{\frac{\gamma -\beta }{2}},\end{array}$$

(24)

where C is a positive constant independent of $t,s$.

Proof of Theorem 2. 

Before proving (23) and (24), one can readily show that

$$\begin{array}{c}\hfill \underset{s\in [0,\infty )}{sup}{\parallel F(X(s))\parallel }_{L^p(\Omega ;H)}\le C(1+\underset{s\in [0,\infty )}{sup}{\parallel X(t)\parallel }_{L^p(\Omega ;H)})<\infty .\end{array}$$

(25)

Further, this together with (10) and (11) and the Burkholder–Davis–Gundy type inequality yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \underset{s\in [0,\infty )}{sup}{\parallel X(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}\le \underset{s\in [0,\infty )}{sup}({\parallel E(s)X_0\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}\hfill \\ \hfill & +{\int }_0^s{\parallel E(s-r)F(X(r))\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}\mathrm{d}s+\parallel {\int }_0^{s}E(s-r)\mathrm{d}W(r){\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })})\hfill \\ \hfill & \le \parallel X_0{\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}+C\underset{s\in [0,\infty )}{sup}({\int }_0^{s}C{(s-r)}^{-\frac{\gamma }{2}}{e}^{-\frac{{\lambda }_1(s-r)}{2}}{\parallel F(X(r))\parallel }_{L^p(\Omega ;H)}\mathrm{d}r\hfill \\ \hfill & +{\left({\int }_0^s{\parallel E(s-r)A^{\frac{\gamma }{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2\mathrm{d}r\right)}^{\frac{1}{2}})\hfill \\ \hfill & \le C\left(\parallel X_0{\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}+\underset{s\in [0,\infty )}{sup}\left({\int }_0^t{(s-r)}^{-\frac{\gamma }{2}}{e}^{-\frac{{\lambda }_1(t-s)}{2}}\mathrm{d}r\right)+{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}\right)\hfill \\ \hfill & <\infty ,\hfill \end{array}\end{array}$$

(26)

where in the last step we used the well-known fact of the Gamma function as follows

$$\begin{array}{c}\hfill {\int }_0^{\infty }{s}^{\rho -1}{e}^{-s}\mathrm{d}s<\infty ,\rho >0.\end{array}$$

(27)

For the regularity in time we apply (10), (11) and (25)–(27) and the Burkholder–Davis–Gundy type inequality to obtain, for $0\le s\le t$ and any $\beta \in [0,\gamma ]$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\parallel X(t)-X(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\beta })}\le {\parallel (I-E(t-s))X(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\beta })}\hfill \\ \hfill & +{\int }_s^t{\parallel E(t-r)F(X(r))\parallel }_{L^p(\Omega ;{\dot{H}}^{\beta })}\mathrm{d}r+\parallel {\int }_s^{t}E(t-r)\mathrm{d}W(r){\parallel }_{L^p(\Omega ;{\dot{H}}^{\beta })}\hfill \\ \hfill \le & C{(t-s)}^{\frac{\gamma -\beta }{2}}{\parallel X(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}+C{\int }_s^t{(t-r)}^{-\frac{\beta }{2}}{e}^{-\frac{{\lambda }_1(t-r)}{2}}{\parallel F(X(r))\parallel }_{L^p(\Omega ;H)}\mathrm{d}r\hfill \\ \hfill & +C{\left({\int }_s^t{\parallel A^{\frac{\beta }{2}}E(t-r)Q^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2\mathrm{d}r\right)}^{\frac{1}{2}}\hfill \\ \hfill \le & C{(t-s)}^{\frac{\gamma -\beta }{2}}({\parallel X(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}+{\int }_s^t{(t-r)}^{-\frac{\gamma }{2}}{e}^{-\frac{{\lambda }_1(t-r)}{2}}\mathrm{d}r\hfill \\ \hfill & +\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2(H)})\hfill \\ \hfill \le & C{(t-s)}^{\frac{\gamma -\beta }{2}}.\hfill \end{array}\end{array}$$

(28)

Thus we complete the proof. □

2.3. Ergodicity

In this part, we consider the ergodicity of the mild solution $X(t)$. Before that, we introduce some concepts related to the ergodicity of ${\left\{X(t)\right\}}_{t\ge 0}$. For any $\Phi \in {\mathcal{B}}_b(H)$, the mapping

$$P_t\Phi (X(t)):=\mathbb{E}[\Phi (X(t))],$$

(29)

is a transition semigroup from $[0,\infty )$ into the Banach space $\mathcal{L}({\mathcal{B}}_b(H))$ and it also is a Markov semigroup on ${\mathcal{B}}_b(H)$. Assuming that $\mu$ is a probability measure of $P_t$ on $(H,\mathcal{B}(H))$, $\mu$ is said to be invariant for ${\left\{P_t\right\}}_{t\ge 0}$, if

$$\begin{array}{c}\hfill {\int }_H{P}_t\Phi dt={\int }_H\Phi \mathrm{d}\mu ,\Phi \in {\mathcal{B}}_b(H),t\ge 0.\end{array}$$

(30)

It is well known that Von Neumann theorem (Theorem 5.12 in [33]) ensures that the limit

$$\begin{array}{c}\hfill \underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T{P}_t\Phi (y)\mathrm{d}t,forall\Phi \in L^2(H,\mu ),\end{array}$$

(31)

always exists in $L^2(H,\mu )$. If in addition, it happens that

$$\begin{array}{c}\hfill \underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T{P}_t\Phi (y)\mathrm{d}t={\int }_H\Phi (y)\mu (dy)in{L}^2(H,\mu ),\end{array}$$

(32)

for all $\Phi \in L^2(H,\mu )$, $P_t$ and the mild solution $X(t)$ are said to be ergodic.

Assumptions 1–4 are sufficient conditions to show that ${\left\{X(t)\right\}}_{t\ge 0}$ is ergodic, see (Section 8.6 in [23], [16,25]).

Theorem 3. 

Under Assumptions 1–4, the mild solution ${\left\{X(t)\right\}}_{t\ge 0}$ is ergodic with a unique invariant probability measure ν.

2.4. The Stochastic Integral and Malliavin Calculus

Malliavin calculus is a standard technique to obtain weak convergence rates of numerical approximation of stochastic partial differential equations, for instance, see [30,34,35]. In this part, we introduce some concepts related to Malliavin calculus, especially the notation of Malliavin derivative and Malliavin integration by parts formula. For a more detailed introduction to Malliavin calculus, we refer to the classical monograph [36].

We now introduce the Malliavin derivative, which is an important operator of the Malliavin calculus. For a deterministic mapping $\Psi \in L^2\left([0,T];{\mathcal{L}}_2(U_0,\mathbb{R})\right)$, we define an isonormal process $M:L^2\left([0,T];{\mathcal{L}}_2(U_0,\mathbb{R})\right)\to L^2(\Omega ;\mathbb{R})$ by

$$M(\Psi ):={\int }_0^T\Psi (t)\mathrm{d}W(t),$$

(33)

where the integral on the right-hand side is the usual Itô-integral. With this, we define $\mathcal{S}(H)$ to be the set of all smooth cylindrical random variables, for ${\Psi }_j\in L^2\left([0,T];{\mathcal{L}}_2(U_0,\mathbb{R})\right)$, $j=1,\cdots ,m$, $m\in \mathbb{N}$

$$\mathcal{S}(H)=\left\{F=\sum _{i=1}^n{f}_i\left(M({\Psi }_1),\cdots ,M({\Psi }_m)\right)h_i,f_i\in C_p^{\infty }({\mathbb{R}}^m,\mathbb{R}),h_i\in H,n\in \mathbb{N}\right\},$$

(34)

where $C_p^{\infty }({\mathbb{R}}^m,\mathbb{R})$ represents the space of all real-valued $C^{\infty }$-functions on ${\mathbb{R}}^m$ with polynomial growth. Obviously, $\mathcal{S}(H)$ is a subset of the space $L^2(\Omega ;H)$. The Malliavin derivative of F, at time s, is defined as

$$\begin{array}{c}\hfill D_{s}F:=\sum _{i=1}^n\sum _{j=1}^m{\partial }_j{f}_i\left(M({\Psi }_1),\cdots ,M({\Psi }_m)\right)h_i\otimes {\Psi }_j(s),\end{array}$$

(35)

where $h_i\otimes {\Psi }_j(s)$ denotes the tensor product of $h_i\in H$ and ${\Psi }_j\in {\mathcal{L}}_2(U_0,\mathbb{R})$, that is for $1\le i\le n$ and $1\le j\le m$

$$\begin{array}{c}\hfill \left(h_i\otimes {\Psi }_j(t)\right)(u)=\left({\Psi }_j(t)(u)\right)h_i\in H,u\in U_0,t\in [0,T].\end{array}$$

(36)

Thanks to the fact $h_i\otimes {\Psi }_j(t)\in {\mathcal{L}}_2^0$, the operator $D:\mathcal{S}(H)\subset L^2(\Omega ;H)\to L^2\left(\Omega ;L^2([0,T];{\mathcal{L}}_2^0)\right)$ is well-defined and closable. Then we define by ${\mathbb{D}}^{1,2}(H)$ the closure of the set of smooth random variables $\mathcal{S}(H)$ in the space $L^2(\Omega ;H)$ with the respective to the norm

$${\parallel F\parallel }_{{\mathbb{D}}^{1,2}(H)}={\left(\mathbb{E}\left[{\parallel F\parallel }^2\right]+\mathbb{E}{\int }_0^T{\parallel D_{t}F\parallel }_{{\mathcal{L}}_2^0}^2\mathrm{d}t\right)}^{\frac{1}{2}},$$

(37)

and we obtain a well-defined extension of the operator $D:{\mathbb{D}}^{1,2}(H)\subset L^2(\Omega ;H)\to L^2(\Omega ;L^2([0,T];{\mathcal{L}}_2^0))$. Additionally, we define the process $D_s^{u}F$ by $⟨D_{s}F,u⟩=D_s^{u}F$, which represents Malliavin derivative in the direction $u\in U_0$. Moreover, the chain rule of the Malliavin derivative is valid. For another separable Hilbert space $\mathcal{H}$, if $\rho \in C_b^1(H,\mathcal{H})$, then $\rho (F)\in {\mathbb{D}}^{1,2}(\mathcal{H})$ and $D_t^{\mu }(\rho (F))={\rho }^{\prime }(F)·D_t^{u}F$. Finally, the Malliavin derivative of the Itô integral ${\int }_0^t\Psi (s)\mathrm{d}W(s)$ with predictable $\Psi (t)\in L^2\left(\Omega ;L^2\left([0,T],{\mathcal{L}}_2^0\right)\right)$ and $F\in {\mathbb{D}}^{1,2}(H)$, for all $t\in [0,T]$ satisfies the equation:

$$D_s^u{\int }_0^t\Psi (r)\mathrm{d}W(r)={\int }_0^t{D}_s^u\Psi (r)\mathrm{d}W(r)+\Psi (s)u,0\le s\le t\le T.$$

(38)

If $s>t$, then $D_s^u{\int }_0^t\Psi (r)\mathrm{d}W(r)=0$, since the integral is ${\mathcal{F}}_t$-measurable.

The remainder of this section is concerned with the Mallivin integration by parts formula, which is significant in the weak analysis provided below. For any $F\in {\mathbb{D}}^{1,2}(H)$ and adapted process $\Psi (t)\in L^2(\Omega ;L^2\left([0,T],{\mathcal{L}}_2^0\right)$, the following integration by parts formula is valid, (Lemma 2.1 in [37])

$$\mathbb{E}{⟨DF,\Psi ⟩}_{L^2([0,T],{\mathcal{L}}_2^0)}=\mathbb{E}{⟨F,{\int }_0^T\Psi (t)\mathrm{d}W(t)⟩}_H.$$

(39)

3. Spatial Semi-Discretization

In this section, we consider the spatial semi-discrete spectral Galerkin method for the considering problem (1) and show that the weak error of the spatial semi-discrete scheme does not depend on the time interval and the weak order is optimal. Then applying the weak error implies the convergence order of $\nu$ and ${\nu }^N$, where $\nu$ and ${\nu }^N$ are invariant measures of the mild solution $X(t)$ and that of the semi-discrete problem, respectively.

3.1. Spectral Galerkin Method and Its Ergodicity

For $N\in \mathbb{N}$, we define a finite-dimensional subspace of H by $H_N:=$ span$\{e_1,e_2,\cdots ,e_N\}$ and the projection operator $P_N:{\dot{H}}^{\beta }\to H_N$ by

$$P_{N}v=\sum _{j=1}^N⟨v,e_j⟩e_j,forallv\in {\dot{H}}^{\beta },\beta \ge -2,$$

(40)

where ${\left\{e_j\right\}}_{j=1}^N$ are the N first eigenvectors of the dominant linear operator A. By the definition of $P_N$, one can imply $\parallel P_N{v\parallel }_{{\dot{H}}^{\alpha }}\le {\parallel v\parallel }_{{\dot{H}}^{\alpha }}$, for $v\in {\dot{H}}^{\alpha }$, $\alpha \in \mathbb{R}$ and for $v\in {\dot{H}}^{\beta },\beta \ge 0$

$$\parallel (I-P_N)v\parallel ={\left(\sum _{j=N+1}^{\infty }{⟨v,e_j⟩}^2\right)}^{\frac{1}{2}}\le {\lambda }_{N+1}^{-\frac{\beta }{2}}{\left(\sum _{j=N+1}^{\infty }{\lambda }_j^{\beta }{⟨v,e_j⟩}^2\right)}^{\frac{1}{2}}\le {\lambda }_{N+1}^{-\frac{\beta }{2}}{\parallel v\parallel }_{{\dot{H}}^{\beta }}.$$

(41)

Now we introduce a Galerkin approximation of (1) in the finite-dimension space $H_N$ as follows

$$\mathrm{d}{X}_N(t)+A_N{X}_N(t)\mathrm{d}t=P_{N}F(X_N(t))\mathrm{d}t+P_N\mathrm{d}W(t),X_N(0)=P_N{X}_0,$$

(42)

where $A_N:H_N\to H_N$ is defined by $A_N:=P_{N}A$ and generates a strongly continuous semigroup $E_N(t)=e^{-t{A}_N}$, $t\ge 0$ in $H_N$. Note that the operators A and $P_N$ are commutable, e.g., $A{P}_N=P_{N}A=A_N$. Analogously to the stochastic problem (1), the unique mild solution of (42) is given by

$$X_N(t)=E_N(t)P_N{X}_0+{\int }_0^t{E}_N(t-s)P_{N}F(X_N(s))\mathrm{d}s+{\int }_0^t{E}_N(t-s)P_N\mathrm{d}W(s).$$

(43)

Assumptions 1–4 sufficiently ensure that the mild solution $X_N(t)$ admits a unique invariant measure ${\nu }^N$, see (Theorem 3.2 in [25]) and enjoys a similar temporal-spatial regularity as the mild solution (21) in Theorem 2.

Lemma 1. 

Let Assumptions 1–4 hold. Then the mild solution (43) is ergodic with a unique invariant measure ${\nu }^N$. Additionally, there exists a constant $C=C(X_0,\gamma )$ independent of $t,s$ and N such that, for $p\in (1,\infty )$

$$\begin{array}{c}\hfill \underset{N\in {\mathbb{N}}^{+}}{sup}\underset{s\in [0,\infty )}{sup}{\parallel X_N(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}<\infty ,\end{array}$$

(44)

for $\beta \in [0,\gamma ]$

$$\begin{array}{c}\hfill \underset{N\in {\mathbb{N}}^{+}}{sup}\parallel X_N(t)-X_N{(s)\parallel }_{L^p(\Omega ;{\dot{H}}^{\beta })}\le C{|t-s|}^{\frac{\gamma -\beta }{2}}.\end{array}$$

(45)

3.2. Weak Convergence for Spatial Semi-Discretization over Long Time

This part is devoted to the weak convergence of spectral Galerkin method (42). Before starting the proof of the weak convergence rate, we need to give the regularity of the Malliavin derivative of $X^N(t)$ over a long time, which will play an essential role in our weak convergence analysis.

Lemma 2. 

Let Assumptions 1–4 hold. Then the Malliavin derivative of $X_N(t)$ satisfies, for $0\le s<t$

$$\begin{array}{c}\hfill \underset{N\in {\mathbb{N}}^{+}}{sup}\mathbb{E}\left[\parallel D_s{X}_N{(t)\parallel }_{{\mathcal{L}}_2^0}^2\right]\le C\left(1+{(t-s)}^{\gamma -1}\right),\end{array}$$

(46)

where C is a constant independent of $s,t$ and N.

Proof of Lemma 2. 

Differentiating the equation (43) formally in the direction $y\in U_0$ and using (38), chain rule and the fact that the initial value is deterministic imply, for $0\le s<t$

$$\begin{array}{c}\hfill D_s^y{X}_N(t)=E_N(t-s)P_{N}y+{\int }_s^t{E}_N(t-r)P_N{F}^{\prime }(X_N(r))D_s^y{X}_N(r)\mathrm{d}r.\end{array}$$

(47)

It is not difficult to check that this equation has a unique solution. Then we obtain

$$\begin{array}{cc}\hfill \parallel D_s^y{X}_N{(t)\parallel }_{L^2(\Omega ;H)}& \le \parallel E_N(t-s)P_N{y\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +{\int }_s^t{\parallel E_N(t-r)P_N{F}^{\prime }(X_N(r))D_s^y{X}_N(r)\parallel }_{L^2(\Omega ;H)}\mathrm{d}r.\hfill \end{array}$$

(48)

Note that $\parallel P_N{v\parallel }_{{\dot{H}}^{\beta }}\le {\parallel v\parallel }_{{\dot{H}}^{\beta }}$, for $\beta \in \mathbb{R}$ and the operators A and $P_N$ are commutable. In view of (10) and the boundedness of $F^{\prime }(·)$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel D_s^y{X}_N{(t)\parallel }_{L^2(\Omega ;H)}\le & C{e}^{-\frac{{\lambda }_1(t-s)}{2}}{(t-s)}^{\frac{\gamma -1}{2}}{\parallel A^{\frac{\gamma -1}{2}}y\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +C{\int }_s^t{e}^{-\frac{{\lambda }_1(t-r)}{2}}{\parallel D_s^y{X}_N(r)\parallel }_{L^2(\Omega ;H)}\mathrm{d}r.\hfill \end{array}\end{array}$$

(49)

Then by (27) and applying the Gronwall inequality, one can easily observe that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel D_s^y& X_N{(t)\parallel }_{L^2(\Omega ;H)}\le C{e}^{-\frac{{\lambda }_1(t-s)}{2}}{(t-s)}^{\frac{\gamma -1}{2}}{\parallel A^{\frac{\gamma -1}{2}}y\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +C{\int }_s^t{(t-r)}^{\frac{\gamma -1}{2}}{e}^{-{\lambda }_1(t-r)}{\parallel A^{\frac{\gamma -1}{2}}y\parallel }_{L^2(\Omega ;H)}{e}^{{\int }_r^t{e}^{-\frac{{\lambda }_1(t-\tau )}{2}}\mathrm{d}\tau }\mathrm{d}r\hfill \\ \hfill \le & C\left(1+{(t-s)}^{\frac{\gamma -1}{2}}\right){\parallel A^{\frac{\gamma -1}{2}}y\parallel }_{L^2(\Omega ;H)}.\hfill \end{array}\end{array}$$

(50)

Finally, by taking an ON-basis ${\left\{e_i\right\}}_{i=1}^{\infty }\subset H$, we can compute the ${\mathcal{L}}_2^0$-norm as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}\left[\parallel D_s{X}_N{(t)\parallel }_{{\mathcal{L}}_2^0}^2\right]& =\sum _{i=1}^{\infty }\mathbb{E}\left[\parallel D_s^{Q^{\frac{1}{2}}{e}_i}{X}_N{(t)\parallel }^2\right]\hfill \\ \hfill & \le C\left(1+{(t-s)}^{\gamma -1}\right)\sum _{i=1}^{\infty }{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{e}_i\parallel }^2\hfill \\ \hfill & \le C\left(1+{(t-s)}^{\gamma -1}\right){\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{}_{{\mathcal{L}}_2(H)}}^2.\hfill \end{array}\end{array}$$

(51)

Hence, the proof of this lemma is complete. □

With the above preparation, we will follow the strategy used in [24] to derive the following time-independent weak error for the spectral Galerkin scheme.

Theorem 4. 

Suppose that Assumptions 1–4 are valid. Let $X(t)$ and $X_N(t)$ be the mild solutions of (1) and (42), respectively. For any $T>0$, $N\in \mathbb{N}$ and $\Phi \in C_b^2(H,\mathbb{R})$, there exists a constant C independent of T and N such that

$$\begin{array}{c}\hfill \left|\mathbb{E}\right[\Phi (X(T))]-\mathbb{E}[\Phi (X_N(T))\left]\right|\le C{\lambda }_N^{-\gamma }.\end{array}$$

(52)

Proof of Theorem 4. 

By introducing two auxiliary processes $\tilde{X}(t):=X(t)-\mathcal{O}(t)$ and ${\tilde{X}}_N(t):=X_N(t)-P_N\mathcal{O}(t)$, we can separate the considered error term $\mathbb{E}[\Phi (X(T))]-\mathbb{E}[\Phi (X_N(T))]$ as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \mathbb{E}[\Phi (X(T))]-\mathbb{E}[\Phi (X_N(T))]\hfill \\ \hfill & =\left(\mathbb{E}[\Phi (\tilde{X}(T)+\mathcal{O}(T))\right]-\mathbb{E}[\Phi ({\tilde{X}}_N(T)+\mathcal{O}(T))])\hfill \\ \hfill & +\left(\mathbb{E}[\Phi ({\tilde{X}}_N(T)+\mathcal{O}(T))\right]-\mathbb{E}[\Phi ({\tilde{X}}_N(T)+P_N\mathcal{O}(T))])\hfill \\ \hfill & =:I_1+I_2.\hfill \end{array}\end{array}$$

(53)

Firstly, we bound the term $I_2$. By applying the second-order Taylor expansion and the Malliavin integration by parts formula (39) and using (17) and (41), one can find that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |I_2|& =\left|\mathbb{E}\right[{\Phi }^{\prime }(X_N(T))(I-P_N)\mathcal{O}(T)\hfill \\ \hfill +& {\int }_0^1{\Phi }^{\prime \prime }(X_N(T)+\lambda (I-P_N)\mathcal{O}(T))\left((I-P_N)\mathcal{O}(T),(I-P_N)\mathcal{O}(T)\right)(1-\lambda )\mathrm{d}\lambda \left]\right|\hfill \\ \hfill \le & \left|\mathbb{E}{\int }_0^T{⟨(I-P_N)E(T-s),D_s{\Phi }^{\prime }(X_N(T))⟩}_{{\mathcal{L}}_2^0}\mathrm{d}s\right|+C\mathbb{E}[\parallel (I-P_N)\mathcal{O}(T){\parallel }^2]\hfill \\ \hfill \le & \underset{\mathbb{L}}{\underbrace{\left|\mathbb{E}{\int }_0^T{⟨(I-P_N)E(T-s),D_s{\Phi }^{\prime }(X_N(T))⟩}_{{\mathcal{L}}_2^0}\mathrm{d}s\right|}}+C{\lambda }_N^{-\gamma }.\hfill \end{array}\end{array}$$

(54)

Further, applying the chain rule of the Malliavin derivative and (47) enables us to obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{L}=& \left|\mathbb{E}{\int }_0^T{⟨(I-P_N)E(T-s),{\Phi }^{\prime \prime }(X_N(T))D_s{X}_N(T)⟩}_{{\mathcal{L}}_2^0}\mathrm{d}s\right|\hfill \\ \hfill \le & \left|\mathbb{E}{\int }_0^T{⟨(I-P_N)E(T-s),{\Phi }^{\prime \prime }(X_N(T))E_N(T-s)⟩}_{{\mathcal{L}}_2^0}\mathrm{d}s\right|\hfill \\ \hfill & +|\mathbb{E}{\int }_0^T<(I-P_N)E(T-s),{\Phi }^{\prime \prime }(X_N(T))·\hfill \\ \hfill & {\int }_s^T{E}_N(T-r)P_N{F}^{\prime }(X_N(r))D_s{X}_N(r)\mathrm{d}r{>}_{{\mathcal{L}}_2^0}\mathrm{d}s|\hfill \\ \hfill :=& {\mathbb{L}}_1+{\mathbb{L}}_2.\hfill \end{array}\end{array}$$

(55)

Thanks to (10), (27), (41) and (46), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{L}}_2\le & C{\int }_0^T{\parallel (I-P_N)E(T-s)\parallel }_{{\mathcal{L}}_2^0}·\hfill \\ \hfill & {\int }_s^T\mathbb{E}\parallel E_N(T-r)P_N{F}^{\prime }(X_N(r))D_s{X}_N(r){\parallel }_{{\mathcal{L}}_2^0}\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }{\int }_0^T{e}^{-\frac{{\lambda }_1(T-s)}{2}}{(T-s)}^{-\frac{\gamma +1}{2}}{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}·\hfill \\ \hfill & {\int }_s^T\mathbb{E}\parallel D_s{X}_N(r){\parallel }_{{\mathcal{L}}_2^0}\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2(H)}^2{\lambda }_N^{-\gamma }{\int }_0^T{e}^{-\frac{{\lambda }_1(T-s)}{2}}{(T-s)}^{-\frac{\gamma +1}{2}}·\hfill \\ \hfill & {\int }_s^T{(1+(r-s)}^{\frac{\gamma -1}{2}})\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }.\hfill \end{array}\end{array}$$

(56)

In order to treat the term ${\mathbb{L}}_1$, we rewrite it as

$${\mathbb{L}}_1=\left|\sum _{j=1}^{\infty }{\int }_0^T⟨(I-P_N)E(T-s)Q^{\frac{1}{2}}{e}_j,{\Phi }^{\prime \prime }(X_N(T))E_N(T-s)Q^{\frac{1}{2}}{e}_j⟩\mathrm{d}s\right|.$$

(57)

Then we use the fact A and Q are commutable to derive

$$\begin{array}{cc}\hfill {\mathbb{L}}_1=& \left|\sum _{j=N+1}^{\infty }{\int }_0^T{e}^{-2{\lambda }_j(T-s)}\mathrm{d}s⟨Q^{\frac{1}{2}}{e}_j,{\Phi }^{\prime \prime }(X_N(T))Q^{\frac{1}{2}}{e}_j⟩\right|\hfill \\ \hfill \le & C\sum _{j=N+1}^{\infty }{\lambda }_j^{-1}\left|⟨Q^{\frac{1}{2}}{e}_j,{\Phi }^{\prime \prime }(X_N(T))Q^{\frac{1}{2}}{e}_j⟩\right|\hfill \\ \hfill \le & C\sum _{j=N+1}^{\infty }{\lambda }_j^{-\gamma }\left|⟨Q^{\frac{1}{2}}{A}^{\frac{\gamma -1}{2}}{e}_j,{\Phi }^{\prime \prime }(X_N(T))Q^{\frac{1}{2}}{A}^{\frac{\gamma -1}{2}}{e}_j⟩\right|\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }\sum _{j=1}^{\infty }\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{e}_j\parallel \parallel {\Phi }^{\prime \prime }(X_N(T))A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{e}_j\parallel \hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2,\hfill \end{array}$$

(58)

which together with (56) yields

$$\mathbb{L}\le C{\lambda }_N^{-\gamma }.$$

(59)

Thus, this in combination with (54) and (59), we arrive at

$$I_2\le C{\lambda }_N^{-\gamma }.$$

(60)

Now it remains to bound $I_1$. It follows from the Taylor formula and the condition $\Phi \in C_b^2(H,\mathbb{R})$ that

$$\begin{array}{cc}\hfill |I_1|=& \left|\mathbb{E}\right[\Phi (\tilde{X}(T)+\mathcal{O}(T))]-\mathbb{E}[\Phi ({\tilde{X}}_N(T)+\mathcal{O}(T))\left]\right|\hfill \\ \hfill =& \left|\mathbb{E}{\int }_0^1{\Phi }^{\prime }\left(X(T)+s({\tilde{X}}_N(T)-\tilde{X}(T))\right)\left({\tilde{X}}_N(T)-\tilde{X}(T)\right)\mathrm{d}s\right|\hfill \\ \hfill \le & C\mathbb{E}\left[\parallel {\tilde{X}}_N(T)-P_N\tilde{X}(T)\parallel \right]+C\mathbb{E}\left[\parallel P_N\tilde{X}(T)-\tilde{X}(T)\parallel \right]\hfill \\ \hfill :=& C\mathbb{E}\left[\parallel e_1(T)\parallel \right]+C\mathbb{E}\left[\parallel e_2(T)\parallel \right].\hfill \end{array}$$

(61)

Applying (10)–(12), (24), (27), and (41), we deduce

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}[\parallel e_2(T)& \parallel ]=\mathbb{E}\left[\parallel (I-P_N)\left(E(T)X_0+{\int }_0^{T}E(T-s)F(X(s))\mathrm{d}s\right)\parallel \right]\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }\mathbb{E}\left[\parallel X_0{\parallel }_{{\dot{H}}^{2\gamma }}+\parallel {\int }_0^{T}E(T-s)F(X(s))\mathrm{d}s{\parallel }_{{\dot{H}}^{2\gamma }}\right]\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }({\parallel X_0\parallel }_{{\dot{H}}^{2\gamma }}+\mathbb{E}\left[\parallel {\int }_0^T{A}^{\gamma }E(T-s)F(X(T))\mathrm{d}s\parallel \right]\hfill \\ \hfill & +{\int }_0^T\mathbb{E}\left[\parallel A^{\gamma }E(T-s)\left(F(X(s))-F(X(T))\right)\parallel \right]\mathrm{d}s)\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }({\parallel X_0\parallel }_{{\dot{H}}^{2\gamma }}+\mathbb{E}\left[\parallel F(X(T))\parallel \right]\hfill \\ \hfill & +{\int }_0^T{e}^{-\frac{{\lambda }_1(T-s)}{2}}{(T-s)}^{-\gamma }\mathbb{E}\parallel F(X(s))-F(X(T))\parallel \mathrm{d}s)\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }\left(\parallel X_0{\parallel }_{{\dot{H}}^{2\gamma }}+\mathbb{E}\left[\parallel F(X(T))\parallel \right]+{\int }_0^T{e}^{-\frac{{\lambda }_1(T-s)}{2}}{(T-s)}^{-\frac{\gamma }{2}}\mathrm{d}s\right)\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }.\hfill \end{array}\end{array}$$

(62)

Finally, we turn our attention to the error $e_1(T)={\tilde{X}}_N(T)-P_N\tilde{X}(T)$. Recalling the two definitions ${\tilde{X}}_N(t)=X_N(t)-P_N\mathcal{O}(t)$ and $\tilde{X}(t)=X(t)-\mathcal{O}(t)$, we obtain by (21) and (43)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill e_1(t)=& {\int }_0^t{E}_N(t-s)P_N\left(F({\tilde{X}}_N(s)+P_N\mathcal{O}(s))-F(\tilde{X}(s)+\mathcal{O}(s))\right)\mathrm{d}s\hfill \\ \hfill =& {\int }_0^t{E}_N(t-s)P_N\left(F({\tilde{X}}_N(s)+P_N\mathcal{O}(s))-F(P_N\tilde{X}(s)+P_N\mathcal{O}(s))\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{E}_N(t-s)P_N\left(F(P_{N}X(s))-F(X(s))\right)\mathrm{d}s.\hfill \end{array}\end{array}$$

(63)

Then employing (10) and (12) implies

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel e_1{(t)\parallel }_{L^2(\Omega ;H)}\le & {\int }_0^t\parallel E_N(t-s)P_N(F({\tilde{X}}_N(s)+P_N\mathcal{O}(s))\hfill \\ \hfill & -F(P_N\tilde{X}(s)+P_N\mathcal{O}(s)){)\parallel }_{L^2(\Omega ;H)}\mathrm{d}s\hfill \\ \hfill & +\parallel {\int }_0^t\parallel E_N(t-s)P_N(F(P_{N}X(s))-F(X(s))\parallel \mathrm{d}s{\parallel }_{L^2(\Omega ;\mathbb{R})}\hfill \\ \hfill \le & C{\int }_0^t{e}^{-\frac{{\lambda }_1(t-s)}{2}}{\parallel e_1(s)\parallel }_{L^2(\Omega ;H)}\mathrm{d}s\hfill \\ \hfill & +\underset{J}{\underbrace{{\int }_0^t{\parallel E_N(t-s)P_N\left(F(P_{N}X(s))-F(X(s))\right)\parallel }_{L^2(\Omega ;H)}\mathrm{d}s}}.\hfill \end{array}\end{array}$$

(64)

Thus to control $\parallel e_1{\parallel }_{L^2(\Omega ;H)}$, it suffices to bound J. Owing to (13), (23), (27), (41) and the first-order Taylor expansion, we find

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill J\le & {\int }_0^t{\int }_0^1\parallel E_N(t-s)P_N{F}^{\prime }\left((I+\theta (I-P_N))X(s)\right)\hfill \\ \hfill & \times (I-P_N)X(s){\parallel }_{L^2(\Omega ;H)}\mathrm{d}\theta \mathrm{d}s\hfill \\ \hfill \le & C_{\eta }{\int }_0^t{\int }_0^1{e}^{-\frac{{\lambda }_1(t-s)}{2}}{(t-s)}^{-\frac{\eta }{2}}\left(1+\parallel (I+\theta (I-P_N))X(s){\parallel }_{L^4(\Omega ;{\dot{H}}^{\gamma })}\right)\hfill \\ \hfill & \times \parallel (I-P_N)X(s){\parallel }_{L^4(\Omega ;{\dot{H}}^{-\gamma })}\mathrm{d}\theta \mathrm{d}s\hfill \\ \hfill \le & C{\lambda }_N^{-\gamma }{\int }_0^t{e}^{-\frac{{\lambda }_1(t-s)}{2}}{(t-s)}^{-\frac{\eta }{2}}{\parallel X(s)\parallel }_{L^4(\Omega ;{\dot{H}}^{\gamma })}^2\mathrm{d}s\le C{\lambda }_N^{-\gamma }.\hfill \end{array}\end{array}$$

(65)

Using the Gronwall inequality, one can derive

$$\parallel e_1{(T)\parallel }_{L^2(\Omega ;H)}\le C{\lambda }_N^{-\gamma }+CL{\lambda }_N^{-\gamma }{\int }_0^T{e}^{-\frac{{\lambda }_1(T-s)}{2}}{e}^{L{\int }_s^T{e}^{-\frac{{\lambda }_1(T-r)}{2}}\mathrm{d}r}\mathrm{d}s\le C{\lambda }_N^{-\gamma }.$$

(66)

This together with (54)–(62) verifies the desired result (52). □

3.3. Spatial Semi-Discrete Approximation of the Invariant Law $\nu$

Theorem 5. 

Suppose that Assumptions 1–4 are valid. Let ν and ${\nu }^N$ be the corresponding unique invariant measures of ${\left\{X(t)\right\}}_{t\ge 0}$ and ${\left\{X_N(t)\right\}}_{t\ge 0}$, respectively. For any $N\in \mathbb{N}$, there exists a constant C independent of N such that

$$\begin{array}{c}\hfill |{\int }_H\Phi (y)\nu (\mathrm{d}y)-{\int }_{H_N}\Phi (y){\nu }^N(\mathrm{d}y)|\le C{\lambda }_N^{-\gamma }.\end{array}$$

(67)

Proof of Theorem 5. 

By the definition of ergodicity, we have the following two equations

$$\begin{array}{c}\hfill \underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T\mathbb{E}[\Phi (X(t))]\mathrm{d}t={\int }_H\Phi (y)\nu (\mathrm{d}y),\end{array}$$

(68)

$$\begin{array}{c}\hfill \underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T\mathbb{E}[\Phi (X_N(t))]\mathrm{d}t={\int }_{H_N}\Phi (y){\nu }^N(\mathrm{d}y).\end{array}$$

(69)

Then, from the time-independent weak error in Theorem 4, it follows that

$$\begin{array}{cc}\hfill & |{\int }_H\Phi (y)\nu (\mathrm{d}y)-{\int }_{H_N}\Phi (y){\nu }^N(\mathrm{d}y)|\hfill \\ \hfill & \le \underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T|\mathbb{E}[\Phi (X(t))]-\mathbb{E}[\Phi (X_N(t))]|\mathrm{d}t\le C{\lambda }_N^{-\gamma },\hfill \end{array}$$

(70)

as required. □

Remark 2. 

Note, that (15) is fulfilled with $\gamma <\frac{1}{2}$ for the space-time white noise in one dimension. In this case, our convergence result yields a convergence order of $O({\lambda }_N^{-\gamma })$, which is identical to the result in [25]. For the trace class noise ($\gamma =1$), our convergence result gives a convergence order of $O({\lambda }_N^{-1})$, which improves the error bound $O({\lambda }^{-1+ϵ})$, for arbitrarily small $ϵ>0$ in [25]. From the above analysis and Remark 1, one can know that our results improve that in [25] under a weaker setting.

4. Fully-Discretization

In this section, we first proceed to study a full discretization of (1) and provide some regularity estimates. Secondly, with the help of these estimates, the time-independent weak error is obtained. Finally, based on the ergodicity of the numerical solution and the time-independent weak error, we derive convergence order between invariant measures $\nu$ and ${\nu }_{\tau }^N$, where ${\nu }_{\tau }^N$ is a unique invariant measure of the fully discrete numerical solution.

4.1. Fully Discrete Scheme and Its Ergodicity

Let $\tau =T/M$, $M\in \mathbb{N}$ be the uniform time-step size and $t_m=m\tau$, $m=1,2,\cdots ,M$. We discretize (42) with the linear implicit Euler method in time and the resulting fully-discrete problem is to find ${\mathcal{F}}_{t_m}$-adapted random variable $X_N^m\in H_N$ such that, for $m=1,2,\cdots ,M$

$$\begin{array}{cc}\hfill X_N^m-X_N^{m-1}+\tau A_N{X}_N^m=& \tau P_{N}F(X_N^{m-1})+P_N\Delta W_m,X_N^0=P_N{X}_0,\hfill \\ \hfill & with\Delta W_m=W(t_m)-W(t_{m-1}).\hfill \end{array}$$

(71)

After introducing a family operators $E_N^m:={(I+\tau A_N)}^{-m}$, $m=0,1,2,\cdots ,M$, the solution of (71), similar to the semi-discrete case, can be expressed by the following form

$$X_N^m=E_N^m{P}_N{X}_0+\tau \sum _{i=0}^{m-1}{E}_N^{m-i}{P}_{N}F(X_N^i)+\sum _{i=0}^{m-1}{E}_N^{m-i}{P}_N\Delta W_{i+1}.$$

(72)

The following lemma concerns the ergodicity and the spatial regularity of ${\left\{X_N^m\right\}}_{m\in \mathbb{N}}$ over a long time.

Lemma 3. 

Let Assumptions 1–4 hold and $\tau \le {\tau }_0\le \frac{{\lambda }_1-L_F}{4L^2}$. Then the solution of the fully-discrete problem (71) is ergodic with a unique invariant measure ${\nu }_{\tau }^N$. Additionally, there exists a constant $C=C(X_0,\gamma )$ independent of $m\in \{1,2,\cdots ,M\}$ and N such that

$$\begin{array}{c}\hfill \underset{N\in {\mathbb{N}}^{+}}{sup}\underset{m\in \{1,2,\cdots ,M\}}{sup}{\parallel X_N^m\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}<\infty ,\end{array}$$

(73)

and, for any $\beta \in [0,\gamma ]$ and $1\le n<m$

$$\begin{array}{c}\hfill \underset{N\in {\mathbb{N}}^{+}}{sup}{\parallel X_N^m-X_N^n\parallel }_{L^2(\Omega ;{\dot{H}}^{\beta })}\le C{t}_{m-n}^{\frac{\gamma -\beta }{2}}.\end{array}$$

(74)

To show this lemma, we need to introduce some smooth properties of the operators $E_N^m$. With the notation $r(z)={(1+z)}^{-1}$, one can write $E_N^m=r{(\tau A_N)}^m{P}_N$. As shown in the proof of (Theorem 7.1 in [38]), there exist two constants C and c such that

$$\begin{array}{c}\hfill |r(z)-e^{-z}|\le C{z}^2,z\in [0,1],\end{array}$$

(75)

and

$$\begin{array}{c}\hfill r(z)\le e^{-cz},z\in [0,1].\end{array}$$

(76)

These two inequalities suffice to ensure that, for $m=1,2,3,\cdots ,$

$$\begin{array}{cc}\hfill {|r(z)}^m-e^{-zm}|& \le \left|(r(z)-e^{-z})\sum _{l=0}^{m-1}r{(z)}^{m-1-l}{e}^{-zl}\right|\hfill \\ \hfill & \le Cm{z}^2{e}^{-c(m-1)z},z\in [0,1].\hfill \end{array}$$

(77)

Lemma 4. 

Under Assumption 1, there exists a constant C independent of $N\in {\mathbb{N}}^{+}$ and $m\in \{1,2,\cdots ,M\}$ such that the following estimates for $E_N^m$ hold, for any $x\in H$

$$\begin{array}{cc}\hfill \parallel A^{\frac{\mu }{2}}{E}_N^m{P}_{N}x\parallel \le & C\varphi (\mu ,t_m)\parallel x\parallel ,\mu \in [0,2],\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill {\left(\tau \sum _{i=n}^m{\parallel A^{\frac{\rho }{2}}{E}_N^i{P}_{N}x\parallel }^2\right)}^{\frac{1}{2}}\le & C{t}_{m-n}^{\frac{1-\rho }{2}}\parallel x\parallel ,\rho \in [0,1],\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill \parallel A^{-\frac{\nu }{2}}(I-E_N^m)P_{N}x\parallel \le & C{t}_m^{\frac{\nu }{2}}\parallel x\parallel ,\nu \in [0,2],\hfill \end{array}$$

(80)

where $\varphi (\mu ,t)=\left\{\begin{array}{cc}C{t}^{-\frac{\mu }{2}},\hfill & t\in (0,1],\hfill \\ C(t^{-\frac{\mu }{2}}{e}^{-ct}+t^{-2}),\hfill & t\ge 1.\hfill \end{array}\right.$

Proof of Lemma 4. 

The result (80) can be found in (Lemma 5.2 in [39]). The proof of (79) with $\rho =1$ is contained in the proof of (Lemma 5.2 in [39]). The case $\rho =0$ can be settled by the stability of $E_N^m$. Thus, the intermediate cases follow by the interpolation technique. The estimates (78) in the case of $t\in (0,1]$ can be shown in (Lemma 5.2 in [39]). It remains to show (78) for $t\ge 1$. By using the expansion of $P_{N}x$ in terms of ${\left\{e_j\right\}}_{j=1}^{\infty }$, we know

$$\begin{array}{c}\hfill \parallel A^{\frac{\mu }{2}}{E}_N^m{P}_N{x\parallel }^2=\sum _{j=1}^N{\lambda }_j^{\mu }r{({\lambda }_j\tau )}^{2m}{⟨x,e_j⟩}^2.\end{array}$$

(81)

Thus, it suffices to show that there exists a constant C such that, for $m=1,2\cdots$

$${\lambda }_j^{\frac{\mu }{2}}r{({\lambda }_j\tau )}^m\le \varphi (\mu ,t_m).$$

(82)

Next, we consider two cases: $\tau {\lambda }_j\le 1$ and $\tau {\lambda }_j>1$. For the case $\tau {\lambda }_j\le 1$, we obtain by (76)

$${\lambda }_j^{\frac{\mu }{2}}r{({\lambda }_j\tau )}^m\le {\lambda }_j^{\frac{\mu }{2}}{e}^{-c{t}_m{\lambda }_j}\le C{t}_m^{-\frac{\mu }{2}}{e}^{-\frac{c{t}_m{\lambda }_j}{2}}.$$

(83)

For the case of $\tau {\lambda }_j>1$, one can easily observe that, for $m=1$

$$\begin{array}{c}\hfill {\lambda }_j^{\frac{\mu }{2}}r({\lambda }_j\tau )\le C{\tau }^{-1}{\lambda }_j^{-1+\frac{\mu }{2}}\le C{\tau }^{-\frac{\mu }{2}}\le C{\tau }^{2-\frac{\mu }{2}}{t}_1^{-2},\end{array}$$

(84)

and for any $m\ge 2$

$$\begin{array}{cc}\hfill {\lambda }_j^{\frac{\mu }{2}}r{({\lambda }_j\tau )}^m& \le C{\tau }^{-\frac{\mu }{2}}r{({\lambda }_j\tau )}^{m-1}\le C{\tau }^{-\frac{\mu }{2}}\underset{\lambda \ge 1}{sup}r{(\lambda )}^{m-1}\hfill \\ \hfill & \le C{\tau }^{-\frac{\mu }{2}}{(m-1)}^{-2}\le C{\tau }^{2-\frac{\mu }{2}}{t}_m^{-2},\hfill \end{array}$$

(85)

which in conjunction with (83) and (84) implies the desired assertion (82). □

Proof of Lemma 3. 

Under Assumptions 1–4, we can show the ergodicity of ${\left\{X_N^m\right\}}_{m\in \mathbb{N}}$ and the existence and uniqueness of the invariant measure by following the similar arguments as in the proof of (Theorem 4.7 in [25]). Hence, we omit it and only prove (73) and (74). For (73), we start at showing

$$\begin{array}{c}\hfill \underset{N\in {\mathbb{N}}^{+}}{sup}\underset{m\in \{1,2,\cdots ,M\}}{sup}{\parallel F(X_N^m)\parallel }_{L^2(\Omega ;H)}<\infty .\end{array}$$

(86)

To do this, we assume ${\mathcal{O}}_N^m:={\sum }_{i=0}^{m-1}{E}_N^{m-i}{P}_N\Delta W_{i+1}$ and ${\tilde{X}}_N^m:=X_N^m-{\mathcal{O}}_N^m$ and, then rewrite (72) as

$$\begin{array}{c}\hfill {\tilde{X}}_N^m=E_N^m{P}_N{X}_0+\tau \sum _{i=0}^{m-1}{E}_N^{m-i}{P}_{N}F({\tilde{X}}_N^i+{\mathcal{O}}_N^i),\end{array}$$

(87)

which immediately implies

$$\begin{array}{c}\hfill {\tilde{X}}_N^m=E_N{P}_N{\tilde{X}}_N^{m-1}+\tau E_N{P}_{N}F({\tilde{X}}_N^{m-1}+{\mathcal{O}}_N^{m-1}).\end{array}$$

(88)

Thanks to (79) and the Burkholder–Davis–Gundy type inequality, there exists a constant C independent of N and m such that, $\forall p\ge 1$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\mathcal{O}}_N^m{\parallel }_{L^p(\Omega ;{\dot{H}}^{\gamma })}\le & C{\left(\tau \sum _{i=0}^{m-1}{\parallel A^{\frac{\gamma }{2}}{E}_N^{m-i}{P}_N{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill =& C{\left(\tau \sum _{i=0}^{m-1}{\parallel A^{\frac{1}{2}}{E}_N^{m-i}{P}_N{A}^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill \le & C\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2(H)}.\hfill \end{array}\end{array}$$

(89)

This together with (12) implies

$$\begin{array}{cc}\hfill \underset{N\in {\mathbb{N}}^{+}}{sup}\underset{m\in \{1,2,\cdots ,M\}}{sup}{\parallel F({\mathcal{O}}_N^m)\parallel }_{L^2(\Omega ;H)}& \le L\underset{N\in {\mathbb{N}}^{+}}{sup}\underset{m\in \{1,2,\cdots ,M\}}{sup}{\parallel {\mathcal{O}}_N^m\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +{\parallel F(0)\parallel }_{L^2(\Omega ;H)}<\infty .\hfill \end{array}$$

(90)

For (86), it suffices to bound $\parallel {\tilde{X}}_N^m{\parallel }_{L^2(\Omega ;H)}$. Therefore, by (12), (14) and the fact $\parallel E_N{\parallel }_{\mathcal{L}(H)}\le {(1+{\lambda }_1\tau )}^{-1}$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\tilde{X}}_N^m{\parallel }^2\le & \parallel E_N{\parallel }_{\mathcal{L}(H)}^2(\parallel {\tilde{X}}_N^{m-1}{\parallel }^2+{\tau }^2{\parallel F({\tilde{X}}_N^{m-1}+{\mathcal{O}}_N^{m-1})\parallel }^2\hfill \\ \hfill & +2\tau ⟨{\tilde{X}}_N^{m-1},F({\tilde{X}}_N^{m-1}+{\mathcal{O}}_N^{m-1})⟩)\hfill \\ \hfill \le & {(1+{\lambda }_1\tau )}^{-2}(\parallel {\tilde{X}}_N^{m-1}{\parallel }^2+2{\tau }^2{\parallel F({\tilde{X}}_N^{m-1}+{\mathcal{O}}_N^{m-1})-F({\mathcal{O}}_N^{m-1})\parallel }^2\hfill \\ \hfill & +2{\tau }^2{\parallel F({\mathcal{O}}_N^{m-1})\parallel }^2+2\tau ⟨{\tilde{X}}_N^{m-1},F({\tilde{X}}_N^{m-1}+{\mathcal{O}}_N^{m-1})-F({\mathcal{O}}_N^{m-1})⟩\hfill \\ \hfill & +2\tau ⟨{\tilde{X}}_N^{m-1},F({\mathcal{O}}_N^{m-1})⟩\hfill \\ \hfill \le & \frac{1}{{(1+{\lambda }_1\tau )}^2}(\left(1+2\tau L_F+2{\tau }^2{L}^2+\frac{{\lambda }_1-L_F}{2}\tau \right){\parallel {\tilde{X}}_N^{m-1}\parallel }^2\hfill \\ \hfill & +\frac{2\tau \left(1+({\lambda }_1-L_F)\tau \right)}{{\lambda }_1-L_F}\parallel F({\mathcal{O}}_N^{m-1}{\parallel }^2),\hfill \end{array}\end{array}$$

(91)

where we used the Young inequality $xy\le \epsilon x^2+\frac{y^2}{4\epsilon }$ for all $x,y\in \mathbb{R}$ with $\epsilon =\frac{{\lambda }_1-L_F}{2}>0$. Since ${\lambda }_1>L_F$ and $\tau <{\tau }_0\le \frac{{\lambda }_1-L_F}{4L^2}$, we have

$$\begin{array}{cc}\hfill 1+2\tau L_F+2{\tau }^2{L}^2+\frac{{\lambda }_1-L_F}{2}\tau \le & 1+2\tau L_F+({\lambda }_1-L_F)\tau \hfill \\ \hfill \le & 1+(L_F+{\lambda }_1)\tau <{(1+{\lambda }_1\tau )}^2.\hfill \end{array}$$

(92)

Therefore, using (90) and (91) and summation on m results in

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}[\parallel {\tilde{X}}_N^m{\parallel }^2]\le & \frac{1+(L_F+{\lambda }_1)\tau }{{(1+{\lambda }_1\tau )}^2}\mathbb{E}\left[\parallel {\tilde{X}}_N^{m-1}{\parallel }^2\right]\hfill \\ \hfill & +\frac{C\left({\tau }^2({\lambda }_1-L_F)+\tau \right)}{{(1+{\lambda }_1\tau )}^2}\underset{N\in {\mathbb{N}}^{+}}{sup}\underset{i\in \{1,2,\cdots ,M\}}{sup}{\parallel F({\mathcal{O}}_N^i)\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill \le & {\left(\frac{1+(L_F+{\lambda }_1)\tau }{{(1+{\lambda }_1\tau )}^2}\right)}^m\mathbb{E}\left[\parallel {\tilde{X}}_N^0{\parallel }^2\right]\hfill \\ \hfill & +\frac{C\left({\tau }^2({\lambda }_1-L_F)+\tau \right)}{{(1+{\lambda }_1\tau )}^2}\sum _{i=1}^m{\left(\frac{1+(L_F+{\lambda }_1)\tau }{{(1+{\lambda }_1\tau )}^2}\right)}^{i-1}\hfill \\ \hfill \le & \parallel X_0{\parallel }^2+\frac{C(1+({\lambda }_1-L_F)\tau )}{{\lambda }_1^2\tau +{\lambda }_1-L_F}\hfill \\ \hfill \le & \parallel X_0{\parallel }^2+C\left(\frac{{\lambda }_1-L_F}{{\lambda }_1^2}+\frac{1}{{\lambda }_1-L_F}\right),\hfill \end{array}\end{array}$$

(93)

where in the last step we used the fact

$$\frac{1+({\lambda }_1-L_F)\tau }{{\lambda }_1^2\tau +{\lambda }_1-L_F}=\frac{{\lambda }_1-L_F}{{\lambda }_1^2}+\frac{{\lambda }_1^2-{({\lambda }_1-L_F)}^2}{{\lambda }_1^2({\lambda }_1-L_F+{\lambda }_1^2\tau )}\le \frac{{\lambda }_1-L_F}{{\lambda }_1^2}+\frac{1}{{\lambda }_1-L_F}.$$

This together with (89) shows (86). From (78), (86), (89) and the fact $\parallel E_N^m{\parallel }_{\mathcal{L}(H)}\le 1$, it follows that

$$\begin{array}{cc}\hfill \parallel X_N^m{\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}\le & \parallel E_N^m{P}_N{X}_0{\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}+\tau \sum _{i=0}^{m-1}{\parallel E_N^{m-i}F(X_N^i)\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}\hfill \\ \hfill & +\parallel {\mathcal{O}}_N^m{\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}\hfill \\ \hfill \le & \parallel X_0{\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}+C\tau \sum _{i=0}^{m-1}\varphi (\gamma ,t_{m-i}){\parallel F(X_N^i)\parallel }_{L^2(\Omega ;H)}+C\hfill \\ \hfill \le & \parallel X_0{\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}+C\tau \sum _{i=1}^m\varphi (\gamma ,t_i)+C<\infty ,\hfill \end{array}$$

(94)

which shows (73). Concerning the temporal regularity of $X_N^m$, we utilize (78)–(80) and the Itô isometry to obtain, for $\beta \in [0,\gamma ]$

$$\begin{array}{cc}\hfill & \parallel X_N^m-X_N^n{\parallel }_{L^2(\Omega ;{\dot{H}}^{\beta })}={\parallel (I-E_N^{m-n})X_N^n\parallel }_{L^2(\Omega ;{\dot{H}}^{\beta })}\hfill \\ \hfill & +\sum _{i=n}^{m-1}\tau {\parallel E_N^{m-i}{P}_{N}F(X_N^i)\parallel }_{L^2(\Omega ;{\dot{H}}^{\beta })}+{\left(\sum _{i=n}^{m-1}\tau {\parallel A^{\frac{\beta }{2}}{E}_N^{m-i}{P}_N{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill \le & C{t}_{m-n}^{\frac{\gamma -\beta }{2}}\parallel X_N^n{\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}+C\tau \sum _{i=n}^{m-1}\varphi (\beta ,t_{m-i})\underset{N\in {\mathbb{N}}^{+}}{sup}\underset{m\in \{1,2,\cdots ,M\}}{sup}{\parallel F(X_N^m)\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +C{t}_{m-n}^{\frac{\gamma -\beta }{2}}{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}\hfill \\ \hfill \le & C{t}_{m-n}^{\frac{\gamma -\beta }{2}},\hfill \end{array}$$

(95)

where in the last inequality we used the following estimate

$$\begin{array}{cc}\hfill \tau \sum _{i=n}^{m-1}\varphi (\beta ,t_{m-i})\le & C{t}_{m-n}^{\frac{\gamma -\beta }{2}}\tau \sum _{i=n}^{m-1}\varphi (\beta ,t_{m-i})t_{m-i}^{\frac{\beta -\gamma }{2}}\hfill \\ \hfill \le & C{t}_{m-n}^{\frac{\gamma -\beta }{2}}\tau \sum _{i=1}^{m-n}\varphi (\gamma ,t_i)\le C{t}_{m-n}^{\frac{\gamma -\beta }{2}}.\hfill \end{array}$$

(96)

The proof of this lemma is complete. □

4.2. Weak Convergence for Full-Discretization over Long Time

Theorem 6. 

Suppose that Assumptions 1–4 are valid and $\tau <{\tau }_0\le \frac{{\lambda }_1-L_F}{4L^2}$. Let $X_N(t)$ and $X_N^M$ be the mild solution of (42) and the solution of (71), respectively. For any $T>0$, $M,N\in {\mathbb{N}}^{+}$ and $\Phi \in C_b^2(H,\mathbb{R})$, there exists a constant C independent of T and $N,M$ such that

$$\begin{array}{c}\hfill \left|\mathbb{E}\right[\Phi (X_N(T))]-\mathbb{E}[\Phi (X_N^M)\left]\right|\le C{\tau }^{\gamma }.\end{array}$$

(97)

Its proof is postponed. Define the fully discrete approximation operators ${\Psi }_{\tau ,N}(t)$, $t\in [0,T]$ as

$$\begin{array}{c}\hfill {\Psi }_{\tau ,N}(t)=E(t)P_N-E_N^m,t\in [t_{m-1},t_m).\end{array}$$

(98)

The following results on the error operators ${\Psi }_{\tau ,N}(t)$ play a significant role in the time-independent weak error estimates of the fully discrete approximation.

Lemma 5. 

Under Assumption 1, the following estimates hold.

(i) 

For $0\le \nu \le \mu \le 2$, it holds that for any $t\in (0,\infty )$

$$\begin{array}{c}\hfill \parallel {\Psi }_{\tau ,N}(t)x\parallel \le C{\tau }^{\frac{\mu }{2}}{t}^{-\frac{\mu -\nu }{2}}{\parallel x\parallel }_{{\dot{H}}^{\nu }},forallx\in {\dot{H}}^{\nu }.\end{array}$$

(99)

(ii) 

For $\nu \in [0,1]$, it holds that for any $t\in (0,\infty )$

$$\begin{array}{c}\hfill \parallel {\Psi }_{\tau ,N}(t)x\parallel \le C\varphi (1+\nu ,t){\tau }^{\nu }{\parallel x\parallel }_{{\dot{H}}^{\nu -1}},forallx\in {\dot{H}}^{\nu -1},\end{array}$$

(100)

where $\varphi (·,·)$ is a piecewise function defined in Lemma 4.

(iii) 

For $0\le \varrho \le 2$, it holds that for any $t\in (0,\infty )$

$$\begin{array}{c}\hfill {\left({\int }_0^t{\parallel {\Psi }_{\tau ,N}(s)x\parallel }^2\mathrm{d}s\right)}^{\frac{1}{2}}\le C{\tau }^{\frac{\varrho }{2}}{\parallel x\parallel }_{\varrho -1},forallx\in {\dot{H}}^{\varrho }.\end{array}$$

(101)

(iv) 

For $0\le \rho \le 1$, it holds that for any $t\in (0,\infty )$

$$\begin{array}{c}\hfill \parallel {\int }_0^t{\Psi }_{\tau ,N}(s)x\mathrm{d}s\parallel \le C{\tau }^{\frac{2-\rho }{2}}{\parallel x\parallel }_{{\dot{H}}^{-\rho }},forallx\in {\dot{H}}^{-\rho }.\end{array}$$

(102)

Proof of Lemma 5. 

By the similar arguments of the proof of (Lemma 4.3 (i) in [26]), we can show (99). The estimates (101) and (102) can be handled by a simple modification of the proof of (Lemma 4.4 in [26]). It remains to prove (100). In order to validate (100), one can use (10) to obtain, for $t\in [t_{m-1},t_m)\cap (0,\infty )$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\Psi }_{\tau ,N}(t)x\parallel & \le \parallel \left(E(t)-E(t_m)\right)P_{N}x\parallel +\parallel \left(E_N(t_m)-E_N^m\right)x\parallel \hfill \\ \hfill \le & \parallel A^{\frac{\nu +1}{2}}E(t)A^{-\nu }(I-E(t_m-t))A^{\frac{\nu -1}{2}}{P}_{N}x\parallel +\parallel (E_N(t_m)-E_N^m)x\parallel \hfill \\ \hfill \le & C{\tau }^{\nu }{t}^{-\frac{1+\nu }{2}}{e}^{-\frac{{\lambda }_{1}t}{2}}{\parallel x\parallel }_{{\dot{H}}^{\nu -1}}+\parallel (E_N(t_m)-E_N^m)x\parallel .\hfill \end{array}\end{array}$$

(103)

It remains to bound $\parallel (E_N(t_m)-E_N^m)x\parallel .$ As in (81), Parseval’s identity implies

$$\begin{array}{c}\hfill \parallel (E_N(t_m)-E_N^m){x\parallel }^2=\sum _{j=1}^N{|e^{-{\lambda }_j{t}_m}-r{(\tau {\lambda }_j)}^m|}^2{⟨x,e_j⟩}^2.\end{array}$$

(104)

Thus, it suffices to show that there exists a constant C independent of t and $m\in {\mathbb{N}}^{+}$ such that

$$\begin{array}{c}\hfill |e^{-{\lambda }_j{t}_m}-r{(\tau {\lambda }_j)}^m|\le C{\tau }^{\nu }\varphi (1+\nu ,t){\lambda }_j^{\frac{\nu -1}{2}}.\end{array}$$

(105)

For this, we consider two cases: $\tau {\lambda }_j\le 1$ and $\tau {\lambda }_j>1$. For the case $\tau {\lambda }_j\le 1$, using (77) and ${sup}_{s\in [0,\infty )}s{e}^{-cs}<\infty$ implies

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |e^{-{\lambda }_j{t}_m}-r{(\tau {\lambda }_j)}^m|\le & Cm{\tau }^2{\lambda }_j^2{e}^{-c{\lambda }_j{t}_{m-1}}\hfill \\ \hfill \le & C{\tau }^{\nu }{\lambda }_j^{\frac{\nu -1}{2}}{(\tau {\lambda }_j)}^{1-\nu }{\lambda }_j^{\frac{1+\nu }{2}}{e}^{-\frac{c{\lambda }_j{t}_m}{2}}{t}_m{\lambda }_j{e}^{-\frac{c{\lambda }_j{t}_m}{2}}\hfill \\ \hfill \le & C{\tau }^{\nu }{\lambda }_j^{\frac{\nu -1}{2}}{t}_m^{-\frac{1+\nu }{2}}{e}^{-\frac{c{\lambda }_1{t}_m}{4}}.\hfill \end{array}\end{array}$$

(106)

For the case $\tau {\lambda }_j>1$, using (85) with $\mu =1-\nu$, (84) with $\mu =1-\nu$ and employing the fact ${sup}_{\lambda \ge 1}{e}^{-\frac{m\lambda }{2}}\le C{m}^{-\nu }$ lead to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |e^{-{\lambda }_j{t}_m}-r{(\tau {\lambda }_j)}^m|\le & |e^{-{\lambda }_j{t}_m}|+|r{(\tau {\lambda }_j)}^m|\hfill \\ \hfill \le & C{\lambda }_j^{\frac{\nu -1}{2}}{\lambda }_j^{\frac{1-\nu }{2}}{e}^{-\frac{{\lambda }_j{t}_m}{2}}\underset{\lambda \ge 1}{sup}{e}^{-\frac{m\lambda }{2}}+C{\tau }^{2-\frac{1-\nu }{2}}{t}_m^{-2}{\lambda }_j^{\frac{\nu -1}{2}}\hfill \\ \hfill \le & C{\lambda }_j^{\frac{\nu -1}{2}}{t}_m^{-\frac{1-\nu }{2}}{e}^{-\frac{{\lambda }_j{t}_m}{4}}{m}^{-\nu }+C{\tau }^{\nu }{t}_m^{-2}{\lambda }_j^{\frac{\nu -1}{2}}\hfill \\ \hfill \le & C{\tau }^{\nu }{\lambda }_j^{\frac{\nu -1}{2}}(t^{-\frac{1+\nu }{2}}{e}^{-ct}+t^{-2}),\hfill \end{array}\end{array}$$

(107)

which together with (106) shows (105) and completes the proof. □

Proof of Theorem 6. 

Recalling the definition of ${\tilde{X}}_N^m$ in (87), we separate the error $\mathbb{E}[\Phi (X_N(T))]-\mathbb{E}[\Phi (X_N^M)]$ as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}[\Phi (X_N(T))]-\mathbb{E}[\Phi (X_N^M)]=& \mathbb{E}[\Phi ({\tilde{X}}_N(T)+{\mathcal{O}}_N(T))]-\mathbb{E}[\Phi ({\tilde{X}}_N(T)+{\mathcal{O}}_N^M)]\hfill \\ \hfill & +\mathbb{E}[\Phi ({\tilde{X}}_N(T)+{\mathcal{O}}_N^M)]-\mathbb{E}[\Phi ({\tilde{X}}_N^M+{\mathcal{O}}_N^M)]\hfill \\ \hfill :=& {\mathbb{I}}_1+{\mathbb{I}}_2.\hfill \end{array}\end{array}$$

(108)

For ${\mathbb{I}}_1$, we use the Taylor expansion and Malliavin integration by parts formula (39) to obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & |{\mathbb{I}}_1|=|\mathbb{E}[{\Phi }^{\prime }(X_N(T))({\mathcal{O}}_N(T)-{\mathcal{O}}_N^M)+{\int }_0^1{\Phi }^{\prime \prime }(X_N(T)+\lambda ({\mathcal{O}}_N(T)-{\mathcal{O}}_N^M))·\hfill \\ \hfill & \left(({\mathcal{O}}_N(T)-{\mathcal{O}}_N^M),({\mathcal{O}}_N(T)-{\mathcal{O}}_N^M)\right)(1-\lambda )\mathrm{d}\lambda \left]\right|\hfill \\ \hfill \le & \underset{\mathbb{L}}{\underbrace{\left|\mathbb{E}{\int }_0^T{⟨{\Psi }_{\tau ,N}(T-s)P_N,D_s{\Phi }^{\prime }(X_N(T))⟩}_{{\mathcal{L}}_2^0}\mathrm{d}s\right|}}+C\underset{\mathbb{J}}{\underbrace{\mathbb{E}[\parallel {\mathcal{O}}_N(T)-{\mathcal{O}}_N^M{\parallel }^2]}}.\hfill \end{array}\end{array}$$

(109)

To bound $\mathbb{J}$, employing (101) and the Itô isometry enables us to derive

$$\begin{array}{cc}\hfill \mathbb{J}& =\mathbb{E}\left[\parallel {\int }_0^T{\Psi }_{\tau ,N}(T-s)\mathrm{d}W(s){\parallel }^2\right]={\int }_0^T\parallel {\Psi }_{\tau ,N}(T-s)Q^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2(H)}^2\mathrm{d}s\hfill \\ \hfill & \le C{\tau }^{\gamma }{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2.\hfill \end{array}$$

(110)

With regard to $\mathbb{L}$, we use (47) to make a further decomposition as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{L}=& \left|\mathbb{E}{\int }_0^T{⟨{\Psi }_{\tau ,N}(T-s)P_N,{\Phi }^{\prime \prime }(X_N(T))D_s{X}_N(T)⟩}_{{\mathcal{L}}_2^0}\mathrm{d}s\right|\hfill \\ \hfill \le & \left|\mathbb{E}{\int }_0^T{⟨{\Psi }_{\tau ,N}(T-s)P_N,{\Phi }^{\prime \prime }(X_N(T))E_N(T-s)⟩}_{{\mathcal{L}}_2^0}\mathrm{d}s\right|\hfill \\ \hfill & +|\mathbb{E}{\int }_0^T<{\Psi }_{\tau ,N}(T-s)P_N,{\Phi }^{\prime \prime }(X_N(T))\hfill \\ \hfill & \times {\int }_s^T{E}_N(T-r)P_N{F}^{\prime }(X_N(r))D_s{X}_N(r)\mathrm{d}r{>}_{{\mathcal{L}}_2^0}\mathrm{d}s|\hfill \\ \hfill :=& {\mathbb{L}}_1+{\mathbb{L}}_2.\hfill \end{array}\end{array}$$

(111)

In view of (10), (46) and (100), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{L}}_2\le & C{\int }_0^T{\parallel {\Psi }_{\tau ,N}(T-s)P_N\parallel }_{{\mathcal{L}}_2^0}{\int }_s^T\mathbb{E}\parallel E_N(T-r)P_N{F}^{\prime }(X_N(r))·\hfill \\ \hfill & D_s{X}_N(r){\parallel }_{{\mathcal{L}}_2^0}\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C{\tau }^{\gamma }{\int }_0^T\varphi (1+\gamma ,T-s){\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}·\hfill \\ \hfill & {\int }_s^T{e}^{-\frac{{\lambda }_1(T-r)}{2}}\mathbb{E}\parallel D_s{X}_N(r){\parallel }_{{\mathcal{L}}_2^0}\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}{\parallel }_{{\mathcal{L}}_2(H)}^2{\tau }^{\gamma }{\int }_0^T\varphi (1+\gamma ,T-s){\int }_s^T{e}^{-\frac{{\lambda }_1(T-r)}{2}}·\hfill \\ \hfill & (1+{(r-s)}^{\frac{\gamma -1}{2}})\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C{\tau }^{\gamma },\hfill \end{array}\end{array}$$

(112)

where in the last inequality we used the fact that applying (27) and ${sup}_{s\in (0,\infty )}s{e}^{-cs}<\infty$ yields

$$\begin{array}{cc}\hfill & {\int }_0^T\varphi (1+\gamma ,T-s){\int }_s^T{e}^{-\frac{{\lambda }_1(T-r)}{2}}(1+{(r-s)}^{\gamma -1})\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C{\int }_0^T\varphi (1+\gamma ,T-s)({(T-s)}^{\frac{\gamma }{2}}{\int }_s^T{e}^{-\frac{{\lambda }_1(T-r)}{2}}{(T-r)}^{-\frac{\gamma }{2}}\mathrm{d}r\hfill \\ \hfill & +{\int }_s^T{(T-r)}^{-\frac{\gamma }{2}}{(r-s)}^{\gamma -1}\mathrm{d}r)\mathrm{d}s\hfill \\ \hfill \le & C{\int }_0^T\varphi (1+\gamma ,T-s){(T-s)}^{\frac{\gamma }{2}}\mathrm{d}s<\infty .\hfill \end{array}$$

As in (57), we reformulate the term ${\mathbb{L}}_1$ as

$$\begin{array}{c}\hfill {\mathbb{L}}_1=\left|\sum _{j=1}^N{\int }_0^T⟨{\Psi }_{\tau ,N}(T-s)P_N{Q}^{\frac{1}{2}}{e}_j,{\Phi }^{\prime \prime }(X_N(T))E_N(T-s)Q^{\frac{1}{2}}{e}_j⟩\mathrm{d}s\right|,\end{array}$$

(113)

and then, use (99) with $\mu =\nu =2\gamma$ and the fact A and Q are commutable to derive

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{L}}_1\le & \sum _{j=1}^N{\int }_0^T\parallel {\Psi }_{\tau ,N}(T-s)P_N{Q}^{\frac{1}{2}}{e}_j\parallel \parallel {\Phi }^{\prime \prime }(X_N(T))E_N(T-s)Q^{\frac{1}{2}}{e}_j\parallel \mathrm{d}s\hfill \\ \hfill \le & C{\tau }^{\gamma }\sum _{j=1}^N{\int }_0^T\parallel A^{\gamma }{Q}^{\frac{1}{2}}{e}_j\parallel \parallel E_N(T-s)Q^{\frac{1}{2}}{e}_j\parallel \mathrm{d}s\hfill \\ \hfill \le & C{\tau }^{\gamma }\sum _{j=1}^N{\lambda }_j^{\gamma }{\int }_0^T{e}^{-{\lambda }_{j}s}\mathrm{d}s{\parallel Q^{\frac{1}{2}}{e}_j\parallel }^2\hfill \\ \hfill \le & C{\tau }^{\gamma }\sum _{j=1}^N{\lambda }_j^{\gamma -1}\parallel Q^{\frac{1}{2}}{e}_j{\parallel }^2\le C{\tau }^{\gamma }{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}^2.\hfill \end{array}\end{array}$$

(114)

This together with (110)–(112) implies

$$\begin{array}{c}\hfill |{\mathbb{I}}_1|\le C{\tau }^{\gamma }.\end{array}$$

(115)

Now we focus on the term ${\mathbb{I}}_2$. Similarly to the semi-discrete case, we use the Taylor formula and the condition $\Phi \in C_b^2(H,\mathbb{R})$ to decompose it as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathbb{I}}_2|=& \left|\mathbb{E}\right[\Phi ({\tilde{X}}_N(T)+{\mathcal{O}}_N^M)]-\mathbb{E}[\Phi ({\tilde{X}}_N^M+{\mathcal{O}}_N^M)\left]\right|\hfill \\ \hfill =& \left|\mathbb{E}{\int }_0^1{\Phi }^{\prime }\left(X_N^M+s({\tilde{X}}_N^M-{\tilde{X}}_N(T))\right)\left({\tilde{X}}_N^M-{\tilde{X}}_N(T)\right)\mathrm{d}s\right|\hfill \\ \hfill \le & C\mathbb{E}\left[\parallel {\tilde{\mathcal{X}}}_N^M-{\tilde{X}}_N(T)\parallel \right]+C\mathbb{E}\left[\parallel {\tilde{X}}_N^M-{\tilde{\mathcal{X}}}_N^M\parallel \right]\hfill \\ \hfill \le & C\parallel {\tilde{\mathcal{X}}}_N^M-{\tilde{X}}_N{(T)\parallel }_{L^2(\Omega ;H)}+C{\parallel {\tilde{X}}_N^M-{\tilde{\mathcal{X}}}_N^M\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill :=& C\parallel {\mathbf{e}}_1^M{\parallel }_{L^2(\Omega ;H)}+C{\parallel {\mathbf{e}}_2^M\parallel }_{L^2(\Omega ;H)},\hfill \end{array}\end{array}$$

(116)

where ${\tilde{\mathcal{X}}}_N^M:={\mathcal{X}}_N^M-{\mathcal{O}}_N^M$ and ${\mathcal{X}}_N^M$ is given by

$$\begin{array}{c}\hfill {\mathcal{X}}_N^m=E_N^m{P}_N{X}_0+\tau \sum _{i=0}^{m-1}{E}_N^{m-i}{P}_{N}F({\tilde{X}}_N(t_i)+{\mathcal{O}}_N^i)+{\mathcal{O}}_N^m.\end{array}$$

(117)

To bound the first error term $\parallel {\mathbf{e}}_1^m{\parallel }_{L^2(\Omega ;H)}$, we decompose it into four terms:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\mathbf{e}}_1^m{\parallel }_{L^2(\Omega ;H)}\le & \parallel {\Psi }_{\tau ,N}(t_m)P_N{X}_0{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +\parallel {\int }_0^{t_m}{\Psi }_{\tau ,N}(t_m-s)F(X_N(s))\mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +\parallel \sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}{E}_N^{m-i}{P}_N\left(F(X_N(\left[s\right]))-F(X_N(s))\right)\mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +\parallel \sum _{i=0}^{m-1}\tau E_N^{m-i}{P}_N\left(F({\tilde{X}}_N(t_i))+{\mathcal{O}}_N^i)-F(X_N(t_i))\right){\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill :=& {\mathbb{J}}_1+{\mathbb{J}}_2+{\mathbb{J}}_3+{\mathbb{J}}_4.\hfill \end{array}\end{array}$$

(118)

For ${\mathbb{J}}_1$, we utilize (99) with $\mu =\nu =2\gamma$ to derive

$$\begin{array}{c}\hfill {\mathbb{J}}_1\le C{\tau }^{\gamma }{\parallel X_0\parallel }_{{\dot{H}}^{2\gamma }}.\end{array}$$

(119)

Employing (45) and (100) with $\nu =1$ and (102) with $\rho =0$ enables us to obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{J}}_2\le & \parallel {\int }_0^{t_m}{\Psi }_{\tau ,N}(t_m-s)F(X_N(t_m))\mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +{\int }_0^{t_m}\parallel {\Psi }_{\tau ,N}(t_m-s)\left(F(X_N(t_m))-F(X_N(s))\right){\parallel }_{L^2(\Omega ;H)}\mathrm{d}s\hfill \\ \hfill \le & C\tau \parallel F(X_N(t_m)){\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +C\tau {\int }_0^{t_m}C\varphi (2,t_m-s){\parallel F(X_N(t_m))-F(X_N(s))\parallel }_{L^2(\Omega ;H)}\mathrm{d}s\hfill \\ \hfill \le & C\tau (1+\parallel X_N(t_m){\parallel }_{L^2(\Omega ;H)})+C\tau {\int }_0^{t_m}\varphi (2,t_m-s){(t_m-s)}^{\frac{\gamma }{2}}\mathrm{d}s\le C\tau .\hfill \end{array}\end{array}$$

(120)

To bound the term ${\mathbb{J}}_3$, we assume $\lambda (X_N(s),X_N(\left[s\right])):=X_N(\left[s\right])+\lambda (X_N(\left[s\right])-X_N(s))$ and use Taylor’s formula to split it into three terms:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{J}}_3=& \parallel \sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}{\int }_0^1{E}_N^{m-i}{P}_N{F}^{\prime }\left(\lambda (X_N(s),X_N(\left[s\right])\right)\hfill \\ \hfill & \times \left(X_N(\left[s\right])-X_N(s)\right)\mathrm{d}\lambda \mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill \le & \parallel \sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}{\int }_0^1{E}_N^{m-i}{P}_N{F}^{\prime }\left(\lambda (X_N(s),X_N(\left[s\right])\right)\hfill \\ \hfill & \times \left(I-E(s-[s])\right)P_N{X}_N(\left[s\right])\mathrm{d}\lambda \mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +\parallel \sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}{\int }_0^1{E}_N^{m-i}{P}_N{F}^{\prime }\left(\lambda (X_N(s),X_N(\left[s\right])\right)\hfill \\ \hfill & \times {\int }_{t_i}^{s}E(s-r)P_{N}F(X_N(r))\mathrm{d}r\mathrm{d}\lambda \mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill & +\parallel \sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}{\int }_0^1{E}_N^{m-i}{P}_N{F}^{\prime }\left(\lambda (X_N(s),X_N(\left[s\right])\right)\hfill \\ \hfill & \times {\int }_{t_i}^{s}E(s-r)P_N\mathrm{d}W(r)\mathrm{d}\lambda \mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill :=& {\mathbb{J}}_3^1+{\mathbb{J}}_3^2+{\mathbb{J}}_3^3,\hfill \end{array}\end{array}$$

(121)

where in the equality we used the fact

$$\begin{array}{cc}\hfill X_N(s)=& E(s-\left[s\right])X_N(\left[s\right])+{\int }_{\left[s\right]}^{s}E(s-r)P_{N}F(X_N(r))\mathrm{d}r\hfill \\ \hfill & +{\int }_{\left[s\right]}^{s}E(s-r)P_N\mathrm{d}W(r).\hfill \end{array}$$

(122)

From (10), (13) and (78), it follows that

$$\begin{array}{cc}\hfill {\mathbb{J}}_3^1\le & C\sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}\varphi (\eta ,t_{m-i}){\int }_0^1\parallel A^{-\frac{\eta }{2}}{F}^{\prime }\left(\lambda (X_N(\left[s\right]),X_N(s)\right))\hfill \\ \hfill & \times \left(I-E(s-[s])\right)X_N{(\left[s\right])\parallel }_{L^2(\Omega ;H)}\mathrm{d}\lambda \mathrm{d}s\hfill \\ \hfill \le & C\sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}\varphi (\eta ,t_{m-i})\left[1+\parallel X_N{(\left[s\right])\parallel }_{L^4(\Omega ;{\dot{H}}^{\gamma })}+{\parallel X_N(s)\parallel }_{L^4(\Omega ;{\dot{H}}^{\gamma })}\right]\hfill \\ \hfill & \times \parallel \left(I-E(s-[s])\right)X_N{(\left[s\right])\parallel }_{L^4(\Omega ;{\dot{H}}^{-\gamma })}\mathrm{d}s\hfill \\ \hfill \le & C{\tau }^{\gamma }\sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}\varphi (\eta ,t_{m-i}){\parallel X_N(\left[s\right])\parallel }_{L^4(\Omega ;{\dot{H}}^{\gamma })}\mathrm{d}s\le C{\tau }^{\gamma }.\hfill \end{array}$$

(123)

As to ${\mathbb{J}}_3^2$, with the help of (12), (44) and (78), we can conclude that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{J}}_3^2\le & C\sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}\varphi (0,t_{m-i}){\int }_0^1\parallel F^{\prime }\left(\lambda (X_N(\left[s\right]),X_N(s)\right))\hfill \\ \hfill & \times {\int }_{t_i}^{s}E(s-r)P_{N}F(X_N(r)){\mathrm{d}r\parallel }_{L^2(\Omega ;H)}\mathrm{d}\lambda \mathrm{d}s\hfill \\ \hfill \le & C\sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}\varphi (0,t_{m-i}){\int }_{t_i}^s{\parallel E(s-r)P_{N}F(X_N(r))\parallel }_{L^2(\Omega ;H)}\mathrm{d}r\mathrm{d}s\hfill \\ \hfill \le & C\tau \sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}\varphi (0,t_{m-i})\mathrm{d}s\le C\tau .\hfill \end{array}\end{array}$$

(124)

Concerning ${\mathbb{J}}_3^3$, we employ (11) and (78), the Hölder inequality, the Itô isometry and the stochastic Fubini theorem(e.g., see Theorem 4.18 in [40]) to obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{J}}_3^3=& \parallel \sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_0^1{E}_N^{m-i}{P}_N{F}^{\prime }\left(\lambda (X_N(s),X_N(\left[s\right]))\right)(1-\lambda ){\chi }_{[t_i,s)}(r)\hfill \\ \hfill & \times E(s-r)P_N\mathrm{d}\lambda \mathrm{d}s\mathrm{d}W(r){\parallel }_{L^2(\Omega ;{\dot{H}}^{\gamma })}\hfill \\ \hfill =& \left[\sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}\mathbb{E}\right[\parallel {\int }_{t_i}^{t_{i+1}}{\int }_0^1{E}_N^{m-i}{P}_N{F}^{\prime }\left(\lambda (X_N(s),X_N(\left[s\right]))\right){\chi }_{[t_i,s)}(r)\hfill \\ \hfill & \times E(s-r)P_N\mathrm{d}\lambda \mathrm{d}s{\parallel }_{{\mathcal{L}}_2^0}^2\mathrm{d}r{]}^{\frac{1}{2}}\hfill \\ \hfill \le & C{\tau }^{\frac{1}{2}}{\left[\sum _{i=0}^{m-1}{\int }_{t_i}^{t_{i+1}}{\left(\varphi (0,t_{m-i})\right)}^2{\int }_{t_i}^s\parallel E(s-r)P_N{\parallel }_{{\mathcal{L}}_2^0}^2\mathrm{d}r\mathrm{d}s\right]}^{\frac{1}{2}}\hfill \\ \hfill \le & C{\tau }^{\frac{1+\gamma }{2}}{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)}{\left[\tau \sum _{i=0}^{m-1}{\left(\varphi (0,t_{m-i})\right)}^2\right]}^{\frac{1}{2}}\le C{\tau }^{\frac{1+\gamma }{2}}.\hfill \end{array}\end{array}$$

(125)

For the term ${\mathbb{J}}_4$, we first apply the Burkholder–Davis–Gundy type inequality and (101) with $\varrho =2\gamma$ to obtain

$$\begin{array}{cc}\hfill \parallel {\mathcal{O}}_N^i-{\mathcal{O}}_N(t_i){\parallel }_{L^4(\Omega ;{\dot{H}}^{-\gamma })}& \le {\left({\int }_0^{t_i}{\parallel {\Psi }_{\tau ,N}(t_i-s)A^{-\frac{\gamma }{2}}\parallel }_{{\mathcal{L}}_2^0}^2\mathrm{d}s\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le C{\tau }^{\gamma }{\parallel A^{\frac{\gamma -1}{2}}{Q}^{\frac{1}{2}}\parallel }_{{\mathcal{L}}_2(H)},\hfill \end{array}$$

(126)

and, then use (13), (17) and (89) to derive

$$\begin{array}{cc}\hfill {\mathbb{J}}_4\le & \parallel \sum _{i=0}^{m-1}\tau E_N^{m-i}{P}_N\left(F({\tilde{X}}_N(t_i)+O_N^i)-F(X_N(t_i))\right){\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill \le & C\tau \sum _{i=0}^{m-1}\varphi (\eta ,t_{m-i})\parallel A^{-\frac{\eta }{2}}{\int }_0^1{F}^{\prime }(X_N(t_i)+s({\mathcal{O}}_N^i-{\mathcal{O}}_N(t_i)))\hfill \\ \hfill & \times ({\mathcal{O}}_N^i-{\mathcal{O}}_N(t_i))(1-s)\mathrm{d}s{\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill \le & C\tau \sum _{i=0}^{m-1}\varphi (\eta ,t_{m-i})(1+\parallel X_N(t_i){\parallel }_{L^4(\Omega ;{\dot{H}}^{\gamma })}+{\parallel {\mathcal{O}}_N^i-{\mathcal{O}}_N(t_i)\parallel }_{L^4(\Omega ;{\dot{H}}^{\gamma })})\hfill \\ \hfill & \times \parallel {\mathcal{O}}_N^i-{\mathcal{O}}_N(t_i){\parallel }_{L^4(\Omega ;{\dot{H}}^{-\gamma })}\hfill \\ \hfill \le & C{\tau }^{\gamma }\tau \sum _{i=0}^{m-1}\varphi (\eta ,t_{m-i})\le C{\tau }^{\gamma }.\hfill \end{array}$$

(127)

As a result, the above estimates result in

$$\begin{array}{c}\hfill \parallel {\mathbf{e}}_1^m{\parallel }_{L^2(\Omega ;H)}\le C{\tau }^{\gamma }.\end{array}$$

(128)

Next, we turn our attention to the error $e_2^m={\tilde{X}}_N^m-{\tilde{\mathcal{X}}}_N^m$, which obeys

$$\begin{array}{cc}\hfill e_2^m=& E_N{e}_2^{m-1}+\tau E_N{P}_N(F(X_N^{m-1})-F({\tilde{X}}_N(t_{m-1})+{\mathcal{O}}_N^{m-1}))\hfill \\ \hfill :=& E_N{e}_2^{m-1}+\tau E_N{P}_N(F(X_N^{m-1})-F({\tilde{\mathcal{X}}}_N^{m-1}+{\mathcal{O}}_N^{m-1}))\hfill \\ \hfill & +\tau E_N{P}_N\underset{F^{m-1}}{\underbrace{\left(F({\tilde{\mathcal{X}}}_N^{m-1}+{\mathcal{O}}_N^{m-1})-F({\tilde{X}}_N(t_{m-1})+{\mathcal{O}}_N^{m-1})\right)}}.\hfill \end{array}$$

(129)

By the similar argument in the proof of (91) together with (92), we arrive that

$$\begin{array}{c}\hfill \parallel e_2^m{\parallel }^2\le \frac{1+(L_F+{\lambda }_1)\tau }{{(1+{\lambda }_1\tau )}^2}\parallel e_2^{m-1}{\parallel }^2+C\tau \frac{\tau ({\lambda }_1-L_F)+1}{({\lambda }_1-L_F){(1+{\lambda }_1\tau )}^2}{\parallel F^{m-1}\parallel }^2.\end{array}$$

(130)

Then by (12) and (128), we have

$$\begin{array}{cc}\hfill \parallel F^{m-1}{\parallel }_{L^2(\Omega ;H)}=& \parallel F({\tilde{\mathcal{X}}}_N^{m-1}+{\mathcal{O}}_N^{m-1})-F({\tilde{X}}_N(t_{m-1})+{\mathcal{O}}_N^{m-1}){\parallel }_{L^2(\Omega ;H)}\hfill \\ \hfill \le & L\parallel e_1^{m-1}{\parallel }_{L^2(\Omega ;H)}\le C{\tau }^{\gamma }.\hfill \end{array}$$

(131)

With the above estimate and the fact $e_2^0=0$, one can follow the same lines of the proof of (93) to show

$$\begin{array}{c}\hfill \mathbb{E}[\parallel e_2^m{\parallel }^2]\le C{\tau }^{2\gamma }.\end{array}$$

(132)

Finally, in combination with (115), (116), (128) and (132), we complete the proof. □

4.3. Fully-Discrete Approximation of the Invariant Law $\nu$

Theorem 7. 

Suppose that Assumptions 1–4 are valid and $\tau <{\tau }_0\le \frac{{\lambda }_1-L_F}{4L^2}$. Let ν and ${\nu }_{\tau }^N$ be the corresponding unique invariant measures of ${\left\{X(t)\right\}}_{t\ge 0}$ and ${\left\{X_N^m\right\}}_{m\ge 1}$, respectively. For any $N\in {\mathbb{N}}^{+}$, there exists a constant C independent of N, τ such that

$$|{\int }_H\Phi (y)\nu (\mathrm{d}y)-{\int }_{H_N}\Phi (y){\nu }_{\tau }^N(\mathrm{d}y)|\le C({\lambda }_N^{-\gamma }+{\tau }^{\gamma }).$$

(133)

Proof of Theorem 7. 

Owing to Theorem 5, it suffices to bound $|{\int }_{H_N}\Phi (y){\nu }^N(\mathrm{d}y)$$-{\int }_{H_N}\Phi (y){\nu }_{\tau }^N(\mathrm{d}y)|$. By the definition of ergodicity of ${\nu }_{\tau }^N$, we have

$$\begin{array}{c}\hfill \underset{M\to \infty }{lim}\frac{1}{M}\sum _{m=0}^{M-1}\mathbb{E}\left[\Phi (X_N^m)\right]={\int }_{H_N}\Phi (y){\nu }_{\tau }^N(\mathrm{d}y),\end{array}$$

(134)

which together with (6), (69) and (97) arrives at

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\int }_{H_N}\Phi (y)& {\nu }^N(\mathrm{d}y)-{\int }_{H_N}\Phi (y){\nu }_{\tau }^N(\mathrm{d}y)|\hfill \\ \hfill \le & \underset{\begin{array}{c}M\to \infty \\ T=M\tau \end{array}}{lim}\frac{1}{T}\sum _{m=0}^{M-1}{\int }_{t_m}^{t_{m+1}}\left|\mathbb{E}\right[\Phi (X_N(t))]-\mathbb{E}[\Phi (X_N^m)\left]\right|\mathrm{d}t\hfill \\ \hfill \le & \underset{\begin{array}{c}M\to \infty \\ T=M\tau \end{array}}{lim}\frac{1}{T}\sum _{m=0}^{M-1}{\int }_{t_m}^{t_{m+1}}\left|\mathbb{E}\right[\Phi (X_N(t))]-\mathbb{E}[\Phi (X_N(t_m))\left]\right|\mathrm{d}t\hfill \\ \hfill & +\underset{M\to \infty }{lim}\frac{1}{M}\sum _{m=0}^{M-1}\left|\mathbb{E}\right[\Phi (X_N(t_m))]-\mathbb{E}[\Phi (X_N^m)\left]\right|\hfill \\ \hfill \le & \underset{\mathbb{F}}{\underbrace{{lim}_{\begin{array}{c}M\to \infty \\ T=M\tau \end{array}}\frac{1}{T}{\sum }_{m=0}^{M-1}{\int }_{t_m}^{t_{m+1}}\left|\mathbb{E}\right[\Phi (X_N(t))]-\mathbb{E}[\Phi (X_N(t_m))\left]\right|\mathrm{d}t}}+C{\tau }^{\gamma }.\hfill \end{array}\end{array}$$

(135)

To control $\mathbb{F}$, it suffices to bound $\left|\mathbb{E}[\Phi (X_N(t))]-\mathbb{E}[\Phi (X_N(t_m))\right]|$. By (45) and the second-order Taylor expansion, we obtain

$$\begin{array}{cc}\hfill & \left|\mathbb{E}[\Phi (X_N(t))]-\mathbb{E}[\Phi (X_N(t_m))\right]|\hfill \\ \hfill =& \left|\mathbb{E}\right[{\Phi }^{\prime }(X_N(t_m))(X_N(t_m)-X_N(t))+{\int }_0^1{\Phi }^{\prime \prime }(X_N(t_m)+\lambda (X_N(t_m)-X_N(t)))\hfill \\ \hfill & \times (X_N(t_m)-X_N(t),X_N(t_m)-X_N(t))(1-\lambda )\mathrm{d}\lambda \left]\right|\hfill \\ \hfill \le & \left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m))(X_N(t_m)-X_N(t))\right]\right|+C\mathbb{E}\left[\parallel X_N(t)-X_N(t_m){\parallel }^2\right]\hfill \\ \hfill \le & \underset{\mathbb{K}}{\underbrace{\left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m))(X_N(t_m)-X_N(t))\right]\right|}}+C{\tau }^{\gamma }.\hfill \end{array}$$

(136)

In order to treat $\left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m))(X_N(t_m)-X_N(t))\right]\right|$, we utilize (12) and (44) and apply the fact ${\Phi }^{\prime }(X_N(t_m))$ and ${\int }_{t_m}^{t}E(t-s)P_N\mathrm{d}W(s)$ are independent of each other

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{K}\le & \left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m))(I-E(t-t_m))X_N(t_m)\right]\right|\hfill \\ \hfill & +\left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m)){\int }_{t_m}^{t}E(t-s)P_{N}F(X_N(s))\mathrm{d}s\right]\right|\hfill \\ \hfill & +\left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m)){\int }_{t_m}^{t}E(t-s)P_N\mathrm{d}W(s)\right]\right|\hfill \\ \hfill \le & \left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m))(I-E(t-t_m))X_N(t_m)\right]\right|\hfill \\ \hfill & +C{\int }_{t_m}^t\left|\mathbb{E}\left[\parallel E(t-s)P_{N}F(X_N(t_m))\parallel \right]\right|\mathrm{d}s\hfill \\ \hfill \le & \underset{\mathbb{M}}{\underbrace{\left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m))(I-E(t-t_m))X_N(t_m)\right]\right|}}+C\tau .\hfill \end{array}\end{array}$$

(137)

For $\mathbb{M}$, we follow the same argument of the proof of (59) and (62) to derive

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{M}\le & \left|\mathbb{E}\right[{\Phi }^{\prime }(X_N(t_m))(I-E(t-t_m))(E(t_m)P_N{X}_0\hfill \\ \hfill & +{\int }_0^{t_m}E(t_m-s)P_{N}F(X_N(s))\mathrm{d}s)]|\hfill \\ \hfill & +\left|\mathbb{E}\left[{\Phi }^{\prime }(X_N(t_m))(I-E(t-t_m)){\int }_0^{t}E(t_m-s)P_N\mathrm{d}W(s)\right]\right|\hfill \\ \hfill \le & C{\tau }^{\gamma }.\hfill \end{array}\end{array}$$

(138)

Hence, the proof of this theorem is complete. □

Remark 3. 

For the space-time white noise in one dimension ((15) is fulfilled with $\gamma <\frac{1}{2}$), Theorem 7 yields a temporal convergence rate of order $O({\tau }^{\gamma })$ for the error between ν and ${\nu }_{\tau }^N$, which coincides with that in [14] for the backward Euler time semi-discretization and that in [25] for a fully-discrete exponential Euler scheme. Further, by specializing Theorem 7 to the trace class noise, we acquire the temporal convergence rate of order $O(\tau )$, which improves the bound $O({\tau }^{1-ϵ})$, for arbitrarily small $ϵ>0$ in [25]. To the best of our knowledge, the existing papers ([14,15,25]) analyzing the approximations of invariant measures for parabolic SPDEs with global Lipschitz nonlinearity, require that F is usually assumed to be two differentiable with (20). Hence, our improved results are derived based on a weaker condition.

5. Numerical Experiments

Some numerical tests are presented in this section to illustrate the previous findings. We consider the following semilinear stochastic parabolic equation in one dimension

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\partial u}{\partial t}-\frac{{\partial }^{2}u}{\partial x^2}=\frac{1-u}{1+u^2}+\dot{W}(t),\hfill & t>0,x\in (0,1),\hfill \\ u(0,x)=0,\hfill & x\in (0,1),\hfill \\ u(t,0)=u(t,1)=0,\hfill & t>0.\hfill \end{array}\right.\end{array}$$

(139)

In order to fulfill (15), we consider two kinds of noise including a space-time white noise case (STWN, $Q=I$) and a trace class noise case (TCN, $Q=A^{-0.5005})$. Note, that Assumptions 1–4 are satisfied in our setting. Since the explicit solution is not available, it will be numerically approximated by a numerical method with a sufficiently small step-size. Additionally, the expectation is approximated by the Monte-Carlo approximation using an average of over 100 samples.

Firstly, we examine the ergodicity of the solution of (139). In Table 1 and Table 2, we present the expected value of the temporal averages $\frac{1}{M+1}{\sum }_{m=0}^M\mathbb{E}[\Phi (X_N^m)]$. Numerical results suggest the temporal averages tend to a constant as M tends to infinity, for a fixed $\tau$ and all initial values in the whole space and may vary for different test functions $\Phi \in C_b^2(H,\mathbb{R})$, which indicates the solution $X_N^m$ of (71) is ergodic. Additionally, both the spatial and temporal weak errors listed in Table 3 show that these weak errors are independent of time T.

Table 1. The temporal averages for different initial values.

$\frac{1}{M+1}{\sum }_{m=0}^M\mathbb{E}[\Phi (X_N^m)],N=2^8,M=\frac{T}{\tau },\tau =2^{-6},\Phi (x)=e^{-{\left|x\right|}^2},x\in {\mathbb{R}}^N$
T	$u_0^1=0,u_0^2=\sqrt{2}sin(\pi x),u_0^3={\sum }_{i=1}^{\infty }sin(i\pi x)/i$
	space-time white noise			trace class noise
	$u_0^1$	$u_0^2$	$u_0^3$	$u_0^1$	$u_0^2$	$u_0^3$
10	0.938520	0.934366	0.933958	0.976648	0.973443	0.973234
20	0.938801	0.936645	0.935726	0.977459	0.976364	0.975307
50	0.938380	0.937762	0.937845	0.978112	0.977335	0.977075
100	0.938787	0.938444	0.938621	0.978162	0.977858	0.977849
200	0.938645	0.938690	0.938908	0.978225	0.978067	0.978207
500	0.938970	0.938813	0.938745	0.978258	0.978184	0.978265

Table 2. The temporal averages for different test functions.

$\frac{1}{M+1}{\sum }_{m=0}^M\mathbb{E}[\Phi (X_N^m)],N=2^8,M=\frac{T}{\tau },\tau =2^{-6},u_0(x)=0,x\in {\mathbb{R}}^N$
T	${\Phi }_1(x)=e^{-{\left|x\right|}^2},{\Phi }_2(x)=sin(|x|),{\Phi }_3(x)=cos(|x|),x\in {\mathbb{R}}^N$
	space-time white noise			trace class noise
	${\Phi }_1$	${\Phi }_2$	${\Phi }_3$	${\Phi }_1$	${\Phi }_2$	${\Phi }_3$
10	0.934366	0.231008	0.964474	0.973443	0.134676	0.985927
20	0.936645	0.227015	0.966441	0.976364	0.130701	0.987420
50	0.937762	0.225179	0.967019	0.977335	0.128184	0.988272
100	0.938444	0.224777	0.967361	0.977858	0.127321	0.988650
200	0.938690	0.224838	0.967327	0.978067	0.126869	0.988804
500	0.938813	0.224186	0.967617	0.978184	0.126772	0.988870

Table 3. The spatial weak errors and the temporal weak errors.

$T=M\tau ,u_0(x)=0,\Phi (y)=e^{-{\left|y\right|}^2},y\in {\mathbb{R}}^N$
T	$\mathbb{E}[\Phi (X(T))]-\mathbb{E}[\Phi (X_N(T))]$		$\mathbb{E}[\Phi (X_N(T))]-\mathbb{E}[\Phi (X_N^M)]$
	$N_{exact}=2^7,N=2^5,\tau =2^{-6}$		$N=2^{-7},{\tau }_{exact}=2^{-9},\tau =2^{-6}$
	STWN	TCN	STWN	TCN
10	4.565652060317671 × 10${}^{-7}$	1.508034616815035 × 10${}^{-7}$	0.006991321567161	0.001120026352536
20	5.186095901610343 × 10${}^{-8}$	7.060159254335119 × 10${}^{-8}$	0.007891500709643	0.001064185885398
50	4.048828477143385 × 10${}^{-7}$	1.345511102057717 × 10${}^{-7}$	0.007417254806891	0.001197879886755
100	1.594043779840071 × 10${}^{-7}$	1.518749788198548 × 10${}^{-7}$	0.006896090700224	0.001245121673112
200	1.797148238380508 × 10${}^{-7}$	1.130844673224995 × 10${}^{-7}$	0.007802558404298	0.001220756375257
500	1.616685430105846 × 10${}^{-7}$	1.533591053748396 × 10${}^{-7}$	0.007628212596405	0.001350136656459

Next, we choose a time point $T=50$ and check the weak orders with $u_0(x)=0$ being the initial value. In the left figure of Figure 1, we depict the weak errors in the space discretization by varying space step-sizes $\frac{T}{N}$, $N=2^i,i=1,2,3,4,5$, on a log-log scale, with a fixed parameter $\tau =2^{-16}$. One can observe that the weak error converges with order 2 for the trace class noise case and with order 1 for the space-white noise case, which is consistent with the theoretical estimate of Theorem 4. Note that here we take $N_{exact}=2^8$ to compute the exact solution for the spatial discretization.

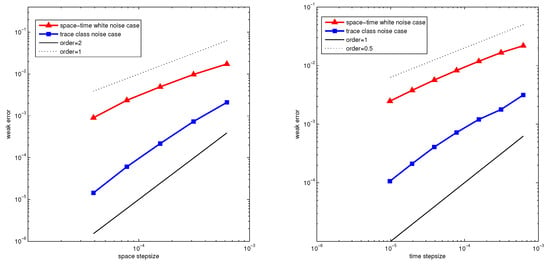
Figure 1. The spatial weak convergence orders (left) and the temporal weak convergence orders (right).

We now fix $N=100$ and test the convergence rates in time of the proposed full-discrete scheme (71) by using the step-sizes $\tau =2^{-i},i=5,6,7,8,9,10,11$. Again, the “exact” solution is computed by the proposed scheme (71) with a sufficiently small time step-size ${\tau }_{exact}=2^{-15}$. In the right picture of Figure 1, the resulting weak errors in temporal direction are plotted. It can be seen that the decay of the error is consistent with our theoretical results.

6. Conclusions

This paper is devoted to the long-time behavior of the full discretization of an ergodic semilinear stochastic partial differential equation driven by additive noise. The full discretization is realized by a spectral Galerkin method in spatial direction and an Euler scheme in temporal direction, which admits a unique invariant probability measure. Compared with the existing works, we relax the condition on the nonlinearity F by assuming that F is once differentiable. Under the weaker condition, the optimal convergence orders of the numerical invariant measures are obtained based on the time-independent weak error, but not relying on the associated Kolmogorov equation. Finally, numerical examples confirm the theoretical findings. In the future, we will consider the ergodic non-globally Lipschitz continuous stochastic partial differential equation and are expected to the optimal convergence order of its numerical method.