Conditioning Theory for Generalized Inverse $C_A^{‡}$ and Their Estimations

Abstract

The conditioning theory of the generalized inverse $C_A^{‡}$ is considered in this article. First, we introduce three kinds of condition numbers for the generalized inverse $C_A^{‡}$, i.e., normwise, mixed and componentwise ones, and present their explicit expressions. Then, using the intermediate result, which is the derivative of $C_A^{‡}$, we can recover the explicit condition number expressions for the solution of the equality constrained indefinite least squares problem. Furthermore, using the augment system, we investigate the componentwise perturbation analysis of the solution and residual of the equality constrained indefinite least squares problem. To estimate these condition numbers with high reliability, we choose the probabilistic spectral norm estimator to devise the first algorithm and the small-sample statistical condition estimation method for the other two algorithms. In the end, the numerical examples illuminate the obtained results.

1. Introduction

Throughout this paper, ${\mathbb{R}}^{m\times n}$ denotes the set of real $m\times n$ matrices. For a matrix $A\in {\mathbb{R}}^{m\times n}$, $A^T$ is the transpose of A, $rank\left(A\right)$ denotes the rank of A, ${\parallel A\parallel }_2$ is the spectral norm of A, and ${\parallel A\parallel }_F$ is the Frobenius norm of A. For a vector a, ${\parallel a\parallel }_{\infty }$ is its ∞-norm, and ${\parallel a\parallel }_2$ the 2-norm. The notation $\left|A\right|$ is a matrix whose components are the absolute values of the corresponding components of A. For any matrix A, the following four equations uniquely define the Moore–Penrose inverse $A^{†}$ of A [1]:

$$\begin{array}{c}\hfill A{A}^{†}A=A,A^{†}A{A}^{†}=A^{†},{\left(A{A}^{†}\right)}^T=A{A}^{†},{\left(A^{†}A\right)}^T=A^{†}A.\end{array}$$

(1)

The generalized inverse $C_A^{‡}$ is defined by

$$\begin{array}{c}\hfill C_A^{‡}=(I-{\left(PQP\right)}^{†}Q)C^{†},\end{array}$$

(2)

where $Q=A^{T}JA$, $A\in {\mathbb{R}}^{(p+q)\times n}$ denotes weight matrix and $P=I-C^{†}C$ is the orthogonal projection onto the null space of C and $C\in {\mathbb{R}}^{s\times n}$ may not have full rank and J is a signature matrix defined by

$$J=\left[\begin{array}{cc}{I}_p& 0\\ 0& -I_q\end{array}\right],p+q=m.$$

The generalized inverse $C_A^{‡}$ originated from the equality constrained indefinite least squares problem (EILS), which is stated as follows [2,3,4,5]:

$$\mathrm{EILS}:\underset{{∥Cx-h∥}_2}{min}{(g-Ax)}^{T}J(g-Ax),$$

(3)

where $g\in {\mathbb{R}}^m$ and $h\in {\mathbb{R}}^s$. The EILS problem has a unique solution:

$$x=C_A^{‡}h+{\left(PQP\right)}^{†}{A}^{T}Jg$$

(4)

under the following condition:

$$\mathrm{rank}\left(C\right)=s,x^{T}Qx>0\mathrm{for}\mathrm{all}\mathrm{nonzero}x\in \mathrm{null}\left(C\right).$$

The above condition implies

$$\begin{array}{c}\hfill p\ge n-s,\mathrm{rank}\left(\begin{array}{c}A\\ C\end{array}\right)=n,\end{array}$$

(5)

then (5) ensures the existence and uniqueness of generalized inverse $C_A^{‡}$ (see [2,6]). The generalized inverse $C_A^{‡}$ has significant applications in the study of EILS algorithms, the analysis of large-scale structure, error analysis, perturbation theory, and the solution of the EILS problem [2,3,4,5,7,8,9,10]. The EILS problem was first demonstrated by Bojanczyk  et al. [5]. Additionally, we reveal some detailed work on the perturbation analysis of this problem. The perturbation theory of the EILS problem was discussed by Wang [11] and extended by Shi and Liu [8] based on the hyperbolic MGS elimination method. Diao and Zhou [12] recovered the linearized estimate of the backward error of this problem. Later, Li et al. [13] investigated the componentwise condition numbers for the EILS problem. Recently, Wang and Meng [14] studied the condition numbers and normwise perturbation analysis of the EILS problem.

Componentwise perturbation analysis has received significant attention in recent years; for references, see [15,16,17,18,19]. The motivation for studying componentwise perturbation analysis is reasonable for research because, if the perturbation in the input data is measured componentwise rather than by norm, it may help us to measure the sensitivity of a function more accurately [15], and improve the exactness and effectiveness of the EILS solution computation. It has attracted many authors’ attention to consider the componentwise perturbation analysis in which the least squares problem [16] and the weighted least squares problem [17] are included. In this article, we continue the research on componentwise perturbation analysis of the EILS problem. We can recover the componentwise perturbation bounds of the indefinite least squares problem with the intermediate result.

The generalized inverse $C_A^{‡}$ reduce to K-weighted pseudoinverse $L_K^{†}$ when $q=0$ and K has a full row rank. This pseudoinverse was expanded to the MK-weighted pseudoinverse $L_{MK}^{†}$ by Wei and Zhang [6], which describes its structure and uniqueness. Its algorithm was developed by Elden [20]. According to Wei [21], the expression of $L_K^{†}$ based on GSVD was investigated. A perturbation equation for $L_K^{†}$ was given by Gulliksson et al. [22]. The condition numbers for the K-weighted pseudoinverse $L_K^{†}$ and their statistical estimate were recently provided by Mahvish et al. [23].

The condition number is a well-known research topic in numerical analysis that estimates the worst-case sensitivity of input data to small perturbations on it (see [24,25,26] and references therein). The normwise condition number [25] has the disadvantage of disregarding the scaling structure of both input and output data. To address this issue, the terms mixed and componentwise condition numbers are introduced [26]. Mixed condition numbers employ componentwise error analysis for input data and normwise error analysis for output data. On the other hand, the componentwise condition numbers employ componentwise error analysis for input and output data. In fact, due to rounding errors and data storage difficulties, it is more practical to estimate input errors componentwise rather than normwise. However, the condition numbers of the generalized inverse $C_A^{‡}$ have not been discussed until now. Inspired by this, we attempt to present the explicit expressions of normwise, mixed and componentwise condition numbers for the generalized inverse $C_A^{‡}$, as well as their statistical estimation due to their importance in EILS research.

The rest of this manuscript is organized as follows: Section 2 provides some preliminaries that will be helpful for the upcoming discussions. With the intermediate result, i.e., the derivative of $C_A^{‡}$, we can recover the explicit expression of condition numbers for the solution of the EILS problem in Section 3. Section 4 will present the componentwise perturbation analysis for the EILS problem. In Section 5, we propose the first two algorithms for the normwise condition number by using the probabilistic spectral norm estimator [27] and the small-sample statistical condition estimation [28] method. Additionally, we construct the third algorithm for the mixed and componentwise condition numbers by using the small-sample statistical condition estimation [28] method. To check the efficiency of these algorithms, we demonstrate them through numerical experiments in Section 6.

2. Preliminaries

In this part, we introduce some definitions and important results, which will be used in the upcoming sections.

Firstly, we define the entrywise division between two vectors $v={\left[v_1,\dots ,v_p\right]}^{\mathrm{T}}\in {\mathbb{R}}^p$ and $w={\left[w_1,\dots ,w_p\right]}^{\mathrm{T}}\in {\mathbb{R}}^p$ by $\frac{v}{w}={\left[{\eta }_1,\dots ,{\eta }_p\right]}^{\mathrm{T}}$ with

$${\eta }_i=\left\{\begin{array}{cc}\frac{v_i}{w_i},\hfill & \mathrm{if}{w}_i\ne 0\hfill \\ v_i,\hfill & \mathrm{if}{w}_i=0.\hfill \end{array}\right.$$

Following [1,26,29], the componentwise distance between v and w is defined by

$$\begin{array}{c}\hfill d(v,w)={∥\frac{v-w}{w}∥}_{\infty }={\displaystyle \underset{i=1,\dots ,p}{max}}\left\{\frac{\left|v_i-w_i\right|}{\left|w_i\right|}\right\}=\left\{\begin{array}{cc}\frac{\left|v_{i*}-w_{i*}\right|}{\left|w_{i*}\right|},\hfill & \mathrm{if}{w}_{i*}\ne 0\hfill \\ \left|v_{i*}\right|,\hfill & \mathrm{if}{w}_{i*}=0.\hfill \end{array}\right.\end{array}$$

Note that when $w_{i*}\ne 0,\forall i=1,\cdots ,p$, $d(v,w)$ gives the relative distance from v to w with respect to w, while the absolute distance for $w_{i*}=0$. We describe the distance between the matrices $V,W\in {\mathbb{R}}^{n\times n}$ as follows:

$$d(V,W)=d\left(\mathrm{vec}\right(V),\mathrm{vec}(W\left)\right).$$

In order to define the mixed and componentwise condition numbers, we also need to define the set $B^{\circ }(v,\epsilon )=\{u\in {\mathbb{R}}^p\left|\right|u_i-v_i|\le ϵ|v_i|,i=1,\cdots ,p\}$ and $B(v,\epsilon )=\{u\in {\mathbb{R}}^p\mid \parallel u-v{\parallel }_2⩽\epsilon \parallel v{\parallel }_2\}$ for given $\epsilon >0.$

Definition 1 

([29]). Let $\aleph :{\mathbb{R}}^p\to {\mathbb{R}}^q$ be a continuous mapping defined on an open set $Dom(\aleph )\subset {\mathbb{R}}^p$, and $v\in Dom(\aleph ),v\ne 0$ such that $\aleph \left(v\right)\ne 0$.

(i) 

The normwise condition number of ℵ at v is given by

$$\begin{array}{ccc}\hfill n(\aleph ,v)& =& {\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{\begin{array}{c}u\in B(v,\epsilon )\\ u\ne v\end{array}}{sup}}\left(\frac{{\parallel \aleph \left(u\right)-\aleph \left(v\right)\parallel }_2}{{\parallel \aleph \left(v\right)\parallel }_2}/\frac{{\parallel u-v\parallel }_2}{{\parallel v\parallel }_2}\right).\hfill \end{array}$$

(ii) 

The mixed condition number of ℵ at v is given by

$$\begin{array}{ccc}\hfill m(\aleph ,v)& =& {\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{\begin{array}{c}u\in B^o(v,\epsilon )\\ u\ne v\end{array}}{sup}}\frac{{\parallel \aleph \left(u\right)-\aleph \left(v\right)\parallel }_{\infty }}{{\parallel \aleph \left(v\right)\parallel }_{\infty }}\frac{1}{d(u,v)}.\hfill \end{array}$$

(iii) 

The componentwise condition number of ℵ at v is given by

$$\begin{array}{ccc}\hfill c(\aleph ,v)& =& {\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{\begin{array}{c}u\in B^o(v,\epsilon )\\ u\ne v\end{array}}{sup}}\frac{d\left(\aleph \left(u\right),\aleph \left(v\right)\right)}{d(u,v)}.\hfill \end{array}$$

When the map ℵ in Definition 1 is Fréchet differentiable, the following lemma given in [29] makes the computation of condition numbers easier.

Lemma 1 

([29]). Under the assumptions of Definition 1, and supposing ℵ is $Fréchet$ differentiable at v, we have

$$n(\aleph ,v)=\frac{{\parallel \mathrm{d}\aleph \left(v\right)\parallel }_2{\parallel v\parallel }_2}{{\parallel \aleph \left(v\right)\parallel }_2}, m(\aleph ,v)=\frac{{\parallel |\mathrm{d}\aleph \left(v\right)|\left|v\right|\parallel }_{\infty }}{{\parallel \aleph \left(v\right)\parallel }_{\infty }}, c(\aleph ,v)={∥\frac{|\mathrm{d}\aleph (v\left)\right|\left|v\right|}{|\aleph (v\left)\right|}∥}_{\infty },$$

where $\mathrm{d}\aleph \left(v\right)$ stands for the Fréchet derivative of ℵ at v.

To obtain the explicit expressions of the above condition numbers, we need some properties of the Kronecker product [30] between X and Y:

$$\begin{array}{ccc}\hfill \mathrm{vec}\left(YZX\right)& =& \left(X^T\otimes Y\right)\mathrm{vec}\left(Z\right),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \mathrm{vec}\left(Y^T\right)& =& {\mathrm{\Pi }}_{mn}\mathrm{vec}\left(Y\right),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\parallel Y\otimes X\parallel }_2& =& {\parallel Y\parallel }_2{\parallel X\parallel }_2,\hfill \end{array}$$

(8)

where the matrix Z has a suitable dimension, and ${\mathrm{\Pi }}_{mn}\in {\mathbb{R}}^{mn\times mn}$ is the vec-permutation matrix, which depends only on the dimensions m and n.

Now, we present the following two lemmas, which will be helpful for obtaining condition numbers and their upper bounds.

Lemma 2 

([31], p. 174, Theorem 5). Let S be an open subset of ${\mathbb{R}}^{n\times q}$, and let $\aleph :S⟶{\mathbb{R}}^{m\times p}$ be a matrix function defined and $k\ge 1$ times (continuously) differentiable on S. If $\mathrm{rank}(\aleph (X\left)\right)$ is constant on $S,$ then ${\aleph }^{†}:S⟶{\mathbb{R}}^{p\times m}$ is k times (continuously) differentiable on S, and 

$$\begin{array}{ccc}\hfill \mathrm{d}{\aleph }^{†}& =& -{\aleph }^{†}\mathrm{d}\aleph {\aleph }^{†}+{\aleph }^{†}{\aleph }^{{†}^T}\mathrm{d}{\aleph }^T(I_m-\aleph {\aleph }^{†})+(I_p-{\aleph }^{†}\aleph )\mathrm{d}{\aleph }^T{\aleph }^{{†}^T}{\aleph }^{†}.\hfill \end{array}$$

(9)

Lemma 3 

([1]). For any matrices $E,$ $F,$ $G,$ $H,$ $U$ and $V$ with dimensions making the following well defined

$$[E\otimes F+(G\otimes H\left)\mathrm{\Pi }\right]\mathrm{vec}\left(U\right),$$

$$\frac{[E\otimes F+(G\otimes H\left)\mathrm{\Pi }\right]\mathrm{vec}\left(U\right)}{V},$$

$$FU{E}^{T}andH{U}^T{G}^T,$$

we have

$${∥\left|\right[E\otimes F+(G\otimes H)\mathrm{\Pi }\left]\right|\mathrm{vec}\left(\right|U\left|\right)∥}_{\infty }\le {∥\mathrm{vec}\left(\right|F\left|\right|U\left|\right|E{|}^T+\left|H\right|\left|U{|}^T\right|G{|}^T)∥}_{\infty }$$

and

$${∥\frac{\left|\right[E\otimes F+(G\otimes H)\mathrm{\Pi }\left]\right|\mathrm{vec}\left(\right|U\left|\right)}{\left|V\right|}∥}_{\infty }\le {∥\frac{\mathrm{vec}\left(\right|F\left|\right|U\left|\right|E{|}^T+\left|H\right|\left|U{|}^T\right|G{|}^T)}{\left|V\right|}∥}_{\infty }.$$

3. Condition Numbers

First, we define a mapping $\varphi \left(u\right):{\mathbb{R}}^{mn+sn}\to {\mathbb{R}}^{ns}$ by

$$\begin{array}{c}\hfill \varphi \left(u\right)=\mathrm{vec}\left(C_A^{‡}\right).\end{array}$$

(10)

Here, $u={(\mathrm{vec}{\left(A\right)}^T,\mathrm{vec}{\left(C\right)}^T)}^T$, $\Delta u={(\mathrm{vec}{(\Delta A)}^T,\mathrm{vec}{(\Delta C)}^T)}^T$, and for matrix $X=\left(x_{ij}\right)$, ${\parallel X\parallel }_F={\parallel \mathrm{vec}\left(X\right)\parallel }_2$ and ${\parallel X\parallel }_{max}={\parallel \mathrm{vec}\left(X\right)\parallel }_{\infty }=\underset{i,j}{max}\left|x_{ij}\right|.$

Then, using Definition 1, we present the definitions of the normwise, mixed, and componentwise condition numbers for generalized inverse $C_A^{‡}$ as given in [32]:

$$\begin{array}{cc}\hfill n^{‡}(A,C)=n(\varphi ,u)& :={\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{{\parallel [\Delta A,\Delta C]\parallel }_F\le \epsilon {\parallel [A,C]\parallel }_F}{sup}}\frac{{\parallel (C+\Delta C)}_A^{‡}-C_A^{‡}{\parallel }_F/{\parallel C_A^{‡}\parallel }_F}{{\parallel [\Delta A,\Delta C]\parallel }_F/{\parallel [A,C]\parallel }_F},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill m^{‡}(A,C)=m(\varphi ,u)& :={\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{\begin{array}{c}{\parallel \Delta A/A\parallel }_{max}\le \epsilon \\ {\parallel \Delta C/C\parallel }_{max}\le \epsilon \end{array}}{sup}}\frac{{\parallel (C+\Delta C)}_A^{‡}-C_A^{‡}{\parallel }_{max}}{\parallel C_A^{‡}{\parallel }_{max}}\frac{1}{d(u+\Delta u,u)},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill c^{‡}(A,C)=c(\varphi ,u)& :={\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{\begin{array}{c}{\parallel \Delta A/A\parallel }_{max}\le \epsilon \\ {\parallel \Delta C/C\parallel }_{max}\le \epsilon \end{array}}{sup}}\frac{1}{d(u+\Delta u,u)}{∥\frac{{(C+\Delta C)}_A^{‡}-C_A^{‡}}{C_A^{‡}}∥}_{max}.\hfill \end{array}$$

(13)

With the help of the $\mathrm{vec}$ operator, Frobenius, spectral, and Max norms, we can rewrite the definitions of normwise, mixed and componentwise condition numbers as follows:

$$\begin{array}{cc}\hfill n^{‡}(A,C)=n(\varphi ,u)& :={\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{{∥\left[\begin{array}{c}\mathrm{vec}(\Delta A)\\ \mathrm{vec}(\Delta C)\end{array}\right]∥}_2\le \epsilon {∥\left[\begin{array}{c}\mathrm{vec}\left(A\right)\\ \mathrm{vec}\left(C\right)\end{array}\right]∥}_2}{sup}}\frac{\parallel \mathrm{vec}({(C+\Delta C)}_A^{‡}-C_A^{‡}){\parallel }_2}{\parallel \mathrm{vec}\left(C_A^{‡}\right){\parallel }_2}/\frac{{∥\left[\begin{array}{c}\mathrm{vec}(\Delta A)\\ \mathrm{vec}(\Delta C)\end{array}\right]∥}_2}{{∥\left[\begin{array}{c}\mathrm{vec}\left(A\right)\\ \mathrm{vec}\left(C\right)\end{array}\right]∥}_2},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill m^{‡}(A,C)=m(\varphi ,u)& :={\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{\begin{array}{c}{\parallel \mathrm{vec}(\Delta A)/\mathrm{vec}\left(A\right)\parallel }_{\infty }\le \epsilon \\ {\parallel \mathrm{vec}(\Delta C)/\mathrm{vec}\left(C\right)\parallel }_{\infty }\le \epsilon \end{array}}{sup}}\frac{\parallel \mathrm{vec}({(C+\Delta C)}_A^{‡}-C_A^{‡}){\parallel }_{\infty }}{\parallel \mathrm{vec}\left(C_A^{‡}\right){\parallel }_{\infty }}\frac{1}{d(u+\Delta u,u)},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill c^{‡}(A,C)=c(\varphi ,u)& :={\displaystyle \underset{\epsilon \to 0}{lim}}{\displaystyle \underset{\begin{array}{c}{\parallel \mathrm{vec}(\Delta A)/\mathrm{vec}\left(A\right)\parallel }_{\infty }\le \epsilon \\ {\parallel \mathrm{vec}(\Delta C)/\mathrm{vec}\left(C\right)\parallel }_{\infty }\le \epsilon \end{array}}{sup}}\frac{1}{d(u+\Delta u,u)}{∥\frac{\mathrm{vec}({(C+\Delta C)}_A^{‡}-C_A^{‡})}{\mathrm{vec}\left(C_A^{‡}\right)}∥}_{\infty }.\hfill \end{array}$$

(16)

In the following, we find the expression of the Fréchet derivative of $\varphi$ at u.

Lemma 4. 

Let the mapping ϕ be continuous. Then, the Fréchet differential at u is:

$$\begin{array}{c}\hfill {\varphi }^{\prime }\left(u\right)=[W\left(A\right),W\left(C\right)],\end{array}$$

(17)

where

$$\begin{array}{cc}\hfill W\left(A\right)& =-[(C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J)+({\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn}],\hfill \\ \hfill W\left(C\right)& =-[(C_A^{{‡}^T}\otimes C_A^{‡})-({(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}-{\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{sn}].\hfill \end{array}$$

(18)

Proof. 

Differentiating both sides of (2), we obtain

$$\begin{array}{ccc}\hfill \mathrm{d}\left(C_A^{‡}\right)& =& \mathrm{d}\left[(I-{\left(PQP\right)}^{†}Q)C^{†}\right].\hfill \end{array}$$

(19)

From ([3], Theorem 2.2), we obtain

$$\begin{array}{cc}\hfill & {\left(PQP\right)}^{†}=P{\left(PQP\right)}^{†}={\left(PQP\right)}^{†}P=P{\left(PQP\right)}^{†}P,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & P(I-{\left(PQP\right)}^{†}QP)=0,{\left(PQP\right)}^{†}QP=P.\hfill \end{array}$$

(21)

Thus, substituting (20) into (19) and differentiating both sides of the equation, we can deduce

$$\begin{array}{cc}\hfill \mathrm{d}\left(C_A^{‡}\right)& =\mathrm{d}\left[(I-P{\left(PQP\right)}^{†}Q)C^{†}\right]=\mathrm{d}{C}^{†}-\mathrm{d}\left(P{\left(PQP\right)}^{†}Q{C}^{†}\right)\hfill \\ \hfill & =(I-P{\left(PQP\right)}^{†}Q)\mathrm{d}{C}^{†}-\mathrm{d}P{\left(PQP\right)}^{†}Q{C}^{†}-P\mathrm{d}{\left(PQP\right)}^{†}Q{C}^{†}-P{\left(PQP\right)}^{†}\mathrm{d}Q{C}^{†}.\hfill \end{array}$$

Further, using (9), we have

$$\begin{array}{cc}\hfill \mathrm{d}\left(C_A^{‡}\right)& =(I-P{\left(PQP\right)}^{†}Q)[-C^{†}\mathrm{d}C{C}^{†}+C^{†}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})+(I-C^{†}C)\mathrm{d}{C}^T{C}^{{†}^T}{C}^{†}]\hfill \\ \hfill & -\mathrm{d}(I-C^{†}C){\left(PQP\right)}^{†}Q{C}^{†}+P[{\left(PQP\right)}^{†}\mathrm{d}\left(PQP\right){\left(PQP\right)}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}{\left(PQP\right)}^{{†}^T}\mathrm{d}{\left(PQP\right)}^T(I-\left(PQP\right){\left(PQP\right)}^{†})\hfill \\ \hfill & -(I-{\left(PQP\right)}^{†}\left(PQP\right))\mathrm{d}{\left(PQP\right)}^T{\left(PQP\right)}^{{†}^T}{\left(PQP\right)}^{†}]Q{C}^{†}-P{\left(PQP\right)}^{†}\mathrm{d}Q{C}^{†}.\hfill \end{array}$$

Noting (20), (2), and $(I-P{\left(PQP\right)}^{†}Q)(I-C^{†}C)=P(I-{\left(PQP\right)}^{†}QP)$, the previous equation may be expressed as

$$\begin{array}{cc}\hfill \mathrm{d}\left(C_A^{‡}\right)& =-C_A^{‡}\mathrm{d}C{C}^{†}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})+P(I-{\left(PQP\right)}^{†}QP)\mathrm{d}{C}^T{C}^{{†}^T}{C}^{†}+\mathrm{d}{C}^{†}C{\left(PQP\right)}^{†}Q{C}^{†}\hfill \\ \hfill & +C^{†}\mathrm{d}C{\left(PQP\right)}^{†}Q{C}^{†}+{\left(PQP\right)}^{†}\mathrm{d}\left(PQP\right){\left(PQP\right)}^{†}Q{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}{\left(PQP\right)}^{{†}^T}\mathrm{d}{\left(PQP\right)}^T(I-\left(PQP\right){\left(PQP\right)}^{†})Q{C}^{†}\hfill \\ \hfill & -P(I-{\left(PQP\right)}^{†}QP)\mathrm{d}{\left(PQP\right)}^T{\left(PQP\right)}^{{†}^T}{\left(PQP\right)}^{†}Q{C}^{†}-{\left(PQP\right)}^{†}\mathrm{d}Q{C}^{†}.\hfill \end{array}$$

Further, by the fact $PQ={\left(QP\right)}^T=QP$, (21), and 

$$\begin{array}{cc}\hfill CP{\left(PQP\right)}^{†}& =C{\left(PQP\right)}^{†}=0,\hfill \end{array}$$

(22)

the above equation may be simplified as follows:

$$\begin{array}{cc}\hfill \mathrm{d}\left(C_A^{‡}\right)& =-C_K^{‡}\mathrm{d}C{C}^{†}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})+C^{†}\mathrm{d}C{\left(PQP\right)}^{†}Q{C}^{†}-{\left(PQP\right)}^{†}\mathrm{d}Q{C}^{†}\hfill \\ \hfill & +{\left(PQP\right)}^{†}\mathrm{d}QP{\left(PQP\right)}^{†}Q{C}^{†}+{\left(PQP\right)}^{†}Q\mathrm{d}P{\left(PQP\right)}^{†}Q{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}{\left(PQP\right)}^{{†}^T}\mathrm{d}{Q}^T{P}^T(I-\left(PQP\right){\left(PQP\right)}^{†})Q{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}{\left(PQP\right)}^{{†}^T}{Q}^T\mathrm{d}{P}^T(I-\left(PQP\right){\left(PQP\right)}^{†})Q{C}^{†}.\hfill \\ \hfill & =-C_K^{‡}\mathrm{d}C{C}^{†}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})+C^{†}\mathrm{d}C{\left(PQP\right)}^{†}Q{C}^{†}-{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}JA{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A{C}^{†}+{\left(PQP\right)}^{†}P\mathrm{d}{A}^{T}JA{\left(PQP\right)}^{†}Q{C}^{†}+{\left(PQP\right)}^{†}P{A}^{T}J\mathrm{d}A{\left(PQP\right)}^{†}Q{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}{\left(PQP\right)}^{{†}^T}\mathrm{d}{Q}^{T}P(I-QP{\left(PQP\right)}^{†})Q{C}^{†}+{\left(PQP\right)}^{†}Q\mathrm{d}P{\left(PQP\right)}^{†}Q{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}\left(PQP\right){\left(PQP\right)}^{†}\mathrm{d}{P}^T(I-QP{\left(PQP\right)}^{†})Q{C}^{†}.\hfill \end{array}$$

(23)

Considering $PQ={\left(QP\right)}^T=QP$, we obtain

$$\begin{array}{c}\hfill P((I-QP{\left(PQP\right)}^{†})=0QP{\left(PQP\right)}^{†}=P\end{array}$$

(24)

Substituting this fact into (23) implies

$$\begin{array}{cc}\hfill \mathrm{d}\left(C_A^{‡}\right)& =-C_A^{‡}\mathrm{d}C{C}^{†}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})+C^{†}\mathrm{d}C{\left(PQP\right)}^{†}Q{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A(I-P{\left(PQP\right)}^{†}Q)C^{†}-{\left(PQP\right)}^{†}Q{C}^{†}\mathrm{d}C{\left(PQP\right)}^{†}Q{C}^{†}\hfill \\ \hfill & -{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}JA(I-{\left(PQP\right)}^{†}Q)C^{†}+{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}Q(I-{\left(PQP\right)}^{†}Q)C^{†}.\hfill \end{array}$$

We can rewrite the above equation by using (2) and (20) as

$$\begin{array}{cc}\hfill \mathrm{d}\left(C_A^{‡}\right)& =-C_A^{‡}\mathrm{d}C{C}_A^{‡}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})+{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}Q{C}_A^{‡}-{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A{C}_A^{‡}\hfill \\ \hfill & -{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}JA{C}_A^{‡}.\hfill \end{array}$$

(25)

By applying “vec” operator on (25), and using (6) and (7), we obtain

$$\begin{array}{cc}\hfill \mathrm{vec}\left(\mathrm{d}\left(C_A^{‡}\right)\right)& =-(C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J)\mathrm{vec}\left(\mathrm{d}A\right)-({\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†})\mathrm{vec}\left(\mathrm{d}{A}^T\right)\hfill \\ \hfill & -(C_A^{{‡}^T}\otimes C_A^{‡})\mathrm{vec}\left(\mathrm{d}C\right)+({(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T})\mathrm{vec}\left(\mathrm{d}{C}^T\right)\hfill \\ \hfill & +({\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†})\mathrm{vec}\left(\mathrm{d}{C}^T\right)\mathrm{by}\left(\right)\hfill \\ \hfill & =-[(C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J)+({\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn}]\mathrm{vec}\left(\mathrm{d}A\right)\hfill \\ \hfill & -[(C_A^{{‡}^T}\otimes C_A^{‡})-({(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}-{\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{sn}]\mathrm{vec}\left(\mathrm{d}C\right)\hfill \\ \hfill & \mathrm{by}\left(\right)\hfill \\ \hfill & =[-(C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J)-({\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn},\hfill \\ \hfill & -(C_A^{{‡}^T}\otimes C_A^{‡})+({(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}+{\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}\left){\mathrm{\Pi }}_{sn}\right]\left[\begin{array}{c}\mathrm{vec}\left(\mathrm{d}A\right)\\ \mathrm{vec}\left(\mathrm{d}C\right)\end{array}\right].\hfill \end{array}$$

That is,

$$\mathrm{d}\left(\mathrm{vec}\left(C_A^{‡}\right)\right)=[W\left(A\right),W\left(C\right)]\mathrm{d}v.$$

Thus, we have obtained the required result by using the definition of Fréchet derivative.    □

Remark 1. 

Setting $C=L$, $K=A$, $q=0$ and C as full row rank, we have $C_A^{‡}=L_K^{†}$ and

$$\begin{array}{cc}\hfill \tilde{W}\left(A\right)& =-[(C_A^{{†}^T}\otimes {\left(AP\right)}^{†})+({\left(A{C}_A^{†}\right)}^T\otimes {\left(AP\right)}^{†}{\left(AP\right)}^{{†}^T}){\mathrm{\Pi }}_{mn}],\hfill \\ \hfill \tilde{W}\left(C\right)& =-[(C_A^{{†}^T}\otimes C_A^{†})-{\left({\left(A{C}^{†}\right)}^{T}A{C}_A^{†}\right)}^T\otimes {\left(AP\right)}^{†}{\left(AP\right)}^{{†}^T}){\mathrm{\Pi }}_{sn}],\hfill \end{array}$$

where the latter is just the result of ([23], Lemma 3.1), with which we can recover the condition numbers for K-weighted pseudoinverse $L_K^{†}$ [23].

Using the straightforward results of Lemmas 1 and 4, we derive the following condition numbers for $C_A^{‡}.$

Theorem 1. 

The normwise, mixed and componentwise condition numbers for $C_A^{‡}$ defined in (11)–(13) are

$$\begin{array}{ccc}\hfill n^{‡}(A,C)& =& \frac{{\parallel [W\left(A\right),W\left(C\right)]\parallel }_2{∥\left[\begin{array}{c}\mathrm{vec}\left(A\right)\\ \mathrm{vec}\left(C\right)\end{array}\right]∥}_2}{\parallel \mathrm{vec}\left(C_A^{‡}\right){\parallel }_2},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill m^{‡}(A,C)& =& \frac{{∥\left|W\right(A\left)\right|\mathrm{vec}\left(\right|A\left|\right)+\left|W\right(C\left)\right|\mathrm{vec}\left(\right|C\left|\right)∥}_{\infty }}{\parallel \mathrm{vec}\left(C_A^{‡}\right){\parallel }_{\infty }},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill c^{‡}(A,C)& =& {∥\frac{\left|W\right(A\left)\right|\mathrm{vec}\left(\right|A\left|\right)+\left|W\right(C\left)\right|\mathrm{vec}\left(\right|C\left|\right)}{\mathrm{vec}\left(C_A^{‡}\right)}∥}_{\infty }.\hfill \end{array}$$

(28)

Next, we provide easier computable upper bounds by minimizing the cost of computing the above condition numbers. The estimation of the upper bounds will be demonstrated by numerical experiments in Section 6.

Corollary 1. 

The upper bounds of normwise, mixed and componentwise condition numbers for $C_A^{‡}$ are

$$\begin{array}{cc}\hfill n^{‡}(A,C)& \le n^{upper}(A,C)\hfill \\ \hfill & =[\parallel C_A^{‡}{\parallel }_2\parallel {\left(PQP\right)}^{†}{A}^{T}J{\parallel }_2+\parallel JA{C}_A^{‡}{\parallel }_2\parallel {\left(PQP\right)}^{†}{\parallel }_2+\parallel C_A^{‡}{\parallel }_2\parallel C_A^{‡}{\parallel }_2+\parallel (I-C{C}^{†}){\parallel }_2\parallel C_A^{‡}{C}^{{†}^T}{\parallel }_2\hfill \\ \hfill & +\parallel C^{{†}^T}Q{C}_A^{‡}{\parallel }_2{\parallel \left(PQP\right)}^{†}{\parallel }_2]\frac{{\parallel [A,C]\parallel }_F}{\parallel C_A^{‡}{\parallel }_F},\hfill \\ \hfill m^{‡}(A,C)& \le m^{upper}(A,C)\hfill \\ \hfill & =\parallel \left[\right|{\left(PQP\right)}^{†}{A}^{T}J\left|\right|A\left|\right|C_A^{{‡}^T}|+|{\left(PQP\right)}^{†}\left|\right|A^T\left|\right|JA{C}_A^{‡}|+|C_A^{‡}\left|\right|C\left|\right|C_A^{{‡}^T}|+|C_A^{‡}{C}^{{†}^T}\left|\right|C^T\left|\right|(I-C{C}^{†})|\hfill \\ \hfill & {+|\left(PQP\right)}^{†}\left|\right|C^T\left|\right|C^{{†}^T}Q{C}_A^{‡}{\left|\right]\parallel }_{max}/{\parallel C_A^{‡}\parallel }_{max},\hfill \\ \hfill c^{‡}(A,C)& \le c^{upper}(A,C)\hfill \\ \hfill & =\parallel \left[\right|{\left(PQP\right)}^{†}{A}^{T}J\left|\right|A\left|\right|C_A^{{‡}^T}|+|{\left(PQP\right)}^{†}\left|\right|A^T\left|\right|JA{C}_A^{‡}|+|C_A^{‡}\left|\right|C\left|\right|C_A^{{‡}^T}|+|C_A^{‡}{C}^{{†}^T}\left|\right|C^T\left|\right|(I-C{C}^{†})|\hfill \\ \hfill & {+|\left(PQP\right)}^{†}\left|\right|C^T\left|\right|C^{{†}^T}Q{C}_A^{‡}\left|\right]/C_A^{‡}{\parallel }_{max}.\hfill \end{array}$$

Proof. 

For any two matrices X and Y, it is well-known that ${\parallel [X,Y]\parallel }_2\le {\parallel X\parallel }_2+{\parallel Y\parallel }_2$. With the help of Theorem 1, and (8), we obtain

$$\begin{array}{cc}\hfill n^{‡}(A,C)& \le [\parallel -(C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J)-({\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn}{\parallel }_2\hfill \\ \hfill & +\parallel -(C_A^{{‡}^T}\otimes C_A^{‡})+({(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}+{\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{sn}{\parallel }_2]\hfill \\ \hfill & \times \frac{{\parallel [A,C]\parallel }_F}{\parallel C_A^{‡}{\parallel }_F}\hfill \\ \hfill & \le [\parallel C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J{\parallel }_2+\parallel {\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}{\parallel }_2+\parallel C_A^{{‡}^T}\otimes C_A^{‡}{\parallel }_2\hfill \\ & +\parallel {(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T}{\parallel }_2+\parallel {\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}{\parallel }_2]\frac{{\parallel [A,C]\parallel }_F}{\parallel C_A^{‡}{\parallel }_F}\hfill \\ \hfill & =[\parallel C_A^{‡}{\parallel }_2\parallel {\left(PQP\right)}^{†}{A}^{T}J{\parallel }_2+\parallel JA{C}_A^{‡}{\parallel }_2\parallel {\left(PQP\right)}^{†}{\parallel }_2+\parallel C_A^{‡}{\parallel }_2\parallel C_A^{‡}{\parallel }_2+\parallel (I-C{C}^{†}){\parallel }_2\parallel C_A^{‡}{C}^{{†}^T}{\parallel }_2\hfill \\ \hfill & +\parallel C^{{†}^T}Q{C}_A^{‡}{\parallel }_2{\parallel \left(PQP\right)}^{†}{\parallel }_2]\frac{{\parallel [A,C]\parallel }_F}{\parallel C_A^{‡}{\parallel }_F}.\hfill \end{array}$$

Secondly, by using Lemma 3 and Theorem 1, we obtain

$$\begin{array}{cc}\hfill m^{‡}(A,C)& =\parallel |-(C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J)-({\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn}\left|\mathrm{vec}\right(\left|A\right|)+|-(C_A^{{‡}^T}\otimes C_A^{‡})\hfill \\ \hfill & +({(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}+{\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{sn}{\left|\mathrm{vec}\right(\left|C\right|)\parallel }_{\infty }/{\parallel \mathrm{vec}\left(C_A^{‡}\right)\parallel }_{\infty }\hfill \\ \hfill & \le \parallel \left[\right|{\left(PQP\right)}^{†}{A}^{T}J\left|\right|A\left|\right|C_A^{{‡}^T}|+|{\left(PQP\right)}^{†}\left|\right|A^T\left|\right|JA{C}_A^{‡}|+|C_A^{‡}\left|\right|C\left|\right|C_A^{{‡}^T}|+|C_A^{‡}{C}^{{†}^T}\left|\right|C^T\left|\right|(I-C{C}^{†})|\hfill \\ \hfill & {+|\left(PQP\right)}^{†}\left|\right|C^T\left|\right|C^{{†}^T}Q{C}_A^{‡}{\left|\right]\parallel }_{max}/{\parallel C_A^{‡}\parallel }_{max},\hfill \end{array}$$

and finally, we have

$$\begin{array}{cc}\hfill c^{‡}(A,C)& =\parallel |-(C_A^{{‡}^T}\otimes {\left(PQP\right)}^{†}{A}^{T}J)-({\left(JA{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn}\left|\mathrm{vec}\right(\left|A\right|)+|-(C_A^{{‡}^T}\otimes C_A^{‡})\hfill \\ \hfill & +({(I-C{C}^{†})}^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}+{\left(C^{{†}^T}Q{C}_A^{‡}\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{sn}\left|\mathrm{vec}\right(\left|C\right|)/|\mathrm{vec}\left(C_A^{‡}\right){|\parallel }_{\infty }\hfill \\ \hfill & \le \parallel \left[\right|{\left(PQP\right)}^{†}{A}^{T}J\left|\right|A\left|\right|C_A^{{‡}^T}|+|{\left(PQP\right)}^{†}\left|\right|A^T\left|\right|JA{C}_A^{‡}|+|C_A^{‡}\left|\right|C\left|\right|C_A^{{‡}^T}|+|C_A^{‡}{C}^{{†}^T}\left|\right|C^T\left|\right|(I-C{C}^{†})|\hfill \\ \hfill & {+|\left(PQP\right)}^{†}\left|\right|C^T\left|\right|C^{{†}^T}Q{C}_A^{‡}\left|\right]/C_A^{‡}{\parallel }_{max}.\hfill \end{array}$$

   □

Remark 2. 

Using the GHQR factorization [3] on A and C in (2) and (5):

$$\begin{array}{cc}\hfill H^{T}AQ=& \left(\begin{array}{cc}{L}_{11}& 0\\ L_{21}& L_{22}\end{array}\right),U^{T}CQ=\left(\begin{array}{cc}{K}_{11}& 0\\ 0& 0\end{array}\right),\hfill \end{array}$$

(29)

where $U\in {\mathbb{R}}^{s\times s}$ and $Q\in {\mathbb{R}}^{n\times n}$ and a $J$-orthogonal matrix, $H\in {\mathbb{R}}^{(p+q)\times (p+q)}$ (i.e., $HJ{H}^T=J$), $L_{22}$ and $K_{11}$ are lower triangular and non-singular. We have

$$C_A^{‡}=Q\left(\begin{array}{c}I\\ -L_{22}^{-1}{L}_{21}\end{array}\right)K_{11}^{-1}{U}_1^T,{\left(PQP\right)}^{†}{A}^{T}J=Q\left(\begin{array}{c}0\\ L_{22}^{-1}\end{array}\right)H_2^T,{\left(PQP\right)}^{†}=Q\left(\begin{array}{c}0\\ -{\left(L_{22}^T{L}_{22}\right)}^{-1}\end{array}\right)Q^T,$$

$$C_A^{‡}{C}^{{†}^T}=\left(\begin{array}{c}0\\ -L_{22}^{-1}{L}_{22}\end{array}\right){\left(K_{11}^{-1}\right)}^T{Q}^T,C^{{†}^T}Q{C}_A^{‡}=U_1^{-T}{K}_{11}^{-T}{L}_{11}^{-1}J{L}_{11}{K}_{11}^{-1}{U}_1^T,$$

$$JA{C}_A^{‡}=J{L}_{11}{K}_{11}^{-T}{U}_1^T,C_A^{‡}{C}_A^{{‡}^T}=Q\left(\begin{array}{c}I\\ -L_{22}^{-1}{L}_{21}\end{array}\right)K_{11}^{-1}{K}_{11}^{-T}\left(\begin{array}{cc}I& -L_{22}^{-1}{L}_{21}\end{array}\right)Q^T,C{C}^{†}=U_1\left(\begin{array}{cc}{K}_{11}{K}_{11}^{-1}& 0\end{array}\right)U_1^T,$$

where $U=(U_1,U_2)$, $H=[H_1,H_2]$; $U_1$ and $H_1$ are, respectively, the submatrices of U and H obtained by taking the first r columns. Putting all the above terms into (18) leads to

$$\begin{array}{cc}\hfill W_1\left(A\right)& =-[\left(U_1{K}_{11}^{-T}\left(\begin{array}{cc}I& -L_{22}^{-1}{L}_{21}\end{array}\right)Q^T\otimes Q\left(\begin{array}{c}0\\ L_{22}^{-1}\end{array}\right)H_2^T\right)\hfill \\ \hfill & +\left(K_{11}^{-T}{U}_1{K}_{11}{L}_{11}^{T}J\otimes Q\left(\begin{array}{c}0\\ -{\left(L_{22}^T{L}_{22}\right)}^{-1}\end{array}\right)Q^T\right){\mathrm{\Pi }}_{mn}],\hfill \\ \hfill W_1\left(C\right)& =-[\left(U_1{K}_{11}^{-T}\left(\begin{array}{cc}I& -L_{22}^{-1}{L}_{21}\end{array}\right)Q^T\otimes Q\left(\begin{array}{c}I\\ -L_{22}^{-1}{L}_{21}\end{array}\right)K_{11}^{-1}{U}_1^T\right)\hfill \\ \hfill & -\left({\left(I-U_1\left(\begin{array}{cc}{K}_{11}{K}_{11}^{-1}& 0\end{array}\right)U_1^T\right)}^T\otimes \left(\begin{array}{c}0\\ -L_{22}^{-1}{L}_{22}\end{array}\right){\left(K_{11}^{-1}\right)}^T{Q}^T\right){\mathrm{\Pi }}_{sn}\hfill \\ \hfill & -\left(U_1{K}_{11}^{-T}{L}_{11}^{T}J{L}_{11}^{-T}{K}_{11}^{-1}{U}_1^{-1}\right)\otimes Q\left(\begin{array}{c}0\\ -{\left(L_{22}^T{L}_{22}\right)}^{-1}\end{array}\right)Q^T){\mathrm{\Pi }}_{sn}].\hfill \end{array}$$

Remark 3. 

We can obtain $\mathrm{d}x$ using the $\mathrm{d}\left(C_A^{‡}\right)$ expression, where (4) is the solution of EILS problem (3). By differentiating (4), we obtain

$$\begin{array}{cc}\hfill \mathrm{d}x& =\mathrm{d}(C_A^{‡}h+{\left(PQP\right)}^{†}{A}^{T}Jg).\hfill \end{array}$$

Thus, using (20), we obtain

$$\begin{array}{ccc}\hfill \mathrm{d}x& =& \mathrm{d}(C_A^{‡}h+P{\left(PQP\right)}^{†}{A}^{T}Jg)=\mathrm{d}\left(C_A^{‡}\right)h+C_A^{‡}\mathrm{d}h+\mathrm{d}P{\left(PQP\right)}^{†}{A}^{T}Jg+P\mathrm{d}{\left(PQP\right)}^{†}{A}^{T}Jg\hfill \\ & & +P{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}Jg+P{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}g.\hfill \end{array}$$

Substituting (25) into above equation and using (9), we have

$$\begin{array}{ccc}\hfill \mathrm{d}x& =& [-C_A^{‡}\mathrm{d}C{C}_A^{‡}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})+{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}Q{C}_A^{‡}-{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A{C}_A^{‡}\hfill \\ & & -{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}JA{C}_A^{‡}]h+\mathrm{d}(I-C^{†}C){\left(PQP\right)}^{†}{A}^{T}Jg+P[-{\left(PQP\right)}^{†}\mathrm{d}\left(PQP\right){\left(PQP\right)}^{†}\hfill \\ & & +{\left(PQP\right)}^{†}{\left(PQP\right)}^{{†}^T}\mathrm{d}{\left(PQP\right)}^T(I-\left(PQP\right){\left(PQP\right)}^{†})\hfill \\ & & +(I-{\left(PQP\right)}^{†}\left(PQP\right))\mathrm{d}{\left(PQP\right)}^T{\left(PQP\right)}^{{†}^T}{\left(PQP\right)}^{†}]A^{T}Jg\hfill \\ & & +P{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}Jg+P{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}g+C_A^{‡}\mathrm{d}h,\hfill \end{array}$$

which together with (20)–(22) give

$$\begin{array}{ccc}\hfill \mathrm{d}x& =& -C_A^{‡}\mathrm{d}C{C}_A^{‡}h+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})h+{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}Q{C}_A^{‡}h-{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A{C}_A^{‡}h\hfill \\ & & -{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}JA{C}_A^{‡}h-C^{†}\mathrm{d}C{\left(PQP\right)}^{†}{A}^{T}Jg-{\left(PQP\right)}^{†}\mathrm{d}QP{\left(PQP\right)}^{†}{A}^{T}Jg\hfill \\ & & -{\left(PQP\right)}^{†}Q\mathrm{d}P{\left(PQP\right)}^{†}{A}^{T}Jg+{\left(PQP\right)}^{†}PQP{\left(PQP\right)}^{†}\mathrm{d}{P}^T(I-\left(QP\right){\left(PQP\right)}^{†})A^{T}Jg\hfill \\ & & +{\left(PQP\right)}^{†}{\left(PQP\right)}^{{†}^T}\mathrm{d}{Q}^{T}P(I-\left(QP\right){\left(PQP\right)}^{†})A^{T}Jg+P{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}Jg+P{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}g+C_A^{‡}\mathrm{d}h.\hfill \end{array}$$

Noting (24), the above equation can be rewritten as

$$\begin{array}{ccc}\hfill \mathrm{d}x& =& -C_A^{‡}\mathrm{d}C{C}_A^{‡}h+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})h+{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}{A}^{T}JA{C}_A^{‡}h-{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A{C}_A^{‡}h\hfill \\ & & -{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}JA{C}_A^{‡}h-C^{†}\mathrm{d}C{\left(PQP\right)}^{†}{A}^{T}Jg+{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}J(g-A{\left(PQP\right)}^{†}{A}^{T}Jg)\hfill \\ & & -{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A{\left(PQP\right)}^{†}{A}^{T}Jg+{\left(PQP\right)}^{†}Q{C}^{†}\mathrm{d}C{\left(PQP\right)}^{†}{A}^{T}Jg\hfill \\ & & -{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}{A}^{T}J(g-A{\left(PQP\right)}^{†}{A}^{T}Jg)+{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}g+C_A^{‡}\mathrm{d}h.\hfill \end{array}$$

Further, by (20) and (4), we have

$$\begin{array}{ccc}\hfill \mathrm{d}x& =& -C_A^{‡}\mathrm{d}C(C_A^{‡}h+{\left(PQP\right)}^{†}{A}^{T}Jg)+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T(I-C{C}^{†})h-{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}A(C_A^{‡}h+{\left(PQP\right)}^{†}{A}^{T}Jg)\hfill \\ & & -{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}{A}^{T}J(g-A(C_A^{‡}h+{\left(PQP\right)}^{†}{A}^{T}Jg))\hfill \\ & & +{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}J(g-A(C_A^{‡}h+{\left(PQP\right)}^{†}{A}^{T}Jg))+{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}g+C_A^{‡}\mathrm{d}h\mathrm{by} \left(20\right)\hfill \\ & =& -C_A^{‡}\mathrm{d}Cx+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}^T\rho -{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}Ax-{\left(PQP\right)}^{†}\mathrm{d}{C}^T{C}^{{†}^T}{A}^{T}Jr\hfill \\ & & +{\left(PQP\right)}^{†}\mathrm{d}{A}^{T}Jr+{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}g+C_A^{‡}\mathrm{d}h,\mathrm{by} \left(4\right)\hfill \end{array}$$

(30)

where $s=Jr=J(g-Ax)$, $\beta =(I-C{C}^{†})h$. By utilizing operator “vec” on (30), and using (6) and (7), we obtain

$$\begin{array}{ccc}\hfill \mathrm{d}x& =& -(x^T\otimes {\left(PQP\right)}^{†}{A}^{T}J)\mathrm{vec}\left(\mathrm{d}A\right)+(s^T\otimes {\left(PQP\right)}^{†})\mathrm{vec}\left(\mathrm{d}{A}^T\right)-(x^T\otimes C_A^{‡})\mathrm{vec}\left(\mathrm{d}C\right)\hfill \\ & & +({\beta }^T\otimes C_A^{‡}{C}^{{†}^T})\mathrm{vec}\left(\mathrm{d}{C}^T\right)+{\left(C^{{†}^T}{A}^{T}s\right)}^T\otimes {\left(PQP\right)}^{†})\mathrm{vec}\left(\mathrm{d}{C}^T\right)+{\left(PQP\right)}^{†}\mathrm{d}g+C_A^{‡}\mathrm{d}h\mathrm{by}\left(\right)\hfill \\ & =& [-(x^T\otimes {\left(PQP\right)}^{†}{A}^{T}J)+(s^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn}]\mathrm{vec}\left(\mathrm{d}A\right)-[(x^T\otimes C_A^{‡})-({\beta }^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}\hfill \\ & & -({\left(C^{{†}^T}{A}^{T}s\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{sn}]\mathrm{vec}\left(\mathrm{d}C\right)+{\left(PQP\right)}^{†}\mathrm{d}g+C_A^{‡}\mathrm{d}h\mathrm{by}\left(\right)\hfill \\ & =& [-(x^T\otimes {\left(PQP\right)}^{†}{A}^{T}J)+(s^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{mn},-(x^T\otimes C_A^{‡})+({\beta }^T\otimes C_A^{‡}{C}^{{†}^T}){\mathrm{\Pi }}_{sn}\hfill \\ & & +({\left(C^{{†}^T}{A}^{T}s\right)}^T\otimes {\left(PQP\right)}^{†}){\mathrm{\Pi }}_{sn},{\left(PQP\right)}^{†},C_A^{‡}]\left[\begin{array}{c}\mathrm{vec}\left(\mathrm{d}A\right)\\ \mathrm{vec}\left(\mathrm{d}C\right)\\ \mathrm{d}g\\ \mathrm{d}h\end{array}\right].\hfill \end{array}$$

From the above result, we can recover the condition numbers of the EILS problem provided in [3,13,14]. Further, we observe that $r=(g-A(C_A^{‡}h+{\left(PQP\right)}^{†}{A}^{T}Jg))$. Applying the same procedure, we can determine $\mathrm{d}r$ and condition numbers for residuals of EILS.

4. Componentwise Perturbation Analysis

In the following section, we derive a componentwise perturbation analysis of the augmented system for the EILS problem.

Let the perturbations $\mathrm{d}A\in {\mathbb{R}}^{(p+q)\times n}$, $\mathrm{d}C\in {\mathbb{R}}^{s\times n}$, $\mathrm{d}g\in {\mathbb{R}}^m$ and $\mathrm{d}h\in {\mathbb{R}}^s$ satisfy $\left|\mathrm{d}A\right|\le ϵ\left|A\right|$, $\left|\mathrm{d}C\right|\le ϵ\left|C\right|$$\left|\mathrm{d}g\right|\le ϵ\left|g\right|$ and $\left|\mathrm{d}h\right|\le ϵ\left|h\right|$ for a small $ϵ$ and $s=Jr$. Suppose that the perturbed augmented system is

$$\left[\begin{array}{ccc}0& 0& C+\mathrm{d}C\\ 0& J+\mathrm{d}J& A+\mathrm{d}A\\ {(C+\mathrm{d}C)}^{\mathrm{T}}& {(A+\mathrm{d}A)}^{\mathrm{T}}& 0\end{array}\right]\left[\begin{array}{c}\lambda +\mathrm{d}\lambda \hfill \\ s+\mathrm{d}s\hfill \\ x+\mathrm{d}x\hfill \end{array}\right]=\left[\begin{array}{c}h+\mathrm{d}h\\ g+\mathrm{d}g\\ 0\end{array}\right].$$

Denoting

$$S=\left[\begin{array}{ccc}0& 0& C\\ 0& J& A\\ C^{\mathrm{T}}& A^{\mathrm{T}}& 0\end{array}\right],u=\left[\begin{array}{c}g\hfill \\ h\hfill \\ 0\hfill \end{array}\right],v=\left[\begin{array}{c}\lambda \hfill \\ s\hfill \\ x\hfill \end{array}\right]$$

and the perturbations

$$\mathrm{d}S=\left[\begin{array}{ccc}0& 0& \mathrm{d}C\\ 0& \mathrm{d}J& \mathrm{d}A\\ {\left(\mathrm{d}C\right)}^{\mathrm{T}}& {\left(\mathrm{d}A\right)}^{\mathrm{T}}& 0\end{array}\right],\mathrm{d}\mathrm{f}=\left[\begin{array}{c}\mathrm{d}g\\ \mathrm{d}h\\ 0\end{array}\right],\mathrm{d}\mathrm{z}=\left[\begin{array}{c}\mathrm{d}\lambda \\ \mathrm{d}s\\ \mathrm{d}x\end{array}\right].$$

When A is of full column rank and C has full row rank, S is invertible. It can be verified that

$$S^{-1}=\left[\begin{array}{ccc}{C_A^{‡}}^{T}Q{C}_A^{‡}& -{\left(JA{C}_A^{‡}\right)}^T& {C_A^{‡}}^T\\ -JA{C}_A^{‡}& J-JA{\left(PQP\right)}^{†}{A}^{T}J& JA{\left(PQP\right)}^{†}\\ C_A^{‡}& {\left(PQP\right)}^{†}{A}^{T}J& -{\left(PQP\right)}^{†}\end{array}\right].$$

If the spectral radius

$$\begin{array}{c}\hfill \rho \left(\left|S^{-1}\right|\left|\mathrm{d}S\right|\right)<1\end{array}$$

(31)

then $I_{m+n}+S^{-1}\mathrm{d}S$ is invertible. Clearly, the condition

$$\begin{array}{c}\hfill ϵ<{\rho }^{-1}\left(\left[\begin{array}{ccc}|{C_A^{‡}}^T{\left|\right|C|}^{\mathrm{T}}& |{C_A^{‡}}^T{\left|\right|A|}^{\mathrm{T}}& |{C_A^{‡}}^{T}Q{C}_A^{‡}\left|\right|C|+|{\left(JA{C}_A^{‡}\right)}^T\left|\right|A|\\ \left|JA{\left(PQP\right)}^{†}\right|{\left|C\right|}^{\mathrm{T}}& \left|JA{\left(PQP\right)}^{†}\right|{\left|A\right|}^{\mathrm{T}}& \left|JA{C}_A^{‡}\right|\left|A\right|+\left|J-JA{\left(PQP\right)}^{†}{A}^{T}J\right|\left|C\right|\\ {|\left(PQP\right)}^{†}{\left|\right|C|}^{\mathrm{T}}& {|\left(PQP\right)}^{†}{\left|\right|A|}^{\mathrm{T}}& |C_A^{‡}{\left|\right|C|+|\left(PQP\right)}^{†}{A}^{T}J\left|\right|A|\end{array}\right]\right),\end{array}$$

(32)

implies (31). The following results [24] are important for Theorem 2.

Lemma 5. 

The perturbed system of a linear system $Sv=u$ is defined as follows:

$$(S+\mathrm{d}S)(v+\mathrm{d}v)=u+\mathrm{d}u,$$

where $v+\mathrm{d}v$ is the solution to the perturbed system, when the perturbations $\mathrm{d}S$ and $\mathrm{d}u$ are sufficiently small such that $S+\mathrm{d}S$ is invertible, the perturbation $\mathrm{d}v$ in the solution v satisfies

$$\mathrm{d}v={\left(I+S^{-1}\mathrm{d}S\right)}^{-1}{S}^{-1}(\mathrm{d}u-\mathrm{d}Sv),$$

which implies

$$\left|\mathrm{d}v\right|\le \left|{\left(I+S^{-1}\mathrm{d}S\right)}^{-1}\right|\left|S^{-1}\right|\left(\right|\mathrm{d}u|+\left|\mathrm{d}S\right|\left|v\right|).$$

Furthermore, when the spectral radius $\rho \left(\left|S^{-1}\right|\left|\mathrm{d}S\right|\right)<1$, we have

$$\begin{array}{cc}\hfill \left|\mathrm{d}v\right|& \le {\left(I-\left|S^{-1}\right|\left|\mathrm{d}S\right|\right)}^{-1}\left|S^{-1}\right|\left(\right|\mathrm{d}u|+\left|\mathrm{d}S\right|\left|v\right|)\hfill \\ \hfill & =\left(I+O\left(\left|S^{-1}\right|\left|\mathrm{d}S\right|\right)\right)\left|S^{-1}\right|\left(\right|\mathrm{d}u|+\left|\mathrm{d}S\right|\left|v\right|).\hfill \end{array}$$

(33)

Now, we have the following bounds for the perturbations in the equality constrained indefinite least squares solution and residual.

Theorem 2. 

Under the above assumption, for any $ϵ>0$ satisfying the condition (32), when the componentwise perturbations $\left|\mathrm{d}A\right|\le ϵ\left|A\right|$, $\left|\mathrm{d}C\right|\le ϵ\left|C\right|$$\left|\mathrm{d}g\right|\le ϵ\left|g\right|$ and $\left|\mathrm{d}h\right|\le ϵ\left|h\right|$, the error in the solution is bounded by

$$\begin{array}{cc}\hfill {\parallel \mathrm{d}x\parallel }_{\infty }& \le ϵ\left(\parallel C_A^{‡}\left(\right|h|+{\left|C\right|\left|x\right|)\parallel }_{\infty }+{∥{\left(PQP\right)}^{†}{A}^{T}J\left(\right|g|+\left|A\right|\left|x\right|)∥}_{\infty }+{∥{\left(PQP\right)}^{†}{\left(\right|C|}^T\left|\lambda \right|+{\left|A\right|}^T\left|r\right|)∥}_{\infty }\right)\hfill \\ \hfill & +O\left({ϵ}^2\right)\hfill \end{array}$$

(34)

and error in the residual is bounded by

$$\begin{array}{cc}\hfill {\parallel \mathrm{d}r\parallel }_{\infty }& \le ϵ(\parallel JA{C}_A^{‡}\left(\right|h|+{\left|C\right|\left|x\right|)\parallel }_{\infty }{+\parallel J-JA\left(PQP\right)}^{†}{A}^{T}J\left(\right|g|+{\left|A\right|\left|x\right|)\parallel }_{\infty }\hfill \\ \hfill & {+\parallel JA\left(PQP\right)}^{†}{\left(\right|C|}^T\left|\lambda \right|+{\left|A\right|}^T{\left|r\right|)\parallel }_{\infty })+O\left({ϵ}^2\right).\hfill \end{array}$$

(35)

Proof. 

Since the condition (32) implies (31), applying (33) in Lemma 5, we obtain

$$\left[\begin{array}{c}\mathrm{d}\lambda \\ \mathrm{d}s\\ \mathrm{d}x\end{array}\right]\le \left(I+O\left(\left|S^{-1}\right|\left|\mathrm{d}S\right|\right)\right)\left|S^{-1}\right|\left[\begin{array}{c}\left|\mathrm{d}h\right|+\left|\mathrm{d}C\right|\left|x\right|\\ \left|\mathrm{d}g\right|+\left|\mathrm{d}A\right|\left|x\right|\\ {\left|\mathrm{d}C\right|}^{\mathrm{T}}\left|\lambda \right|+{\left|\mathrm{d}\mathrm{A}\right|}^{\mathrm{T}}\left|r\right|\end{array}\right..$$

Finally, using the conditions $\left|\mathrm{d}A\right|\le ϵ\left|A\right|$, $\left|\mathrm{d}C\right|\le ϵ\left|C\right|$$\left|\mathrm{d}g\right|\le ϵ\left|g\right|$ and $\left|\mathrm{d}h\right|\le ϵ\left|h\right|$, and the explicit form of $S^{-1}$, the upper bounds (34) and (35) can be obtained.    □

Furthermore, we can obtain the componentwise perturbation bounds of the indefinite least squares solution and its residual.

Remark 4. 

Assume that C is a zero matrix, $\lambda =0$, and $h=0$. Using the above notations, for any $ϵ>0$, if the componentwise perturbations satisfy $\left|\mathrm{d}A\right|\le ϵ\left|A\right|$ and $\left|\mathrm{d}g\right|\le ϵ\left|g\right|$, then the error in the solution is bounded by

$${\parallel \mathrm{d}\mathbf{x}\parallel }_{\infty }\le ϵ\left(\parallel |\left({\left(A^{\mathrm{T}}JA\right)}^{-1}\right)A^{\mathrm{T}}J\left|\right(\left|g\right|+{\left|A\right|\left|\mathbf{x}\right|)\parallel }_{\infty }+\parallel {\left(A^{\mathrm{T}}JA\right)}^{-1}{\left|\right|A|}^{\mathrm{T}}{\left|r\right|\parallel }_{\infty }\right)+O\left({ϵ}^2\right)$$

and the error in the residual is bounded by

$${\parallel \mathrm{d}r\parallel }_{\infty }\le ϵ\left(\parallel |J-JA{\left(A^{\mathrm{T}}JA\right)}^{-1}{A}^{\mathrm{T}}J\left|\right(\left|g\right|+{\left|A\right|\left|\mathbf{x}\right|)\parallel }_{\infty }+\parallel |JA{\left(A^{\mathrm{T}}JA\right)}^{-1}{\left|\right|A|}^{\mathrm{T}}{\left|r\right|\parallel }_{\infty }\right)+O\left({ϵ}^2\right).$$

5. Statistical Condition Estimates

This section proposes three algorithms for estimating the normwise, mixed and componentwise condition numbers for the generalized inverse $C_A^{‡}.$ Algorithm 1 is based on a probabilistic condition estimator method [27] and utilized to examine the normwise condition number for K-weighted pseudoinverse $L_K^{†}$ [23], ILS problem [33], constrained and weighted least squares problem [34] and Tikhonov regularization of total least squares problem [35]. Based on the SSCE method [28], we develop Algorithm 2 to estimate the normwise condition number; for details, see [23,33,36,37,38].   

Algorithm 1: Probabilistic condition estimator for the normwise condition number

Compute the derivative $\mathrm{d}\varphi \left(u\right)=\left[W\right(A),W(C\left)\right]$, and choose a starting vector $u_0$ uniformly and randomly from the unit t-sphere $S_{t-1}$ with $t=n^2$. Using the probabilistic spectral norm estimator [27], compute the certain lower bound ${\alpha }_1$ and the probabilistic upper bound ${\alpha }_2$ of $\mathrm{d}\varphi \left(u\right)$. Compute the normwise condition number by using (26) $$\begin{array}{ccc}\hfill n_p^{‡}(A,C)=\frac{n_p(A,C){\parallel [A,C]\parallel }_F}{\parallel C_A^{‡}{\parallel }_F}\mathrm{with}{n}_p(A,C)& =& \sqrt{\frac{{\alpha }_1+{\alpha }_2}{2}}.\hfill \end{array}$$

Algorithm 2: Small-sample statistical condition estimation method for the normwise condition number

Generate matrices $\left[\mathrm{d}{A}_1,\mathrm{d}{C}_1\right],\left[\mathrm{d}{A}_2,\mathrm{d}{C}_2\right],\dots ,\left[\mathrm{d}{A}_q,\mathrm{d}{C}_q\right]$ with each entry in $\mathcal{N}(0,1)$ and Orthonormalize the following matrix $$\left[\begin{array}{cccc}vec\left(\mathrm{d}{A}_1\right)& vec\left(\mathrm{d}{A}_2\right)& \cdots & vec\left(\mathrm{d}{A}_q\right)\\ vec\left(\mathrm{d}{C}_1\right)& vec\left(\mathrm{d}{C}_2\right)& \cdots & vec\left(\mathrm{d}{C}_q\right)\end{array}\right]$$ to obtain $\left[{\tau }_1,{\tau }_2,\dots ,{\tau }_q\right]$ by modified Gram-Schmidt orthogonalization process. Each ${\tau }_i$ can be converted into the corresponding matrices $\left[\mathrm{d}{A}_i,\mathrm{d}{C}_i\right]$ by applying the unvec operation. Let $p=m+mn$. Approximate ${\omega }_p$ and ${\omega }_q$ by $$\begin{array}{c}\hfill {\omega }_k\approx \sqrt{\frac{2}{\pi (k-\frac{1}{2})}}\end{array}$$ (36) For $i=1,2,\dots ,q,$ compute $${\theta }_i=-C_A^{‡}\mathrm{d}{C}_i{C}_A^{‡}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}_i^T(I-C{C}^{†})+{\left(PQP\right)}^{†}\mathrm{d}{C}_i^T{C}^{{†}^T}Q{C}_A^{‡}-{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}{A}_i{C}_A^{‡}-{\left(PQP\right)}^{†}\mathrm{d}{A}_i^{T}JA{C}_A^{‡}.$$ Compute the absolute condition vector by $$\begin{array}{c}\hfill {\kappa }_{\mathrm{abs}}^{‡}:=\frac{{\omega }_q}{{\omega }_p}\sqrt{{\left|{\theta }_1\right|}^2+{\left|{\theta }_2\right|}^2+\cdots +{\left|{\theta }_q\right|}^2},\end{array}$$ (37) where the square operation is applied to each entry of ${\theta }_i,i=1,2,\dots ,q$ and the square root is also applied componentwise. Estimate the normwise condition number (26) by $$\begin{array}{c}\hfill n^{‡}(A,C)=\frac{N_{\mathrm{SCE}}^{‡}{\parallel [A,C]\parallel }_F}{{∥C_A^{‡}∥}_F},\end{array}$$ (38) where $N_{\mathrm{SCE}}^{‡}:=\frac{{\omega }_q}{{\omega }_p}\sqrt{{∥{\sigma }_1∥}_2^2+{∥{\sigma }_2∥}_2^2+\cdots +{∥{\sigma }_q∥}_2^2}={∥{\kappa }_{\mathrm{abs}}^{‡}∥}_F$.

To estimate the mixed and componentwise condition numbers, we need the following SSCE method, which is from [28] and has been applied to many problems (see, e.g., [23,32,33,34,35]).

6. Numerical Experiments

In the following section, we illustrate two specific examples. The first compares the normwise, mixed and componentwise condition numbers and their upper bounds. The second is used to present the efficiency of statistical condition estimators.

Example 1. 

In this example, we first compute the condition numbers and their upper bounds by using the below matrix pair, then we demonstrate the reliability of Algorithms 1–3. Matlab2018a has been used to perform all the numerical experiments. We examine 200 matrices that are created by repeatedly applying the matrices $A\in {\mathbb{R}}^{m\times n}$ from [33] and $C\in {\mathbb{R}}^{s\times n}$ below.

$$A=\left[\begin{array}{cc}{U}_p& 0\\ 0& U_q\end{array}\right]\left[\begin{array}{c}D\hfill \\ 0\hfill \end{array}\right]V,U_p=I_p-2u_p{u}_p^T,U_q=I_q-2u_q{u}_q^T,\mathrm{and}V=I_n-2v{v}^T,$$

where $u_p\in {\mathbb{R}}^p,u_q\in {\mathbb{R}}^q$ and $v\in {\mathbb{R}}^n$ are unit random vectors obtained from Matlab function randn( $\left.·,1\right)$ and $D=$$n^{-l}diag\left(n^l,{(n-1)}^l,\cdots ,1^l\right)$. It is simple to determine that the condition number of A, i.e., $\kappa \left(A\right)={\parallel A\parallel }_2{∥A^{†}∥}_2$, is $n^l$. $C=\left[C_1,0\right]$, where $C_1$ is a nonsymmetric Gaussian random Toeplitz matrix generated by the Matlabs function $\mathrm{toeplitz}(c,r)$ with $c=\mathrm{randn}(s,1)$, $r=\mathrm{randn}(s,1)$. From Table 1, we can see the numerical outcomes of the ratios given by

$$\begin{array}{cc}\hfill {\omega }_1=& n^{\mathrm{upper}}(A,C)/n^{‡}(A,C),{\omega }_2=m^{\mathrm{upper}}(A,C)/m^{‡}(A,C)\mathrm{and}{\omega }_3=c^{\mathrm{upper}}(A,C)/c^{‡}(A,C).\hfill \end{array}$$

Table 1. Comparison of condition numbers and their upper bounds by choosing different values of $p,q,s$ and n.

		Mean	Max	Mean	Max	Mean	Max
$n^1$	$p,q,n,s$	${\omega }_1$		${\omega }_2$		${\omega }_3$
	$25,15,20,10$	1.0763 $\times {10}^0$	4.8422 $\times {10}^0$	1.0647 $\times {10}^0$	2.8373 $\times {10}^0$	1.1538 $\times {10}^0$	3.9657 $\times {10}^0$
	$50,30,40,20$	1.3146 $\times {10}^0$	6.7089 $\times {10}^0$	1.0861 $\times {10}^0$	4.4630 $\times {10}^0$	1.2845 $\times {10}^0$	5.9123 $\times {10}^0$
	$75,45,60,30$	1.7422 $\times {10}^0$	1.6402 $\times {10}^1$	1.1965 $\times {10}^0$	1.2847 $\times {10}^1$	1.0784 $\times {10}^0$	1.5766 $\times {10}^1$
	$100,60,80,40$	2.6043 $\times {10}^0$	1.9461 $\times {10}^1$	1.4574 $\times {10}^0$	1.6783 $\times {10}^1$	1.7540 $\times {10}^0$	1.8452 $\times {10}^1$
$n^2$	$p,q,n,s$	${\omega }_1$		${\omega }_2$		${\omega }_3$
	$25,15,20,10$	1.4032 $\times {10}^0$	5.7654 $\times {10}^0$	1.2433 $\times {10}^0$	4.6501 $\times {10}^0$	1.3601 $\times {10}^0$	5.3752 $\times {10}^0$
	$50,30,40,20$	1.7341 $\times {10}^0$	8.2074 $\times {10}^0$	1.5623 $\times {10}^0$	6.4738 $\times {10}^0$	1.7320 $\times {10}^0$	7.2004 $\times {10}^0$
	$75,45,60,30$	2.5254 $\times {10}^0$	2.8732 $\times {10}^1$	1.8510 $\times {10}^0$	1.6062 $\times {10}^1$	2.0653 $\times {10}^0$	2.2903 $\times {10}^1$
	$100,60,80,40$	2.7034 $\times {10}^0$	3.9543 $\times {10}^1$	2.0312 $\times {10}^0$	2.0106 $\times {10}^1$	2.3871 $\times {10}^0$	2.4803 $\times {10}^1$
$n^3$	$p,q,n,s$	${\omega }_1$		${\omega }_2$		${\omega }_3$
	$25,15,20,10$	1.7301 $\times {10}^0$	7.9662 $\times {10}^0$	1.4607 $\times {10}^0$	6.8606 $\times {10}^0$	1.5296 $\times {10}^0$	8.0651 $\times {10}^0$
	$50,30,40,20$	1.9674 $\times {10}^0$	3.7649 $\times {10}^1$	1.7065 $\times {10}^0$	8.5963 $\times {10}^0$	1.8472 $\times {10}^0$	9.7063 $\times {10}^0$
	$75,45,60,30$	2.7055 $\times {10}^0$	5.6570 $\times {10}^1$	2.0276 $\times {10}^0$	3.2613 $\times {10}^1$	2.3601 $\times {10}^0$	4.6904 $\times {10}^1$
	$100,60,80,40$	2.9867 $\times {10}^0$	7.1601 $\times {10}^1$	2.2760 $\times {10}^0$	4.9013 $\times {10}^1$	2.5935 $\times {10}^0$	5.9721 $\times {10}^1$
$n^4$	$p,q,n,s$	${\omega }_1$		${\omega }_2$		${\omega }_3$
	$25,15,20,10$	1.8271 $\times {10}^0$	2.3021 $\times {10}^1$	1.6354 $\times {10}^0$	1.4032 $\times {10}^1$	1.7925 $\times {10}^0$	1.5102 $\times {10}^1$
	$50,30,40,20$	2.3064 $\times {10}^0$	3.7632 $\times {10}^1$	1.9642 $\times {10}^0$	1.5210 $\times {10}^1$	1.9862 $\times {10}^0$	1.6082 $\times {10}^1$
	$75,45,60,30$	2.8063 $\times {10}^0$	7.4310 $\times {10}^1$	2.0513 $\times {10}^0$	5.0471 $\times {10}^1$	2.6743 $\times {10}^0$	6.0437 $\times {10}^1$
	$100,60,80,40$	2.9887 $\times {10}^0$	8.6501 $\times {10}^1$	2.3810 $\times {10}^0$	7.1089 $\times {10}^1$	2.7011 $\times {10}^0$	7.4810 $\times {10}^1$

To show the efficiency of the three algorithms discussed above, we run some numerical tests and choose parameters $\delta =0.01$ and $ϵ=0.001$ for Algorithm 1 and $k=2$ for Algorithms 2 and 3. The ratios between the exact condition numbers and their estimated values are determined as follows:

$$\begin{array}{ccc}\hfill r_p& =& n_p^{‡}(A,C)/n^{‡}(A,C),r_s=n_s^{‡}(A,C)/n^{‡}(A,C),\hfill \\ \hfill r_m& =& m_s^{‡}(A,C)/m^{‡}(A,C),r_c=c_s^{‡}(A,C)/c^{‡}(A,C),\hfill \end{array}$$

where $r_p$ is the ratio between the exact normwise condition number and the estimated value of Algorithm 1, $r_s$ is the ratio between the exact normwise condition number and the estimated value of Algorithm 2, and $r_m$ and $r_c$ are the ratios between the exact mixed and componentwise condition numbers and estimated values of Algorithm 3.

The results in Table 2 demonstrate that Algorithms 1–3 can reliably estimate the condition numbers in most situations, supporting the statement in ([39], Chapter 15) that an estimate of the condition number that is correct to within a factor 10 is generally appropriate because it is the magnitude of an error bound that is of interest, not its precise value. For the normwise condition number, Algorithm 1 works more effectively and stably.

Table 2. Results by choosing different values of $p,q,s$ and n for Algorithms 1–3.

		Mean	Variance	Mean	Variance	Mean	Variance	Mean	Variance
$n^1$	$p,q,n,s$	$r_p$		$r_s$		$r_m$		$r_c$
	$25,15,20,10$	1.0000 $\times {10}^0$	5.3577 $\times {10}^{-11}$	1.0322 $\times {10}^0$	1.2063 $\times {10}^{-1}$	1.0067 $\times {10}^0$	1.3505 $\times {10}^{-2}$	1.2785 $\times {10}^0$	1.0431 $\times {10}^{-2}$
	$50,30,40,20$	1.0000 $\times {10}^0$	7.0635 $\times {10}^{-9}$	1.1439 $\times {10}^0$	3.5027 $\times {10}^{-1}$	1.0134 $\times {10}^0$	3.9054 $\times {10}^{-2}$	1.3744 $\times {10}^0$	3.6397 $\times {10}^{-2}$
	$75,45,60,30$	1.0001 $\times {10}^0$	1.5165 $\times {10}^{-11}$	1.2906 $\times {10}^0$	4.6021 $\times {10}^{-1}$	1.1075 $\times {10}^0$	4.1653 $\times {10}^{-2}$	1.5043 $\times {10}^0$	3.9428 $\times {10}^{-2}$
	$100,60,80,40$	1.0001 $\times {10}^0$	1.7940 $\times {10}^{-12}$	1.3482 $\times {10}^0$	5.7803 $\times {10}^{-1}$	1.2306 $\times {10}^0$	4.9563 $\times {10}^{-2}$	1.8732 $\times {10}^0$	4.6543 $\times {10}^{-2}$
$n^2$	$p,q,n,s$	$r_p$		$r_s$		$r_m$		$r_c$
	$25,15,20,10$	1.0000 $\times {10}^0$	6.5102 $\times {10}^{-9}$	1.2654 $\times {10}^0$	2.7360 $\times {10}^{-1}$	1.3405 $\times {10}^0$	3.4605 $\times {10}^{-2}$	1.2765 $\times {10}^0$	2.6123 $\times {10}^{-2}$
	$50,30,40,20$	1.0000 $\times {10}^0$	7.4738 $\times {10}^{-11}$	1.4783 $\times {10}^0$	4.4925 $\times {10}^{-1}$	1.7169 $\times {10}^0$	4.8543 $\times {10}^{-2}$	1.5063 $\times {10}^0$	4.3326 $\times {10}^{-2}$
	$75,45,60,30$	1.0001 $\times {10}^0$	1.6062 $\times {10}^{-9}$	1.6295 $\times {10}^0$	6.8732 $\times {10}^{-1}$	1.8206 $\times {10}^0$	6.4890 $\times {10}^{-2}$	1.7422 $\times {10}^0$	5.0542 $\times {10}^{-2}$
	$100,60,80,40$	1.0001 $\times {10}^0$	2.5106 $\times {10}^{-13}$	1.8693 $\times {10}^0$	7.9543 $\times {10}^{-1}$	2.1456 $\times {10}^0$	7.4293 $\times {10}^{-2}$	2.0361 $\times {10}^0$	6.3702 $\times {10}^{-2}$
$n^3$	$p,q,n,s$	$r_p$		$r_s$		$r_m$		$r_c$
	$25,15,20,10$	1.0000 $\times {10}^0$	1.7029 $\times {10}^{-8}$	1.2063 $\times {10}^0$	4.2083 $\times {10}^{-1}$	1.6710 $\times {10}^0$	5.7862 $\times {10}^{-2}$	1.3722 $\times {10}^0$	4.7031 $\times {10}^{-2}$
	$50,30,40,20$	1.0000 $\times {10}^0$	2.4771 $\times {10}^{-11}$	1.7033 $\times {10}^0$	7.2035 $\times {10}^{-1}$	1.8041 $\times {10}^0$	6.0165 $\times {10}^{-2}$	1.5760 $\times {10}^0$	5.7402 $\times {10}^{-2}$
	$75,45,60,30$	1.0002 $\times {10}^0$	6.1041 $\times {10}^{-12}$	2.0654 $\times {10}^0$	7.5293 $\times {10}^{-1}$	2.2054 $\times {10}^0$	8.3014 $\times {10}^{-2}$	2.0113 $\times {10}^0$	7.2461 $\times {10}^{-2}$
	$100,60,80,40$	1.0003 $\times {10}^0$	5.6854 $\times {10}^{-13}$	2.1976 $\times {10}^0$	8.2063 $\times {10}^{-1}$	2.2593 $\times {10}^0$	8.6458 $\times {10}^{-2}$	2.1263 $\times {10}^0$	7.9432 $\times {10}^{-2}$
$n^4$	$p,q,n,s$	$r_p$		$r_s$		$r_m$		$r_c$
	$25,15,20,10$	1.0000 $\times {10}^0$	5.6321 $\times {10}^{-7}$	1.6305 $\times {10}^0$	6.2092 $\times {10}^{-1}$	1.9455 $\times {10}^0$	6.7402 $\times {10}^{-2}$	1.8240 $\times {10}^0$	6.0461 $\times {10}^{-2}$
	$50,30,40,20$	1.0000 $\times {10}^0$	6.0573 $\times {10}^{-9}$	1.7002 $\times {10}^0$	8.0210 $\times {10}^{-1}$	1.9822 $\times {10}^0$	8.0549 $\times {10}^{-2}$	1.9701 $\times {10}^0$	7.4322 $\times {10}^{-2}$
	$75,45,60,30$	1.0003 $\times {10}^0$	8.6021 $\times {10}^{-11}$	2.1533 $\times {10}^0$	9.0425 $\times {10}^{-1}$	2.4003 $\times {10}^0$	9.3614 $\times {10}^{-2}$	2.2764 $\times {10}^0$	8.4681 $\times {10}^{-2}$
	$100,60,80,40$	1.0004 $\times {10}^0$	2.8543 $\times {10}^{-12}$	2.4187 $\times {10}^0$	9.2054 $\times {10}^{-1}$	2.6005 $\times {10}^0$	9.5370 $\times {10}^{-2}$	2.5711 $\times {10}^0$	9.4502 $\times {10}^{-2}$

Algorithm 3: Small-sample statistical condition estimation method for the mixed and componentwise condition numbers

Generate matrices $\left[\mathrm{d}{A}_1,\mathrm{d}{C}_1\right],\left[\mathrm{d}{A}_2,\mathrm{d}{C}_2\right],\dots ,\left[\mathrm{d}{A}_q,\mathrm{d}{C}_q\right]$ with each entry in $\mathcal{N}(0,1)$ and Orthonormalize the following matrix: $$\left[\begin{array}{cccc}vec\left(\mathrm{d}{A}_1\right)& vec\left(\mathrm{d}{A}_2\right)& \cdots & vec\left(\mathrm{d}{A}_q\right)\\ vec\left(\mathrm{d}{C}_1\right)& vec\left(\mathrm{d}{C}_2\right)& \cdots & vec\left(\mathrm{d}{C}_q\right)\end{array}\right]$$ to obtain $\left[{\tau }_1,{\tau }_2,\dots ,{\tau }_q\right]$ by modified Gram-Schmidt orthogonalization process. Each ${\tau }_i$ can be converted into the corresponding matrices $\left[\mathrm{d}{A}_i,\mathrm{d}{C}_i\right]$ by applying the unvec operation. Let $\left[\mathrm{d}{A}_i,\mathrm{d}{C}_i\right]$ be the matrix $\left[\widetilde{\mathrm{d}{A}_i},\widetilde{\mathrm{d}{C}_i}\right]$ multiplied by $[A,C]$ componentwise. Let $p=mn+sn$. Approximate ${\omega }_p$ and ${\omega }_q$ by (36). For $i=1,2,\dots ,q,$ compute $${\theta }_i=-C_A^{‡}\mathrm{d}{C}_i{C}_A^{‡}+C_A^{‡}{C}^{{†}^T}\mathrm{d}{C}_i^T(I-C{C}^{†})+{\left(PQP\right)}^{†}\mathrm{d}{C}_i^T{C}^{{†}^T}Q{C}_A^{‡}-{\left(PQP\right)}^{†}{A}^{T}J\mathrm{d}{A}_i{C}_A^{‡}-{\left(PQP\right)}^{†}\mathrm{d}{A}_i^{T}JA{C}_A^{‡}.$$ Using the approximations for ${\omega }_p$ and ${\omega }_q,$ compute the absolute condition vector $${\kappa }_{sce}^{†}=\frac{{\omega }_q}{{\omega }_p}\sqrt{{\left|{\theta }_1\right|}^2+{\left|{\theta }_2\right|}^2+\cdots +{\left|{\theta }_q\right|}^2}$$ Estimate the mixed and componentwise condition estimations $m_{sce}^{‡}(A,C)$ and $c_{sce}^{‡}(A,C)$ as follows: $$m_s^{‡}(A,C)=\frac{\parallel {\kappa }_{sce}^{†}{\parallel }_{\infty }}{\parallel \mathrm{vec}\left(C_A^{‡}\right){\parallel }_{\infty }},c_s^{‡}(A,C)={∥\frac{{\kappa }_{sce}^{†}}{\mathrm{vec}\left(C_A^{‡}\right)}∥}_{\infty }.$$

Example 2. 

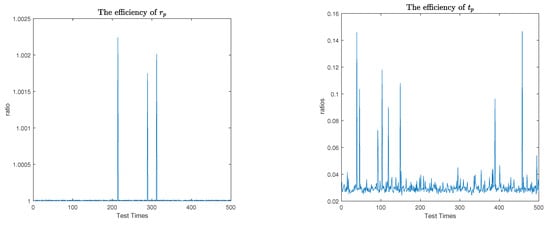
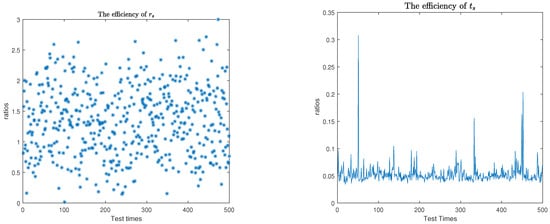
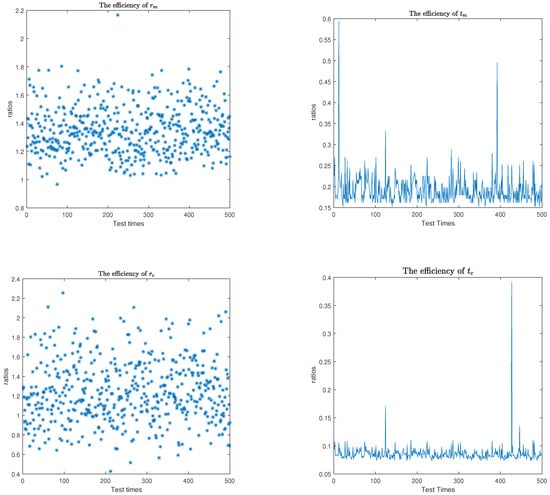
On similar patrons given in [2,3,5], we generate A and C matrices using the GHQR factorization.

$$H^{T}AQ=\left[\begin{array}{cc}{L}_{11}& 0\\ L_{21}& L_{22}\end{array}\right],U^{T}CQ=\left[\begin{array}{cc}{K}_{11}& 0\\ 0& 0\end{array}\right],$$

where $H\in {\mathbb{R}}^{(p+q)\times (p+q)}$ is J-orthogonal, i.e., $HJ{H}^T=J$, Q is orthogonal, and $L_{22}\in {\mathbb{R}}^{(n-s)\times (n-s)}$ and $K_{11}\in {\mathbb{R}}^{(s\times s)}$ are lower triangular and non-singular, respectively. In our experiment, we let $L_{11}$ $L_{21}$ be random matrices. H is a random J-orthogonal matrix with a specific condition number generated using the method described in [40]. $Q\in {\mathbb{R}}^{(n\times n)}$ and $U\in {\mathbb{R}}^{(s\times s)}$ generated randomly (by Matlabs gallery (‘qmult ’, …)), $L_{22}$, and $K_{11}$ are generated by QR factorization of random matrices with specified condition numbers and pre-assigned singular value distributions (generated via Matlabs gallery (‘randsvd’, …)). To examine the above algorithms’ performance, we use 500 matrix pairs, variate the condition numbers of A and C, and set $p=50$, $q=30$, $n=40$, and $s=20$. The ratios between the exact condition numbers and their estimated values are below.

$$\begin{array}{ccc}\hfill r_p& =& n_p^{‡}(A,C)/n^{‡}(A,C),r_s=n_s^{‡}(A,C)/n^{‡}(A,C),\hfill \\ \hfill r_m& =& m_s^{‡}(A,C)/m^{‡}(A,C),r_c=c_s^{‡}(A,C)/c^{‡}(A,C),\hfill \end{array}$$

where the parameters δ, ϵ, k, and ratios $r_p$, $r_s$, $r_m$ and $r_c$ are the same as given in Example 1. We present these numerical results and CPU time in Figure 1 and Figure 2. The time ratios are defined by

$$\begin{array}{ccc}\hfill t_p:=\frac{t_1}{t},t_s:=\frac{t_2}{t},t_m& :=& \frac{t_3}{t},t_c:=\frac{t_4}{t},\hfill \end{array}$$

where t is the CPU time of computing the generalized inverse $C_A^{‡}$ by GHQR decomposition [20]. $t_1$ is the CPU time of Algorithm 1, $t_2$ is the CPU time of Algorithm 2, and $t_3$ and $t_4$ are the CPU times of Algorithm 3. From Figure 1 and Figure 2, we can see that these three algorithms are highly efficient in estimating condition numbers. However, Table 3 shows that the CPU times of Algorithms 1 and 2 are smaller than Algorithm 3.

Figure 1. Efficiency of normwise condition estimators and CPU times of Algorithms 1 and 2.

Figure 2. Efficiency of mixed and componentwise condition estimators and CPU time of Algorithm 3.

Table 3. CPU times for Algorithms 1–3 by choosing different values of $p,q,s$ and n.

$\mathit{p},\mathit{q},\mathit{n},\mathit{s}$	${\mathit{t}}_{\mathit{p}}$	${\mathit{t}}_{\mathit{s}}$	${\mathit{t}}_{\mathit{m}}$	${\mathit{t}}_{\mathit{c}}$
$25,15,20,10$	0.1065	0.2742	0.7601	0.4643
$75,45,60,30$	0.3784	0.5204	1.3644	1.1677
$100,60,80,40$	0.4842	0.6032	1.4569	1.2658
$120,80,100,50$	0.5643	0.7411	1.6345	1.5403

7. Conclusions

In this paper, we provided the explicit expressions and upper bounds for the normwise, mixed, and componentwise condition numbers for the generalized inverse $C_A^{‡}$. Additionally, the corresponding results for the K-weighted pseudoinverse $L_K^{†}$ can be obtained as a special case. We also show how to recover the previous condition numbers of the EILS solution from the generalized inverse $C_A^{‡}$ condition numbers. We also developed the componentwise perturbation analysis of the EILS problem. Moreover, we designed three algorithms that efficiently estimate the normwise, mixed, and componentwise conditions for the generalized inverse $C_A^{‡}$ using the probabilistic condition estimation method and the small-sample statistical condition estimation method. Finally, numerical results demonstrated the performance of these algorithms. In the future, we will continue our research on the MK-weighted generalized inverse.