An Inertial Forward–Backward Splitting Method for Solving Modified Variational Inclusion Problems and Its Application

Abstract

In this paper, we propose an inertial forward–backward splitting method for solving the modified variational inclusion problem. The concept of the proposed method is based on Cholamjiak’s method. and Khuangsatung and Kangtunyakarn’s method. Cholamjiak’s inertial technique is utilized in the proposed method for increased acceleration. Moreover, we demonstrate that the proposed method strongly converges under appropriate conditions and apply the proposed method to solve the image restoration problem where the images have been subjected to various obscuring processes. In our example, we use the proposed method and Khuangsatung and Kangtunyakarn’s method to restore two medical images. To compare image quality, we also evaluate the signal-to-noise ratio (SNR) of the proposed method to that of Khuangsatung and Kangtunyakarn’s method.

1. Introduction

One of the most significant aspects of image processing is image restoration. Image restoration refers to the technique of removing or reducing image degradation that may occur during the acquisition process. This has a number of useful applications in environmental design, motion picture special effects, old photo restoration and removing text and obstructions from photographs. Image restoration’s objective is to recreate a high-quality image X from a low-quality or damaged image Y. It is a classic, inadequately linear inverse problem, which can be formulated as

$$Y=SX+c$$

(1)

where X and Y are the original and degraded images, respectively, S is the matrix representing the linear irreversible degenerate operator and c is usually noise.

Many inverse problems necessitate the use of optimization. In fact, inversion is frequently presented as a solution to an optimization problem. As a result, many of these inversions are non-linear, non-convex and large-scale, posing some difficult optimization challenges. To find x such that the following is correct, optimization problems can be formulated as follows:

$$\underset{x\in {\mathbf{R}}^n}{min}g(x)$$

(2)

where $g:{\mathbf{R}}^n\to \mathbf{R}$ is continuously differentiable. The variational inclusion problem (VIP) is one of the most fundamental optimizations for determining minimization. The following problems can be resolved: image restoration, machine learning, transportation and engineering. These problems will be solved by finding u in a real Hilbert space H such that the following holds.

$$0\in Su+Tu$$

(3)

where operators $S:H\to H$ and $T:H\to 2^H$. Tseng’s technique [1,2], the proximal point method [3,4,5], the forward–backward splitting method [6,7,8,9] and other methods for the variational inclusion problem have received great attention from an increasing number of researchers. The forward–backward splitting method is one of the most commonly used. This is how it is defined:

$$u_{n+1}=J_r^T(u_n-rS{u}_n),n\ge 1$$

(4)

where $J_r^T={(I+rT)}^{-1}$ with $r>0$. Additionally, researchers have refined these methods by using relaxation and inertial techniques to give them more flexibility and acceleration. Alvarez and Attouch developed the inertial concept and proposed the inertial forward–backward approach, which is represented as follows:

$$\left\{\begin{array}{c}{v}_n=u_n+{\theta }_n(u_n-u_{n-1})\hfill \\ u_{n+1}=J_r^T(I-rS)v_n,n\ge 1.\hfill \end{array}\right.$$

(5)

The term ${\theta }_n(u_n-u_{n-1})$ is the technique for speeding up this method. The extrapolation factor ${\theta }_n$ is well-known in the inertial term. The inertial technique significantly improves the algorithm’s performance and has better convergence properties. Secondly, the convergence theorem was demonstrated for non-smooth convex minimization problems and monotone inclusions. The relaxed inertial forward–backward methods [10,11], the inertial proximal point algorithm [12,13] and the inertial Tseng’s type method [2,14] were all created as a consequence of this concentration on both methods.

Lorenz and Pock [10] recommended that the inertial forward–backward method for monotone operators be as follows:

$$\left\{\begin{array}{c}{v}_n=u_n+{\theta }_n(u_n-u_{n-1})\hfill \\ u_{n+1}=J_{r_n}^T(I-r_{n}S)v_n,n\ge 1.\hfill \end{array}\right.$$

(6)

It has been determined that algorithm (6) differs from algorithm (5) because $J_{r_n}^T={(I+r_{n}T)}^{-1}$ where $\left\{r_n\right\}$ is a positive real sequence. The above-mentioned algorithms for the inertial term have weak convergence. Cholamjiak et al. [11] presented an improved forward–backward method for solving VIP using the inertial technique. The following describes their algorithm:

$$\left\{\begin{array}{c}{v}_n=u_n+{\theta }_n(u_n-u_{n-1})\hfill \\ u_{n+1}={\omega }_{n}p+{\xi }_n{v}_n+{\gamma }_n{J}_{r_n}^T(I-r_{n}S)v_n,n\ge 1\hfill \end{array}\right.$$

(7)

where $r_n\in (0,2\alpha ]$. The numerical experiments and proof that the algorithm generated strong convergence results have been provided.

Khuangsatung and Kangtunyakarn’s modified variational inclusion problem (MVIP) [15,16] aims to determine $u\in H$ such that

$$0\in \sum _{i=1}^N{a}_i{S}_{i}u+Tu,$$

(8)

where $a_i\in (0,1)$ with ${\sum }_{i=1}^N{a}_i=1$, $S_i:H\to H$ and $T:H\to 2^H$. Obviously, if $S_i\equiv S$ for every $i=1,2,\dots ,N$, then MVIP implies VIP. Under the required conditions, they were able to devise a method to solve a family of nonexpansive fixed point mapping problems with finite dimensions and a family of finite variational inclusion problems. The following provides their method:

$$\left\{\begin{array}{c}{q}_n^i={\beta }_n{p}_n+(1-{\beta }_n)T_i{p}_n,\forall n\ge 1\hfill \\ p_{n+1}={\omega }_{n}f(p_n)+{\xi }_n{\gamma }_n{J}_{\lambda }^T(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)p_n+{\gamma }_n\sum _{i=1}^N{a}_i{q}_n^i.\hfill \end{array}\right.$$

(9)

This paper’s purpose is to demonstrate an inertial forward–backward splitting method for solving the modified variational inclusion problem based on the concept of [11,15,16]. The proposed method modifies = method (18) for higher acceleration by using the inertial technique of Cholamjiak et al. [11]. We further show that it strongly converges under appropriate conditions. In addition, we apply the proposed method to solve the image restoration problem. Image restoration is an essential problem in digital image processing. During data collection, images usually suffer degradation. Blurring, information loss due to sampling and quantization effects and different noise sources can all be part of the degradation. The goal of image restoration is to estimate the original image from degraded data. Therefore, the proposed method could be used to solve image restoration problems where the images have suffered a variety of blurring operations. Medical imaging is the technique and process of imaging the interior of a body for clinical analysis and medical intervention, as well as providing a visual representation of the function of certain organs or tissues (physiology). Medical imaging also creates a database of normal anatomy and physiology so that abnormalities can be identified. Occasionally, disturbances occur during the photographing process, such as when X-ray film images are blurred or segments of the X-ray film are absent. In our example, we use the proposed method and the method of Khuangsatung and Kangtunyakarn to restore blurred and motion-damaged X-ray films of the brain and the right shoulder. We also compare the signal-to-noise ratio (SNR) of the proposed method to that of Khuangsatung and Kangtunyakarn’s method in order to determine the image quality.

An overview of the contents of this research is presented below: Section 2 compiles fundamental lemmas and definitions. In Section 3, the suggested methods are completely detailed. Applications for image restoration and numerical experimentation are covered in Section 4. The last section of the work presents the conclusion.

2. Preliminaries

This section involves the use of preliminary statements, lemmas and definitions. Assume H is a real Hilbert space and $K\subset H$ is nonempty, closed and convex with a norm $\parallel ·\parallel$ and inner product $⟨·,·⟩$. The nearest point projection of H onto K is denoted by $P_K$; that is, $\parallel u-P_{K}u\parallel \le \parallel u-v\parallel$ for all $u\in H$ and $v\in K$. It implies that $⟨u-P_{K}u,v-P_{K}u⟩\le 0$ holds for all $u\in H$ and $v\in K$ [17,18].

Lemma 1 

([18]). For every $u,v\in H.$ The following statements are accurate:

(i) 

${\parallel u\parallel }^2-{\parallel v\parallel }^2-2⟨u-v,v⟩\ge {\parallel u-v\parallel }^2$;

(ii) 

${\parallel u\parallel }^2+2⟨v,u+v⟩\ge {\parallel u+v\parallel }^2$;

(iii) 

${t\parallel u\parallel }^2+{(1-t)\parallel v\parallel }^2{-t(1-t)\parallel u-v\parallel }^2={\parallel tu+(1-t)v\parallel }^2$, $\forall t\in [0,1]$.

A mapping $S:K\to H$ is called $\alpha$-inverse strongly monotone. If there exists $\alpha >0$ such that for every $u,v\in K$,

$$\begin{array}{c}\hfill ⟨Su-Sv,u-v⟩\ge {\alpha \parallel Su-Sv\parallel }^2.\end{array}$$

(10)

Remark 1. 

S is monotone and Lipschitz continuous, if S is α- inverse strongly monotone.

A self mapping Z on H is said to be nonexpansive if for all $u,v\in H$,

$$\parallel Zu-Zv\parallel \le \parallel u-v\parallel .$$

(11)

A self mapping Z on H is said to be firmly nonexpansive if for all $u,v\in H$,

$${\parallel Zu-Zv\parallel }^2\le {\parallel u-v\parallel }^2-{\parallel (I-Z)u-(I-Z)v\parallel }^2,$$

(12)

or equivalently

$${\parallel Zu-Zv\parallel }^2\le ⟨Zu-Zv,u-v⟩.$$

(13)

Remark 2 

([17]). Z is firmly nonexpansive iff $I-Z$ is firmly nonexpansive. Obviously, the projection $P_K$ is firmly nonexpansive.

Theorem 1 

([19]). Assume that $Z:K\to K$ is a nonexpansive mapping with a fixed point. For $t\in (0,1)$ and fixed $p\in K$, the unique fixed point $u_t\in K$ of the contraction $u⟼tp+(1-t)Zu$ converges strongly as $t\to 0$ to a fixed point of Z.

Lemma 2 

([20]). Assume that $\left\{x_n\right\}$ and $\left\{y_n\right\}$ are sequences of nonnegative real numbers such that

$$x_{n+1}⩽(1-{\omega }_n)x_n+y_n+z_n,\forall n\ge 1,$$

where $\left\{{\omega }_n\right\}\in (0,1)$ and ${\displaystyle \sum _{n=1}^{\infty }{z}_n<\infty }$. Then, the following holds:

(i) 

$\left\{x_n\right\}$ is a bounded sequence, if $y_n\le {\omega }_{n}M$ for some $M\ge 0;$

(ii) 

$\underset{n\to \infty }{lim}{x}_n=0$, if ${\displaystyle \sum _{n=1}^{\infty }{\omega }_n=\infty }$ and $\underset{n\to \infty }{lim\; sup}\frac{y_n}{{\omega }_n}\le 0$.

Lemma 3 

([21]). Assume $\left\{z_n\right\}$ is a sequence of nonnegative real numbers such that

$$z_{n+1}\le (1-{\omega }_n)z_n+{\gamma }_n{t}_n,n\ge 1,$$

and

$$z_{n+1}\le z_n-{\eta }_n+{\rho }_n,n\ge 1,$$

where $\left\{{\omega }_n\right\}$ is a sequence in $(0,1),\left\{{\eta }_m\right\}$ is a sequence of nonnegative real numbers and $\left\{t_n\right\}$ and $\left\{{\rho }_n\right\}$ are real sequences such that

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\omega }_n=\infty }$;

(ii) 

$\underset{n\to \infty }{lim}{\rho }_n=0$;

(iii) 

$\underset{k\to \infty }{lim}{\eta }_{n_k}=0$ implies $\underset{k\to \infty }{lim\; sup}{t}_n\le 0$ for each subsequence of real number $\left\{n_k\right\}$ of $\left\{n\right\}$.

Then $\underset{n\to \infty }{lim}{z}_n=0$.

Proposition 1 

([22]). Let H be a real Hilbert space. Let $j\in N$ be fixed. Let ${\left\{x_i\right\}}_{i=1}^j\subset H$ and $t_i\ge 0$ for all $i=1,2,...,j$ with ${\displaystyle \sum _{i=1}^j{t}_i\le 1}$. Then, we have

$${\displaystyle \parallel \sum _{i=1}^j{t}_i{x}_i{\parallel }^2\le {\displaystyle \frac{{\displaystyle \sum _{i=1}^j{t}_i{\parallel x_i\parallel }^2}}{{\displaystyle 2-(\sum _{i=1}^j{t}_i)}}}.}$$

3. Main Result

A set-valued mapping $T:H\to 2^H$ is called monotone if for all $u,v\in H,g\in T(u),$ and $h\in T(v)$ implies $⟨u-v,g-h⟩\ge 0.$ A monotone mapping T is maximal if its graph $G(T):=\{(g,u)\in H\times H:g\in T(u)\}$ of T is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping T is maximal if and only if for $(u,g)\in H\times H,⟨u-v,g-h⟩\ge 0$ for all $(v,h)\in G(T)$ implies $g\in T(u).$ A maximal monotone operator $T:H\to 2^H$ and $\lambda >0$; its associated resolvent of order $\lambda$, defined by

$$J_{\lambda }^T:={(I+\lambda T)}^{-1},$$

(14)

where I denotes the identily operator, which is a firmly nonexpansive mapping from H to H with full domain, and the set of fixed points of $J_{\lambda }^T$ coincides with the set of zeros of S. Note that

$${\displaystyle G_{\lambda }:=J_{\lambda }^T{(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)}^{-1}={(I+\lambda T)}^{-1}(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i).}$$

(15)

Lemma 4. 

Let $T:H\to 2^H$ be a maximal monotone and for any $i=1,2,3,...,N,S_i:H\to H$ be ${\alpha }_i$ inverse strongly monotone with $\alpha =min\{\alpha {}_i,i=1,2,...,n\}$. Then, for $\lambda >0$,

(i) ${\displaystyle F(G_{\lambda })={(\sum _{i=1}^N{\delta }_i{S}_i+T)}^{-1}(0)}$;

(ii) $\parallel u-G_{r}u\parallel \le 2\parallel u-G_{\lambda }u\parallel$ for $0<r\le \lambda$;

(iii) $\begin{array}{ll}{\displaystyle \parallel G_{\lambda }u-G_{\lambda }{v\parallel }^2\le }& {\parallel u-v\parallel }^2-\lambda (2\alpha -\lambda ){\parallel {\displaystyle \sum _{i=1}^N}{\delta }_i{S}_{i}u-{\displaystyle \sum _{i=1}^N}{\delta }_i{S}_{i}v\parallel }^2\\ & {\displaystyle -\parallel (I-J_{\lambda }^T)(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)u-(I-J_{\lambda }^T)(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i){v\parallel }^2}\end{array}$ for all $u,v\in T_{\lambda }=\{p\in H:\parallel p\parallel \le \lambda \}$. It follows that $G_{\lambda }$ is nonexpansive mapping.

Proof. 

(i) By the definition of $G_{\lambda }$,

$$\begin{array}{cc}\hfill u\in F(G_{\lambda })& \iff u=G_{\lambda }u\hfill \\ \hfill & {\displaystyle \iff u={(I+\lambda T)}^{-1}(u-\lambda \sum _{i=1}^N{\delta }_i{S}_{i}u)}\hfill \\ \hfill & {\displaystyle \iff u-\lambda \sum _{i=1}^N{\delta }_i{S}_{i}u\in u+\lambda Tu}\hfill \\ \hfill & {\displaystyle \iff 0\in \sum _{i=1}^N{\delta }_i{S}_{i}u+Tu}\hfill \\ \hfill & {\displaystyle \iff u\in {(\sum _{i=1}^N{\delta }_i{S}_i+T)}^{-1}(0).}\hfill \end{array}$$

(ii)

Since ${\displaystyle G_{\lambda }u={(I+\lambda T)}^{-1}(u-\lambda \sum _{i=1}^N{\delta }_i{S}_{i}u),}$ then ${\displaystyle {\displaystyle \frac{u-G_{\lambda }u}{\lambda }}-\sum _{i=1}^N{\delta }_i{S}_{i}u\in T(G_{\lambda }u).}$ Let $0<r\le \lambda$; by the monotone of T, we obtain that

$$⟨{\displaystyle \frac{u-G_{\lambda }u}{r}}-{\displaystyle \frac{u-G_{\lambda }u}{\lambda }},G_{r}u-G_{\lambda }u⟩\ge 0.$$

It follows that

$$\begin{array}{cc}\hfill 0& \le r⟨{\displaystyle \frac{u-G_{\lambda }u}{r}}-{\displaystyle \frac{u-G_{\lambda }u}{\lambda }},G_{r}u-G_{\lambda }u⟩\hfill \\ \hfill & =⟨{\displaystyle \frac{\lambda -r}{\lambda }}u-{\displaystyle \frac{\lambda -r}{\lambda }}{G}_{\lambda }u,G_{r}u-G_{\lambda }u⟩-⟨G_{r}u-G_{\lambda }u,G_{r}u-G_{\lambda }u⟩.\hfill \end{array}$$

Since $0<r\le \lambda ,$ we obtain that

$$\begin{array}{cc}\hfill \parallel G_{r}u-G_{\lambda }{u\parallel }^2& \le 1-{\displaystyle \frac{r}{\lambda }}⟨u-G_{\lambda }u,G_{r}u-G_{\lambda }u⟩\hfill \\ \hfill & \le \parallel u-G_{\lambda }u\parallel \parallel G_{r}u-G_{\lambda }u\parallel .\hfill \end{array}$$

Hence, $\parallel u-G_{r}u\parallel \le \parallel u-G_{\lambda }u\parallel +\parallel G_{r}u-G_{\lambda }u\parallel \le 2\parallel u-G_{\lambda }u\parallel .$

(iii)

Since T is maximal monotone, it is know that $J_{\lambda }^T$ is firmly nonexpaxsive and so we have

$$\begin{array}{cc}\hfill \parallel G_{\lambda }u-G_{\lambda }{v\parallel }^2& {\displaystyle {=\parallel (I+\lambda T)}^{-1}(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)u-{(I+\lambda T)}^{-1}(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i){v\parallel }^2}\hfill \\ \hfill & =\parallel J_{\lambda }^T{u}^{\prime }-J_{\lambda }^T{v}^{\prime }{\parallel }^2\hfill \\ \hfill & \le \parallel u^{\prime }-v^{\prime }{\parallel }^2-{\parallel (I-J_{\lambda }^T)u^{\prime }-(I-J_{\lambda }^T)v^{\prime }\parallel }^2\hfill \end{array}$$

(16)

where ${\displaystyle u^{\prime }=(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)u}$ and ${\displaystyle v^{\prime }=(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)v.}$

Since $S_i$ is ${\alpha }_i$-inverse strongly monotone with $\alpha =min\{{\alpha }_i:i=1,2,...,n\}$, we derive that

$$\begin{array}{cc}\hfill \parallel u^{\prime }-v^{\prime }{\parallel }^2& {\displaystyle =\parallel (u-v)-\lambda (\sum _{i=1}^N{\delta }_i{S}_{i}u-(\sum _{i=1}^N{\delta }_i{S}_{i}v){\parallel }^2}\hfill \\ \hfill & {\displaystyle \le {\parallel u-v\parallel }^2+{\lambda }^2\parallel \sum _{i=1}^N{\delta }_i{S}_{i}u-\sum _{i=1}^N{\delta }_i{S}_i{v\parallel }^2-2\lambda \alpha \parallel \sum _{i=1}^N{\delta }_i{S}_{i}u-\sum _{i=1}^N{\delta }_i{S}_{i}v\parallel \parallel u-v\parallel }\hfill \\ \hfill & {\displaystyle ={\parallel u-v\parallel }^2-\lambda (2\alpha -\lambda ){\parallel \sum _{i=1}^N{\delta }_i{S}_{i}u-\sum _{i=1}^N{\delta }_i{S}_{i}v\parallel }^2.}\hfill \end{array}$$

(17)

From (16) and (17), we obtain that

$${\displaystyle \parallel G_{\lambda }u-G_{\lambda }{v\parallel }^2\le {\parallel u-v\parallel }^2-\lambda (2\alpha -\lambda )\parallel \sum _{i=1}^N{\delta }_i{S}_{i}u-\sum _{i=1}^N{\delta }_i{S}_i{v\parallel }^2-{\parallel (I-J_{\lambda }^T)u^{\prime }-(I-J_{\lambda }^T)v^{\prime }\parallel }^2.}$$

Obviously, the mapping $G_{\lambda }$ is nonexpansive. □

The following theorem is the strong convergence theorem under sutiable conditions of an inertial forward–backward splitting algorithm for solving the modified variational inclusion in a real Hilbert space.

Theorem 2. 

Let K be a nonempty closed convex subset of a real Hilbert space H. Let $S_i:H\to H$ be ${\alpha }_i$-inverse strongly monotone mapping with $\eta =min\left\{{\alpha }_i\right\}$ and let $T:H\to 2^H$ be a multi-valued maximal monotone mapping such that ${\displaystyle \Omega ={(\sum _{i=1}^N{\delta }_i{S}_i+T)}^{-1}(0)\ne \varnothing }$. Suppose that the sequence $\left\{u_n\right\}$, generated by $u_1\in H$ and

$$\left\{\begin{array}{c}{v}_n=u_n+{\theta }_n(u_n-u_{n-1}),\hfill \\ {\displaystyle u_{n+1}={\omega }_{n}u+{\xi }_n{J}_{\lambda }^T(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)v_n+{\gamma }_n{v}_n,}\hfill \end{array}\right.$$

(18)

for all ${\delta }_i⩽1,0<\lambda <2\eta ,\left\{{\theta }_n\right\}\subset [0,\theta ]$ with $\theta \in [0,1)$ and $n\in N.$ Let $\left\{{\omega }_n\right\},\left\{{\xi }_n\right\},\left\{{\gamma }_n\right\}\in [0,1]$ and ${\omega }_n+{\xi }_n+{\gamma }_n=1.$ Assume that the following conditions hold:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\theta }_n|u_n-u_{n-1}|<\infty }$,

(ii) 

$\underset{n\to \infty }{lim}{\omega }_n=0$ and ${\displaystyle \sum _{n=0}^{\infty }{\omega }_n=\infty ,\sum _{n=0}^{\infty }|{\omega }_{n+1}-{\omega }_n|<\infty }$,

(iii) 

$0<c⩽{\xi }_n⩽d<1$ for all $n\ge 1$ and ${\displaystyle \sum _{n=0}^{\infty }|{\xi }_{n+1}-{\xi }_n|<\infty }$,

(iv) 

${\displaystyle \sum _{n=1}^N{\delta }_i=1.}$

Then, the sequence $\left\{u_n\right\}$ converges strongly to $z=P_{\Omega }p$.

Proof. 

For each $n\in N$, we put ${\displaystyle G_{\lambda }=J_{\lambda }^T(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)}$. Let $\left\{z_n\right\}$ be defined by

$$z_{n+1}={\omega }_{n}p+{\xi }_n{G}_{\lambda }{z}_n+{\gamma }_n{z}_n.$$

Using Lemma 1, we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-z_{n+1}\parallel & \le {\xi }_n\parallel G_{\lambda }{v}_n-G_{\lambda }{z}_n\parallel +{\gamma }_n\parallel v_n-z_n\parallel \hfill \\ \hfill & \le {\xi }_n\parallel v_n-z_n\parallel +{\gamma }_n\parallel v_n-z_n\parallel \hfill \\ \hfill & =(1-{\omega }_n)\parallel v_n-z_n\parallel \hfill \\ \hfill & \le (1-{\omega }_n)\parallel u_n-z_n\parallel +{\theta }_n\parallel u_n-u_{n-1}\parallel .\hfill \end{array}$$

(19)

By our assumptions and Lemma 2(ii), we obtain that

$$\underset{n\to \infty }{lim}\parallel u_n-z_n\parallel =0.$$

(20)

Let $z=P_{\Omega }p.$ Then

$$\begin{array}{cc}\hfill \parallel z_{n+1}-z\parallel & \le {\omega }_n\parallel p-z\parallel +{\xi }_n\parallel G_{\lambda }{z}_n-z\parallel +{\gamma }_n\parallel z_n-z\parallel \hfill \\ \hfill & \le {\omega }_n\parallel p-z\parallel +{\xi }_n\parallel z_n-z\parallel +{\gamma }_n\parallel z_n-z\parallel \hfill \\ \hfill & ={\omega }_n\parallel p-z\parallel +(1-{\omega }_n)\parallel z_n-z\parallel .\hfill \end{array}$$

(21)

This show that $\left\{z_n\right\}$ is bounded by Lemma 2(i). Therefore, $\left\{u_n\right\}$ and $\left\{v_n\right\}$ are also bounded. We observe that

$$\begin{array}{cc}\hfill \parallel v_n{-z\parallel }^2& =\parallel u_n+{\theta }_n(u_n-u_{n-1}){-z\parallel }^2\hfill \\ \hfill & \le \parallel u_n{-z\parallel }^2+2{\theta }_n⟨u_n-u_{n-1},v_n-z⟩\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill \parallel u_{n+1}{-z\parallel }^2& =\parallel {\omega }_{n}p+{\xi }_n{G}_{\lambda }{v}_n+{\gamma }_n{v}_n{-z\parallel }^2\hfill \\ \hfill & \le \parallel {\xi }_n(G_{\lambda }{v}_n-z)+{\gamma }_n(v_n-z){\parallel }^2+2{\omega }_n⟨p-z,u_{n+1}-z⟩.\hfill \end{array}$$

(23)

On the other hand, by Proposition 1 and Lemma 4(iii), we obtain that

$$\begin{array}{cc}\hfill \parallel {\xi }_n(G_{\lambda }{v}_n-z)+{\gamma }_n(v_n-z){\parallel }^2& \le {\displaystyle \frac{1}{1+{\omega }_n}}({\xi }_n\parallel G_{\lambda }{v}_n{-z\parallel }^2+{\gamma }_n\parallel v_n-z{\parallel }^2)\hfill \\ \hfill & {\displaystyle \le {\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}(\parallel v_n{-z\parallel }^2-\lambda (2\alpha -\lambda ){\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_n-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }^2}\hfill \\ \hfill & {\displaystyle -\parallel (I-J_{\lambda }^T)(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)v_n-(I-J_{\lambda }^T)(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)z\parallel )}\hfill \\ \hfill & +{\displaystyle \frac{{\gamma }_n}{1+{\omega }_n}}{\parallel v_n-z\parallel }^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\displaystyle ={\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}\parallel v_n{-z\parallel }^2-{\displaystyle \frac{{\xi }_n\lambda (2\alpha -\lambda )}{1+{\omega }_n}}{\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_n-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }^2}\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}\parallel (I-J_{\lambda }^T)(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)v_n-(I-J_{\lambda }^T)(I-\lambda \sum _{i=1}^N{\delta }_i{S}_i)z\parallel }\hfill \\ \hfill & +{\displaystyle \frac{{\gamma }_n}{1+{\omega }_n}}{\parallel v_n-z\parallel }^2\hfill \\ \hfill & {\displaystyle \le {\displaystyle \frac{1-{\omega }_n}{1+{\omega }_n}}\parallel v_n{-z\parallel }^2-{\displaystyle \frac{{\xi }_n\lambda (2\alpha -\lambda )}{1+{\omega }_n}}{\parallel \sum _{i=1}^N{\delta }_i{S}_i(v_n-z)\parallel }^2}\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}\parallel v_n-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_n-G_{\lambda }{v}_n+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel .}\hfill \end{array}$$

(24)

Substituting (22) and (24) into (23), we obtain that

$$\begin{array}{cc}\hfill \parallel u_{n+1}{-z\parallel }^2& {\displaystyle \le {\displaystyle \frac{1-{\omega }_n}{1+{\omega }_n}}\parallel v_n{-z\parallel }^2-{\displaystyle \frac{{\xi }_n\lambda (2\alpha -\lambda )}{1+{\omega }_n}}{\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_n-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }^2}\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}\parallel v_n-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_n-G_{\lambda }{v}_n+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel +2{\omega }_n⟨p-z,u_{n+1}-z⟩}\hfill \\ \hfill & \le {\displaystyle \frac{1-{\omega }_n}{1+{\omega }_n}}(\parallel u_n-z{\parallel }^2+2{\theta }_n⟨u_n-u_{n-1},v_n-z⟩)\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{{\xi }_n\lambda (2\alpha -\lambda )}{1+{\omega }_n}}{\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_n-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }^2}\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}\parallel v_n-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_n-G_{\lambda }{v}_n+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel +2{\omega }_n⟨p-z,u_{n+1}-z⟩}\hfill \\ \hfill & {\displaystyle =(1-{\displaystyle \frac{2{\omega }_n}{1+{\omega }_n}})\parallel u_n{-z\parallel }^2-{\displaystyle \frac{{\xi }_n\lambda (2\alpha -\lambda )}{1+{\omega }_n}}{\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_n-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }^2}\hfill \\ \hfill & +({\displaystyle \frac{2{\omega }_n}{1+{\omega }_n}})({\displaystyle \frac{1-{\omega }_n}{{\omega }_n}}{\theta }_n⟨u_n-u_{n-1},v_n-z⟩+(1+{\omega }_n)⟨p-z,u_{n+1}-z⟩)\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}\parallel v_n-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_n-G_{\lambda }{v}_n+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel .}\hfill \end{array}$$

(25)

We can check that ${\displaystyle \frac{2{\omega }_n}{1+{\omega }_n}}$ in $(0,1)$. From (25), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}{-z\parallel }^2& \le (1-{\displaystyle \frac{2{\omega }_n}{1+{\omega }_n}}){\parallel u_n-z\parallel }^2\hfill \\ \hfill & +({\displaystyle \frac{2{\omega }_n}{1+{\omega }_n}})({\displaystyle \frac{1-{\omega }_n}{{\omega }_n}}{\theta }_n⟨u_n-u_{n-1},v_n-z⟩+(1+{\omega }_n)⟨p-z,u_{n+1}-z⟩)\hfill \end{array}$$

(26)

and

$$\begin{array}{cc}\hfill \parallel u_{n+1}{-z\parallel }^2& {\displaystyle \le \parallel u_n{-z\parallel }^2-{\displaystyle \frac{{\xi }_n\lambda (2\alpha -\lambda )}{1+{\omega }_n}}{\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_n-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }^2}\hfill \\ \hfill & {\displaystyle -{\displaystyle \frac{{\xi }_n}{1+{\omega }_n}}\parallel v_n-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_n-G_{\lambda }{v}_n+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }\hfill \\ \hfill & +{\displaystyle \frac{2(1-{\omega }_n)}{1+{\omega }_n}}{\theta }_n⟨u_n-u_{n-1},v_n-z⟩+2{\omega }_n⟨p-z,u_{n+1}-z⟩).\hfill \end{array}$$

(27)

Then, (26) and (27) are reduced to the following

$$a_{n+1}⩽(1-{\omega }_n)a_n+{\omega }_n{b}_n,n\ge 1$$

and

$$a_{n+1}⩽a_n-t_n+s_n,n\ge 1$$

where $b_n={\displaystyle \frac{1-{\omega }_n}{{\omega }_n}}{\theta }_n⟨u_n-u_{n-1},v_n-z⟩+(1+{\omega }_n)⟨p-z,u_{n+1}-z⟩$

$$\begin{array}{c}{\displaystyle t_n=-{\displaystyle \frac{{\xi }_n\lambda (2\alpha -\lambda )}{1+{\omega }_n}}\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_n-\sum _{i=1}^N{\delta }_i{S}_i{z\parallel }^2-{\displaystyle \frac{{\xi }_n}{1+{\alpha }_n}}\parallel v_n-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_n-G_{\lambda }{v}_n+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }\hfill \\ s_n={\displaystyle \frac{2(1-{\omega }_n)}{1+{\omega }_n}}{\theta }_n⟨u_n-u_{n-1},v_n-z⟩+2{\omega }_n⟨p-z,u_{n+1}-z⟩.\hfill \end{array}$$

(28)

Since ${\displaystyle \sum _{n=0}^{\infty }{\omega }_n=\infty }$, it follows that ${\displaystyle \sum _{n=0}^{\infty }{\displaystyle \frac{2{\omega }_n}{1+{\omega }_n}}=\infty }$. By the boundedness of $\left\{v_n\right\}$, $\parallel u_n\parallel$, $\underset{n\to \infty }{lim}{\omega }_n=0$ and condition (1), we see that $\underset{n\to \infty }{lim}{s}_n=0.$ In order to complete the proof, using Lemma 3, it remains to show that $\underset{k\to \infty }{lim}{t}_{n_k}=0$ implies that $\underset{k\to \infty }{lim\; sup}{b}_{n_k}⩽0$ for any subsequence $\left\{t_{n_k}\right\}$ of $\left\{t_n\right\}$. Let $\left\{t_{n_k}\right\}$ be a subsequence of $\left\{t_n\right\}$ such that $\underset{k\to \infty }{lim}{t}_{n_k}=0.$ With these assumptions, we can deduce that

$$\begin{array}{cc}\hfill {\displaystyle \underset{k\to \infty }{lim}{\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_{n_k}-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }^2}& {\displaystyle =\underset{k\to \infty }{lim}\parallel v_{n_k}-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_{n_k}-G_{\lambda }{v}_{n_k}+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }\hfill \\ \hfill & =0.\hfill \end{array}$$

By the triangle inequality

$$\begin{array}{cc}\hfill {\displaystyle \underset{k\to \infty }{lim}\parallel v_{n_k}-\lambda \sum _{i=1}^N{\delta }_i{S}_i{v}_{n_k}-G_{\lambda }{v}_{n_k}+\lambda \sum _{i=1}^N{\delta }_i{S}_{i}z\parallel }& \le \underset{k\to \infty }{lim}\parallel v_{n_k}-G_{\lambda }{v}_{n_k}\parallel \hfill \\ \hfill & {\displaystyle +\underset{k\to \infty }{lim}\parallel \sum _{i=1}^N{\delta }_i{S}_i{v}_{n_k}-\sum _{i=1}^N{\delta }_i{S}_{i}z\parallel .}\hfill \end{array}$$

Then, we have

$$\underset{k\to \infty }{lim}\parallel v_{n_k}-G_{\lambda }{v}_{n_k}\parallel =0.$$

(28)

Since $\underset{n\to \infty }{lim\; inf}{\lambda }_n>0$, there is $\lambda >0$ such that ${\lambda }_n\ge \lambda$ for all $n\ge 1.$ In particular, ${\lambda }_{n_k}\ge \lambda$ for all $k\ge 1$. By Lemma 4(ii), we have

$$\parallel G_{\lambda }{v}_{n_k}-v_{n_k}\parallel \le 2\parallel G_{{\lambda }_n}{v}_{n_k}-v_{n_k}\parallel .$$

Then, by (28), we obtain

$$\underset{k\to \infty }{lim\; sup}\parallel G_{\lambda }{v}_{n_k}-v_{n_k}\parallel ⩽0.$$

(29)

This implies that

$$\underset{k\to \infty }{lim}\parallel G_{\lambda }{v}_{n_k}-v_{n_k}\parallel =0.$$

(30)

On the other hand, we have

$$\begin{array}{cc}\hfill \parallel G_{\lambda }{v}_{n_k}-u_{n_k}\parallel & \le \parallel G_{\lambda }{v}_{n_k}-v_{n_k}\parallel +\parallel v_{n_k}-u_{n_k}\parallel \hfill \\ \hfill & =\parallel G_{\lambda }{v}_{n_k}-v_{n_k}\parallel +\parallel u_{n_k}+{\theta }_{n_k}(u_{n_k}-u_{n_k-1})-u_{n_k}\parallel \hfill \\ \hfill & =\parallel G_{\lambda }{v}_{n_k}-v_{n_k}\parallel +{\theta }_{n_k}\parallel u_{n_k}-u_{n_k-1}\parallel .\hfill \end{array}$$

(31)

By condition (i) and (30), we obtain

$$\underset{k\to \infty }{lim}\parallel G_{\lambda }{v}_{n_k}-u_{n_k}\parallel =0.$$

(32)

Let $z_t=tu+(1-t)G_{\lambda }{z}_t$, for all $t\in (0,1).$ Then, by Theorem 1, we have $\underset{t\to 0}{lim}{z}_t=z\in F(G_{\lambda }).$

By Lemma 1(ii) and Lemma 4(iii), we know that $G_{\lambda }$ is nonexpansive. Thus

$$\begin{array}{cc}\hfill \parallel z_t-u_{n_k}{\parallel }^2& =\parallel tp+(1-t)G_{\lambda }{z}_t-u_{n_k}{\parallel }^2\hfill \\ \hfill & =\parallel t(p-u_{n_k})+(1-t)(G_{\lambda }{z}_t-u_{n_k}){\parallel }^2\hfill \\ \hfill & \le {(1-t)}^2{\parallel G_{\lambda }{z}_t-u_{n_k}\parallel }^2+2t⟨p-u_{n_k},z_t-u_{n_k}⟩\hfill \\ \hfill & ={(1-t)}^2\parallel G_{\lambda }{z}_t-u_{n_k}{\parallel }^2+2t⟨p-z_t,z_t-u_{n_k}⟩+2t{\parallel z_t-u_{n_k}\parallel }^2\hfill \\ \hfill & \le {(1-t)}^2(\parallel G_{\lambda }{z}_t-G_{\lambda }{v}_{n_k}\parallel +\parallel G_{\lambda }{v}_{n_k}-u_{n_k}{\parallel )}^2+2t⟨p-z_t,z_t-u_{n_k}⟩+2t{\parallel z_t-u_{n_k}\parallel }^2\hfill \\ \hfill & \le {(1-t)}^2(\parallel z_t-v_{n_k}\parallel +\parallel G_{\lambda }{v}_{n_k}-u_{n_k}{\parallel )}^2+2t⟨p-z_t,z_t-u_{n_k}⟩+2t{\parallel z_t-u_{n_k}\parallel }^2\hfill \\ \hfill & \le {(1-t)}^2(\parallel z_t-u_{n_k}\parallel +{\theta }_n\parallel u_{n_k}-u_{n_k-1}\parallel +\parallel G_{\lambda }{v}_{n_k}-u_{n_k}{\parallel )}^2\hfill \\ \hfill & -2t⟨z_t-p,z_t-u_{n_k}⟩+2t{\parallel z_t-u_{n_k}\parallel }^2.\hfill \end{array}$$

(33)

This shows that

$$\begin{array}{cc}\hfill ⟨z_t-p,z_t-u_{n_k}⟩& \le {\displaystyle \frac{{(1-t)}^2}{2t}}(\parallel z_t-u_{n_k}\parallel +{\theta }_n\parallel u_{n_k}-u_{n_k-1}\parallel +\parallel G_{\lambda }{v}_{n_k}-u_{n_k}{\parallel )}^2\hfill \\ \hfill & +{\displaystyle \frac{(2t-1)}{2t}}{\parallel z_t-u_{n_k}\parallel }^2.\hfill \end{array}$$

(34)

From conditon (i), (32) and (34), we obtain for some $T>0$ large enough

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; sup}⟨z_t-p,z_t-u_{n_k}⟩& \le {\displaystyle \frac{t{T}^2}{2}}.\hfill \end{array}$$

(35)

Taking $t\to 0$ in (35), we obtain

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; sup}⟨z-p,z-u_{n_k}⟩& \le 0.\hfill \end{array}$$

(36)

On the other hand, we have

$$\begin{array}{cc}\hfill \parallel u_{n_k+1}-u_{n_k}\parallel & \le {\omega }_{n_k}\parallel p+u_{n_k}\parallel +{\xi }_{n_k}\parallel G_{\lambda }{v}_{n_k}-u_{n_k}\parallel +{\gamma }_{n_k}\parallel v_{n_k}-u_{n_k}\parallel \hfill \\ \hfill & \le {\omega }_{n_k}\parallel p+u_{n_k}\parallel +{\xi }_{n_k}\parallel G_{\lambda }{v}_{n_k}-u_{n_k}\parallel +(1-{\omega }_{n_k})\parallel v_{n_k}-u_{n_k}\parallel \hfill \\ \hfill & ={\omega }_{n_k}\parallel p+u_{n_k}\parallel +{\xi }_{n_k}\parallel G_{\lambda }{v}_{n_k}-u_{n_k}\parallel +(1-{\omega }_{n_k}){\theta }_{n_k}\parallel u_{n_k}-u_{n_k-1}\parallel .\hfill \end{array}$$

(37)

By conditions (i), (ii), (36) and (37), we obtain that

$$\underset{k\to \infty }{lim}\parallel u_{n_k+1}-u_{n_k}\parallel =0.$$

(38)

Combining (36) and (38),

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; sup}⟨z-p,z-u_{n_k+1}⟩& \le 0.\hfill \end{array}$$

(39)

Therefore,

$$\begin{array}{cc}\hfill {\displaystyle \frac{1-{\omega }_{n_k}}{{\omega }_{n_k}}}{\theta }_{n_k}⟨u_{n_k}-u_{n_k-1},v_{n_k}-z⟩& \le {\displaystyle \frac{1-{\omega }_{n_k}}{{\omega }_{n_k}}}{\theta }_{n_k}\parallel u_{n_k}-u_{n_k-1}\parallel \parallel v_{n_k}-z\parallel .\hfill \end{array}$$

From condition (i), it also follows that

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; sup}{\displaystyle \frac{1-{\omega }_{n_k}}{{\omega }_{n_k}}}{\theta }_{n_k}⟨u_{n_k}-u_{n_k-1},v_{n_k}-z⟩& \le 0.\hfill \end{array}$$

(40)

Hence, we obtain that $\underset{k\to \infty }{lim\; sup}{b}_{n_k}\le 0.$ By Lemma 3, we conclude that $\underset{n\to \infty }{lim}{\parallel u_n-z\parallel }^2\le 0.$ Therefore, $u_n\to z$ as $n\to \infty$. This completes the proof. □

4. Numerical Result

In this section, we will demonstrate how our proposed method can be applied to solve the image recovery problem. In the example, we also compare the proposed method with the method of Theorem 3.1 [16] in terms of the signal-to-noise ratio (SNR) of the recovered image. This demonstrates the capacity of our proposed algorithm. We consider a linear inverse problem $y=Mx+ϵ$, where $x\in {\mathbb{R}}^{n\times 1}$ is an original image, $y\in {\mathbb{R}}^{m\times 1}$ is the observed image, $ϵ$ is additive noise and $M\in {\mathbb{R}}^{m\times n}$ is the blurring operation. We recover an approximation of the original image x using the Basis Pursuit denoise technique:

$$\begin{array}{c}\hfill \underset{x\in {\mathbb{R}}^{n\times 1}}{min}P(x)=\frac{1}{2}{\parallel y-Mx\parallel }^2+\tau {\parallel x\parallel }_1\end{array}$$

(41)

where ${\parallel x\parallel }_1={\sum }_i\left|x_i\right|$ and $\tau$ is a parameter that is relate to noise $ϵ$. Problem (41) is widely recognized as the least absolute selection and shrinkage operator problem (LASSO).

We focus on minimizing a special case of the LASSO problem (41)$:{\delta }_i{A}_i+B$, where $A_i=\frac{1}{2}{\parallel y_i-M_{i}x\parallel }^2$ and $B={\tau \parallel x\parallel }_1$, where x is the original image, $M_i$ is the blurred matrix, $y_i$ is the blurred image by the blurred matrix $M_i$ for all $i=1,2,...,N$. Observe that $A_i$ is evidently a smooth function with an $L_i$-Lipschitz continuous gradient $\nabla A_i=M_i^T(M_{i}x-y_i)$, where $L_i=\parallel M_i^T{M}_i\parallel$.

Example 1 

(Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10). Let $\tilde{x}$ be the deblurred image. We show how to solve the special case of the LASSO problem by using the flowchart in Figure 1. We will recover an original image $x\in {\mathbb{R}}^{n\times 1}$. Let $N=4.$ Consider a linear operator, which is a filtering $M_{i}x={\phi }_i*x$, for a simple linearized model of image recovery, where ${\phi }_1$ is a motion blur specifying with motion length 21 pixels (len $=21$) and motion orientation ${11}^{\circ }$ ($\theta =11$), ${\phi }_2$ is a Gaussian blur of filter size $9\times 9$ with standard deviation $\sigma =2$, ${\phi }_3$ is a circular averaging filter with radius $r=4$ and ${\phi }_4$ is an averaging blur of filter size $9\times 9$. In this experiment, we will use our proposed algorithm to solve problem (41). All parameters are set to the following values: ${\omega }_n=\frac{1}{2n+2},{\xi }_n=\frac{1}{{(2n+2)}^2},u=0.01,{\theta }_n=0.1,{\delta }_n=0.25$ and $\lambda =0.001$. As a basic stopping criterion, we deem 350 iterations sufficient.

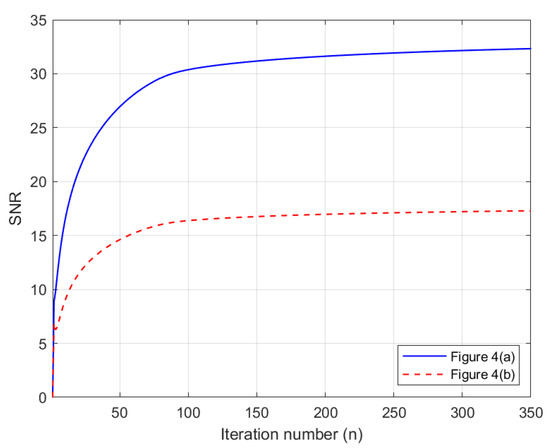
The following numerical results are proposed: Figure 2 presents the original grayscale images for (a) X-ray film of the brain and (b) X-ray film of the right shoulder. Figure 3 and Figure 6 are blurred X-ray films of the brain and the right shoulder images with filtering $M_{i}x$ in the part of degradation of Figure 1. In this example, we set $N=4$. So, we have $M_{1}x,M_{2}x,M_{3}x,$ and $M_{4}x$. Figure 4a, X-ray films of the brain and the right shoulder images were obtained via Theorem 2. Figure 4b, X-ray films of the brain and the right shoulder images were obtained via Theorem 3.1 in [16] (Khuangsatung and Kangtunyakarn’s method). Figure 9 is an X-ray film of the brain image that was recovered via the proposed method that was tuned for the parameter λ.

Additionally, we use the signal-to-noise ratio (SNR),

$$SNR=20{log}_{10}\frac{{\parallel x\parallel }_2}{\parallel x-x_{n+1}{\parallel }_2},$$

to measure the quality of recovery; a higher SNR indicates a higher quality of recovery. The following numerical results are proposed: Figure 5 is the SNR results of Figure 4a,b. We see that the SNR of Figure 4a is higher than that of Figure 4b. This means that Figure 4a is better than Figure 4b. Figure 8 is the SNR results of Figure 7a,b. We also see that the SNR of Figure 7a is higher than that of Figure 7b. This means that Figure 7a is better than Figure 7b. Figure 10 is the SNR of Figure 9 when we select a higher $\lambda$ value inside the specified range to produce a higher quality image than a lower $\lambda$ value.

Remark 3. 

Experimentally, the SNR value demonstrates that our proposed algorithm is more effective than the algorithm that was introduced by Khuangsatung and Kangtunyakarn [15,16] in solving the image recovery problem (41).

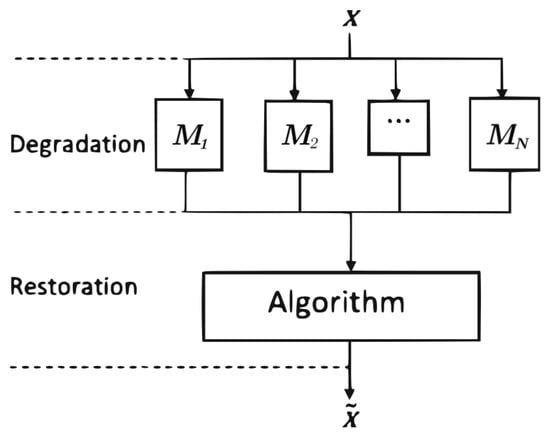
Figure 1. The image restoration process flowchart.

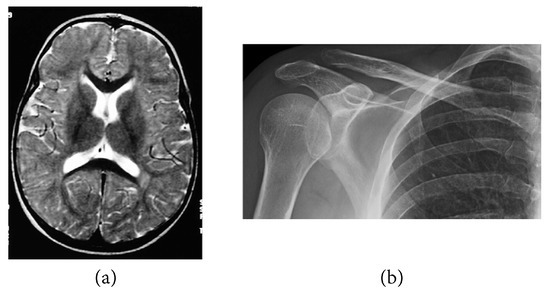
Figure 2. Original grayscale images. (a) X-ray film of the brain image and (b) X-ray film of the right shoulder image.

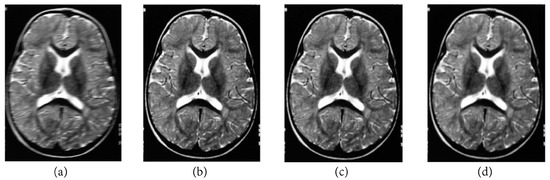
Figure 3. Blurred X-ray film of the brain image with filtering $M_{i}x$ by (a) $M_{1}x$, (b) $M_{2}x$, (c) $M_{3}x$ and (d) $M_{4}x$.

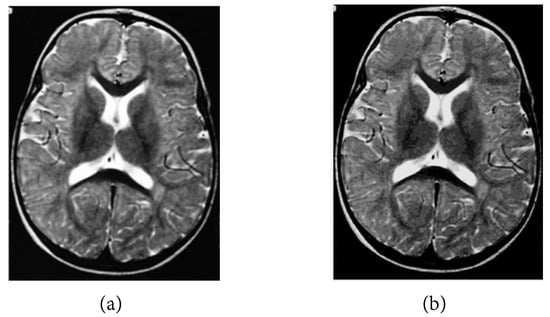
Figure 4. (a) X-ray film of the brain image obtained via Theorem 2 and (b) X-ray film of the brain image obtained via Theorem 3.1 in [16].

Figure 5. SNR results of X-ray films of the brain images between Figure 4a and Figure 4b.

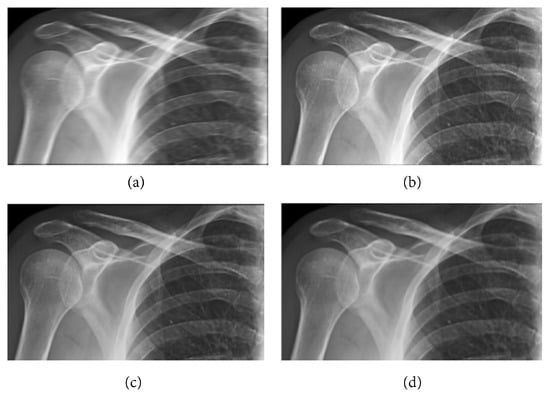
Figure 6. Blurred X-ray film of the right shoulder image with filtering $M_{i}x$ by (a) $M_{1}x$, (b) $M_{2}x$, (c) $M_{3}x$ and (d) $M_{4}x$.

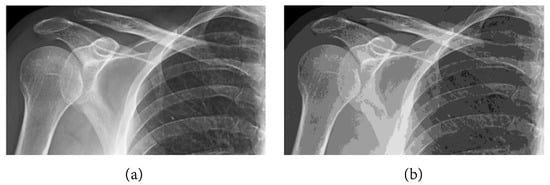
Figure 7. (a) X-ray film of the right shoulder image obtained via Theorem 2 and (b) X-ray film of the right shoulder image obtained via Theorem 3.1 in [16].

Figure 8. The SNR results of X-ray film of the right shoulder images between Figure 7a and Figure 7b.

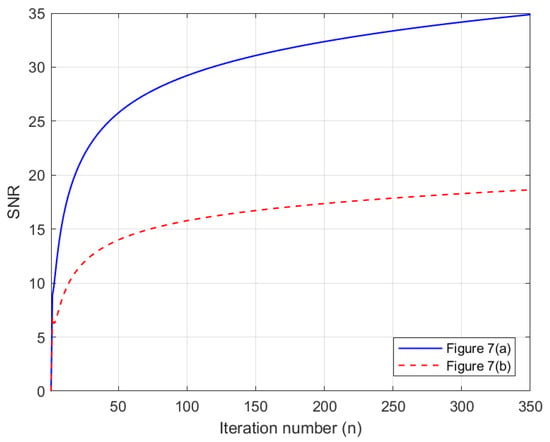
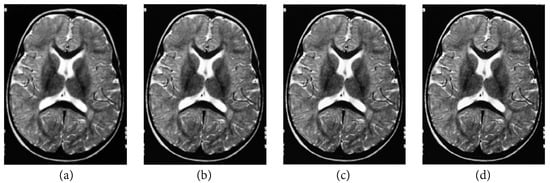
Figure 9. X-ray film of the brain image obtained via Theorem 2 when Example 1 was tuned for the parameter $\lambda$ by setting (a) $\lambda$ = 0.25, (b) $\lambda$ = 0.5, (c) $\lambda$ = 0.75, (d) $\lambda$ = 1.

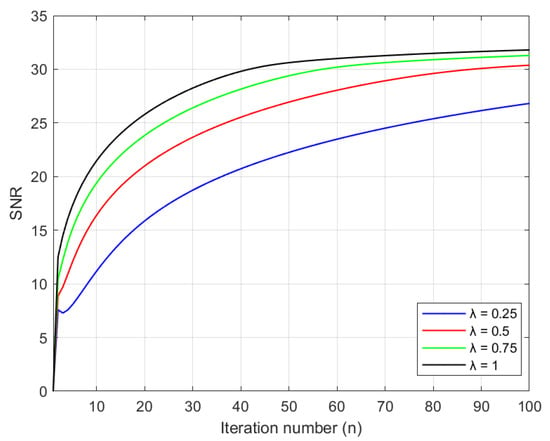
Figure 10. The SNR of Figure 9a–d.

5. Conclusions

An inertial forward–backward splitting method is presented for solving modified variational inclusion problems. Obviously, under appropriate conditions, we demonstrate its strong convergence. Moreover, we apply the proposed method to solve the image restoration problem. In our application, we use the proposed method and Khuangsatung and Kangtunyakarn’s method to restore two medical images. To compare image quality, we also evaluate the signal-to-noise ratio (SNR) of the proposed method to that of Khuangsatung and Kangtunyakarn’s method. Finally, the SNR value demonstrates that our proposed algorithm is more effective than the algorithm that was introduced by Khuangsatung and Kangtunyakarn in solving the image recovery problem.