Iterative Schemes Involving Several Mutual Contractions

Abstract

In this paper, we introduce the new concept of mutual Reich contraction that involves a pair of operators acting on a distance space. We chose the framework of strong b-metric spaces (generalizing the standard metric spaces) in order to add a more extended underlying structure. We provide sufficient conditions for two mutually Reich contractive maps in order to have a common fixed point. The result is extended to a family of operators of any cardinality. The dynamics of iterative discrete systems involving this type of self-maps is studied. In the case of normed spaces, we establish some relations between mutual Reich contractivity and classical contractivity for linear operators. Then, we introduce the new concept of mutual functional contractivity that generalizes the concept of classical Banach contraction, and perform a similar study to the Reich case. We also establish some relations between mutual functional contractions and Banach contractivity in the framework of quasinormed spaces and linear mappings. Lastly, we apply the obtained results to convolutional operators that had been defined by the first author acting on Bochner spaces of integrable Banach-valued curves.

1. Introduction

A standard way of constructing a fractal set is its definition as the fixed point of a contractive operator in a suitable metric space; for instance, the space of compact sets of some distance space endowed with the Hausdorff metric. Thus, the fractal set is the limit of an iteration of the contractive operator. If this operator is replaced by a family and a different self-map intervenes at each step, the problem of convergence is far from solved. In the case of fractal functions, a usual construction procedure is to consider an operator on a complete space of mappings and define the fractal function as the result of a Picard iteration. However, if the operator is replaced by a family of mappings, we face an open problem of fractal theory.

The well-known Banach contraction theorem is one of the most useful results in nonlinear analysis and applied mathematics. A huge number of numerical algorithms and mathematical methods were established by using this principle (for instance, the solution of equations of all types: algebraic, differential, integral). The Banach theorem was extended by many authors to some larger and different classes of contractive mappings; see more details in [1,2,3,4,5,6,7] and the references therein. Here, we introduce two generalizations of the classical (Banach) contraction involving two operators on a metric space instead of a single map. In some instances, we obtain the singular case studied in the recent bibliography [8]. We establish theorems of the existence of a common fixed point when there are mutual relations of contraction between operators. We then generalize the results to a family of operators and study the convergence of the iterative schemes when a different operator is taken at each step of the algorithm. This type of iteration was studied in [9] for the case of Banach contractions. In the last section, we consider the problem of convergence of iterations related to the fractal convolution of mappings valued in Banach spaces and algebras [10].

Definition 1.

Let X be a metric space, and $T:X\to X$. T a Reich contraction on X if it satisfies the following condition for any $x,y\in X$:

$$d(Tx,Ty)\le ad(x,y)+bd(x,Tx)+cd(y,Ty),\mathit{for}a,b,c\ge 0\mathit{and}a+b+c<1.$$

(1)

If X is complete, the Reich contraction admits a unique fixed point [3].

Remark 1.

Reich contractivity contains Kannan and Banach contractions as particular cases, taking $a=0$ and $b=c$ for Kannan contractions [1,2,5], and $b=c=0$ for Banach contractions. Reich’s theorem is stronger than Banach and Kannan’s theorems. For example, let $X=[0,1]$ and $T\left(x\right)=\frac{x}{2},0\le x<1,T\left(1\right)=\frac{1}{4}$. Then, T is not a Banach contraction, as it is not continuous at $x=1$. If we take $x=0,y=\frac{1}{2}$, then $d\left(T\left(0\right),T\left(\frac{1}{2}\right)\right)=d\left(0,T\left(0\right)\right)+d\left(\frac{1}{2},T\left(\frac{1}{2}\right)\right)$, T does not satisfy the required condition to be Kannan’s contraction. However, for values $a=\frac{1}{2},b=\frac{1}{4},c=\frac{1}{6}$, T satisfies the condition of Reich’s contraction.

Remark 2.

Banach’s contraction is trivially a Reich contraction, but the converse is not true in general. For instance, map $T:[0,1]\to [0,1]$, defined as $T\left(x\right)=0$ for any $x\in [0,1)$ and $T\left(1\right)=1/4,$ is not Banach contractive, but it is a Reich contraction for $a=b=c=1/4.$

A Reich contraction does not need to be continuous, unlike a classical contraction. In this sense, the Reich concept is much more general than classical contractivity. The applications of Reich contractions include those of Kannan and Banach maps. Thus, their study is greatly important in applied mathematics and generally the sciences. The applications of the Banach contraction principle are well-known. Next, we define the concept of mutual Reich contractivity for two mappings and show the existence of a common fixed point for a given collection under some suitable conditions of mutual contraction. This is conducted in the framework of strong b-metric spaces that contain the metric spaces as a remarkable particular case.

2. Strong $\mathit{b}$-Metric Spaces

In this section, we first outline the rudiments of the structure of strong b-metric spaces (see, for instance, [11,12,13]).

Definition 2.

A strong b-metric space X is a set endowed with mapping $d_s:X\times X\to {\mathbb{R}}^{+}$ with the following properties:

1.

$d_s(x,y)\ge 0,$ $d_s(x,y)=0$ if and only if $x=y$.

2.

$d_s(x,y)=d_s(y,x)$ for any $x,y\in X.$

3.

There exists $s\ge 1$, such that $d_s(x,y)\le d_s(x,z)+s{d}_s(z,y)$ for any $x,y,z\in X.$

Constant s is the index of the strong b-metric space, and $d_s$ is called a strong b-metric. If the inequality in Property (3) is substituted by

$$d_s(x,y)\le s(d_s(x,z)+d_s(z,y)),$$

(2)

for any $x,y,z\in X$, X is a b-metric space, and $d_s$ is a b-metric (see, for instance, [14]). In both cases, s is the index of the metric.

Remark 3.

A metric space is a strong b-metric space taking $s=1.$

Remark 4.

As the inequality in Property (3) implies (2), a strong b-metric space is a b-metric space.

Example 1.

Let set $X=\{x,y,z\}$ be endowed with map $d_s:X\times X\to {\mathbb{R}}^{+}$ defined as $d_s(x,x)=d_s(y,y)=d_s(z,z)=0,$ $d_s(x,y)=d_s(y,x)=1/2,$ $d_s(y,z)=d_s(z,y)=5$ and $d_s(x,z)=d_s(z,x)=6.$ Then, X is a strong b-metric space with index $s=2$ (see Example 2.3 of [11]).

Example 2.

Let us consider set $X=\{x,y,z\}$ with $d_s:X\times X\to {\mathbb{R}}^{+}$ defined as $d_s(x,x)=d_s(y,y)=d_s(z,z)=0,$ $d_s(x,y)=d_s(y,x)=2,$ $d_s(y,z)=d_s(z,y)=1$ and $d_s(x,z)=d_s(z,x)=6.$ Then, X is a strong b-metric space with index $s=4$ (see Example 2.1 of [12]).

Example 3.

Lebesgue space ${\mathcal{L}}^p\left(I\right)$, where I is a real bounded interval and $0<p<1,$ with $d_s$ defined as

$$d_s(f,g)=({\int }_I{|f-g|}^p{dt)}^{1/p},$$

is a b-metric space with index $s=2^{\frac{1}{p}-1}.$

Example 4.

Let us consider set $X=\{x_1,x_2,x_3,x_4\}$ with $d_s:X\times X\to {\mathbb{R}}^{+}$ defined as $d_s(x_i,x_i)=0,$ for any i, $d_s(x_1,x_2)=4,$ $d_s(x_1,x_3)=d_s(x_1,x_4)=d_s(x_2,x_3)=d_s(x_2,x_4)=d_s(x_3,x_4)=1,$ $d_s(x_i,x_j)=d_s(x_j,x_i),$ for any $i,j.$ Then, X is a b-metric space with index $s=2$ (see Example 2.1 of [13]).

Let us consider a strong b-metric space X. Sometimes, we write the b-metric space as BMS.

Definition 3.

A sequence $\left(x_n\right)\subseteq X$ is Cauchy if $d_s(x_m,x_n)\to 0$ as $m,n$ tend to infinity.

Definition 4.

Sequence $\left(x_n\right)\subseteq X$ is convergent if there exists $x\in X$, such that $d_s(x_n,x)\to 0$ as n tends to infinity.

Definition 5.

Subset $A\subseteq X$ is complete if every Cauchy sequence in A is convergent to an element of A.

Remark 5.

The strong b-metric spaces described in Examples 1 and 2 are complete (see [11,12]).

Definition 6.

A self-map $T:X\to X$, where X is a strong BMS, is continuous if $x_n\to x$ implies $T{x}_n\to Tx.$

3. Mutual Reich Contractions

This section searches for the existence of common fixed points for a set of operators with mutual relations of the Reich type. We first propose the definition of mutual Reich contractions.

Definition 7.

Let $T_1,T_2:X\to X$ and X be a strong BMS. $T_1,T_2$ are mutually Reich contractive if $\exists a,b,c\ge 0,a+b+c<1$, such that for all $x,y\in X$

$$d_s(T_{1}x,T_{2}y)\le a{d}_s(x,y)+b{d}_s(x,T_{1}x)+c{d}_s(y,T_{2}y).$$

(3)

Remark 6.

The definition of a mutual Reich contraction generalizes that of Kannan mutual contractions introduced in [8] by taking $a=0$, and mutual Banach contraction for $b=c=0$ and $x\ne y$.

Lemma 1.

If $(X,d_s)$ is a strong BMS for any finite collection of elements $x_0,x_1,\dots ,x_j\in X$ the following inequality is satisfied:

$$d_s(x_0,x_j)\le s\left(\sum _{k=0}^{j-1}{d}_s(x_k,x_{k+1})\right).$$

Proof. 

We used induction on $j\in \mathbb{N}$. For $j=1$ the proposed inequality holds trivially. Let us assume that it is true for $j=n$. Applying the third condition of a strong b-metric:

$$d_s(x_0,x_{n+1})\le d_s(x_0,x_n)+s{d}_s(x_n,x_{n+1})\le s\sum _{k=0}^{n-1}{d}_s(x_k,x_{k+1})+s{d}_s(x_n,x_{n+1})$$

and the result is obtained.  □

Theorem 1.

Let $(X,d_s)$ be a complete strong b-metric space with index $s\ge 1$ and $T_1,T_2$ be mutual Reich contractions with constants $a,b,c$ such that $a+b+c<1$ and $max\{b,c\}<s^{-1}$. Then, $T_1,T_2$ have a unique common fixed point.

Proof. 

Let $x\in X$. Let us define sequence $x_0=x,x_1=T_1\left(x_0\right),x_2=T_2\left(x_1\right),x_3=T_1\left(x_2\right),x_4=T_2\left(x_3\right)$. Then, according to the definition of mutual Reich contractivity,

$$\begin{array}{cc}\hfill d_s(x_1,x_2)& =d_s(T_1\left(x_0\right),T_2\left(x_1\right))\le a{d}_s(x_0,x_1)+b{d}_s(x_0,T_1{x}_0)+c{d}_s(x_1,T_2{x}_1)\hfill \\ \hfill & =a{d}_s(x_0,x_1)+b{d}_s(x_0,x_1)+c{d}_s(x_1,x_2).\hfill \end{array}$$

Therefore, we obtained $d_s(x_1,x_2)\le \frac{(a+b)}{(1-c)}{d}_s(x_0,x_1)$. Analogously,

$$\begin{array}{cc}\hfill d_s(x_2,x_3)& =d_s(T_1\left(x_2\right),T_2\left(x_1\right))\le a{d}_s(x_1,x_2)+b{d}_s(x_2,T_1{x}_2)+c{d}_s(x_1,T_2{x}_1)\hfill \\ \hfill & =a{d}_s(x_1,x_2)+b{d}_s(x_2,x_3)+c{d}_s(x_1,x_2).\hfill \end{array}$$

Consequently, we obtained $d_s(x_2,x_3)\le \frac{(a+c)}{(1-b)}{d}_s(x_1,x_2)\le {\lambda }^2{d}_s(x_0,x_1),$ where

$$\lambda =max\left\{\frac{(a+b)}{(1-c)},\frac{(a+c)}{(1-b)}\right\}<1.$$

Thus, $d_s(x_n,x_{n+1})\le {\lambda }^n{d}_s(x_0,x_1)$. We show that $\left(x_n\right)$ is a Cauchy sequence. For $p\ge 1$, applying Lemma 1,

$$d_s(x_n,x_{n+p})\le s\left(\sum _{j=0}^{p-1}{d}_s(x_{n+j},x_{n+j+1})\right)\le s\left(\sum _{k=n}^{n+p-1}{\lambda }^k\right)d_s(x_0,x_1).$$

Since ${\displaystyle \sum _{k=0}^{\infty }}{\lambda }^k$ is convergent, $\left(x_n\right)$ is a Cauchy sequence with a limit $x^{*}\in X$. We now show that $x^{*}$ is a common fixed point of $T_1$ and $T_2$. For instance, for $n\in \mathbb{N}$, n even,

$$\begin{array}{cc}\hfill d_s(x^{*},T_1{x}^{*})& \le d_s(x^{*},x_n)+s{d}_s(x_n,T_1{x}^{*})=d_s(x^{*},x_n)+s{d}_s(T_2\left(x_{n-1}\right),T_1{x}^{*}).\hfill \end{array}$$

Applying the definition of Reich contractivity for $T_1,T_2$,

$$\begin{array}{cc}\hfill d_s(x^{*},T_1{x}^{*})& \le d_s(x^{*},x_n)+as{d}_s(x_{n-1},x^{*})+bs{d}_s(x^{*},T_1{x}^{*})+cs{d}_s(x_{n-1},T_2\left(x_{n-1}\right))\hfill \\ \hfill & \Rightarrow (1-bs)d_s(x^{*},T_1{x}^{*})\le d_s(x^{*},x_n)+as{d}_s(x_{n-1},x^{*})+cs{d}_s(x_{n-1},x_n).\hfill \end{array}$$

Since all the right terms tend to 0, $x^{*}=T_1{x}^{*}$. The same analysis can be performed for $T_2$ taking an odd natural n. Now, we show that $x^{*}$ is unique. Let us assume that there is another common fixed point $\overline{x}$.

$$\begin{array}{c}\hfill d_s(\overline{x},x^{*})=d_s(T_1\left(\overline{x}\right),T_2\left(x^{*}\right))\le a{d}_s(\overline{x},x^{*})+b{d}_s(x^{*},T_1\left(x^{*}\right))+c{d}_s(\overline{x},T_2\left(\overline{x}\right))=a{d}_s(\overline{x},x^{*}).\end{array}$$

Since $a<1,\overline{x}=x^{*}$.  □

Corollary 1.

If X is a complete strong b-metric space with index s and $T:X\to X$ is a Reich contraction with $max\{b,c\}<s^{-1}$, then T has a unique fixed point.

Remark 7.

In this way, the Reich’s Theorem is generalized to the framework of a complete strong b-metric space.

Corollary 2.

If X is a complete strong b-metric space and $T:X\to X$ is a Banach contraction, then T has a unique fixed point.

Corollary 3.

If X is a complete strong b-metric space and $T:X\to X$ is a Kannan contraction with constant $\beta <s^{-1}$, then T has a unique fixed point.

Remark 8.

T is a Reich contraction if and only if it is mutually Reich contractive with respect to itself. In this sense the concept of mutual Reich contraction generalizes the usual Reich contractivity.

Example 5.

Let $T_1,T_2:[0,1]\to [0,1]$ be defined by

$$T_1\left(x\right)=\frac{x}{6}\mathit{and}{T}_2\left(x\right)=\frac{x}{8}$$

and $[0,1]$ be endowed with the usual metric. It is easy to check that

$$\begin{array}{cc}\hfill d(T_1\left(x\right),T_2\left(y\right))& =|\frac{x}{6}-\frac{y}{8}|\le \left|\frac{x}{6}\right|+\left|\frac{y}{8}\right|\le \frac{1}{5}\left\{|x-\frac{x}{6}|+|y-\frac{y}{8}|\right\}\hfill \\ \hfill & \le \left\{ad(x,y)+bd(x,T_{1}x)+cd(y,T_{2}y)\right\},\hfill \end{array}$$

where $a=b=c=\frac{1}{5}.$ Thus, $T_1$ and $T_2$ are mutual Reich contractions.

Below, we find the existence of a common fixed point for a set of operators of any cardinality on a strong b-metric space.

Definition 8.

Let $(X,d_s)$ be a strong b-metric space and $\mathcal{F}=\{T_i:X\to X;i\in \mathcal{I}\}$. $x^{*}\in X$ is a fixed point of $\mathcal{F}$ if $T_i\left(x^{*}\right)=x^{*}\forall i\in \mathcal{I}$.

Example 6.

Let X be interval $[0,1]$ with the usual metric, and set $\mathcal{F}$ composed of the maps $T_i:[0,1]\to [0,1]$, defined as $T_i\left(x\right)=x^i$ for $i\in \mathbb{N}.$ Real $0,1$ are fixed points of $\mathcal{F}$.

Definitions concerning discrete dynamical systems can be found (for instance) in [15].

For all $r\ge 1,x_0\in X,T_{i_r}\in \mathcal{F}$, consider the iterative scheme

$$x_r=T_{i_r}{x}_{r-1}.$$

(4)

Definition 9.

$x\in X$ is a global attractor for the scheme (4) if $\underset{n\to \infty }{lim}{\omega }_n\left(x\right)=x^{*}$ $\forall x\in X$, where ${\omega }_n:=T_{i_n}\circ T_{i_{n-1}}\circ \dots T_{i_2}\circ T_{i_1}$.

Example 7.

Let X be the interval $[0,1)$ with the usual metric, and the set $\mathcal{F}$ composed of the maps $T_i:[0,1)\to [0,1)$, defined as $T_i\left(x\right)=x^i$ for $i\in \mathbb{N}.$ The point 0 is a global attractor for the iteration (4).

Theorem 2.

Let $(X,d)$ be a complete strong b-metric space and $\mathcal{F}=\{T_i:X\to X,i\in \mathcal{I}\}$. If there exists $i_0\in \mathcal{I}$ such that $\forall i\in \mathcal{I}$, $T_i,T_{i_0}$ are mutually Reich contractive with constants $a_i,b_i,c_i$ such that ${sup}_i{b}_i<s^{-1}$, ${sup}_i{c}_i<s^{-1}$; then the following hold:

1.

$\mathcal{F}$ has a unique fixed point $x^{*}\in X$.

2.

$x^{*}$ is the only fixed point of each $T_i$ $\forall i\in \mathcal{I}$.

Proof. 

According to Corollary 1, since $T_{i_0}$ is a Reich contraction, it has a unique fixed point $x^{*}\in X,$ $T_{i_0}\left(x^{*}\right)=x^{*}$. Let us examine if this element is a fixed point of every $T_i$. The definition of mutual Reich contraction implies that

$$d_s(T_i\left(x^{*}\right),T_{i_0}\left(x^{*}\right))\le b_i{d}_s(x^{*},T_i\left(x^{*}\right))+c_i{d}_s(x^{*},T_{i_0}\left(x^{*}\right)),$$

then

$$d_s(T_i\left(x^{*}\right),x^{*})\le b_i{d}_s(x^{*},T_i\left(x^{*}\right)).$$

Since $b_i<1$ then $d_s(T_i\left(x^{*}\right),x^{*})=0$ and $x^{*}$ is a fixed point of any $T_i$. Let us prove now that $x^{*}$ is the only fixed point of $T_i$. If there were another fixed point, $T_i\left(y^{*}\right)=y^{*}$,

$$d_s(y^{*},T_{i_0}\left(y^{*}\right))=d_s(T_i\left(y^{*}\right),T_{i_0}\left(y^{*}\right))\le c_i{d}_s(y^{*},T_{i_0}\left(y^{*}\right)),$$

as $c_i<1$ then $y^{*}$ would be another fixed point of $T_{i_0}$ and consequently $x^{*}=y^{*}.$  □

Theorem 3.

Let $(X,d_s)$ be a complete strong b-metric space and $\mathcal{F}=\{T_i:X\to X,i\in \mathcal{I}\}$, such that $\forall i,j\in \mathcal{I}$, $T_i,T_j$ are mutually Reich with constants $a_{ij},b_{ij},c_{ij},$ such that $max\{sup{b}_{ij},sup{c}_{ij}\}<s^{-1}$ for any $i,j\in \mathcal{I}$. Then, $\mathcal{F}$ has a unique fixed point $x^{*}$ that is a global attractor for any scheme of type (4).

Proof. 

According to Theorem 2, $\mathcal{F}$ has a unique fixed point $x^{*}.$ For any $x\in X$ let us define $x_0=x$, $x_1=T_{i_1}\left(x_0\right),$ $x_2=T_{i_2}\left(x_1\right),$ $\dots ,$ $x_n=T_{i_n}\left(x_{n-1}\right).$ Then

$$d_s(x_1,x_2)=d_s(T_{i_1}\left(x_0\right),T_{i_2}\left(x_1\right))\le a_{i_1{i}_2}{d}_s(x_0,x_1)+b_{i_1{i}_2}{d}_s(x_0,T_{i_1}\left(x_0\right))+c_{i_1{i}_2}{d}_s(x_1,T_{i_2}\left(x_1\right)),$$

and

$$d_s(x_1,x_2)\le a_{i_1{i}_2}{d}_s(x_0,x_1)+b_{i_1{i}_2}{d}_s(x_0,x_1)+c_{i_1{i}_2}{d}_s(x_1,x_2).$$

Let us define $a:=sup{a}_{ij}$, $b:=sup{b}_{ij}$, $c:=sup{c}_{ij}$, then

$$d_s(x_1,x_2)\le \frac{a+b}{1-c}{d}_s(x_0,x_1).$$

we Iteratively obtain

$$d_s(x_n,x_{n+1})\le {\lambda }^n{d}_s(x_0,x_1),$$

(5)

where $\lambda :=max\{\frac{a+b}{1-c},\frac{a+c}{1-b}\}<1.$ It is easy to check that $\left(x_n\right)$ is a Cauchy sequence as in the proof of Theorem 1. Thus, there exists $\tilde{x}\in X$ such that $\tilde{x}=\underset{n\to \infty }{lim}{x}_n$.

We now show that $\tilde{x}$ is the fixed point of $\mathcal{F}$. For $i\in \mathcal{I}$ and $n\in \mathbb{N}$:

$$d_s(\tilde{x},T_i\left(\tilde{x}\right))\le d_s(\tilde{x},x_n)+s{d}_s(T_{i_n}\left(x_{n-1}\right),T_i\left(\tilde{x}\right)).$$

Applying condition (3) for $T_{i_n}$ and $T_i$,

$$d_s(\tilde{x},T_i\left(\tilde{x}\right))\le d_s(\tilde{x},x_n)+as{d}_s(x_{n-1},\tilde{x})+bs{d}_s(x_{n-1},T_{i_n}\left(x_{n-1}\right))+cs{d}_s(\tilde{x},T_i\left(\tilde{x}\right))$$

and

$$(1-cs)d_s(\tilde{x},T_i\left(\tilde{x}\right))\le d_s(\tilde{x},x_n)+as{d}_s(x_{n-1},x_n)+bs{d}_s(x_{n-1},\tilde{x}).$$

The terms of the right hand tend to zero, and consequently $\tilde{x}=T_i\tilde{x}$, and $\tilde{x}=x^{*}.$ Additionally $\underset{n\to \infty }{lim}{x}_n=x^{*}$ and consequently $x^{*}$ is the limit of the orbit of any point x defined by iteration (4).  □

Definition 10.

Subset M of X is called an invariant set of the sequence ${\left\{T_i\right\}}_{i\in \mathcal{I}}$ if for all $i\in \mathcal{I}$ and $\forall x\in M,T_i\left(x\right)\in M$.

Example 8.

Let X be the real line with the usual metric, and the $\mathcal{F}$ composed of the maps $T_i\left(x\right)=x^i$ for $i\in \mathbb{N}.$ Interval $[0,1]$ is an invariant set of $\mathcal{F}.$

Definition 11.

$\tilde{x}\in X$ is Lyapunov stable for System (4) if $\forall \epsilon >0$, $\exists \delta >0$ such that $d(x,\tilde{x})<\delta$ implies $d({\omega }_n\left(x\right),{\omega }_n\left(\tilde{x}\right))<\epsilon$, where ${\omega }_n:=T_{i_n}\circ T_{i_{n-1}}\circ \dots \circ T_{i_1}$ for all n. An element $\tilde{x}\in X$ is asymptotically stable if it is stable and attractor ($\underset{n\to \infty }{lim}{\omega }_n\left(x\right)=\tilde{x}$ for any $x\in X$).

Example 9.

Let X be interval $[0,1)$ with the usual metric, and set $\mathcal{F}$ composed of the maps $T_i\left(x\right)=k_{i}x,$ where $sup{k}_i<1$ for $i\in \mathbb{N}.$ The origin is asymptotically stable.

Proposition 1.

Let us consider the assumptions of Theorem 2, and let $x^{*}$ be the fixed point of $\mathcal{F}.$ If the constants $a:=sup{a}_i$, $b:=sup{b}_i$ and $c:=sup{c}_i$ are such that $a+b+ds<1,$ where $d:=max\{b,c\}$, then for $r>0$ any ball $B_r=B(x^{*},r)$ is an invariant set of $\mathcal{F}$.

Proof. 

Let $z\in B_r$, and $i,j\in \mathcal{I}$. Since $x^{*}=T_{i_0}{x}^{*}$,

$$d_s(T_i\left(z\right),x^{*})\le a_i{d}_s(z,x^{*})+b_i{d}_s(z,T_i\left(z\right))$$

$$d_s(T_i\left(z\right),x^{*})\le (a+b)d_s(z,x^{*})+bs{d}_s(x^{*},T_i\left(z\right)).$$

Consequently,

$$d_s(T_i\left(z\right),x^{*})\le \frac{a+b}{1-bs}{d}_s(z,x^{*})\le d_s(z,x^{*})<r$$

and $T_i\left(z\right)\in B_r$. Since $i\in \mathcal{I}$ is arbitrary, $B_r$ is an invariant set of $\mathcal{F}$.  □

Theorem 4.

Under the assumptions of Theorem 3, if $a:=sup{a}_{ij},$ $b:=sup{b}_{ij},$ $c:=sup{c}_{ij}$ are such that $a+b+ds<1$ where $d:=max\{b,c\}$, the fixed point of $\mathcal{F}$ is asymptotically stable for the scheme (4).

Proof. 

$x^{*}$ is a fixed point of ${\omega }_n$ for all n. For any $\epsilon >0$, let us take $\delta =\epsilon$. If $d_s(x,x^{*})<\delta$ then, from the previous proposition $T_{i_1}\left(x\right)\in B(x^{*},\delta )$, ${\omega }_2\left(x\right)=T_{i_2}\circ T_{i_1}\left(x\right)\in B(x^{*},\delta )$, etc. In general, we have $d_s({\omega }_n\left(x\right),x^{*})<\delta =\epsilon$.

Since $x^{*}$ is a global attractor and stable, $x^{*}$ is asymptotically stable for the scheme (4).  □

Definition 12.

Let $x\in X$. The orbit of x is the sequence ${\left\{{\omega }_n\left(x\right)\right\}}_{n\ge 0},$ where ${\omega }_0:=Id$.

We now find the rate of convergence of the orbits ${\omega }_n\left(x\right)$ to $x^{*}$:

$$d_s({\omega }_n\left(x\right),x^{*})=d_s(T_{i_n}\left(x_{n-1}\right),T_{i_n}\left(x^{*}\right))\le a{d}_s(x_{n-1},x^{*})+b{d}_s(x_{n-1},T_{i_n}\left(x_{n-1}\right))+c{d}_s(x^{*},T_{i_n}\left(x^{*}\right)),$$

then,

$$d_s({\omega }_n\left(x\right),x^{*})\le a{d}_s(x_{n-1},x^{*})+b{d}_s(x_{n-1},x_n)\le a{d}_s(x_n,x^{*})+as{d}_s(x_n,x_{n-1})+b{d}_s(x_{n-1},x_n).$$

Bearing in mind that ${\omega }_n\left(x\right)=x_n$, according to (5),

$$d_s({\omega }_n\left(x\right),x^{*})\le \frac{as+b}{1-a}{d}_s(x_{n-1},x_n)\le \frac{as+b}{1-a}{\lambda }^{n-1}{d}_s(x_0,x_1),$$

where

$$\lambda =max\{\frac{a+b}{1-c},\frac{a+c}{1-b}\}$$

and the convergence is of exponential type. For the convergence of different orbits, $d({\omega }_n\left(x\right),{\omega }_n\left(y\right))$ for all $x,y\in X$ as

$$d_s({\omega }_n\left(x\right),{\omega }_n\left(y\right))=d_s(T_{i_n}\left(x_{n-1}\right),T_{i_n}\left(y_{n-1}\right))\le k{\lambda }^n\left[d_s(x,T_{i_1}\left(x\right))+d_s(y,T_{i_1}\left(y\right))\right].$$

Other Properties of Mutual Reich Contractions

Using Theorem 1, we obtain the following generalization of [3] (Theorem 4). We need a previous lemma.

Lemma 2.

If $(X,d_s)$ is a strong BMS, mapping $d_s$ is continuous.

Proof. 

Let us consider that, for any $x,x_0,y,y_0\in X$

$$|d_s(x,y)-d_s(x_0,y_0)|\le |d_s(x,y)-d_s(x_0,y)|+|d_s(x_0,y)-d_s(x_0,y_0)|\le s(d_s(x,x_0)+d_s(y,y_0)).$$

Taking $x=x_n$, $y=y_n$, $x_0=\underset{n\to \infty }{lim}{x}_n$, $y_0=\underset{n\to \infty }{lim}{y}_n$ we obtain the convergence of $d_s(x_n,y_n)$ to $d_s(x_0,y_0).$  □

Remark 9.

Distance $d_s$ of a general b-metric space need not be continuous. However, if $d_s$ is continuous, balls $B(x,r)=\{y\in X:d_s(y,x)<r\}$, where $r>0,$ are open sets and $\overline{B}(x,r)=\{y\in X:d_s(y,x)\le r\}$ are closed sets (see [14], Proposition 3.5).

Theorem 5.

Let $(X,d)$ be a complete strong b-metric space, and $S_n,T_n(n=1,2,\dots )$ be convergent and mutually Reich contractive with convergent constants $a_n,b_n,c_n$ such that $\underset{n\to \infty }{lim}{a}_n+\underset{n\to \infty }{lim}{b}_n+\underset{n\to \infty }{lim}{c}_n<1,$ ${sup}_n{a}_n<1,$ ${sup}_n{b}_n<s^{-1}$ and ${sup}_n{c}_n<s^{-1}$. Let $z_n$ be the common fixed point of $S_n,T_n$. Suppose that mappings $S,T:X\to X$ are defined as $S\left(x\right)=\underset{n\to \infty }{lim}{S}_n\left(x\right),T\left(x\right)=\underset{n\to \infty }{lim}{T}_n\left(x\right)$ for any $x\in X$; then $S,T$ are mutually Reich contractive and $z=\underset{n\to \infty }{lim}{z}_n$ is the common unique fixed point of $S,T$.

Proof. 

Since $d_s$ is a continuous function, and $S,T$ are the limit functions of $S_n,T_n$, it immediately follows that $S,T$ satisfy the mutual Reich condition and hence have a unique common fixed point, $z\in X$.

Now,

$$\begin{array}{cc}\hfill d_s(z_n,z)& =d_s(S_n\left(z_n\right),T\left(z\right))\le d_s(S_n\left(z_n\right),T_n\left(z\right))+s{d}_s(T_n\left(z\right),T\left(z\right))\hfill \\ \hfill & \le a_n{d}_s(z_n,z)+b_n{d}_s(S_n\left(z_n\right),z_n)+c_n{d}_s(T_n\left(z\right),z)+s{d}_s(T_n\left(z\right),T\left(z\right))\hfill \\ \hfill & =a_n{d}_s(z_n,z)+(c_n+s)d_s(T_n\left(z\right),z).\hfill \end{array}$$

Then,

$$d_s(z_n,z)\le \frac{s+c_n}{1-a_n}{d}_s(T_n\left(z\right),z).$$

(6)

Hence, z is the limit of the sequence $z_n$.  □

Remark 10.

An analogous expression of (6) can be found for the sequence $S_n$. The rate of convergence of sequence $z_n$ to z depends on those of $T_n\left(z\right),S_n\left(z\right)$ to z.

Remarks 1 and 2 show that operators with mutual relation of the Reich type do not need to be contractive. Our next objective is to find a relation between contractivity and mutual Reich contractivity for linear operators.

Proposition 2.

Let X be a Banach space and $T_1,T_2:X\to X$ be linear and mutually Reich contractive with constants $a,b,c$ such that $b\le c.$ Then $T_1$ is bounded, contractive,

$$\parallel T_1\parallel \le \frac{a+b}{1-b}<1$$

and $Id-T_1$ is invertible. If $c\le b$ then $T_2$ is bounded, contractive,

$$\parallel T_2\parallel \le \frac{a+c}{1-c}<1$$

and $Id-T_2$ is invertible.

Proof. 

Using Definition 1 for $x\in X$ and $y=0$, and the condition $b\le c$, we have

$$\parallel T_{1}x\parallel \le a\parallel x\parallel +b\parallel T_{1}x-x\left|\right|\le (a+b)\parallel x\parallel +b\parallel T_{1}x\parallel .$$

Thus, obtaining

$$\parallel T_1\parallel \le \frac{a+b}{1-b}<1.$$

Therefore, $T_1$ is contractive and $Id-T_1$ is invertible. Similarly, if $c\le b$ then $T_2$ is contractive,

$$\parallel T_2\parallel \le \frac{a+c}{1-c}<1$$

and $Id-T_2$ is invertible.  □

Proposition 3.

Let X be a normed space and $T:X\to X$ be linear and mutually Reich contractive with the null operator with constants $a,b,c$ such that $b\le c$. Then, T is contractive. If T is linear and contractive, then T is mutually Reich contractive with the null operator.

Proof. 

If T is mutually Reich contractive with the null operator, for any $x\in X,$

$$\parallel Tx\parallel \le a\left|\right|x\left|\right|+b\parallel x-Tx\parallel +c\parallel y\parallel .$$

Taking $y=0,$

$$\parallel Tx\parallel \le (a+b)\left|\right|x\left|\right|+b\parallel Tx\parallel$$

and

$$\parallel Tx\parallel \le \frac{(a+b)}{(1-b)}\left|\right|x\left|\right|.$$

With the conditions on the constants, $\left|\right|T\left|\right|<1$ and T is contractive.

For the second statement, let T be contractive with ratio $\alpha$. Then, for any $x\in X,$

$$\parallel Tx\parallel \le \alpha \left|\right|x\left|\right|\le \alpha \left|\right|x\left|\right|+b\parallel x-Tx\parallel +c\parallel y\parallel .$$

Taking $b,c\ge 0$ such that $b+c<1-\alpha$, we obtain the mutual Reich condition for T and the null operator.  □

Let $X,Y$ be Banach spaces and let us denote the set of all bounded invertible linear operators as $L(X,Y)$. If $X=Y$, the space is denoted as $L\left(X\right)$.

Lemma 3

([16]). Let $T:X\to X$ be a linear operator. If there exist constants $k_1,k_2\in [0,1)$ such that $\parallel Tx-x\parallel \le k_1\parallel x\parallel +k_2\parallel Tx\parallel$, then $T\in L\left(X\right)$ and

$$\frac{1-k_1}{1+k_2}\parallel x\parallel \le \parallel Tx\parallel \le \frac{1+k_1}{1-k_2}\parallel x\parallel ,$$

$$\frac{1-k_2}{1+k_1}\parallel x\parallel \le \parallel T^{-1}x\parallel \le \frac{1+k_2}{1-k_1}\parallel x\parallel ,$$

for $x\in X.$

Proposition 4.

Let X be a Banach space and $T_1:X\to X$ be linear and mutually Reich contractive with $T_2\in L\left(X\right)$ such that $\left|\right|I-T_2^{-1}\left|\right|<1$. Then, $T_1$ is bounded, invertible and

$$\frac{1-(a+b+c)}{1+b}\parallel x\parallel \le \parallel T_{1}x\parallel \le \frac{1+(a+b+c)}{1-b}\parallel x\parallel ,$$

(7)

$$\frac{1-b}{1+(a+b+c)}\parallel x\parallel \le \parallel T_1^{-1}x\parallel \le \frac{1+b}{1-(a+b+c)}\parallel x\parallel .$$

(8)

Proof. 

Let us consider $y=T_2^{-1}x$ in Equation (3), then

$$\parallel T_{1}x-x\parallel =\parallel T_{1}x-T_{2}y\parallel \le a\left|\right|x-y\left|\right|+b\parallel x-T_{1}x\parallel +c\parallel y-T_{2}y\parallel .$$

$$\parallel T_{1}x-x\parallel \le a\left|\right|x-T_2^{-1}x\left|\right|+b\parallel x-T_{1}x\parallel +c\parallel x-T_2^{-1}x\parallel .$$

Since $\left|\right|I-T_2^{-1}\left|\right|<1$,

$$\parallel T_{1}x-x\parallel \le (a+c)\left|\right|x\left|\right|+b\parallel x\parallel +b\parallel T_{1}x\parallel$$

and

$$\parallel T_{1}x-x\parallel \le (a+b+c)\left|\right|x\left|\right|+b\parallel T_{1}x\parallel .$$

Thus, as per Lemma 3, we have $k_1=a+b+c<1,k_2=b<1.$ Consequently $T_1\in L\left(X\right)$, and Inequalities (7) and (8) hold.  □

Proposition 5.

Let X be a Banach space, and $T_1:X\to X$ be linear and mutually Reich contractive with $T_2\in L\left(X\right)$ such that $\left|\right|T_2^{-1}x\left|\right|\le \left|\right|T_{1}x\left|\right|$ for any $x\in X$. Then, $T_1$ is bounded, invertible, and

$$\frac{1-(a+b+c)}{1+(a+b+c)}\parallel x\parallel \le \parallel T_{1}x\parallel \le \frac{1+(a+b+c)}{1-(a+b+c)}\parallel x\parallel ,$$

(9)

$$\frac{1-(a+b+c)}{1+(a+b+c)}\parallel x\parallel \le \parallel T_1^{-1}x\parallel \le \frac{1+(a+b+c)}{1-(a+b+c)}\parallel x\parallel .$$

(10)

Proof. 

Let us consider $y=T_2^{-1}x$ in Equation (3), then

$$\parallel T_{1}x-x\parallel =\parallel T_{1}x-T_{2}y\parallel \le a\left|\right|x-y\left|\right|+b\parallel x-T_{1}x\parallel +c\parallel y-T_{2}y\parallel .$$

$$\parallel T_{1}x-x\parallel \le a\left|\right|x-T_2^{-1}x\left|\right|+b\parallel x-T_{1}x\parallel +c\parallel x-T_2^{-1}x\parallel .$$

Since $\left|\right|T_2^{-1}x\left|\right|\le \left|\right|T_{1}x\left|\right|$,

$$\parallel T_{1}x-x\parallel \le (a+b+c)\left|\right|x\left|\right|+(a+b+c)\parallel T_{1}x\parallel .$$

Thus, as per Lemma 3, we have $k_1=a+b+c<1,k_2=a+b+c<1.$ Consequently $T_1\in L\left(X\right)$ and the stated inequalities hold.  □

4. Systems of Mutually Functional Contractive Operators

In this section, we define a mutual functional contraction and find the existence of common fixed point for systems of operators with mutual relations of functional Banach contractivity.

Definition 13.

Operators $T,S:X\to X$, where X is a strong b-metric space are mutually functional contractive if there exists $\alpha :X\times X\to {\mathbb{R}}^{+}$ such that $0<\alpha (x,y)<1$ and for $x,y\in X$, $x\ne y$,

$$d_s(T\left(x\right),S\left(y\right))\le \alpha (x,y)d_s(x,y).$$

(11)

The map $\alpha (x,y)$ is the functional factor of the mutual contraction.

Case $\alpha (x,y)=r$ for any $x,y\in X$, where $0<r<1,$ was treated in [8] for the usual metric spaces. The following results generalize the given propositions for mutually functional contractive operators on strong b-metric spaces.

Let $\mathcal{F}$ be a set of self-maps on a strong b-metric space X:

$$\mathcal{F}=\{T_i:X\to X;i\in \mathcal{I}\},$$

where $\mathcal{I}$ may have any cardinality (finite or infinite). As before, $x^{*}$ is a fixed point of $\mathcal{F}$ if $T_i\left(x^{*}\right)=x^{*},$ for any $T_i\in \mathcal{F}.$

In the following results, we provide the conditions for the existence of a common fixed point of a family of operators with relations of mutual functional contraction.

Theorem 6.

Let X be a complete strong b-metric space, and $\mathcal{F}$ be a set of self-maps $\mathcal{F}=\{T_i:X\to X,i\in \mathcal{I}\}$. If there exists $T_{i_0}\in \mathcal{F}$ such that $\forall i\in \mathcal{I},$ $T_{i_0}$ and $T_i$ are mutually functional contractive with factor ${\alpha }_i(x,y)$ such that $a:=sup\{{\alpha }_i(x,y):x,y\in X,i\in \mathcal{I}\}<s^{-1}/3$, then

1.

$T_i$ is contractive $\forall i\in \mathcal{I}$.

2.

$\mathcal{F}$ has a unique fixed point.

Proof. 

Since $T_{i_0}$ is contractive, according to Corollary 2, it has a unique fixed point $\overline{x}$. For $i\ne i_0$, if $x\ne y$, using Lemma 1,

$$d_s(T_i\left(x\right),T_i\left(y\right))\le s(d_s(T_i\left(x\right),T_{i_0}\left(y\right))+d_s(T_{i_0}\left(y\right),T_{i_0}\left(x\right))+d_s(T_{i_0}\left(x\right),T_i\left(y\right)))\le 3as{d}_s(x,y).$$

Consequently $T_i$ is also contractive. Let ${\overline{x}}_i$ be its fixed point. If $\overline{x}\ne {\overline{x}}_i$ then

$$d_s(\overline{x},{\overline{x}}_i)=d_s(T_{i_0}\left(\overline{x}\right),T_i\left({\overline{x}}_i\right))\le a{d}_s(\overline{x},{\overline{x}}_i).$$

Since $a<1$ agree.  □

Theorem 7.

Let X be a complete strong BMS and $\mathcal{F}$ a set of self-maps $\mathcal{F}=\{T_i:X\to X,i\in \mathcal{I}\}$. Let $T_{i_0}\in \mathcal{F}$ be such that, $\forall i\in \mathcal{I},$ $T_{i_0}$ and $T_i$ be mutually functional contractive with factor ${\alpha }_i(x,y)$ and $a:=sup\{{\alpha }_i(x,y):x,y\in X,i\in \mathcal{I}\}$ be such that $s^{-1}/3\le a<1$. Let us assume that there exists $y\in X$ such that the sequence $y_n:={\left(T_{i_0}\right)}^n\left(y\right),y_0:=y,$ tends to $\overline{x}$ and satisfies the inequalities $y_n\ne \overline{x}$, for all $n>n_0,$ where $n_0$ is a natural number such that $n_0\ge 1,$ and $\overline{x}$ is the fixed point of $T_{i_0}$. Then

1.

$\mathcal{F}$ has a unique fixed point $\overline{x}\in X$.

2.

$\overline{x}$ is the only fixed point of every $T_i\in \mathcal{F}$.

Proof. 

Since $T_{i_0}$ is a contraction and X is a complete strong BMS, according to Corollary 2, there exists $\overline{x}\in X$ such that $\overline{x}$ is the fixed point of $T_{i_0}$. Given $y\in X$ such that the sequence $y_n={\left(T_{i_0}\right)}^n\left(y\right),$ $y_0=y$, satisfies the conditions described in the statement, let us consider for $i\ne i_0$ and $n>n_0$. Then

$$d_s(\overline{x},T_i\left(\overline{x}\right))\le d_s(\overline{x},y_n)+sd(y_n,T_i\left(\overline{x}\right))\le d_s(\overline{x},y_n)+s{d}_s(T_{i_0}\left(y_{n-1}\right),T_i\left(\overline{x}\right))$$

and

$$d_s(\overline{x},T_i\left(\overline{x}\right))\le d_s(\overline{x},y_n)+as{d}_s(y_{n-1},\overline{x}).$$

Since both summands on the right hand tend to zero, $\overline{x}=T_i\left(\overline{x}\right)$ and $\overline{x}$ is a fixed point of $T_i$, $\forall i\in \mathcal{I}.$ $T_{i_0}$ has a unique fixed point and consequently $\mathcal{F}$ has only the fixed point $\overline{x}$.

For $i\ne i_0$, if ${\overline{x}}_i$ is another fixed point of $T_i$ and ${\overline{x}}_i\ne \overline{x}$, then

$$d_s({\overline{x}}_i,\overline{x})=d_s(T_i\left({\overline{x}}_i\right),T_{i_0}\left(\overline{x}\right))\le a{d}_s({\overline{x}}_i,\overline{x}),$$

where $a<1.$ Hence ${\overline{x}}_i=\overline{x}$, and $T_i$ has only a fixed point (equal to $\overline{x}$).  □

Theorem 8.

Let X be a complete strong b-metric space and $\mathcal{F}=\{T_i:X\to X;i\in \mathcal{I}\}$ satisfying the conditions of Theorems 6 or 7. Let us define $\forall x\in X$ the sequence $x_0=x$, and for $k\ge 1$

$$x_k=T_{i_k}\left(x_{k-1}\right),$$

where $T_{i_k}\in \mathcal{F}$. Let $\overline{x}$ be the fixed point of $\mathcal{F}$. Then

1.

For any $x\in X$

$$\underset{n\to \infty }{lim}{\tau }_n\left(x\right)=\underset{n\to \infty }{lim}{T}_{i_n}\circ T_{i_{n-1}}\circ \cdots \circ T_{i_1}\left(x\right)=\overline{x}.$$

2.

$\overline{x}$ is globally asymptotically stable.

Proof. 

Let us consider any $x\in X$ and define the sequence $x_n={\tau }_n\left(x\right)=T_{i_n}\circ T_{i_{n-1}}\circ \cdots \circ T_{i_1}\left(x\right),$ $x_0=x.$ If $x_n\ne \overline{x}$ $\forall n\ge 0$, then

$$d_s(x_n,\overline{x})=d_s(T_{i_n}\left(x_{n-1}\right),T_{i_0}\left(\overline{x}\right))\le a{d}_s(x_{n-1},\overline{x})\le \dots a^n{d}_s(x_0,\overline{x}).$$

(12)

If there exists $m>0$ such that $x_m=\overline{x}$, then $x_{m+1}=T_{i_{m+1}}\left(x_m\right)=x_m=\overline{x}$ and so on. In any case, $d_s(x_n,\overline{x})\le a^{n}d(x_0,\overline{x}).$ Consequently, $\underset{n\to \infty }{lim}{\tau }_n\left(x\right)=\overline{x}$, and therefrom the attraction.

For any $\epsilon >0$, if $d_s(x,\overline{x})<\delta$, then via (12) $d_s({\tau }_n\left(x\right),\overline{x})\le a^n{d}_s(x,\overline{x})<a^n\delta <\delta .$ Selection $\delta =\epsilon$ satisfies the definition of stability. Hence, $\overline{x}$ is asymptotically stable.  □

Proposition 6.

In the hypotheses of Theorems 6 or 7, any ball $B(\overline{x},r)$, where $\overline{x}$ is the fixed point of $\mathcal{F}$ and $r>0$, is an invariant set of $\mathcal{F}$.

Proof. 

Let $\overline{x}$ be the fixed point of $\mathcal{F}$. If $x\in B(\overline{x},r)$ and $x\ne \overline{x}$,

$$d_s(T_i\left(x\right),\overline{x})=d_s(T_i\left(x\right),T_{i_0}\left(\overline{x}\right))\le a{d}_s(x,\overline{x})<ar<r.$$

Thus, $T_i\left(x\right)\in B(\overline{x},r)$ $\forall i\in \mathcal{I}$.

If $x=\overline{x}$, $T_i\left(x\right)=T_i\left(\overline{x}\right)=\overline{x}\in B(\overline{x},r)$.  □

Theorem 9.

Let $(X,d_s)$ be a complete strong b-metric space and $S_n,T_n$ ($n=1,2,\dots$) be mutual functional contractions with functional factors ${\alpha }_n(x,y)$ such that $a:=sup\{{\alpha }_n(x,y):x,y\in X,n\in \mathbb{N}\}<s^{-1}/3$. If $T_n$ is contractive with factor ${\beta }_n(x,y)$ such that $b:=sup\{{\beta }_n(x,y):x,y\in X,n\in \mathbb{N}\}<s^{-1}/3,$ according to Theorem 6, $S_n,T_n$ have a common fixed point $z_n$. Suppose $S_n,T_n$ are convergent to the mappings $S,T$ respectively. Then, $S,T$ are mutually functional contractive, the sequence $z_n$ is convergent and $z=\underset{n\to \infty }{lim}{z}_n$ is the unique common fixed point of $S,T$.

Proof. 

Via the continuity of $d_s$, $S,T$ satisfy Definition 13, and T is contractive; hence, they have a unique common fixed point z.

Now, if $z_n\ne z$,

$$\begin{array}{cc}\hfill d_s(z_n,z)& =d_s(S_n\left(z_n\right),T\left(z\right))\le d_s(S_n\left(z_n\right),T_n\left(z\right))+s{d}_s(T_n\left(z\right),T\left(z\right))\hfill \\ \hfill & \le a{d}_s(z_n,z)+s{d}_s(T_n\left(z\right),T\left(z\right))\hfill \\ \hfill \Rightarrow d_s(z_n,z)& \le \frac{s}{1-a}{d}_s(T_n\left(z\right),T\left(z\right)).\hfill \end{array}$$

If $z_n=z$, then $d_s(z_n,z)=0$ and the last inequality is also true. Since the right=hand term tends to zero, $z=\underset{n\to \infty }{lim}{z}_n.$  □

Let us recall the concept of the quasinorm (see, for instance, [17]).

Definition 14.

If B is a real linear space, mapping $\left|\right|·{\left|\right|}_q:B\times B\to {\mathbb{R}}^{+}$ is a quasinorm of index s if

1.

${\left|\right|x\left|\right|}_q\ge 0$; $x=0$ if and only if ${\left|\right|x\left|\right|}_q=0.$

2.

${\left|\right|\lambda x\left|\right|}_q={\left|\lambda \right|\left|\right|x\left|\right|}_q$.

3.

There exists $s\ge 1$, such that $\left|\right|x+{y\left|\right|}_q\le {s\left(\right|\left|x\right||}_q+{\left|\right|y\left|\right|}_q)$ for any $x,y\in B.$

and space B is quasinormed.

Distance associated with a quasinorm $d_s(u,v):=\left|\right|u-{v\left|\right|}_q$ is a b-metric since:

$$\left|\right|u-{v\left|\right|}_q=\left|\right|u-w+w-{v\left|\right|}_q\le s\left(\right||u-{w\left|\right|}_q+\left|\right|w-{v\left|\right|}_q)=s(d_s(u,w)+d_s(w,v)).$$

Proposition 7.

Let X be a quasinormed space with quasinorm ${\parallel ·\parallel }_q$ and let us define the b-metric:

$$d(x,y):={\parallel x-y\parallel }_q+{\parallel x\parallel }_q+{\parallel y\parallel }_q.$$

(13)

Let $L,L^{\prime }:X\to X$ be two linear and bounded operators such that $k:=max\{\parallel L-L^{\prime }{\parallel }_q,\parallel L{\parallel }_q,\parallel L^{\prime }{\parallel }_q\}$ $<1/(s+1)$. Then, $L,L^{\prime }$ are mutually functional contractive with respect to any functional factor $\alpha (x,y)$ such that $(s+1)k<\alpha (x,y)<1$ for any $x,y\in X,$ with respect to the b-metric d.

Proof. 

Let us prove the relaxed triangular inequality for map d:

$$d(x,z)={\parallel x-z\parallel }_q+{\parallel x\parallel }_q+{\parallel z\parallel }_q\le {s\parallel x-y\parallel }_q{+s\parallel y-z\parallel }_q+{\parallel x\parallel }_q+{\parallel z\parallel }_q,$$

where s is the index of the quasi-norm. The quantity on the right is lower than or equal to $s\left(d\right(x,y)+d(y,z\left)\right).$ Now, let us prove the property of being mutually contractive:

$$\begin{array}{cc}\hfill d(L\left(x\right),L^{\prime }\left(y\right))& =\parallel L\left(x\right)-L^{\prime }{\left(y\right)\parallel }_q+{\parallel L\left(x\right)\parallel }_q+{\parallel L^{\prime }\left(y\right)\parallel }_q\hfill \\ \hfill & \le s\parallel L\left(x\right)-L^{\prime }{\left(x\right)\parallel }_q+s\parallel L^{\prime }\left(x\right)-L^{\prime }{\left(y\right)\parallel }_q+{\parallel L\left(x\right)\parallel }_q+{\parallel L^{\prime }\left(y\right)\parallel }_q,\hfill \end{array}$$

and

$$d(L\left(x\right),L^{\prime }\left(y\right))\le s\parallel L-L^{\prime }{\parallel }_q{\parallel x\parallel }_q+s\parallel L^{\prime }{\parallel }_q{\parallel x-y\parallel }_q+{\parallel L\parallel }_q{\parallel x\parallel }_q+\parallel L^{\prime }{\parallel }_q{\parallel y\parallel }_q.$$

This quantity is lower than or equal to

$$(s+1)kd(x,y),$$

Thus,

$$d(L\left(x\right),L^{\prime }\left(y\right))\le \alpha (x,y)d(x,y),$$

for any map $\alpha (x,y)$ with the described conditions.  □

Example 10.

Maps $f\left(x\right)=(1/4)x$ and $g\left(x\right)=(1/6)x$ are mutually contractive with respect to metric d in $\mathbb{R}$ according to the previous proposition with functional factor $\alpha (x,y)$ such that $1/2<\alpha (x,y)<1.$

We now give an inverse of the previous result.

Proposition 8.

Let X be a quasinormed space with quasinorm ${\parallel ·\parallel }_q$ and $L,L^{\prime }:X\to X$ be two linear and bounded operators. If $L,L^{\prime }$ are mutually functional contractive with functional factor $\alpha (x,y)$ such that $\alpha (x,y)\le k<1,$ where $k:=max\{\parallel L-L^{\prime }{\parallel }_q{,\parallel L\parallel }_q{\}<(s+1)}^{-1}.$ Then, L is contractive with respect to the distance d defined in (13).

Proof. 

Applying the contractivity condition of $L,L^{\prime }$ for $x\ne y$:

$$\begin{array}{cc}\hfill {\parallel L\left(x\right)-L\left(y\right)\parallel }_q& \le s\parallel L^{\prime }{\left(x\right)-L\left(y\right)\parallel }_q+s{\parallel L\left(x\right)-L^{\prime }\left(x\right)\parallel }_q\hfill \\ \hfill & \le {(s+1)k\parallel x-y\parallel }_q+s\parallel L-L^{\prime }{\parallel }_q{\parallel x\parallel }_q.\hfill \end{array}$$

Thus

$$\begin{array}{cc}\hfill d\left(L\right(x),L(y\left)\right)& ={\parallel L\left(x\right)-L\left(y\right)\parallel }_q+{\parallel L\left(x\right)\parallel }_q+{\parallel L\left(y\right)\parallel }_q\hfill \\ \hfill & \le {(s+1)k\parallel x-y\parallel }_q+{sk\parallel x\parallel }_q+{k\parallel x\parallel }_q+k{\parallel y\parallel }_q\hfill \\ \hfill & \le (s+1)k(\parallel x-y{\parallel }_q+\parallel x{\parallel }_q+\parallel y{\parallel }_q)=(s+1)kd(x,y).\hfill \end{array}$$

 □

In particular, for linear operators, the following results were obtained.

Theorem 10.

If X is a quasinormed space, $\mathcal{F}$ is a family of linear and bounded operators, and there exists $j_0\in \mathcal{I}$ such that the constants $k_i:=max\{\parallel L_i-L_{j_0}{\parallel }_q,\parallel L_i{\parallel }_q,\parallel L_{j_0}{\parallel }_q\}$ satisfy the condition $(s+1)k<1$, where $k:=sup{k}_i$, then $L_i,L_{j_0}$ are mutually functional contractive for any $i\in \mathcal{I}$ with respect to distance d defined in (13) and

1.

0 is an equilibrium asymptotically stable for the system $x_k=L_{i_k}\left(x_{k-1}\right)$ for $k\ge 1$.

2.

1 does not belong to the point spectrum of $L_i$ for any i.

Proof. 

According to Proposition 7, $L_i,L_{j_0}$ are mutually contractive with respect to the distance d. Set $\mathcal{F}$ has the fixed point zero. If some $L_i$ has another fixed point ${\overline{x}}_i\ne 0$ then, following the proof of Proposition 7,

$$d({\overline{x}}_i,0)=d(L_i\left({\overline{x}}_i\right),L_{j_0}\left(0\right))\le (s+1)k_{i}d({\overline{x}}_i,0).$$

Since $(s+1)k<1$, $d({\overline{x}}_i,0)=0$, and $L_i$ has a single fixed point. Let us consider any $x\in X$ and define the sequence $x_n={\tau }_n\left(x\right)=L_{i_n}\circ L_{i_{n-1}}\circ \cdots \circ L_{i_1}\left(x\right),$ $x_0=x.$ Then, if $c=(s+1)k$,

$$d_s(x_n,0)=d_s(L_{i_n}\left(x_{n-1}\right),L_{j_0}\left(0\right))\le c{d}_s(x_{n-1},0)\le \dots \le c^n{d}_s(x_0,0).$$

(14)

The proof for stability is similar to that in Theorem 8.  □

5. A Problem of Convergence of Iterations of a Family of Convolution Operators on Bochner Spaces

In this section, we apply the results of previous sections to the iterations of a system of linear operators on Bochner spaces related to fractal convolution [10].

We consider a real Banach space $\mathbb{A}$ with norm $\left|\right|·\left|\right|$, and remind the definitions of the Bochner spaces of order $p,$ ${\mathcal{B}}^p(I,\mathbb{A})$:

Definition 15.

Let the map $u:I\to \mathbb{A}$ be strongly measurable, then $u\in {\mathcal{B}}^p(I,\mathbb{A})$, for $0<p<\infty$ if the function $t\hookrightarrow {\left|\right|u\left(t\right)\left|\right|}^p$ is Lebesgue integrable. In this case we define:

$${\left|\right|u\left|\right|}_p=({\int }_I{\left|\right|u\left(t\right)\left|\right|}^p{dt)}^{1/p}.$$

The map u belongs to the class ${\mathcal{B}}^{\infty }(I,\mathbb{A}),$ $u\in {\mathcal{B}}^{\infty }(I,\mathbb{A}),$ if the function $t\hookrightarrow \left|\right|u\left(t\right)\left|\right|$ is essentially bounded. Then

$${\left|\right|u\left|\right|}_{\infty }=esssu{p}_{t\in I}\left|\right|u\left(t\right)\left|\right|.$$

If $1\le p\le +\infty ,$ ${\mathcal{B}}^p(I,\mathcal{A})$ is a real Banach space with respect to the norm $\left|\right|·{\left|\right|}_p.$

For $0<p<1$,

$${\left|\right|u\left|\right|}_p=({\int }_I{\left|\right|u\left(t\right)\left|\right|}^p{dt)}^{1/p}$$

is a quasinorm with index $s=2^{1/p-1}.$ In both cases, Bochner spaces are complete b-metric spaces.

We first introduce the formalism of a type of an iterated function system (IFS).

Let us define in $E=I\times \mathbb{A},$ where $\mathbb{A}$ is a Banach space or algebra and $I=[a,b]$ is a real compact interval, an IFS $\{w_n:n=1,\dots ,N\}$ associated with a partition of the interval, $a=t_0<t_1<t_2<\dots t_N=b$, where $N>1,$ and a set of scale factors $\{{\alpha }_n,n=1,\dots ,N\}$ such that $|{\alpha }_n|<1$ for all n. Let us denote $I_n=[t_{n-1},t_n)$, for $i=1,2,N-1$ and $I_N=[t_{N-1},t_n].$

The IFS is composed of the mappings $w_n(t,x)=(h_n\left(t\right),F_n(t,x))$ where $h_n:I\to I_n$ are affine and such that $h_n\left(t_0\right)=t_{n-1},h_n\left(t_N\right)=t_n$ and $F_n:I\times \mathbb{A}\to \mathbb{A}$ given by $F_n(t,x)={\alpha }_n(x-b\left(t\right))+v\circ h_n\left(t\right),$ for $n=1,\dots N,$ where $v,b$ are Bochner integrable.

The described iterated function system has an associated operator, $T_{v,b}:{\mathcal{B}}^p(I,\mathbb{A})\to {\mathcal{B}}^p(I,\mathbb{A})$ defined as:

$$T_{v,b}w=F_n(h_n^{-1}\left(t\right),w\circ h_n^{-1}\left(t\right))$$

for $t\in I_n$. Then,

$$|T_{v,b}\left(w\right)-T_{v,b}\left(w^{\prime }\right){|}_p\le a{|w-w^{\prime }|}_p,$$

where

$$a:=sup\left\{\right|{\alpha }_n|:n=1,2,\dots ,N\}.$$

If $a<1$ the operator is a Banach contraction and it has a fixed point $v^{\alpha }:I\to \mathbb{A},$ whose graph has a fractal structure [10].

$v^{\alpha }$ can be seen as the result of an operation between v and b. This operation is the fractal convolution of v and b. Thus

$$v^{\alpha }=v\ast b.$$

Let us now consider the case $1\le p\le +\infty$, and the space of linear and bounded operators on the space of Bochner p-integrable mappings, $\mathcal{L}\left({\mathcal{B}}^p(I,\mathbb{A})\right)$. This set is a Banach algebra, since ${\mathcal{B}}^p(I,\mathbb{A})$ is a Banach space. Let us denote as ${|·|}_p$ the operator norm with respect to $\left|\right|·{\left|\right|}_p$.

For $S,T$ linear and bounded operators on ${\mathcal{B}}^p(I,\mathbb{A})$, let us define the convolution $S\ast T$ as

$$(S\ast T)\left(u\right)=S\left(u\right)\ast T\left(u\right),$$

for any $u\in {\mathcal{B}}^p(I,\mathbb{A}).$ The next result is proved in [10].

Proposition 9.

The convolution of operators satisfies the following properties:

• $S\ast S=S$ for any $S\in \mathcal{L}\left({\mathcal{B}}^p(I,\mathbb{A})\right).$
• $S\ast T\in \mathcal{L}\left({\mathcal{B}}^p(I,\mathbb{A})\right)$ if $S,T\in \mathcal{L}\left({\mathcal{B}}^p(I,\mathbb{A})\right)$ and

  $${|S\ast T|}_p\le \frac{{\left|S\right|}_p+a{\left|T\right|}_p}{1-a}.$$

  (15)
• For any $S,T,S^{\prime },T^{\prime }\in \mathcal{L}\left({\mathcal{B}}^p(I,\mathbb{A})\right),$

  $$|S\ast T-S\ast T^{\prime }{|}_p\le \frac{a}{1-a}{|T-T^{\prime }|}_p,$$

  (16)

  $$|S\ast T-S^{\prime }{\ast T|}_p\le \frac{1}{1-a}{|S-S^{\prime }|}_p.$$

The convolution of operators satisfies all the conditions required to be a metric convolution in the metric space $\mathcal{L}\left({\mathcal{B}}^p(I,\mathbb{A})\right)$ as defined in [18] and the properties deduced for the operation are applicable to it.

Let us consider for instance a family of operators defined by convolution: $\mathcal{F}=\{S\ast T_i:i\in \mathcal{I}\}$, where $S,T_i$ are linear and bounded operators defined on ${\mathcal{B}}^p(I,\mathbb{A})$ as:

$$Sf\left(t\right)=f\left(t\right)·u\left(t\right)$$

for some $u\in {\mathcal{B}}^{\infty }(I,\mathbb{A})$ (the dot represents the product in the algebra $\mathbb{A}$), and

$$T_{i}f\left(t\right)=c_{i}f\left(t\right),$$

where $c_i\in {\mathbb{R}}^{+}$. S and $T_i$ are linear and bounded:

$${\left|\right|Sf\left|\right|}_p=({\int }_I\left|\right|f\left(t\right)·{u\left(t\right)\left|\right|}^p{dt)}^{1/p}\le {\left|\right|u\left|\right|}_{\infty }{\left|\right|f\left|\right|}_p,$$

and clearly

$$\left|\right|T_i{f\left|\right|}_p=c_i{\left|\right|f\left|\right|}_p.$$

Let us define $L_i=S\ast T_i,$ for $i\in \mathcal{I}$. Inequality (16) implies that

$$|L_i-L_{j_0}{|}_p\le \frac{a}{1-a}{|T_i-T_{j_0}|}_p\le \frac{aK}{1-a},$$

where $K={sup}_i|c_i-c_{j_0}|.$ Moreover, bearing in mind (15),

$$|L_i{|}_p\le \frac{{\left|\right|u\left|\right|}_{\infty }+a{K}^{\prime }}{1-a},$$

where $K^{\prime }={sup}_i{c}_i.$ According to Theorem 10, if

$$max\left\{\frac{aK}{1-a},\frac{{\left|\right|u\left|\right|}_{\infty }+a{K}^{\prime }}{1-a}\right\}<\frac{1}{2},$$

the null function is an equilibrium asymptotically stable for the system $f_k=L_{i_k}\left(f_{k-1}\right)$ for $k\ge 1$, $f_0=f$.

Let us illustrate the procedure in a real case. Let us consider the interval $I=[0,2\pi ],$ and a partition of $N=10$ subintervals, the maps $h_n$ are affine satisfying the join-up conditions prescribed. Let the scale vector associated with the partition $\alpha =(0.3,-0.2,0.3,-0.2,0.1,-0.2,0.3,0.1,$ $0.2,-0.2).$ Let us define the operators $Sf\left(t\right)=f\left(t\right)·u\left(t\right)$, where $u\left(t\right)=cos\left(t\right)/6$, and the self-maps $T_i\left(f\right)=c_{i}f$ where $c_1=1/2,$ $c_2=1/3$ and $c_3=1/4$. The family of convolved operators $\{L_i:=S\ast T_i;i\in \{1,2,3\}\}$ satisfies the conditions described, being ${\left|S\right|}_p\le {\left|\right|u\left|\right|}_{\infty }=1/6$, $a=0.3,$ $K=1/4$ and $K^{\prime }=1/2.$ Consequently, by applying Theorem 10, any Picard iteration

$$f_n=L_{i_n}\circ L_{i_{n-1}}\circ L_{i_1}\left(f\right)$$

tends asymptotically to zero for $f\in {\mathcal{L}}^p\left(I\right)$.

Figure 1 represents the graph of function $f\left(t\right)=exp(-t/2)sin\left(5t\right)$ (zero-th iteration).

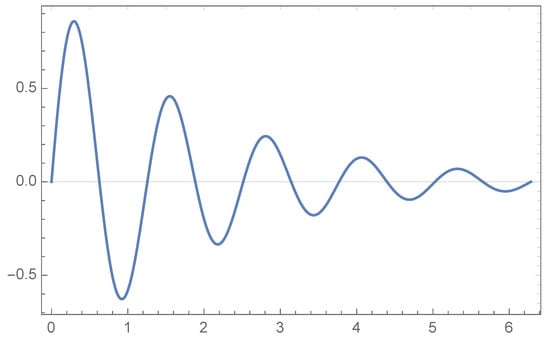
Figure 1. Graph of function $f\left(t\right)=exp(-t/2)sin\left(5t\right)$ (zero-th iteration).

Figure 2 represents the outcome of the action of the first iteration on the map f taking $i_1=1$ ($L_{1}f=(S\ast T_1)f$).

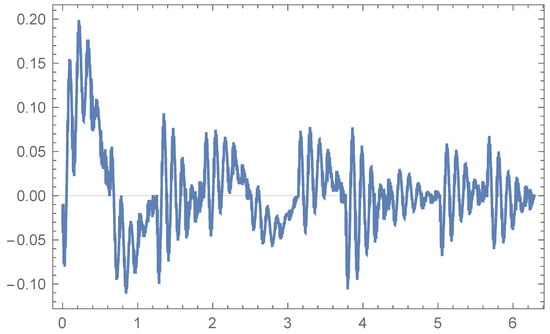
Figure 2. Graph of the first iteration of the function $f\left(t\right)=exp(-t/2)sin\left(5t\right)$ by the operator $L_1=S\ast T_1$ in the interval $I=[0,2\pi ]$.

6. Conclusions

In this paper, we introduced the concept of mutual Reich contraction between operators $T_1$ and $T_2$ defined on a strong b-metric space $(X,d_s)$ (that generalizes the structure of metric space). Mutual Reich contractivity extends the concept of Reich contraction on a metric space to a pair of self-maps. When $T_1=T_2$, we obtained the classical Reich maps.

We provided sufficient conditions for the existence of a common fixed point for $T_1$ and $T_2$ when they are mutually Reich contractive. This result was then considered in a set $\mathcal{F}$ of operators of any cardinality (finite or infinite). We also studied the convergence of iterative schemes of the type

$$x_k=T_{i_k}\left(x_{k-1}\right),$$

where $x_k\in X$ and $T_{i_k}\in \mathcal{F}.$ Under some conditions, the common fixed point of $\mathcal{F}$ is a global attractor for this kind of systems.

Further results established some relations between classical (Banach) contractivity and mutual Reich contractions in the case where X was a normed space and $T_1,T_2$ were linear.

We also introduced the new concept of mutual functional contractivity for two operators, and provided results similar to the Reich case. For quasinormed spaces, we also set some relations between mutual functional contractivity and single classical contractions, in the case of linear operators. In the last section we study the latter case for convolution operators, defined in ([10]), acting on Bochner spaces ${\mathcal{B}}^p(I,\mathbb{A})$ of integrable curves in a Banach space or algebra $\mathbb{A}$.