Abstract
In this article, we develop a simple mathematical GNU Octave/MATLAB code that is easy to modify for the simulation of mathematical models governed by fractional-order differential equations, and for the resolution of fractional-order optimal control problems through Pontryagin’s maximum principle (indirect approach to optimal control). For this purpose, a fractional-order model for the respiratory syncytial virus (RSV) infection is considered. The model is an improvement of one first proposed by the authors in 2018. The initial value problem associated with the RSV infection fractional model is numerically solved using Garrapa’s fde12 solver and two simple methods coded here in Octave/MATLAB: the fractional forward Euler’s method and the predict-evaluate-correct-evaluate (PECE) method of Adams–Bashforth–Moulton. A fractional optimal control problem is then formulated having treatment as the control. The fractional Pontryagin maximum principle is used to characterize the fractional optimal control and the extremals of the problem are determined numerically through the implementation of the forward-backward PECE method. The implemented algorithms are available on GitHub and, at the end of the paper, in appendixes, both for the uncontrolled initial value problem as well as for the fractional optimal control problem, using the free GNU Octave computing software and assuring compatibility with MATLAB.
Keywords:
numerical algorithms; fractional optimal control; Octave; respiratory syncytial virus infection; open source code for fractional optimal control MSC:
34A08; 49M05; 92D30
1. Introduction
In 1695, L’Hôpital asked Leibniz in a letter about the possible meaning of a derivative of order [1]. This episode is considered the kilometer zero of the Fractional Calculus road. In recent years, the modeling of real-phenomenon with fractional-order derivatives has caught the attention of many researchers. The associated problems have been modeled and studied using fractional-order derivatives to better understand their dynamics. For problems that arise in biology, ecology, engineering, physics, and some other fields of applied sciences, see, e.g., [2,3,4,5].
Mathematical models can predict the evolution of an infectious disease, show the predictable result of an epidemic, and support public health possible interventions. Compartmental models serve as a basic mathematical structure in epidemiology to comprehend the dynamics of such systems. In the simplest case, the compartments divide the population into two health states: susceptible to the infection of the pathogen agent, usually denoted by S, and infected by the pathogen, usually denoted by the letter I. Phenomenological assumptions explain the way that these compartments interact, and the model is constructed from there. Usually, these models are investigated through systems of ordinary differential equations. Other compartments could be included. Depending on the disease, the recovered/immune/removed compartment, usually denoted by R, is very common. To give further realism to the mathematical models and consider the influence of the past on the current and future state of the disease, recently, fractional order differential equations have been considered. In this regard, one can find, for example, research on dengue, Ebola, tuberculosis, and HIV/AIDS [6,7,8].
Respiratory syncytial virus (RSV) is a prominent cause of acute lower respiratory infection in young children. Consequently, RSV is a considerable burden on healthcare systems.
In a recent study of RSV in Portugal [9], it is shown that RSV is accountable for a substantial number of hospitalizations in children, especially when they have less than one year old. Hospitalizations are mainly motivated by healthy children. The authors of [9] conclude their study claiming that the creation of a universal RSV surveillance system to guide prevention strategies are crucial.
In another context, a surveillance system was already implemented in Florida in 1999, to support clinical decision-making for the prophylaxis of premature newborns. Since this infection is seasonal, a local periodic SEIRS mathematical model was proposed in [10] to describe real data collected by Florida’s system. Later, a nonlocal fractional (non-integer order) model was proposed in [11], where a fractional optimal control problem was formulated and solved.
In this work, we start by introducing dimension corrections to the SEIRS- epidemic model presented in [11]. Afterwards, we apply fractional optimal control to the model having treatment as the control variable. Differently from previous works, our computer codes are presented in the text and they are intentionally easy to modify in order to motivate readers to use them and adapt them to their own models and to their own contexts.
When , a fractional compartmental model represents a classical compartmental model. Therefore, the presented codes can also solve classical optimal control models; although, in that case, we suggest the reference [12] as a preferential option in such a scenario.
By providing the code of algorithms in an open programming language, we believe that our work contributes to reducing the alleged “replication crisis” in science and, in particular, in the field of dynamic optimization and control in biomedical research. This is a crisis due to the fact that many scientific studies are difficult or impossible to validate through replication [13].
The organization of the paper is as follows. In Section 2, we introduce the fractional-order RSV model, correcting the model first presented in [11]. The numerical resolution of the fractional RSV model is presented by three algorithms, being the subject of Section 3. The fractional optimal control of RSV transmission is the subject of Section 4. We end with conclusions and possible future work in Section 5.
2. A Fractional-Order RSV Model
We consider that the population under study consists of susceptible (S), infected but not yet infectious (E), infected and infectious (I), and recovered (R) individuals. A characteristic feature of RSV is that immunity after infection is temporary, so the recovered individuals become susceptible again [14]. Let parameter denote the birth rate, which we assume equal to the mortality rate; individuals leave the latency period and become infectious at a rate ; be the rate of loss of immunity; and be the rate of loss of infectiousness. We assume the latency period to be equal to the time between infection and the first symptoms. The influence of seasonality on the transmission parameter is modeled by the cosine function. As in [15], we consider that the annual recruitment rate is seasonal due to school opening/closing periods. Our system of fractional differential equations, the SEIR- epidemic model presented in [11] is given by
where and denote the left Caputo derivative of order [2]. The parameter is the mean of the transmission parameter and is the amplitude of the seasonal fluctuation in the transmission parameter, . Here, is the recruitment rate (including newborns and immigrants), where parameter is the amplitude of the seasonal fluctuation in the recruitment parameter, , while is an angle that is chosen in agreement with real data. Note that in the particular case of we obtain from (2) the SEIRS model of [16].
Equations of model (1) do not have appropriate time dimensions. Indeed, on the left-hand side the dimension is (time), while on the right-hand side the dimension is (time). We can conclude that model (1) is only consistent when . For more details about the importance of consistency of dimensions, we refer the reader to [17,18] and the references therein. Hence, we correct system (1) as follows:
where and .
3. Numerical Resolution of the Fractional RSV Model
In this section, we consider an initial value problem that consists of the fractional system (2) and the following initial conditions in terms of percentage of total population:
The values of (3) correspond to the endemic equilibrium of the fractional system (2). Note that because we have introduced the dimension correction into the initial model, the resulting model differs from the one presented in [11].
The RSV model parameters are presented in Table 1. The parameter values , , and were obtained from [14]. The birth rate, , is borrowed from [19] for the state of Florida. The birth rate is assumed equal to the mortality rate, which results in a constant population during the duration of the study. Analogously to [10], the fractional model was fitted to the data of the State of Florida, not including the north region, between September 2011 and July 2014. The data was collected from the Florida Department of Health [20]. In that process, values of the following parameters were determined by fitting the model: (i) the mean of the transmission parameter, ; (ii) and its relative seasonal amplitude, . As previously in [10], we assume here that the amplitude of the seasonal fluctuation in the recruitment parameter, , is equal to . The angle is assumed to be . This value allows the initial value of the transmission parameter to be the average, , and the initial value of the recruitment rate to also be the average, .

Table 1.
RSV model parameters that, with the exception of , and , are borrowed from [10] and references cited therein.
The new fractional model maintains a better fit to real data than the classical model (the absolute error is equal to 1716.12, which surpasses the value of 1719.12 corresponding to the classical model. For more details see [11]. The best adjustment to real data is achieved with a derivative order slightly different than the one determined before: . This value is the one we consider in what follows.
Algorithms designed to obtain the numerical solution of the initial value problem, (2) and (3), are now implemented under the free GNU Octave software (version 7.3.0), a high-level language primarily intended for numerical computations. Octave uses a language that is mostly compatible with MATLAB, being free [21]. In that regard, two known numerical techniques are implemented: the forward Euler’s and the predict-evaluate-correct-evaluate (PECE) methods. The obtained solutions are compared with the ones obtained through the known and freely available fde12 routine.
3.1. The fde12 Solver
Currently, neither GNU Octave nor MATLAB installation includes a built-in routine dedicated to the resolution of nonlinear differential equations of fractional order. Nevertheless, in the “MATLAB Central File Exchange”, there exists a routine, named fde12, whose implementation, based on Adams–Bashforth–Moulton scheme, is due to Garrapa [22]. This Octave/MATLAB routine solves fractional order differential equations in the Caputo sense. Convergence and accuracy of the numerical method are available in [23]. The stability properties of the algorithm implemented by fde12 are studied in [24].
The initial value problem of Equation (2), with initial conditions (3), can be solved with the fde12 function employing the implementation available in Appendix A.
The solution through Garrapa’s routine can then be obtained by introducing the following instructions in the GNU Octave interface:
>> N = 400; alpha = 0.995;
>> [t,y] = model_SEIRS_fde12(N, alpha)
3.2. Fractional Forward Euler’s Method
Let us consider the initial value problem (IVP):
where is a given function that satisfies some smooth conditions [25].
The function , known as the exact solution, that satisfies the IVP (4) is not what we will obtain with this procedure. Instead, an approximation of it is computed in as many points as we deem necessary.
The interval is subdivided into n subintervals of equal size using the nodes , for .
Applying on both sides of (4), we obtain the following equivalent Volterra integral equation [23]:
According to [25], is then approximated by a left fractional rectangular formula in such a way
where
This method was elected here since this approach agrees with the fact that fractional derivatives are given by an integral.
Applying the fractional forward Euler’s method to approximate the four variables of our fractional ordinary differential system of equations, we obtain the GNU Octave routine implementation that can be found in Appendix B.
In Figure 1, the solution of the system of fractional differential Equation (2), with initial conditions (3), obtained by the fde12 solver (solid line) is compared with the correspondent solution of the forward Euler’s method (dashed line). The same discretization is used by both implementations in the interval , considering 400 knots and the step size . We can verify that the graphics of system variables have strong oscillations. As a consequence, the approximations obtained by the forward Euler’s method, a very simple algorithm, have difficulty following the solution of a more sophisticated and robust implementation like the one provided by the fde12 solver.
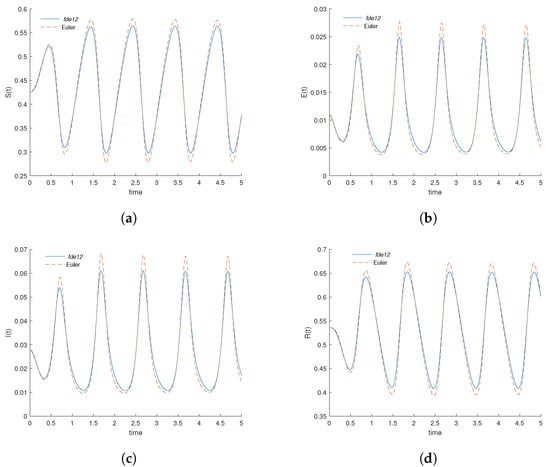
Figure 1.
State variables of the fractional differential system (2), considering , determined with the fde12 solver and with Euler’s method: (a) Variation of the number of susceptible individuals; (b) Variation of the number of exposed individuals; (c) Variation of the number of infected individuals; (d) Variation of the number of recovered individuals.
The solver fde12 is a sophisticated routine that, in some cases, considers a number of knots different from the one proposed by the user. We tested a few numbers of knots and verified that the number 400 was not changed by the solver. This allows the direct comparison with the approximations obtained by other routines, dispensing the use of other tools (e.g., interpolation) and their associated errors.
For illustration purposes, we follow the instructions used in the GNU Octave interface to obtain Figure 1a, which exhibits the variation of the number of susceptible individuals:
- figure
- hold on
- plot( t,yf(1,:),t,ye(1,:),'--')
- xlabel('time')
- ylabel('S(t)')
- legend( '\it fde12','Euler');
- legend('boxoff')
- set(gca,'XTick',[0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5])
- hold off
where yf(1,:) is the vector of values of variable (susceptibles) determined by fde12 solver, while ye(1,:) is the vector of values of variable determined by Forward Euler’s method.
The norm of the difference vector, the absolute difference between the results obtained by the fde12 solver and the ones obtained by the proposed implementation of Euler’s method, is presented in Table 2 using norms 1, 2, and ∞. Since Euler’s method has a global error of order one [25], the error bound depends linearly on the step size, h. Therefore, reducing the step size should lead to greater accuracy in the approximations.

Table 2.
Difference between results of fde12 solver and Euler’s method with norms 1, 2, and ∞.
3.3. PECE Algorithm
Based on [26] and the references cited therein, we now propose an implementation of the predict-evaluate-correct-evaluate (PECE) method of Adams–Basforth–Moulton. The code is relatively simple, easy to modify, and can be tailored to solve a particular nonlinear fractional differential model with constant, or time-varying, coefficients.
Applying the PECE method to approximate the four variables of our fractional ordinary differential system of equations, we obtain the GNU Octave routine implementation that can be found in Appendix C.
In Figure 2, the solution of the system of fractional differential Equation (2), with initial conditions (3), obtained by the fde12 solver (solid line) is compared with the corresponding solution of the PECE method (dashed line). We observe that the PECE method produces a better approximation than Euler’s method since both curves in each plot are almost indistinguishable. As before, here the same discretization is also used by both implementations in the interval , considering 400 knots and the step size .
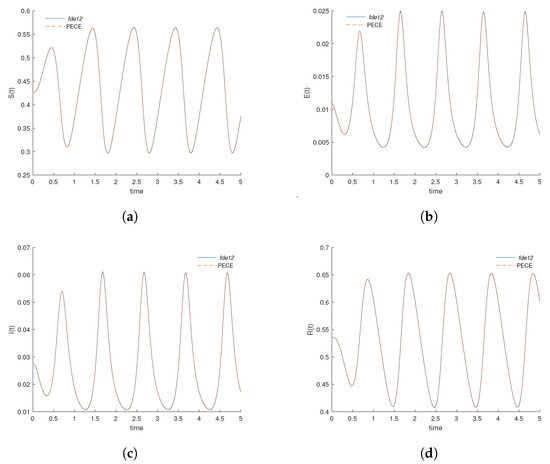
Figure 2.
State variables of the fractional differential system (2), considering , determined with the fde12 solver and with our PECE implementation: (a) Variation of the number of susceptible individuals; (b) Variation of the number of exposed individuals; (c) Variation of the number of infected individuals; (d) Variation of the number of recovered individuals.
The norm of the absolute difference between the results obtained by the fde12 solver and the proposed implementation of the PECE method are presented in Table 3 making use of norms 1, 2, and ∞. Since PECE’s method has a global error of order two [27], the error bound depends quadratically on the step size, h. This explains why the results obtained from the PECE implementation are better than those obtained from the forward Euler’s method.

Table 3.
Difference between results of the fde12 solver and the PECE implementation with norms 1, 2, and ∞.
In Section 4, a fractional optimal control problem of the model is presented. The computation of the corresponding optimal solution is carried out in a forward-backward scheme with the PECE algorithm because custom made dedicated algorithms are, in general, more efficient and can handle more complex models comparatively with generic codes.
4. Fractional Optimal Control of RSV Transmission
The evolution of the variables of the model depends on some circumstances that can be controlled. In what concerns RSV disease, treatment is commonly used as the control due to its relevance in a hospital context (limitation in the number of beds and other resources). Hence, we consider the following fractional optimal control problem: to minimize the number of infectious individuals and the cost associated to control the disease with the treatment of the patients, that is,
with given , subject to the fractional control system
and given initial conditions
Here, is the control variable, which designates treatment. Note that in absence of treatment, that is, for , then the control system (6) reduces to the SEIRS- dynamical system (2). The set of admissible control functions is
Two approaches can be chalked to solve optimal control problems: direct and indirect. In direct methods, the resolution of the fractional optimal control problem is performed through the application of a variety of discretization and numerical tools [28]. Indirect methods are based on Pontryagin’s maximum principle and are more robust, although less widespread in biological applications since they are not as easy to solve as direct approaches [29]. In what follows, we show how one can take advantage of Octave/MATLAB to solve fractional optimal control problems through Pontryagin’s maximum principle, reducing the problem to the solution of a boundary value problem.
Pontryagin’s maximum principle (PMP) for fractional optimal control can be used to solve the problem [29,30]. The Hamiltonian of our optimal control problem is
the optimality condition of PMP ensures that the optimal control is given by
while the adjoint system asserts that the co-state variables , , satisfy
which is a fractional system of right Riemann–Liouville derivatives, whose operator is represented by . In addition, the following transversality conditions hold:
where is the right Riemann–Liouville fractional integral of order .
Numerical Resolution of the RSV Fractional Optimal Control Problem
The optimal control problem (5)–(8) is numerically solved with the help of Pontryagin’s maximum principle and its optimality conditions, as discussed at the beginning of Section 4, implementing a forward-backward predict-evaluate-correct-evaluate (PECE) method of Adams–Basforth–Moulton (see Section 3.3 for the PECE algorithm). The presented forward-backward algorithm generalizes the algorithm proposed in reference [31].
First, we solve system (6) by the PECE procedure with initial conditions for the state variables (7) given in terms of the percentage of the total population, that is, , and a guess for the control over the time interval , and obtain the values of the state variables S, E, I and R.
Applying the change of variable
to the system of adjoint Equation (10) and to the transversality conditions (11), we obtain the following left Riemann–Liouville fractional initial value problem (12)–(13):
with initial conditions
In turn, conditions (13) imply that
which means that the adjoint system (12) can be treated as a Caputo system of fractional differential equations (see, e.g., [29], Section 3.3).
Given the initial conditions (13), we solve (12) with the PECE procedure and obtain the values of the co-state variables , . The control is then updated by a convex combination of the previous control and the value from (9). This procedure is repeated iteratively until the values of the controls at the previous iteration are very close to the ones at the current iteration.
In our numerical computations, we consider that and the other parameters are fixed according to Table 1. Such values allow the transmission parameter’s initial value to be the average, , and the recruitment rate initial value to also be the average, . Our initial conditions, given by (3), guarantee the existence of a nontrivial endemic equilibrium for the system (6) in the absence of control (), corresponding to the population system (2) prior introduction of treatment. Because the World Health Organization’s goals for most diseases are usually fixed for five-year periods, we assumed .
The algorithm is implemented in GNU Octave divided into four functions, the main function named FOCP_PECE. The implementation of all those functions is available in Appendix D.
The numerical solution of the fractional optimal control problem (5)–(13) with initial conditions (3), determined by our FOCP_PECE routine and associated functions, is exhibited in Figure 3. The introduction of treatment as control forces a reduction in the level of infected individuals as we can see in Figure 3c.
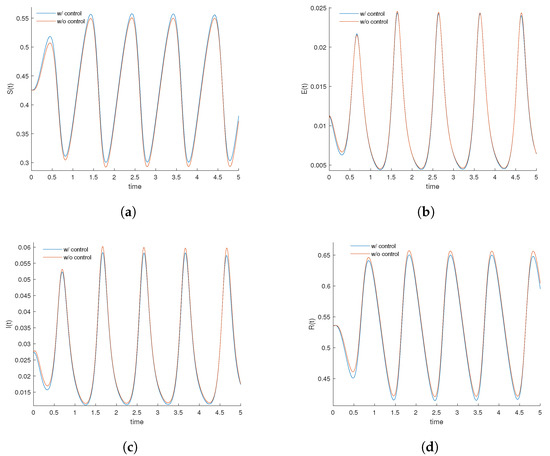
Figure 3.
Comparison of optimal state variables for the FOCP, defined by (5)–(13), subject to the initial conditions (3) with homonymous variables of the original model prior to the use of control treatment. (a) Evolution of susceptible individuals. (b) Evolution of exposed individuals. (c) Evolution of infected individuals. (d) Evolution of recovered individuals.
The evolution of the control treatment is traced in Figure 4 and follows the seasonality of the RSV infection.
5. Conclusions
Respiratory syncytial virus (RSV) is the most common cause of lower respiratory tract infection in infants and children worldwide. In addition, RSV causes serious diseases in elderly and immune-compromised individuals [10]. In this work, we improved a fractional compartmental model for RSV and applied optimal control to the resulting model. The Octave/MATLAB codes, developed in the computation of numerical solutions, are available in appendixes and were purposely simplified in order to be easily adapted to other contexts and models. We trust this will motivate more researchers to use fractional optimal control in the modeling of real applications. As future work, we plan to investigate the use of others measures to control the transmission of the disease and the benefit of the fractional approach in other contexts and geographical regions.
Author Contributions
Conceptualization, S.R. and D.F.M.T.; methodology, S.R. and D.F.M.T.; software, S.R. and D.F.M.T.; validation, S.R. and D.F.M.T.; formal analysis, S.R. and D.F.M.T.; investigation, S.R. and D.F.M.T.; writing—original draft preparation, S.R. and D.F.M.T.; writing—review and editing, S.R. and D.F.M.T.; visualization, S.R. and D.F.M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Portuguese Foundation for Science and Technology (FCT—Fundação para a Ciência e a Tecnologia), grants number UIDB/50008/2020 (S.R.) and UIDB/04106/2020 (D.F.M.T.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are very grateful to three anonymous Reviewers for several important comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Resolution of the IVP with the fde12 Function
Here, the initial value problem (2) and (3) is solved in Octave/MATLAB with the help of the fde12 function [22].
function [t, y] = model_SEIRS_fde12(N,alpha)
% initial conditions
y0=[0.426282; 0.0109566; 0.0275076; 0.535254];
% Values of parameters
miu = 0.0113; niu = 36; epsilon = 91; b0 = 85; b1 = 0.167; c1 = 0.167;
gama = 1.8; tfinal = 5; phi = pi/2;
ft = linspace(0,tfinal,N); h = tfinal/(N-1);
% Correction of values of parameters
miu_ = miu^alpha; niu_ = niu^alpha; epsilon_ = epsilon^alpha;
gama_ = gama^alpha;
% time-dependent parameters
flambda = @(t) miu.^alpha.*(1 + c1.* cos( 2.* pi.* t + phi) );
fbeta = @(t) b0.^alpha.* (1 + b1.* cos( 2.* pi.* t + phi ) );
% Differential system of equations of the model
fdefun = @(t,y,ft)[flambda(t)-miu_*y(1)-fbeta(t)*y(1)*y(3)+gama_*y(4); ...
fbeta(t)*y(1)*y(3)-(miu_+epsilon_)*y(2);
epsilon_*y(2)-(miu_+niu_)*y(3); ...
niu_*y(3)-miu_*y(4)-gama_*y(4)];
% resolution of system with solver fde12
[t,y] = fde12(alpha,fdefun,0,tfinal,y0,h,ft);
end
Appendix B. Resolution of the IVP with the Forward Euler Method
Here, the initial value problem (2) and (3) is solved in Octave/MATLAB by using the fractional forward Euler’s method to approximate the four variables of the fractional system of equations.
function [t,y] = model_SEIRS_EULER(N,alpha)
% Values of parameters
miu = 0.0113; niu = 36; epsilon = 91; gama = 1.8; tfinal = 5; b0 = 85;
b1 = 0.167; c1 = 0.167; phi = pi/2;
% initial conditions
S0 = 0.426282; E0 = 0.0109566; I0 = 0.0275076; R0 = 0.535254;
% Correction of values of parameters
miu_ = miu^alpha; niu_ = niu^alpha; epsilon_ = epsilon^alpha;
gama_ = gama^alpha;
% time-dependent parameters
flambda = @(t) miu_*(1 + c1 * cos( 2 * pi * t + phi) );
fbeta = @(t) b0^alpha.* (1 + b1 * cos( 2 * pi * t + phi ) );
% Initialization of variables
t = linspace(0,tfinal,N); h = tfinal/N; init = zeros(1,N);
S = init; E = init; I = init; R = init;
S(1) = S0; E(1) = E0; I(1) = I0; R(1) = R0;
beta = fbeta(t); lambda = flambda(t);
for j = 2:N
aux_s = 0; aux_e = 0; aux_i = 0; aux_r = 0;
for k = 1:j-1
bk = (j-k+1)^alpha-(j-k)^alpha;
% Differential system of equations of the model
aux_s = aux_s+bk*(lambda(k)-miu_*S(k)-beta(k)*S(k)*I(k) ...
+gama_*R(k));
aux_e = aux_e+bk*(beta(k)*S(k)*I(k)-(miu_+epsilon_)*E(k));
aux_i = aux_i+bk*(epsilon_*E(k)-(miu_+niu_)*I(k));
aux_r = aux_r+bk*(niu_*I(k)-miu_*R(k)-gama_*R(k));
end
S(j) = S0+h^alpha/gamma(1+alpha)*aux_s;
E(j) = E0+h^alpha/gamma(1+alpha)*aux_e;
I(j) = I0+h^alpha/gamma(1+alpha)*aux_i;
R(j) = R0+h^alpha/gamma(1+alpha)*aux_r;
end
y(1,:) = S; y(2,:) = E; y(3,:) = I; y(4,:) = R;
end
Appendix C. Resolution of the IVP with the PECE Method
Now, the initial value problem (2) and (3) is solved in Octave/MATLAB by using the predict-evaluate-correct-evaluate (PECE) method of Adams–Bashforth–Moulton.
function [t,y] = model_SEIRS_PECE(N,alpha)
% Values of parameters
miu = 0.0113; niu = 36; epsilon = 91; gama = 1.8; tfinal = 5;
b0 = 85; b1 = 0.167; c1=0.167; phi = pi/2;
% initial conditions
S0 = 0.426282; E0 = 0.0109566; I0 = 0.0275076; R0 = 0.535254;
% Correction of values of parameters
miu_ = miu^alpha; niu_ = niu^alpha; epsilon_ = epsilon^alpha;
gama_ = gama^alpha;
% time-dependent parameters
flambda = @(t) miu_*(1 + c1 * cos( 2 * pi * t + phi) );
fbeta = @(t) b0^alpha.* (1 + b1 * cos( 2 * pi * t + phi ) );
% Initialization of variables
t = linspace(0,tfinal,N); h = tfinal/N; init = zeros(1,N);
beta = fbeta(t); lambda = flambda(t);
S = init; E = init; I = init; R = init; b = init; a = init;
S(1) = S0; E(1) = E0; I(1) = I0; R(1) = R0;
Sp = S; Ep = E; Ip = I; Rp = R;
% computation of coefficients a_k and b_k
for k = 1:N
b(k) = k^alpha-(k-1)^alpha;
a(k) = (k+1)^(alpha+1)-2*k^(alpha+1)+(k-1)^(alpha+1);
end
for j = 2:N
% First part: prediction
aux_s = 0; aux_e = 0; aux_i = 0; aux_r = 0;
for k = 1:j
% Differential system of equations of the model
aux_s = aux_s+b(j-k+1)*(lambda(k)-miu_*S(k)...
-beta(k)*S(k)*I(k)+gama_*R(k));
aux_e = aux_e+b(j-k+1)*(beta(k)*S(k)*I(k)...
-(miu_+epsilon_)*E(k));
aux_i = aux_i+b(j-k+1)*(epsilon_*E(k)-(miu_+niu_)*I(k));
aux_r = aux_r+b(j-k+1)*(niu_*I(k)-miu_*R(k)-gama_*R(k));
end
Sp(j) = S0+h^alpha/gamma(1+alpha)*aux_s;
Ep(j) = E0+h^alpha/gamma(1+alpha)*aux_e;
Ip(j) = I0+h^alpha/gamma(1+alpha)*aux_i;
Rp(j) = R0+h^alpha/gamma(1+alpha)*aux_r;
% Second part: correction
aux_ss = lambda(j)-miu_*Sp(j)-beta(j)*Sp(j)*Ip(j)+gama_*Rp(j);
aux_ee = beta(j)*Sp(j)*Ip(j)-(miu_+epsilon_)*Ep(j);
aux_ii = epsilon_*Ep(j)-(miu_+niu_)*Ip(j);
aux_rr = niu_*Ip(j)-miu_*Rp(j)-gama_*Rp(j);
auxx = ((j-1)^(alpha+1)-(j-1-alpha)*j^alpha);
aux_s0 = auxx*(lambda(1)-miu_*S(1)-beta(1)*S(1)*I(1)+gama_*R(1));
aux_e0 = auxx* (beta(1)*S(1)*I(1)-(miu_+epsilon_)*E(1));
aux_i0 = auxx*(epsilon_*E(1)-(miu_+niu_)*I(1));
aux_r0 = auxx*(niu_*I(1)-miu_*R(1)-gama_*R(1));
aux_s = 0; aux_e = 0; aux_i = 0; aux_r = 0;
for k = 1:j-1
% Differential system of equations of the model
aux_s = aux_s+a(j-k)*(lambda(k)-miu_*S(k)-beta(k)*S(k)*I(k)...
+gama_*R(k));
aux_e = aux_e+a(j-k)*(beta(k)*S(k)*I(k)-(miu_+epsilon_)*E(k));
aux_i = aux_i+a(j-k)*(epsilon_*E(k)-(miu_+niu_)*I(k));
aux_r = aux_r+a(j-k)*(niu_*I(k)-miu_*R(k)-gama_*R(k));
end
S(j) = S0+h^alpha/gamma(2+alpha)*(aux_ss+aux_s0+aux_s);
E(j) = E0+h^alpha/gamma(2+alpha)*(aux_ee+aux_e0+aux_e);
I(j) = I0+h^alpha/gamma(2+alpha)*(aux_ii+aux_i0+aux_i);
R(j) = R0+h^alpha/gamma(2+alpha)*(aux_rr+aux_r0+aux_r);
end
y(1,:) = S; y(2,:) = E; y(3,:) = I; y(4,:) = R;
end
Appendix D. Numerical Resolution of the Fractional Optimal Control Problem
Here, we provide our Octave/MATLAB code for the numerical solution of the fractional optimal control problem (5)–(13) with initial conditions (3).
function [t,y] = FOCP_PECE(N,alpha);
% values assumed as global
global tfinal miu niu epsilon gama b0 b1 c1 phi k1 k2 S0 E0 I0 R0;
% Values of parameters
miu = 0.0113; niu = 36; epsilon = 91; gama = 1.8; tfinal = 5;
b0 = 85; b1 = 0.167; phi = pi/2; c1 = .167;
% parameters of the algorithm
k1 = 1; k2 = 0.001; trmax = 1.0; tol = 0.001; test = 1;
% initial conditions
S0 = 0.426282; E0 = 0.0109566; I0 = 0.0275076; R0 = 0.535254;
% initialization of variables
t = linspace(0,tfinal,N);
init = zeros(1,N); S = init; E = init; I = init; R = init;
p1 = init; p2 = init; p3 = init; p4 = init; Ta = init;
% iterations of the numerical method
while test>tol,
oldS = S; oldE = E; oldI = I; oldR = R;
oldp1 = p1; oldp2 = p2; oldp3 = p3; oldp4 = p4; oldTa = Ta;
% forward PECE iterations
[y1] = system1_control(Ta,t,N,alpha);
S = y1(1,:); E = y1(2,:); I = y1(3,:); R = y1(4,:);
% backward PECE iterations
[y2] = system2_adjoint(S,I,Ta,t,N,alpha);
p1 = y2(1,:); p2 = y2(2,:); p3 = y2(3,:); p4 = y2(4,:);
% new control
Ta = projection((p3-p4).*I/(2*k2),trmax);
Ta = ( Ta + oldTa ) / 2;
% Relative error values for convergence
vector = [max(abs(S-oldS))/(max(abs(S))),...
max(abs(oldE-E))/(max(abs(E))),...
max(abs(oldI-I))/(max(abs(I))),...
max(abs(oldR-R))/(max(abs(R))),...
max(abs(oldp1-p1))/(max(abs(p1))),...
max(abs(oldp2-p2))/(max(abs(p2))),...
max(abs(oldp3-p3))/(max(abs(p3))),...
max(abs(oldp4-p4))/(max(abs(p4))), ...
max(abs(oldTa-Ta))/(max(abs(Ta)))]*100;
test = max(vector);
end
y(1,:) = S; y(2,:) = E; y(3,:) = I; y(4,:) = R; y(5,:) = Ta;
y(6,:) = p1; y(7,:) = p2; y(8,:) = p3; y(9,:) = p4;
end
% function II: resolution of the fractional control system
function [y]= system1_control(Ta,t,N,alpha)
global b0 b1 c1 phi miu gama epsilon niu tfinal S0 E0 I0 R0;
% time-dependent parameters
flambda = @(t) miu^alpha*(1 + c1 * cos( 2 * pi * t + phi) );
fbeta = @(t) b0^alpha.* (1 + b1 * cos( 2 * pi * t + phi ) );
% Correction of values of parameters
miu_ = miu^alpha; niu_ = niu^alpha; epsilon_ = epsilon^alpha;
gama_ = gama^alpha;
% initialization of variables
beta = fbeta(t); lambda = flambda(t);
h = tfinal/N; init = zeros(1,N);
S = init; E = init; I = init; R = init; a = init; b = init;
S(1) = S0; E(1) = E0; I(1) = I0; R(1) = R0;
Sp = init; Ep = init; Ip = init; Rp = init;
% computation of coefficients a_k and b_k
for k = 1:N
b(k) = k^alpha-(k-1)^alpha;
a(k) = (k+1)^(alpha+1)-2*k^(alpha+1)+(k-1)^(alpha+1);
end
for j = 2:N
% First part: predict
% differential equations of control system
aux_s = 0; aux_e = 0; aux_i = 0; aux_r = 0;
for k = 1:j
aux_s = aux_s+b(j-k+1)*(lambda(k)-miu_*S(k)...
-beta(k)*S(k)*I(k)+gama_*R(k));
aux_e = aux_e+b(j-k+1)*(beta(k)*S(k)*I(k)...
-(miu_+epsilon_)*E(k));
aux_i = aux_i+b(j-k+1)*(epsilon_*E(k)-(miu_+niu_+Ta(k))*I(k));
aux_r = aux_r+b(j-k+1)*(niu_*I(k)-miu_*R(k)-gama_*R(k)...
+Ta(k)*I(k));
end
Sp(j) = S0+h^alpha/gamma(1+alpha)*aux_s;
Ep(j) = E0+h^alpha/gamma(1+alpha)*aux_e;
Ip(j) = I0+h^alpha/gamma(1+alpha)*aux_i;
Rp(j) = R0+h^alpha/gamma(1+alpha)*aux_r;
% Second part: correct
aux_ss = lambda(j)-miu_*Sp(j)-beta(j)*Sp(j)*Ip(j)+gama_*Rp(j);
aux_ee = beta(j)*Sp(j)*Ip(j)-(miu_+epsilon_)*Ep(j);
aux_ii = epsilon_*Ep(j)-(miu_+niu_+Ta(j))*Ip(j);
aux_rr = niu_*Ip(j)-miu_*Rp(j)-gama_*Rp(j)+Ta(j)*Ip(j);
auxx = ((j-1)^(alpha+1)-(j-1-alpha)*j^alpha);
aux_s0 = auxx*(lambda(1)-miu_*S(1)-beta(1)*S(1)*I(1)+gama_*R(1));
aux_e0 = auxx* (beta(1)*S(1)*I(1)-(miu_+epsilon_)*E(1));
aux_i0 = auxx*(epsilon_*E(1)-(miu_+niu_+Ta(1))*I(1));
aux_r0 = auxx*(niu_*I(1)-miu_*R(1)-gama_*R(1)+Ta(1)*I(1));
aux_s = 0; aux_e = 0; aux_i = 0; aux_r = 0;
for k = 1:j-1
aux_s = aux_s+a(j-k)*(lambda(k)-miu_*S(k)-beta(k)*S(k)*I(k)...
+gama_*R(k));
aux_e = aux_e+a(j-k)*(beta(k)*S(k)*I(k)-(miu_+epsilon_)*E(k));
aux_i = aux_i+a(j-k)*(epsilon_*E(k)-(miu_+niu_+Ta(k))*I(k));
aux_r = aux_r+a(j-k)*(niu_*I(k)-miu_*R(k)...
-gama_*R(k)+Ta(k)*I(k));
end
S(j) = S0+h^alpha/gamma(2+alpha)*(aux_ss+aux_s0+aux_s);
E(j) = E0+h^alpha/gamma(2+alpha)*(aux_ee+aux_e0+aux_e);
I(j) = I0+h^alpha/gamma(2+alpha)*(aux_ii+aux_i0+aux_i);
R(j) = R0+h^alpha/gamma(2+alpha)*(aux_rr+aux_r0+aux_r);
end
y(1,:) = S; y(2,:) = E; y(3,:) = I; y(4,:) = R;
end
% function III: resolution of the fractional adjoint system
function [y] = system2_adjoint(S,I,Ta,t,N,alpha)
global miu gama epsilon niu tfinal k1 b0 b1 phi;
% time-dependent parameter
fbeta = @(t) b0^alpha.* (1 + b1 * cos( 2 * pi * t + phi ) );
% Correction of values of parameters
miu_=miu^alpha; niu_=niu^alpha; epsilon_=epsilon^alpha;
gama_=gama^alpha;
% initialization of variables
beta = fbeta(t);
h = tfinal/N; init = zeros(1,N); a = init; b = init;
p1 = init; p2 = init; p3 = init; p4 = init;
p1p = init; p2p = init; p3p = init; p4p = init;
% First part: predict
S = S(end:-1:1); I = I(end:-1:1);
Ta = Ta(end:-1:1); beta = beta(end:-1:1);
% computation of coefficients a_k and b_k
for k = 1:N
b(k) = k^alpha-(k-1)^alpha;
a(k) = (k+1)^(alpha+1)-2*k^(alpha+1)+(k-1)^(alpha+1);
end
for j = 2:N
% differential equations of adjoint system
aux_p1 = 0; aux_p2 = 0; aux_p3 = 0; aux_p4 = 0;
for k = 1:j
aux_p1 = aux_p1+b(j-k+1)*(-1)*(p1(k)*(miu_+beta(k)*I(k))- ...
beta(k)*I(k)*p2(k));
aux_p2 = aux_p2+b(j-k+1)*(-1)*(p2(k)*(miu_+epsilon_)...
-epsilon_*p3(k));
aux_p3 = aux_p3+b(j-k+1)*(-1)*(-k1+beta(k)*p1(k)*S(k)...
-p2(k)*beta(k)*S(k)+p3(k)*(miu_+niu_+Ta(k))...
-p4(k)*(niu_+Ta(k)));
aux_p4 = aux_p4+b(j-k+1)*(-1)*(-gama_*p1(k)...
+p4(k)*(miu_+gama_));
end
p1p(j) = h^alpha/gamma(1+alpha)*aux_p1;
p2p(j) = h^alpha/gamma(1+alpha)*aux_p2;
p3p(j) = h^alpha/gamma(1+alpha)*aux_p3;
p4p(j) = h^alpha/gamma(1+alpha)*aux_p4;
% Second part: correct
aux_pp1 = (-1)*(p1p(j)*(miu_+beta(j)*I(j))-beta(j)*I(j)*p2p(j));
aux_pp2 = (-1)*(p2p(j)*(miu_+epsilon_)-epsilon_*p3p(j));
aux_pp3 = (-1)*(-k1+beta(j)*p1p(j)*S(j)-p2p(j)*beta(j)*S(j)...
+p3p(j)*(miu_+niu_+Ta(j))-p4p(j)*(niu_+Ta(j)));
aux_pp4 = (-1)*(-gama_*p1p(j)+p4p(j)*(miu_+gama_));
auxx = (-1)*((j-1)^(alpha+1)-(j-1-alpha)*j^alpha);
aux_p10 = auxx*(p1(1)*(miu_+beta(1)*I(1))-beta(1)*I(1)*p2(1));
aux_p20 = auxx*(p2(1)*(miu_+epsilon_)-epsilon_*p3(1));
aux_p30 = auxx*(-k1+beta(1)*p1(1)*S(1)-p2(1)*beta(1)*S(1)...
+p3(1)*(miu_+niu_+Ta(1))-p4(1)*(niu_+Ta(1)));
aux_p40 = auxx*(-gama_*p1(1)+p4(1)*(miu_+gama_));
aux_p1 = 0; aux_p2 = 0; aux_p3 = 0; aux_p4 = 0;
for k = 1:j-1
aux_p1 = aux_p1+a(j-k)*(-1)*(p1(k)*(miu_+beta(k)*I(k))- ...
beta(k)*I(k)*p2(k));
aux_p2 = aux_p2+a(j-k)*(-1)*( p2(k)*(miu_+epsilon_)...
-epsilon_*p3(k));
aux_p3 = aux_p3+a(j-k)*(-1)*( -k1+beta(k)*p1(k)*S(k)...
-p2(k)*beta(k)*S(k)+p3(k)*(miu_+niu_+Ta(k))...
-p4(k)*(niu_+Ta(k)));
aux_p4 = aux_p4+a(j-k)*(-1)*(-gama_*p1(k)+p4(k)*(miu_+gama_));
end
p1(j) = h^alpha/gamma(2+alpha)*(aux_pp1+aux_p10+aux_p1);
p2(j) = h^alpha/gamma(2+alpha)*(aux_pp2+aux_p20+aux_p2);
p3(j) = h^alpha/gamma(2+alpha)*(aux_pp3+aux_p30+aux_p3);
p4(j) = h^alpha/gamma(2+alpha)*(aux_pp4+aux_p40+aux_p4);
end
y(1,:) = p1(end:-1:1); y(2,:) = p2(end:-1:1); y(3,:) = p3(end:-1:1);
y(4,:) = p4(end:-1:1);
end
% function IV: control projection over the set of admissible controls
function [v] = projection(vect,trmax)
isNeg = vect<0; vect(isNeg) = 0;
isHuge = vect>trmax; vect(isHuge) = trmax;
v = vect;
end
References
- Leibniz, G.W. Letter from Hanover, Germany to GFA L’Hospital, September 30, 1695. Math. Schriften 1849, 2, 301–302. [Google Scholar]
- Podlubny, I. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. In Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1999; Volume 198, p. xxiv+340. [Google Scholar]
- Rezapour, S.; Etemad, S.; Agarwal, R.P.; Nonlaopon, K. On a Lyapunov-Type Inequality for Control of a Ψ-Model Thermostat and the Existence of Its Solutions. Mathematics 2022, 10, 4023. [Google Scholar] [CrossRef]
- Shah, K.; Ali, A.; Zeb, S.; Khan, A.; Alqudah, M.A.; Abdeljawad, T. Study of fractional order dynamics of nonlinear mathematical model. Alex. Eng. J. 2022, 61, 11211–11224. [Google Scholar] [CrossRef]
- Sintunavarat, W.; Turab, A. Mathematical analysis of an extended SEIR model of COVID-19 using the ABC-fractional operator. Math. Comput. Simul. 2022, 198, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Area, I.; Losada, J.; Ndaïrou, F.; Nieto, J.J.; Tcheutia, D.D. Mathematical modeling of 2014 Ebola outbreak. Math. Methods Appl. Sci. 2017, 40, 6114–6122. [Google Scholar] [CrossRef]
- Carvalho, A.R.M.; Pinto, C.M.A.; Baleanu, D. HIV/HCV coinfection model: A fractional-order perspective for the effect of the HIV viral load. Adv. Differ. Equ. 2018, 1, 1–22. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; Rehan, K.; Mushtaq, M. HIV/AIDS epidemic fractional-order model. J. Differ. Equ. Appl. 2017, 23, 1298–1315. [Google Scholar] [CrossRef]
- Bandeira, T.; Carmo, M.; Lopes, H.; Gomes, C.; Martins, M.; Guzman, C.; Bangert, M.; Rodrigues, F.; Januário, G.; Tomé, T.; et al. Burden and severity of children’s hospitalizations by respiratory syncytial virus in Portugal, 2015–2018. Influenza Other Respir. Viruses 2022, 17, e13066. [Google Scholar] [CrossRef]
- Rosa, S.; Torres, D.F.M. Parameter estimation, sensitivity analysis and optimal control of a periodic epidemic model with application to HRSV in Florida. Stat. Optim. Inf. Comput. 2018, 6, 139–149. [Google Scholar] [CrossRef]
- Rosa, S.; Torres, D.F.M. Optimal control of a fractional order epidemic model with application to human respiratory syncytial virus infection. Chaos Solitons Fractals 2018, 117, 142–149. [Google Scholar] [CrossRef]
- Campos, C.; Silva, C.J.; Torres, D.F.M. Numerical optimal control of HIV transmission in Octave/MATLAB. Math. Comput. Appl. 2020, 25, 1. [Google Scholar] [CrossRef]
- An, G. The Crisis of Reproducibility, the Denominator Problem and the Scientific Role of Multi-scale Modeling. Bull. Math. Biol. 2018, 80, 3071–3080. [Google Scholar] [CrossRef] [PubMed]
- Weber, A.; Weber, M.; Milligan, P. Modeling epidemics caused by respiratory syncytial virus (RSV). Math. Biosci. 2001, 172, 95–113. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, J.; Teng, Z. Existence of positive periodic solutions of an SEIR model with periodic coefficients. Appl. Math. 2012, 57, 601–616. [Google Scholar] [CrossRef]
- Mateus, J.P.; Rebelo, P.; Rosa, S.; Silva, C.M.; Torres, D.F.M. Optimal control of non-autonomous SEIRS models with vaccination and treatment. Discret. Contin. Dyn. Syst. Ser. S 2018, 11, 1179–1199. [Google Scholar] [CrossRef]
- Almeida, R. Analysis of a fractional SEIR model with treatment. Appl. Math. Lett. 2018, 84, 56–62. [Google Scholar] [CrossRef]
- Carvalho, A.R.M.; Pinto, C.M.A. Immune response in HIV epidemics for distinct transmission rates and for saturated CTL response. Math. Model. Nat. Phenom. 2019, 14, 307. [Google Scholar] [CrossRef]
- FLHealthCHARTS. 2015. Available online: http://www.flhealthcharts.com/charts/default.aspx (accessed on 31 January 2023).
- Florida Department of Health. Available online: http://www.floridahealth.gov/diseases-and-conditions/respiratory-syncytial-virus/ (accessed on 3 May 2017).
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave Version 7.3.0 Manual: A High-Level Interactive Language for Numerical Computations; Network Theory Limited: Boston, MA, USA, 2022. [Google Scholar]
- Garrapa, R. Predictor-Corrector PECE Method for Fractional Differential Equations. In Matlab Central File Exchange, File ID: 32918; MathWorks: Natick, MA, USA, 2023. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Garrappa, R. On linear stability of predictor-corrector algorithms for fractional differential equations. Int. J. Comput. Math. 2010, 87, 2281–2290. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; Volume 24. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Salati, A.B.; Shamsi, M.; Torres, D.F.M. Direct transcription methods based on fractional integral approximation formulas for solving nonlinear fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 334–350. [Google Scholar] [CrossRef]
- Almeida, R.; Pooseh, S.; Torres, D.F.M. Computational Methods in the Fractional Calculus of Variations; Imperial College Press: London, UK, 2015; p. xii+266. [Google Scholar] [CrossRef]
- Bergounioux, M.; Bourdin, L. Pontryagin maximum principle for general Caputo fractional optimal control problems with Bolza cost and terminal constraints. ESAIM Control Optim. Calc. Var. 2020, 26, 35. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman & Hall/CRC Mathematical and Computational Biology Series; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; p. xii+261. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).