Two New Modified Regularized Methods for Solving the Variational Inclusion and Null Point Problems

Abstract

In this article, based on the regularization techniques, we construct two new algorithms combining the forward-backward splitting algorithm and the proximal contraction algorithm, respectively. Iterative sequences of the new algorithms can converge strongly to a common solution of the variational inclusion and null point problems in real Hilbert spaces. Multi-inertial extrapolation steps are applied to expedite their convergence rate. We also give some numerical experiments to certify that our algorithms are viable and efficient.

1. Introduction

Let H be a real Hilbert space such that norm is $\parallel ·\parallel$ and the inner product is $⟨·,·⟩$, respectively. We recall that the variational inclusion problem (VIP):

$$\mathrm{Find}{v}^{*}\in H\mathrm{such} \mathrm{that} 0\in A\left(v^{*}\right)+B\left(v^{*}\right),$$

(1)

where $A:H\to 2^H$ is a set-valued operator and $B:H\to H$ is a single-valued operator. We denote the solution set of (1) by $\Phi$. The variational inclusion problem is a crucial extension of the variational inequality problem. Many nonlinear problems such as problems of saddle point, minimization, and split feasibility can be transformed into variational inclusion problems which can be applied to signal processing, neural networks, medical image reconstruction, machine learning, and data mining, etc., see [1,2,3,4,5,6,7].

As we all know, (1) can be converted to the fixed point equation $v^{*}=J_{\lambda A}(v^{*}-\lambda B{v}^{*})$ for some $\lambda >0$, where $J_{\lambda A}={(I+\lambda A)}^{-1}$ is the resolvent operator of A. The famous forward–backward splitting method (FBSM) was proposed by Lions and Mercier [8] in 1979:

$$x_{n+1}=J_{\lambda A}(I-\lambda B)x_n,$$

where A and B are maximally monotone and $\eta$-inverse strongly monotone, respectively, $\lambda \in (0,2\eta )$. Note that the Lipschitz continuity of an operator is a weaker property than the inverse strong monotonicity. So the algorithm has a shortcoming: the convergence requires a strong hypothesis. In order to overcome this difficulty, Tseng [9] constructed a modified forward–backward splitting algorithm (TFBSM) in 2000:

$$\left\{\begin{array}{c}{y}_n=J_{\lambda A}(I-\lambda B)x_n,\hfill \\ x_{n+1}=y_n-\lambda (B{y}_n-B{x}_n),\hfill \end{array}\right.$$

where B is monotone and Lipschitz continuous.

On the other hand, a famous method for solutions of variational inequalities is the projection and contraction method which was first introduced by He [10] for the variational inequality problem in Euclidean space. Inspired by this, the following proximal contraction method (PCM) was proposed by Zhang and Wang [11] in 2018:

$$\left\{\begin{array}{c}{y}_n=J_{{\lambda }_{n}A}(x_n-{\lambda }_{n}B{x}_n),\hfill \\ h_n=x_n-y_n-{\lambda }_n(B{x}_n-B{y}_n),\hfill \\ x_{n+1}=x_n-r{\beta }_n{h}_n,\hfill \end{array}\right.$$

where $r\in (0,2)$,

$${\beta }_n=\left\{\begin{array}{cc}0,\hfill & h_n=0,\hfill \\ \frac{\varphi (x_n,y_n)}{\parallel h_n{\parallel }^2},\hfill & h_n\ne 0,\hfill \end{array}\right.$$

$\varphi (x_n,y_n)=⟨x_n-y_n,h_n⟩$, and the sequence of variable stepsizes $\left\{{\lambda }_n\right\}$ satisfies some conditions. Notice that both (TFBSM) and (PCM) can only get weak convergent results in real Hilbert spaces. In general, weakly convergent results are obviously less popular than strongly convergent ones. In order to get the strong convergence, Hieu et al. [12] gave an algorithm named the regularization proximal contraction method (RPCM), for solving (1) in 2021:

$$\left\{\begin{array}{c}{y}_n=J_{{\lambda }_{n}A}(x_n-{\lambda }_n(B+{\alpha }_{n}F)x_n),\hfill \\ h_n=x_n-y_n-{\lambda }_n(B{x}_n-B{y}_n),\hfill \\ x_{n+1}=x_n-r{\beta }_n{h}_n,\hfill \end{array}\right.$$

where $r\in (0,2)$, $\varphi (x_n,y_n)=⟨w_n-y_n,h_n⟩$, ${\beta }_n=min\left\{\beta ,\frac{\varphi (x_n,y_n)}{\parallel h_n{\parallel }^2}\right\}$ and $\left\{{\lambda }_n\right\}$ satisfies some appropriate conditions. Before this, some scholars successfully applied this technique to the variational inequality problem. Very recently, Song and Bazighifan [13] introduced an inertial regularized method for solving the variational inequality and null point problem.

In recent years, there has been interest in methods with inertia which are considered effective methods to expedite the convergence. The inertial method is favored by many scholars because of its simple structure and easy operation, which is promoted by many scholars and in-depth research. In 2003, Moudafi and Oliny [14] combined (FBSM) with the inertial method to construct a new algorithm:

$$\left\{\begin{array}{c}{y}_n=x_n+{\vartheta }_n(x_n-x_{n-1}),\hfill \\ x_{n+1}=J_{{\lambda }_{n}A}(y_n-{\lambda }_{n}B{x}_n),\hfill \end{array}\right.$$

where $\left\{{\lambda }_n\right\}$ is a positive real sequence. Furthermore, some scholars have proposed multi-step inertial methods. In 2021, Wang et al. [15] proposed the multi-step inertial hybrid method to solve the problem (1).

Inspired by [12,13,15], we consider the variational inclusion and null point problem:

$$\mathrm{Find}{x}^{\S }\in \Phi \cap G^{-1}\left(0\right)\mathrm{such} \mathrm{that} ⟨F{x}^{\S },x-x^{\S }⟩\ge 0,\forall x\in \Phi \cap G^{-1}\left(0\right),$$

(2)

where G and F are nonlinear operators. We propose two modified regularized multi-step inertial methods to solve the above problem. These two algorithms are the modified forward-backward splitting algorithm and the proximal contraction algorithm. Using regularization techniques, the new algorithms converge strongly under mild conditions. Some numerical examples are given to show that our algorithms are efficient.

This article is arranged as follows: we introduce some notations, fundamental definitions, and results that are used in later proofs in Section 2. In Section 3, we present the new algorithms and discuss their convergence. In Section 4, we report some numerical experiments to support our theoretical results obtained.

2. Preliminaries

Let H be a real Hilbert space. The weak convergence and strong convergence of sequence $\left\{x_n\right\}$ are denoted by $x_n\rightharpoonup x$ and $x_n\to x$, respectively.

Definition 1

([16]). The mapping T: $H\to H$ is called

(i)

monotone, if

$$⟨Ty-Tx,y-x⟩\ge 0,\forall x,y\in H;$$

(ii)

γ-strongly monotone ($\gamma >0$), if

$$⟨Ty-Tx,y-x⟩\ge {\gamma \parallel y-x\parallel }^2,\forall x,y\in H;$$

(iii)

δ-inverse strongly monotone ($\delta >0$), if

$$⟨Ty-Tx,y-x⟩\ge {\delta \parallel Ty-Tx\parallel }^2,\forall x,y\in H;$$

(iv)

l-Lipschitz continuous ($l>0$), if

$$\parallel Ty-Tx\parallel \le l\parallel y-x\parallel ,\forall x,y\in H;$$

(v)

firmly nonexpansive, if

$$⟨Ty-Tx,y-x⟩\ge {\parallel Ty-Tx\parallel }^2,\forall x,y\in H;$$

(vi)

nonexpansive, if

$$\parallel Ty-Tx\parallel \le \parallel y-x\parallel ,\forall x,y\in H.$$

Definition 2

([16]). Let $T:H\to 2^H$ be a set-valued mapping. The graph of T is defined by $\mathrm{Graph}\left(T\right)=\left\{\right(x,u):x\in H,u\in Tx\}$. The mapping T is said to be

(i)

monotone, if

$$⟨v-u,y-x⟩\ge 0,\forall u\in Tx,v\in Ty;$$

(ii)

maximally monotone, if T is monotone on H and for any $(y,v)\in H\times H$,

$$⟨v-u,y-x⟩\ge 0,\forall (x,u)\in \mathrm{Graph}\left(T\right)indicates(y,v)\in \mathrm{Graph}\left(T\right).$$

Lemma 1

([17]). Let $A:H\to 2^H$ be a maximally monotone operator, and $B:H\to H$ be a monotone Lipschitz continuous operator. Then $A+B$ is maximally monotone.

Lemma 2

([18]). Let $\left\{t_n\right\}$ be a of nonnegative real sequence satisfying

$$t_{n+1}\le (1-{\beta }_n)t_n+{\beta }_n{d}_n+{\varrho }_n,\forall x,y\in H,$$

where $\left\{{\beta }_n\right\},\left\{d_n\right\}$ and $\left\{{\varrho }_n\right\}$ satisfying the conditions:

(i)

$\left\{{\beta }_n\right\}\subset (0,1)$, ${\sum }_{n=1}^{\infty }{\beta }_n=\infty$;

(ii)

${\mathrm{limsup}}_{n\to \infty }{d}_n\le 0$;

(iii)

${\varrho }_n\ge 0$ with ${\sum }_{n=1}^{\infty }{\varrho }_n<\infty$.

Then ${\lim }_{n\to \infty }{t}_n=0.$

Lemma 3

([19]). Let C be a nonempty closed convex subset of H and $T:C\to C$ be a nonexpansive mapping. Then, the mapping $I-T$ is demiclosed at zero, i.e., if $x_n\rightharpoonup x$ and $(I-T)x_n\to 0$, then $x\in Fix\left(T\right).$

3. Main Results

We mainly introduce our new algorithms and analyze their convergence in this section. Let H be a real Hilbert space. The following assumptions will be needed throughout the paper:

(A1)

$A:H\to 2^H$ is maximally monotone.

(A2)

$B:H\to H$ is monotone and L-Lipschitz continuous.

(A3)

$F:H\to H$ is $\xi$-strongly monotone and k-Lipschitz continuous.

(A4)

$G:H\to H$ is $\gamma$-inverse strongly monotone.

(A5)

$\Omega :=\Phi \cap G^{-1}\left(0\right)\ne \varnothing$, where $\Phi$ is the solution set of (1).

To solve (2), we construct a auxiliary problem:

$$\mathrm{Find}x\in H,\mathrm{such} \mathrm{that} 0\in A\left(x\right)+B\left(x\right)+{\alpha }^{\omega }G\left(x\right)+\alpha F\left(x\right),$$

(3)

for each $\alpha >0$ and $0<\omega <1$, the solution of the problem (3) denoted by $x_{\alpha }$.

Lemma 4.

Under the assumptions (A1)–(A4), for each $\alpha >0$ and $0<\omega <1$, the problem (3) has a unique solution $x_{\alpha }$.

Proof. 

Since the properties of A, B, G, and F in the hypothesis, we can conclude that $A+B+{\alpha }^{\omega }G+\alpha F$ is strongly monotone. It is well known that strong monotone operators have unique solutions (see [20]). Therefore, the problem (3) has a unique solution $x_{\alpha }$. □

Lemma 5.

The net $\left\{x_{\alpha }\right\}$ is bounded.

Proof. 

For each $p\in \Omega$ and $\alpha >0$, we have $0\in Ap+Bp$, $Gp=0$ and $0\in A{x}_{\alpha }+B{x}_{\alpha }+{\alpha }^{\omega }G{x}_{\alpha }+\alpha F{x}_{\alpha }$. Thus,

$$-\alpha F{x}_{\alpha }\in A{x}_{\alpha }+B{x}_{\alpha }+{\alpha }^{\omega }G{x}_{\alpha },$$

and

$$0\in Ap+Bp+{\alpha }^{\omega }Gp.$$

Using the monotonic property of $A,B$ and G, we derive

$$⟨p-x_{\alpha },\alpha F{x}_{\alpha }⟩\ge 0.$$

(4)

By (4) and the $\xi$-strong monotonicity, it follows that

$$\begin{array}{cc}\hfill ⟨p-x_{\alpha },Fp⟩& =⟨p-x_{\alpha },F{x}_{\alpha }⟩+⟨p-x_{\alpha },Fp-F{x}_{\alpha }⟩\hfill \\ \hfill & \ge \xi \parallel p-x_{\alpha }{\parallel }^2.\hfill \end{array}$$

(5)

Consequently (5) and the Cauchy-Schwarz inequality, we find $\parallel Fp\parallel \parallel p-x_{\alpha }\parallel \ge \xi \parallel p-x_{\alpha }{\parallel }^2$, then $\parallel p-x_{\alpha }\parallel \le \parallel Fp\parallel /\xi$, we get

$$\begin{array}{cc}\hfill \parallel x_{\alpha }\parallel & \le \parallel p\parallel +\parallel p-x_{\alpha }\parallel \hfill \\ \hfill & \le \parallel p\parallel +\frac{\parallel Fp\parallel }{\xi }.\hfill \end{array}$$

So the net $\left\{x_{\alpha }\right\}$ is bounded. □

Lemma 6.

For all ${\alpha }_1,{\alpha }_2\in (0,1)$, there exists $M>0$ such that,

$$\parallel x_{{\alpha }_1}-x_{{\alpha }_2}\parallel \le \frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}M.$$

Proof. 

According to the assumption, $x_{{\alpha }_1},x_{{\alpha }_2}$ are solutions of the problem (3), let us suppose that $0<{\alpha }_2<{\alpha }_1<1$. Then,

$$0\in A{x}_{{\alpha }_1}+B{x}_{{\alpha }_1}+{\alpha }_1^{\omega }G{x}_{{\alpha }_1}+{\alpha }_{1}F{x}_{{\alpha }_1}$$

and

$$0\in A{x}_{{\alpha }_2}+B{x}_{{\alpha }_2}+{\alpha }_2^{\omega }G{x}_{{\alpha }_2}+{\alpha }_{2}F{x}_{{\alpha }_2},$$

which implies

$$-{\alpha }_1^{\omega }G{x}_{{\alpha }_1}-{\alpha }_{1}F{x}_{{\alpha }_1}\in (A+B)x_{{\alpha }_1}$$

and

$$-{\alpha }_2^{\omega }G{x}_{{\alpha }_2}-{\alpha }_{2}F{x}_{{\alpha }_2}\in (A+B)x_{{\alpha }_2}.$$

By Lemma 1, we know that

$$⟨x_{{\alpha }_1}-x_{{\alpha }_2},-{\alpha }_{1}F{x}_{{\alpha }_1}-{\alpha }_1^{\omega }G{x}_{{\alpha }_1}+{\alpha }_{2}F{x}_{{\alpha }_2}+{\alpha }_2^{\omega }G{x}_{{\alpha }_2}⟩\ge 0,$$

or, equivalently,

$$\begin{array}{ccc}& & ⟨x_{{\alpha }_1}-x_{{\alpha }_2},({\alpha }_2-{\alpha }_1)F{x}_{{\alpha }_2}⟩+⟨x_{{\alpha }_1}-x_{{\alpha }_2},{\alpha }_1(F{x}_{{\alpha }_2}-F{x}_{{\alpha }_1})⟩\hfill \\ & & +⟨x_{{\alpha }_1}-x_{{\alpha }_2},({\alpha }_2^{\omega }-{\alpha }_1^{\omega })G{x}_{{\alpha }_2}⟩+⟨x_{{\alpha }_1}-x_{{\alpha }_2},{\alpha }_1^{\omega }(G{x}_{{\alpha }_2}-G{x}_{{\alpha }_1})⟩\ge 0.\hfill \end{array}$$

The properties of G and F and the Cauchy-Schwarz inequality imply that

$$\begin{array}{ccc}\hfill {\alpha }_1\xi {\parallel x_{{\alpha }_1}-x_{{\alpha }_2}\parallel }^2& \le & ({\alpha }_2^{\omega }-{\alpha }_1^{\omega })⟨x_{{\alpha }_1}-x_{{\alpha }_2},G{x}_{{\alpha }_2}⟩+({\alpha }_2-{\alpha }_1)⟨x_{{\alpha }_1}-x_{{\alpha }_2},F{x}_{{\alpha }_2}⟩\hfill \\ & \le & |{\alpha }_2^{\omega }-{\alpha }_1^{\omega }|\parallel x_{{\alpha }_1}-x_{{\alpha }_2}\parallel \parallel G{x}_{{\alpha }_2}\parallel +|{\alpha }_2-{\alpha }_1|\parallel x_{{\alpha }_1}-x_{{\alpha }_2}\parallel \parallel F{x}_{{\alpha }_2}\parallel \hfill \end{array}$$

which equal to

$$\parallel x_{{\alpha }_1}-x_{{\alpha }_2}\parallel \le \frac{|{\alpha }_2^{\omega }-{\alpha }_1^{\omega }|\parallel G{x}_{{\alpha }_2}\parallel +|{\alpha }_2-{\alpha }_1|\parallel F{x}_{{\alpha }_2}\parallel }{{\alpha }_1\xi }.$$

(6)

The Lipschitz continuity of the mapping F and G imply they are bounded. Combining the Lagrange’s mean-value theorem, we deduce that

$$|{\alpha }_2^{\omega }-{\alpha }_1^{\omega }|={\alpha }_1^{\omega }-{\alpha }_2^{\omega }\le \omega {\alpha }_2^{\omega -1}({\alpha }_1-{\alpha }_2)\le \omega {\alpha }_2^{-1}({\alpha }_1-{\alpha }_2)\le {\alpha }_2^{-1}({\alpha }_1-{\alpha }_2),$$

this together with (6), implies that

$$\parallel x_{{\alpha }_1}-x_{{\alpha }_2}\parallel \le \frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}\frac{\parallel G{x}_{{\alpha }_2}\parallel }{\xi }+\frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}\frac{\parallel F{x}_{{\alpha }_2}\parallel }{\xi }\le \frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}M,$$

(7)

where $M=\frac{1}{\xi }{\sup }_{\alpha \in (0,1)}\{\parallel G{x}_{\alpha }\parallel +\parallel F{x}_{\alpha }\parallel \}$. Indeed, since F and G are Lipschitz continuous, the net $\{\parallel G{x}_{\alpha }\parallel \}$ and $\{\parallel F{x}_{\alpha }\parallel \}$ is bounded. If $0<{\alpha }_1\le {\alpha }_2<1$, we can also get the same results. □

Lemma 7.

${lim}_{\alpha \to 0^{+}}{x}_{\alpha }=x^{\S }.$

Proof. 

According to the conclusion of Lemma 5, there exists a subsequence $\left\{x_{{\alpha }_m}\right\}$ of the net $\left\{x_{\alpha }\right\}$ such that $x_{{\alpha }_m}\rightharpoonup \overline{x}$ and ${\alpha }_m\to 0^{+}$ as $m\to \infty$. From RVI, we have that $-B{x}_{\alpha }-{\alpha }^{\omega }G{x}_{\alpha }-\alpha F{x}_{\alpha }\in A{x}_{\alpha }$. Let us take a point $(u,v)$ in $\mathrm{Graph}(A+B)$, that is, $v\in Au+Bu$. Thus, we derive by the assumption (A1),

$$⟨u-x_{\alpha },v-Bu+B{x}_{\alpha }+{\alpha }^{\omega }G{x}_{\alpha }+\alpha F{x}_{\alpha }⟩\ge 0.$$

Replace $\alpha$ with ${\alpha }_m$, we deduce from the monotonicity of B that

$$\begin{array}{ccc}\hfill 0& \le & ⟨u-x_{{\alpha }_m},v-Bu+B{x}_{{\alpha }_m}+{\alpha }_m^{\omega }G{x}_{{\alpha }_m}+{\alpha }_{m}F{x}_{{\alpha }_m}⟩\hfill \\ & =& ⟨u-x_{{\alpha }_m},{\alpha }_m^{\omega }G{x}_{{\alpha }_m}+{\alpha }_{m}F{x}_{{\alpha }_m}⟩+⟨u-x_{{\alpha }_m},v⟩-⟨x_{{\alpha }_m}-u,B{x}_{{\alpha }_m}-Bu⟩\hfill \\ & \le & ⟨u-x_{{\alpha }_m},{\alpha }_m^{\omega }G{x}_{{\alpha }_m}+{\alpha }_{m}F{x}_{{\alpha }_m}⟩+⟨u-x_{{\alpha }_m},v⟩.\hfill \end{array}$$

(8)

It obtains that the sequence $\left\{F{x}_{{\alpha }_m}\right\}$ is bounded by the boundedness of the sequence $\left\{x_{{\alpha }_m}\right\}$ and the Lipschitz continuity of F. Letting $m\to \infty$ in relation (8) and we infer that

$$⟨u-\overline{x},v⟩\ge 0,\forall (u,v)\in \mathrm{Graph}(A+B),$$

$$\overline{x}\in {(A+B)}^{-1}\left(0\right).$$

(9)

For every $q\in \Omega$, $0\in Aq+Bq$ and $Gq=0$. By (3), we obtain

$$-{\alpha }_m^{\omega }G{x}_{{\alpha }_m}-{\alpha }_{m}F{x}_{{\alpha }_m}\in A{x}_{{\alpha }_m}+B{x}_{{\alpha }_m},$$

due to the definition of $A+B$, we know that

$$⟨x_{{\alpha }_m}-q,-{\alpha }_m^{\omega }G{x}_{{\alpha }_m}-{\alpha }_{m}F{x}_{{\alpha }_m}⟩\ge 0,$$

by the monotonicity of F,

$$\begin{array}{cc}\hfill {\alpha }_m^{\omega }⟨G{x}_{{\alpha }_m},x_{{\alpha }_m}-q⟩& \le {\alpha }_m⟨F{x}_{{\alpha }_m},q-x_{{\alpha }_m}⟩\hfill \\ \hfill & \le {\alpha }_m⟨Fq,q-x_{{\alpha }_m}⟩,\hfill \end{array}$$

which leads to

$$⟨G{x}_{{\alpha }_m},x_{{\alpha }_m}-q⟩\le {\alpha }_m^{1-\omega }⟨Fq,q-x_{{\alpha }_m}⟩\to 0.$$

(10)

By the property of G, noting (10) and $Gq=0$, we obtain

$$\begin{array}{cc}\hfill \gamma \parallel G{x}_{{\alpha }_m}{\parallel }^2& =\gamma \parallel G{x}_{{\alpha }_m}{-Gq\parallel }^2\hfill \\ \hfill & =⟨G{x}_{{\alpha }_m}-Gq,x_{{\alpha }_m}-q⟩\hfill \\ \hfill & \le ⟨G{x}_{{\alpha }_m},x_{{\alpha }_m}-q⟩\to 0,\hfill \end{array}$$

which yields that

$$\underset{m\to \infty }{lim}G{x}_{{\alpha }_m}=0.$$

For any $\iota \in (0,2\gamma ]$, $G_{\iota }=I-\iota G$ is nonexpansive obviously holds. Owing to Lemma 3, we obtain that $\overline{x}\in \mathrm{Fix}\left(G_{\iota }\right)$,

$$\overline{x}\in G^{-1}\left(0\right),$$

together with (9), implies

$$\overline{x}\in \Omega .$$

Noting (5), we obtain $⟨Fp,p-x_{\alpha }⟩\ge 0$ for all $p\in \Omega$. Letting $\alpha ={\alpha }_m\to 0^{+}$, we have

$$⟨Fp,p-\overline{x}⟩\ge 0,\forall p\in \Omega .$$

By Minty lemma [21], we get

$$⟨F\overline{x},p-\overline{x}⟩\ge 0,\forall p\in \Omega .$$

Due to uniqueness of the solution $x^{\S }$ to the problem (2), we have $\overline{x}=x^{\S }$. Since $\overline{x}$ is any point in ${\omega }_w\left(x_{\alpha }\right)$, ${\omega }_w\left(x_{\alpha }\right)=\{x^{\S }\}$, that is, the net $\left\{x_{\alpha }\right\}$ converges weakly to $x^{\S }$. After that, applying (5) for $p=x^{\S }$, we get

$$\xi \parallel x^{\S }-x_{\alpha }{\parallel }^2\le ⟨F{x}^{\S },x^{\S }-x_{\alpha }⟩.$$

(11)

Taking limit in (11) as $\alpha \to 0^{+}$, we obtain

$$\underset{\alpha \to 0^{+}}{lim}\xi {\parallel x^{\S }-x_{\alpha }\parallel }^2\le \underset{\alpha \to 0^{+}}{lim}⟨F{x}^{\S },x^{\S }-x_{\alpha }⟩=0.$$

Thus, ${lim}_{\alpha \to 0^{+}}\parallel x^{\S }-x_{\alpha }\parallel =0$. □

Remark 1.

${\alpha }_n$ can be chosen as ${\alpha }_n=\frac{1}{n^p}$, where $0<p<\frac{1}{2}$.

Lemma 8.

Under the condition (A2), the sequence $\left\{{\lambda }_n\right\}$ generated by Algorithm 1 or Algorithm 2 is convergent and

$$\underset{n\to \infty }{lim}{\lambda }_n=\lambda >0.$$

To be more precise, we have $\lambda \ge min\left\{{\lambda }_1,\frac{\mu }{L}\right\}>0$.

Algorithm 1 Modified multi-steps inertial forward-backward splitting method with regularization

Initialization: Let $x_0,x_1\in H$ be arbitrary, $\mu \in (0,1)$, ${\lambda }_1\in (0,(1-\mu )\gamma )$ and set $n:=1$. Choose a sequence $\left\{{\tau }_n\right\}\subset [0,+\infty )$ such that ${\sum }_{n=1}^{\infty }{\tau }_n=\tau <\infty$ and $0<\mu +\frac{{\lambda }_1+\tau }{\gamma }<1$. Choose a sequence $\left\{{\alpha }_n\right\}\subset [0,+\infty )$ satisfying: $$\sum _{n=1}^{\infty }{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0,\underset{n\to \infty }{lim}\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_{n+1}{\alpha }_n^2}=0.$$ For a given positive integer N, choose a sequence $\left\{{ϵ}_{i,n}\right\}\subset [0,+\infty )$$(i=1,2,\dots ,N)$ satisfying $$\underset{n\to +\infty }{lim}\frac{{ϵ}_{i,n}}{{\alpha }_n}=0.$$ Iterative steps: Calculate $x_{n+1}$ as follows: Step 1. Compute $$w_n=x_n+\sum _{i=1}^{min\{n,N\}}{\theta }_{i,n}(x_{n-i+1}-x_{n-i}),$$ where $0\le {\theta }_{i,n}\le {\theta }_i$ for some ${\theta }_i\in \mathbb{R}$ with $${\theta }_{i,n}=\left\{\begin{array}{cc}\min \left\{{\theta }_i,\frac{{ϵ}_{i,n}}{\parallel x_{n-i+1}-x_{n-i}\parallel }\right\},\hfill & \mathrm{if}{x}_{n-i+1}\ne x_{n-i},\hfill \\ {\theta }_i,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Step 2. Compute $$y_n=J_{{\lambda }_{n}A}\left(w_n-{\lambda }_n(B+{\alpha }_n^{\omega }G+{\alpha }_{n}F)w_n\right).$$ Step 3. Compute $$x_{n+1}=y_n-{\lambda }_n(B{y}_n-B{w}_n+{\alpha }_n^{\omega }G{y}_n-{\alpha }_n^{\omega }G{w}_n),$$ and $${\lambda }_{n+1}=\left\{\begin{array}{cc}min\left\{{\lambda }_n+{\tau }_n,\frac{\mu \parallel w_n-y_n\parallel }{\parallel B{w}_n-B{y}_n\parallel }\right\},\hfill & \mathrm{if}B{w}_n\ne B{y}_n,\hfill \\ {\lambda }_n+{\tau }_n,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Set $n=n+1$ and go to Step 1.

Algorithm 2 Modified multi-steps inertial proximal contraction method with regularization

Initialization: Let $x_0,x_1\in H$ be arbitrary, $r\in (0,2)$, $\beta >0$, $\mu \in (0,1)$, and ${\lambda }_1\in (0,(1-\mu )\gamma )$ and set $n:=1$. Choose a sequence $\left\{{\tau }_n\right\}\subset [0,+\infty )$ such that ${\sum }_{n=1}^{\infty }{\tau }_n=\tau <\infty$ and $0<\mu +\frac{{\lambda }_1+\tau }{\gamma }<1$. Choose a sequence $\left\{{\alpha }_n\right\}\subset [0,+\infty )$ satisfying: $$\sum _{n=1}^{\infty }{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0,\underset{n\to \infty }{lim}\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_{n+1}{\alpha }_n^2}=0.$$ For a given positive integer N, choose a sequence $\left\{{ϵ}_{i,n}\right\}\subset [0,+\infty )$$(i=1,2,\dots ,N)$ satisfying $$\underset{n\to \infty }{lim}\frac{{ϵ}_{i,n}}{{\alpha }_n}=0.$$ Iterative steps: Calculate $x_{n+1}$ as follows: Step 1. Compute $$w_n=x_n+\sum _{i=1}^{min\{N,n\}}{\theta }_{i,n}(x_{n-i+1}-x_{n-i}),$$ where $0\le {\theta }_{i,n}\le {\theta }_i$ for some ${\theta }_i\in \mathbb{R}$ with $${\theta }_{i,n}=\left\{\begin{array}{cc}min\left\{{\theta }_i,\frac{{ϵ}_{i,n}}{\parallel x_{n-i+1}-x_{n-i}\parallel }\right\},\hfill & \mathrm{if}{x}_{n-i+1}\ne x_{n-i},\hfill \\ {\theta }_i,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Step 2. Compute $$y_n=J_{{\lambda }_{n}A}\left(w_n-{\lambda }_n(B+{\alpha }_n^{\omega }G+{\alpha }_{n}F)w_n\right).$$ and $${\lambda }_{n+1}=\left\{\begin{array}{cc}min\left\{{\lambda }_n+{\tau }_n,\frac{\mu \parallel w_n-y_n\parallel }{\parallel B{w}_n-B{y}_n\parallel }\right\},\hfill & \mathrm{if}B{w}_n\ne B{y}_n,\hfill \\ {\lambda }_n+{\tau }_n,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ step 3. Compute $$\left\{\begin{array}{c}{h}_n=w_n-y_n-{\lambda }_n\left((B{w}_n-B{y}_n)+{\alpha }_n^{\omega }(G{w}_n-G{y}_n)\right),\hfill \\ \varphi (w_n,y_n)=⟨w_n-y_n,h_n⟩.\hfill \end{array}\right.$$ Step 4. Compute $$x_{n+1}=w_n-r{\beta }_n{h}_n,$$ where $${\beta }_n=\left\{\begin{array}{cc}\frac{\varphi (w_n,y_n)}{\parallel h_n{\parallel }^2},\hfill & \mathrm{if}\parallel h_n\parallel \ne 0,\hfill \\ \beta ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Set $n=n+1$ and go to Step 1.

Proof. 

Since

$$\parallel B{w}_n-B{y}_n\parallel \le L\parallel w_n-y_n\parallel ,$$

in the case of $B{w}_n\ne B{y}_n$,

$$\frac{\mu \parallel w_n-y_n\parallel }{\parallel B{w}_n-B{y}_n\parallel }\ge \frac{\mu \parallel w_n-y_n\parallel }{L\parallel w_n-y_n\parallel }=\frac{\mu }{L}.$$

By induction, can draw the sequence $\left\{{\lambda }_n\right\}$ has the lower bound $min\left\{{\lambda }_1,\frac{\mu }{L}\right\}$. Since the computation of ${\lambda }_{n+1}$, we can get

$${\lambda }_{n+1}\le {\lambda }_n+{\tau }_n,$$

that is

$${\lambda }_{n+1}-{\lambda }_n\le {\tau }_n.$$

Let ${\left[a\right]}_{+}$ represent $max\{a,0\}$ for all $a\in \mathbb{R}$. And we know ${\tau }_n\ge 0$, then

$${[{\lambda }_{n+1}-{\lambda }_n]}_{+}\le {\tau }_n.$$

Because ${\sum }_{n=1}^{\infty }{\tau }_n<\infty$, obviously

$$\sum _{n=1}^{\infty }{[{\lambda }_{n+1}-{\lambda }_n]}_{+}<\infty .$$

Besides ${\left[a\right]}_{+}=\frac{1}{2}a+\frac{1}{2}\left|a\right|$, we infer

$$|{\lambda }_{n+1}-{\lambda }_n|=2{[{\lambda }_{n+1}-{\lambda }_n]}_{+}-{\lambda }_{n+1}+{\lambda }_n,$$

then,

$$\sum _{n=1}^k|{\lambda }_{n+1}-{\lambda }_n|=2\sum _{n=1}^k{[{\lambda }_{n+1}-{\lambda }_n]}_{+}-{\lambda }_{k+1}+{\lambda }_1.$$

Since $\left\{{\lambda }_n\right\}$ has the lower bound $min\left\{{\lambda }_1,\frac{\mu }{L}\right\}$, we know ${\lambda }_{k+1}>0$. So we have

$$\sum _{n=1}^k|{\lambda }_{n+1}-{\lambda }_n|<2\sum _{n=1}^k{[{\lambda }_{n+1}-{\lambda }_n]}_{+}+{\lambda }_1,$$

furthermore,

$$\sum _{n=1}^{\infty }|{\lambda }_{n+1}-{\lambda }_n|<\infty .$$

Therefore, $\left\{{\lambda }_n\right\}$ is convergent. □

Theorem 1.

If the conditions (A1)–(A5) hold, $x^{\S }$ is the unique solution of problem (2) and the sequence $\left\{x_n\right\}$ is generated by Algorithm 1, then $x_n$ converges strongly to $x^{\S }$.

Proof. 

Setting $s_n=B{y}_n-B{w}_n+{\alpha }_n^{\omega }G{y}_n-{\alpha }_n^{\omega }G{w}_n$,

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2& =\parallel y_n-{\lambda }_n{s}_n-x_{{\alpha }_n}{\parallel }^2\hfill \\ \hfill & =\parallel y_n-x_{{\alpha }_n}{\parallel }^2+{\lambda }_n^2{\parallel s_n\parallel }^2-2{\lambda }_n⟨y_n-x_{{\alpha }_n},s_n⟩.\hfill \end{array}$$

(12)

Since $x_{{\alpha }_n}$ is the solution of (3), we get

$$x_{{\alpha }_n}=J_{{\lambda }_{n}A}\left(x_{{\alpha }_n}-{\lambda }_n(B{x}_{{\alpha }_n}+{\alpha }_n^{\omega }G{x}_{{\alpha }_n}+{\alpha }_{n}F{x}_{{\alpha }_n})\right),$$

and $J_{{\lambda }_{n}A}$ is firmly nonexpansive,

$$\begin{array}{ccc}& & ⟨y_n-x_{{\alpha }_n},w_n-x_{{\alpha }_n}-{\lambda }_n(B{w}_n+{\alpha }_n^{\omega }G{w}_n+{\alpha }_{n}F{w}_n\hfill \\ & & -B{x}_{{\alpha }_n}-{\alpha }_n^{\omega }G{x}_{{\alpha }_n}-{\alpha }_{n}F{x}_{{\alpha }_n})⟩\ge \parallel y_n-x_{{\alpha }_n}{\parallel }^2,\hfill \end{array}$$

which implies

$$\begin{array}{ccc}\hfill & & ⟨y_n-x_{{\alpha }_n},w_n-x_{{\alpha }_n}⟩-{\lambda }_n⟨y_n-x_{{\alpha }_n},B{w}_n+{\alpha }_n^{\omega }G{w}_n-B{x}_{{\alpha }_n}-{\alpha }_n^{\omega }G{x}_{{\alpha }_n}⟩\hfill \\ & & -{\alpha }_n{\lambda }_n⟨y_n-x_{{\alpha }_n},F{w}_n-F{x}_{{\alpha }_n}⟩\ge {\parallel y_n-x_{{\alpha }_n}\parallel }^2.\hfill \end{array}$$

(13)

Since the monotony of B and G, we find

$${\lambda }_n⟨y_n-x_{{\alpha }_n},B{y}_n-B{x}_{{\alpha }_n}+{\alpha }_n^{\omega }G{y}_n-{\alpha }_n^{\omega }G{x}_{{\alpha }_n}⟩\ge 0,$$

(14)

combining (13) and (14), we derive

$$\begin{array}{ccc}& & {\lambda }_n⟨y_n-x_{{\alpha }_n},B{y}_n-B{w}_n+{\alpha }_n^{\omega }G{y}_n-{\alpha }_n^{\omega }G{w}_n⟩\hfill \\ & \ge & ⟨y_n-x_{{\alpha }_n},x_{{\alpha }_n}-w_n⟩+{\alpha }_n{\lambda }_n⟨y_n-x_{{\alpha }_n},F{w}_n-F{x}_{{\alpha }_n}⟩+{\parallel y_n-x_{{\alpha }_n}\parallel }^2,\hfill \end{array}$$

or, equivalently,

$$\begin{array}{ccc}\hfill & & ⟨y_n-x_{{\alpha }_n},s_n⟩\hfill \\ & \ge & \frac{1}{{\lambda }_n}⟨y_n-x_{{\alpha }_n},x_{{\alpha }_n}-w_n⟩+{\alpha }_n⟨y_n-x_{{\alpha }_n},F{w}_n-F{x}_{{\alpha }_n}⟩\hfill \\ & & +\frac{1}{{\lambda }_n}{\parallel y_n-x_{{\alpha }_n}\parallel }^2.\hfill \end{array}$$

(15)

Combining (12) and (15), we get that

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2& \le {\lambda }_n^2{\parallel s_n\parallel }^2-2⟨y_n-x_{{\alpha }_n},x_{{\alpha }_n}-w_n⟩\hfill \\ \hfill & -2{\alpha }_n{\lambda }_n⟨y_n-x_{{\alpha }_n},F{w}_n-F{x}_{{\alpha }_n}⟩-{\parallel y_n-x_{{\alpha }_n}\parallel }^2,\hfill \end{array}$$

(16)

and the fact of

$$2⟨y_n-x_{{\alpha }_n},x_{{\alpha }_n}-w_n⟩=\parallel y_n-w_n{\parallel }^2-\parallel w_n-x_{{\alpha }_n}{\parallel }^2-{\parallel x_{{\alpha }_n}-y_n\parallel }^2,$$

(17)

imply that

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2& \le & \parallel x_{{\alpha }_n}-w_n{\parallel }^2-\parallel w_n-y_n{\parallel }^2+{\lambda }_n^2{\parallel s_n\parallel }^2\hfill \\ & & -2{\alpha }_n{\lambda }_n⟨y_n-x_{{\alpha }_n},F{w}_n-F{x}_{{\alpha }_n}⟩.\hfill \end{array}$$

(18)

Since

$$\begin{array}{ccc}\hfill {\lambda }_n^2{\parallel s_n\parallel }^2& =& {\lambda }_n^2\parallel B{y}_n-B{w}_n{\parallel }^2+{\lambda }_n^2{\alpha }_n^{2\omega }{\parallel G{y}_n-G{w}_n\parallel }^2\hfill \\ & & +2{\lambda }_n^2{\alpha }_n^{\omega }⟨B{y}_n-B{w}_n,G{y}_n-G{w}_n⟩\hfill \\ & \le & \frac{{\lambda }_n^2{\mu }^2}{{\lambda }_{n+1}^2}\parallel w_n-y_n{\parallel }^2+\frac{{\lambda }_n^2{\alpha }_n^{2\omega }}{{\gamma }^2}\parallel w_n-y_n{\parallel }^2+\frac{2{\lambda }_n^2\mu {\alpha }_n^{\omega }}{\gamma {\lambda }_{n+1}}{\parallel w_n-y_n\parallel }^2\hfill \\ & \le & {\left(\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}+\frac{{\lambda }_1+\tau }{\gamma }\right)}^2{\parallel w_n-y_n\parallel }^2.\hfill \end{array}$$

(19)

Let $t_1,t_2$ and $t_3$ be three positive numbers such that

$$2\xi -k{t}_1-t_2-t_3>0.$$

By virtue of Lemma 8, ${\alpha }_n\to 0$ and $\frac{{ϵ}_{i,n}}{{\alpha }_n}\to 0$, there exists $n_0\ge 1$, $\forall n\ge n_0$ such that

$$\begin{array}{cc}\hfill & 1-\frac{{\alpha }_n{\lambda }_{n}k}{t_1}-{\left(\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}+\frac{{\lambda }_1+\tau }{\gamma }\right)}^2>0,\hfill \\ \hfill & 1-t_3{\alpha }_n{\lambda }_n>0,\hfill \\ \hfill & \sum _{i=1}^N{ϵ}_{i,n}\le t_3{\lambda }_n{\alpha }_n.\hfill \end{array}$$

Because F is strongly monotone,

$$\begin{array}{ccc}\hfill & & ⟨y_n-x_{{\alpha }_n},F{w}_n-F{x}_{{\alpha }_n}⟩\hfill \\ & =& ⟨w_n-x_{{\alpha }_n},F{w}_n-F{x}_{{\alpha }_n}⟩+⟨y_n-w_n,F{w}_n-F{x}_{{\alpha }_n}⟩\hfill \\ & \ge & \xi \parallel w_n-x_{{\alpha }_n}{\parallel }^2-k\parallel w_n-x_{{\alpha }_n}\parallel \parallel y_n-w_n\parallel \hfill \\ & \ge & \xi \parallel w_n-x_{{\alpha }_n}{\parallel }^2-\frac{k{t}_1}{2}\parallel w_n-x_{{\alpha }_n}{\parallel }^2-\frac{k}{2t_1}{\parallel y_n-w_n\parallel }^2\hfill \\ & =& \left(\xi -\frac{k{t}_1}{2}\right)\parallel w_n-x_{{\alpha }_n}{\parallel }^2-\frac{k}{2t_1}{\parallel y_n-w_n\parallel }^2.\hfill \end{array}$$

(20)

In views of (18)–(20), we get

$$\begin{array}{ccc}\hfill & & \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2\hfill \\ & \le & \left(1-{\alpha }_n{\lambda }_n(2\xi -k{t}_1)\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & -\left(1-\frac{{\alpha }_n{\lambda }_{n}k}{t_1}-{\left(\frac{{\lambda }_1+\tau }{\gamma }+\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\right)}^2\right){\parallel w_n-y_n\parallel }^2.\hfill \end{array}$$

(21)

which implies,

$$\parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2\le \left(1-{\alpha }_n{\lambda }_n(2\xi -k{t}_1)\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2,\forall n\ge n_0.$$

(22)

By Lemma 6, for all $n\ge n_0$, we have

$$\begin{array}{ccc}\hfill & & \parallel x_{n+1}-x_{{\alpha }_{n+1}}{\parallel }^2\hfill \\ & =& 2⟨x_{{\alpha }_n}-x_{{\alpha }_{n+1}},x_{n+1}-x_{{\alpha }_n}⟩+\parallel x_{{\alpha }_n}-x_{{\alpha }_{n+1}}{\parallel }^2+{\parallel x_{n+1}-x_{{\alpha }_n}\parallel }^2\hfill \\ & \le & 2\parallel x_{{\alpha }_n}-x_{{\alpha }_{n+1}}\parallel \parallel x_{n+1}-x_{{\alpha }_n}\parallel +\parallel x_{{\alpha }_{n+1}}-x_{{\alpha }_n}{\parallel }^2+{\parallel x_{n+1}-x_{{\alpha }_n}\parallel }^2\hfill \\ & \le & \frac{1}{t_2{\alpha }_n{\lambda }_n}\parallel x_{{\alpha }_n}-x_{{\alpha }_{n+1}}{\parallel }^2+t_2{\alpha }_n{\lambda }_n\parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2+{\parallel x_{n+1}-x_{{\alpha }_{n+1}}\parallel }^2\hfill \\ & & +\parallel x_{{\alpha }_n}-x_{{\alpha }_{n+1}}{\parallel }^2\hfill \\ & =& \left(1+\frac{1}{t_2{\alpha }_n{\lambda }_n}\right)\parallel x_{{\alpha }_n}-x_{{\alpha }_{n+1}}{\parallel }^2+(1+t_2{\alpha }_n{\lambda }_n){\parallel x_{n+1}-x_{{\alpha }_n}\parallel }^2\hfill \\ & \le & \left(1+\frac{1}{t_2{\alpha }_n{\lambda }_n}\right){\left(\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_n{\alpha }_{n+1}}\right)}^2{M}^2+(1+t_2{\alpha }_n{\lambda }_n){\parallel x_{n+1}-x_{{\alpha }_n}\parallel }^2,\hfill \end{array}$$

(23)

where M appears in Lemma 6. Substituting (23) into (22), for all $n\ge n_0$, we deduce

$$\begin{array}{ccc}\hfill & & \parallel x_{n+1}-x_{{\alpha }_{n+1}}{\parallel }^2\hfill \\ & \le & (1+t_2{\alpha }_n{\lambda }_n)\left(1-{\alpha }_n{\lambda }_n(2\xi -k{t}_1)\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & +\left(1+\frac{1}{t_2{\alpha }_n{\lambda }_n}\right){\left(\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_n{\alpha }_{n+1}}\right)}^2{M}^2\hfill \\ & =& (1-(2\xi -k{t}_1-t_2){\alpha }_n{\lambda }_n-(2\xi -k{t}_1)t_2{\alpha }_n^2{\lambda }_n^2){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & +\left(1+\frac{1}{t_2{\alpha }_n{\lambda }_n}\right){\left(\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_n{\alpha }_{n+1}}\right)}^2{M}^2\hfill \\ & \le & (1-(2\xi -k{t}_1-t_2){\alpha }_n{\lambda }_n){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & +\frac{(1+t_2{\alpha }_n{\lambda }_n){({\alpha }_{n+1}-{\alpha }_n)}^2}{t_2{\lambda }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2.\hfill \end{array}$$

(24)

In the view of, for all $n\ge n_0$,

$$\begin{array}{ccc}\hfill & & \parallel w_n-x_{{\alpha }_n}{\parallel }^2\hfill \\ & =& \parallel x_n+\sum _{i=1}^N{\theta }_{i,n}(x_{n-i+1}-x_{n-i})-x_{{\alpha }_n}{\parallel }^2\hfill \\ & \le & {\left(\parallel x_n-x_{{\alpha }_n}\parallel +\sum _{i=1}^N{\theta }_{i,n}\parallel x_{n-i+1}-x_{n-i}\parallel \right)}^2\hfill \\ & =& \parallel x_n-x_{{\alpha }_n}{\parallel }^2+\sum _{i=1}^N{\theta }_{i,n}^2{\parallel x_{n-i+1}-x_{n-i}\parallel }^2\hfill \\ & & +2\sum _{1\le i<j\le N}{\theta }_{i,n}{\theta }_{j,n}\parallel x_{n-i+1}-x_{n-i}\parallel \parallel x_{n-j+1}-x_{n-j}\parallel \hfill \\ & & +2\sum _{i=1}^N{\theta }_{i,n}\parallel x_n-x_{{\alpha }_n}\parallel \parallel x_{n-i+1}-x_{n-i}\parallel \hfill \\ & \le & \left(1+\sum _{i=1}^N{ϵ}_{i,n}\right){\parallel x_n-x_{{\alpha }_n}\parallel }^2+\sum _{i=1}^N{ϵ}_{i,n}^2+\sum _{i=1}^N{ϵ}_{i,n}+2\sum _{1\le i<j\le N}{ϵ}_{i,n}{ϵ}_{j,n}\hfill \\ & =& \left(1+\sum _{i=1}^N{ϵ}_{i,n}\right){\parallel x_n-x_{{\alpha }_n}\parallel }^2+{\overline{ϵ}}_n\hfill \\ & \le & (1+t_3{\alpha }_n{\lambda }_n){\parallel x_n-x_{{\alpha }_n}\parallel }^2+{\overline{ϵ}}_n,\hfill \end{array}$$

(25)

where ${\overline{ϵ}}_n={\sum }_{i=1}^N{ϵ}_{i,n}^2+{\sum }_{i=1}^N{ϵ}_{i,n}+2{\sum }_{1\le i<j\le N}{ϵ}_{i,n}{ϵ}_{j,n}$. The condition of $\left\{{ϵ}_{i,n}\right\}$ implies that ${lim}_{n\to \infty }\frac{{\overline{ϵ}}_n}{{\alpha }_n}=0$. Substituting (25) into (24), for all $n\ge n_0$,

$$\begin{array}{ccc}& & \parallel x_{n+1}-x_{{\alpha }_{n+1}}{\parallel }^2\hfill \\ & \le & (1-(2\xi -k{t}_1-t_2){\alpha }_n{\lambda }_n)(1+t_3{\alpha }_n{\lambda }_n){\parallel x_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & +\frac{(1+t_2{\alpha }_n{\lambda }_n){({\alpha }_{n+1}-{\alpha }_n)}^2}{t_2{\lambda }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2+{\overline{ϵ}}_n\hfill \\ & \le & (1-(2\xi -k{t}_1-t_2-t_3){\alpha }_n{\lambda }_n){\parallel x_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & +\frac{(1+t_2{\alpha }_n{\lambda }_n){({\alpha }_{n+1}-{\alpha }_n)}^2}{t_2{\lambda }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2+{\overline{ϵ}}_n\hfill \\ & =& (1-(2\xi -k{t}_1-t_2-t_3){\alpha }_n{\lambda }_n){\parallel x_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & +(2\xi -k{t}_1-t_2-t_3){\alpha }_n{\lambda }_n\frac{(1+t_2{\alpha }_n{\lambda }_n){({\alpha }_{n+1}-{\alpha }_n)}^2}{(2\xi -k{t}_1-t_2-t_3)t_2{\lambda }_n^2{\alpha }_n^4{\alpha }_{n+1}^2}{M}^2+{\overline{ϵ}}_n\hfill \\ & \le & (1-{\phi }_n){\parallel x_n-x_{{\alpha }_n}\parallel }^2+{\phi }_n{M}^{\prime }{\left(\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_{n+1}{\alpha }_n^2}\right)}^2+{\overline{ϵ}}_n\hfill \\ & =& (1-{\phi }_n){\parallel x_n-x_{{\alpha }_n}\parallel }^2+{\phi }_n{\zeta }_n,\hfill \end{array}$$

where ${\phi }_n=(2\xi -k{t}_1-t_2-t_3){\alpha }_n{\lambda }_n$, $M^{\prime }={\sup }_{n\in N}\left\{\frac{(1+t_2{\alpha }_n{\lambda }_n)M^2}{(2\xi -k{t}_1-t_2-t_3)t_2{\lambda }_n^2}\right\}$ is positive and ${\zeta }_n=M^{\prime }{\left(\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_{n+1}{\alpha }_n^2}\right)}^2+\frac{{\overline{ϵ}}_n}{{\phi }_n}$. Because the constraints of $\left\{{\lambda }_n\right\}$ and $\left\{{\alpha }_n\right\}$, we know that ${\phi }_n\to 0$, ${\sum }_{n=1}^{\infty }{\phi }_n=\infty$, and ${\zeta }_n\to 0$. We deduce from Lemma 2 that $\parallel x_n-x_{{\alpha }_n}{\parallel }^2\to 0$ as $n\to \infty$. □

Theorem 2.

If the conditions (A1)–(A5) hold, $x^{\S }$ is the unique solution of problem (2) and the sequence $\left\{x_n\right\}$ is generated by Algorithm 2, then $x_n$ converges strongly to $x^{\S }$.

Proof. 

We have ${lim}_{n\to \infty }1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}-\frac{{\lambda }_1+\tau }{\gamma }=1-\mu -\frac{{\lambda }_1+\tau }{\gamma }>0$ by Lemma 8, so for all $n\ge n_0$, there exists $\delta >0$ and $n_0\ge 1$ such that $1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}-\frac{{\lambda }_1+\tau }{\gamma }>\delta >0$. We can also obtain ${lim}_{n\to \infty }1+\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}+\frac{{\lambda }_1+\tau }{\gamma }=1+\mu +\frac{{\lambda }_1+\tau }{\gamma }>0$, then $\left\{1+\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}+\frac{{\lambda }_1+\tau }{\gamma }\right\}$ is bounded. We will use the letter V to denote ${sup}_{n\in \mathbb{N}}\left\{1+\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}+\frac{{\lambda }_1+\tau }{\gamma }\right\}$, obviously $V>0$.

In the remainder proof, we assume that $n\ge n_0$. Setting $s_n=B{y}_n-B{w}_n+{\alpha }_n^{\omega }G{y}_n-{\alpha }_n^{\omega }G{w}_n$, then

$$\begin{array}{ccc}& & \parallel h_n\parallel \hfill \\ & \ge & \parallel w_n-y_n\parallel -{\lambda }_n\parallel B{w}_n-B{y}_n\parallel -{\lambda }_n{\alpha }_n^{\omega }\parallel G{w}_n-G{y}_n\parallel \hfill \\ & \ge & \parallel w_n-y_n\parallel -\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\parallel w_n-y_n\parallel -\frac{{\lambda }_1+\tau }{\gamma }\parallel w_n-y_n\parallel \hfill \\ & =& \left(1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}-\frac{{\lambda }_1+\tau }{\gamma }\right)\parallel w_n-y_n\parallel \hfill \\ & \ge & \delta \parallel w_n-y_n\parallel .\hfill \end{array}$$

In the meantime,

$$\begin{array}{ccc}\hfill & & \parallel h_n\parallel \hfill \\ & \le & \parallel w_n-y_n\parallel +{\lambda }_n\parallel s_n\parallel \hfill \\ & \le & \parallel w_n-y_n\parallel +{\lambda }_n(\parallel B{w}_n-B{y}_n\parallel +{\alpha }_n^{\omega }\parallel G{w}_n-G{y}_n\parallel )\hfill \\ & \le & \left(1+\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}+\frac{{\lambda }_1+\tau }{\gamma }\right)\parallel w_n-y_n\parallel \hfill \\ & \le & V\parallel w_n-y_n\parallel .\hfill \end{array}$$

(26)

For any $n\ge n_0$, $w_n=y_n$ is equivalent to $h_n=0$. Since

$$\begin{array}{ccc}\hfill & & \varphi (w_n,y_n)\hfill \\ & =& ⟨w_n-y_n,w_n-y_n+{\lambda }_n{s}_n⟩\hfill \\ & =& \parallel w_n-y_n{\parallel }^2-⟨w_n-y_n,{\lambda }_n(B{w}_n-B{y}_n)+{\alpha }_n^{\omega }{\lambda }_n(G{w}_n-G{y}_n)⟩\hfill \\ & \ge & \parallel w_n-y_n{\parallel }^2-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\parallel w_n-y_n{\parallel }^2-\frac{{\lambda }_1+\tau }{\gamma }{\parallel w_n-y_n\parallel }^2\hfill \\ & =& \left(1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}-\frac{{\lambda }_1+\tau }{\gamma }\right){\parallel w_n-y_n\parallel }^2\hfill \\ & \ge & \delta \parallel w_n-y_n{\parallel }^2,\hfill \end{array}$$

(27)

combining (26) and (27), if $h_n\ne 0$, then

$${\beta }_n=\frac{\varphi (w_n,y_n)}{\parallel h_n{\parallel }^2}\ge \frac{\delta }{V^2}>0,$$

hence ${\beta }_n\ge min\left\{\beta ,\frac{\delta }{V^2}\right\}>0$. Then observe that

$$\begin{array}{ccc}\hfill & & \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2\hfill \\ & =& \parallel w_n-x_{{\alpha }_n}{\parallel }^2-r{\beta }_n{h}_n\hfill \\ & =& \parallel w_n-x_{{\alpha }_n}{\parallel }^2+r^2{\beta }_n^2{\parallel h_n\parallel }^2-2r{\beta }_n⟨w_n-x_{{\alpha }_n},h_n⟩.\hfill \end{array}$$

(28)

By the definition of ${\beta }_n$,

$$\varphi (w_n,y_n)={\beta }_n{\parallel h_n\parallel }^2,$$

which and (28) imply

$$\parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2={\parallel w_n-x_{{\alpha }_n}\parallel }^2+r^2{\beta }_n\varphi (w_n,y_n)-2r{\beta }_n⟨w_n-x_{{\alpha }_n},h_n⟩.$$

(29)

By the definition of $h_n$,

$$\begin{array}{c}\hfill \varphi (w_n,y_n)={\parallel w_n-y_n\parallel }^2+{\lambda }_n⟨w_n-y_n,s_n⟩,\end{array}$$

(30)

and

$$\begin{array}{ccc}\hfill & & ⟨w_n-x_{{\alpha }_n},h_n⟩\hfill \\ & =& ⟨w_n-x_{{\alpha }_n},w_n-y_n⟩+{\lambda }_n⟨w_n-y_n,s_n⟩+{\lambda }_n⟨y_n-x_{{\alpha }_n},s_n⟩.\hfill \end{array}$$

(31)

Substituting (30) and (31) into (29), we infer

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2& =\parallel w_n-x_{{\alpha }_n}{\parallel }^2+r^2{\beta }_n{\parallel w_n-y_n\parallel }^2-(2-r)r{\beta }_n{\lambda }_n⟨w_n-y_n,s_n⟩\hfill \\ \hfill & -2r{\beta }_n{\lambda }_n⟨y_n-x_{{\alpha }_n},s_n⟩-2r{\beta }_n⟨w_n-x_{{\alpha }_n},w_n-y_n⟩.\hfill \end{array}$$

(32)

And then, by the properties of B and G, we infer that

$$\begin{array}{ccc}\hfill ⟨w_n-y_n,s_n⟩& =& -⟨w_n-y_n,B{w}_n-B{y}_n⟩-{\alpha }_n^{\omega }⟨w_n-y_n,G{w}_n-G{y}_n⟩\hfill \\ & \ge & -\left(\frac{\mu }{{\lambda }_{n+1}}+\frac{1}{\gamma }\right){\parallel w_n-y_n\parallel }^2.\hfill \end{array}$$

(33)

Using the same method in the Theorem 1, we get

$$\begin{array}{ccc}& & \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2\hfill \\ & \le & \left(1-r{\beta }_n{\alpha }_n{\lambda }_n(2\xi -k{t}_1)\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & -r{\beta }_n\left(2-r-(2-r){\lambda }_n\left(\frac{\mu }{{\lambda }_{n+1}}+\frac{1}{\gamma }\right)-\frac{{\alpha }_{n}k{\lambda }_n}{t_1}\right){\parallel w_n-y_n\parallel }^2\hfill \\ & \le & \left(1-r{\beta }_n{\alpha }_n{\lambda }_n(2\xi -k{t}_1)\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & -r{\beta }_n\left((2-r)\left(1-\frac{\mu }{{\lambda }_{n+1}}-\frac{{\lambda }_1+\tau }{\gamma }\right)-\frac{{\alpha }_{n}k{\lambda }_n}{t_1}\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & \le & \left(1-r{\beta }_n{\alpha }_n{\lambda }_n(2\xi -k{t}_1)\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2\hfill \\ & & -r{\beta }_n\left((2-r)\eta -\frac{{\alpha }_{n}k{\lambda }_n}{t_1}\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2.\hfill \end{array}$$

where $t_1\in (0,\frac{2\xi }{k})$. Cause ${\alpha }_n\to 0$, we assume $(2-r)\eta -\frac{{\alpha }_{n}k{\lambda }_n}{t_1}>0$. Hence

$$\begin{array}{ccc}& & \parallel x_{n+1}-x_{{\alpha }_n}{\parallel }^2\hfill \\ & \le & \left(1-r{\beta }_n{\alpha }_n{\lambda }_n(2\xi -k{t}_1)\right){\parallel w_n-x_{{\alpha }_n}\parallel }^2.\hfill \end{array}$$

The remaining proofs are the same as Theorem 1. □

4. Numerical Experiments

Three examples are given to show the performances of our algorithms. When the coefficients of inertia are equal to zero, let us use MFBMR and MPCMR for Algorithms 1 and 2, respectively. We denote Algorithm 1 for $N=1,2,3$ by MIFBMR, 2-MMIFBMR and 3-MMIFBMR, respectively. Similarly denote Algorithm 2 for $N=1,2,3$ by MIPCMR, 2-MMIPCMR and 3-MMIPCMR, respectively. All the programmes are written in Matlab 9.0 and performed on PC Desktop Intel(R) Core(TM) i5-1035G1 CPU @ 1.00 GHz 1.19 GHz, RAM 16.0 GB.

Example 1.

Suppose $H=\mathbb{R}$. Let $A:\mathbb{R}\to 2^{\mathbb{R}}$ be a mapping defined as

$$Ax:=\left\{\frac{1}{4}x\right\},\forall x\in \mathbb{R},$$

and $B:\mathbb{R}\to \mathbb{R}$ as

$$Bx:=xarctanx-\frac{1}{2}ln(1+x^2)+\frac{\pi }{2}x,\forall x\in \mathbb{R}.$$

Set mapping $G:\mathbb{R}\to \mathbb{R}$ as

$$Gx:=x-sinx,\forall x\in \mathbb{R}.$$

It is obvious that A is maximally monotone. We can prove that B is monotone and Lipschitz continuous. We know G is $\frac{1}{2}$-inverse strongly monotone by calculation. Let $F=0.4I$.

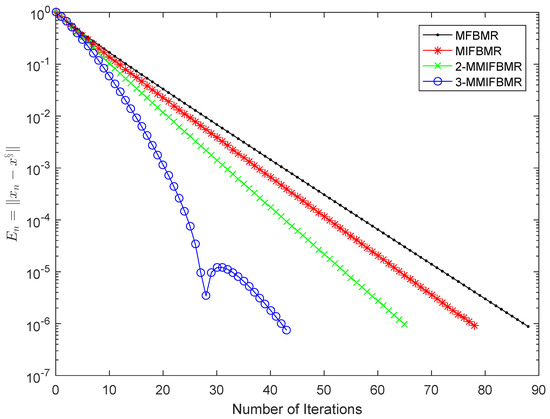
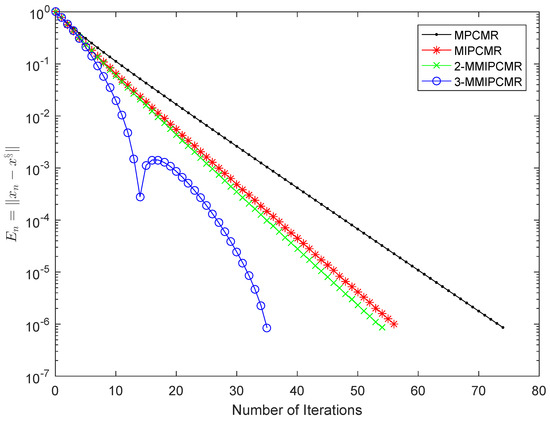
Choose ${\theta }_i=0.1$, $x_0=1$ and ${ϵ}_{i,n}=n^{-2}$ for MIFBMR, 2-MMIFBMR, 3-MMIFBMR, MIPCMR, 2-MMIPCMR and 3-MMIPCMR. Choose $x_1=1$, $\omega =0.6$, ${\lambda }_1=0.08$, $\mu =0.6$, ${\tau }_n=0.1{(n+1)}^{-4}$ and ${\alpha }_n=n^{-1/3}$ for each algorithm. Choose $r=1$, $\beta =2$ for MPCMR, MIPCMR, 2-MMIPCMR, and 3-MMIPCMR. It is obvious that $\Omega =\left\{0\right\}$ and $x^{\S }=0$ is the only one solution of problem (2). The numerical results of this example are represented in Figure 1 and Figure 2.

Figure 1. Comparison of MFBMR, MIFBMR, 2-MMIFBMR and 3-MMIFBMR in Example 1.

Figure 2. Comparison of MPCMR, MIPCMR, 2-MMIPCMR and 3-MMIPCMR in Example 1.

Example 2.

Let $H={\mathbb{R}}^s$. Let $F=I$. Let $A:{\mathbb{R}}^s\to 2^{{\mathbb{R}}^s}$ be defined by

$$Ax:=\left\{Jx\right\},\forall x\in {\mathbb{R}}^s,$$

where J is an upper triangular matrix whose nonzero elements are all 1 in ${\mathbb{R}}^{s\times s}$. Let $B:{\mathbb{R}}^s\to {\mathbb{R}}^s$ be a mapping defined as

$$Bx:=Ex,\forall x\in {\mathbb{R}}^s,$$

where

$$E=C{C}^{\mathrm{T}}+S+D,$$

here C is a matrix, S is a skew-symmetric matrix and D is a diagonal matrix whose diagonal entries are positive. They all in ${\mathbb{R}}^{s\times s}$. Therefore E is positive definite. Obviously, B is monotone and Lipschitz continuous. Define $G:{\mathbb{R}}^s\to {\mathbb{R}}^s$ as

$$Gx:=x-\frac{1}{\parallel Q\parallel }Qx,\forall x\in {\mathbb{R}}^s,$$

where Q is a nonzero matrix in ${\mathbb{R}}^{s\times s}$. We know G is $\frac{1}{2}$-inverse strongly monotone by calculation.

Choose $x_0={(1,1,\cdots ,1)}^{\mathrm{T}}$, ${ϵ}_{i,n}=n^{-2}$ and ${\theta }_i=0.1$ for MIFBMR, 2-MMIFBMR, 3-MMIFBMR, MIPCMR, 2-MMIPCMR and 3-MMIPCMR. Choose $x_1={(1,1,\cdots ,1)}^{\mathrm{T}}$, $\omega =0.5$, $\mu =0.5$, ${\lambda }_1=0.2$, ${\tau }_n=0.1{(n+1)}^{-4}$ and ${\alpha }_n=n^{-1/4}$ for each algorithm. Choose $r=1$, $\beta =2$ for MPCMR, MIPCMR, 2-MMIPCMR and 3-MMIPCMR. All the diagonal elements of D are arbitrary in $(0,2)$, the elements of C, S and Q are generated randomly in $(-2,2)$, $(-2,2)$ and $(0,1)$, respectively. It is obvious that $\Omega =\{{(0,0,\cdots ,0)}^{\mathrm{T}}\}$ and hence the solution of (2) $x^{\S }={(0,0,\cdots ,0)}^{\mathrm{T}}$ is unique. The numerical results are represented in Figure 3 and Figure 4.

Figure 3. Comparison of MFBMR, MIFBMR, 2-MMIFBMR and 3-MMIFBMR in Example 2 with $s=10$.

Figure 4. Comparison of MPCMR, MIPCMR, 2-MMIPCMR and 3-MMIPCMR in Example 2 with $s=10$.

Example 3.

Let $H={\mathbb{R}}^2$. Let $A:{\mathbb{R}}^2\to 2^{{\mathbb{R}}^2}$ be a mapping defined as

$$A{(u,v)}^{\mathrm{T}}:=\left\{\left(\begin{array}{cc}2& -5\\ -5& 13\end{array}\right){(u,v)}^{\mathrm{T}}\right\},\forall {(u,v)}^{\mathrm{T}}\in {\mathbb{R}}^2,$$

$B:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be a mapping defined as

$$B{(u,v)}^{\mathrm{T}}:={(u+v+sinu,-u+v+sinv)}^{\mathrm{T}},\forall {(u,v)}^{\mathrm{T}}\in {\mathbb{R}}^2,$$

and $F:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be a mapping defined as

$$F{(u,v)}^{\mathrm{T}}:={(2u+2v+sinu,-2u+2v+sinv)}^{\mathrm{T}},\forall {(u,v)}^{\mathrm{T}}\in {\mathbb{R}}^2.$$

Define $G:{\mathbb{R}}^2\to {\mathbb{R}}^2$ as

$$G{(u,v)}^{\mathrm{T}}:=\frac{3}{28}\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right){(u,v)}^{\mathrm{T}},\forall {(u,v)}^{\mathrm{T}}\in {\mathbb{R}}^2.$$

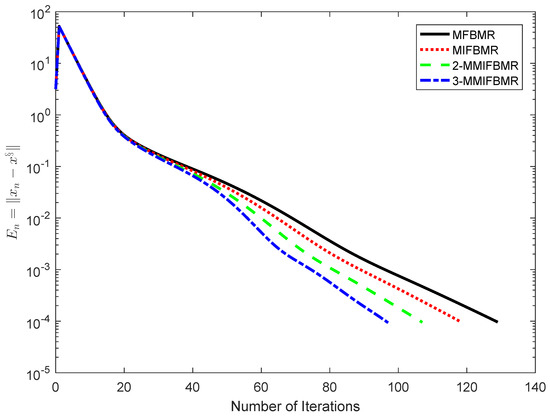
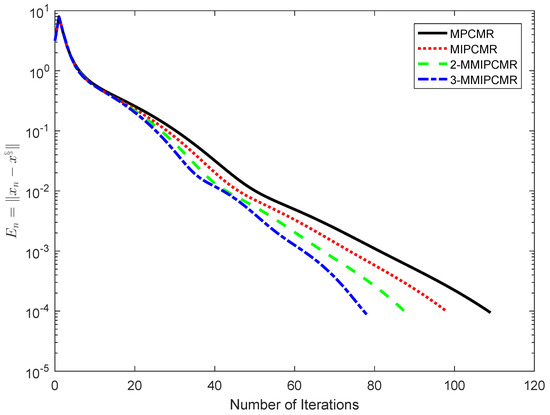
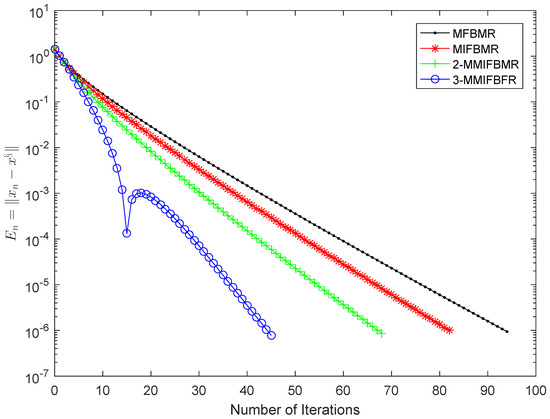
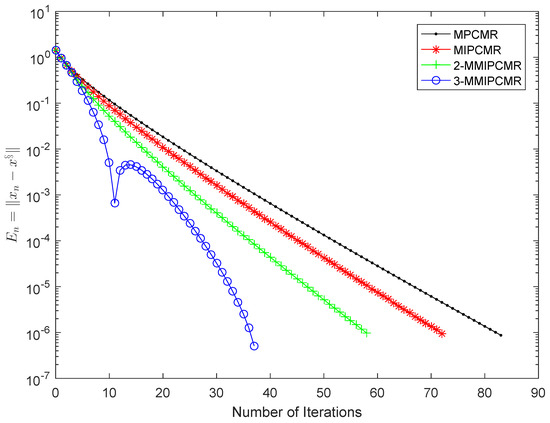
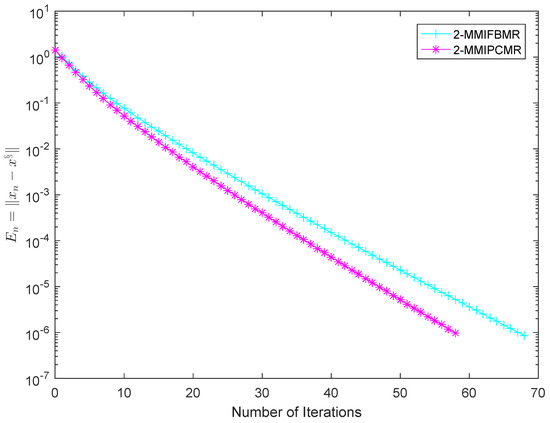
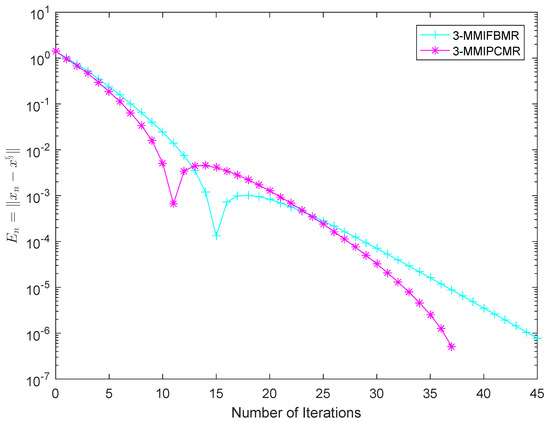
We can claim that B is monotone and $\sqrt{10}$-Lipschitz continuous, F is 1-strongly monotone and $\sqrt{26}$-Lipschitz continuous. We know G is 2-inverse strongly monotone by calculation. Choose ${\theta }_i=0.1$,$x_0={(1,1)}^{\mathrm{T}}$ and ${ϵ}_{i,n}=n^{-2}$ for MIFBMR, 2-MMIFBMR, 3-MMIFBMR, MIPCMR, 2-MMIPCMR and 3-MMIPCMR. Choose $x_1={(1,1)}^{\mathrm{T}}$, $\omega =0.8$, ${\lambda }_1=0.05$, $\mu =0.2$, ${\tau }_n=0.1{(n+1)}^{-6}$ and ${\alpha }_n=n^{-2/5}$ for each algorithm. Choose $r=1$, $\beta =2$ for MPCMR, MIPCMR, 2-MMIPCMR and 3-MMIPCMR. It is obvious that $\Omega =\{{(0,0)}^{\mathrm{T}}\}$ and $x^{\S }={(0,0)}^{\mathrm{T}}$ is the only solution of problem (2). The numerical results are represented in Figure 5, Figure 6, Figure 7 and Figure 8.

Figure 5. Comparison of MFBMR, MIFBMR, 2-MMIFBMR and 3-MMIFBMR in Example 3.

Figure 6. Comparison of MPCMR, MIPCMR, 2-MMIFBMR and 3-MMIPCMR in Example 3.

Figure 7. Comparison of 2-MMIFBMR and 2-MMIPCMR in Example 3.

Figure 8. Comparison of 3-MMIFBMR and 3-MMIPCMR in Example 3.

Remark 2.

In Algorithms 1 and 2, the values of L, k and ξ are not necessary to be known.

5. Conclusions

We have introduce two improved regularized algorithms with multi-step inertia to solve the variational inclusion and null point problem in Hilbert spaces. Then we can get strong convergence without using the inverse strongly monotone assumption. Another advantage of our algorithms is that the stepsizes do not need to use the Lipschitz constant of the operator. In addition, the values of k, L, and $\xi$ are not needed in the calculation process, and the choice of ${\alpha }_n$ seems harsh but is actually available, such as ${\alpha }_n=n^{-p}$, $0<p<1/2$. Finally, the feasibility and effectiveness of our algorithms can be seen in the figures of the numerical experiments. After this, a question is how to get strong convergence under weaker conditions. We will discuss and study this issue in the future.