A One-Parameter Memoryless DFP Algorithm for Solving System of Monotone Nonlinear Equations with Application in Image Processing

Abstract

In matrix analysis, the scaling technique reduces the chances of an ill-conditioning of the matrix. This article proposes a one-parameter scaling memoryless Davidon–Fletcher–Powell (DFP) algorithm for solving a system of monotone nonlinear equations with convex constraints. The measure function that involves all the eigenvalues of the memoryless DFP matrix is minimized to obtain the scaling parameter’s optimal value. The resulting algorithm is matrix and derivative-free with low memory requirements and is globally convergent under some mild conditions. A numerical comparison showed that the algorithm is efficient in terms of the number of iterations, function evaluations, and CPU time. The performance of the algorithm is further illustrated by solving problems arising from image restoration.

1. Introduction

The classical quasi–Newton methods are numerically efficient due to their ability to use approximate Jacobian matrices. Consider the following system of monotone nonlinear equations (SMNE) with convex constraints

$$F\left(x\right)=0,x\in \mathcal{X},$$

(1)

where $x={(x_1,x_2,x_3,...,x_n)}^T$, $\mathcal{X}\subseteq R^n$ is a nonempty closed convex set and $F:R^n\to R^n$ is a continuous and monotone function. The system $F=F_i(i=1,2,3,...,n)$ is monotone if

$${(F\left(x\right)-F\left(y\right))}^T(x-y)\ge 0,x,y\in R^n.$$

(2)

The solution of system (1) is important in many fields of science and engineering such as control systems [1], signal recovery and image restoration in compressive sensing [2,3,4,5], communications and networking [6], data estimation and modeling [7], and geophysics [8].

Newton’s method is one of the old techniques for solving a system (1) if the Jacobian matrix is invertible [9]. Initially, Davidon [10] derived a method, which was later on reformulated by Fletcher and Powell [11] known as the Davidon–Fletcher–Powell (DFP) method for approximating the Hessian matrix of the unconstrained optimization problems. The method has been widely used for solving nonlinear optimization problems [12,13,14,15].

In recent years, there has been a lot of interest in developing methods for solving the convex-constrained nonlinear monotone problems. Some examples include: Levenberg–Marquardt method [16], scaled trust–region method [17], interior global method [18], Dogleg method [19], Polak–Ribière–Polyak (PRP) method [20], Dai and Yuan method [21], descent derivative–free method [22], projection–based method [23], double projection method [24], multivariate spectral gradient method [25], extension of CG_DESCENT projection method [26], new derivative–free SCG–type projection method [27], partially symmetrical derivative–free Liu–Storey projection method [28], modified spectral gradient projection method [29], efficient generalized conjugate gradient (CG) algorithm [30], modified Fletcher–Reeves method [31], modified decent three–term CG method [32], new hybrid CG projection method [33], self–adaptive three–term CG method [34], efficient three–term CG method [35], derivative–free RMIL CG method [36], and spectral three–term conjugate descent method [37]. A new technique called the inexact Newton method has been introduced by Solodov and Svaiter [9] having an interesting property that the entire system converges to a solution without any assumptions. Later on, Zhou and Toh [38] proved that Solodov and Svaiter method has superlinear convergence under some assumptions. Furthermore, this algorithm was extended by Zhou and Li [39,40] to the Broyden–Fletcher–Goldfarb–Shanno (BFGS) and limited memory BFGS methods. Zhang and Zhou proposed a new method named spectral gradient projection method [41] for the solution of the system (1), which is the combination of spectral gradient method [42] and the projection method [9]. Wang et al. [43] extended the work of Solodov and Svaiter [9] for the solution of monotone equations with convex constraints. Yu et al. [44] extended the spectral gradient projection method for convex constraint problems. Xiao and Zhu [45] extended the CG_DESCENT method [46,47] for large–scale nonlinear convex-constrained monotone equations. Moreover, Awwal et al. [48] derived a new hybrid spectral gradient projection method for the solution of the system (1). Currently, Sabi’u et al. [49] modified the Hager–Zhang CG method by using singular value analysis for solving the system (1).

Inspired by the work of Sabi’u et al. [50,51] for finding some optimal choices of non–negative constants that are involved in some nonlinear CG methods and measure function scaling techniques introduced by Neculai Andrei [52,53]

• We scaled one term of the DFP update formula and found the optimal value of the scaled parameter using the idea of measure function.
• Based on the optimal value of the scaled parameter, we derived a new search direction for the DFP algorithm.
• We proposed a projection-based DFP algorithm for solving large-scale systems of nonlinear monotone equations.
• We provided the global convergence result for the proposed algorithm under some mild assumptions.
• The algorithm is successfully implemented for solving some image restoration problems.

The remainder of this paper is organized as follows. The derivation of the proposed algorithm is given in Section 2. The global convergence of the algorithm is given in Section 3. The numerical results are presented in Section 4. Section 5 contains some applications from the image restoration with its physical explanation. The conclusion is provided in Section 6.

2. One-Parameter Scaled DFP Algorithm

Quasi-Newton schemes are efficient due to their ability to use the Jacobian approximation in the scheme. The DFP update is some of the popular quasi-Newton schemes used for solving large-scale systems of algebraic nonlinear equations. In this section, we present a one-parameter scaled DFP algorithm for solving the system (1). The default iterative formula for the DFP algorithm is as follows

$$x_{k+1}=x_k+{\alpha }_k{d}_k,k=0,1,2,...,$$

(3)

where $x_k$ is the previous iteration, $x_{k+1}$ is the current iteration, ${\alpha }_k$ is the step–length and $d_k$ is the DFP direction defined as

$$d_k=-H_k{F}_k,k=0,1,2,...,$$

(4)

with $F_k=F\left(x_k\right)$ and $H_k$ is the DFP matrix at $x_k$. The updating formula for DFP can be found in [10,54] as

$$H_{k+1}=H_k-\frac{H_k{y}_k{y}_k^T{H}_k}{y_k^{T}H{y}_k}+\frac{s_k{s}_k^T}{s_k^T{y}_k},k=0,1,2,...,$$

(5)

where $s_k=x_{k+1}-x_k$, and $y_k=F_{k+1}-F_k$. The symmetry of $H_{k+1}$ is directly concern with the symmetry of $H_k$. One of the well-known properties of the DFP update is that $H_{k+1}$ is positive definite for $s_k^T{y}_k>0$ [54]. The main contribution of the scaling technique in the DFP update formula is that it reduces the chances of an ill–conditioning of the matrix $H_k$ for all $k\ge 0$. Now, by multiplying the third term on right-hand side of (5) with a positive scalar ${\gamma }_k$, we have

$$H_{k+1}=H_k-\frac{H_k{y}_k{y}_k^T{H}_k}{y_k^{T}H{y}_k}+{\gamma }_k\frac{s_k{s}_k^T}{s_k^T{y}_k},k=0,1,2,...,$$

(6)

where ${\gamma }_k$ needs to be determined.

The memoryless concept is applied to the DFP formula to avoid the computation and storage of the matrix $H_k$ at each iteration. In this way, we are replacing the $H_k$ with an identity matrix $I_n$ (where n is dimension of the problem) in (6), so that formula (6) becomes

$$H_{k+1}=I_n-\frac{y_k{y}_k^T}{y_k^T{y}_k}+{\gamma }_k\frac{s_k{s}_k^T}{s_k^T{y}_k},k=0,1,2,...,.$$

(7)

In addition, we want to utilize the concept of measure function $\phi$ on (7), introduced by Byrd and Nocedal [55];

$$\phi \left(H_{k+1}\right)=\mathrm{tr}\left(H_{k+1}\right)-ln(det\left(H_{k+1}\right)),$$

(8)

where tr denotes trace of a positive definite matrix $H_{k+1}$, ln is the natural logarithm, and det is the determinant of $H_{k+1}$. The measure function $\phi$ works with tr and det of $H_{k+1}$ at the same time to modify the quasi–Newton method and to collect information about the behavior of the quasi–Newton method. It is the measure of matrices involving all the eigenvalues of $H_{k+1}$ [56]. If $H_{k+1}=I$, then the function $\phi$ is strictly convex [57], while $\phi$ becomes unbounded in case of either $H_{k+1}$ is singular or infinite.

Now, the determinant of $H_{k+1}$ can be calculated by the Sherman–Morrison formula [58], i.e.,

$$det(I+v_1{v}_2^T+v_3{v}_4^T)=(1+v_1^T{v}_2)(1+v_3^T{v}_4)-\left(v_1^T{v}_4\right)\left(v_2^T{v}_3\right),$$

(9)

to have

$$\begin{array}{c}\hfill det\left(H_{k+1}\right)={\gamma }_k\frac{y_k^T{s}_k}{{∥y_k∥}^2}.\end{array}$$

(10)

Using simple algebra on (7), the trace of $H_{k+1}$ is given by

$$\begin{array}{cc}\hfill \mathrm{tr}\left(H_{k+1}\right)& =\mathrm{tr}\left(I_n\right)-\mathrm{tr}\left(\frac{y_k{y}_k^T}{y_k^T{y}_k}\right)+{\gamma }_k\mathrm{tr}\left(\frac{s_k{s}_k^T}{s_k^T{y}_k}\right)\hfill \\ \hfill & =\mathrm{tr}\left(I_n\right)-\frac{y_k^T{y}_k}{y_k^T{y}_k}+{\gamma }_k\frac{s_k^T{s}_k}{s_k^T{y}_k}\hfill \\ \hfill & =n-\frac{{∥y_k∥}^2}{{∥y_k∥}^2}+{\gamma }_k\frac{{∥s_k∥}^2}{s_k^T{y}_k}\hfill \\ \hfill & =n-1+{\gamma }_k\frac{{∥s_k∥}^2}{s_k^T{y}_k}.\hfill \end{array}$$

(11)

Now, putting (10) and (11) into (8), we have

$$\begin{array}{cc}\hfill \phi \left(H_{k+1}\right)& =n-1+{\gamma }_k\frac{{∥s_k∥}^2}{s_k^T{y}_k}-ln\left({\gamma }_k\frac{y_k^T{s}_k}{{∥y_k∥}^2}\right)\hfill \\ \hfill & =n-1+{\gamma }_k\frac{{∥s_k∥}^2}{s_k^T{y}_k}-ln\left({\gamma }_k\right)-ln\left(y_k^T{s}_k\right)+ln\left({∥y_k∥}^2\right).\hfill \end{array}$$

(12)

Differentiating (12) with respect to ${\gamma }_k$, we have

$$\frac{\partial \phi }{\partial {\gamma }_k}=\frac{{∥s_k∥}^2}{s_k^T{y}_k}-\frac{1}{{\gamma }_k}.$$

(13)

Using the optimality condition on (13), i.e.,$\frac{\partial \phi }{\partial {\gamma }_k}=0$, we have

$$\frac{{∥s_k∥}^2}{s_k^T{y}_k}=\frac{1}{{\gamma }_k},$$

(14)

implies that

$${\gamma }_k=\frac{s_k^T{y}_k}{{∥s_k∥}^2}.$$

(15)

Using (15) into (7), we have

$$\begin{array}{cc}\hfill H_{k+1}& =I_n-\frac{y_k{y}_k^T}{y_k^T{y}_k}+\frac{s_k^T{y}_k}{{∥s_k∥}^2}\frac{s_k{s}_k^T}{s_k^T{y}_k}\hfill \\ \hfill & =I_n-\frac{y_k{y}_k^T}{y_k^T{y}_k}+\frac{s_k{s}_k^T}{{∥s_k∥}^2}.\hfill \end{array}$$

(16)

Next, using (16) in (4), the search direction is

$$\begin{array}{cc}\hfill d_{k+1}& =-\left(I_n-\frac{y_k{y}_k^T}{{∥y_k∥}^2}+\frac{s_k{s}_k^T}{{∥s_k∥}^2}\right)F_{k+1}\hfill \\ \hfill & =-F_{k+1}+\frac{y_k^T{F}_{k+1}}{{∥y_k∥}^2}{y}_k-\frac{s_k^T{F}_{k+1}}{{∥s_k∥}^2}{s}_k.\hfill \end{array}$$

(17)

Furthermore, Solodov and Svaiter [9] proposed a predictor-corrector method, in which

$$z_k=x_k+{\alpha }_k{d}_k,\left(\mathrm{predictor}\right)$$

(18)

and

$$x_{k+1}=x_k-{\lambda }_{k}F\left(z_k\right),\left(\mathrm{corrector}\right)$$

(19)

where

$${\lambda }_k=\frac{F{\left(z_k\right)}^T(x_k-z_k)}{{∥F\left(z_k\right)∥}^2}.$$

(20)

In this work, we use an iterative scheme as

$$x_{k+1}=P_{\chi }\left[x_k-\xi {\lambda }_{k}F\left(z_k\right)\right],$$

(21)

where $\xi$ is any positive constant and P is the projection operator on a convex subset $\chi$ defined by

$$P_{\chi }\left[x\right]=argmin\left\{\parallel y-x\parallel \mid y\in \chi \right\},\forall x\in R^n.$$

(22)

We recommend that readers read [59] for further details on the advantages and applications of the projection operator. Now, the One-parameter Scaled Memoryless DFP (SMDFP) algorithm for solving system (1) is summarized in Algorithm 1:

Algorithm 1: Scaled Memoryless DFP (SMDFP) Method

Step 0 Given a starting point $x_0\in R^n$.  Step 1 Choose values for $\xi ,ϵ,\rho >0$ with $\theta \in (0,1)$. Compute $d_0=-F\left(x_0\right)$, set $k=0$.  Step 2 Compute $F\left(x_k\right)$, while testing the stopping criteria, i.e. If $∥F_k∥\le ϵ$, then stop, otherwise move to the next step.  Step 3 Compute the step size ${\alpha }_k=max\left\{{\rho }^i;i=0,1,2,\dots \right\}$ satisfying the line search $$-F{(x_k+{\alpha }_k{d}_k)}^T{d}_k\ge \theta {\alpha }_k∥F(x_k+{\alpha }_k{d}_k)∥{∥d_k∥}^2.$$ (23)  Step 4 Compute the difference $s_k=x_{k+1}-x_k$ and $y_k=F_{k+1}-F_k$.  Step 5 Compute the search direction $d_{k+1}$ using (17).  Step 6 Compute iterative relations $x_{k+1}$ using (21).  Step 7 Set $k=k+1$ and go to Step 2.

Remark 1. 

The proposed SMDFP algorithm is a matrix-free and also derivative-free approach. These make the proposed algorithm more efficient in solving large-scale problems.

3. Convergence Analysis

This section provides the global convergence of the SMDFP algorithm using the following assumptions:

(a)

The solution set of system (1) is nonempty and the function F is monotone on $R^n$, i.e.,

$${(F\left(x\right)-F\left(y\right))}^T(x-y)\ge 0,\forall x,y\in R^n.$$

(24)

(b)

For a constant $\mu >0$, the function F is Lipschitz continuous on $R^n$, i.e.,

$$∥F\left(x\right)-F\left(y\right)∥\le \mu ∥x-y∥,\forall x,y\in R^n.$$

(25)

(c)

Let $x^{*}\in \mathcal{X}$ be the solution of the problem (1) such that $F\left(x^{*}\right)=0$.

Now, we will proceed with a non–expansive property of projection operator [60].

Lemma 1. 

Suppose χ is a nonempty closed and convex subset of $R^n$. Then the projection operator P can be written as

$$∥P_{\chi }\left[x\right]-P_{\chi }\left[y\right]∥\le \parallel x-y\parallel ,\forall x,y\in R^n,$$

(26)

which shows that, P is a Lipschitz continuous on $R^n$ with $\mu =1$.

Lemma 2. 

Our search direction $d_{k+1}$ defined by (17) satisfies the descent condition, i.e.,

$$F_{k+1}^{\mathrm{T}}{d}_{k+1}\le 0,\forall k\ge 0.$$

(27)

Proof. 

Multiplying (17) by $F_{k+1}^{\mathrm{T}}$, we have

$$\begin{array}{cc}\hfill F_{k+1}^{\mathrm{T}}{d}_{\mathrm{k}+1}& =F_{k+1}^{\mathrm{T}}\left(-F_{k+1}+\frac{y_k^T{F}_{k+1}}{{∥y_k∥}^2}{y}_k-\frac{s_k^T{F}_{k+1}}{{∥s_k∥}^2}{s}_k\right)\hfill \\ \hfill & =-{∥F_{k+1}∥}^2+\frac{\left(y_k^T{F}_{k+1}\right)F_{k+1}^{\mathrm{T}}}{{∥y_k∥}^2}{y}_k-\frac{\left(s_k^T{F}_{k+1}\right)F_{k+1}^{\mathrm{T}}}{{∥s_k∥}^2}{s}_k\hfill \\ \hfill & =-{∥F_{k+1}∥}^2+\frac{{\left(y_k^T{F}_{k+1}\right)}^2}{{∥y_k∥}^2}-\frac{{\left(s_k^T{F}_{k+1}\right)}^2}{{∥s_k∥}^2}\hfill \\ \hfill & \le -{∥F_{k+1}∥}^2+\frac{{\left(y_k^T{F}_{k+1}\right)}^2}{{∥y_k∥}^2}\hfill \\ \hfill & \le -{∥F_{k+1}∥}^2+\frac{{∥y_k∥}^2{∥F_{k+1}∥}^2}{{∥y_k∥}^2}\hfill \\ \hfill & =-{∥F_{k+1}∥}^2+{∥F_{k+1}∥}^2=0,\hfill \end{array}$$

(28)

where the second inequality follows from the Cauchy–Schwarz inequality. Hence

$$F_{k+1}^{\mathrm{T}}{d}_{k+1}\le 0,\forall k\ge 0.$$

(29)

□

Lemma 3. 

Let the assumptions (a), (b), and (c) hold, then the sequences $\left\{z_k\right\}$ and $\left\{x_k\right\}$ generated by the SMDFP algorithm are bounded. Moreover, we have

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}∥x_k-z_k∥=0,\end{array}$$

(30)

and

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}∥x_{k+1}-x_k∥=0.\end{array}$$

(31)

Proof. 

Firstly, we will show that the sequences $\left\{z_k\right\}$ and $\left\{x_k\right\}$ are bounded. Let $x^{*}\in \mathcal{X}$ be any solution of the problem (1). By monotonicity of F, we get

$$\begin{array}{cc}\hfill ⟨F\left(z_k\right),x_k-x^{*}⟩& =⟨F\left(z_k\right),x_k-z_k⟩+⟨F\left(z_k\right),z_k-x^{*}⟩\hfill \\ \hfill & \ge ⟨F\left(z_k\right),x_k-z_k⟩+⟨F\left(x^{*}\right),z_k-x^{*}⟩\hfill \\ \hfill & =⟨F\left(z_k\right),x_k-z_k⟩,\hfill \end{array}$$

(32)

and from the definition of $z_k$ and line search (23), we have

$$\begin{array}{cc}\hfill ⟨F\left(z_k\right),x_k-z_k⟩& =-{\alpha }_k⟨F\left(z_k\right),d_k⟩\hfill \\ \hfill & \ge \theta {\alpha }_k^2∥F\left(z_k\right)∥{∥d_k∥}^2\hfill \\ \hfill & =\theta ∥F\left(z_k\right)∥{∥x_k-z_k∥}^2>0.\hfill \end{array}$$

(33)

Now, by using (21) and (26), we get

$$\begin{array}{cc}\hfill {∥x_{k+1}-x^{*}∥}^2& ={∥P_X\left[x_k-\xi {\lambda }_{k}F\left(z_k\right)\right]-x^{*}∥}^2\hfill \\ \hfill & \le {∥x_k-\xi {\lambda }_{k}F\left(z_k\right)-x^{*}∥}^2\hfill \\ \hfill & ={∥x_k-x^{*}∥}^2-2\xi {\lambda }_k⟨F\left(z_k\right),x_k-x^{*}⟩+{∥\xi {\lambda }_{k}F\left(z_k\right)∥}^2.\hfill \end{array}$$

(34)

Putting (32) into (34), and then using the value of ${\lambda }_k$ from (20), we have

$$\begin{array}{cc}\hfill {∥x_{k+1}-x^{*}∥}^2& \le {∥x_k-x^{*}∥}^2-2\xi {\lambda }_k⟨F\left(z_k\right),x_k-z_k⟩+{\xi }^2{\lambda }_k^2{∥F\left(z_k\right)∥}^2\hfill \\ \hfill & ={∥x_k-x^{*}∥}^2-2\xi \left(\frac{F{\left(z_k\right)}^T(x_k-z_k)}{{∥F\left(z_k\right)∥}^2}\right)⟨F\left(z_k\right),x_k-z_k⟩\hfill \\ & +{\xi }^2{\left(\frac{F{\left(z_k\right)}^T(x_k-z_k)}{{∥F\left(z_k\right)∥}^2}\right)}^2{∥F\left(z_k\right)∥}^2\hfill \\ \hfill & ={∥x_k-x^{*}∥}^2-2\xi {\left(\frac{⟨F\left(z_k\right),x_k-z_k⟩}{∥F\left(z_k\right)∥}\right)}^2+{\xi }^2{\left(\frac{⟨F\left(z_k\right),x_k-z_k⟩}{∥F\left(z_k\right)∥}\right)}^2\hfill \\ \hfill & ={∥x_k-x^{*}∥}^2-\xi (2-\xi ){\left(\frac{⟨F\left(z_k\right),x_k-z_k⟩}{∥F\left(z_k\right)∥}\right)}^2.\hfill \end{array}$$

(35)

Now, by using (33) on (35), we have

$$\begin{array}{cc}\hfill {∥x_{k+1}-x^{*}∥}^2& \le {∥x_k-x^{*}∥}^2-\xi (2-\xi ){\left(\frac{\theta ∥F\left(z_k\right)∥{∥x_k-z_k∥}^2}{∥F\left(z_k\right)∥}\right)}^2\hfill \\ \hfill & ={∥x_k-x^{*}∥}^2-\xi (2-\xi ){\theta }^2{∥x_k-z_k∥}^4.\hfill \end{array}$$

(36)

Hence the sequence $\left\{∥x_k-x^{*}∥\right\}$ is decreasing and convergent. Moreover, the sequence $\left\{∥x_k∥\right\}$ is bounded. Furthermore, from (36), we can write

$$\begin{array}{cc}\hfill {∥x_{k+1}-x^{*}∥}^2& \le {∥x_k-x^{*}∥}^2,\forall k\ge 0,\hfill \end{array}$$

(37)

and repeating the same process, we get the result that

$$\begin{array}{c}\hfill {∥x_k-x^{*}∥}^2\le {∥x_0-x^{*}∥}^2,\forall k\ge 0.\end{array}$$

(38)

Moreover, from assumption (b), we have

$$\begin{array}{c}\hfill ∥F\left(x_k\right)∥=∥F\left(x_k\right)-F\left(x^{*}\right)∥\le \mu ∥x_k-x^{*}∥\le \mu ∥x_0-x^{*}∥.\end{array}$$

(39)

We suppose that $\mu ∥x_0-x^{*}∥=\omega$, then the sequence $\left\{F\left(x_k\right)\right\}$ is bounded, i.e.,

$$\begin{array}{c}\hfill ∥F\left(x_k\right)∥\le \omega ,\forall k\ge 0.\end{array}$$

(40)

By the Cauchy–Schwarz inequality, monotonicity of F and inequality (33), it holds that

$$\begin{array}{c}\hfill 0<\theta ∥F\left(z_k\right)∥{∥x_k-z_k∥}^2\le ⟨F\left(z_k\right),x_k-z_k⟩\le ∥F\left(z_k\right)∥∥x_k-z_k∥.\end{array}$$

(41)

From the inequality (41), it implies that

$$\begin{array}{c}\hfill \theta ∥x_k-z_k∥\le 1,\end{array}$$

(42)

which shows that the sequence $\left\{z_k\right\}$ is also bounded. Moreover, from inequality (36), it follows that

$$\begin{array}{cc}\hfill \xi (2-\xi ){\theta }^2\sum _{k=1}^{\infty }{∥x_k-z_k∥}^4& \le \sum _{k=1}^{\infty }\left({∥x_k-x^{*}∥}^2-{∥x_{k+1}-x^{*}∥}^2\right)\hfill \\ \hfill & \le ∥x_0-x_{*}∥<\infty ,\hfill \end{array}$$

(43)

which implies that

$$\underset{k\to \infty }{lim}∥x_k-z_k∥=0.$$

(44)

Since $x_k\in X$, so by using (26) and then putting the value of ${\lambda }_k$ from (20), we have

$$\begin{array}{cc}\hfill ∥x_{k+1}-x_k∥& =∥P_X\left[x_k-\xi {\lambda }_{k}F\left(z_k\right)\right]-x^{*}∥\hfill \\ \hfill & \le ∥x_k-\xi {\lambda }_{k}F\left(z_k\right)-x_k∥\hfill \\ \hfill & =∥\xi {\lambda }_{k}F\left(z_k\right)∥\hfill \\ \hfill & =\xi \left(\frac{⟨F\left(z_k\right),x_k-z_k⟩}{{∥F\left(z_k\right)∥}^2}\right)∥F\left(z_k\right)∥\hfill \\ \hfill & =\xi \frac{⟨F\left(z_k\right),x_k-z_k⟩}{∥F\left(z_k\right)∥}.\hfill \end{array}$$

(45)

Now using the Cauchy–Schwarz inequality on (45), we have

$$\begin{array}{cc}\hfill ∥x_{k+1}-x_k∥& \le \xi \frac{∥F\left(z_k\right)∥{∥x_k-z_k∥}^2}{∥F\left(z_k\right)∥}\hfill \\ \hfill & =\xi {∥x_k-z_k∥}^2,\forall k\ge 0.\hfill \end{array}$$

(46)

Thus, by using (30), we have

$$\underset{k\to \infty }{lim}∥x_{k+1}-x_k∥=0.$$

Hence, the proof of (31) is completed. □

Remark 2. 

Let the sequence $\left\{x_k\right\}$ be generated by the SMDFP method. Then, using (18) on (44), we have

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim}∥z_k-x_k∥& =\underset{k\to \infty }{lim}∥x_k+{\alpha }_k{d}_k-x_k∥\hfill \\ & =\underset{k\to \infty }{lim}{\alpha }_k∥d_k∥=0,\forall k\ge 0.\hfill \end{array}$$

(47)

Lemma 4. 

The direction generated by the SMDFP algorithm is bounded. That is

$$∥d_{k+1}∥\le q,\forall k\ge 0,$$

(48)

where q is some positive constant.

Proof. 

It follows from (17) that

$$\begin{array}{cc}\hfill ∥d_{k+1}∥& =∥-F_{k+1}+\frac{y_k^T{F}_{k+1}}{{∥y_k∥}^2}{y}_k-\frac{s_k^T{F}_{k+1}}{{∥s_k∥}^2}{s}_k∥\hfill \\ \hfill & \le ∥F_{k+1}∥+∥\frac{y_k^T{F}_{k+1}}{{∥y_k∥}^2}{y}_k∥+∥\frac{s_k^T{F}_{k+1}}{{∥s_k∥}^2}{s}_k∥\hfill \\ \hfill & \le ∥F_{k+1}∥+∥F_{k+1}∥+∥F_{k+1}∥\hfill \\ \hfill & =3∥F_{k+1}∥\le 3\omega =q,\hfill \end{array}$$

(49)

where the second inequity follows from Cauchy–Schwarz inequality. Thus,

$$\begin{array}{c}\hfill ∥d_{k+1}∥\le q,\forall k\ge 0.\end{array}$$

(50)

□

Theorem 1. 

Let the sequences $\left\{z_k\right\}$ and $\left\{x_k\right\}$ be generated by the SMDFP algorithm, then

$$\underset{k\to \infty }{lim\; inf}∥F_k∥=0.$$

(51)

Proof. 

To prove that (51) holds, we consider the following two cases;

Case 1. Suppose the sequence $\left\{x_k\right\}$ is generated by the SMDFP method. Then we have

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}{\alpha }_k∥d_k∥=0.\end{array}$$

(52)

Assume that if

$$\underset{k\to \infty }{lim\; inf}∥d_k∥=0,$$

then

$$\underset{k\to \infty }{lim\; inf}∥F_k∥=0.$$

Then by continuity property of F, there will be some accumulation point $x^{*}$ in sequence $\left\{x_k\right\}$ such that $F\left(x^{*}\right)=0$. Since $\left\{∥x_k-x^{*}∥\right\}$ is going to converge and $\left\{x_k\right\}$ has an accumulation point $x^{*}$, $\left\{x_k\right\}$ is going to converge to $x^{*}$.

Case 2. Suppose (51) is not true, and then there exists some positive constant $\delta$ such that

$$∥F_k∥\ge \delta >0,\forall k\ge 0.$$

(53)

By using Cauchy–Schwarz inequality on descent condition, we have

$$\begin{array}{cc}\hfill ∥F_k∥∥d_k∥& \ge -{F_k}^T{d}_k\ge {∥F_k∥}^2\ge 0,\forall k\ge 0,\hfill \end{array}$$

(54)

which implies that

$$\begin{array}{c}\hfill ∥d_k∥\ge ∥F_k∥>0,\forall k\ge 0.\end{array}$$

(55)

Using (52) and (55), we have

$$\underset{k\to \infty }{lim\; inf}∥d_k∥>0.$$

(56)

Now, by using (52) and (56), we have

$$\underset{k\to \infty }{lim}{\alpha }_k=0.$$

(57)

Since (57) is true, by the definition of ${\alpha }_k$, ${\rho }^{-1}{\alpha }_k$ does not satisfy the line search, i.e.,

$$-F{(x_k+{\alpha }_k{\rho }^{-1}{d}_k)}^T{d}_k<\theta {\alpha }_k{\rho }^{-1}∥F(x_k+{\alpha }_k{\rho }^{-1}{d}_k)∥{∥d_k∥}^2,$$

(58)

and from the boundedness of $\left\{x_k\right\}$ and $\left\{d_k\right\}$, we can choose a sub–sequence such that k approaches to infinity in the above inequality results, then (58) becomes

$$-F{\left(x^{*}\right)}^T\overline{d}<0.$$

(59)

Moreover, k approaches to ∞ in (29), which implies that

$$-F{\left(x^{*}\right)}^T\overline{d}\ge 0.$$

(60)

From (59) and (60), we concluded that it is a clear contradiction to each other. Hence,

$$\underset{k\to \infty }{lim\; inf}∥F_k∥=0,$$

is true and the proof is complete. □

4. Numerical Experimentation

In this section, we perform some numerical experiments to validate the SMDFP algorithm by comparing the computed results with the conjugate gradient hybrid (CGH) method [61] and with the generalized hybrid CGPM–based (GHCGP) method [62]. All algorithms are written in Matlab R2014 on an HP CORE i5 Intel 8th Gen personal computer. In our experiment with the uniform stopping condition, we used the published initial values for the comparison algorithms. However, we used $\theta =0.0001$ and $\rho =0.9$ in the SMDFP algorithm. The numerical simulations are stopped either exceeding the dimension or $∥F\left(x_k\right)∥\le {10}^{-11}$. For the following problems see [63,64,65,66,67,68].

Problem 1 

([63,64]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_i\left(x\right)=exp\left(x_i\right)-1$, for $i=1,2,3,\dots ,n$.

Problem 2 

([65]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_1\left(x\right)=cos\left(x_1\right)+3x_1+8exp\left(x_2\right)-9$,

$F_i\left(x\right)=cos\left(x_i\right)+3x_i+8exp\left(x_{i-1}\right)-9$, for $i=2,3,4,\dots ,n$.

Problem 3 

([66]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_i\left(x\right)=x_i-0.1x_{i+1}^2$, for $i=2,3,4,\dots ,n-1$,

$F_n\left(x\right)=x_n-0.1x_1^2$.

Problem 4 

([67]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_i\left(x\right)=x_{i}cos(x_i-\frac{1}{n})-x_n\left[sin\left(x_i\right)-1-{(x_i-1)}^2-\frac{1}{n}{\sum }_{i=1}^n{x}_i\right]$, for $i=1,2,3,\dots ,n$.

Problem 5 

([68]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_i\left(x\right)=x_i^2+10x_i$, for $i=1,2,3,\dots ,n$.

Problem 6 

([63]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_i\left(x\right)=log\left(∥x_i∥+1\right)-\frac{x_i}{n}$, for $i=1,2,3,\dots ,n$.

Problem 7 

([63,64]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_i\left(x\right)=2x_i-sin∥x_i∥$, for $i=1,2,3,\dots ,n$.

Problem 8 

([63]). Set $\mathcal{X}={\mathbb{R}}_{+}^n$ and function $F\left(x\right)$ is described as

$F_1\left(x\right)=exp\left(x_1\right)-1$,

$F_i\left(x\right)=exp\left(x_i\right)+x_i-1$, for $i=2,3,4,\dots ,n$.

In Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, we used the initial points $x_1=(1,1,\dots ,1)$, $x_2=(1,\frac{1}{2},\frac{1}{3},\dots ,\frac{1}{n})$, $x_3=(0.1,0.1,\dots ,0.1)$, $x_4=(\frac{1}{n},\frac{2}{n},\dots ,1)$, $x_5=(1-\frac{1}{n},1-\frac{2}{n},\dots ,0)$, $x_6=(-1,-1,\dots ,-1)$, $x_7=(n-\frac{1}{n},n-\frac{2}{n},\dots ,n-1)$ and $x_8=(\frac{1}{2},1,\frac{2}{3},\dots ,\frac{2}{n})$. Moreover, the terms ITER, FEV, CPUT, and NORM stand for the number of iterations, the number of function evaluations, CPU times (in seconds), and the norm of the function evaluations, respectively. The failure of a certain algorithm is denoted by “_”. We further show the numerical performance of the SMDFP algorithm along with the CGH [61] and GHCGP [62] methods in terms of the number of iterations, function evaluations, CPU times, and error estimation.

Table 1. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 1			SMDFP				CGH				GHCGP
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	1	3	0.035122	0	130	1680	2.236476	8.41 $\times {10}^{-9}$	30	61	0.143056	7.2$\times {10}^{-9}$
	$x_2$	1	3	0.014751	0	1	3	0.007694	0	31	64	0.030084	9.34$\times {10}^{-9}$
	$x_3$	1	3	0.00864	0	1	3	0.004303	0	32	68	0.028365	9.12$\times {10}^{-9}$
	$x_4$	1	3	0.004609	0	1	3	0.003516	0	31	66	0.026267	6.23$\times {10}^{-9}$
	$x_5$	1	3	0.004232	0	1	3	0.003499	0	1	3	0.003961	0
	$x_6$	1	3	0.0045	0	107	1392	0.141467	8.73$\times {10}^{-9}$	30	61	0.02529	8.66$\times {10}^{-9}$
	$x_7$	1	3	0.004224	0	95	1236	0.147844	9.5$\times {10}^{-9}$	29	59	0.025136	5.33$\times {10}^{-9}$
	$x_8$	1	3	0.004219	0	1	3	0.003311	0	1	3	0.004024	0
5000	$x_1$	1	3	0.01969	0	134	1732	1.826228	8.17$\times {10}^{-9}$	31	63	0.282029	8.05$\times {10}^{-9}$
	$x_2$	1	3	0.01655	0	1	3	0.007681	0	33	68	0.460068	5.22$\times {10}^{-9}$
	$x_3$	1	3	0.013203	0	1	3	0.006739	0	34	72	0.461073	5.1$\times {10}^{-9}$
	$x_4$	1	3	0.03535	0	1	3	0.006651	0	32	68	0.605644	6.97$\times {10}^{-9}$
	$x_5$	1	3	0.011906	0	1	3	0.020484	0	1	3	0.013328	0
	$x_6$	1	3	0.016778	0	111	1444	0.63665	8.47$\times {10}^{-9}$	31	63	0.548416	9.68$\times {10}^{-9}$
	$x_7$	1	3	0.01269	0	99	1288	0.62048	9.22$\times {10}^{-9}$	30	61	0.629381	5.95$\times {10}^{-9}$
	$x_8$	1	3	0.015683	0	1	3	0.006559	0	1	3	0.017017	0
15,000	$x_1$	1	3	0.01634	0	135	1745	1.434341	9.38$\times {10}^{-9}$	32	65	0.986364	5.69$\times {10}^{-9}$
	$x_2$	1	3	0.017012	0	1	3	0.007016	0	33	68	1.136386	7.38$\times {10}^{-9}$
	$x_3$	1	3	0.021289	0	1	3	0.007927	0	34	72	1.153497	7.21$\times {10}^{-9}$
	$x_4$	1	3	0.014781	0	1	3	0.009047	0	32	68	1.039588	9.86$\times {10}^{-9}$
	$x_5$	1	3	0.015541	0	1	3	0.006813	0	1	3	0.025195	0
	$x_6$	1	3	0.015866	0	112	1457	1.40839	9.72$\times {10}^{-9}$	32	65	1.296489	6.85$\times {10}^{-9}$
	$x_7$	1	3	0.020727	0	101	1314	1.66346	8.59$\times {10}^{-9}$	30	61	1.407296	8.42$\times {10}^{-9}$
	$x_8$	1	3	0.014068	0	1	3	0.014423	0	1	3	0.02878	0
50,000	$x_1$	1	3	0.035269	0	139	1797	8.660152	9.1$\times {10}^{-9}$	33	67	2.698926	6.36$\times {10}^{-9}$
	$x_2$	1	3	0.036429	0	1	3	0.026383	0	34	70	2.620559	8.25$\times {10}^{-9}$
	$x_3$	1	3	0.04011	0	1	3	0.02646	0	35	74	2.367671	8.06$\times {10}^{-9}$
	$x_4$	1	3	0.033272	0	1	3	0.029999	0	34	72	2.239652	5.51$\times {10}^{-9}$
	$x_5$	1	3	0.032413	0	1	3	0.158757	0	1	3	0.080205	0
	$x_6$	1	3	0.069492	0	116	1509	39.25009	9.44$\times {10}^{-9}$	33	67	2.284177	7.65$\times {10}^{-9}$
	$x_7$	1	3	0.031998	0	105	1366	8.375691	8.34$\times {10}^{-9}$	31	63	2.439808	9.42$\times {10}^{-9}$
	$x_8$	1	3	0.042604	0	1	3	0.024109	0	1	3	0.0487	0
100,000	$x_1$	1	3	0.072912	0	141	1823	15.78274	8.48$\times {10}^{-9}$	33	67	2.800037	9$\times {10}^{-9}$
	$x_2$	1	3	0.090527	0	1	3	0.044907	0	35	72	3.262603	5.84$\times {10}^{-9}$
	$x_3$	1	3	0.078645	0	1	3	0.045901	0	36	76	3.094576	5.7$\times {10}^{-9}$
	$x_4$	1	3	0.075346	0	1	3	0.054425	0	34	72	2.737321	7.79$\times {10}^{-9}$
	$x_5$	1	3	0.126657	0	1	3	0.051759	0	1	3	0.128415	0
	$x_6$	1	3	0.071292	0	118	1535	14.85632	8.8$\times {10}^{-9}$	34	69	3.082105	5.41$\times {10}^{-9}$
	$x_7$	1	3	0.091889	0	106	1379	12.69957	9.57$\times {10}^{-9}$	32	65	2.589503	6.66$\times {10}^{-9}$
	$x_8$	1	3	0.111511	0	1	3	0.03606	0	1	3	0.084673	0

Table 2. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 2			SMDFP				CGH				GHCGP
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	1	3	0.005111	0	1	3	0.201878	0	13	55	0.057429	1.93$\times {10}^{-9}$
	$x_2$	1	3	0.004934	0	1	3	0.004667	0	12	50	0.02292	2.44$\times {10}^{-9}$
	$x_3$	1	3	0.004862	0	1	3	0.004516	0	14	61	0.02838	2$\times {10}^{-9}$
	$x_4$	1	3	0.00481	0	1	3	0.004824	0	15	69	0.030771	1.66$\times {10}^{-9}$
	$x_5$	1	3	0.004774	0	1	3	0.004738	0	12	55	0.023997	2.48$\times {10}^{-9}$
	$x_6$	1	3	0.004873	0	1	3	0.004792	0	12	50	0.022978	1.78$\times {10}^{-9}$
	$x_7$	1	3	0.004563	0	1	3	0.004552	0	11	45	0.01946	1.91$\times {10}^{-9}$
	$x_8$	1	3	0.005762	0	1	3	0.004795	0	14	67	0.028311	2.31$\times {10}^{-9}$
5000	$x_1$	1	3	0.018152	0	1	3	0.016958	0	13	55	1.230151	4.31$\times {10}^{-9}$
	$x_2$	1	3	0.01962	0	1	3	0.054983	0	12	50	0.988219	5.45$\times {10}^{-9}$
	$x_3$	1	3	0.021361	0	1	3	0.071534	0	14	61	2.208304	4.46$\times {10}^{-9}$
	$x_4$	1	3	0.049504	0	1	3	0.028522	0	15	69	2.334171	3.72$\times {10}^{-9}$
	$x_5$	1	3	0.028837	0	1	3	0.026218	0	12	55	0.976465	5.54$\times {10}^{-9}$
	$x_6$	1	3	0.014489	0	1	3	0.023154	0	12	50	1.120086	3.97$\times {10}^{-9}$
	$x_7$	1	3	0.020818	0	1	3	0.036165	0	11	45	1.011787	4.27$\times {10}^{-9}$
	$x_8$	1	3	0.035658	0	1	3	0.023837	0	14	67	1.645371	5.18$\times {10}^{-9}$
15,000	$x_1$	1	3	0.024338	0	1	3	0.042924	0	13	55	1.554233	6.09$\times {10}^{-9}$
	$x_2$	1	3	0.025928	0	1	3	0.0635	0	12	50	2.311009	7.71$\times {10}^{-9}$
	$x_3$	1	3	0.028652	0	1	3	0.033185	0	14	61	1.574	6.31$\times {10}^{-9}$
	$x_4$	1	3	0.027035	0	1	3	0.049415	0	15	69	1.408958	5.26$\times {10}^{-9}$
	$x_5$	1	3	0.028536	0	1	3	0.231511	0	12	55	1.176572	7.84$\times {10}^{-9}$
	$x_6$	1	3	0.020113	0	1	3	0.03914	0	12	50	1.131856	5.62$\times {10}^{-9}$
	$x_7$	1	3	0.033993	0	1	3	0.086277	0	11	45	1.110647	6.04$\times {10}^{-9}$
	$x_8$	1	3	0.024769	0	1	3	0.102031	0	14	67	1.089978	7.32$\times {10}^{-9}$
50,000	$x_1$	1	3	0.100548	0	1	3	0.081128	0	14	59	1.840833	1.63$\times {10}^{-9}$
	$x_2$	1	3	0.059629	0	1	3	0.107223	0	13	54	1.495333	2.07$\times {10}^{-9}$
	$x_3$	1	3	0.060439	0	1	3	0.089753	0	15	65	2.181382	1.69$\times {10}^{-9}$
	$x_4$	1	3	0.066735	0	1	3	0.083639	0	16	73	2.307287	1.41$\times {10}^{-9}$
	$x_5$	1	3	0.057437	0	1	3	0.09488	0	13	59	1.942567	2.1$\times {10}^{-9}$
	$x_6$	1	3	0.060867	0	1	3	0.111695	0	13	54	1.833159	1.51$\times {10}^{-9}$
	$x_7$	1	3	0.064029	0	1	3	0.156286	0	12	49	1.23558	1.62$\times {10}^{-9}$
	$x_8$	1	3	0.065988	0	1	3	0.326879	0	15	71	2.245318	1.96$\times {10}^{-9}$
100,000	$x_1$	1	3	0.119022	0	1	3	0.172609	0	14	59	2.501767	2.31$\times {10}^{-9}$
	$x_2$	1	3	0.127509	0	1	3	0.314452	0	13	54	2.947286	2.93$\times {10}^{-9}$
	$x_3$	1	3	0.132327	0	1	3	0.224496	0	15	65	2.886944	2.4$\times {10}^{-9}$
	$x_4$	1	3	0.120837	0	1	3	0.28043	0	16	73	3.275997	2$\times {10}^{-9}$
	$x_5$	1	3	0.163017	0	1	3	0.218818	0	13	59	2.979261	2.97$\times {10}^{-9}$
	$x_6$	1	3	0.147234	0	1	3	0.317258	0	13	54	1.977479	2.13$\times {10}^{-9}$
	$x_7$	1	3	0.114379	0	1	3	0.164473	0	12	49	2.349758	2.29$\times {10}^{-9}$
	$x_8$	1	3	0.155111	0	1	3	0.164645	0	15	71	2.860774	2.78$\times {10}^{-9}$

Table 3. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 3			SMDFP				CGH				GHCGP
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	27	352	0.117364	7.01$\times {10}^{-9}$	104	1353	0.318394	9.22$\times {10}^{-9}$	32	65	0.061522	9.06$\times {10}^{-9}$
	$x_2$	28	365	0.123548	7.87$\times {10}^{-9}$	2	16	0.006879	0	34	69	0.031974	5.68$\times {10}^{-9}$
	$x_3$	29	378	0.120701	6.79$\times {10}^{-9}$	2	16	0.00681	0	35	71	0.031623	5.47$\times {10}^{-9}$
	$x_4$	30	391	0.134075	9.73$\times {10}^{-9}$	2	16	0.007006	0	36	73	0.032578	8.43$\times {10}^{-9}$
	$x_5$	33	430	0.146445	7.54$\times {10}^{-9}$	9	73	0.018668	9.97$\times {10}^{-9}$	39	79	0.036347	8.49$\times {10}^{-9}$
	$x_6$	26	339	0.112825	7.14$\times {10}^{-9}$	102	1327	0.297255	8.12$\times {10}^{-9}$	31	63	0.028116	8.15$\times {10}^{-9}$
	$x_7$	24	313	0.100542	6.87$\times {10}^{-9}$	94	1223	0.285619	9.71$\times {10}^{-9}$	29	59	0.0284	6.01$\times {10}^{-9}$
	$x_8$	-	-	-	-	-	-	-	-	-	-	-	-
5000	$x_1$	28	365	2.139238	6.82$\times {10}^{-9}$	108	1405	13.72612	8.95$\times {10}^{-9}$	34	69	2.214968	5.06$\times {10}^{-9}$
	$x_2$	29	378	2.203859	7.66$\times {10}^{-9}$	2	16	0.095661	0	35	71	2.019577	6.35$\times {10}^{-9}$
	$x_3$	30	391	2.179331	6.61$\times {10}^{-9}$	2	16	0.100748	0	36	73	1.722336	6.12$\times {10}^{-9}$
	$x_4$	31	404	1.693619	9.47$\times {10}^{-9}$	2	16	0.168732	0	37	75	1.493552	9.43$\times {10}^{-9}$
	$x_5$	34	443	1.419028	7.34$\times {10}^{-9}$	9	73	0.611932	2.23$\times {10}^{-9}$	40	81	3.0625	9.49$\times {10}^{-9}$
	$x_6$	27	352	0.746712	6.95$\times {10}^{-9}$	105	1366	7.824971	9.71$\times {10}^{-9}$	32	65	2.277345	9.11$\times {10}^{-9}$
	$x_7$	25	326	0.761351	6.69$\times {10}^{-9}$	98	1275	5.246163	9.43$\times {10}^{-9}$	30	61	1.597036	6.72$\times {10}^{-9}$
	$x_8$	-	-	-	-	-	-	-	-	-	-	-	-
10,000	$x_1$	28	365	1.48354	9.65$\times {10}^{-9}$	110	1431	6.355567	8.34$\times {10}^{-9}$	34	69	1.958965	7.16$\times {10}^{-9}$
	$x_2$	30	391	1.390034	4.71$\times {10}^{-9}$	2	16	0.074192	0	35	71	2.865596	8.98$\times {10}^{-9}$
	$x_3$	30	391	1.431256	9.35$\times {10}^{-9}$	2	16	0.067912	0	36	73	2.382778	8.65$\times {10}^{-9}$
	$x_4$	32	417	1.53683	5.83$\times {10}^{-9}$	2	16	0.052701	0	38	77	2.529481	6.66$\times {10}^{-9}$
	$x_5$	35	456	1.352757	4.52$\times {10}^{-9}$	9	73	0.584748	3.15$\times {10}^{-9}$	41	83	3.048691	6.71$\times {10}^{-9}$
	$x_6$	27	352	0.924018	9.83$\times {10}^{-9}$	107	1392	5.41707	9.05$\times {10}^{-9}$	33	67	2.122735	6.44$\times {10}^{-9}$
	$x_7$	25	326	0.898503	9.46$\times {10}^{-9}$	100	1301	4.89272	8.78$\times {10}^{-9}$	30	61	1.577585	9.5$\times {10}^{-9}$
	$x_8$	-	-	-	-	-	-	-	-	-	-	-	-
50,000	$x_1$	29	378	4.140748	9.39$\times {10}^{-9}$	113	1470	11.60575	9.98$\times {10}^{-9}$	35	71	2.654783	8.01$\times {10}^{-9}$
	$x_2$	31	404	4.157986	4.58$\times {10}^{-9}$	2	16	0.120349	0	37	75	2.537268	5.02$\times {10}^{-9}$
	$x_3$	31	404	3.655449	9.1$\times {10}^{-9}$	2	16	0.140539	0	37	75	2.57247	9.67$\times {10}^{-9}$
	$x_4$	33	430	3.891895	5.67$\times {10}^{-9}$	2	16	0.14212	0	39	79	2.641795	7.45$\times {10}^{-9}$
	$x_5$	36	469	4.213919	4.39$\times {10}^{-9}$	9	73	0.730919	7.05$\times {10}^{-9}$	42	85	3.088176	7.51$\times {10}^{-9}$
	$x_6$	28	365	3.438646	9.56$\times {10}^{-9}$	111	1444	10.96663	8.78$\times {10}^{-9}$	34	69	2.17434	7.2$\times {10}^{-9}$
	$x_7$	26	339	3.296482	9.2$\times {10}^{-9}$	104	1353	9.567916	8.53$\times {10}^{-9}$	32	65	1.841247	5.31$\times {10}^{-9}$
	$x_8$	-	-	-	-	-	-	-	-	-	-	-	-
100,000	$x_1$	30	391	7.675792	5.78$\times {10}^{-9}$	115	1496	18.44836	9.29$\times {10}^{-9}$	36	73	3.191328	5.66$\times {10}^{-9}$
	$x_2$	31	404	7.127316	6.48$\times {10}^{-9}$	2	16	0.173612	0	37	75	3.53366	7.1$\times {10}^{-9}$
	$x_3$	32	417	7.365149	5.6$\times {10}^{-9}$	2	16	0.260983	0	38	77	3.179414	6.84$\times {10}^{-9}$
	$x_4$	33	430	7.323262	8.02$\times {10}^{-9}$	2	16	0.238622	0	40	81	3.479403	5.27$\times {10}^{-9}$
	$x_5$	36	469	7.954414	6.21$\times {10}^{-9}$	9	73	1.261594	9.97$\times {10}^{-9}$	43	87	4.137574	5.31$\times {10}^{-9}$
	$x_6$	29	378	6.641638	5.89$\times {10}^{-9}$	113	1470	21.35079	8.19$\times {10}^{-9}$	35	71	2.87259	5.09$\times {10}^{-9}$
	$x_7$	27	352	6.081961	5.66$\times {10}^{-9}$	105	1366	15.93775	9.79$\times {10}^{-9}$	32	65	2.929885	7.51$\times {10}^{-9}$
	$x_8$	-	-	-	-	-	-	-	-	-	-	-	-

Table 4. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 4			SMDFP				CGH				GHCGP
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	1	3	0.005096	0	-	-	-	-	25	75	0.074388	5.14$\times {10}^{-9}$
	$x_2$	1	3	0.005338	0	1	3	0.003663	0	26	78	0.046803	4.09$\times {10}^{-9}$
	$x_3$	1	3	0.005816	0	1	3	0.005606	0	26	79	0.04716	6.99$\times {10}^{-9}$
	$x_4$	1	3	0.00575	0	1	3	0.005469	0	26	80	0.046384	7.42$\times {10}^{-9}$
	$x_5$	1	3	0.005851	0	1	3	0.005245	0	26	81	0.047634	5.28$\times {10}^{-9}$
	$x_6$	1	3	0.005918	0	1	3	0.005187	0	26	79	0.048149	4.88$\times {10}^{-9}$
	$x_7$	1	3	0.004853	0	1	3	0.005062	0	23	70	0.042655	7.88$\times {10}^{-9}$
	$x_8$	1	3	0.005734	0	1	3	0.005934	0	26	84	0.051013	7.34$\times {10}^{-9}$
5000	$x_1$	1	3	0.038406	0	-	-	-	-	26	78	2.150775	4.61$\times {10}^{-9}$
	$x_2$	1	3	0.026129	0	1	3	0.021583	0	26	78	1.483384	9.18$\times {10}^{-9}$
	$x_3$	1	3	0.019968	0	1	3	0.017991	0	27	82	2.751638	6.28$\times {10}^{-9}$
	$x_4$	1	3	0.030478	0	1	3	0.027568	0	27	83	2.081753	6.66$\times {10}^{-9}$
	$x_5$	1	3	0.034382	0	1	3	0.023907	0	27	84	2.040673	4.75$\times {10}^{-9}$
	$x_6$	1	3	0.019777	0	1	3	0.025307	0	27	82	2.46602	4.37$\times {10}^{-9}$
	$x_7$	1	3	0.035994	0	1	3	0.040065	0	24	73	2.228755	7.05$\times {10}^{-9}$
	$x_8$	1	3	0.031355	0	1	3	0.039022	0	27	87	1.830332	6.58$\times {10}^{-9}$
10,000	$x_1$	1	3	0.028243	0	-	-	-	-	26	78	1.677716	6.53$\times {10}^{-9}$
	$x_2$	1	3	0.02932	0	1	3	0.021768	0	27	81	2.064659	5.2$\times {10}^{-9}$
	$x_3$	1	3	0.033628	0	1	3	0.043117	0	27	82	2.812976	8.88$\times {10}^{-9}$
	$x_4$	1	3	0.029182	0	1	3	0.027671	0	27	83	2.747761	9.42$\times {10}^{-9}$
	$x_5$	1	3	0.05026	0	1	3	0.023297	0	27	84	1.791871	6.72$\times {10}^{-9}$
	$x_6$	1	3	0.029588	0	1	3	0.017539	0	27	82	2.440435	6.18$\times {10}^{-9}$
	$x_7$	1	3	0.031805	0	1	3	0.032294	0	24	73	1.648455	9.97$\times {10}^{-9}$
	$x_8$	1	3	0.038152	0	1	3	0.02327	0	27	87	1.710434	9.31$\times {10}^{-9}$
50,000	$x_1$	1	3	0.078573	0	-	-	-	-	27	81	2.742683	5.84$\times {10}^{-9}$
	$x_2$	1	3	0.103523	0	1	3	0.052539	0	28	84	3.509985	4.65$\times {10}^{-9}$
	$x_3$	1	3	0.096328	0	1	3	0.060336	0	28	85	3.07001	7.95$\times {10}^{-9}$
	$x_4$	1	3	0.087426	0	1	3	0.055083	0	28	86	2.848744	8.43$\times {10}^{-9}$
	$x_5$	1	3	0.094959	0	1	3	0.059838	0	28	87	3.496331	6.01$\times {10}^{-9}$
	$x_6$	1	3	0.092829	0	1	3	0.054967	0	28	85	3.266481	5.53$\times {10}^{-9}$
	$x_7$	1	3	0.092697	0	1	3	0.063267	0	25	76	2.269198	8.92$\times {10}^{-9}$
	$x_8$	1	3	0.096316	0	1	3	0.074379	0	28	90	2.783691	8.33$\times {10}^{-9}$
100,000	$x_1$	1	3	0.150145	0	-	-	-	-	27	81	4.25115	8.26$\times {10}^{-9}$
	$x_2$	1	3	0.1847	0	1	3	0.084738	0	28	84	4.937926	6.58$\times {10}^{-9}$
	$x_3$	1	3	0.174993	0	1	3	0.096997	0	29	88	4.278757	4.5$\times {10}^{-9}$
	$x_4$	1	3	0.248637	0	1	3	0.124909	0	29	89	4.49134	4.77$\times {10}^{-9}$
	$x_5$	1	3	0.178261	0	1	3	0.126066	0	28	87	4.322899	8.5$\times {10}^{-9}$
	$x_6$	1	3	0.155795	0	1	3	0.125207	0	28	85	4.35602	7.81$\times {10}^{-9}$
	$x_7$	1	3	0.153226	0	1	3	0.120531	0	26	79	4.062214	5.04$\times {10}^{-9}$
	$x_8$	1	3	0.182843	0	1	3	0.288392	0	29	93	4.299852	4.71$\times {10}^{-9}$

Table 5. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 5			SMDFP				CGH				GHCGP
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	1	4	0.004742	0	1	3	0.095815	0	15	61	0.019106	5.85$\times {10}^{-9}$
	$x_2$	1	10	0.006129	0	1	3	0.004263	0	1	3	0.004059	0
	$x_3$	1	14	0.007935	0	1	7	0.004939	0	1	3	0.004083	0
	$x_4$	1	14	0.007325	0	1	12	0.006223	0	1	3	0.004035	0
	$x_5$	1	14	0.007355	0	1	14	0.006378	0	1	3	0.003865	0
	$x_6$	1	3	0.004434	0	1	3	0.004388	0	15	61	0.018663	3.98$\times {10}^{-9}$
	$x_7$	1	3	0.004	0	1	3	0.004763	0	14	57	0.017273	4.93$\times {10}^{-9}$
	$x_8$	1	14	0.007555	0	1	14	0.006207	0	1	3	0.005359	0
5000	$x_1$	1	4	0.037256	0	1	3	0.030271	0	16	65	0.675961	2.62$\times {10}^{-9}$
	$x_2$	1	10	0.082444	0	1	3	0.0317	0	1	3	0.022237	0
	$x_3$	1	14	0.084766	0	1	7	0.071499	0	1	3	0.022972	0
	$x_4$	1	14	0.10313	0	1	12	0.104274	0	1	3	0.026511	0
	$x_5$	1	3	0.031836	0	1	14	0.106067	0	1	3	0.048799	0
	$x_6$	1	3	0.034784	0	1	3	0.025469	0	15	61	0.887118	8.9$\times {10}^{-9}$
	$x_7$	1	3	0.049976	0	1	3	0.030696	0	15	61	1.163482	2.2$\times {10}^{-9}$
	$x_8$	1	3	0.039773	0	1	14	0.100821	0	1	3	0.025777	0
10,000	$x_1$	1	4	0.054014	0	1	3	0.397306	0	16	65	1.078513	3.7$\times {10}^{-9}$
	$x_2$	1	10	0.099402	0	1	3	0.400362	0	1	3	0.029786	0
	$x_3$	1	14	0.133006	0	1	7	0.096216	0	1	3	0.042265	0
	$x_4$	1	14	0.114411	0	1	12	0.148145	0	1	3	0.040303	0
	$x_5$	1	3	0.033535	0	1	14	0.248653	0	1	3	0.031149	0
	$x_6$	1	3	0.030994	0	1	3	0.24238	0	16	65	1.292146	2.52$\times {10}^{-9}$
	$x_7$	1	3	0.026189	0	1	3	0.059157	0	15	61	1.200833	3.12$\times {10}^{-9}$
	$x_8$	1	3	0.02614	0	1	14	0.139992	0	1	3	0.043985	0
50,000	$x_1$	1	4	0.071046	0	1	3	0.099884	0	16	65	1.572604	8.28$\times {10}^{-9}$
	$x_2$	1	10	0.169775	0	1	3	0.083629	0	1	3	0.090689	0
	$x_3$	1	14	0.227858	0	1	7	0.187958	0	1	3	0.099092	0
	$x_4$	1	3	0.081543	0	1	12	0.510994	0	1	3	0.3273	0
	$x_5$	1	3	0.065031	0	1	14	0.193226	0	1	3	0.067268	0
	$x_6$	1	3	0.094322	0	1	3	0.077699	0	16	65	3.255643	5.63$\times {10}^{-9}$
	$x_7$	1	3	0.060192	0	1	3	0.06505	0	15	61	2.191639	6.97$\times {10}^{-9}$
	$x_8$	1	3	0.059951	0	1	14	0.498453	0	1	3	0.136817	0
100,000	$x_1$	1	4	0.136362	0	1	3	0.112411	0	17	69	3.476377	2.34$\times {10}^{-9}$
	$x_2$	1	10	0.33991	0	1	3	0.484194	0	1	3	0.116341	0
	$x_3$	1	3	0.120604	0	1	7	0.237996	0	1	3	0.10336	0
	$x_4$	1	3	0.123234	0	1	12	0.323803	0	1	3	0.299915	0
	$x_5$	1	3	0.105494	0	1	14	0.291497	0	1	3	0.107072	0
	$x_6$	1	3	0.10725	0	1	3	0.1356	0	16	65	2.42926	7.96$\times {10}^{-9}$
	$x_7$	1	3	0.095151	0	1	3	0.412831	0	15	61	1.704192	9.85$\times {10}^{-9}$
	$x_8$	1	3	0.123426	0	1	14	0.293479	0	1	3	0.084475	0

Table 6. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 6			SMDFP				CGHM				GHCGPM
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	28	365	0.177863	6.4$\times {10}^{-9}$	101	1314	0.509568	8.63$\times {10}^{-9}$	33	67	0.034528	8.84$\times {10}^{-9}$
	$x_2$	30	391	0.18942	5.21$\times {10}^{-9}$	101	1314	0.390828	9.95$\times {10}^{-9}$	35	71	0.036322	8.9$\times {10}^{-9}$
	$x_3$	31	404	0.193811	6.75$\times {10}^{-9}$	101	1314	0.412585	9.85$\times {10}^{-9}$	37	75	0.037483	6.28$\times {10}^{-9}$
	$x_4$	33	430	0.212529	7.34$\times {10}^{-9}$	100	1301	0.433422	9.8$\times {10}^{-9}$	39	79	0.039543	8.22$\times {10}^{-9}$
	$x_5$	36	469	0.229279	5.1$\times {10}^{-9}$	93	1210	0.365524	8.57$\times {10}^{-9}$	42	85	0.043653	7.71$\times {10}^{-9}$
	$x_6$	27	352	0.174778	4.76$\times {10}^{-9}$	99	1288	0.390179	9.68$\times {10}^{-9}$	32	65	0.03258	5.96$\times {10}^{-9}$
	$x_7$	24	313	0.161837	7.74$\times {10}^{-9}$	94	1223	0.368178	8.53$\times {10}^{-9}$	29	59	0.029921	6.68$\times {10}^{-9}$
	$x_8$	37	482	0.24653	7.75$\times {10}^{-9}$	3	40	0.014419	0	44	89	0.045735	6.28$\times {10}^{-9}$
5000	$x_1$	29	378	2.980886	6.05$\times {10}^{-9}$	105	1366	16.49603	8.52$\times {10}^{-9}$	34	69	2.016212	9.63$\times {10}^{-9}$
	$x_2$	31	404	3.319602	4.92$\times {10}^{-9}$	105	1366	9.604319	9.83$\times {10}^{-9}$	36	73	1.871193	9.68$\times {10}^{-9}$
	$x_3$	32	417	2.993108	6.36$\times {10}^{-9}$	105	1366	6.839324	9.74$\times {10}^{-9}$	38	77	2.428632	6.81$\times {10}^{-9}$
	$x_4$	34	443	2.798318	6.89$\times {10}^{-9}$	104	1353	4.096109	9.74$\times {10}^{-9}$	40	81	3.588929	8.89$\times {10}^{-9}$
	$x_5$	37	482	2.724222	4.76$\times {10}^{-9}$	97	1262	2.361667	9.43$\times {10}^{-9}$	43	87	3.421294	8.29$\times {10}^{-9}$
	$x_6$	28	365	1.821698	4.51$\times {10}^{-9}$	103	1340	2.711408	9.55$\times {10}^{-9}$	33	67	2.189047	6.5$\times {10}^{-9}$
	$x_7$	25	326	1.464441	7.35$\times {10}^{-9}$	98	1275	2.886032	8.4$\times {10}^{-9}$	30	61	1.821143	7.3$\times {10}^{-9}$
	$x_8$	38	495	1.908881	7.2$\times {10}^{-9}$	3	40	0.079459	0	45	91	2.789199	6.72$\times {10}^{-9}$
10,000	$x_1$	29	378	1.898784	8.53$\times {10}^{-9}$	106	1379	4.306217	9.8$\times {10}^{-9}$	35	71	2.232917	6.79$\times {10}^{-9}$
	$x_2$	31	404	2.069526	6.93$\times {10}^{-9}$	107	1392	4.291552	9.18$\times {10}^{-9}$	37	75	2.195953	6.82$\times {10}^{-9}$
	$x_3$	32	417	1.831673	8.96$\times {10}^{-9}$	107	1392	4.323227	9.1$\times {10}^{-9}$	38	77	3.49647	9.6$\times {10}^{-9}$
	$x_4$	34	443	1.879557	9.69$\times {10}^{-9}$	106	1379	3.935484	9.1$\times {10}^{-9}$	41	83	2.109302	6.26$\times {10}^{-9}$
	$x_5$	37	482	2.073277	6.69$\times {10}^{-9}$	99	1288	3.094513	8.92$\times {10}^{-9}$	44	89	2.172212	5.83$\times {10}^{-9}$
	$x_6$	28	365	1.65292	6.35$\times {10}^{-9}$	105	1366	3.4379	8.91$\times {10}^{-9}$	33	67	1.488057	9.17$\times {10}^{-9}$
	$x_7$	26	339	1.462072	4.51$\times {10}^{-9}$	99	1288	3.260719	9.66$\times {10}^{-9}$	31	63	2.113036	5.15$\times {10}^{-9}$
	$x_8$	39	508	2.136944	4.4$\times {10}^{-9}$	3	40	0.098955	0	45	91	2.322794	9.46$\times {10}^{-9}$
50,000	$x_1$	30	391	5.510234	8.28$\times {10}^{-9}$	110	1431	12.02104	9.53$\times {10}^{-9}$	36	73	2.310523	7.57$\times {10}^{-9}$
	$x_2$	32	417	5.422092	6.72$\times {10}^{-9}$	111	1444	11.20052	8.93$\times {10}^{-9}$	38	77	2.429677	7.6$\times {10}^{-9}$
	$x_3$	33	430	5.211846	8.69$\times {10}^{-9}$	111	1444	10.38166	8.85$\times {10}^{-9}$	40	81	2.63147	5.35$\times {10}^{-9}$
	$x_4$	35	456	5.418886	9.4$\times {10}^{-9}$	110	1431	9.864932	8.86$\times {10}^{-9}$	42	85	2.592365	6.97$\times {10}^{-9}$
	$x_5$	38	495	5.911243	6.48$\times {10}^{-9}$	103	1340	9.243294	8.77$\times {10}^{-9}$	45	91	2.887271	6.5$\times {10}^{-9}$
	$x_6$	29	378	4.547813	6.16$\times {10}^{-9}$	109	1418	9.68457	8.67$\times {10}^{-9}$	35	71	3.069208	5.11$\times {10}^{-9}$
	$x_7$	27	352	4.509685	4.38$\times {10}^{-9}$	103	1340	8.983611	9.39$\times {10}^{-9}$	32	65	2.150055	5.74$\times {10}^{-9}$
	$x_8$	39	508	6.3106	9.8$\times {10}^{-9}$	3	40	0.315881	0	47	95	3.4158	$5.26\times {10}^{-9}$
100,000	$x_1$	31	404	9.124879	5.09$\times {10}^{-9}$	112	1457	19.99888	8.88$\times {10}^{-9}$	37	75	3.532723	5.35$\times {10}^{-9}$
	$x_2$	32	417	9.267631	9.5$\times {10}^{-9}$	113	1470	18.60411	8.32$\times {10}^{-9}$	39	79	3.615499	5.37$\times {10}^{-9}$
	$x_3$	34	443	9.769236	5.34$\times {10}^{-9}$	113	1470	19.53358	8.25$\times {10}^{-9}$	40	81	3.712092	7.56$\times {10}^{-9}$
	$x_4$	36	469	10.3297	5.78$\times {10}^{-9}$	112	1457	21.29243	8.25$\times {10}^{-9}$	42	85	4.354342	9.86$\times {10}^{-9}$
	$x_5$	38	495	10.86344	9.16$\times {10}^{-9}$	105	1366	20.03786	8.18$\times {10}^{-9}$	45	91	4.165578	9.18$\times {10}^{-9}$
	$x_6$	29	378	8.410524	8.71$\times {10}^{-9}$	110	1431	18.72643	9.95$\times {10}^{-9}$	35	71	3.300663	7.23$\times {10}^{-9}$
	$x_7$	27	352	7.737803	6.19$\times {10}^{-9}$	105	1366	16.81034	8.76$\times {10}^{-9}$	32	65	3.313093	8.12$\times {10}^{-9}$
	$x_8$	40	521	11.275	6.03$\times {10}^{-9}$	3	40	0.561181	0	47	95	4.430573	7.44$\times {10}^{-9}$

Table 7. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 7			SMDFP				CGH				GHCGP
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	1	3	0.004846	0	108	1405	0.349376	8.21$\times {10}^{-9}$	32	65	0.030379	5.96$\times {10}^{-9}$
	$x_2$	1	3	0.004706	0	119	1548	0.356497	9.04$\times {10}^{-9}$	32	65	0.030191	6.4$\times {10}^{-9}$
	$x_3$	1	3	0.005136	0	-	-	-	-	29	59	0.028313	8.3$\times {10}^{-9}$
	$x_4$	1	3	0.0051	0	1	3	0.003102	0	31	64	0.028523	9.58$\times {10}^{-9}$
	$x_5$	1	3	0.004344	0	-	-	-	-	32	65	0.030716	6.9$\times {10}^{-9}$
	$x_6$	1	3	0.00465	0	103	1340	0.339387	8.52$\times {10}^{-9}$	31	63	0.028804	6.97$\times {10}^{-9}$
	$x_7$	1	3	0.004371	0	95	1236	0.277541	8.16$\times {10}^{-9}$	29	59	0.027149	5.88$\times {10}^{-9}$
	$x_8$	1	3	0.005142	0	1	3	0.004269	0	35	74	0.03332	6.36$\times {10}^{-9}$
5000	$x_1$	1	3	0.020114	0	111	1444	4.909827	9.82$\times {10}^{-9}$	33	67	1.929645	6.66$\times {10}^{-9}$
	$x_2$	1	3	0.013025	0	123	1600	6.337627	8.77$\times {10}^{-9}$	33	67	2.086561	7.15$\times {10}^{-9}$
	$x_3$	1	3	0.02639	0	-	-	-	-	30	61	1.893546	9.28$\times {10}^{-9}$
	$x_4$	1	3	0.016253	0	1	3	0.010931	0	33	68	1.390724	5.36$\times {10}^{-9}$
	$x_5$	1	3	0.026679	0	-	-	-	-	33	67	2.23439	7.72$\times {10}^{-9}$
	$x_6$	1	3	0.027297	0	107	1392	1.259304	8.27$\times {10}^{-9}$	32	65	1.953112	7.79$\times {10}^{-9}$
	$x_7$	1	3	0.031613	0	98	1275	1.840177	9.76$\times {10}^{-9}$	30	61	1.349774	6.57$\times {10}^{-9}$
	$x_8$	1	3	0.036752	0	1	3	0.009336	0	36	76	2.060581	7.11$\times {10}^{-9}$
10,000	$x_1$	1	3	0.031447	0	113	1470	3.136975	9.15$\times {10}^{-9}$	33	67	1.818738	9.42$\times {10}^{-9}$
	$x_2$	1	3	0.033583	0	125	1626	3.851012	8.18$\times {10}^{-9}$	34	69	1.954061	5.06$\times {10}^{-9}$
	$x_3$	1	3	0.024303	0	-	-	-	-	31	63	2.357244	6.56$\times {10}^{-9}$
	$x_4$	1	3	0.052224	0	1	3	0.011473	0	33	68	3.237999	7.57$\times {10}^{-9}$
	$x_5$	1	3	0.046682	0	-	-	-	-	34	69	1.586711	5.46$\times {10}^{-9}$
	$x_6$	1	3	0.046979	0	108	1405	2.024726	9.49$\times {10}^{-9}$	33	67	1.704647	5.51$\times {10}^{-9}$
	$x_7$	1	3	0.057642	0	100	1301	3.125811	9.09$\times {10}^{-9}$	30	61	1.669927	9.29$\times {10}^{-9}$
	$x_8$	1	3	0.025922	0	1	3	0.011375	0	37	78	2.068357	5.03$\times {10}^{-9}$
50,000	$x_1$	1	3	0.064974	0	117	1522	10.18713	8.89$\times {10}^{-9}$	35	71	2.75523	5.27$\times {10}^{-9}$
	$x_2$	1	3	0.061701	0	128	1665	10.09225	9.78$\times {10}^{-9}$	35	71	2.387113	5.66$\times {10}^{-9}$
	$x_3$	1	3	0.064387	0	-	-	-	-	32	65	2.055857	7.34$\times {10}^{-9}$
	$x_4$	1	3	0.067186	0	1	3	0.019284	0	34	70	1.99498	8.47$\times {10}^{-9}$
	$x_5$	1	3	0.089911	0	-	-	-	-	35	71	2.415085	6.1$\times {10}^{-9}$
	$x_6$	1	3	0.059953	0	112	1457	5.988195	9.21$\times {10}^{-9}$	34	69	2.627024	6.16$\times {10}^{-9}$
	$x_7$	1	3	0.059474	0	104	1353	7.026984	8.83$\times {10}^{-9}$	32	65	2.161008	5.19$\times {10}^{-9}$
	$x_8$	1	3	0.102486	0	1	3	0.028383	0	38	80	2.533343	5.62$\times {10}^{-9}$
100,000	$x_1$	1	3	0.150496	0	119	1548	18.04442	8.28$\times {10}^{-9}$	35	71	3.709317	7.45$\times {10}^{-9}$
	$x_2$	1	3	0.119297	0	130	1691	17.32583	9.11$\times {10}^{-9}$	35	71	4.106231	8$\times {10}^{-9}$
	$x_3$	1	3	0.120414	0	-	-	-	-	33	67	3.193129	5.19$\times {10}^{-9}$
	$x_4$	1	3	0.167358	0	1	3	0.055669	0	35	72	3.486973	5.99$\times {10}^{-9}$
	$x_5$	1	3	0.14736	0	-	-	-	-	35	71	3.104115	8.63$\times {10}^{-9}$
	$x_6$	1	3	0.123877	0	114	1483	12.50694	8.59$\times {10}^{-9}$	34	69	3.558606	8.71$\times {10}^{-9}$
	$x_7$	1	3	0.113269	0	106	1379	14.34735	8.22$\times {10}^{-9}$	32	65	3.108505	7.35$\times {10}^{-9}$
	$x_8$	1	3	0.111948	0	1	3	0.046828	0	38	80	3.532805	7.95$\times {10}^{-9}$

Table 8. Numerical comparison of the SMDFP, CGH [61], and GHCGP [62] methods.

Problem 8			SMDFP				CGH				GHCGP
DIMENSION	INITIAL POINT	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM	ITER	FEV	CPUT	NORM
1000	$x_1$	2	5	0.006257	0	7	26	0.064518	0	-	-	-	-
	$x_2$	1	3	0.004575	0	9	30	0.013856	0	50	108	0.060925	0
	$x_3$	2	5	0.005677	0	6	24	0.011035	0	-	-	-	-
	$x_4$	2	5	0.006564	0	131	1671	0.415251	8.78$\times {10}^{-9}$	-	-	-	-
	$x_5$	2	5	0.005898	0	7	26	0.012663	0	4	17	0.007869	0
	$x_6$	2	5	0.005661	0	7	26	0.013313	0	-	-	-	-
	$x_7$	2	5	0.006256	0	135	1679	0.398362	8.98$\times {10}^{-9}$	-	-	-	-
	$x_8$	3	7	0.006335	0	5	11	0.00916	0	-	-	-	-
5000	$x_1$	2	5	0.071744	0	7	26	0.278915	0	-	-	-	-
	$x_2$	1	3	0.032757	0	9	30	0.335638	0	19	46	0.321704	6.24$\times {10}^{-9}$
	$x_3$	2	5	0.074475	0	6	24	0.227703	0	-	-	-	-
	$x_4$	2	5	0.150227	0	139	1786	10.12413	9.92$\times {10}^{-9}$	17	42	0.140003	7.16$\times {10}^{-9}$
	$x_5$	2	5	0.054634	0	5	22	0.309578	0	5	20	0.054782	0
	$x_6$	2	5	0.102503	0	7	26	0.290641	0	-	-	-	-
	$x_7$	2	5	0.067849	0	129	1623	9.42968	8.65$\times {10}^{-9}$	-	-	-	-
	$x_8$	2	5	0.12588	0	4	9	0.179896	0	6	26	0.033651	0
10,000	$x_1$	2	5	0.109853	0	7	26	0.429911	0	-	-	-	-
	$x_2$	1	3	0.064967	0	9	30	0.433819	0	18	44	0.113456	6.24$\times {10}^{-9}$
	$x_3$	2	5	0.109943	0	6	24	0.249119	0	-	-	-	-
	$x_4$	2	5	0.101969	0	140	1799	11.30977	9.87$\times {10}^{-9}$	16	40	0.094243	7.16$\times {10}^{-9}$
	$x_5$	2	5	0.066711	0	5	22	0.339357	0	5	20	0.047766	0
	$x_6$	2	5	0.069338	0	7	26	0.247131	0	-	-	-	-
	$x_7$	2	5	0.086838	0	9	30	0.300432	0	-	-	-	-
	$x_8$	2	5	0.083051	0	4	9	0.115857	0	7	29	0.056413	0
50,000	$x_1$	2	5	0.131377	0	7	26	3.688616	0	-	-	-	-
	$x_2$	1	3	0.070502	0	9	30	0.623855	0	15	38	0.261414	9.98$\times {10}^{-9}$
	$x_3$	2	5	0.257994	0	6	24	0.577014	0	-	-	-	-
	$x_4$	2	5	0.15874	0	135	1734	17.44768	9.73$\times {10}^{-9}$	14	36	0.241642	5.73$\times {10}^{-9}$
	$x_5$	2	5	0.144073	0	5	22	0.37145	0	6	23	0.157215	0
	$x_6$	2	5	0.128614	0	7	26	0.426915	0	-	-	-	-
	$x_7$	2	5	0.152141	0	9	30	3.662605	0	-	-	-	-
	$x_8$	2	5	0.171881	0	5	22	3.374986	0	7	29	0.172393	0
100,000	$x_1$	2	5	0.383221	0	7	26	12.88737	0	-	-	-	-
	$x_2$	1	3	0.256944	0	9	30	0.769409	0	14	36	0.546488	9.98$\times {10}^{-9}$
	$x_3$	2	5	0.231476	0	6	24	0.52902	0	-	-	-	-
	$x_4$	2	5	0.327778	0	133	1708	22.37772	8.54$\times {10}^{-9}$	13	34	0.497945	5.73$\times {10}^{-9}$
	$x_5$	2	5	0.25519	0	5	22	0.330482	0	6	23	0.358825	0
	$x_6$	2	5	0.312419	0	7	26	0.487292	0	-	-	-	-
	$x_7$	2	5	0.228052	0	9	30	11.78943	0	-	-	-	-
	$x_8$	2	5	0.320283	0	5	22	7.510984	0	7	29	0.39418	0

In Table 1 and Table 2, the SMDFP algorithm has fewer iterations and function evaluations, shorter CPU times, and smaller errors compared to CGH [61] and GHCGP [62] methods. However, the SMDFP algorithm has more number of iterations, function evaluations, shorter CPU times, and smaller errors than the two compared methods in Table 3, Table 5 and Table 6. The CGH method failed for Problems 4 and 7, as shown in Table 4 and Table 7. Further from Table 8, it is noted that the GHCGP algorithm failed for Problem 8. It is concluded that the overall performance of the SMDFP algorithm is more efficient than both the CGH approach and GHCGP algorithm in terms of the number of iterations, function evaluations, CPU times, and error estimation, as shown in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8.

Next, the robustness of the SMDFP algorithm is illustrated by Figure 1, Figure 2 and Figure 3 showing the performance profiles based on Dolan and Moré procedure [69]. In Figure 1, the top curve showed the SMDFP algorithm with respect to the number of iterations, which leads the remaining curves of CGH [61] and GHCGP methods [62]. Similarly, in the case of function evaluations and CPU times, the SMDFP algorithm has better performance, as shown in Figure 2 and Figure 3, respectively. All of the above factors clearly showed that our proposed algorithm is leading and the best in all aspects, i.e., in terms of iterations, function evaluations, and CPU times.

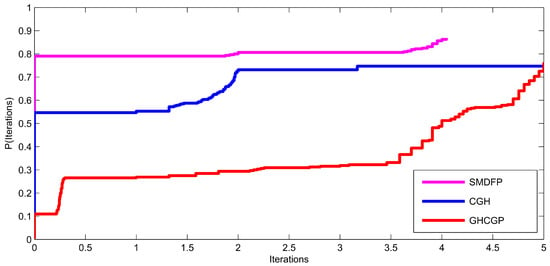
Figure 1. Performance of the SMDFP, CGH [61], and GHCGP [62] methods for the number of iterations.

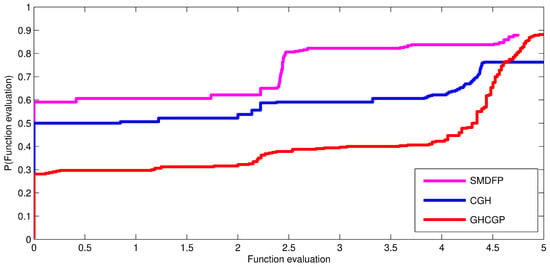
Figure 2. Performance of the SMDFP, CGH [61], and GHCGP [62] methods for the number of function evaluations.

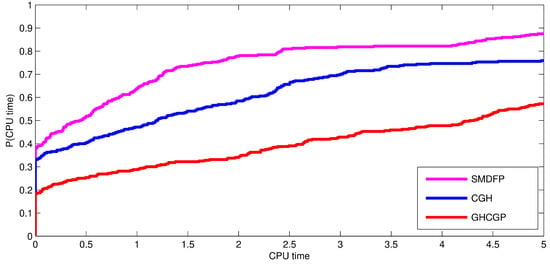
Figure 3. Performance of the SMDFP, CGH [61], and GHCGP [62] methods for the number of CPU time.

5. Applications

5.1. Image Restoration

This section describes techniques for reducing noise and recovering lost image resolutions. Its applications are in the field of medical imaging [70], astronomical imaging [71], file restoration [72], and image coding [73]. Let $x^{*}$ be the original sparse signal, and $t\in R^m$ be an observation satisfying

$$t=U{x}^{*},$$

(61)

where $U\in R^{m\times n}(m<<n)$ is a linear operator. This problem is used for finding solutions to the sparse ill-conditioned linear system of equations. According to Bruckstein et al. [74], a function containing a quadratic $\left(l_2\right)$ error term as well as a sparse $l_1$–regularization term is minimized as,

$$\underset{x}{min}\left\{\frac{1}{2}{∥t-Ux∥}_2^2+\beta {∥x∥}_1\right\},$$

(62)

where $x\in R^n$, and $\beta$ is a nonnegative balance parameter, ${\parallel x\parallel }_2$ denotes the Euclidean norm of x, and ${\parallel x\parallel }_1$ is the $l_1$–norm of x. Problem (62) is a convex unconstrained minimization problem commonly used in compressive sensing if the original signal is sparse or near to sparse on some orthogonal basis.

Many iterative techniques have been introduced in literature such as Figueiredo et al. [75], Hale et al. [76], Figueiredo et al. [77], Van Den Berg et al. [78], Beck et al. [79], and Hager et al. [80] for finding a solution to (62). The GPRS method has the following steps to present (62) as a quadratic problem.

Let $x\in {\mathbb{R}}^n$ be categorized into two different classes, namely, its positive and negative parts:

$$x=q-r,q\ge 0,r\ge 0,$$

(63)

where $q_i={\left(x_i\right)}_{+},r_i={\left(-x_i\right)}_{+}$ for all $i=1,2,\dots ,n$, and ${(.)}_{+}=max\{0,.\}.$ Since, by definition of ${\ell }_1$–norm, we have ${\parallel x\parallel }_1=e_n^{T}q+e_n^{T}r$, where $e_n={(1,1,\dots ,1)}^T\in R^n$. Thus, (62) can be written as:

$$\underset{q,r}{min}\frac{1}{2}{\parallel t-U(q-r)\parallel }_2^2+\beta e_n^{T}q+\beta e_n^{T}r,q\ge 0,r\ge 0,$$

(64)

which is a bound–constrained and quadratic problem. Moreover, following Figueiredo et al. [77], a standard form of problem (64) can be written as:

$$\underset{v}{min}\frac{1}{2}{v}^{T}Av+c^{T}v,\mathrm{such}\mathrm{that}v\ge 0,$$

(65)

where $v=\left(\begin{array}{c}q\hfill \\ r\hfill \end{array}\right),b=U^{T}t,c=\beta e_{2n}+\left(\begin{array}{c}-b\\ b\end{array}\right)$, and $A=\left(\begin{array}{cc}{U}^{T}U& -U^{T}U\\ -U^{T}U& U^{T}U\end{array}\right)$. Problem (65) is convex quadratic because A is a positive semi-definite matrix as proved by Xiao et al. [5]. He also transformed (65) into a linear variable inequality problem, which is equivalent to a linear complementarity problem. However, v is a solution to the linear complementarity problem if and only if it is a solution to the nonlinear equation

$$f\left(v\right)=min\{v,Av+c\}=0,$$

(66)

which is continuously monotone, as shown by Xiao et al. [5]. So, problem (66) can be solved using the SMDFP method.

5.2. Implementation

Table 9 shows the numerical comparison for four different methods, namely; SMDFP method, CGD method [45], PSGM method [81], and TPRP method [82] by applying on seven different images, namely, baby, COMSATS, fox, horse, Lena, and Thai-Culture.The mean of squared error (MSE) [45] between the blurred $x^{*}$ and restored x images is

$$\mathrm{MSE}=\frac{1}{n}{∥x^{*}-x∥}^2,$$

and the signal–to–ratio (SNR) [45] of the recovered images is

$$\mathrm{SNR}=20\times {\log }_{10}\left(\frac{\parallel x^{*}\parallel }{\parallel x-x^{*}\parallel }\right).$$

Table 9. Numerical comparison of SMDFP, CGD [45], PSGM [81], and TPRP [82] methods.

	SMDFP					CGD					PSGM					TPRP
Pictures	ITER	CPUT	MSE	SNR	SSIM	ITER	CPUT	MSE	SNR	SSIM	ITER	CPUT	MSE	SNR	SSIM	ITER	CPUT	MSE	SNR	SSIM
Baby	69	4.55	3.88$\times {10}^1$	22.79	0.92	713	42.19	4.46$\times {10}^1$	22.19	0.93	27	1.55	3.87$\times {10}^1$	22.8	0.93	317	1366.58	4.56$\times {10}^1$	22.09	0.92
COMSATS	14	0.64	1.83$\times {10}^2$	23.9	0.87	671	49.02	1.69$\times {10}^2$	24.24	0.86	23	1.88	1.52$\times {10}^2$	24.71	0.87	50	1020.66	1.87$\times {10}^2$	23.79	0.87
Fox	39	4.25	7.33$\times {10}^1$	24.45	0.84	474	62.83	7.45$\times {10}^1$	24.38	0.86	18	2.36	7.37$\times {10}^1$	24.42	0.84	58	228.41	7.76$\times {10}^1$	24.2	0.84
Horse	16	1.16	1.20$\times {10}^2$	19.52	0.81	645	44.06	1.06$\times {10}^2$	20.07	0.85	42	2.59	1.07$\times {10}^2$	20	0.83	109	248.86	1.10$\times {10}^2$	19.9	0.81
Lena	14	0.78	6.30$\times {10}^1$	22.88	0.84	491	34.63	6.05$\times {10}^1$	23.05	0.88	26	2.05	5.81$\times {10}^1$	23.23	0.87	101	1175.6	5.91$\times {10}^1$	23.16	0.84
Marwat	34	2.02	1.52$\times {10}^2$	20.43	0.81	856	58.33	1.53$\times {10}^2$	20.4	0.84	38	2.42	1.46$\times {10}^2$	20.61	0.82	472	707.05	1.61$\times {10}^2$	20.18	0.81
Thai fabric pattern in Phetchabun	12	0.97	2.46$\times {10}^2$	17.69	0.66	565	48.23	2.47$\times {10}^2$	17.67	0.7	22	1.84	2.38$\times {10}^2$	17.83	0.68	156	1445.32	2.31$\times {10}^2$	17.97	0.69

By both MSE and SNR, we measure the image restoration quality by taking $\rho =6$ and $\theta =0.0001$. We studied a compressive sensing situation in which the aim was to reconstruct a length-n sparse signal from m observations, where $m<<n$. We test a modest size signal with $n=211$, $m=29$, and the original has 26 randomly non-zero elements due to the PC’s storage restrictions. The random U is the Gaussian matrix created by the Matlab command $randn(m,n)$. The measurement t in this test involves noise,

$$t=U{x}^{*}+\varphi ,$$

(67)

where $\varphi$ is the Gaussian noise distributed as $N(0,{\sigma }^{2}I)$ with ${\sigma }^2={10}^{-4}$. We used $f\left(x\right)=\frac{1}{2}{∥t-Ux∥}_2^2+\beta {∥x∥}_1$ as the merit function, $x_0=U^{T}t$, $\beta$ is compelled to decrease as adopted in [75], and the iteration terminates if

$$\mathit{Tolerance}=\frac{∥f\left(x_k\right)-f\left(x_{k-1}\right)∥}{∥f\left(x_{k-1}\right)∥}<{10}^{-10}.$$

(68)

 All of the codes in this section are also executed on the same machine and software as described in Section 4. In summary, the performance of the SMDFP method is better than CGD [45], PSGM [81], and TPRP [82] methods for the number of iterations, CPU time, and recovered images SNR quality as clear from Table 9. Consequently, it can be seen from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 that the proposed method has restored all the problems with fewer iterations and CPU time.

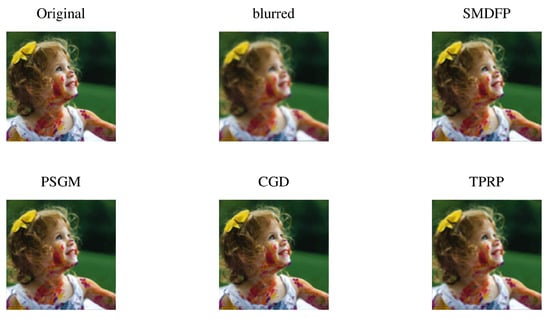
Figure 4. Comparison of the original image, blurred image, SMDFP image, CGD image, PSGM image, and TPRP image for the number of iterations, CPU time, MSE, and SNR.

Figure 5. Comparison of the original image, blurred image, SMDFP image, CGD image, PSGM image, and TPRP image for the number of iterations, CPU time, MSE, and SNR.

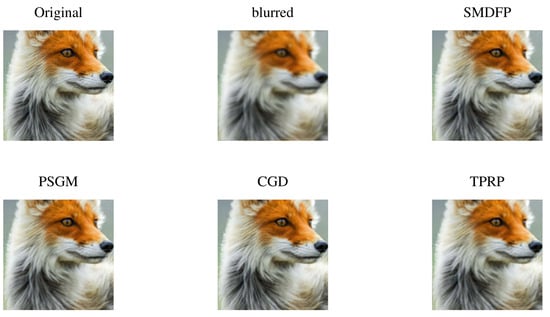
Figure 6. Comparison of the original image, blurred image, SMDFP image, CGD image, PSGM image, and TPRP image for the number of iterations, CPU time, MSE, and SNR.

Figure 7. Comparison of the original image, blurred image, SMDFP image, CGD image, PSGM image, and TPRP image for the number of iterations, CPU time, MSE, and SNR.

Figure 8. Comparison of the original image, blurred image, SMDFP image, CGD image, PSGM image, and TPRP image for the number of iterations, CPU time, MSE, and SNR.

Figure 9. Comparison of the original image, blurred image, SMDFP image, CGD image, PSGM image, and TPRP image for the number of iterations, CPU time, MSE, and SNR.

Figure 10. Comparison of the original image, blurred image, SMDFP image, CGD image, PSGM image, and TPRP image for the number of iterations, CPU time, MSE, and SNR.

6. Conclusions

This paper presents a one-parameter SMDFP method for solving a system of monotone nonlinear equations with convex constraints. We scaled one term of the DFP update formula and found the optimal value of the scaled parameter using the idea of measure function. Based on the new optimal value of the scaled parameter, we derived a modified search direction for the DFP algorithm. The proposed method is globally convergent using the monotonicity and Lipschitz continuous assumptions. The method’s robustness is demonstrated by solving large-scale monotone nonlinear equations and making comparisons with the related CGH and GHCGP methods. Lastly, the algorithm is successfully implemented for solving some image restoration problems. The proposed scale DFP direction can further be applied to solve unconstrained optimization problems, motion control of two coplanar joint robot manipulators, and many more problems.