Abstract
This study proposes a strategy for improving the thrust performance of fixed-wing UAV turbine engines from the perspective of aircraft/engine integration. In the UAV engine control process, the inlet distortion caused by the angle of attack change is taken into account, the inlet distortion index is calculated in real time by predicting the angle of attack, and the influence of the inlet distortion on the engine model is analyzed mechanically. Then, the pressure ratio command is adjusted according to the new compressor surge margin requirement caused by the inlet distortion to finally improve the engine thrust performance. To verify the effectiveness of the algorithm, an adaptive disturbance rejection controller is designed for the flight control of a fixed-wing UAV to complete the simulation of horizontal acceleration. The simulation results show that, with this strategy, the UAV turbofan engine can improve the turbofan engine thrust performance by more than 8% under the safety conditions.
Keywords:
unmanned aerial vehicle; aircraft/engine integration; thrust optimization; adaptive margin model; adaptive disturbance rejection control MSC:
37M10
1. Introduction
The unmanned aerial vehicle (UAV), as a rapidly developing aircraft technology, plays an important role in many fields [1,2,3], such as large-scale display activities, aerial photography entertainment, mapping and geological exploration, agricultural spraying, police patrol, electric power inspection, etc. [4]. UAV propulsion systems have a decisive influence on the performance, cost, and reliability of UAVs. With the continuous enrichment of application scenarios, different types of power units have been developed for different requirements of UAVs in terms of flight speed, flight altitude, maneuvering overload, landing and take-off methods, range, and economic indicators [5]. Most of the power units currently installed on advanced UAVs are turbofan engines, and this status quo will not change for a long time to come. Li conducted work related to the prediction of future UAV power development trends [6], summarized the overloaded advanced typical combat UAVs and the main parameters of power, and compared the payloads of several types of UAVs under development with those of manned fighter aircraft in service. The study shows that the development of large-thrust turbofan engines is one of the future unmanned fighter power development trends. Hu analyzed the requirements of various unmanned aircraft systems for propulsion systems and the impact of propulsion system technology on the performance of UAVs [7,8]. Chen analyzed the development requirements of different types of engines for UAVs and proposed the integrated design of the full authority digital engine control (FADEC) system of a vehicle/engine/propeller for optimal performance matching output [9]. In summary, the research on the improvement of the thrust performance of future UAV turbine engines has considerable value, and this part of the work is not abundant at present. Cheng [10] proposed a turbofan engine Turbine Inter Burner (TIB) supplemental combustion and thrust augmentation thermodynamic cycle scheme based on ultra-compact combustion UCC technology, increasing the engine unit thrust significantly. Dong [11] analyzed the effect of jet pre-cooling on the high- and low-pressure shaft torque, obtained the characteristics of the effect of jet pre-cooling on the control scheme, and also designed the relevant control scheme to adjust the nozzle and buck ratio limiting strategies, thus improving the engine speed performance. Sun [12] established a piecewise linear model of the turbofan engine and used a weighted prediction method to effectively estimate the thrust of the engine and track the set expected thrust to achieve maximum compensation for the thrust loss, and the simulation results showed that the whole thrust control system can ensure the safe operation of the engine and achieve effective thrust boost.
The existing related work lacks the ability to improve powertrain performance from an aircraft/engine integration perspective, and the integrated control of UAVs and engines can seek the best match of their performance. In the aircraft/engine integration research, the stability control technology of the turbo-fan engine is essential. The influence of inlet distortion on the performance and stability of turbine engines is first considered, which is a common phenomenon that occurs widely in turbo-fan engines; the geometric asymmetry of the inlet airflow channel of the compressor, the obstruction of the local inlet airflow by the leading edge of the compressor inlet when the aircraft is flying at a large angle of attack, and the uneven distribution of the temperature and density of the compressor inlet flow field by the missile trailing combustion airflow are the main reasons [13,14]. In order to solve the problem of the unmeasurable engine surge margin in super maneuvering flight, Wang [15] proposed a modeling method of the engine surge margin and verified that the above scheme can accurately control the engine surge margin at 11~13% by the numerical simulation of maneuvering flight with a large angle of attack, which ensures the stability and high efficiency of engine operation. Liu [16] concluded that inlet distortion is an important factor affecting engine stability. To meet the inlet distortion requirements, the engine design needs to make large concessions; in other words, the inlet distortion required for the surge margin greatly reduces the performance of the design point of the compression system. This reduction in margin translates directly into improved system capabilities.
Indeed, the current strategy, which considering flight control and engine control separately, is capable of achieving the optimal performance of each subsystem. However, the overall performance cannot be optimized since the change in engine operation caused by the angle of attack is not taken into account. A large margin of surge is usually given in the control in order to ensure the safety of the compressor operation, which sacrifices a certain engine performance. Inspired by the development of aero-engine stability control technology, this paper proposes a method for improving the thrust performance of future UAVs. This method incorporates engine stability assessment into the engine control process, calculates the requirement of the compressor surge margin associated with the engine stability influence factor in real time, and evaluates the compressor stability, allowing the control system to minimize the surge margin to improve the engine performance and thus enhance the engine thrust performance.
2. Dynamical Modeling and Problem Description
In order to evaluate the UAV thrust performance improvement, UAV flight simulation under certain flight profiles is required, so the UAV dynamics model is first established.
2.1. UAV Dynamics Modeling
2.1.1. UAV Modeling Assumptions
Considering that the mass of the turbine engine-powered UAV is time-varying during flight and its structure is strong and elastic, there are also centrifugal and Gauche accelerations; thus, the aerodynamic forces acting on the UAV are affected by many variables such as its aerodynamic layout, structural elasticity, and flight state, which sometimes cannot be modeled mathematically accurately. Therefore, the primary factors should be considered when modeling the UAV, ignoring the secondary factors. Figure 1 shows a diagram of the coordinate system of the UAV body. The following assumptions need to be considered in the mathematical modeling of scaled-down UAVs.
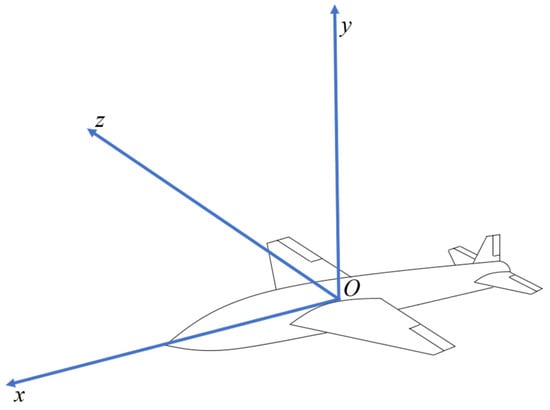
Figure 1.
Diagram of the UAV body coordinate system.
- The mass of the UAV does not change during flight for a short period of time.
- The UAV is an ideal rigid body, and the effects of aircraft elasticity are ignored.
- The UAV is affected only by the acceleration of gravity, and the curvature of the Earth is neglected.
- Since the UAV is symmetric about the plane, and .
- The change in the aircraft center of mass with fuel is neglected during the UAV.
2.1.2. Dynamics Equations
The dynamics equations for the motion of the center of mass of the UAV are established as follows.
where m is the UAV mass, V is the UAV velocity, X,Y,Z are the drag lift and lateral force, respectively, P is the UAV thrust, α, β are the angle of attack and sideslip angle, θ is the flight path angle, γV is the speed tilt angle, and ψV is the trajectory deflection angle.
The dynamics equations of the UAV rotational motion are as follows
where are the angular velocities of rotation of the UAV relative to the ground coordinate system, are the components of the moments of all external forces acting on the UAV on the center of mass in the UAV body coordinate system, and are inertia tensor elements.
2.1.3. Kinematic Equations
In the modeling, it is assumed that the UAV is a rigid body and that the six-degrees-of-freedom motion of the UAV is the displacement and rotation around the center of mass. With the help of the transformation matrix of the ground inertial system and the aircraft dynamic system, the kinematic equations are obtained as follows [17,18].
where are the center-of-mass position components of the man-machine, is the pitch angle, and is the roll angle.
2.2. UAV Turbofan Engine Modeling
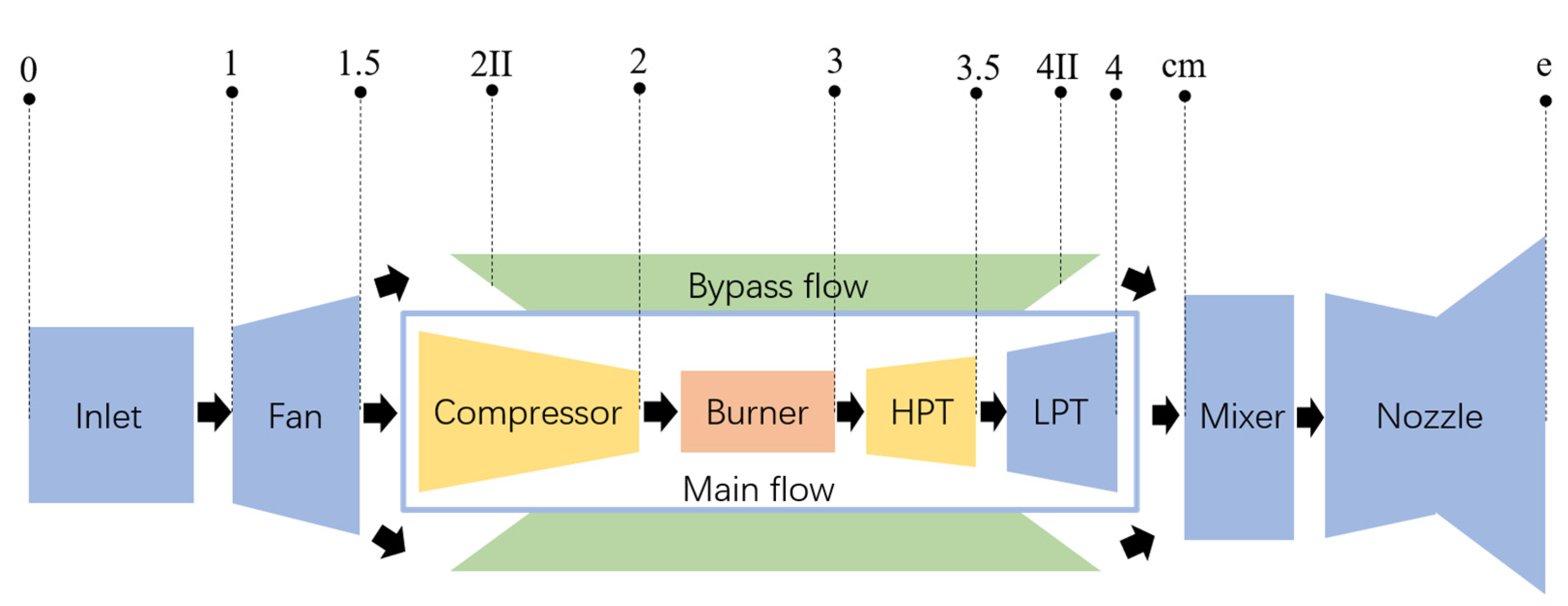
The object of this study is a twin-shaft small-culvert-ratio mixed-exhaust turbofan engine containing no afterburner. The main components of the engine include the inlet, fan, compressor, burner, high-pressure turbine, low-pressure turbine, bypass, mixer, and nozzle; its structural schematic diagram is shown in Figure 2.
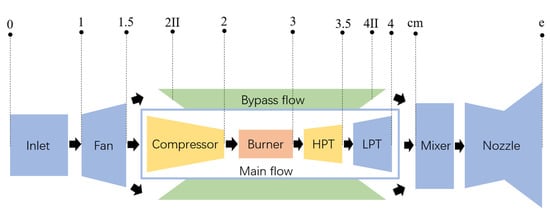
Figure 2.
UAV turbofan engine structure schematic.
The aerodynamic and thermal processes during the operation of an aero-engine are very complex, and, when modeling them, the real physical processes need to be suitably simplified, and the following assumptions are usually made when modeling at the component level [19].
- Ignore the effect of the Reynolds number variation on the characteristics of the engine components; ignore the effect of atmospheric humidity on the parameters of the thermodynamic properties of the gas; the effect of rotor inertia is considered.
- The flow of air in the engine is treated as quasi one-dimensional flow, i.e., the airflow parameters are considered to be the same in the same cross-section of the engine.
The idea of component-level modeling is to first establish each component sub-model; then, build a non-linear system of equations based on the aerodynamic thermodynamic laws governing the gas flow process, combined with the assumptions of flow continuity and energy balance; finally, determine the engine operating state by solving the system of common operating equations to construct the engine model.
When a small-culvert-ratio turbofan engine enters into quasi-steady-state operation, each component needs to satisfy a series of common operating conditions in mechanical and aerodynamic aspects, including flow continuity and power balance. It is generally accepted that the inlet and outlet sections of each component meet the flow continuity condition and the two rotors meet the power balance condition, i.e., the power from the high-pressure turbine is balanced with the power consumed by the fan and booster stage, and the power from the low-pressure turbine is balanced with the power consumed by the high-pressure compressor. The dynamic engine simulation process also requires an iterative solution of the common set of operating equations, unlike the steady-state simulation, where the flow continuity balance condition is still satisfied, but the power balance condition is no longer satisfied. The high- and low-pressure rotor speeds are no longer used as initial guess variables but are determined by the speed and acceleration at the previous moment, i.e., the power balance conditions are transformed into the rotor dynamics equations.
2.2.1. Inlet
As the inlet section of the engine, the calculation of the relevant parameters of the air inlet tract is related to the height of the engine. The main parameters of the inlet cross-section—atmospheric pressure in and atmospheric temperature in at different altitudes (H km)—can be obtained by the atmoscoesa function in MATLAB. The inlet pressure , temperature , and flight speed of the engine are calculated as follows.
in the above equation, is the Mach number; is the total pressure recovery factor, where ; k is the adiabatic index; and is the local speed of sound.
2.2.2. Fan
Assuming the same main and bypass flow pressure ratios and efficiencies of the fan, we have:
where , represent the pressure ratios of the main and bypass flow and ,. represent the overall efficiencies of the main and bypass flow.
The exit section airflow parameters of the turbofan engine fan are calculated as follows.
in the above equation, , where ; is the total air flow through the fan; is the converted air flow; is the fan adjustable parameter; is the converted speed at different temperatures. The last two equations in Formula (6) show that the specific values of and are obtained by interpolating the variables associated with each of them.
2.2.3. Compressor
Similar to the fan characteristics, the generic characteristics of a compressor are calculated as follows.
where is the converted air flow; is the compressor adjustable parameter; is the converted speed of the compressor.
If the fan control law is known, then the mathematical relationship between the conversion speed and the rotational speed , and we can obtain and . Then, from , and , we can calculate and , where the relevant parameters for the outlet section of the compressor are calculated as follows:
2.2.4. Burner
The burner characteristics are generally given by the component characteristics test; in general, the burner efficiency and the total pressure recovery coefficient are the main characteristics parameters of the combustion chamber and are calculated as follows.
in the above equation, is the residual gas coefficient of the gas mixture; is the gas flow rate; is the heating ratio.
The is calculated from , and (the burner characteristics), and then the is calculated from the energy balance (by iteration). The energy balance equation is calculated as follows.
in the formula above, is the fuel temperature, and , , and denote the enthalpy per unit (kg) of mass of air, fuel, and fuel after vaporization, respectively.
In summary, the combustion chamber output parameters can be calculated as follows.
2.2.5. High-Pressure Turbine (HPT) and Low-Pressure Turbine (LPT)
The efficiencies of the high-pressure turbine , the gas flow rate , and the conversion speed are related to the expansion ratio , i.e., its operating state can be determined from and . The mathematical representation of and , obtained from the characteristic curve diagram, is as follows.
where , and is the engine turbine inlet section temperature in the design condition.
In summary, the high-pressure turbine outlet parameters are calculated as follows.
in the above equation, , where is the adiabatic coefficient of fuel oil after vaporization.
The structures of the high-pressure turbine and the low-pressure turbine are the same, as are the models, and the parameters of the low-pressure turbine outlet section can be obtained.
in the above equation, , and is the thermal insulation index. , , and correspond to , , representing the characteristics of the low-pressure turbine.
2.2.6. Mixer
The gas flow rate contained in the mixing chamber is calculated as follows:
Equivalently, the above equation is transformed as:
where , is the gas constant, , and is the cross-sectional area of the inner culvert (main flow) into the mixing room.
Additionally, since can be expressed as
the above equation leads to , which, in turn, gives
Again, the main flow and bypass flow pressures are equal, i.e., , so we have
So, there is
where indicates the area of the bypass duct at the entrance to the mixing room.
The mixer outlet pressure is calculated as follows.
where is the total pressure recovery coefficient of the mixer.
can be calculated from , and then and can be calculated from the pneumatic function calculation formula. In summary, the gas flow and temperature at the outlet section of the mixing chamber are calculated as follows.
where , , and .
2.2.7. Nozzle
According to the different relationship between the ratio of the total pressure of the nozzle outlet and the total atmospheric pressure and the nozzle pressure ratio , the engine nozzle can be divided into subcritical, critical, and supercritical operating conditions.
When , the nozzle is operating in a sub-critical condition. At this point, the calculation of and are as follows.
At this point, the exit section of the nozzle airflow velocity is less than the speed of sound, so < 1. The gas in the nozzle is completely expanded; at this time, the nozzle exit section pressure and the external atmospheric pressure are the same, that is, .
From and , we have
from , we obtain and find .
When , the nozzle works in the critical state; at this time, = 1 and = l. At this time, the gas in the nozzle is completely expanded, and the nozzle outlet section pressure and the external atmospheric pressure are the same, that is, .
When , the nozzle operation is in the supercritical state; at this time, = 1 and = l. At this time, the gas in the nozzle is not fully expanded, and the nozzle outlet cross-section pressure is greater than the atmospheric pressure, that is, .
Therefore, its operating condition can be determined from the nozzle parameters (), and the parameters related to the exit section of the tail nozzle are calculated as follows.
In the above equation, is the nozzle outlet flow rate, is the exhaust velocity, is the critical speed of sound, and is the nozzle flow loss coefficient number.
2.3. Problem Description
As mentioned in the introduction, the aim of this paper is to improve the thrust performance of the UAV by reducing the surge margin reserve of the turbine engine. The real-time estimation of the surge margin is caused by many factors, including inlet distortion, and calculations of the proper pressure ratio of the fan and the compressor are carried out to satisfy the surge margin requirements through multivariable control.
From a mathematical point of view, the thrust lifting problem under this line of thought can be described as the optimization problem of engine thrust regulation control.
where is the current state of the engine output thrust; in this optimization problem, the engine output thrust considered is related to the compressor pressurization ratio , the compressor converted air flow rate , the fan speed , the ambient altitude , and the flight Mach number . and represent the current surge margin and the current allowable surge margin, respectively. and are the turbine front temperature and the threshold of the turbine front temperature protection, and represent the current total compressor outlet pressure and the overpressure protection threshold. is described as
The problem is constrained by three inequalities: the first is the surge margin of the engine, that is, the compressor does not surge; the second is, in the optimization process, the turbine front temperature cannot exceed the overtemperature protection temperature while the engine is working; the third inequality constraint is that the total compressor outlet pressure of the engine cannot exceed the limit pressure.
In this optimization problem, the independent variables are ,,, , and , where and are environment variables that change with the motion of the vehicle and the surrounding environment. The value of can be determined by , so the independent variables that can be adjusted in this optimization problem are , , and the dependent variable is the thrust .
According to the engine model established in Section 2.2, for a known compressor operating state, we can obtain a set of engine operating parameters. In the engine control, , as one of the main parameters controlling the compressor operating catch state, can directly affect the working state of the compressor. The physical principle is to change the deflection angle of the guide vane and increase the work carried out by the compressor on the airflow such that the pressure of the airflow at the exit of the compressor is greater. The gas mixture entering the burner carries more energy, so it can increase the overall reasoning performance; however, if is too large, it will lead to a reduction in , that is, it will lead to the occurrence of the gas turbulence of the compressor, so another control parameter should be adjusted at the same time to limit the appearance of dangerous situations.
3. Major Studies
3.1. Thrust Optimization Based on the Adaptive Margin Model
In the introduction, the idea of thrust promotion is introduced, which is to reduce the compressor surge margin reserve and increase the propulsion performance under the premise of ensuring the safe operation of the engine; a detailed description of this strategy is provided below.
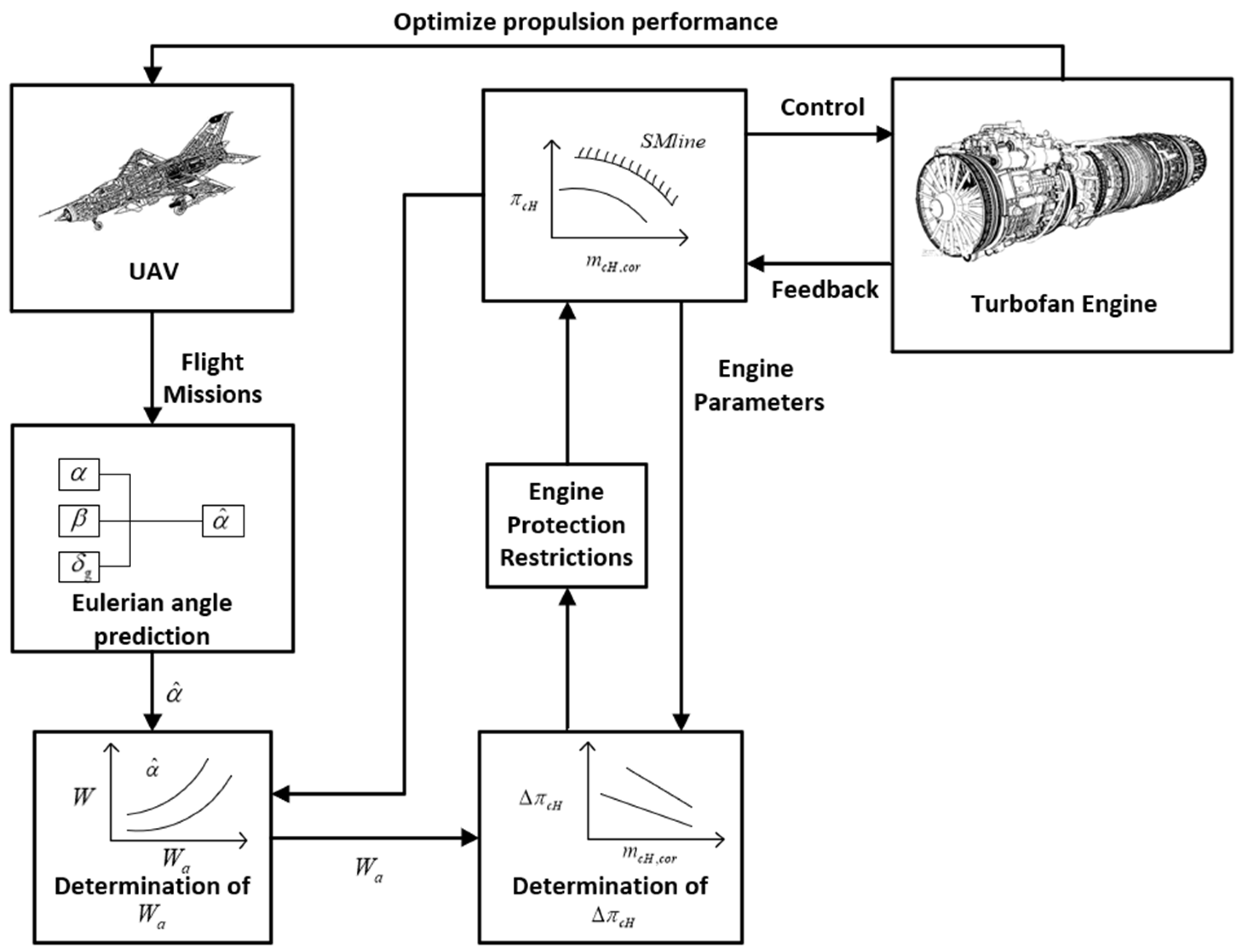
As shown in Figure 3, the first step is to predict the angle of attack in a short period of time in the future by building a dynamic model of the UAV, which is combined with the current mission; then, the distortion index is determined by the current compressor gas conversion flow , and the available pressure ratio increment is determined by the distortion index and the current surge margin value of the engine; then, the final pressure ratio correction plan is given according to the protection limit of the turbine engine, and the instruction correction quantity is transmitted to the controller to achieve the goal of thrust lifting.
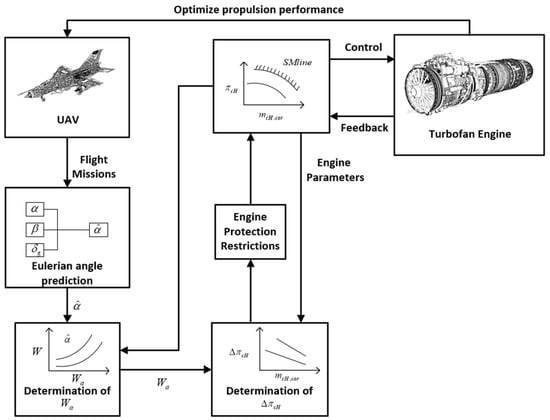
Figure 3.
Optimal thrust strategy schematic diagram based on the adaptive margin model.
3.1.1. Angle of Attack Prediction for UAV
Based on the symmetry and small perturbation approximations theory [20], the UAV dynamic model is expanded on the point of longitudinal motion equilibrium and rewritten as perturbation equation. The following equations of motion for the longitudinal disturbance of the UAV are given.
where denote the disturbance force due to the disturbance introduced during the small disturbance linearization process and the disturbance torque . denotes the elevator deflection angle. … are known as the power factors, which characterize the dynamics of the UAV. The specific expressions are shown in Table 1.

Table 1.
The symbol of the dynamic coefficient and its expression.
In the table above, represent the partial derivative of parameters such as the aerodynamic torque and thrust with respect to the parameter .
In the longitudinal motion of UAV, the outputs of the airframe are , while the input is . If there is external interference, the input is , , and . In order to obtain the transfer function of UAV short-period longitudinal perturbation motion, the long-period output is first ignored, and the Equation (40) are transformed by Laplace transform as
Then, the transfer function from the elevator to the angle of attack is obtained as
So far, we have obtained the transfer function from the elevator deflection command to the change in the angle of attack in the short-period longitudinal motion of the UAV, by which the current flight parameters of the UAV and the elevator command can be combined, and the angle of attack can be predicted in a short time.
3.1.2. Engine Model under the Influence of Inlet Distortion
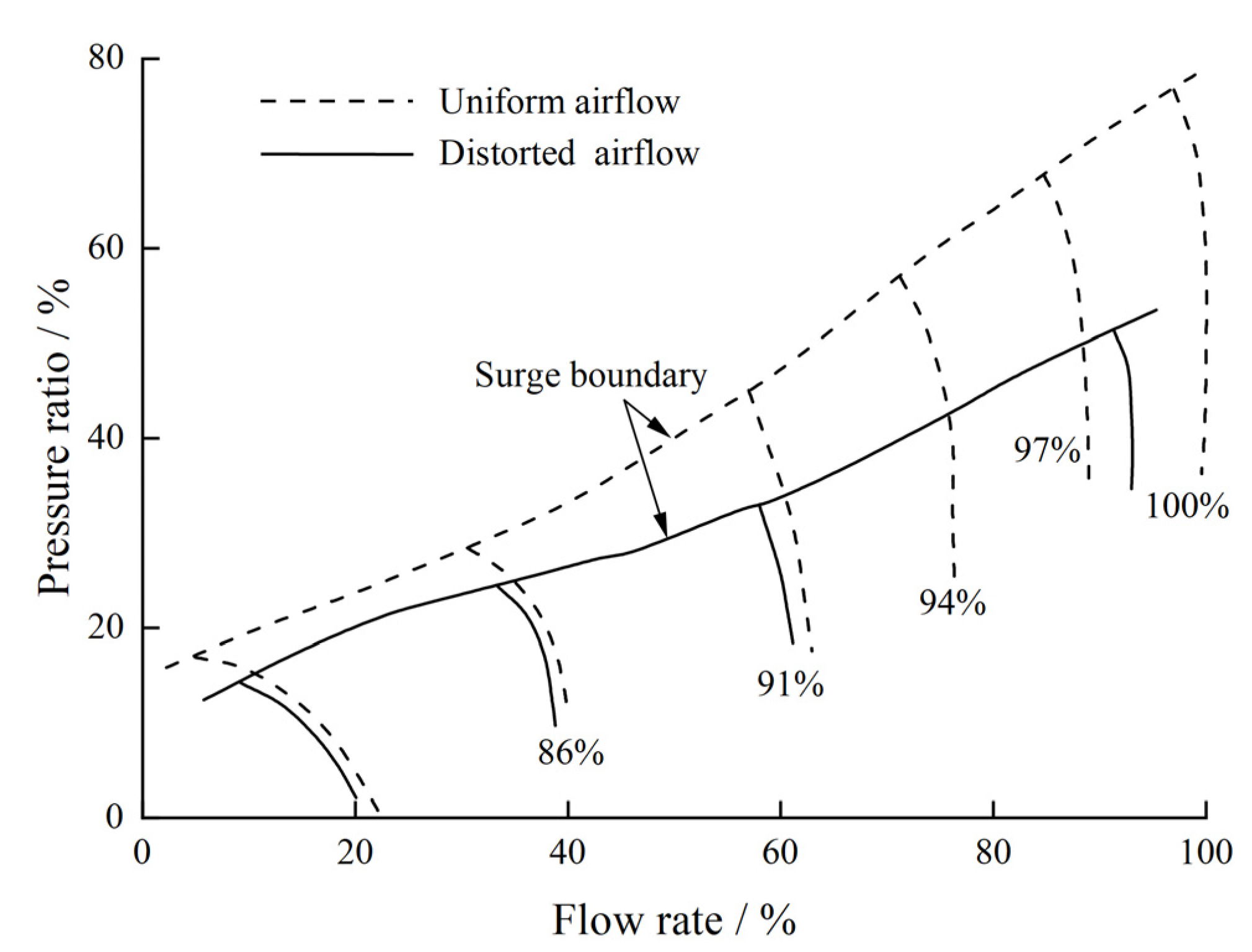
The inlet distortion creates an uneven flow field at the engine inlet, which leads to stall boundary degradation and steady-state characteristic decay of the entire engine, causing the stall point of the entire compressor to move to the lower right [21] (Figure 4), that is to say, the inlet distortion affects the performance parameters of each component of the engine and results in the offset of the common working line and the reduction in the surge margin.
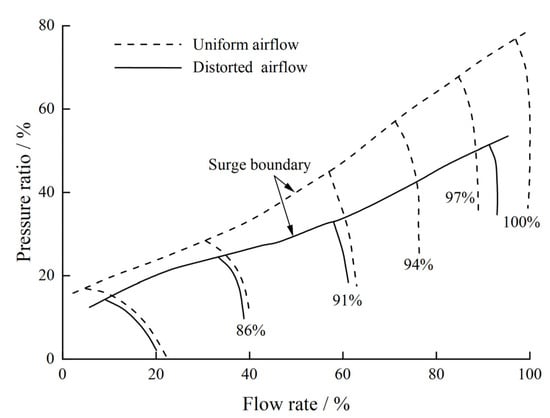
Figure 4.
Sketch of the compressor surge boundary movement caused by inlet distortion.
The inhomogeneous air flow caused by the inlet distortion changes the inlet total pressure and affects the thermodynamic process of the subsequent parts. The average total pressure recovery coefficient σ of the inlet cross-section is generally used to measure the inlet total pressure after the inlet distortion. The main formulas are as follows.
in the formula, is the radial mean total pressure recovery coefficient function, and the expression is
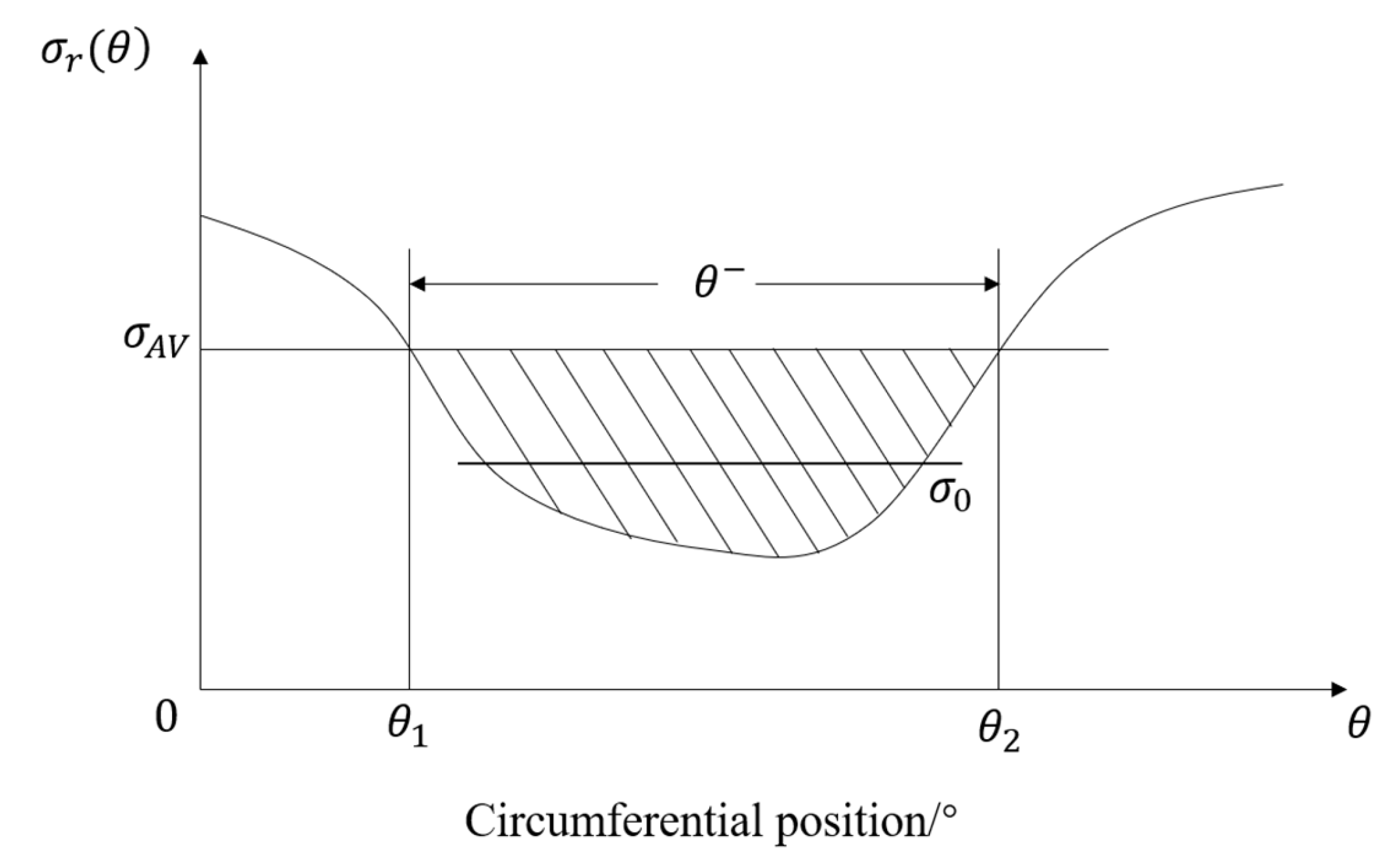
where is the relative radius of the wheel hub and is the circumferential angle of ; the total pressure recovery coefficient is a function of the relative radius , and the schematic diagram of the parameters is shown in Figure 5. The shaded area is below in the low-pressure region . and are the starting and ending points of the low-pressure region, respectively.
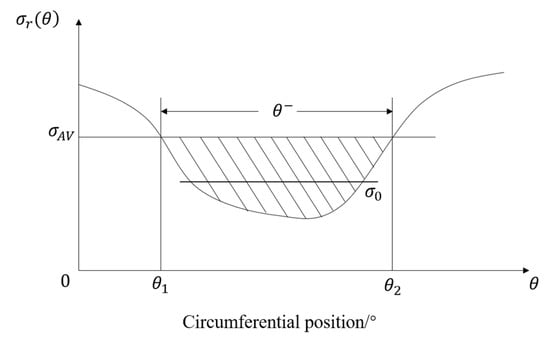
Figure 5.
Radial mean total pressure recovery coefficient .
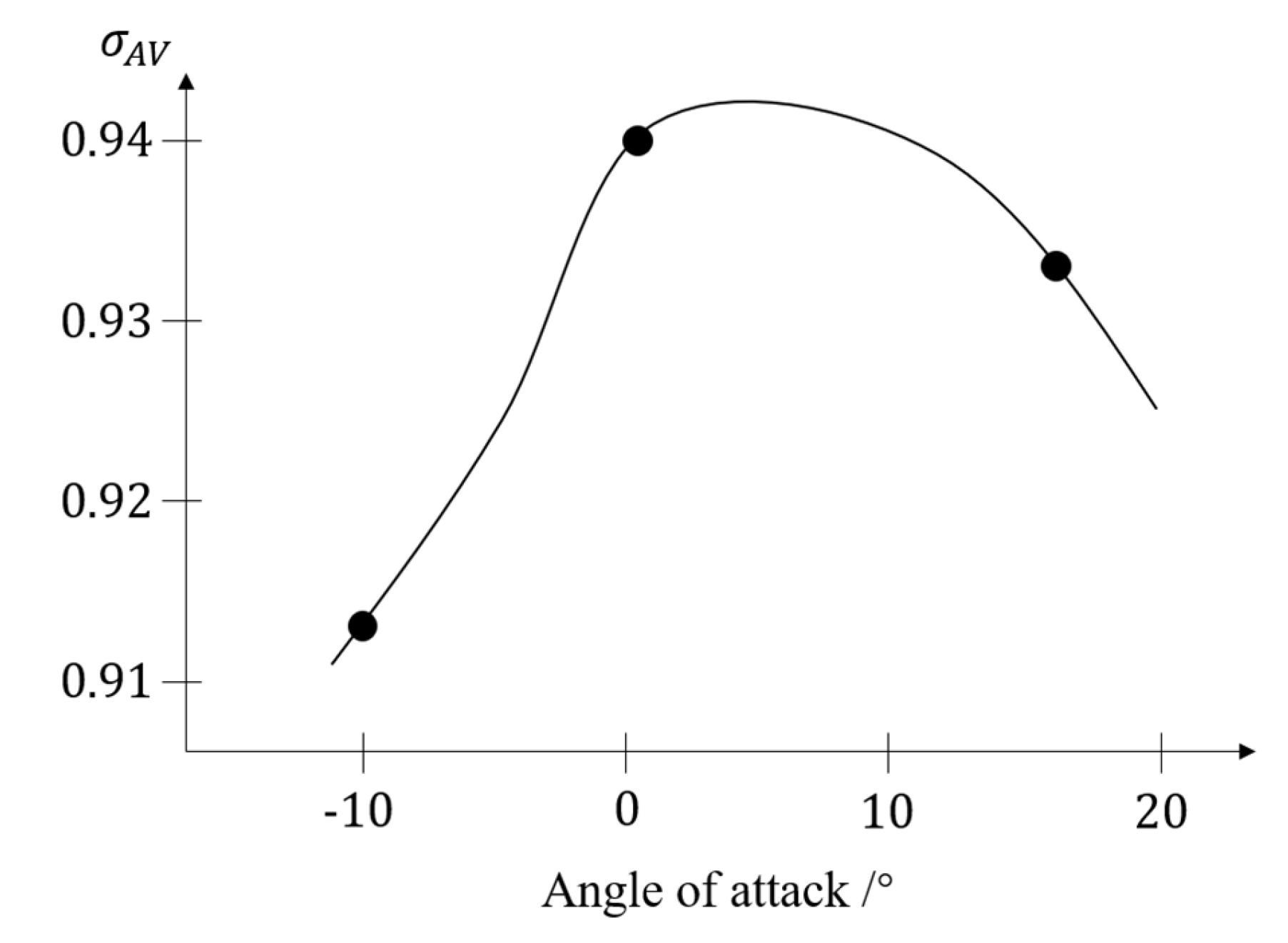
The recovery coefficient of the surface mean total pressure directly reflects the variation in total pressure after distortion [17]. Figure 6 shows the surface mean total pressure recovery coefficient and the mean total pressure of the distorted low-pressure sector of an inlet at different angles of attack during subsonic and sonic travel. The angle of attack is directly related to the distortion. The larger the angle of attack, the stronger the distortion is. As can be seen from Figure 6, the total pressure recovery coefficient is closely related to the angle of attack. The attenuates rapidly from the 0° angle of attack to both sides, and the attenuation is faster at a negative angle of attack. It can be concluded that is closely related to the distortion strength and increases with the increase in distortion strength. Therefore, the inlet total pressure in the component-level model needs to be corrected according to the inlet distortion.
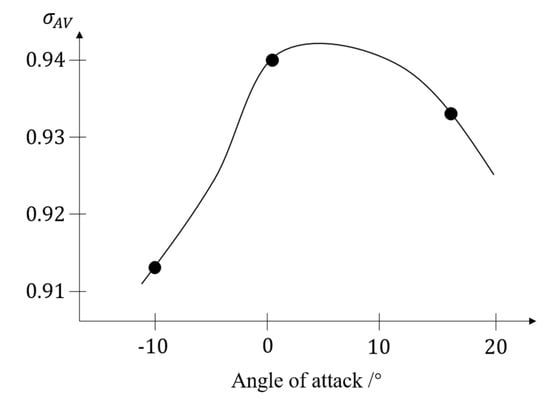
Figure 6.
The surface mean total pressure recovery coefficient of an inlet at different angles of attack during subsonic operation.
In order to quantify the impact of inlet distortion, it is necessary to select a distortion index that can reflect the magnitude of the distortion. The distortion index is mainly used to measure the degree of distortion quantitatively. At present, different countries use different calculation methods, so there is not a universal definition of the distortion index. Because the Russian comprehensive distortion index is widely used in engine stability assessment and experimental research, the research work in this paper is based on the definition of the distortion index. The distortion index only considers the total pressure distortion, not the total temperature distortion, and mainly consists of three parts, namely, the circumferential total pressure unevenness, the radial total pressure unevenness, and the mean surface turbulence. However, a large number of statistical data show that the influence of radial total pressure unevenness on the stability of different types of engine structures is very small, so it is not considered. Therefore, the total pressure distortion index can be expressed as
The composite distortion index is the sum of the steady-state circumferential total pressure distortion index and the surface mean turbulence degree . For the convenience of description, the s in this paper are all percentages. The indicates the difference between the surface mean total pressure recovery coefficient and the total pressure recovery coefficient in the low-pressure area.
The mean surface turbulence represents the quantitative characteristics of the total pressure fluctuation at the aerodynamic interface.
is the ratio of the root-mean-square value of the pulsating pressure to the mean value of the total pressure .
In the formula above, T is the sampling time of the pulse airflow.
In Section 2.2.1, we present the calculation of inlet and outlet flow parameters, and in Formula (4), we refer to the total inlet pressure recovery factor , which is used to characterize the total pressure loss of the inlet flow. The general total pressure recovery coefficient is calculated by the following formula.
For the total pressure recovery coefficient with inlet distortion, it is correlated not only with but also with . The total pressure recovery coefficient in this paper is:
The conventional fan component calculation module obtains the conversion flow and efficiency based on the interpolation of the fan relative conversion speed, and the calculation expression is
Similarly, in Section 2.2.2, some modifications are made to the fan characteristics by taking into account the inlet distortion index in the fan converted air flow and the overall efficiency calculations, i.e., Formula (6) is changed to:
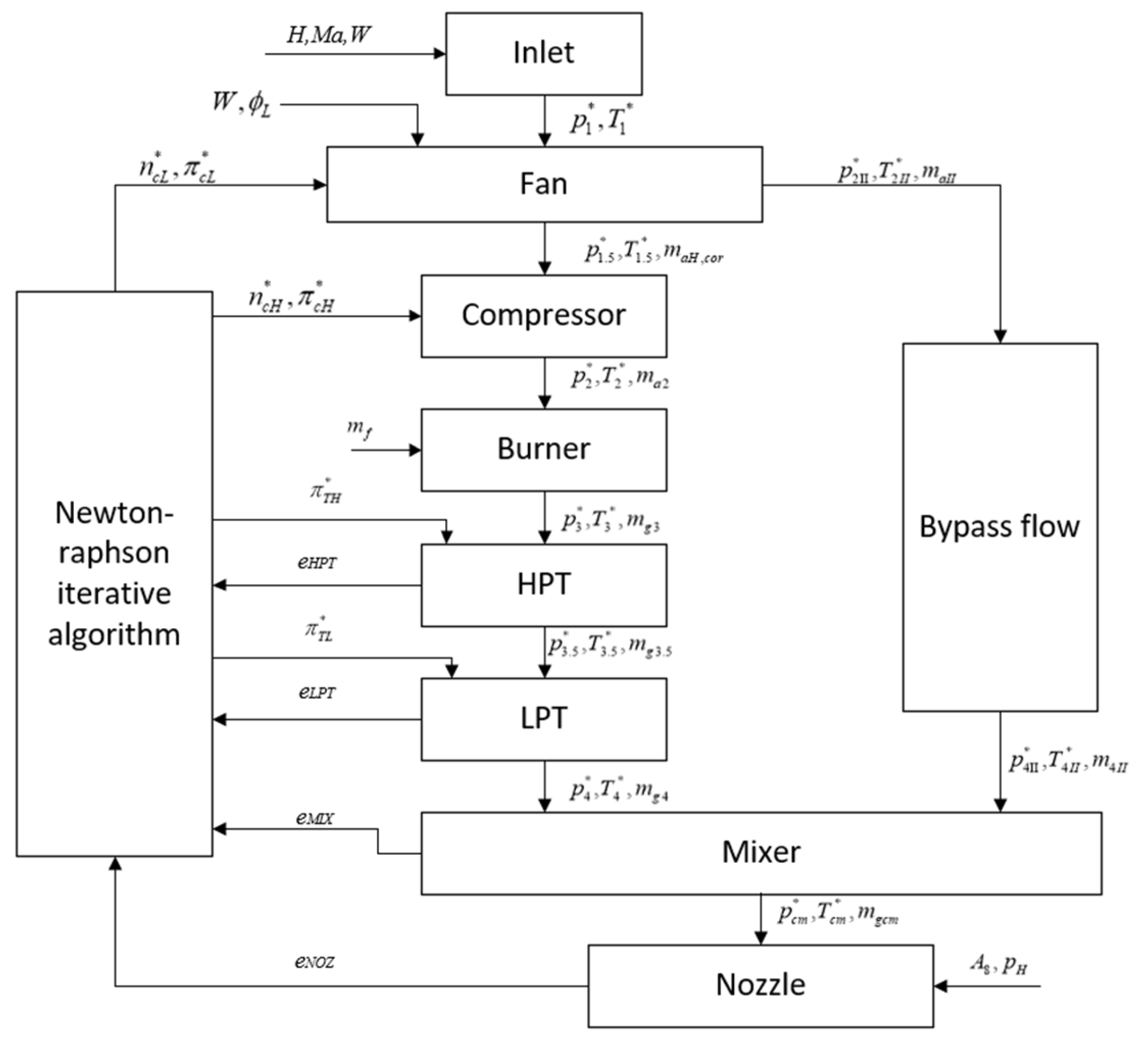
So far, the calculation flow of the components related to the inlet distortion has been modified and combined with the existing engine component-level modeling methods. The nonlinear engine component-level model with the inlet distortion can be formed, and the schematic diagram of its main calculation flow is shown in Figure 7.
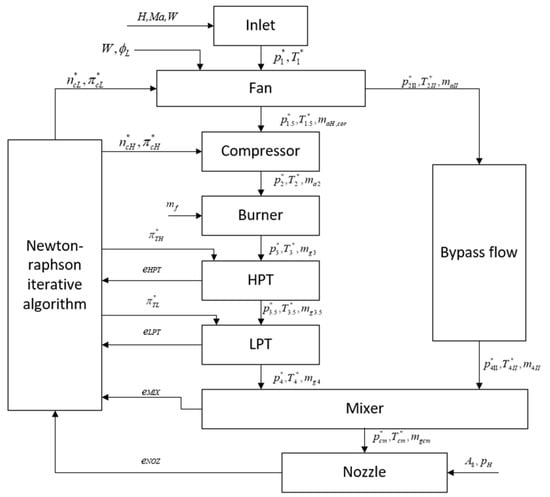
Figure 7.
Flow chart of the turbine engine component-level model with inlet distortion.
3.2. Adaptive Disturbance Rejection Control
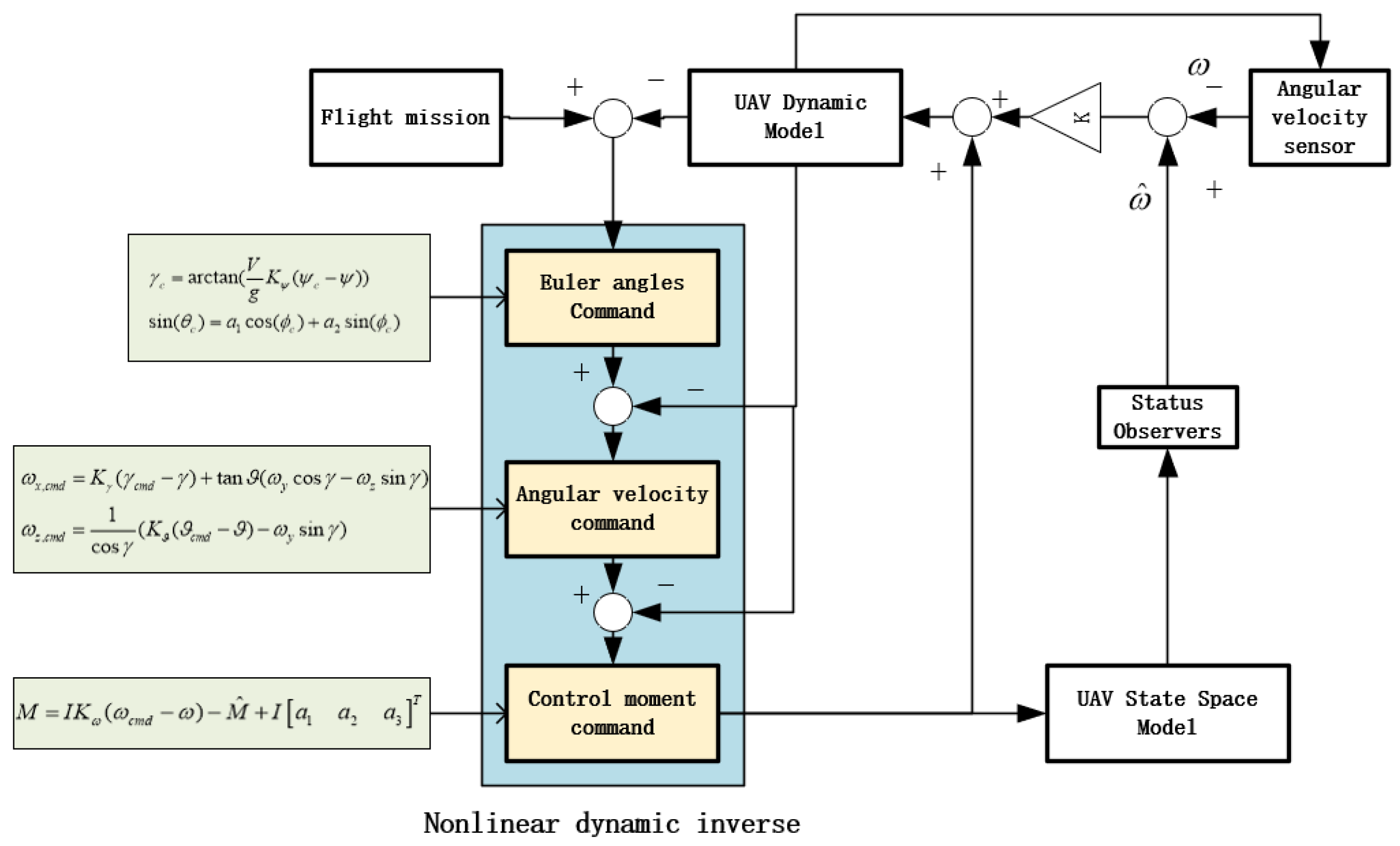
The basic configuration of adaptive disturbance rejection control is a nonlinear dynamic inverse (NDI) control law. The control logic is shown in Figure 8.
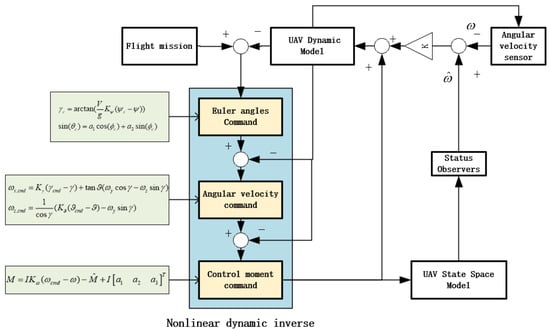
Figure 8.
Control Structure chart of adaptive disturbance rejection.
Taking the tilt-turn dynamics model of UAV as an example, first, according to the dynamics of UAV established in Section 2.1, the instruction design rule is that the time scale of the state variable is separated, and the control instructions are generated by dynamic inversion according to the response speed of the variable.
3.2.1. Design of Slow Loop Control Instruction
The desired angular rate command and can be obtained from the desired attitude angular response, and the expression is as follows:
The angular rate instructions can be obtained by associating with the dynamic equations. The results are as follows:
Observing the dynamic model, the angular acceleration model can be considered as the result of the interaction of the moment part and the non-moment part, and the non-moment control parts are .
The above equation can be rewritten as
The control quantities are , and the control instruction is designed according to the above expected response method.
which is associated with the kinetic equations:
3.2.2. Design of Adaptive Disturbance Rejection Control
In the above derivation process, the body torque of the UAV is strongly nonlinear during the flight process, and it cannot accurately rely on the existing data to calculate it during the flight process. Similarly, when the moment control command is calculated, the rudder surface efficiency cannot be obtained accurately, and the exact value of rudder surface deflection cannot be determined to realize the control moment; the original control law is improved to overcome its dependence on an accurate model. The adaptive disturbance rejection control operates by comparing the measured response with an internal model of the desired dynamics. It then adjusts the control signal based on the difference between the desired and measured behaviors. First, the desired angular rate is designed as follows:
Because of the simplified assumptions, model uncertainty, external disturbance, and so on, dynamic inversion cannot achieve its goal completely. Therefore, is introduced to describe all the uncertainty errors of the system. The system dynamics are written in a form similar to the expected behavior as follows.
Among them, brings the angular acceleration increment for the adaptive control moment, . The angular rate internal model instruction is designed as.
where is an output of the UAV state space model. is defined. The difference between the true angular rate and the internal model angular rate is obtained.
According to the solution of the first-order non-homogeneous differential equation, the functional relationship of with time can be solved.
From the above, we know that, in a certain period of time, converges to , and in the same way, in this period of time, converges to 0, that is, converges to 0. Based on the actual differential equation, the can be substituted into Formula (61) to obtain:
According to the solution of the first-order non-homogeneous linear differential equation,
In this case, converges to within a certain time, so can suppress the effect of error .
According to the dynamic inversion of the above dynamic equations, the adaptive input is added to the NDI control torque command to generate the total torque command.
4. Simulation Results
In the preceding paragraph, we build the dynamics model of UAV and the engine model of UAV and add the influence of inlet distortion into the engine model. Then, the strategy of thrust optimization based on the adaptive margin model and the method of adaptive disturbance rejection flight control for UAV are proposed. In order to verify this, the flight control strategy and the thrust optimization strategy proposed earlier are simulated and verified successively. The parameters of a certain type of UAV are given in Table 2. The simulation is based on the model and strategy established in the previous paper, which are implemented in code in MATLAB, where the turbine engine model is built by Simulink of MATLAB.

Table 2.
Parameters of a certain type of UAV.
4.1. Simulation Results of Thrust Optimization Based on the Adaptive Margin Model
In order to verify the optimization results of the engine thrust performance, we use the acceleration performance improvement of the UAV at the altitude of 7500 m as a way to test the engine thrust optimization, to increase the speed of the UAV from 150 m/s to 250 m/s with the altitude change, and to check the time of the engine acceleration plan as well as the thrust output of the engine. The simulation results are as follows:
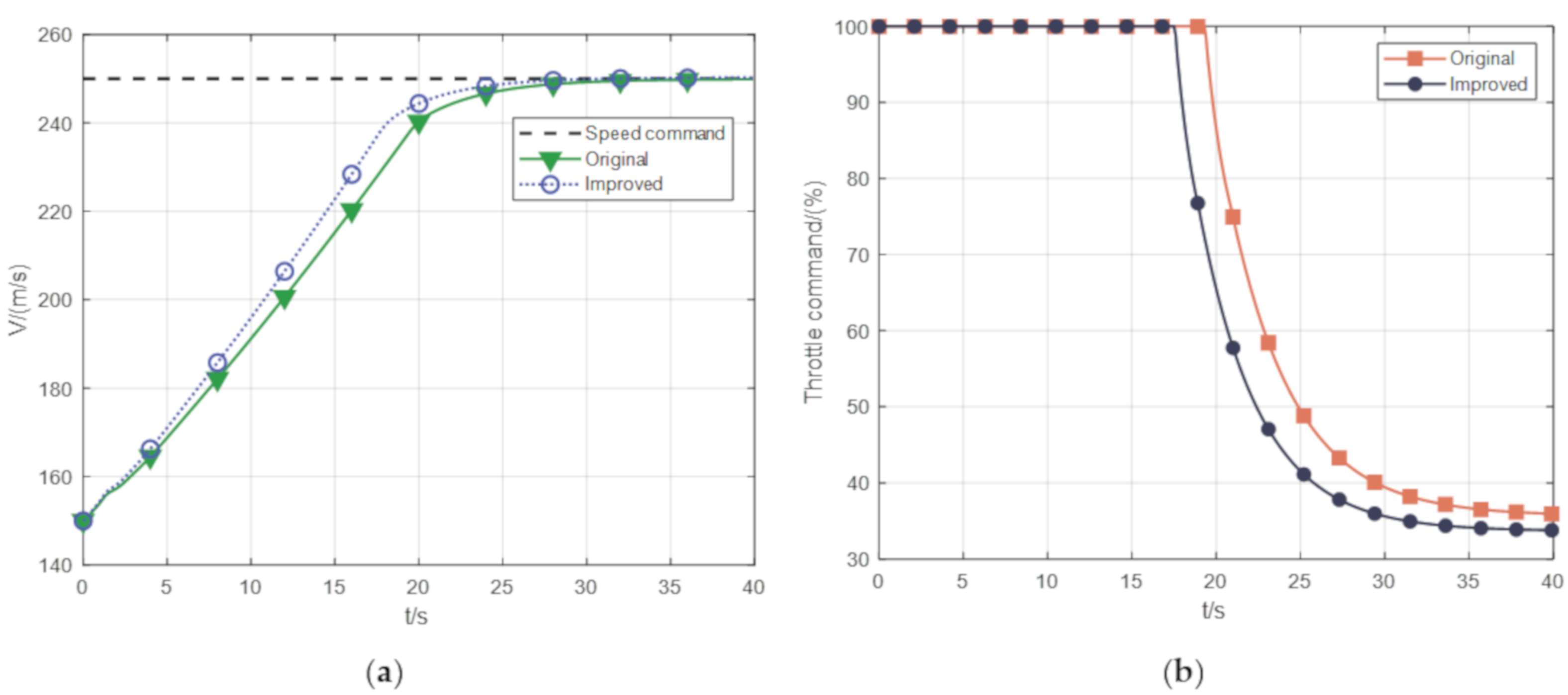
Figure 9a shows the speed simulation results of the UAV for a given speed command, and we compare the speed results after the thrust performance optimization with the original case. It can be seen that the acceleration performance of the UAV after the thrust lift is obviously improved compared with the original situation. In the original acceleration plan, the UAV used 28.9 s to accelerate the speed to 249 m/s, the speed was increased to 250 m/s in 40 s, the time of acceleration to 249 m/s was advanced to 25.5 s, and the time of acceleration to 250 m/s was reduced to 29.9 s after the thrust optimization. This shows that, under the same engine acceleration control parameters, the engine thrust optimization strategy proposed in this paper can significantly improve the acceleration capability of UAV and shorten the acceleration time. It is also possible to see this by the slope of the velocity resultant curve in plot 9(a), i.e., the maximum acceleration of the UAV.
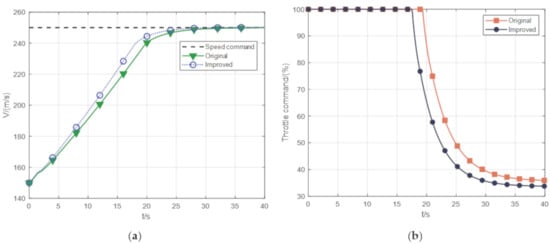
Figure 9.
The result graph of engine thrust lifting: (a) Speed result of the UAV acceleration process, (b) Result of the UAV engine throttle command.
Figure 9b shows the result of UAV engine throttle command. Under the original condition, the engine throttle command needs to keep 19.3 s fully open, but after improvement, the change time is reduced to 17.5 s. The result shows that the full throttle time of UAV is shorter after the thrust performance is improved. In the acceleration control program of the UAV, the controller parameters used in the two simulated scenarios are exactly the same. Therefore, the optimized throttle command maximum output time is shorter than the original one, which can also indicate that the optimized case has an increased maximum thrust output compared to the original case.
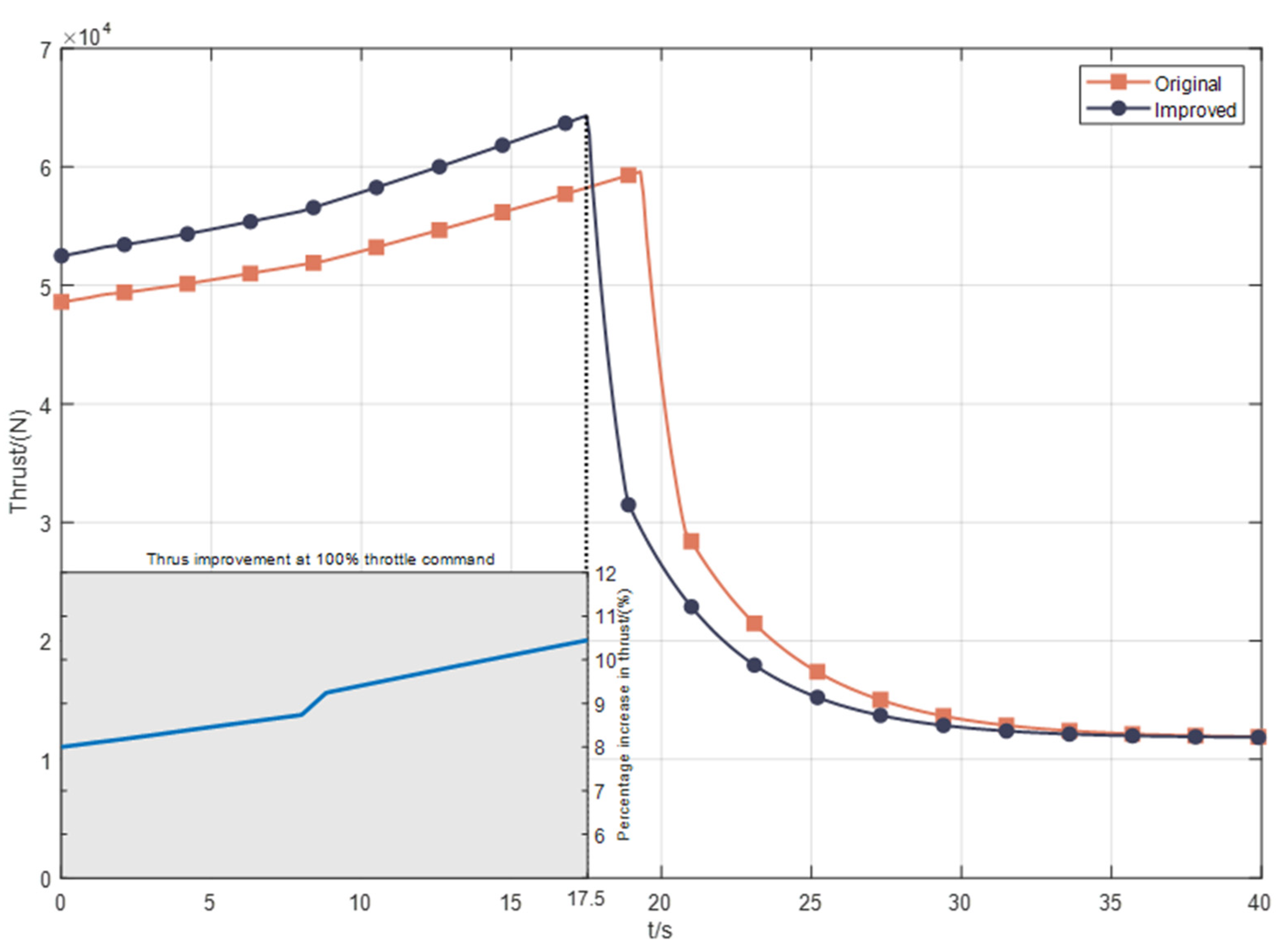
To visualize the thrust improvement, Figure 10 shows the UAV thrust output during this acceleration; the percentage increase in the thrust of the engine at 100% throttle is in the corner of the image (take the first 17.5 s, which is 100% of the time for the engine throttle command in both cases). The right axis of the small graph is the label, and the unit is the percentage of thrust performance improvement. It can be seen that the maximum thrust output of the engine can be increased by at least 8% under the condition of maximum throttle command and also increases with the increase in the UAV speed, reaching 10.4% at 17.5 s.
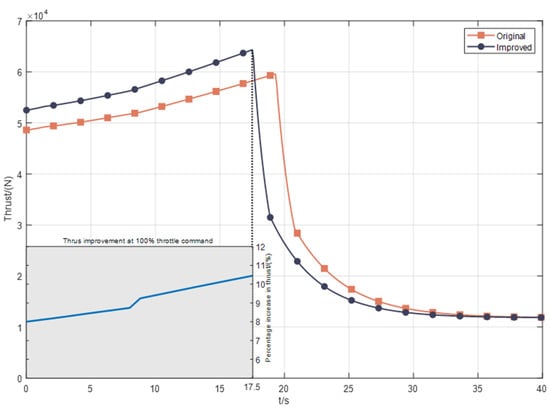
Figure 10.
Thrust output diagram.
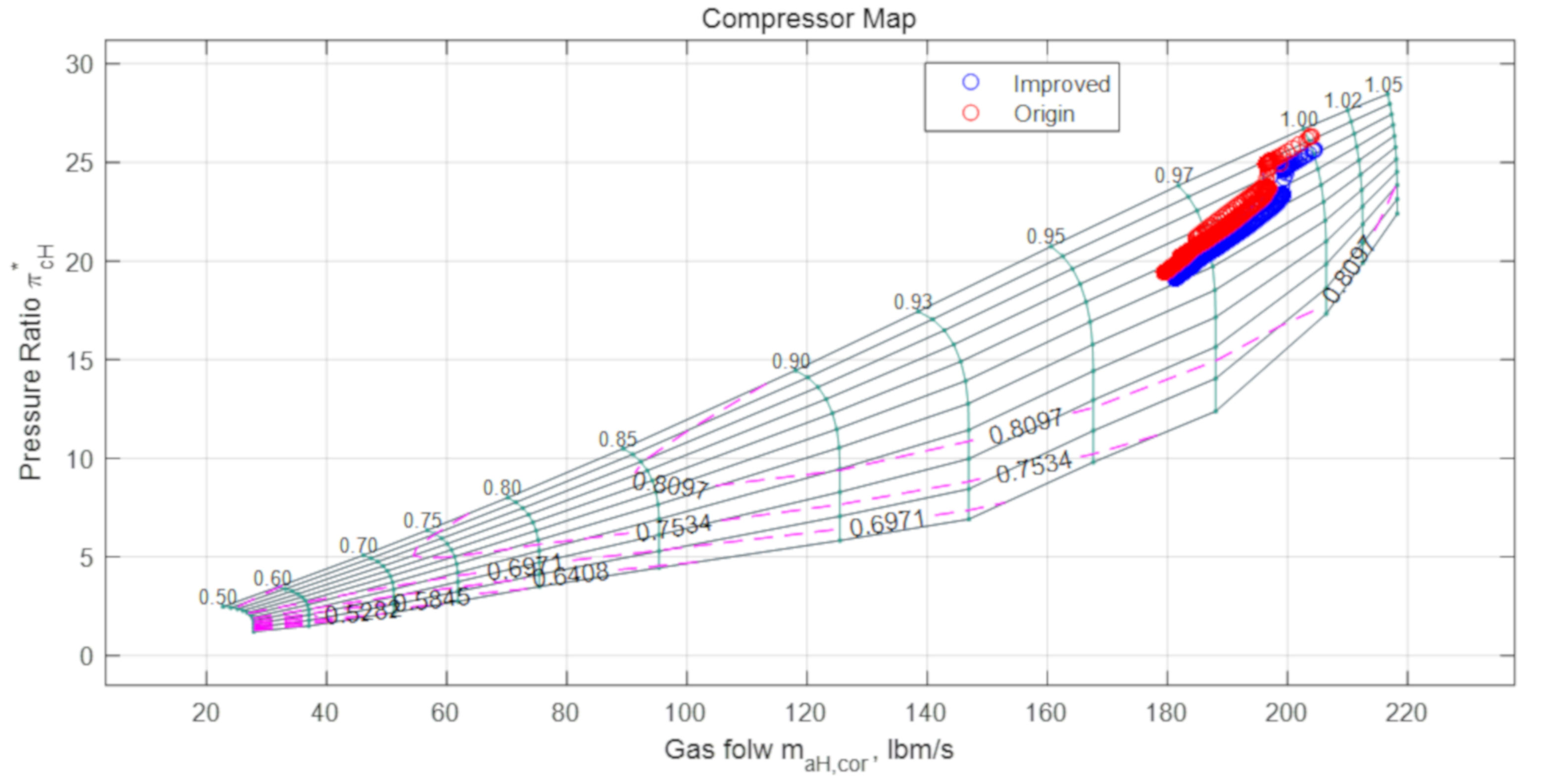
Figure 11 is the result diagram of the working state of the compressor. It can be seen that the working point of the engine is closer to the surge boundary after the more reasonable order of the turbocharging ratio, that is, the surge margin reserve of the engine is reduced but still kept in safe working conditions, and the engine did not surge.
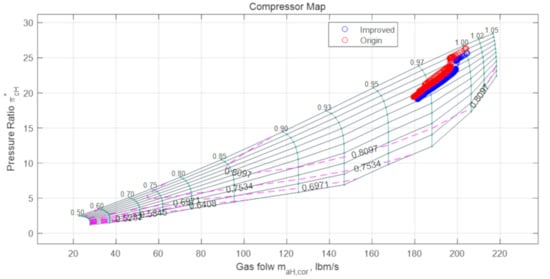
Figure 11.
Compressor working state diagram.
Brief summary:
- Under the same acceleration control parameters, the thrust optimization strategy proposed in this paper can significantly improve the acceleration capability of UAV and shorten the acceleration time.
- With improved thrust performance, the UAV requires a shorter full throttle time.
- At the same flat flying speed, the throttle command of the engine after thrust optimization is smaller than the original throttle command.
- At maximum throttle, the engine’s maximum thrust output can be increased by at least 8%.
4.2. Simulation Results of Adaptive Disturbance Rejection Control
In order to verify the designed adaptive disturbance rejection control strategy, the UAV is given different flight instructions in the longitudinal and rolling directions, and the advantages and disadvantages of the control method and the traditional PID control were observed. The flight environment is given under two conditions: altitude 7500 m, speed 150 m/s.
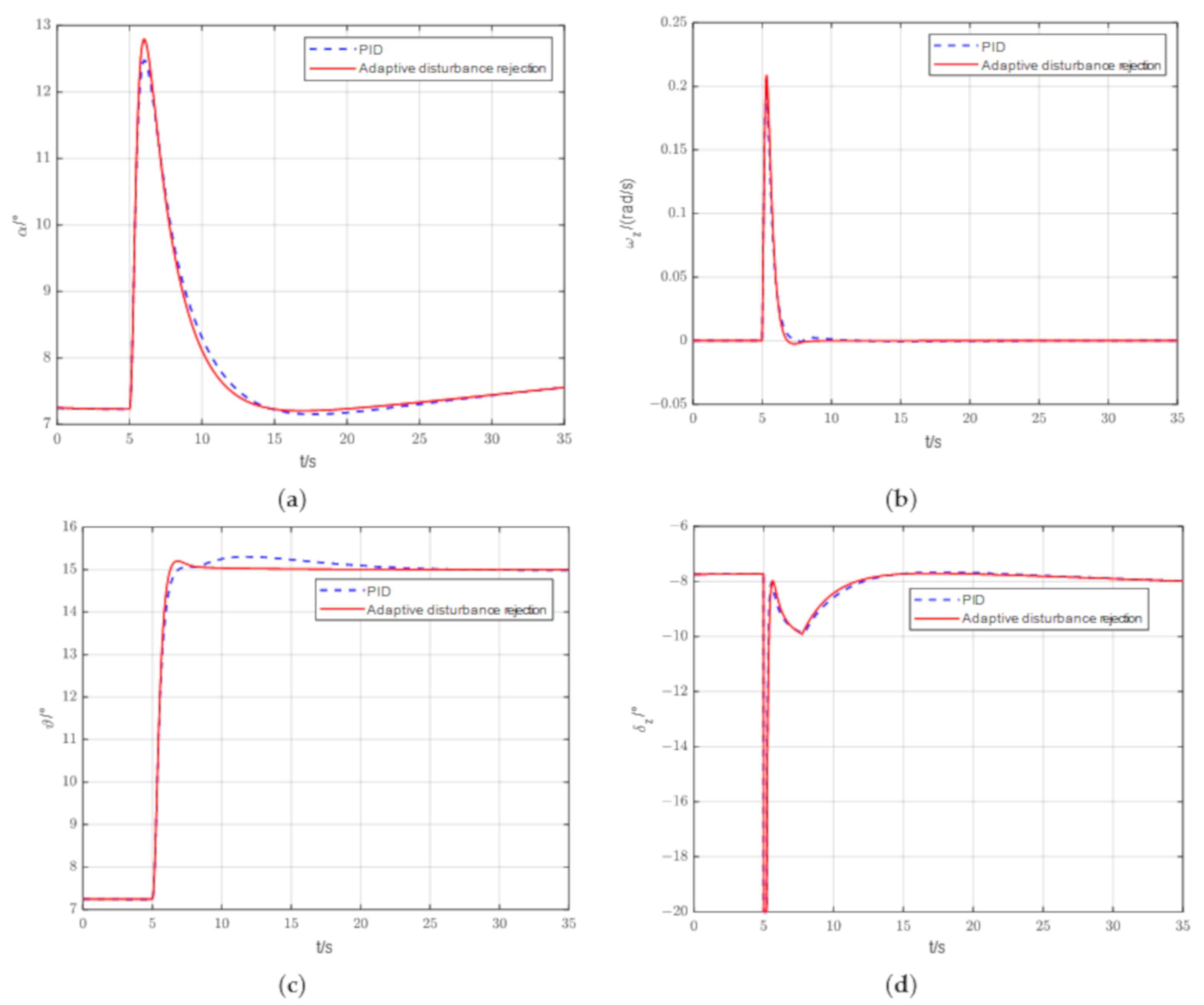
The first is the longitudinal simulation results, the initial pitch angle is 7.2°, the initial track angle is 0°, the UAV is controlled in the first 5 s of the flat flight, the UAV is given a 15° pitch command at 5 s, and the UAV is made to climb quickly. Observe the response of the pitch angle and the command output of the rudder deviation.
For the PID control case in the simulation, we used the Ziegler–Nichols tuning method. This method provides a good starting point for the PID gains, which can then be refined through further tuning. Start by adjusting the proportional gain Kp until the system’s response is close to the desired response. Then, adjust the integral gain Ki until the steady-state error is reduced to an acceptable level. Finally, adjust the derivative gain Kd to reduce the overshoot and dampen the oscillations caused by the proportional and integral gains. A set of PID controller parameters with the fastest response time and the smallest overshoot is obtained by the above method.
As shown in Figure 12c, it took 17.39 s for the PID controller to make the pitch angle converge to the command, while the adaptive disturbance rejection control took 3.62 s to achieve the equivalent situation (0.05 degrees of static difference). Compared with the PID control, the pitch angle of the adaptive disturbance rejection control method converges to the given instruction more rapidly, the overshoot is smaller, and the overshoot arrival time is shorter.
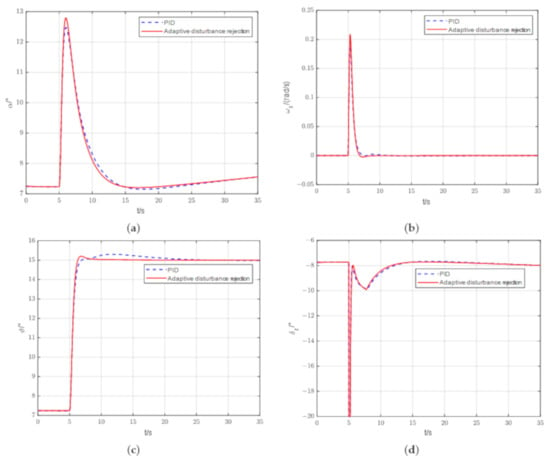
Figure 12.
Simulation results of UAV adaptive disturbance rejection control in longitudinal flight: (a) Result of the angle of attack response graph; (b) Result of the pitch angular velocity response graph; (c) Result of the pitch angular response graph; (d) Result graph of the elevator deflection command.
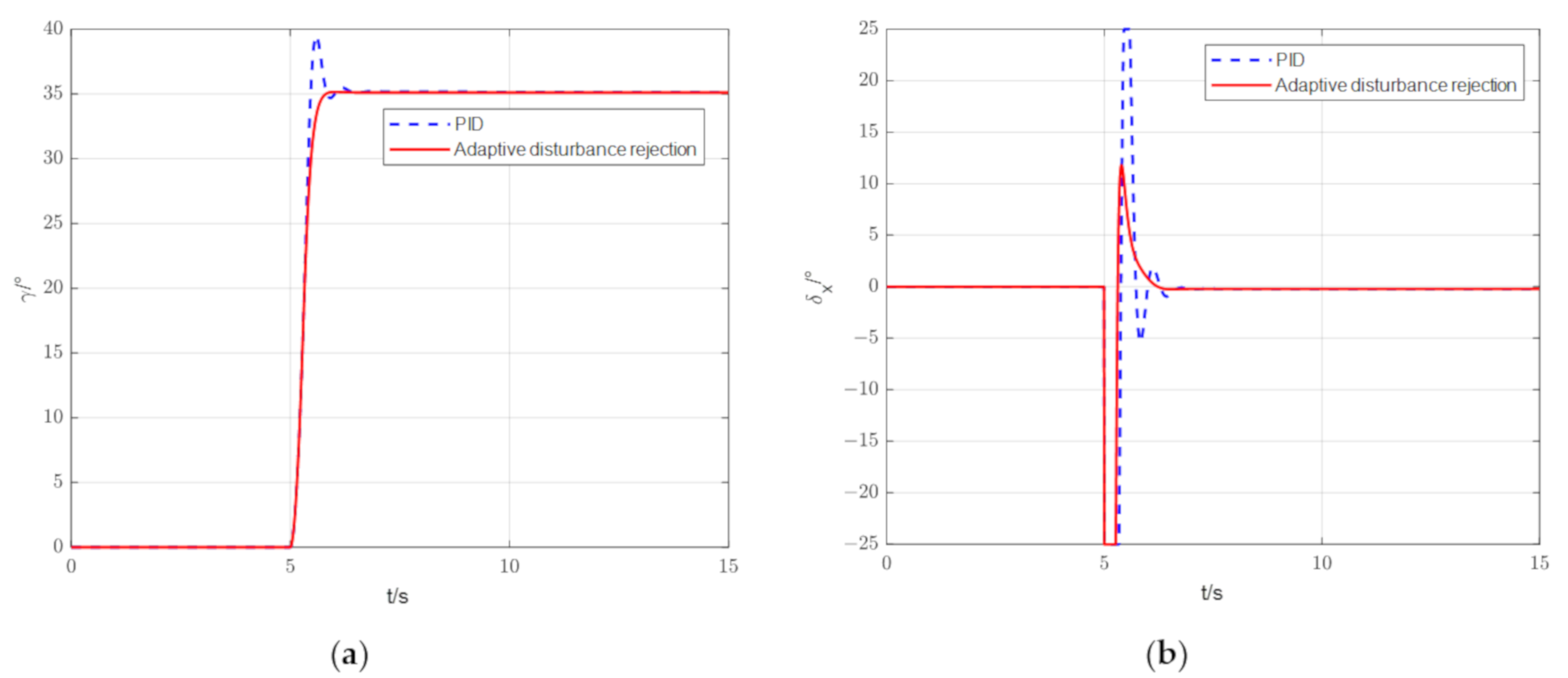
Similarly, the simulation results for the roll direction are given in Figure 13. The initial tilt angle is 0°, and the control UAV will fly horizontally in the first 5 s. The UAV is given a 35° tilt command at 5 s to make the UAV roll quickly. Observe the response of the tilt angle and the command output of the rudder.
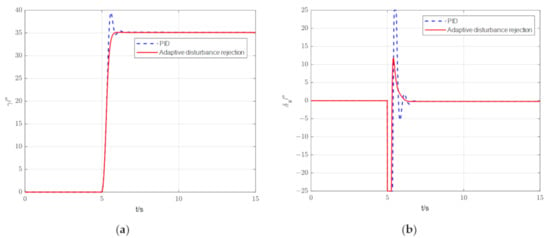
Figure 13.
Flight simulation results of UAV adaptive interference suppression control roll direction: (a) The resulting graph of the tilt-angle response; (b) Result diagram of aileron deflection command.
As shown in Figure 13a, The PID controller produces a large overshoot in the tilt angle (12.82% overshoot), which is obviously undesirable in this case, while the adaptive disturbance rejection control method has only 0.4% overshoot. Compared to the result of PID control, the tilt angle of the adaptive disturbance rejection control mode converges to the given instruction more quickly, the overshoot is smaller, and the overshoot arrival time is shorter. The aileron command, compared with the PID control in the case of swing, greatly reduced. This increases the potential of the UAV to perform other maneuvers. The results of both the longitudinal and rolling flight simulation show that the adaptive disturbance rejection control method proposed in this paper can achieve fast attitude maneuvers; compared with PID control, it can complete the maneuver command more accurately in a short time and improve the overshoot and rudder surface jitter caused by PID control.
5. Conclusions
We designed a strategy for exchanging the surge margin of the engine for the improvement of the thrust performance in order to meet the requirement of the development of the propulsion system for UAVs. First, the dynamic equation of UAV is established, which describes the straight motion of the center of mass and the rotation motion of the body around the center of mass. A mathematical model of the turbofan’s components is built. Then, an optimal thrust algorithm based on the adaptive margin model is designed. The internal working environment of the engine and the angle of attack in flight dynamics are considered. From the angle of aircraft/engine integration, the way to improve the performance of the engine propulsion system is studied; in this part, the UAV body transfer function is obtained from the UAV dynamic equation, and the UAV angle of attack is predicted by the transfer function. Then, the inlet and fan models are modified by adding a correction term considering inlet distortion. For further flight simulation, a flight control strategy based on adaptive disturbance rejection control is designed. In order to compensate for the external loop control law, a disturbance observer is introduced to estimate the flight disturbance of the UAV.
Finally, the feasibility of the proposed strategy is verified by numerical simulation. The numerical simulation results show that the thrust lifting strategy based on the adaptive margin model can ensure the safety of the flight and the stability of the compressor; the maximum thrust of the UAV is increased by at least 8% by reducing the surge margin reserve and improving the maneuverability of the UAV. The adaptive disturbance rejection control method can suppress the attitude fluctuation quickly and has strong robustness and adaptive ability.
Nowadays, there are more and more research works on aircraft/engine integration, and in this paper, we meet the demand of the thrust performance improvement of UAVs from this perspective, which has some implementability in engineering practice. However, the strategy still has some limitations, namely, a high accuracy requirement for the engine model. In fact, turbine engine power system modeling is a complex discipline, and the engine model has strong nonlinearity. The component-level modeling method used in this paper, at the cost of a lengthy and complex mechanism model and in exchange for a higher accuracy, sacrifices a certain amount of computing speed. We plan to continue to explore the thrust optimization method based on the adaptive margin model and, on the other hand, to seek a more accurate and faster engine modeling method.
Author Contributions
Conceptualization, Y.W. and H.L.; methodology, Y.W.; software, K.L.; validation, K.L. and H.L.; formal analysis, Y.W., H.L. and K.L.; investigation, H.L.; resources, Y.W.; data curation, Y.W. and H.L.; writing—original draft preparation, H.L. and K.L.; writing—review and editing, Y.W. and H.L.; visualization, Y.W. and H.L.; supervision, Y.W.; project administration, Y.W.; funding acquisition, K.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number U2141229, and the foundation under grant JCJQ, grant number 2019-JCJQ-DA-001-131.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bello, A.B.; Navarro, F.; Raposo, J.; Miranda, M.; Zazo, A.; Álvarez, M. Fixed-Wing UAV Flight Operation under Harsh Weather Conditions: A Case Study in Livingston Island Glaciers, Antarctica. Drones 2022, 6, 384. [Google Scholar] [CrossRef]
- Cao, S.; Yu, H. An Adaptive Control Framework for the Autonomous Aerobatic Maneuvers of Fixed-Wing Unmanned Aerial Vehicle. Drones 2022, 6, 316. [Google Scholar] [CrossRef]
- Liu, Z.; Han, W.; Wu, Y.; Su, X.; Guo, F. Automated Sortie Scheduling Optimization for Fixed-Wing Unmanned Carrier Aircraft and Unmanned Carrier Helicopter Mixed Fleet Based on Offshore Platform. Drones 2022, 6, 375. [Google Scholar] [CrossRef]
- Ming, Z. Research on Uav Application Development and Airworthiness Standard Management in China. Acad. J. Eng. Technol. Sci. 2020, 4, 37–46. [Google Scholar]
- Cui, Y.P.; Xing, Q.H. The challenge and inspiration of UAVs to field air defense from the Russia-Ukraine War. Aerosp. Electron. Warf. 2022, 38, 1–3. [Google Scholar]
- Li, R.J.; Gong, S. Development Direction Analysis of Future UCAV Power Plant. Aeronaut. Sci. Technol. 2015, 26, 1–5. [Google Scholar]
- Hu, X.Y. UAV Propulsion System Technology Research. Gas Turbine Exp. Res. 2008, 1, 58–61. [Google Scholar]
- Hu, X.Y. Development of High Altitude Long Endurance UAV Propulsion Technology. Gas Turbine Exp. Res. 2006, 4, 56–60. [Google Scholar]
- Chen, D.; Tian, H.J.; Li, M.X.; Lei, Q.Q. Analysis to the Development of Power Systems for MALE UAVs. Aerosp. Power 2022, 5, 16–19. [Google Scholar]
- Cheng, B.L.; Tang, H.; Xu, X.; Li, X.P. Performance Study on Turbofan Engine with Turbine Inter Burner. Aeroengine 2010, 36, 18–22. [Google Scholar]
- Dong, H.B.; Shang, G.J.; Guo, Y.Q. Effect and verification of mass injecting pre-compressor cooling on control plan of turbonfan engine. J. Aerosp. Power 2022, 37, 404–408. [Google Scholar]
- Sun, H.G.; Li, J.; Li, H.C.; Ye, B. The Analysis on Surge Margin’S Influence on Aeroengine Thrust Control System. Comput. Simul. 2017, 34, 84–89. [Google Scholar]
- Longley, J.P. A review of non-steady flow models for compressor stability. J. Turbomach. 1994, 116, 202–215. [Google Scholar] [CrossRef]
- Longley, J.P.; Shin, H.W.; Plumley, R.E. Effects of rotating inlet distortion on multistage compressor stability. ASME J. Turbomach. 1996, 118, 181–188. [Google Scholar] [CrossRef]
- Wang, J.K.; Zhang, H.B.; Chen, K.; Sun, F.Y.; Zhou, X. High stability control of engine based on surge margin estimation model. J. Aerosp. Power 2013, 28, 2145–2154. [Google Scholar]
- Liu, D.X. Aviation Gas turbine Engine Stability Design and Evaluation Technology, 6th ed.; Aviation Industry Press: Beijing, China, 2004; pp. 45–182. [Google Scholar]
- Bodó, Z.; Lantos, B. Modeling and control of fixed wing UAVs. In Proceedings of the IEEE 13th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 29–31 May 2019; pp. 332–337. [Google Scholar]
- Kim, C. Development of unified high-fidelity flight dynamic modeling technique for unmanned compound aircraft. Int. J. Aerosp. Eng. 2021, 2021, 5513337. [Google Scholar]
- Zhou, W.X. Research on Object-Oriented Modeling and Simulation for Aeroengine and Control System; DR, Nanjing University of Aeronautics and Astronautics the Graduate School: Nanjing, China, 2006. [Google Scholar]
- Iliff, K.W. Flight-Determined Subsonic Longitudinal Stability and Control Derivatives of the F-18 High Angle of Attack Research Vehicle (HARV) with Thrust Vectoring; NASA, Dryden Flight Research Center: Edwards, CA, USA, 1997; pp. 17–19.
- Lee, K.; Lee, B.; Kang, S.; Yang, S.; Lee, D. Inlet Distortion Test with Gas Turbine Engine in the Altitude Engine Test Facility. In Proceedings of the 27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Chicago, IL, USA, 30 June 2010; p. 4337. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).