A New Class of Generalized Probability-Weighted Moment Estimators for the Pareto Distribution

Abstract

Estimation based on probability-weighted moments is a well-established method and an excellent alternative to the classic method of moments or the maximum likelihood method, especially for small sample sizes. In this research, we developed a new class of estimators for the parameters of the Pareto type I distribution. A generalization of the probability-weighted moments approach is the foundation for this new class of estimators. It has the advantage of being valid in the entire parameter space of the Pareto distribution. We established the asymptotic normality of the new estimators and applied them to simulated and real datasets in order to illustrate their finite sample behavior. The results of comparisons with the most used estimation methods were also analyzed.

1. Introduction

The Pareto distribution has resulted from the work of the economist Vilfredo Pareto [1]. Pareto observed that the number of taxpayers with an income greater than x could be approximated by $b{x}^{-a}$, where a and b are positive parameters. This fact led to the introduction of several variants of the Pareto distribution, with a survival function proportional to $x^{-a}$. The most common Pareto distribution, often referred to as Pareto type I, will be investigated in this work. Given a random variable X with a Pareto type I distribution, the distribution function (d.f.) is as follows:

$$F\left(x\right|a,c)=1-{\left(\frac{x}{c}\right)}^{-a},x>c,a>0,c>0,$$

(1)

where a and c are the shape and scale parameters, respectively. The corresponding probability density function is

$$f\left(x\right|a,c)=\frac{a{c}^a}{x^{a+1}},x>c,a>0,c>0.$$

(2)

The parameter c corresponds to the lower bound for the support of the random variable, whereas the parameter a quantifies the heaviness of the right tail and is also referred to as the tail or Pareto index [2,3]. As a decreases, the tail becomes heavier. The d.f. in (1) is inverted to produce the associated quantile function of X, which is represented by

$$Q\left(p\right|a,c)=c{(1-p)}^{-1/a},0<p<1,a>0,c>0,$$

(3)

where the lower tail probability is denoted by p. Despite the simple analytic expressions in Equations (1)–(3), this model has been successfully applied in a large number of different fields, such as bibliometrics, demography, economy, geology, insurance and finance, among others. An alternative form of the Pareto model results from the change in location $X-c$. This alternative form is known as the Pareto type II or the Lomax ([4,5]) distribution. Another related model is the generalized Pareto distribution [6]. Under a semiparametric framework, the Pareto type I distribution is often used in the analysis of extreme events. Under such a framework, we use Equation (1) as an upper tail model and work with the reciprocal parameter $\xi =1/a$, the so-called extreme value index. Detailed discussions and reviews of $\xi$ estimation for Pareto-tailed models can be found in works by Beirlant et al. [7,8,9], Gomes and Guillou [10] and Peng and Qi [11], among others.

The estimation of the shape and scale parameters a and c is an important and popular research topic. Although maximum likelihood estimators have optimal properties, such properties are only guaranteed asymptotically. Thus, different estimation methods, which performed better than the maximum likelihood method for small or moderate sample sizes, have been proposed in the literature by many authors. Quandt [12] compared the performance of the maximum likelihood estimator with that of the moments estimator, a least squares estimator and four quantile estimators. Different least squares estimators were examined by Lu and Tau [13], Caeiro et al. [14], Kantar [15] and Kim et al. [16]. Robust estimators of the shape parameter were introduced by Brazauskas and Serfling [17] and Vandewalle et al. [18]. Bayesian estimators can be found in Arnold and Press [19], Rasheed and Al-Gazi [20] and Han [21]. Singh and Guo [22], Caeiro and Gomes [23,24] and Munir et al. [25] considered probability-weighted moment estimators. Bhatti et al. [26,27] proposed modified maximum likelihood estimators and Chen et al. [28] dealt with the estimation of the Pareto parameters with a modification of ranked set sampling.

The purpose of this article is to examine a new method for estimating the shape and scale parameters of a Pareto model. The remainder of the paper is structured as follows. In Section 2, we review the most common estimators for the parameters of the Pareto distribution and introduce the new class of estimators. These estimators, called log-generalized probability-weighted moment estimators, are derived from a modification of the classic probability-weighted moments method. In Section 3, we study the asymptotic results for the new class of estimators. A Monte Carlo simulation study and two real data applications are provided in Section 4 to illustrate the performance of the estimators. Some concluding remarks are given in Section 5.

2. Traditional and New Techniques for Estimating the Parameters of the Pareto Distribution

This section covers some common estimation methods for the shape and scale parameters from the Pareto distribution in (1) and introduces a new estimation procedure. Assume that $X_1,X_2,\cdots ,X_n$ is a sample of independent and identically distributed (i.i.d.) random variables, from a Pareto distribution, as defined in (1), with both parameters, a and c, unknown. The sample of non-decreasing order statistics is denoted as $X_{1:n},X_{2:n},\cdots ,X_{n:n}$.

2.1. Maximum Likelihood Estimators

The maximum likelihood (ML) estimators are found by maximizing the log-likelihood function and have the closed-form expressions

$${\widehat{a}}^{ML}={\left(\frac{1}{n}\sum _{i=1}^{n}ln{X}_i-ln{X}_{1:n}\right)}^{-1},{\widehat{c}}^{ML}=X_{1:n}.$$

(4)

2.2. Moment Estimators

It is well known that the non-central moments of order k for the Pareto model are expressed as follows:

$$E\left(X^k\right)=\frac{a{c}^k}{a-k},\mathrm{if}a>k.$$

In applications, the approach of moments based on the two first moments is unpopular because the second moment only exists for $a>2$, and other moment-based estimators have emerged in the literature. To extend the domain of validity of the estimators based on moments, Quandt [12] considered the first non-central moment of X, $E\left(X\right)$, and the first moment of the sample minimum, $E\left(X_{1:n}\right)$. The sample minimum of a Pareto distribution has a Pareto distribution whose scale and shape parameters are c and $an$, respectively. Quandt obtained the moment (M) estimators by equating two aforementioned theoretical moments to the corresponding sample moments and solving the system of equations following the parameters of the distribution. The estimators obtained are consistent for $a>1$ and given by

$${\widehat{a}}^M=\frac{n\overline{X}-X_{1:n}}{n(\overline{X}-X_{1:n})},{\widehat{c}}^M=\left(1-\frac{1}{n{\widehat{a}}^M}\right)X_{1:n},$$

(5)

where $\overline{X}$ denotes the arithmetic sample mean.

2.3. Probability Weighted Moment Estimators

The probability-weighted moment (PWM) method (Greenwood et al. [29]) is currently a well-established estimation procedure in the field of hydrology. Studies using Monte Carlo simulations demonstrated that, for small sample sizes, PWM estimators outperform other estimation techniques (Hosking et al. [30]). The PWMs of a random variable X, with d.f. F, are defined as

$$M_{k,r,s}=E\left(X^k{\left(F\left(X\right)\right)}^r{(1-F\left(X\right))}^s\right)$$

(6)

where k, r and s are real numbers. If the mean value $M_{1,0,0}$ exists, then $M_{1,r,s}$ exists for any real positive values r and s. The PWM method generalizes the classic method of moments: when $r=s=0$, $M_{k,0,0}$ are the non-central moments of order k. For models that have a closed-form quantile function, Q, it may be more convenient to compute the PWMs as

$$M_{k,r,s}={\int }_0^1{\left(Q\left(u\right)\right)}^k{u}^r{(1-u)}^{s}du.$$

More recently, this method was modified for models without an analytic d.f. and quantile function (see Jing et al. [31]). The PWM estimators are derived by equating $M_{k,r,s}$ with their respective sample moments and then solving those equations following the parameters of the distribution. Greenwood et al. [29] and Hosking et al. [30] recommend using $M_{1,r,s}$, since the relations between parameters and moments are usually much simpler. The empirical estimate of $M_{1,r,s}$ is usually less sensitive to outliers and has good properties when the sample size is small. For convenience, several authors chose to use $k=1$ and non-negative integer values for r and s. This approach will be referred to as the classic PWM method. In addition, when r and s are non-negative integers, it is more convenient to work with the PWMs

$${\alpha }_r=M_{1,0,r}=E\left(X{(1-F\left(X\right))}^r\right),r=0,1,\cdots ,$$

(7)

or

$${\beta }_r=M_{1,r,0}=E\left(X{\left(F\left(X\right)\right)}^r\right),r=0,1,\cdots .$$

(8)

It should be noted that $F{\left(X\right)}^r{(1-F\left(X\right))}^s$ can be represented as a linear combination of powers of $F\left(X\right)$ or $1-F\left(X\right)$ for non-negative integers r and s. As a result, we may use the following equations to relate ${\alpha }_r$ and ${\beta }_r$:

$${\alpha }_r=\sum _{j=0}^r{(-1)}^j\left(\genfrac{}{}{0pt}{}{r}{j}\right){\beta }_j\mathrm{and}{\beta }_r=\sum _{j=0}^r{(-1)}^j\left(\genfrac{}{}{0pt}{}{r}{j}\right){\alpha }_j,$$

where $\left(\genfrac{}{}{0pt}{}{r}{j}\right)$ denotes the binomial coefficient. Using ${\alpha }_r$ or ${\beta }_r$ is equivalent as long as the values for r are non-negative integers that are as small as possible. For non-negative integer values of r, the unbiased estimators of the PWMs ${\alpha }_r$ and ${\beta }_r$, defined in (7) and (8), are, respectively (Landwehr et al. [32]),

$${\widehat{\alpha }}_r=\frac{1}{n}\sum _{i=1}^{n-r}\frac{\left(\genfrac{}{}{0pt}{}{n-i}{r}\right)}{\left(\genfrac{}{}{0pt}{}{n-1}{r}\right)}{X}_{i:n}\mathrm{and}{\widehat{\beta }}_r=\frac{1}{n}\sum _{i=r+1}^n\frac{\left(\genfrac{}{}{0pt}{}{i-1}{r}\right)}{\left(\genfrac{}{}{0pt}{}{n-1}{r}\right)}{X}_{i:n}.$$

(9)

Instead of the unbiased estimators, one may prefer to use the biased estimators

$${\tilde{\alpha }}_r=\frac{1}{n}\sum _{i=1}^n{(1-p_{i:n})}^r{X}_{i:n}\mathrm{and}{\tilde{\beta }}_r=\frac{1}{n}\sum _{i=1}^n{p}_{i:n}^r{X}_{i:n},$$

(10)

where r can be a real number and $p_{i:n}$ are the plotting positions; that is, empirical estimates of $F\left(X_{i:n}\right)$. The options that are most frequently used for plotting positions are

$$p_{i:n}=\frac{i-b}{n},0\le b\le 1$$

or

$$p_{i:n}=\frac{i-b}{n+1-2b},-0.5\le b\le 0.5$$

where b is a continuity correction factor. Landwehr et al. [33] concluded empirically that moderated biased estimators of the PWMs could produce more accurate estimates of upper quantiles.

For the Pareto distribution in (1), the PWMs in (6) are given by

$$M_{k,r,s}=c^k\mathrm{B}\left(s+1-\frac{k}{a},r+1\right),s-k/a>-1,r>-1,$$

where $\mathrm{B}$ stands for the complete beta function. By setting the exponents $(k,r)=(1,0)$, we obtain the classical PWMs for the Pareto distribution, valid for $a>{(1+s)}^{-1}$ and given by

$${\alpha }_s=M_{1,0,s}=\frac{c}{(s+1-1/a)},s>\frac{1}{a}-1.$$

Singh and Guo [22], Caeiro and Gomes [23,34], Munir et al. [25] and Caeiro et al. [35] took the PWMs ${\alpha }_0$ and ${\alpha }_1$ into account and deduced the associated PWM estimators for the shape and scale parameters of the Pareto distribution. Those estimators are

$${\widehat{a}}^{PWM}=\frac{{\widehat{\alpha }}_0-{\widehat{\alpha }}_1}{{\widehat{\alpha }}_0-2{\widehat{\alpha }}_1}and{\widehat{c}}^{PWM}={\widehat{\alpha }}_0\left(\frac{{\widehat{\alpha }}_1}{{\widehat{\alpha }}_0-{\widehat{\alpha }}_1}\right),$$

(11)

with ${\widehat{\alpha }}_0$ and ${\widehat{\alpha }}_1$ given in (9). As stated earlier, the PWM estimators in (11) are only defined for a Pareto model with finite mean value ($a>1$).

2.4. Extended Class of PWM Estimators

The theoretical PWMs defined in (6) can have any real values for the exponents k, r and s; however, early applications only considered non-negative integer exponents. Rasmussen [36] explored PWMs with real exponents and referred to this method as generalized PWM (GPWM) to distinguish it from the classic PWM approach. He found that, in most cases, the GPWM method outperforms the classic PWM method. To simplify the GPWM method, it is recommended to limit the class of GPWMs by setting $(k,r)=(1,0)$ or $(k,s)=(1,0)$. This restriction leads to the use of simpler analytical formulas for GPWMs. The GPWM estimators are the ones in (10) for any real value of r. Another version of the PWM method was introduced by Caeiro and Prata Gomes [37]. The authors worked in the context of Pareto-type tails and considered a different type of PWM, specified by

$$M_{g,r,s}^{*}=E\left(g\left(X\right){\left(F\left(X\right)\right)}^r{(1-F\left(X\right))}^s\right)$$

(12)

with $g\left(x\right)=ln\left(x\right)$, $r=0$, $s=0,1$. Such a class of PWMs was named log PWM (LPWM) and has the advantage of extending the domain of validity of the estimators to the complete parameter space for the Pareto model. Caeiro and Mateus [38] considered the LPWMs in (12) with $r=0$ and studied the corresponding LPWMs for the Pareto model.

$$l_s=M_{ln,0,s}^{*}=\frac{ln\left(c\right)}{1+s}+\frac{1}{a{(1+s)}^2},s>-1.$$

(13)

If we take into consideration the LPWMs $l_0$ and $l_1$, the respective LPWM estimators of the shape and scale parameters of the Pareto distribution in (1) are, respectively,

$${\widehat{a}}^{LPWM}=\frac{1}{2\widehat{l_0}-4\widehat{l_1}}and{\widehat{c}}^{LPWM}=exp(4\widehat{l_1}-\widehat{l_0})$$

(14)

where ${\widehat{l}}_s$, $s=0,1$ are the unbiased empirical estimator of $l_s$ given by

$${\widehat{l}}_s=\frac{1}{n}\sum _{i=1}^{n-s}\frac{\left(\genfrac{}{}{0pt}{}{n-i}{s}\right)}{\left(\genfrac{}{}{0pt}{}{n-1}{s}\right)}ln{X}_{i:n}.$$

(15)

Recently, Chen [39] introduced an extended class of GPWMs by evaluating the PWMs in (12) with g a suitable continuous function and r and s any real values. Mateus and Caeiro [40] considered the extended class of GPWMs with $g\left(x\right)=ln\left(x\right)$ for a rescaled sample of the Pareto model. This approach, called log-generalized probability-weighted (LGPWM), uses one theoretical moment and only provides an estimator for the shape parameter of the Pareto distribution. For the estimation of the scale parameter, Mateus and Caeiro [40] used an estimator similar to the moment estimator, ${\widehat{c}}^M$.

2.5. New Class of LGPWM Estimators

We now introduce a new LGPWM class of estimators for the Pareto distribution that provides shape and scale estimators and generalizes the LPWM estimators in (14). The new LGPWM estimators are built using the moments $l_s$ in (13) for any real value of $s>-1$. Then, for each real s, the corresponding empirical (biased) estimator is provided by

$${\tilde{l}}_s=\frac{1}{n}\sum _{i=1}^n{(1-p_{i:n})}^{s}ln{X}_{i:n}.$$

(16)

where $p_{i:n}$ are the plotting positions. To estimate the two parameters of the Pareto distribution, we shall consider the theoretical moments $l_{s_1}$ and $l_{s_2}$ in (13) with $s_1<s_2$. Equating the moments $l_{s_1}$ and $l_{s_2}$ to the corresponding empirical estimate in (16) and solving the system of equations in the order of the parameters a and c, we obtain the following estimators:

$${\widehat{a}}^{LGPWM}=\frac{s_2-s_1}{(1+s_1)(1+s_2)[(1+s_1){\tilde{l}}_{s_1}-(1+s_2){\tilde{l}}_{s_2}]},$$

(17)

and

$${\widehat{c}}^{LGPWM}=exp\left(\frac{{(1+s_1)}^2{\tilde{l}}_{s_1}-{(1+s_2)}^2{\tilde{l}}_{s_2}}{s_2-s_1}\right)$$

(18)

where $s_1<s_2$. The tuning parameters $s_1$ and $s_2$ should be chosen carefully in order to obtain a good fit of the sample data. A possible selection of $s_1$ and $s_2$ will be presented in Section 4.

3. Distributional Behavior of the LGPWM Estimators

To better understand the behavior of the estimators under consideration, and in order to compare their relative performance with other established estimators from the literature, it is important to study their sampling distribution. Unfortunately, for the estimators depending on a weighted average of the complete set of order statistics, the exact distribution cannot be derived analytically. As a compromise, we will study the asymptotic sampling distribution of the estimators considered here. Such asymptotic distributions can be used as an approximation to the exact distribution for large values of n and usually provide a good approximation for samples of sizes larger than 50.

In the following, $\stackrel{d}{⟶}$ and $\stackrel{d}{=}$ stand, respectively, for convergence and equality in distribution. Next, we present, without proof, in Proposition 1 and Proposition 2, the non-degenerated asymptotic distribution of the commonly known estimators from the literature given in (4), (5) and (11).

Proposition 1

(Mateus and Caeiro [40,41]). Suppose that $(X_1,X_2,\dots ,X_n)$ is an i.i.d. sample from the Pareto population with d.f. in (1). Then,

$$\sqrt{n}\left({\widehat{a}}^{ML}-a\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,a^2\right),$$

(19)

$$\sqrt{n}\left({\widehat{a}}^M-a\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{a{(a-1)}^2}{a-2}\right),\mathrm{if}a>2,$$

(20)

and

$$\sqrt{n}\left({\widehat{a}}^{PWM}-a\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{a(a-1){(2a-1)}^2}{(a-2)(3a-2)}\right),\mathrm{if}a>2,$$

(21)

where $N(\mu ,{\sigma }^2)$ represents a normal random variable with mean value μ and variance ${\sigma }^2$.

Proposition 2.

Under the conditions of Proposition 1, we have

$$({(1-n^{-1})}^{-1/a}-1)\left(\frac{{\widehat{c}}^{ML}}{c}-1\right)\underset{n\to \infty }{\overset{d}{⟶}}Exp\left(1\right),$$

(22)

$$({(1-n^{-1})}^{-1/a}-1)\left(\frac{{\widehat{c}}^M}{c}-1\right)\underset{n\to \infty }{\overset{d}{⟶}}Exp\left(1\right),\mathrm{if}a>2,$$

(23)

and

$$\sqrt{n}\left(\frac{{\widehat{c}}^{PWM}}{c}-1\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{a-1}{a(3a-2)(a-2)}\right),\mathrm{if}a>2,$$

(24)

where $Exp\left(1\right)$ refers to a standard exponential random variable with d.f.

$$F_E\left(x\right)=1-e^{-x},x>0.$$

(25)

The following lemma and proposition are required to state the non-degenerate asymptotic limit behavior of the LGPWM estimators.

Lemma 1.

Let X be a Pareto random variable with d.f. given in (1) and E a standard exponential random variable with d.f. given in Equation (25). Then, $lnX$ has a shifted and re-scaled standard exponential distribution (Arnold [42]):

$$lnX\stackrel{d}{=}lnc+\frac{1}{a}E.$$

Moreover, since the previous relation between the Pareto and exponential distributions is strictly increasing, it follows that, for a sample of size n,

$$ln{X}_{i:n}\stackrel{d}{=}lnc+\frac{1}{a}{E}_{i:n}.$$

where $E_{1:n}\le E_{2:n}\le \cdots \le E_{n:n}$ are the non-decreasing order statistics from n mutually independent and identically distributed standard exponentially random variables.

Proposition 3.

Consider a sample of size n from a Pareto population and define

$$D_{s_1,s_2}\left(\omega \right)=\frac{1}{n}\sum _{i=1}^n\left[{(1+s_1)}^{\omega }{\left(1-\frac{i}{n}\right)}^{s_1}-{(1+s_2)}^{\omega }{\left(1-\frac{i}{n}\right)}^{s_2}\right]ln{X}_{i:n},$$

(26)

with $-0.5<s_1<s_2$ and any real ω. The asymptotic limit distribution

$$\sqrt{n}\left(D_{s_1,s_2}\left(\omega \right)-{\mu }_{D\left(\omega \right)}\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,{\sigma }_{D\left(\omega \right)}^2\right)$$

(27)

holds true, with

$${\mu }_{D\left(\omega \right)}=ln\left(c\right)[{(1+s_1)}^{\omega -1}-{(1+s_2)}^{\omega -1}]+\frac{{(1+s_1)}^{\omega -2}-{(1+s_2)}^{\omega -2}}{a},$$

and

$${\sigma }_{D\left(\omega \right)}^2=\frac{1}{a^2}\left[\frac{{(1+s_1)}^{2(\omega -1)}}{1+2s_1}+\frac{{(1+s_2)}^{2(\omega -1)}}{1+2s_2}-\frac{2{(1+s_1)}^{\omega -1}{(1+s_2)}^{\omega -1}}{1+s_1+s_2}\right].$$

Proof of Proposition 3.

Using Lemma 1 we can write

$$D_{s_1,s_2}\left(\omega \right)=ln\left(c\right)T_0+\frac{1}{a}{T}_n,$$

with

$$T_0=\frac{1}{n}\sum _{i=1}^{n}J(i/n),T_n=\frac{1}{n}\sum _{i=1}^{n}J(i/n)E_{i:n},$$

and

$$J\left(\frac{i}{n}\right)={(1+s_1)}^{\omega }{\left(1-\frac{i}{n}\right)}^{s_1}-{(1+s_2)}^{\omega }{\left(1-\frac{i}{n}\right)}^{s_2}.$$

Hence, note that $T_0$ converges toward ${\int }_0^{1}J\left(x\right)dx={(1+s_1)}^{\omega -1}-{(1+s_2)}^{\omega -1}$. By utilizing the asymptotic result in the study by Arnold et al. [43] (p.229), for linear functions of order statistics, we obtain

$$\sqrt{n}(T_n-{\mu }_{T_n})\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,{\sigma }_{T_n}^2\right),-0.5<s_1<s_2$$

(28)

with

$$\begin{array}{cc}\hfill {\mu }_{T_n}& ={\int }_0^{1}xJ(1-e^{-x})e^{-x}dx={(1+s_1)}^{\omega -2}-{(1+s_2)}^{\omega -2}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\sigma }_{T_n}^2& =2{\int }_0^{\infty }J(1-e^{-x})(1-e^{-x})\left({\int }_x^{\infty }xJ(1-e^{-y})e^{-y}dy\right)dx\hfill \\ \hfill & =\frac{{(1+s_1)}^{2(\omega -1)}}{1+2s_1}+\frac{{(1+s_2)}^{2(\omega -1)}}{1+2s_2}-\frac{2{(1+s_1)}^{\omega -1}{(1+s_2)}^{\omega -1}}{1+s_1+s_2}.\hfill \end{array}$$

Combining the asymptotic results for $T_0$ and $T_n$, the limit distribution in (27) follows straightforwardly. □

Next, we establish the non-degenerate asymptotic behavior of the LGPWM estimators in (17) and (18).

Proposition 4.

Let us consider the conditions of Proposition 3. Then,

$$\sqrt{n}\left({\widehat{a}}^{LGPWM}-a\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{2a^2{(1+s_1)}^2{(1+s_2)}^2}{(1+2s_1)(1+2s_2)(1+s_1+s_2)}\right),$$

(29)

and

$$\sqrt{n}({\widehat{c}}^{LGPWM}-c)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{c^2}{a^2{(s_2-s_1)}^2}\left(\frac{{(1+s_1)}^2}{1+2s_1}+\frac{{(1+s_2)}^2}{1+2s_2}-\frac{2(1+s_1)(1+s_2)}{1+s_1+s_2}\right)\right),$$

(30)

with $-0.5<s_1<s_2$.

Proof. 

First, notice that we can write the LGPWM estimators in (17) and (18) as

$${\widehat{a}}^{LGPWM}=\frac{s_2-s_1}{(1+s_1)(1+s_2)D_{s_1,s_2}\left(1\right)}$$

(31)

and

$${\widehat{c}}^{LGPWM}=exp\left\{\frac{-D_{s_1,s_2}\left(2\right)}{s_2-s_1}\right\},$$

(32)

with $D_{s_1,s_2}\left(\omega \right)$ in (26).

Let ${\xi }_n=\frac{(1+s_1)(1+s_2)}{s_2-s_1}{D}_{s_1,s_2}\left(1\right)$. Then, invoking Proposition 3 with $\omega =1$, we obtain

$$\sqrt{n}\left({\widehat{\xi }}_n-\frac{1}{a}\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{2{(1+s_1)}^2{(1+s_2)}^2}{a^2(1+2s_1)(1+2s_2)(1+s_1+s_2)}\right).$$

Noticing that ${\widehat{a}}^{LGPWM}=1/{\widehat{\xi }}_n$ and applying the delta method, the asymptotic result in (29) is established. Then, defining ${\widehat{\gamma }}_n=\frac{-D_{s_1,s_2}\left(2\right)}{s_2-s_1}$ and using the result from Proposition 3 again, with $\omega =2$, we obtain

$$\sqrt{n}({\widehat{\gamma }}_n-ln\left(c\right))\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{\frac{{(1+s_1)}^2}{1+2s_1}+\frac{{(1+s_2)}^2}{1+2s_2}-\frac{2(1+s_1)(1+s_2)}{1+s_1+s_2}}{a^2{(s_2-s_1)}^2}\right).$$

Applying the delta method to $\sqrt{n}\left(exp\left({\widehat{\gamma }}_n\right)-c\right)$, we obtain the limit distribution in (30). □

Remark 1.

Since ${\widehat{l}}_s$ and ${\tilde{l}}_s$ defined in (15) and (16), respectively, are asymptotic equivalent, straightforward computations to the result of Proposition 2 allow us to obtain the following asymptotic limit distribution for the LPWM estimators in (14):

$$\sqrt{n}\left({\widehat{a}}^{LPWM}-a\right)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{4a^2}{3}\right)$$

and

$$\sqrt{n}({\widehat{c}}^{LPWM}-c)\underset{n\to \infty }{\overset{d}{⟶}}N\left(0,\frac{c^2}{3a^2}\right).$$

4. Numerical Results

In this section, we analyze simulated and real datasets to assess the performance of the estimation procedures discussed in Section 2. For the LGPWM estimators in (17) and (18), we used the empirical values of (16) with plotting positions $p_{i:n}=(i-0.35)/n$, where $1\le i\le n$. Since the LGPWM estimation method requires two tuning parameters, we first present a data-driven algorithm to determine these parameters.

4.1. Data-Driven Tuning Parameter Selection for the LGPWM Estimator

Consider the LGPWM estimators $\widehat{a}$ and $\widehat{c}$ with tuning parameters $s_1$ and $s_2$ taking values in $(-0.5,4]$, with $s_1<s_2$, discretized in small steps of length 0.1. For each pair of values ($s_1,s_2$), we analyze the fit of the Pareto model by comparing the empirical cumulative distribution function, $F_n\left(x\right)$, with the fitted cumulative distribution function, $\widehat{F}\left(x\right)=F\left(x\right|\widehat{a},\widehat{c})$, as defined in (1), using an appropriate goodness-of-fit statistic. Lastly, we select the set of parameters that provides the best fit. To measure the agreement between the observations and the model, the following goodness-of-fit statistic tests were considered:

• Kolmogorov–Smirnov (KS) statistic:

  $$D_n=\underset{x}{sup}|F_n\left(x\right)-F\left(x\right)|=max\left\{D_n^{+},D_n^{-}\right\}$$

  (33)

  with

  $$D_n^{+}=\underset{1\le i\le n}{max}\left(\left|\frac{i}{n}-F\left(X_{i:n}\right|\widehat{a},\widehat{c})\right|\right),$$

  and

  $$D_n^{-}=\underset{1\le i\le n}{max}\left(\left|\frac{i-1}{n}-F\left(X_{i:n}\right|\widehat{a},\widehat{c})\right|\right).$$
• Cramér–von Mises (CvM) statistic:

  $$W_n^2=\sum _{i=1}^n{\left(\frac{2i-1}{2n}-F\left(X_{i:n}\right|\widehat{a},\widehat{c})\right)}^2+\frac{1}{12n}.$$

  (34)
• Modified Anderson–Darling (MAD) statistic (Ahmad et al. [44]):

  $$A{U}_n^2=\frac{n}{2}-\sum _{i=1}^n\left(2-\frac{2i-1}{n}\right)log(1-F\left(X_{i:n}\right|\widehat{a},\widehat{c}))-2\sum _{i=1}^{n}F\left(X_{i:n}\right|\widehat{a},\widehat{c}).$$

  (35)

Relative to the usual Anderson–Darling statistic, the $A{U}_n^2$ statistic in (35) gives more weight to the data in the upper tail. Smaller values of the statistics in (33)–(35) correspond to a better fit of the Pareto model. For a statistical power comparison between some of the aforementioned statistical tests, see Razali and Wah [45] or Singla et al. [46].

4.2. Simulation Study

In this subsection, we conduct a Monte Carlo simulation experiment to illustrate the performance of the aforementioned estimation methods for the shape and scale parameters of the Pareto model. We refer to the LGPWM estimators as LGPWM-KS, LGPWM-CvM and LGPWM-MAD when the tuning parameters $s_1$ and $s_2$ are selected using the data-driven method described in Section 4.1 based on the statistics in (33), (34) and (35), respectively. All computation was performed in software R. We simulated $r=200$ samples of sizes $n=15$, 20, 30, 40, 50, 75, 100, 150 and 200 from the Pareto distribution, taking the following combination of shape and scale parameters: $(a,c)$ = $(0.1,0.25)$, $(0.25,0.5)$, $(0.75,0.5)$ and $(1,1)$. To evaluate the accuracy and efficiency of the various estimators, we computed the simulated bias and the root mean squared error (RMSE) for each sample size, each set of parameters and the estimator under study.

The simulated results are summarized in Table 1 and Table 2. As can be seen from these tables, the estimated biases and root mean squared errors generally tend toward zero for all estimation methods as the sample size increases, except for the M and PWM. This can be explained by the fact that the M estimator of a and both PWM estimators are not consistent if $a\le 1$. Moreover, most of the estimators usually overestimate the target parameter. Regarding the LGPWM estimator, the optimal selection of tuning parameters is obtained through the data-driven method outlined in Section 4.1 using the MAD statistic.

Table 1. Bias and RMSE of the estimators of the shape parameter a for the Pareto distribution.

	ML	M	PWM	LGPWM-KS	LGPWM-CvM	LGPWM-MAD
	Bias/RMSE	Bias/RMSE	Bias/RMSE	Bias/RMSE	Bias/RMSE	Bias/RMSE
	Pareto model with $a=0.1$ and $c=0.25$
15	0.016/0.037	0.900/0.900	0.906/0.906	0.014/0.042	0.015/0.041	0.008/0.036
20	0.012/0.030	0.900/0.900	0.904/0.904	0.010/0.030	0.010/0.032	0.006/0.029
30	0.007/0.020	0.900/0.900	0.903/0.903	0.006/0.023	0.005/0.022	0.003/0.021
40	0.006/0.019	0.900/0.900	0.902/0.902	0.006/0.022	0.005/0.022	0.003/0.020
50	0.004/0.014	0.900/0.900	0.902/0.902	0.004/0.016	0.004/0.016	0.002/0.015
75	0.003/0.011	0.900/0.900	0.901/0.901	0.003/0.013	0.002/0.013	0.001/0.012
100	0.002/0.010	0.900/0.900	0.901/0.901	0.003/0.011	0.002/0.012	0.001/0.011
150	0.001/0.008	0.900/0.900	0.901/0.901	0.002/0.009	0.001/0.009	0.000/0.009
200	0.001/0.007	0.900/0.900	0.900/0.900	0.001/0.008	0.001/0.008	0.000/0.008
	Pareto model with $a=0.25$ and $c=0.5$
15	0.040/0.093	0.753/0.753	0.776/0.778	0.036/0.106	0.037/0.103	0.020/0.089
20	0.029/0.074	0.751/0.751	0.770/0.770	0.025/0.076	0.026/0.081	0.016/0.072
30	0.017/0.050	0.750/0.750	0.763/0.764	0.015/0.058	0.012/0.055	0.008/0.051
40	0.015/0.047	0.750/0.750	0.759/0.759	0.014/0.054	0.013/0.054	0.009/0.049
50	0.011/0.036	0.750/0.750	0.757/0.757	0.011/0.041	0.010/0.041	0.006/0.038
75	0.007/0.027	0.750/0.750	0.754/0.754	0.008/0.032	0.006/0.033	0.003/0.030
100	0.006/0.025	0.750/0.750	0.753/0.753	0.006/0.029	0.005/0.029	0.002/0.027
150	0.003/0.020	0.750/0.750	0.752/0.752	0.004/0.023	0.003/0.023	0.001/0.022
200	0.002/0.017	0.750/0.750	0.752/0.752	0.003/0.020	0.002/0.020	0.000/0.020
	Pareto model with $a=0.75$ and $c=0.5$
15	0.120/0.280	0.429/0.467	0.524/0.577	0.118/0.318	0.115/0.309	0.069/0.277
20	0.088/0.223	0.397/0.422	0.479/0.524	0.089/0.238	0.086/0.252	0.052/0.219
30	0.052/0.151	0.363/0.375	0.435/0.463	0.051/0.180	0.040/0.166	0.025/0.155
40	0.046/0.141	0.346/0.357	0.401/0.421	0.048/0.167	0.042/0.163	0.027/0.146
50	0.033/0.107	0.330/0.338	0.379/0.398	0.036/0.122	0.033/0.124	0.019/0.114
75	0.021/0.080	0.315/0.319	0.354/0.364	0.026/0.099	0.020/0.098	0.009/0.090
100	0.018/0.075	0.310/0.314	0.347/0.355	0.021/0.087	0.015/0.087	0.008/0.081
150	0.010/0.059	0.301/0.304	0.333/0.340	0.014/0.071	0.008/0.069	0.003/0.067
200	0.007/0.052	0.297/0.300	0.327/0.332	0.010/0.060	0.006/0.060	0.001/0.059
	Pareto model with $a=1$ and $c=1$
15	0.160/0.373	0.363/0.462	0.475/0.593	0.138/0.410	0.143/0.410	0.077/0.354
20	0.118/0.298	0.318/0.393	0.416/0.519	0.097/0.299	0.098/0.318	0.063/0.289
30	0.069/0.202	0.269/0.316	0.356/0.429	0.054/0.227	0.047/0.218	0.029/0.206
40	0.061/0.188	0.244/0.291	0.309/0.370	0.054/0.216	0.052/0.216	0.034/0.195
50	0.044/0.143	0.217/0.256	0.276/0.335	0.041/0.160	0.041/0.164	0.024/0.152
75	0.028/0.107	0.195/0.221	0.244/0.282	0.029/0.129	0.025/0.130	0.011/0.119
100	0.024/0.100	0.190/0.213	0.236/0.270	0.024/0.115	0.019/0.116	0.010/0.108
150	0.013/0.078	0.173/0.193	0.214/0.245	0.016/0.092	0.011/0.094	0.004/0.090
200	0.009/0.069	0.167/0.186	0.205/0.232	0.011/0.079	0.008/0.080	0.001/0.080

Table 2. Bias and RMSE of the estimators of the scale parameter c for the Pareto distribution.

	ML	M	PWM	LGPWM-KS	LGPWM-CvM	LGPWM-MAD
	Bias/RMSE	Bias/RMSE	Bias/RMSE	Bias/RMSE	Bias/RMSE	Bias/RMSE
	Pareto model with $a=0.1$ and $c=0.25$
15	0.517/2.489	0.466/2.319	*/*	0.428/1.439	0.525/1.852	0.366/1.248
20	0.199/0.350	0.176/0.326	*/*	0.345/1.376	0.328/1.362	0.294/1.193
30	0.111/0.200	0.099/0.189	*/*	0.097/0.302	0.112/0.470	0.100/0.384
40	0.077/0.131	0.069/0.124	*/*	0.064/0.221	0.066/0.262	0.066/0.279
50	0.059/0.087	0.053/0.082	*/*	0.058/0.204	0.060/0.219	0.051/0.216
75	0.036/0.052	0.032/0.050	*/*	0.025/0.113	0.022/0.127	0.025/0.217
100	0.025/0.035	0.022/0.033	*/*	0.018/0.088	0.013/0.089	0.011/0.117
150	0.016/0.021	0.014/0.020	*/*	0.012/0.069	0.009/0.084	0.008/0.103
200	0.012/0.016	0.010/0.015	*/*	0.009/0.062	0.004/0.061	0.001/0.079
	Pareto model with $a=0.25$ and $c=0.5$
15	0.179/0.335	0.134/0.296	*/*	0.122/0.345	0.133/0.381	0.086/0.332
20	0.112/0.168	0.081/0.144	*/*	0.095/0.303	0.093/0.299	0.071/0.301
30	0.070/0.108	0.051/0.094	*/*	0.043/0.149	0.039/0.173	0.028/0.180
40	0.052/0.078	0.039/0.068	*/*	0.029/0.119	0.026/0.128	0.019/0.147
50	0.042/0.059	0.031/0.051	*/*	0.025/0.114	0.025/0.121	0.013/0.133
75	0.026/0.037	0.019/0.032	*/*	0.011/0.078	0.007/0.083	0.001/0.111
100	0.019/0.026	0.014/0.022	*/*	0.009/0.063	0.004/0.065	−0.001/0.081
150	0.012/0.016	0.009/0.014	*/*	0.007/0.052	0.003/0.057	−0.001/0.071
200	0.009/0.013	0.007/0.011	*/*	0.004/0.046	0.000/0.047	−0.005/0.060
	Pareto model with $a=0.75$ and $c=0.5$
15	0.048/0.073	0.016/0.054	0.514/2.059	0.034/0.084	0.034/0.084	0.018/0.090
20	0.033/0.046	0.009/0.033	0.356/0.720	0.028/0.072	0.026/0.074	0.014/0.078
30	0.021/0.031	0.006/0.023	0.370/0.682	0.015/0.045	0.012/0.046	0.006/0.054
40	0.016/0.023	0.004/0.017	0.321/0.456	0.011/0.037	0.008/0.038	0.003/0.045
50	0.013/0.018	0.004/0.013	0.316/0.409	0.009/0.036	0.007/0.036	0.002/0.043
75	0.009/0.012	0.002/0.008	0.302/0.346	0.004/0.026	0.002/0.027	−0.001/0.034
100	0.006/0.008	0.001/0.006	0.306/0.349	0.004/0.021	0.002/0.021	−0.001/0.026
150	0.004/0.005	0.001/0.004	0.299/0.321	0.002/0.017	0.001/0.017	−0.001/0.023
200	0.003/0.004	0.001/0.003	0.308/0.329	0.002/0.015	−0.000/0.016	−0.002/0.020
	Pareto model with $a=1$ and $c=1$
15	0.070/0.105	0.015/0.075	0.293/0.625	0.033/0.120	0.035/0.122	0.011/0.131
20	0.048/0.068	0.010/0.047	0.238/0.343	0.026/0.102	0.024/0.103	0.009/0.114
30	0.032/0.046	0.004/0.032	0.233/0.328	0.012/0.063	0.009/0.068	0.002/0.080
40	0.024/0.034	0.003/0.024	0.198/0.262	0.008/0.053	0.007/0.056	0.001/0.067
50	0.020/0.027	0.003/0.018	0.183/0.239	0.007/0.052	0.007/0.054	−0.000/0.064
75	0.013/0.018	0.001/0.012	0.173/0.215	0.002/0.037	0.000/0.040	−0.004/0.052
100	0.009/0.012	0.001/0.008	0.173/0.209	0.002/0.030	0.000/0.031	−0.003/0.040
150	0.006/0.008	0.000/0.005	0.165/0.193	0.001/0.025	−0.000/0.027	−0.003/0.034
200	0.005/0.006	0.000/0.004	0.163/0.184	0.001/0.023	−0.001/0.024	−0.004/0.030

* value greater than 10.

For the estimation of the shape parameter a, the LGPWM-MAD estimator always has the smallest absolute bias and the smallest RMSE if the sample size is small. For larger sample sizes, the ML estimators have the lowest RMSE. In addition, the performance of the ML estimator is always quite close to the LGPWM-MAD estimator. Comparing the performance of all of the estimators for the scale parameter c, it is observed that the M estimator usually has the smallest RMSE. The LGPWM-MAD provides generally good results in terms of absolute bias.

4.3. Real Data Analysis

We now analyze the fit of a Pareto model to two real datasets: the population of the 150 largest metropolitan areas in the world and the estimated number of deaths from major earthquakes.

4.3.1. Population of the Largest Metropolitan Areas in the World

This dataset has the 150 largest cities in the world, by population, and was retrieved from the worldatlas website [47]. Since the webpage with the dataset is no longer available, data can be retrieved using the Wayback Machine website (https://web.archive.org/ (accessed on 15 May 2021)) or in Appendix A. Values were converted to millions ($\times {10}^{-6}$). In Table 3 we provide the descriptive statistics obtained with the function summary in R software.

Table 3. Summary statistics for the population data.

Min.	1st Quart.	Median	Mean	3rd Quart.	Max.
2.916	3.571	4.907	7.082	8.744	38.001

If data come from a Pareto distribution, high-order moments might not exist. Therefore, to assess the skewness, we computed the Bowley [48] coefficient of skewness,

$$S_b=\frac{q_3+q_1-2q_2}{q_3-q_1}=0.483,$$

where $q_1$, $q_2$ and $q_3$ are the first, second and third empirical quartiles, respectively. This measure of skewness is robust against extreme values. For other robust measures of skewness, see, among others, Horn [49], Kim and White [50] and Brys et al. [51]. Since $S_b>0$ and the median is smaller than the mean, we conclude that the underlying model is positively skewed. The histogram and the boxplot of these observations, in Figure 1, confirm the skewness of the data.

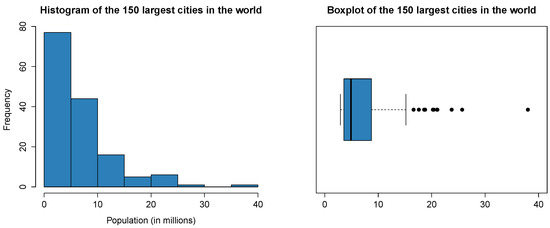
Figure 1. Histogram and boxplot for the population data.

Figure 2 suggests a Paretian behavior of the data. For more details regarding the construction of the Pareto Q-Q plot, see refs. [7,52].

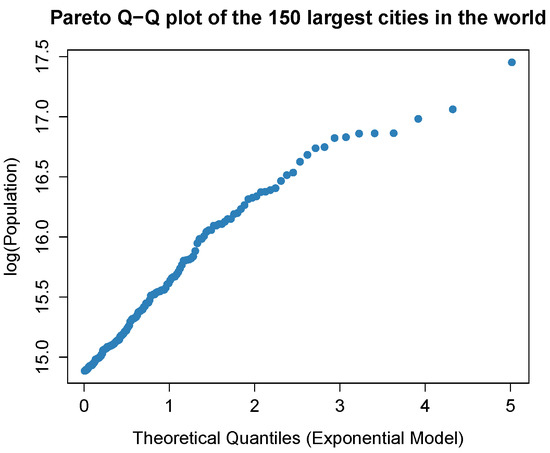
Figure 2. Pareto Q-Q Plot for the population data.

The parameter estimates for the fitted Pareto distribution, provided by the ML, L, PWM and LGPWM estimators, and the values of $D_n$, $W_n^2$ and $A{U}_n^2$ test statistics in (33), (34) and (35), respectively, are shown in Table 4. The smallest value of each test statistic is presented in bold. We took all possible combinations of values $(s_1,s_2)$ and chose the three combinations that provided the smallest values for each of the aforementioned test statistics. The values of the test statistics show that the new LGPWM estimators are relatively better than any other considered estimators. The choice of parameters $s_1=0.9$ and $s_2=1.0$ for the LGPWM estimators provides the smallest or second smallest value of the test statistics $D_n$, $W_n^2$ and $A{U}_n^2$. Note that not all methods perform well: the ${\widehat{c}}^{PWM}$ estimator produced an inadequate estimate (${\widehat{c}}^{PWM}>x_{1:150}$).

Table 4. Parameter estimates and goodness-of-fit statistics for the population data.

	$\widehat{\mathit{a}}$	$\widehat{\mathit{c}}$	${\mathit{D}}_{\mathit{n}}$	${\mathit{W}}_{\mathit{n}}^2$	${\mathit{AU}}_{\mathit{n}}^2$
ML	1.4599	2.9162	0.0595	0.0979	0.4462
M	1.6953	2.9047	0.1167	0.5929	2.1937
PWM	1.8835	3.3222	0.1800	0.9749	2.1406
LGPWM ($s_1=0.7,s_2=1.1$)	1.3933	2.9129	0.0437	0.0529	0.3408
LGPWM ($s_1=1.4,s_2=1.5$)	1.3325	2.8694	0.0502	0.0408	0.3686
LGPWM ($s_1=0.9,s_2=1.0$)	1.3824	2.9056	0.0447	0.0488	0.3398

4.3.2. Estimated Number of Deaths in Major Earthquakes

The second data set is available in Clark [53] and contains the estimated number of deaths in international earthquakes (from 1900 to 2011). The values of the data are as follows: 316,000, 242,769, 227,898, 200,000, 142,800, 110,000, 87,587, 86,000, 72,000, 70,000, 50,000, 40,900, 32,700, 32,610, 31,000, 30,000, 28,000, 25,000, 23,000, 20,896, 20,085. Values were converted to thousands ($\times {10}^{-3}$). Table 5 shows the descriptive statistics of the data.

Table 5. Summary statistics for the estimated number of deaths.

Min.	1st Quart.	Median	Mean	3rd Quart.	Max.
20.09	30.00	50.00	89.96	110.00	316.00

The Bowley coefficient of skewness is 0.5. Figure 3 shows the histogram and the boxplot, which are clearly right skewed.

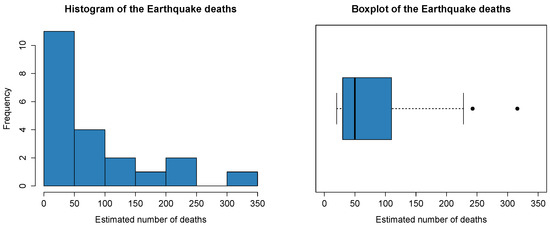
Figure 3. Histogram and boxplot for the estimated number of deaths.

The Q-Q plot in Figure 4 suggests a Paretian behavior of the data.

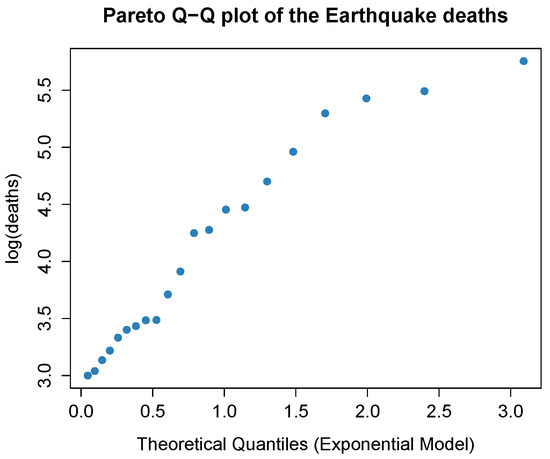
Figure 4. Pareto Q-Q Plot for the estimated number of deaths.

The parameter estimates of the Pareto model and the empirical value of the Kolmogorov–Smirnov, Cramér–von Mises and modified Anderson–Darling criteria are shown in Table 6. Overall, the LGPWM method provides a good fit. From Table 6, it is seen that there is no significant difference between using the Cramér–von Mises or modified Anderson–Darling criteria. In addition, notice that the scale PWM estimate is again invalid, since it is greater than the sample minimum.

Table 6. Parameter estimates and goodness-of-fit statistics for estimated number of deaths.

	$\widehat{\mathit{a}}$	$\widehat{\mathit{c}}$	${\mathit{D}}_{\mathit{n}}$	${\mathit{W}}_{\mathit{n}}^2$	${\mathit{AU}}_{\mathit{n}}^2$
ML	0.9034	20.0850	0.1525	0.0615	0.2479
M	1.2737	19.3341	0.2820	0.4347	1.7498
PWM	1.5046	30.1704	0.3145	0.5197	1.1743
LGPWM ($s_1=0.9,s_2=1.5$)	0.7536	18.0595	0.1159	0.0520	0.2421
LGPWM ($s_1=0.7,s_2=0.8$)	0.8149	19.0483	0.1300	0.0467	0.2179
LGPWM ($s_1=0.6,s_2=0.7$)	0.8323	19.3380	0.1334	0.0468	0.2161

5. Conclusions

In this research, we propose a new class of estimators for the shape and scale parameters of a Pareto distribution, named the log-generalized probability-weighted moment. This new class can be viewed as a generalization of the well-known probability-weighted moments and offers the advantage of extending the domain of the validity of the estimators to the complete parameter space of the Pareto distribution. Additionally, the asymptotic sampling distribution of the estimators provided by this method can be used as an approximation of the exact distribution for large sample sizes. The usefulness of the new estimation method was illustrated through a simulation study and two real data applications. It is concluded that, with appropriate choices of the tuning parameters $s_1$ and $s_2$, the proposed LGPWM estimators are capable of competing with the most commonly used estimation methods. As future research, we plan to examine the utilization of other goodness-of-fit statistics in the data-driven method for selecting the tuning parameters.