Abstract
Testing for complex serial dependence in economic and financial time series is a crucial task that bears many practical implications. However, the linear paradigm remains pervasive among practitioners as the autocorrelation function, because, despite its known shortcomings, it is still one of the most used tools in time series analysis. We propose a solution to the problem, by introducing the R package tseriesEntropy, dedicated to testing for serial/cross dependence and nonlinear serial dependence in time series, based on the entropy metric . The package implements tests for both continuous and categorical data. The nonparametric tests, based on , rely on minimal assumptions and have also been shown to be powerful for small sample sizes. The measure can be used as a nonlinear auto/cross-dependence function, both as an exploratory tool, or as a diagnostic measure, if computed on the residuals from a fitted model. Different null hypotheses of either independence or linear dependence can be tested by means of resampling methods, backed up by a sound theoretical background. We showcase our methods on a panel of commodity price time series. The results hint at the presence of a complex dependence in the conditional mean, together with conditional heteroskedasticity, and indicate the need for an appropriate nonlinear specification.
Keywords:
nonlinear time series; entropy; Hellinger distance; testing for nonlinear serial dependence; bootstrap; surrogate time series; tseriesEntropy; commodity prices MSC:
37M10
1. Introduction
The problem of measuring and testing dependence between two or more random variables is as old as statistics itself; still, it is subject to very active development and research. In the time series context, especially in economics and finance, there is a clear need to measure the serial/cross dependence beyond the information conveyed by the linear paradigm through the correlograms. For instance, a proper diagnostic test on the residuals of a statistical model should enforce the null hypothesis of serial independence. Testing for nonlinear serial dependence is also important in view of the practical implications of the nonlinear nature of the series. Departures from the linear hypothesis can occur in many different directions, since, contrarily to the linear case, there is no formal operational definition of a nonlinear process that can be tested directly. As a result, a test for a nonlinear effect is often either a test for a specific feature or the comparison of two specifications. For instance, it is well known that the business cycle is strongly asymmetric, since it is characterised by a slow growth phase, followed by a fast recession. As a result, all the macroeconomic time series that depend upon the economic activity present an asymmetry, which is not possible to describe through linear models. These include, for instance, unemployment rates, strikes rates, and wages. Another peculiar nonlinear feature observed in many economic and financial time series is the presence of multiple regimes. This is observed, for instance, in the dynamics of real exchange rates, where mean reversion is triggered by crossing a certain threshold. One way to model regime switching time series is to adopt the well known threshold autoregressive models (TAR) [1] and their moving-average extension (TARMA) [2]. Nonlinearity and complexity is also present in the conditional variance and this is especially observed in financial time series, as witnessed by the proliferation of ARCH-/GARCH-type models and the associated tests aimed at detecting conditional heteroskedasticity. The interested reader is referred to [3,4,5,6] and references therein for different accounts on the topic and on various testing procedures, on both the conditional mean and the conditional variance. Recent tests for threshold effects in the TAR/TARMA framework are introduced in [7,8,9].
The present paper moves from the works of [10,11], that propose nonparametric tests for serial/cross dependence and nonlinear serial dependence, relying on minimal assumptions, and can be used in many different scenarios. Such omnibus tests have good size and high power against many alternatives for sample sizes as small as 50. Both works are based upon the entropy-based dependence metric , that possesses many desirable properties. We describe the usage of the R package tseriesEntropy [12], which implements and extends such results and provides user-friendly routines, together with plotting and summary abilities, so that the measure can be used as a dropout replacement of the overly-used correlograms. Most tests can be applied both to continuous and categorical data. We describe the theoretical background underlying inference and testing with the entropy-based metric . Then, we focus on describing in detail all the routines present in the tseriesEntropy package by means of examples and code snippets that can be used to exactly reproduce some of the results of the paper. Different null hypotheses of either independence or linear dependence can be tested and the tests can be used both as exploratory tools or as diagnostic measures, if computed on the residuals from a fitted model. We also illustrate the practical usage of the package on a panel of time series of commodities.
Before describing in some detail the functionalities available in tseriesEntropy, together with providing a sketch of the underlying theoretical background, we provide a selective review of the software libraries dedicated to the theme of testing for serial/cross dependence in time series. We also mention some of the packages that are not explicitly dedicated to time series, but which implement recent notable theoretical results, especially in the multivariate case. The review is by no means exhaustive and we have selected those packages that appear to rely upon a sound theoretical background with available mathematical results on the validity of the associated inferences. The package np [13] contains bootstrap tests for serial and pairwise independence, based on the metric entropy . These are implemented in the functions npsdeptest and npdeptest, respectively. The measure is the same we use in tseriesEntropy, that also implements a similar test in its function Srho.test.ts and that encompasses both tests. The package NTS [14] contains some tests for threshold nonlinearity and lack of fit. The package testcorr [15] contains functions that implement robust tests based on auto/cross-correlation functions and for serial independence. Weighted portmanteau tests for goodness-of-fit and serial correlation, based on the trace of the square of the autocorrelation matrix, are implemented in the package WeightedPortTest [16]. There, a gamma-based approximation is used to derive the asymptotic null distribution of the test statistics. The package SDD [17] implements bootstrap tests for serial independence, based on generalized divergence functionals, that include, as a special case, the Hellinger distance. The authors use a nonparametric kernel density estimator for the densities, based upon Gaussian kernels. Then, the divergence measures are approximated by summation over a finite grid of values. The null distribution is obtained through permutation. The core function ADF also implements the serial independence test, based on grouping values in a contingency table and then using Pearson’s Chi-squared statistic. The package dCovTS [18] includes tests for pairwise/multivariate dependence in time series, based on the distance covariance/correlation function. The null distribution is approximated through either the iid or the wild bootstrap scheme. A portmanteau diagnostic test for vector autoregressive moving average (VARMA) models, based on the determinant of the standardized multivariate residual autocorrelations, is implemented in the portes package [19]. The package tsextreme [20] characterises the extreme dependence structure of time series through Bayesian methods. The package extremogram [21] implements permutation tests for serial and cross independence based on the extremogram. The package copula [22] contains tests of serial and multivariate independence, based on the empirical copula process. Finally, the package tseries [23], which is probably the first R package dedicated to time series to have appeared on CRAN, implements two neural network tests for nonlinearity in the mean, either in a single series or in a bivariate (regression) framework. We mention them even if they are not directly based upon the idea of measuring the serial/cross dependence. Both tests are asymptotic.
Besides the R packages specifically dedicated to time series, there are a number of packages that propose tests for independence/goodness-of-fit through diverse approaches. The packages wdm [24] and testforDEP [25] implement several measures of dependence and the associated tests for bivariate/multivariate independence. The package LIStest [26] implements a test for bivariate independence for continuous data, based on the longest increasing subsequence. The package USP [27] implements various independence tests for discrete, continuous, and infinite-dimensional data. These are permutation tests based on U-statistics. The package IndepTest [28] provides implementations of the weighted Kozachenko–Leonenko entropy estimator and permutation tests of independence based on it. The package dHSIC [29] contains an implementation of the d-variable Hilbert Schmidt multivariate independence criterion and several hypothesis tests based on it. A similar test is also implemented in the package EDMeasure [30], together with several other tests based upon measures of mutual dependence and conditional mean dependence. Multivariate independence tests, based on the notion of distance multivariance, are implemented in the package multivariance [31]. The package steadyICA [32] also implements a similar set of tests, but these rely on the notion of distance covariance instead. A test for conditional univariate/multivariate independence, based on the generalized covariance measure, is implemented in the package GeneralisedCovarianceMeasure [33].
The article is structured as follows: in Section 2 we introduce the entropy metric and describe the routines for its nonparametric estimation, both for continuous and dicrete/categorical time series. The S4 class Srho is also introduced and briefly illustrated. In Section 3 we introduce the routines to test for serial/cross independence with . As in Section 2, there are separate routines for testing both continuous and discrete/categorical time series and we also describe the S4 class Srho.test designed to work with all the tests based upon . Section 4 describes the theoretical background and the routines dedicated to testing for nonlinear serial dependence in time series. In particular, Section 4.1 illustrates the routines that implement the test where the null hypothesis is that of a linear Gaussian random process. The null distribution is based on surrogate data and Simulated Annealing. The test where the null hypothesis is that of a generic linear process (not necessarily Gaussian) is described in Section 4.2. In such cases, the null distribution is derived by means of a smoothed sieve bootstrap scheme. Finally, in Section 5 we show an application of the tests upon a panel of four monthly commodity price time series.
2. The Measure for Serial and Cross Dependence
Let and , , be two stationary random processes, where , , . Then, the metric entropy at lag k is a normalized version of the Bhattacharya–Hellinger–Matusita distance, defined as
In the case where for all t, measures the serial dependence of at lag k, this can be interpreted as a nonlinear auto/cross-correlation function that overcomes the limits of Pearson’s correlation coefficient. As pointed out in [10,11,34], satisfies many desirable properties, including the seven Rényi axioms and the additional properties described in [34]. Moreover, it satisfies the so-called generalized data processing inequality of Information Theory that, inter alia, implies independence from the margins in the continuous case (see also [35], for a discussion).
As concerns the relation to Pearson’s correlation coefficient in the Gaussian case, we have the following:
Proposition 1
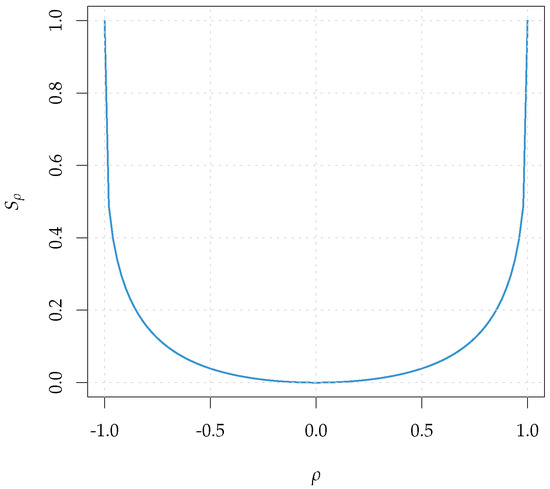
([11]). Let be a standard Normal random vector with correlation coefficient . Then
The relation, depicted in Figure 1, presents a sharp steepness around the maximum value of in modulus. The package tseriesEntropy implements the measure both for continuous and categorical data.

Figure 1.
Relation between and the correlation coefficient under the bivariate Gaussian setting.
2.1. Continuous State Space Time Series
In the case of continuous state–space processes that admit a probability density function with respect to the Lebesgue measure, the entropy measure becomes:
From now on, for simplicity, we use in place of . The nonparametric estimator of is the following:
and is implemented through kernel density estimation of the bivariate density and of the marginal densities and :
Here, K is a univariate kernel function and are the corresponding bandwidths. is a bivariate kernel function and is the bandwidth matrix. The function Srho.ts implements the nonparametric estimator of Equation (6). The syntax is the following:
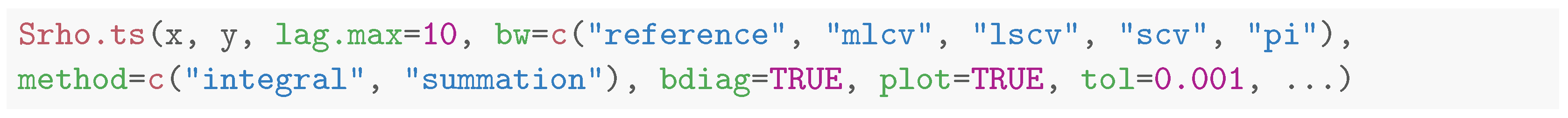
Here, x and y are numeric vectors/time series. If y is not missing, then the function computes the entropy measure between and , where the lag k ranges from -lag.max to lag.max. As a simple illustration, we generate a time series x of 50 observations from an AR(1) process and induce a nonlinear dependence at lag 1 in the series y.
The results are shown in Figure 2 that shows the peak at lag 1.
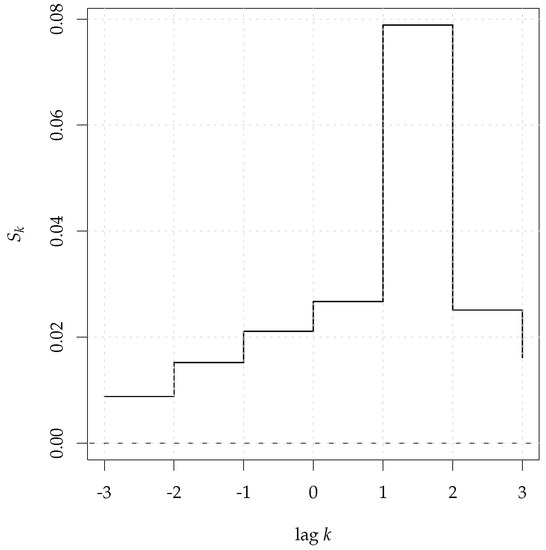
Figure 2.
Cross entropy between and () from Equation (9).

Plots can be suppressed by setting plot = FALSE. The choice of the kernel functions in the nonparametric estimator of Equation (6) has a limited impact and is taken to be Gaussian for the univariate densities and the product of two Gaussians for the bivariate density.
The bandwidth selection method plays an important role so that tseriesEntropy implements several options and some of these rely on the package ks [36]. They are controlled through the option bw and are presented in Table 1.

Table 1.
Overview of the bandwidth selection options in Srho.ts.
If the bandwidth selector is either reference or mlcv, then the bandwidth matrix for estimating the bivariate density is diagonal and this implies a spherical Gaussian kernel. The methods that rely on the package ks, namely, lscv, scv, pi can use both a diagonal or an unstructured bandwidth matrix through the option bdiag. If bdiag = TRUE (the default), then a diagonal matrix is used. This option has been introduced in version 0.7-0.
The double integral is computed by means of adaptive cubature methods, implemented in the function hcubature of the package cubature [41]. The maximum tolerance tol is passed to hcubature and usually there is no need to change its default value. The option method = “summation” selects an alternative estimator based on summation. As also remarked in [10], the estimator based upon adaptive integration is generally preferable.
If y is missing, then Srho.ts computes the serial version of the measure. This is shown in the next example, where we compute , with the Likelihood Cross Validation bandwidth selector, on a realization from an MA(1) process:

The result is shown in Figure 3, where the dependence at lag 1 is detected.
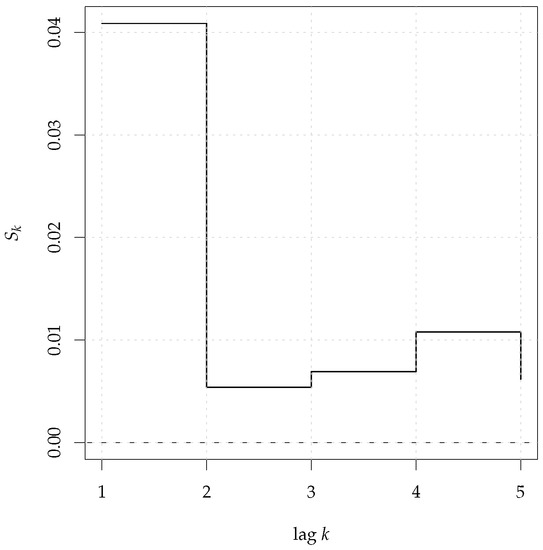
Figure 3.
Entropy () computed on a realization of a MA(1) process.
2.2. Categorical/Discrete State Space Time Series
The package implements the maximum likelihood estimator of based on relative frequencies in the function Srho:
where
and is the indicator function that takes value 1 if A is true, 0 otherwise. The syntax of Srho is the following:

The main difference with Srho.ts lies in the option nor, which has been introduced to deal with the effects of the margins. While the measure, based on the distance between densities, is free from the effects of the marginal probability distributions, this is not the case with discrete/categorical data, so that the maximum reachable value of the measure is not 1 but depends upon the marginal probabilities. As is pointed out below, this has no practical effects if is used in hypothesis testing. However, if the actual value of the measure matters, as is the case when, for instance, one compares the level of dependence of different series, then the option nor = TRUE normalizes the measure against its maximum theoretical attainable level so that the actual range is the interval , as it should be. This effect is illustrated in the following example, where we generate 1000 random variates from a discrete uniform distribution on the first 5 integers and correlate the sequence with itself so that we should observe perfect dependence at lag 0.

The results are shown in Figure 4. Note that, even if we are in the perfect dependence scenario, the maximum theoretical attainable level of is not 1 but results in (left panel, red dashed line) and this is confirmed by the estimate (blue line). By using the option nor = TRUE the normalized measure reaches 1 at lag zero (right panel).
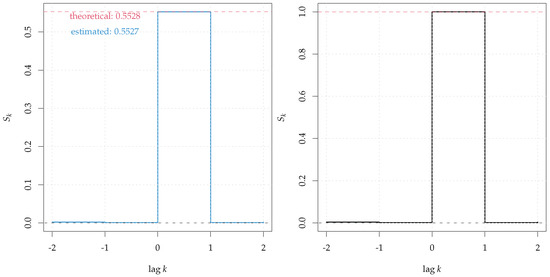
Figure 4.
Cross Entropy for categorical data, in the presence of perfect dependence at lag 1. The left panel shows the unnormalized measure (blue, solid line), where the maximum attainable level is indicated in red. The right panel shows the normalized version of the measure (black, solid line).
The option stationary = TRUE assumes stationarity, so that the marginal probabilities are estimated on the whole sample and this leads to more efficient estimators, even if its effect on large samples is negligible.
2.3. The S4 Classes Srho-class and Srho.ts-class
The S4 classes Srho-class and its extension Srho.ts-class are designed to store and manage the results coming from Srho and Srho.ts, respectively. These are equipped with methods show and plot.

In particular, the plot method allows the achievement of fine tuning and customizations, as shown in Figure 5.
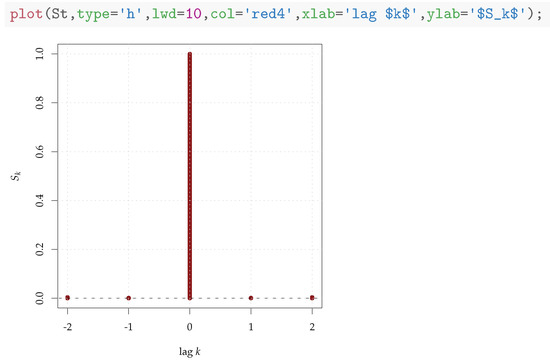
Figure 5.
The same as Figure 4 (right) but with plot customizations.
3. Tests for Serial and Cross Dependence
The package tseriesEntropy offers specialized functions for testing for serial and cross dependence. The entropy measure has been shown to provide powerful tests that overcome many of the issues of the auto- and cross-correlation functions [10]. They can be used both as exploratory tools to investigate the dependence structure of time series and as diagnostic tools to assess the presence of residual dependence from a fitted model. Being based upon a nonparametric estimator, it is model-free and is able to detect departures from independence in any possible direction. Given two time series of size n, realizations of stationary random processes and we test the null hypotheses that and are independent, for each k ranging in [-lag.max, lag.max]. The distribution of the test statistic under is obtained by resampling/permutation.
3.1. Tests for Continuous Time Series
In case of continuous state–space time series, the package implements a test for serial/cross dependence through the routine Srho.test.ts:

Besides the parameters relevant to Srho.ts, the user needs to specify the number B of bootstrap resamples used to build the distribution of the test statistic under the null hypothesis. As before, if y is missing, the routine tests for serial dependence in . We illustrate this in the following example where we compute on w and x, realizations from a Gaussian white noise and an AR(1) process, respectively. For convenience, we use the parallel version of the routine Srho.test.ts.p and B = 40. In practice, the choice of B depends upon the experimenter. In general, 100 replications are enough to have a rough idea of the result and the number can be increased for a finer assessment of the significance level.

The results are displayed in Figure 6. The output is similar to that of Srho.ts, but the rejection bands at levels, specified by quant, are added, and, by default, they are 95% (green dashed line) and 99% (blue dashed line). No lag of exceeds the confidence bands for the white noise w (left panel). As for the AR(1) series x, the test statistic points correctly to the presence of dependence in the 5 lags. In its serial version, the null distribution of is obtained by random permutation, as also put forward in [10].
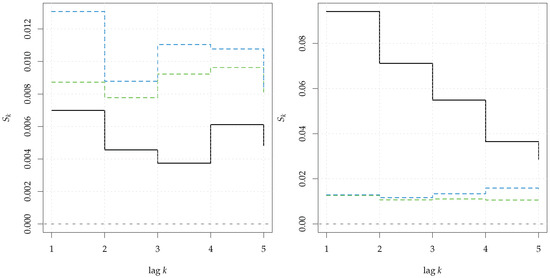
Figure 6.
Serial Entropy for (black, solid line) computed on a realization from a white noise (left panel) and a AR(1) process (right panel). The rejection bands at 95% (green dashed line) and 99% (blue dashed line) correspond to the null hypothesis of serial independence.
Srho.test.ts.p is the parallel version of the routine that uses the parallel package. The user only needs to specify the number of workers to be used through the option nwork. By default, all the available cores are used.
In the next example, we show testing for cross dependence and the effect of the resampling scheme selected with ci.type. First, we generate two independent realizations of the following AR(1) process:

Then, we compute the cross entropy between x and y. Since the two time series are independent realizations, the test should not reject the null hypothesis at all lags, but the presence of strong serial dependence in the time series affects the results.

This is clear from the left panel of Figure 7 where the null distribution is obtained by randomly permuting the two series (ci.type = "perm"). This also destroys the serial correlation of the two series and biases the result of the test since the variance of the null distribution of the test statistic depends upon the autocorrelation of the series. One way to overcome this problem would be to prewhiten the series before applying the cross-entropy test (see e.g., ref. [42,43]). Such an approach has its limits, in that it is tailored to be used for testing with the cross-correlation function, but its use for general measures of dependence is questionable. The solution adopted in Srho.test.ts is to resample the series by means of a moving block bootstrap that preserves the serial dependence structure of the series [44]. This is selected by setting ci.type = "mbb", which is the default if y is not missing. The block length is equal to lag.max. The result of the right panel shows correctly that no lag of the cross-entropy exceeds the rejection bands at 99%.
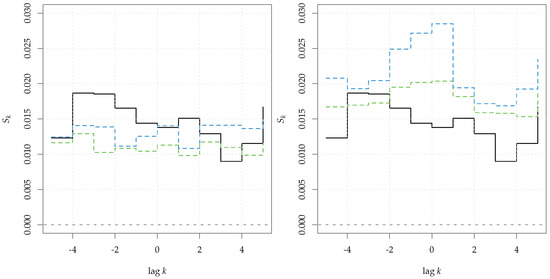
Figure 7.
Cross Entropy for (black, solid line), computed between two independent realizations of a AR(1) process. The rejection bands at 95% and 99% are indicated as green and blue dashed lines, respectively. In the left panel they are computed by permutation (ci.type=‘perm’), whereas in the right panel the bands are computed through a moving block bootstrap (ci.type=‘mbb’).
3.2. Tests for Discrete/Categorical Time Series
The test for serial/cross independence for categorical time series is implemented in the routine Srho.test:

There are no new options with respect to Srho.test.ts; moreover, for the cross-entropy version, only the permutation option is available. The moving block bootstrap is implemented in a future version of the package. In the next example, we generate y, a correlated binary sequence (at lag 2) by thresholding over the origin a realization x of a MA process:
The results are shown in Figure 8.

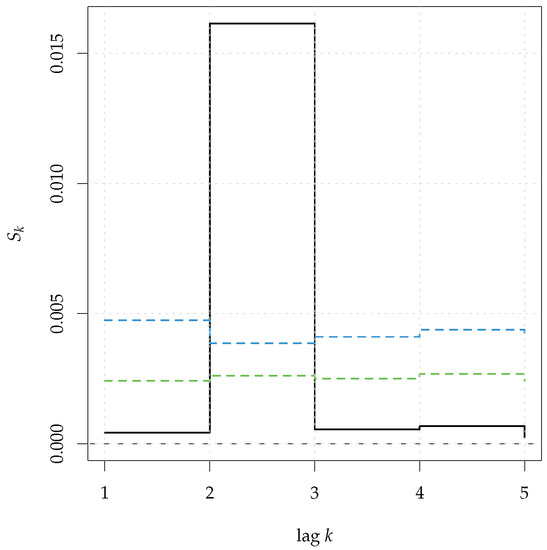
Figure 8.
Serial Entropy for (black, solid line) computed on a correlated binary time series generated from discretizing a MA(2) process. The rejection bands at 95% (green dashed line) and 99% (blue dashed line) correspond to the null hypothesis of serial independence.
3.3. The S4 Class Srho.test-class
The S4 class Srho.test-class is an extension of Srho-class, to allow dealing with the results coming from all the tests implemented in the package.


The show method prints both the significant lags at levels set by quant and the p-values of the test at each lag. As shown in the previous examples, the plot method adds the rejection bands of the tests computed on the null distribution at the levels specified in quant.
4. Tests for Nonlinear Serial Dependence
The most important functions of the package tseriesEntropy implement the tests for nonlinear serial dependence introduced in [11] where the formal definition of linear processes is discussed along the lines of [45]. In particular, the null hypothesis assumes that the data generating process follows a zero-mean AR as follows:
where both and are finite. The nature of the innovation process determines the two null hypotheses discussed:
where f is a generic probability distribution. In practice, specifies the hypothesis of a linear Gaussian process and the alternative hypothesis can include linear non-Gaussian processes, whereas defines a generic linear process driven by possibly non-Gaussian innovations. In the latter case, the alternative hypothesis is that of a (fully) non-linear process that does not admit the AR representation of Equation (19). The two hypotheses and are tested by means of the two statistics and , where is a restricted parametric estimator of based upon Equation (3).
Since the derivation of the asymptotic distribution of the two statistics and is either unfeasible, or requires large sample sizes to hold in practice, Ref. [11] discusses two resampling schemes and prove their asymptotic validity. These are summarized in the following two sections.
4.1. Tests for Linear Gaussian Dependence with Surrogate Data
The first scheme is based upon surrogate data, a class of Monte Carlo-based tests for nonlinearity where the null distribution is derived by generating random time series that possess the same mean and linear dependence as the original series. This can be achieved by randomizing the phase of the Fourier transform of the original time series, and this was the original proposal of [46]. The asymptotic validity of the proposal under the null hypothesis of a (circular) linear Gaussian process was established in [47]. Subsequent studies showed that the phase-randomization approach led to tests with biased size [48]. One solution to this problem is to see the generation of time series under the null hypothesis as a constrained stochastic optimization problem that can be solved by Simulated Annealing. This is implemented in the function surrogate.SA:
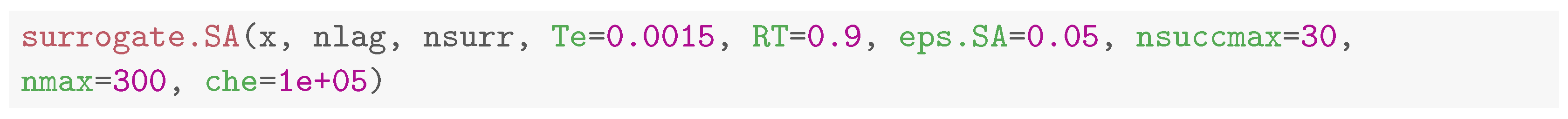
The function takes, as input, the original time series x, the number of lags of the autocorrelation to be matched by surrogates (nlag), and the number of surrogates nsurr. The remaining parameters pertain to the Simulated Annealing algorithm and are further discussed below in Section 4.1.1. We illustrate the use of the routine in the following example. First, we generate the original time series x from a AR(1) process. Then, we generate 2 surrogates and plot all the series, see Figure 9.
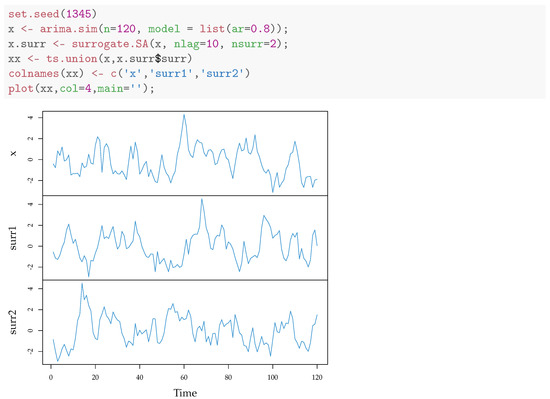
Figure 9.
Time series from a AR(1) process together with two surrogate time series generated through Simulated Annealing.
Now, we check that the surrogates have the same ACF of x (up to eps.SA).

As expected, for each lag, the difference between the ACF of the original series and that of the surrogates does not exceed eps.SA = 0.05.
The routine Trho.test.SA, and its parallel version Trho.test.SA.p, implement the test statistic together with the surrogate data approach based on Simulated Annealing. The null hypothesis tested is that of Equation (20) and the syntax is the following:

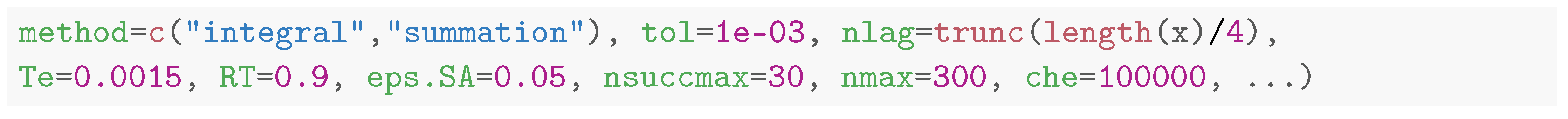
Most options are passed either to Srho.ts or surrogate.SA so that they are not discussed again. Note that even if the syntax allows for the presence of the bivariate version of the test, this has not yet been implemented. Indeed, it requires the extension of the theory put forward in [11] and is the subject of future investigations. We illustrate the typical usage of the routine in the following example, where we generate two realizations of a linear MA(1) process: x1 has Gaussian innovations, whereas x2 has Student’s t innovations (with 3 degrees of freedom). In both cases, in order to expedite the computations, the number of surrogates was 40 and the target criterion was set to 0.1.

The results are displayed in Figure 10. The test did reject the null hypothesis for x1 (left panel), while it rejected it for x2 (right panel). Note that, as suggested in [11], the mlcv bandwidth selector was used and gave the best performance in conjunction with . The Simulated Annealing algorithm for generating surrogate time series is discussed in some detail in the next section.
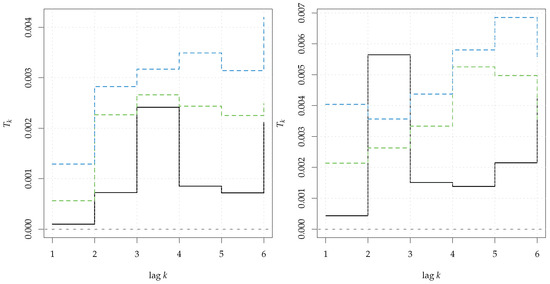
Figure 10.
Test statistic for (black, solid line), computed on a linear Gaussian MA(1) process (left panel) and on a linear MA(1) process driven by Student’s t innovations (right panel). The rejection bands at 95% (green dashed line) and 99% (blue dashed line) correspond to the null hypothesis of a linear Gaussian process.
4.1.1. Generating Surrogate Time Series with Simulated Annealing
The simulated annealing is stochastic optimization algorithm that can minimize complex multidimensional functions with many false minima (see e.g., ref. [49]). The cost function C can be interpreted as the energy of a thermodynamic system and the annealing is used to bring a glassy solid close to the optimal state by first heating it and then cooling it. The simulation of this tempering procedure exploited the fact that, in thermodynamic equilibrium at some finite temperature T, the configurations of the system are visited with a probability according to the Boltzmann distribution of the canonical ensemble . Hence, the algorithm accepts changes of the configuration with a probability if the energy is decreased () or if the energy is increased () (Metropolis step). The temperature T is the parameter of the Boltzmann distribution that determines the probability of accepting the unfavourable changes needed to avoid false minima.
Let be an observed series of length n and let , be its sample autocorrelation function. We denoted with the candidate surrogate, with autocorrelation function . The cost function implemented is:
The algorithm starts with a temperature Te = T and with , a random permutation of the original series . For each temperature value T:
- swap two observations of and obtain the series ;
- compute ;
- if accept the swap, that is,if accept the swap with probability ;
- repeat step (1)–(3) until either the number of accepted swaps reaches nsuccmax×n or the number of trials reaches nmax×n;
- lower the temperature T, for instance by setting where = RT < 1;
- repeat the whole procedure until the cost function reaches a specified threshold eps.SA.
In general, the choice of the parameters for the algorithm is problem-specific and a certain amount of experimentation and tuning is expected in order to obtain good results. The following parameter settings can be used almost automatically as follows:
Ideally, eps.SA should depend upon the sample size n and one can try increasing it to speed up the computations.
| Parameter | Value | Description |
| Te | 0.001 | initial temperature |
| RT | 0.9 | reduction factor for Te |
| eps.SA | 0.05 | threshold |
| nsuccmax | 30 | Te is decreased after nsuccmax×n successes |
| nmax | 300 | Te is decreased after nmax×n trials |
| che | 1 × | after che× 2n global iterations the algorithm starts again |
4.2. Tests for General Nonlinear Serial Dependence
The hypothesis of a generic non-linear serial dependence of Equation (21) was tested by means of the entropy metric of Equation (6), paired with a smoothed sieve bootstrap scheme [50]. The smoothed version of the sieve bootstrap extends the classic sieve bootstrap for AR processes [51]. While the latter is valid for smooth functions of linear statistics, the smoothed sieve bootstrap leads to valid inferences for statistics, like , that are compactly differentiable nonlinear functionals of empirical measures. The main steps of the scheme are the following:
- Given a time series (), fit an AR model upon itand obtain the estimated parameters ;
- derive the centered residuals :
- compute the kernel density estimate of :where is a bandwidth such that and ;
- draw the bootstrap innovations from the kernel density estimate
- obtain the bootstrapped time series according to:where the initial values are .
- Repeat steps (4)–(5) B times.
The scheme is similar to the classic sieve bootstrap, except for the key idea of resampling from the smooth density of the residuals, which ensures that the bootstrap process inherits the mixing properties needed to prove asymptotic results. The scheme is implemented in the routine surrogate.ARs:

The routine uses stats::ar to fit the AR model and the arguments order.max and fit.methods are passed to it. The default options ensure that the best AR model, where p ranges from 1 to order.max, is selected by means of the AIC and order.max depends upon the length of the series. The following example illustrates the usage of the routine and the results are presented in Figure 11.

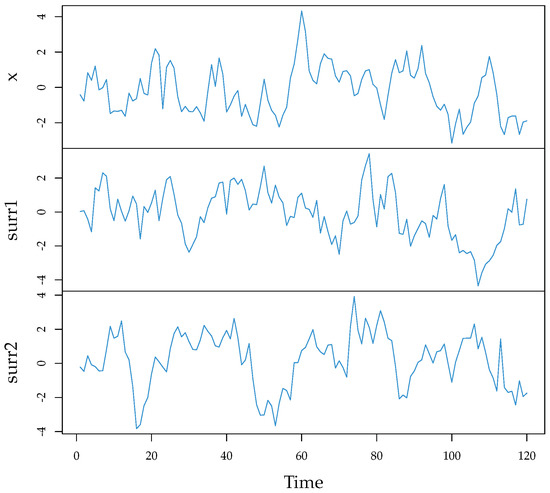
Figure 11.
Time series from a AR(1) process together with two surrogate/resampled time series generated through the smoothed sieve bootstrap scheme.
Now we compare the correlograms of the series.

Note that the package also contains the routine surrogate.AR that implements the standard sieve bootstrap [51].
The routines Srho.test.AR and Srho.test.AR.p implement the test statistic together with the sieve bootstrap scheme. The null hypothesis tested is that of Equation (21) and the syntax is the following:

The option smoothed selects either the smoothed sieve scheme of surrogate.ARs or the standard sieve of surrogate.AR. The remaining option has already been discussed above. According to the results of [11], this is the most powerful and flexible test and its use is recommended in conjunction with the reference bandwidth selection criterion. We show its use on a time series from a nonlinear moving average process with nonlinear dependence at lag k.
With this aim in mind, we introduce the nlma function:

First, we generate a series x of 50 observations from nlma and show the inability of the analysis based upon the autocorrelation, to detect the nonlinear dependence, see Figure 12. Then, we compute the bootstrap test of nonlinear serial dependence, based on and present the results in Figure 13:

Even with a sample size as small as 50 the test correctly identified the nonlinear dependence at lag 2.
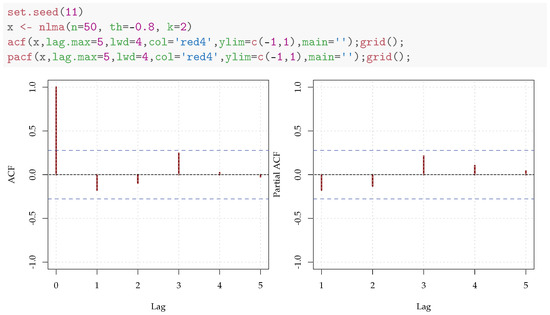
Figure 12.
Correlograms computed on a realization of a nonlinear MA process.
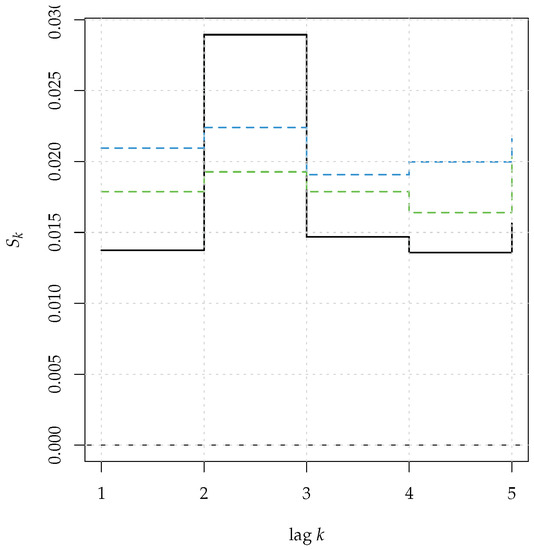
Figure 13.
Serial entropy for (black, solid line), computed on a realization of a nonlinear MA(1) process. The rejection bands at 95% (green dashed line) and 99% (blue dashed line) correspond to the null hypothesis of a general linear process.
4.3. Discussion
In this section, we highlight the difference between the test for serial dependence Srho.test.ts and that of nonlinear serial dependence Srho.test.AR and address why the two cannot be used interchangeably. In literature, several diagnostic tests to verify the independence of the residuals of a fitted model have been proposed. These can be based upon dependence measures, akin to , or rely on ad hoc measures, such as generalized correlations. Contrarily to some of the claims, finding structure in the residuals of a linear model does not necessarily imply a nonlinear specification, but can simply point to a misspecified (linear) model. Hence, a proper test for nonlinear serial dependence should explicitly enforce the null hypothesis of linearity on the test statistic and this is the approach adopted here. We illustrate the matter in the following example, where the time series x came from an ARMA(1,1) process. Then, we fitted a MA(1) model to the series and tested for independence of both x and the residuals res with the permutation test of Srho.test.ts.

From Figure 14 it is clear that the test rejected the null hypothesis of serial independence for both the original series x (left panel) and the residuals res of the fitted MA(1) (right panel). In the latter case, rejection implied lack of fit but not nonlinearity. This was further confirmed by applying the test for nonlinear serial dependence of Srho.test.AR. The results are plotted in Figure 15:

This time, the test did not reject the null hypothesis in both series and correctly indicated that the data generating process was linear.
Being based upon resampling methods, most of the tests presented a high computational burden. In particular, as shown in the supplement of [11], the test Trho.test.SA, based upon Simulated Annealing and paired with the mlcv bandwidth selector, had a computational complexity of (n being the length of the series), whereas the test Srho.test.AR, paired with the reference criterion, had a complexity of , which made it generally preferable, in view of its superior performance. In order to (partly) overcome the burden, and to parallelize the functions, the key code portions for estimating , and for the resampling schemes, were coded in Fortran. In any case, we recommend running the tests with a small initial number of resamples, especially if the series is long.
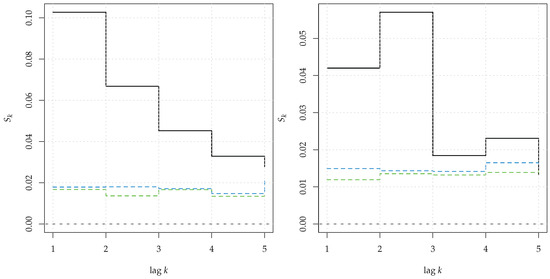
Figure 14.
Serial entropy for (black, solid line), computed on a realization of a linear ARMA(1,1) process (left panel) and on the residuals of a fitted MA(1) model upon the series (right panel). The rejection bands at 95% (green dashed line) and 99% (blue dashed line) corresponded to the null hypothesis of serial independence.
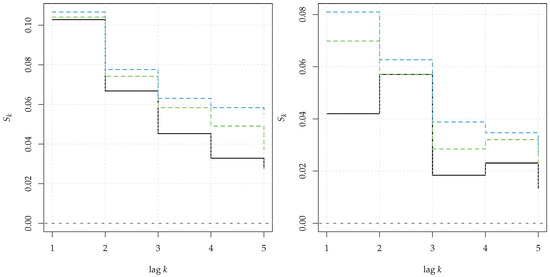
Figure 15.
Serial entropy for (black, solid line), computed on a realization of a linear ARMA(1,1) process (left panel) and on the residuals of a fitted MA(1) model upon the series. The rejection bands at 95% (green dashed line) and 99% (blue dashed line) corresponded to the null hypothesis of a general linear process.
5. Detecting Complex Dependence in Commodity Prices
In this section we apply the entropy-based tests to a panel of 4 commodity price time series. Commodities are primary agricultural products or raw materials and they are used in the production of other goods. Their prices are crucial in individual, country-level economies, in that they respond quickly to economic shocks, such as increase in demand. Hence, they are used to predict the behavior of other economic variables, and they are traded in the cash market, or as derivatives [52].
We considered 347 monthly observations, from January, 1994, to November, 2022, for the price of the four commodities. The two energy commodities were the WTI crude oil price index and the US natural gas spot price at the Henry Hub in Louisiana. The two precious commodities were gold and silver prices traded in London, with afternoon fixing. The series were obtained from the World Bank website https://www.worldbank.org/en/research/commodity-markets (accessed on 27 December 2022). For each commodity, we modeled log returns of their prices, that is , where denoted the price of commodity i () at time t. The time plot reported in Figure 16 highlighted that the series had different variabilities, which were lower for gold, while more pronounced for WTI oil and natural gas.
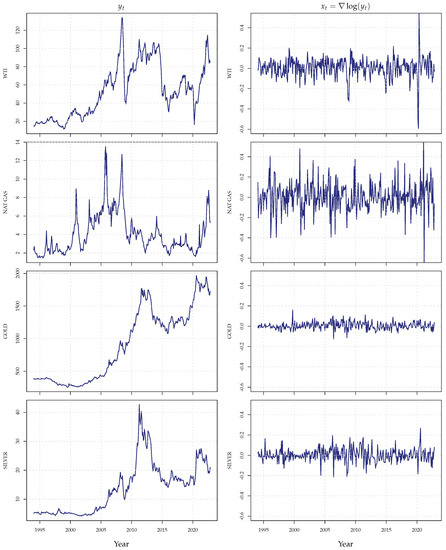
Figure 16.
Time plots of the four monthly commodities series January 1994–November 2022. Left column: raw commodities . Right column: log-returns .
The correlograms of the series, presented in Figure 17, showed a white noise-like structure, whereas the correlograms of the squared series, shown in Figure 18, pointed to the possible presence of a nonlinear structure in the conditional variance (ARCH effect).
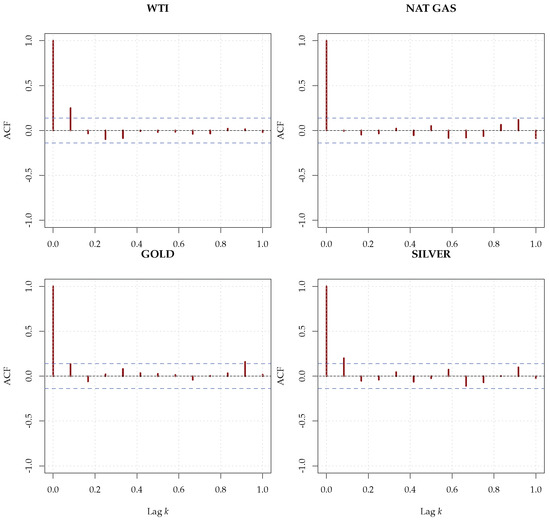
Figure 17.
Sample correlograms for the four commodities up to one year. The confidence bands at level under the white noise hypothesis are indicated as blue dashed horizontal lines.
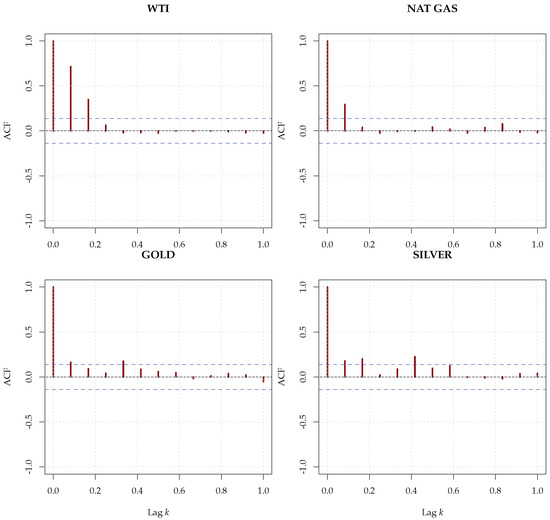
Figure 18.
Sample correlograms for the squared series of the four commodities up to one year. The confidence bands at level under the white noise hypothesis are indicated as blue dashed horizontal lines.
As a first step, we tested the series of the log-returns for the presence of general nonlinear dependence up to lag 13, by using the smoothed sieve bootstrap version implemented in Srho.test.AR. In all the tests, the number of bootstrap replications was set to 1000 and we used the reference bandwidth, as suggested in [11].
As shown in Figure 19, the entropy measure exceeded the rejection bands under the null hypothesis of linearity for all the four series, but at different lags. Furthermore, the evidence was less striking for silver, where the test rejected only for lag 7, at level 95%. Now, since in [11] it was shown that the test had power against nonlinear serial dependence both in the conditional mean and in the conditional variance, we repeated the test on the residuals of a ARMA–GARCH model fitted upon the series. The order of the ARMA model was chosen by means of the consistent Hannan–Rissanen criterion, see [53,54] for more details.
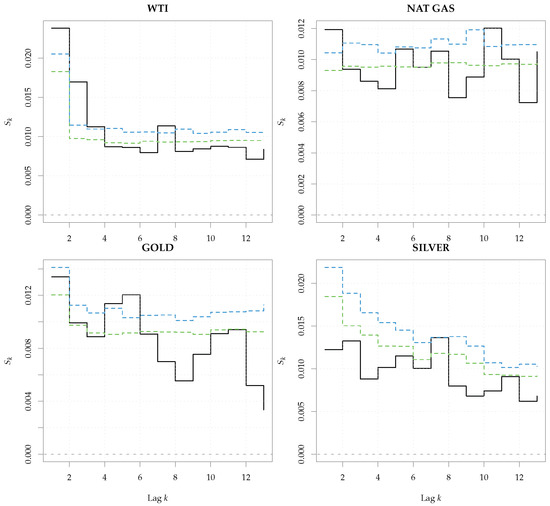
Figure 19.
Serial entropy for lag (black, solid line), computed on the commodity price series. The rejection bands at 95% (green dashed line) and 99% (blue dashed line) correspond to the null hypothesis of a general linear process.
The results are presented in Figure 20 and clearly show rejections for all the series. In particular, the energy commodities presented a significant nonlinear dependence at lag 1 that could not be ascribed to conditional heteroskedasticity, but hinted at a nonlinearity in the conditional mean dynamics. The results were consistent with those of [55], where the authors showed the predictive superiority of a threshold ARMA model over linear specifications. Overall, the entropy-based tests were used both as an exploratory tool, when applied to the raw series, and as a diagnostic tool, if applied to the residuals of a fitted model. They seemed to indicate the presence of a complex (nonlinear) dependence in the conditional mean, together with conditional heteroskedasticity. The complexity of commodity prices was recognised in literature and investigated from different perspectives. For instance, Ref. [56] studied the presence of spillover effects in commodity prices through the continuous wavelet transform, whereas [57] investigated the presence of long-range dependence in hourly electricity prices.
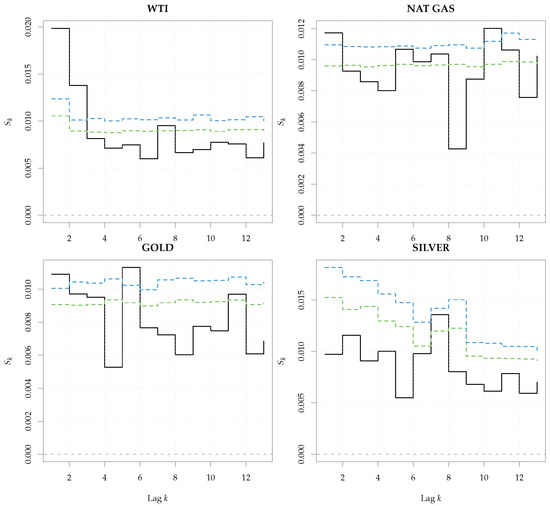
Figure 20.
Serial entropy for lag (black, solid line), computed on the residuals of a ARMA–GARCH model fitted upon the series of commodity prices. The rejection bands at 95% (green dashed line) and 99% (blue dashed line) correspond to the null hypothesis of a general linear process.
The procedures followed in the article should provide some guidance to the practitioner on how to deal with complex dependence and/or perform diagnostic analysis upon the residuals of a fitted model, which should go beyond the simple usage of the autocorrelation function. As mentioned in the introduction, nonlinearity has many different aspects and each of them would require a separate, specific treatment. The tests presented are general, in that they have power against all sorts of dependence and nonlinearity so they can be used in many different situations and at various steps of the investigation, from exploratory analysis to the diagnostic phase.
Author Contributions
Conceptualization, S.G. and G.G.; methodology, S.G.; software, S.G. and G.G.; data curation, S.G. and G.G.; writing—original draft preparation, S.G. and G.G.; writing—review and editing, S.G. and G.G.; visualization, S.G. and G.G.; funding acquisition, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was covered with the support of the Free University of Bozen-Bolzano.
Data Availability Statement
The commodity time series are available from the World Bank website https://www.worldbank.org/en/research/commodity-markets (accessed on 27 December 2022). The latest version of the R package tseriesEntropy is available on CRAN at https://cran.r-project.org/web/packages/tseriesEntropy/ (accessed on 27 December 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AR | Autoregressive |
| MA | Moving Average |
| ARMA | Autoregressive Moving Average |
| TAR | Threshold Autoregressive |
| TARMA | Threshold Autoregressive Moving Average |
| AIC | Akaike Information Criterion |
References
- Tong, H.; Lim, K. Threshold autoregression, limit cycles and cyclical data. J. R. Stat. Soc. Ser. B (Methodol.) 1980, 42, 245–292. [Google Scholar] [CrossRef]
- Tong, H. Nonlinear Time Series. A Dynamical System Approach; Oxford University Press: Oxford, UK, 1990; p. xvi+564. [Google Scholar]
- Fan, J.; Yao, Q. Nonlinear Time Series. Nonparametric and Parametric Methods; Springer: New York, NY, USA, 2003; p. xx+551. [Google Scholar]
- Enders, W. Applied Econometric Time Series, 4th ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- De Gooijer, J. Elements of Nonlinear Time Series Analysis and Forecasting; Springer Series in Statistics; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Tsay, R.; Chen, R. Nonlinear Time Series Analysis; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Giannerini, S.; Goracci, G.; Rahbek, A. The validity of bootstrap testing in the threshold framework. J. Econom. 2023, in press. [Google Scholar] [CrossRef]
- Goracci, G.; Giannerini, S.; Chan, K.S.; Tong, H. Testing for threshold effects in the TARMA framework. Stat. Sin. 2023, 33, 3. [Google Scholar] [CrossRef]
- Chan, K.S.; Giannerini, S.; Goracci, G.; Tong, H. Testing for threshold regulation in presence of measurement error. Stat. Sin. 2023, 34, 3. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Maasoumi, E.; Racine, J. A Dependence Metric for Possibly Nonlinear Processes. J. Time Ser. Anal. 2004, 25, 649–669. [Google Scholar] [CrossRef]
- Giannerini, S.; Maasoumi, E.; Dagum, E.B. Entropy Testing for Nonlinear Serial Dependence in Time Series. Biometrika 2015, 102, 661–675. [Google Scholar] [CrossRef]
- Giannerini, S. tseriesentropy: Entropy Based Analysis and Tests for Time Series. R Package Version 0.7-0. 2021. Available online: https://CRAN.R-project.org/package=tseriesEntropy (accessed on 27 December 2022).
- Hayfield, T.; Racine, J.S. Nonparametric Econometrics: The np Package. J. Stat. Softw. 2008, 27, 1–32. [Google Scholar] [CrossRef]
- Tsay, R.; Chen, R.; Liu, X. NTS: Nonlinear Time Series Analysis. R Package Version 1.1.2. 2020. Available online: https://CRAN.R-project.org/package=NTS (accessed on 27 December 2022).
- Dalla, V.; Giraitis, L.; Phillips, P.C.B. testcorr: Testing Zero Correlation. R Package Version 0.1.2. 2020. Available online: https://CRAN.R-project.org/package=testcorr (accessed on 27 December 2022).
- Fisher, T.J.; Gallagher, C.M. WeightedPortTest: Weighted Portmanteau Tests for Time Series Goodness-of-Fit. R Package Version 1.0. 2012. Available online: https://CRAN.R-project.org/package=WeightedPortTest (accessed on 27 December 2022).
- Bagnato, L.; De Capitani, L.; Mazza, A.; Punzo, A. SDD: An R Package for Serial Dependence Diagrams. J. Stat. Softw. 2015, 64, 1–19. [Google Scholar] [CrossRef]
- Pitsillou, M.; Fokianos, K. dCovTS: Distance Covariance and Correlation for Time Series Analysis. R Package Version 1.1. 2016. Available online: https://CRAN.R-project.org/package=dCovTS (accessed on 27 December 2022).
- Mahdi, E.; McLeod, A.I. Improved Multivariate Portmanteau Diagnostic Test. J. Time Ser. Anal. 2012, 33, 211–222. [Google Scholar] [CrossRef]
- Lugrin, T.; Davison, A.C.; Tawn, J.A. Bayesian Uncertainty Management in Temporal Dependence of Extremes. Extremes 2016, 19, 491–515. [Google Scholar] [CrossRef]
- Frolova, N.; Cribben, I. extremogram: Estimation of Extreme Value Dependence for Time Series Data. R Package Version 1.0.2. 2016. Available online: https://CRAN.R-project.org/package=extremogram (accessed on 27 December 2022).
- Hofert, M.; Kojadinovic, I.; Maechler, M.; Yan, J. copula: Multivariate Dependence with Copulas. R Package Version 1.0-1. 2020. Available online: https://CRAN.R-project.org/package=copula (accessed on 27 December 2022).
- Trapletti, A.; Hornik, K. tseries: Time Series Analysis and Computational Finance. R Package Version 0.10-48. 2020. Available online: https://CRAN.R-project.org/package=tseries (accessed on 27 December 2022).
- Nagler, T. wdm: Weighted Dependence Measures. R Package Version 0.2.2. 2020. Available online: https://CRAN.R-project.org/package=wdm (accessed on 27 December 2022).
- Miecznikowski, J.C.; Hsu, E.S.; Chen, Y.; Vexler, A. testforDEP: Dependence Tests for Two Variables. R Package Version 0.2.0. 2017. Available online: https://CRAN.R-project.org/package=testforDEP (accessed on 27 December 2022).
- Garcia, J.E.; Gonzalez-Lopez, V.A. LIStest: Tests of Independence Based on the Longest Increasing Subsequence. R Package Version 2.1. 2014. Available online: https://CRAN.R-project.org/package=LIStest (accessed on 27 December 2022).
- Berrett, T.B.; Kontoyiannis, I.; Samworth, R.J. USP: U-Statistic Permutation Tests of Independence for All Data Types. R Package Version 0.1.1. 2020. Available online: https://CRAN.R-project.org/package=USP (accessed on 27 December 2022).
- Berrett, T.B.; Grose, D.J.; Samworth, R.J. IndepTest: Nonparametric Independence Tests Based on Entropy Estimation. R Package Version 0.2.0. 2018. Available online: https://CRAN.R-project.org/package=IndepTest (accessed on 27 December 2022).
- Pfister, N.; Peters, J. dHSIC: Independence Testing via Hilbert Schmidt Independence Criterion. R Package Version 2.1. 2019. Available online: https://CRAN.R-project.org/package=dHSIC (accessed on 27 December 2022).
- Jin, Z.; Yao, S.; Matteson, D.S.; Shao, X. EDMeasure: Energy-Based Dependence Measures. R Package Version 1.2. 2018. Available online: https://search.r-project.org/CRAN/refmans/EDMeasure/html/EDMeasure-package.html (accessed on 27 December 2022).
- Böttcher, B. multivariance: Measuring Multivariate Dependence Using Distance Multivariance. R Package Version 2.3.0. 2020. Available online: https://CRAN.R-project.org/package=multivariance (accessed on 27 December 2022).
- Risk, B.B.; James, N.A.; Matteson, D.S. steadyICA: ICA and Tests of Independence via Multivariate Distance Covariance. R Package Version 1.0. 2015. Available online: https://CRAN.R-project.org/package=steadyICA (accessed on 27 December 2022).
- Peters, J.; Shah, R.D. GeneralisedCovarianceMeasure: Test for Conditional Independence Based on the Generalized Covariance Measure (GCM). R Package Version 0.1.0. 2019. Available online: https://CRAN.R-project.org/package=GeneralisedCovarianceMeasure (accessed on 27 December 2022).
- Maasoumi, E. A Compendium to Information Theory in Economics and Econometrics. Econom. Rev. 1993, 12, 137–181. [Google Scholar] [CrossRef]
- Geenens, G.; de Micheaux, P.L. The Hellinger Correlation. J. Am. Stat. Assoc. 2022, 117, 639–653. [Google Scholar] [CrossRef]
- Duong, T. ks: Kernel Smoothing. R Package Version 1.12.0. 2021. Available online: https://CRAN.R-project.org/package=ks (accessed on 27 December 2022).
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Bowman, A.W. An Alternative Method of Cross-Validation for the Smoothing of Density Estimates. Biometrika 1984, 71, 353–360. [Google Scholar] [CrossRef]
- Duong, T.; Hazelton, M.L. Cross-Validation Bandwidth Matrices for Multivariate Kernel Density Estimation. Scand. J. Stat. 2005, 32, 485–506. [Google Scholar] [CrossRef]
- Duong, T.; Hazelton, M. Plug-in Bandwidth Matrices for Bivariate Kernel Density Estimation. J. Nonparametric Stat. 2003, 15, 17–30. [Google Scholar] [CrossRef]
- Narasimhan, B.; Johnson, S.G.; Hahn, T.; Bouvier, A.; Kiêu, K. cubature: Adaptive Multivariate Integration over Hypercubes. R Package Version 2.0.4.1. 2020. Available online: https://CRAN.R-project.org/package=cubature (accessed on 27 December 2022).
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer: New York, NY, USA, 1991. [Google Scholar]
- Li, W. Diagnostic Checks in Time Series, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Bühlmann, P. Bootstraps for Time Series. Stat. Sci. 2002, 17, 52–72. [Google Scholar] [CrossRef]
- Bickel, P.J.; Bühlmann, P. Closure of Linear Processes. J. Theor. Probab. 1997, 10, 445–479. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J. Testing for Nonlinearity in Time Series: The Method of Surrogate Data. Physica D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Chan, K.S. On the Validity of the Method of Surrogate Data. Fields Inst. Commun. 1997, 11, 77–97. [Google Scholar]
- Schreiber, T.; Schmitz, A. Surrogate Time Series. Physica D 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Vidal, R.V.V. Applied Simulated Annealing; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin, Germany, 1993; Volume 396. [Google Scholar]
- Bickel, P.J.; Bühlmann, P. A New Mixing Notion and Functional Central Limit Theorems for a Sieve Bootstrap in Time Series. Bernoulli 1999, 5, 413–446. [Google Scholar] [CrossRef]
- Bühlmann, P. Sieve Bootstrap for Time Series. Bernoulli 1997, 3, 123–148. [Google Scholar] [CrossRef]
- Ravazzolo, F.; Rothman, P. Oil and U.S. GDP: A Real-Time Out-of-Sample Examination. J. Money Credit Bank. 2013, 45, 449–463. [Google Scholar] [CrossRef]
- Hannan, E.; Rissanen, J. Recursive Estimation of Mixed Autoregressive-Moving Average Order. Biometrika 1982, 69, 81–94. [Google Scholar] [CrossRef]
- Choi, B. ARMA Model Identification; Springer: New York, NY, USA, 1992. [Google Scholar] [CrossRef]
- Goracci, G.; Ferrari, D.; Giannerini, S.; Ravazzolo, F. Robust Estimation for Threshold Autoregressive Moving-Average Models. arXiv 2022, arXiv:2211.08205. [Google Scholar]
- Dimitriou, D.; Kenourgios, D.; Simos, T. Are there any other safe haven assets? Evidence for “exotic” and alternative assets. Int. Rev. Econ. Financ. 2020, 69, 614–628. [Google Scholar] [CrossRef]
- Ergemen, Y.E.; Haldrup, N.; Rodríguez-Caballero, C.V. Common long-range dependence in a panel of hourly Nord Pool electricity prices and loads. Energy Econ. 2016, 60, 79–96. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).