Abstract
In this paper, we examine deflation-based algebraic multigrid methods for solving large systems of linear equations. Aggregation of the unknown terms is applied for coarsening, while deflation techniques are proposed for improving the rate of convergence. More specifically, the V-cycle strategy is adopted, in which, at each iteration, the solution is computed by initially decomposing it utilizing two complementary subspaces. The approximate solution is formed by combining the solution obtained using multigrids and deflation. In order to improve performance and convergence behavior, the proposed scheme was coupled with the Modified Generic Factored Approximate Sparse Inverse preconditioner. Furthermore, a parallel version of the multigrid scheme is proposed for multicore parallel systems, improving the performance of the techniques. Finally, characteristic model problems are solved to demonstrate the applicability of the proposed schemes, while numerical results are given.
Keywords:
multigrid; deflation; approximate inverses; aggregation-based algebraic multigrid; iterative methods; linear systems MSC:
65F08; 65F10; 65F50; 65N55
1. Introduction
Lately, research efforts for efficiently solving large sparse linear systems have focused on multigrid methods [,]. Their applicability and efficiency are based on the use of a stationary method as a smoother for higher frequency components of the error, while the lower frequency components are transferred to a coarser level with higher frequency, which can reduce the error [,]. Multigrid algorithms consider a recursive application with two-grid coarse grid-correction schemes []. In the coarse level, a smoother is used for defecting correction, which is interpolated to the finer level and then added to the solution [,].
An algebraic multigrid (AMG) requires the information of the coefficient matrix of the linear system []. The only difference between the geometrical and algebraic approaches is the coarsening algorithm; however, they both consist of a smoother and a coarse grid correction. The smoother, is usually the application of some iterations of a fixed-point iterative method (such as Jacobi and Gauss–Seidel) and coarse grid correction is the transformation of the approximate residual to the finest grid. It should be noted that the notion of aggregation has multiple applications in several scientific fields, including gene regulatory networks [,].
Moreover, approximate inverses have been extensively used for approximating the inverse of the coefficient matrix of a linear system, resulting in efficient preconditioners for Krylov subspace iterative methods. Their efficiency relies on the fact that they have inherent parallelism and can be computed quickly in parallel [,,]. Additionally, approximate inverse techniques have been efficiently used in conjunction with multigrid methods for solving partial differential equations discretized with finite difference methods [], and for a variety of other applications [,].
In this paper, a class of Modified Generic Factored Approximate Sparse Inverses (MGenFAspI) based on approximate inverse sparsity patterns is used to solve two-dimensional and three-dimensional partial differential equations, discretized with high-order finite difference schemes. For the computation of these approximate inverses, a fill-in parameter is required which affects the density, in terms of nonzero elements, of the preconditioner []. A deflation technique is also utilized in this work, splitting the problem at each multigrid level into two complementary subspaces, aiming to further improve the convergence rate.
The paper is organized as follows: Section 2 introduces the deflation technique and the corresponding algorithm used for the solution of linear systems. Section 3 presents the aggregation-based algebraic multigrid method in conjunction with the deflation techniques and the Modified Generic Factored Approximate Sparse Inverses. The algorithmic procedures for the pairwise aggregation and the preconditioned multigrid are also given. The parallel aspects and techniques for accelerating the computations required by the Modified Generic Factored Approximate Sparse Inverses in hybrid parallel environments are discussed in Section 4. Finally, numerical results regarding the efficiency and convergence behavior of the proposed techniques are presented and discussed in Section 5, by solving characteristic model problems. Concluding remarks and directions for future research are provided in Section 6.
2. Deflation Techniques
Deflation techniques were introduced by Nicolaides in 1987 for improving the rate of convergence of the conjugate gradient method []. The main idea is based on the projection of the linear system into two complementary subspaces, in order to separately solve the two produced linear systems. The efficiency of this technique is based on the fact that the projected linear systems could be solved faster than the initial system, and then their solution can be combined for formulating the solution of the initial problem [].
Let us consider an linear system of the form:
where A is a symmetric and positive definite matrix, b is the right-hand side vector and x is the solution vector. The deflation subspace can be represented by a full-rank matrix with such that:
Then, the projection matrix Q can be defined as follows:
where I is the identity matrix. The matrix Q is the orthogonal projection on the subspace , while is the orthogonal projection on the subspace V. For the selection of the subspace V, we can use the deflation technique for the generation of the basis of V, proposed in [], where the domain is decomposed into m nonoverlapping subdomains , , where:
The solution of the linear system can be computed as follows
where is the solution vector of the projection to subspace V, while is the solution vector from the projection to the subspace . These vectors can be computed as follows:
where x is an initial approximation for the solution. By applying matrix operations, the solution vector can be defined as:
Then, the vector can be computed by solving iteratively the following linear system:
The procedure for the solution of the linear system with the deflation technique can be summarized by Algorithm 1.
| Algorithm 1 Deflation technique for solving linear systems |
|
The use of the deflation technique in conjunction with an efficient preconditioning scheme can accelerate the convergence behavior of the solution of the system []. Preconditioning techniques yield the solution of a linear system of the form:
where M is a symmetric positive definite preconditioner. An efficient preconditioner should be efficiently computed in parallel, should have a “clustered” spectrum, and the M × vector should be fast to compute in parallel [,,]. Then, the preconditioner can be used in conjunction with a Krylov-subspace iterative method, such as the conjugate gradient or the generalized minimum residual methods for the solution of the linear system [,].
3. Aggregation Multigrid Method
Multigrid methods have been widely used by the scientific community for solving linear systems, due to their convergence behavior and efficiency [,]. The design of these methods is based on the fact that high-frequency error components can be damped by a stationary iterative method, while low-frequency error components are handled by coarser grids with a higher discretization step, where the high-frequency modes of the error are more oscillatory and can be damped efficiently by a stationary iterative method [,]. Multigrid methods are composed of four components: (a) the stationary iterative method (iterative methods such as the Richardson, Jacobi and Gauss–Seidel methods), (b) the restriction operator (transfer operators from finer to coarser grids), (c) the prolongation operator (transfer operators from coarser to finer grids) and (d) the cycle strategy (the sequence in which the grids are visited until a solution with the predefined tolerance is achieved) [].
The method utilized for grid coarsening in this paper is the aggregation multigrid, first introduced in [] and developed by Notay []. The nodes of the grid are combined into pairs, creating aggregates, based on a weighting rule.
The coarsening algorithm constructs a prolongation matrix P from the coefficient matrix A, which is the transformation matrix from the coarse to the fine grid. The dimensions of the prolongation matrix are , where is the number of the nodes of the coarser grid. The transformation from the fine to the coarser grid can be managed by the restriction matrix R, which is computed as follows:
and the coarse coefficient matrix is estimated by Galerkin’s formula:
For the formulation of the prolongation matrix, the aggregates , which are disjoint subsets of the variable set, have to be defined. The number of these variables, , is, then, the number of the subsets and is used to define the prolongation matrix P:
Therefore, P is a Boolean matrix with one nonzero entry in each row. In order to define the aggregates, the algorithm searches for the set of nodes to which i is strongly negatively coupled, using a strong/weak coupling threshold :
Then, one unmarked node at a time is selected, giving priority to the node with the minimal , where is the number of unmarked nodes which are strongly negatively coupled to I [,]. Next, one can pick an unmarked node j, which consists of the column of the matrix A with the minimal element in line i. Then, an aggregate is created between the node i and the node j. The algorithm of the pairwise aggregation is given in Algorithm 2 []. It should be noted that the parameter is optional and confirms if matrix A is diagonal-dominant [].
For the solution of a linear system with an algebraic aggregation multigrid, the V-cycle strategy can be used. The linear system is smoothed and the residual is transferred to the coarser level until the resulting linear system is small enough to be solved directly. Then, the solution vector is subject to the procedure of coarse grid correction, by means of the appropriate prolongation [,].
During each iteration of the V-cycle, the deflation technique is used to split the problem into two complementary subspaces, and the approximate solution is computed, which is transferred to the coarser level of the grid. The combination of the multigrid and deflation techniques is depicted in Figure 1.
| Algorithm 2 Pairwise aggregation |
Inputs: matrix with n rows, Threshold , Logical parameter Outputs: number of coarse variables , Aggregates , (such as
|
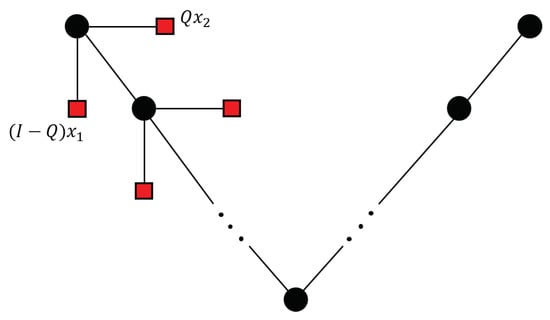
Figure 1.
A V-cycle of aggregation multigrid in conjunction with deflation.
Algorithm 3 depicts the procedure of using a multigrid as preconditioner for a V-cycle.
| Algorithm 3 Preconditioned V cycle |
Inputs: Residual vector Grid matrix at level k: Deflation matrix Prolongation matrix Matrix of next grid Outputs:
|
The function is executed once at the higher level for using the matrix , and iteratively calls itself until the parameter k reduces to 1. For smoothing, the symmetric Gauss–Seidel method is used, where
where , and are the lower, diagonal and upper submatrices of [].
In this paper, the coarse coefficient matrix is inverted by the Modified Generic Factored Approximate Sparse Inverse (MGenFAspI) technique []. For a coefficient matrix A, we consider its incomplete factorization, i.e.,
where L and U are, respectively, the upper and lower triangular factors and E is the error matrix. The GenFAspI matrix can be computed using the following procedure:
considering and . In order to compute the G and H, an “a-priori” sparsity pattern is required, []. These patterns occur when utilizing a predetermined drop tolerance (droptol) and then raising to a predefined power (level of fill or lfill) the upper and lower triangular factors. After that, the GenFAspI matrix is constructed by solving the following system:
where denote the elements of G, , the elements of H; are the elements of the identity matrix and m the order of the coefficient matrix of the linear system []. A modified version of GenFAspI (MGenFAspI) is used in order to enhance the performance during the computation of the approximate inverse []. The MGenFAspI matrix is used to compute each column of the factor of the approximate inverse, separately, by a restricted solution process of only the factors. The elements that do not belong to G and H factors are set to zero; thus, Equation (17) is rewritten as:
The advantage of the modified version of GenFAspI is that the construction of the approximate inverse can be easily parallelized, since the elements of the matrices G and H or L and U are not required to be identified. The algorithmic procedure of MGenFAspI is given in [].
4. Parallel Techniques
In this section, the parallel algorithm for the Modified Generic Factored Approximate Sparse Inverse and the parallel V-cycle are discussed. The matrices G and H can be computed by solving the following equations:
where U and L are the upper and lower triangular matrices that are derived from the incomplete LU factorization of the coefficient matrix A. Thus, for calculating the columns of the matrices G and H, the linear system of Equation (18) should be solved.
The MGenFAspI algorithm allows the individual computation of the columns of matrices G and H, and, due to this inherent parallelism, it can be efficiently implemented on hybrid parallel systems that consist of distributed and multicore CPUs. Each node of the distributed system can be assigned into a block of columns of the matrices, while, within each node, the multiple cores can further distribute the workload.
The computation of the elements of each column of matrices G and H does not require all rows of matrices U or L, respectively, but only the rows that correspond to nonzero elements of each column. For this reason, there is no need to broadcast the whole matrices U and L, yielding a reduced communication cost, especially for large-scale matrices. A visual representation of the distribution of matrix G on the available nodes is given in Figure 2, while the workload of two cores of a distributed node is depicted in Figure 3.
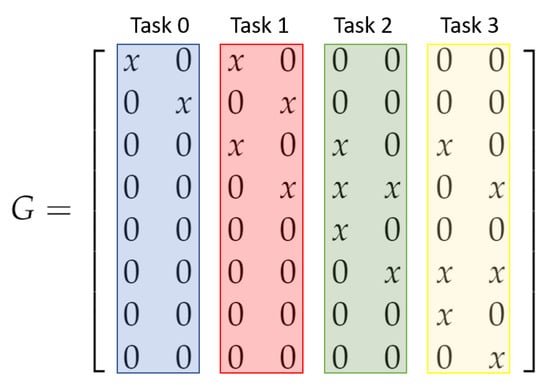
Figure 2.
Distribution of columns of matrix G on four tasks.
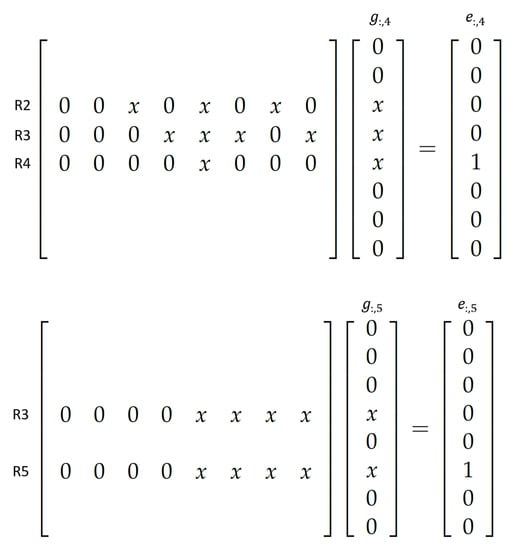
Figure 3.
Computations performed from the two cores of Task 2 for the formulation of fourth and fifth columns of matrix G of the MGenFAspI.
The same process was implemented for the computation of the elements of matrix H, where the rows of matrix L were used. Since this technique does not require any communication between the distributed processes, the parallel speedup and parallel efficiency are expected to be high. The derived matrices (G and H) are distributed on the nodes; however, they can be used on any distributed system for executing a column-wise matrix×vector multiplication. The algorithm for the parallelization of the MGenFAspI has been presented in []. In the context of this work, the parallelization on multicore systems was considered.
5. Numerical Results
The applicability, performance and convergence behavior of the proposed schemes are given in this section. Various model problems are considered and numerical results are obtained, experimentally demonstrating the behavior of the proposed methods. It should be noted that the experimental results were obtained on an Intel Xeon 2420v2 with 6 cores and 12 threads, 48GB of RAM memory, running Linux CentOS 7. All algorithmic techniques were implemented in C++ 11.
For the evaluation of the aggregation-based multigrid method with V-cycle, the 2D Poisson problem was initially selected with the number of elements per direction . Four iterations of the Jacobi method were performed as a pre-smoother and four iterations of the Jacobi method were used for post-smoothing in each level of grid hierarchy. In the last level of the multigrid, the linear system is solved by a direct method, such as LU factorization. The termination criterion is , where is the norm of the residual vector of the i-th iteration, is the norm of the residual of the initial problem and . In the parallel experiments, the resolution at the lowest level was held by the PARDISO method (parallel direct solver) contained in the parallel libraries of Intel [].
It should be noted that the choice of pre-smoothing and post-smoothing iterations affects the convergence behavior, e.g., increased values lead to better overall performance. However, since the stationary iterative methods in the context of multigrids are used to damp the high-frequency components of the error, an arbitrary increase does not guarantee substantial improvements. In the context of an algebraic multigrid, the choices for pre-smoothing and post-smoothing iterations vary between 1 and 4 for smoothers, such as Jacobi or Gauss–Seidel, in the literature. Thus, determination of the optimal parameters in the context of a multigrid depends on the problem to be solved and can be determined by experimentation [,].
The convergence behavior and the performance of the AGAMG method for different numbers of the unknowns per dimension for the 2D Poisson problem are given in Table 1.

Table 1.
Convergence behavior and performance of V cycle of AGAMG for 2D Poisson model problem.
The number of iterations required for convergence slightly increases as the size of matrix A increases, for the different number of levels. Moreover, increasing the number of levels while increasing the number of points per dimension () yields reduced execution time. This is due to the size of the matrix at the last level, which is solved by a direct method. Thus, for large-scale systems, an increased number of levels is recommended.
In order to examine the applicability and efficiency of the deflation techniques, the same model problem was executed by considering deflation with V-cycle. For the integration of the two methods, the four Jacobi pre-smoothing iterations were replaced with one deflation iteration. The deflation algorithm computes, using a direct method, the solution in subspace :
by inverting the matrix E with the Jacobi method (i.e., inverting only the main diagonal). The solution in subspace Q is computed with six iterations of the BiCGStab method for the following linear system:
The efficiency and convergence behavior of the aggregation-based algebraic multigrid method with deflation are given in Table 2, for various numbers of levels and . It should be noted that the Jacobi method with was used as post-smoother.

Table 2.
Convergence behavior and performance of V cycle of AGAMG in combination with deflation technique for 2D Poisson model problem.
To further improve the convergence behavior, the Modified Generic Factored Approximate Sparse Inverse (MGenFAspI) was used for approximating matrix . The parameter was set to 1 and the to zero. The corresponding results are given in Table 3, for various values of and numbers of levels for the 2D Poisson problem. It can be seen that in most of the cases, the number of iterations is reduced.

Table 3.
Convergence behavior and performance of V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 2D Poisson model problem.
In Table 4, the convergence behavior and the performance of the proposed scheme with the use of MGenFAspI preconditioner for various values of and number of levels for solving the 3D Poisson problem are given. Moreover, in Table 5 and Table 6, numerical results are given for the 2D and 3D Poisson problem with and for various numbers of levels.

Table 4.
Convergence behavior and performance of V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem.

Table 5.
Convergence behavior and performance of V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 2D Poisson model problem.

Table 6.
Convergence behavior and performance of V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem.
The convergence behavior and the performance of the proposed schemes with the use of MGenFAspI for various numbers of the parameter and number of levels for the 2D Poisson problem with is given in Table 7.

Table 7.
Convergence behavior and performance of V cycle of AGAMG in combination with deflation technique and MGenFAspI with and different values of for 2D Poisson model problem with .
The performance and applicability were also tested against the Sherman problem (https://sparse.tamu.edu/HB/sherman1 (accessed on 28 November 2022)). In Table 8, the convergence behavior and performance of the proposed schemes with the use of the MGenFAspI preconditioner, for various values of the parameter and number of levels for the Sherman1 problem, are given in Table 8. In Table 9, the parallel aggregation-based algebraic multigrid method in conjunction with deflation and Modified Generic Factored Approximate Sparse Inverses for the 3D Poisson problem, with and , is given.

Table 8.
Convergence behavior and performance of V cycle of AGAMG in combination with deflation technique and MGenFAspI with and different values of for Sherman1 problem.

Table 9.
Convergence behavior and performance of a parallel V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem with .
The addition of deflation is expected to increase the computational time, since it involves matrix inversion operations (approximate) and matrix-by-matrix products. However, for difficult problems, e.g., Sherman1, where iterations increase substantially when following the original AGMG approach, deflation leads to substantial improvements and even ensures convergence within the prescribed maximum iterations. Moreover, the additional computational work is composed of inherently parallel operations which can be accelerated on modern hardware, leading to an efficient solution approach.
Direct parallelization of algebraic multigrid algorithms has been studied extensively in the literature and has been shown to be limited []. The advantages of a truncated approach, which is similar to the one adopted in this manuscript, for the parallelization of the V cycle have been discussed extensively in [].
Finally, the speedups and efficiency of the parallel aggregation-based algebraic multigrid method in conjunction with deflation and Modified Generic Factored Approximate Sparse Inverses for the 3D Poisson problem, with and , are given in Table 10 and Table 11, respectively. The corresponding figures for the execution times, speedups and efficiency are given in Figure 4, Figure 5 and Figure 6, respectively.

Table 10.
Speedup of parallel V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem with .

Table 11.
Efficiency of parallel V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem with .
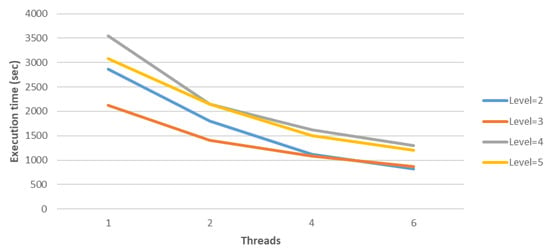
Figure 4.
Execution times (in seconds) of parallel V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem with .
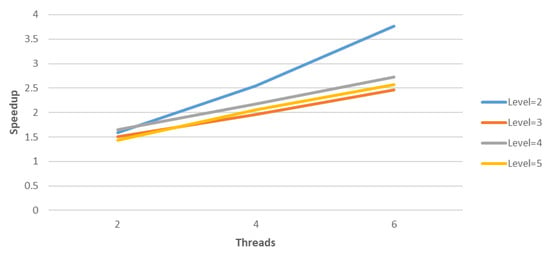
Figure 5.
Speedups of parallel V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem with .
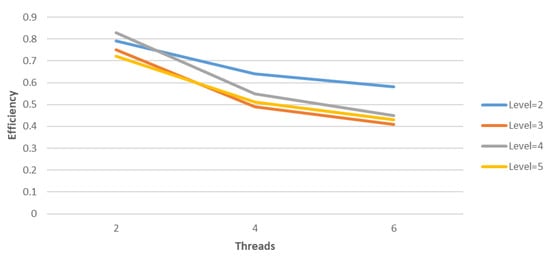
Figure 6.
Efficiency of parallel V cycle of AGAMG in combination with deflation technique and MGenFAspI with and for 3D Poisson model problem with .
6. Discussion and Conclusions
The Modified Generic Factored Approximate Sparse Inverse technique based on incomplete factorization has been recently proposed and used as a preconditioner for Krylov subspace methods. In this work, algebraic multigrid methods were examined that are based on aggregation, while a V cycle was used in conjunction with deflation techniques to improve the convergence behavior. The proposed schemes were discussed and numerical results from solving two model problems were presented.
The evaluation of the proposed methods demonstrates the improvement in the rate of convergence of the multigrid techniques using deflation, for various values of the parameters and . The extensive experimentation that was carried out validated that the V cycle of AGAMG in combination with deflation and MGenFAspI was the most efficient approach in terms of convergence behavior; however, with greater execution time. For this, the paper took advantage of the inherent parallelism of the approximate inverse scheme and the aggregation-based multigrid method, and resulted in reduced execution times on a shared memory parallel system. The parallel numerical results obtained demonstrated good parallel results with good potential for large-scale parallel systems.
Future work includes the use of the aggregation-based multigrid method in conjunction with deflation techniques and approximate inverses as preconditioners for Krylov-subspace iterative methods. Moreover, the use of domain decomposition methods will be examined, in order to further improve the parallel efficiency of the methods.
Author Contributions
Conceptualization, G.A.G. and C.K.F.-P.; Investigation, A.A.N., G.A.G., C.K.F.-P. and K.M.G.; Methodology, A.A.N., G.A.G., C.K.F.-P. and K.M.G.; Software, A.A.N. and C.K.F.-P.; Supervision, G.A.G.; Validation, A.A.N., C.K.F.-P. and K.M.G.; Visualization, C.K.F.-P. and K.M.G.; Writing—original draft, A.A.N., G.A.G., C.K.F.-P. and K.M.G.; Writing—review and editing, A.A.N., G.A.G., C.K.F.-P. and K.M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMG | Algebraic multigrid |
| AGAMG | Aggregation-based algebraic multigrid |
| CPU | Central processing unit |
| GenFAspI | Generic Factored Approximate Sparse Inverse |
| MGenFAspI | Modified Generic Factored Approximate Sparse Inverse |
References
- Paludetto Magri, V.A.; Franceschini, A.; Janna, C. A Novel Algebraic Multigrid Approach Based on Adaptive Smoothing and Prolongation for Ill-Conditioned Systems. SIAM J. Sci. Comput. 2019, 41, A190–A219. [Google Scholar] [CrossRef]
- Demidov, D. AMGCL: An efficient, flexible, and extensible algebraic multigrid implementation. Lobachevskii J. Math. 2019, 40, 535–546. [Google Scholar] [CrossRef]
- Briggs, W.L.; Henson, V.E.; McCormick, S.F. A Multigrid Tutorial; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Wesseling, P. Theoretical and Practical Aspects of a Multigrid Method. SIAM J. Sci. Stat. Comput. 1982, 3, 387–407. [Google Scholar] [CrossRef]
- Notay, Y. An aggregation-based algebraic multigrid method. Electron. Trans. Numer. Anal. 2008, 37, 123–146. [Google Scholar]
- Li, H.; Liu, Y.; Wang, S.; Niu, B. State Feedback Stabilization of Large-Scale Logical Control Networks via Network Aggregation. IEEE Trans. Autom. Control. 2021, 66, 6033–6040. [Google Scholar] [CrossRef]
- Wang, S.; Li, H. Aggregation method to reachability and optimal control of large-size Boolean control networks. Sci. China Inf. Sci. 2022, 66, 1869–1919. [Google Scholar] [CrossRef]
- Bröker, O.; Grote, M.J.; Mayer, C.; Reusken, A. Robust Parallel Smoothing for Multigrid Via Sparse Approximate Inverses. SIAM J. Sci. Comput. 2001, 23, 1396–1417. [Google Scholar] [CrossRef]
- Giannoutakis, K.M.; Gravvanis, G.A. High performance finite element approximate inverse preconditioning. Appl. Math. Comput. 2008, 201, 293–304. [Google Scholar] [CrossRef]
- Filelis-Papadopoulos, C.; Gravvanis, G. A class of generic factored and multi-level recursive approximate inverse techniques for solving general sparse systems. Eng. Comput. 2016, 33, 74–99. [Google Scholar] [CrossRef]
- Filelis-Papadopoulos, C.K.; Gravvanis, G.A. On the Multigrid Method Based on Finite Difference Approximate Inverses. Comput. Model. Eng. Sci. 2013, 90, 233–253. [Google Scholar]
- Gravvanis, G.; Filelis-Papadopoulos, C.; Matskanidis, P. Algebraic Multigrid Methods Based on Generic Approximate Banded Inverse Matrix Techniques. Comput. Model. Eng. Sci. 2014, 100, 323–345. [Google Scholar]
- Kyziropoulos, P.; Filelis-Papadopoulos, C.; Gravvanis, G. Parallel N-body simulation based on the PM and P3M methods using multigrid schemes in conjunction with generic approximate sparse inverses. Math. Probl. Eng. 2015, 2015, 450980. [Google Scholar] [CrossRef]
- Nicolaides, R.A. Deflation of Conjugate Gradients with Applications to Boundary Value Problems. SIAM J. Numer. Anal. 1987, 24, 355–365. [Google Scholar] [CrossRef]
- Frank, J.; Vuik, C. On the Construction of Deflation-Based Preconditioners. SIAM J. Sci. Comput. 2001, 23, 442–462. [Google Scholar] [CrossRef]
- Gravvanis, G.; Filelis-Papadopoulos, C. On the multigrid cycle strategy with approximate inverse smoothing. Eng. Comput. Int. J. Comput.-Aided Eng. 2014, 31, 110–122. [Google Scholar] [CrossRef]
- Haelterman, R.; Vierendeels, J.; Van Heule, D. Non-stationary two-stage relaxation based on the principle of aggregation multi-grid. In Proceedings of the Computational Fluid Dynamics 2006; Deconinck, H., Dick, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 243–248. [Google Scholar]
- Hackbusch, W. Multi-Grid Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1985; Volume 4. [Google Scholar] [CrossRef]
- Bulgakov, V.E. Multi-level iterative technique and aggregation concept with semi-analytical preconditioning for solving boundary-value problems. Commun. Numer. Methods Eng. 1993, 9, 649–657. [Google Scholar] [CrossRef]
- Emans, M. Aggregation schemes for k-cycle AMG. Proc. Conf. Algoritm. 2015, 141–150. Available online: http://www.iam.fmph.uniba.sk/amuc/ojs/index.php/algoritmy/article/view/324 (accessed on 28 November 2022).
- Chow, E. A Priori Sparsity Patterns for Parallel Sparse Approximate Inverse Preconditioners. SIAM J. Sci. Comput. 2000, 21, 1804–1822. [Google Scholar] [CrossRef]
- Grylonakis, E.N.G.; Filelis-Papadopoulos, C.K.; Gravvanis, G.A. On the Numerical Solution of the Generalized Dirichlet-Neumann Map for the 2D Laplace Equation Using Modified Generic Factored Approximate Sparse Inverse Preconditioning. In Proceedings of the 19th Panhellenic Conference on Informatics, Athens, Greece, 1–3 October 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 13–18. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. PARDISO. In Encyclopedia of Parallel Computing; Padua, D., Ed.; Springer: Boston, MA, USA, 2011; pp. 1458–1464. [Google Scholar] [CrossRef]
- Trottenberg, U.; Oosterlee, C.V.; Schuller, A. Multigrid; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Filelis-Papadopoulos, C.K.; Gravvanis, G.A. Parallel multigrid algorithms based on generic approximate sparse inverses: An SMP approach. J. Supercomput. 2014, 67, 384–407. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).