Fixed-Point Approximation of Operators Satisfying (RCSC)—Condition in CAT(0) Spaces

Abstract

In this research article, we have proved strong and $\mathrm{\Delta }$-convergence results for mapping satisfying $\left(RCSC\right)$ condition via M-iteration process in CAT(0) spaces. Numerical examples are provided to show the superiority of our results over other existing results and to illustrate the faster convergence of the M iterative scheme as compared to many well-known iterative schemes. In this process, many results are improved in the current literature of CAT(0) spaces.

1. Introduction

The theory of fixed points plays a vital role in solving the nonlinear problems that arise in pure and applied sciences. Banach [1] studied the existence of fixed points for contraction mappings in 1922. He proved that a contraction mapping T defined on a closed nonempty subset N of a Banach space $(S,d)$ has a unique fixed point. To approximate the fixed point, he used the Picard iterative method (or successive approximation method), i.e., $u_{n+1}=T{u}_n$. But in the case of nonexpansive mappings, the Picard iterative method fails to converge to the fixed point. So, for the case of nonexpansive mappings, Browder [2] and Gohde [3] independently proved the same results in the framework of a uniformly convex Banach space. They stated that a nonexpansive mapping T on a nonempty bounded closed and convex subset N of a uniformly convex Banach space $(S,d)$ admits a fixed point. Similarly, for the fixed point approximation of different mappings, many iterative methods have been developed. Some of these iteration processes are in Maan [4], Ishikawa [5], Agarwal et al. [6], Thakur [7], Noor [8] and Abbas [9]. For more details on iteration processes, see [10,11,12,13,14,15,16,17] and references therein.

In 2008, Suzuki [18] studied the non-expansive mappings and introduced a new notion of Suzuki generalized non-expansive mapping (or mappings satisfying condition-$\left(C\right)$). Many results have been obtained for this type of mapping in $CAT\left(0\right)$ spaces (see, [9,19,20]).

In 2012, Karapinar [21] studied the condition $\left(C\right)$ and introduced a new condition called $\left(RCSC\right)$ condition (Riech Chatterjee Suzuki $\left(C\right)$) as a generalization of condition (C).

In 2018, Ullah and Arshad [22] introduced a new three-step iteration process to approximate the fixed point of mapping satisfying condition (C), known as the M-iteration process, which is defined as:

Let $\varnothing \ne N\subseteq S$(Banach space) and $T:N\to N$ be a selfmap. Then, for any real sequence $\left\{{\gamma }_k\right\}\subset (0,1)$ for $k\ge 0$, we have

$$\left\{\begin{array}{c}\hfill r_0\in N,\hfill \\ \hfill s_k=(1-{\gamma }_k)r_k+{\gamma }_{k}T{r}_k,\hfill \\ \hfill t_k=T{s}_k,\hfill \\ \hfill r_{k+1}=T{t}_k.\hfill \end{array}\right.$$

(1)

They proved the speedier convergence behavior of the M-iteration process and compared it with Picard-$(S,d)$ and $(S,d)$-iterative schemes with the help of a numerical example. They also proved the weak and strong convergence results in Banach spaces.

Let $[0,m]\subset \mathbb{R}$ and $(S,d)$ be a metric space. Then a mapping $\xi :[0,m]\to S$ is a geodesic joining the two points $j^{\prime },k^{\prime }\in S$ such that $\xi \left(0\right)=j^{\prime }$, $\xi \left(m\right)=k^{\prime }$ and $d(\xi \left(s_1\right),\xi \left(s_2\right))=|s_1-s_2|$ for all $s_1,s_2\in [0,m]$. The mapping $\xi$ is isometry and $d(j^{\prime },k^{\prime })=m$. The image of the geodesic $\left(\xi \right)$ is called a geodesic segment joining the points $j^{\prime },k^{\prime }\in S$ denoted by $[j^{\prime },k^{\prime }]$ whenever it exists uniquely. The space $(S,d)$ is called a geodesic space whenever for every two points $j^{\prime },k^{\prime }\in S$ there exists a geodesic joining these points. If the space $(S,d)$ has only one geodesic joining each two points $j^{\prime },k^{\prime }\in S$, then the space is called uniquely geodesic. A subset N is convex in $(S,d)$ if each geodesic segment (joining $j^{\prime },k^{\prime }\in N$) contained in N.

Let $(S,d)$ is a geodesic space, then a triangle $\mathrm{\Delta }(u_1,v_1,w_1)$ in $(S,d)$ is called a geodesic triangle having three elements of $(S,d)$, which denote the vertices of the triangle $\mathrm{\Delta }$, i.e., $u_1,v_1,w_1$ and three geodesic segments, which denote the edges of $\mathrm{\Delta }$, i.e., $[u_1,v_1],[v_1,w_1]$, $[w_1,u_1]$. For any geodesic triangle $\mathrm{\Delta }(u_1,v_1,w_1)\in S$, a triangle $\overline{\mathrm{\Delta }}(\overline{u_1},\overline{v_1},\overline{w_1})\subset {\mathbb{R}}^2$ is called a comparison triangle if it satisfies

$$\begin{array}{c}\hfill d_{{\mathbb{R}}^2}(\overline{u_1},\overline{v_1})=d(u_1,v_1)\\ \hfill d_{{\mathbb{R}}^2}(\overline{v_1},\overline{w_1})=d(v_1,w_1)\\ \hfill and{d}_{{\mathbb{R}}^2}(\overline{w_1},\overline{u_1})=d(w_1,u_1).\end{array}$$

If $x\in [u_1,u_2]$, then an element $\overline{x}\in [\overline{u_1},\overline{u_2}]$ is called a comparison element, if $d(u_1,x)=d(\overline{u_1},\overline{x})$.

A geodesic space $(S,d)$ is called a $CAT\left(0\right)$ space if there exists a comparison triangle $\overline{\mathrm{\Delta }}\subset {\mathbb{R}}^2$ for a geodesic triangle $\mathrm{\Delta }\subset S$ such that

$$d(j^{\prime },k^{\prime })\le d_{{\mathbb{R}}^2}(\overline{j^{\prime }},\overline{k^{\prime }}),$$

where $j^{\prime },k^{\prime }\in \mathrm{\Delta }\subset S$ and $\overline{j^{\prime }},\overline{k^{\prime }}\in \overline{\mathrm{\Delta }}\subset {\mathbb{R}}^2$.

This research article aims to prove some strong and $\mathrm{\Delta }$-convergence theorems for mapping with $\left(RCSC\right)$ condition using the M-iteration process in the $CAT\left(0\right)$ spaces. The M-iteration in $CAT\left(0\right)$ space is defined as:

$$\left\{\begin{array}{c}\hfill r_0\in N,\hfill \\ \hfill s_k=(1-{\gamma }_k)r_k\oplus {\gamma }_{k}T{r}_k,\hfill \\ \hfill t_k=T{s}_k,\hfill \\ \hfill r_{k+1}=T{t}_k,\hfill \end{array}\right.$$

(2)

where $k\ge 0$ and $\left\{{\gamma }_k\right\}$ can be any real sequence in (0,1).

2. Preliminaries

Let $N\ne \varnothing \subseteq S$ where $(S,d)$ is a metric space and $T:N\to N$ is a self mapping, then a point $p_0\in N$ is a fixed point of the mapping T if $T{p}_0=p_0$. The set $F_T$, i.e., $F_T$ = $\{p_0\in N:T{p}_0=p_0\}$ denotes the set of all fixed points of mapping T.

Definition 1.

The mapping T is called non-expansive mapping if for $j^{\prime },k^{\prime }\in N$, we have

$$\begin{array}{c}\hfill d(T{j}^{\prime },T{k}^{\prime })\le d(j^{\prime },k^{\prime }).\end{array}$$

Definition 2.

A self-mapping $T:N\to N$ is said to be quasi if the set of fixed point $F_T\ne \varnothing$ and for all $j^{\prime }\in N$ and $p_0\in F_T$, we have

$$\begin{array}{c}\hfill d(T{j}^{\prime },p_0)\le d(j^{\prime },p_0).\end{array}$$

Definition 3.

Let $N\ne \varnothing \subseteq S$ where $(S,d)$ is a metric space. Then $T:N\to N$ satisfies condition (C) if for each $j^{\prime },k^{\prime }\in N$, we have

$$\begin{array}{c}\hfill \frac{1}{2}d(j^{\prime },T{j}^{\prime })\le d(j^{\prime },k^{\prime })\Rightarrow d(T{j}^{\prime },T{k}^{\prime })\le d(j^{\prime },k^{\prime }).\end{array}$$

Definition 4

([21]). Let $N\ne \varnothing \subseteq S$ (metric space). Then $T:N\to N$ satisfies $\left(RCSC\right)$ condition if for $j^{\prime },k^{\prime }\in N$ the mapping T satisfy

$$\frac{1}{2}d(j^{\prime },T{j}^{\prime })\le d(j^{\prime },k^{\prime })\Rightarrow d(T{j}^{\prime },T{k}^{\prime })\le \frac{1}{3}(d(j^{\prime },k^{\prime })+d(j^{\prime },T{k}^{\prime })+d(k^{\prime },T{j}^{\prime })).$$

Example 1.

Suppose that $N=[1,4]$ and $T:N\to N$ defined by

$$T\left(\mathit{h}\right)=\left\{\begin{array}{ccc}1& if& \mathit{h}=4,\\ \frac{1+\mathit{h}}{2}& if& \mathit{h}\ne 4.\end{array}\right.$$

It is easy to show that T satisfies the (RCSC) condition but does not satisfy condition (C) at $j^{\prime }=3.2$ and ${\mathit{k}}^{\prime }=4$.

Remark 1.

The above example shows that $\left(RCSC\right)$ condition is the extension of condition (C).

Lemma 1

([23]). Let $(S,d)$ be a $CAT\left(0\right)$ space. Then for $\zeta \in [0,1]$ and $j^{\prime },k^{\prime }\in S$, there is a unique line segment $z=(1-\zeta )j^{\prime }\oplus \zeta k^{\prime }$ i.e., $z\in [j^{\prime },k^{\prime }]$ such that

$$d(j^{\prime },z)=\zeta d(j^{\prime },k^{\prime })\mathit{and}d(k^{\prime },z)=(1-\zeta )d(j^{\prime },k^{\prime }).$$

Lemma 2

([23]). For any $j^{\prime },k^{\prime },l^{\prime }\in S$ and $\zeta \in [0,1]$ in Lemma 1, we have

$$d(l^{\prime },\zeta j^{\prime }\oplus (1-\zeta )k^{\prime })\le \zeta d(l^{\prime },j^{\prime })+(1-\zeta )d(l^{\prime },k^{\prime }).$$

Lemma 3

([21]). Let $\varnothing \ne N\subseteq S$ where $(S,d)$ is a $CAT\left(0\right)$ space and $T:N\to N$ be a self mapping with $\left(RCSC\right)$ condition. Then for any $j^{\prime }\in N$ and $p_0\in F_T$, T satisfies that

$$\begin{array}{c}\hfill d(T{j}^{\prime },T{p}_0)\le d(j^{\prime },p_0).\end{array}$$

Lemma 4

([21]). Let $N\ne \varnothing$ such that N is closed and convex in $CAT\left(0\right)$ space $(S,d)$. Then for any $j^{\prime },k^{\prime }\in N$, the self mapping $T:N\to N$ with $\left(RCSC\right)$ condition holds that

$$\begin{array}{c}\hfill d(j^{\prime },T{k}^{\prime })\le 9d(j^{\prime },T{j}^{\prime })+d(j^{\prime },k^{\prime }).\end{array}$$

Lemma 5

([9]). Let $N\ne \varnothing$ such that N is closed in $CAT\left(0\right)$ space $(S,d)$. Let $T:N\to N$ be a mapping with $\left(RCSC\right)$ condition and a sequence $\left\{r_k\right\}$ bounded in N with ${lim}_{k}d(r_k,T{r}_k)=0$ and $\mathrm{\Delta }-{lim}_k{r}_k=r$, then $r=Tr$.

Lemma 6

([24]). Suppose that $\left\{{\eta }_k\right\}$ be a sequence in the interval $[k,l]$ for some $k,l\in (0,1)$. Let $\left\{r_k\right\},\left\{t_k\right\}$ are sequences in the $CAT\left(0\right)$ space $(S,d)$ such that, for some $\varsigma \ge 0$

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}supd(r_k,r)\le \varsigma ,\underset{k\to \infty }{lim}supd(t_k,r)\le \varsigma \\ \hfill \underset{k\to \infty }{lim}d({\eta }_k{r}_k\oplus (1-{\eta }_k)t_k,r)=\varsigma ;\end{array}$$

then

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}d(r_k,t_k)=0.\end{array}$$

Let $(S,d)$ is a $CAT\left(0\right)$ space and $N\ne \varnothing$ is closed in $(S,d)$. If a sequence $\left\{r_k\right\}$ is bounded in N, then for any $k^{\prime }\in S$, we define

(i) Asymptotic radius of the sequence $\left\{r_k\right\}$ at the point $k^{\prime }$

$$r(k^{\prime },\left\{r_k\right\})=\underset{k\to \infty }{lim}supd(k^{\prime },r_k)$$

(ii) Asymptotic radius of the sequence $\left\{r_k\right\}$ relative to the set N

$$r(N,\left\{r_k\right\})=inf\{r(k^{\prime },\left\{r_k\right\}):k^{\prime }\in N\}$$

(iii) Asymptotic center of the sequence $\left\{r_k\right\}$ relative to the set N

$$A(N,\left\{r_k\right\})=\{r(k^{\prime },\left\{r_k\right\})=r(N,\left\{r_k\right\}):k^{\prime }\in N\}.$$

We know that $A(N,\left\{r_k\right\})$ has only one element (see [25]).

In 2008, Kirk and Panyanak [26] proved a weak convergence result in the framework of Banach spaces. They studied Lim’s [27] concept of $\mathrm{\Delta }$-convergence and proved that a nonexpansive mapping $T:N\to N$ admits a fixed point, where N is closed, convex, and bounded in $CAT\left(0\right)$ space $(S,d)$.

Definition 5

([26]). Let $(S,d)$ be a $CAT\left(0\right)$ space. Then a sequence $\left\{r_k\right\}\in S$Δ-converges to an element $r\in S$ if r is the unique asymptotic center of every sub sequence $\left\{t_k\right\}$ of $\left\{r_k\right\}$. Here r is the called $\mathrm{\Delta }-lim$ of $\left\{r_k\right\}$ and written as $\mathrm{\Delta }-{lim}_{k\to \infty }{r}_k=r$.

From the definition of $\mathrm{\Delta }$-convergence we know that each $CAT\left(0\right)$ space $(S,d)$ satisfies the Opial’s condition [28].

Lemma 7

([26]). Let $(S,d)$ is a $CAT\left(0\right)$ space. Then every sequence $\left\{r_k\right\}$ bounded in $(S,d)$ has a sub-sequence $\left\{t_k\right\}$, which is Δ-convergent.

Lemma 8

([23]). Let N be a closed convex and non-empty subset of $(S,d)$. Then the asymptotic center of a bounded sequence $\left\{r_k\right\}\subset N$ is in the set N.

3. Convergence Results for Mapping with (RCSC) Condition

Some results of strong and $\mathrm{\Delta }$-convergence are proved for the mapping satisfying $\left(RCSC\right)$ condition via M iteration process in the framework of $CAT\left(0\right)$ space $(S,d)$. We start from a key lemma.

Lemma 9.

Let $(S,d)$ be a complete $CAT\left(0\right)$ space and $N\ne \varnothing$, closed and convex in $(S,d)$. Assume that $T:N\to N$ is a self mapping with (RCSC) condition and $F_T\ne \varnothing$. If $\left\{r_k\right\}$ is a sequence defined by (2), then ${lim}_{k\to \infty }d(r_k,p_0)$ exists for each $p_0\in F_T$.

Proof. 

Assume that $p_0\in F_T$ and $k\in \mathbb{N}$. Since T is a self-mapping with $\left(RCSC\right)$ condition by Lemmas 2 and 3, we obtain

$$\begin{array}{ccc}\hfill d(s_k,p_0)& =& \hfill d[((1-{\gamma }_k)r_k\oplus {\gamma }_{k}T{r}_k),p_0]\hfill \\ & \le & \hfill (1-{\gamma }_k)d(r_k,p_0)+{\gamma }_{k}d(T{r}_k,p_0)\hfill \\ & \le & \hfill (1-{\gamma }_k)d(r_k,p_0)+{\gamma }_{n}d(r_k,p_0)\hfill \\ & =& \hfill d(r_k,p_0).\hfill \end{array}$$

(3)

Using the inequality (3) we have

$$\begin{array}{ccc}\hfill d(t_k,p_0)& =& \hfill d(T{s}_k,p_0)\hfill \\ & =& \hfill d(T((1-{\gamma }_k)r_k\oplus {\gamma }_{k}T{r}_k),p_0)\hfill \\ & \le & \hfill d((1-{\gamma }_k)r_k\oplus {\gamma }_{k}T{r}_k,p_0)\hfill \\ & \le & \hfill (1-{\gamma }_k)d(r_k,p_0)+{\gamma }_{k}d(r_k,p_0)\hfill \\ & =& \hfill d(r_k,p_0).\hfill \end{array}$$

(4)

Similarly using the inequality (4) we have,

$$\begin{array}{ccc}\hfill d(r_{k+1},p_0)& =& \hfill d(T{t}_k,p_0)\hfill \\ & \le & \hfill d(t_k,p_0)\hfill \\ & =& \hfill d(r_k,p_0).\hfill \end{array}$$

(5)

Hence the sequence $\left\{d(r_{k+1},p_0)\right\}$ is a non-increasing and bounded, which implies that, ${lim}_{k\to \infty }d(r_k,p_0)$ exists for each $p_0\in F_T$. □

Theorem 1.

Let $(S,d)$ be a complete $CAT\left(0\right)$ space and $N\ne \varnothing$, closed and convex in $(S,d)$. Assume that $T:N\to N$ is a self mapping with (RCSC) condition. Then a sequence $\left\{r_k\right\}$ defined by (2), is bounded if and only if $F_T\ne \varnothing$ and ${lim}_{k\to \infty }d(r_k,T{r}_k)=0$.

Proof. 

Suppose that a sequence $\left\{r_k\right\}$ is bounded and ${lim}_{k\to \infty }d(r_k,T{r}_k)=0$. We need to prove that $F_T\ne \varnothing$. For this we choose any $p_0\in A(N,\left\{r_k\right\})$. We are going to show that $p_0=T{p}_0$ (i.e., $p_0\in F_T$). Since T satisfies $\left(RCSC\right)$ condition, so Lemma 4 suggests that

$$\begin{array}{ccc}\hfill r(T{p}_0,\left\{r_k\right\})& =& \hfill \underset{k\to \infty }{lim\; sup}d(r_k,T{p}_0)\hfill \\ & \le & \hfill 9\underset{k\to \infty }{lim\; sup}d(r_k,T{r}_k)+\underset{k\to \infty }{lim\; sup}d(r_k,p_0)\hfill \\ & =& \hfill \underset{k\to \infty }{lim\; sup}d(r_k,p_0)\hfill \\ & =& \hfill r(p_0,\left\{r_k\right\}).\hfill \end{array}$$

Hence $T{p}_0\in A(N,\left\{r_k\right\})$. Since the space $(S,d)$ is uniformly convex, so $A(N,\left\{r_k\right\})$ contains only one element and thus we have $p_0=T{p}_0$. Hence it is proved that $p_0$ is the element of $F_T$, i.e., $F_T\ne \varnothing$.

Conversely, suppose that $F_T\ne \varnothing$. We need to prove that ${lim}_{k\to \infty }d(r_k,T{r}_k)=0$ and the sequence $\left\{r_k\right\}$ is bounded. For this we assume that $p_0\in F_T$ be fix, then in Lemma 9, we have already proved that the sequence $\left\{r_k\right\}$ is bounded and ${lim}_{k\to \infty }d(r_k,p_0)$ exists. Put

$$\underset{k\to \infty }{lim}d(r_k,p_0)=\varrho .$$

(6)

Using inequality (3) and Equation (6), we have

$$d(s_k,p_0)\le d(r_k,p_0)=\varrho .$$

Taking limsup on both sides, we have

$$\underset{k\to \infty }{lim\; sup}d(s_k,p_0)\le \underset{k\to \infty }{lim\; sup}d(r_k,p_0)=\varrho .$$

(7)

By using Lemma 3, we have

$$\underset{k\to \infty }{lim\; sup}d(t_k,p_0)\le \underset{k\to \infty }{lim\; sup}d(r_k,p_0)=\varrho .$$

(8)

Also by Lemma 9, we know that

$$d(r_{k+1},p_0)\le d(r_k,p_0).$$

Therefore

$$\varrho \le \underset{k\to \infty }{lim\; inf}d(s_k,p_0).$$

(9)

Using inequalities (7) and (9), we have

$$\varrho =\underset{k\to \infty }{lim}d(s_k,p_0).$$

(10)

From Equation (10), we have

$$\begin{array}{c}\hfill \varrho =\underset{k\to \infty }{lim}d(s_k,p_0)=\underset{k\to \infty }{lim}d((1-{\gamma }_k)r_k+{\gamma }_{k}T{r}_k,p_0).\end{array}$$

Using Lemma 6, we obtain

$$\underset{k\to \infty }{lim}d(r_k,T{r}_k)=0.$$

This completes the proof. □

Next, we prove a strong convergence result for mapping with $\left(RCSC\right)$ condition in a compact domain.

Theorem 2.

Let $(S,d)$ be a complete $CAT\left(0\right)$ space, $N\ne \varnothing$ is a closed convex and compact subset of $(S,d)$, a self mapping $T:N\to N$ satisfying (RCSC) condition and $F_T\ne \varnothing$. Then, $\left\{r_k\right\}$ is a sequence defined by iteration (2) that will strongly converge to the fixed point of T.

Proof. 

Since $F_T\ne \varnothing$, so by Theorem 1, we know that $\left\{r_k\right\}$ is bounded and ${lim}_{k\to \infty }d(r_k,T{r}_k)$ $=0$. Since N is a compact in $(S,d)$, so $\left\{r_k\right\}$ has a sub-sequence $\left\{r_{k_j}\right\}$ such that ${lim}_{j\to \infty }d(r_{k_j},p_0)=0$, for some $p_0\in N$ i.e., $\left\{r_{k_j}\right\}$ converges strongly to $p_0$.

Using Lemma 4, we have

$$d(r_{k_j},T{p}_0)\le 9d(r_{k_j},T{r}_{k_j})+d(r_{k_j},p_0).$$

(11)

Taking ${lim}_{j\to \infty }$ on both sides we have

$$\underset{j\to \infty }{lim}d(r_{k_j},T{p}_0)\le 9\underset{j\to \infty }{lim}d(r_{k_j},T{r}_{k_j})+\underset{j\to \infty }{lim}d(r_{k_j},p_0).$$

(12)

In the view of Theorem 1, ${lim}_{j\to \infty }d(r_{k_j},T{r}_{k_j})=0$. Now using ${lim}_{j\to \infty }d(r_{k_j},T{r}_{k_j})=0$ and ${lim}_{j\to \infty }d(r_{k_j},p_0)=0$ in the inequality (12), we obtain

$$\underset{j\to \infty }{lim}d(r_{k_j},T{p}_0)=0.$$

(13)

This means that the sequence $\left\{r_{k_j}\right\}$ converges to $T{p}_0$, so $T{p}_0=p_0$ i.e., $p_0\in F_T$. Lemma 9, suggests that ${lim}_{k\to \infty }d(r_k,p_0)$ exists. Therefore the strong limit of $\left\{r_k\right\}$ is $p_0$. □

Now, we will prove the strong convergence results based on condition $\left(I\right)$ which was defined by Sentor and Dotson in [29].

Definition 6

([29]). Let $N\ne \varnothing$ subset of $(S,d)$. Then a self mapping $T:N\to N$ satisfies condition $\left(I\right)$, if there exists a non-decreasing mapping $\zeta :[0,\infty )\to [0,\infty )$ with $\zeta \left(q\right)=0$, $\zeta \left(q\right)>0$ for each $q\in (0,\infty )$ and $d(u^{\prime },T{u}^{\prime })\ge \zeta \left(d(u^{\prime },F_T)\right)$ for all $u^{\prime }\in N$, where $d(u^{\prime },F_T)$ = ${inf}_{p_0\in F_T}d(u^{\prime },p_0)$.

Theorem 3.

Let $(S,d)$ is a complete $CAT\left(0\right)$ space and $N\ne \varnothing$, closed and convex in $(S,d)$. Since $T:N\to N$ be a self mapping satisfy (RCSC) condition with $F_T\ne \varnothing$ and a sequence $\left\{r_k\right\}$ defined by iteration (2). If the mapping T satisfies condition $\left(I\right)$, then the sequence $\left\{r_k\right\}$ strongly converges to the fixed point of T.

Proof. 

By Lemma 9, we know that ${lim}_{k\to \infty }d(r_k,p_0)$ exists for all $p_0\in F_T$, so ${lim}_{k\to \infty }d(r_k,F_T)$ exists. Let ${lim}_{k\to \infty }d(r_k,p_0)=\eta$ for some $\eta \ge 0$. If $\eta =0$ then the equation is true. Let $\eta >0$. Now, $d(r_{k+1},p_0)\le d(r_k,p_0)$ for all $p_0\in F_T$ gives that

$$\begin{array}{c}\hfill \underset{p_0\in F_T}{inf}d(r_{k+1},p_0)\le \underset{p_0\in F_T}{inf}d(r_k,p_0),\end{array}$$

yields the inequality

$$\begin{array}{c}\hfill d(r_{k+1},F_T)\le d(r_k,F_T).\end{array}$$

This shows that $\left\{d(r_k,F_T)\right\}$ is bounded below and non-increasing, so ${lim}_{k\to \infty }d(r_k,F_T)$ exists. Also, Theorem 1 suggests that ${lim}_{k\to \infty }d(r_k,T{r}_k)=0$. It follows from the condition $\left(I\right)$ that

$$\underset{k\to \infty }{lim}\zeta \left(d(r_k,F_T)\right)\le \underset{k\to \infty }{lim}d(r_k,T{r}_k)=0.$$

(14)

Also by the proof of Theorem 1, we know that ${lim}_{k\to \infty }d(T{r}_k,r_k)=0$. So inequality (14) becomes

$$\underset{k\to \infty }{lim}\zeta d(r_k,F_T)=0.$$

(15)

Since the mapping $\zeta :[0,\infty ]\to [0,\infty ]$ is nondecreasing with $\zeta \left(0\right)=0$ and $\zeta \left(q\right)>0$ for each $q\in (0,\infty )$. Now from (15), we have

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}d(r_k,F_T)=0.\end{array}$$

(16)

Next, we need to prove that $\left\{r_k\right\}$ is a Cauchy sequence in N. Let $ϵ>0$ be chosen arbitrarily. Since ${lim}_{k\to \infty }d(r_k,F_T)=0$, so there exists a natural $k_0\in \mathbb{N}$ such that for each $k\ge k_0$

$$\begin{array}{c}\hfill d(r_k,F_T)<\frac{ϵ}{4}.\end{array}$$

In particular,

$$\begin{array}{c}\hfill inf\{d(r_{k_0},p_0):p_0\in F_T\}<\frac{ϵ}{4}.\end{array}$$

So there must be $q\in F_T$ such that

$$\begin{array}{c}\hfill d(r_{k_0},q)<\frac{ϵ}{2}.\end{array}$$

Now, for any $k,l\ge k_0$, we have

$$\begin{array}{ccc}\hfill d(r_{k+l},r_k)& \le & \hfill d(r_{k+l},q)+d(r_k,q)\hfill \\ & \le & \hfill 2d(r_{k_0},q)\hfill \\ & <& \hfill 2\frac{ϵ}{2}\hfill \\ & =& \hfill ϵ.\hfill \end{array}$$

Thus we see that the sequence $\left\{r_k\right\}$ is a Cauchy sequence in N. Since N is closed in $(S,d)$, so N is complete and therefore $\left\{r_k\right\}$ must be converged to the point $r\in N$. As ${lim}_{k\to \infty }d(r_k,F_T)=0$, this gives that $d(r,F_T)=0$. Since N is closed and T satisfies $\left(RCSC\right)$ condition, so $F_T$ is closed and hence r is the fixed point of T. Thus, the sequence $\left\{r_k\right\}$ strongly converges to fixed point r of T. □

Finally, we suggest the $\mathrm{\Delta }$-convergence results for mapping having $\left(RCSC\right)$-condition via the M-iteration process.

Theorem 4.

Let $(S,d)$ is complete $CAT\left(0\right)$ space and $N\ne \varnothing$, closed and convex in $(S,d)$. Assume that $T:N\to N$ is a self mapping satisfying (RCSC) condition with $F_T\ne \varnothing$. Then a sequence $\left\{r_k\right\}$ defined by iteration (2) Δ-converges to a fixed point of T.

Proof. 

By Theorem 1, we know that the sequence $\left\{r_k\right\}$ is bounded and ${lim}_{k\to \infty }d(r_k,T{r}_k)=0$. Now we assume that $W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right):=\bigcup A\left(\left\{r{\prime }_k\right\}\right)$ where $\left\{r{\prime }_k\right\}$ is the subsequence of $\left\{r_k\right\}$. In order to prove that $\left\{r_k\right\}$$\mathrm{\Delta }$-converges to the fixed point of T, we follow the two steps.

(I)

We prove that $W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right)\subseteq F_T$.

(II)

$W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right)$ contains exactly one point.

Step-I To show $W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right)\subseteq F_T$. Let $r\in W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right)$, then there is a sub-sequence $\left\{r_k^{\prime }\right\}$ of $\left\{r_k\right\}$ such that $A\left(\left\{r_k^{\prime }\right\}\right)=r$. Using Lemmas 7 and 8, the sequence $\left\{r_k^{\prime }\right\}$ has a sub-sequence $\left\{s_k^{\prime }\right\}$ with $\mathrm{\Delta }-{lim}_{k\to \infty }{s}_k^{\prime }=s\in N$. Since $\left\{s_k^{\prime }\right\}$ is a sub-sequence of $\left\{r_k\right\}$ and ${lim}_{k\to \infty }d(r_k,T{r}_k)=0,$ so ${lim}_{k\to \infty }d(s_k^{\prime },T{s}_k^{\prime })=0$. Also, the mapping T satisfies the condition $\left(RCSC\right)$, using Lemma 4, we have

$$\begin{array}{c}\hfill d(s_k^{\prime },Ts)\le 9d(s_k^{\prime },T{s}_k^{\prime })+d(s_k^{\prime },s).\end{array}$$

Taking limsup on both sides of the above inequality, we have

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim}supd(s_k^{\prime },Ts)& \le & \hfill \underset{k\to \infty }{lim}sup\{9d(s_k^{\prime },T{s}_k^{\prime })+d(s_k^{\prime },s)\}\hfill \\ & \le & \hfill \underset{k\to \infty }{lim}supd(s_k^{\prime },s).\hfill \end{array}$$

As ${lim}_{k\to \infty }{s}_k^{\prime }=s$, using Opial condition, we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}supd(s_k^{\prime },s)\le \underset{k\to \infty }{lim}supd(s_k^{\prime },Ts).\end{array}$$

Hence, $Ts=s$, i.e., $s\in F_T$.

Now, from Lemma 9, we have ${lim}_{k\to \infty }d(r_k,s)$ exists. So we need to prove that $r=s$. On contrary, assume that $r\ne s$, then by uniqueness property of asymptotic centers, we have

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim\; sup}d(s_k^{\prime },s)& <& \hfill \underset{k\to \infty }{lim\; sup}d(s_k^{\prime },r)\le \underset{k\to \infty }{lim\; sup}d(r_k^{\prime },r)\hfill \\ & <& \hfill \underset{k\to \infty }{lim\; sup}d(r_k^{\prime },s)=\underset{k\to \infty }{lim\; sup}d(r_k.s)\hfill \\ & =& \hfill \underset{k\to \infty }{lim\; sup}d(s_k^{\prime },s).\hfill \end{array}$$

Consequently, ${lim\; sup}_{k\to \infty }d(s_k^{\prime },s)<{lim\; sup}_{k\to \infty }d(s_k^{\prime },r)$. This is a contradiction and so $r=s\in F_T$. Hence, $W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right)\subseteq F_T$.

Step-II: To prove the $\mathrm{\Delta }$-convergent of the sequence $\left\{r_k\right\}$ in the set $F_T,$ we will prove that $W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right)$ has only one element. If $\left\{r_k^{\prime }\right\}$ is a sub-sequence of $\left\{r_k\right\}$, then Lemmas 7 and 8 suggest that the sequence $\left\{r_k^{\prime }\right\}$ has a subsequence $\left\{s_k^{\prime }\right\}$ such that $\mathrm{\Delta }-{lim}_{k\to \infty }{s}_k^{\prime }=s\in N$. Let $A\left(\left\{r_k^{\prime }\right\}\right)=\left\{r^{\prime }\right\}$ and $A\left(\left\{r_k\right\}\right)=\left\{r\right\}$. We have already proved that $r=s$ and $r\in F_T$. We contrarily suppose that $r\ne s$, then ${lim}_{k\to \infty }d(r_k,s)$ exists and the asymptotic centers are unique, so we have

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim\; sup}d(s_k^{\prime },s)& <& \hfill \underset{k\to \infty }{lim\; sup}d(s_k^{\prime },r)\le \underset{k\to \infty }{lim\; sup}d(r_k,r)\hfill \\ & <& \hfill \underset{k\to \infty }{lim\; sup}d(r_k,s)=\underset{k\to \infty }{lim\; sup}d(s_k^{\prime },s).\hfill \end{array}$$

which is a contradiction, so $r=s\in F_T$. Therefore, $W_{\mathrm{\Delta }}\left(\left\{r_k\right\}\right)=\left\{r\right\}$. This completes the proof. □

4. Numerical Example

Now, we will construct a numerical example for mapping with (RCSC) condition to observe the efficiency of the M iteration process with the already-existing iteration process in the current literature.

Example 2.

Suppose that $N=[5,8]$ and the self mapping T are defined by

$$T\left(\mathit{h}\right)=\left\{\begin{array}{ccc}5& if& \mathit{h}=8,\\ \frac{5+\mathit{h}}{2}& if& \mathit{h}\ne 8.\end{array}\right.$$

(17)

We will show that

(i)

T satisfies (RCSC) condition.

(ii)

T does not satisfy condition (C).

To prove these conditions, we have the following cases:

Case (a): Let $\mathit{h},{\mathit{h}}^{\prime }\in \left\{8\right\}$, then $T\mathit{h}=5$ and $T{\mathit{h}}^{\prime }=5$.

$$\begin{array}{c}d(T\mathit{h},T{\mathit{h}}^{\prime })=\left|5-5\right|=0\le \frac{1}{3}(d(\mathit{h},{\mathit{h}}^{\prime })+d(\mathit{h},T{\mathit{h}}^{\prime })+d({\mathit{h}}^{\prime },T\mathit{h}))\end{array}$$

Case (b): Let $\mathit{h},{\mathit{h}}^{\prime }\in [5,8)$, then $T\mathit{h}$ = $\frac{5+\mathit{h}}{2},$ and $T{\mathit{h}}^{\prime }$ = $\frac{5+{\mathit{h}}^{\prime }}{2}$. Now

$$\begin{array}{ccc}d(T\mathit{h},T{\mathit{h}}^{\prime })& =& \hfill \left|\frac{5+\mathit{h}}{2}-\frac{5+{\mathit{h}}^{\prime }}{2}\right|\hfill \\ & =& \hfill \left|\frac{\mathit{h}-{\mathit{h}}^{\prime }}{2}\right|\hfill \\ & \le & \hfill \frac{1}{3}\left|\mathit{h}-{\mathit{h}}^{\prime }\right|+\frac{1}{2}\left|\mathit{h}-{\mathit{h}}^{\prime }\right|\hfill \\ & =& \hfill \frac{1}{3}\left|\mathit{h}-{\mathit{h}}^{\prime }\right|+\frac{1}{3}\left|\frac{3\mathit{h}-3{\mathit{h}}^{\prime }}{2}\right|\hfill \\ & =& \hfill \frac{1}{3}\left|\mathit{h}-{\mathit{h}}^{\prime }\right|+\frac{1}{3}\left|\left(\begin{array}{c}\mathit{h}-\left(\begin{array}{c}\frac{5+{\mathit{h}}^{\prime }}{2}\end{array}\right)\end{array}\right)-\left(\begin{array}{c}{\mathit{h}}^{\prime }-\left(\begin{array}{c}\frac{5+\mathit{h}}{2}\end{array}\right)\end{array}\right)\right|\hfill \\ & \le & \hfill \frac{1}{3}\left|\mathit{h}-{\mathit{h}}^{\prime }\right|+\frac{1}{3}\left|\mathit{h}-\left(\begin{array}{c}\frac{5+{\mathit{h}}^{\prime }}{2}\end{array}\right)\right|+\frac{1}{3}\left|{\mathit{h}}^{\prime }-\left(\begin{array}{c}\frac{5+\mathit{h}}{2}\end{array}\right)\right|\hfill \\ & =& \hfill \frac{1}{3}\left(\begin{array}{c}d(\mathit{h}-{\mathit{h}}^{\prime })+d(\mathit{h},T{\mathit{h}}^{\prime })+d({\mathit{h}}^{\prime },T\mathit{h})\end{array}\right).\hfill \end{array}$$

Case (c): When $\mathit{h}\in \left\{8\right\}$ and ${\mathit{h}}^{\prime }\in [5,8)$. Then $T\mathit{h}=5$ and $T{\mathit{h}}^{\prime }=\frac{5+{\mathit{h}}^{\prime }}{2}$. Now

$$\begin{array}{ccc}\hfill d(T\mathit{h},T{\mathit{h}}^{\prime })& =& \hfill \left|\frac{5+{\mathit{h}}^{\prime }}{2}-5\right|=\left|\frac{{\mathit{h}}^{\prime }-5}{2}\right|\hfill \\ & =& \hfill \frac{1}{3}\left|\frac{3{\mathit{h}}^{\prime }-15}{2}\right|=\frac{1}{3}\left(\begin{array}{c}\left|\frac{{\mathit{h}}^{\prime }-5}{2}+({\mathit{h}}^{\prime }-5)\right|\end{array}\right)\hfill \\ & \le & \hfill \frac{1}{3}\left|\frac{{\mathit{h}}^{\prime }-5}{2}\right|+\frac{1}{3}\left|{\mathit{h}}^{\prime }-5\right|\hfill \\ & =& \hfill \frac{1}{3}\left|\left(\begin{array}{c}({\mathit{h}}^{\prime }-\mathit{h})+(\mathit{h}-\left(\frac{5+{\mathit{h}}^{\prime }}{2}\right)\end{array}\right)\right|+\frac{1}{3}\left|{\mathit{h}}^{\prime }-5\right|\hfill \\ & \le & \hfill \frac{1}{3}\left|{\mathit{h}}^{\prime }-\mathit{h}\right|+\frac{1}{3}\left|\mathit{h}-\frac{5+{\mathit{h}}^{\prime }}{2}\right|+\frac{1}{3}\left|{\mathit{h}}^{\prime }-5\right|\hfill \\ & =& \hfill \frac{1}{3}\left(\begin{array}{c}d(\mathit{h},{\mathit{h}}^{\prime })+d(\mathit{h},T{\mathit{h}}^{\prime })+d({\mathit{h}}^{\prime },T\mathit{h})\end{array}\right)\hfill \end{array}$$

Case (d): When $\mathit{h}\in [5,8)$ and ${\mathit{h}}^{\prime }\in \left\{8\right\}$. Then $T\mathit{h}=\frac{5+\mathit{h}}{2}$ and $T{\mathit{h}}^{\prime }=5$. Now

$$\begin{array}{ccc}\hfill d(T\mathit{h},T{\mathit{h}}^{\prime })& =& \hfill \left|\frac{5+\mathit{h}}{2}-5\right|=\left|\frac{\mathit{h}-5}{2}\right|=\frac{1}{3}\left|\frac{3\mathit{h}-15}{2}\right|\hfill \\ & =& \hfill \frac{1}{3}\left(\begin{array}{c}\left|\frac{\mathit{h}-5}{2}+(\mathit{h}-5)\right|\end{array}\right)\le \frac{1}{3}\left|\frac{\mathit{h}-5}{2}\right|+\frac{1}{3}\left|\mathit{h}-5\right|\hfill \\ & =& \hfill \frac{1}{3}\left|\left(\begin{array}{c}\mathit{h}-{\mathit{h}}^{\prime }\end{array}\right)+\left(\begin{array}{c}{\mathit{h}}^{\prime }-\left(\begin{array}{c}\frac{5+\mathit{h}}{2}\end{array}\right)\end{array}\right)\right|+\frac{1}{3}\left|\mathit{h}-5\right|\hfill \\ & \le & \hfill \frac{1}{3}\left(\begin{array}{c}d(\mathit{h},{\mathit{h}}^{\prime })+d({\mathit{h}}^{\prime },T\mathit{h})+d(\mathit{h},T{\mathit{h}}^{\prime })\end{array}\right)\hfill \end{array}$$

Hence, (i) is proved.

Next, we will prove the condition (ii). For this, we let $\mathit{h}=7.2$ and ${\mathit{h}}^{\prime }=8$, then $T\mathit{h}=\frac{5+7.2}{2}=6.1andT{\mathit{h}}^{\prime }=5andd(\mathit{h},{\mathit{h}}^{\prime })=\left|\mathit{h}-{\mathit{h}}^{\prime }\right|=\left|7.2-8\right|=0.8.$

$Since\frac{1}{2}d(\mathit{h},T{\mathit{h}}^{\prime })<d(\mathit{h},{\mathit{h}}^{\prime })i.e.,\frac{1}{2}\left|7.2-6.1\right|=0.55<0.8=d(\mathit{h},{\mathit{h}}^{\prime })$ but

$$d(T\mathit{h},T{\mathit{h}}^{\prime })=\left|6.1-5\right|=1.2>0.8=\left|\mathit{h}-{\mathit{h}}^{\prime }\right|$$

.

Hence, we prove that T satisfies (RCSC) condition but fails to satisfy condition (C).

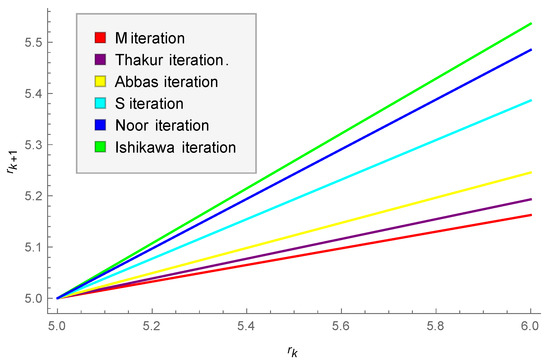
Now we let the parameters ${\alpha }_k=0.90$, ${\beta }_k=0.65$ and ${\gamma }_k=0.70$, for all $k\in \mathbb{N}$. Table 1 and Figure 1 clearly show the speedy convergence of the M-iteration process to the fixed point of mapping T as compared to the other iteration processes, i.e., the Thakur, Abbas, S, Noor and Ishikawa iteration processes.

Table 1. Computational values generated by the different iteration processes for the mapping T as given in Example 2.

k	M	Thakur	Abbas	S	Noor	Ishikawa
1	6	6	6	6	6	6
2	5.1625	5.1931	5.2456	5.3863	5.4851	5.5363
3	5.0264	5.0373	5.0603	5.1492	5.2353	5.2876
4	5.0043	5.0072	5.0148	5.0576	5.1141	4.0236
5	5.0007	5.0014	5.0036	5.0223	5.0554	5.1542
6	5.0001	5.0003	5.0009	5.0086	5.0269	5.0827
7	5.0000	5.0001	5.0002	5.0033	5.0130	5.0443
8	5.0000	5.0000	5.0001	5.0013	5.0063	5.0238
9	5.0000	5.0000	5.0000	5.0005	5.0031	5.0128
10	5.0000	5.0000	5.0000	5.0002	5.0015	5.0068
11	5.0000	5.0000	5.0000	5.0001	5.0007	5.0037
12	5.0000	5.0000	5.0000	5.0000	5.0003	5.0020
13	5.0000	5.0000	5.0000	5.0000	5.0002	5.0011
14	5.0000	5.0000	5.0000	5.0000	5.0001	5.0006
15	5.0000	5.0000	5.0000	5.0000	5.0000	5.0003
16	5.0000	5.0000	5.0000	5.0000	5.0000	5.0002
17	5.0000	5.0000	5.0000	5.0000	5.0000	5.0001
18	5.0000	5.0000	5.0000	5.0000	5.0000	5.0000

Figure 1. Convergence behaviors of M-iteration, Thakur, Abbas, S, Noor, Ishikawa to a fixed point $p_0=5$ of the self mapping T with parameters ${\alpha }_k=0.90$, ${\beta }_k=0.65$ and ${\gamma }_k=0.70$ and initial guess $r_0=6$.

5. Conclusions

The fixed-point results extending from the domain of linear spaces to the domain of nonlinear spaces has his own significance. Takahashi [30] suggests a new notion of convexity in the framework of metric spaces. This discovery initiated the study of different convexity structures in the context of metric spaces. Here in this paper, we have extended the linear version convergence results of mapping with (RCSC) condition (which is the extension of mapping with condition (C)) to the nonlinear framework of CAT(0) spaces for the M-iteration process. In this sense, our results Theorem 2, Theorem 3 and Theorem 4 are the two-fold extensions of Theorem $3.5$, Theorem $3.6$ and Theorem $3.4$ of [22], respectively.